Microsoft excel решение задач презентации - Word и Excel - помощь в работе с программами

Материал содержит конспеат+презентацию по данной теме.

Скачать:

Предварительный просмотр:

№2.

Составить таблицу, подсчитывающую выручку в газетном киоске за день.

Порядок работы:

Выделить ячейки А1:С1 и включить кнопку Объединить и поместить по центру .
Ввести в ячейкуА1 текст Газетный киоск.
Переместиться в А2 и установить дату:

ЛКМ по кнопке Мастер функций;
В раскрывшемся списке выбрать категорию Дата и время и функцию Сегодня, ЛКМ по кнопке Ок;
ЛКМ по кнопке Ок;
В сервис меню выбрать пункт Формат – Ячеки,
Вкладка Число, Числовой формат –Дата, установить нужный тип и ЛКМ по кнопке Ок.

Ввести заголовки таблицы, выделить третью строку и включить выравнивание по центру (Формат – Ячейка – Выравнивание – установить в окошках по горизонтали и вертикали выравнивание по центру).
Выделить ячейки А4:А10 и включить перенос по словам(Формат–Ячейки–Выравнивание –установить флажок Перенос по словам)
Ввести названия газет в соответствующие ячейки.
Внести цифры в столбцы В и С.
Выделить ячейки А11:С11 и включить кнопку Объединить и поместить по центру и ввести текст Общая выручка=
В ячейку D4 занести формулу =В4*С4. Для этого:
– нажать =
– мышкой установить курсор в ячейку В4
– нажать на дополнительной клавиатуре *
– мышкой установить курсор в ячейку С4
– нажать Enter
Занести формулы в ячейки D5:D9 с помощью автозаполнения(встать на маркер размножения в ячейке D4 и растянуть до ячейки D10)
Подсчитать общую выручку с помощью Автосуммирования. Установить курсор в ячейку D11 и включить кнопку .
Установить для ячеек В4:В10 денежный формат числа (выделить их и Формат – Ячейки –Число –Денежный).
Установить для ячеек D4:D11денежный формат числа.
Выполнить обрамление таблицы с помощью кнопки.
Изменить оформление, используя Автоформат.

Задание №3.

В таблицу собраны данные о крупнейших озерах мира.

Найти глубину самого мелкого озера, площадь самого обширного озера и среднюю высоту озер над уровнем моря.

Порядок работы:

Заполнить таблицу в соответствии с образцом.
Добавить в ячейки А8, А9, А10 соответственно текст Миним.Глубина, Максим.Площадь, Средн.Высота
В ячейку В8 занести функцию Мин(С2:С7). Для этого:

Включить кнопку
Выбрать категорию Статистические, Мин(), Ок
Сместить окно мастера так, чтобы была видна таблица(переместить за любую область окна при прижатой ЛКМ)
Выделить ЛКМ ячейки С2:С7
Нажать Ok

В ячейку В9 занести функцию МАКС(В2:В7) тем же способом что и в пункте 3.
В ячейку В10 поместить формулу СРЗНАЧ(D2:D7), с помощью которой вычисляется средняя высота озера над уровнем моря.

По теме: методические разработки, презентации и конспекты

Мне нравится

Источник

Решение прикладных задач в Excel.

Учитель: Латышева Е.В.

Цели урока:

1. Формирование у учащихся новых понятий и способов действий в среде Excel;
2. Знакомство с основными технологическими приемами при решении задач оптимизации;
3. Приобретение навыков работы с надстройками Excel, а именно использование инструментов Excel Поиск решения и Подбор параметра.

Задача.

Задача.
Предположим, что мы решили производить 2 вида полок А и В. На изготовление модели А требуется 3 м3 досок, на изготовление модели В — 4 м3 досок. За неделю можно получить не более 1800 м3 досок. На изготовление модели А требуется – 15 минут, модели В – 30 минут. Рабочая неделя для 4 сотрудников составляет 160 часов. Сколько полок А и В надо изготовить, чтобы получить максимальную прибыль, если полка А стоит 3500 рублей, полка В – 4800 рублей.

	А	В
1	Наименование
2	А
3	В
4
5	Прибыль	=3500x+4800y
6
7	Затраты на материалы	=3x+4y
8	Затраты по времени	=0,25x+0,5y
9

Выделим ячейку В5 и выберем меню Данные, после чего активизируем команду Поиск решения. Заполним ячейки этого окна следующим образом:

На экране увидим:
Пусть мы хотим получать максимальную прибыль в размере 2500000 рублей. Используем функцию Подбор параметра для определения новых значений. Выберем эту команду и заполним ячейки окна следующим образом:

На экране увидим:
Выберем в качестве Изменения значения ячейки количество полок вида А.

На экране увидим:
Самостоятельная работа:

Предположим, что мы решили производить несколько видов конфет. Назовем их условно «А», «В», «С». Известно, что реализация 10 килограммов конфет «А» дает прибыль 9 у.е., «В» — 10 у.е., «С» — 16 у.е. Конфеты можно производить в любых количествах (сбыт обеспечен), но запасы сырья ограничены. Необходимо определить, каких конфет и сколько десятков килограммов необходимо произвести, чтобы общая прибыль от реализации была максимальной. Нормы расхода сырья на производство 10 кг конфет каждого вида приведены ниже:

Сырье	Нормы расхода сырья			Запас сырья
	А	В	С
Какао	18	15	12	360
Сахар	6	4	8	192
Накопитель	5	3	3	180
Прибыль	9	10	16

Литература:

Литература:
1. Макарова, Н. В. Информатика. Задачник по моделированию. — 9 класс. – СПб.: Питер, 2001.
2. Чернов, А. А., Чернов, А. Ф. Информатика. Сборник элективных курсов. – 9 класс. – Волгоград: Учитель, 2007.

Спасибо за урок.

Спасибо за урок.

Источник

Скачать презентацию (1.44 Мб)
65 загрузок
4.0 оценка

Ваша оценка презентации

Оцените презентацию по шкале от 1 до 5 баллов

Аннотация к презентации

Смотреть презентацию онлайн с анимацией на тему «Решение задач оптимизации в MS Excel» по информатике. Презентация состоит из 18 слайдов. Для учеников 10-11 класса. Материал добавлен в 2016 году. Средняя оценка: 4.0 балла из 5.. Возможность скчачать презентацию powerpoint бесплатно и без регистрации. Размер файла 1.44 Мб.

Формат

pptx (powerpoint)
Количество слайдов

18
Аудитория
Слова
Конспект

Отсутствует

Содержание

Слайд 1

Решение задач оптимизации в MS Excel

ГБОУ Центр образования № 133 Невского района
авт. Баринова Е.А.
Слайд 2

Для решения задач оптимизации необходимо:

Задать целевую функцию
Создать математическую модель задачи
Решить задачу на компьютере
Слайд 3

Математическая модель

Математическая модель – это приближенное описание какого-либо класса явлений средствами математической символики.
При составлении математической модели решения задачи оптимизации искомые величины принимаются за неизвестные и составляется система неравенств, наиболее полно характеризующих решение поставленной задачи.
В любую математическую модель входят две составляющие:
Ограничения, которые устанавливают зависимости между переменными.
Граничные условия показывают, в каких пределах могут быть значения искомых переменных в оптимальном решении.
Слайд 4

Задача

Компания производит полки для ванных комнат двух типов — А и В. Агенты по продаже считают, что за неделю на рынке может быть реализовано до 550 полок. Для каждой полки типа А требуется 2 м2 материала, для полки типа В — 3 м2 материала. Компания может получить до 1200 м2 материала в неделю. Для изготовления одной полки типа А требуется 12 мин. работы оборудования, а для изготовления одной полки типа В — 30 мин. Оборудование можно использовать 160 час. в неделю. Если прибыль от продажи полок типа А составляет 3 долл., а от полок типа В — 4 долл., то сколько полок надо выпускать в неделю, чтобы получить максимальную прибыль?
Слайд 5

Целевая функция

Очевидно, что в качестве критерия оптимизации в данном случае выступает функция прибыли. Оптимальным будет считаться тот из вариантов решения, в котором значение прибыли будет максимальным. Учитывая, что «…прибыль от продажи полок типа А составляет 3 долл., а от полок типа В — 4 долл.…» целевая функция будет выглядеть следующим образом:
3×1 + 4×2 max, где
x1 – объем производства полок типа A
x2 – объем производства полок типа B
Слайд 6

Ограничение на объем производства:

«…Агенты по продаже считают, что неделю на рынке может быть реализовано до 550 полок…» Очевидно, что совокупный объем производства полок не должен превышать 550 единиц, или, в математическом виде:
x1 + x2  550
Слайд 7

Ограничение на использование оборудования:

«…Для изготовления одной полки типа А требуется 12 мин. работы оборудования, а для изготовления одной полки типа В — 30 мин. Оборудование можно использовать 160 часов в неделю…» На основе этой информации можно сделать вывод, что общее время использования оборудования в рамках данного проекта не должно превышать 160 часов в неделю. Переведя время, необходимое для изготовления одной полки в часы (с целью сопоставимости единиц измерения правой и левой части неравенства) получим:
0,2×1 + 0,5×2  160
Слайд 8

Ограничение на использование материалов:

«…Для каждой полки типа А требуется 2 м2 материала, для полки типа В — 3 м2 материала. Компания может получить до 1200 м2 материала в неделю…» На основе этой информации можно сделать вывод, что общее количество материала, затрачиваемого для реализации данного проекта, не должно превышать 1200 м2:
2×1 + 3×2  1200
Слайд 9

Граничные условия

В качестве граничных условий в данном примере могут быть использованы следующие утверждения, вытекающие из сути поставленной задачи:
Объем производства полок типа А и полок типа В – неотрицательное значение.
Объем производства полок типа А и полок типа В – целое число, запишем таким образом:
x1, x2  0
x1, x2 – целое
Слайд 10

Ввод условий задачи

Ввод условий задачи состоит из следующих основных шагов:
Создание формы для ввода данных, необходимых для последующего решения.
Ввод исходных данных и зависимостей из математической модели.
Указание целевой ячейки (ячейки, в которую введена целевая функция), ввод ограничений и граничных условий в диалоговом окне Поиск решения.
Слайд 11

Создание формы для ввода данных

Такая форма должна содержать возможность ввода всех данных, необходимых для решения поставленной задачи:
искомых переменных;
целевой функции;
правой и левой части неравенств, описывающих ограничения, налагаемые на возможные варианты решения поставленной задачи.
Слайд 12

Ввод исходных данных

Отметим, что целевая функция и левые части неравенств, определяющих возможные варианты решения поставленной задачи, вводятся формулой, в которой роль искомых переменных играют адреса ячеек, зарезервированных для вывода их значений после решения задачи, а роль коэффициентов – адреса ячеек, содержащих соответственные коэффициенты.
Слайд 13

Назначение целевой функции, ввод ограничений и граничных условий

Данная стадия ввода условия задачи осуществляется в диалоговом окне Поиск решения
Слайд 14

Назначить целевую ячейку

Для этого в поле «Установить целевую ячейку:» вводится адрес ячейки, содержащей целевую функцию. Затем устанавливается направление последней – значение, к которому она должна стремиться исходя из условий задачи (минимальное, максимальное, конкретное, задаваемое пользователем).
В поле «Изменяя ячейки:» ввести адреса ячеек, зарезервированных для искомых переменных.
Слайд 15

Ввести ограничения и граничные условия

Ввести ограничения и граничные условия. Для этого в диалоговом окне Поиск решения нажать на кнопку Добавить. В открывшемся диалоговом окне Добавление ограничений:

в поле «Ссылка на ячейку:» ввести адрес ячейки листа, содержащей формулу для расчета показателя, используемого в качестве левой части неравенства, из списка знаков неравенств выбрать необходимый знак, в поле «Ограничение:» указать адрес ячейки, содержащей показатель, используемый в качестве правой части неравенства.
Слайд 16

Получение результата

После нажатия на кнопку Выполнить диалогового окна Поиск решения на экране появляется диалоговое окно Результаты поиска решения.
Слайд 18

Оптимальное решение поставленной задачи

полок типа А — в количестве 450 штук (В3);
полок типа В – в количестве 100 штук (С3).
При этом максимальная прибыль будет составлять 1720 единиц, а ресурсы используются следующим образом:
потребление материала – 1200 единиц (D10);
использование оборудования – 140 часов (D11).

Посмотреть все слайды

Сообщить об ошибке

Похожие презентации

Спасибо, что оценили презентацию.

Мы будем благодарны если вы поможете сделать сайт лучше и оставите отзыв или предложение по улучшению.

Добавить отзыв о сайте

Источник

1

Решение прикладных задач в Excel. Учитель: Латышева Е.В.

2

Цели урока: 1. Формирование у учащихся новых понятий и способов действий в среде Excel; 2. Знакомство с основными технологическими приемами при решении задач оптимизации; 3. Приобретение навыков работы с надстройками Excel, а именно использование инструментов Excel Поиск решения и Подбор параметра.

3

Задача. Предположим, что мы решили производить 2 вида полок А и В. На изготовление модели А требуется 3 м 3 досок, на изготовление модели В — 4 м 3 досок. За неделю можно получить не более 1800 м 3 досок. На изготовление модели А требуется – 15 минут, модели В – 30 минут. Рабочая неделя для 4 сотрудников составляет 160 часов. Сколько полок А и В надо изготовить, чтобы получить максимальную прибыль, если полка А стоит 3500 рублей, полка В – 4800 рублей.

4

АВ 1 Наименование 2 А 3 В 4 5 Прибыль=3500*x+4800*y 6 7 Затраты на материалы=3*x+4*y 8 Затраты по времени=0,25*x+0,5*y 9

5

Выделим ячейку В5 и выберем меню Данные, после чего активизируем команду Поиск решения. Заполним ячейки этого окна следующим образом:

6

На экране увидим:

7

Пусть мы хотим получать максимальную прибыль в размере рублей. Используем функцию Подбор параметра для определения новых значений. Выберем эту команду и заполним ячейки окна следующим образом:

8

На экране увидим:

9

Выберем в качестве Изменения значения ячейки количество полок вида А.

10

На экране увидим:

11

Самостоятельная работа: Предположим, что мы решили производить несколько видов конфет. Назовем их условно «А», «В», «С». Известно, что реализация 10 килограммов конфет «А» дает прибыль 9 у.е., «В» — 10 у.е., «С» — 16 у.е. Конфеты можно производить в любых количествах (сбыт обеспечен), но запасы сырья ограничены. Необходимо определить, каких конфет и сколько десятков килограммов необходимо произвести, чтобы общая прибыль от реализации была максимальной. Нормы расхода сырья на производство 10 кг конфет каждого вида приведены ниже:

12

СырьеНормы расхода сырьяЗапас сырья АВС Какао Сахар Накопит ель Прибыль91016

13

Литература: 1. Макарова, Н. В. Информатика. Задачник по моделированию. — 9 класс. – СПб.: Питер, Чернов, А. А., Чернов, А. Ф. Информатика. Сборник элективных курсов. – 9 класс. – Волгоград: Учитель, 2007.

14

Спасибо за урок.

Источник

Решение экономических задач в Excel

Полезные хитрости, которые облегчат работу с Excel

Функции в Excel

Функции — программы , которые можно вызывать по имени для выполнения определенных действий.

( Функции представляют собой заранее определенные формулы, которые выполняют вычисления по заданным величинам, называемым аргументами, и в указанном порядке)

Пример:

Функция

=ОСТАТ(5; 2)

Описание

Результат

Остаток от деления 5 на 2

Формулы могут включать функции. Функции могут вводиться в таблицу в составе формул либо отдельно. Функцию так же, как и число, можно считать частным случаем формулы.

Синтаксис функции

= ИМЯ_ФУНКЦИИ ( аргумент1;аргумент2 ;…)

Например:

= КОРЕНЬ (9) – расчет корня квадратного числа 9

= СЕГОДНЯ () – определение текущей даты, данные не нужны

= SIN (С8) – расчет синуса угла, заданного в ячейке С8

Скобки — обязательная принадлежность функции, даже если у нее нет аргументов, например функция =ПИ() — 3,1416… (Если аргументов нет, то скобки остаются пустыми.)

Если аргументов несколько, то один аргумент от другого отделяется точкой с запятой .

Для вызова Мастера функций можно использовать:

Excel содержит более 300 встроенных функций, условно разделенных на несколько категорий: Математические, Статистические, Финансовые, Текстовые, Логические, Дата и время и др.

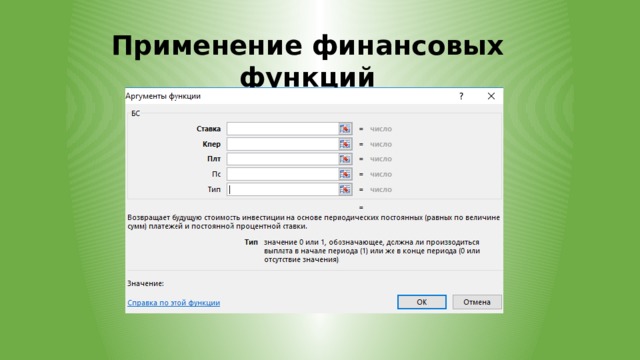
Применение финансовых функций

Аргументы финансовых функций:

БС – будущая (конечная) сумма

Ставка – процентная ставка за 1 период выплат

КПЕР – кол-во периодов выплаты (вклада, кредита)

ПЛТ – размер выплат за 1 период

ПС – начальное значение суммы

Тип – выплата в конце (0) или начале периода (1)

Очень важно! Запомните правило:

Если мы платим деньги, даже если помещаем их на свой счет в банке, и в нашем кошельке деньги уменьшаются , то соответствующий аргумент будет иметь знак « — ».

Если деньги платят нам , даже если мы получаем их со своего счета в банке, и в нашем кошельке деньги увеличиваются , то аргумент будет иметь знак « + ».

КПЕР – сколько раз будут производиться платежи.

Например, если вы выплачиваете кредит 2 года каждый месяц, то КПЕР=2×12=24.

Если вы выплачиваете этот же кредит один раз в год, то КПЕР=2.

СТАВКА – процентная ставка за период.

Например, если вы берете кредит под 12% годовых и выплачиваете его каждый месяц, то СТАВКА=12%÷12мес.=1%.

А если за этот же кредит вы будете расплачиваться только один раз в год, то

СТАВКА=12%.

ПС – приведенная стоимость на

начальный момент времени.

Например, если вы помещаете в банк

10000 руб., то ПС=-10000.

А если вы берете кредит 50000 руб., то ПС=50000.

ПЛТ – выплата, производимая в каждый момент времени.

Например, если вы каждый месяц пополняете свой счет в банке на 5000 руб., то ПЛТ=-5000.

А если вы каждый месяц получаете доход с инвестиций, равный 5000 руб.,

то ПЛТ=5000.

Функция БС (ставка;кпер;плт ;[пс];[тип] )

возвращает будущую стоимость инвестиций на основе периодических постоянных платежей и процентной ставки.

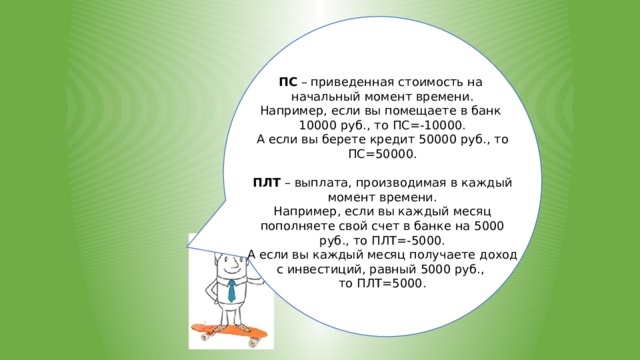
Пример 1. Мы помещаем 20000 руб. в банк с начислением 7% годовых. Начисления проводятся каждый месяц.

Вопрос:

Сколько денег окажется на нашем счету через 5 лет?

Мы помещаем 20000 руб. в банк с начислением 7% годовых. Начисления проводятся каждый месяц.

Решение задачи

Определяем ставку за 1 период, который у нас равен

1 месяцу:

7% в год / 12 мес.

Определяем количество периодов начисления процентов:

5 лет  12 мес=60.

Аргумент ПЛТ=0, т.к. в течение 5 лет мы вклад не пополняем и деньги не забираем.
Аргумент ПС будет иметь знак «-», т.к. первоначально мы вкладываем деньги, а не получаем их.

Ответ : на нашем счету окажется

28352,5 руб.

Функция ПС ( ставка; кпер; плт; [бс]; [тип] )

возвращает приведенную к начальному времени стоимость инвестиций.

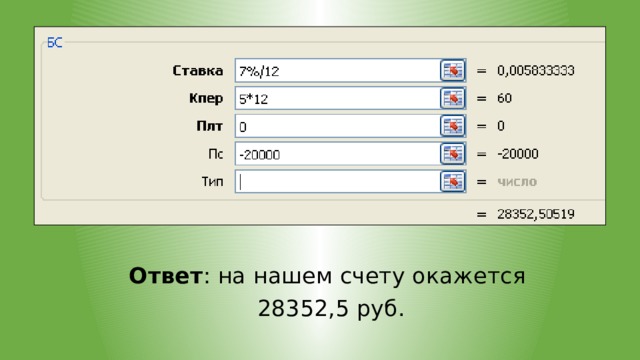
Пример 2. Мы хотим накопить 100000 руб. через 5 лет, вложив в банк под 9% годовых определенную сумму. Проценты будут начисляться каждый месяц.

Вопрос:

Какую сумму мы должны положить в банк?

Мы хотим накопить 100000 руб. через 5 лет, вложив в банк под 9% годовых определенную сумму. Проценты будут начисляться каждый месяц.

Решение

Определяем ставку за 1 период, который у нас равен 1 месяцу:

9% в год / 12 месяцев.

Определяем количество периодов начисления процентов:

5 лет  12 мес.=60.

Аргумент ПЛТ=0, т.к. размер периодических платежей=0.
Аргумент БС=100000 – это та сумма, которую мы хотим получить через 5 лет.

Ответ : мы должны вложить 63869,97 руб.

Функция ПЛТ (ставка; кпер; плт; [бс]; [тип])

возвращает сумму постоянных периодических платежей при условии неизменной процентной ставки.

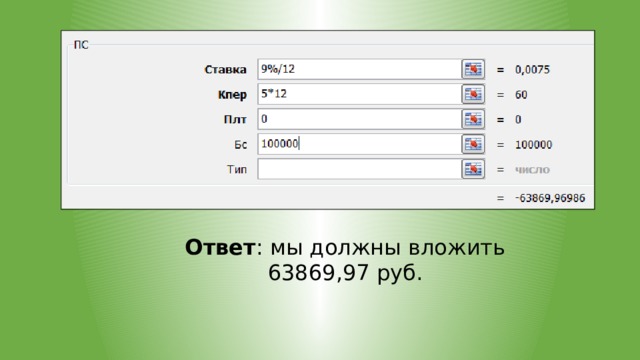
Пример 3. Мы берем ипотеку 1000000 руб. Годовая ставка — 12%. Хотим полностью рассчитаться с банком за 15 лет, выплачивая долг каждый месяц.

Вопрос:

Чему будут равны наши платежи?

Мы берем ипотеку 1000000 руб. Годовая ставка — 12%. Хотим полностью рассчитаться с банком за 15 лет, выплачивая долг каждый месяц.

Решение

Определяем ставку за 1 период, который у нас равен

1 месяцу:

12% в год / 12 месяцев.

Определяем количество выплат:

15 лет  12 мес.=180.

Аргумент ПС=1000000 – сумма, которую мы берем в долг.
Аргумент БС=0 – через 15 лет наш долг должен быть равен 0 рублей.

Ответ : ежемесячно мы должны выплачивать 12001,68 руб.

Функция КПЕР (ставка;плт;пс;[бс];[тип])

возвращает количество периодов выплат при постоянных платежах и неизменной процентной ставке.

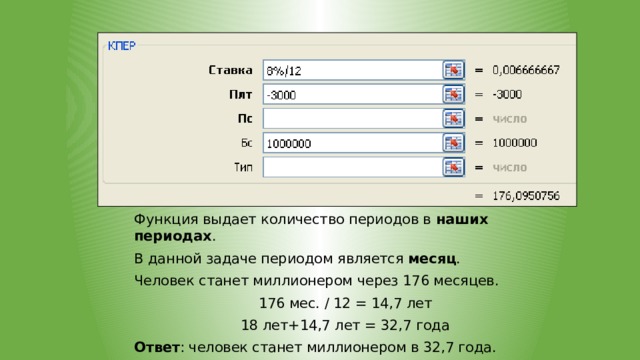
Пример 4. Человек, начиная с 18-летнего возраста, начинает каждый месяц вкладывать в банк 3000 руб. Годовая ставка банка 8%.

Вопрос:

В каком возрасте человек станет миллионером?

Человек, начиная с 18-летнего возраста, начинает каждый месяц вкладывать в банк 3000 руб.

Годовая ставка банка 8%.

Решение

Определяем величину процентной ставки за период: 8%/12 мес.=0,66%.

Аргумент ПЛТ=-3000 – сумма, которую человек ежемесячно добавляет на свой счет.
Аргумент БС=1000000 – человек хочет стать миллионером!
Аргумент ПС=0 – накапливать деньги человек будет начинать с нуля.

Функция выдает количество периодов в наших периодах .

В данной задаче периодом является месяц .

Человек станет миллионером через 176 месяцев.

176 мес. / 12 = 14,7 лет

18 лет+14,7 лет = 32,7 года

Ответ : человек станет миллионером в 32,7 года.

Источник

Скачать:

Предварительный просмотр:

По теме: методические разработки, презентации и конспекты

Комментарии

Аннотация к презентации

Содержание

Решение задач оптимизации в MS Excel

Для решения задач оптимизации необходимо:

Математическая модель

Задача

Целевая функция

Ограничение на объем производства:

Ограничение на использование оборудования:

Ограничение на использование материалов:

Граничные условия

Ввод условий задачи

Создание формы для ввода данных

Ввод исходных данных

Назначение целевой функции, ввод ограничений и граничных условий

Назначить целевую ячейку

Ввести ограничения и граничные условия

Получение результата

Оптимальное решение поставленной задачи

Похожие презентации