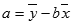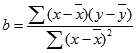Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ОТРЕЗОК в Microsoft Excel.
Описание
Вычисляет точку пересечения линии с осью y, используя значения аргументов «известные_значения_x» и «известные_значения_y». Точка пересечения находится на оптимальной линии регрессии, проведенной через точки, заданные аргументами «известные_значения_x» и «известные_значения_y». Функция ОТРЕЗОК используется, если нужно определить значение зависимой переменной при нулевом значении независимой переменной. Например, с помощью функции ОТРЕЗОК можно предсказать электрическое сопротивление металла при температуре 0°C, если имеются данные измерений при комнатной температуре и выше.
Синтаксис
ОТРЕЗОК(известные_значения_y; известные_значения_x)
Аргументы функции ОТРЕЗОК описаны ниже.
-
Известные_значения_y — обязательный аргумент. Зависимое множество наблюдений или данных.
-
Известные_значения_x — обязательный аргумент. Независимое множество наблюдений или данных.
Замечания
-
Аргументы могут быть числами либо содержащими числа именами, массивами или ссылками.
-
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения пропускаются; ячейки, содержащие нулевые значения, учитываются.
-
Если аргументы «известные_значения_y» и «известные_значения_x» содержат разное количество точек данных или вовсе не содержат точек данных, функция ОТРЕЗОК возвращает значение ошибки #Н/Д.
-
Уравнение для точки пересечения линии линейной регрессии a с осью y имеет следующий вид:
где наклон b вычисляется следующим образом:
где x и y — средние значения выборок СРЗНАЧ(известные_значения_x) и СРЗНАЧ(известные_значения_y).
-
Алгоритм, лежащий в основе работы функций ОТРЕЗОК и НАКЛОН, отличается от алгоритма, на котором основана функция ЛИНЕЙН. Результаты вычислений по этим алгоритмам могут не совпадать в случае неопределенных и коллинеарных данных. Например, если точками данных аргумента «известные_значения_y» являются нули, а аргумента «известные_значения_x» — единицы, то справедливо указанное ниже.
-
От ПЕРЕХВАТ и НАКЛОН возвращают #DIV/0! ошибку «#ВЫЧИС!». Алгоритмы ОТОКП и НАКЛОН предназначены для поиска одного и только одного ответа, и в этом случае может быть несколько ответов.
-
Функция ЛИНЕЙН возвратит нулевое значение. Алгоритм, используемый в функции ЛИНЕЙН, предназначен для возврата правдоподобных результатов для коллинеарных данных, а в этом случае может быть найдено по меньшей мере одно решение.
-
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Известные значения y |
Известные значения x |
|
|
2 |
6 |
|
|
3 |
5 |
|
|
9 |
11 |
|
|
1 |
7 |
|
|
8 |
5 |
|
|
Формула |
Описание |
Результат |
|
=ОТРЕЗОК(A2:A6; B2:B6) |
Определяет точку пересечения линии с осью y, используя приведенные выше известные значения x и известные значения y |
0,0483871 |
Нужна дополнительная помощь?
Функция ОТРЕЗОК в Excel на основе значений x и y находит точку пересечения линейного графика с осью Y. Точка пересечения определяется на оптимальной линии регрессии, коэффициентами которой являются «известные значения x» и «известные значения y». К функции обращаются чаще всего, если необходимо найти значение зависимой переменной при равной нулю независимой переменной.
Особенности и синтаксис функции ОТРЕЗОК
Описание аргументов и параметров:
- Заданные значения y. Массив зависимых переменных, данных или результатов наблюдений.
- Заданные значения x. Массив независимых переменных, данных или результатов наблюдений.
Оба аргумента обязательные. Способы выражения – числа, содержащие числа имена, массивы или ссылки.
Особенности работы функции ОТРЕЗОК:
- Функция игнорирует пустые ячейки, ячейки с текстовыми и логическими значениями. Нулевые значения учитываются.
- Если аргументы содержат разное количество значений либо данные вовсе отсутствуют, появляется ошибка #Н/Д.
- Точка пересечения графика линейной регрессии с осью Y имеет уравнение Где x и y рассчитаны с помощью функции СРЗНАЧ (средние значения выборок множества данных x и y).
Примеры функции ОТРЕЗОК в Excel
При моделировании экономических, физических, технических или социальных процессов в Excel применяются различные способы расчета приблизительных значений функций по известным данным в некоторых фиксированных точках.
Некоторые статистические функции Excel позволяют получать регрессии (линии тренда) сразу на основе исходных табличных данных (без построения диаграммы). Самый простой вариант моделирования исследуемого процесса – линейная регрессия. Модель хороша в том случае, когда значения характеристик растут или уменьшаются с постоянной скоростью.
Для построения линейной регрессии в Excel можно использовать статистическую функцию ОТРЕЗОК. Она определяет отрезок, отсекаемый регрессией на оси ординат.
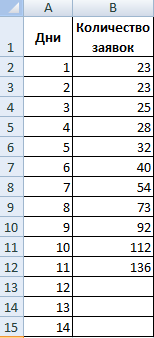
Имеются наблюдения, выраженные числовыми значениями, о количестве оказанных предприятием услуг с 1 по 11 число текущего месяца.
Необходимо составить прогноз на 12-14 число.
Получим ряды данных для линейной регрессии с помощью функции ОТРЕЗОК.
! Сама функция не является регрессией. Она лишь определяет необходимые параметры регрессии.
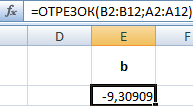
Ставим курсор в ячейку Е2 и вызываем «Мастер функций». В категории «Статистические» находим функцию ОТРЕЗОК. Известные значения y – В2:В12. Известные значения x – А2:А12.
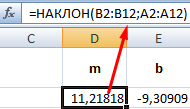
Мы получили значение свободного члена b уравнения линейной регрессии y = mx + b. Для построения линейной регрессии и выполнения поставленной задачи нужно найти другие неизвестные. В частности, угловой коэффициент регрессии m. Воспользуемся встроенной функцией НАКЛОН.
Аргументы заполняем аналогично:
Чтобы получить искомый ряд данных, подставим известные значения в уравнение:
Абсолютные ссылки на ячейки D2 и E2 не позволяют адресу меняться при копировании формулы. Так как количество услуг не может быть дробным числом, на вкладке «Формат ячеек» ставим 0 десятичных знаков для числового формата.
Преимущества данного метода регрессионного анализа:
- простой и однотипный процесс построения рядов данных для функции ОТРЕЗОК (и функции НАКЛОН);
- стандартный способ построения линии тренда;
- возможность составления прогноза исследуемого явления на нужное число шагов вперед или назад.
Существенный недостаток метода – с помощью встроенной функции ОТРЕЗОК можно создать только линейный тип линии тренда. Отсутствие других типов часто не позволяет получить максимально реальный прогноз и подобрать точную модель исследуемого явления.
Содержание
- Функция ОТРЕЗОК в Excel для прогнозирования явления
- Особенности и синтаксис функции ОТРЕЗОК
- Примеры функции ОТРЕЗОК в Excel
- Функция ОТРЕЗОК
- Описание
- Синтаксис
- Замечания
- Пример
- Функция ОТРЕЗОК
- Описание
- Синтаксис
- Замечания
- Пример
- Примеры использования функции ОТРЕЗОК в Excel на оси ординат
- Поиск зависимости значений оси ординат по функции ОТРЕЗОК в Excel
- Расчет потребления энергии отопления в Excel в зависимости от температуры
- Прогноз затрат с учетом посещаемости и потребления в Excel
- Функция ОТРЕЗОК в Excel и особенности ее использования
Функция ОТРЕЗОК в Excel для прогнозирования явления
Функция ОТРЕЗОК в Excel на основе значений x и y находит точку пересечения линейного графика с осью Y. Точка пересечения определяется на оптимальной линии регрессии, коэффициентами которой являются «известные значения x» и «известные значения y». К функции обращаются чаще всего, если необходимо найти значение зависимой переменной при равной нулю независимой переменной.
Особенности и синтаксис функции ОТРЕЗОК
Описание аргументов и параметров:
- Заданные значения y. Массив зависимых переменных, данных или результатов наблюдений.
- Заданные значения x. Массив независимых переменных, данных или результатов наблюдений.
Оба аргумента обязательные. Способы выражения – числа, содержащие числа имена, массивы или ссылки.
Особенности работы функции ОТРЕЗОК:
- Функция игнорирует пустые ячейки, ячейки с текстовыми и логическими значениями. Нулевые значения учитываются.
- Если аргументы содержат разное количество значений либо данные вовсе отсутствуют, появляется ошибка #Н/Д.
- Точка пересечения графика линейной регрессии с осью Y имеет уравнение Где x и y рассчитаны с помощью функции СРЗНАЧ (средние значения выборок множества данных x и y).
Примеры функции ОТРЕЗОК в Excel
При моделировании экономических, физических, технических или социальных процессов в Excel применяются различные способы расчета приблизительных значений функций по известным данным в некоторых фиксированных точках.
Некоторые статистические функции Excel позволяют получать регрессии (линии тренда) сразу на основе исходных табличных данных (без построения диаграммы). Самый простой вариант моделирования исследуемого процесса – линейная регрессия. Модель хороша в том случае, когда значения характеристик растут или уменьшаются с постоянной скоростью.
Для построения линейной регрессии в Excel можно использовать статистическую функцию ОТРЕЗОК. Она определяет отрезок, отсекаемый регрессией на оси ординат.
Имеются наблюдения, выраженные числовыми значениями, о количестве оказанных предприятием услуг с 1 по 11 число текущего месяца.
Необходимо составить прогноз на 12-14 число.
Получим ряды данных для линейной регрессии с помощью функции ОТРЕЗОК.
! Сама функция не является регрессией. Она лишь определяет необходимые параметры регрессии.
Ставим курсор в ячейку Е2 и вызываем «Мастер функций». В категории «Статистические» находим функцию ОТРЕЗОК. Известные значения y – В2:В12. Известные значения x – А2:А12.
Мы получили значение свободного члена b уравнения линейной регрессии y = mx + b. Для построения линейной регрессии и выполнения поставленной задачи нужно найти другие неизвестные. В частности, угловой коэффициент регрессии m. Воспользуемся встроенной функцией НАКЛОН.
Аргументы заполняем аналогично:
Чтобы получить искомый ряд данных, подставим известные значения в уравнение:
Абсолютные ссылки на ячейки D2 и E2 не позволяют адресу меняться при копировании формулы. Так как количество услуг не может быть дробным числом, на вкладке «Формат ячеек» ставим 0 десятичных знаков для числового формата.
Преимущества данного метода регрессионного анализа:
- простой и однотипный процесс построения рядов данных для функции ОТРЕЗОК (и функции НАКЛОН);
- стандартный способ построения линии тренда;
- возможность составления прогноза исследуемого явления на нужное число шагов вперед или назад.
Существенный недостаток метода – с помощью встроенной функции ОТРЕЗОК можно создать только линейный тип линии тренда. Отсутствие других типов часто не позволяет получить максимально реальный прогноз и подобрать точную модель исследуемого явления.
Источник
Функция ОТРЕЗОК
В этой статье описаны синтаксис формулы и использование функции ОТРЕЗОК в Microsoft Excel.
Описание
Вычисляет точку пересечения линии с осью y, используя значения аргументов «известные_значения_x» и «известные_значения_y». Точка пересечения находится на оптимальной линии регрессии, проведенной через точки, заданные аргументами «известные_значения_x» и «известные_значения_y». Функция ОТРЕЗОК используется, если нужно определить значение зависимой переменной при нулевом значении независимой переменной. Например, с помощью функции ОТРЕЗОК можно предсказать электрическое сопротивление металла при температуре 0°C, если имеются данные измерений при комнатной температуре и выше.
Синтаксис
Аргументы функции ОТРЕЗОК описаны ниже.
Известные_значения_y — обязательный аргумент. Зависимое множество наблюдений или данных.
Известные_значения_x — обязательный аргумент. Независимое множество наблюдений или данных.
Замечания
Аргументы могут быть числами либо содержащими числа именами, массивами или ссылками.
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения пропускаются; ячейки, содержащие нулевые значения, учитываются.
Если аргументы «известные_значения_y» и «известные_значения_x» содержат разное количество точек данных или вовсе не содержат точек данных, функция ОТРЕЗОК возвращает значение ошибки #Н/Д.
Уравнение для точки пересечения линии линейной регрессии a с осью y имеет следующий вид:
где наклон b вычисляется следующим образом:
где x и y — средние значения выборок СРЗНАЧ(известные_значения_x) и СРЗНАЧ(известные_значения_y).
Алгоритм, лежащий в основе работы функций ОТРЕЗОК и НАКЛОН, отличается от алгоритма, на котором основана функция ЛИНЕЙН. Результаты вычислений по этим алгоритмам могут не совпадать в случае неопределенных и коллинеарных данных. Например, если точками данных аргумента «известные_значения_y» являются нули, а аргумента «известные_значения_x» — единицы, то справедливо указанное ниже.
От ПЕРЕХВАТ и НАКЛОН возвращают #DIV/0! ошибку «#ВЫЧИС!». Алгоритмы ОТОКП и НАКЛОН предназначены для поиска одного и только одного ответа, и в этом случае может быть несколько ответов.
Функция ЛИНЕЙН возвратит нулевое значение. Алгоритм, используемый в функции ЛИНЕЙН, предназначен для возврата правдоподобных результатов для коллинеарных данных, а в этом случае может быть найдено по меньшей мере одно решение.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Источник
Функция ОТРЕЗОК
В этой статье описаны синтаксис формулы и использование функции ОТРЕЗОК в Microsoft Excel.
Описание
Вычисляет точку пересечения линии с осью y, используя значения аргументов «известные_значения_x» и «известные_значения_y». Точка пересечения находится на оптимальной линии регрессии, проведенной через точки, заданные аргументами «известные_значения_x» и «известные_значения_y». Функция ОТРЕЗОК используется, если нужно определить значение зависимой переменной при нулевом значении независимой переменной. Например, с помощью функции ОТРЕЗОК можно предсказать электрическое сопротивление металла при температуре 0°C, если имеются данные измерений при комнатной температуре и выше.
Синтаксис
Аргументы функции ОТРЕЗОК описаны ниже.
Известные_значения_y — обязательный аргумент. Зависимое множество наблюдений или данных.
Известные_значения_x — обязательный аргумент. Независимое множество наблюдений или данных.
Замечания
Аргументы могут быть числами либо содержащими числа именами, массивами или ссылками.
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения пропускаются; ячейки, содержащие нулевые значения, учитываются.
Если аргументы «известные_значения_y» и «известные_значения_x» содержат разное количество точек данных или вовсе не содержат точек данных, функция ОТРЕЗОК возвращает значение ошибки #Н/Д.
Уравнение для точки пересечения линии линейной регрессии a с осью y имеет следующий вид:
где наклон b вычисляется следующим образом:
где x и y — средние значения выборок СРЗНАЧ(известные_значения_x) и СРЗНАЧ(известные_значения_y).
Алгоритм, лежащий в основе работы функций ОТРЕЗОК и НАКЛОН, отличается от алгоритма, на котором основана функция ЛИНЕЙН. Результаты вычислений по этим алгоритмам могут не совпадать в случае неопределенных и коллинеарных данных. Например, если точками данных аргумента «известные_значения_y» являются нули, а аргумента «известные_значения_x» — единицы, то справедливо указанное ниже.
От ПЕРЕХВАТ и НАКЛОН возвращают #DIV/0! ошибку «#ВЫЧИС!». Алгоритмы ОТОКП и НАКЛОН предназначены для поиска одного и только одного ответа, и в этом случае может быть несколько ответов.
Функция ЛИНЕЙН возвратит нулевое значение. Алгоритм, используемый в функции ЛИНЕЙН, предназначен для возврата правдоподобных результатов для коллинеарных данных, а в этом случае может быть найдено по меньшей мере одно решение.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Источник
Примеры использования функции ОТРЕЗОК в Excel на оси ординат
Функция ОТРЕЗОК в Excel используется для прогнозирования некоторого события. Она находит координаты точки пересечения графика с осью ординат (OY), построенного по координатам точек X (независимая переменная) и Y (зависимая переменная).
Поиск зависимости значений оси ординат по функции ОТРЕЗОК в Excel
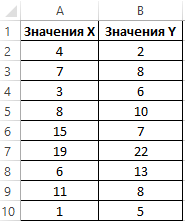
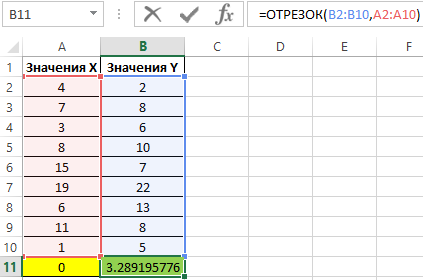
Пример 1. Два массива данных характеризуют показатели одной величины (Y) относительной другой (X). Предположить, каким будет значение величины Y, если X примет значение 0 (нуль).
Таблица исходных данных:
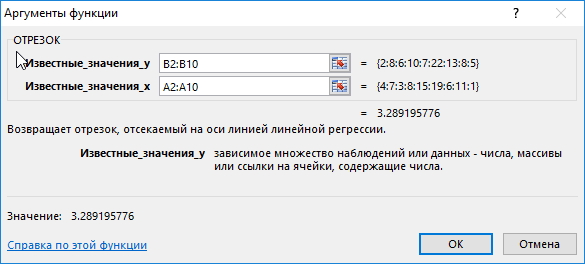
Для нахождения координаты пересечения с осью Ординат введем следующую формулу:
- B2:B10 – диапазон ячеек, со значениями для изменяемого параметра Y;
- A2:A10 – диапазон ячеек, с исходными значениями неизменяемых величин X.
В результате получим:
То есть, координата Y точки пересечения графика с осью Ординат равна примерно 3,29.
Расчет потребления энергии отопления в Excel в зависимости от температуры
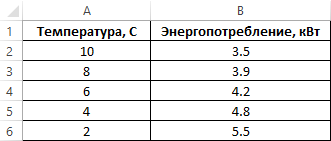
Пример 2. Потребление энергии отопительного прибора зависит от температуры окружающей среды. Известны значения энергопотребления при плюсовой температуре окружающей среды. Определить, сколько энергии будет потреблять котел, если температура на улице снизится до 0 °C и показать это на графике.
Запишем данные в таблицу:
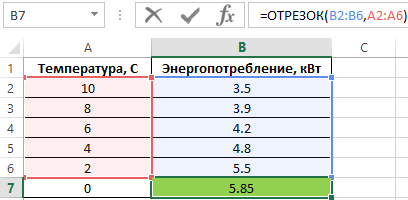
Определим значение энергопотребления при 0 °C:
- B2:B6 – массив значений энергопотребления для определенных температур;
- A2:A6 – массив значений температур, для которых была определена характеристика энергопотребления.
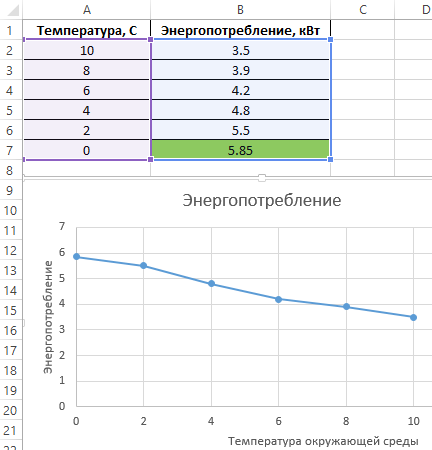
Построим график на основе известных значений:
Как видно, между двумя значениями установилась почти линейная зависимость.
Прогноз затрат с учетом посещаемости и потребления в Excel
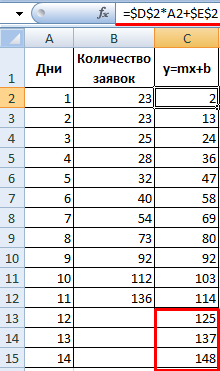
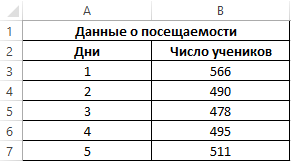
Пример 3. Для расчета необходимого количества продуктов в столовую учебного заведения выполняют учет общей посещаемости учеников. Имеются данные за последнюю неделю. Необходимо спрогнозировать посещаемость на два последующих дня.
Запишем данные в таблицу:
Для расчетов используем метод линейной регрессии. То есть, нам необходимо получить уравнение типа y=kx+b, где:
- y – количество учеников (посещаемость);
- x – номер дня, в который учитывалась посещаемость;
- b – некоторый свободный член уравнения;
- k – угловой коэффициент регрессии.
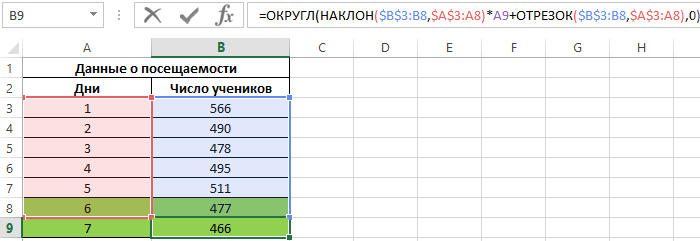
Для решения поставленной задачи запишем следующую формулу:
Описание логики формулы:
- Запись НАКЛОН(B3:B7;A3:A7)*A8+ОТРЕЗОК(B3:B7;A3:A7) соответствует записи kx+b, где угловой коэффициент регрессии вычисляется с помощью функции НАКЛОН, а свободный член b – с использованием функции ОТРЕЗОК.
- Обе функции принимают массивы значений посещаемости (Y) и номеров дней (X).
- Значение Y (посещаемость) округляется до целого значения функцией ОКРУГЛ, поскольку посещаемость должна быть целым числом.
Аналогично вычисляем посещаемость для следующего дня. В результате получим:
Примечание: представленный в Примере 3 способ не применима для моделирования процессов с высокой точностью, поскольку функция ОТРЕЗОК позволяет создавать линии тренда только линейного типа. Наибольшая точность достигается при изучении процесса с пропорциональным приростом/уменьшением величин.
Функция ОТРЕЗОК в Excel и особенности ее использования
Данная функция имеет следующую синтаксическую запись:
- известные_значения_y – массив данных или ссылка на диапазон ячеек, хранящих некоторые данные, которые характеризуют изменчивость одной величины относительно другой. Аргумент обязателен для заполнения.
- известные_значения_x – массив либо ссылка на ячейки, в которых хранятся данные, на основании которых выполняются вычисления значений, содержащихся в первом аргументе данной функции.
- В алгебре при построении графиков функций типа y(x) составляют таблицу величин Y (зависимой) и X (независимой), при этом расчет значений Y выполняют на основании известных значений X путем их подстановки в уравнение функции. Аналогичный смысл имеют аргументы функции известные_значения_y и известные_значения_x, то есть их можно рассматривать как готовые таблицы известных значений, используемых для построения графика функции.
- Функция ОТРЕЗОК принимает в качестве аргументов числовые данные, имена, содержащие числа, ссылки на диапазоны значений и массивы данных.
- Данная функция пропускает объекты данных (ячейки), содержащие логические ИСТИНА или ЛОЖЬ, текстовые строки, пустые значения. Нулевые значения функцией ОТРЕЗОК учитываются.
- Если в массивах данных, принимаемых в качестве аргументов рассматриваемой функции, содержится неодинаковое количество элементов, либо эти массивы являются пустыми, результатом работы функции ОТРЕЗОК будет код ошибки #Н/Д.
- Функция ОТРЕЗОК завершит свою работу с кодом ошибки #ДЕЛ/0!, если в качестве аргумента известные_значения_y будет передан массив данных, содержащий только нули, а в качестве известные_значения_x – массив данных, все элементы которого являются единицами.
- При вычислении точки пересечения определяется оптимальная линия регрессии, при этом координаты X и Y вычисляются с использованием функции СРЗНАЧ.
- Функция ОТРЕЗОК позволяет определить значение переменной Y в тот момент, когда переменная X принимает значение 0 (нуль). Например, функция может быть использована для предсказания значения относительной влажности воздуха при температуре 0 °C, если имеются известные значения этой величины при температурах 10 °C, 15 °C, 20 °C и т. д.
Источник
В этом учебном материале вы узнаете, как использовать Excel функцию ОТРЕЗОК с синтаксисом и примерами.
Описание
Microsoft Excel функция ОТРЕЗОК возвращает точку пересечения оси Y линии с использованием известные_значения_y и известные_значения_x.
Функция ОТРЕЗОК является встроенной функцией Excel, которая относится к категории статистических функций.
Её можно использовать как функцию рабочего листа (WS) в Excel.
Как функцию рабочего листа, функцию ОТРЕЗОК можно ввести как часть формулы в ячейку рабочего листа.
Синтаксис
Синтаксис функции ОТРЕЗОК в Microsoft Excel:
ОТРЕЗОК(известные_значения_y; известные_значения_x)
Аргументы или параметры
- известные_значения_y
- Известные значения y, используемые для расчета пересечения.
- известные_значения_x
- Известные значения x, используемые для вычисления пересечения.
Возвращаемое значение
Функция ОТРЕЗОК возвращает числовое значение. Если параметры известные_значения_y и известные_значения_x содержат разное количество элементов, функция вернет ошибку #Н/Д.
Применение
- Excel для Office 365, Excel 2019, Excel 2016, Excel 2013, Excel 2011 для Mac, Excel 2010, Excel 2007, Excel 2003, Excel XP, Excel 2000
Тип функции
- Функция рабочего листа (WS)
Пример (как функция рабочего листа)
Рассмотрим несколько примеров функции ОТРЕЗОК, чтобы понять, как использовать Excel функцию ОТРЕЗОК в качестве функции рабочего листа в Microsoft Excel:
На основании, приведенной выше электронной таблицы Excel, будут возвращены следующие примеры функции ОТРЕЗОК:
|
=ОТРЕЗОК(A2:A5; B2:B5) Результат:25 =ОТРЕЗОК({1;2;3;4}; {10;11;12;13}) Результат: —9 =ОТРЕЗОК({10;20;30}; {10;20;30}) Результат: 0 |
Линейная регрессия (функции ЛИНЕЙН, НАКЛОН, ОТРЕЗОК, ПРЕДСКАЗ, ТЕНДЕНЦИЯ)
Так как задача отыскания
функциональной зависимости очень важна, в Excel введен набор функций, которые
позволяют решать эту задачу. Эти функции основаны на методе наименьших
квадратов. В
качестве результата выдаются не только коэффициенты аппроксимирующей функции, но и статистические характеристики полученных результатов.
Функция ЛИНЕЙН
Функция ЛИНЕЙН вычисляет коэффициенты m и b прямой линии y=mx+b, которая наилучшим образом аппроксимирует имеющиеся данные, а также дополнительную регрессионную статистику. Функция возвращает массив данных, который описывает полученную прямую. Синтаксис функции:
ЛИНЕЙН(известные_y, [известные_x], [константа], [статистика])
Известные_y. Обязательный аргумент. Множество значений y, которые уже известны для соотношения y=mx+b.
Известные_x. Необязательный аргумент. Множество значений x, которые уже известны для соотношения y=mx+b.
Константа. Необязательный аргумент. Логическое значение. Если аргумент Константа = 0, то b принудительно полагается равным нулю, т.е. y=mx.
Статистика. Необязательный аргумент. Логическое значение. Если аргумент Статистика = 0 или опущен, то вычисляются только
коэффициенты m и b, а если = 1, то выдаются дополнительные статистические характеристики.
Пример 1
Даны x и y: (0, 3), (1,
1), (2, 6), (3, 3), (4, 7). Найти коэффициенты m и b прямой линии y=mx+b, наилучшим образом
аппроксимирующей эти данные по критерию наименьших квадратов.
Решение
Подготовим таблицу как показано ниже. Ячейки E2:F6 не заполняйте, они будут заполнены автоматически.
- В A2:A6 введены значения x, блоку присвоено имя х.
- В В2:В6 введены значения y, блоку присвоено имя y.
- В E2:F6 введена табличная формула {=ЛИНЕЙН(y;x;1;1)}. Для того чтобы ввести табличную формулу, надо выделить блок ячеек E2:F6, ввести формулу и нажать комбинацию клавиш Ctrl Shift Enter. Фигурные скобки вводить вручную не надо.
Пояснение к блоку статистических результатов функции Линейн.
- В E2 записан коэффициент m, в F2 — коэффициент b.
- В E3:F3 стандартные отклонения для этих коэффициентов.
- В E4 записан так называемый
коэффициент детерминации R2. Этот коэффициент
лежит на отрезке [0; 1]. Считается, что чем ближе этот коэффициент к 1, тем
лучше регрессионное уравнение описывает зависимость. Иногда к
такой интерпретации надо относиться с осторожностью. - В F4 находится стандартная
ошибка для оценки у. - В E5 записано значение F-статистики, а в F5 —
количество степеней свободы. - В E6:F6 записана регрессионная сумма квадратов (10) и остаточная сумма квадратов (14).
Функция НАКЛОН
Функция НАКЛОН вычисляет коэффициент m — тангенс угла наклона прямой регрессии. Например: =НАКЛОН(y;x)
Функция ОТРЕЗОК
Функция ОТРЕЗОК вычисляет коэффициент b —
отрезок, отсекаемый прямой на оси ординат. Например: =ОТРЕЗОК(y;x)
Функция ПРЕДСКАЗ
Вычисляет или предсказывает будущее значение
по существующим значениям. Предсказываемое значение — это y-значение,
соответствующее заданному x-значению. x- и y-значения — известны; новое
значение предсказывается с использованием линейной регрессии. Этой
функцией можно воспользоваться для прогнозирования.
ПРЕДСКАЗ(x;известные_y;известные_x)
x — точка данных, для которой предсказывается значение.
Функция ТЕНДЕНЦИЯ
Возвращает значения в соответствии с линейным трендом. Аппроксимирует прямой линией (по методу наименьших квадратов) массивы «известные_y» и «известные_x». Возвращает значения y, соответствующие этой прямой для заданного массива «новые_x».
ТЕНДЕНЦИЯ(известные_y;[известные_x];[новые_x];[константа])
Новые_x — новые значения x, для которых функция ТЕНДЕНЦИЯ возвращает соответствующие значения y.
Не забывайте, что функция ТЕНДЕНЦИЯ может возвращать массив результатов, поэтому для неё надо указывать блок ячеек и вводить как табличную формулу.
Пример 2.
Постройте таблицу по образцу. В примечаниях показаны имена ячеек или формулы. В A5:A9 известныеX, в B5:B9 известныеY. Блоку A5:A12 присвоено имя Х. Рассчитайте Предсказ, Тенденцию и прямую mx+b.
Постройте диаграмму по образцу. На диаграмме видно, что прямая пересекает ось ординат в точке 2 (b=2), а наклон прямой равен 45° (m=1). Прямые Предсказ, Тенденция и mx+b слились в одну линию.