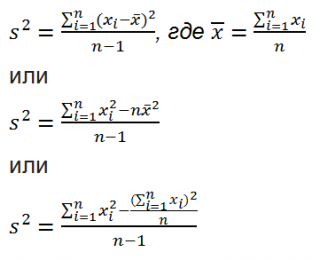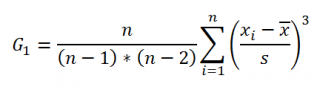Microsoft excel для статистических данных - Word и Excel - помощь в работе с программами

Содержание

Использование описательной статистики
- Подключение «Пакета анализа»
- Применение инструмента «Описательная статистика»
Вопросы и ответы

Пользователи Эксель знают, что данная программа имеет очень широкий набор статистических функций, по уровню которых она вполне может потягаться со специализированными приложениями. Но кроме того, у Excel имеется инструмент, с помощью которого производится обработка данных по целому ряду основных статистических показателей буквально в один клик.

Этот инструмент называется «Описательная статистика». С его помощью можно в очень короткие сроки, использовав ресурсы программы, обработать массив данных и получить о нем информацию по целому ряду статистических критериев. Давайте взглянем, как работает данный инструмент, и остановимся на некоторых нюансах работы с ним.

Использование описательной статистики

Под описательной статистикой понимают систематизацию эмпирических данных по целому ряду основных статистических критериев. Причем на основе полученного результата из этих итоговых показателей можно сформировать общие выводы об изучаемом массиве данных.

В Экселе существует отдельный инструмент, входящий в «Пакет анализа», с помощью которого можно провести данный вид обработки данных. Он так и называется «Описательная статистика». Среди критериев, которые высчитывает данный инструмент следующие показатели:

Медиана;
Мода;
Дисперсия;
Среднее;
Стандартное отклонение;
Стандартная ошибка;
Асимметричность и др.

Рассмотрим, как работает данный инструмент на примере Excel 2010, хотя данный алгоритм применим также в Excel 2007 и в более поздних версиях данной программы.

Подключение «Пакета анализа»

Как уже было сказано выше, инструмент «Описательная статистика» входит в более широкий набор функций, который принято называть Пакет анализа. Но дело в том, что по умолчанию данная надстройка в Экселе отключена. Поэтому, если вы до сих пор её не включили, то для использования возможностей описательной статистики, придется это сделать.

Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».

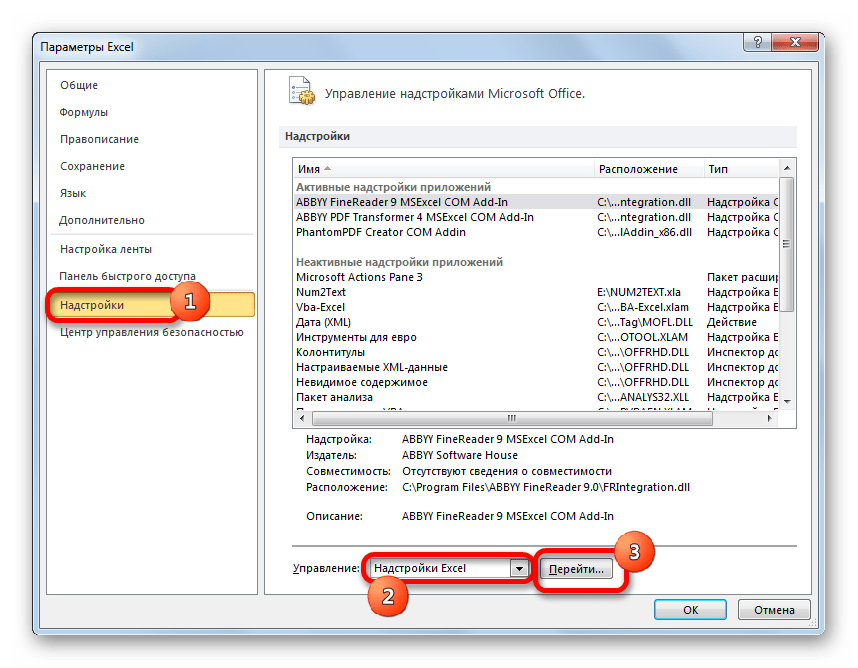
В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».

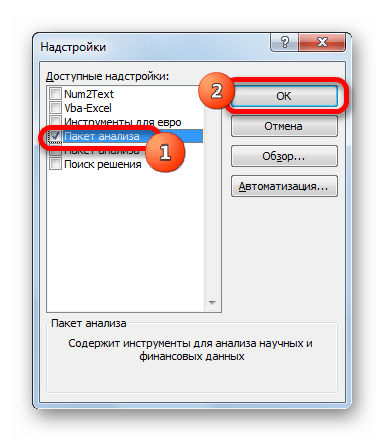
Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».

После вышеуказанных действий надстройка Пакет анализа будет активирована и станет доступной во вкладке «Данные» Эксель. Теперь мы сможем использовать на практике инструменты описательной статистики.

Применение инструмента «Описательная статистика»

Теперь посмотрим, как инструмент описательная статистика можно применить на практике. Для этих целей используем готовую таблицу.

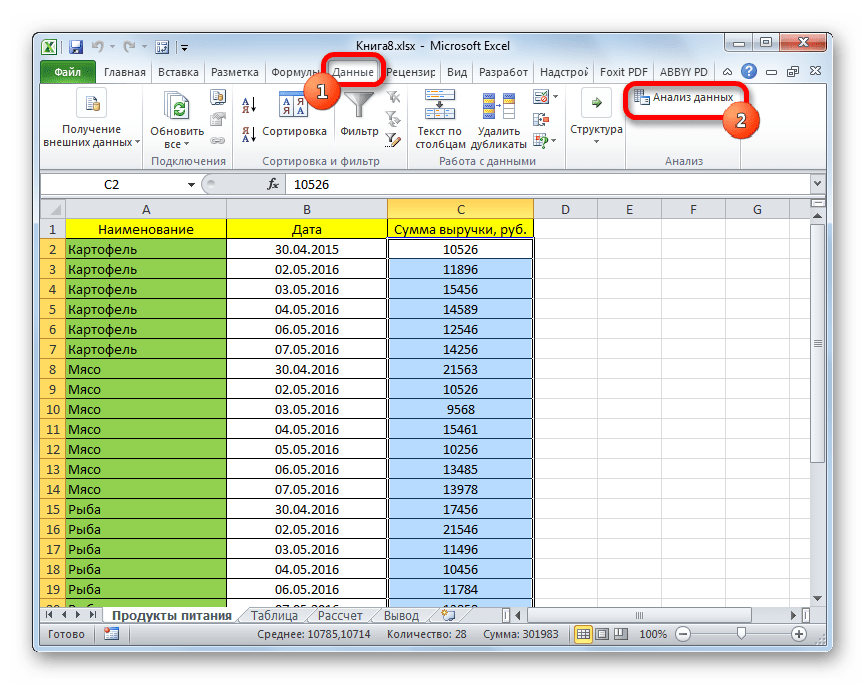
Переходим во вкладку «Данные» и выполняем щелчок по кнопке «Анализ данных», которая размещена на ленте в блоке инструментов «Анализ».

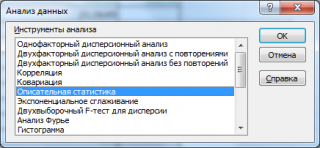
Открывается список инструментов, представленных в Пакете анализа. Ищем наименование «Описательная статистика», выделяем его и щелкаем по кнопке «OK».

После выполнения данных действий непосредственно запускается окно «Описательная статистика».
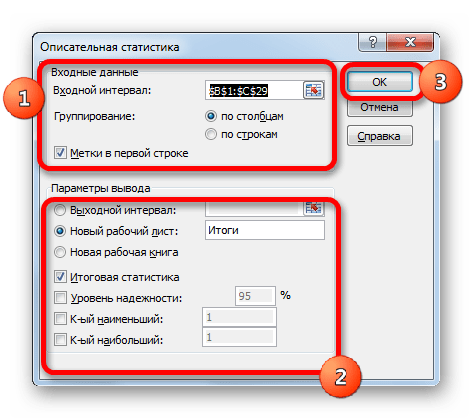
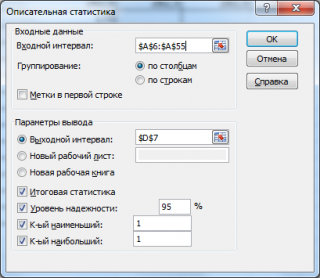
В поле «Входной интервал» указываем адрес диапазона, который будет подвергаться обработке этим инструментом. Причем указываем его вместе с шапкой таблицы. Для того, чтобы внести нужные нам координаты, устанавливаем курсор в указанное поле. Затем, зажав левую кнопку мыши, выделяем на листе соответствующую табличную область. Как видим, её координаты тут же отобразятся в поле. Так как мы захватили данные вместе с шапкой, то около параметра «Метки в первой строке» следует установить флажок. Тут же выбираем тип группирования, переставив переключатель в позицию «По столбцам» или «По строкам». В нашем случае подходит вариант «По столбцам», но в других случаях, возможно, придется выставить переключатель иначе.

Выше мы говорили исключительно о входных данных. Теперь переходим к разбору настроек параметров вывода, которые расположены в этом же окне формирования описательной статистики. Прежде всего, нам нужно определиться, куда именно будут выводиться обработанные данные:
- Выходной интервал;
- Новый рабочий лист;
- Новая рабочая книга.
В первом случае нужно указать конкретный диапазон на текущем листе или его верхнюю левую ячейку, куда будет выводиться обработанная информация. Во втором случае следует указать название конкретного листа данной книги, где будет отображаться результат обработки. Если листа с таким наименованием в данный момент нет, то он будет создан автоматически после того, как вы нажмете на кнопку «OK». В третьем случае никаких дополнительных параметров указывать не нужно, так как данные будут выводиться в отдельном файле Excel (книге). Мы выбираем вывод результатов на новом рабочем листе под названием «Итоги».

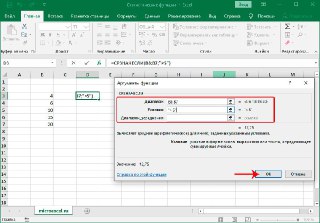
Далее, если вы хотите чтобы выводилась также итоговая статистика, то нужно установить флажок около соответствующего пункта. Также можно установить уровень надежности, поставив галочку около соответствующего значения. По умолчанию он будет равен 95%, но его можно изменить, внеся другие числа в поле справа.

Кроме этого, можно установить галочки в пунктах «K-ый наименьший» и «K-ый наибольший», установив значения в соответствующих полях. Но в нашем случае этот параметр так же, как и предыдущий, не является обязательным, поэтому флажки мы не ставим.

После того, как все указанные данные внесены, жмем на кнопку «OK».

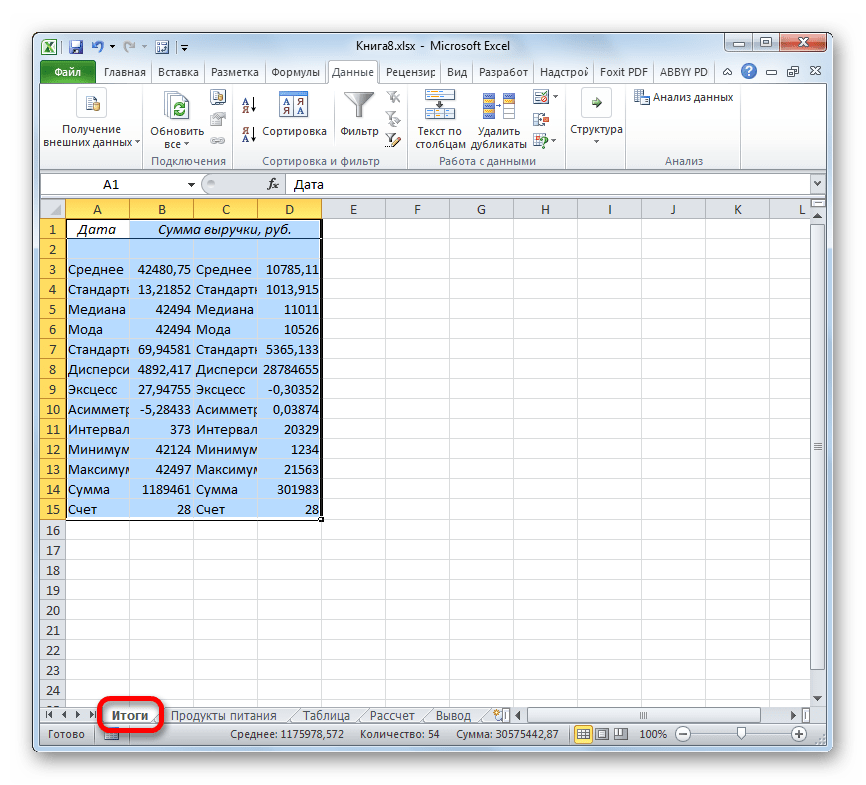
После выполнения этих действий таблица с описательной статистикой выводится на отдельном листе, который был нами назван «Итоги». Как видим, данные представлены сумбурно, поэтому их следует отредактировать, расширив соответствующие колонки для более удобного просмотра.

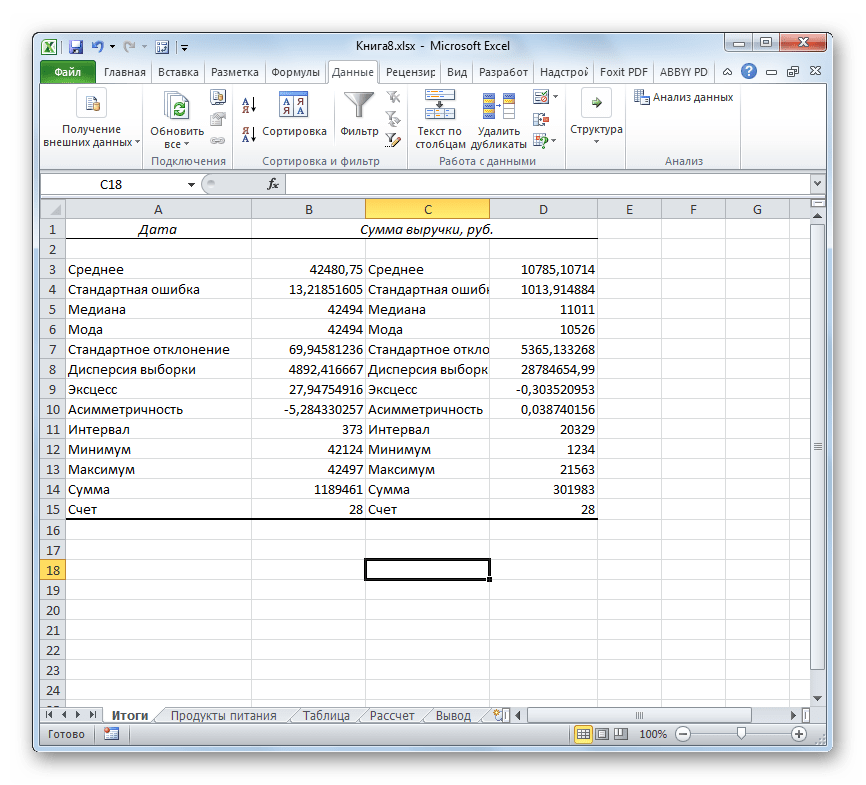
После того, как данные «причесаны» можно приступать к их непосредственному анализу. Как видим, при помощи инструмента описательной статистики были рассчитаны следующие показатели:
- Асимметричность;
- Интервал;
- Минимум;
- Стандартное отклонение;
- Дисперсия выборки;
- Максимум;
- Сумма;
- Эксцесс;
- Среднее;
- Стандартная ошибка;
- Медиана;
- Мода;
- Счет.

Если какие-то из вышеуказанных данных для конкретного вида анализа не нужны, то их можно удалить, чтобы они не мешали. Далее производится анализ с учетом статистических закономерностей.

Урок: Статистические функции в Excel

Как видим, с помощью инструмента «Описательная статистика» можно сразу получить результат по целому ряду критериев, которые в ином случае рассчитывались с применением отдельно предназначенной для каждого расчета функцией, что заняло бы значительное время у пользователя. А так, все эти расчеты можно получить практически в один клик, использовав соответствующий инструмент — Пакета анализа.

Еще статьи по данной теме:

Помогла ли Вам статья?

Источник

Рассмотрим инструмент Описательная статистика, входящий в надстройку Пакет Анализа. Рассчитаем показатели выборки: среднее, медиана, мода, дисперсия, стандартное отклонение и др.

Задача

описательной статистики

(descriptive statistics) заключается в том, чтобы с использованием математических инструментов свести сотни значений

выборки

к нескольким итоговым показателям, которые дают представление о

выборке

.В качестве таких статистических показателей используются:

среднее

медиана

мода

дисперсия, стандартное отклонение

и др.

Опишем набор числовых данных с помощью определенных показателей. Для чего нужны эти показатели? Эти показатели позволят сделать определенные

статистические выводы о распределении

, из которого была взята

выборка

. Например, если у нас есть

выборка

значений толщины трубы, которая изготавливается на определенном оборудовании, то на основании анализа этой

выборки

мы сможем сделать, с некой определенной вероятностью, заключение о состоянии процесса изготовления.

Содержание статьи:

Надстройка Пакет анализа;
Среднее выборки

;
Медиана выборки

;
Мода выборки

;
Мода и среднее значение

;
Дисперсия выборки

;
Стандартное отклонение выборки

;
Стандартная ошибка

;
Ассиметричность

;
Эксцесс выборки

;
Уровень надежности

.

Надстройка Пакет анализа

Для вычисления статистических показателей одномерных

выборок

, используем

надстройку Пакет анализа

. Затем, все показатели рассчитанные надстройкой, вычислим с помощью встроенных функций MS EXCEL.

СОВЕТ

: Подробнее о других инструментах надстройки

Пакет анализа

и ее подключении – читайте в статье

Надстройка Пакет анализа MS EXCEL

Выборку

разместим на

листе

Пример

в файле примера

в диапазоне

А6:А55

(50 значений).

Примечание

: Для удобства написания формул для диапазона

А6:А55

создан

Именованный диапазон

Выборка.

В диалоговом окне

Анализ данных

выберите инструмент

Описательная статистика

.

После нажатия кнопки

ОК

будет выведено другое диалоговое окно,

в котором нужно указать:

входной интервал

(Input Range) – это диапазон ячеек, в котором содержится массив данных. Если в указанный диапазон входит текстовый заголовок набора данных, то нужно поставить галочку в поле

Метки в первой строке (

Labels

in

first

row

).

В этом случае заголовок будет выведен в

Выходном интервале.

Пустые ячейки будут проигнорированы, поэтому нулевые значения необходимо обязательно указывать в ячейках, а не оставлять их пустыми;
выходной интервал

(Output Range). Здесь укажите адрес верхней левой ячейки диапазона, в который будут выведены статистические показатели;
Итоговая статистика (

Summary

Statistics

)

. Поставьте галочку напротив этого поля – будут выведены основные показатели выборки:

среднее, медиана, мода, стандартное отклонение

и др.;
Также можно поставить галочки напротив полей

Уровень надежности (

Confidence

Level

for

Mean

)

,

К-й наименьший

(Kth Largest) и

К-й наибольший

(Kth Smallest).

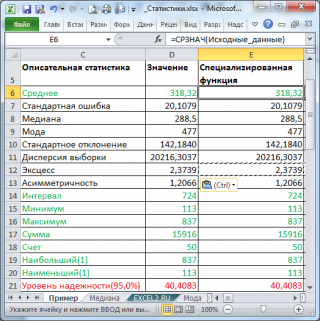
В результате будут выведены следующие статистические показатели:

Все показатели выведены в виде значений, а не формул. Если массив данных изменился, то необходимо перезапустить расчет.

Если во

входном интервале

указать ссылку на несколько столбцов данных, то будет рассчитано соответствующее количество наборов показателей. Такой подход позволяет сравнить несколько наборов данных. При сравнении нескольких наборов данных используйте заголовки (включите их во

Входной интервал

и установите галочку в поле

Метки в первой строке

). Если наборы данных разной длины, то это не проблема — пустые ячейки будут проигнорированы.

Зеленым цветом на картинке выше и в

файле примера

выделены показатели, которые не требуют особого пояснения. Для большинства из них имеется специализированная функция:

Интервал

(Range) — разница между максимальным и минимальным значениями;
Минимум

(Minimum) – минимальное значение в диапазоне ячеек, указанном во

Входном интервале

(см.

статью про функцию

МИН()

);
Максимум

(Maximum)– максимальное значение (см.

статью про функцию

МАКС()

);
Сумма

(Sum) – сумма всех значений (см.

статью про функцию

СУММ()

);
Счет

(Count) – количество значений во

Входном интервале

(пустые ячейки игнорируются, см.

статью про функцию

СЧЁТ()

);
Наибольший

(Kth Largest) – выводится К-й наибольший. Например, 1-й наибольший – это максимальное значение (см.

статью про функцию

НАИБОЛЬШИЙ()

);
Наименьший

(Kth Smallest) – выводится К-й наименьший. Например, 1-й наименьший – это минимальное значение (см.

статью про функцию

НАИМЕНЬШИЙ()

).

Ниже даны подробные описания остальных показателей.

Среднее выборки

Среднее

(mean, average) или

выборочное среднее

или

среднее выборки

(sample average) представляет собой

арифметическое среднее

всех значений массива. В MS EXCEL для вычисления среднего выборки используется функция

СРЗНАЧ()

.

Выборочное среднее

является «хорошей» (несмещенной и эффективной) оценкой

математического ожидания

случайной величины (подробнее см. статью

Среднее и Математическое ожидание в MS EXCEL

Медиана выборки

Медиана

(Median) – это число, которое является серединой множества чисел (в данном случае выборки): половина чисел множества больше, чем

медиана

, а половина чисел меньше, чем

медиана

. Для определения

медианы

необходимо сначала

отсортировать множество чисел

. Например,

медианой

для чисел 2, 3, 3,

4

, 5, 7, 10 будет 4.

Если множество содержит четное количество чисел, то вычисляется

среднее

для двух чисел, находящихся в середине множества. Например,

медианой

для чисел 2, 3,

3

,

5

, 7, 10 будет 4, т.к. (3+5)/2.

Если имеется длинный хвост распределения, то

Медиана

лучше, чем

среднее значение

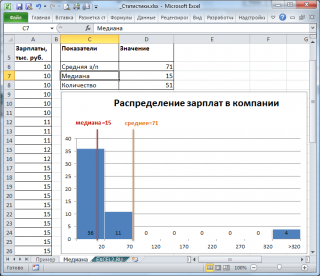
, отражает «типичное» или «центральное» значение. Например, рассмотрим несправедливое распределение зарплат в компании, в которой руководство получает существенно больше, чем основная масса сотрудников.

Очевидно, что средняя зарплата (71 тыс. руб.) не отражает тот факт, что 86% сотрудников получает не более 30 тыс. руб. (т.е. 86% сотрудников получает зарплату в более, чем в 2 раза меньше средней!). В то же время медиана (15 тыс. руб.) показывает, что

как минимум

у 50% сотрудников зарплата меньше или равна 15 тыс. руб.

Для определения

медианы

в MS EXCEL существует одноименная функция

МЕДИАНА()

, английский вариант — MEDIAN().

Медиану

также можно вычислить с помощью формул

=КВАРТИЛЬ.ВКЛ(Выборка;2) =ПРОЦЕНТИЛЬ.ВКЛ(Выборка;0,5).

Подробнее о

медиане

см. специальную статью

Медиана в MS EXCEL

СОВЕТ

: Подробнее про

квартили

см. статью, про

перцентили (процентили)

см. статью.

Мода выборки

Мода

(Mode) – это наиболее часто встречающееся (повторяющееся) значение в

выборке

. Например, в массиве (1; 1;

2

;

2

;

2

; 3; 4; 5) число 2 встречается чаще всего – 3 раза. Значит, число 2 – это

мода

. Для вычисления

моды

используется функция

МОДА()

, английский вариант MODE().

Примечание

: Если в массиве нет повторяющихся значений, то функция вернет значение ошибки #Н/Д. Это свойство использовано в статье

Есть ли повторы в списке?

Начиная с

MS EXCEL 2010

вместо функции

МОДА()

рекомендуется использовать функцию

МОДА.ОДН()

, которая является ее полным аналогом. Кроме того, в MS EXCEL 2010 появилась новая функция

МОДА.НСК()

, которая возвращает несколько наиболее часто повторяющихся значений (если количество их повторов совпадает). НСК – это сокращение от слова НеСКолько.

Например, в массиве (1; 1;

2

;

2

;

2

; 3;

4

;

4

;

4

; 5) числа 2 и 4 встречаются наиболее часто – по 3 раза. Значит, оба числа являются

модами

. Функции

МОДА.ОДН()

и

МОДА()

вернут значение 2, т.к. 2 встречается первым, среди наиболее повторяющихся значений (см.

файл примера

, лист

Мода

).

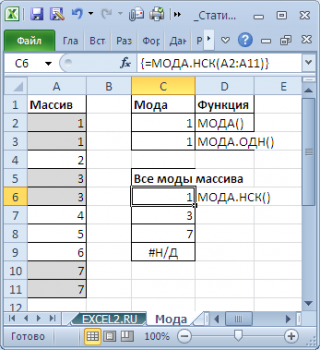
Чтобы исправить эту несправедливость и была введена функция

МОДА.НСК()

, которая выводит все

моды

. Для этого ее нужно ввести как

формулу массива

Как видно из картинки выше, функция

МОДА.НСК()

вернула все три

моды

из массива чисел в диапазоне

A2:A11

: 1; 3 и 7. Для этого, выделите диапазон

C6:C9

, в

Строку формул

введите формулу

=МОДА.НСК(A2:A11)

и нажмите

CTRL+SHIFT+ENTER

. Диапазон

C

6:

C

9

охватывает 4 ячейки, т.е. количество выделяемых ячеек должно быть больше или равно количеству

мод

. Если ячеек больше чем м

о

д, то избыточные ячейки будут заполнены значениями ошибки #Н/Д. Если

мода

только одна, то все выделенные ячейки будут заполнены значением этой

моды

.

Теперь вспомним, что мы определили

моду

для выборки, т.е. для конечного множества значений, взятых из

генеральной совокупности

. Для

непрерывных случайных величин

вполне может оказаться, что выборка состоит из массива на подобие этого (0,935; 1,211; 2,430; 3,668; 3,874; …), в котором может не оказаться повторов и функция

МОДА()

вернет ошибку.

Даже в нашем массиве с

модой

, которая была определена с помощью

надстройки Пакет анализа

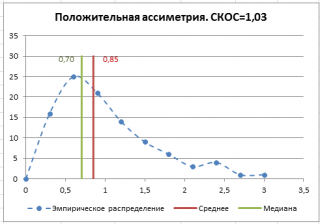
, творится, что-то не то. Действительно,

модой

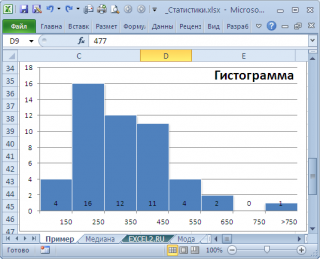
нашего массива значений является число 477, т.к. оно встречается 2 раза, остальные значения не повторяются. Но, если мы посмотрим на

гистограмму распределения

, построенную для нашего массива, то увидим, что 477 не принадлежит интервалу наиболее часто встречающихся значений (от 150 до 250).

Проблема в том, что мы определили

моду

как наиболее часто встречающееся значение, а не как наиболее вероятное. Поэтому,

моду

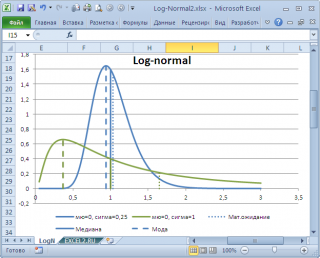
в учебниках статистики часто определяют не для выборки (массива), а для функции распределения. Например, для

логнормального распределения

мода

(наиболее вероятное значение непрерывной случайной величины х), вычисляется как

exp

(

m

—

s
²
)

, где m и s параметры этого распределения.

Понятно, что для нашего массива число 477, хотя и является наиболее часто повторяющимся значением, но все же является плохой оценкой для

моды

распределения, из которого взята

выборка

(наиболее вероятного значения или для которого плотность вероятности распределения максимальна).

Для того, чтобы получить оценку

моды

распределения, из

генеральной совокупности

которого взята

выборка

, можно, например, построить

гистограмму

. Оценкой для

моды

может служить интервал наиболее часто встречающихся значений (самого высокого столбца). Как было сказано выше, в нашем случае это интервал от 150 до 250.

Вывод

: Значение

моды

для

выборки

, рассчитанное с помощью функции

МОДА()

, может ввести в заблуждение, особенно для небольших выборок. Эта функция эффективна, когда случайная величина может принимать лишь несколько дискретных значений, а размер

выборки

существенно превышает количество этих значений.

Например, в рассмотренном примере о распределении заработных плат (см. раздел статьи выше, о Медиане),

модой

является число 15 (17 значений из 51, т.е. 33%). В этом случае функция

МОДА()

дает хорошую оценку «наиболее вероятного» значения зарплаты.

Примечание

: Строго говоря, в примере с зарплатой мы имеем дело скорее с

генеральной совокупностью

, чем с

выборкой

. Т.к. других зарплат в компании просто нет.

О вычислении

моды

для распределения

непрерывной случайной величины

читайте статью

Мода в MS EXCEL

Мода и среднее значение

Не смотря на то, что

мода

– это наиболее вероятное значение случайной величины (вероятность выбрать это значение из

Генеральной совокупности

максимальна), не следует ожидать, что

среднее значение

обязательно будет близко к

моде

.

Примечание

:

Мода

и

среднее

симметричных распределений совпадает (имеется ввиду симметричность

плотности распределения

Представим, что мы бросаем некий «неправильный» кубик, у которого на гранях имеются значения (1; 2; 3; 4; 6; 6), т.е. значения 5 нет, а есть вторая 6.

Модой

является 6, а среднее значение – 3,6666.

Другой пример. Для

Логнормального распределения

LnN(0;1)

мода

равна =EXP(m-s2)= EXP(0-1*1)=0,368, а

среднее значение

1,649.

Дисперсия выборки

Дисперсия выборки

или

выборочная дисперсия (

sample

variance

) характеризует разброс значений в массиве, отклонение от

среднего

.

Из формулы №1 видно, что

дисперсия выборки

это сумма квадратов отклонений каждого значения в массиве

от среднего

, деленная на размер выборки минус 1.

В MS EXCEL 2007 и более ранних версиях для вычисления

дисперсии выборки

используется функция

ДИСП()

. С версии MS EXCEL 2010 рекомендуется использовать ее аналог — функцию

ДИСП.В()

.

Дисперсию

можно также вычислить непосредственно по нижеуказанным формулам (см.

файл примера

):

=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1) =(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1)

– обычная формула

=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1)

–

формула массива

Дисперсия выборки

равна 0, только в том случае, если все значения равны между собой и, соответственно, равны

среднему значению

.

Чем больше величина

дисперсии

, тем больше разброс значений в массиве относительно

среднего

.

Размерность

дисперсии

соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность

дисперсии

будет кг
²
. Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из

дисперсии – стандартное отклонение

.

Подробнее о

дисперсии

см. статью

Дисперсия и стандартное отклонение в MS EXCEL

Стандартное отклонение выборки

Стандартное отклонение выборки

(Standard Deviation), как и

дисперсия

, — это мера того, насколько широко разбросаны значения в выборке

относительно их среднего

.

По определению,

стандартное отклонение

равно квадратному корню из

дисперсии

:

Стандартное отклонение

не учитывает величину значений в

выборке

, а только степень рассеивания значений вокруг их

среднего

. Чтобы проиллюстрировать это приведем пример.

Вычислим стандартное отклонение для 2-х

выборок

: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у

выборок

существенно отличается.

В MS EXCEL 2007 и более ранних версиях для вычисления

Стандартного отклонения выборки

используется функция

СТАНДОТКЛОН()

. С версии MS EXCEL 2010 рекомендуется использовать ее аналог

СТАНДОТКЛОН.В()

.

Стандартное отклонение

можно также вычислить непосредственно по нижеуказанным формулам (см.

файл примера

):

=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))

Подробнее о

стандартном отклонении

см. статью

Дисперсия и стандартное отклонение в MS EXCEL

Стандартная ошибка

В

Пакете анализа

под термином

стандартная ошибка

имеется ввиду

Стандартная ошибка среднего

(Standard Error of the Mean, SEM).

Стандартная ошибка среднего

— это оценка

стандартного отклонения

распределения

выборочного среднего

Примечание

: Чтобы разобраться с понятием

Стандартная ошибка среднего

необходимо прочитать о

выборочном распределении

(см. статью

Статистики, их выборочные распределения и точечные оценки параметров распределений в MS EXCEL

) и статью про

Центральную предельную теорему

.

Стандартное отклонение распределения выборочного среднего

вычисляется по формуле σ/√n, где n — объём

выборки, σ — стандартное отклонение исходного

распределения, из которого взята

выборка

. Т.к. обычно

стандартное отклонение

исходного распределения неизвестно, то в расчетах вместо

σ

используют ее оценку

s

—

стандартное отклонение выборки

. А соответствующая величина s/√n имеет специальное название —

Стандартная ошибка среднего.

Именно эта величина вычисляется в

Пакете анализа.

В MS EXCEL

стандартную ошибку среднего

можно также вычислить по формуле

=СТАНДОТКЛОН.В(Выборка)/ КОРЕНЬ(СЧЁТ(Выборка))

Асимметричность

Асимметричность

или

коэффициент асимметрии

(skewness) характеризует степень несимметричности распределения (

плотности распределения

) относительно его

среднего

.

Положительное значение

коэффициента асимметрии

указывает, что размер правого «хвоста» распределения больше, чем левого (относительно среднего). Отрицательная асимметрия, наоборот, указывает на то, что левый хвост распределения больше правого.

Коэффициент асимметрии

идеально симметричного распределения или выборки равно 0.

Примечание

:

Асимметрия выборки

может отличаться расчетного значения асимметрии теоретического распределения. Например,

Нормальное распределение

является симметричным распределением (

плотность его распределения

симметрична относительно

среднего

) и, поэтому имеет асимметрию равную 0. Понятно, что при этом значения в

выборке

из соответствующей

генеральной совокупности

не обязательно должны располагаться совершенно симметрично относительно

среднего

. Поэтому,

асимметрия выборки

, являющейся оценкой

асимметрии распределения

, может отличаться от 0.

Функция

СКОС()

, английский вариант SKEW(), возвращает коэффициент

асимметрии выборки

, являющейся оценкой

асимметрии

соответствующего распределения, и определяется следующим образом:

где n – размер

выборки

, s –

стандартное отклонение выборки

.

В

файле примера на листе СКОС

приведен расчет коэффициента

асимметрии

на примере случайной выборки из

распределения Вейбулла

, которое имеет значительную положительную

асимметрию

при параметрах распределения W(1,5; 1).

Эксцесс выборки

Эксцесс

показывает относительный вес «хвостов» распределения относительно его центральной части.

Для того чтобы определить, что относится к хвостам распределения, а что к его центральной части, можно использовать границы μ +/-

σ

.

Примечание

: Не смотря на старания профессиональных статистиков, в литературе еще попадается определение

Эксцесса

как меры «остроконечности» (peakedness) или сглаженности распределения. Но, на самом деле, значение

Эксцесса

ничего не говорит о форме пика распределения.

Согласно определения,

Эксцесс

равен четвертому

стандартизированному моменту:

Для

нормального распределения

четвертый момент равен 3*σ
⁴
, следовательно,

Эксцесс

равен 3. Многие компьютерные программы используют для расчетов не сам

Эксцесс

, а так называемый Kurtosis excess, который меньше на 3. Т.е. для

нормального распределения

Kurtosis excess равен 0. Необходимо быть внимательным, т.к. часто не очевидно, какая формула лежит в основе расчетов.

Примечание

: Еще большую путаницу вносит перевод этих терминов на русский язык. Термин Kurtosis происходит от греческого слова «изогнутый», «имеющий арку». Так сложилось, что на русский язык оба термина Kurtosis и Kurtosis excess переводятся как

Эксцесс

(от англ. excess — «излишек»). Например, функция MS EXCEL

ЭКСЦЕСС()

на самом деле вычисляет Kurtosis excess.

Функция

ЭКСЦЕСС()

, английский вариант KURT(), вычисляет на основе значений выборки несмещенную оценку

эксцесса распределения

случайной величины и определяется следующим образом:

Как видно из формулы MS EXCEL использует именно Kurtosis excess, т.е. для выборки из

нормального распределения

формула вернет близкое к 0 значение.

Если задано менее четырех точек данных, то функция

ЭКСЦЕСС()

возвращает значение ошибки #ДЕЛ/0!

Вернемся к

распределениям случайной величины

.

Эксцесс

(Kurtosis excess) для

нормального распределения

всегда равен 0, т.е. не зависит от параметров распределения μ и σ. Для большинства других распределений

Эксцесс

зависит от параметров распределения: см., например,

распределение Вейбулла

или

распределение Пуассона

, для котрого

Эксцесс

= 1/λ.

Уровень надежности

Уровень

надежности

— означает вероятность того, что

доверительный интервал

содержит истинное значение оцениваемого параметра распределения.

Вместо термина

Уровень

надежности

часто используется термин

Уровень доверия

. Про

Уровень надежности

(Confidence Level for Mean) читайте статью

Уровень значимости и уровень надежности в MS EXCEL

Задав значение

Уровня

надежности

в окне

надстройки Пакет анализа

, MS EXCEL вычислит половину ширины

доверительного интервала для оценки среднего (дисперсия неизвестна)

Тот же результат можно получить по формуле (см.

файл примера

):

=ДОВЕРИТ.СТЬЮДЕНТ(1-0,95;s;n)

s —

стандартное отклонение выборки

, n – объем

выборки

.

Подробнее см. статью про

построение доверительного интервала для оценки среднего (дисперсия неизвестна)

Источник

Содержание

Статистические функции в Excel. Описание всех функций, как их использовать
Как пользоваться статистическими функциями
Перечень статистических функций
Функция СРГЕОМ
Функция СТАНДОТКЛОН
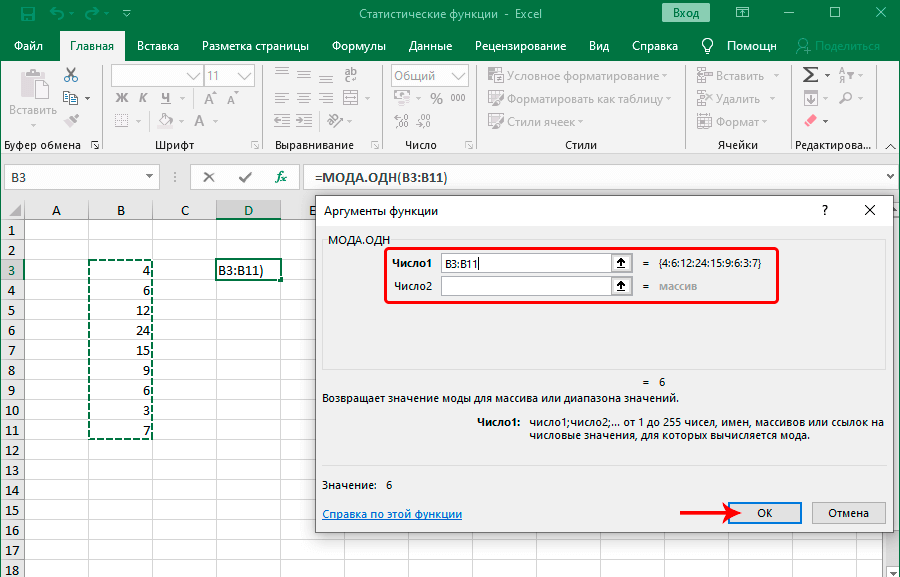
Функция МОДА.ОДН
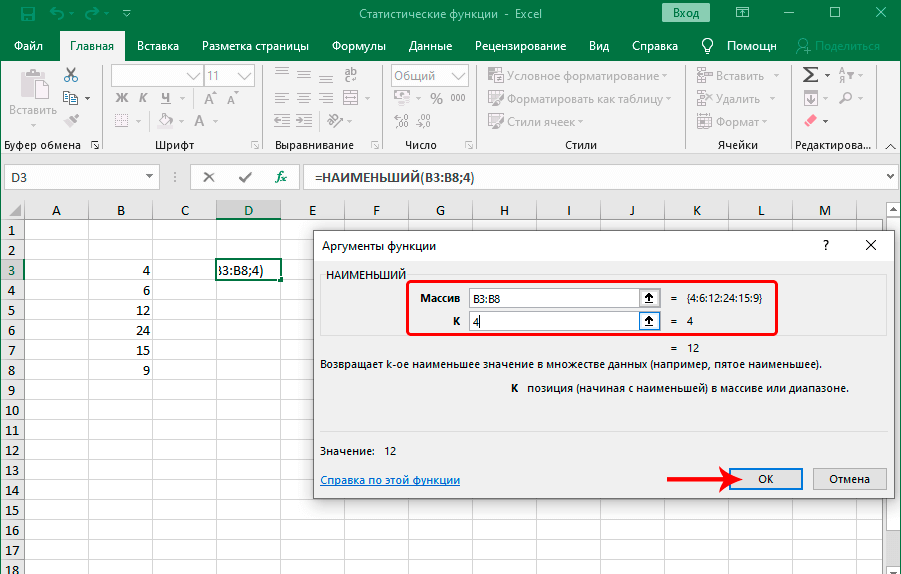
Функция НАИМЕНЬШИЙ
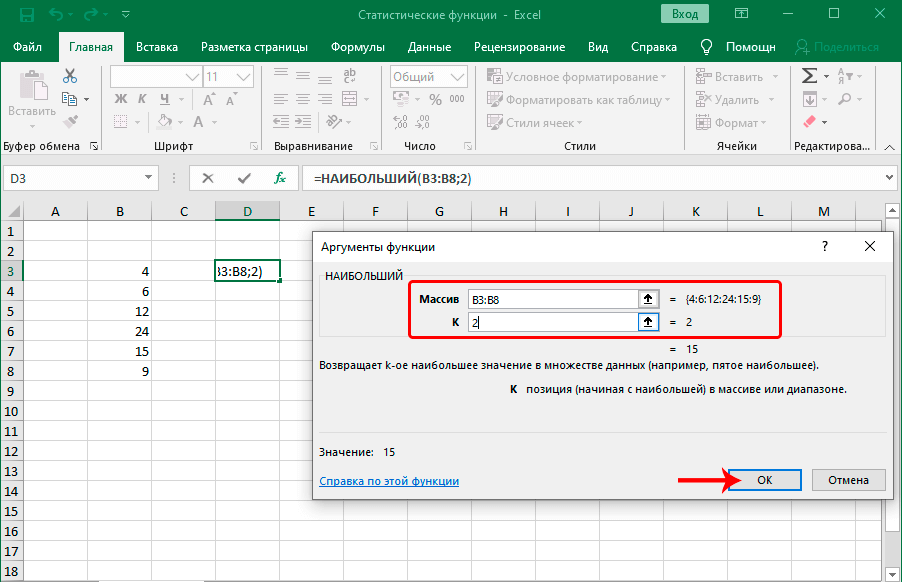
Функция НАИБОЛЬШИЙ
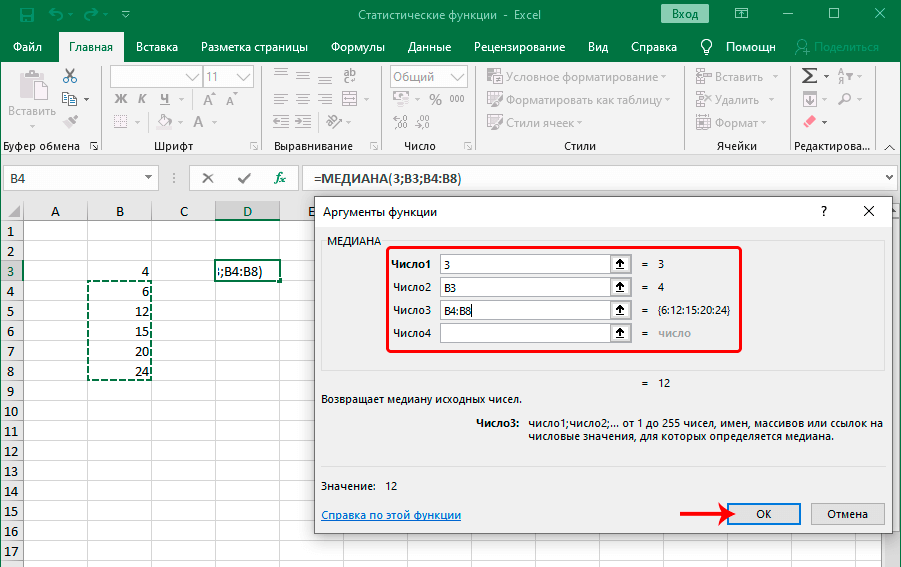
Функция МЕДИАНА
Функция СРЗНАЧЕСЛИ
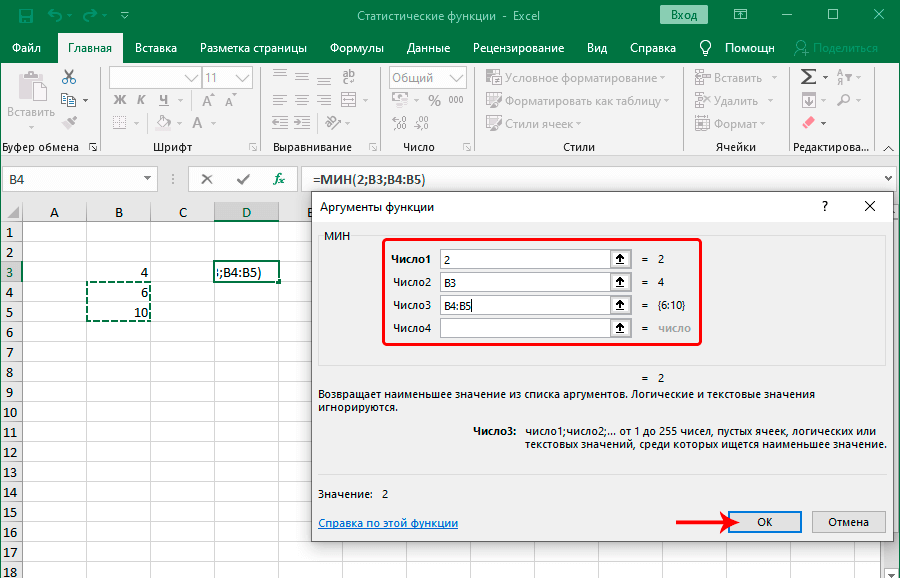
Функция МИН
Функция МАКС
Функции СРЗНАЧ и СРЗНАЧА
Функция РАНГ.СР
Лекция 2. Microsoft excel. Средства статистической обработки ms Excel
Статистические функции в ms Excel

Статистические функции в Excel. Описание всех функций, как их использовать

Статистика – наука, которая используется для любых других исследований, а также обработки большого количества количественных и даже качественных данных. И что важно, это одно из главных применений электронных таблиц Excel, поэтому давайте более подробно рассмотрим, статистические формулы. Во-первых, что они нам дают? Прежде всего, они позволяют структурировать информацию и осуществить ее анализ. Статистические функции в Excel относятся к совершенно отдельной категории.

Как пользоваться статистическими функциями

Есть несколько способов ввода любой функции, и статистические не являются исключением:

Ввести непосредственно в ячейке, предварительно нажав клавишу =. Это касается самых простых функций, несложных для запоминания и содержащих один или два аргумента. Например, так можно делать для операции умножения, сложения, вычитания и деления. А вот если функция сложная, то можно воспользоваться помощником. Это уже второй способ.
Помощник по использованию функций. Он не только подсказывает, какая формула что означает, а и помогает ввести правильные аргументы применительно к конкретной функции.

Вызвать помощник можно несколькими способами:

Воспользоваться кнопкой «Вставить функцию», расположенной слева от строки формул.
Вызвать мастер ввода функций через кнопку «Вставить функцию», которая находится в левой части панели, которая открывается по клику на вкладку «Формулы».
Воспользовавшись горячими клавишами Shift+F3.

Любой из этих методов приводит к одному результату – вызову мастера функций. Можно использовать тот, который больше всего подходит в конкретной ситуации. После того, как окно откроется, нам первым делом нужно выбрать категорию: статистические функции.

После того, как тип функции будет выбран, нам нужно выбрать подходящую формулу из списка. Под перечнем видим, что есть описание, в котором рассказывается, что конкретная функция делает.

Чтобы подтвердить выбор функции, которая будет вводиться, нужно нажать клавишу ОК. После этого появится такое окно, в котором можно ввести параметры функции (или, как их еще называют, аргументы).

Интересный факт. Можно выбрать функцию еще одним способом. Для этого нужно перейти на вкладку «Формулы» и нажать на кнопку «Другие функции», расположенной на ленте.

Далее будет пункт «Другие функции» – «Статистические» и в появившемся списке ищем подходящую функцию и выбираем ее. Этот перечень может прокручиваться.

Перечень статистических функций

А теперь давайте перейдем непосредственно к рассмотрению статистических функций.

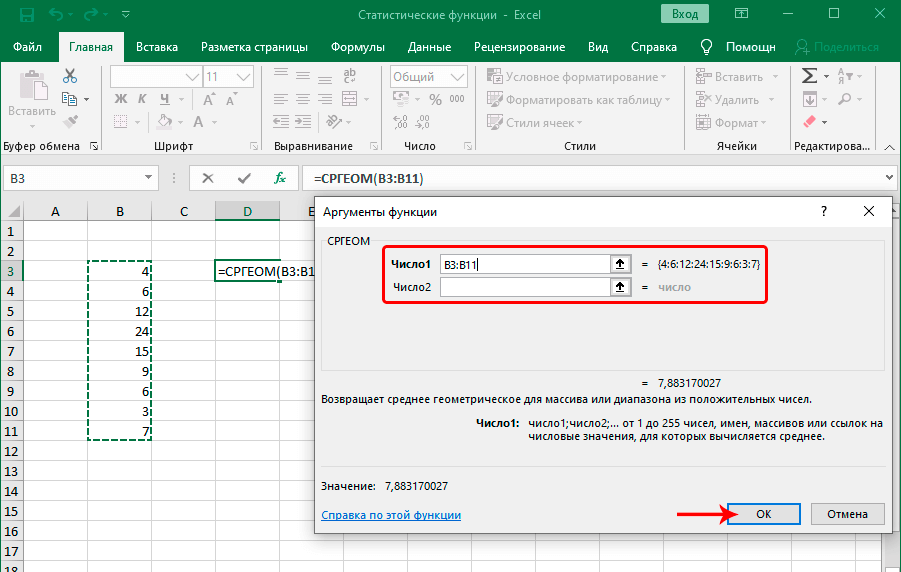
Функция СРГЕОМ

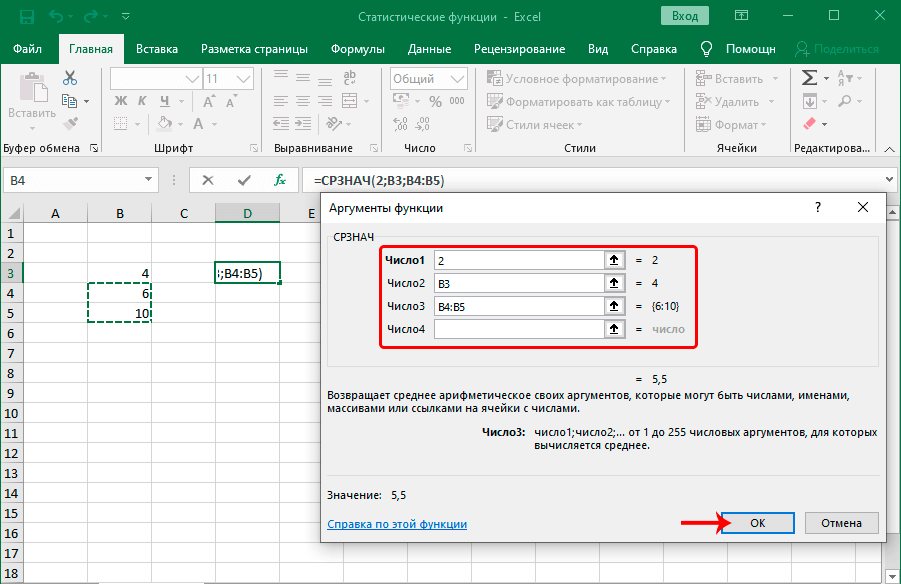
Много кто знает о таком параметре, как среднее арифметическое. Вычисляется оно с помощью функции, о которой мы еще сегодня обязательно поговорим. Но есть еще одна функция, которая определяет среднее геометрическое.

Формула очень простая: =СРГЕОМ(число1;число2;…). Кроме чисел также можно указать диапазон значений, которые учитываются этой функцией. Что же такое среднее геометрическое? Это число, которое может заменять любое из чисел в последовательности таким образом, чтобы не менялось произведение этих значений. Еще один часто используемый термин – среднее пропорциональное. Это синоним к среднему геометрическому. Такой второй термин используется, потому что среднее геометрическое пропорционально к первому и второму числам.

Функция СТАНДОТКЛОН

Один из главных статистических параметров, который должен рассчитываться вместо со средним арифметическим – стандартное отклонение. Это мера, демонстрирующая степень разброса значений. Выполняет ту же функцию, что и дисперсия, просто представлена в том же виде, что и среднее значение, в отличие от дисперсии.

Вообще, стандартное отклонение рассчитывается, как квадратный корень из дисперсии. Но в Эксель есть специальная формула, которая сразу вычисляет степень дисперсии, после чего на основе полученного значения получает стандартное (или среднеквадратическое) отклонение.

Сама эта формула довольно старая, но знать о ней надо, потому что время от времени ее можно найти в готовых таблицах. Сейчас уже есть более новые версии этой функции – СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г. Последняя функция находит среднеквадратическое отклонение по генеральной совокупности, в то время как первая ориентируется исключительно на выборку.

В остальном, синтаксис обеих функций такой же, как и для вычисления среднего арифметического (об этом мы поговорим позже) – числа, которые перечислены через скобку.

Функция МОДА.ОДН

Мода выборки абсолютно не связана с одеждой или популярными машинами. Но при этом она связана со словом «популярный». Если говорить о статистике, то это значение в выборке, которое встречается наиболее часто. Соответственно, функция МОДА.ОДН дает возможность определить это значение.

Если говорить о синтаксисе, то он похож на многие другие статистические функции. Сначала пишется оператор, после чего в скобках записываются его аргументы, которые являют собой числа, разделенные запятой. В качестве значения аргумента может выступать не только число, но и отдельные ячейки, диапазоны значений. Это дает возможность более гибко управлять выборкой. На этом скриншоте отчетливо видно, как это работает на практике.

Эта функция подходит для горизонтальных массивов. Если же нужно определить моду выборки для вертикального массива, используется похожая функция МОДА.НСК. Общий внешний вид функции следующий: =МОДА.ОДН(аргумент 1, аргумент 2; аргумент …).

Функция НАИМЕНЬШИЙ

Задача этой функции – выполнение поиска из того набора значений, который был указан пользователем. Принцип ее работы такой же, как и следующий, только поиск осуществляется по направлению снизу вверх, от наименьшего числа к самому большому. Синтаксис этой функции предельно простой: =НАИМЕНЬШИЙ(массив;k).

Функция имеет два основных аргумента: массив данных, по которым будет осуществляться поиск и порядковый номер элемента, который надо найти. Далее функция работает следующим образом: сначала она ищет самое маленькое значение, потом начинает перебирать цифры снизу вверх. Первое значение считается 1. То есть, если использовать число 1 во втором аргументе, то результат будет эквивалентным функции МИН, о которой мы поговорим немного позже.

Функция НАИБОЛЬШИЙ

Функция НАИБОЛЬШИЙ является аналогичной, только отсчет выполняет, начиная с самого большого значения. После того, как передать ей коэффициент, она ищет в порядковом ряду с большего в меньший число, занимающее соответствующее место и возвращает его. Работают обе функции аналогичным образом. Предположим, у нас есть числовой ряд. Если в нем в качестве числа k указать 2, то в результате получится число 15, поскольку оно является вторым по величине в диапазоне, который прописан в первом аргументе.

Эта функция может быть полезной в ситуациях, например, когда товар поступал в определенной последовательности, и нужно определить, сколько стоила, например, шубка, которая пришла второй по счету.

Функция МЕДИАНА

В статистике медиана – это разновидность среднего числа, которое находится ровно посередине числового ряда. Очень часто медиана является лучшим решением, чем стандартное среднее арифметическое, потому что позволяет определить действительно среднестатистическое значение. Синтаксис этой функции аналогичен тому, который имеет любой другой оператор, определяющий среднее значение – перечень цифр, ячеек или диапазонов, из которых данные будут получаться.

На этом примере видно, как на практике осуществляется работа с функцией. В диалоговом окне «Аргументы функции» можно вводить большое количество чисел, ячеек и диапазонов. На картинке мы попробовали ввести число в первую строку, ячейку во вторую и диапазон значений в третью. Получили в результате число 12. Максимальное количество аргументов этой функции – 255, что более, чем достаточно для полноценного использования этой функции.

Функция СРЗНАЧЕСЛИ

Это улучшенная версия функции СРЗНАЧ, задача которой – находить среднее арифметическое, но лишь при условии, что определенное условие выполняется. Эта функция уже несколько сложнее тех, которые приводились выше: =СРЗНАЧЕСЛИ(диапазон;условие;диапазон_усреднения). Давайте рассмотрим каждый аргумент более подробно:

Диапазон. Это ячейки, которые проверяются на предмет соответствия определенному условию.
Условие. Это критерий, на предмет соответствия которому проверяется диапазон.
Диапазон усреднения. Это тот диапазон, из которого будет доставаться среднее арифметическое. Этот аргумент вводить необязательно, поскольку диапазон ячеек и диапазон усреднения могут совпадать.

Функция МИН

В статистических подсчетах нередко нужно не только определить среднее значение, среднеквадратическое отклонение и вычислить другие показатели. Также важно значение наименьшего и наибольшего числа, в том числе, для получения указанных показателей. Практическое применение этой функции довольно обширное:

На рынке акций для определения времени, когда цела была наиболее низкой.
Для определения слабых мест в годовом бюджете (например, в каком месяце доходы компании были минимальными) с целью их дальнейшего исправления. Например, можно определить наименее доходный месяц и проанализировать факторы, которые этому способствовали.

Существует огромное количество других ситуаций, когда можно использовать функцию МИН. В самом общем виде она выглядит следующим образом: =МИН(число1;число2;…). Принцип заполнения аргументов этой функции аналогичен функции МАКС.

Функция МАКС

Как становится понятно из названия, эта функция ищет максимальное значение в определенной числовой выборке. Ситуации, в которых она может использоваться, в принципе, те же за тем лишь исключением, что все в противоположную сторону. Например, компания может с помощью функции МАКС определить самый доходный месяц и понять, каковы причины этого успеха.

Функции СРЗНАЧ и СРЗНАЧА

Стандартная функция СРЗНАЧ определяет среднее арифметическое в числовой выборке. Общий вид формулы такой же, как и для любой другой выборки значений. Сначала пишется название функции, после чего в скобках приводятся числа и диапазоны, которые необходимо обработать с помощью этой функции. То есть, общий вид формулы следующий: =СРЗНАЧ(число1;число2;…).

Как мы поняли, можно использовать как обычные числа (очень полезно для использования значений, которые не будут меняться в течение ближайшего времени), ссылки на ячейку (они применяются для тех значений, которые в будущем изменятся) и на диапазон (в этом случае будет использоваться целый набор чисел за один раз). Чтобы после ввода одного аргумента начать записывать другой, достаточно нажать на соответствующее поле в мастере функций или просто нажать на клавишу Tab.

Максимальное количество аргументов, которые можно использовать в этой функции – 255. При этом обязательным аргументом является только первое число. В качестве аргументов не могут использоваться текстовые и логические значения. Они просто не учитываются формулой, в которой используется указанный оператор. Основное отличие функции СРЗНАЧА от СРЗНАЧ заключается в том, что текстовые значения и «ЛОЖЬ» считаются нулевыми, а значение «Истина» приравнивается к единице.

Функция РАНГ.СР

С помощью функции РАНГ.СР пользователь может вернуть ранг числа. Если несколько чисел в одном диапазоне относятся к одному рангу, то возвращается среднее. Имеет три аргумента, два из которых – обязательные:

Число. Это то число, для которого осуществляется определение ранга.
Ссылка. Это массив чисел, или ссылка на этот массив.
Порядок. Это число, которое влияет на способ, в который значения будут упорядочиваться.

Таким образом, статистические функции Excel – это превосходный инструмент для обработки больших массивов информации.

Источник

Лекция 2. Microsoft excel. Средства статистической обработки ms Excel

1. Систематизировать знания о статистических функциях в Excel, получить представление о способах обработки статистические данных в табличном процессоре.

2. Ознакомиться с возможностями Пакета анализа в Excel.

3. Привести примеры работы со списками в Excel.

Статистические функции в ms Excel

Пусть представлены следующие статистические данные (см. таб. 1), по которым надо вычислить:

количество опрошенных женщин;

процент женщин среди опрошенных;

процент мужчин среди опрошенных;

средний возраст опрошенных (среднеарифметическое);

средний возраст (медиана);

минимальный и максимальный возраст опрошенных;

количество женщин с высшим образованием;

средний возраст женщин с высшим образованием;

Данные социологического опроса

Для такого рода вычислений будем пользоваться встроенными функциями. Рассмотрим некоторые из них.

1) СЧЕТ(значение1; значение2;…), которая подсчитывает количество чисел в списке аргументов. Функция СЧЁТ используется для получения количества числовых ячеек в интервалах или массивах ячеек.

Аргументы: значение1; значение2; …— это от 1 до 30 аргументов, которые могут содержать или ссылаться на данные различных типов, но в подсчете участвуют только числа.

2) СЧЕТЕСЛИ(диапазон;критерий), где диапазон – диапазон, в котором нужно подсчитать ячейки. Критерий – критерий в форме числа, выражения или текста, который определяет, какие ячейки надо подсчитывать.

3) СРЗНАЧ, которая возвращает среднее (арифметическое) своих аргументов. СРЗНАЧ(число1; число2; . )

Число1, число2, . – это от 1 до 30 аргументов, для которых вычисляется среднее.

4) МЕДИАНА(число1;число2;. ). Число1, число2. – от 1 до 30 чисел, для которых определяется медиана. Медиана – это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана.

5) МОДА(число1;число2;. ). Число1, число2. – от 1 до 30 чисел, для которых определяется мода. МОДА определяет значение, которое чаще других встречается во множестве чисел.

6) МАКС(число1;число2; . ). Число1, число2. – от 1 до 30 чисел, среди которых требуется найти наибольшее.

7) МИН(число1;число2; . ). Число1, число2. – от 1 до 30 чисел, среди которых требуется найти наименьшее.

если числовые значения образуют полную генеральную совокупность, то для вычисления дисперсии и стандартного отклонения (среднего квадратического отклонения) используются функции ДИСПР и СТАНДОТКЛОНП.

9) функции ДИСП и СТАНДОТКЛОН используются, если необходимо произвести вычисления дисперсии и стандартного отклонения по выборке.

Источник

Лекция 2

Цель

1. Систематизировать знания о статистических
функциях в Excel, получить
представление о способах обработки
статистические данных в табличном
процессоре.

2. Ознакомиться с возможностями Пакета
анализа в Excel.

3. Привести примеры работы со списками
в Excel.

Статистические функции в ms Excel

Пусть представлены следующие статистические
данные (см. таб. 1), по которым надо
вычислить:

количество опрошенных;
количество опрошенных женщин;
процент женщин среди опрошенных;
процент мужчин среди опрошенных;
средний возраст опрошенных
(среднеарифметическое);
средний возраст (медиана);
минимальный и максимальный
возраст опрошенных;
количество женщин с высшим
образованием;
средний возраст женщин с высшим
образованием;

Таблица 1

Данные социологического опроса
пол	возраст	образование
м	41	высшее
ж	53	среднее
ж	48	незаконченное высшее
м	47	среднее специальное
ж	22	среднее
м	32	высшее
ж	39	среднее специальное
м	49	незаконченное высшее
м	52	незаконченное высшее
м	28	высшее
м	55	среднее
ж	41	среднее специальное
м	32	высшее
м	40	среднее
м	41	среднее
ж	32	высшее
м	41	высшее
м	20	высшее
ж	48	высшее
м	61	высшее
нет ответа	32	среднее специальное
ж	19	среднее специальное
ж	49	среднее специальное
м	22	среднее
м	40	среднее
м	60	высшее

Для такого рода вычислений будем
пользоваться встроенными функциями.
Рассмотрим некоторые из них.

1) СЧЕТ(значение1; значение2;…), которая
подсчитывает количество чисел в списке
аргументов. Функция СЧЁТ используется
для получения количества числовых ячеек
в интервалах или массивах ячеек.

Аргументы: значение1; значение2; …— это
от 1 до 30 аргументов, которые могут
содержать или ссылаться на данные
различных типов, но в подсчете участвуют
только числа.

2) СЧЕТЕСЛИ(диапазон;критерий), где
диапазон – диапазон, в котором нужно
подсчитать ячейки. Критерий – критерий
в форме числа, выражения или текста,
который определяет, какие ячейки надо
подсчитывать.

3) СРЗНАЧ, которая возвращает среднее
(арифметическое) своих аргументов.
СРЗНАЧ(число1; число2; …)

Число1, число2, …– это от 1 до 30 аргументов,
для которых вычисляется среднее.

4) МЕДИАНА(число1;число2;…). Число1,
число2,…– от 1 до 30 чисел, для которых
определяется медиана. Медиана – это
число, которое является серединой
множества чисел, то есть половина чисел
имеют значения большие, чем медиана, а
половина чисел имеют значения меньшие,
чем медиана.

5) МОДА(число1;число2;…). Число1,
число2,…– от 1 до 30 чисел, для которых
определяется мода. МОДА определяет
значение, которое чаще других встречается
во множестве чисел.

6) МАКС(число1;число2; …). Число1,
число2,…– от 1 до 30 чисел, среди которых
требуется найти наибольшее.

7) МИН(число1;число2; …). Число1,
число2,…– от 1 до 30 чисел, среди которых
требуется найти наименьшее.

если числовые значения образуют
полную генеральную совокупность, то
для вычисления дисперсии и стандартного
отклонения (среднего квадратического
отклонения) используются функции ДИСПР
и СТАНДОТКЛОНП.

9) функции ДИСП и СТАНДОТКЛОН
используются, если необходимо
произвести вычисления дисперсии и
стандартного отклонения по выборке.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Содержание

1 Использование описательной статистики
- 1.1 Подключение «Пакета анализа»
- 1.2 Применение инструмента «Описательная статистика»
- 1.3 Помогла ли вам эта статья?
- 1.4 Статистические процедуры Пакета анализа
- 1.5 Статистические функции библиотеки встроенных функций Excel

Этот инструмент называется «Описательная статистика». С его помощью можно в очень короткие сроки, использовав ресурсы программы, обработать массив данных и получить о нем информацию по целому ряду статистических критериев. Давайте взглянем, как работает данный инструмент, и остановимся на некоторых нюансах работы с ним.

Использование описательной статистики

В Экселе существует отдельный инструмент, входящий в «Пакет анализа», с помощью которого можно провести данный вид обработки данных. Он так и называется «Описательная статистика». Среди критериев, которые высчитывает данный инструмент следующие показатели:

Медиана;
Мода;
Дисперсия;
Среднее;
Стандартное отклонение;
Стандартная ошибка;
Асимметричность и др.

Подключение «Пакета анализа»

Как уже было сказано выше, инструмент «Описательная статистика» входит в более широкий набор функций, который принято называть Пакет анализа. Но дело в том, что по умолчанию данная надстройка в Экселе отключена. Поэтому, если вы до сих пор её не включили, то для использования возможностей описательной статистики, придется это сделать.

Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».
В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».
Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».

После вышеуказанных действий надстройка Пакет анализа будет активирована и станет доступной во вкладке «Данные» Эксель. Теперь мы сможем использовать на практике инструменты описательной статистики.

Применение инструмента «Описательная статистика»

Переходим во вкладку «Данные» и выполняем щелчок по кнопке «Анализ данных», которая размещена на ленте в блоке инструментов «Анализ».
Открывается список инструментов, представленных в Пакете анализа. Ищем наименование «Описательная статистика», выделяем его и щелкаем по кнопке «OK».
После выполнения данных действий непосредственно запускается окно «Описательная статистика».
В поле «Входной интервал» указываем адрес диапазона, который будет подвергаться обработке этим инструментом. Причем указываем его вместе с шапкой таблицы. Для того, чтобы внести нужные нам координаты, устанавливаем курсор в указанное поле. Затем, зажав левую кнопку мыши, выделяем на листе соответствующую табличную область. Как видим, её координаты тут же отобразятся в поле. Так как мы захватили данные вместе с шапкой, то около параметра «Метки в первой строке» следует установить флажок. Тут же выбираем тип группирования, переставив переключатель в позицию «По столбцам» или «По строкам». В нашем случае подходит вариант «По столбцам», но в других случаях, возможно, придется выставить переключатель иначе.

Выше мы говорили исключительно о входных данных. Теперь переходим к разбору настроек параметров вывода, которые расположены в этом же окне формирования описательной статистики. Прежде всего, нам нужно определиться, куда именно будут выводиться обработанные данные:
- Выходной интервал;
- Новый рабочий лист;
- Новая рабочая книга.
В первом случае нужно указать конкретный диапазон на текущем листе или его верхнюю левую ячейку, куда будет выводиться обработанная информация. Во втором случае следует указать название конкретного листа данной книги, где будет отображаться результат обработки. Если листа с таким наименованием в данный момент нет, то он будет создан автоматически после того, как вы нажмете на кнопку «OK». В третьем случае никаких дополнительных параметров указывать не нужно, так как данные будут выводиться в отдельном файле Excel (книге). Мы выбираем вывод результатов на новом рабочем листе под названием «Итоги».

Далее, если вы хотите чтобы выводилась также итоговая статистика, то нужно установить флажок около соответствующего пункта. Также можно установить уровень надежности, поставив галочку около соответствующего значения. По умолчанию он будет равен 95%, но его можно изменить, внеся другие числа в поле справа.

Кроме этого, можно установить галочки в пунктах «K-ый наименьший» и «K-ый наибольший», установив значения в соответствующих полях. Но в нашем случае этот параметр так же, как и предыдущий, не является обязательным, поэтому флажки мы не ставим.

После того, как все указанные данные внесены, жмем на кнопку «OK».
После выполнения этих действий таблица с описательной статистикой выводится на отдельном листе, который был нами назван «Итоги». Как видим, данные представлены сумбурно, поэтому их следует отредактировать, расширив соответствующие колонки для более удобного просмотра.
После того, как данные «причесаны» можно приступать к их непосредственному анализу. Как видим, при помощи инструмента описательной статистики были рассчитаны следующие показатели:
- Асимметричность;
- Интервал;
- Минимум;
- Стандартное отклонение;
- Дисперсия выборки;
- Максимум;
- Сумма;
- Эксцесс;
- Среднее;
- Стандартная ошибка;
- Медиана;
- Мода;
- Счет.

Урок: Статистические функции в Excel

Как видим, с помощью инструмента «Описательная статистика» можно сразу получить результат по целому ряду критериев, которые в ином случае рассчитывались с применением отдельно предназначенной для каждого расчета функцией, что заняло бы значительное время у пользователя. А так, все эти расчеты можно получить практически в один клик, использовав соответствующий инструмент — Пакета анализа.

Мы рады, что смогли помочь Вам в решении проблемы.

Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.

Помогла ли вам эта статья?

Да Нет

Сортировка данных в Excel

Таблицы Excel можно использовать для создания баз данных, т.е. совокупности определенным образом организованной информации. В таблицах хранят информацию о сотрудниках, клиентах, поставщиках различной продукции, ценах, книгах, фильмах, фотографиях и т.д. Как правило, для таких баз данных используется табличный способ организации. Они содержат большое количество данных, а с большим количеством данных не всегда просто работать. Для этого и необходима обработка данных.

сортировку списков;
выборку данных по определенным критериям;
вычисление промежуточных сумм;
вычисление средних значений;
вычисление отклонений от определенного значения;
построение сводных таблиц.

Как сделать фильтр в Excel

Базы данных очень удобны для хранения информации, но мы создаем их для того, чтобы получать нужную для нас справку, когда возникает подобная необходимость.

Например, нам нужно расписание железнодорожных поездов, которые отправляются в Москву в пятницу после четырех часов дня и т.п.

Поиск нужной информации осуществляется путем отбора строк, удовлетворяющих некоторому критерию. В большинстве случаев критерием отбора является равенство содержимого ячейки определенному значению.

Помимо сравнения на равенство, при отборе записей можно использовать и другие операции сравнения. Например, больше, меньше, больше или равно, меньше или равно. Использование этих операций позволяет сформулировать критерий запроса менее строго. Например, если требуется найти информацию о человеке, фамилия которого начинается с «Ку», то в качестве критерия можно использовать правило «содержимое ячейки Фамилия больше или равно Ку и содержимое ячейки Фамилия меньше Л».

Промежуточные итоги в Excel

Одним из методов обработки данных является подведение итогов. Пусть, например, есть таблица расходов. Для того чтобы узнать, сколько потрачено в каждом месяце, необходимо подвести итог за каждый месяц.

1. Выделить диапазон, содержащий данные и заголовки столбцов, в которых данные находятся. В рассматриваемом примере это вся таблица, на фото представлена только ее часть.
2. На вкладке Данные -> Структура выбрать команду Промежуточный итог.
3. В появившемся диалоговом окне Промежуточные итоги в поле — При каждом изменении в:, требуется задать столбец, при изменении содержимого которого будет вычислена промежуточная сумма. В данном случае это Дата. В поле Операция выбрать операцию из списка, которую нужно выполнить над обрабатываемыми данными. В нашем случае это Сумма. В поле — Добавить итоги по:, установить флажок в том столбце, в котором находятся обрабатываемые данные.

Сводные таблицы Excel 2010

Сводная таблица позволяет выполнить более тонкий анализ данных, чем простое подведение итога. Что такое сводная таблица и как ее построить, рассмотрим на примере.

Пусть есть таблица, в которой находится информация о расходах.

Основными средствами анализа статистических данных в Excel являются статистические процедуры надстройки Пакет анализа (Analysis ToolРак) и статистические функции библиотеки встроенных функций. Основные сведения обо всех этих средствах имеются в электронной справочной системе Excel.

Однако качество описаний статистических процедур и функций, приведенных в этой системе, заставляет желать лучшего. Некоторые из этих описаний не очень понятны, в них имеются неточности, а подчас и просто ошибки (это относится как к англоязычному оригиналу, так и к русскому переводу). Эти недостатки с завидным постоянством повторяются и во многих пособиях по Excel. Найти необходимые пособия в интернете можно быстро если скачать бесплатно Амиго браузер с усовершенствованным поисковым алгоритмом.

Статистические процедуры Пакета анализа

Наиболее развитыми средствами анализа данных являются статистические процедуры Пакета анализа. Они обладают большими возможностями, чем статистические функции. С их помощью можно решать более сложные задачи обработки статистических данных и выполнять более тонкий анализ этих данных.

В Пакет анализа входят следующие статистические процедуры:

генерация случайных чисел (Random number generation);
выборка (Sampling);
гистограмма (Histogram);
описательная статистика (Descriptive statistics);
ранги персентиль (Rank and percentile);
двухвыборочный z-тест для средних (z-Test: Two Sample for Means);
двухвыборочный t-тест для средних с одинаковыми дисперсиями (t-Test: Two-Sample Assuming Equal Variances);
двухвыборочный t-тест для средних с различными дисперсиями (t-Test: Two-Sample Assuming Unequal Variances);
парный двухвыборочный t-тест для средних (t-Test: Paired Two Sample for Means);
двухвыборочный F-тест да я дисперсий (F-Test: Two Sample for Variances);
коварнация (Covariance);
корреляция (Correlation);
рецессия (Regression);
однофакторный дисперсионный анализ (ANOVA: Single Factor);
двухфакторный дисперсионный анализ без повторений (ANOVA: Two Factor Without Replication);
двухфакторный дисперсионный анализ с повторениями (ANOVA: Two Factor With Replication);
скользящее среднее (Moving Average);
экспоненциальное сглаживание (Exponential Smoothing);
анализ Фурье (Fourier Analysis).

Для доступа к процедурам Пакета анализа необходимо в меню Сервис (Tools) щелкнуть указателем мыши на строке Анализ данных (Data Analysis). Откроется диалоговое окно с соответствующим названием, в котором перечислены процедуры статистического анализа данных (рис. 1).

Рис.1. Диалоговое окно Анализ данных

Для того чтобы запустить в работу нужную статистическую процедуру, нужно выделить ее указателем мыши и щелкнуть на кнопке ОК. На экране появится диалоговое окно вызванной процедуры. На рис. 2 для примера показано диалоговое окно процедуры Описательная статистика (Descriptive statistics).

Рис.2. Диалоговое окно процедуры Описательная статистика

Диалоговое окно каждой процедуры содержит элементы управления: поля ввода, раскрывающиеся списки, переключатели, флажки и т. п. Эти элементы позволяют задать нужные параметры используемой процедуры. Некоторые элементы управления имеют специфический характер, присущий одной процедуре или небольшой группе процедур. Назначение таких элементов управления будет рассмотрено при описании соответствующих процедур. Другие элементы управления присутствуют в диалоговых окнах почти всех статистических процедур.

К числу общих для большинства процедур элементов управления относятся:

поле ввода Входной интервал (Input Range). В это поле вводится ссылка на диапазон, содержащий статистические данные, подлежащие обработке. Входной диапазон может быть столбцом пли группой столбцов (строкой или группой строк);
переключатель Группирование (Grouped By). В том случае, когда входной диапазон представляет собой столбец или группу столбцов, переключатель устанавливается в положение по столбцам (Columns). Если же входной диапазон представляет собой строку или группу строк, то переключатель устанавливается в положение по строкам (Rows). Более точным названием этого переключателя было бы название Расположение;
флажок Метки (Labels in First Row). Флажок устанавливается в тех случаях, когда первая строка (первый столбец) входного диапазона содержит заголовки. Если такие заголовки отсутствуют, флажок Метки не устанавливают. При этом Excel автоматически создает и выводит на экран стандартные названия для данных выходного диапазона (Столбец1, Столбец2,… или Строка 1. Строка2,…);
переключатели Выходной интервал/Новый рабочий лист/Новая книга (Output Range/New Worksheet/New Workbook). Эти переключатели определяют место вывода таблицы, содержащей результаты реализации статистической процедуры. В группе может быть выбран только одни переключатель.

При выборе переключателя Выходной интервал таблица результатов решения выводится на тот же рабочий лист, на котором находятся исходные данные. Справа от переключателя открывается поле ввода, в которое надо ввести ссылку на левую верхнюю ячейку таблицы результатов. Если возникает опасность наложения таблицы результатов на уже заполненные ячейки, на экране появляется сообщение о такой опасности. В ответ на это сообщение пользователь должен разрешить удаление старых данных и вывод на их место новых.

В положении Новый рабочий лист открывается новый лист рабочей книги. На этот лист, начиная с ячейки А1, и выводится таблица результатов решения. Справа от переключателя имеется поле ввода, в которое в случае необходимости можно ввести имя нового рабочего листа. При выборе переключателя Новая рабочая книга открывается новая рабочая книга. На первый лист этой новой книги, начиная с ячейки А1, выводится таблица результатов решения.

Следует заметить, что результаты;, получаемые с помощью статистических процедур Пакета анализа, не имеют постоянной связи с исходными данными — в случае изменения исходных данных результаты решения автоматически не изменяются. В том случае, когда необходимо получить результаты, автоматически изменяющиеся вместе с исходными данными, нужно использовать подходящие статистические функции библиотеки встроенных функций.

Эффективным и очень удобным в использовании средством парного регрессионного анализа и анализа временных рядов является процедура Добавить линию тренда (Add Trendline), входящая в комплекс графических средств Excel.

Статистические функции библиотеки встроенных функций Excel

Табличный процессор Excel имеет библиотеку встроенных функции рабочего листа (Worksheet function). Одним из разделов этой библиотеки является раздел Статистические функции. В этот раздел входят 83 функции, предназначенные для решения некоторых наиболее востребованных задач теории вероятностей и математической статистики.

Аргументы статистических функций должны быть числами или ссылками на диапазоны, которые содержат числа Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются, однако ячейки с нулевыми значениями учитываются.

Когда в качестве какого-либо аргумента встроенной статистической функции введен текст, функция выдает сообщение об ошибке #ЗНАЧ! (#VALUE!). Если в качестве аргумента, который по определению должен быть целым числом, введено число не целое, Excel использует в качестве аргумента целую часть этот числа. Никакие сообщения об этом «несанкционированном округлении» на экран не выводятся.

Источник