Методика расчета рисков excel

ППП
EXCEL
предлагает широкий набор средств
автоматизации статистического
моделирования данных от вычисления
параметров описательной статистики до
построения сложных прогнозных моделей.
Для этих целей в нем реализована
специальная группа статистических и
математических функций, большинство
из которых содержится в дополнении
Пакет анализа.
Список и форматы некоторых функций,
использованных в процессе анализа
рисков, приведены в табл. 1.1.

	Таблица 1.1.
Наименование функции	Формат функции
СРЗНАЧ	СРЗНАЧ(блок ячеек)
ДИСПР	ДИСПР(блок ячеек)
СКОС	СКОС(блок ячеек)
СТАНДОТКЛОНП	СТАНДОТКЛОНП(блок ячеек)
НОЕМОБР	НОРМОБР(вероятность; средн_энач; станд отклон)
НОРМРАСП	НОРМРАСП (х; средн знач ; станд откл; интегральная)

4.3. Анализ рисков финансовых операций

Рассмотрим
типовые задачи, которые можно решать с
использованием стандартных функций
ППП EXCEL.

Определение
основных характеристик распределения
случайной величины (СВ). Возможны
два варианта расчетов: случай, когда
вероятность осуществления случайного
события не задана и , наоборот, вероятность
осуществления случайного события задана
явно.

Определение
характеристик СВ при незаданной
вероятности осуществления событий.
В этом случае полагаем вероятность
осуществления всех событий одина­ковой,
т.е. p₁
= p₂
=…= p_n=
1/n
и можем непосредственно применить
статистические функций ППП EXCEL,
вычисляющие основные характеристики
распределения СВ (среднее значение
М(Е), дисперсию VAR(E),
стандартное отклонение (Е)).
Продемонстрируем технику их расчетов
с применением встроенных функций ППП
EXCEL.

Подготовьте исходную таблицу (рис. 1.1. ) с данными следующего примера.

Пример
1.1. Рассмотрим
возможность покупки акции недавно
образованной фирмы «Н». Предполагается,
что прогнозируется доходность по акциям
этой фирмы через год будет зависеть от
состояния спроса на ее продукцию в
течение данного периода и соответственно
равна: 12% — в случае повышенного спроса;
9% — при обычном спросе; 6% — при пониженном
спросе.

	А	В	С
1	Анализ рисков (акции фирмы «Н»)
2
3	Прогноз	Доходность
4	Пессимистический	6%
5	Вероятный	9%
6	Оптимистический	12%
7
8	Ожидаемая доходность (r )
9	Дисперсия (VAR)
10	Стандартное отклонение
11	Коэффициент вариации (CV)

Рис.
1.1. Исходная таблица для решения примера
1.1.

Осуществим
анализ риска этой операции. Прежде всего
определим среднюю доходность по акциям
фирмы «Н». Поскольку наступление
любого события в данном примере считается
равновероятным, для расчета искомой
величины можно воспользоваться функцией
СРЗНАЧ (),
указав ей в качестве аргументов блок
ячеек В4,
В6,
содержащий предполагаемые значения
доходности. Введите в ячейку В8
формулу: =СРЗНАЧ
(В4: В6) (Результат
0,09, или 9%).

Для
вычисления дисперсии и стандартного
отклонения в ячейках В9
и В10
необходимо задать следующие формулы:

=ДИСПР(В4:В6) (Результат
0,0006)

=СТАНДОТКЛОНП
(В4: В6) (Результат
0,0245, или 2,45%)

Теперь
можно легко определить значение
коэффициента ва­риации из соотношения
(11). Для этого
в ячейке В11
вычислим результат отношения стандартного
отклонения (В10)
к ве­личине среднего значения (В8):

=В10/В8 (Результат
0,27)

Полученные
значения параметров позволяют сделать
вывод о невысоком риске акций фирмы
«Н».

Определение
характеристик СВ при заданной вероятности
осуществления событий.

Рассчитаем
вероятность того, что доходность по
акциям «Н» будет меньше величины
а—
(9 — 2,45 = 6,55). При этом будем исходить из
предполо­жения, что величина доходности
r
распределена по нормальному закону
Тогда из (10)

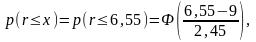
где
Ф — функция Лапласа.

Для
автоматизации расчетов, связанных с
нормальным распределением вероятностей,
в ППП EXCEL
реализован ряд специальных функций. Мы
будем использовать две функции —
НОРМРАСП()
и НОРМОБР().

Функция
НОРМРАСП (х; средн_знач; станд_откл;
интегральная)

Функция
НОРМРАСП ()
имеет следующие параметры:

х
— исследуемое значение случайной
величины,

средн_знач
— среднее значение;

станд_откл
— стандартное отклонение;

интегральная
— 0 или 1.

В
зависимости от заданного параметра
интегральная
— О (ложь) или 1 (истина) — она возвращает
плотность распределения (х)
или значение кумулятивной функции
распределения вероятностей F(x)
для нормальной случайной величины.

Определим
искомую вероятность р
(r
<. 6,55) Для
этого в ячейку В14
введем формулу:

=НОРМРАСП(6,55;
9; 2,45; 1)
(Результат 0,1586), или

=НОРМРАСП(В8-В10;
В8; В10; 1)
(Результат 0,1586)

Таким
образом, эта вероятность приблизительно
равна 16%. Соответственно вероятность
Р(r
> 6,55) будет
равна:

=1
— НОPМРАСП(В8-В10;
В8; В10; 1)
(Результат 0,8414)

На
рис. 1.2. приведен фрагмент ЭТ с расчетами
вероятностей для различных значений
ставки доходности r.
Выполнить эти расчеты самостоятельно.

Построить
графики плотности и кумулятивной функции
распределения вероятностей для примера
1.1. Для построения графиков необходимо
предварительно выполнить табуляцию
функций (х)
на интервале [а ± 3]
и F(x).
Для определения значений (х)
также используется функция НОРМРАСП
(), однако
значение параметра интегральная
при этом задается равным 0 (ложь).

	А	В	С
1	Анализ рисков (акции фирмы «Н»)
2
3	Прогноз	Доходность
4	Пессимистический	6%
5	Вероятный	9%
6	Оптимистический	12%
7
8	Ожидаемая доходность (r )	9,00%
9	Дисперсия (VAR)	0,0006
10	Стандартное отклонение	2,45%
11	Коэффициент вариации (CV)	0,27
12
13	P (r<=6,55%)	0,1587
14	P (r<=11,45%)	0,8413
15	P (r<=0%)	0,0001
16
17

рис.
1.2. Анализ риска (пример 1.1)

По
графикам убедиться, функция распределения
F(x)
возрастает на интервале от 0 до 1. Согласно
правилу сложения вероятностей при x₁<x₂
вероятность попадания значения случайной
величины Е
в интервал (x₁;
x₂)
равна
приращению функции распределения
вероятностей:

p(x₁

E
< x₂)=F(x₂)
– F(x₁)

Определим
вероятность попадания r
в интервал (а + ):

=НОРМРАСП(В8+В10;
В8; В10;1) — НОЕМРАСП(В8; В8; В10;1)

(Результат:
0,3414)

Соответственно
вероятность попадания r
в интервал (а ± )
будет равна:

=НОЕМРАСП(В8+В10;В8;В10;1)
— НОБМРАСП(В8-В10; В8; В10;1)

(Результат:
0,6828)

Вероятность
попадания г в интервал (а ± 2)
и (а ± З)
определите самостоятельно.

Полученные
результаты служат числовой иллюстрацией
правила трех сигм для нормального закона
распределения.

Функция
НОРМОБР (вероятность; средн_энач;
станд__откл)

Функция
имеет следующие параметры:

вероятность
—вероятность нормального распределения;

средн_знач
—среднее значение;

станд_откл
—стандартное отклонение.

Она
возвращает обратное нормальное
распределение для указанного среднего
и стандартного отклонения. Другими
словами, она позволяет по заданной
вероятности определить величину
исследуемой переменной (в нашем примере
доходности).

Определим
предельную величину доходности для
вероятности 84%:

=НОРМОБР
(0,84 ;В8 ;В10) (Результат:
11,45%).

Таким
образом, для заданной вероятности
величина доходности составит не более
11,45%: р(х 0,1145)
= 0,84.

Функции
ППП EXCEL,
определяющие значения параметров
распределения М(Е),
VAR(E)
и (Е),
следует применять только в тех случаях,
когда
вероятности событий равны.
Если же распределение вероятностей
задано (например, известно из преды­дущего
опыта или получено методом экспертных
оценок), среднее значение, дисперсия и
стандартное отклонение рассчитываются
путем непосредственной реализации
средствами ППП EXCEL
соответствующих соотношений — (4),
(6), (7). Продемонстрируем
один из вариантов подобной реализации
на решении примера 1.2.

Пример
1.2.
Рассматривается возможность приобретения
акций двух фирм «А» и «В». Полученные
экспертные оценки предполагаемых
значений доходности по акциям и их
вероятности представлены в таблице
1.2.

Таблица
1.2.

Прогноз	Вероятность	Доходность, %
Фирма «А»	Фирма «В»
Пессимистический	0,3	-70	10
Вероятный	0,4	15	15
Оптимистический	0,3	100	20

Подготовьте
исходную таблицу с данными примера, как
показано на рис. 1.3.

	А	В	С	D
1	Анализ рисков (акции фирмы «А»)	Взвешенные квадраты отклонений
2
3	Прогноз	Вероятность	Доходность
5	Пессимистический	0,30	-70,00%
6	Вероятный	0,40	15,00%
7	Оптимистический	0,30	100,00%
8
9	Ожидаемая доходность (r )
10	Стандартное отклонение
11	Коэффициент вариации (CV)
12
14		Интервал ставки (r1; r2)	Вероятность (r1<=R<=r2)
15		r1	r2

Рис.
1.3. Исходная таблица для решения примера
1.2.

Прежде
всего необходимо определить среднюю
величину доходности (соотношение (4)).
Наиболее простой способ — последовательно
перемножить каждую ячейку блока В5.
В7
на соответствующую ей ячейку блока С5.
С7 и суммировать
полученные значения. Нетрудно заметить,
что данная последовательность действий
представляет собой операцию нахождения
суммы произведений элементов двух
матриц. Поскольку матричные операции
достаточно часто встречаются в прикладном
анализе, для автоматизации их выполнения
в ППП EXCEL
реализована специальная группа
математических
функции..

В
частности, для выполнения необходимой
нам операции удобно использовать функцию
СУММПРОИЗВ (). Как следует из табл. 1.3.,
аргументами функции являются матрицы
одинакового размера. Введем в ячейку и
формулу:

=СУММПРОИЗВ
(В5: В7; С5: С7) (Результат:
0,15, или 15%)

Для
определения величины стандартного
отклонения необходимо сперва вычислить
дисперсию. Из (6) следует, что дисперсия
случайной величины представляет собой
сумму квадратов отклонений от среднего,
взвешенных на соответствующие вероятности.
Зададим в ячейке D5
формулу вычисления дисперсии для первого
события:

=В5*
(С5-$В$9) ^2 (Результат:
0,2165).

Обратите
внимание на то, что для задания ячейки,
содержащей среднее значение (В9),
используется способ абсолютной адресации.
Это позволяет безболезненно скопировать
данную формулу в ячейки D6,D7
(в противном случае адрес ячейки,
содержащей среднее значение, был бы
настроен неправильно). Теперь можно
вычислить величину стандартного
отклонения, которая равна квадратному
корню из дисперсии (суммы ячеек D5:D7).
Для этого воспользуемся функцией КОРЕНЬ
() (см. табл. 1.3.). Введите в ячейку В10:

=КОРЕНЬ(СУММ(D5:D7)) (Результат:
0,6584, или 65,84%).

Вычисление
коэффициента вариации не представляет
особых трудностей. Для этого достаточно
просто разделить значение ячейки В10 на
значение В9. Введите в ячейку В11:

=В10/В9 (Результат:
4,39).

Вычислив
основные параметры распределения
случайной величины, можно определить
вероятность ее попадания в некоторый
интервал. В приведенной на рис. 1.4. таблице
границы первого интервала задаются в
ячейках В16
и С 16.
Определим вероятность того, что значение
доходности попадет в интервал (-70; 0).
Введите границы анализируемого интервала
в ячейки В16
и С16.
Формула вычисления вероятности в ячейке
D16
реализована с использованием уже
известной нам функцией НОРМРАСП
() и имеет
следующий вид:

=НОРМРАСП
(С16;$В$9;$В$10;1)-НОРМРАСП (В16;$В$9;$В$10;1)

(Результат:
0,31).

Снова
обращаем внимание на использование
абсолютной адресации при задании в
формулах ячеек, содержащих среднее
значение и стандартное отклонение.

	А	В	С	D
1	Анализ рисков (акции фирмы «А»)
3	Прогноз	Вероятность	Доходность	Взвешенные квадраты отклонений
4
5	Пессимистический	0,30	-70,00%	0,21675
6	Вероятный	0,40	15,00%	0
7	Оптимистический	0,30	100,00%	0,21675
9	Ожидаемая доходность (r )	15,00%
10	Стандартное отклонение	65,84%
11	Коэффициент вариации (CV)	4,39
14		Интервал ставки (r1; r2)	Вероятность (r1<=R<=r2)
15		r1	r2
16		-70%	0%	0,31
17		15%	65%	0,28
18		15%	100%	0,4
19		-70%	100%	0,8

Рис.
1.4. Итоговая таблица анализа рисков
(фирма «А»).

Для
дальнейшего анализа достаточно указать
интересующие интервалы и скопировать
формулу в ячейке
D16
необходимое число раз. На рис 1.4. приведена
итоговая таблица, содержащая некоторые
результаты анализа риска по акциям
фирмы «А» (пример 2.) Аналогичная
таблица на рис 1.5. содержит результаты
анализа риска по акциям фирмы «В».

В
качестве упражнения попробуйте
разработать таблицу анализа рисков для
фирмы «В» самостоятельно, используя
рис 1.3. в качестве образца. Сравните
полученные результаты.

	А	В	С	D
1	Анализ рисков (акции фирмы «В»)
2
3	Прогноз	Вероятность	Доходность	Взвешенные квадраты отклонений
4
5	Пессимистический	0,3	10%	0,00075
6	Вероятный	0,4	15%	0
7	Оптимистический	0,3	20%	0,00075
8
9	Ожидаемая доходность (r )	15,00%
10	Стандартное отклонение	3,87%
11	Коэффициент вариации (CV)	0,26
12
13
14		Интервал ставки (r1; r2)	Вероятность (r1<=R<=r2)
15		r1	r2
16		0%	20%	0,9
17		15%	20%	0,4
18		10%	20%	0,8
19		-10%	0%	0

Рис.
1.5. Итоговая таблица анализа рисков
(фирма «В»).

Пример
1.3.
Прогнозируемые
доходности по акциям фирм «К» и «Р»
имеют следующие распределения вероятностей
(табл.1.5)

Таблица
1.5.

Вероятность	Доходность
Акции «К»	Акции «Р»
0,15	-15%	—25%
0,20	0%	10%
0,40	15%	20%
0,20	20%	30%
0,05	35%	45%

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

В этом видео я знакомлю вас с методикой расчета риска в трейдинге в EXCEL, расчетом стоп-лосса и базовыми принципами управления капиталом. Привожу наглядные примеры для расчета риска по акциям, фьючерсам и CFD.

Также в вводной части высказываю свое мнение о проблемах неопытных трейдеров и об ошибках, которые приводят к потере депозита. У высказанной мысли имеется научное обоснование, поэтому пару слов сказал о Теории перспектив и ее влиянии на финрезультаты трейдеров.

Первая часть. Эту часть можно просто послушать.

00:00 — вступительное слово. Что вас ждет в этом видео, почему принципы управления капиталом так важны для трейдера, почему все новички сливаются и как этого избежать? Пара слов о теории перспектив и философия риск-менеджмента.

12:00 Вторая часть: работа в excel

12:01 — расчет риска для акций на примере акций Сбербанка;

19:42 — расчет риска для CFD на примерах валютных пар EUR/USD, USD/JPY, CFD на серебро;

33:02 — расчет риска для фьючерсов на примере фьючерсов на Московской бирже (РТС, нефть) и на Чикагской товарной бирже (Нефть, фьючерс на EUR/USD).

Все видео пропитано размышлениями и комментариями относительно риск-менеджмента и принципами управления капиталом.

====================================================================

За оперативной информацией по финансовым рынкам приглашаю всех желающих в свой канал Телеграмм: https://teleg.run/khtrader

КУРС

ИНВЕСТИЦИОННЫЙ АНАЛИТИК

Инвестору чрезвычайно важно знать степень риска, которому подвержены открытые позиции. Определить меру риска VaR (Value-at-Risk) для единичного актива можно по формуле:

95% VaR = 1.65 X Волатильность * Размер позиции * SQRT(Время)

где
(SQRT – корень квардатный) и 95% – это 95%-ный доверительный уровень;
Волатильность – стандартное отклонение изменения цен (выясняется как натуральный логарифм «сегодня/вчера»);
Размер позиции – лицевая стоимость торгуемого контракта;
Время – горизонт оценки.

Полученный результат трактуют так: ценовые изменения в данный промежуток времени не приведут к потерям выше полученного результата в 95% случаев. Иными словами, есть только 5%-ная вероятность потери, превышающей значение 95% VaR.

В банковской практике чаще применяется 99% VaR, отличие которого от представленной формулы в коэффициенте: 2.33 вместо 1.65. Соответственно, 99% VaR говорит нам, что цены с вероятностью 99% не способны измениться настолько, чтобы убытки превысили вычисленное значение.

Пользуясь указанной выше формулой, можно определить риск широкого спектра финансовых активов, попадающих в категорию простых инструментов и линейных производных. К ним относятся: акции, иностранные валюты, облигации обычные и с плавающим купоном (не имеющие высокую дюрацию), процентные и валютные свопы, валютные форвардные контракты, FRA. Тем самым формулировка доступна для применения практически на всех рынках, традиционно вызывающих интерес у отечественных инвесторов, в первую очередь – на рынке акций и FOREX.

Обычно проблемы оценки риска рассматриваются на стадии портфеля, состоящего из двух активов. Для большего числа инструментов предлагаются формулы, труднопонимаемые без специальной математической подготовки. Но данная задача решается просто, если подойти к ней сугубо с практической точки зрения, исключив теоретические аспекты.

Поэтому здесь дается только то, что необходимо знать, чтобы самостоятельно составить программу в электронных таблицах (Excel), обеспечивающую вычисления VaR портфеля. Для иллюстрации использованы случайно выбранные пять российских акций в произвольно взятый период времени: с 1 по 29 апреля 2003 года.

Шаг 1. Первичная обработка данных

Сначала выясним значение среднего изменения цен и волатильности. Для этого нам потребуется как минимум объем данных, удовлетворяющих выбранному периоду оценки.

Предположим, используется 20-периодный цикл, тогда нужно не менее 21 дня, если анализ выполняется по дневным данным. Для каждого дня необходимо выяснить натуральный логарифм отношения цен «сегодня/вчера» (см. значение «Изм.» в табл. 1).

«Изменение» = ln (сегодня / вчера)

Теперь можно найти среднедневное изменение и величину стандартного отклонения, используя полученный ряд (колонки «Изм.»).

Среднедневное изменение – это среднеарифметическое, которое в Excel записывается «=average()», а стандартное отклонение как «=stdev()», которое и является дневной волатильностью.

При этом калькуляция охватывает область переменных, находящихся на строчках от 2 до 21 в колонке «Изм.» (результат см. в табл. 2).

Следует иметь в виду: предлагаемый алгоритм оценки волатильности основан на методе постоянных, а не экспоненциально взвешенных ковариаций. Но к ним можно перейти, используя полученные ряды изменения цен, для чего необходимо ввести соответствующие поправки, обеспечивающие больший вклад более поздних наблюдений.

Хороший аналог данного метода оценки волатильности – взвешенная скользящая средняя по сравнению с обычной скользящей средней. Характерно, что множитель, практикуемый в методологии J.P. Morgan RiskMetrics, равен 0.98, как и в установках по умолчанию в программах, предназначенных для технического анализа рынка.

Шаг 2. Необходимый минимум теории

Прежде чем перейти к вычислению VaR портфеля, обратимся к некоторым сведениям, которые дают понимание расчетных алгоритмов. В целом VaR портфеля из многих активов можно определить по следующей формуле:

VaR портфеля = Среднее изменение – К * Волатильность портфеля,

где
Среднее изменение – просто сумма средних изменений всех компонентов портфеля;
К – число стандартных отклонений, требуемых для заданного доверительного уровня, вычисляемое по формуле в Excel «=NORMSINV()», где аргумент – соответствующий доверительный уровень.

Волатильность портфеля калькулируется с использованием формулы, предложенной Г. Марковицем:

Волатильность портфеля = SQRT (Вектор волатильной компоненты *Корреляционная матрица * Транспонированный вектор волатильной компоненты)

Вектор волатильной компоненты можно вычислить, пользуясь формулой:

Компонента волатильности = Стоимость позиции * Волатильность позиции

Помимо уже выполненных расчетов для вычисления VaR портфеля потребуется построить корреляционную матрицу, основываясь на данных, обработанных в шаге 1.

Она представляет собой совокупность коэффициентов, отражающих корреляцию между каждым из инструментов, входящих в портфель.

Вычисления в Excel выполняются с помощью соответствующей функции «=correl()», причем построение матрицы лучше выполнить на странице, где будут размещены все прочие расчеты, в том числе и VaR. Это уже будет шаг 3.

КУРС

ИНВЕСТИЦИОННЫЙ АНАЛИТИК

Шаг 3. Вычисление VaR портфеля

Протокол расчета, позволяющий видеть все промежуточные этапы, представлен в таблице 3. Здесь же даны формулы, с помощью которых производятся вычисления.

Следует иметь в виду: данная таблица есть копия рабочего листа Excel, поэтому при написании программы рекомендуется придерживаться указанного порядка, пользуясь для подсказки формулами, выложенными в крайней колонке «Н» справа. Позже, если возникнет желание, структуру таблицы можно изменить.

Остается сделать ряд важных замечаний

Во-первых, в зависимости от задачи число входящих в портфель активов можно увеличить или уменьшить.

Во-вторых, при оценке по ценам внутри дня при вычислениях надо придерживаться единого масштаба, поэтому VaR будет получаться для задаваемого числа часов в параметре «время». Для перевода в дневной масштаб следует учесть число торговых часов в одном дне.

Для обращающихся на бирже активов обычно это не вызывает трудностей, но в ряде случаев можно столкнуться с проблемами. Как, скажем, на рынке FOREX, где трудно предложить однозначное решение, поскольку приходится учитывать неравномерный характер торговой активности.

В-третьих, следует иметь в виду: портфель может содержать различные активы. Единственное условие – они должны быть выражены в одной валюте.

Например, если бы мы пожелали оценить риск портфеля, состоящего из акций в рублях, валютной позиции по евро/доллар и процентного фьючерса в британских фунтах, нам пришлось бы прежде выбрать счетную валюту.

Если мы выбрали евро, то потребуется пересчитать все ценовые ряды в евро по соответствующему курсу для каждого дня. После этого нам удастся без труда получить результирующую цифру, которая также будет в евро.

Шаг 4. Оптимизация портфеля

Поняв процедуру оценки риска, можно решать такие серьезные задачи, как поиск более эффективных решений. В Excel существует опция «Solver» в разделе «Tools», позволяющая выполнять поиск решений по заданным условиям. О других полезных функциях Excel мы рассказываем на нашем открытом курсе «Аналитика в Excel».

Например, если мы укажем, что нас устраивает иное значение 95% VaR – скажем, -500, а не -844 – и определим при этом возможность изменения числа всех акций, то программа вычислит: «Акция 1» следует иметь 119 акций, «Акция 2» – 1193, «Акция 3» – 11, «Акция 4» – 2 и «Акция 5» – 227 акций. Причем с длинными позициями по всем бумагам.

Легко заметить: подобный подход отличается ограниченностью, поскольку мы никак не определяем имеющийся в нашем распоряжении капитал, а указываем лишь уровень принимаемого риска.

Эта проблема легко разрешима: имеющиеся данные позволяют производить любые вычисления, необходимые для определения стоимости портфеля, а также размера требуемого капитала как при торговле с маржой, так и без нее. После этого определить степень риска в относительных величинах не представляет труда, это будет частное от VaR и рабочего капитала или размера счета – в зависимости от того, что необходимо оценить.

С полученной величиной мы можем обращаться точно так же, как и со значением VaR в денежных единицах. Скажем, если нам для создания портфеля, представленного в таблице 3, потребуется капитал в размере 42 тыс. руб. (исходя из правил брокера), то 1-дневный 95% VaR составит 2.01%, а 10-дневный – 3.41%.

Данные цифры говорят: существует 95%-ная вероятность, что потери портфеля за 1 день не превысят 2.01% от работающего капитала, а за 10 дней – 3.41%. Естественно, если нам нужна более полная картина, следует проводить расчеты также и для всего капитала, с учетом резервов.

Опираясь на эти цифры, можно выполнять оптимизацию, пользуясь алгоритмом, описанным выше. Например, задавая 1-дневные потери в размере 1% от работающего капитала при доверительном уровне в 95%, мы узнаем, что это достигается за счет увеличения короткой позиции в «Акция 3» (с 20 до 23 акций) и покупки 18, а не одной, акций «Акция 4», при неизменности числа прочих бумаг.

Обратите внимание: не введя в данную процедуру ограничений на капитал, мы обнаружим, что эта возможность для нас нереальна или не отвечает нашим намерениям, поскольку для создания портфеля требуется 163 тыс. руб. Поэтому следующий этап усложнения алгоритмов оценки риска – ввод ограничений.

Шаг 5. Ввод ограничений

Ввод ограничений, позволяющих решать проблему оптимизации, требует немного больше знаний об электронных таблицах. Полностью описать то, как можно решить ту или иную задачу, здесь не представляется возможным.

Во-первых, можно найти немало подходящих алгоритмов, позволяющих достичь поставленной цели. Во-вторых, многие из них связаны с уровнем квалификации инвесторов – пользователей среды Windows, а обучение не является нашей задачей. В-третьих, как показывает практика, пользователям лучше всего самостоятельно создавать интерфейс, если работа ведется с Excel.

Поэтому в шаге 5 только указывается путь, ведущий к построению потокового процесса контроля над риском и управления им.

Наиболее простой способ решить задачу – ввести условия, опираясь на соотношение между показателем меры риска и размером имеющегося в нашем распоряжении капитала. Если одновременно мы хотим автоматизировать процесс, нам потребуется ввести дополнительные ограничения, описывающие наши реальные возможности. Обычно это реализуется через совместное использование таких функций, как «=IF(), OR(), AND()».

Дополнительные возможности появляются, если изменениям будет подвергаться не число акций, а их доля в портфеле. Описание связей в таком случае будет легче, так как мы заранее указываем размер капитала, под который формируется портфель. Число акций уже будет не задаваться пользователем, как это предложено в таблице 3, а вычисляться на основе весовой доли в портфеле.

Причем подходы, основанные на оценке веса, могут иметь и другие решения. Вводя граничные условия с целью автоматизации процесса оценки риска, мы неминуемо столкнемся с проблемой управления резервами.

И здесь следует обратить внимание на важную деталь. Дело в том, что непосредственное применение VaR – это определение, какой капитал необходимо резервировать, чтобы иметь достаточное покрытие рыночного риска. В практике рядового инвестора – это решение вопроса, сколько надо иметь свободных средств на счете, чтобы не потерять свыше заданной величины или не получить margin call (при маржевой торговле).

В банковской практике рекомендуемые резервы – 3-кратный 10-дневный 99% VaR (для портфеля из таблицы 3 такие резервы составят 8299 рублей). Поскольку резервы, оцениваемые через VaR, – величина «плавающая» и зависит от волатильности, этот аспект может оказаться для кого-то привлекательным. В таком случае вполне естественно включить данный параметр в алгоритмы, обеспечивающие обсчет риска.

Наконец, следует включить и ожидаемую прибыль. Это дополнение позволяет получать новые оценочные коэффициенты, играющие важную роль в торговой практике. Скажем, мы можем вывести соотношение «прибыль/возможный убыток». Если при этом учтены издержки на транзакции, а также соответствуют горизонты, использованные для оценки потерь и прибыли, то у нас получится формулировка для оценки рисков RAROC по методике Bankers Trust.

Решений автоматизации процедур, связанных с риск-менеджментом, существует много. Окажутся ли они эффективными, в значительной степени зависит от точности поставленной задачи и желания получить действительно простую и понятную процедуру оценки меры риска.

Вершиной здесь является построение потокового процесса управления ценовыми и финансовыми рисками, решающего с максимально возможной эффективностью основную задачу инвестора – как понадежней заработать.

Автор: Михаил Чекулаев

КУРС

ИНВЕСТИЦИОННЫЙ АНАЛИТИК

Рассмотрим  методы оценки риска, в частности рыночного, с помощью меры риска VaR (Value at Risk). Для этого разберем практический пример оценки риска для акции компании ОАО «Газпром».

Рыночный риск. Определение

Рыночный риск (англ. Market risk) – это вероятность неблагоприятного изменения стоимости активов. На изменение стоимости влияют множество макро-, мезо-, микроэкономических факторов, к которым можно отнести цены на сырье (нефть, сталь, платина и т.д.); цены на драгоценные металлы (золото, серебро); изменения отраслевых индексов производства, национальных показателей (ВВП, безработица, ключевая процентная ставка, инфляция), уровня спроса и предложения и т.д.

★ Инвестиционная оценка в Excel. Расчет NPV, IRR, DPP, PI за 5 минут

Рыночные риски находятся в системе финансовых рисков и можно выделить их следующие виды:

• Фондовый риск (Equity risk) – вероятность потерь в случае неблагоприятного изменения стоимости ценных бумаг на фондовом рынке.
• Процентный риск (Interest rate risk) – вероятность потерь при изменении банковских процентных ставок.
• Товарный риск (Commodity risk) – вероятность непредвиденных потерь в случае изменения стоимости товаров.
• Валютный риск (Currency risk) – вероятность потерь из-за изменения курса валют.

Рыночные риски оценивают различные инвестиционные компании, инвестиционные и хеджевые фонды, частные инвесторы, банки, предприятия, финансовые агенты, поставщики и т.д. для минимизации возможных убытков и создания резервов. Как мы видим, рыночные риски влияют на самых различных участников финансового рынка.

Методы оценки риска

Для того чтобы управлять возможными потерями и определять резервы для страхования потерь необходима количественная оценка риска. Основная аксиома любого управления заключается в том, что управлять можно только тем, что можно количественно измерить. Все методы оценки рыночных риском можно условно разделить на две группы:

1. Статистические методы оценки риска
   1. Стандартное отклонение доходностей (σ)
   2. Метод Value at Risk (Var)
   3. Метод CVaR
2. Экспертные методы оценки риска
   1. Рейтинговые методы
   2. Бальные методы
   3. Метод Дельфи

К преимуществам статистических методов можно отнести возможность объективной оценки вероятности возникновения непредвиденных убытков и их абсолютного размера. Экспертные методы оценки позволяют учесть слабоформализуемые факторы риска и разработать различные сценарии его снижения.

Г.Марковиц в начале 60-х годов предложил оценивать риск как изменчивость стоимости ценных бумаг на фондовом рынке. То есть чем сильнее изменяется цена актива, тем выше риск вложения в него. Недостатками данного способа были в неспособности спрогнозировать размер и вероятность будущих убытков.

Метод оценки рыночного риска. Мера риска VaR (Value at Risk). Что такое VaR?

В 80-е годы был предложен новый критерий риска – VaR (Value at Risk), который позволил комплексно оценить возможные убытки в будущем с выбранной вероятностью и за определенный промежуток времени. Для расчета меры риска VaR на практике используют несколько способов:

• Метод исторического моделирования («дельта нормальный», «ручной способ»).
• Метод параметрической модели.
• Статистическое (имитационное) моделирование с помощью метода Монте-Карло.

Оценка риска по методу VaR на основе исторического моделирования в Excel

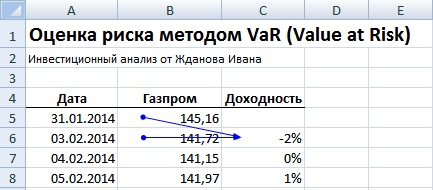
Рассмотрим пример оценки риска актива на фондовом рынке по модели VaR на основе дельта нормального моделирования вероятности и размера убытка. Возьмем котировки акции ОАО «Газпром» и рассчитаем возможные убытки по данному виду актива. Для этого необходимо закачать котировки с сервиса finam.ru («Экспорт данных») или с сайта finance.yahoo.com, если вы будете оценивать рыночный риск  для иностранных компаний. По рекомендации Bank of International Settlements для расчета VaR необходимо использовать не менее 250 данных по стоимости акции. Были взяты дневные котировки по ОАО «Газпром» за период 31.01.2014 – 31.01.2015.

На следующем этапе необходимо рассчитать дневную доходность акции ОАО «Газпром», воспользовавшись следующей формулой.

Доходность акции ОАО «Газпром» =LN(B6/B5)

Следует отметить, что корректность использования дельта нормального метода оценки риска достигается только при подчинении факторов риска (доходности) нормальному закону распределения (Гауссовому). Для определения принадлежности распределения доходности Гауссовому распределению можно воспользоваться классическими статистическими критериями ­– Коломогорова-Смирнова или Пирсона.

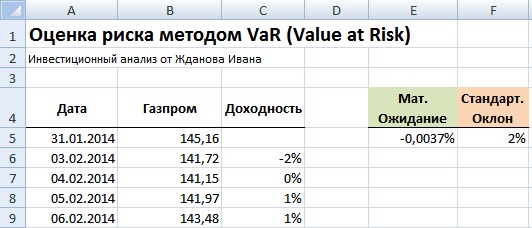
На  следующем шаге необходимо рассчитать основные параметры распределения доходности: математическое ожидание и стандартное отклонение. Для этого воспользуемся встроенными формулами в Excel:

Математическое ожидание =СРЗНАЧ(C5:C255)

Стандартное отклонение =СТАНДОТКЛОН(C5:C255)

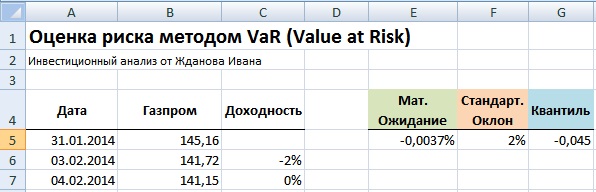
Следующим этапом в расчете меры риска VaR является определение квантиля данного нормального распределения. В статистике под квантилем понимают – значение функции распределения (Гаусса) по заданным параметрам (математического ожидания и стандартного отклонения) при которых функция не превышает данное значение с заданной вероятностью. В нашем примере уровень вероятности был взят 99%.

Рассчитаем в Excel значение квантиля для распределения доходностей акции ОАО «Газпром».

Квантиль =НОРМОБР(1%;E5;F5)

Прогнозирование будущей стоимости акции на основе метода VaR

Далее необходимо оценить какой возможно будет стоимость акции при заданных параметрах распределения доходности. Для этого можно воспользоваться следующей формулой:

где:

q – квантиль распределения доходностей акции;

P_t – стоимость акции в момент времени t;

P_t+1 – минимальная стоимость акции в следующем периоде времени t с заданным уровнем квантиля.

Для прогнозирования будущей стоимости акции (актива) на несколько периодов вперед следует использовать модификацию формулы:

 где:

q – квантиль распределения доходностей акции;

P_t – стоимость акции в момент времени t;

P_t+1 – минимальная стоимость акции в следующем периоде времени t при заданном уровне квантиля;

n – глубина прогноза возможной минимальной стоимости акции.

Формула расчета будущей стоимости акции в Excel будет иметь вид:

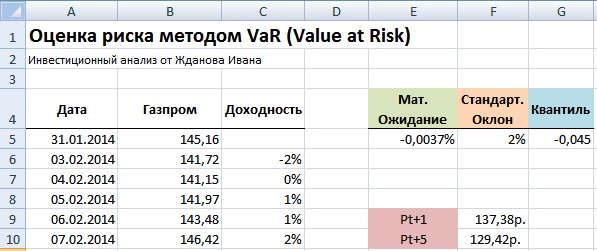
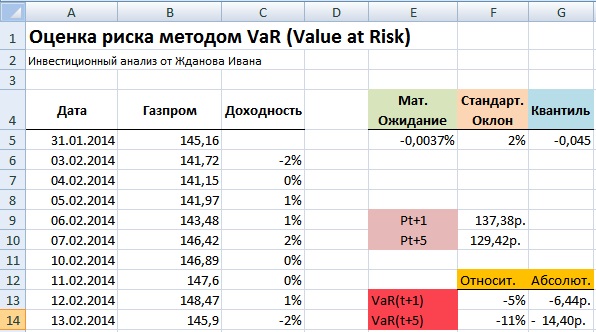
Минимальная стоимость акции ОАО «Газпром» на следующий день =(1+G5)*B255

Минимальная стоимость акции ОАО «Газпром» через 5 дней =B255*(1+G5*КОРЕНЬ(5))

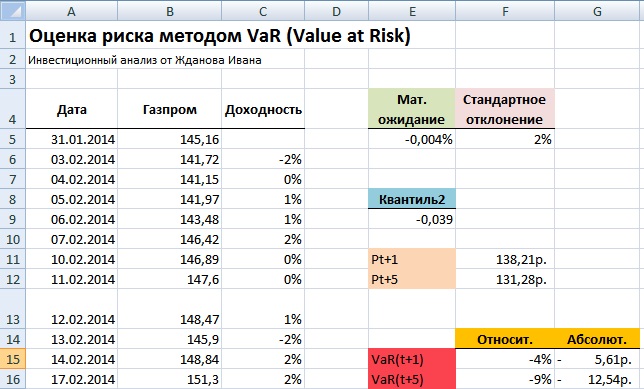
Значения P_t+1 показывает, что с вероятностью 99% акции ОАО «Газпром» не опустятся ниже цены равной 137.38руб, а значение P_t+5 показывает возможную минимальную стоимость акции с вероятностью 99% на 5 следующих дней. Для расчета абсолютного значения возможного убытка следует определить процентное изменение стоимости акции. Формулы расчета в Excel будут следующие:

Относительное изменение стоимости акции

Относительное снижение стоимости акции на следующий день =LN(F9/B255)

Относительное снижение стоимости акции за пять дней =LN(F10/B255)

Абсолютное изменение стоимости акции

Абсолютное снижение стоимости акции на следующий день =F9-B255

Абсолютное снижение стоимости акции за пять дней =F10-B255

Таким образом читать экономический смысл показателя VaR заключается в следующем: в течение следующего дня стоимость акции ОАО «Газпром» с вероятностью 99% не окажется ниже 137,38руб. и абсолютные убытки не превысят 6,44руб (5%) на акцию. И аналогично для оценки VaR на пять дней вперед: в течение пяти дней стоимость акции ОАО «Газпром» с вероятностью 99% не опуститься ниже 129,42 руб., и потеря капитала не превысит 11% (14,4руб на акцию).

Оценка меры риска VaR на основе «ручного способа» в Excel

Второй метод расчета меры риска VaR называется «ручным способом», так как позволяет не привязываться к распределению, по которому изменяется стоимость актива. Это одно из его главных преимуществ по отношению к дельта нормальному методу. Для оценки рыночного рискам будем использовать те же входные данные – котировки ОАО «Газпром». Этапы расчета VaR следующие:

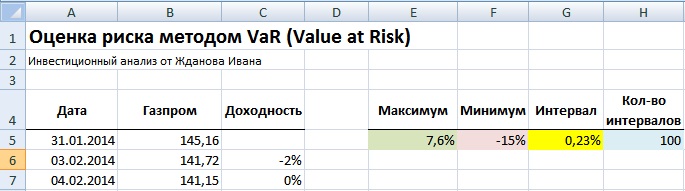
Расчет максимума и минимума доходностей акции ОАО «Газпром»

По рассчитанной доходности акции ОАО «Газпром» определяем максимум и минимум доходности. Для этого воспользуемся формулами:

Максимальное значение доходности акции =МАКС(C5:C255)

Минимальное значение доходности акции =МИН(C5:C255)

Выбор количества интервалов группировки доходностей/убытков акции

Для ручного способа оценки риска необходимо взять количество интервалов деления группировки доходностей. Количество может быть любое, в нашем примере мы возьмем N=100.

Определение ширины интервала группировки доходностей

Ширина интервала или шаг изменения группы необходим для построения гистограммы и рассчитывается как деление максимального разброса доходностей к количеству интервалов. Формула расчета интервала следующая:

Размер интервала доходностей акции =(E5-F5)/H5

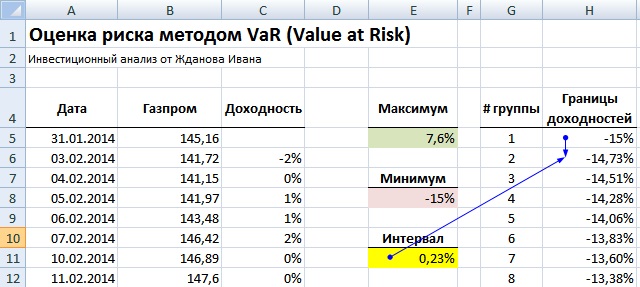
На следующем этапе необходимо построить гистограмму распределения доходностей по выбранным интервалам. Для этого рассчитываем границы всех групп доходностей (всего их 100). Формула расчета следующая:

Граница доходностей акции =H5+$E$11

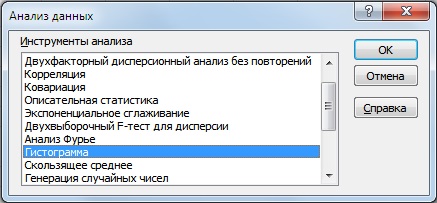
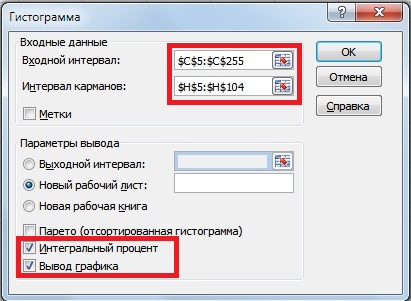
После определения границ групп доходностей строим накопительную гистограмму. Для этого заходим в надстройку «Данные» → «Анализ данных» → «Гистограмма».

В открывшемся окне заполняем «Входные интервалы», «Интервалы карманов», также выбираем опцию «Интегральный процент» и «Вывод графика».

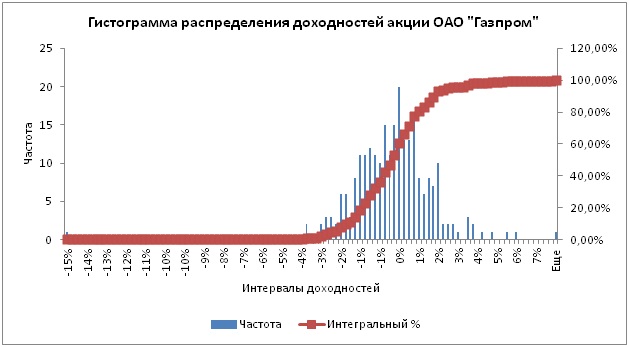
В результате будет сформирован новый рабочий лист с графиком и частотой попадания доходности/убытка в тот или иной интервал. График накопительным итогом имеет следующий вид:

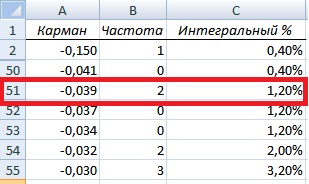
Итак первый столбец полученной таблицы это квантиль данного для распределения доходностей/убытков, вторая частота попадания доходностей в тот или иной интервал, третья отражает вероятность появления убытков. В таблице с накопительной вероятностью попадания в тот или иной интервал необходимо найти уровень ~1%.

Значение квантиля соответствует -0,039, тогда как при дельта нормальном способе оценки риска квантиль составил -0,045. Для оценки рисков воспользуемся уже полученными формулами оценки и рассчитаем размер убытков. На рисунке ниже показана оценка возможных убытков на следующий день и в течение пяти дней с вероятностью 1% составят 4 и 9% соответственно.

Сложность использования метода оценки риска VaR

Отечественный фондовый рынок имеет достаточно высокую степень волатильности, на рынке наблюдаются «тяжелые хвосты» – то есть возникновение частых кризисов с большим размером убытков. В результате модель VaR не может точно спрогнозировать возможные будущие потери инвестора. Следует отметить, что данная модель хорошо применима для товарных низковолательных рынков нежели фондовых.

Резюме

В данной статье мы рассмотрели методы оценки риска на примере акции ОАО «Газпром», для этого пошагово разобрали, как строится современная оценка риска Value at Risk (VaR) в Excel двумя способами: дельта нормальным моделированием и «ручным способом».

Автор: к.э.н. Жданов Иван Юрьевич

Оценивание рисков представляет собой анализ каждого риска и определение его влияния на проект, в случае если данный риск воплотится в соответствующее нежелательное событие. Конечной целью процесса оценивания является определение рисков, для которых необходимо составить планы реагирования.

Например, мы определили, что одним из рисков, связанных с выполнением проекта Grant St.Move, является возможное увольнение главного исполнительного директора. Наша команда выяснила, что на данном этапе увольнение главного исполнительного директора не окажет существенного влияния на проект, поскольку договор об аренде нового здания на улице Grant St. уже подписан, а уведомление о прекращении действия договоров аренды старых зданий разослано в соответствующие инстанции. Иными словами, переезд в новое здание состоится независимо от появления в организации нового главного исполнительного директора, который если и посчитает переезд плохой идеей, повернуть данный процесс вспять (т.е. остановить выполнение проекта) все равно не сможет, поскольку это обошлось бы организации слишком дорого.

Таким образом, для указанного риска план реагирования не требуется. Это вовсе не означает, что событие, связанное с этим риском, не может наступить. Просто команда приняла осознанное решение такого плана не составлять, независимо от того, произойдет событие или нет. Проанализировав все риски в этом списке и взяв за основу степень серьезности каждого из них, мы должны решить, нуждаются ли они в составлении соответствующих планов реагирования. Прежде чем приступать к рассмотрению методов анализа, мы должны уяснить уровни допустимости рисков в нашей организации. Именно этот вопрос мы и рассмотрим.

Допустимость рисков

Риск, подобно другим процессам планирования проекта, связан с проблемой баланса. Определяя черту, до которой следует идти, чтобы извлечь из этого проекта выгоду, вы тем самым пытаетесь сбалансировать свою готовность рисковать со стремлением избежать последствий наступления соответствующего неблагоприятного события. У организаций, как и у людей, есть определенные уровни допустимости рисков. Вам нужно определить эти уровни для всех заинтересованных сторон, руководства организации, клиентов и других лиц, имеющих отношение к выполняемому проекту, т.е. необходимо заранее определить готовность тех или иных лиц брать на себя риск.

Возможно, разные категории риска будут характеризоваться разными уровнями допустимости рисков. Например, лица, заинтересованные в выполнении вашего проекта, могут быть в большей степени готовы к риску, связанному с календарным планом проекта, чем к финансовому риску. Воспользуйтесь методами интервьюирования: возможно, кому-то из исполнителей или руководителей других проектов уже приходилось работать с кем-то из лиц, заинтересованных в выполнении вашего проекта. Определяя уровни допустимости рисков для своего проекта, не забудьте ознакомиться с информацией о предыдущих проектах. Вы можете использовать специальные опросные листы, разместите их на press wall свадебный и периодически проверяйте заполнение их.

Определение уровней допустимости рисков

Рассмотрим понятие уровня допустимости риска на примере повседневной деятельности. Большинство из нас регулярно принимает ванну. И хотя всегда существует риск наступить на кусок мыла, случайно упавший на дно ванны, поскользнуться и ушибиться (или даже заработать серьезную травму), удерживает ли вас осознание этого риска от регулярного приема ванны или душа? Разумеется, нет (в противном случае вам следовало бы обратиться к психиатру, а не читать книги по управлению проектами). Таким образом, ваш уровень допустимости этого риска чрезвычайно высок. Иными словами, вы готовы мириться с возможностью весьма тяжелых последствий (в случае наступления события, связанного с этим риском) во имя того, чтобы воспользоваться таким благом современной цивилизации, как ванна.

Рассмотрим другой пример. Допустим, каждое утро по дороге на работу вам приходится пересекать оживленный перекресток. Этот перекресток печально известен тем, что здесь почти каждый день случаются дорожные происшествия, жертвами которых становятся как водители, так и пешеходы. Готовы ли вы перебегать этот перекресток на красный свет, лавируя между автомобилями с риском для жизни, только для того, чтобы вовремя прибыть на работу, или вы все же предпочитаете ждать минуту-другую, пока загорится зеленый сеет светофора, даже когда опаздываете на работу? Смеем предположить, что около 80% читателей будут ждать, пока загорится зеленый свет. Оставшиеся 20% еще приближаясь к перекрестку будут внимательно следить за сигналами светофора и постараются проскочить на зеленый свет, даже если останется всего пару секунд. Как нетрудно догадаться, у этих 20% пешеходов уровень допустимости риска, связанного с переходом оживленного перекрестка, выше, чем у тех, кто предпочитает дожидаться зеленого света.

Вероятность риска и его влияние

Есть несколько способов, с помощью которых можно определить вероятность риска и его влияние, из которых мы рассмотрим только два. Но сначала давайте разберемся, что же такое вероятность риска и в чем заключается его влияние.

Вероятность риска — это возможность наступления события, связанного с соответствующим риском. Например, когда вы подбрасываете монетку, вероятность выпадения «орла» и «решки» примерно одинакова и равняется 50%. Однако определить вероятность того или иного риска далеко не так просто. Как правило, для определения вероятности рисков, связанных с выполнением вашего проекта, приходится прибегать к помощи экспертов, которые высказывают собственные «предположения» относительно этих вероятностей. И зачастую такие предположения экспертов являются достаточно обоснованными, поскольку базируются на опыте выполнения аналогичных проектов в прошлом. В любом случае пользоваться оценками экспертов все же лучше, чем подбрасывать монетку.

Разумеется, точность оценки вероятности рисков зависит от того, насколько грамотно вы подберете экспертов и заинтересованных лиц, которые будут оценивать эти вероятности. Чтобы не попасть в ловушку так называемого группового мышления, вам потребуются эксперты с разным опытом работы. Если, например, все ваши эксперты являются специалистами по информационным технологиям и имеют соответствующий опыт работы, то вполне возможно, что им не удастся правильно оценить уровни вероятности рисков, связанных с бюджетами или маркетингом.

Влияние риска — это, так сказать, уровень неприятностей, которые может причинить событие, связанное с соответствующим отрицательным риском, или уровень «позитива», который может обусловить событие, связанное с соответствующим положительным риском. Влияние, как правило, зависит от конкретного риска и едва ли является более определенным, чем вероятность. Например, для определения влияния утраты какого-либо из ключевых ресурсов (специалиста редкой квалификации) по нашему проекту Grant St. Move нам нужно оценить приблизительно время, на которое задержится исполнение календарного плана этого проекта, пока мы будем подыскивать другого специалиста с аналогичной квалификацией (и пока этот специалист будет входить в курс дел и выходить на требуемый уровень производительности). Кроме того, нам потребуется оценить приблизительные затраты, связанные с задержкой выполнения заказов, продлением договоров с поставщиками (вызванным указанной задержкой) и т.п.

Схемы вероятности рисков и их влияния

Вероятность риска и его влияние можно выразить либо в виде числа, либо уровня. Числа всегда выражаются долями в диапазоне от 0,0 (означающем, что вероятность наступления события, связанного с соответствующим риском, равняется нулю) до 1,0 (а это означает, что вероятность наступления события, связанного с соответствующим риском, равняется единице, т.е. наступление этого события неизбежно). Уровни обычно измеряются по шкале «высокий-средненизкий» или с помощью того или иного отклонения. На рис. 1 представлен шаблон схемы вероятности рисков и их влияния. В этом шаблоне предусмотрен столбец «Величина риска» (Risk Score), который представляет собой интегральную оценку вероятности риска и его влияния. Ниже мы покажем (на примере проекта Grant St. Move), как заполнять такой шаблон.

В нашей схеме вероятности рисков и их влияния мы использовали уровни (высокий, средний и низкий). Их можно применять для небольших и средних проектов, а иногда и для крупных проектов с минимальным количеством рисков. На рис. 2 показаны риски, обнаруженные нами для проекта Grant St.Move, причем для каждого из этих рисков указан соответствующий уровень. (Разумеется, этот перечень рисков ни в коем случае не является исчерпывающим.)

Рассмотрим подробно первый риск — «стабилизаторы электропитания выбраны неправильно». Вероятность этого риска («низкая») базируется на мнении наших экспертов. Однако влияние этого риска велико. Специалисты рассуждали так: если событие, связанное с этим риском, случится, то в лучшем случае серверы будут работать со сбоями, т.е. пользователи не смогут передавать электронную почту, запускать компьютерные программы, требующиеся для выполнения их работы, или обращаться в Интернет. А значит, наш проект не достигнет своей цели, поскольку его назначение в том, чтобы не допустить снижения производительности и простоев. Показатель «Величина риска» представляет собой интегральную оценку вероятности риска и его влияния (в данном случае эта интегральная оценка риска такова: «низкая-высокая»).

Чтобы определить уровни вероятности риска и его влияния, вы можете воспользоваться любым методом — мозгового штурма, номинально-групповым или интервью, задав такие вопросы: «Если событие, связанное с этим риском, действительно произойдет, то каким может быть самое негативное его влияние на выполняемый проект, клиентов, организацию и т.д.? И как в этом случае вы оцените уровень влияния этого риска (высокое, среднее, низкое)?»

Шкалы влияния риска

Теперь мы займемся созданием матрицы вероятности рисков и их влияния (Probability and Impact Matrix — PI matrix). Эта матрица похожа на только что рассмотренную схему в том отношении, что вы определяете вероятность и влияние событий, связанных с каждым из рисков, и присваиваете каждому такому риску соответствующую интегральную оценку вероятности/влияния. Как правило, в матрице PI вместо уровней используются числа. Поскольку до сих пор мы пользовались лишь такими оценками, как низкая, средняя и высокая, нам нужно в качестве первого шага построить шкалу влияния рисков.

Командам, по-видимому, гораздо легче при использовании шкалы влияния присваивать рискам привычные для себя уровни, нежели некий процент (долю). Разница в данном случае заключается лишь в том, что мы будем сопоставлять с уровнями определенные числа, что даст нам возможность затем использовать эти числа в матрице PI. Следующим этапом является шкала влияния рисков: она описывает диапазон возможных влиянии или последствий, что позволяет нам уточнить оценки влияния чех пли иных рисков. При оценке влияния рисков почти всегда учитываются факторы времени и затрат. В зависимости от природы выполняемого проекта вашей команде придется определять для своих шкал какие-то другие критерии. Для проекта Grant St. Move мы добавили в качестве еще одного критерия «Производительность» (невозможность использования компьютеров или телефонов). Соответствующая шкала влияния рисков показана на рис. 3.

С учетом такой шкалы команда сказала нам, что вследствие неправильного выбора стабилизаторов электропитания может пострадать производительность. Они определили, что влияние этого риска является высоким — 0,7. Теперь мы можем перейти к определению вероятности.

Если вы хотите также при оценке вероятности пользовать ся шкалой с уровнями от «очень низкой» до «очень высокой», то можно разработать такие шкалы, подобно разработанным нами шкалам влияния риска. Например, очень низкая вероятность для критерия «Производительность» может оцениваться величиной 0,05. У нас сложилось впечатление, что командам гораздо легче присвоить тот или иной процент вероятности события, связанного с риском, чем присвоить некий процент влияния этого риска на выполнение проекта.

Вероятность риска, связанного с неправильным выбором стабилизаторов электропитания, оценивается как низкая, поэтому вероятности такого события мы присвоили значение 0,2. Чтобы получить интегральную оценку этого риска, нужно вероятность умножить на влияние (0,2×0,7). Итак, в нашем случае интегральная оценка риска равняется 0.14. Чтобы определить, нужно ли для этого риска составлять план реагирования, следует рассмотреть матрицу PI.

Чтобы облегчить себе задачу определения интегральной оценки риска, можно воспользоваться электронной таблицей, которую мы сформировали в подразделе «Схемы вероятности рисков и их влияния» (см. рис. 1). Эту электронную таблицу необходимо модифицировать таким образом, чтобы в столбце «Величина риска» содержалась формула умножения вероятности на влияние.