Метод золотого сечения excel

VBA Excel. Нахождение экстремума функции Методом Золотого Сечения.

О методе Золотого Сечения:

Безусловно, простой и быстрый метод. И как водится, скорость не способствует аккуратности.
Это я о том, что если на заданном интервале поиска будут находиться несколько минимумов (максимумов),
то данный алгоритм легко может вернуть локальный (не самый большой, не абсолютный) экстремум.

Задание:

Составить программу позволяющую протестировать алгоритм поиска экстремума методом Золотого Сечения
на примере пяти произвольных функций. Исходными данными для поиска должны являться границы интервала,
точность и тип экстремума (MAX или MIN). Программа должна отображать график функции
на заданном интервале и координаты точки экстремума.

В программе есть смысл оформить следующие классы и модули:

1. Модуль листа Excel (SheetGoldCutting), на котором как на форме будут располагаться необходимые органы управления ходом тестирования;
2. Форма для ввода данных FormDann;
3. Класс ExtremGC, вычисляющий координаты точки экстремума с заданной точностью, а также массив точек
   графика функции на заданном интервале (для отображения на диаграмме);
4. Стандартный модуль GoldCutting для описания глобальных констант, переменных и функций.

Например, так…

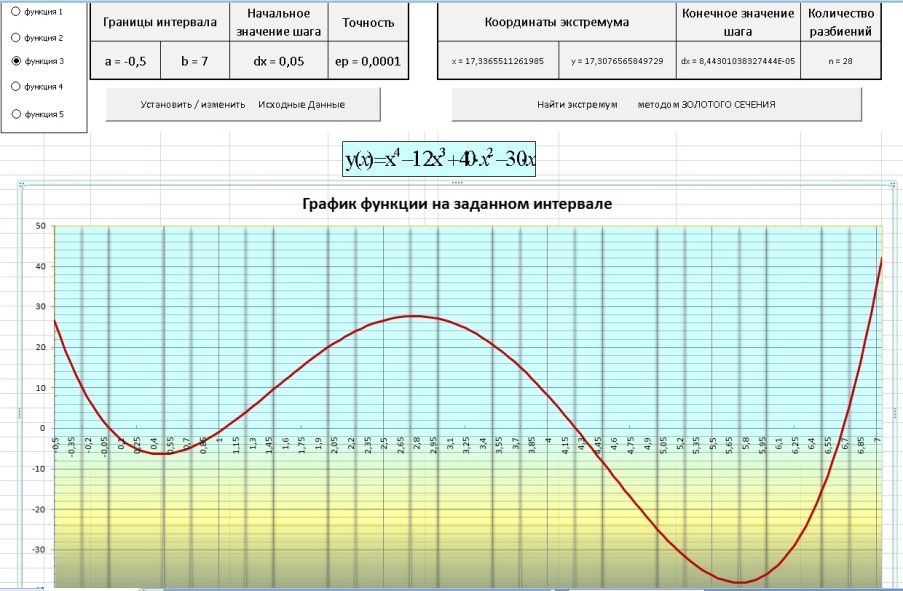
Рис.1 Рабочий лист Excel с диаграммой, двумя командными кнопками и кнопками выбора функции

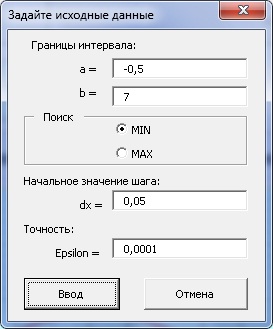
Рис.2 Форма для ввода исходных данных

Данная форма вызывается явно при щелчке по первой командной кнопке (расположенной на листе Excel)
или косвенно, если в момент нажатия на вторую командную кнопку (расположенную на листе Excel),
исходные данные не обеспечивают необходимых условий начала выполнения алгоритма.
Для удобства пользователя, все элементы TextBox допускают ввод только числовых значений.
При щелчке по кнопке «Отмена» все
переменные получат значения, которые существовали на момент открытия формы.

При открытии файла (если макросы включены) или включении макросов (если они были отключены на момент
открытия файла) выполняется обработчик события с целью задать (определить) одну из заготовленных функций,
как функцию для тестирования по умолчанию. Для этого достаточно отметить одну (например, первую) OptionButton
(или как часто называют — радиокнопку) и вызвать макрос назначенный этой кнопке.


Private Sub Workbook_Open()
   ' радиокнопки нумеруются в этой книге от 5 до 9.

   ' Поэтому по умолчанию выделяю первую кнопку.
    Sheets(1).Shapes("Option Button 5").ControlFormat.Value = 1
    SheetGoldCutting.OptBut1_Click
End Sub


Метод theAlgoritm класса ExtremGC, который, собственно, и выполняет
определение координат точки экстремума выглядит приблизительно так:


'Нахождение экстремума функции на отрезке. Метод золотого сечения
Public Sub theAlgoritm(v1 As Double, v2 As Double, v3 As Double, v4 As Double, findMax As Boolean)
Dim x1 As Double, x2 As Double, y1 As Double, y2 As Double, sme As Double
FullArrayOnly v1, v2, v3, v4 'для проверки допустимости аргумента

If Not BadDann Then

    zc = (1 + Sqr(5)) / 2
    n = 0 'количество разбиений (переменная модуля класса)
    Do While b - a > ep
       sme = (b - a) / zc
       x1 = b - sme: x2 = a + sme
       y1 = theFunc(x1): y2 = theFunc(x2)
       If findMax Then
             'поиск максимума
             If y1 <= y2 Then
                   a = x1
             Else
                   b = x2
             End If
       Else
             'поиск минимума
             If y1 >= y2 Then
                   a = x1
             Else
                   b = x2
             End If
       End If
       n = n + 1 'количество разбиений (переменная модуля класса)
    Loop
    dxk = Abs(b - a) ' конечное значение шага
    xe = (a + b) / 2: ye = theFunc(xe) ' результат: координаты точки экстремума

End If
End Sub

Где
FullArrayOnly — закрытый метод класса для проверки допустимости аргумента и заполнения массива точек графика;
BadDann – флаг допустимости аргумента;

zc – константа золотого сечения;
a, b – границы интервала;
ep – заданная точность поиска ε;
findMax – параметр, характеризующий режим поиска (при true ищется максимум, при false – минимум);
theFunc(x As Double) As Double – метод класса, возвращающий значение тестируемой функции в зависимости от значение аргумента.

Кому интересен остальной код – обращайтесь…
Если нужно что-то изменить в проекте под Ваши требования (например, заменить функции) – пожалуйста, проблем не будет!

скачать xlsm-файл для тестирования,

исходный код уже открыт. Используйте !

Если у Вас не появляется форма ввода данных, значит вы забыли включить макросы…

Хочу обратить внимание, что для первой функции значения аргумента не могут быть меньше или равны нулю.

Чтобы увидеть, как ошибается алгоритм и находит локальный экстремум вместо абсолютного,
задайте достаточно большой интервал (например: от 0 до 25) для 4 или 5 функций, имеющих явную периодичность…

Если на этой странице не нашлось того, что Вы так искали…

        
Не расстраивайтесь, не все потеряно… Смело щелкайте…

       телефон:

+7(919) 572-59-92
+7(987) 848-79-61

Метод золотого сечения

При построении процесса оптимизации
стараются сократить объем вычислений
и время поиска. Этого достигают обычно
путем сокращения количества вычислений
значений целевой функции f(x).Одним из наиболее эффективных методов,
в которых при ограниченном количестве
вычисленийf(x)достигается наилучшая точность, является
метод золотого сечения.

Если известно, что функция f(x)унимодальная на отрезке[a;b],
то положение точки минимума можно
уточнить, вычисливf(x)
в двух внутренних точках отрезка. При
этом возможны две ситуации:

	f(x1)<f(x2) минимум находится на отрезке [a, x2].
	f(x1)>f(x2) минимум находится на отрезке [x1, b].

В методе золотого сечения каждая из
точек x₁иx₂
делит исходный интервал на две части
так, что отношение целого к большей
части равно отношении большей части к
меньшей, т.е. равно так называемому
«золотому отношению». Это соответствует
следующему простому геометрическому
представлению:

Здесь

или

^{Обозначив
,
получаем
,
откуда}

Итак, длины отрезков равны и составляют
0,382от длины интервала(a,b).
Соотношением значенийf(x₁)
иf(x₂)определяется новый отрезок[a;
x₁]или[x_2; b],
в котором локализован минимум. Найденный
интервал снова делится двумя точками
в том же отношении, причем одна из новых
точек деления совпадает с уже
использованной. Поэтому, начиная со
второй итерации, расчет функции необходимо
производить только в одной точке, что
для сложныхf(x)
позволяет существенно сократить
время решения задачи.

Алгоритм метода

1. Ввод исходных
   данных: a, b,
   ε.

2. Определение
   положения точек x₁,
   x₂:
   x₁=a+0,0,382×(b—a);
   x₂=a+0,0,618×(b—a).

3. Проверка условия
   f(x₁)
   < f(x₂).
   Если условие выполняется, то b=
   x₂,
   иначе a=
   x₁.

4. Проверка условия
   (b-a)<=
   ε. Если
   условие выполняется, то переход к пункту
   5, иначе переход к пункту 2.

5. Расчет закончен.
   Минимум находится в точке х*=(a+b)/2,
   минимальное значение функции на отрезке
   [a;b]
   равно f(x^*).

Реализация
метода золотого сечения в MS Excel

Дано: функция
и точность ε=0,01. Найти минимум функции
на отрезке [0; 1].

Заполнение клеток листа MS
Excel:

Адрес клетки	Содержание	Тип
A1	a	Текст
B1	b	Текст
C1	x1	Текст
D1	x2	Текст
E1	f(x1)	Текст
F1	f(x2)	Текст
G1	b-a	Текст
I1	точность	Текст
J1	0,01	Число
A2	0 — значение a	Число
B2	1 — значение b	Число
C2	=A2+0,318*(B2-A2)	Формула
D2	=A2+0,618*(B2-A2)	Формула
E2	=(0,25*C2+LN(0,5*C2+1)-EXP(-C2*0,75))^2	Формула
F2	=(0,25*D2+LN(0,5*D2+1)-EXP(-D2*0,75))^2	Формула
G2	=B2-A2	Формула
A3	=ЕСЛИ(E2<F2;A2;C2)	Формула
B3	=ЕСЛИ(E2<F2;D2;B2)	Формула
C3	=ЕСЛИ(E2<F2;A3+0,318*(B3-A3);D2)	Формула
D3	=ЕСЛИ(E2<F2;C2;A3+0,618*(B3-A3))	Формула
E3	=ЕСЛИ(E2<F2;(0,25*C3+LN(0,5*C3+1)- EXP(-C3*0,75))^2;F2)	Формула
F3	=ЕСЛИ(E2<F2;E2;(0,25*D3+LN(0,5*D3+1)-EXP(-D3*0,75))^2)	Формула
G3	Автозаполнение формулой из клетки G2	Формула

Первая итерация
закончена. Последующие итерации реализуем
копированием диапазона ячеек A3: G3 в
диапазон ячеек от A4: G4 до A22: G22. Выделим
первую строку, где значение (b-a)<=
точности. Результат получен за 11 итераций.
Итоговые значения запишем в ячейки
J4->=( A13+ B13)/2, J5->
=(0,25*J4+LN(0,5*J4+1)-EXP(-J4*0,75))^2.

Вид листа MS
Excel:

Ответ:х*=0,813
f(x*)=
0,0 n=11.

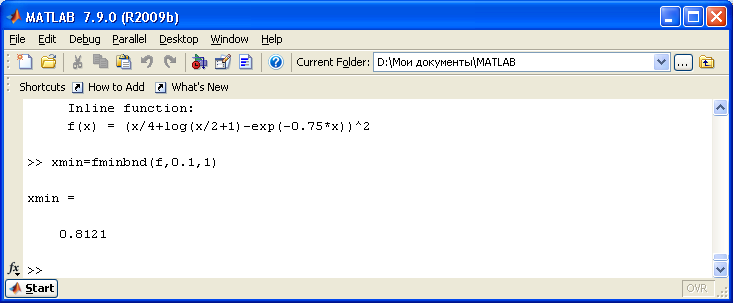
Реализация метода
в MatLab

В MatLab вычисление минимума
функции одной переменной можно выполнить
с помощью функции fminbnd(fun,x1,x2), которая
возвращает значение х, являющееся
локальным минимумом функции fun(x) на
интервале x1<x<x2. Функцию fun(x) зададим,
используя функцию inline:
f=inline(‘(x/4+log(x/2+1)-exp(-0,75*x))^2’, ‘x’).

Результаты решения
представлены на рисунке:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

jogano, К сожалению, я абсолютно ничего не понимаю в этом.. Это так решается? К примеру в решении приводится один из локальных экстремумов — min функции

Если решение верное, то мне надо таким же образом получить max функции, хотя я не уверен, что именно так должно решаться, даже не имею представления

При изучении дисциплины “Математика” в
средних специальных учебных заведениях
предполагается рассмотрение темы: “Элементы
численных методов”. Использование MathCAD 2000 и Microsoft
Excel для реализации численных методов позволяет
сформировать понимание математического
содержания конкретного метода и умение
использовать современные программные средства.
При использовании MathCAD 2000 и Microsoft Excel в ходе
выполнения лабораторных работ студенты получают
возможность использовать знания, полученные при
изучении дисциплины “Информатика”.

Возможности MathCAD 2000 позволяют строить графики
зависимостей, графически отделять корни
уравнений, решать уравнения и системы уравнений,
преобразовывать полученные выражения, проверять
правильность полученного приближённого решения.

Возможности Microsoft Excel позволяют не тратить
время на проведение однотипных расчетов, быстро
исправлять возникающие ошибки в вычислениях.

Использование MathCAD 2000 и Microsoft Excel для
приближённого решения систем линейных
алгебраических уравнений методом итераций.

На первом этапе приближённого решения СЛАУ
методом простой итерации необходимо привести
систему к нормальному виду. Для этого нужно
выразить х из первого уравнения, y из
второго уравнения и т.д. Это можно сделать с
помощью Math CAD 2000. При этом можно использовать один
из способов решения уравнений: набирается
уравнение, причём равно ставится жирное
(<Ctrl>+<=>) и даётся команда solve из панели
“Символика”, после указания переменной,
относительно которой необходимо разрешить
уравнение, получим результат.

На втором этапе решения необходимо проверить
для полученной системы, приведённой к
нормальному виду условие сходимости
итерационного процесса, т. е. сравнить нормы
матрицы с единицей. Например, проверить условие,
что наибольшая из сумм модулей элементов
столбцов меньше 1. Это также можно сделать с
помощью Math CAD 2000. При этом используется функция norm1(А)
из стандартного набора функций.

Итерационный процесс удобнее осуществить в
Microsoft Excel. В столбец А заносится номер
итерационного шага, в столбцы В, С, D – значения х_k,
y_k, z_k в столбцы E,F,G – значения х_k+1,
y_k+1, z_k+1, в столбце Н можно вычислять
значение погрешности вычислений на данном шаге
итерации, чтобы выполнить вычисления с заданной
степенью точности.

При заполнении ячеек В3, С3, D3 лучше ссылаться на
ячейки E2, F2, G2, а не вводить данные вручную, это
позволит рациональнее использовать время, лучше
использовать автозаполнение и проще исправлять
ошибки.

В правильности полученных результатов можно
убедиться, если решить систему с помощью MathCAD 2000.
Это можно сделать с помощью команд given и find.

Для решения данной системы методом Зейделя
достаточно будет лишь изменить формулы для
вычисления , y_k, z_k.

Пример использование MathCAD 2000 и Microsoft Excel для
приближённого решения системы линейных
алгебраических уравнений методом простых
итераций и методом Зейделя можно увидеть на рис.1.

Использование MathCAD 2000 и Microsoft Excel для
интерполирования кубическими сплайнами

Сейчас широкое распространение для
интерполяции получило использование кубических
сплайн–функций – специальным образом
построенных многочленов третьей степени.

При осуществлении этого метода для функции,
заданной четырьмя точками, необходимо составить
и решить систему девяти уравнений с девятью
неизвестными. Составлять эту систему приходится
вручную. Решить, полученную систему лучше в MathCAD
2000, это сэкономит время и позволит быстро
исправить возможные ошибки. Это можно сделать с
помощью команд given и find, или матричным
способом.

Проверить правильность выполнения
сплайн–интерполирования можно, построив график
данной функции и полученного сплайна в MathCAD 2000.
Для этого задаются: матрицы Х и У исходных данных,
три отрезка на которых строится сплайн–функция.
Потом задаются все три функции, определяющие
сплайн–функцию (аргумент у каждой должен быть
разный, соответствующий отрезку на котором эта
функция построена). Последний этап – построение
графика. Чтобы задать несколько аргументов и
функций используется запятая. Если щёлкнуть по
полю графика 2 раза, то появится окно
форматирования графиков, в закладке Х–У Axec
можно задать линию сетки, а в закладке Traces задать
вид линии графика и построить график исходных
данных точками, а график полученной
сплайн–функции сплошной линией.

Пример использование Math CAD 2000 для
интерполирования кубическими сплайнами можно
увидеть на рис.2.

Быстро просчитать варианты заданий
преподавателю поможет шаблон, заготовленный в
MathCAD 2000 (рис. 3). Полученные ответы помогут быстро
найти ошибку, допущенную студентом, и помочь ему
исправить её.

Использование MathCAD 2000 и Microsoft Excel для поиска
экстремума функции методом золотого сечения

При решении задачи на поиск экстремума функции
методом золотого сечения необходимо сначала
определить отрезок, которому принадлежит
минимум или максимум. Это можно сделать, построив
график данной функции в MathCAD 2000. Выполнив
форматирование графика, можно указать
достаточно малый отрезок, которому принадлежит
экстремум функции.

Уточнять значение экстремума с заданной
степенью точности лучше в Microsoft Excel. В столбцы A и D
удобно занести значение концов отрезка на данном
шаге, а в столбцы B и C – формулы для нахождения
точек, которые осуществляют золотое сечение
данного отрезка. В столбцах E и F вычисляются
значения функции в этих точках, а в столбце G –
вычисляется длина рассматриваемого отрезка, т. е.
точность вычисления на данном шаге. Для
наглядности выбора следующего рассматриваемого
отрезка можно выделять ячейки цветом.
Последующие строки заполняются с использованием
автозаполнения.

Правильность решения можно проверить в MathCAD 2000.
Для этого необходимо воспользоваться правилами
нахождения экстремума функции средствами
математического анализа. Найти производную
функции и решить полученное уравнение помогут
панели “Калькулус” и “Символика”.

Пример использование MathCAD 2000 и Microsoft Excel для
нахождения экстремума функции методом золотого
сечения можно увидеть на рис.4.

Использование MathCAD 2000 и Microsoft Excel для поиска
экстремума функции методом Ньютона

При нахождении экстремума функции методом
Ньютона MathCAD 2000 поможет не только определить
отрезок, которому принадлежит экстремум, но и
вычислить необходимые для выбора начального
приближения первую, вторую, третью производные и
значения их на концах рассматриваемого отрезка.

Найти экстремум с заданной степенью точности
можно в Microsoft Excel. В столбец А заносится начальное
значение экстремума, в столбцах В и С вычисляются
значения первой и второй производных в этой
точке. В столбце D вычисляется по формуле Ньютона
уточнённое значение экстремума, а в столбце Е –
точность вычисления на данном шаге.

Пример использование Math CAD 2000 и Microsoft Excel для
нахождения экстремума функции методом Ньютона
можно увидеть на рис.5

Использование MathCAD 2000 и Microsoft Excel для
аппроксимации функций методом наименьших
квадратов

При осуществлении линейной аппроксимации
функций методом наименьших квадратов для
составления уравнения регрессии сначала
необходимо вычислить числа М_х, М_ху, М_у,
М_х², это удобно сделать в Microsoft Excel,
используя автосуммирование.

По полученным значениям М_х, М_ху, М_у,
М_х² составляется система, после
решения которой можно будет записать уравнение
регрессии. Решить систему можно с помощью MathCAD 2000.

Правильность вычислений можно проверить в MathCAD
2000. Функции interсept(Х,У) и slope(Х,У) вычисляют по
заданным векторам экспериментальных данных Х, У
значения а₀ и а₁ для записи уравнения
линейной регрессии в виде j (х)=а₀+а₁х.

Затем с помощью MathCAD 2000 можно убедиться в том,
что полученное уравнение регрессии
аппроксимирует таблично заданную функцию,
построив в одной системе координат график данной
функции и полученного уравнения регрессии.
Возможности

Пример использование MathCAD 2000 и Microsoft Excel для
составления уравнения линейной регрессии можно
увидеть на рис.6.

Аналогично используются MathCAD 2000 и Microsoft Excel для
выполнения аппроксимации функций многочленами
второй степени и составления уравнений
регрессии, преобразуемых в линейную. Примеры
этого представлены на рис.7 и рис.8.

Использование MathCAD 2000 для численного решения
дифференциальных уравнений методом Рунге–Кутта

Осуществление численного решения
дифференциального уравнения методом
Рунге–Кутта даже в Microsoft Excel весьма трудоёмкий
процесс. MathCAD 2000 позволяет облегчить эту задачу.

Решить дифференциальное уравнение методом
Рунге–Кутта в MathCAD 2000 можно двумя способами: с
помощью встроенной функции и непосредственно по
формулам.

При непосредственном осуществлении метода
Рунге–Кутта задаются формулы для вычисления
необходимых коэффициентов, а затем создаётся
цикл для вычисления с помощью их искомых
значений у.

Встроенная функция rkfixed позволяет
осуществить метод Рунге–Кутта, не производя
никаких вычислений. С помощью этой функции можно
предложить студентам проверить вычисления,
выполненные ими по формулам, а преподавателю
быстро просчитать различные варианты.

Пример использование MathCAD 2000 для реализации
метода Рунге–Кутта численного решения
дифференциального уравнения можно увидеть на
рис.9.

Применение MathCAD 2000 и Microsoft Excel для реализации
численных методов и для решения других
математических задач поможет студентам не
только лучше понять приёмы решения задач, не
теряя время на рутинные вычисления, но и создаст
возможности для использования этих программ при
дальнейшем обучении и в профессиональной
деятельности.