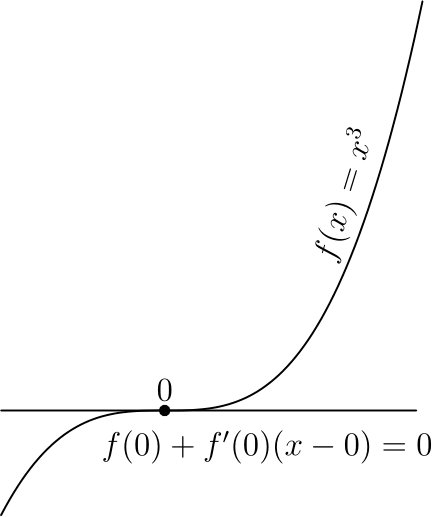Метод тяжелого шарика excel

Лабораторная
работа № 5

Решение
задачи одномерной оптимизации методом
«тяжелого шарика»

Задание

Найти
интервалы унимодальности заданной
функции на интервале [-1 ; 3] с точностью
0,2.

Минимизировать
заданную функцию с точностью =0,0001
методом «тяжелого шарика».

Используя
окно диалога «Поиск решения»,
уточнить координаты всех экстремумов
(минимумов и максимумов) заданной функции
на заданном интервале.

Варианты

1. f(x)
= x3-2×2-5arctg(2,5x)

2. f(x)
= x3-2,5×2-1,5arctg(10x)

3. f(x)
= x3-2×2-0,7arctg(3x)

4. f(x)
= x3-2,1×2-0,8arctg(4x)

5. f(x)
= x3-2,8×2-0,2arctg(5x)

6. f(x)
= x3-2,9×2-0,7arctg(2x)

7. f(x)
= x3-2,2×2-1,7arctg(0,8x)

8. f(x)
= x3-1,8×2-0,7arctg(0,2x)

9. f(x)
= x3-1,5×2-1,5arctg(5x)

10. f(x)
= x3-2,1×2-5arctg(1,5x)

11. f(x)
= x3-2,3×2-3arctg(1,8x)

12. f(x)
= x3-1,4×2-4arctg(1,9x)

Отчет о выполнении
работы в лабораторном журнале

Отчет
о выполнении работы в лабораторном
журнале должен содержать следующие
численные результаты:

  • Результаты
    поиска интервалов унимодальности и
    график функции;

  • Уточненный
    методом «тяжелого шарика» минимум
    функции и достигнутую точность;

  • Уточненные
    поиском решения значения всех экстремумов
    функции на заданном интервале.

Пример
выполнения лабораторной работы в MS
Excel

Этапы
выполнения работы

1. Создать
электронную таблицу для поиска экстремумов
функции одной переменной.

Поиск
экстремумов функции состоит из двух
этапов. Нахождение интервалов
унимодальности (интервалов, на которых
функция имеет один экстремум и не имеет
точек перегиба) выполняется табулированием
функции и графически. Уточнение
экстремумов выполняется двумя способами:
А) методом тяжелого шарика (минимум
функции в соответствии с заданием); Б)
при помощи окна диалога MS «Поиск
решения» (уточняются все экстремумы).

В
первой строке таблицы расположить
название работы. Во вторую строку ввести
уравнение в соответствии с номером
варианта. Обе строки текста выделить
жирным шрифтом и выровнять по ширине
5-ти столбцов.

2. Поиск
интервалов унимодальности.

Для
поиска интервалов унимодальности
функции необходимо построить таблицу
значений заданной функции на заданном
отрезке [xнач;xкон].
В третью строку ввести название таблицы
– «Поиск интервалов унимодальности».
Названия столбцов X
и f(X)
выделить жирным шрифтом. Для расчета
значения аргумента X
от xнач
до xкон
с заданным шагом использовать формулу.
Значения аргумента X
должны иметь 1 знак после запятой.
Значения функции f(X)
должны иметь 2 знака после запятой.
Интервалы унимодальности должны быть
обведены рамкой.

Построить
график функции на заданном отрезке.
Диаграмму расположить справа от таблицы
значений функции. Название диаграммы
должно содержать исследуемую функцию.
Шкалы осей должны содержать целые числа.
Область построения диаграммы должна
быть белого цвета.

Выписать
результаты поиска интервалов
унимодальности. Под диаграммой ввести
текст – «Интервалы унимодальности» и
выделить его жирным шрифтом. В следующих
строках ввести тексты – найденные
отрезки, содержащие ровно один экстремум
с точностью до 0,2.

3. Построить
таблицу для уточнения заданного
экстремума функции.
Ниже результатов
отделения поиска интервалов унимодальности
ввести текст – «Уточнение минимума
методом «Тяжелого шарика»» и
выделить его жирным шрифтом. Ввести
названия столбцов таблицы жирным шрифтом
и заполнить расчетную таблицу формулами.

Название
столбца

Значения
в столбце

n

Номер
итерации (0 для начального приближения)

x

Левая
граница интервала унимодальности

на текущем шаге вычислений xнов=x+h

F(x)

Значение
функции на этом шаге вычислений

h

Значение
шага

d

Достигнутая
точность на текущем шаге d
= |h|

?

Достигнута
ли заданная точность вычислений (да
или нет)

В
качестве начального приближения
использовать найденный на этапе отделения
корней отрезок, содержащий один экстремум.
Для определения новых границ отрезка
и проверки достигнутой точности
вычислений использовать логическую
функцию ЕСЛИ.

hнов
= {

h,
если f(x)<f(x+h)

-h/2,
если
f(x)>f(x+h)

}

Выделить
светло-желтым фоном ячейки, содержащие
начальное приближение, уточненное
значение экстремума, достигнутую
точность решения и количество итераций.

4. Уточнение
экстремумов при помощи окна диалога MS
«Поиск решения»

Ниже
найденного методом тяжелого шарика
минимума функции ввести текст –
«Уточнение экстремумов «Поиском
решения»». Скопировать из таблицы
значений функции заголовки столбцов и
первую строку с формулами. Исправить
название столбца с аргументом X
на X1. В
качестве начального приближения
использовать одну из границ первого
отделенного отрезка. Уточнить значения
экстремума, используя окно диалога
«Поиск решения». Убедиться, что уточненное
значение принадлежит отделенному
отрезку. Ниже аналогично уточнить
остальные экстремумы функции.

Соседние файлы в папке 29-10-2013_01-02-33

  • #
  • #
Источник

Обзор градиентных методов в задачах математической оптимизации

Время на прочтение
11 мин

Количество просмотров 87K

Предисловие

В этой статье речь пойдет о методах решения задач математической оптимизации, основанных на использовании градиента функции. Основная цель — собрать в статье все наиболее важные идеи, которые так или иначе связаны с этим методом и его всевозможными модификациями.

UPD. В комментариях пишут, что на некоторых браузерах и в мобильном приложении формулы не отображаются. К сожалению, не знаю, как с этим бороться. Могу лишь сказать, что использовал макросы «inline» и «display» хабравского редактора. Если вдруг знаете, как это исправить — напишите в комментариях, пожалуйста.

Примечание от автора

На момент написания я защитил диссертацию, задача которой требовала от меня глубокое понимание теоретических основно методов математической оптимизации. Тем не менее, у меня до сих пор (как и у всех) расплываются глаза от страшных длинных формул, поэтому я потратил немалое время, чтобы вычленить ключевые идеи, которые бы характеризовали разные вариации градиентных методов. Моя личная цель — написать статью, содержащую минимальное количество информации, необходимое для более менее подробного понимания тематики. Но будьте готовы, без формул так или иначе не обойтись.

Постановка задачи

Прежде чем описывать метод, следует сначала описать задачу, а именно: «Даны множество $mathcal{K}$ и функция $f:mathcal{K}rightarrow mathbb{R}$, требуется найти точку $x^*in mathcal{K}$, такую что $ f(x)geq f(x^*)$ для всех $xin mathcal{K}$», что обычно записывается например вот так

$f(x)rightarrow min_{xin mathcal{K}}.$

В теории обычно предполагается, что $f$ — дифференцируемая и выпуклая функция, а $mathcal{K}$ — выпуклое множество (а еще лучше, если вообще $mathcal{K}=mathbb{R}^n$), это позволяет дать какие-то гарантии успешности применения градиентного спуска. На практике градиентный спуск успешно применяется даже когда у задачи нет ни одного из вышеперечисленных свойств (пример дальше в статье).

Немного математики

Допустим пока что нам нужно просто найти минимум одномерной функции

$f(x)rightarrow min_{xin mathbb{R}}.$

Еще в 17 веке Пьером Ферма был придуман критерий, который позволял решать простые задачи оптимизации, а именно, еcли $x^* $ — точка минимума $f^* $, то

$f'(x^*)=0 $

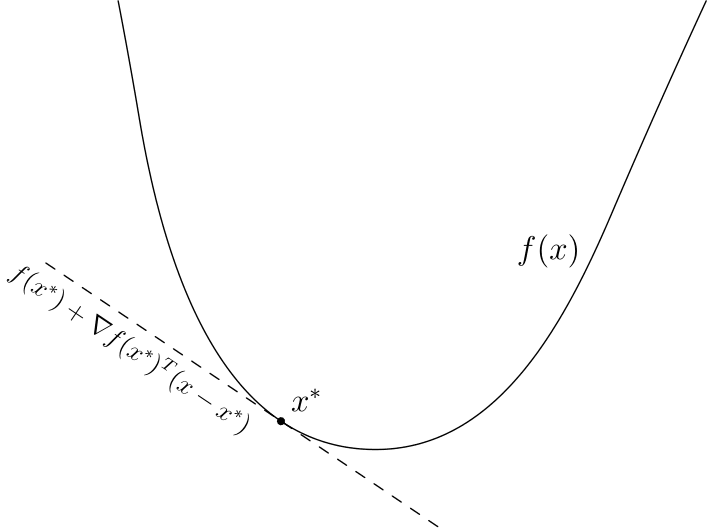
где $f'$ — производная $f$. Этот критерий основан на линейном приближении

$ f(x)approx f(x^*)+f'(x^*)(x-x^*).$

Чем ближе $x$ к $x^*$, чем точнее это приближение. В правой части — выражение, которое при $f'(x^*)neq 0$ может быть как больше $f(x^*)$ так и меньше — это основная суть критерия. В многомерном случае аналогично из линейного приближения $f(x)approx f(x^*)+nabla f(x^*)^T(x-x^*)$ (здесь и далее $x^Ty=sum_{i=1}^nx_iy_i$ — стандартное скалярное произведение, форма записи обусловлена тем, что скалярное произведение — это то же самое, что матричное произведение вектор-строки на вектор-столбец) получается критерий

$nabla f(x^*)=0. $

Величина $nabla f(x^*)$ — градиент функции $f$ в точке $x^*$. Также равенство градиента нулю означает равенство всех частных производных нулю, поэтому в многомерном случае можно получить этот критерий просто последовательно применив одномерный критерий по каждой переменной в отдельности.

Стоит отметить, что указанные условия являются необходимыми, но не достаточными, самый простой пример — 0 для $f(x)=x^2$ и $f(x)=x^3$

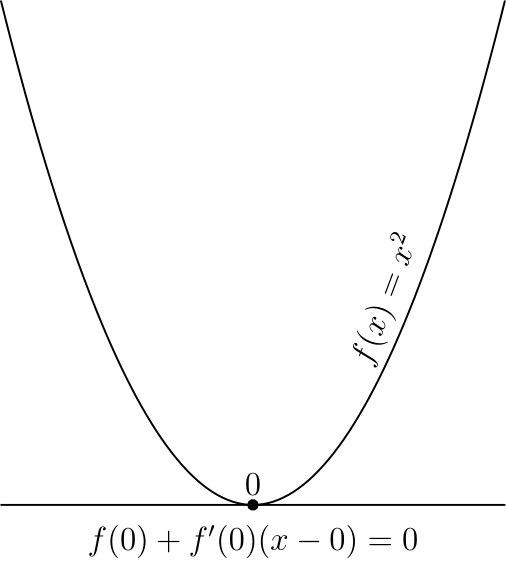
Этот критерий является достаточным в случае выпуклой функции, во многом из-за этого для выпуклых функций удалось получить так много результатов.

Квадратичные функции

Квадратичные функции в $mathbb{R}^n$ — это функция вида

$ f(x) = f(x_1, x_2, ldots, x_n)=frac{1}{2}sum_{i,j=1}^na_{ij}x_ix_j-sum_{i=1}^n b_ix_i+c $

Для экономии места (да и чтобы меньше возиться с индексами) такую функцию обычно записывают в матричной форме:

$ f(x) = frac{1}{2}x^TAx-b^Tx+c, $

где $x=(x_1, ldots, x_n)^T$, $b=(b_1, ldots, b_n)^T$, $A$ — матрица, у которой на пересечении $i$ строки и $j$ столбца стоит величина
$frac{1}{2}(a_{ij}+a_{ji})$ ($A$ при этом получается симметричной — это важно). Далее. при упомянании квадратичной функции я буду иметь указанную выше функцию.

Зачем я об этом рассказываю? Дело в том, что квадратичные функции важны в оптимизации по двум причинам:

  1. Они тоже встречаются на практике, например при построении линейной регрессии методом наименьших квадратов
  2. Градиент квадратичной функции — линейная функция, в частности для функции выше

    $ frac{partial}{partial x_i} f(x_1, x_2, ldots, x_n) = a_{ii} x_i + sum_{jneq i}frac{1}{2}(a_{ij}+a_{ji})x_j -b_i, $

    Или в матричной форме

    $ nabla f(x) = Ax-b, $

    Таким образом система $nabla f(x)=0$ — линейная система. Системы, проще чем линейная, просто не существует. Мысль, к которой я старался подобраться — оптимизация квадратичной функции — самый простой класс задач оптимизации. С другой стороны, тот факт, что $nabla f(x^*)=0$ — необходимые условия минимума дает возможность решать линейные системы через задачи оптимизации. Чуть позже я постараюсь вас убедить в том, что это имеет смысл.

Полезные свойства градиента

Хорошо, мы вроде бы выяснили, что если функция дифференцируема (у нее существуют производные по всем переменным), то в точке минимума градиент должен быть равен нулю. А вот несет ли градиент какую-нибудь полезную информацию в случае, когда он отличен от нуля?

Попробуем пока решить более простую задачу: дана точка $x$, найти точку $bar{x}$ такую, что $f(bar{x})<f(x)$. Давайте возьмем точку рядом с $x$, опять же используя линейное приближение $f(bar{x})approx f(x)+nabla f(x)^T(bar{x}-x)$. Если взять $bar{x}=x-alphanabla f(x)$, $ alpha>0$ то мы получим

$ f(bar{x})approx f(x)-alpha|nabla f(x)|^2<f(x). $

Аналогично, если $ alpha<0 $, то $f(bar{x})$ будет больше $f(x)$ (здесь и далее $||x||=sqrt{x_1^2+x_2^2+ldots+x_n^2}~$). Опять же, так как мы использовали приближение, то эти соображения будут верны только для малых $alpha$. Подытоживая вышесказанное, если $nabla f(x)neq 0$, то градиент указывает направление наибольшего локального увеличения функции.

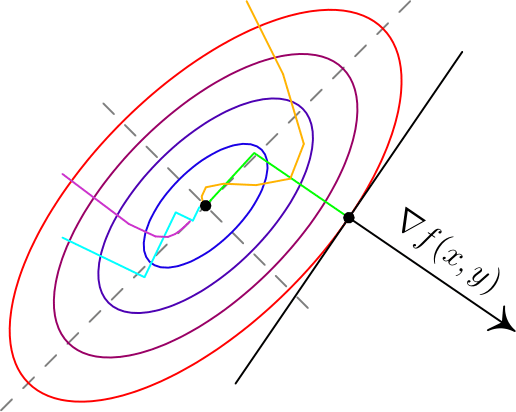
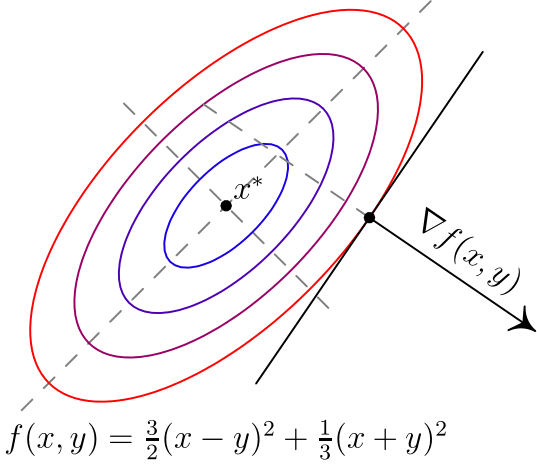
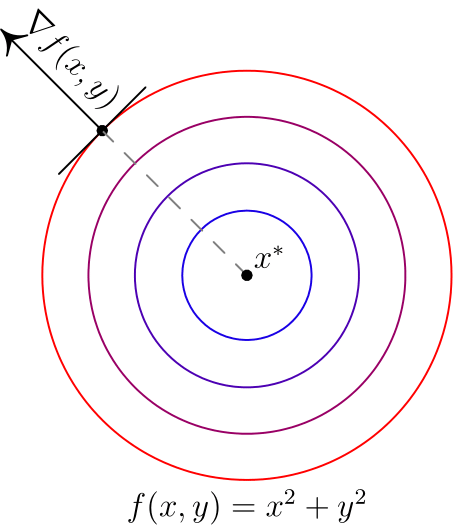
Вот два примера для двумерных функций. Такого рода картинки можно часто увидеть в демонстрациях градиентного спуска. Цветные линии — так называемые линии уровня, это множество точек, для которых функция принимает фиксированное значений, в моем случае это круги и эллипсы. Я обозначил синими линии уровня с более низким значением, красными — с более высоким.

Обратите внимание, что для поверхности, заданной уравнением вида $f(x)=c$, $nabla f(x) $ задает нормаль (в простонародии — перпендикуляр) к этой поверхности. Также обратите внимание, что хоть градиент и показывает в направлении наибольшего увеличения функции, нет никакой гарантии, что по направлению, обратному к градиенту, можно найти минимум (пример — левая картинка).

Градиентный спуск

До базового метода градиентного спуска остался лишь малый шажок: мы научились по точке $x$ получать точку $bar{x}$ с меньшим значением функции $ f$. Что мешает нам повторить это несколько раз? По сути, это и есть градиентный спуск: строим последовательность

$ x_{k+1}=x_k-alpha_knabla f(x_k). $

Величина $alpha_k$ называется размером шага (в машинном обучении — скорость обучения). Пару слов по поводу выбора $alpha_k$: если $alpha_k$ — очень маленькие, то последовательность медленно меняется, что делает алгоритм не очень эффективным; если же $alpha_k$ очень большие, то линейное приближение становится плохим, а может даже и неверным. На практике размер шага часта подбирают эмпирически, в теории обычно предполагается липшицевость градиента, а именно, если

$ |nabla f(x)-nabla f(y)|leq L|x-y| $

для всех $x,y$, то $alpha_k< frac{2}{L}$ гарантирует убывание $f(x_k)$.

Анализ для квадратичных функций

Если $A$ — симметричная обратимая матрица, $Ax^*=b$, то для квадратичной функции $f(x)=frac{1}{2}x^TAx-b^Tx+c$ точка $x^*$ является точкой минимума (UPD. при условии, что этот минимум вообще существует — $f$ не принимает сколько угодно близкие к $-infty$ значения только если $A$ положительно определена), а для метода градиентного спуска можно получить следующее

$ x_{k+1}-x^* = x_k-alpha_k nabla f(x_k)-x^* = x_k-alpha_k(Ax_k-b)-x^*= $

$ (x_k-x^*)-alpha_kA(x_k-x^*)=(I-alpha_k A)(x_k-x^*), $

где $ I $ — единичная матрица, т.е. $ Ix=x$ для всех $ x$. Если же $alpha_kequivalpha$, то получится

$ |x_{k}-x^*|=|(I-alpha A)^k(x_0-x^*)|leq |I-alpha A|^k |x_0-x^*|. $

Выражение слева — расстояние от приближения, полученного на шаге $k$ градиентного спуска до точки минимума, справа — выражение вида $lambda^k beta$, которое сходится к нулю, если $|lambda|<1$ (условие, которое я писал на $alpha$ в предыдущем пункте как раз это гарантирует). Эта базовая оценка гарантирует, что градиентный спуск сходится.

Модификации градиентного спуска

Теперь хотелось бы рассказать немного про часто используемые модификации градиентного спуска, в первую очередь так называемые

Инерционные или ускоренные градиентные методы

Все методы такого класса выражаются в следующем виде

$ x_{k+1}=x_k-alpha_knabla f(x_k)+beta_k(x_k-x_{k-1}). $

Последнее слагаемое характеризует эту самую «инерционность», алгоритм на каждом шаге старается двигаться против градиента, но при этом по инерции частично двигается в том же направлении, что и на предыдущей итерации. Такие методы обладают двумя важными свойствами:

  1. Они практически не усложняют обычный градиентный спуск в вычислительном плане.
  2. При аккуратном подборе $alpha_k, beta_k$ такие методы на порядок быстрее, чем обычный градиентный спуск даже с оптимально подобранным шагом.

Один из первых таких методов появился в середине 20 века и назывался метод тяжелого шарика, что передавало природу инерционности метода: в этом методе $alpha_k, beta_k$ не зависят от $k$ и аккуратно подбираются в зависимости от целевой функции. Стоит отметить, что $alpha_k$ может быть какой угодно, а $beta_k$ — обычно лишь чуть-чуть меньше единицы.

Метод тяжелого шарика — самый простой инерционный метод, но не самый первый. При этом, на мой взгляд, самый первый метод довольно важен для понимания сути этих методов.

Метод Чебышева

Да да, первый метод такого типа был придуман еще Чебышевым для решения систем линейных уравнений. В какой-то момент при анализе градиентного спуска было получено следующее равенство

$ x_{k+1}-x^* = (I-alpha_k A) (x_k-x^*)=ldots= $

$ (I-alpha_kA)(I-alpha_{k-1}A)ldots(I-alpha_1A)(x_0-x^*)=P_k(A)(x_0-x^*), $

где $P_k$ — некоторый многочлен степени $k$. Почему бы не попробовать подобрать $alpha_k$ таким образом, чтобы $P_k(A)(x_0-x^*)$ было поменьше? Один уз универсальных многочленов, которые меньше всего отклоняются от нуля — многочлен Чебышева. Метод Чебышева по сути заключается в том, чтобы подобрать параметры спуска так, чтобы $P_k$ был многочленом Чебышева. Есть правда одна небольшая проблема: для обычного градиентного спуска это просто невозможно. Однако для инерционных методов это оказывается возможным. В основном это происходит из-за того, что многочлены Чебышева удовлетворяют рекуррентному соотношению второго порядка

$ T_{n+1}(x)=2xT_n(x)-T_{n-1}(x), $

поэтому их невозможно построить для градиентного спуска, который вычисляет новое значение лишь по одному предыдущему, а для инерционных становится возможным за счет того, что используется два предыдущих значения. При этом оказывается, что сложность вычисления $alpha_k,beta_k$ не зависит ни от $k$, ни от размера пространства $n$.

Метод сопряженных градиентов

Еще один очень интересный и важный факт (следствие теоремы Гамильтона-Кэли): для любой квадратной матрицы $A$ размера $ntimes n$ существует многочлен $P$ степени не больше $n$, для которого $P(A)=0$. Чем это интересно? Все дело в том же равенстве

$ x_{k+1}-x^* = P_k(A)(x_0-x^*). $

Если бы мы могли подбирать размер шага в градиентном спуске так, чтобы получать именно этот обнуляющий многочлен, то градиентный спуск сходился бы за фиксированное число итерации не большее размерности $A$. Как уже выяснили — для градиентного спуска мы так делать не можем. К счастью, для инерционных методов — можем. Описание и обоснование метода довольно техническое, я ограничусь сутью:на каждой итерации выбираются параметры, дающие наилучший многочлен, который можно построить учитывая все сделанные до текущего шага измерения градиента. При этом

  1. Одна итерация градиентного спуска (без учета вычислений параметров) содежит одно умножение матрицы на вектор и 2-3 сложения векторов
  2. Вычисление параметров также требует 1-2 умножение матрицы на вектор, 2-3 скалярных умножения вектор на вектор и несколько сложений векторов.

Самое сложное в вычислительном плане — умножение Матрицы на вектор, обычно это делается за время $mathcal{O}(n^2)$, однако для со специальной реализацией это можно сделать за $mathcal{O}(m) $, где $m$ — количество ненулевых элементов в $A$. Учитывая сходимость метода сопряженных градиентов не более, чем за $n$ итерации получаем общую сложность алгоритма $mathcal{O}(nm)$, что во всех случаях не хуже $mathcal{O}(n^3)$ для метода Гаусса или Холесского, но намного лучше в случае, если $m<<n^2$, что не так редко встречается.

Метод сопряженных градиентов хорошо работает и в случае, если $f$ не является квадратичной функцией, но при этом уже не сходится за конечное число шагов и часто требует небольших дополнительных модификаций

Метод Нестерова

Для сообществ математической оптимизации и машинного обучения фамилия «Нестеров» уже давно стало нарицательной. В 80х годах прошлого века Ю.Е. Нестеров придумал интересный вариант инерционного метода, который имеет вид

$ x_{k+1}=x_k-alpha_knabla f(x_k+beta_k(x_k-x_{k-1}))+beta_k(x_k-x_{k-1}), $

при этом не предполагается какого-то сложного подсчета $alpha_k,beta_k$ как в методе сопряженных градиентов, в целом поведение метода похоже на метод тяжелого шарика, но при этом его сходимость обычно гораздо надежнее как в теории, так и на практике.

Стохастический градиентный спуск

Единственное формальное отличие от обычного градиентного спуска — использование вместо градиента функции $g(x, theta)$ такой, что $E_theta g(x,theta)=nabla f(x)$ ($E_theta$ — математическое ожидание по случайной величине $theta$), таким образом стохастический градиентный спуск имеет вид

$ x_{k+1}=x_k-alpha_kg(x_k, theta_k). $

$theta_k$ — это некоторый случайный параметр, на который мы не влияем, но при этом в среднем мы идем против градиента. В качестве примера рассмотрим функции

$ f(x)=frac{1}{2m}sum_{j=1}^m|x-y_j|^2,~~nabla f(x)=frac{1}{m}sum_{j=1}^m(x-y_j) $

и

$ g(x, i)=x-y_i. $

Если $i$ принимает значения $1,ldots, m$ равновероятно, то как раз в среднем $g$ — это градиент $f$. Этот пример показателен еще и следующим: сложность вычисления градиента в $m$ раз больше, чем сложность вычисления $g$. Это позволяет стохастическому градиентному спуску делать за одно и то же время в $m$ раз больше итераций. Несмотря на то, что стохастический градиентный спуск обычно сходится медленней обычного, за счет такого большого увеличения числа итераций получается улучшить скорость сходимости на единицу времени. Насколько мне известно — на данный момент стохастический градиентный спуск является базовым методом обучения большинства нейронных сетей, реализован во всех основных библиотеках по ML: tensorflow, torch, caffe, CNTK, и т.д.

Стоит отметить, что идеи иннерционных методов применяются для стохастического градиентного спуска и на практике часто дают прирост, в теории же обычно считается, что асимптотическая скорость сходимости не меняется из-за того, что основная погрешность в стохастическом градиентном спуске обусловлена дисперсией $g$.

Субградиентный спуск

Эта вариация позволяет работать с недифференцируемыми функциями, её я опишу более подробно. Придется опять вспомнить линейное приближение — дело в том, что есть простая характеристика выпуклости через градиент, дифференцируемая функция $f$ выпукла тогда и только тогда, когда выполняется $f(y)geq f(x)+nabla f(x)^T(y-x)$ для всех $x, y$ . Оказывается, что выпуклая функция не обязаны быть дифференцируемой, но для любой точки $x$ обязательно найдется такой вектор $g$, что $f(y)geq f(x)+g^T(y-x)$ для всех $y$. Такой вектор $g$ принято называть субградиентом $f$ в точке $x$, множество всех субградиентов в точки $x$ называют субдифференциалом $x$ и обозначают $partial f(x)$ (несмотря на обозначение — не имеет ничего общего с частными производными). В одномерном случае $g$ — это число, а вышеуказанное свойство просто означает, что график $f$ лежит выше прямой, проходящей через $(x, f(x))$ и имеющей тангенс угла наклона $g$ (смотрите рисунки ниже). Отмечу, что субградиентов для одной точки может быть несколько, даже бесконечное число.

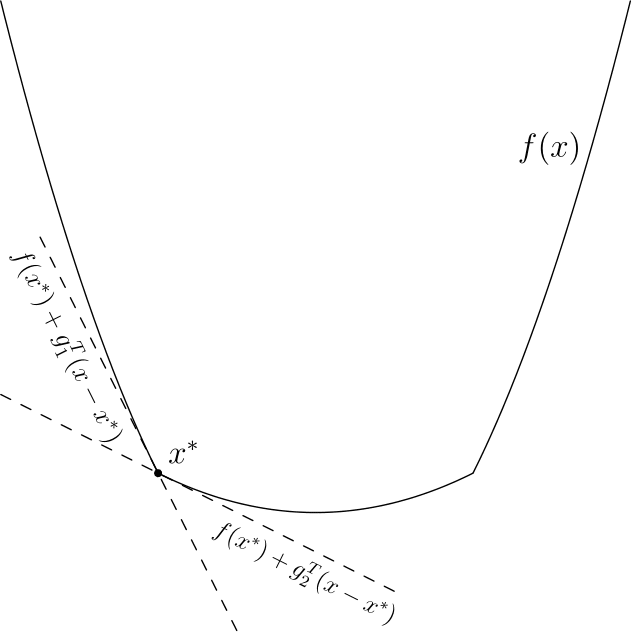
Вычислить хотя бы один субградиент для точки обычно не очень сложно, субградиентный спуск по сути использует субградиент вместо градиента. Оказывается — этого достаточно, в теории скорость сходимости при этом падает, однако например в нейронных сетях недифференцируемую функцию $ReLU(x)=max(0, x)$ любят использовать как раз из-за того, что с ней обучение проходит быстрее (это кстати пример невыпуклой недифференцируемой функции, в которой успешно применяется (суб)градиентный спуск. Сама по себе функция $ReLU$ выпукла, но многослойная нейронная сеть, содержащая $ReLU$, невыпукла и недифференцируема). В качестве примера, для функции $f(x)=|x|$ субдифференциал вычисляется очень просто

$ partial f(x)=begin{cases} 1, & x>0, \ -1, & x < 0, \ [-1, 1], & x=0. end{cases} $

Пожалуй, последняя важная вещь, которую стоит знать, — это то, что субградиентный спуск не сходится при постоянном размере шага. Это проще всего увидеть для указанной выше функции $f(x)=|x|$. Даже отсутствие производной в одной точке ломает сходимость:

  1. Допустим мы начали из точки $x_0$.
  2. Шаг субградиентного спуска:

    $ x_{k+1}=begin{cases} x_{k}-1, & x>0, \ x_k+1, & x < 0, \ ??? & x=0. end{cases} $

  3. Если $x_0>0$, то первые несколько шагов мы будет вычитать единицу, если $x_0<0$, то прибавлять. Так или иначе мы в какой-то момент окажемся на интервале $[0, 1)$, из которого попадем в $[-1, 0)$, а дальше будем прыгать между двумя точками этих интервалов.

В теории для субградиентного спуска рекомендуется брать последовательность шагов

$ alpha_k=frac{1}{(k+1)^c}. $

Где $c$ обычно $1$ или $frac{1}{2}$. На практике я часто видел успешное применение шагов $alpha_k=e^{-ck}$, хоть и для таких шагов вообще говоря не будет сходимости.

Proximal методы

К сожалению я не знаю хорошего перевода для «proximal» в контексте оптимизации, поэтому просто так и буду называть этот метод. Proximal-методы появились как обобщение проективных градиентных методов. Идея очень простая: если есть функция $f$, представимая в виде суммы $f(x)=varphi(x)+h(x)$, где $varphi$ — дифференцируемая выпуклая функция, а $h(x)$ — выпуклая, для которой существует специальный proximal-оператор $prox_h(x)$ (в этой статье ограничусь лишь примерами, описывать в общем виде не буду), то свойства сходимости градиентного спуска для $varphi$ остаются и для градиентного спуска для $f$, если после каждой итерации применять этот proximal-оператор для текущей точки $x_k$, другими словами общий вид proximal-метода выглядит так:

$ x_{k+1}=prox_{alpha_kh}(x_k-alpha_knabla varphi(x_k)) $

Думаю, пока что совершенно непонятно, зачем это может понадобиться, особенно учитывая то, что я не объяснил, что такое proximal-оператор. Вот два примера:

  1. $h(x)$ — индикатор-функция выпуклого множества $mathcal{K}$, то есть

    $ h(x)=begin{cases} 0, & xin mathcal{K},\ +infty, & xnotin mathcal{K}.\ end{cases} $

    В этом случае $prox_{alpha_kh}(x)$ — это проекция на множество $mathcal{K}$, то есть «ближайшая к $x$ точка множества $mathcal{K}$». Таким образом, мы ограничиваем градиентный спуск только на множество $mathcal{K}$, что позволяет решать задачи с ограничениями. К сожалению, вычисление проекции в общем случае может быть еще более сложной задачей, поэтому обычно такой метод применяется, если ограничения имеют простой вид, например так называемые box-ограничения: по каждой координате

    $ l_ileq x_ileq r_i $

  2. $h(x)=lambda |x|_1=lambdasum_{i=1}^n|x_i|$ — $ell_1$-регуляризация. Такое слагаемое любят добавлять в задачи оптимизации в машинном обучении, чтобы избежать переобучения. Регуляризация такого вида еще и имеет тенденцию обнулять наименее значимые компоненты. Для такой функции proximal-оператор имеет вид (ниже описано выражение для одной координаты):

    $ [prox_{alpha h}(x)]_i=begin{cases} x_i-alpha, & x_i>alpha,\ x_i+alpha, & x_i <-alpha,\ 0, & x_iin [-alpha, alpha], end{cases} $

    что довольно просто вычислить.

Заключение

На этом заканчиваются основные известные мне вариации градиентного метода. Пожалуй под конец я бы отметил, что все указанные модификации (кроме разве что метода сопряженных градиентов) могут легко взаимодействовать друг с другом. Я специально не стал включать в эту перечень метод Ньютона и квазиньютоновские методы (BFGS и прочие): они хоть и используют градиент, но при этом являются более сложными методами, требуют специфических дополнительных вычислений, которые обычно более вычислительно затратны, нежели вычисление градиента. Тем не менее, если этот текст будет востребован, я с удовольствием сделаю подобный обзор и по ним.

Использованная / рекомендованная литература

Boyd. S, Vandenberghe L. Convex Optimization
Shewchuk J. R. An Introduction to the Conjugate Gradient Method Without the Agonizing Pain
Bertsekas D. P. Convex Optimization Theory

Нестеров Ю. Е. Методы выпуклой оптимизации
Гасников А. В. Универсальный градиентный спуск

Источник

Лекция: Составить алгоритм поиска экстремума функции двух переменных

F (x1, x2) = x14 +x12 + x1x2 – 2 x22

методом «тяжелого шарика

Метод тяжелого шарика.

Градиентный метод решения задачи безусловной минимизации

где f: Rm → R, можно интерпретировать в терминах обыкновенных дифференциальных уравнений следующим образом. Рассмотрим дифференциальное уравнение

(здесь точка над x обозначает производную по независимой переменной t, а f ′(x) как обычно обозначает градиент отображения f: Rm → R; предполагается, что p > 0). Простейший разностный аналог уравнения (2), а именно, явная схема Эйлера

p xn+1 – xn h + f ′(xn) = 0

и есть градиентный метод для задачи (1):

Рассмотрим теперь вместо уравнения (2) уравнение

описывающее движение шарика массы m в потенциальном поле f ′ при наличии силы трения. Потери энергии на трение вынудят шарик спуститься в точку минимума потенциала f, а силы инерции не дадут ему осциллировать так, как это изображено на рис. 8. Это позволяет надеяться, что изменение уравнения (2) введением в него инерционного члена mx··улучшит сходимость градиентного метода (3). Конечно-разностный аналог уравнения, описыавющего движение шарика — это, например, уравнение

m xn+1 – 2xn + xn–1h2 + p xn – xn–1h + f ′(xn) = 0.

После простых преобразований и очевидных обозначений мы получаем

xn+1 = xn – αf ′(xn) + β(xn – xn–1). (4)

Итерационная формула (4) задает метод тяжелого шарика решения задачи безусловной оптимизации (см. рис. 14; ср. с рис. 8).

Рис. 14.

Можно доказать, что в условиях теоремы 3.7 метод тяжелого шарика при α = 2/(√Λ + √λ)2 и β = (√Λ – √λ)/(√Λ +√λ)2сходится со скоростью геометрической прогрессии со знаменателем q = (√Λ –√λ)/(√Λ + √λ).

Если теперь сравнить знаменатели qгм = (Λ – λ)/(Λ + λ) и qмтш = (√Λ – √λ)/(√Λ + √λ), характеризующие скорости сходимости градиентного метода и метода тяжелого шарика, соответственно, то для плохо обусловленных функций, т. е. для функций с μ = Λ /λ >> 1, очевидно, qгм ≈ 1– 2/μ, а qмтш ≈ 1 – 2/√μ. Поэтому для уменьшения погрешности в e ≈ 2.718 раз градиентный метод с постоянным оптимальным шагом требует –[ln(1 – 2/μ)]–1 ≈ μ)/2 итераций, а метод тяжелого шарика –ln(1 – 2/√μ)]–1 ≈ √μ/2. Для больших μ это весьма значительный выигрыш, поскольку объем вычислений в методе тяжелого шарика почти не отличается от объема вычислений в градиентном методе.

    Реферат по информатике

    Состав персонального компьютера

    30 Декабря 2015

    Реферат по информатике

    Состав интегрированной системы автоматизации предприятия.

    30 Декабря 2015

    Реферат по информатике

    Состав внутрифирменной интегрированной системы управления

    30 Декабря 2015

    Реферат по информатике

    Состав Microsoft Office

    30 Декабря 2015



Источник

Обновлено: 15.04.2023

метод ведет себя как метод первого порядка, а в окрестностях оп тимума приближается к методам второго порядка.

Первый шаг аналогичен первому шагу метода наискорейшег спуска, второй и следующий шаги выбираются каждый раз в на правлении, образуемом в виде линейной комбинащси векторо градиента в данной точке и предшествующего направления.

.Алгоритм метода можно записать следующим образом (в век торной форме):

Величина а может быть приближенно найдена из выражени

Алгоритм работает следующим образом. Из начальной точки х° ищут тсапЩх) в направлении градиента (методом наискорей шего спуска), затем, начиная с найденной точки и далее, направ ление поиска min определяется по второму вьфажению. Поис минимума по направлению может осуществляться любым спосо бом: можно использовать метод последовательного сканирова ния без коррекции шага сканирования при переходе минимума поэтому точность достижения минимума по направлению зави сит от величины шага h.

Для квадратичной функции R(x) решение может быть найден за п шагов (п — размерность задачи). Для других функций поис будет медленнее, а в ряде случаев может вообще не достигнут оптимума вследствие сильного влияния вычислительных оши бок.

Одна из возможных траекторий поиска минимума двумерной функции методом сопряженных градиентов приведена на рис. 17

Для сравнения рассмотрим решение предыдущего примера. Первый шаг делаем по методу наискорейшего спуска

Найдена наилучшая точка. Вычисляем производные в этой точке: dRIdx^ =-2^0%, dR/dx2 =1,600; вычисляем коэффищ1еш а, учитывающий влияние градиента в предыдущей точке а =3,31920-3,3192/8,3104^=0,160. Делаем рабочий шаг в соот ветствии с алгоритмом метода, получаем д:, =0,502, Xj =1,368 Далее все повторяется аналогично. Ниже, в табл. 23 приведены текущие координаты поиска следующих шагов.

МЕТОД ТЯЖЕЛОГО ШАРИКА

Метод базируется на аналогии с движением «тяжелого» мате риального шарика по наклонной поверхности. Скорость шарика при движении вниз будет возрастать, и он будет стремиться занять нижнее положение, т.е. точку минимума. При выводе дифферен циального уравнения движения шарика учитывается его масса и вязкость среды, которые влияют на характер его движения, т.е поиска min R

В дискретном варианте траектория поиска описывается сле дующим алгоритмом:

При а =0 метод превращается в обыкновенный градиентный. При а = 1 поиск не затухает, следовательно, при О < а < 1 можно получать различную эффективность метода, которая будет зави­ сеть и от А.

Вдали от оптимума поиск будет ускоряться, а вблизи возмож­ ны колебания около точки min R(x).

К недостаткам метода относится необходимость задания сра­ зу двух неформальных параметров, определяющих эффектив­ ность поиска. К достоинствам метода, помимо ускорения дви­ жения вдали от оптимума, относится возможность «проскока» мелких локальных «ямок» (минимумов) за счет «инерционности шарика», т.е. можно решать и задачу глобальной оптимизации для функции R(x) с одним явно выраженным минимумом и мно­ гими «мелкими».

Одна из возможных траекторий поиска минимума двумерной функции методом тяжелого шарика приведена на рис. 17.

Для сравнения методов рассмотрим решение предыдущего примера. Результаты вычислений при а =0,5 и Л =0,1 приведены ниже в кратком изложении, так как никаких принципиально но­ вых элементов здесь нет, кроме формулы для вычисления рабоче­ го шага. Обратим внимание на то, что первый шаг делается обыч­ ным методом градиента (результаты полностью совпадают с результатами метода градиента), так как мы еще не имеем преды­ дущей точки (табл. 24).

Метод не оказался более эффективным по сравнению с други­ ми. Это обусловлено проблемами с подбором параметров поиска а иА.

Для наглядного сравнения методов целесообразно по приве­ денным результатам поиска различными методами самостоятель­ но построить траектории поиска в координатах дс, -Х2, соединив отрезками прямых все точки для каждого метода.

1. При каком из алгоритмов выбора направления поиска max R

2. Как изменяется угол между двумя соседними направлениями поиска при приближении к оптимуму?

3. Что называется градиентом функции Щх^ .дгз)?

4. Свойства градиента функции/

5. Как оценивается эффективность поиска градиентным мето­ дом?

6. Какой алгоритм коррекции шага предпочтительнее вблизи оптимума?

7. Почему в районе оптимума величина шага Дх убывает при использовании алгоритмах-^ = х^ *-Agrad/?(A:)?

8. В чем отличие двух алгоритмовградиентного метода:

где созф у — направляющие косинусы градиента.

9. Исходя из определения grad^(x) как вектора, указывающего направление возрастания функщ1и, что лучше искать: min или max?

10. Что дает вычисление производных по методу с парными про­ бами?

Метод наискорейшего спуска

1. В чем основные отличия метода наискорейшего спуска от ме­ тода градиента?

2. По какому направлению осуществляется поиск из каждой те­ кущей точки при поиске пипЛ(х)?

3. Как вычисляется градиент Щх) в методе наискорейшего спуска?

5. Каковы условия окончания поиска?

6. Область наивысшей эффективности к^етода.

7. Какой метод вычисления шага при поиске min/?(jc) по grad/?(x) более предпочтителен?

8. Можно ли методом наискорейшего спуска найти тахЛ(л;)?

9. Можно ли применять алгоритм корреющи шага поиска, опре­ деляемый изменением угла между градиентами в текущей и предыдущей точках?

10. Какое влияние оказывают вычислительные погрешности при поиске ттаК<х) в направлении градиента на точность полу­ чения решения?

Метод сопрямсенных градиентов

1. Чем отличаются квадратичные методы оптимизащш от ли­ нейных?

2. Какова сравнительная эффективность метода сопряженных градиентов и наискорейшего спуска вблизи от оптимума?

3. Как записывается алгоритм метода сопряженных градиен тов?

4. Как влияют вычислительные погрешности на эффективность метода сопряженных градиентов?

5. Для каких функций R(x) метод сопряженных градиентов наи более эффективен?

6. В чем недостатки использования методов второго порядка?

7. В чем отличие первого шага в методах наискорейшего спуска

и сопряженных градиентов?

8. Какая процедура поиска осуществляется на каждом шаге?

9. Сравнительная эффективность метода градиента и метода со­ пряженных градиентов вдали от оптимума.

10. Возможно ли применение метода для недифференцируемых функций?

Метод тяжелого шарика

1. Как влияет масса шарика на характер поиска, учитывая, что траектория поиска аналогична движению шарика в вязкой среде?

2. Может ли поиск ускоряться?

3. Можно ли найти тахЛ(х), а не пйпЛ(дс) методом тяжелого шарика?

4. В чем заключаются недостатки метода тяжелого шарика?

5. Является ли метод тяжелого шарика пригодным для одно­ мерной оптимизации (т.е. когда у «шарика» нет объема, а сле­ довательно, и массы)?

6. Можно ли найти глобальный минимум R(x) методом тяжело­ го шарика?

7. Зачем «помещают шарик в вязкую среду»?

8. Какой путь можно выбрать для затухания поиска в районе оп­

тимума при использовании алгоритма х^»^’ =х^-а(х’-х^

9. Можно ли отнести метод тяжелого шарика к методам второго порядка?

10. В каких условиях предпочтительнее использовать метод тя­ желого шарика?

МНОГОМЕРНАЯ БЕЗГРАДИЕНТНАЯ ОПТИМИЗАЦИЯ

В данном разделе рассматриваются численные методы опти­ мизации, у которых величина и направление шага к оптимуму формируются однозначно по определенным детерминированным функциям в зависимости от свойств критерия оптимальности в окрестности текущей точки без использования производных (т.е. градиента). Все алгоритмы имеют итерационный характер и вы­ ражаются формулой

Основная особенность рассматриваемой группы методов — отсутствие вычисления градиента критерия оптимальности. Ряд

методов прямого поиска ба­ зируется на последователь­ ном применении одномер­ ного поиска по переменным или по другим задаваемым направлениям, что облегча­ ет их алгоритмизацию и применение.

Как и для градиентных методов, на рис. 18 приво­ дятся лишь по одной из воз­ можных траекторий поиска каждым из ниже рассмат­ риваемых методов. Кроме того, также для всех приве­ денных траекторий выбра­ ны различные начальные условия, с тем чтобы не за­ громождать построения.

Рис. 18. Иллюстрация траекторий поиска минимума функции безгра­ диентными детерминированными методами: / — оптимум; 2 — тра­ ектория метода параллельных ка­ сательных; 5— траектория метода Гаусса — Зайделя; 4 — траектория метода Розенброка; 5 — траекто­ рия симплексного метода; б —

начальные точки поиска

МЕТОД ГАУССА — ЗАЙДЕЛЯ

Метод Гаусса — Зайделя (в математической литературе ис пользуется и другое название — метод покоординатного спуска заключается в последовательном поиске оптимума R(x) пооче редно по каждой переменной. Причем после завершения перебо ра всех переменных (т.е. после завершения одного цикла) опять общем случае приходится перебирать все переменные до тех под пока не придем к оптимуму.

В ряде случаев (для сепарабельных критериев оптимальности т.е. таких R

удается получить решение всего за один цикл. В случае тесной нелинейной взаимосвязи переменных (например, при наличии произведения переменных и т.п.) для получения решения прихо дится делать очень много циклов.

Метод обладает низкой эффективностью в овражных функци ях, может застревать в «ловушках», особенно при сравнительно больших шагах h при поиске оптимума по каждой переменной очень чувствителен и к выбору системы координат. Метод прос в реализации. На эффективность метода влияет порядок чередо вания переменных.

Одна из возможных траекторий поиска минимума двумерной функции методом Гаусса — Зайделя приведена на рис. 18. В ка честве начальной изменяемой переменной в каждом цикле при нята дсг-

Условием окончания поиска является малость изменения кри терия оптимальности за один цикл или невозможность улучше ния критерия оптимальности ни по одной из переменных.

Для нейтрализации недостатков разработаны модификации алгоритма, среди которых рассмотрим метод поиска с последей ствием.

При нахождении оптимума по каждой переменной пре1фаща ют поиск не в точке оптимума, а несколько пройдя ее. При этом

удается «выскочить из ловушек», за меньшее число циклов выйтн в район оптимума. В районе оптимума наблюдается зациклива ние, и в этом случае последовательно уменьшают величину по следействия.

В двумерных задачах метод Гаусса — Зайделя фактически сводится к методу наискорейшего спуска, так как в обоих методах траектория поиска представляет собой последовательность вза имноортогональных отрезков.

Пример. Требуется найти минимум функции

2. Интервал поиска: JC,„, = -2, x^^ = 2, x,^^ = -2, x^^„ = 2.

3. Начальная точка: jc,j = 1,4962, дг^д = — 1 .

4. Параметры поиска: шаг А = 0,1, погрешность = 0,01. Результаты вычислений. Из начальной точки

Найти интервалы унимодальности заданной функции на интервале [-1 ; 3] с точностью 0,2.

Минимизировать заданную функцию с точностью =0,0001 методом «тяжелого шарика».

Используя окно диалога «Поиск решения», уточнить координаты всех экстремумов (минимумов и максимумов) заданной функции на заданном интервале.

Варианты

1. f(x) = x3-2×2-5arctg(2,5x)

2. f(x) = x3-2,5×2-1,5arctg(10x)

3. f(x) = x3-2×2-0,7arctg(3x)

4. f(x) = x3-2,1×2-0,8arctg(4x)

5. f(x) = x3-2,8×2-0,2arctg(5x)

6. f(x) = x3-2,9×2-0,7arctg(2x)

7. f(x) = x3-2,2×2-1,7arctg(0,8x)

8. f(x) = x3-1,8×2-0,7arctg(0,2x)

9. f(x) = x3-1,5×2-1,5arctg(5x)

10. f(x) = x3-2,1×2-5arctg(1,5x)

11. f(x) = x3-2,3×2-3arctg(1,8x)

12. f(x) = x3-1,4×2-4arctg(1,9x)

Отчет о выполнении работы в лабораторном журнале

Отчет о выполнении работы в лабораторном журнале должен содержать следующие численные результаты:

Результаты поиска интервалов унимодальности и график функции;

Уточненный методом «тяжелого шарика» минимум функции и достигнутую точность;

Уточненные поиском решения значения всех экстремумов функции на заданном интервале.

Пример выполнения лабораторной работы в MS Excel

Этапы выполнения работы

1. Создать электронную таблицу для поиска экстремумов функции одной переменной.

Поиск экстремумов функции состоит из двух этапов. Нахождение интервалов унимодальности (интервалов, на которых функция имеет один экстремум и не имеет точек перегиба) выполняется табулированием функции и графически. Уточнение экстремумов выполняется двумя способами: А) методом тяжелого шарика (минимум функции в соответствии с заданием); Б) при помощи окна диалога MS «Поиск решения» (уточняются все экстремумы).

В первой строке таблицы расположить название работы. Во вторую строку ввести уравнение в соответствии с номером варианта. Обе строки текста выделить жирным шрифтом и выровнять по ширине 5-ти столбцов.

2. Поиск интервалов унимодальности.

Для поиска интервалов унимодальности функции необходимо построить таблицу значений заданной функции на заданном отрезке [xнач;xкон]. В третью строку ввести название таблицы – «Поиск интервалов унимодальности». Названия столбцов X и f(X) выделить жирным шрифтом. Для расчета значения аргумента X от xнач до xкон с заданным шагом использовать формулу. Значения аргумента X должны иметь 1 знак после запятой. Значения функции f(X) должны иметь 2 знака после запятой. Интервалы унимодальности должны быть обведены рамкой.

Построить график функции на заданном отрезке. Диаграмму расположить справа от таблицы значений функции. Название диаграммы должно содержать исследуемую функцию. Шкалы осей должны содержать целые числа. Область построения диаграммы должна быть белого цвета.

Выписать результаты поиска интервалов унимодальности. Под диаграммой ввести текст – «Интервалы унимодальности» и выделить его жирным шрифтом. В следующих строках ввести тексты – найденные отрезки, содержащие ровно один экстремум с точностью до 0,2.

3. Построить таблицу для уточнения заданного экстремума функции. Ниже результатов отделения поиска интервалов унимодальности ввести текст – «Уточнение минимума методом «Тяжелого шарика»» и выделить его жирным шрифтом. Ввести названия столбцов таблицы жирным шрифтом и заполнить расчетную таблицу формулами.

Значения в столбце

Номер итерации (0 для начального приближения)

Левая граница интервала унимодальности на текущем шаге вычислений xнов=x+h

В этой статье речь пойдет о методах решения задач математической оптимизации, основанных на использовании градиента функции. Основная цель — собрать в статье все наиболее важные идеи, которые так или иначе связаны с этим методом и его всевозможными модификациями.

Примечание от автора

На момент написания я защитил диссертацию, задача которой требовала от меня глубокое понимание теоретических основно методов математической оптимизации. Тем не менее, у меня до сих пор (как и у всех) расплываются глаза от страшных длинных формул, поэтому я потратил немалое время, чтобы вычленить ключевые идеи, которые бы характеризовали разные вариации градиентных методов. Моя личная цель — написать статью, содержащую минимальное количество информации, необходимое для более менее подробного понимания тематики. Но будьте готовы, без формул так или иначе не обойтись.

Постановка задачи

Прежде чем описывать метод, следует сначала описать задачу, а именно: «Даны множество и функция , требуется найти точку , такую что для всех », что обычно записывается например вот так

В теории обычно предполагается, что — дифференцируемая и выпуклая функция, а — выпуклое множество (а еще лучше, если вообще ), это позволяет дать какие-то гарантии успешности применения градиентного спуска. На практике градиентный спуск успешно применяется даже когда у задачи нет ни одного из вышеперечисленных свойств (пример дальше в статье).

Немного математики

Допустим пока что нам нужно просто найти минимум одномерной функции

Еще в 17 веке Пьером Ферма был придуман критерий, который позволял решать простые задачи оптимизации, а именно, еcли — точка минимума , то

где — производная . Этот критерий основан на линейном приближении

Чем ближе к , чем точнее это приближение. В правой части — выражение, которое при может быть как больше так и меньше — это основная суть критерия. В многомерном случае аналогично из линейного приближения (здесь и далее — стандартное скалярное произведение, форма записи обусловлена тем, что скалярное произведение — это то же самое, что матричное произведение вектор-строки на вектор-столбец) получается критерий

Величина — градиент функции в точке . Также равенство градиента нулю означает равенство всех частных производных нулю, поэтому в многомерном случае можно получить этот критерий просто последовательно применив одномерный критерий по каждой переменной в отдельности.

Стоит отметить, что указанные условия являются необходимыми, но не достаточными, самый простой пример — 0 для и

Этот критерий является достаточным в случае выпуклой функции, во многом из-за этого для выпуклых функций удалось получить так много результатов.

Квадратичные функции

Для экономии места (да и чтобы меньше возиться с индексами) такую функцию обычно записывают в матричной форме:

где , , — матрица, у которой на пересечении строки и столбца стоит величина
( при этом получается симметричной — это важно). Далее. при упомянании квадратичной функции я буду иметь указанную выше функцию.

Зачем я об этом рассказываю? Дело в том, что квадратичные функции важны в оптимизации по двум причинам:

  1. Они тоже встречаются на практике, например при построении линейной регрессии методом наименьших квадратов
  2. Градиент квадратичной функции — линейная функция, в частности для функции выше

Или в матричной форме

Полезные свойства градиента

Хорошо, мы вроде бы выяснили, что если функция дифференцируема (у нее существуют производные по всем переменным), то в точке минимума градиент должен быть равен нулю. А вот несет ли градиент какую-нибудь полезную информацию в случае, когда он отличен от нуля?

Попробуем пока решить более простую задачу: дана точка , найти точку такую, что . Давайте возьмем точку рядом с , опять же используя линейное приближение . Если взять , то мы получим

Аналогично, если , то будет больше (здесь и далее ). Опять же, так как мы использовали приближение, то эти соображения будут верны только для малых . Подытоживая вышесказанное, если , то градиент указывает направление наибольшего локального увеличения функции.

Вот два примера для двумерных функций. Такого рода картинки можно часто увидеть в демонстрациях градиентного спуска. Цветные линии — так называемые линии уровня, это множество точек, для которых функция принимает фиксированное значений, в моем случае это круги и эллипсы. Я обозначил синими линии уровня с более низким значением, красными — с более высоким.


Обратите внимание, что для поверхности, заданной уравнением вида , задает нормаль (в простонародии — перпендикуляр) к этой поверхности. Также обратите внимание, что хоть градиент и показывает в направлении наибольшего увеличения функции, нет никакой гарантии, что по направлению, обратному к градиенту, можно найти минимум (пример — левая картинка).

Градиентный спуск

До базового метода градиентного спуска остался лишь малый шажок: мы научились по точке получать точку с меньшим значением функции . Что мешает нам повторить это несколько раз? По сути, это и есть градиентный спуск: строим последовательность

Величина называется размером шага (в машинном обучении — скорость обучения). Пару слов по поводу выбора : если — очень маленькие, то последовательность медленно меняется, что делает алгоритм не очень эффективным; если же очень большие, то линейное приближение становится плохим, а может даже и неверным. На практике размер шага часта подбирают эмпирически, в теории обычно предполагается липшицевость градиента, а именно, если

для всех , то гарантирует убывание .

Анализ для квадратичных функций

Если — симметричная обратимая матрица, , то для квадратичной функции точка является точкой минимума (UPD. при условии, что этот минимум вообще существует — не принимает сколько угодно близкие к значения только если положительно определена), а для метода градиентного спуска можно получить следующее

где — единичная матрица, т.е. для всех . Если же , то получится

Выражение слева — расстояние от приближения, полученного на шаге градиентного спуска до точки минимума, справа — выражение вида , которое сходится к нулю, если (условие, которое я писал на в предыдущем пункте как раз это гарантирует). Эта базовая оценка гарантирует, что градиентный спуск сходится.

Модификации градиентного спуска

Теперь хотелось бы рассказать немного про часто используемые модификации градиентного спуска, в первую очередь так называемые

Инерционные или ускоренные градиентные методы

Все методы такого класса выражаются в следующем виде

Последнее слагаемое характеризует эту самую «инерционность», алгоритм на каждом шаге старается двигаться против градиента, но при этом по инерции частично двигается в том же направлении, что и на предыдущей итерации. Такие методы обладают двумя важными свойствами:

  1. Они практически не усложняют обычный градиентный спуск в вычислительном плане.
  2. При аккуратном подборе такие методы на порядок быстрее, чем обычный градиентный спуск даже с оптимально подобранным шагом.

Метод тяжелого шарика — самый простой инерционный метод, но не самый первый. При этом, на мой взгляд, самый первый метод довольно важен для понимания сути этих методов.

Метод Чебышева

Да да, первый метод такого типа был придуман еще Чебышевым для решения систем линейных уравнений. В какой-то момент при анализе градиентного спуска было получено следующее равенство

где — некоторый многочлен степени . Почему бы не попробовать подобрать таким образом, чтобы было поменьше? Один уз универсальных многочленов, которые меньше всего отклоняются от нуля — многочлен Чебышева. Метод Чебышева по сути заключается в том, чтобы подобрать параметры спуска так, чтобы был многочленом Чебышева. Есть правда одна небольшая проблема: для обычного градиентного спуска это просто невозможно. Однако для инерционных методов это оказывается возможным. В основном это происходит из-за того, что многочлены Чебышева удовлетворяют рекуррентному соотношению второго порядка

поэтому их невозможно построить для градиентного спуска, который вычисляет новое значение лишь по одному предыдущему, а для инерционных становится возможным за счет того, что используется два предыдущих значения. При этом оказывается, что сложность вычисления не зависит ни от , ни от размера пространства .

Метод сопряженных градиентов

Еще один очень интересный и важный факт (следствие теоремы Гамильтона-Кэли): для любой квадратной матрицы размера существует многочлен степени не больше , для которого . Чем это интересно? Все дело в том же равенстве

Если бы мы могли подбирать размер шага в градиентном спуске так, чтобы получать именно этот обнуляющий многочлен, то градиентный спуск сходился бы за фиксированное число итерации не большее размерности . Как уже выяснили — для градиентного спуска мы так делать не можем. К счастью, для инерционных методов — можем. Описание и обоснование метода довольно техническое, я ограничусь сутью:на каждой итерации выбираются параметры, дающие наилучший многочлен, который можно построить учитывая все сделанные до текущего шага измерения градиента. При этом

  1. Одна итерация градиентного спуска (без учета вычислений параметров) содежит одно умножение матрицы на вектор и 2-3 сложения векторов
  2. Вычисление параметров также требует 1-2 умножение матрицы на вектор, 2-3 скалярных умножения вектор на вектор и несколько сложений векторов.

Метод сопряженных градиентов хорошо работает и в случае, если не является квадратичной функцией, но при этом уже не сходится за конечное число шагов и часто требует небольших дополнительных модификаций

Метод Нестерова

Для сообществ математической оптимизации и машинного обучения фамилия «Нестеров» уже давно стало нарицательной. В 80х годах прошлого века Ю.Е. Нестеров придумал интересный вариант инерционного метода, который имеет вид

при этом не предполагается какого-то сложного подсчета как в методе сопряженных градиентов, в целом поведение метода похоже на метод тяжелого шарика, но при этом его сходимость обычно гораздо надежнее как в теории, так и на практике.

Стохастический градиентный спуск

Единственное формальное отличие от обычного градиентного спуска — использование вместо градиента функции такой, что ( — математическое ожидание по случайной величине ), таким образом стохастический градиентный спуск имеет вид

— это некоторый случайный параметр, на который мы не влияем, но при этом в среднем мы идем против градиента. В качестве примера рассмотрим функции

Если принимает значения равновероятно, то как раз в среднем — это градиент . Этот пример показателен еще и следующим: сложность вычисления градиента в раз больше, чем сложность вычисления . Это позволяет стохастическому градиентному спуску делать за одно и то же время в раз больше итераций. Несмотря на то, что стохастический градиентный спуск обычно сходится медленней обычного, за счет такого большого увеличения числа итераций получается улучшить скорость сходимости на единицу времени. Насколько мне известно — на данный момент стохастический градиентный спуск является базовым методом обучения большинства нейронных сетей, реализован во всех основных библиотеках по ML: tensorflow, torch, caffe, CNTK, и т.д.

Стоит отметить, что идеи иннерционных методов применяются для стохастического градиентного спуска и на практике часто дают прирост, в теории же обычно считается, что асимптотическая скорость сходимости не меняется из-за того, что основная погрешность в стохастическом градиентном спуске обусловлена дисперсией .

Субградиентный спуск

Эта вариация позволяет работать с недифференцируемыми функциями, её я опишу более подробно. Придется опять вспомнить линейное приближение — дело в том, что есть простая характеристика выпуклости через градиент, дифференцируемая функция выпукла тогда и только тогда, когда выполняется для всех . Оказывается, что выпуклая функция не обязаны быть дифференцируемой, но для любой точки обязательно найдется такой вектор , что для всех . Такой вектор принято называть субградиентом в точке , множество всех субградиентов в точки называют субдифференциалом и обозначают (несмотря на обозначение — не имеет ничего общего с частными производными). В одномерном случае — это число, а вышеуказанное свойство просто означает, что график лежит выше прямой, проходящей через и имеющей тангенс угла наклона (смотрите рисунки ниже). Отмечу, что субградиентов для одной точки может быть несколько, даже бесконечное число.


Вычислить хотя бы один субградиент для точки обычно не очень сложно, субградиентный спуск по сути использует субградиент вместо градиента. Оказывается — этого достаточно, в теории скорость сходимости при этом падает, однако например в нейронных сетях недифференцируемую функцию любят использовать как раз из-за того, что с ней обучение проходит быстрее (это кстати пример невыпуклой недифференцируемой функции, в которой успешно применяется (суб)градиентный спуск. Сама по себе функция выпукла, но многослойная нейронная сеть, содержащая , невыпукла и недифференцируема). В качестве примера, для функции субдифференциал вычисляется очень просто

Пожалуй, последняя важная вещь, которую стоит знать, — это то, что субградиентный спуск не сходится при постоянном размере шага. Это проще всего увидеть для указанной выше функции . Даже отсутствие производной в одной точке ломает сходимость:

  1. Допустим мы начали из точки .
  2. Шаг субградиентного спуска:

Где обычно или . На практике я часто видел успешное применение шагов , хоть и для таких шагов вообще говоря не будет сходимости.

Proximal методы

К сожалению я не знаю хорошего перевода для «proximal» в контексте оптимизации, поэтому просто так и буду называть этот метод. Proximal-методы появились как обобщение проективных градиентных методов. Идея очень простая: если есть функция , представимая в виде суммы , где — дифференцируемая выпуклая функция, а — выпуклая, для которой существует специальный proximal-оператор (в этой статье ограничусь лишь примерами, описывать в общем виде не буду), то свойства сходимости градиентного спуска для остаются и для градиентного спуска для , если после каждой итерации применять этот proximal-оператор для текущей точки , другими словами общий вид proximal-метода выглядит так:

    — индикатор-функция выпуклого множества , то есть

В этом случае — это проекция на множество , то есть «ближайшая к точка множества ». Таким образом, мы ограничиваем градиентный спуск только на множество , что позволяет решать задачи с ограничениями. К сожалению, вычисление проекции в общем случае может быть еще более сложной задачей, поэтому обычно такой метод применяется, если ограничения имеют простой вид, например так называемые box-ограничения: по каждой координате

Заключение

На этом заканчиваются основные известные мне вариации градиентного метода. Пожалуй под конец я бы отметил, что все указанные модификации (кроме разве что метода сопряженных градиентов) могут легко взаимодействовать друг с другом. Я специально не стал включать в эту перечень метод Ньютона и квазиньютоновские методы (BFGS и прочие): они хоть и используют градиент, но при этом являются более сложными методами, требуют специфических дополнительных вычислений, которые обычно более вычислительно затратны, нежели вычисление градиента. Тем не менее, если этот текст будет востребован, я с удовольствием сделаю подобный обзор и по ним.

Метод базируется на аналогии с движением «тяжелого» материального шарика по наклонной поверхности. Скорость шарика при движении вниз будет возрастать, и он будет стремиться занять нижнее положение, т.е. точку минимума. При выводе дифференциального уравнения движения шарика учитывается его масса и вязкость среды, которые влияют на характер его движения, т.е. поиска min R(x).

В дискретном варианте траектория поиска описывается следующим алгоритмом:

x i +1 = x i – α (x i – x i –1 ) – h grad R(x i )

При α =0 метод превращается в обыкновенный градиентный. При α = 1 поиск не затухает, следовательно, при 0 < α < 1 можно получать различную эффективность метода, которая будет зависеть и от h.

Вдали от оптимума поиск будет ускоряться, а вблизи возможны колебания около точки min R(x).

К недостаткам метода относится необходимость задания сразу двух неформальных параметров, определяющих эффективность поиска. К достоинствам метода, помимо ускорения движения вдали от оптимума, относится возможность «проскока» мелких локальных «ямок» (минимумов) за счет «инерционности шарика», т.е. можно решать и задачу глобальной оптимизации для функции R(x) с одним явно выраженным минимумом и многими «мелкими».

Одна из возможных траекторий поиска минимума двумерной функции методом тяжелого шарика приведена на рис. 1.

Алгоритм метода тяжёлого шарика для поиска минимума.

Начальный этап. Выполнение градиентного метода.

Задаём начальное приближение x1 0 , х2 0 . Определяем значение критерия R(x1 0 , х2 0 ). Положить k = 0 и перейти к шагу 1 начального этапа.

Шаг 1. Вычислить R(x1 k + g, x2 k ), R(x1 k – g, x2 k ), R(x1 k , x2 k + g), R(x1 k , x2 k ). В соответствии с алгоритмом с центральной или парной пробы вычислить значение частных производных и . Вычислить значение модуля градиента .

Шаг 2. Если модуль градиента , то расчёт остановить, а точкой оптимума считать точку (x1 k , x2 k ). В противном случае перейти к шагу 3.

Шаг 3. Выполнить рабочий шаг, рассчитав по формуле

x k+1 = x k – h grad R(x k )).

Шаг 4. Определить значение критерия R(x1 k +1 , х2 k +1 ). Если R(x1 k +1 , х2 k +1 ) < R(x1 k , х2 k ), то положить k = k+1 и перейти к шагу 3. Если R(x1 k +1 , х2 k +1 ) ≥ R(x1 k , х2 k ), то перейти к основному этапу.

Шаг 1. Вычислить R(x1 k + g, x2 k ), R(x1 k – g, x2 k ), R(x1 k , x2 k + g), R(x1 k , x2 k ). В соответствии с алгоритмом с центральной или парной пробы вычислить значение частных производных и . Вычислить значение модуля градиента .

Шаг 2. Если модуль градиента , то расчёт остановить, а точкой оптимума считать точку (x1 k , x2 k ). В противном случае перейти к шагу 3.

Шаг 3. Выполнить рабочий шаг, рассчитав по формуле

x k +1 = x k – α (x k – x k –1 ) – h grad R(x k )

Шаг 4. Определить значение критерия R(x1 k +1 , х2 k +1 ). Положить k = k+1 и перейти к шагу 1.

Пример.

Для сравнения методов рассмотрим решение предыдущего примера. Результаты вычислений при α =0,5 и h =0,1 приведены ниже в кратком изложении, так как никаких принципиально новых элементов здесь нет, кроме формулы для вычисления рабочего шага. Обратим внимание на то, что первый шаг делается обычным методом градиента (результаты полностью совпадают с результатами метода градиента), так как мы еще не имеем предыдущей точки (табл. 7).

Читайте также:

      

  • Asus smart gesture как удалить полностью

    •   

  • Где формат в автокаде 2019

    •   

  • Как загрузить vba в автокад

    •   

  • Удалить из mac os программу из launchpad

    •   

  • Убрать нависшее веко фотошоп

Источник
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163

#include "stdafx.h"
#include <cmath>
 
bool sravn(double x[], double y[], double eps, int n)
{
    int i;
    int k = 0;
    bool s = true;
    for (i = 0; i<n; i++)
        if (fabs(x[i] - y[i]) <= eps)
        {
            k++;
        }
    if (k == n) s = false;
    return s;
}
 
double pr(double (*f) (double*) , double eps, double *x, int i, int n)
{
    double f1 = 0, f2 = 0;
    double *x1 = new double[n];
    double *x2 = new double[n];
    for (int j = 0; j < n; j++)
    {
        x1[j] = x2[j] = x[j];
    }
    double dx = 0.1;
    x1[i] += dx;
    x2[i] -= dx;
    f1 = (f(x1) - f(x2)) / (2 * dx);
    dx = dx / 10;
    for (int j = 0; j < n; j++)
    {
        x1[j] = x2[j] = x[j];
    }
    x1[i] += dx;
    x2[i] -= dx;
    f2 = (f(x1) - f(x2)) / (2 * dx);
    while (fabs(f2 - f1) > eps)
    {
        f1 = f2;
        dx /= 10;
        for (int j = 0; j < n; j++)
        {
            x1[j] = x2[j] = x[j];
        }
        x1[i] += dx;
        x2[i] -= dx;
 
        f2 = (f(x1) - f(x2)) / (2 * dx);
        if (f2 == 0)
            break;
    }
    return f1;
}
 
//double *proizv(double *x, int n, double eps, double(*fu) (double*))
//{
//  double *f = new double[n];
//  for (int i = 0; i < n; i++)
//  {
//      f[i] = pr(fu, eps, x, i, n);
//  }
//  return f;
//}
 
double rosenbr(double *x)
{
    return (1 - x[0])*(1 - x[0]) + 100 * (x[1] - x[0] * x[0])*(x[1] - x[0] * x[0]);
}
 
double fo(double *x)
{
    return pow(x[0], 3) + 2 * pow(x[1], 2) - 3 * x[0] - 4 * x[1];
}
double fo1(double *x)
{
    return x[0] * x[0]-4;
}
double fo2(double *x)
{
    return 3 * x[0] * x[0] + x[0] * x[1] + 2 * x[1] * x[1] - x[0] - 4 * x[1];
}
double fo3(double *x)
{
    return -x[0] * x[0] - 5 * x[1] * x[1] - 3 * x[2] * x[2] + x[0] * x[1] - 2 * x[0] * x[2] + 2 * x[1] * x[2] + 11 * x[0] + 2 * x[1] + 18 * x[2] + 10;
}
 
double pr11(double x)
{
    return 3 * x*x - 3;
}
 
double pr22(double x)
{
    return 4 * x - 4;
}
int main()
{
    double(*f) (double*);
    f = &fo;
    double ff;
    double eps = 0.00000001;
    int n=2;
    int k=0, p=0, iter=0;
    double a=0.5, b=0.2;
    double *T = new double[n];
    double *x0 = new double[n];
    for (int i = 0; i < n; i++)
    {
        scanf("%lf", &x0[i]);
    }
    double *x1 = new double[n];
    for (int i = 0; i < n; i++)
    {
        scanf("%lf", &x1[i]);
    }
    double *x = new double[n];
    double f0, f1;
    f0 = f(x0);
    f1 = f(x1);
    //printf("%lf %lf", f0, f1);
    if (f1 > f0)
    {
        T = x0;
        x0 = x1;
        x1 = T;
    }
 
    do
    {
        if (k == 1)
        {
            x0 = x1;
            x1 = x;
        }
        k = 0;
        iter++;
        for (int i = 0; i < n; i++)
        {
            x[i] = x1[i] - a*pr(f, 0.000001, x1, i, n)+b*(x1[i]-x0[i]);
        }
        //x[0]=x1[0]-a*pr11(x1[0])+b*(x1[0] - x0[0]);
        //x[1] = x1[1] - a*pr11(x1[1]) + b*(x1[1] - x0[1]);
        ff = f(x);
        if (ff > f1 && p == 0 && b > 0.1)
            b -= 0.1;
        else
        {
            if (b <= 0.1) p = 1;
            if (ff > f1 && p == 1 && a >= eps) a /= 2;
            if (ff<f1) k = 1;
        }
    } while (sravn(x1,x,eps,n) && a>eps);
    printf("%lf %lf ", x[0], x[1]);
    printf("%lf   iter %d  a %lf  b %lf", f(x), iter, a ,b);
 
 
 
 
    system("pause");
    return 0;
}
Источник

Понравилась статья? Поделить с друзьями:
  • Метод тренда это в excel
  • Метод трапеций для интеграла в excel
  • Метод суммы лет excel
  • Метод стьюдента в excel
  • Метод сопоставимых рыночных цен пример расчета в excel