history 27 ноября 2022 г.
- Группы статей
Вычислим в MS EXCEL определенный интеграл методом Симпсона (англ. Simpson’s rule). Покажем как оценить ошибку интегрирования, построим график функции.
Примечание: Основная статья про численное интегрирование — Интегрирование в MS EXCEL. Метод трапеций. В этой статье дана небольшая теория.
В данной статье используем тот же полином третьего порядка, что и в статье про Метод трапеций. Т.к. метод Симпсона использует параболу для аппроксимации подинтегральной функции, то при нахождении этим методом интеграла от полинома третьего порядка (и ниже) мы будем получать точное значение (это можно доказать строго математически). Т.е. ошибка интегрирования точно равна 0.
Построение модели
Для определенности вычислим интеграл для функции-многочлена f(𝑥)=𝑥3−5𝑥2+6𝑥+1. График этой функции в диапазоне от 0 до 4 выглядит следующим образом (см. файл примера).
Примечание: про тонкости построения графика функции можно прочитать в этой статье https://excel2.ru/articles/grafik-vs-tochechnaya-diagramma-v-ms-excel.
В файле примера построим таблицу значений функции для 41 точки (от 0 до 40), что составляет 40 интервалов (для метода Симпсона обязательно должно быть ЧЕТНОЕ количество интервалов).
Формула для вычисления интеграла Методом Симпсона следующая:
Примечание: В файле примера вместо Δх (шаг по х) будем использовать символ h, который используется в математических формулах численного интегрирования гораздо чаще, чем Δх. Хотя для первого знакомства, конечно, Δх является более знакомым обозначением шага изменения х.
Как видно из формулы, чтобы вычислить значение интеграла достаточно сложить значения y=f(x) в узлах сетки с определенным весом:
- Значения в узлах 0 и n, которые соответствуют пределам интегрирования а и b, берутся с весом 1;
- Значения в узлах с нечетным индексом берутся с весом 4;
- Значения в узлах с четным индексом берутся с весом 2.
В MS EXCEL вычислить веса по этому правилу можно с помощью простой формулы =ЕСЛИ(ИЛИ(A19=0;A19=$E$12);1; ЕСЛИ(ЕНЕЧЁТ(A19);4;2)). В файле примера это реализовано в столбце D (дополнительно вес домножен на соответствующее значение y).
В итоге, значение определенного интеграла, вычисленное по методу Симпсона, можно записать простой формулой =СУММ(D19:D59)*E13/3
Вычислив интеграл аналитически, можно убедиться, что полученное значение точно равно значению, вычисленного формулами (напомним, что это справедливо только для полиномов не выше третьего порядка).
Ошибка интегрирования
Формула для оценки ошибки интегрирования основана на вычислении 4-й (!) производной, что достаточно трудоемко и совсем не удобно для реализации в MS EXCEL.
После вычисления 4-й производной подинтегральной функции нужно найти ее максимум в интервале интегрирования, а затем подставить в вышеуказанную формулу. Понятно, что для полиномов не выше третьего порядка оценка будет равна 0, а значит точность метода Симпсона для таких функций выше чем Метод трапеций.
Для более сложных функций нахождение 4-й производной будет трудоемко, но к счастью есть много сайтов, которые помогут в этом вопросе, например https://www.derivative-calculator.net/
Настраиваемый интервал
На листе Настраиваемый интервал сделана удобная форма для вычисления интеграла при различных значениях шага интегрирования. График функции также перестраивается динамически благодаря использованию Имен и функции СМЕЩ().
Данная форма удобна когда необходимо ответить на вопрос «Какой шаг сетки нужно выбрать, чтобы точность интегрирования была не хуже заданному значению?». Правда, для этого потребуется вычислить 4-ю производную, найти максимум этой функции и, наконец, по формуле оценить ошибку.
Лирическое отступление
Зачем оценивать ошибку интегрирования? Можно ведь взять «маленький» шаг сетки и заведомо получить «точный» результат, и не важно что потребуется сделать 1000 или более шагов интегрирования, ведь вычислительные мощности так дешевы!
На этот счет есть 2 замечания: для больших интервалов интегрирования может потребоваться слишком много шагов и если вычисление интеграла лишь часть задачи, да еще и если оно находится в цикле, то это может замедлить работу программы. И второй момент: если мы не знаем ошибки, то как мы можем быть уверены, что вычисленное значение нам подходит? Например, мы вычисляем интеграл, чтобы получить значение, которое мы будем затем сравнивать с неким критерием. Если значение больше критерия, то мы принимаем одно решение, а если нет, то другое. Из-за недостаточной точности вычисления интеграла может случиться, что будет принято неверное решение, что соответственно приведет к некорректной работе программы (в определенной ситуации).
Опубликовано 10 Авг 2015
Рубрика: Справочник Excel | 13 комментариев

Формулировка в предыдущем предложении определяет сущность понятия интегрирования.
Интеграл чего-либо – это сумма всех малых частей этого чего-либо. Чем больше количество этих малых частей, тем точнее значение интеграла соответствует действительности, определяя признак изучаемого объекта.
Интегрирование применимо для изучения свойств физических и философских объектов при условии, что эти свойства остаются неизменными как для «мелкой» части, так и для всего объекта в целом.
Функция – это описание зависимости некоторого признака или свойства объекта от аргумента.
Например:
Объект – плоская фигура между графиком функции и осью абсцисс.
Признак (значение функции) – высота фигуры.
Аргумент (независимая переменная) – ширина фигуры.
Функция – описание зависимости высоты от ширины.
Определенный интеграл функции – площадь фигуры. Площадь тоже является признаком фигуры, но зависит от двух переменных – высоты и ширины – и представляет собой качественно иной новый признак.
Теория.
Подробно рассмотрим два наиболее точных метода численного интегрирования функции одной переменной – метод трапеций и метод парабол или метод Симпсона. Есть еще метод прямоугольников, но мы его проигнорируем из-за невысокой точности.
Все, что требуется для понимания и применения метода трапеций и метода Симпсона на практике представлено далее на рисунке.
Площадь под кривой y = f (x) разбиваем на n-1 криволинейных трапеций, у которых три стороны – это прямые линии, а одна сторона – участок кривой y=f (x). Суммарная площадь под графиком функции на участке от x1 до xn – это и есть искомая величина, которая является определенным интегралом функции на этом участке и находится как сумма площадей всех криволинейных трапеций.
Точно вычислить аналитически площадь криволинейной трапеции бывает сложно или даже невозможно.
Для приближенного вычисления площади криволинейной трапеции можно заменить участок кривой прямой линией и, получив простую фигуру – обычную трапецию, найти по известной формуле ее площадь. В этом суть метода трапеций.
Если участок кривой линии над двумя криволинейными трапециями заменить параболой, проведенной через три характерные точки, то получим новую криволинейную трапецию с одной из сторон в виде параболы. Количество новых фигур будет в два раза меньше, чем количество исходных трапеций. Площадь этих новых фигур вычисляется по простой формуле. В этом смысл метода Симпсона.
Идею замены участка любой кривой участком параболы высказывал Исаак Ньютон, но первым вывел формулу английский математик Томас Симпсон. Метод Симпсона для вычисления интегралов является самым точным из приближенных численных методов.
Если вычисление интегралов методом трапеций не имеет ограничений, то для того, чтобы реализовать метод Симпсона необходимо выполнить два условия.
1. Разбить площадь на четное количество частей, то есть n должно быть нечетным числом!
2. Расстояния между точками по оси x должны быть одинаковыми!
Практика вычисления интегралов в Excel.
Определенной сложностью является связать вычисление интегралов с реальными задачами из жизни. Рассмотрение примеров – лучший способ устранения подобных препятствий.
Определение тепловой энергии.
Мой знакомый из города Улан-Удэ Алексей Пыкин проводит испытания воздушных солнечных PCM-коллекторов производства КНР. Воздух из помещения подается вентилятором в коллекторы, нагревается от солнца и поступает назад в помещение. Каждую минуту измеряется и записывается температура воздуха на входе в коллекторы и на выходе при постоянном воздушном потоке. Требуется определить количество тепловой энергии полученной в течение суток.
Более подробно о преобразовании солнечной энергии в тепловую и электрическую и об экспериментах Алексея я постараюсь рассказать в отдельной статье. Многим, я думаю, это будет интересно.
Запускаем MS Excel и начинаем работу – выполняем вычисление интеграла.
Заполним таблицу.
1. В столбец B вписываем время проведения измерения τi.
2. В столбец C заносим температуры нагретого воздуха t2i, измеренные на выходе из коллекторов в градусах Цельсия.
3. В столбец D записываем температуры холодного воздуха t1i, поступающего на вход коллекторов.
4. В столбце E вычисляем разности температур dti на выходе и входе
dti=t2i—t1i
5. Зная удельную теплоемкость воздуха c=1005 Дж/(кг*К) и его постоянный массовый расход (измеренная производительность вентилятора) G=0,02031 кг/с, определяем мощность установки Ni в КВт в каждый из моментов времени в столбце F
Ni=c*G*dti
На графике ниже показана экспериментальная кривая зависимости мощности, развиваемой коллекторами, от времени.
Количество тепловой энергии, выработанной за промежуток времени – это интеграл этой функции, и значение интеграла – это заштрихованная площадь под кривой.
6. Вычисляем в ячейках столбца G площади трапеций, суммируем их и находим общее количество энергии, выработанной за день
Qi=(Ni+1+Ni)*(τi+1—τi)/2
Q=ΣQi=10,395 КВт*час
7. Рассчитываем в ячейках столбца H элементарные площади по методу парабол, суммируем их и находим общее количество энергии по методу Симпсона
Qj=(Ni+4*Ni+1+Ni+2)*(τi+1—τi)/3
Q=ΣQj=10,395 КВт*час
Как видим, значения не отличаются друг от друга. Оба метода демонстрируют одинаковые результаты!
Исходная таблица содержит 421 строку. Давайте уменьшим её в 30 раз и оставим всего 15 строк, увеличив тем самым интервалы между замерами с 1 минуты до 30 минут.
По методу трапеций: Q=10,220 КВт*час (-1,684%)
По методу Симпсона: Q=10,309 КВт*час (-0,827%)
Не смотря на оставшуюся неожиданно весьма высокую точность полученных результатов, метод трапеций дает в данном случае относительную ошибку в 2 раза большую, чем метод Симпсона.
Общие выводы.
Вычисление интегралов численными методами в Excel позволяет эффективно и быстро решать сложные практические задачи, обеспечивая очень высокую точность результатов.
Так как мы существуем в пространстве и времени, то и всё окружающее нас изменяется или в пространстве или во времени. Это означает, что аргументом x функций y интересующих нас процессов или объектов чаще всего являются длина или время. Например, пройденный путь – это интеграл функции скорости (аргумент – время), площадь плотины – это интеграл функции высоты (аргумент – длина), и т.д.
Понимание сути интегрального исчисления и умение использовать его на практике вооружает вас, как специалиста, мощным оружием в осознанном изучении окружающего мира!
Ссылка на скачивание файла с примером: vychisleniye-integralov (xls 216,0KB).
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
Simpson’s rule is a method for evaluating definite integrals. Simpson’s rule uses quadratic polynomials. It often provides more accurate estimates than the trapezoidal rule. If the function you are integrating can be evaluated in Excel, then you can implement Simpson’s rule in Excel.
Subtract the lower endpoint from the upper endpoint and divide by 2. For example, if you want to find the definite integral of cos(x) between 0 and pi/2 radians, subtract 0 from pi/2 and divide by 2 to get pi/4. (Radians are the usual method of measuring angles in calculus; Excel also assumes that angles are measured in radians).
Enter column headers in Excel. Enter «value» in cell A1 and «function» in cell B1, where «function» is the function you are evaluating. In the example, put cos(x) in cell B1.
Enter the lower endpoint, the midpoint and the upper endpoint of the integral in cells A2, A3 and A4 respectively. In the example, put 0 in cell A2, =PI/4 in cell A3 and =PI()/2 in cell A4.
Use Excel to evaluate the function at these three points. In cell B2, enter =function(A2). In the example, put =COS(A2) in cell B2 and copy this to cells B3 and B4.
Evaluate Simpson’s rule. In cell A5, enter =(A3-A2)_(B2+4_B3+B4)/3. The result is the approximation of the integral by Simpson’s rule.
Вместо звёздочки в записи 143* поставьте цифру так,что бы полученное число было кратно 3 — Знания.site
Последние вопросы
-
Математика
51 секунд назад
кошек взвесили попарно на весах во всех возможных комбинациях получилось веса 7,8,9,10,11,12. Сколько весит каждая кошка? Даю 40 баллов
-
Математика
51 секунд назад
номер789 срочнопожалуйста
-
Математика
51 секунд назад
помогите пожалуйста (30 баллов)
-
Математика
52 секунд назад
В трех мешках 105,2 кг капусты Сколько капусты в каждом мешке если в первом 0,3 всей капусты а во втором -1,2 раза больше чем в первомПОМОГИТЕ УМОЛЯЮЮЮЮЮЮЮЮЮ НОРМ ОТВЕТ ПЖ ДАМ 100 БАЛЛОВ
-
Математика
2 минуты назад
Дан треугольник ABC.
Прямая MС перпендикулярна плоскости ABC, ∠AMB=90
∠MAC=30
∠MBC=45
MD⊥AB.
Найдите угол между прямой MD и плоскостью ABC.
-
Математика
5 минут назад
5. Составь задачу по выражению 40 : 5 + 20 . помогите пж
-
Математика
5 минут назад
Помогите решить 3 примера
-
Математика
5 минут назад
3. Реши задачу. Аян выучила 6 считалок, а загадок — в 2 раза больше. Сколько загадок выучила Аян?
-
Математика
5 минут назад
5.
Расстояние от села до города 20км. Путник прошел метров осталось ему идти? NIS 2 этого расстояния. Сколько кило-. помогите пожалуйста пжпжпж даю сто балла. по Сочу пж.
-
Математика
5 минут назад
4. (x-5) >-28 неравенство
-
Математика
5 минут назад
тато приніс 6 кг овочів зних 4 кг картоплі а решта цибуля. скільки кг цибулі приніс тато.
-
Математика
10 минут назад
14•x=0,14помогите14 times x = 0.14
-
Математика
10 минут назад
Першого дня продали 13,5ц картоплі,а другого— у 1,2 раза більше.
Скільки центнерів картоплі продали за два дні?
-
Математика
10 минут назад
Контрольна робота з теми «Раціональні числа»
1. За день температура повітря піднялась на 6,7°С. Якою температура повітря стала
ввечері, якщо зранку вона становила — 5,5°С?
a. 1,2ºC
в. — 12,2°С
б. — 1,2ºC
2
г. 12,2°С -
Математика
10 минут назад
No8. Найдите число, в котором отсутствует единицы первого класса: a) 75000 6) 70050 в) 70070 г) 23001
Все предметы
Выберите язык и регион
English
United States
Polski
Polska
Português
Brasil
English
India
Türkçe
Türkiye
English
Philippines
Español
España
Bahasa Indonesia
Indonesia
Русский
Россия
How much to ban the user?
1 hour
1 day
100 years
Mathway | Популярные задачи
| 1 | Множитель | x^2-4 | |
| 2 | Множитель | 4x^2+20x+16 | |
| 3 | График | y=-x^2 | |
| 4 | Вычислить | 2+2 | |
| 5 | Множитель | x^2-25 | |
| 6 | Множитель | x^2+5x+6 | |
| 7 | Множитель | x^2-9 | |
| 8 | Множитель | x^3-8 | |
| 9 | Вычислить | квадратный корень из 12 | |
| 10 | Вычислить | квадратный корень из 20 | |
| 11 | Вычислить | квадратный корень из 50 | |
| 12 | Множитель | x^2-16 | |
| 13 | Вычислить | квадратный корень из 75 | |
| 14 | Множитель | x^2-1 | |
| 15 | Множитель | x^3+8 | |
| 16 | Вычислить | -2^2 | |
| 17 | Вычислить | квадратный корень из (-3)^4 | |
| 18 | Вычислить | квадратный корень из 45 | |
| 19 | Вычислить | квадратный корень из 32 | |
| 20 | Вычислить | квадратный корень из 18 | |
| 21 | Множитель | x^4-16 | |
| 22 | Вычислить | квадратный корень из 48 | |
| 23 | Вычислить | квадратный корень из 72 | |
| 24 | Вычислить | квадратный корень из (-2)^4 | |
| 25 | Множитель | x^3-27 | |
| 26 | Вычислить | -3^2 | |
| 27 | Множитель | x^4-1 | |
| 28 | Множитель | x^2+x-6 | |
| 29 | Множитель | x^3+27 | |
| 30 | Множитель | x^2-5x+6 | |
| 31 | Вычислить | квадратный корень из 24 | |
| 32 | Множитель | x^2-36 | |
| 33 | Множитель | x^2-4x+4 | |
| 34 | Вычислить | -4^2 | |
| 35 | Множитель | x^2-x-6 | |
| 36 | Множитель | x^4-81 | |
| 37 | Множитель | x^3-64 | |
| 38 | Вычислить | 4^3 | |
| 39 | Множитель | x^3-1 | |
| 40 | График | y=x^2 | |
| 41 | Вычислить | 2^3 | |
| 42 | Вычислить | (-12+ квадратный корень из -18)/60 | |
| 43 | Множитель | x^2-6x+9 | |
| 44 | Множитель | x^2-64 | |
| 45 | График | y=2x | |
| 46 | Множитель | x^3+64 | |
| 47 | Вычислить | (-8+ квадратный корень из -12)/40 | |
| 48 | Множитель | x^2-8x+16 | |
| 49 | Вычислить | 3^4 | |
| 50 | Вычислить | -5^2 | |
| 51 | Множитель | x^2-49 | |
| 52 | Вычислить | (-20+ квадратный корень из -75)/40 | |
| 53 | Множитель | x^2+6x+9 | |
| 54 | Множитель | 4x^2-25 | |
| 55 | Вычислить | квадратный корень из 28 | |
| 56 | Множитель | x^2-81 | |
| 57 | Вычислить | 2^5 | |
| 58 | Вычислить | -8^2 | |
| 59 | Вычислить | 2^4 | |
| 60 | Множитель | 4x^2-9 | |
| 61 | Вычислить | (-20+ квадратный корень из -50)/60 | |
| 62 | Вычислить | (-8+ квадратный корень из -20)/24 | |
| 63 | Множитель | x^2+4x+4 | |
| 64 | Множитель | x^2-10x+25 | |
| 65 | Вычислить | квадратный корень из -16 | |
| 66 | Множитель | x^2-2x+1 | |
| 67 | Вычислить | -7^2 | |
| 68 | График | f(x)=2^x | |
| 69 | Вычислить | 2^-2 | |
| 70 | Вычислить | квадратный корень из 27 | |
| 71 | Вычислить | квадратный корень из 80 | |
| 72 | Множитель | x^3+125 | |
| 73 | Вычислить | -9^2 | |
| 74 | Множитель | 2x^2-5x-3 | |
| 75 | Вычислить | квадратный корень из 40 | |
| 76 | Множитель | x^2+2x+1 | |
| 77 | Множитель | x^2+8x+16 | |
| 78 | График | y=3x | |
| 79 | Множитель | x^2+10x+25 | |
| 80 | Вычислить | 3^3 | |
| 81 | Вычислить | 5^-2 | |
| 82 | График | f(x)=x^2 | |
| 83 | Вычислить | квадратный корень из 54 | |
| 84 | Вычислить | (-12+ квадратный корень из -45)/24 | |
| 85 | Множитель | x^2+x-2 | |
| 86 | Вычислить | (-3)^3 | |
| 87 | Множитель | x^2-12x+36 | |
| 88 | Множитель | x^2+4 | |
| 89 | Вычислить | квадратный корень из (-8)^2 | |
| 90 | Множитель | x^2+7x+12 | |
| 91 | Вычислить | квадратный корень из -25 | |
| 92 | Множитель | x^2-x-20 | |
| 93 | Вычислить | 5^3 | |
| 94 | Множитель | x^2+8x+15 | |
| 95 | Множитель | x^2+7x+10 | |
| 96 | Множитель | 2x^2+5x-3 | |
| 97 | Вычислить квадратный корень | квадратный корень из 116 | |
| 98 | Множитель | x^2-x-12 | |
| 99 | Множитель | x^2-x-2 | |
| 100 | Вычислить | 2^2 |
кратно 11 | Каковы кратные 11 до 1000?
Кратные 11 : К кратным 11 можно отнести список чисел, которые полностью делятся на 11.
В этой статье вы можете получить четкое представление о том, что такое кратные 11, как их вычислить с помощью метода умножения и повторного сложения, список кратных до 1000 и несколько решенных примеров, связанных с кратными 11. Прокрутите вниз, чтобы узнать больше!
Сколько кратно 11?
Число, кратное 11, — это список чисел, которые могут полностью делиться на 11, то есть остаток будет равен нулю. Число, кратное 11, можно вычислить, умножив 11 на последовательность чисел, например 1, 2, 3, 4 и т. д. В приведенной ниже таблице вы видите, что 9 многократно умножается на последовательность чисел от 1 до 10. Полученные результаты называются кратными 11.
Кратные 11
Первые 10 кратных 11: 11, 22, 33, 44, 55, 66, 77, 88, 99, 110
Как найти кратные 11?
Чтобы найти числа, кратные числу 11, мы должны выполнить многократное сложение числа 11 или умножить число 11 на последовательность натуральных чисел.
| 11 кратных методом сложения | 11 мультипликации с методом деления |
| 11 | 11 x 1 = 11 |
| 11 + 11 = 22 | 11 x 2 = 22 |
| 22 + 11 = 33 | 111111111111102 33 |
| 32 + 11 = 44 | 11 x 4 = 44 |
| 44 + 11 = 55 | 11 x 5 = 55 |
. В приведенной ниже таблице мы показали первые 20 кратных 11:
Шаг 1: Чтобы вычислить первые 20 кратных 11, сначала создайте таблицу с последовательностью чисел от 1 до 20.
Шаг 2: Теперь, используя метод повторного умножения, умножьте 11 на последовательность чисел numbers from 1 to 20, as shown in the table below:
| Multiply 11 by the numbers 1 to 20 | Multiples of 11 |
| 11 x 1 | 11 |
| 11 х 2 | 22 |
| 11 x 3 | 33 |
| 11 x 4 | 44 |
| 11 x 5 | 55 |
| 11 x 6 | 66 |
| 11 x 7 | 77 |
| 11 x 8 | 88 |
| 11 x 9 | 99 |
| 11 x 10 | 110 |
| 11 x 11 | 121 |
| 11 x 12 | 132 |
| 11 x 13 | 143 |
| 11 x 14 | 154 |
| 11 x 15 | 165 |
| 11 x 16 | 176 |
| 11 x 17 | 187 |
| 11 x 18 | 198 |
| 11 x 19 | 209 |
| 11 x 20 | 220 |
First 20 Multiples of 11
What Are the Multiples of 11 up до 1000?
The 11 multiples up to 1000 are given below:
| 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 |
| 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 231 | 242 | 253 | 264 | 275 | 286 | 297 | 308 | 319 | 330 |
| 341 | 352 | 363 | 374 | 385 | 396 | 407 | 418 | 429 | 440 |
| 451 | 462 | 473 | 484 | 495 | 506 | 517 | 528 | 539 | 550 |
| 561 | 572 | 583 | 594 | 605 | 616 | 627 | 638 | 649 | 660 |
| 671 | 682 | 693 | 704 | 715 | 726 | 737 | 748 | 759 | 770 |
| 781 | 792 | 803 | 814 | 825 | 836 | 847 | 858 | 869 | 880 |
| 891 | 902 | 913 | 924 | 935 | 946 | 957 | 968 | 979 | 990 |
Properties of Multiples of 11
Here are some следует помнить о свойствах кратных 11:
- Когда число 11 умножается на одно число, произведение записывается в два раза больше натурального числа.
- Все числа, кратные 11, больше или равны числу 11.
- Число, которое делится на 11, представляет собой сумму чисел, стоящих в нечетных местах
- Существует бесконечное число кратных числа 11.
Разница между кратными и множителями 11 11 можно суммировать как:
- Кратные 11 — это список натуральных чисел, которые при делении на 11 оставляют ноль в остатке. В качестве альтернативы, числа, кратные 11, — это числа, которые полностью делятся на 11. Первые 10 кратных 11 равны 9.0003 11, 22, 33, 44, 55, 66, 77, 88, 99 и 110 .
- Принимая во внимание, что множители 11 — это числа, произведение которых кратно 11. Делители числа 11 равны 1 и 11.
Решенные примеры на числа, кратные 11
Вот несколько решенных примеров для учащихся:
Вопрос 1: Какие числа кратны 11 между 20 и 150?
A 1: Число 11 может быть кратно 14 от 20 до 150.
А числа между 22, 33, 44, 55, 66, 77, 88, 99, 110, 121, 132 и 143 являются 14 кратными от 20 до 150.
Вопрос 2: Как найти кратные 11?
A 2: Чтобы найти числа, кратные 11, вам нужно будет умножить число 11 на последовательность натуральных чисел. В качестве альтернативы, используя метод повторного сложения, вы можете найти числа, кратные 11.
Вопрос 3: Каковы первые 6 кратных 11?
A 3: 11, 22, 33, 44, 55 и 66 — первые 6 кратных 11.
11 x 1 = 11
11 x 2 = 22
11 x 3 = 33
11 x 4 = 44
11 x 5 = 55
11 x 6 = 66
Вопрос 4: Какова сумма первых 5 кратно 11?
A 4: первые 5 множителей из 11: 11, 22, 33, 44 и 55.
11 + 22 + 33 + 44 + 55 = 165
Итак, 165 есть сумма первых 5 множителей из 11.
Вопрос 5: Каковы нечетные числа, кратные 11?
A 5: Некоторые нечетные числа, кратные 11, равны 11, 33, 55, 77, 9.
Вопрос 6: 165 кратно 11, да или нет?
A 6: да, это кратное 11.
Так как 11 x 15 = 165.
Вопрос 7: 72 кратно 11, да или нет?
A 7: Нет, так как после деления 72 на 11 в остатке осталось 6.
Вопрос 8: Чему может быть от 11 до 100?
A 8: Кратность 11 меньше 100 равна 11, 22, 33, 44, 55, 66, 77, 88 и 99.
Q 9: Какие числа, кратные 11, меньше 270?
А 9: 11, 22, 33, 44, 55, 66, 77, 88, 99, 110, 121, 132, 143, 154, 165, 176, 187, 198, 209, 220, 231, 242, 253 , а 264 — это 11 множеств, меньших 270.
Вопрос 10: Чему равно число, кратное 11?
A 10: Некоторые из четных кратных 11: 22, 44, 66, 88, 110, 132, 154, 176, 198, 220, 242, 264, 286, 308, 330 и т. д.
Хочу учиться Математика? Изучите онлайн-услуги Wiingy по обучению математике, чтобы учиться у ведущих математиков и экспертов.
Часто задаваемые вопросы о числах, кратных 11
Что такое 5 кратных 11?
11, 22, 33, 44 и 55 5 кратны 11
Сколько кратно 11 до 100?
Число, кратное от 11 до 100, равно 11, 22, 33, 44, 55, 66, 77, 88 и 99 .
Каковы первые три числа, кратные 11?
Первые три числа, кратные 11, это 11, 22 и 33.
Какие числа кратны 11 до 500?
11, 22, 33, 44, 55, 66, 77, 88, 99, 110, 121, 132, 143, 154, 165, 176, 187, 198, 209, 220, 231, 242, 253, 264 , 275, 286, 297, 308, 319, 330, 341, 352, 363, 374, 385, 396, 407, 418, 429, 440, 451, 462, 473, 484 и 495 кратны 11 до 500.
Сколько всего кратно 11?
Так как существует бесконечное число натуральных чисел, которые можно умножить на 11, то число, кратное 11, может быть бесконечным. Некоторые из кратных 11 равны 11, 22, 33, 44, 55, 66, 77, 88, 99, 110, 121, 132, 143, 154 и 165 .
Сколько кратно 11 до 80?
11, 22, 33, 44, 55, 66 и 77 — это числа, кратные 11 до 80.
Всегда ли числа, кратные 11, четны?
Некоторые четные, а некоторые нет, когда речь идет об 11 кратных.
Сумма трех последовательных чисел, кратных 11, равна 363. Найдите эти три числа.
Сумма трех последовательных множителей 11, составляющих 363, равна 110, 121 и 132.
11 х 11 = 110
11 х 12 = 121
11 х 13 = 132.
Сколько общих кратных чисел 11 и 3?
Общие кратные 11 и 3 равны 33.
Сколько кратных 11 существует между 100 и 500?
Всего существует 36 кратных 11 от 100 до 500.
Каковы общие кратные 3 и 11 от 1 до 100?
Кратность 3 от 1 до 100: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96 и 99.
Число, кратное 11, от 1 до 100 : 11, 22, 33, 44, 55, 66, 77, 88 и 99.
Следовательно, общие кратные 3 и 11 между 1 и 100: 33, 66 и 99.
Какое наименьшее общее кратное из 14, 11 и 3?
Кратность 14 : 14, 28, 42, 56, 70, 84, 98, 112, 126, 140, 154, 168, 182, 196, 210, 224, 238, 252, 266, 284, 294, 294 308, 322, 336, 350, 364, 378, 392, 406, 420, 434, 448 и 462.
Кратность 11: 11, 22, 33, 44, 55, 66, 77, 88, 99, 110, 121, 132, 143, 154, 165, 176, 187, 198, 209, 220, 231, 242 , 253, 264, 275, 286, 297, 308, 319, 330, 341, 352, 363, 374, 385, 396, 407, 418, 429, 440, 451 и 462.
Кратность 3:5 , 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78 , 81, 84, 87, 90, 93, 96, 99, 102 105 108 111 114 117 120 123 126 129 132 135 138 141 144 147 150 153 156 159 162 165 168 171 174 177 180 183 186 189192 195 198 201 204 207 210 213 216 219 222 225 228 231 234 237 240 243 246 249 252 255 258 261 264 267 270 273 276 279 282 285 288 291 294 297 300 303 306 309 312 315 318 321 324 327 330 333 336 339 342 345 348 351 354 357 360 363 366 369 372 375 378 381 384 387 390 393 396 399 402 405 408 411 414 417 420 423 426.
Следовательно, наименее изящные из 14, 11, и 3 — 426.
. надеюсь, что эта статья о числах, кратных 11, будет вам полезна.
Что такое LCM 143 и 156?
Калькулятор «наименьшего общего кратного»
Что такое наименьшее общее кратное (НОК) чисел 143 и 156?
Ответ: LCM 143 и 156 — 1 716
(тысяча, семь сотен шестнадцати)
LCM для чисел 143 и 156 состоит в том, чтобы найти наибольший общий делитель (GCF) этих чисел. Вот формула:
lcm = (number1 × number2) ÷ gcf
gcf чисел 143 и 156 IS 13 , поэтому
Lcm = (143 × 156) ÷ 13
= 22308 ÷ 13
lcm = 1716
9002
9004
9004
9004
Нахождение НОК для чисел 143 и 156 путем перечисления кратных
Второй метод нахождения НОК для чисел 143 и 156 состоит в том, чтобы перечислить общие кратные для обоих чисел и выбрать первое, которое соответствует: 286, 429, 572, 715, 858, 1001, 1144, 1287, 1430, 1573, 1716, 1859, 2002
Клажу 156 : 156, 312, 468, 624, 780, 936, 1092, 1248, 1404, 1560, 1716, 1872, 2028
SO 156 равно 1716
Нахождение НОК для 143 и 156 с помощью простой факторизации
Другой метод нахождения МОК для чисел 143 и 156 состоит в том, чтобы перечислить все простые множители для обоих чисел и умножить наибольшую степень простых множителей:
Все Простые множители числа 143: 11, 13 (показатель степени: 11 1 , 13 1 )
All Prime Factors of 156: 2, 2, 3, 13 (exponent form: 2 2 , 3 1 , 13 1 )
11 1 × 13 1 × 2 2 × 3 1 = 1716
of/143—156
Оставить комментарий on 143 кратно 3: «вместо звёздочек в записи 143* поставьте цифру так, чтобы полученное число было кратным 3»? » — Яндекс Кью/
Урок математики в 1 классе на тему «Знаки плюс, минус, равно» | План-конспект урока по математике (1 класс) на тему:
ГБОУ ООШ № 2
п.г.т. Новосемейкино Красноярского района Самарской области
Урок по математике в 1 классе по теме :
Знаки +, -, =.
Разработан учителем начальных классов:
Костиной А. А.
2016 год
Цель:
познакомить с названиями и значением знаков +, -, =.
Планируемые результаты:
— предметные: уметь понимать значение знаков +, -, =; читать полученные равенства;
метапредметные
— регулятивные: уметь организовывать своё рабочее место под руководством учителя; определять цель выполнения заданий на уроке;
— коммуникативные: уметь обмениваться мнениями, слушать другого ученика, учителя, обсуждать, делать умозаключения;
— познавательные: уметь самостоятельно выделять и формулировать познавательную цель, сравнивать, группировать;
— личностные: уметь оценивать себя, границы своего знания и незнания, работать в паре, оценивать товарища, стремиться к повышению культуры речевого общения.
Материально-техническое обеспечение:
Проектор, экран, компьютер, слайды, учебник, тетрадь на печатной основе, карточки со знаками и цифрами, знаки дорожного движения – картинки, ободки для выступления, раздаточный материал – геометрические фигуры, тренажёр Базарного.
Ход урока
- Организационный момент.
Проверить готовность принадлежностей, приветствие учителя стоя.
Парта – это не кровать
И на ней нельзя лежать.
Прозвенел звонок и смолк.
Начинается урок.
Тихо девочки за парты сели,
Тихо мальчики за парты сели,
На меня все посмотрели.
- Повторение изученного материала.
— Прежде, чем мы приступим к изучению новой темы, предлагаю вам математическую разминку.
а) логическая разминка:
— Сколько хвостов у трех китов? (3 хвоста)
— Сколько ушей и двух мышей? (4 уха)
— У кого больше лап, у утки или у утенка? (одинаково, по 2 лапы)
б) устный счет:
— Посчитайте:
От 1 до 10 и обратно хором;
На доске корзина с грибами
— Составьте вопросы со словом «сколько» и ответьте на них.
(сколько грибов в корзине, сколько грибов на поляне, сколько грибов всего в корзине и на поляне)
- Работа по теме урока.
- Целеполагание.
На доске знаки (+, -, =, 1, 2, 3 и знаки дорожного движения «Автобусная остановка», «Пешеходный переход», «Пункт первой медицинской помощи», «Осторожно, дети!»)
— Что изображено на первом рисунке? (Автобусная остановка)
— Как вы понимаете значение слова «знак»?
— Представьте, что вы оказались в незнакомом районе города, спросить не у кого, но вы знаете, что в ваш район идет автобус № 410. Что вы будете делать?
(Предлагают найти автобусную остановку с помощью знака.)
— Верно. Знак молчит, но и сообщает нам о чем- то. Указывает на место, где останавливается автобус.
— А какие еще дорожные знаки вы знаете и что они сообщают?
— Теперь вы можете мне сказать, что такое знак?
Рефлексия: Знак — это указание или сообщение о каком-либо объекте.
— Нас окружает множество знаков.
(Версии разные: цифры, числа, знаки.)
— Эти записи являются тоже знаками, но математическими. Цифра это тоже математический знак, который используют для записи чисел.
— Какие из этих знаков вам знакомы?
— Какие новые? Кто знает, что это за знаки? (Гипотеза, предположение)
— Догадались, какая тема сегодняшнего урока? (Знаки плюс, минус, равно)
— Чему вы хотели бы научиться сегодня? (пользоваться знаками: плюс, минус, равно).
- Знакомство со знаками «плюс» (+), «минус» (–), равно (=).
Практическая работа.
— Положите два оранжевых треугольника.
Какой цифрой мы это обозначим? ( один ученик к доске находит и крепит цифру 2)
— Рядом положите синий квадрат.
Какой цифрой обозначим?( 1).
— Фигур стало больше или меньше? Сколько фигур получилось?
— Какими словами можно заменить слово положили? (прибавили, добавили)
— Чтобы записать это выражение в математике используются цифры и математический знак «+».
запись: 2+1
— Плюс – знак добрый, он всем дает, прибавляет и всего становится больше.
Ученик (Сизяков Рома) рассказывает стихотворение:
Я – плюс,
И этим я горжусь.
Я для сложения гожусь
Я – добрый знак соединенья
И в том мое предназначение.
— Какую работу он выполняет? (Он всем дает, прибавляет, всего становится больше.)
— Сколько у вас т фигур на столе? (3 фигуры)
Уберите синий квадрат. Фигур стало больше или меньше? Сколько фигур осталось? (2 фигуры)
— Слово уберите, тоже можно заменить знаком. Этот математический знак называется – минус.
Запись: 3-1
— Этот знак у всех отбирает, отнимает и всего становится меньше. Действие при этом называется вычитание.
Ученик (Спиридонов Никита) рассказывает стихотворение:
Я – минус.
Тоже добрый знак.
Ведь не со зла я отнимаю
Я свою роль лишь выполняю.
— Как называется математический знак, который у всех отнимает и при этом всего становится меньше? (Знак минус)
— Посмотрите на записи, которые у нас получились. Кто сможет их прочитать? (читают записанные на доске выражения)
Запись: 2+1 3
3 – 1 2
— Какого знака не хватает?
— Чтобы записать слово получится, используют знак равно (=) .
Запись: 2+1=3
3 – 1=2
Такие записи называют выражения.
— Давайте вместе прочитаем выражения, используя новые термины.
— Итак, какие же знаки используют математики, для записи выражений?
- Работа в тетради на печатной основе.
— Откройте тетрадь на стр.10.
«Я тетрадь свою открою
И наклонно положу.
А ручку я вот так держу.
Сяду прямо, не согнусь,
За работу я возьмусь.»
— Посмотрите на клеточки, какие знаки написаны?
— Посмотрите внимательно, а по какому правилу расположены здесь знаки? (через клетку)
(Показ, как правильно пишутся знаки «+», «–».
— Поменяйтесь тетрадями со своим соседом. Оцените работу. Посмотрите внимательно, получилось ли прописать красиво, аккуратно? Сохранили ли вы закономерность, все ли знаки у вас прописаны через клетку? Если всё верно – зелёный светофорик, если ошибка – жёлтый, если совсем неверно – красный.
- Закрепление.
- Работа по учебнику.
— Откройте учебник на стр.28.
— Посмотрите, о ком мы сейчас будем говорить? (О ежах.)
— Сколько было ежиков сначала? (1 ёжик)
— Что изменилось потом? (подбежал еще 1)
— Сколько их стало? (2)
(Чтение под картинкой рассказа) – Правильно вы ответили на вопросы?
— Какое слово заменили знаком «плюс» (подбежал). Прочитайте полученное выражение в учебнике.
2) Работа в парах:
— Посмотрите на картинку ниже и составьте рассказ. О ком вы будете составлять рассказ? Аналогично разбирается рисунок с зайцами.
– Данную запись можно прочитать так: «Три минус два равно одному». (Чтение детьми вслух.) Или по-другому: «Из трёх вычесть два, получится один». (Чтение детьми вслух.)
V. Подведение итогов.
– Давайте вспомним, что мы хотели узнать в начале урока? (Хотели узнать, как пользоваться знаками плюс, минус, равно)
— Вы достигли результата?
– Каким знаком будем пользоваться, если услышим слова: «убежали, убрали»? (Знаком минус)
— Каким знаком будет пользоваться, если услышите слова: «добавили, пришли»? (Знаком плюс)
— А какие это знаки + и – и =? (дорожные или математические)
VI. Рефлексия.
— оцените себя с помощью светофора: если вы всё поняли, всё удалось выполнить – зелёный свет;
если что-то осталось непонятно и были допущены ошибки – жёлтый. И после урока подойдёте ко мне – я ещё раз вам объясню;
если всё было непонятно – красный, и тогда нужно подробно ещё раз разобрать тему.
Спасибо вам большое за урок, завтра мы продолжим учиться пользоваться нашими новыми знаками и познакомимся с новой цифрой.
Приложение.
В течении урока, проводится 2-3 физминутки. Время проведения первой через 7-10 минут после начала урока, следующие по усмотрению учителя и временной промежуток зависит от работоспособности класса.
Физминутка
Раз – подняться, потянуться,
Два – согнуться, разогнуться,
Три – в ладоши три хлопка,
Головою три кивка.
На четыре руки шире,
Пять – руками помахать,
Шесть за парту тихо сесть.
Пальчиковая физминутка
Этот пальчик бабушка, (большие)
Этот пальчик дедушка, (указательные)
Этот пальчик мамочка, (средние)
Этот пальчик папочка. (безымянные)
Этот пальчик я. (мизинцы)
Это вся моя семья! (хлопки и встряхивание кистями рук)
Физминутка для глаз
Тренажёр Базарного на доске
Математика. Сложение и вычитание | Сайт Леонида Некина
«Вот смотри, я написал на бумаге
$6 + 2$
Это называется шесть плюс два. Это значит, что ты вначале берешь у папы шесть конфет, а потом еще две.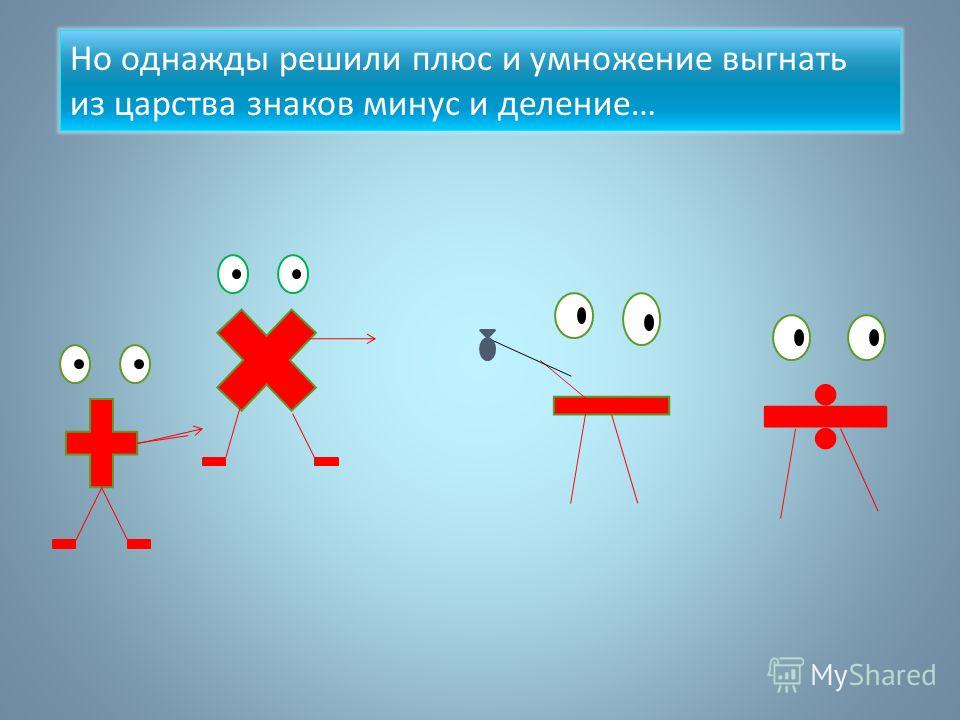
$6 + 2 = underline{,8,}$
Шесть плюс два равно восемь. Мы решили пример на сложение: мы сложили числа $6$ и $2$ и в результате получили $8$. Вот, держи восемь конфет. (Разумеется, речь идет о крошечных конфетах-горошинах.)
А теперь, смотри, я написал
$5 — 3$
Это называется пять минус три. Это значит, что у нас на двоих пять конфет. Три из них я отдаю тебе. Сколько же тогда конфет остается у меня? Давай отложим на счетах вначале пять бусинок, а потом из них в обратную сторону переложим три. Что получается в результате? Правильно, пять минус три равно два:
$5 — 3 = underline{,2,}$
Мы решили пример на вычитание. Из числа $5$ вычли число $3$ и получили $2$».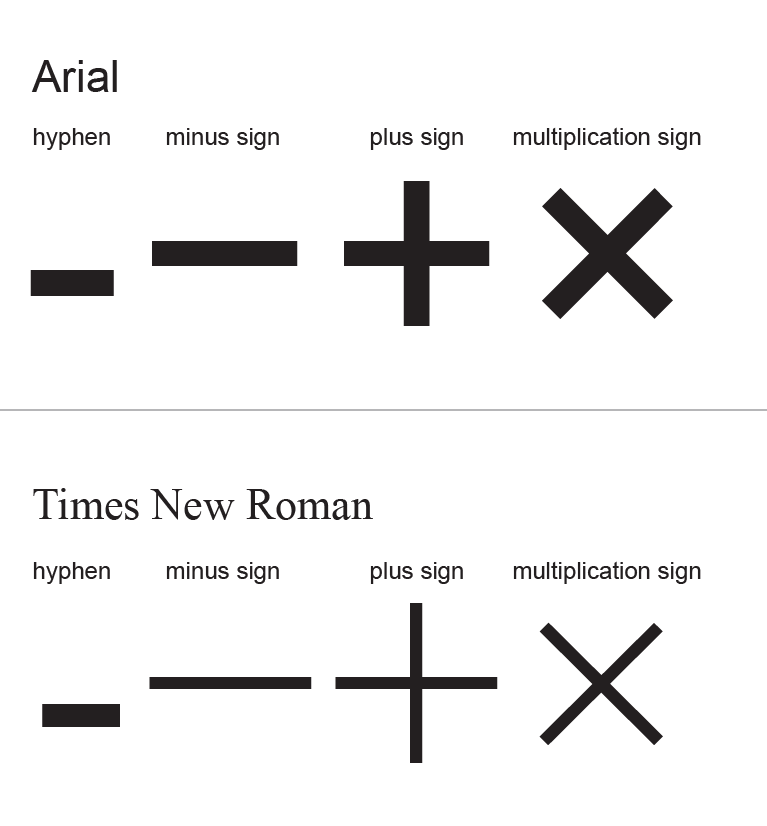
После такого объяснения ребенок уже способен самостоятельно делать упражнения на сложение и вычитание. Взрослый вручает ему листок бумаги, на котором написано, например, следующее:
$7 + 3 =$
$7 — 3 =$
$10 + 2 =$
$10 — 2 =$
и так далее.
В задачу ребенка входит выполнить на счетах указанные действия и записать ответ. После того как все ответы будут записаны, он показывает их взрослому. Взрослый восхищается правильными ответами, обводит их в кружочек, а неправильные просит пересчитать еще раз. Если один и тот же неправильный ответ появляется снова и снова, взрослый разбирается вместе с ребенком, где источник ошибки. Постепенно числа в примерах становятся всё больше и больше, однако второе число нет смысла делать больше тридцати, пока ребенку приходится пересчитывать его по бусинкам от начала до конца. Важно, чтобы ребенок не просто понял принцип сложения и вычитания, но и выработал соответствующий навык, то есть почти никогда не ошибался. Движения руки должны стать уверенными, — чтобы, откладывая одну бусинку, не задевать соседние.
После того как ребенок начнет обращаться со счетами более или менее уверенно, ему можно подсказать одну «хитрость» (если он сам до нее не додумается): второе число, точно так же, как и первое, необязательно пересчитывать по бусинкам от начала до конца: можно вначале отложить десятки (пусть даже десяток получится «рваный» — часть бусинок с одного ряда, часть — со следующего) и только потом продолжать считать по отдельным бусинкам.
Еще на одно открытие можно натолкнуть ребенка, давая ему примеры такими парами:
$1 + 26 =$
$26 + 1 =$
Оказывается, удобнее вначале отложить большее число, а потом прибавлять к нему меньшее. Результат всё равно остается один и тот же.
Необязательное дополнение 1: «уравнения»
Постепенно можно переходить к более сложным заданиям. В следующем примере вместо многоточия надо поставить такое число, чтобы получился правильный ответ:
$ldots + 3 = 9$
Подобного рода задачи решаются методом обращения времени вспять.
$underline{,6,} + 3 = 9$
Впрочем, очень скоро становится ясно, что перекладываемые бусинки можно считать и обычным образом: раз-бусинка, два-бусинка, три-бусинка. Результат от этого не изменится. Интересно отметить, что мы выполняем в точности такие же действия, как если бы решали пример «${9 — 3}$».
Подобным же образом можно найти, какое число должно стоять вместо многоточия в таком примере:
$ldots — 2 = 5$
Снова обращаем время вспять, и обнаруживается, что мы выполняем такие действия, как будто решаем пример «${5 + 2}$». В итоге получаем:
$underline{,7,} — 2 = 5$
Но вот еще один пример с многоточием:
$9 + ldots = 12$
Здесь многоточие стоит не на первом месте, а на втором, поэтому вспять обратить время не получится.
$9 + underline{,3,} = 12$
Тут можно ввести небольшое усовершенствование. Давайте, после того как мы отложили $9$ бусинок, пометим еще как-нибудь бусинку номер двенадцать. Например, сдвинем ее чуть-чуть влево — не до конца, а так, чтобы сразу после нее в ряду бусинок образовался небольшой разрыв. Теперь мы сразу видим, какие именно бусинки надо добавить к первым девяти, чтобы всего получилось двенадцать. Остается их только пересчитать: раз, два, три — ответ готов. Но посмотрим внимательно на счеты. Здесь у нас отмечено $12$ бусинок, поскольку именно после $12$-ой бусинки идет разрыв. Из них $9$ стоят особняком — сдвинуты до упора влево, — а остальные нам надо было пересчитать. То есть получается, что мы на самом-то деле отвечали на вопрос, сколько будет «${12 — 9}$».
Теперь мы так же легко можем справиться и с таким примером:
$14 — ldots = 8$
Откладываем $14$ бусинок, помечаем бусинку номер $8$ — например, сдвигая ее немножко вправо — и сразу видим, какие бусинки надо отнять от четырнадцати, чтобы получить восемь. Простым пересчетом находим, что их ровно $6$. Таким образом, многоточие надо заменить на шестерку:
$14 — underline{,6,} = 8$
И снова приглядимся к счетам. По расположению бусинок мы видим, что фактически решали пример «${14 — 8}$».
Необязательное дополнение 2: «отрицательные числа»
Пусть теперь дано:
$3 — 3 =$
Тут всё просто: откладываем сначала три бусинки, а потом те же три бусинки отправляем обратно. В результате получается «ничто» — ноль. А как быть, если встретится такое задание?
$3 — 5 =$
Мы привычным движением откладываем справа налево три бусинки, затем начинаем перекладывать по бусинке обратно: раз-бусинка, два-бусинка, три-бусинка — мы еще не успели переложить столько бусинок, сколько требуется, а они уже кончились.
$3 — 5 = underline{-2,}$
Такие числа со знаком минус впереди, полученные хитрым способом, называются отрицательными. Нам еще предстоит много иметь с ними дело в будущем. Заметим, что мы всего переложили слева направо $5$ бусинок, из них $3$ на лицевой стороне счет, а остальные на обратной. Поэтому мы с тем же успехом могли бы решить пример «${5 — 3}$» и приписать к ответу знак минус.
Но вот еще один пример с многоточием:
$7 — ldots = -3$
Откладываем $7$ бусинок и начинаем действовать методом подбора. Отнимаем для начала одну бусинку.
$7 — underline{,10,} = -3$
Поучается, что с лицевой стороны мы насчитали $7$ бусинок, а с обратной стороны — еще $3$ бусинки. Значит, мы фактически решили пример «$7 + 3$».
Конспект
1. Сложение. Пусть у нас в одной кучке шесть конфет, а в другой — две. Смешаем эти кучки в одну. Сколько в ней оказалось конфет? Ответ на эту задачу записывается в виде ${6 + 2 = 8}$ (шесть плюс два равно восемь). Мы выполнили пример на сложение: сложили шесть и два и получили восемь. Для решения этого примера на счетах откладываем вначале шесть бусинок, потом две и пересчитываем отложенные бусинки.
2. Вычитание. Пусть у нас есть кучка из пяти конфет. Мы взяли из нее три конфеты. Сколько осталось? Ответ записывается в виде ${5 — 3 = 2}$ (пять минус три равно два). Это пример на вычитание: мы вычли из пяти три и получили два. Для решения этого примера на счетах откладываем пять бусинок, возвращаем обратно три и пересчитываем оставшиеся.
3. Уравнения. Допустим в решенном примере на сложение «потерялось» первое число: ${ldots + 3 = 9}$. Какое число потерялось? Представляем себе, что мы решили этот пример на счетах, и после этого «обращаем время вспять», фактически выполняя те же действия, которые мы совершаем при решении примера ${9 — 3 = 6}$. Подобным же образом, обращая время вспять, можно найти «потерянное» число в примере на вычитание: ${ldots — 2 = 5}$, а именно: ${5 + 2 = 7}$. Глядя на бусинки, нетрудно также установить, что в примере ${9 + ldots = 12}$ потерялось число ${12 — 9 = 3}$, а в примере ${14 — ldots = 8}$ потерянным оказалось число ${14 — 8 = 6}$.
4. Отрицательные числа. Решая на счетах пример ${3 — 5}$, обнаруживаем, что из трех отложенных бусинок можно в обратную сторону переложить только три. Оставшиеся две бусинки перекладываем, развернув счеты обратной стороной. Ответ записываем в виде: ${3 — 5 = -2}$ (три минус пять равно минус два). С тем же успехом мы могли бы вычесть из пяти три и приписать перед результатом знак минус.
Задачи
1.2.1. «Мама дала Денису $7$ конфет, а папа $5$ конфет. Сколько конфет стало у Дениса?» Такого рода задач можно придумать множество, и хорошо, если они поначалу будут полностью соответствовать реальности. Главное действующее лицо — сам ребенок, и речь идет о приятных вещах. Мама в самом деле дает ему вкусные конфеты и спрашивает: «Сколько конфет я тебе дала?» Ребенок отвечает: «Семь». Потом он получает конфеты от папы, пересчитывает их и говорит: «Пять». Теперь он готов с радостью подумать над вопросом: «А сколько у тебя всего конфет?». Опять-таки, имеются в виду маленькие конфетки, не больше горошины.
1.2.2. Задачи на вычитание придумывать несколько труднее. Не следует повторять ошибку Мальвины, взявшуюся обучать арифметике Буратино. Если ребенок не любит делиться конфетами с младшим братиком, то это неподходящая тема для первых занятий по математике. Не слишком хорошо начинать и с таких задачек: «У Дениса было $10$ конфет. $4$ из них он съел. Сколько конфет осталось?» Здесь недостает наглядности: съеденных конфет-то не видно! Пожалуй, лучше так: «У папы было $10$ конфет. $4$ из них он оставил себе, а остальные дал Денису. Сколько конфет папа дал Денису?»
1.2.3. К вычитанию можно подойти еще и с другой стороны.
— Денис, сколько тебе дать конфет, — спрашивает папа.
— Двенадцать, — отвечает Денис.
— Хорошо, — говорит папа и дает Денису девять конфет. — Сколько конфет я должен тебе еще дать, чтобы получилось двенадцать?
Примеры из «динамических» прописей
Сложение и вычитание в пределах 20-ти («серый» шрифт для обводки)
То же с «уравнениями» (т.
Сложение и вычитание в пределах 20-ти (разность может быть отрицательной)
То же с «уравнениями»
Origin Story: «+» и «-» основные знаки арифметики | от Edtech Board | Edtech Board
Мы никогда не сможем думать о математике без знаков «+» плюс и «-» минус. Хотя у нас есть множество математических символов для деления (÷), умножения (×), интеграла (∫) и т. д., по своей сути это всегда символы «+» и «-». С самого раннего детства нас учили этим двум неотъемлемым символам. Их можно было бы рассматривать как азбуку математики, и без них все было бы иначе. Одни и те же символы используются везде, по всему миру. Немного любопытства, чтобы узнать, как они возникли и эволюционировали в нынешнюю форму, не повредит.
Знаки плюс и минус (+ и −) — это математические символы, используемые для обозначения операций сложения и вычитания, а также понятий положительного и отрицательного. Более того, плюс и минус — это латинские термины, означающие «больше» и «меньше» соответственно.
Зарегистрировано, что знак «+» происходит от латинского слова «et», означающего «и». Николь д’Оресм, астроном и автор книги «Книга неба и мира» 14 века, использовала знак «+» в качестве сокращения для слова «et». Использование знака «-» впервые было зарегистрировано в 1481 году в рукописи по немецкой алгебре, хранящейся в Дрезденской библиотеке. Иоганнес Видман, знаменитый немецкий математик, опубликовал первую печатную книгу под названием «Торговая арифметика» в Лейпциге, 1489 г.
Но именно Роберт Рекорд, известный валлийский математик и создатель знака равенства (=), ввел в Британии в 1557 году те же плюс и минус, которыми мы пользуемся до сих пор. Он описал эти два знака следующими словами:
«Есть еще два часто используемых знака, из которых первый сделан таким образом + и означает большее; другой сделан таким образом — и означает меньшее».
Кажется, разные люди использовали разные версии этих знаков, но именно Роберт Рекорд дал нам знаки, которыми мы пользуемся до сих пор, которые передавались из поколения в поколение, прежде чем получили всеобщее признание.
Первое уравнение, когда-либо написанное Робертом Рекордом в его трактате «Точильный камень Витте» в 1557 году. Уравнение, представленное в современных терминах, «14x+15=71» с помощью , и его решение равно 4.
A Еврейская традиция, которая восходит к 1920-го века пишет символ плюса, используя что-то, напоминающее перевернутую букву Т, и даже сейчас используется в еврейских начальных школах. Объяснение этому заключается в том, что он избегает обычного символа «+», который выглядит ужасно похожим на христианский крест.
Первоначально опубликовано по адресу www.edtechboard.com 20 марта 2013 г.
Где и когда появились символы «+» и «–»?
Символы для арифметических операций сложения (плюс; «+») и вычитания (минус; «–») настолько распространены сегодня, что мы вряд ли когда-нибудь задумываемся о том, что они не всегда существовали. На самом деле кто-то должен был сначала изобрести эти символы (или, по крайней мере, другие символы, которые позже превратились в текущую форму), и, безусловно, должно было пройти некоторое время, прежде чем символы стали общепринятыми. Когда я начал изучать историю этих знаков, я с удивлением обнаружил, что они не имеют своего происхождения в древности.
Древние греки выражали сложение в основном путем сопоставления, но время от времени использовали косую черту «/» для сложения и полуэллиптическую кривую для вычитания. В знаменитом египетском папирусе Ahmes пара ног, идущих вперед, обозначала сложение, а отходящее — вычитание. У индусов, как и у греков, обычно не было знака для сложения, за исключением того, что « ю » использовалось в рукописи Бахшали Арифметика (которая, вероятно, относится к третьему или четвертому веку). К концу пятнадцатого века французский математик Шюке (в 1484 г.) и итальянец Пачоли (в 1494 г.) использовали «p» или «p» (обозначает плюс) для сложения и «» или «m» (обозначает минус) для вычитания.
Нет никаких сомнений в том, что наш знак + имеет свои корни в одной из форм слова » et , что означает «и» на латыни.
Advertisement
Происхождение знака — гораздо менее ясно, и предположения варьируются от иероглифического или александрийского грамматического происхождения до символа полосы, используемого торговцами для отделения тары от общего веса товаров.
Первое использование современного алгебраического знака появляется в немецкой рукописи по алгебре 1481 года, которая была найдена в Дрезденской библиотеке. В латинском манускрипте того же периода (также в Дрезденской библиотеке) встречаются оба символа + и –. Известно, что Йоханнес Видман изучил и прокомментировал обе эти рукописи. В 1489 году в Лейпциге он издал первую печатную книгу ( Торговая арифметика ), в которой встречались два знака + и – (рис.
Рис. 1. Первое использование символов + и – в печати в книге Йоханнеса Видмана Behëde und Lubsche Rechenung auff allen Kauffmanschafft, Аугсбургское издание 1526 года.
В Италии символы + и – были приняты астрономом Кристофером Клавиус (немец, живший в Риме), математики Глориози и Кавальери в начале XVII века.
Реклама
Первое появление + и – в английском языке было в 1551 году в книге по алгебре Точильный камень Витте оксфордского математика Роберта Рекорда, который также ввел знак равенства как более длинный, чем сегодняшний символ «═». Описывая знаки «плюс» и «минус», Рекорд писал: «Есть два других знака, при частом использовании которых первый сделан таким образом + и означает больше: другой сделан таким образом — и означает меньше».
В качестве исторического любопытства я должен отметить, что даже после принятия не все использовали один и тот же символ для +. Сам Видман представил его как греческий крест + (знак, который мы используем сегодня), с горизонтальной чертой, иногда немного более длинной, чем вертикальная. Эту форму использовали такие математики, как Рекорд, Харриот и Декарт. Другие (например, Юм, Гюйгенс и Ферма) использовали латинский крест «✝», иногда располагаемый горизонтально, с перекладиной на одном конце или на другом. Наконец, некоторые (например, Де Ортега, Галлей) использовали более декоративную форму «✠».
Практика обозначения вычитания была несколько менее причудливой, но, возможно, более запутанной (по крайней мере, для нас), поскольку вместо простого – в немецких, швейцарских и голландских книгах иногда использовался символ «÷», который мы теперь используем для разделение. В нескольких книгах семнадцатого века (например, Декарта и Мерсенна) для вычитания использовались две точки «∙∙» или три точки «∙∙∙».
so3, h4P, Ba3N2, N2O, HMnO — Знания.site
Последние вопросы
-
Химия
36 минут назад
назовите минусы фарфора
-
Химия
51 минут назад
Помогите, пожалуйста, разобраться в задании по химии
-
Химия
51 минут назад
Для синтезу естеру із запахом яблука (метилбутаноат) було використано бутанова кислота масою 200 г з масовою часткою 8,8 %. Визнач масу одержаного естеру.
-
Химия
51 минут назад
Під час кислотного гідролізу етилетаноату утворюються.
..
Етан й етанова кислота;
Етанол і метанова кислота;
Етаналь й етанова кислота;
Етанол й етанова кислота -
Химия
1 час назад
Химия 8 класс
-
Химия
1 час назад
Помогите с химией
-
Химия
1 час назад
Помогите по химии !!!! составить уравнение реакции для гидроксида меди 2
-
Химия
1 час назад
де більше міститься молекул у 4,6 л сульфуру 4 оксиду SO4 або в 11,2л кисню O2
-
Химия
2 часа назад
Помогите , пожайлуста.
Записати рівняння реакцій між металами з порядковими номерами 3, 13, 20, 25, 26, 28, 30, 37, 47, 56 з водою і сульфатною кислотою.
-
Химия
2 часа назад
Решить методом ПОЛУРЕАНЦИИ!!
-
Химия
2 часа назад
При взаємодії магнію з сульфатною кислотою виділився газ обʼємом 6,72 л. Які ° маси магнію та сульфатної кислоти прореагували?
-
Химия
2 часа назад
Спалили фосфор масою 6,2г. Який обʼєм кисню витратився?
-
Химия
2 часа назад
Яка маса розчину з масовою часткою солі 18% містить 34г солі?
РЕШИТЕ ПЛИЗ -
Химия
2 часа назад
Задачи по химии
-
Химия
2 часа назад
Чёрный чай взбадривает также как и кофк?
Все предметы
Выберите язык и регион
English
United States
Polski
Polska
Português
Brasil
English
India
Türkçe
Türkiye
English
Philippines
Español
España
Bahasa Indonesia
Indonesia
Русский
Россия
How much to ban the user?
1 hour
1 day
100 years
Тест «Щелочные и щелочноземельные металлы»
Тест « Щелочные и щелочноземельные металлы»
(контрольный срез знаний)
Цель: проверить знания и умения учащихся то теме «Щелочные и щелочноземельные металлы»
Умения:
определять положение металлов в периодической системе Д.
определять строение атома;
определять степень окисления;
составлять полные и сокращенные ионные уравнения
определять продукты реакции;
решать цепочки уравнений;
определять окислитель и восстановитель, писать электронный баланс;
расставлять коэффициенты;
определять молярную массу и молярный объем;
составлять пропорцию.
Знания:
тривиальные названия соединений;
химические свойства металлов, оксидов и гидроксидов;
качественные реакции;
историю открытия металлов.
Предлагаемые тестовые задания содержат теоретические и практические вопросы, соответствующие требованиям государственного стандарта химического образования: основные понятия, законы химии, строение, свойства, получение важнейших классов веществ, изучаемых в 8 классе и 9 классе (I и II четверть)
Количество вариантов: 2
На решение варианта, состоящего из 15 заданий, отводится 40 минут.
Оценивание заданий:
Часть А – 1 балл
Часть Б:
Цепочка превращений:
— получение оксида – 1 балл;
— получение гидроксида – 1 балл;
— получение соли – 1 балл;
— метод электронного баланса – 2 балла;
— ионные уравнения – 1 балл.
Задача:
— составление уравнения – 1 балл;
— определение молярной массы – 1 балл;
— определение молярного объема – 1 балл;
— составление пропорции – 1 балл;
— ответ – 1 балл;
— оформление задачи – 1 балл.
Критерии для оценивания тематического теста:
«2» — менее 12 баллов
«3» — 12 — 17 баллов
«4» — 18 — 23 баллов
«5» — 24 — 25 баллов
Тест «Щелочные и щелочноземельные металлы»
Вариант I
Ученик (ца)_____________________________________________________________
Класс ___________________
Дата ____________________
ФИО учителя ___________________________________________________________
|
№ п/п |
Задание |
Ответ |
|
Блок А (1 балл) Выберите правильный вариант ответа |
||
|
1 |
Щелочноземельные металлы находятся в: 1) I A группе; 2) II А группе; 3) IV А группе 4) VIII А группе |
2 |
|
2 |
Какой из указанных металлов является щелочным: 1) Mg; 2) Zn; 3) Ba; 4) K |
4 |
|
3 |
Степень окисления щелочных металлов: 1) +1; 2) +2; 3) -2; 4) +3 |
1 |
|
4 |
Распределение электронов по энергетическим уровням в атоме магния: 1) 2,8,2; 2) 2,8,1; 3) 2,8,8,1; 4) 1,8,8,1 |
1 |
|
5 |
Щелочноземельные металлы: А. Б. Легко режутся ножом. В. Неактивные металлы. 1) Все утверждения не верны; 2) Верны А и Б; 3) Верны А и С |
2 |
|
6 |
При взаимодействии с кислородом натрий образует: 1) оксид; 2) пероксид; 3) натрий не реагирует с кислородом. |
2 |
|
7 |
Каустическая сода: 1) NaOH; 2) KOH; 3) Mg (OH)2; 4) NaCl |
1 |
|
8 |
С каким из следующих веществ реагирует кальций? 1) Na2O; 2) NaCl; 3) Cu; 4) h3O |
4 |
|
9 |
С каким из следующих веществ реагирует гидроксид калия? 1) СO2; 2) NaCl; 3) KNO3; 4) Ba(OH)2 |
1 |
|
10 |
Какой осадок образуется при взаимодействии растворов солей Na3PO4 и Ca(NO3)2 1) NaNO3; 2) Ca (OH)2; 3) Ca3(PO4)2; 4) NaOH |
3 |
|
11 |
Какая из следующих реакций относится к реакциям ионного обмена? 1) CaO + h3O → Ca (OH)2 2) Ba (NO3)2 + Na2SO4 → BaSO4 + 2 NaNO3 3) 2 Mg + TiO2 → 2 MgO + Ti 4) 3 Ba + N2 → Ba3N2 |
2 |
|
12 |
Соли калия окрашивают пламя в: 1) зеленый цвет; 2) красный цвет; 3) желтый цвет; 4) фиолетовый цвет |
4 |
|
13 |
Английский химик впервые получивший магний в 1808г. 1) Г.Дэви; 2) У. Гилберт; 3) Й. Берцелиус; 4) А.Арфведсон |
1 |
Блок Б
1. Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения (6 баллов):
Ba → BaO → Ba(OH)2 → BaSO4
В первом уравнении определите окислитель и восстановитель (метод электронного баланса), третье уравнение напишите в ионном виде
1) 2 Ba0 + O02 → 2 Ba+2O-2
Ba0 – 2e → Ba+2 2 (восстановитель/окисление)
4
O2 + 4e → 2O-2 1 (окислитель/восстановление)
2) BaO + h3O → Ba(OH)2
3) Ba(OH)2 + h3SO4 → BaSO4 + 2 h3O
Ba2+ + 2OH- + 2H+ + SO42- → BaSO4 + 2 h3O
2. Решите задачу (6 баллов). При взаимодействии натрия массой 10 г с водой выделился водород. Определите объём водорода (н.у.).
|
Дано |
Решение |
|
m(Na) = 10г |
0. 2Na + 2 h3O → 2NaOH + h3 2 моль 1 моль 1) 2) х = 0,215 (моль) 3) Ответ: V(h3) = 4.816 (л) |
|
Найти: V(h3) — ? |
Тест «Щелочные и щелочноземельные металлы»
Вариант II
Ученик (ца)_____________________________________________________________
Класс ___________________
Дата ____________________
ФИО учителя ___________________________________________________________
|
№ п/п |
Задание |
Ответ |
|
Блок А (1 балл) Выберите правильный вариант ответа |
||
|
1 |
Щелочные металлы находятся в: 1) I A группе; 2) III А группе; 3) VII Б группе 4) VI А группе |
1 |
|
2 |
Какой из указанных металлов является щелочноземельным: 1) Sr; 2) Cs; 3) Na; 4) Al |
1 |
|
3 |
Степень окисления щелочноземельных металлов: 1) +2; 2) +4; 3) +3; 4) -1 |
1 |
|
4 |
Распределение электронов по энергетическим уровням в атоме калия: 1) 2,8,7,2; 2) 2,8,8,1; 3) 2,8,1; 4) 1,8,8,2 |
2 |
|
5 |
Щелочные металлы: А. Б. Легко режутся ножом. В. Неактивные металлы. 1) Все утверждения верны; 2) Верны А и Б; 3) Верны А и В |
2 |
|
6 |
Реакция сжигания магния сопровождается: 1) взрывом; 2) вспышкой; 3) нет ярко выраженных признаков химической реакции. |
2 |
|
7 |
Английская соль: 1) CaSO4; 2) Ca (OH)2; 3) MgSO4; 4) CaCO3 |
3 |
|
8 |
С каким из перечисленных веществ реагирует калий? 1) Na2O; 2) h3O; 3) Ca (OH)2; 4) Mg |
2 |
|
9 |
С каким веществом реагирует гидроксид кальция? 1) NaOH; 2) Na2O; 3) HCl; 4) h3O |
1 |
|
10 |
Какой осадок образуется при взаимодействии растворов солей Ba (NO3)2 и Na2SO4 1) NaNO3; 2)BaSO4; 3)NaHSO4; 4) Ba (OH)2 |
2 |
|
11 |
Какая из следующих реакций выражается сокращенным ионным уравнением H + + OH — → h3O 1) 2 HCl + Cu (OH)2 → CuCl2 + 2 h3O 2) HBr + KOH → KBr + h3O 3) h3SO3 + 2 RbOH → Rb2SO3 + 2 h3O |
2 |
|
12 |
Соли натрия окрашивают пламя в: 1) зеленый цвет; 2) красный цвет; 3) желтый цвет; 4) фиолетовый цвет |
3 |
|
13 |
Шведский химик, открывший литий в 1817г: 1) Г. |
4 |
Блок Б
1. Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения (6 баллов):
Li → Li2O→ LiOH → Li3PO4
В первом уравнении определите окислитель и восстановитель (метод электронного баланса), третье уравнение напишите в ионном виде.
1) 4 Li0 + O02 → 2 Li+2O-2
Li0 – 1e → Li+ 4 (восстановитель/окисление)
4
O2 + 4e → 2O-2 1 (окислитель/восстановление)
2) Li2O + h3O → 2 LiOH
3) 3LiOH + h4PO4 → Li3PO4 + 3 h3O
3 Li+ + 3OH- + 3H+ + PO43- → Li3PO4 + 3 h3O
2. Решите задачу (6 баллов). При взаимодействии магния с хлором объемом 11,2 л (н.у.), образуется хлорид магния. Определите массу хлорида магния.
|
Дано |
Решение |
|
V(Cl2) = 11. |
0.5 моль х моль 2Mg + Cl2 → MgCl2 1 моль 1 моль 1) 2) х = 0,5 (моль) 3) Ответ: m(MgCl2) = 45.5 (г) |
|
Найти: m(MgCl2) — ? |
The Periodic Table at KnowledgeDoor
Ссылки (Нажмите рядом со значением выше, чтобы увидеть полную информацию о цитировании для этой записи)
Allred, A.L. «Значения электроотрицательности на основе термохимических данных». Журнал неорганической и ядерной химии, том 17, номера 3–4, 1961 г., стр. 215–221. doi:10.1016/ 0022-1902(61)80142-5
Андерс, Эдвард и Николя Гревесс. «Изобилие элементов:
Метеоритный и солнечный.» Geochimica et Cosmochimica Acta, том 53, номер 1, 1989, стр. 197–214. doi:10.1016/ 0016-7037(89)
-X
Андерсен Т., Х.К. Хауген и Х.
Барсан, Майкл Э., редактор. Карманный справочник NIOSH по химическим опасностям. Цинциннати, Огайо: Публикации NIOSH, 2007.
Бацанов С.С. «Ван-дер-Ваальсовы радиусы элементов». Неорганические материалы, том 37, номер 9, 2001 г., стр. 871–885. См. аннотацию
Бонди, А. «Объемы и радиусы Ван-дер-Ваальса». Журнал физической химии, том 68, номер 3, 1964 г., стр. 441–451. doi: 10.1021/ j100785a001
Боуэн, Х. Дж. М. Экологическая химия элементов. Лондон: Academic Press, Inc., 1979.
Брач, Стивен Г. «Пересмотренные электроотрицательности Малликена: I. Расчет и преобразование в единицы Полинга». Журнал химических
Образование, том 65, номер 1, 1988 г., стр. 34–41. дои: 10.1021/ ed065p34
Кэмпбелл, Дж. Л. «Урожайность флуоресценции и вероятности Костера-Кронига для атомных подоболочек L.
Таблицы данных и ядерных данных, том 95, номер 1, 2009 г., стр. 115–124. doi: 10.1016/ j.adt.2008.08.002
Кэмпбелл, Дж. Л. «Урожайность флуоресценции и вероятности Костера-Кронига для атомных L подоболочек». Атомные данные и таблицы ядерных данных,
том 85, номер 2, 2003 г., стр. 291–315. дои: 10.1016/ S0092-640X(03)00059-7
Кардарелли, Франсуа. Справочник по материалам: краткий настольный справочник, 2-е издание. Лондон: Springer-Verlag, 2008.
Клементи, Э., Д.Л. Раймонди и В.П. Рейнхардт. «Константы атомного экранирования из функций SCF. II. Атомы с 37–86 электронами». Журнал химической физики, том 47, номер 4, 1967 г., стр. 1300–1307. doi:10.1063/ 1.1712084
Коэн, Э. Ричард, Дэвид Р. Лайд и Джордж Л. Тригг, редакторы. Справочник по физике AlP, 3-е издание. Нью-Йорк: Springer-Verlag New York, Inc., 2003.
Коннелли, Нил Г., Туре Дамхус, Ричард М. Хартсхорн и Алан Т.
Кордеро, Беатрис, Вероника Гомес, Ана Э. Платеро-Пратс, Марк Ревес, Хорхе Эчеверриа, Эдуард Кремадес, Флавия Барраган и Сантьяго Альварес. «Возвращение ковалентных радиусов». Dalton Transactions, номер 21, 2008 г., стр. 2832–2838. doi:10.1039/ b801115j
Кокс, П. А. Элементы: их происхождение, изобилие и распространение. Оксфорд: Издательство Оксфордского университета, 1989.
Кронан, Д.С. «Базальные металлоносные отложения восточной части Тихого океана». Бюллетень Геологического общества Америки, том 87,
№ 6, 1976 г., стр. 928–934. doi:10.1130/ 0016-7606(1976)872.0.CO;2
де Подеста, Майкл. Понимание свойств материи, 2-е издание. Лондон: Тейлор и Фрэнсис, 2002.
Дебессай, М., Дж. Дж. Хэмлин и Дж. С. Шиллинг. «Сравнение зависимостей Tc от давления в трехвалентных d-электронных сверхпроводниках Sc, Y, La и Lu до давлений в мегабарах».
Дронсковски, Ричард. Вычислительная химия твердотельных материалов. Вайнхайм, Германия: WILEY-VCH Verlag GmbH & Co. KGaA, 2005.
Эббинг, Даррелл Д. и Стивен Д. Гэммон. Общая химия, 8-е издание. Бостон, Массачусетс: Компания Houghton Mifflin, 2005.
Эмсли, Джон. Строительные блоки природы: Путеводитель по А-Я
элементы. Оксфорд: Издательство Оксфордского университета, 2003.
Эмсли, Джон. Элементы, 3-е издание. Оксфорд: Издательство Оксфордского университета, 1998.
Файерстоун, Ричард Б. Таблица изотопов, 8-е издание, том 2. Под редакцией Вирджинии С. Ширли с помощниками редактора Корал М. Бэглин, С. Ю. Фрэнк Чу и Джин Зипкин. Нью-Йорк: John Wiley & Sons, Inc., 1996.
Галассо, Фрэнсис С. Структура и свойства
Неорганические твердые вещества. Oxford: Pergamon Press, 1970.
Гринвуд, Н. Н. и А. Эрншоу. Химия элементов, 2-е издание.
Гвин Уильямс. Энергии связи электронов. http:// www.jlab.org/ ~gwyn/ ebindene.html . Проверено 30 апреля 2010 г.
Хо, С.Ю., Р.В. Пауэлл и П.Е. Лили. «Теплопроводность элементов: всесторонний обзор». Журнал физических и химических справочных данных, том 3, приложение 1, 1974 г., стр. с I–1 по I–796.
Хорват, А.Л. «Критическая температура элементов и периодическая система». Журнал химического образования, том 50, номер 5, 1973 г., стр. 335–336. doi:10.1021/ ed050p335
Хотоп Х. и В. К. Линебергер. «Энергии связи в атомных отрицательных ионах: II». Журнал физических и
Химические справочные данные, том 14, номер 3, 1985 г., стр. 731–750.
Хьюи, Джеймс Э., Эллен А. Кейтер и Ричард Л. Кейтер. Неорганическая химия: принципы строения и реакционной способности, 4-е издание. Нью-Йорк: Издательство HarperCollins College Publishers, 1993.
Ихде, Аарон Дж. Развитие современной химии.
Международная организация труда (МОТ). Международный
Карта химической безопасности для таллия. http:// www.ilo.org/ legacy/ english/ protection/ safework/ cis/ products/ icsc/ dtasht/ _icsc00/ icsc0077.htm . По состоянию на 4 мая 2010 г.
Международная организация труда (МОТ). Международная карта химической безопасности для таллия. http:// www.ilo.org/ Legacy/ английский/ Защита/ Safework/ CIS/ Продукты/ ICSC/ DTASHT/ _ICSC00/ ICSC0077.HTM . По состоянию на 5 мая 2010 г.
Jr., Элберт Дж. Литтл и Марк М. Джонс. «Полная таблица электроотрицательностей». Журнал химического образования, том 37, номер 5, 1960 г., стр. 231–233. doi: 10.1021/ ed037p231
Кинг, Х.
Кинг, Х.В. «Температурно-зависимые аллотропные структуры элементов». Бюллетень фазовых диаграмм сплавов, том 3, номер 2, 1982 г., стр. 275–276. doi:10.1007/ BF02892394
Киттель, Чарльз. Введение в физику твердого тела, 8-е издание. Хобокен, Нью-Джерси: John Wiley & Sons, Inc., 2005.
Киттель, Чарльз. Введение в физику твердого тела, 5-е издание. Нью-Йорк: John Wiley & Sons, Inc., 1976.
Ли, Ю.-Х. и Дж. Э. Шунмейкеры. «Химический состав и минералогия
Морские отложения». Стр. 1–36 в «Осадочных породах, диагенезе и осадочных породах». Под редакцией Фреда Т. Маккензи. Оксфорд: Elsevier Ltd., 2005.
Либофф, Ричард Л. Введение в квантовую механику, 3-е издание. Рединг, Массачусетс. : Addison Wesley Longman, Inc., 1998.
Лиде, Дэвид Р., редактор CRC Handbook of Chemistry and Physics, 88th edition.
2008.
Манн, Джозеф Б., Терри Л. Мик и Леланд С. Аллен. «Конфигурационные энергии элементов основной группы». Журнал Американского химического общества, том 122, номер 12, 2000 г., стр. 2780–2783. doi:10.1021/ ja992866e
Мануэль О., изд. Происхождение элементов в Солнечной системе: последствия наблюдений после 1957 года. Нью-Йорк: Kluwer Academic Publishers, 2000.
Маршалл, Джеймс Л. Открытие элементов: поиск фундаментальных принципов Вселенной, 2-е издание. Бостон, Массачусетс: Pearson Custom Publishing, 2002.
Мартин В.К. «Электронная структура элементов». Европейский физический журнал C — Частицы и поля, том 15, номера 1–4, 2000 г., стр. 78–79. doi: 10.1007/ BF02683401
McDonough, WF «Композиционная модель ядра Земли». стр. 547–568 в «Мантии и ядре». Под редакцией Ричарда В. Карлсона. Оксфорд: Elsevier Ltd., 2005.
Мечтли, Юджин А. «Свойства материалов». стр. 4–1–4–33 в Справочные данные для инженеров: радио, электроника, компьютер и связь.
Мислер, Гэри Л. и Дональд А. Тарр. Неорганическая химия, 3-е издание. Река Аппер-Сэдл, Нью-Джерси: Pearson Prentice Hall, 2004.
Мур, Шарлотта Э. Потенциалы ионизации и пределы ионизации, полученные на основе анализа оптических спектров. Вашингтон, округ Колумбия: Национальный
Бюро стандартов, 1970.
Нэгл, Джеффри К. «Атомная поляризуемость и электроотрицательность». Журнал Американского химического общества, том 112, номер 12, 19.90, стр. 4741–4747. doi:10.1021/ ja00168a019
Национальный институт охраны труда и здоровья (NIOSH). Международная карта химической безопасности для таллия. http:// www.cdc.gov/ niosh/ ipcsneng/ neng0077.html . По состоянию на 5 мая 2010 г.
Национальный институт охраны труда и здоровья (NIOSH).
Национальный институт охраны труда и здоровья (NIOSH). Реестр токсического действия химических веществ на таллий. http:// www.cdc.gov/ niosh-rtecs/ xg3442e8.html . Проверено 5 мая 2010 г.
Орем, У. Х. и Р. Б. Финкельман. «Углеобразование и геохимия». стр. 191–222 в Отложениях, диагенезе и осадочных породах. Под редакцией Фреда Т. Маккензи. Оксфорд: Elsevier Ltd., 2005.
Окстоби, Дэвид В., Х. П. Гиллис и Алан Кэмпион. Основы современной химии, 6-е издание. Бельмонт, Калифорния: Thomson Brooks/Cole, 2008.
Пальме, Х. и Х. Бир. «Метеориты и состав солнечной
Фотосфера». Стр. 204–206 в Ландольте-Бёрнштейне — Группа VI: Астрономия и астрофизика. Под редакцией HH Voigt. Нью-Йорк: Springer-Verlag, 1993. doi: 10.1007/ 10057790_59
Пальме, Х.
Состав». С. 1–38 в The Mantle and Core. Под редакцией Ричарда В. Карлсона. Оксфорд: Elsevier Ltd., 2005.
Полинг, Лайнус. Природа химической связи, 3-е издание. Итака, Нью-Йорк: Издательство Корнельского университета, 1960.
Пирсон, Ральф Г. «Абсолютная электроотрицательность и твердость: приложение к неорганической химии». Неорганическая химия, том 27, номер 4, 1988 г., стр. 734–740. doi:10.1021/ ic00277a030
Пекка Пюйккё. Самосогласованные ковалентные радиусы 2009 года. http:// www.chem.helsinki.fi/ ~pyykko/ Radii09.pdf . Проверено 20 ноября 2010 г.
Прохаска, Томас, Йоханна Ирргехер, Жаклин Бенефилд, Джон К. Бёлке, Лесли А. Чессон, Тайлер Б. Коплен, Типинг Динг, Филип Дж. Х. Данн, Манфред Грёнинг, Норман Э. Холден, Харро А. Дж. Мейер, Хайко Муссен, Антонио Посоло, Йошио Такахаши, Йохен Фогль, Томас Вальчик, Джун Ван, Майкл Э. Визер, Сигеказу Йонеда,
Сян-Кун Чжу и Юрис Мейджа.
Пюикко, Пекка и Митико Атсуми. «Ковалентные радиусы молекулярных двойных связей для элементов Li-E112». Химия — Европейский журнал, том 15, номер 46, 2009 г., стр. 12770–12779. doi:10.1002/ chem.200
2
Пьюкко, Пекка и Мичико Атсуми. «Ковалентные радиусы молекулярных одинарных связей для элементов 1-118». Химия — Европейский журнал, том 15, номер 1, 2009 г., стр. 186–197. doi:10.1002/ chem.200800987
Pyykkö, Pekka, Sebastian Riedel, and Michael Patzschke. «Ковалентные радиусы тройной связи». Химия — Европейский журнал, том 11, номер 12, 2005 г., стр. 3511–3520. дои: 10.1002/ chem.200401299
Рорер, Грегори С. Структура и связь в кристаллических материалах. Кембридж: Издательство Кембриджского университета, 2001.
Самсонов Г.В., изд.
Сандерсон, Р. Т. Простые неорганические вещества. Малабар, Флорида: Robert E. Krieger Publishing Co., Inc., 1989.
Сандерсон, Р. Т. «Принципы электроотрицательности: Часть I. Общая природа». Журнал химического образования, том 65, номер 2, 1988, стр. 112–118. doi:10.1021/ ed065p112
Сандерсон, Р. Т. Полярная ковалентность. Нью-Йорк: Academic Press, Inc., 1983.
Сансонетти, Дж. Э. и У. К. Мартин. «Справочник по основным данным атомной спектроскопии». Журнал физических и химических справочных данных, том 34, номер 4, 2005 г., стр. 1559–2259. doi:10.1063/ 1.1800011
Научная группа Thermodata Europe (SGTE). Чистый
Вещества: Часть 1 — Элементы и соединения от AgBr до Ba3N2. Под редакцией И. Уртадо и Д. Нойшюца. Берлин: Springer-Verlag, 19.99. doi:10.1007/ 10652891_3
Шеннон, Р. Д. «Пересмотренные эффективные ионные радиусы и систематические исследования
Межатомные расстояния в галогенидах и халькогенидах».
Сингман, Чарльз Н. «Атомный объем и аллотропия элементов». Журнал химического образования, том 61, номер 2. , 1984, стр. 137–142. doi: 10.1021/ ed061p137
Слейтер, Дж. К. «Атомные радиусы в кристаллах». Журнал химической физики, том 41, номер 10, 1964 г., стр. 3199–3204. doi: 10.1063/ 1.1725697
Смит, Дерек В. «Электроотрицательность в двух измерениях: переоценка и разрешение парадокса Пирсона-Полинга». Журнал химического образования, том 67, номер 11, 1990 г., стр. 911–914. doi:10.1021/ ed067p911
Смит, Дерек В. Неорганические вещества: прелюдия к изучению описательной неорганической химии. Кембридж: Издательство Кембриджского университета, 1990.
Стюарт, Г. Р. «Измерение низкотемпературной удельной теплоемкости». Обзор научных инструментов, том 54, номер 1, 1983 г.
Стюарт, Г. Р. «Измерение низкотемпературной удельной теплоемкости». Обзор научных инструментов, том 54, номер 1, 1983 г., стр. 1–11. doi:10.1063/ 1.1137207
Тари А. Удельная теплоемкость вещества при низких температурах. Лондон: Imperial College Press, 2003.
Министерство транспорта США (DOT), Transport Canada (TC), Секретариат транспорта и коммуникаций Мексики (SCT) и Centro de Información Química para Emergencias (CIQUIME). 2008 Чрезвычайная ситуация
Руководство по ответу.
Вайнштейн, Борис К., Владимир М. Фридкин и Владимир Л. Инденбом. Структура кристаллов, 2-е издание. Современная кристаллография 2. Под редакцией Бориса К. Вайнштейна, А.А. Чернова и Л.А. Шувалова. Берлин: Springer-Verlag, 1995.
Voigt, HH, редактор. Ландольт-Бёрнштейн — Группа VI Астрономия и астрофизика. Берлин: Springer-Verlag, 1993.
Вабер, Дж. Т. и Дон Т. Кромер. «Орбитальные радиусы атомов и ионов».
Вагман, Дональд Д., Уильям Х. Эванс, Вивиан Б. Паркер, Ричард Х. Шумм,
Ива Халоу, Сильвия М. Бейли, Кеннет Л. Чёрни и Ральф Л. Наттолл. «Теплопроводность элементов: всесторонний обзор». Журнал физических и химических справочных данных, том 11, приложение 2, 1982 г., стр. 2–1–2–392.
Уолдрон, Кимберли А., Эрин М. Ферингер, Эми Э. Стриб, Дженнифер Э. Троски и Джошуа Дж. Пирсон. «Отбор в процентах на основе эффективного заряда ядра Слейтера как универсальный инструмент для изучения периодических тенденций». Журнал химического образования, том 78, номер 5, 2001 г., стр. 635–639.. doi:10.1021/ ed078p635
Уикс, Мэри Эльвира и Генри М. Лестер. Открытие элементов, 7-е издание. Истон, Пенсильвания: Журнал химического образования, 1968.
Йос, Карл Л. «Плотность элементов в жидкости». Химическая инженерия, том 114, номер 12, 2007 г., стр. 44–46.
Yaws, Карл Л.
Химический элемент: Азот (N)
Химический элемент: Азот (N)
0 00342 3.
| Atomic Number: | 7 | ||||
| Element Symbol: | N | ||||
| Element Name: | Nitrogen | ||||
| Atomic Weight: | 14.0067 | ||||
| Номер группы: | 15 | ||||
| Название группы: | Pnictogen | ||||
| 4 Номер периода 40: 41 | |||||
| Block: | p-block | ||||
| Ground State Configuration: | 1s2 2s2 2p3 | ||||
| Ground State Level: | 4So3/2 | ||||
| Standard State : | Газ | ||||
| Общие валеня: | 3 | ||||
| Длина Бонда: | 109. 76 76 |
Длина Бонда: | 09.76976 | .0340 | 65 |
| Atomic Radius Calculated: | 56 | ||||
| Covalent Radius Empirical: | 75 | ||||
| Vander Waals Radius: | 155 | ||||
| Electron Affinity : | 7 | ||||
| Энергия первой ионизации: | 1402.3 | ||||
| Полинг Электроотрицательность: | |||||
| Sanderson Electronegativity: | 3.19 | ||||
| Allred Rochow Electronegativity: | 3.07 | ||||
| Mulliken Jaffe Electronegativity: | 2.90 | ||||
| Allen Electronegativity: | 3,066 | ||||
| Молярный объем: | 13,54 | ||||
| Скорость звука: | 333.6 | ||||
| Refractive Index: | 1. 000298 (gas; liquid 1.197) 000298 (gas; liquid 1.197) |
||||
| Melting Point: | -210.1 | ||||
| Boiling Point: | -195.79 | ||||
| Критическая температура: | -146,9 | ||||
| Теплопроводность: | 0,02583 | ||||
| 0.36 (per mol N atoms) | |||||
| Enthalpy Of Vaporization: | 2.79 (per mole N atoms) | ||||
| Enthalpy Of Atmization: | 473 | ||||
| Most Common Oxidation Numbers : | 5,3, -3 | ||||
| Цвет: | Классификация | ||||
| Классификация: | |||||
| : | : | : | |||
| : | |||||
| : | |||||
| : | |||||
. Discovered By: Discovered By: |
Daniel Rutherford | ||||
| Discovered At: | Scotland | ||||
| Discovered When: | 1772 | ||||
| Origin Of Name: | From the Greek words nitron genes означает нитр и образование и латинское слово nitrum (нитр – это общее название нитрата калия, KNO#) |
04 90 Enthalpy: 1 7 7
Рассчитайте молекулярную массу азота или
молекулярная масса N.
См. также полный список химических элементов и атомных весов.
Acetanilide C6H5NH(COCh4)
Acetonitrile Ch4CN
Ethidium Bromide C21h30BrN3
Ethylamine Ch4Ch3Nh3
Glycine Nh3Ch3COOH
Histidine C6H9N3O2
Lysine HO2CCH(Nh3)(Ch3)4Nh3
Phenacetin Ch4CONHC6h5OC2H5
Valine C5h21NO2
Aluminium Nitride AlN
Aluminium Nitrate Al(NO3) 3
Аммиак Nh4
Ацетат аммония Ch4COONh5
Бикарбонат аммония (Nh5)HCO3
Ammonium Chloride Nh5Cl
Ammonium Hydroxide Nh5OH
Ammonium Nitrate Nh5NO3
Ammonium Sulfate (Nh5)2SO4
Barium Nitrate Ba(NO3)2
Boron Nitride BN
Cadmium Nitrate Cd(NO3)2
Calcium Cyanamide CaCN2
Carboplatin C6h22N2O4Pt
Cyanogen (CN )2
Цианогенхлорид CNCl
Цианурхлорид C3Cl3N3
Нитрид галлия GaN
Гидразин N2h5
Гидразиновая кислота HN3
Нитрид индия Mercury InN
Нитрат лития0671 Nitric Acid HNO3
Nitric Oxide NO
Nitrogen Dioxide NO2
Nitrosylsulfuric Acid NOHSO4
Nitrous Acid HNO2
Nitrous Oxide N2O
Potassium Nitrate KNO3
Rubidium Nitrate RbNO3
Silver Nitrate AgNO3
Sodium Cyanide NaCN
Sodium Nitrate NaNO3
Sodium Nitrite NaNO2
Strontium Нитрат Sr(NO3)2
Сульфаминовая кислота h4NSO3
Тетранитрид тетрасеры S4N4
Нитрид титана TiN
Тринитротолуол C6h3(NO2)3Ch4
Тринитроглицерин C3H5(NO3)3
Uranyl Nitrate UO2(NO3)2
Zinc Cyanide Zn(CN)2
Zirconium Nitride ZrN
Acetaminophen C8H9NO2
Acridine C13H9N
Acrylamide C3H5NO
Cadaverine Nh3(Ch3)5Nh3
Cinnoline C8H6N2
Cytosine C4H5N3O
Epinephrine C9h23NO3
Hexamine (Ch3) 6N4
Метиленовый синий C16h28N3SCl
N-Метилпирролидон C5H9NO
Нитроглицерин C3H5(NO3)3
Фенилтиокарбамид C7H8N2S
Клавуланат калия C8H8KNO5
Путресцин 4Ch30671 Pyridine C5H5N
Tetryl C7H5N5O8
Tyrosine C9h21NO3
Urea CO(Nh3)2
Uric Acid C5h5N4O3
Yohimbine Hydrochloride C21h36N2O3.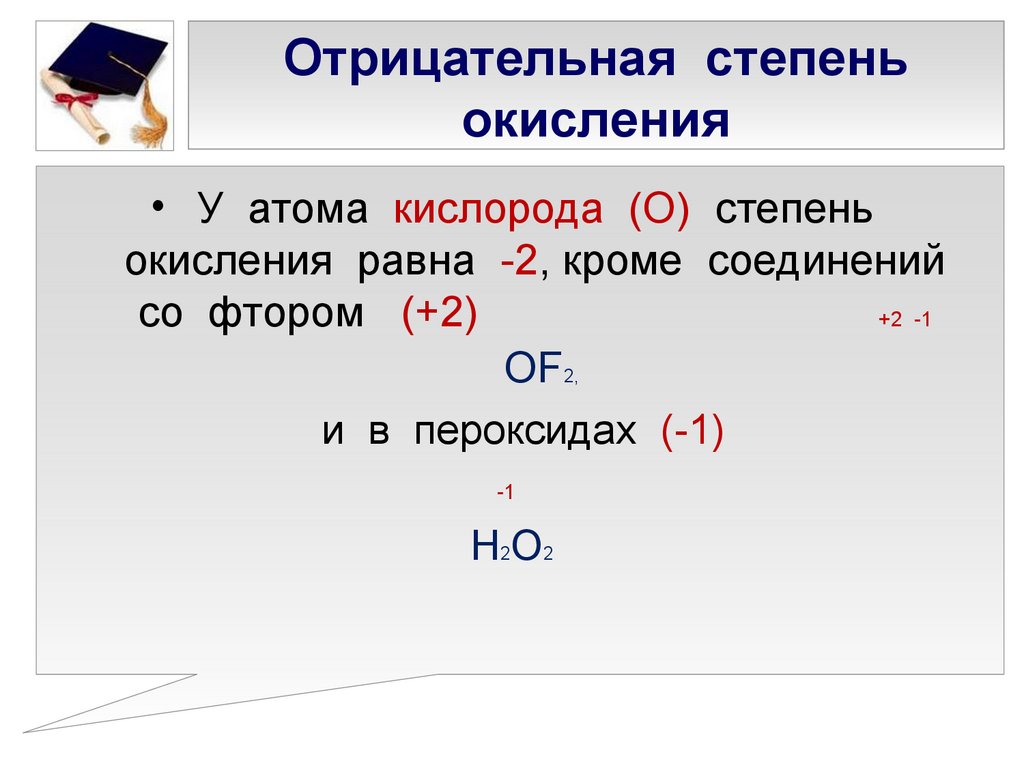
Ammonium Carbonate (Nh5)2CO3
Magnesium Nitride Mg3N2
Lead Nitrate Pb(NO3)2
Alanine Ch4CH(Nh3 ) COOH
Аммоний NH5
Аргинин C6H24N4O2
Нитроглицерина C3H5 (NO3) 3
MAGITRINE C6H5NH3
CAFFEIN0671 Calcium Nitrate Ca(NO3)2
Sulfanilic acid C6H7NO3S
Methyl isocyanate C2h4NO
Silver Cyanide AgCN
Silver Azide AgN3
Silver Fulminate AgONC
Silver Thiocyanate AgSNC
Gold(I) Cyanide AuCN
Barium Cyanide Ba(CN)2
Barium Nitrite Ba(NO2)2
Азид бария BaN6
Тиоцианат бария Ba(SCN)2
Нитрид бария Ba3N2
Нитрат бериллия Be(NO3)2
Тетрагидрат нитрата бериллия Be(NO3)2.4h3O
Тригидрат нитрата бериллия 93hNO3O2 .Be(NO3)2 .Be0671 Нитрид бериллия Be3N2
Оксинитрат висмута(III) BiONO3
Субнитрат висмута(IV) Bi5O(OH)9(NO3)4
Азид брома BrN3
Цианид кальция Ca(7CN)2
Цианид кадмия Cd(CN)2
Азид кадмия Cd(N3)2
Нитрид кадмия Cd3N2
Нитрид церия(III) CeN
Цианид кобальта(II) Co(CN)2
Нитрат кобальта(II) 9Co(06712) Гексагидрат нитрата кобальта(II) Co(NO3)2,6h3O
Нитрат кобальта(III) Co(NO3)3
Феррицианид кобальта(II) Co3(Fe(CN)6)2
Пиколинат хрома(III) Cr(C6h5NO2)3
Нитрид хрома(III) CrN
Нитрат хрома(III) Cr(NO3)3
Цианид цезия CsCN
Цезий Амид CsNh3
Нитрит цезия CsNO2
Нитрат цезия CsNO3
Азид цезия CsN3
Цианид меди (I) CuCN
Цианид меди (II) Cu(CN)2
Азид меди (I) (CuN3) Азид меди (Nu3)
Тиоцианат меди(I) CuSCN
Ферроцианид меди(II) Cu2Fe(CN)6
Нитрид диспрозия(III) DyN
Нитрид эрбия(III) ErN
Нитрид европия(III) EuN
Нитрат фтора FNO3
Нитрат железа(II) Fe(NO3)2
Ферроцианид железа(III) Fe4(Fe(CN)6)3
Нитрат галлия(III) Ga(NO3)3
Нитрид гадолиния(III) GdN
Нитрид германия(IV) Ge3N4
Нитрид гафния HfN
Нитрат ртути(II) Hg(NO3)2
Тиоцианат ртути(II) Hg(SCN)2
Нитрид гольмия 90 6 HoN Моноазид йода IN3
Цианид калия KCN
Цианат калия KCNO
Диметилдитиокарбамат калия KC3H7NS2
Potassium Nitrite KNO2
Potassium Azide KN3
Potassium Thiocyanate KSCN
Potassium Ferricyanide K3(Fe(CN)6)
Lanthanum Nitride LaN
Lithium Diisopropylamide LiN(C3H7)2
Lithium Amide LiNh3
Lithium Azide LiN3
Lithium Nitride Li3N
Lutetium Nitride LuN
Нитрат лютеция Lu(NO3)3
Нитрат марганца(II) Mn(NO3)2
Нитрид молибдена(III) MoN
Трибромид азота NBr3
Трихлорид азота NCl3
Трифторид азота NF3
Nitrogen Triiodide NI3
Dinitrogen Difluoride N2F2
Dinitrogen Tetrafluoride N2F4
Dinitrogen Trioxide N2O3
Dinitrogen Tetroxide N2O4
Dinitrogen Pentoxide N2O5
Sodium Cyanoborohydride NaBh4CN
Sodium Cyanate NaCNO
Sodium Hydromethylglycinate NaC3H6NO3
Sodium Amide NaNh3
Sodium Azide NaN3
Sodium Thiocyanate NaSCN
Sodium Нитрит кобальта Na3Co(NO2)6
Ферроцианид натрия Na4Fe(CN)6
Нитрид ниобия(III) NbN
Нитрид неодима(III) NdN
Нитрат неодима(III) Nd(NO3)3
Цианид никеля(II) Ni(CN)2
Нитрат никеля(II) Ni(NO3)2
Нитрид нептуния(III) NpN
Свинец( II) Цианид Pb(CN)2
Тиоцианат свинца(II) Pb(SCN)2
Азид свинца(II) Pb(N3)2
Цианид палладия(II) Pd(CN)2
Нитрат палладия(II) Pd(NO3) )2
Нитрид празеодима(III) PrN
Цианид платины(II) Pt(CN)2
Нитрид плутония(III) PuN
Нитрат радия RaNO3
Нитрат родия(III) Rh(NO3)3
Тринитрид SBN
SCN
(III) NITRATE SC (NO3) 3
Силиконовый нитрид Si3n4
нитрит стронция (NO2) 2
Thiocyanate Srscn
Tantalum (III) nitride tan 9067.
Коэффициенты Стьюдента | это… Что такое Коэффициенты Стьюдента?
Толкование
- Коэффициенты Стьюдента
-
Кванти́ли (проценти́ли) распределе́ния Стью́дента (коэффициенты Стьюдента) — числовые характеристики, широко используемые в задачах математической статистики таких как построение доверительных интервалов и проверка статистических гипотез.
Содержание
- 1 Определение
- 2 Замечания
- 3 Таблица квантилей
- 3.1 Пример
- 4 См. также
Определение
Пусть Fn — функция распределения Стьюдента t(n) с n степенями свободы, и . Тогда α-квантилью этого распределения называется число tα,n такое, что
- .
Замечания
- Прямо из определения следует, что случайная величина, имеющая распределение Стьюдента с n степенями свободы, не превышает значение tα,n с вероятностью α и превышает его с вероятностью 1 − α.
- Функция Fnстрого возрастает для любого . Следовательно, определена её обратная функция , и
- .
- Функция не имеет простого представления. Однако, возможно вычислить её значения численно.
- Распределение t(n) симметрично. Следовательно,
- t1 − α,n = − tα,n.
Таблица квантилей
Нижеприведённая таблица получена с помощью функции tinv пакета tα,n, необходимо найти строку, соответствующую нужному n, и колонку, соответствующую нужному α. Искомое число находится в таблице на их пересечении.
Пример
- t0.2,4 = 0.2707;
- t0.8,4 = − t0.2,4 = − 0.2707.
См. также
- Распределение Стьюдента;
- Доверительный интервал для математического ожидания нормальной выборки.
Квантили tα,n
two-tailed test 1-0. 9/2
1-0.8/2 1-0.7/2 1-0.6/2 1-0.5/2 1-0.4/2 1-0.3/2 1-0.2/2 1-0.1/2 1-0.05/2 1-0.02/2 one-tailed test 1-0.9 1-0.8 1-0.7 1-0.6 1-0.5 1-0.4 1-0.3 1-0.2 1-0.1 1-0.05 1-0.02 1 0.1584 0.3249 0.5095 0.7265 1.0000 1.3764 1.9626 3.0777 6.3138 12.7062 31.8205 2 0.1421 0.2887 0.4447 0.6172 0.8165 1.0607 1.3862 1.8856 2.9200 4.3027 6.9646 3 0.1366 0.2767 0.4242 0.5844 0.7649 0.9785 1.2498 1.6377 2.3534 3.1824 4.5407 4 0.1338 0. 2707
0.4142 0.5686 0.7407 0.9410 1.1896 1.5332 2.1318 2.7764 3.7469 5 0.1322 0.2672 0.4082 0.5594 0.7267 0.9195 1.1558 1.4759 2.0150 2.5706 3.3649 6 0.1311 0.2648 0.4043 0.5534 0.7176 0.9057 1.1342 1.4398 1.9432 2.4469 3.1427 7 0.1303 0.2632 0.4015 0.5491 0.7111 0.8960 1.1192 1.4149 1.8946 2.3646 2.9980 8 0.1297 0.2619 0.3995 0.5459 0.7064 0.8889 1.1081 1.3968 1.8595 2.3060 2.8965 9 0.1293 0.2610 0.3979 0. 5435
0.7027 0.8834 1.0997 1.3830 1.8331 2.2622 2.8214 10 0.1289 0.2602 0.3966 0.5415 0.6998 0.8791 1.0931 1.3722 1.8125 2.2281 2.7638 11 0.1286 0.2596 0.3956 0.5399 0.6974 0.8755 1.0877 1.3634 1.7959 2.2010 2.7181 12 0.1283 0.2590 0.3947 0.5386 0.6955 0.8726 1.0832 1.3562 1.7823 2.1788 2.6810 13 0.1281 0.2586 0.3940 0.5375 0.6938 0.8702 1.0795 1.3502 1.7709 2.1604 2.6503 14 0.1280 0.2582 0.3933 0.5366 0. 6924
0.8681 1.0763 1.3450 1.7613 2.1448 2.6245 15 0.1278 0.2579 0.3928 0.5357 0.6912 0.8662 1.0735 1.3406 1.7531 2.1314 2.6025 16 0.1277 0.2576 0.3923 0.5350 0.6901 0.8647 1.0711 1.3368 1.7459 2.1199 2.5835 17 0.1276 0.2573 0.3919 0.5344 0.6892 0.8633 1.0690 1.3334 1.7396 2.1098 2.5669 18 0.1274 0.2571 0.3915 0.5338 0.6884 0.8620 1.0672 1.3304 1.7341 2.1009 2.5524 19 0.1274 0.2569 0.3912 0.5333 0.6876 0. 8610
1.0655 1.3277 1.7291 2.0930 2.5395 20 0.1273 0.2567 0.3909 0.5329 0.6870 0.8600 1.0640 1.3253 1.7247 2.0860 2.5280 21 0.1272 0.2566 0.3906 0.5325 0.6864 0.8591 1.0627 1.3232 1.7207 2.0796 2.5176 22 0.1271 0.2564 0.3904 0.5321 0.6858 0.8583 1.0614 1.3212 1.7171 2.0739 2.5083 23 0.1271 0.2563 0.3902 0.5317 0.6853 0.8575 1.0603 1.3195 1.7139 2.0687 2.4999 24 0.1270 0.2562 0.3900 0.5314 0.6848 0.8569 1. 0593
1.3178 1.7109 2.0639 2.4922 25 0.1269 0.2561 0.3898 0.5312 0.6844 0.8562 1.0584 1.3163 1.7081 2.0595 2.4851 26 0.1269 0.2560 0.3896 0.5309 0.6840 0.8557 1.0575 1.3150 1.7056 2.0555 2.4786 27 0.1268 0.2559 0.3894 0.5306 0.6837 0.8551 1.0567 1.3137 1.7033 2.0518 2.4727 28 0.1268 0.2558 0.3893 0.5304 0.6834 0.8546 1.0560 1.3125 1.7011 2.0484 2.4671 29 0.1268 0.2557 0.3892 0.5302 0.6830 0.8542 1.0553 1. 3114
1.6991 2.0452 2.4620 30 0.1267 0.2556 0.3890 0.5300 0.6828 0.8538 1.0547 1.3104 1.6973 2.0423 2.4573 31 0.1267 0.2555 0.3889 0.5298 0.6825 0.8534 1.0541 1.3095 1.6955 2.0395 2.4528 32 0.1267 0.2555 0.3888 0.5297 0.6822 0.8530 1.0535 1.3086 1.6939 2.0369 2.4487 33 0.1266 0.2554 0.3887 0.5295 0.6820 0.8526 1.0530 1.3077 1.6924 2.0345 2.4448 34 0.1266 0.2553 0.3886 0.5294 0.6818 0.8523 1.0525 1.3070 1. 6909
2.0322 2.4411 35 0.1266 0.2553 0.3885 0.5292 0.6816 0.8520 1.0520 1.3062 1.6896 2.0301 2.4377 36 0.1266 0.2552 0.3884 0.5291 0.6814 0.8517 1.0516 1.3055 1.6883 2.0281 2.4345 37 0.1265 0.2552 0.3883 0.5289 0.6812 0.8514 1.0512 1.3049 1.6871 2.0262 2.4314 38 0.1265 0.2551 0.3882 0.5288 0.6810 0.8512 1.0508 1.3042 1.6860 2.0244 2.4286 39 0.1265 0.2551 0.3882 0.5287 0.6808 0.8509 1.0504 1.3036 1.6849 2. 0227
2.4258 40 0.1265 0.2550 0.3881 0.5286 0.6807 0.8507 1.0500 1.3031 1.6839 2.0211 2.4233 41 0.1264 0.2550 0.3880 0.5285 0.6805 0.8505 1.0497 1.3025 1.6829 2.0195 2.4208 42 0.1264 0.2550 0.3880 0.5284 0.6804 0.8503 1.0494 1.3020 1.6820 2.0181 2.4185 43 0.1264 0.2549 0.3879 0.5283 0.6802 0.8501 1.0491 1.3016 1.6811 2.0167 2.4163 44 0.1264 0.2549 0.3878 0.5282 0.6801 0.8499 1.0488 1.3011 1.6802 2.0154 2. 4141
45 0.1264 0.2549 0.3878 0.5281 0.6800 0.8497 1.0485 1.3006 1.6794 2.0141 2.4121 46 0.1264 0.2548 0.3877 0.5281 0.6799 0.8495 1.0483 1.3002 1.6787 2.0129 2.4102 47 0.1263 0.2548 0.3877 0.5280 0.6797 0.8493 1.0480 1.2998 1.6779 2.0117 2.4083 48 0.1263 0.2548 0.3876 0.5279 0.6796 0.8492 1.0478 1.2994 1.6772 2.0106 2.4066 49 0.1263 0.2547 0.3876 0.5278 0.6795 0.8490 1.0475 1.2991 1.6766 2.0096 2.4049 50 0. 1263
0.2547 0.3875 0.5278 0.6794 0.8489 1.0473 1.2987 1.6759 2.0086 2.4033 100 0.1260 0.2540 0.3864 0.5261 0.6770 0.8452 1.0418 1.2901 1.6602 1.9840 2.3642 1000 0.1257 0.2534 0.3854 0.5246 0.6747 0.8420 1.0370 1.2824 1.6464 1.9623 2.3301
Wikimedia Foundation.
2010.
Игры ⚽ Поможем сделать НИР
- Коэффициенты Ламэ
- Коялович, Войцех
Полезное
Классические методы статистики: t-критерий Стьюдента
Начать, пожалуй, стоит с математических допущений, на которых основан критерий Стьюдента. Основных таких допущений, как известно, два:
Кроме того, в своей исходной форме, t-критерий предполагает независимость сравниваемых выборок.
Проверка указанных требований к данным должна всегда предшествовать формальному статистическому анализу, в котором задействован критерий Стьюдента (к сожалению, многие исследователи забывают об этом). Способы проверки этих требований я рассмотрю в будущих сообщениях. Сейчас же пока отметим, что условие нормальности распределения данных становится не таким жестким при «больших» объемах выборок, а для выборок с разными дисперсиями существует особая модификация t-критерия (критерий Уэлча; см. также ниже).
Этот вариант критерия Стьюдента служит для проверки нулевой гипотезы о равенстве среднего значения ((mu_1)) генеральной совокупности, из которой была взята выборка, некоторому известному значению ((mu_0)):
Рассчитанное значение критерия мы можем далее интерпретировать следующим образом, исходя из свойств t-распределения: если это значение попадает в т.н. область отклонения нулевой гипотезы (см. рисунок ниже), то мы вправе отклонить проверяемую нулевую гипотезу.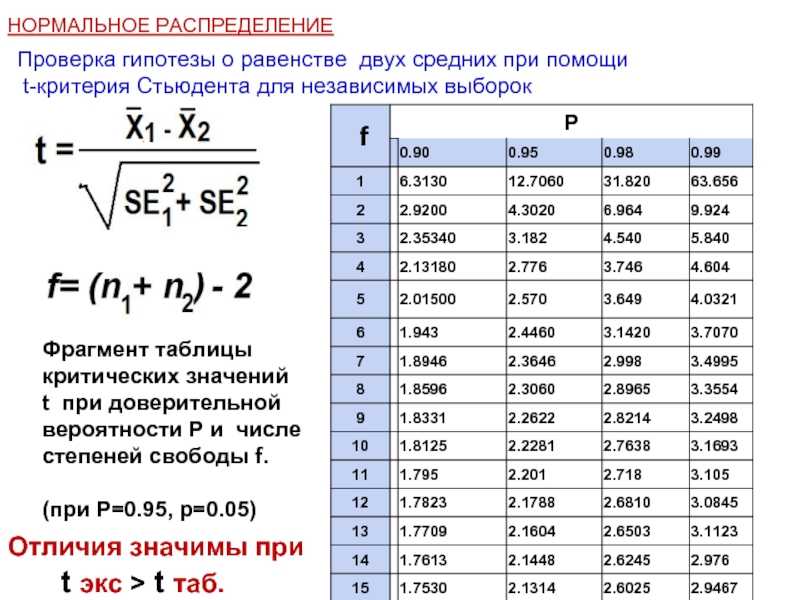
Эквивалентным подходом к интерпретации результатов теста будет следующий: допустив, что нулевая гипотеза верна, мы можем рассчитать, насколько велика вероятность получить t-критерий, равный или превышающий то реальное значение, которое мы рассчитали по имеющимся выборочным данным. Если эта вероятность оказывается меньше, чем заранее принятый уровень значимости (например, (P < 0.05)), мы вправе отклонить проверяемую нулевую гипотезу. Именно такой подход сегодня используется чаще всего: исследователи приводят в своих работах P-значение, которое легко рассчитывается при помощи статистических программ. Рассмотрим, как это можно сделать в системе R.
Предположим, у нас имеются данные по суточному потреблению энергии, поступающей с пищей (кДж/сутки), для 11 женщин (пример заимствован из книги Altman D.
d.intake <- c(5260, 5470, 5640, 6180, 6390, 6515, 6805, 7515, 7515, 8230, 8770)
Среднее значение для этих 11 наблюдений составляет:
mean(d.intake) [1] 6753.6
Вопрос: отличается ли это выборочное среднее значение от установленной нормы в 7725 кДж/сутки? Разница между нашим выборочным значением и этим нормативом довольно прилична: 7725 — 6753.6 = 971.4. Но насколько велика эта разница статистически? Ответить на этот вопрос поможет одновыборочный t-тест. Как и другие варианты t-теста, одновыборочный тест Стьюдента выполняется в R при помощи функции t.test():
t.test(d.intake, mu = 7725)
One Sample t-test
data: d.intake
t = -2.8208, df = 10, p-value = 0.01814
alternative hypothesis: true mean is not equal to 7725
95 percent confidence interval:
5986.348 7520.925
sample estimates:
mean of x
6753. 636
636
Видим, что для имеющихся выборочных данных t-критерий составляет -2.821 при 10 степенях свободы (df). Вероятность получить такое (либо большее) значение t при условии, что проверяемая нулевая гипотеза верна, оказалась весьма мала: p-value = 0.01814 (во всяком случае, это меньше 5%). Следовательно (см. выше), мы можем отклонить проверяемую нулевую гипотезу о равенстве выборочного среднего значения нормативу и принять альтернативную гипотезу (alternative hypothesis: true mean is not equal to 7725). Делая это, мы рискуем ошибиться с вероятностью менее 5%.
Помимо t-критерия, количества степеней свободы, Р-значения и выборочного среднего (sample estimates: mean of x), программа рассчитала также 95%-ный доверительный интервал (95 percent confidence interval) для истинной разницы между выборочным средним значением суточного потребления энергии и нормативом. Если бы мы повторили аналогичный тест много раз для разных групп из 11 женщин, то в 95% случаев эта разница оказалась бы в диапазоне от 5986.
Рассмотрим пример о суточном расходе энергии (expend) у худощавых женщин (lean) и женщин с избыточным весом (obese), приведенный в книге Питера Дальгаарда (Dalgaard P (2008) Introductory statistics with R. Springer). Данные из этого примера (подробнее см. ?energy) входят в состав пакета ISwR, сопровождающего книгу (если он у Вас не установлен, выполните команду install.packages(«ISwR»)):
library(ISwR) data(energy) attach(energy) energy expend stature 1 9.21 obese 2 7.53 lean 3 7.48 lean 4 8.08 lean 5 8.09 lean 6 10.15 lean 7 8.40 lean 8 10.88 lean 9 6.13 lean 10 7.90 lean 11 11.51 obese 12 12.79 obese 13 7.05 lean 14 11.85 obese 15 9.97 obese 16 7.48 lean 17 8.79 obese 18 9.69 obese 19 9.68 obese
Соответствующие средние значения потребления энергии в рассматриваемых группах пациенток составляют (подробнее о примененной ниже функции tapply() см. здесь):
tapply(expend, stature, mean) lean obese 8.07 10.30
Различаются ли эти средние значения статистически? Проверим гипотезу об отсутствии разницы при помощи t-теста:
t.test(expend ~ stature)
Welch Two Sample t-test
data: expend by stature
t = -3.8555, df = 15.919, p-value = 0.001411
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-3.459167 -1.004081
sample estimates:
mean in group lean mean in group obese
8.066154 10.297778
Обратите внимание на использование знака ~ в вызове функции t.test(). Это стандартный для R способ записи формул, описывающих связь между переменными.
Согласно полученному значению P (p-value = 0.001411), средние значения потребления энергии у женщин из рассматриваемых весовых групп статистически значимо различаются. Отвергая нулевую гипотезу о равенстве этих средних значений, мы рискуем ошибиться с вероятностью лишь около 0.1%. При этом истинная разница между средними значениями с вероятностью 95% находится в диапазоне от -3.5 до -1.0 (см. 95 percent confidence interval).
Следует подчеркнуть, что при выполнении двухвыборочного t-теста R по умолчанию принимает, что дисперсии сравниваемых совокупностей не равны, и, как следствие, выполняет t-тест в модификации Уэлча (подробнее см. здесь). Мы можем изменить такое поведение программы, воспользовавшись аргументом var.equal = TRUE: (от variance — дисперсия, и equal — равный):
t.test(expend ~ stature, var.equal = TRUE) Two Sample t-test data: expend by stature t = -3.9456, df = 20, p-value = 0.000799 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -3.411451 -1.051796 sample estimates: mean in group lean mean in group obese 8.066154 10.297778
Р-значение стало еще меньше, и мы так же, как и после теста в модификации Уэлча, можем сделать вывод о наличии существенной разницы между средними. Однако такое совпадение выводов будет иметь место не всегда и, следовательно, на разницу между групповыми дисперсиями (или ее отсутствие) следует обращать серьезное внимание при выборе и интерпретации того или иного варианта t-теста.
Сравнение двух зависимых (= парных) выборок
Зависимыми, или парными, являются две выборки, содержащие результаты измерений какого-либо количественного признака, выполненных на одних и тех же объектах. Во многих исследованиях какой-то определенный отклик измеряется у одних и тех же объектов до и после экспериментального воздействия.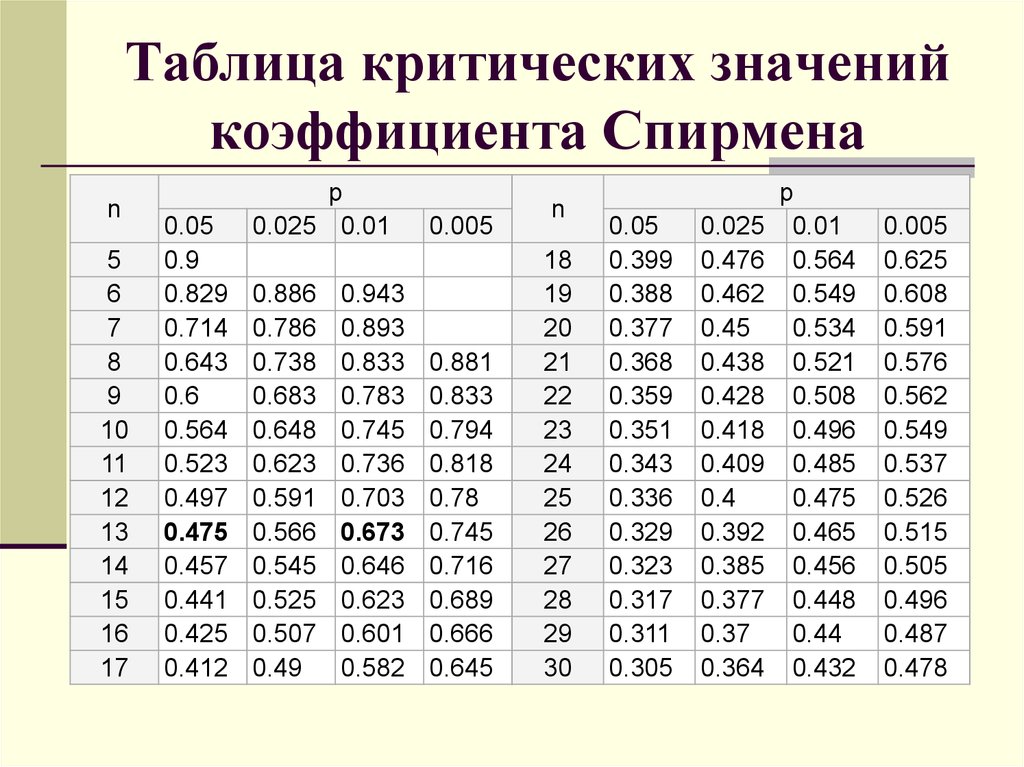
Но как в таких случаях оценить наличие эффекта от воздействия статистически? В общем виде критерий Стьюдента можно представить как
[t = frac{text{оценка параметра} — text{истинное значение параметра}}{text{ст. ошибка оценки параметра}}]
Нас интересует «истинное значение параметра» — среднее изменение какого-либо количественного признака как результат экспериментального воздействия — обозначим его (delta). Оценкой этого истинного параметра является наблюдаемое (выборочное) среднее изменение признака. Тогда t-критерий примет вид
[t = frac{bar{d} — delta}{S_{bar{d}}} ]
Если нулевая гипотеза заключается в равенстве истинного эффекта нулю, формула для парного критерия Стьюдента примет вид
[t = frac{bar{d}}{S_{bar{d}}} ]
В книге П.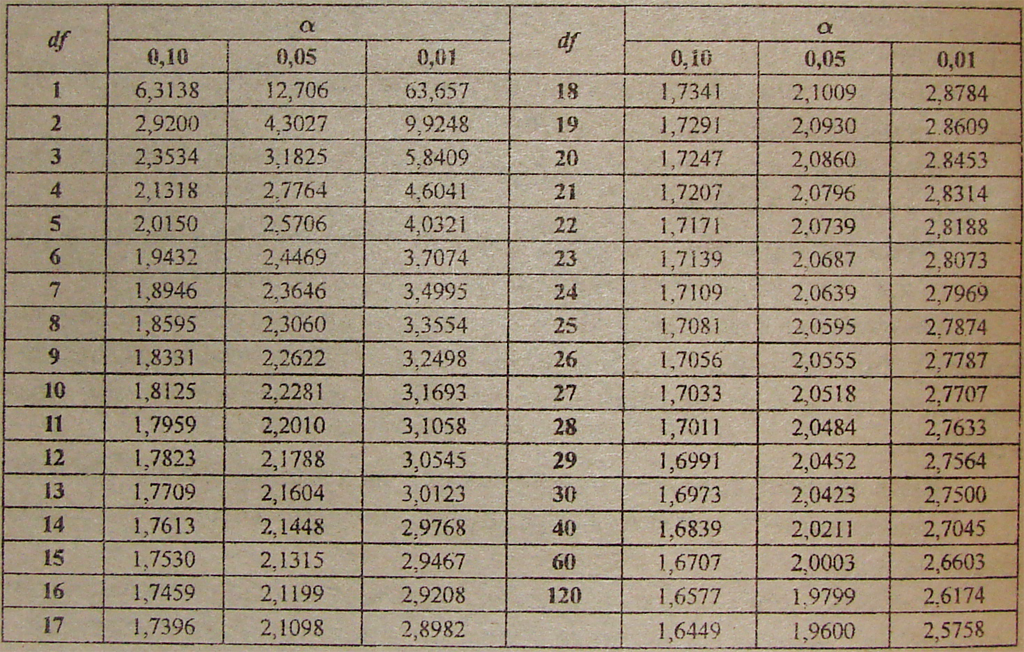
data(intake) # из пакета ISwR
attach(intake)
intake
pre post
1 5260 3910
2 5470 4220
3 5640 3885
4 6180 5160
5 6390 5645
6 6515 4680
7 6805 5265
8 7515 5975
9 7515 6790
10 8230 6900
11 8770 7335
Индивидуальные разницы в потреблении энергии у этих женщин составляют:
post - pre [1] -1350 -1250 -1755 -1020 -745 -1835 -1540 -1540 [9] -725 -1330 -1435
Усреднив эти индивидуальные разницы, получим
mean(post - pre) [1] -1320.5
Задача заключается в том, чтобы оценить, насколько статистически значимо эта средняя разница отличается от нуля. Применим парный критерий Стьюдента (обратите внимание на использование аргумента paired = TRUE):
t.test(pre, post, paired = TRUE)
Paired t-test
data: pre and post
t = 11. 9414, df = 10, p-value = 3.059e-07
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
1074.072 1566.838
sample estimates:
mean of the differences
1320.455
9414, df = 10, p-value = 3.059e-07
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
1074.072 1566.838
sample estimates:
mean of the differences
1320.455
Как видим, рассчитанное программой P-значение оказалось намного меньше 0.05, что позволяет нам сделать заключение о наличии существенной разницы в потреблении энергии у исследованных женщин до и после менструации. Истинная величина эффекта (в абсолютном выражении) с вероятностью 95% находится в интервале от 1074.1 до 1566.8 кДж/сутки.
Приведенные выше примеры охватывают наиболее типичные случаи применения критерия Стьюдента. За рамками этого сообщения остаются т.н. односторонние варианты t-теста, когда проверяемая нулевая гипотеза заключается в том, что одно из сравниваемых средних значений больше (или меньше) другого. Однако можно отметить, что односторонний вариант t-теста легко реализуется при помощи функции t.
Распределение | Что это такое и как его использовать (с примерами)
Опубликован в
28 августа 2020 г.
к
Ребекка Беванс.
Отредактировано
9 июля 2022 г.
Распределение t , также известное как t -распределение Стьюдента, представляет собой способ описания данных, которые следуют кривой нормального распределения при нанесении на график, с наибольшим количеством наблюдений, близких к среднему, и меньшим количеством наблюдений в хвосты.
Это тип нормального распределения, используемый для небольших выборок, когда дисперсия данных неизвестна.
В статистике t -распределение чаще всего используется для:
- Найдите критические значения для доверительного интервала, когда данные примерно нормально распределены.
- Найдите соответствующее p -значение из статистического теста, использующего t -распределение ( t -тесты, регрессионный анализ).
- Что такое t-распределение?
- T-распределение и стандартное нормальное распределение
- T-распределение и t-показатели
- Часто задаваемые вопросы о t-распределении
- Академический стиль
- Расплывчатые предложения
- Грамматика
- Согласованность стиля
- Верхняя и нижняя границы доверительного интервала, когда данные примерно нормально распределены.
- p -значение тестовой статистики для t -тестов и регрессионных тестов.
-
Что такое t-распределение?
-
t -значение (также известное как t -значение) эквивалентно количеству стандартных отклонений от среднего значения t -распределения.
Показатель t — это тестовая статистика, используемая в t -тестах и регрессионных тестах.
Его также можно использовать для описания того, насколько далеко от среднего находится наблюдение, когда данные следуют т -распределение.
-
Что такое тестовая статистика?
-
Статистика теста — это число, рассчитанное с помощью статистического теста. Он описывает, насколько ваши наблюдаемые данные далеки от нулевой гипотезы об отсутствии связи между переменными или отсутствии различий между группами выборок.
Тестовая статистика показывает, насколько две или более группы отличаются от общего среднего значения генеральной совокупности или насколько линейный наклон отличается от наклона, предсказанного нулевой гипотезой. В разных статистических тестах используются разные статистические данные.
-
Что такое критическое значение?
-
Вы уже проголосовали. Спасибо 🙂
Ваш голос сохранен 🙂
Обработка вашего голоса…Ребекка работает над докторской диссертацией по почвенной экологии, а в свободное время пишет. Она очень рада, что может поболтать о статистике со всеми вами.
т Распределение Основные понятия | Реальная статистика с использованием Excel
Основные понятия
Проверка гипотезы с одной выборкой, описанная в разделе «Проверка гипотез с использованием центральной предельной теоремы с использованием нормального распределения», подходит, когда известно стандартное отклонение распределения совокупности, а совокупность либо нормально распределена или выборка достаточно велика, чтобы применить центральную предельную теорему.
Проблема в том, что стандартное отклонение генеральной совокупности обычно неизвестно. Один из подходов к решению этой проблемы заключается в использовании стандартного отклонения s выборки в качестве аппроксимации стандартного отклонения σ для генеральной совокупности. Лучшим подходом является использование t-распределения.
Pdf и основные свойства
Определение 1 : ( Студенческий ) т распределение с к степеней свободы , сокращенно T ( k ) имеет функцию распределения вероятностей (pdf)
, где Γ(y) — гамма-функция, как описано в разделе Гамма-функция.
Ключевые статистические свойства распределения t:
- Среднее = 0 для k > 0
- Медиана = 0
- Режим = 0
- Диапазон = (-∞, ∞)
- Дисперсия = тыс. ⁄ ( тыс. – 2) для тыс.
> 2
- Асимметрия = 0 для k > 3
- Эксцесс = 6 ⁄ ( к – 4) для к > 4
Общая форма функции плотности вероятности распределения t напоминает колоколообразную форму нормально распределенной случайной величины со средним значением 0 и дисперсией 1, за исключением того, что она немного ниже и шире. По мере роста числа степеней свободы распределение t приближается к стандартному нормальному распределению, и в действительности приближение довольно близкое для K ≥ 30.
Рисунок 1 — Диаграмма T -распределения по градусам свободы
Другие свойства
свойство 1 : если x имеет нормальное дистрибьютор 555555555 года. , ?
Щелкните здесь для доказательства свойства 1.
свойство 2 : для выборок достаточно большого размера n со средним x̄ и стандартным отклонением s случайная величина
3 имеет распределение 0 T
3
( н – 1).
Доказательство: Это следует из свойства 1 центральной предельной теоремы.
Наблюдения
Тестовая статистика в свойствах 1 и 2 такая же, как
из центральной предельной теоремы с заменой стандартного отклонения совокупности σ на стандартное отклонение выборки s . Что делает это настолько полезным, так это то, что обычно стандартное отклонение совокупности неизвестно, в то время как стандартное отклонение выборки известно.
Если выборка составляет значительную часть (конечной) совокупности (например, более 5%), то стандартную ошибку s/ в свойствах 1 и 2 следует заменить на
, где N – численность населения.
Функции рабочего листа
Excel Functions : Excel обеспечивает следующие функции для распределения T:
T.DIST ( x , DF , CUM 9006). f ( x ) для распределения t, когда cum = FALSE и соответствующая кумулятивная функция распределения F ( x ), когда включая = ИСТИНА.
T.ОБР ( p,df ) = значение x такое, что T.DIST( x, df , TRUE) = p df , т.е. х, df , ИСТИНА).
Кроме того, Excel предоставляет следующие функции рабочего листа:
T.DIST.RT ( x , df ) = правая часть распределения t с размерами x и df степеней свободы.0003
T.DIST.2T ( x , df ) = сумма правого хвоста распределения t с df степеней свободы при x плюс левый хвост при -06,
5 -x6,
где x ≥ 0 (функция выдает значение ошибки, когда x < 0).
T.ОБР.2T ( p , df ) = значение x такое, что T.DIST.2T( x , df ) = 9000 .РАСП.2T( x , df )
Обратите внимание, что правый хвост на x , T.DIST.RT( x , df ) = 1 – T.
DIST( x 0d 0 , TRUE 0, , ). Поскольку распределение t симметрично относительно x = 0, левый хвост при — x также равен T.DIST.RT( x , df ) и сумме правого и левого хвостов, T.DIST .2T( x , df ) равно 2* T.DIST.RT( x , df ).
Так как распределение t симметрично относительно x = 0, мы имеем следующие эквивалентности:
T.DIST (- x , df , ИСТИНА) = 1 – T.DIST ( x , df , TRUE) = T.DIST .RT( x , df )
T.DIST.RT(- x , df ) = 1 – T.DIST.RT( x , df ) 900 x , df , ИСТИНА)
T.ОБР(1- p , df ) = T.ОБР.2T(2* p , df
) для
Как правило, мы используем T.DIST.RT и T.DIST.2T для одностороннего и двустороннего t-тестов соответственно. Мы используем T.ОБР.(1- p, df ) и T.ОБР.2T( p, df ) для односторонних и двусторонних критических значений соответственно.
Функции рабочего листа для более ранних версий Excel
Функции Excel : Вышеуказанные функции недоступны для версий Excel до Excel 2010. В Excel 2007 и более ранних версиях вместо них используются следующие функции, где x ≥ 0, DF > 0 и Хвосты = 1 или 2:
TDIST ( x, DF , Хвосты ) = T.DIST.RT ( x, DF ), если хвосты = 1 и = T.DIST.2T( x, df ) if tails = 2
TINV ( p, df ) = T.INV.2T( p, df )
функции более подробно описаны в разделе Встроенные статистические функции.
На рис. 2 приведены примеры использования этих функций рабочего листа Excel.
Рисунок 2 – Примеры функций распределения t
Функции для нецелочисленных df округляется до ближайшего меньшего целого числа. Таким образом, df = 3,7 обрабатывается так же, как df = 3.
Содержание
Что такое
t -распределение?
Распределение t — это тип нормального распределения, который используется для небольших выборок. Нормально распределенные данные образуют форму колокола при нанесении на график, с большим количеством наблюдений около среднего и меньшим количеством наблюдений в хвостах.
t -распределение используется, когда данные примерно нормально распределены, что означает, что данные имеют форму колокола, но дисперсия совокупности неизвестна. Дисперсия в t -распределении оценивается на основе степеней свободы набора данных (общее количество наблюдений минус 1).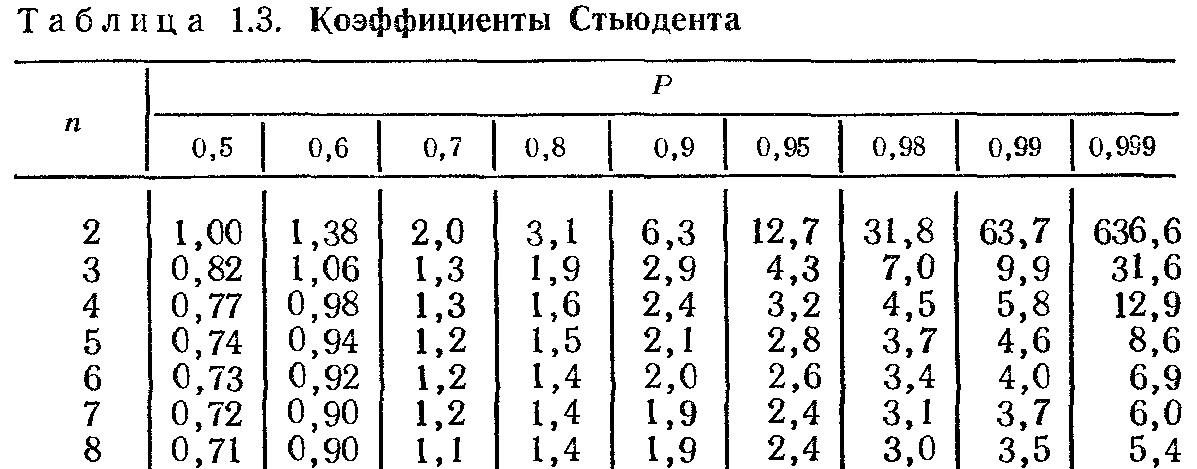
Это более консервативная форма стандартного нормального распределения , также известного как распределение z . Это означает, что оно дает более низкую вероятность центру и более высокую вероятность хвостам, чем стандартное нормальное распределение.
Пример: t -распределение по сравнению с z -распределение Если вы измеряете средний балл теста по выборке только из 20 учащихся, вы должны использовать t -распределение для оценки доверительного интервала вокруг среднего значения. Если вы используете распределение z , ваш доверительный интервал будет искусственно точным.
T — распределение и стандартное нормальное распределение
При увеличении степеней свободы (общее количество наблюдений минус 1) 9Распределение 0005 t будет все ближе и ближе соответствовать стандартному нормальному распределению, также известному как распределение z , пока они не станут почти идентичными.
Свыше 30 степеней свободы распределение t примерно совпадает с распределением z . Таким образом, распределение z можно использовать вместо распределения t при больших размерах выборки.
Распределение z предпочтительнее t -распределение, когда дело доходит до статистических оценок, потому что оно имеет известную дисперсию. Он может дать более точные оценки, чем t -распределение, дисперсия которого аппроксимируется с использованием степеней свободы данных.
Получение отзывов о языке, структуре и форматировании
Профессиональные редакторы вычитывают и редактируют вашу статью, уделяя особое внимание:
См. пример
Т -распределение и т -баллы
t -оценка представляет собой число стандартных отклонений от среднего в t -распределении.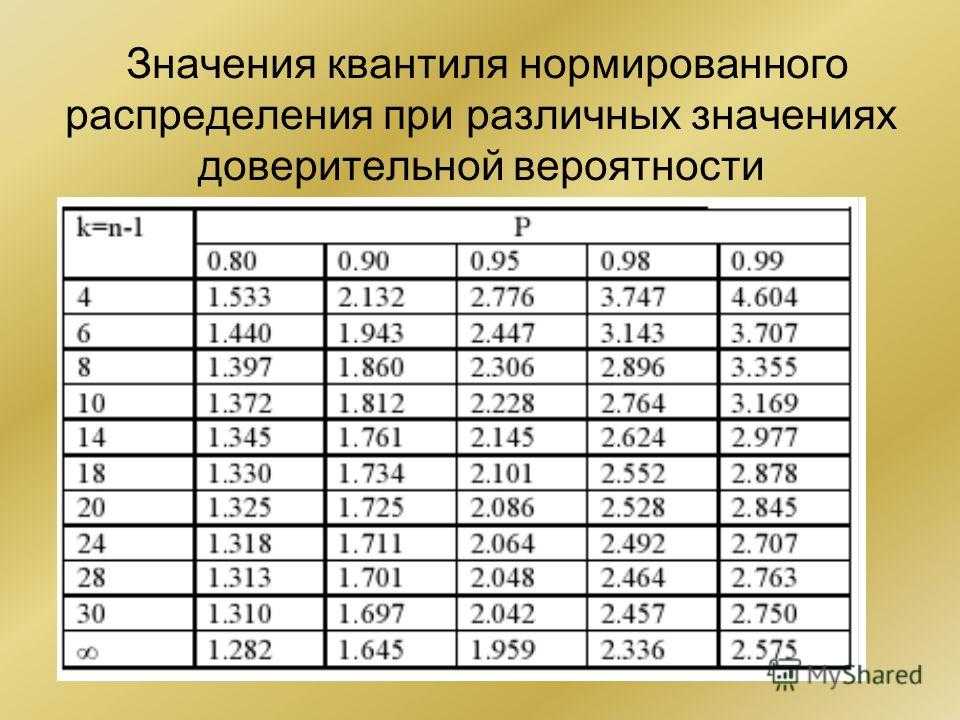
В статистике t -оценки в основном используются для нахождения двух вещей:
T — баллы и доверительные интервалы
Доверительные интервалы используют t -показателей для вычисления верхней и нижней границ интервала прогнозирования. Оценка t , используемая для получения верхней и нижней границ, также известна как критическое значение из t или t *.
Пример доверительного интервалаВы выбрали 20 учащихся из двух разных классов для оценки средних результатов стандартизированного теста и хотите узнать, есть ли разница между двумя группами.
Используя двусторонний t -критерий, вы получаете оценку разницы между двумя классами и доверительный интервал вокруг этой оценки. Из теста t вы обнаружите, что разница в среднем балле между классом 1 и классом 2 составляет 4,61, с 95% доверительный интервал от 3,87 до 5,35.
Поскольку доверительный интервал не пересекает ноль и на самом деле очень далек от нуля, маловероятно, что эта разница в результатах тестов могла возникнуть при нулевой гипотезе об отсутствии различий между группами.
T -баллы и p -значения
Статистические тесты генерируют тестовую статистику, показывающую, насколько далеки ваши данные от нулевой гипотезы статистического теста. Затем они вычисляют p — значение, описывающее вероятность того, что ваши данные появятся, если нулевая гипотеза верна.
Статистика теста для t -тестов и регрессионных тестов представляет собой t -оценку. В то время как большинство статистических программ автоматически вычисляют соответствующее значение p для оценки t , вы также можете найти значения в таблице t , используя ваши степени свободы и t -оценку, чтобы найти значение p .
Значение t , которое дает значение p ниже вашего порога статистической значимости, известно как критическое значение t или t *.
Пример p-значения. Двусторонний t -критерий разницы результатов теста дает t -значение 12,79. Это означает, что разница в средних групповых значениях составляет 12,79 стандартных отклонений от среднего значения распределения нулевой гипотезы.
Степени свободы 38 (n–1 для каждой группы). Глядя на это в t -table (или вычислив его в вашей любимой статистической программе) вы найдете p -значение < 0,001.
Этот вывод, как и вывод из доверительного интервала, предполагает, что вы вряд ли обнаружите такую большую разницу, если истинная разница в средних результатах теста равна нулю.
Часто задаваемые вопросы о t-распределении
Онлайн калькулятор периметра вписанного в круг квадрата. Как узнать периметр вписанного в круг квадрата.
При помощи нашего калькулятора вы легко сможете узнать периметр вписанного в круг квадрата.
| Вычислить периметр вписанного квадрата через: | R — радиус кругаD — диаметр кругаS — площадь кругаP — периметр круга |
| Радиус круга R: |
Для того что бы найти периметр вписанного в круг квадрата, нам необходимо узнать длину ребра этого квадрата. Для этого нам необходимо разделить квадрат по диагонали на два равнобедренных треугольника, при этом основание у этих треугольников будет равно диаметру круга.
Следующим действиям мы должны определиться с известной нам величиной круга в которую вписан квадрат, а именно нам должна быть известна:
- либо площадь круга, обозначаемая буквой S,
- либо периметр круга, обозначаемый буквой P,
- либо радиус круга, обозначаемый буквой R,
- либо диаметр круга, обозначаемый буквой D.
Начнем по порядку, мы имеем равнобедренный прямоугольный треугольник и для того, что бы узнать длину его ребер нам необходимо воспользоваться теоремой Пифагора исходя из которой
c2 = 2a2,
Таким образом
a = √c2/2
Теперь для того что бы найти длину ребра треугольника (которое равно стороне нашего квадрата) нам необходимо узнать длину основания треугольника, которое равно диаметру круга
D = c
1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
D=2√S/π
2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
D=P/π
3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
D=2R
Соответственно если мы знаем диаметр круга который равен основанию треугольника полученного путем разделения квадрата на две части по диагонали,
c=D
мы можем узнать длину сторон квадрата используя теорему Пифагора
a = √c2/2
после того как мы получили значение длины стороны вписанного квадрата равную a, для получения его периметра нам необходимо полученное значение умножить на 4.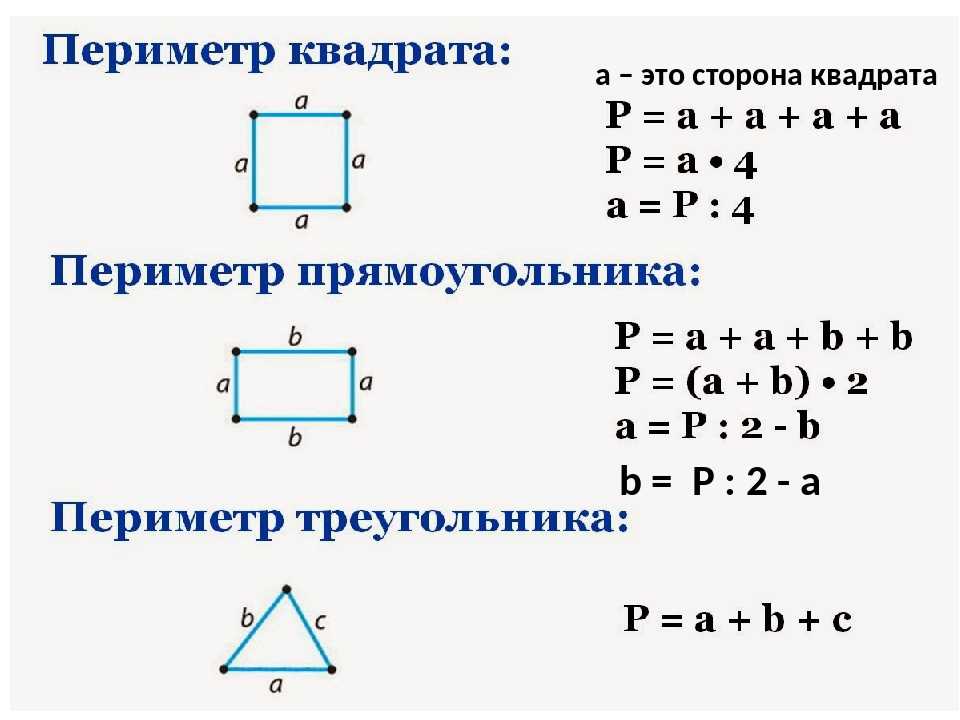
S = 4a
Вычислить периметр вписанного квадрата через R — радиус круга |
Вычислить периметр вписанного квадрата через D — диаметр круга |
Вычислить периметр вписанного квадрата через S — площадь круга |
Вычислить периметр вписанного квадрата через P — периметр круга |
Периметр квадрата и прямоугольника. Способы определения и примеры решения. :: SYL.ru
Часто на просторах интернета можно найти насмешки по поводу того, как знания по математике — интегралы, дифференциалы, тригонометрические функции и прочие разделы предмета — не помогают облегчить жизнь человека.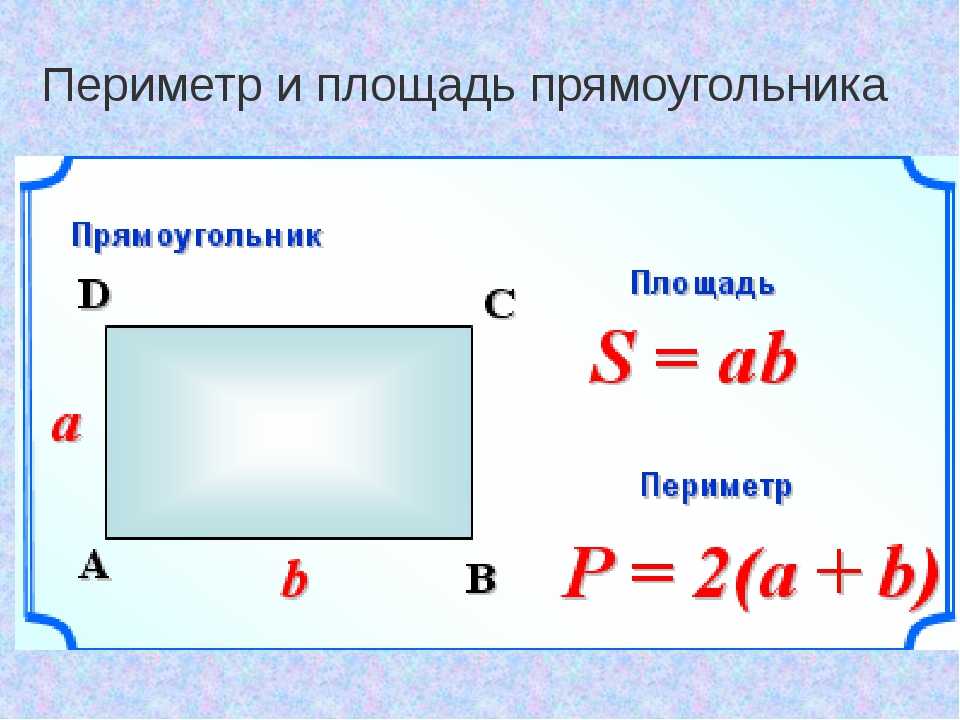
Свойства квадрата
Любые вычисления в математике базируются на свойствах объекта. Чтобы ответить на вопрос: «Чему равен периметр квадрата?» — рекомендуется вспомнить отличительные характеристики этой фигуры.
- Равенство всех сторон.
- Наличие четырех углов величиной 90 градусов.
- Параллельность сторон.
- Поворотная симметрия. При вращении фигуры ее вид остается неизменным.
- Возможность описать и вписать окружность.
- Диагонали при пересечении делят друг друга пополам.
- Площадь фигуры характеризует заполненное квадратом место в двухмерном пространстве.
- Периметр фигуры не что иное, как сумма длин его сторон.
- Из предыдущего свойства вытекает, что единицами измерения величины периметра будут единицы длины: м, см, дм и другие.
Для подсчета плинтусов для завершения ремонта в квадратном помещении, необходимо знать длину комнаты. Для этого необходимо посчитать ее периметр.
Периметр
В переводе с греческого языка слово означает «измерять вокруг». Термин применим ко всем замкнутым фигурам: квадрату, окружности, прямоугольнику, треугольнику, трапеции и прочим. Знания по определению периметра элементарных фигур необходимы для решения сложных геометрических задач с объектами неправильной формы. Например, для расчета плинтусов в комнату планировкой типа «Г», или как еще называют, «сапожком», потребуется определить периметр квадрата и прямоугольника. Ведь форма помещения состоит из этих элементарных фигур.
Общепринятое обозначение такой величины – буква Р. Каждой фигуре с учетом ее свойств присуща своя формула для определения периметра.
Свойства прямоугольника
- Равенство противоположных сторон.
- Равенство диагоналей.
- Возможность описать окружность.
- Высоты прямоугольника равны его сторонам.
- Сумма углов равна 360 градусов, и все углы прямые.
- Параллельность противоположных сторон.
- Перпендикулярность прилегающих сторон.
- Сумма квадратов диагоналей прямоугольника равна сумме квадратов его сторон.
- Пересекаясь, диагонали делят друг друга пополам.
- Невозможность вписать в фигуру окружность.
Периметр квадрата
В зависимости от установленных (известных) параметров квадрата, существуют разные формулы для определения его периметра. Простой задачей является расчет периметра при установленной длине его стороны (с). В этом случае Р=с+с+с+с или 4*с. Например, длина стороны квадрата 7 см, тогда периметр фигуры буде 28 см (4*7).
В первом случае все понятно, но как найти периметр квадрата, зная его площадь? И тут все предельно ясно. Поскольку площадь фигуры определяется умножением одной стороны на другую, а у квадрата все стороны равны, необходимо извлечь корень из известной величины. Пример: есть квадрат с площадью 25 дм2.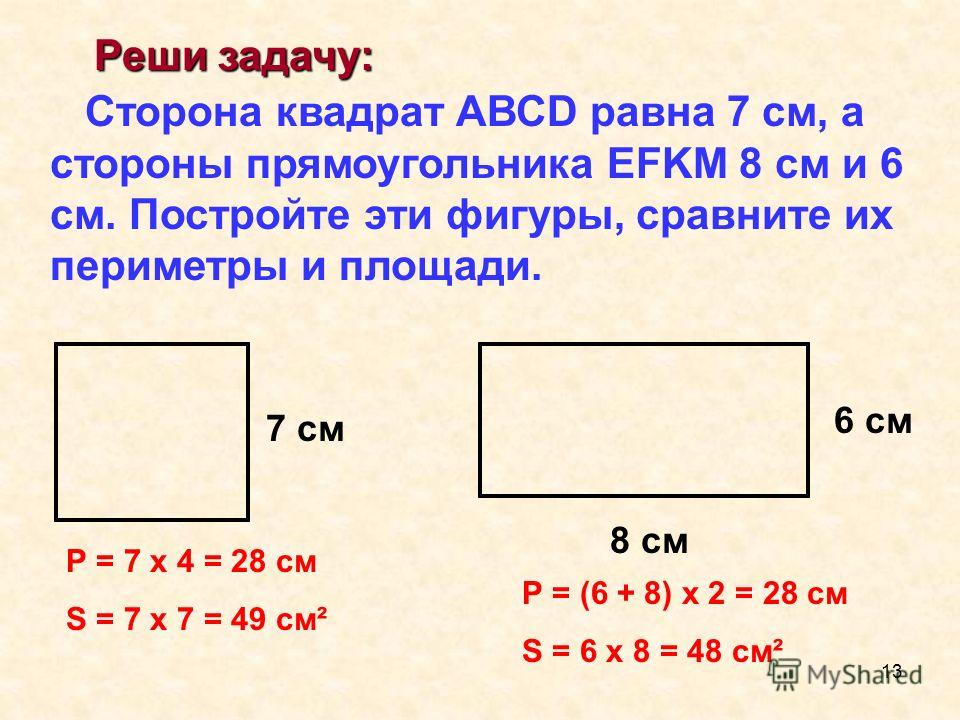
Квадрат и окружность
Из свойств рассматриваемой фигуры выплывает, что в квадрат можно вписать окружность и также ее описать вокруг фигуры.
Первый вариант – нахождение периметра по радиусу описанной окружности. Вписанным считается квадрат, вершины которого находятся на окружности. Радиус окружности равен 1/2 длине диагонали. Выходит, что диаметр равен диагонали. Теперь необходимо рассмотреть прямоугольный треугольник, который получился в результате деления диагональю квадрата. Решение задачи сводится к нахождению сторон этого треугольника. ВС – это известная величина, диаметр описанной окружности. Допустим, он равен 3 см. Теорема Пифагора в случае с равными сторонами треугольника, будет выглядеть так: 2с2=32 .
Особенностью вписанной окружности является деление сторон квадрата пополам. Поэтому радиус равняется половине длины стороны квадрата. Тогда сторона с=2*радиус. Периметр квадрата в этом случае равен 4*2*радиус или 8 радиусам окружности.
Периметр прямоугольника
Самая элементарная формула определения периметра прямоугольника через известные величины его сторон выглядит так: Р=2(а+b), где а и b — длины сторон фигуры.
Диагональ прямоугольника аналогично квадрату делит фигуру пополам, образуя прямоугольный треугольник. Однако задача усложняется тем, что стороны этого треугольника неравные. В случае с известной величиной одной из сторон и диагонали, вторую можно найти, следуя теореме Пифагора: д2=а2+в2, где а и в – стороны фигуры, а д – диагональ.
Если неизвестна ни одна из сторон, тогда в дело вступают знания тригонометрии: синусы, косинусы и другие функции.
Нахождение периметра по описанной окружности и известному диаметру сводится к тому, что диаметр равен длине диагонали фигуры. Дальше решение задачи определяется по наличию известных величин. Если даны углы, тогда через тригонометрические функции. Если дана сторона, ответ будет найден через теорему Пифагора.
Прямоугольник и тригонометрические функции
Для наглядности приведен пример решения задачи. Дано: прямоугольник АВСД; длина диагонали (d) 20 см; угол ф – 30°. Найти периметр фигуры.
Из тригонометрии необходимо вспомнить следующее: синус угла в прямоугольном треугольнике равен отношению противоположного катета к гипотенузе. Синус 30° (существуют таблицы, по которым можно определить значения тригонометрических функций для правильных углов) равен 1/2. Получается 1/2 = отношению в к d. Неизвестная величина в будет равна d/2=20/2=10 см.
Для расчета периметра следует найти вторую сторону фигуры. Можно через теорему Пифагора, так как известны длины гипотенузы и одного из катетов или опять через отношение сторон для косинуса угла.
Косинус угла ф выражается как отношение прилежащего катета к гипотенузе и равен √3/2.
√3/2=n/d, n=(d*√3)/2 или 10*√3. После извлечения корня из 3, получаем длину стороны треугольника: 10*1,73=17,3 см.
Периметр равен 2(17,3+10)=2*27,3=54,6 см.
Периметр и отношение сторон
В школьной программе встречаются задачи по геометрии, когда длины сторон прямоугольника выражены их отношением друг к другу. Рассмотрение решения подобной задачи представлено ниже.
Известно, что сумма длин всех сторон прямоугольника, то есть его периметр, равен 84 см. Отношение длины (д) к ширине (ш) – 3:2. Найти стороны фигуры.
Решение: пусть длина будет 3х, а ширина 2х, согласно соотношению из условия задачи. Формула периметра прямоугольника с полученными данными длин сторон будет следующей: 3х+3х+2х+2х = 84. Далее, 10х = 84, х=8,4 см. Подставив х в выражение длины и ширины прямоугольника, можно найти искомые величины. Длина будет: 3*8,4 = 25,2 см; ширина: 2*8,4 = 16,8 см.
Статья посвящена решению наиболее часто встречаемых задач в школьной программе. И это далеко не все способы нахождения периметра квадрата и прямоугольника.
Программа Python для нахождения периметра квадрата
Питон
Джава
С
С++
HTML
CSS
JavaScript
PHP
SQL
Контрольный опрос
В этой статье мы создали несколько программ на Python, чтобы найти и распечатать периметр квадрата на основе длины
его стороны, введенной пользователем во время выполнения. Вот список программ:
- Найти периметр квадрата без функции
- Использование определяемой пользователем функции
- Использование класса
Прежде чем запускать эти программы, давайте сначала напомним вам об используемой здесь формуле.
Формула для нахождения периметра квадрата
Чтобы найти периметр любого квадрата, используйте следующую формулу:
per = 4*side
Здесь per указывает периметр, а сторона указывает длину стороны квадрата.
То есть, как вы все знаете, периметр квадрата можно вычислить, сложив все его четыре стороны, или просто
умножение любой стороны на 4.
Следовательно, если длина стороны квадрата равна 2 метрам, то его периметр будет равен 2+2+2+2 или 4*2 ,
что равно 16 .
Найти периметр квадрата без функции
Чтобы вычислить периметр квадрата в Python, вы должны попросить пользователя ввести длину стороны квадрата,
затем используйте приведенную выше формулу и рассчитайте периметр, как показано в программе, приведенной ниже:
print("Введите длину стороны квадрата:")
с = интервал (ввод ())
р = 4*с
print("nПериметр = ", p)
Приведенный ниже снимок показывает начальный вывод, созданный этой программой Python:
Теперь введите ввод, скажем, 5 в качестве длины стороны квадрата, и нажмите клавишу ENTER , чтобы найти и
напечатайте значение периметра, как показано на снимке ниже:
Модифицированная версия предыдущей программы
В этой программе end= используется для пропуска автоматического перехода на новую строку с помощью print() .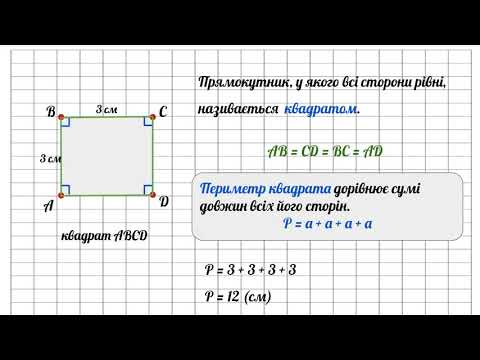
используется с format() для печати значения p только до двух знаков после запятой.
print("Введите длину стороны: ", end="")
с = с плавающей запятой (ввод ())
р = 4*с
print("nPerimeter = {:.2f}".format(p))
Вот пример запуска с пользовательским вводом 3.4 в качестве длины стороны квадрата:
Найти периметр квадрата с помощью функции
Эта программа делает то же задание, что и предыдущее, но с использованием определяемой пользователем функции с именем findPerSqr() . Этот
Функция получает в качестве аргумента длину любой стороны квадрата и возвращает значение площади.
по определению findPerSqr(x):
вернуть 4*х
print("Введите длину стороны: ", end="")
с = с плавающей запятой (ввод ())
p = найтиPerSqr(s)
print("nPerimeter = {:.2f}".format(p))
Эта программа выводит тот же результат, что и предыдущая программа.
Найти периметр квадрата с помощью класса
Это последняя программа в этой статье, созданная с использованием класса , объектно-ориентированной функции Python.
Доступ к функции-члену класса осуществляется через его объект. Поэтому мы создали объект с именем об и
через этот объект мы получили доступ к функции-члену с именем findPerSqr() класса CodesCracker .
класс CodesCracker:
def найтиPerSqr (я, х):
вернуть 4*х
print("Введите длину стороны: ", end="")
с = с плавающей запятой (ввод ())
ob = Взломщик кодов()
p = ob.findPerSqr(s)
print("nPerimeter = {:.2f}".format(p))
Та же программа на других языках
- Java Вычислить периметр квадрата
- C Расчет периметра квадрата
- С++ Вычисление периметра квадрата
Онлайн-тест Python
« Предыдущая программаСледующая программа »
Поделись, пожалуйста:
Подпишитесь на нас/Нравится на Facebook
Подпишитесь на нас на YouTube
Калькулятор периметра квадрата
Периметр квадрата — Периметр квадрата определяется как длина границы квадрата.
Примеры расчетов периметра квадрата
Квадрат представляет собой плоскую форму с четырьмя сторонами равной длины, с прямым углом 90° на каждой стороне.
Этот небольшой калькулятор предназначен для вычисления периметра квадрата. Это бесплатный онлайн-инструмент для автоматического определения области, которая задается в заданном вопросе.
Формула периметра квадрата
Универсальная формула для вычисления периметра квадрата:
4a= 4*a, где a равно стороне квадрата.
Чтобы измерить периметр квадрата, нам нужно знать длину его сторон и умножить длину сторон на 4. Все четыре стороны имеют одинаковую длину. Они обозначаются единицей измерения или сантиметром.
Необходимые шаги:
Шаг 1- Запишите длины сторон, указанные в вопросе
Шаг 2- Обозначьте длину как «а»
Шаг 3- Напишите формулу- 4a = 4*a
Шаг 4- вставьте значения, указанные в вопросе, так, как написано в формуле.
Шаг 5- умножить данные стороны на 4
Шаг 6- Полученный результат является мерой периметра в назначенных ему единицах измерения
Пример 1- Найдите периметр квадрата со стороной 100 см
Решение-
Шаг 1- данная сторона как «а» равна 100 см.
Шаг 2- 4a=4*a
Шаг 3- 4*100= 400
Шаг 4- Периметр квадрата равен 400 см
Пример 2- Нас могут попросить найти сторону квадрата квадрат. Например, найдите сторону квадрата, периметр которого равен 196 м.
Решение-
Шаг 1- площадь = 196 м
Шаг 2- 4a= 4*a
Шаг 3- 196= 4*a => 196/4= a => a=49
Шаг 4- сторона квадрата равна 49
Пример 3- Можно задать отношение периметров 2-х квадратов. Например, если отношение площадей двух квадратов 225:256, то отношение их периметров будет-
Решение-
Шаг 1- сторона квадрата будет «а».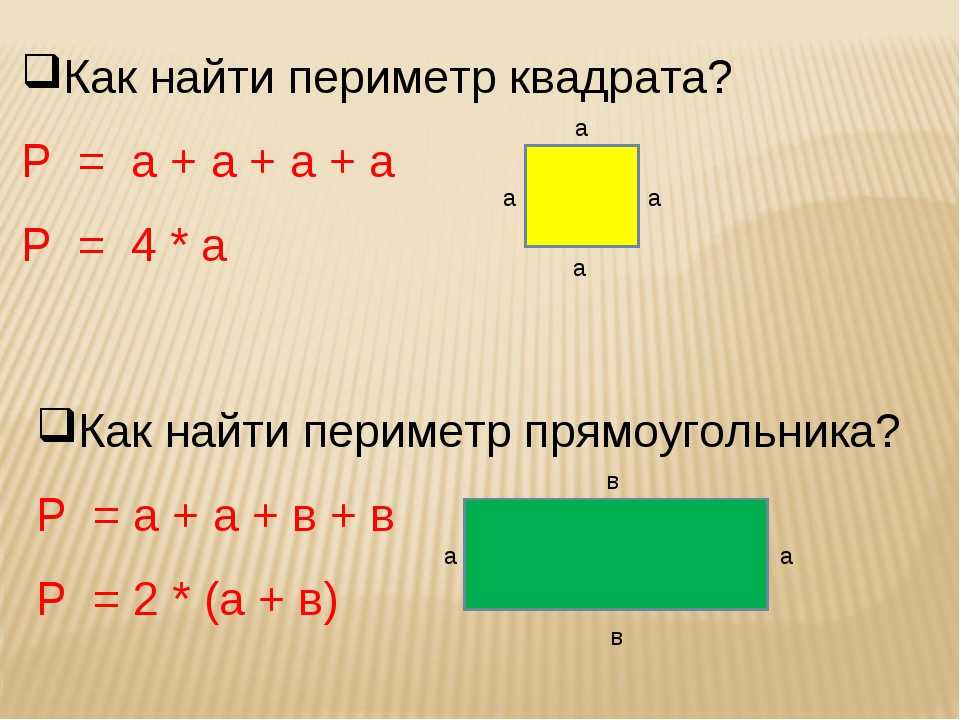
circ }.) Найдите периметр трапеции.
Ответ
ОТВЕТ: 75.
Задача 18. Дана равнобедренная трапеция ABCD с основаниями AD и BC. Периметр треугольника ABM равен 25, AB = 10, MD = 8, (BMparallel CD.) Найдите периметр трапеции.
Ответ
ОТВЕТ: 41.
Задача 19. Дана прямоугольная трапеция ABCD (см. рис.). Найдите длину меньшего основания BC.
Ответ
ОТВЕТ: 6.
Задача 20. В равнобедренной трапеции ABCD с основаниями AD и BC диагонали AC и BD перпендикулярны. Найдите высоту трапеции, если сумма оснований равна 23.
Ответ
ОТВЕТ: 11,5.
Реклама
Поддержать нас
Решение Ященко ОГЭ 2023 Вариант №16 (36 вариантов) Математика
Решение заданий варианта №16 из сборника ОГЭ 2023 по математике И. В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ решебник для 9 класса. Ответы с решением. Полный разбор всех заданий.
ЧАСТЬ 1
Задание 1-5.
В жилых домах установлены бытовые электросчётчики, которые фиксируют расход электроэнергии в киловатт-часах (кВт·ч). Учёт расхода электроэнергии может быть однотарифным, двухтарифным или трёхтарифным.
При однотарифном учёте стоимость 1 кВт · ч электроэнергии не меняется в течение суток. При двухтарифном и трёхтарифном учёте она различна в зависимости от времени суток (сутки разбиты на периоды, называемые тарифными зонами).
В таблице дана стоимость 1 кВт · ч электроэнергии в рублях в 2021 году.
В квартире у Петра Сергеевича установлен трёхтарифный счётчик, и в 2021 году Николай Андреевич оплачивал электроэнергию по трёхтарифному учёту.
На рисунке точками показан расход электроэнергии в квартире Петра Сергеевича по тарифным зонам за каждый месяц 2021 года.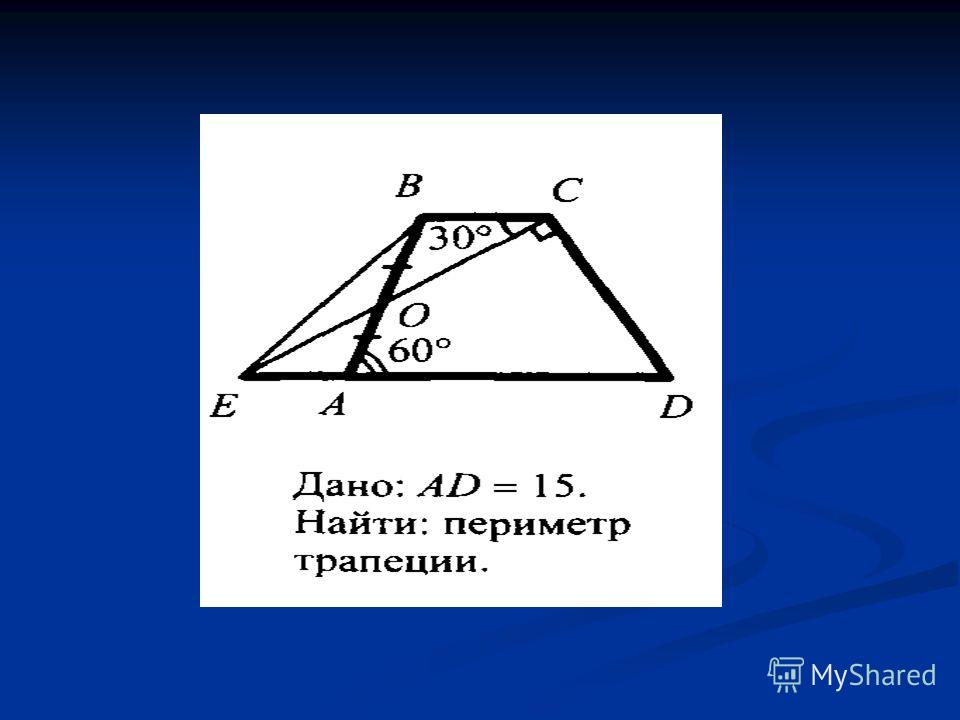
Задание 6.
Найдите значение выражения (frac{2}{15}+frac{5}{12})cdot frac{16}{11}.
Задание 7.
На координатной прямой точки А, В, С и D соответствуют числам -frac{1}{50}; frac{1}{50}; -frac{11}{15}; -frac{11}{50}.
Какой точке соответствует число -frac{11}{50}?
1) A 2) B 3) C 4) D
Задание 8.
Найдите значение выражения 9√7·2√2·√14.
Задание 9.
Решите уравнение x2 – 4 = 2x – 1.
Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Задание 10.
Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,14. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Задание 11.
Установите соответствие между графиками функций и формулами, которые их задают.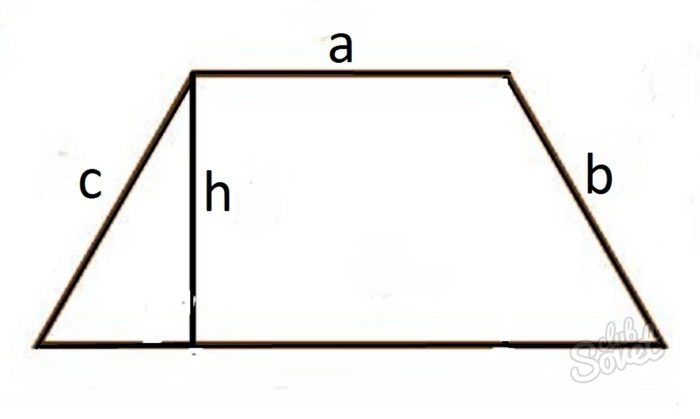
ФОРМУЛЫ
А) y=frac{1}{6x}
Б) y=-frac{6}{x}
В) y=frac{6}{x}
ГРАФИКИ
В таблице под буквой укажите соответствующий номер.
Задание 12.
Потенциальная энергия тела (в джоулях) в поле тяготения Земли вблизи её поверхности вычисляется по формуле Е = mgh, где m – масса тела (в килограммах), g – ускорение свободного падения (в м/с2), a h – высота (в метрах), на которой находится это тело, относительно поверхности. Пользуясь этой формулой, найдите m (в килограммах), если g = 9,8 м/с2, h = 5 м, а E = 196 Дж.
Задание 13.
Укажите неравенство, решение которого изображено на рисунке.
1) x2 – 16 ≤ 0
2) x2 – 4x ≤ 0
3) x2 – 4x ≥ 0
4) x2 – 16 ≥ 0
Задание 14.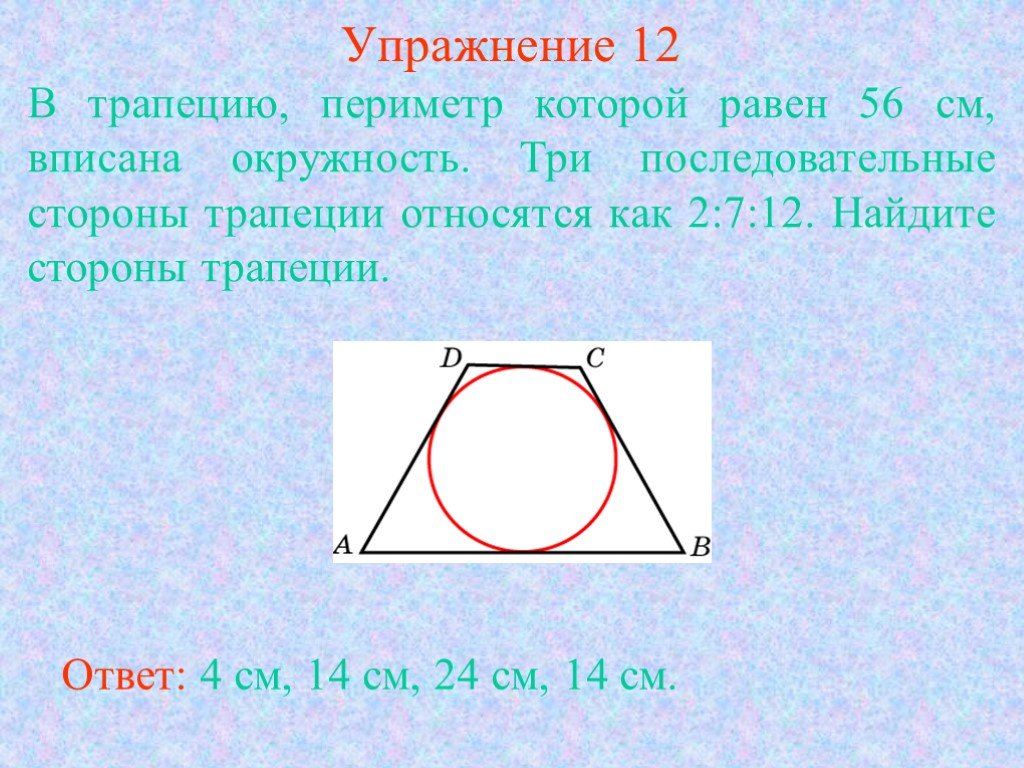
В ходе распада радиоактивного изотопа его масса уменьшается вдвое каждые 6 минут. В начальный момент масса изотопа составляла 640 мг. Найдите массу изотопа через 42 минуты. Ответ дайте в миллиграммах.
Задание 15.
В треугольнике ABC угол С равен 90°, М – середина стороны АВ, АВ = 64, ВС = 44. Найдите СМ.
Задание 16.
Касательные в точках A и В к окружности с центром в точке О пересекаются под углом 56°. Найдите угол АВО. Ответ дайте в градусах.
Задание 17.
Высота равнобедренной трапеции, проведённая из вершины С, делит основание AD на отрезки длиной 8 и 17. Найдите длину основания ВС.
Задание 18.
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Задание 19.
Какое из следующих утверждений верно?
1) Диагонали ромба равны.
Определите, при каких значениях k прямая у = kx имеет с графиком ровно одну общую точку.
Задание 23.
Отрезки АВ и DC лежат на параллельных прямых, а отрезки АС и BD пересекаются в точке М. Найдите МС, если АВ = 14, DC = 30, АС = 39.
Задание 24.
В остроугольном треугольнике ABC проведены высоты AA1 и BB1. Докажите, что углы BB1A1 и BAA1 равны.
Задание 25.
В равнобедренную трапецию, периметр которой равен 20, а площадь равна 20, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
Источник варианта: Сборник ОГЭ 2023 по математике. Типовые экзаменационные варианты. 36 вариантов. Под редакцией И.В. Ященко.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5.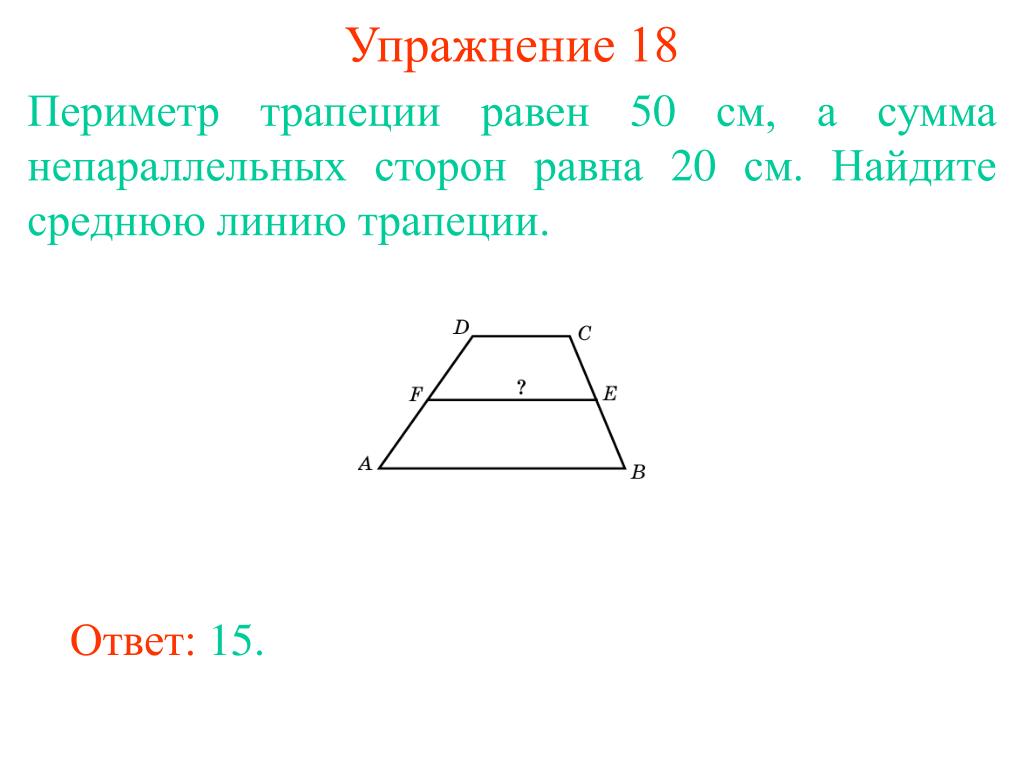
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
- Запись опубликована:
Введение.
Интегральное исчисление имеет многочисленные приложения в геометрии, механике, физике и технике. Оно дает общий метод нахождения площадей, объемов, центров тяжести и т.д.
Курс математического анализа содержит разнообразный материал, однако, одним из его центральных разделов является определенный интеграл. Интегрирование многих видов функций подчас представляет собой одну из труднейших проблем математического анализа.
Вычисление определенного интеграла имеет не только теоретический интерес. К его вычислению сводятся иногда задачи, связанные с практической деятельностью человека.
Также понятие определенного интеграла широко используется в физике.
Если же говорить о программе Excel, которая является одной из наиболее известных в обработке электронных таблиц, то без преувеличения можно утверждать, что ее возможности практически неисчерпаемы.
Обработка текста, управление базами данных — программа настолько мощна, что во многих случаях превосходит специализированные программы — редакторы или программы баз данных. Такое многообразие функций может поначалу запутать, нежели заставить применять их на практике. Но по мере приобретения опыта начинаешь по достоинству ценить то, что границ возможностей Excel тяжело достичь.
За всю историю табличных расчетов с применением персональных компьютеров требования пользователей к подобным программам существенно изменились. В начале основной акцент в такой программе, как, например, Visi Calc, ставился на счетные функции. Сегодня, положение другое. Наряду с инженерными и бухгалтерскими расчетами организация и графическое изображение данных приобретают все возрастающее значение. Кроме того, многообразие функций, предлагаемое такой расчетной и графической программой, не должно осложнять работу пользователя. Программы для Windows создают для этого идеальные предпосылки.
Ряд технологических задач требует увязки в математическое описание всей информации о процессе. Например, для математических моделей химико-технологических процессов одними из основных параметров, характеризующих процессы, являются концентрации реагирующих веществ, температура процесса и др. Как правило, большинство балансовых уравнений в химической технологии представлены системой интегральных и дифференциальных уравнений, в результате решения которых могут быть получены зависимости, характеризующие протекание процесса.
Часто на практике не удается вычислить интеграл аналитическим путем. В этих случаях применяют приближенные методы численного интегрирования.
Постановка задачи
Вычислить определенный интеграл
при условии, что а и b конечны и F(х) является непрерывной функцией х на всем интервале х[a,b]. Во многих случаях, когда подынтегральная функция задана в аналитическом виде, интеграл от этой функции в пределах от а до b может быть вычислен по формуле Ньютона-Лейбница:
Однако этой формулой часто нельзя воспользоваться по следующим причинам:
- первообразная функция f(x) слишком сложна и ее нельзя выразить в элементарных функциях;
- функция f(x) задана в виде таблицы, что особенно часто встречается в задачах химической технологии при обработке экспериментальных данных.
В этих случаях используются методы численного интегрирования.
Задача численного интегрирования состоит в нахождении приближенного значения интеграла по заданным или вычисленным значениям.
Общий подход к решению задачи будет следующим. Определенный интеграл I представляет собой площадь, ограниченную кривой f(x), осью х и переменными х=а и х=b. Необходимо вычислить интеграл, разбивая интервал [a,b] на множество меньших интервалов, находя приблизительно площадь каждой полоски и суммируя их.
В зависимости от способа вычисления подынтегральной суммы существуют различные методы численного интегрирования (методы прямоугольников, трапеций, парабол, сплайнов и др.).
Все методы будут рассматриваться на примере вычисления следующего интеграла:
Метод прямоугольников.
Существует несколько видов формул прямоугольников:
Формула левых прямоугольников.
В общем виде формула левых прямоугольников на отрезке [x0;xn] выглядит следующим образом:
Формула правых прямоугольников.
В общем виде формула правых прямоугольников на отрезке [x0;xn] выглядит следующим образом:
В данной формуле x0=a, xn=b.
Формула средних прямоугольников.
В общем виде формула средних прямоугольников на отрезке [x0;xn] выглядит следующим образом:
где xi=xi-1+h.
В данной формуле, как и в предыдущих, требуется h умножать сумму значений функции f(x), но уже не просто подставляя соответствующие значения x0,x1,…,xn-1 в функцию f(x), а прибавляя к каждому из этих значений h/2 (x0+h/2, x1+h/2,…, xn-1+h/2), а затем только подставляя их в заданную функцию.
На практике данные способы реализуются следующим образом:
Для того, чтобы вычислить интеграл по формуле левых прямоугольников в Excel, необходимо выполнить следующие действия:
Ввести в ячейку A1 текст a=.
Ввести в ячейку B1 число 0.
Ввести в ячейку A2 текст b=.
Ввести в ячейку B2 число 3,2.
Ввести в ячейку A3 текст n=.
Ввести в ячейку B3 число 10.
Ввести в ячейку A4 текст h=.
Ввести в ячейку B4 формулу =(B2-B1)/B3.
Вести в ячейку A6 текст i, в B6 — x, в C6 — y0,…,y(n-1).
Ввести в ячейку A7 число 0.
Ввести в ячейку A8 формулу =A7+1, скопировать эту формулу методом протягивания в диапазон ячеек A8:A17.
Ввести в ячейку B7 число 0.
Ввести в ячейку B8 формулу =B7+$B$4, скопировать эту формулу методом протягивания в диапазон ячеек B8:B17.
Ввести в ячейку C7 формулу =КОРЕНЬ(B7^4-B7^3+8), скопировать эту формулу методом протягивания в диапазон ячеек C8:C16.
Ввести в ячейку B18 текст сумма:.
Ввести в ячейку B19 текст интеграл=.
Ввести в ячейку C18 формулу =СУММ(C7:C16).
Ввести в ячейку C19 формулу =B4*C18.
Ввести в ячейку C20 текст левых.
В итоге получаем следующее:
Ответ: значение заданного интеграла равно 12,500377.
Для того, чтобы вычислить интеграл по формуле правых прямоугольников в Excel, необходимо выполнить следующие действия:
Продолжить работу в том же документе, что и при вычислении интеграла по формуле левых прямоугольников.
В ячейку D6 ввести текст y1,…,yn.
Ввести в ячейку D8 формулу =КОРЕНЬ(B8^4-B8^3+8), скопировать эту формулу методом протягивания в диапазон ячеек D9:D17
Ввести в ячейку D18 формулу =СУММ(D7:D17).
Ввести в ячейку D19 формулу =B4*D18.
Ввести в ячейку D20 текст правых.
В итоге получаем следующее:
Ответ: значение заданного интеграла равно 14,45905.
Для того, чтобы вычислить интеграл по формуле средних прямоугольников в Excel, необходимо выполнить следующие действия:
Продолжить работу в том же документе, что и при вычислении интеграла по формулам левых и правых прямоугольников.
В ячейку E6 ввести текст xi+h/2, а в F6 — f(xi+h/2).
Ввести в ячейку E7 формулу =B7+$B$4/2, скопировать эту формулу методом протягивания в диапазон ячеек E8:E16
Ввести в ячейку F7 формулу =КОРЕНЬ(E7^4-E7^3+8), скопировать эту формулу методом протягивания в диапазон ячеек F8:F16
Ввести в ячейку F18 формулу =СУММ(F7:F16).
Ввести в ячейку F19 формулу =B4*F18.
Ввести в ячейку F20 текст средних.
В итоге получаем следующее:
Ответ: значение заданного интеграла равно 13,40797.
Исходя из полученных результатов, можно сделать вывод, что формула средних прямоугольников является наиболее точной, чем формулы правых и левых прямоугольников.
Метод трапеций.
В общем виде формула трапеций на отрезке [x0;xn] выглядит следующим образом:
В данной формуле x0=a, xn=b, так как любой интеграл в общем виде выглядит:
h можно вычислить по следующей формуле: h=(b-a)/n (19).
y0, y1,…, yn — это значения соответствующей функции f(x) в точках x0, x1,…, xn (xi=xi-1+h)» [3].
На практике данный способ реализуется следующим образом:
Для того, чтобы вычислить интеграл по формуле трапеций в Excel, необходимо выполнить следующие действия:
Ввести в ячейку A1 текст n=.
Ввести в ячейку B1 число 10.
Ввести в ячейку A2 текст a=.
Ввести в ячейку B2 число -1.
Ввести в ячейку A3 текст b=.
Ввести в ячейку B3 число 1.
Ввести в ячейку A4 текст h=(b-a)/n.
Ввести в ячейку B4 формулу =(B3-B2)/B1.
Заполнить диапазон ячеек A6:D6 следующим образом:
Ввести в ячейку A7 число 0.
Ввести в ячейку A8 формулу =A7+1, скопировать эту формулу методом протягивания в диапазон ячеек A8:A17.
Ввести в ячейку B7 число -1.
Ввести в ячейку B8 формулу =B7+$B$4, скопировать эту формулу методом протягивания в диапазон ячеек B8:B17.
Ввести в ячейку C7 формулу =КОРЕНЬ(B7^4-B7^3+8), а в ячейку C17 формулу =КОРЕНЬ(B17^4-B17^3+8).
Ввести в ячейку D8 формулу =КОРЕНЬ(B8^4-B8^3+8), скопировать эту формулу методом протягивания в диапазон ячеек D8:B16.
Ввести в ячейку B18 текст суммы:.
Ввести в ячейку C18 формулу =СУММ(C7;C17).
Ввести в ячейку D18 формулу =СУММ(D8:D16).
Ввести в ячейку A19 текст интеграл=.
Ввести в ячейку B19 формулу =B4*(C18/2+D18).
Метод парабол или Симпсона.
Этот метод более точный по сравнению с методами прямоугольников и трапеций, а поэтому наиболее широко известный и применяемый метод численного интегрирования.
Метод аналогичен рассмотренным ранее методам прямоугольников и трапеций: интервал интегрирования разбивается на множество более мелких отрезков; однако для вычисления площади под каждым из отрезков через три последовательных ординаты разбиения проводится квадратичная парабола.
Формулу Симпсона получаем, проводя параболу через три ординаты на концах двух соседних интервалов и складывая получившиеся при этом площади.
Поскольку в методе Симпсона парабола проводится через три ординаты на концах двух соседних интервалов, то при реализации этого метода необходимо требовать, чтобы «n» было четным числом.
На практике данный способ реализуется следующим образом:
Для того, чтобы вычислить интеграл по формуле Симпсона в Excel, необходимо выполнить следующие действия:
Ввести в ячейку A1 текст n=.
Ввести в ячейку B1 число 10.
Ввести в ячейку A2 текст a=.
Ввести в ячейку B2 число 0.
Ввести в ячейку A3 текст b=.
Ввести в ячейку B3 число 3,2.
Ввести в ячейку A4 текст h=.
Ввести в ячейку B4 формулу =(B3-B2)/B1.
Заполнить диапазон ячеек A6:D6 следующим образом:
Ввести в ячейку A7 число 0.
Ввести в ячейку A8 формулу =A7+1, скопировать эту формулу методом протягивания в диапазон ячеек A8:A17.
Ввести в ячейку B7 число 0.
Ввести в ячейку B8 формулу =B7+$B$4, скопировать эту формулу методом протягивания в диапазон ячеек B8:B17.
Ввести в ячейку C7 формулу =КОРЕНЬ(B7^4-B7^3+8), а в ячейку C17 формулу =КОРЕНЬ(B17^4-B17^3+8).
Заполнить нижеприведенные ячейки:
Ввести в ячейку C18 формулу =(C7-C17)/2.
Ввести в ячейку D18 формулу =2*D8+2*D10+2*D12+2*D14+2*D16.
Ввести в ячейку E18 формулу =E9+E11+E13+E15+E17.
Ввести в ячейку A19 текст интеграл=.
Ввести в ячейку B19 формулу =(2*B4/3)*(C18+D18+E18).
В итоге получаем следующее:
Заключение
Рассмотренные выше примеры практических задач, дают нам ясное представление значимости определенного интеграла для их разрешимости.
Трудно назвать научную область, в которой бы не применялись методы интегрального исчисления, в общем, и свойства определенного интеграла, в частности. Так в процессе выполнения работы нами были рассмотрены примеры практических задач в области физики, геометрии, механики, биологии и экономики. Конечно, это еще далеко не исчерпывающий список наук, которые используют интегральный метод для поиска устанавливаемой величины при решении конкретной задачи, и установлении теоретических фактов.
Также определенный интеграл используется для изучения собственно самой математики. Например, при решении дифференциальных уравнений, которые в свою очередь вносят свой незаменимый вклад в решение задач практического содержания. Можно сказать, что определенный интеграл — это некоторый фундамент для изучения математики. Отсюда и важность знания методов их решения.
Из всего выше сказанного понятно, почему знакомство с определенным интегралом происходит еще в рамках средней общеобразовательной школы, где ученики изучают не только понятие интеграла и его свойства, но и некоторые его приложения.
Литература
- Волков Е.А. Численные методы. М., Наука, 1988.
- Пискунов Н.С. Дифференциальное и интегральное исчисление. М., Интеграл-Пресс, 2004. Т. 1.
- Шипачев В.С. Высшая математика. М., Высшая школа, 1990.
- Бронштейн И.Н., Семендяев К.А. Справочник по высшей математике для инженеров и учащихся втузов. — М.: Наука , 1981 . — 718 с.
- Белецкий Я. Excel с графикой для персональных компьютеров перевод с польского Д.И.Юренкова. -М.: Машиностроение , 1991. — 320 с.
- Самарский А.А, Гулин А.В. Численные методы.М.:Наука,1989. – 430 с.
- http://tgspa.ru/info/education/faculties
- http://www.machinelearning.ru/wiki

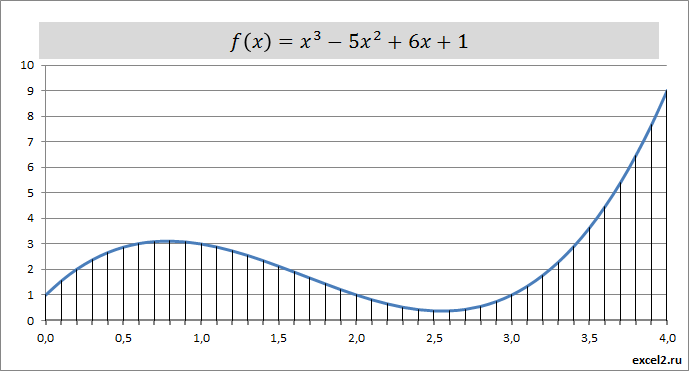
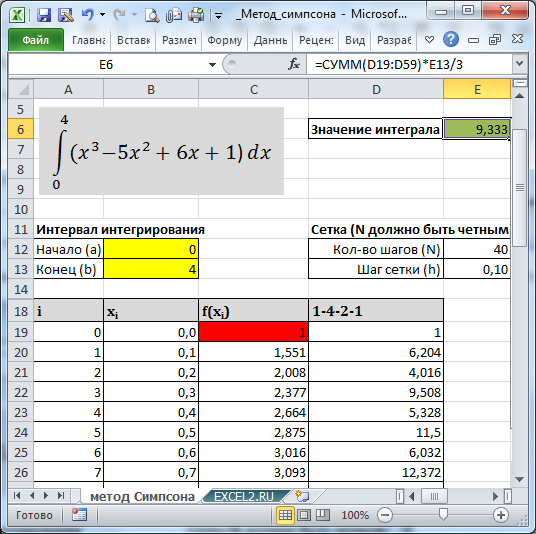
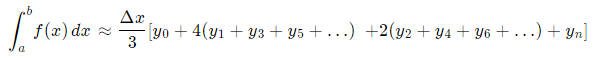
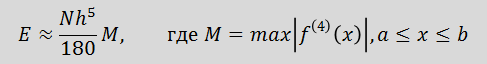
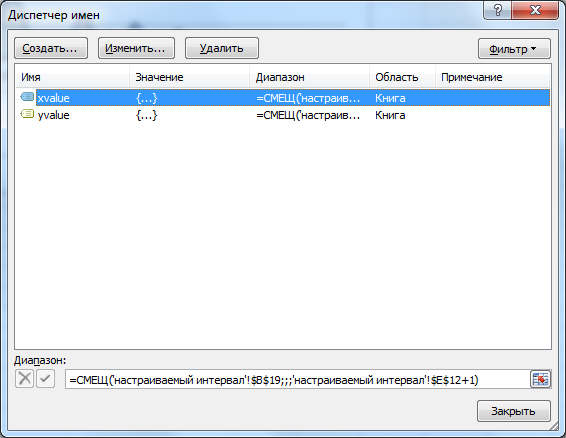
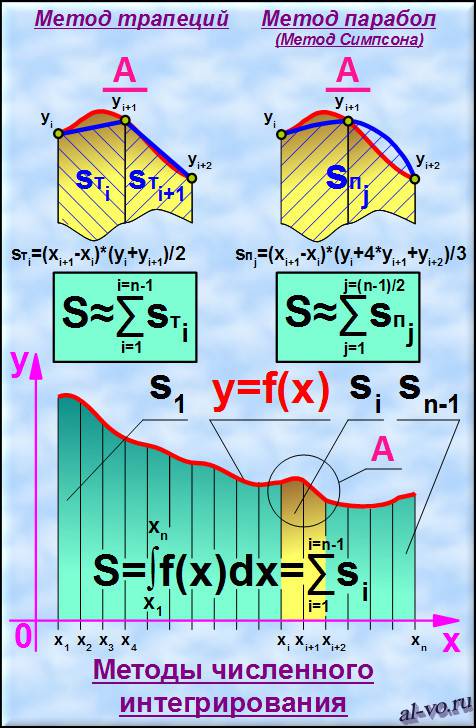
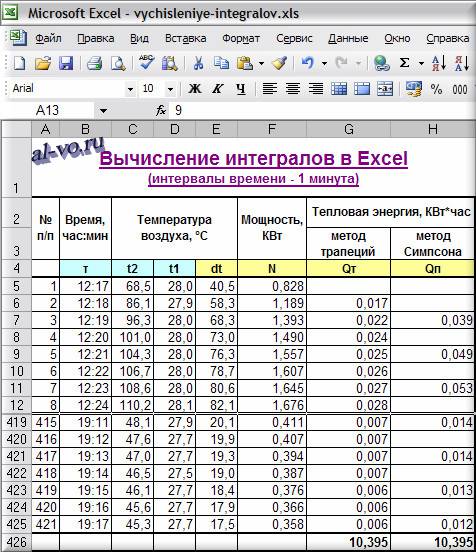
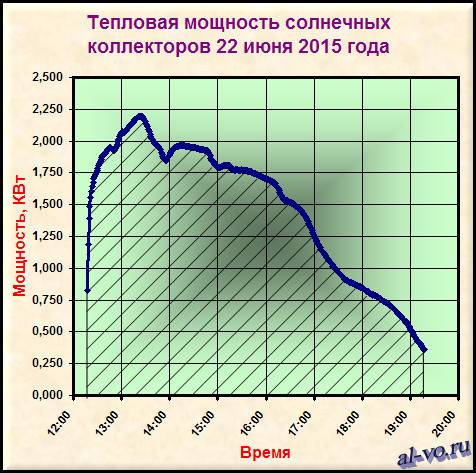
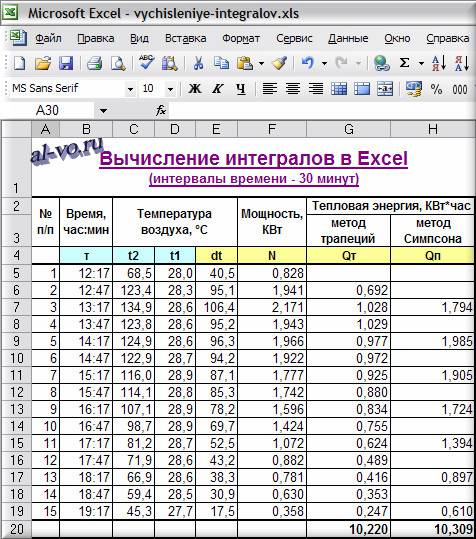
 Расстояние от села до города 20км. Путник прошел метров осталось ему идти? NIS 2 этого расстояния. Сколько кило-. помогите пожалуйста пжпжпж даю сто балла. по Сочу пж.
Расстояние от села до города 20км. Путник прошел метров осталось ему идти? NIS 2 этого расстояния. Сколько кило-. помогите пожалуйста пжпжпж даю сто балла. по Сочу пж.
 Скільки центнерів картоплі продали за два дні?
Скільки центнерів картоплі продали за два дні?

 Записати рівняння реакцій між металами з порядковими номерами 3, 13, 20, 25, 26, 28, 30, 37, 47, 56 з водою і сульфатною кислотою.
Записати рівняння реакцій між металами з порядковими номерами 3, 13, 20, 25, 26, 28, 30, 37, 47, 56 з водою і сульфатною кислотою. Серебристо – белые.
Серебристо – белые. :
: 43 моль х моль
43 моль х моль Серебристо – белые.
Серебристо – белые. Дэви; 2) У. Гилберт; 3) Й. Берцелиус; 4) А.Арфведсон
Дэви; 2) У. Гилберт; 3) Й. Берцелиус; 4) А.Арфведсон 2 л
2 л
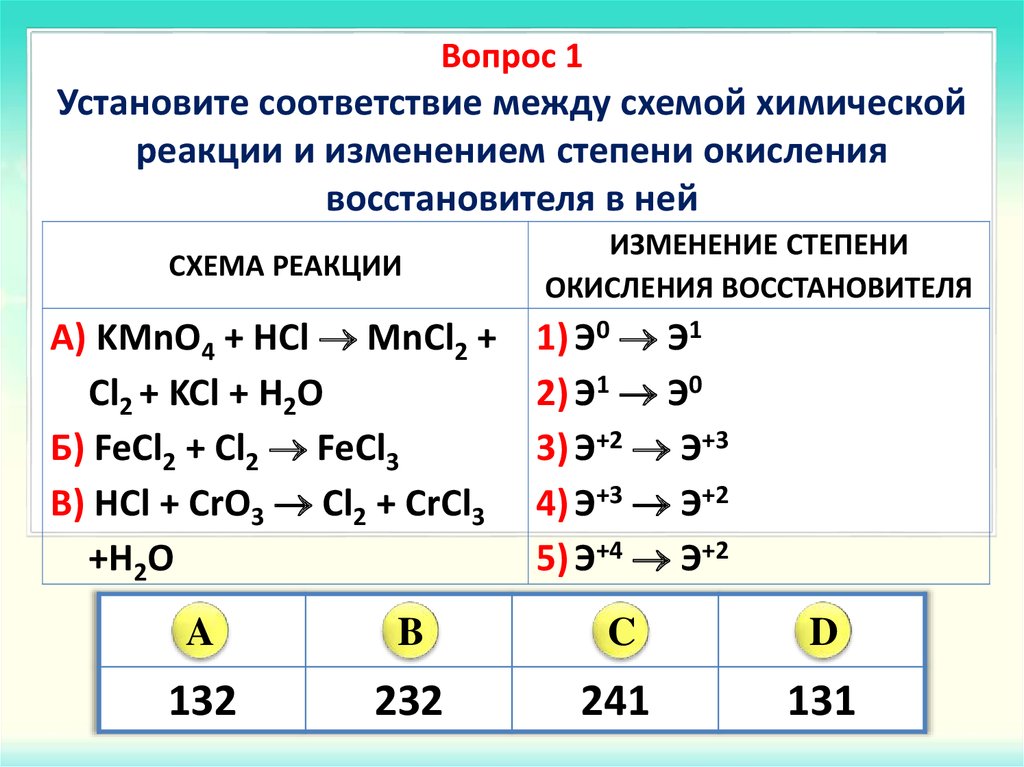
 9/2
9/2 2707
2707 5435
5435 6924
6924 8610
8610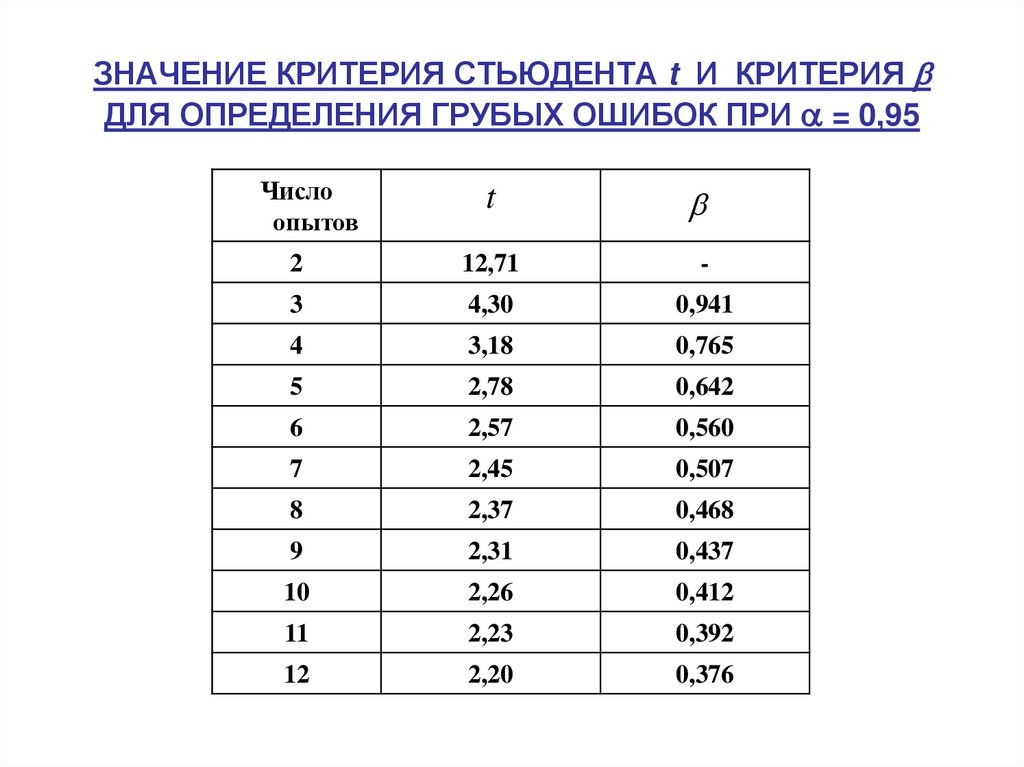 0593
0593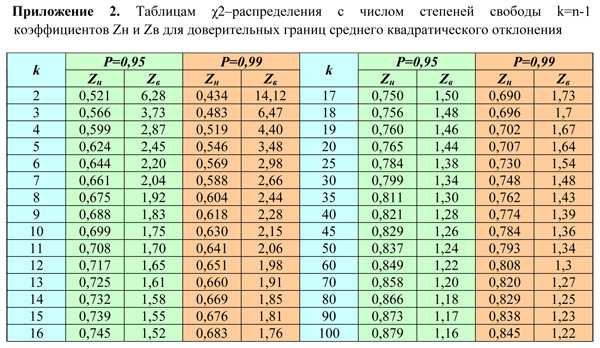 3114
3114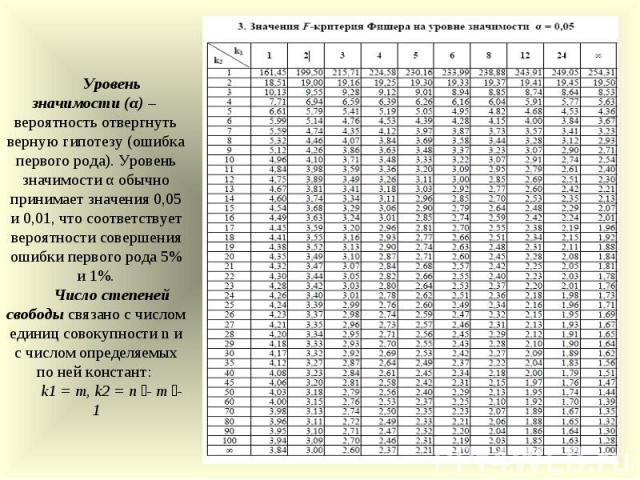 6909
6909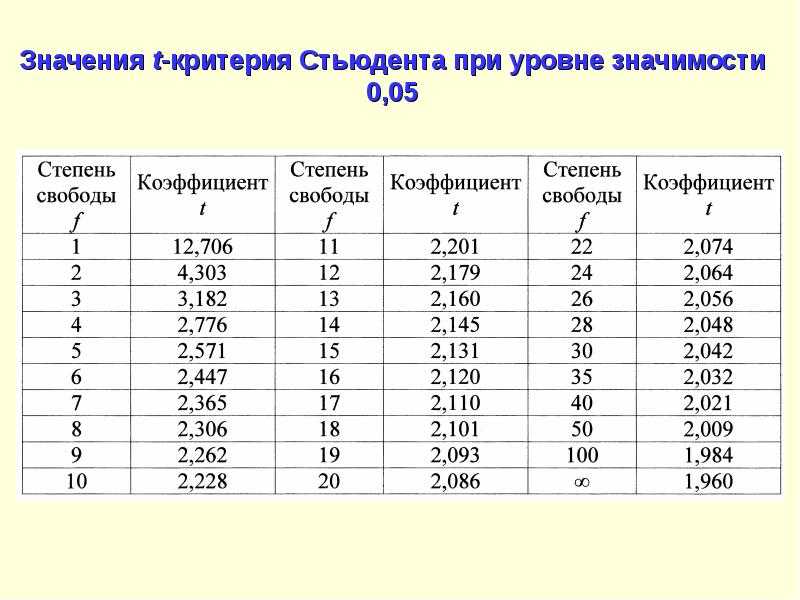 0227
0227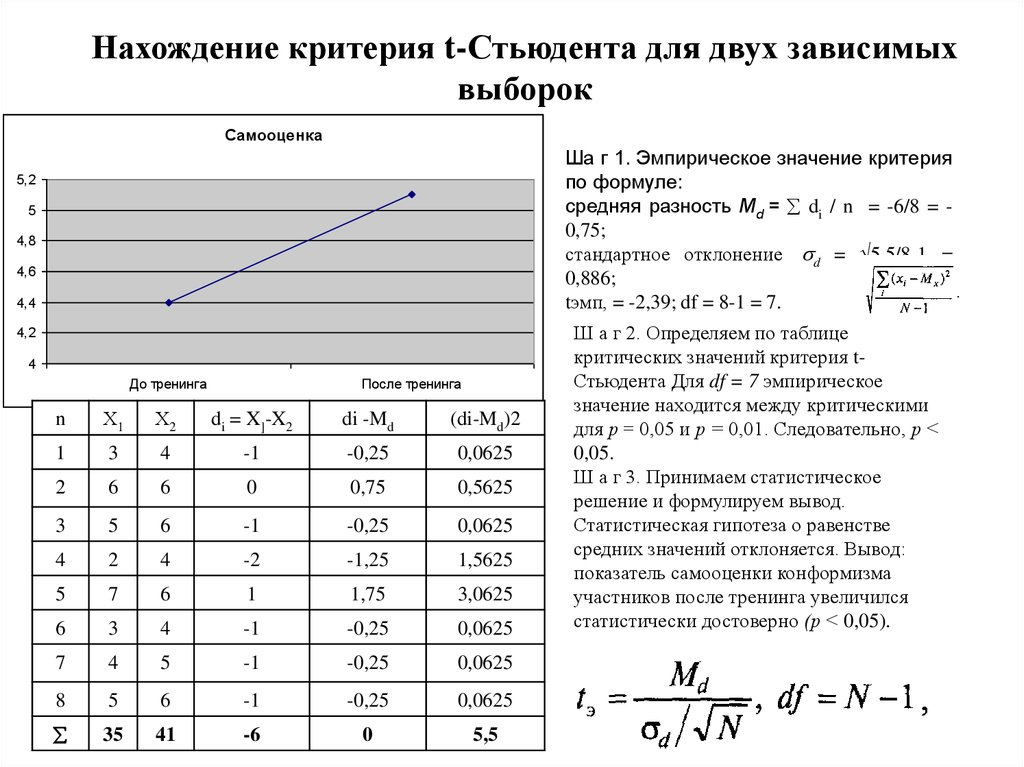 4141
4141 1263
1263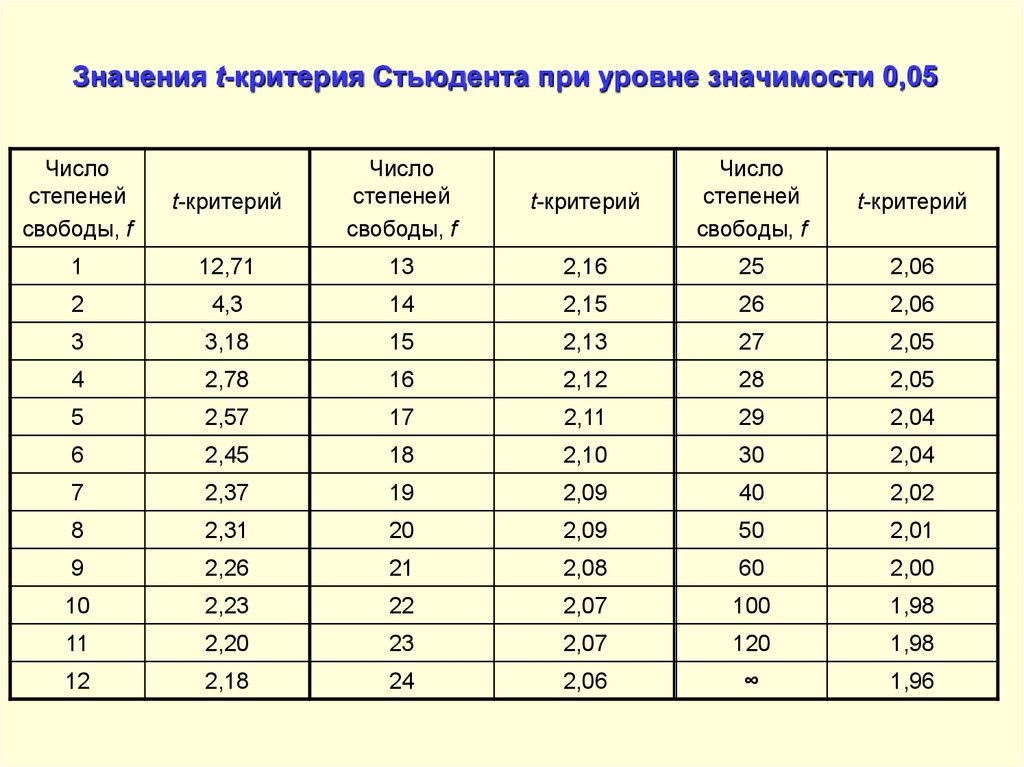 636
636 05 lean
14 11.85 obese
15 9.97 obese
16 7.48 lean
17 8.79 obese
18 9.69 obese
19 9.68 obese
05 lean
14 11.85 obese
15 9.97 obese
16 7.48 lean
17 8.79 obese
18 9.69 obese
19 9.68 obese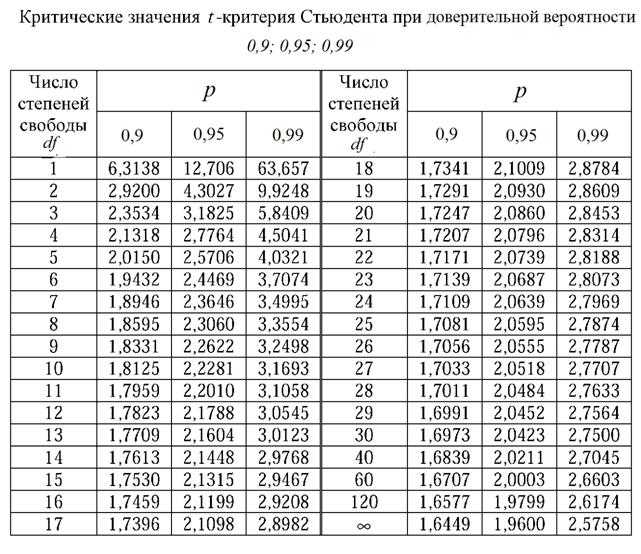 test(expend ~ stature, var.equal = TRUE)
Two Sample t-test
data: expend by stature
t = -3.9456, df = 20, p-value = 0.000799
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-3.411451 -1.051796
sample estimates:
mean in group lean mean in group obese
8.066154 10.297778
test(expend ~ stature, var.equal = TRUE)
Two Sample t-test
data: expend by stature
t = -3.9456, df = 20, p-value = 0.000799
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-3.411451 -1.051796
sample estimates:
mean in group lean mean in group obese
8.066154 10.297778 9414, df = 10, p-value = 3.059e-07
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
1074.072 1566.838
sample estimates:
mean of the differences
1320.455
9414, df = 10, p-value = 3.059e-07
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
1074.072 1566.838
sample estimates:
mean of the differences
1320.455
 Его также можно использовать для описания того, насколько далеко от среднего находится наблюдение, когда данные следуют т -распределение.
Его также можно использовать для описания того, насколько далеко от среднего находится наблюдение, когда данные следуют т -распределение. 
 > 2
> 2 

 DIST( x 0d 0 , TRUE 0, , ). Поскольку распределение t симметрично относительно x = 0, левый хвост при — x также равен T.DIST.RT( x , df ) и сумме правого и левого хвостов, T.DIST .2T( x , df ) равно 2* T.DIST.RT( x , df ).
DIST( x 0d 0 , TRUE 0, , ). Поскольку распределение t симметрично относительно x = 0, левый хвост при — x также равен T.DIST.RT( x , df ) и сумме правого и левого хвостов, T.DIST .2T( x , df ) равно 2* T.DIST.RT( x , df ).