Рунге-Кутта VBA EXCEL
Решение дифференциальных уравнений первого порядка
методом Рунге-Кутта.
Данный проект VBA позволяет решать дифференциальные уравнения первого порядка одним из численных методов, а именно, методом Рунге-Кутта.
Исходные данные:
- границы интервала a и b;
- шаг интегрирования h;
- начальное значение для решения y(a), позволяющее правильно определить константу…
вводятся в соответствующие ячейки столбца «J».
И самое главное (самая ответственная часть) необходимо без ошибок ввести формулу в ячейку «D3». Эта формула получается из заданного уравнения и представляет функцию, являющуюся производной от решения. Ее параметрами может быть как только х (т.е. ячейка «D4»), так и х совместно с у (т.е. ячейкой «D5»). На рисунке показан пример ввода формулы для заданного уравнения…
В ячейки «D4» и «D5» вводить ничего не нужно… Туда значения будет подставлять макрос…
Если не удалось запустить видео, воспользуйтесь этой ссылкой . видео на YouTube
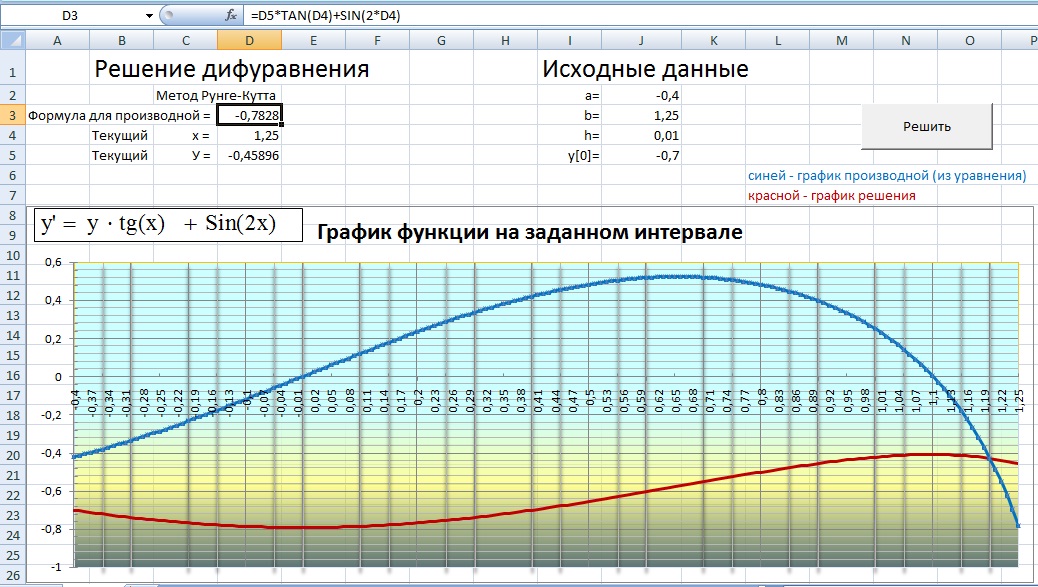
После этого остается нажать кнопку «Решить» и … если Вы не забыли включить макросы, то увидите, быстро меняющиеся текущие значения в ячейках столбца «D», а после окончания цикла расчета значений у, произойдет изменение графиков.
Графики должны быть построены на заданном Вами интервале (на рисунке от -0,4 до 1,25)…
В каждой точке, где производная (график синего цвета) пересекает ось 0У, функция решения(красная) должна иметь экстремум (максимум или минимум)…
Если терпением Вы не отличаетесь, то не задавайте очень длинный интервал и/или очень мелкий шаг…
Подсказка:
Собственно, процедура заполнения массивов х и у по методу Рунге-Кутта будет выглядеть так:
(при этом глобальная переменная D3formula предварительно инициализируется: D3formula = Range(«D3»).Formula)
Private Function func(x As Double, y As Double) As Double ‘производная
Dim f As String
‘функция вычисляется по формуле, введенной пользователем в ячейку D3 (гед D4 — это x, D5 — это y)
f = Replace(D3formula, «D4», CStr(x))
f = Replace(f, «D5», CStr(y))
Range(«D3»).FormulaLocal = f
func = Range(«D3»)
End Function
Sub MethodRungeKutta()
‘вспомогательные переменные
Dim k1 As Double, k2 As Double, k3 As Double, k4 As Double
Dim i As Integer
For i = 1 To n ‘нулевые значения уже есть
x(i) = x(0) + i * h
k1 = func(x(i — 1), y(i — 1))
k2 = func(x(i — 1) + h / 2, y(i — 1) + k1 * h / 2)
k3 = func(x(i — 1) + h / 2, y(i — 1) + k2 * h / 2)
k4 = func(x(i), y(i — 1) + k3 * h)
y(i) = y(i — 1) + h / 6 * (k1 + 2 * k2 + 2 * k3 + k4) ‘значения вычисляются
p(i — 1) = k1 ‘сохранение в массив для графика
Чтобы на диаграмме отобразились рассчитанные графики, производится заполнение соответствующих диапазонов в столбцах «AA-AB-AC»… Можете сравнить результаты с этим табличным вариантом.
Обзор методов решения в Excel
Введение
Уравнение 
называется обыкновенным дифференциальным n-го порядка, если F определена и непрерывна в некоторой области 
и, во всяком случае, зависит от 
. Его решением является любая функция u(x), которая этому уравнению удовлетворяет при всех x в определённом конечном или бесконечном интервале. Дифференциальное уравнение, разрешенное относительно старшей производной имеет вид 
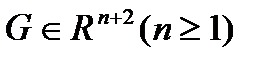
Решением этого уравнения на интервале I=[a,b] называется функция u(x).
Решить дифференциальное уравнение у / =f(x,y) численным методом — это значит для заданной последовательности аргументов х0, х1…, хn и числа у0, не определяя функцию у=F(x), найти такие значения у1, у2,…, уn, что уi=F(xi)(i=1,2,…, n) и F(x0)=y0.
Таким образом, численные методы позволяют вместо нахождения функции y=F(x) (3) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=xk-xk-1 называется шагом интегрирования.
Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.
Метод Эйлера для обыкновенных дифференциальных уравнений используется для решений многих задач естествознания в качестве математической модели. Например задачи электродинамики системы взаимодействующих тел (в модели материальных точек), задачи химической кинетики, электрических цепей. Ряд важных уравнений в частных производных в случаях, допускающих разделение переменных, приводит к задачам для обыкновенных дифференциальных уравнений – это, как правило, краевые задачи (задачи о собственных колебаниях упругих балок и пластин, определение спектра собственных значений энергии частицы в сферически симметричных полях и многое другое)
Обзор методов решения в Excel
1.1 Метод Рунге-Кутта четвертого порядка для решения уравнения первого порядка
Идея Рунге-Кута состоит в том, чтобы использовать метод неопределённых коэффициентов. Наиболее употребительным методом Рунге-Кутта решения уравнения первого порядка y’ = F(x,y) (1) является метод четвертого порядка, в котором вычисления производятся по формуле:
yk+1 = yk +(k1 +2k2 +2k3 +k4 )/6, (2)
k1 = Fk h = F(xk , yk )h
Рассмотрим задачу Коши для уравнений первого порядка на отрезке [a,b]:
, 
(4)
Разобьём промежуток [a,b] на N частей 
. Обозначим , где u(x) –точное решение задачи Коши, и через 
значения приближенного решения в точках 
. Существует 2 типа численных схем :
1. явные: 
) (5)
2. неявные: 
(6)
Здесь F некоторая функция, связывающая приближения. В явных схемах приближенное значение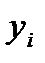 
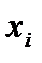
в точке определяется через некоторое число k уже определённых приближенных значений. В неявных схемах определяется не рекурентным способом, как в явных схемах, а для его определения возникает уравнение, поскольку равенство (6) представляет из себя именно уравнение на . Явные схемы проще, однако зачастую неявные схемы предпочтительнее
1.3 Метод Эйлера
Решить дифференциальное уравнение у / =f(x,y) численным методом — это значит для заданной последовательности аргументов х0, х1…, хn и числа у0, не определяя функцию у=F(x), найти такие значения у1, у2,…, уn, что
Таким образом, численные методы позволяют вместо нахождения функции У=F(x) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=xk-xk-1 называется шагом интегрирования.
Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.
Рассмотрим дифференциальное уравнение первого порядка (7) с начальным условием
Требуется найти решение уравнения (7) на отрезке [а,b].
Разобьем отрезок [a, b] на n равных частей и получим последовательность х0, х1, х2,…, хn, где xi=x0+ih (i=0,1,…, n), а h=(b-a)/n-шаг интегрирования.
В методе Эйлера приближенные значения у(хi)»yi вычисляются последовательно по формулам уi+hf(xi, yi) (i=0,1,2…).
При этом искомая интегральная кривая у=у(х), проходящая через точку М0(х0, у0), заменяется ломаной М0М1М2… с вершинами Мi(xi, yi) (i=0,1,2,…); каждое звено МiMi+1 этой ломаной, называемой ломаной Эйлера, имеет направление, совпадающее с направлением той интегральной кривой уравнения (7), которая проходит через точку Мi. Если правая часть уравнения (7) в некотором прямоугольнике R<|x-x0|£a, |y-y0|£b>удовлетворяет условиям:
|df/dx|=|df/dx+f(df/dy)| £ M (M=const),
то имеет место следующая оценка погрешности:
где у(хn)-значение точного решения уравнения (7) при х=хn, а уn— приближенное значение, полученное на n-ом шаге.
Формула (13) имеет в основном теоретическое применение. На практике иногда оказывается более удобным двойной просчет: сначала расчет ведется с шагом h, затем шаг дробят и повторный расчет ведется с шагом h/2. Погрешность более точного значения уn * оценивается формулой
Метод Эйлера легко распространяется на системы дифференциальных уравнений и на дифференциальные уравнения высших порядков. Последние должны быть предварительно приведены к системе дифференциальных уравнений первого порядка.
1.4 Модифицированный метод Эйлера
Рассмотрим дифференциальное уравнение (7) y / =f(x,y) с начальным условием y(x0)=y0. Разобьем наш участок интегрирования на n равных частей. На малом участ интегральную кривую заменим прямой линией.
Рисунок 1 Метод Эйлера в графическом виде
Получаем точку Мк(хк,ук). Через Мк проводим касательную:
Получаем точку Nk / . В этой точке строим следующую касательную:
Из точки Мк проводим прямую с угловым коэффициентом αк и определяем точку пересечения этой прямой с прямой Хк1. Получаем точку Мк / . В качестве ук+1 принимаем ординату точки Мк / . Тогда:
(14)-рекурентные формулы метода Эйлера.
Сначала вычисляют вспомогательные значения искомой функции ук+1/2 в точках хк+1/2, затем находят значение правой части уравнения (11) в средней точке y / k+1/2=f(xk+1/2, yk+1/2) и определяют ук+1.
Для оценки погрешности в точке хк проводят вычисления ук с шагом h, затем с шагом 2h и берут 1/3 разницы этих значений:
где у(х)-точное решение дифференциального уравнения.
Таким образом, методом Эйлера можно решать уравнения любых порядков. Например, чтобы решить уравнение второго порядка y // =f(y / ,y,x) c начальными условиями y / (x0)=y / 0, y(x0)=y0, выполняется замена
Тем самым преобразуются начальные условия
1.5 Практическая часть
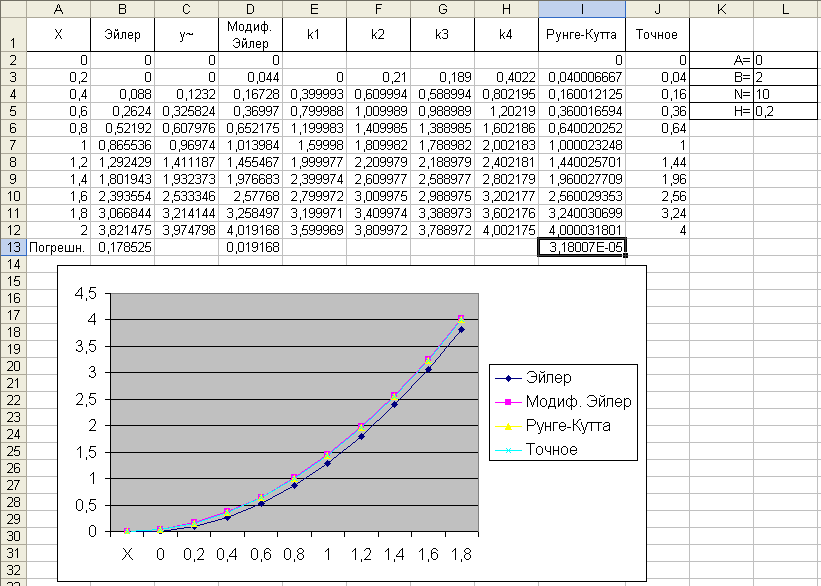
Здесь решается уравнение dy/dx = 2x-y+x 2 на интервале [0,2], начальное значение y(0)=0, для оценки точности задано также точное решение в виде функции u(x)=x 2 . Оценка погрешности делается в нормеL1, как и принято в данном случае
Методы решения дифференциальных уравнений
Метод Эйлера
- 1. При разложении функции в ряд Тейлора, отбрасываются производные 2-го и более порядков. Получаем: yn+1=yn+h*y'(xn),y'(x)=f(x,y).
- 2. Можно вывести формулу, рекуррентную методу Эйлера: yn+1=yn+h*y'(xn,yn).
- 3. Ошибкой метода имеет порядок h 2
Рисунок 3.1.1 — Метод Эйлера в MS Excel в режиме отображения значений
Рисунок 3.1.2 — Метод Эйлера в MS Excel в режиме отображения формул
Модифицированный метод Эйлера
- 1. Сначала по методу Эйлера вычисляется значение функции в следующей точке, которое используется для вычисления приближённого значения производной в конце интервала.
- 2. Вычислив среднее между производной и ее значением в начале интервала найдем более точное значение по формуле: yi+1+1=yi+1/2h(f(xi;yi)+f(xi+1;yi+1)).
- 3. Ошибкой метода составляет величина, равная h 2
Рисунок 3.2.1 — Модифицированный метод Эйлера в MS Excel в режиме отображения значений
Рисунок 3.2.2 — Модифицированный метод Эйлера в MS Excel в режиме отображения формул
Метод Рунге-Кутта
- 1. Для повышения тонности вычисления значения функции требуется проведение дополнительных вычислений внутри интервала h, т.е. между xi и xi+1.
- 2. Этот метод даёт набор формул для расчета координат внутренних точек, требуемых для достижения точности. Для решения используется формула:
3. Ошибкой метода составляет величина, равная h 4
Рисунок 3.3.1 — Метод Рунге-Кутта в MS Excel в режиме отображения значений
Рисунок 3.3.2 — Метод Рунде-Кутта в MS Excel в режиме отображения формул
Рисунок 3.3.3 — График с четырьмя кривыми
источники:
http://poisk-ru.ru/s7554t17.html
http://vuzlit.com/837119/metody_resheniya_differentsialnyh_uravneniy
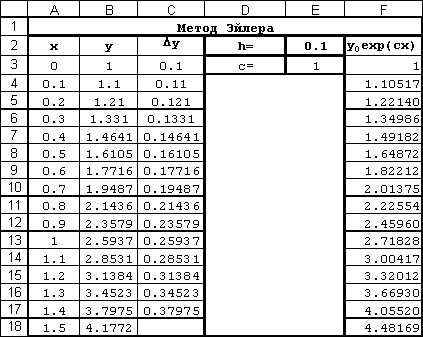
4. Вычисление третьего
столбца:
Копируем формулу из ячейки C3
в ячейки C4:C17
5.
Вычислим в узловых точках отрезка
[a, b] аналитическое решение по формуле (2.2). Для этого
введем в ячейку F3 формулу
=$B$3*EXP($E$3*A4). Затем копируем ее в ячейки F4:F18
Расчетная таблица,
скопированная с рабочего листа MS Excel, показана на рис. 2.1.
Рис. 2.1. Фрагмент
рабочего листа с решением примера методом Эйлера
2.1.4.Численное решение методом Рунге-Кутта
в Excel
Расчетные
формулы для конкретного примера запишем, исходя из общих формул и подставляя в
них конкретные функции, определяемые видом уравнения (2.1). Отметим, что
исходное уравнение должно быть приведен к виду (1.1).
Задаемся
начальным значением y0 и
вычисляем
, (2.6)
(2.7)
Приведем
также пример расчетных формул для уравнения другого вида, а именно уравнения,
содержащего x в правой части.
Рассмотрим
уравнение
Для него расчетные формулы
имеют вид:
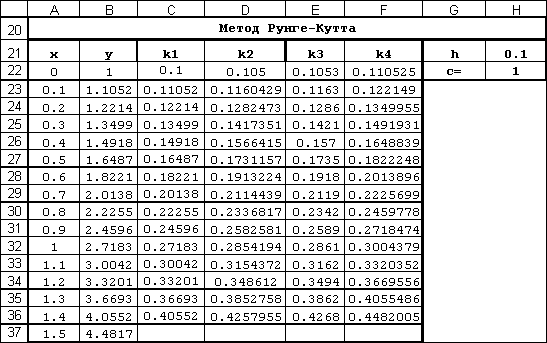
Расчетная таблица,
скопированная из Excel, представлена на рис. 2.2. Ниже указан порядок ее
заполнения
Первая
строка заполнена именами переменных
Две
ячейки H21, H22 отводятся под значения констант h, c и
еще две ячейки G21?G22 под их имена
Первый
столбец заполняется значениями x
В
ячейку B22 вводим значение y0,
В
ячейки С22,D22, E22, F22 вводим соответственно формулы:
= $H$22*B22*$H$21
=$H$22*(B22+C22/2)*$H$21
=$H$22*(B22+D22/2)*$H$21
=$H$22*(B22+E22)*$H$21
В
ячейку B23 вводим формулу:
=B22+(C22+2*D22+2*E22+F22)/6
В
ячейки B24:B37 копируем формулу из ячейки B23
В
ячейки C22:F36 копируем формулы из ячеек C22:F22.
Рис. 2.2. Фрагмент
рабочего листа с решением примера по методу Рунге-Кутта
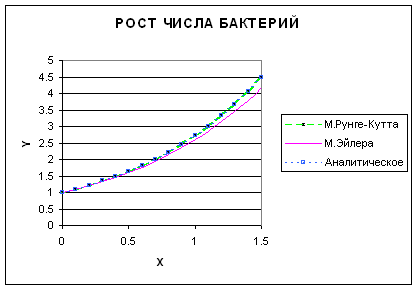
Построим
графики численного решения данного уравнения в Excel методами Эйлера и Рунге-Кутта, а также график
аналитического решения. Все три графика строим на одной диаграмме. При
построении графика с помощью Мастера диаграмм следует:
1.
На первом шаге
выбрать Тип диаграммы — Точечная
2.
На втором шаге последовательно
задать ряды данных для каждого графика:
3.
На третьем шаге задать параметры
Диаграммы: заголовок, названия осей. В случае абстрактного уравнения
заголовок диаграммы можно опустить. В легенде следует указать, какому методу
данный ряд соответствует.
4.
На последнем шаге помещаем
диаграмму на имеющемся рабочем листе.
Примечания.
1.
Если графики трудно различимы,
можно изменить формат рядов данных (на графике), выделяя соответствующий ряд и
вызывая контекстное меню правой кнопкой мыши
2.
Если шкалы по осям x или
y не соответствуют диапазону изменения x, y,
нужно изменить их минимальные и максимальные значения по команде формат оси,
вызываемой в контекстном меню.
Графики решения данного
уравнения различными методами представлены на рис. 2.3.
Рис. 2.3. Графики решений уравнения (2.1) различными
способами
2.1.5. Численное решение задачи методом
Рунге-Кутта в Турбо Паскале
Расчетные формулы.
Решим
уравнение (2.1) методом Рунге-Кутта четвертого порядка, используя формулы
(1.8)-(1.9). Т.к. неизвестные значения функции y(x) вычисляются рекуррентно, требуется задать ее
начальное значение.
Обзор методов решения в Excel
Введение
Уравнение называется обыкновенным дифференциальным n-го порядка, если F определена и непрерывна в некоторой области и, во всяком случае, зависит от . Его решением является любая функция u(x), которая этому уравнению удовлетворяет при всех x в определённом конечном или бесконечном интервале. Дифференциальное уравнение, разрешенное относительно старшей производной имеет вид
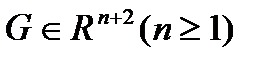
Решением этого уравнения на интервале I=[a,b] называется функция u(x).
Решить дифференциальное уравнение у / =f(x,y) численным методом — это значит для заданной последовательности аргументов х0, х1…, хn и числа у0, не определяя функцию у=F(x), найти такие значения у1, у2,…, уn, что уi=F(xi)(i=1,2,…, n) и F(x0)=y0.
Таким образом, численные методы позволяют вместо нахождения функции y=F(x) (3) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=xk-xk-1 называется шагом интегрирования.
Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.
Метод Эйлера для обыкновенных дифференциальных уравнений используется для решений многих задач естествознания в качестве математической модели. Например задачи электродинамики системы взаимодействующих тел (в модели материальных точек), задачи химической кинетики, электрических цепей. Ряд важных уравнений в частных производных в случаях, допускающих разделение переменных, приводит к задачам для обыкновенных дифференциальных уравнений – это, как правило, краевые задачи (задачи о собственных колебаниях упругих балок и пластин, определение спектра собственных значений энергии частицы в сферически симметричных полях и многое другое)
Обзор методов решения в Excel
1.1 Метод Рунге-Кутта четвертого порядка для решения уравнения первого порядка
Идея Рунге-Кута состоит в том, чтобы использовать метод неопределённых коэффициентов. Наиболее употребительным методом Рунге-Кутта решения уравнения первого порядка y’ = F(x,y) (1) является метод четвертого порядка, в котором вычисления производятся по формуле:
Решение дифференциальных уравнений в эксель
Pers.narod.ru. Обучение. Excel: Решение обыкновенных дифференциальных уравнений (задача Коши)
Решение обыкновенных дифференциальных уравнений (ОДУ) — популярный раздел численных методов, немного теории можно почитать здесь.
В приведённом примере решается задача Коши, то есть, ищется решение дифференциального уравнения первого порядка вида dy/dx = f(x,y) на интервале x ∈ [x0,xn] при условии y(x0)=y0 и равномерном шаге сетки по x .
Решение выполняется методами Эйлера, «предиктор-корректор» (он же модифицированный метод Эйлера) и методом Рунге-Кутта 4 порядка точности. Пример может служить образцом для Ваших решений, правда, функцию придётся перепрограммировать несколько раз при различных значениях аргумента — поскольку без применения макросов на VBA Excel не позволяет создать полноценную функцию, которую было бы удобно вызывать с разными значениями аргументов.
Здесь решается уравнение dy/dx = 2x-y+x 2 на интервале [0,2] , начальное значение y(0)=0 , для оценки точности задано также точное решение в виде функции u(x)=x 2 . Оценка погрешности делается в норме L1 , как и принято в данном случае.
Скачать пример в Excel XP/2003 (28 Кб)
Рунге-Кутта VBA EXCEL
Решение дифференциальных уравнений первого порядка
методом Рунге-Кутта.
Данный проект VBA позволяет решать дифференциальные уравнения первого порядка одним из численных методов, а именно, методом Рунге-Кутта.
Исходные данные:
- границы интервала a и b;
- шаг интегрирования h;
- начальное значение для решения y(a), позволяющее правильно определить константу…
вводятся в соответствующие ячейки столбца «J».
И самое главное (самая ответственная часть) необходимо без ошибок ввести формулу в ячейку «D3». Эта формула получается из заданного уравнения и представляет функцию, являющуюся производной от решения. Ее параметрами может быть как только х (т.е. ячейка «D4»), так и х совместно с у (т.е. ячейкой «D5»). На рисунке показан пример ввода формулы для заданного уравнения…
В ячейки «D4» и «D5» вводить ничего не нужно… Туда значения будет подставлять макрос…
Если не удалось запустить видео, воспользуйтесь этой ссылкой . видео на YouTube
После этого остается нажать кнопку «Решить» и … если Вы не забыли включить макросы, то увидите, быстро меняющиеся текущие значения в ячейках столбца «D», а после окончания цикла расчета значений у, произойдет изменение графиков.
Графики должны быть построены на заданном Вами интервале (на рисунке от -0,4 до 1,25)…
В каждой точке, где производная (график синего цвета) пересекает ось 0У, функция решения(красная) должна иметь экстремум (максимум или минимум)…
Если терпением Вы не отличаетесь, то не задавайте очень длинный интервал и/или очень мелкий шаг…
Подсказка:
Собственно, процедура заполнения массивов х и у по методу Рунге-Кутта будет выглядеть так:
(при этом глобальная переменная D3formula предварительно инициализируется: D3formula = Range(«D3»).Formula)
Private Function func(x As Double, y As Double) As Double ‘производная
Dim f As String
‘функция вычисляется по формуле, введенной пользователем в ячейку D3 (гед D4 — это x, D5 — это y)
f = Replace(D3formula, «D4», CStr(x))
f = Replace(f, «D5», CStr(y))
Range(«D3»).FormulaLocal = f
func = Range(«D3»)
End Function
Sub MethodRungeKutta()
‘вспомогательные переменные
Dim k1 As Double, k2 As Double, k3 As Double, k4 As Double
Dim i As Integer
For i = 1 To n ‘нулевые значения уже есть
x(i) = x(0) + i * h
k1 = func(x(i — 1), y(i — 1))
k2 = func(x(i — 1) + h / 2, y(i — 1) + k1 * h / 2)
k3 = func(x(i — 1) + h / 2, y(i — 1) + k2 * h / 2)
k4 = func(x(i), y(i — 1) + k3 * h)
y(i) = y(i — 1) + h / 6 * (k1 + 2 * k2 + 2 * k3 + k4) ‘значения вычисляются
p(i — 1) = k1 ‘сохранение в массив для графика
Чтобы на диаграмме отобразились рассчитанные графики, производится заполнение соответствующих диапазонов в столбцах «AA-AB-AC»… Можете сравнить результаты с этим табличным вариантом.
источники:
http://pers.narod.ru/study/excel_odu.html
http://orenstudent.ru/RungeKuttaVBA_change_formula.htm
|
Diana001020 0 / 0 / 0 Регистрация: 26.03.2020 Сообщений: 1 |
||||
|
1 |
||||
|
Excel Метод Рунге-Кутта26.03.2020, 16:49. Показов 3838. Ответов 14 Метки нет (Все метки)
0 |
|
ᴁ®
3070 / 1736 / 361 Регистрация: 13.12.2016 Сообщений: 5,938 Записей в блоге: 4 |
|
|
29.03.2020, 09:12 |
2 |
|
Diana001020, не понятно что не получается? Не понятно что за код.
0 |
|
Модератор
34709 / 19230 / 4040 Регистрация: 12.02.2012 Сообщений: 32,197 Записей в блоге: 13 |
|
|
29.03.2020, 14:48 |
3 |
|
CallByName — встроенная функция, позволяющая вызывать метод COM-объекта по string-имени
0 |
|
Burk 1813 / 1135 / 346 Регистрация: 11.07.2014 Сообщений: 4,002 |
||||
|
29.03.2020, 15:00 |
4 |
|||
|
Diana001020, я сделал предположение, что DEqn это и есть функция, которую надо проинтегрировать, Проверьте такой код (запустить макрос proba)
0 |
|
Catstail Модератор
34709 / 19230 / 4040 Регистрация: 12.02.2012 Сообщений: 32,197 Записей в блоге: 13 |
||||||
|
29.03.2020, 15:04 |
5 |
|||||
|
Diana001020, понятно, что не работает. Ты сама писала этот код? Вот что должно быть на самом деле:
Вложения
0 |
|
Модератор
34709 / 19230 / 4040 Регистрация: 12.02.2012 Сообщений: 32,197 Записей в блоге: 13 |
|
|
29.03.2020, 15:06 |
6 |
|
Burk, это правая часть диф. уравнения, которое решается методом Рунге-Кутта Добавлено через 1 минуту
0 |
|
Burk 1813 / 1135 / 346 Регистрация: 11.07.2014 Сообщений: 4,002 |
||||
|
29.03.2020, 15:17 |
7 |
|||
|
Diana001020, в строках 9, 10, 11 забыл заменить DEqn на аналог строки 8
Добавлено через 3 минуты
0 |
|
Модератор
34709 / 19230 / 4040 Регистрация: 12.02.2012 Сообщений: 32,197 Записей в блоге: 13 |
|
|
29.03.2020, 15:34 |
8 |
|
DEqn это и есть функция, которую надо проинтегрировать, — проинтегрировать функцию и проинтегрировать дифференциальное уравнение — не одно и то же
0 |
|
1813 / 1135 / 346 Регистрация: 11.07.2014 Сообщений: 4,002 |
|
|
29.03.2020, 15:40 |
9 |
|
Catstail, давайте мы на форуме по программированию не будем изощряться в точностях определений, понимаю, что хотите чтобы последнее слово осталось за вами, ради бога, но не увлекайтесь.
0 |
|
Модератор
34709 / 19230 / 4040 Регистрация: 12.02.2012 Сообщений: 32,197 Записей в блоге: 13 |
|
|
29.03.2020, 15:43 |
10 |
|
Burk, Программирование — программированием, а математика — математикой. Я просто Вас поправил, не стоит обижаться
0 |
|
1813 / 1135 / 346 Регистрация: 11.07.2014 Сообщений: 4,002 |
|
|
29.03.2020, 15:44 |
11 |
|
Catstail, а вот у вас претензии к моему коду есть?
0 |
|
Catstail Модератор
34709 / 19230 / 4040 Регистрация: 12.02.2012 Сообщений: 32,197 Записей в блоге: 13 |
||||
|
29.03.2020, 15:54 |
12 |
|||
|
Burk, немного есть…
но это легко поправить. Можно упрекнуть код и в том, что работать он будет только в Excel, а код с CallByName — и в чистом VB. Но и это не столь важно. Ну, и последнее: обычно интегрирование дифф. уравнений делают ради поведения функции на отрезке интегрирования. А в Вашем коде (как и в коде ТС) функция просто возвращает последнее значение y. Что почти бесполезно. Я вставил отладочную печать внутрь кода. Ну, хоть так. Впрочем, еще раз, все это легко правится и не столь уж и важно.
0 |
|
1813 / 1135 / 346 Регистрация: 11.07.2014 Сообщений: 4,002 |
|
|
29.03.2020, 16:04 |
13 |
|
Catstail, после вашего сообщения, в котором вы мне объясняли про правую часть, стоит моё, в котором я объяснял, что забыл заменить явную ссылку на вызов по символическому имени и показал автору как нужно исправить. Читайте внимательно и странности исчезнут. Добавлено через 3 минуты
функция просто возвращает последнее значение y я всегда стараюсь делать как у автора. Для себя, конечно, вывел бы промежуточные значения. И мне такие вещи объяснять не надо, это к автору.
0 |
|
Модератор
34709 / 19230 / 4040 Регистрация: 12.02.2012 Сообщений: 32,197 Записей в блоге: 13 |
|
|
29.03.2020, 16:08 |
14 |
|
Burk, да, не обратил внимание на следующий коммент… Но замечание про неуниверсальность остается. И не стоит так реагировать на замечания.
0 |
|
1813 / 1135 / 346 Регистрация: 11.07.2014 Сообщений: 4,002 |
|
|
29.03.2020, 16:31 |
15 |
|
Catstail, меня не интересуют универсальности, я работаю только в вба, поэтому, если вы увидите в моих кодах что-то, что не пойдет в ВБ, можете мне об этом и не сообщать. Главная задача помочь и, если возможно, научить создателей тем чему-то. А промежуточные значения пусть делают сами, если появится нужда. А то сделаете всё от А до Я, а им что останется?
1 |
Решение обыкновенных дифференциальных уравнений (ОДУ) — популярный раздел численных методов, немного теории можно почитать здесь.
В приведённом примере решается задача Коши, то есть, ищется решение дифференциального уравнения первого порядка вида dy/dx = f(x,y) на интервале x ∈ [x0,xn] при условии y(x0)=y0 и равномерном шаге сетки по x.
Решение выполняется методами Эйлера, «предиктор-корректор» (он же модифицированный метод Эйлера) и методом Рунге-Кутта 4 порядка точности. Пример может служить образцом для Ваших решений, правда, функцию придётся перепрограммировать несколько раз при различных значениях аргумента — поскольку без применения макросов на VBA Excel не позволяет создать полноценную функцию, которую было бы удобно вызывать с разными значениями аргументов.
Здесь решается уравнение dy/dx = 2x-y+x2 на интервале [0,2], начальное значение y(0)=0, для оценки точности задано также точное решение в виде функции u(x)=x2.
Оценка погрешности делается в норме L1, как и принято в данном случае.
Скачать пример в Excel XP/2003 (28 Кб)
