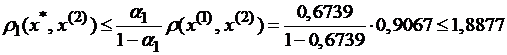Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
- Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
Теперь для нахождения корней уравнения, прежде всего, нам нужно отыскать матрицу, обратную существующей. К счастью, в Эксель имеется специальный оператор, который предназначен для решения данной задачи. Называется он МОБР. Он имеет довольно простой синтаксис:
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Запускается окно аргументов функции МОБР. Оно по числу аргументов имеет всего одно поле – «Массив». Тут нужно указать адрес нашей таблицы. Для этих целей устанавливаем курсор в это поле. Затем зажимаем левую кнопку мыши и выделяем область на листе, в которой находится матрица. Как видим, данные о координатах размещения автоматически заносятся в поле окна. После того, как эта задача выполнена, наиболее очевидным было бы нажать на кнопку «OK», но не стоит торопиться. Дело в том, что нажатие на эту кнопку является равнозначным применению команды Enter. Но при работе с массивами после завершения ввода формулы следует не кликать по кнопке Enter, а произвести набор сочетания клавиш Ctrl+Shift+Enter. Выполняем эту операцию.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
-
Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
-
Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
-
Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12768 полезных инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Вычисления СЛАУ методом простой итерации
Традиционный способ решения СЛАУ
1. Проверьте условие сходимости
2. Приведите систему к нормальному виду, т.е. из первого уравнения выразите x1, из второго x2, из третьего x3.
3. Разделите первое уравнение на 200, второе на 400, третье на 600.
4. Выберите начальное приближение
- 5. Итерационный процесс
- 1-я итерация
Требуемая точность не достигнута



Требуемая точность достигнута
Решение СЛАУ с помощью MS Excel
- 1. Переименуйте Лист2 в метод простых итераций.
- 2. Запишите коэффициенты при неизвестных (а1, а2, а3) и свободные члены bi, т.е. сформируйте матрицу систему.
- 3. В ячейки G2:G4 введите точное решение уравнений, используя ссылки на ячейки С17:С19 листа Матричный метод.
- 4. В ячейку E1 введите точность , равной 0,01.
Результаты выполненных действий
5. Проверьте условие сходимости с помощью функции ЕСЛИ
6. Введите в ячейки C19:E19 формулы, вычисляющие начальные приближения к точному значению x1, x2 x3, в ячейки C20:E20 — итерационные формулы, вычисляющие последовательные приближения к точному значению x1, x2, x3.
7. В ячейки G20:I20 введите формулы, вычислите критерии окончания итерационного процесса для x1, x2 и x3.
8. В ячейку K20 введите условие окончания итерационного процесса с помощью функции ЕСЛИ.
9. Копируйте формулы итерационного процесса, критериев и условия окончания итерационного процесса до тех пор, пока критерии 1, 2 и 3 не достигнут значения, меньше заданного (=0,01).
Решение СЛАУ методом простой итерации
Назначение сервиса . Онлайн-калькулятор предназначен для решения СЛАУ методом простой итерации в онлайн режиме (см. пример решения). Для проверки решения генерируется шаблон в Excel .
- Шаг №1
- Шаг №2
- Видеоинструкция
Рассмотрим достаточные условия сходимости итерационной последовательности n>.
Практически, для применения метода итерации систему линейных уравнений удобно «погрузить» в одну из трёх следующих метрик:

Для того, чтобы отображение F, заданное в метрическом пространстве соотношениями (3.2), было сжимающим, достаточно выполнение одного из следующих условий:
а) в пространстве с метрикой ρ1: 
б) в пространстве с метрикой ρ2: 
в) в пространстве с метрикой ρ3: 
Пример . Вычислить два приближения методом простой итерации. Оценить погрешность второго приближения. В качестве начального приближения выбрать x 0 =(0; 0; 0).
Так как диагональные элементы системы являются преобладающими, то приведем систему к нормальному виду:
Последовательные приближения будем искать по формулам:
Получаем:
x 1 =(-1.9022; 0.4889; 2.1456), x 2 =(-1.1720; 0.6315; 1.2389).
Для оценки погрешности в метрике ρ1 вычисляем коэффициент μ 
Вычисляем погрешность:
При большом числе неизвестных схема метода Гаусса, дающая точное решение, становится весьма сложной. В этом случае для решения СЛАУ иногда удобнее пользоваться методом простой итерации.
Метод итераций для системы уравнений в Excel
Для вычисления точности epsilon .
Итерация №1: =ABS(B7)-ABS(B6);=ABS(C7)-ABS(C6);=ABS(D7)-ABS(D6)
Итерация №2: =ABS(B8)-ABS(B7);=ABS(C8)-ABS(C7);=ABS(D8)-ABS(D7)
Скачать шаблон решения.
источники:
http://vuzlit.com/968834/vychisleniya_slau_metodom_prostoy_iteratsii
http://math.semestr.ru/optim/iter.php
Тема: Решение систем линейных уравнений методом простой итерации.
Цель работы: изучить особенности различных методов решения систем линейных алгебраических уравнений (далее — СЛАУ), приобрести навыки решения СЛАУ с помощью средств MS Excel выполнения задания
Задание 1. Используя методы Гаусса, простых итераций и Зейделя, разработайте схемы соответствующих алгоритмов решения СЛАУ в среде MS Excel.
1.1. Метод Гаусса в среде MS Excel
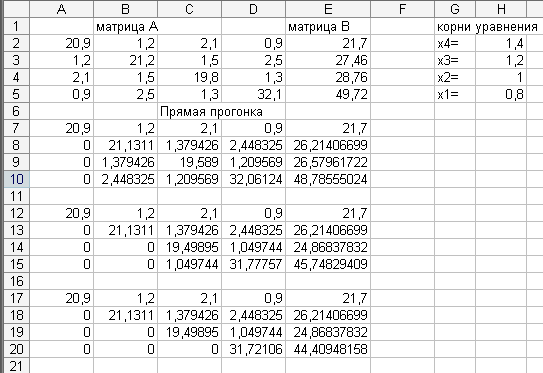
1.1.1. В ячейки А2:Е5 введите расширенную матрицу системы (рис. 1.1), скопируйте ее в диапазоны ячеек А7:Е10.
a)предположите, что в ячейке А2 не ноль. Если это не так, то переставьте строки таким образом, чтобы число в ячейке А2 было отлично от нуля;
нажмите клавиши + + . В результате формула примет вид:
в) протянув за маркер автозаполнения, скопируйте формулу в ячейки А9:Е10. В результате этих операций коэффициенты при х1 во всех уравнениях кроме первого обратятся в ноль;
г) выделите диапазон А7:Е10 и скопируйте значения, хранящиеся в нем в ячейки диапазонов А12:Е15. Для копирования значений нужно воспользоваться специальной вставкой. Ей соответствует пункт меню Правка-Специальная вставка. После выбора этого пункта появляется диалоговое окно Специальная вставка, в котором нужно выбрать Вставить-Значения и нажать ОК;
д) аналогичным образом обратите в ноль коэффициенты при х2. В диапазон ячеек В14:Е14 введите формулу
е) протяните маркер автозаполнения этого диапазона так, чтобы заполнить ячейки диапазона В15:Е15. Это обратит в ноль коэффициенты при х2 в последних двух уравнениях.
ж) далее содержимое (только значения!) диапазона A12:Е15 скопируйте в ячейки диапазона A17:Е20;
з) выделите диапазон С20:Е20, введите в него формулу
{=C15:E15–$C$14:$E$14*C15/$C$14},
что обратит в ноль коэффициент при х3 в последнем уравнении;
и) в результате этих преобразований матрица системы примет треугольный вид.
1.1.3.Обратный ход метода Гаусса:
а)в ячейки G2, G3, G4 и G5 введите х4, x3, x2 и х1 соответственно, а в ячейки Н2:Н5 — формулы из таблицы 1.1;
Таблица 1.1 — Обратный ход метода Гаусса
|
Ячейка |
Формула |
|
Н2 |
= E20 / D20 |
|
Н3 |
= (E19 – D19 * H2) / C19 |
|
Н4 |
= (E18 – D18 * H2 – C18 * H3) / B18 |
|
Н5 |
= (E17 – D17*H2 – C17 * H3 – B17 * H4) / A17 |
б) в результате чего в диапазоне Н2:Н5 будет получено решение системы (рис. 1.1).
1.2. Метод простых итераций в среде MS Excel:
а) в ячейки А2:Е5 введите расширенную матрицу системы (рис. 1.2) и сделайте пояснительные записи;
б) приведите систему к нормальному виду, т. е. все коэффициенты первого уравнения разделите на а11, все коэффициенты второго уравнения на а22 и т. д. Для этого в диапазон ячеек А8:А11 введите надписи: х1=, х2=, х3=, х4=. Выделите блок ячеек В8:Е8, в строке формул введите формулу =$B$2:$E$2/$A$2 и нажмите клавиши + + (операция над матрицей);
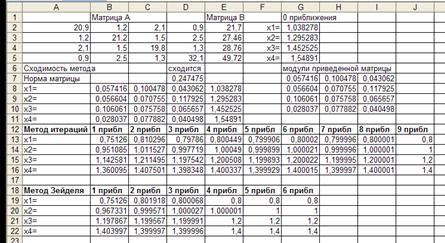
Рисунок 1.2 – Вид решения СЛАУ методом простых итераций и методом Зейделя в Excel
б) в ячейку В9 введите формулу =А3/В3. Далее выделите диапазон ячеек С9:Е9 и введите формулу =С3:Е3/В3, используя операцию над матрицей;
в) в блок ячеек В10:С10 внесите формулу =А4:В4/С4, а в блок D10:E10 — соответственно =D4:E4/C4, используя операцию над матрицами. Для блока В11:D11 введите формулу =А5:С5/D5, а в ячейку Е5 — формулу = E5/D5;
г) из полученной системы определите норму матрицы и признак сходимости метода. Для этого найдите модули полученных коэффициентов и в ячейку G7 введите формулу =ABS(B8), которую скопируйте на блок G7:I10. В ячейке D6 проверьте один из признаков сходимости и введите формулу =ЕСЛИ(МАКС (G7 + G8 + G9 + G10; H7 + H8 + H9 + H10; I7 + I8 + I9 + I10)
д) в ячейке D7 определите норму матрицы по формуле: =МАКС(G7 + H7 + I7; G8 + H8 + I8; G9 + H9 + I9; G10 + H10 + I10). Если полученный ответ меньше 1, то метод сходится при любых начальных приближениях. За начальное (нулевое) приближение возьмите полученные свободные члены и внесите их в ячейки G2:G5. Вычислим первые приближенные значения: х1(1), х2(1), х3(1), х4(1) по формулам (табл. 1.2);
Таблица 1.2 – Вычисление первых приближенных значений
|
Ячейка |
Формула |
|
В13 |
= E8 – B8*G3 – C8 * G4 – D8 * G5 |
|
В14 |
= E9 – B9 * G2 – C9 * G4 – D9 * G5 |
|
В15 |
= E10 – B10 * G2 – C10 * G3 – D10 * G5 |
|
В16 |
= E11 – B11 * G2 – C11 * G3 – D11 * G4 |
е) таким образом получите первые приближенные значения х1, х2, х3, х4. Далее в ячейки С13:С16 введите формулы, используя уже новые полученные приближения из В13:В16 (табл. 1.3).
Таблица 1.3 – Продолжение вычислений
|
Ячейка |
Формула |
|
С13 |
= $E$8 – $B$8 * B14 – $C$8 * B15 – $D$8 * B16 |
|
С14 |
= $E$9 – $B$9 * B13 – $C$9 * B15 – $D$9 * B16 |
|
С15 |
= $E$10 – $B$10 * B13 – $C$10 * B14 – $D$10 * B16 |
|
С16 |
= $E$11 – $B$11 * B13 – $C$11 * B14 – $D$11 * B15 |
ж) используя полученные вторые приближения, скопируйте формулы из ячеек С13:С16 на блок ячеек D13:D16. В результате получите новые приближенные значения корней. Продолжайте операцию копирования, получая новые приближения. Момент прекращения вычислений определите эмпирическим правилом.
1.3.Метод Зейделя в среде MS Excel:
а) в блоке ячеек В19:В22введите формулы вычисления корней уравнения по методу Зейделя (табл. 1.4).
Таблица 1.4 – Вычисление корней уравнения по методу Зейделя
|
Ячейка |
Формула |
|
В19 |
= $E$8 – $B$8 * G3 – $C$8 * G4 – $D$8 * G5 |
|
В20 |
= $E9 – $B$9 * B19 – $C$9 * G4 – $D$9 * G5 |
|
В21 |
= $E$10 – $B$10 * B19 –$C$10 * B20 – $D$10 * G5 |
|
В22 |
= $E$11 – $B$11 * B19 – $C$11 * B20 – $D$11 * B21 |
б) рассуждая аналогично, введите формулы в ячейки C19:C22, используя соответственно полученные данные из В19:В22 (табл. 1.5).
Таблица 1.5 – Продолжение вычислений
|
Ячейка |
Формула |
|
С19 |
=$E$8 – $B$8 * B20 – $C$8 * B21 – $D$8 * B22 |
|
С20 |
=$E$9 – $B$9 * C19 – $C$9 * B21 – $D$9 * B22 |
|
С21 |
=$E$10 – $B$10 * C19 – $C$10 * C20 – $D$10 * B22 |
|
С22 |
=$E$11 – $B$11 * C19 – $C$11 * C20 – $D$11 * C21 |
в) скопируйте формулы из ячеек С19:С22 на блоки: D19:D22, Е19:Е22 и т.д. Момент прекращения вычислений определяется, как и в методе простых итераций, эмпирическим правилом.
3. Выполненной задание прислать по эл.почте [email protected]
или в л/с ВК (Елена Ленина)
Метод простой итерации даёт возможность получить последовательность приближённых значений, сходящуюся к точному решению системы.
Преобразуем систему (3.1) к нормальному виду:
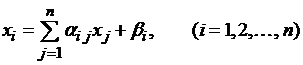
Правая часть системы (3.2) определяет отображение:
x=(x1, x2, …, xn), преобразующее точку n-мерного метрического пространства в точку y=(y1, y2, …, yn) того же пространства.
Выбрав начальную точку x0=(x01, x02, …, x0n), можно построить итерационную последовательность точек n — мерного пространства: x0, x1=F(x0), … , xn+1=F(xn)
При определённых условиях данная последовательность сходится.
Так, для исследования сходимости таких последовательностей используется принцип сжимающих отображений, который состоит в следующем.
Если F– сжимающее отображение, определённое в полном метрическом пространстве с метрикой ρ(x,y), то существует единственная неподвижная точка x*, такая, что x*=F(x*). При этом итерационная последовательность, {xn}, полученная с помощью отображения F с любым начальным членом х(0), сходится к x*.
Оценка расстояния между неподвижной точкой x* отображения F и приближением х(к) даётся формулами:
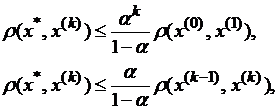
где α – множитель, определяемый достаточными условиями сжимаемости отображения F.
Значение множителя α, определяется выбором метрики, в которой проверяется сходимость последовательности значений xi.
Рассмотрим достаточные условия сходимости итерационной последовательности {xn}.
Практически, для применения метода итерации систему линейных уравнений удобно «погрузить» в одну из трёх следующих метрик:
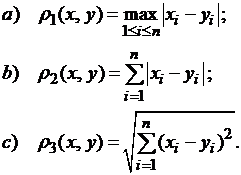
Для того, чтобы отображение F, заданное в метрическом пространстве соотношениями (3.2), было сжимающим, достаточно выполнение одного из следующих условий:
а) в пространстве с метрикой ρ1: 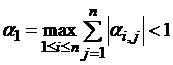
б) в пространстве с метрикой ρ2: 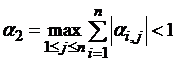
в) в пространстве с метрикой ρ3: 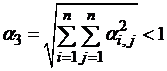
ПРИМЕР. Вычислить два приближения методом простой итерации. Оценить погрешность второго приближения. В качестве начального приближения выбрать x0=(0; 0; 0).
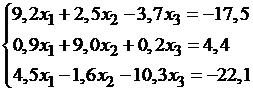
Так как диагональные элементы системы являются преобладающими, то приведем систему к нормальному виду:
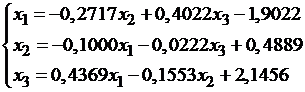
Последовательные приближения будем искать по формулам:
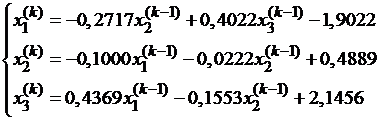
Получаем:
x1=(-1.9022; 0.4889; 2.1456), x2=(-1.1720; 0.6315; 1.2389).
Для оценки погрешности в метрике ρ1 вычисляем коэффициент μ
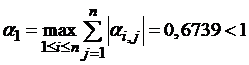
Вычисляем погрешность:
При большом числе неизвестных схема метода Гаусса, дающая точное решение, становится весьма сложной. В этом случае для решения СЛАУ иногда удобнее пользоваться методом простой итерации.
Метод итераций для системы уравнений в Excel
На листе Excel организуется таблица в три зоны: первая зона состоит из одного столбца (номер итерации), вторая зона определяет переменные x, третья зона под вычисления точности epsilon.
Во второй зоне по итерационной схеме организуется расчет переменных x (в примере для случая трех переменных):
Итерация №1:=$F$2/$B$2-C6*$C$2/$B$2-D6*$D$2/$B$2;=$F$3/$C$3-B6*$B$3/$C$3-D6*$D$3/$C$3;=$F$4/$D$4-B6*$B$4/$D$4-C6*$C$4/$D$4
Итерация №2:=$F$2/$B$2-C7*$C$2/$B$2-D7*$D$2/$B$2;=$F$3/$C$3-B7*$B$3/$C$3-D7*$D$3/$C$3;=$F$4/$D$4-B7*$B$4/$D$4-C7*$C$4/$D$4
Для вычисления точности epsilon.
Итерация №1:=ABS(B7)-ABS(B6);=ABS(C7)-ABS(C6);=ABS(D7)-ABS(D6)
Итерация №2:=ABS(B8)-ABS(B7);=ABS(C8)-ABS(C7);=ABS(D8)-ABS(D7)
Скачать шаблон решения.
ПРИМЕР. Методом итераций решить систему линейных алгебраических уравнений предварительно приведя ее к диагональному преобладанию.
Решение. Приведем матрицу к диагональному преобладанию.
Умножаем матрицы ATA.
Умножаем матрицы ATb.
Приведем к виду:
x1=7.25-1.5x3
x2=-0.8+0.24x3
x3=-3.67-0.5x1+0.5x2
Покажем вычисления на примере нескольких итераций.
N=1
x1=7.25 — 0 • 0 — 0 • (-1.5)=7.25
x2=-0.8 — 0 • 0 — 0 • 0.24=-0.8
x3=-3.67 — 0 • (-0.5) — 0 • 0.5=-3.67
N=2
x1=7.25 — (-0.8) • 0 — (-3.67) • (-1.5)=1.75
x2=-0.8 — 7.25 • 0 — (-3.67) • 0.24=0.0588
x3=-3.67 — 7.25 • (-0.5) — (-0.8) • 0.5=0.36
N=3
x1=7.25 — 0.0588 • 0 — 0.36 • (-1.5)=7.79
x2=-0.8 — 1.75 • 0 — 0.36 • 0.24=-0.89
x3=-3.67 — 1.75 • (-0.5) — 0.0588 • 0.5=-2.82
Остальные расчеты сведем в таблицу.
| N | x1 | x2 | x3 | e1 | e2 | e3 |
| 7.25 | -0.8 | -3.67 | 7.25 | 0.8 | 3.67 | |
| 1.75 | 0.0588 | 0.36 | -5.5 | -0.75 | -3.31 | |
| 7.79 | -0.89 | -2.82 | 6.04 | 0.83 | 2.46 | |
| 3.02 | -0.14 | 0.67 | -4.77 | -0.75 | -2.15 | |
| 8.26 | -0.96 | -2.09 | 5.24 | 0.82 | 1.41 | |
| 4.12 | -0.31 | 0.94 | -4.14 | -0.65 | -1.14 | |
| 8.67 | -1.03 | -1.45 | 4.55 | 0.71 | 0.51 | |
| 5.07 | -0.46 | 1.18 | -3.59 | -0.56 | -0.27 | |
| 9.02 | -1.08 | -0.9 | 3.95 | 0.62 | -0.28 | |
| 5.9 | -0.59 | 1.38 | -3.12 | -0.49 | 0.49 | |
| 9.33 | -1.13 | -0.42 | 3.42 | 0.54 | -0.96 | |
| 6.62 | -0.71 | 1.56 | -2.7 | -0.42 | 1.14 | |
| 9.59 | -1.17 | -0.00351 | 2.97 | 0.47 | -1.56 | |
| 7.24 | -0.8 | 1.71 | -2.35 | -0.37 | 1.71 | |
| 9.82 | -1.21 | 0.36 | 2.58 | 0.4 | -1.36 | |
| 7.79 | -0.89 | 1.85 | -2.04 | -0.32 | 1.49 | |
| 10.02 | -1.24 | 0.67 | 2.24 | 0.35 | -1.18 | |
| 8.26 | -0.96 | 1.96 | -1.77 | -0.28 | 1.29 |
После N-ой итерации получаем: x1 = 7.5, x2 = -0.75, x3 = 0.25
Практикум
Цель работы: изучить особенности различных методов решения систем линейных алгебраических уравнений (далее — слау), приобрести навыки решения слау с помощью средств ms Excel и MathCad.
Задание 1. Используя методы Гаусса, простых итераций и Зейделя, разработайте схемы соответствующих алгоритмов решения слау в среде ms Excel.
Пример выполнения задания
Найдите
решение системы
(1.9)
1.1.
Метод Гаусса
в среде MS Excel
1.1.1.
В ячейки А2:Е5 введите расширенную матрицу
системы (рис. 1.1), скопируйте ее в диапазоны
ячеек А7:Е10.
Рисунок
1.1 – Вид решения СЛАУ методом Гаусса в
Excel
-
Прямой ход метода Гаусса:
a)
предположите,
что в ячейке А2 не ноль. Если это не так,
то переставьте строки таким образом,
чтобы число в ячейке А2 было отлично от
нуля;
б)
выделите диапазон А8:Е8 и в строке формул
введите формулу
=A3:E3–$A$2:$E$2*A3/$A$2,
нажмите
клавиши
<Ctrl> + <Shift> + <Enter>.
В результате
формула примет вид:
{=A3:E3–$A$2:$E$2*A3/$A$2},
где
фигурные скобки указывают на операции
над матрицами;
в)
протянув за маркер автозаполнения,
скопируйте формулу в ячейки А9:Е10. В
результате этих операций коэффициенты
при х1
во всех уравнениях кроме первого
обратятся в ноль;
г)
выделите диапазон А7:Е10 и скопируйте
значения, хранящиеся в нем в ячейки
диапазонов А12:Е15. Для копирования
значений нужно воспользоваться
специальной вставкой. Ей соответствует
пункт меню Правка-Специальная
вставка.
После выбора этого пункта появляется
диалоговое окно Специальная
вставка, в
котором нужно выбрать Вставить-Значения
и нажать ОК;
д)
аналогичным образом обратите в ноль
коэффициенты при х2.
В диапазон ячеек В14:Е14 введите формулу
=B9:E9–$B$8:$E$8*B9/$B$8,
нажмите
клавиши
<Ctrl> + <Shift> + <Enter>;
е)
протяните маркер автозаполнения этого
диапазона так, чтобы заполнить ячейки
диапазона В15:Е15. Это обратит в ноль
коэффициенты при х2
в последних двух уравнениях.
ж)
далее содержимое (только значения!)
диапазона A12:Е15
скопируйте в ячейки диапазона A17:Е20;
з)
выделите диапазон С20:Е20, введите в него
формулу
{=C15:E15–$C$14:$E$14*C15/$C$14},
что
обратит в ноль коэффициент при х3
в последнем уравнении;
и)
в результате этих преобразований матрица
системы примет треугольный вид.
1.1.3.
Обратный ход метода Гаусса:
а)
в ячейки G2,
G3,
G4
и G5
введите х4,
x3,
x2
и х1
соответственно, а в ячейки Н2:Н5 — формулы
из таблицы 1.1;
Таблица
1.1 — Обратный ход метода Гаусса
|
Ячейка |
Формула |
|
Н2 |
= E20 / D20 |
|
Н3 |
= (E19 – D19 * H2) / C19 |
|
Н4 |
= (E18 – D18 * H2 – C18 * H3) / B18 |
|
Н5 |
= (E17 – D17*H2 – C17 * H3 – B17 * H4) / A17 |
б)
в результате чего в диапазоне Н2:Н5 будет
получено решение системы (рис. 1.1).
1.2.
Метод простых итераций в
среде MS Excel:
а)
в ячейки А2:Е5 введите расширенную матрицу
системы (рис. 1.2) и сделайте пояснительные
записи;
б)
приведите систему к нормальному виду,
т. е. все коэффициенты первого уравнения
разделите на а11,
все коэффициенты второго уравнения на
а22
и т. д. Для этого в диапазон ячеек
А8:А11 введите надписи: х1=,
х2=,
х3=,
х4=.
Выделите блок ячеек В8:Е8, в строке формул
введите формулу =$B$2:$E$2/$A$2
и нажмите клавиши <Ctrl> + <Shift> + <Enter>
(операция над матрицей);
Рисунок
1.2 – Вид решения СЛАУ методом простых
итераций и методом Зейделя в Excel
б)
в ячейку В9 введите формулу =А3/В3. Далее
выделите диапазон ячеек С9:Е9 и введите
формулу =С3:Е3/В3, используя операцию над
матрицей;
в)
в блок ячеек В10:С10 внесите формулу
=А4:В4/С4, а в блок D10:E10
— соответственно =D4:E4/C4,
используя операцию над матрицами. Для
блока В11:D11 введите формулу =А5:С5/D5, а в
ячейку Е5 — формулу = E5/D5;
г)
из полученной
системы определите норму матрицы и
признак сходимости метода. Для этого
найдите модули полученных коэффициентов
и в ячейку G7 введите формулу =ABS(B8), которую
скопируйте на блок G7:I10. В ячейке D6
проверьте один из признаков сходимости
и введите
формулу
=ЕСЛИ(МАКС (G7 + G8 + G9 + G10; H7 + H8 + H9 + H10; I7 + I8 + I9 + I10) < 1; «сходится»;
«не сходится»);
д)
в ячейке D7 определите норму матрицы по
формуле:
=МАКС(G7 + H7 + I7; G8 + H8 + I8; G9 + H9 + I9; G10 + H10 + I10).
Если полученный ответ меньше 1, то метод
сходится при любых начальных приближениях.
За начальное (нулевое) приближение
возьмите полученные свободные члены и
внесите их в ячейки G2:G5. Вычислим первые
приближенные значения: х1(1),
х2(1),
х3(1),
х4(1)
по формулам (табл. 1.2);
Таблица
1.2 – Вычисление первых приближенных
значений
|
Ячейка |
Формула |
|
В13 |
= E8 – B8*G3 – C8 * G4 – D8 * G5 |
|
В14 |
= E9 – B9 * G2 – C9 * G4 – D9 * G5 |
|
В15 |
= E10 – B10 * G2 – C10 * G3 – D10 * G5 |
|
В16 |
= E11 – B11 * G2 – C11 * G3 – D11 * G4 |
е)
таким образом получите первые приближенные
значения х1,
х2,
х3,
х4.
Далее в ячейки С13:С16 введите формулы,
используя уже новые полученные приближения
из В13:В16 (табл. 1.3).
Таблица
1.3 – Продолжение вычислений
|
Ячейка |
Формула |
|
С13 |
= $E$8 – $B$8 * B14 – $C$8 * B15 – $D$8 * B16 |
|
С14 |
= $E$9 – $B$9 * B13 – $C$9 * B15 – $D$9 * B16 |
|
С15 |
= $E$10 – $B$10 * B13 – $C$10 * B14 – $D$10 * B16 |
|
С16 |
= $E$11 – $B$11 * B13 – $C$11 * B14 – $D$11 * B15 |
ж)
используя полученные вторые приближения,
скопируйте формулы из ячеек С13:С16 на
блок ячеек D13:D16.
В результате получите новые приближенные
значения корней. Продолжайте операцию
копирования, получая новые приближения.
Момент прекращения вычислений определите
эмпирическим правилом.
1.3.Метод
Зейделя в
среде MS Excel:
а)
в блоке ячеек В19:В22
введите
формулы вычисления корней уравнения
по методу Зейделя (табл. 1.4).
Таблица
1.4 – Вычисление корней уравнения по
методу Зейделя
|
Ячейка |
Формула |
|
В19 |
= $E$8 – $B$8 * G3 – $C$8 * G4 – $D$8 * G5 |
|
В20 |
= $E9 – $B$9 * B19 – $C$9 * G4 – $D$9 * G5 |
|
В21 |
= $E$10 – $B$10 * B19 –$C$10 * B20 – $D$10 * G5 |
|
В22 |
= $E$11 – $B$11 * B19 – $C$11 * B20 – |
б)
рассуждая аналогично, введите формулы
в ячейки C19:C22,
используя соответственно полученные
данные из В19:В22 (табл. 1.5).
Таблица
1.5 – Продолжение вычислений
|
Ячейка |
Формула |
|
С19 |
=$E$8 |
|
С20 |
=$E$9 |
|
С21 |
=$E$10 |
|
С22 |
=$E$11 |
в)
скопируйте формулы из ячеек С19:С22 на
блоки: D19:D22,
Е19:Е22 и т.д. Момент прекращения вычислений
определяется, как и в методе простых
итераций, эмпирическим правилом.
Задание
2. Изучите возможности математического
пакета MathCad при решении СЛАУ и разработайте
схемы программ решения СЛАУ с использованием
средств: lsolve( ), Given … Find( ), метода обратной
матрицы и метода Гаусса.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Решение уравнений методом подбора параметров Excel
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: {=B12:E12/D12}.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки ({=(B11:E11-B16:E16*D11)/C11}). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
Хn+1 = Xn– F (Xn) / M, n = 0, 1, 2, … .
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х3 – 1. М = 11.
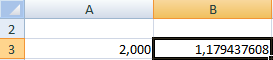
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
Скачать решения уравнений в Excel
Корень на заданном промежутке один.