Метод последовательных уступок excel

Рассмотрим решения этой задачи с помощью
различных методов решения многокритериальных
задач, которые мы рассматривали во
второй главе данной работы. Для вычисления,
мы воспользуемся стандартной программой
поиска решения в MS
Excel.

3.3.1. Метод последовательных уступок

Из двух приведенных критерий, мы
максимизируем первый, наиболее важный
критерий, затем назначаем величину
допустимого снижения значения этого
критерия. В данном случае, размер уступка
равна 20000.

рис.3.19.
Целевые, переменные значения и ограничения

В «В1» вводим надпись «Переменные»,
следующая строка это имя наших переменных
.
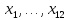
В ячейках «В3:M3» вводим
значения переменных, то есть наши.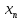
Это могут быть произвольные числа,
допустим, запишем нули,
далее они будут оптимизироваться.

Ячейку «A5» назовем
«Целевые», в соседние ячейки записываем
значения переменных первой целевой
функции, которая мы хотим максимизировать.
В «Р5», вводим «=B5*$B$3 +C5*$C$3 +D5*$D$3
+E5*$E$3+F5*$F$3+G5*$G$3+H5*$H$3+I5*$I$3+J5*$J$3+K5*$K$3+L5*$L$3+M5*$M$3»,
или «=СУММПРОИЗВ(B3:M3;B5:M5)». Таким образом,
мы задали первую целевую функцию.

Ячейка «А8» будет называться «Ограничения».
Левые части ограничений распишем от
«B9:M18»,
правые части находятся в диапазоне от
«P9:P18». В
ячейке «О9» вводим формулу «=B9*$B$3+ C9*$C$3+
D9*$D$3
+E9*$E$3+F9*$F$3+G9*$G$3+H9*$H$3+I9*$I$3+J9*$J$3+K9*$K$3+L9*$L$3+M9*$M$3»,
номера столбцов и номера строк ряда
переменных зафиксировано, далее
воспользуемся автозаполнением, чтобы
заполнить ячейки «O10:O18».

Предварительные действия завершены.
Вызываем надстройку «Поиск решения»,
«P5» — это наша целевая
функция.

рис.3.20.
Параметры поиска решения

В связи с тем, что функция максимизируется,
мы ставим флажок в поле напротив надписи
«Максимум». Изменяем ячейки переменных
$B$3:$M$3. Добавляем следующие ограничения:

1. $B$3: $M$3 ≥
0

2. $O$16:$O$18 ≥
$P$16:$P$18

3. $O$9:$O$15 ≤
$P$9:$P$15

Выбираем «Поиск решения линейных задач
симплекс-методом». Запускаем решения
и сохраняем найденное решение.
Теперь
мы можем увидеть следующие результаты:

рис.3.21.
Определение размер уступка

На следующем этапе оптимизируем вторую
целевую функцию, для этого, нам необходимо
ввести уступок в размере 20000. Теперь,
значения первой целевой функции может
быть не менее, чем 2637985 (2637985 = 2657985-20000).

Начиная с «B6:M6»
мы записываем значения переменных
второй целевой функции, которая
минимизируется. В «Р6», вводим саму
функцию «=B6*$B$3
+C6*$C$3+D6*$D$3+E6*$E$3+F6*$F$3+G6*$G$3+H6*$H$3+I6*$I$3+J6*$J$3+K6*$K$3+L6*$L$3+M6*$M$3»,
или «=СУММПРОИЗВ(B3:M3;B6:M6)».

Снова вызываем надстройку «Поиск
решения», прежние данные остались
введенными.

Меняем ссылку на целевую функцию, теперь
это будет ячейка «Р6». Так, как вторая
целевая минимизируется, то ставим флажок
в поле напротив надписи «Минимум».
Вводим дополнительное ограничение,
связанное с уступкой по первому критерию
«Р5» «≥» «С21».

рис.3.22. Параметры поиска решения

Выбираем «Поиск решения линейных задач
симплекс-методом». Запускаем решения
и сохраняем найденное решение.
Теперь
мы можем увидеть окончательные результаты:

рис.3.23.
Окончательный результат решения по
методу последовательных уступок

Согласно методу последовательных
уступок, оптимальный план производства,
при данных условиях, состоит в том, что
продукцию 2-ого, 6-ого и 11-ого видов
необходимо производить в объеме 135, 198
и 160 единиц соответственно, а продукции
1-ого, 3-ого, 4-ого, 5-ого, 7-ого, 9-ого, 10-ого
и 12-ого видов не стоит выпускать в
производство. При этом обеспечивается
максимальная выручка в размере 32110,65 ₴
и размер минимальной себестоимости
ресурса в размере 24104,22 ₴.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Всероссийский заочный финансово-экономический институт Кафедра экономико-математический методов и моделей

• Тема:

• Решение многокритериальных задач линейного программирования методом последовательных уступок в Excel

• Работу выполнила: студентка 3-го курса

• спец. Финансы и кредит

• Сущевская Лилия С.

• Руководитель: к.т.н., доц. Уродовских

• Виктор Николаевич

Цель работы: изучить алгоритм решения многокритериальных ЗЛП с помощью ЭВМ с использованием метода последовательных уступок.

• Цель работы: изучить алгоритм решения многокритериальных ЗЛП с помощью ЭВМ с использованием метода последовательных уступок.

• В экономических задачах могут использоваться несколько критериев оптимизации.

• Например, при производстве продукции одновременно максимизируется ее качество и минимизируется себестоимость, при выдаче ссуды в банке максимизируется кредитный срок и минимизируется процентная ставка, и др.

• Существуют различные методы решения многокритериальных задач.

Наиболее эффективным методом решения много-критериальных задач является метод последова-тельных уступок. Он применяется, когда частные критерии (Ц.Ф.) могут быть упорядочены в порядке убывающей важности.

• Наиболее эффективным методом решения много-критериальных задач является метод последова-тельных уступок. Он применяется, когда частные критерии (Ц.Ф.) могут быть упорядочены в порядке убывающей важности.

• Предположим, что все критерии максимизируются и пронумерованы в порядке убывания их важности.

• Находим максимальное значение Z1 , первого по важности критерия в области допустимых решений, решив задачу

• Затем исходя из практических соображений и принятой точности, назначается допустимое отклонение (экономически оправданная уступка) критерия Z1 и отыскивается максимальное значение второго критерия Z2 при условии, что значение первого должно отклоняться от максимального не более чем на величину допустимой уступки.

Далее решается задача

• Далее решается задача

• Затем снова назначается величина уступки по второму критерию, которая вместе с первой использу-ется при нахождении условного экстремума третьего частного критерия, и т.д.

• В конце, выявляется экстремальное значение последнего по важности критерия Zm при условии, что значение каждого из первых m-1 частных критериев отличается от экстремального не более чем на величину допустимой уступки. Полученное на последнем этапе решение считается оптимальным.

• Недостаток – метод не всегда дает эффективное решение.

ПРИМЕР 1. Найти оптимальное решение для трехкритериальной задачи:

• ПРИМЕР 1. Найти оптимальное решение для трехкритериальной задачи:

Оптимальное решение найти методом последовательных уступок, выбрав уступку по первому критерию 1 = 4, а по второму 2 = 5.

• Оптимальное решение найти методом последовательных уступок, выбрав уступку по первому критерию 1 = 4, а по второму 2 = 5.

• Алгоритм решения задачи.

• 1. Вначале решаем однокритериальную задачу с первой целевой функцией.

• В ячейку С1 записываем «Переменные», а в ячейку А3 — «значение».

• В соседние три ячейки В3, С3 и D3 вводим произвольные числа для переменных (Х1, Х2, Х3), например, единицы. В дальнейшем эти числа будут оптимизироваться.

2. В следующей строке задаем целевые функции.

• 2. В следующей строке задаем целевые функции.

• В А4 вводим подпись «Целевые», а в В4 формулу «= 2*B3 + C3 — 3*D3» задаем первую целе-вую функцию. Аналогично в ячейку С4 вводим вторую целевую функцию «= B3+3*C3-2*D3», и в ячейку третью D4 – третью «= — B3+2*C3+4*D3».

3. В следующую строку вводим левые части ограничений.

• 3. В следующую строку вводим левые части ограничений.

• Для этого в А5 вводим подпись «Ограничения», в В5 формулу «=B3+3*C3+2*D3»,

• в С5 формулу «=2*B3- C3+D3»

• и в D5 формулу «=B3+2*C3».

4. Вызываем надстройку «Поиск решения» (Solver).

• 4. Вызываем надстройку «Поиск решения» (Solver).

• После открытия окна «Поиск решения» в поле «Установить целевую ячейку» ставим курсор и делаем ссылку на ячейку В4, щелкая по ней мышью.

• Поскольку целевая функция максимизируется, то нужно убедиться в том, что флажок стоит напротив надписи «Равной: максимальному значению».

Затем ставим курсор в поле «^ » и выделяем блок ячеек В3, С3 и D3 с переменными. В поле появиться $B$3:$D$3.

• Затем ставим курсор в поле «Изменяя ячейки» и выделяем блок ячеек В3, С3 и D3 с переменными. В поле появиться $B$3:$D$3.

• В поле «Ограничения» нажатием кнопки «Добавить» поочередно вводятся ссылки на ограничения – ячейку В5, в центральном окне определяем знак ≥ и в правом «Ограничения» набираем правую часть ограничения – число 1.

• Аналогично вводим «С5» «» и «16». Вновь нажимаем «Добавить», вводим «D5» «≤» и «24».

• Для ввода дополнительных ограничений (условия неотрицательности) нажимаем «Добавить», ставим курсор в левое поле и обводим ячейки В3, С3 и D3 (результат $B$3:$D$3) в среднем окне ставим «» и в правом число 0.

Для запуска вычислений нажимаем кнопку «Выполнить».

• Для запуска вычислений нажимаем кнопку «Выполнить».

В открывшемся диалоговом окне «Результаты поиска решения» выбираем «Сохранить найденное решение» (Keep Solver Solution) и подтверждаем «ОК». В ячейках В3, С3 и D3 находятся оптимальные значения переменных: 11,2; 6,4 и 0. В ячейки В4 – значение целевой функции 28,8.

• В открывшемся диалоговом окне «Результаты поиска решения» выбираем «Сохранить найденное решение» (Keep Solver Solution) и подтверждаем «ОК». В ячейках В3, С3 и D3 находятся оптимальные значения переменных: 11,2; 6,4 и 0. В ячейки В4 – значение целевой функции 28,8.

5. После этого оптимизируется вторая целевая функция. При этом первую Ц.Ф., в соответствии с методом последовательных уступок можно ухудшить на величину не более, чем 1= 4. С учетом этого значение в ячейке В4 (где хранится первая целевая функция) может быть не меньшее, чем 28,8 – 4 = 24,8.

• 5. После этого оптимизируется вторая целевая функция. При этом первую Ц.Ф., в соответствии с методом последовательных уступок можно ухудшить на величину не более, чем 1= 4. С учетом этого значение в ячейке В4 (где хранится первая целевая функция) может быть не меньшее, чем 28,8 – 4 = 24,8.

• Далее вызываем надстройку «Поиск решения», в ней все данные остались прежними.

• Меняем ссылку на целевую функцию. Ставим курсор в поле «Установить целевую ячейку» и щелкаем по ячейке С4, в которой находится ссылка на вторую целевую функцию.

• Поскольку вторая целевая функция миними-зируется, то ставим флажок напротив надписи «Равной минимальному значению».

В поле «Ограничения» нажимаем кнопку «Добавить» и вводим дополнительное ограничение, связанное с уступкой по первому критерию. В появившемся окне «Добавление ограничения» в трех окнах (слева на право) вводим данные «В4», «≥», «24,8».

• В поле «Ограничения» нажимаем кнопку «Добавить» и вводим дополнительное ограничение, связанное с уступкой по первому критерию. В появившемся окне «Добавление ограничения» в трех окнах (слева на право) вводим данные «В4», «≥», «24,8».

В результате решения – переменные равны 10,2; 4,4; 0. Вторая целевая функция равна 23,4 (ячейка С4). Первая равна своему минимальному значению 24,8 (ячейка В4).

• В результате решения – переменные равны 10,2; 4,4; 0. Вторая целевая функция равна 23,4 (ячейка С4). Первая равна своему минимальному значению 24,8 (ячейка В4).

6. На третьем этапе делаем уступку по второму крите-рию, равную 2 = 5.

• 6. На третьем этапе делаем уступку по второму крите-рию, равную 2 = 5.

• Поскольку вторая функция минимизируется, то ее значение не должно превышать 23,4 + 5 = 28,4. Вызываем надстройку «Поиск решения» и меняем ссылку на целевую функцию. Для этого ставим курсор в поле «Установить целевую ячейку» и щелкаем по ячейке D4, содержащую третью целевую функцию.

• Поскольку третья Ц.Ф. максимизируется, то ставим флажок в поле напротив надписи «Равной максималь-ному значению».

• В поле «Ограничения» и нажимаем кнопку «Добавить» вводим дополнительное ограничение с учетом уступки по второму критерию.

• В окне «Добавление ограничения» вводим данные «С4», «≤», «28,4».

В поле «Ограничения» нажимаем кнопки «Добавить» вводим дополнительное ограничение с учетом уступки по второму критерию. В окне «Добавление ограничения» вводим данные «С4», «≤», «28,4».

В результате расчета найдены:

• В результате расчета найдены:

• X1 = 10,76; X2 = 6,62; X3 = 1,11.

• Целевые функции равны:

• max Z1 = 24,8; min Z2 = 28,4 и max Z3 = 28,4, при удовлетворении всех ограничений

Рассмотрим решения этой задачи с помощью различных методов решения многокритериальных задач, которые мы рассматривали во второй главе данной работы. Для вычисления, мы воспользуемся стандартной программой поиска решения в MS Excel.

Метод последовательных уступок

Из двух приведенных критерий, мы максимизируем первый, наиболее важный критерий, затем назначаем величину допустимого снижения значения этого критерия. В данном случае, размер уступка равна 20000.

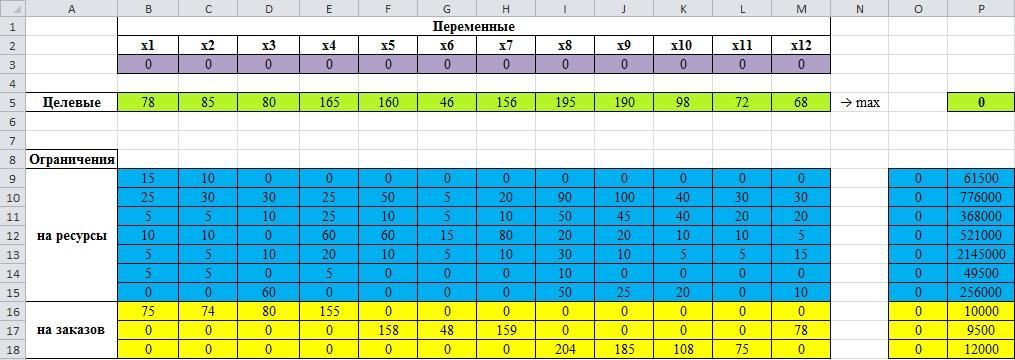
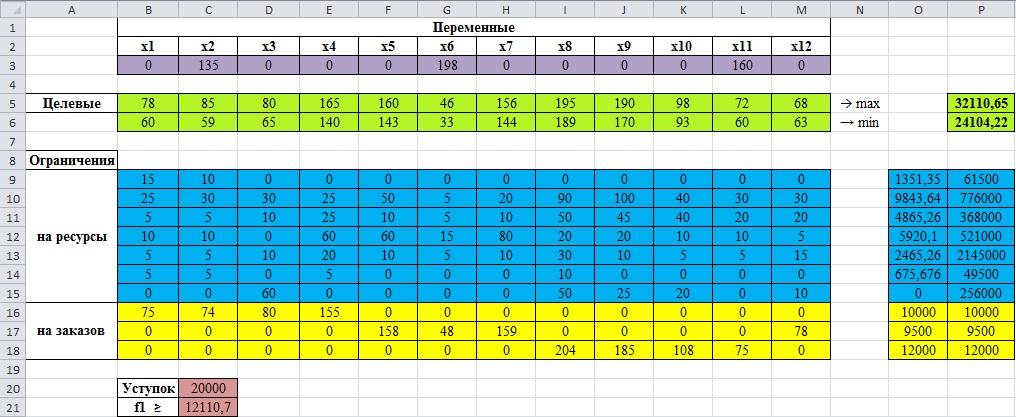
рис.3.19. Целевые, переменные значения и ограничения

В «В1» вводим надпись «Переменные», следующая строка это имя наших переменных . В ячейках «В3:M3» вводим значения переменных, то есть наши . Это могут быть произвольные числа, допустим, запишем нули, далее они будут оптимизироваться.

Ячейку «A5» назовем «Целевые», в соседние ячейки записываем значения переменных первой целевой функции, которая мы хотим максимизировать. В «Р5», вводим «=B5*$B$3 +C5*$C$3 +D5*$D$3 +E5*$E$3+F5*$F$3+G5*$G$3+H5*$H$3+I5*$I$3+J5*$J$3+K5*$K$3+L5*$L$3+M5*$M$3», или «=СУММПРОИЗВ(B3:M3;B5:M5)». Таким образом, мы задали первую целевую функцию.

Ячейка «А8» будет называться «Ограничения». Левые части ограничений распишем от «B9:M18», правые части находятся в диапазоне от «P9:P18». В ячейке «О9» вводим формулу «=B9*$B$3+ C9*$C$3+ D9*$D$3 +E9*$E$3+F9*$F$3+G9*$G$3+H9*$H$3+I9*$I$3+J9*$J$3+K9*$K$3+L9*$L$3+M9*$M$3», номера столбцов и номера строк ряда переменных зафиксировано, далее воспользуемся автозаполнением, чтобы заполнить ячейки «O10:O18».

Предварительные действия завершены. Вызываем надстройку «Поиск решения», «P5» — это наша целевая функция.

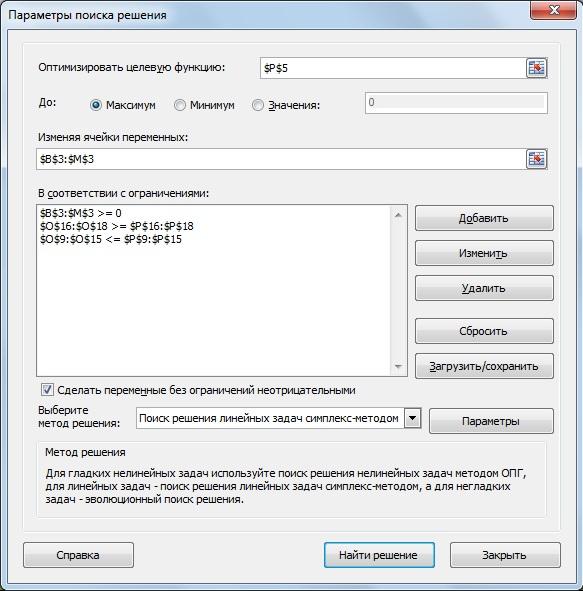
рис.3.20. Параметры поиска решения

В связи с тем, что функция максимизируется, мы ставим флажок в поле напротив надписи «Максимум». Изменяем ячейки переменных $B$3:$M$3. Добавляем следующие ограничения:

1. $B$3: $M$3 ? 0

2. $O$16:$O$18 ? $P$16:$P$18

3. $O$9:$O$15 ? $P$9:$P$15

Выбираем «Поиск решения линейных задач симплекс-методом». Запускаем решения и сохраняем найденное решение. Теперь мы можем увидеть следующие результаты:

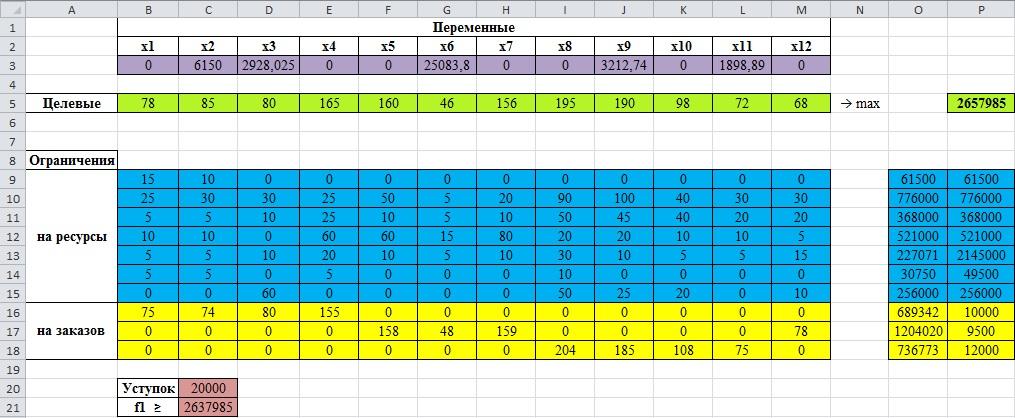
рис.3.21. Определение размер уступка

На следующем этапе оптимизируем вторую целевую функцию, для этого, нам необходимо ввести уступок в размере 20000. Теперь, значения первой целевой функции может быть не менее, чем 2637985 (2637985 = 2657985-20000).

Начиная с «B6:M6» мы записываем значения переменных второй целевой функции, которая минимизируется. В «Р6», вводим саму функцию

«=B6*$B$3 +C6*$C$3+D6*$D$3+E6*$E$3+F6*$F$3+G6*$G$3+H6*$H$3+I6*$I$3+J6*$J$3+K6*$K$3+L6*$L$3+M6*$M$3», или «=СУММПРОИЗВ(B3:M3;B6:M6)».

Снова вызываем надстройку «Поиск решения», прежние данные остались введенными.

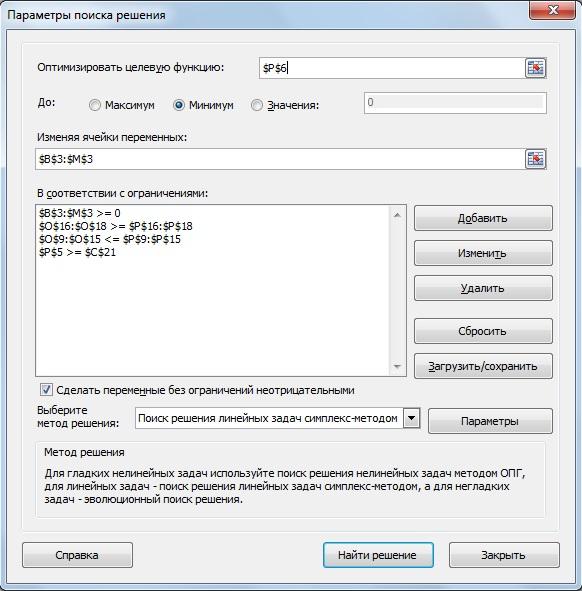
Меняем ссылку на целевую функцию, теперь это будет ячейка «Р6». Так, как вторая целевая минимизируется, то ставим флажок в поле напротив надписи «Минимум». Вводим дополнительное ограничение, связанное с уступкой по первому критерию «Р5» «?» «С21».

рис.3.22. Параметры поиска решения

Выбираем «Поиск решения линейных задач симплекс-методом». Запускаем решения и сохраняем найденное решение. Теперь мы можем увидеть окончательные результаты:

рис.3.23. Окончательный результат решения по методу последовательных уступок

Согласно методу последовательных уступок, оптимальный план производства, при данных условиях, состоит в том, что продукцию 2-ого, 6-ого и 11-ого видов необходимо производить в объеме 135, 198 и 160 единиц соответственно, а продукции 1-ого, 3-ого, 4-ого, 5-ого, 7-ого, 9-ого, 10-ого и 12-ого видов не стоит выпускать в производство. При этом обеспечивается максимальная выручка в размере 32110,65 ? и размер минимальной себестоимости ресурса в размере 24104,22 ?.

1


Всероссийский заочный финансово-экономический институт Кафедра экономико-математический методов и моделей Тема: Решение многокритериальных задач линейного программирования методом последовательных уступок в Excel Работу выполнила:студентка 3-го курса спец. Финансы и кредит Сущевская Лилия С. Руководитель:к.т.н., доц.Уродовских Виктор Николаевич

2


Цель работы: изучить алгоритм решения многокритериальных ЗЛП с помощью ЭВМ с использованием метода последовательных уступок. В экономических задачах могут использоваться несколько критериев оптимизации. Например, при производстве продукции одновременно максимизируется ее качество и минимизируется себестоимость, при выдаче ссуды в банке максимизируется кредитный срок и минимизируется процентная ставка, и др. Существуют различные методы решения многокритериальных задач.

3


метод последова- тельных уступок Наиболее эффективным методом решения много- критериальных задач является метод последова- тельных уступок. Он применяется, когда частные критерии (Ц.Ф.) могут быть упорядочены в порядке убывающей важности. Предположим, что все критерии максимизируются и пронумерованы в порядке убывания их важности. Находим максимальное значение Z 1, первого по важности критерия в области допустимых решений, решив задачу Затем исходя из практических соображений и принятой точности, назначается допустимое отклонение (экономически оправданная уступка) критерия Z 1 и отыскивается максимальное значение второго критерия Z 2 при условии, что значение первого должно отклоняться от максимального не более чем на величину допустимой уступки.

4


Далее решается задача Затем снова назначается величина уступки по второму критерию, которая вместе с первой использу- ется при нахождении условного экстремума третьего частного критерия, и т.д. В конце, выявляется экстремальное значение последнего по важности критерия Z m при условии, что значение каждого из первых m-1 частных критериев отличается от экстремального не более чем на величину допустимой уступки. Полученное на последнем этапе решение считается оптимальным. Недостаток – метод не всегда дает эффективное решение.

5


ПРИМЕР 1. Найти оптимальное решение для трехкритериальной задачи:

6


Оптимальное решение найти методом последовательных уступок, выбрав уступку по первому критерию 1 = 4, а по второму 2 = 5. Алгоритм решения задачи Алгоритм решения задачи. 1. Вначале решаем однокритериальную задачу с первой целевой функцией. В ячейку С1 записываем «Переменные», а в ячейку А3 — «значение». В соседние три ячейки В3, С3 и D3 вводим произвольные числа для переменных (Х1, Х2, Х3), например, единицы. В дальнейшем эти числа будут оптимизироваться.

7


2. В следующей строке задаем целевые функции. В А4 вводим подпись «Целевые», а в В4 формулу «= 2*B3 + C3 — 3*D3» задаем первую целе- вую функцию. Аналогично в ячейку С4 вводим вторую целевую функцию «= B3+3*C3-2*D3», и в ячейку третью D4 – третью «= — B3+2*C3+4*D3 ».

8


3. В следующую строку вводим левые части ограничений. Для этого в А5 вводим подпись «Ограничения», в В5 формулу «=B3+3*C3+2*D3», в С5 формулу «=2*B3- C3+D3» и в D5 формулу «=B3+2*C3».

9


4. Вызываем надстройку «Поиск решения» (Solver). После открытия окна «Поиск решения» в поле «Установить целевую ячейку» ставим курсор и делаем ссылку на ячейку В4, щелкая по ней мышью. Поскольку целевая функция максимизируется, то нужно убедиться в том, что флажок стоит напротив надписи «Равной: максимальному значению».

10


Затем ставим курсор в поле «Изменяя ячейки» и выделяем блок ячеек В3, С3 и D3 с переменными. В поле появиться $B$3:$D$3. В поле «Ограничения» нажатием кнопки «Добавить» поочередно вводятся ссылки на ограничения – ячейку В5, в центральном окне определяем знак и в правом «Ограничения» набираем правую часть ограничения – число 1. Аналогично вводим «С5» « » и «16». Вновь нажимаем «Добавить», вводим «D5» «» и «24». Для ввода дополнительных ограничений (условия неотрицательности) нажимаем «Добавить», ставим курсор в левое поле и обводим ячейки В3, С3 и D3 (результат $B$3:$D$3) в среднем окне ставим « » и в правом число 0.

11


Для запуска вычислений нажимаем кнопку «Выполнить».

12


В открывшемся диалоговом окне «Результаты поиска решения» выбираем «Сохранить найденное решение» (Keep Solver Solution) и подтверждаем «ОК». В ячейках В3, С3 и D3 находятся оптимальные значения переменных: 11,2; 6,4 и 0. В ячейки В4 – значение целевой функции 28,8.

13


5. После этого оптимизируется вторая целевая функция. При этом первую Ц.Ф., в соответствии с методом последовательных уступок можно ухудшить на величину не более, чем 1= 4. С учетом этого значение в ячейке В4 (где хранится первая целевая функция) может быть не меньшее, чем 28,8 – 4 = 24,8. Далее вызываем надстройку «Поиск решения», в ней все данные остались прежними. Меняем ссылку на целевую функцию. Ставим курсор в поле «Установить целевую ячейку» и щелкаем по ячейке С4, в которой находится ссылка на вторую целевую функцию. Поскольку вторая целевая функция миними- зируется, то ставим флажок напротив надписи «Равной минимальному значению».

14


В поле «Ограничения» нажимаем кнопку «Добавить» и вводим дополнительное ограничение, связанное с уступкой по первому критерию. В появившемся окне «Добавление ограничения» в трех окнах (слева на право) вводим данные «В4», «», «24,8».

15


В результате решения – переменные равны 10,2; 4,4; 0. Вторая целевая функция равна 23,4 (ячейка С4). Первая равна своему минимальному значению 24,8 (ячейка В4).

16


6. На третьем этапе делаем уступку по второму крите- рию, равную 2 = 5. Поскольку вторая функция минимизируется, то ее значение не должно превышать 23,4 + 5 = 28,4. Вызываем надстройку «Поиск решения» и меняем ссылку на целевую функцию. Для этого ставим курсор в поле «Установить целевую ячейку» и щелкаем по ячейке D4, содержащую третью целевую функцию. Поскольку третья Ц.Ф. максимизируется, то ставим флажок в поле напротив надписи «Равной максималь- ному значению». В поле «Ограничения» и нажимаем кнопку «Добавить» вводим дополнительное ограничение с учетом уступки по второму критерию. В окне «Добавление ограничения» вводим данные «С4», «», «28,4».

17


В поле «Ограничения» нажимаем кнопки «Добавить» вводим дополнительное ограничение с учетом уступки по второму критерию. В окне «Добавление ограничения» вводим данные «С4», «», «28,4».

18


В результате расчета найдены: X 1 = 10,76; X 2 = 6,62; X 3 = 1,11. Целевые функции равны: max Z 1 = 24,8 ; min Z 2 = 28,4 и max Z 3 = 28,4, при удовлетворении всех ограничений

ЛЕКЦИЯ 8.
Многокритериальные задачи
(продолжение)
Метод последовательных уступок
Другой способ носит название метода последовательных уступок. В
этом методе критерии нумеруются в порядке убывания важности. Пусть
критерии f1 , f 2 ,…, f K записаны в порядке уменьшения их важности. Тогда
должны быть выполнены следующие действия.
1-й шаг. Решается однокритериальная задача по 1-му критерию:
z1*  max f1 ( X ) .
XD
2-й шаг. Назначается разумная с инженерной точки зрения уступка
z1 , составляется и решается новая задача оптимизации по 2-му критерию:
z 2* 
max
X D
f1  X  z1*  z1
f2 (X ) .
3-й шаг. Назначается уступка для 2-го критерия z 2 , составляется и
решается задача оптимизации по 3-му критерию:
z 3* 
max
X D
f1  X  z1*  z1
f 2  X  z *2  z 2
f3 ( X ) .
Процесс назначения уступок по каждому критерию и решения однокритериальных задач продолжается, пока не дойдем до последнего K -го
шага.
K -й
шаг. Назначается уступка для ( K  1)-го критерия z K 1 , состав-
ляется и решается задача оптимизации по последнему K -му критерию:
10
z K* 
max
X D
f1  X  z1*  z1
f 2  X  z *2  z 2
….
f K 1  X  z *K 1  z K 1
fK (X ) .
Основной недостаток методов, использующих ограничения на критерии, состоит в субъективности выбора контрольных показателей и в
субъективности выбора уступок. При использовании метода последовательных уступок следует помнить, что уступки могут быть несоизмеримы
между собой, поэтому надо предварительно организовать нормировку критериев. Кроме того, в общем случае уже со 2-го шага решение может оказаться не оптимальным по Парето.
Пример 5.
Рассмотрим сначала однокритериальную задачу, заключающуюся в
максимизации общей прибыли от реализации готовой продукции.
На лесоперерабатывающем предприятии установлено три группы
оборудования (строгальные, фрезерные и шлифовальные станки). На этих
станках производится два типа продукция: шкафы и столы. Известны нормы затрат машинного времени, эффективный фонд времени станков, прибыль от реализации единицы продукции (таблица 2).
Таблица 2
Станки
Строгальные
Фрезерные
Шлифовальные
Прибыль, ден.ед.
Затраты машинного времени на обработку
одного изделия, час
Шкаф
Стол
4
3
2
1
2
3
8
7
Фонд времени станков, час
144
64
120
Определить количество изделий каждого вида, которое необходимо
изготовить на предприятии с целью получения наибольшей общей прибыли от реализации готовой продукции.
11
Количество шкафов и столов, которое необходимо изготовить на
предприятии, обозначим соответственно через x1 и x2 . Общая прибыль от
их изготовления выражается функцией
z  8 x1  7 x 2 .
(*)
Определим фактическую загрузку по каждой группе оборудования.
Она будет равна
4 x1  3 x 2 – для строгальных станков,
2 x1  x 2 – для фрезерных станков,
2 x1  3 x 2 – для шлифовальных станков.
Коэффициенты при неизвестных обозначают здесь нормы затрат
машинного времени на обработку одного шкафа и одного стола соответственно.
Ресурсы машинного времени ограниченны. Следовательно, загрузка
по каждой группе оборудования не должна превышать имеющихся ресурсов машинного времени. Математически это означает, что
4 x1  3x 2  144

2 x1  x 2  64 .
2 x  3x  120
2
 1
(**)
Ограничительные условия для решения данной задачи мы получили
в виде системы линейных неравенств (**). Очевидно, что неизвестные задачи являются целыми числами и удовлетворяют условиям
x1  0 , x 2  0 .
(***)
Таким образом, математическая модель задачи состоит в максимизации целевой функции (*) при условиях, что неизвестные x1 и x 2 удовлетворяют системе ограничений (**) и неравенствам (***).
Согласно оптимальному плану предприятие должно изготовить 12
шкафов и 32 стола, и наибольшая прибыль составит 320 ден.ед.
12
Дополнительно предположим, что предприятие заинтересовано в
эффективном использовании оборудования. При этом известны цены за 1
час простоя оборудования каждого вида: для строгальных станков – 3
ден.ед., для фрезерных станков – 9 ден.ед., для шлифовальных станков – 2
ден.ед.
Требуется составить задачу оптимизации с двумя критериями и решить ее методом уступок.
Обозначим через z 2 суммарные издержки предприятия за простой
оборудования. Поскольку время простоя равно
144  (4 x1  3x 2 ) – для строгальных станков,
64  (2 x1  x2 ) – для фрезерных станков,
120  (2 x1  3x 2 ) – для шлифовальных станков,
то суммарные издержки равны
z 2  3144  4 x1  3x 2   964  2 x1  x 2   2120  2 x1  3x 2  ,
или
z 2  34 x1  24 x 2  1248  min .
(4)
Система ограничений (**), (***) при этом не изменяется:
4 x1  3x 2  144

2 x1  x 2  64 ,
2 x  3x  120
2
 1
(5)
x1  0 , x 2  0 .
(6)
Задача оптимизации по второму критерию (4) – (6) решается в Excel
с использованием средства «Поиск решения». Исходные данные и результаты оптимизации показаны на рисунке 5.
13
Рисунок 5 – Исходные данные и результаты решения задачи (4) – (6)
Отметим, что целевая функция (4) содержит свободный член, поэтому в ячейку D6 помещается одна из формул таблицы 3.
Таблица 3
= B6*B4+C6*C4+1248
или
=СУММПРОИЗВ(B6:C6;B4:C4)+1248
На рисунке 5 представлен оптимальный план выпуска мебели по
критерию минимизации издержек за простой оборудования: предприятие
должно изготовить 24 шкафа и 16 столов. При этом минимальные издержки составят z 2,min  48 ден.ед. Как видим, этот план существенно отличается от оптимального плана по критерию общей прибыли.
Решим теперь задачу с двумя критериями методом уступок. Для первого критерия z назначим уступку z  8 , и в математическую модель (4)
– (6) добавим еще одно ограничение z  320  8  312 . Тогда получим новую задачу оптимизации по второму критерию:
z 2  34 x1  24 x 2  1248  min
(7)
при ограничениях
14
4 x1  3x 2  144
2 x  x  64
 1
2
,

2
x

3
x

120
2
 1
8 x1  7 x2  312
(8)
x1  0 , x 2  0 .
(9)
Организация исходных данных задачи (7) – (9) на листе Excel приведена на рисунке 6.
Рисунок 6 – Исходные данные и результаты решения задачи МКО
В результате получен компромиссный план выпуска мебели, состоящий в изготовлении 18 шкафов и 24 столов. Издержки за простой оборудования составят z 2  60 ден.ед., а общая прибыль предприятия будет равна z  312 ден.ед.
15
Методы целевого программирования
Название этой группы методов связано с тем, что ЛПР задает определенные цели f1 , f 2 ,…, f K для каждого критерия. Задача МКО в этом случае преобразуется в задачу минимизации суммы отклонений с некоторым
показателем p :
 K
z    wk f k  X   f k
 k 1
1
p
p
  min (при XD),

(10)
где wk – некоторые весовые коэффициенты, характеризующие важность
того или иного критерия.
Задачу (10) можно конкретизировать в зависимости от значений параметра p и заданных целей. В частности, при p  2 и wk  1 получим задачу минимизации суммы квадратов отклонений:
z   f k  X   f k*
K
2
k 1
 min (при XD),
в которой минимизируется евклидово расстояние от множества достижимости F до «абсолютного максимума» f *   f1* , f 2* ,…, f l *  в пространстве
критериев. Здесь f k*  max f k  X  .
X D
Осложнения,
обусловленные
несоизмеримостью
величин
f k  X   f k* , можно преодолеть с помощью нормировки критериев, рас-
сматривая следующую задачу оптимизации:
 f k  X   f k*

z  
f k*
k 1 

K
2


  min (при XD).

(11)
Пример 6. Методом целевого программирования решить задачу
МКО из примера 3.
19
В условиях примера 3 имеем f1*  2 , f 2*  1, поэтому задача (11)
принимает вид
z
x1  22 x2  12
4

1
 min
при условиях
 x1  2 x 2  2
.

x

,
x

 1
2
При постоянном значении z линии уровня целевой функции
x1  22 x 2  12

 1 представляют собой эллипсы с центром в точке
z2
2 z 2
M 2; 1 и полуосями a  2 z и b  z . Необходимо найти минимальное значение z , для которого соответствующий эллипс будет иметь общие точки с
областью D. На рисунке 7 показано графическое решение данной задачи.
Рисунок 7 – Решение задачи методом целевого программирования
 
Оптимальной является точка X *  1; 1 .
2
20
Методы гарантированного результата
Рассматриваются методы, которые дают наилучший результат даже
для самого наименьшего из критериев, а именно, компромиссное решение
находится путем решения следующей задачи оптимизации:
z  min f k  X   max при X  D .
k 1, 2 ,…, K
Это есть максиминная задача. С учетом нормировки критериев методы гарантированного результата образуют наиболее перспективное
направление в решении задач МКО.
Для нормированных критериев k ( X ) 
fk (X )
fk
*
, где f k*  max f k ( X ) ,
X D
максиминная задача формулируется в виде:
z  min k  X   max (при X  D ).
k 1, 2 ,…, K
(12)
Остановимся на рассмотрении двух случаев, когда критерии равнозначны и неравнозначны (с заданным приоритетом).
Равнозначные критерии
Задача (12) эквивалентна задаче
z    max
(13)
при условиях
  k  X , k  1,2,…, K
.

X

D

(14)
Задача (13) – (14) называется  -задачей. Она имеет линейную целевую функцию и m  K ограничений. Если все функции f k и g i линейны,
то  -задача относится к линейному программированию. В этом случае доказано, что оптимальное решение X *  -задачи оптимально по Парето.
21
Пример 7. Требуется решить задачу из примера 3 методом гарантированного результата с равнозначными критериями. Составим  -задачу:
z    max
при условиях
x1




2
  x
.
2

 x1  2 x2  2

 x1  0, x 2  0,   0
 
Оптимальное решение этой задачи есть X *  1; 1 , *  1 .
2
2
Критерии с заданным приоритетом
Рассмотрим только два критерия f1  X  и f 2  X  , и пусть 1  X  и
2  X  – соответствующие нормированные критерии. Разобьем допустимую область на две части D  D1  D2 так, что в области D1 выполняется
неравенство 1  X   2  X  , то есть первый критерий имеет приоритет над
вторым, а в области D2 выполняется неравенство 1  X   2  X  , то есть
второй критерий имеет приоритет над первым.
Для числовой характеристики приоритета вводится коэффициент
связи p  X  : 1  X   p X 2  X  , который показывает, во сколько раз относительная оценка 1  X  больше  2  X  . Если X * – оптимальная точка для
равнозначных критериев, то pX *   1 .
Если X 1* – точка оптимума по первому критерию, то 1 X 1*   1 ,
2 X 1*   1 , то есть X 1*  D1 , и значит pX 1*   1 . Аналогично, если X 2* –
точка оптимума по второму критерию, то 1 X 2*   1 ,  2 X 2*   1 , и значит
pX 2*   1 .
22
Предположим, что первый критерий имеет приоритет над вторым.
Тогда коэффициент p  X  необходимо задать в интервале 1; p X 1*  , а затем составить и решить  -задачу, включив в систему ограничений равенство 1  X   p X 2  X  . В результате получим точку X * , которая будет
принадлежать множеству D1 , где первый критерий имеет приоритет над
вторым.
Доказано, что для выпуклых задач МКО точка X * , являющаяся решением  -задачи, единственная и оптимальна по Парето.
Пример 8. Требуется решить задачу из примера 3 методом гарантированного результата с неравнозначными критериями при условии, что
первый критерий имеет приоритет над вторым.
Так как
pX 1*  
X 1*  2; 0 , то 1 X 1*   1 , 2 X 1*   0 , следовательно,
1
  . В интервале 1;   зададим коэффициент связи p X   2 .
Тогда 1  X   22  X  , или
x1
 2 x2 .
2
Составим  -задачу:
z    max
при условиях
x1




2

  x 2
 x
1
.
  2 x2
2

 x1  2 x 2  2
 x  0, x  0,   0
2
 1

23
В результате решения задачи получим оптимальное решение


X *  4 ; 1 , *  1 .
3 3
3
Недостаток рассмотренного метода состоит в субъективности задания коэффициента связи p  X  .
Решение задачи МКО методом гарантированного результата, как
правило, проходит следующие этапы.
1.
Разработка математической модели системы на основе заданных
целей и ограничений; при этом часто используется мнение экспертов.
2.
Предварительный анализ системы отдельно по каждому крите-
рию; используются методы и программные средства оптимизации с одним
критерием.
3.
Нормировка критериев.
4.
Решение задачи МКО при равнозначных критериях.
5.
Задание приоритетов критериев и решение задачи МКО с назна-
ченными приоритетами.
24