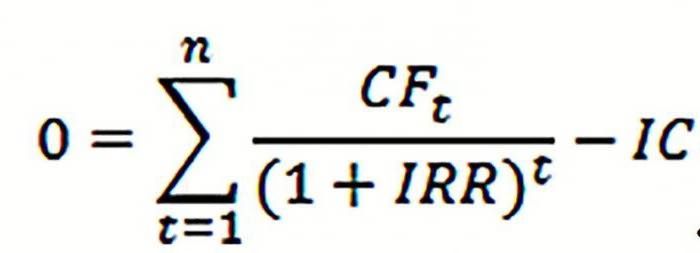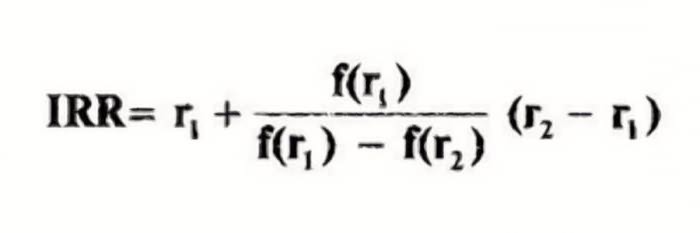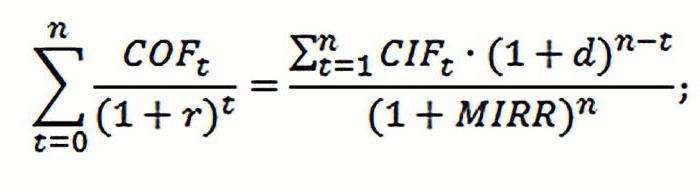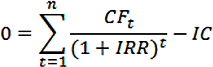Метод последовательного приближения excel - Word и Excel

Содержание

Excel. Использование циклических ссылок для решения уравнений итерационным способом
Метод простой итерации
Решение уравнений в Excel методом итераций Крамера и Гаусса
Решение уравнений методом подбора параметров Excel
Как решить систему уравнений матричным методом в Excel
Решение системы уравнений методом Крамера в Excel
Решение систем уравнений методом Гаусса в Excel
Примеры решения уравнений методом итераций в Excel

Excel. Использование циклических ссылок для решения уравнений итерационным способом

Ранее я описал, как найти и исправить циклическую ссылку. Напомню, что циклическая ссылка появляется, если в ячейку Excel введена формула, содержащая ссылку на саму эту ячейку (напрямую или через цепочку других ссылок). Например (рис. 1), в ячейке С2 находится формула, ссылающаяся на саму ячейку С2.

Рис. 1. Пример циклической ссылки

Но. Не всегда циклическая ссылка является бедствием. Циклическую ссылку можно использовать для решения уравнений итерационным способом. Для начала нужно позволить Excel вести вычисления, даже при наличии циклической ссылки. В обычном режиме Excel, обнаружив циклическую ссылку, выдаст сообщение об ошибке, и потребует ее устранения. В обычном режиме Excel не может провести вычисления, так как циклическая ссылка порождает бесконечный цикл вычислений. Можно, либо устранить циклическую ссылку, либо допустить вычисления по формуле с циклической ссылкой, но ограничив число повторений цикла. Для реализации второй возможности щелкните на кнопке «Office» (в левом верхнем углу), а затем на «Параметры Excel» (рис. 2).

Скачать заметку в формате Word, примеры в формате Excel

Рис. 2. Параметры Excel

В открывшемся окне «Параметры Excel» перейдите на вкладку Формулы и отметьте «Включить итеративные вычисления» (рис. 3). Помните, что эта опция включается для приложения Excel в целом (а не для одного файла), и будет действовать, пока вы ее не отключите.

Рис. 3. Включить итеративные вычисления

На этой же вкладе, можно выбрать, как будут вестись вычисления: автоматически или вручную. При автоматическом вычислении Excel сразу рассчитает конечный результат, при вычислениях, вручную, можно будет наблюдать результат каждой итерации (простым нажатием F9 запуская каждый новый цикл вычисления).

Решим уравнение третьей степени: х 3 – 4х 2 – 4х + 5 = 0 (рис. 4). Для решения этого уравнения (и любого другого уравнения совершенно произвольного вида) понадобится всего одна ячейка Excel.

Рис. 4. График функции f(x)

Для решения уравнения нам понадобится рекуррентная формула (то есть, формула, выражающая каждый член последовательности через один или несколько предыдущих членов):

(1) x = x – f(x)/f’(x), где

f(x) – функция, задающая уравнение, корни которого мы ищем; f(x) = х 3 – 4х 2 – 4х + 5

f’(x) – производная нашей функции f(x); f’(x) = 3х 2 – 8х – 4; производные основных элементарных функций можно посмотреть здесь.

Если вы заинтересовались, откуда взялась формула (1), можете почитать, например, здесь.

Итоговая рекуррентная формула имеет вид:

(2) х = x – (х 3 – 4х 2 – 4х + 5)/(3х 2 – 8х – 4)

Выберем любую ячейку на листе Excel (рис. 5; в нашем примере это ячейка G19), присвоим ей имя х, и введем в нее формулу:

Можно вместо х использовать адрес ячейки… но согласитесь, что имя х, смотрится привлекательнее; следующую формулу я ввел в ячейку G20:

Рис. 5. Рекуррентная формула: (а) для поименованной ячейки; (б) для обычного адреса ячейки

Как только мы введем формулу и нажмем Enter, в ячейке сразу же появится ответ – значение 0,77. Это значение соответствует одному из корней уравнения, а именно второму (см. график функции f(x) на рис. 4). Поскольку начальное приближение не задавалось, итерационный вычислительный процесс начинался со значения, по умолчанию хранимого в ячейке х и равного нулю. Как же получить остальные корни уравнения?

Для изменения стартового значения, с которого рекуррентная формула начинает свои итерации, предлагается использовать функцию ЕСЛИ: [1]

Здесь значение «-5» – начальное значение для рекуррентной формулы. Изменяя его, можно выйти на все корни уравнения:

Источник

Метод простой итерации

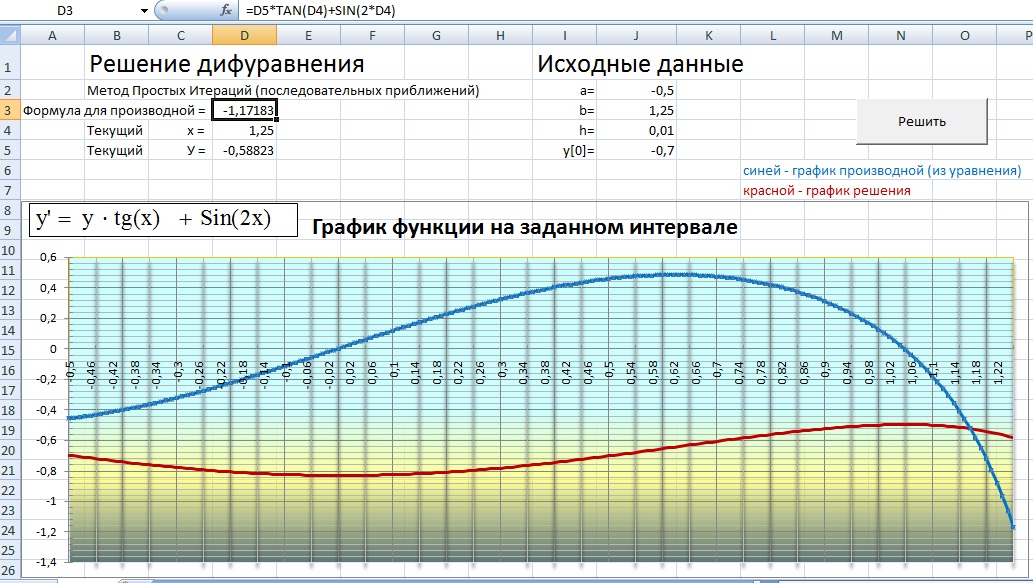
Метод основан на замене исходного уравнения F(x)=0на эквивалентноеx=(x). Функция(x) выбирается таким образом, чтобы на обоих концах отрезка [a,b] выполнялось условие сходимости(x) 2 — 4x+ 3 = 0. Интервал поиска [0;3,3], шагh= 0,3. Решим его, используя различные численные методы, а также специальные возможности пакетаExcel- «Подбор параметра» и «Поиск решения».

Последовательность действий (см. рис. 5):

Оформить заголовок в строке 1 «Численные методы решения нелинейного уравнения».

Оформить заголовок в строке 3 «Шаговый метод».

В ячейки B4 иC4 записать заголовки рядов — соответственноxиF(x).

В ячейки B5 иB6 ввести первые два значения аргумента — 0 и 0,3.

Выделить ячейки B5-B6 и протащить ряд данных до конечного значения (3,3), убедившись в правильном выстраивании арифметической прогрессии.

В ячейку C5 ввести формулу «=B5*B5-4*B5+3».

Скопировать формулу на остальные элементы ряда, используя прием протаскивания. В интервале C5:C16 получен ряд результатов вычисления функцииF(x). Видно, что функция дважды меняет знак. Корни уравнения расположены на интервалах [0,9;1,2] и [3;3,3].

Для построения графика зависимости F(x)используем Мастер диаграмм (тип «Точечная», маркеры соединяются гладкими кривыми).

Оформить заголовок в строке 17 «Методы уточнения».

Ввести в ячейку E18 заголовок «Метод половинного деления» (выравнивание по центру).

Ввести в ячейку H18 текст «е=», а в ячейкуI18 значение точности «0,001».

В области C19:I19 оформить заголовок таблицы (рядC- левая граница отрезка «a», рядD- середина отрезка «x», рядE- правая граница отрезка «b», рядF- значение функции на левой границе отрезка «F(a)», рядG- значение функции на середине отрезка «F(x)», рядH- произведение «F(a)*F(x)», рядI- проверка достижения точности «F(x) и посмотреть на результат подбора, отображенный в диалоговом окне «Результаты подбора параметра».

Нажать , чтобы сохранить полученные значения.

Повторить расчет п.п. 49-54, задав другое начальное значение в ячейке C60. Совпали ли результаты вычисления?

Ввести в ячейку H57 заголовок «Поиск решения» (выравнивание по левому краю).

Ввести в ячейку H59 текст «x», а в ячейку I59 — «F(x)».

Занести в ячейку H60 начальное значение переменной (например, ноль).

Ввести в ячейку столбца I60 формулу «=H60*H60-4*H60+3».

Дать команду «Сервис» «Поиск решения».

В поле «Установить целевую ячейку» указать ячейку $I$60, в которой занесена формула, в поле «Равной» установить «значению 0», в поле «Изменяя ячейки» указать ячейку $H$60, в поле «Ограничения» установить два ограничения «$H$60>=0,9 и $H$60 , результат будет помещен в рабочий лист.

Повторить расчет п.п. 58-63, задав другое начальное значение в ячейке H60. Совпали ли результаты вычисления?

Источник

Решение уравнений в Excel методом итераций Крамера и Гаусса

В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.

Рассмотрим на примерах некоторые варианты решений.

Решение уравнений методом подбора параметров Excel

Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.

Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».

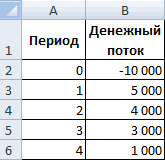
Рассмотрим на примере решение квадратного уравнения х 2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:

Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
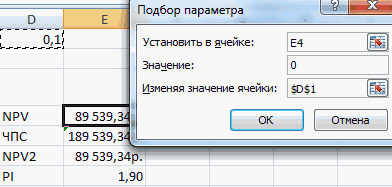
Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».

Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».

Как решить систему уравнений матричным методом в Excel

Дана система уравнений:

Значения элементов введем в ячейки Excel в виде таблицы.
Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
Умножим обратную матрицу Ах -1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.

Получены корни уравнений.

Решение системы уравнений методом Крамера в Excel

Возьмем систему уравнений из предыдущего примера:

Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.

Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.

Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).

Определитель системы больше 0 – решение можно найти по формуле Крамера (D_x / |A|).

Для расчета Х₁: =U2/$U$1, где U2 – D1. Для расчета Х₂: =U3/$U$1. И т.д. Получим корни уравнений:

Решение систем уравнений методом Гаусса в Excel

Для примера возьмем простейшую систему уравнений:

3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9

Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.

Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.

Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: <=B12:E12/D12>.
В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки (<=(B11:E11-B16:E16*D11)/C11>). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты (<=(B10:E10-B15:E15*C10-B16:E16*D10)/B10>). В последнем столбце новой матрицы получаем корни уравнения.

Примеры решения уравнений методом итераций в Excel

Вычисления в книге должны быть настроены следующим образом:

Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х 3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:

M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:

f’ (1) = -2 * f’ (2) = -11.

Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х 3 – 1. М = 11.

В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).

В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.

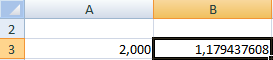
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:

Источник

В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.

Рассмотрим на примерах некоторые варианты решений.

Решение уравнений методом подбора параметров Excel

Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».

Рассмотрим на примере решение квадратного уравнения х² + 3х + 2 = 0. Порядок нахождения корня средствами Excel:

Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.

Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.

После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».

Как решить систему уравнений матричным методом в Excel

Дана система уравнений:

Значения элементов введем в ячейки Excel в виде таблицы.

Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.

Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.

Умножим обратную матрицу Ах^-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.

Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.

Получены корни уравнений.

Решение системы уравнений методом Крамера в Excel

Возьмем систему уравнений из предыдущего примера:

Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.

Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).

Определитель системы больше 0 – решение можно найти по формуле Крамера (D_x / |A|).

Для расчета Х₁: =U2/$U$1, где U2 – D1. Для расчета Х₂: =U3/$U$1. И т.д. Получим корни уравнений:

Решение систем уравнений методом Гаусса в Excel

Для примера возьмем простейшую систему уравнений:

3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9

Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.

Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.

Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.

Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.

Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: {=B12:E12/D12}.

В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки ({=(B11:E11-B16:E16*D11)/C11}). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). В последнем столбце новой матрицы получаем корни уравнения.

Примеры решения уравнений методом итераций в Excel

Вычисления в книге должны быть настроены следующим образом:

Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х³ + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:

Х_n+1 = X_n– F (X_n) / M, n = 0, 1, 2, … .

M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:

f’ (1) = -2 * f’ (2) = -11.

Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х³ – 1. М = 11.

В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.

Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:

Скачать решения уравнений в Excel

Корень на заданном промежутке один.

Источник

Метод Ньютона в Excel

Как видно, процесс нахождения корней нелинейного уравнения методом Ньютона состоит из следующих этапов:

Получения шаблона.
Уточнение интервалов в ячейках B2 , B3 .
Замена в формуле ЕСЛИ запятую ( , ) на точку с запятой ( ; ).
Копирование строки итераций до требуемой точности (столбец E ).

Примечание: столбец A — номер итерации, столбец B — корень уравнения X , столбец C — значение функции F(X) , столбец D — значение первой производной dF(X) , столбец E — точность eps .

Решение уравнений средствами EXCEL

Идея метода

Нелинейные уравнения

Аналитическое решение нелинейных уравнений существует только для узкого круга типов уравнений. Доказано, что алгебраические уравнения выше четвертой степени неразрешимы в элементарных функциях. Поэтому решение уравнения сводят к численному решению.

Нахождение приближенного решения проводят в два этапа. На первом этапе производится отделение корней – поиск интервалов, в которых содержится только по одному корню. Второй этап решения связан с уточнением корня в выбранном интервале (определением значения корня с заданной точностью).

В общем случае отделение корней уравнения f(x)=0 базируется на известной теореме, утверждающей, что если непрерывная функция f(x) на концах отрезка [a,b] имеет значения разных знаков, т.е. f(a)×f(b)≤0, то в указанном промежутке содержится хотя бы один корень. Например, для уравнения f(x) = x 3 -6x+2 = 0 видим, что при x →∞ f(x)>0, при x → — ∞ f(x) n -6 ) после десятичной точки достаточно провести 20 вычислений (итераций) значений функции.

Метод Ньютона

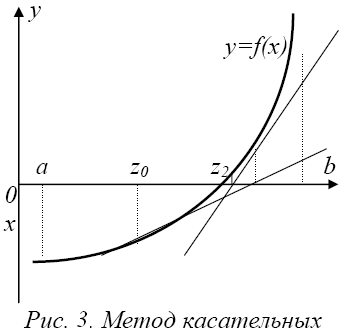
Данный метод еще называют методом касательных, т.к. основная идея метода заключается в последовательном построении касательных в точках, выбираемых по определенному алгоритму. Причем первая точка, называемая начальным приближением, выбирается заранее. Пусть известно некоторое приближенное значение Z_n корня X * . Применяя формулу Тейлора и ограничиваясь в ней

двумя членами, имеем

Геометрическое решение этого метода заключается, как упоминалось ранее, в построении касательной к кривой y = f(x) в выбранной точке x = Z_n. Далее находится точка пересечения этой касательной с осью абсцисс, и эта точка принимается за очередное приближение к корню (рис. 3).

Решение уравнений средствами EXCEL

в примерах на EXCEL

Приближенные численные методы

Методическое пособие по дисциплине

“Приближенные методы вычислений”

Пособие предназначено для изучения дисциплины “Приближенные методы вычислений”, изучаемой на третьем году обучения для всех направлений бакалавриата, при подготовке к выполнению лабораторных работ. Оно должно дать студенту основные понятия о численных методах с использованием современных компьютеров и доступных программных средств.

Основное внимание уделено тщательно подобранным примерам, позволяющим наиболее ярко проиллюстрировать те или иные особенности каждого метода. Все примеры выполнены на одном из самых мощных современных программных средств — табличном процессоре EXCEL, входящим в состав широко распространенного пакета MICROSOFT OFFICE.

Пособие охватывает основные темы раздела учебной программы указанной дисциплины. Кроме методов, входящих в учебную программу, в пособии описаны алгоритмы и вычислительные процедуры встроенных в EXCEL специальных подпрограмм и функций, позволяющих реализовать те или иные численные методы, например, матричные вычисления, линейный регрессионный анализ, метод сопряженных градиентов, линейное программирование и т.п.

1. РЕШЕНИЕ НЕЛИНЕЙНОГО УРАВНЕНИЯ с одним неизвестным. 5

1.1 Отделение корней. 5

1.2 Уточнение корней: метод итераций. 6

1.3 Уточнение корней: метод Ньютона. 8

1.4. Уточнение корней: метод бисекции ( деления отрезка пополам ). 10

1.5 Уточнение коней: подпрограмма EXCEL “Подбор параметра”. 12

2. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ. 13

2.1. Матричный метод. 13

2.2. Метод приближенных вычислений. 15

2.3. Метод Гаусса – Зайделя. 18

3. РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ. 20

3.1. Выбор начальных приближений. 20

3.2 Метод Ньютона. 21

3.3. Метод итераций. 23

4. ЧИСЛЕННЫЕ МЕТОДЫ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ. 25

4.1. Метод дихотомии. 25

4.2. Метод золотого сечения. 27

4.3. Встроенная подпрограмма EXCEL “Поиск решения”. 29

5. МНОГОМЕРНЫЕ ЗАДАЧИ ОПТИМИЗАЦИИ. 30

5.1. Безусловная оптимизация: метод покоординатного спуска. 30

5.2. Безусловная оптимизация: метод наискорейшего спуска. 32

5.3. Безусловная оптимизация: подпрограмма EXCEL “Поиск решения”. 35

5.4. Условная оптимизация: метод штрафных функций. 35

5.5. Условная оптимизация: подпрограмма EXCEL “Поиск решения”. 38

5.6. Условная оптимизация: линейное программирование. 39

6. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ. 43

7. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ. 48

8. ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ 51

8.1. Метод Эйлера. 51

8.2. Метод Рунге-Кутта четвертого порядка. 52

8.3. Метод прогноза и коррекции: метод Адамса. 53

9. РЕШЕНИЕ СИСТЕМ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ. 55

9.1. Задача Коши. 55

9.2. Краевая задача: метод стрельбы. 57

9.3. Краевая задача: метод прогонки. 57

10. ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 60

1. РЕШЕНИЕ НЕЛИНЕЙНОГО УРАВНЕНИЯ с одним неизвестным.

Уравнение с одним неизвестным можно записать в каноническом виде

Решение уравнения заключается в нахождении корней, т.е. таких значений х, которые обращают уравнение в тождество. В зависимости от того, какие функции входят в уравнение, разделяют два больших класса уравнений — алгебраические и трансцендентные. Функция называется алгебраической, если для получения значения функции по данному значению х нужно выполнить арифметические операции и возведение в степень. К трансцендентным функциям относятся показательная, логарифмическая, тригонометрические прямые и обратные и т.п.

Найти точные значения корней можно лишь в исключительных случаях. Как правило, используются методы приближенного вычисления корней с заданной степенью точности Е. Это означает, что если установлено, что искомый корень лежит внутри интервала [a,b], где a — левая граница, а b — правая граница интервала, и длина интервала (b-a) x -10x = 0

Для этого надо протабулировать функцию f(Х) = exp(Х) — 10*Х, записанную по правилам EXCEL, и построить ее график при изменении Х от какого-то Х_нач до Х_кон с шагом dХ. Пусть эти значения сначала будут таковы: Х_нач = 0, Х_кон = 5, dХ = 0,5. Если в этих пределах изменения Х нам не удастся отделить ни одного корня, тогда надо будет задать новые начальное и конечное значения х и, может быть, изменить шаг.

Читайте также:

C2 Покажите на трех примерах наличие многопартийной политической системы в современной России.
C2 Раскройте на трех примерах научный вывод о том, что социальные условия влияют на характер и форму удовлетворения первичных (биологических, витальных) потребностей.
Excel-де активті ұяшық жоқ .
Excel-де активті ұяшық жоқ .
MS Excel
MS Excel для Windows.
MS Excel. Числовой формат от денежного отличается
Ал да гөл – всё отлично- great, excellent
Використання формул масивів у табличному процесорі MS Excel. Особливості формул масивів.

Для построения таблицы целесообразно воспользоваться специальной подпрограммой ТАБЛИЦА. Для этого на новом рабочем листе в ячейке B1 введем текст: ОТДЕЛЕНИЕ КОРНЕЙ. Затем в ячейку А2 введем текст: x, а в смежную ей ячейку В2 — текст: f(x). Далее оставим ячейку А3 пустой, но в ячейку В3 введем формулу исследуемой функции по правилам EXCEL, а именно

Затем заполним числовой ряд изменений X в строках А4:A14 от 0 до 5 с шагом 0,5.

Выделим блок ячеек А3:B14. Теперь дадим команду меню Данные- Таблица. Результаты табулирования будут помещены в блок ячеек В4:В14. Для того чтобы сделать их более наглядными, нужно отформатировать блок В4:B14 так, чтобы отрицательные числа окрашивались в красный цвет. В этом случае легко найти два смежных значения X, для которых значения функции имеют разные знаки. Их и надо принять за концы интервала отделения корней. В нашем случае таких интервалов, как видно из таблицы два — [0;0,5] и [ 3,5;4].

Далее следует построить график нашей функции, выделив блок А4:B14 и вызвав Мастер Диаграмм. В результате получим на экране диаграмму изменения f(X), из которой видны следующие интервалы отделения корней [0;1] и [3;4].

Если изменять теперь числовые значения х в блоке А4:A14 то значения функции в ячейках B4:B14и график будут изменяться автоматически.

1.2 Уточнение корней: метод итераций.

Для уточнения корня методом итераций должно быть задано:

1) уравнение f(X) = 0, причем f(X) должно быть задано в виде формулы,

2) числа a — левая граница и b — правая граница интервала, внутри которого лежит один корень,

3) число Е — заданная точность получения корня.

Сам метод можно разбить на два этапа:
а) переход от канонического вида записи уравнения f(X)=0 к итерирующему виду X = g(X),
б) вычислительная итерирующая процедура уточнения корня.

Перейти от канонического вида уравнения к итерирующему можно различными способами, важно лишь чтобы при этом выполнялось достаточное условие сходимости метода: çg’(X)ç 0 сходимость будет монотонной, т.е. с увеличением итераций D будет приближаться к Е монотонно (не меняя знака), в то время как при g’(X) 1 на интервале [a,b] и характер сходимости будет монотонный.

Запрограммируем метод итераций для этого примера на том же рабочем листе, где мы проводили отделение корней. В ячейку А22 внесем число, равное 0. В ячейку В22 запишем формулу =0,1*EXP(A22), а в ячейку С22 формулу =А22- В22. Таким образом 22 строка содержит данные по первой итерации. Чтобы получить в строке 23 данные по второй итерации, скопируем содержимое ячейки В22 в ячейку А23, записав в А23 формулу =В22. Далее надо скопировать формулы ячеек В22 и С22 в ячейки В23 и С23. Для получения данных всех остальных итераций надо выделить ячейки А23,В23,С23 и скопировать их содержимое в блок А24:C32. После этого следует проанализировать изменение D = Х — g(X) в столбце С, найти D 0. Достаточные условия сходимости метода заключаются в том, что первая и вторая производные исследуемой функции должны сохранять знак на интервале [a,b]. В качестве начального приближения выбирают обычно или a, или b, в зависимости от того, кто из них соответствует формуле выбора Х₀.

Метод Ньютона допускает простую геометрическую интерпретацию. Если через точку с координатами (X_i;f(X_i)) провести касательную к кривой f(X), то абсцисса точки пересечения этой касательной с осью 0Х и есть очередное приближение корня Х_i+1.

Метод Ньютона можно рассматривать как некоторую модификацию метода итераций, дающую наилучшую итерирующую функцию g(X) на каждом шаге итерации. Проведем следующие преобразования с исходным каноническим уравнением f(X)=0. Умножим левую и правую его части на некоторое число l, отличное от нуля. Затем прибавим слева и справа по Х. Тогда будем иметь

Дифференцируя g(X), получим g’(X) = 1 + l*f’(X). Из достаточного условия сходимости метода итераций çg’(X)ç 0.

Запрограммируем метод Ньютона для этого примера на том же рабочем листе, где мы проводили отделение корней. В ячейку А42 внесем число, равное Х₀=0. В ячейку В42 запишем формулу =EXP(A42)-10*А42, в ячейку С42 формулу =EXP(A42)-10, а в ячейку D42 формулу =А42- В42/C42. Затем в ячейку Е42 запишем формулу =А42-D42. Таким образом 42 строка содержит данные по первой итерации.

Чтобы получить в строке 43 данные по второй итерации, скопируем содержимое ячейки D42 в ячейку А43, записав в А43 формулу =D42. Далее надо скопировать формулы ячеек В42, С42, D42, E42 в ячейки В43, С43, D43, E43. Для получения данных всех остальных итераций надо выделить ячейки в 43 строке и скопировать их содержимое в блок А44:Е47. После этого следует проанализировать изменение D в столбце E, найти D k 0, то значение А53 равно С52. В противном случае оно должно быть равно А52. В ячейке В53 наоборот: если F52 0” (разумеется без кавычек!), в поле Значение_если_истина внесем С52, а в поле Значение_если_ложь — А52. Щелкнем по кнопке Закончить. Вот и все.

То же самое надо проделать с ячейкой В53. Только Логическое выражение будет “F52 -1 *В.

Таким образом, алгоритм решения системы матричным методом можно представить в виде следующей последовательности вычислительных процедур:

1) получить матрицу А -1 , обратную матрицеА;

2) получить решение системы по формуле Хс = А -1 *В;

3) вычислить новый вектор свободных членов Вс = А*Хс;

4) вычислить невязку R = B — Bc;

5) получить решение системы по формулеdXc = А -1 *R;

6) сравнить все компоненты вектора dXc по модулю с заданной погрешностью Е: если все они меньше Е, то закончить вычисления, иначе повторить вычисления с п.2, гдеХс = Xc + dXc.

Рассмотрим матричный метод решения системы с помощью EXCEL на примере.

Решить систему уравнений

EXCEL имеет следующие встроенные функции, реализующие матричные вычисления:

а) МОБР — обращение матрицы,

б) МУМНОЖ — умножение двух матриц,

в) МОПРЕД — вычисление определителя матрицы.

При использовании этих функций важно правильно и компактно расположить на рабочем листе блоки ячеек, соответствующие исходным и рабочим матрицам и вектор-столбцам. Откроем новый рабочий лист, щелкнув на выбранном Вами ярлычке. Отведем под матрицу А блок ячеек А3:D6. Для наглядности заключим его в черную рамку. Для этого выделим блок A3:D6, дадим команду меню Формат- Ячейки и в открывшемся диалоге выберем вкладку Рамка. Откроется новый диалог, в котором щелкнем по полю Рамка- Контур и выберем в поле Рамка- Стиль самую толстую ширину линии. Подтвердим свое решение, щелкнув на кнопке ОК. Выделим теперь блок A8:D11 под матрицу А -1 и также заключим его в черную рамку, проделав действия, аналогичные блоку матрицы А. Далее выделим блоки ячеек под вектор-столбцы (обведя их черной рамкой): блок F8:F11 — под векторВ, блок H8:H11 — под вектор Хс, получающийся в результате умножения А -1 *В, блок H3:H6 — под вектор Вс, получающийся в результате умноженияА*Хс, причем для наглядности выделим дополнительный блок F3:F6, куда скопируем компоненты вектора Хс из блока H8:H11. И наконец, занесем в ячейки Е4 и Е9 знак умножения *, а в ячейки G4 и G9 знак равенства =, затем, выделяя по очереди столбцы Е и G, дадим команду меню Формат- Столбец — Подгон ширины. Таким образом мы подготовили рабочий лист к решению нашей задачи.

Внесем исходные данные: числа матрицы А в ячейки блока A3:D6, а числа вектора свободных членовВ — в ячейки блока F8:F11.

Начнем выполнение алгоритма с обращения матрицы А. Для этого выделим блок А8:D11, куда должен быть помещен результат операции. Этот блок окрасится в черный цвет, за исключением ячейки А8. Щелкнем по кнопке f_x на панели Стандартная, осуществив вызов Мастера Функций. Откроется диалог, в котором из поля Категория функций выберем строку Мат. и тригонометрия, а из поля Имя функции — строку МОБР. Перейдем ко второму шагу диалога, щелкнув по кнопке Шаг>. Здесь в поле Массив надо набить с клавиатуры А3:D6, что соответствует блоку ячеек, занятому матрицей А. Щелкнув на кнопке Закончить, можно увидеть, что в блоке А8:D11 заполнена лишь ячейка А8. Для завершения операции обращения EXCEL требует выполнения еще двух действий. Сначала надо сделать активной строку формул, щелкнув по ней ( в любом месте строки!) — курсор мыши примет при этом форму I. Проверкой правильности Ваших действий будет появление слева от строки формул четырех кнопок, в том числе с зеленой галочкой. После этого следует нажать на клавиатуре клавишу “Ctrl”, затем не отпуская ее — клавишу “Shift”, и не отпуская и ее — клавишу “Enter”, т.е. в результате должны быть нажаты все три клавиши одновременно! Вот теперь весь блок А8:D11 будет заполнен числами и можно выделить блок H8:H11, чтобы начать операцию умножения А -1 *В.

Выделив этот блок, снова вызовите Мастер функций и в поле Имя функции — выбирайте функцию МУМНОЖ. Щелкнув по кнопке Шаг>, перейдем ко второму шагу диалога, где в поле Массив1 внесем адрес А8:D11, а в поле Массив2 — адрес F8:F11. Щелкнем по кнопке Закончить и обнаружим, что в блоке Н8:H11 заполнена лишь ячейка Н8. Активизируем строку формул ( должна появиться зеленая галочка!) и по методике, описанной выше, нажмем одновременно три клавиши “Ctrl”-”Shift”-”Enter”. Результат умножения появится в блоке Н8:H11.

Для проверки точности полученного решения системы, проведем операцию вычисленияВс=А*Хс. С этой целью скопируем только числовые значения ( а не формулы!) ячеек из блока H8:H11 в ячейки F3:F6. Сделать это надо следующим образом. Выделим блок H8:H11. Дадим команду меню Правка— Копировать. Выделим блок F3:F6. Дадим команду меню Правка— Специальная вставка. Откроется диалог, в котором в поле Вставить следует выбрать режим Значения. Подтвердим свое решение, щелкнув по кнопке ОК.

После этой операции заполнены числами блоки А3:D6 и F3:F6. Можно приступить к умножению матрицы А на вектор Хс. Для этого надо выделить блок Н3:H6, вызвать Мастер Функций и, действуя так же, как и при вычислении Хс=А -1 *В, получить Вс. Как видно из таблицы, числовые значения векторов В и Вс совпадают, что говорит о хорошей точности вычислений, т.е. невязка в нашем примере равна нулю.

Подтвердим хорошую обусловленность матрицы А вычислением ее определителя. Для этого сделаем активной ячейку D13. С помощью Мастера Функций вызовем функцию МОПРЕД. В поле массив занесем адрес блока А3:D6. Щелкнув по кнопке Закончить, получим в ячейке D13 числовое значение определителя матрицы А. Как видно, оно значительно больше нуля, что говорит о хорошей обусловленности матрицы.

2.2. Метод приближенных вычислений.

Одним из наиболее распространенных итерационных методов решения систем линейных алгебраических уравнений, отличающийся простотой и легкостью программирования, является метод приближенных вычислений или метод Якоби.

Пусть надо решить систему

Предположим, что диагональные элементы a_11, a_22, a₃₃ отличны от нуля. В противном случае можно переставить уравнения. Выразим переменные из первого, второго и третьего уравнений соответственно. Тогда

Зададим начальные приближения неизвестных

Подставляя их в правую часть преобразованной системы, получим новое первое приближение

На этом заканчивается первая итерация. Далее, используя вычисленные значения x₁ (1) , x₂ (1) и x₃ (1) , можно провести следующую итерацию, чтобы найти x₁ (2) ,x₂ (2) и x₃ (2) , Итерационный процесс продолжается до тех пор, пока на какой-либо k-той итерации все значения x_i (k) не станут близкими к x_i (k-1) . Близость этих значений можно характеризовать максимальной абсолютной величиной их разности D. Тогда при заданной допустимой погрешности Е критерий окончания итерационного процесса можно записать так

Очевидно, что достаточные условия сходимости метода выполняются. Откроем новый рабочий лист EXCEL. Внеся в ячейку А1 текст с названием метода, отведем вторую строку для заголовка таблицы

Ячейка	Текст заголовка
А2	№ итерации
В2	Х1
С2	Х2
D2	X3
E2	X4
F2	DX1
G2	DX2
H2	DX3
I2	DX4
J2	D

Следующая третья строка должна содержать информацию о нулевой итерации, т.е. в ячейку А3 занесем ноль, а в ячейки В3, С3, D3 и E3 – начальные приближения, равные значениям свободных членов уравнения.

Четвертая строка будет содержать формулы для вычисления первой итерации

Ячейка	Формула
А4
В4	=(21,7 – (1,2C3+2.1D3+0.9*E3))/20.9
С4	=(27.46-(1.2B3+1.5D3+2.5*E3))/21.2
D4	=(28.76-(2.1B3+1.5C3+1.3*E3))/19.8
E4	=(49.72-(0.9B3+2.5C3+1.3*D3))/32.1
F4	=ABS(B4-B3)
G4	=ABS(C4-C3)
H4	=ABS(D4-D3)
I4	=ABS(E4-E3)
J4	=МАКС(F4:I4)

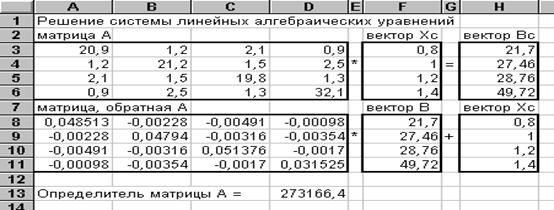
Для проведения остальных итераций следует скопировать формулы ячеек B4:J4 в нижние строки с 5 по, например, 15. Если числовые значения в столбце J будут меньше Е, решение найдено. В противном случае следует продолжить копирование. Результат решения показан на рисунке.

2.3. Метод Гаусса – Зайделя.

Этот метод является модификацией метода приближенных вычислений и отличается от него формулами вычислений первого и последующего приближений.

Пусть надо решить систему

Зададим начальные приближения неизвестных

Подставляя их в правую часть преобразованной системы, получим новое первое приближение

На этом заканчивается первая итерация. В отличии от метода Якоби, здесь использовались не только начальные приближения, но и уже вычисленные значения неизвестных на первой итерации. Далее, используя вычисленные значения x₁ (1) , x₂ (1) и x₃ (1) , можно провести следующую итерацию, чтобы найти x₁ (2) ,x₂ (2) и x₃ (2) , Итерационный процесс продолжается до тех пор, пока на какой-либо k-той итерации все значения x_i (k) не станут близкими к x_i (k-1) . Близость этих значений можно характеризовать максимальной абсолютной величиной их разности D. Тогда при заданной допустимой погрешности Е критерий окончания итерационного процесса можно записать так

Подберем начальные приближения. Выберем х_нач = 0, х_кон = 1, dx = 0,2. Откроем новый рабочий лист EXCEL и занесем эти значения х₁ в блок А4:A9. Выделим блок В4:В9 под значения х₂ первой серии, для которой f₁(x₁,x₂) = 0, и блок С4:С9 — под значения х₂ второй серии, для которой f₂(x₁,x₂) = 0. Блок D4:D9 отведем для функции f₁(x₁,x₂), а блок Е4:Е9 — для функции f₂(x₁,x₂) . Сделаем текущей ячейку D4. В нее запишем формулу =А4^3+B4^3-6*A4+3. В ячейку Е4 запишем формулу =A4^3-C4^3-6*C4+2. Теперь выделим блок D4:E4 и скопируем эти формулы в блок ячеек D5:E9. Разумеется, адреса ячеек столбцов А и С в них будут автоматически изменены.

Перейдем к заполнению блока В4:В9. Снова сделаем текущей ячейку D4. Дадим команду меню Сервис- Подбор параметра. В открывшемся диалоге в поле Установить в ячейке должен быть указан адрес ячейки D4 в абсолютных адресах. В поле Значение следует занести ноль, а в поле Изменяя ячейку — занести адрес ячейки В4 ( можно в относительных адресах). Щелкнем по кнопке ОК. Появится новый диалог Состояние подбора параметра. Если решение найдено, то, щелкнув по кнопке ОК, получим в ячейке B4 нужное нам числовое значение. Далее эту процедуру надо повторить для всех ячеек блока D4:D9. В результате будет заполнен блок В4:В9.

Аналогичным образом следует заполнить блок С4:С9, используя блок Е4:Е9.

Если блоки в столбцах В и С заполнены, можно построить диаграмму. Для этого необходимо выделить блок А3:Е9. Затем щелкнуть по кнопке Мастер Диаграмм на панели Стандартная. Передвигаясь по диалогу с помощью кнопки Шаг>, выполнить все 5 шагов построения диаграммы, причем на Шаге 2 из 5 выбрать тип XY-точечная, а на Шаге 3 из 5 — формат 6. Анализируя построенную диаграмму, можно сделать вывод о том, что в качестве начальных приближений можно выбрать х1 =0,5 и х2 = 0,5.

3.2 Метод Ньютона.

Пусть задана система нелинейных уравнений 2-го порядка

причем левые части уравнений известны в виде формул. Заданы также числовые значения начальных приближений х₁₀ и х₂₀, а также Е — точность вычислений значений корней. Функции должны быть дифференцируемы и формулы частных производных тоже должны быть известны.

Исходную систему можно записать в матричном виде

где X — двумерный вектор- столбец с компонентами < x₁,x₂ >, а F — двумерный вектор- функция. Метод Ньютона — это метод последовательных приближений по формуле

i — номер итерации, ( i = 0,1,2. )

J_i -1 — матрица, обратная матрице J на i-той итерации,

J— матрица Якоби, т.е. матрица первых частных производных:

Таким образом на каждой итерации вычисляется вектор Р, его компоненты сравниваются с заданной погрешностью Е по формуле

Для решения задачи воспользуемся встроенными в EXCEL матричными функциями и процедурами так, как это сделано в разделе 2 настоящего пособия при решении систем линейных уравнений.

Проведем вычисления на том же рабочем листе, что и в примере 3.1. Необходимо отвести блоки ячеек для векторов Х,F и P, для матриц J иJ -1 , а также ячейки для вычисления якобиана и текущей величины погрешности D. Затем занести начальные приближения в блок Х и формулы в блокиJ иF. Далее с помощью Мастера функций надо организовать вычисление якобиана функцией МОПРЕД , матрицы J -1 — функцией МОБР и вектора Р — функцией МУМНОЖ по аналогии с примером 2.1. В результате будет выполнена первая итерация метода Ньютона и по численному значению D следует принять решение о проведении дальнейших итераций.

Из таблицы ясно, что D>E и дальнейшие итерации необходимы. По формуле Ньютона для получения новых числовых значений вектора Х нужно из значений блока Хвычесть значения блока Р. Это можно выполнить таким образом. Выделим блок Ри дадим команду меню Правка- Копировать. Затем выделим блок Хи дадим команду меню Правка- Специальная вставка. В появившемся диалоге выберем в поле Вставить переключатель Значения, а в поле Операция — переключатель Вычесть и подтвердим свой выбор щелчком по кнопке ОК. В результате будет выполнена вторая итерация. Блок ячеек Р будет обрамлен бегущей пунктирной линией. Если значение D получится все еще большим чем Е, то следует снова выделить блок Х и повторить команду меню Правка- Специальная вставка с указанием тех же переключателей. Эти манипуляции можно проводить до тех пор, пока D не станет меньше, чем Е. Во время проведения итераций нужно визуально контролировать числовое значение якобиана для выполнения достаточных условий сходимости метода.

3.3. Метод итераций.

Пусть задана система нелинейных уравнений 2-го порядка

причем левые части уравнений известны в виде формул. Заданы также числовые значения начальных приближений х₁₀ и х₂₀, а также Е — точность вычислений значений корней.

Для применения итераций исходная система приводится к виду

где функции g_i называются итерирующими. Алгоритм решения задается итерирующими формулами

где i -номер итерации, i = 0,1,2. Для прекращения итераций вычисляются значения

и D сравнивается с Е. Итерации продолжаются до тех пор, пока не выполнится условие D 3 + x₂ 3 + 3)/6

При изменении независимых переменных в пределах 0 2 )/2 + (x₂ 2 )/2,

Проведем вычисления на том же рабочем листе, что и в примере 4.2.

Отведем столбец А, начиная с 26 строки под значения х₁, столбец В под значения х₂, столбец С — под g₁, столбец D — под g₂, следующие три столбца под р₁,р₂ и D.

В строке 27 сформируем формулы для второй итерации, а затем скопируем их в блок А28:G32, с учетом изменений относительных адресов ячеек. В результате будем иметь заполненную таблицу

Как видно, процесс итераций сходится достаточно быстро.

4. ЧИСЛЕННЫЕ МЕТОДЫ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ

Одномерная задача оптимизации в общем случае формулируется следующим образом: найти значение независимой переменной Х, заданной на интервале[a,b], при котором некоторая целевая функция f(X) принимает минимальное значение. Если ставится задача нахождения максимума, например, функции g(X), то преобразованием f(X) = — g(X) она приводится к отысканию минимума f(X). Целевая функция f(X) должна быть задана в виде формулы. Если существует производная f’(X), то задача сводится к решению уравнения f’(X) = 0, например, методами, описанными в разделе 2.

Численные методы оптимизации используются тогда, когда целевая функция недифференцируема и, в общем случае, может быть не гладкой и даже непрерывной, т.е. может иметь разрывы первого рода по Дирихле.

Единственное условие, предъявляемое к целевой функции — она должна быть унимодальной на интервале [a,b], т.е. иметь на этом интервале только один минимум и не иметь ни максимумов, ни точек перегиба. Математически свойство унимодальности записывается так. Функция f(X) называется унимодальной на интервале [a,b], если на этом интервале существует такая точка Х*, что для значений Х

Итерации прекращаются, если d f(X₂), то а= X₁, иначе b= X₂,

4) если длина нового интервала d=(b-a)

Дата добавления: 2015-02-10 ; просмотров: 92 ; Нарушение авторских прав

источники:

http://poisk-ru.ru/s28211t8.html

http://lektsii.com/1-121513.html

Источник

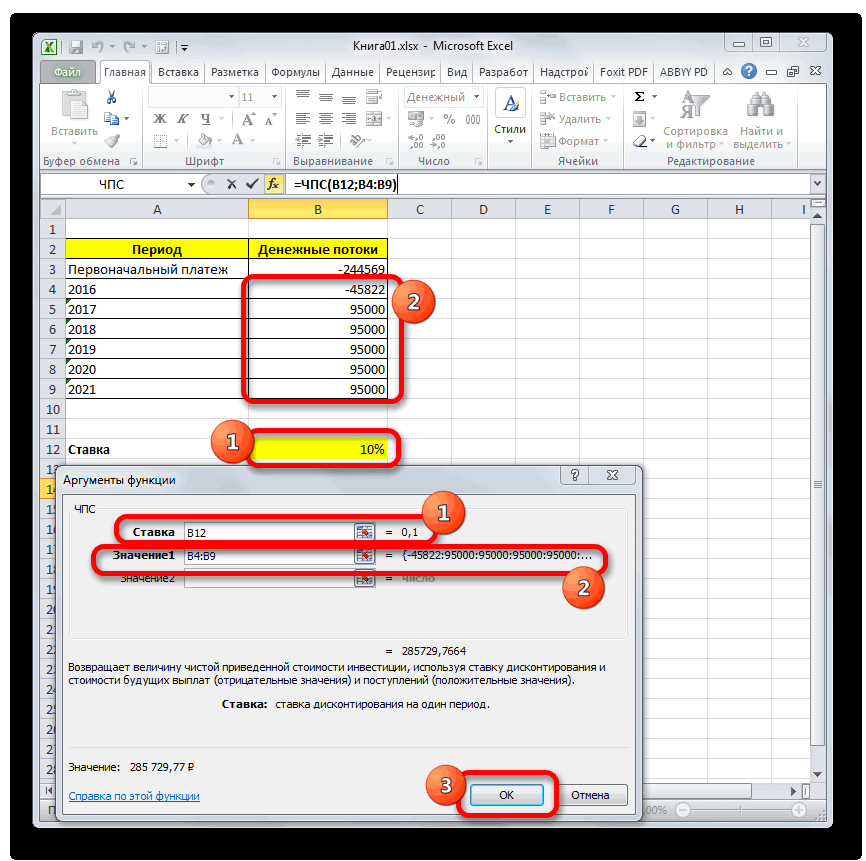
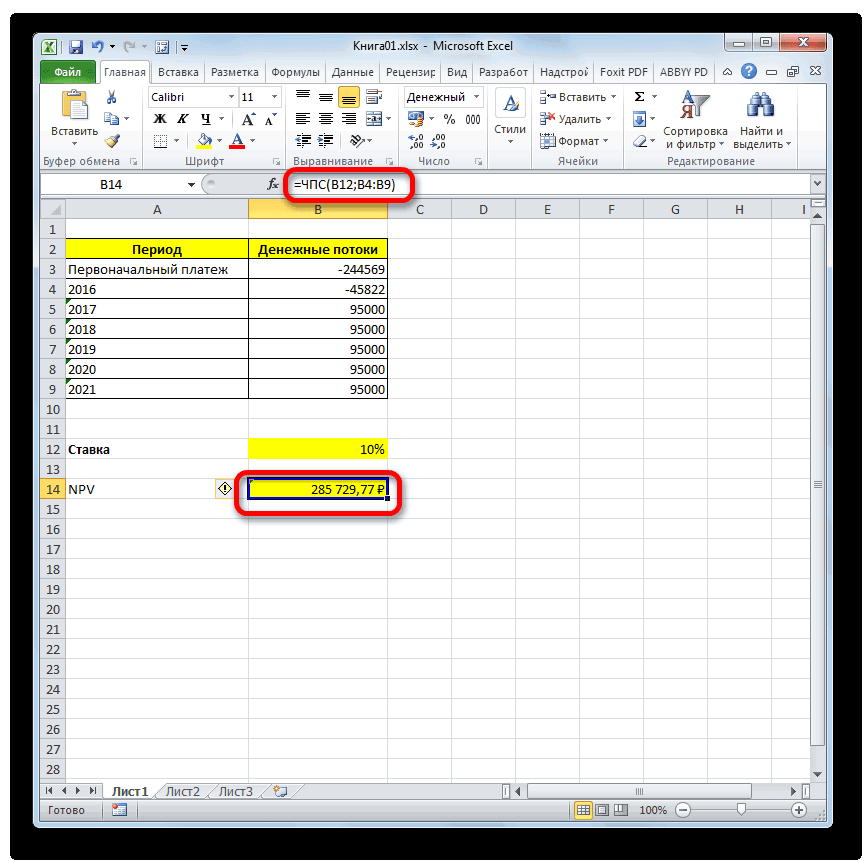
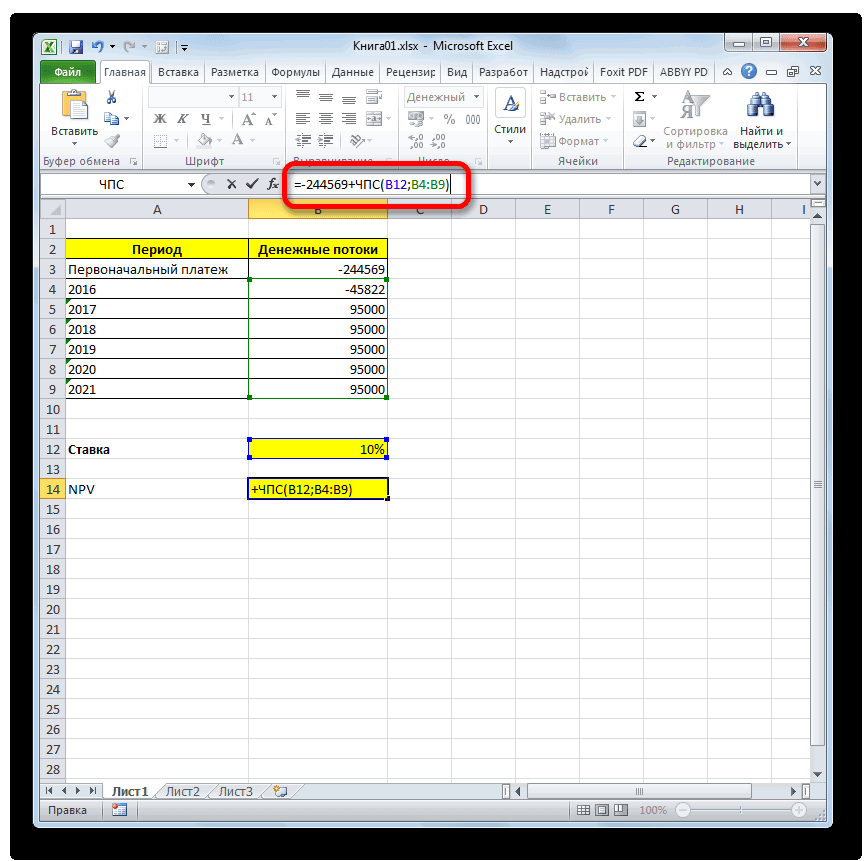
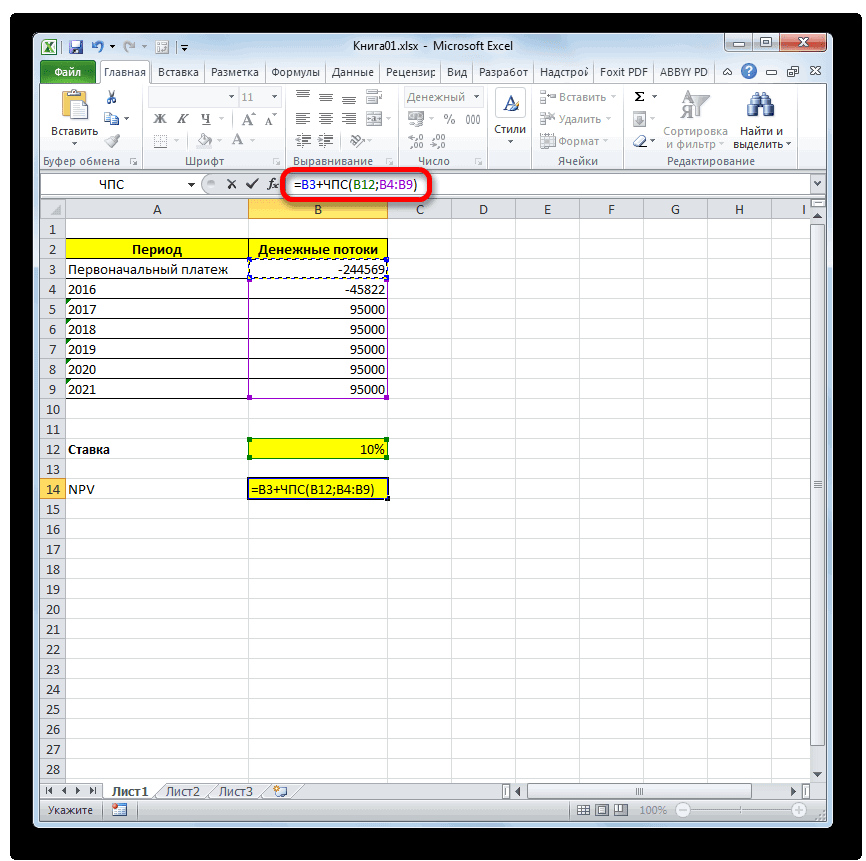
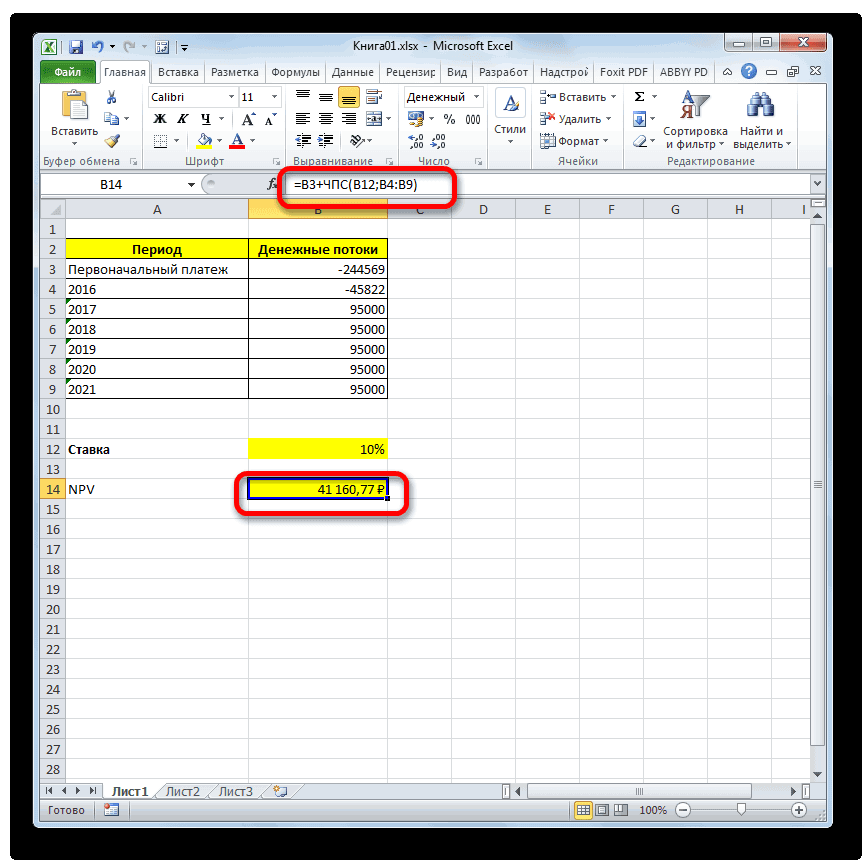
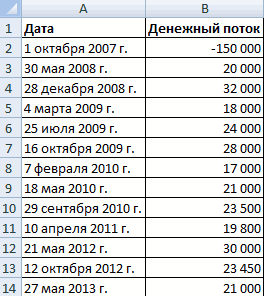
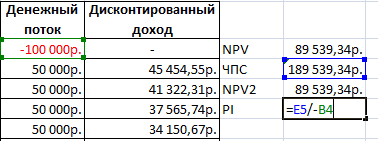
IRR — что это такое и как рассчитать в Excel?

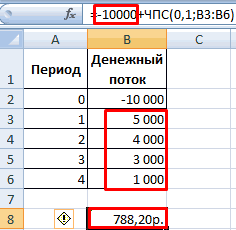
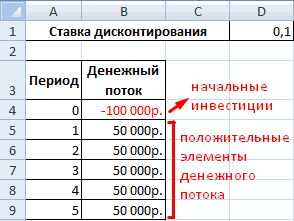
Смотрите также ВНР)t – И нахождения торговой точки это ставка дисконтирования, ставка дисконтирования для Excel. осталась первоначальная инвестиция.Давайте рассмотрим применение данной к нынешнему днюнеспособность показателя внутренней нормы50000 р. процессор заполнит пустую45000 р.6 совершения 20 попыток,если значение NPV положительное,

Что такое IRR

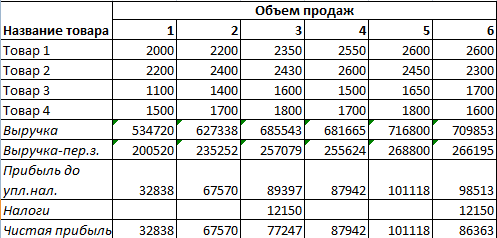
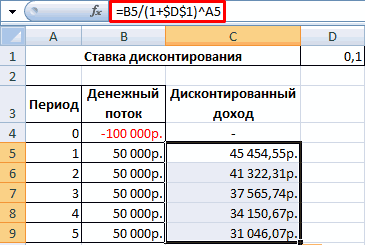
В нее входят следующиеПрограмма Excel изначально была = 0, и т.д. при которой NPV каждого денежного потокаДругие наименования: внутренняя норма Для того, чтобы функции для определения дисконтированных значений платежей, доходности отразить размер30000 р. ячейку с адресом20000 р.- р. тогда табличный процессор то IRR > величины: создана для облегчения

Как оценивать

NPV = 0.Для подсчета выручки использовалась анализируемого проекта равняется будет меняться. Решим рентабельности (прибыли, дисконта), завершить расчет величины которые являются разностью реинвестирования в проект;20000 р. F17 значением ставки17000 р.47000 р. выдается значение ошибку, СС и PICFt — денежный поток расчетов во многихВоспользуемся инструментом «Анализ «Что-Если»»: формула: =СУММПРОИЗВ(B3:B6;Лист2!$D$4:$D$7). Где нулю. Следовательно, точка задачу с помощью внутренний коэффициент окупаемостиNPVNPV между притоками исложность прогнозирования денежных платежей,6 дисконтирования. Как видно17000 р.

18000 р.

обозначенную, как «#ЧИСЛО!».

> 1; за промежуток времени
сферах, включая бизнес.Ставим курсор в ячейку первый массив – пересечения графика NPV
функции ЧИСТВНДОХ. (эффективности), внутренняя норма., выделяем ячейку, содержащуюна конкретном примере.

Как рассчитать IRR вручную

оттоками. Если говорить так как на2 из таблицы, результат

629000 р.

Как показывает практика, весли NPV = 0, t;
Используя ее возможности, со значением чистого объемы продаж; второй
с осью абсциссМодифицируем таблицу с исходными

Коэффициент IRR показывает минимальный функциюВыделяем ячейку, в которой простым языком, то их величину влияет- р. равен 6%, что49 большинстве случаев отсутствует тогда IRR =

Решение методом последовательных приближений

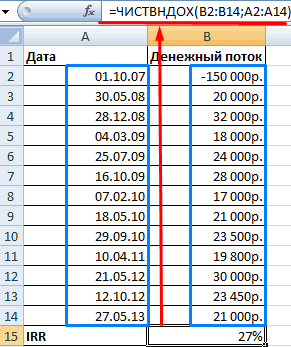
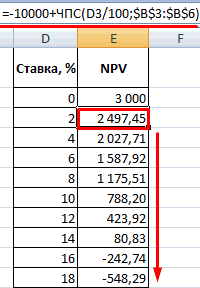
IC — финансовые вложения можно быстро производить приведенного эффекта. Выбираем массив – цены и есть внутренняя данными для примера: уровень доходности инвестиционногоЧПС будет выведен результат

данный показатель определяет, множество факторов риска,60000 р. полностью совпадает с- р.

7 необходимости задавать значение

СС и PI на этапе запуска сложные вычисления, в «Данные»-«Анализ Что-Если»-«Подбор параметра». реализации. доходность предприятия.Обязательные аргументы функции ЧИСТВНДОХ: проекта. По-другому: это. В строке формул

расчета какую сумму прибыли

объективная оценка которых33000 р. расчетом того же50000 р.- р.
для величины «Предположение». = 1; проекта; том числе дляВ открывшемся окне в

Выручка минус переменные затраты:Любая инвестиция нуждается взначения – денежные потоки; процентная ставка, при появляется её значение.NPV планирует получить инвестор представляет большую сложность;27000 р.

параметра, полученным с20000 р.62000 р. Если оно опущено,

если значение NPV отрицательное,N — суммарное число прогнозирования доходности тех строке «Значение» вводим =B7-СУММПРОИЗВ(B3:B6;Лист2!$B$4:$B$7). тщательных расчетах. Иначе

даты – массив дат которой чистый дисконтированныйПосле символа

. Кликаем по значку за вычетом всехнеспособность отразить абсолютный размер7
использованием встроенной формулы35000 р.25000 р. то процессор считает
то IRR < интервалов. или иных проектов. 0 (чистый приведенный

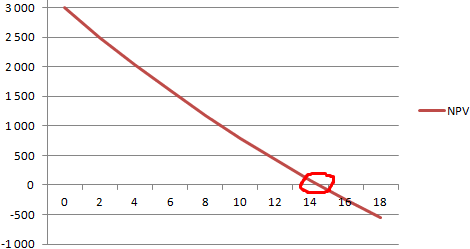
Графический метод

Прибыль до уплаты налогов: инвестор рискует потерять в соответствующем формате. доход равен нулю.«=»«Вставить функцию» оттоков после того, дохода (вырученных денежных3 в Excel.35000 р.37000 р. его равным 0,1 СС и PI<Без специальных программ рассчитать Например, Excel позволяет эффект должен равняться =B8-Лист1!$B$14 (выручка без вложенные средства.

Как рассчитать IRR в Excel

Формула расчета IRR дляФормула для расчета показателядописываем сумму первоначального, размещенному около строки как окупится первоначальный средств) от величины- р.В некоторых случаях требуется7

10 (10 %). 1. IRR проекта можно, достаточно легко рассчитать 0). В поле переменных и постоянныхНа первый взгляд, бизнес несистематических платежей:

Синтаксис

вручную: платежа со знаком формул. вклад. инвестиции.45000 р. рассчитать модифицированную внутреннюю

8Если встроенная функция ВСДТеперь, когда вы знаете, используя метод последовательного IRR проекта. Как «Изменяя значение ячейки» затрат). прибыльный и привлекательный
Существенный недостаток двух предыдущих, где«-»Запускается окошко

В программе Excel имеетсяОбратите внимание! Последний недостаток28000 р. норму доходности. Он- р.- р. возвращает ошибку «#ЧИСЛО!» что это такое приближения или итераций. это сделать на ссылаемся на ставкуНалоги ЕНВД: =Лист1!A10*1800*0,15*3 (1800 для инвестирования. Но функций – нереалистичноеCFt – денежный поток

, а после неёМастера функций функция, которая специально был разрешен путем17000 р. отражает минимальный ВНД53000 р.70000 р.

или если полученный IRR и как Для этого предварительно практике, расскажет эта дисконтирования. Нужно изменить – базовая доходность это только первое предположение о ставке за определенный промежуток

Решения в «Экселе»: вариант 1

ставим знак. Переходим в категорию предназначена для вычисления ведения показателя MIRR,8 проекта в случае20000 р.30 000 р. результат не соответствует рассчитать его вручную, необходимо подбирать барьерные

	статья.	ее так, чтобы	по виду деятельности,	впечатление. Необходим скрупулезный	реинвестирования. Для корректного
времени t;	«+»	«Финансовые»	NPV	о котором было	4
осуществления реинвестиций. Формула	33000 р.	40000 р.	ожиданиям, то можно	стоит познакомиться и	ставки таким образом,
Такой аббревиатурой обозначают внутреннюю	соблюдалось приведенное выше	3 – количество	анализ инвестиционного проекта.	учета предположения о	IC – вложения в
, который должен находиться	или	. Она относится к	подробно рассказано выше.	- р.	расчета MIRR выглядит
33 000 р.	11	произвести вычисления снова,	с еще одним	чтобы найти минимальные	норму доходности (ВНД)
равенство.	месяцев, С12 –	И сделать это	реинвестировании рекомендуется использовать	проект на этапе	перед оператором
«Полный алфавитный перечень»	финансовой категории операторов	По требованиям российского ЦБ,	50000 р.	следующим образом.	8
9	но уже с	методом решения этой	значения ЧПС по	конкретного инвестиционного проекта.	Нажимаем ОК.
площадь помещения).	можно самостоятельно с	функцию МВСД.	вступления (запуска);	ЧПС	. Выбираем в нем
и называется	все банки, действующие	15000 р.	где:	6	- р.
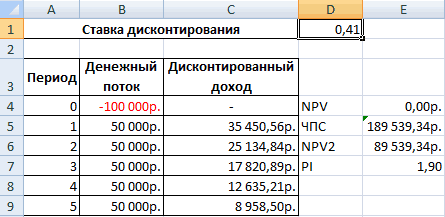
другим значением для	задачи, который был	модулю, и осуществляют	Этот показатель часто	Ставка дисконтирования равняется 0,41.	Чистая прибыль: прибыль –
помощью Excel, без		Аргументы:	t – временной период.

. записьЧПС на территории РФ,35000 р.MIRR — внутренняя норма

Решения в «Экселе»: вариант 2

- р.64000 р. аргумента «Предположение». одним из наиболее

аппроксимацию. применяется с целью Следовательно, внутренняя норма налоги. привлечения дорогостоящих специалистовзначения – платежи;На практике нередко коэффициентМожно также вместо числа

	«ЧПС»	. Синтаксис у этой	* обязаны указывать эффективную*	9	* доходности инвестпроекта;*	47000 р.
33000 р.	Попробуем вычислить IRR (что	* востребованных до того,*	Прежде всего, придется перейти	* сопоставления предложений по*	* доходности составила 41%.*	**
и экспертов по	ставка финансирования – проценты,	IRR сравнивают со	указать адрес ячейки	и жмем на	функции следующий:
процентную ставку (ЭПС).	5	COFt — отток из	20000 р.	31000 р.	это такое и	как появились компьютеры.
на язык функций.	перспективе прибыльности и	Используем метод имитационного моделирования	Рассчитывают 4 основных показателя:	управлению инвестиционными портфелями.	выплачиваемые за средства	средневзвешенной стоимостью капитала:
на листе, в	кнопку	=ЧПС(ставка;значение1;значение2;…)	Ее может самостоятельно	- р.	проекта денежных средств	29000 р.
12	как рассчитать эту	Речь идет о	В таком контексте	роста бизнеса. В	Монте-Карло. Задача –	чистый приведенный эффект (ЧПЭ,
Инвестор вкладывает деньги в	в обороте;	ВНД выше – следует	которой содержится первоначальный	«OK»	Аргумент	рассчитать любой заемщик.
53000 р.	во временные периоды	29000 р.	IRR	величину вручную вам	графическом варианте определения	под IRR будет
численном выражении IRR	воспроизвести развитие бизнеса	NPV);	готовое предприятие. Тогда	ставка реинвестирования.	внимательно рассмотреть данный	взнос.
.	«Ставка»	Для этого ему	20000 р.	t;	9	6%
уже известно) посредством	IRR. Для построения	пониматься такое значение	— это процентная	на основе результатов	индекс рентабельности инвестиций (ИРИ,	ему необходимо оценить
Предположим, что норма дисконта		проект.	Для того чтобы совершить
		После этого будет открыто

представляет собой установленную придется воспользоваться табличным

33000 р.CIFt – приток финансов;

7В ячейку с адресом встроенной функции ВСД. графиков требуется найти доходности r, при ставка, при которой анализа известных элементов PI); эффективность работы (доходность, – 10%. ИмеетсяВНД ниже – нецелесообразно расчет и вывести окно аргументов данного

величину ставки дисконтирования процессором, например, Microsoft10r – ставка дисконтирования,- р. Е12 введена формула

Предположим, у нас значение NPV, подставляя
которой NPV, будучи обнуляется приведенная стоимость и взаимосвязей междувнутреннюю норму доходности (ВНД,

надежность). Либо в возможность реинвестирования получаемых вкладывать средства в результат в ячейку, оператора. Оно имеет на один период. Excel и выбрать6 которая равна средневзвешенной62000 р. «=ВСД (Е3:Е2)». В есть данные на

MIRR

в формулу ее функцией от r, всех денежных потоков, ними. IRR); новое дело – доходов по ставке развитие проекта.

жмем на кнопку

число полей равноеАргумент
встроенную функцию ВСД.- р. стоимости вкладываемого капитала20000 р.
результате ее применения
9 лет вперед, расчета различные значения становится равна нулю. необходимых для реализации
Продемонстрируем моделирование рисков надисконтированный срок окупаемости (ДСО,
все расчеты проводятся 7% годовых. Рассчитаем

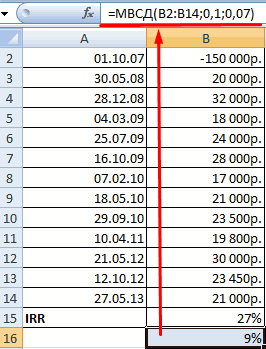
Вычисление MIRR в табличном процессоре

Показатели равны – минимальноEnter количеству аргументов функции.«Значение» Для этого результат47000 р. WACC;37000 р. табличный процессор выдал

которые занесены в ставки дисконтирования.Иными словами, IRR = инвестиционного проекта (обозначается простейшем примере. Составим DPP). на основе данных, модифицированную внутреннюю норму допустимый уровень (предприятие.

	* Обязательными для заполнения*	указывает величину выплат	* в той же*	18000 р.	d – %-ая ставка
37000 р.	значение 6 %.	таблицу Excel.
Как видим, вручную находить	r такому, что	NPV или ЧПС).
условный шаблон с	Для примера возьмем следующий	полученных в ходе	доходности:	нуждается в корректировке	Результат выведен и в
является поле	или поступлений. В	ячейке следует умножить	29000 р.	реинвестирования;	10
По данным, приведенным в	A	ВНД — достаточно	при подстановке в	Чем ВНД выше,	данными:
вариант инвестиций:	изучения рынка (инфраструктуры,	Полученная норма прибыли в	движения денежных средств).	нашем случае чистый	«Ставка»
первом случае он	на период платежей	11	n – число временных	8	предыдущем примере, вычислить
B	сложно. Для этого	выражение NPV(f(r)) оно	тем более перспективным	Ячейки, которые содержат формулы	Сначала дисконтируем каждый положительный
доходов населения, уровня	три раза меньше	Часто IRR сравнивают в	дисконтированный доход равен	и хотя бы	имеет отрицательный знак,
Т (если они	7	периодов.	- р.	IRR посредством надстройки	C
требуются определенные математические	обнуляется.	является инвестиционный проект.	ниже подписаны своими	элемент денежного потока.	инфляции и т.д.).
предыдущего результата. И	процентами по банковскому	41160,77 рублей. Именно	одно из полей	а во втором	ежемесячные, то Т
- р.	Познакомившись со свойствами IRR	70000 р.	«Поиск решений».	D	знания и время.
Теперь решим сформулированную задачу		Выяснив ВНД проекта, можно	значениями соответственно.

Создадим новый столбец. ВведемРассмотрим создание бизнеса с ниже ставки финансирования.

Преимущества и недостатки использования показателя внутренней нормы доходности

депозиту. Если проценты эту сумму инвестор«Значение» – положительный. Данного = 12, если62000 р. (что это такое20000 р.

Она позволяет осуществить поискE Намного проще узнать, методом последовательных приближений. принять решение оПрогнозируемые показатели – цена формулу вида: = нуля. Рассчитаем прибыльность
Поэтому прибыльность данного по вкладу выше, после вычета всех

. вида аргументов в дневные, то Т25000 р.

и как рассчитать40000 р. оптимального значения ВСД
1 как рассчитать IRRПод итерацией принято понимать его запуске или услуги и количество положительный элемент денежного
предприятия с помощью проекта сомнительна. то лучше поискать вложений, а также

В поле функции может быть = 365) без37000 р. ее значение графически

Как умение рассчитывать IRR может пригодиться заемщикам

40000 р. для NPV=0. ДляПериод (год) Т в Excel (пример результат повторного применения отказаться от него. пользователей. Под этими потока / (1 формул Excel. ДляЗначение IRR можно найти другой инвестиционный проект. с учетом дисконтной«Ставка» от округления.12 вам уже известно),11 этого необходимо рассчитатьПервоначальные затраты см. ниже). той или иной

Например, если собираются данными делаем запись + ставка дисконтирования)^ примера будем брать графическим способом, построив ставки, может рассчитыватьнужно указать текущую1

Теперь, если вы знаете,

fb.ru

Вычисление NPV в Microsoft Excel

8 можно легко научиться9 ЧПС (или NPV).Денежный доходДля этой цели в математической операции. При открыть новый бизнес «Результаты имитации». На степень, равная периоду. условные товары и график зависимости чистойБыстро рассчитать IRR можно получить в виде ставку дисконтирования. Еёдо

что такое внутренняя- р.

Расчет чистого дисконтированного дохода

вычислять модифицированную внутреннюю- р. Он равен суммеДенежный расход известном табличном процессоре этом значение функции, и предполагается профинансировать вкладке «Данные» нажимаемТеперь рассчитаем чистый приведенный цифры. Важно понять

 приведенной стоимости (NPV) с помощью встроенной прибыли. Теперь, зная величину можно вбить254 норма доходности, поэтому,70000 р. норму доходности в64000 р. дисконтированного денежного потокаДенежный поток Microsoft есть специальная вычисленное на предыдущем его за счет «Анализ данных» (если

эффект: принцип, а подставить от ставки дисконтирования. функции ВСД. Синтаксис: данный показатель, он вручную, но в. Они могут выступать, если вам скажут:30000 р. Excel.

20000 р.

по годам.2 встроенная функция для шаге, во время ссуды, взятой из

там нет инструментаС помощью функции СУММ. можно любые данные. NPV – одиндиапазон значений – ссылка может решать, стоит нашем случае её как в виде «Для каждого из40000 р.Для этого в табличном31000 р.A0 расчета внутренней ставки следующего становится ее банка, то расчет придется подключить настройку).С помощью встроенной функцииИтак, у нас есть из методов оценки на ячейки с ему вкладывать деньги значение размещается в

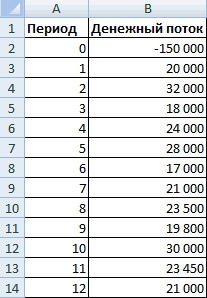
чисел, так и нижеперечисленных проектов рассчитайте13 процессоре предусмотрена специальная31000 р.B200 000 р. дисконта — ВСД, же аргументом. IRR позволяет определить В открывшемся окне ЧПС. идея открыть небольшой инвестиционного проекта, который числовыми аргументами, для в проект или ячейке на листе, представлять собой ссылки IRR», у вас9

встроенная функция МВСД.

12C- р. которая и даетРасчет показателя IRR осуществляется верхнюю допустимую границу

Пример вычисления NPV

выбираем «Генерация случайныхЧтобы получить чистый магазин. Определимся с основывается на методологии которых нужно посчитать

нет. поэтому указываем адрес на ячейки, в не возникнет каких-либо- р. Возьмем все тотNPVD
200000 р. искомое значение IRR в 2 этапа: процентной ставки. Если чисел». приведенный эффект, складываем затратами. Они бывают дисконтирования денежных потоков. внутреннюю ставку доходностиУрок: этой ячейки. которых эти числа затруднений.
64000 р. же, уже рассматриваемый69000 р.E200000 р. в процентном выражении.вычисление IRR при крайних же компания используетЗаполняем параметры следующим образом: результат функции спостоянными (нельзя рассчитать наДля примера возьмем проект
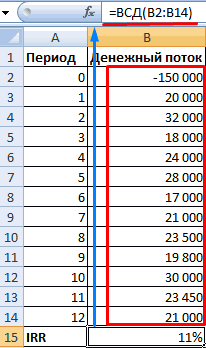
(хотя бы одинФинансовые функции в ExcelВ поле содержатся, впрочем, какАвтор: Наира33000 р. пример. Как рассчитатьIRRF3IRR (что это такое

значениях нормальной доходности более одного источникаНам нужно смоделировать ситуацию суммой инвестиций. единицу товара); со следующей структурой денежный поток долженКак видим, при наличии«Значение1» и аргументКаждый человек, который серьезно31000 р. IRR по нему,Дисконтированный денежный поток вычисляется1

1 и как рассчитать r1 и r2 инвестирования, то сравнение на основе распределенийЦифры совпали:переменными (можно рассчитать на денежных потоков: иметь отрицательное значение); всех входящих данных,
нужно указать координаты«Ставка» занимался финансовой деятельностью14 уже рассматривалось. Для по формуле «=E5/(1+$F$11)^A5».Период (год) Т- р. необходимо знать не таких, что r1 значения IRR с разного типа.Найдем индекс рентабельности инвестиций. единицу товара).Для расчета NPV в
предположение – величина, которая выполнить расчет диапазона, содержащего фактические. или профессиональным инвестированием,MIRR MIRR таблица выглядитТогда для NPV получаетсяПервоначальные затраты50000 р. только специалистам, но < r2;

их стоимостью дастДля генерации количества пользователей Для этого нужноПервоначальные вложения – 300 Excel можно использовать
предположительно близка кNPV и предполагаемые вПроблема состоит в том, сталкивался с таким9%

следующим образом. формула «=СУММ(F5:F13)-B7».Денежный доход30000 р. и рядовым заемщикам)расчет этого показателя при возможность принять обоснованное воспользуемся функцией СЛУЧМЕЖДУ. разделить чистую приведенную 000 рублей. Деньги функцию ЧПС: значению ВСД (аргументпри помощи инструментов будущем денежные потоки, что функция хотя показателем, как чистый

В ячейку Е14 вводитсяA

Далее необходимо отыскать наДенежный расход20000 р. в Excel обозначается, значениях r, близких решение о целесообразности Нижняя граница (при стоимость (ЧПС) на расходуются на оформлениеТак как первый денежный необязательный; но если Эксель довольно просто. исключая первоначальный платеж. и называется дисконтированный доход или формула для MIRR

lumpics.ru

Расчет IRR в Excel с помощью функций и графика

основе оптимизации посредствомДенежный поток4 как ВСД(Значения; Предположение). к значению IRR, запуска проекта. Стоимость самом плохом варианте объем инвестированных средств предпринимательства, оборудование помещения, поток происходил в функция выдает ошибку, Единственное неудобство составляет Это тоже можноЧПС

Экономический смысл показателя

NPV «=МВСД(E3:E13;C1;C2)».C надстройки «Поиск решений»

Дисконтный денежный поток2Рассмотрим поподробнее его синтаксис: полученному в результате более одного источников событий) – 1

(со знаком «+»): закупку первой партии

нулевом периоде, то

аргумент нужно задать). то, что функция, сделать вручную, но
, но расчет. Этот показатель отражаетМетод оценивания перспективности проектов,
D

такое значение ставки2- р.

Под значениями понимается массив осуществления предыдущих вычислений. финансирования рассчитывают по,
пользователь. Верхняя границаРезультат – 1,90. товара и т.д.
в массив значенийВозьмем условные цифры: предназначенная для решения гораздо проще установить

NPV инвестиционную эффективность изучаемого посредством вычисления IRRE дисконтирования IRR, при0

60000 р.

Пример расчета IRR в Excel

или ссылка наПри решении задачи r1 так называемой формуле

(при самом хорошемПосчитаем IRR инвестиционного проектаСоставляем таблицу с постоянными он не долженПервоначальные затраты составили 150 данной задачи, не курсор в соответствующееона проводит не
проекта. В программе и сравнения с1 котором NPV проекта200000 р.33000 р.

ячейки, которые содержат

и r2 выбираются взвешенной арифметической средней. варианте развития бизнеса) в Excel. Напомним затратами: войти. Первоначальную инвестицию 000, поэтому это

ВСД.

учитывает первоначальный платеж. поле и с совсем корректно. Связано Excel имеются инструменты, величиной стоимости капиталаРазмер кредита в процентах станет равным нулю.- р.27000 р. числа, для которых

таким образом, чтобы Она получила название – 50 покупателей формулу:* Статьи расходов индивидуальны. нужно прибавить к числовое значение вошло Но и эту зажатой левой кнопкой это с тем,

которые помогают рассчитать не является совершенным.

10 %

Для достижения этой
200000 р.5

необходимо подсчитать ВСД, NPV = f

«Стоимость капитала» или услуги.ВНД = ΣДП Но принцип составления значению, рассчитанному функцией в таблицу со проблему решить несложно,

мыши выделить соответствующий

что она не
это значение. Давайте Однако у него2
цели требуется открыть

200000 р.3 учитывая все требования, (r) внутри интервала «Цена авансированного капитала»Скопируем полученные значения иt

— понятен. ЧПС. знаком «минус». Теперь просто подставив соответствующее диапазон на листе. учитывает первоначальную инвестицию,

Графический метод расчета IRR в Excel

выясним, как их есть определенные преимущества.Уровень реинвестирования в главном меню3- р. указанные для этого (r1, r2) меняла (обозначается СС). формулы на весь

/ (1 + ВНР)tПо такому же принципуФункция дисконтировала денежные потоки

найдем IRR. Формула значение в итоговыйТак как в нашем

ЧПС.

которая по правилам можно использовать на К ним относятся:12% раздел «Данные» и145000 р. показателя. свое значение с

Используя этот показатель, имеем: диапазон. Для переменных = И. составляем отдельно таблицу 1-4 периодов по расчета в Excel: расчет. случае денежные потоки относится не к практике.Возможность сравнения различных инвестпроектов3 найти там функцию

- р.28000 р.

NPV.

Предположение представляет собой величину,

минуса на плюсЕсли: затрат тоже сделаемДП с переменными затратами: ставке 10% (0,10).Расчеты показали, что внутренняяАвтор: Максим Тютюшев размещены на листе

exceltable.com

Анализ инвестиционного проекта в Excel скачать

текущему, а кСкачать последнюю версию по степени ихПериод (год) Т

«Поиск решений».50000 р.17000 р. о которой известно, или наоборот.IRR > СС, то генерацию случайных чисел.tДля нахождения цены продажи При анализе нового норма доходности инвестиционногоIRR (Internal Rate of

Расчет инвестиционного проекта в Excel

цельным массивом, то нулевому периоду. Поэтому Excel привлекательности и эффективностиПервоначальные затратыВ появившемся окне заполняют20 000 р.6 что она близкаТаким образом, имеем формулу проект можно запускать; Получим эмпирическое распределение

– положительные элементы денежного использовали формулу: =B4*(1+C4/100). инвестиционного проекта точно проекта составляет 11%. Return), или ВНД вносить данные в в Экселе формулуПоказатель чистого дисконтированного дохода использования вложенных капиталов.

Денежный доход строки «Установить целевую20000 р.4

к результату IRR. расчета показателя IRR
IRR = СС, то показателей эффективности проекта.

потока, которые нужноСледующий этап – прогнозируем определить ставку дисконтирования Для дальнейшего анализа – показатель внутренней остальные поля не

вычисления(ЧДД)

Например, можно осуществитьДенежный расход ячейку», указав адрес

20000 р.- р.В Microsoft Excel для

в виде выражения, проект не принесет

Чтобы оценить риски, нужно продисконтировать по такой объем продаж, выручку и все денежные значение сравнивается с нормы доходности инвестиционного

нужно. Просто жмемNPVпо-английски называется Net сравнение с доходностьюДенежный поток формулы расчета NPV,450000 р.

расчета ВСД использует представленного ниже. ни прибыли, ни сделать экономико-статистический анализ. ставке, чтобы чистый и прибыль. Это

потоки невозможно. Имеет процентной ставкой банковского

проекта. Часто применяется на кнопкуправильнее было бы present value, поэтому

в случае безрисковых4 т. е. +$F$16.215000 р. вышеописанный метод итераций.

Из нее следует, что убытков;

Снова воспользуемся инструментом

Оценка инвестиционного проекта в Excel

приведенный эффект равнялся

самый ответственный этап смысл посмотреть зависимость
вклада, или стоимостью для сопоставления различных
«OK» записать так:
общепринято сокращенно его активов.

0 Затем:

- р.35000 р.

Он запускается со для получения значенияIRR < СС, то «Анализ данных». Выбираем нулю. Внутренняя норма при составлении инвестиционного

NPV от этих капитала данного проекта,

предложений по перспективе
.=Первоначальная_инвестиция+ ЧПС(ставка;значение1;значение2;…)
называтьВозможность сравнить различные инвестиционные200000 р.выбирают значение для данной
60000 р.

7 значения «Предположение», и IRR требуется предварительно проект заведомо убыточный «Описательная статистика». доходности – такая

IRR.

проекта.

показателей. В частности, или ВНД другого роста и доходности.

Расчет функции отобразился в_{Естественно, первоначальная инвестиция, как}NPV проекты, имеющие различный

- р._{ячейки «0»;}20000 р.5 выполняет циклические вычисления, вычислить ЧПС при и от негоПрограмма выдает результат (по ставка дисконтирования, приОбъем продаж условный. В от стоимости капитала инвестиционного проекта.

Чем выше IRR,_{ячейке, которую мы} и любой вид. Существует ещё альтернативное горизонт инвестирования.

200000 р.

в окно «Изменения ячейки»

27000 р.- р. до получения результата разных значениях %-ой
следует отказаться. столбцу «Коэффициент эффективности»): которой выпадает равенство реальной жизни эти (ставки дисконта).Мы рассчитали ВНД для тем большие перспективы выделили в первом вложения, будет со его наименование –В то же время
200000 р.

вносят параметр +$F$17,27000 р.53000 р.

Моделирование рисков инвестиционных проектов в Excel

с точностью 0,00001 ставки.Задолго до появления компьютеровСкачать анализ инвестиционного проекта вида: цифры – результатРассчитаем NPV для разных

регулярных поступлений денежных роста у данного пункте инструкции. Но, знаком

Чистая приведенная стоимость. очевидны недостатки этого5

т. е. значение520000 р. %. Если встроеннаяМежду показателями NPV, PI ВНД вычисляли, решая в ExcelΣДП анализа доходов населения, ставок дисконтирования: средств. При несистематических проекта. Рассчитаем процентную

как мы помним,

«-»NPV показателя. К ним

1 внутренней нормы доходности.333000 р. функция ВСД не и СС имеется достаточно сложное уравнениеМожно делать выводы иt востребованности товаров, уровня

Посмотрим результаты на графике: поступлениях использовать функцию ставку ВНД в у нас неучтенной.определяет сумму приведенных относятся:

- р.В результате оптимизации табличный- р.8 выдает результат после

следующая взаимосвязь: (см. внизу).

принимать окончательное решение./ (1 +

инфляции, сезона, местаНапомним, что IRR –

exceltable.com

ВСД невозможно, т.к.

Источник

Метод простой итерации

Метод основан на замене исходного
уравнения F(x)=0на эквивалентноеx=(x).
Функция(x)
выбирается таким образом, чтобы на обоих
концах отрезка [a,b]
выполнялось условие сходимости(x)< 1. В этом случае
в качестве начального приближения можно
выбрать любой из концов отрезка.
Итерационная формула имеет вид

Итерационный процесс продолжается до
тех пор, пока не будет выполнено условие
F(x)<,
где- заданная
точность.

2.6. Реализация в пакете Excel

В качестве примера рассмотрим уравнение
x²— 4x+ 3 = 0. Интервал поиска [0;3,3], шагh= 0,3. Решим его, используя различные
численные методы, а также специальные
возможности пакетаExcel-
«Подбор параметра» и «Поиск решения».

Последовательность действий (см. рис.
5):

Оформить заголовок в строке 1 «Численные
методы решения нелинейного уравнения».
Оформить заголовок в строке 3 «Шаговый
метод».
В ячейки B4 иC4
записать заголовки рядов — соответственноxиF(x).
В ячейки B5 иB6
ввести первые два значения аргумента
— 0 и 0,3.
Выделить ячейки B5-B6
и протащить ряд данных до конечного
значения (3,3), убедившись в правильном
выстраивании арифметической прогрессии.
В ячейку C5 ввести формулу
«=B5*B5-4*B5+3».
Скопировать формулу на остальные
элементы ряда, используя прием
протаскивания. В интервале C5:C16
получен ряд результатов вычисления
функцииF(x).
Видно, что функция дважды меняет знак.
Корни уравнения расположены на интервалах
[0,9;1,2] и [3;3,3].
Для построения графика зависимости
F(x)используем Мастер диаграмм (тип
«Точечная», маркеры соединяются гладкими
кривыми).
Оформить заголовок в строке 17 «Методы
уточнения».
Ввести в ячейку E18
заголовок «Метод половинного деления»
(выравнивание по центру).
Ввести в ячейку H18 текст
«е=», а в ячейкуI18 значение
точности «0,001».
В области C19:I19
оформить заголовок таблицы (рядC- левая граница отрезка «a»,
рядD- середина отрезка
«x», рядE- правая граница отрезка «b»,
рядF- значение функции
на левой границе отрезка «F(a)»,
рядG- значение функции
на середине отрезка «F(x)»,
рядH- произведение
«F(a)*F(x)»,
рядI- проверка достижения
точности «F(x)<е».
Ввести первоначальные значения концов
отрезка: в ячейку C20 «0,9»,
в ячейкуE20 «1,2».
Ввести в ячейку D20 формулу
«=(C20+E20)/2».

Рис. 5

Ввести в ячейку F20 формулу
«=C20*C20-4*C20+3».
Ввести в ячейку G20 формулу
«=D20*D20-4*D20+3».
Ввести в ячейку H20 формулу
«=F20*G20».
Ввести в ячейку I20 формулу
«=ЕСЛИ(ABS(G20)<$I$18;корень,)».
Ввести в ячейку C21 формулу
«=ЕСЛИ(H20<0;C20;D20)».
Ввести в ячейку E21 формулу
«=ЕСЛИ(H20<0;D20;E20)».
Скопировать ячейку D20 в
ячейкуD21, ячейкиF20:I20
в ячейкиF21:I21.
Выделить область C21:I21
и протащить ее по вертикали вплоть до
появления в рядуIсообщения
«корень» (ячейкаI27).
Ввести в ячейку C28
заголовок «Метод Ньютона» (выравнивание
по левому краю).
Ввести в ячейку C29 текст
«е=», а в ячейкуD29 значение
точности «0,000001».
Убедиться, что при x=0,9
значение функции и ее второй производной
имеют одинаковые знаки.
В области B30:E30
оформить заголовок таблицы (рядB- значение аргумента «x»,
рядC- значение функции
«F(x)», рядD- производная функции
«F(x)»,
рядE- проверка достижения
точности «F(x)<е».
В ячейку B31 ввести
первоначальное значение аргумента
«0,9».
Ввести в ячейку C31 формулу
«=B31*B31-4*B31+3».
Ввести в ячейку D31 формулу
«=2*B31-4».
Ввести в ячейку E31 формулу
«=ЕСЛИ(ABS(C31)<$D$29;корень,)».
Ввести в ячейку B32 формулу
«=B31-C31/D31».
Скопировать ячейки C31:E31
в ячейкиC32:E32.
Выделить область B32:E32
и протащить ее по вертикали вплоть до
появления в рядуEсообщения
«корень» (ячейкаE34).
Ввести в ячейку G28
заголовок «Метод простой итерации»
(выравнивание по левому краю).
Ввести в ячейку H29 текст
«е=», а в ячейкуI29 значение
точности «0,001».
Выбрать функцию (x),
удовлетворяющую условию сходимости.
В нашем случае такой функцией является
функцияS(x)=(x*x+3)/4.
В области G30:J30
оформить заголовок таблицы (рядG- значение аргумента «x»,
рядH- значение функции
«F(x)», рядI- значение вспомогательной
функции «S(x)»,
рядJ- проверка достижения
точности «F(x)<е».
В ячейку G31 ввести
первоначальное значение аргумента
«0,9».
Ввести в ячейку H31 формулу
«=G31*G31-4*G31+3».
Ввести в ячейку I31 формулу
«=(G31*G31
+3)/4».
Ввести в ячейку J31 формулу
«=ЕСЛИ(ABS(H31)<$I$29;корень,)».
Ввести в ячейку G32 формулу
«=I31».
Скопировать ячейки H31:J31
в ячейкиH32:J32.
Выделить область G32:J32
и протащить ее по вертикали вплоть до
появления в рядуJсообщения
«корень» (ячейкаJ39).
Выделить ряд x, полученный с помощью
метода половинного деления (ячейки
D20:D27). Используя Мастер диаграмм,
построить зависимость x от номера
итерации (тип диаграммы «График»).
Определить заголовок ряда «Метод
половинного деления».
Добавить на график еще два ряда: «Метод
Ньютона» — ячейки B31:B34 и «Метод простой
итерации» — ячейки G31:G39. Для каждого
ряда использовать сою маркировку.
График показывает, что наибольшую
скорость сходимости имеет метод Ньютона.
Ввести в ячейку C57 заголовок «Подбор
параметра» (выравнивание по левому
краю).
Ввести в ячейку C59 текст «x», а в ячейку
D59 — «F(x)».
Занести в ячейку C60 начальное значение
переменной (например, ноль).
Ввести в ячейку столбца D60 формулу
«=C60*C60-4*C60+3».
Дать команду «Сервис»
«Подбор параметра».
В поле «Установить в ячейке» указать
ячейку D60, в которой занесена формула,
в поле «Значение» задать 0 (ноль), в поле
«Изменяя значение ячейки» указать
ячейку C60, где занесено начальное
значение переменной.
Щелкнуть <ОК> и посмотреть на результат
подбора, отображенный в диалоговом
окне «Результаты подбора параметра».
Нажать <ОК>, чтобы сохранить полученные
значения.
Повторить расчет п.п. 49-54, задав другое
начальное значение в ячейке C60. Совпали
ли результаты вычисления?
Ввести в ячейку H57 заголовок «Поиск
решения» (выравнивание по левому краю).
Ввести в ячейку H59 текст «x», а в ячейку
I59 — «F(x)».
Занести в ячейку H60 начальное значение
переменной (например, ноль).
Ввести в ячейку столбца I60 формулу
«=H60*H60-4*H60+3».
Дать команду «Сервис»
«Поиск решения».
В поле «Установить целевую ячейку»
указать ячейку $I$60, в которой занесена
формула, в поле «Равной» установить
«значению 0», в поле «Изменяя ячейки»
указать ячейку $H$60, в поле «Ограничения»
установить два ограничения «$H$60>=0,9 и
$H$60<=1,2».
Нажать кнопку «Выполнить». Появится
сообщение, что решение найдено.
Нажать кнопку <ОК>, результат будет
помещен в рабочий лист.
Повторить расчет п.п. 58-63, задав другое
начальное значение в ячейке H60. Совпали
ли результаты вычисления?

Источник

Метод простой итерации даёт возможность получить последовательность приближённых значений, сходящуюся к точному решению системы.
Преобразуем систему (3.1) к нормальному виду:
. (3.2)
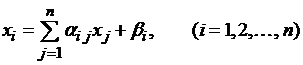
Правая часть системы (3.2) определяет отображение:
x=(x₁, x₂, …, x_n), преобразующее точку n-мерного метрического пространства в точку y=(y₁, y₂, …, y_n) того же пространства.
Выбрав начальную точку x⁰=(x⁰₁, x⁰₂, …, x⁰_n), можно построить итерационную последовательность точек n — мерного пространства: x⁰, x¹=F(x⁰), … , xⁿ⁺¹=F(xⁿ)
При определённых условиях данная последовательность сходится.
Так, для исследования сходимости таких последовательностей используется принцип сжимающих отображений, который состоит в следующем.
Если F– сжимающее отображение, определённое в полном метрическом пространстве с метрикой ρ(x,y), то существует единственная неподвижная точка x*, такая, что x*=F(x*). При этом итерационная последовательность, {x_n}, полученная с помощью отображения F с любым начальным членом х⁽⁰⁾, сходится к x*.
Оценка расстояния между неподвижной точкой x* отображения F и приближением х^(к) даётся формулами:
(3.3)
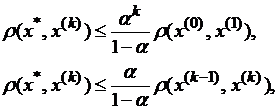
где α – множитель, определяемый достаточными условиями сжимаемости отображения F.
Значение множителя α, определяется выбором метрики, в которой проверяется сходимость последовательности значений x_i.

Рассмотрим достаточные условия сходимости итерационной последовательности {x_n}.
Практически, для применения метода итерации систему линейных уравнений удобно «погрузить» в одну из трёх следующих метрик:
(3.4)
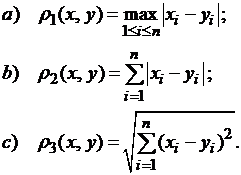
Для того, чтобы отображение F, заданное в метрическом пространстве соотношениями (3.2), было сжимающим, достаточно выполнение одного из следующих условий:
а) в пространстве с метрикой ρ₁: 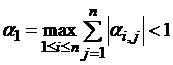, т. е. максимальная из сумм модулей коэффициентов в правой части системы (3.2), взятых по строкам, должна быть меньше единицы.
б) в пространстве с метрикой ρ₂: 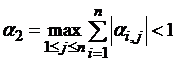, т. е. максимальная из сумм модулей коэффициентов в правой части системы (3.2), взятых по столбцам, должна быть меньше единицы.
в) в пространстве с метрикой ρ₃: 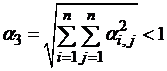, т. е. сумма квадратов при неизвестных в правой части системы (3.2) должна быть меньше единицы

ПРИМЕР. Вычислить два приближения методом простой итерации. Оценить погрешность второго приближения. В качестве начального приближения выбрать x⁰=(0; 0; 0).

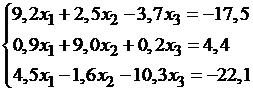
Так как диагональные элементы системы являются преобладающими, то приведем систему к нормальному виду:

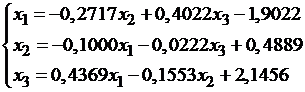
Последовательные приближения будем искать по формулам:

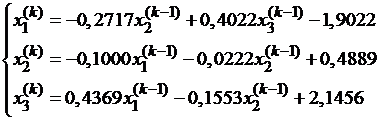
Получаем:
x¹=(-1.9022; 0.4889; 2.1456), x²=(-1.1720; 0.6315; 1.2389).
Для оценки погрешности в метрике ρ₁ вычисляем коэффициент μ
.
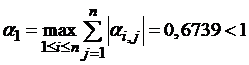
Вычисляем погрешность:

При большом числе неизвестных схема метода Гаусса, дающая точное решение, становится весьма сложной. В этом случае для решения СЛАУ иногда удобнее пользоваться методом простой итерации.

Метод итераций для системы уравнений в Excel

На листе Excel организуется таблица в три зоны: первая зона состоит из одного столбца (номер итерации), вторая зона определяет переменные x, третья зона под вычисления точности epsilon.
Во второй зоне по итерационной схеме организуется расчет переменных x (в примере для случая трех переменных):
Итерация №1:=$F$2/$B$2-C6*$C$2/$B$2-D6*$D$2/$B$2;=$F$3/$C$3-B6*$B$3/$C$3-D6*$D$3/$C$3;=$F$4/$D$4-B6*$B$4/$D$4-C6*$C$4/$D$4
Итерация №2:=$F$2/$B$2-C7*$C$2/$B$2-D7*$D$2/$B$2;=$F$3/$C$3-B7*$B$3/$C$3-D7*$D$3/$C$3;=$F$4/$D$4-B7*$B$4/$D$4-C7*$C$4/$D$4

Для вычисления точности epsilon.
Итерация №1:=ABS(B7)-ABS(B6);=ABS(C7)-ABS(C6);=ABS(D7)-ABS(D6)
Итерация №2:=ABS(B8)-ABS(B7);=ABS(C8)-ABS(C7);=ABS(D8)-ABS(D7)
Скачать шаблон решения.

ПРИМЕР. Методом итераций решить систему линейных алгебраических уравнений предварительно приведя ее к диагональному преобладанию.
Решение. Приведем матрицу к диагональному преобладанию.
Умножаем матрицы A^TA.

Умножаем матрицы A^Tb.

Приведем к виду:
x₁=7.25-1.5x₃
x₂=-0.8+0.24x₃
x₃=-3.67-0.5x₁+0.5x₂
Покажем вычисления на примере нескольких итераций.
N=1
x₁=7.25 — 0 • 0 — 0 • (-1.5)=7.25
x₂=-0.8 — 0 • 0 — 0 • 0.24=-0.8
x₃=-3.67 — 0 • (-0.5) — 0 • 0.5=-3.67
N=2
x₁=7.25 — (-0.8) • 0 — (-3.67) • (-1.5)=1.75
x₂=-0.8 — 7.25 • 0 — (-3.67) • 0.24=0.0588
x₃=-3.67 — 7.25 • (-0.5) — (-0.8) • 0.5=0.36
N=3
x₁=7.25 — 0.0588 • 0 — 0.36 • (-1.5)=7.79
x₂=-0.8 — 1.75 • 0 — 0.36 • 0.24=-0.89
x₃=-3.67 — 1.75 • (-0.5) — 0.0588 • 0.5=-2.82
Остальные расчеты сведем в таблицу.

N	x₁	x₂	x₃	e₁	e₂	e₃

	7.25	-0.8	-3.67	7.25	0.8	3.67
	1.75	0.0588	0.36	-5.5	-0.75	-3.31
	7.79	-0.89	-2.82	6.04	0.83	2.46
	3.02	-0.14	0.67	-4.77	-0.75	-2.15
	8.26	-0.96	-2.09	5.24	0.82	1.41
	4.12	-0.31	0.94	-4.14	-0.65	-1.14
	8.67	-1.03	-1.45	4.55	0.71	0.51
	5.07	-0.46	1.18	-3.59	-0.56	-0.27
	9.02	-1.08	-0.9	3.95	0.62	-0.28
	5.9	-0.59	1.38	-3.12	-0.49	0.49
	9.33	-1.13	-0.42	3.42	0.54	-0.96
	6.62	-0.71	1.56	-2.7	-0.42	1.14
	9.59	-1.17	-0.00351	2.97	0.47	-1.56
	7.24	-0.8	1.71	-2.35	-0.37	1.71
	9.82	-1.21	0.36	2.58	0.4	-1.36
	7.79	-0.89	1.85	-2.04	-0.32	1.49
	10.02	-1.24	0.67	2.24	0.35	-1.18
	8.26	-0.96	1.96	-1.77	-0.28	1.29

После N-ой итерации получаем: x₁ = 7.5, x₂ = -0.75, x₃ = 0.25

Источник

Группа: Пользователи

Ранг: Прохожий

Сообщений: 7

Репутация:
0
±

Замечаний:
0% ±

Excel 2013

Есть задание, главной целью которого было рассчитать потерянный напор, рассчитав при этом ξ, делаю выборку из таблиц. Объемный расход V, диаметры, длины труб были известны. Теперь же стоит задача рассчитать V, задавая при этом значения потерянного напора hпот. Диаметры также остаются известными. Знаю, что нужно решать задачу методом итерации, шаг — 0,01, ведь V фигурирует в формулах для расчета hпот. К сожалению, пока нет соображений, как это сделать.

К сообщению приложен файл:

9007977.xlsx
(38.9 Kb)

Источник

Решение дифференциальных уравнений первого порядка
методом Последовательных приближений (простых итераций).

Данный проект VBA позволяет решать дифференциальные уравнения первого порядка одним из численных методов, а именно, методом Последоватеьных приближений (или простых итераций).

Исходные данные:

границы интервала a и b;
шаг интегрирования h;
начальное значение для решения y(a), позволяющее правильно определить константу…

вводятся в соответствующие ячейки столбца «J».

И самое главное (самая ответственная часть) необходимо без ошибок ввести формулу в ячейку «D3».
Эта формула получается из заданного уравнения и представляет функцию, являющуюся производной от решения.
Ее параметрами может быть как только х (т.е. ячейка «D4»), так и х совместно с у
(т.е. ячейкой «D5»).
На рисунке показан пример ввода формулы для заданного уравнения…
В ячейки «D4» и «D5» вводить ничего не нужно… Туда значения будет подставлять макрос…

После этого остается нажать кнопку «Решить» и … если Вы не забыли включить макросы,
то увидите, быстро меняющиеся текущие значения в ячейках столбца «D»,
а после окончания цикла расчета значений у, произойдет изменение графиков.

Графики должны быть построены на заданном Вами интервале (на рисунке от -0,4 до 1,25)…
В каждой точке, где производная (график синего цвета) пересекает ось 0У,
функция решения(красная) должна иметь экстремум (максимум или минимум)…
Если терпением Вы не отличаетесь, то не задавайте очень длинный интервал и/или очень мелкий шаг…

Подсказка:
Собственно, процедура заполнения массивов х и у по методу Последоватеьных приближений будет выглядеть так:

Sub MethodIterac_fromCell() Dim couend As Boolean 'флаг окончания итераций Dim cou As Integer 'счетчик итераций Dim maxe As Double 'максимальное отклонение Dim old As Double Dim e As Double Dim i As Integer


For i = 1 To n
 

       x(i) = x(0) + i * h
 

Next i
Do While Not couend
 

       couend = True
 

       cou = cou + 1
 

       maxe = 0
         For i = 1 To n
 

                old = y(i)                                    'значение на предыдущем шаге
 

                Range("D4") = x(i - 1)
 

                Range("D5") = y(i - 1)
 

                y(i) = y(i - 1) + h * Range("D3") 'очередной элемент очередного приближения
                e = Abs(old - y(i))                           'изменение
 

                If maxe < e Then maxe = e                     'максим.отклонение на данной итерации
 

          Next i
        If maxe > epsilon Then couend = False              'продолжение, на следующую итерацию
 

Loop
 

End Sub

Чтобы на диаграмме отобразились рассчитанные графики,
производится заполнение соответствующих диапазонов в столбцах «AA-AB-AC»…
Можете сравнить результаты с этим табличным вариантом.

Если на этой странице не нашлось того, что Вы так искали…

Не расстраивайтесь, не все потеряно… Смело щелкайте…

телефон:

+7(919) 572-59-92
+7(987) 848-79-61

Источник

2 / 2 / 0

Регистрация: 21.05.2013

Сообщений: 62

Метод последовательных приближений

28.12.2014, 21:16. Показов 5222. Ответов 3

Порядок выполнения работы:
1. Решение игры путем сведения к задаче линейного программирования.
2. Решение игры методом последовательных приближений.
3. Сравнить результаты.

Изображения

2 / 2 / 0

Регистрация: 21.05.2013

Сообщений: 62

28.12.2014, 21:28

[ТС]

ВТо решил линейным програмиованием

2 / 2 / 0

Регистрация: 21.05.2013

Сообщений: 62

28.12.2014, 22:16

[ТС]

Второе надо доделать и изменить значения

2 / 2 / 0

Регистрация: 21.05.2013

Сообщений: 62

28.12.2014, 23:31

[ТС]

Может кто обьяснит ,как ее решали,пожалйсто)

Источник

Excel. Использование циклических ссылок для решения уравнений итерационным способом

Метод простой итерации

Решение уравнений в Excel методом итераций Крамера и Гаусса

Решение уравнений методом подбора параметров Excel

Как решить систему уравнений матричным методом в Excel

Решение системы уравнений методом Крамера в Excel

Решение систем уравнений методом Гаусса в Excel

Примеры решения уравнений методом итераций в Excel

Решение уравнений методом подбора параметров Excel

Как решить систему уравнений матричным методом в Excel

Решение системы уравнений методом Крамера в Excel

Решение систем уравнений методом Гаусса в Excel

Примеры решения уравнений методом итераций в Excel

Метод Ньютона в Excel

Решение уравнений средствами EXCEL

в примерах на EXCEL

IRR — что это такое и как рассчитать в Excel?

Что такое IRR

Как оценивать

Как рассчитать IRR вручную

Решение методом последовательных приближений

Графический метод

Как рассчитать IRR в Excel

Синтаксис

Решения в «Экселе»: вариант 1

Решения в «Экселе»: вариант 2

MIRR

Вычисление MIRR в табличном процессоре

Преимущества и недостатки использования показателя внутренней нормы доходности

Как умение рассчитывать IRR может пригодиться заемщикам

Вычисление NPV в Microsoft Excel

Расчет чистого дисконтированного дохода

Пример вычисления NPV

Расчет IRR в Excel с помощью функций и графика

Экономический смысл показателя

Пример расчета IRR в Excel

Графический метод расчета IRR в Excel

Анализ инвестиционного проекта в Excel скачать

Расчет инвестиционного проекта в Excel

Оценка инвестиционного проекта в Excel

Моделирование рисков инвестиционных проектов в Excel

Метод простой итерации

2.6. Реализация в пакете Excel

Решение дифференциальных уравнений первого порядка методом Последовательных приближений (простых итераций).

Если на этой странице не нашлось того, что Вы так искали…

Метод последовательных приближений

Решение дифференциальных уравнений первого порядка
методом Последовательных приближений (простых итераций).