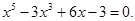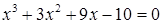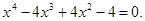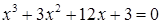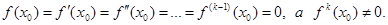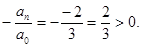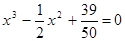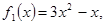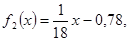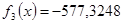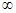Метод половинного деления в excel для уравнения

Решение уравнений в EXCEL методом половинного деления, методом хорд и касательных.

При прохождении темы численные методы учащиеся уже умеют работать с электронными таблицами и составлять программы на языке паскаль. Работа комбинированного характера.Расчитана на 40 минут. Цель работы повторить и закрепить навыки паботы с программами EXCEL, ABCPascal. Материал содержит 2 файла. Один содержит теоретический материал, так как он и предлагается ученику . Во 2-м файле пример работы ученика Иванова Ивана.

Скачать:

Вложение	Размер
материал для ученика	57.5 КБ
работа ученика	27 КБ

Предварительный просмотр:

Аналитическое решение некоторых уравнений, содержащих, например тригонометрические функции может быть получено лишь для единичных частных случаев. Так, например, нет способа решить аналитически даже такое простое уравнение, как cos x=x

Численные методы позволяют найти приближенное значение корня с любой заданной точностью.

Приближённое нахождение обычно состоит из двух этапов:

1) отделение корней, т.е. установление возможно точных промежутков [a,b], в которых содержится только один корень уравнения;

2) уточнение приближённых корней, т.е. доведение их до заданной степени точности.

Мы будем рассматривать решения уравнений вида f(x)=0. Функция f(x) определена и непрерывна на отрезке [а.Ь]. Значение х 0 называется корнем уравнения если f(х 0 )=0

Для отделения корней будем исходить из следующих положений:

• Если f(a)* f(b] a, b существует, по крайней мере, один корень
• Если функция y = f(x) непрерывна на отрезке [a, b], и f(a)*f(b) и f ‘(x) на интервале (a, b) сохраняет знак, то внутри отрезка [а, b] существует единственный корень уравнения

Приближённое отделение корней можно провести и графически. Для этого уравнение (1) заменяют равносильным ему уравнением р(х) = ф(х), где функции р(х) и ф(х] более простые, чем функция f(x). Тогда, построив графики функций у = р(х) и у = ф(х), искомые корни получим, как абсциссы точек пересечения этих графиков

Для уточнения корня разделим отрезок [а, b] пополам и вычислим значение функции f(х) в точке x sr =(a+b)/2. Выбираем ту из половин [a, x sr ] или [x sr ,b], на концах которых функция f(x) имеет противоположные знаки.. Продолжаем процесс деления отрезка пополам и проводим то же рассмотрение до тех пор, пока. длина [a,b] станет меньше заданной точности . В последнем случае за приближённое значение корня можно принять любую точку отрезка [a,b] (как правило, берут его середину). Алгоритм высокоэффективен, так как на каждом витке (итерации) интервал поиска сокращается вдвое; следовательно, 10 итераций сократят его в тысячу раз. Сложности могут возникнуть с отделением корня у сложных функций.

Для приближенного определения отрезка на котором находится корень можно воспользоваться табличным процессором, построив график функции

ПРИМЕР : Определим графически корень уравнения . Пусть f1(х) = х , a и построим графики этих функций. (График). Корень находится на интервале от 1 до 2. Здесь же уточним значение корня с точностью 0,001(на доске шапка таблицы)

Алгоритм для программной реализации

1. а:=левая граница b:= правая граница
2. m:= (a+b)/2 середина
3. определяем f(a) и f(m)
4. если f(a)*f(m)
5. если (a-b)/2>e повторяем , начиная с пункта2

Точки графика функции на концах интервала соединяются хордой. Точка пересечения хорды и оси Ох (х*) и используется в качестве пробной. Далее рассуждаем так же, как и в предыдущем методе: если f(x a ) и f(х*) одного знака на интервале , нижняя граница переносится в точку х*; в противном случае – переносим верхнюю границу. Далее проводим новую хорду и т.д.

Осталось только уточнить, как найти х*. По сути, задача сводится к следующей: через 2 точки с неизвестными координатами (х 1 , у 1 ) и (х 2 , у 2 ) проведена прямая; найти точку пересечения этой прямой и оси Ох.

Запишем уравнение прямой по двум точках:

В точке пересечения этой прямой и оси Ох у=0, а х=х*, то есть

, откуда

процесс вычисления приближённых значений продолжается до тех пор, пока для двух последовательных приближений корня х„ и х п _1 не будет выполняться условие abs(xn-x n-1 ) е — заданная точность

Сходимость метода гораздо выше предыдущего

Алгоритм различается только в пункте вычисления серединной точки- пересечения хорды с осью абсцисс и условия останова (разность между двумя соседними точками пересечения)

Уравнения для самостоятельного решения: (отрезок в excel ищем самостоятельно)

1 Численный метод решения нелинейных уравнений

1.1 Область локализации корней

В общем виде любое уравнение одной переменной принято записывать так , при этом корнем (решением) называется такое значение x*, что оказывается верным тождеством. Уравнение может иметь один, несколько (включая бесконечное число) или ни одного корня. Как легко видеть, для действительных корней задача отыскания решения уравнения легко интерпретируется графически: корень есть такое значение независимой переменной, при котором происходит пересечение графика функции, стоящей в левой части уравнения f ( x ), с осью абсцисс.

Например , для уравнения выполним преобразование и приведем его к виду f(x)= 0 т.е. . График этой функции представлен на рисунке 1. Очевидно, что данное уравнение имеет два действительных корня – один на отрезке [-1, 0] , а второй – [1, 2].

Рисунок 1. График функции

Таким образом, можно приблизительно определять область локализации корней уравнения. Заметим, что отделить корень можно не единственным образом: если корень отделён на каком-либо отрезке, то годится и любой меньший отрезок, содержащий этот корень. Вообще говоря, чем меньше отрезок, тем лучше, но при этом не следует забывать о том, что на отделение корня на меньших отрезках также тратятся вычислительные усилия, и, быть может, весьма значительные. Таким образом, часто для начала довольствуются весьма широким отрезком, на котором корень отделён.

Некоторые виды уравнений допускают аналитическое решение. Например, степенные алгебраические уравнения степени n при n ≤ 4. Однако, в общем виде, аналитическое решение, как правило, отсутствует. В этом случае, применяются численные методы. Все численные методы решения уравнений представляют собой итерационные алгоритмы последовательного приближения к корню уравнения. То есть, выбирается начальное приближение к корню x ₀ и затем с помощью итерационной формулы генерируется последовательность x ₁, x ₂, …, x_k сходящаяся к корню уравнения .

1.2 Критерии сходимости при решении уравнений

Ø Абсолютная погрешность — абсолютное изменение приближения на соседних шагах итерации

Ø Относительная погрешность — относительное изменение приближения на соседних шагах итерации

Ø Близость к нулю вычисленного значения левой части уравнения (иногда это значение называют невязкой уравнения, так как для корня невязка равна нулю)

1.3 Метод половинного деления (метод дихотомии)

Метод половинного деления основан на последовательном делении отрезка локализации корня пополам.

Для этого выбирается начальное приближение к отрезку [ a , b ], такое, что f ( a ) × f ( b ) — середине отрезка [ a , b ]. Если он противоположен знаку функции в точке a, то корень локализован на отрезке [ a , c ], если же нет – то на отрезке [ c , b ]. Схема метода дихотомии приведен на рис у нке 2.

Рисунок 2. Последовательное деление отрезка пополам и приближение к корню

Алгоритм метода дихотомии можно записать так:

1. представить решаемое уравнение в виде

2. выбрать a, b и вычислить

3. если f(a) × f( с ) то a=a; b = c иначе a = c; b=b

4. если критерий сходимости не выполнен, то перейти к п. 2

Пример решения уравнения методом дихотомии

Найти решение заданного уравнения методом дихотомии с точностью до 10 -5 .

Пример создания расчетной схемы на основе метода дихотомии на примере уравнения: на отрезке [1, 2]

Данный метод заключается в проверке на каждой итерации условия:

если f ( a ) × f (с) и выбор соответствующего отрезка для следующей итерации.

Рисунок 3. Последовательность итераций метода дихотомии при поиске корня уравнения на отрезке [1, 2]

a ) схема расчета (зависимые ячейки); b) режим отображения формул;

Для нашего примера итерационная последовательность для нахождения решения принимает вид:

Точность до пятой значащей цифры достигается за 20 итераций.

Скорость сходимости этого метода является линейной.

При выполнении начального условия он сходится к решению всегда.

Метод половинного деления удобен при решении физически реальных уравнений, когда заранее известен отрезок локализации решения уравнения.

2 Решение уравнений , используя “Подбор параметра ”

Используя возможности Excel можно находить корни нелинейного уравнения вида f(x)=0 в допустимой области определения переменной. Последовательность операций нахождения корней следующая:

1. Производится табулирование функции в диапазоне вероятного существования корней;

2. По таблице фиксируются ближайшие приближения к значениям корней;

3. Используя средство Excel Подбор параметра, вычисляются корни уравнения с заданной точностью.

При подборе параметра Excel использует итерационный (циклический) процесс. Количество итераций и точность устанавливаются в меню Сервис/Параметры/вкладка Вычисления. Если Excel выполняет сложную задачу подбора параметра, можно нажать кнопку Пауза в окне диалога Результат подбора параметра и прервать вычисление, а затем нажать кнопку Шаг, чтобы выполнить очередную итерацию и просмотреть результат. При решении задачи в пошаговом режиме появляется кнопка П родолжить — для возврата в обычный режим подбора параметра.

2.1 Пример решения уравнения, используя “Подбор параметра”

Например , найдем все корни уравнения 2x 3 -15sin(x)+0,5x-5=0 на отрезке [-3 ; 3].

Для локализации начальных приближений необходимо определить интервалы значений Х, внутри которых значение функции пересекает ось абсцисс, т.е. функция меняет знак. С этой целью табулируем функцию на отрезке [–3; 3] с шагом 0,2, получим табличные значения функции. Из полученной таблицы находим, что значение функции трижды пересекает ось Х, следовательно, исходное уравнение имеет на заданном отрезке все три корня.

Рисунок 4. Поиск приближенных значений корней уравнения

Выполните команду меню Сервис/Параметры, во вкладке Вычисления установите относительную погрешность вычислений E=0,00001, а число итераций N=1000, установите флажок Итерации.

Выполните команду меню Сервис/Подбор параметра. В диалоговом окне (рисунок 9) заполните следующие поля:

þ Установить в ячейке : в поле указывается адрес ячейки, в которой записана формула правой части функции;

þ Значение : в поле указывается значение, которое должен получить полином в результате вычислений, т.е. правая часть уравнения (в нашем случае 0);

þ Изменяя значение : в поле указывается адрес ячейки (где записано начальное приближение), в которой будет вычисляться корень уравнения и на которую ссылается формула.

Рисунок 5. Диалоговое окно Подбор параметра для поиска первого корня

После щелчка на ОК получим значение первого корня -1,65793685 .

Выполняя последовательно операции аналогичные предыдущим, вычислим значения остальных корней: -0,35913476 и 2,05170101 .

3 Решение уравнений и систем уравнений, используя надстройку “Поиск решения”

Для решения уравнений можно также использовать команду Поиск решения, доступ к которой реализуется через пункт меню Сервис/Поиск решения.

Последовательность операций нахождения корней следующая:

1. Найти приближенное значение корня уравнения

2. Открыть диалог Поиск решения и установить следующие параметры (рисунок 10):

þ в поле У становить целевую ячейку ввести адрес ячейки, содержащей формулу (левую часть уравнения);

þ установить переключатель в положение ‘ значению’ и ввести значение 0 (правая часть уравнения);

þ в поле Изменяя ячейки ввести адреса изменяемых ячеек, т.е. аргумента x целевой функции,;

þ в поле Ограничения с помощью кнопки Д обавить ввести все ограничения, которым должен отвечать результат поиска (область поиска корня уравнения);

þ для запуска процесса поиска решения нажать кнопку В ыполнить.

þ Для сохранения полученного решения необходимо использовать переключатель С охранить найденное решение в открывшемся окне диалога Результаты поиска решения.

Рисунок 6. Диалоговое окно Поиск решения

Полученное решение зависит от выбора начального приближения. Поиск начальных приближений рассмотрен выше.

Рассмотрим некоторые Опции, управляющие работой Поиска решения, задаваемые в окне Параметры (окно появляется, если нажать на кнопку Параметры окна Поиск решения):

þ Максимальное время — ограничивает время, отведенное на процесс поиска решения (по умолчанию задано 100 секунд, что достаточно для задач, имеющих около 10 ограничений, если задача большой размерности, то время необходимо увеличить).

þ Относительная погрешность — задает точность, с которой определяется соответствие ячейки целевому значению или приближение к указанным ограничениям (десятичная дробь от 0 до 1).

þ Неотрицательные значения — этим флажком можно задать ограничения на переменные, что позволит искать решения в положительной области значений, не задавая специальных ограничений на их нижнюю границу.

þ Показывать результаты итераций — этот флажок позволяет включить пошаговый процесс поиска, показывая на экране результаты каждой итерации.

þ Метод поиска — служит для выбора алгоритма оптимизации. Метод Ньютона был рассмотрен ранее. В Методе сопряженных градиентов запрашивается меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно велика и если итерации дают слишком малое отличие в последовательных приближениях.

Рисунок 7. Вкладка Параметры окна Поиск решения

3.1 Пример решения уравнения, используя надстройку “Поиск решения”

Например , найдем все корни уравнения 2x 3 -15sin(x)+0,5x-5=0 на отрезке [-3 ; 3]. Для локализации начальных приближений необходимо определить интервалы значений Х, внутри которых значение функции пересекает ось абсцисс, т.е. функция меняет знак. С этой целью табулируем функцию на отрезке [–3;3] с шагом 0,2, получим табличные значения функции. Из полученной таблицы находим, что значение функции трижды пересекает ось Х, следовательно, исходное уравнение имеет на заданном отрезке все три корня. На рисунке 12 представлен пример заполнения окна Поиск решения для нахождения первого корня на отрезке [-2; -1].

Рисунок 8. Пример решения уравнения при помощи надстройки Поиск решения

Задание 1. Решение уравнений численным методом

На листе 1 (название листа: Численные методы) для заданного уравнения вида f(x)=0 (Таблица 1. Индивидуальные задания ) реализовать итерационные расчетные схемы методов, указанных в Таблице 1 для нахождения хотя бы одного корня на заданном интервале. Количество итераций просчитать, оценивая , .

Задания 2. Решение уравнений встроенными средствами “Подбор параметра” и “Поиск решения”

На листе 2 (название листа: Подбор Поиск) для заданного уравнения вида f(x)=0 (Таблица 1. Индивидуальные задания) на заданном интервале и с некоторым шагом (шаг выбрать самостоятельно) построить таблицу значений функции f(x) и определить количество корней уравнения и выделить интервалы, на которых находятся корни. Построить график функции. Уточнить на заданных интервалах с точностью до 10 -6 корни уравнения с помощью встроенных средств: Подбор параметра, Поиск решения

Решение нелинейных уравнений в Excel и Mathcad (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

Кафедра прикладной математики и вычислительной техники

Решение нелинейных уравнений в Excel и Mathcad

к выполнению лабораторных работ

по дисциплине «Вычислительная математика»

Решение нелинейных уравнений в Excel и Mathcad: Метод. указ. / Сост. , — Самара: СГАСУ, 20с.

Методические указания разработаны в соответствии с Государственным образовательным стандартом изучения дисциплины «Вычислительная математика».

Рассмотрена реализация численных методов при решении нелинейных уравнений и систем уравнений в Excel и MathCad. Приведены варианты заданий для индивидуального выполнения и вопросы для самоконтроля и тестирования.

Предназначены для студентов специальности 230201 – «Информационные системы и технологии» всех форм обучения.

Рецензент к. ф-м. н.

Ó , составление, 2012

1 Решение нелинейного уравнения

1.1 Общие сведения о решении нелинейного уравнения

1.2 Отделение корней

1.3 Уточнение корней стандартными средствами Excel и Mathcad

1.4 Метод деления отрезка пополам

1.6 Метод Ньютона (касательных)

1.7 Комбинированный метод

1.8 Метод итераций

2 Решение систем нелинейных уравнений

2.1 Общие сведения о решении систем нелинейных уравнений

2.2 Решение систем нелинейных уравнений методом Ньютона

2.3 Решение систем нелинейных уравнений методами итераций

3 Задания к лабораторным работам

Лабораторная № 1. Отделение корней и стандартные инструменты решения нелинейного уравнения

Лабораторная № 2. Сравнение методов уточнения корней нелинейного уравнения

Лабораторная № 3. Решение систем нелинейных уравнений

Лабораторная № 4. Программирование методов решения нелинейных уравнений и систем

4 Вопросы и тесты для самоконтроля

Список рекомендуемой литературы

1 Решение нелинейного уравнения

1.1 Общие сведения о решении нелинейного уравнения

Как правило, нелинейное уравнения общего вида f(х)=0 невозможно решить аналитически. Для практических задач достаточно найти приближенное значение x, в определенном смысле близкое к точному решению уравнения хточн.

В большинстве случаев поиск приближенного решения включает два этапа. На первом этапе отделяют корни, т. е. находят такие отрезки, внутри которых находится строго один корень. На втором этапе уточняют корень на одном из таких отрезков, т. е. находят его значение с требуемой точностью.

Достигнутая точность может оцениваться либо «по функции» (в найденной точке x, функция достаточно близка к 0, т. е. выполняется условие |f(x)|≤ ef, где ef требуемая точность по оси ординат), либо «по аргументу» (найден достаточно маленький отрезок [a,b], внутри которого находится корень, т. е. |b–a|≤ ex, где ex требуемая точность по оси абсцисс).

1.2 Отделение корней

Отделение корней может производиться сочетанием графического и аналитического исследования функции. Такое исследование опирается на теорему Вейерштрасса, в соответствии с которой для непрерывной на отрезке [a,b] функции f(х) и любого числа y, отвечающего условию f(a)≤y≤f(b), существует на этом отрезке точка x, в которой функция равна y. Следовательно, для непрерывной функции достаточно найти отрезок, на концах которого функция имеет разные знаки, и можно быть уверенным, что на этом отрезке есть корень уравнения f(х)=0.

Для ряда методов уточнения желательно, чтобы найденный на первом этапе отрезок содержал только один корень уравнения. Это условие выполняется, если функция на отрезке монотонна. Монотонность, можно проверить либо по графику функции, либо по знаку производной.

Пример Найти с точностью до целых все корни нелинейного уравнения y(x)=x3 ‑ 10x + 7=0 а) построив таблицу и б) построив график. Найти корень уравнения на выделенном отрезке, используя опции «Подбор параметра» и «Поиск решения».

Решение Создадим в Excel таблицу, содержащую аргументы и значения функции и по ней построим точечную диаграмму. На рисунке 1 приведен снимок решения.

На графике видно, что уравнение имеет три корня, принадлежащие отрезкам [-4, -3], [0, 1] и [2, 3]. Эти отрезки можно выявить и наблюдая за сменой знаков функции в таблице. По построенному графику можно сделать вывод, что на указанных отрезках функция f(x) монотонна и, следовательно, на каждом из них содержится только по одному корню.

Такой же анализ может быть выполнен и в пакете Mathcad. Для этого достаточно набрать определение функции f(x), используя оператор присваивания (:=) и естественные общепринятые обозначения математических операций и стандартных функций, задать цикл для изменения аргумента, например, а затем вывести на экран таблицу значений функции (располо­жен­ными в одной строке командами x= f(x)=) и график. Цикл можно задать, например, командой x:=-5,-4.5…5. Шаг цикла формируется путем задания начального и следующего за ним значений переменной, а перед конечным значением переменной ставится точка с запятой, которая будет визуально отображена на экране в виде многоточия.

Рисунок 1 – Таблица и график для отделения корней нелинейного уравнения

1.3 Уточнение корней стандартными средствами Excel и Mathcad

Во всех методах уточнения корней необходимо задать начальное прибли­же­ние, которое затем и будет уточняться. Если уравнение имеет несколько кор­ней, в зависимости от выбранного начального приближения будет найден один из них. При неудачно выбранном начальном приближении решение может и не быть найдено. Если в результате первого этапа расчетов уже выделен отрезок, содержа­щий единственный корень уравнения, в качестве начального приближения можно взять любую точку этого отрезка.

В Excel для уточнения значений корней можно использовать опции «Подбор параметра» и «Поиск решения». Пример оформления решения приведен на рисунках 2 и 3.

Рисунок 2 – Ввод значений для использования средств решения уравнения в Excel

Рисунок 3 – Результаты использования средств решения уравнения в Excel

В Mathcad для уточнения корней уравнения можно использовать функцию root(….) или блок решения. Пример использования функции root(…) приведен на рисунке 4, а блока решения на рисунке 5. Следует обратить внимание, что в блоке решения (после заголовка блока Given) между левой и правой частями уравнения должен стоять жирный знак равенства (тождества), который можно получить выбором из соответствующей палитры инструментов, либо нажатием одновременно клавиши Ctrl и =.

Рисунок 4 – Решение уравнения с использованием функции root(…) в Mathcad

Рисунок 5 – Решение уравнения с использованием блока решения в Mathcad

Как видим, каждый стандартный инструмент находит решение уравнения с определенной точностью. Эта точность зависит от метода, используемого в пакете и, в определенной степени, настроек пакета. Управлять точностью результата здесь достаточно сложно, а часто и невозможно.

В то же время, очень просто построить собственную таблицу или написать программу, реализующие один из методов уточнения корней. Здесь можно использовать критерии точности расчета, задаваемые пользователем. При этом достигается и понимание процесса расчетов без опоры на принцип Митрофанушки: «Извозчик есть, довезет».

Далее рассмотрены несколько наиболее распространенных методов. Отметим очевидный момент: при прочих равных условиях тот метод уточнения корней будет более эффективен, в котором результат с той же погрешностью найден с меньшим числом вычислений функции f(x) (при этом достигается и максимальная точность при одинаковом числе вычислений функции).

1.4 Метод деления отрезка пополам

В этом методе на каждом шаге отрезок делится на две равные части. Затем сравнивают знаки функции на концах каждой из двух половинок (например, по знаку произведения значений функций на концах), определяют ту из них, в которой содержится решение (знаки функции на концах должны быть разные), и. сужают отрезок, перенося в найденную точку его границу (а или b). Условием окончания служит малость отрезка, где содержится корень («точность по x»), либо близость к 0 значения функции в средине отрезка («точность по y»). Решением уравнения считают середину отрезка, найденного на последнем шаге.

Пример. Построить таблицу для уточнения корня уравнения x3 –10x+7=0 на отрезке [-4, -3] методом деления отрезка пополам. Определить сколько шагов надо сделать методом деления отрезка пополам и какая при этом достигается точность по х, для достижения точности по y, равной 0,1; 0,01; 0, 001.

Решение Для решения можно использовать табличный процессор Excel, позволяющий автоматически продолжать строки. На первом шаге заносим в таблицу значения левого и правого концов выбранного начального отрезка и вычисляем значение середины отрезка с=(a+b)/2, а затем вводим формулу для вычисления функции в точке a (f(a)) и растягиваем (копируем) её для вычисления f(c) и f(b). В последнем столбца вычисляем выражение (b—a)/2, характеризующего степень точности вычислений. Все набранные формулы можно скопировать во вторую строку таблицы.

На втором шаге нужно автоматизировать процесс поиска той половины отрезка, где содержится корень. Для этого испльзуется логическая функция ЕСЛИ (Меню: ВставкаФункцияЛогические). Для нового левого края отрезка мы проверяем истинность условия f(a)*f(c)>0, если оно верно, то мы в качестве нового значения левого конца отрезка берем число c (т. к. это условие показывает, что корня на отрезке [a, c] нет), иначе оставляем значение a. Аналогично, для нового правого края отрезка мы проверяем истинность условия f(c)*f(b)>0, если оно верно, то мы в качестве нового значения правого конца отрезка берем число c (т. к. это условие показывает, что корня на отрезке [c, b] нет), иначе оставляем значение b.

Вторую строку таблицы можно продолжить (скопировать) на необходимое число последующих строк.

Итерационный процесс завершается, когда очередное значение в последнем столбце становится меньшим, чем заданный показатель точности ex. При этом, значение середины отрезка в последнем приближении, принимается в качестве приближенного значения искомого корня нелинейного уравнения. На рисунке 6 приведен снимок решения. Для построения аналогичного процесса в Mathcad можно использовать бланк, подобный приведенному на рисунке 7. Число шагов N может варьиро­вать­ся до достижения в таблице результатов требуемой точности. При этом таблица будет автоматически удлиняться или укорачиваться.

Итак, одним из трех корней нелинейного уравнения x3 – 10x + 7=0, найденным с точностью e=0,0001, является x= — 3,46686. Как мы видим, он действительно принадлежит отрезку [-4; -3].

Рисунок 6 – Уточнение корня методом деления отрезка пополам в Excel

Рисунок 7 – Уточнение корня методом деления отрезка пополам в Mathcad

1.5 Метод хорд

В этом методе нелинейная функция f(x) на отделенном интервале [а, b] заменяется линейной – уравнением хорды, т. е. прямой соединяющей граничные точки графика на отрезке. Условие применимости метода – монотонность функции на начальном отрезке, обеспечивающая единственность корня на этом отрезке. Расчет по методу хорд аналогичен расчету методом деления отрезка пополам, но теперь на каждом шаге новая точка x внутри отрезка [a,b] рассчитывается по любой из следующих формул:

.

1.6 Метод Ньютона (касательных)

Идея, на которой основан метод, аналогична той, которая реализована в методе хорд, только на каждом шаге кривая f(x) заменяется касательной к ней, проведенной в предыдущей найденной точке. В качестве начальной точки в зависимости от свойств функции берется или левая граница отрезка, содержащего корень – x0 = а (если f(а) f»(х) > 0), или правая его граница: x0 = b (если f(b) f»(х)>0). Расчет нового приближения на следующем шаге i+1 производится по формуле:

.

Алгоритм применим для монотонных функций, сохраняющих выпуклость или вогнутость в промежутке между начальным приближением и корнем уравнения (т. е. должен сохраняться знак первой и второй производных функции f(x)). работоспособен при выпуклых и монотонных функциях f(x). В расчетах нет необходимости отслеживать две границы отрезка, поэтому достаточно на каждом шаге вычислять значения x, f(x) и f′(x). При этом легко оценить «точность по y», по значению левой части уравнения на очередном шаге. Для оценки «точности по x» нужно отслеживать разницу приближений на предыдущем и последующих шагах, которая связана с разницей между найденным приближением и точным значением корня.

Следует обратить внимание на следующую особенность метода: последовательность x1, x2, x3,… приближается к корню с другой стороны, в отличие от использования метода хорд при прочих равных условиях.

Главным достоинством метода касательных является квадратичная скорость сходимости, что во многих случаях может привести к сокращению числа вычислений функции.

Уточнить корень уравнения tg (0,55x+0,1) – x2=0 на отрезке [0.6, 0.8] методом касательных до точности 0,001.

Точность вычислений можно оценить из соотношения

2 Решение систем нелинейных уравнений

2.1 Общие сведения о решении систем нелинейных уравнений

Систему n нелинейных уравнений с n неизвестными x1, x2, . xn записывают в виде:

где F1, F2,…, Fn – функции независимых переменных, среди которых есть нелинейные.

Как и в случае систем линейных уравнений, решением системы является такой вектор X*, который при подстановке обращает одновременно все уравнения системы в тождества.

Система уравнений может не иметь решений, иметь единственное решение, конечное или бесконечное количество решений. Вопрос о количестве решений должен решаться для каждой конкретной задачи отдельно.

Численные методы решения системы уравнений носят итерационный характер и требуют задания начального приближения X0.

Рассмотрим две группы таких методов: метод Ньютона с различными его модификациями и методы итераций (простых итераций и Зейделя).

2.2 Решение систем нелинейных уравнений методом Ньютона

Будем рассматривать этот метод на примере системы двух нелинейных уравнений с двумя неизвестными:

Начальные значения x0 и y0 определяются графически. Для нахождения каждого последующего приближения (xi+1, yi+1) используют вектор значений функций и матрицу значений их первых производных, рассчитанные в предыдущей точке (xi, yi).

,

Для расчета новых приближений на шаге i+1 используется матричная формула

.

Следует обратить внимание, что в последней формуле используется вычисление матрицы, обратной к матрице первых производных.

Расчет останавливают при выполнении одного (а иногда и обоих) из двух условий. Первое из них заключается в том, что на очередном шаге максимальное по модулю из изменений аргументов x и y становится меньше заданная погрешность по аргументам. В соответствии со вторым из условий, на очередном шаге максимальное по модулю значение левых частей уравнений должно отличаться от нуля меньше, чем заданная погрешность по функциям.

В упрощенном методе Ньютона матрица производных и матрица, обратная к ней вычисляются только один раз (в начальной точке) и для расчетов используется матричная формула

.

Приведенные формулы особенно легко записать в Mathcad, где имеются операторы для вычисления производных и действий с матрицами. Однако при правильном использовании матричных операций эти формулы достаточно просто записываются и в Excel. Правда, здесь придется заранее получить формулы для вычисления производных. Для аналитического вычисления производных также может быть использован Mathcad.

2.3 Решение систем нелинейных уравнений методами итераций

Для реализации этих методов исходную систему уравнений необходимо путем алгебраических преобразований явно выразить каждую переменную через остальные. Для случая двух уравнений с двумя неизвестными новая система будет иметь вид

.

Для решения такой системы задаются начальным приближением x0, y0. Уточненные решения получают по шагам, подставляя в правые части уравнений значения, найденные на предыдущем шаге. В методе простых итераций для уточнения решения используют формулы:

.

Если одно из решений системы и начальные значения x0 и y0 лежат в области D, задаваемой неравенствами: a ≤ x ≤ b, c ≤ y ≤ d, то расчет по методу простых итераций сходится при выполнении в области D соотношений:

Метод половинного деления

Метод половинного деления

Пусть корень уравнения (1) отделен на отрезке [a;b]. Требуется найти значение корня с точностью ε.

«Процедура уточнения положения корня заключается в построении последовательности вложенных друг в друга отрезков, каждый из которых содержит корень уравнения. Для этого находится середина текущего интервала неопределенности (6):

В в качестве следующего интервала неопределенности из двух возможных выбирается тот, на концах которых функция F(x)=0имеет разные знаки»[8]. «Точность будет достигнута, если:

Корень уравнения вычисляется по формуле x=(a_n+b_n)/2 (7)«[1].

Пусть дана задача следующего характера: Уточнить корни уравнения cos(2x)+x-5=0 методом половинного деления с точностью до 0,00001, используя:

1. Mathcad;

Excel.

Для того чтобы уточнить корни уравнения cos(2x)+x-5=0 методом половинного деления, используя Excel, необходимо выполнить следующие действия:

1. Заполнить ячейки A1:H1 последовательно следующим образом: a, b, c=(a+b)/2, f(a), f(b), f(c), |b-a|<=2*e, e.

2. Ввести в ячейку A2 число 5, в ячейку B2 — число 6.

3. В ячейку B2 ввести формулу: =(A2+B2)/2.

4. В ячейку D2 ввести формулу: =cos(2*A2)+A2-5, скопировать эту формулу в ячейки E2:F2.

5. Ввести в ячейку G2 формулу: =ЕСЛИ(ABS(B2-A2)<=2*$H$2;C2;»-«).

6. Ввести в ячейку H2 число 0,00001.

7. В ячейку A3 ввести формулу: =ЕСЛИ(D2*F2<0;A2;C2).

8. В ячейку B3 ввести формулу: =ЕСЛИ(D2*F2<0;C2;B2).

9. Диапазон ячеек C2:G2 скопировать в диапазон ячеек C3:G3.

10. Выделить диапазон ячеек A3:G3 и с помощью маркера заполнения заполнить все нижестоящие ячейки до получения результата в одной из ячеек столбца G (это ячейки A3:G53).

В итоге получаем следующее:

Ответ: Корень уравнения cos(2x)+x-5=0 равен 5,32977.

1. Метод хорд

Берілген әдісті шешу үшін y=F(x) функциясын құру керек

» Для реализации данного метода, нужно построить исходную функциюy=F(x)и найти значения функции на концах отрезка F(a) и F(b). Затем провести хорду М₁M₂c концами в точкахМ₁(a, F(a)) и M₂(b, F(b)). Абсцисса точки пересечения хорды М₁M₂с осью OX это и есть приближенный кореньx₁. Далее найти точкуM₃(X₁ ,F(x₁ )), построить следующую хорду и найти второй приближенный корень x₂. И так далее. В зависимости от поведения функции возможны два случая:

Для первого случая (Рис. 1) справедлива следующая формула (8):

и справедливо неравенство: F(a)*F»(a)>0, где x=b.

Для второго случая (Рис. 2) справедлива следующая формула (9):

и справедливо неравенство: F(b)*F»(b)>0, где x=a.

Условия сходимости метода секущих аналогичны условиям сходимости метода Ньютона, т. е.»[1]

Пусть дана задача: Уточнить корни уравнения cos(2x)+x-5=0 методом хорд с точностью до 0,00001, используя:

1. Mathcad;

Excel.

Для того чтобы уточнить корни уравнения cos(2x)+x-5=0 методом хорд, используя Excel, необходимо выполнить следующие действия:

1. Выбрать одну из двух предложенных формул для решения задачи, для этого:

o Найти производную первого порядка от функции f(x)=cos(2x)+x-5. Она будет выглядеть следующим образом: f1(x)=-2sin(2x)+1.

o Найти производную второго порядка от функции f(x)=cos(2x)+x-5. Она будет выглядеть следующим образом: f2(x)=-4cos(2x).

o Заполнить ячейки следующим образом:

— В ячейку A1 ввести a.

— В ячейку A2 ввести цифру 5.

— В ячейку B1 ввести b.

— В ячейку B2 ввести цифру 6.

— В ячейку C1 ввести f(x)=cos(2x)+x-5.

— В ячейку C2 ввести формулу =COS(2*A2)+A2-5.

— В ячейку D1 ввести f1(x)=-2sin(2x)+1.

— В ячейку E1 ввести f2(x)=-4cos(2x).

— В ячейку E2 ввести формулу =-4*COS(2*A2).

— В ячейку F1 ввести Выбор формулы.

— В ячейку F2 ввести формулу =ЕСЛИ(C2*E2>0;»Воспользоваться формулой 8″;»Воспользоваться формулой 9″).

— В ячейку G1 ввести e.

— В ячейку G2 ввести цифру 0,00001.

o В итоге получается следующее:

2. Исходя из того, что выбрана формула 9, в Excel необходимо выполнить следующие действия:

o В ячейку A4 ввести xn.

o В ячейку B4 ввести f(xn).

o В ячейку C4 ввести b-xn.

o В ячейку D4 ввести f(xn)*(b-xn).

o В ячейку E4 ввести f(b).

o В ячейку F4 ввести f(b)-f(xn).

o В ячейку G4 ввести xn-f(xn)*(b-xn)/f(b)-f(xn).

o В ячейку H4 ввести |f(xn)|<=e.

o В ячейку A5 ввести цифру 5.

o В ячейку B5 ввести формулу =COS(2*A5)+A5-5.

o В ячейку C5 ввести формулу =$B$2-A5.

o В ячейку D5 ввести формулу =B5*C5.

o В ячейку E5 ввести формулу =COS(2*$B$2)+$B$2-5.

o В ячейку F5 ввести формулу =$E$5-B5.

o В ячейку G5 ввести формулу =A5-(B5*C5/F5).

o В ячейку H5 ввести формулу =ЕСЛИ(ABS(B5)<=$G$2;A5;»-«).

o В ячейку A6 ввести формулу =G5.

o Выделить диапазон ячеек B5:D5 и скопировать его методом протягивания в диапазон ячеек B6:D6.

o Выделить диапазон ячеек F5:H5 и скопировать его методом протягивания в диапазон ячеек F6:H6.

o Выделить диапазон ячеек A6:H6 и скопировать его методом протягивания в диапазон ячеек ниже до получения результата в одной из ячеек столбца H (A6:H9).

В итоге получаем следующее:

Ответ: Корень уравнения cos(2x)+x-5=0 равен 5,32976.

studopedia.org — Студопедия.Орг — 2014-2021 год. Студопедия не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования (0.004 с) .

Постановка задачи

Дано нелинейное алгебраическое уравнение

f(x)=0 (1)

Нелинейность уравнения означает, что график функции не есть прямая линия, т.е. в f(x) входит x в некоторой степени или под знаком функции.

Решить уравнение – это найти такое x* ∈ R: f(x*)=0. Значение x* называют корнем уравнения. Нелинейное уравнение может иметь несколько корней. Геометрическая интерпретация корней уравнения представлена на рис. 1. Корнями уравнения (1) являются точки x₁*, x₂*, x₃*, в которых функция f(x) пересекает ось x.

Методы решения нелинейного уравнения (1) можно разделить на точные (аналитические) и приближенные (итерационные). В точных методах корень представляется некоторой алгебраической формулой. Например, решение квадратных уравнений, некоторых тригонометрических уравнений и т. д.

В приближенных методах процесс нахождения решения, вообще говоря, бесконечен. Решение получается в виде бесконечной последовательности <x_n>, такой, что . По определению предела, для любого (сколь угодно малого) ε, найдется такое N, что при n>N, |x_n – x*|< ε. Члены этой последовательности x_n называются последовательными приближениями к решению, или итерациями. Наперёд заданное число ε называют точностью метода, а N – это количество итераций, которое необходимо выполнить, чтобы получить решение с точностью ε.

Существует различные методы нахождения приближенного решения, т.е. способы построения последовательности итераций <x_n>, однако все они имеют общие этапы, изображенные на рисунке.

Наиболее часто используется следующий критерий остановки итерационного процесса: |x_n+1–x_n|<ε, т.е. разница между соседними итерациями становится малой. Также для окончания итерационного процесса используется условие |f(x_n)|<ε , где f(x_n) – невязка метода.

Прежде чем использовать приближенный метод, уравнение надо исследовать его на наличие корней и уточнить, где эти корни находятся, т.е. найти интервалы изоляции корней. Интервалом изоляции корня называется отрезок, на котором корень уравнения существует и единственен.

Необходимое условие существования корня уравнения на отрезке [a,b]: Пусть f(x) непрерывна и f(a)f(b)<0 (т.е., на концах интервала функция имеет разные знаки). Тогда внутри отрезка [a, b] существует хотя бы один корень уравнения f(x)=0.

Достаточное условие единственности корня на отрезке [a,b]:

Корень будет единственным, если f(a)f(b)<0 и f / (x) не меняет знак на отрезке [a, b], т.е. f(x) – монотонная функция, в этом случае отрезок [a,b] будет интервалом изоляции.

Если корней несколько, то для каждого нужно найти интервал изоляции.

Существуют различные способы исследования функции: аналитический, табличный, графический.

Аналитический способ состоит в нахождении экстремумов функции f(x), исследование ее поведения при и нахождение участков возрастания и убывания функции.

Графический способ – это построение графика функции f(x) и определение числа корней по количеству пересечений графика с осью x.

Табличный способ – это построение таблицы, состоящей из столбца аргумента x и столбца значений функции f(x). О наличии корней свидетельствуют перемены знака функции. Чтобы не произошла потеря корней, шаг изменения аргумента должен быть достаточно мелким, а интервал изменения достаточно широким.

Решить уравнение x 3 ‑ 6x 2 +3x+11=0, т.е. f(x)= x 3 ‑ 6x 2 +3x+11.

Найдем производную f / (x)=3x 2 -12x+3.

Найдем нули производной f / (x)=3x 2 -12x+3=0; D=144-4*3*3=108;

Так как f / ( )>0, то f / (x)>0 при , f / (x)<0 при и f / (x)>0 при . Кроме того, f( )= <0, f( )= >0. Следовательно, на интервале возрастает от до f(x₁)= 3x₁ 2 -12x₁+3=11.39; на интервале — убывает до f(x₂)= 3x₂ 2 -12x₂+3=-9.39 и на интервале возрастает до , т.е. уравнение имеет три корня.

Найдем интервалы изоляции для каждого из корней.

Рассмотрим для первого корня отрезок [-2, -1]:

f(-2)= -27<0, f(-1)= 1>0, f / (x)>0 при т.е. этот отрезок является интервалом изоляции корня.

Рассмотрим для второго корня отрезок [1, 3]:

f(1)= 9>0, f(3)= -7<0, f / (x)<0 при т.е. этот отрезок является интервалом изоляции корня.

Рассмотрим для третьего корня отрезок [4, 5]:

f(4)= -9<0, f(5)=1>0, f / (x)>0 при т.е. этот отрезок является интервалом изоляции корня.

Трансцендентные уравнения? «Подбор параметра» в Excel!

Нелинейные, трансцендентные уравнения функции одной переменной – это уравнения вида f (x) = 0, в которых нельзя найти алгебраическими методами корни. Функция f (x) – это, как правило, достаточно сложная и громоздкая функция, содержащая в своем составе.

. тригонометрические, логарифмические, степенные и иные нелинейные функции с различной глубиной вложенности. Например: f (x) = sin (3,14^x) + cos (x) = 0. Уравнения такого вида решаются численными методами.

В этой статье я постараюсь доступно и кратко рассказать и показать на примерах, как и когда такие задачи возникают и как их сегодня быстро и просто можно решать в Excel.

Чуть-чуть истории и теории.

Вы задумывались когда-нибудь — откуда и зачем в головах людей, живших в XVI…XVII веках, родились понятия дифференциалов, производных, интегралов? Объяснение, в общем-то, достаточно простое и понятное – эти ученые искали аналитические пути решения прикладных практических задач. И успешно находили.

Мне сегодня видится приблизительно такая «лестница» с качественными «ступенями инструментов» математики для решения практических и научных задач, которую изобрело человечество:

1. Арифметика — сложение, вычитание, умножение, деление.

2. Алгебра – применение элементарных функций (степенной, логарифмической, тригонометрической, …) и алгебраических уравнений функции одной переменной.

3. Гауссовские системы линейных уравнений.

4. Численные методы решения трансцендентных уравнений.

5. Численные методы решения систем трансцендентных уравнений функций нескольких переменных.

6. Дифференцирование и интегрирование функций одной переменной.

7. Дифференцирование и интегрирование функций нескольких переменных.

8. Системы дифференциальных и интегральных уравнений.

9. Масса разнообразных новых и старых специальных методик и подходов мне не известных и известных, но, безусловно, существующих и работающих.

Предлагаю остановиться и разобраться с достаточно высокой четвертой ступенью «лестницы».

Для численного решения нелинейных уравнений успешно применяются: метод половинного деления, метод простых итераций, метод хорд, метод касательных Ньютона, комбинированный метод секущих-хорд на основе итерационной формулы Ньютона. Для чего ученые-математики придумали множество различных методов решения трансцендентных уравнений? Они старались упростить и ускорить процесс расчетов. Надо помнить и понимать, что у них компьютеров не было, и расчеты выполнялись вручную.

Каждый из методов имеет свои достоинства и недостатки — они подробно описаны в литературе, и углубляться в них мы не будем. Скажу только, что из вышеперечисленных методов мне на практике довелось использовать все. При решении различных (в основном геометрических и теплотехнических) задач по разным причинам было удобно использовать то один, то другой подход. Метод Ньютона хорош своей быстрой сходимостью и простотой формулы. Комбинированный метод секущих-хорд на основе итерационной формулы Ньютона не требует нахождения производных, быстро «сходится», и главное – не требует анализа функции на сходимость. Метод половинного деления медленно сходится, но не требует никакого предварительного анализа функции.

Трансцендентные уравнения. Два метода решения в Excel.

Если у вас на компьютере нет программы MS Excel, то расчеты можно выполнить в программе OOo Calc из бесплатного пакета Open Office.

Задач, которые требуют для получения ответа составления и решения трансцендентных уравнений, вокруг нас очень много. Это — задачи и физики, и теплотехники, и астрономии, и элементарной геометрии в обычной жизни… Инженерам-конструкторам и программистам в повседневной работе необходимо уметь составлять и быстро решать численными методами нелинейные уравнения. На мой взгляд — это один из критериев профессионализма. Более того, уравнения, которые решаются аналитически, сегодня иногда гораздо проще и быстрее при наличии вычислительной техники решить численными методами, поэтому нужно уметь это делать.

Вычисление угла зацепления зубчатой передачи методом Ньютона (методом касательных)

Рассмотрим пример из статьи «Расчет геометрии зубчатой передачи». Необходимо найти угол зацепления зубчатой передачи atw . Я обещал в той статье рассказать, как это делается. Выполняю обещание.

Если расстояние между центрами колеса и шестерни не задано, то угол зацепления можно вычислить путем решения трансцендентного уравнения:

inv ( atw )=tg ( atw ) — atw =2* xs *tg ( a )/( z2 + T * z1 )+ tg ( at ) — at

Подставив данные из примера, рассмотренного в вышеупомянутой статье, получим после преобразований следующее уравнение:

inv ( atw )=0,020910

f ( atw )=tg ( atw )— atw -0,020910=0

Используем метод Ньютона, потому что взять производную представленной выше функции элементарно просто, а итерационная формула очень проста и компактна:

f’( atw )=1/(cos ( atw ))^2—1

atw (i+1) = atw i — f ( atw ) i/ f’( atw ) i

Открываем файл Excel и начинаем работу.

Исходные данные будем традиционно писать в ячейки со светло-бирюзовой заливкой. Результаты расчетов будем считывать в ячейках со светло-желтой заливкой.

1. Инволюту угла зацепления inv( atw ) заносим

в ячейку D3: 0,020910

2. Значение угла зацепления в нулевом приближении atw в радианах записываем

3. Итерационную формулу atw (i+1)= atw i— f( atw )i/ f’( atw )i заносим

в D5: =D4- (TAN (D4) -D4-$D$3)/(1/(COS (D4))^2-1) =0,591706

atw 1= atw 0- (tg ( atw 0) — atw 0- inv ( atw ))/(1/(cos ( atw 0))^2-1)

и копируем в ячейки D6… D14

4. Видим, что уже после шестой итерации угол зацепления atw в радианах вычислен с нулевой абсолютной и относительной ошибкой:

atw =D13- (TAN (D13) -D13-$D$3)/(1/(COS (D13))^2-1) =0,389140

Решение найдено, расчет в Excel завершен!

Решение задачи ландшафтного дизайна с помощью сервиса «Подбор параметра» в Excel

Задача:

Вдоль отмостки стены дома длиной 14 метров необходимо разбить цветник в виде сегмента круга площадью ровно 16 квадратных метров. На сколько метров цветник будет отстоять от края отмостки по центру стены? Каким радиусом необходимо выполнить границу цветника?

1. Длину отмостки стены дома — хорды сегмента круга x в метрах записываем

в ячейку D17: 14,000

2. Площадь цветника – сегмента круга S в квадратных метрах вписываем

в D18: 16,000

3. Предположительное произвольное (не нулевое) значение центрального угла сегмента a в радианах пишем

в D19: 1,000

Трансцендентное уравнение a / sin( a /2 ) -2*cos ( a /2) — (8* S / x ^2) *sin( a /2)=0 вводим

в объединенную ячейку E19F19: =D19/SIN (D19/2) -2*COS (D19/2) — (8*D18/D17^2)*SIN (D19/2)

Включаем сервис «Подбор параметра» в Excel: «Сервис» – «Подбор параметра». Пишем в появившемся окне все как на рисунке слева и нажимаем кнопку OK.

В появившемся новом окне видим, что решение найдено, снова нажимаем на кнопку OK.

Считываем искомое значение центрального угла сегмента a в радианах

в D19: 0,950057

При этом видим, что значение трансцендентного уравнения равно нулю; считываем

в объединенной ячейке E19F19: =D19/SIN (D19/2) -2*COS (D19/2) — (8*D18/D17^2)*SIN (D19/2) =0

4. Радиус наружной границы цветника – радиус сегмента круга r в метрах рассчитывается

в D20: =D17/2/SIN (D19/2) =15,305

r = x /2/sin( a /2)

5. Максимальная ширина цветника – высота сегмента круга h в метрах рассчитывается

в ячейке D21: =D20*(1-COS (D19/2)) =1.695

h = r *(1- cos( a /2))

Ответы получены, вторая задача успешно решена!

Я не приводил вывода использованных формул потому, что это не по теме поста, и, думаю, с геометрией и тригонометрией вы легко разберетесь. Будут вопросы – обращайтесь.

Чтобы получать информацию о выходе новых статей вам нужно подписаться на анонсы в окне, расположенном вверху страницы. Введите адрес своей электронной почты и нажмите на кнопку «Получать анонсы статей». С этого момента к вам на почтовый ящик будет приходить небольшое уведомление о появлении на моем блоге новой статьи.

Краткие выводы

1. Итерационными численными методами удобно и быстро можно решать трансцендентные уравнения и громоздкие нелинейные алгебраические.

2. При написании расчетных модулей программ в Excel, если нежелательны лишние остановки по ходу вычислений, можно использовать вставки блоков с классическими методами решения нелинейных уравнений или макросов с вызовом инструмента «Подбор параметра».

3. Использование инструмента «Подбор параметра» в Excel является сегодня, безусловно, наиболее оптимальным и эффективным методом решения нелинейных, трансцендентных уравнений функций одной переменной, а также проведения анализа типа «Что будет? Если…».

Умение применять в работе сервис «Подбор параметра» существенно повышает ваш уровень, как специалиста вообще, так и как пользователя Excel – в частности.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ — Тема: Решение алгебраических и трансцендентных уравнений методом половинного деления и методом итераций.

Решение алгебраических и трансцендентных уравнений методом половинного деления и методом итераций.

Цель работы:

— применить умения отделять корни алгебраических уравнений;

— применить умения решать алгебраические уравнений приближенными методами (метод половинного деления, метод хорд, метод касательных);

Оборудование:

1. Рабочая тетрадь в клетку.

2. Раздаточный материал: инструкционные карты-20шт.

3. Калькулятор простой.

1. Методом половинного деления с точностью 0,01 найдите приближенное значение наибольшего действительного корня следующего алгебраического уравнения

1. Методом итераций решить уравнение с точностью до 0,001

1. Методом половинного деления с точностью 0,01 найдите приближенное значение наибольшего действительного корня следующего алгебраического уравнения

2. Методом итераций решить с точностью до 0,001 уравнение.

Порядок выполнения:

1. Внимательно прочитать тему и цель практической работы .

2. Изучить учебный материал по теме.

3. Ответить на вопросы.

4. Выполнить задания.

5. Подготовить отчет.

Пояснения к работе (учебный материал):

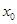
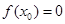
Число из области определения функции называется корнем уравнения , если .

Процесс нахождения корней уравнения распадается на несколько этапов:

1) определяются границы интервала, в котором находятся все корни уравнения ;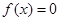

2) устанавливаются возможно малые промежутки, в каждом из которых содержатся ровно один корень.

3) каждый из корней вычисляется с заданной точностью.

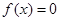
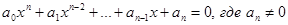
К сожалению, определение в общем виде границ интервала, в котором находятся все корни уравнения , можно дать только для алгебраического уравнения в каноническом виде, т.е. для уравнения вида:

(1)

В дальнейшем будем находить действительные корни алгебраических уравнений.

Теорема 1 (основная теорема алгебры).

Уравнения вида (1) имеет ровно n корней, действительных или комплексных, если корень кратности k считать за k корней.

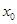
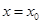
Число называется корнем кратности k уравнения (1), если при обращается в нуль сама функция и ее производные до ( k -1 )-го порядка включительно, т.е.

Корень кратности 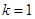называется простым.

1) Число действительных корней уравнения (1) четной степени с действительными коэффициентами всегда четно (в том числе и может равняться нулю).

Если кроме этого 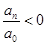, то уравнение четной степени имеет, по крайней мере, два действительных корня разного знака.

2) Уравнение (1) нечетной степени имеет по крайней мере один действительный корень того же знака, что и « ».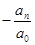

Теорема 3 (теорема Декарта).

Число положительных корней уравнения (1) равно или на четное число меньше числа перемен знака в ряду коэффициентов 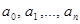уравнения. Так как при замене «х» на «-у» корни уравнения (1) меняют знаки, то с помощью этой теоремы можно оценить и число отрицательных корней.

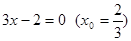
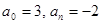
1. В уравнении нечетной степени коэффициенты и

Кроме этого, число перемен знаков равно 1.

Следовательно, по теоремам 2 и 3, оно имеет один действительный положительный корень.

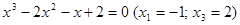
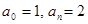
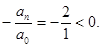
2. В уравнении нечетной степени коэффициенты и Следовательно по теореме 2, оно имеет по крайней мере один действительный отрицательный корень.

Число перемен знаков в данном уравнении равно двум, следовательно, по теореме 3, оно имеет либо два, либо 0 положительных действительных корней.

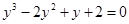
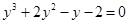
Оценим число действительных отрицательных корней. Для этого заменим «х» на «-у». Получим уравнение, или , или . Число перемен знаков в этом уравнении равно 1, следовательно, исходное уравнение имеет один действительный отрицательный корень.

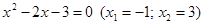
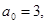
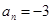
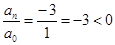
3. В уравнении четной степени коэффициенты и . Следовательно, по теореме 2, оно имеет два действительных корня разного знака.

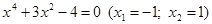
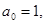
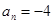
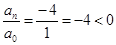
4. В уравнении четной степени коэффициенты и . Следовательно, по теореме 2, оно имеет по крайней мере два действительных корня разного знака.

Число перемен знаков в данном уравнении равно 1, следовательно, по теореме 3, оно имеет один положительный действительный корень.

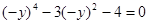
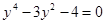
Оценим число действительных отрицательных корней. Для этого заменим «х» на «-у». Получим уравнение или . Число перемен знаков в этом уравнении равно 1, следовательно, исходное уравнение имеет один действительный корень.

Дадим теперь формулировку теоремы, позволяющей достаточно грубо определять границы интервала, в котором находятся все действительные корни уравнения (1).

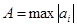
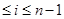
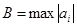
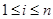
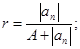
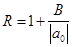
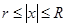
1) Если , где 0 ; , где , и , то .

2) Все положительные действительные корни уравнения находятся в промежутке , а все отрицательные действительные корни уравнения (1) находятся в промежутке .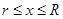

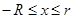
Если непрерывная и дифференцируемая функции , определяющая алгебраическое уравнение , на концах отрезка принимает значения разных знаков, т.е. , и ее первая производная сохраняет знак внутри этого отрезка, но на находится ровно один действительный корень данного уравнения.

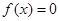
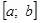
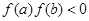
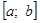
Замечание. Для алгебраических уравнений (1), степень которых больше трех, трудно аналитически находить интервалы знакопостоянства функции . Поэтому для нахождения возможно малых промежутков, содержащих ровно один действительный корень можно на практике использовать следующие способы:

1) средствами машинной графики функция />представляется на дисплее и приближенно определяются возможно малые промежутки, содержащие ровно один корень (т.е. промежутки содержащие одну точку пересечения графика функции />с осью Ох);

2) если график функции построить трудно, то формируют простые функции и , такие, что уравнение преобразуется в виде = . Затем строятся графики функций у= и y = и приближенно определяются промежутки, содержащие абсциссы точек пересечения этих графиков.

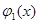
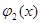
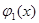
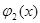
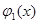
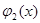
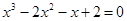
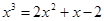
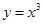
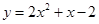
Так, например, уравнение можно преобразовать к виду и затем построить графики функции и .

Начиная третий этап, дадим формулировку теоремы, позволяющей оценивать погрешность приближенного решения.

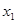
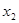
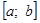
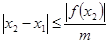
Если точный, а — приближенный, корни уравнения (1), принадлежащие одному и тому же промежутку , то справедливая оценка: , где m – наименьшее значение модуля производной функции на промежутке .

Графически решить уравнение x ln ( x )=1 .

Решение. Запишем исходное уравнение в виде: , т.е. и . Таким образом, корни данного уравнения могут быть найдены как абсциссы точек пересечения кривых и .

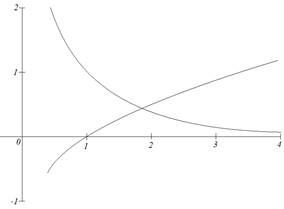
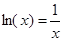
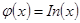
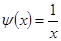
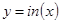
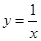
Теперь построим графики функций и определим интервал изоляции корня.

Аналитически отделить корни данного алгебраического уравнения, используя теорему Штурма:

,

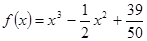
Построим таблицу для подсчета смены знаков:

—

ЛАБОРАТОРНАЯ РАБОТА «МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ (ДИХОТОМИИ)»

1 ЛАБОРАТОРНАЯ РАБОТА «МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ (ДИХОТОМИИ)» Морарь А.А. Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Южно-Российский государственный политехнический университет (Новочеркасский политехнический институт) имени М.И. Платова Новочеркасск, Россия LABORATORY WORK «METHOD HALF DIVISION (DICHOTOMY)» Morar A. A. Federal State Budget Educational Institution of Higher Professional University «Platov South-Russian State Polytechnic University (NPI)» Novocherkassk, Russia Цель работы: овладеть практическими навыками численного нахождения локального минимума функции одной переменной на заданном отрезке в среде электронных таблиц Microsoft Excel, пакета Mathcad и среде программирования Pascal-АВС. Теоретическая часть Экстремум максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум, точка экстремума называется точкой минимума, а если максимум точкой максимума. Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума локальным минимумом данной функции. Максимум и минимум функции называются её локальными экстремумами.

2 Термин «локальный экстремум» обусловлен тем, что введённое понятие экстремума связано с окрестностью данной точки в области определения функции, а не со всей этой областью. Функция может иметь несколько экстремумов, причём минимум в одной точке может быть больше максимума в другой. Определение. Точка x 0 называется точкой локального минимума функции f(x), если существует такая окрестность точки x 0, что для всех x из этой окрестности f(x) f(x 0 ). Суть нахождение локального минимума методом половинного деления состоит в уменьшении длины отрезка [a ; b] таким образом, что минимум остается всегда внутри отрезка. Процесс продолжается до тех пор, пока длина отрезка не станет меньше заданной точности нахождения экстремума ε. Уменьшение длины отрезка производится выбором двух точек x 1 и x 2, расположенных симметрично относительно середины отрезка, т.е. точки = + Абсциссы этих точек находятся по формулам: = 2 ; = + 2 где δ величина различимости точек, при этом δ < ε. При этом возможны три случая, приводящие к сужению длины отрезка: 1) f(x 1 ) > f(x 2 ) В этом случае в промежутке [a ; x 1 ] функция монотонно убывает, значит минимума нет. Поэтому новый уменьшенный отрезок на котором расположен экстремум, это [x 1 ; b]. Для получения отрезка [a ; b] меньшей длины переносим точку a в точку x 1, полагая a:= x 1 a x 1 x 2 b

3 2) f(x 1 ) < f(x 2 ) В этом случае в промежутке [x 2 ; b] функция возрастает, значит минимума нет. Поэтому новый уменьшенный отрезок на котором расположен экстремум, это [a ; x 2 ]. Для получения отрезка [a ; b] меньшей длины переносим точку a в точку x 1, полагая b:= x 2 a x 1 x 2 b 3) f(x 1 ) = f(x 2 ) В этом случае истинный экстремум находится на интервале [x 1 ; x 2 ]. В этом случае получаем новый уменьшенный отрезок [a ; b], полагая a:= x 1, b:= x 2. a x x2 b Получив новый отрезок [a ; b] меньшей длины повторяем алгоритм заново, до тех пор пока b — a ε. В этом случае выполняя последнее деление пополам полагая =. После чего находим значение y min = f(x min ).

4 Блок-схема алгоритма метода дихотомии имеет вид: Начало a, b, eps del : = 0.01*eps b-a < eps Да = + 2 ; 1:= 2 ; 2 = + ; 2 xmin :=(a+b)/2 xmin, fmin Да Конец f(x1) f(x2) Да a := x1 ; f(x1)<f(x2) b := x2 a := x1 b:= x2 Выполнение задания Найти минимум функции = + + на интервале [-1 ; 2]. 1. Реализация в среде MS Excel 1.1 Надстройка «Поиск решения» Найдем минимум функции с помощью надстройки «Поиск решения». Для этого создадим таблицу со значениями x и f(x), и по ним построим график функции, а так же построим еще одну таблицу для определения x min и f min, в ячейку для результата минимального значения функции заносим формулу нашей функции.

5 Набираем команду Данные Поиск решения. В появившемся диалоговом окне Поиск решения необходимо выполнить необходимые установки, указанные ниже. 1.2 Метод половинного деления Решим данную задачу, используя алгоритм, указанный ранее. Формулы, в MS Excel для данного способа, представлены на следующей странице.

7 В итоге имеем следующие результаты вычислений. 2. Реализация в Pascal-ABC Паскаль-программа и результаты вычислений имеют вид:

8 Модернизируем данную программу, так чтобы она подсчитывала количество разбиений, выполняемых для достижения заданной точности. Из полученных данных заполним таблицу для трех разных значений ε. Таблица количества разбиений в зависимости от точности ε: п/п ε K Как мы видим, с увеличением заданной точности увеличивается количество разбиений, что вполне логично.

9 3. Реализация в математическом пакете MathCad Осуществим метод половинного деления в среде MathCad с применением программирования: Так же, в MathCad можно использовать более простой метод нахождения минимума функции, а именно минимизацию функции с помощью Minimize.

10 Вывод: в ходе лабораторной работы были изучены различные средства нахождения минимума функции методом половинного деления (дихотомии), который является довольно простым и легко реализуемым.