31
Различают задачи
безусловной оптимизации и условной.
Задача безусловной минимизации –
различают методы:
-
Метод
прямого поиска -
Градиентный
метод 1-го порядка. -
Градиентный
метод 2-го порядка.
Методы прямого поиска
относятся к ГМ нулевого порядка. К ним
относятся поиск по симплексу, метод
поиска Хука-Дживса, метод Пауэла. К ГМ
1-го порядка относится метод Коши, метод
Флетчера-Ривза. К ГМ 2-го порядка относятся
методы Ньютона, Марквардта, Девидона
Флетчера-Пауэла.
Методы прямого
поиска
Метод поиска
в узлах решётки.
Метод эволюционной
оптимизации(Метод Бокса).
-
Выбор х (0)
– начальная точка -
построение
квадрата (сторона задается самостоятельно) -
Вычисление
-
Точка с
минимальным значением функции начинает
выполнять роль точки х (0) – центр
квадрата. На рис. 2 точка х (0) на
каждой итерации выбирается в качестве
начальной, уменьшается в заданное
количество раз величина стороны квадрата.
На рис. 1 точка х (3) стала центром
нового квадрата. В большинстве случаев
встречается комбинация рис. 1 и рис. 2
Метод симплекса.
Если в методе Бокса в
качестве образца выбран квадрат, то в
этом методе – правильный треугольник.
В методе
строится правильный треугольник с
вершинами х (0), х (1), х (2).
Вычисляется значение функции, после
чего отбрасывается вершина с максимальным
значением функции. В нашем примере х
(0) . Относительно отбрасываемой
точки строится её зеркальное отражение
точка х (3), которое находится на
прямой, проходящей через отбрасываемую
точку и середину противоположного
отрезка. (центр тяжести прямой х (1),
х (2)) В полученном треугольнике х
(1) , х (2) , х (3) вычисляем
значение функции только в одной точке
х (3), после чего сравниваем значение
в точках х (1) х (2) х (3).
На каком то этапе может произойти
зацикливание, т.е. в новой точке значение
функции оказывается больше, чем в
предыдущих точках. Для устранения
зацикливания выбирается точка с
наименьшим значением функции и
относительно её строится треугольник
с меньшей длинной стороны.
Метод поиска
Хука-Дживса
2
основные части:
-
Исследующий
поиск -
Поиск по
образцу
Исследующий
поиск. Производится вдоль координатных
осей заранее заданным приращением по
каждой координате. Возможны случаи
успешного и не успешного поиска. В случае
успешного поиска по данной координате
заканчивается и начинается поиск по
другой координате.
Пример:
УСПЕХ.
Поиск по образцу:
Исследующий поиск:
Останавливаемся на точке
Поиск по образу
Можно показать, что найденная точка
соответствует точке минимума. Но есть
—
коэффициент приращения.
Метод сопряженных
направлений Пауэла.
П
ример:
Все методы оптимизации заключаются:
Найдем следующую точку: двигаемся в
другом направлении
Изменение направления поиска:
Нормируем новое направление:
Положим
конец поиска
Градиентные
методы.
Метод Каши.
—
длина шага
Формула (2)
используется в методе Каши. Поиск ведётся
в направлении обратном градиенту.
Значением
определится путём решения задачи
минимизации. Метод устойчивости
используется в качестве начальной
процедуры. При реализации градиентных
методов, т.к. позволяет существенно
уменьшить значение целевой функции
при движении из точки, расположенной
на значительном расстоянии от точки
минимума.
Пример:
Поиск окончен.
Метод
Фледчера-Ривса
При k=0
метод вырождается в метод Коши(начальную
процедуру). Рассмотрим пример:
Метод Ньютона.
Модифицированный
метод Ньютона.
Метод Марквардта.
В этом методе
Маркварда уменьшается величина показателя
,
котоорый первоначально принимается
достаточно большой().
Решение задач
условной оптимизации.
Метод понижения
размерности.
Используется
при m<n.
Использование метода затр-но случае:
-
большого
значения m -
невозможности
аналитического разрешения управления
для целевой функции относительно
независимой переменной
Пример 1.
Пример 2.
Метод множителей
Лагранжа
считая переменную
V известной находим минимум
функции
для
этого определяем
-частные производные. Решаем полученную
систему уравнений и определяем
Строим матрицу
Гессе:
Для того чтобы
найд. точка
была точкой минимума необходимо, чтобы
матрица Гессе была положительно
определённой, т.е.
Пример 1.
Пример 2.
Пример 3.
Пример 4.
Пример 5
Если матрица
Гессе положительно определена, то
определяем значение ().
Подставляем в уравнение для ограничений
значение
и решаем полученное уравнение с учётом
условия положительной определённости
матрицы Гессе. Вычисляем окончательное
значение
путём подстановки выбранного значения
переменной
.
Задача:
найдём частные
производные:
Второй способ
решения задачи.
Состоит в
том, что в сумме уравнений
добавляется
уравнение для ограничения
.
В результате решения системы уравнений
определяется значение
.
Составляем матрицу Гессе в случае, если
она положительно определена, то нашли
точку минимума.
Случай нескольких
ограничений равенств.
-два значения,
которые надо исследовать
Вариант 1.
Вариант не
подходит.
Вариант 2.
Методы оптимизации
на основе преобразования задачи.
Квадратичный
штраф.
На практике задаётся начальные значения
параметра R, а за тем
изменяют его так, чтобы получить наилучшее
приближение к ограничениям.
|
R |
1/R |
|
|
h (x) |
h (x) |
|
|
0 |
4,00 |
0 |
0 |
3 |
|
10 |
0,1 |
3,75 |
0,75 |
0,125 |
2,5 |
|
1 |
1 |
3,00 |
3 |
2 |
1 |
|
0,1 |
10 |
2,5714 |
4,2857 |
4 |
0,14 |
|
0,01 |
100 |
2,5075 |
4,4776 |
4,49 |
0,05 |
|
10 |
|
2,5000 |
4,500 |
4,5 |
0 |
Основные типы
штрафных функций в случае ограничений
неравенств.
Штраф типа
квадрата срезки.
Пример.
Логарифмический
штраф.
Пример:
Значение
отбрасывается т.к. соответствует
недопустимой точке.
Штраф, выдаваемый
обратной функцией.
|
R |
|
|
|
|
|
|
100 |
0,59 |
23,3 |
3,83 |
26,13 |
49,43 |
|
10 |
1,75 |
10,1 |
1,49 |
6,70 |
16,79 |
|
1 |
2,23 |
6,2 |
0,53 |
1,88 |
8,12 |
|
0,1 |
2,41 |
5,0 |
0,18 |
0,56 |
5,61 |
|
0,01 |
2,47 |
4,7 |
0,06 |
0,17 |
4,85 |
|
0,001 |
2,49 |
4,6 |
0,02 |
0,05 |
4,61 |
|
0 |
2,50 |
4,5 |
0,00 |
0,00 |
4,50 |
Метод исключения
переменных при наличии нескольких
ограничений.
Метод комплекса
(Бокс 1965)
В качестве модификации
метода поиска по симплексу.
Наличие
ограничений в задачах условий оптимизаций
приводит к недопустимости отдельных
точек симплекса. Их уточняют, передвигая
вдоль прямой по направлению к центру
тяжести. Для построения симплекса
берётся начальная точка, остальные
строятся случайным образом. Для каждой
переменной определяются нижняя и верхняя
границы, генерируются псевдослучайные
числа, равномерно распределяемые на
отрезке [0,1], после чего рассматриваются
координаты точек.
—
нижняя и верхняя граница,
—
псевдослучайное число.
Для получения
точки в n-мерном пространстве
требуется n случайных
чисел. Каждая точка проверяется на
допустимость. Если ограничение нарушено
то точку двигают к центру тяжести уже
построенных точек до тех пор, пока она
не станет допустимой. Общее число точек
должно быть не менее n+1.
После построения множества точек в
каждой из них вычисляется целевая
функция. Отбрасывается точка с наибольшим
значением функции. Новая точка получается
путём отражения отбрасываемой точки
через центр тяжести остальных точек.
Возможны
случаи
-
Новая
точка допустимая, но не мах. Операция
отражения выполняется для мах точки. -
Новая
точка — допустимое и мах значение. Вместо
отражения новую точку передвигают на
половину расстояния до центра тяжести
(чтобы исключить зацикливание) -
Новая
точка не допустимая. Уменьшаем в два
раза состояние до центра тяжести.
Процедура поиска продолжается пока
многогранник не будет стянут в центре
тяжести в пределах заданной точности
и (или) пока разница между значениями
целевой функции в вершинах не станет
достаточно малой.
Бокс рекомендует
значения:
Выбор
компенсирует
сжатие комплекса. А большее число вершин
предотвращает (уплощение) и вырождение
комплекса при поиске вблизи границы
допустимой области.
Пусть
Так как
не удовлетворяет ограничению
,
поэтому определяется центр тяжести для
точек
и
.
Вновь используется
генератор случайных чисел.
Имея четыре
дополнительных точки, вычисляем для
них значение целевой функции.
|
№ точки |
X1 |
X2 |
F(X) |
Замена точки |
|
1 |
1,00 |
1,00 |
18,00 |
|
|
2 |
1,15 |
2,50 |
10,37 |
|
|
3 |
-1,20 |
2,00 |
31,04 |
|
|
4 |
0,60 |
3,00 |
12,06 |
3 |
|
5 |
2,35 |
2,38 |
5,68 |
1 |
Из таблицы
видно, что исключению подлежит точка с
наибольшим значением функции – точка
.
Определяем центр тяжести точек
В точке
не выполняется ограничение
,
поэтому двигаем её в направлении центра
тяжести.
Исключению
подлежит точка
.
Определяем центр тяжести х…
Расчёт оформляется
в виде приведённой ранее таблицы. Условие
окончания поиска:
Задачи спец.
структуры
Геометрическое
программирование.
Разработано в
1961г. Зелиром
В геометрическом
программировании имеют дело с позиномами,
а с индексами n,t
, может принимать различные значения.
Позином отличается от много члена тем,
что показатели степеней его переменных
могут быть натуральными числами Для
реализации поставленной задачи составляют
двойственную задачу:
Пример:
Пример:
Стратегии
оптимизационных исследований.
Преобразование
функций и ограничений
1.
—
линейная функция по х.
-
Ограничения
вида:
.
Что позволяет
иногда отбросить одно из неравенств.
Соседние файлы в папке MIAPR
- #
- #
- #
- #
- #
- #
- #
Решетчатый поиск
| Рис. 5-1. Решетчатый поиск — две переменные. | 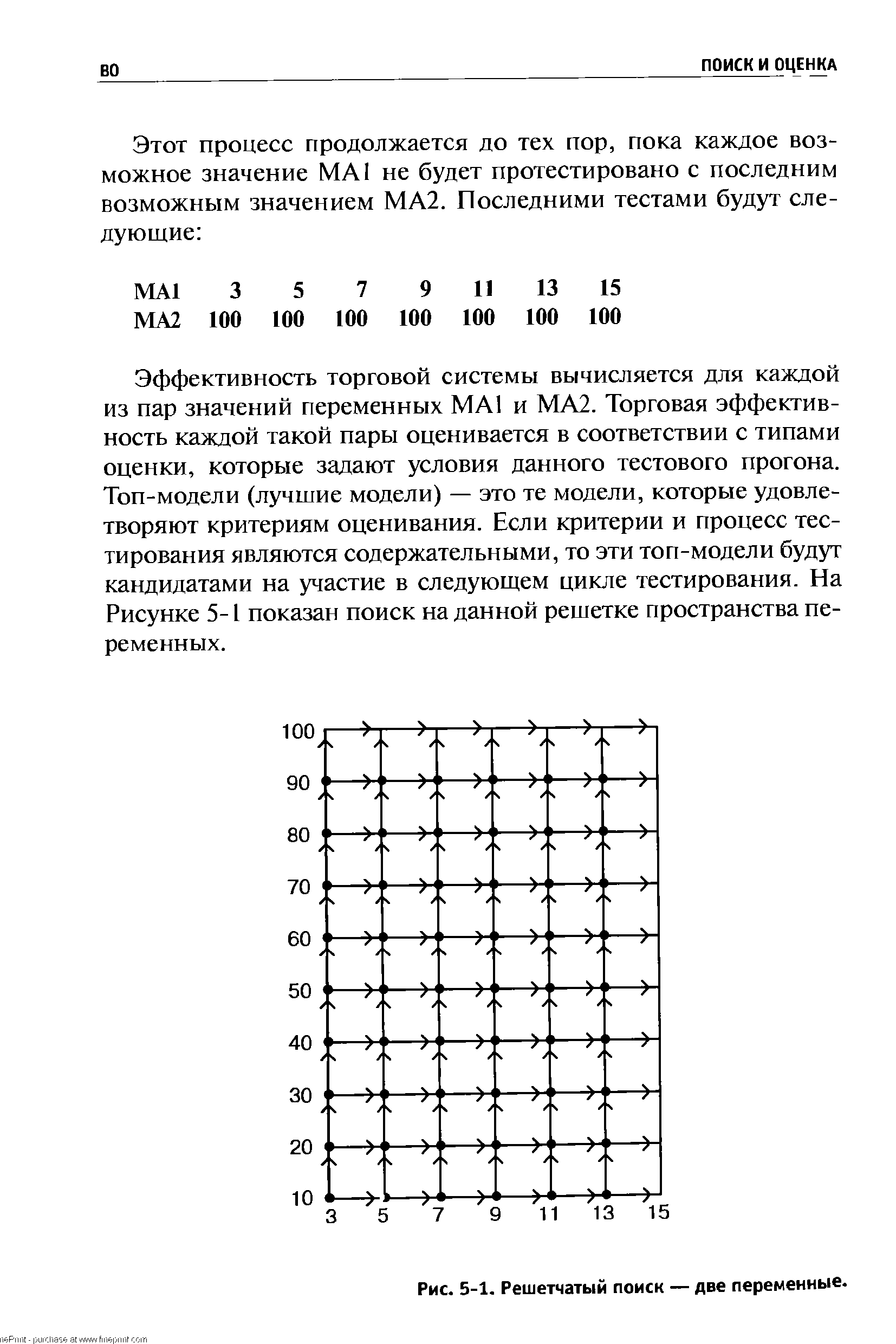 |
Этот метод поиска известен как решетчатый поиск. Два диапазона переменных задают решетку комбинаций переменных. Оценивается эффективность каждой комбинации. Другими словами, исследуются все узлы решетки. Это самый распространенный метод поиска. Существует и много других методов. Преимущество поиска по узлам решетки в его скрупулезности. Поскольку оценена каждая возможная комбинация, пропустить лучшую невозможно, за исключением случая, когда сам метод оценивания был плохим. Это будет обсуждаться позже. [c.81]
То, что по временным затратам делало решетчатый поиск непригодным для проведения данного теста, то для метода поиска с приоритетом шагов вполне по силам. Тестовый прогон будет состоять всего из 166 тестов (15+49+51+51=166), а это совсем другое дело. Как это делается И в чем недостаток этого метода [c.82]
Сочетание локального решетчатого поиска с методом направленного поиска — одна из вариаций на тему комбинирования некоторых лучших моментов обоих методов способом, призванным компенсировать слабые стороны каждого из них. Этот метод быстрее, чем поиск по узлам решетки, и медленнее, чем чистый направленный поиск. Он менее тщателен, чем поиск по узлам решетки, и более тщателен, чем направленный поиск. Он менее подвержен попаданию в локальный максимум, чем направленный поиск. [c.85]
Недостаток решетчатого выбора — его низкая скорость. В небольших тестах, подобных предыдущему примеру, время прогона было незначительным, особенно на быстрых современных персональных компьютерах. Предположив, что на один тест требуется одна секунда, поиск на решетке из 133 тестов занял бы всего 133 секунды, или 2.2 минуты. [c.81]
Смотреть страницы где упоминается термин Решетчатый поиск
:
[c.79]
Смотреть главы в:
Разработка,тестирование и оптимизация торговых систем -> Решетчатый поиск
Содержание
- Методика и специфика решения задач нелинейной оптимизации в msExcel
- Задание для самостоятельного решения
- Функция в Excel: поиск решения
- Как включить функцию “Поиск решения”
- Подготовительный этап
- Применение функции и ее настройка
- Заключение
Методика и специфика решения задач нелинейной оптимизации в msExcel
Задачу оптимизации нелинейной функции (6) можно было бы решить не путем анализа с использованием производной, и используя инструмент «Поиск решения» в MS Excel.
Если реализовать вычисления функции (6) по значению переменной в ячейке (см. рис. 2), то можно определить оптимально значение переменной в этой ячейке.
Рис. 2. Реализация вычисления функции прибыли в MSExcel
Для оптимизации используем инструмент «Поиск решения». Настраиваем параметры поиска решения (рис. 3) следующим образом:
Рис. 3. Настройка инструмента «Поиск решения»
в поле «Оптимизировать целевую функцию» указываем ячейку, где реализована формула для прибыли;
в поле «До» указываем «Максимум»;
в поле «Изменяя ячейки переменных» указываем ячейку, предназначенную для значения переменной 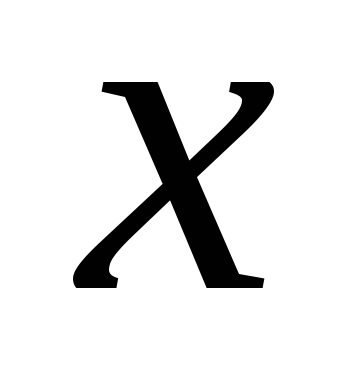
в поле «В соответствии с ограничениями» добавляем ограничение невозможности большого увольнения 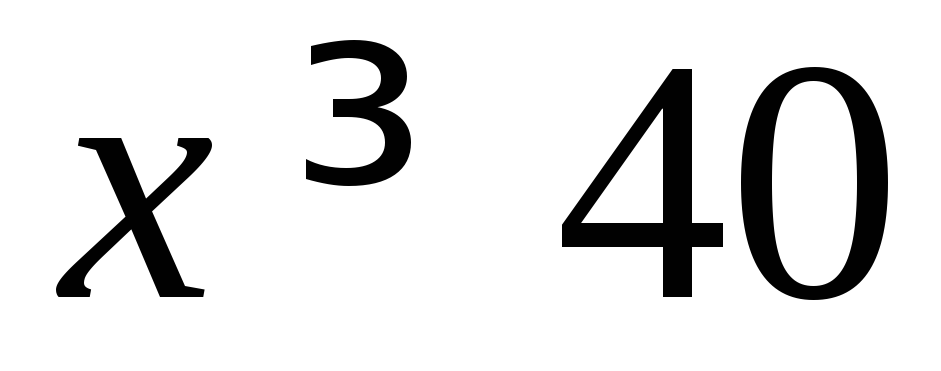
состояние поля «Сделать переменные без ограничений неотрицательными» в нашей задаче безразлично, так как единственная переменная ограничена;
в поле «Выберите метод решения» выбираем «Поиск решения нелинейных задач методом ОПГ» (так как наша задача нелинейная).
Нажав кнопку «Найти решение» получаем форму «Результаты поиска решения» (рис. 4). Убедившись, что в этом окне написано «Решение найдено. Все ограничения и условия выполнены», выбираем «Сохранить найденное решение» и нажимаем кнопку «Ок».
Рис. 4. Форма «Результаты поиска решения»
В ячейке переменной получаем оптимальное решение (рис. 5).
Рис. 5. Значения переменных после оптимизации
Как видим, нам удалось найти правильное решение автоматически.
Замечание: небольшое отличие значения в ячейке для искомой переменной от точного (получилось 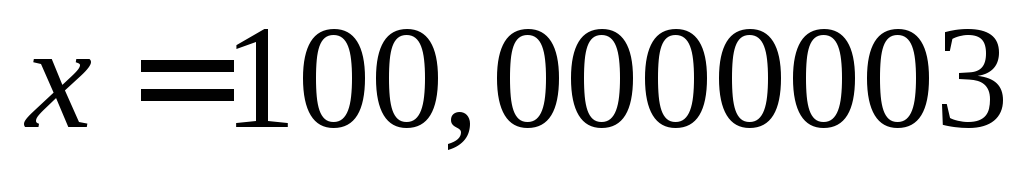
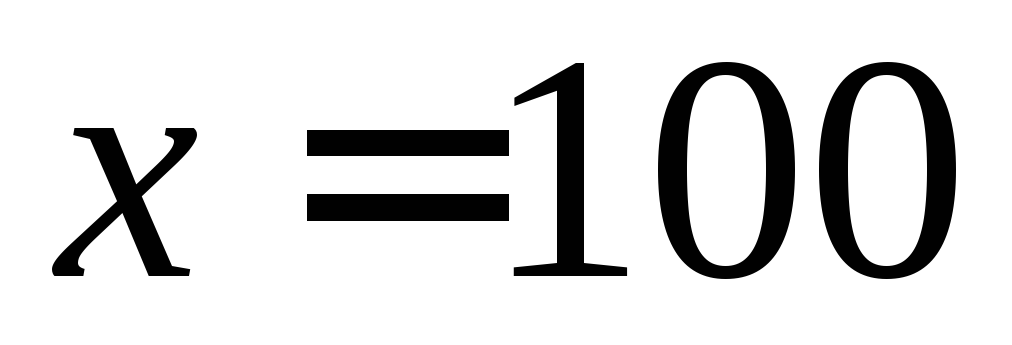
Важно отметить такую специфику решения нелинейных задач в MS Excel. Поиск решения методом ОПГ ищет значения переменных от начального заданного, обеспечивая постоянное улучшение результата с текущего места. Такая реализация приводит к поиску локального, а не глобального экстремума. Так, «начав» поиск от 70 рабочих мы нашли оптимальное значение 100 человек. Начав же, например, со 160 человек, получим «оптимальное» количество 150 (рис. 6). Выбрав же вначале 200 человек можно снова прийти к оптимальному значению 100.
Рис. 6. Изменение решения при смене начального приближения
Описанное свойство является характерным для большинства алгоритмов численного поиска оптимумов в задачах нелинейной оптимизации. Для того, чтобы получить действительно глобальный максимум необходимо попробовать определить оптимальное решение для нескольких начальных приближений (в задачах экономики они, как правило, выбираются легко из смысла задачи). В задачах с одной и двумя переменными очень помогает построение графиков.
Задание для самостоятельного решения
Числовые условия задания формируются на основе двух последних цифр зачетной книжки или студенческого билета. Выполнение чужого варианта задания не допускается.
В задании данной темы:
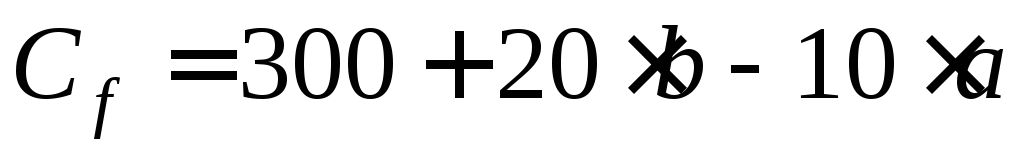
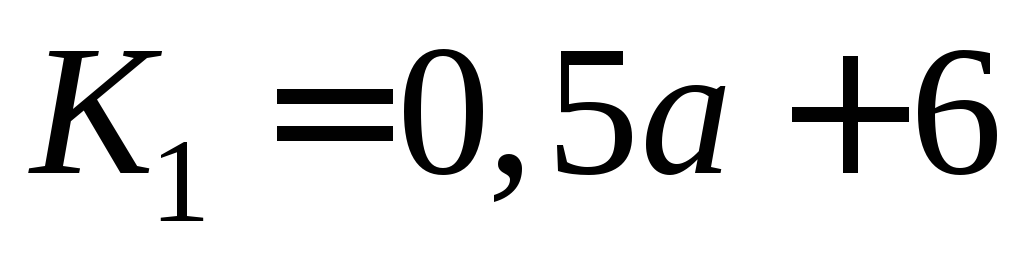
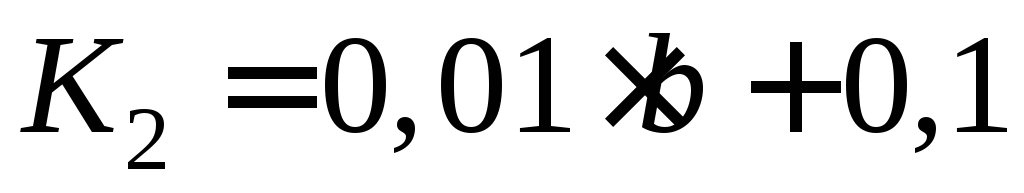
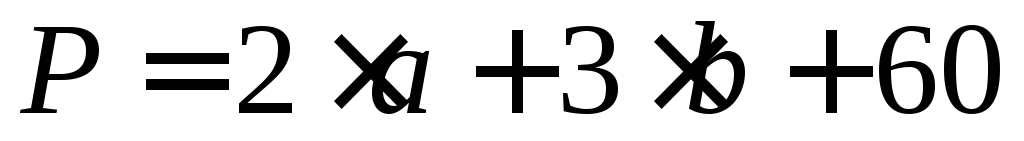
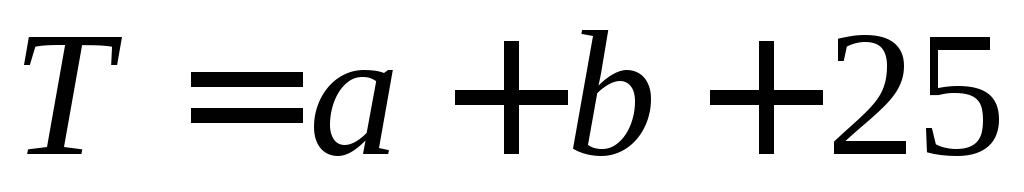
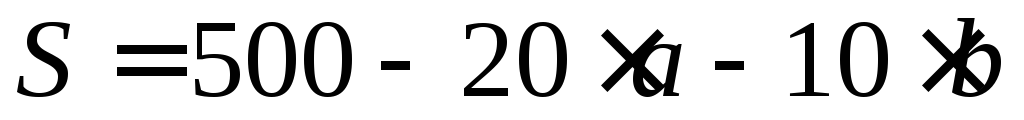
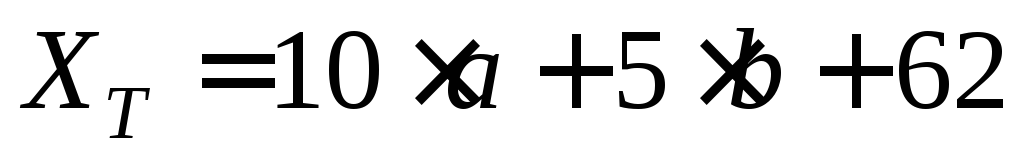
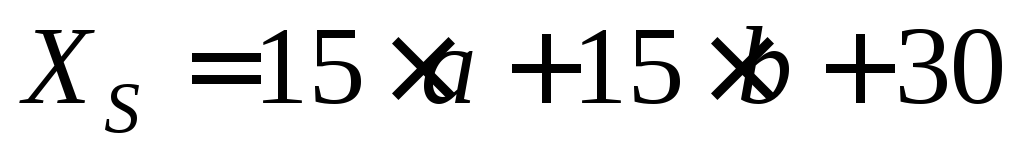

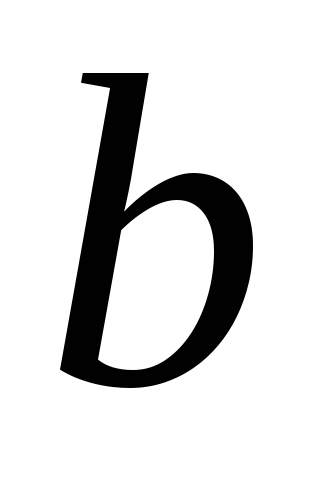
Вы – новый руководитель фирмы, производящей дорогостоящие автоматизированные станки. В настоящее время фирма производит 100 станков в год. Вам необходимо проанализировать и при возможности оптимизировать работу фирмы.
Определите оптимальное количество станков 
Цена продажи одного станка равна 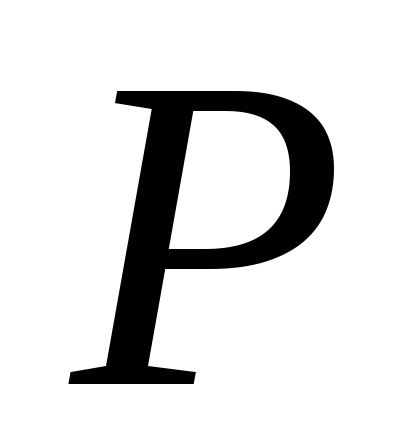
Постоянные издержки фирмы равны 

На отечественном рынке возможно продать только 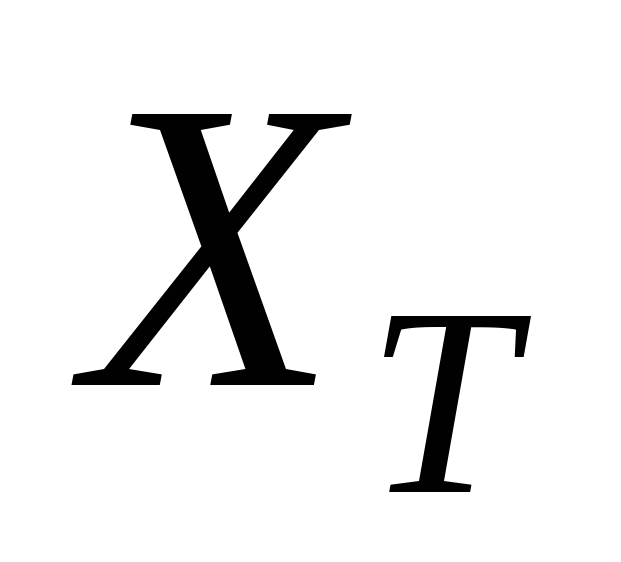
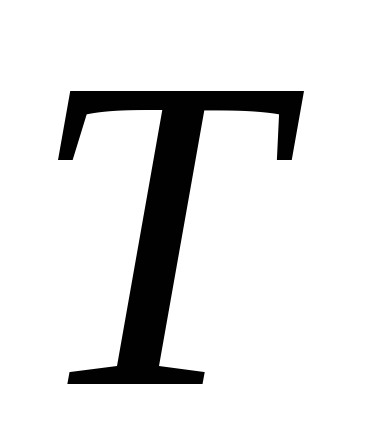
Для крупного выпуска продукции (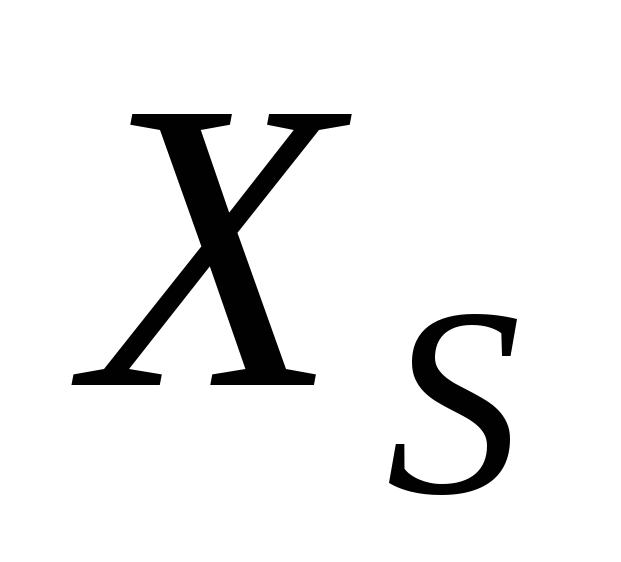
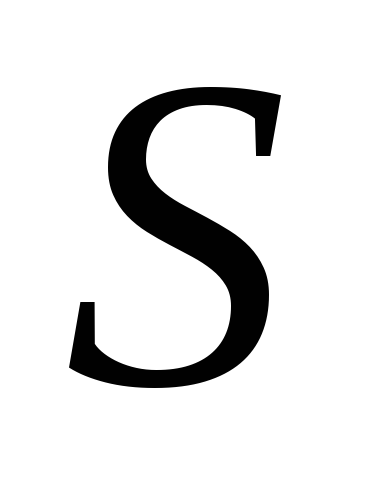
Сформулируйте оптимальное экономико-управленческое решение в имеющихся условиях.
Дайте экономическое обоснование полученного решения.
Приведите сравнение предлагаемого Вами плана выпуска станков с используемым ранее вариантом. Обоснуйте необходимость изменений.
Приведите график зависимости прибыли от количества выпускаемой продукции. Обоснуйте свое решение с помощью графика.
Источник
Функция в Excel: поиск решения
Наряду со множеством других возможностей, в Microsoft Excel есть одна малоизвестная, но очень полезная функция под названием “Поиск решения”. Несмотря на то, что найти и освоить ее, может быть, непросто, ее изучение и применение может помочь в решении огромного количества задач. Функция берет данные, перебирает их и выдает самое оптимальное решение из возможных. Итак, давайте разберемся, как именно работает поиск решения и попробуем применить данную функцию на практике
Как включить функцию “Поиск решения”
Несмотря на свою эффективность, функция “Поиск решения” не находится в первых рядах панели инструментов или контекстного меню. Многие пользователи, работающие в Excel годами, даже не подозревают о ее существовании. Дело в том, что по умолчанию она вообще отключена и для ее добавления на ленту нужно проделать следующие шаги:
- Открываем меню “Файл”, кликнув по соответствующему названию.
- Кликаем по разделу “Параметры”, который находится внизу вертикального перечня с левой стороны.
- Далее щелкаем по подразделу “Надстройки”. Здесь отображаются все надстройки программы, а внизу будет надпись “Управление”. Справа от нее представлено выпадающее меню, в котором должны быть выбраны “Надстройки Excel”, обычно уже установленные по умолчанию. Нажимаем кнопку “Перейти”.
- На экране появится новое вспомогательное окно “Надстройки”. Устанавливаем флажок напротив опции “Поиск решения” и нажимаем ОК.
- Все готово. Требуемая функция появится на ленте в правой части вкладки “Данные”.
Подготовительный этап
Добавить функцию на ленту программы – половина дела. Нужно еще понять принцип ее работы.
Итак, у нас есть данные про продаже товаров, представленные в табличном виде.
И перед нами стоит задача – назначить каждому товару скидку таким образом, чтобы сумма по всем скидкам составила 4,5 млн. рублей. Она должна отобразиться в отдельной ячейке, которая называется целевой. Ориентируясь на нее мы должны рассчитать остальные значения.
Наша задача – вычислить скидку, на которую будут умножены все суммы по продажам всех наименований. Она и будет найдена с помощью функции “Поиск решения”, а ячейка с этой скидкой будет называется искомой.
Данные ячейки (искомая и целевая) связываем вместе формулой, которую пишем в целевой ячейке следующим образом: =D13*$G$2, где ячейка D13 содержит итоговую сумму по продажам всех товаров, а ячейка $G$2 – абсолютные (неизменные) координаты искомой ячейки.
Применение функции и ее настройка
Формула готова. Теперь нужно применить саму функцию.
- Переключаемся во вкладку “Данные” и нажимаем кнопку “Поиск решения”.
- Откроются “Параметры”, где необходимо задать нужные настройки. В поле “Оптимизировать целевую функцию:” указываем адрес целевой ячейки, где планируется вывести сумму по всем скидкам. Можно прописать координаты вручную, либо выбрать из таблицы, для чего сначала кликаем по области ввода, затем – по нужной ячейке.
- Переходим к настройке других параметров. В пункте “До:” можно задать максимальную границу, минимальную границу или же точное число. Исходя из поставленной задачи ставим отметку рядом с опцией “Значение” и набираем “4500000” – сумма скидок по всем наименованиям.
- Следующее для заполнения поле – “Изменяя значения переменных:”. В него нужно внести координаты искомой ячейки, содержащей определенное значение. Это значение и есть та самая скидка, которую мы пытаемся вычислить. Также, как и с выбором целевой ячейки, координаты можно написать вручную, либо кликнуть по нужной ячейке в самой таблице.
- Теперь нужно отредактировать раздел “В соответствии с ограничениями:”, в котором задаем ограничения используемых данных. Например, можно исключить десятичные дроби или, скажем, отрицательные числа. Это делается через кнопку “Добавить”.
- Откроется вспомогательно окно, позволяющее добавить ограничения во время вычислений. В первом поле указываем координаты определенной ячейки или области ячеек, для которых это условие должно действовать. Согласно нашей задаче, указываем координаты искомой ячейки, в которой будет выводиться значение скидки. Следующий шаг – определить знак сравнения. Устанавливаем “больше или равно”, чтобы итоговое число не могло быть отрицательным. “Ограничение”, которое устанавливается в третьем поле, в этом случае будет равно цифре 0, поскольку именно относительно этого значения задается условие.
Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK.
- После выполнения описанных выше действий в самом большом поле окна появится установленное только что ограничение. Список может быть довольно большим и зависит от сложности предполагаемых расчетов, но в данном случае будет достаточно и одного условия.
Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.
- Также можно задать немалое количество дополнительных настроек. Чуть ниже справа есть кнопка “Параметры”, позволяющая это сделать. Нажимаем на нее и открываем новое окно.
- В этих настройках у нас есть возможность установить “Точность ограничения” и “Пределы решения”. В нашем случае задавать данные параметры нет необходимости, поэтому после ознакомления с представленным окном, его можно закрыть, нажав OK.
- Итак, все настройки выполнены и параметры установлены. Пора запускать функцию – для этого нажимаем кнопку “Найти решение”.
- После этого программа сделает все необходимые расчеты и выдаст результаты в нужных ячейках. При этом сразу же откроется окно “Результаты поиска решения”, где можно сохранить/отменить результаты или настроить параметры поиска заново. Если результаты нас устраивают, оставляем отметку напротив опции “Сохранить найденное решение” и нажимаем ОК. При этом, если мы предварительно установим галочку слева от надписи “Вернуться в диалоговое окно параметров поиска решения”, после того, как мы щелкнем OK, мы обратно переключимся к настройке функции поиска решения.
- Вполне вероятно, что расчеты могут показаться неправильными, либо возникнет желание немного изменить исходные данные и получить другой результат. В этом случае нужно снова открыть окно с параметрами поиска решения и внимательно посмотреть поля с введенными данными.
- Если с данными все нормально, можно попробовать задействовать другой метод решения. Для этого щелкаем по текущему варианту и из раскрывшегося перечня выбираем способ, который нам кажется наиболее подходящим:
- Первый – ищет решение методом обобщенного приведенного градиента (ОПГ) для нелинейных задач. Стандартно выбран именно этот вариант, но можно попробовать и другие.
- Второй – пытается отыскать решение для линейных задач, используя симплекс-метод.
- Третий – для выполнения поставленной задачи использует эволюционный поиск.
- В том случае, если ни один из методов не принес удовлетворительных результатов, стоит проверить данные в таблице и параметрах еще раз, поскольку именно это является самой частой ошибкой в подобного рода задачах.
- Теперь, когда мы получили требуемую скидку, осталось ее применить, чтобы рассчитать суммы скидок по всем наименованиям. Для этого отмечаем первую ячейку столбца “Сумма скидки”, пишем в ней формулу “=D2*$G$2” и нажимаем Enter. Знаки доллара ставятся для того, чтобы при растягивании/копировании формулы на другие строки, ячейка G2 со скидкой оставалась неизменной в расчетах.
- Мы получили сумму скидки для первого наименования. Теперь наводим курсор на нижний правый угол ячейки с результатом, как только он поменяет форму на крестик, зажав левую кнопку мыши растягиваем формулу на все строки, по которым хотим посчитать аналогичную сумму.
- Теперь наша таблица полностью готова в соответствии с поставленной задачей.
Заключение
Таким образом, функция “Поиск решения” в Эксель может помочь в решении определенных задач, которые достаточно сложно или невозможно решить простыми методами. Однако, проблема в использовании данного способа заключается в том, что по умолчанию данная функция скрыта в программе, из-за чего многие пользователи не догадываются о ее существовании. Также функция довольно трудна в освоении и использовании, но при ее должном изучении, она может принести значительную пользу и облегчить работу.
Источник
Решение СЛАУ с помощью надстройки «Поиск решения»
Систему линейных алгебраических уравнений можно также решить, используя надстройку «Поиск решения». При использовании данной надстройки строится последовательность приближений 
Назовем вектором невязок следующий вектор:
Задача Excel заключается в том, чтобы найти такое приближение 

В качестве примера рассмотрим СЛАУ (3.27).
Последовательность действий:
1. Оформим таблицу, как показано на рис.3.4. Введем коэффициенты системы (матрицу А) в ячейки А3:С5.
Рис.3.4. Решение СЛАУ с помощью надстройки «Поиск решения»
2. В ячейках А8:С8 будет сформировано решение системы (х1, х2, х3). Первоначально они остаются пустыми, т.е. равными нулю. В дальнейшем будем их называть изменяемыми ячейками.. Однако для контроля правильности вводимых далее формул, удобно ввести в эти ячейки какие-либо значения, например, единицы. Эти значения можно рассматривать как нулевое приближение решения системы, 
3. В столбец D введем выражения для вычисления левых частей исходной системы. Для этого в ячейкуD3 введем и затем скопируем вниз до конца таблицы формулу:
Используемая функция СУММПРОИЗВ принадлежит категории Математические.
4. В столбец Е запишем значения правых частей системы (матрицу В).
5. В столбец F введем невязки в соответствии с формулой (3.29), т.е. введем формулу F3=D3-E3 и скопируем ее вниз до конца таблицы.
6. Будет не лишним проверить правильность вычислений для случая 
7. Выберем команду ДанныеАнализПоиск решения.
Рис. 3.5. Окно надстройки «Поиск решения»
В окне Поиск решения (рис.3.5) в поле Изменяемые ячейки укажем блок $А$8:$С$8, а в поле Ограничения – $F$3:$F$5=0. Далее щелкнем по кнопке Добавить и введем эти ограничения. И затем — кнопка Выполнить
Реализация метода Якоби средствами приложения MS Excel
В качестве примера рассмотрим систему уравнений (3.19), решение которой методом Якоби получено выше (пример 3.2)
Приведем эту систему к нормальному виду:
Последовательность действий
1. Оформим таблицу, как показано на рис.3.6.:
• Матрицы 
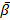
• Значение e–в Н5.
• Номер итерации k сформируем в столбце А таблицы с помощью автозаполнения.
• В качестве нулевого приближения выберем вектор

2. Используя выражения (3.29), в ячейки В12:D12 запишем формулы для вычисления первого приближения:
Эти формулы можно записать иначе, используя функцию Excel СУММПРОИЗВ.
В ячейку Е12 введем формулу: E12=ABS(B11-B12) и скопируем ее вправо, в ячейки F12:G12.
Рис.3.6. Схема решения СЛАУ методом Якоби
3. В ячейку Н12 введем формулу для вычисления M (k) , используя выражение (3.18): Н12 = МАКС(E12:G12). Функция МАКС находится в категории статистические.
4. Выделим ячейки В12:Н12 и скопируем их вниз до конца таблицы. Таким образом, получим k приближений решения СЛАУ.
5. Определим приближенное решение системы и количество итераций, необходимое для достижения заданной точности e.
Для этого оценим степень близости двух соседних итераций по формуле (3.18). Воспользуемся Условным форматированиемв ячейках столбца.
Результат такого форматирования виден на рис.3.6. Ячейки столбца Н, значения которых удовлетворяют условию (3.18), т.е. меньше e=0,1, тонированы.
Анализируя результаты, принимаем за приближенное решение исходной системы с заданной точностью e=0,1 четвертую итерацию, т.е.
Исследуем характер итерационного процесса. Для этого выделим блок ячеек А10:D20 и, используя Мастер диаграмм, построим графики изменения каждой компоненты вектора решения в зависимости от номера итерации,
Приведенные графики (рис.3.7) подтверждают сходимость итерационного процесса.
Рис. 3.7. Иллюстрация сходящегося итерационного процесса
Изменяя значение eв ячейке Н5, получим новое приближенное решение исходной системы с новой точностью.
Реализация метода прогонки средствами приложения Excel
Рассмотрим решение следующей системы линейных алгебраических уравнений методом «прогонки», используя таблицы Excel.
Векторы:
Последовательность действий
1. Оформим таблицу, как показано на рис.3.8. Исходные данные расширенной матрицы системы (3.30), т.е. вектора 

2. Про гоночные коэффициенты U0=0 и V0=0 введем в ячейки G4 и H4 соответственно.
3. Вычислим прогоночные коэффициенты Li, Ui, Vi. Для этого в ячейках F5, G5, H5 вычислим L1, U1, V1. по формуле (3.8). Для этого введем формулы:
F5 = B5*G4+C5; G5=-D5/F5, H5 = (E5-B5*H4)/F5, и затем скопируем их вниз.
Рис.3.8. Расчетная схема метода «прогонки»
4. В ячейке I10 вычислим x6 по формуле (3.10)
5. По формуле (3.7) вычислим все остальные неизвестные x5 x4, x3, x2, x1. Для этого в ячейке I9 вычислим x5 по формуле (3.6): I9=G9*I10+H9 . А далее копируем эту формуле вверх.
Контрольные вопросы
1. Система линейных алгебраических уравнений (СЛАУ). Что является решением СЛАУ. Когда существует единственное решение СЛАУ.
2. Общая характеристика прямых (точных) методов решения СЛАУ. Методы Гаусса и прогонки.
3. Общая характеристика итерационных методов решения СЛАУ. Методы Якоби (простых итераций) и Гаусса-Зейделя.
4. Условия сходимости итерационных процессов.
5. Что понимают под терминами обусловленности задач и вычислений, корректности задачи решения СЛАУ.
Глава 4.
Численное интегрирование
При решении достаточно большого круга технических задач приходится сталкиваться с необходимостью вычисления определенного интеграла:
Вычисление площадей, ограниченных кривыми, работы, моментов инерции, перемножение эпюр по формуле Мора и т.д. сводится к вычислению определенного интеграла.
Если непрерывная на отрезке [a, b] функция y = f(x) имеет на этом отрезке первообразную F(x), т.е. F ’ (x) = f(x) , то интеграл (4.1) может быть вычислен по формуле Ньютона – Лейбница:
Однако, только для узкого класса функций y=f(x) первообразная F(x) может быть выражена в элементарных функциях. Кроме того, функция y=f(x) может задаваться графически или таблично. В этих случаях применяют различные формулы для приближенного вычисления интегралов.
Такие формулы называют квадратурными формулами или формулами численного интегрирования.
Формулы численного интегрирования хорошо иллюстрируются графически. Известно [1, 12], что значение определенного интеграла (4.1) пропорционально площади криволинейной трапеции, образованной подынтегральной функцией y=f(x), прямыми х=а и х=b, осью ОХ (рис.4.1).
Задачу вычисления определенного интеграла (4.1) заменяем задачей вычисления площади этой криволинейной трапеции. Однако задача нахождения площади криволинейной не является простой.
Отсюда идея численного интегрирования [3, 6] будет заключатся в замене криволинейной трапеции фигурой, площадь которой вычисляется достаточно просто.
Рис.4.1. Геометрическая интерпретация численного интегрирования
Для этого отрезок интегрирования [a, b] разобьем на n равных элементарных отрезков [xi ,xi+1] (i=0, 1, 2, …. n-1), с шагом h=(b-a)/n. При этом криволинейная трапеция разобьется на n элементарных криволинейных трапеций с основаниями равными h (рис.4.1).
Каждая элементарная криволинейная трапеция заменяется фигурой, площадь которой вычисляется довольно просто. Обозначим эту площадь Si . Сумма всех этих площадей называется интегральной суммой и вычисляется по формуле
Тогда приближенная формула вычисления определенного интеграла (4.1) имеет вид
Точность вычисления по формуле (4.4) зависит от шага h, т.е. от числа разбиений n. С увеличением n интегральная сумма 
Это хорошо проиллюстрировано на рис.4.2.
Точное значение интеграла
Рис.4.2. Зависимость точности вычисления интеграла
от числа разбиений
В математике доказывается теорема: если функция y=f(x) непрерывна на [a, b], то предел интегральной суммы бn существует и не зависит от способа разбиения отрезка [a,b] на элементарные отрезки.
Формулу (4.4) можно использовать, если известна степень точности такого приближения. Существуют различные формулы для оценки погрешности выражения (4.4), но, как правило, они достаточно сложны. Будем проводить оценку точности приближения (4.4) методом половинного шага.
Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
-
Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
-
Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
-
Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
-
Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12677 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Решение систем линейных уравнений
Эта страничка поможет решить Системы Линейных Алгебраических Уравнений (СЛАУ) методом Гаусса, матричным методом или методом Крамера, исследовать их на совместность (теорема Кронекера-Капелли), определить количество решений, найти общее, частное и базисные решения.
Введите коэффициенты при неизвестных в поля. Если Ваше уравнение имеет меньшее количество неизвестных, то оставьте пустыми поля при переменных, не входящих в ваше уравнение. Можно использовать дроби ( 13/31 ).
источники:
http://lumpics.ru/how-solve-system-equations-excel/
http://matrixcalc.org/slu.html
Решение краевой задачи методом конечных разностей: Методические указания по выполнению лабораторной работы в курсе “Информатика”
Страницы работы
Фрагмент текста работы
ячейках от C3 до C8 вычисляем
значения вспомогательной функции 1/(2 хi+1), входящей взнаменатели
функций p(x), q(x) и f(x). Вводим в C3 формулу «=1/(2*B3+1)» и протягиваем эту формулу до ячейкиC8;
5.
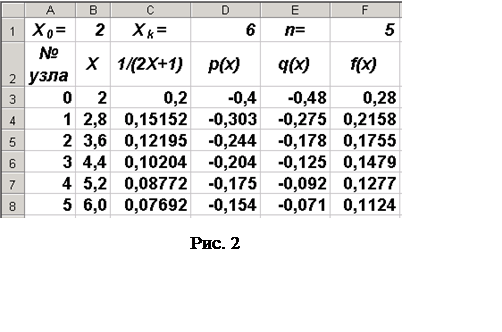 |
В ячейки D3, E3 и
F3 записываем формулы, соответствующие (13), для вычисления значений
функций p(x), q(x) и f(x). Запись этих формул при
вводе их в ячейки таблицы имеет следующий вид: «=-2*C3», «= ‑12*C3*C3»
и «=(3*B3+1)*C3*C3» соответственно. При протягивании этих
формул по столбцам D, Е и F до восьмой строки таблица заполняется
так, как показано на рис. 2.
6.
Далее начинаем
заполнение столбцов G, H, I и J значениями коэффициентов Ai, Ci,
Bi и Fi в соответствии с форматом системы
уравнений (11). В ячейки G3, H3, I3 записываем значения, определяемые
форматом первого уравнения системы (11): A0=0, C0=-1,
В0=0. В ячейку J3 записываем ссылку на ячейку J1, в которой записано начальное значение F0=Y0:
«=J1″.
7.
В ячейки G8,
H8, I8 записываем значения, определяемые конечными условиями A5=0,
C5=-1, В5=0. В ячейку J8 записываем ссылку на ячейку
L1, в которой записано начальное значение Fk=
F5 = Yk :»=L1″.
8.
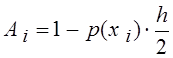 |
Далее заполняем столбцы G,
H, I и J
значениями коэффициентов Ai , Ci , Bi и Fi. В
ячейку G4 вводим формулу «=1-D4*$H$1/2″, соответствующую формуле
для вычисления коэффициента A1. После
чего протягиваем эту формулу до ячейки G7.
9.
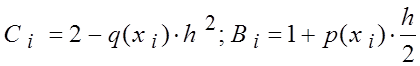 |
Аналогично в ячейку Н4
вводим формулу для вычисления коэффициента С1: «2-Е4*$H$1*$H$1″, а в ячейку I4 вводим формулу для вычисления коэффициента B1: «1+D4*$H$1/2″, реализуя соответствующие формулы
Протягиваем эти формулы до ячеек Н7 иI7.
10.
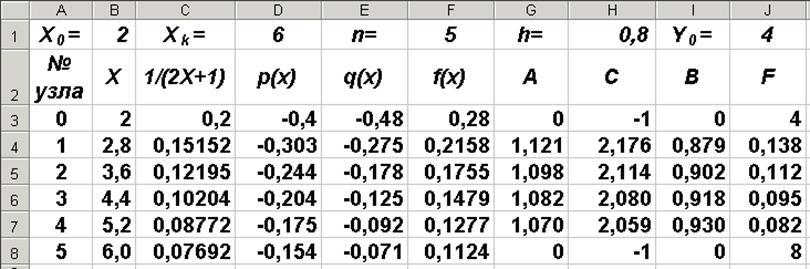 |
В ячейках столбца J формируем вектор правых частей
системы уравнений (11). В ячейку J4
вводим формулу “=F4*$H$1*$H$1”, соответствующую формуле Fi = fih2. Протягиваем эту формулу до ячейки J7. В результате получаем таблицу, показанную на рис. 3.
Следует отметить, что в столбцах G, H, I и J этой таблицы записаны элементы
матрицы, решаемой системы уравнений (11).
Рис. 3
11.
Используя
вычисленные значения коэффициентов Ai, Ci, Bi
и Fi, находим в соответствии с формулами (18) и (19) значения
коэффициентов ai и bi. В ячейку K3 запишем формулу для вычисления a0 : «=I3/H3″, а в ячейку L3 формулу для вычисления b0.: «=-J3/H3″. И далее в ячейки K4 и L4 вводим
формулы, соответствующие (19), для вычисления коэффициентов
a1 :«=I4/(H4-K3*G4)», и b1: «=(G4*L3‑J4)/(
H4‑K3*G4)».
Протягиваем эти формулы до ячеек K8 и L8 соответственно.
Результаты вычисления показаны на рис. 4.
12.
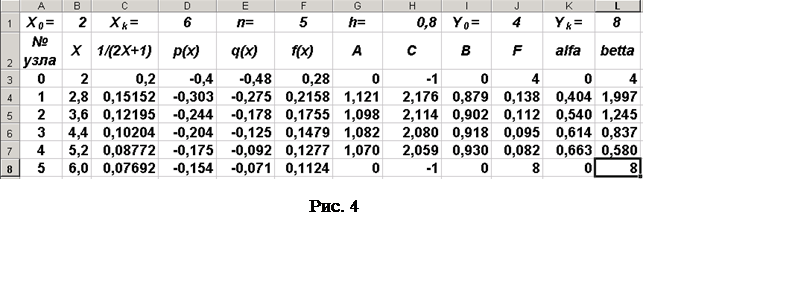 |
Дальнейшие вычисления
выполняются в столбце М по формулам обратного хода (21) и (22). В ячейку
М8 введем формулу «=L8″, представляющую ссылку на значение bn. В ячейку М7 введем формулу «=L7+K7*M8»,
соответствующую и протянем ее до ячейки М3. Результаты вычислений
показаны на рис. 5.
13.
Построим график
функции Y(X), используя возможности мастера диаграмм программы MS Excel.
Для этого выделим ячейки столбца значений функции Y(X) от ячейки М3 до М8 ивыполним
процедуру создания диаграммы, используя средства «мастера
диаграмм» программы MS Excel. Окончательный результат
показан на рис. 5.
Проверка правильности
полученного решения
Для
проверки правильности полученного в столбце М решения Y(X) выполняется подстановкой полученного решения в
уравнения исходной системы. В ячейки столбца N последовательно вводим формулы, реализующие
вычислительный алгоритм, определяемый системой уравнений (11). В N3 введём формулу «=M3″. Затемв N4 введём формулу «=G4*M3‑H4*M4+I4*M5″, реализующую левую часть уравнения
(9). Эту формулу протягиваем до N8, получаясоответственно – «=G5*M4‑H5*M5+I5*M6″ вN5, «=G6*M5-H6*M6+I6*M7″ в N6, «=G7*M6‑H7*M7+I7*M8″ вN7 и «=G8*M7-H8*M8+I8*M9″ вN8. Полученные в столбце N значения совпадают со значениями в столбце J, что позволяет судить о правильности
полученного решения.
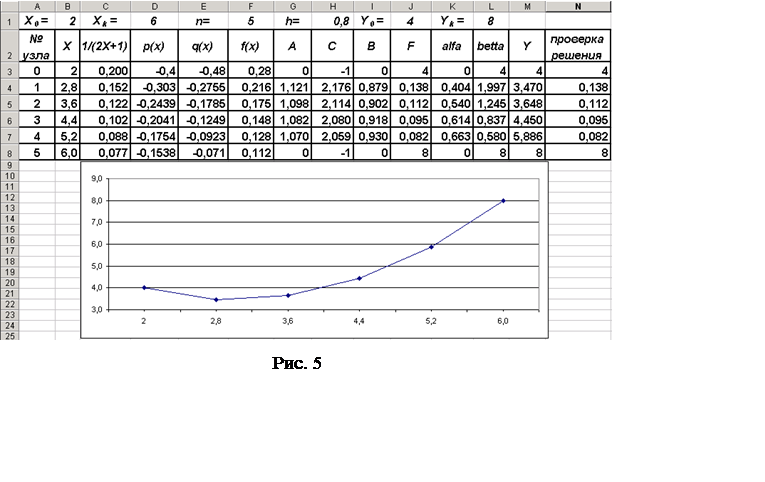 |
Варианты
заданий для выполнения самостоятельной работы
Методом конечных разностей найти решение краевой задачи на
сетке из 6 узлов.
Вариант 1
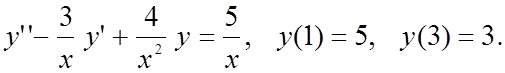 |
Вариант 2
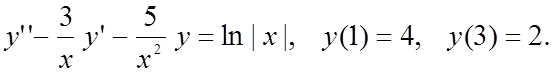 |
Вариант 3
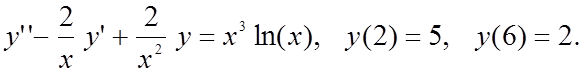 |
Вариант 4
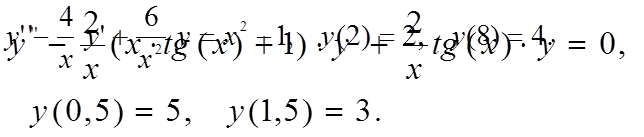 |
Вариант 5
Вариант 6
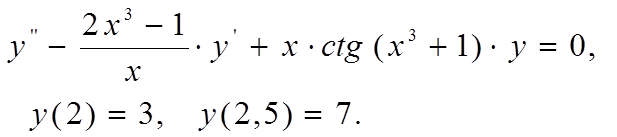 |
Вариант 7
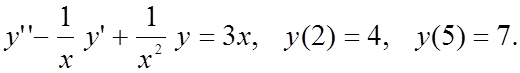 |
Вариант 8
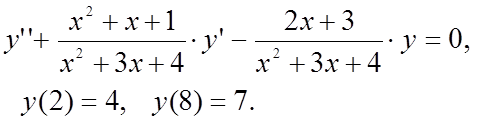 |
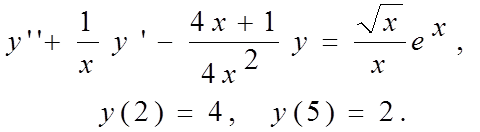 |
Вариант 9
Вариант 10
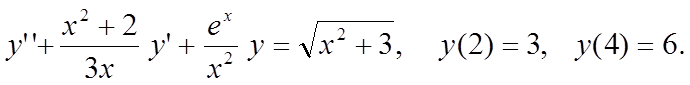 |
Вариант 11
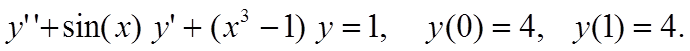 |
Вариант 12
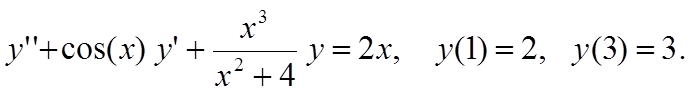 |
Вариант 13
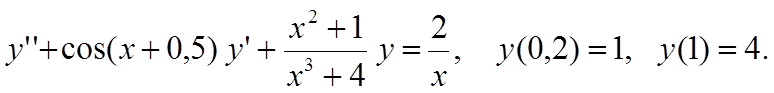 |
Вариант 14
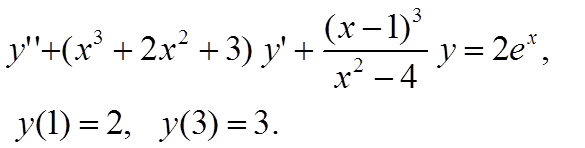 |
Вариант 15
Литература
1. Пискунов Н.С.
Дифференциальное и интегральное исчисления. М.:Физматгиз, 1963. – 856 с.
2. Карпов В.В.,
Коробейников А.В. Математические модели задач строительного профиля и численные
методы их исследования: Учеб. пособие. – СПб., СПбГАСУ, 1996. – 134 с.
3. Бахвалов Н.С.
Численные методы. – М.:Наука, 1973. – 632 с.
4. Вагер Б.Г.
Численные методы решения дифференциальных уравнений: Учеб. пособие – СПбГАСУ. –
СПб. 2003. 114 с.
5. Любимов Е.Б. и
др. Решение систем линейных алгебраических уравнений средствами программы Microsoft Excel:
Метод. указ. – СПб., СПбГАСУ, 2005. – 22 c.
СОДЕРЖАНИЕ
Основные понятия, используемые
в постановках краевых задач. 3
Применение метода прогонки для решения систем линейных
алгебраических уравнений с трёхдиагональными ленточными матрицами. 6
Реализация метода прогонки в среде программы
MS Excel 6
Постановка задачи. 6
Проверка правильности полученного решения. 12
Варианты заданий для выполнения самостоятельной работы.. 13
Литература. 16
[1]
) Формулы вводятся в ячейки таблиц, начиная с символа “=” (равно). Двойные
кавычки использованы в тексте для выделения формулы. Вводить их в ячейки
таблицы не нужно.
[2]
) Терминология и сокращения, используемые в тексте методических указаний,
приведены в начальном разделе методических указаний к первой лабораторной
Похожие материалы
- Visual Basic for Application. Свойства, методы и события объектов VBA. Переменная
- Обзорная лекция по основным разделам (дидактическим единицам ГОС) дисциплины «Информатика»
- Интерполяция. Введение. Общая постановка задачи (Решение задач в среде программ Microsoft Excel или OpenOffice.org Calc)
Информация о работе
Тип:
Методические указания и пособия
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
Содержание материала
- Включение функции
- Видео
- Поиску решения не удалось найти решения (Solver could not find a feasible solution)
- Конкретные примеры использования
- Изготовление йогурта
- Затраты на рекламу
- Применение функции и ее настройка
- Подготовка оптимизационной модели в MS EXCEL
- Обзор и возможности функции
- Решение эконометрики в Excel
- Пример использования поиска решений
- Подготовка таблицы
Включение функции
Можно долго искать на ленте, где находится Поиск решения, но так и не найти данный инструмент. Просто, для активации данной функции, нужно её включить в настройках программы.
Для того, чтобы произвести активацию Поиска решений в программе Microsoft Excel 2010 года, и более поздних версий, переходим во вкладку «Файл». Для версии 2007 года, следует нажать на кнопку Microsoft Office в левом верхнем углу окна. В открывшемся окне, переходим в раздел «Параметры».
В окне параметров кликаем по пункту «Надстройки». После перехода, в нижней части окна, напротив параметра «Управление» выбираем значение «Надстройки Excel», и кликаем по кнопке «Перейти».
Открывается окно с надстройками. Ставим галочку напротив наименования нужной нам надстройки – «Поиск решения». Жмем на кнопку «OK».
После этого, кнопка для запуска функции Поиска решений появится на ленте Excel во вкладке «Данные».
Поиску решения не удалось найти решения (Solver could not find a feasible solution)
Это сообщение появляется, когда Поиск решения не смог найти сочетаний значений переменных, которые одновременно удовлетворяют всем ограничениям. Если вы используете Симплекс метод решения линейных задач , то можно быть уверенным, что решения действительно не существует. Если вы используете метод решения нелинейных задач, который всегда начинается с начальных значений переменных, то это может также означать, что допустимое решение далеко от этих начальных значений. Если вы запустите Поиск решения с другими начальными значениями переменных, то, возможно, решение будет найдено. Представим, что при решении задачи нелинейным методом, ячейки с переменными были оставлены не заполненными (т.е. начальные значения равны 0), и Поиск решения не нашел решения. Это не означает, что решения действительно не существует (хотя это может быть и так). Теперь, основываясь на результатах некой экспертной оценки, в ячейки с переменными введем другой набор значений, который, по Вашему мнению, близок к оптимальному (искомому). В этом случае, Поиск решения может найти решение (если оно действительно существует).
Примечание . О влиянии нелинейности модели на результаты расчетов можно прочитать в последнем разделе статьи Поиск решения MS EXCEL (4.3). Выбор места открытия нового представительства .
В любом случае (линейном или нелинейном), Вы должны сначала проанализировать модель на непротиворечивость ограничений, то есть условий, которые не могут быть удовлетворены одновременно. Чаще всего это связано с неправильным выбором соотношения (например, <= вместо >=) или граничного значения. Если, например, в рассмотренном выше примере, значение максимального объема установить 16 м3 вместо 32 м3, то это ограничение станет противоречить ограничению по минимальному количеству мест (110), т.к. минимальному количеству мест соответствует объем равный 16,5 м3 (110*0,15, где 0,15 – объем коробки, т.е. самой маленькой тары). Установив в качестве ограничения максимального объема 16 м3, Поиск решения не найдет решения.
При ограничении 17 м3 Поиск решения найдет решение.
Видео
Конкретные примеры использования
Закончив с виртуальным примером, который помог разобраться с особенностями построения таблицы и задачи условий перейдём к более приземлённым и конкретным примерам. С их помощью в задаче будет разобраться немного проще.
Формулы в Excel – создание простых формул
Изготовление йогурта
Попробуем рассчитать какой из видов йогурта при разной концентрации компонентов производить лучше, чем остальные. Для этого определим компоненты, их соотношение и стоимость конечного продукта, при условии ограниченности запасов:
В раздел «Расход сырья» внесены формулы, которые опираются на «количество» и нормы расхода. Прибыль является произведением стоимости и количества. Количество и будет переменной, которая будет изменяться в пределах «запасы». Для этого формируется следующий набор условий:
В результате вычислений (с учётом дробного остатка, поскольку условие работы только с целыми числами добавлено не было), получилось, что эффективнее всего производить 1 и 3 йогурты, а второй полностью игнорировать.
Затраты на рекламу
Другим вопросом, с которым поможет эта функция будет «оптимизация расходов на рекламу». В этом случае перед пользователем стоит задача: повысить возможную прибыль посредством изменения рекламных вложений в определённые месяцы.
Итак, прибыль является целевой ячейкой (выделена изумрудным цветом). Зелёным выделены расходы на рекламу, а красным максимальные затраты. При поиске решения ограничиваем подстановку переменных в значениях рекламы максимумом, а в качестве цели ставим максимизацию прибыли.
В результате получаем максимизированную прибыль в указанном месяце, посредством грамотного распределения рекламного бюджета между остальными месяцами.
Отсюда и вытекает главный недостаток «поиска решений». Он оперирует лишь конечной (одной) ячейкой. Чтобы максимизировать прибыль требуется работать с последней ячейкой (прибыль – всего), что сопряжено с вероятностью появления ошибки в программе, если формулы настроены неверно.
Применение функции и ее настройка
Смотрите также: “Как построить график в Excel”
Формула готова. Теперь нужно применить саму функцию.
- Переключаемся во вкладку “Данные” и нажимаем кнопку “Поиск решения”.
- Откроются “Параметры”, где необходимо задать нужные настройки. В поле “Оптимизировать целевую функцию:” указываем адрес целевой ячейки, где планируется вывести сумму по всем скидкам. Можно прописать координаты вручную, либо выбрать из таблицы, для чего сначала кликаем по области ввода, затем – по нужной ячейке.
- Переходим к настройке других параметров. В пункте “До:” можно задать максимальную границу, минимальную границу или же точное число. Исходя из поставленной задачи ставим отметку рядом с опцией “Значение” и набираем “4500000” – сумма скидок по всем наименованиям.
- Следующее для заполнения поле – “Изменяя значения переменных:”. В него нужно внести координаты искомой ячейки, содержащей определенное значение. Это значение и есть та самая скидка, которую мы пытаемся вычислить. Также, как и с выбором целевой ячейки, координаты можно написать вручную, либо кликнуть по нужной ячейке в самой таблице.
- Теперь нужно отредактировать раздел “В соответствии с ограничениями:”, в котором задаем ограничения используемых данных. Например, можно исключить десятичные дроби или, скажем, отрицательные числа. Это делается через кнопку “Добавить”.
- Откроется вспомогательно окно, позволяющее добавить ограничения во время вычислений. В первом поле указываем координаты определенной ячейки или области ячеек, для которых это условие должно действовать. Согласно нашей задаче, указываем координаты искомой ячейки, в которой будет выводиться значение скидки. Следующий шаг – определить знак сравнения. Устанавливаем “больше или равно”, чтобы итоговое число не могло быть отрицательным. “Ограничение”, которое устанавливается в третьем поле, в этом случае будет равно цифре 0, поскольку именно относительно этого значения задается условие.
Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK.
- После выполнения описанных выше действий в самом большом поле окна появится установленное только что ограничение. Список может быть довольно большим и зависит от сложности предполагаемых расчетов, но в данном случае будет достаточно и одного условия.
Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.
- Также можно задать немалое количество дополнительных настроек. Чуть ниже справа есть кнопка “Параметры”, позволяющая это сделать. Нажимаем на нее и открываем новое окно.
- В этих настройках у нас есть возможность установить “Точность ограничения” и “Пределы решения”. В нашем случае задавать данные параметры нет необходимости, поэтому после ознакомления с представленным окном, его можно закрыть, нажав OK.
- Итак, все настройки выполнены и параметры установлены. Пора запускать функцию – для этого нажимаем кнопку “Найти решение”.
- После этого программа сделает все необходимые расчеты и выдаст результаты в нужных ячейках. При этом сразу же откроется окно “Результаты поиска решения”, где можно сохранить/отменить результаты или настроить параметры поиска заново. Если результаты нас устраивают, оставляем отметку напротив опции “Сохранить найденное решение” и нажимаем ОК. При этом, если мы предварительно установим галочку слева от надписи “Вернуться в диалоговое окно параметров поиска решения”, после того, как мы щелкнем OK, мы обратно переключимся к настройке функции поиска решения.
- Вполне вероятно, что расчеты могут показаться неправильными, либо возникнет желание немного изменить исходные данные и получить другой результат. В этом случае нужно снова открыть окно с параметрами поиска решения и внимательно посмотреть поля с введенными данными.
- Если с данными все нормально, можно попробовать задействовать другой метод решения. Для этого щелкаем по текущему варианту и из раскрывшегося перечня выбираем способ, который нам кажется наиболее подходящим:
- Первый – ищет решение методом обобщенного приведенного градиента (ОПГ) для нелинейных задач. Стандартно выбран именно этот вариант, но можно попробовать и другие.
- Второй – пытается отыскать решение для линейных задач, используя симплекс-метод.
- Третий – для выполнения поставленной задачи использует эволюционный поиск.
- В том случае, если ни один из методов не принес удовлетворительных результатов, стоит проверить данные в таблице и параметрах еще раз, поскольку именно это является самой частой ошибкой в подобного рода задачах.
- Теперь, когда мы получили требуемую скидку, осталось ее применить, чтобы рассчитать суммы скидок по всем наименованиям. Для этого отмечаем первую ячейку столбца “Сумма скидки”, пишем в ней формулу “=D2*$G$2” и нажимаем Enter. Знаки доллара ставятся для того, чтобы при растягивании/копировании формулы на другие строки, ячейка G2 со скидкой оставалась неизменной в расчетах.
- Мы получили сумму скидки для первого наименования. Теперь наводим курсор на нижний правый угол ячейки с результатом, как только он поменяет форму на крестик, зажав левую кнопку мыши растягиваем формулу на все строки, по которым хотим посчитать аналогичную сумму.
- Теперь наша таблица полностью готова в соответствии с поставленной задачей.
Подготовка оптимизационной модели в MS EXCEL
Поиск решения оптимизирует значение целевой функции. Под целевой функцией подразумевается формула, возвращающая единственное значение в ячейку. Результат формулы должен зависеть от переменных модели (не обязательно напрямую, можно через результат вычисления других формул). Ограничения модели могут быть наложены как на диапазон варьирования самих переменных, так и на результаты вычисления других формул модели, зависящих от этих переменных. Все ячейки, содержащие переменные и ограничения модели должны быть расположены только на одном листе книги. Ввод параметров в диалоговом окне Поиска решения возможен только с этого листа. Целевая функция (ячейка) также должна быть расположена на этом листе. Но, промежуточные вычисления (формулы) могут быть размещены на других листах.
Совет . Организуйте данные модели так, чтобы на одном листе MS EXCEL располагалась только одна модель. В противном случае, для выполнения расчетов придется постоянно сохранять и загружать настройки Поиска решения (см. ниже).
Приведем алгоритм работы с Поиском решения , который советуют сами разработчики ( ]]> www.solver.com ]]> ):
- Определите ячейки с переменными модели (decision variables);
- Создайте формулу в ячейке, которая будет рассчитывать целевую функцию вашей модели (objective function);
- Создайте формулы в ячейках, которые будут вычислять значения, сравниваемые с ограничениями (левая сторона выражения);
- С помощью диалогового окна Поиск решения введите ссылки на ячейки содержащие переменные, на целевую функцию, на формулы для ограничений и сами значения ограничений;
- Запустите Поиск решения для нахождения оптимального решения.
Проделаем все эти шаги на простом примере.
Обзор и возможности функции
Надстройка «Поиск решений» — специфическая возможность Excel 2007, 2010, 2013, 2016, которая предназначена для работы с формулой при наличии определённых условий. Описать её логику можно следуя принципу «что если?». То есть, просчитать изменение конечной ячейки при условии изменения других. Хотя и звучит это сложно, но описать данный принцип удобнее на конкретном примере: как будет изменяться остаток средств в конце месяца, если изменить разные статьи расходов.
Ожидать, что функция сработает в обратном порядке можно, но для этого потребуется изменять формулу и вводные данные для этой формулы. Фактически Excel следует строгой логике и сама по себе функция не решит проблему, но поможет прийти к корректному решению подбором или перебором вводных данных.
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:
Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).
Пример использования поиска решений
Теперь перейдем к самой функции.
1) Чтобы включить «Поиск решений», выполните следующие шаги:
- нажмите «Параметры Excel», а затем выберите категорию «Надстройки»;
- в поле «Управление» выберите значение «Надстройки Excel» и нажмите кнопку «Перейти»;
- в поле «Доступные надстройки» установите флажок рядом с пунктом «Поиск решения» и нажмите кнопку ОК.


2) Теперь упорядочим данные в виде таблицы, отражающей связи между ячейками. Советуем использовать цветовые обозначения: на примере красным выделена целевая функция, бежевым — ограничения, а желтым — изменяемые ячейки.

Не забудьте ввести формулы. Стоимость заказа рассчитывается как «Оплата труда за 1 изделие» умножить на «Число заготовок, передаваемых в работу». Для того, чтобы узнать «Время на выполнение заказа», нужно «Число заготовок, передаваемых в работу» разделить на «Производительность».


3) Выделите целевую ячейку, которая должна показать максимум, минимум или определенное значение при заданных условиях. Для этого на панели нажмите «Данные» и выберете функцию «Поиск решений» (обычно она в верхнем правом углу).

4) Заполните параметры «Поиска решений» и нажмите «Найти решение».
Совокупная стоимость 1000 изделий рассчитывается как сумма стоимостей количества изделий от каждого работника. Данная ячейка (Е13) — это целевая функция. D9:D12 — изменяемые ячейки. «Поиск решений» определяет их оптимальные значения, чтобы целевая функция достигла минимума при заданных ограничениях.
В нашем примере следующие ограничения:
- общее количество изделий 1000 штук ($D$13 = $D$3);
- число заготовок, передаваемых в работу — целое и больше нуля либо равно нулю ($D$9:$D$12 = целое, $D$9:$D$12 > = 0);
- количество дней меньше либо равно 30 ($F$9:$F$12 < = $D$6, либо как в примере в ячейке F13 задать функцию МАКС(F9:F12) и поставить ограничение $F$13 < = $D$6).

5) В конце проверьте полученные данные на соответствие заданному целевому значению. Если что-то не сходится — нужно пересмотреть исходные данные, введенные формулы и ограничения.

Хотите научиться решать задачи в Excel, как это делают в компаниях-лидерах? Приходите на наш онлайн-курс, на котором вы освоите этот инструмент на уровне профи. Вашими преподавателями будут эксперты-практики, а после обучения вы сможете дополнить резюме весомой строчкой. Регистрируйтесь!
Подготовка таблицы
Теперь, после того, как мы активировали функцию, давайте разберемся, как она работает. Легче всего это представить на конкретном примере. Итак, у нас есть таблица заработной платы работников предприятия. Нам следует рассчитать премию каждого работника, которая является произведением заработной платы, указанной в отдельном столбце, на определенный коэффициент. При этом, общая сумма денежных средств, выделяемых на премию, равна 30000 рублей. Ячейка, в которой находится данная сумма, имеет название целевой, так как наша цель подобрать данные именно под это число.
Коэффициент, который применяется для расчета суммы премии, нам предстоит вычислить с помощью функции Поиска решений. Ячейка, в которой он располагается, называется искомой.
Целевая и искомая ячейка должны быть связанны друг с другом с помощью формулы. В нашем конкретном случае, формула располагается в целевой ячейке, и имеет следующий вид: «=C10*$G$3», где $G$3 – абсолютный адрес искомой ячейки, а «C10» — общая сумма заработной платы, от которой производится расчет премии работникам предприятия.
Теги
Почему в Экселе вместо цифр значки решеточки
Как Убрать Решетки в Excel Вместо Цифр
Excel
В этой статье – как убрать решетки в excel вместо цифр.
Решетки вместо цифр появляются, когда количество символов в ячейке не может быть отображено.
Также решетки могут быть:
- из-за неправильно набранной формулы
- если есть некорректные расчеты в ссылающихся ячейках
- если есть ошибки в тексте
- ошибка в программе (Можно проверить так – установите курсор в эту ячейку. Если в строке формул всё отображается, то решетка из-за большого количества символов.)
Как убрать решетки в excel вместо цифр
Убрать решетки в эксель можно разными способами:
Способ 1 – вручную расширить границы ячейки
Это самый простой способ решения проблемы.
- откройте документ excel
- кликните по ячейке с решеткой
- наведите курсор мыши, на правую границу названия столбца
- когда курсор будет в виде двухсторонней стрелки, нажмите на границу и перемещайте вправо до тех пор пока вместо решеток не появятся все символы
Способ 2 – уменьшить шрифт
Данный метод лучше всего применять, если размер шрифта не важен в вашей таблице.
- выделите ячейку или несколько ячеек с решетками
- на вкладке “Главная” найдите раздел “Шрифт“
- в поле “Размера шрифта” установите меньшее значение шрифта
Способ 3 – автоподбор ширины столбца
Если решетки есть в нескольких столбцах, примените данный метод.
- выделите диапазон ячеек, в которых надо убрать решетки
- на вкладке “Главная” в разделе “Ячейки” нажмите на команду “Формат“
- в списке кликните по команде “Автоподбор ширины столбца“
Способ 4 – изменить формат ячейки
Если в ячейке был установлен Текстовый формат, также можете попробовать этот метод.
- кликните по ячейке с текстовым форматом
- на вкладке “Главная” найдите раздел “Число“
- в поле “Числовой формат” вместо “Текстовый” выберите “Общий“
Видео – как убрать решетки в excel вместо цифр
Чтобы узнать как в Excel убрать решетки, вы можете посмотреть
Другие статьи по теме Excel
Кроме этой статьи, вы можете прочитать другие статьи на сайте. Здесь вы найдёте много интересного о работе в программе Excel и других программах.
Приглашаем в наш канал на youtube:
Видеокурсы по обучению программе Excel
- Excel: эффективная обработка массивов данных –
Чтобы не пропустить новые статьи, добавьте наш сайт в закладки.
Была ли эта информация полезной? Оставьте комментарий и поделитесь с друзьями.
Решетки вместо цифр в Excel. Что делать, если вместо цифр отображаются решетки в Эксель
Часто случается, что при вводе данных в программу Microsoft Excel вместо определенных цифр отображаются спецсимволы, например, решетки. Такое обстоятельство препятствует нормальной работе с электронным документом, поэтому нужно знать, как можно устранить данную неполадку. В этой статье представлено несколько эффективных способов для оперативного решения проблемы.
Причины появления решеток
Решетки в ячейках появляются, когда количество символов, введенное в них, превышает лимит. При этом программа запоминает данные, которые вы вводили, однако корректно отображать их не будет до тех пор, пока не будет удалено лишнее количество знаков. Если при вводе цифр в ячейку Excel 2003 превышено количество 255 единиц, то вместо чисел будет отображаться октоторп. Именно так называется решетка на языке программирования.
Таким же образом покажет себя текст, если ввести его в ячейку более свежей версии. Максимально допустимое количество букв, которые разрешается прописывать в поле Excel 2007 — 1024. Это характерно для продуктов Excel до 2010 года. Более новые версии уже не предусматривают лимит. Также причинами могут стать:
- наличие грамматических ошибок в тексте или недопустимых символов;
- ошибочно посчитанные суммы;
- неправильное применение формул и некорректные расчеты в ячейках;
- сбои на программном уровне (определяется это следующим путем: если при наведении курсора на ячейку все отображается корректно, а при нажатии на «Enter» значение превращается в октоторп, значит дело все-таки в лишнем количестве символов).
Обратите внимание! Появление решеток в полях Excel может быть следствием неправильно установленной раскладки клавиатуры.
Также подобная проблема может появится, если для суммирования данных были выбраны неправильные наименования ячеек. Решить проблему с отображением личных данных можно с помощью нескольких действенных способов.
Решение проблемы
Простого удаления лишнего количества символов бывает недостаточно. Придется воспользоваться методами, которые заставляют исчезнуть некорректные символы. Будем двигаться от более простых к сложным.
Способ 1: ручное расширение границ
Чтобы расширить границы в Microsoft Excel, достаточно их растянуть вручную. Это надежный и простой способ, который поможет решить проблему даже новичкам, которые впервые воспользовались функционалом офисного приложения. Следуйте инструкции:
- В открывшемся окне Microsoft Excel кликаем по той ячейке, в которой появились решетки.
- Наводим курсор на правую границу, где установлено название ячейки. Границы ячейки могут растягиваться и влево, но при таком направлении ячейки, расположенные впереди, будут смещаться.
- Ждем, когда курсор приобретет вид двухсторонней стрелочки. Затем нажимаем на границу и тянем до того положения, пока не покажутся все символы.
- По окончанию процедуры все решетки отобразятся в виде введенных ранее цифр.
Данный способ работает для всех версий Excel.
Способ 2: уменьшение шрифта
Первый вариант решения проблемы более подходит для тех случаев, когда на листе занято всего 2-3 столбика и данных не много. Но чтобы исправить спецсимволы в электронной книге масштабно, необходимо воспользоваться инструкцией ниже.
- Выделяем ячейку или диапазон ячеек, в которых хотим визуализировать числовые данные.
- Убеждаемся в том, что находимся во вкладке «Главная», если нет, то кликаем по ней в верхней части страницы. В разделе «Шрифт» находим его размер и уменьшаем до тех пор, пока нужное количество символов не отобразится в ячейках в требуемом цифровом формате. Для изменения шрифта можно просто прописать предполагаемый размер в соответствующем поле.
На заметку! При редактировании шрифта и изменении формата ячейка примет ту ширину, которой соответствует самое длинное числовое значение, которое записано внутри нее.
Способ 3: автоподбор ширины
Изменение шрифта в ячейках доступно и способом, который описан ниже. Он подразумевает подбор ширины с помощью встроенных инструментов Microsoft Excel.
- Необходимо выделить диапазон ячеек, которые нуждаются в форматировании (то есть те, которые содержат некорректные символы вместо цифр). Далее следует кликнуть правой кнопкой мыши по выделенному фрагменту и во всплывающем окне найти инструмент «Формат ячеек». В более ранних версиях Excel меню может менять расположение инструментов.
- В появившемся окне выбираем раздел «Выравнивание». Мы будем работать с ним и в дальнейшем, затем проставляем галочку напротив записи «Автоподбор ширины». Она находится снизу в блоке «Отображение». В конце нажимаем на кнопку «ОК». После проделанных действий значения уменьшаются и приобретают формат, соответствующий размеру окошка в электронной книге.
Данная методика очень удобна и отличается своей оперативностью. Оформить лист Excel должным образом можно всего за считанные секунды.
Обратите внимание! Все способы редактирования допустимы только в том случае, если вы являетесь автором файла или он открыт для редактирования.
Способ 4: смена числового формата
Данный метод подходит исключительно тем, кто пользуется старой версией Microsoft Excel. Дело в том, что на введение цифр есть лимит, как говорилось в начале статьи. Рассмотрим процесс исправления пошагово:
- Выделяем ячейку или диапазон ячеек, которые нуждаются в форматировании. Далее кликаем по ним правой кнопкой мыши. В появившемся перечне функций находим инструмент «Формат ячеек», делаем по нему клик.
- После нажимаем на вкладку «Число», видим, что там установлен формат «Текстовый». Меняем его на «Общий» в подразделе «Числовые форматы». Для этого кликаем по последнему и подтверждаем свое действие нажатием на кнопку «ОК» в нижней части окна форматирования.
Обратите внимание! В обновленных версиях Excel формат «Общий» устанавливается по умолчанию.
После того, как данное ограничение будет снято, все числа отобразятся в нужном формате. После проделанной манипуляции можно сохранять файл. После повторного открытия все ячейки будут отображаться в корректном виде.
Изменить числовой формат можно еще одним удобным способом:
- Для этого войдите в файл табличного процессора Excel, где некорректным образом обозначены числовые значения, перейдите во вкладке «Главная» к разделу «Число».
- Кликните по стрелке, чтобы вызвать выпадающий список и поменяйте установленный режим с «Текстового» на «Общий».
- Отформатировать одну из ячеек, в которой присутствует некоторое количество решеток, можно в одиночном порядке, не прибегая к выбору форматов для всего листа. Для это кликаем по нужном окошку, жмем правой кнопкой мыши.
- Во всплывающем окне находим инструмент «Формат с разделителями», кликаем по нему.
- Далее все параметры необходимо изменить так, как было описано в предыдущем методе.
На заметку! Чтобы быстро выполнить переход к форматам ячеек, достаточно воспользоваться комбинацией клавиш «CTRL+1». Здесь легко внести изменения, как для одной конкретной ячейки, так и для целого диапазона.
Чтобы убедиться в правильности выполненных действий, рекомендуем ввести текстовые или числовые символы в большом количестве. Если после исчерпания лимита решетки не появились, соответственно, вы все сделали верно.
Способ 5: меняем формат ячейки
Сменить формат ячейки для корректного отображения символов возможно с помощью нескольких инструментов, по умолчанию задействованных в табличном процессоре Microsoft Excel. Рассмотрим данным метод более подробно:
- Для начала следует выделить проблемную ячейку, затем кликнуть по ней правой кнопкой мыши. Всплывает меню, в котором необходимо нажать «Формат ячеек». Форматирование ячеек выполняется только в «Числовой» вид, если в книге предусмотрены цифры.
- В открывшемся блоке «Число» из списка выбираем тот формат, которому будет соответствовать введенное значение в ячейках. В данном примере рассмотрен «Денежный» формат. После выбора подтверждаем свои действия нажатием на кнопку «ОК» в нижней части окна настроек. В случае, если нужно, чтобы в числах появилась запятая, необходимо кликнуть по варианту форматирования «Финансовый».
- Если вы не нашли в списке подходящий вариант для форматирования, попробуйте вернуться на страницу «Главная» и перейти в раздел «Число». Здесь следует открыть список с форматами, а в самом низу нажать на «Другие числовые форматы», как показано на скриншоте. Запустив данную опцию, произойдет перемещение к уже знакомым нам настройкам изменения формата ячеек.
Если ни один из способов не помог, можно попробовать вводить значения не в ячейку, а в строку, расположенную под панелью управления электронной книгой Microsoft Excel. Достаточно кликнуть по ней и начать вводить нужные данные.
Заключение
В большинстве случаев отображение решеток вместо числовых или буквенных выражений в ячейках программы Microsoft Excel не является ошибкой. В основном подобное отображение символов зависит исключительно от действий пользователя, поэтому важно обращать внимание на соблюдение лимита при использовании более старых версий табличного процессора.
Что делать, если вместо цифр отображаются решетки в Эксель
Во время работы в Эксель многие пользователи могут столкнуться с ситуацией, когда вместо набранных цифр в ячейке отображаются решетки (#), что делает невозможным дальнейшую работу с ними. В данной статье мы выясним, почему так происходит, и как это исправить.
Причина появления решеток и методы устранения проблемы
Довольно часто содержимое ячейки не умещается в ее текущих границах. И когда слишком длинным оказывается какое-то число, вместо него отображаются символы решетки (#) или, другими словами, октоторп. При этом программа хранит в памяти реальные значения, которые используются при расчетах, но из-за такого визуального представления даных, их невозможно идентифицировать, следовательно, работать с ними становится затруднительно или даже невозможно. В данном случае, просмотреть полное содержимое ячейки, конечно же, можно в строке формул, но это, вряд ли, можно назвать оптимальным решением.
Примечание: в более ранних версиях программы подобные решетки появлялись, в том числе, при наборе текста, который содержал более 1024 символов. Правда, с версии 2010 такое не наблюдается.
Итак, теперь, когда мы выяснили, почему появляются решетки, давайте разберемся, как их убрать.
Метод 1: сдвигаем границу ячейки вручную
Для начала рассмотрим, пожалуй, самый простой метод, который позволяет решить проблему путем сдвига границы ячеек.
- На горизонтальной панели координат наводим указатель мыши на правую границу столбца, который хотим расширить. Когда появится характерный плюсик со стрелками в обе стороны, зажав левую кнопку мыши тянем линию границы вправо.
- Отпустив кнопку мыши мы должны увидеть содержимое ячейки. Если этого не произошло, и до сих пор отображаются решетки, значит мы недостаточно сдвинули границу и нужно повторить первое действие.
Метод 2: выравниваем границу по содержимому ячейки
Здесь нам не придется вручную двигать границу, пытаясь угадать ее новое расположение, которе позволит отобразить содержимое ячейки. Дело в том, что в Excel существует возможность выполнить данное действие автоматически.
- Также, наводим указатель мыши на правую границу столбца, который хотим расширить (на горизонтальной панели координат), затем вместо захвата и сдвига линии границы просто дважды щелкаем по ней.
- Ширина столбца автоматически подстроится под содержимое ячейки.
Примечание: если данное действие будет выполнено в отношении столбца с ячейками, содержащими данные разной длины, ширина столбца подстроится под ячейку, содержащую наибольшее количество символов.
Метод 3: уменьшаем размер шрифта
Данный метод подойдет, если нет возможности сдвинуть границы ячеек, или когда их слишком много. В подобных ситуациях можно попробовать уменьшить размер шрифта. Рассмотрим на примере одного столбца.
- Для начала нужно выделить диапазон, внутри которого планируется уменьшение шрифта.
- Переключаемся во вкладку “Главная” (если мы не в ней), щелкаем по стрелке вниз рядом с текущим размером шрифта (группа инструментов “Шрифт”) и в раскрывшемся списке выбираем значение поменьше, которое, по-нашему мнению, позволит вместить все содержимое в ячейке.
Также, размер шрифта можно сразу указать в поле для ввода значений, предварительно щелкнув внутри него.
- Все готово, не сдвигая границу столбца, нам удалось сделать данные видимыми.
Если после уменьшения шрифта мы, по-прежнему, видим решетки, пробуем выбрать значение еще меньше.
Метод 4: используем автоподбор ширины
Способ также позволяет изменить размер шрифта в ячейках, однако, в данном случае, он будет разным, в зависимости от количества символов. Использоваться будет форматирование ячеек.
- Производим выделение области, для которой нужно настроить размер шрифта. Щелчком правой кнопки мыши по ней открываем меню, в котором кликаем по пункту “Формат ячеек”.
- В появившемся окне “Формат ячеек” переключаемся во вкладку “Выравнивание”. В блоке параметров “Отображение” ставим галочку напротив опции “автоподбор ширины”, после чего жмем OK.
- В результате, размер шрифта в ячейках уменьшиться (для каждой ячейки по-разному, в зависимости от количества символов), что позволит сделать всю информацию видимой.
Метод 5: меняем формат ячейки
Ранее мы уже упомянули о том, что в более ранних версиях программы решетки могли отображаться и при слишком длинном тексте. Для решения проблемы нужно поменять формат ячейки с “текстового” на “общий”. Сделать это можно:
- В окне форматирования (вкладка “Число”), которое открывается выбором пункта “Формат ячеек” в контекстном меню ячейки.
- На ленте программы, во вкладке “Главная”, группа инструментов “Число”.
Заключение
Решетки в таблице Excel вовсе не означают наличие какой-либо ошибки. Они лишь дают пользователю понять, что ширины ячейки недостаточно, чтобы отобразить все ее содержимое при заданном размере шрифта. В данном случае можно либо сдвинуть границы, либо уменьшить шрифт.
Почему в Excel вместо числа появляется решетка?
Решетки в ячейках появляются, когда количество символов, введенное в них, превышает лимит. … Если при вводе цифр в ячейку Excel 2003 превышено количество 255 единиц, то вместо чисел будет отображаться октоторп. Именно так называется решетка на языке программирования.
Как в Экселе убрать решетки вместо цифр?
Что делать, если вместо цифр отображаются решетки в Эксель
- Метод 1: сдвигаем границу ячейки вручную
- Метод 2: выравниваем границу по содержимому ячейки
- Метод 3: уменьшаем размер шрифта
- Метод 4: используем автоподбор ширины
- Метод 5: меняем формат ячейки
Почему в Экселе вместо числа?
Решение проблемы отображения числа как даты Единственной причиной, почему данные в ячейке могут отображаться как дата, является то, что в ней установлен соответствующий формат. Таким образом, чтобы наладить отображение данных, как ему нужно, пользователь должен его поменять.
Как убрать решетку в Excel?
Для того чтобы убрать сетку таблицы Excel существует еще два способа: Настройки программы. «Файл»-«Параметры»-«Дополнительно»-«Параметры для следующего листа:» убираем галочку с опции «показывать сетку».
Почему Excel показывает формулу вместо значения?
Причина При связывании ячеек в Microsoft Excel к связанной ячейке применяется формат исходной ячейки. Таким образом, при вводе формулы, которая связывает одну ячейку с ячейкой, которая форматируется как текст, ячейка с формулой также форматируется как текст.
Как убрать цифры в Excel?
1. Выделите ячейки текстовой строки, из которых нужно удалить числа, и нажмите Kutools > Текст > Удалить символы. 2. В открывшемся диалоговом окне «Удалить символы» установите флажок Числовой и нажмите Ok кнопку.
Как написать несколько строк в одной ячейке?
При необходимости ввода в одну ячейку двух или более строк текста, начните ввод текста и в конце строки нажмите сочетание клавиш [Alt] + [Enter]. После этого в этой же ячейке можно начинать вторую строку текста.
Как отключить Автозамену на дату в Excel?
Автозамена числа на дату в Excel 2003
- Нажмите на круглую кнопку меню Excel 2007 (в левом верхнем углу программы).
- Нажмите на «Параметры Excel». …
- Выберите пункт меню Правописание и, справа, нажмите на кнопку Параметры автозамены:
- В появившемся окне снимите отметку с чекбокса «Заменять при вводе» и нажмите на ОК:
Как в Экселе сделать чтобы число не менялось?
Для этого необходимо задать формат ячейки – что в ней будет находиться число, а не цифра. Для этого, щелкаем правой кнопкой мыши по ячейке и выбираем вкладку “Формат ячеек”. В ней выбираем вариант “Текстовый”. Все, после этого в данной ячейке Excel даже набрав цифры с точкой у вас не появится число и месяц.
Что означает ### в Excel?
Приложение Microsoft Excel может отображать в ячейках символы #####, если ширины столбца недостаточно для отображения всего содержимого ячейки. В формулах, возвращающих дату и время как отрицательные значения, также может отображаться строка #####.
Как убрать пунктирную сетку в Excel?
- Выберите лист.
- Перейдите на вкладку Разметка страницы .
- Чтобы отобразить сетку, установите флажок вид в группе Сетка . Чтобы скрыть сетку, снимите флажок Просмотреть в разделе линии сетки .
Почему в ячейке появляются символы решетка или Октоторп Укажите две причины?
Знак решетки ( # ) или, как его правильнее называть, октоторп появляется в тех ячейках на листе Эксель, у которых данные не вмещаются в границы. Поэтому они визуально подменяются этими символами, хотя фактически при расчетах программа оперирует все-таки реальными значениями, а не теми, которые отображает на экране.
Почему Excel показывает формулу а не результат?
Бывает, что введя формулу и нажав клавишу ENTER пользователь видит в ячейке не результат вычисления формулы, а саму формулу. Причина — Текстовый формат ячейки. … Заставить EXCEL интерпретировать введенное в ячейку выражение как формулу, а не как текст — очень просто: нажмите клавишу F2 , затем ENTER (ВВОД) .
Как отобразить в ячейке формула вместо значения?
В меню типичных задач выберите пункт «Параметры Excel». В окне «Параметры Excel» на вкладке «Дополнительно» в группе «Показать параметры для следующего листа» выбери те в списке лист для настройки, а затем активируйте пункт «Показывать формулы, а не их значения». Закройте окно кнопкой «ОК».






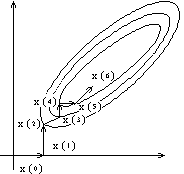
















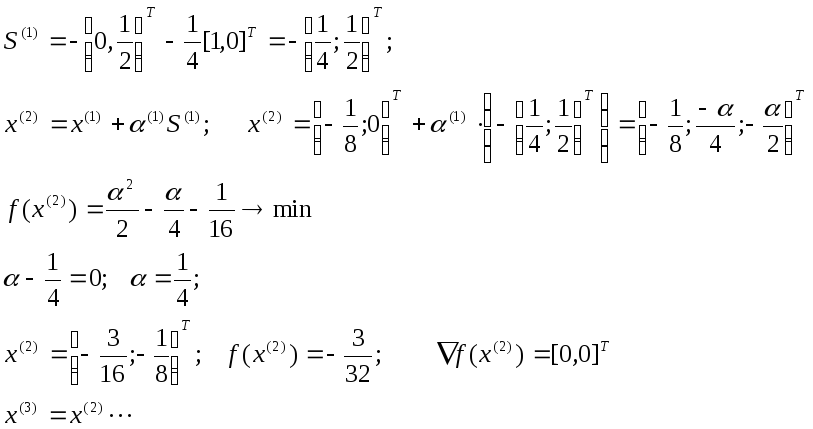


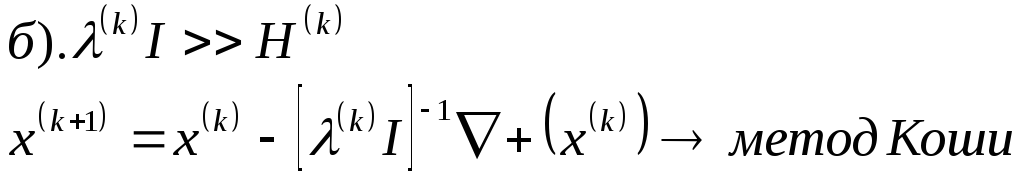

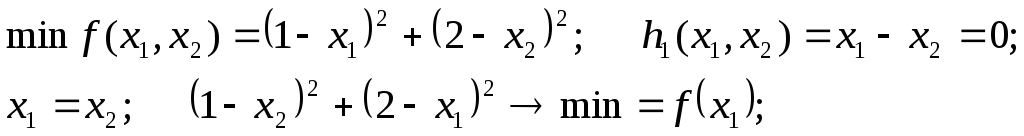















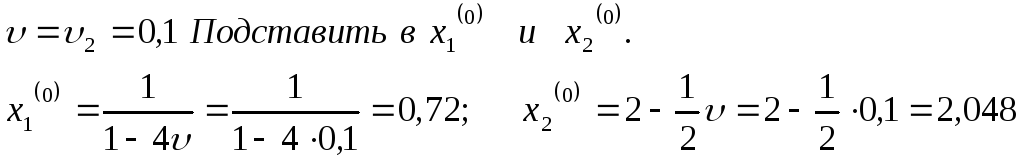













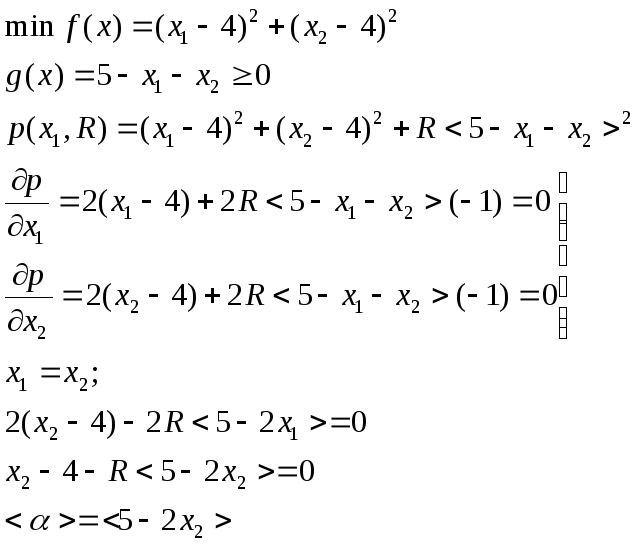














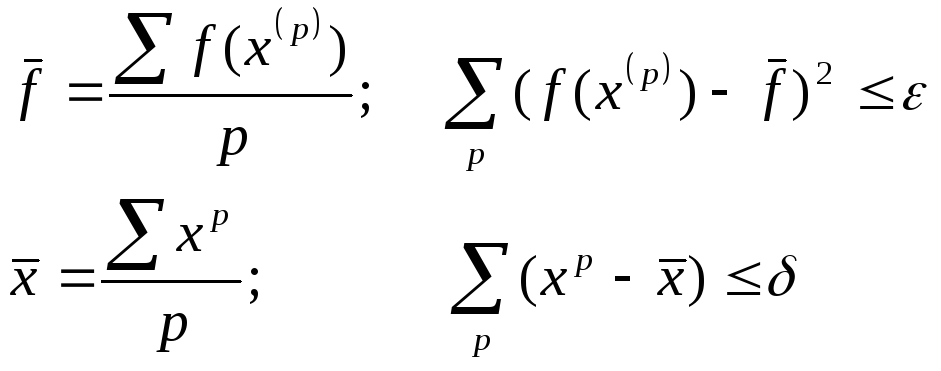






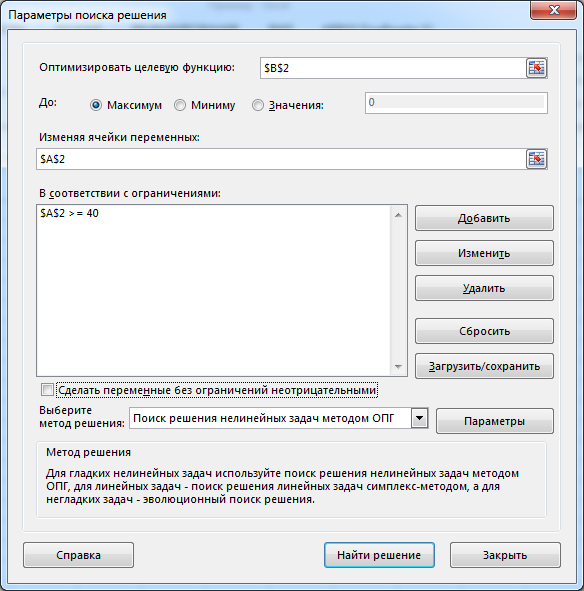
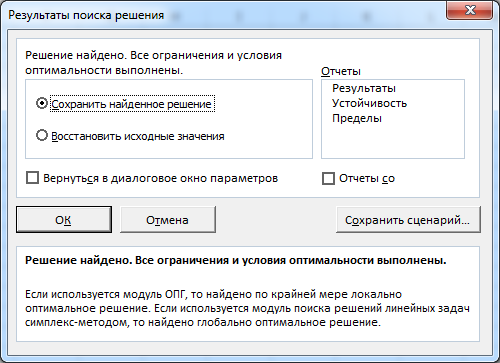















 Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK.
Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK. Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.
Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.







































































 Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK.
Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK. Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.
Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.























 Также, размер шрифта можно сразу указать в поле для ввода значений, предварительно щелкнув внутри него.
Также, размер шрифта можно сразу указать в поле для ввода значений, предварительно щелкнув внутри него.
 Если после уменьшения шрифта мы, по-прежнему, видим решетки, пробуем выбрать значение еще меньше.
Если после уменьшения шрифта мы, по-прежнему, видим решетки, пробуем выбрать значение еще меньше.

