Рассмотрим пример нелинейной оптимизационной экономической задачи, ее экономико-математическую модель и компьютерную реализацию в среде пакета Excel.
Задача (модель) нелинейного программирования (НЛП) формулируется так же, как и общая задача оптимального программирования, со следующими требованиями к целевой функции (ЦФ) и допустимой области: целевая функция /(х,, х2, . хп) и (или) одна из функций ^.(х,, х2. хп) являются нелинейными —
Задачи НЛП несравнимо сложнее задач ЛП, и для них не существует общего, универсального метода решения (аналогично симплексному методу).
Есть целый ряд методов решения задач НЛП, некоторые из них рассмотрены в [25]. В пакете Excel реализован метод множителей Лагранжа [14], идея которого заключается в следующем: задачу условной оптимизации преобразуют в задачу безусловной оптимизации и решают последнюю либо градиентными методами, либо методами Ньютона. Чаще применяются градиентные методы.
Однако необходимо помнить, что существующие методы дают возможность находить только локальные оптимумы (помимо случаев, когда функции обладают соответствующими свойствами выпуклости и вогнутости) [22]. Если же есть подозрение, что в допустимой области целевая функция может иметь несколько оп- тимумов, то эту область следует разбить на ряд областей и в каждой из них определить свои локальные оптимумы, а затем из всех локальных оптимумов выбрать глобальный. При таком подходе задача поиска глобального оптимума сводится к решению ряда задач, в каждой из которых определяется свой (локальный) оптимум.
Следует отметить, что в подавляющем большинстве практических задач оптимизации существует только один оптимум.
Решение задачи НЛП (реализация модели нелинейной оптимизации) средствами Excel отличается от решения ЗЛП следующим:
? назначаются начальные значения искомых переменных x Q j (у = 1, п) так, чтобы ЦФ в начальной точке не была равна нулю:
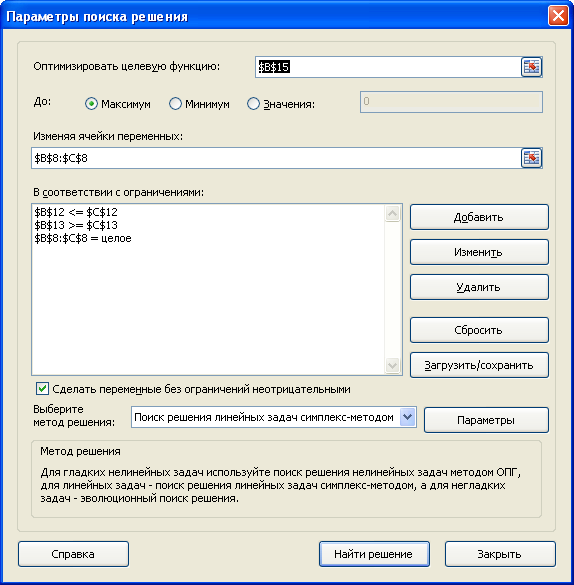
- ? в диалоговом окне Параметры поиска решения не надо ставить флажок Сделать переменные без ограничения неотрицательными;
- ? в поле Выберите метод решения указывается Поиск решения нелинейных задач методом ОПГ.
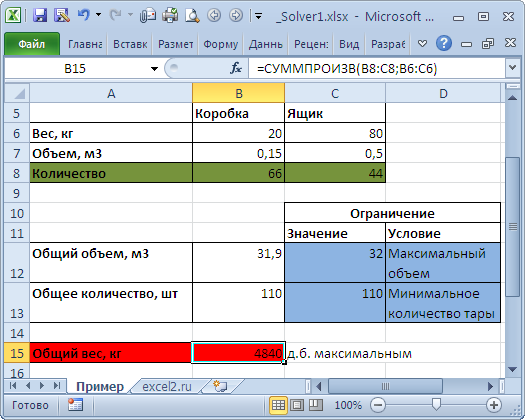
Пример 2.4.6. Задача составления оптимального плана выпуска мебели.
Предприятие может выпускать два вида корпусной мебели. На их изготовление идет древесина трех видов. Запасы древесины на предприятии, нормы их расхода а
(/ = 1,3; j = 1,2), себестоимость Cj и оптовые цены указаны в табл. 2.4.5. Из-за брака в процессе производства расход древесины зависит от объема Xj производства изделий и в первом приближении выражается линейной функцией + Xj, а себестоимость продукции — функцией Cj + 0,Xj. Изделия могут выпускаться в любых соотношениях, так как их сбыт обеспечен. По контракту предприятие обязано выпустить не менее двух комплектов каждого вида мебели. Составить план выпуска изделий, обеспечивающий получение максимальной прибыли.
Запас сырья, м 3
Нормы расхода, м 3 , на изделие вида
«Поиск решения» — это надстройка для Microsoft Excel, которую можно использовать для анализ «что если». С ее помощью можно найти оптимальное значение (максимум или минимум) формула, содержащейся в одной ячейке, называемой целевой, с учетом ограничений на значения в других ячейках с формулами на листе. Надстройка «Поиск решения» работает с группой ячеек, называемых ячейками переменных решения или просто ячейками переменных, которые используются при расчете формул в целевых ячейках и ячейках ограничения. Надстройка «Поиск решения» изменяет значения в ячейках переменных решения согласно пределам ячеек ограничения и выводит нужный результат в целевой ячейке.
Проще говоря, с помощью надстройки «Поиск решения» можно определить максимальное или минимальное значение одной ячейки, изменяя другие ячейки. Например, вы можете изменить планируемый бюджет на рекламу и посмотреть, как изменится планируемая сумма прибыли.
Примечание: В версиях надстройки «Поиск решения», выпущенных до Excel 2007, ячейки переменных решения назывались изменяемыми или регулируемыми. В Excel 2010 надстройка «Поиск решения» была значительно улучшена, так что работа с ней в Excel 2007 будет несколько отличаться.
В приведенном ниже примере количество проданных единиц в каждом квартале зависит от уровня рекламы, что косвенно определяет объем продаж, связанные издержки и прибыль. Надстройка «Поиск решения» может изменять ежеквартальные расходы на рекламу (ячейки переменных решения B5:C5) до ограничения в 20 000 рублей (ячейка F5), пока общая прибыль (целевая ячейка F7) не достигнет максимального значения. Значения в ячейках переменных используются для вычисления прибыли за каждый квартал, поэтому они связаны с формулой в целевой ячейке F7, =СУММ (Q1 Прибыль:Q2 Прибыль).
1. Ячейки переменных
2. Ячейка с ограничениями
3. Целевая ячейка
После выполнения процедуры получены следующие значения.
На вкладке Данные в группе Анализ нажмите кнопку Поиск решения.
Примечание: Если команда Поиск решения или группа анализ недоступна, вам нужно активировать надстройка «Поиск решения». Сведения о том, как активировать надстройку «Поиск решения».
В поле Оптимизировать целевую функцию введите ссылка на ячейку или имя целевой ячейки. Целевая ячейка должна содержать формулу.
Выполните одно из следующих действий.
Чтобы значение целевой ячейки было максимальным из возможных, установите переключатель в положение Макс.
Чтобы значение целевой ячейки было минимальным из возможных, установите переключатель в положение Мин.
Чтобы задать для целевой ячейки конкретное значение, установите переключатель в положение Значение и введите в поле нужное число.
В поле Изменяя ячейки переменных введите имена диапазонов ячеек переменных решения или ссылки на них. Несмежные ссылки разделяйте запятыми. Ячейки переменных должны быть прямо или косвенно связаны с целевой ячейкой. Можно задать до 200 ячеек переменных.
В поле В соответствии с ограничениями введите любые ограничения, которые требуется применить. Для этого выполните указанные ниже действия.
В диалоговом окне Параметры поиска решения нажмите кнопку Добавить.
В поле Ссылка на ячейку введите ссылку на ячейку или имя диапазона ячеек, на значения которых налагаются ограничения.
Щелкните отношение ( =, >=, int, binили DIF ), которое вы хотите использовать между указанной ячейкой и ограничением. Если в поле « ограничение » выбрано значение « int», это значит. Если щелкнуть ячейку, в поле ограничение появится двоичный файл . Если выбрать параметр DIF, аллдифферент отображается в поле ограничение .
Если в поле Ограничение было выбрано отношение =, введите число, ссылку на ячейку (или имя ячейки) или формулу.
Выполните одно из указанных ниже действий.
Чтобы принять данное ограничение и добавить другое, нажмите кнопку Добавить.
Чтобы сохранить ограничение и вернуться в диалоговое окно Параметры поиска решения, нажмите кнопку ОК.
Примечание Отношения int, binи DIF можно применять только в ограничениях ячеек переменной решения.
Чтобы изменить или удалить существующее ограничение, выполните указанные ниже действия.
В диалоговом окне Параметры поиска решения щелкните ограничение, которое требуется изменить или удалить.
Нажмите кнопку Изменить и внесите изменения либо нажмите кнопку Удалить.
Нажмите кнопку Найти решение и выполните одно из указанных ниже действий.
Чтобы сохранить значения решения на листе, в диалоговом окне Результаты поиска решения выберите вариант Сохранить найденное решение.
Чтобы восстановить исходные значения перед нажатием кнопки Найти решение, выберите вариант Восстановить исходные значения.
Вы можете прервать поиск решения, нажав клавишу ESC. Лист Excel будет пересчитан с учетом последних найденных значений для ячеек переменных решения.
Чтобы создать отчет, основанный на найденном решении, выберите тип отчета в поле Отчеты и нажмите кнопку ОК. Отчет будет помещен на новый лист книги. Если решение не найдено, будут доступны только некоторые отчеты или они вообще не будут доступны.
Чтобы сохранить значения ячейки переменной решения в качестве сценария, который можно будет отобразить позже, нажмите кнопку Сохранить сценарий в диалоговом окне Результаты поиска решения, а затем введите имя этого сценария в поле Название сценария.
После постановки задачи нажмите кнопку Параметры в диалоговом окне Параметры поиска решения.
Чтобы просмотреть значения всех найденных решений, в диалоговом окне Параметры установите флажок Показывать результаты итераций и нажмите кнопку ОК.
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение.
В диалоговом окне Показать предварительное решение выполните одно из указанных ниже действий.
Чтобы остановить поиск решения и вывести на экран диалоговое окно Результаты поиска решения, нажмите кнопку Стоп.
Чтобы продолжить процесс поиска решения и просмотреть следующий вариант решения, нажмите кнопку Продолжить.
В диалоговом окне Параметры поиска решения нажмите кнопку Параметры.
В диалоговом окне на вкладках Все методы, Поиск решения нелинейных задач методом ОПГ и Эволюционный поиск решения выберите или введите значения нужных параметров.
В диалоговом окне Параметры поиска решения нажмите кнопку Загрузить/сохранить.
Введите диапазон ячеек для области модели и нажмите кнопку Сохранить или Загрузить.
При сохранении модели введите ссылку на первую ячейку вертикального диапазона пустых ячеек, в котором следует разместить модель оптимизации. При загрузке модели введите ссылку на весь диапазон ячеек, содержащий модель оптимизации.
Совет: Чтобы сохранить последние параметры, настроенные в диалоговом окне Параметры поиска решения, вместе с листом, сохраните книгу. Каждый лист в книге может иметь свои параметры надстройки «Поиск решения», и все они сохраняются. Кроме того, для листа можно определить более одной задачи, если нажимать кнопку Загрузить или сохранить для сохранения задач по отдельности.
В диалоговом окне Параметры поиска решения можно выбрать любой из указанных ниже алгоритмов или методов поиск решения.
Нелинейный метод обобщенного понижающего градиента (ОПГ). Используется для гладких нелинейных задач.
Симплекс-метод. Используется для линейных задач.
Эволюционный метод Используется для негладких задач.
Важно: Сначала нужно включить надстройку «Поиск решения». Дополнительные сведения см. в статье Загрузка надстройки «Поиск решения».
В приведенном ниже примере количество проданных единиц в каждом квартале зависит от уровня рекламы, что косвенно определяет объем продаж, связанные издержки и прибыль. Надстройка «Поиск решения» может изменять ежеквартальные расходы на рекламу (ячейки переменных решения B5:C5) до ограничения в 20 000 рублей (ячейка D5), пока общая прибыль (целевая ячейка D7) не достигнет максимального значения. Значения в ячейках переменных используются для вычисления прибыли за каждый квартал, поэтому они связаны с формулой в целевой ячейке D7, =СУММ (Q1 Прибыль:Q2 Прибыль).
В результате выполнения получены следующие значения:
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
В разделе Оптимизировать целевую функцию, введите ссылка на ячейку или имя целевой ячейки.
Примечание: Целевая ячейка должна содержать формулу.
Выполните одно из указанных ниже действий.
Сделать так, чтобы значение целевой ячейки было максимальным из возможных
Выберите значение Макс.
Сделать так, чтобы значение целевой ячейки было минимальным из возможных
Выберите значение Мин.
Сделать так, чтобы целевая ячейка имела определенное значение
Щелкните Значение, а затем введите нужное значение в поле.
В поле Изменяя ячейки переменных введите имена диапазонов ячеек переменных решения или ссылки на них. Несмежные ссылки разделяйте запятыми.
Ячейки переменных должны быть прямо или косвенно связаны с целевой ячейкой. Можно задать до 200 ячеек переменных.
В поле В соответствии с ограничениями введите любые ограничения, которые требуется применить.
Для этого выполните следующие действия:
В диалоговом окне Параметры поиска решения нажмите кнопку Добавить.
В поле Ссылка на ячейку введите ссылку на ячейку или имя диапазона ячеек, на значения которых налагаются ограничения.
Во всплывающем меню =, или >= в поле Ограничение, введите число, имя ячейки, ссылку на нее или формулу.
Примечание: Отношения int, бин и раз можно использовать только в ограничениях для ячеек, в которых находятся переменные решения.
Выполните одно из указанных ниже действий.
Принять ограничение и добавить другое
Нажмите кнопку Добавить.
Принять ограничение и вернуться в диалоговое окно Параметры поиска решения
Нажмите кнопку ОК.
Нажмите кнопку Найти решение и выполните одно из следующих действий:
Сохранить значения решения на листе
В диалоговом окне Результаты поиска решения выберите вариант Сохранить найденное решение.
Восстановить исходные значения
Щелкните Восстановить исходные значения.
Чтобы прервать поиск решения, нажмите клавишу ESC. Лист Excel будет пересчитан с учетом последних найденных значений для ячеек переменных.
Чтобы создать отчет, основанный на найденном решении, выберите тип отчета в поле Отчеты и нажмите кнопку ОК. Отчет будет помещен на новый лист книги. Если решение не найдено, отчет не будет доступен.
Чтобы сохранить значения ячейки переменной решения в качестве сценария, который можно будет отобразить позже, нажмите кнопку Сохранить сценарий в диалоговом окне Результаты поиска решения, а затем введите имя этого сценария в поле Название сценария.
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
После постановки задачи нажмите кнопку Параметры в диалоговом окне Параметры поиска решения.
Чтобы просмотреть значения всех предварительных решений, установите флажок Показывать результаты итераций и нажмите кнопку ОК.
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение.
В диалоговом окне Показать предварительное решение выполните одно из следующих действий:
Остановить поиск решения и вывести на экран диалоговое окно Результаты поиска решения
Нажмите кнопку Стоп.
Продолжить поиск и просмотреть следующее предварительное решение
Нажмите кнопку Продолжить.
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
Нажмите кнопку Параметры, а затем в диалоговом окне Параметры или Поиск решения выберите один или несколько из следующих вариантов:
Настроить время решения и число итераций
На вкладке Все методы в разделе Пределы решения в поле Максимальное время (в секундах) введите количество секунд, в течение которых можно будет искать решение. Затем в поле Итерации укажите максимальное количество итераций, которое вы хотите разрешить.
Примечание: Если будет достигнуто максимальное время поиска решения или количество итераций, а решение еще не будет найдено, средство «Поиск решения» выведет диалоговое окно Показать предварительное решение.
На вкладке Все методы введите в поле Точность ограничения нужное значение погрешности. Чем меньше число, тем выше точность.
Задать степень сходимости
На вкладке Поиск решения нелинейных задач методом ОПГ или Эволюционный поиск решения в поле Сходимость укажите, насколько должны отличаться результаты последних пяти итераций, чтобы средство прекратило поиск решения. Чем меньше число, тем меньше должно быть изменение.
Нажмите кнопку ОК.
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение или Закрыть.
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
Щелкните Загрузить/сохранить, укажите диапазон ячеек для области модели и нажмите кнопку Сохранить или Загрузить.
При сохранении модели введите ссылку на первую ячейку вертикального диапазона пустых ячеек, в котором следует разместить модель оптимизации. При загрузке модели введите ссылку на весь диапазон ячеек, содержащий модель оптимизации.
Совет: Чтобы сохранить последние параметры, настроенные в диалоговом окне Параметры поиска решения, вместе с листом, сохраните книгу. Каждый лист в книге может иметь свои параметры надстройки «Поиск решения», и все они сохраняются. Кроме того, для листа можно определить более одной задачи, если нажимать кнопку Загрузить/сохранить для сохранения задач по отдельности.
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
Во всплывающем меню Выберите метод решения выберите одно из следующих значений:
Нелинейный метод обобщенного понижающего градиента (ОПГ)
Используется по умолчанию для моделей со всеми функциями Excel, кроме ЕСЛИ, ВЫБОР, ПРОСМОТР и другие ступенчатые функции.
Поиск решения линейных задач симплекс-методом
Используйте этот метод для задач линейного программирования. В формулах модели, которые зависят от ячеек переменных, должны использоваться функции СУММ, СУММПРОИЗВ, +, — и *.
Эволюционный поиск решения
Этот метод, основанный на генетических алгоритмах, лучше всего подходит в том случае, если в модели используются функции ЕСЛИ, ВЫБОР и ПРОСМОТР с аргументами, которые зависят от ячеек переменных.
Примечание: Авторские права на части программного кода надстройки «Поиск решения» версий 1990–2010 принадлежат компании Frontline Systems, Inc. Авторские права на части версии 1989 принадлежат компании Optimal Methods, Inc.
Поскольку надстройки не поддерживаются в Excel в Интернете, вы не сможете использовать надстройку «Поиск решения» для выполнения анализа «что если» для ваших данных, чтобы помочь найти оптимальные решения.
Если у вас есть классическое приложение Excel, вы можете открыть книгу с помощью кнопки Открыть в Excel , чтобы использовать надстройку «Поиск решения».
Дополнительная справка по надстройке «Поиск решения»
За дополнительной справкой по надстройке «Поиск решения» обращайтесь по этим адресам:
Рядовые Systems, Inc.
Поле П.О. 4288
Наклонная деревня, NV 89450-4288
(775) 831-0300
Веб-сайт:
http://www.Solver.com Электронная почта:
Справка по [email protected] поиску по адресу www.Solver.com.
Авторские права на части программного кода надстройки «Поиск решения» версий 1990-2009 принадлежат компании Frontline Systems, Inc. Авторские права на части версии 1989 принадлежат компании Optimal Methods, Inc.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community, попросить помощи в сообществе Answers community, а также предложить новую функцию или улучшение на веб-сайте Excel User Voice.
См. также
Примечание: Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Была ли информация полезной? Для удобства также приводим ссылку на оригинал (на английском языке).
Get expert help now
Don’t have time to figure this out? Our expert partners at Excelchat can do it for you, 24/7.
Одной из самых интересных функций в программе Microsoft Excel является Поиск решения. Вместе с тем, следует отметить, что данный инструмент нельзя отнести к самым популярным среди пользователей в данном приложении. А зря. Ведь эта функция, используя исходные данные, путем перебора, находит наиболее оптимальное решение из всех имеющихся. Давайте выясним, как использовать функцию Поиск решения в программе Microsoft Excel.
Включение функции
Можно долго искать на ленте, где находится Поиск решения, но так и не найти данный инструмент. Просто, для активации данной функции, нужно её включить в настройках программы.
Для того, чтобы произвести активацию Поиска решений в программе Microsoft Excel 2010 года, и более поздних версий, переходим во вкладку «Файл». Для версии 2007 года, следует нажать на кнопку Microsoft Office в левом верхнем углу окна. В открывшемся окне, переходим в раздел «Параметры».
В окне параметров кликаем по пункту «Надстройки». После перехода, в нижней части окна, напротив параметра «Управление» выбираем значение «Надстройки Excel», и кликаем по кнопке «Перейти».
Открывается окно с надстройками. Ставим галочку напротив наименования нужной нам надстройки – «Поиск решения». Жмем на кнопку «OK».
После этого, кнопка для запуска функции Поиска решений появится на ленте Excel во вкладке «Данные».
Подготовка таблицы
Теперь, после того, как мы активировали функцию, давайте разберемся, как она работает. Легче всего это представить на конкретном примере. Итак, у нас есть таблица заработной платы работников предприятия. Нам следует рассчитать премию каждого работника, которая является произведением заработной платы, указанной в отдельном столбце, на определенный коэффициент. При этом, общая сумма денежных средств, выделяемых на премию, равна 30000 рублей. Ячейка, в которой находится данная сумма, имеет название целевой, так как наша цель подобрать данные именно под это число.
Коэффициент, который применяется для расчета суммы премии, нам предстоит вычислить с помощью функции Поиска решений. Ячейка, в которой он располагается, называется искомой.
Целевая и искомая ячейка должны быть связанны друг с другом с помощью формулы. В нашем конкретном случае, формула располагается в целевой ячейке, и имеет следующий вид: «=C10*$G$3», где $G$3 – абсолютный адрес искомой ячейки, а «C10» — общая сумма заработной платы, от которой производится расчет премии работникам предприятия.
Запуск инструмента Поиск решения
После того, как таблица подготовлена, находясь во вкладке «Данные», жмем на кнопку «Поиск решения», которая расположена на ленте в блоке инструментов «Анализ».
Открывается окно параметров, в которое нужно внести данные. В поле «Оптимизировать целевую функцию» нужно ввести адрес целевой ячейки, где будет располагаться общая сумма премии для всех работников. Это можно сделать либо пропечатав координаты вручную, либо кликнув на кнопку, расположенную слева от поля введения данных.
После этого, окно параметров свернется, а вы сможете выделить нужную ячейку таблицы. Затем, требуется опять нажать по той же кнопке слева от формы с введенными данными, чтобы развернуть окно параметров снова.
Под окном с адресом целевой ячейки, нужно установить параметры значений, которые будут находиться в ней. Это может быть максимум, минимум, или конкретное значение. В нашем случае, это будет последний вариант. Поэтому, ставим переключатель в позицию «Значения», и в поле слева от него прописываем число 30000. Как мы помним, именно это число по условиям составляет общую сумму премии для всех работников предприятия.
Ниже расположено поле «Изменяя ячейки переменных». Тут нужно указать адрес искомой ячейки, где, как мы помним, находится коэффициент, умножением на который основной заработной платы будет рассчитана величина премии. Адрес можно прописать теми же способами, как мы это делали для целевой ячейки.
В поле «В соответствии с ограничениями» можно выставить определенные ограничения для данных, например, сделать значения целыми или неотрицательными. Для этого, жмем на кнопку «Добавить».
После этого, открывается окно добавления ограничения. В поле «Ссылка на ячейки» прописываем адрес ячеек, относительно которых вводится ограничение. В нашем случае, это искомая ячейка с коэффициентом. Далее проставляем нужный знак: «меньше или равно», «больше или равно», «равно», «целое число», «бинарное», и т.д. В нашем случае, мы выберем знак «больше или равно», чтобы сделать коэффициент положительным числом. Соответственно, в поле «Ограничение» указываем число 0. Если мы хотим настроить ещё одно ограничение, то жмем на кнопку «Добавить». В обратном случае, жмем на кнопку «OK», чтобы сохранить введенные ограничения.
Как видим, после этого, ограничение появляется в соответствующем поле окна параметров поиска решения. Также, сделать переменные неотрицательными, можно установив галочку около соответствующего параметра чуть ниже. Желательно, чтобы установленный тут параметр не противоречил тем, которые вы прописали в ограничениях, иначе, может возникнуть конфликт.
Дополнительные настройки можно задать, кликнув по кнопке «Параметры».
Здесь можно установить точность ограничения и пределы решения. Когда нужные данные введены, жмите на кнопку «OK». Но, для нашего случая, изменять эти параметры не нужно.
После того, как все настройки установлены, жмем на кнопку «Найти решение».
Далее, программа Эксель в ячейках выполняет необходимые расчеты. Одновременно с выдачей результатов, открывается окно, в котором вы можете либо сохранить найденное решение, либо восстановить исходные значения, переставив переключатель в соответствующую позицию. Независимо от выбранного варианта, установив галочку «Вернутся в диалоговое окно параметров», вы можете опять перейти к настройкам поиска решения. После того, как выставлены галочки и переключатели, жмем на кнопку «OK».
Если по какой-либо причине результаты поиска решений вас не удовлетворяют, или при их подсчете программа выдаёт ошибку, то, в таком случае, возвращаемся, описанным выше способом, в диалоговое окно параметров. Пересматриваем все введенные данные, так как возможно где-то была допущена ошибка. В случае, если ошибка найдена не была, то переходим к параметру «Выберите метод решения». Тут предоставляется возможность выбора одного из трех способов расчета: «Поиск решения нелинейных задач методом ОПГ», «Поиск решения линейных задач симплекс-методом», и «Эволюционный поиск решения». По умолчанию, используется первый метод. Пробуем решить поставленную задачу, выбрав любой другой метод. В случае неудачи, повторяем попытку, с использованием последнего метода. Алгоритм действий всё тот же, который мы описывали выше.
Как видим, функция Поиск решения представляет собой довольно интересный инструмент, который, при правильном использовании, может значительно сэкономить время пользователя на различных подсчетах. К сожалению, далеко не каждый пользователь знает о его существовании, не говоря о том, чтобы правильно уметь работать с этой надстройкой. В чем-то данный инструмент напоминает функцию «Подбор параметра…», но в то же время, имеет и существенные различия с ним.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Оптимизация доставки
Постановка задачи
Предположим, что компания, где вы работаете, имеет три складских помещения, откуда товар поступает в пять ваших магазинов, разбросанных по всей Москве.
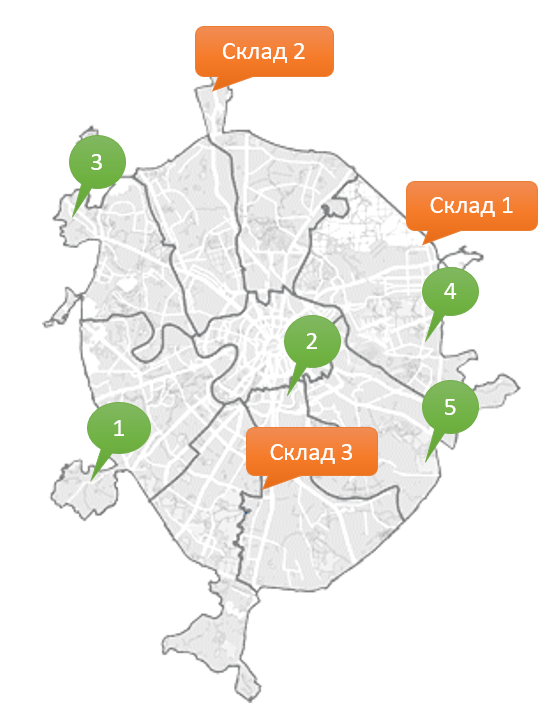
Каждый магазин в состоянии реализовать определенное, известное нам количество товара. Каждый из складов имеет ограниченную вместимость. Задача состоит в том, чтобы рационально выбрать – с какого склада в какие магазины нужно доставлять товар, чтобы минимизировать общие транспортные расходы.
Перед началом оптимизации необходимо будет составить несложную таблицу на листе Excel – нашу математическую модель, описывающую ситуацию:
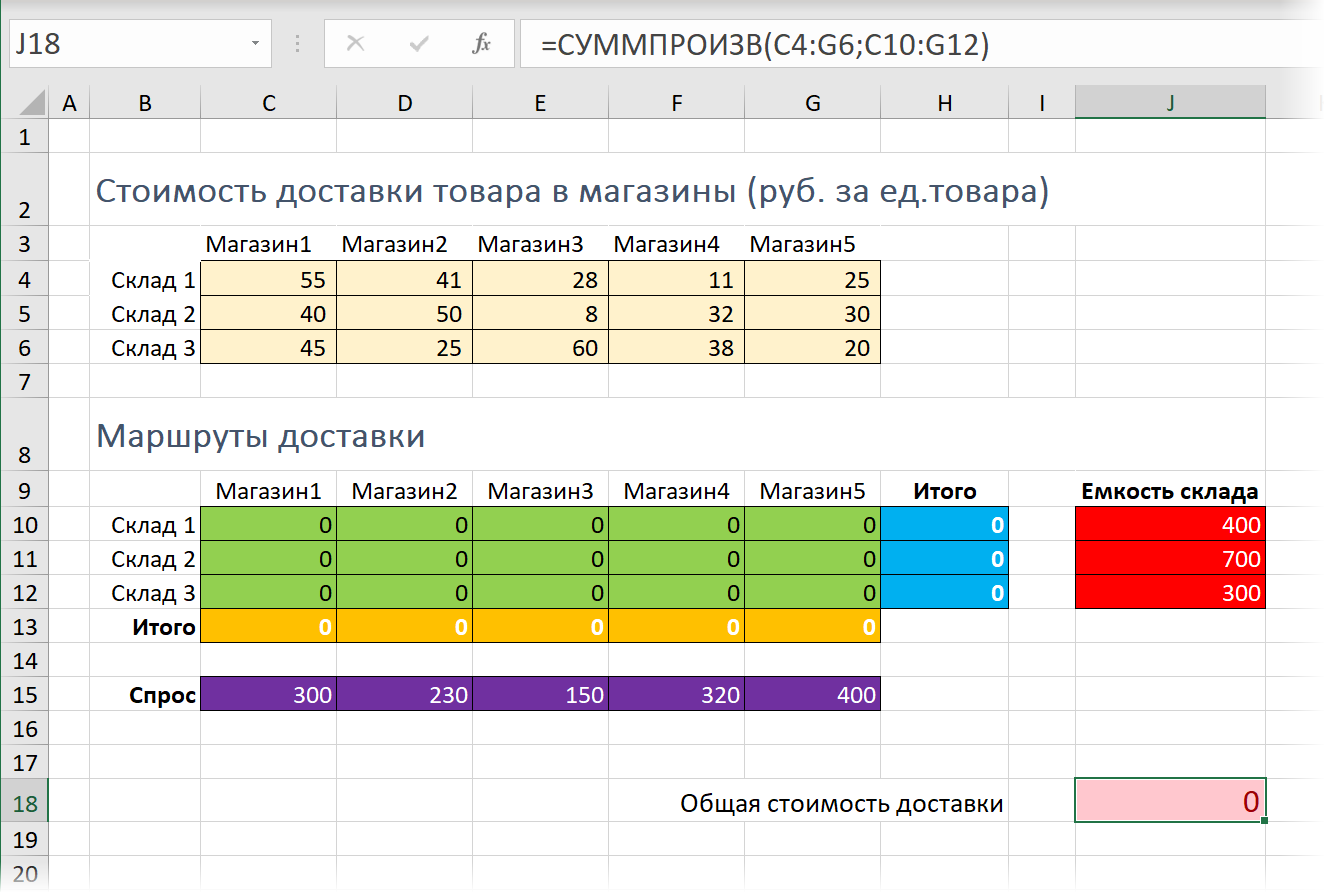
Подразумевается, что:
- Светло-желтая таблица (C4:G6) описывает стоимость доставки одной единицы товара от каждого склада до каждого магазина.
- Лиловые ячейки (C15:G14) описывают необходимое для каждого магазина количество товаров на реализацию.
- Красные ячейки (J10:J13) отображают емкость каждого склада – предельное количество товара, которое склад вмещает.
- Желтые (C13:G13) и синие (H10:H13) ячейки – соответственно, суммы по строке и столбцу для зеленых ячеек.
- Общая стоимость доставки (J18) вычисляется как сумма произведений количества товаров на соответствующие им стоимости доставки — для подсчёта здесь используется функция СУММПРОИЗВ (SUMPRODUCT).
Таким образом, наша задача сводится к подбору оптимальных значений зеленых ячеек. Причем так, чтобы общая сумма по строке (синие ячейки) не превышала вместимости склада (красные ячейки), и при этом каждый магазин получил необходимое ему количество товаров на реализацию (сумма по каждому магазину в желтых ячейках должна быть как можно ближе к требованиям – лиловым ячейкам).
Решение
В математике подобные задачи выбора оптимального распределения ресурсов сформулированы и описаны уже давно. И, конечно же, давно разработаны способы их решения не тупым перебором (что очень долго), а за весьма небольшое количество итераций. Excel предоставляет пользователю такой функционал с помощью надстройки Поиск решения (Solver) с вкладки Данные (Data):

Если на вкладке Данные вашего Excel такой команды нет – ничего страшного — значит надстройка просто еще не подключена. Для ее активации откройте Файл, далее выберите Параметры – Надстройки – Перейти (Options — Add-Ins — Go To). В открывшемся окне поставьте галочку напротив нужной нам строки Поиск решения (Solver).
Запустим надстройку:
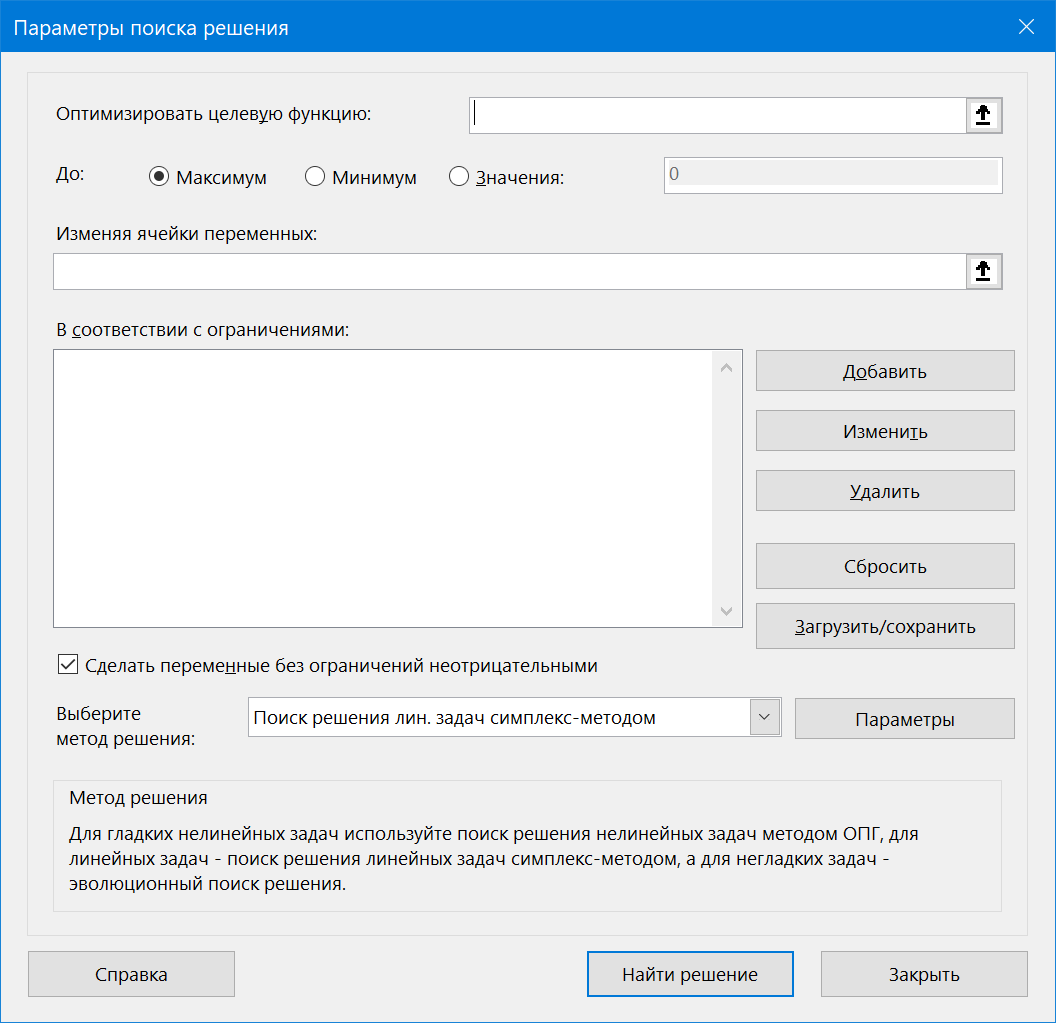
В этом окне нужно задать следующие параметры:
- Оптимизировать целевую функцию (Set target cell) – тут необходимо указать конечную главную цель нашей оптимизации, т.е. розовую ячейку с общей стоимостью доставки (J18). Целевую ячейку можно минимизировать (если это расходы, как в нашем случае), максимизировать (если это, например, прибыль) или попытаться привести к заданному значению (например, вписаться ровно в выделенный бюджет).
- Изменяя ячейки переменных (By changing cells) – здесь укажем зеленые ячейки (C10:G12), варьируя значения которых мы хотим добиться нашего результата – минимальных затрат на доставку.
- В соответствии с ограничениями (Subject to the Constraints) – список ограничений, которые надо учитывать при проведении оптимизации. Для добавления ограничений в список нужно нажать кнопку Добавить (Add) и ввести условие в появившееся окно. В нашем случае, это будет ограничение на спрос:
и ограничение на предельный объем складов:
Кроме очевидных ограничений, связанных с физическими факторами (вместимость складов и средств перевозки, ограничения бюджета и сроков и т.д.) иногда приходится добавлять ограничения «специально для Excel». Так, например, Excel легко может устроить вам «оптимизацию» стоимости доставки, предложив возить товары из магазинов обратно на склад — расходы при этом станут отрицательными, т.е. мы получим прибыль! 
Чтобы этого не случилось лучше оставить включенным флажок Сделать переменные без ограничений неотрицательными или даже иногда явно прописать такие моменты в списке ограничений.
После настройки всех необходимых параметров окно должно выглядеть следующим образом:
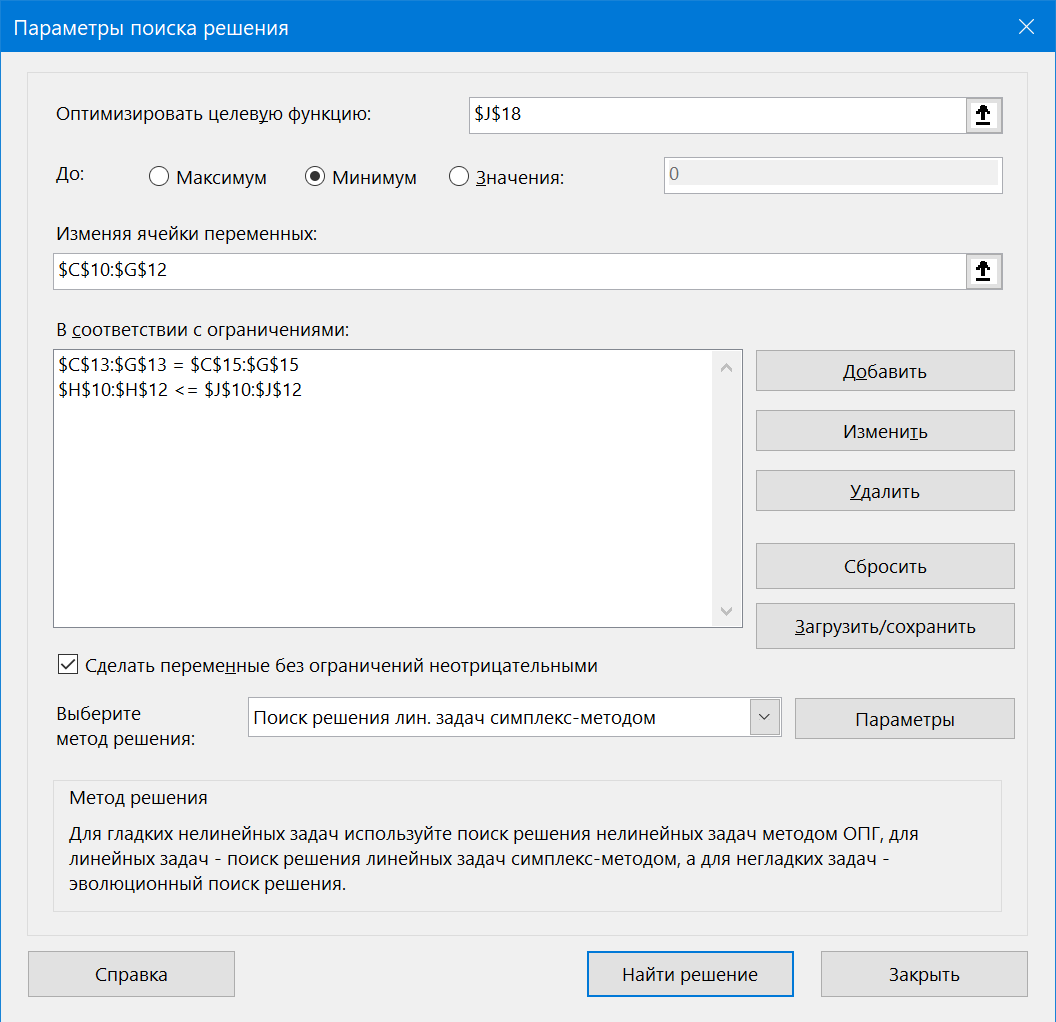
В выпадающем списке Выберите метод решения (Select a solving method) дополнительно требуется подобрать подходящий математический метод для решения на выбор из трех вариантов:
- Симплекс-метод — простой и быстрый метод для решения линейных задач, т.е. задач, где выход линейно зависит от входа.
- Метод общего понижающего градиента (ОПГ) — для нелинейных задач, где между входными и выходными данными есть сложные нелинейные зависимости (например, зависимость продаж от расходов на рекламу).
- Эволюционный поиск решения — относительно новый метод оптимизации, основанный на принципах биологической эволюции (привет Дарвину). Этот метод работает в разы дольше первых двух, но может решать практически любые задачи (нелинейные, дискретные).
Наша задача явно относится к линейным: доставили 1 шт — затратили 40 р., доставили 2 шт — затратили 80 р. и т.д., так что симплекс-метод будет наилучшим выбором.
Теперь, когда данные для расчета введены, нажмем кнопку Найти решение (Solve), чтобы начать оптимизацию. В тяжелых случаях с большим количеством изменяемых ячеек и ограничений нахождение решения может занять продолжительное время (особенно с эволюционным методом), но наша задача для Excel проблемы не составит – через пару мгновений мы получим следующие результаты:
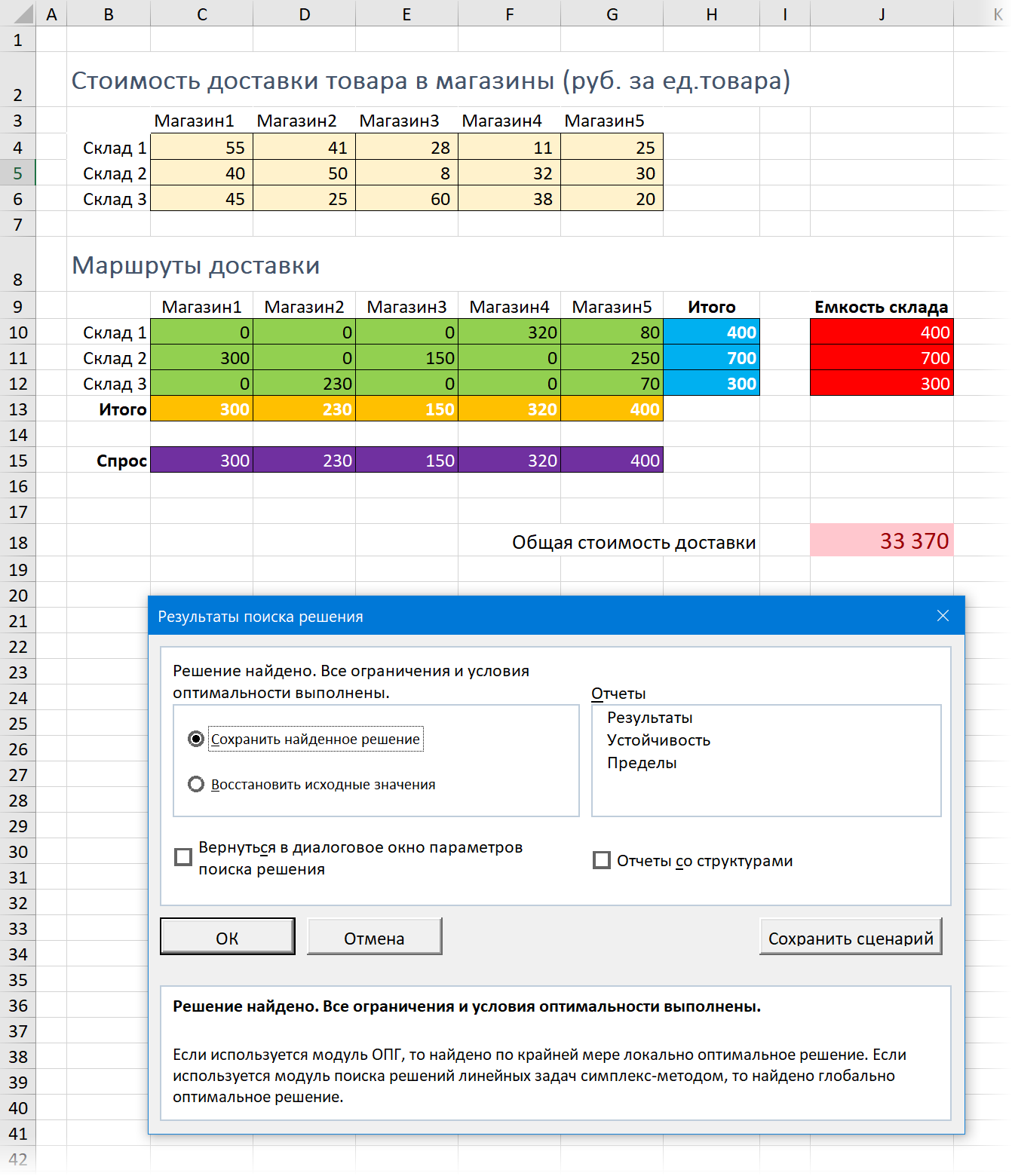
Обратите внимание на то, как интересно распределились объемы поставок по магазинам, не превысив при этом емкости наших складов и удовлетворив все запросы по требуемому количеству товаров для каждого магазина.
Если найденное решение нам подходит, то можно его сохранить, либо откатиться назад к исходным значениям и попробовать еще раз с другими параметрами. Также можно сохранить подобранную комбинацию параметров как Сценарий. По желанию пользователя Excel может построить три типа Отчетов по решаемой задаче на отдельных листах: отчет по результатам, отчет по математической устойчивости решения и отчет по пределам (ограничениям) решения, однако они, в большинстве случаев, интересны только специалистам.
Бывают, однако, ситуации, когда Excel не может найти подходящего решения. Имитировать такой случай можно, если указать в нашем примере требования магазинов в сумме большие, чем общая вместимость складов. Тогда при выполнении оптимизации Excel попытается приблизиться к решению, насколько это возможно, а затем выдаст сообщение о невозможности найти решение. Тем не менее, даже в этом случае мы имеем массу полезной информации – в частности можем видеть «слабые звенья» наших бизнес-процессов и понять направления совершенствования.
Рассмотренный пример, конечно, является относительно простым, но легко масштабируется под решение гораздо более сложных задач. Например:
- Оптимизация распределения финансовых средств по статьям расходов в бизнес-плане или бюджете проекта. Ограничениями, в данном случае, будут являться объемы финансирования и сроки выполнения проекта, а целью оптимизирования – максимизация прибыли и минимизация расходов на проект.
- Оптимизация расписания сотрудников с целью минимизации фонда заработной платы предприятия. Ограничениями, в этом случае, будут пожелания каждого сотрудника по графику занятости и требования штатного расписания.
- Оптимизация инвестиционных вложений – необходимость грамотно распределить средства между несколькими банками, ценными бумагами или акциями предприятий с целью, опять же, максимизации прибыли или (если это более важно) минимизации рисков.
В любом случае, надстройка Поиск решения (Solver) является весьма мощным и красивым инструментом Excel и достойна того, чтобы вы обратили на нее свое внимание, поскольку может выручить во многих сложных ситуациях, с которыми приходится сталкиваться в современном бизнесе.
«Поиск решения» — это надстройка для Microsoft Excel, которую можно использовать для анализ «что если». С ее помощью можно найти оптимальное значение (максимум или минимум) формула, содержащейся в одной ячейке, называемой целевой, с учетом ограничений на значения в других ячейках с формулами на листе. Надстройка «Поиск решения» работает с группой ячеек, называемых ячейками переменных решения или просто ячейками переменных, которые используются при расчете формул в целевых ячейках и ячейках ограничения. Надстройка «Поиск решения» изменяет значения в ячейках переменных решения согласно пределам ячеек ограничения и выводит нужный результат в целевой ячейке.
Проще говоря, с помощью надстройки «Поиск решения» можно определить максимальное или минимальное значение одной ячейки, изменяя другие ячейки. Например, вы можете изменить планируемый бюджет на рекламу и посмотреть, как изменится планируемая сумма прибыли.
Примечание: В версиях надстройки «Поиск решения», выпущенных до Excel 2007, ячейки переменных решения назывались изменяемыми или регулируемыми. В Excel 2010 надстройка «Поиск решения» была значительно улучшена, так что работа с ней в Excel 2007 будет несколько отличаться.
В приведенном ниже примере количество проданных единиц в каждом квартале зависит от уровня рекламы, что косвенно определяет объем продаж, связанные издержки и прибыль. Надстройка «Поиск решения» может изменять ежеквартальные расходы на рекламу (ячейки переменных решения B5:C5) до ограничения в 20 000 рублей (ячейка F5), пока общая прибыль (целевая ячейка F7) не достигнет максимального значения. Значения в ячейках переменных используются для вычисления прибыли за каждый квартал, поэтому они связаны с формулой в целевой ячейке F7, =СУММ (Q1 Прибыль:Q2 Прибыль).
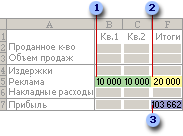
1. Ячейки переменных
2. Ячейка с ограничениями
3. Целевая ячейка
После выполнения процедуры получены следующие значения.

-
На вкладке Данные в группе Анализ нажмите кнопку Поиск решения.
-
В поле Оптимизировать целевую функцию введите ссылка на ячейку или имя целевой ячейки. Целевая ячейка должна содержать формулу.
-
Выполните одно из следующих действий.
-
Чтобы значение целевой ячейки было максимальным из возможных, установите переключатель в положение Макс.
-
Чтобы значение целевой ячейки было минимальным из возможных, установите переключатель в положение Мин.
-
Чтобы задать для целевой ячейки конкретное значение, установите переключатель в положение Значение и введите в поле нужное число.
-
В поле Изменяя ячейки переменных введите имена диапазонов ячеек переменных решения или ссылки на них. Несмежные ссылки разделяйте запятыми. Ячейки переменных должны быть прямо или косвенно связаны с целевой ячейкой. Можно задать до 200 ячеек переменных.
-
-
В поле В соответствии с ограничениями введите любые ограничения, которые требуется применить. Для этого выполните указанные ниже действия.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Добавить.
-
В поле Ссылка на ячейку введите ссылку на ячейку или имя диапазона ячеек, на значения которых налагаются ограничения.
-
Щелкните связь (<=, =, >=, int,binили dif), которая требуется между ячейкой, на которую ссылается ссылка, и ограничением. Если щелкнуть int, в поле Ограничение появится integer. Если щелкнуть бин,в поле Ограничение появится двоичное поле. Если нажать кнопку dif,в поле Ограничение появится ссылкаalldifferent.
-
Если в поле Ограничение было выбрано отношение <=, = или >=, введите число, ссылку на ячейку (или имя ячейки) или формулу.
-
Выполните одно из указанных ниже действий.
-
Чтобы принять данное ограничение и добавить другое, нажмите кнопку Добавить.
-
Чтобы принять ограничение и вернуться в диалоговое окно Параметрырешения, нажмите кнопку ОК.
Примечание Отношения int,binи dif можно применять только в ограничениях для ячеек переменных решения.Чтобы изменить или удалить существующее ограничение, выполните указанные ниже действия.
-
-
В диалоговом окне Параметры поиска решения щелкните ограничение, которое требуется изменить или удалить.
-
Нажмите кнопку Изменить и внесите изменения либо нажмите кнопку Удалить.
-
-
Нажмите кнопку Найти решение и выполните одно из указанных ниже действий.
-
Чтобы сохранить значения решения на листе, в диалоговом окне Результаты поиска решения выберите вариант Сохранить найденное решение.
-
Чтобы восстановить исходные значения перед нажатием кнопки Найти решение, выберите вариант Восстановить исходные значения.
-
Вы можете прервать поиск решения, нажав клавишу ESC. Лист Excel будет пересчитан с учетом последних найденных значений для ячеек переменных решения.
-
Чтобы создать отчет, основанный на найденном решении, выберите тип отчета в поле Отчеты и нажмите кнопку ОК. Отчет будет помещен на новый лист книги. Если решение не найдено, будут доступны только некоторые отчеты или они вообще не будут доступны.
-
Чтобы сохранить значения ячейки переменной решения в качестве сценария, который можно будет отобразить позже, нажмите кнопку Сохранить сценарий в диалоговом окне Результаты поиска решения, а затем введите имя этого сценария в поле Название сценария.
-
-
После постановки задачи нажмите кнопку Параметры в диалоговом окне Параметры поиска решения.
-
Чтобы просмотреть значения всех найденных решений, в диалоговом окне Параметры установите флажок Показывать результаты итераций и нажмите кнопку ОК.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение.
-
В диалоговом окне Показать предварительное решение выполните одно из указанных ниже действий.
-
Чтобы остановить поиск решения и вывести на экран диалоговое окно Результаты поиска решения, нажмите кнопку Стоп.
-
Чтобы продолжить процесс поиска решения и просмотреть следующий вариант решения, нажмите кнопку Продолжить.
-
-
В диалоговом окне Параметры поиска решения нажмите кнопку Параметры.
-
В диалоговом окне на вкладках Все методы, Поиск решения нелинейных задач методом ОПГ и Эволюционный поиск решения выберите или введите значения нужных параметров.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Загрузить/сохранить.
-
Введите диапазон ячеек для области модели и нажмите кнопку Сохранить или Загрузить.
При сохранении модели введите ссылку на первую ячейку вертикального диапазона пустых ячеек, в котором следует разместить модель оптимизации. При загрузке модели введите ссылку на весь диапазон ячеек, содержащий модель оптимизации.
Совет: Чтобы сохранить последние параметры, настроенные в диалоговом окне Параметры поиска решения, вместе с листом, сохраните книгу. Каждый лист в книге может иметь свои параметры надстройки «Поиск решения», и все они сохраняются. Кроме того, для листа можно определить более одной задачи, если нажимать кнопку Загрузить или сохранить для сохранения задач по отдельности.
В диалоговом окне Параметры поиска решения можно выбрать любой из указанных ниже алгоритмов или методов поиск решения.
-
Нелинейный метод обобщенного понижающего градиента (ОПГ). Используется для гладких нелинейных задач.
-
Симплекс-метод. Используется для линейных задач.
-
Эволюционный метод Используется для негладких задач.
В приведенном ниже примере количество проданных единиц в каждом квартале зависит от уровня рекламы, что косвенно определяет объем продаж, связанные издержки и прибыль. Надстройка «Поиск решения» может изменять ежеквартальные расходы на рекламу (ячейки переменных решения B5:C5) до ограничения в 20 000 рублей (ячейка D5), пока общая прибыль (целевая ячейка D7) не достигнет максимального значения. Значения в ячейках переменных используются для вычисления прибыли за каждый квартал, поэтому они связаны с формулой в целевой ячейке D7, =СУММ (Q1 Прибыль:Q2 Прибыль).
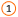
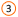
В результате выполнения получены следующие значения:

-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
В разделе Оптимизировать целевую функцию, введите ссылка на ячейку или имя целевой ячейки.
Примечание: Целевая ячейка должна содержать формулу.
-
Выполните одно из следующих действий.
Задача
Необходимые действия
Сделать так, чтобы значение целевой ячейки было максимальным из возможных
Выберите значение Макс.
Сделать так, чтобы значение целевой ячейки было минимальным из возможных
Выберите значение Мин.
Сделать так, чтобы целевая ячейка имела определенное значение
Щелкните Значение, а затем введите нужное значение в поле.
-
В поле Изменяя ячейки переменных введите имена диапазонов ячеек переменных решения или ссылки на них. Несмежные ссылки разделяйте запятыми.
Ячейки переменных должны быть прямо или косвенно связаны с целевой ячейкой. Можно задать до 200 ячеек переменных.
-
В поле В соответствии с ограничениями введите любые ограничения, которые требуется применить.
Для этого выполните следующие действия:
-
В диалоговом окне Параметры поиска решения нажмите кнопку Добавить.
-
В поле Ссылка на ячейку введите ссылку на ячейку или имя диапазона ячеек, на значения которых налагаются ограничения.
-
Во всплывающем меню <= задайте требуемое отношение между целевой ячейкой и ограничением. Если вы выбрали <=, =, или >= в поле Ограничение, введите число, имя ячейки, ссылку на нее или формулу.
Примечание: Отношения int, бин и раз можно использовать только в ограничениях для ячеек, в которых находятся переменные решения.
-
Выполните одно из указанных ниже действий.
Задача
Необходимые действия
Принять ограничение и добавить другое
Нажмите кнопку Добавить.
Принять ограничение и вернуться в диалоговое окно Параметры поиска решения
Нажмите кнопку ОК.
-
-
Нажмите кнопку Найти решение и выполните одно из следующих действий:
Задача
Необходимые действия
Сохранить значения решения на листе
В диалоговом окне Результаты поиска решения выберите вариант Сохранить найденное решение.
Восстановить исходные значения
Щелкните Восстановить исходные значения.
Примечания:
-
Чтобы прервать поиск решения, нажмите клавишу ESC. Лист Excel будет пересчитан с учетом последних найденных значений для ячеек переменных.
-
Чтобы создать отчет, основанный на найденном решении, выберите тип отчета в поле Отчеты и нажмите кнопку ОК. Отчет будет помещен на новый лист книги. Если решение не найдено, отчет не будет доступен.
-
Чтобы сохранить значения ячейки переменной решения в качестве сценария, который можно будет отобразить позже, нажмите кнопку Сохранить сценарий в диалоговом окне Результаты поиска решения, а затем введите имя этого сценария в поле Название сценария.
-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
После постановки задачи нажмите кнопку Параметры в диалоговом окне Параметры поиска решения.
-
Чтобы просмотреть значения всех предварительных решений, установите флажок Показывать результаты итераций и нажмите кнопку ОК.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение.
-
В диалоговом окне Показать предварительное решение выполните одно из следующих действий:
Задача
Необходимые действия
Остановить поиск решения и вывести на экран диалоговое окно Результаты поиска решения
Нажмите кнопку Стоп.
Продолжить поиск и просмотреть следующее предварительное решение
Нажмите кнопку Продолжить.
-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
Нажмите кнопку Параметры, а затем в диалоговом окне Параметры или Поиск решения выберите один или несколько из следующих вариантов:
Задача
Необходимые действия
Настроить время решения и число итераций
На вкладке Все методы в разделе Пределы решения в поле Максимальное время (в секундах) введите количество секунд, в течение которых можно будет искать решение. Затем в поле Итерации укажите максимальное количество итераций, которое вы хотите разрешить.
Примечание: Если будет достигнуто максимальное время поиска решения или количество итераций, а решение еще не будет найдено, средство «Поиск решения» выведет диалоговое окно Показать предварительное решение.
Задать точность
На вкладке Все методы введите в поле Точность ограничения нужное значение погрешности. Чем меньше число, тем выше точность.
Задать степень сходимости
На вкладке Поиск решения нелинейных задач методом ОПГ или Эволюционный поиск решения в поле Сходимость укажите, насколько должны отличаться результаты последних пяти итераций, чтобы средство прекратило поиск решения. Чем меньше число, тем меньше должно быть изменение.
-
Нажмите кнопку ОК.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение или Закрыть.
-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
Щелкните Загрузить/сохранить, укажите диапазон ячеек для области модели и нажмите кнопку Сохранить или Загрузить.
При сохранении модели введите ссылку на первую ячейку вертикального диапазона пустых ячеек, в котором следует разместить модель оптимизации. При загрузке модели введите ссылку на весь диапазон ячеек, содержащий модель оптимизации.
Совет: Чтобы сохранить последние параметры, настроенные в диалоговом окне Параметры поиска решения, вместе с листом, сохраните книгу. Каждый лист в книге может иметь свои параметры надстройки «Поиск решения», и все они сохраняются. Кроме того, для листа можно определить более одной задачи, если нажимать кнопку Загрузить/сохранить для сохранения задач по отдельности.
-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
Во всплывающем меню Выберите метод решения выберите одно из следующих значений:
|
Метод решения |
Описание |
|---|---|
|
Нелинейный метод обобщенного понижающего градиента (ОПГ) |
Используется по умолчанию для моделей со всеми функциями Excel, кроме ЕСЛИ, ВЫБОР, ПРОСМОТР и другие ступенчатые функции. |
|
Поиск решения линейных задач симплекс-методом |
Используйте этот метод для задач линейного программирования. В формулах модели, которые зависят от ячеек переменных, должны использоваться функции СУММ, СУММПРОИЗВ, +, — и *. |
|
Эволюционный поиск решения |
Этот метод, основанный на генетических алгоритмах, лучше всего подходит в том случае, если в модели используются функции ЕСЛИ, ВЫБОР и ПРОСМОТР с аргументами, которые зависят от ячеек переменных. |
Примечание: Авторские права на части программного кода надстройки «Поиск решения» версий 1990–2010 принадлежат компании Frontline Systems, Inc. Авторские права на части версии 1989 принадлежат компании Optimal Methods, Inc.
Поскольку надстройки не поддерживаются в Excel в Интернете, вы не сможете использовать надстройку «Поиск решения» для анализа данных «что если», чтобы найти оптимальные решения.
Если у вас есть Excel, вы можете нажать кнопку Открыть в Excel, чтобы открыть книгу для использования надстройки «Поиск решения».
Дополнительная справка по надстройке «Поиск решения»
За дополнительной справкой по надстройке «Поиск решения» обращайтесь по этим адресам:
Frontline Systems, Inc.
P.O. Box 4288
Incline Village, NV 89450-4288
(775) 831-0300
Веб-сайт: http://www.solver.com
Электронная почта: info@solver.com
«Решение» на www.solver.com.
Авторские права на части программного кода надстройки «Поиск решения» версий 1990-2009 принадлежат компании Frontline Systems, Inc. Авторские права на части версии 1989 принадлежат компании Optimal Methods, Inc.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Использование «Решения» для бюджетов с использованием средств на счете вех
Использование «Решение» для определения оптимального сочетания продуктов
Введение в анализ гипотетических вариантов
Полные сведения о формулах в Excel
Рекомендации, позволяющие избежать появления неработающих формул
Обнаружение ошибок в формулах
Сочетания клавиш в Excel
Функции Excel (по алфавиту)
Функции Excel (по категориям)
Наряду со множеством других возможностей, в Microsoft Excel есть одна малоизвестная, но очень полезная функция под названием “Поиск решения”. Несмотря на то, что найти и освоить ее, может быть, непросто, ее изучение и применение может помочь в решении огромного количества задач. Функция берет данные, перебирает их и выдает самое оптимальное решение из возможных. Итак, давайте разберемся, как именно работает поиск решения и попробуем применить данную функцию на практике
Содержание
- Как включить функцию “Поиск решения”
- Подготовительный этап
- Применение функции и ее настройка
- Заключение
Как включить функцию “Поиск решения”
Несмотря на свою эффективность, функция “Поиск решения” не находится в первых рядах панели инструментов или контекстного меню. Многие пользователи, работающие в Excel годами, даже не подозревают о ее существовании. Дело в том, что по умолчанию она вообще отключена и для ее добавления на ленту нужно проделать следующие шаги:
- Открываем меню “Файл”, кликнув по соответствующему названию.
- Кликаем по разделу “Параметры”, который находится внизу вертикального перечня с левой стороны.
- Далее щелкаем по подразделу “Надстройки”. Здесь отображаются все надстройки программы, а внизу будет надпись “Управление”. Справа от нее представлено выпадающее меню, в котором должны быть выбраны “Надстройки Excel”, обычно уже установленные по умолчанию. Нажимаем кнопку “Перейти”.
- На экране появится новое вспомогательное окно “Надстройки”. Устанавливаем флажок напротив опции “Поиск решения” и нажимаем ОК.
- Все готово. Требуемая функция появится на ленте в правой части вкладки “Данные”.
Подготовительный этап
Добавить функцию на ленту программы – половина дела. Нужно еще понять принцип ее работы.
Итак, у нас есть данные про продаже товаров, представленные в табличном виде.
И перед нами стоит задача – назначить каждому товару скидку таким образом, чтобы сумма по всем скидкам составила 4,5 млн. рублей. Она должна отобразиться в отдельной ячейке, которая называется целевой. Ориентируясь на нее мы должны рассчитать остальные значения.
Наша задача – вычислить скидку, на которую будут умножены все суммы по продажам всех наименований. Она и будет найдена с помощью функции “Поиск решения”, а ячейка с этой скидкой будет называется искомой.
Данные ячейки (искомая и целевая) связываем вместе формулой, которую пишем в целевой ячейке следующим образом: =D13*$G$2, где ячейка D13 содержит итоговую сумму по продажам всех товаров, а ячейка $G$2 – абсолютные (неизменные) координаты искомой ячейки.
Применение функции и ее настройка
Формула готова. Теперь нужно применить саму функцию.
- Переключаемся во вкладку “Данные” и нажимаем кнопку “Поиск решения”.
- Откроются “Параметры”, где необходимо задать нужные настройки. В поле “Оптимизировать целевую функцию:” указываем адрес целевой ячейки, где планируется вывести сумму по всем скидкам. Можно прописать координаты вручную, либо выбрать из таблицы, для чего сначала кликаем по области ввода, затем – по нужной ячейке.
- Переходим к настройке других параметров. В пункте “До:” можно задать максимальную границу, минимальную границу или же точное число. Исходя из поставленной задачи ставим отметку рядом с опцией “Значение” и набираем “4500000” – сумма скидок по всем наименованиям.
- Следующее для заполнения поле – “Изменяя значения переменных:”. В него нужно внести координаты искомой ячейки, содержащей определенное значение. Это значение и есть та самая скидка, которую мы пытаемся вычислить. Также, как и с выбором целевой ячейки, координаты можно написать вручную, либо кликнуть по нужной ячейке в самой таблице.
- Теперь нужно отредактировать раздел “В соответствии с ограничениями:”, в котором задаем ограничения используемых данных. Например, можно исключить десятичные дроби или, скажем, отрицательные числа. Это делается через кнопку “Добавить”.
- Откроется вспомогательно окно, позволяющее добавить ограничения во время вычислений. В первом поле указываем координаты определенной ячейки или области ячеек, для которых это условие должно действовать. Согласно нашей задаче, указываем координаты искомой ячейки, в которой будет выводиться значение скидки. Следующий шаг – определить знак сравнения. Устанавливаем “больше или равно”, чтобы итоговое число не могло быть отрицательным. “Ограничение”, которое устанавливается в третьем поле, в этом случае будет равно цифре 0, поскольку именно относительно этого значения задается условие.
Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK.
- После выполнения описанных выше действий в самом большом поле окна появится установленное только что ограничение. Список может быть довольно большим и зависит от сложности предполагаемых расчетов, но в данном случае будет достаточно и одного условия.
Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.
- Также можно задать немалое количество дополнительных настроек. Чуть ниже справа есть кнопка “Параметры”, позволяющая это сделать. Нажимаем на нее и открываем новое окно.
- В этих настройках у нас есть возможность установить “Точность ограничения” и “Пределы решения”. В нашем случае задавать данные параметры нет необходимости, поэтому после ознакомления с представленным окном, его можно закрыть, нажав OK.
- Итак, все настройки выполнены и параметры установлены. Пора запускать функцию – для этого нажимаем кнопку “Найти решение”.
- После этого программа сделает все необходимые расчеты и выдаст результаты в нужных ячейках. При этом сразу же откроется окно “Результаты поиска решения”, где можно сохранить/отменить результаты или настроить параметры поиска заново. Если результаты нас устраивают, оставляем отметку напротив опции “Сохранить найденное решение” и нажимаем ОК. При этом, если мы предварительно установим галочку слева от надписи “Вернуться в диалоговое окно параметров поиска решения”, после того, как мы щелкнем OK, мы обратно переключимся к настройке функции поиска решения.
- Вполне вероятно, что расчеты могут показаться неправильными, либо возникнет желание немного изменить исходные данные и получить другой результат. В этом случае нужно снова открыть окно с параметрами поиска решения и внимательно посмотреть поля с введенными данными.
- Если с данными все нормально, можно попробовать задействовать другой метод решения. Для этого щелкаем по текущему варианту и из раскрывшегося перечня выбираем способ, который нам кажется наиболее подходящим:
- Первый – ищет решение методом обобщенного приведенного градиента (ОПГ) для нелинейных задач. Стандартно выбран именно этот вариант, но можно попробовать и другие.
- Второй – пытается отыскать решение для линейных задач, используя симплекс-метод.
- Третий – для выполнения поставленной задачи использует эволюционный поиск.
- В том случае, если ни один из методов не принес удовлетворительных результатов, стоит проверить данные в таблице и параметрах еще раз, поскольку именно это является самой частой ошибкой в подобного рода задачах.
- Теперь, когда мы получили требуемую скидку, осталось ее применить, чтобы рассчитать суммы скидок по всем наименованиям. Для этого отмечаем первую ячейку столбца “Сумма скидки”, пишем в ней формулу “=D2*$G$2” и нажимаем Enter. Знаки доллара ставятся для того, чтобы при растягивании/копировании формулы на другие строки, ячейка G2 со скидкой оставалась неизменной в расчетах.
- Мы получили сумму скидки для первого наименования. Теперь наводим курсор на нижний правый угол ячейки с результатом, как только он поменяет форму на крестик, зажав левую кнопку мыши растягиваем формулу на все строки, по которым хотим посчитать аналогичную сумму.
- Теперь наша таблица полностью готова в соответствии с поставленной задачей.
Заключение
Таким образом, функция “Поиск решения” в Эксель может помочь в решении определенных задач, которые достаточно сложно или невозможно решить простыми методами. Однако, проблема в использовании данного способа заключается в том, что по умолчанию данная функция скрыта в программе, из-за чего многие пользователи не догадываются о ее существовании. Также функция довольно трудна в освоении и использовании, но при ее должном изучении, она может принести значительную пользу и облегчить работу.
|
18 / 18 / 7 Регистрация: 20.03.2012 Сообщений: 549 |
|
|
1 |
|
|
22.04.2013, 22:38. Показов 22118. Ответов 4
Как работает метод ОПГ («Метод обобщенного градиента») надстройки «Поиск решения» Excel? Есть ли синонимы у этого метода? Где можно почитать информацию?
0 |
|
0 / 0 / 0 Регистрация: 12.03.2014 Сообщений: 3 |
|
|
19.03.2014, 14:14 |
2 |
|
Здравствуйте, Вы нашли что то по этому методу?
0 |
|
18 / 18 / 7 Регистрация: 20.03.2012 Сообщений: 549 |
|
|
19.03.2014, 15:12 [ТС] |
3 |
|
Здравствуйте, Вы нашли что то по этому методу? Нет. Как именно работает Excel на настоящий момент мне неизвестно.
0 |
|
0 / 0 / 0 Регистрация: 12.03.2014 Сообщений: 3 |
|
|
19.03.2014, 15:18 |
4 |
|
znseday
0 |
|
18 / 18 / 7 Регистрация: 20.03.2012 Сообщений: 549 |
|
|
19.03.2014, 23:03 [ТС] |
5 |
|
mr_art91, Не по теме: могу, но не могу сообразить, как отправить ЛС Что именно Вас интересует? Я ограничился методами градиентного спуска и исследующим методом Хука-Дживса. Оба метода для моей задачи работают «так себе», т.к сильно зависят от начальных параметров.
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
19.03.2014, 23:03 |
|
Помогаю со студенческими работами здесь Задача на «Поиск решения в exel» Оптимальный метод Надстройка «Поиск решения» и функции Excel Excel («Поиск решения») Как заменить код «метод правых прямоугольников» на «метод трапеции» на примере данной программы var x, s, h, minlim, maxlim, funcabspog:real; Как написать регулярное выражение для выдергивания английских букв и символов: «+», «,», «:», «-«, » «, «!», «?» и «.» Классы «Студент» ,»Группа» — не работает метод ввода и вывода Задание 1. Создайте класс «Группа». Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 5 |
Одной из самых интересных функций в программе Microsoft Excel является Поиск решения. Вместе с тем, следует отметить, что данный инструмент нельзя отнести к самым популярным среди пользователей в данном приложении. А зря. Ведь эта функция, используя исходные данные, путем перебора, находит наиболее оптимальное решение из всех имеющихся. Давайте выясним, как использовать функцию Поиск решения в программе Microsoft Excel.
Включение функции
Можно долго искать на ленте, где находится Поиск решения, но так и не найти данный инструмент. Просто, для активации данной функции, нужно её включить в настройках программы.
Для того, чтобы произвести активацию Поиска решений в программе Microsoft Excel 2010 года, и более поздних версий, переходим во вкладку «Файл». Для версии 2007 года, следует нажать на кнопку Microsoft Office в левом верхнем углу окна. В открывшемся окне, переходим в раздел «Параметры».
В окне параметров кликаем по пункту «Надстройки». После перехода, в нижней части окна, напротив параметра «Управление» выбираем значение «Надстройки Excel», и кликаем по кнопке «Перейти».
Открывается окно с надстройками. Ставим галочку напротив наименования нужной нам надстройки – «Поиск решения». Жмем на кнопку «OK».
После этого, кнопка для запуска функции Поиска решений появится на ленте Excel во вкладке «Данные».
Подготовка таблицы
Теперь, после того, как мы активировали функцию, давайте разберемся, как она работает. Легче всего это представить на конкретном примере. Итак, у нас есть таблица заработной платы работников предприятия. Нам следует рассчитать премию каждого работника, которая является произведением заработной платы, указанной в отдельном столбце, на определенный коэффициент. При этом, общая сумма денежных средств, выделяемых на премию, равна 30000 рублей. Ячейка, в которой находится данная сумма, имеет название целевой, так как наша цель подобрать данные именно под это число.
Коэффициент, который применяется для расчета суммы премии, нам предстоит вычислить с помощью функции Поиска решений. Ячейка, в которой он располагается, называется искомой.
Целевая и искомая ячейка должны быть связанны друг с другом с помощью формулы. В нашем конкретном случае, формула располагается в целевой ячейке, и имеет следующий вид: «=C10*$G$3», где $G$3 – абсолютный адрес искомой ячейки, а «C10» — общая сумма заработной платы, от которой производится расчет премии работникам предприятия.
Запуск инструмента Поиск решения
После того, как таблица подготовлена, находясь во вкладке «Данные», жмем на кнопку «Поиск решения», которая расположена на ленте в блоке инструментов «Анализ».
Открывается окно параметров, в которое нужно внести данные. В поле «Оптимизировать целевую функцию» нужно ввести адрес целевой ячейки, где будет располагаться общая сумма премии для всех работников. Это можно сделать либо пропечатав координаты вручную, либо кликнув на кнопку, расположенную слева от поля введения данных.
После этого, окно параметров свернется, а вы сможете выделить нужную ячейку таблицы. Затем, требуется опять нажать по той же кнопке слева от формы с введенными данными, чтобы развернуть окно параметров снова.
Под окном с адресом целевой ячейки, нужно установить параметры значений, которые будут находиться в ней. Это может быть максимум, минимум, или конкретное значение. В нашем случае, это будет последний вариант. Поэтому, ставим переключатель в позицию «Значения», и в поле слева от него прописываем число 30000. Как мы помним, именно это число по условиям составляет общую сумму премии для всех работников предприятия.
Ниже расположено поле «Изменяя ячейки переменных». Тут нужно указать адрес искомой ячейки, где, как мы помним, находится коэффициент, умножением на который основной заработной платы будет рассчитана величина премии. Адрес можно прописать теми же способами, как мы это делали для целевой ячейки.
В поле «В соответствии с ограничениями» можно выставить определенные ограничения для данных, например, сделать значения целыми или неотрицательными. Для этого, жмем на кнопку «Добавить».
После этого, открывается окно добавления ограничения. В поле «Ссылка на ячейки» прописываем адрес ячеек, относительно которых вводится ограничение. В нашем случае, это искомая ячейка с коэффициентом. Далее проставляем нужный знак: «меньше или равно», «больше или равно», «равно», «целое число», «бинарное», и т.д. В нашем случае, мы выберем знак «больше или равно», чтобы сделать коэффициент положительным числом. Соответственно, в поле «Ограничение» указываем число 0. Если мы хотим настроить ещё одно ограничение, то жмем на кнопку «Добавить». В обратном случае, жмем на кнопку «OK», чтобы сохранить введенные ограничения.
Как видим, после этого, ограничение появляется в соответствующем поле окна параметров поиска решения. Также, сделать переменные неотрицательными, можно установив галочку около соответствующего параметра чуть ниже. Желательно, чтобы установленный тут параметр не противоречил тем, которые вы прописали в ограничениях, иначе, может возникнуть конфликт.
Дополнительные настройки можно задать, кликнув по кнопке «Параметры».
Здесь можно установить точность ограничения и пределы решения. Когда нужные данные введены, жмите на кнопку «OK». Но, для нашего случая, изменять эти параметры не нужно.
После того, как все настройки установлены, жмем на кнопку «Найти решение».
Далее, программа Эксель в ячейках выполняет необходимые расчеты. Одновременно с выдачей результатов, открывается окно, в котором вы можете либо сохранить найденное решение, либо восстановить исходные значения, переставив переключатель в соответствующую позицию. Независимо от выбранного варианта, установив галочку «Вернутся в диалоговое окно параметров», вы можете опять перейти к настройкам поиска решения. После того, как выставлены галочки и переключатели, жмем на кнопку «OK».
Если по какой-либо причине результаты поиска решений вас не удовлетворяют, или при их подсчете программа выдаёт ошибку, то, в таком случае, возвращаемся, описанным выше способом, в диалоговое окно параметров. Пересматриваем все введенные данные, так как возможно где-то была допущена ошибка. В случае, если ошибка найдена не была, то переходим к параметру «Выберите метод решения». Тут предоставляется возможность выбора одного из трех способов расчета: «Поиск решения нелинейных задач методом ОПГ», «Поиск решения линейных задач симплекс-методом», и «Эволюционный поиск решения». По умолчанию, используется первый метод. Пробуем решить поставленную задачу, выбрав любой другой метод. В случае неудачи, повторяем попытку, с использованием последнего метода. Алгоритм действий всё тот же, который мы описывали выше.
Как видим, функция Поиск решения представляет собой довольно интересный инструмент, который, при правильном использовании, может значительно сэкономить время пользователя на различных подсчетах. К сожалению, далеко не каждый пользователь знает о его существовании, не говоря о том, чтобы правильно уметь работать с этой надстройкой. В чем-то данный инструмент напоминает функцию «Подбор параметра…», но в то же время, имеет и существенные различия с ним.
Решим задачу об оптимизации плана-графика работ по проекту с помощью Поиска решений MS EXCEL 2010. В качестве примера разберем задачу из сборника «Методы оптимизации управления и принятия решений» авторы Зайцев М.Г. и Варюхин С.Е. (2008г.). Задача 3.7 «Проект комапании Мегашоп».
Сборник задач «Методы оптимизации управления и принятия решений» довольно популярен в качестве задачника для Вузов, поэтому ссылки на него встречаются повсеместно в интернете. Приятно, что для каждой задачи имеется ответ в конце книги — можно сравнить получившееся решение с решением, которое найдено авторами
с помощью Поиска решения
(в году так 2000-м, я полагаю).
Условия задачи
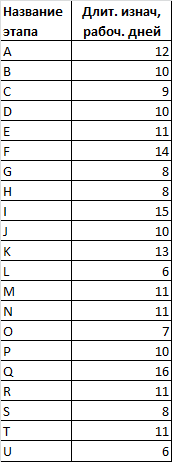
Компания МегаШоп планирует развертывание сети магазинов в южном регионе России. Отдел развития компании составил план работы по развертыванию сети, состоящий из 21 этапа (здесь они обозначены буквами от A до U). В таблице приведена информация длительности этапов в рабочих днях:
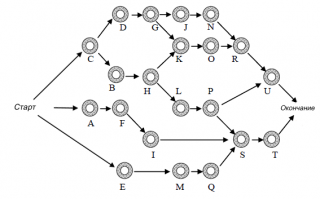
Сетевая диаграмма проекта, показывающая порядок выполнения работ приведена на рисунке.
После того, как план был доложен на совещании в присутствии директора по логистике, выяснилось, что план никуда не годится. Товар под новую сеть уже заказан и поставки начнутся примерно за 4 недели до планируемого завершения проекта. При этом излишки товара вынужден будет оставить у себя центральный склад, что полностью парализует его работу. Для нормализации ситуации необходимо сократить длительность проекта не менее чем на две недели.
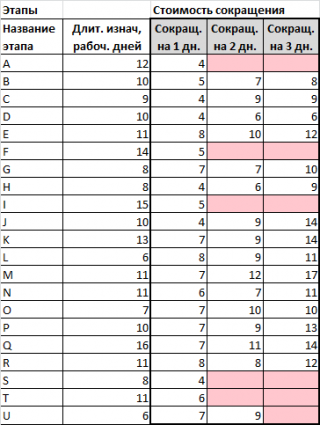
Срочный запрос служащим и подразделениям, исполняющим отдельные этапы проекта, выявил, что некоторые этапы можно сократить на три дня. В таблице указаны стоимости ускорения выполнения этапов проекта. Если стоимость не указана, сокращение невозможно.
Задания
:
a. Определите минимальную стоимость сокращения длительности проекта на две недели.
b. Допустим, что альтернативой сокращению проекта на 2 недели является найм дополнительных складских площадей по соседству, но это обойдется в 15 единиц в день (оплата услуги, перегрузки товара, доп. охрана и проч.). Какой срок сокращения длительности проекта оптимален по издержкам?
В сборнике сразу доступен ответ. Вот он.
Разбор условия задачи
Сначала несколько слов о стилистике формулирования условия (по мелочи).
Работы по проекту называются то работами («порядок выполнения работ»), то этапами. Будем называть их работами. Каждой работе соответствует точка на сетевой диаграмме с соответствующей буквой.
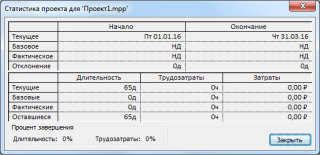
В ответе на вопрос а) приведен ответ о длительности проекта (65 дн.). Но, об этом нас не спрашивают в задании, спрашивают только о стоимости сокращения (109 условных единиц денег). Сразу возникает вопрос: «это изначальная длительность проекта или длительность после сокращения?». Выясним это в ходе решения.
Решение
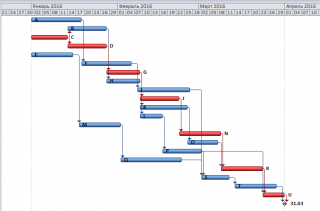
Сначала рассчитаем изначальную длительность проекта. Сделаем это в MS Project. Для этого введем 21 работу, укажем их длительность и связи.
Работы, выделенные красным, лежат на критическом пути. MS Project показывает, что первые работы С, А, Е начинаются 01.01.2016, проект заканчивается 31.03.2016. Длительность проекта — 65 дней.
Напомним, что у проекта длительность может быть указана в календарных днях (31.03.2016-01.01.2016+1=91 дней) и в рабочих днях (без учета выходных, 65 дней). Так как длительность работ указана в рабочих днях, то и длительность проекта разумно вычислять в рабочих днях. Т.е. в ответе указана изначальная длительность проекта
в рабочих днях
.
Теперь вычислим стоимость сокращения проекта на 2 недели. Обратите внимание на формулировку — 2 недели, а не 14 дней! 2 недели — это календарные дни, т.е. с учетом выходных длительность проекта нужно сократить на 10 дней! Но, сейчас это только наша догадка. Построим модель в MS EXCEL и покажем, что на 14 рабочих дней проект нельзя сократить в принципе, а вот на 10 можно.
Построение модели
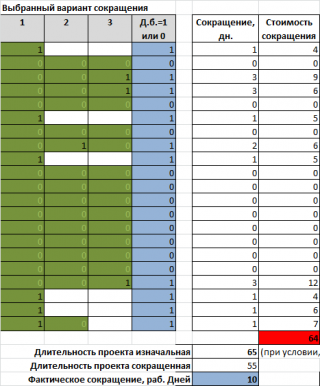
Как известно из условия задачи, существует возможность сократить длительность каждой задачи от 1 до 3 дней. Но, за это придется заплатить. Таким образом, нам нужно перебрать все варианты сокращения длительности проекта ровно на «2 недели», чтобы выбрать из них вариант, имеющий минимальную стоимость сокращения.
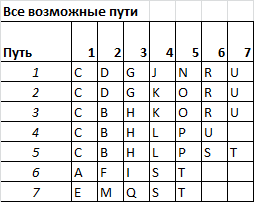
Сначала определим на сколько вообще возможно сократить длительность проекта (без учета затрат на это). Для этого нам потребуется вычислить длину критического пути проекта, т.е. путь, который имеет максимальную длительность. Для этого определим все пути в рамках проекта. Проще всего это сделать визуально, используя сетевую диаграмму.
Сначала отправимся из работы (точки) С, затем D; G; J; N; R; U; Окончание. Т.е. обойдем сетевую диаграмму по самому верхнему пути. Последнюю веху
Окончание
можно не указывать, т.к. ее длительность равна 0. Второй путь располагается чуть ниже: С; D; G; K; O; R; U. Всего путей 7. Вот они.
Как рассчитать длительность путей показано в
файле примера
(ссылка внизу статьи). Для этого понадобится только простая формула на основе
функции ВПР()
.
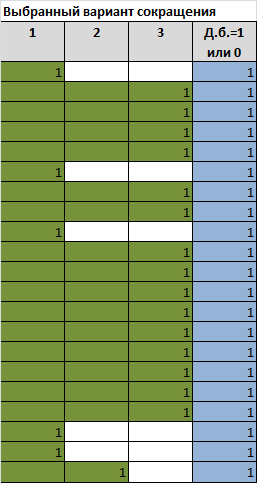
Также нам понадобится табличка, в которой будем указывать выбранные варианты сокращения длительности работ.
На картинке выше показан вариант, когда все работы сокращены по максимуму (по условию, не все работы можно сократить на 3 или даже на 2 дня). Это как раз и соответствует максимально возможному сокращению работ проекта, т.е. максимальному сокращению общей длительности проекта.
Как мы и предполагали, в этом случае сокращение общей длительности проекта составит 10 рабочих дней. Нет, конечно, это 2 календарные недели, но ведь и не 14 дней ))). Не сомневаюсь, что авторы сборника, очень креативные люди, которые формулируют заковыристые условия для студентов (чтобы те подумали), но, лично мое мнение, таких студентов не более 10%. Остальные просто запутаются и сдадутся не получив ответ. Тем более, что точный ответ (109 ед.) и получить-то проблематично в сегодняшних условиях. Об этом ниже.
Для нахождения оптимального варианта сокращения длительности проекта на 2 недели будем использовать инструмент
MS EXCEL Поиск решения
.
Чтобы построить модель для
Поиска решения
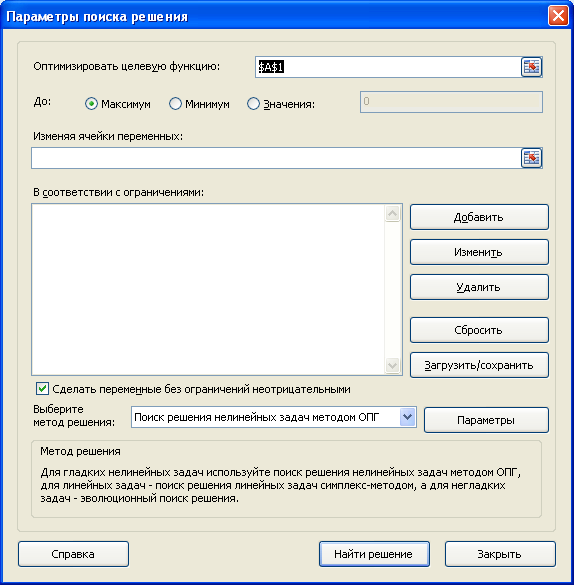
(ПР) в EXCEL нужно определить 3 ее составляющих:
-
целевая функция (то, что мы будем оптимизировать, например в нашем случае — минимизировать стоимость сокращения длительности проекта), это формула в одной ячейке (
ячейку выделим красным
); -
переменные модели, это то что будет изменять ПР в ходе поиска (
ячейки выделим зеленым
). В нашем случае — это вариант сокращения длительности каждой работы на 1, 2 или 3 дня; -
ограничения модели, например, вариант сокращения длительности работы должен быть только один (либо сократить на 1 день, либо на 2 (если можно по условию), либо на 3 (если можно) или вообще не сокращать) (
ячейки выделим синим/голубым
). Также потребуется несколько технических ограничений: все переменные должны быть бинарными, т.е. 0 или 1.
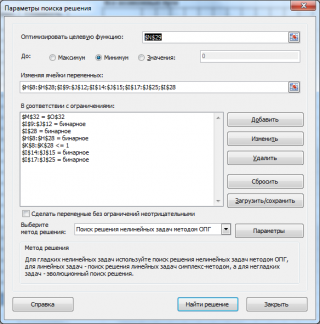
Заполним окно Поиска решения.
В качестве еще одного ограничения добавим, что длительность проекта должна сократиться ровно на 10 рабочих дней. Задача нелинейная, т.к. для вычисления целевой функции мы использовали функцию
ВПР()
, а не только линейные операции умножения и сложения. Запустим ПР с использованием нелинейного метода ОПГ. Через несколько секунд получим решение: 81 условная денежная единица. Т.е. меньше 109 ед.!
Почему можно получить разные ответы с помощь Поиска решения (в нелинейном случае)? Причин может быть несколько.
1) Разные модели. Обе правильные (надеюсь), но разные;
2) Разные методы решения: Нелинейный метод ОПГ или Эволюционный;
3) Разные параметры решения (точность ограничения, число подзадач и т.д.), которые устанавливаются пользователем в окне ПР (кнопка Параметры).
4) Версия MS EXCEL. Алгоритм оптимизации надстройки Solver (Поиск решения) может отличаться в зависимости от версии. Так в EXCEL 2010 в надстройку был включен новый метод решения нелинейных задач
Эволюционный поиск решения (
Evolution solver)
, основанный на генетических алгоритмах. Возможно были внесены и другие изменения в алгоритм расчета нелинейных задач.
Например, мной с помощью Эволюционного метода был получен вариант со стоимостью сокращения 64! Это на 40% лучше ответа, приведенного в ответе сборника (это полностью заслуга разработчиков Поиска решения). Правда, эволюционный метод требует более тонких настроек параметров, в отличие от Нелинейного ОПГ, а также он считает дольше.
Но, может, 109 ед., приведенные в ответе, это просто ошибка? Существует ли такой вариант сокращения длительности работ, который приводит к такой стоимости? Да, существует и расчет приведен на листе
Как в ответе
в
файле примера
.
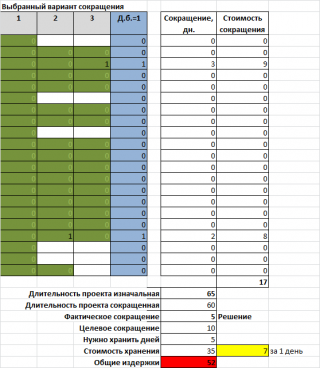
Теперь решим вторую часть задачи:
Альтернативой сокращению проекта на 2 недели является найм дополнительных складских площадей по соседству, но это обойдется в 15 единиц в день (оплата услуги, перегрузки товара, доп. охрана и проч.). Какой срок сокращения длительности проекта оптимален по издержкам
?
Расчет приведен на листе
Задание Б
в
файле примера
.
Сразу зададим себе вопрос: «Почему стоимость хранения на дополнительных складах составляет именно 15 ед., а не 100 ед. или 5 ед.». Понятно, что если эта стоимость будет слишком высока, то арендовать новые склады будет слишком дорого и бессмысленно (проще сократить проект на 2 недели за 64 ед.). Если наоборот, склады будут слишком дешевы, то тратить деньги на сокращение длительности проекта не имеет смысла, дешевле будет арендовать доп.склады.
Так как в нашем распоряжении более мощный Поиск решения, который позволяет найти очень эффективный (более дешевый) вариант сокращения длительности проекта, то 15 ед. будет слишком высокой ценой за склады. Выгоднее сокращать длительность проекта. Снизим стоимость аренды складов до 7 единиц и немного подкорректируем модель: общая стоимость минимизируемых затрат будет складываться из затрат на сокращение длительности проекта (как раньше) + затраты на хранение (хранить будем то количество дней, которое не хватает, чтобы сократить проект на 10 рабочих дней). Ниже приведен один из найденных вариантов: сокращение длительности — 5 дней, остальные 5 дней (10-5) храним на складе за 7 ед./день.
Конечно, в модели убрано одно из ограничений — количество дней, на которое нужно сократить проект, теперь оно не обязательно должно быть равно 10.
Решение уравнения с помощью инструмента «Поиск решения».
Практическая работа № 17.
Тема: Решение линейных и нелинейных уравнений с помощью MS Excel.
Цель: научиться решать линейные и нелинейные уравнения различными способами.
Теоретические сведения и задания:
Графический метод решения уравнения.
Известно, что графическим решением уравнения f(x)=0 является точка пересечения графика функции f(x) с осью абсцисс, т.е. такое значение x, при котором функция обращается в ноль.
Разберем графический метод решения уравнения на примере: пусть необходимо решить уравнение x 3 — 0,01x 2 — 0,7044x + 0,139104 = 0.
На листе 1 проведем табулирование нашей функции на интервале от -1 до 1 с шагом 0,2, для этого построим таблицу значений. Затем по таблице построим точечную диаграмму. Результаты вычислений приведены на рисунке, где в ячейку В2 была введена формула: = A2^3 — 0,01*A2^2 — 0,7044*A2 + 0,139104. На графике видно, что функция три раза пересекает ось Оx, а так как полином третьей степени имеет не более трех вещественных корней, то графическое решение поставленной задачи найдено. Иначе говоря, была проведена локализация корней, т.е. определены интервалы, на которых находятся корни данного полинома: [-1,-0.8], [0.2,0.4] и [0.6,0.8] (можно получить более точное решение если выбрать шаг 0,1).
Лист 1 переименовать в Задание1 и сохранить работу в своей папке с именем Фамилия пр17.xls
Решение уравнения с помощью инструмента «Подбор параметра».
Перейти на лист 2.
Чтобы решить нелинейное уравнение можно воспользоваться средством Подбор параметра, выбрав команду Подбор параметра в меню Сервис. При подборе параметра Excel изменяет значение в одной конкретной ячейке до тех пор, пока вычисления по формуле, ссылающейся на эту ячейку, не дадут нужного результата.
Возьмем в качестве примера квадратное уравнение х 2 -5х+6=0. Для нахождения корней уравнения выполним следующие действия:
В ячейку С3 введем формулу для вычисления значения функции, стоящей в уравнении слева от знака равенства. В качестве аргумента используем ссылку на ячейку С2, т.е. =С2^2-5*C2+6.
· В окне диалога Подбор параметра в поле Установить в ячейке введем ссылку на ячейку с формулой, в поле Значение — ожидаемый результат, в поле Изменяя значения ячейки — ссылку на ячейку, в которой будет храниться значение подбираемого параметра (содержимое этой ячейки не может быть формулой).
· После нажатия на кнопку Ok Excel выведет окно диалога Результат подбора параметра. Если подобранное значение необходимо сохранить, то нажмите на Оk, и результат будет сохранен в ячейке, заданной ранее в поле Изменяя значения ячейки. Для восстановления значения, которое было в ячейке С2 до использования команды Подбор параметра, нажмите кнопку Отмена.
При подборе параметра Excel использует итерационный (циклический) процесс. Количество итераций и точность устанавливаются в меню Сервис/Параметры/вкладка Вычисления. Если Excel выполняет сложную задачу подбора параметра, можно нажать кнопку Пауза в окне диалога Результат подбора параметра и прервать вычисление, а затем нажать кнопку Шаг, чтобы выполнить очередную итерацию и просмотреть результат. При решении задачи в пошаговом режиме появляется кнопка Продолжить — для возврата в обычный режим подбора параметра.
Вернемся к примеру. Возникает вопрос: как получить второй корень? Для того чтобы найти второй корень, достаточно в качестве начального приближения в ячейку C2 поместить константу 5 и после этого запустить процесс Подбор параметра.
Лист 2 переименовать в Задание2.
Решение уравнения с помощью инструмента «Поиск решения».
Команда Подбор параметра является удобной для решения простых уравнений. Для более сложных задач следует использовать команду Поиск решения, доступ к которой реализован через пункт меню Сервис/Поиск решения. При решении уравнений с помощью Поиска решений можно учитывать различные дополнительные ограничения, например, ОДЗ (область допустимых значений).
Перейти на лист 3.
Рассмотрим, как воспользоваться Поиском решения на примере того же квадратного уравнения.
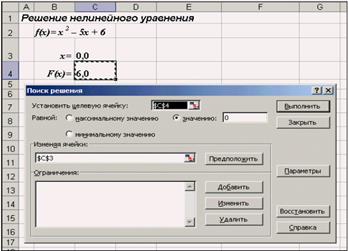
После открытия диалога Поиск решения необходимо выполнить следующие действия:
1. в поле Установить целевую ячейку ввести адрес ячейки, содержащей формулу для вычисления значений оптимизируемой функции, в нашем примере целевая ячейка — это С4, а формула в ней имеет вид: = C3^2 — 5*C3 + 6;
2. для максимизации значения целевой ячейки, установить переключатель максимальному значению, для минимизации используется переключатель минимальному значению, в нашем случае устанавливаем переключатель в положение значению и вводим значение 0;
3. в поле Изменяя ячейки ввести адреса изменяемых ячеек, т.е. аргументов целевой функции (С3), разделяя их знаком «;» (или щелкая мышью при нажатой клавише Сtrl на соответствующих ячейках), для автоматического поиска всех влияющих на решение ячеек используется кнопка Предположить;
4. в поле Ограничения с помощью кнопки Добавить ввести все ограничения, которым должен отвечать результат поиска: для нашего примера ограничений задавать не нужно;
5. для запуска процесса поиска решения нажать кнопку Выполнить.

Для сохранения полученного решения необходимо использовать переключатель Сохранить найденное решение в открывшемся окне диалога Результаты поиска решения. После чего рабочий лист примет вид, как на рисунке. Полученное решение зависит от выбора начального приближения, которое задается в ячейке С4 (аргумент функции). Если в качестве начального приближения в ячейку С4 ввести значение, равное 1,0, то с помощью Поиска решения найдем второй корень, равный 2,0.
Поиск решения EXCEL. Знакомство
history 23 марта 2015 г.
-
Группы статей
- Надстройка «Поиск решения»
Поиск решения — это надстройка Microsoft Excel, с помощью которой можно найти оптимальное решение задачи с учетом заданных пользователем ограничений.
Поиск решения будем рассматривать в MS EXCEL 2010 (эта надстройка претерпела некоторые изменения по сравнению с предыдущей версией в MS EXCEL 2007) . В этой статье рассмотрим:
- создание оптимизационной модели на листе MS EXCEL
- настройку Поиска решения;
- простой пример (линейная модель).
Установка Поиска решения
Команда Поиск решения находится в группе Анализ на вкладке Данные .
Если команда Поиск решения в группе Анализ недоступна, то необходимо включить одноименную надстройку. Для этого:
- На вкладке Файл выберите команду Параметры , а затем — категорию Надстройки ;
- В поле Управление выберите значение Надстройки Excel и нажмите кнопку Перейти;
- В поле Доступные надстройки установите флажок рядом с пунктом Поиск решения и нажмите кнопку ОК.
Примечание . Окно Надстройки также доступно на вкладке Разработчик . Как включить эту вкладку читайте здесь .
После нажатия кнопки Поиск решения в группе Анализ, откроется его диалоговое окно .
При частом использовании Поиска решения его удобнее запускать с Панели быстрого доступа, а не из вкладки Данные. Чтобы поместить кнопку на Панель, кликните на ней правой клавишей мыши и выберите пункт Добавить на панель быстрого доступа .
О моделях
Этот раздел для тех, кто только знакомится с понятием Оптимизационная модель.
Совет . Перед использованием Поиска решения настоятельно рекомендуем изучить литературу по решению оптимизационных задач и построению моделей.
Ниже приведен небольшой ликбез по этой теме.
Надстройка Поиск решения помогает определить лучший способ сделать что-то :
- «Что-то» может включать в себя выделение денег на инвестиции, загрузку склада, доставку товара или любую другую предметную деятельность, где требуется найти оптимальное решение.
- «Лучший способ» или оптимальное решение в этом случае означает: максимизацию прибыли, минимизацию затрат, достижение наилучшего качества и пр.
Вот некоторые типичные примеры оптимизационных задач:
- Определить план производства , при котором доход от реализации произведенной продукции максимальный;
- Определить схему перевозок , при которой общие затраты на перевозку были бы минимальными;
- Найти распределение нескольких станков по разным видам работ , чтобы общие затраты на производство продукции были бы минимальными;
- Определить минимальный срок исполнения всех работ проекта (критический путь).
Для формализации поставленной задачи требуется создать модель, которая бы отражала существенные характеристики предметной области (и не включала бы незначительные детали). Следует учесть, что модель оптимизируется Поиском решения только по одному показателю (этот оптимизируемый показатель называется целевой функцией ). В MS EXCEL модель представляет собой совокупность связанных между собой формул, которые в качестве аргументов используют переменные. Как правило, эти переменные могут принимать только допустимые значения с учетом заданных пользователем ограничений. Поиск решения подбирает такие значения этих переменных (с учетом заданных ограничений), чтобы целевая функция была максимальной (минимальной) или была равна заданному числовому значению.
Примечание . В простейшем случае модель может быть описана с помощью одной формулы. Некоторые из таких моделей могут быть оптимизированы с помощью инструмента Подбор параметра . Перед первым знакомством с Поиском решения имеет смысл сначала детально разобраться с родственным ему инструментом Подбор параметра . Основные отличия Подбора параметра от Поиска решения :
- Подбор параметра работает только с моделями с одной переменной;
- в нем невозможно задать ограничения для переменных;
- определяется не максимум или минимум целевой функции, а ее равенство некому значению;
- эффективно работает только в случае линейных моделей, в нелинейном случае находит локальный оптимум (ближайший к первоначальному значению переменной).
Подготовка оптимизационной модели в MS EXCEL
Поиск решения оптимизирует значение целевой функции. Под целевой функцией подразумевается формула, возвращающая единственное значение в ячейку. Результат формулы должен зависеть от переменных модели (не обязательно напрямую, можно через результат вычисления других формул). Ограничения модели могут быть наложены как на диапазон варьирования самих переменных, так и на результаты вычисления других формул модели, зависящих от этих переменных. Все ячейки, содержащие переменные и ограничения модели должны быть расположены только на одном листе книги. Ввод параметров в диалоговом окне Поиска решения возможен только с этого листа. Целевая функция (ячейка) также должна быть расположена на этом листе. Но, промежуточные вычисления (формулы) могут быть размещены на других листах.
Совет . Организуйте данные модели так, чтобы на одном листе MS EXCEL располагалась только одна модель. В противном случае, для выполнения расчетов придется постоянно сохранять и загружать настройки Поиска решения (см. ниже).
Приведем алгоритм работы с Поиском решения , который советуют сами разработчики ( ]]> www.solver.com ]]> ):
- Определите ячейки с переменными модели (decision variables);
- Создайте формулу в ячейке, которая будет рассчитывать целевую функцию вашей модели (objective function);
- Создайте формулы в ячейках, которые будут вычислять значения, сравниваемые с ограничениями (левая сторона выражения);
- С помощью диалогового окна Поиск решения введите ссылки на ячейки содержащие переменные, на целевую функцию, на формулы для ограничений и сами значения ограничений;
- Запустите Поиск решения для нахождения оптимального решения.
Проделаем все эти шаги на простом примере.
Простой пример использования Поиска решения
Необходимо загрузить контейнер товарами, чтобы вес контейнера был максимальным. Контейнер имеет объем 32 куб.м. Товары содержатся в коробках и ящиках. Каждая коробка с товаром весит 20кг, ее объем составляет 0,15м3. Ящик — 80кг и 0,5м3 соответственно. Необходимо, чтобы общее количество тары было не меньше 110 штук.
Данные модели организуем следующим образом (см. файл примера ).
Переменные модели (количество каждого вида тары) выделены зеленым. Целевая функция (общий вес всех коробок и ящиков) – красным. Ограничения модели: по минимальному количеству тары (>=110) и по общему объему ( =СУММПРОИЗВ(B8:C8;B6:C6) – это общий вес всех коробок и ящиков, загруженных в контейнер. Аналогично рассчитываем общий объем — =СУММПРОИЗВ(B7:C7;B8:C8) . Эта формула нужна, чтобы задать ограничение на общий объем коробок и ящиков ( =СУММ(B8:C8) . Теперь с помощью диалогового окна Поиск решения введем ссылки на ячейки содержащие переменные, целевую функцию, формулы для ограничений и сами значения ограничений (или ссылки на соответствующие ячейки). Понятно, что количество коробок и ящиков должно быть целым числом – это еще одно ограничение модели.
После нажатия кнопки Найти решение будут найдены такие количества коробок и ящиков, при котором общий их вес (целевая функция) максимален, и при этом выполнены все заданные ограничения.
Совет : в статье » Поиск решения MS EXCEL. Экстремум функции с несколькими переменными. Граничные условия заданы уравнениями » показано решение задачи, в которой функция и граничные условия заданы в явном виде, т.е. математическими выражениями типа F(x1, x2, x3)=x1+2*x2+6*x3, что существенно облегчает построение модели, т.к. не требуется особо осмыслять задачу: можно просто подставить переменные x в поле переменные, а ограничения ввести в соответствующее поле окна Поиска решения.
Резюме
На самом деле, основной проблемой при решении оптимизационных задач с помощью Поиска решения является отнюдь не тонкости настройки этого инструмента анализа, а правильность построения модели, адекватной поставленной задаче. Поэтому в других статьях сконцентрируемся именно на построении моделей, ведь «кривая» модель часто является причиной невозможности найти решение с помощью Поиска решения . Зачастую проще просмотреть несколько типовых задач, найти среди них похожую, а затем адаптировать эту модель под свою задачу. Решение классических оптимизационных задач с помощью Поиска решения рассмотрено в этом разделе .
Поиску решения не удалось найти решения (Solver could not find a feasible solution)
Это сообщение появляется, когда Поиск решения не смог найти сочетаний значений переменных, которые одновременно удовлетворяют всем ограничениям. Если вы используете Симплекс метод решения линейных задач , то можно быть уверенным, что решения действительно не существует. Если вы используете метод решения нелинейных задач, который всегда начинается с начальных значений переменных, то это может также означать, что допустимое решение далеко от этих начальных значений. Если вы запустите Поиск решения с другими начальными значениями переменных, то, возможно, решение будет найдено. Представим, что при решении задачи нелинейным методом, ячейки с переменными были оставлены не заполненными (т.е. начальные значения равны 0), и Поиск решения не нашел решения. Это не означает, что решения действительно не существует (хотя это может быть и так). Теперь, основываясь на результатах некой экспертной оценки, в ячейки с переменными введем другой набор значений, который, по Вашему мнению, близок к оптимальному (искомому). В этом случае, Поиск решения может найти решение (если оно действительно существует).
Примечание . О влиянии нелинейности модели на результаты расчетов можно прочитать в последнем разделе статьи Поиск решения MS EXCEL (4.3). Выбор места открытия нового представительства .
В любом случае (линейном или нелинейном), Вы должны сначала проанализировать модель на непротиворечивость ограничений, то есть условий, которые не могут быть удовлетворены одновременно. Чаще всего это связано с неправильным выбором соотношения (например, =) или граничного значения. Если, например, в рассмотренном выше примере, значение максимального объема установить 16 м3 вместо 32 м3, то это ограничение станет противоречить ограничению по минимальному количеству мест (110), т.к. минимальному количеству мест соответствует объем равный 16,5 м3 (110*0,15, где 0,15 – объем коробки, т.е. самой маленькой тары). Установив в качестве ограничения максимального объема 16 м3, Поиск решения не найдет решения.
При ограничении 17 м3 Поиск решения найдет решение.
Некоторые настройки Поиска решения
Метод решения Рассмотренная выше модель является линейной, т.е. целевая функция (M – общий вес, который может быть максимален) выражена следующим уравнением M=a1*x1+a2*x2, где x1 и x2 – это переменные модели (количество коробок и ящиков), а1 и а2 – их веса. В линейной модели ограничения также должны быть линейными функциями от переменных. В нашем случае ограничение по объему V=b1*x1+b2*x2 также выражается линейной зависимостью. Очевидно, что другое ограничение — Максимальное количество тары (n) – также линейно x1+x2
Постановка и решение задачи с помощью надстройки «Поиск решения»
«Поиск решения» — это надстройка для Microsoft Excel, которую можно использовать для анализ «что если». С ее помощью можно найти оптимальное значение (максимум или минимум) формула, содержащейся в одной ячейке, называемой целевой, с учетом ограничений на значения в других ячейках с формулами на листе. Надстройка «Поиск решения» работает с группой ячеек, называемых ячейками переменных решения или просто ячейками переменных, которые используются при расчете формул в целевых ячейках и ячейках ограничения. Надстройка «Поиск решения» изменяет значения в ячейках переменных решения согласно пределам ячеек ограничения и выводит нужный результат в целевой ячейке.
Проще говоря, с помощью надстройки «Поиск решения» можно определить максимальное или минимальное значение одной ячейки, изменяя другие ячейки. Например, вы можете изменить планируемый бюджет на рекламу и посмотреть, как изменится планируемая сумма прибыли.
Примечание: В версиях надстройки «Поиск решения», выпущенных до Excel 2007, ячейки переменных решения назывались изменяемыми или регулируемыми. В Excel 2010 надстройка «Поиск решения» была значительно улучшена, так что работа с ней в Excel 2007 будет несколько отличаться.
В приведенном ниже примере количество проданных единиц в каждом квартале зависит от уровня рекламы, что косвенно определяет объем продаж, связанные издержки и прибыль. Надстройка «Поиск решения» может изменять ежеквартальные расходы на рекламу (ячейки переменных решения B5:C5) до ограничения в 20 000 рублей (ячейка F5), пока общая прибыль (целевая ячейка F7) не достигнет максимального значения. Значения в ячейках переменных используются для вычисления прибыли за каждый квартал, поэтому они связаны с формулой в целевой ячейке F7, =СУММ (Q1 Прибыль:Q2 Прибыль).
1. Ячейки переменных
2. Ячейка с ограничениями
3. Целевая ячейка
После выполнения процедуры получены следующие значения.
На вкладке Данные в группе Анализ нажмите кнопку Поиск решения.
Примечание: Если команда «Найти решение» или «Анализ» недоступна, необходимо активировать надстройка. См. также: Активация надстройки «Надстройка».
В поле Оптимизировать целевую функцию введите ссылка на ячейку или имя целевой ячейки. Целевая ячейка должна содержать формулу.
Выполните одно из следующих действий.
Чтобы значение целевой ячейки было максимальным из возможных, установите переключатель в положение Макс.
Чтобы значение целевой ячейки было минимальным из возможных, установите переключатель в положение Мин.
Чтобы задать для целевой ячейки конкретное значение, установите переключатель в положение Значение и введите в поле нужное число.
В поле Изменяя ячейки переменных введите имена диапазонов ячеек переменных решения или ссылки на них. Несмежные ссылки разделяйте запятыми. Ячейки переменных должны быть прямо или косвенно связаны с целевой ячейкой. Можно задать до 200 ячеек переменных.
В поле В соответствии с ограничениями введите любые ограничения, которые требуется применить. Для этого выполните указанные ниже действия.
В диалоговом окне Параметры поиска решения нажмите кнопку Добавить.
В поле Ссылка на ячейку введите ссылку на ячейку или имя диапазона ячеек, на значения которых налагаются ограничения.
Щелкните связь ( =, >=, int, binили dif), которая требуется между ячейкой, на которую ссылается ссылка, и ограничением. Если щелкнуть int, в поле Ограничение появится integer. Если щелкнуть бин, в поле Ограничение появится двоичное поле. Если нажать кнопку dif,в поле Ограничение появится ссылка alldifferent.
Если в поле Ограничение было выбрано отношение =, введите число, ссылку на ячейку (или имя ячейки) или формулу.
Выполните одно из указанных ниже действий.
Чтобы принять данное ограничение и добавить другое, нажмите кнопку Добавить.
Чтобы принять ограничение и вернуться в диалоговое окно Параметрырешения, нажмите кнопку ОК.
Примечание Отношения int, binи dif можно применять только в ограничениях для ячеек переменных решения.
Чтобы изменить или удалить существующее ограничение, выполните указанные ниже действия.
В диалоговом окне Параметры поиска решения щелкните ограничение, которое требуется изменить или удалить.
Нажмите кнопку Изменить и внесите изменения либо нажмите кнопку Удалить.
Нажмите кнопку Найти решение и выполните одно из указанных ниже действий.
Чтобы сохранить значения решения на листе, в диалоговом окне Результаты поиска решения выберите вариант Сохранить найденное решение.
Чтобы восстановить исходные значения перед нажатием кнопки Найти решение, выберите вариант Восстановить исходные значения.
Вы можете прервать поиск решения, нажав клавишу ESC. Лист Excel будет пересчитан с учетом последних найденных значений для ячеек переменных решения.
Чтобы создать отчет, основанный на найденном решении, выберите тип отчета в поле Отчеты и нажмите кнопку ОК. Отчет будет помещен на новый лист книги. Если решение не найдено, будут доступны только некоторые отчеты или они вообще не будут доступны.
Чтобы сохранить значения ячейки переменной решения в качестве сценария, который можно будет отобразить позже, нажмите кнопку Сохранить сценарий в диалоговом окне Результаты поиска решения, а затем введите имя этого сценария в поле Название сценария.
После постановки задачи нажмите кнопку Параметры в диалоговом окне Параметры поиска решения.
Чтобы просмотреть значения всех найденных решений, в диалоговом окне Параметры установите флажок Показывать результаты итераций и нажмите кнопку ОК.
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение.
В диалоговом окне Показать предварительное решение выполните одно из указанных ниже действий.
Чтобы остановить поиск решения и вывести на экран диалоговое окно Результаты поиска решения, нажмите кнопку Стоп.
Чтобы продолжить процесс поиска решения и просмотреть следующий вариант решения, нажмите кнопку Продолжить.
В диалоговом окне Параметры поиска решения нажмите кнопку Параметры.
В диалоговом окне на вкладках Все методы, Поиск решения нелинейных задач методом ОПГ и Эволюционный поиск решения выберите или введите значения нужных параметров.
В диалоговом окне Параметры поиска решения нажмите кнопку Загрузить/сохранить.
Введите диапазон ячеек для области модели и нажмите кнопку Сохранить или Загрузить.
При сохранении модели введите ссылку на первую ячейку вертикального диапазона пустых ячеек, в котором следует разместить модель оптимизации. При загрузке модели введите ссылку на весь диапазон ячеек, содержащий модель оптимизации.
Совет: Чтобы сохранить последние параметры, настроенные в диалоговом окне Параметры поиска решения, вместе с листом, сохраните книгу. Каждый лист в книге может иметь свои параметры надстройки «Поиск решения», и все они сохраняются. Кроме того, для листа можно определить более одной задачи, если нажимать кнопку Загрузить или сохранить для сохранения задач по отдельности.
В диалоговом окне Параметры поиска решения можно выбрать любой из указанных ниже алгоритмов или методов поиск решения.
Нелинейный метод обобщенного понижающего градиента (ОПГ). Используется для гладких нелинейных задач.
Симплекс-метод. Используется для линейных задач.
Эволюционный метод Используется для негладких задач.
Важно: Сначала нужно включить надстройку «Поиск решения». Дополнительные сведения см. в статье Загрузка надстройки «Поиск решения».
В приведенном ниже примере количество проданных единиц в каждом квартале зависит от уровня рекламы, что косвенно определяет объем продаж, связанные издержки и прибыль. Надстройка «Поиск решения» может изменять ежеквартальные расходы на рекламу (ячейки переменных решения B5:C5) до ограничения в 20 000 рублей (ячейка D5), пока общая прибыль (целевая ячейка D7) не достигнет максимального значения. Значения в ячейках переменных используются для вычисления прибыли за каждый квартал, поэтому они связаны с формулой в целевой ячейке D7, =СУММ (Q1 Прибыль:Q2 Прибыль).
В результате выполнения получены следующие значения:
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
В разделе Оптимизировать целевую функцию, введите ссылка на ячейку или имя целевой ячейки.
Примечание: Целевая ячейка должна содержать формулу.
Выполните одно из следующих действий.
Сделать так, чтобы значение целевой ячейки было максимальным из возможных
Выберите значение Макс.
Сделать так, чтобы значение целевой ячейки было минимальным из возможных
Выберите значение Мин.
Сделать так, чтобы целевая ячейка имела определенное значение
Щелкните Значение, а затем введите нужное значение в поле.
В поле Изменяя ячейки переменных введите имена диапазонов ячеек переменных решения или ссылки на них. Несмежные ссылки разделяйте запятыми.
Ячейки переменных должны быть прямо или косвенно связаны с целевой ячейкой. Можно задать до 200 ячеек переменных.
В поле В соответствии с ограничениями введите любые ограничения, которые требуется применить.
Для этого выполните следующие действия:
В диалоговом окне Параметры поиска решения нажмите кнопку Добавить.
В поле Ссылка на ячейку введите ссылку на ячейку или имя диапазона ячеек, на значения которых налагаются ограничения.
Во всплывающем меню =, или >= в поле Ограничение, введите число, имя ячейки, ссылку на нее или формулу.
Примечание: Отношения int, бин и раз можно использовать только в ограничениях для ячеек, в которых находятся переменные решения.
Выполните одно из указанных ниже действий.
Принять ограничение и добавить другое
Нажмите кнопку Добавить.
Принять ограничение и вернуться в диалоговое окно Параметры поиска решения
Нажмите кнопку ОК.
Нажмите кнопку Найти решение и выполните одно из следующих действий:
Сохранить значения решения на листе
В диалоговом окне Результаты поиска решения выберите вариант Сохранить найденное решение.
Восстановить исходные значения
Щелкните Восстановить исходные значения.
Чтобы прервать поиск решения, нажмите клавишу ESC. Лист Excel будет пересчитан с учетом последних найденных значений для ячеек переменных.
Чтобы создать отчет, основанный на найденном решении, выберите тип отчета в поле Отчеты и нажмите кнопку ОК. Отчет будет помещен на новый лист книги. Если решение не найдено, отчет не будет доступен.
Чтобы сохранить значения ячейки переменной решения в качестве сценария, который можно будет отобразить позже, нажмите кнопку Сохранить сценарий в диалоговом окне Результаты поиска решения, а затем введите имя этого сценария в поле Название сценария.
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
После постановки задачи нажмите кнопку Параметры в диалоговом окне Параметры поиска решения.
Чтобы просмотреть значения всех предварительных решений, установите флажок Показывать результаты итераций и нажмите кнопку ОК.
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение.
В диалоговом окне Показать предварительное решение выполните одно из следующих действий:
Остановить поиск решения и вывести на экран диалоговое окно Результаты поиска решения
Нажмите кнопку Стоп.
Продолжить поиск и просмотреть следующее предварительное решение
Нажмите кнопку Продолжить.
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
Нажмите кнопку Параметры, а затем в диалоговом окне Параметры или Поиск решения выберите один или несколько из следующих вариантов:
Настроить время решения и число итераций
На вкладке Все методы в разделе Пределы решения в поле Максимальное время (в секундах) введите количество секунд, в течение которых можно будет искать решение. Затем в поле Итерации укажите максимальное количество итераций, которое вы хотите разрешить.
Примечание: Если будет достигнуто максимальное время поиска решения или количество итераций, а решение еще не будет найдено, средство «Поиск решения» выведет диалоговое окно Показать предварительное решение.
На вкладке Все методы введите в поле Точность ограничения нужное значение погрешности. Чем меньше число, тем выше точность.
Задать степень сходимости
На вкладке Поиск решения нелинейных задач методом ОПГ или Эволюционный поиск решения в поле Сходимость укажите, насколько должны отличаться результаты последних пяти итераций, чтобы средство прекратило поиск решения. Чем меньше число, тем меньше должно быть изменение.
Нажмите кнопку ОК.
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение или Закрыть.
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
Щелкните Загрузить/сохранить, укажите диапазон ячеек для области модели и нажмите кнопку Сохранить или Загрузить.
При сохранении модели введите ссылку на первую ячейку вертикального диапазона пустых ячеек, в котором следует разместить модель оптимизации. При загрузке модели введите ссылку на весь диапазон ячеек, содержащий модель оптимизации.
Совет: Чтобы сохранить последние параметры, настроенные в диалоговом окне Параметры поиска решения, вместе с листом, сохраните книгу. Каждый лист в книге может иметь свои параметры надстройки «Поиск решения», и все они сохраняются. Кроме того, для листа можно определить более одной задачи, если нажимать кнопку Загрузить/сохранить для сохранения задач по отдельности.
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
Во всплывающем меню Выберите метод решения выберите одно из следующих значений:
Нелинейный метод обобщенного понижающего градиента (ОПГ)
Используется по умолчанию для моделей со всеми функциями Excel, кроме ЕСЛИ, ВЫБОР, ПРОСМОТР и другие ступенчатые функции.
Поиск решения линейных задач симплекс-методом
Используйте этот метод для задач линейного программирования. В формулах модели, которые зависят от ячеек переменных, должны использоваться функции СУММ, СУММПРОИЗВ, +, — и *.
Эволюционный поиск решения
Этот метод, основанный на генетических алгоритмах, лучше всего подходит в том случае, если в модели используются функции ЕСЛИ, ВЫБОР и ПРОСМОТР с аргументами, которые зависят от ячеек переменных.
Примечание: Авторские права на части программного кода надстройки «Поиск решения» версий 1990–2010 принадлежат компании Frontline Systems, Inc. Авторские права на части версии 1989 принадлежат компании Optimal Methods, Inc.
Поскольку надстройки не поддерживаются в Excel в Интернете, вы не сможете использовать надстройку «Поиск решения» для анализа данных «что если», чтобы найти оптимальные решения.
Если у вас есть Excel, вы можете нажать кнопку Открыть в Excel, чтобы открыть книгу для использования надстройки «Поиск решения».
Дополнительная справка по надстройке «Поиск решения»
За дополнительной справкой по надстройке «Поиск решения» обращайтесь по этим адресам:
Frontline Systems, Inc.
P.O. Box 4288
Incline Village, NV 89450-4288
(775) 831-0300
Веб-сайт: http://www.solver.com
Электронная почта: info@solver.com
«Решение» на www.solver.com.
Авторские права на части программного кода надстройки «Поиск решения» версий 1990-2009 принадлежат компании Frontline Systems, Inc. Авторские права на части версии 1989 принадлежат компании Optimal Methods, Inc.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
источники:
http://excel2.ru/articles/poisk-resheniya-ms-excel-znakomstvo
http://support.microsoft.com/ru-ru/office/%D0%BF%D0%BE%D1%81%D1%82%D0%B0%D0%BD%D0%BE%D0%B2%D0%BA%D0%B0-%D0%B8-%D1%80%D0%B5%D1%88%D0%B5%D0%BD%D0%B8%D0%B5-%D0%B7%D0%B0%D0%B4%D0%B0%D1%87%D0%B8-%D1%81-%D0%BF%D0%BE%D0%BC%D0%BE%D1%89%D1%8C%D1%8E-%D0%BD%D0%B0%D0%B4%D1%81%D1%82%D1%80%D0%BE%D0%B9%D0%BA%D0%B8-%D0%BF%D0%BE%D0%B8%D1%81%D0%BA-%D1%80%D0%B5%D1%88%D0%B5%D0%BD%D0%B8%D1%8F-5d1a388f-079d-43ac-a7eb-f63e45925040



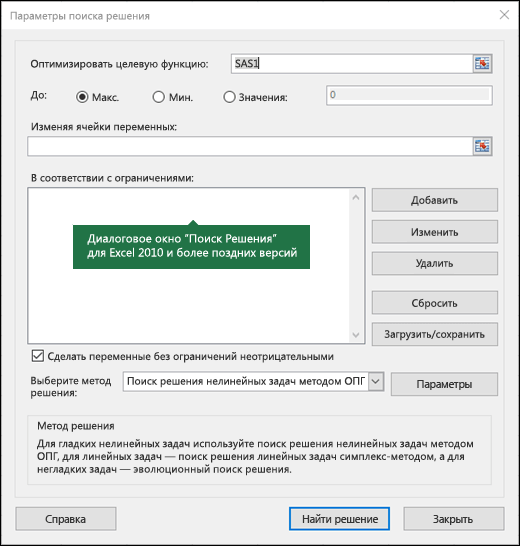



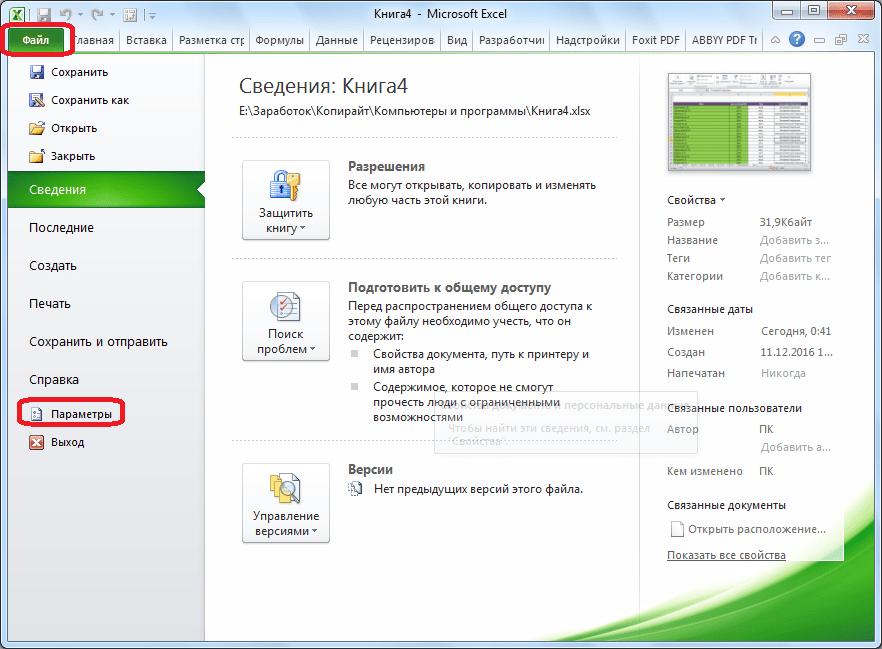
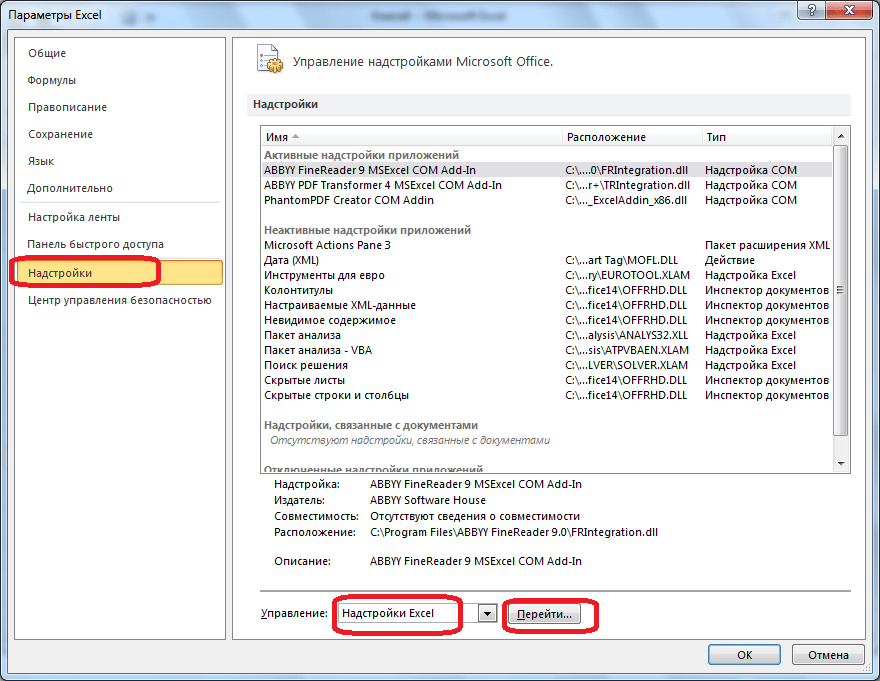
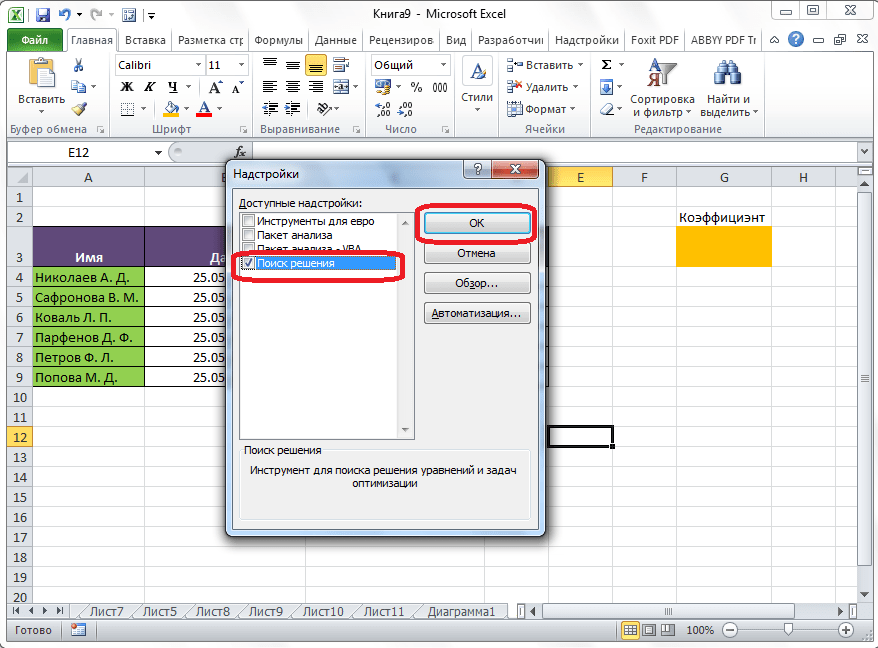
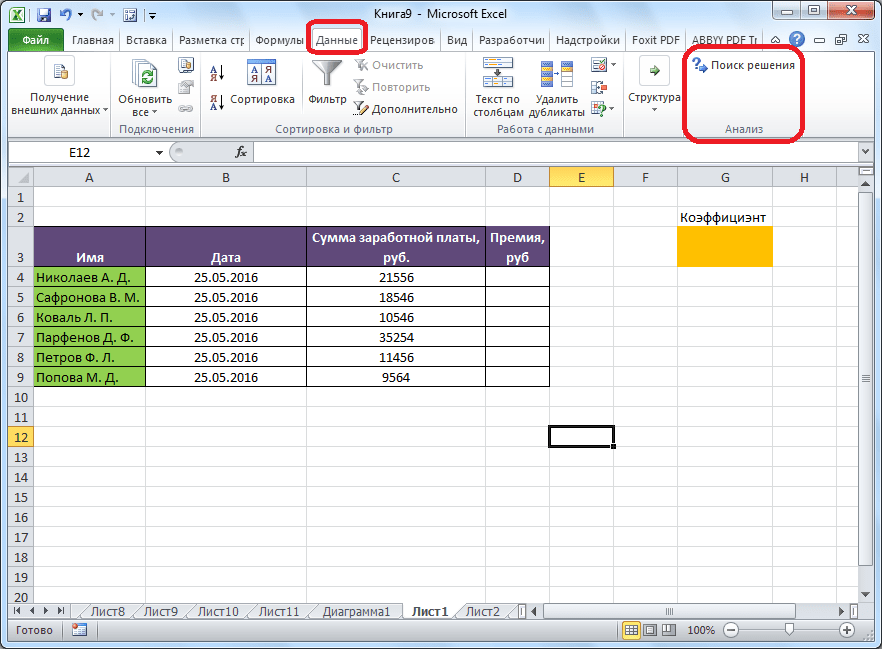
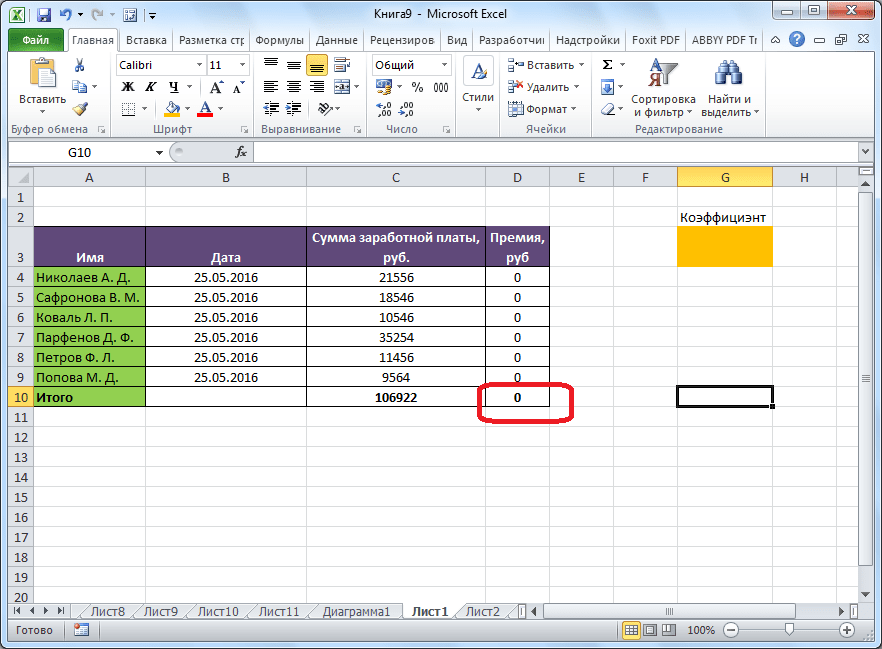
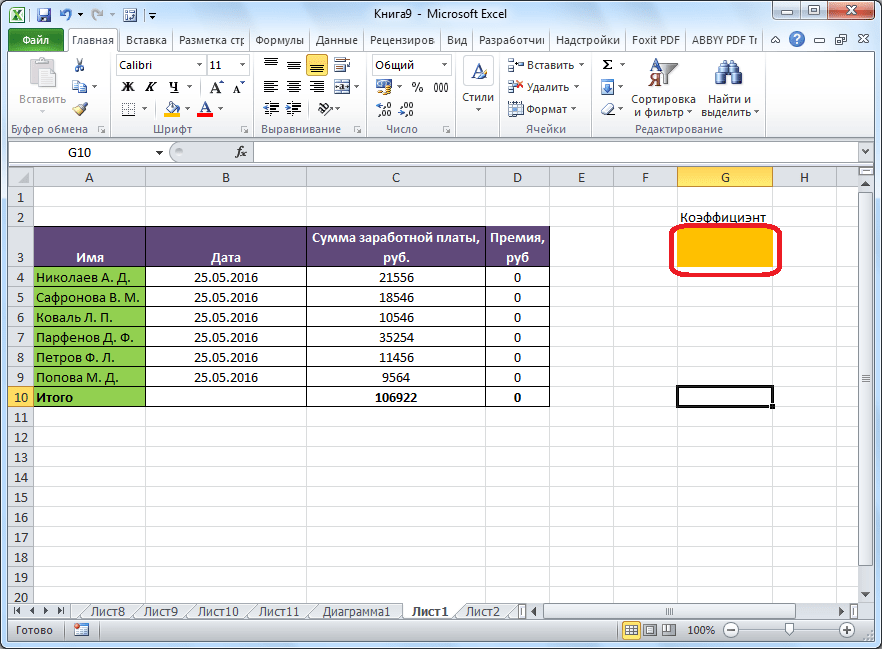
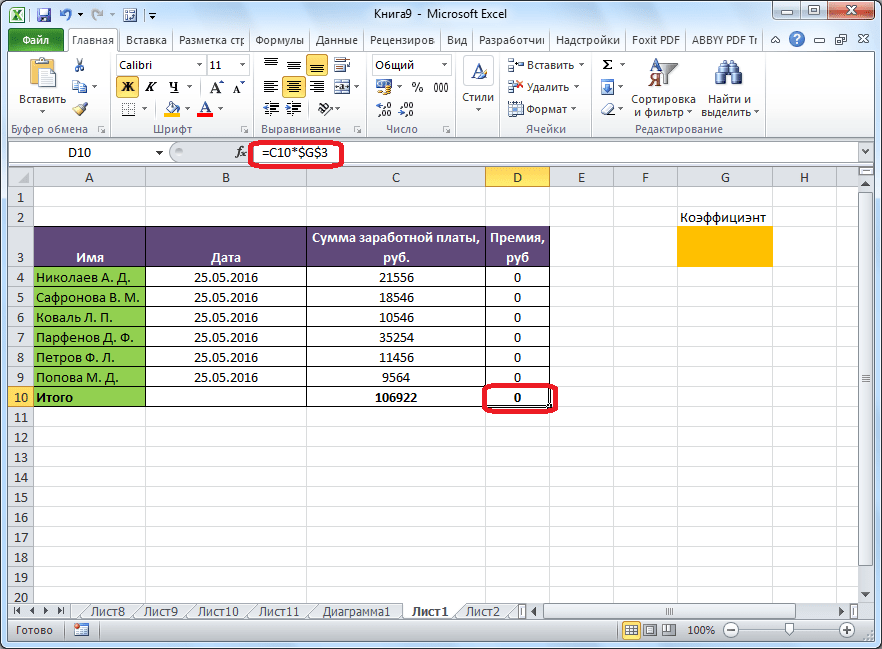
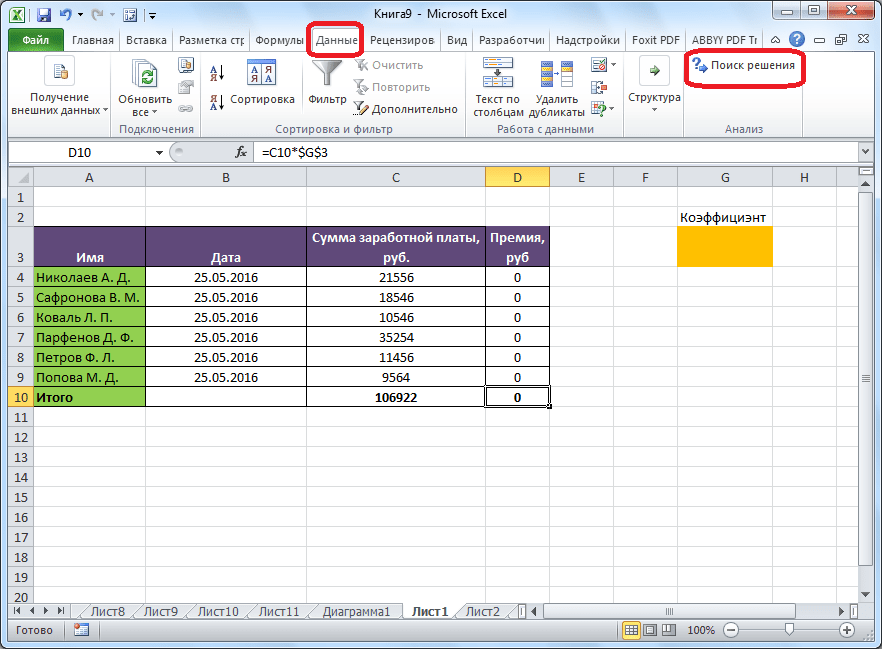
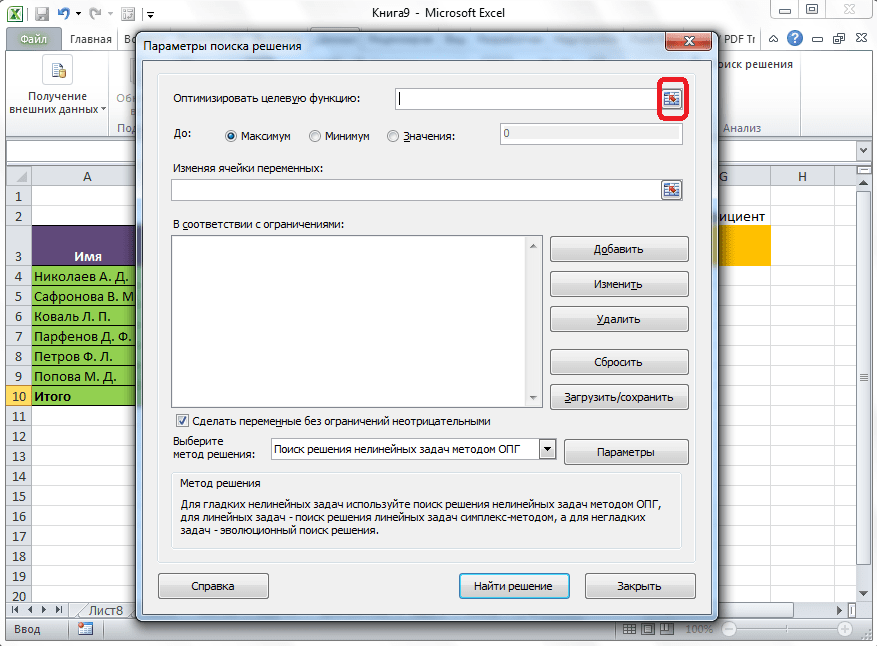
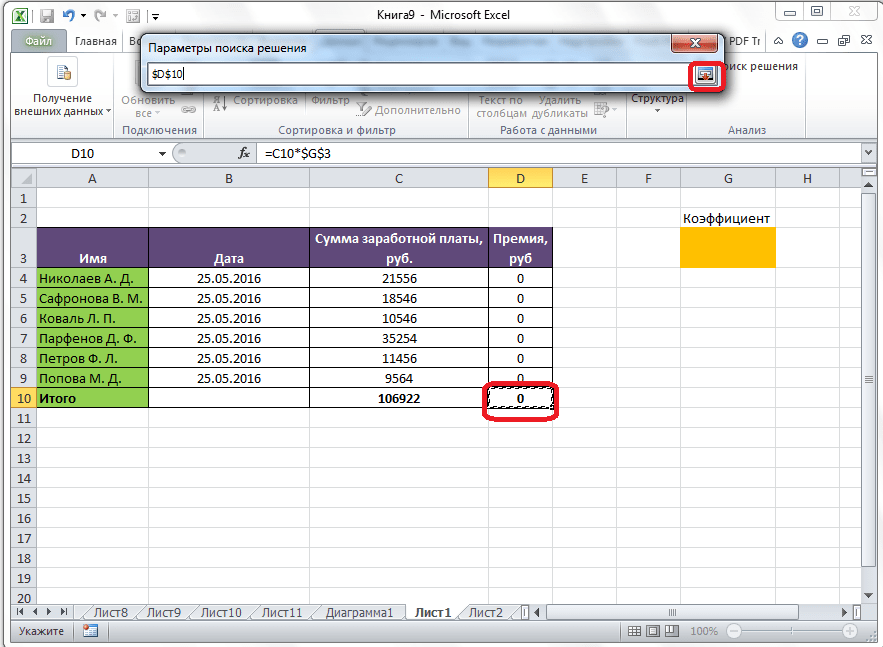
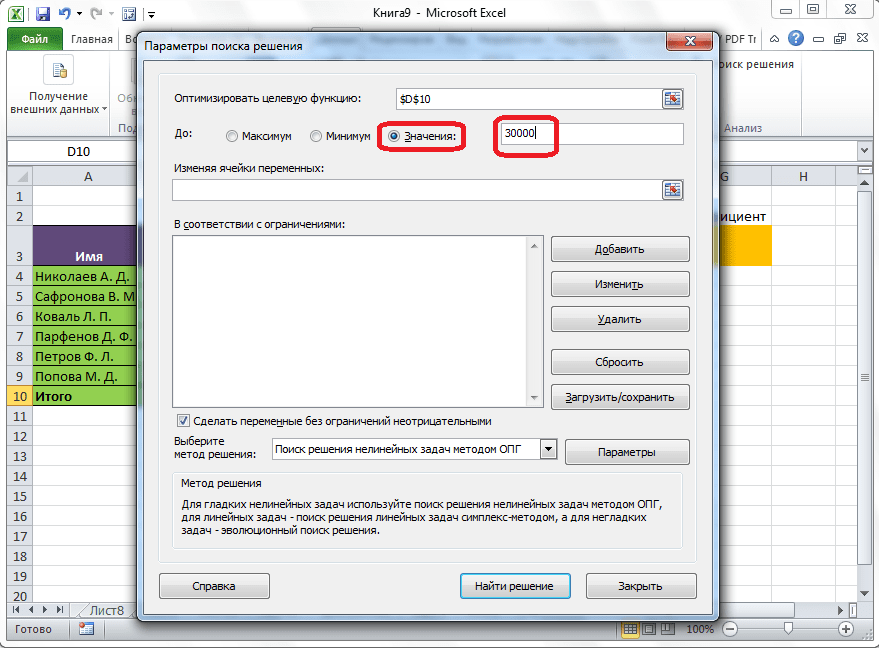
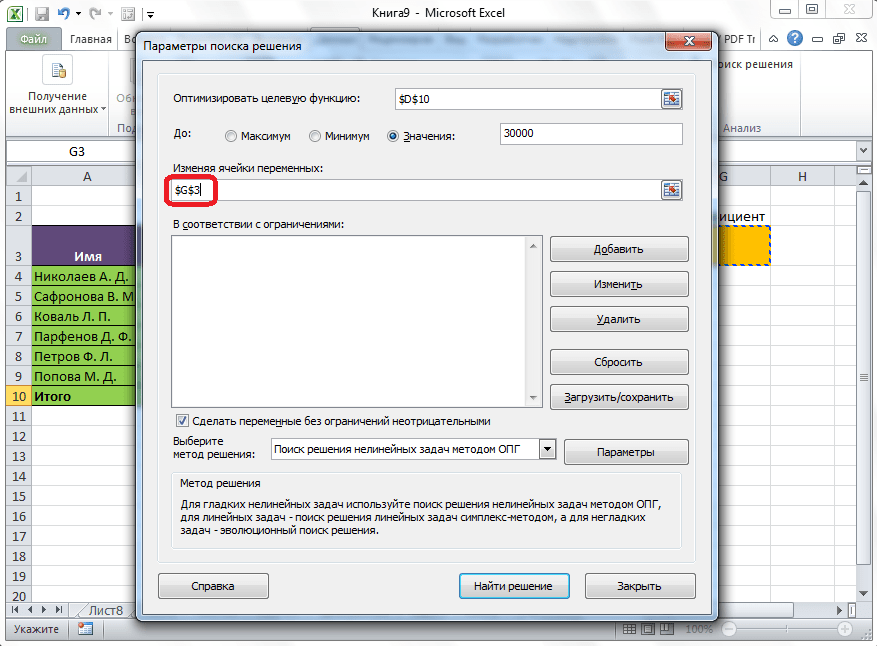
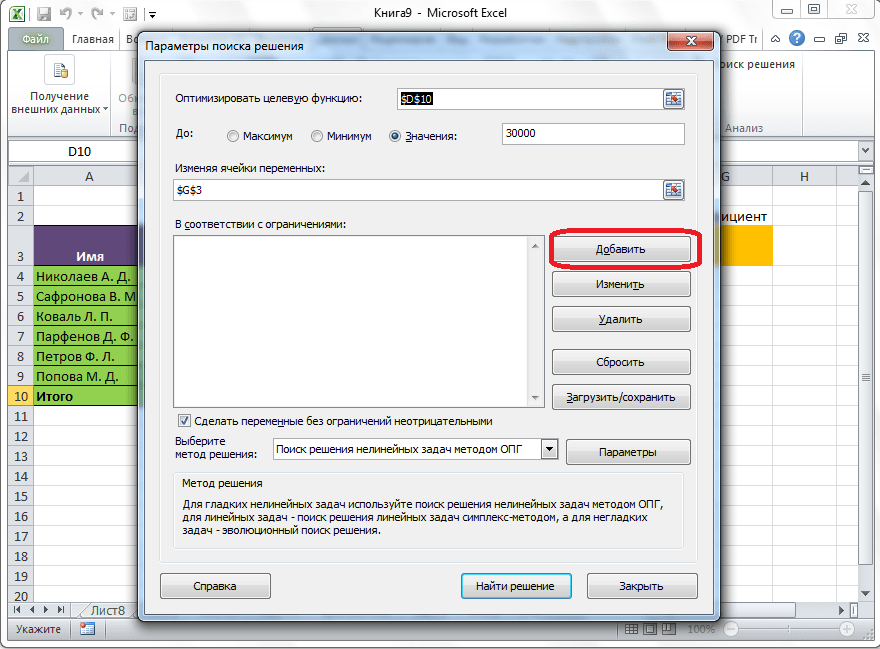
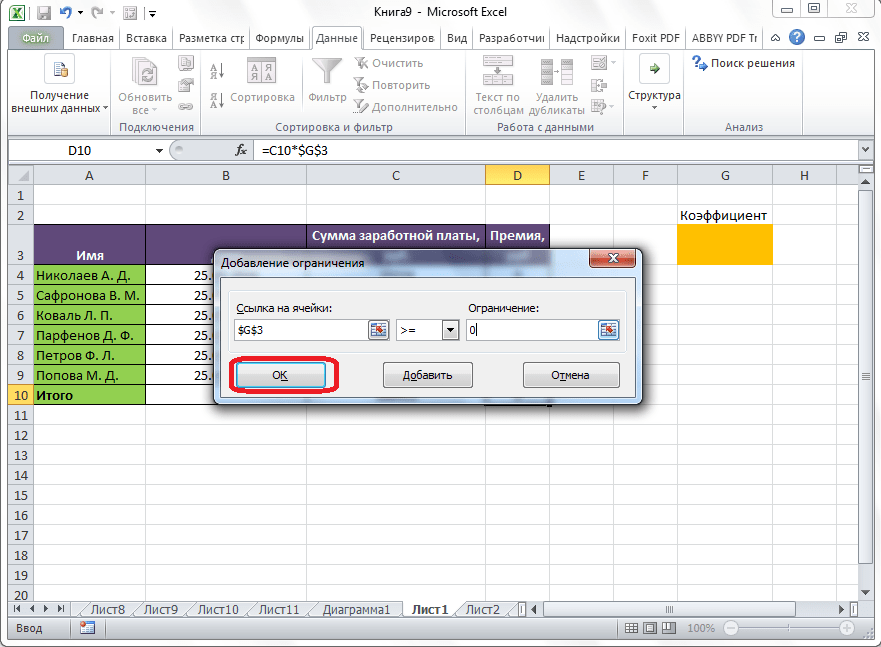
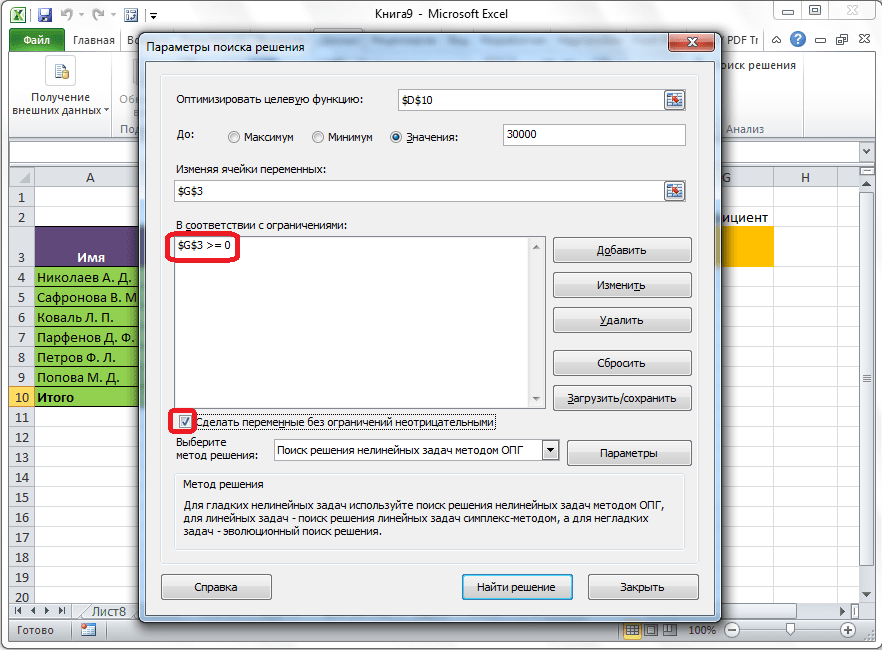
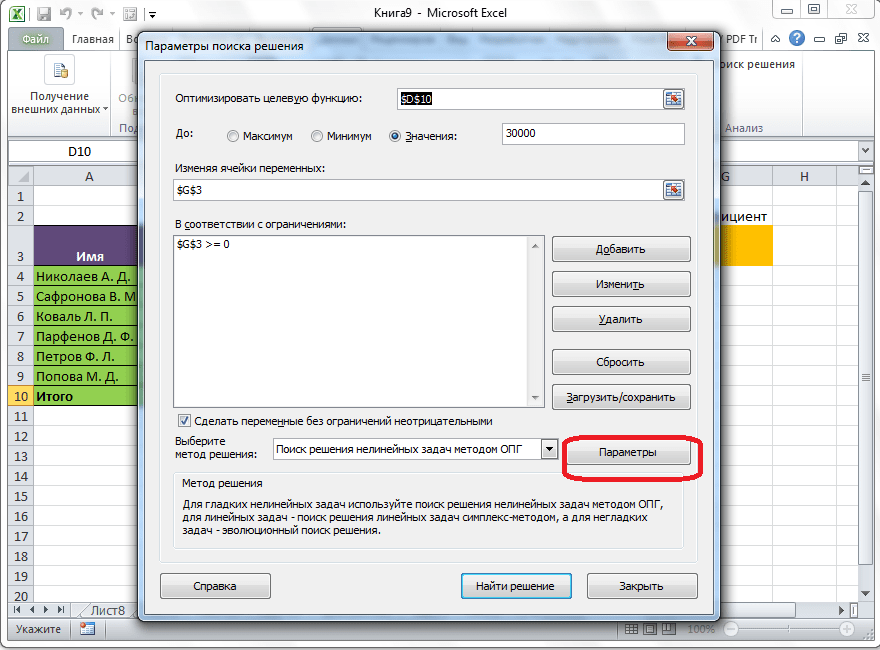
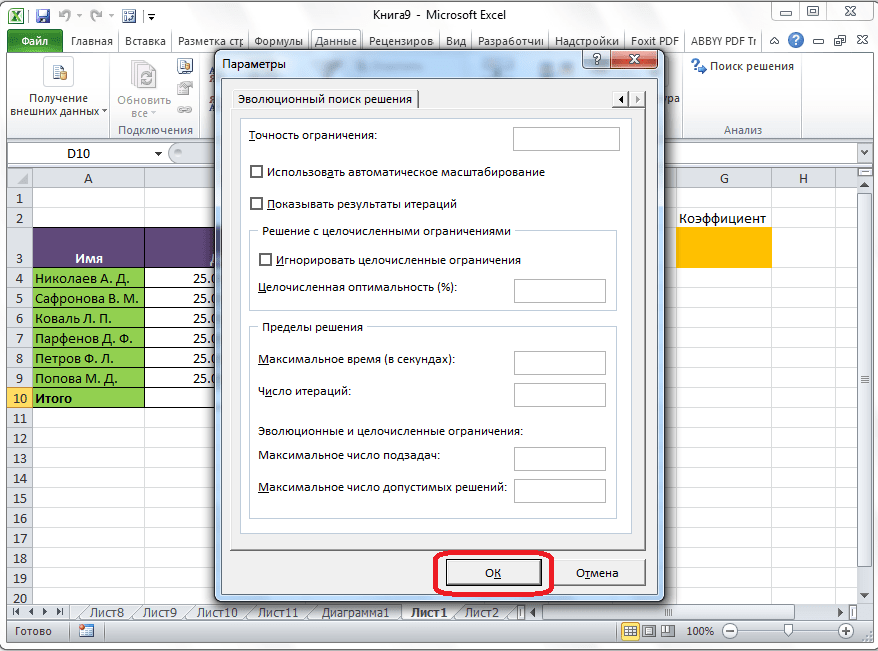
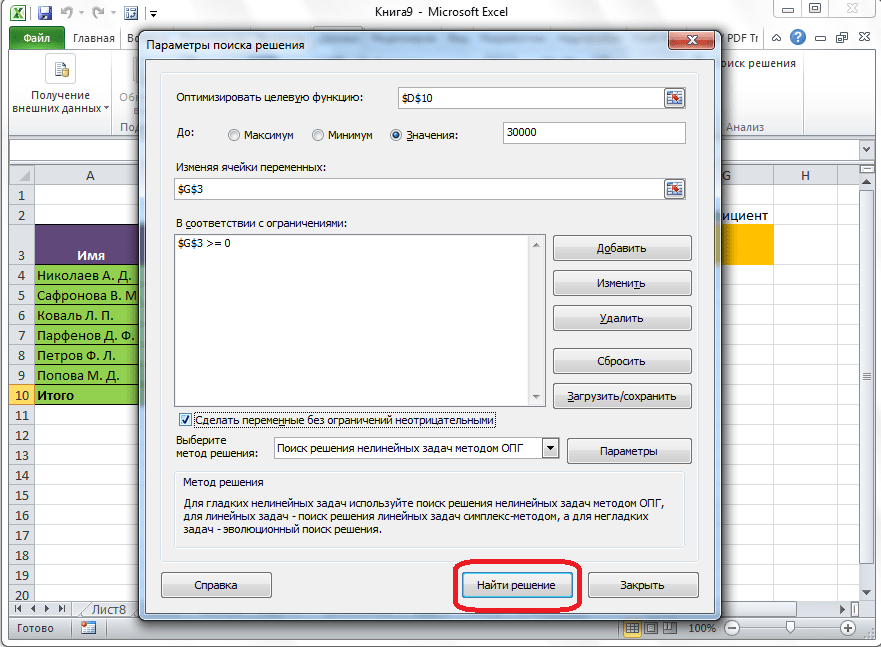
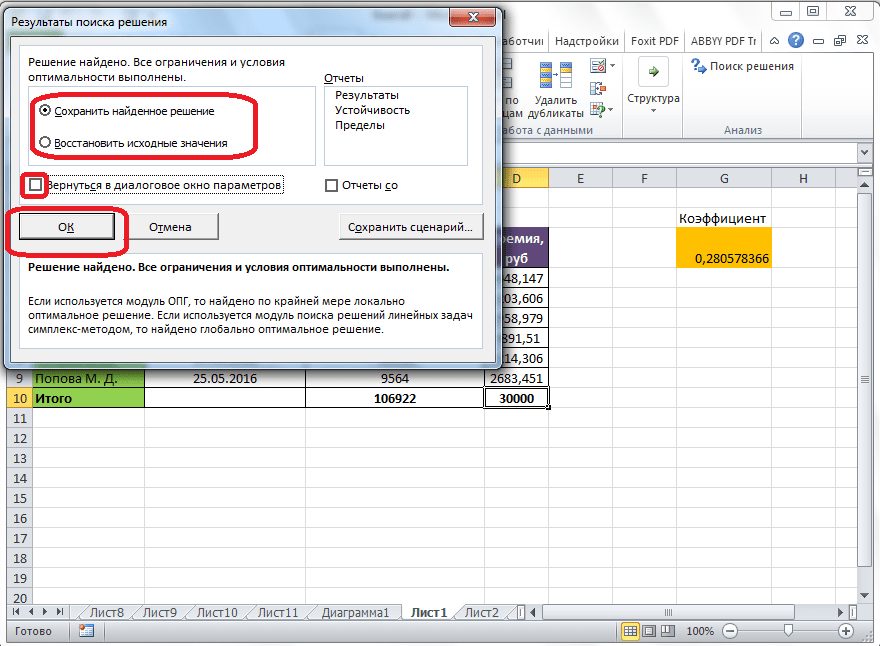
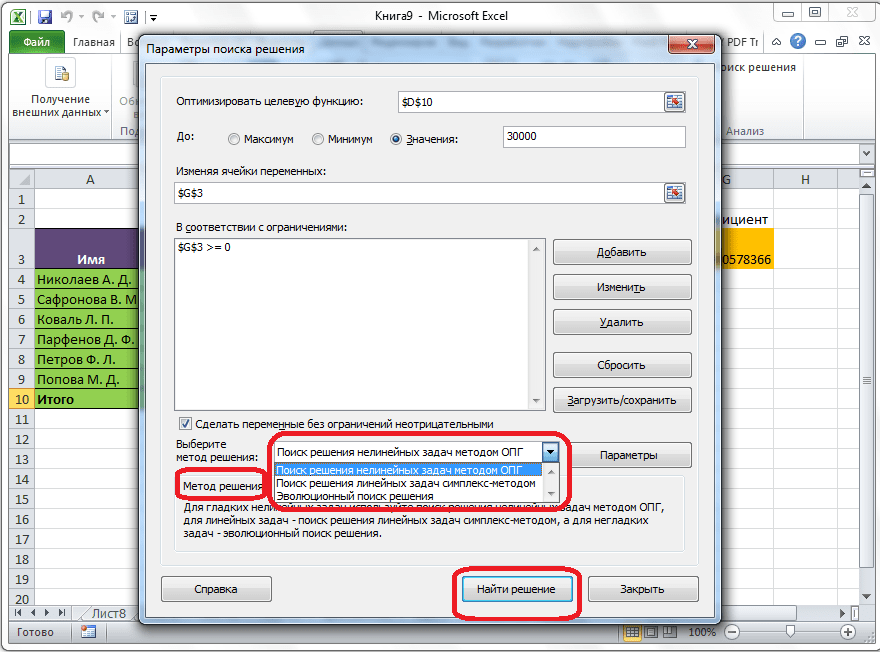
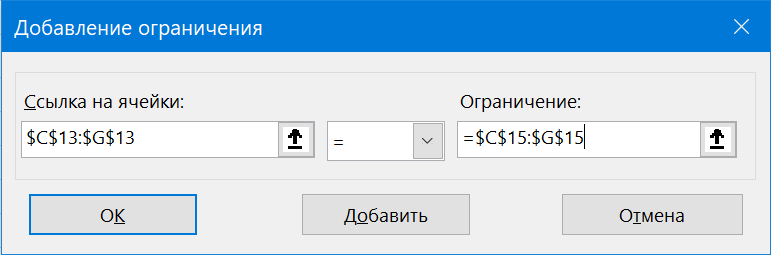
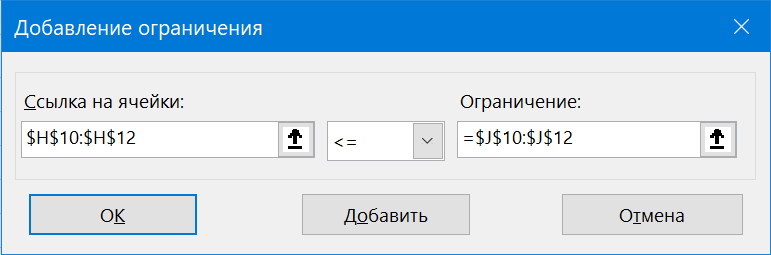













 Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK.
Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK. Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.
Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.