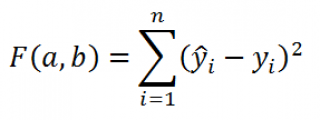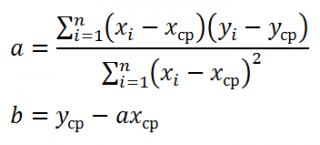Sub aprox()
Dim x() As Single, y() As Single, eps() As Single, yNew() As Single
Dim i As Integer, j As Integer, h As Integer, m As Integer
m = 20
n = InputBox("Введіть кількість відрізків", "Кількість відрізків")
ReDim x(n) As Single
ReDim y(n) As Single
ReDim yNew(n) As Single
ReDim eps(m) As Single
mes = "Апроксимація функції за МНК:"
mes = mes & vbNewLine & vbNewLine
For i = 1 To n
x(i) = InputBox("Введіть " & i & "-e значення x", "Значення х")
Next i
For j = 1 To n
y(j) = InputBox("Введіть " & j & "-e значення y", "Значення у")
Next j
For j = 1 To n
For h = 1 To n
If j = h Then
yNew(h) = y(j)
End If
Next h
Next j
xAr = (x(1) + x(n)) / 2
xGeom = (x(1) * x(n)) ^ 0.5
xGarm = 2 * x(1) * x(n) / (x(1) + x(n))
yAr = (y(1) + y(n)) / 2
yGeom = (y(1) * y(n)) ^ 0.5
yGarm = 2 * y(1) * y(n) / (y(1) + y(n))
minimum = 100
minimum2 = 100
minimum3 = 100
For i = 1 To n
j = i
If xAr = x(i) Then
yzAr = y(j)
ElseIf Abs(xAr - x(i)) < minimum Then
minimum = Abs(xAr - x(i))
yzAr = y(j) + (y(j + 1) - y(j)) / (x(i + 1) - x(i)) * (xGeom - x(i))
End If
If xGeom = x(i) Then
yzGeom = y(j)
ElseIf Abs(xGeom - x(i)) < minimum2 Then
yzGeom = y(j) + (y(j + 1) - y(j)) / (x(i + 1) - x(i)) * (xGeom - x(i))
minimum2 = Abs(xGeom - x(i))
End If
If xGarm = x(i) Then
yzGarm = y(j)
ElseIf Abs(xGarm - x(i)) < minimum3 Then
minimum3 = Abs(xGarm - x(i))
yzGarm = y(j) + (y(j + 1) - y(j)) / (x(i + 1) - x(i)) * (xGarm - x(i))
End If
Next i
eps(1) = Abs(yzAr - yAr)
eps(2) = Abs(yzAr - yGeom)
eps(3) = Abs(yzAr - yGarm)
eps(4) = Abs(yzGeom - yAr)
eps(5) = Abs(yzGeom - yGeom)
eps(6) = Abs(yzGarm - yAr)
eps(7) = Abs(yzGarm - yGarm)
epsMin = eps(1)
For m = 2 To 7
If eps(m) < epsMin Then
epsMin = eps(m)
End If
Next m
If epsMin = eps(1) Then
Text = "Данна залежність є лінійною"
For j = 1 To n
For i = 1 To n
If j = i Then
y(j) = y(j)
x(i) = x(i)
End If
Next i
Next j
ElseIf epsMin = eps(2) Then
Text = "Дана залежність є показниковою"
For j = 1 To n
For i = 1 To n
If j = i Then
y(j) = Log(y(j)) / Log(10)
x(i) = x(i)
End If
Next i
Next j
ElseIf epsMin = eps(3) Then
Text = "Дана залежність є дробово-раціональною"
For j = 1 To n
For i = 1 To n
If j = i Then
x(i) = x(i)
y(j) = 1 / y(j)
End If
Next i
Next j
ElseIf epsMin = eps(4) Then
Text = "Дана залежність є логарифмічною"
For j = 1 To n
For i = 1 To n
If j = i Then
x(i) = Log(x(i))
y(j) = y(j)
End If
Next i
Next j
ElseIf epsMin = eps(5) Then
Text = "Дана залежність є степеневою"
For j = 1 To n
For i = 1 To n
If j = i Then
y(j) = Log(y(j)) / Log(10)
x(i) = Log(x(i)) / Log(10)
End If
Next i
Next j
ElseIf epsMin = eps(6) Then
Text = "Дана залежність є гіперболічною"
For j = 1 To n
For i = 1 To n
If j = i Then
x(i) = 1 / x(i)
y(j) = y(j)
End If
Next i
Next j
ElseIf epsMin = eps(7) Then
Text = "Дана залежність є добово-раціональною"
For j = 1 To n
For i = 1 To n
If j = i Then
y(j) = 1 / y(j)
x(i) = 1 / x(i)
End If
Next i
Next j
End If
mes = mes & Text & vbNewLine & vbNewLine & "y(задане) " & "y(апроксимоване)" & vbNewLine
sumX2 = 0
sumX = 0
For i = 1 To n
sumX = sumX + x(i)
sumX2 = sumX2 + x(i) ^ 2
Next i
sumY = o
For j = 1 To n
sumY = sumY + y(j)
Next j
summ = o
For i = 1 To n
For j = 1 To n
If i = j Then
summ = summ + x(i) * y(j)
End If
Next j
Next i
del = n * sumX2 - (sumX * sumX)
del1 = sumY * sumX2 - (summ * sumX)
del2 = n * summ - (sumX * sumY)
b0 = del1 / del
b1 = del2 / del
For j = 1 To n
For i = 1 To n
If j = i Then
y(j) = b0 + b1 * x(i)
End If
Next i
Next j
If epsMin = eps(1) Then
For j = 1 To n
For i = 1 To n
If j = i Then
y(j) = y(j)
x(i) = x(i)
End If
Next i
Next j
ElseIf epsMin = eps(2) Then
For j = 1 To n
For i = 1 To n
If j = i Then
y(j) = Exp(y(j) * Log(10))
x(i) = x(i)
End If
Next i
Next j
ElseIf epsMin = eps(3) Then
For j = 1 To n
For i = 1 To n
If j = i Then
x(i) = x(i)
y(j) = 1 / y(j)
End If
Next i
Next j
ElseIf epsMin = eps(4) Then
For j = 1 To n
For i = 1 To n
If j = i Then
x(i) = Exp(x(i))
y(j) = y(j)
End If
Next i
Next j
ElseIf epsMin = eps(5) Then
For j = 1 To n
For i = 1 To n
If j = i Then
y(j) = Exp(y(j) * Log(10))
x(i) = Exp(x(i) * Log(10))
End If
Next i
Next j
ElseIf epsMin = eps(6) Then
For j = 1 To n
For i = 1 To n
If j = i Then
x(i) = 1 / x(i)
y(j) = y(j)
End If
Next i
Next j
ElseIf epsMin = eps(7) Then
For j = 1 To n
For i = 1 To n
If j = i Then
y(j) = 1 / y(j)
x(i) = 1 / x(i)
End If
Next i
Next j
End If
For h = 1 To n
For j = 1 To n
If h = j Then
vseEps = vseEps + (yNew(h) - y(j)) ^ 2
mes = mes & yNew(h) & " " & y(j) & vbNewLine
End If
Next j
Next h
poh = (vseEps / (n - 1)) ^ 0.5
mes = mes & vbNewLine & vbNewLine & "Середньоквадратична похибка: " & poh
MsgBox mes
End Sub
Подборка по базе: основные статистические показатели (характеристики) данных агрон, При измерении сопротивления обмотки якоря методом амперметра и в, Визуализация данных.ти ЭБС 63 вопроса.docx, Курсовая по информатике на тему _Спроектированная база данных ма, Тема 3.1 Понятия сводки и группировки статистических данных.pdf, АОУ. Лабораторная работа 3. Определение настроек регулятора мето, Положение о персональных данных.docx, Практическая работа №5_ Анализ данных о результатах оценочных пр, 3.13 Измерение сопротивление методом моста Уитстона..docx, Инструкция по выгрузке и загрузке данных.docx
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Санкт-Петербургский горный университет»
КУРСОВАЯ РАБОТА
По дисциплине
: ________Информатика__________________________
(наименование учебной дисциплины согласно учебному плану)
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Тема:
Аппроксимация данных методом наименьших квадратов
Автор: студент гр.
ЭРБ-16 _ _____________ /Акульшин Д.А./
(шифр группы) (подпись) (Ф.И.О.)
ОЦЕНКА: ___________
Дата: _______________
ПРОВЕРИЛ:
Руководитель проекта
доцент _____________ / Ильин А.Е./
(должность) (подпись) (Ф.И.О.)
Санкт-Петербург
2017 г.
Министерство Образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
Санкт-Петербургский горный Университет
УТВЕРЖДАЮ
Заведующий кафедрой
Доцент Маховиков А.Б.
___________/________/
«___»__________2017 г.
Кафедра информатики и компьютерных технологий
КУРСОВАЯ РАБОТА
По дисциплине
Информатика
_________________________________________________________________________
(наименование учебной дисциплины согласно учебному плану)
ЗАДАНИЕ
Студенту группы
ЭРБ-16 Акульшин Д.А.
(шифр группы) (Ф.И.О.)
1. Тема работы:
Аппроксимация функции методом наименьших квадратов
2. Исходные данные к проекту: Вариант №1
3. Содержание пояснительной записки: Пояснительная записка включает в себя задание на выполнение работы, расчётные формулы, расчёты с помощью электронных таблиц MicrosoftExcel, расчёты с использованием пакетов MathCAD, программу расчёта (на языке VBA), графическое решение, заключение, библиографический список
4. Перечень графического материала: таблицы и графики.
5. Срок сдачи законченного проекта:
02.05.2017
Руководитель проекта доцент ________________ / Ильин А.Е. /
(должность) (подпись) (Ф.И.О.)
Дата выдачи задания:
15.02.2017.
Аннотация
Пояснительная записка представляет собой отчет о выполнении курсовой работы. В ней рассматриваются вопросы по нахождению эмпирических формул методом наименьших квадратов (МНК) посредством возможностей пакетов Microsoft Excel, а также рассматривается решение данной задачи в программе MathCAD и VBA. В работе получены уравнения различных видов с помощью аппроксимации линейной, квадратичной и экспоненциальной зависимостей. По окончании работы сделан вывод, каким методом задача решена лучше всего.
Страниц 34, таблиц 10, рисунков 12.
Abstract
The explanatory note represents the report on performance of term paper performance. In it questions of empirical formulas by a method of the least squares (МNK) by means of possibilities of package Microsoft Excel are considered, and also the decision of the given problem in MathCAD and VBA is considered. In work the equations of various kinds by means of approximation linear, square-law and exponential dependences are received. Upon termination of work the conclusion is drawn, the problem is solved by what method is better.
Pages 34, tables 10, figures 124.
Оглавление
Введение 5
1.Постановка задачи 6
2. Математические методы и средства решения 7
2.1. Построение эмпирических формул методом наименьших квадратов 7
2.2. Линейная зависимость 10
2.3. Квадратичная зависимость 10
2.4. Линеаризация экспоненциальной зависимости 11
2.5. Элементы теории корреляции 11
2.6. Коэффициент детерминированности 14
3.Исходные данные 15
4.Аппроксимация функции с помощью Excel 16
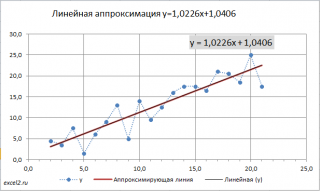
4.1.Линейная аппроксимация 17
4.2.Квадратичная аппроксимация 18
4.3.Экспоненциальная аппроксимация 19
4.4.Коэффициент корреляции. Коэффициенты детерминированности 20
4.5.Графический способ в Excel 22
4.6. Использование функции ЛИНЕЙН 25
4.6.1. Назначение функции ЛИНЕЙН 25
4.6.2. Получение числовых характеристик зависимости 25
5. Аппроксимация функции с помощью MathCAD 27
5.1. Исходные данные 27
5.2. Линейная аппроксимация 28
5.3. Полиномиальная регрессия 29
5.4. Экспоненциальная регрессия 30
6. Программа для аппроксимации функций методом наименьших квадратов на языке VBA 32
Выводы 37
Рекомендательный библиографический список 38
|
0 / 0 / 0 Регистрация: 31.10.2017 Сообщений: 7 |
|
|
1 |
|
Макрос. Аппроксимация31.10.2017, 16:16. Показов 5178. Ответов 14
Буду очень рад помощи) Есть следующий рад данных в виде таблицы exel Миниатюры
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
31.10.2017, 16:16 |
|
14 |
|
oh my god 1454 / 793 / 161 Регистрация: 05.01.2016 Сообщений: 2,307 Записей в блоге: 8 |
|
|
31.10.2017, 16:20 |
2 |
|
Вы знаете что такое аппроксимация ?
0 |
|
0 / 0 / 0 Регистрация: 31.10.2017 Сообщений: 7 |
|
|
31.10.2017, 16:29 [ТС] |
3 |
|
да, обобщение данных при помощи заданной функции
0 |
|
31 / 28 / 1 Регистрация: 06.01.2017 Сообщений: 297 |
|
|
31.10.2017, 16:47 |
4 |
|
Прежде чем строить аппроксимацию надо задать критерий аппроксимации, т.е. чем одна аппроксимация лучше другой. Традиционно в качестве критерия выступает сумма квадратов разностей, оптимальной аппроксимацией считается та, у которой эта сумма наименьшая, почему и называется «метод наименьших квадратов». Но строить эти разности можно по разному. Скорее всего, Вам надо сделать напрямую:
0 |
|
6169 / 934 / 309 Регистрация: 25.02.2011 Сообщений: 1,359 Записей в блоге: 1 |
|
|
31.10.2017, 16:59 |
5 |
|
Обязательно нужно решать через VBA? Полином очень хорошо описывает указанный набор данных
0 |
|
15136 / 6410 / 1730 Регистрация: 24.09.2011 Сообщений: 9,999 |
|
|
31.10.2017, 17:00 |
6 |
|
Есть следующий рад данных в виде таблицы exel Так приложите файл Eхcel, а не картинку.
0 |
|
0 / 0 / 0 Регистрация: 31.10.2017 Сообщений: 7 |
|
|
31.10.2017, 17:27 [ТС] |
7 |
|
Скорее всего, Вам надо сделать напрямую: Если бы вопрос был в линейной аппроксимации все было бы на много проще, но увы мне нужна именно такая функция Добавлено через 15 секунд
Скорее всего, Вам надо сделать напрямую: Если бы вопрос был в линейной аппроксимации все было бы на много проще, но увы мне нужна именно такая функция Добавлено через 55 секунд
Обязательно нужно решать через VBA? А можно пожалуйста поподробнее?
0 |
|
oh my god 1454 / 793 / 161 Регистрация: 05.01.2016 Сообщений: 2,307 Записей в блоге: 8 |
|
|
31.10.2017, 17:30 |
8 |
|
А можно пожалуйста поподробнее? Это надстройка в excel Миниатюры
1 |
|
31 / 28 / 1 Регистрация: 06.01.2017 Сообщений: 297 |
|
|
31.10.2017, 17:33 |
9 |
|
Причем тут линейная аппроксимация? Говоря «напрямую» я имел в виду, что разности надо строить напрямую: dY(i) = Y(i) — (A/(X(i)+C) + B) Но можно и не напрямую, сначала проведя преобразования, сведя Вашу зависимость к линейной: y*(x+c)= a + b*(x+c) Или Z = x*y
1 |
|
6169 / 934 / 309 Регистрация: 25.02.2011 Сообщений: 1,359 Записей в блоге: 1 |
|
|
31.10.2017, 17:37 |
10 |
|
поиск решения по вашим данным нашел следующие коэффициенты: Y = -2023,25099599718/(X-13,6971883429513)+8,86941820361647 Если взять модель полинома третей степени, то уравнение аппроксимирующей кривой будет следующим:
1 |
|
oh my god 1454 / 793 / 161 Регистрация: 05.01.2016 Сообщений: 2,307 Записей в блоге: 8 |
|
|
31.10.2017, 17:38 |
11 |
|
Ну вот, перепишите то что на картинке, задайте целевые ячейки как в преведенных уравнениях
0 |
|
0 / 0 / 0 Регистрация: 31.10.2017 Сообщений: 7 |
|
|
31.10.2017, 19:34 [ТС] |
12 |
|
поиск решения по вашим данным нашел следующие коэффициенты: Вот в matcad такие же коэффициенты получились (вот только matcad как оказалось не общедоступная среда, поэтому потребовали сделать в exel). Но в exele я понимаю как подобрать решение для одной ячейки, А как это сделать для всего диапазона?
0 |
|
0 / 0 / 0 Регистрация: 31.10.2017 Сообщений: 7 |
|
|
31.10.2017, 19:35 [ТС] |
13 |
|
поиск решения по вашим данным нашел следующие коэффициенты: Вот в matcad такие же коэффициенты получились (вот только matcad как оказалось не общедоступная среда, поэтому потребовали сделать в exel). Но в exele я понимаю как подобрать решение для одной ячейки, А как это сделать для всего диапазона?
0 |
|
15136 / 6410 / 1730 Регистрация: 24.09.2011 Сообщений: 9,999 |
|
|
31.10.2017, 20:05 |
14 |
|
Решениеnik_art, я брал числа из текста, они немного не такие, как на картинке, поэтому коэффициенты получились немного другие. Запустите Поиск решения, в файле хранятся его параметры.
1 |
|
0 / 0 / 0 Регистрация: 31.10.2017 Сообщений: 7 |
|
|
31.10.2017, 20:50 [ТС] |
15 |
|
Огромное спасибо
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
31.10.2017, 20:50 |
|
Помогаю со студенческими работами здесь Макрос делает копию листа и сохраняет в новую книгу, но макрос в новой не работает Макрос, чтобы другой макрос распихал сам по N файлам Макрос, запускающий макрос из другого закрытого файла Сделать макрос в Word, вводишь строку и макрос произвольно меняет шрифт, цвет и размер для каждого слова из этого активного вордовского документа. Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 15 |
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью линейной функции
y
=
a
x
+
b
.
Метод наименьших квадратов
(англ.
Ordinary
Least
Squares
,
OLS
) является одним из базовых методов регрессионного анализа в части оценки неизвестных параметров
регрессионных моделей
по выборочным данным.
Рассмотрим приближение функциями, зависящими только от одной переменной:
- Линейная: y=ax+b (эта статья)
-
Логарифмическая
: y=a*Ln(x)+b
-
Степенная
: y=a*x
m
-
Экспоненциальная
: y=a*EXP(b*x)+с
-
Квадратичная
: y=ax
2
+bx+c
Примечание
: Случаи приближения полиномом с 3-й до 6-й степени рассмотрены в этой статье. Приближение тригонометрическим полиномом рассмотрено здесь.
Линейная зависимость
Нас интересует связь 2-х переменных
х
и
y
. Имеется предположение, что
y
зависит от
х
по линейному закону
y
=
ax
+
b
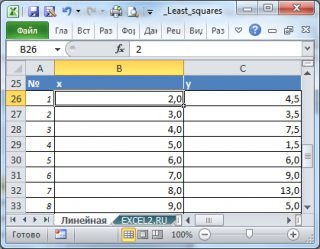
. Чтобы определить параметры этой взаимосвязи исследователь провел наблюдения: для каждого значения х
i
произведено измерение y
i
(см.
файл примера
). Соответственно, пусть имеется 20 пар значений (х
i
; y
i
).
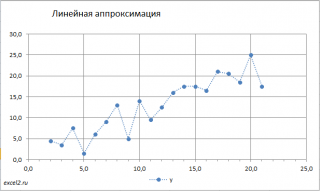
Для наглядности рекомендуется построить диаграмму рассеяния.
Примечание:
Если шаг изменения по
х
постоянен, то для построения
диаграммы рассеяния
можно использовать
тип График
, если нет, то необходимо использовать тип диаграммы
Точечная
.
Из диаграммы очевидно, что связь между переменными близка к линейной. Чтобы понять какая из множества прямых линий наиболее «правильно» описывает зависимость между переменными, необходимо определить критерий, по которому будут сравниваться линии.
В качестве такого критерия используем выражение:
где
ŷ
i
=
a
*
x
i
+
b
;
n – число пар значений (в нашем случае n=20)
Вышеуказанное выражение представляет собой сумму квадратов расстояний между наблюденными значениями y
i
и ŷ
i
и часто обозначается как SSE (
Sum
of
Squared
Errors
(
Residuals
), сумма квадратов ошибок (остатков)
)
.
Метод наименьших квадратов
заключается в подборе такой линии
ŷ
=
ax
+
b
, для которой вышеуказанное выражение принимает минимальное значение.
Примечание:
Любая линия в двухмерном пространстве однозначно определяется значениями 2-х параметров:
a
(наклон) и
b
(сдвиг).
Считается, что чем меньше сумма квадратов расстояний, тем соответствующая линия лучше аппроксимирует имеющиеся данные и может быть в дальнейшем использована для прогнозирования значений y от переменной х. Понятно, что даже если в действительности никакой взаимосвязи между переменными нет или связь нелинейная, то МНК все равно подберет «наилучшую» линию. Таким образом, МНК ничего не говорит о наличии реальной взаимосвязи переменных, метод просто позволяет подобрать такие параметры функции
a
и
b
, для которых вышеуказанное выражение минимально.
Проделав не очень сложные математические операции (подробнее см.
статью про квадратичную зависимость
), можно вычислить параметры
a
и
b
:
Как видно из формулы, параметр
a
представляет собой отношение ковариации и
дисперсии
, поэтому в MS EXCEL для вычисления параметра
а
можно использовать следующие формулы (см.
файл примера лист Линейная
):
=
КОВАР(B26:B45;C26:C45)/ ДИСП.Г(B26:B45)
или
=
КОВАРИАЦИЯ.В(B26:B45;C26:C45)/ДИСП.В(B26:B45)
Также для вычисления параметра
а
можно использовать формулу =
НАКЛОН(C26:C45;B26:B45)
. Для параметра
b
используйте формулу =
ОТРЕЗОК(C26:C45;B26:B45)
.
И наконец, функция
ЛИНЕЙН()
позволяет вычислить сразу оба параметра. Для ввода формулы
ЛИНЕЙН(C26:C45;B26:B45)
необходимо выделить в строке 2 ячейки и нажать
CTRL
+
SHIFT
+
ENTER
(см. статью про
формулы массива, возвращающими несколько значений
). В левой ячейке будет возвращено значение
а
, в правой –
b
.
Примечание
: Чтобы не связываться с вводом
формул массива
потребуется дополнительно использовать функцию
ИНДЕКС()
. Формула =
ИНДЕКС(ЛИНЕЙН(C26:C45;B26:B45);1)
или просто =
ЛИНЕЙН(C26:C45;B26:B45)
вернет параметр, отвечающий за наклон линии, т.е.
а
. Формула =
ИНДЕКС(ЛИНЕЙН(C26:C45;B26:B45);2)
вернет параметр, отвечающий за пересечение линии с осью Y, т.е.
b
.
Вычислив параметры, на
диаграмме рассеяния
можно построить соответствующую линию.
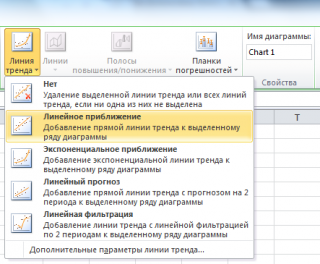
Инструмент диаграммы Линия тренда
Еще одним способом построения прямой линии по методу наименьших квадратов является инструмент диаграммы
Линия тренда
. Для этого выделите диаграмму, в меню выберите
вкладку Макет
, в
группе Анализ
нажмите
Линия тренда
, затем
Линейное приближение
.
Поставив в диалоговом окне галочку в поле «показывать уравнение на диаграмме» можно убедиться, что найденные выше параметры совпадают со значениями на диаграмме.
Примечание
: Для того, чтобы параметры совпадали необходимо, чтобы тип у диаграммы был
Точечная, а не График
. Дело в том, что при построении диаграммы
График
значения по оси Х не могут быть заданы пользователем (пользователь может указать только подписи, которые не влияют на расположение точек). Вместо значений Х используется последовательность 1; 2; 3; … (для нумерации категорий). Поэтому, если строить
линию тренда
на диаграмме типа
График
, то вместо фактических значений Х будут использованы значения этой последовательности, что приведет к неверному результату (если, конечно, фактические значения Х не совпадают с последовательностью 1; 2; 3; …).
СОВЕТ
: Подробнее о построении диаграмм см. статьи
Основы построения диаграмм
и
Основные типы диаграмм
.
4.1.
Использование встроенных функций
Вычисление
коэффициентов
регрессии
осуществляется с помощью функции
ЛИНЕЙН(Значения_y;
Значения_x;
Конст;
статистика),
где
Значения_y
— массив значений y,
Значения_x—
необязательный массив значений x,
если массив х
опущен, то предполагается, что это массив
{1;2;3;…} такого же размера, как и Значения_y,
Конст—
логическое значение, которое указывает,
требуется ли, чтобы константа b
была равна 0. Если Конст
имеет значение ИСТИНА
или опущено, то b
вычисляется обычным образом. Если
аргумент Конст
имеет значение ЛОЖЬ, то b
полагается равным 0 и значения a
подбираются так, чтобы выполнялось
соотношение y=ax.
Статистика—
логическое значение, которое указывает,
требуется ли вернуть дополнительную
статистику по регрессии. Если аргумент
Статистика
имеет значение ИСТИНА,
то функция ЛИНЕЙН
возвращает дополнительную регрессионную
статистику. Если аргумент Статистика
имеет значение ЛОЖЬ
или опущен, то функция ЛИНЕЙН
возвращает только коэффициент a
и постоянную b.
Необходимо
помнить, что результатом функций ЛИНЕЙН()
является
множество значений – массив.
Для
расчета коэффициента
корреляции
используется функция
КОРРЕЛ(Массив1;Массив2),
возвращающая
значения коэффициента корреляции, где
Массив1
— массив значений y,
Массив2
— массив значений x.
Массив1
и Массив2
должны быть одной размерности.
ПРИМЕР
1. Зависимость
y(x)
представлена в таблице. Построить линию
регрессии
и вычислить коэффициент
корреляции.
|
y |
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
4 |
|
x |
1 |
2.39 |
2.81 |
3.25 |
3.75 |
4.11 |
4.45 |
4.85 |
5.25 |
Введем
таблицу значений в лист MS
Excel
и построим точечный график. Рабочий
лист примет вид изображенный на рис. 2.
Рис. 2
Для
того чтобы рассчитать значения
коэффициентов регрессии а
и b
выделим
ячейки A7:B7,
обратимся к мастеру функций и в категории
Статистические
выберем функцию ЛИНЕЙН.
Заполним появившееся диалоговое окно
так, как показано на рис. 3 и нажмем ОK.
Рис. 3
В
результате вычисленное значение появится
только в ячейке A6
(рис.4). Для того чтобы значение появилось
и в ячейке B6
необходимо войти в режим редактирования
(клавиша F2),
а затем нажать комбинацию клавиш
CTRL+SHIFT+ENTER.
Для
расчета значения коэффициента корреляции
в ячейку С6
была введена следующая формула:
С7=КОРРЕЛ(B3:J3;B2:J2).
Рис. 4
Зная
коэффициенты
регрессии а
и b
вычислим значения функции y=ax+b
для заданных x.
Для этого
введем формулу
B5=$A$7*B2+$B$7
и
скопируем ее в диапазон С5:J5
(рис. 5).
Рис. 5
Изобразим
линию регрессии на диаграмме. Выделим
экспериментальные точки на графике,
щелкнем правой кнопкой мыши и выберем
команду Исходные
данные. В
появившемся диалоговом окне (рис. 5)
выберем вкладку Ряд
и щелкнем по кнопке Добавить.
Заполним поля ввода, так как показано
на рис. 6 и нажмем кнопку ОК.
К графику экспериментальных данных
будет добавлена линия регрессии. По
умолчанию ее график будет изображен в
виде точек, не соединенных сглаживающими
линиями.
Р
6
Чтобы
изменить вид линии регрессии, выполним
следующие действия. Щелкнем правой
кнопкой мыши по точкам, изображающим
график линии, выберем команду Тип
диаграммы и
установим вид точечной диаграммы, так
как показано на рис. 7.
Рис.
7
Тип
линии, ее цвет и толщину можно изменить
следующим образом. Выделить линию на
диаграмме, нажать правую кнопку мыши и
в контекстном меню выбрать команду
Формат рядов
данных…
Далее сделать установки, например, так
как показано на рис. 8.
Рис. 8
В
результате всех преобразований получим
график экспериментальных данных и линию
регрессии в одной графической области
(рис. 9).
Рис. 9
4.2.
Использование линии тренда.
Построение
различных аппроксимирующих зависимостей
в MS
Excel
реализовано в виде свойства диаграммы
– линия
тренда.
ПРИМЕР
2. В результате
эксперимента была определена некоторая
табличная зависимость.
-
0.15
0.16
0.17
0.18
0.19
0.20
4.4817
4.4930
5.4739
6.0496
6.6859
7.3891
Выбрать
и построить аппроксимирующую зависимость.
Построить графики табличной и подобранной
аналитической зависимости.
Решение
задачи можно разбить на следующие этапы:
ввод исходных данных, построение
точечного графика и добавление к этому
графику линии тренда.
Рассмотрим
этот процесс подробно. Введем исходные
данные в рабочий лист и построим график
экспериментальных данных. Далее выделим
экспериментальные точки на графике,
щелкнем правой кнопкой мыши и воспользуемся
командой Добавить
линию
тренда (рис.
10).
Рис. 10
Появившееся
диалоговое окно позволяет построить
аппроксимирующую зависимость.
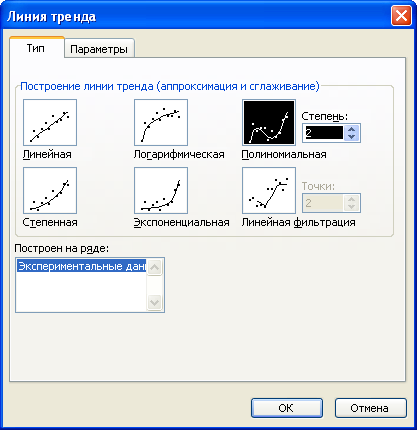
На
первой вкладке (рис. 11) этого окна
указывается вид аппроксимирующей
зависимости.
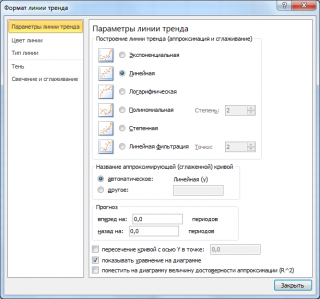
На
второй (рис. 12) определяются параметры
построения:
-
название
аппроксимирующей зависимости; -
прогноз
вперед (назад) на n
единиц (этот параметр определяет, на
какое количество единиц вперед (назад)
необходимо продлить линию тренда); -
показывать
ли точку пересечения кривой с прямой
y=const; -
показывать
аппроксимирующую функцию на диаграмме
или нет (параметр показывать уравнение
на диаграмме); -
помещать
ли на диаграмму величину среднеквадратичного
отклонения или нет (параметр поместить
на диаграмму величину достоверности
аппроксимации).
Рис. 11
Рис. 12
Выберем
в качестве аппроксимирующей зависимости
полином второй степени (рис. 11) и выведем
уравнение, описывающее этот полином на
график (рис. 12). Полученная диаграмма
представлена на рис. 13.
Рис.
13
Аналогично
с помощью линии
тренда можно
подобрать параметры таких зависимостей
как
-
линейная
y=a∙x+b, -
логарифмическая
y=a∙ln(x)+b, -
экспоненциальная
y=a∙eb, -
степенная
y=a∙xb, -
полиномиальная
y=a∙x2+b∙x+c,
y=a∙x3+b∙x2+c∙x+d
и так далее, до полинома 6-й степени
включительно, -
линейная
фильтрация.
4.3.
Использование решающего блока
Значительный
интерес представляет реализация в MS
Excel
подбора параметров методом наименьших
квадратов с использованием решающего
блока. Эта методика позволяет подобрать
параметры функции любого вида. Рассмотрим
эту возможность на примере следующей
задачи.
ПРИМЕР
3. В результате
эксперимента получена зависимость z(t)
представленная в таблице
|
0,66 |
0,9 |
1,17 |
1,47 |
1,7 |
1,74 |
2,08 |
2,63 |
3,12 |
|
38,9 |
68,8 |
64,4 |
66,5 |
64,95 |
59,36 |
82,6 |
90,63 |
113,5 |
Подобрать
коэффициенты зависимости Z(t)=At4+Bt3+Ct2+Dt+K
методом наименьших квадратов.
Эта
задача эквивалентна задаче нахождения
минимума функции пяти переменных
(10).
Рассмотрим
процесс решения задачи оптимизации
(рис. 14).
Рис. 14
Пусть
значения А,
В,
С,
D
и К
хранятся в ячейках A7:E7.
Рассчитаем теоретические значения
функции Z(t)=At4+Bt3+Ct2+Dt+K
для заданных t
(B2:J2).
Для этого в ячейку B4
введем значение функции в первой точке
(ячейка B2):
B4=$A$7*B2^4+$B$7*B2^3+$C$7*B2^2+$D$7*B2+$E$7.
Скопируем
эту формулу в диапазон С4:J4
и получим ожидаемое значение функции
в точках, абсциссы которых хранится в
ячейках B2:J2.
В
ячейку B5
введем формулу, вычисляющую квадрат
разности между экспериментальными и
расчетными точками:
B5=(B4-B3)^2,
и
скопируем ее в диапазон С5:J5.
В ячейке F7
будем хранить суммарную квадратичную
ошибку (10). Для этого введем формулу:
F7
=
СУММ(B5:J5).
Воспользуемся
командой СервисПоиск
решения
и решим задачу оптимизации без ограничений.
Заполним соответствующим образом поля
ввода в диалоговом окне, показанном на
рис. 14 и нажмем кнопку Выполнить.
Если решение будет найдено, то появится
окно, изображенное на рис. 15.
Результатом
работы решающего блока будет вывод в
ячейки A7:E7
значений
параметров
функции Z(t)=At4+Bt3+Ct2+Dt+K.
В ячейках B4:J4
получим ожидаемые
значение функции
в исходных точках. В ячейке F7
будет храниться суммарная
квадратичная ошибка.
Изобразить
экспериментальные точки и подобранную
линию в одной графической области можно,
если выделить диапазон B2:J4,
вызвать
Мастер
диаграмм,
а затем отформатировать внешний вид
полученных графиков.
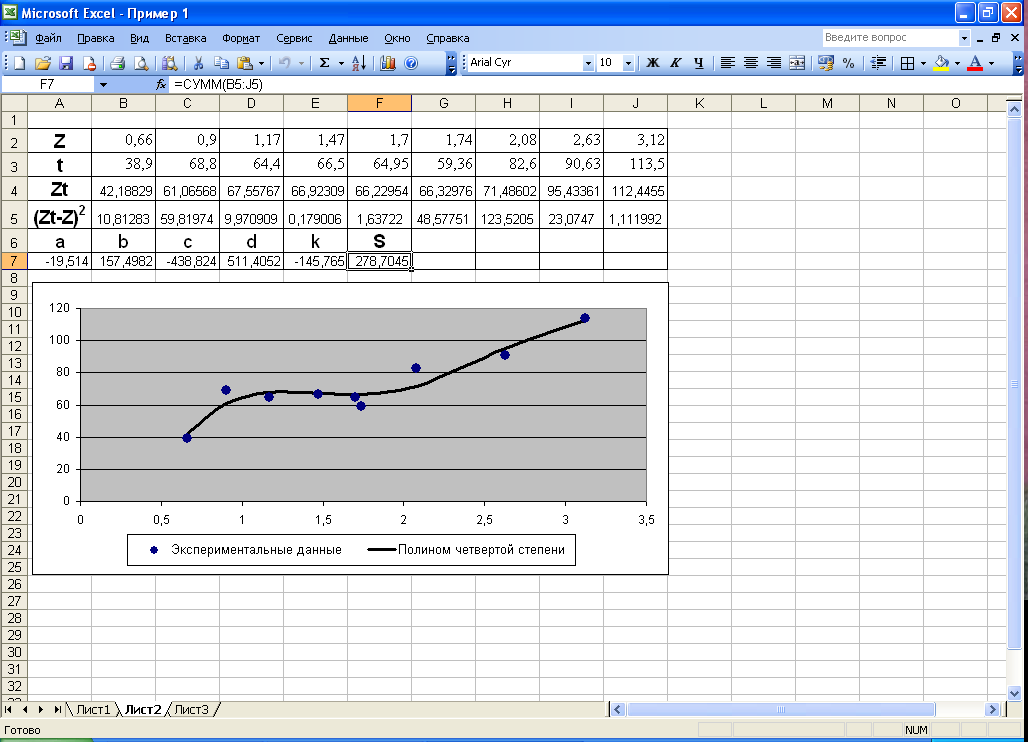
Рис.
17 отображает рабочий лист MS
Excel
после проведенных вычислений.
Рис.
15
Рис. 16
Рис. 17
5.
СПИСОК ЛИТЕРАТУРЫ
1.
Алексеев Е.Р., Чеснокова О.В., Решение
задач вычислительной математики в
пакетах Mathcad12,
MATLAB7,
Maple9.
– НТ Пресс, 2006.–596с. :ил. –(Самоучитель)
2.
Алексеев Е.Р., Чеснокова О.В., Е.А. Рудченко,
Scilab,
решение инженерных и математических
задач. –М., БИНОМ, 2008.–260с.
3.
Березин И.С., Жидков Н.П., Методы
вычислений.–М.:Наука, 1966.–632с.
4.
Гарнаев А.Ю., Использование MS
EXCEL
и VBA
в экономике и финансах. – СПб.: БХВ —
Петербург, 1999.–332с.
5.
Демидович Б.П., Марон И А., Шувалова В.З.,
Численные методы анализа.–М.:Наука,
1967.–368с.
6.
Корн Г., Корн Т., Справочник по математике
для научных работников и инженеров.–М.,
1970, 720с.
7.
Алексеев
Е.Р., Чеснокова О.В. Методические указания
к выполнению лабораторных работ в MS
EXCEL.
Для студентов всех специальностей.
Донецк,
ДонНТУ, 2004. 112 с.
25
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #




 Сообщение было отмечено nik_art как решение
Сообщение было отмечено nik_art как решение