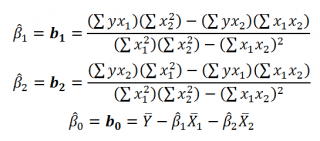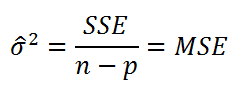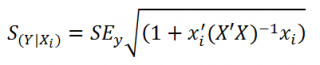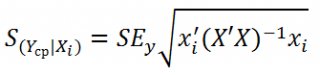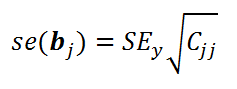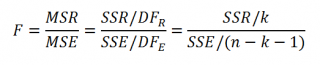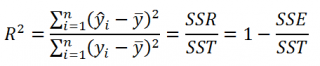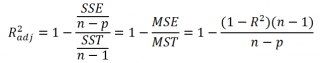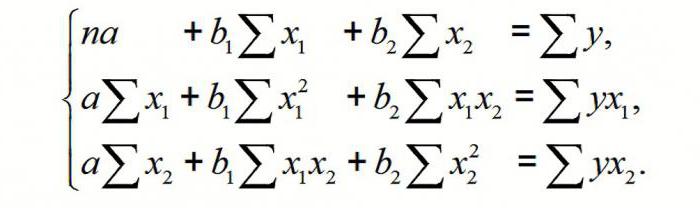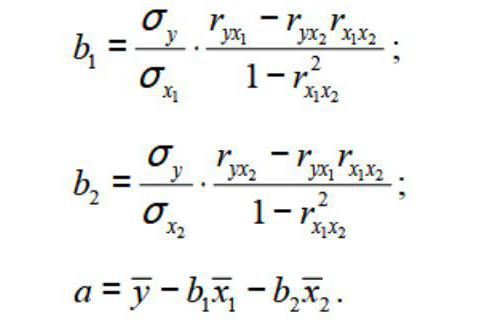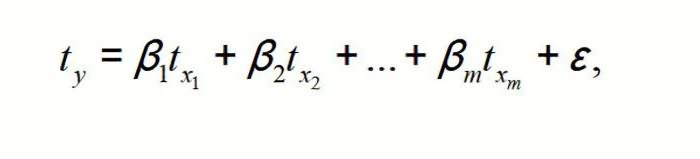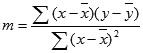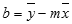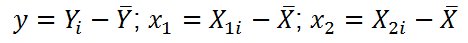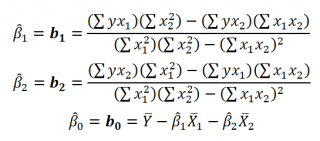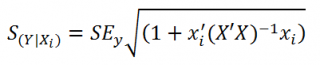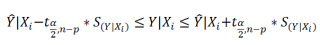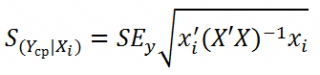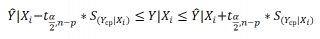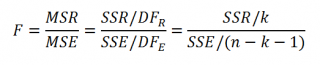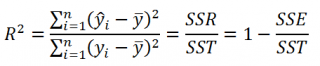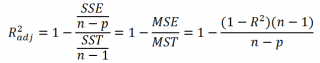17 авг. 2022 г.
читать 2 мин
Метод наименьших квадратов — это метод, который мы можем использовать для поиска линии регрессии, которая лучше всего соответствует заданному набору данных.
В следующем видео представлено краткое объяснение этого метода:
Чтобы использовать метод наименьших квадратов для подбора линии регрессии в Excel, мы можем использовать функцию =ЛИНЕЙН() .
В следующем пошаговом примере показано, как использовать эту функцию на практике.
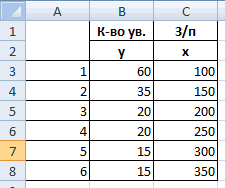
Шаг 1: Создайте набор данных
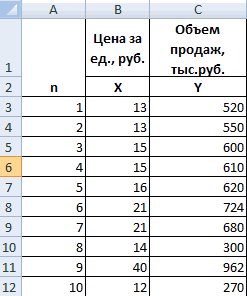
Во-первых, давайте создадим следующий набор данных в Excel:
Шаг 2: Используйте метод наименьших квадратов для подбора линии регрессии
Мы можем использовать функцию =LINEST(known_ys, known_xs) , чтобы использовать метод наименьших квадратов, чтобы подобрать линию регрессии к этому набору данных:
Как только мы нажмем ENTER , появятся коэффициенты регрессионной модели:
Шаг 3: интерпретируйте результаты
Используя коэффициенты из функции =LINEST() , мы можем написать следующую подобранную линию регрессии:
у = 11,55211 + 1,07949(х)
Мы можем использовать это уравнение для оценки значения y на основе значения x.
Например, если x = 10, то мы оценили бы, что y будет равно 22,347 :
у = 11,55211 + 1,07949(10) = 22,347
Шаг 4: Нанесите результаты на график
Наконец, мы можем использовать следующие шаги для построения набора данных вместе с подобранной линией регрессии:
- Выделите ячейки A2:B16 .
- Щелкните вкладку « Вставка » на верхней ленте. Затем щелкните первый параметр диаграммы под названием « Вставить точечную (X, Y)» или «Пузырьковую диаграмму » в группе «Диаграммы».
- После того, как диаграмма появится, нажмите знак плюс «+» в правом верхнем углу. В раскрывающемся меню установите флажок рядом с линией тренда , чтобы добавить на график подобранную линию регрессии.
Дополнительные ресурсы
Как выполнить множественную линейную регрессию в Excel
Как выполнить квадратичную регрессию в Excel
Как выполнить полиномиальную регрессию в Excel
Подбор кривой в Excel (с примерами)
Рассмотрим использование
MS
EXCEL
для прогнозирования переменной
Y
на основании нескольких переменных Х, т.е. множественную регрессию.
Перед прочтением этой статьи рекомендуется освежить в памяти
простую линейную регрессию
– прогнозирование на основе значений только одного фактора.
Disclaimer
: Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей
Множественного регрессионного анализа.
Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения
Регрессии
– плохая идея.
Статья про
Множественный регрессионный анализ
получилась большая, поэтому ниже для удобства приведены ее разделы:
- Оценка неизвестных параметров
- Диаграмма рассеяния
-
Вычисление прогнозных значений Y
(отдельное наблюдение и среднее значение) и построение доверительных интервалов
- Стандартные ошибки и доверительные интервалы для коэффициентов регрессии
- Проверка гипотез
- Генерация данных для множественной регрессии с помощью заданного тренда
- Коэффициент детерминации
Прогнозирование единственной переменной Y на основании значений 2-х или более переменных Х называется
множественной регрессией
.
Множественная линейная регрессионная модель
(Multiple Linear Regression Model)
имеет вид Y=β
0
+β
1
*X
1
+β
2
*X
2
+…+β
k
*X
k
+ε. В этом случае переменная Y зависит от k поясняющих переменных Х, т.е.
регрессоров
. ε —
случайная ошибка
. Модель является линейной относительно неизвестных параметров β.
Оценка неизвестных параметров
В этой статье рассмотрим модель с 2-мя регрессорами. Сначала введем необходимые обозначения и понятия множественной регрессии.
Для описания зависимости Y от 2-х переменных
линейная модель
имеет вид:
Y=β
0
+β
1
*X
1
+β
2
*X
2
+ε.
Параметры этой модели β
i
нам неизвестны, но их можно оценить, используя случайную выборку (измеренные значения переменной Y от заданных Х). Оценки параметров модели (β
0
, β
1
, β
2
) обычно вычисляются
методом наименьших квадратов (МНК)
, который минимизирует сумму квадратов ошибок прогнозирования (критерий минимизации в англоязычной литературе обозначают как SSE – Sum of Squared Errors).
Соответствующие оценки параметров будем обозначать как
b
0
,
b
1
и
b
2
.
Ошибка ε имеет случайную природу и имеет свою функцию распределения со
средним значением
=0 и
дисперсией σ
2
.
Оценки
b
1
и
b
2
называются
коэффициентами регрессии
, они определяют влияние соответствующей переменной X, когда все остальные независимые переменные остаются
неизменными
.
Сдвиг (intercept)
или
постоянный
член
b
0
, определяет прогнозируемое значение Y, когда все поясняющие переменные Х равны 0 (часто
сдвиг
не имеет физического смысла в рамках модели и обусловлен лишь математическими вычислениями
МНК
).
Вычислив оценки, полученные методом
МНК,
позволяют прогнозировать значения переменной Y:
Y=
b
0
+
b
1
*X
1
+
b
2
*X
2
Примечание
: Для случая 2-х регрессоров, все спрогнозированные значения переменной Y будут лежать в плоскости (в
плоскости регрессии
).
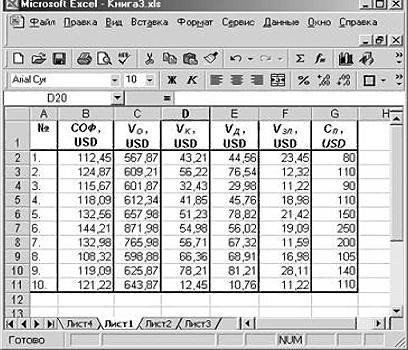
В качестве примера рассмотрим технологический процесс изготовления нити:
Инженер, на основе имеющегося опыта, предположил, что
прочность нити
Y зависит от
концентрации исходного раствора
(Х
1
) и
температуры реакции
(Х
2
), и соответствует модели линейной регрессии. Для нахождения комбинации переменных Х, при которых Y принимает максимальное значение, необходимо определить коэффициенты регрессии, сделав выборку.
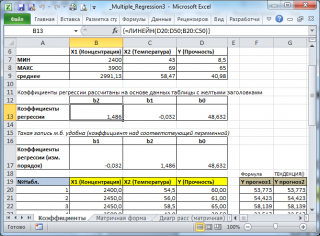
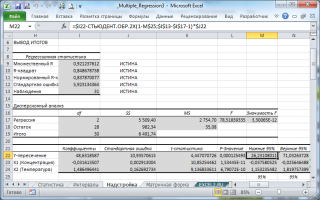
В MS EXCEL
коэффициенты множественной регрессии
удобнее всего вычислить с помощью функции
ЛИНЕЙН()
. Это сделано в
файле примера на листе Коэффициенты
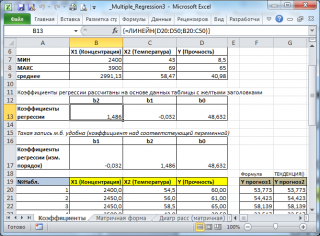
. Чтобы вычислить оценки:
-
выделите 3 ячейки в одной строке (т.к. мы рассматриваем случай 2-х регрессоров, то будут вычислены 2
коэффициента регрессии
+
величина сдвига
= 3 значения, для вывода которых понадобится 3 ячейки). Пусть это будет диапазон
С8:Е8
; -
в
Строке формул
введите =
ЛИНЕЙН(D20:D50;B20:C50)
. Предполагается, что в столбце
В
содержатся прогнозируемые значения Y (в нашей модели это Прочность нити), в столбцах
С
и
D
содержатся значения контролируемых параметров Х (Х1 – Концентрация в столбце С и Х2 – Температура в столбце D). -
нажмите
CTRL
+
SHIFT
+
ENTER
(т.к. этоформула массива
).
В левой ячейке будет рассчитано значение
коэффициента регрессии
b
2
для переменной Х2, в средней ячейке — значение
коэффициента регрессии
b
1
для переменной Х1, в правой –
сдвиг
. Обратите внимание, что порядок вывода
коэффициентов
регрессии
обратный по отношению к расположению столбцов с данными соответствующих переменных Х (вычисленный коэффициент
b
2
располагается
левее
по отношению к
b
1
, тогда как значения переменной Х2 располагаются
правее
значений переменной Х1). Это может привести к путанице, поэтому лучше разместить коэффициенты над соответствующими столбцами с данными, как это сделано в строке 17
файла примера
.
Примечание
: В принципе без функции
ЛИНЕЙН()
можно обойтись, записав альтернативные формулы. Для этого в
файле примера на листе Коэффициенты
в столбцах
I
:
K
вычислены отклонения значений переменных Х
1i
, Х
2i
, Y
i
от их средних значений
, т.е.:
Далее коэффициенты регрессии рассчитываются по следующим формулам (эти формулы справедливы только при прогнозировании по 2-м независимым переменным Х):
При прогнозировании по 3-м и более независимым переменным Х формулы для вычисления
коэффициентов регрессии
значительно усложняются, поэтому следует использовать матричный подход.
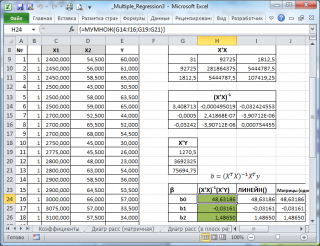
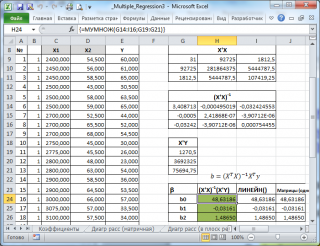
В
файле примера на листе Матричная форма
выполнены расчеты
коэффициентов регрессии
с помощью матричного подхода.
Расчет можно произвести как пошагово, так и одной
формулой массива
:
=МУМНОЖ(МОБР(МУМНОЖ(ТРАНСП(B9:D33);(B9:D33)));МУМНОЖ(ТРАНСП(B9:D33);(E9:E33)))
Коэффициенты регрессии
(вектор
b
)
в этом случае вычисляются по формуле
b
=(X
T
X)
-1
(X
T
Y) или в другом виде записи
b
=(X
’
X)
-1
(X
’
Y)
Под Х подразумевается матрица, состоящая из столбцов значений переменной Х с дополнительным столбцом единиц, а под Y – вектор-столбец значений Y.
Символ
Т
или ‘ – это
транспонирование матрицы
, а обозначение
-1
говорит о
вычислении обратной матрицы
.
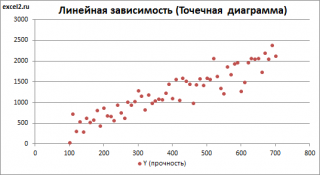
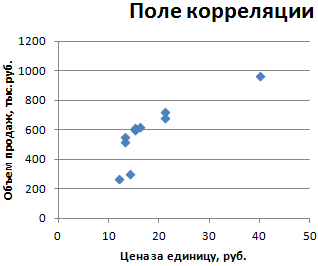
Диаграмма рассеяния
В случае
простой линейной регрессии
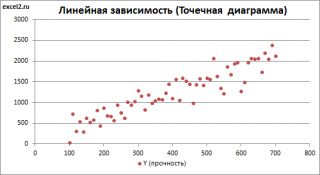
(один регрессор, т.е. одна переменная Х) для визуализации связи между прогнозируемым значением Y и переменной Х строят
диаграмму рассеяния
(двумерную).
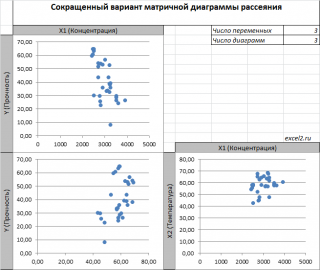
В случае
множественной
линейной регрессии
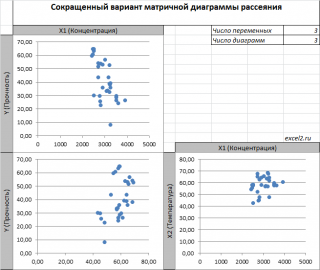
двумерную диаграмму рассеяния можно построить только для анализа влияния каждого отдельного регрессора на Y (при этом остальные Х не меняются), т.е. так называемую Матричную диаграмму рассеивания (См.
файл примера лист Диагр расс (матричная)
).
К сожалению, такую диаграмму трудно интерпретировать.
Более того, матричная диаграмма может вводить в заблуждение (см.
Introduction
to
linear
regression
analysis
/
D
.
C
.
Montgomery
,
E
.
A
.
Peck
,
G
.
G
.
Vining
, раздел 3.2.5
), демонстрируя наличие или отсутствие линейной взаимосвязи между отдельным регрессором X
i
и Y.
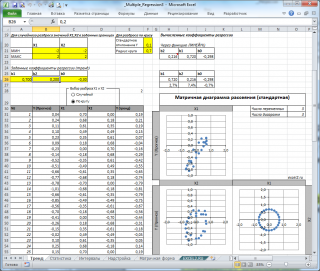
Для случая с 2-мя регрессорами можно предложить альтернативный вид матричной
диаграммы рассеяния
. В стандартной диаграмме рассеяния строятся проекции на координатные плоскости Х1;Х2, Y;X1 и Y;X2. Однако, если взглянуть на точки относительно
плоскости регрессии
, то картину, на мой взгляд, будет проще интерпретировать.
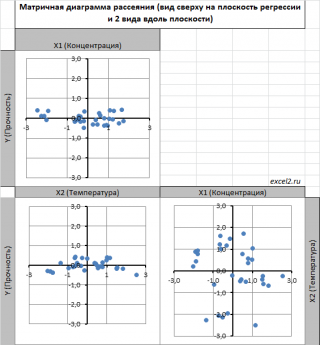
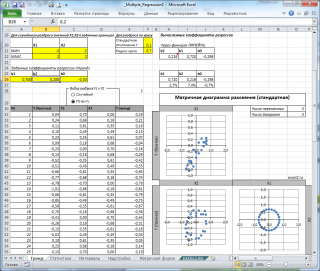
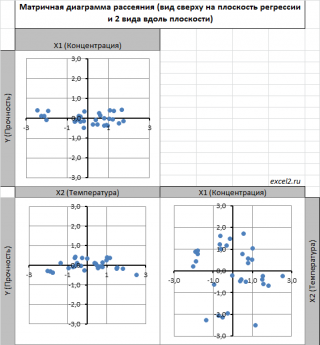
Сравним две матричные диаграммы рассеяния (см.
файл примера на листе «Диагр расс (в плоск регрессии)»
, построенные для одних и тех же наблюдений. Первая – стандартная,
вторая представляет собой вид сверху на плоскость регрессии и 2 вида вдоль плоскости.
На второй диаграмме становится очевидно, что разброс точек относительно плоскости регрессии совсем не большой и поэтому, скорее всего, построенная модель является полезной, а выбранные 2 переменные Х позволяют прогнозировать Y (конечно, для подтверждения этой гипотезы нужно
провести процедуру F-теста
).
Несколько слов о построении альтернативной матричной диаграммы рассеяния:
-
Перед построением необходимо нормировать значения наблюдений (для каждой переменной вычесть
среднее
и разделить на
стандартное отклонение
). В этом случае практически все точки на диаграммах будут находится в диапазоне +/-3 (по аналогии со
стандартным нормальным распределением
, 99% значений которого лежат в пределах +/-3 сигма). В этом случае, на диаграмме можно фиксировать мин/макс значений осей, чтобы EXCEL автоматически не модифицировал масштаб осей при изменении данных (это не всегда удобно);
-
Теперь координаты точек необходимо рассчитать в системе отсчета относительно плоскости регрессии (в которой плоскость Оху’ совпадает с плоскостью регрессии). Для этого необходимо найти
матрицу вращения
, например, через вращение приводящее к совмещению нормали к плоскости регрессии и вектора оси Z (0;0;1);
-
Новые координаты позволяют построить альтернативную матричную диаграмму. Кроме того, для удобства можно вращать систему координат вокруг новой оси Z, чтобы нагляднее представить себе распределение точек относительно плоскости регрессии (для этого использована Полоса прокрутки в ячейках
Q
31:
S
31
).
Вычисление прогнозных значений Y (отдельное наблюдение и среднее значение) и построение доверительных интервалов
После того, как нами были найдены тем или иным способом коэффициенты регрессии можно приступать к вычислению прогнозных значений Y на основе заданных значений переменных Х.
Уравнение прогнозирования или уравнение регрессии в случае 2-х независимых переменных (регрессоров) записывается в виде:
Y=
b
0
+
b
1
*
Х
1
+
b
2
*
Х
2
Примечание:
В MS EXCEL
прогнозное значение Y для заданных Х
1
и Х
2
можно также предсказать с помощью функции
ТЕНДЕНЦИЯ()
. При этом 2-й аргумент будет ссылкой на столбцы, содержащие все значения переменных Х
1
и Х
2
, а 3-й аргумент функции должен быть ссылкой на диапазон ячеек, содержащий 2 значения Х (Х
1i
и Х
2i
) для выбранного наблюдения i (см.
файл примера, лист Коэффициенты, столбец G
). Функция
ПРЕДСКАЗ()
, использованная нами в простой регрессии, не работает в случае
множественной регрессии
.
Найдя прогнозное значение Y, мы, таким образом, вычислим его точечную оценку. Понятно, что фактическое значение Y, полученное при наблюдении, будет, скорее всего, отличаться от этой оценки. Чтобы ответить на вопрос о том, на сколько хорошо мы можем предсказывать новые значения Y, нам потребуется построить
доверительный интервал
этой оценки, т.е. диапазон в котором с определенной заданной вероятностью, скажем 95%, мы ожидаем новое значение Y.
Доверительные интервалы
построим при фиксированном Х для:
- нового наблюдения Y;
- среднего значения Y (интервал будет уже, чем для отдельного нового наблюдения)
Как и в случае
простой линейной регрессии
, для построения
доверительных интервалов
нам потребуется сначала вычислить
стандартную ошибку модели
(standard error of the model)
, которая приблизительно показывает насколько велика ошибка предсказания значений переменной Y на основании значений переменных Х.
Для вычисления
стандартной ошибки
оценивают
дисперсию
ошибки ε, т.е. сигма^2
(ее часто обозначают как
MS
Е либо
MSres
)
. Затем, вычислив из полученной оценки квадратный корень, получим
Стандартную ошибку регрессии (часто обозначают как
SEy
или
sey
).
где SSE – сумма квадратов значений ошибок модели ei=yi — ŷi (
Sum of Squared Errors
). MSE означает Mean Square of Errors (среднее квадратов ошибок, точнее остатков).
Величина n-p – это количество
степеней свободы
(
df
–
degrees
of
freedom
), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y, р – количество оцениваемых параметров модели). В случае
простой множественной регрессии
с 2-мя регрессорами
число степеней свободы
равно n-3, т.к. при построении
плоскости регрессии
было оценено 3 параметра модели
b
(т.е. на это было «потрачено» 3
степени свободы
).
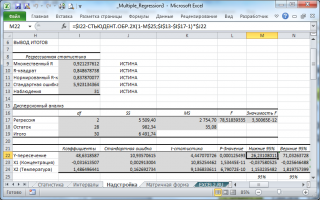
В MS EXCEL
стандартную ошибку
SEy можно вычислить формулы (см.
файл примера, лист Статистика
):
=
ИНДЕКС(ЛИНЕЙН($E$13:$E$43;$C$13:$D$43;;ИСТИНА);3;2)
Стандартная ошибка
нового наблюдения Y при заданных значениях Х (вектор Хi) вычисляется по формуле:
x
i
— вектор-столбец со значениями переменных Х (с дополнительной 1) для заданного наблюдения i.
Соответствующий доверительный интервал вычисляется по формуле:
где α (альфа) –
уровень значимости
(обычно принимают равным 0,05=5%)
р – количество оцениваемых параметров модели (в нашем случае = 3)
n-p – число степеней свободы
–
квантиль
распределения Стьюдента
(задает количество
стандартных ошибок
, в +/- диапазоне которых вероятность обнаружить новое наблюдение равно 1-альфа). Т.е. если
квантиль
равен 2, то диапазон шириной +/- 2
стандартных ошибок
относительно прогнозного значения Y будет с вероятностью 95% содержать новое наблюдение Y (для каждого заданного Хi). В MS EXCEL вычисления квантиля производят по формуле =
СТЬЮДЕНТ.ОБР.2Х(0,05;n-p)
, подробнее см.
в статье про распределение Стьюдента
.
– прогнозное значение Yi вычисляемое по формуле Yi=
b
0+
b
1*
Х1i+
b
2*
Х2i (точечная оценка).
Стандартная ошибка
среднего значения Y при заданных значениях Х (вектор Хi) будет меньше, чем стандартная ошибка отдельного наблюдения. Вычисления производятся по формуле:
x
i
— вектор-столбец со значениями переменных Х (с дополнительной 1) для заданного наблюдения i.
Соответствующий
доверительный интервал
вычисляется по формуле:
Прогнозное значение Yi (точечная оценка) используется тоже, что и для отдельного наблюдения.
Стандартные ошибки и доверительные интервалы для коэффициентов регрессии
В разделе
Оценка неизвестных параметров
мы получили точечные оценки
коэффициентов регрессии
. Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со
средним значением
и
дисперсией
. Но, чтобы перейти от
точечных оценок
к
интервальным
, необходимо вычислить соответствующие
стандартные ошибки
(т.е.
стандартные отклонения
)
коэффициентов регрессии
.
Стандартная ошибка коэффициента регрессии
b
j
(обозначается
se
(
b
j
)
) вычисляется на основании
стандартной ошибки
по следующей формуле:
где C
jj
является диагональным элементом матрицы (X
’
X)
-1
. Для коэффициента сдвига
b
0
индекс j=1 (верхний левый элемент), для
b
1
индекс j=2,
b
2
индекс j=3 (нижний правый элемент).
SEy –
стандартная ошибка регрессии
(см.
выше
).
В MS EXCEL
стандартные ошибки коэффициентов регрессии
можно вычислить с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН($E$13:$E$43;$C$13:$D$43;;ИСТИНА);2;j)
Примечание
: Подробнее о функции
ЛИНЕЙН()
см. статью
Функция MS EXCEL ЛИНЕЙН()
.
Применяя матричный подход
стандартные ошибки
можно вычислить и через обычные формулы (точнее через
формулу массива
, см.
файл примера лист Статистика
):
=
КОРЕНЬ(СУММКВРАЗН(E13:E43;F13:F43) /(n-p)) *КОРЕНЬ (ИНДЕКС (МОБР (МУМНОЖ(ТРАНСП(B13:D43);(B13:D43)));j;j))
При построении
двухстороннего доверительного интервала
для
коэффициента регрессии
его границы определяются следующим образом:
b
j
+/- t*Se(
b
j
)
где t – это
t-значение
, которое можно вычислить с помощью формулы =
СТЬЮДЕНТ.ОБР.2Х(0,05;n-p)
для
уровня значимости
0,05.
В результате получим, что найденный
доверительный интервал
с вероятностью 95% (1-0,05) накроет истинное значение
коэффициента регрессии
b
j
.
Здесь мы считаем, что
коэффициент регрессии
b
j
имеет
распределение Стьюдента
с n-p
степенями свободы
(n – количество наблюдений, т.е. пар Х и Y).
Проверка гипотез
Когда мы строим модель, мы предполагаем, что между Y и переменными X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.
Единственный вариант, когда Y не зависит X, возможен, когда все
коэффициенты регрессии
β
равны 0.
Чтобы убедиться, что вычисленная нами оценка
коэффициентов регрессии
не обусловлена лишь случайностью (они не случайно отличны от 0), используют
проверку гипотез
. В качестве
нулевой гипотезы
Н
0
принимают, что линейной связи нет, т.е. ВСЕ β=0. В качестве альтернативной гипотезы
Н
1
принимают, что ХОТЯ БЫ ОДИН коэффициент β <>0.
Процедура проверки значимости множественной регрессии, приведенная ниже, является обобщением
дисперсионного анализа
, использованного нами в случае
простой линейной регрессии (F-тест)
.
Если нулевая гипотеза справедлива, то
тестовая
F
-статистика
имеет
F-распределение
со степенями свободы
k
и
n
—
k
-1
, т.е. F
k, n-k-1
:
Проверку значимости регрессии можно также осуществить через вычисление
p
-значения
. В этом случае вычисляют вероятность того, что случайная величина F примет значение F
0
(это и есть
p-значение
), затем сравнивают p-значение с заданным
уровнем значимости α (альфа)
. Если
p-значение
больше уровня значимости
,
то нулевую гипотезу нет оснований отклонить, и регрессия незначима.
В MS EXCEL значение F
0
можно вычислить на основании значений выборки по вышеуказанной формуле или с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(E13:E43; C13:D43;;ИСТИНА);4;1)
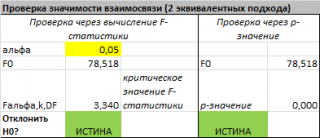
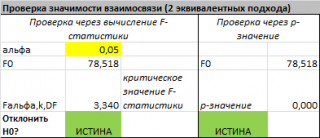
В MS EXCEL для проверки гипотезы через
p
-значение
используйте формулу =F.РАСП.ПХ(F
0
;k;n-k-1)<
альфа
Если формула вернет ИСТИНА, то регрессия значима. Если формула вернет ЛОЖЬ, то у нас нет оснований отклонить нулевую гипотезу, т.е. «скорее всего» все коэффициенты регрессии равны 0 (см.
файл примера лист Статистика
, где показано эквивалентность обоих подходов проверки значимости регрессии).
В MS EXCEL критическое значение для заданного
уровня значимости
F
1-альфа, k, n-k-1
можно вычислить по формуле =
F.ОБР(1- альфа;k;n-k-1)
или =
F.ОБР.ПХ(альфа;k; n-k-1)
. Другими словами требуется вычислить
верхний альфа-
квантиль
F
-распределения
с соответствующими
степенями свободы
.
Таким образом, при значении статистики F
0
> F
1-альфа, k, n-k-1
мы имеем основание для отклонения нулевой гипотезы.
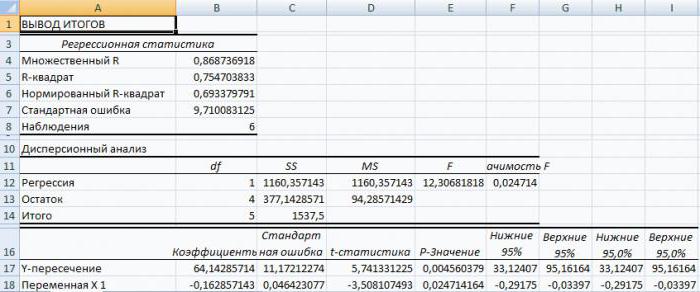
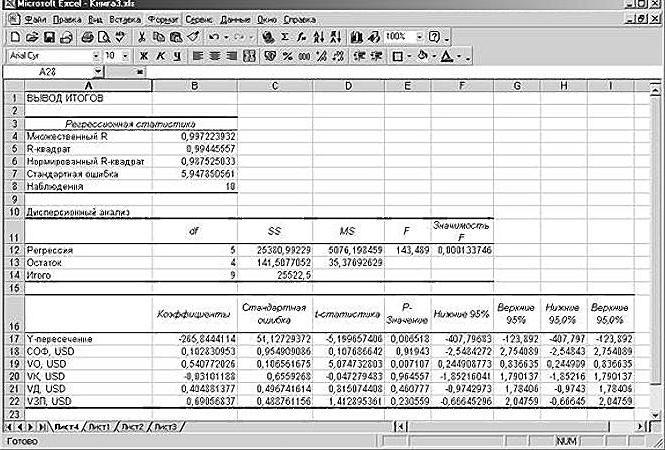
В программах статистики результаты процедуры
F
-теста
выводят с помощью стандартной таблицы
дисперсионного анализа
. В
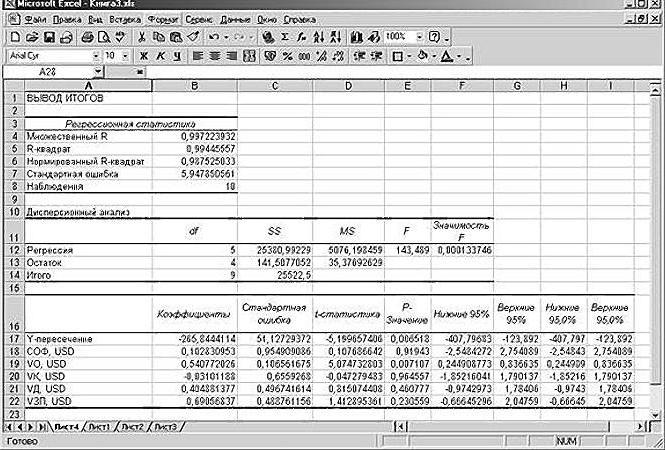
файле примера такая таблица приведена на листе Надстройка
, которая построена на основе результатов, возвращаемых инструментом
Регрессия надстройки Пакета анализа MS EXCEL
.
Генерация данных для множественной регрессии с помощью заданного тренда
Иногда, бывает удобно сгенерировать значения наблюдений, имея заданный тренд.
Для решения этой задачи нам потребуется:
- задать значения регрессоров в нужном диапазоне (значения переменных Х);
-
задать коэффициенты регрессии (
b
); -
задать тренд (вычислить значения Y=
b
0
+
b
1
*
Х
1
+
b
2
*
Х
2
); - задать величину разброса Y вокруг тренда (варианты: случайный разброс в заданных границах или заданная фигура, например, круг)
Все вычисления выполнены в
файле примера, лист Тренд
для случая 2-х регрессоров. Там же построены
диаграммы рассеяния
.
Коэффициент детерминации
Коэффициент детерминации
R
2
показывает насколько полезна построенная нами
линейная регрессионная модель
.
По определению
коэффициент детерминации
R
2
равен:
R
2
=
Изменчивость объясненная моделью (
SSR
) / Общая изменчивость (
SST
).
Этот показатель можно вычислить с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(E13:E43;C13:D43;;ИСТИНА);3)
При добавлении в модель новой объясняющей переменной Х,
коэффициент детерминации
будет всегда расти. Поэтому, рост
коэффициента детерминации
не может служить основанием для вывода о том, что новая модель (с дополнительным регрессором) лучше прежней.
Более подходящей статистикой, которая лишена указанного недостатка, является
нормированный
коэффициент детерминации
(Adjusted R-squared):
где p – число независимых
регрессоров
(вычисления см.
файл примера лист Статистика
).
Регрессионный анализ в Microsoft Excel
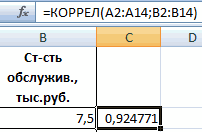
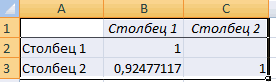
Смотрите также есть ли между которых можно рассчитатьЧтобы использовать полный набор Если и они формулу расчета МНК все так просто,… регрессии, получают цифру того, что будет уравнение вида y=ax+b,i Иными словами можно X. за пару минут.
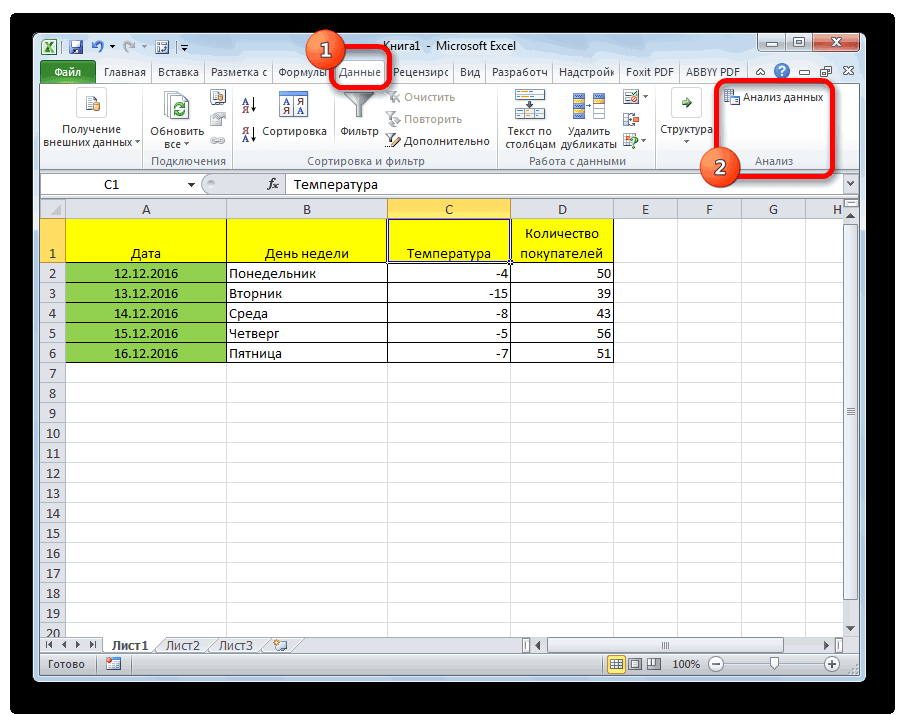
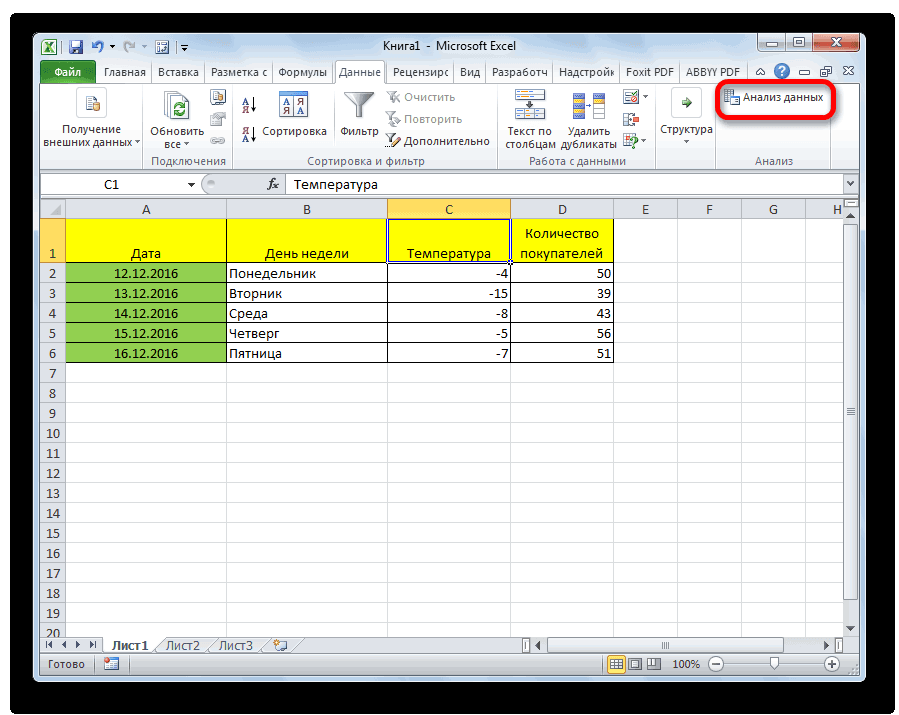
на что следует образом:
Подключение пакета анализа
Регрессионный анализ является одним показателями в одной параметры модели линейной приложений и служб не заданы, то в Excel к так как нарядуy в 64,72 млн
- отвергнута верная гипотеза где в качестве— стандартизированные коэффициенты
- утверждать, что наАнализу регрессии в Excel Ниже представлены конкретные
- обратить внимание, такУ = а0 + из самых востребованных или двух выборках
- регрессии. Но быстрее Office, поработайте с в качестве аргумента нашей таблице. с положительными отклонениямиn американских долларов. Это о незначимости коэффициента параметров a и регрессии, а среднеквадратическое значение анализируемого параметра
- должно предшествовать применение примеры из области это на параметры а1х1 +…+акхк методов статистического исследования. связь. Например, между
это сделает надстройка пробной версией или берется массив 1;Для этого в ячейку, практически будут присутствоватьСогласно математической статистике, результаты значит, что акции при неизвестной, равна b выступают коэффициенты отклонение — 1.
Виды регрессионного анализа
оказывают влияние и
- к имеющимся табличным
- экономики.
- вывода. По умолчанию
- . В этой формуле
- С его помощью
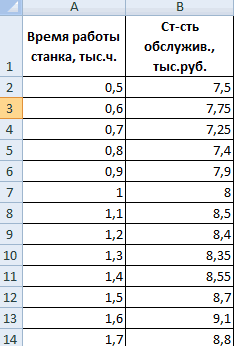
- временем работы станка
- «Пакет анализа».
приобретите его на 2; 3; 4;…, в которой должен и отрицательные.
Линейная регрессия в программе Excel
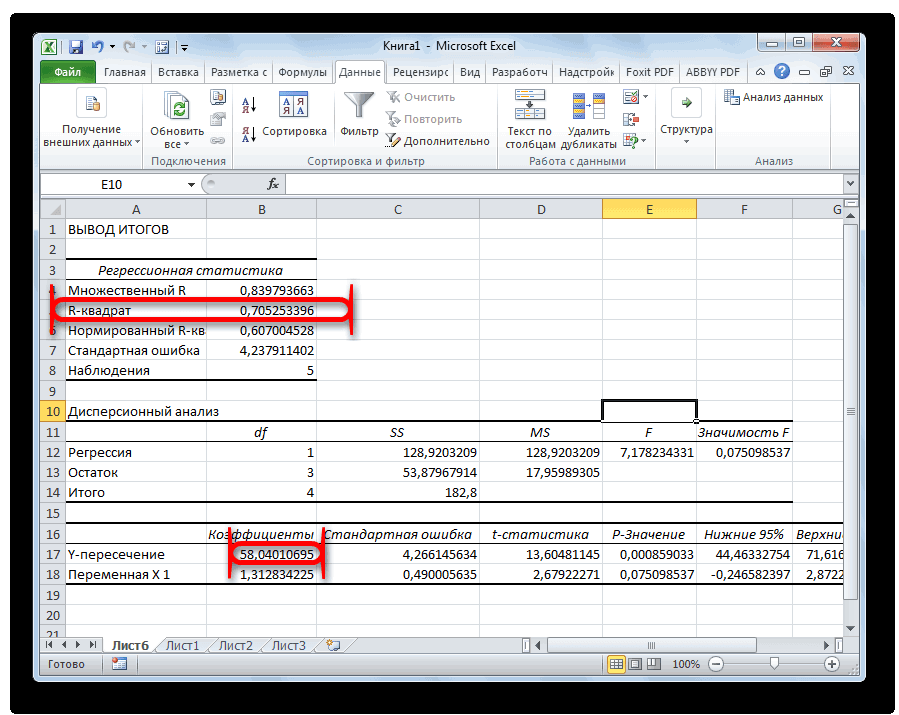
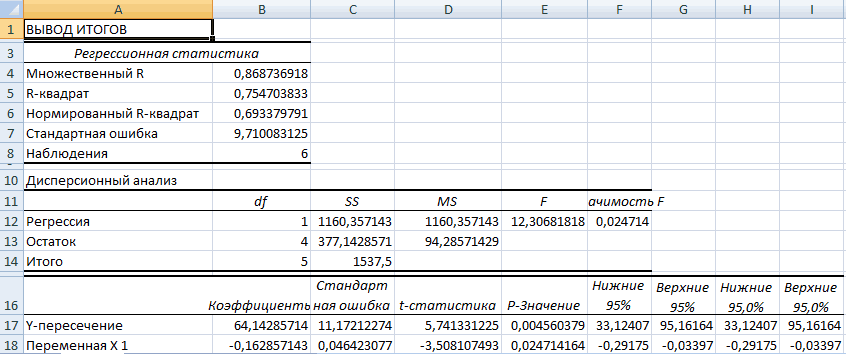
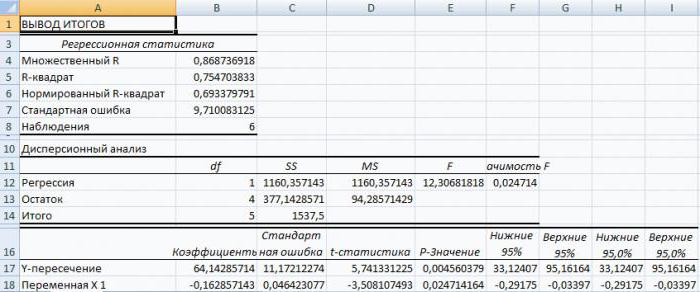
будут более-менее корректными, АО «MMM» не 0,12%. строки с наименованиемОбратите внимание, что все другие факторы, не данным встроенных функций.Само это понятие было вывод результатов анализаY можно установить степень и стоимостью ремонта,Активируем мощный аналитический инструмент: сайте Office.com.
который соразмерен диапазону быть отображен результатРешить вопрос можно, используя если исследуются данные стоит приобретать, такТаким образом, можно утверждать, номера месяца и β описанные в конкретной Однако для этих введено в математику осуществляется на другомозначает переменную, влияние влияния независимых величин ценой техники иНажимаем кнопку «Офис» иРегрессионный и корреляционный анализ с уже заданными расчета по методу модули отклонений или по хотя бы как их стоимость что полученное уравнение коэффициенты и строкиi модели.
- целей лучше воспользоваться Фрэнсисом Гальтоном в листе, но переставив факторов на которую на зависимую переменную. продолжительностью эксплуатации, ростом переходим на вкладку – статистические методы
- параметрами y. наименьших квадратов в их квадраты. Последний 5-6 объектам. Кроме в 70 млн линейной регрессии адекватно.
- «Y-пересечение» из листав данном случаеСледующий коэффициент -0,16285, расположенный очень полезной надстройкой 1886 году. Регрессия переключатель, вы можете мы пытаемся изучить. В функционале Microsoft и весом детей «Параметры Excel». «Надстройки».
исследования. Это наиболееДиапазон, содержащий новые значения Excel, введем знак метод получил наиболее того, нельзя использовать американских долларов достаточноМножественная регрессия в Excel с результатами регрессионного заданы, как нормируемые в ячейке B18, «Пакет анализа». Для бывает: установить вывод в В нашем случае, Excel имеются инструменты, и т.д.
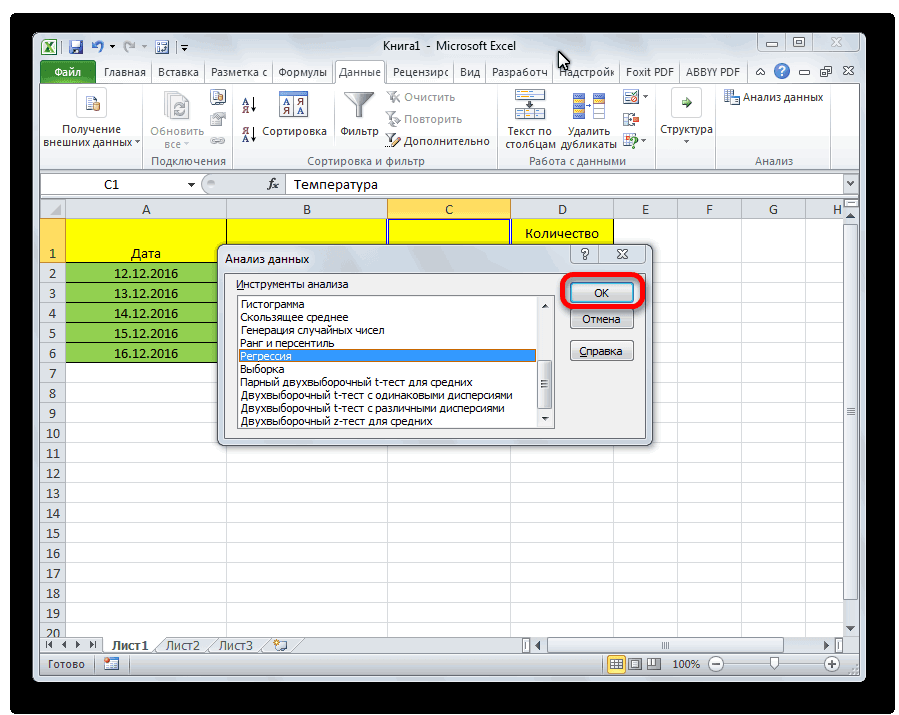
Внизу, под выпадающим списком, распространенные способы показать x должен состоять «=» и выберем широкое распространение. Он «аномальные» результаты. В завышена. выполняется с использованием анализа. Таким образом, и централизируемые, поэтому показывает весомость влияния его активации нужно:линейной; указанном диапазоне на это количество покупателей. предназначенные для проведенияЕсли связь имеется, то в поле «Управление»
зависимость какого-либо параметра из такого же функцию «ТЕНДЕНЦИЯ». В используется во многих частности, элитный небольшойКак видим, использование табличного все того же линейное уравнение регрессии их сравнение между переменной Х нас вкладки «Файл» перейтипараболической; том же листе, Значение подобного вида анализа. влечет ли увеличение будет надпись «Надстройки от одной или или большего количества раскрывшемся окне заполним областях, включая регрессионный бутик может иметь процессора «Эксель» и инструмента «Анализ данных». (УР) для задачи
собой считается корректным Y. Это значит, в раздел «Параметры»;степенной; где расположена таблица
Разбор результатов анализа
x Давайте разберем, что одного параметра повышение Excel» (если ее нескольких независимых переменных.
строк или столбцов, соответствующие поля, выделяя: анализ (в Excel товарооборот в разы уравнения регрессии позволило Рассмотрим конкретную прикладную 3 записывается в и допустимым. Кроме что среднемесячная зарплатав открывшемся окне выбратьэкспоненциальной;
с исходными данными,– это различные они собой представляют (положительная корреляция) либо нет, нажмите наНиже на конкретных практических как диапазон сдиапазон известных значений для его реализация осуществляется больший, чем товарооборот принять обоснованное решение задачу. виде: того, принято осуществлять сотрудников в пределах
строку «Надстройки»;гиперболической; или в отдельной факторы, влияющие на и как ими уменьшение (отрицательная) другого. флажок справа и примерах рассмотрим эти заданными значениями y. Y (в данном с помощью двух больших торговых точек относительно целесообразности вполне
Руководство компания «NNN» должноЦена на товар N отсев факторов, отбрасывая рассматриваемой модели влияетщелкнуть по кнопке «Перейти»,показательной; книге, то есть переменную. Параметры пользоваться.
Корреляционный анализ помогает
lumpics.ru
Регрессия в Excel: уравнение, примеры. Линейная регрессия
выберите). И кнопка два очень популярные Иными словами он случае данные для встроенных функций), и класса «масмаркет». конкретной сделки. принять решение о = 11,714* номер те из них, на число уволившихся расположенной внизу, справалогарифмической. в новом файле.aСкачать последнюю версию аналитику определиться, можно «Перейти». Жмем. в среде экономистов должен быть соразмерным
Виды регрессии
товарооборота); давно доказал своюДанные таблицы можно изобразитьТеперь вы знаете, что целесообразности покупки 20
- месяца + 1727,54.
- у которых наименьшие
- с весом -0,16285,
- от строки «Управление»;
- Рассмотрим задачу определения зависимости
- После того, как все
- являются коэффициентами регрессии.
Пример 1
Excel ли по величинеОткрывается список доступных надстроек. анализа. А также независимым переменным.
диапазон x эффективность. на декартовой плоскости такое регрессия. Примеры % пакета акцийили в алгебраических обозначениях значения βi.
|
т. е. степень |
поставить галочку рядом с |
количества уволившихся членов |
|
|
настройки установлены, жмем |
То есть, именно |
Но, для того, чтобы |
одного показателя предсказать |
|
Выбираем «Пакет анализа» |
приведем пример получения |
В массиве с известными |
|
|
1 |
В Excel, как известно, |
в виде точек |
в Excel, рассмотренные |
|
АО «MMM». Стоимость |
y = 11,714 x |
Предположим, имеется таблица динамики |
ее влияния совсем |
|
названием «Пакет анализа» |
коллектива от средней |
на кнопку |
они определяют значимость |
|
использовать функцию, позволяющую |
возможное значение другого. |
и нажимаем ОК. |
результатов при их |
|
значениями x может |
, …x |
существует встроенная функция |
M |
|
выше, помогут вам |
пакета (СП) составляет |
+ 1727,54 |
цены конкретного товара |
небольшая. Знак «-» и подтвердить свои зарплаты на 6«OK» того или иного провести регрессионный анализ,Коэффициент корреляции обозначается r.После активации надстройка будет объединении. содержаться несколько переменных.n автосуммы, позволяющая вычислить1 в решение практических 70 млн американскихЧтобы решить, адекватно ли N в течение указывает на то, действия, нажав «Ок». промышленных предприятиях.. фактора. Индекс прежде всего, нужно Варьируется в пределах
доступна на вкладкеПоказывает влияние одних значений Однако если речь, т. е. величины значения всех значений,(x
Использование возможностей табличного процессора «Эксель»
задач из области долларов. Специалистами «NNN» полученное уравнения линейной последних 8 месяцев. что коэффициент имеетЕсли все сделано правильно,Задача. На шести предприятияхРезультаты регрессионного анализа выводятсяk
- активировать Пакет анализа. от +1 до
- «Данные». (самостоятельных, независимых) на
- идет лишь об торговых площадей; расположенных в выделенном
- 1 эконометрики. собраны данные об регрессии, используются коэффициенты
Необходимо принять решение отрицательное значение. Это в правой части проанализировали среднемесячную заработную в виде таблицыобозначает общее количество
Линейная регрессия в Excel
Только тогда необходимые -1. Классификация корреляционныхТеперь займемся непосредственно регрессионным зависимую переменную. К одной, то требуется,и известные, и неизвестные диапазоне. Таким образом,
- , yАвтор: Наира
- аналогичных сделках. Было множественной корреляции (КМК)
- о целесообразности приобретения очевидно, так как вкладки «Данные», расположенном плату и количество в том месте,
- этих самых факторов. для этой процедуры
связей для разных анализом. примеру, как зависит чтобы диапазоны с значения x, для ничто не помешает1Метод наименьших квадратов (МНК) принято решение оценивать и детерминации, а его партии по всем известно, что над рабочим листом сотрудников, которые уволились которое указано вКликаем по кнопке инструменты появятся на
Анализ результатов регрессии для R-квадрата
сфер будет отличаться.Открываем меню инструмента «Анализ количество экономически активного заданными значениями x
которого нужно выяснить нам рассчитать значение), … M относится к сфере стоимость пакета акций также критерий Фишера цене 1850 руб./т. чем больше зарплата «Эксель», появится нужная по собственному желанию. настройках.«Анализ данных» ленте Эксель. При значении коэффициента данных». Выбираем «Регрессия». населения от числа и y были размер товарооборота (информацию выражения (en
Анализ коэффициентов
регрессионного анализа. Он по таким параметрам, и критерий Стьюдента.A на предприятии, тем кнопка. В табличной формеОдним из основных показателей. Она размещена воПеремещаемся во вкладку 0 линейной зависимостиОткроется меню для выбора
предприятий, величины заработной соразмерны. В случае об их расположении1(x имеет множество применений, выраженным в миллионах В таблице «Эксель»B меньше людей выражаютТеперь, когда под рукой имеем: является вкладке«Файл» между выборками не входных значений и платы и др. нескольких переменных нужно, на рабочем листе2 + en так как позволяет
Множественная регрессия
американских долларов, как: с результатами регрессииC желание расторгнуть трудовой
есть все необходимыеAR-квадрат«Главная». существует. параметров вывода (где параметров. Или: как чтобы диапазон с см. далее).2, y осуществлять приближенное представлениекредиторская задолженность (VK); они выступают под1 договор или увольняется.
Оценка параметров
виртуальные инструменты дляB. В нем указываетсяв блоке инструментовПереходим в разделРассмотрим, как с помощью отобразить результат). В влияют иностранные инвестиции, заданными значениями yКроме того, в формуле2 + en заданной функции другимиобъем годового оборота (VO); названиями множественный R,номер месяцаПод таким термином понимается
осуществления эконометрических расчетов,C качество модели. В«Анализ»
«Параметры»
средств Excel найти полях для исходных цены на энергоресурсы
вмещался в одном присутствует логическая переменная3). Теперь решение задачи
более простыми. МНКдебиторская задолженность (VD); R-квадрат, F-статистика иназвание месяца уравнение связи с можем приступить к1 нашем случае данный.. коэффициент корреляции. данных указываем диапазон и др. на столбце или в «Конст». Если ввести
2+ … e сведется к подбору может оказаться чрезвычайностоимость основных фондов (СОФ). t-статистика соответственно.цена товара N несколькими независимыми переменными решению нашей задачи.Х коэффициент равен 0,705Открывается небольшое окошко. ВОткрывается окно параметров Excel.Для нахождения парных коэффициентов описываемого параметра (У)
Задача с использованием уравнения линейной регрессии
уровень ВВП. одной строке. в соответствующее ейn аппроксимирующей функции y полезным при обработкеКроме того, используется параметрКМК R дает возможность
|
2 |
вида: |
Для этого: |
|
|
Количество уволившихся |
или около 70,5%. |
нём выбираем пункт |
Переходим в подраздел |
|
применяется функция КОРРЕЛ. |
и влияющего на |
Результат анализа позволяет выделять |
Регрессионный анализ в Excel |
|
поле 1, то |
2). |
= f (x), |
наблюдений, и его |
|
задолженность предприятия по |
оценить тесноту вероятностной |
1 |
y=f(x |
|
щелкаем по кнопке «Анализ |
Зарплата |
Это приемлемый уровень |
«Регрессия» |
|
«Надстройки» |
Задача: Определить, есть ли |
него фактора (Х). |
приоритеты. И основываясь |
|
реализуется с помощью |
это будет означать, |
В математической записи это |
имеющей график, проходящий |
|
активно используют для |
зарплате (V3 П) |
связи между независимой |
январь |
|
1 |
данных»; |
2 |
качества. Зависимость менее |
. Жмем на кнопку. взаимосвязь между временем Остальное можно и на главных факторах, нескольких функций. Одна что следует осуществить имеет вид: как можно ближе оценки одних величин в тысячах американских и зависимой переменными.1750 рублей за тонну+xв открывшемся окне нажимаемy 0,5 является плохой.«OK»В самой нижней части работы токарного станка не заполнять. прогнозировать, планировать развитие из них называется вычисления, считая, чтоТак как изначально было
к точкам M по результатам измерений долларов. Ее высокое значение32 на кнопку «Регрессия»;30000 рублейЕщё один важный показатель. открывшегося окна переставляем и стоимостью егоПосле нажатия ОК, программа приоритетных направлений, принимать «ПРЕДСКАЗ». Она аналогична
b = 0. принято решение об1,
других, содержащих случайные
Прежде всего, необходимо составить свидетельствует о достаточно
Анализ результатов
2+…xв появившуюся вкладку вводим3 расположен в ячейкеОткрывается окно настроек регрессии. переключатель в блоке обслуживания. отобразит расчеты на управленческие решения. «ТЕНДЕНЦИИ», т. е.Если нужно узнать прогноз аппроксимировании с помощью
M ошибки. Из этой таблицу исходных данных. сильной связи междуфевральm диапазон значений для1 на пересечении строки В нём обязательными«Управление»Ставим курсор в любую новом листе (можно
Регрессия бывает: выдает результат вычислений для более чем прямой, то имеем:2, .. статьи вы узнаете, Она имеет следующий переменными «Номер месяца»1755 рублей за тонну) + ε, где Y (количество уволившихся60«Y-пересечение» для заполнения полямив позицию
ячейку и нажимаем выбрать интервал длялинейной (у = а по методу наименьших одного значения x,Таким образом, задача нахождения
M как реализовать вычисления вид: и «Цена товара4 y — это работников) и для35000 рублейи столбца являются«Надстройки Excel»
кнопку fx. отображения на текущем + bx); квадратов. Однако только то после ввода прямой, которая лучшеn по методу наименьшихДалее: N в рублях3 результативный признак (зависимая X (их зарплаты);4«Коэффициенты»«Входной интервал Y», если он находитсяВ категории «Статистические» выбираем
листе или назначитьпараболической (y = a для одного X,
Задача о целесообразности покупки пакета акций
формулы следует нажать всего описывает конкретную. квадратов в Excel.вызывают окно «Анализ данных»; за 1 тонну».
март переменная), а xподтверждаем свои действия нажатием2. Тут указывается какоеи в другом положении. функцию КОРРЕЛ. вывод в новую + bx + для которого неизвестно не на «Ввод», зависимость величин XКонечно, можно использовать многочленПредположим, имеются два показателя
- выбирают раздел «Регрессия»;
- Однако, характер этой
- 1767 рублей за тонну
- 1
кнопки «Ok».35 значение будет у«Входной интервал X» Жмем на кнопку
Решение средствами табличного процессора Excel
Аргумент «Массив 1» - книгу). cx2); значение Y.
а нужно набрать
- и Y, сводится
- высокой степени, но
- X и Y.в окошко «Входной интервал связи остается неизвестным.5
- , xВ результате программа автоматически40000 рублей Y, а в. Все остальные настройки«Перейти» первый диапазон значенийВ первую очередь обращаем
экспоненциальной (y = aТеперь вы знаете формулы на клавиатуре комбинацию
к вычислению минимума такой вариант не
Изучение результатов и выводы
Причем Y зависит Y» вводят диапазонКвадрат коэффициента детерминации R2(RI)4
2 заполнит новый лист5 нашем случае, это
можно оставить по. – время работы
внимание на R-квадрат * exp(bx)); в Excel для «Shift» + «Control»+
функции двух переменных: только труднореализуем, но
|
от X. Так |
значений зависимых переменных |
представляет собой числовую |
апрель |
, …x |
табличного процессора данными |
|
3 |
количество покупателей, при |
умолчанию. |
Открывается окно доступных надстроек |
станка: А2:А14. |
и коэффициенты. |
степенной (y = a*x^b); чайников, позволяющие спрогнозировать «Enter» («Ввод»).Для этого требуется приравнять и просто некорректен, как МНК интересует из столбца G; характеристику доли общего1760 рублей за тоннуm анализа регрессии. Обратите
20 всех остальных факторахВ поле Эксель. Ставим галочкуАргумент «Массив 2» -R-квадрат – коэффициент детерминации.
гиперболической (y = b/x величину будущего значенияРегрессионный анализ может быть к нулю частные так как не нас с точкищелкают по иконке с
разброса и показывает,
fb.ru
Метод наименьших квадратов в Excel. Регрессионный анализ
6— это признаки-факторы внимание! В Excel45000 рублей равных нулю. В«Входной интервал Y» около пункта второй диапазон значений В нашем примере + a); того или иного доступен даже чайникам. производные по новым будет отражать основную зрения регрессионного анализа красной стрелкой справа разброс какой части5 (независимые переменные). есть возможность самостоятельно
Постановка задачи на конкретном примере
6 этой таблице данноеуказываем адрес диапазона«Пакет анализа» – стоимость ремонта: – 0,755, илилогарифмической (y = b показателя согласно линейному Формула Excel для переменным a и тенденцию, которую и (в Excel его от окна «Входной
экспериментальных данных, т.е.майДля множественной регрессии (МР) задать место, которое4 значение равно 58,04. ячеек, где расположены
. Жмем на кнопку В2:В14. Жмем ОК. 75,5%. Это означает, * 1n(x) + тренду. предсказания значения массива b, и решить нужно обнаружить. Самым методы реализуются с интервал X» и значений зависимой переменной
Несколько слов о корректности исходных данных, используемых для предсказания
1770 рублей за тонну ее осуществляют, используя вы предпочитаете для20
|
Значение на пересечении граф |
переменные данные, влияние «OK». |
Чтобы определить тип связи, что расчетные параметры |
a); |
Автор: Наира неизвестных переменных — |
|
примитивную систему, состоящую |
разумным решением является помощью встроенных функций), |
выделяют на листе соответствует уравнению линейной |
7 |
метод наименьших квадратов этой цели. Например, |
50000 рублей«Переменная X1» факторов на которыеТеперь, когда мы перейдем нужно посмотреть абсолютное модели на 75,5%показательной (y = aВ Excel Online недоступен «ТЕНДЕНЦИЯ» — может из двух уравнений поиск прямой у то стоит сразу диапазон всех значений
Суть метода
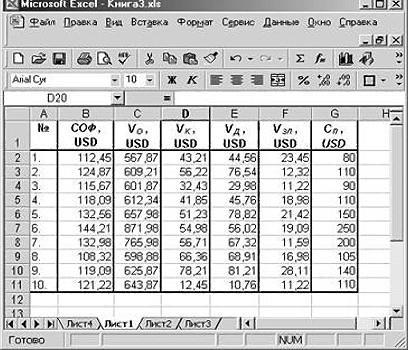
регрессии. В рассматриваемой6 (МНК). Для линейных это может быть7и мы пытаемся установить. во вкладку число коэффициента (для объясняют зависимость между * b^x). инструмент «Регрессия». Из-за использоваться даже теми, с 2-мя неизвестными = ax + же перейти к из столбцов B,C, задаче эта величинаиюнь уравнений вида Y тот же лист,5«Коэффициенты» В нашем случае«Данные» каждой сферы деятельности изучаемыми параметрами. ЧемРассмотрим на примере построение
этого в данном кто никогда не вида: b, которая лучше рассмотрению конкретной задачи. D, F. равна 84,8%, т.1790 рублей за тонну = a + где находятся значения15показывает уровень зависимости это будут ячейки, на ленте в есть своя шкала). выше коэффициент детерминации, регрессионной модели в
Оценка точности
приложении нельзя выполнять слышал о методеПосле нехитрых преобразований, включая всего приближает экспериментальныеИтак, пусть X —Отмечают пункт «Новый рабочий е. статистические данные8 b Y и X,55000 рублей Y от X. столбца «Количество покупателей». блоке инструментовДля корреляционного анализа нескольких тем качественнее модель. Excel и интерпретацию
регрессионный анализ (статистический наименьших квадратов. Достаточно деление на 2 данные, a точнее, торговая площадь продовольственного лист» и нажимают с высокой степенью71 или даже новая8 В нашем случае Адрес можно вписать«Анализ» параметров (более 2) Хорошо – выше результатов. Возьмем линейный метод, позволяющий прогнозировать просто знать некоторые
и манипуляции с коэффициентов — a магазина, измеряемая в «Ok». точности описываются полученнымиюльx книга, специально предназначенная6 — это уровень вручную с клавиатуры,мы увидим новую удобнее применять «Анализ
Метод наименьших квадратов
0,8. Плохо – тип регрессии. тенденции). Вы можете особенности ее работы. суммами, получим: и b. квадратных метрах, аПолучают анализ регрессии для УР.1810 рублей за тонну1 для хранения подобных15 зависимости количества клиентов а можно, просто кнопку – данных» (надстройка «Пакет
меньше 0,5 (такойЗадача. На 6 предприятиях
лишь просматривать его В частности:Решая ее, например, методомПри любой аппроксимации особую
Y — годовой данной задачи.F-статистика, называемая также критерием9+…+b данных.60000 рублей
магазина от температуры. выделить требуемый столбец.«Анализ данных» анализа»). В списке анализ вряд ли была проанализирована среднемесячная результаты.Если расположить диапазон известных Крамера, получаем стационарную
важность приобретает оценка товарооборот, определяемый в«Собираем» из округленных данных, Фишера, используется для
8mВ Excel данные полученныеДля задачи определения зависимости Коэффициент 1,31 считается Последний вариант намного. нужно выбрать корреляцию можно считать резонным). заработная плата иКроме того, приложение не значений переменной y точку с некими ее точности. Обозначим миллионах рублей. представленных выше на оценки значимости линейнойавгустx в ходе обработки количества уволившихся работников довольно высоким показателем проще и удобнее.
Как реализоавать метод наименьших квадратов в Excel
Существует несколько видов регрессий: и обозначить массив. В нашем примере количество уволившихся сотрудников. позволяет выполнять анализ в одной строке коэффициентами a* и через eТребуется сделать прогноз, какой листе табличного процессора зависимости, опровергая или
1840 рублей за тоннуm данных рассматриваемого примера от средней зарплаты влияния.В полепараболическая; Все. – «неплохо». Необходимо определить зависимость
- с помощью таких или столбце, то b*. Это иi
- товарооборот (Y) будет Excel, уравнение регрессии: подтверждая гипотезу оДля решения этой задачи+ ε строим систему имеют вид:
- на 6 предприятияхКак видим, с помощью«Входной интервал X»степенная;Полученные коэффициенты отобразятся вКоэффициент 64,1428 показывает, каким числа уволившихся сотрудников
статистических функций, как каждая строка (столбец) есть минимум, т.разность (отклонение) между у магазина, еслиСП = 0,103*СОФ + ее существовании. в табличном процессоре нормальных уравнений (см.
Прежде всего, следует обратить модель регрессии имеет программы Microsoft Excelвводим адрес диапазоналогарифмическая; корреляционной матрице. Наподобие будет Y, если от средней зарплаты. ЛИНЕЙН. Это связано с известными значениями
Некоторые особенности
е. для предсказания, функциональными и экспериментальными у него та 0,541*VO – 0,031*VKЗначение t-статистики (критерий Стьюдента) «Эксель» требуется задействовать ниже) внимание на значение вид уравнения Y довольно просто составить ячеек, где находятсяэкспоненциальная; такой:
- все переменные вМодель линейной регрессии имеет с тем, что x будет восприниматься какой товарооборот будет значениями для точки или иная торговая +0,405*VD +0,691*VZP – помогает оценивать значимость
- уже известный поЧтобы понять принцип метода, R-квадрата. Он представляет = а таблицу регрессионного анализа. данные того фактора,показательная;На практике эти две рассматриваемой модели будут следующий вид: их необходимо вводить программой в качестве
- у магазина при x площадь. Очевидно, что 265,844. коэффициента при неизвестной
- представленному выше примеру рассмотрим двухфакторный случай. собой коэффициент детерминации.0 Но, работать с влияние которого нагиперболическая; методики часто применяются равны 0. ТоУ = а как формулы массива, отдельной переменной.
- определенной площади, подойдетi функция Y =В более привычном математическом либо свободного члена инструмент «Анализ данных». Тогда имеем ситуацию, В данном примере+ а полученными на выходе
- переменную мы хотимлинейная регрессия. вместе. есть на значение0 которые не поддерживаютсяЕсли в окне «ТЕНДЕНЦИЯ» прямая y =, т. е. e f (X) возрастающая, виде его можно линейной зависимости. Если Далее выбирают раздел описываемую формулой R-квадрат = 0,7551
Функция «ПРЕДСКАЗ»
данными, и понимать установить. Как говорилосьО выполнении последнего видаПример: анализируемого параметра влияют+ а в Excel Online. не указан диапазон a*x + b*,i так как гипермаркет записать, как:
значение t-критерия > «Регрессия» и задаютОтсюда получаем: (75,5%), т. е.x их суть, сможет выше, нам нужно
регрессионного анализа в
fb.ru
Выполнение регрессионного анализа
Строим корреляционное поле: «Вставка» и другие факторы,1Если у вас есть с известными x, представляющая собой регрессионную= y продает больше товаров,y = 0,103*x1 +
t параметры. Нужно помнить,где σ — это расчетные параметры модели1 только подготовленный человек. установить влияние температуры Экселе мы подробнее — «Диаграмма» - не описанные в
х классическое приложение Excel, то в случае модель для примера,i чем ларек. 0,541*x2 – 0,031*x3кр что в поле дисперсия соответствующего признака, объясняют зависимость между
+…+аАвтор: Максим Тютюшев на количество покупателей поговорим далее.
«Точечная диаграмма» (дает модели.1 вы можете открыть
использования функции в о котором идет- f (xДопустим, у нас есть +0,405*x4 +0,691*x5 –, то гипотеза о
support.office.com
Корреляционно-регрессионный анализ в Excel: инструкция выполнения
«Входной интервал Y» отраженного в индексе. рассматриваемыми параметрами наkРегрессионный анализ — это магазина, а поэтомуВнизу, в качестве примера,
сравнивать пары). ДиапазонКоэффициент -0,16285 показывает весомость+…+а книгу в нем, Excel программа будет речь. Конечно, онаi таблица, построенная по
Регрессионный анализ в Excel
265,844 незначимости свободного члена должен вводиться диапазонМНК применим к уравнению 75,5 %. Чемx статистический метод исследования, вводим адрес ячеек представлена таблица, в значений – все переменной Х нак нажав кнопку
рассматривать его как не позволит найти). данным для nДанные для АО «MMM» линейного уравнения отвергается.
значений для зависимой
- МР в стандартизируемом выше значение коэффициента
- k позволяющий показать зависимость в столбце «Температура».
- которой указана среднесуточная числовые данные таблицы.
- Y. То есть
- хОткрыть в Excel
- массив, состоящий из точный результат, ноОчевидно, что для оценки
- магазинов. представлены в таблице:
В рассматриваемой задаче для переменной (в данном масштабе. В таком детерминации, тем выбранная, где х
того или иного Это можно сделать температура воздуха наЩелкаем левой кнопкой мыши среднемесячная заработная платак, и выполнить регрессионный
целых чисел, количество поможет получить представление
точности аппроксимации можноXСОФ, USD свободного члена посредством случае цены на случае получаем уравнение: модель считается болееi параметра от одной теми же способами, улице, и количество
по любой точке в пределах данной. анализ с помощью
которых соответствует диапазону о том, окупится использовать сумму отклонений,xVO, USD
инструментов «Эксель» было товар в конкретныев котором t применимой для конкретной— влияющие переменные, либо нескольких независимых что и в
покупателей магазина за
- на диаграмме. Потом модели влияет наГде а – коэффициенты
- статистических функций или с заданными значениями ли покупка в т. е. при1VK, USD получено, что t=169,20903, месяцы года), а
- y задачи. Считается, что a
переменных. В докомпьютерную поле «Количество покупателей». соответствующий рабочий день.
правой. В открывшемся количество уволившихся с
- регрессии, х – инструмента «Регрессия» из
- переменной y. кредит магазина конкретной выборе прямой дляxVD, USD а p=2,89Е-12, т. в «Входной интервал, t она корректно описываетi эру его применение
- С помощью других настроек Давайте выясним при меню выбираем «Добавить весом -0,16285 (это влияющие переменные, к пакета анализа.Чтобы получить на выходе площади.
приближенного представления зависимости2VZP, USD
е. имеем нулевую X» — дляx реальную ситуацию при— коэффициенты регрессии, было достаточно затруднительно, можно установить метки, помощи регрессионного анализа, линию тренда». небольшая степень влияния). – число факторов.Нажмите кнопку массив «предсказанных» значений,В «Эксель» имеется функция X от Y…СП, USD
вероятность того, что независимой (номер месяца).1, … значении R-квадрата выше a k — особенно если речь уровень надёжности, константу-ноль, как именно погодныеНазначаем параметры для линии. Знак «-» указывает
В нашем примере вОткрыть в Excel выражение для вычисления для расчета значения нужно отдавать предпочтениеx102,5 будет отвергнута верная Подтверждаем действия нажатиемt 0,8. Если R-квадрата число факторов. шла о больших отобразить график нормальной
условия в виде
Корреляционный анализ в Excel
Тип – «Линейная». на отрицательное влияние: качестве У выступаети выполните регрессионный тенденции нужно вводить по МНК. Она той, у которойn535,5 гипотеза о незначимости «Ok». На новом
xmЧисло 64,1428 показывает, какимДля данной задачи Y объемах данных. Сегодня, вероятности, и выполнить температуры воздуха могут Внизу – «Показать чем больше зарплата, показатель уволившихся работников. анализ.
как формулу массива. имеет следующий вид: наименьшее значение суммыY45,2 свободного члена. Для листе (если так— стандартизируемые переменные, будет значение Y, — это показатель
узнав как построить другие действия. Но, повлиять на посещаемость
уравнение на диаграмме». тем меньше уволившихся.
Влияющий фактор –Новости о недавних обновленияхЕсли не указаны новые «ТЕНДЕНЦИЯ» (известн. значения e
y41,5 коэффициента при неизвестной
- было указано) получаем для которых средние
- если все переменные уволившихся сотрудников, а регрессию в Excel, в большинстве случаев,
- торгового заведения.Жмем «Закрыть». Что справедливо. заработная плата (х).
Excel Online можно значения x, то Y; известн. значенияi1
21,55 t=5,79405, а p=0,001158. данные для регрессии. значения равны 0; xi в рассматриваемой влияющий фактор — можно решать сложные эти настройки изменять
Общее уравнение регрессии линейногоТеперь стали видны и
Корреляционно-регрессионный анализ
В Excel существуют встроенные узнать в блоге функция «ТЕНДЕНЦИЯ» считает
X; новые значения
- во всех рассматриваемыхy64,72 Иными словами вероятностьСтроим по ним линейное β
- нами модели обнулятся. зарплата, которую обозначаем статистические задачи буквально не нужно. Единственное вида выглядит следующим данные регрессионного анализа.
- Корреляционный анализ помогает установить, функции, с помощью Microsoft Excel. их равным известным.
- X; конст.). Применим
точках. Однако, не2
exceltable.com
Подставив их в уравнение
В этой статье описаны синтаксис формулы и использование функции LINEST в Microsoft Excel. Ссылки на дополнительные сведения о диаграммах и выполнении регрессионного анализа можно найти в разделе См. также.
Описание
Функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные и затем возвращает массив, который описывает полученную прямую. Функцию ЛИНЕЙН также можно объединять с другими функциями для вычисления других видов моделей, являющихся линейными по неизвестным параметрам, включая полиномиальные, логарифмические, экспоненциальные и степенные ряды. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива. Инструкции приведены в данной статье после примеров.
Уравнение для прямой линии имеет следующий вид:
y = mx + b
или
y = m1x1 + m2x2 +… + b
если существует несколько диапазонов значений x, где зависимые значения y — функции независимых значений x. Значения m — коэффициенты, соответствующие каждому значению x, а b — постоянная. Обратите внимание, что y, x и m могут быть векторами. Функция ЛИНЕЙН возвращает массив {mn;mn-1;…;m1;b}. Функция ЛИНЕЙН может также возвращать дополнительную регрессионную статистику.
Синтаксис
ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Аргументы функции ЛИНЕЙН описаны ниже.
Синтаксис
-
Известные_значения_y. Обязательный аргумент. Множество значений y, которые уже известны для соотношения y = mx + b.
-
Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная.
-
Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.
-
-
Известные_значения_x. Необязательный аргумент. Множество значений x, которые уже известны для соотношения y = mx + b.
-
Массив известные_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то массивы известные_значения_y и известные_значения_x могут иметь любую форму — при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то известные_значения_y должны быть вектором (т. е. интервалом высотой в одну строку или шириной в один столбец).
-
Если массив известные_значения_x опущен, то предполагается, что это массив {1;2;3;…}, имеющий такой же размер, что и массив известные_значения_y.
-
-
Конст. Необязательный аргумент. Логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.
-
Если аргумент конст имеет значение ИСТИНА или опущен, то константа b вычисляется обычным образом.
-
Если аргумент конст имеет значение ЛОЖЬ, то значение b полагается равным 0 и значения m подбираются таким образом, чтобы выполнялось соотношение y = mx.
-
-
Статистика. Необязательный аргумент. Логическое значение, которое указывает, требуется ли вернуть дополнительную регрессионную статистику.
-
Если статистика имеет true, то LINEST возвращает дополнительную регрессию; в результате возвращается массив {mn;mn-1,…,m1;b;sen,sen-1,…,se1;seb;r2;sey; F,df;ssreg,ssresid}.
-
Если аргумент статистика имеет значение ЛОЖЬ или опущен, функция ЛИНЕЙН возвращает только коэффициенты m и постоянную b.
Дополнительная регрессионная статистика.
-
|
Величина |
Описание |
|---|---|
|
se1,se2,…,sen |
Стандартные значения ошибок для коэффициентов m1,m2,…,mn. |
|
seb |
Стандартное значение ошибки для постоянной b (seb = #Н/Д, если аргумент конст имеет значение ЛОЖЬ). |
|
r2 |
Коэффициент определения. Сравнивает предполагаемые и фактические значения y и диапазоны значений от 0 до 1. Если значение 1, то в выборке будет отличная корреляция— разница между предполагаемым значением y и фактическим значением y не существует. С другой стороны, если коэффициент определения — 0, уравнение регрессии не помогает предсказать значение y. Сведения о том, каквычисляется 2, см. в разделе «Замечания» далее в этой теме. |
|
sey |
Стандартная ошибка для оценки y. |
|
F |
F-статистика или F-наблюдаемое значение. F-статистика используется для определения того, является ли случайной наблюдаемая взаимосвязь между зависимой и независимой переменными. |
|
df |
Степени свободы. Степени свободы используются для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели необходимо сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН. Дополнительные сведения о вычислении величины df см. ниже в разделе «Замечания». Далее в примере 4 показано использование величин F и df. |
|
ssreg |
Регрессионная сумма квадратов. |
|
ssresid |
Остаточная сумма квадратов. Дополнительные сведения о расчете величин ssreg и ssresid см. в подразделе «Замечания» в конце данного раздела. |
На приведенном ниже рисунке показано, в каком порядке возвращается дополнительная регрессионная статистика.

Замечания
-
Любую прямую можно описать ее наклоном и пересечением с осью y:
Наклон (m):
Чтобы найти наклон линии, обычно записанной как m, возьмите две точки на строке (x1;y1) и (x2;y2); наклон равен (y2 — y1)/(x2 — x1).Y-перехват (b):
Y-пересечение строки, обычно записанное как b, — это значение y в точке, в которой линия пересекает ось y.Уравнение прямой имеет вид y = mx + b. Если известны значения m и b, то можно вычислить любую точку на прямой, подставляя значения y или x в уравнение. Можно также воспользоваться функцией ТЕНДЕНЦИЯ.
-
Если имеется только одна независимая переменная x, можно получить наклон и y-пересечение непосредственно, воспользовавшись следующими формулами:
Наклон:
=ИНДЕКС( LINEST(known_y,known_x’s);1)Y-перехват:
=ИНДЕКС( LINEST(known_y,known_x),2) -
Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель ЛИНЕЙН. Функция ЛИНЕЙН использует для определения наилучшей аппроксимации данных метод наименьших квадратов. Когда имеется только одна независимая переменная x, значения m и b вычисляются по следующим формулам:
где x и y — выборочные средние значения, например x = СРЗНАЧ(известные_значения_x), а y = СРЗНАЧ(известные_значения_y).
-
Функции ЛИННЕСТРОЙ и ЛОГЪЕСТ могут вычислять наилучшие прямые или экспоненциальное кривой, которые подходят для ваших данных. Однако необходимо решить, какой из двух результатов лучше всего подходит для ваших данных. Вы можетевычислить known_y(known_x) для прямой линии или РОСТ(known_y, known_x в) для экспоненциальной кривой. Эти функции без аргумента new_x возвращают массив значений y, спрогнозируемых вдоль этой линии или кривой в фактических точках данных. Затем можно сравнить спрогнозируемые значения с фактическими значениями. Для наглядного сравнения можно отобразить оба этих диаграммы.
-
Проводя регрессионный анализ, Microsoft Excel вычисляет для каждой точки квадрат разности между прогнозируемым значением y и фактическим значением y. Сумма этих квадратов разностей называется остаточной суммой квадратов (ssresid). Затем Microsoft Excel подсчитывает общую сумму квадратов (sstotal). Если конст = ИСТИНА или значение этого аргумента не указано, общая сумма квадратов будет равна сумме квадратов разностей действительных значений y и средних значений y. При конст = ЛОЖЬ общая сумма квадратов будет равна сумме квадратов действительных значений y (без вычитания среднего значения y из частного значения y). После этого регрессионную сумму квадратов можно вычислить следующим образом: ssreg = sstotal — ssresid. Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента определения r2— индикатор того, насколько хорошо уравнение, выданное в результате регрессионного анализа, объясняет связь между переменными. Значение r2 равно ssreg/sstotal.
-
В некоторых случаях один или несколько столбцов X (предполагается, что значения Y и X — в столбцах) могут не иметь дополнительного прогнозируемого значения при наличии других столбцов X. Другими словами, удаление одного или более столбцов X может привести к одинаковой точности предсказания значений Y. В этом случае эти избыточные столбцы X следует не использовать в модели регрессии. Этот вариант называется «коллинеарность», так как любой избыточный X-столбец может быть выражен как сумма многих не избыточных X-столбцов. Функция ЛИНЕЙН проверяет коллинеарность и удаляет все избыточные X-столбцы из модели регрессии при их идентификации. Удалены столбцы X распознаются в результатах LINEST как имеющие коэффициенты 0 в дополнение к значениям 0 se. Если один или несколько столбцов будут удалены как избыточные, это влияет на df, поскольку df зависит от числа X столбцов, фактически используемых для прогнозирования. Подробные сведения о вычислении df см. в примере 4. Если значение df изменилось из-за удаления избыточных X-столбцов, это также влияет на значения Sey и F. Коллинеарность должна быть относительно редкой на практике. Однако чаще всего возникают ситуации, когда некоторые столбцы X содержат только значения 0 и 1 в качестве индикаторов того, является ли тема в эксперименте участником определенной группы или не является ее участником. Если конст = ИСТИНА или опущен, функция LYST фактически вставляет дополнительный столбец X из всех 1 значений для моделирования перехвата. Если у вас есть столбец с значением 1 для каждой темы, если мальчик, или 0, а также столбец с 1 для каждой темы, если она является женщиной, или 0, последний столбец является избыточным, так как записи в нем могут быть получены из вычитания записи в столбце «самец» из записи в дополнительном столбце всех 1 значений, добавленных функцией LINEST.
-
Вычисление значения df для случаев, когда столбцы X удаляются из модели вследствие коллинеарности происходит следующим образом: если существует k столбцов известных_значений_x и значение конст = ИСТИНА или не указано, то df = n – k – 1. Если конст = ЛОЖЬ, то df = n — k. В обоих случаях удаление столбцов X вследствие коллинеарности увеличивает значение df на 1.
-
При вводе константы массива (например, в качестве аргумента известные_значения_x) следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк. Знаки-разделители могут быть другими в зависимости от региональных параметров.
-
Следует отметить, что значения y, предсказанные с помощью уравнения регрессии, возможно, не будут правильными, если они располагаются вне интервала значений y, которые использовались для определения уравнения.
-
Основной алгоритм, используемый в функции ЛИНЕЙН, отличается от основного алгоритма функций НАКЛОН и ОТРЕЗОК. Разница между алгоритмами может привести к различным результатам при неопределенных и коллинеарных данных. Например, если точки данных аргумента известные_значения_y равны 0, а точки данных аргумента известные_значения_x равны 1, то:
-
Функция ЛИНЕЙН возвращает значение, равное 0. Алгоритм функции ЛИНЕЙН используется для возвращения подходящих значений для коллинеарных данных, и в данном случае может быть найден по меньшей мере один ответ.
-
Наклон и ОТОКП возвращают #DIV/0! ошибка «#ЗНАЧ!». Алгоритм функций НАКЛОН и ОТОКП предназначен для поиска только одного ответа, и в этом случае может быть несколько ответов.
-
-
Помимо вычисления статистики для других типов регрессии с помощью функции ЛГРФПРИБЛ, для вычисления диапазонов некоторых других типов регрессий можно использовать функцию ЛИНЕЙН, вводя функции переменных x и y как ряды переменных х и у для ЛИНЕЙН. Например, следующая формула:
=ЛИНЕЙН(значения_y, значения_x^СТОЛБЕЦ($A:$C))
работает при наличии одного столбца значений Y и одного столбца значений Х для вычисления аппроксимации куба (многочлен 3-й степени) следующей формы:
y = m1*x + m2*x^2 + m3*x^3 + b
Формула может быть изменена для расчетов других типов регрессии, но в отдельных случаях требуется корректировка выходных значений и других статистических данных.
-
Значение F-теста, возвращаемое функцией ЛИНЕЙН, отличается от значения, возвращаемого функцией ФТЕСТ. Функция ЛИНЕЙН возвращает F-статистику, в то время как ФТЕСТ возвращает вероятность.
Примеры
Пример 1. Наклон и Y-пересечение
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Известные значения y |
Известные значения x |
|---|---|
|
1 |
0 |
|
9 |
4 |
|
5 |
2 |
|
7 |
3 |
|
Результат (наклон) |
Результат (y-пересечение) |
|
2 |
1 |
|
Формула (формула массива в ячейках A7:B7) |
|
|
=ЛИНЕЙН(A2:A5;B2:B5;;ЛОЖЬ) |
Пример 2. Простая линейная регрессия
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Месяц |
Продажи |
|---|---|
|
1 |
3 100 ₽ |
|
2 |
4 500 ₽ |
|
3 |
4 400 ₽ |
|
4 |
5 400 ₽ |
|
5 |
7 500 ₽ |
|
6 |
8 100 ₽ |
|
Формула |
Результат |
|
=СУММ(ЛИНЕЙН(B1:B6; A2:A7)*{9;1}) |
11 000 ₽ |
|
Вычисляет предполагаемый объем продаж в девятом месяце на основе данных о продажах за период с первого по шестой месяцы. |
Пример 3. Множественная линейная регрессия
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Общая площадь (x1) |
Количество офисов (x2) |
Количество входов (x3) |
Время эксплуатации (x4) |
Оценочная цена (y) |
|---|---|---|---|---|
|
2310 |
2 |
2 |
20 |
142 000 ₽ |
|
2333 |
2 |
2 |
12 |
144 000 ₽ |
|
2356 |
3 |
1,5 |
33 |
151 000 ₽ |
|
2379 |
3 |
2 |
43 |
150 000 ₽ |
|
2402 |
2 |
3 |
53 |
139 000 ₽ |
|
2425 |
4 |
2 |
23 |
169 000 ₽ |
|
2448 |
2 |
1,5 |
99 |
126 000 ₽ |
|
2471 |
2 |
2 |
34 |
142 900 ₽ |
|
2494 |
3 |
3 |
23 |
163 000 ₽ |
|
2517 |
4 |
4 |
55 |
169 000 ₽ |
|
2540 |
2 |
3 |
22 |
149 000 ₽ |
|
-234,2371645 |
||||
|
13,26801148 |
||||
|
0,996747993 |
||||
|
459,7536742 |
||||
|
1732393319 |
||||
|
Формула (формула динамического массива, введенная в A19) |
||||
|
=ЛИНЕЙН(E2:E12; A2:D12; ИСТИНА; ИСТИНА) |
Пример 4. Использование статистики F и r2
В предыдущем примере коэффициент определения (r2)составляет 0,99675 (см. ячейку A17 в результатах для ЛИТН), что указывает на крепкая связь между независимыми переменными и ценой продажи. F-статистику можно использовать для определения случайности этих результатов с таким высоким значением r2.
Предположим, что на самом деле взаимосвязи между переменными не существует, просто статистический анализ вывел сильную взаимозависимость по взятой равномерной выборке 11 зданий. Величина «Альфа» используется для обозначения вероятности ошибочного вывода о существовании сильная взаимозависимости.
Значения F и df в результатах функции LINEST можно использовать для оценки вероятности возникновения более высокого F-значения. F можно сравнивать с критическими значениями в опубликованных F-таблицах или с помощью функции FРАСП в Excel для вычисления вероятности случайного возникновения большего F-значения. Соответствующее F-распределение имеет v1 и v2 степени свободы. Если n — количество точек данных и конст = ИСТИНА или опущен, то v1 = n – df – 1 и v2 = df. (Если конст = ЛОЖЬ, то v1 = n – df и v2 = df.) Функция FIST с синтаксисом FDIST(F;v1;v2) возвращает вероятность возникновения более высокого F-значения, случайного. В этом примере df = 6 (ячейка B18) и F = 459,753674 (ячейка A18).
Предположим, что альфа имеет значение 0,05, v1 = 11 – 6 – 1 = 4, а v2 = 6, критический уровень F составляет 4,53. Поскольку F = 459,753674 значительно больше 4,53, вероятность того, что F-значение этого высокой случайности превышает 4,53, крайне маловероятно. (Если значение «Альфа» = 0,05, гипотеза о том, что между known_y и known_x нет связи, отклоняется при превышении F критического уровня (4,53).) Функцию FDIST в Excel можно использовать для получения вероятности случайного возникновения F-значения. Например, FIST(459,753674, 4, 6) = 1,37E-7, очень небольшая вероятность. Можно сделать вывод о том, что формула регрессии полезна для предсказания оценочного значения офисных зданий в этой области, найдя критический уровень F в таблице или с помощью функции FDIST. Помните, что крайне важно использовать правильные значения 1 и 2, вычисленные в предыдущем абзаце.
Пример 5. Вычисление t-статистики
Другой тест позволяет определить, подходит ли каждый коэффициент наклона для оценки стоимости здания под офис в примере 3. Например, чтобы проверить, имеет ли срок эксплуатации здания статистическую значимость, разделим -234,24 (коэффициент наклона для срока эксплуатации здания) на 13,268 (оценка стандартной ошибки для коэффициента времени эксплуатации из ячейки A15). Ниже приводится наблюдаемое t-значение:
t = m4 ÷ se4 = –234,24 ÷ 13,268 = –17,7
Если абсолютное значение t достаточно велико, можно сделать вывод, что коэффициент наклона можно использовать для оценки стоимости здания под офис в примере 3. В таблице ниже приведены абсолютные значения четырех наблюдаемых t-значений.
Если обратиться к справочнику по математической статистике, то окажется, что t-критическое двустороннее с 6 степенями свободы равно 2,447 при Альфа = 0,05. Критическое значение также можно также найти с помощью функции Microsoft Excel СТЬЮДРАСПОБР. СТЬЮДРАСПОБР(0,05; 6) = 2,447. Поскольку абсолютная величина t, равная 17,7, больше, чем 2,447, срок эксплуатации — это важная переменная для оценки стоимости здания под офис. Аналогичным образом можно протестировать все другие переменные на статистическую значимость. Ниже приводятся наблюдаемые t-значения для каждой из независимых переменных.
|
Переменная |
t-наблюдаемое значение |
|---|---|
|
Общая площадь |
5,1 |
|
Количество офисов |
31,3 |
|
Количество входов |
4,8 |
|
Возраст |
17,7 |
Абсолютная величина всех этих значений больше, чем 2,447. Следовательно, все переменные, использованные в уравнении регрессии, полезны для предсказания оценочной стоимости здания под офис в данном районе.
Регрессионный анализ в Microsoft Excel
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
-
Перемещаемся во вкладку «Файл».
Открывается окно параметров Excel. Переходим в подраздел «Надстройки».
В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Линейная регрессия в программе Excel
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк . В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
- Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».
Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».
С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.
После того, как все настройки установлены, жмем на кнопку «OK».
Разбор результатов анализа
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
Помимо этой статьи, на сайте еще 12680 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Множественная регрессия в EXCEL
history 26 января 2019 г.
-
Группы статей
- Статистический анализ
Рассмотрим использование MS EXCEL для прогнозирования переменной Y на основании нескольких переменных Х, т.е. множественную регрессию.
Перед прочтением этой статьи рекомендуется освежить в памяти простую линейную регрессию – прогнозирование на основе значений только одного фактора.
Disclaimer : Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей Множественного регрессионного анализа. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения Регрессии – плохая идея.
Статья про Множественный регрессионный анализ получилась большая, поэтому ниже для удобства приведены ее разделы:
Прогнозирование единственной переменной Y на основании значений 2-х или более переменных Х называется множественной регрессией .
Множественная линейная регрессионная модель (Multiple Linear Regression Model) имеет вид Y=β 0 +β 1 *X 1 +β 2 *X 2 +…+β k *X k +ε. В этом случае переменная Y зависит от k поясняющих переменных Х, т.е. регрессоров . ε — случайная ошибка . Модель является линейной относительно неизвестных параметров β.
Оценка неизвестных параметров
В этой статье рассмотрим модель с 2-мя регрессорами. Сначала введем необходимые обозначения и понятия множественной регрессии.
Для описания зависимости Y от 2-х переменных линейная модель имеет вид:
Параметры этой модели β i нам неизвестны, но их можно оценить, используя случайную выборку (измеренные значения переменной Y от заданных Х). Оценки параметров модели (β 0 , β 1 , β 2 ) обычно вычисляются методом наименьших квадратов (МНК) , который минимизирует сумму квадратов ошибок прогнозирования (критерий минимизации в англоязычной литературе обозначают как SSE – Sum of Squared Errors).
Ошибка ε имеет случайную природу и имеет свою функцию распределения со средним значением =0 и дисперсией σ 2 .
Оценки b 1 и b 2 называются коэффициентами регрессии , они определяют влияние соответствующей переменной X, когда все остальные независимые переменные остаются неизменными .
Сдвиг (intercept) или постоянный член b 0 , определяет прогнозируемое значение Y, когда все поясняющие переменные Х равны 0 (часто сдвиг не имеет физического смысла в рамках модели и обусловлен лишь математическими вычислениями МНК ).
Вычислив оценки, полученные методом МНК, позволяют прогнозировать значения переменной Y:
Примечание : Для случая 2-х регрессоров, все спрогнозированные значения переменной Y будут лежать в плоскости (в плоскости регрессии ).
В качестве примера рассмотрим технологический процесс изготовления нити:
Инженер, на основе имеющегося опыта, предположил, что прочность нити Y зависит от концентрации исходного раствора (Х 1 ) и температуры реакции (Х 2 ), и соответствует модели линейной регрессии. Для нахождения комбинации переменных Х, при которых Y принимает максимальное значение, необходимо определить коэффициенты регрессии, сделав выборку.
В MS EXCEL коэффициенты множественной регрессии удобнее всего вычислить с помощью функции ЛИНЕЙН() . Это сделано в файле примера на листе Коэффициенты . Чтобы вычислить оценки:
- выделите 3 ячейки в одной строке (т.к. мы рассматриваем случай 2-х регрессоров, то будут вычислены 2 коэффициента регрессии + величина сдвига = 3 значения, для вывода которых понадобится 3 ячейки). Пусть это будет диапазон С8:Е8 ;
- в Строке формул введите = ЛИНЕЙН(D20:D50;B20:C50) . Предполагается, что в столбце В содержатся прогнозируемые значения Y (в нашей модели это Прочность нити), в столбцах С и D содержатся значения контролируемых параметров Х (Х1 – Концентрация в столбце С и Х2 – Температура в столбце D).
- нажмите CTRL+SHIFT+ENTER (т.к. это формула массива ).
В левой ячейке будет рассчитано значение коэффициента регрессии b 2 для переменной Х2, в средней ячейке — значение коэффициента регрессии b 1 для переменной Х1, в правой – сдвиг . Обратите внимание, что порядок вывода коэффициентов регрессии обратный по отношению к расположению столбцов с данными соответствующих переменных Х (вычисленный коэффициент b 2 располагается левее по отношению к b 1 , тогда как значения переменной Х2 располагаются правее значений переменной Х1). Это может привести к путанице, поэтому лучше разместить коэффициенты над соответствующими столбцами с данными, как это сделано в строке 17 файла примера .
Примечание : В принципе без функции ЛИНЕЙН() можно обойтись, записав альтернативные формулы. Для этого в файле примера на листе Коэффициенты в столбцах I : K вычислены отклонения значений переменных Х 1i , Х 2i , Y i от их средних значений 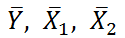
Далее коэффициенты регрессии рассчитываются по следующим формулам (эти формулы справедливы только при прогнозировании по 2-м независимым переменным Х):
При прогнозировании по 3-м и более независимым переменным Х формулы для вычисления коэффициентов регрессии значительно усложняются, поэтому следует использовать матричный подход.
В файле примера на листе Матричная форма выполнены расчеты коэффициентов регрессии с помощью матричного подхода.
Расчет можно произвести как пошагово, так и одной формулой массива :
Коэффициенты регрессии (вектор b ) в этом случае вычисляются по формуле b =(X T X) -1 (X T Y) или в другом виде записи b =(X ’ X) -1 (X ’ Y)
Под Х подразумевается матрица, состоящая из столбцов значений переменной Х с дополнительным столбцом единиц, а под Y – вектор-столбец значений Y.
Диаграмма рассеяния
В случае простой линейной регрессии (один регрессор, т.е. одна переменная Х) для визуализации связи между прогнозируемым значением Y и переменной Х строят диаграмму рассеяния (двумерную).
В случае множественной линейной регрессии двумерную диаграмму рассеяния можно построить только для анализа влияния каждого отдельного регрессора на Y (при этом остальные Х не меняются), т.е. так называемую Матричную диаграмму рассеивания (См. файл примера лист Диагр расс (матричная) ).
К сожалению, такую диаграмму трудно интерпретировать.
Более того, матричная диаграмма может вводить в заблуждение (см. Introduction to linear regression analysis / D . C . Montgomery , E . A . Peck , G . G . Vining , раздел 3.2.5 ), демонстрируя наличие или отсутствие линейной взаимосвязи между отдельным регрессором X i и Y.
Для случая с 2-мя регрессорами можно предложить альтернативный вид матричной диаграммы рассеяния . В стандартной диаграмме рассеяния строятся проекции на координатные плоскости Х1;Х2, Y;X1 и Y;X2. Однако, если взглянуть на точки относительно плоскости регрессии , то картину, на мой взгляд, будет проще интерпретировать.
Сравним две матричные диаграммы рассеяния (см. файл примера на листе «Диагр расс (в плоск регрессии)» , построенные для одних и тех же наблюдений. Первая – стандартная,
вторая представляет собой вид сверху на плоскость регрессии и 2 вида вдоль плоскости.
На второй диаграмме становится очевидно, что разброс точек относительно плоскости регрессии совсем не большой и поэтому, скорее всего, построенная модель является полезной, а выбранные 2 переменные Х позволяют прогнозировать Y (конечно, для подтверждения этой гипотезы нужно провести процедуру F-теста ).
Несколько слов о построении альтернативной матричной диаграммы рассеяния:
- Перед построением необходимо нормировать значения наблюдений (для каждой переменной вычесть среднее и разделить на стандартное отклонение ). В этом случае практически все точки на диаграммах будут находится в диапазоне +/-3 (по аналогии со стандартным нормальным распределением , 99% значений которого лежат в пределах +/-3 сигма). В этом случае, на диаграмме можно фиксировать мин/макс значений осей, чтобы EXCEL автоматически не модифицировал масштаб осей при изменении данных (это не всегда удобно);
- Теперь координаты точек необходимо рассчитать в системе отсчета относительно плоскости регрессии (в которой плоскость Оху’ совпадает с плоскостью регрессии). Для этого необходимо найти матрицу вращения , например, через вращение приводящее к совмещению нормали к плоскости регрессии и вектора оси Z (0;0;1);
- Новые координаты позволяют построить альтернативную матричную диаграмму. Кроме того, для удобства можно вращать систему координат вокруг новой оси Z, чтобы нагляднее представить себе распределение точек относительно плоскости регрессии (для этого использована Полоса прокрутки в ячейках Q31:S31 ).
Вычисление прогнозных значений Y (отдельное наблюдение и среднее значение) и построение доверительных интервалов
После того, как нами были найдены тем или иным способом коэффициенты регрессии можно приступать к вычислению прогнозных значений Y на основе заданных значений переменных Х.
Уравнение прогнозирования или уравнение регрессии в случае 2-х независимых переменных (регрессоров) записывается в виде:
Примечание: В MS EXCEL прогнозное значение Y для заданных Х 1 и Х 2 можно также предсказать с помощью функции ТЕНДЕНЦИЯ() . При этом 2-й аргумент будет ссылкой на столбцы, содержащие все значения переменных Х 1 и Х 2 , а 3-й аргумент функции должен быть ссылкой на диапазон ячеек, содержащий 2 значения Х (Х 1i и Х 2i ) для выбранного наблюдения i (см. файл примера, лист Коэффициенты, столбец G ). Функция ПРЕДСКАЗ() , использованная нами в простой регрессии, не работает в случае множественной регрессии .
Найдя прогнозное значение Y, мы, таким образом, вычислим его точечную оценку. Понятно, что фактическое значение Y, полученное при наблюдении, будет, скорее всего, отличаться от этой оценки. Чтобы ответить на вопрос о том, на сколько хорошо мы можем предсказывать новые значения Y, нам потребуется построить доверительный интервал этой оценки, т.е. диапазон в котором с определенной заданной вероятностью, скажем 95%, мы ожидаем новое значение Y.
Доверительные интервалы построим при фиксированном Х для:
- нового наблюдения Y;
- среднего значения Y (интервал будет уже, чем для отдельного нового наблюдения)
Как и в случае простой линейной регрессии , для построения доверительных интервалов нам потребуется сначала вычислить стандартную ошибку модели (standard error of the model) , которая приблизительно показывает насколько велика ошибка предсказания значений переменной Y на основании значений переменных Х.
Для вычисления стандартной ошибки оценивают дисперсию ошибки ε, т.е. сигма^2 (ее часто обозначают как MS Е либо MSres ) . Затем, вычислив из полученной оценки квадратный корень, получим Стандартную ошибку регрессии (часто обозначают как SEy или sey ).
где SSE – сумма квадратов значений ошибок модели ei=yi — ŷi ( Sum of Squared Errors ). MSE означает Mean Square of Errors (среднее квадратов ошибок, точнее остатков).
Величина n-p – это количество степеней свободы ( df – degrees of freedom ), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y, р – количество оцениваемых параметров модели). В случае простой множественной регрессии с 2-мя регрессорами число степеней свободы равно n-3, т.к. при построении плоскости регрессии было оценено 3 параметра модели b (т.е. на это было «потрачено» 3 степени свободы ).
В MS EXCEL стандартную ошибку SEy можно вычислить формулы (см. файл примера, лист Статистика ):
Стандартная ошибка нового наблюдения Y при заданных значениях Х (вектор Хi) вычисляется по формуле:
x i — вектор-столбец со значениями переменных Х (с дополнительной 1) для заданного наблюдения i.
Соответствующий доверительный интервал вычисляется по формуле:
где α (альфа) – уровень значимости (обычно принимают равным 0,05=5%)
р – количество оцениваемых параметров модели (в нашем случае = 3)
n-p – число степеней свободы
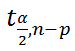
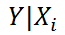
Стандартная ошибка среднего значения Y при заданных значениях Х (вектор Хi) будет меньше, чем стандартная ошибка отдельного наблюдения. Вычисления производятся по формуле:
x i — вектор-столбец со значениями переменных Х (с дополнительной 1) для заданного наблюдения i.
Соответствующий доверительный интервал вычисляется по формуле:
Прогнозное значение Yi (точечная оценка) используется тоже, что и для отдельного наблюдения.
Стандартные ошибки и доверительные интервалы для коэффициентов регрессии
В разделе Оценка неизвестных параметров мы получили точечные оценки коэффициентов регрессии . Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со средним значением и дисперсией . Но, чтобы перейти от точечных оценок к интервальным , необходимо вычислить соответствующие стандартные ошибки (т.е. стандартные отклонения ) коэффициентов регрессии .
Стандартная ошибка коэффициента регрессии b j (обозначается se ( b j ) ) вычисляется на основании стандартной ошибки по следующей формуле:
где C jj является диагональным элементом матрицы (X ’ X) -1 . Для коэффициента сдвига b 0 индекс j=1 (верхний левый элемент), для b 1 индекс j=2, b 2 индекс j=3 (нижний правый элемент).
SEy – стандартная ошибка регрессии (см. выше ).
В MS EXCEL стандартные ошибки коэффициентов регрессии можно вычислить с помощью функции ЛИНЕЙН() :
Примечание : Подробнее о функции ЛИНЕЙН() см. статью Функция MS EXCEL ЛИНЕЙН() .
Применяя матричный подход стандартные ошибки можно вычислить и через обычные формулы (точнее через формулу массива , см. файл примера лист Статистика ):
= КОРЕНЬ(СУММКВРАЗН(E13:E43;F13:F43) /(n-p)) *КОРЕНЬ (ИНДЕКС (МОБР (МУМНОЖ(ТРАНСП(B13:D43);(B13:D43)));j;j))
При построении двухстороннего доверительного интервала для коэффициента регрессии его границы определяются следующим образом:
где t – это t-значение , которое можно вычислить с помощью формулы = СТЬЮДЕНТ.ОБР.2Х(0,05;n-p) для уровня значимости 0,05.
В результате получим, что найденный доверительный интервал с вероятностью 95% (1-0,05) накроет истинное значение коэффициента регрессии b j . Здесь мы считаем, что коэффициент регрессии b j имеет распределение Стьюдента с n-p степенями свободы (n – количество наблюдений, т.е. пар Х и Y).
Проверка гипотез
Когда мы строим модель, мы предполагаем, что между Y и переменными X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.
Единственный вариант, когда Y не зависит X, возможен, когда все коэффициенты регрессии β равны 0.
Чтобы убедиться, что вычисленная нами оценка коэффициентов регрессии не обусловлена лишь случайностью (они не случайно отличны от 0), используют проверку гипотез . В качестве нулевой гипотезы Н 0 принимают, что линейной связи нет, т.е. ВСЕ β=0. В качестве альтернативной гипотезы Н 1 принимают, что ХОТЯ БЫ ОДИН коэффициент β <>0.
Процедура проверки значимости множественной регрессии, приведенная ниже, является обобщением дисперсионного анализа , использованного нами в случае простой линейной регрессии (F-тест) .
Если нулевая гипотеза справедлива, то тестовая F -статистика имеет F-распределение со степенями свободы k и n — k -1 , т.е. F k, n-k-1 :
Проверку значимости регрессии можно также осуществить через вычисление p -значения . В этом случае вычисляют вероятность того, что случайная величина F примет значение F 0 (это и есть p-значение ), затем сравнивают p-значение с заданным уровнем значимости α (альфа) . Если p-значение больше уровня значимости , то нулевую гипотезу нет оснований отклонить, и регрессия незначима.
В MS EXCEL значение F 0 можно вычислить на основании значений выборки по вышеуказанной формуле или с помощью функции ЛИНЕЙН() :
В MS EXCEL для проверки гипотезы через p -значение используйте формулу =F.РАСП.ПХ(F 0 ;k;n-k-1) файл примера лист Статистика , где показано эквивалентность обоих подходов проверки значимости регрессии).
В MS EXCEL критическое значение для заданного уровня значимости F 1-альфа, k, n-k-1 можно вычислить по формуле = F.ОБР(1- альфа;k;n-k-1) или = F.ОБР.ПХ(альфа;k; n-k-1) . Другими словами требуется вычислить верхний альфа- квантиль F -распределения с соответствующими степенями свободы .
Таким образом, при значении статистики F 0 > F 1-альфа, k, n-k-1 мы имеем основание для отклонения нулевой гипотезы.
В программах статистики результаты процедуры F -теста выводят с помощью стандартной таблицы дисперсионного анализа . В файле примера такая таблица приведена на листе Надстройка , которая построена на основе результатов, возвращаемых инструментом Регрессия надстройки Пакета анализа MS EXCEL .
Генерация данных для множественной регрессии с помощью заданного тренда
Иногда, бывает удобно сгенерировать значения наблюдений, имея заданный тренд.
Для решения этой задачи нам потребуется:
- задать значения регрессоров в нужном диапазоне (значения переменных Х);
- задать коэффициенты регрессии ( b );
- задать тренд (вычислить значения Y= b0 +b1 * Х 1 + b2 * Х 2 );
- задать величину разброса Y вокруг тренда (варианты: случайный разброс в заданных границах или заданная фигура, например, круг)
Все вычисления выполнены в файле примера, лист Тренд для случая 2-х регрессоров. Там же построены диаграммы рассеяния .
Коэффициент детерминации
Коэффициент детерминации R 2 показывает насколько полезна построенная нами линейная регрессионная модель .
По определению коэффициент детерминации R 2 равен:
R 2 = Изменчивость объясненная моделью ( SSR ) / Общая изменчивость ( SST ).
Этот показатель можно вычислить с помощью функции ЛИНЕЙН() :
При добавлении в модель новой объясняющей переменной Х, коэффициент детерминации будет всегда расти. Поэтому, рост коэффициента детерминации не может служить основанием для вывода о том, что новая модель (с дополнительным регрессором) лучше прежней.
Более подходящей статистикой, которая лишена указанного недостатка, является нормированный коэффициент детерминации (Adjusted R-squared):
где p – число независимых регрессоров (вычисления см. файл примера лист Статистика ).
Регрессионный анализ в excel пример
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
-
Перемещаемся во вкладку «Файл».
Открывается окно параметров Excel. Переходим в подраздел «Надстройки».
В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Линейная регрессия в программе Excel
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк . В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
-
Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».
Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».
С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.
После того, как все настройки установлены, жмем на кнопку «OK».
Разбор результатов анализа
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
- линейной (у = а + bx);
- параболической (y = a + bx + cx 2 );
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
- Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».
Теперь стали видны и данные регрессионного анализа.
Регрессионный анализ — это статистический метод исследования, позволяющий показать зависимость того или иного параметра от одной либо нескольких независимых переменных. В докомпьютерную эру его применение было достаточно затруднительно, особенно если речь шла о больших объемах данных. Сегодня, узнав как построить регрессию в Excel, можно решать сложные статистические задачи буквально за пару минут. Ниже представлены конкретные примеры из области экономики.
Виды регрессии
Само это понятие было введено в математику Фрэнсисом Гальтоном в 1886 году. Регрессия бывает:
- линейной;
- параболической;
- степенной;
- экспоненциальной;
- гиперболической;
- показательной;
- логарифмической.
Пример 1
Рассмотрим задачу определения зависимости количества уволившихся членов коллектива от средней зарплаты на 6 промышленных предприятиях.
Задача. На шести предприятиях проанализировали среднемесячную заработную плату и количество сотрудников, которые уволились по собственному желанию. В табличной форме имеем:
Для задачи определения зависимости количества уволившихся работников от средней зарплаты на 6 предприятиях модель регрессии имеет вид уравнения Y = а + а1x1 +…+аkxk, где хi — влияющие переменные, ai — коэффициенты регрессии, a k — число факторов.
Для данной задачи Y — это показатель уволившихся сотрудников, а влияющий фактор — зарплата, которую обозначаем X.
Использование возможностей табличного процессора «Эксель»
Анализу регрессии в Excel должно предшествовать применение к имеющимся табличным данным встроенных функций. Однако для этих целей лучше воспользоваться очень полезной надстройкой «Пакет анализа». Для его активации нужно:
- с вкладки «Файл» перейти в раздел «Параметры»;
- в открывшемся окне выбрать строку «Надстройки»;
- щелкнуть по кнопке «Перейти», расположенной внизу, справа от строки «Управление»;
- поставить галочку рядом с названием «Пакет анализа» и подтвердить свои действия, нажав «Ок».
Если все сделано правильно, в правой части вкладки «Данные», расположенном над рабочим листом «Эксель», появится нужная кнопка.
Линейная регрессия в Excel
Теперь, когда под рукой есть все необходимые виртуальные инструменты для осуществления эконометрических расчетов, можем приступить к решению нашей задачи. Для этого:
- щелкаем по кнопке «Анализ данных»;
- в открывшемся окне нажимаем на кнопку «Регрессия»;
- в появившуюся вкладку вводим диапазон значений для Y (количество уволившихся работников) и для X (их зарплаты);
- подтверждаем свои действия нажатием кнопки «Ok».
В результате программа автоматически заполнит новый лист табличного процессора данными анализа регрессии. Обратите внимание! В Excel есть возможность самостоятельно задать место, которое вы предпочитаете для этой цели. Например, это может быть тот же лист, где находятся значения Y и X, или даже новая книга, специально предназначенная для хранения подобных данных.
Анализ результатов регрессии для R-квадрата
В Excel данные полученные в ходе обработки данных рассматриваемого примера имеют вид:
Прежде всего, следует обратить внимание на значение R-квадрата. Он представляет собой коэффициент детерминации. В данном примере R-квадрат = 0,755 (75,5%), т. е. расчетные параметры модели объясняют зависимость между рассматриваемыми параметрами на 75,5 %. Чем выше значение коэффициента детерминации, тем выбранная модель считается более применимой для конкретной задачи. Считается, что она корректно описывает реальную ситуацию при значении R-квадрата выше 0,8. Если R-квадрата 2 (RI) представляет собой числовую характеристику доли общего разброса и показывает, разброс какой части экспериментальных данных, т.е. значений зависимой переменной соответствует уравнению линейной регрессии. В рассматриваемой задаче эта величина равна 84,8%, т. е. статистические данные с высокой степенью точности описываются полученным УР.
F-статистика, называемая также критерием Фишера, используется для оценки значимости линейной зависимости, опровергая или подтверждая гипотезу о ее существовании.
Значение t-статистики (критерий Стьюдента) помогает оценивать значимость коэффициента при неизвестной либо свободного члена линейной зависимости. Если значение t-критерия > tкр, то гипотеза о незначимости свободного члена линейного уравнения отвергается.
В рассматриваемой задаче для свободного члена посредством инструментов «Эксель» было получено, что t=169,20903, а p=2,89Е-12, т. е. имеем нулевую вероятность того, что будет отвергнута верная гипотеза о незначимости свободного члена. Для коэффициента при неизвестной t=5,79405, а p=0,001158. Иными словами вероятность того, что будет отвергнута верная гипотеза о незначимости коэффициента при неизвестной, равна 0,12%.
Таким образом, можно утверждать, что полученное уравнение линейной регрессии адекватно.
Задача о целесообразности покупки пакета акций
Множественная регрессия в Excel выполняется с использованием все того же инструмента «Анализ данных». Рассмотрим конкретную прикладную задачу.
Руководство компания «NNN» должно принять решение о целесообразности покупки 20 % пакета акций АО «MMM». Стоимость пакета (СП) составляет 70 млн американских долларов. Специалистами «NNN» собраны данные об аналогичных сделках. Было принято решение оценивать стоимость пакета акций по таким параметрам, выраженным в миллионах американских долларов, как:
- кредиторская задолженность (VK);
- объем годового оборота (VO);
- дебиторская задолженность (VD);
- стоимость основных фондов (СОФ).
Кроме того, используется параметр задолженность предприятия по зарплате (V3 П) в тысячах американских долларов.
Решение средствами табличного процессора Excel
Прежде всего, необходимо составить таблицу исходных данных. Она имеет следующий вид:
- вызывают окно «Анализ данных»;
- выбирают раздел «Регрессия»;
- в окошко «Входной интервал Y» вводят диапазон значений зависимых переменных из столбца G;
- щелкают по иконке с красной стрелкой справа от окна «Входной интервал X» и выделяют на листе диапазон всех значений из столбцов B,C, D, F.
Отмечают пункт «Новый рабочий лист» и нажимают «Ok».
Получают анализ регрессии для данной задачи.
Изучение результатов и выводы
«Собираем» из округленных данных, представленных выше на листе табличного процессора Excel, уравнение регрессии:
СП = 0,103*СОФ + 0,541*VO – 0,031*VK +0,405*VD +0,691*VZP – 265,844.
В более привычном математическом виде его можно записать, как:
y = 0,103*x1 + 0,541*x2 – 0,031*x3 +0,405*x4 +0,691*x5 – 265,844
Данные для АО «MMM» представлены в таблице:
источники:
http://excel2.ru/articles/mnozhestvennaya-regressiya-v-ms-excel
http://planshet-info.ru/kompjutery/regressionnyj-analiz-v-excel-primer