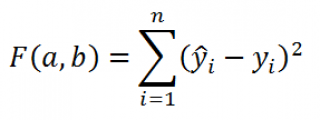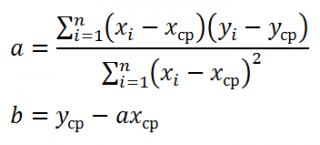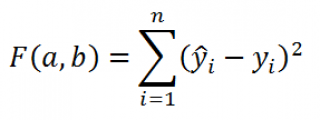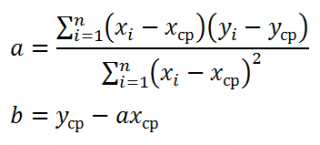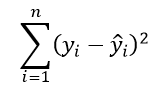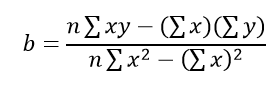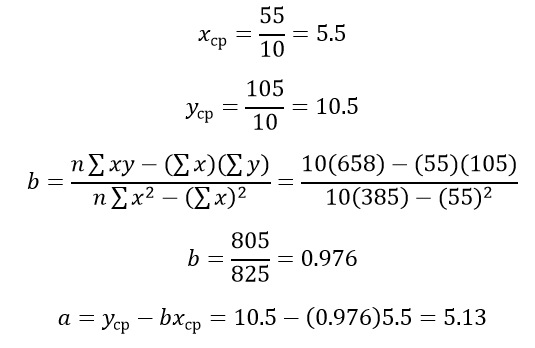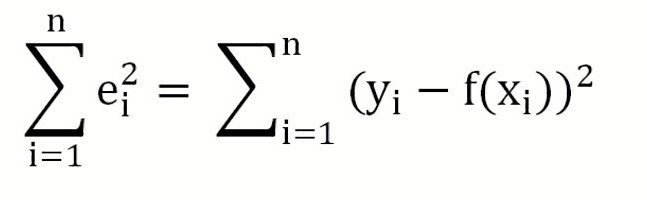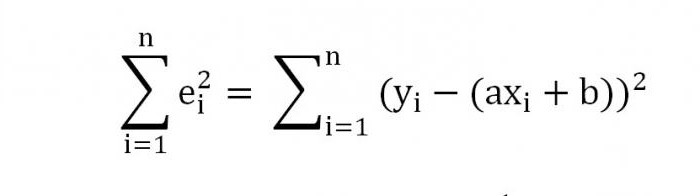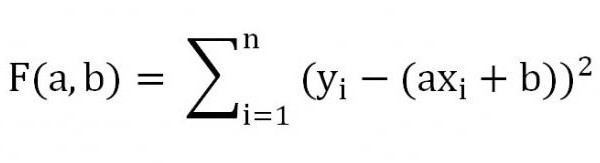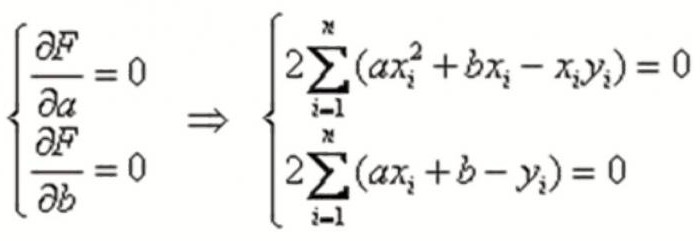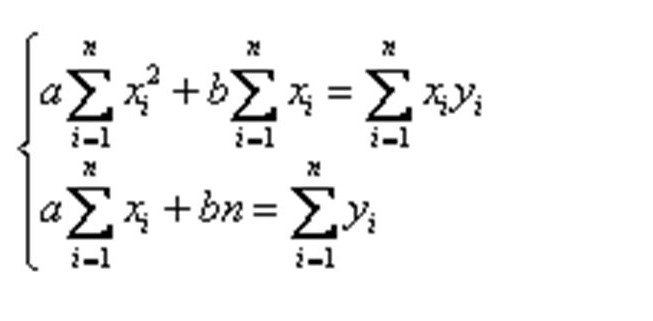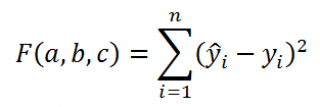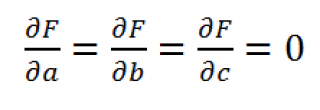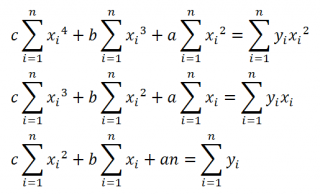Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью линейной функции
y
=
a
x
+
b
.
Метод наименьших квадратов
(англ.
Ordinary
Least
Squares
,
OLS
) является одним из базовых методов регрессионного анализа в части оценки неизвестных параметров
регрессионных моделей
по выборочным данным.
Рассмотрим приближение функциями, зависящими только от одной переменной:
- Линейная: y=ax+b (эта статья)
-
Логарифмическая
: y=a*Ln(x)+b
-
Степенная
: y=a*x
m
-
Экспоненциальная
: y=a*EXP(b*x)+с
-
Квадратичная
: y=ax
2
+bx+c
Примечание
: Случаи приближения полиномом с 3-й до 6-й степени рассмотрены в этой статье. Приближение тригонометрическим полиномом рассмотрено здесь.
Линейная зависимость
Нас интересует связь 2-х переменных
х
и
y
. Имеется предположение, что
y
зависит от
х
по линейному закону
y
=
ax
+
b
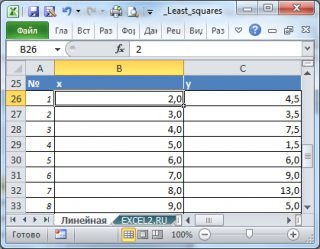
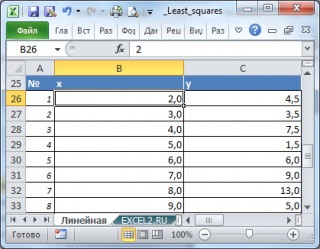
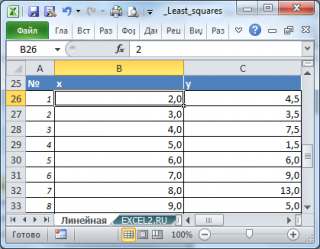
. Чтобы определить параметры этой взаимосвязи исследователь провел наблюдения: для каждого значения х
i
произведено измерение y
i
(см.
файл примера
). Соответственно, пусть имеется 20 пар значений (х
i
; y
i
).
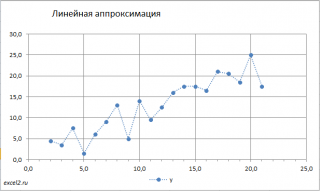
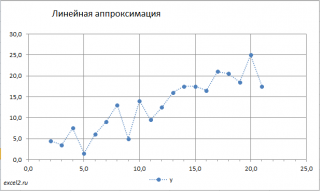
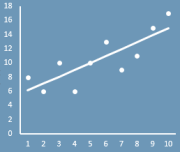
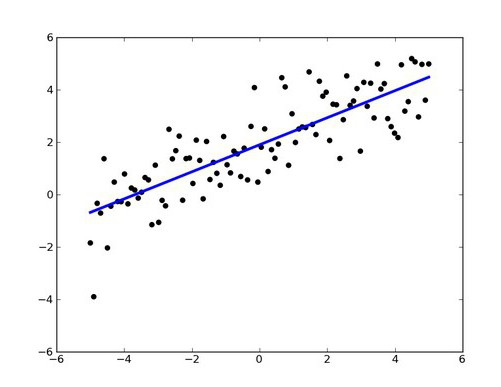
Для наглядности рекомендуется построить диаграмму рассеяния.
Примечание:
Если шаг изменения по
х
постоянен, то для построения
диаграммы рассеяния
можно использовать
тип График
, если нет, то необходимо использовать тип диаграммы
Точечная
.
Из диаграммы очевидно, что связь между переменными близка к линейной. Чтобы понять какая из множества прямых линий наиболее «правильно» описывает зависимость между переменными, необходимо определить критерий, по которому будут сравниваться линии.
В качестве такого критерия используем выражение:
где
ŷ
i
=
a
*
x
i
+
b
;
n – число пар значений (в нашем случае n=20)
Вышеуказанное выражение представляет собой сумму квадратов расстояний между наблюденными значениями y
i
и ŷ
i
и часто обозначается как SSE (
Sum
of
Squared
Errors
(
Residuals
), сумма квадратов ошибок (остатков)
)
.
Метод наименьших квадратов
заключается в подборе такой линии
ŷ
=
ax
+
b
, для которой вышеуказанное выражение принимает минимальное значение.
Примечание:
Любая линия в двухмерном пространстве однозначно определяется значениями 2-х параметров:
a
(наклон) и
b
(сдвиг).
Считается, что чем меньше сумма квадратов расстояний, тем соответствующая линия лучше аппроксимирует имеющиеся данные и может быть в дальнейшем использована для прогнозирования значений y от переменной х. Понятно, что даже если в действительности никакой взаимосвязи между переменными нет или связь нелинейная, то МНК все равно подберет «наилучшую» линию. Таким образом, МНК ничего не говорит о наличии реальной взаимосвязи переменных, метод просто позволяет подобрать такие параметры функции
a
и
b
, для которых вышеуказанное выражение минимально.
Проделав не очень сложные математические операции (подробнее см.
статью про квадратичную зависимость
), можно вычислить параметры
a
и
b
:
Как видно из формулы, параметр
a
представляет собой отношение ковариации и
дисперсии
, поэтому в MS EXCEL для вычисления параметра
а
можно использовать следующие формулы (см.
файл примера лист Линейная
):
=
КОВАР(B26:B45;C26:C45)/ ДИСП.Г(B26:B45)
или
=
КОВАРИАЦИЯ.В(B26:B45;C26:C45)/ДИСП.В(B26:B45)
Также для вычисления параметра
а
можно использовать формулу =
НАКЛОН(C26:C45;B26:B45)
. Для параметра
b
используйте формулу =
ОТРЕЗОК(C26:C45;B26:B45)
.
И наконец, функция
ЛИНЕЙН()
позволяет вычислить сразу оба параметра. Для ввода формулы
ЛИНЕЙН(C26:C45;B26:B45)
необходимо выделить в строке 2 ячейки и нажать
CTRL
+
SHIFT
+
ENTER
(см. статью про
формулы массива, возвращающими несколько значений
). В левой ячейке будет возвращено значение
а
, в правой –
b
.
Примечание
: Чтобы не связываться с вводом
формул массива
потребуется дополнительно использовать функцию
ИНДЕКС()
. Формула =
ИНДЕКС(ЛИНЕЙН(C26:C45;B26:B45);1)
или просто =
ЛИНЕЙН(C26:C45;B26:B45)
вернет параметр, отвечающий за наклон линии, т.е.
а
. Формула =
ИНДЕКС(ЛИНЕЙН(C26:C45;B26:B45);2)
вернет параметр, отвечающий за пересечение линии с осью Y, т.е.
b
.
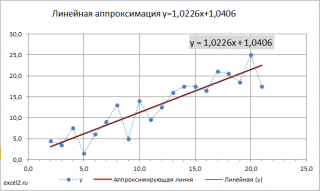
Вычислив параметры, на
диаграмме рассеяния
можно построить соответствующую линию.
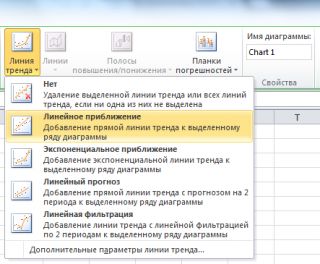
Инструмент диаграммы Линия тренда
Еще одним способом построения прямой линии по методу наименьших квадратов является инструмент диаграммы
Линия тренда
. Для этого выделите диаграмму, в меню выберите
вкладку Макет
, в
группе Анализ
нажмите
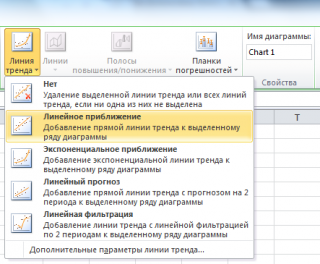
Линия тренда
, затем
Линейное приближение
.
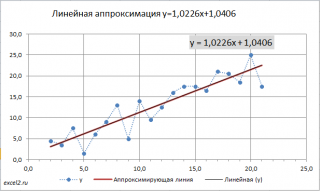
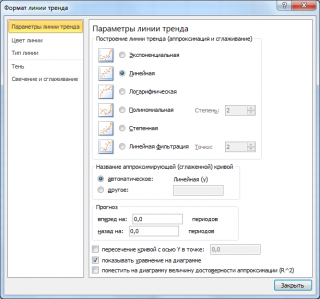
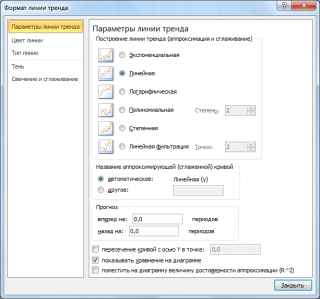
Поставив в диалоговом окне галочку в поле «показывать уравнение на диаграмме» можно убедиться, что найденные выше параметры совпадают со значениями на диаграмме.
Примечание
: Для того, чтобы параметры совпадали необходимо, чтобы тип у диаграммы был
Точечная, а не График
. Дело в том, что при построении диаграммы
График
значения по оси Х не могут быть заданы пользователем (пользователь может указать только подписи, которые не влияют на расположение точек). Вместо значений Х используется последовательность 1; 2; 3; … (для нумерации категорий). Поэтому, если строить
линию тренда
на диаграмме типа
График
, то вместо фактических значений Х будут использованы значения этой последовательности, что приведет к неверному результату (если, конечно, фактические значения Х не совпадают с последовательностью 1; 2; 3; …).
СОВЕТ
: Подробнее о построении диаграмм см. статьи
Основы построения диаграмм
и
Основные типы диаграмм
.
17 авг. 2022 г.
читать 2 мин
Метод наименьших квадратов — это метод, который мы можем использовать для поиска линии регрессии, которая лучше всего соответствует заданному набору данных.
В следующем видео представлено краткое объяснение этого метода:
Чтобы использовать метод наименьших квадратов для подбора линии регрессии в Excel, мы можем использовать функцию =ЛИНЕЙН() .
В следующем пошаговом примере показано, как использовать эту функцию на практике.
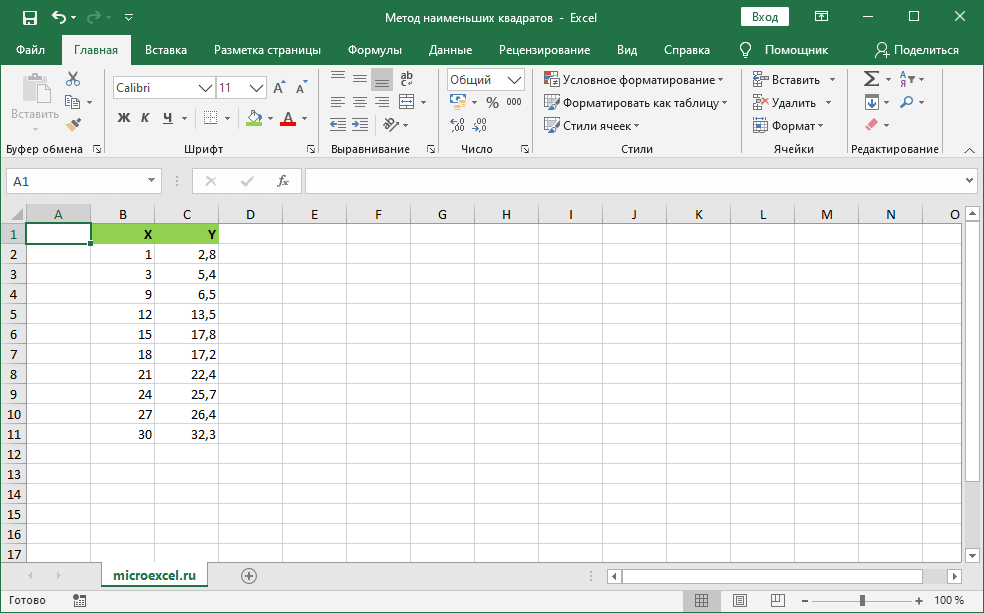
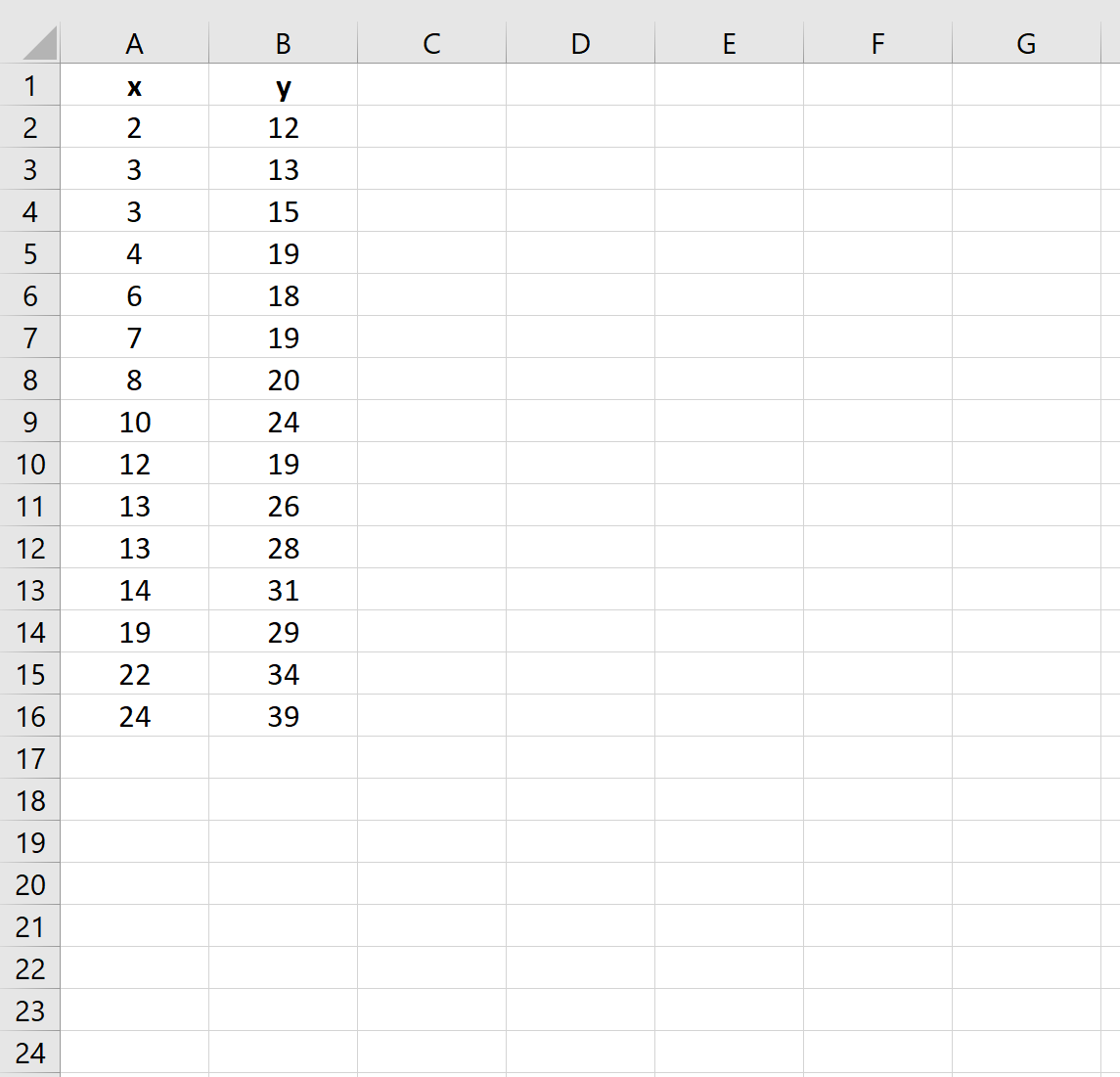
Шаг 1: Создайте набор данных
Во-первых, давайте создадим следующий набор данных в Excel:
Шаг 2: Используйте метод наименьших квадратов для подбора линии регрессии
Мы можем использовать функцию =LINEST(known_ys, known_xs) , чтобы использовать метод наименьших квадратов, чтобы подобрать линию регрессии к этому набору данных:
Как только мы нажмем ENTER , появятся коэффициенты регрессионной модели:
Шаг 3: интерпретируйте результаты
Используя коэффициенты из функции =LINEST() , мы можем написать следующую подобранную линию регрессии:
у = 11,55211 + 1,07949(х)
Мы можем использовать это уравнение для оценки значения y на основе значения x.
Например, если x = 10, то мы оценили бы, что y будет равно 22,347 :
у = 11,55211 + 1,07949(10) = 22,347
Шаг 4: Нанесите результаты на график
Наконец, мы можем использовать следующие шаги для построения набора данных вместе с подобранной линией регрессии:
- Выделите ячейки A2:B16 .
- Щелкните вкладку « Вставка » на верхней ленте. Затем щелкните первый параметр диаграммы под названием « Вставить точечную (X, Y)» или «Пузырьковую диаграмму » в группе «Диаграммы».
- После того, как диаграмма появится, нажмите знак плюс «+» в правом верхнем углу. В раскрывающемся меню установите флажок рядом с линией тренда , чтобы добавить на график подобранную линию регрессии.
Дополнительные ресурсы
Как выполнить множественную линейную регрессию в Excel
Как выполнить квадратичную регрессию в Excel
Как выполнить полиномиальную регрессию в Excel
Подбор кривой в Excel (с примерами)
Содержание
- Использование метода в Экселе
- Включение надстройки «Поиск решения»
- Условия задачи
- Решение
- Вопросы и ответы
Метод наименьших квадратов представляет собой математическую процедуру построения линейного уравнения, которое бы наиболее точно соответствовало набору двух рядов чисел. Целью применения данного способа является минимизация общей квадратичной ошибки. В программе Excel имеются инструменты, с помощью которых можно применять данный метод при вычислениях. Давайте разберемся, как это делается.
Использование метода в Экселе
Метод наименьших квадратов (МНК) является математическим описанием зависимости одной переменной от второй. Его можно использовать при прогнозировании.
Включение надстройки «Поиск решения»
Для того, чтобы использовать МНК в Экселе, нужно включить надстройку «Поиск решения», которая по умолчанию отключена.
- Переходим во вкладку «Файл».
- Кликаем по наименованию раздела «Параметры».
- В открывшемся окне останавливаем выбор на подразделе «Надстройки».
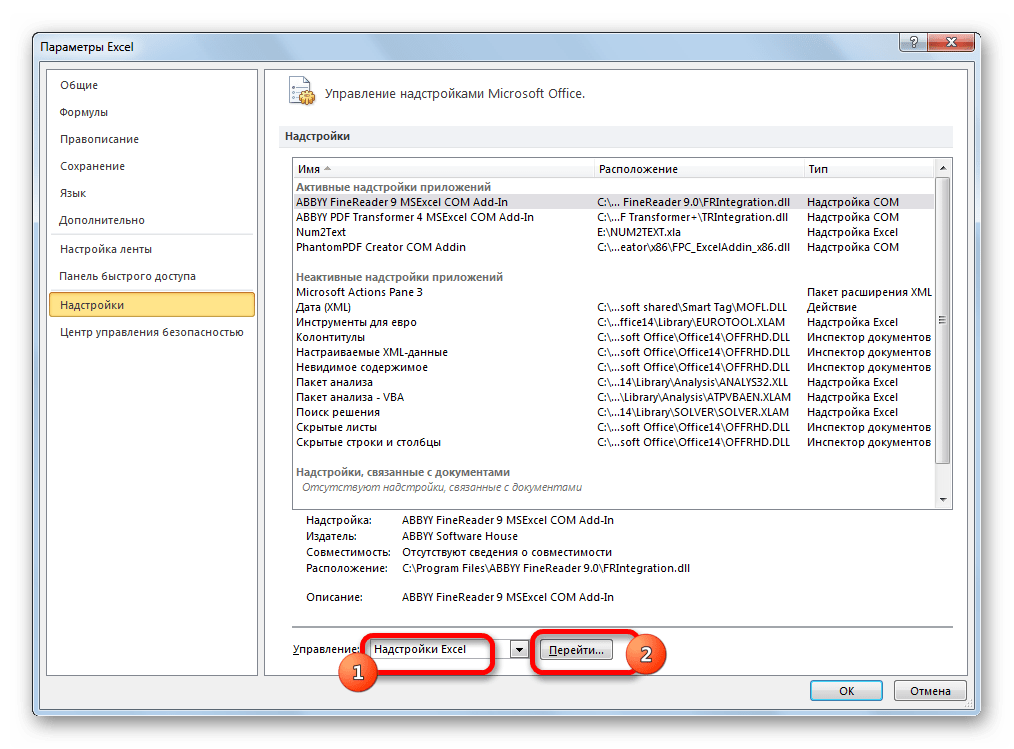
- В блоке «Управление», который расположен в нижней части окна, устанавливаем переключатель в позицию «Надстройки Excel» (если в нём выставлено другое значение) и жмем на кнопку «Перейти…».
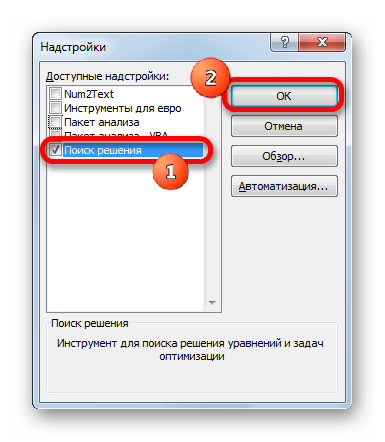
- Открывается небольшое окошко. Ставим в нём галочку около параметра «Поиск решения». Жмем на кнопку «OK».
Теперь функция Поиск решения в Excel активирована, а её инструменты появились на ленте.
Урок: Поиск решения в Экселе
Условия задачи
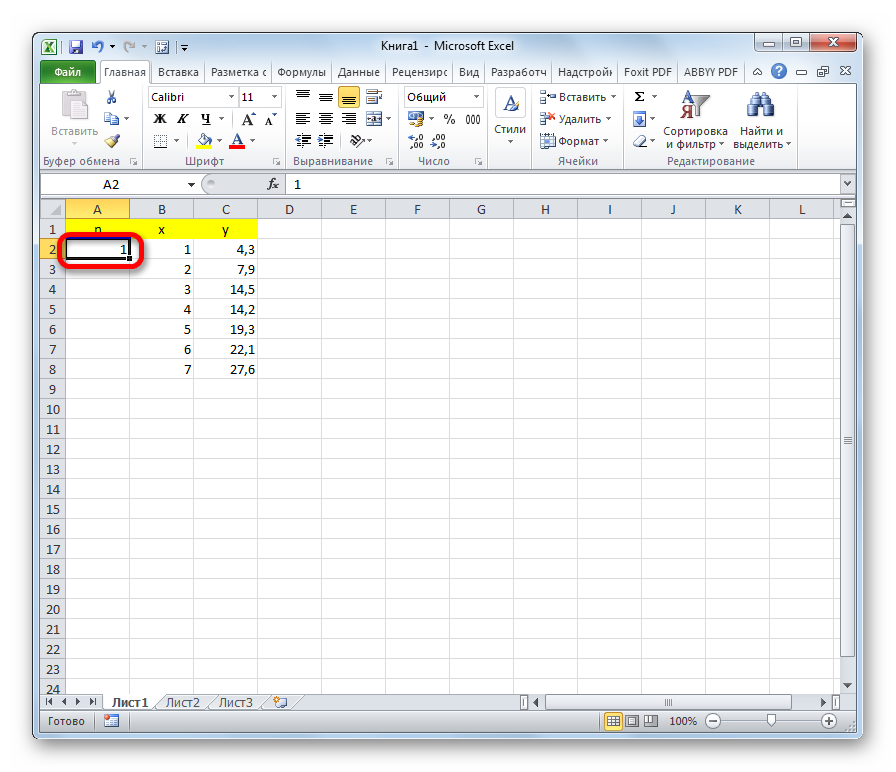
Опишем применение МНК на конкретном примере. Имеем два ряда чисел x и y, последовательность которых представлена на изображении ниже.
Наиболее точно данную зависимость может описать функция:
y=a+nx
При этом, известно что при x=0 y тоже равно 0. Поэтому данное уравнение можно описать зависимостью y=nx.
Нам предстоит найти минимальную сумму квадратов разности.
Решение
Перейдем к описанию непосредственного применения метода.
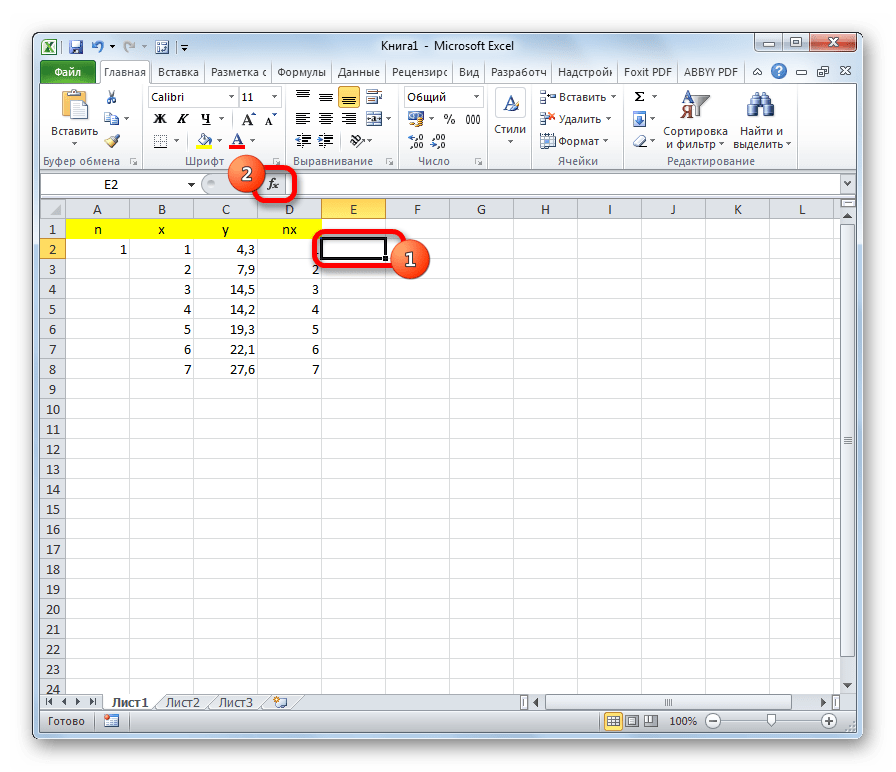
- Слева от первого значения x ставим цифру 1. Это будет приближенная величина первого значения коэффициента n.
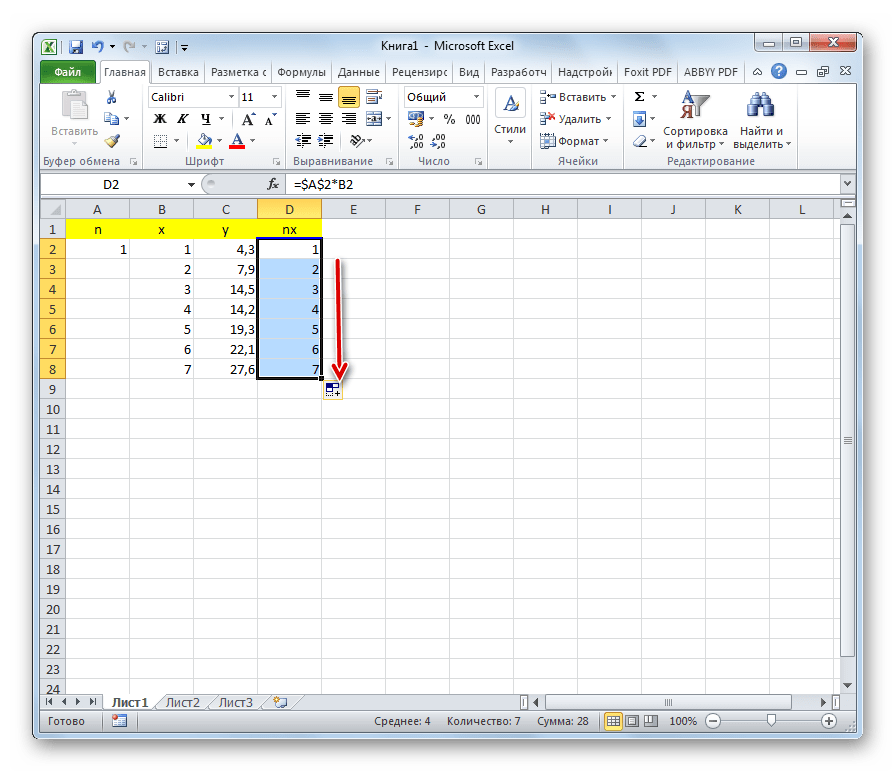
- Справа от столбца y добавляем ещё одну колонку – nx. В первую ячейку данного столбца записываем формулу умножения коэффициента n на ячейку первой переменной x. При этом, ссылку на поле с коэффициентом делаем абсолютной, так как это значение меняться не будет. Кликаем по кнопке Enter.
- Используя маркер заполнения, копируем данную формулу на весь диапазон таблицы в столбце ниже.
- В отдельной ячейке высчитываем сумму разностей квадратов значений y и nx. Для этого кликаем по кнопке «Вставить функцию».
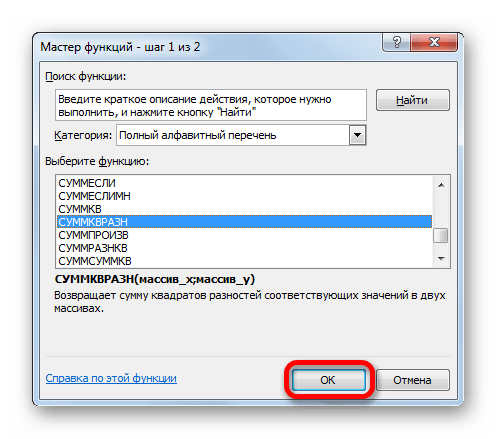
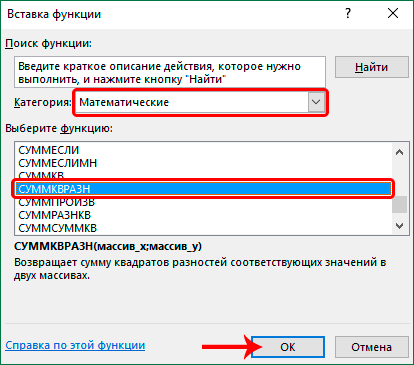
- В открывшемся «Мастере функций» ищем запись «СУММКВРАЗН». Выбираем её и жмем на кнопку «OK».
- Открывается окно аргументов. В поле «Массив_x» вводим диапазон ячеек столбца y. В поле «Массив_y» вводим диапазон ячеек столбца nx. Для того, чтобы ввести значения, просто устанавливаем курсор в поле и выделяем соответствующий диапазон на листе. После ввода жмем на кнопку «OK».
- Переходим во вкладку «Данные». На ленте в блоке инструментов «Анализ» жмем на кнопку «Поиск решения».
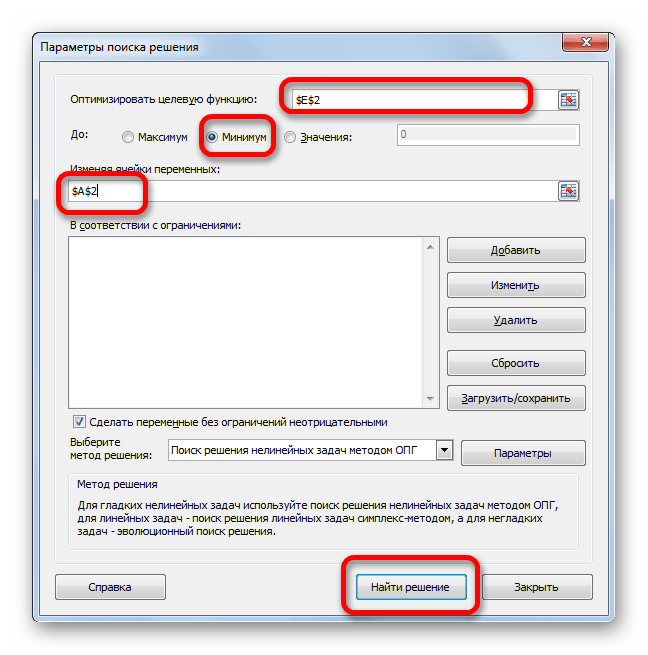
- Открывается окно параметров данного инструмента. В поле «Оптимизировать целевую функцию» указываем адрес ячейки с формулой «СУММКВРАЗН». В параметре «До» обязательно выставляем переключатель в позицию «Минимум». В поле «Изменяя ячейки» указываем адрес со значением коэффициента n. Жмем на кнопку «Найти решение».
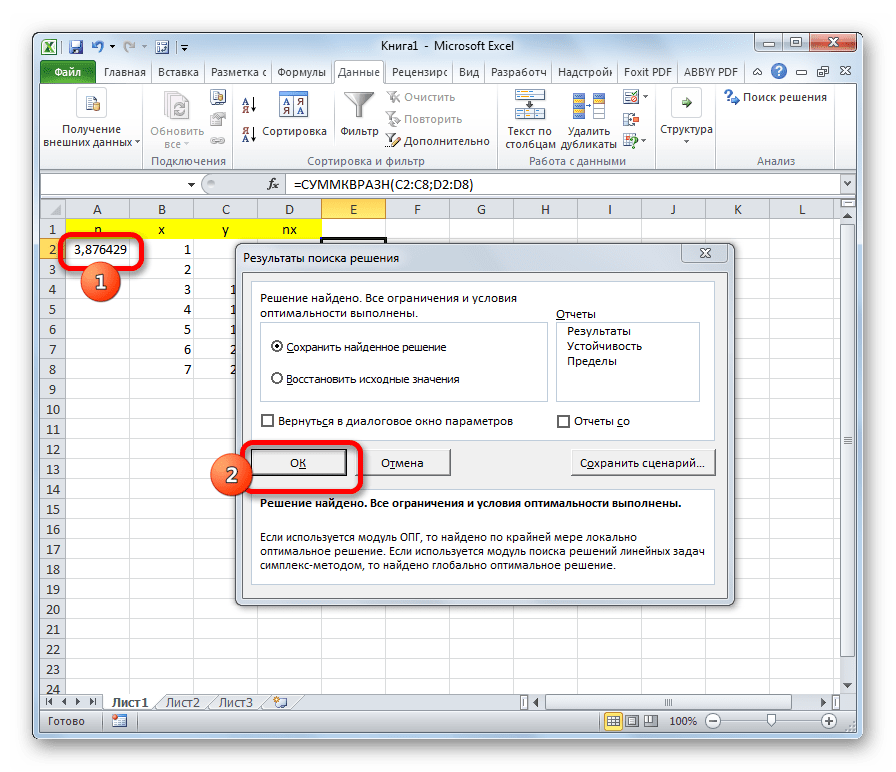
- Решение будет отображаться в ячейке коэффициента n. Именно это значение будет являться наименьшим квадратом функции. Если результат удовлетворяет пользователя, то следует нажать на кнопку «OK» в дополнительном окне.
Как видим, применение метода наименьших квадратов довольно сложная математическая процедура. Мы показали её в действии на простейшем примере, а существуют гораздо более сложные случаи. Впрочем, инструментарий Microsoft Excel призван максимально упростить производимые вычисления.
Еще статьи по данной теме:
Помогла ли Вам статья?
Программа Excel – мощный табличный редактор, позволяющий выполнять огромное количество различных операций и задач. В данной статье мы разберем, как можно применить метод наименьших квадратов (МНК), который используется для решения различных задач с минимизацией суммы квадратов отклонений некоторых функций от искомых переменных.
Содержание
- Подготовительный этап: активируем надстройку “Поиск Решения”
- Этап 1: исходные данные
- Этап 2: решаем задачу с применением МНК
- Заключение
Подготовительный этап: активируем надстройку “Поиск Решения”
Прежде, чем приступить к решению основной задачи, потребуется активировать надстройку “Поиск решения” в программе.
- Идем в меню “Файл”.
- В перечне слева выбираем пункт “Параметры”.
- В правой части подраздела “Надстройки” выбираем для параметра “Управление” вариант “Надстройки Excel” и жмем “Перейти”.
- Появится окно для выбора нужных надстроек. Устанавливаем галочку напротив пункта “Поиск решения” и щелкаем OK.
Этап 1: исходные данные
Давайте разберем применение метода наименьших квадратов, решив конкретный пример. Допустим, у нас есть два ряда числовых значений – X и Y.
Данная зависимость может быть описана уравнением ниже:
Y=A+NX
Также, мы знаем, что если X=0, то и Y=0. А значит, данное уравнение можно записать так:
Y=NX
Приступим к выполнению нашей задачи, которая заключается в нахождении суммы квадратов разности.
Этап 2: решаем задачу с применением МНК
- Столбцу, находящемся слева от X, задаем имя N пишем число “1” (примерное значение первого коэф. N) напротив первого значения ряда X.
- Столбцу с правой стороны от Y задаем название NX. Затем в самой верхней ячейке (напротив первых значений рядов X и Y) пишем формулу произведения коэф. N на соответствующее ему значение из столбца X. При этом адрес ячейки с коэффициентом нужно сделать абсолютным, чтобы он не менялся при копировании формулы. По готовности жмем Enter.
- Наводим указатель мыши на ячейку с полученным результатом. Как только появится черный плюсик (маркер заполнения), зажав левую кнопку мыши тянем его вниз до последней строки таблицы.
- Получаем результаты расчетов в каждой ячейке столбца NX.
- Теперь нужно посчитать сумму разностей квадратов значений Y и NX. Встаем в самую верхнюю ячейку столбца справа от NX (не считая шапки таблицы) и щелкаем по значку “Вставить функцию” (fx).
- В окне вставки функции выбираем категорию “Математические”, находим оператор “СУММКВРАЗН” и щелкаем OK.
- Теперь нужно заполнить аргументы функции:
- в поле “Массив_x” указываем координаты диапазона ячеек столбца Y (без шапки). Адреса ячеек можно указать как вручную, напечатав их с клавиатуры, так и путем выделения с помощью зажатой левой кнопки мыши в самой таблице.
- в поле “Массив_y” указываем диапазон ячеек столбца NX.
- жмем Enter, когда все готово.
- Переключаемся во вкладку “Данные”. В группе “Анализ” щелкаем по функции “Поиск решения”.
- Нам предстоит заполнить параметры поиска решения:
- в поле “Оптимизировать целевую функцию” следует указать ссылку на ячейку с функцией “СУММКВРАЗН”. Сделать это можно вручную или выбрав элемент в таблице.
- для опции “До” выбираем вариант – “Минимум”.
- в поле “Изменяя ячейки переменных” нужно указать координаты ячейки, в которой находится соответствующее значение коэф. N.
- по готовности нажимаем “Найти решение”.
- После выполнения функции появится окно с результатами поиска решения и произойдет замена значения в столбце N. Найденная величина является наименьшим квадратом функции. Нажимаем OK, если полученный результат удовлетворителен.
Заключение
Итак, мы только что разобрали на практическом примере, каким образом можно применить метод наименьших квадратов в Эксель. На практике могут встречаться более сложные задачи, однако, в целом логика действий схожа с той, что мы описали.
history 11 ноября 2018 г.
-
Группы статей
- Статистический анализ
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью линейной функции y = a x + b .
Метод наименьших квадратов (англ. Ordinary Least Squares , OLS ) является одним из базовых методов регрессионного анализа в части оценки неизвестных параметров регрессионных моделей по выборочным данным.
Рассмотрим приближение функциями, зависящими только от одной переменной:
- Линейная: y=ax+b (эта статья)
- Логарифмическая : y=a*Ln(x)+b
- Степенная : y=a*x m
- Экспоненциальная : y=a*EXP(b*x)+с
- Квадратичная : y=ax 2 +bx+c
Примечание : Случаи приближения полиномом с 3-й до 6-й степени рассмотрены в этой статье. Приближение тригонометрическим полиномом рассмотрено здесь.
Линейная зависимость
Нас интересует связь 2-х переменных х и y . Имеется предположение, что y зависит от х по линейному закону y = ax + b . Чтобы определить параметры этой взаимосвязи исследователь провел наблюдения: для каждого значения х i произведено измерение y i (см. файл примера ). Соответственно, пусть имеется 20 пар значений (х i ; y i ).
Для наглядности рекомендуется построить диаграмму рассеяния.
Примечание: Если шаг изменения по х постоянен, то для построения диаграммы рассеяния можно использовать тип График , если нет, то необходимо использовать тип диаграммы Точечная .
Из диаграммы очевидно, что связь между переменными близка к линейной. Чтобы понять какая из множества прямых линий наиболее «правильно» описывает зависимость между переменными, необходимо определить критерий, по которому будут сравниваться линии.
В качестве такого критерия используем выражение:
где ŷ i = a * x i + b ; n – число пар значений (в нашем случае n=20)
Вышеуказанное выражение представляет собой сумму квадратов расстояний между наблюденными значениями y i и ŷ i и часто обозначается как SSE ( Sum of Squared Errors ( Residuals ), сумма квадратов ошибок (остатков) ) .
Метод наименьших квадратов заключается в подборе такой линии ŷ = ax + b , для которой вышеуказанное выражение принимает минимальное значение.
Примечание: Любая линия в двухмерном пространстве однозначно определяется значениями 2-х параметров: a (наклон) и b (сдвиг).
Считается, что чем меньше сумма квадратов расстояний, тем соответствующая линия лучше аппроксимирует имеющиеся данные и может быть в дальнейшем использована для прогнозирования значений y от переменной х. Понятно, что даже если в действительности никакой взаимосвязи между переменными нет или связь нелинейная, то МНК все равно подберет «наилучшую» линию. Таким образом, МНК ничего не говорит о наличии реальной взаимосвязи переменных, метод просто позволяет подобрать такие параметры функции a и b , для которых вышеуказанное выражение минимально.
Проделав не очень сложные математические операции (подробнее см. статью про квадратичную зависимость ), можно вычислить параметры a и b :
Как видно из формулы, параметр a представляет собой отношение ковариации и дисперсии , поэтому в MS EXCEL для вычисления параметра а можно использовать следующие формулы (см. файл примера лист Линейная ):
= КОВАР(B26:B45;C26:C45)/ ДИСП.Г(B26:B45) или
Также для вычисления параметра а можно использовать формулу = НАКЛОН(C26:C45;B26:B45) . Для параметра b используйте формулу = ОТРЕЗОК(C26:C45;B26:B45) .
И наконец, функция ЛИНЕЙН() позволяет вычислить сразу оба параметра. Для ввода формулы ЛИНЕЙН(C26:C45;B26:B45) необходимо выделить в строке 2 ячейки и нажать CTRL + SHIFT + ENTER (см. статью про формулы массива, возвращающими несколько значений ). В левой ячейке будет возвращено значение а , в правой – b .
Примечание : Чтобы не связываться с вводом формул массива потребуется дополнительно использовать функцию ИНДЕКС() . Формула = ИНДЕКС(ЛИНЕЙН(C26:C45;B26:B45);1) или просто = ЛИНЕЙН(C26:C45;B26:B45) вернет параметр, отвечающий за наклон линии, т.е. а . Формула = ИНДЕКС(ЛИНЕЙН(C26:C45;B26:B45);2) вернет параметр, отвечающий за пересечение линии с осью Y, т.е. b .
Вычислив параметры, на диаграмме рассеяния можно построить соответствующую линию.
Еще одним способом построения прямой линии по методу наименьших квадратов является инструмент диаграммы Линия тренда . Для этого выделите диаграмму, в меню выберите вкладку Макет , в группе Анализ нажмите Линия тренда , затем Линейное приближение .
Поставив в диалоговом окне галочку в поле «показывать уравнение на диаграмме» можно убедиться, что найденные выше параметры совпадают со значениями на диаграмме.
Примечание : Для того, чтобы параметры совпадали необходимо, чтобы тип у диаграммы был Точечная, а не График . Дело в том, что при построении диаграммы График значения по оси Х не могут быть заданы пользователем (пользователь может указать только подписи, которые не влияют на расположение точек). Вместо значений Х используется последовательность 1; 2; 3; … (для нумерации категорий). Поэтому, если строить линию тренда на диаграмме типа График , то вместо фактических значений Х будут использованы значения этой последовательности, что приведет к неверному результату (если, конечно, фактические значения Х не совпадают с последовательностью 1; 2; 3; …).
СОВЕТ : Подробнее о построении диаграмм см. статьи Основы построения диаграмм и Основные типы диаграмм .
Exceltip
Блог о программе Microsoft Excel: приемы, хитрости, секреты, трюки
Метод наименьших квадратов в Excel — использование функции ТЕНДЕНЦИЯ
Метод наименьших квадратов — это математическая процедура составления линейного уравнения, максимально соответствующего набору упорядоченных пар, путем нахождения значений для a и b, коэффициентов в уравнении прямой. Цель метода наименьших квадратов состоит в минимизации общей квадратичной ошибки между значениями y и ŷ. Если для каждой точки мы определяем ошибку ŷ, метод наименьших квадратов минимизирует:
где n = число упорядоченных пар вокруг линии. максимально соответствующей данным.
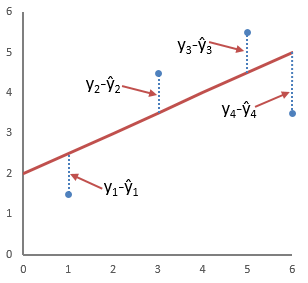
Это понятие проиллюстрировано на рисунке
Судя по рисунку, линия, максимально соответствующая данным, линия регрессии, минимизирует общую квадратичную ошибку четырех точек на графике. Я покажу вам, как определять это уравнение регрессии с помощью метода наименьших квадратов на следующем примере.
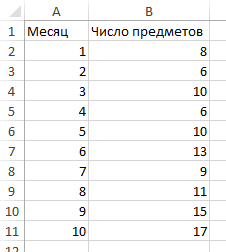
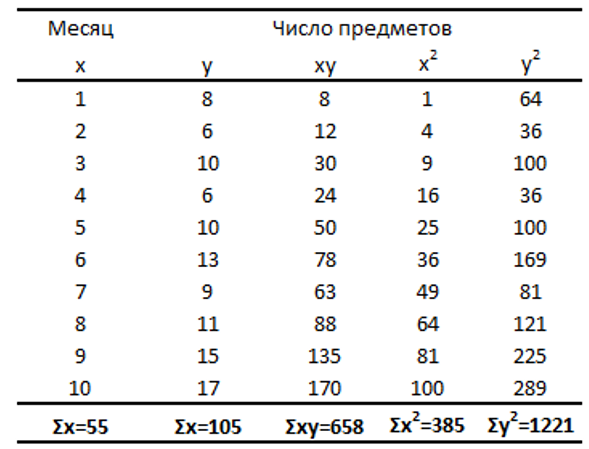
Представьте себе молодую пару, которые, с недавних пор, живут вместе и совместно делят столик для косметических принадлежностей в ванной. Молодой человек начал замечать, что половина его столика неумолимо сокращается, сдавая свои позиции муссам для волос и соевым комплексам. За последние несколько месяцев парень внимательно следил за тем, с какой скоростью увеличивается число предметов на ее части стола. В таблице ниже представлено число предметов девушки на столике в ванной, накопившихся за последние несколько месяцев.
Поскольку своей целью мы определили задачу узнать, увеличивается ли со временем число предметов, «Месяц» будет независимой переменной, а «Число предметов» — зависимой.
С помощью метода наименьших квадратов определяем уравнение, максимально соответствующее данным, путем вычисления значений a, отрезка на оси y, и b, наклона линии:
где xср — среднее значение x, независимой переменной, yср — среднее значение y, независимой переменной.
В таблице ниже суммированы необходимые для этих уравнений вычисления.
Кривая эффекта для нашего примера с ванной будет определяться следующим уравнением:
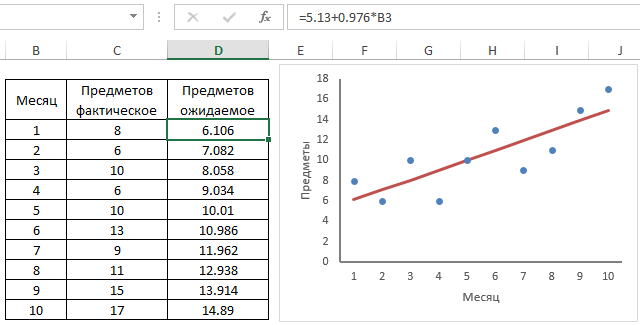
Поскольку наше уравнение имеет положительный наклон — 0.976, парень имеет доказательство того, что число предметов на столике со временем увеличивается со средней скоростью 1 предмет в месяц. На графике представлена кривая эффекта с упорядоченными парами.
Ожидание в отношении числа предметов в течение следующего полугода (месяца 16) будет вычисляться так:
ŷ = 5.13 + 0.976x = 5.13 + 0.976(16)
20.7 = 21 предмет
Так что, пора нашему герою предпринимать какие-нибудь действия.
Функция ТЕНДЕНЦИЯ в Excel
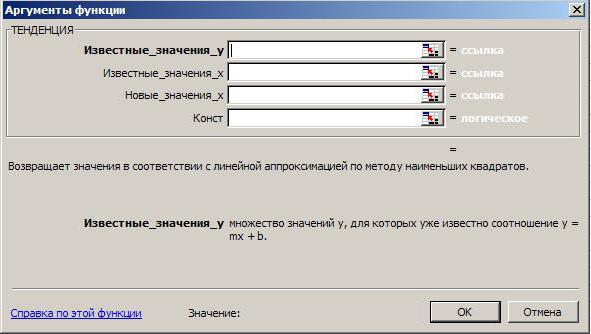
Как вы уже, наверное, догадались в Excel имеется функция для расчета значения по методу наименьших квадратов. Это функция называется ТЕНДЕНЦИЯ. Синтаксис у нее следующий:
ТЕНДЕНЦИЯ (известные значения Y; известные значения X; новые значения X; конст)
известные значения Y – массив зависимых переменных, в нашем случае, количество предметов на столике
известные значения X – массив независимых переменных, в нашем случае это месяц
новые значения X – новые значения X (месяца) для которого функция ТЕНДЕНЦИЯ возвращает ожидаемое значение зависимых переменных (количество предметов)
конст — необязательный. Логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.
Например, на рисунке показана функция ТЕНДЕНЦИЯ, используемая для определения ожидаемого количества предметов на столике в ванной для 16-го месяца.
Применение метода наименьших квадратов в Excel
Метод наименьших квадратов представляет собой математическую процедуру построения линейного уравнения, которое бы наиболее точно соответствовало набору двух рядов чисел. Целью применения данного способа является минимизация общей квадратичной ошибки. В программе Excel имеются инструменты, с помощью которых можно применять данный метод при вычислениях. Давайте разберемся, как это делается.
Использование метода в Экселе
Метод наименьших квадратов (МНК) является математическим описанием зависимости одной переменной от второй. Его можно использовать при прогнозировании.
Включение надстройки «Поиск решения»
Для того, чтобы использовать МНК в Экселе, нужно включить надстройку «Поиск решения», которая по умолчанию отключена.
- Переходим во вкладку «Файл».
Кликаем по наименованию раздела «Параметры».
В открывшемся окне останавливаем выбор на подразделе «Надстройки».
Теперь функция Поиск решения в Excel активирована, а её инструменты появились на ленте.
Условия задачи
Опишем применение МНК на конкретном примере. Имеем два ряда чисел x и y, последовательность которых представлена на изображении ниже.
Наиболее точно данную зависимость может описать функция:
При этом, известно что при x=0 y тоже равно 0. Поэтому данное уравнение можно описать зависимостью y=nx.
Нам предстоит найти минимальную сумму квадратов разности.
Решение
Перейдем к описанию непосредственного применения метода.
-
Слева от первого значения x ставим цифру 1. Это будет приближенная величина первого значения коэффициента n.
Справа от столбца y добавляем ещё одну колонку – nx. В первую ячейку данного столбца записываем формулу умножения коэффициента n на ячейку первой переменной x. При этом, ссылку на поле с коэффициентом делаем абсолютной, так как это значение меняться не будет. Кликаем по кнопке Enter.
Используя маркер заполнения, копируем данную формулу на весь диапазон таблицы в столбце ниже.
В отдельной ячейке высчитываем сумму разностей квадратов значений y и nx. Для этого кликаем по кнопке «Вставить функцию».
В открывшемся «Мастере функций» ищем запись «СУММКВРАЗН». Выбираем её и жмем на кнопку «OK».
Открывается окно аргументов. В поле «Массив_x» вводим диапазон ячеек столбца y. В поле «Массив_y» вводим диапазон ячеек столбца nx. Для того, чтобы ввести значения, просто устанавливаем курсор в поле и выделяем соответствующий диапазон на листе. После ввода жмем на кнопку «OK».
Переходим во вкладку «Данные». На ленте в блоке инструментов «Анализ» жмем на кнопку «Поиск решения».
Открывается окно параметров данного инструмента. В поле «Оптимизировать целевую функцию» указываем адрес ячейки с формулой «СУММКВРАЗН». В параметре «До» обязательно выставляем переключатель в позицию «Минимум». В поле «Изменяя ячейки» указываем адрес со значением коэффициента n. Жмем на кнопку «Найти решение».
Как видим, применение метода наименьших квадратов довольно сложная математическая процедура. Мы показали её в действии на простейшем примере, а существуют гораздо более сложные случаи. Впрочем, инструментарий Microsoft Excel призван максимально упростить производимые вычисления.

Добавьте сайт Lumpics.ru в закладки и мы еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.

Метод наименьших квадратов в Excel
Табличный процессор Эксель способен реализовывать большое число математических операций. Из статьи вы узнаете, как используется метод наименьших квадратов, который применяется для осуществления решения разнообразных задач.
Первоначальные настройки: включение параметра «Поиск решения»
Изначально необходимо включить «Поиск решения», так как по умолчанию он находится в выключенном состоянии. Пошаговое руководство выглядит следующим образом:
- Переходим в раздел «Файл», который находится в левом верхнем углу интерфейса табличного процессора.
- На экране отобразилось новое окошко. Здесь, в левой колонке, необходимо кликнуть на элемент «Параметры».
- В появившемся окне выбираем раздел «Надстройки». В правой части окошка находим надпись «Управление:» и раскрываем список. В списке выбираем пункт «Надстройки Excel». Щёлкаем кнопку «ОК».
- Появилось еще одно окошко с названием «Надстройки». Около элемента «Поиск решения» ставим галочку. После проведения всех манипуляций кликаем «ОК».
- Готово! Параметр включился, и теперь мы можем приступить к разбору метода наименьших квадратов.
Что такое метод наименьших квадратов
Для начала вспомним, что метод наименьших квадратов — математический метод, используемый для решения задач, основанный на минимизации суммы квадратов отклонений некоторых функций от изначальных значений.
Он может применяться для «решения» переопределенных систем уравнений (когда число уравнений больше числа неизвестных), для поиска решения в случае стандартных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функции.
Шаг первый: исходные данные решаемой задачи
На конкретном примере начнем разбор метода наименьших квадратов. К примеру, у нас есть 2 колонки – X и Y:
5
Эта зависимость описывается уравнением: Y=A+NX.
Мы прекрасно знаем, что если Х равен нулю, то и Y равен нулю. Следовательно, это уравнение можно привести к следующему виду: Y=NX. Начнём реализацию этой задачи. Нам нужно найти сумму квадратов разности.
Шаг второй: решение задачки с использованием МНК
Пошаговое руководство выглядит следующим образом:
- Столбику, который располагается левее показателя Х, даем название N и прописываем единицу рядом с 1-м показателем колонки Х. Единица – это примерное значение 1-го коэффициента N.
- Столбику, который располагается правее показателя Y, даем наименование NX.
- В ячейку D1, находящуюся около первых показателей X и Y, прописываем специальную формулу произведения коэффициента N на показатель из столбика Х. Сама формула выглядит следующим образом: =$А$2*В2. Стоит заметить, что адрес ячейки с коэффициентом необходимо привести к абсолютному типу. Абсолютный тип в табличном процессоре позволяет зафиксировать строчку или столбик (или все вместе одновременно). Иными словами, при копировании значений в другие ячейки абсолютные ссылки не будут меняться. После проведения всех манипуляций жмем клавишу «Enter».
- Перемещаем курсор мышки на сектор с выведенным результатом. Наведя указатель в правый верхний уголок, он превратится в маленький плюсик темного цвета, который называется маркером заполнения. Зажимаем ЛКМ и перетягиваем маркер в самый низ до крайней строчки табличных данных.
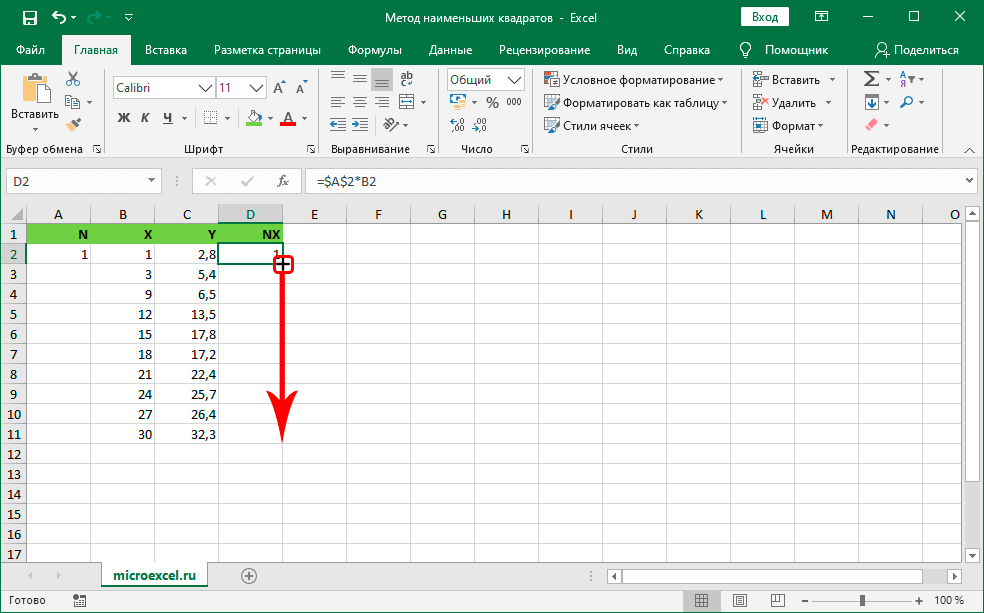
- После проведения этих манипуляций мы получили результаты вычислений во всех секторах колонки NX.
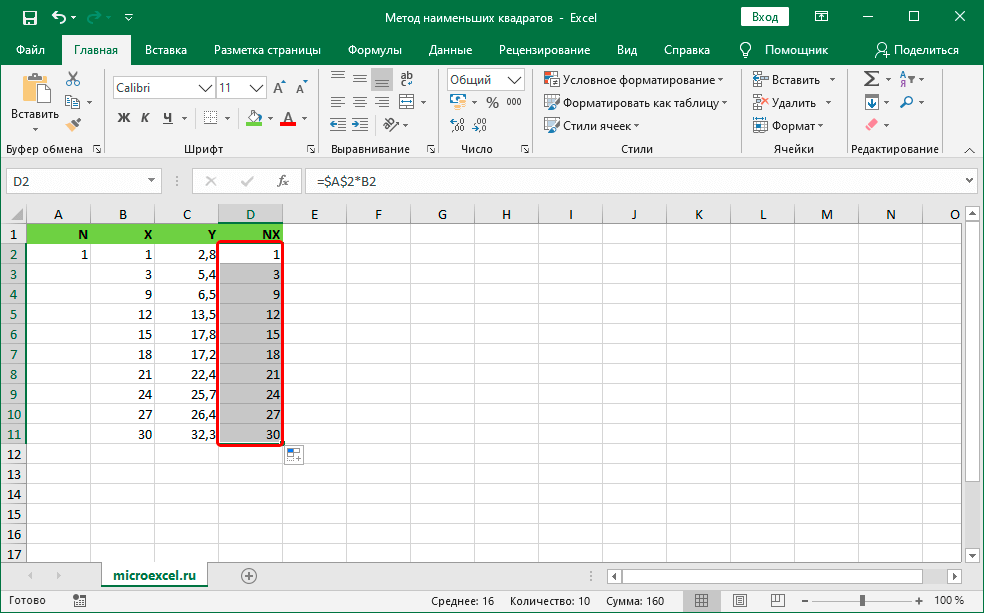
- Далее переходим к подсчету суммы разностей квадратов показателей Y и NX. Перемещаемся в ячейку E1, располагающуюся правее от показателя NX, нажимаем на элемент «Вставить функцию», который находится рядом со строкой для ввода формул, и имеет внешний вид «fx».
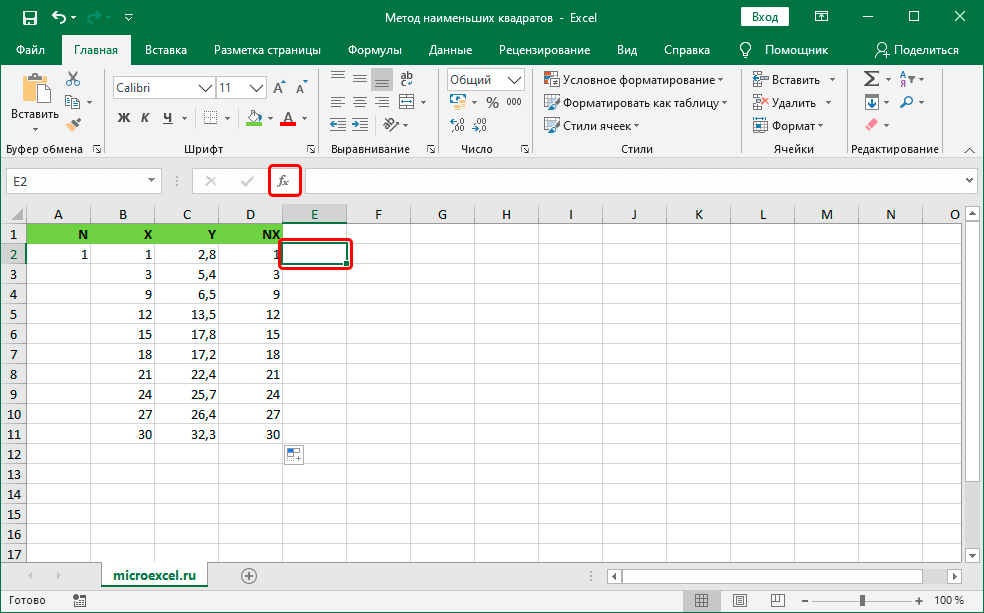
- Первым делом, находим надпись «Категории:» и раскрываем список, находящийся рядом. В обширном списке выбираем элемент «Математические». В блоке «Выберите функцию:» отыскиваем функцию «СУММКВРАЗН» и выбираем ее. После проведения всех манипуляций жмем на кнопку «ОК».
- Открылось небольшое окошко «Аргументы функции». Для дальнейшей работы необходимо заполнить все строки формы. В строчку «Массив_х» вводим адрес диапазона ячеек столбика Y. Координаты можно вписать самостоятельно ручным вводом, используя клавиатуру, или же путем их выбора в самих табличных данных.
- В строчку «Массив_у» вводим адрес диапазона ячеек столбика NX. После проведения всех манипуляций щёлкаем клавишу «Enter».
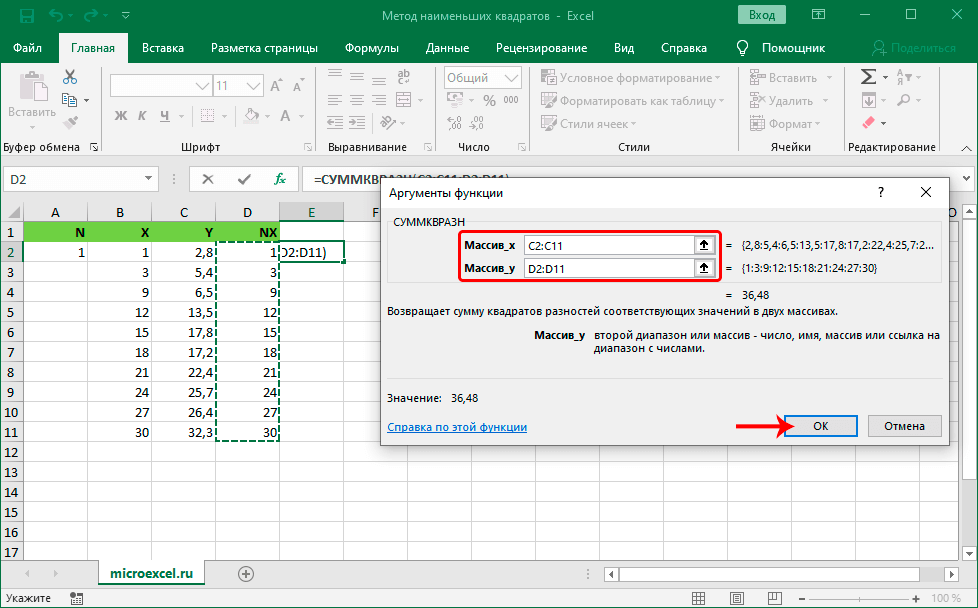
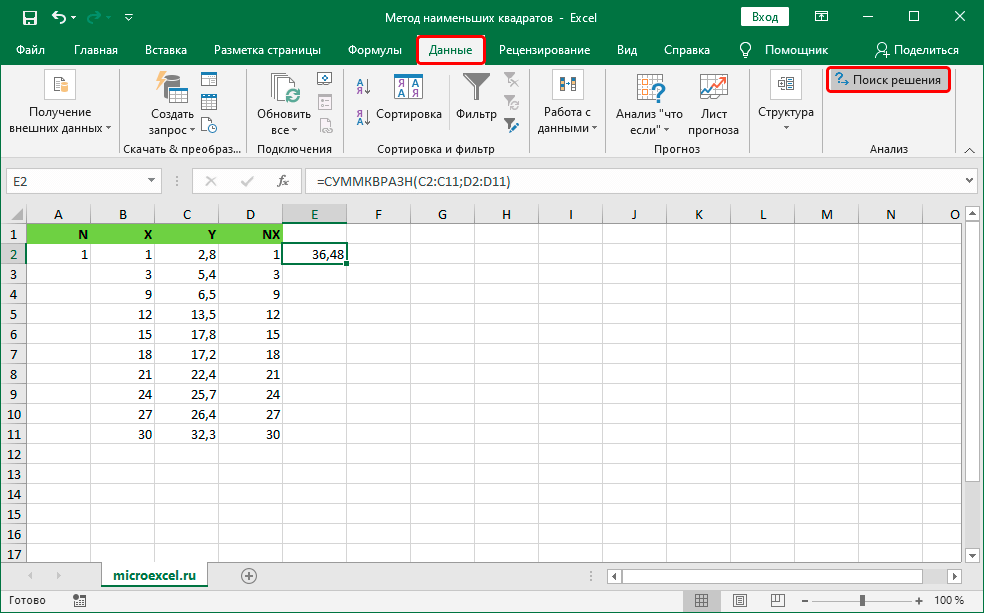
- Перемещаемся в раздел «Данные», который находится в верхней части интерфейса табличного процессора. Находим блок команд под названием «Анализ» и выбираем элемент «Поиск решения».
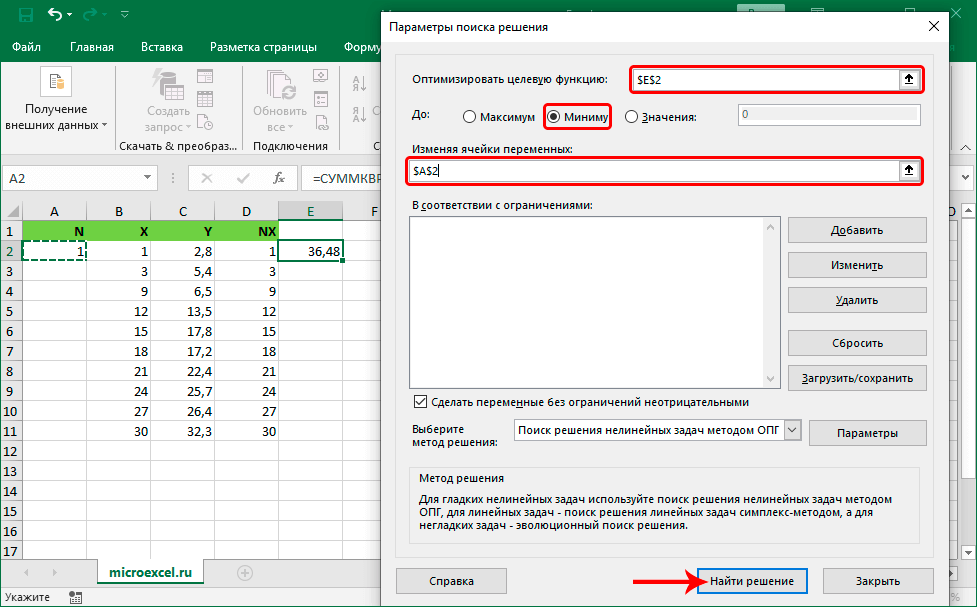
- На экране отобразилось окошко с огромным количеством настроек, которые необходимо заполнить. В строчку «Оптимизировать целевую функцию» вводим ссылку на ячейку с оператором «СУММКВРАЗН». Реализовать это действие можно самостоятельно ручным вводом, используя клавиатуру, или же выбрав сектор в самой табличке. Ставим отметку около надписи «Минимум», которая располагается в блоке «До:». В строчку «Изменяя ячейки переменных» вбиваем адрес сектора, в котором располагается показатель коэффициента N – $A$2. После проведения всех манипуляций щелкаем на «Найти решение».
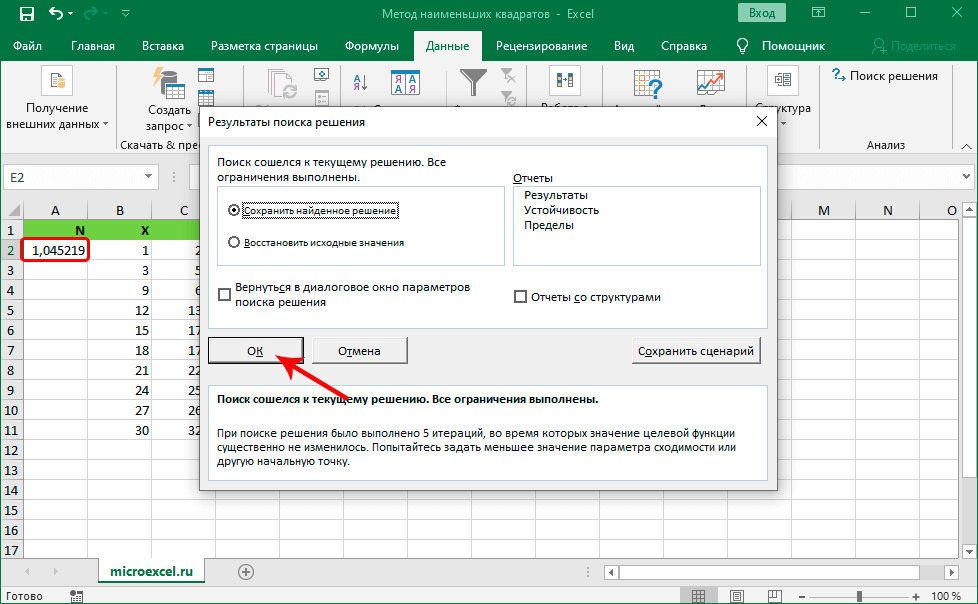
- После того, как «Поиск решения» будет выполнен, на экране компьютера отобразится окошко с выведенными результатами поиска решения, а затем реализуется замена числовых значений в столбике N. Отображенный результат – это наименьший квадрат функции. Если выведенный результат удовлетворяет тому, что нужно было найти, то нажимаем «ОК».
Заключение
Таким образом, мы на конкретном примере рассмотрели способ использования метода наименьших квадратов в табличном процессоре Microsoft Excel и ознакомились со стандартным алгоритмом действий при решении похожих задач.
Метод наименьших квадратов в Excel
Программа Excel – мощный табличный редактор, позволяющий выполнять огромное количество различных операций и задач. В данной статье мы разберем, как можно применить метод наименьших квадратов (МНК), который используется для решения различных задач с минимизацией суммы квадратов отклонений некоторых функций от искомых переменных.
Подготовительный этап: активируем надстройку “Поиск Решения”
Прежде, чем приступить к решению основной задачи, потребуется активировать надстройку “Поиск решения” в программе.
- Идем в меню “Файл”.
- В перечне слева выбираем пункт “Параметры”.
- В правой части подраздела “Надстройки” выбираем для параметра “Управление” вариант “Надстройки Excel” и жмем “Перейти”.
Появится окно для выбора нужных надстроек. Устанавливаем галочку напротив пункта “Поиск решения” и щелкаем OK.
Этап 1: исходные данные
Давайте разберем применение метода наименьших квадратов, решив конкретный пример. Допустим, у нас есть два ряда числовых значений – X и Y.
Данная зависимость может быть описана уравнением ниже:
Также, мы знаем, что если X=0, то и Y=0. А значит, данное уравнение можно записать так:
Приступим к выполнению нашей задачи, которая заключается в нахождении суммы квадратов разности.
Этап 2: решаем задачу с применением МНК
- Столбцу, находящемся слева от X, задаем имя N пишем число “1” (примерное значение первого коэф. N) напротив первого значения ряда X.





- в поле “Массив_x” указываем координаты диапазона ячеек столбца Y (без шапки). Адреса ячеек можно указать как вручную, напечатав их с клавиатуры, так и путем выделения с помощью зажатой левой кнопки мыши в самой таблице.
- в поле “Массив_y” указываем диапазон ячеек столбца NX.
- жмем Enter, когда все готово.

- в поле “Оптимизировать целевую функцию” следует указать ссылку на ячейку с функцией “СУММКВРАЗН”. Сделать это можно вручную или выбрав элемент в таблице.
- для опции “До” выбираем вариант – “Минимум”.
- в поле “Изменяя ячейки переменных” нужно указать координаты ячейки, в которой находится соответствующее значение коэф. N.
- по готовности нажимаем “Найти решение”.

Заключение
Итак, мы только что разобрали на практическом примере, каким образом можно применить метод наименьших квадратов в Эксель. На практике могут встречаться более сложные задачи, однако, в целом логика действий схожа с той, что мы описали.
Метод наименьших квадратов в Excel. Регрессионный анализ
Метод наименьших квадратов (МНК) относится к сфере регрессионного анализа. Он имеет множество применений, так как позволяет осуществлять приближенное представление заданной функции другими более простыми. МНК может оказаться чрезвычайно полезным при обработке наблюдений, и его активно используют для оценки одних величин по результатам измерений других, содержащих случайные ошибки. Из этой статьи вы узнаете, как реализовать вычисления по методу наименьших квадратов в Excel.
Постановка задачи на конкретном примере
Предположим, имеются два показателя X и Y. Причем Y зависит от X. Так как МНК интересует нас с точки зрения регрессионного анализа (в Excel его методы реализуются с помощью встроенных функций), то стоит сразу же перейти к рассмотрению конкретной задачи.
Итак, пусть X — торговая площадь продовольственного магазина, измеряемая в квадратных метрах, а Y — годовой товарооборот, определяемый в миллионах рублей.
Требуется сделать прогноз, какой товарооборот (Y) будет у магазина, если у него та или иная торговая площадь. Очевидно, что функция Y = f (X) возрастающая, так как гипермаркет продает больше товаров, чем ларек.
Несколько слов о корректности исходных данных, используемых для предсказания
Допустим, у нас есть таблица, построенная по данным для n магазинов.
Согласно математической статистике, результаты будут более-менее корректными, если исследуются данные по хотя бы 5-6 объектам. Кроме того, нельзя использовать «аномальные» результаты. В частности, элитный небольшой бутик может иметь товарооборот в разы больший, чем товарооборот больших торговых точек класса «масмаркет».
Суть метода
Данные таблицы можно изобразить на декартовой плоскости в виде точек M1 (x1, y1), … Mn (xn, yn). Теперь решение задачи сведется к подбору аппроксимирующей функции y = f (x), имеющей график, проходящий как можно ближе к точкам M1, M2, ..Mn.
Конечно, можно использовать многочлен высокой степени, но такой вариант не только труднореализуем, но и просто некорректен, так как не будет отражать основную тенденцию, которую и нужно обнаружить. Самым разумным решением является поиск прямой у = ax + b, которая лучше всего приближает экспериментальные данные, a точнее, коэффициентов — a и b.
Оценка точности
При любой аппроксимации особую важность приобретает оценка ее точности. Обозначим через ei разность (отклонение) между функциональными и экспериментальными значениями для точки xi, т. е. ei = yi — f (xi).
Очевидно, что для оценки точности аппроксимации можно использовать сумму отклонений, т. е. при выборе прямой для приближенного представления зависимости X от Y нужно отдавать предпочтение той, у которой наименьшее значение суммы ei во всех рассматриваемых точках. Однако, не все так просто, так как наряду с положительными отклонениями практически будут присутствовать и отрицательные.
Решить вопрос можно, используя модули отклонений или их квадраты. Последний метод получил наиболее широкое распространение. Он используется во многих областях, включая регрессионный анализ (в Excel его реализация осуществляется с помощью двух встроенных функций), и давно доказал свою эффективность.
Метод наименьших квадратов
В Excel, как известно, существует встроенная функция автосуммы, позволяющая вычислить значения всех значений, расположенных в выделенном диапазоне. Таким образом, ничто не помешает нам рассчитать значение выражения (e1 2 + e2 2 + e3 2 + . en 2 ).
В математической записи это имеет вид:
Так как изначально было принято решение об аппроксимировании с помощью прямой, то имеем:
Таким образом, задача нахождения прямой, которая лучше всего описывает конкретную зависимость величин X и Y, сводится к вычислению минимума функции двух переменных:
Для этого требуется приравнять к нулю частные производные по новым переменным a и b, и решить примитивную систему, состоящую из двух уравнений с 2-мя неизвестными вида:
После нехитрых преобразований, включая деление на 2 и манипуляции с суммами, получим:
Решая ее, например, методом Крамера, получаем стационарную точку с некими коэффициентами a * и b * . Это и есть минимум, т. е. для предсказания, какой товарооборот будет у магазина при определенной площади, подойдет прямая y = a * x + b * , представляющая собой регрессионную модель для примера, о котором идет речь. Конечно, она не позволит найти точный результат, но поможет получить представление о том, окупится ли покупка в кредит магазина конкретной площади.
Как реализоавать метод наименьших квадратов в Excel
В «Эксель» имеется функция для расчета значения по МНК. Она имеет следующий вид: «ТЕНДЕНЦИЯ» (известн. значения Y; известн. значения X; новые значения X; конст.). Применим формулу расчета МНК в Excel к нашей таблице.
Для этого в ячейку, в которой должен быть отображен результат расчета по методу наименьших квадратов в Excel, введем знак «=» и выберем функцию «ТЕНДЕНЦИЯ». В раскрывшемся окне заполним соответствующие поля, выделяя:
- диапазон известных значений для Y (в данном случае данные для товарооборота);
- диапазон x1, …xn, т. е. величины торговых площадей;
- и известные, и неизвестные значения x, для которого нужно выяснить размер товарооборота (информацию об их расположении на рабочем листе см. далее).
Кроме того, в формуле присутствует логическая переменная «Конст». Если ввести в соответствующее ей поле 1, то это будет означать, что следует осуществить вычисления, считая, что b = 0.
Если нужно узнать прогноз для более чем одного значения x, то после ввода формулы следует нажать не на «Ввод», а нужно набрать на клавиатуре комбинацию «Shift» + «Control»+ «Enter» («Ввод»).
Некоторые особенности
Регрессионный анализ может быть доступен даже чайникам. Формула Excel для предсказания значения массива неизвестных переменных — «ТЕНДЕНЦИЯ» — может использоваться даже теми, кто никогда не слышал о методе наименьших квадратов. Достаточно просто знать некоторые особенности ее работы. В частности:
- Если расположить диапазон известных значений переменной y в одной строке или столбце, то каждая строка (столбец) с известными значениями x будет восприниматься программой в качестве отдельной переменной.
- Если в окне «ТЕНДЕНЦИЯ» не указан диапазон с известными x, то в случае использования функции в Excel программа будет рассматривать его как массив, состоящий из целых чисел, количество которых соответствует диапазону с заданными значениями переменной y.
- Чтобы получить на выходе массив «предсказанных» значений, выражение для вычисления тенденции нужно вводить как формулу массива.
- Если не указаны новые значения x, то функция «ТЕНДЕНЦИЯ» считает их равным известным. Если и они не заданы, то в качестве аргумента берется массив 1; 2; 3; 4;…, который соразмерен диапазону с уже заданными параметрами y.
- Диапазон, содержащий новые значения x должен состоять из такого же или большего количества строк или столбцов, как диапазон с заданными значениями y. Иными словами он должен быть соразмерным независимым переменным.
- В массиве с известными значениями x может содержаться несколько переменных. Однако если речь идет лишь об одной, то требуется, чтобы диапазоны с заданными значениями x и y были соразмерны. В случае нескольких переменных нужно, чтобы диапазон с заданными значениями y вмещался в одном столбце или в одной строке.
Функция «ПРЕДСКАЗ»
Регрессионный анализ в Excel реализуется с помощью нескольких функций. Одна из них называется «ПРЕДСКАЗ». Она аналогична «ТЕНДЕНЦИИ», т. е. выдает результат вычислений по методу наименьших квадратов. Однако только для одного X, для которого неизвестно значение Y.
Теперь вы знаете формулы в Excel для чайников, позволяющие спрогнозировать величину будущего значения того или иного показателя согласно линейному тренду.
На чтение 5 мин Опубликовано 27.12.2020
Табличный процессор Эксель способен реализовывать большое число математических операций. Из статьи вы узнаете, как используется метод наименьших квадратов, который применяется для осуществления решения разнообразных задач.
Содержание
- Первоначальные настройки: включение параметра «Поиск решения»
- Что такое метод наименьших квадратов
- Шаг первый: исходные данные решаемой задачи
- Шаг второй: решение задачки с использованием МНК
- Заключение
Первоначальные настройки: включение параметра «Поиск решения»
Изначально необходимо включить «Поиск решения», так как по умолчанию он находится в выключенном состоянии. Пошаговое руководство выглядит следующим образом:
- Переходим в раздел «Файл», который находится в левом верхнем углу интерфейса табличного процессора.
- На экране отобразилось новое окошко. Здесь, в левой колонке, необходимо кликнуть на элемент «Параметры».
- В появившемся окне выбираем раздел «Надстройки». В правой части окошка находим надпись «Управление:» и раскрываем список. В списке выбираем пункт «Надстройки Excel». Щёлкаем кнопку «ОК».
- Появилось еще одно окошко с названием «Надстройки». Около элемента «Поиск решения» ставим галочку. После проведения всех манипуляций кликаем «ОК».
- Готово! Параметр включился, и теперь мы можем приступить к разбору метода наименьших квадратов.
Что такое метод наименьших квадратов
Для начала вспомним, что метод наименьших квадратов — математический метод, используемый для решения задач, основанный на минимизации суммы квадратов отклонений некоторых функций от изначальных значений.
Он может применяться для «решения» переопределенных систем уравнений (когда число уравнений больше числа неизвестных), для поиска решения в случае стандартных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функции.
Шаг первый: исходные данные решаемой задачи
На конкретном примере начнем разбор метода наименьших квадратов. К примеру, у нас есть 2 колонки – X и Y:
Эта зависимость описывается уравнением: Y=A+NX.
Мы прекрасно знаем, что если Х равен нулю, то и Y равен нулю. Следовательно, это уравнение можно привести к следующему виду: Y=NX. Начнём реализацию этой задачи. Нам нужно найти сумму квадратов разности.
Шаг второй: решение задачки с использованием МНК
Пошаговое руководство выглядит следующим образом:
- Столбику, который располагается левее показателя Х, даем название N и прописываем единицу рядом с 1-м показателем колонки Х. Единица – это примерное значение 1-го коэффициента N.
- Столбику, который располагается правее показателя Y, даем наименование NX.
- В ячейку D1, находящуюся около первых показателей X и Y, прописываем специальную формулу произведения коэффициента N на показатель из столбика Х. Сама формула выглядит следующим образом: =$А$2*В2. Стоит заметить, что адрес ячейки с коэффициентом необходимо привести к абсолютному типу. Абсолютный тип в табличном процессоре позволяет зафиксировать строчку или столбик (или все вместе одновременно). Иными словами, при копировании значений в другие ячейки абсолютные ссылки не будут меняться. После проведения всех манипуляций жмем клавишу «Enter».
- Перемещаем курсор мышки на сектор с выведенным результатом. Наведя указатель в правый верхний уголок, он превратится в маленький плюсик темного цвета, который называется маркером заполнения. Зажимаем ЛКМ и перетягиваем маркер в самый низ до крайней строчки табличных данных.
- После проведения этих манипуляций мы получили результаты вычислений во всех секторах колонки NX.
- Далее переходим к подсчету суммы разностей квадратов показателей Y и NX. Перемещаемся в ячейку E1, располагающуюся правее от показателя NX, нажимаем на элемент «Вставить функцию», который находится рядом со строкой для ввода формул, и имеет внешний вид «fx».
- Первым делом, находим надпись «Категории:» и раскрываем список, находящийся рядом. В обширном списке выбираем элемент «Математические». В блоке «Выберите функцию:» отыскиваем функцию «СУММКВРАЗН» и выбираем ее. После проведения всех манипуляций жмем на кнопку «ОК».
- Открылось небольшое окошко «Аргументы функции». Для дальнейшей работы необходимо заполнить все строки формы. В строчку «Массив_х» вводим адрес диапазона ячеек столбика Y. Координаты можно вписать самостоятельно ручным вводом, используя клавиатуру, или же путем их выбора в самих табличных данных.
- В строчку «Массив_у» вводим адрес диапазона ячеек столбика NX. После проведения всех манипуляций щёлкаем клавишу «Enter».
- Перемещаемся в раздел «Данные», который находится в верхней части интерфейса табличного процессора. Находим блок команд под названием «Анализ» и выбираем элемент «Поиск решения».
- На экране отобразилось окошко с огромным количеством настроек, которые необходимо заполнить. В строчку «Оптимизировать целевую функцию» вводим ссылку на ячейку с оператором «СУММКВРАЗН». Реализовать это действие можно самостоятельно ручным вводом, используя клавиатуру, или же выбрав сектор в самой табличке. Ставим отметку около надписи «Минимум», которая располагается в блоке «До:». В строчку «Изменяя ячейки переменных» вбиваем адрес сектора, в котором располагается показатель коэффициента N – $A$2. После проведения всех манипуляций щелкаем на «Найти решение».
- После того, как «Поиск решения» будет выполнен, на экране компьютера отобразится окошко с выведенными результатами поиска решения, а затем реализуется замена числовых значений в столбике N. Отображенный результат – это наименьший квадрат функции. Если выведенный результат удовлетворяет тому, что нужно было найти, то нажимаем «ОК».
Заключение
Таким образом, мы на конкретном примере рассмотрели способ использования метода наименьших квадратов в табличном процессоре Microsoft Excel и ознакомились со стандартным алгоритмом действий при решении похожих задач.
Оцените качество статьи. Нам важно ваше мнение:
Содержание
- Как использовать метод наименьших квадратов в Excel
- Шаг 1: Создайте набор данных
- Шаг 2: Используйте метод наименьших квадратов для подбора линии регрессии
- Шаг 3: интерпретируйте результаты
- Шаг 4: Нанесите результаты на график
- МНК: Метод Наименьших Квадратов в EXCEL
- Линейная зависимость
- Инструмент диаграммы Линия тренда
- МНК: Квадратичная зависимость в EXCEL
- МНК: Экспоненциальная зависимость в EXCEL
- Функция РОСТ()
- Функция ЛГРФПРИБЛ()
Как использовать метод наименьших квадратов в Excel
Метод наименьших квадратов — это метод, который мы можем использовать для поиска линии регрессии, которая лучше всего соответствует заданному набору данных.
В следующем видео представлено краткое объяснение этого метода:
Чтобы использовать метод наименьших квадратов для подбора линии регрессии в Excel, мы можем использовать функцию =ЛИНЕЙН() .
В следующем пошаговом примере показано, как использовать эту функцию на практике.
Шаг 1: Создайте набор данных
Во-первых, давайте создадим следующий набор данных в Excel:
Шаг 2: Используйте метод наименьших квадратов для подбора линии регрессии
Мы можем использовать функцию =LINEST(known_ys, known_xs) , чтобы использовать метод наименьших квадратов, чтобы подобрать линию регрессии к этому набору данных:
Как только мы нажмем ENTER , появятся коэффициенты регрессионной модели:
Шаг 3: интерпретируйте результаты
Используя коэффициенты из функции =LINEST() , мы можем написать следующую подобранную линию регрессии:
у = 11,55211 + 1,07949(х)
Мы можем использовать это уравнение для оценки значения y на основе значения x.
Например, если x = 10, то мы оценили бы, что y будет равно 22,347 :
у = 11,55211 + 1,07949(10) = 22,347
Шаг 4: Нанесите результаты на график
Наконец, мы можем использовать следующие шаги для построения набора данных вместе с подобранной линией регрессии:
- Выделите ячейки A2:B16 .
- Щелкните вкладку « Вставка » на верхней ленте. Затем щелкните первый параметр диаграммы под названием « Вставить точечную (X, Y)» или «Пузырьковую диаграмму » в группе «Диаграммы».
- После того, как диаграмма появится, нажмите знак плюс «+» в правом верхнем углу. В раскрывающемся меню установите флажок рядом с линией тренда , чтобы добавить на график подобранную линию регрессии.
Источник
МНК: Метод Наименьших Квадратов в EXCEL
history 11 ноября 2018 г.
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью линейной функции y = a x + b .
Метод наименьших квадратов (англ. Ordinary Least Squares , OLS ) является одним из базовых методов регрессионного анализа в части оценки неизвестных параметров регрессионных моделей по выборочным данным.
Рассмотрим приближение функциями, зависящими только от одной переменной:
Примечание : Случаи приближения полиномом с 3-й до 6-й степени рассмотрены в этой статье. Приближение тригонометрическим полиномом рассмотрено здесь.
Линейная зависимость
Нас интересует связь 2-х переменных х и y . Имеется предположение, что y зависит от х по линейному закону y = ax + b . Чтобы определить параметры этой взаимосвязи исследователь провел наблюдения: для каждого значения х i произведено измерение y i (см. файл примера ). Соответственно, пусть имеется 20 пар значений (х i ; y i ).
Для наглядности рекомендуется построить диаграмму рассеяния.
Примечание: Если шаг изменения по х постоянен, то для построения диаграммы рассеяния можно использовать тип График , если нет, то необходимо использовать тип диаграммы Точечная .
Из диаграммы очевидно, что связь между переменными близка к линейной. Чтобы понять какая из множества прямых линий наиболее «правильно» описывает зависимость между переменными, необходимо определить критерий, по которому будут сравниваться линии.
В качестве такого критерия используем выражение:
Вышеуказанное выражение представляет собой сумму квадратов расстояний между наблюденными значениями y i и ŷ i и часто обозначается как SSE ( Sum of Squared Errors ( Residuals ), сумма квадратов ошибок (остатков) ) .
Метод наименьших квадратов заключается в подборе такой линии ŷ = ax + b , для которой вышеуказанное выражение принимает минимальное значение.
Примечание: Любая линия в двухмерном пространстве однозначно определяется значениями 2-х параметров: a (наклон) и b (сдвиг).
Считается, что чем меньше сумма квадратов расстояний, тем соответствующая линия лучше аппроксимирует имеющиеся данные и может быть в дальнейшем использована для прогнозирования значений y от переменной х. Понятно, что даже если в действительности никакой взаимосвязи между переменными нет или связь нелинейная, то МНК все равно подберет «наилучшую» линию. Таким образом, МНК ничего не говорит о наличии реальной взаимосвязи переменных, метод просто позволяет подобрать такие параметры функции a и b , для которых вышеуказанное выражение минимально.
Проделав не очень сложные математические операции (подробнее см. статью про квадратичную зависимость ), можно вычислить параметры a и b :
Как видно из формулы, параметр a представляет собой отношение ковариации и дисперсии , поэтому в MS EXCEL для вычисления параметра а можно использовать следующие формулы (см. файл примера лист Линейная ):
= КОВАР(B26:B45;C26:C45)/ ДИСП.Г(B26:B45) или
Также для вычисления параметра а можно использовать формулу = НАКЛОН(C26:C45;B26:B45) . Для параметра b используйте формулу = ОТРЕЗОК(C26:C45;B26:B45) .
И наконец, функция ЛИНЕЙН() позволяет вычислить сразу оба параметра. Для ввода формулы ЛИНЕЙН(C26:C45;B26:B45) необходимо выделить в строке 2 ячейки и нажать CTRL + SHIFT + ENTER (см. статью про формулы массива, возвращающими несколько значений ). В левой ячейке будет возвращено значение а , в правой – b .
Примечание : Чтобы не связываться с вводом формул массива потребуется дополнительно использовать функцию ИНДЕКС() . Формула = ИНДЕКС(ЛИНЕЙН(C26:C45;B26:B45);1) или просто = ЛИНЕЙН(C26:C45;B26:B45) вернет параметр, отвечающий за наклон линии, т.е. а . Формула = ИНДЕКС(ЛИНЕЙН(C26:C45;B26:B45);2) вернет параметр, отвечающий за пересечение линии с осью Y, т.е. b .
Вычислив параметры, на диаграмме рассеяния можно построить соответствующую линию.
Инструмент диаграммы Линия тренда
Еще одним способом построения прямой линии по методу наименьших квадратов является инструмент диаграммы Линия тренда . Для этого выделите диаграмму, в меню выберите вкладку Макет , в группе Анализ нажмите Линия тренда , затем Линейное приближение .
Поставив в диалоговом окне галочку в поле «показывать уравнение на диаграмме» можно убедиться, что найденные выше параметры совпадают со значениями на диаграмме.
Примечание : Для того, чтобы параметры совпадали необходимо, чтобы тип у диаграммы был Точечная, а не График . Дело в том, что при построении диаграммы График значения по оси Х не могут быть заданы пользователем (пользователь может указать только подписи, которые не влияют на расположение точек). Вместо значений Х используется последовательность 1; 2; 3; … (для нумерации категорий). Поэтому, если строить линию тренда на диаграмме типа График , то вместо фактических значений Х будут использованы значения этой последовательности, что приведет к неверному результату (если, конечно, фактические значения Х не совпадают с последовательностью 1; 2; 3; …).
СОВЕТ : Подробнее о построении диаграмм см. статьи Основы построения диаграмм и Основные типы диаграмм .
Источник
МНК: Квадратичная зависимость в EXCEL
history 24 ноября 2018 г.
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью квадратичной функции y=ax 2 +bx+с .
Метод наименьших квадратов (англ. Ordinary Least Squares , OLS ) является одним из базовых методов регрессионного анализа в части оценки неизвестных параметров регрессионных моделей по выборочным данным. Основная статья про МНК — МНК: Метод Наименьших Квадратов в MS EXCEL .
Для построения графика квадратичной зависимости y=ax 2 +bx+с вспомним исходный критерий МНК, который необходимо минимизировать:
Теперь ŷ i = a*x i 2 +b*x i +с и мы имеем зависимость от 3-х параметров полинома второй степени: a , b и с .
Вышеуказанное выражение примет минимальное значение при таких параметрах a , b и с , при которых соответствующие 3 частные производные функции F равны нулю, т.е.:
В результате вычислений и преобразований получим систему из 3-х линейных уравнений:
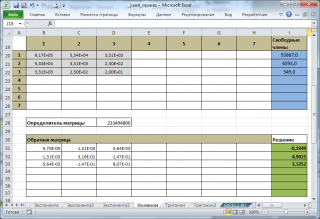
Сначала вычислим выражения со знаком суммирования. Для этого возьмем исходные данные таблицы и произведем с ними арифметические действия (см. файл примера ).
Затем получившуюся систему линейных уравнений нужно решить относительно параметров a , b и с. Для этого можно использовать, например метод обратной матрицы или функцию ЛИНЕЙН() (эти подходы реализованы в файле примера ).
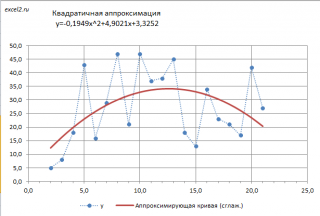
В результате вычислений будут найдены три параметра квадратичного полинома a , b и с, а также построена соответствующая парабола.
Примечание : Три параметра можно также найти с помощью замены переменных – это сделано в более общем случае для полинома .
Источник
МНК: Экспоненциальная зависимость в EXCEL
history 11 ноября 2018 г.
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью экспоненциальной функции.
Метод наименьших квадратов (англ. Ordinary Least Squares , OLS ) является одним из базовых методов регрессионного анализа в части оценки неизвестных параметров регрессионных моделей по выборочным данным. Основная статья про МНК — МНК: Метод Наименьших Квадратов в MS EXCEL .
В этой статье рассмотрена только экспоненциальная зависимость, но ее выводы можно применить и к показательной зависимости, т.к. любую показательную функцию можно свести к экспоненциальной:
y=a*m x =a*(e ln(m) ) x = a*e x*ln(m) =a*e bx , где b= ln(m))
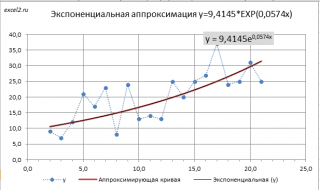
В свою очередь экспоненциальную зависимость y=a*EXP(b*x) при a>0 можно свести к случаю линейной зависимости с помощью замены переменных (см. файл примера ).
После замены переменных Y=ln(y) и A=ln(a) вычисления полностью аналогичны линейному случаю Y=b*x+A. Для нахождения коэффициента a необходимо выполнить обратное преобразование a= EXP(A) .
Примечание : Построить линию тренда по методу наименьших квадратов можно также с помощью инструмента диаграммы Линия тренда ( Экспоненциальная линия тренда ). Поставив в диалоговом окне галочку в поле «показывать уравнение на диаграмме» можно убедиться, что найденные выше параметры совпадают со значениями на диаграмме. Подробнее о диаграммах см. статью Основы построения диаграмм в MS EXCEL .
Следствием замены Y=ln(y) и A=ln(a) являются дополнительные ограничения: a>0 и y>0. При уменьшении х (в сторону больш и х по модулю отрицательных чисел) соответствующее значение y асимптотически стремится к 0. Именно такую линию тренда и строит инструмент диаграммы Линия тренда. Если среди значений y есть отрицательные, то с помощью инструмента Линия тренда экспоненциальную линию тренда построить не удастся.
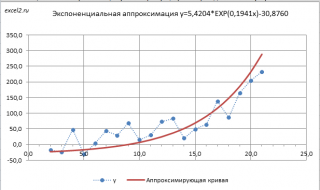
Чтобы обойти это ограничение используем другое уравнение экспоненциальной зависимости y=a*EXP(b*x)+с, где по прежнему a>0, т.е. при росте х значения y также будут увеличиваться. В качестве с можно взять некую заранее известную нижнюю границу для y , ниже которой у не может опускаться, т.е. у>с. Далее заменой переменных Y=ln(y-c) и A=ln(a) опять сведем задачу к линейному случаю (см. файл примера лист Экспонента2 ).
Если при росте х значения y уменьшаются по экспоненциальной кривой, т.е. a файл примера лист Экспонента3 ).
Функция РОСТ()
Еще одним способом построить линию экспоненциального тренда является использование функции РОСТ() , английское название GROWTH.
Синтаксис функции следующий:
РОСТ( известные_значения_y; [известные_значения_x]; [новые_значения_x]; [конст] )
Для работы функции нужно просто ввести ссылки на массив значений переменной Y (аргумент известные_значения_y ) и на массив значений переменной Х (аргумент известные_значения_x ). Функция рассчитает прогнозные значения Y для Х, указанных в аргументе новые_значения_x . Если требуется, чтобы экспоненциальная кривая y=a*EXP(b*x) имела a=1, т.е. проходила бы через точку (0;1), то необязательный аргумент конст должен быть установлен равным ЛОЖЬ (или 0).
Если среди значений y есть отрицательные, то с помощью функции РОСТ() аппроксимирующую кривую построить не удастся.
Безусловно, использование функции РОСТ() часто удобно, т.к. не требуется делать замену переменных и сводить задачу к линейному случаю.
Наконец, покажем как с помощью функции РОСТ() вычислить коэффициенты уравнения y= a *EXP( b *x).
Примечание : В MS EXCEL имеется специальная функция ЛГРФПРИБЛ() , которая позволяет вычислить коэффициенты уравнения y=a*EXP(b*x). Об этой функции см. ниже.
Чтобы вычислить коэффициент a (значение Y в точке Х=0) используйте формулу =РОСТ(C26:C45;B26:B45;0) . В диапазонах C26:C45 и B26:B45 должны находиться массивы значений переменной Y и X соответственно.
Чтобы вычислить коэффициент b используйте формулу:
= LN(РОСТ(C26:C45;B26:B45;МИН(B26:B45))/ РОСТ(C26:C45;B26:B45;МАКС(B26:B45)))/ (МИН(B26:B45)-МАКС(B26:B45))
Функция ЛГРФПРИБЛ()
Функция ЛГРФПРИБЛ() на основе имеющихся значений переменных Х и Y подбирает методом наименьших квадратов коэффициенты а и m уравнения y= a * m ^x.
Используя свойство степеней a mn =(a m ) n приведем уравнение экспоненциального тренда y= a *EXP( b *x)= a *e b *x = a *(e b ) x к виду y= a * m ^x, сделав замену переменной m= e b =EXP( b ).
Чтобы вычислить коэффициенты уравнения y= a *EXP( b *x) используйте следующие формулы:
= LN(ЛГРФПРИБЛ(C26:C45;B26:B45)) — коэффициент b
= ИНДЕКС(ЛГРФПРИБЛ(C26:C45;B26:B45);;2) — коэффициент a
Примечание : Функция ЛГРФПРИБЛ() , английское название LOGEST, является формулой массива, возвращающей несколько значений . Поэтому, например, для вывода коэффициентов уравнения необходимо выделить 2 ячейки в одной строке, в Строке формул ввести = ЛГРФПРИБЛ(C26:C45;B26:B45) , затем для ввода формулы вместо обычного ENTER нажать CTRL + SHIFT + ENTER .
Функция ЛГРФПРИБЛ() имеет линейный аналог – функцию ЛИНЕЙН() , которая рассмотрена в статье про простую линейную регрессию. Если 4-й аргумент этой функции ( статистика ) установлен ИСТИНА, то ЛГРФПРИБЛ() возвращает регрессионную статистику: стандартные ошибки для оценок коэффициентов регрессии, коэффициент детерминации, суммы квадратов: SSR , SSE и др.
Примечание : Особой нужды в функции ЛГРФПРИБЛ() нет, т.к. с помощью логарифмирования и замены переменной показательную функцию y= a * m ^x можно свести к линейной ln(y)=ln(a)+x*ln(m)=> Y=A+bx. То же справедливо и для экспоненциальной функции y= a *EXP( b *x).
Источник
Метод наименьших квадратов — это математическая процедура составления линейного уравнения, максимально соответствующего набору упорядоченных пар, путем нахождения значений для a и b, коэффициентов в уравнении прямой. Цель метода наименьших квадратов состоит в минимизации общей квадратичной ошибки между значениями y и ŷ. Если для каждой точки мы определяем ошибку ŷ, метод наименьших квадратов минимизирует:
где n = число упорядоченных пар вокруг линии. максимально соответствующей данным.
Это понятие проиллюстрировано на рисунке
Судя по рисунку, линия, максимально соответствующая данным, линия регрессии, минимизирует общую квадратичную ошибку четырех точек на графике. Я покажу вам, как определять это уравнение регрессии с помощью метода наименьших квадратов на следующем примере.
Представьте себе молодую пару, которые, с недавних пор, живут вместе и совместно делят столик для косметических принадлежностей в ванной. Молодой человек начал замечать, что половина его столика неумолимо сокращается, сдавая свои позиции муссам для волос и соевым комплексам. За последние несколько месяцев парень внимательно следил за тем, с какой скоростью увеличивается число предметов на ее части стола. В таблице ниже представлено число предметов девушки на столике в ванной, накопившихся за последние несколько месяцев.
Поскольку своей целью мы определили задачу узнать, увеличивается ли со временем число предметов, «Месяц» будет независимой переменной, а «Число предметов» — зависимой.
С помощью метода наименьших квадратов определяем уравнение, максимально соответствующее данным, путем вычисления значений a, отрезка на оси y, и b, наклона линии:
a = yср — bxср
где xср — среднее значение x, независимой переменной, yср — среднее значение y, независимой переменной.
В таблице ниже суммированы необходимые для этих уравнений вычисления.
Кривая эффекта для нашего примера с ванной будет определяться следующим уравнением:
ŷ=5.13+0.976x
Поскольку наше уравнение имеет положительный наклон — 0.976, парень имеет доказательство того, что число предметов на столике со временем увеличивается со средней скоростью 1 предмет в месяц. На графике представлена кривая эффекта с упорядоченными парами.
Ожидание в отношении числа предметов в течение следующего полугода (месяца 16) будет вычисляться так:
ŷ = 5.13 + 0.976x = 5.13 + 0.976(16) ~ 20.7 = 21 предмет
Так что, пора нашему герою предпринимать какие-нибудь действия.
Как вы уже, наверное, догадались в Excel имеется функция для расчета значения по методу наименьших квадратов. Это функция называется ТЕНДЕНЦИЯ. Синтаксис у нее следующий:
ТЕНДЕНЦИЯ (известные значения Y; известные значения X; новые значения X; конст)
где:
известные значения Y – массив зависимых переменных, в нашем случае, количество предметов на столике
известные значения X – массив независимых переменных, в нашем случае это месяц
новые значения X – новые значения X (месяца) для которого функция ТЕНДЕНЦИЯ возвращает ожидаемое значение зависимых переменных (количество предметов)
конст — необязательный. Логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.
Например, на рисунке показана функция ТЕНДЕНЦИЯ, используемая для определения ожидаемого количества предметов на столике в ванной для 16-го месяца.
Скачать файл с примером расчета значений по методу наименьших квадратов
4.1.
Использование встроенных функций
Вычисление
коэффициентов
регрессии
осуществляется с помощью функции
ЛИНЕЙН(Значения_y;
Значения_x;
Конст;
статистика),
где
Значения_y
— массив значений y,
Значения_x—
необязательный массив значений x,
если массив х
опущен, то предполагается, что это массив
{1;2;3;…} такого же размера, как и Значения_y,
Конст—
логическое значение, которое указывает,
требуется ли, чтобы константа b
была равна 0. Если Конст
имеет значение ИСТИНА
или опущено, то b
вычисляется обычным образом. Если
аргумент Конст
имеет значение ЛОЖЬ, то b
полагается равным 0 и значения a
подбираются так, чтобы выполнялось
соотношение y=ax.
Статистика—
логическое значение, которое указывает,
требуется ли вернуть дополнительную
статистику по регрессии. Если аргумент
Статистика
имеет значение ИСТИНА,
то функция ЛИНЕЙН
возвращает дополнительную регрессионную
статистику. Если аргумент Статистика
имеет значение ЛОЖЬ
или опущен, то функция ЛИНЕЙН
возвращает только коэффициент a
и постоянную b.
Необходимо
помнить, что результатом функций ЛИНЕЙН()
является
множество значений – массив.
Для
расчета коэффициента
корреляции
используется функция
КОРРЕЛ(Массив1;Массив2),
возвращающая
значения коэффициента корреляции, где
Массив1
— массив значений y,
Массив2
— массив значений x.
Массив1
и Массив2
должны быть одной размерности.
ПРИМЕР
1. Зависимость
y(x)
представлена в таблице. Построить линию
регрессии
и вычислить коэффициент
корреляции.
|
y |
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
4 |
|
x |
1 |
2.39 |
2.81 |
3.25 |
3.75 |
4.11 |
4.45 |
4.85 |
5.25 |
Введем
таблицу значений в лист MS
Excel
и построим точечный график. Рабочий
лист примет вид изображенный на рис. 2.
Рис. 2
Для
того чтобы рассчитать значения
коэффициентов регрессии а
и b
выделим
ячейки A7:B7,
обратимся к мастеру функций и в категории
Статистические
выберем функцию ЛИНЕЙН.
Заполним появившееся диалоговое окно
так, как показано на рис. 3 и нажмем ОK.
Рис. 3
В
результате вычисленное значение появится
только в ячейке A6
(рис.4). Для того чтобы значение появилось
и в ячейке B6
необходимо войти в режим редактирования
(клавиша F2),
а затем нажать комбинацию клавиш
CTRL+SHIFT+ENTER.
Для
расчета значения коэффициента корреляции
в ячейку С6
была введена следующая формула:
С7=КОРРЕЛ(B3:J3;B2:J2).
Рис. 4
Зная
коэффициенты
регрессии а
и b
вычислим значения функции y=ax+b
для заданных x.
Для этого
введем формулу
B5=$A$7*B2+$B$7
и
скопируем ее в диапазон С5:J5
(рис. 5).
Рис. 5
Изобразим
линию регрессии на диаграмме. Выделим
экспериментальные точки на графике,
щелкнем правой кнопкой мыши и выберем
команду Исходные
данные. В
появившемся диалоговом окне (рис. 5)
выберем вкладку Ряд
и щелкнем по кнопке Добавить.
Заполним поля ввода, так как показано
на рис. 6 и нажмем кнопку ОК.
К графику экспериментальных данных
будет добавлена линия регрессии. По
умолчанию ее график будет изображен в
виде точек, не соединенных сглаживающими
линиями.
Р
6
Чтобы
изменить вид линии регрессии, выполним
следующие действия. Щелкнем правой
кнопкой мыши по точкам, изображающим
график линии, выберем команду Тип
диаграммы и
установим вид точечной диаграммы, так
как показано на рис. 7.
Рис.
7
Тип
линии, ее цвет и толщину можно изменить
следующим образом. Выделить линию на
диаграмме, нажать правую кнопку мыши и
в контекстном меню выбрать команду
Формат рядов
данных…
Далее сделать установки, например, так
как показано на рис. 8.
Рис. 8
В
результате всех преобразований получим
график экспериментальных данных и линию
регрессии в одной графической области
(рис. 9).
Рис. 9
4.2.
Использование линии тренда.
Построение
различных аппроксимирующих зависимостей
в MS
Excel
реализовано в виде свойства диаграммы
– линия
тренда.
ПРИМЕР
2. В результате
эксперимента была определена некоторая
табличная зависимость.
-
0.15
0.16
0.17
0.18
0.19
0.20
4.4817
4.4930
5.4739
6.0496
6.6859
7.3891
Выбрать
и построить аппроксимирующую зависимость.
Построить графики табличной и подобранной
аналитической зависимости.
Решение
задачи можно разбить на следующие этапы:
ввод исходных данных, построение
точечного графика и добавление к этому
графику линии тренда.
Рассмотрим
этот процесс подробно. Введем исходные
данные в рабочий лист и построим график
экспериментальных данных. Далее выделим
экспериментальные точки на графике,
щелкнем правой кнопкой мыши и воспользуемся
командой Добавить
линию
тренда (рис.
10).
Рис. 10
Появившееся
диалоговое окно позволяет построить
аппроксимирующую зависимость.
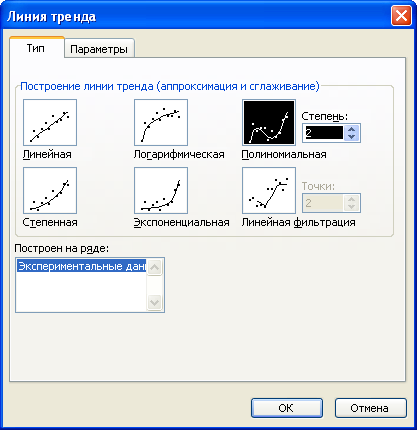
На
первой вкладке (рис. 11) этого окна
указывается вид аппроксимирующей
зависимости.
На
второй (рис. 12) определяются параметры
построения:
-
название
аппроксимирующей зависимости; -
прогноз
вперед (назад) на n
единиц (этот параметр определяет, на
какое количество единиц вперед (назад)
необходимо продлить линию тренда); -
показывать
ли точку пересечения кривой с прямой
y=const; -
показывать
аппроксимирующую функцию на диаграмме
или нет (параметр показывать уравнение
на диаграмме); -
помещать
ли на диаграмму величину среднеквадратичного
отклонения или нет (параметр поместить
на диаграмму величину достоверности
аппроксимации).
Рис. 11
Рис. 12
Выберем
в качестве аппроксимирующей зависимости
полином второй степени (рис. 11) и выведем
уравнение, описывающее этот полином на
график (рис. 12). Полученная диаграмма
представлена на рис. 13.
Рис.
13
Аналогично
с помощью линии
тренда можно
подобрать параметры таких зависимостей
как
-
линейная
y=a∙x+b, -
логарифмическая
y=a∙ln(x)+b, -
экспоненциальная
y=a∙eb, -
степенная
y=a∙xb, -
полиномиальная
y=a∙x2+b∙x+c,
y=a∙x3+b∙x2+c∙x+d
и так далее, до полинома 6-й степени
включительно, -
линейная
фильтрация.
4.3.
Использование решающего блока
Значительный
интерес представляет реализация в MS
Excel
подбора параметров методом наименьших
квадратов с использованием решающего
блока. Эта методика позволяет подобрать
параметры функции любого вида. Рассмотрим
эту возможность на примере следующей
задачи.
ПРИМЕР
3. В результате
эксперимента получена зависимость z(t)
представленная в таблице
|
0,66 |
0,9 |
1,17 |
1,47 |
1,7 |
1,74 |
2,08 |
2,63 |
3,12 |
|
38,9 |
68,8 |
64,4 |
66,5 |
64,95 |
59,36 |
82,6 |
90,63 |
113,5 |
Подобрать
коэффициенты зависимости Z(t)=At4+Bt3+Ct2+Dt+K
методом наименьших квадратов.
Эта
задача эквивалентна задаче нахождения
минимума функции пяти переменных
(10).
Рассмотрим
процесс решения задачи оптимизации
(рис. 14).
Рис. 14
Пусть
значения А,
В,
С,
D
и К
хранятся в ячейках A7:E7.
Рассчитаем теоретические значения
функции Z(t)=At4+Bt3+Ct2+Dt+K
для заданных t
(B2:J2).
Для этого в ячейку B4
введем значение функции в первой точке
(ячейка B2):
B4=$A$7*B2^4+$B$7*B2^3+$C$7*B2^2+$D$7*B2+$E$7.
Скопируем
эту формулу в диапазон С4:J4
и получим ожидаемое значение функции
в точках, абсциссы которых хранится в
ячейках B2:J2.
В
ячейку B5
введем формулу, вычисляющую квадрат
разности между экспериментальными и
расчетными точками:
B5=(B4-B3)^2,
и
скопируем ее в диапазон С5:J5.
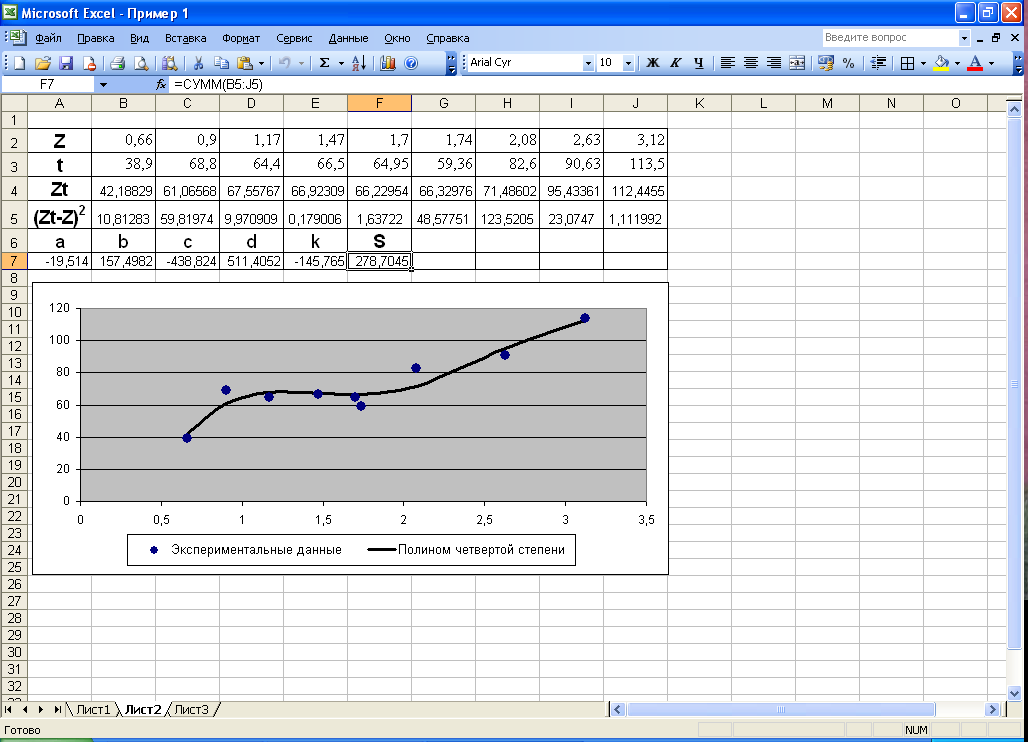
В ячейке F7
будем хранить суммарную квадратичную
ошибку (10). Для этого введем формулу:
F7
=
СУММ(B5:J5).
Воспользуемся
командой СервисПоиск
решения
и решим задачу оптимизации без ограничений.
Заполним соответствующим образом поля
ввода в диалоговом окне, показанном на
рис. 14 и нажмем кнопку Выполнить.
Если решение будет найдено, то появится
окно, изображенное на рис. 15.
Результатом
работы решающего блока будет вывод в
ячейки A7:E7
значений
параметров
функции Z(t)=At4+Bt3+Ct2+Dt+K.
В ячейках B4:J4
получим ожидаемые
значение функции
в исходных точках. В ячейке F7
будет храниться суммарная
квадратичная ошибка.
Изобразить
экспериментальные точки и подобранную
линию в одной графической области можно,
если выделить диапазон B2:J4,
вызвать
Мастер
диаграмм,
а затем отформатировать внешний вид
полученных графиков.
Рис.
17 отображает рабочий лист MS
Excel
после проведенных вычислений.
Рис.
15
Рис. 16
Рис. 17
5.
СПИСОК ЛИТЕРАТУРЫ
1.
Алексеев Е.Р., Чеснокова О.В., Решение
задач вычислительной математики в
пакетах Mathcad12,
MATLAB7,
Maple9.
– НТ Пресс, 2006.–596с. :ил. –(Самоучитель)
2.
Алексеев Е.Р., Чеснокова О.В., Е.А. Рудченко,
Scilab,
решение инженерных и математических
задач. –М., БИНОМ, 2008.–260с.
3.
Березин И.С., Жидков Н.П., Методы
вычислений.–М.:Наука, 1966.–632с.
4.
Гарнаев А.Ю., Использование MS
EXCEL
и VBA
в экономике и финансах. – СПб.: БХВ —
Петербург, 1999.–332с.
5.
Демидович Б.П., Марон И А., Шувалова В.З.,
Численные методы анализа.–М.:Наука,
1967.–368с.
6.
Корн Г., Корн Т., Справочник по математике
для научных работников и инженеров.–М.,
1970, 720с.
7.
Алексеев
Е.Р., Чеснокова О.В. Методические указания
к выполнению лабораторных работ в MS
EXCEL.
Для студентов всех специальностей.
Донецк,
ДонНТУ, 2004. 112 с.
25
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #