Excel для Microsoft 365 Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Еще…Меньше
Эта статья была адаптирована на основе Microsoft Excel анализа данных и бизнес-моделирования, автором Wayne L. Winston.
-
Кто использует метод Монте-Карло?
-
Что происходит при введите =СЛЛ() в ячейку?
-
Как имитировать значения дискретной случайной переменной?
-
Как имитировать значения обычной случайной переменной?
-
Как компания с поздравительной открыткой определяет, сколько карточек нужно создать?
Мы хотим точно оценить вероятность неопределяемых событий. Например, какова вероятность того, что денежные потоки нового продукта будут иметь положительное чистое значение (ЧПС)? Каков коэффициент риска для нашего портфеля инвестиций? С помощью моделирования Монте-Карло мы моделируем ситуации, которые представляют неопределенность, а затем играем их на компьютере тысячи раз.
Примечание: Название методом Монте-Карло является названием компьютера, которое было выполнено в 30-40-е гг. для оценки вероятности успешной реакции на цепочку, необходимую для этого. Вехи, вовлеченные в эту работу, были большим поклонником заверверять, поэтому они предоставили им кодовое имя Монте-Карло.
В следующих пяти главах вы увидите примеры использования Excel по методу Монте-Карло.
Многие компании используют метод Монте-Карло в качестве важной части процесса принятия решений. Вот несколько примеров.
-
Для оценки средней прибыли и коэффициента риска для новых продуктов используются general Elis, Proctor и Tos, Pfizer, Bristol-Myers Squibb и Илья Елисеев. В компании GM эта информация используется директором для определения продуктов, которые будут вы рынок.
-
В gm используются такие виды деятельности, как прогнозирование чистой прибыли для корпорации, прогнозирование структурных и покупок, определение его чувствительности к различным типам рисков (например, изменение процентной ставки и изменение курсов обмена валют).
-
Для определения оптимальной емкости растений для каждого растения Будет использована омывная химя.
-
Для моделирования и оптимального снижения риска обмена валюты профессиональный менеджер и менеджер использует моделирование.
-
В Sears используется моделирование, чтобы определить, сколько единиц каждой строки товаров следует заказать у поставщиков ( например, количество пар поставщиков Dockers, которые должны быть заказано в этом году).
-
В компаниях, работающих с экспортом, используются неявные условия, чтобы получить «реальные параметры», например значение варианта для расширения, срыв или отложенного проекта.
-
Финансовые планировщики используют метод Монте-Карло для определения оптимальных стратегий инвестиций для выхода клиентов из системы.
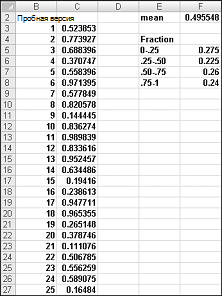
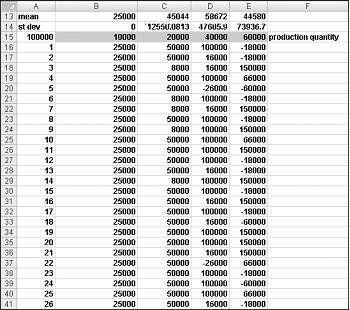
При введите формулу =СЛЛ() в ячейку, вы получаете число, которое с равной вероятностью будет принимать любое значение от 0 до 1. Таким образом, примерно 25 процентов времени должно получить число, меньшее или равное 0,25; примерно 10 процентов времени, когда нужно получить число не менее 0,90, и так далее. Чтобы продемонстрировать, как работает функция СЛЛ, посмотрите на Randdemo.xlsx, показанную на рисунке 60-1.
Примечание: При Randdemo.xlsx файла случайные числа, показанные на рисунке 60-1, не будут одинаковыми. Функция СЛЧИС всегда автоматически пересчитирует числа, которые она генерирует при открытие или при входе на него новых данных.
Сначала скопируйте формулу =СЛДД()из ячейки C3 в ячейку C4:C402. Затем назовем диапазон C3:C402 Data (ДанныеC3:C402). Затем в столбце F можно отследить среднее значение 400 случайных чисел (ячейка F2) и использовать функцию СЧЁТЕIF для определения дробей от 0 до 0,25, 0,25 и 0,50, 0,50 и 0,75 и 0,75 и 1. При нажатии клавиши F9 пересчитываются случайные числа. Обратите внимание на то, что среднее значение 400 чисел всегда составляет приблизительно 0,5, а 25 процентов результатов находятся с интервалами 0,25. Эти результаты соответствуют определению случайного числа. Кроме того, обратите внимание на то, что значения, генерируемые СЛ RAND в разных ячейках, являются независимыми. Например, если случайное число, сгенеризированное в ячейке C3, является большим числом (например, 0,99), оно ничего не сообщает нам о значениях других сгенеремых случайных чисел.
Предположим, что запрос календаря регулируется следующей дискретной случайной переменной:
|
Спрос |
Вероятность |
|
10 000 |
0,10 |
|
20 000 |
0.35 |
|
40,000 |
0,3 |
|
60 000 |
0,25 |
Как можно многократно Excel или имитировать это требование к календарям? Все возможные значения функции СЛ RAND можно связать с запросами календарей. Следующее задание гарантирует, что потребность в 10 000 будет выполняться в 10 процентов времени и так далее.
|
Спрос |
Назначенное случайное число |
|
10 000 |
Меньше 0,10 |
|
20 000 |
Больше или равно 0,10 и меньше 0,45 |
|
40,000 |
Больше или равно 0,45 и меньше 0,75 |
|
60 000 |
Больше или равно 0,75 |
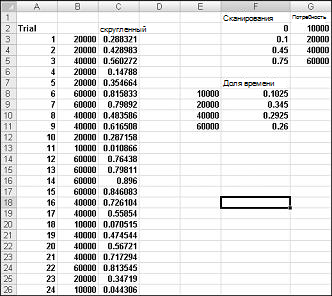
Чтобы показать, как выглядит потребность, посмотрите на файл Discretesim.xlsx, показанный на рисунке 60-2 на следующей странице.
Ключ к нашему моделированию — использовать случайное число для инициировать подставку из диапазона таблицы F2:G5 (именоваемого подсмотра). Случайные числа, которые больше или равны 0 и меньше 0,10, при этом будет требоваться 10 000; случайные числа, которые больше или равны 0,10 и меньше 0,45, будут требоваться 20 000; случайные числа, которые больше или равны 0,45 и меньше 0,75, будут требоваться 40 000; и случайные числа, которые больше или равны 0,75, при этом будет требоваться 60 000. Вы создаете 400 случайных чисел, копируя формулу СЛДД()из C3 в C4:C402. Затем вы создаете 400 пробных испытаний или итерации по запросу календаря, скопируя формулу В.В.В402 из B3 в B4:B402. Эта формула гарантирует, что любое случайное число меньше 0,10 создает запрос в 10 000, любое случайное число в период от 0,10 до 0,45 создает запрос на 20 000 и так далее. В диапазоне ячеок F8:F11 с помощью функции СЧЁТЕФ можно определить долю 400 итерации, которая дает каждому запросу. При нажатии F9 для пересчета случайных чисел имитация вероятностей ближе к предполагаемым вероятностям запроса.
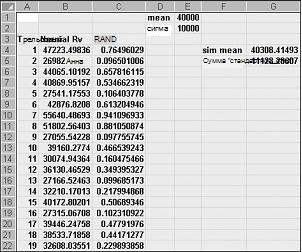
Если ввести в любую ячейку формулу NORMINV(rand(),mu,sigma),будет сгенерировано имитация нормальной случайной переменной со значением «мю» и сигмой стандартного отклонения. Эта процедура показана в файле Normalsim.xlsx, показанном на рисунке 60-3.
Предположим, что мы хотим имитировать 400 испытаний или итерации для обычной случайной переменной со значением 40 000 и стандартным отклонением 10 000. (Вы можете ввести эти значения в ячейки E1 и E2 и назвать эти ячейки под именем «сигма» соответственно.) При копировании формулы =СЛЛ() из C4 в C5:C403 создается 400 различных случайных чисел. При копировании из B4 в B5:B403 формула НОРМОРВ(C4;mean,sigma) генерирует 400 различных пробных значений из обычной случайной переменной со значением 40 000 и стандартным отклонением 10 000. При нажатии клавиши F9 для пересчета случайных чисел их значение остается близко к 40 000, а стандартное отклонение близко к 10 000.
По сути, для случайного числа x формула НОРМОНОРМКВ(p,му,сигма) генерирует p-юпроцентиль нормальной случайной переменной со значением «му» и сигмой стандартного отклонения. Например, случайное число 0,77 в ячейке C4 (см. рисунок 60-3) создает в ячейке B4 примерно 77-ю процентиль нормальной случайной переменной со значением 40 000 и стандартным отклонением 10 000.
В этом разделе вы увидите, как метод методом принятия решений можно использовать метод Монте-Карло. Предположим, что потребность в открытке «День Валентинки» регулируется следующей дискретной случайной переменной:
|
Спрос |
Вероятность |
|
10 000 |
0,10 |
|
20 000 |
0.35 |
|
40,000 |
0,3 |
|
60 000 |
0,25 |
Открытка продается за 4,00 долларов США, а переменная стоимость создания каждой карточки составляет 1,50 долларов США. Остаточные карточки необходимо удалять по цене 0,20 долларов США на карточку. Сколько карточек нужно распечатать?
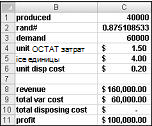
Фактически мы имитируем все возможные количества (10 000, 20 000, 40 000 или 60 000) многократно (например, 1000 итераций). Затем мы определяем, какой объем заказов дает максимальную среднюю прибыль за 1000 итерации. Данные для этого раздела можно найти в файле Valentine.xlsx, показанном на рисунке 60-4. Имена диапазонов в ячейках B1:B11 назначаются ячейкам C1:C11. Диапазону ячеев G3:H6 назначена подпапь с именем. Наши параметры цены и стоимости продаж ввели в ячейки C4:C6.
В ячейку C1 можно ввести пробное производственное количество (в данном примере — 40 000). Затем создайте случайное число в ячейке C2 с помощью формулы =СЛП(). Как было описано выше, имитация запроса на карточку в ячейке C3 с помощью формулы ВЛОП(сл,просмотр;2). (В формуле ВЛП слдд — это имя ячейки, назначенное ячейке C3, а не функции СЛЛ.)
Количество проданных единиц меньше количества и потребности в продукции. В ячейке C8 доход вычисляется с помощью формулы МИН(произведено,потребность)*unit_price. В ячейке C9 суммарные производственные затраты вычисляются с помощью формулы произведено*unit_prod_cost.
Если мы выпускаем больше карт, чем нужно, количество остатых единиц равно производственному минус потребностью; в противном случае единицы не будут оставлены. Затраты на удаление вычисляются в ячейке C10 с помощью формулы unit_disp_cost*ЕСЛИ(произведено>,произведено-потребность;0). Наконец, в ячейке C11 мы вычисляем прибыль как доход — total_var_cost-total_disposing_cost.
Мы хотели бы эффективно нажимать F9 много раз (например, 1000) для каждого производственного количества, а также обработать ожидаемую прибыль для каждого из них. Это ситуация, в которой нам приходит на помощь двустоятельная таблица данных. (Подробные сведения о таблицах данных см. в главе 15 «Анализ конфиденциальности с таблицами данных».) Таблица данных, используемая в этом примере, показана на рисунке 60-5.
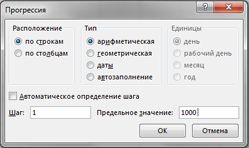
В диапазоне ячеев A16:A1015 введите числа от 1 до 1000 (соответствует 1000 испытаний). Один из простых способов создать эти значения — начать с ввода 1 в ячейку A16. Вы выберите ячейку, а затем на вкладке Главная в группе Редактирование нажмите кнопку Заливка ивыберите ряд, чтобы отобразить диалоговое окно Ряд. В диалоговом окне Ряд, показанном на рисунке 60–6, введите шаг 1 и значение остановки 1000. В области Ряд выберите параметр Столбцы и нажмите кнопку ОК. Числа от 1 до 1000 будут введены в столбец A, начиная с ячейки A16.
Далее мы введите возможные производственные объемы (10 000, 20 000, 40 000, 60 000) в ячейки B15:E15. Мы хотим вычислить прибыль для каждого пробного номера (от 1 до 1000) и для каждого производственного количества. Мы ссылаемся на формулу прибыли (вычисляемую в ячейке C11) в левой верхней ячейке таблицы данных (A15), введите =C11.
Теперь мы готовы обманным Excel, чтобы совместить 1000 итераций запроса для каждого производственного количества. Выберем диапазон таблицы (A15:E1014), а затем в группе Средства данных на вкладке Данные нажмите кнопку Анализ «что если» и выберите таблицу данных. Чтобы настроить двухстолевую таблицу данных, выберите производственное количество (ячейка C1) в качестве ячейки ввода строки, а в качестве ячейки ввода столбца выберите любую пустую ячейку (выбрана ячейка I14). Нажав кнопку ОК, Excel сымитировать 1000 значений запроса для каждого количества заказов.
Чтобы понять, почему это работает, рассмотрите значения из таблицы данных в диапазоне ячеев C16:C1015. Для каждой из этих ячеек Excel будет использовать значение 20 000 в ячейке C1. В ячейке C16 значение ячейки ввода 1 помещается в пустую ячейку, а случайное число в ячейке C2 пересчитыется. Соответствующая прибыль будет записана в ячейке C16. Затем значение ячейки столбца 2 помещается в пустую ячейку, а случайное число в ячейке C2 повторно пересчитыется. Соответствующий доход будет введен в ячейку C17.
Копируя формулу СРЦЕН(B16:B1015)из ячейки B13 в ячейку C13:E13, мы вычисляем среднюю имитацию прибыли для каждого производственного количества. Копируя формулу СТАНДEV(B16:B1015)из ячейки B14 в ячейку C14:E14, мы вычисляем стандартное отклонение имитации прибыли для каждого количества заказов. Каждый раз, когда мы нажимаем F9, 1000 итерации запроса имитация для каждого количества заказов. Создание 40 000 карточек всегда дает наибольший ожидаемый доход. Поэтому, похоже, правильнее всего будет сделать 40 000 карточек.
Влияние риска на наше решение Если мы выпустили 20 000 вместо 40 000 карточек, ожидаемая прибыль снижается примерно на 22 процента, а риск (в виде стандартного отклонения прибыли) — почти 73 процента. Поэтому, если мы высмеем риск, то лучше всего получить 20 000 карточек. К сожалению, при создании 10 000 карточек стандартное отклонение всегда составляет 0, так как если мы выготовим 10 000 карточек, мы всегда будем продавать все без остатка.
Примечание: В этой книге параметр Вычисление имеет параметр Автоматически, кроме таблиц. (Используйте команду Вычисление в группе Вычисления на вкладке Формулы.) Этот параметр гарантирует, что таблица данных не будет повторно пересчитироваться, если только не нажмем F9. Это хорошая идея, так как при каждом введите данные в таблицу с большими данными. Обратите внимание на то, что в этом примере при нажатии F9 будет меняться его пример. Это происходит потому, что при каждом нажатии F9 для создания требований для каждого количества заказов используется другая последовательность из 1000 случайных чисел.
Доверительный интервал для «Промежуток прибыли» В такой ситуации естественно задать вопрос: с какого интервала мы на 95 процентов уверены в том, что будет выпадет настоящая убывая убывляемая прибыль? Этот интервал называется доверительный интервал в 95 процентов для доходности. Доверительный интервал в 95 процентов для всех результатов моделирования вычисляется по следующей формуле:
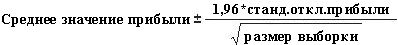
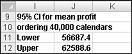
В ячейке J11 вычисляется нижний предел доверительных интервалов в 95 процентов для получения 40 000 календарей с формулой D13–1,96*D14/SQRT(1000). В ячейке J12 для вычисления верхнего предела доверительный интервал в 95 процентов вычисляется с помощью формулы D13+1,96*D14/SQRT(1000). Эти вычисления показаны на рисунке 60-7.
Мы 95 процентов уверены, что при заказе 40 000 календарей мы можем получить сумму от 56 687 до 62 589 рублей.
-
По мнению эксперта, потребность в 2005 ярлах будет нормально распределена со стандартным отклонением 200 и 30. Его стоимость получения 15 000 рублей, а он продает его за 40 000 рублей. Половина всех товаров, которые не продаются по полной цене, можно продать за 30 000 рублей. Он рассматривает возможность заказа 200, 220, 240, 260, 280 или 300 . Сколько нужно заказать?
-
Небольшая группа пытается определить, сколько копий журнала «Люди» следует заказывать каждую неделю. Они считают, что запросы на людей регулируются следующей дискретной случайной переменной:
Спрос
Вероятность
15
0,10
20
0.20
25
0.30
30
0,25
35
0,15
-
При этом за каждую копию «Люди» будет выплачиваться по 1,00 долларов США, а затем продается за 1,95 долларов США. Каждую непроданную копию можно вернуть за 0,50 долларов США. Сколько копий людей должны быть заказана в магазине?
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Нужна дополнительная помощь?
| Срок выполнения | от 1 дня |
| Цена | от 100 руб./задача |
| Предоплата | 50 % |
| Кто будет выполнять? | преподаватель или аспирант |
ЗАКАЗАТЬ РЕШЕНИЕ ЗАДАЧ МЕТОДОМ МОНТЕ-КАРЛО
Один из самых прикладных методов статистической оценки риска. К нему нужно отнестись с большим участием. В данной статье будет рассмотрен пример имитационного моделирования с использованием данного подхода.
Метод Монте-Карло получил своё название за то, что предназначен осуществить оценку предельно случайных событий. А что, как ни казино, которых в Монте-Карло много, связано со случайностью больше всего?
В процессе работы нам понадобится «генератор случайных чисел» из MS Excel и функция «Описательная статистика».
Оценка риска инвестиционного проекта
Есть следующие условия задачи:
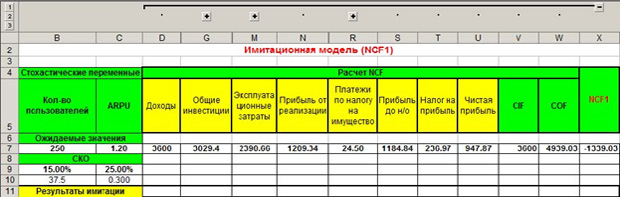
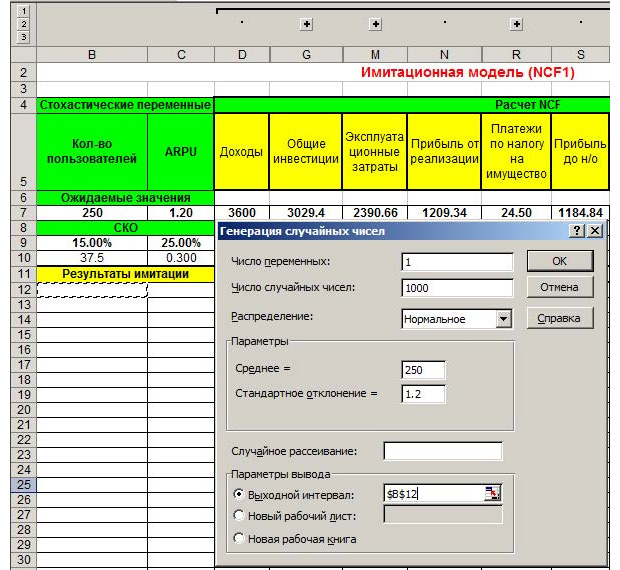
Таким образом, нам нужно оценить три периода – за три года. Запишем все исходные данные в таблицу. Значения, полученные в ячейках D5-X5, имеют формулу для вычисления или есть в условиях задачи. Вы, как экономист, с формулами должны быть знакомы. Обратите внимание на заголовок, выделенный красным цветом на рисунке ниже – «Имитационная модель NCF1». Это говорит о том, что мы имитируем первый год, а всего их будет три на разных листах в MS Excel. На новый лист переключиться внизу окна программы.
Теперь в MS Excel переключаемся на «Данные» и выбираем пункт «Анализ данных».
В появившемся окне выбираем «Генерация случайных чисел». Выполняем генерацию с параметрами, продемонстрированными на картинке ниже, для пункта «Кол-во пользователей».
Параметры будут отталкиваться от среднего значения 250, оно есть в ожидаемых значениях в нашей таблице. Нужно выполнить 1000 генераций. Если вы знакомы со статистикой, то понимаете, что большее количество испытаний даёт более точную оценку. Используя метод Монте-Карло, можно имитировать и 10 000 значений для большей точности.
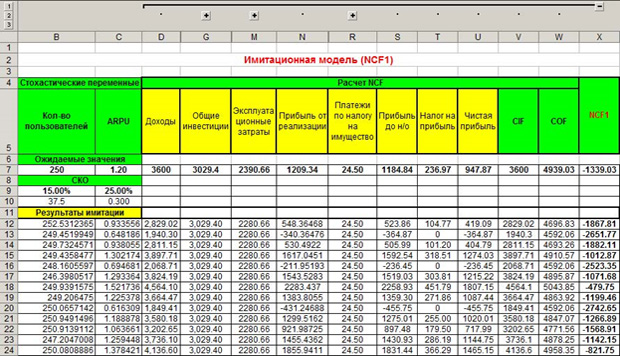
После мы имитируем все стохастические, то есть, меняющиеся значения по аналогии, как показано выше. Копируем формулы переменных или констант из ячеек D7-X7 под «Результаты имитации» с учетом имитированных значений. Получаем следующий результат.
Как видим, платежи по налогам за имущество, например, являются постоянным значением на весь год, поэтому это значение везде одинаковое, а другие меняются, потому что рассчитываются по формулам, и в эти формулы входят меняющиеся значение, имитированные нами. Не забывайте, что значений в каждом столбце должно быть по тысяче.
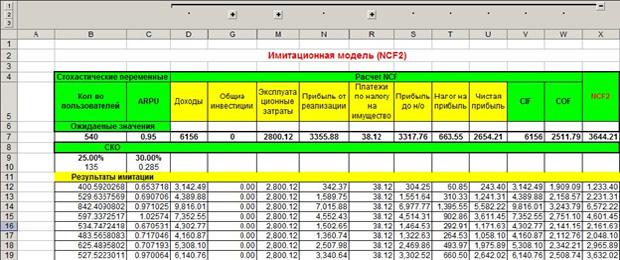
Теперь делаем то же самое, но для имитационной модели NCF2.
Это второй год работы проекта. Как видим, под «СКО» процентные соотношения увеличились. Об этом говорится в условии задачи, что налоги и зарплата должны расти каждый год.
Повторяем это действие в третий раз, увеличивая налоги и зарплаты, как говорит условие.
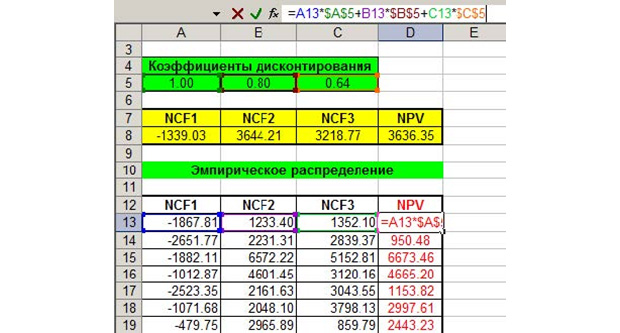
Наибольшую важность в оценке инвестиционного проекта имеет параметр NCF – чистый денежный поток. Копируем все значения NCF на четвертый лист с каждой из трёх предыдущих страниц.
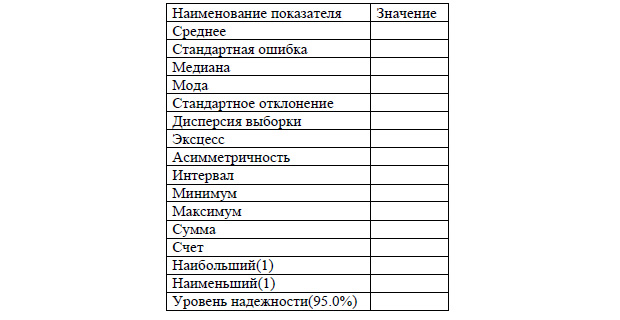
Формула для расчета NPV есть вверху картинки. Используем её. Теперь точно так же заходим в «Данные», жмём на «Анализ данных» и выбираем там «Описательная статистика». Вот, что в появившемся окне вам нужно указать.
Во входном интервале выбирается 1000 полученных значений NPV. Выходной интервал можете выбрать произвольно. На выходе у вас будет таблица со статистическими данными.
Вы, как экономист, должны понимать, о чем говорит каждое значение, если нет, то нужно прочитать отдельную статью или главу учебника. Наша статья о том, метод Монте-Карло применяется с использованием функций MS Excel.
Заключение
Генерация случайных чисел – наше всё. Именно в оценке того, к чему может привести случайность, заключается статистический метод Монте-Карло. Это работает не только в экономике, но и везде, где есть случайность. Можете посмотреть, как это делается, применительно к зоологии в видео ниже.
Содержание
- 1 Оценка риска инвестиционного проекта
- 2 Заключение
- 3 Моделирование Монте-Карло
- 4 Игра в кости
- 5 Шаг 1: События прокатки в кости
- 6 Шаг 2: Диапазон результатов
- 7 Шаг 3: Выводы
- 8 Шаг 4: Количество рулонов кости
- 9 Шаг 5: Моделирование
- 10 Шаг 6: Вероятность
| Срок выполнения | от 1 дня |
| Цена | от 100 руб./задача |
| Предоплата | 50 % |
| Кто будет выполнять? | преподаватель или аспирант |
ЗАКАЗАТЬ РЕШЕНИЕ ЗАДАЧ МЕТОДОМ МОНТЕ-КАРЛО
Один из самых прикладных методов статистической оценки риска. К нему нужно отнестись с большим участием. В данной статье будет рассмотрен пример имитационного моделирования с использованием данного подхода.
Метод Монте-Карло получил своё название за то, что предназначен осуществить оценку предельно случайных событий. А что, как ни казино, которых в Монте-Карло много, связано со случайностью больше всего?
В процессе работы нам понадобится «генератор случайных чисел» из MS Excel и функция «Описательная статистика».
Оценка риска инвестиционного проекта
Есть следующие условия задачи:
Таким образом, нам нужно оценить три периода – за три года. Запишем все исходные данные в таблицу. Значения, полученные в ячейках D5-X5, имеют формулу для вычисления или есть в условиях задачи. Вы, как экономист, с формулами должны быть знакомы. Обратите внимание на заголовок, выделенный красным цветом на рисунке ниже – «Имитационная модель NCF1». Это говорит о том, что мы имитируем первый год, а всего их будет три на разных листах в MS Excel. На новый лист переключиться внизу окна программы.
Теперь в MS Excel переключаемся на «Данные» и выбираем пункт «Анализ данных».
В появившемся окне выбираем «Генерация случайных чисел». Выполняем генерацию с параметрами, продемонстрированными на картинке ниже, для пункта «Кол-во пользователей».
Параметры будут отталкиваться от среднего значения 250, оно есть в ожидаемых значениях в нашей таблице. Нужно выполнить 1000 генераций. Если вы знакомы со статистикой, то понимаете, что большее количество испытаний даёт более точную оценку. Используя метод Монте-Карло, можно имитировать и 10 000 значений для большей точности.
После мы имитируем все стохастические, то есть, меняющиеся значения по аналогии, как показано выше. Копируем формулы переменных или констант из ячеек D7-X7 под «Результаты имитации» с учетом имитированных значений. Получаем следующий результат.
Как видим, платежи по налогам за имущество, например, являются постоянным значением на весь год, поэтому это значение везде одинаковое, а другие меняются, потому что рассчитываются по формулам, и в эти формулы входят меняющиеся значение, имитированные нами. Не забывайте, что значений в каждом столбце должно быть по тысяче.
Теперь делаем то же самое, но для имитационной модели NCF2.
Это второй год работы проекта. Как видим, под «СКО» процентные соотношения увеличились. Об этом говорится в условии задачи, что налоги и зарплата должны расти каждый год.
Повторяем это действие в третий раз, увеличивая налоги и зарплаты, как говорит условие.
Наибольшую важность в оценке инвестиционного проекта имеет параметр NCF – чистый денежный поток. Копируем все значения NCF на четвертый лист с каждой из трёх предыдущих страниц.
Формула для расчета NPV есть вверху картинки. Используем её. Теперь точно так же заходим в «Данные», жмём на «Анализ данных» и выбираем там «Описательная статистика». Вот, что в появившемся окне вам нужно указать.
Во входном интервале выбирается 1000 полученных значений NPV. Выходной интервал можете выбрать произвольно. На выходе у вас будет таблица со статистическими данными.
Вы, как экономист, должны понимать, о чем говорит каждое значение, если нет, то нужно прочитать отдельную статью или главу учебника. Наша статья о том, метод Монте-Карло применяется с использованием функций MS Excel.
Заключение
Генерация случайных чисел – наше всё. Именно в оценке того, к чему может привести случайность, заключается статистический метод Монте-Карло. Это работает не только в экономике, но и везде, где есть случайность. Можете посмотреть, как это делается, применительно к зоологии в видео ниже.
31.01.2014 Григорий Цапко Бизнес-планирование, Калькуляторы, шаблоны, форматы, Малый бизнес
Предлагаю вашему вниманию шаблон для анализа инвестиционного проекта методом Монте-Карло.
Предлагаемый шаблон на основе анализа инвестиционного проекта служит иллюстрацией реализации метода моделирования получившим название «Монте-Карло». Название метода говорит само за себя: в основе моделирования будущих событий лежит использование большого количества случайных величин.
Подобный метод моделирования событий приемлем в тех случаях, когда существует неопределенность относительно значений тех или иных величин.
Считается, что данный метод был использован в работах над атомной бомбой, когда пытались рассчитать количество обогащённого урана необходимое для производства заряда. Слишком маленькое количество могло не дать развиться цепной реакции, а слишком большое было чревато дополнительными месяцами работы над получением необходимого количества урана.
Итак, мы имеем инвестиционный проект, который будет реализован в течение, предположим, 5 лет.
Нам точно не известна цена за которую мы будем реализовывать нашу продукцию, неизвестно точное количество продукции и неизвестно точное значение переменных затрат на ее производство. Это будут случайные величины.
Однако экспертным путем мы определили некий диапазон, в котором будут лежать эти значения.
Например, цена будет не ниже 30 руб. и не выше 40 руб., количество не меньше 150 и не больше 300 единиц, переменные затраты в диапазоне 15 до 20 руб. Цифры могут быть совершенно различными. Важно то, что мы имеем представление о диапазоне их вероятных значений.
Именно значения в этих диапазонах мы и будем моделировать для оценки общей привлекательности проекта.
Для генерации случайных величин мы будем использовать функцию СЛУЧМЕЖДУ, с указанием в качестве аргументов нижней и верхней границы диапазона.
Полученные величины будут использоваться для расчета денежных потоков и чистой приведенной стоимости проекта (NPV).
Генерируется достаточно большое количество вариантов (опытов) и все они обрабатываются методами статистического анализа. В нашем шаблоне мы используем 5 000 опытов, но их может быть и 1 000 000, правда кардинально на результаты это не повлияет.
Это основная философия данного метода. Далее лишь техника реализации.
На листе «Имитация» указываем диапазоны изменения величин, указываем постоянные параметры проекта, а также формируем таблицу в 5 000 строк.
В каждой строке у нас есть случайное значение объема производства, переменных затрат и цены реализации. Также по каждой строке на основе этих данных рассчитываются такие показатели как выручка, прибыль (за минусом постоянных расходов и налога), денежный поток и чистая приведенная стоимость проекта за 5 лет с учетом заданной ставки дисконтирования.
Далее переходим к анализу полученных результатов.
На листе «Результаты анализа» выводим значение минимума, максимума, среднего значения, стандартного отклонения и коэффициента вариации интересующих нас показателей.
По большому счету, нас интересует показатель NPV.
Для него мы рассчитываем также количество случаев, когда NPV0 для всей совокупности в 5000 опытов.
Вместе с сумой убытков и суммой доходов, эти значения могут дать представление о мере рискованности проекта и масштабе возможных потерь.
Далее, используя стандартное распределение оцениваем вероятность получения того или иного значения NPV. Например, безубыточный проект имеет NPV > 0.
Установив в качестве значения Х (это наше NPV) ноль, мы получим вероятность получения убытка в 3%.
Для определения вероятности используем функцию НОРМ.СТ.РАСП, имеющую следующий синтаксис:
=НОРМ.СТ.РАСП(z,интегральная)
Z Обязательный. Значение, для которого строится распределение.
Интегральная Обязательный. Логическое значение, определяющее форму функции. Если аргумент «интегральная» имеет значение ИСТИНА, функция НОРМ.СТ.РАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается весовая функция распределения.
Для определения значения Z используем функцию НОРМАЛИЗАЦИЯ, имеющую следующий синтаксис:
=НОРМАЛИЗАЦИЯ(x, среднее, стандартное_откл)
x Обязательный. Нормализуемое значение. В нашем случае это NPV.
Среднее Обязательный. Среднее арифметическое распределения.
Стандартное_откл Обязательный. Стандартное отклонение распределения.
Среднее значение и стандартное отклонение для NPV мы рассчитали в таблице «Результаты анализа».
Мы разработаем симуляцию Монте-Карло с использованием Microsoft Excel и игра в кости. Моделирование Монте-Карло — математический численный метод, который использует случайные ничьи для выполнения вычислений и сложных проблем. Сегодня он широко используется и играет ключевую роль в различных областях, таких как финансы, физика, химия, экономика и многие другие.
Моделирование Монте-Карло
Метод Монте-Карло был изобретен Николаем Метрополисом в 1947 году и направлен на решение сложных проблем с использованием случайных и вероятностных методов. Термин «Монте-Карло» происходит от административного района Монако, широко известного как место, где европейские элиты играют в азартные игры. Мы используем метод Монте-Карло, когда проблема слишком сложна и сложна при непосредственном вычислении. Большое количество итераций позволяет моделировать нормальное распределение.
Метод моделирования методом Монте-Карло вычисляет вероятности для интегралов и решает уравнения в частных производных, тем самым вводя статистический подход к риску в вероятностном решении. Несмотря на то, что существует множество современных статистических инструментов для создания симуляций Монте-Карло, проще моделировать нормальный закон и единообразный закон с использованием Microsoft Excel и обходить математические основы.
Для моделирования Монте-Карло мы выделяем ряд ключевых переменных, которые контролируют и описывают результат эксперимента и назначают распределение вероятности после выполнения большого количества случайных выборок. Давайте возьмем игру в кости как модель.
Игра в кости
Вот как игра в кости играется:
• Игрок бросает три кости, которые имеют 6 сторон 3 раза.
• Если общее количество 3 бросков составляет 7 или 11, игрок выигрывает.
• Если общее количество 3 бросков: 3, 4, 5, 16, 17 или 18, проигрыватель проигрывает.
• Если общий результат — любой другой результат, игрок снова играет и повторно свертывает штамп.
• Когда игрок снова бросает кубик, игра продолжается таким же образом, за исключением того, что игрок выигрывает, когда сумма равна сумме, определенной в первом раунде.
Рекомендуется также использовать таблицу данных для генерации результатов. Более того, для подготовки моделирования методом Монте-Карло требуется 5 000 результатов.
Шаг 1: События прокатки в кости
Сначала мы разрабатываем ряд данных с результатами каждого из 3 кубиков для 50 рулонов. Для этого предлагается использовать функцию «RANDBETWEEN (1. 6)». Таким образом, каждый раз, когда мы нажимаем F9, мы генерируем новый набор результатов каротажа. Ячейка «Результат» — это сумма итогов трех рулонов.
.
Шаг 2: Диапазон результатов
Затем нам нужно разработать ряд данных для определения возможных результатов для первого раунда и последующих раундов. Ниже приведен диапазон данных с тремя столбцами.В первом столбце у нас есть числа от 1 до 18. Эти цифры представляют собой возможные результаты после того, как катятся кости 3 раза: максимум составляет 3 * 6 = 18. Вы заметите, что для ячеек 1 и 2 результаты N / A, так как невозможно получить 1 или 2, используя 3 кости. Минимальное значение равно 3.
Во втором столбце включены возможные выводы после первого раунда. Как указано в первоначальном заявлении, либо игрок выигрывает (выигрывает), либо проигрывает (проигрывает), либо повторяет его (Re-roll), в зависимости от результата (всего 3 кубика).
В третьей колонке регистрируются возможные выводы для последующих раундов. Мы можем достичь этих результатов, используя функцию «If. «Это гарантирует, что если полученный результат будет эквивалентен результату, полученному в первом раунде, мы выиграем, иначе мы будем следовать первоначальным правилам первоначальной игры, чтобы определить, будем ли мы повторно бросать кости.
.
Шаг 3: Выводы
На этом этапе мы определяем результат 50 кубиков. Первый вывод можно получить с помощью индексной функции. Эта функция выполняет поиск возможных результатов первого раунда, вывод, соответствующий полученному результату. Например, при получении 6, как это имеет место на рисунке ниже, мы снова играем.
Можно получить результаты других рулонов кости, используя функцию «Or» и функцию индекса, вложенную в функцию «If». Эта функция сообщает Excel: «Если предыдущий результат -« Выиграть или проиграть », перестаньте бросать кости, потому что как только мы выиграли или проиграли, мы закончили. В противном случае мы переходим к столбцу следующих возможных выводов, и мы определяем вывод результата.
…
Шаг 4: Количество рулонов кости
Теперь мы определяем количество бросков кубиков, необходимых до проигрыша или выигрыша. Для этого мы можем использовать функцию «Countif», которая требует, чтобы Excel подсчитывал результаты «Re-Roll» и добавлял номер 1 к ней. Он добавляет один, потому что у нас есть один дополнительный раунд, и мы получаем окончательный результат (выигрываем или проигрываем).
.
Шаг 5: Моделирование
Мы разрабатываем диапазон для отслеживания результатов различных симуляций. Для этого мы создадим три столбца. В первом столбце одна из приведенных цифр — 5 000. Во второй колонке мы будем искать результат после 50 кубиков. В третьем столбце, в заголовке столбца, мы будем искать количество бросков кубиков, прежде чем получить окончательный статус (выиграть или проиграть).
Затем мы создадим таблицу анализа чувствительности с использованием данных характеристик или таблицы данных таблицы (эта чувствительность будет вставлена во вторую таблицу и в третьи столбцы). В этом анализе чувствительности номера событий 1 — 5, 000 должны быть вставлены в ячейку A1 файла. Фактически, можно было выбрать любую пустую ячейку. Идея состоит в том, чтобы просто произвести перерасчет каждый раз и таким образом получить новые броски кубиков (результаты новых симуляций), не повредив формулы на месте.
Шаг 6: Вероятность
Мы можем, наконец, вычислить вероятности выигрыша и проигрыша. Мы делаем это с помощью функции «Countif».Формула подсчитывает количество «выигрышей» и «проиграет», а затем делит на общее количество событий, 5, 000, чтобы получить соответствующую долю одного и другого. Наконец, мы видим, что вероятность получить выигрыш составляет 73. 2%, а результат Lose — 26,8%.
Не так давно я прочитал замечательную книгу Дугласа Хаббарда Как измерить всё, что угодно. Оценка стоимости нематериального в бизнесе. В кратком конспекте книги я обещал, что одному из разделов – Оценка риска: введение в моделирование методом Монте-Карло – я посвящу отдельную заметку. Да всё как-то не складывалось. И вот недавно я стал более внимательно изучать методы управления валютными рисками. В материалах, посвященных этой тематике, часто упоминается моделирование методом Монте-Карло. Так что обещанный материал перед вами.
* * *
Приведу простой пример моделирования методом Монте-Карло для тех, кто никогда не работал с ним ранее, но имеет определенное представление об использовании электронных таблиц Excel.
Предположим, что вы хотите арендовать новый станок. Стоимость годовой аренды станка 400 000 дол., и договор нужно подписать на несколько лет. Поэтому, даже не достигнув точки безубыточности, вы всё равно не сможете сразу вернуть станок. Вы собираетесь подписать договор, думая, что современное оборудование позволит сэкономить на трудозатратах и стоимости сырья и материалов, а также считаете, что материально-техническое обслуживание нового станка обойдется дешевле.
Скачать заметку в формате Word, примеры в формате Excel
Ваши калиброванные специалисты по оценке дали следующие интервалы значений ожидаемой экономии и годового объема производства:
| экономия на материально-техническом обслуживании (maintenance savings, MS) | от 10 до 20 дол. на единицу продукции |
| экономия на трудозатратах (labour savings, LS) | от «–2» до 8 дол. на единицу продукции |
| экономия на сырье и материалах (raw materials savings, RMS) | от 3 до 9 дол. на единицу продукции |
| объем производства (production level, PL) | от 15 000 до 35 000 единиц продукции в год |
| стоимость годовой аренды (точка безубыточности — breakeven) | 400 000 дол. |
Годовая экономия составит: (MS + LS + RMS) х PL
Конечно, этот пример слишком прост, чтобы быть реалистичным. Объем производства каждый год меняется, какие-то затраты снизятся, когда рабочие окончательно освоят новый станок, и т.д. Но мы в этом примере намеренно пожертвовали реализмом ради простоты.
Если мы возьмем медиану (среднее) каждого из интервалов значений, то получим годовую экономию: (15 + 3 + 6) х 25 000 = 600 000 (дол.)
Похоже, что мы не только добились безубыточности, но и получили кое-какую прибыль, но не забывайте – существуют неопределенности. Как же оценить рискованность этих инвестиций? Давайте, прежде всего, определим, что такое риск в данном контексте. Чтобы получить риск, мы должны наметить будущие результаты с присущими им неопределенностями, причем какие-то из них – с вероятностью понести ущерб, поддающийся количественному определению. Один из способов взглянуть на риск – представить вероятность того, что мы не добьемся безубыточности, то есть что наша экономия окажется меньше годовой стоимости аренды станка. Чем больше нам не хватит на покрытие расходов на аренду, тем больше мы потеряем. Сумма 600 000 дол. – это медиана интервала. Как определить реальный интервал значений и рассчитать по нему вероятность того, что мы не достигнем точки безубыточности?
Поскольку точные данные отсутствуют, нельзя выполнить простые расчеты для ответа на вопрос, сможем ли мы добиться требуемой экономии. Есть методы, позволяющие при определенных условиях найти интервал значений результирующего параметра по диапазонам значений исходных данных, но для большинства проблем из реальной жизни такие условия, как правило, не существуют. Как только мы начинаем суммировать и умножать разные типы распределений, задача обычно превращается в то, что математики называют неразрешимой или не имеющей решения обычными математическими методами проблемой. Поэтому взамен мы пользуемся методом прямого подбора возможных вариантов, ставшим возможным благодаря появлению компьютеров. Из имеющихся интервалов мы выбираем наугад множество (тысячи) точных значений исходных параметров и рассчитываем множество точных значений искомого показателя.
Моделирование методом Монте-Карло – превосходный способ решения подобных проблем. Мы должны лишь случайным образом выбрать в указанных интервалах значения, подставить их в формулу для расчета годовой экономии и рассчитать итог. Одни результаты превысят рассчитанную нами медиану 600 000 дол., а другие окажутся ниже. Некоторые будут даже ниже требуемых для безубыточности 400 000 дол.
Вы легко сможете осуществить моделирование методом Монте-Карло на персональном компьютере с помощью программы Excel, но для этого понадобится чуть больше информации, чем 90%-ный доверительный интервал. Необходимо знать форму кривой распределения. Для разных величин больше подходят кривые одной формы, чем другой. В случае 90%-ного доверительного интервала обычно используется кривая нормального (гауссова) распределения. Это хорошо знакомая всем колоколообразная кривая, на которой большинство возможных значений результатов группируются в центральной части графика и лишь немногие, менее вероятные, распределяются, сходя на нет к его краям (рис. 1).
Вот как выглядит нормальное распределение:
Рис.1. Нормальное распределение. По оси абсцисс число сигм.
Особенности:
- значения, располагающиеся в центральной части графика, более вероятны, чем значения по его краям;
- распределение симметрично; медиана находится точно посредине между верхней и нижней границами 90%-ного доверительного интервала (CI);
- «хвосты» графика бесконечны; значения за пределами 90%-ного доверительного интервала маловероятны, но все же возможны.
Для построения нормального распределения в Excel можно воспользоваться функцией =НОРМРАСП(Х; Среднее; Стандартное_откл; Интегральная), где
Х – значение, для которого строится нормальное распределение;
Среднее – среднее арифметическое распределения; в нашем случае = 0;
Стандартное_откл – стандартное отклонение распределения; в нашем случае = 1;
Интегральная – логическое значение, определяющее форму функции; если аргумент «интегральная» имеет значение ИСТИНА, функция НОРМРАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается функция плотности распределения; в нашем случае = ЛОЖЬ.
Говоря о нормальном распределении, необходимо упомянуть о таком связанном с ним понятии, как стандартное отклонение. Очевидно, не все обладают интуитивным пониманием, что это такое, но поскольку стандартное отклонение можно заменить числом, рассчитанным по 90%-ному доверительному интервалу (смысл которого интуитивно понимают многие), я не буду здесь подробно на нем останавливаться. Рисунок 1 показывает, что в одном 90%-ном доверительном интервале насчитывается 3,29 стандартного отклонения, поэтому нам просто нужно будет сделать преобразование.
В нашем случае следует создать в электронной таблице генератор случайных чисел для каждого интервала значений. Начнем, например, с MS – экономии на материально-техническом обслуживании. Воспользуемся формулой Excel: =НОРМОБР(вероятность;среднее;стандартное_откл), где
Вероятность – вероятность, соответствующая нормальному распределению;
Среднее – среднее арифметическое распределения;
Стандартное_откл – стандартное отклонение распределения.
В нашем случае:
Среднее (медиана) = (Верхняя граница 90%-ного CI + Нижняя граница 90%-ного СI)/2;
Стандартное отклонение = (Верхняя граница 90%-ного CI – Нижняя граница 90%-ного СI)/3,29.
Для параметра MS формула имеет вид: =НОРМОБР(СЛЧИС();15;(20-10)/3,29), где
СЛЧИС – функция, генерирующая случайные числа в диапазоне от 0 до 1;
15 – среднее арифметическое диапазона MS;
(20-10)/3,29 = 3,04 – стандартное отклонение; напомню, что смысл стандартного отклонения в следующем: в интервал 3,29*Стандарт_откл, расположенный симметрично относительного среднего, попадает 90% всех значений случайной величины (в нашем случае MS)
Распределение величины экономии на материально-техническом обслуживании для 100 случайных нормально распределенных значений:
Рис. 2. Вероятность распределения MS по диапазонам значений; о том, как построить такое распределение с помощью сводной таблицы см. Вычисления в сводной таблице (в области значений) в Excel 2013
Поскольку мы использовали «лишь» 100 случайных значений, распределение получилось не таким уж и симметричным. Тем не менее, около 90% значений попали в диапазон экономии на MS от 10 до 20 долл. (если быть точным, то 91%).
Построим таблицу на основе доверительных интервалов параметров MS, LS, RMS и PL (рис. 3). Два последних столбца показывают результаты расчетов на основе данных других столбцов. В столбце «Общая экономия» показана годовая экономия, рассчитанная для каждой строки. Например, в случае реализации сценария 1 общая экономия составит (14,3 + 5,8 + 4,3) х 23 471 = 570 834 долл. Столбец «Достигается ли безубыточность?» вам на самом деле не нужен. Я включил его просто для информативности. Создадим в Excel 10 000 строк-сценариев.
Рис. 3. Расчет сценариев методом Монте-Карло в Excel
Чтобы оценить полученные результаты, можно использовать, например, сводную таблицу, которая позволяет подсчитать число сценариев в каждом 100-тысячном диапазоне. Затем вы строите график, отображающий результаты расчета (рис. 4). Этот график показывает, какая доля из 10 000 сценариев будут иметь годовую экономию в том или ином интервале значений. Например, около 3% сценариев дадут годовую экономию более 1М дол.
Рис. 4. Распределение общей экономии по диапазонам значений. По оси абсцисс отложены 100-тысячные диапазоны размера экономии, а по оси ординат доля сценариев, приходящихся на указанный диапазон
Из всех полученных значений годовой экономии примерно 15% будут меньше 400К дол. Это означает, что вероятность ущерба составляет 15%. Данное число и представляет содержательную оценку риска. Но риск не всегда сводится к возможности отрицательной доходности инвестиций. Оценивая размеры вещи, мы определяем ее высоту, массу, обхват и т.д. Точно так же существуют и несколько полезных показателей риска. Дальнейший анализ показывает: есть 4%-ная вероятность того, что завод вместо экономии будет терять ежегодно по 100К дол. Однако полное отсутствие доходов практически исключено. Вот что подразумевается под анализом риска – мы должны уметь рассчитывать вероятности ущерба разного масштаба. Если вы действительно измеряете риск, то должны делать именно это.
В некоторых ситуациях можно пойти более коротким путем. Если все распределения значений, с которыми мы работаем, будут нормальными и нам надо просто сложить интервалы этих значений (например, интервалы затрат и выгод) или вычесть их друг из друга, то можно обойтись и без моделирования методом Монте-Карло. Когда необходимо суммировать три вида экономии из нашего примера, следует провести простой расчет. Чтобы получить искомый интервал, используйте шесть шагов, перечисленных ниже:
1) вычтите среднее значение каждого интервала значений из его верхней границы; для экономии на материально-техническом обслуживании 20 – 15 = 5 (дол.), для экономии на трудозатратах – 5 дол. и для экономии на сырье и материалах – 3 дол.;
2) возведите в квадрат результаты первого шага 52 = 25 (дол.) и т.д.;
3) суммируйте результаты второго шага 25 + 25 + 9 = 59 (дол.);
4) извлеките квадратный корень из полученной суммы: получится 7,7 дол.;
5) сложите все средние значения: 15 + 3 + 6 = 24 (дол.);
6) прибавьте к сумме средних значений результат шага 4 и получите верхнюю границу диапазона: 24 + 7,7 = 31,7 дол.; вычтите из суммы средних значений результат шага 4 и получите нижнюю границу диапазона 24 – 7,7 = 16,3 дол.
Таким образом, 90%-ный доверительный интервал для суммы трех 90%-ных доверительных интервалов по каждому виду экономии составляет 16,3–31,7 дол.
Мы использовали следующее свойство: размах суммарного интервала равен квадратному корню из суммы квадратов размахов отдельных интервалов .
Иногда нечто похожее делают, суммируя все «оптимистические» значения верхней границы и «пессимистические» значения нижней границы интервала. В данном случае мы получили бы на основе наших трех 90%-ных доверительных интервалов суммарный интервал 11–37 дол. Этот интервал несколько шире, чем 16,3–31,7 дол. Когда такие расчеты выполняются при обосновании проекта с десятками переменных, расширение интервала становится чрезмерным, чтобы его игнорировать. Брать самые «оптимистические» значения для верхней границы и «пессимистические» для нижней – все равно что думать: бросив несколько игральных костей, мы во всех случаях получим только «1» или только «6». На самом же деле выпадет некое сочетание низких и высоких значений. Чрезмерное расширение интервала – распространенная ошибка, которая, несомненно, часто приводит к принятию необоснованных решений. В то же время описанный мной простой метод прекрасно работает, когда у нас есть несколько 90%-ных доверительных интервалов, которые необходимо суммировать.
Однако наша цель не только суммировать интервалы, но и умножить их на объем производства, значения которого также даны в виде диапазона. Простой метод суммирования годится только для вычитания или сложения интервалов значений.
Моделирование методом Монте-Карло требуется и тогда, когда не все распределения являются нормальными. Хотя другие типы распределений не входят в предмет данной книги, упомянем о двух из них — равномерном и бинарном (рис. 5, 6).
Рис. 5. Равномерное распределение (не идеальное, а построенное с помощью функции СЛЧИС в Excel)
Особенности:
- вероятность всех значений одинакова;
- распределение симметрично, без перекосов; медиана находится точно посредине между верхней и нижней границами интервала;
- значения за пределами интервала невозможны.
Для построения данного распределения в Excel была использована формула: СЛЧИС()*(UB – LB) + LB, где UB – верхняя граница; LB – нижняя граница; с последующим разбиением всех значений на диапазоны с помощью сводной таблицы.
Рис. 6. Бинарное распределение (распределение Бернулли)
Особенности:
- возможны только два значения;
- существует единственная вероятность одного значения (в данном случае 60%); вероятность другого значения равна единице минус вероятность первого значения
Для построения случайного распределения данного вида в Excel использовалась функция: =ЕСЛИ(СЛЧИС()
A Monte Carlo simulation can be developed using Microsoft Excel and a game of dice. A Monte Carlo simulation is a method for modeling probabilities by using random numbers to approximate and simulate possible outcomes. Today, it is widely used as an analysis tool. It plays a key part in various fields such as finance, physics, chemistry, and economics.
Key Takeaways
- The Monte Carlo method seeks to improve the analysis of data using random data sets and probability calculations.
- A Monte Carlo simulation can be developed using Microsoft Excel and a game of dice.
- A data table can be used to generate the results—a total of5,000 results are needed to prepare the Monte Carlo simulation.
Monte Carlo Simulation
The Monte Carlo method was invented by John von Neumann and Stanislaw Ulam in the 1940s and seeks to solve complex problems using random and probabilistic methods. The term Monte Carlo refers the administrative area of Monaco popularly known as a place where European elites gamble.
The Monte Carlo simulation method computes the probabilities for integrals and solves partial differential equations, thereby introducing a statistical approach to risk in a probabilistic decision. Although many advanced statistical tools exist to create Monte Carlo simulations, it is easier to simulate the normal law and the uniform law using Microsoft Excel and bypass the mathematical underpinnings.
When to Use the Monte Carlo Simulation
We use the Monte Carlo method when a problem is too complex and difficult to do by direct calculation. Using the simulation can help provide solutions for situations that prove uncertain. A large number of iterations allows a simulation of the normal distribution. It can also be used to understand how risk works, and to comprehend the uncertainty in forecasting models.
As noted above, the simulation is often used in many different disciplines including finance, science, engineering, and supply chain management—especially in cases where there are far too many random variables in play. For example, analysts may use Monte Carlo simulations in order to evaluate derivatives including options or to determine risks including the likelihood that a company may default on its debts.
Game of Dice
For the Monte Carlo simulation, we isolate a number of key variables that control and describe the outcome of the experiment, then assign a probability distribution after a large number of random samples is performed. In order to demonstrate, let’s take a game of dice as a model. Here’s how the dice game rolls:
• The player throws three dice that have six sides three times.
• If the total of the three throws is seven or 11, the player wins.
• If the total of the three throws is: three, four, five, 16, 17, or 18, the player loses.
• If the total is any other outcome, the player plays again and re-rolls the dice.
• When the player throws the dice again, the game continues in the same way, except that the player wins when the total is equal to the sum determined in the first round.
It is also recommended to use a data table to generate the results. Moreover, 5,000 results are needed to prepare the Monte Carlo simulation.
To prepare the Monte Carlo simulation, you need 5,000 results.
Step 1: Dice Rolling Events
First, we develop a range of data with the results of each of the three dice for 50 rolls. To do this, it is proposed to use the «RANDBETWEEN(1,6)» function. Thus, each time we click F9, we generate a new set of roll results. The «Outcome» cell is the sum total of the results from the three rolls.
Step 2: Range of Outcomes
Then, we need to develop a range of data to identify the possible outcomes for the first round and subsequent rounds. There is a three-column data range. In the first column, we have the numbers one to 18. These figures represent the possible outcomes following rolling the dice three times: The maximum being 3 x 6 = 18. You will note that for cells one and two, the findings are N/A since it is impossible to get a one or a two using three dice. The minimum is three.
In the second column, the possible conclusions after the first round are included. As stated in the initial statement, either the player wins (Win) or loses (Lose), or they replay (Re-roll), depending on the result (the total of three dice rolls).
In the third column, the possible conclusions to subsequent rounds are registered. We can achieve these results using the «IF» function. This ensures that if the result obtained is equivalent to the result obtained in the first round, we win, otherwise we follow the initial rules of the original play to determine whether we re-roll the dice.
Step 3: Conclusions
In this step, we identify the outcome of the 50 dice rolls. The first conclusion can be obtained with an index function. This function searches the possible results of the first round, the conclusion corresponding to the result obtained. For example, when we roll a six, we play again.
One can get the findings of other dice rolls, using an «OR» function and an index function nested in an «IF» function. This function tells Excel, «If the previous result is Win or Lose,» stop rolling the dice because once we have won or lost we are done. Otherwise, we go to the column of the following possible conclusions and we identify the conclusion of the result.
Step 4: Number of Dice Rolls
Now, we determine the number of dice rolls required before losing or winning. To do this, we can use a «COUNTIF» function, which requires Excel to count the results of «Re-roll» and add the number one to it. It adds one because we have one extra round, and we get a final result (win or lose).
Step 5: Simulation
We develop a range to track the results of different simulations. To do this, we will create three columns. In the first column, one of the figures included is 5,000. In the second column, we will look for the result after 50 dice rolls. In the third column, the title of the column, we will look for the number of dice rolls before obtaining the final status (win or lose).
Then, we will create a sensitivity analysis table by using the feature data or Table Data table (this sensitivity will be inserted in the second table and third columns). In this sensitivity analysis, the numbers of events of one to 5,000 must be inserted into cell A1 of the file. In fact, one could choose any empty cell. The idea is simply to force a recalculation each time and thus get new dice rolls (results of new simulations) without damaging the formulas in place.
Step 6: Probability
We can finally calculate the probabilities of winning and losing. We do this using the «COUNTIF» function. The formula counts the number of «win» and «lose» then divides by the total number of events, 5,000, to obtain the respective proportion of one and the other. We finally see that the probability of getting a Win outcome is 73.2% and getting a Lose outcome is therefore 26.8%.
Просмотров 2.9к. Опубликовано 28.07.2021
Обновлено 29.07.2021
Метод Монте-Карло назван в честь района Монако, известного своими казино. В этой статье мы будем использовать метод Монте-Карло для изучения зависимости эффективности ставок от фактора везения.
Что такое метод Монте-Карло?
Метод Монте-Карло используется в тех случаях, когда применение других математических подходов сопряжено с большим количеством трудностей.
Суть метода заключается в многократном использовании генератора случайных чисел. На основе полученных данных вычисляются вероятности в рассматриваемом процессе.
Он особенно полезен тем бетторам, которые в меньшей степени осведомлены о традиционных методах статистического тестирования, поскольку не требует обширных математических знаний.
Анализ эффективности ставок
Допустим, есть история из 1500 ставок одинакового размера с доходностью (Yield) 0,85 %. Но как понять, является ли это оправданной закономерностью или же результатом влияния удачи или невезения?
Смотрите также: Что такое ROI и Yield (доходность)
Первый шаг предполагает сравнение этой величины со значением математического ожидания. Концепция используемой методологии предполагает оценку справедливого коэффициента каждой ставки и, следовательно, величины ценности (валуйности).
Например, коэффициент букмекера 2,10 при справедливом коэффициенте 2,00 содержит ценность (value) 5 % или 1,05 (рассчитанное путем деления 2,10 ⁄ 2,00).
Справедливый (или объективный) коэффициент 2,00 предполагает вероятность выигрыша 50 %. Если сделать 100 ставок, 50 из которых будут выигрышными (прибыль по каждой ставке 1,10 доллара), а 50 — проигрышными (убыток по каждой ставке — 1 доллар), то размер чистой прибыли составит 5 долл. (или 5 % от оборота в 100 долл.).
Аналогичным образом, КФ букмекера 3,30 при справедливом коэффициенте 2,95 будет содержать ценность 11,8 %. В приведенной ниже таблице представлены данные прогнозирования.
| Матч | Ставка | Кэф БК | Справедливый КФ | Валуйность |
|---|---|---|---|---|
| Рубин — Спартак | П2 | 2,1 | 1,9 | 10,5% |
| Левски — Славия | П2 | 3,2 | 3 | 6,7% |
| Вердер — Ганновер | П1 | 2 | 1,95 | 2,3% |
| Ганза — Карлсруэ | П2 | 3,3 | 2,95 | 11,9% |
| Шабаб — Видад | П2 | 2,2 | 2,15 | 2,3% |
| Хуарес — Толука | П1 | 2,35 | 2,2 | 6,8% |
Определить общую валуйность и размер ожидаемой прибыли для полной истории ставок достаточно просто, поскольку нужно просто вычислить среднее значение.
Для портфеля из 1500 ставок оно было равно 4,1 %, и это указывает на то, что если бы использованная система ставок функционировала точно так, как прогнозировалось, ожидаемая прибыль по ставкам на сумму 1500 доллар составляла бы 61,5 доллара.
В действительности же доход для этих ставок был равен 13,7 доллара. По-видимому, такой низкий результат объясняется невезением (при условии, конечно, что использованная модель прогнозирования функционировала должным образом).
Вопрос заключается в том, насколько сильна эта зависимость? Для поиска ответа на этот вопрос можно воспользоваться методом Монте-Карло.
Моделирование Монте-Карло в Excel
Выполнить моделирование по методу Монте-Карло в Excel достаточно просто.
- Рассчитайте ожидаемую вероятность выигрыша для каждой ставки, выраженную в виде десятичной цифры от нуля до единицы. Эта величина является обратной значению справедливого коэффициента ( 1 ⁄ КФ).
- Используйте функцию «СЛЧИС()» в Excel для вывода случайного числа от нуля до единицы для каждой ставки. Для того чтобы с помощью Excel определить, принесет ли ставка в моделировании прибыль или убыток, необходимо просто выяснить, является ли случайное число, связанное со ставкой, меньше величины ожидаемой вероятности выигрыша.
- Если выпавшее случайное число меньше вероятности, то засчитывается выигрыш (коэффициент минус 1), если случайное число больше — то проигрыш (−1).
- Суммируйте прибыли и убытки по всем ставкам. Затем просто разделите сумму прибыли на количество ставок.
- Используйте функцию таблицы данных в Excel и обновите случайные числа для определенного количества моделирований.
| Матч | Ставка | Справедливый КФ | Вероятность выигрыша | Случайное число | Прибыль |
|---|---|---|---|---|---|
| Рубин — Спартак | П2 | 1,9 | 0,53 | 0,46 | +0,9 |
| Левски — Славия | П2 | 3 | 0,33 | 0,15 | +2 |
| Вердер — Ганновер | П1 | 1,95 | 0,51 | 0,8 | -1 |
| Ганза — Карлсруэ | П2 | 2,95 | 0,34 | 0,70 | -1 |
| Шабаб — Видад | П2 | 2,15 | 0,47 | 0,53 | -1 |
| Хуарес — Толука | П1 | 2,2 | 0,45 | 0,54 | -1 |
Нажатие клавиши F9 позволяет выполнить перерасчет всех случайных чисел для совершенно нового моделирования и вычисления теоретической доходности новой выборки.
Размер доходности можно фиксировать вручную каждый раз при запуске нового моделирования, но если мы хотим повторять процесс сотни или тысячи раз, для этого потребуются большие затраты времени и усилий.
К счастью, в Excel предусмотрен быстрый и простой способ выполнения множества моделирований за один раз с помощью функции таблицы данных. Для доступа к ней перейдите в Данные ⇒ Анализ «что если» ⇒ Таблица данных.
Вычислите доходность своей выборки в любой свободной ячейке Excel, как описано в шаге три выше.
Затем выделите несколько ячеек, которые вы хотите заполнить значениями доходности для новых моделирований, включая один столбец слева.
После этого вызовите таблицу данных в Excel. Отобразится окно, подобное приведенному ниже.
В ячейке ввода столбца просто введите ссылку на одну ячейку. Это может быть любая ячейка при условии, что она не является одной из тех ячеек, которые были выделены ранее.
Нажмите ОК и посмотрите, что сделает Excel. Ячейки, выделенные ниже первой, будут заполнены новыми вычисленными значениями доходности, каждое из которых представляет собой одно моделирование. В рамках этого примера было выполнено 10 моделирований, как показано ниже.
Измерение влияния удачи на результаты ставок
Можно выполнить столько моделирований, сколько мы захотим, хотя чем больше их количество, тем больше времени займут вычисления в Excel. Для целей этой статьи было выполнено 100 000 моделирований (что заняло около пяти минут).
Еще один важный момент, который можно вынести из этого эксперимента, касается влияния невезения на результаты игроков с положительным матожиданием и довольно значительными историями ставок.
Средняя доходность составила 4,05 %, что почти совпадает с величиной ценностного ожидания данной истории ставок. Однако наблюдается широкий разброс значений от –12,23 % (самый низкий показатель эффективности) до 23,26 % (самый высокий показатель).
Действительно, убыточными оказались почти 17 % моделирований, хотя величина теоретического ценностного ожидания для использованной истории ставок превышала 4 %, в то время как доходность могла быть выше фактического показателя 0,85 % в 76 % случаев.
Фактически, используя эти данные, мы могли бы вычислить вероятность достижения какого-либо определенного порогового значения доходности в Excel без необходимости в проведении каких-либо статистических тестирований.
Метод Монте-Карло позволяет сделать все это с минимумом усилий с нашей стороны. Полное распределение 100 000 результатов моделирования доходности приведено в таблице ниже (с шагом 0,1 % по оси X). Тот, кто имеет представление о нормальном распределении, может увидеть, что это совпадение почти идеальное.
Конечно, если бы фактический размер доходности был равен, скажем, –5 % или ниже (что возможно только в 1 % случаев), можно было бы задуматься о несовершенстве использованной системы ставок. Таким образом, метод Монте-Карло является полезным инструментом для проведения таких субъективных оценок.
Несовершенная система ставок или невезение?
Еще один важный момент, который можно вынести из этого эксперимента, касается влияния невезения на результаты игроков с положительным ожиданием и довольно значительными историями ставок.
Использованная в этой статье история ставок включала более 1500 ставок с прогнозируемым математическим ожиданием свыше 4 %. Несмотря на это преимущество, результаты моделирований по методу Монте-Карло продемонстрировали, что проигрыш возможен более чем в одном случае из пяти.
Если бы ваша стратегия ставок содержала похожее преимущество, как бы вы повели себя, сделав 1500 ставок, которые ничего бы вам не принесли? Сохранили бы уверенность в своей методологии, списали бы низкие результаты на невезение или потеряли бы веру в свой подход?
Один из способов, который может помочь в решении этой дилеммы, предполагает увеличение размера выборки. Опять же, для того чтобы понять, как меняется общая картина при увеличении размера истории ставок, можно обратиться к методу Монте-Карло.
В рамках мысленного эксперимента первоначальное количество ставок (1500) было увеличено в десять раз (путем простого воспроизведения исходной выборки коэффициентов ставок еще девять раз). Дополнительное моделирование, проведенное 100 000 раз, позволило получить приведенные далее значения доходности.
- Среднее значение доходности = 4,04 %
- Наименьшее значение доходности = –1,21 %
- Наибольшее значение доходности = 10,17 %
- Вероятность доходности < 0 % = 0,1 %
- Вероятность доходности > 0,85 % = 99,2 %
Ниже представлено новое распределение, которое было получено после выполнения 100 000 моделирований, наложенное на исходное распределение для первоначальной выборки из 1500 ставок.
Очевидная разница между двумя выборками — это размер спреда или диапазона возможных значений доходности, который намного ýже в случае с большей историей ставок. Такой результат вполне предсказуем и является просто следствием закона больших чисел.
Оценка результатов моделирования по методу Монте-Карло
Чем больше история ставок, тем вероятнее, что фактическая эффективность будет ближе к ожидаемой — конечно, при условии, что система прогнозирования функционирует должным образом.
Напрашивающийся вывод состоит в том, что если после более 15 000 ставок доходность будет оставаться на отметке 0,85 % или ниже, это утверждение следует поставить под сомнение.
В конечном счете, метод Монте-Карло не позволит вам точно понять, какие факторы, не считая везения, определяют результативность вашей системы ставок. Тем не менее это действительно полезный инструмент, который поможет в формировании обоснованных суждений в этом отношении, а также даст вам возможность оценить диапазон обоснованно ожидаемых исходов, возможных в пределах действия удачи и невезения.
В качестве бонуса вы можете скачать файл Excel с моделированием Монте-Карло. Его можно модифицировать и использовать для анализа эффективности своей игровой стратегии.
Скачать “Монте-карло для эффективности системы ставок”
monte-karlo-1.xlsx – Загружено 560 раз – 10,28 КБ