Метод конечных разностей в расчете прогибов пластин
Опубликовано 10 Апр 2016
Рубрика: Механика | 5 комментариев

Получить точные аналитические решения так называемых краевых задач для дифференциальных уравнений в частных производных зачастую бывает очень сложно, поэтому приближенные методы нашли широкое распространение на практике. Метод сеток или метод конечных разностей – один из наиболее известных приближенных методов.
Мы не будем писать дифференциальные уравнения, а воспользуемся готовой схемой замещения и составим систему уравнений в конечных разностях при помощи простого оператора формулы, а затем легко решим эту систему, используя мощь MS Excel.
Приступим к рассмотрению практической задачи и научимся применять в реальных расчетах метод конечных разностей.
Расчет в Excel прогибов пластины в узлах сетки.
Квадратная стальная пластина нагружена равномерно распределенной нагрузкой по всей площади. Границы пластины шарнирно оперты на основание — пластина свободно лежит, опираясь контуром.
Необходимо рассчитать прогибы в разных точках пластины.
Исходные данные:
Наносим на чертеж пластины сетку с шагом a/4. В точках пересечения линий сетки находятся узлы, в которых и будем определять величину прогибов wi (i— номер узла).
Присваиваем номера узлам, начиная с «0».
Номер «0» назначаем всем узлам, расположенным на контуре. Эти узлы по условиям задачи лежат на опорной поверхности и после приложения нагрузки остаются на прежнем месте – прогиб этих узлов равен нулю w0=0.
Из условий приложения и характера нагрузки, а также квадратной формы пластины (условия центральной симметрии) очевидно, что прогиб будет одинаковым во всех узлах «1». Поэтому этим узлам и присвоен одинаковый номер.
Руководствуясь теми же признаками симметрии, назначаем характерным внутренним узлам номер «2».
Понятно, что наибольший прогиб будет в центре пластины, назначаем этому узлу номер «3». Он один, других узлов на пластине, имеющих такой же прогиб нет.
На рисунке вы видите законтурные (зеркальные или мнимые) узлы. Они участвуют в расчете, поэтому нам нужны. Номера им присвоим исходя из простых правил:
1. Если линия контура опирается в этом месте шарнирно, то законтурному (зеркальному) узлу присваивается номер «-N» Где «N» — номер симметричного относительно линии контура внутреннего узла (w— N=-wN).
2. Если контур жестко закреплен (жесткое защемление), то соответствующему зеркальному узлу присваивается номер «N» — такой же, как и симметричному внутреннему узлу (wN=+wN).
Числовые исходные данные о материале и размере пластины, а также о нагрузке записываем в таблицу MS Excel в ячейки D3…D7.
Расчет:
1. В рассматриваемом варианте расчета пластина делится сеткой на 4 квадрата по горизонтали и вертикали. Определяем шаг сетки в мм
в ячейке D9: δ=a/4
2. Цилиндрическую жесткость пластины в Н*мм вычисляем по общеизвестной формуле
в D10: D=(E*h3)/(12*(1- μ2)
3. Для каждого узла, в котором мы хотим найти прогиб, составляем уравнение, применив метод конечных разностей.
Для составления уравнений используем оператор формулы, изображенный выше на схеме пластины.
Мысленно накладываем оператор центральной клеткой сначала на узел «1» и каждой периферийной клеточкой на соответствующие соседние узлы. Пишем уравнение:
20*w1-8*(w0+w2+w3+w2)+2*(w0+w0+w1+w1)+1*(w-1+w0+
w1+w0)=k*q*δ4/D
Думаю, понятно, как оно получилось? Уясните этот шаг, он ключевой при составлении уравнений!
После преобразований получим:
24*w1-16*w2-8*w3=k*q*δ4/D
Выражение в правой части уравнения справедливо для распределенной нагрузки q.
Для сосредоточенной силы F выражение имеет вид: F*δ2/D
Если в точке действуют несколько различных нагрузок, то выражения их характеризующие суммируются в правой части уравнения.
Что такое коэффициент веса k? Если бы распределенная нагрузка была приложена только к центральной части пластины, ограниченной квадратом с узлами «2» по углам, то:
для узлов «2»: k=0,25
для узлов «1»: k=0,5
для узла «3»: k=1
Так как в нашем примере распределенная нагрузка приложена ко всей поверхности пластины, то для всех внутренних узлов k=1.
Накладывая оператор формулы метода конечных разностей последовательно на все уникальные внутренние узлы, нужно составить все уравнения. Из-за равномерности сплошной нагрузки и симметрии формы в нашем примере таких узлов 3, а, следовательно, и уравнений будет тоже 3.
Запишем эти уравнения в таблицу Excel в виде матрицы, заполнив область ячеек O5…Q7.
4. Заполним область R5…R7 значениями коэффициентов k.
5. Вычислим свободные члены уравнений в мм
в ячейках S5…S7: k*q*δ4/D
6. Определим коэффициенты обратной матрицы. Для этого впишем формулу массива
в область O9…Q11: {=МОБР(O5:Q7)}
Чтобы правильно ввести формулу массива напишем
в O9: =МОБР(O5:Q7)
Выделим область для обратной матрицы равную по размеру исходной матрице – O9…Q11, нажмем на клавиатуре клавишу F2, затем – Ctrl+Shift+Enter. Excel мгновенно рассчитал коэффициенты обратной матрицы.
7. Для вычисления корней уравнений системы (читай: искомых прогибов) нужно перемножить обратную матрицу с матрицей свободных членов уравнений. Для этого запишем формулу массива
в область ячеек S9…S11: {=МУМНОЖ(O9:Q11;S5:S7)}
Всё, задача решена. Используя метод конечных разностей, мы определили прогибы в узлах «1», «2» и «3». Наибольший прогиб ожидаемо оказался в центре пластины в узле «3».
Ниже приведены скриншоты решения этой же задачи при уменьшенном в 2,5 раза шаге сетки δ. Excel легко решает в этом случае систему из 15-и уравнений!
Что в итоге?
Расчет прогиба в центре пластины из рассмотренного примера по «точным» аналитическим формулам дает следующие результаты при μ=0,3:
wц=0,00406*q*a4/D=3,632 мм (Тимошенко С.П.)
wц=0,0443*q*a4/(E*h3)=3,629 мм (Вайнберг Д.В.)
Прогибы, определенные методом конечных разностей:
При шаге сетки δ=a/4:
wц=w3=3,604 мм (относительная погрешность -0,8%)
При шаге сетки δ=a/10:
wц=w15=3,630 мм (относительная погрешность 0,0%)
Как видим, метод конечных разностей даже при большом шаге сетки дает незначительную погрешность результатов!
Используя рассмотренную методику, можно выполнять расчеты прямоугольных пластин с разными способами закрепления контуров и произвольным расположением распределенных и концентрированных нагрузок. Составление уравнений даже без навыка использования оператора формулы не займет, поверьте, у вас много времени. На вариант с 15-ю узлами было затрачено не более получаса.
Развитие программы возможно для решения других похожих задач.
Ссылка на скачивание файла с программой: metod-konechnyh-raznostej (xls 164KB).
Статьи с близкой тематикой
Отзывы
Задание.
Решить
краевую задачу методом конечных
разностей, построив два приближения
(две итерации) с шагом h и с шагом h/2.
Проанализировать
полученные результаты. Варианты заданий
приведены в приложении 4.
Порядок выполнения работы
-
Постройте
вручную
конечноразностную аппроксимацию
краевой задачи (конечноразностную
СЛАУ) с шагом h,
заданным вариантом. -
Используя
метод конечных разностей, сформируйте
в Excel
систему
линейных алгебраических конечно-разностных
уравнений для шага h
разбивки отрезка [a,
b].
Запишите эту СЛАУ на рабочем листе
книги Excel.
Расчетная схема приведена на рис.4.1. -
Полученную
СЛАУ решите методом прогонки. -
Проверьте
правильность решения СЛАУ с помощью
надстройки Excel
Поиск решения. -
Уменьшите
шаг сетки в 2 раза и еще раз решите
задачу. Результаты представьте в
графическом виде. -
Сравните
полученные результаты. Сделайте вывод
о необходимости продолжения или о
прекращении счета.
Решение краевой задачи с использованием электронных таблиц Microsoft Excel.
Пример
4.1. Методом
конечных разностей найти решение краевой
задачи
,
y(1)=1, y’
(2)=0,5
на отрезке
x[1,
2] с шагом
h=0,2 и с шагом h=0,1. Сравнить полученные
результаты и сделать вывод о необходимости
продолжения или о прекращении счета.
Расчетная схема
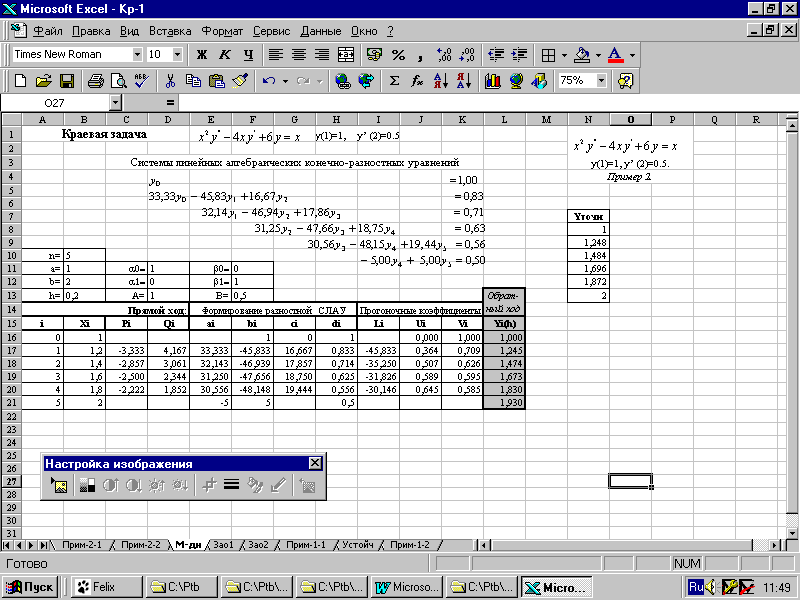
для шага h=0,2 приведена на рис.4.1.
Полученное
решение (сеточную функцию) Y{1.000,
1.245, 1.474, 1.673, 1.829, 1.930}, Х
{1; 1,2; 1,4; 1,6; 1,8;2} в столбце L
и B
можно принять за первую итерацию (первое
приближение) исходной задачи.
Рис.4.1.
Д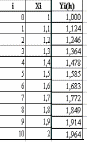
нахождениявторой
итерации
сделайте сетку вдвое гуще (n=10, шаг h=0,1)
и повторите приведенный выше алгоритм.
Это
можно проделать на том же или на другом
листе книги Excel.
Решение (второе приближение) приведено
на рис.4.2.
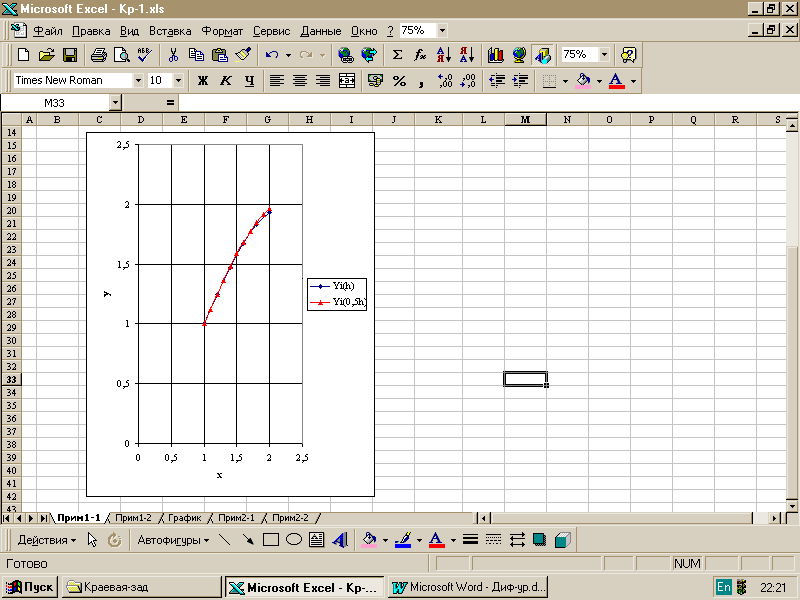
Сравните
полученные приближенные решения. Для
наглядности можно построить графики
этих двух приближений (двух сеточных
функций), рис.4.3.
Рис.4.2.
Порядок построения графиков приближенных решений краевой задачи
-
Постройте
график решения задачи для разностной
сетки с шагом h=0,2
(n=5). -
Активизируйте
уже построенный график и выберите
команду меню
ДиаграммаДобавить данные -
В
окне Новые
данные
укажите данные xi,
yi
для разностной сетки с шагом h/2 (n=10). -
В
окне Специальная
вставка
установите флажки в полях:
-
новые
ряды, -
категории(значение
оси х) в первом столбце.
Как
видно из приведенных данных, два
приближенных решения краевой задачи
(две сеточные функции) отличаются друг
от друга не более, чем на 5%. Поэтому за
приближенное решение исходной задачи
принимаем вторую итерацию, т.е.
Y
{1, 1.124,
1.246, 1.364, 1.478, 1.584, 1.683, 1.772, 1.849, 1.914, 1.964}
Рис.4.3.
Лабораторная работа №5 Тема. Численные методы оптимизации. Графический метод
Задание.
Решить задачу
линейного программирования, приведенную
в приложении 5, графическим методом и
на ЭВМ. Сравнить полученные решения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Решение краевой задачи методом конечных разностей: Методические указания по выполнению лабораторной работы в курсе “Информатика”
Страницы работы
Фрагмент текста работы
ячейках от C3 до C8 вычисляем
значения вспомогательной функции 1/(2 хi+1), входящей взнаменатели
функций p(x), q(x) и f(x). Вводим в C3 формулу «=1/(2*B3+1)» и протягиваем эту формулу до ячейкиC8;
5.
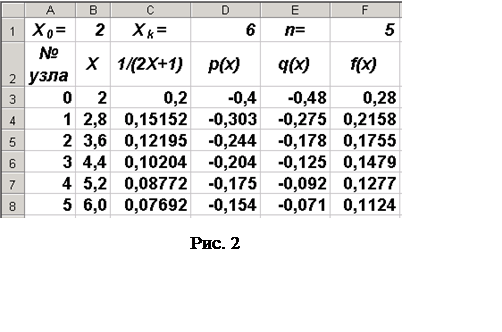 |
В ячейки D3, E3 и
F3 записываем формулы, соответствующие (13), для вычисления значений
функций p(x), q(x) и f(x). Запись этих формул при
вводе их в ячейки таблицы имеет следующий вид: «=-2*C3», «= ‑12*C3*C3»
и «=(3*B3+1)*C3*C3» соответственно. При протягивании этих
формул по столбцам D, Е и F до восьмой строки таблица заполняется
так, как показано на рис. 2.
6.
Далее начинаем
заполнение столбцов G, H, I и J значениями коэффициентов Ai, Ci,
Bi и Fi в соответствии с форматом системы
уравнений (11). В ячейки G3, H3, I3 записываем значения, определяемые
форматом первого уравнения системы (11): A0=0, C0=-1,
В0=0. В ячейку J3 записываем ссылку на ячейку J1, в которой записано начальное значение F0=Y0:
«=J1″.
7.
В ячейки G8,
H8, I8 записываем значения, определяемые конечными условиями A5=0,
C5=-1, В5=0. В ячейку J8 записываем ссылку на ячейку
L1, в которой записано начальное значение Fk=
F5 = Yk :»=L1″.
8.
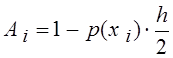 |
Далее заполняем столбцы G,
H, I и J
значениями коэффициентов Ai , Ci , Bi и Fi. В
ячейку G4 вводим формулу «=1-D4*$H$1/2″, соответствующую формуле
для вычисления коэффициента A1. После
чего протягиваем эту формулу до ячейки G7.
9.
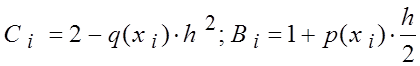 |
Аналогично в ячейку Н4
вводим формулу для вычисления коэффициента С1: «2-Е4*$H$1*$H$1″, а в ячейку I4 вводим формулу для вычисления коэффициента B1: «1+D4*$H$1/2″, реализуя соответствующие формулы
Протягиваем эти формулы до ячеек Н7 иI7.
10.
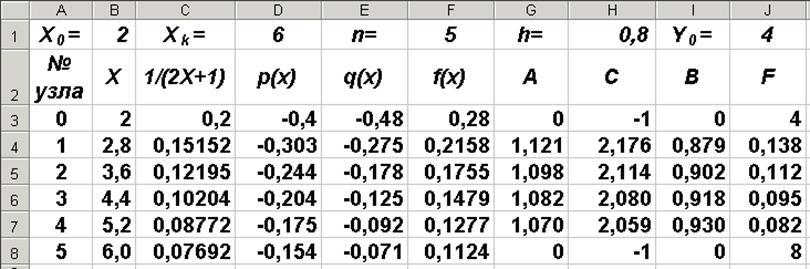 |
В ячейках столбца J формируем вектор правых частей
системы уравнений (11). В ячейку J4
вводим формулу “=F4*$H$1*$H$1”, соответствующую формуле Fi = fih2. Протягиваем эту формулу до ячейки J7. В результате получаем таблицу, показанную на рис. 3.
Следует отметить, что в столбцах G, H, I и J этой таблицы записаны элементы
матрицы, решаемой системы уравнений (11).
Рис. 3
11.
Используя
вычисленные значения коэффициентов Ai, Ci, Bi
и Fi, находим в соответствии с формулами (18) и (19) значения
коэффициентов ai и bi. В ячейку K3 запишем формулу для вычисления a0 : «=I3/H3″, а в ячейку L3 формулу для вычисления b0.: «=-J3/H3″. И далее в ячейки K4 и L4 вводим
формулы, соответствующие (19), для вычисления коэффициентов
a1 :«=I4/(H4-K3*G4)», и b1: «=(G4*L3‑J4)/(
H4‑K3*G4)».
Протягиваем эти формулы до ячеек K8 и L8 соответственно.
Результаты вычисления показаны на рис. 4.
12.
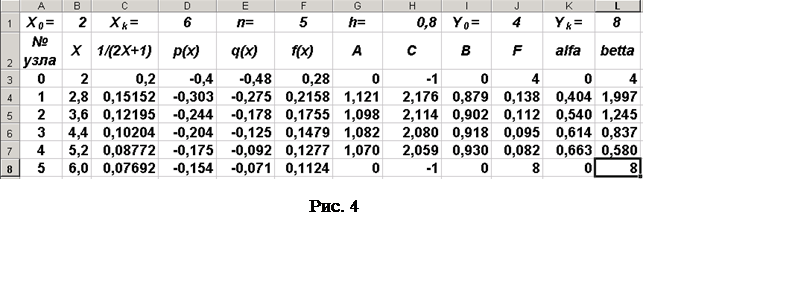 |
Дальнейшие вычисления
выполняются в столбце М по формулам обратного хода (21) и (22). В ячейку
М8 введем формулу «=L8″, представляющую ссылку на значение bn. В ячейку М7 введем формулу «=L7+K7*M8»,
соответствующую и протянем ее до ячейки М3. Результаты вычислений
показаны на рис. 5.
13.
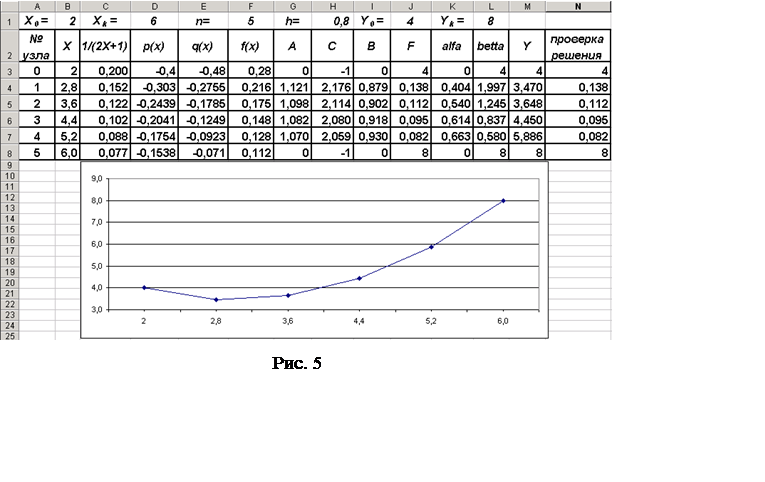
Построим график
функции Y(X), используя возможности мастера диаграмм программы MS Excel.
Для этого выделим ячейки столбца значений функции Y(X) от ячейки М3 до М8 ивыполним
процедуру создания диаграммы, используя средства «мастера
диаграмм» программы MS Excel. Окончательный результат
показан на рис. 5.
Проверка правильности
полученного решения
Для
проверки правильности полученного в столбце М решения Y(X) выполняется подстановкой полученного решения в
уравнения исходной системы. В ячейки столбца N последовательно вводим формулы, реализующие
вычислительный алгоритм, определяемый системой уравнений (11). В N3 введём формулу «=M3″. Затемв N4 введём формулу «=G4*M3‑H4*M4+I4*M5″, реализующую левую часть уравнения
(9). Эту формулу протягиваем до N8, получаясоответственно – «=G5*M4‑H5*M5+I5*M6″ вN5, «=G6*M5-H6*M6+I6*M7″ в N6, «=G7*M6‑H7*M7+I7*M8″ вN7 и «=G8*M7-H8*M8+I8*M9″ вN8. Полученные в столбце N значения совпадают со значениями в столбце J, что позволяет судить о правильности
полученного решения.
 |
Варианты
заданий для выполнения самостоятельной работы
Методом конечных разностей найти решение краевой задачи на
сетке из 6 узлов.
Вариант 1
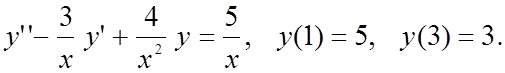 |
Вариант 2
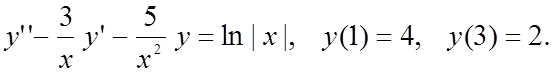 |
Вариант 3
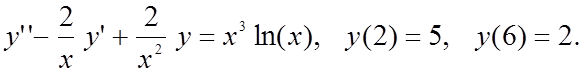 |
Вариант 4
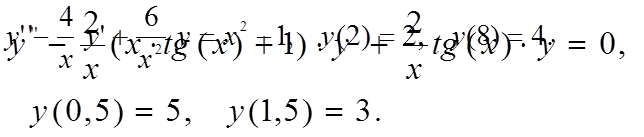 |
Вариант 5
Вариант 6
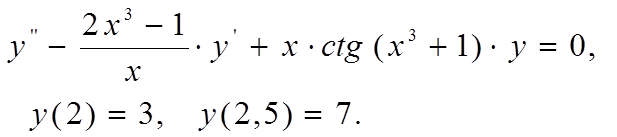 |
Вариант 7
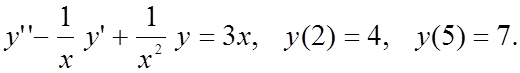 |
Вариант 8
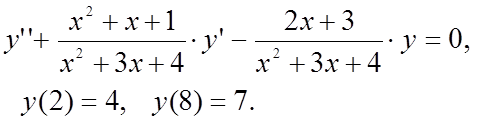 |
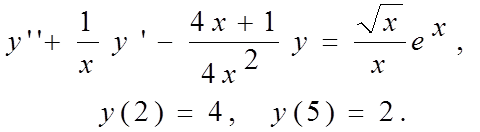 |
Вариант 9
Вариант 10
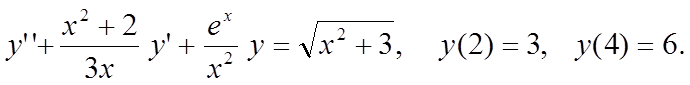 |
Вариант 11
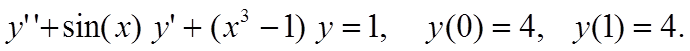 |
Вариант 12
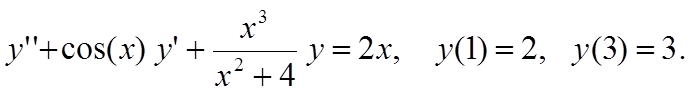 |
Вариант 13
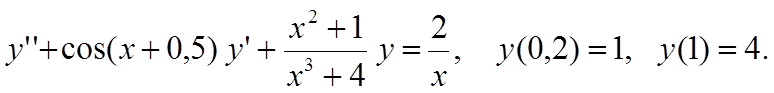 |
Вариант 14
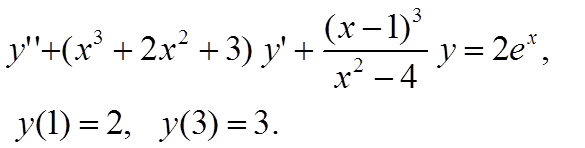 |
Вариант 15
Литература
1. Пискунов Н.С.
Дифференциальное и интегральное исчисления. М.:Физматгиз, 1963. – 856 с.
2. Карпов В.В.,
Коробейников А.В. Математические модели задач строительного профиля и численные
методы их исследования: Учеб. пособие. – СПб., СПбГАСУ, 1996. – 134 с.
3. Бахвалов Н.С.
Численные методы. – М.:Наука, 1973. – 632 с.
4. Вагер Б.Г.
Численные методы решения дифференциальных уравнений: Учеб. пособие – СПбГАСУ. –
СПб. 2003. 114 с.
5. Любимов Е.Б. и
др. Решение систем линейных алгебраических уравнений средствами программы Microsoft Excel:
Метод. указ. – СПб., СПбГАСУ, 2005. – 22 c.
СОДЕРЖАНИЕ
Основные понятия, используемые
в постановках краевых задач. 3
Применение метода прогонки для решения систем линейных
алгебраических уравнений с трёхдиагональными ленточными матрицами. 6
Реализация метода прогонки в среде программы
MS Excel 6
Постановка задачи. 6
Проверка правильности полученного решения. 12
Варианты заданий для выполнения самостоятельной работы.. 13
Литература. 16
[1]
) Формулы вводятся в ячейки таблиц, начиная с символа “=” (равно). Двойные
кавычки использованы в тексте для выделения формулы. Вводить их в ячейки
таблицы не нужно.
[2]
) Терминология и сокращения, используемые в тексте методических указаний,
приведены в начальном разделе методических указаний к первой лабораторной
Похожие материалы
- Visual Basic for Application. Свойства, методы и события объектов VBA. Переменная
- Обзорная лекция по основным разделам (дидактическим единицам ГОС) дисциплины «Информатика»
- Интерполяция. Введение. Общая постановка задачи (Решение задач в среде программ Microsoft Excel или OpenOffice.org Calc)
Информация о работе
Тип:
Методические указания и пособия
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
Помогаю со студенческими работами здесь
Методом конечных разностей найти решение краевой задачи
Методом конечных разностей найти решение краевой задачи
y»-7*x*y’-y=5*x^2
u(0)-u'(0)=0; u(1)=1…

Помогите пожалуйста. Надо написать программу, которая решает краевую задачу для ОДУ 2 порядка…
Решение краевой задачи для дифференциального уравнения методом сеток
Мне в университете задали данную программу написать. но к сожалению на паре мы не успели пройти…

Доброе время суток, прошу помочь решить задачку методом конечных разностей в маткад, или хотя бы…
Искать еще темы с ответами
Или воспользуйтесь поиском по форуму:
You should upgrade or use an alternative browser.
-
Forums
-
Homework Help
-
Engineering and Comp Sci Homework Help
Using Finite Difference Method In Excel
-
Thread starter
elliottmarter -
Start date
Mar 24, 2010
- Mar 24, 2010
- #1
Investigate the derivative over the range x = [0,1], using finite differences of 0.1
b)Plot the results from each method onto one graph, along with the analytical derivative of the function. Make sure your plot includes a legend.
i can see that this is a really (really) easy question if you know how to utilise the finite differences method in excel, however as you can see from the question were weren’t taught it and we have to research it, so i went to wikipedia (obviously!)
so anyway i see on wikipedia they have this:
which i can partially understand, you just insert your function where it says f(x) and then link you x values to a table of values 0-1 in 0.1 steps, but i don’t understand what the «h» stands for, then for part b i guess by analytical derivative it means just standard differentiation so:
[tex]stackrel{dy}{dx}[/tex]=3x2-2x+0.5
if anyone could lend a hand or a link to a good «dummies guide» web page I’d be very grateful.
Thanks
Elliott M
Answers and Replies
- Mar 24, 2010
- #2
That is kind of intuitive when you look at the equations. For the forward difference calculation you are adding +h which gives you the «forward difference» while for the backward difference calculation you subtract h in order to get the backward difference. Of course the central difference you add and subtract half your step to be in the middle. As for part B you are correct. The point of this excersize is probably to compare the accuracy of analytical differentiation with numerical differentiation (finite difference).
Suggested for: Using Finite Difference Method In Excel
- Dec 10, 2022
- Jan 18, 2021
- Oct 11, 2022
- Jun 24, 2022
- Nov 1, 2018
- Oct 27, 2020
- Apr 7, 2022
- Jun 11, 2022
- Jun 11, 2021
- Mar 30, 2023
-
Forums
-
Homework Help
-
Engineering and Comp Sci Homework Help