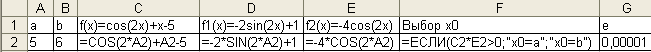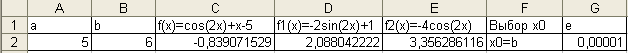»
В отличие от метода хорд, в методе
касательных вместо хорды на каждом шаге
проводится касательная к кривой y=F(x)
при x=xn
и
ищется точка пересечения касательной
с осью абсцисс:
Формула
для (n+1) приближения имеет вид:
Если
F(a)*F»(a)>0,
x0=a,
в противном случае x0=b.
Итерационный
процесс продолжается до тех пор, пока
не будет обнаружено, что:
.
Пример:
Пусть
дана задача следующего характера:
Уточнить корни уравнения cos(2x)+x-5=0
методом касательных с точностью до
0,00001.
Для
решения такой задачи, используя Excel,
необходимо выполнить следующие действия:
Изначально
необходимо определиться с тем, чему
равно x0: либо a, либо b. Для этого необходимо
выполнить следующие действия:
Найти
производную первого порядка от функции
f(x)=cos(2x)+x-5. Она будет выглядеть следующим
образом: f1(x)=-2sin(2x)+1.
Найти
производную второго порядка от функции
f(x)=cos(2x)+x-5. Она будет выглядеть следующим
образом: f2(x)=-4cos(2x).
Заполнить
ячейки следующим образом (обратить
внимание на названия и номера столбцов
при заполнении — они должны быть такими
же, как на рисунке):
В
итоге получается следующее:
Так
как x0=b, то необходимо выполнить следующие
действия:
Заполнить
ячейки следующим образом (обратить
внимание на названия и номера столбцов
при заполнении — они должны быть такими
же, как на рисунке):
В
ячейку A6 ввести формулу =D5.
Выделить
диапазон ячеек B5:E5 и методом протягивания
заполнить диапазон ячеек B6:E6.
Выделить
диапазон ячеек A6:E5 и методом протягивания
заполнить диапазон нижерасположенных
ячеек до получения в одной из ячеек
столбца E результата (диапазон ячеек
A6:E9).
В
итоге получаем следующее:
Ответ:
Корень уравнения cos(2x)+x-5=0 равен 5,32976.
4. Комбинированный метод хорд и касательных
Для
того чтобы достичь наиболее точной
погрешности, нужно одновременно
использовать методы хорд и касательных.
«По формуле хорд находят xn+1
, а по формуле касательных —
zn+1
. Процесс нахождения приближенного
корня прекращается, как только:
В
качестве приближенного корня берут
значение, равное (11):»[2]
Пример:
Пусть
требуется уточнить корни уравнения
cos(2x)+x-5=0 комбинированным методом с
точностью до 0,00001.
Для
решения такой задачи, используя Excel,
необходимо выполнить следующие действия:
-
Так
как в комбинированном методе необходимо
использовать одну из формул хорд и
формулу касательных, то для упрощения
следует ввести следующие обозначения:
-
Для
формул хорд обозначить:
—
xn как mn.
—
Переменная c будет играть роль a или b в
зависимости от ситуации.
—
Остальные обозначения аналогичны
приведенным в формулах хорд, только
учитывая выше введенные переменные.
-
Для
формулы касательных обозначить:
—
xn как nn.
—
Остальные обозначения аналогичны
приведенным в формуле касательных,
только учитывая выше введенные переменные.
-
Найти
производную первого порядка от функции
f(x)=cos(2x)+x-5. Она будет выглядеть следующим
образом: f1(x)=-2sin(2x)+1. -
Найти
производную второго порядка от функции
f(x)=cos(2x)+x-5. Она будет выглядеть следующим
образом: f2(x)=-4cos(2x). -
Заполнить
ячейки следующим образом (обратить
внимание на названия и номера столбцов
при заполнении — они должны быть такими
же, как на рисунке):
-
В
итоге получается следующее:
-
В
ячейку G1 ввести e, а в G2 ввести число
0,00001. -
В
ячейку H1 ввести c, а в H2 ввести число 6,
так как c=b (см. ячейку F2). -
В
ячейку I1 ввести f(c), а в I2 ввести формулу
=COS(2*H2)+H2-5. -
Заполнить
ячейки последовательно следующим
образом (обратить внимание на названия
и номера столбцов при заполнении — они
должны быть такими же, как на рисунке):
-
В
ячейку A6 ввести формулу =E5. -
В
ячейку F6 ввести формулу =I5. -
Выделить
диапазон ячеек B5:E5 и маркером автозаполнения
заполнить диапазон ячеек B6:E6. -
Выделить
диапазон ячеек G5:K5 и маркером автозаполнения
заполнить диапазон ячеек G6:K6. -
Выделить
диапазон ячеек A6:K6 и методом протягивания
заполнить все нижестоящие ячейки до
получения ответа в одной из ячеек
столбца K (диапазон ячеек A6:K9).
В
итоге получаем следующее:
Ответ:
Корень уравнения cos(2x)+x-5=0 равен 5,32976.
Соседние файлы в папке Численные_методы
- #
- #
- #
- #
- #
- #
Решите нелинейное уравнение методом касательных в экселе
Найдем корень нелинейного уравнения в табличном процессоре Excel методом касательных с использованием циклических ссылок. Для нахождения корня будем использовать формулу:
Для включения режима циклических вычислений в Excel 2003 в меню Сервис/Параметры/вкладка Вычисления следует поставить флажок Итерации и флажок выбора вида ведения вычислений: автоматически. В MS Excel 2010 следует зайти в меню Файл/Параметры/Формулы и поставить флажок в поле «Включить итеративные вычисления» :
Найдем производную функции f(x)=x-x 3 +1
f’(x)=1-3x 2
В ячейку А3 введем значение а =1, ячейку В3 введем формулу расчета текущего значения х: =ЕСЛИ(B3=0;A3;B3-(B3-СТЕПЕНЬ(B3;3)+1)/(1-3*СТЕПЕНЬ(B3;2)))
В ячейку С3 введем формулу для контроля значения f(x): =B3-СТЕПЕНЬ(B3;3)+1.
Получим корень уравнения в ячейке В3 х=1,325.
Введем начальное приближение в ячейку А3 =2. Но для того чтобы вычисления были правильные, недостаточно изменить число в ячейке А3 и запустить процесс вычислений. Потому что в этом случае вычисления продолжаться с последнего вычисленного ранее значения. Это значение, в ячейке В3, необходимо обнулить, для этого можно заново записать туда формулу или просто выбрать ячейку с формулой и дважды щелкнуть мышью на ней . После этого поставить курсор на ячейку с формулой и нажать клавишу Enter для запуска процесса итерационных вычислений.
Получим тот же результат, значит корень на данном промежутке один.
Решение уравнений в EXCEL методом половинного деления, методом хорд и касательных.
При прохождении темы численные методы учащиеся уже умеют работать с электронными таблицами и составлять программы на языке паскаль. Работа комбинированного характера.Расчитана на 40 минут. Цель работы повторить и закрепить навыки паботы с программами EXCEL, ABCPascal. Материал содержит 2 файла. Один содержит теоретический материал, так как он и предлагается ученику . Во 2-м файле пример работы ученика Иванова Ивана.
Скачать:
| Вложение | Размер |
|---|---|
| материал для ученика | 57.5 КБ |
| работа ученика | 27 КБ |
Предварительный просмотр:
Аналитическое решение некоторых уравнений, содержащих, например тригонометрические функции может быть получено лишь для единичных частных случаев. Так, например, нет способа решить аналитически даже такое простое уравнение, как cos x=x
Численные методы позволяют найти приближенное значение корня с любой заданной точностью.
Приближённое нахождение обычно состоит из двух этапов:
1) отделение корней, т.е. установление возможно точных промежутков [a,b], в которых содержится только один корень уравнения;
2) уточнение приближённых корней, т.е. доведение их до заданной степени точности.
Мы будем рассматривать решения уравнений вида f(x)=0. Функция f(x) определена и непрерывна на отрезке [а.Ь]. Значение х 0 называется корнем уравнения если f(х 0 )=0
Для отделения корней будем исходить из следующих положений:
- Если f(a)* f(b] a, b существует, по крайней мере, один корень
- Если функция y = f(x) непрерывна на отрезке [a, b], и f(a)*f(b) и f ‘(x) на интервале (a, b) сохраняет знак, то внутри отрезка [а, b] существует единственный корень уравнения
Приближённое отделение корней можно провести и графически. Для этого уравнение (1) заменяют равносильным ему уравнением р(х) = ф(х), где функции р(х) и ф(х] более простые, чем функция f(x). Тогда, построив графики функций у = р(х) и у = ф(х), искомые корни получим, как абсциссы точек пересечения этих графиков
Для уточнения корня разделим отрезок [а, b] пополам и вычислим значение функции f(х) в точке x sr =(a+b)/2. Выбираем ту из половин [a, x sr ] или [x sr ,b], на концах которых функция f(x) имеет противоположные знаки.. Продолжаем процесс деления отрезка пополам и проводим то же рассмотрение до тех пор, пока. длина [a,b] станет меньше заданной точности . В последнем случае за приближённое значение корня можно принять любую точку отрезка [a,b] (как правило, берут его середину). Алгоритм высокоэффективен, так как на каждом витке (итерации) интервал поиска сокращается вдвое; следовательно, 10 итераций сократят его в тысячу раз. Сложности могут возникнуть с отделением корня у сложных функций.
Для приближенного определения отрезка на котором находится корень можно воспользоваться табличным процессором, построив график функции
ПРИМЕР : Определим графически корень уравнения . Пусть f1(х) = х , a и построим графики этих функций. (График). Корень находится на интервале от 1 до 2. Здесь же уточним значение корня с точностью 0,001(на доске шапка таблицы)
Алгоритм для программной реализации
- а:=левая граница b:= правая граница
- m:= (a+b)/2 середина
- определяем f(a) и f(m)
- если f(a)*f(m)
- если (a-b)/2>e повторяем , начиная с пункта2
Точки графика функции на концах интервала соединяются хордой. Точка пересечения хорды и оси Ох (х*) и используется в качестве пробной. Далее рассуждаем так же, как и в предыдущем методе: если f(x a ) и f(х*) одного знака на интервале , нижняя граница переносится в точку х*; в противном случае – переносим верхнюю границу. Далее проводим новую хорду и т.д.
Осталось только уточнить, как найти х*. По сути, задача сводится к следующей: через 2 точки с неизвестными координатами (х 1 , у 1 ) и (х 2 , у 2 ) проведена прямая; найти точку пересечения этой прямой и оси Ох.
Запишем уравнение прямой по двум точках:
В точке пересечения этой прямой и оси Ох у=0, а х=х*, то есть
, откуда
процесс вычисления приближённых значений продолжается до тех пор, пока для двух последовательных приближений корня х„ и х п _1 не будет выполняться условие abs(xn-x n-1 ) е — заданная точность
Сходимость метода гораздо выше предыдущего
Алгоритм различается только в пункте вычисления серединной точки- пересечения хорды с осью абсцисс и условия останова (разность между двумя соседними точками пересечения)
Уравнения для самостоятельного решения: (отрезок в excel ищем самостоятельно)
Метод Ньютона в Excel
Как видно, процесс нахождения корней нелинейного уравнения методом Ньютона состоит из следующих этапов:
- Получения шаблона.
- Уточнение интервалов в ячейках B2 , B3 .
- Замена в формуле ЕСЛИ запятую ( , ) на точку с запятой ( ; ).
- Копирование строки итераций до требуемой точности (столбец E ).
Примечание: столбец A — номер итерации, столбец B — корень уравнения X , столбец C — значение функции F(X) , столбец D — значение первой производной dF(X) , столбец E — точность eps .
источники:
http://nsportal.ru/ap/library/drugoe/2015/08/20/reshenie-uravneniy-v-excel-metodom-polovinnogo-deleniya-metodom-hord-i
http://math.semestr.ru/optim/newton-excel.php
Слайд 1
Тема: АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ В MICROSOFT EXCEL Выполнил: Мурзин Дмитрий Алексеевич, студент 2 курса Научный руководитель: преподаватель специальных дисциплин Соколова Марина Анатольевна Серпухов 2022г . ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ МОСКОВСКОЙ ОБЛАСТИ «СЕРПУХОВСКИЙ КОЛЛЕДЖ»
Слайд 2
Актуальность На практике при решении различных физических и технических задач составляются и решаются уравнения. Уравнения – аналитическая запись задачи о нахождении значений аргументов, при которых значения двух данных функций равны . Аргументы-неизвестные, а значение неизвестных-корни уравнения. В школьном курсе математике рассматриваются различные способы аналитического решения простейших уравнений. Но существуют алгебраические уравнения ,для которых нет общего случая решения в радикалах, их решение можно найти только приближенно. Например, ш ар радиуса r плавает в воде, погрузившись на глубину d .Пусть r =10см, сделан он из сосны, имеющей плотность 0,638 г / .Плотность воды 1 г / . Требуется найти глубину погружения шарика d . В своей работе я буду рассматривать различные методы решения алгебраических и трансцендентных уравнений, с применением электронных таблиц Microsoft Excel .
Слайд 3
Объект исследования: уравнения; Предмет исследования: методы решения алгебраических и трансцендентных уравнений. Цель работы: Выполнить в Microsoft Excel различные методы решения алгебраических и трансцендентных уравнений. Задачи работы: 1. Изучить и провести анализ литературы, интернет-ресурсов теоретической и практической основы методов решения уравнений; 2. Исследовать различные методы решения трансцендентных и алгебраических уравнений; 3. Выполнить в Microsoft Excel различные методы решения алгебраических и трансцендентных уравнений.
Слайд 4
Введение: Возможности электронных таблиц не ограничиваются вычислениями по формулам и построением графиков и диаграмм. В своей работе я рассмотрю практическое применение Microsoft Excel . Остановимся на решении уравнений. Конечно, это не означает, что Microsoft Excel решит уравнение в алгебраическом виде и выдаст все его корни. В Microsoft Excel встроены методы нахождения приближенных значений. Один из них называется методом подбора параметра. Она подберет один из корней уравнения. Электронные таблицы располагают серьезными возможностями по оптимизации решений, то есть нахождению наилучшего результата при заданных условиях. Для этого в Microsoft Excel можно рассмотреть различные методы приближенного решения уравнений.
Слайд 5
Общая постановка задачи Найти действительные корни уравнения f(x) = 0, где f(x) – алгебраическая или трансцендентная функция. Точные методы решения уравнений подходя только для узкого класса уравнений (квадратные, биквадратные и т. д.). Задача численного нахождения корней уравнения состоит из двух этапов: 1. Отделение (локализация) корня; 2. Приближенное вычисление корня до заданной точности (уточнение корней). Уточнение корня может производить разными методами[1][3]: 1. Графический метод; 2.Метод подбора параметра; 3. Метод половинного деления; 4. Метод итераций; 5. Метод хорд (метод секущих); 6. Метод касательных (метод Ньютона); 7. Комбинированный метод. Применяя электронные таблицы Microsoft Excel , я выполнил решение задачи перечисленными методами.
Слайд 6
Пример: Найдите приближенное значение уравнения заданного функцией с точностью е=0,001 . Представьте графически поставленную задачу;
Слайд 7
Графический метод . X= 1,100586 Отрезок [ 0 , 1 ]
Слайд 8
Метод подбора параметра: Подбор параметра — простейший метод нахождения оптимального желаемого решения за счет изменения одного из параметров. Алгоритм для программной реализации : 1.Составить таблицу значений данной функции . 2.Построить график функции . 3.По графику грубо приближенно определить корень уравнения . 4.Выяснить в какой ячейке находится это значение (адрес ячейки будет использоваться далее ) 5.Ввести команду Сервис – Подбор параметра . 6.На панели Подбор параметра в поле Значение ввести требуемое значение функции . 7.В поле Изменяя значение ячейки ввести адрес ячейки, в которой будет производиться подбор значения аргумента (адрес ячейки определенный в пункте 4 ) 8.На панели Результат подбора параметра будет выведена информация о величине подбираемого и подобранного значений. Щелкните кнопку ОК . 9.В ячейке аргумента из пункта 4 появится подобранное значение. Это и есть корень уравнения, найденный с заданной точностью. Точность подбора зависит от заданной точности представления чисел в ячейках таблицы . Однако не все задачи могут быть решены путем подбора параметра. Решение не будет найдено, если изменяемая и целевая ячейки логически связаны. При такой сходимости в окне Результат подбора параметра можно установить Шаг ( Step ) и Паузу ( Pause ) и с их помощью осуществлять процесс подбора параметра.
Слайд 9
Таблица. Расчет уравнения по методу подбора параметра: x= 1,001
Слайд 10
Метод половинного деления: Постановка задачи: Пусть дано уравнение f(x) = 0, (a, b) — интервал, на котором f(x) имеет единственный корень. Нужно приближенно вычислить этот корень с заданной точностью. Примечание: Заметим, что если f(x) имеет k корней, то нужно выделить соответственно k интервалов. Метод половинного деления или дихотомии (дихотомия — сопоставленность или противопоставленность двух частей целого): Метод основан на той идее, что корень лежит либо на середине интервала (a, b) , либо справа от середины, либо — слева, что следует из существования единственного корня на интервале (a, b) . Алгоритм для программной реализации: а:=левая граница b:= правая граница m:= ( a+b )/2 середина определяем f(a) и f(m) если f(a)*f(m)<0 то b:=m иначе a:=m если (a-b)/2>e повторяем , начиная с пункта2 m- искомый корень.
Слайд 11
Таблица. Расчет уравнения по методу половинного деления: x= 1,00586
Слайд 12
Метод простой итерации: Смысл метода простой итерации состоит в том, что мы представляем уравнение f(x) в виде ) и по формуле будем строить итерации, которые сходятся к искомому корню с интересующей степенью точности, но тут есть проблемы: возможно f(x) очень сложно представить в таком виде, да и не факт, что любая будет строить сходящиеся итерации, поэтому алгорим сводится к тому, чтобы оптимально найти . Подготовка: Ищем числа m и M такие, что на (a, b) ; Представляем , где ; Алгоритм: 1. Выбираем х0 из (a, b) ; 2.Вычисляем ; 3.Проверяем условие , где q=(M-m)/( M+m ) ; 4.Если оно ложно, то переходим к пункту 7; 5. х0=х1; 6.Переходим к пункту 2; 7. х1–искомый корень.
Слайд 13
Таблица. Расчет уравнения по методу простой итерации: x^3-10x+1=0,
Слайд 14
Метод хорд Метод хорд заключается в замене кривой у = f ( x ) отрезком прямой, проходящей через точки ( а , f ( a )) и ( b , f ( b )) . Абсцисса точки пересечения прямой с осью ОХ принимается за очередное приближение. Чтобы получить расчетную формулу метода хорд, запишем уравнение прямой, проходящей через точки ( a , f ( a )) и ( b , f ( b )) и, приравнивая у к нулю, найдем х : Алгоритм метода хорд : 1) П усть k = 0; 2) В ычислим следующий номер итерации: k = k + 1. Найдем очередное k -e приближение по формуле: x k = a — f ( a )( b — a )/( f ( b ) — f ( a )). Вычислим f ( x k ); 3) Е сли f ( x k )= 0 (корень найден), то переходим к п. 5. Если f ( x k ) × f ( b )>0, то b = x k , иначе a = x k ; 4) Е сли |x k – x k -1 | > ε , то переходим к п. 2; 5) В ыводим значение корня x k ; 6) К онец.
Слайд 15
Таблица. Расчет уравнения по методу хорд: x= 0,1001
Слайд 16
Метод касательных В точке пересечения касательной с осью Оx переменная у = 0. Приравнивая у к нулю, выразим х и получим формулу метода касательных: Теорема. Пусть на отрезке [а, b]выполняются условия: 1) функция f(x)и ее производные f ‘(х)и f »(x)непрерывны; 2) производные f ‘(x)и f »(x)отличны от нуля и сохраняют определенные постоянные знаки; 3) f(a)× f(b) < 0 (функция f(x)меняет знак на отрезке). Тогда существует отрезок [α, β], содержащий искомый корень уравнения f(x) = 0, на котором итерационная последовательность сходится. Если в качестве нулевого приближения х0 выбрать ту граничную точку [α, β], в которой знак функции совпадает со знаком второй производной, т.е. f(x0)× f»(x0)>0, то итерационная последовательность сходится монотонно
Слайд 17
Таблица. Расчетное уравнение по методу касательных: x= 0,1001
Слайд 18
Результаты: Исследование методов показало различные методы решения алгебраических и трансцендентных уравнений с помощью электронной таблицы Microsoft Excel . Следующие методы были изучены: • Графический метод; • Подбор параметра; • Метод половинного деления; • Метод итераций; • Метод хорд (метод секущих); • Метод касательных (метод Ньютона); • Комбинированный метод.
Слайд 19
Вывод: Я изучил методы решения алгебраических и трансцендентных уравнений на примере задачи с физическим содержанием с помощью Microsoft Excel . В данной работе я показал методы решение алгебраических и трансцендентных уравнений в среде Microsoft Excel : 1)методом бисекции;2)методом итераций;3)методом секущих;4)методом Ньютона;5)метод подбора параметра;
Слайд 20
Список использованных источников : 1. Lectures on Numerical Analysis /Dennis Deturck , Herbert S. Wilf. — 1- е издание . — Philadelphia: Department of Mathematics University of Pennsylvania, 2002. — 125 с . 2. Numerical analysis [ Электронный ресурс ] / Wikipedia contributors. — Электрон . текстовые дан . — San Francisco: Wikipedia, The Free Encyclopedia, 2019. — Режим доступа : https://en.wikipedia.org/w/index.php?title=Numerical_analysis&oldid=895278527, свободный . — Online encyclopedia ( Дата обращения : 13.05.2019); 3. Numerical methods /John D. Fenton. — 1- е издание . — Vienna: Institute of Hydraulic Engineering and Water Resources Management. Vienna University of Technology, 2019. — 33 с .; 4. Numerical Methods for Physicists [ Электронный ресурс ] / Anthony O’Hare. — Электрон . текстовые дан . — Belton: MMHB. Department of Computer Science and Engineering, 2005. — Режим доступа : http://mars.umhb.edu/~wgt/engr2311/NMfP.pdf, свободный ( Дата обращения : 12.05.2019)
Метод Ньютона (метод касательных).
Суть метода состоит в том, что на -й итерации в точке строится касательная к кривой и ищется точка пересечения касательной с осью абсцисс (рис. 1.6). Если задан интервал изоляции корня , то за начальное приближение принимается тот конец отрезка, на котором
Уравнение касательной, проведенной к кривой в точке с координатами и , имеет вид:
За следующее приближение корня примем абсциссу точки пересечения касательной с ocью OX. Из (1.2) при , получим
Аналогично могут быть найдены и следующие приближения как точки пересечения с осью абсцисс касательных, проведенных в точках , и т.д. Формула для -го приближения имеет вид:
Для завершения итерационного процесса можно использовать условия или .
Объем вычислений в методе Ньютона больше, чем в других методах, поскольку приходится находить значение не только функции , но и ее производной. Однако скорость сходимости здесь значительно выше.
Пример 1.2. Решить уравнение на отрезке методом Ньютона c точностью .
Решение. Определим первые и вторые производные заданной функции : ; . Проверим выполнение условия сходимости на концах заданного интервала: — не выполняется, — выполняется. За начальное приближение корня можно принять . Находим первое приближение:
Так как , итерационный процесс заканчивается. Таким образом, приближенным решением данного уравнения является .
На рис. 1.7 приведена программа решения данного уравнения методом Ньютона. В качестве исходных данных вводятся начальное приближение и точность вычисления.
Пример 1.3. Решить уравнение на отрезке методом Ньютона c точностью с помощью программы Excel.
| A | B | C | D |
| x | F(x) | F'(x) | погрешность |
| 1,00000 | |||
| 0,75000 | 1,00000 | 4,00000 | 0,25000 |
| 0,68605 | 0,17188 | 2,68750 | 0,06395 |
| 0,68234 | 0,00894 | 2,41198 | 0,00371 |
| 0,68233 | 0,00003 | 2,39676 | 0,00001 |
| Рис. 1.8. Решение уравнения методом Ньютона с помощью программы Excel. |
1) Ввести в ячейки A1:D1 заголовки столбцов.
2) В ячейку A2 – значение начального приближения
3) В ячейку B3 – формулу функции =A2^3+A2-1
4) В ячейку C3 – формулу производной функции =3*A2^2+1
5) В ячейку A3 – формулу первого приближения =A2-B3/C3
6) В ячейку D3 – погрешность =ABS(A3-A2)
7) Выделить ячейки A3:D3 и скопировать формулы в соседние ячейки расположенных ниже строк A4:D4, A5:D5, и т.д. при помощи маркера заполнения. Каждая новая строка содержит результаты очередного приближения.
В столбце A найти значение корня, соответствующее заданной точности.
Приближенное решение данного уравнения содержится в ячейке A6 (погрешность в ячейке D6).
Для использования этого метода исходное нелинейное уравнение необходимо привести к виду .
В качестве можно принять функцию ,где M ‑ неизвестная постоянная величина, которая определяется из условия сходимости метода простой итерации . При этом для определения M условие сходимости записывается в следующем виде:
Если известно начальное приближение корня , подставляя это значение в правую часть уравнения , получаем новое приближение .
Далее подставляя каждый раз новое значение корня в уравнение , получаем последовательность значений:
, ,. , k = 1,2. n.
Итерационный процесс прекращается, если результаты двух последовательных итераций близки, т.е. .
| а) | б) |
| Рис. 1.9. Геометрическая интерпретация метода простой итерации. |
Пример 1.4. Решить уравнение на отрезке методом простой итерации c точностью .
Решение. Из условия сходимости (1.5) , при определяем .Пусть .
Подставляя каждый раз новое значение корня в уравнение
Теперь и приближенным решением данного уравнения c точностью является .
На рис.1.10 приведена программа решения данного уравнения методом простой итерации. В качестве исходных данных вводятся начальное приближение, точность вычисления и значение постоянной М.
Пример 1.4. Решить уравнение на отрезке методом простой итерации c точностью с помощью программы Excel.
| A | B | C | D |
| x | f(x) | M | погрешность |
| 0,8 | 0,2 | ||
| 0,7376 | 0,312 | 0,0624 | |
| 0,70982 | 0,13889 | 0,02777881 | |
| 0,69633 | 0,06746 | 0,01349237 | |
| 0,68954 | 0,03396 | 0,00679209 | |
| 0,68606 | 0,01738 | 0,0034769 | |
| 0,68427 | 0,00897 | 0,00179463 | |
| Рис.1.11. Решение уравнения методом простой итерации с помощью программы Excel. |
1) Ввести в ячейки A1:D1 заголовки столбцов.
2) В ячейку A2 – значение начального приближения
3) В ячейку B3 – формулу функции =A2^3+A2-1
4) В ячейку C2 – значение M 5
5) В ячейку A3 – формулу первого приближения =A2-B3/$C$2
6) В ячейку D3 – погрешность =ABS(A3-A2)
7) Выделить ячейки A3:D3 и скопировать формулы в соседние ячейки расположенных ниже строк A4:D4, A5:D5, и т.д. при помощи маркера заполнения. Каждая новая строка содержит результаты очередного приближения.
В столбце A найти значение корня, соответствующее заданной точности.
Приближенное решение данного уравнения содержится в ячейке A9 (погрешность в ячейке D9).
[expert_bq id=»1570″]при сохранении книги Excel после поиска решения все значения, введенные в окнах диалога Поиск решения , сохраняются вместе с данными рабочего листа. Если же вы хотите что-то уточнить, обращайтесь ко мне![/expert_bq]
· Метод поиска – служит для выбора алгоритма оптимизации. Метод Ньютона был рассмотрен ранее. В Методе сопряженных градиентов запрашивается меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно велика и необходимо экономить память, а также если итерации дают слишком малое отличие в последовательных приближениях.
Метод Ньютона (метод касательных).
Очевидно, что этот метод обеспечивает сходящийся процесс приближений лишь при выполнении некоторых условий (например при непрерывности и знакопостоянстве первой и второй производной функции в окрестности корня) и при их нарушении либо дает расходящийся процесс (4), либо приводит к другому корню (5).
| а) | б) |
| Рис. 1.9. Геометрическая интерпретация метода простой итерации. |