Метод дихотомии в excel это

Решение уравнений в EXCEL методом половинного деления, методом хорд и касательных.

При прохождении темы численные методы учащиеся уже умеют работать с электронными таблицами и составлять программы на языке паскаль. Работа комбинированного характера.Расчитана на 40 минут. Цель работы повторить и закрепить навыки паботы с программами EXCEL, ABCPascal. Материал содержит 2 файла. Один содержит теоретический материал, так как он и предлагается ученику . Во 2-м файле пример работы ученика Иванова Ивана.

Скачать:

Вложение	Размер
материал для ученика	57.5 КБ
работа ученика	27 КБ

Предварительный просмотр:

Аналитическое решение некоторых уравнений, содержащих, например тригонометрические функции может быть получено лишь для единичных частных случаев. Так, например, нет способа решить аналитически даже такое простое уравнение, как cos x=x

Численные методы позволяют найти приближенное значение корня с любой заданной точностью.

Приближённое нахождение обычно состоит из двух этапов:

1) отделение корней, т.е. установление возможно точных промежутков [a,b], в которых содержится только один корень уравнения;

2) уточнение приближённых корней, т.е. доведение их до заданной степени точности.

Мы будем рассматривать решения уравнений вида f(x)=0. Функция f(x) определена и непрерывна на отрезке [а.Ь]. Значение х 0 называется корнем уравнения если f(х 0 )=0

Для отделения корней будем исходить из следующих положений:

• Если f(a)* f(b] a, b существует, по крайней мере, один корень
• Если функция y = f(x) непрерывна на отрезке [a, b], и f(a)*f(b) и f ‘(x) на интервале (a, b) сохраняет знак, то внутри отрезка [а, b] существует единственный корень уравнения

Приближённое отделение корней можно провести и графически. Для этого уравнение (1) заменяют равносильным ему уравнением р(х) = ф(х), где функции р(х) и ф(х] более простые, чем функция f(x). Тогда, построив графики функций у = р(х) и у = ф(х), искомые корни получим, как абсциссы точек пересечения этих графиков

Для уточнения корня разделим отрезок [а, b] пополам и вычислим значение функции f(х) в точке x sr =(a+b)/2. Выбираем ту из половин [a, x sr ] или [x sr ,b], на концах которых функция f(x) имеет противоположные знаки.. Продолжаем процесс деления отрезка пополам и проводим то же рассмотрение до тех пор, пока. длина [a,b] станет меньше заданной точности . В последнем случае за приближённое значение корня можно принять любую точку отрезка [a,b] (как правило, берут его середину). Алгоритм высокоэффективен, так как на каждом витке (итерации) интервал поиска сокращается вдвое; следовательно, 10 итераций сократят его в тысячу раз. Сложности могут возникнуть с отделением корня у сложных функций.

Для приближенного определения отрезка на котором находится корень можно воспользоваться табличным процессором, построив график функции

ПРИМЕР : Определим графически корень уравнения . Пусть f1(х) = х , a и построим графики этих функций. (График). Корень находится на интервале от 1 до 2. Здесь же уточним значение корня с точностью 0,001(на доске шапка таблицы)

Алгоритм для программной реализации

1. а:=левая граница b:= правая граница
2. m:= (a+b)/2 середина
3. определяем f(a) и f(m)
4. если f(a)*f(m)
5. если (a-b)/2>e повторяем , начиная с пункта2

Точки графика функции на концах интервала соединяются хордой. Точка пересечения хорды и оси Ох (х*) и используется в качестве пробной. Далее рассуждаем так же, как и в предыдущем методе: если f(x a ) и f(х*) одного знака на интервале , нижняя граница переносится в точку х*; в противном случае – переносим верхнюю границу. Далее проводим новую хорду и т.д.

Осталось только уточнить, как найти х*. По сути, задача сводится к следующей: через 2 точки с неизвестными координатами (х 1 , у 1 ) и (х 2 , у 2 ) проведена прямая; найти точку пересечения этой прямой и оси Ох.

Запишем уравнение прямой по двум точках:

В точке пересечения этой прямой и оси Ох у=0, а х=х*, то есть

, откуда

процесс вычисления приближённых значений продолжается до тех пор, пока для двух последовательных приближений корня х„ и х п _1 не будет выполняться условие abs(xn-x n-1 ) е — заданная точность

Сходимость метода гораздо выше предыдущего

Алгоритм различается только в пункте вычисления серединной точки- пересечения хорды с осью абсцисс и условия останова (разность между двумя соседними точками пересечения)

Уравнения для самостоятельного решения: (отрезок в excel ищем самостоятельно)

1 Численный метод решения нелинейных уравнений

1.1 Область локализации корней

В общем виде любое уравнение одной переменной принято записывать так , при этом корнем (решением) называется такое значение x*, что оказывается верным тождеством. Уравнение может иметь один, несколько (включая бесконечное число) или ни одного корня. Как легко видеть, для действительных корней задача отыскания решения уравнения легко интерпретируется графически: корень есть такое значение независимой переменной, при котором происходит пересечение графика функции, стоящей в левой части уравнения f ( x ), с осью абсцисс.

Например , для уравнения выполним преобразование и приведем его к виду f(x)= 0 т.е. . График этой функции представлен на рисунке 1. Очевидно, что данное уравнение имеет два действительных корня – один на отрезке [-1, 0] , а второй – [1, 2].

Рисунок 1. График функции

Таким образом, можно приблизительно определять область локализации корней уравнения. Заметим, что отделить корень можно не единственным образом: если корень отделён на каком-либо отрезке, то годится и любой меньший отрезок, содержащий этот корень. Вообще говоря, чем меньше отрезок, тем лучше, но при этом не следует забывать о том, что на отделение корня на меньших отрезках также тратятся вычислительные усилия, и, быть может, весьма значительные. Таким образом, часто для начала довольствуются весьма широким отрезком, на котором корень отделён.

Некоторые виды уравнений допускают аналитическое решение. Например, степенные алгебраические уравнения степени n при n ≤ 4. Однако, в общем виде, аналитическое решение, как правило, отсутствует. В этом случае, применяются численные методы. Все численные методы решения уравнений представляют собой итерационные алгоритмы последовательного приближения к корню уравнения. То есть, выбирается начальное приближение к корню x ₀ и затем с помощью итерационной формулы генерируется последовательность x ₁, x ₂, …, x_k сходящаяся к корню уравнения .

1.2 Критерии сходимости при решении уравнений

Ø Абсолютная погрешность — абсолютное изменение приближения на соседних шагах итерации

Ø Относительная погрешность — относительное изменение приближения на соседних шагах итерации

Ø Близость к нулю вычисленного значения левой части уравнения (иногда это значение называют невязкой уравнения, так как для корня невязка равна нулю)

1.3 Метод половинного деления (метод дихотомии)

Метод половинного деления основан на последовательном делении отрезка локализации корня пополам.

Для этого выбирается начальное приближение к отрезку [ a , b ], такое, что f ( a ) × f ( b ) — середине отрезка [ a , b ]. Если он противоположен знаку функции в точке a, то корень локализован на отрезке [ a , c ], если же нет – то на отрезке [ c , b ]. Схема метода дихотомии приведен на рис у нке 2.

Рисунок 2. Последовательное деление отрезка пополам и приближение к корню

Алгоритм метода дихотомии можно записать так:

1. представить решаемое уравнение в виде

2. выбрать a, b и вычислить

3. если f(a) × f( с ) то a=a; b = c иначе a = c; b=b

4. если критерий сходимости не выполнен, то перейти к п. 2

Пример решения уравнения методом дихотомии

Найти решение заданного уравнения методом дихотомии с точностью до 10 -5 .

Пример создания расчетной схемы на основе метода дихотомии на примере уравнения: на отрезке [1, 2]

Данный метод заключается в проверке на каждой итерации условия:

если f ( a ) × f (с) и выбор соответствующего отрезка для следующей итерации.

Рисунок 3. Последовательность итераций метода дихотомии при поиске корня уравнения на отрезке [1, 2]

a ) схема расчета (зависимые ячейки); b) режим отображения формул;

Для нашего примера итерационная последовательность для нахождения решения принимает вид:

Точность до пятой значащей цифры достигается за 20 итераций.

Скорость сходимости этого метода является линейной.

При выполнении начального условия он сходится к решению всегда.

Метод половинного деления удобен при решении физически реальных уравнений, когда заранее известен отрезок локализации решения уравнения.

2 Решение уравнений , используя “Подбор параметра ”

Используя возможности Excel можно находить корни нелинейного уравнения вида f(x)=0 в допустимой области определения переменной. Последовательность операций нахождения корней следующая:

1. Производится табулирование функции в диапазоне вероятного существования корней;

2. По таблице фиксируются ближайшие приближения к значениям корней;

3. Используя средство Excel Подбор параметра, вычисляются корни уравнения с заданной точностью.

При подборе параметра Excel использует итерационный (циклический) процесс. Количество итераций и точность устанавливаются в меню Сервис/Параметры/вкладка Вычисления. Если Excel выполняет сложную задачу подбора параметра, можно нажать кнопку Пауза в окне диалога Результат подбора параметра и прервать вычисление, а затем нажать кнопку Шаг, чтобы выполнить очередную итерацию и просмотреть результат. При решении задачи в пошаговом режиме появляется кнопка П родолжить — для возврата в обычный режим подбора параметра.

2.1 Пример решения уравнения, используя “Подбор параметра”

Например , найдем все корни уравнения 2x 3 -15sin(x)+0,5x-5=0 на отрезке [-3 ; 3].

Для локализации начальных приближений необходимо определить интервалы значений Х, внутри которых значение функции пересекает ось абсцисс, т.е. функция меняет знак. С этой целью табулируем функцию на отрезке [–3; 3] с шагом 0,2, получим табличные значения функции. Из полученной таблицы находим, что значение функции трижды пересекает ось Х, следовательно, исходное уравнение имеет на заданном отрезке все три корня.

Рисунок 4. Поиск приближенных значений корней уравнения

Выполните команду меню Сервис/Параметры, во вкладке Вычисления установите относительную погрешность вычислений E=0,00001, а число итераций N=1000, установите флажок Итерации.

Выполните команду меню Сервис/Подбор параметра. В диалоговом окне (рисунок 9) заполните следующие поля:

þ Установить в ячейке : в поле указывается адрес ячейки, в которой записана формула правой части функции;

þ Значение : в поле указывается значение, которое должен получить полином в результате вычислений, т.е. правая часть уравнения (в нашем случае 0);

þ Изменяя значение : в поле указывается адрес ячейки (где записано начальное приближение), в которой будет вычисляться корень уравнения и на которую ссылается формула.

Рисунок 5. Диалоговое окно Подбор параметра для поиска первого корня

После щелчка на ОК получим значение первого корня -1,65793685 .

Выполняя последовательно операции аналогичные предыдущим, вычислим значения остальных корней: -0,35913476 и 2,05170101 .

3 Решение уравнений и систем уравнений, используя надстройку “Поиск решения”

Для решения уравнений можно также использовать команду Поиск решения, доступ к которой реализуется через пункт меню Сервис/Поиск решения.

Последовательность операций нахождения корней следующая:

1. Найти приближенное значение корня уравнения

2. Открыть диалог Поиск решения и установить следующие параметры (рисунок 10):

þ в поле У становить целевую ячейку ввести адрес ячейки, содержащей формулу (левую часть уравнения);

þ установить переключатель в положение ‘ значению’ и ввести значение 0 (правая часть уравнения);

þ в поле Изменяя ячейки ввести адреса изменяемых ячеек, т.е. аргумента x целевой функции,;

þ в поле Ограничения с помощью кнопки Д обавить ввести все ограничения, которым должен отвечать результат поиска (область поиска корня уравнения);

þ для запуска процесса поиска решения нажать кнопку В ыполнить.

þ Для сохранения полученного решения необходимо использовать переключатель С охранить найденное решение в открывшемся окне диалога Результаты поиска решения.

Рисунок 6. Диалоговое окно Поиск решения

Полученное решение зависит от выбора начального приближения. Поиск начальных приближений рассмотрен выше.

Рассмотрим некоторые Опции, управляющие работой Поиска решения, задаваемые в окне Параметры (окно появляется, если нажать на кнопку Параметры окна Поиск решения):

þ Максимальное время — ограничивает время, отведенное на процесс поиска решения (по умолчанию задано 100 секунд, что достаточно для задач, имеющих около 10 ограничений, если задача большой размерности, то время необходимо увеличить).

þ Относительная погрешность — задает точность, с которой определяется соответствие ячейки целевому значению или приближение к указанным ограничениям (десятичная дробь от 0 до 1).

þ Неотрицательные значения — этим флажком можно задать ограничения на переменные, что позволит искать решения в положительной области значений, не задавая специальных ограничений на их нижнюю границу.

þ Показывать результаты итераций — этот флажок позволяет включить пошаговый процесс поиска, показывая на экране результаты каждой итерации.

þ Метод поиска — служит для выбора алгоритма оптимизации. Метод Ньютона был рассмотрен ранее. В Методе сопряженных градиентов запрашивается меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно велика и если итерации дают слишком малое отличие в последовательных приближениях.

Рисунок 7. Вкладка Параметры окна Поиск решения

3.1 Пример решения уравнения, используя надстройку “Поиск решения”

Например , найдем все корни уравнения 2x 3 -15sin(x)+0,5x-5=0 на отрезке [-3 ; 3]. Для локализации начальных приближений необходимо определить интервалы значений Х, внутри которых значение функции пересекает ось абсцисс, т.е. функция меняет знак. С этой целью табулируем функцию на отрезке [–3;3] с шагом 0,2, получим табличные значения функции. Из полученной таблицы находим, что значение функции трижды пересекает ось Х, следовательно, исходное уравнение имеет на заданном отрезке все три корня. На рисунке 12 представлен пример заполнения окна Поиск решения для нахождения первого корня на отрезке [-2; -1].

Рисунок 8. Пример решения уравнения при помощи надстройки Поиск решения

Задание 1. Решение уравнений численным методом

На листе 1 (название листа: Численные методы) для заданного уравнения вида f(x)=0 (Таблица 1. Индивидуальные задания ) реализовать итерационные расчетные схемы методов, указанных в Таблице 1 для нахождения хотя бы одного корня на заданном интервале. Количество итераций просчитать, оценивая , .

Задания 2. Решение уравнений встроенными средствами “Подбор параметра” и “Поиск решения”

На листе 2 (название листа: Подбор Поиск) для заданного уравнения вида f(x)=0 (Таблица 1. Индивидуальные задания) на заданном интервале и с некоторым шагом (шаг выбрать самостоятельно) построить таблицу значений функции f(x) и определить количество корней уравнения и выделить интервалы, на которых находятся корни. Построить график функции. Уточнить на заданных интервалах с точностью до 10 -6 корни уравнения с помощью встроенных средств: Подбор параметра, Поиск решения

Решение уравнения с помощью методов дихотомии, хорд, Ньютона в MSExcel и в VisualBasic

Страницы работы

Содержание работы

Министерство образования и науки Российской Федерации

Санкт-Петербургский Государственный архитектурно-строительный университет

кафедра прикладной математики и информатики

по информатике и ИКТ

Работу выполнила студентка

1 курса группы 1-РРАН-I

специальности «Реставрация и

наследия» Богданова М. А.

Работу проверила ассистент

Григорьева Ксения Владимировна

Содержание

Метод деления отрезка пополам.. 3

Приближенное решение уравнений методом касательных. 4

Метод Ньютона. 4

Решение уравнения методом деления отрезка пополам в MS Excel. 5

Решение уравнения методом хорд в MS Excel. 7

Решение уравнения методом Ньютона в MS Excel. 8

User Form по решению уравнения x 3 +2,56*x 2 -1,3251*x+4,395006=0 указанными методами.. 9

Метод деления отрезка пополам

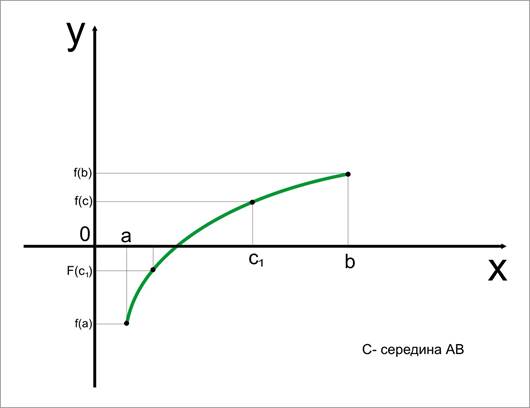
Пустьf(x) непрерывна на концах отрезка [a;b] имеет разные знаки, т.е. f(a)*f(b) 0

Точка A(a;f(a)) и B(b;f(b)) соединим хордой. За исходное приближенное значение исходного корня примем абсциссу х₁ – точка пересечения АВ с осью x