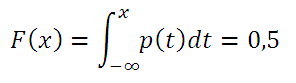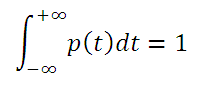Median на русском excel

Функция МЕДИАНА в Excel используется для анализа диапазона числовых значений и возвращает число, которое является серединой исследуемого множества (медианой). То есть, данная функция условно разделяет множество чисел на два подмножества, первое из которых содержит числа меньше медианы, а второе – больше. Медиана является одним из нескольких методов определения центральной тенденции исследуемого диапазона.

Примеры использования функции МЕДИАНА в Excel

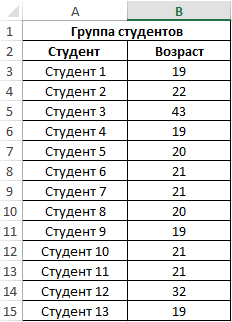
Пример 1. При исследовании возрастных групп студентов использовались данные случайно выбранной группы учащихся в ВУЗе. Задача – определить срединный возраст студентов.

Исходные данные:

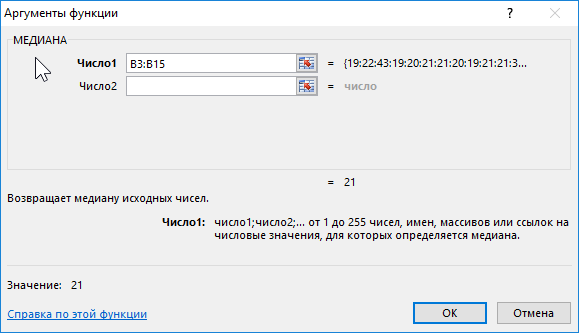
Формула для расчета:

Описание аргумента:

• B3:B15 – диапазон исследуемых возрастов.

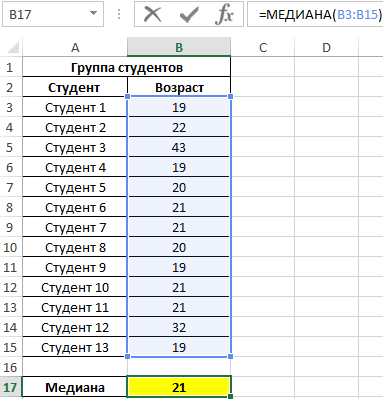
Полученный результат:

То есть в группе есть студенты, возраст которых меньше 21 года и больше этого значения.



Сравнение функций МЕДИАНА и СРЗНАЧ для вычисления среднего значения

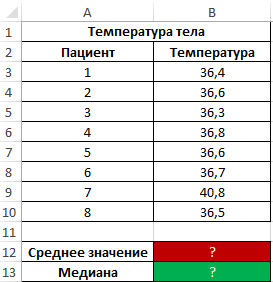
Пример 2. Во время вечернего обхода в больнице каждому больному была замерена температура тела. Продемонстрировать целесообразность использования параметра медиана вместо среднего значения для исследования ряда полученных значений.

Исходные данные:

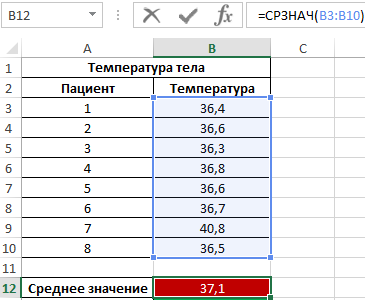
Формула для нахождения среднего значения:

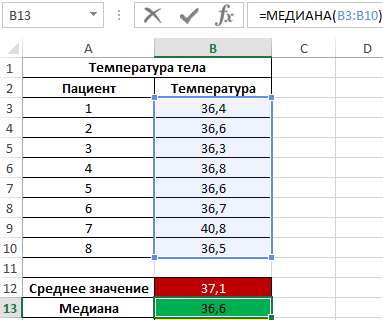
Формула для нахождения медианы:

Как видно из показателя среднего значения, в среднем температура у пациентов выше нормы, однако это не соответствует действительности. Медиана показывает, что как минимум у половины пациентов наблюдается нормальная температура тела, не превышающая показатель 36,6.

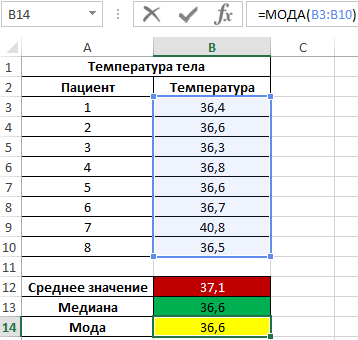
Внимание! Еще одним методом определения центральной тенденции является мода (наиболее часто встречающееся значение в исследуемом диапазоне). Чтобы определить центральную тенденцию в Excel следует использовать функцию МОДА. Обратите внимание: в данном примере значения медианы и моды совпадают:

То есть срединная величина, делящая одно множество на подмножества меньших и больших значений также является и наиболее часто встречающимся значением в множестве. Как видно, у большинства пациентов температура составляет 36,6.

Пример расчета медианы при статистическом анализе в Excel

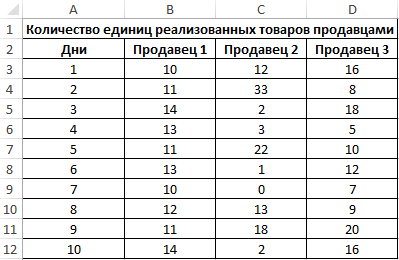
Пример 3. В магазине работают 3 продавца. По результатам последних 10 дней необходимо определить работника, которому будет выдана премия. При выборе лучшего работника учитывается степень эффективности его работы, а не число проданных товаров.

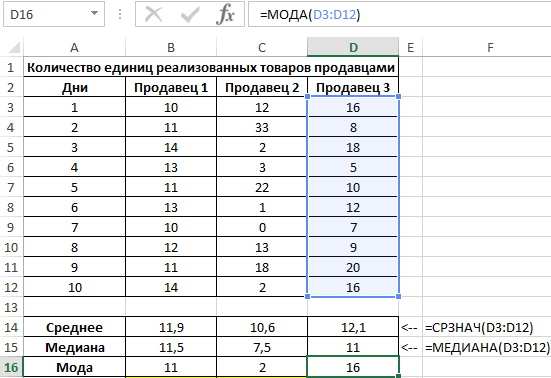
Исходная таблица данных:

Для характеристики эффективности будем использовать сразу три показателя: среднее значение, медиана и мода. Определим их для каждого работника с использованием формул СРЗНАЧ, МЕДИАНА и МОДА соответственно:

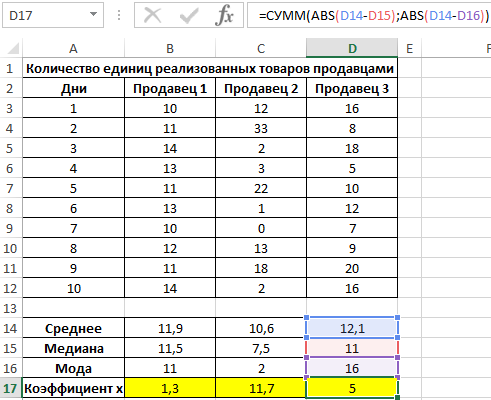
Для определения степени разброса данных используем величину, которая является суммарным значением модуля разницы среднего значения и моды, среднего значения и медианы соответственно. То есть коэффициент x=|av-med|+|av-mod|, где:

• av – среднее значение;
• med – медиана;
• mod – мода.

Рассчитаем значение коэффициента x для первого продавца:

Аналогично проведем расчеты для остальных продавцов. Полученные результаты:

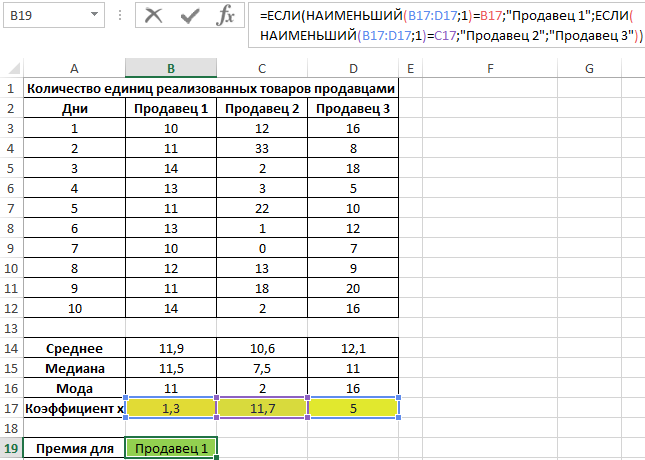
Определим продавца, которому будет выдана премия:

Примечание: функция НАИМЕНЬШИЙ возвращает первое минимальное значение из рассматриваемого диапазона значений коэффициента x.

Коэффициент x является некоторой количественной характеристикой стабильности работы продавцов, которую ввел экономист магазина. С его помощью удалось определить диапазон с наименьшими отклонениями значений. Этот способ демонстрирует, как можно использовать сразу три метода определения центральной тенденции для получения наиболее достоверных результатов.

Особенности использования функции МЕДИАНА в Excel

Функция имеет следующий синтаксис:

=МЕДИАНА(число1;[число2];…)

Описание аргументов:

• число1 – обязательный аргумент, характеризующий первое числовое значение, содержащееся в исследуемом диапазоне;
• [число2] – необязательный второй (и последующие аргументы, всего до 255 аргументов), характеризующий второе и последующие значения исследуемого диапазона.

Примечания 1:

1. При расчетах удобнее передавать сразу весь диапазон исследуемых значений вместо последовательного ввода аргументов.
2. В качестве аргументов принимаются данные числового типа, имена, содержащие числа, данные ссылочного типа и массивы (например, =МЕДИАНА({1;2;3;5;7;10})).
3. При расчете медианы учитываются ячейки, содержащие пустые значения или логические ИСТИНА, ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно. Например, результат выполнения функции с логическими значениями в аргументах (ИСТИНА;ЛОЖЬ) эквивалентен результату выполнения с аргументами (1;0) и равен 0,5.
4. Если один или несколько аргументов функции принимают текстовые значения, которые не могут быть преобразованы в числовые, или содержат коды ошибок, результатом выполнения функции будет код ошибки #ЗНАЧ!.
5. Для определения медианы выборки могут быть использованы другие функции Excel: ПРОЦЕНТИЛЬ.ВКЛ, КВАРТИЛЬ.ВКЛ, НАИБОЛЬШИЙ Примеры использования:

• =ПРОЦЕНТИЛЬ.ВКЛ(A1:A10;0,5), поскольку по определению медиана – 50-я процентиль.
• =КВАРТИЛЬ.ВКЛ(A1:A10;2), так как медиана – 2-я квартиль.
• =НАИБОЛЬШИЙ(A1:A9;СЧЁТ(A1:A9)/2), но только если количество чисел в диапазоне является нечетным числом.

Примечания 2:

1. Если в исследуемом диапазоне все числа распределены симметрично относительно среднего значения, среднее арифметическое и медиана для данного диапазона будут эквивалентны.
2. При больших отклонениях данных в диапазоне («разбросе» значений) медиана лучше отражает тенденцию распределения значений, чем среднее арифметическое. Отличным примером является использование медианы для определения реального уровня зарплат у населения государства, в котором чиновники получают на порядок больше обычных граждан.
3. Диапазон исследуемых значений может содержать:

Скачать примеры функции МЕДИАНА для статистического анализа в Excel

• Нечетное количество чисел. В этом случае медианой будет являться единственное число, разделяющее диапазон на два подмножества больших и меньших значений соответственно;
• Четное количество чисел. Тогда медиана вычисляется как среднее арифметическое для двух числовых значений, разделяющих множество на два указанных выше подмножества.

В этой статье описаны синтаксис формулы и использование функции МЕДИАНА в Microsoft Excel.

Описание

Возвращает медиану заданных чисел. Медиана — это число, которое является серединой множества чисел.

Синтаксис

МЕДИАНА(число1;[число2];…)

Аргументы функции МЕДИАНА описаны ниже.

• Число1, число2,…    Аргумент «число1» является обязательным, последующие числа необязательные. От 1 до 255 чисел, для которых требуется определить медиану.

Замечания

• Если в наборе имеется ряду чисел, медиана вычисляет среднее значение двух чисел в середине. См. вторую формулу в примере.

• Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.

• Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.

• Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения пропускаются; однако ячейки, которые содержат нулевые значения, учитываются.

• Аргументы, которые являются значениями ошибки или текстами, не преобразуемыми в числа, приводят в возникновению ошибок.

Примечание: Функция МЕДИАНА измеряет центральную тенденцию, которая является центром множества чисел в статистическом распределении. Существует три наиболее распространенных способа определения центральной тенденции:

• Среднее значение     — это среднее арифметическое, которое вычисляется путем сложения набора чисел с последующим делением полученной суммы на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.

• Медиана     — это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4.

• Мода     — это число, наиболее часто встречающееся в данном наборе чисел. Например, модой для чисел 2, 3, 3, 5, 7 и 10 будет 3.

При симметричном распределении множества чисел все три значения центральной тенденции будут совпадать. При смещенном распределении множества чисел значения могут быть разными.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные
1
2
3
4
5
6
Формула	Описание	Результат
=МЕДИАНА(A2:A6)	Медиана пяти чисел в диапазоне A2:A6. Так как имеется пять значений, третье из них является медианой.	3
=МЕДИАНА(A2:A7)	Медиана шести чисел в диапазоне A2:A6. Так как имеется шесть чисел, медианой является средняя точка между третьим и четвертым числами.	3,5

Для вычисления медианы в MS EXCEL существует специальная функция

МЕДИАНА()

. В этой статье дадим определение медианы и научимся вычислять ее для выборки и для заданного закона распределения случайной величины.

Начнем с

медианы

для

выборок

(т.е. для фиксированного набора значений).

Медиана выборки

Медиана

(median) – это число, которое является серединой множества чисел: половина чисел множества больше, чем

медиана

, а половина чисел меньше, чем

медиана

.

Для вычисления

медианы

необходимо сначала

отсортировать множество чисел

(значения в

выборке

). Например,

медианой

для выборки (2; 3; 3;

4

; 5; 7; 10) будет 4. Т.к. всего в

выборке

7 значений, три из них меньше, чем 4 (т.е. 2; 3; 3), а три значения больше (т.е. 5; 7; 10).

Если множество содержит четное количество чисел, то вычисляется

среднее

для двух чисел, находящихся в середине множества. Например,

медианой

для выборки (2; 3;

3

;

6

; 7; 10) будет 4,5, т.к. (3+6)/2=4,5.

Для определения

медианы

в MS EXCEL существует одноименная функция

МЕДИАНА()

, английский вариант MEDIAN().

Медиана

не обязательно совпадает со

средним значением (mean, average) в

выборке

. Совпадение имеет место только в том случае, если значения в выборке распределены симметрично относительно

среднего

. Например, для

выборки

(1; 2;

3

;

4

; 5; 6)

медиана

и

среднее

равны 3,5.

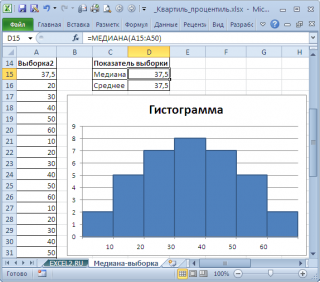
Чтобы в этом убедиться —

построим гистограмму

для симметричной выборки, состоящую из 36 значений, и вычислим

среднее

и

медиану

(см.

файл примера

лист

Медиана-выборка

).

В чем же ценность

медианы

? Почему ее используют зачастую наравне со

средним значением

?

Оба параметра используются для определения «центральной тенденции»

выборки

. Для

выборки

с несимметричным распределением,

медиана

будет отличаться от

среднего

. Например, для (1; 2;

3

;

4

; 5; 600)

медиана

равна 3,5, а вот

среднее

равно 103,5 (смещено в сторону б

о

льшего значения).

То есть, если имеется длинный хвост распределения, то

медиана

лучше, чем

среднее

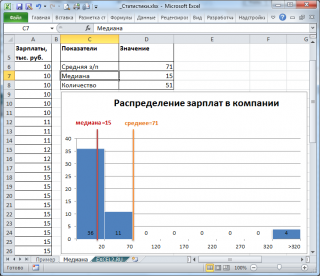
значение, отражает «типичное» или «центральное» значение. Например, рассмотрим пример несправедливого распределения зарплат в компании, в которой руководство получает существенно больше, чем основная масса сотрудников (также см.

статью Описательная статистика

, раздел

Медиана

).

Очевидно, что средняя зарплата (71 тыс. руб.) не отражает тот факт, что 86% сотрудников получает не более 30 тыс. руб. (т.е. 86% сотрудников получает зарплату в более, чем в 2 раза меньше средней!). В то же время медиана (15 тыс. руб.) показывает, что

как минимум

у половины сотрудников зарплата меньше или равна 15 тыс. руб.

Примечание

: Так как медиана является 50-й

процентилью

и 2-й

квартилью

, ее также можно вычислить с помощью формул

=ПРОЦЕНТИЛЬ.ВКЛ(

Выборка;0,5

)

и

=КВАРТИЛЬ.ВКЛ(

Выборка;2

)

, где

Выборка

– это ссылка на диапазон, содержащий значения выборки.

Если выборка содержит нечетное количество чисел, то для вычисления медианы можно также воспользоваться формулой:

НАИБОЛЬШИЙ(Выборка;СЧЁТ(Выборка)/2)

.

Медиана непрерывного распределения

Если

Функция распределения

F

(х)

случайной величины

х

непрерывна, то

медиана

является решением уравнения

F(х)

=0,5.

Примечание

: подробнее о

Функции распределения

см. статью

Функция распределения и плотность вероятности в MS EXCEL

.

Если известна

Функция распределения

F(х) или

функция плотности вероятности

p

(х)

, то

медиану

можно найти из уравнения:

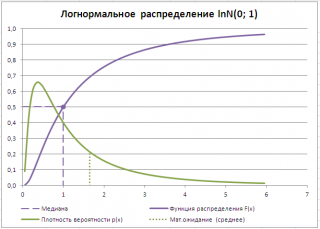
Например, решив аналитическим способом это уравнение для Логнормального распределения lnN(μ; σ

²

), получим, что

медиана

вычисляется по формуле =EXP(μ). При μ=0, медиана равна 1.

Обратите внимание на точку

Функции распределения

, для которой

F

(х)=0,5

(см. картинку выше)

.

Абсцисса этой точкиравна1. Это и есть значение медианы, что естественно совпадает с ранее вычисленным значением по формуле em.

В MS EXCEL

медиану

для

логнормального распределения

LnN(0;1) можно вычислить по формуле

=ЛОГНОРМ.ОБР(0,5;0;1)

.

Примечание

: Напомним, что интеграл от

функции плотности вероятности

по всей области задания случайной величины равен единице.

Поэтому, линия медианы (х=Медиана) делит площадь под графиком

функции плотности вероятности

на две равные части.

Примечание

: В

статье о распределениях MS EXCEL

приведены ссылки на распределения для которых в MS EXCEL существуют специальные функции (

нормальное распределение

,

гамма-распределение

,

Экспоненциальное

и др.). Используя эти функции можно вычислить

медиану

соответствующего распределения.

Функция МЕДИАНА возвращает медиану заданных чисел.

Описание функции МЕДИАНА

Возвращает медиану заданных чисел. Медиана — это число, которое является серединой множества чисел.

Синтаксис

=МЕДИАНА(число1; [число2]; …)

Аргументы

Замечания

• Если в множество содержит четное количество чисел, функция МЕДИАНА вычисляет среднее для двух чисел, находящихся в середине множества.
• Аргументы должны быть либо числами, либо содержащими числа именами, массивами или ссылками.
• Учитываются логические значения и текстовые представления чисел, которые введены непосредственно в список аргументов.
• Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения игнорируются; ячейки, содержащие нулевые значения, учитываются.
• Аргументы, которые являются значениями ошибки или текстами, не преобразуемыми в числа, приводят в возникновению ошибок.
• Функция МЕДИАНА измеряет центральную тенденцию, которая является центром множества чисел в статистическом распределении. Существует три наиболее распространенных способа определения центральной тенденции:
• Среднее значение     — среднее арифметическое, которое вычисляется сложением множества чисел с последующим делением полученной суммы на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
• Медиана     — число, которое является серединой множества чисел: половина чисел имеют значения большие, чем медиана, а половина чисел — меньшие. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4.
• Мода     — число, наиболее часто встречающееся в данном множестве чисел. Например, модой для чисел 2, 3, 3, 5, 7 и 10 будет 3.

Пример