Meaning of the word mean in math - Word и Excel - помощь в работе с программами

This article is about the mathematical concept. For other uses, see Mean (disambiguation). For the state of being mean or cruel, see Meanness. For broader coverage of this topic, see Average.

There are several kinds of mean in mathematics, especially in statistics. Each mean serves to summarize a given group of data, often to better understand the overall value (magnitude and sign) of a given data set.

Pythagorean means consist of arithmetic mean (AM), geometric mean (GM), and harmonic mean (HM). The AM is the sum of numbers divided by the number of numbers, GM is an average for sets of positive numbers based on their product, and HM is an average for sets of numbers defined in relation to a unit of measurement. The relationship between AM, GM, and HM is represented by the inequality AM ≥ GM ≥ HM.

Statistical location covers mean, median, and mode, where mean may not always be the same as the median or mode for skewed distributions. The mean of a probability distribution is the long-run average value of a random variable with that distribution.

Generalized means include power mean and f-mean. The power mean is an abstraction of quadratic, arithmetic, geometric, and harmonic means, while the f-mean generalizes the concept further.

Other specialized means discussed are weighted arithmetic mean, truncated mean, interquartile mean, mean of a function, mean of angles and cyclical quantities, Fréchet mean, triangular sets, and Swanson’s rule.

For a data set, the arithmetic mean, also known as «arithmetic average», is a measure of central tendency of a finite set of numbers: specifically, the sum of the values divided by the number of values. The arithmetic mean of a set of numbers x₁, x₂, …, x_n is typically denoted using an overhead bar, .^{[note 1]} If the data set were based on a series of observations obtained by sampling from a statistical population, the arithmetic mean is the sample mean () to distinguish it from the mean, or expected value, of the underlying distribution, the population mean (denoted or $mu _{x}$ ^{[note 2]}).^[1]

Outside probability and statistics, a wide range of other notions of mean are often used in geometry and mathematical analysis; examples are given below.

Types of meansEdit

Pythagorean meansEdit

Arithmetic mean (AM)Edit

The arithmetic mean (or simply mean) of a list of numbers, is the sum of all of the numbers divided by the number of numbers. Similarly, the mean of a sample , usually denoted by , is the sum of the sampled values divided by the number of items in the sample.

For example, the arithmetic mean of five values: 4, 36, 45, 50, 75 is:

Geometric mean (GM)Edit

The geometric mean is an average that is useful for sets of positive numbers, that are interpreted according to their product (as is the case with rates of growth) and not their sum (as is the case with the arithmetic mean):

^[2]

For example, the geometric mean of five values: 4, 36, 45, 50, 75 is:

Harmonic mean (HM)Edit

The harmonic mean is an average which is useful for sets of numbers which are defined in relation to some unit, as in the case of speed (i.e., distance per unit of time):

For example, the harmonic mean of the five values: 4, 36, 45, 50, 75 is

Relationship between AM, GM, and HMEdit

AM, GM, and HM satisfy these inequalities:

Equality holds if all the elements of the given sample are equal.

Statistical locationEdit

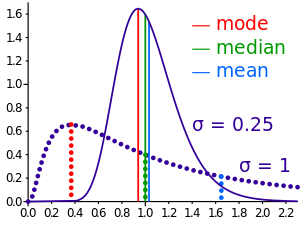
Geometric visualization of the mode, median and mean of an arbitrary probability density function.^[3]

In descriptive statistics, the mean may be confused with the median, mode or mid-range, as any of these may incorrectly be called an «average» (more formally, a measure of central tendency). The mean of a set of observations is the arithmetic average of the values; however, for skewed distributions, the mean is not necessarily the same as the middle value (median), or the most likely value (mode). For example, mean income is typically skewed upwards by a small number of people with very large incomes, so that the majority have an income lower than the mean. By contrast, the median income is the level at which half the population is below and half is above. The mode income is the most likely income and favors the larger number of people with lower incomes. While the median and mode are often more intuitive measures for such skewed data, many skewed distributions are in fact best described by their mean, including the exponential and Poisson distributions.

Mean of a probability distributionEdit

The mean of a probability distribution is the long-run arithmetic average value of a random variable having that distribution. If the random variable is denoted by , then it is also known as the expected value of (denoted ). For a discrete probability distribution, the mean is given by , where the sum is taken over all possible values of the random variable and is the probability mass function. For a continuous distribution, the mean is , where is the probability density function.^[4] In all cases, including those in which the distribution is neither discrete nor continuous, the mean is the Lebesgue integral of the random variable with respect to its probability measure. The mean need not exist or be finite; for some probability distributions the mean is infinite (+∞ or −∞), while for others the mean is undefined.

Generalized meansEdit

Power meanEdit

The generalized mean, also known as the power mean or Hölder mean, is an abstraction of the quadratic, arithmetic, geometric, and harmonic means. It is defined for a set of n positive numbers x_i by

^[2]

By choosing different values for the parameter m, the following types of means are obtained:

: maximum of
: quadratic mean
: arithmetic mean
: geometric mean
: harmonic mean
: minimum of

f-meanEdit

This can be generalized further as the generalized f-mean

and again a suitable choice of an invertible f will give

Weighted arithmetic meanEdit

The weighted arithmetic mean (or weighted average) is used if one wants to combine average values from different sized samples of the same population:

^[2]

Where and are the mean and size of sample respectively. In other applications, they represent a measure for the reliability of the influence upon the mean by the respective values.

Truncated meanEdit

Sometimes, a set of numbers might contain outliers (i.e., data values which are much lower or much higher than the others). Often, outliers are erroneous data caused by artifacts. In this case, one can use a truncated mean. It involves discarding given parts of the data at the top or the bottom end, typically an equal amount at each end and then taking the arithmetic mean of the remaining data. The number of values removed is indicated as a percentage of the total number of values.

Interquartile meanEdit

The interquartile mean is a specific example of a truncated mean. It is simply the arithmetic mean after removing the lowest and the highest quarter of values.

assuming the values have been ordered, so is simply a specific example of a weighted mean for a specific set of weights.

Mean of a functionEdit

In some circumstances, mathematicians may calculate a mean of an infinite (or even an uncountable) set of values. This can happen when calculating the mean value of a function . Intuitively, a mean of a function can be thought of as calculating the area under a section of a curve, and then dividing by the length of that section. This can be done crudely by counting squares on graph paper, or more precisely by integration. The integration formula is written as:

In this case, care must be taken to make sure that the integral converges. But the mean may be finite even if the function itself tends to infinity at some points.

Mean of angles and cyclical quantitiesEdit

Angles, times of day, and other cyclical quantities require modular arithmetic to add and otherwise combine numbers. In all these situations, there will not be a unique mean. For example, the times an hour before and after midnight are equidistant to both midnight and noon. It is also possible that no mean exists. Consider a color wheel—there is no mean to the set of all colors. In these situations, you must decide which mean is most useful. You can do this by adjusting the values before averaging, or by using a specialized approach for the mean of circular quantities.

Fréchet meanEdit

The Fréchet mean gives a manner for determining the «center» of a mass distribution on a surface or, more generally, Riemannian manifold. Unlike many other means, the Fréchet mean is defined on a space whose elements cannot necessarily be added together or multiplied by scalars.
It is sometimes also known as the Karcher mean (named after Hermann Karcher).

Trianglar setsEdit

In geometry, there are thousands of different
definitions for the center of a triangle that can all be interpretted as the mean of a triangular set of points in the plane.^{[citation needed]}

Swanson’s ruleEdit

This is an approximation to the mean for a moderately skewed distribution.^[5] It is used in hydrocarbon exploration and is defined as:

where P₁₀, P₅₀ and P₉₀ 10th, 50th and 90th percentiles of the distribution.

Other meansEdit

Arithmetic-geometric mean
Arithmetic-harmonic mean
Cesàro mean
Chisini mean
Contraharmonic mean
Elementary symmetric mean
Geometric-harmonic mean
Grand mean
Heinz mean
Heronian mean
Identric mean
Lehmer mean
Logarithmic mean
Moving average
Neuman–Sándor mean
Quasi-arithmetic mean
Root mean square (quadratic mean)
Rényi’s entropy (a generalized f-mean)
Spherical mean
Stolarsky mean
Weighted geometric mean
Weighted harmonic mean

NotesEdit

^ Pronounced «x bar».
^ Greek letter μ, for «mean», pronounced /’mjuː/.

ReferencesEdit

^ Underhill, L.G.; Bradfield d. (1998) Introstat, Juta and Company Ltd. ISBN 0-7021-3838-X p. 181
^ ^a ^b ^c «Mean | mathematics». Encyclopedia Britannica. Retrieved 2020-08-21.
^ «AP Statistics Review — Density Curves and the Normal Distributions». Archived from the original on 2 April 2015. Retrieved 16 March 2015.
^ Weisstein, Eric W. «Population Mean». mathworld.wolfram.com. Retrieved 2020-08-21.
^ Hurst A, Brown GC, Swanson RI (2000) Swanson’s 30-40-30 Rule. American Association of Petroleum Geologists Bulletin 84(12) 1883-1891

Источник

What Is a Mean?

Mean is the simple mathematical average of a set of two or more numbers.

The mean for a given set of numbers can be computed in more than one way, including the arithmetic mean method, which uses the sum of the numbers in the series, and the geometric mean method, which is the average of a set of products. However, all the primary methods of computing a simple average produce the same approximate result most of the time.

Key Takeaways

The mean is the mathematical average of a set of two or more numbers.
The arithmetic mean and the geometric mean are two types of mean that can be calculated.
The formula for calculating the arithmetic mean is to add up the numbers in a set and divide by the total quantity of numbers in the set.
The formula for calculating the geometric mean is to multiply all the values in a data set, then take the root of the sum equal to the quantity of values within that data set.
A mean helps you to assess a set of numbers by telling you the average, helping to contextualize each data point.

Calculating The Means

Understanding Mean

The mean is a statistical indicator that can be used to gauge performance over time. Specific to investing, the mean is used to understand the performance of a company’s stock price over a period of days, months, or years.

An analyst who wants to measure the trajectory of a company’s stock value in, say, the last 10 days would sum up the closing price of the stock in each of the 10 days. The sum total would then be divided by the number of days to get the arithmetic mean. The geometric mean will be calculated by multiplying all of the values together. The nth root of the product total is then taken—in this case, the 10^th root—to get the mean.

Formulas for Arithmetic Mean and Geometric Mean

Calculations for both the arithmetic and geometric means are fairly similar. The calculated amount for one will not substantially vary from another. However, there are subtle differences between the two approaches that do lead to different numbers.

Arithmetic Mean

The formula for calculating the arithmetic mean is to add up all figures and divide by the quantity of figures used. For example, the arithmetic mean of the numbers 4 and 9 is found by adding 4 and 9 together, then dividing by 2 (the quantity of numbers we are using). The arithmetic mean in this example is 6.5.

Arithmetic Mean

Pros

It is easier to calculate.
It is simpler for following along and audit results.
Its calculated value is a finite number.
It has more widespread use in algebraic computations.
It is often the fastest type of mean to calculate.

Cons

It is highly affected by material outliers or extreme numbers outside of a data set.
It is not as useful for skewed distributions.
It is not useful when using time series data (or other series of data with varying basis).
It weighs every item equally, diminishing the importance of more impactful data points.

Geometric Mean

The geometric mean is more complicated and uses a more complex formula. To get the formula for calculating the geometric mean is to multiply all values within a data set. Then, take the root of the sum equal to the quantity of values within that data set. For example, to calculate the geometric of the values 4 and 9, multiply the two numbers together to get 36. Then, take the square root (since there are two values). The geometric mean in this example is 6.

Geometric Mean

Pros

It is less likely to be impacted by extreme outliers.
It returns a more accurate measurement for more volatile data sets.
It considers the effects of compounding.
It is more accurate when using a data set over a long period of time (due to compounding).

Cons

It can’t be used if any value within the data set is 0 or negative.
Its formula is more complex and not easily used.
Its calculation is not transparent and more difficult to audit.
It is less prevalent and not used as much as other methods.

Example Mean Calculations

Let’s put this into practice by examining the price of a stock over a 10-day period. Imagine an investor purchased one share of stock for $148.01. The price of the stock over the next 10 days is also included.

Image by Sabrina Jiang © Investopedia 2022

The arithmetic mean is 0.67%, and is simply the sum total of the returns divided by 10. However, the arithmetic mean of returns is only accurate when there is no volatility, which is nearly impossible with the stock market.

In addition to the arithmetic and geometric means, the harmonic mean is calculated by dividing the number of observations by the reciprocal (one over the value) of each number in the series. Harmonic means are often used in finance to average data that occurs in fractions, ratios, or percentages, such as yields, returns, or price multiples.

The geometric mean factors in compounding and volatility, making it a better metric of average returns. Because it is impossible to take the root of a negative value, add one to all the percentage returns so that the product total yields a positive number. Take the 10^th root of this number and remember to subtract from one to get the percentage figure. The geometric mean of returns for the investor in the last five days is 0.61%. As a mathematical rule, the geometric mean will always be equal to or less than the arithmetic mean.

Arithmetic Mean

(

0.0045

)

0.0121

0.0726

0.0043

(

0.0049

)

0.0376

0.0067

0.67

begin{aligned}text{Arithmetic Mean} &= tiny{frac{ (0.0045) + 0.0121 + 0.0726 + … + 0.0043 + (0.0049) + 0.0376 }{ 10 } } \&= 0.0067 \&= 0.67% \end{aligned}

Arithmetic Mean=10(0.0045)+0.0121+0.0726+…+0.0043+(0.0049)+0.0376=0.0067=0.67%

Geometric Mean

0.9955

1.0121

1.0726

1.0043

0.9951

1.0376

−

0.0061

0.61

begin{aligned}text{Geometric Mean} &= tiny{sqrt[10]{ 0.9955 times 1.0121 times 1.0726 times … times 1.0043 times 0.9951 times 1.0376 } — 1} \&= 0.0061 \&= 0.61% \end{aligned}

Geometric Mean=100.9955×1.0121×1.0726×…×1.0043×0.9951×1.0376−1=0.0061=0.61%

Analyzing the table shows why the geometric mean provides a better value. When the arithmetic mean of 0.67% is applied to each of the stock prices, the end value is $152.63. However, the stock traded for $157.32 on the last day. This means that the arithmetic mean of returns is understated.

On the other hand, when each of the closing prices is raised by the geometric average return of 0.61%, the exact price of $157.32 is calculated. In this example, and often in many calculations, the geometric mean is a more accurate reflection of the true return of a portfolio.

While the mean is a good tool to evaluate the performance of a company or portfolio, it should also be used with other fundamentals and statistical tools to get a better and broader picture of the investment’s historical and future prospects.

Examples of When Means Are Important in Investing

Within business and investing, mean is used extensively to analyze performance. Examples of situations in which you may encounter mean include:

Determining whether an equity is trading above or below its average over a specified time period.
Looking back to see how comparative trading activity may determine future outcomes. For example, seeing the average rate of return for broad markets during prior recessions may guide decision making in future economic downturns.
Seeing whether trading volume or the quantity of market orders is in line with recent market activity.
Analyzing the operational performance of a company. For instance, some financial ratios like days sales outstanding require determining the average accounts receivable balance for the numerator.
Quantifying macroeconomic data like average unemployment over a period of time to determine general health of an economy.

What is a mean in math?

In mathematics and statistics, the mean refers to the average of a set of values. The mean can be computed in a number of ways, including the simple arithmetic mean (add up the numbers and divide the total by the number of observations), the geometric mean, and the harmonic mean.

How do you find the mean?

The mean is a characteristic of a set of data that describes some sort of average. To find the mean, you can compute it mathematically using one of several methods, depending on the structure of the data and the type of average you need. You can also visually identify the mean in many cases by plotting the data distribution. In a normal distribution, the mean, mode, and median are all the same value that occurs at the center of the plot.

What is the difference between mean, median, and mode?

The mean is the average that appears in a set of data.

The median is the midway point above (below) where 50% of the values in the data sits.

The mode refers to the most frequently observed value in the data (the one that occurs the most).

Why is mean important?

Mean is a valuable statistical measurement that tells you what the expected outcome is when comparing all data points together. Although it doesn’t guarantee future results, the mean helps set the expectation of a future outcome based on what already has happened.

Is a mean the same as an average?

Yes. A mean is the mathematical average of a set of two or more numbers.

The Bottom Line

The mean is another word for a mathematical «average.» The simple or arithmetic mean is the average calculated by summing up the values of some observations and dividing by the number of observations. The geometric mean is calculated by multiplying all the numbers in a dataset and then taking the n^th root of the product, where n is the total number of values in the dataset. The geometric mean is particularly useful when dealing with quantities that have a multiplicative or exponential relationship, such as growth rates, percentages, or ratios. The harmonic mean is calculated by dividing the total number of values in the dataset by the sum of the reciprocals of the individual values. It is also used when dealing with rates, ratios, or situations where the relationship between the values is inversely proportional.

The mean is an important descriptive statistic, but should not be interpreted in isolation. One should also keep in mind the shape of the data distribution and other metrics like the standard deviation, median, and mode.

Источник

From Wikipedia, the free encyclopedia

For broader coverage of this topic, see Mean.

In mathematics and statistics, the arithmetic mean ( arr-ith-MET-ik), arithmetic average, or just the mean or average (when the context is clear), is the sum of a collection of numbers divided by the count of numbers in the collection.^[1] The collection is often a set of results from an experiment, an observational study, or a survey. The term «arithmetic mean» is preferred in some mathematics and statistics contexts because it helps distinguish it from other types of means, such as geometric and harmonic.

In addition to mathematics and statistics, the arithmetic mean is frequently used in economics, anthropology, history, and almost every academic field to some extent. For example, per capita income is the arithmetic average income of a nation’s population.

While the arithmetic mean is often used to report central tendencies, it is not a robust statistic: it is greatly influenced by outliers (values much larger or smaller than most others). For skewed distributions, such as the distribution of income for which a few people’s incomes are substantially higher than most people’s, the arithmetic mean may not coincide with one’s notion of «middle». In that case, robust statistics, such as the median, may provide a better description of central tendency.

Definition[edit]

Given a data set ${displaystyle X={x_{1},ldots ,x_{n}}}$ , the arithmetic mean (also mean or average), denoted (read bar), is the mean of the values $x_{1},ldots ,x_{n}$ .^[2]

The arithmetic mean is a data set’s most commonly used and readily understood measure of central tendency. In statistics, the term average refers to any measurement of central tendency. The arithmetic mean of a set of observed data is equal to the sum of the numerical values of each observation, divided by the total number of observations. Symbolically, for a data set consisting of the values , the arithmetic mean is defined by the formula:

${displaystyle {bar {x}}={frac {1}{n}}left(sum _{i=1}^{n}{x_{i}}right)={frac {x_{1}+x_{2}+dots +x_{n}}{n}}}$

^[3]

(For an explanation of the summation operator, see summation.)

For example, if the monthly salaries of employees are , then the arithmetic mean is:

${displaystyle {frac {2500+2700+2400+2300+2550+2650+2750+2450+2600+2400}{10}}=2530}$

If the data set is a statistical population (i.e., consists of every possible observation and not just a subset of them), then the mean of that population is called the population mean and denoted by the Greek letter . If the data set is a statistical sample (a subset of the population), it is called the sample mean (which for a data set is denoted as ).

The arithmetic mean can be similarly defined for vectors in multiple dimensions, not only scalar values; this is often referred to as a centroid. More generally, because the arithmetic mean is a convex combination (meaning its coefficients sum to ), it can be defined on a convex space, not only a vector space.

Motivating properties[edit]

The arithmetic mean has several properties that make it interesting, especially as a measure of central tendency. These include:

The arithmetic mean is independent of scale of the units of measurement, in the sense that ${displaystyle {text{avg}}(ca_{1},cdots ,ca_{n})=ccdot {text{avg}}(a_{1},cdots ,a_{n}).}$ So, for example, calculating a mean of liters and then converting to gallons is the same as converting to gallons first and then calculating the mean. This is also called first order homogeneity.

Additional properties[edit]

The arithmetic mean of a sample is always between the largest and smallest values in that sample.
The arithmetic mean of any amount of equal-sized number groups together is the arithmetic mean of the arithmetic means of each group.

Contrast with median[edit]

The arithmetic mean may be contrasted with the median. The median is defined such that no more than half the values are larger, and no more than half are smaller than it. If elements in the data increase arithmetically when placed in some order, then the median and arithmetic average are equal. For example, consider the data sample . The mean is 2.5 , as is the median. However, when we consider a sample that cannot be arranged to increase arithmetically, such as , the median and arithmetic average can differ significantly. In this case, the arithmetic average is , while the median is . The average value can vary considerably from most values in the sample and can be larger or smaller than most.

There are applications of this phenomenon in many fields. For example, since the 1980s, the median income in the United States has increased more slowly than the arithmetic average of income.^[4]

Generalizations[edit]

Weighted average[edit]

A weighted average, or weighted mean, is an average in which some data points count more heavily than others in that they are given more weight in the calculation.^[5] For example, the arithmetic mean of and is ${displaystyle {frac {3+5}{2}}=4}$ , or equivalently ${displaystyle 3{frac {1}{2}}+5{frac {1}{2}}=4}$ . In contrast, a weighted mean in which the first number receives, for example, twice as much weight as the second (perhaps because it is assumed to appear twice as often in the general population from which these numbers were sampled) would be calculated as ${displaystyle 3{frac {2}{3}}+5{frac {1}{3}}={frac {11}{3}}}$ . Here the weights, which necessarily sum to one, are ${frac {2}{3}}$ and ${frac {1}{3}}$ , the former being twice the latter. The arithmetic mean (sometimes called the «unweighted average» or «equally weighted average») can be interpreted as a special case of a weighted average in which all weights are equal to the same number ( ${frac {1}{2}}$ in the above example and ${frac {1}{n}}$ in a situation with numbers being averaged).

Continuous probability distributions[edit]

If a numerical property, and any sample of data from it, can take on any value from a continuous range instead of, for example, just integers, then the probability of a number falling into some range of possible values can be described by integrating a continuous probability distribution across this range, even when the naive probability for a sample number taking one certain value from infinitely many is zero. In this context, the analog of a weighted average, in which there are infinitely many possibilities for the precise value of the variable in each range, is called the mean of the probability distribution. The most widely encountered probability distribution is called the normal distribution; it has the property that all measures of its central tendency, including not just the mean but also the median mentioned above and the mode (the three Ms^[6]), are equal. This equality does not hold for other probability distributions, as illustrated for the log-normal distribution here.

Angles[edit]

Particular care is needed when using cyclic data, such as phases or angles. Taking the arithmetic mean of 1° and 359° yields a result of 180°.
This is incorrect for two reasons:

In general application, such an oversight will lead to the average value artificially moving towards the middle of the numerical range. A solution to this problem is to use the optimization formulation (that is, define the mean as the central point: the point about which one has the lowest dispersion) and redefine the difference as a modular distance (i.e., the distance on the circle: so the modular distance between 1° and 359° is 2°, not 358°).

Symbols and encoding[edit]

The arithmetic mean is often denoted by a bar (vinculum or macron), as in .^[2]

Some software (text processors, web browsers) may not display the «x̄» symbol correctly. For example, the HTML symbol «x̄» combines two codes — the base letter «x» plus a code for the line above (̄ or ¯).^[7]

In some document formats (such as PDF), the symbol may be replaced by a «¢» (cent) symbol when copied to a text processor such as Microsoft Word.

References[edit]

^ Jacobs, Harold R. (1994). Mathematics: A Human Endeavor (Third ed.). W. H. Freeman. p. 547. ISBN 0-7167-2426-X.
^ ^a ^b ^c Medhi, Jyotiprasad (1992). Statistical Methods: An Introductory Text. New Age International. pp. 53–58. ISBN 9788122404197.
^ Weisstein, Eric W. «Arithmetic Mean». mathworld.wolfram.com. Retrieved 21 August 2020.
^ Krugman, Paul (4 June 2014) [Fall 1992]. «The Rich, the Right, and the Facts: Deconstructing the Income Distribution Debate». The American Prospect.
^ «Mean | mathematics». Encyclopedia Britannica. Retrieved 21 August 2020.
^ Thinkmap Visual Thesaurus (30 June 2010). «The Three M’s of Statistics: Mode, Median, Mean June 30, 2010». www.visualthesaurus.com. Retrieved 3 December 2018.
^ «Notes on Unicode for Stat Symbols». www.personal.psu.edu. Retrieved 14 October 2018.
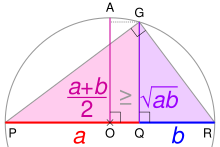
^ If AC = a and BC = b. OC = AM of a and b, and radius r = QO = OG.
Using Pythagoras’ theorem, QC² = QO² + OC² ∴ QC = √QO² + OC² = QM.
Using Pythagoras’ theorem, OC² = OG² + GC² ∴ GC = √OC² − OG² = GM.
Using similar triangles, HC/GC = GC/OC ∴ HC = GC²/OC = HM.

External links[edit]

Calculations and comparisons between arithmetic mean and geometric mean of two numbers
Calculate the arithmetic mean of a series of numbers on fxSolver

Источник

Types of meansEdit

Pythagorean meansEdit

Arithmetic mean (AM)Edit

Geometric mean (GM)Edit

Harmonic mean (HM)Edit

Relationship between AM, GM, and HMEdit

Statistical locationEdit

Mean of a probability distributionEdit

Generalized meansEdit

Power meanEdit

f-meanEdit

Weighted arithmetic meanEdit

Truncated meanEdit

Interquartile meanEdit

Mean of a functionEdit

Mean of angles and cyclical quantitiesEdit

Fréchet meanEdit

Trianglar setsEdit

Swanson’s ruleEdit

Other meansEdit

See alsoEdit

NotesEdit

ReferencesEdit

What Is a Mean?

Key Takeaways

Calculating The Means

Understanding Mean

Formulas for Arithmetic Mean and Geometric Mean

Arithmetic Mean

Arithmetic Mean

Geometric Mean

Geometric Mean

Example Mean Calculations

Examples of When Means Are Important in Investing

What is a mean in math?

How do you find the mean?

What is the difference between mean, median, and mode?

Why is mean important?

Is a mean the same as an average?

The Bottom Line

Definition[edit]

Motivating properties[edit]

Additional properties[edit]

Contrast with median[edit]

Generalizations[edit]

Weighted average[edit]

Continuous probability distributions[edit]

Angles[edit]

Symbols and encoding[edit]

See also[edit]

References[edit]

Further reading[edit]

External links[edit]