Цель работы:
получить
представление о работе с матричными
объектами, изучить встроенные функции
для обработки массивов.
Краткие
теоретические сведения
Электронные таблицы
представляют собой естественную среду
для работы с матрицами, поскольку
в их ячейках удобно размещать матричные
элементы. В Excel термин
матрица (набор значений, упорядоченный
в виде строк и столбцов) и термин вектор
(матрица, состоящая из одной строки
или столбца) заменяются понятием массив
(набор значений, расположенных в виде
строк или столбцов и представляющих
собой единую структуру).
Функции, предназначенные для выполнения
операций с массивами или возвращающие
массивы, называются функциями массива.
В программе Excel
есть возможности для выполнения любой
стандартной матричной операции,
однако эти операции осуществляются
по-разному. Для
сложения (вычитания) двух матриц и
умножения матрицы
на скаляр служат обычные арифметические
функции, производящие
операции с содержимым ячеек. Нахождение
определителя, перемножение и обращение
матриц выполняется с помощью функций
массива.
Функции, предназначенные для выполнения
операций с массивами, располагаются в
категории Математические мастера
функций:
МУМНОЖО – служит для перемножения
двух матриц (две матрицы
можно перемножить при условии, что
количество столбцов первой матрицы
равно количеству строк второй матрицы);
МОБРО – находит обратную матрицу
(обратная матрица существует только
для невырожденной квадратной матрицы);
МОПРЕДО – служит для вычисления
определителя (детерминанта) матрицы. В
качестве аргумента должна использоваться
квадратная матрица.
Практическая
часть
Постановка
задачи
Решить систему уравнений с тремя
неизвестными:
Порядок
выполнения работы
-
Данную систему уравнений можно записать
в матричной форме
Ах=b,
где
– матрица
коэффициентов системы;
– вектор
неизвестных;
– правая часть системы.
Решение системы
находится как произведение обратной
матрицы А-1 на
правую часть b:
х=А-1b.
-
Занесем исходные данные в таблицу (рис.
28).
Рис. 28. Исходные данные задачи
-
С помощью функции
МОБР()
найдем матрицу, обратную матрице А:
выделим диапазон
для размещения результата (обратной
матрицы) А7:С9
(три строки и три столбца);
в строке формул
запишем {=МОБР(А2:С4)}
или вызовем Мастер функций и выберем
функцию МОБР()
из категории Математические,
введя в качестве аргумента диапазон
А2:С4;
завершим ввод
нажатием комбинации клавиш Ctrl+Shift+Enter.
-
Умножим обратную матрицу А-1 на правую
часть системы b:
выделим диапазон
для вывода результата (вектора неизвестных)
Е7:Е9
(три строки и один столбец);
в строке формул
запишем {=МУМНОЖ(А7:С9;Е2:Е4)}
или вызовем Формулы-Вставить
функцию и
выберем функцию МУМНОЖ()
из категории
Математические,
введя в качестве аргумента Массив1
в диапазон А7:С9,
а Массив2
в диапазон Е2:Е4;
завершим ввод
нажатием комбинации клавиш Ctrl+Shift+Enter.
Рис. 29. Результаты расчета задачи
-
Таким образом, при
умножении обратной матрицы А-1
на правую часть b получили вектор
неизвестных х (рис. 29).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Матрицы
Операции с матрицами
Транспонирование
Вычисление определителя матрицы
Нахождение обратной матрицы
Сложение и вычитание матриц
Умножение матрицы на число
Умножение матриц
Список литературы
2
4
4
6
7
9
10
11
14
Средства MSExcel оказываются весьма полезны в линейной алгебре, прежде всего для операций с сматрицами и решения систем линейных уравнений.
Матрицы
Значительная часть математических моделей различных объектов и процессов записывается в достаточно простой и компактной матричной форме. В частности, при решении линейных уравнений мы имеем дело с матрицами и арифметическими действиями с ними. Что же такое матрица? Как выполняются действия с матрицами?
Матрицей размера m × n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Матрицы обозначаются прописными (заглавными) буквами латинского алфавита. Числа, составляющие матрицу, называются элементами матрицы и обозначаются строчными буквами с двойной индексацией: aij, где I – номер строки, а j – номер столбца. Например, матрица А размером m × n может быть представлена в виде:
где i=1, …, m; j=1, …, n.
Две матрицы А и В одного размера называются равными, если они совпадают поэлементно, то есть aij =bij для любых i=1,2, …, m; j=1,2, …, n.
Матрица, состоящая из одной строки, называется матрицей (вектором)-строкой:
а из одного столбца – матрицей (вектором)-столбцом:
Если число строк матрицы равно числу столбцов и равно n, то такую матрицу называют квадратной n-го порядка. Например, квадратная матрица 2-го порядка:
Если у элемента матрицы aij номер столбца равен номеру строки (i=j), то такой элемент называется диагональным. Диагональные элементы образуют главную диагональ матрицы
Квадратная матрица с равными нулю всеми недиагональными элементами называется диагональной.
Квадратная матрица называется единичной, если она диагональная, и все диагональные элементы равны единице. Единичная матрица имеет следующий вид:
Различают единичные матрицы первого, второго, третьего и т. д. порядков:
Матрица любого размера называется нулевой или нуль-матрицей, если все её элементы равны нулю:
Операции с матрицами
Как и над числами, над матрицами можно проводить ряд операций, причём в случае с матрицами некоторые из операций являются специфическими.
Транспонирование
Транспонированной называется матрица (АТ ), в которой столбцы исходной матрицы (А) заменяются строками с соответствующими номерами.
В сокращённой записи, если А= (aij ), то АТ = (aji ).
Для обозначения транспонированной матрицы иногда используют символ «’» (A’). Транспонированием называется операция перехода от исходной матрицы (А) к транспонированной (АТ ).
Из определения транспонированной матрицы следует, что если исходная матрица А имеет размер m × n , то транспонированная матрицаАТ имеет размер n × m .
Для осуществления транспонирования в Excel используется функция ТРАНСП, которая позволяет поменять ориентацию массива на рабочем листе с вертикальной на горизонтальную и наоборот.
Функция имеет вид ТРАНСП (массив). Здесь массив – это транспонируемый массив или диапазон ячеек на рабочем листе. Транспонирование массива заключается в том, что первая строка массива становится первым столбцом нового массива, вторая строка массива становится вторым столбцом нового массива и т. д. Рассмотрим это на примере.
Пример 1.1 Предположим, что диапазон ячеек A1:E2 введена матрица размера 2×5
Необходимо получить транспонированную матрицу.
Решение.
1. Выделите (указателем мыши при нажатой левой кнопке) блок ячеек под транспонированную матрицу (52). Например, A4:B8.
2. Нажмите на панели инструментов Стандартная кнопку Вставка функции.
3. В появившемся диалоговом окне Мастер функций в рабочем поле Категория выберите Ссылки и массивы, а в рабочем поле Функция – имя функции ТРАНСП (рис. 1.1). После этого щелкните на кнопке ОК.
Рис. 1.1. Пример выбора вида функции в диалоговом окне Мастер функций
4. Появившееся диалоговое окно ТРАНСП мышью отодвиньте в сторону от исходной матрицы A1:E2 в рабочее поле Массив (указателем мыши при нажатой левой кнопке). После чего нажмите сочетание клавиш CTRL+SHIFT+ENTER (рис. 1.2).
Рис. 1.2. Пример заполнения диалогового окна ТРАНСП
5. Если транспонированная матрица не появилась в диапазоне A4:B8, то следует щелкнуть указателем мыши в строке формул и повторить нажатие CTRL+SHIFT+ENTER.
В результате в диапазоне A4:B8 появится транспонированная матрица:
Вычисление определителя матрицы
Важной характеристикой квадратных матриц является их определитель. Определитель матрицы – это число, вычисляемое на основе значений элементов массива. Определитель матрицы А обозначается как |А| или ∆.
Определителем матрицы первого порядка А = (а11 ), или определителем первого порядка, называется элемент а11 .
∆1 = |А| = а11
Определителем матрицы второго порядка А = (aij ), или определителем второго порядка, называется число, которое вычисляется по формуле:
Произведения а11 а22 и а12 а21 называются членами определителя второго порядка.
С ростом порядка матрицы n резко увеличивает число членов определителя (n!). Например, при n=4 имеем 24 слагаемых. Существуют специальные правила, облегчающие вычисление определителей вручную, учитываются свойства определителей и т. п. При применении компьютера в использовании этих приемов нет необходимости.
В MSExcel для вычисления определителя квадратной матрицы используется функция МОПРЕД.
Функция имеет вид МОПРЕД(массив).
Здесь массив – это числовой массив, в котором хранится матрица с равным количеством строк и столбцов. При этом массив может быть задан как интервал ячеек, например, А1: С3; или как массив констант, например, {1;2;3;4;5;6;7;8;9}. Для массива А1: С3, состоящего из трёх строк и трёх столбцов (матрица размером 3×3), определитель вычисляется следующим образом:
Рассмотрим пример нахождения определителя матрицы.
Пример 1.2. Предположим, что в диапазон ячеек А1: С3 введена матрица:
Необходимо вычислить определитель этой матрицы.
Решение
1. Табличный курсор поставьте в ячейку, в которую требуется получить значение определителя, например, А4.
2. Нажмите на панели инструментов Стандартная кнопку Вставка функции.
3. В появившемся диалоговом окне Мастер функций в рабочем поле Категория выберите Математические, а в рабочем поле Функция – имя функции МОПРЕД. После этого щелкните на кнопке ОК.
4. Появившееся диалоговое окно МОПРЕД мышью отодвиньте от исходной матрицы и введите диапазон исходной матрицы А1: С3 в рабочее поле Массив (указателем мыши при нажатой левой кнопке) Нажмите кнопку ОК (рис. 1.3).
Рис. 1.3. Пример заполнения диалогового окна МОПРЕД
В ячейке А4 появится значение определителя – 6.
Нахождение обратной матрицы
Для каждого числа а≠0 существует обратное число а-1, и для квадратных матриц вводится аналогичное понятие. Обратные матрицы обычно используются для решения систем уравнений с несколькими неизвестными.
Матрица А-1 называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную как слева, так и справа получается единичная матрица:
как следует из определения, обратная матрица является квадратной того же порядка, что и исходная матрица.
Необходимым и достаточным условием существования обратной матрицы является невырожденность исходной матрицы. Матрица называется невырожденной или неособенной, если её определитель отличен от нуля (|А|≠0); в противном случае (|А|=0) матрица называется вырожденной или особенной.
Существуют специальные достаточно сложные алгоритмы для ручного вычисления обратных матриц. В качестве примера того, как вычисляется обратная матрица, рассмотрим квадратную матрицу второго порядка
Тогда обратная матрица вычисляется следующим образом:
В MSExcel для нахождения обратной матрицы используется функция МОБР, которая вычисляет обратную матрицу для матрицы, хранящейся в таблице в виде массива.
Функция имеет вид МОБР(массив).
Здесь массив – это числовой массив с равным количеством строк и столбцов. Массив может быть задан как диапазон ячеек, например А1: С3; как массив констант, например, {1;2;3;4;5;6;7;8;9} или как имя диапазона или массива.
Рассмотрим пример нахождения обратной матрицы.
Пример 1.3. Пусть в диапазон ячеек А1: С3 введена матрица
Необходимо получить обратную матрицу.
Решение
1. Выделите блок ячеек под обратную матрицу, например блок ячеек А5: С7 (указателем мыши при нажатой левой кнопке).
2. Нажмите на панели инструментов Стандартная кнопку Вставка функции. В появившемся диалоговом окне Мастер функций в рабочем поле Категория выберите Математические, а в рабочем поле Функция – имя функции МОБР. После этого щелкните на кнопке ОК.
3. Появившееся диалоговое окно МОПРЕД мышью отодвиньте от исходной матрицы и введите диапазон исходной матрицы А1: С3 в рабочее поле Массив (указателем мыши при нажатой левой кнопке).
4. Нажмите сочетание клавиш CTRL+SHIFT+ENTER (рис. 1.4).
Рис. 1.4. Пример заполнения диалогового окна МОБР
5. Если обратная матрица не появилась в диапазоне А5: С7, то следует щелкнуть указателем мыши в строке формул и повторить нажатие CTRL+SHIFT+ENTER.
В результате в диапазоне А5: С7 появится обратная матрица:
Сложение и вычитание матриц
Складывать (вычитать) можно матрицы одного размера. Суммой матриц А = (aij ) и В = (bij ) размера m×n называется матрица C = A + B, элементы которой cij = aij + bij для i = 1,2, …, m; j = 1,2, …, n (то есть матрица складывается поэлементно). Например, если:
то С = А + В:
В частном случае А + 0 = А.
Аналогично определяют разность двух матриц С = А – В.
В MSExcel для выполнения операций суммирования и вычитания матриц могут быть использованы формулы, вводимые в соответствующие ячейки.
Пример 1.4. Пусть матрица А из рассмотренного примера, введена в диапазон А1: С2, а матрица В – в диапазон А4: С5. Необходимо найти матрицу С, являющуюся их суммой.
Решение.
1. Табличный курсор установите в левый верхний угол результирующей матрицы, например в А7.
2. Введите формулу для вычисления первого элемента результирующей матрицы = А1 + А4
3. Скопируйте введённую формулу в остальные ячейки результирующей матрицы: установите табличный курсор в ячейку А7; наведите указатель мыши на точку в правом нижнем углу ячейки так, чтобы указатель принял вид тонкого крестика; при нажатой левой кнопке мыши протяните указатель до ячейки С7; затем так же протяните указатель мыши до ячейки С8.
В результате в ячейках А7: С8 появится матрица, равная сумме исходных матриц. Подобным образом вычисляется разность матриц, только в формуле для вычисления первого элемента вместо знака «+» ставят знак «-».
Умножение матрицы на число
Произведением матрицы А на число k называется матрица В = kA, элементы которой bij = kaij для I = 1,2, …, m; j = 1,2, …, n. Иначе говоря, при умножении матрицы на постоянную каждый элемент этой матрицы умножается на эту постоянную: k*Aij = (k*aij ).
Например, для матриц А и В из предыдущего примера:
В частности, произведение матрицы А на число 0 есть нулевая матрица, то есть 0 × А = 0.
В MSExcel для выполнения операции умножения матрицы на число могут быть использованы формулы, вводимые в соответствующие ячейки.
Пример 1.5. Пусть, как и в предыдущем примере матрица А введена в диапазон А1: С2. Необходимо получить матрицу С = 3 × А.
Решение
1. Табличный курсор поставить в левый верхний угол результирующей матрицы, например в Е1.
2. Введите формулу для вычисления первого элемента результирующей матрицы = 3*А1.
3. Скопируйте введённую формулу в остальные ячейки результирующей матрицы: установите табличный курсор в ячейку Е1; наведите указатель мыши на точку в правом нижнем углу ячейки так, чтобы указатель принял вид тонкого крестика; при нажатой левой кнопке мыши протяните указатель до ячейки G1; затем так же протяните указатель мыши до ячейки G2.
В результате в ячейках E1:G2 появится матрица, равная исходной матрице, умноженной на постоянную – 3.
Умножение матриц
Произведение матриц определено, если число столбцов первой матрицы равно числу строк второй.
Пусть А = (aij ) m×n, B = (bij ) n×p, тогда размерность произведения А×В равна m×p. При этом матрица С называется произведением матриц А и В, если каждый её элемент cij равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В:
Таким образом, перемножение матриц осуществляется по следующему правилу:
Пусть, например,
Многие свойства, присущие операциям над числами, справедливы и для операций умножения матриц.
Для матриц верны общие свойства операции умножения.
1. А(ВС) = (АВ)С – ассоциативность.
2. А(В+С) = АВ + АС – дистрибутивность.
3. (А + В)С + АС + ВС.
4. (αА)В = А(αВ) = α(АВ), α – константа.
Однако имеются и специфические свойства операций умножения матриц.
5. Умножение матриц некоммутативно – АВ ≠ ВА.
В частном случае коммутативным законом обладает произведение любой квадратной матрицы А n-го порядка на единичную матрицу Е того же порядка, причем это произведение равно А.
6. Если Е – единичная матрица, то ЕА = А; ЕВ = В.
Таким образом, единичная матрица играет при умножении ту же роль, что и число 1 при умножении чисел.
7. Из того, что А × В = 0, не следует, что А = 0 или В = 0.
В алгебре матриц нет действия деления. Выражение А/В не имеет смысла. Его заменяют два различных выражения В-1 × А и А × В-1, если существует В-1 .
Для квадратных матриц возможна операция возведения в степень. По определении. полагают, что А0= Е и А1 = А. Целой положительной степенью Am (m>1) квадратной матрицей А называется произведение m матриц, равных А, то есть:
Для нахождения произведения двух матриц в Excel используется функция МУМНОЖ, которая вычисляет произведение матриц.
Функция имеет вид МУМНОЖ(массив1; массив2).
Здесь массив1 и массив2 – это перемножаемые массивы. При этом количество столбцов аргумента массив1 должно быть таким же, как количество строк аргумента массив2, и оба массива должны содержать только числа. Результатом является массив с таким же числом строк, как массив1 и с таким же числом столбцов, как массив2.
Массив С, который является произведением двух массивов А и В, определяется следующим образом:
где I – номер строки, а j – номер столбца.
Рассмотрим пример умножения матриц.
Пример 1.6. Пусть матрица А из примера 1.2 введена в диапазон А1:D3, а матрица В – в диапазон А4: В7. Необходимо найти произведение этих матриц С.
Решение
1. Выделите блок ячеек под результирующую матрицу. Для этого требуется найти размер матрицы-произведения. Её размером будет mp, в данном примере 32. Например, выделите блок ячеек F1:G3.
2. Нажмите на панели инструментов Стандартная кнопку Вставка функции.
3. В появившемся диалоговом окне Мастер функций в рабочем поле Категория выберите Математические, а в рабочем поле Функция – имя функции МУМНОЖ. После этого щелкните на кнопке ОК.
4. Появившееся диалоговое окно МУМНОЖ мышью отодвиньте от исходной матрицы и введите диапазон исходной матрицы А — А1:D3 в рабочее поле Массив1 (указателем мыши при нажатой левой кнопке), а диапазон матрицы В – А4: В7 введите в рабочее поле Массив2 (рис. 1.5). Нажмите сочетание клавиш CTRL+SHIFT+ENTER.
Рис. 1.5. Пример заполнения рабочих полей диалогового окна МУМНОЖ
5. Если произведение матриц А×В не появилось в диапазоне F1:G3, то следует щёлкнуть указателем мыши в строке формул и ещё раз нажать комбинацию клавиш CTRL+SHIFT+ENTER.
В результате в диапазоне F1:G3 появится произведение матриц:
Список литературы:
1 . www.office.microsoft.com
2. В. Я. Гельман «Решение математических задач средствами Excel », стр. 49-60
Лабораторная работа № 4
Электронные таблицы: работа с
матрицами
Время выполнения – 2 часа.
Цель работы: научиться приемам работы с матрицами.
Задачи работы
1.
Изучить приемы работы с матрицами.
2.
Научиться решать системы линейных алгебраических
уравнений.
3.
Научиться выполнять проверку решения.
Перечень обеспечивающих средств
Для выполнения работы необходимо иметь компьютер с
операционной системой MS Windows, офисным пакетом MS Office 2010
и выше и методические указания по выполнению работы.
Общие теоретические сведения
Система mn чисел,
расположенных в прямоугольной таблице из m строк и n столбцов, называется матрицей. Если m = n, то матрица называется квадратной, иначе – прямоугольной. Над
матрицами могут быть выполнены операции: сложение матриц, умножение матрицы на
число, на вектор.
Если матрица имеет размер 1 × n, то она называется вектором-строкой, а m ×
1 – вектором-столбцом.
Если в матрице переставить строки и столбцы местами,
то получим транспонированную матрицу.
Обратной матрицей по отношению к
данной называется матрица, которая, будучи умноженной как справа, так и слева
на данную матрицу, дает единичную матрицу. При умножении матриц результирующая
матрица имеет такое количество строк, как матрица слева, а количество столбцов
– как матрица справа. Для освоения методов работы с матрицами рассмотрим
пример.
Рассмотрим пример перемножения матриц.
Необходимо умножить матрицу А2,3 на
матрицу В3,3, результат представить в виде матрицы С2,3.
Решение.
1.
Задать значения элементам матриц A2,3, В3,3 (табл. 6.1).
2.
Выделить место для результирующей матрицы С2,3.
3.
Нажать на кнопку Вставить функцию,
расположенную рядом со строкой формул или на вкладке Формулы.
4.
В открывшемся диалоговом окне Вставка функции
открыть категорию Математические и выбрать из списка функцию МУМНОЖ.
5.
Задать аргументы функции: выбрать мышью массив 1 – A2,3 и массив 2 – В3,3
(рис. 6.1).
6.
Нажать одновременно 3 клавиши Ctrl + Shift + Enter.
7.
В выделенной области В8:D9
получим результат перемножения матриц (рис. 6.2).
Таблица 6.1. Элементы матриц A2,3, В3,3
|
А |
В |
С |
D |
E |
F |
|
|
1 |
A2,3= |
1 |
3 |
2 |
||
|
2 |
3 |
4 |
5 |
|||
|
3 |
||||||
|
4 |
1 |
2 |
3 |
|||
|
5 |
В3,3= |
1 |
4 |
1 |
||
|
6 |
2 |
3 |
3 |
|||
|
7 |
||||||
|
8 |
С2,3= |
|||||
|
9 |
||||||
|
10 |
Рис. 6.1. Заполнение аргументов функции
Рис. 6.2. Результат перемножения исходных матриц
В следующем примере рассмотрим решение системы
линейных алгебраических уравнений методом обратной матрицы.
Задана система линейных уравнений с тремя
неизвестными:
x1 + 2·x2 + 3·x3 = 4;
4·x1 + 3·x2 + 2·x3 = 1; (6.1)
x1 + 3·x2 + 2·x3 = 4.
В матричной форме система (6.1) имеет вид:
А3,3 · Х3,1 = В3,1, (6.2)
где А3,3 – матрица коэффициентов
при неизвестных
A3,3: = 
B3,1 – вектор
правых частей
B3,1: = . (6.4)
Вектор неизвестных Х3,1 может быть
найден по формуле:
Х3,1 = А3,3-1 · В3,1, (6.5)
где А3,3-1 – обратная
матрица;
Решение.
1.
Заполнить электронную таблицы исходными данными. Пример
расположения матрицы исходных коэффициентов, вектора правых частей, обратной
матрицы и вектора неизвестных приведен в табл. 6.2.
Таблица 6.2. Решение системы линейных алгебраических
уравнений
|
A |
B |
C |
D |
E |
F |
H |
|
|
1 |
Матрица исходных коэффициентов |
Вектор правых частей |
|||||
|
2 |
1 |
2 |
3 |
4 |
|||
|
3 |
А3,3 = |
4 |
3 |
2 |
В3,1 = |
1 |
|
|
4 |
1 |
3 |
2 |
4 |
|||
|
5 |
Обратная матрица |
Вектор неизвестных |
|||||
|
6 |
|||||||
|
7 |
А3,3-1 = |
Х3,1 = |
|||||
|
8 |
|||||||
2.
Ввести в таблицу матрицу коэффициентов А3,3.
3.
Ввести в таблицу вектор правых частей В3,1.
4.
Выделить место для обратной матрицы А3,3-1.
5.
Нажать на кнопку Вставить функцию,
расположенную рядом со строкой формул или на вкладке Формулы.
6.
Выбрать функцию МОБР для вычисления обратной
матрицы.
7.
Ввести в диалоговое окно Аргументы функции
адрес исходной матрицы коэффициентов, выделив ее мышью.
8.
Нажать на клавиатуре одновременно Ctrl + Shift + Enter.
9.
В выделенных ячейках появится обратная матрица.
10.
Выделить место для вектор неизвестных Х3,1.
11.
Нажать на кнопку Вставить функцию,
расположенную рядом со строкой формул или на вкладке Формулы.
12.
Выбрать функцию МУМНОЖ.
—
В качестве аргументов выбрать обратную матрицу
(массив1) и вектор правых частей (массив2).
13.
Нажать на клавиатуре одновременно Ctrl + Shift + Enter.
14.
В выделенных ячейках появится вектор неизвестных
(результат решения системы линейных уравнений) (рис. 6.3).
Рис. 6.3. Решение системы линейных алгебраических
уравнений методом обратной матрицы
Рассмотрим пример решения системы линейных
алгебраических уравнений методом Крамера (через определители).
Если данные для каких-то таблиц повторяются, то их
лучше набирать в режиме «выделенных листов». Можно выделять стоящие подряд
листы, не подряд стоящие или вообще все листы рабочей книги.
Пусть необходимо выделить три подряд стоящих листа
(Лист1, Лист2, Лист3). Для этого производим щелчок левой кнопки мыши по ярлычку
Лист1, затем нажимаем клавишу Shift и производим
щелчок по ярлычку Лист3. Тогда все три ярлычка станут светлее. Чтобы отменить
выделение группы листов, в контекстном меню ярлыка листа выбрать команду Разгруппировать
листы или нажать на ярлык любого листа.
Для выполнения задания следует выделить одновременно
4 листа. Матрицу исходных коэффициентов и вектор правых частей поместить на
выделенные листы. Затем разгруппировать листы. На листах 2, 3, 4 столбцы при
неизвестных заменить векторами правых частей для вычисления определителей
неизвестных: на листе2 – в 1-й столбец, на листе3 – во 2-й столбец и на листе4
– в 3-й столбец. Вычислить определители на каждом листе, используя функцию МОПРЕД.
Для вычисления значений неизвестных разделить определитель для соответствующей
переменной на общий определитель для матрицы исходных коэффициентов, так для
вычисления х1 разделить определитель на листе2 на определитель на
листе1, для х2 – определитель на листе3 на определитель на листе1 и
т. д. Ввод формул выполнять только в строку формул.
Задание
1.
Найти для матрицы A2,3 в таблице 6.1 транспонированную матрицу,
используя функцию ТРАНСП.
2.
Для матрицы В3,3 в таблице 6.1
найти обратную матрицу с помощью функции МОБР.
3.
Решить систему линейных алгебраических уравнений
(СЛАУ) методом обратной матрицы и методом Крамера по заданному варианту.
|
1 вариант |
2 вариант |
|
2·х1 + х2 х1 – 3·х2 2·х2 – х3 х1 + 4·х2 |
1·х1 – 5·х3 5·х1 – 3·х2 х1 + 2·х2 4·х1 – х2 + 2·х3 + 2·х4 = –4 |
|
3 вариант |
4 вариант |
|
–2·х2 + 5·х3 2·х1 + х2 х1 + 2·х2 –х2 + 2·х3 + х4 = –3 |
–2·х1 – 2·х2 3·х1 + х2 –4·х1 + 2·х3 х1 – х2 + 4·х4 = –5 |
|
5 вариант |
6 вариант |
|
2·х1 – х2 –х1 + 2·х2 –3·х1 + 4·х2 5·х1 + 4·х2 – 2·х3 + 2·х4 = –2 |
х1 – 5·х2 –3·х1 + 3·х2 –2·х1 + 8·х2 7·х1 – 2·х2 + 3·х3 + 7·х4 = –10 |
|
7 вариант |
8 вариант |
|
–6·х1 + 6·х2 –х1 – 5·х2 –х1 – х2 –х1 + 2·х2 + 6·х3 + 2·х4 = 11 |
–7·х1 + 3·х2 –10·х1 – 2·х3 –4·х1 – 9·х2 2·х1 + 7·х2 + х3 – х4 = –27 |
|
9 вариант |
10 вариант |
|
7·х1 – 3·х2 9·х1 – 7·х2 – 10·х2 – 5·х3 –10·х1 – х2 – 2·х3 + 5·х4 = –33 |
7·х1 – 4·х2 –7·х1 + 5·х2 –10·х1 + 9·х2 –10·х1 + 7·х2 + 4·х3 – 9·х4 = –48 |
Сравнить результаты решений системы уравнений методом
обратной матрицы и методом Крамера.
Решение системы уравнений проверить, умножив матрицу
исходных коэффициентов на вектор неизвестных, в результате должен получиться
вектор правых частей. Результаты выполнения заданий сохранить в файле
Фио_студента_Матрицы_№вар.xlsx.
Контрольные вопросы
1.
Кратко опишите ход работы решения системы линейных
уравнений методом обратной матрицы.
2.
Какие три клавиши нужно нажать, чтобы получить
результат при работе с матрицами?
3.
Какие функции можно использовать в Excel для работы с матрицами?
4.
Как выполнить проверку решения СЛАУ?
Содержание и оформление отчета
1.
Цель работы.
2.
Формулировка задания.
3.
Скриншоты рабочих листов электронной таблицы с
выполненными заданиями.
4.
Ответы на контрольные вопросы.
5.
Общий вывод о проделанной работе.
Цель работы: познакомиться с приемами решения задач линейной алгебры.
Типичными задачами линейной алгебры являются задачи, связанные с решением систем линейных уравнений. При этом приходится работать с массивами чисел. Для их обработки в Excel предусмотрен ряд математических функций:
- МОПРЕД(массив) — функция для нахождения определителя квадратной матрицы. Здесь массив — числовой массив с равным количеством строк и столбцов;
- МОБР(массив) — функция для нахождения обратной матрицы. Здесь массив — числовой массив с равным количеством строк и столбцов;
- МУМНОЖ(массив1;массив2) — функция для нахождения произведения массива1на массив2.Результатом является массив с таким же числом строк, как массив1, и с таким же числом столбцов, как массив2. При этом если обозначить буквой С результат произведения двух массивов А и В, то элементы массива С определяются по формуле
, где i — номер строки, а j — номер столбца;
- ТРАНСП(массив) — функция для транспонирования массива ячеек на рабочем листе. Транспонирование массива заключается в том, что первая строка массива становится первым столбцом нового массива, вторая строка массива становится вторым столбцом нового массива и т.д.
Особенностью вычислений, связанных с массивами, является то, что результат вычисления распространяется в виде формулы на целый блок ячеек. Такие формулы называются формулами массива. При вводе формул массива необходимо соблюдать определенную последовательность действий:
Шаг 1. Сначала формула вводится в первую ячейку результирующего массива.
Шаг 2.Выделяется весь блок ячеек результирующего массива.
Шаг 3.Нажимается клавишаклавиатуры.
Шаг 4.Нажимается комбинация клавиш Ctrl+Shift+Enter. При этом формула распознается как формула массива и заключается в фигурные скобки { }.
Важно!
При работе с массивами чисел всегда контролируйте размерность результирующего массива!
ЗАДАНИЕ 1. Решение задач линейной алгебры
Рассмотрим решение некоторых задач линейной алгебры на простейших примерах. Пусть дана квадратная матрица 3-го порядка 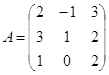
- Найдите матрицу А-1, обратную к данной матрице А.
- Найдите определитель матрицы А.
- Проверьте, что найденная матрица А-1 действительно является обратной для матрицы А.
1. Откройте чистый рабочий лист. Переименуйте его в Обратная матрица.
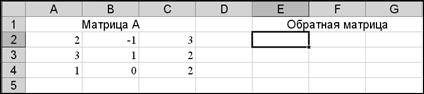
2. Заполните рабочий лист исходными данными, как показано на рис. 14:
Рис. 14
3. Установите курсор в ячейку Е2 и введите формулу =МОБР(А2:С4). После нажатия клавиши Enter в ячейке Е2 появится число 0,4.
4. Для получения обратной матрицы формулу в этом примере необходимо ввести как формулу массива. Для этого выделите диапазон ячеек Е2:G4, соответствующий обратной матрице (размерность матрицы А-1 очевидно будет такая же, как и у матрицы А). Нажмите клавишу , а затем комбинацию клавиш Ctrl+Shift+Enter. В результате ячейки Е2:G4 будут заполнены элементами обратной матрицы.
5. В ячейку А6 введите текст Определитель(A).
6. Установите курсор в ячейку В6 и введите формулу = МОПРЕД(А2:С4). Нажмите клавишу Enter. В ячейке должно получиться значение определителя матрицы А, равное 5. Внимание!В этом случае формулу для расчета определителя не нужно вводить как формулу массива, так как определитель является не массивом, а одним числом.
7. Для проверки правильности нахождения обратной матрицы вспомним, что должно выполняться условие: А А-1=Е, где Е — единичная матрица того же порядка, что и матрица А. Установите курсор в ячейку Е6 и введите текст Произведение матриц.
8. В ячейку Е7 введите формулу = МУМНОЖ(А2:С4; Е2:G4). Нажмите клавишу Enter.
9. Формулу в этом случае также вводим как формулу массива. В результате ячейки Е7:G9 будут заполнены элементами единичной матрицы (по главной диагонали будут записаны 1, остальные элементы будут равны 0). Если числа имеют много десятичных знаков, то выделите ячейки Е7:G9 и уменьшите разрядность либо при помощи команды меню Формат/Ячейки/закладка Число, либо при помощи кнопки Уменьшить разрядность 
ТЕСТОВОЕ ЗАДАНИЕ 1. Решение систем линейных уравнений
Вариант вашего задания задает преподаватель!
Откройте чистый рабочий лист. Переименуйте его в Тест 1.Решите систему линейных уравнений (см. табл. 5) по формулам Крамера.
Формулы Крамера имеют вид:
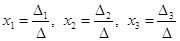
Здесь D- определитель системы, а Di — вспомогательный определитель, который получается из исходного определителя D путем замены i-го столбца на столбец свободных членов уравнений системы.
Таблица 5
| № | Решить систему | № | Решить систему |
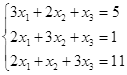 |
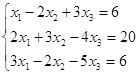 |
||
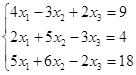 |
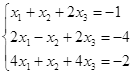 |
||
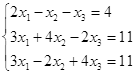 |
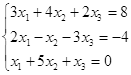 |
||
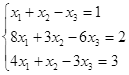 |
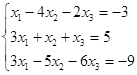 |
||
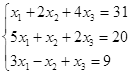 |
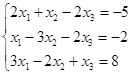 |
||
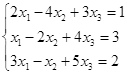 |
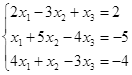 |
||
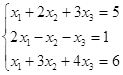 |
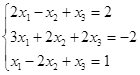 |
||
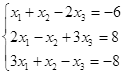 |
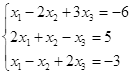 |
||
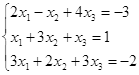 |
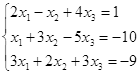 |
||
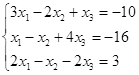 |
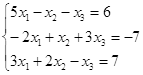 |
||
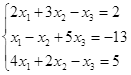 |
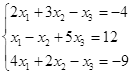 |
||
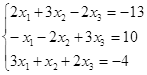 |
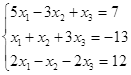 |
||
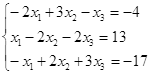 |
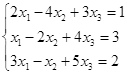 |
||
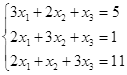 |
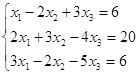 |
||
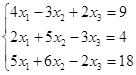 |
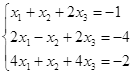 |
ТЕСТОВОЕ ЗАДАНИЕ 2. Решение уравнений, записанных в матричной форме
Вариант вашего задания задает преподаватель!
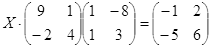
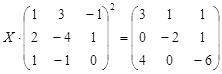
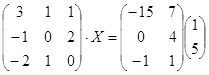
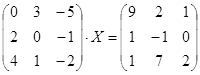
Откройте чистый рабочий лист. Переименуйте его в Тест 2.Решите матричные уравнения, выбрав свой вариант из таблицы 6.
Примечание. Заданное уравнение нужно свести к одному из двух видов:
1) А Х=В, здесь решение находится по формуле Х=А-1 В
или
2) Х А =В, в этом случае решение находится по формуле Х=В А-1.
Если исходное уравнение имеет вид С Х А =В, то его предварительно приведите к виду: Х А = С-1 В, рассчитайте правую часть системы и затем воспользуйтесь предложенными формулами для нахождения решения системы.
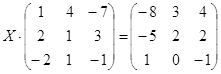
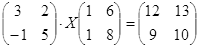
Таблица 6
| № | Уравнение | № | Уравнение |
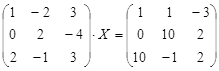 |
 |
||
 |
 |
||
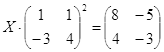 |
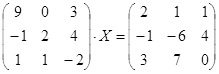 |
||
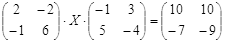 |
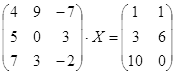 |
||
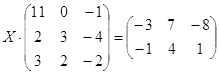 |
 |
||
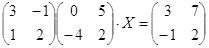 |
 |
||
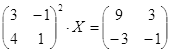 |
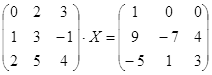 |
||
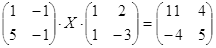 |
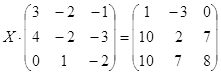 |
||
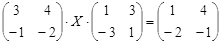 |
 |
||
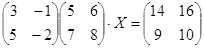 |
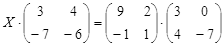 |
||
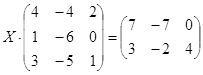 |
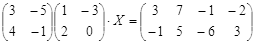 |
||
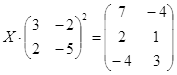 |
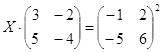 |
||
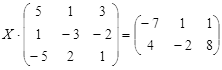 |
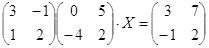 |
||
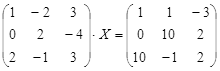 |
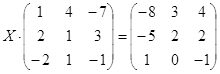 |
||
 |
 |
Статьи к прочтению:
- Лабораторная работа № 6. шифрование данных на жестком диске при помощи системы pgp
- Лабораторная работа №6. создание idef3-диаграммы
Курс Excel_Базовый — Урок №8. Абсолютные и относительные ссылки
Похожие статьи:
-
Лабораторная работа №1. основы работы с программой ms excel
САМАРСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ПУТЕЙ СООБЩЕНИЯ Кафедра информатики ИНФОРМАТИКА Табличный процессор MS Excel Методические указания к выполнению…
-
Лабораторная работа №5. вычисление сумм и произведений в ms excel
Цель работы: познакомиться с возможностями организации циклических вычислений на примере расчетов сумм и произведений. Обычно при расчетах сумм или…
Лабораторная работа № 6.
Электронные таблицы MS Excel: работа с матрицами
Время выполнения
2 часа
Цель работы
Научиться приемам работы с матрицами.
Задачи лабораторной работы
После выполнения работы студент должен:
- знать приемы работы с матрицами;
- уметь решать системы линейных алгебраических уравнений;
- уметь выполнять проверку решения.
Перечень обеспечивающих средств
Для обеспечения выполнения работы необходимо иметь компьютер со следующим обеспечением: операционная система Windows и MS Office 2007 и выше.
Общие теоретические сведения
Система mn чисел, расположенных в прямоугольной таблице из m строк и n столбцов, называется матрицей. Если m=n, то матрица называется квадратной, иначе прямоугольной. Над матрицами могут быть выполнены операции сложение матриц, умножение матрицы на число, на вектор.
Если матрица имеет размер 1 x n, то она называется вектором-строкой, а m x 1 – вектором-столбцом.
Если в матрице переставить строки и столбцы местами, то получим транспонированную матрицу.
Обратной матрицей по отношению к данной, называется матрица, которая, будучи умноженной как справа, так и слева на данную матрицу, дает единичную матрицу. При умножении матриц результирующая матрица имеет такое количество строк, как матрица слева, а количество столбцов как матрица справа. Для освоения методов работы с матрицами рассмотрим пример.
Пример 1. Умножить матрицу А2,3 на матрицу В3,3 и получить матрицу С2,3.
1. Задать значения элементам матриц A2,3, В3,3.
| A | B | C | D | E | F | |
| 1 | A2,3= | 1 | 3 | 2 | ||
| 2 | 3 | 4 | 5 | |||
| 3 | ||||||
| 4 | 1 | 2 | 3 | |||
| 5 | В3,3= | 1 | 4 | 1 | ||
| 6 | 2 | 3 | 3 | |||
| 7 | ||||||
| 8 | С2,3= | |||||
| 9 | ||||||
| 10 |
2. Выделить место для результирующей матрицы С2,3.
3. В строку формул записать знак равно (=).
4. С помощью мастера функций найти функцию МУМНОЖ.
5. Задать для нее исходные данные (указать с помощью мыши адреса матриц А и В).
6. Активизировать строку формул.
7. Нажать 3 клавиши Ctrl+Shift+Enter.
8. В результирующей матрице получим результат (рис. 1).
Рис. 1. Результат перемножения матриц
Пример 2. Решение системы линейных алгебраических уравнений.
Задана система линейных уравнений (1)
x1+2•x2+3•x3 = 4
4•x1+3•x2+2•x3=1 (1)
x1+3•x2+2мx3 = 4
В матричной форме система (1) имеет вид
А3,3 • Х3,1 =В3,1 (2), где А3,3-матрица коэффициентов при неизвестных
B3,1 – вектор правых частей.
Вектор неизвестных Х3,1 может быть найден по формуле
Х3,1=А3,3-1 • В3,1 (5)
А3,3-1 – обратная матрица.
Решение задачи выполнить в таблице.
| A | B | C | D | E | F | H | |
| 1 | Матрица исходных коэффициентов | Вектор правых частей | |||||
| 2 | 1 | 2 | 3 | 4 | |||
| 3 | А3,3= | 4 | 3 | 2 | В3,1= | 1 | |
| 4 | 1 | 3 | 2 | 4 | |||
| 5 | Обратная матрица | Вектор неизвестных | |||||
| 6 | |||||||
| 7 | А3,3-1= | Х3,1= | |||||
| 8 |
1. Ввести в таблицу значения матрицы коэффициентов А3,3.
2. Ввести в таблицу значения вектора В3,1.
3. Выделить место для обратной матрицы А3,3-1.
4. Вызвать мастер функций, отыскать функцию МОБР для вычисления обратной матрицы.
5. Ввести в диалоговое окно параметров функции адрес исходной матрицы коэффициентов мышью. Проверить записанный адрес. Если все нормально, щелкнуть мышью по строке формул (в ней появится курсор) и нажать 3 клавиши одновременно Ctrl+Shift+Enter. В выделенных ячейках появятся значения обратной матрицы.
6. Выделить место для результата (вектор неизвестных) Х3,1.
7. С помощью мастера функций найти функцию МУМНОЖ.
8. Ввести в диалоговое окно два адреса:
- адрес обратной матрицы (массив1);
- адрес вектора правых частей (массив2).
9. Активизировать строку формул, чтобы в ней появился курсор и нажать клавиши Ctrl+Shift+Enter (рис. 2).
Рис. 2. Решение системы линейных алгебраических уравнений
Пример 3. Решение системы линейных алгебраических уравнений методом Крамера (через определители). Работа со склеенными листами.
Если данные для каких-то таблиц повторяются, то их лучше набирать в режиме «склеенных листов». Можно склеивать подряд стоящие листы, не подряд стоящие или вообще все листы рабочей книги.
Пусть необходимо склеить три подряд стоящих листа (Лист1, Лист2, Лист3). Для этого производим щелчок левой кнопки мыши по ярлычку Лист1, затем нажимаем клавишу Shift и производим щелчок по ярлычку Лист3. Тогда все три ярлычка станут светлее. Чтобы расклеить листы, выполнить щелчок правой кнопкой мыши по ярлычку Лист1 и выбрать команду Разгруппировать листы.
Для выполнения задания склеим 4 листа. Матрицу исходных коэффициентов и вектор правых частей поместить на склеенные листы. Затем расклеить листы. На листах 2, 3, 4 столбцы при неизвестных заменить векторами правых частей для вычисления определителей неизвестных: на листе2 в 1-ый столбец, на листе3 во 2-ой столбец и на листе4 в третий столбец. Вычислить определители на каждом листе, используя функцию МОПРЕД. Для вычисления значения неизвестных разделить определитель для соответствующей переменной на общий определитель для матрицы исходных коэффициентов, так для вычисления х1 разделить определитель на листе2 на определитель на листе1, для х2 – определитель на листе3 на определитель на листе1 и т. д. Ввод формул выполнять только в строку формул.
С дополнительным материалом по теме можно ознакомиться в литературе [1, 3, 4, 7].
Видеоурок по выполнению заданий лабораторной работы
Задание
Отчетом является файл Матрицы_№вар_Фио_студента.xlsx, созданный в результате выполнения задания.
Технология выполнения работы
Заполнение файла Матрицы_№вар_Фио_студента.xlsx по заданному варианту должно быть выполнено с использованием приемов работы с матрицами. Решение системы уравнений должно быть выполнено двумя методами с проверкой решения.
Вопросы для защиты работы
- Какие СЛАУ можно решать методом обратной матрицы?
- Какие три клавиши нужно нажать, чтобы получить результат при работе с матрицами?
- Можно ли матрицу отнести к структурированным данным?
- Как выполнить проверку решения СЛАУ?
- Какие методы вы знаете для решения СЛАУ?



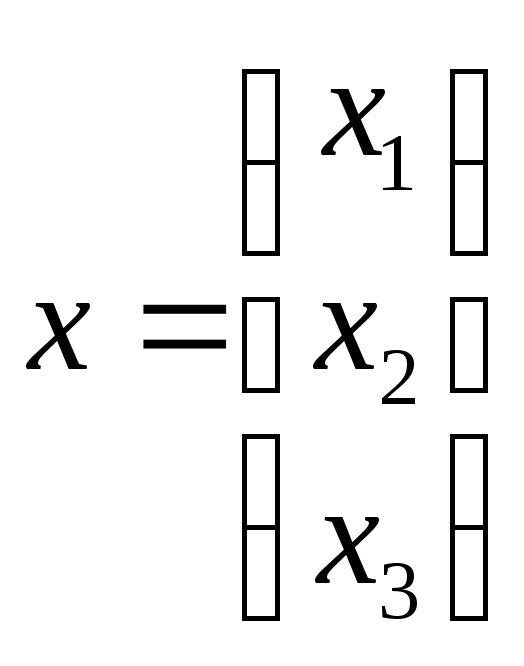





 , где i — номер строки, а j — номер столбца;
, где i — номер строки, а j — номер столбца;