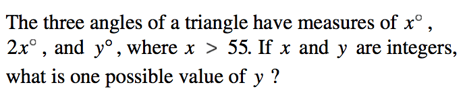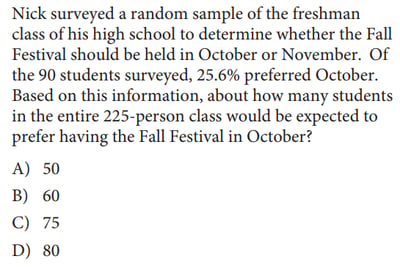Free Math Word Problems Collection for Grades 1-5
The LogicLike team has collected over 500+ math problems on various topics! We provide word
problems and math puzzles designed by experienced teachers. LogicLike helps children improve
their math skills in a playfull way!

Educational platform LogicLike.com helps children to build critical
thinking, math & logic skills. Adults improve mental abilities and develop
ingenuity.
Choose Word Problems by Grade
Our team has created word math problems for grades 1-5! Choose your grade, learn math and have
fun with LogicLike!
1st Grade Math Word Problems
In first grade, an important task for students is to learn addition and subtraction. Word
problems will help them do it!
Go to Math Word
Problems for 1st Grade.
2nd Grade Math Word Problems
In second grade children learn to add and subtract more complex numbers. We offer
our own collection of word math problems for 2nd grade students to practice!
Go to Math Word
Problems for 2nd Grade.
3rd Grade Math Word Problems
In grade 3 children begin to master multiplication and division, two-step word problems, solve
time and measurement problems!
Go to Math Word
Problems for 3rd Grade.
4th Grade Math Word Problems
In 4th grade, it is very important to consolidate all your knowledge from previous years and
learn how to apply it to more difficult word problems!
Go to Math Word
Problems for 4th Grade.
5th Grade Math Word Problems
In fifth grade, children begin to learn fractions, variable equations and mixed numbers.
LogicLike will help them do just that!
Go to Math Word
Problems for 5th Grade.
Children ages 5-12 enjoy the LogicLike course in a playful way. In the meantime,
they learn to reason, develop their math and logical skills, and interest in
knowledge.
Choose Word Problems by Topic
LogicLike has made over 13 themed picks for learning important topics in math! You can solve the
best word problems for addition and subtraction, multiplication and division, fractions and
mixed numbers, and more!
Money Word Problems
Tom has 50 cents, and his mother gives him 4 quarters.
How much money does Tom have?
Sara wants to buy 14 ChocoPies. The ChocoPies cost 35 cents each.
How much money will 14 ChocoPies cost?
Michael had $9,896.00 in his checking account.
Then, he spent $3,458.00 on the account.
How much money is left in Michael’s checking account?
Mixed Addition and Subtraction Word Problems
Sam caught 4 fish in the morning. Later, he caught 1 more fish.
How many fish did Sam catch in all?
At the birthday party, there were 12 cups but 4 cups were broken.
Mom goes out and buys 10 cups.
How many cups are there after she returns?
The pirate has a chest with coins.
Inside there are 328 gold, 264 silver and 136 copper coins.
How many coins are in the chest in total?

Multi-Step (Multiple Step) Word Problems
There were 6 yellow apples and 4 red apples on the plate. We ate 7
apples.
How many apples are left on the plate?
The clown had balloons of 3 colors, 6 pieces of each color.
He gave the kids 4 balls of 2 colors.
How many balloons does the clown have left?
Mary bought 15 pounds of strawberries at $1.68 per pound.
Marion bought 14 pounds of strawberries at $1.80 per pound.
Who paid more?
Multiplication Word Problems
Jessica saw 4 dozen doves in the park.
How many doves did Jessica see?
The chef of the restaurant prepares an omelet from 3 eggs.
If the chef has 72 omelets to make, how many eggs will he need?
Brenda’s kitten weighs 3 3/5 pounds.
Oliver’s dog weighs 4 times more.
How much does Oliver’s dog weigh?
Mixed Multiplication and Division Word Problems
Each crayon costs $3.00.
How much do 18 crayons cost?
A concert hall contains 6 sections of seats with the same number of seats in
each section. If there are 768 seats, how many seats are in each section?
The online store has $ 21,000 to buy online ads.
If each ad costs $ 6, how many ads can an online store purchase in a
month?
Is this enough to get 300 ads per month for a year?
Division Word Problems
There are 3 students in the class and 21 pens.
If the pens are divided equally among the students,
how many does each student get?
Monika earned $216 babysitting in 9 months.
She earned the same amount each month.
How much did Tina earn babysitting each month?
The toy company makes Teddy bears in two sizes — big and small.
The company produced 1,620 Teddy Bears last week.
They made 11 times more small Teddies than large ones.
How many big size toys did they make?
Fraction Word Problems
Sarah made nine chocolate bars.
She put powdered sugar on three chocolate bars.
Which part of the bars now have powdered sugar?
Jessica had $200, 1/4 of this money she spent on cosmetics.
How much money did Jessica spend?
The perimeter of the triangle is 40 inches.
The first side is 3/10 of the perimeter,
the other is 3/2 of the first side.
What is the third side of the triangle?
Proportion Word Problems and Worksheets
The cinema has 400 seats, 260 of which are occupied by spectators.
Express the attendance at a percent of capacity.
Molly has 45 markers. 20% of the markers write poorly.
How many markers are bad at writing?
In an exam, Shawna secured 340 marks.
If she secured 85% makes, find the maximum marks.

Ratio Word Problems
The ratio of green and red apples in a bag is 2 : 5.
If there are only green and red apples in a bag,
what is the smallest total number of apples possible?
65 children are swimming in the pool.
There are 15 more boys than girls.
What is the ratio of boys to girls?
James gives Kathy a box of building blocks and tells her that the ratio of
red blocks to total is 3 to 19. He also tells her there are 3 times as many
yellow blocks as red, and that there are 2 more green than red.
What is the ratio of yellow blocks to green?
Dividing Decimals Word Problems
Jack paid $99 for 6 pizzas.
How much did he pay per pizza?
Mark has run a total of 84.24 miles in 32.4 days of running training.
How many miles did he run on average per day?
An Olive Oil Factory made 809.9 pounds of olive oil in 6.5 minutes.
How much oil, on average, did the factory make each minute?
Volume Word Problems
Ship container has a length of 40 feet, width 8 feet, and 9.6 feet in
height.
Find the volume of the container in cubic feet.
The volume of a cylinder is 441 cubic inches. The height of the cylinder is
9 in.
Find the radius of the cylinder to the nearest tenth of an inch.
A cylindrical hole with a diameter of 8 inches is bored through a cub 10
inches on a side. Find the surface area and volume of this solid casting.
Measurement Word Problems
Jack was 5 feet 9 inches tall last year.
He grew 7 inches in the past year.
How tall is he now?
The turkey is 18 lb 11 oz and the stuffing inside the turkey is 5 oz.
What is the total weight of the roasted turkey?
From 10g of instant coffee, 120 ml of coffee can be brewed.
In a can of instant coffee is 200 g.
How much coffee (in liters) can you make from a can?
Mila is 5 years older than her brother, but 3 times younger than her
mother.
How old is Mila and how old is her mother, if Mila’s brother is 6 years old?
In 8 years, Mary will be 3 times as old as she is today.
How old is Mary today?
Felix is twice as old as his friend Greg.
Greg is 5 years older than Rachel.
In 5 years, Felix will be three times as old as Rachel.
How old is Greg now?
Have a look at some age word
problems that the LogicLike team creates for
children and adults.
This article is for parents who think about how to help with math and support their children. The math word problems below provide a gentle introduction to common math operations for schoolers of different grades.
What are math word problems?
During long-time education, kids face various hurdles that turn into real challenges. Parents shouldn’t leave their youngsters with their problems. They need an adult’s possible help, but what if the parents themselves aren’t good at mathematics? All’s not lost. You can provide your kid with different types of support. Not let a kid burn the midnight oil! Help him/ her to get over the challenges thanks to these captivating math word examples.
Math word problems are short math questions formulated into one or several sentences. They help schoolers to apply their knowledge to real-life scenarios. Besides, this kind of task helps kids to understand this subject better.
Addition for the first and second grades
These math examples are perfect for kids that just stepped into primary school. Here you find six easy math problems with answers:
1. Peter has eight apples. Dennis gives Peter three more. How many apples does Peter have in all?
Show answer
Answer: 8 apples + 3 apples = 11 apples.
2. Ann has seven candies. Lack gives her seven candies more. How many candies does Ann have in all?
Show answer
Answer: 7 candies + 7 candies = 14 candies.
3. Walter has two books. Matt has nine books. If Matt gives all his books to Walter, how many books will Walter have?
Show answer
Answer: 2 books + 9 books = 11 books.
4. There are three crayons on the table. Albert puts five more crayons on the table. How many crayons are on the table?
Show answer
Answer: 3 crayons + 5 crayons = 8 crayons.
5. Bill has nine oranges. His friend has one orange. If his friend gives his orange to Bill, how many oranges will Bill have?
Show answer
Answer: 9 oranges + 1 orange = 10 oranges.
6. Jassie has four leaves. Ben has two leaves. Ben gives her all his leaves. How many leaves does Jessie have in all?
Show answer
Answer: 4 leaves + 2 leaves = 6 leaves.
Subtraction for the first and second grades
1. There were three books in total at the book shop. A customer bought one book. How many books are left?
Show answer
Answer: 3 books – 1 book = 2 books.
2. There are five pizzas in total at the pizza shop. Andy bought one pizza. How many pizzas are left?
Show answer
Answer: 5 pizzas – 1 pizza = 4 pizzas.
3. Liza had eleven stickers. She gave one of her stickers to Sarah. How many stickers does Liza have?
Show answer
Answer: 11 stickers – 1 sticker = 10 stickers.
4. Adrianna had ten stones. But then she left two stones. How many stones does Adrianna have?
Show answer
Answer: 10 stones – 2 stones = 8 stones.
5. Mary bought a big bag of candy to share with her friends. There were 20 candies in the bag. Mary gave three candies to Marissa. She also gave three candies to Kayla. How many candies were left?
Show answer
Answer: 20 candies – 3 candies – 3 candies = 14 candies.
6. Betty had a pack of 25 pencil crayons. She gave five to her friend Theresa. She gave three to her friend Mary. How many pencil crayons does Betty have left?
Show answer
Answer: 25 crayons – 5 crayons – 3 crayons = 17 crayons.
Multiplication for the 2nd grade and 3rd grade
See the simple multiplication word problems. Make sure that the kid has a concrete understanding of the meaning of multiplication before.
Bill is having his friends over for the game night. He decided to prepare snacks and games.
1. He makes mini sandwiches. If he has five friends coming over and he made three sandwiches for each of them, how many sandwiches did he make?
Show answer
Answer: 5 x 3 = 15 sandwiches.
2. He also decided to get some juice from fresh oranges. If he used two oranges per glass of juice and made six glasses of juice, how many oranges did he use?
Show answer
Answer: 2 x 6 = 12 oranges.
3. Then Bill prepared the games for his five friends. If each game takes 7 minutes to prepare and he prepared a total of four games, how many minutes did it take for Bill to prepare all the games?
Show answer
Answer: 7 x 4 = 28 minutes.
4. Bill decided to have takeout food as well. If each friend and Bill eat three slices of pizza, how many slices of pizza do they have in total?
Show answer
Answer: 6 (5 friends and Bill) x 3 slices of pizza = 18 slices of pizza.
Mike is having a party at his house to celebrate his birthday. He invited some friends and family.
1. He and his mother prepared cupcakes for dessert. Each box had 8 cupcakes, and they prepared four boxes. How many cupcakes have they prepared in the total?
Show answer
Answer: 8 x 4 = 32 cupcakes.
2. They also baked some cookies. If they baked 6 pans of cookies, and there were 7 cookies per pan, how many cookies did they bake?
Show answer
Answer: 6 x 7 = 42 cookies.
3. Mike planned to serve some cold drinks as well. If they make 7 pitchers of drinks and each pitcher can fill 5 glasses, how many glasses of drinks are they preparing?
Show answer
Answer: 7 x 5 = 35 glasses.
4. At the end of the party, Mike wants to give away some souvenirs to his 6 closest friends. If he gives 2 souvenir items for each friend, how many souvenirs does Mike prepare?
Show answer
Answer: 6 x 2 = 12 souvenirs.
Division: best for 3rd and 4th grades
1. If you have 10 books split evenly into 2 bags, how many books are in each bag?
Show answer
Answer: 10 : 2 = 5 books.
2. You have 40 tickets for the fair. Each ride costs 2 tickets. How many rides can you go on?
3. The school has $20,000 to buy new equipment. If each piece of equipment costs $100, how many pieces can the school buy in total?
Show answer
Answer: $20,000 : $100= 200.
4. Melissa has 2 packs of tennis balls for $10 in total. How much does 1 pack of tennis balls cost?
5. Jack has 25 books. He has a bookshelf with 5 shelves on it. If Jack puts the same number of books on each shelf, how many books will be on each shelf?
6. Matt is having a picnic for his family. He has 36 cookies. There are 6 people in his family. If each person gets the same number of cookies, how many cookies will each person get?
Division with remainders for fourth and fifth grades
1. Sarah sold 35 boxes of cookies. How many cases of ten boxes, plus extra boxes does Sarah need to deliver?
Show answer
Answer: 35 boxes divided by 10 boxes per case = 3 cases and 5 boxes.
2. Candies come in packages of 16. Mat ate 46 candies. How many whole packages of candies did he eat, and how many candies did he leave? 46 candies divided by 16 candies = 2 packages and 2 candies left over.
3. Mary sold 24 boxes of chocolate biscuits. How many cases of ten boxes, plus extra boxes does she need to deliver?
Show answer
Answer: 24 boxes divided by 10 boxes per case = 2 cases and four boxes.
4. Gummy bears come in packages of 25. Suzie and Tom ate 30 gummy bears. How many whole packages did they eat? How many gummy bears did they leave?
Show answer
Answer: 30 divided by 25 = 1 package they have eaten and 20 gummy bears left over.
5. Darel sold 55 ice-creams. How many cases of ten boxes, plus extra boxes does he need to deliver?
Show answer
Answer: 55 boxes divided by 10 boxes per case = 5 cases and 5 boxes.
6. Crackers come in packages of 8. Mat ate 20 crackers. How many whole packages of crackers did he eat, and how many crackers did he leave?
Show answer
Answer: 20 divided by 8 = 2 packages eaten and 4 crackers are left.
Mixed operations for the fifth grade
These math word problems involve four basic operations: addition, multiplication, subtraction, and division. They suit best for the fifth-grade schoolers.
200 planes are taking off from the airport daily. During the Christmas holidays, the airport is busier — 240 planes are taking off every day from the airport.
1. During the Christmas holidays, how many planes take off from the airport in each hour if the airport opens 12 hours daily?
Show answer
Answer: 240÷12=20 planes take off from this airport each hour during the Christmas holidays.
2. Each plane takes 220 passengers. How many passengers depart from the airport every hour during the Christmas holidays? 20 x 220 = 4400.
Show answer
Answer: 4400 passengers depart from the airport every hour.
3. Compared with a normal day, how many more passengers are departing from the airport in a day during the Christmas holidays?
Show answer
Answer: (240-200) x 220 = 8800 more passengers departing from the airport in a day during the Christmas holidays.
4. During normal days on average 650 passengers are late for their plane daily. During the Christmas holidays, 1300 passengers are late for their plane. That’s why 14 planes couldn’t take off and are delayed. How many more passengers are late for their planes during Christmas week?
Show answer
Answer: 1300 – 650 = 650 more passengers are late for their planes each day during the Christmas holidays.
5. According to the administration’s study, an additional 5 minutes of delay in the overall operation of the airport is caused for every 27 passengers that are late for their flights. What is the delay in the overall operation if there are 732 passengers late for their flights?
Show answer
Answer: 732 ÷ 27 × 5 = 136. There will be a delay of 136 minutes in the overall operation of the airport.
Extra info math problems for the fifth grade
1. Ann has 7 pairs of red socks and 8 pairs of pink socks. Her sister has 12 pairs of white socks. How many pairs of socks does Ann have?
2. Kurt spent 17 minutes doing home tasks. He took a 3-minute snack break. Then he studied for 10 more minutes. How long did Kurt study altogether?
Show answer
Answer: 17 + 10 = 27 minutes.
3. There were 15 spelling words on the test. The first schooler spelled 9 words correctly. Miguel spelled 8 words correctly. How many words did Miguel spell incorrectly?
4. In the morning, Jack gave his friend 2 gummies. His friend ate 1 of them. Later Jack gave his friend 7 more gummies. How many gummies did Jack give his friend in all?
5. Peter wants to buy 2 candy bars. They cost 8 cents, and the gum costs 5 cents. How much will Peter pay?
Finding averages for 5th grade
We need to find averages in many situations in everyday life.
1. The dog slept 8 hours on Monday, 10 hours on Tuesday, and 900 minutes on Wednesday. What was the
average number of hours the dog slept per day?
Show answer
Answer: (8+10+(900:60)) : 3 = 11 hours.
2. Jakarta can get a lot of rain in the rainy season. The rainfall during 6 days was 90 mm, 74 mm, 112 mm, 30 mm, 100 mm, and 44 mm. What was the average daily rainfall during this period?
Show answer
Answer: (90+74+112+30+100+44) : 6 = 75 mm.
3. Mary bought 4 books. The prices of the first 3 books were $30, $15, and $18. The average price she paid for the 4 books was $25 per books. How much did she pay for the 4th books?


Math & logic courses for kids
Times more complex than school, extremely fun, interactive and rewarding to keep 7-13 years old kids engaged. We’re gonna make them love math!
learn more
Ordering and number sense for the 5th grade
1. There are 135 pencils, 200 pens, 167 crayons, and 555 books in the bookshop. How would you write these numbers in ascending order?
Show answer
Answer: 135, 167, 200, 555
2. There are five carrots, one cabbage, eleven eggs, and 15 apples in the fridge. How would you write these numbers in descending order?
3. Peter has completed exercises on pages 279, 256, 264, 259, and 192. How would you write these numbers in ascending order?
Show answer
Answer: 192, 256, 259, 264, 279.
4. Mary picked 32 pants, 15 dresses, 26 pairs of socks, 10 purses. Put all these numbers in order.
5. The family bought 12 cans of tuna, 23 potatoes, 11 onions, and 33 pears. Put all these numbers in order.
Fractions for the 6th-8th grades
1. Jannet cooked 12 lemon biscuits for her daughter, Jill. She ate up 4 biscuits. What fraction of lemon biscuits did Jill eat?
Show answer
Answer: 1/3 of the lemon biscuits.
2. Guinet travels a distance of 7 miles to reach her school. The bus covers only 5 miles. Then she has to walk 2 miles to reach the school. What fraction of the distance does Guinet travel by bus?
Show answer
Answer: 5/7 of the distance
3. Bob has 24 pencils in a box. Eighteen pencils have #2 marked on them, and the 6 are marked #3. What fraction of pencils are marked #3?
Show answer
Answer: 1/4 of the pencils.
4. My mother places 15 tulips in a glass vase. It holds 6 yellow tulips and 9 red tulips. What fraction of tulips are red?
Show answer
Answer: 3/5 of the tulips.
5. Bill owns 14 pairs of socks, of which 7 pairs are white, and the rest are brown. What fraction of pairs of socks are brown?
Show answer
Answer: 1/2 of the pairs of socks.
6. Bred spotted a total of 39 birds in an aviary at the Zoo. He counted 18 macaws and 21 cockatoos. What fraction of macaws did Bred spot at the aviary?
Show answer
Answer: 6/13 of the birds.
Decimals for the 6th grade
Write in words the following decimals:
- 0,004
- 0,07
- 2,1
- 0,725
- 46,36
- 2000,19
Show answer
Answer:
- 0,004 = four thousandths.
- 0,07 = seven hundredths.
- 2,1 = two and one tenth.
- 0,725 = seven hundred twenty five thousandths.
- 46,36 = foury six and thirty six hundredths.
- 2000,19 = two thousand and nineteen hundredths.
Comparing and sequencing for the 6th grade
1. The older brother picked 42 apples at the orchard. The younger brother picked only 22 apples. How many more apples did the older brother pick?
Show answer
Answer: 42 – 22 = 20 apples more.
2. There were 16 oranges in a basket and 66 oranges in a barrel. How many fewer oranges were in the basket than were in the barrel?
Show answer
Answer: 66 – 16 = 50 fewer oranges.
3. There were 40 parrots in the flock. Some of them flew away. Then there were 25 parrots in the flock. How many parrots flew away?
Show answer
Answer: 40 – 25 = 15 parrots flew away.
4. One hundred fifty is how much greater than fifty-three?
5. On Monday, the temperature was 13°C. The next day, the temperature dropped by 8 degrees. What was the temperature on Tuesday?
6. Zoie picked 15 dandelions. Her sister picked 22 ones. How many more dandelions did her sister pick than Zoie?
Show answer
Answer: 22-15 = 7 dandelions more.
Time for the 4th grade
1. The bus was scheduled to arrive at 7:10 p.m. However, it was delayed for 45 minutes. What time was it when the bus arrived?
2. My mother starts her 7-hour work at 9:15 a.m. What time does she get off from work?
3. Jack’s walk started at 6:45 p.m. and ended at 7:25 p.m. How long did his walk last?
4. The school closes at 9:00 p.m. Today, the school’s principal left 15 minutes after the office closed, and his secretary left the office 25 minutes after he left. When did the secretary leave work?
5. Suzie arrives at school at 8:20 a.m. How much time does she need to wait before the school opens? The school opens at 8:35 a.m.
6. The class starts at 9:15 a.m.. The first bell will ring 20 minutes before the class starts. When will the first bell ring?
Money word problems for the fourth grade
1. James had $20. He bought a chocolate bar for $2.30 and a coffee cup for $5.50. How much money did he have left?
Show answer
Answer: $20.00 – $2.30 – $5.50 = $12.20. James had $12.20 left.
2. Coffee mugs cost $1.50 each. How much do 7 coffee mugs cost?
Show answer
Answer: $1.5 x 7 = $10.5.
3. The father gives $32 to his four children to share equally. How much will each of his children get?
4. Each donut costs $1.20. How much do 6 donuts cost?
Show answer
Answer: $1.20 * 6 = $7,2.
5. Bill and Bob went out for takeout food. They bought 4 hamburgers for $10. Fries cost $2 each. How much does one hamburger with fries cost?
Show answer
Answer: $10 ÷ 4 = $2.50. One hamburger costs $2.50. $2.50 + $2.00 = $4.50. One hamburger with fries costs $4.50.
6. A bottle of juice costs $2.80, and a can is $1.50. What would it cost to buy two cans of soft drinks and a bottle of juice?
Show answer
Answer: $1.50 x 2 + $2.80 = $5.80.
Measurement word problems for the 6th grade
The task is to convert the given measures to new units. It best suits the sixth-grade schoolers.
- 55 yd = ____ in.
- 43 ft = ____ yd.
- 31 in = ____ ft.
- 29 ft = ____ in.
- 72 in = ____ ft.
- 13 ft = ____ yd.
- 54 lb = ____ t.
- 26 t = ____ lb.
- 77 t = ____ lb.
- 98 lb = ____ t.
- 25 lb = ____ t.
- 30 t = ____ lb.
Show answer
Answer:
- 55 yd = 1.980 in
- 43 ft = 14 yd 1 ft
- 31 in = 2 ft 7 in
- 29 ft = 348 in
- 72 in = 6 ft
- 13 ft = 4 yd 1 ft.
- 54 lb = 0,027 t
- 26 t = 52.000 lb
- 77 t = 154.000 lb
- 98 lb = 0,049 t
- 25 lb = 0?0125 t
- 30 t = 60.000 lb.
Ratios and percentages for the 6th-8th grades
It is another area that children can find quite difficult. Let’s look at simple examples of how to find percentages and ratios.
1. A chess club has 25 members, of which 13 are males, and the rest are females. What is the ratio of males to all club members?
2. A group has 8 boys and 24 girls. What is the ratio of girls to all children?
3. A pattern has 4 red triangles for every 12 yellow triangles. What is the ratio of red triangles to all triangles?
4. An English club has 21 members, of which 13 are males, and the rest are females. What is the ratio of females to all club members?
5. Dan drew 1 heart, 1 star, and 26 circles. What is the ratio of circles to hearts?
6. Percentages of whole numbers:
- 50% of 60 = …
- 100% of 70 = …
- 90% of 70 = …
- 20% of 30 = …
- 40% of 10 = …
- 70% of 60 = …
- 100% of 20 = …
- 80% of 90 = …
Show answer
Answer:
- 50% of 60 = 30
- 100% of 70 = 70
- 90% of 70 = 63
- 20% of 30 = 6
- 40% of 10 = 4
- 70% of 60 = 42
- 100% of 20 = 20
- 80% of 90 = 72.
Probability and data relationships for the 8th grade
1. John ‘s probability of winning the game is 60%. What is the probability of John not winning the game?
2. The probability that it will rain is 70%. What is the probability that it won’t rain?
3. There is a pack of 13 cards with numbers from 1 to 13. What is the probability of picking a number 9 from the pack?
4. A bag had 4 red toy cars, 6 white cars, and 7 blue cars. When a car is picked from this bag, what is the probability of it being red or blue?
5. In a class, 22 students like orange juice, and 18 students like milk. What is the probability that a schooler likes juice?
Geometry for the 7th grade
The following task is to write out equations and find the angles. Complementary angles are two angles that sum up to 90 degrees, and supplementary angles are two angles that sum up to 180 degrees.
1. The complement of a 32° angle = …
2. The supplement of a 10° angle = …
3. The complement of a 12° angle = …
4. The supplement of a 104° angle = …
Variables/ equation word problems for the 5th grades
1. The park is 𝑥 miles away from Jack’s home. Jack had to drive to and from the beach with a total distance of 36 miles. How many miles is Jack’s home away from the park?
Show answer
Answer: 2𝑥 = 36 → 𝑥 = 18 miles.
2. Larry bought some biscuits which cost $24. He paid $x and got back $6 of change. Find x.
Show answer
Answer: x = 24 + 6 = $30.
3. Mike played with his children on the beach for 90 minutes. After they played for x minutes, he had to remind them that they would be leaving in 15 minutes. Find x.
Show answer
Answer: x = 90 – 15 = 75 minutes.
4. At 8 a.m., there were x people at the orchard. Later at noon, 27 of the people left the orchard, and there were 30 people left in the orchard. Find x.
Show answer
Answer: x = 30 + 27 = 57 people
Travel time word problems for the 5th-7th grades
1. Tony sprinted 22 miles at 4 miles per hour. How long did Tony sprint?
Show answer
Answer: 22 miles divided by 4 miles per hour = 5.5 hours.
2. Danny walked 15 miles at 3 miles per hour. How long did Danny walk?
Show answer
Answer: 15 miles divided by 3 miles per hour = 5 hours.
3. Roy sprinted 30 miles at 6 miles per hour. How long did Roy sprint?
Show answer
Answer: 30 miles divided by 6 miles per hour = 5 hours.
4. Harry wandered 5 hours to get Pam’s house. It is 20 miles from his house to hers. How fast did Harry go?
Show answer
Answer: 20 miles divided by 5 hours = 4 miles per hour.
STEM subjects for kids
STEM courses for kids ages 7-13 in physics, chemistry, math and logic in interactive game format
learn more
From Wikipedia, the free encyclopedia
This article is about algorithmic word problems in mathematics and computer science. For other uses, see Word problem.
In computational mathematics, a word problem is the problem of deciding whether two given expressions are equivalent with respect to a set of rewriting identities. A prototypical example is the word problem for groups, but there are many other instances as well. A deep result of computational theory is that answering this question is in many important cases undecidable.[1]
Background and motivation[edit]
In computer algebra one often wishes to encode mathematical expressions using an expression tree. But there are often multiple equivalent expression trees. The question naturally arises of whether there is an algorithm which, given as input two expressions, decides whether they represent the same element. Such an algorithm is called a solution to the word problem. For example, imagine that 

EQUAL, and similarly produce NOT_EQUAL from 
The most direct solution to a word problem takes the form of a normal form theorem and algorithm which maps every element in an equivalence class of expressions to a single encoding known as the normal form — the word problem is then solved by comparing these normal forms via syntactic equality.[1] For example one might decide that 



While the word problem asks whether two terms containing constants are equal, a proper extension of the word problem known as the unification problem asks whether two terms 


while 

History[edit]
One of the most deeply studied cases of the word problem is in the theory of semigroups and groups. A timeline of papers relevant to the Novikov-Boone theorem is as follows:[3][4]
- 1910: Axel Thue poses a general problem of term rewriting on tree-like structures. He states «A solution of this problem in the most general case may perhaps be connected with unsurmountable difficulties».[5][6]
- 1911: Max Dehn poses the word problem for finitely presented groups.[7]
- 1912: Dehn presents Dehn’s algorithm, and proves it solves the word problem for the fundamental groups of closed orientable two-dimensional manifolds of genus greater than or equal to 2.[8] Subsequent authors have greatly extended it to a wide range of group-theoretic decision problems.[9][10][11]
- 1914: Axel Thue poses the word problem for finitely presented semigroups.[12]
- 1930 – 1938: The Church-Turing thesis emerges, defining formal notions of computability and undecidability.[13]
- 1947: Emil Post and Andrey Markov Jr. independently construct finitely presented semigroups with unsolvable word problem.[14][15] Post’s construction is built on Turing machines while Markov’s uses Post’s normal systems.[3]
- 1950: Alan Turing shows the word problem for cancellation semigroups is unsolvable,[16] by furthering Post’s construction. The proof is difficult to follow but marks a turning point in the word problem for groups.[3]: 342
- 1955: Pyotr Novikov gives the first published proof that the word problem for groups is unsolvable, using Turing’s cancellation semigroup result.[17][3]: 354 The proof contains a «Principal Lemma» equivalent to Britton’s Lemma.[3]: 355
- 1954 – 1957: William Boone independently shows the word problem for groups is unsolvable, using Post’s semigroup construction.[18][19]
- 1957 – 1958: John Britton gives another proof that the word problem for groups is unsolvable, based on Turing’s cancellation semigroups result and some of Britton’s earlier work.[20] An early version of Britton’s Lemma appears.[3]: 355
- 1958 – 1959: Boone publishes a simplified version of his construction.[21][22]
- 1961: Graham Higman characterises the subgroups of finitely presented groups with Higman’s embedding theorem,[23] connecting recursion theory with group theory in an unexpected way and giving a very different proof of the unsolvability of the word problem.[3]
- 1961 – 1963: Britton presents a greatly simplified version of Boone’s 1959 proof that the word problem for groups is unsolvable.[24] It uses a group-theoretic approach, in particular Britton’s Lemma. This proof has been used in a graduate course, although more modern and condensed proofs exist.[25]
- 1977: Gennady Makanin proves that the existential theory of equations over free monoids is solvable.[26]
The word problem for semi-Thue systems[edit]
The accessibility problem for string rewriting systems (semi-Thue systems or semigroups) can be stated as follows: Given a semi-Thue system 




The accessibility and word problems are undecidable, i.e. there is no general algorithm for solving this problem.[28] This even holds if we limit the systems to have finite presentations, i.e. a finite set of symbols and a finite set of relations on those symbols.[27] Even the word problem restricted to ground terms is not decidable for certain finitely presented semigroups.[29][30]
The word problem for groups[edit]
Given a presentation 
The word problem in combinatorial calculus and lambda calculus[edit]
One of the earliest proofs that a word problem is undecidable was for combinatory logic: when are two strings of combinators equivalent? Because combinators encode all possible Turing machines, and the equivalence of two Turing machines is undecidable, it follows that the equivalence of two strings of combinators is undecidable. Alonzo Church observed this in 1936.[32]
Likewise, one has essentially the same problem in (untyped) lambda calculus: given two distinct lambda expressions, there is no algorithm which can discern whether they are equivalent or not; equivalence is undecidable. For several typed variants of the lambda calculus, equivalence is decidable by comparison of normal forms.
The word problem for abstract rewriting systems[edit]
Solving the word problem: deciding if 

The word problem for an abstract rewriting system (ARS) is quite succinct: given objects x and y are they equivalent under 

The Knuth-Bendix completion algorithm can be used to transform a set of equations into a convergent term rewriting system.
The word problem in universal algebra[edit]
In universal algebra one studies algebraic structures consisting of a generating set A, a collection of operations on A of finite arity, and a finite set of identities that these operations must satisfy. The word problem for an algebra is then to determine, given two expressions (words) involving the generators and operations, whether they represent the same element of the algebra modulo the identities. The word problems for groups and semigroups can be phrased as word problems for algebras.[1]
The word problem on free Heyting algebras is difficult.[34]
The only known results are that the free Heyting algebra on one generator is infinite, and that the free complete Heyting algebra on one generator exists (and has one more element than the free Heyting algebra).
The word problem for free lattices[edit]
|
|
The word problem on free lattices and more generally free bounded lattices has a decidable solution. Bounded lattices are algebraic structures with the two binary operations ∨ and ∧ and the two constants (nullary operations) 0 and 1. The set of all well-formed expressions that can be formulated using these operations on elements from a given set of generators X will be called W(X). This set of words contains many expressions that turn out to denote equal values in every lattice. For example, if a is some element of X, then a ∨ 1 = 1 and a ∧ 1 = a. The word problem for free bounded lattices is the problem of determining which of these elements of W(X) denote the same element in the free bounded lattice FX, and hence in every bounded lattice.
The word problem may be resolved as follows. A relation ≤~ on W(X) may be defined inductively by setting w ≤~ v if and only if one of the following holds:
- w = v (this can be restricted to the case where w and v are elements of X),
- w = 0,
- v = 1,
- w = w1 ∨ w2 and both w1 ≤~ v and w2 ≤~ v hold,
- w = w1 ∧ w2 and either w1 ≤~ v or w2 ≤~ v holds,
- v = v1 ∨ v2 and either w ≤~ v1 or w ≤~ v2 holds,
- v = v1 ∧ v2 and both w ≤~ v1 and w ≤~ v2 hold.
This defines a preorder ≤~ on W(X), so an equivalence relation can be defined by w ~ v when w ≤~ v and v ≤~ w. One may then show that the partially ordered quotient set W(X)/~ is the free bounded lattice FX.[35][36] The equivalence classes of W(X)/~ are the sets of all words w and v with w ≤~ v and v ≤~ w. Two well-formed words v and w in W(X) denote the same value in every bounded lattice if and only if w ≤~ v and v ≤~ w; the latter conditions can be effectively decided using the above inductive definition. The table shows an example computation to show that the words x∧z and x∧z∧(x∨y) denote the same value in every bounded lattice. The case of lattices that are not bounded is treated similarly, omitting rules 2 and 3 in the above construction of ≤~.
Example: A term rewriting system to decide the word problem in the free group[edit]
Bläsius and Bürckert
[37]
demonstrate the Knuth–Bendix algorithm on an axiom set for groups.
The algorithm yields a confluent and noetherian term rewrite system that transforms every term into a unique normal form.[38]
The rewrite rules are numbered incontiguous since some rules became redundant and were deleted during the algorithm run.
The equality of two terms follows from the axioms if and only if both terms are transformed into literally the same normal form term. For example, the terms
, and
share the same normal form, viz. 
As another example, the term 



| A1 |  |

|
| A2 |  |

|
| A3 |  |

|
| R1 |  |

|
| R2 |  |

|
| R3 |  |

|
| R4 |  |

|
| R8 |  |

|
| R11 |  |

|
| R12 |  |

|
| R13 |  |

|
| R14 |  |

|
| R17 |  |

|
See also[edit]
- Conjugacy problem
- Group isomorphism problem
References[edit]
- ^ a b c d Evans, Trevor (1978). «Word problems». Bulletin of the American Mathematical Society. 84 (5): 790. doi:10.1090/S0002-9904-1978-14516-9.
- ^ Cohen, Joel S. (2002). Computer algebra and symbolic computation: elementary algorithms. Natick, Mass.: A K Peters. pp. 90–92. ISBN 1568811586.
- ^ a b c d e f g Miller, Charles F. (2014). Downey, Rod (ed.). «Turing machines to word problems» (PDF). Turing’s Legacy: 330. doi:10.1017/CBO9781107338579.010. hdl:11343/51723. ISBN 9781107338579. Retrieved 6 December 2021.
- ^ Stillwell, John (1982). «The word problem and the isomorphism problem for groups». Bulletin of the American Mathematical Society. 6 (1): 33–56. doi:10.1090/S0273-0979-1982-14963-1.
- ^ Müller-Stach, Stefan (12 September 2021). «Max Dehn, Axel Thue, and the Undecidable». p. 13. arXiv:1703.09750 [math.HO].
- ^ Steinby, Magnus; Thomas, Wolfgang (2000). «Trees and term rewriting in 1910: on a paper by Axel Thue». Bulletin of the European Association for Theoretical Computer Science. 72: 256–269. CiteSeerX 10.1.1.32.8993. MR 1798015.
- ^ Dehn, Max (1911). «Über unendliche diskontinuierliche Gruppen». Mathematische Annalen. 71 (1): 116–144. doi:10.1007/BF01456932. ISSN 0025-5831. MR 1511645. S2CID 123478582.
- ^ Dehn, Max (1912). «Transformation der Kurven auf zweiseitigen Flächen». Mathematische Annalen. 72 (3): 413–421. doi:10.1007/BF01456725. ISSN 0025-5831. MR 1511705. S2CID 122988176.
- ^ Greendlinger, Martin (June 1959). «Dehn’s algorithm for the word problem». Communications on Pure and Applied Mathematics. 13 (1): 67–83. doi:10.1002/cpa.3160130108.
- ^ Lyndon, Roger C. (September 1966). «On Dehn’s algorithm». Mathematische Annalen. 166 (3): 208–228. doi:10.1007/BF01361168. hdl:2027.42/46211. S2CID 36469569.
- ^ Schupp, Paul E. (June 1968). «On Dehn’s algorithm and the conjugacy problem». Mathematische Annalen. 178 (2): 119–130. doi:10.1007/BF01350654. S2CID 120429853.
- ^ Power, James F. (27 August 2013). «Thue’s 1914 paper: a translation». arXiv:1308.5858 [cs.FL].
- ^ See History of the Church–Turing thesis. The dates are based on On Formally Undecidable Propositions of Principia Mathematica and Related Systems and Systems of Logic Based on Ordinals.
- ^ Post, Emil L. (March 1947). «Recursive Unsolvability of a problem of Thue» (PDF). Journal of Symbolic Logic. 12 (1): 1–11. doi:10.2307/2267170. JSTOR 2267170. S2CID 30320278. Retrieved 6 December 2021.
- ^ Mostowski, Andrzej (September 1951). «A. Markov. Névožmoinost’ nékotoryh algoritmov v téorii associativnyh sistém (Impossibility of certain algorithms in the theory of associative systems). Doklady Akadémii Nauk SSSR, vol. 77 (1951), pp. 19–20». Journal of Symbolic Logic. 16 (3): 215. doi:10.2307/2266407. JSTOR 2266407.
- ^ Turing, A. M. (September 1950). «The Word Problem in Semi-Groups With Cancellation». The Annals of Mathematics. 52 (2): 491–505. doi:10.2307/1969481. JSTOR 1969481.
- ^ Novikov, P. S. (1955). «On the algorithmic unsolvability of the word problem in group theory». Proceedings of the Steklov Institute of Mathematics (in Russian). 44: 1–143. Zbl 0068.01301.
- ^ Boone, William W. (1954). «Certain Simple, Unsolvable Problems of Group Theory. I». Indagationes Mathematicae (Proceedings). 57: 231–237. doi:10.1016/S1385-7258(54)50033-8.
- ^ Boone, William W. (1957). «Certain Simple, Unsolvable Problems of Group Theory. VI». Indagationes Mathematicae (Proceedings). 60: 227–232. doi:10.1016/S1385-7258(57)50030-9.
- ^ Britton, J. L. (October 1958). «The Word Problem for Groups». Proceedings of the London Mathematical Society. s3-8 (4): 493–506. doi:10.1112/plms/s3-8.4.493.
- ^ Boone, William W. (1958). «The word problem» (PDF). Proceedings of the National Academy of Sciences. 44 (10): 1061–1065. Bibcode:1958PNAS…44.1061B. doi:10.1073/pnas.44.10.1061. PMC 528693. PMID 16590307. Zbl 0086.24701.
- ^ Boone, William W. (September 1959). «The Word Problem». The Annals of Mathematics. 70 (2): 207–265. doi:10.2307/1970103. JSTOR 1970103.
- ^ Higman, G. (8 August 1961). «Subgroups of finitely presented groups». Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences. 262 (1311): 455–475. Bibcode:1961RSPSA.262..455H. doi:10.1098/rspa.1961.0132. S2CID 120100270.
- ^ Britton, John L. (January 1963). «The Word Problem». The Annals of Mathematics. 77 (1): 16–32. doi:10.2307/1970200. JSTOR 1970200.
- ^ Simpson, Stephen G. (18 May 2005). «A Slick Proof of the Unsolvability of the Word Problem for Finitely Presented Groups» (PDF). Retrieved 6 December 2021.
- ^ «Subgroups of finitely presented groups». Mathematics of the USSR-Sbornik. 103 (145): 147–236. 13 February 1977. doi:10.1070/SM1977v032n02ABEH002376.
- ^ a b Matiyasevich, Yuri; Sénizergues, Géraud (January 2005). «Decision problems for semi-Thue systems with a few rules». Theoretical Computer Science. 330 (1): 145–169. doi:10.1016/j.tcs.2004.09.016.
- ^ Davis, Martin (1978). «What is a Computation?» (PDF). Mathematics Today Twelve Informal Essays: 257–259. doi:10.1007/978-1-4613-9435-8_10. ISBN 978-1-4613-9437-2. Retrieved 5 December 2021.
- ^ a b Baader, Franz; Nipkow, Tobias (5 August 1999). Term Rewriting and All That. Cambridge University Press. pp. 59–60. ISBN 978-0-521-77920-3.
- ^
- Matiyasevich, Yu. V. (1967). «Простые примеры неразрешимых ассоциативных исчислений» [Simple examples of undecidable associative calculi]. Doklady Akademii Nauk SSSR (in Russian). 173 (6): 1264–1266. ISSN 0869-5652.
- Matiyasevich, Yu. V. (1967). «Simple examples of undecidable associative calculi». Soviet Mathematics. 8 (2): 555–557. ISSN 0197-6788.
- ^ Novikov, P. S. (1955). «On the algorithmic unsolvability of the word problem in group theory». Trudy Mat. Inst. Steklov (in Russian). 44: 1–143.
- ^ Statman, Rick (2000). «On the Word Problem for Combinators». Rewriting Techniques and Applications. Lecture Notes in Computer Science. 1833: 203–213. doi:10.1007/10721975_14. ISBN 978-3-540-67778-9.
- ^ Beke, Tibor (May 2011). «Categorification, term rewriting and the Knuth–Bendix procedure». Journal of Pure and Applied Algebra. 215 (5): 730. doi:10.1016/j.jpaa.2010.06.019.
- ^ Peter T. Johnstone, Stone Spaces, (1982) Cambridge University Press, Cambridge, ISBN 0-521-23893-5. (See chapter 1, paragraph 4.11)
- ^ Whitman, Philip M. (January 1941). «Free Lattices». The Annals of Mathematics. 42 (1): 325–329. doi:10.2307/1969001. JSTOR 1969001.
- ^ Whitman, Philip M. (1942). «Free Lattices II». Annals of Mathematics. 43 (1): 104–115. doi:10.2307/1968883. JSTOR 1968883.
- ^ K. H. Bläsius and H.-J. Bürckert, ed. (1992). Deduktionsssysteme. Oldenbourg. p. 291.; here: p.126, 134
- ^ Apply rules in any order to a term, as long as possible; the result doesn’t depend on the order; it is the term’s normal form.
>Addition word problems
>Subtraction word problems
>Multiplication word problems
>Division word problems
>Multi-Step word problems
Welcome to the math word problems worksheets page at Math-Drills.com! On this page, you will find Math word and story problems worksheets with single- and multi-step solutions on a variety of math topics including addition, multiplication, subtraction, division and other math topics. It is usually a good idea to ensure students already have a strategy or two in place to complete the math operations involved in a particular question. For example, students may need a way to figure out what 7 × 8 is or have previously memorized the answer before you give them a word problem that involves finding the answer to 7 × 8.
There are a number of strategies used in solving math word problems; if you don’t have a favorite, try the Math-Drills.com problem-solving strategy:
- Question: Understand what the question is asking. What operation or operations do you need to use to solve this question? Ask for help to understand the question if you can’t do it on your own.
- Estimate: Use an estimation strategy, so you can check your answer for reasonableness in the evaluate step. Try underestimating and overestimating, so you know what range the answer is supposed to be in. Be flexible in rounding numbers if it will make your estimate easier.
- Strategize: Choose a strategy to solve the problem. Will you use mental math, manipulatives, or pencil and paper? Use a strategy that works for you. Save the calculator until the evaluate stage.
- Calculate: Use your strategy to solve the problem.
- Evaluate: Compare your answer to your estimate. If you under and overestimated, is the answer in the correct range. If you rounded up or down, does the answer make sense (e.g. is it a little less or a little more than the estimate). Also check with a calculator.
Most Popular Math Word Problems this Week
Various Word Problems
Various word problems for students who have mastered basic arithmetic and need a further challenge.
Addition word problems

Subtraction word problems

Multiplication word problems

Division word problems

Multi-Step word problems

Click below to see contributions from other visitors to this page…
Riddle Me Numbers
Divide me by 10 and 3 remains. A square number my first digit to be. My second digit is the product of 1 and 3. All together I’m greater than 50.
…
A Tricky Percentage Math Problem
If someone wants to make $10.00 when selling an item and I get 40%. How much do I need to add to $10.00? It’s not coming out when I add 40% to 10.00. …
Problem solving: Least common multiple
During a car race, two competitors will stop to fill up the fuel tank. One does it every 4 laps, and the other every 5 laps.
When the race begins, …
A word problem about discount Not rated yet
The $580 computer Nancy purchased was on sale for 15% off. How much was deducted from the original price?
Solution
The amount that was deducted …
A football team and percentage Not rated yet
A football team has 60 players. 42 of the players are seniors. What percentage of the team are seniors?
The percentage that are seniors is 42/60 = 7/10 …
Multiplying fractions and total distance Not rated yet
Adam needs to drive a distance of 372 miles to New York to attend a seminar. He stops to grab a quick bite after he covers one third the total distance. …
Recipe, brownies and math Not rated yet
A recipe that makes 16 brownies calls for 1/3 nuts. How many nuts are needed to make 24 brownies?
Solution
If 16 brownies require 1/3 nuts, 8 …
Multiplying Similar and Dissimilar Fractions Not rated yet
Problem:
Jane has 1/6 of marbles in her hand from her bag of marbles. She wants to share it with her 3 friends, but she wants the same amount as the …
Mind Twisting vacation Trip with Proportion Not rated yet
Danny and Melissa decided to rent a campervan from a motorhome company for their 20-day vacation. They are already up from packing up their stuffs when …
Sugar cookie recipe and multiplying fractions Not rated yet
Problem
A sugar cookie recipe calls for 4 1/2 cups of sugar. Alison wants to make 2/3 of the normal amount of sugar. How much sugar will Alison use …
When will beepers beep at the same time Not rated yet
Maria has 2 electronic beepers. One beeps after every 5 seconds and the second beeps after every 9 second.
1) At what time both beepers will beep at …
find consecutive odd positive integers Not rated yet
The sum of squares of two consecutive odd positive integers is 202. Find the integers.
Solution
Let 2x + 1 be the first odd integer
Then, 2x …
cost to copy 4757 pages Not rated yet
How much does it cost to copy 4,757 pages if the cost is as following?
Pages 1-25 cost 1.00 each.
Pages 26-500 cost 50 cents each.
Pages 501-finish …
Looking for 2 numbers (CNA) Not rated yet
The larger of two numbers is 4 less than five times the smaller. When the smaller number is subtracted from the larger, the difference is 4. Find the numbers. …
Sleep and fraction Not rated yet
If I live to be 80 years old and sleep 8 hours a day, How many years have I slept?
Solution
A day has 24 hours
24 = 8 + 8 + 8
So you spent …
Solving an age problem with basic math Not rated yet
Janet and younger brother Jared are 5 years apart. The sum of their ages is 13. How old is each?
Solution by Trial and error
13 = 12 + 1 The difference …
Debra : Ounces and quarts problem Not rated yet
A restaurant serves 8 fluid ounces of soup to each customer. How many quarts of soup should be prepared in order to serve 185 customers?
Solution …
Click here to write your own.
About 25% of your total SAT Math section will be word problems, meaning you will have to create your own visuals and equations to solve for your answers. Though the actual math topics can vary, SAT word problems share a few commonalities, and we’re here to walk you through how to best solve them.
This post will be your complete guide to SAT Math word problems. We’ll cover how to translate word problems into equations and diagrams, the different types of math word problems you’ll see on the test, and how to go about solving your word problems on test day.
Feature Image: Antonio Litterio/Wikimedia
What Are SAT Math Word Problems?
A word problem is any math problem based mostly or entirely on a written description. You will not be provided with an equation, diagram, or graph on a word problem and must instead use your reading skills to translate the words of the question into a workable math problem. Once you do this, you can then solve it.
You will be given word problems on the SAT Math section for a variety of reasons. For one, word problems test your reading comprehension and your ability to visualize information.
Secondly, these types of questions allow test makers to ask questions that’d be impossible to ask with just a diagram or an equation. For instance, if a math question asks you to fit as many small objects into a larger one as is possible, it’d be difficult to demonstrate and ask this with only a diagram.
Translating Math Word Problems Into Equations or Drawings
In order to translate your SAT word problems into actionable math equations you can solve, you’ll need to understand and know how to utilize some key math terms. Whenever you see these words, you can translate them into the proper mathematical action.
For instance, the word «sum» means the value when two or more items are added together. So if you need to find the sum of a and b, you’ll need to set up your equation like this: a+b.
Also, note that many mathematical actions have more than one term attached, which can be used interchangeably.
Here is a chart with all the key terms and symbols you should know for SAT Math word problems:
| Key Terms | Mathematical Action |
| Sum, increased by, added to, more than, total of | + |
| Difference, decreased by, less than, subtracted from | − |
| Product, times, __ times as much, __ times as many (a number, e.g., “three times as many”) | * or x |
| Divided by, per, __ as many, __ as much (a fraction, e.g., “one-third as much”) | / or ÷ |
| Equals, is, are, equivalent | = |
| Is less than | < |
| Is greater than | > |
| Is less than or equal to | ≤ |
| Is greater than or equal to | ≥ |
Now, let’s look at these math terms in action using a few official examples:
We can solve this problem by translating the information we’re given into algebra. We know the individual price of each salad and drink, and the total revenue made from selling 209 salads and drinks combined. So let’s write this out in algebraic form.
We’ll say that the number of salads sold = S, and the number of drinks sold = D. The problem tells us that 209 salads and drinks have been sold, which we can think of as this:
S + D = 209
Finally, we’ve been told that a certain number of S and D have been sold and have brought in a total revenue of 836 dollars and 50 cents. We don’t know the exact numbers of S and D, but we do know how much each unit costs. Therefore, we can write this equation:
6.50S + 2D = 836.5
We now have two equations with the same variables (S and D). Since we want to know how many salads were sold, we’ll need to solve for D so that we can use this information to solve for S. The first equation tells us what S and D equal when added together, but we can rearrange this to tell us what just D equals in terms of S:
S + D = 209
Now, just subtract S from both sides to get what D equals:
D = 209 − S
Finally, plug this expression in for D into our other equation, and then solve for S:
6.50S + 2(209 − S) = 836.5
6.50S + 418 − 2S = 836.5
6.50S − 2S = 418.5
4.5S = 418.5
S = 93
The correct answer choice is (B) 93.
This word problem asks us to solve for one possible solution (it asks for «a possible amount»), so we know right away that there will be multiple correct answers.
Wyatt can husk at least 12 dozen ears of corn and at most 18 dozen ears of corn per hour. If he husks 72 dozen at a rate of 12 dozen an hour, this is equal to 72 / 12 = 6 hours. You could therefore write 6 as your final answer.
If Wyatt husks 72 dozen at a rate of 18 dozen an hour (the highest rate possible he can do), this comes out to 72 / 18 = 4 hours. You could write 4 as your final answer.
Since the minimum time it takes Wyatt is 4 hours and the maximum time is 6 hours, any number from 4 to 6 would be correct.
Though the hardest SAT word problems might look like Latin to you right now, practice and study will soon have you translating them into workable questions.
Typical SAT Word Problems
Word problems on the SAT can be grouped into three major categories:
- Word problems for which you must simply set up an equation
- Word problems for which you must solve for a specific value
- Word problems for which you must define the meaning of a value or variable
Below, we look at each world problem type and give you examples.
Word Problem Type 1: Setting Up an Equation
This is a fairly uncommon type of SAT word problem, but you’ll generally see it at least once on the Math section. You’ll also most likely see it first on the section.
For these problems, you must use the information you’re given and then set up the equation. No need to solve for the missing variable—this is as far as you need to go.
Almost always, you’ll see this type of question in the first four questions on the SAT Math section, meaning that the College Board consider these questions easy. This is due to the fact that you only have to provide the setup and not the execution.
To solve this problem, we’ll need to know both Armand’s and Tyrone’s situations, so let’s look at them separately:
Armand: Armand sent m text messages each hour for 5 hours, so we can write this as 5m—the number of texts he sent per hour multiplied by the total number of hours he texted.
Tyrone: Tyrone sent p text messages each hour for 4 hours, so we can write this as 4p—the number of texts he sent per hour multiplied by the total number of hours he texted.
We now know that Armand’s situation can be written algebraically as 5m, and Tyrone’s can be written as 4p. Since we’re being asked for the expression that represents the total number of texts sent by Armand and Tyrone, we must add together the two expressions:
5m + 4p
The correct answer is choice (C) 5m + 4p
Word Problem Type 2: Solving for a Missing Value
The vast majority of SAT Math word problem questions will fall into this category. For these questions, you must both set up your equation and solve for a specific piece of information.
Most (though not all) word problem questions of this type will be scenarios or stories covering all sorts of SAT Math topics, such as averages, single-variable equations, and ratios. You almost always must have a solid understanding of the math topic in question in order to solve the word problem on the topic.
Let’s try to think about this problem in terms of x. If Type A trees produced 20% more pears than Type B did, we can write this as an expression:
x + 0.2x = 1.2x = # of pears produced by Type A
In this equation, x is the number of pears produced by Type B trees. If we add 20% of x (0.2x) to x, we get the number of pears produced by Type A trees.
The problem tells us that Type A trees produced a total of 144 pears. Since we know that 1.2x is equal to the number of pears produced by Type A, we can write the following equation:
1.2x = 144
Now, all we have to do is divide both sides by 1.2 to find the number of pears produced by Type B trees:
x = 144 / 1.2
x = 120
The correct answer choice is (B) 120.
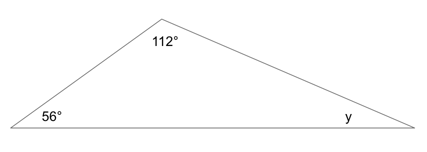
You might also get a geometry problem as a word problem, which might or might not be set up with a scenario, too. Geometry questions will be presented as word problems typically because the test makers felt the problem would be too easy to solve had you been given a diagram, or because the problem would be impossible to show with a diagram. (Note that geometry makes up a very small percentage of SAT Math.)
This is a case of a problem that is difficult to show visually, since x is not a set degree value but rather a value greater than 55; thus, it must be presented as a word problem.
Since we know that x must be an integer degree value greater than 55, let us assign it a value. In this case, let us call x 56°. (Why 56? There are other values x could be, but 56 is guaranteed to work since it’s the smallest integer larger than 55. Basically, it’s a safe bet!)
Now, because x = 56, the next angle in the triangle—2x—must measure the following:
56*2 = 112
Let’s make a rough (not to scale) sketch of what we know so far:
Now, we know that there are 180° in a triangle, so we can find the value of y by saying this:
y = 180 − 112 − 56
y = 12
One possible value for y is 12. (Other possible values are 3, 6, and 9.)
Word Problem Type 3: Explaining the Meaning of a Variable or Value
This type of problem will show up at least once. It asks you to define part of an equation provided by the word problem—generally the meaning of a specific variable or number.
This question might sound tricky at first, but it’s actually quite simple.
We know that P is the number of phones Kathy has left to fix, and d is the number of days she has worked in a week. If she’s worked 0 days (i.e., if we plug 0 into the equation), here’s what we get:
P = 108 − 23(0)
P = 108
This means that, without working any days of the week, Kathy has 108 phones to repair. The correct answer choice, therefore, is (B) Kathy starts each week with 108 phones to fix.
To help juggle all the various SAT word problems, let’s look at the math strategies and tips at our disposal.
Ready to go beyond just reading about the SAT? Then you’ll love the free five-day trial for our SAT Complete Prep program. Designed and written by PrepScholar SAT experts, our SAT program customizes to your skill level in over 40 subskills so that you can focus your studying on what will get you the biggest score gains.
Click on the button below to try it out!
SAT Math Strategies for Word Problems
Though you’ll see word problems on the SAT Math section on a variety of math topics, there are still a few techniques you can apply to solve word problems as a whole.
#1: Draw It Out
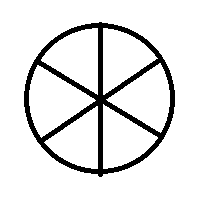
Whether your problem is a geometry problem or an algebra problem, sometimes making a quick sketch of the scene can help you understand what exactly you’re working with. For instance, let’s look at how a picture can help you solve a word problem about a circle (specifically, a pizza):
If you often have trouble visualizing problems such as these, draw it out. We know that we’re dealing with a circle since our focus is a pizza. We also know that the pizza weighs 3 pounds.
Because we’ll need to solve the weight of each slice in ounces, let’s first convert the total weight of our pizza from pounds into ounces. We’re given the conversion (1 pound = 16 ounces), so all we have to do is multiply our 3-pound pizza by 16 to get our answer:
3 * 16 = 48 ounces (for whole pizza)
Now, let’s draw a picture. First, the pizza is divided in half (not drawn to scale):
We now have two equal-sized pieces. Let’s continue drawing. The problem then says that we divide each half into three equal pieces (again, not drawn to scale):
This gives us a total of six equal-sized pieces. Since we know the total weight of the pizza is 48 ounces, all we have to do is divide by 6 (the number of pieces) to get the weight (in ounces) per piece of pizza:
48 / 6 = 8 ounces per piece
The correct answer choice is (C) 8.
As for geometry problems, remember that you might get a geometry word problem written as a word problem. In this case, make your own drawing of the scene. Even a rough sketch can help you visualize the math problem and keep all your information in order.
#2: Memorize Key Terms
If you’re not used to translating English words and descriptions into mathematical equations, then SAT word problems might be difficult to wrap your head around at first. Look at the chart we gave you above so you can learn how to translate keywords into their math equivalents. This way, you can understand exactly what a problem is asking you to find and how you’re supposed to find it.
There are free SAT Math questions available online, so memorize your terms and then practice on realistic SAT word problems to make sure you’ve got your definitions down and can apply them to the actual test.
#3: Underline and/or Write Out Important Information
The key to solving a word problem is to bring together all the key pieces of given information and put them in the right places. Make sure you write out all these givens on the diagram you’ve drawn (if the problem calls for a diagram) so that all your moving pieces are in order.
One of the best ways to keep all your pieces straight is to underline your key information in the problem, and then write them out yourself before you set up your equation. So take a moment to perform this step before you zero in on solving the question.
#4: Pay Close Attention to What’s Being Asked
It can be infuriating to find yourself solving for the wrong variable or writing in your given values in the wrong places. And yet this is entirely too easy to do when working with math word problems.
Make sure you pay strict attention to exactly what you’re meant to be solving for and exactly what pieces of information go where. Are you looking for the area or the perimeter? The value of x, 2x, or y?
It’s always better to double-check what you’re supposed to find before you start than to realize two minutes down the line that you have to begin solving the problem all over again.
#5: Brush Up on Any Specific Math Topic You Feel Weak In
You’re likely to see both a diagram/equation problem and a word problem for almost every SAT Math topic on the test. This is why there are so many different types of word problems and why you’ll need to know the ins and outs of every SAT Math topic in order to be able to solve a word problem about it.
For example, if you don’t know how to find an average given a set of numbers, you certainly won’t know how to solve a word problem that deals with averages!
Understand that solving an SAT Math word problem is a two-step process: it requires you to both understand how word problems work and to understand the math topic in question. If you have any areas of mathematical weakness, now’s a good time to brush up on them—or else SAT word problems might be trickier than you were expecting!
All set? Let’s go!
Test Your SAT Math Word Problem Knowledge
Finally, it’s time to test your word problem know-how against real SAT Math problems:
Word Problems
1. No Calculator
2. Calculator OK
3. Calculator OK
4. Calculator OK
Answers: C, B, A, 1160
Answer Explanations
1. For this problem, we have to use the information we’re given to set up an equation.
We know that Ken spent x dollars, and Paul spent 1 dollar more than Ken did. Therefore, we can write the following equation for Paul:
x + 1
Ken and Paul split the bill evenly. This means that we’ll have to solve for the total amount of both their sandwiches and then divide it by 2. Since Ken’s sandwich cost x dollars and Paul’s cost x + 1, here’s what our equation looks like when we combine the two expressions:
x + x + 1
2x + 1
Now, we can divide this expression by 2 to get the price each person paid:
(2x + 1) / 2
x + 0.5
But we’re not finished yet. We know that both Ken and Paul also paid a 20% tip on their bills. As a result, we have to multiply the total cost of one bill by 0.2, and then add this tip to the bill. Algebraically, this looks like this:
(x + 0.5) + 0.2(x + 0.5)
x + 0.5 + 0.2x + 0.1
1.2x + 0.6
The correct answer choice is (C) 1.2x + 0.6
2. You’ll have to be familiar with statistics in order to understand what this question is asking.
Since Nick surveyed a random sample of his freshman class, we can say that this sample will accurately reflect the opinion (and thus the same percentages) as the entire freshman class.
Of the 90 freshmen sampled, 25.6% said that they wanted the Fall Festival held in October. All we have to do now is find this percentage of the entire freshmen class (which consists of 225 students) to determine how many total freshmen would prefer an October festival:
225 * 0.256 = 57.6
Since the question is asking «about how many students»—and since we obviously can’t have a fraction of a person!—we’ll have to round this number to the nearest answer choice available, which is 60, or answer choice (B).
3. This is one of those problems that is asking you to define a value in the equation given. It might look confusing, but don’t be scared—it’s actually not as difficult as it appears!
First off, we know that t represents the number of seconds passed after an object is launched upward. But what if no time has passed yet? This would mean that t = 0. Here’s what happens to the equation when we plug in 0 for t:
h(0) = -16(0)2 + 110(0) + 72
h(0) = 0 + 0 + 72
h(0) = 72
As we can see, before the object is even launched, it has a height of 72 feet. This means that 72 must represent the initial height, in feet, of the object, or answer choice (A).
4. You might be tempted to draw a diagram for this problem since it’s talking about a pool (rectangle), but it’s actually quicker to just look at the numbers given and work from there.
We know that the pool currently holds 600 gallons of water and that water has been hosed into it at a rate of 8 gallons a minute for a total of 70 minutes.
To find the amount of water in the pool now, we’ll have to first solve for the amount of water added to the pool by hose. We know that 8 gallons were added each minute for 70 minutes, so all we have to do is multiply 8 by 70:
8 * 70 = 560 gallons
This tells us that 560 gallons of water were added to our already-filled, 600-gallon pool. To find the total amount of water, then, we simply add these two numbers together:
560 + 600 = 1160
The correct answer is 1160.
Aaaaaaaaaaand time for a nap.
Key Takeaways: Making Sense of SAT Math Word Problems
Word problems make up a significant portion of the SAT Math section, so it’s a good idea to understand how they work and how to translate the words on the page into a proper expression or equation. But this is still only half the battle.
Though you won’t know how to solve a word problem if you don’t know what a product is or how to draw a right triangle, you also won’t know how to solve a word problem about ratios if you don’t know how ratios work.
Therefore, be sure to learn not only how to approach math word problems as a whole, but also how to narrow your focus on any SAT Math topics you need help with. You can find links to all of our SAT Math topic guides here to help you in your studies.
What’s Next?
Want to brush up on SAT Math topics? Check out our individual math guides to get an overview of each and every topic on SAT Math. From polygons and slopes to probabilities and sequences, we’ve got you covered!
Running out of time on the SAT Math section? We have the know-how to help you beat the clock and maximize your score.
Been procrastinating on your SAT studying? Learn how you can overcome your desire to procrastinate and make a well-balanced prep plan.
Trying to get a perfect SAT score? Take a look at our guide to getting a perfect 800 on SAT Math, written by a perfect scorer.
Want to improve your SAT score by 160 points?
Check out our best-in-class online SAT prep program. We guarantee your money back if you don’t improve your SAT score by 160 points or more.
Our program is entirely online, and it customizes what you study to your strengths and weaknesses. If you liked this Math strategy guide, you’ll love our program. Along with more detailed lessons, you’ll get thousands of practice problems organized by individual skills so you learn most effectively. We’ll also give you a step-by-step program to follow so you’ll never be confused about what to study next.
Check out our 5-day free trial:
Have friends who also need help with test prep? Share this article!
About the Author
Courtney scored in the 99th percentile on the SAT in high school and went on to graduate from Stanford University with a degree in Cultural and Social Anthropology. She is passionate about bringing education and the tools to succeed to students from all backgrounds and walks of life, as she believes open education is one of the great societal equalizers. She has years of tutoring experience and writes creative works in her free time.
In this section, we are going to see word problems and step by step solutions for them in different topics of mathematics.
Before look at the word problems, click here to know how to solve word problems in math step by step.
Topic Wise Word Problems in Mathematics
Please click on the topics given below in which you would like to have word problems.
HCF and LCM word problems
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Word problems on trains
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on unit price
Word problems on unit rate
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Double facts word problems
Trigonometry word problems
Percentage word problems
Profit and loss word problems
Markup and markdown word problems
Decimal word problems
Word problems on fractions
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Time and work word problems
Word problems on sets and Venn diagrams
Word problems on ages
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Word problems for third grade
Math word problems help deepen a student’s understanding of mathematical concepts by relating mathematics to everyday life.
These worksheets are best attempted after a student has studied the underlying skill; for example, our ‘addition in columns» word problem worksheets should not be attempted until students are comfortable with addition in columns.
In many of our word problems we intentionally include superfluous data, so that students need to read and think about the questions carefully, rather than simply applying a computation pattern to solve the problems.
Addition word problems for third grade
Simple addition word problems
Column form addition word problems
Mixed add and subtract word problems
Subtraction word problems
Simple subtraction word problems
Subtraction in columns word problems
Multiplication word problems
Simple multiplication word problems
Multiples of 10
Multiplying in columns
More multiplication word problems
Mixed multiply & divide word problems
Division word problems
Simple division word problems
Long division word problems
Fraction word problems
Identifying and comparing fractions word problems
Adding and subtracting fractions word problems
Mixed 3rd grade word problems
The following worksheets contain a mix of grade 3 addition, subtraction, multiplication and division word problems. Mixing math word problems tests the understanding mathematical concepts, as it forces students to analyze the situation rather than mechanically apply a solution.
Mixed word problems — mental math
Mixed word problems — column math
Mixed word problems — simpler form (shorter texts, no superfluous data)
Measurement word problems for grade 3
These word problems combine the 4 operations with real world units of length, time, volume and mass. There is no conversion of units.
Length word problems
Time word problems
Mass & weight word problems
Volume & capacity word problems.
Word problems with variables
These grade 3 word problems introduce students to using variables («x, y, etc.») to represent unknowns. The problems are relatively simple, but emphasize the use of variables and the writing of equations.
Word problems with variables (variable is chosen for the student)
Writing variables to solve word problems (student chooses the variable)