Даже если ваша профессиональная деятельность никак не связана с точными науками, хотя бы основные математические действия на английском знать нужно. Они встречаются не только в специальной литературе, но и в фильмах, книгах, повседневной речи. В этой статье мы рассмотрим термины, связанные с арифметическими задачами, дробями, процентами. В конце я привожу озвученные карточки со основными словами на тему математики.
Обратите внимание, здесь рассматриваются только математические термины. Если вы ищете сведения о числительных, рекомендую эту статью: Числительные в английском языке.
Содержание:
- Основные математические действия на английском: сложение, вычитание, умножение и деление.
- Дроби и проценты на английском языке.
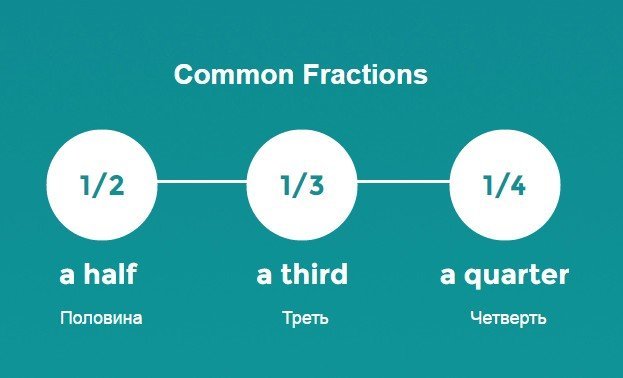
- Простые дроби — common fractions.
- Десятичные дроби — decimal fractions, decimals.
- Проценты в английском языке, трудности с числом глагола.
- Возведение в степень в английском.
- Математические выражения со скобками.
- Карточки с английскими словами на тему «Математика».
Основные математические действия на английском: сложение, вычитание, умножение и деление
Наиболее употребительные математические термины относятся к арифметике. Обратите внимание, в русском языке у нас есть такие слова, как:
- Сложение, вычитание, деление, умножение — название действия.
- Складывать, вычитать, делить, умножать — глагол, обозначающий действие.
- Плюс, минус, разделить, умножить — название действия, которое мы используем в речи, когда читаем выражение, именно оно используется чаще всего.
В английском языке точно так же, поэтому представим арифметические действия в виде таблицы:
| Название действия (сущ.) | Название действия (глагол) | Используется в речи |
|---|---|---|
| Addition — сложение | Add — прибавлять | Plus — плюс |
| Subtraction — вычитание | Subtract — вычитать | Minus — минус |
| Multiplication — умножение | Multiply by — умножать на | Times — умножить |
| Division — деление | Divide by — делить на | Divided by — разделить |
| Equality — равенство | Equals to is equal to — равняться чему-то | Equals to is equal to is — равно |
Сама арифметическая задача (например, 2+2) называется problem (по-научному) или sum (разговорный вариант), решение или ответ — answer, а глагол «решать» — to solve (the problem).
Приведу примеры:
- 2+2=4 — Two plus two equals four.
- 7-2=5 — Seven minus two equals five.
Часто вместо equals или is equal to говорят просто is.
- 5×3=15 — Five times three is fifteen.
- 8÷4=2 — Eight divided by four is two.
Дроби на английском языке
Простые дроби — common fractions
Если у вас с математикой так же «прекрасно», как у меня, напомню самое основное о дробях.
Простые дроби (common fractions) состоят из числителя (numerator) и знаменателя (denominator). Напоминаю, числитель сверху, знаменатель снизу 🙂 Если число состоит из целого и дроби, например 1½, — это называется смешанная дробь или смешанное число (mixed numeral).
Числитель выражается количественным числительным, а знаменатель порядковым. Наиболее употребительные в речи дроби 1/2, 1/3, 1/4 в русском языке имеют не только «умные» называния «одна вторая», «одна третья», одна четвертая, но и простые: половина, треть, четверть. В английском точно так же.
- 1/2 — a half, one half.
- 1/3 — a third, one third.
- 1/4 — a quarter, one fourth.
- 1/5 — one fifth.
- 1/6 — one sixth.
- 2/3 — two thirds.
- 3/4 — three fourths.
- 1/8 — one eighth.
- 1/10 — a tenth.
- 1/100 — a hundredth.
- 1¼ — one and a quarter.
- 1½ — one and a half.
- 1¾ — one and three quarters.
Обратите внимание, когда числитель больше одного, к окончанию добавляется -s, так как знаменатель используется во множественном числе (как и в русском: две третьих, три четвертых).
Существительное, которое определяется дробью, используется с предлогом of:
- 3/4 mile — Three fourths of a mile.
- 1/4 bottle — A quarter of a bottle.
Существительное, определяемое смешанной дробью, используется без предлога, но во множественном числе:
- 2 ½ miles — Two and a half miles.
- 1¼ bottles — One and a quarter bottles.
Десятичные дроби — decimal fractions, decimals
В английском в десятичных дробях (decimals) целое от дроби отделяется точкой (point), а не запятой, как у нас.
Ноль перед точкой называется zero или (британский вариант) nought. Ноль после точки может называться oh (как буква «o»), zero, nought. Лично я для простоты всегда говорю zero, потому что это слово проще выговорить и расслышать. Если целое число в дроби равно нулю, его часто опускают в речи, начиная говорить сразу с «point».
Целое число читается как обычное количественное числительное, например 45.1 — forty five point one. Но в дробной части каждая цифра читается отдельно тоже как количественное: 2.45 — two point four five (а не two point forty five).
Примеры:
- 0.1 — Point one, zero point one.
- 0.35 — Point three five, zero point three five.
- 1.25 — One point two five.
- 35.158 — Thirty five point one five eight.
- 15.05 — Fifteen point zero five.
Проценты в английском языке, трудности с числом глагола
Сотые доли могут выражаться с помощью процентов, тогда используется стандартный значок % и слово percent, всегда использующееся в единственном числе.
- 1% — One percent.
- 10% — Ten percent.
- 17% — Seventeen percent.
Трудность может вызвать число глагола в выражениях с процентами. Например:
- Twenty percent of the students are/is present. — 20% студентов присутствуют.
- The remaining twenty percent of the script has/have been rewritten. — Оставшиеся 20% сценария были переписаны.
В таких случаях глагол согласуется в числе с существительным после of:
- Twenty percent of the students are present (т. к. students — мн. число).
- The remaining twenty percent of the script has been rewritten (т. к. script — ед. число).
Возведение в степень в английском
Для обозначение степени используются выражения to the power of five, to the fifth power, raised to the power of five, raised to the fifth power. Для 2-ой и 3-ей степени используются термины «в квадрате» (squared) и «в кубе» (cubed).
- 32 — Three squared, three to the second power.
- 33 — Three cubed, three to the third power.
- 104 — Ten to the fourth power, ten to the power of four.
- 3024 — Thirty to the power of twenty four.
Квадратный корень называется square root:
- √16 = 4 — The square root of sixteen is four.
- √25 = 5 — The square root of twenty five is five.
Математические выражения со скобками
Круглые скобки называются parentheses (ед. число parenthesis) или, проще, round brackets. Если выражение стоит в скобках, и к нему применяется операция, используется слово quantity.
- (2+3)×4=24 — Two plus three quantity times four equals to twenty four.
- (3+5)2=64 Three plus five quantity squared is sixty four.
Карточки с английскими словами на тему «Математика»
Математические термины из этой статьи можно выучить с помощью карточек на Quizlet и PDF-карточек для распечатки.
| math (mathematics) | математика |
| do the math | считать (матем. действия) |
| problem (sum) | арифметическая задача |
| to solve | решать |
| answer | ответ |
| digit | цифра |
| number | число |
| odd number | нечетное число |
| even number | четное число |
| to add | прибавлять |
| to subtract | вычитать |
| to multiply by | умножать на |
| to divide by | делить на |
| to be equal to | равняться |
| plus | плюс |
| minus | минус |
| times | умножить |
| divided by | разделить |
| equals to | равно |
| common fractions | простые дроби |
| numerator | числитель |
| denominator | знаменатель |
| mixed number | смешанное число (дробь) |
| half | половина |
| quarter | четверть |
| decimals (decimal fractions) | десятичные дроби |
| point | точка (в дес. дробях) |
| percent | процент |
| to the power of five | в пятой степени |
| two squared | два в квадрате |
| two cubed | два в кубе |
| square root | квадратный корень |
| round brackets | круглые скобки |
| brackets | квадратные скобки |
| to round up the numbers | округлять числа |
Здравствуйте! Меня зовут Сергей Ним, я автор этого сайта, а также книг, курсов, видеоуроков по английскому языку.
Подпишитесь на мой Телеграм-канал, чтобы узнавать о новых видео, материалах по английскому языку.
У меня также есть канал на YouTube, где я регулярно публикую свои видео.

Below is a summary of the common mathematical symbols discussed below, along with the words in English used to describe them.
| SYMBOL | SYMBOL NAME | CALCULATION TYPE | CALCULATION WORD |
|---|---|---|---|
| + | Plus sign | Addition | …plus… |
| — | Minus sign | Subtraction | …minus… |
| ± | Plus-minus sign | N/A | …plus or minus… |
| × ⋅ ∗ | Multiplication sign | Multiplication | …times… …multiplied by… |
| ÷ / | Division sign | Division | …divided by… |
| = | Equals sign | Equation | …equals… |
| ≠ | Not-equals sign | N/A | …is not equal to… |
| ≈ | Almost-equals sign | Approximation | …equals… |
| > | Greater-than sign | Inequality | …is greater than… |
| < | Less-than sign | Inequality | …is less than… |
| ≥ | Greater-than-or-equal-to sign | Inequality | …is greater than or equal to… |
| ≤ | Less-than-or-equal-to sign | Inequality | …is less than or equal to… |
| % | Percent sign | Percentage | …percent |
| xy | Exponent | Exponentiation | …to the power of… …squared, cubed, etc. …to the… |
| x√ | Radical sign | Root | The square root of… The cube root of… …root… |
| log | Log | Logarithm | Log base…of… |
| ln | Natural log | Natural logarithm | The natural log of… |
| ! | Factorial | Factorial | …factorial… |
- Addition
- Equation
- Not-equals sign
- Subtraction
- Plus-minus sign
- Multiplication
- Division
- Inequality
- Decimal
- Approximation
- Ratio
- Improper fraction
- Percentage
- Exponential
- Square root
- Imaginary number
- Logarithm
- Per
- Infinity
- Factorial
- Equation of those number
Math can be frustrating enough in your own language. But when learning a new language, you may find that you’ll need to relearn not just numbers, but many of the terms used in the world of math.
For example, it might be difficult for you to calculate a tip at a restaurant out loud for your English-speaking friend, but something like that can definitely come in handy. To help, here are a bunch of terms (and example equations) that English speakers use when rattling their brains with numbers and equations.
Addition
6 + 4 = 12
Six plus four equals twelve.
This type of calculation is called addition, which is when you add two or more numbers together. When saying the equation out loud, we use the word “plus,” and the “+” symbol is called a plus sign. The result of an addition equation is called a sum.
Equation
Usually, we say that one expression equals another, and the “=” symbol is fittingly called an equals sign. Though it is fairly common in English to say the word “equals,” it is also fine to use the singular “is.” For example, two plus three is five. Any mathematical statement involving an equals sign is called an equation.
Not-equals sign
6 + 4 ≠ 13
Six plus four is not equal to thirteen.
The “≠” symbol is called a not-equals sign, and we say that one expression is not equal to another.
Subtraction
15 – 8 = 7
Fifteen minus eight equals seven.
This type of calculation is called subtraction, which is when you subtract one number from the other to get a difference. When saying the equation out loud, we use the word “minus,” and the “-” symbol is called—you guessed it—a minus sign. However, the word “minus” is not used when describing negative numbers (as opposed to positive numbers). For example, three minus four is not “minus one,” but “negative one.”
More for you:
Ordinal Numbers in English!
Numbers, Years, Length, Dates in English!
Plus-minus sign
4 ± 3 = 1 or 7
Four plus or minus three equals one or seven.
The “±” symbol is called the plus-minus sign, and when used in an equation, we say that one number plus or minus another results in two possible sums.
Multiplication
5 × 2 = 10
Five times two equals ten.
Five multiplied by two equals ten.
Now we’ve gotten to multiplication, and there are two ways to recite such a calculation. One way is to say that one number times another results in a product. The other way is to use the logical term “multiplied by.” The “×” symbol is considered to be the multiplication sign, although you can also use a dot (⋅) or an asterisk (∗).
Division
21 ÷ 7 = 3
Twenty-one divided by seven equals three.
When dealing with division, we say that one number is divided by another number to get a quotient. We call the “÷” symbol a division sign, but it is also common to use a slash (/), a symbol also used for fractions. If an answer contains a remainder, then you simply say “remainder” where the “r” is. For example, 22 ÷ 7 = 3r1 would be “twenty-two divided by seven equals three remainder one.”
Inequality
18.5 > 18
Eighteen point five is greater than eighteen.
This type of equation is called an inequality, and it is usually read from left to right. So logically, the “>” symbol is called a “greater-than sign” and the “<” symbol is called a “less-than sign.” You can also use the “≥” or “≤” symbols if a number, usually a variable, may be greater than or equal to another number, or less than or equal to it.
More for you:
Don’t Count Your Chickens Before They Hatch idiom meaning
List of Most Common Political Terms with Their Meanings [Infographic]
Decimal
3.141
three point one four one
18.5 is considered a decimal, and the period used to write this number is called a decimal point.
When said out loud, we usually use the word “point,” followed by a string of individual numbers. For example, 3.141 would be pronounced “three point one four one.” However, with simpler numbers, it is common to use a fraction like “five-tenths.” Don’t worry, this will be covered next.
Money tends to be recited a little differently. For example, if something costs $5.75, you wouldn’t say “five point seven five dollars.” Instead you would say “five dollars and seventy-five cents” or simply “five seventy-five.”
Approximation
π ≈ 3.14
Pi is approximately equal to 3.14
This type of equation is called an approximation, where one value is approximately equal to another value. The “≈” symbol is called an almost-equals sign.
The fields of math and science tend to borrow a lot of letters from the Greek alphabet as commonplace symbols, and English tends to put a twist on the pronunciation of these letters. For example, the letter π is not pronounced /pi/ as it normally would be, but rather as /paj/, like the word “pie.”
Be careful about pronouncing Greek letters in English because oftentimes, it won’t be the same.
Ratio (numerator, denominator)
1 ÷ 3 = ⅓
One divided by three equals a third.
In a fraction, the top number is called the numerator and the bottom number is called the denominator. When saying fractions out loud, we usually treat the denominator like an ordinal number. That means ⅓ is pronounced “a third,” ¼ is pronounced “a fourth,” etc. One exception is ½, which is usually called “a half,” not “a second.” Similarly, ¼ can be called “a quarter,” as well as a fourth, but those are the only irregularities.
With all of these fractions, it’s acceptable to use the word “one” instead of “a,” so ½ can be called “one half” as well as “a half.” And if the numerator is a number greater than one, simply say that number out loud. ¾ would be “three-fourths,” ⅖ would be “two-fifths,” etc. Notice the use of a hyphen when writing out the fraction.
With any fraction, it is also possible to simply say that one number is “over” another. While ⅖ can be pronounced “two-fifths,” it is also perfectly fine to say “two over five.” In fact, when dealing with variables (letters that represent numbers), it is actually the only convenient way to say it. For example, x/y would be said as “x over y,” while nobody would ever say “x-yth.”
Improper fraction
2 ÷ 3 = 1½
Two divided by three equals one and a half.
An improper fraction is a combination of a whole number (integer) and a fraction and involves the use of the word “and.” So 1½ would be one and a half, 2¾ would be two and three-fourths, etc. As stated before, decimals can occasionally be stated as an improper fraction. While it is normal to pronounce 0.7 as “zero point seven” or “point seven,” it can also be said as “seven-tenths,” since it is technically equal to 7/10. Similarly, 0.75 can be said as “seventy-five hundredths.”
However, this method of reading decimals can become clunky and confusing, and so it is much more common and convenient to stick with the “point” method.
More for you:
65 Football Phrases and Idioms to Use in English
Formal and Informal Email Phrases Starting with Greetings
Percentage
20 × 40% = 8
Twenty times forty percent equals eight.
Forty percent of twenty is eight.
The percent sign (%) is used to indicate a percentage. When reading a percentage, you simply say the number and the word “percent” after it, so 50% would be read as “fifty percent.” When calculating something that involves a percentage, you can simply pronounce it as a standard multiplication equation, or you can say that a certain percent of another number results in a product.
In computer science, the percent sign tends to have a different function and is actually used as the modulo operator, which acts as a division calculation but outputs only the remainder. Where the percent sign is, you would say “modulo” or “mod” for short. For example, 15 % 6 == 3 would be “fifteen mod six equals three” (a double percent sign is usually used in computer languages, but it is read the same).
Exponential
33 = 27
Three cubed equals twenty-seven.
Three to the third equals twenty-seven.
Three to the power of three equals twenty-seven.
An exponent is when you take a number and multiply it by itself a certain number of times, an operation called exponentiation. In other words, you take one number to the power of another number. This is the easiest way to read an exponent out loud, since it works easily with decimals and fractions (“four to the seven point five,” “three to the four-fifths,” etc.).
However, it is also common to use an ordinal number when reading aloud an exponent. For example, x3 reads “x to the third,” x4 reads “x to the fourth,” etc. Note that this is different from saying “x-thirds” or “x-fourths,” which would turn the number into a fraction.
It is not common to say x2 as “x to the second.” Instead, the convention is to say “x squared,” which relates to concepts of geometry. Similarly, it is common to say x3 as “x cubed.”
However, there is no equivalent for x4 and numbers beyond that. “Squared” and “cubed” are also used when talking about units of length in two or three dimensions. For example, 5 ft2 would be read as “five feet squared,” and 50 km3 would be read as “fifty kilometers cubed.
Square root
√16 = 4
The square root of sixteen is four.
The result of this equation is called a square root, and the “√” symbol is called a radical sign (“radical” literally means “root”). It is typical to state that the square root of one number equals another number.
A square root is essentially a number to the power of a half. In other words, √16 is the same as 161/2. However, if the number is to the power of a different fraction, say ⅓, then the root becomes a cube root, written as 3√16.
For this, you can say “the cube root of sixteen,” but you can also say “sixteen root three.” Similarly, 4√16 would be “sixteen root four,” etc.
Imaginary number
√(–4) = 2i
The square root of negative four is two i.
An imaginary number is the result of taking the square root of a negative number. When reading an imaginary number aloud, simply pronounce the letter “i” as it is. 2i is pronounced “two i,” 3i is “three i,” etc.
More for you:
19 Email Templates for Business Communication
English Vocabulary For Information Technology Professionals and …
Logarithm
log28 = 3
Log base two of eight equals three.
A logarithm is basically an inverse of an exponential equation, and though it seems complicated, reading one may actually be easier and more consistent.
In the case of log28, since the “2” is considered to be the base of the logarithm, you would say that log base two of eight equals three. An expression containing “ln” is called a natural log. For example, lnx would be stated as “the natural log of x.”
Per
12m / 4s = 3m/s
Twelve meters divided by four seconds equals three meters per second.
When dealing with rates, we use the word per between units. This applies to even mundane rates that don’t require the use of scientific units. For example:
- This class will meet five times per (Five times a week)
- I usually assist ten customers per (Ten customers every shift)
The word “per” also appears in the abbreviation “mph,” which stands for “miles per hour.” Instead of using a slash like most scientific rates, this abbreviation shortens the word “per” with the letter “p.”
- I usually go 80mph on the highway.
Infinity
0 < x < ∞
X is greater than zero and less than infinity.
Infinity (∞) is an abstraction of the largest number imaginable, the opposite of which is negative infinity (–∞). The “∞” symbol is called the infinity symbol, sometimes called a lemniscate because of its figure-eight shape. Notice that it’s different from the word “infinite,” which is an adjective that describes something that is endless or limitless.
Factorial
5! = 120
Five factorial equals 120.
A factorial is represented by an exclamation point, and you simply say the word “factorial” after the number. Things don’t get much easier…
Equation of those number
5 x (4 + 3) = 35
Five times the quantity of four plus three equals thirty-five.
Saying equations out loud can get a bit tricky when there are parentheses involved.
One method is to take short pauses before saying numbers grouped in parentheses. But a more effective way would be to call them the quantity of those numbers, almost as if you’re making a calculation within a calculation, which is essentially what you’re doing.
This phrase also comes in handy when you’re dealing with complex fractions. For example, an easy way to say x / (y + z) would be “x over the quantity of y plus z.”
More for you:
Essential Academic Writing Examples and Phrases!
Useful English Phrases For Running A Business Meeting
Learn Math Vocabulary in English through pictures and videos.
The language of mathematics is the system used by a mathematician to communicate mathematical ideas among themselves. This language consists of a substrate of some natural language (for example English) using technical terms and grammatical conventions that are peculiar to mathematical discourse, supplemented by a highly specialized symbolic notation for mathematical formulas.
Below is the list of math vocabulary in English.
- +: plus/add
- –: minus/take
- x: multiply/times
- :: divide
- =: equals
- <: less than
- >: more than
- %: percentage
- #: is not equal to
How to Say and Write Numbers in English
“Angles” Vocabulary
- An angle equal to 1/4 turn (90° or π/2 radians) is called a right angle. Two lines that form a right angle are said to be normal, orthogonal, or perpendicular.
- A pair of angles opposite each other, formed by two intersecting straight lines that form an “X”-like shape, are called vertical angles or opposite angles or vertically opposite angles.
- Angles larger than a right angle and smaller than a straight angle (between 90° and 180°) are called obtuse angles (“obtuse” meaning “blunt”).
- An angle equal to 1/2 turn (180° or π radians) is called a straight angle.
- Angles larger than a straight angle but less than 1 turn (between 180° and 360°) are called reflex angles.
- An angle equal to 1 turn (360° or 2π radians) is called a full angle, complete angle, or a perigon.
- Angles that are not right angles or a multiple of a right angle are called oblique angles.
- …
Даже если вы никак не связаны с точными науками, знание математической лексики на английском вам пригодится. Такие слова бытуют не только в научных изданиях, но и в повседневном общении носителей языка. Их можно услышать в современных фильмах и популярных песнях. Каждый из нас ежедневно выполняет математические действия: мы делаем покупки, высчитываем сумму чека в кафе, оплачиваем проезд, переводим деньги, пополняем счет. А как сделать это по-английски? Давайте познакомимся поближе с увлекательным миром английской математики. Знание профессиональной лексики существенно обогатит ваш словарный запас.
Арифметические действия
Основные математические понятия и их функции в английском такие же, как в русском. Британцы делят, складывают, умножают и вычитают по тем же правилам, что и мы. Рассмотрим, при помощи каких языковых средств они это делают.
Division. / Деление.
Multiplication. / Умножение.
Addition. / Сложение.
Subtraction. / Вычитание.
Add. / Прибавить.
Divide by. / Разделить на.
Subtract. / Вычесть.
Multiply by. / Умножить на.
Однако такую терминологию британцы редко используют в непосредственном общении. Она больше характерна для академической речи и специализированной литературы. В обычном разговоре часто употребляются упрощенные формы:
Times. / Умножить.
Plus. / Плюс.
Divided by. / Разделить.
Minus. / Минус.
Так в разговоре встречаются оба варианта. Они полностью равнозначны. Например, чтобы сказать «31 + 4», англичане во время беседы используют обе конструкции: как «31 plus 4», так и «Add 31 to 4».
Для того, чтобы выполнить какую-либо математическую задачу, носители языка говорят: «sum» (задача). В научных изданиях для этой цели применяется более формальное слово «problem». Теперь перейдем к самим компонентам, с помощью которых совершаются арифметические действия.
Элементы математических задач
Зная, как звучат основные команды в математике, вам не составит труда назвать их компонентный состав. Лексически такие слова являются производными от арифметических задач, но не все.
Addend. / Слагаемое.
Subtrahend. / Вычитаемое.
Multiplier. / Множитель.
Divisor. / Делитель.
Результаты проведенной математической операции тоже имеют свои обозначения. Причем для каждого действия есть свой термин, как и в русском.
Total. / Сумма сложения.
Difference. / Итог вычитания.
Product. / Результат умножения.
Quotient R Remainder. / Частное и остаток от деления.
При решении любой задачки часто нужна специальная терминология. Она иллюстрирует не только теоретический результат, но и полученное от выполненного упражнения число.
Термины математических операций
Когда мы делим или вычитаем, у нас всегда остается какой-то итог. Как его объяснить на русском, известно со школьной скамьи. Английская терминология по звучанию и написанию немного отличается от нашей, но обозначает то же самое.
Derivative of. / Производное от.
Remainder. / Остаток.
Even number. / Четное число.
Common denominator. / Общий знаменатель.
Decimal number. / Десятеричное число.
Square root of. / Квадратный корень из.
Percentage. / Процент.
Cube root of. / Кубический корень из.
Fraction. / Дробь.
Denominator. / Знаменатель (нижняя дробная часть).
Numerator. / Числитель (верхняя дробная часть).
Все эти слова необходимы, чтобы задать систему отсчета («reference frame») или составить уравнение («equation»). Но употребляются они не по отдельности, а в синтаксической связке. Предложения в математике строятся по стандартным правилам английского языка. Но чтобы объяснить какое-то упражнение, понадобится профессиональная лексика.
Устойчивые математические обороты
Они пригодятся не только для устного общения, но и для письменной речи. Все конструкции формальны и нейтральны по окраске, поэтому одинаково используются и в научных изданиях, и во время беседы на профессиональную тему.
Write an equation. / Написать уравнение.
Look for a pattern. / Искать закономерность.
Poll. / Подсчитывать.
Clarify thinking. / Пояснить рассуждение.
Formulate conclusions from graphs. / Сделать выводы на основании графиков.
Use manipulatives. / Использовать счётный материал.
Round a number. / Округлить число.
To extract a root. / Извлекать корень из.
Raise to a power to. / Возводить в степень.
Count backwards — count on. / Считать в порядке убывания – в порядке возрастания.
Математические термины пригодятся, если вам предстоит сдавать профильные международные экзамены. Умея изъясняться по-английски в арифметической плоскости, ваши шансы получить заветный сертификат по английскому языку существенно возрастают. Осваивать профессиональную лексику всегда непросто. Если вы готовитесь к языковым тестам по математике, советуем вам делать это на английском. Старайтесь по-английски произносить вслух все упражнения и ваши действия. Тогда вы быстрее запомните основную терминологию и во время экзамена без проблем сможете использовать устойчивые фразы, чтобы объяснить какое-либо математическое понятие на иностранном языке.
Приветствуем всех любителей английского языка на нашем очередном онлайн-уроке! Мы рады, что вы продолжаете совершенствовать свои знания, и сегодня предлагаем вам разобрать тему «Математика» по-английски. Многим кажется, что математические знания в жизни пригождаются редко. Но если задуматься, то счет, процессы деления или сложения, а вместе с тем и упоминание дробей встречаются в окружающем человека информационном поле практически изо дня в день. Поэтому, несомненно, без запаса математической лексики полноценно общаться на английском языке невозможно. Так что давайте поскорее устраним этот пробел!
Как пишется и произносится слово «математика» по-английски
Прежде всего разберемся, какой получает математика перевод на английский язык. Ведь назвать Королеву наук британцы и американцы могут несколькими способами.
Первый и самый главный – это термин mathematics [ˌmæθəˈmætɪks]. Интересно, что слово математика по-английски пишется с окончанием –s, но при этом относится к числу существительных, которые могут употребляться только в единственном числе! Так что не обманывайтесь конечной буквой «-s» и при необходимости употребляйте вместе с mathematics глагол в форме единственного числа.
- Mathematics is the only truly universal language. — Единственный универсальный язык на свете – это математика.
- Mathematics has always been a closed book to me. — Математика всегда была и остается для меня закрытой книгой.
- Mathematics includes the study of many topics. — Математика включает в себя изучение многих тем.
Важно обговорить и сферу употребления данного термина. Если речь идет о научной дисциплине или предмете изучения, то слово mathematics будет идеальным вариантом для применения. Но в разговорной речи более уместен будет сокращенный вариант – maths. Причем здесь следует сделать важную оговорку: в Великобритании принято использовать в речи сокращение maths [maθs], а в США широко распространено применение еще более укороченного варианта math [mæθ]. Также обратите внимание, что в данном случае произношение слова Математика по-английски изменяется в зависимости от выбранного типа сокращения.
- My son has always been good at maths [масс]. — Мой сын всегда был хорош в математике.
- Her favourite subject is math [мэс]. — Ее любимый школьный предмет – это математика.
И раз уж мы так подробно рассматриваем название самой дисциплины, то нельзя оставить в стороне и расхожее однокоренное слово – математик. Чтобы обозначить профессию или увлечение человека, необходимо прибавить к основе слова Mathematics специальный суффикс – cian. В итоге термин «математик» по-английски будет писаться как mathematician [maθəməˈtɪʃn].
- Bernard Roy is a famous French mathematician. — Бернард Рой – знаменитый французский математик.
Что ж, как будет по-английски математика и математик, мы выяснили, наступило время поговорить об основных математических операциях. Им и посвятим следующий раздел статьи.
Простейшие математические действия на английском языке
Иногда мы и сами не замечаем, как в нашей речи то тут, то там мелькают математические термины. Конечно, математика – сложная наука, освоить даже фундаментальную базу которой удается не всем. Тем не менее простейшие математические операции должен знать каждый, поэтому мы и прорабатываем сегодня топик Математика на английском языке. И конкретно сейчас предлагаем пополнить свой словарный запас полезной лексикой по данной теме. Итак, термины, фразы и выражения представим в виде таблицы. Причем на каждое английское слово будут предусмотрены перевод и транскрипция по-английски, чтобы произношение математических терминов не вызывало затруднений.
| Слово | Транскрипция | Перевод |
| plus | [plʌs] | плюс, складывать |
| minus | [ˈmaɪnəs] | минус, отнимать |
| add | [æd] | прибавлять |
| subtract | [səbˈtrækt] | вычитать |
| multiply by | [ˈmʌltɪplaɪ baɪ] | умножать |
| times | [taɪmz] | умножить (разговорное) |
| divide by | [dɪˈvaɪd baɪ] | делить |
| equals to | [ˈiːkwəlz tuː] | равнять |
| is equal | [ɪz ˈiːkwəl] | равно |
| to solve | [tuː sɒlv] | решать |
| answer | [ˈɑːnsə] | ответ |
Вот такой мини-словарик у нас получился. А для лучшего понимания и запоминания терминов покажем, как написал бы по-английски простое математическое действие любой коренной житель Соединенного Королевства или Америки.
- 2+5=7 – two plus five equals seven — Два плюс пять равняется семи
- 5*5=25 — five times five is twenty-five. — Пятью пять – двадцать пять
- 17-7=10 — Seventeen minus seven is ten. — Семнадцать минус семь равно десять
- 15:3=5 — Fifteen divided by three equals five — Пятнадцать, разделенное на три, равняется пяти
Как видно, все фразы достаточно простые и по своей сути аналогичны примерам из русского языка.
Дробные числа, проценты, степени и другие термины математики по-английски
Итак, мы уже умеем обозначать простейшие математические действия и называть Королеву наук как общелитературным, так и разговорным терминами. Но ведь математика сложнейшая дисциплина, включающая в себя множество различных тем. И даже для общения на самом простом уровне изученной нами информации пока будет недостаточно. Поэтому мы дополним тему Математика на английском языке еще одной подборкой полезной лексики. В частности, в таблице расскажем, как обозначить проценты, дробные числа, математические скобки и другие важные элементы. Присоединяйтесь к изучению или же распечатайте приведенную таблицу и пополняйте свой словарный запас в любую свободную минуту.
| Слово | Транскрипция | Перевод |
| mathematical sign | [ˌmæθɪˈmætɪkəl saɪn] | математический знак |
| quotient | [ˈkwəʊʃənt] | частное |
| difference | [ˈdɪfrəns] | разница |
| remainder | [rɪˈmeɪndə] | остаток |
| multiplication table | [ˌmʌltɪplɪˈkeɪʃən ˈteɪbl] | таблица умножения |
| odd number | [ɒd ˈnʌmbə] | нечетное число |
| even number | [ˈiːvən ˈnʌmbə] | четное число |
| percent | [pəˈsɛnt] | процент |
| mixed number | [mɪkst ˈnʌmbə] | смешанное число |
| decimal fractions | [ˈdɛsɪməl ˈfrækʃənz] | десятичная дробь |
| common fractions | [ˈkɒmən ˈfrækʃənz] | обыкновенная дробь |
| numerator | [ˈnjuːməreɪtə] | числитель |
| denominator | [dɪˈnɒmɪneɪtə] | знаменатель |
| point | [pɔɪnt] | точка |
| half | [hɑːf] | половина |
| quarter | [ˈkwɔːtə] | четверть |
| to round up the number | [tuː raʊnd ʌp ðə ˈnʌmbə] | округлить число |
| squared | [skweəd] | в квадрате |
| cubed | [kjuːbd] | в кубе |
| the square root of | [ðə skweə ruːt ɒv] | корень квадратный от |
| parentheses или round brackets | [pəˈrɛnθɪsiːz] (raʊnd ˈbrækɪts) | скобки |
Вот теперь топик Математика для среднего уровня владения английским языком освоен в достаточно объеме. Успехов в дальнейшем обучении и до новых встреч!
Просмотры: 4 086
Математика на английском: подборка
В статье вы узнаете лексику из математики на английском языке.
Mathematical terms — Математические термины
odd numbers — нечетные числа
even numbers — четные
times — (умножить) на
to multiply — умножить
to divide — делить
equals — равно
square root — квадратный корень
minus — минус
addition — прибавление
multiplication — умножение
subtraction — вычитание
division — деление
arithmetic — арифметика
algebra — алгебра
geometry — геометрия
to add — прибавлять
to subtract — вычитать
to take away — вычитать
squared — в квадрате
parallel — параллель
circumference — окружность
length — длина
width — ширина
height — высота
fraction — дробь
decimal — десятичная дробь
decimal point — точка в десятичной дроби, отделяющая целое от дроби
plus — плюс
total — равно
Shapes — Формы
circle — круг
square — квадрат
triangle — треугольник
rectangle — прямоугольник
pentagon — пятиугольник
hexagon — шестиугольник
oval — овал
cube — куб
pyramid — пирамида
sphere — сфера; шар
percent — процент
percentage — процент
volume — объём, масса
straight line — прямая
curve — кривая
angle — угол
right angle — прямой угол
radius — радиус
diameter — диаметр
Fractions — дроби
1⁄2 (“a half”) — половина
1⁄3 (“a third”) — треть
1⁄4 (“a quarter”) — четверть
1⁄5 (“a fifth”) — одна пятая
1⁄6 (“a sixth”) — одна шестая
2⁄3 (“two thirds”) — две трети
3⁄4 (“three quarters”) — три четверти
1⁄8 (“an eighth”) — одна восьмая
1⁄10 (“a tenth”) — одна десятая
1⁄100 (“a hundredth”) — одна сотая
1½ (“one and a half”) — полтора
2¾ (“two and three quarters”) — три четверти и два
Чтобы учить английский дальше, переходите на эту статью с лексикой английского языка о физике.
Оставить комментарий
Для комментирования необходимо войти через Вконтакте
Numbers
-187 : minus one hundred and eighty seven
33,333 : thirty-three thousand, three hundred and thirty-three
1,000,000 : one million
2,000,000,000 : two billion
9,000,000,000,000 : nine trillion
Notes:
- always use a comma with numbers greater than 999.
- don’t say ‘3 millions’ – although you might hear people say things like ‘It cost millions and millions of dollars’.
- if you have an old dictionary you might read that there are two options for billion – that is no longer true.
54.25 : fifty-four point two five
110 : one to the power of ten
-5.5 x 1010 : minus five point five times ten to the power of ten
8 x 10-3 : eight times ten to the minus three
Fractions
1 ½ : one and a half
2 ⅓ : two and a third
-3 ¼ : minus three and a quarter
4 ⅕ : four and a fifth
⅜ : three-eighths
0.002 : two thousandths
Equations and Operations
3n + 4x : three n plus four x
1 – 2n : one minus two n
3+3=6 : three plus three equals six
18-8=10 : eighteen minus eight equals ten
3/5=0.6 : three divided by five equals zero point six
5! = five factorial
Notes:
- For 0.6 you can also say nought point six
Greater and Less Than
x>y : x is greater than y
x≥y : x is greater than or equal to y
x<y : x is less than y
x≤y : x is less than or equal to y
Notes:
You can also say ‘x is smaller than y’
Exponentials and Roots
22 : two squared
43 : four cubed
64 : six to the power of four
810 : eight to the power of ten
10-1 : ten to the minus one
√3 : the square root of three
3√32 : the cube root of thirty two
5√64 : the fifth root of sixty four
Miscellaneous Maths Vocabulary
odd number : 1,3,5,7, etc
even number : 2,4,6, etc
denominator : the number below the line
numerator : the number above the line
left bracket : [
right bracket : ]
curly bracket (AKA braces) : { }
exponent : how many times to use that number in a multiplication
factorial : the product of a number and all the numbers below it. (4! = 4 x 3 x 2 x 1)
infinity : ∞ : a number greater than all the atoms of ice cream I’ve ever eaten
product : the answer when numbers are multiplied
ratio : the relationship between two numbers
integer : a whole number
rational number : a number that can be made by dividing two integers
irrational number : a real number that cannot be made by dividing two integers
prime : a number that is divisible only by itself and 1
coefficient : a number used to multiply a variable
Fractions in English
It so happens that seeing a fraction in a text or article, we do not know how to read it correctly. And if you are going to study Business English and use it in your professional activities, then you should not doubt the correctness of the data you have provided. And in everyday life you can’t do without fractions.
In this article, we will learn the rules for reading different types of fractional numbers in English, remembering which, you will always be sure that you are speaking correctly.
Fractions are of two types: ordinary, which are written with a dash (common fractions or simple fractions) and decimal, which have a period (decimals).
Ordinary fractions
Reading simple fractions is quite simple, and very similar to how we read them in Russian. An ordinary fraction has two components: the numerator (the number above the line) and the denominator (the number below the line). The upper number (numerator) is read as a cardinal number (how much?), And the lower number (denominator) is read as an ordinal (which order?). In this case, the numerator one can be read as the article a:
1/3 — one third / a third 1/7 — one seventh / a seventh
1/9 — one ninth / a ninth
If the numerator is greater than one, then the denominator acquires a plural ending:
2/3 — two thirds
3/5 — three fifths
Remember that half when reading fractions is half, and a quarter can be read as (a / one) quarter or (a / one) fourth:
1/2 — one half / a half NOT one second 1/4 — one quarter / a quarter / one fourth
3/4 — three quarters / three fourths
If there is an integer in the fraction, then it is associated with a fraction using the word and:
1 1/2 — one and a half 3 2/3 — three and two thirds
2 1/4 — two and a quarter / two and a forth
Reading decimals
First of all, it is important to remember that English decimal fractions use a full stop, not a comma. In English decimal fractions, we do not say the words: tenths, hundredths, thousandths, but simply call numbers. And when reading decimal fractions, the word point is said and each digit is called separately:
2.25 — two point twentyfive
1.4 — one point four
6.785 — six point seven eight five
If there is no whole number, and there are numbers only after the dot, then they say nought or zero (in American English), or even miss zero in speech and writing:
0.2 — nought (zero) point two / point two 0.75 — nought (zero) point seven five / point seven five
0.03 — nought (zero) point nought three / point nought three
Interest
Often percentages are indicated in decimal fractions: per cent [pəˈsent] (percent AmE). The word per cent is used in the singular:
2.2% — two point two per cent 3.5% — three point five per cent 50% — fifty per cent
99% — ninety-nine per cent
The use of the word percents is possible only in relation to the school topic «Percents», but cannot be used with specific numbers.
Phone numbers, dates, and prices are also in doubt. It would seem that nothing complicated, but even the best students make mistakes when talking about these numbers. I recommend remembering the rules, and perhaps learning something new: Phone numbers, dates and prices in English.
See a mistake in the text? Select it and click on the arrow that appears or CTRL + Enter.
Pokemon, thanks! We tried to make the information as accessible as possible.
Ira, Maria, Fatima thank you for reading and giving feedback!
Anatoly, please clarify your question.
Thank you so much!!
Source: https://enginform.com/article/drobi-na-angliyskom
Math Actions in English
The most common simple fractions.
Even if your professional activity is in no way connected with the exact sciences, you need to know at least basic mathematical operations in English. They are found not only in special literature, but also in films, books, and everyday speech. In this article, we will look at terms related to arithmetic problems, fractions, percentages. At the end, I provide the voiced flashcards with basic words on the topic of mathematics.
Please note that only mathematical terms are discussed here. If you’re looking for information on numerals, I recommend this article: Numbers in English.
:
Basic math in English: addition, subtraction, multiplication and division
The most common mathematical terms are related to arithmetic. Please note that in Russian we have words such as:
- Addition, subtraction, division, multiplication is the name of the action.
- Add, subtract, divide, multiply is a verb denoting an action.
- Plus, minus, divide, multiply — the name of the action that we use in speech, when we read the expression, it is this that is used most often.
In English, the same is true, so we represent arithmetic operations in the form of a table:
Action name (n) Action name (verb) Used in speech
| Addition — addition | Add — add | Plus — plus |
| Subtraction — subtraction | Subtract — subtract | Minus — minus |
| Multiplication — multiplication | Multiply by — multiply by | Times — multiply |
| Division — division | Divide by — divide by | Divided by — to divide |
| Equality — equality | Equals to is equal to — equal to something | Equals to is equal to is — equals |
The arithmetic problem itself (for example, 2 + 2) is called problem (scientifically) or catfish (colloquial), solution or answer — answer, and the verb «decide» — to solve (the problem).
I will give examples:
- 2 + 2 = 4 — Two plus two equals four.
- 7 — 2 = 5 — Seven minus two equals five.
Often instead of equals: or is equal to they just say is.
- 5 × 3 = 15 — Five times three is fifteen.
- 8 ÷ 4 = 2 — Eight divided by four is two.
Common fractions — common fractions
If your math is as “excellent” as mine, let me remind you the most basic thing about fractions.
Common fractions consist of numerator and denominator… Remember, the numerator is on top, the denominator is on the bottom
Source: https://langformula.ru/math-in-english/
:
- Addition and subtraction
- Multiplication and division in English
- Additional vocabulary related to mathematics
When learning English, many learners overlook simple vocabulary topics that they think will never be useful to them. The same thing happens with words and phrases that denote mathematical actions.
However, mathematics can be useful in areas of activity completely unexpected for us. Therefore, in English, it is also worth learning a couple of simple expressions that will help you do basic calculations.
There are 4 mathematical operations in total, but to begin with, consider only 2:
- Addition (addition);
- Subtraction
In order to correctly describe addition and subtraction in English, the following vocabulary is useful:
- to add — add;
- to subtract — subtract;
- summand / addend — term;
- answer — the answer;
- minuend — minified;
- subtrahend — subtracted;
- sum — the sum (of numbers);
- difference — the difference.
Signs:
= equal mark — equal sign.
Let’s look at some examples of how to correctly read arithmetic operations:
| 4 11 = | Four and seven is eleven |
| Four plus seven equals eleven | |
| Four plus seven is equal to eleven | |
| Four added to seven makes eleven | |
| 4 and 7 are summands, 11 is sum | 4 and 7 are terms, 11 is the sum |
| 12-8 4 = | Twelve minus eight is equal to / equals four |
| Eight from twelve is four | |
| Twelve minus makes eight four | |
| Eight from twelve leave four | |
| 12 is minuend, 8 is subtrahend, 4 is difference | 12 — reduced, 8 — subtracted, 4 — difference. |
Multiplication and division in English
- Multiplication;
The following vocabulary is useful to describe the multiplication and division formulas:
- multiply (by) — multiply (by);
- multiplicanda — multiplicable;
- multiplier — multiplier;
- product — product;
- divide (by) — divide (by);
- dividend — dividend;
- divisor — divider;
- quotient — private.
Signs:
х multiplication sign — multiplication sign;
: division sign — division sign
Source: https://www.study.ru/article/grammar/matematicheskie-deystviya-na-angliyskom-yazyke
How the language we learn to count in affects math ability
Anand Jagashia BBC Future
Image copyright Getty Images
Four times 20 plus 12? Four and a half times 20? What is this number? Learning to count in a particular European language can affect how a child’s math skills develop.
If I ask you to write the number ninety-two, you won’t think too much. By the time we become adults, the connection between numbers and their names in our language has already been established and we recognize numbers almost automatically.
You may be surprised, but 92 in English is not the best description for this number. And in some other languages it’s even worse.
And in some it is better. But it’s not just semantics. As scientists believed back in 1798, the language in which we learn to count can influence the development of our mathematical abilities.
And one European country in the XNUMXth century even completely revised its counting system and made it simpler and easier — both for teaching and for mathematical calculations.
What’s the best way to count?
Almost all countries today use the decimal (base 10) number system. The most logical counting systems use words that reflect a decimal structure and have clear rules. However, in many languages these rules are complex and confusing.
For example, in French the number 92 is ninety-two or «four times 20 and 12». Danish 92 — TooghalvfemsWhere halvfems means 90 (an abbreviated Old Norse word halvfemsindstyve, «Four and a half times 20».
Image copyright Javier Hirschfeld / Getty Images Image caption 90 is halvfems in Danish. This is an abbreviation of the Old Norse halvfemsindstyve, or «four and a half times 20»
And in English, such numbers as twelve (12) or eleven (11) tell us practically nothing about the structure of the number as such. These words originated from ancient Saxon ellevan и twelif (meaning «one left» and «two left» — after subtracting 10).
Now compare this with the literary Chinese language (Mandarin), in which the relationship between tens and ones is absolutely clear. 92, for example, the direct translation would be «nine ten two». Japanese and Korean have similar rules.
Psychologists call such systems transparent, transparent, the connection between numbers and their names is clear and logical.
How language affects math ability
There is growing evidence that this kind of transparency in the counting system can influence the way we handle numbers. For example, children from East Asian countries can better understand decimal education.
In one study, first grade students were asked to represent numbers (such as 42) using cubes representing tens and ones.
Children from the United States, France, or Sweden added 42 out of forty-two cubes, while the little Koreans and Japanese used four decimal cubes and two ones. From this, we can assume that language already at this age influences how a person imagines numbers.
Of course, there may be many other reasons why children from different countries have different mathematical abilities: how they are taught mathematics, how they generally care about education, and so on. These factors are difficult to account for when it comes to representatives of different cultures. But the language helps to explain something.
The formation of numerals in modern Welsh is very clear and transparent. 92 — naw deg dau, that is, «nine ten two», almost like in the East Asian languages. But in the old, traditional Welsh system (which is still used to convey dates and ages), 92 in the letter will be dau ar ddeg a phedwar ugain, that is, «two to ten and four times twenty.»
The new system was created by a businessman from the Welsh diaspora in Argentina — solely to make accounting easier. But in the end, in the 1940s, the system was adopted in the schools of Wales.
Image copyright Javier Hirschfeld / Getty Images Image caption In traditional Welsh language, the number 92 was written dau ar ddeg a phedwar ugain — two to ten and four times twenty
Today in Wales, about 80% of schoolchildren study mathematics in English, but 20% are taught in modern Welsh. And this opens up an ideal opportunity for experiment: after all, children study the same school curriculum in two different languages. In addition, they are from the same social environment, from the same country, with the same cultural characteristics.
Let’s look at their example, is the system created in the East Asian style more effective than the system that we adhere to in the West?
Six-year-old children studying English and Welsh were tested for their ability to locate two-digit numbers on a blank horizontal line, one end of which was labeled «0» and the other end «100».
Both groups performed equally well on the arithmetic tests, but the Welsh children performed better on the task of determining the position of the numbers.
“We think this is because the Welsh kids had a clearer understanding of double-digit numbers,” says Ann Dowker, lead author of the study and experimental psychologist at the University of Oxford. «They had a better idea of the relationship between numbers, how much one is larger than the other.»
From changing places
In some other languages, tens and ones in two-digit numbers are reversed. For example, in Dutch 94 is written as vierennegentig (that is, «four and 90»), and one study showed how this might affect the performance of certain math tasks.
For example, Dutch kindergarteners are worse than English kindergartners at adding double-digit numbers. And this despite the fact that they were a little older and with a more developed working memory (kindergarten in the Netherlands starts later than in Britain).
But in all other respects (the ability to count, add and compare the number of points, the addition of single-digit numbers), the two groups of children showed the same results.
In Dutch, extra mental effort is required to rearrange the numbers in a numeral
“This shows the role of language,” said Iro Zinidou-Dervo, lead author of the study and lecturer in mathematical cognition at Loughborough University in England.
As Zinida-Derva explains, when children see a number like 38, for example, they say it to themselves, and then draw its place on the line in front of them.
In Dutch, it takes extra mental effort to rearrange the numbers in a numeral that sounds like «eight and 30». This additional mental load ultimately affects the final result.
And, as it turns out, this happens not only with children. Scientists have tested these results in adults, only using software that tracks the participants’ eye movements.
“Eye movements reveal to us how cognitive processing of information occurs at a deep level. We could see at what point the participant was looking in which direction, ”comments Zinida-Derva.
Image copyright Javier Hirschfeld / Getty Images Image caption Dutch children have to swap two-digit numbers to understand it
Both adult groups performed equally well in terms of the final direction of the participants’ gaze. But when the numbers were pronounced, and not written in front of them, the Dutch representatives experienced a slight hitch and looked in the direction where the first digit in the number should be located, that is, in the opposite direction (for example, when they called the number 94, the first instinctive movement of the Dutch eyes was to the side 49).
The results are surprising, since it was always believed that in adults, the identification of numerals occurs automatically and no language influences this. But it turns out that the less transparent language system for the education of numerals in the Dutch language makes math problems more difficult for Dutch adults as well.
“The influence is very weak, but since we, as adults, do a lot of mathematical calculations in our daily life, sometimes difficult ones, the language system potentially acts as an additional obstacle in these calculations,” notes Zinida-Derva.
So how can we teach math to our children if everything in our language is not as transparent as we want it to be?
“Well, it seems to me that the question should not be so — in what language to teach children to count,” says Dowker. “You just have to remember that some difficulties in the study of mathematics may be associated with a particular language system.”
Zinidou-Dervo thinks so too. “It would be nice if the double-digit numbers were explained to Dutch children a little earlier. It is useful to remember that such an obstacle exists. «
So, even if we use the same numbers, the words we call these numbers can influence how we perceive them.
It is often said that mathematics is a universal language. It seems that this is not entirely true.
—
You can read the original of this article in English at BBC Future.
Source: https://www.bbc.com/russian/vert-fut-50560541
English for Mathematicians: Words You Need to Know!
The practice of English and the need to replenish vocabulary arises constantly. Therefore, we will continue the topic of using the English language in various fields of activity.
If you are thinking about going to a university abroad, looking for a job in a technical specialty abroad or in an international company in your city, we can say with confidence that you cannot do without mathematics. Even if you are fluent in English, think about it: have you succumbed to mathematical terms in English? It is one thing to have knowledge in the field of study in your native language, it is quite another to be able to understand the relevant English terminology.
We suggest considering a list of basic mathematical signs, symbols, fractions, mathematical operations that will definitely come in handy.
Signs and Symbols in Mathematics in English
Signs and symbols in mathematics, both in Russian and in English, have the same meaning. Therefore, there will be no problems with their recognition:
+ plus (more);
— minus (minus);
x, ∙ multiplication signs (the signs of multiplication);
÷, /,: division signs (the signs of division);
: proportion sign (the sign proportion) reads as is to: A: B = C: DA is to B as C is to D;
, comma (Comma) — used to indicate the position of every three numbers: 10,000,000 (10 million);
# if placed before a number, then the sign value is a number: # 3, # 85; if this sign is placed after the number, its value is a pound (measure of weight): 7 # (seven pounds — seven pounds);
% percent (per cent);
> in equations — more than; includes (is greater than, includes);
<in equations — less than; included (is less than, is included);
≥ in equations — equal or more (is equal to, or greater than);
≤ in equations — equal or less (is equal to, or less than);
∑ sum sign (the sum, summation of);
√, ³√ square root, cubic (the sign of the root or the radical sign: square root, cube root);
F (x), f (x) function of x (function of x);
∞ sign of an infinitely large number, as well as proportional changes (an infinitely large number, to vary proportionally).
Maths in English
Since school, everyone knows simple arithmetic operations, and now we will study them in English:
- + (plus) — addition (addition);
- — (minus) — subtraction;
- ÷ (divided by) — division;
- × (times / multiplied by) — multiplication;
- = (equals / is) — equals.
There are several options for reading examples for each action:
| Additiona + b = c1) a plus b equals c; 2) a and b is equal to c; 3) a added to b makes c; 4) a plus b is c. | Subtraction4-3 = 11) three from four is one; 2) four minus three is one; 3) four minus three is equal to one; 4) the difference between four and three is one. |
| Multiplication2 × 3 = 61) two multiplied by three is six; 2) twice three is six; 3) three times two is six. | Division35 ÷ 5 = 71) thirty five divided by five is seven; 2) five into thirty five goes seven times; 3) thirty five divided by five equals seven. |
Fractions and decimals
Common fractions express the numerator through the cardinal number, and the denominator through the ordinal number.
Ordinals are formed using the -th suffix and answer the question which (which): six (six) — sixth (sixth), ten (ten) — tenth (tenth). The only exceptions are the words first — first, second — second, third — third. The ending -y when forming an ordinal number changes to -i and the suffix -eth is added: twenty (twenty) — twentieth (twentieth), forty (forty) — fortieth (fortieth).
More about numbers in our article Numbers in English
How to read fractions in English correctly?
- 1/12: one-twelfth (one twelfth) — one twelfth;
- 1/7: one-seventh (one seventh) — one seventh.
But 1/2 and ¼ are read as one half and one quarter — in Russian it is just one second and one fourth.
If the numerator is more than one, the denominator is plural:
- 5/6: five-sixths (five sixths) — five sixths;
- 8/10: eight-tenths (eight tenths) — eight tenths.
In mixed numbers, the fractional part with the whole is connected by the union and, and the nouns associated with the fractional number are used in the singular and with the preposition of:
- 5 1/3: five and one-third (five and a third) — five and one-third;
- 1/4 mile: one quarter of a mile — one quarter of a mile;
- 5 1/7 kilograms: five and one seventh kilograms — five point and one-seventh kilograms.
In decimal fractions, numbers are read separately. Unlike Russian, where numbers are separated by commas, English uses a period:
- 0.1: nought (zero) point one / point one — zero point one;
- 0.01: nought (zero) point nought one / point nought (zero) one — zero point zero one;
- 3.36: three point three six — three point thirty six;
- 64.705: six four point seven nought five — sixty-four point seven hundred and five.
We made sure that English is as important for mathematicians as it is for other professions and specialties. Using simple words alone is not enough for professional and general development. In order to understand and possess knowledge at the highest level, of course, you need to delve deeper into the study of the subject.
Sign up for lessons in the NES at a convenient time for you and come to improve your level of English!
Source: https://native-english.com.ua/blog/anglijskij-dlja-matematikov-slova-kotorye-nuzhno-znat/
Math in English for kids
It’s no secret that the mathematics curriculum in Russian educational institutions is quite strong, often stronger than the Western one. The main difficulty is at different ages of presentation of the material.
In the Western system, there are more tasks on logic, statistics, probability, while in the Russian system these concepts are given much later — in the senior grades.
The Russian program in mathematics is more like «layers» of information, while the Western system is like a «spiral», new material is first studied superficially, so that the student has an idea of this concept or phenomenon, after a year more deeply, then another deeper.
Purpose of math lessons in English for children — to teach the student to think independently, and not only to solve typical problems in English, to develop mathematical thinking, to increase attentiveness.
Very often, the subject of the task may be familiar to the student, but the formulation of the task itself can cause difficulties due to the specific terminology. Top British schools, when offering a student to take an entrance test in mathematics, often offer him unusual tasks in logic and statistics, which require the ability to quickly combine the solution algorithm and derive the answer itself.
Teachers from the UK prepare children of different ages (from 10 to 15 years old) for admission to private British schools and taking a math test in English. Problems of the problem solving type, which for the most part are the most difficult for incoming children and students, are dealt with in detail during classes.
The program of the Russian school is often called upon to give a specific task in which it is required to find a solution, while the British program gives a situation where it is necessary to first develop an algorithm for the solution, to draw up several equations / graphs / examples to obtain the final answer.
This implies the development of logical thinking and working with data.
The mathematics course in English for children entering English schools includes such basic sections as:
- Numbers (integers, fractions and operations with them, roots, powers, problems with percentages, rounding, proportions, etc.)
- Algebra (formulas, algebraic expressions, equations, functions, identities, etc.)
- Shape and measures (geometric shapes: circles, triangles, quadrangles, prism vectors, the theorem of sines and cosines, rotation, reflection, etc.)
- Handling Data (theory of probability, working with data, working with tables, analyzing and comparing data.)
In the context of a tight time frame before the entrance exams in mathematics to school, we invite children to «solve» as many tests of the past years in mathematics in English from different schools as possible in order to identify and get acquainted with the typology of problems, get a clear understanding of the requirements, the assessment system and identify their own strengths and weaknesses.
We recommend that children prepare for the entrance tests a year before the exams themselves, but there are times when people turn to us 2 months before the mathematics exams in English, in this case, you usually only need to practice with the child typical tasks with which he is usually already familiar, the mathematical vocabulary and vocabulary also do not cause special problems for such students.
Mathematics is a fundamental subject in both Russian and Western education systems, it speaks about the level and abilities of children to think logically, apply rules and theories, count, and solve multi-stage problems.
Purpose of the math course in English for children — to prepare a person of different age categories (9+, 11+, 13+) for passing entrance exams in mathematics in English. These exams include GCSE Mathematics and A-Level Mathematics.
In mathematics in English for children, topics are studied such as:
- Coordinates
- Angles
- Fractions Percentages decimals
- Addition subtraction
- Multiplication / division
- Statistical problems
- prime factors
- Assorted problems
- Square and cube numbers and many others
Do Russian schoolchildren need additional training in mathematics in English?
It is generally accepted that the mathematics course is stronger in Russian schools — you cannot argue with that. The main difficulty in performing the tests is that the mathematics course in English in British schools contains many tasks on logic, statistics, probability at an early stage, while we study these topics in high school.
This is what leads to great confusion in the exams, to a misunderstanding of tasks and an inability to find their solutions. A mathematics course in English in Western educational institutions places great emphasis on problems such as problem solving, where you first need to develop an algorithm for solving, compose several actions equations examples to obtain the final result.
These are the skills of working with data and analyzing information.
In the classroom, we offer students to pass a large number of practice tests or tests of previous years from different schools, we have accumulated a decent archive of such tests, which allows the child to practice on the performance of examination papers, identify all weaknesses and incomprehensible points, get a clear understanding of the requirements and the assessment system …
Math textbooks in English for kids
Source: https://thetutorsofmoscow.ru/podgotovka/matematika-na-angliyskom-dlya-detey.html
Enjoy learning English online with Puzzle English for free
Autumn is a time not only for walking in the park and enjoying the fallen leaves, but also for the beginning of school days. Do you love English classes as much as we love them? We hope so! What about the rest of the lessons?
In this article we will tell you what are the names of school subjects in English and how they are translated. And also, what is the difference between the lessons of the English and our Russian lessons.
Schools in England
In September, millions of children around the world pack up their school bag and go to their first classes in the new school year. True, education systems in Russia and England are fundamentally different from each other.
In England, a 100-point system for assessing knowledge has been adopted, which is not always clear to Russian pupils and foreign students. So, a score of 70 or higher is called the First Class Honors classification and is equal to our «five».
Next come the categories, separated by tens of points: 60-69 points — Upper Second Class Honors classification («four»);
50-59 points — Lower Second Class Honors classification («four with a minus»);
40-49 points — Third Class Honors classification («three»);
30-39 points — Referral.
And finally, if a student gets from 0 to 29 points, he is given a Fail or Unsatisfactory mark, which equates to our “two”.
In terms of the classes themselves and the training system, there are also significant differences between the UK and Russia.
Our first-graders go to school from 6-7 years old, and they usually study there from 8 in the morning. There are not so many classes for the pupils of the elementary grades: there are about 3-5 lessons of 45 minutes a day, which continue until lunchtime. Middle and high school students take an average of 5-6 lessons a day, and after that they stay for additional subjects or other extracurricular activities.
Students in Russia of all ages have about the same number of days, including not only summer and New Year’s holidays, but also spring and autumn holidays. In England, children go to primary school from the age of 5, and the total duration of complete secondary education is 13 years.
The average schoolchildren graduate at the age of 18 and then can go to university for higher education. Standard school classes everywhere begin at 9 am and continue until 3 pm. The youngest primary school students do not immediately sit down at their desks: there are many games and outdoor lessons in their schedule.
Every year kids are taught more and more discipline and different sciences. This prepares them for a smooth transition to high school.
As in many countries, there are two types of schools in England: public and private. True, the quality of education and the difference between them are not as noticeable as in Russian schools. All students of private schools in England must wear a school uniform, which is distinguished by the corporate color of the educational institution. A prestigious school always has its own coat of arms and other symbols that are widely known outside its borders.
An interesting feature of schools in England is that they can differ by gender: there are schools for boys only, only for girls and mixed educational institutions. Even in the modern world, many parents choose to send their children to such schools. Also, the British have access to a large selection of schools with special biases: sports, humanitarian, mathematics, art schools and many others.
In middle and high school, regardless of its bias, special attention is paid to the development of qualities that will help the child form his own view of the world and bring up a strong independent personality. Many activities are aimed at developing leadership skills, discipline, a sense of responsibility and the ability to express one’s opinion. Much time is also devoted to sports training and, in general, the comprehensive development of the student.
Lessons in English
The basic set of subjects (school subjects) of any student includes the study of the native language, mathematics, natural sciences, literature, as well as work and physical education classes. As for the study of foreign languages, in Russian schools, as a rule, students are asked to choose between English or German. In English schools, they study mainly French and German. Below are the main Russian school subjects with translation into English:
Algebra [ˈældʒəbrə] — algebra
Biology [baɪˈɒlədʒi] — biology
Drawing [ˈdrɔːɪŋ] — drawing
Chemistry [ˈkemɪstri] — chemistry
Geography [dʒiˈɒɡrəfi] — geography
Geometry [dʒiˈɒmətri] — geometry
History [ˈhɪstəri] — history
Literature [ˈlɪtrətʃər] — literature
Mathematics [ˌmæθˈmætɪks] / Math [mæθ] — mathematics
Music [ˈmjuːzɪk] — music
Physical education [ˈfɪzɪkəl ˌedʒuˈkeɪʃən] / PE [pɪː ˈɪː] — physical education
Physics [ˈfɪzɪks] — physics
Technology [tekˈnɒlədʒi] — works
Regarding the standard set of subjects for students in the UK, it is different from what we know. So, physics, chemistry and biology are combined into one subject — science (science), and English (that is, their native language) and literature — into general English. Similarly, algebra and geometry, which are usually taught separately in our country, are united in Math in England.
There are compulsory subjects in the UK school course that we do not have. For example, citizenship (bases of legal responsibility). Below you will find a complete list of compulsory subjects in British schools:
Art and design — art and design
Citizenship — Legal Responsibility Basics
Computing — informatics
Design and technology — design and technology
English — English language and literature
Geography — geography
History — history
Maths — mathematics
Modern foreign languages - modern foreign languages
Music — music
Physical education — physical education
Science — science
A significant difference from our education system is that all UK schools are required to provide lessons in religious education and sex and relationship education. True, parents of students who have not yet turned 18 have the right to refuse these classes in whole or in part. After 18, the student makes this decision himself.
In addition to all of the above, schools can introduce other subjects, at their discretion or depending on the specialization.
School vocabulary
In addition to the list of school subjects in English, we suggest remembering important words that will be useful to all students:
Bell — call
Break — change
Chalk — chalk
Classroom — classroom
Copybook — notebook
Curriculum — curriculum
Desk — desk
Duster — duster
Exam — exam
Exercise book — exercise book
Grade / year — class
Headmaster — Director
Homework — homework
Instructor — instructor, trainer
Lesson / class — lesson
Mark / grade — grade
Notebook — notepad
Pen — pen
Pencil — pencil
Prom — school ball, graduation
Pupil / student — student
Quiz / test — test, control work
Seat / chair — a chair, a place at a desk
School uniform — school uniform
Schoolboy — schoolboy
Schoolgirl — schoolgirl
Semester — semester
Teacher — teacher
Term — quarter
Terminal — exam at the end of a quarter or semester
Textbook — tutorial
Timetable — schedule
Vacation (US) / holidays (UK) — holidays
Whiteboard — board
Enjoy!
Source: https://puzzle-english.com/directory/school-subjects
Math in English — how to say it correctly, useful vocabulary,
›Learning a language› Vocabulary ›How to say in English› Math topic in English — useful vocabulary, grammar and pronunciation
Welcome all English lovers to our next online lesson! We are glad that you continue to improve your knowledge, and today we invite you to analyze the topic «Mathematics» in English. It seems to many that mathematical knowledge rarely comes in handy in life.
But if you think about it, then counting, the processes of division or addition, and at the same time the mention of fractions are found in the information field around a person almost every day. Therefore, of course, without a stock of mathematical vocabulary, it is impossible to fully communicate in English.
So let’s fill that gap as soon as possible!
How to spell and pronounce math in English
First of all, let’s figure out how mathematics gets translated into English. After all, the British and Americans can call the Queen of Sciences in several ways.
The first and foremost is the term mathematics [ˌmæθəˈmætɪks]. Interestingly, the word mathematics in English is written with the ending -s, but at the same time it belongs to the number of nouns that can only be used in the singular! So don’t be fooled by the final «-s» and use the singular verb with mathematics if necessary.
- Mathematics is the only truly universal language. — The only universal language in the world is mathematics.
- Mathematics has always been a closed book to me. — Mathematics has always been and remains a closed book for me.
- Mathematics includes the study of many topics. — Mathematics includes the study of many topics.
It is also important to discuss the scope of this term. When it comes to a scientific discipline or subject of study, then the word mathematics would be an ideal option to apply. But in colloquial speech, an abbreviated version — maths will be more appropriate.
And here an important caveat should be made: in the UK it is customary to use the abbreviation maths [maθs] in speech, and in the United States, the use of an even shorter version of math [mæθ] is widespread.
Also note that in this case, the pronunciation of the word Math in English changes depending on the type of abbreviation selected.
- My son has always been good at maths [masses]. — My son has always been good at math.
- Her favorite subject is math [mes]. — Her favorite school subject is mathematics.
And since we are considering the name of the discipline itself in such detail, we cannot leave aside the common word of the same root — mathematician. To denote a person’s profession or hobby, it is necessary to add a special suffix — cian to the base of the word Mathematics. As a result, the term «mathematician» in English will be written as mathematician [maθəməˈtɪʃn].
- Bernard Roy is a famous French mathematician. — Bernard Roy is a famous French mathematician.
Well, what is the English math and mathematician, we figured out, it’s time to talk about basic math operations. We will devote the next section of the article to them.
The simplest mathematical operations in English
Sometimes we ourselves do not notice how mathematical terms flicker here and there in our speech. Of course, mathematics is a complex science, and not everyone succeeds in mastering even the fundamental basis.
Nevertheless, everyone should know the simplest mathematical operations, which is why we are working on the topic Mathematics in English today. And right now we propose to replenish your vocabulary with useful vocabulary on this topic. So, the terms, phrases and expressions will be presented in the form of a table.
Moreover, for each English word, translation and transcription in English will be provided so that the pronunciation of mathematical terms does not cause difficulties.
| Word | Transcription | Transfer |
| plus | [plʌs] | plus, fold |
| minus | [ˈMaɪnəs] | minus, subtract |
| add | [æd] | add |
| subtract | [səbˈtrækt] | subtract |
| multiply by | [ˈMʌltɪplaɪ baɪ] | multiply |
| teams | [taɪmz] | multiply (colloquial) |
| divide by | [dɪˈvaɪdbaɪ] | share |
| equals to | [ˈIːkwəlz tuː] | equate |
| is equal | [ɪzˈiːkwəl] | equally |
| to solve | [tuːsɒlv] | solve |
| answer | [ˈⱭːnsə] | answer |
Here’s a mini-dictionary we got. And for a better understanding and memorization of the terms, we will show how any native resident of the United Kingdom or America would write a simple mathematical action in English.
- 2 + 5 = 7 — two plus five equals seven — Two plus five equals seven
- 5 * 5 = 25 — five times five is twenty-five. — Five five — twenty five
- 17-7 = 10 — Seventeen minus seven is ten. — Seventeen minus seven equals ten
- 15: 3 = 5 — Fifteen divided by three equals five — Fifteen divided by three equals five
As you can see, all phrases are quite simple and in essence similar to examples from the Russian language.
Fractional numbers, percentages, degrees, and other mathematics terms in English
So, we already know how to designate the simplest mathematical operations and call the Queen of Sciences in both general literary and colloquial terms. But after all, mathematics is a very complex discipline, which includes many different topics. And even for communication at the simplest level, the information we have studied will not be enough.
Therefore, we will supplement the topic Mathematics in English with another collection of useful vocabulary. In particular, the table will tell you how to indicate percentages, fractional numbers, mathematical brackets, and other important elements.
Join the study or print out the table below and expand your vocabulary whenever you have free time.
| Word | Transcription | Transfer |
| mathematical sign | [ˌMæθɪˈmætɪkəl saɪn] | mathematical sign |
| quotient | [ˈKwəʊʃənt] | private |
| difference | [ˈDɪfrance] | difference |
| remaining | [rɪˈmeɪndə] | the remainder |
| multiplication table | [ˌMʌltɪplɪˈkeɪʃən ˈteɪbl] | multiplication table |
| odd number | [ɒdˈnʌmbə] | odd number |
| even number | [ˈIːvən ˈnʌmbə] | even number |
| percent | [pəˈsɛnt] | percentage |
| mixed number | [mɪkst ˈnʌmbə] | mixed number |
| decimal fractions | [ˈDɛsɪməl ˈfrækʃənz] | decimal |
| common fractions | [ˈKɒmən ˈfrækʃənz] | common fraction |
| numerator | [ˈNjuːməreɪtə] | numerator |
| denominator | [dɪˈnɒmɪneɪtə] | denominator |
| point | [pɔɪnt] | point |
| half | [hɑːf] | half |
| quarter | [ˈKwɔːtə] | fourth |
| to round up the number | [tuːraʊndʌpðə ˈnʌmbə] | round a number |
| squared | [skweəd] | squared |
| cubed | [kjuːbd] | cubed |
| the square root of | [ðə skweə ruːt ɒv] | square root of |
| parentheses or round brackets | [pəˈrɛnθɪsiːz] (raʊnd ˈbrækɪts) | parentheses |
Now the topic Mathematics for the intermediate level of English proficiency has been mastered in sufficient volume. I wish you success in your further training and see you soon!
Topic «Mathematics» in English — useful vocabulary, grammar and pronunciation Link to main publication
Source: https://speakenglishwell.ru/tema-matematika-po-anglijski-poleznaya-leksika/
Mathematics, Russian, English: where to apply?
Perhaps the thought of entering has already visited your head more than once, but your reflections have not ended with anything constructive. If you need a push from the outside — here it is. We want to tell you about 3 specializations, each of which is interesting and promising in its own way.
Management
Code: 38.03.02
Professions: manager (logistics, procurement, advertising, personnel, etc.), marketer, auditor, manager, financial analyst.
This option of where you can go with English and specialized mathematics is, to a certain extent, a «hodgepodge». In the general sense of the word, management is management, but you can manage many people and many things.
Therefore, future specialists in this profile study psychology (from the point of view of human resource management), economics, advertising, finance, and strategic planning.
It is up to you to decide which area to bias, but during your studies at the university you will have to master:
- development, assessment and analysis of business ideas and business plans;
- development of a marketing strategy, its preparation and implementation, assessment of its effectiveness;
- preparation of financial documentation, analysis of financial and investment projects;
- planning and managing the work of the team, organizing an audit of human resources, carrying out activities aimed at finding new employees;
- work with the regulations and laws of our country.
You can enroll in this direction with mathematics and English, for example, at the All-Russian Academy of Foreign Trade and Trade of the Ministry of Economic Development of Russia. It offers full-time education, 43 places for education on a budgetary basis, and a passing score of 85.0. Another good option is St. Petersburg State University. Here there are more budget places — 70, the passing score is at the level of 87.7, the form of study is also full-time.
Business Informatics
Code: 38.03.05
Professions: programmer, business consultant, system analyst, web administrator, sap specialist.
This specialty is a kind of combination of the IT industry and the financial industry.
Future professionals in the field of business informatics study programming, the creation and use of information systems and databases, as well as logistics, business process modeling, strategies for managing human, financial and other resources, and even some areas of law.
As a result, they can work in any company where IT tools are used or are planned to be used, and which, in principle, are focused on development and profit growth. While studying at a university in such a specialization, you will need to study:
- analysis and research of the current state of the IT market;
- design, implementation and implementation of information technologies in the work of enterprises;
- development of projects aimed at optimizing business processes;
- management of information products used in the enterprise;
- training users in the use of information systems;
- development of business plans and new business structures using IT tools.
To become a business analyst, you can enroll, for example, at the Higher School of Economics. Here in Moscow, 85 budget places are allocated for this profile, they offer full-time education, and the passing score is at the level of 96.0.
Or you can pay attention to Peter the Great SPbPU with 30 budget places and a passing score of 86.3.
There are both full-time and part-time forms of study, but for admission to the full-time department, you will need to additionally take a foreign language at the university.
Fundamental and Applied Linguistics
Code: 45.03.03
Professions: linguistic expert, translator, linguist, computer linguist, proofreader, editor, content manager, foreign language teacher.
Mathematics and language are a combination, whatever one may say, rather rare, and this specialty embodied the fusion of these two subjects to the fullest. On the one hand, students in this direction deeply study languages, phonetic, grammatical, syntactic, morphological rules and patterns. On the other hand, in their studies, considerable attention is paid to the development of mathematical statistics, probability theory, logic, mathematical modeling.
The result is the study of languages not so much at the literary level, but in the context of the laws and algorithms to which they obey. Therefore, graduates can engage in linguistic expertise, the development of electronic dictionaries, control systems and any other information products, for the quality of which the competent use of languages plays a decisive role.
So, in the process of getting education, future linguistic experts master the following skills:
- organization, preparation and implementation of linguistic experiments and research;
- development, implementation and service support of linguistic information products;
- execution of written, oral and simultaneous translation (from Russian into foreign and vice versa) in compliance with linguistic ethics;
- the use of information technology to work on a linguistic profile;
- creation, design and optimization of text content of web resources.
This option of where you can go with the exam in Russian, mathematics and English cannot be called widespread — but that is why it does not become less interesting. You can get an appropriate education, for example, at Moscow State University. M.V. Lomonosov. The passing mark here is set at 94.
0, the number of budget places is 20, the form of study is full-time. Additionally, you will need to pass an exam in a foreign language at the university. Another good option is the Russian State Humanitarian University. Full-time training is also conducted here, 10 places are allocated for free training, and the passing score is 87.7.
We hope that we managed to stir your thoughts towards a successful choice of your future profession!
Source: https://www.profguide.io/article/mat_rus_angl_kuda_postupit.html

Хотелось бы начать с числительных (numerals), ведь это первое, с чем мы сталкиваемся в математическом контексте. Напомню, что числительные бывают двух видов: количественные (отвечают на вопрос «сколько?») и порядковые (отвечают на вопрос «который по счёту?»).
Давайте обратим особое внимание на произношение тех или иных числительных, так как этот, казалось бы, простой момент иногда вызывает замешательство даже у опытных «пользователей» языка.
| Тип | Правило | Пример | Особенность |
|---|---|---|---|
| Сотни | And между сотнями и десятками. | “101 (one hundred and one) Dalmatians” is my favourite cartoon. |
– |
| Тысячи | And не ставится между тысячами и сотнями. | The population of my village is almost 6500 (six thousand five hundred) people.
1 253 (one thousand two hundred and fifty-three) candidates passed this exam last year. |
Американцы иногда произносят тысячи и сотни так: 1500 = fifteen hundred = 15 сотен. |
| Сотни и десятки тысяч | And между сотнями тысяч и десятками тысяч. | The population of Liverpool is 466 415 (four hundred and sixty-six thousand, four hundred and fifteen) people. | Американцы используют and намного реже британцев. Так, они сказали бы: 466 415 = four hundred sixty-six thousand, four hundred fifteen. |
| Миллионы | And не ставится между миллионами и тысячами. | There are 2 629 743 (2 million, 6 hundred and 29 thousand, 7 hundred and 43) seconds in one month. |
– |
| Миллиарды | And не ставится между миллиардами и миллионами. | The world population was 5 320 816 000 (5 billion, 3 hundred and 20 million, 8 hundred and 16 thousand) people in 1990. |
– |
Ряд чисел (series of numbers): произнося ряд чисел, из которых состоит банковский счет, номер кредитной карты или телефона, мы называем каждую цифру отдельно. При этом ноль произносится как oh в британском варианте, и как zero – в американском:
His credit card number is 5368 7208 0944 0699 (five three six eight, seven two oh/zero eight…). – Номер его кредитной карты – 5368 7208 0944 0699.
При этом, если в номере телефона присутствуют две одинаковые цифры, стоящие рядом, говорится, например double nine:
My friend’s number is 2290 4566 (double two nine oh four five double six). – Телефон моего друга – 2290…
Называя десятичные дроби (decimals), мы используем слова nought (британский английский) и zero (американский английский): 10.39 (ten point thirty-nine) – десять целых и тридцать девять сотых. Более подробно ознакомиться с особенностями произношения дробных числительных можно в нашей статье.
Указывая ту или иную дату, мы, конечно же, очень далеки от математики, однако дата – одна из самых популярных сфер употребления числительных. Если вам необходимо освежить в памяти, как именно указываются даты в английском, то советую прочитать статью «Даты и порядковые числительные в английском языке».
И наконец переходим к математическим действиям (mathematical operations): сложению (addition), вычитанию (subtraction), умножению (multiplication) и делению (division).
- To add to / to plus – прибавлять.
- To minus / to subtract from – вычитать.
- To multiply by – умножать.
- To divide by – делить.
- To equal – равняться
| Действие | Пример по-английски | Перевод |
|---|---|---|
Пример: 7 + 8 = 15 |
7 plus/and 8 equals/is 15.
Add 7 to 8 and you’ll get 15. |
7 прибавить 8 равняется 15.
Прибавь 7 к 8 и получишь 15. |
Пример: 23 – 3 = 20 |
Twenty-three minus three equals/is twenty.
If you subtract 3 from 23, the answer is 20. |
23 минус 3 будет 20.
|

Пример: 6 * 4 = 24 |
6 multiplied by 4 / 6 times 4 equals/is 24.
Multiply 6 by 4 and you’ll get 24. |
6 умножить на 4 равно 24.
|

Пример: 9 ÷ 3 = 3 |
9 divided by 3 equals/is 3.
If you divide 9 by 3, the answer is 3. |
9 разделить на 3 равно 3.
Если разделить 9 на 3, ответ будет 3. |
Глоссарий на тему «Математика»
- To do sums / to solve problems – решать примеры, задачи.
He is the best at doing sums in our class. – Он решает примеры лучше всех в нашем классе.
- Сommon denominator – общий знаменатель.
The task is to reduce to the common denominator. – Задача – привести к общему знаменателю.
- Difference – разность.
The difference of 15 and 10 is 5. – Разность пятнадцати и десяти – пять.
- Equation /ɪˈkweɪʒ(ə)n/ – уравнение.
Solve the equation. – Решите уравнение.
- Improper fraction – неправильная дробь.
“Improper fractions” are not an easy topic for him. – «Неправильные дроби» – непростая тема для него.
- Mixed fraction – смешанная дробь.
He knows exactly what a mixed fraction is. – Он точно знает, что такое смешанная дробь.
- Numerator /ˈnjuːməˌreɪtə(r)/ – числитель.
Numerator is the number above the line in a common fraction showing how many of the parts indicated by the denominator are taken. – Числитель – это число над линией простой дроби, показывающее сколько частей, указанных знаменателем, взято.
- Quotient /ˈkwəʊʃ(ə)nt/ – частное (при делении).
Quotient is a result obtained by dividing one quantity by another. – Частное – это значение, полученное путем деления некого числа на другое.
- Remainder – остаток.
Remainder is the number that is left over in a division in which one quantity does not exactly divide another – Остаток – это число, которое осталось в результате деления, когда одно число не делится на другое без остатка.
- Сube root of – корень кубический из.
Find the cube root of 15. – Найдите кубический корень из 15.
- Inequality /ˌɪnɪˈkwɒləti/ – неравенство.
Inequality is the relation between two expressions that are not equal. – Неравенство – это соотношение между двумя выражениями, которые не являются одинаковыми.
- Equality /ɪˈkwɒləti/ – равенство.
Equality is the condition of being equal in number or amount. – Равенство – это идентичность числа или величины.
- Mathematical sign – математический знак.
Minus is an example of a mathematical sign. – Минус – это пример математического знака.
- Multiplication table – таблица умножения.
Schoolchildren learn the multiplication table all over the world. – Школьники по всему миру учат таблицу умножения.
- Parentheses /pəˈrenθəsɪs/ или round brackets – круглые/овальные скобки.
Parentheses are widely used in mathematics. – Круглые скобки широко используются в математике.
- Right angle – прямой угол.
The right angle is 90˚ (degrees). – Прямой угол равняется 90 градусам.
И в завершение статьи хотелось бы предложить вам пройти небольшой тест. Но не волнуйтесь! Это не урок математики! 
Тест
Говорим о математике на английском
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
acute angle (noun): any angle measuring between 0° and 90° – The leaves protrude out of the stem at an acute angle.
add (verb): to combine two numbers to get a total – If we add 2 to 4, we get 6.
addition (noun): the bringing together of two or more numbers to find a total – The addition of 2 new students to the class of 20 brought the total number of students to 22.
ALGEBRA (noun): a branch of mathematics in which letters and other symbols can be used to represent numbers – It wasn’t until I studied algebra that I got the concept of E = mc2.
algorithm (noun): a set of rules used to carry out any calculation – Following this algorithm will make the problem easier to solve.
angle (noun): the space (measured in degrees) between two lines which meet at a certain point – A square has four angles, whereas a triangle has three.
arc (noun): a curved shape, the distance between any two points on the of the circumference of a circle – The sun moved in an arc across the cloudless sky from sunrise to sunset.
area (noun): the two-dimensional space occupied by an object or shape – Malta is a small country with a surface area of 316 km2.
ARITHMETIC (noun): the oldest and most basic branch of maths, dealing with numbers and their basic operations: addition, subtraction, multiplication, and division – There were 10 students in one class and 15 in the other, which if my arithmetic serves me right comes to 25 in total.
ascending order (noun): increasing; arranged from smallest to largest – They told us to line up in ascending order of height, with the shortest on the left.
average (noun): a mean; a number that is a typical representation of a set of numbers – To calculate the average of four different numbers for example, simply add the four numbers, then divide the total by four. So the average of 2, 4, 6 and 8 is 20 divided by 4 which is 5.
axis (noun): an imaginary straight line around which a body rotates – The earth rotates on its axis which runs from North Pole to South Pole.
base (noun): in geometry a base is the bottom line of a 2D shape such as a square or triangle, or the bottom surface of a 3D shape such as a pyramid – The statue stood on a heavy stone base.
binary (adjective): relating to a system of numbers based on 2. See decimal – Computers use a «base-2» binary system of numbers 0 and 1.
CALCULUS (noun): a branch of mathematics that studies continuous rates of change – Astronomers use calculus to track the orbits of different planets.
capacity: (noun): the maximum volume that a container can hold – The tank has a capacity of 64 litres.
cardinal number (noun): a number that expresses quantity (one, two, three etc), as opposed to an ordinal number which expresses position (first, second, third) – We started the lesson by learning about cardinal numbers.
circle (noun): see shapes
circumference (noun): The boundary of a circle or other curved geometric figure – The circumference of the wedding cake was 140 centimetres.
common fraction (noun):
a fraction expressed as a numerator above and denominator below, for example ½ (as opposed to decimal 0.5). Also called vulgar fraction – In practice, common fractions are often simply called fractions.
cone (noun): see shapes
consecutive numbers (noun): whole numbers that follow each other in ascending order without gaps – We can say that 7, 8, 9, 10, 11, 12 are consecutive numbers but 7, 9, 12 or 12, 8, 11 are not.
coordinates (noun): usually a pair of numbers indicating a point on a graph (or map etc) – We read the first coordinate along the graph (left to right) and the second coordinate up the graph (bottom to top).
cube (verb): when you cube a number you multiply it by itself three times – If you cube 3 you get 33 = 3 x 3 x 3 = 27. Three cubed is twenty-seven.
cube (noun): see shapes
cube root (noun): the cube root of a number is the factor that we multiply by itself three times to get that number. – 3 × 3 × 3 = 27 so the cube root of 27 is 3. The cube root of 8 is 2 because 2 x 2 x 2 = 8.
curve (noun): a line that flows smoothly without any sharp turns – In maths a curve can be a straight line.
cylinder (noun): see shapes
decimal (adjective): relating to a system of numbers based on 10. This «base-10» system of numbers using 0-9 is derived from the Hindu-Arabic number system – Computers don’t work with decimal numbers: they have to convert them into binary first.
decimal point (noun): A full point or dot placed after the figure representing units in a decimal fraction – In English the decimal point is like a period (12.5) but in some languages, French for example, the decimal symbol is a comma (12,5).
degree (noun): a unit of measurement for angles. The symbol is °. There are 90° in a right angle (an interior corner of a square) – Any angle less than 90° is called an acute angle.
denominator (noun): The number below the line in a vulgar fraction – The teacher pointed to the denominator at the bottom of each fraction on the board.
descending order (noun): decreasing; arranged from largest to smallest – Our exam scores were listed in descending order with the best at the top.
diagonal (noun): a line that connects any two corners, but is not an edge – If you have a square and you join the top left corner to the bottom right corner, you get a diagonal.
diameter (noun): The measurement of the longest distance across a circle, from one point to another – The table is over a metre in diameter and can easily seat four people.
digit (noun): any of the ten Arabic numerals from 0 to 9 – The number 9 has only one digit, whereas 11 and 12 both have two digits.
divide (verb): to break up a number into equal parts. We use the symbol ÷ (or the symbol / ) to mean divide – We write 12 ÷ 3 = 4 and we say twelve divided by three equals four. We can also write 12 / 3 = 4.
division (noun): The process of breaking up a number into equal parts. It is the opposite of multiplication. Division is represented by the ÷ symbol – The division of the class into four groups of 3 meant that we all got a chance to speak.
edge (noun): a line between corners in 2D and 3D shapes – A square has four edges and a cube has 12 edges.
equal sign (noun): the symbol = indicating that two amounts are of the same value, for example 2 + 2 = 4 – I wrote down the answer on the right side of the equal sign.
equation (noun): A mathematical statement which uses an equal sign ( = ) to indicate that two mathematical expressions are of the same value – The most famous equation ever is probably Einstein’s E = mc2.
equilateral (adjective): having all sides the same length – By definition all squares are equilateral, but other shapes can be equilateral too.
even number (noun): any integer (never a fraction) that can be divided exactly by two – The houses on the right side of the road all have even numbers | 2 and 4 are even numbers, whereas 1 and 3 are odd numbers.
factor (noun): a number which produces another number when it is multiplied – Both 2 and 3 are factors of 6.
formula (noun): a mathematical rule that can be written with numbers, letters and symbols – The formula V = l x w x h will give the volume of a box where V = volume, l = length, w = width and h = height.
fraction (noun): a numerical representation of equal parts of a whole. If you cut a whole orange into two equal pieces, each piece is a fraction of the whole and can be expressed as 0.5 (decimal), ½ (common fraction), or 50% (percentage) – After the hungry children had finished their lunch, only a fraction of the pie remained.
geometric, geometrical (adjective): relating to geometry – Much ancient Greek pottery was characterized by geometric patterns.
geometry (noun): the branch of mathematics dealing with points, lines, surfaces, solids etc – I have a geometry test tomorrow.
graph (noun): A diagram expressing the relationship of a set of numbers or measurements, usually with lines – The seasonal temperatures were shown on a graph with a single line going up and down.
greater than: the symbol > means greater than or bigger than. See also < less than – If we write 5 > 3 we are saying that five is greater than three.
hemisphere (noun): half of a sphere or three-dimensional round object – The earth’s northern hemisphere and southern hemisphere are separated by the equator.
infinity (noun): in maths, an imaginary number that is greater than any countable number; the symbol for infinity is ∞ – The infinity symbol is a closed figure of eight loop on its side indicating its unending nature.
integer (noun): A whole number with no fractional parts – 3 is an integer, whereas 3.5 is not.
less than: the symbol < means less than or smaller than. See also > greater than – If we write 3 < 5 we are saying that three is less than five.
mean (noun): see average
minus (preposition): with the subtraction of – Does 25 minus 10 equal 15?
minus sign (noun): the symbol ( — ) indicating subtraction or a negative value – An example of the minus sign for subtraction is 5 — 3 = 2. An example of the minus sign for a negative value is that -10℃ is ten degrees below freezing.
multiplication (noun): the process of taking a number and adding it together multiple times. Multiplication is represented in expressions by the times symbol ( x ) – An example of multiplication is four times three ( 4 x 3 ) which is the same as 4 + 4 + 4 = 12.
multiply (verb): to apply multiplication; to take a number and add it together multiple times – If you multiply 3 by 4, you get 12.
negative number (noun): a number that is less than zero, typically preceded by a minus sign ( — ) or sometimes written in red – In 2 — 5 = -3, the result is a negative number.
numerator (noun): the number above the line in a common or vulgar fraction – In ⅔ the numerator is 2 and the denominator is 3.
obtuse angle (noun): an angle that is greater than 90° but less than 180° – The door was wide open at an obtuse angle.
odd number (noun): any whole number that cannot be divided exactly by two. See even number – The number 23 is an odd number because it cannot be divided by 2.
ordinal number↗ (noun): a number indicating the position of something within a list. Ordinal numbers show the «order» of things. They can be written in full (first, second, third etc.) or abbreviated (1st, 2nd, 3rd) – Unfortunately my horse came in third so I lost my money. | She was born on the 2nd of May.
oval (noun): see shapes
parallel (adjective): (of two lines) placed side by side with an equal distance between them at all points – The two planks of wood ran parallel to each other on the floor. Parallel lines never meet.
percent (adverb): parts per hundred. The symbol is % – We sleep for about 30% of our lives.
perimeter (noun): the total distance around a two-dimensional shape. The perimeter can usually be calculated by adding the length of all the edges together – Each edge of this square is 10cm, so the perimeter is 40cm.
plus sign (noun): the symbol ( + ) placed between two numbers to indicate that the second number is being added to the first – An example of the plus sign for addition is 5 + 3 = 8, spoken as five plus three equals eight.
pi (noun): the ratio of a circle’s circumference to its diameter (circumference divided by diameter). Pi is approximately 3.14159 and is represented by the Greek symbol π – I calculated the circle’s circumference by multiplying its diameter by pi. The value of pi is always the same regardless of a circle’s size.
polygon (noun): see shapes
prime number (noun): a whole number greater than 1 that cannot be exactly divided by any whole number except itself and 1 – Four can be divided by 2, so it is not a prime number. Seven can only be exactly divided by 1 and 7, so it is a prime number.
PROBABILITY (noun): a branch of mathematics that predicts how likely something is to happen – When we toss a coin, the probability of it landing heads up is 50%.
radius (noun): a straight line representing the distance from the centre of a circle to its circumference – The radius of the circle is half the length of the diameter.
ratio (noun): a comparison of the quantity of one thing with the quantity of another thing – In our school there are 3000 students and 100 teachers, so the ratio of students to teachers is 30 to 1 (also written as 30 : 1).
rectangle (noun): see shapes
remainder (noun): an amount left over after division when the first number cannot be divided exactly by the other – 4 goes into 10 two times with the remainder of 2.
right angle (noun): an angle measuring exactly 90°, such as an interior corner of a square. – If you draw a triangle with sides that are 3, 4 and 5 units in length, then you can create a perfect right angle using just a ruler.
round up/down (verb): if you round a number, you make it simpler to use but keep it close to its original value — For example, you might round 43 down to 40. And you might round 47 up to 50.
Shapes
shape (noun): a geometric figure which can be 2D or two-dimensional (square, circle, triangle etc) or 3D or three-dimensional (cube, sphere, pyramid etc) – Geometry involves the study of all kinds of shapes, both 2D and 3D.
2D or two-dimensional shapes (flat)
circle (noun): a round flat shape whose boundary is equidistant from its centre at all points
oval (noun): any round flat shape that looks like an egg or «stretched circle»
triangle (noun): a flat shape with 3 sides
square (noun): a flat shape with 4 equal sides and 4 equal angles of 90°
rectangle (noun): a flat shape with 4 sides and 4 equal angles of 90°. Opposite sides are parallel and of equal length
trapezium (noun): any flat shape with 4 sides, none them parallel
quadrilateral (noun): any flat shape with 4 sides
pentagon (noun): a flat shape with 5 equal sides
hexagon (noun): – a flat shape with 6 equal sides
heptagon (noun): a flat shape with 7 equal sides
octagon (noun): a flat shape with 8 equal sides
polygon (noun): any flat shape with 3 or more equal sides
3D or three-dimensional shapes (solid or hollow)
sphere (noun): a round 3D shape like a ball or globe. Every point on its surface is equidistant from its centre
cone (noun): a 3D shape that tapers to a point from a flat circular base
cube (noun): a symmetrical 3D shape with 6 equal square faces
cuboid (noun): a 3D shape with 6 rectangular faces
cylinder (noun): a 3D shape with straight parallel sides and a circular cross-section
octahedron (noun): a 3D shape consisting of eight equal faces, twelve edges, and six corners
prism (noun): a 3D flat-sided object with two identical ends
tetrahedron (noun): a 3D shape with four triangular faces
sphere (noun): see shapes
square (noun): see shapes
square root (noun): a number’s square root (symbol √ ) is a smaller number whose product is the original number when multiplied by itself – The square root of 9 is 3 ( √9 = 3 ).
subtract (verb): to take one amount or quantity away from another – If you subtract 3 from 10, you get 7.
subtraction (noun): the process of subtracting one number from another. We use the minus sign ( — ) to indicate subtraction in maths – We practised our subtraction by removing pennies from the pile on the table.
sum (noun): the amount which results from the addition of two or more numbers – 7 is the sum of 1, 2 and 4.
three-dimensional, 3D (adjective): having 3 dimensions: length, breadth, depth. See 2D – Objects like boxes and buildings are 3D.
times sign (noun): the symbol ( x ) that indicates multiplication – In multiplication we write 2 x 3 = 6 and say two times three equals six (or two multiplied by three equals six).
triangle (noun): see shapes
TRIGONOMETRY (noun): the branch of mathematics that studies triangles, their angles and lengths etc – Astronomers use trigonometry to figure out the distance of stars from earth.
two-dimensional, 2D (adjective): having two dimensions: length, breadth. See 3D – Flat shapes like a triangle or a piece of paper are basically 2D.
volume (noun): the amount of space occupied by any three-dimensional object, or that a three-dimensional object can contain; capacity – Three-dimensional objects have volume whereas two-dimensional objects have area.
whole number (noun): integer; any number without fractional or decimal parts – 7 and 51 are whole numbers but 7½ and 51.3 are not.