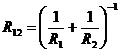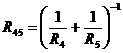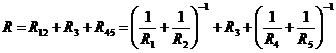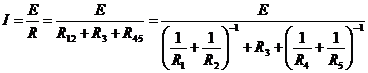Математическое моделирование в excel задания

Цели урока:


  1. Обучающие: Повторить и закрепить навыки
    работы в MS Excel; научить применять современное
    программное обеспечение в решении
    математических задач, строить математические
    модели в среде MS Excel.


  2. Развивающие: Развивать: практические и
    исследовательские навыки по составлению моделей
    в электронных таблицах, научное мировоззрение
    через связь информационных технологий с другими
    школьными предметами, логическое и
    алгоритмическое мышление, аналитические
    способности, внимание, память.


  3. Воспитательные: Воспитание общей и
    информационной культуры, творческого подхода к
    работе, желания экспериментировать,
    самостоятельности в учебном труде.

Тип урока: Комплексного применения
знаний, обобщения и систематизации.

Программное и техническое обеспечение
урока:


  • компьютеры с ОС MS Windows XP;


  • пакет Microsoft Office;
  • мультимедийный проектор

Время проведения урока: один из
последних уроков в разделе «Информационное
моделирование».

План урока: (40 минут)

  1. Орг. момент. (1 мин)
  2. Проверка и актуализация знаний. / Тестирование
    по теме (4 мин)./ Разминка (5 мин)
  3. Теоретическая часть. (10 мин)
  4. Практическая часть. (10 мин)
  5. Самостоятельная работа. (8 мин)
  6. Подведение итогов. Д/з (2 мин)

Ход урока:

1. Организационный момент.

Приветствие, проверка присутствующих.

С помощью проектора демонстрируется
на экране первый слайд презентации. Приложение 1

Сообщается тема урока: «Математическое
моделирование в среде электронных таблиц MS Excel
«.Озвучить цели и план урока.

2. Актуализация опорных знаний.

Пройденная нами тема «Электронные
таблицы»– одна из наиболее практически
значимых, востребованных, после текстового
редактора Word и его возможностей. Но электронные
таблицы не только позволяют автоматизировать
расчеты, но и являются эффективным средством
моделирования различных вариантов и ситуаций.
Меняя значения исходных данных, можно проследить
за изменением получаемых результатов и из
множества вариантов решения задачи выбрать
наиболее подходящий.

Перечислите, что вы научились делать,
изучая табличный процессор MS Excel?

– выполнять вычислительные операции
при помощи формул;

– составлять таблицы;

– строить графики и диаграммы.

Тестирование по теме «Электронные
таблицы».

Домашним заданием было повторить весь
изученный материал по теме «Электронные
таблицы». Чтобы проверить домашнее задание, я
предлагаю Вам ответить на вопросы электронного
теста. (Дети уже знакомы с работой системы
дистанционного обучения MyTestServer 1.1) Приложение 2

Перед началом работы учащиеся
прослушивают инструкцию по выполнению теста.

Тест состоит из 5 вопросов. Дается
только одна попытка, будьте внимательны, не
торопитесь. Время на тест 3 минуты.

После завершения тестирования каждому
ученику системой выставляется оценка, которую он
видит на экране своего монитора.

Сегодня на уроке мы будем использовать
электронные таблицы с их мощным вычислительным
потенциалом для решения математических задач –
построим математическую модель в среде MS Excel и
проведем небольшое исследование.

А для этого вспомним основные понятия
по теме “моделирование” (проводим устную разминку).

Вопросы разминки: Приложение 1

Моделирование – метод познания
окружающего мира, состоящий..

Модель – это объект, который
используется в качестве..

Различают ____________и ___________модели.

Натурные модели – это…

Информационные модели – это…

Основными видами информационных
моделей являются:_________ ,_________, __________.

А как вы думаете, математическая
модель к какому виду принадлежит?

Математическая модель – это модель,
построенная с использованием…

Приведите пример знаковой
информационной модели, рассматриваемой на
уроках математики.

Основным языком информационного
моделирования в науке является язык математики.

3. Теоретическая часть.

Какую бы жизненную задачу ни взялся
решать человек, первым делом он строит модель
заданного объекта. Очень часто задачи связаны с
потребностями человека.

Сегодня нам предстоит решить
следующую задачу:

Задача 1: Приложение
1

У маленького Васи есть небольшой
бассейн во дворе. Иногда Вася ходит к речке и
приносит воду в бассейн в небольшой цистерне
цилиндрической формы. Известны ширина ШБ, высота
ВБ, ДБ бассейна и объем цистерны Об Ц. Сколько раз
Васе нужно сходить к речке за водой, чтобы
наполнить бассейн наполовину?

Этот текст можно рассматривать как
словесную модель бассейна.

Постановка задачи: выяснение
условий

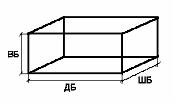
Какую форму может иметь бассейн?
(ответы детей).

А какой формы он в нашей задаче?– В
форме куба или параллелепипеда, потому, что даны
его параметры: ширина, высота, длина. А что еще нам
известно?

– объем цистерны.

Давайте попробуем решить задачу:
узнаем сколько раз (N) Васе нужно сходить к речке
за водой, чтобы наполнить бассейн наполовину.

Что для этого нужно знать?

– сколько цистерн воды помещается в
бассейн.

А как это узнать?

– определить объем бассейна (Об Б)

– сравнить половину объема бассейна и
объем цистерны (Об Б / Об Ц / 2).

4. Практическая часть.

Карточка – задание №1 Приложение 3

Задание для практической работы: Скопировать
в свою папку файл – шаблон Excel Приложение 4

Назвать лист номером задачи «Задача
1» (редактирование названия – двойной щелчок
мыши на «Лист 1»).

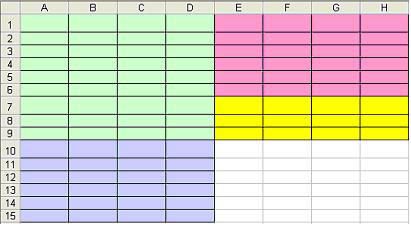
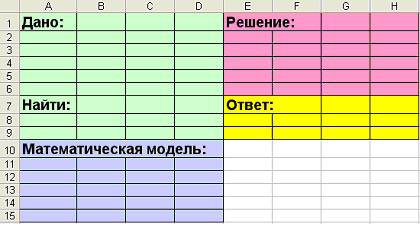
Оформить на листе решения разделы «Дано«,
«Найти«, «Математическая модель«,
«Решение«, «Ответ» (по образцу):

В ячейках А1и А7 напечатать
слова «Дано» и «Найти«.

Объединить ячейки А10, В10 и С10,
ввести текст: «Математическая модель«

Объединить ячейки Е1 и F1,
напечатать слово «Решение«.

В ячейку Е7 – «Ответ«.

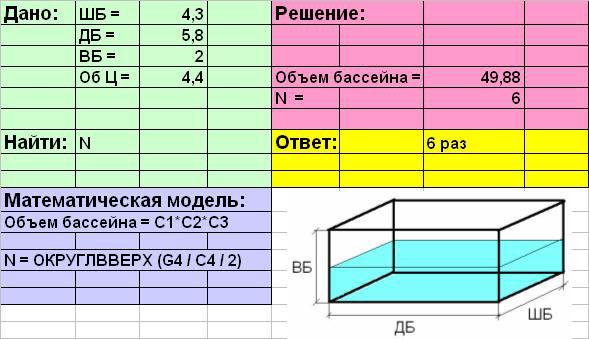
 Заполнить таблицу начальными
данными.

В ячейки В1:В4 ввести текст: ШБ=;
ДБ=; ВБ=; Об Ц=.

В ячейки С1:С4; ввести
соответствующие значения параметров: 4,3; 5,8; 2; 4,5.

Для наглядности, если есть
возможность, можно построить графическую модель
(рисунок задаче) в Painte и скопировать ее в
электронную таблицу или нарисовать бассейн
непосредственно в Excel.

Далее заполнить раздел таблицы
«Математическая модель».

Объединить ячейки А11, В11 и С11,
ввести формулы (тип данных – текст) в раздел
(пробел перед знаком «=»). «Объем бассейна
=С1*С2*С3«

Объединить ячейки А13, В13 и С13
и ввести текст «N = ОКРУГЛВВЕРХ(G4 / C4 / 2)«.
(для получения целого числа используем функцию
округления ОКРУГЛВВЕРХ)

В разделе «Решение»
создать сетку вычислений:

– Обозначить искомые и промежуточные
величины.

– Объединить ячейки Е4 и F4,
ввести текст: «Объем бассейна =«. В ячейку
Е5 – «N =«(тип данных – текст).

В ячейки G4 и G5; ввести
соответствующие формулы (тип данных – формулы):
=С1*С2*С3;

Используем функцию округления
дробного числа до целого:

Вставка-функция – математические –
ОКРУГЛВВЕРХ – число разрядов выбираем «0«.

=ОКРУГЛВВЕРХ(G4 / C4 / 2)

В разделе «Ответ» запишем
искомый результат в ячейку G7 (тип данных –
текст).

 Проведем небольшое исследование:

Вопрос: Сколько раз Васе нужно будет
сходить к речке за водой, если он возьмет
цистерну емкостью 5,6 литров; 4 литра; 3,3
литра?

Меняем в ячейке С4 значение на 5,6
и электронные таблицы автоматически производят
пересчет.

Создадим таблицу значений Об Ц и
будем заносить в нее результаты вычислений N.

Введем в ячейку А20 и В2 текст
«Об Ц» и » N«. Заполним таблицу
данными.

Об Ц

N

3,3

8

4

7

4,5

6

5,6

5

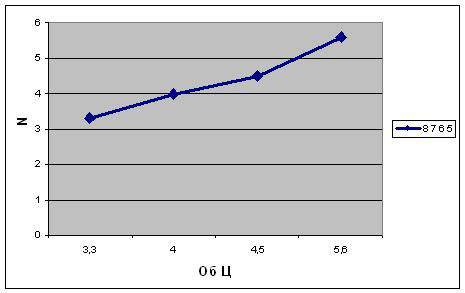
Для графического представления
результатов выделить диапазон А21: В24,
построить график функции, отредактировать его.

 Анализ полученных результатов.

5. Самостоятельная работа.

Задание для самостоятельной разработки:

Карточка – задание №2 Приложение
3

Задача 2. Пешеход начал движение из
начала координат со скоростью V=0,6 м/с.
Найдите, какой путь S прошел пешеход за одну
минуту t после начала движения, если он
двигался равномерно.

Постановка задачи: выяснение
условий

Скажите, что мы будем моделировать? –

– движение

Какие виды движения вы знаете? (ответы
детей)

Какое движение рассматривается в
нашей задаче?

– равномерное. Приложение 1

Давайте вспомним формулу расчета
скорости: V=s/t– отсюда s=V*t

Технология моделирования:

  1. Назвать лист номером задачи «Задача 2»
    (редактирование названия – двойной щелчок мыши
    на «Лист 2»).
  2. Выделить расчетную таблицу на листе «Задача1»
    и скопировать ее на лист «Задача 2«.
  3. Заполнить таблицу новыми начальными данными.
  4. Ввести формулу (тип данных – текст) в раздел
    «Математическая модель» (пробел перед
    знаком «=»).
  5. Ввести фоpмулу (тип данных – формулы) в
    раздел «Решение«.
  6. В разделе «Ответ» записать искомый
    результат (тип данных – текст).


  7. Создать таблицу значений t и занести в нее
    результаты вычислений S. Заполнить таблицу
    данными.
  8. Для графического представления результатов
    выделить область аргументов и функций, построить
    график зависимости пути S от времени при t=40;60;90,
    отредактировать график.

6. Итог урока.


Сегодня на уроке мы узнали, как можно
использовать электронные таблицы в решении
математических задач, научились строить
математические модели в. среде MS Excel

Домашним заданием будет: самим
придумать задачу, разработать ее математическую
модель.

У кого есть вопросы по пройденному материалу?

Спасибо за работу. Вы сегодня молодцы. Можете
быть свободны.

Источник

Урок-практикум по теме «Построение и исследование математической модели с помощью электронной таблицы Excel»

Цели урока: проверка знаний учащихся и формирование умений и навыков в работе с электронными таблицами при моделировании математических задач, побуждение интереса к изучению предмета.

Тип урока: Комбинированный (применение знаний и умений, обобщение и систематизация знаний)

Задачи урока:

Учебная:

  • закрепление знаний по теме «Моделирование»

  • закрепление знаний и навыков проведения расчетов Excel

  • применение диаграмм при исследовании математической модели.

Развивающая:

  • развитие алгоритмического и логического мышления. Научить выделять главное при решении задач.

Воспитательная:

  • на примере решения на компьютере конкретной задачи формировать умение прогнозировать и предвидеть результат своей работы.

  • воспитание информационной культуры.

Материально – техническая база: компьютеры с лицензионным программным обеспечением, проектор, демонстрационный экран, карточки с индивидуальными дифференцированными заданиями (карточки красного цвета — на оценку 5; карточки розового цвета – на 4)

Подготовительный этап:

  • на предыдущем уроке было задано домашнее задание по теме «Моделирование» Учащиеся должны знать определение модели, моделирования, формы представления моделей, выполнять расчеты в среде электронных таблиц, строить диаграммы, анализировать полученные результаты, применять знания по работе в среде электронных таблиц,

  • карточки с индивидуальными заданиями.

План урока:

  1. Организационный момент (Цели и задачи урока)

  2. Повторение изученного материала в виде фронтального опроса, с демонстрацией вопросов с помощью проектора

  3. Объяснение нового материала и самостоятельная работа учащихся на компьютерах.

  4. Выполнение индивидуальных заданий в редакторе Excel.

  5. Подведение итогов.

  6. Домашнее задание.

Ход урока:

I Организационный момент

Учитель:

Здравствуйте, ребята! Сегодня мы с вами в очередной раз убедимся в том, что человек создаёт модели с целью их использования и изучения, на нашем уроке помощником в исследовании модели будет электронная таблица Excel. Модели, позволяют представить в наглядной форме объекты и процессы, недоступные для непосредственного восприятия. Давайте вспомним и что такое модели, какие они бывают и возможности программы Excel.

II Фронтальный опрос. На экране демонстрируются вопросы, дети последовательно на них отвечают.

III Изложение нового материала и самостоятельная работа учащихся на компьютерах.

Проводится одновременно с работой учеников на компьютерах синхронно с учителем (помогают учителю два самых сильных ученика класса). Учитель свои действия показывает на демонстрационном экране.

Учитель: Сегодня на уроке мы с вами строим математическую модель с помощью редактора Excel. Для примера рассмотрим решение системы уравнений.

Из курса математики нам известно, что корнями уравнения являются значения точек пересечения графика функции с осью абсцисс. Решением системы уравнений будут координаты точек пересечения графиков функций. Такой метод нахождения корней называется графическим. В программе Excel, с помощью Мастера диаграмм можно строить практически любые графики. И мы сейчас вместе найдём корни системы уравнений графическим способом.

Д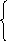ана система уравнений:

Y — X2 = 0

Y – 2X = 9

1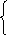) Преобразуем данную систему:

Y = X2

Y = 2X + 9

Отобразим графики обеих функций, используя диаграмму. Вы знаете, что для построения диаграммы необходимо построить таблицу:

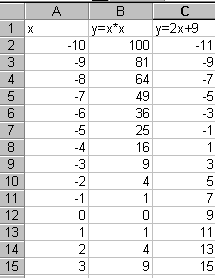
а. первая строка — заголовки

б. в ячейку А2 занесем начальное значение аргумента Х = -10

в. В ячейку А3 заносим формулу =А2 + 1 и копируем её до ячейки А23

г. В ячейку В2 заносим формулу =А2 * А2 и копируем до ячейки В23

д. ячейку С2 заносим формулу = 2 * А2 + 9

С помощью мастера диаграмм выберем тип диаграммы Точечная и построим диаграмму первоначальной оценки решений.

На диаграмме видно, что оба графика имеют точки пересечения – координаты этих точек и есть решения системы. Так как шаг изменения аргумента был достаточно велик, то мы получили приближённые значения решений. Уточним их, построив два графика в интервалах от –3 до 0, где находится первое решение, и от 3 до 5 – где находится второе с шагом 0,1 для более точного построения. Составим новые таблицы:

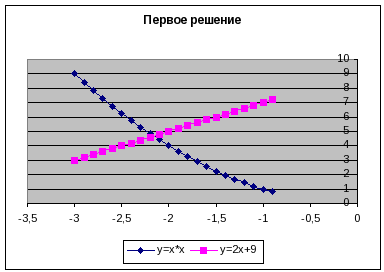
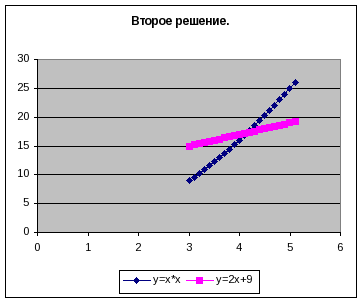
Для первого решения.

Для второго решения.

Решением нашей системы будут координаты точек пересечения графиков:

Х1 = 4,2 У1 = 4,8 Х2 = 4,2 У2 = 17, 5

Как вы уже поняли, графическое решение системы даёт приблизительные результаты, но программа Excel даёт возможность графически решить практически любое уравнение, что мы и сделаем, получив индивидуальные задания.

  2. х = 2 – у

3х — 2у – 11 =

Ответ: х = 3 у = -1

у – 2х = 1

6х – у = 7

Ответ: х = 2 у = 5

7х – 3у = 13

х – 2у = 5

Ответ: х = 1 у = -2

х + у = 6

3х – 5у = 2

Ответ: х = 4 у = 2

у – х = 20

2х – 15у = -1

Ответ: х = -23 у = -3

х2 + у = 14

у– х = 8

Ответ: х1 = -3 у1 = 5

х2 = 2 у2 = 10

у2 – х = -1

х = у + 3

Ответ: х1 = 5 у1 = 2

х2 = 2 у2 = -1

х = 3 – у

– х = 39

Ответ: х1 = 10 у1 = -7

х2 = -3 у2 = 6

у = х – 1

х2 – 2у = 26

Ответ: х1 = -4 у1 = -5

х2 = 6 у2 = 5

у = 1 + х

х + у2 = -1

Ответ: х1 = -1 у1 = 0

х2 = -2 у2 = -1

Фронтальный опрос.

  1. Что такое модель?

Ответ: модель – это некий новый объект, который отражает существенные особенности изучаемого объекта, явления или процесса.

2) Приведите примеры моделей объекта Человек

Ответ: манекен, скелет, фото, рисунок, паспорт, запись о ребёнке в журнале…

  1. Что такое моделирование?

Ответ: это метод познания, состоящий в создании и исследовании моделей.

  1. На какие виды делятся объекты?

Ответ: Материальные и нематериальные (информационные )

  1. Приведите примеры информационных моделей.

Ответ: схемы, рисунки, математические формулы, графики…

6) Дана электронная таблица:

А

В

С

D

1

1

3

4

2

4

2

5

3

3

1

2

В ячейку D1  введена формула, вычисляющая выражение по формуле

= (A2+B1-C1). Какое значение появится в ячейке D1

Ответ: 3

7) Чему равно значение в ячейке С3 электронной таблицы

А

В

С

Ответ: 15

1

3

9

 =В2+$A$1

2

7

15

3

3

45

4

 =C1-C2

8) Дана электронная таблица:

А

В

С

D

1

1

3

4

8

2

3

2

5

3

7

1

2

Значение в ячейке С1 заменили на 7. В результате этого значение в ячейке D1 автоматически изменилось на 11. Можно предположить что в ячейке D1 ……

Ответ: записана формула  СУММ(А1:С1)

9) Дан фрагмент электронной таблицы:

А

В

С

1

3

2

5

2

7

1

3

4

4

Значение ячейки С1 вычисляется по формуле =В1+$A$1

Какое значение появиться в ячейке с3 после копирования формулы?

Ответ: 7

10) При помощи какой команды меню можно построить диаграммы и графики в Excel?

Ответ: с помощью кнопки вызова Мастера диаграмм

Самоанализ урока:

Урок построен на деятельной основе с применением проблемно – исследовательской технологии, что обеспечивает развитие познавательной деятельности учащихся с помощью проблемных заданий, развитие логического мышления детей. Ученики пытаются решить стандартные математические задачи нестандартным способом – применяя современные компьютерные технологии. Этим уроком мы достигаем поставленных целей: не только повторяем и закрепляем материал, но и побуждаем интерес к изучению предмета и показываем его практическое применение в реальной жизни. На уроке ученики показали хорошее владение компьютером, подготовку домашнего задания и с неподдельным интересом выполняли индивидуальные задания.

Источник

Построение математической модели задачи и ее решение в MS Excel

Задание 1

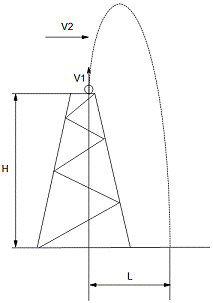
Шарик бросают вертикально вверх с верхней площадки башни со скоростью V1.
Ветер, дующий со скоростью V2,
относит его в сторону.

Требуется:

·  создать математическую модель движения шарика от начала падения до удара
о землю;

·        подготовить компьютерную реализацию математической модели в
среде электронных таблиц.

В ходе проведения компьютерных экспериментов определить:

·  как влияет изменение скорости V1 (шаг изменений 1 м/с) на дальность
падения L;

·        как влияет изменение высоты Н (шаг изменений 1 м) на время
падения t;

·        как влияет высота Н (шаг изменений 1 м) на дальность падения L.

Исходные данные

Номер задания

Скорость V2, м/с

Высота Н, м

Скорость V1, м/с

начальная

конечная

начальная

конечная

7

1,8

6

18

10

24

Решение

Построим модель движения шарика.

) Сначала шарик совершает равнозамедленное движение вверх.

Максимальная высота подъема:

h = V12/(2g)

Время подъема шарика:

t1 = V1/g

) Свободное падение с высоты H+h. Применяя уравнение свободного
падения, получаем (H+h) = gt22/2, где t2 —
время падения.

Выражая t2, получаем:

t2 = .

)
Время шарика в пути

t = t1 + t2 = V1/g +

)
Учитываем боковой ветер. Расстояние L, на которое сместится шарик
после падения, равно:

L = V2t.

Математическая
модель построена.

Строим
модель в MS Office Excel
(лист Задание1).

)
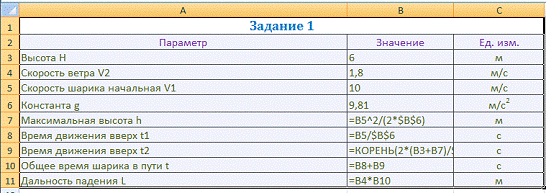
Организуем расположение данных и формул:

математический модель
задача excel

Результат вычислений с заданными исходными значениями:

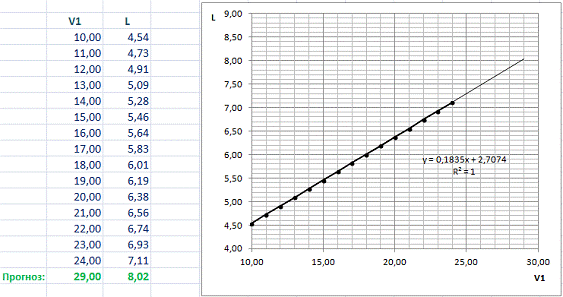
) Проанализируем, как влияет изменение скорости V1 (шаг изменений 1 м/с)
на дальность падения L.
Результаты анализа представим в графическом виде.

Как видим, зависимость дальности падения от начальной скорости линейная.
Достоверность аппроксимации равна 1.

Уравнение зависимости: y =
0,1835x + 2,7024.

Для прогноза значений дальности падения L вне диапазона значений скорости V1 применим полученное уравнение и вычислим L, например при V1 = 29 м/с.

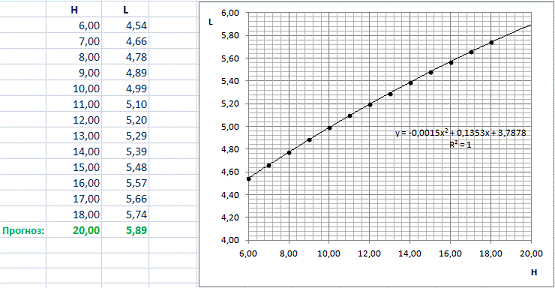
) Проанализируем, как влияет изменение высоты Н (шаг изменений 1 м) на
время падения t.

Аппроксимация графика привела к квадратичной зависимости.

Уравнение зависимости: y =
-0,0015×2 + 0,1353x + 3,7878

Использование этого уравнения позволяет прогнозировать значения t вне диапазона H.

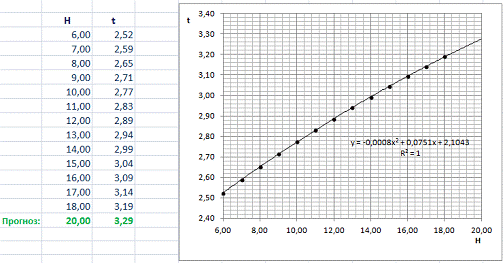
) Проанализируем, как влияет высота Н (шаг изменений 1 м) на дальность
падения L.

Аппроксимация графика привела к квадратичной зависимости.

Уравнение зависимости: y =
-0,0008×2 + 0,0751x + 2,1043

Использование уравнения, приведенного на графике, позволяет
прогнозировать значения L вне
диапазона H.

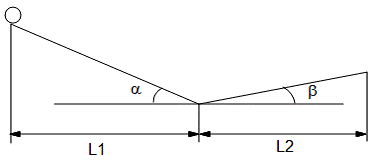
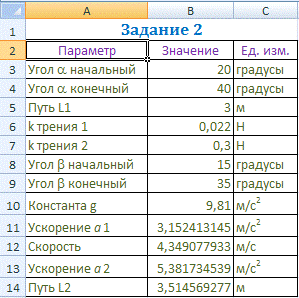
Задание 2

Дана наклонная плоскость, по которой скатывается шарик:

Угол a начальный 200

Угол a конечный 400

L1 = 3
м

kтр1 =
0,022

kтр2 =
0,3

Угол b начальный 150

Угол b конечный 350

Сопротивлением воздуха пренебрегаем.

На начальном этапе шарик движется по наклонной плоскости длиной L1, расположенной под углом a. Коэффициент трения при движении
шарика по наклонной плоскости описывается величиной kтр1. Затем шарик движется по наклонной плоскости вверх.
Коэффициент трения kтр2.

При
спуске с наклонной плоскости и отсутствии дополнительных сил ускорение равно a1 = g(sina — kтр1 · cosa), где g — ускорение свободного падения; kтр1
— коэффициент трения. Поскольку начальная скорость шарика равна нулю, скорость
шарика v = a1t. Путь, который пройдёт шарик, равен L1 = a1t2/2.
Отсюда t = . Значит,
скорость шарика в момент прохождения отрезка пути L1 составит v = a1t = .

Далее
шарик движется по наклонной плоскости вверх. При подъеме по наклонной плоскости
и отсутствии дополнительных сил a2 = g(sinb + kтр2 · cosb), где g — ускорение свободного падения; kтр2
— коэффициент трения. Поскольку у шарика уже есть начальная скорость v,
пройденный путь составит: L2 = vt2 + a2t22/2. Нам необходимо найти максимальный пройденный
путь. В момент остановки шарика ускорение равно 0. Время подъёма. t2 = v / a2.
Тогда пройденный путь равен L2 = vt2 = v2/a2.

Математическая
модель построена.

Строим
модель в MS Office Excel
(лист Задание2).

)
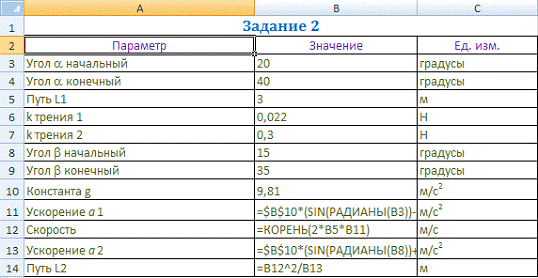
Формулы ячеек:

Результат
вычислений с начальными значениями:

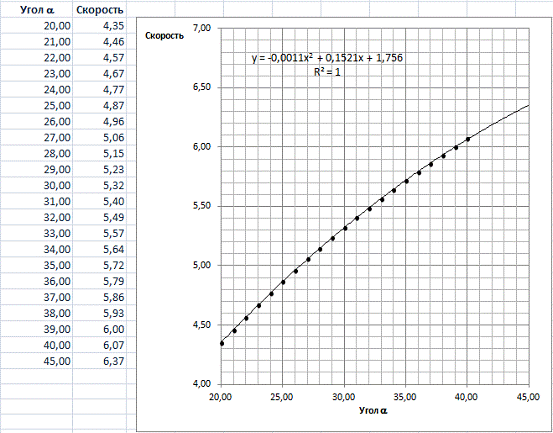
2)
Определим, как влияет изменение значения угла a на скорость
движения шарика в момент нахождения его в конце первой наклонной плоскости.

В
данном случае зависимость получилась квадратичная (полиномиальная второй
степени).

Уравнение
зависимости: y = -0,0011×2 + 0,1521x + 1,756

Использование
уравнения позволяет прогнозировать значения скорости при других углах a. Например, при a = 450 скорость равна 6,37 м/с.

)
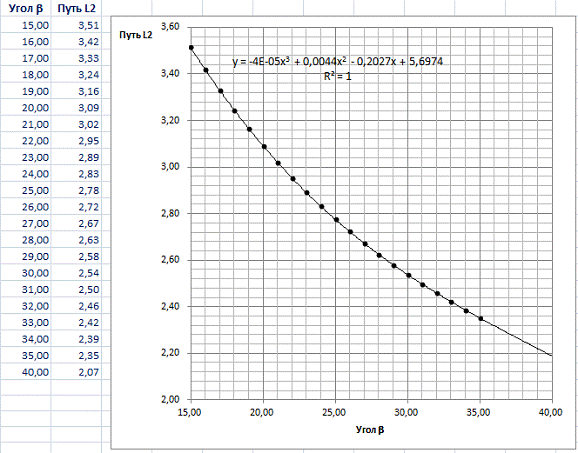
Определим, как влияет изменение значения угла b на длину
пробега шарика L2.

В
данном случае зависимость получилась полиномиальная 3 степени.

Уравнение
зависимости: y = -4×10-5×3 +
0,0044×2 — 0,2027x + 5,6974.

Использование
уравнения позволяет прогнозировать значения пути при других углах b. Например, при b = 400 скорость равна 6,37 м/с.

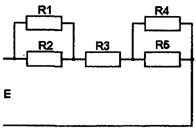
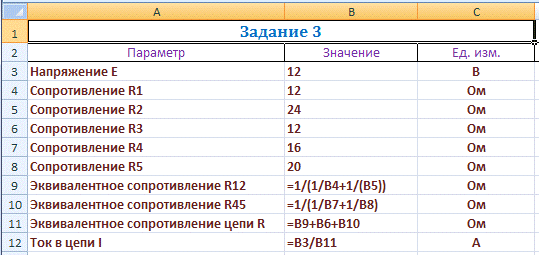
Задание 3

Дана электрическая цепь:

Исходные данные:

Е = 12 В; R1 = 12 Ом; R2 = 24 Ом

R3 =
12 Ом; R4 = 16 Ом; R5 = 20 Ом.

Требуется:

·  создать математическую модель цепи;

·        определить, как влияет изменение значения R4 (таблица) на ток, протекающий в
цепи, с построением диаграммы и определением уравнения зависимости;

·        спрогнозировать по полученному уравнению величину тока при R4 = 150 Ом;

·        определить, как влияет изменение значения R2 (таблица) на ток, протекающий в
цепи, с построением диаграммы и определением уравнения зависимости;

·        спрогнозировать по полученному уравнению величину тока при R2 = 110 Ом;

·        подобрать значение R1, при котором значение протекающего в цепи тока уменьшится на 15 %, и
записать его в одну из ячеек;

·        подобрать значение R3, при котором падение напряжения на нём увеличится на 10 %, и записать
его в одну из ячеек.

Таблица значений сопротивления (Ом):

Решение

Строим математическую модель цепи.

Резисторы 1, 2 связаны параллельно, для них эквивалентное сопротивление
будет

Резисторы
4, 5 связаны параллельно, для них эквивалентное сопротивление будет

Участки
12, 3 и 45 подключены последовательно.

Эквивалентное
сопротивление цепи:

Ток
в цепи определяется законом Ома:

Математическая
модель построена.

Строим
модель в MS Office Excel
(лист Задание3).

)
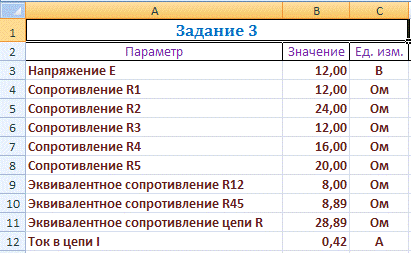
Формулы:

Расчеты по формулам приводят к следующим результатам:

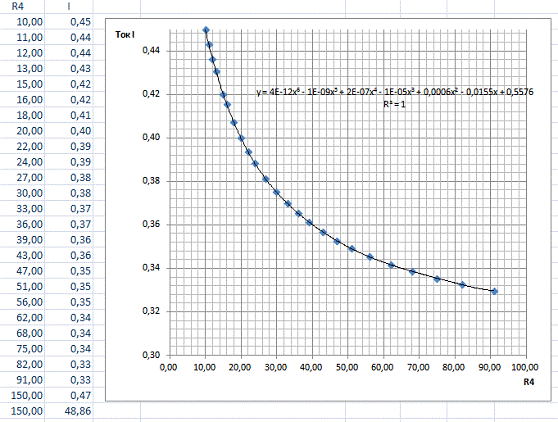
) Определим, как влияет изменение значения R4 (таблица) на ток, протекающий в цепи. Результаты анализа
представим в графическом виде.

Наиболее точное уравнение аппроксимации является полиномом 6 степени: y = 4×10-12×6 — 10-9×5 + 2×10-7×4 — 1×10-5×3 + 0,0006×2 — 0,0155x +
0,5576.

С помощью этого уравнения можно предсказать величину тока при других значениях
R4. Ток в цепи убывает с ростом R4, стремясь к определенному пределу.

Предсказываемое программой Excel
уравнение аппроксимации нельзя использовать для прогноза значения параметра,
сильно выходящего за аппроксимируемый диапазон. Так, попытка спрогнозировать
ток в цепи при R4 = 150 Ом
приводит к неправильному значению силы тока. В этом случае следует пользоваться
расчетной формулой.

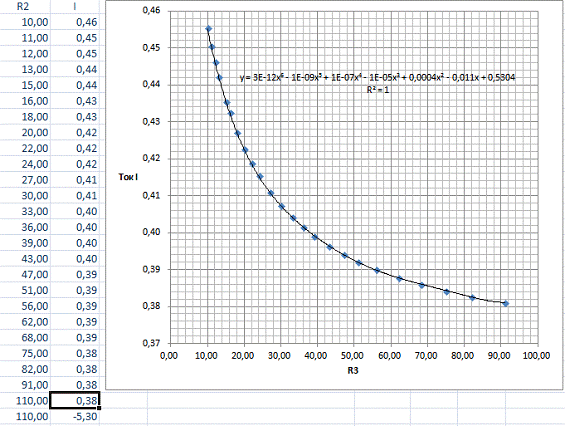
) Определим, как влияет изменение значения R2 (таблица) на ток, протекающий в цепи. Результаты анализа
представим в графическом виде.

Наиболее точное уравнение аппроксимации является полиномом 6 степени:

y = 3×10-12×6 — 1×10-9×5 + 1×10-7×4 — 1×10-5×3 + 0,0004×2 — 0,011x +
0,5304.

Ток в цепи убывает с ростом R2, стремясь к определенному пределу.

При R2 = 110 Ом это уравнение даёт прогноз
-5,30 Ом, что неверно. Следовательно, необходимо пользоваться точными
расчетными формулами, поскольку величина 110 Ом выходит за границы диапазона
сопротивлений.

) Далее необходимо узнать значение R1, при котором ток в цепи снизится на 15%. Воспользуемся
подбором параметра.

Для того, чтобы ток в цепи снизился на 15%, нужно установить
сопротивление R1 = 30,26 Ом.

) Определим значение R3,
при котором падение напряжения на нём увеличится на 10%.

Падение напряжение на R3
равно произведению общего тока I на R3:

E2 = IR3

Воспользуемся инструментом «Поиск решения».

Список
литературы

1. Кашаев С.
Офисные решения с использованием Microsoft Excel 2007 и VBA. — СПб.: Питер,
2009. — 352 с.

2.      Леонов
В. Функции Excel 2010. — СПб.: Эксмо, 2011. — 560 с.

.        Мачула
В. Г. Excel 2007 на практике. — Ростов-на-Дону: Феникс, 2009. — 160 с.

Источник

Понравилась статья? Поделить с друзьями:
  • Математические функции в excel что это такое
  • Математический шрифт для word
  • Математические функции в excel степень
  • Математический функции в excel с примером если
  • Математические функции в excel среднее значение