Надстройка с несколькими пользовательскими функциями вычислительной математики.
Надстройка предназначена для тех пользователей, кто хочет:
- интерполировать табличные данные;
- находить корни уравнения;
- вычислять производные;
- численно интегрировать;
- аппроксимировать экспериментальные данные
Внимание: 21 марта 2020 года выложена новая версия надстройки.
Во вложении к статье — надстройка NMFNC.xla, и файл справки NMFNC_Help.xlsb с примерами.
(для тестирования: извлеките оба файла в одну папку, запустите файл надстройки, затем — файл справки)
Автор: С.М. (реквизиты для связи с автором — в файле справки)
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Еще…Меньше
Если вам нужно разработать сложный статистический или инженерный анализ, вы можете сэкономить время и этапы с помощью этого средства. Вы предоставляете данные и параметры для каждого анализа, а средство использует соответствующие статистические или инженерные функции для вычисления и отображения результатов в выходной таблице. Некоторые средства создают диаграммы в дополнение к выходным таблицам.
Функции анализа данных можно применять только на одном листе. Если анализ данных проводится в группе, состоящей из нескольких листов, то результаты будут выведены на первом листе, на остальных листах будут выведены пустые диапазоны, содержащие только форматы. Чтобы провести анализ данных на всех листах, повторите процедуру для каждого листа в отдельности.
Ниже описаны инструменты, включенные в пакет анализа. Для доступа к ним нажмите кнопкуАнализ данных в группе Анализ на вкладке Данные. Если команда Анализ данных недоступна, необходимо загрузить надстройку «Пакет анализа».
-
Откройте вкладку Файл, нажмите кнопку Параметры и выберите категорию Надстройки.
-
В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
Если вы используете Excel для Mac, в строке меню откройте вкладку Средства и в раскрывающемся списке выберите пункт Надстройки для Excel.
-
В диалоговом окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
-
Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
-
Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
-
Примечание: Чтобы включить Visual Basic для приложений (VBA) для надстройки «Надстройка анализа», вы можете загрузить надстройку VBA так же, как и надстройку «Надстройка анализа». В поле Доступные надстройки выберите «Надстройка анализа — VBA».
Существует несколько видов дисперсионного анализа. Нужный вариант выбирается с учетом числа факторов и имеющихся выборок из генеральной совокупности.
Однофакторный дисперсионный анализ
Этот инструмент выполняет простой анализ дисперсии данных для двух или более выборок. Анализ дает проверку гипотезы о том, что каждая выборка взята из одного и того же распределения вероятности на основе альтернативной гипотезы о том, что для всех выборок распределение вероятности не одно и то же. Если есть только два примера, можно использовать функцию T.ТЕСТ. В более чем двух примерах нет удобного обобщения T.ВМЕСТОэтого можно использовать модель Anova для одного фактора.
Двухфакторный дисперсионный анализ с повторениями
Этот инструмент анализа применяется, если данные можно систематизировать по двум параметрам. Например, в эксперименте по измерению высоты растений последние обрабатывали удобрениями от различных изготовителей (например, A, B, C) и содержали при различной температуре (например, низкой и высокой). Таким образом, для каждой из 6 возможных пар условий {удобрение, температура}, имеется одинаковый набор наблюдений за ростом растений. С помощью этого дисперсионного анализа можно проверить следующие гипотезы:
-
Извлечены ли данные о росте растений для различных марок удобрений из одной генеральной совокупности. Температура в этом анализе не учитывается.
-
Извлечены ли данные о росте растений для различных уровней температуры из одной генеральной совокупности. Марка удобрения в этом анализе не учитывается.
Извлечены ли шесть выборок, представляющих все пары значений {удобрение, температура}, используемые для оценки влияния различных марок удобрений (для первого пункта в списке) и уровней температуры (для второго пункта в списке), из одной генеральной совокупности. Альтернативная гипотеза предполагает, что влияние конкретных пар {удобрение, температура} превышает влияние отдельно удобрения и отдельно температуры.
Двухфакторный дисперсионный анализ без повторений
Этот инструмент анализа применяется, если данные можно систематизировать по двум параметрам, как в случае двухфакторного дисперсионного анализа с повторениями. Однако в таком анализе предполагается, что для каждой пары параметров есть только одно измерение (например, для каждой пары параметров {удобрение, температура} из предыдущего примера).
Функции CORREL и PEARSON вычисляют коэффициент корреляции между двумя переменными измерения, если для каждой переменной наблюдаемы измерения по каждому из N-объектов. (Любые отсутствующие наблюдения по любой теме вызывают игнорирование в анализе.) Средство анализа корреляции особенно удобно использовать, если для каждого субъекта N имеется более двух переменных измерения. Она содержит выходную таблицу — матрицу корреляции, которая показывает значение CORREL (или PEARSON),примененного к каждой из возможных пар переменных измерения.
Коэффициент корреляции, как и ковариана, — это мера степени, в которой две единицы измерения «различаются». В отличие от ковариации коэффициент корреляции масштабирован таким образом, что его значение не зависит от единиц измерения, выраженных в двух переменных измерения. (Например, если двумя переменными измерения являются вес и высота, то значение коэффициента корреляции не изменяется, если вес преобразуется из фунта в фунты.) Значение любого коэффициента корреляции должно быть включительно от -1 до +1 включительно.
Корреляционный анализ дает возможность установить, ассоциированы ли наборы данных по величине, т. е. большие значения из одного набора данных связаны с большими значениями другого набора (положительная корреляция) или наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная корреляция), или данные двух диапазонов никак не связаны (нулевая корреляция).
Средства корреляции и коварианс могут использоваться в одном и том же параметре, если у вас есть N различных переменных измерения, наблюдаемые для набора людей. Каждый из инструментов корреляции и ковариции дает выходную таблицу — матрицу, которая показывает коэффициент корреляции или коварианс между каждой парой переменных измерения соответственно. Разница заключается в том, что коэффициенты корреляции масштабироваться в зависимости от -1 и +1 включительно. Соответствующие ковариансы не масштабироваться. Коэффициент корреляции и коварианс — это показатели степени, в которой две переменные «различаются».
Инструмент Ковариана вычисляет значение функции КОВАРИАНА. P для каждой пары переменных измерения. (Прямое использование КОВАРИАНА. P вместо ковариана является разумной альтернативой, если есть только две переменные измерения, то есть N=2.) Запись в диагонали выходной таблицы средства Коварица в строке i, столбце i — коварианс i-й переменной измерения. Это только дисперсия по численности населения для этой переменной, вычисляемая функцией ДИСПЕРС.P.
Ковариационный анализ дает возможность установить, ассоциированы ли наборы данных по величине, то есть большие значения из одного набора данных связаны с большими значениями другого набора (положительная ковариация) или наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная ковариация), или данные двух диапазонов никак не связаны (ковариация близка к нулю).
Инструмент анализа «Описательная статистика» применяется для создания одномерного статистического отчета, содержащего информацию о центральной тенденции и изменчивости входных данных.
Инструмент анализа «Экспоненциальное сглаживание» применяется для предсказания значения на основе прогноза для предыдущего периода, скорректированного с учетом погрешностей в этом прогнозе. При анализе используется константа сглаживания a, величина которой определяет степень влияния на прогнозы погрешностей в предыдущем прогнозе.
Примечание: Для константы сглаживания наиболее подходящими являются значения от 0,2 до 0,3. Эти значения показывают, что ошибка текущего прогноза установлена на уровне от 20 до 30 процентов ошибки предыдущего прогноза. Более высокие значения константы ускоряют отклик, но могут привести к непредсказуемым выбросам. Низкие значения константы могут привести к большим промежуткам между предсказанными значениями.
Двухвыборочный F-тест применяется для сравнения дисперсий двух генеральных совокупностей.
Например, можно использовать F-тест по выборкам результатов заплыва для каждой из двух команд. Это средство предоставляет результаты сравнения нулевой гипотезы о том, что эти две выборки взяты из распределения с равными дисперсиями, с гипотезой, предполагающей, что дисперсии различны в базовом распределении.
С помощью этого инструмента вычисляется значение f F-статистики (или F-коэффициент). Значение f, близкое к 1, показывает, что дисперсии генеральной совокупности равны. В таблице результатов, если f < 1, «P(F <= f) одностороннее» дает возможность наблюдения значения F-статистики меньшего f при равных дисперсиях генеральной совокупности и F критическом одностороннем выдает критическое значение меньше 1 для выбранного уровня значимости «Альфа». Если f > 1, «P(F <= f) одностороннее» дает возможность наблюдения значения F-статистики большего f при равных дисперсиях генеральной совокупности и F критическом одностороннем дает критическое значение больше 1 для «Альфа».
Инструмент «Анализ Фурье» применяется для решения задач в линейных системах и анализа периодических данных на основе метода быстрого преобразования Фурье (БПФ). Этот инструмент поддерживает также обратные преобразования, при этом инвертирование преобразованных данных возвращает исходные данные.

Инструмент «Гистограмма» применяется для вычисления выборочных и интегральных частот попадания данных в указанные интервалы значений. При этом рассчитываются числа попаданий для заданного диапазона ячеек.
Например, можно получить распределение успеваемости по шкале оценок в группе из 20 студентов. Таблица гистограммы состоит из границ шкалы оценок и групп студентов, уровень успеваемости которых находится между самой нижней границей и текущей границей. Наиболее часто встречающийся уровень является модой диапазона данных.
Совет: В Excel 2016 теперь можно создавать гистограммы и диаграммы Парето.
Инструмент анализа «Скользящее среднее» применяется для расчета значений в прогнозируемом периоде на основе среднего значения переменной для указанного числа предшествующих периодов. Скользящее среднее, в отличие от простого среднего для всей выборки, содержит сведения о тенденциях изменения данных. Этот метод может использоваться для прогноза сбыта, запасов и других тенденций. Расчет прогнозируемых значений выполняется по следующей формуле:
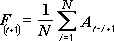
где
-
N — число предшествующих периодов, входящих в скользящее среднее;
-
A
j — фактическое значение в момент времени j; -
F
j — прогнозируемое значение в момент времени j.
Инструмент «Генерация случайных чисел» применяется для заполнения диапазона случайными числами, извлеченными из одного или нескольких распределений. С помощью этой процедуры можно моделировать объекты, имеющие случайную природу, по известному распределению вероятностей. Например, можно использовать нормальное распределение для моделирования совокупности данных по росту людей или использовать распределение Бернулли для двух вероятных исходов, чтобы описать совокупность результатов бросания монеты.
Средство анализа Ранг и процентиль создает таблицу, которая содержит порядковую и процентную ранг каждого значения в наборе данных. Можно проанализировать относительное положение значений в наборе данных. В этом средстве используются функции РАНГ. EQ и PERCENTRANK. INC. Если вы хотите учитывать связанные значения, используйте РАНГ. Функция EQ, которая обрабатывает связанные значения как имеющие одинаковый ранг или использует РАНГ.Функция AVG, которая возвращает средний ранг связанных значений.
Инструмент анализа «Регрессия» применяется для подбора графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или нескольких независимых переменных. Например, на спортивные качества атлета влияют несколько факторов, включая возраст, рост и вес. Можно вычислить степень влияния каждого из этих трех факторов по результатам выступления спортсмена, а затем использовать полученные данные для предсказания выступления другого спортсмена.
В средстве регрессии используется функция LINEST.
Инструмент анализа «Выборка» создает выборку из генеральной совокупности, рассматривая входной диапазон как генеральную совокупность. Если совокупность слишком велика для обработки или построения диаграммы, можно использовать представительную выборку. Кроме того, если предполагается периодичность входных данных, то можно создать выборку, содержащую значения только из отдельной части цикла. Например, если входной диапазон содержит данные для квартальных продаж, создание выборки с периодом 4 разместит в выходном диапазоне значения продаж из одного и того же квартала.
Двухвыборочный t-тест проверяет равенство средних значений генеральной совокупности по каждой выборке. Три вида этого теста допускают следующие условия: равные дисперсии генерального распределения, дисперсии генеральной совокупности не равны, а также представление двух выборок до и после наблюдения по одному и тому же субъекту.
Для всех трех средств, перечисленных ниже, значение t вычисляется и отображается как «t-статистика» в выводимой таблице. В зависимости от данных это значение t может быть отрицательным или неотрицательным. Если предположить, что средние генеральной совокупности равны, при t < 0 «P(T <= t) одностороннее» дает вероятность того, что наблюдаемое значение t-статистики будет более отрицательным, чем t. При t >=0 «P(T <= t) одностороннее» делает возможным наблюдение значения t-статистики, которое будет более положительным, чем t. «t критическое одностороннее» дает пороговое значение, так что вероятность наблюдения значения t-статистики большего или равного «t критическое одностороннее» равно «Альфа».
«P(T <= t) двустороннее» дает вероятность наблюдения значения t-статистики, по абсолютному значению большего, чем t. «P критическое двустороннее» выдает пороговое значение, так что значение вероятности наблюдения значения t- статистики, по абсолютному значению большего, чем «P критическое двустороннее», равно «Альфа».
Парный двухвыборочный t-тест для средних
Парный тест используется, когда имеется естественная парность наблюдений в выборках, например, когда генеральная совокупность тестируется дважды — до и после эксперимента. Этот инструмент анализа применяется для проверки гипотезы о различии средних для двух выборок данных. В нем не предполагается равенство дисперсий генеральных совокупностей, из которых выбраны данные.
Примечание: Одним из результатов теста является совокупная дисперсия (совокупная мера распределения данных вокруг среднего значения), вычисляемая по следующей формуле:
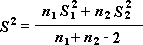
Двухвыборочный t-тест с одинаковыми дисперсиями
Этот инструмент анализа выполняет t-тест для двух образцов учащихся. В этой форме t-test предполагается, что два набора данных поступили из распределения с одинаковыми дисперсиями. Его называют гомике t-тестом. Этот t-тест можно использовать для определения вероятности того, что эти две выборки взяты из распределения с равными средствами распределения.
Двухвыборочный t-тест с различными дисперсиями
Этот инструмент анализа выполняет t-тест для двух образцов учащихся. В этой форме t-test предполагается, что два набора данных были полученными из распределения с неравными дисперсиями. Его называют гетероскестическими t-тестами. Как и в предыдущем примере с равными дисперсиями, этот t-тест можно использовать для определения вероятности того, что эти две выборки взяты из распределения с равными средствами распределения. Этот тест можно использовать, если в двух примерах есть отдельные объекты. Используйте тест Парный, описанный в примере, если существует один набор тем и две выборки представляют измерения по каждой теме до и после обработки.
Для определения тестовой величины t используется следующая формула.
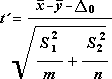
Следующая формула используется для вычисления степеней свободы (df). Так как результат вычисления обычно не является integer, значение df округлится до ближайшего другого, чтобы получить критическое значение из таблицы t. Функция Excel T .Test использует вычисляемую величину df без округлений, так как можно вычислить значение для T.ТЕСТ с неинтегрированной df. Из-за этих разных подходов к определению степеней свободы результаты T.Тест и этот t-тест будут отличаться в случае неравных дисперсий.
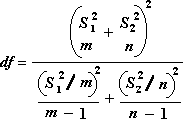
Z-тест. Средство анализа «Две выборки для середины» выполняет два примера z-теста для средств со известными дисперсиями. Этот инструмент используется для проверки гипотезы NULL о том, что между двумя значениями численности населения нет различий между односторонними или двухбокльными альтернативными гипотезами. Если дисперсии не известны, функция Z .Вместо этого следует использовать тест.
При использовании этого инструмента следует внимательно просматривать результат. «P(Z <= z) одностороннее» на самом деле есть P(Z >= ABS(z)), вероятность z-значения, удаленного от 0 в том же направлении, что и наблюдаемое z-значение при одинаковых средних значениях генеральной совокупности. «P(Z <= z) двустороннее» на самом деле есть P(Z >= ABS(z) или Z <= -ABS(z)), вероятность z-значения, удаленного от 0 в том же направлении, что и наблюдаемое z-значение при одинаковых средних значениях генеральной совокупности. Двусторонний результат является односторонним результатом, умноженным на 2. Инструмент «z-тест» можно также применять для гипотезы об определенном ненулевом значении разницы между двумя средними генеральных совокупностей. Например, этот тест можно использовать для определения разницы выступлений на соревнованиях двух автомобилей разных марок.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Создание гистограммы в Excel 2016
Создание диаграммы Парето в Excel 2016
Загрузка средства анализа в Excel
Инженерные функции (справка)
Общие сведения о формулах в Excel
Рекомендации, позволяющие избежать появления неработающих формул
Поиск ошибок в формулах
Сочетания клавиш и горячие клавиши в Excel
Функции Excel (по алфавиту)
Функции Excel (по категориям)
Нужна дополнительная помощь?
Содержание
- Применение математических функций
- СУММ
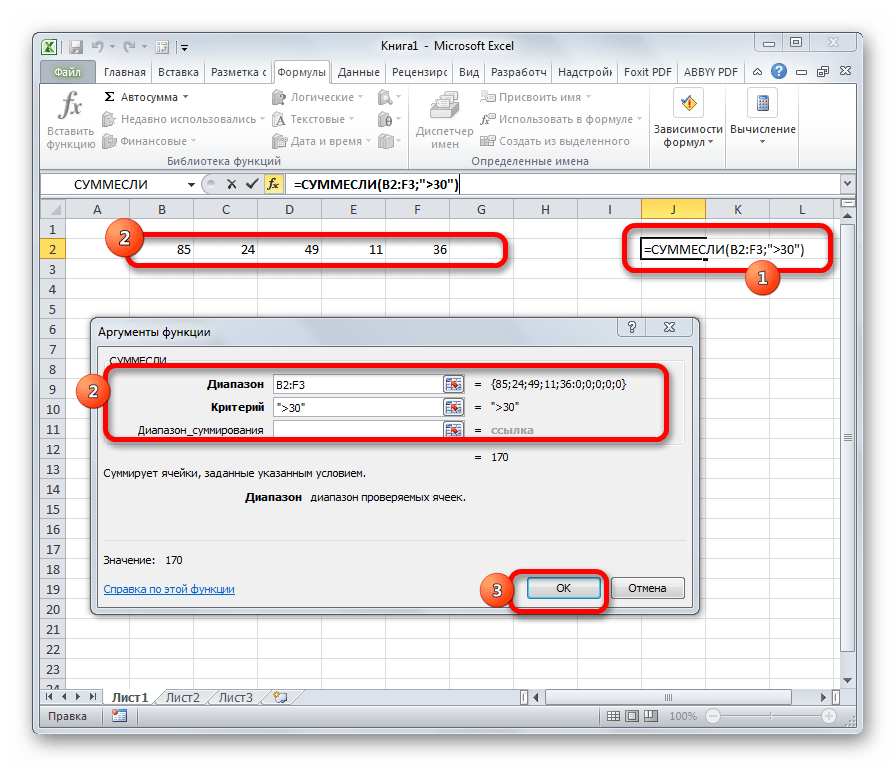
- СУММЕСЛИ
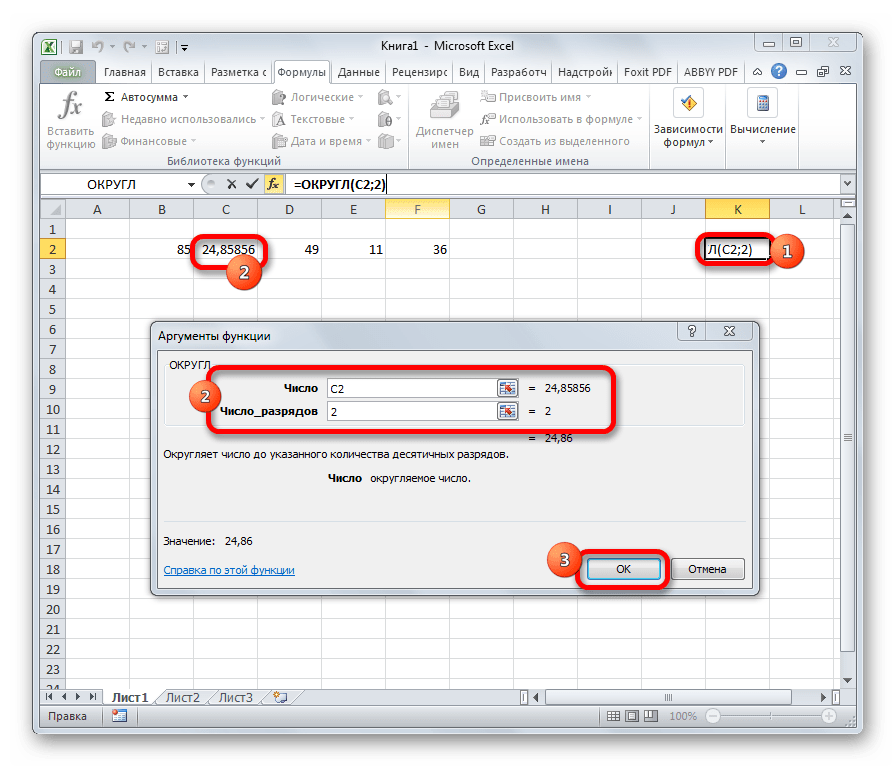
- ОКРУГЛ
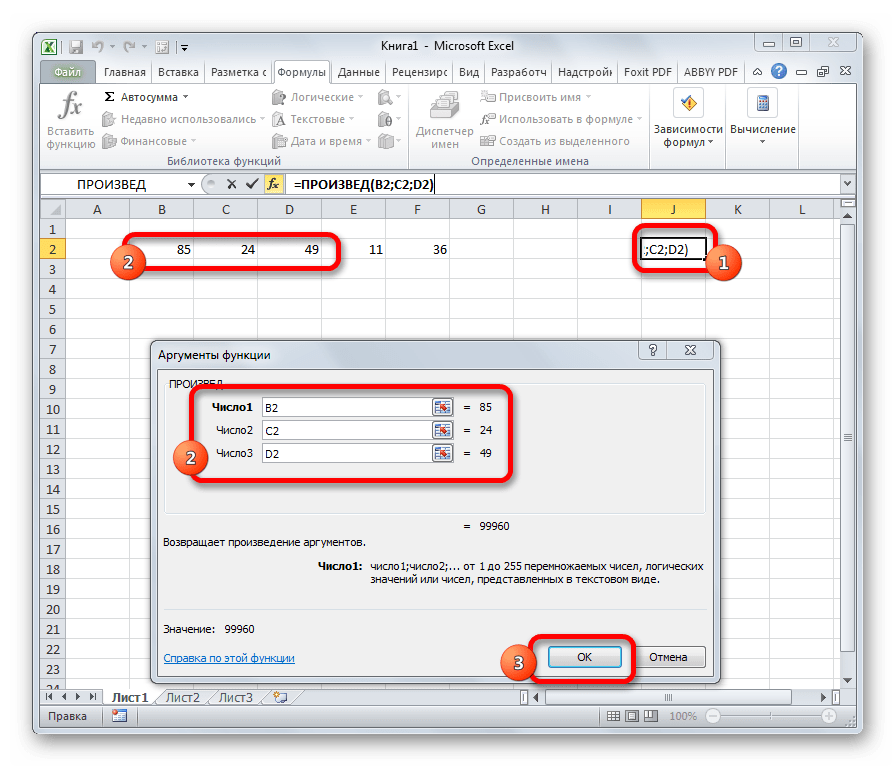
- ПРОИЗВЕД
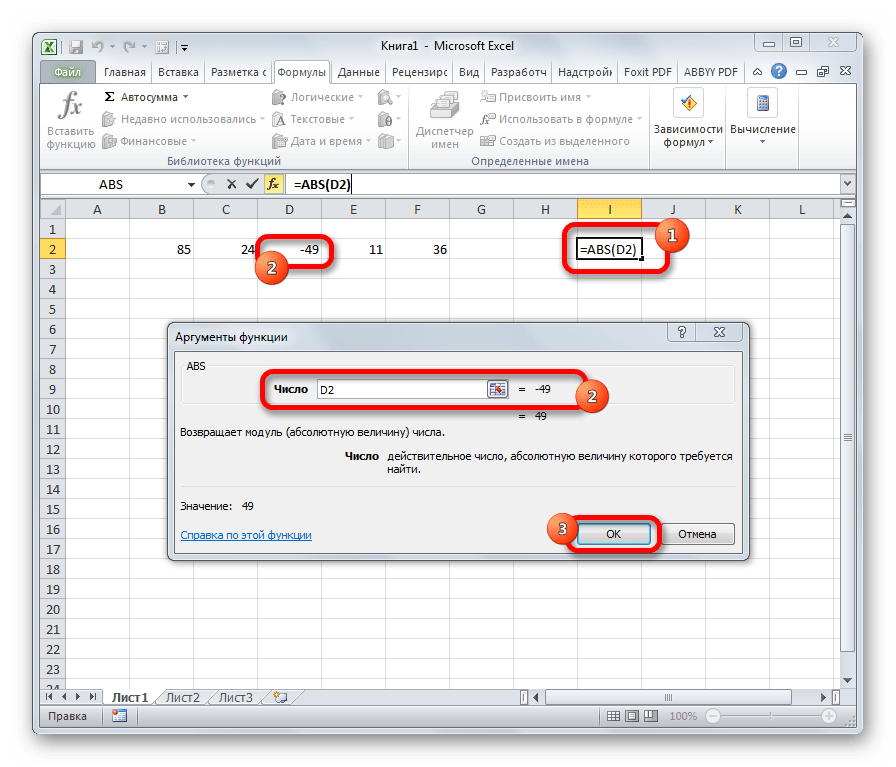
- ABS
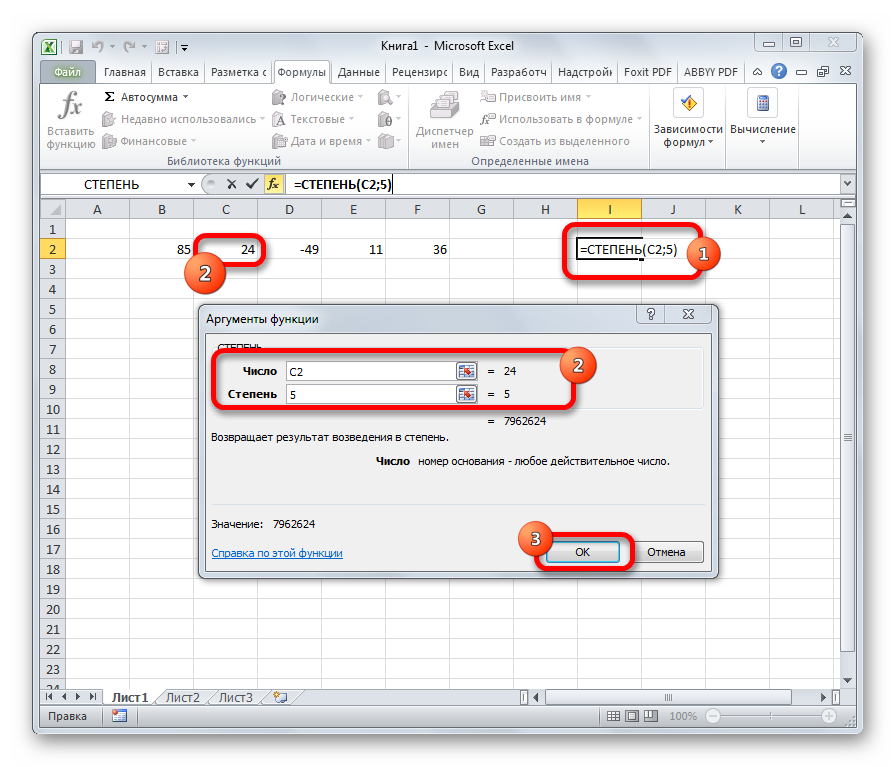
- СТЕПЕНЬ
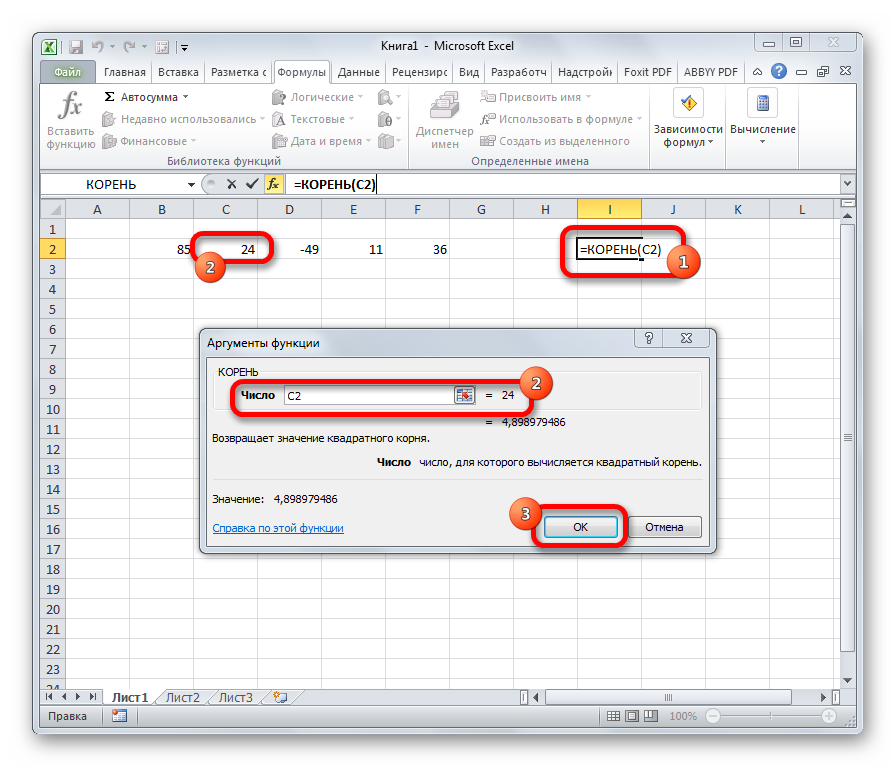
- КОРЕНЬ
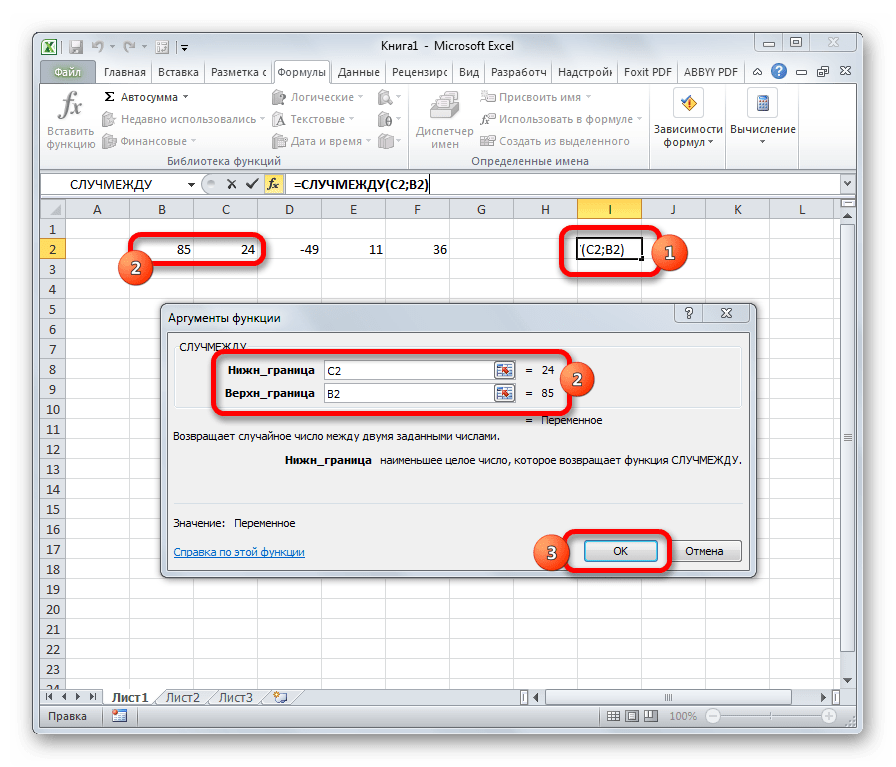
- СЛУЧМЕЖДУ
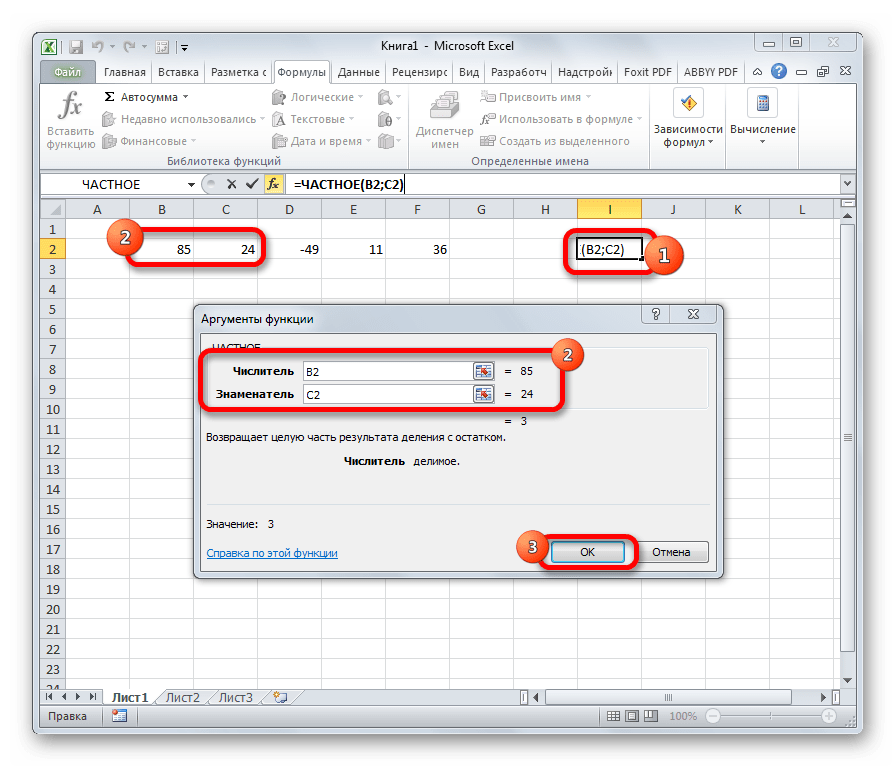
- ЧАСТНОЕ
- РИМСКОЕ
- Вопросы и ответы
Чаще всего среди доступных групп функций пользователи Экселя обращаются к математическим. С помощью них можно производить различные арифметические и алгебраические действия. Их часто используют при планировании и научных вычислениях. Узнаем, что представляет собой данная группа операторов в целом, и более подробно остановимся на самых популярных из них.
Применение математических функций
С помощью математических функций можно проводить различные расчеты. Они будут полезны студентам и школьникам, инженерам, ученым, бухгалтерам, планировщикам. В эту группу входят около 80 операторов. Мы же подробно остановимся на десяти самых популярных из них.
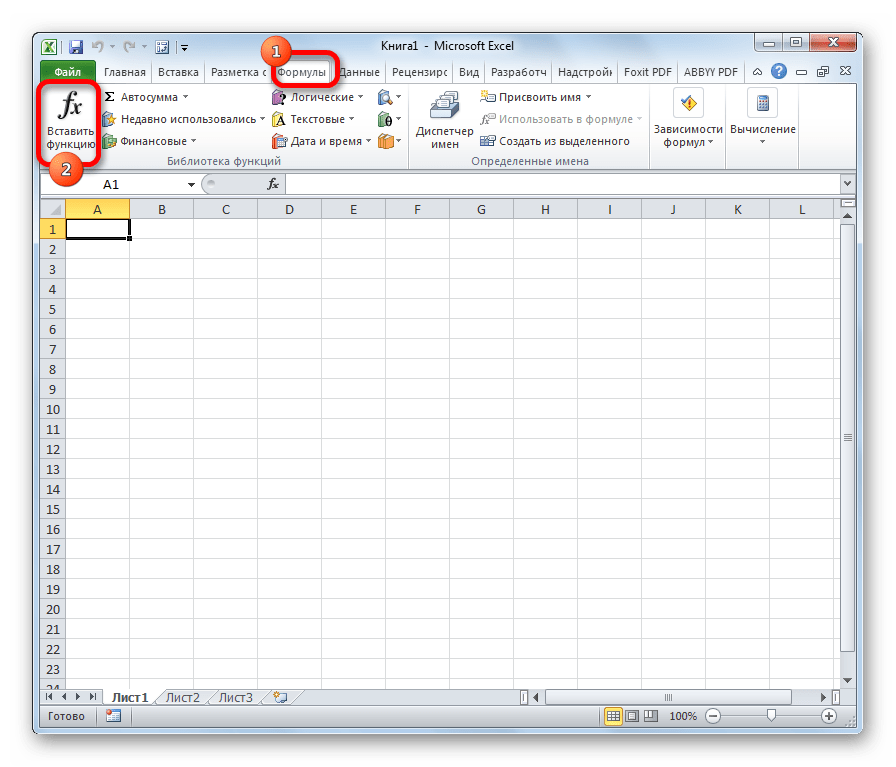
Открыть список математических формул можно несколькими путями. Проще всего запустить Мастер функций, нажав на кнопку «Вставить функцию», которая размещена слева от строки формул. При этом нужно предварительно выделить ячейку, куда будет выводиться результат обработки данных. Этот метод хорош тем, что его можно реализовать, находясь в любой вкладке.
Также можно запустить Мастер функций, перейдя во вкладку «Формулы». Там нужно нажать на кнопку «Вставить функцию», расположенную на самом левом краю ленты в блоке инструментов «Библиотека функций».
Существует и третий способ активации Мастера функций. Он осуществляется с помощью нажатия комбинации клавиш на клавиатуре Shift+F3.
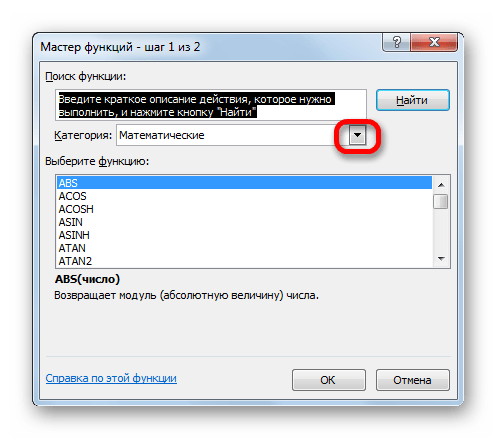
После того, как пользователь произвел любое из вышеуказанных действий, открывается Мастер функций. Кликаем по окну в поле «Категория».
Открывается выпадающий список. Выбираем в нем позицию «Математические».
После этого в окне появляется список всех математических функций в Excel. Чтобы перейти к введению аргументов, выделяем конкретную из них и жмем на кнопку «OK».
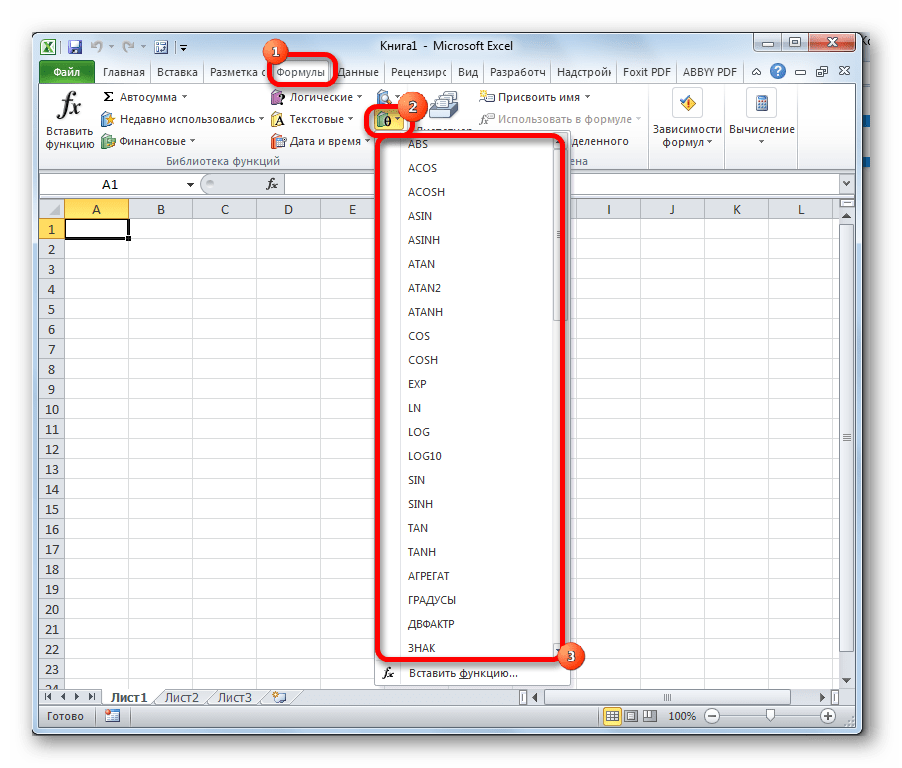
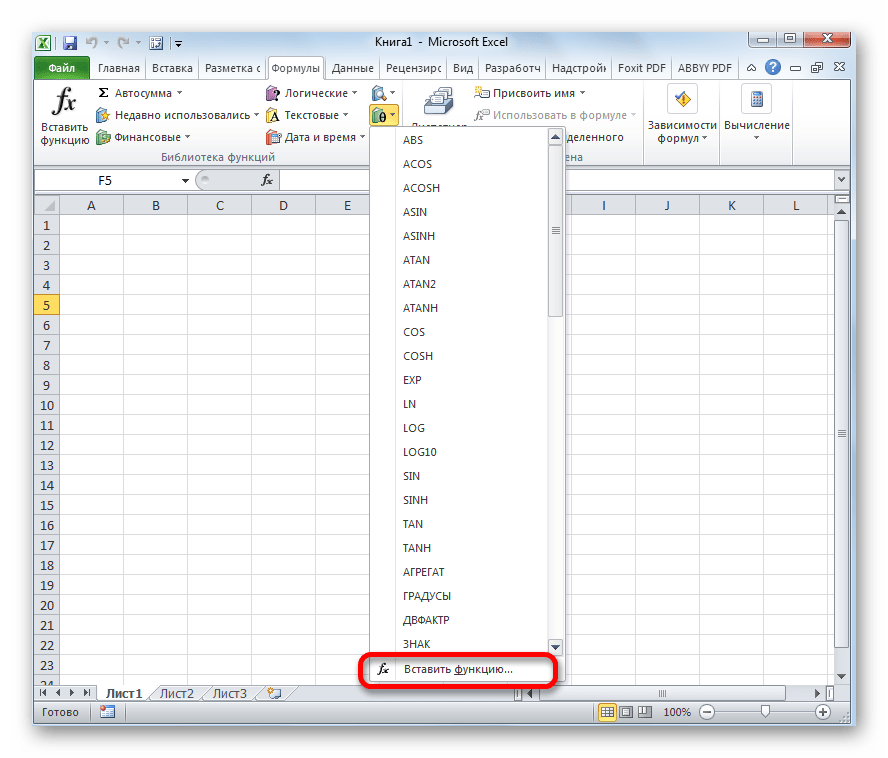
Существует также способ выбора конкретного математического оператора без открытия главного окна Мастера функций. Для этого переходим в уже знакомую для нас вкладку «Формулы» и жмем на кнопку «Математические», расположенную на ленте в группе инструментов «Библиотека функций». Открывается список, из которого нужно выбрать требуемую формулу для решения конкретной задачи, после чего откроется окно её аргументов.
Правда, нужно заметить, что в этом списке представлены не все формулы математической группы, хотя и большинство из них. Если вы не найдете нужного оператора, то следует кликнуть по пункту «Вставить функцию…» в самом низу списка, после чего откроется уже знакомый нам Мастер функций.
Урок: Мастер функций в Excel
СУММ
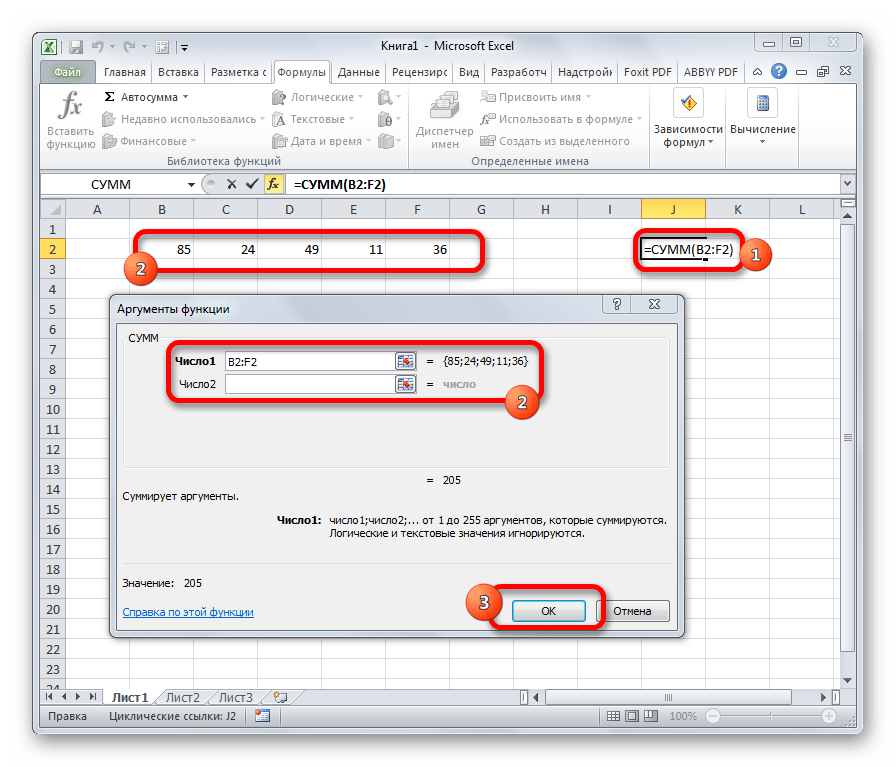
Наиболее часто используется функция СУММ. Этот оператор предназначен для сложения данных в нескольких ячейках. Хотя его можно использовать и для обычного суммирования чисел. Синтаксис, который можно применять при ручном вводе, выглядит следующим образом:
=СУММ(число1;число2;…)
В окне аргументов в поля следует вводить ссылки на ячейки с данными или на диапазоны. Оператор складывает содержимое и выводит общую сумму в отдельную ячейку.
Урок: Как посчитать сумму в Экселе
СУММЕСЛИ
Оператор СУММЕСЛИ также подсчитывает общую сумму чисел в ячейках. Но, в отличие от предыдущей функции, в данном операторе можно задать условие, которое будет определять, какие именно значения участвуют в расчете, а какие нет. При указании условия можно использовать знаки «>» («больше»), «<» («меньше»), «< >» («не равно»). То есть, число, которое не соответствует заданному условию, во втором аргументе при подсчете суммы в расчет не берется. Кроме того, существует дополнительный аргумент «Диапазон суммирования», но он не является обязательным. Данная операция имеет следующий синтаксис:
=СУММЕСЛИ(Диапазон;Критерий;Диапазон_суммирования)
ОКРУГЛ
Как можно понять из названия функции ОКРУГЛ, служит она для округления чисел. Первым аргументом данного оператора является число или ссылка на ячейку, в которой содержится числовой элемент. В отличие от большинства других функций, у этой диапазон значением выступать не может. Вторым аргументом является количество десятичных знаков, до которых нужно произвести округление. Округления проводится по общематематическим правилам, то есть, к ближайшему по модулю числу. Синтаксис у этой формулы такой:
=ОКРУГЛ(число;число_разрядов)
Кроме того, в Экселе существуют такие функции, как ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, которые соответственно округляют числа до ближайшего большего и меньшего по модулю.
Урок: Округление чисел в Excel
ПРОИЗВЕД
Задачей оператора ПРИЗВЕД является умножение отдельных чисел или тех, которые расположены в ячейках листа. Аргументами этой функции являются ссылки на ячейки, в которых содержатся данные для перемножения. Всего может быть использовано до 255 таких ссылок. Результат умножения выводится в отдельную ячейку. Синтаксис данного оператора выглядит так:
=ПРОИЗВЕД(число;число;…)
Урок: Как правильно умножать в Excel
ABS
С помощью математической формулы ABS производится расчет числа по модулю. У этого оператора один аргумент – «Число», то есть, ссылка на ячейку, содержащую числовые данные. Диапазон в роли аргумента выступать не может. Синтаксис имеет следующий вид:
=ABS(число)
Урок: Функция модуля в Excel
СТЕПЕНЬ
Из названия понятно, что задачей оператора СТЕПЕНЬ является возведение числа в заданную степень. У данной функции два аргумента: «Число» и «Степень». Первый из них может быть указан в виде ссылки на ячейку, содержащую числовую величину. Второй аргумент указывается степень возведения. Из всего вышесказанного следует, что синтаксис этого оператора имеет следующий вид:
=СТЕПЕНЬ(число;степень)
Урок: Как возводить в степень в Экселе
КОРЕНЬ
Задачей функции КОРЕНЬ является извлечение квадратного корня. Данный оператор имеет только один аргумент – «Число». В его роли может выступать ссылка на ячейку, содержащую данные. Синтаксис принимает такую форму:
=КОРЕНЬ(число)
Урок: Как посчитать корень в Экселе
СЛУЧМЕЖДУ
Довольно специфическая задача у формулы СЛУЧМЕЖДУ. Она состоит в том, чтобы выводить в указанную ячейку любое случайное число, находящееся между двумя заданными числами. Из описания функционала данного оператора понятно, что его аргументами является верхняя и нижняя границы интервала. Синтаксис у него такой:
=СЛУЧМЕЖДУ(Нижн_граница;Верхн_граница)
ЧАСТНОЕ
Оператор ЧАСТНОЕ применяется для деления чисел. Но в результатах деления он выводит только четное число, округленное к меньшему по модулю. Аргументами этой формулы являются ссылки на ячейки, содержащие делимое и делитель. Синтаксис следующий:
=ЧАСТНОЕ(Числитель;Знаменатель)
Урок: Формула деления в Экселе
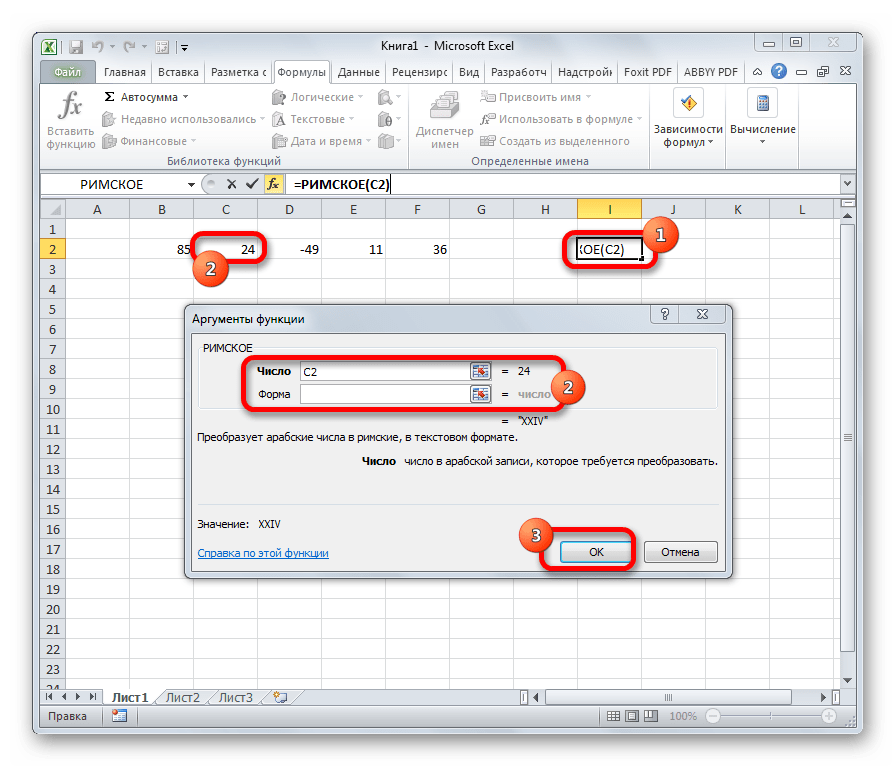
РИМСКОЕ
Данная функция позволяет преобразовать арабские числа, которыми по умолчанию оперирует Excel, в римские. У этого оператора два аргумента: ссылка на ячейку с преобразуемым числом и форма. Второй аргумент не является обязательным. Синтаксис имеет следующий вид:
=РИМСКОЕ(Число;Форма)
Выше были описаны только наиболее популярные математические функции Эксель. Они помогают в значительной мере упростить различные вычисления в данной программе. При помощи этих формул можно выполнять как простейшие арифметические действия, так и более сложные вычисления. Особенно они помогают в тех случаях, когда нужно производить массовые расчеты.
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Microsoft Excel – одна из самых популярных и легкодоступных программ для представителей разный специальностей. Сегодня мы рассмотрим, пожалуй, одну из самых используемых групп формул – математические формулы.
Начнем с того, как найти их среди прочего функционала. Есть несколько путей того, как открыть список математических формул.
Самый простой способ – нажать на кнопку «Формулы» на панели управления. Затем выбрать из перечня тип функций: «Математические».
Перед вами появится выпадающий длинный список всех существующих операторов:

Всего в Excel около 80 математических и тригонометрических функций. Мы рассмотрим не все, только самые распространенные из них, а также обратим внимание на некоторые нюансы, о которых вы, возможно, не знали. Если в статье вы не нашли нужную вам функцию, то скачивайте наш бесплатный гайд «Математические функции в Excel».
Для разминки вспомним самые простые формулы.
1. Формулы СУММ(), ПРОИЗВЕД()
Эти операции имеют схожую структуру и одинаковый тип аргументов, поэтому мы их объединили в один блок. СУММ() служит для сложения данных в нескольких ячейках, ПРОИЗВЕД() – очевидно, для нахождения произведения.
Аргументами этих функций могут быть числа, диапазоны, ссылки на ячейку, в которой содержится числовое значение. Количество элементов не может быть больше 30.
СУММ() и ПРОИЗВЕД() пропускают пустые ячейки, ячейки текстового формата и логические значения. Операторы вносят результат вычислений в отдельную, ранее выделенную курсором ячейку:

Аналогично для формулы ПРОИЗВЕД():

2. Формула ЧАСТНОЕ()
Тоже одна из простых операций в математике. В Excel выполняется тоже несложно: у функции ЧАСТНОЕ() есть два аргумента: делимое и делитель.
В выделенной ячейке выводится частное:

3. Формула СУММЕСЛИ()
Оператор СУММЕСЛИ() находит сумму чисел. Главное отличие этой функции от СУММ() в том, что здесь в качестве аргумента можно задавать условие (только одно), которое будет показывать, какие значения будут использованы в расчетах, а какие – нет.
В качестве условий могут выступать неравенства со знаками больше, меньше или не равно («>», «<», «< >»). Число, которое не соответствует введенному условию, не будет включен в суммирование.
На рисунке 5 изображено суммирование всех чисел, которые больше 0.
Оранжевым выделены те числа, которые будут включены в расчет функцией СУММЕСЛИ().
Остальные числа просто будут игнорироваться:

Кроме постоянных аргументов, существует еще и дополнительный – «Диапазон суммирования». Он добавляется тогда, когда необходимо просуммировать один диапазон, а условия выбирать по другому диапазону.
Например, нужно посчитать общую стоимость всех проданных фруктов.
Для этого воспользуемся следующей формулой:

То есть сначала пишем диапазон, по которому проверяем условие, затем само ограничение и в конце диапазон чисел, которые надо суммировать. В примере на рисунке 6 выше, соответственно, все строки из категории «Овощи» в расчет включены не будут.
4. Формулы ОКРУГЛ(), ОКРУГЛВВЕРХ(), ОКРУГЛВНИЗ()
Функция ОКРУГЛ() предназначена для округления значения до заданного количества знаков после запятой. В качестве первого аргумента выступают, как обычно, числа или диапазон ячеек, второго – разряд, до которого нужно округлить число.
Например, округление значения до второго знака после запятой:

Если в качестве второго аргумента выступает 0, то число будет округляться до ближайшего целого:

Второй аргумент может быть и отрицательным, тогда округление будет происходить до требуемого знака перед запятой:

Если необходимо округлить в сторону меньшего или большего по модулю числа используют функции ОКРУГЛВНИЗ(), ОКРУГЛВВЕРХ(), соответственно:


Замечание: многие могут решить, что функции округления бесполезны, так как можно просто убрать/добавить дополнительный знак после запятой с помощью кнопок увеличить/уменьшить разрядность.
На самом деле, это не так.
Дело в том, что увеличение или уменьшение разрядности влияет только на «внешний вид» ячейки, то есть на то, как мы число видим.
Само число, при этом, не меняется. Функции округления же полностью меняют вид числа, убирая лишние разряды.
5. Формулы ОТБР(), ЦЕЛОЕ()
Эти функции очень похожи на предыдущие, но работают немного по-другому.
ОТБР() убирает все цифры справа от запятой и у положительных, и у отрицательных чисел. На первом месте в скобках после оператора пишется значение, а на втором – разряд, после которого удалятся все знаки.
Если второй аргумент пропущен, то по умолчанию ставится 0:

ЦЕЛОЕ() – функция, которая выдает в качестве результата наименьшее целое число, стоящее перед аргументом:

На положительные числа операторы влияют почти одинаково, а вот на отрицательные – нет.
Функция ЦЕЛОЕ(-5,6) выдаст результат (-6), а ОТБР(-5,6;0) выдаст (-5), хотя в то же время для числа 5,3 результат обеих функций будет одинаковый – число (5).
6. Формула ABS()
Математическая формула ABS() позволяет получить число по модулю. Как обычно, аргументами оператора является число или ссылка на ячейку.

Эту функцию удобно использовать, например, когда необходимо найти количество дней между датами. Из школьной программы многие знают, что нужно из большего вычитать меньшее.
Но что делать если дана огромная таблица, где трудно определить, где какое значение? Здесь нам помогает оператор ABS(), который переводит отрицательное число в положительное.

7. Формула КОРЕНЬ()
КОРЕНЬ() – довольно легкая функция с одним аргументом (числом или ссылкой на ячейку), которая находит квадратный корень числа:

Замечание. Для извлечения корня другой степени (не квадратного) можно пользоваться функцией СТЕПЕНЬ().
8. Формула СТЕПЕНЬ()
Функция СТЕПЕНЬ() позволяет возвести число в любую степень, в том числе извлечь корень (то есть возвести число в дробную степень).
Например, чтобы извлечь кубический корень из числа 8, необходимо воспользоваться формулой, как на рисунке 17.1.


Помимо математической функции СТЕПЕНЬ(), можно пользоваться оператором “^”, но он выглядит менее опрятно в формулах.
Если вам интересно узнать больше о других математических функциях, напишите об этом ниже в комментариях. Записывайтесь на открытый онлайн-курс «Аналитика в Excel», если хотите научиться выполнять рутинную работу в программе быстрее.
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Блог SF Education
Investment Banking
5 примеров экономии времени в Excel
Содержание статьи Что для работодателя главное в сотруднике? Добросовестность, ответственность, профессионализм и, конечно же, умение пользоваться отведенным временем! Предлагаем познакомиться с очень нужными, на…
Как работает сотрудник одной из компаний «большой тройки»?
Ты работаешь в компании «большой тройки (имеются в виду три крупнейших консалтинговых компании: McKinsey, Boston Consulting Group и Bain & Company), в которых мечтают работать тысячи подписчиков наших каналов и читателей vc.ru. Что это значит для тебя?
На сегодняшний день разработано большое количество специализированных программных продуктов для проведения экономических расчетов, однако сотрудники финансово-экономических служб чаще всего пользуются табличным редактором Excel. Причина популярности данного инструмента — обширный функционал Excel и постоянное его развитие практически в каждой новой версии табличного редактора.
В рамках одной статьи невозможно рассмотреть все достоинства Excel, которые экономисты могут применить в своей работе, поэтому остановимся на анализе лучших функций редактора, используемых для решения экономических задач.
Для удобства восприятия материала сгруппируем эти функции в три блока:
1. Функционал расчетных формул в Excel.
2. Функционал Excel для обработки табличных данных.
3. Инструменты Excel для моделирования и анализа экономических данных.
ФУНКЦИОНАЛ РАСЧЕТНЫХ ФОРМУЛ В EXCEL
Расчетные формулы являются изначальным и основополагающим функционалом табличного редактора Excel, поэтому рассмотрим их в первую очередь.
Пакет встроенных расчетных формул включает в себя десятки наименований, но самыми востребованными в работе экономистов являются следующие формулы: ЕСЛИ, СУММЕСЛИ и СУММЕСЛИМН, ВПР и ГПР, СУММПРОИЗВ, СЧЕТЕСЛИ.
Решение экономической задачи с помощью формулы ЕСЛИ
Формула ЕСЛИ — расчетная функция Excel, которую наиболее часто используют для решения несложных экономических расчетов. Она относится к группе логических формул и позволяет рассчитать необходимые данные по условиям, заданным пользователями.
С помощью формулы ЕСЛИ можно сравнить числовые или текстовые значения по прописанным в формуле условиям.
Запись расчетной формулы в заданной ячейке в общем виде выглядит так:
=ЕСЛИ(логическое_выражение;[значение_если_истина];[значение_если_ложь]),
где логическое выражение — данные, которые нужно проверить/сравнить (числовые или текстовые значения в ячейках);
значение_если_истина — результат, который появится в расчетной ячейке, если значение будет верным;
значение_если_ложь — результат, который появится в расчетной ячейке при неверном значении.
Задача № 1. Предприятие реализует три номенклатурные группы продукции: лимонад, минеральная вода и пиво. С 01.09.2020 запланировано установить скидку в размере 15 % на пиво.
Чтобы сформировать новый прайс на продукцию, сохраняем ее перечень в виде таблицы Excel. В первом столбце таблицы отражена номенклатура всей продукции в алфавитном порядке, во втором — признак группы продукции.
Для решения задачи создаем в таблице третий столбец и прописываем в первой ячейке номенклатуры формулу: =ЕСЛИ(C4=»пиво»;15%;0).
Эту формулу продлеваем до конца перечня номенклатуры продукции. В итоге получаем сведения о продукции, на которую с сентября снизится цена (табл. 1).
В данном примере показано использование формулы ЕСЛИ для обработки текстовых значений в исходных данных.
Решение экономической задачи с помощью формулы СУММЕСЛИ
Формулы СУММЕСЛИ и СУММЕСЛИМН также используют для экономических расчетов, но они обладают более широкими возможностями для выборки и обработки данных. Можно задать не одно, а несколько условий отборов и диапазонов.
Задача № 2. На основе ведомости начисления заработной платы сотрудникам магазина нужно определить общую сумму зарплаты продавцов.
Чтобы решить эту задачу, сохраняем ведомость из учетной базы данных в виде таблицы Excel. В данном случае нам нужно не просто произвести выборку значений, но и суммировать их результат. Поэтому будем использовать более сложную разновидность формулы ЕСЛИ — СУММЕСЛИ.
Для решения задачи добавим внизу таблицы еще одну строку «Всего продавцы». В ее ячейке под суммой зарплаты, начисленной сотрудникам магазина, пропишем следующую формулу:=СУММЕСЛИ(C4:C13;»продавец»;D4:D13).
Таким образом мы задали условие, при котором табличный редактор обращается к столбцу с наименованием должностей (столбец С), выбирает в нем значение «Продавец» и суммирует данные ячеек с начисленной заработной платой из столбца D в привязке к этой должности.
Результат решения задачи — в табл. 2.
Решение экономической задачи с помощью формул ВПР и ГПР
Формулы ВПР и ГПР используют для решения более сложных экономических задач. Они популярны среди экономистов, так как существенно облегчают поиск необходимых значений в больших массивах данных. Разница между формулами:
- ВПР предназначена для поиска значений в вертикальных списках (по строкам) исходных данных;
- ГПР используют для поиска значений в горизонтальных списках (по столбцам) исходных данных.
Формулы прописывают в общем виде следующим образом:
=ВПР(искомое значение, которое требуется найти; таблица и диапазон ячеек для выборки данных; номер столбца, из которого будут подставлены данные; [интервал просмотра данных]);
=ГПР(искомое значение, которое требуется найти; таблица и диапазон ячеек для выборки данных; номер строки, из которой будут подставлены данные; [интервал просмотра данных]).
Указанные формулы имеют ценность при решении задач, связанных с консолидацией данных, которые разбросаны на разных листах одной книги Excel, находятся в различных рабочих книгах Excel, и размещении их в одном месте для создания экономических отчетов и подсчета итогов.
Задача № 3. У экономиста есть данные в виде таблицы Excel о реализации продукции за сентябрь в натуральном измерении (декалитрах) и данные о реализации продукции в сумме (рублях) в другой таблице Excel. Экономисту нужно предоставить руководству отчет о реализации продукции с тремя параметрами:
- продажи в натуральном измерении;
- продажи в суммовом измерении;
- средняя цена реализации единицы продукции в рублях.
Для решения этой задачи с помощью формулы ВПР нужно последовательно выполнить следующие действия.
Шаг 1. Добавляем к таблице с данными о продажах в натуральном измерении два новых столбца. Первый — для показателя продаж в рублях, второй — для показателя цены реализации единицы продукции.
Шаг 2. В первой ячейке столбца с данными о продажах в рублях прописываем расчетную формулу: =ВПР(B4:B13;Табл.4!B4:D13;3;ЛОЖЬ).
Пояснения к формуле:
В4:В13 — диапазон поиска значений по номенклатуре продукции в создаваемом отчете;
Табл.4!B4:D13 — диапазон ячеек, где будет производиться поиск, с наименованием таблицы, в которой будет организован поиск;
3 — номер столбца, по которому нужно выбрать данные;
ЛОЖЬ — значение критерия поиска, которое означает необходимость строгого соответствия отбора наименований номенклатуры таблицы с суммовыми данными наименованиям номенклатуры в таблице с натуральными показателями.
Шаг 3. Продлеваем формулу первой ячейки до конца списка номенклатуры в создаваемом нами отчете.
Шаг 4. В первой ячейке столбца с данными о цене реализации единицы продукции прописываем простую формулу деления значения ячейки столбца с суммой продаж на значение ячейки столбца с объемом продаж (=E4/D4).
Шаг 5. Продлим формулу с расчетом цены реализации до конца списка номенклатуры в создаваемом нами отчете.
В результате выполненных действий появился искомый отчет о продажах (табл. 3).
На небольшом количестве условных данных эффективность формулы ВПР выглядит не столь внушительно. Однако представьте, что такой отчет нужно сделать не из заранее сгруппированных данных по номенклатуре продукции, а на основе реестра ежедневных продаж с общим количеством записей в несколько тысяч.
Тогда эта формула обеспечит такую скорость и точность выборки нужных данных, которой трудно добиться другими функциями Excel.
Решение экономической задачи с помощью формулы СУММПРОИЗВ
Формула СУММПРОИЗВ позволяет экономистам справиться практически с любой экономической задачей, для решения которой нужно работать с несколькими массивами данных. Она обладает всеми возможностями рассмотренных выше формул, умеет суммировать произведения данных из списка до 255 источников (массивов).
Задача № 4. Есть реестр продаж различной номенклатуры продукции за сентябрь 2020 г. Нужно рассчитать из общего реестра данные о суммах реализации по основным номенклатурным группам продукции.
Чтобы выполнить задачу, добавим внизу реестра три новые строки с указанием групп продукции и пропишем в ячейке с будущими данными о продажах первой группы (пиво) следующую формулу: =СУММПРОИЗВ(((C4:C13=C16)*D4:D13)). Здесь указано, что в ячейке должно быть выполнено суммирование произведений значений диапазона ячеек столбца с наименованием групп продукции (C4:C13) с условием отбора наименования группы «Пиво» (С16) на значения ячеек столбца с суммами продаж (D4:D13).
Далее копируем эту формулу на оставшиеся две ячейки, заменив в них условия отбора на группу «Лимонад» (С17) и группу «Минеральная вода» (С18).
Выполнив указанные действия, получим искомое решение задачи в табл. 4.
Решение экономической задачи с помощью формулы СЧЕТЕСЛИ
Формула СЧЕТЕСЛИ используется не так широко, как предыдущие, но она выручает экономистов, если нужно минимизировать ошибки при работе с таблицами Excel. Эта формула удобна для проверки корректности вводимых данных и установке различного рода запретов, что особенно важно, если с данными работает несколько пользователей.
Задача № 5. Экономисту поручили провести корректировку справочника номенклатуры ТМЦ в учетной базе данных компании. Справочник долгое время не проверяли, данные в него вносили порядка 10 человек, поэтому появилось много некорректных и дублирующих наименований.
Чтобы повысить качество работы, приняли решение создать обновленный справочник в книге Excel, а затем сопоставить его с данными в учетной базе и исправить их. Проблема заключалась в том, что перечень номенклатуры составляет порядка 3000 наименований. Вносить его в книгу будут шесть человек, а это создает риск дублирования позиций.
Экономист может решить эту проблему с помощью формулы СЧЕТЕСЛИ. Нужно выполнить следующие действия:
- выбираем диапазон ячеек, куда будут вноситься наименования номенклатуры (В5:В3005);
- в меню редактора выбираем путь: Данные → Проверка данных;
- в появившемся диалоговом окне выбираем вкладку Параметры и указываем в выпадающем списке Тип данных вариант Другой;
- в строке Формула указываем: =СЧЕТЕСЛИ($В$5:$В$3005;В5)<=1;
- в диалоговом окне на вкладке Сообщение об ошибке вводим текст сообщения и нажимаем кнопку «ОК».
Если кто-либо из сотрудников будет пытаться ввести в указанный диапазон ячеек наименование ТМЦ, которое уже есть в диапазоне, у него это не получится. Excel выдаст сообщение в таком виде (рис. 1).
ФУНКЦИОНАЛ EXCEL ДЛЯ ОБРАБОТКИ ТАБЛИЧНЫХ ДАННЫХ
Помимо расчетных формул в табличном редакторе Excel присутствует набор инструментов, значительно облегчающих жизнь экономистам, которые работают с большими объемами данных. К наиболее популярным из них можно отнести функцию сортировки данных, функцию фильтрации данных, функцию консолидации данных и функцию создания сводных таблиц.
Решение экономической задачи с применением функции сортировки данных
Функционал сортировки данных позволяет изменить расположение данных в таблице и выстроить их в новой последовательности. Это удобно, когда экономист консолидирует данные нескольких таблиц и ему нужно, чтобы во всех исходных таблицах данные располагались в одинаковой последовательности.
Другой пример целесообразности сортировки данных — подготовка отчетности руководству компании. С помощью функционала сортировки из одной таблицы с данными можно быстро сделать несколько аналитических отчетов.
Сортировку данных выполнить просто:
- выделяем курсором столбцы таблицы;
- заходим в меню редактора: Данные → Сортировка;
- выбираем нужные параметры сортировки и получаем новый вид табличных данных.
Задача № 6. Экономист должен подготовить отчет о заработной плате, начисленной сотрудникам магазина, с последовательностью от самой высокой до самой низкой зарплаты.
Для решения этой задачи берем табл. 2 в качестве исходных данных. Выделяем в ней диапазон ячеек с показателями начисления зарплат (B4:D13).
Далее в меню редактора вызываем сортировку данных и в появившемся окне указываем, что сортировка нужна по значениям столбца D (суммы начисленной зарплаты) в порядке убывания значений.
Нажимаем кнопку «ОК», и табл. 2 преобразуется в новую табл. 5, где в первой строке идут данные о зарплате директора в 50 000 руб., в последней — данные о зарплате грузчика в 18 000 руб.
Решение экономической задачи с использованием функционала Автофильтр
Функционал фильтрации данных выручает при решении задач по анализу данных, особенно если возникает необходимость проанализировать часть исходной таблицы, данные которой отвечают определенным условиям.
В табличном редакторе Excel есть два вида фильтров:
- автофильтр — используют для фильтрации данных по простым критериям;
- расширенный фильтр — применяют при фильтрации данных по нескольким заданным параметрам.
Автофильтр работает следующим образом:
- выделяем курсором диапазон таблицы, данные которого собираемся отфильтровать;
- заходим в меню редактора: Данные → Фильтр → Автофильтр;
- выбираем в таблице появившиеся значения автофильтра и получаем отфильтрованные данные.
Задача № 7. Из общих данных о реализации продукции за сентябрь 2020 г. (см. табл. 4) нужно выделить суммы продаж только по группе лимонадов.
Для решения этой задачи выделяем в таблице ячейки с данными по реализации продукции. Устанавливаем автофильтр из меню: Данные → Фильтр → Автофильтр. В появившемся меню столбца с группой продукции выбираем значение «Лимонад». В итоге в табл. 6 автоматически остаются значения продаж лимонадов, а данные по группам «Пиво» и «Минеральная вода» скрываются.
Для применения расширенного фильтра нужно предварительно подготовить «Диапазон условий» и «Диапазон, в который будут помещены результаты».
Чтобы организовать «Диапазон условий», следует выполнить следующие действия:
- в свободную строку вне таблицы копируем заголовки столбцов, на данные которых будут наложены ограничения (заголовки несмежных столбцов могут оказаться рядом);
- под каждым из заголовков задаем условие отбора данных.
Строка копий заголовков вместе с условиями отбора образуют «Диапазон условий».
Порядок работы с функционалом консолидации данных
Функционал консолидации данных помогает экономистам в решении задач по объединению данных из нескольких источников в одну общую таблицу. Например, экономисты холдинговых компаний часто создают однотипные таблицы с данными по разным компаниям холдинга и им требуется предоставить руководству сводные данные о работе всей группы компаний. Для упрощения формирования сводных показателей как раз и подходит функционал консолидации данных.
Консолидация работает только с идентичными таблицами Excel, поэтому для успеха все объединяемые таблицы должны отвечать следующим требованиям:
- макеты всех консолидируемых таблиц одинаковые;
- названия столбцов во всех консолидируемых таблицах идентичные;
- в консолидируемых таблицах нет пустых столбцов и строк.
Работа с функционалом консолидации включает ряд последовательных действий:
1) открываем файлы со всеми таблицами, из которых собираемся консолидировать данные;
2) в отдельном файле, где будет находиться консолидированный отчет, ставим курсор на первую ячейку диапазона консолидированной таблицы;
3) в меню Excel открываем вкладки: Данные → Работа с данными → Консолидация;
4) в открывшемся диалоговом окне выбираем функцию консолидации (как правило, это «сумма», потому что нам требуется суммировать значения нескольких таблиц);
5) в диалоговом окне консолидации указываем ссылки на диапазоны объединяемых таблиц (диапазоны должны быть одинаковые);
6) если требуется автоматическое обновление данных консолидированной таблицы при изменении данных исходных таблиц, ставим галочку напротив «Создавать связи с исходными данными»;
7) завершаем консолидацию нажатием кнопки «ОК». В итоге получаем сводную структурированную таблицу, объединяющую данные всех исходных таблиц.
Решение экономической задачи с использованием функционала сводной таблицы для создания нового отчета
Функционал сводных таблиц позволяет сформировать различного рода отчеты из одного или нескольких массивов данных с возможностью обновления отчетных данных в случае изменения информации в исходных массивах. Используя сводные таблицы, можно быстро перенастроить параметры отчета.
Для создания сводной таблицы нужно зайти в меню Excel и вызвать Мастера сводных таблиц. В моей версии редактора это выполняется через Вставка → Сводная таблица, в некоторых версиях нужно выбрать Данные → Сводная таблица.
В появившемся диалоговом окне формируем параметры будущей таблицы:
- указываем исходную таблицу или диапазон ячеек Excel, откуда будут взяты данные для сводной таблицы. В последних версиях Excel также можно выбрать вариант обработки данных из внешних источников;
- указываем место, куда размещать создаваемый отчет сводной таблицы (новый лист, ячейки открытого листа);
- в открывшемся конструкторе отчета указываем, какие исходные данные будут выведены в строки и столбцы отчета, при необходимости настраиваем фильтры для показателей сводной таблицы и создаем новый отчет.
Задача № 8. Экономисту нужно создать отчет на основе реестра данных о реализации продукции за сентябрь 2020 г. В отчете должно быть два уровня группировки данных. На первом уровне нужно вывести итоги по группам продукции, на втором уровне — по ее номенклатурным позициям. Чтобы решить эту задачу, вызываем Мастера сводных таблиц. Указываем, что данные берем из ячеек табл. 4, а отчет будем размещать на новом листе книги Excel. В конструкторе отчета указываем, что в первой колонке отчета будут показатели групп и номенклатурных единиц продукции, во второй — данные о суммах реализации. После этого даем команду создать сводную таблицу. Результат — в табл. 7.
ИНСТРУМЕНТЫ EXCEL ДЛЯ МОДЕЛИРОВАНИЯ И АНАЛИЗА ЭКОНОМИЧЕСКИХ ДАННЫХ
Постоянное развитие функционала табличного редактора Excel привело к тому, что появилось много новых инструментов, которые могут помочь экономистам в решении выполняемых ими задач. К числу наиболее значимых можно отнести функцию «Поиск решения», пакет расширенного анализа данных и специализированные надстройки.
Решение экономической задачи с помощью надстройки «Поиск решения»
Функция «Поиск решения» позволяет найти наиболее рациональный способ решения экономической задачи математическими методами. Она может автоматически выполнить расчеты для задач с несколькими вводными данными при условии накладывания определенных ограничений на искомое решение.
Такими экономическими задачами могут быть:
- расчет оптимального объема выпуска продукции при ограниченности сырья;
- минимизация транспортных расходов на доставку продукции покупателям;
- решение по оптимизации фонда оплаты труда.
Функция поиска решения является дополнительной надстройкой, поэтому в стандартном меню Excel мы ее не найдем. Чтобы использовать в своей работе функцию «Поиск решения», экономисту нужно сделать следующее:
- в меню Excel выбрать путь: Файл → Параметры → Надстройки;
- в появившемся списке надстроек выбрать «Поиск решения» и активировать эту надстройку;
- вернуться в меню Excel и выбрать: Данные → Поиск решения.
Задача № 9. Туристической компании необходимо организовать доставку 45 туристов в четыре гостиницы города с трех пунктов прибытия при минимально возможной сумме затрат. Для решения задачи составляем таблицу с исходными данными:
1. Количество прибывающих с каждого пункта — железнодорожный вокзал, аэропорт и автовокзал (ячейки Н6:Н8).
2. Количество забронированных для туристов мест в каждой из четырех гостиниц (ячейки D9:G9).
3. Стоимость доставки одного туриста с каждого пункта прибытия до каждой гостиницы размещения (диапазон ячеек D6:G8).
Исходные данные, размещенные таким образом, показаны в табл. 8.1.
Далее приступаем к подготовке поиска решения.
1. Создаем внизу исходной таблицы такую же таблицу для расчета оптимального количества доставки туристов при условии минимизации затрат на доставку с диапазоном ячеек D15:G17.
2. Выбираем на листе ячейку для расчета искомой функции минимизации затрат (J4) и прописываем в ячейке расчетную формулу: =СУММПРОИЗВ(D6:G8;D15:G17).
3. Заходим в меню Excel, вызываем диалоговое окно надстройки «Поиск решения» и указываем там требуемые параметры и ограничения (рис. 2):
- оптимизировать целевую функцию — ячейка J4;
- цель оптимизации — до минимума;
- изменения ячейки переменных — диапазон ячеек второй таблицы D15:G17;
- ограничения поиска решения:
– в диапазоне ячеек второй таблицы D15:G17 должны быть только целые значения (D15:G17=целое);
– значения диапазона ячеек второй таблицы D15:G17 должны быть только положительными (D15:G17>=0);
– количество мест для туристов в каждой гостинице таблицы для поиска решения должно быть равно количеству мест в исходной таблице (D18:G18 = D9:G9);
– количество туристов, прибывающих с каждого пункта, в таблице для поиска решения должно быть равно количеству туристов в исходной таблице (Н15:Н17 = Н6:Н8).
Далее даем команду найти решение, и надстройка рассчитывает нам результат оптимальной доставки туристов (табл. 8.2).
При такой схеме доставки целевое значение общей суммы расходов действительно минимальное и составляет 1750 руб.
Пакет расширенного анализа данных
Пакет расширенного анализа данных применяют, если нужно исследовать различного рода статистические анализы, ряды данных, спрогнозировать тренды и т. д.
Пакет является надстройкой к Excel, устанавливается в основное меню аналогично функции поиска решений (Файл → Параметры → Надстройки → Пакет анализа). Вызвать его можно командой Данные → Анализ данных через диалоговое окно, в котором отражены все заложенные в надстройке виды анализа (рис. 3).
Специализированные надстройки для финансово-экономической работы
В последние годы значительно расширился перечень специализированных надстроек к табличному редактору Excel, которые могут использовать в своей работе экономисты. Практически все они бесплатные, легко устанавливаются самим пользователем.
Не будем останавливаться на таких надстройках, как Power Query, Power Pivot, Power Quick, так как они в большей степени используются в целях бизнес-аналитики, чем для решения экономических задач.
Есть и другие надстройки к Excel, которые могут облегчить работу специалистов финансово-экономических служб. Интерес представляют две бесплатные надстройки — «Финансист» и PowerFin.
Надстройку «Финансист» можно установить на свою версию Excel как в автоматическом, так и ручном режиме. В надстройке собрано много полезных для экономистов функций. Достаточно перечислить основные блоки данной надстройки:
- финансовые функции (ликвидность, платежеспособность, финансовая устойчивость, рентабельность, оборачиваемость, безубыточность продаж, отсрочка платежа, налоги и т. д.);
- работа с формулами;
- работа с текстом;
- работа с книгами и листами Excel;
- работа с ячейками Excel;
- поиск дубликатов и сравнение диапазонов данных;
- вставка дат и примечаний к диапазонам данных;
- загрузка курсов валют;
- создание выпадающих списков.
Надстройка PowerFin будет полезна прежде всего экономистам, которые работают с кредитами и инвестициями. Она без проблем устанавливается в меню надстроек Excel и имеет следующие функции:
- кредитный калькулятор (с функцией выведения калькулятора на лист, в том числе с возможностью автоматического формирования графика платежей);
- депозитный калькулятор для вычисления основных параметров инвестиций (с функцией выведения калькулятора на лист);
- вычисление требуемой процентной ставки исходя из первоначальной и будущей стоимости инвестиций;
- набор основных формул для расчета эффективности проекта: дисконтированного денежного потока, чистого денежного дохода, внутренней нормы доходности, срока окупаемости.
Статья опубликована в журнале «Планово-экономический отдел» № 10, 2020.