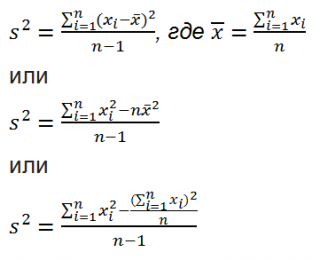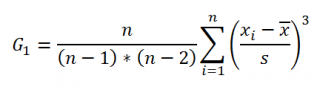Математический анализ в excel примеры

Функция СРОТКЛ в Excel используется для анализа числового ряда, передаваемого в качестве аргумента, и возвращает число, соответствующее среднему значению, рассчитанному для модулей отклонений относительно среднего арифметического для исследуемого ряда.

Примеры методов анализа числовых рядов в Excel

Смысл данной функции становится предельно ясен после рассмотрения примера. Допустим, на протяжении суток каждые 3 часа фиксировались показатели температуры воздуха. Был получен следующий ряд значений: 16, 14, 17, 21, 25, 26, 22, 18. С помощью функции СРЗНАЧ можно определить среднее значение температуры – 19,88 (округлим до 20). Для определения отклонения каждого значения от среднего необходимо вычесть из него полученное среднее значение. Например, для первого замера температуры это будет равно 16-20=-4. Получаем ряд значений: -4, -6, -3, 1, 5, 6, 2, -2. Поскольку СРОТКЛ по определению работает с модулями отклонений, итоговый ряд значений имеет вид: 4, 6, 3, 1, 5, 6, 2, 2. Теперь нужно получить среднее значение для данного ряда с помощью функции СРЗНАЧ – примерно 3,63. Именно таков алгоритм работы рассматриваемой функции.

Таким образом, значение, вычисляемое функцией СРОТКЛ, можно рассчитать с помощью формулы массива без использования этой функции. Допустим, перечисленные результаты замеров температур записаны в столбец (ячейки A1:A8). Тогда для определения среднего значения отклонений можно использовать формулу =СРЗНАЧ(ABS(A1:A8-СРЗНАЧ(A1:A8))). Однако, рассматриваемая функция значительно упрощает расчеты.

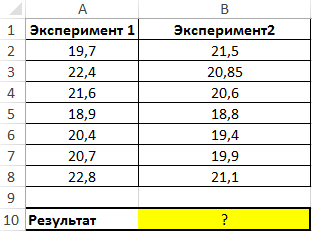
Пример 1. Имеются два ряда значений, представляющих собой результаты наблюдений одного и того же физического явления, сделанные в ходе двух различных экспериментов. Определить, среднее отклонение от среднего значения результатов для какого эксперимента является максимальным?

Вид таблицы данных:

Используем следующую формулу:

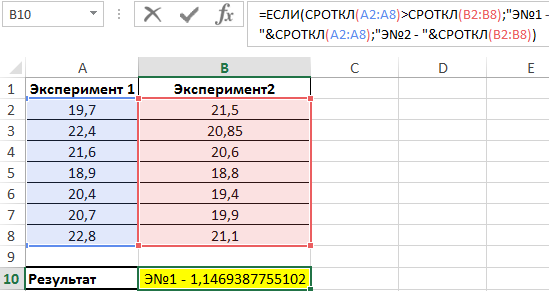
Сравниваем результаты, возвращаемые функцией СРОТКЛ для первого и второго ряда чисел с использованием функции ЕСЛИ, возвращаем соответствующий результат.

Полученное значение:

В результате мы получили среднее отклонение от среднего значения. Это весьма интересная функция для технического анализа финансовых рынков, прогнозов курсов валют и даже позволяет повысить шансы выигрышей в лотереях.



Формула расчета линейного коэффициента вариации в Excel

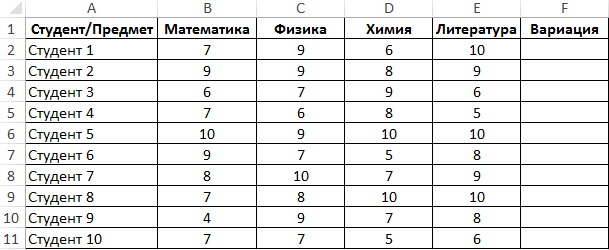
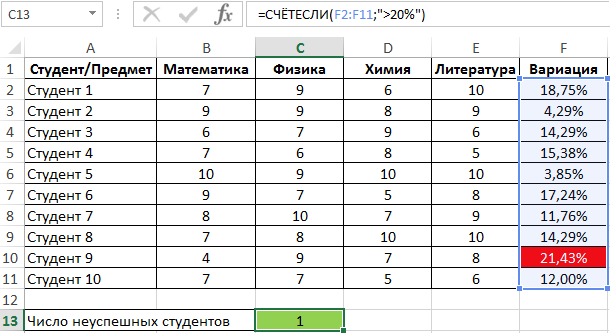
Пример 2. Студенты сдали экзамены по различным предметам. Определить число студентов, которые удовлетворяют следующему критерию успеваемости – линейный коэффициент вариации оценок не превышает 15%.

Вид таблицы данных:

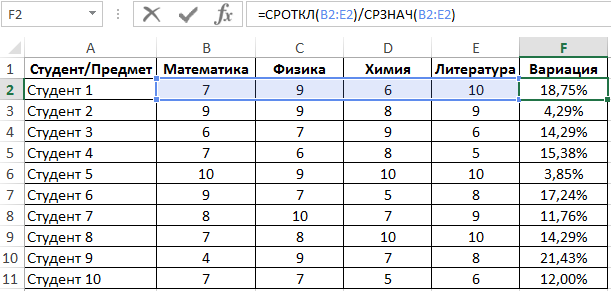
Линейный коэффициент вариации определяется как отношение среднего отклонения к среднему значению. Для расчета используем следующую формулу:

Растянем ее вниз по столбцу и получим следующие значения:

Для определения числа неуспешных студентов по указанному критерию используем функцию:

Полученный результат:

Правила использования функции СРОТКЛ в Excel

Функция имеет следующий синтаксис:

=СРОТКЛ(число1;[число2];…)

Описание аргументов:

• число1 – обязательный, принимает числовое значение, характеризующее первый член ряда значений, для которых необходимо определить среднее отклонение от среднего;
• [число2];… — необязательный, принимает второе и последующие значения из исследуемого числового ряда.

Примечания:

1. При использовании функции СРОТКЛ удобнее задавать первый аргумент в виде ссылки на диапазон ячеек, например =СРОТКЛ(A1:A8) вместо перечисления (=СРОТКЛ(A1;A2:A3…;A8)).
2. В качестве аргумента функции может быть передана константа массива, например =СРОТКЛ({2;5;4;7;10}).
3. Для получения достоверного результата необходимо привести все значения ряда к единой системе измерения величин. Например, если часть длин указана в мм, а остальные – в см, результат расчетов будет некорректен. Необходимо преобразовать все значения в мм или см соответственно.
4. Если в качестве аргументов функции переданы нечисловые данные, которые не могут быть преобразованы к числам, функция вернет код ошибки #ЧИСЛО!. Если хотя бы одно значение из ряда является числовым, функция выполнит расчет, не возвращая код ошибки.
5. Не преобразуемые к числам текстовые строки и пустые ячейки не учитываются в расчете. Если ячейка содержит значение 0 (нуль), оно будет учтено.
6. Логические данные автоматически преобразуются к числовым: ИСТИНА – 1, ЛОЖЬ – 0 соответственно.

КУРС

EXCEL ACADEMY

Научитесь использовать все прикладные инструменты из функционала MS Excel.

Microsoft Excel – одна из самых популярных и легкодоступных программ для представителей разный специальностей. Сегодня мы рассмотрим, пожалуй, одну из самых используемых групп формул – математические формулы.

Начнем с того, как найти их среди прочего функционала. Есть несколько путей того, как открыть список математических формул.

Самый простой способ – нажать на кнопку «Формулы» на панели управления. Затем выбрать из перечня тип функций: «Математические».

Перед вами появится выпадающий длинный список всех существующих операторов:

Всего в Excel около 80 математических и тригонометрических функций. Мы рассмотрим не все, только самые распространенные из них, а также обратим внимание на некоторые нюансы, о которых вы, возможно, не знали. Если в статье вы не нашли нужную вам функцию, то скачивайте наш бесплатный гайд «Математические функции в Excel».

Для разминки вспомним самые простые формулы.

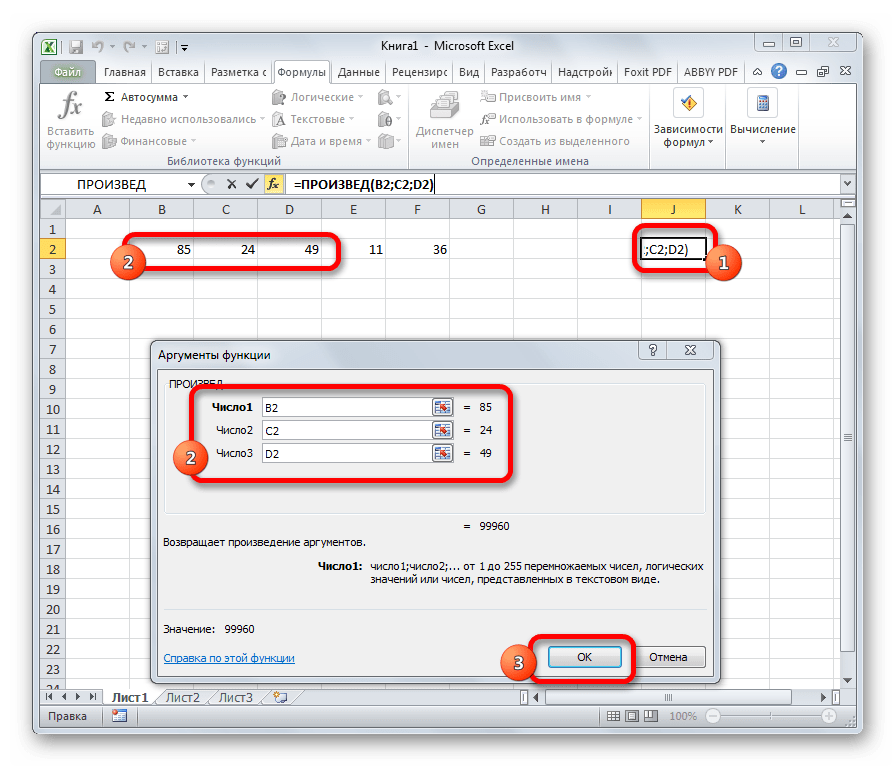
1. Формулы СУММ(), ПРОИЗВЕД()

Эти операции имеют схожую структуру и одинаковый тип аргументов, поэтому мы их объединили в один блок. СУММ() служит для сложения данных в нескольких ячейках, ПРОИЗВЕД() – очевидно, для нахождения произведения.

Аргументами этих функций могут быть числа, диапазоны, ссылки на ячейку, в которой содержится числовое значение. Количество элементов не может быть больше 30.

СУММ() и ПРОИЗВЕД() пропускают пустые ячейки, ячейки текстового формата и логические значения. Операторы вносят результат вычислений в отдельную, ранее выделенную курсором ячейку:

Аналогично для формулы ПРОИЗВЕД():

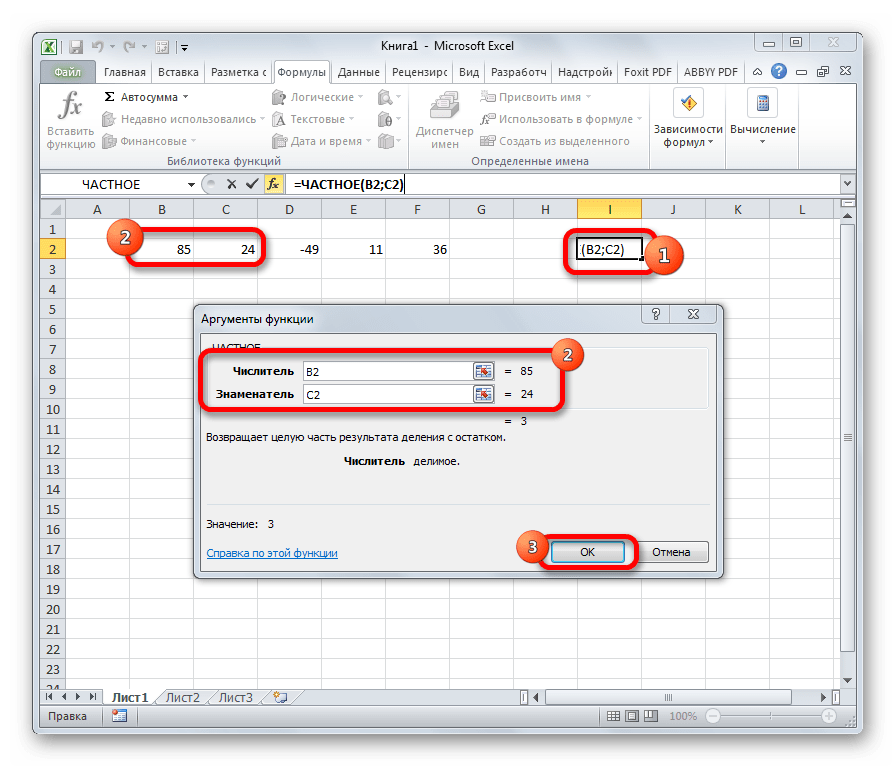
2. Формула ЧАСТНОЕ()

Тоже одна из простых операций в математике. В Excel выполняется тоже несложно: у функции ЧАСТНОЕ() есть два аргумента: делимое и делитель.

В выделенной ячейке выводится частное:

3. Формула СУММЕСЛИ()

Оператор СУММЕСЛИ() находит сумму чисел. Главное отличие этой функции от СУММ() в том, что здесь в качестве аргумента можно задавать условие (только одно), которое будет показывать, какие значения будут использованы в расчетах, а какие – нет.

В качестве условий могут выступать неравенства со знаками больше, меньше или не равно («>», «<», «< >»). Число, которое не соответствует введенному условию, не будет включен в суммирование.

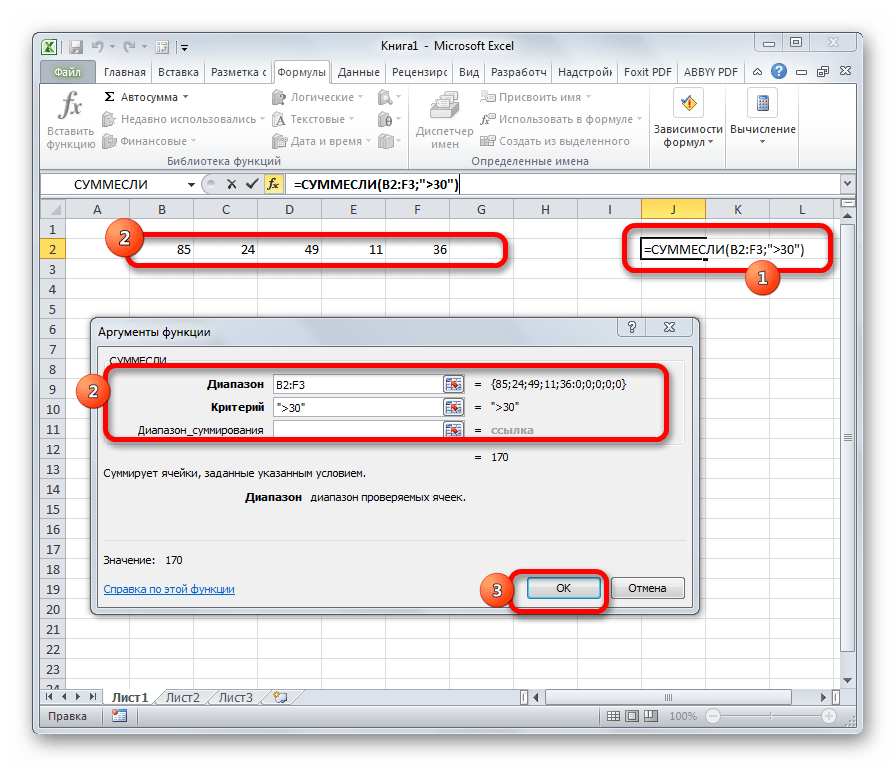
На рисунке 5 изображено суммирование всех чисел, которые больше 0.

Оранжевым выделены те числа, которые будут включены в расчет функцией СУММЕСЛИ().

Остальные числа просто будут игнорироваться:

Кроме постоянных аргументов, существует еще и дополнительный – «Диапазон суммирования». Он добавляется тогда, когда необходимо просуммировать один диапазон, а условия выбирать по другому диапазону.

Например, нужно посчитать общую стоимость всех проданных фруктов.

Для этого воспользуемся следующей формулой:

То есть сначала пишем диапазон, по которому проверяем условие, затем само ограничение и в конце диапазон чисел, которые надо суммировать. В примере на рисунке 6 выше, соответственно, все строки из категории «Овощи» в расчет включены не будут.

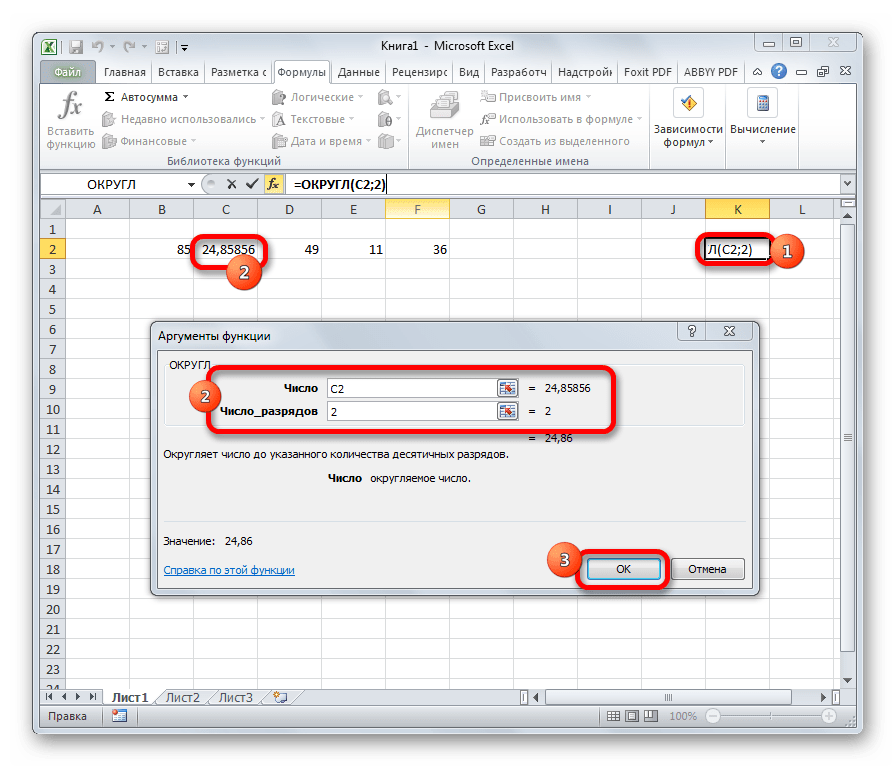
4. Формулы ОКРУГЛ(), ОКРУГЛВВЕРХ(), ОКРУГЛВНИЗ()

Функция ОКРУГЛ() предназначена для округления значения до заданного количества знаков после запятой. В качестве первого аргумента выступают, как обычно, числа или диапазон ячеек, второго – разряд, до которого нужно округлить число.

Например, округление значения до второго знака после запятой:

Если в качестве второго аргумента выступает 0, то число будет округляться до ближайшего целого:

Второй аргумент может быть и отрицательным, тогда округление будет происходить до требуемого знака перед запятой:

Если необходимо округлить в сторону меньшего или большего по модулю числа используют функции ОКРУГЛВНИЗ(), ОКРУГЛВВЕРХ(), соответственно:

Замечание: многие могут решить, что функции округления бесполезны, так как можно просто убрать/добавить дополнительный знак после запятой с помощью кнопок увеличить/уменьшить разрядность.

На самом деле, это не так.

Дело в том, что увеличение или уменьшение разрядности влияет только на «внешний вид» ячейки, то есть на то, как мы число видим.

Само число, при этом, не меняется. Функции округления же полностью меняют вид числа, убирая лишние разряды.

5. Формулы ОТБР(), ЦЕЛОЕ()

Эти функции очень похожи на предыдущие, но работают немного по-другому.

ОТБР() убирает все цифры справа от запятой и у положительных, и у отрицательных чисел. На первом месте в скобках после оператора пишется значение, а на втором – разряд, после которого удалятся все знаки.

Если второй аргумент пропущен, то по умолчанию ставится 0:

ЦЕЛОЕ() – функция, которая выдает в качестве результата наименьшее целое число, стоящее перед аргументом:

На положительные числа операторы влияют почти одинаково, а вот на отрицательные – нет.

Функция ЦЕЛОЕ(-5,6) выдаст результат (-6), а ОТБР(-5,6;0) выдаст (-5), хотя в то же время для числа 5,3 результат обеих функций будет одинаковый – число (5).

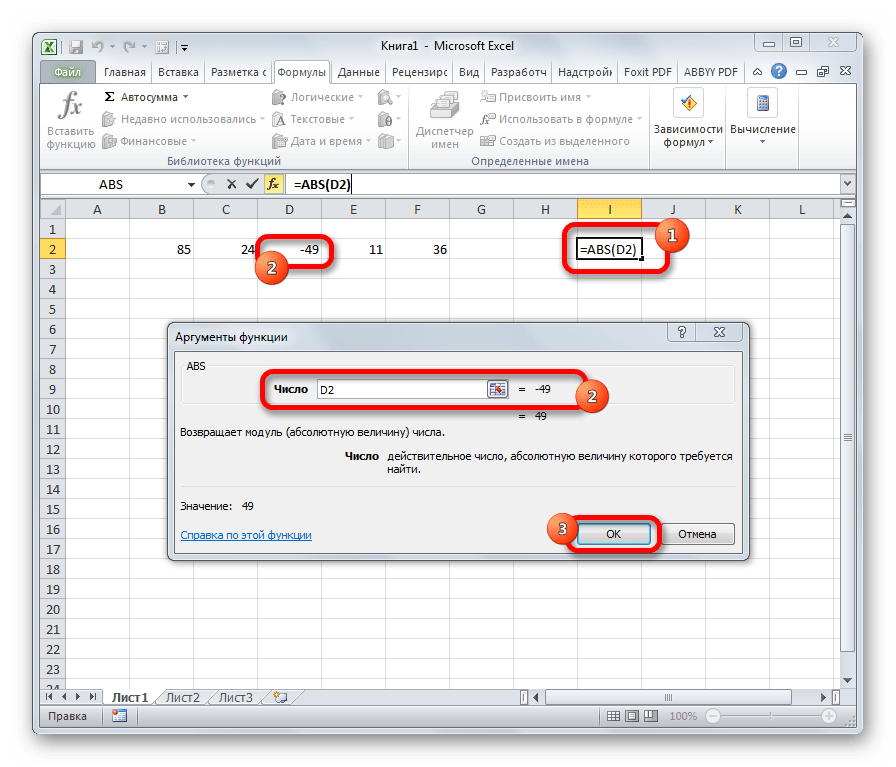
6. Формула ABS()

Математическая формула ABS() позволяет получить число по модулю. Как обычно, аргументами оператора является число или ссылка на ячейку.

Эту функцию удобно использовать, например, когда необходимо найти количество дней между датами. Из школьной программы многие знают, что нужно из большего вычитать меньшее.

Но что делать если дана огромная таблица, где трудно определить, где какое значение? Здесь нам помогает оператор ABS(), который переводит отрицательное число в положительное.

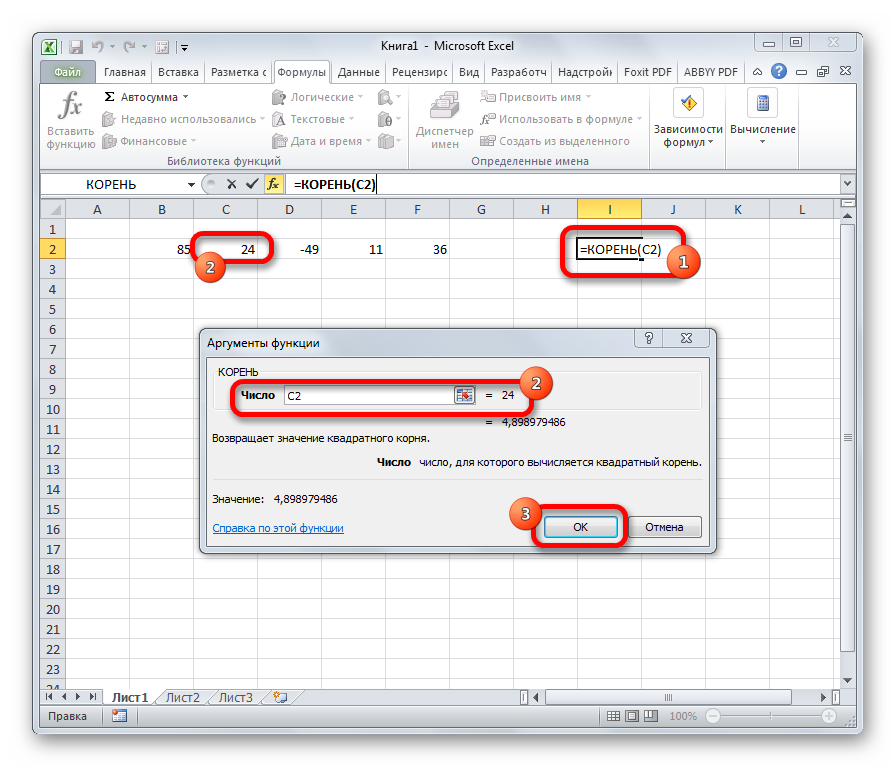
7. Формула КОРЕНЬ()

КОРЕНЬ() – довольно легкая функция с одним аргументом (числом или ссылкой на ячейку), которая находит квадратный корень числа:

Замечание. Для извлечения корня другой степени (не квадратного) можно пользоваться функцией СТЕПЕНЬ().

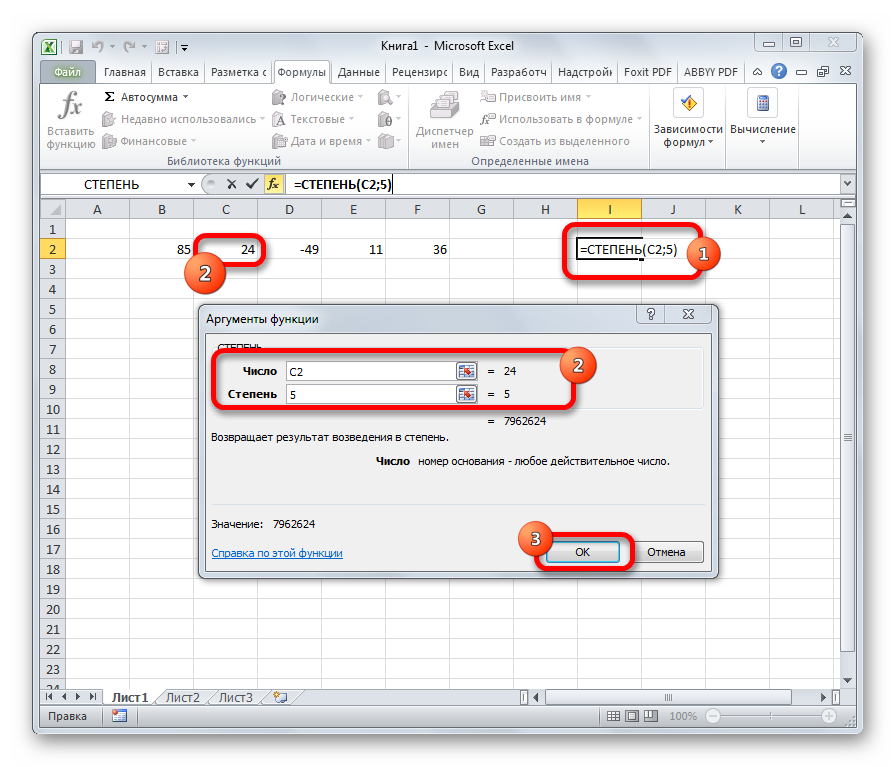
8. Формула СТЕПЕНЬ()

Функция СТЕПЕНЬ() позволяет возвести число в любую степень, в том числе извлечь корень (то есть возвести число в дробную степень).

Например, чтобы извлечь кубический корень из числа 8, необходимо воспользоваться формулой, как на рисунке 17.1.

Помимо математической функции СТЕПЕНЬ(), можно пользоваться оператором “^”, но он выглядит менее опрятно в формулах.

Если вам интересно узнать больше о других математических функциях, напишите об этом ниже в комментариях. Записывайтесь на открытый онлайн-курс «Аналитика в Excel», если хотите научиться выполнять рутинную работу в программе быстрее.

КУРС

EXCEL ACADEMY

Научитесь использовать все прикладные инструменты из функционала MS Excel.

Блог SF Education

Investment Banking

5 примеров экономии времени в Excel

Содержание статьи Что для работодателя главное в сотруднике? Добросовестность, ответственность, профессионализм и, конечно же, умение пользоваться отведенным временем! Предлагаем познакомиться с очень нужными, на…

Как работает сотрудник одной из компаний «большой тройки»?

Ты работаешь в компании «большой тройки (имеются в виду три крупнейших консалтинговых компании: McKinsey, Boston Consulting Group и Bain & Company), в которых мечтают работать тысячи подписчиков наших каналов и читателей vc.ru. Что это значит для тебя?

Рассмотрим инструмент Описательная статистика, входящий в надстройку Пакет Анализа. Рассчитаем показатели выборки: среднее, медиана, мода, дисперсия, стандартное отклонение и др.

Задача

описательной статистики

(descriptive statistics) заключается в том, чтобы с использованием математических инструментов свести сотни значений

выборки

к нескольким итоговым показателям, которые дают представление о

выборке

.В качестве таких статистических показателей используются:

среднее

,

медиана

,

мода

,

дисперсия, стандартное отклонение

и др.

Опишем набор числовых данных с помощью определенных показателей. Для чего нужны эти показатели? Эти показатели позволят сделать определенные

статистические выводы о распределении

, из которого была взята

выборка

. Например, если у нас есть

выборка

значений толщины трубы, которая изготавливается на определенном оборудовании, то на основании анализа этой

выборки

мы сможем сделать, с некой определенной вероятностью, заключение о состоянии процесса изготовления.

Содержание статьи:

• Надстройка Пакет анализа;
• Среднее выборки

  ;

• Медиана выборки

  ;

• Мода выборки

  ;

• Мода и среднее значение

  ;

• Дисперсия выборки

  ;

• Стандартное отклонение выборки

  ;

• Стандартная ошибка

  ;

• Ассиметричность

  ;

• Эксцесс выборки

  ;

• Уровень надежности

  .

Надстройка Пакет анализа

Для вычисления статистических показателей одномерных

выборок

, используем

надстройку Пакет анализа

. Затем, все показатели рассчитанные надстройкой, вычислим с помощью встроенных функций MS EXCEL.

СОВЕТ

: Подробнее о других инструментах надстройки

Пакет анализа

и ее подключении – читайте в статье

Надстройка Пакет анализа MS EXCEL

.

Выборку

разместим на

листе

Пример

в файле примера

в диапазоне

А6:А55

(50 значений).

Примечание

: Для удобства написания формул для диапазона

А6:А55

создан

Именованный диапазон

Выборка.

В диалоговом окне

Анализ данных

выберите инструмент

Описательная статистика

.

После нажатия кнопки

ОК

будет выведено другое диалоговое окно,

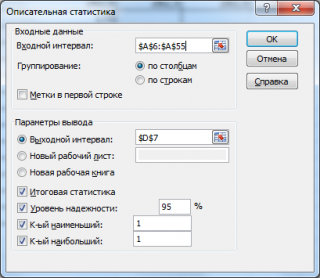
в котором нужно указать:

• 
  входной интервал
  
  (Input Range) – это диапазон ячеек, в котором содержится массив данных. Если в указанный диапазон входит текстовый заголовок набора данных, то нужно поставить галочку в поле
  
  Метки в первой строке (
  
  Labels
  
  in
  
  first
  
  row
  
  ).
  
  В этом случае заголовок будет выведен в
  
  Выходном интервале.
  
  Пустые ячейки будут проигнорированы, поэтому нулевые значения необходимо обязательно указывать в ячейках, а не оставлять их пустыми;
• 
  выходной интервал
  
  (Output Range). Здесь укажите адрес верхней левой ячейки диапазона, в который будут выведены статистические показатели;
• 
  Итоговая статистика (
  
  Summary
  
  Statistics
  
  )
  
  . Поставьте галочку напротив этого поля – будут выведены основные показатели выборки:
  
  среднее, медиана, мода, стандартное отклонение
  
  и др.;
• Также можно поставить галочки напротив полей
  
  Уровень надежности (
  
  Confidence
  
  Level
  
  for
  
  Mean
  
  )
  
  ,
  
  К-й наименьший
  
  (Kth Largest) и
  
  К-й наибольший
  
  (Kth Smallest).

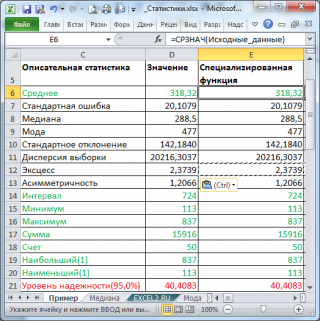
В результате будут выведены следующие статистические показатели:

Все показатели выведены в виде значений, а не формул. Если массив данных изменился, то необходимо перезапустить расчет.

Если во

входном интервале

указать ссылку на несколько столбцов данных, то будет рассчитано соответствующее количество наборов показателей. Такой подход позволяет сравнить несколько наборов данных. При сравнении нескольких наборов данных используйте заголовки (включите их во

Входной интервал

и установите галочку в поле

Метки в первой строке

). Если наборы данных разной длины, то это не проблема — пустые ячейки будут проигнорированы.

Зеленым цветом на картинке выше и в

файле примера

выделены показатели, которые не требуют особого пояснения. Для большинства из них имеется специализированная функция:

• 
  Интервал
  
  (Range) — разница между максимальным и минимальным  значениями;
• 
  Минимум
  
  (Minimum) – минимальное значение в диапазоне ячеек, указанном во
  
  Входном интервале
  
  (см.

  статью про функцию
  
  МИН()
  
  );

• 
  Максимум
  
  (Maximum)– максимальное значение (см.

  статью про функцию
  
  МАКС()
  
  );

• 
  Сумма
  
  (Sum) – сумма всех значений (см.

  статью про функцию
  
  СУММ()
  
  );

• 
  Счет
  
  (Count) – количество значений во
  
  Входном интервале
  
  (пустые ячейки игнорируются, см.

  статью про функцию
  
  СЧЁТ()
  
  );

• 
  Наибольший
  
  (Kth Largest) – выводится К-й наибольший. Например, 1-й наибольший – это максимальное значение (см.

  статью про функцию
  
  НАИБОЛЬШИЙ()
  
  );

• 
  Наименьший
  
  (Kth Smallest) – выводится К-й наименьший. Например, 1-й наименьший – это минимальное значение (см.

  статью про функцию
  
  НАИМЕНЬШИЙ()
  
  ).

Ниже даны подробные описания остальных показателей.

Среднее выборки

Среднее

(mean, average) или

выборочное среднее

или

среднее выборки

(sample average) представляет собой

арифметическое среднее

всех значений массива. В MS EXCEL для вычисления среднего выборки используется функция

СРЗНАЧ()

.

Выборочное среднее

является «хорошей» (несмещенной и эффективной) оценкой

математического ожидания

случайной величины (подробнее см. статью

Среднее и Математическое ожидание в MS EXCEL

).

Медиана выборки

Медиана

(Median) – это число, которое является серединой множества чисел (в данном случае выборки): половина чисел множества больше, чем

медиана

, а половина чисел меньше, чем

медиана

. Для определения

медианы

необходимо сначала

отсортировать множество чисел

. Например,

медианой

для чисел 2, 3, 3,

4

, 5, 7, 10 будет 4.

Если множество содержит четное количество чисел, то вычисляется

среднее

для двух чисел, находящихся в середине множества. Например,

медианой

для чисел 2, 3,

3

,

5

, 7, 10 будет 4, т.к. (3+5)/2.

Если имеется длинный хвост распределения, то

Медиана

лучше, чем

среднее значение

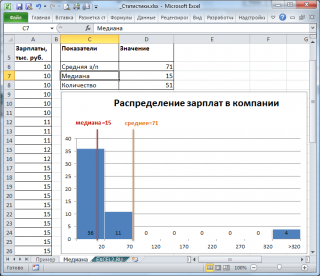
, отражает «типичное» или «центральное» значение. Например, рассмотрим несправедливое распределение зарплат в компании, в которой руководство получает существенно больше, чем основная масса сотрудников.

Очевидно, что средняя зарплата (71 тыс. руб.) не отражает тот факт, что 86% сотрудников получает не более 30 тыс. руб. (т.е. 86% сотрудников получает зарплату в более, чем в 2 раза меньше средней!). В то же время медиана (15 тыс. руб.) показывает, что

как минимум

у 50% сотрудников зарплата меньше или равна 15 тыс. руб.

Для определения

медианы

в MS EXCEL существует одноименная функция

МЕДИАНА()

, английский вариант — MEDIAN().

Медиану

также можно вычислить с помощью формул

=КВАРТИЛЬ.ВКЛ(Выборка;2) =ПРОЦЕНТИЛЬ.ВКЛ(Выборка;0,5).

Подробнее о

медиане

см. специальную статью

Медиана в MS EXCEL

.

СОВЕТ

: Подробнее про

квартили

см. статью, про

перцентили (процентили)

см. статью.

Мода выборки

Мода

(Mode) – это наиболее часто встречающееся (повторяющееся) значение в

выборке

. Например, в массиве (1; 1;

2

;

2

;

2

; 3; 4; 5) число 2 встречается чаще всего – 3 раза. Значит, число 2 – это

мода

. Для вычисления

моды

используется функция

МОДА()

, английский вариант MODE().

Примечание

: Если в массиве нет повторяющихся значений, то функция вернет значение ошибки #Н/Д. Это свойство использовано в статье

Есть ли повторы в списке?

Начиная с

MS EXCEL 2010

вместо функции

МОДА()

рекомендуется использовать функцию

МОДА.ОДН()

, которая является ее полным аналогом. Кроме того, в MS EXCEL 2010 появилась новая функция

МОДА.НСК()

, которая возвращает несколько наиболее часто повторяющихся значений (если количество их повторов совпадает). НСК – это сокращение от слова НеСКолько.

Например, в массиве (1; 1;

2

;

2

;

2

; 3;

4

;

4

;

4

; 5) числа 2 и 4 встречаются наиболее часто – по 3 раза. Значит, оба числа являются

модами

. Функции

МОДА.ОДН()

и

МОДА()

вернут значение 2, т.к. 2 встречается первым, среди наиболее повторяющихся значений (см.

файл примера

, лист

Мода

).

Чтобы исправить эту несправедливость и была введена функция

МОДА.НСК()

, которая выводит все

моды

. Для этого ее нужно ввести как

формулу массива

.

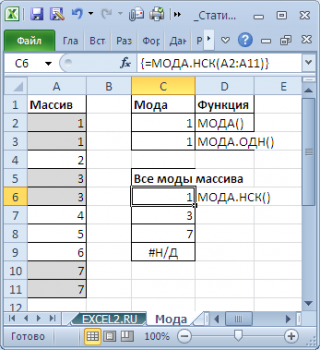
Как видно из картинки выше, функция

МОДА.НСК()

вернула все три

моды

из массива чисел в диапазоне

A2:A11

: 1; 3 и 7. Для этого, выделите диапазон

C6:C9

, в

Строку формул

введите формулу

=МОДА.НСК(A2:A11)

и нажмите

CTRL+SHIFT+ENTER

. Диапазон

C

6:

C

9

охватывает 4 ячейки, т.е. количество выделяемых ячеек должно быть больше или равно количеству

мод

. Если ячеек больше чем м

о

д, то избыточные ячейки будут заполнены значениями ошибки #Н/Д. Если

мода

только одна, то все выделенные ячейки будут заполнены значением этой

моды

.

Теперь вспомним, что мы определили

моду

для выборки, т.е. для конечного множества значений, взятых из

генеральной совокупности

. Для

непрерывных случайных величин

вполне может оказаться, что выборка состоит из массива на подобие этого (0,935; 1,211; 2,430; 3,668; 3,874; …), в котором может не оказаться повторов и функция

МОДА()

вернет ошибку.

Даже в нашем массиве с

модой

, которая была определена с помощью

надстройки Пакет анализа

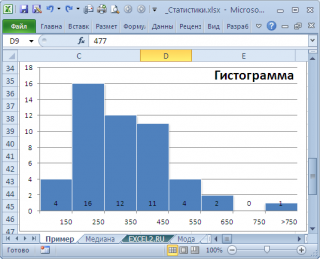
, творится, что-то не то. Действительно,

модой

нашего массива значений является число 477, т.к. оно встречается 2 раза, остальные значения не повторяются. Но, если мы посмотрим на

гистограмму распределения

, построенную для нашего массива, то увидим, что 477 не принадлежит интервалу наиболее часто встречающихся значений (от 150 до 250).

Проблема в том, что мы определили

моду

как наиболее часто встречающееся значение, а не как наиболее вероятное. Поэтому,

моду

в учебниках статистики часто определяют не для выборки (массива), а для функции распределения. Например, для

логнормального распределения

мода

(наиболее вероятное значение непрерывной случайной величины х), вычисляется как

exp

(

m

—

s

²

)

, где m и s параметры этого распределения.

Понятно, что для нашего массива число 477, хотя и является наиболее часто повторяющимся значением, но все же является плохой оценкой для

моды

распределения, из которого взята

выборка

(наиболее вероятного значения или для которого плотность вероятности распределения максимальна).

Для того, чтобы получить оценку

моды

распределения, из

генеральной совокупности

которого взята

выборка

, можно, например, построить

гистограмму

. Оценкой для

моды

может служить интервал наиболее часто встречающихся значений (самого высокого столбца). Как было сказано выше, в нашем случае это интервал от 150 до 250.

Вывод

: Значение

моды

для

выборки

, рассчитанное с помощью функции

МОДА()

, может ввести в заблуждение, особенно для небольших выборок. Эта функция эффективна, когда случайная величина может принимать лишь несколько дискретных значений, а размер

выборки

существенно превышает количество этих значений.

Например, в рассмотренном примере о распределении заработных плат (см. раздел статьи выше, о Медиане),

модой

является число 15 (17 значений из 51, т.е. 33%). В этом случае функция

МОДА()

дает хорошую оценку «наиболее вероятного» значения зарплаты.

Примечание

: Строго говоря, в примере с зарплатой мы имеем дело скорее с

генеральной совокупностью

, чем с

выборкой

. Т.к. других зарплат в компании просто нет.

О вычислении

моды

для распределения

непрерывной случайной величины

читайте статью

Мода в MS EXCEL

.

Мода и среднее значение

Не смотря на то, что

мода

– это наиболее вероятное значение случайной величины (вероятность выбрать это значение из

Генеральной совокупности

максимальна), не следует ожидать, что

среднее значение

обязательно будет близко к

моде

.

Примечание

:

Мода

и

среднее

симметричных распределений совпадает (имеется ввиду симметричность

плотности распределения

).

Представим, что мы бросаем некий «неправильный» кубик, у которого на гранях имеются значения (1; 2; 3; 4; 6; 6), т.е. значения 5 нет, а есть вторая 6.

Модой

является 6, а среднее значение – 3,6666.

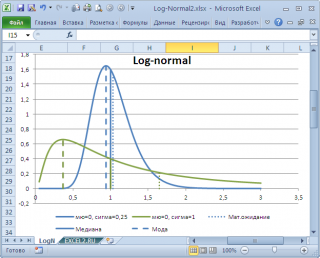
Другой пример. Для

Логнормального распределения

LnN(0;1)

мода

равна =EXP(m-s2)= EXP(0-1*1)=0,368, а

среднее значение

1,649.

Дисперсия выборки

Дисперсия выборки

или

выборочная дисперсия (

sample

variance

) характеризует разброс значений в массиве, отклонение от

среднего

.

Из формулы №1 видно, что

дисперсия выборки

это сумма квадратов отклонений каждого значения в массиве

от среднего

, деленная на размер выборки минус 1.

В MS EXCEL 2007 и более ранних версиях для вычисления

дисперсии выборки

используется функция

ДИСП()

. С версии MS EXCEL 2010 рекомендуется использовать ее аналог — функцию

ДИСП.В()

.

Дисперсию

можно также вычислить непосредственно по нижеуказанным формулам (см.

файл примера

):

=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1) =(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1)

– обычная формула

=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1)

–

формула массива

Дисперсия выборки

равна 0, только в том случае, если все значения равны между собой и, соответственно, равны

среднему значению

.

Чем больше величина

дисперсии

, тем больше разброс значений в массиве относительно

среднего

.

Размерность

дисперсии

соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность

дисперсии

будет кг

²

. Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из

дисперсии – стандартное отклонение

.

Подробнее о

дисперсии

см. статью

Дисперсия и стандартное отклонение в MS EXCEL

.

Стандартное отклонение выборки

Стандартное отклонение выборки

(Standard Deviation), как и

дисперсия

, — это мера того, насколько широко разбросаны значения в выборке

относительно их среднего

.

По определению,

стандартное отклонение

равно квадратному корню из

дисперсии

:

Стандартное отклонение

не учитывает величину значений в

выборке

, а только степень рассеивания значений вокруг их

среднего

. Чтобы проиллюстрировать это приведем пример.

Вычислим стандартное отклонение для 2-х

выборок

: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у

выборок

существенно отличается.

В MS EXCEL 2007 и более ранних версиях для вычисления

Стандартного отклонения выборки

используется функция

СТАНДОТКЛОН()

. С версии MS EXCEL 2010 рекомендуется использовать ее аналог

СТАНДОТКЛОН.В()

.

Стандартное отклонение

можно также вычислить непосредственно по нижеуказанным формулам (см.

файл примера

):

=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))

Подробнее о

стандартном отклонении

см. статью

Дисперсия и стандартное отклонение в MS EXCEL

.

Стандартная ошибка

В

Пакете анализа

под термином

стандартная ошибка

имеется ввиду

Стандартная ошибка среднего

(Standard Error of the Mean, SEM).

Стандартная ошибка среднего

— это оценка

стандартного отклонения

распределения

выборочного среднего

.

Примечание

: Чтобы разобраться с понятием

Стандартная ошибка среднего

необходимо прочитать о

выборочном распределении

(см. статью

Статистики, их выборочные распределения и точечные оценки параметров распределений в MS EXCEL

) и статью про

Центральную предельную теорему

.

Стандартное отклонение распределения выборочного среднего

вычисляется по формуле σ/√n, где n — объём

выборки, σ — стандартное отклонение исходного

распределения, из которого взята

выборка

. Т.к. обычно

стандартное отклонение

исходного распределения неизвестно, то в расчетах вместо

σ

используют ее оценку

s

—

стандартное отклонение выборки

. А соответствующая величина s/√n имеет специальное название —

Стандартная ошибка среднего.

Именно эта величина вычисляется в

Пакете анализа.

В MS EXCEL

стандартную ошибку среднего

можно также вычислить по формуле

=СТАНДОТКЛОН.В(Выборка)/ КОРЕНЬ(СЧЁТ(Выборка))

Асимметричность

Асимметричность

или

коэффициент асимметрии

(skewness) характеризует степень несимметричности распределения (

плотности распределения

) относительно его

среднего

.

Положительное значение

коэффициента асимметрии

указывает, что размер правого «хвоста» распределения больше, чем левого (относительно среднего). Отрицательная асимметрия, наоборот, указывает на то, что левый хвост распределения больше правого.

Коэффициент асимметрии

идеально симметричного распределения или выборки равно 0.

Примечание

:

Асимметрия выборки

может отличаться расчетного значения асимметрии теоретического распределения. Например,

Нормальное распределение

является симметричным распределением (

плотность его распределения

симметрична относительно

среднего

) и, поэтому имеет асимметрию равную 0. Понятно, что при этом значения в

выборке

из соответствующей

генеральной совокупности

не обязательно должны располагаться совершенно симметрично относительно

среднего

. Поэтому,

асимметрия выборки

, являющейся оценкой

асимметрии распределения

, может отличаться от 0.

Функция

СКОС()

, английский вариант SKEW(), возвращает коэффициент

асимметрии выборки

, являющейся оценкой

асимметрии

соответствующего распределения, и определяется следующим образом:

где n – размер

выборки

, s –

стандартное отклонение выборки

.

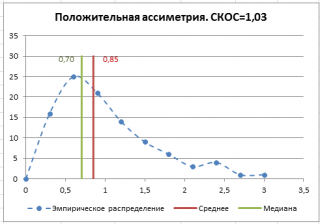
В

файле примера на листе СКОС

приведен расчет коэффициента

асимметрии

на примере случайной выборки из

распределения Вейбулла

, которое имеет значительную положительную

асимметрию

при параметрах распределения W(1,5; 1).

Эксцесс выборки

Эксцесс

показывает относительный вес «хвостов» распределения относительно его центральной части.

Для того чтобы определить, что относится к хвостам распределения, а что к его центральной части, можно использовать границы μ +/-

σ

.

Примечание

: Не смотря на старания профессиональных статистиков, в литературе еще попадается определение

Эксцесса

как меры «остроконечности» (peakedness) или сглаженности распределения. Но, на самом деле, значение

Эксцесса

ничего не говорит о форме пика распределения.

Согласно определения,

Эксцесс

равен четвертому

стандартизированному моменту:

Для

нормального распределения

четвертый момент равен 3*σ

⁴

, следовательно,

Эксцесс

равен 3. Многие компьютерные программы используют для расчетов не сам

Эксцесс

, а так называемый Kurtosis excess, который меньше на 3. Т.е. для

нормального распределения

Kurtosis excess равен 0. Необходимо быть внимательным, т.к. часто не очевидно, какая формула лежит в основе расчетов.

Примечание

: Еще большую путаницу вносит перевод этих терминов на русский язык. Термин Kurtosis происходит от греческого слова «изогнутый», «имеющий арку». Так сложилось, что на русский язык оба термина Kurtosis и Kurtosis excess переводятся как

Эксцесс

(от англ. excess — «излишек»). Например, функция MS EXCEL

ЭКСЦЕСС()

на самом деле вычисляет Kurtosis excess.

Функция

ЭКСЦЕСС()

, английский вариант KURT(), вычисляет на основе значений выборки несмещенную оценку

эксцесса распределения

случайной величины и определяется следующим образом:

Как видно из формулы MS EXCEL использует именно Kurtosis excess, т.е. для выборки из

нормального распределения

формула вернет близкое к 0 значение.

Если задано менее четырех точек данных, то функция

ЭКСЦЕСС()

возвращает значение ошибки #ДЕЛ/0!

Вернемся к

распределениям случайной величины

.

Эксцесс

(Kurtosis excess) для

нормального распределения

всегда равен 0, т.е. не зависит от параметров распределения μ и σ. Для большинства других распределений

Эксцесс

зависит от параметров распределения: см., например,

распределение Вейбулла

или

распределение Пуассона

, для котрого

Эксцесс

= 1/λ.

Уровень надежности

Уровень

надежности

— означает вероятность того, что

доверительный интервал

содержит истинное значение оцениваемого параметра распределения.

Вместо термина

Уровень

надежности

часто используется термин

Уровень доверия

. Про

Уровень надежности

(Confidence Level for Mean) читайте статью

Уровень значимости и уровень надежности в MS EXCEL

.

Задав значение

Уровня

надежности

в окне

надстройки Пакет анализа

, MS EXCEL вычислит половину ширины

доверительного интервала для оценки среднего (дисперсия неизвестна)

.

Тот же результат можно получить по формуле (см.

файл примера

):

=ДОВЕРИТ.СТЬЮДЕНТ(1-0,95;s;n)

s —

стандартное отклонение выборки

, n – объем

выборки

.

Подробнее см. статью про

построение доверительного интервала для оценки среднего (дисперсия неизвестна)

.

Чаще всего среди доступных групп функций пользователи Экселя обращаются к математическим. С помощью них можно производить различные арифметические и алгебраические действия. Их часто используют при планировании и научных вычислениях. Узнаем, что представляет собой данная группа операторов в целом, и более подробно остановимся на самых популярных из них.

Применение математических функций

С помощью математических функций можно проводить различные расчеты. Они будут полезны студентам и школьникам, инженерам, ученым, бухгалтерам, планировщикам. В эту группу входят около 80 операторов. Мы же подробно остановимся на десяти самых популярных из них.

Открыть список математических формул можно несколькими путями. Проще всего запустить Мастер функций, нажав на кнопку «Вставить функцию», которая размещена слева от строки формул. При этом нужно предварительно выделить ячейку, куда будет выводиться результат обработки данных. Этот метод хорош тем, что его можно реализовать, находясь в любой вкладке.

Также можно запустить Мастер функций, перейдя во вкладку «Формулы». Там нужно нажать на кнопку «Вставить функцию», расположенную на самом левом краю ленты в блоке инструментов «Библиотека функций».

Существует и третий способ активации Мастера функций. Он осуществляется с помощью нажатия комбинации клавиш на клавиатуре Shift+F3.

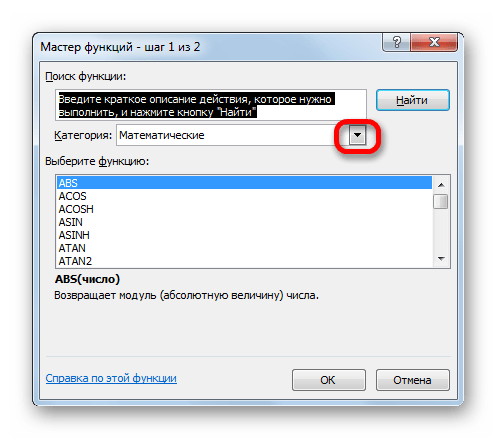
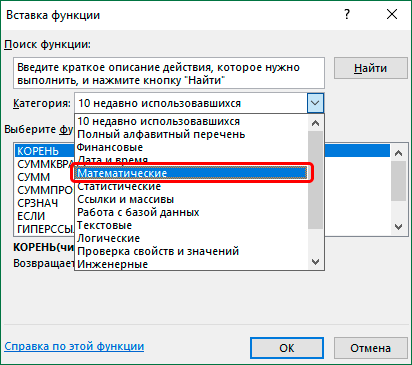
После того, как пользователь произвел любое из вышеуказанных действий, открывается Мастер функций. Кликаем по окну в поле «Категория».

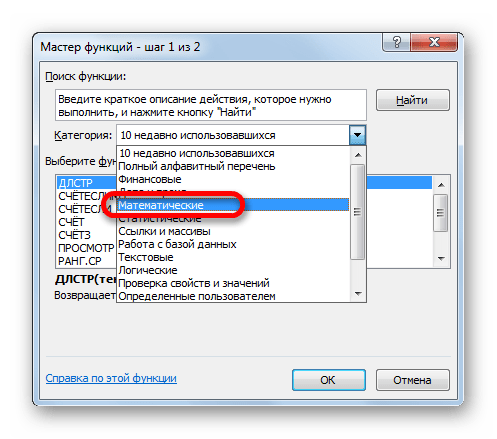
Открывается выпадающий список. Выбираем в нем позицию «Математические».

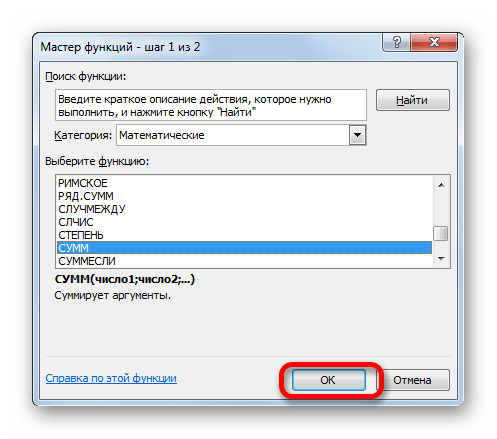
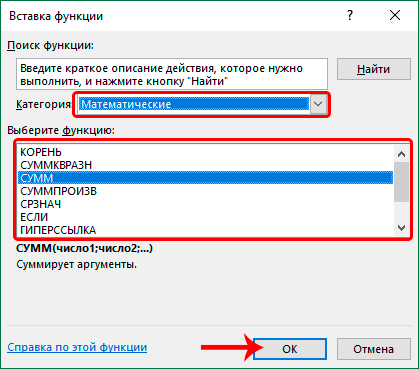
После этого в окне появляется список всех математических функций в Excel. Чтобы перейти к введению аргументов, выделяем конкретную из них и жмем на кнопку «OK».

Существует также способ выбора конкретного математического оператора без открытия главного окна Мастера функций. Для этого переходим в уже знакомую для нас вкладку «Формулы» и жмем на кнопку «Математические», расположенную на ленте в группе инструментов «Библиотека функций». Открывается список, из которого нужно выбрать требуемую формулу для решения конкретной задачи, после чего откроется окно её аргументов.

Правда, нужно заметить, что в этом списке представлены не все формулы математической группы, хотя и большинство из них. Если вы не найдете нужного оператора, то следует кликнуть по пункту «Вставить функцию…» в самом низу списка, после чего откроется уже знакомый нам Мастер функций.

Урок: Мастер функций в Excel

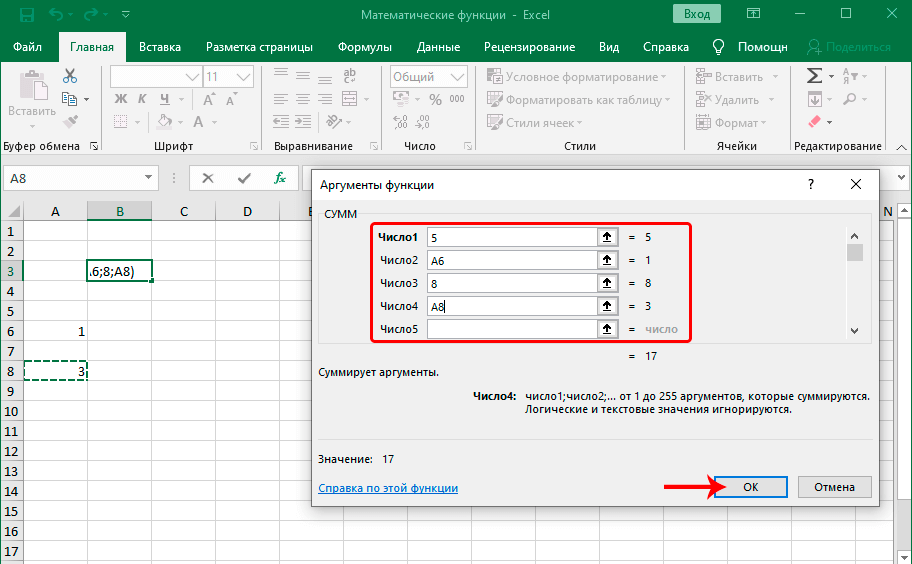
СУММ

Наиболее часто используется функция СУММ. Этот оператор предназначен для сложения данных в нескольких ячейках. Хотя его можно использовать и для обычного суммирования чисел. Синтаксис, который можно применять при ручном вводе, выглядит следующим образом:

=СУММ(число1;число2;…)

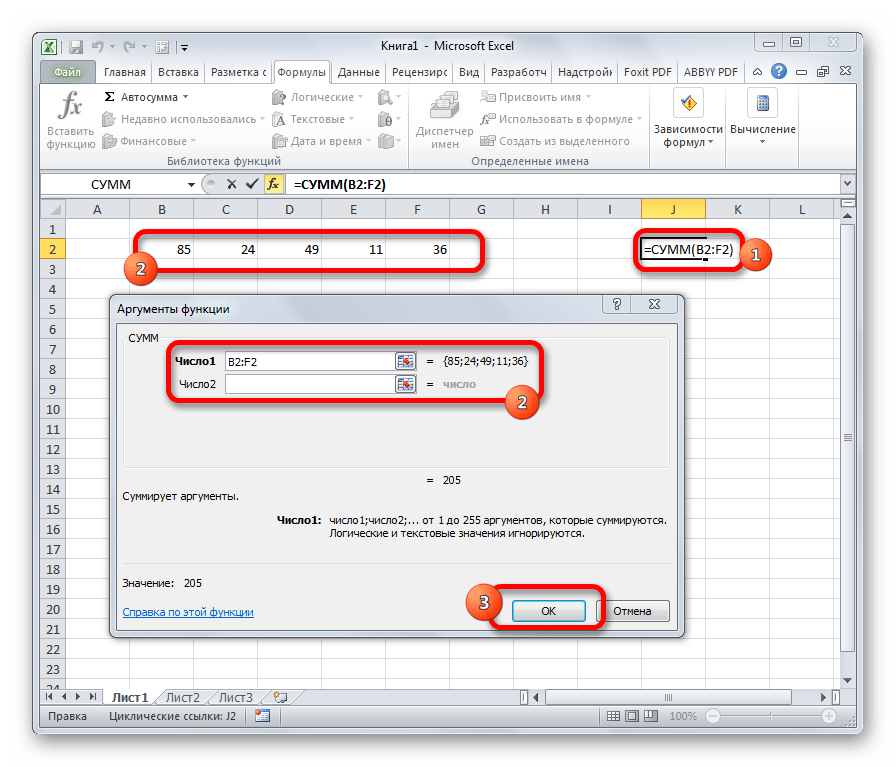
В окне аргументов в поля следует вводить ссылки на ячейки с данными или на диапазоны. Оператор складывает содержимое и выводит общую сумму в отдельную ячейку.

Урок: Как посчитать сумму в Экселе

СУММЕСЛИ

Оператор СУММЕСЛИ также подсчитывает общую сумму чисел в ячейках. Но, в отличие от предыдущей функции, в данном операторе можно задать условие, которое будет определять, какие именно значения участвуют в расчете, а какие нет. При указании условия можно использовать знаки «>» («больше»), «<» («меньше»), «< >» («не равно»). То есть, число, которое не соответствует заданному условию, во втором аргументе при подсчете суммы в расчет не берется. Кроме того, существует дополнительный аргумент «Диапазон суммирования», но он не является обязательным. Данная операция имеет следующий синтаксис:

=СУММЕСЛИ(Диапазон;Критерий;Диапазон_суммирования)

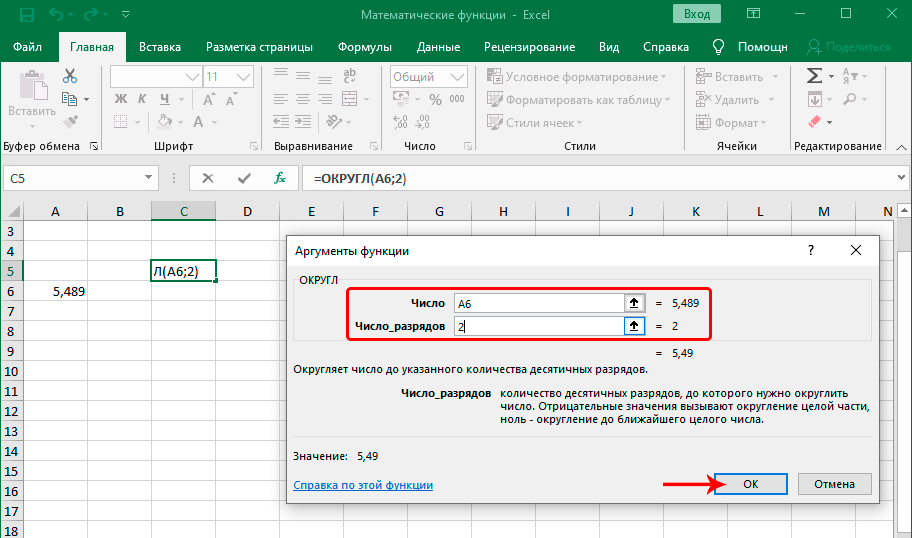
ОКРУГЛ

Как можно понять из названия функции ОКРУГЛ, служит она для округления чисел. Первым аргументом данного оператора является число или ссылка на ячейку, в которой содержится числовой элемент. В отличие от большинства других функций, у этой диапазон значением выступать не может. Вторым аргументом является количество десятичных знаков, до которых нужно произвести округление. Округления проводится по общематематическим правилам, то есть, к ближайшему по модулю числу. Синтаксис у этой формулы такой:

=ОКРУГЛ(число;число_разрядов)

Кроме того, в Экселе существуют такие функции, как ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, которые соответственно округляют числа до ближайшего большего и меньшего по модулю.

Урок: Округление чисел в Excel

ПРОИЗВЕД

Задачей оператора ПРИЗВЕД является умножение отдельных чисел или тех, которые расположены в ячейках листа. Аргументами этой функции являются ссылки на ячейки, в которых содержатся данные для перемножения. Всего может быть использовано до 255 таких ссылок. Результат умножения выводится в отдельную ячейку. Синтаксис данного оператора выглядит так:

=ПРОИЗВЕД(число;число;…)

Урок: Как правильно умножать в Excel

ABS

С помощью математической формулы ABS производится расчет числа по модулю. У этого оператора один аргумент – «Число», то есть, ссылка на ячейку, содержащую числовые данные. Диапазон в роли аргумента выступать не может. Синтаксис имеет следующий вид:

=ABS(число)

Урок: Функция модуля в Excel

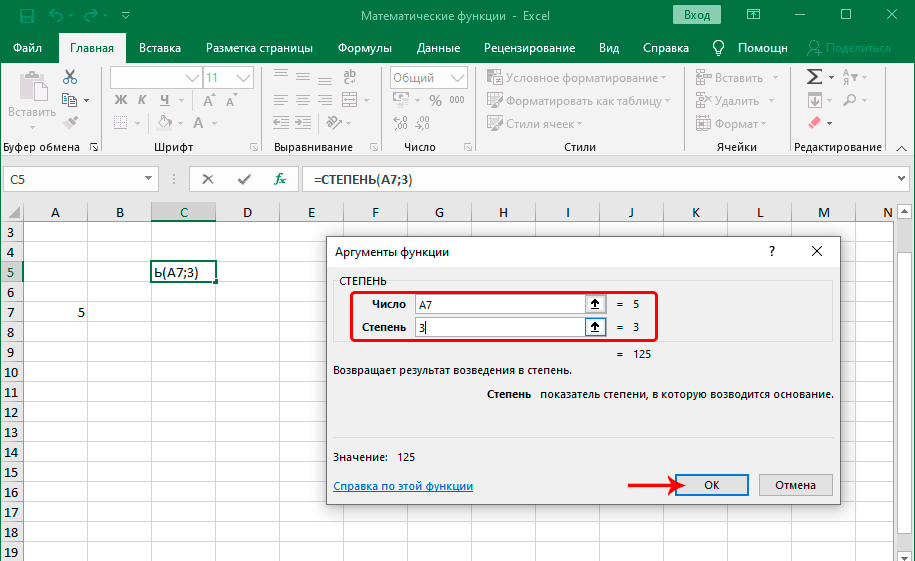
СТЕПЕНЬ

Из названия понятно, что задачей оператора СТЕПЕНЬ является возведение числа в заданную степень. У данной функции два аргумента: «Число» и «Степень». Первый из них может быть указан в виде ссылки на ячейку, содержащую числовую величину. Второй аргумент указывается степень возведения. Из всего вышесказанного следует, что синтаксис этого оператора имеет следующий вид:

=СТЕПЕНЬ(число;степень)

Урок: Как возводить в степень в Экселе

КОРЕНЬ

Задачей функции КОРЕНЬ является извлечение квадратного корня. Данный оператор имеет только один аргумент – «Число». В его роли может выступать ссылка на ячейку, содержащую данные. Синтаксис принимает такую форму:

=КОРЕНЬ(число)

Урок: Как посчитать корень в Экселе

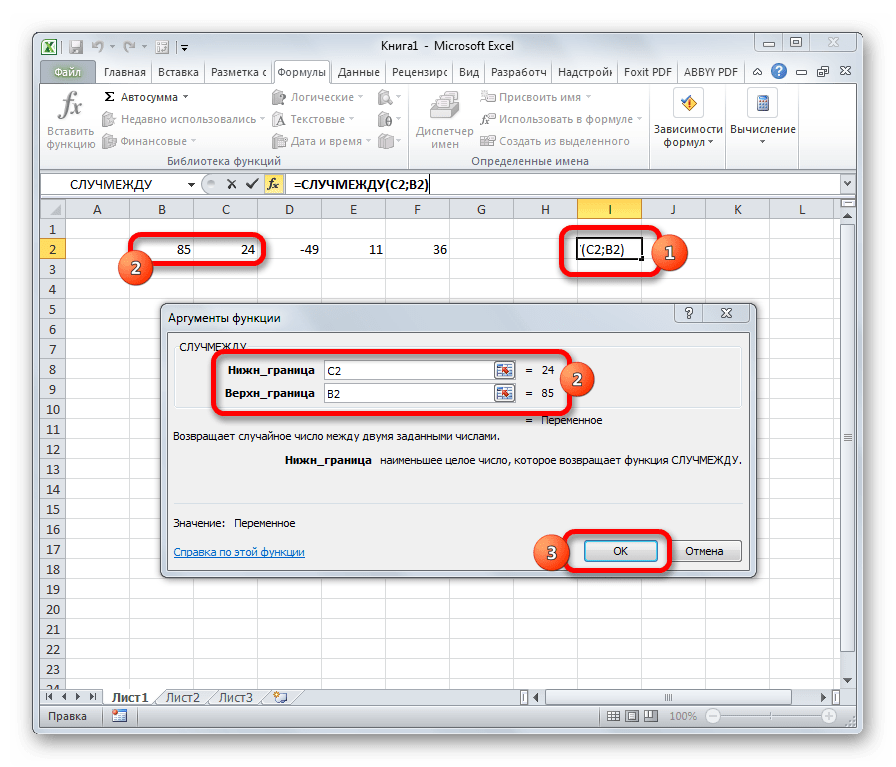
СЛУЧМЕЖДУ

Довольно специфическая задача у формулы СЛУЧМЕЖДУ. Она состоит в том, чтобы выводить в указанную ячейку любое случайное число, находящееся между двумя заданными числами. Из описания функционала данного оператора понятно, что его аргументами является верхняя и нижняя границы интервала. Синтаксис у него такой:

=СЛУЧМЕЖДУ(Нижн_граница;Верхн_граница)

ЧАСТНОЕ

Оператор ЧАСТНОЕ применяется для деления чисел. Но в результатах деления он выводит только четное число, округленное к меньшему по модулю. Аргументами этой формулы являются ссылки на ячейки, содержащие делимое и делитель. Синтаксис следующий:

=ЧАСТНОЕ(Числитель;Знаменатель)

Урок: Формула деления в Экселе

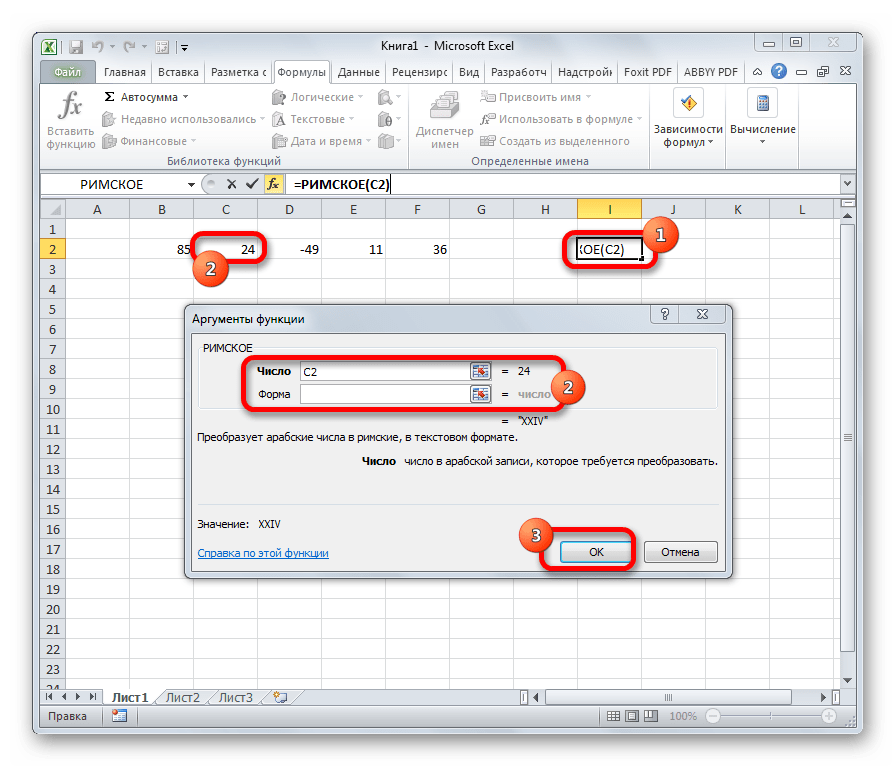
РИМСКОЕ

Данная функция позволяет преобразовать арабские числа, которыми по умолчанию оперирует Excel, в римские. У этого оператора два аргумента: ссылка на ячейку с преобразуемым числом и форма. Второй аргумент не является обязательным. Синтаксис имеет следующий вид:

=РИМСКОЕ(Число;Форма)

Выше были описаны только наиболее популярные математические функции Эксель. Они помогают в значительной мере упростить различные вычисления в данной программе. При помощи этих формул можно выполнять как простейшие арифметические действия, так и более сложные вычисления. Особенно они помогают в тех случаях, когда нужно производить массовые расчеты.

Функция Excel – это оператор, позволяющий автоматизировать определенный процесс работы с базами данных. Они бывают разных типов: математические, логические и другие. Именно они и являются основной фишкой этой программы. Математические функции Excel – одни из наиболее часто используемых. Это не удивительно, поскольку это программа, которая изначально создавалась для упрощения обработки огромных количеств чисел. Существует множество математических функций, но есть 10 тех, которые наиболее полезны. Сегодня мы их собираемся рассмотреть.

Как применять математические функции в программе?

Excel предусматривает возможность воспользоваться более, чем 60 разными математическими функциями, с помощью которых можно проводить все операции. Есть несколько способов, как вставить математическую функцию в ячейку:

1. Использование кнопки «Вставить функцию», которая находится слева от строки ввода формул. Независимо от того, какая вкладка главного меню в данный момент выбрана, можно использовать этот способ.
2. Воспользоваться вкладкой «Формулы». Здесь также есть кнопка с возможностью вставить функцию. Она располагается в самой левой части панели инструментов.
3. Воспользоваться горячими клавишами Shift+F3 для того, чтобы воспользоваться мастером функций.

Последний способ является наиболее удобным, хотя на первый взгляд он сложнее из-за необходимости запоминать комбинацию клавиш. Но в будущем он может сильно сэкономить время в случае, если вы не знаете, с помощью какой функции можно реализовать определенную возможность. После того, как будет вызван мастер функций, появится диалоговое окно.

В нем можно увидеть раскрывающийся список с категориями, и нас интересуют, как могли догадливые читатели понять, математические функции. Далее необходимо выбрать ту, которая нас интересует, после чего подтвердить свои действия путем нажатия клавиши ОК. Также пользователь может посмотреть те, которые интересны именно ему и почитать их описание.

Далее появится окно с аргументами, которые нам нужно передать функции.

Кстати, выбрать математические функции можно сразу с ленты. Для этого нужно самую левую панель, кликнуть по значку, выделенному красным квадратиком, а потом выбрать нужную функцию.

Также можно ввести функцию самостоятельно. Для этого пишется знак равно, после чего вводится вручную название этой функции. Давайте посмотрим, как это работает на практике, приведя конкретные названия функций.

Перечень математических функций

Теперь давайте перечислим самые популярные математические функции, которые применяются во всех возможных сферах жизни человека. Это как стандартная функция, применяющаяся для складывания большого количества чисел за один раз, так и более вычурные формулы типа СУММЕСЛИ, которая выполняет за раз сразу несколько разноплановы операций. Есть также большое количество других функций, которые более подробно рассмотрим прямо сейчас.

Функция СУММ

Эта функция на данный момент используется наиболее часто. Она предназначена для того, чтобы суммировать набор чисел попеременно между собой. Синтаксис этой функции очень прост и содержит минимум два аргумента – числа или ссылки на ячейки, суммирование которых требуется. Как видим, не обязательно записывать в скобках числа, возможен также ввод ссылок. При этом можно указать адрес ячейки как вручную, так и сразу в таблице путем клика по соответствующей ячейке после того, как был помещен курсор в поле ввода. После того, как первый аргумент был введен, достаточно нажать клавишу Tab, чтобы начать заполнять следующий.

СУММЕСЛИ

С помощью формул, в которых записана эта функция, пользователь может осуществлять подсчет суммы значений, которые соответствуют определенным условиям. Они помогут автоматизировать отбор значений, которые подходят под конкретные критерии. Внешний вид формулы следующий: =СУММЕСЛИ(Диапазон;Критерий;Диапазон_суммирования). Видим, что в качестве параметров этой функции приводится несколько параметров:

1. Диапазон ячеек. Сюда входят те ячейки, которые должны проверяться на соответствие условию, заданному во втором аргументе.
2. Условие. Непосредственно само условие, на предмет соответствия которому будет проверяться диапазон, указанный в первом аргументе. Возможные условия следующие: больше (знак >), меньше (знак <), не равно (<>).
3. Диапазон суммирования. Тот диапазон, который будет суммироваться в случае, если условию первый аргумент соответствует. Диапазон ячеек и суммирования может быть и одинаковым.

Третий аргумент не является обязательным для заполнения.

Функция ЧАСТНОЕ

Как правило, пользователи используют стандартную формулу деления двух или нескольких чисел. Для осуществления этой арифметической операции используется знак /. Недостаток такого подхода такой же, как и при ручном выполнении любых других арифметических операций. Если количество данных слишком большое, осуществлять правильный их подсчет довольно непросто. Автоматизировать процесс деления можно с помощью функции ЧАСТНОЕ. Ее синтаксис следующий: =ЧАСТНОЕ(Числитель;Знаменатель). Как видим, у нас здесь два основных аргумента: числитель и знаменатель. Они соответствуют классическим арифметическим числителю и знаменателю.

Функция ПРОИЗВЕД

Это противоположная к прошлой функция, выполняющая умножение чисел или диапазонов, которые туда вводятся в качестве аргументов. Точно так же, как и в предыдущих подобных функциях, это дает возможность вносить информацию не только о конкретных числах, но и диапазонах с числовыми значениями.

Функция ОКРУГЛ

Округление – одно из самых популярных действий в разных сферах человеческой жизни. И хотя после внедрения компьютерных технологий в нем нет такой необходимости, как раньше, эта формула до сих пор используется для приведения числа в красивый вид, не содержащий большого количества знаков после запятой. Ниже вы можете посмотреть на то, как выглядит универсальный синтаксис формулы, использующей этой функцию: =ОКРУГЛ(число;число_разрядов). Видим, что здесь два аргумента: число, которое будет поддаваться округлению и количество разрядов, которые будут видны в конечном итоге.

Округление – это прекрасная возможность упростить читателю электронной таблицы жизнь, если точность не имеет принципиальной важности. Абсолютно любая рутинная задача допускает использование округления, поскольку в бытовых ситуациях очень редко приходится заниматься деятельностью, где нужно осуществлять расчеты с точностью до стотысячной доли числа. Эта функция округляет число по стандартным правилам,

Функция СТЕПЕНЬ

Начинающие пользователи Excel очень часто задаются вопросом, как возводить число в степень. Для этого используется простая формула, которая делает автоматически перемножает число само на себя определенное количество раз. Содержит два обязательных аргумента: =СТЕПЕНЬ(число;степень). Как видно из синтаксиса, первый аргумент дает возможность указать число, которое будет умножаться определенное количество раз. Второй же аргумент – это та степень, в которую будет оно возводиться.

Функция КОРЕНЬ

Эта функция позволяет определить квадратный корень из значения, которое указывается в скобках. Шаблон формулы выглядит следующим образом: =КОРЕНЬ(число). Если вводить эту формулу через ее окно ввода, то видно, что есть только один аргумент, который нужно вводить.

Функция LOG

Это еще одна математическая функция, позволяющая вычислить логарифм определенного числа. Чтобы она работала, требуется два аргумента: число и основание логарифма. Второй аргумент, в принципе, вводить не обязательно. В этом случае значение примет то, которое запрограммировано в Excel как то, которое указывается по умолчанию. То есть, 10.

Кстати, если необходимо вычислить десятичный логарифм, можно воспользоваться функцией LOG10.

Функция ОСТАТОК

Если не получается поделить одно число на другое, чтобы результат получился целым, то нередко приходится получать остаток. Чтобы это сделать, необходимо ввести формулу =ОСТАТОК(число;делитель). Видим, что здесь два аргумента. Первый – это число, над которым осуществляется операция деления. Второй – это делитель, значение, на которое делится число. Можно ввести эту формулу как поставив подходящие значения в скобках при ручном вводе, так и через мастер ввода функции.

Интересный факт: операция деления с остатком также называется целочисленным делением и является отдельной категорией в математике. Также его нередко называют делением по модулю. Но на практике такого термина лучше избегать, потому что возможна путаница в терминологии.

Менее популярные математические функции

Некоторые функции не являются настолько популярными, но они все равно обрели широкое распространение. Прежде всего, это функция, позволяющая выбрать случайное число в определенном коридоре, а также та, которая делает из арабского числа римское. Давайте их рассмотрим более подробно.

Функция СЛУЧМЕЖДУ

Эта функция интересна тем, что выводит любое число, которое находится между значением А и значением Б. Они же и являются ее аргументами. Под значением А подразумевается нижняя граница выборки, а под значением Б – верхняя.

Полностью случайных чисел не бывает. Все они формируются по определенным закономерностям. Но это на практическое использование данной формулы не влияет, просто интересный факт.

Функция РИМСКОЕ

Стандартный формат представления чисел, который используется в Excel – арабский. Но можно также отображать числа в римском формате. Для этого можно воспользоваться специальной функцией, которая имеет два аргумента. Первый из них – это ссылка на ячейку, где содержится число, или само число. Второй аргумент – это форма.

Несмотря на то, что римские числа уже не имеют такого распространения, как раньше, в русском языке они все же иногда используются. В частности, эта форма представления необходима в таких случаях:

1. Если нужно записать век или тысячелетие. В этом случае форма записи следующая: XXI век или II тысячелетие.
2. Спряжение глаголов.
3. Если было несколько монархов с одним именем, то римское число обозначает его порядковый номер.
4. Обозначение корпуса в Вооруженных силах.
5. На военной форме в ВС РФ с помощью римских цифр записывается группа крови, чтобы можно было спасти раненого неизвестного солдата.
6. Номера листов также нередко отображаются римскими цифрами для того, чтобы не было необходимости корректировать ссылки внутри текста, если предисловие изменяется.
7. Для создания особой маркировки циферблатов с целью добавить эффект раритетности.
8. Обозначение порядкового номера важного явления, закона или события. Например, II мировая война.
9. В химии с помощью римских цифр обозначается способность химических элементов создавать определенное количество связей с другими элементами.
10. В сольфеджио (это такая дисциплина, которая изучает строение музыкального ряда и развивает музыкальный слух) римскими цифрами обозначается номер ступени в звуковом ряду.

Римские цифры также используются и в математическом анализе для записи номера производной. Таким образом, спектр применения римских цифр огромный.

Сейчас почти не используются те форматы даты, которые подразумевают запись в виде римских цифр, но подобный способ отображения был довольно популярен в докомпьютерную эпоху. Ситуации, в которых используются римские цифры, могут отличаться в разных странах. Например, в Литве они активно используются на дорожных знаках, для обозначения дней недели, а также на витринах.

Время для подведения небольших итогов. Формулы Excel – это прекрасная возможность сделать свою жизнь проще. Мы привели сегодня ТОП самых популярных математических функций в электронных таблицах, которые позволяют перекрыть большую часть задач. Но для решения специфических проблем лучше подойдут специальные формулы.