Математические встроенные функции excel это

Чаще всего среди доступных групп функций пользователи Экселя обращаются к математическим. С помощью них можно производить различные арифметические и алгебраические действия. Их часто используют при планировании и научных вычислениях. Узнаем, что представляет собой данная группа операторов в целом, и более подробно остановимся на самых популярных из них.

Применение математических функций

С помощью математических функций можно проводить различные расчеты. Они будут полезны студентам и школьникам, инженерам, ученым, бухгалтерам, планировщикам. В эту группу входят около 80 операторов. Мы же подробно остановимся на десяти самых популярных из них.

Открыть список математических формул можно несколькими путями. Проще всего запустить Мастер функций, нажав на кнопку «Вставить функцию», которая размещена слева от строки формул. При этом нужно предварительно выделить ячейку, куда будет выводиться результат обработки данных. Этот метод хорош тем, что его можно реализовать, находясь в любой вкладке.

Также можно запустить Мастер функций, перейдя во вкладку «Формулы». Там нужно нажать на кнопку «Вставить функцию», расположенную на самом левом краю ленты в блоке инструментов «Библиотека функций».

Существует и третий способ активации Мастера функций. Он осуществляется с помощью нажатия комбинации клавиш на клавиатуре Shift+F3.

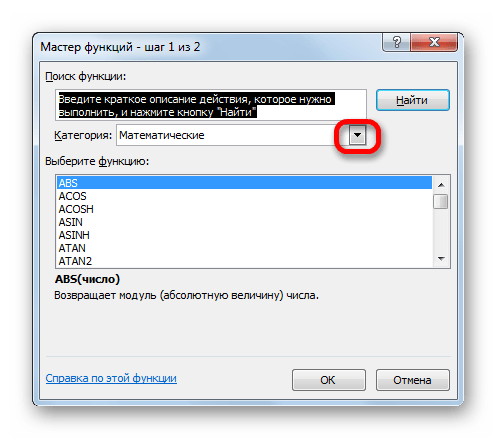
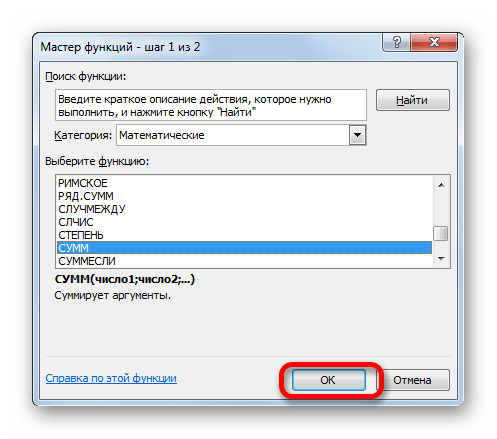
После того, как пользователь произвел любое из вышеуказанных действий, открывается Мастер функций. Кликаем по окну в поле «Категория».

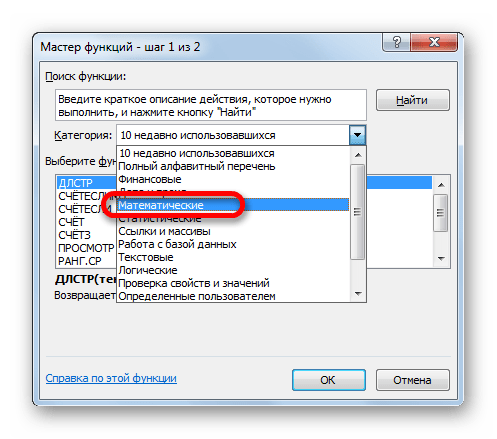
Открывается выпадающий список. Выбираем в нем позицию «Математические».

После этого в окне появляется список всех математических функций в Excel. Чтобы перейти к введению аргументов, выделяем конкретную из них и жмем на кнопку «OK».

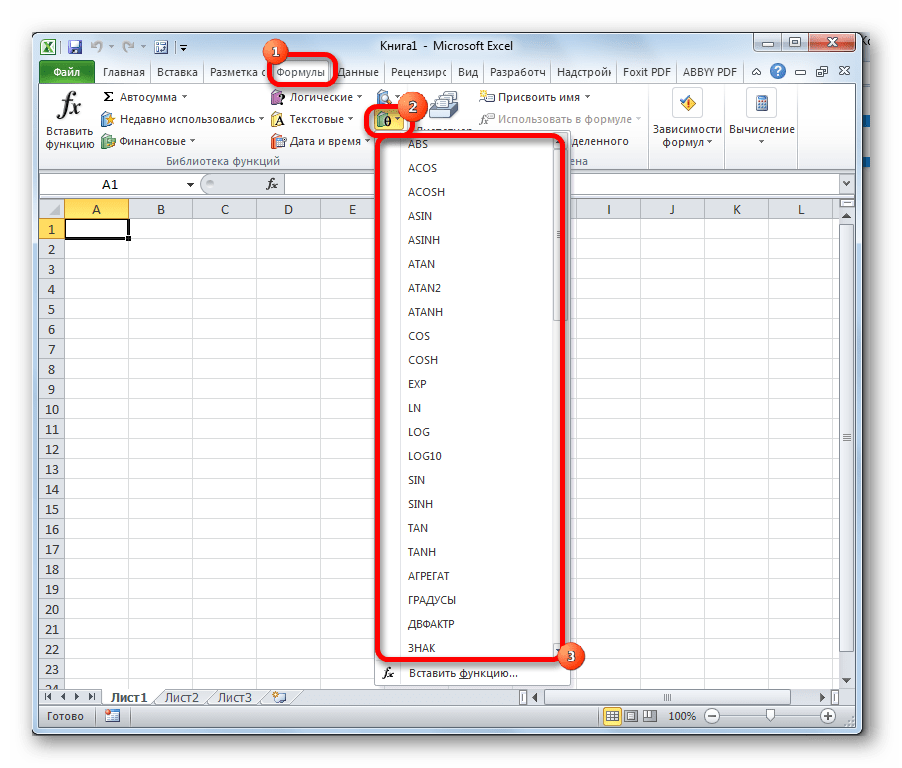
Существует также способ выбора конкретного математического оператора без открытия главного окна Мастера функций. Для этого переходим в уже знакомую для нас вкладку «Формулы» и жмем на кнопку «Математические», расположенную на ленте в группе инструментов «Библиотека функций». Открывается список, из которого нужно выбрать требуемую формулу для решения конкретной задачи, после чего откроется окно её аргументов.

Правда, нужно заметить, что в этом списке представлены не все формулы математической группы, хотя и большинство из них. Если вы не найдете нужного оператора, то следует кликнуть по пункту «Вставить функцию…» в самом низу списка, после чего откроется уже знакомый нам Мастер функций.

Урок: Мастер функций в Excel

СУММ

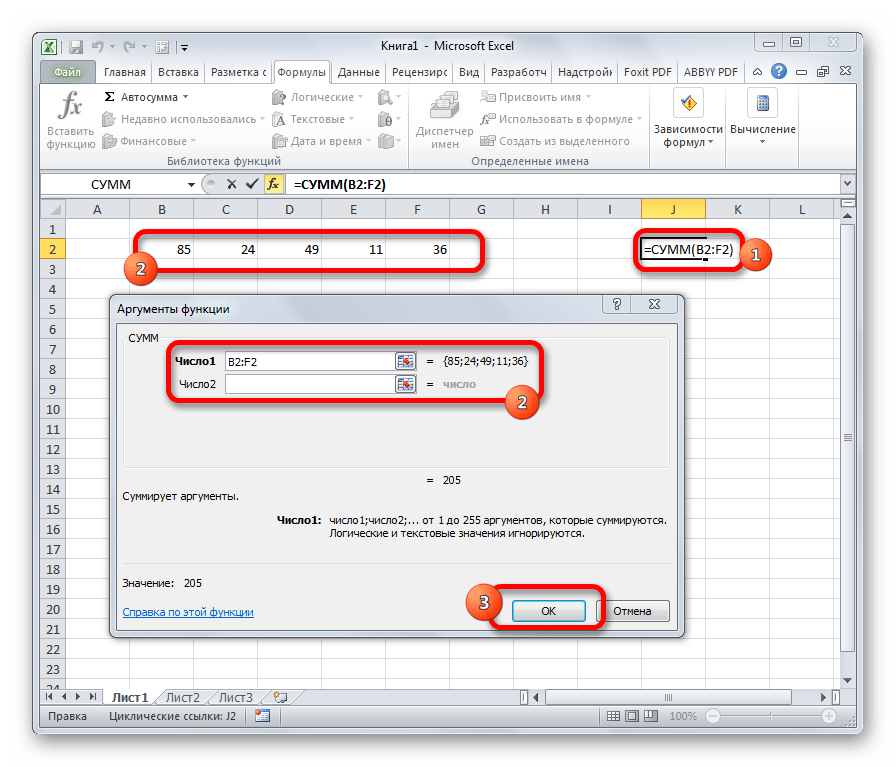
Наиболее часто используется функция СУММ. Этот оператор предназначен для сложения данных в нескольких ячейках. Хотя его можно использовать и для обычного суммирования чисел. Синтаксис, который можно применять при ручном вводе, выглядит следующим образом:

=СУММ(число1;число2;…)

В окне аргументов в поля следует вводить ссылки на ячейки с данными или на диапазоны. Оператор складывает содержимое и выводит общую сумму в отдельную ячейку.

Урок: Как посчитать сумму в Экселе

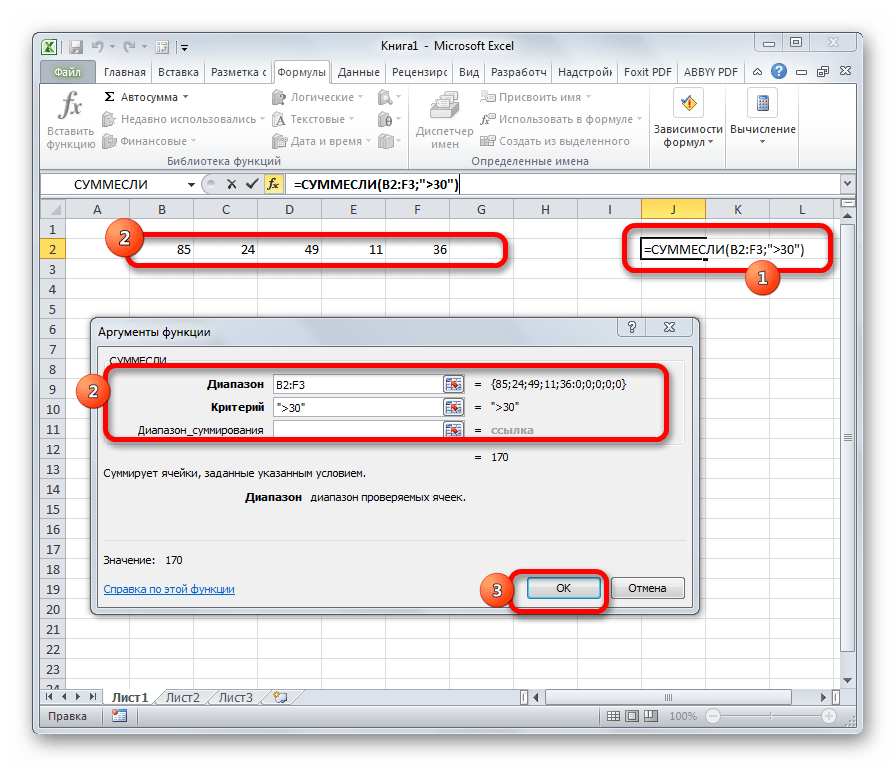
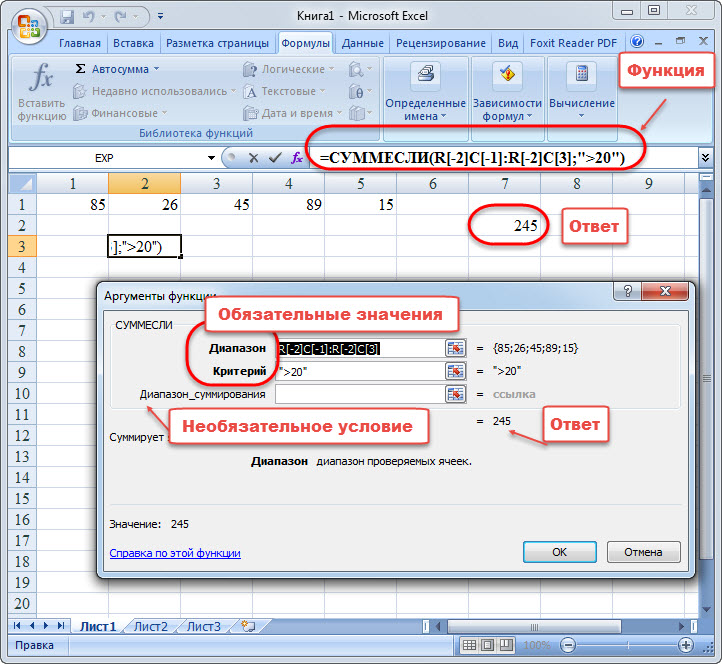
СУММЕСЛИ

Оператор СУММЕСЛИ также подсчитывает общую сумму чисел в ячейках. Но, в отличие от предыдущей функции, в данном операторе можно задать условие, которое будет определять, какие именно значения участвуют в расчете, а какие нет. При указании условия можно использовать знаки «>» («больше»), «<» («меньше»), «< >» («не равно»). То есть, число, которое не соответствует заданному условию, во втором аргументе при подсчете суммы в расчет не берется. Кроме того, существует дополнительный аргумент «Диапазон суммирования», но он не является обязательным. Данная операция имеет следующий синтаксис:

=СУММЕСЛИ(Диапазон;Критерий;Диапазон_суммирования)

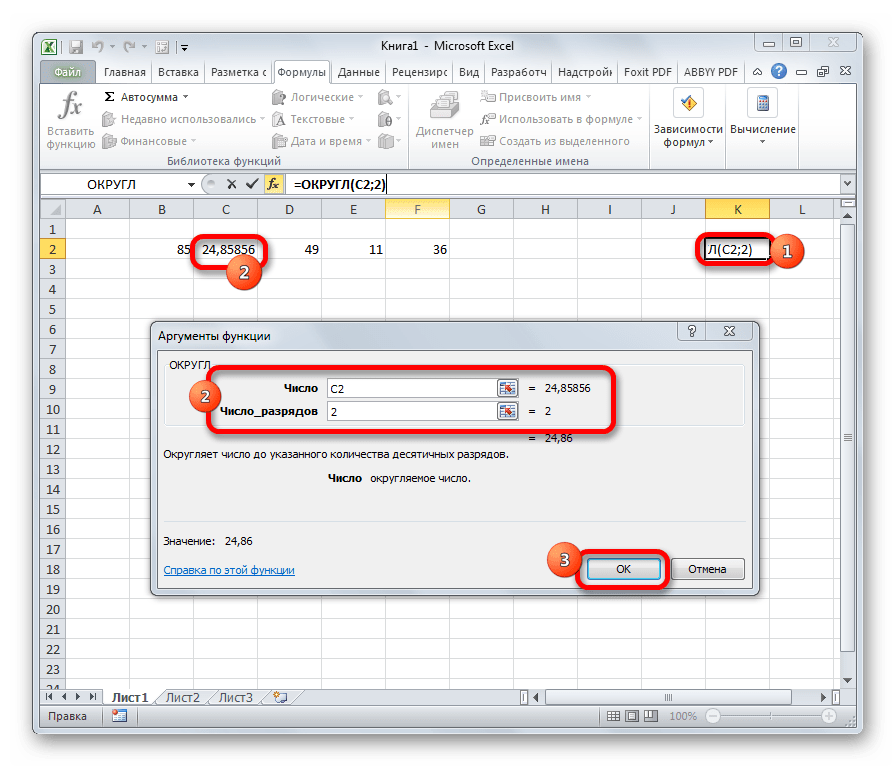
ОКРУГЛ

Как можно понять из названия функции ОКРУГЛ, служит она для округления чисел. Первым аргументом данного оператора является число или ссылка на ячейку, в которой содержится числовой элемент. В отличие от большинства других функций, у этой диапазон значением выступать не может. Вторым аргументом является количество десятичных знаков, до которых нужно произвести округление. Округления проводится по общематематическим правилам, то есть, к ближайшему по модулю числу. Синтаксис у этой формулы такой:

=ОКРУГЛ(число;число_разрядов)

Кроме того, в Экселе существуют такие функции, как ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, которые соответственно округляют числа до ближайшего большего и меньшего по модулю.

Урок: Округление чисел в Excel

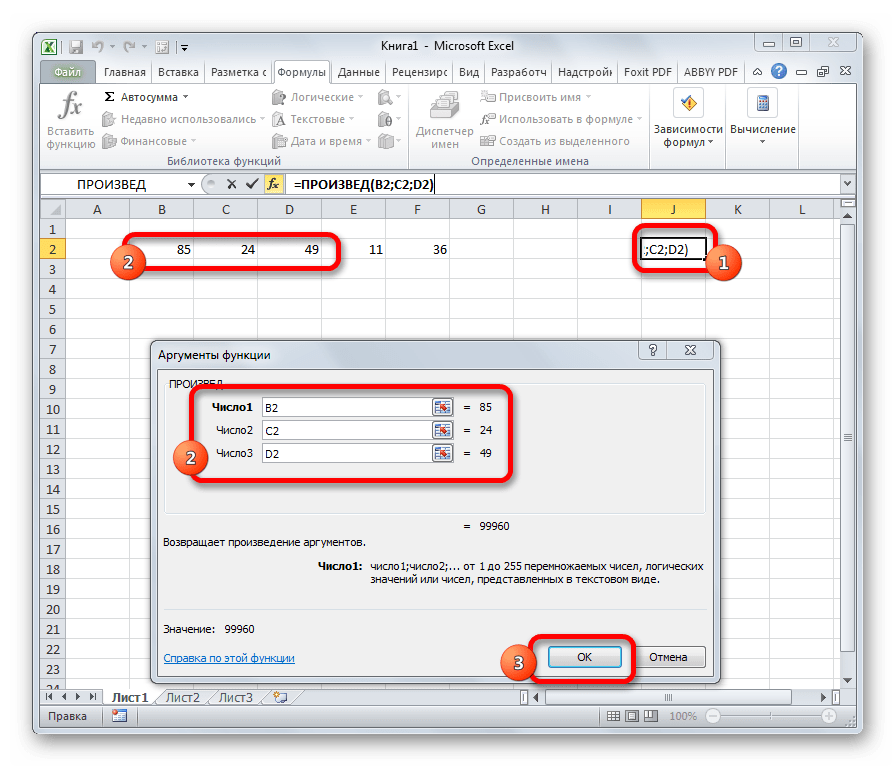
ПРОИЗВЕД

Задачей оператора ПРИЗВЕД является умножение отдельных чисел или тех, которые расположены в ячейках листа. Аргументами этой функции являются ссылки на ячейки, в которых содержатся данные для перемножения. Всего может быть использовано до 255 таких ссылок. Результат умножения выводится в отдельную ячейку. Синтаксис данного оператора выглядит так:

=ПРОИЗВЕД(число;число;…)

Урок: Как правильно умножать в Excel

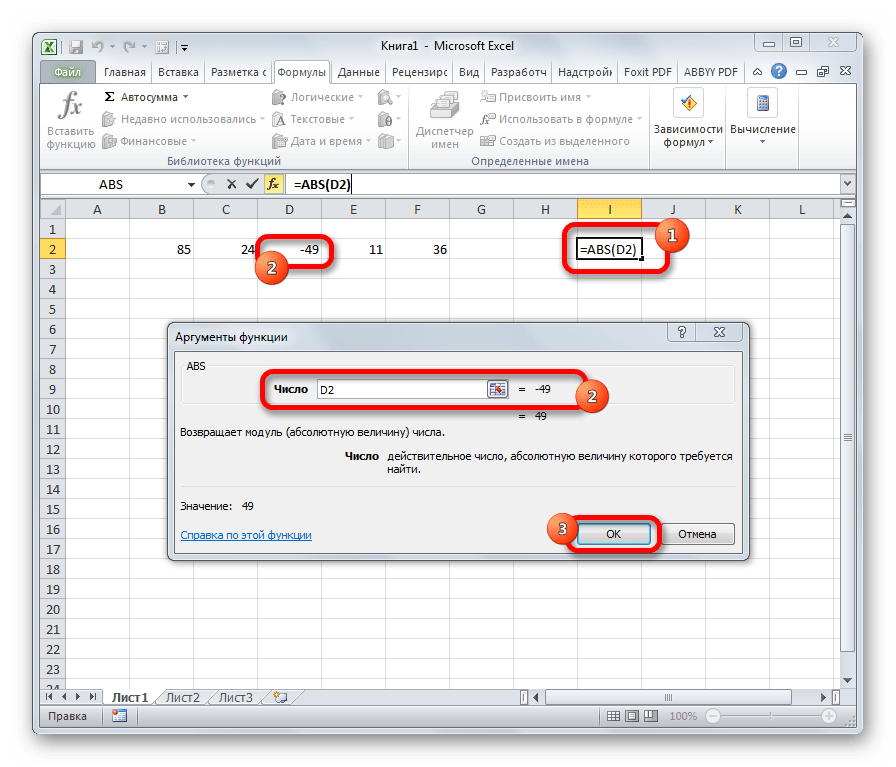
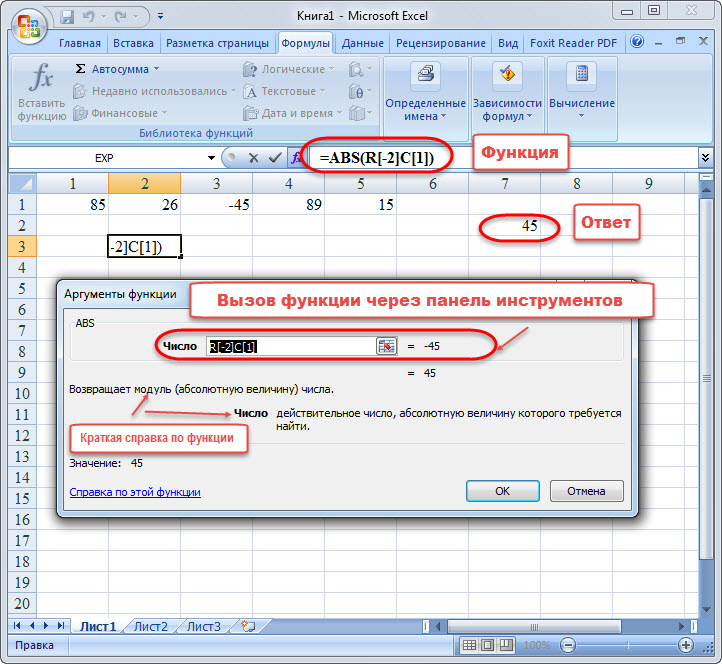
ABS

С помощью математической формулы ABS производится расчет числа по модулю. У этого оператора один аргумент – «Число», то есть, ссылка на ячейку, содержащую числовые данные. Диапазон в роли аргумента выступать не может. Синтаксис имеет следующий вид:

=ABS(число)

Урок: Функция модуля в Excel

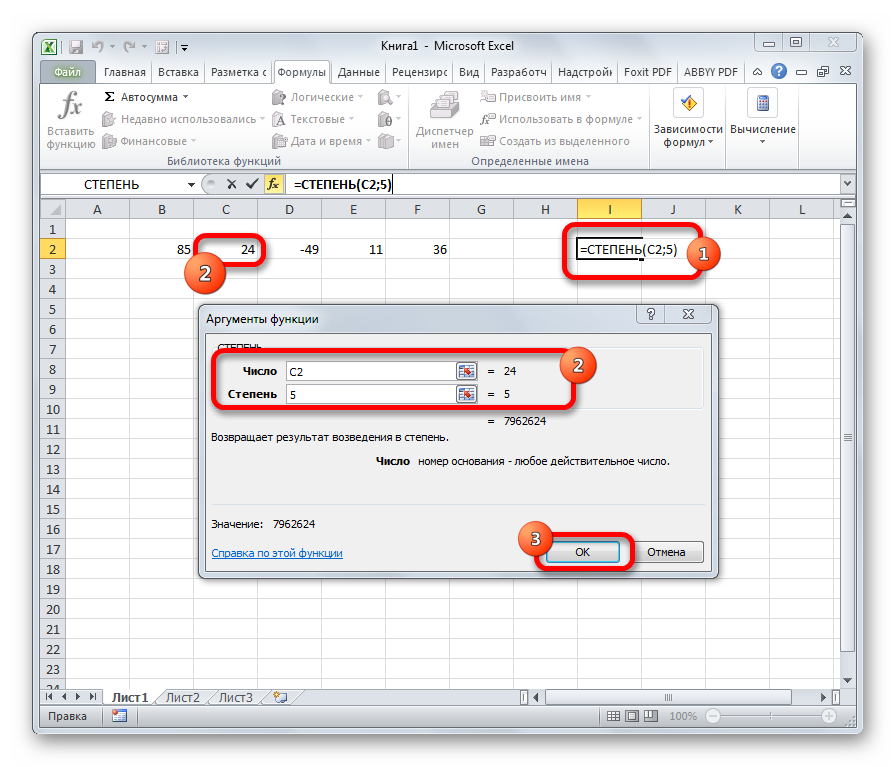
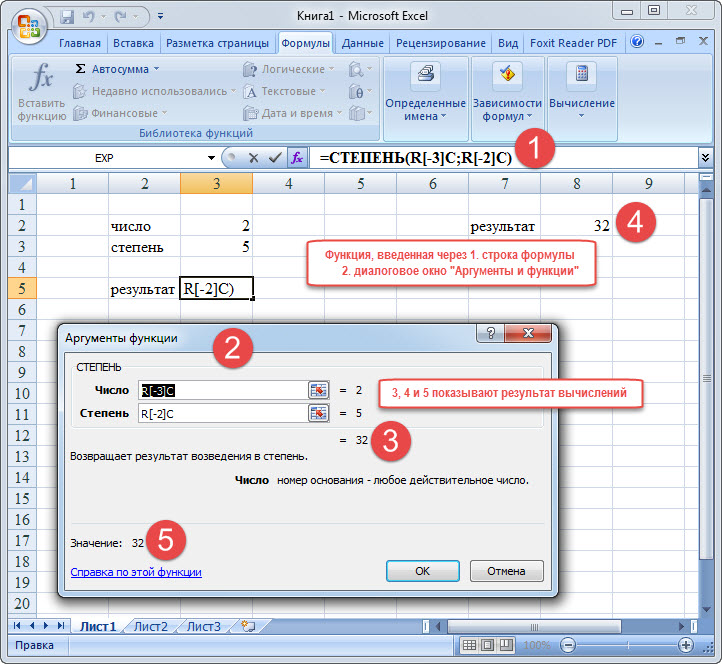
СТЕПЕНЬ

Из названия понятно, что задачей оператора СТЕПЕНЬ является возведение числа в заданную степень. У данной функции два аргумента: «Число» и «Степень». Первый из них может быть указан в виде ссылки на ячейку, содержащую числовую величину. Второй аргумент указывается степень возведения. Из всего вышесказанного следует, что синтаксис этого оператора имеет следующий вид:

=СТЕПЕНЬ(число;степень)

Урок: Как возводить в степень в Экселе

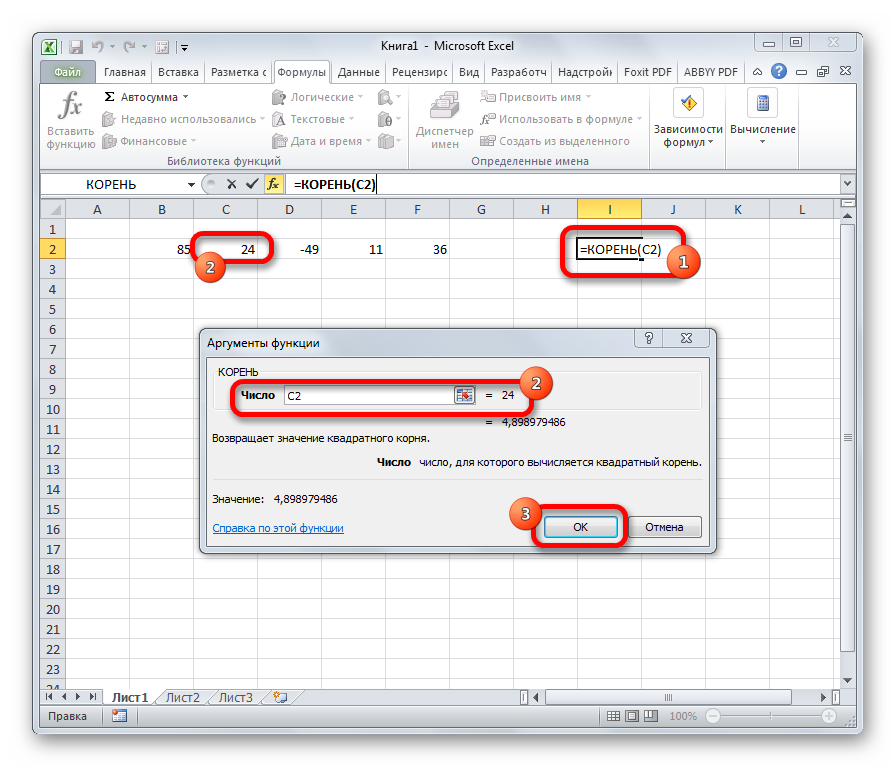
КОРЕНЬ

Задачей функции КОРЕНЬ является извлечение квадратного корня. Данный оператор имеет только один аргумент – «Число». В его роли может выступать ссылка на ячейку, содержащую данные. Синтаксис принимает такую форму:

=КОРЕНЬ(число)

Урок: Как посчитать корень в Экселе

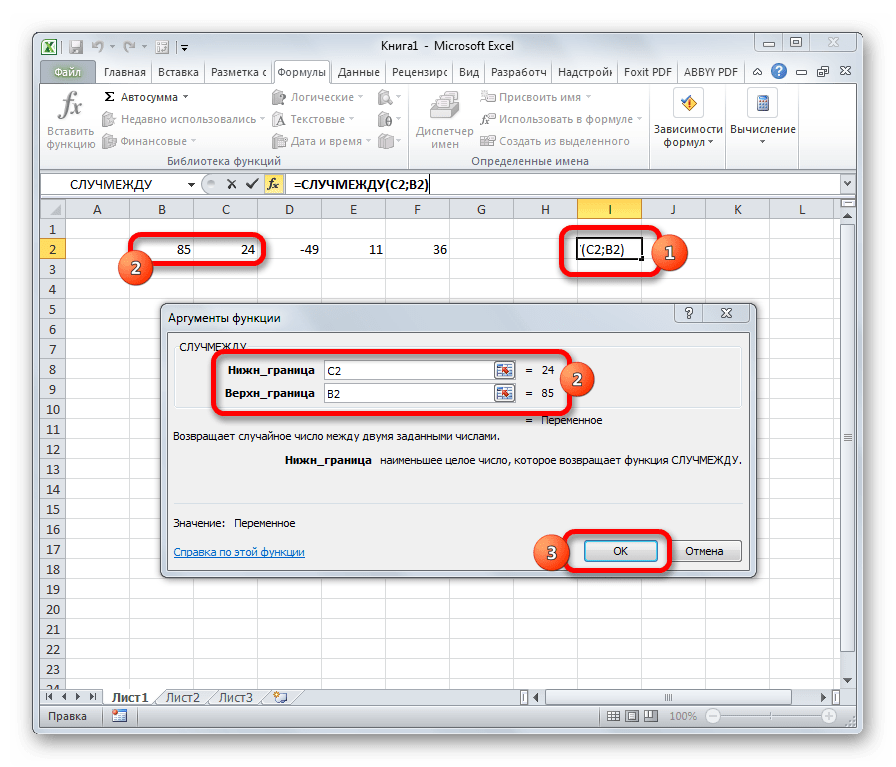
СЛУЧМЕЖДУ

Довольно специфическая задача у формулы СЛУЧМЕЖДУ. Она состоит в том, чтобы выводить в указанную ячейку любое случайное число, находящееся между двумя заданными числами. Из описания функционала данного оператора понятно, что его аргументами является верхняя и нижняя границы интервала. Синтаксис у него такой:

=СЛУЧМЕЖДУ(Нижн_граница;Верхн_граница)

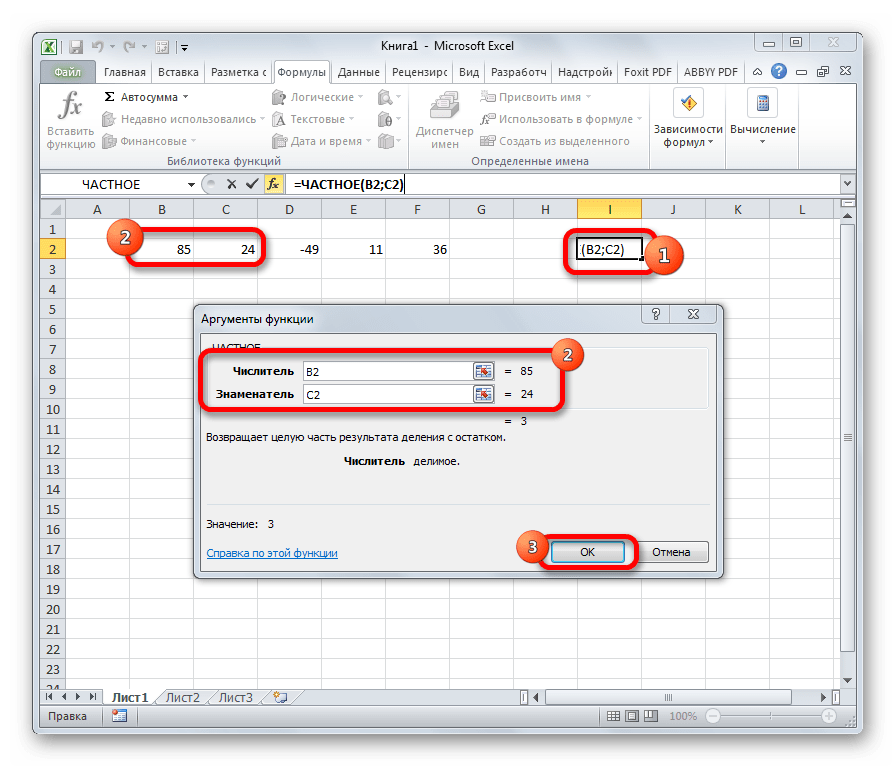
ЧАСТНОЕ

Оператор ЧАСТНОЕ применяется для деления чисел. Но в результатах деления он выводит только четное число, округленное к меньшему по модулю. Аргументами этой формулы являются ссылки на ячейки, содержащие делимое и делитель. Синтаксис следующий:

=ЧАСТНОЕ(Числитель;Знаменатель)

Урок: Формула деления в Экселе

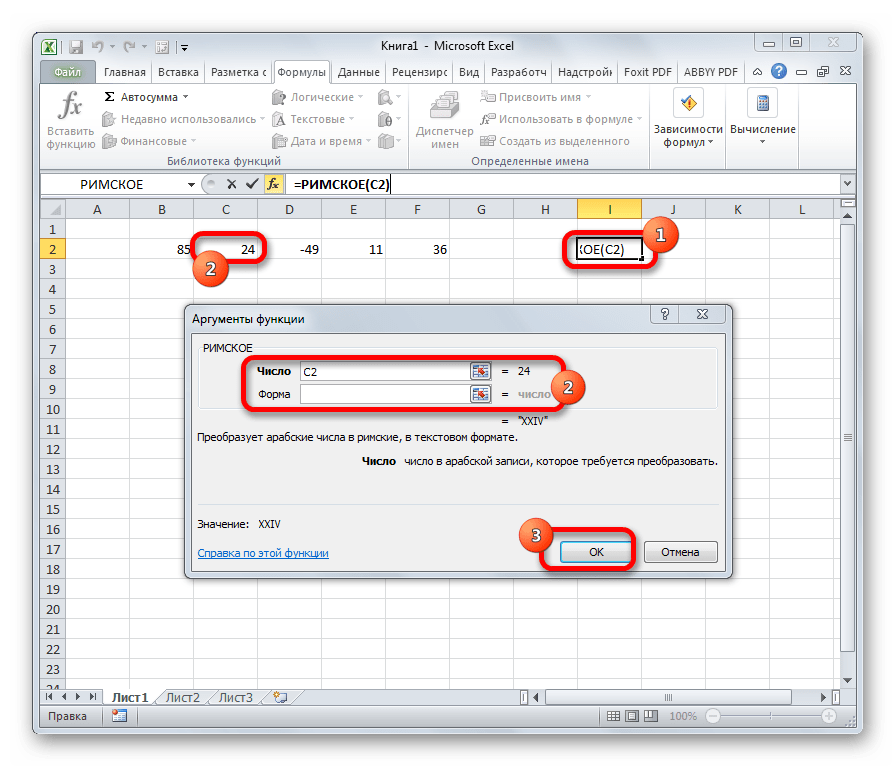
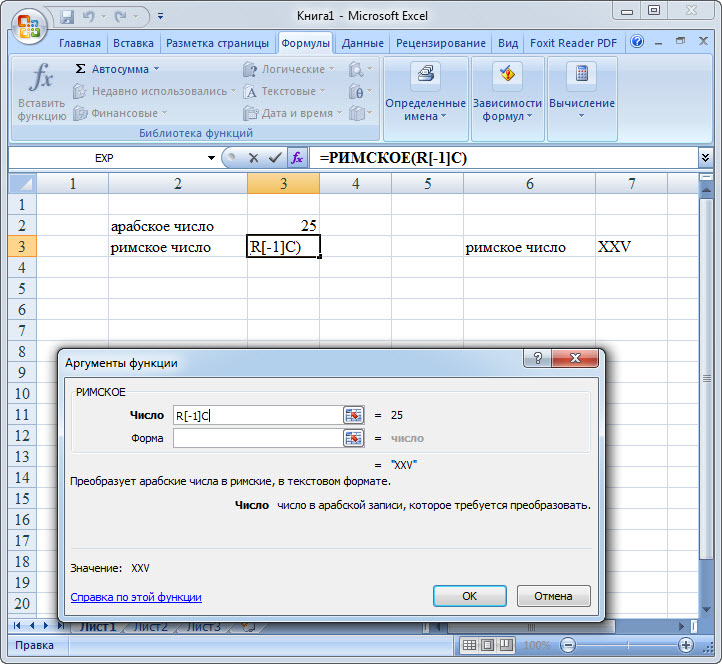
РИМСКОЕ

Данная функция позволяет преобразовать арабские числа, которыми по умолчанию оперирует Excel, в римские. У этого оператора два аргумента: ссылка на ячейку с преобразуемым числом и форма. Второй аргумент не является обязательным. Синтаксис имеет следующий вид:

=РИМСКОЕ(Число;Форма)

Выше были описаны только наиболее популярные математические функции Эксель. Они помогают в значительной мере упростить различные вычисления в данной программе. При помощи этих формул можно выполнять как простейшие арифметические действия, так и более сложные вычисления. Особенно они помогают в тех случаях, когда нужно производить массовые расчеты.

В программе Excel разработчиками заложено огромное количество различных функций, но, пользователи чаще всего пользуются математическими. Давайте рассмотрим их и подробнее остановимся на самых популярных.

Использование математических функций в программе

В категорию математических функций входит более 60 различных операторов, которые позволяют выполнять различные вычисления.

Вставить функцию в свободную ячейку таблицы можно по-разному:

1. Жмем кнопку “Вставить функцию” (fx) слева от строки формул. Выполнить данное действие можно, находясь в любой вкладке.
2. Переключаемся во вкладку “Формулы”. Здесь также представлена кнопка “Вставить функцию” – в левом углу ленты инструментов.
3. Нажимаем комбинацию клавиш Shift+F3, чтобы вызвать Мастер функций.

Результатом любого из вышеописанных способов будет открытие окна вставки функции. Здесь мы выбираем категорию “Математические”.

Теперь, когда категория выбрана, в поле ниже отмечаем требуемую функцию и щелкаем OK. 

После этого откроется окно с аргументами для заполнения.

Примечание: Если мы, находясь во вкладке “Формулы”, в группе инструментов “Библиотека функций” нажмем по значку математических функций, сразу откроется список операторов, которые мы можем выбрать, минуя окно вставки функции.

Стоит учитывать, что в предлагаемом перечне присутствуют не все операторы, но самые необходимые здесь все же есть, и в большинстве случаев их достаточно.

Теперь перейдем к детальному рассмотрению самых популярных функций.

СУММ

Пожалуй, это самая популярная функция, которая используется в Эксель. С помощью нее выполняется суммирование числовых данных. Формула функции:

=СУММ(число1;число2;...)

В аргументах можно указать как конкретные числа, так и ссылки на ячейки, содержащие числовые значения. Причем указать координаты можно вручную (с помощью клавиш клавиатуры) или методом клика/выделения непосредственно в самой таблице.

Для перехода к заполнению следующего аргумента достаточно кликнуть по полю напротив него или нажать клавишу Tab.

СУММЕСЛИ

Данная функция позволяет считать сумму чисел с заданным условиями, с помощью которых будет выполняться отбор значений, учитывающихся в суммировании. Формула выглядит следующим образом:

=СУММЕСЛИ(Диапазон;Критерий;Диапазон_суммирования)

В аргументах функции указывается диапазон ячеек (вручную или путем выделения в таблице), значения которых нужно просуммировать. В качестве критерия можно задать следующие условия (в кавычках):

• больше (“>”)
• меньше (“<“)
• не равно (“<>”)

Аргумент “Диапазон_сумирования” заполнять не обязательно.

ПРОИЗВЕД

С помощью данного оператора выполняется умножение чисел. Синтаксис выглядит следующим образом:

=ПРОИЗВЕД(число;число;…)

В аргументах функции, как и в СУММ, можно указывать как конкретные числа, так и адреса ячеек (диапазоны ячеек), которые содержат числовые значения.

ЧАСТНОЕ

Чаще всего для деления используется формула со знаком “/” между делимым и делителем: =Число1/Число2.

Однако в программе также есть отдельная функция для выполнения деления, синтаксис которой представлен ниже:

=ЧАСТНОЕ(Числитель;Знаменатель)

Заполнить нужно два аргумента: Числитель (Делимое) и Знаменатель (Делитель).

СТЕПЕНЬ

Оператор позволяет возвести число в указанную степень. Формула выглядит так:

=СТЕПЕНЬ(число;степень)

В аргументах функции указывается само число, а также, степень, в которую нужно его возвести.

КОРЕНЬ

С помощью данного оператора можно извлечь квадратный корень из числа. Синтаксис выглядит следующим образом:

=КОРЕНЬ(число)

Заполнить требуется только один аргумент – “Число”.

ОКРУГЛ

Функция применяется для выполнения еще одного распространенного математического действия – округления чисел (по общематематическим правилам, т.е., к ближайшему по модулю значению). Синтаксис функции представлен ниже:

=ОКРУГЛ(число;число_разрядов)

В аргументе “Число” указывается значение, которое требуется округлить. В числе разрядов, соответственно, пишем количество цифр, которые хотим оставить после запятой.

Также, в Excel доступны операторы ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, которые, как следует из их названий, используются для округления до ближайшего верхнего и нижнего числа, соответственно (по модулю).

ABS

Позволяет получить модуль числа. Формула функции представлена ниже:

=ABS(число)

Заполнить нужно всего один аргумент – “Число”, модуль которого требуется найти.

LOG

С помощью этого оператора определяется логарифм числа по заданному основанию. Синтаксис функции представлен в виде:

=LOG(Число;Основание)

Необходимо заполнить два аргумента: Число и Основание логарифма (если его не указать, программа примет значение по умолчанию, равное 10).

Также для десятичного логарифма предусмотрена отдельная функция – LOG10.

ОСТАТОК

Применяется для получения остатка от деления чисел. Формула оператора выглядит следующим образом:

=ОСТАТ(чило;делитель)

Для того, чтобы получить результат, требуется заполнить значения двух аргументов: Число и Делитель.

Заключение

Таким образом, мы разобрали самые популярные математические функции, которые используются в Excel. Однако возможности программы гораздо шире, и в ее инструментарии можно найти функцию для успешного выполнения практически любой задачи.

Главным достоинством данного редактора являются математические функции в Excel. При работе с таблицами, диапазонами и массивами количество времени, потраченное на вычисление тех или иных значений, снижается в разы при умении пользоваться встроенными возможностями. В зависимости от категории математической функции можно получить результат при арифметических действиях, построить график или диаграмму, использовать относительные и абсолютные ссылки.

Excel: общие сведения

Программный продукт позволяет выполнять расчеты с различными типами данных и управлять электронными таблицами. Под последними понимается средство, необходимое для обработки и анализа оцифрованных данных посредством компьютера.

Важная особенность электронной таблицы – автоматический пересчет значений при изменении данных в ячейках. Математические функции в Excel позволяют не только получить искомое, но и построить графики и диаграммы.

Книга – тот файл, с которым работает программный комплекс. Она состоит из листов. К каждому из них можно обратиться при необходимости посредством встроенных функций или ручного ввода формулы.

Основа рабочего листа – таблица, состоящая из строк и столбцов. Их перекрестие составляет ячейка, куда вводятся данные или формулы. Строки названы арабскими цифрами, а столбцы – латинскими буквами. Считалось, что рабочий лист бесконечен в обе стороны, однако это не так. Он содержит 65536 строк и 256 столбцов. По другим данным в рабочем листе содержатся 16384 столбцов и 1048576 строк. Каждой ячейке присваивается уникальный адрес:А5.

Использование ссылок

При работе с Excel можно применять в работе различные виды ссылок. Начинающим пользователям доступны простейшие из них. Важно научиться использовать все форматы в своей работе.

Существуют:

• простые;
• ссылки на другой лист;
• абсолютные;
• относительные ссылки.

Простые адреса используются чаще всего. Простые ссылки могут быть выражены следующим образом:

• пересечение столбца и строки (А4);
• массив ячеек по столбцу А со строки 5 до 20 (А5:А20);
• диапазон клеток по строке 5 со столбца В до R (В5:R5);
• все ячейки строки (10:10);
• все клетки в диапазоне с 10 по 15 строку (10:15);
• по аналогии обозначаются и столбцы: В:В, В:К;
• все ячейки диапазона с А5 до С4 (А5:С4).

Следующий формат адресов: ссылки на другой лист. Оформляется это следующим образом: Лист2!А4:С6. Подобный адрес вставляется в любую функцию.

Абсолютные и относительные ссылки

Особого внимания требуют такие форматы адресов.

Выделяют:

• абсолютные;
• относительные;
• смешанные ссылки.

Под относительными адресами понимают указанные диапазоны или конкретные ячейки, которые при копировании формулы и ее последующей вставке изменяются автоматически. К примеру, необходимо суммировать в столбце С несколько значений. Формула будет выглядеть следующим образом: =сумм(С5:С9). Если допустить, что подобных столбцов несколько, и в каждом нужно найти сумму, проще скопировать формулу и вставить в нужные клетки. После проделанных манипуляций можно заметить, что диапазоны поменялись автоматически.

Под абсолютными ссылками понимаются ячейки, которые в процессе копирования не меняют своего вида. К примеру, имеется клетка А5. Она участвует в формуле вычисления суммы нескольких значений. Чтобы она не изменилась ни при одном копировании, перед обозначением столбца и строки ставят знак $. Абсолютная ссылка будет выглядеть следующим образом: $А$5.

Основные математические функции Excel предпочитают использовать при больших объемах данных смешанные адреса. В таком формате можно зафиксировать только столбец или строку. К примеру, $С5 или С$5. В первом случае не меняется название столбца, во втором – строки.

Ссылки формата R1C1

В новых версиях Excel адреса ячеек видоизменились. Некоторые не могут понять, в чем разница между А1 и R[-1]C[-5].

Разработчики приводят несколько примеров подобных адресов:

• относительный адрес строки, расположенной на 3 позиции выше указанной: R[-3];
• абсолютная ссылка на ячейку, содержащуюся на 10-й строке 10-го столбца: R10C10;
• относительный адрес на ячейку, расположенную на 5 позиций выше в активном столбце (где прописывается формула): R[-5]C;
• абсолютная ссылка на текущую клетку, где прописывается формула: R;
• относительная ссылка на ячейку, расположенную на 8 строк правее и 5 строк ниже активной: R[5]C[8].

Категории математических функций

При выпадающем списке в программе на вкладке «Формулы» содержится 11 групп. В их число входят и математические функции в Excel, которые условно разделяются на следующие категории. Рассмотрим основные. Арифметические операции:

• СУММ: складывает необходимые значения.
• ПРОИЗВЕД: находит произведение заданных чисел или содержимого ячеек.
• ЦЕЛОЕ: необходимо для нахождения целой части.
• СТЕПЕНЬ: возводит число в заданную степень.
• КОРЕНЬ: извлекает корень из содержимого ячейки или заданного вручную числа и т. д.

Также можно выделить тригонометрические функции:

• SIN: находит синус от заданного значения.
• ASIN: необходима для вычисления арксинуса числа.
• LN: находит натуральный логарифм.
• EXP: возводит число Е в заданную пользователем степень и др.

Округление по различным критериям:

• ОКРВВЕРХ: округляет значение до ближайшего целого.
• ОКРУГЛВВЕРХ: находит число, округленное до ближайшего целого по модулю.
• НЕЧЕТ: функция, позволяющая округлить до нечетного числа. Положительное – в большую сторону, отрицательное – в меньшую.
• ОКРУГЛ: необходима для нахождения результата округления с заданием количества десятичных разрядов и др.

Для работы с векторами и матрицами:

• СУММПРОИЗВ: функция, необходимая для возвращения суммы массивов.
• СУММВРАЗН: при наличии 2 диапазонов возвращает сумму квадратов разностей.
• МОБР: функция, необходимая для получения обратной матрицы.
• МОПРЕД: требуется для нахождения определителя матрицы и т. д.

Применение математических функций

Математические функции в Excel могут вводиться тремя способами:

• вручную;
• через панель инструментов;
• посредством диалогового окна «Вставка функции».

В первом случае пользователь вручную вводит формулу на основе своих знаний и умений в специальной строке или конкретной ячейке. Начинающим рекомендуется прибегнуть ко второму и третьему вариантам.

С помощью панели инструментов нужно перейти на вкладку «Формулы» и выбрать необходимую группу формул: логическую, статистическую, математическую и т. д. В выпадающем списке пользователь использует потребовавшуюся функцию. Когда появляется диалоговое окно «Аргументы и функции» проставляются необходимые значения и подтверждаются сделанные манипуляции.

Чтобы воспользоваться третьим вариантом, нужно нажать кнопку Fx или CTRL+F3. На панели инструментов также имеется «Мастер подстановки» на вкладке «Формулы». Послы выполнения одного из перечисленных действий появляется окно, в котором нужно выбрать соответствующую группу, а после – нужную функцию. Далее последует окно «Аргументы и функции», в котором выполняются необходимые манипуляции.

Некоторых пугают особенности вызова встроенных математических функций Excel. Достаточно проделать все шаги представленного алгоритма и в таблице отобразится искомое решение.

Использование встроенных функций

Популярны среди пользователей встроенные математические функции в Excel. Их синтаксис состоит из 2 частей: имени и аргументов. Последних может быть один или несколько. Обязательно формула начинается со знака «=». В противном случае Excel выдаст ошибку о неверном вводе функции.

К примеру, имеется формула «=СУММ(А2:М10)». В таком случае речь пойдет о суммировании всех значений диапазона А2:М10. Аргументы обязательно заключаются в скобки и указываются без пробелов. Писать имя функции с заглавной или строчной буквы – дело каждого. Для программного продукта это не играет никакой роли.

Если указана формула «=СУММ(А2;С7;М10)», это означает, что суммируются только 3 указанные ячейки. В состав функции могут входить до 30 элементов в аргументе.

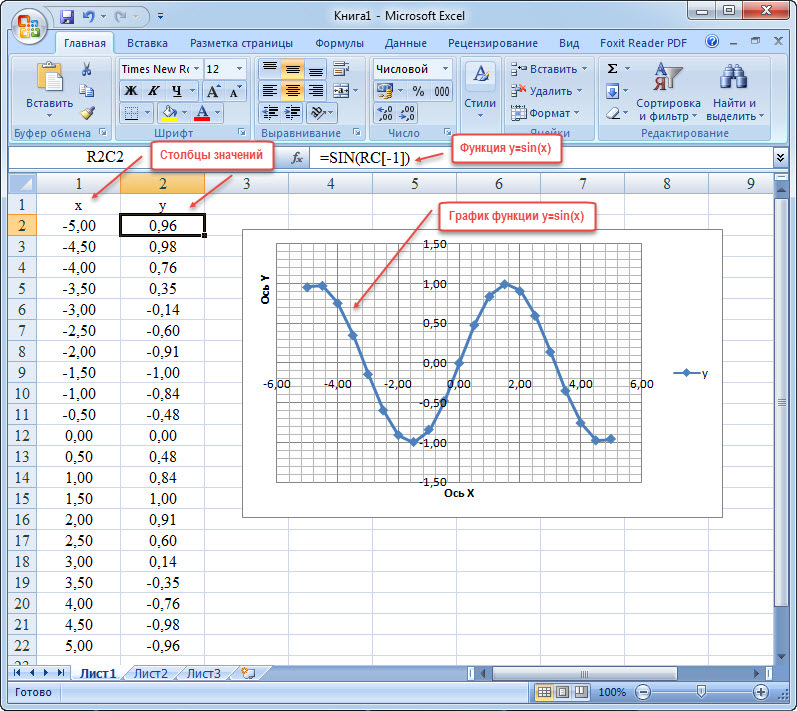
Графики математических функций

Построить графики математических функций в Excel достаточно просто. Важные условия: правильно задать условия и выбрать подходящий тип отображения.

Пример. Построить график функции для оператора sin. Шаг приращения = 0,5.

Примеры математических функций в Excel

Задание 1. Использовать функцию «суммесли». Данный оператор суммирует значения, если они удовлетворяют определенному условию и находятся в нужном диапазоне.

Задание 2. Использовать функцию «abs». Она находит модуль от заданного числа. В диалоговом окне указывают лишь один аргумент в виде одной ячейки. Диапазон участвовать в данном операторе не может.

Задание 3. Применить функцию «степень». Суть заключается в возведении заданного числа в указанную пользователем степень. У функции 2 аргумента.

Задание 4. Получить римскую запись от числа, написанного арабскими цифрами. Для этого понадобится формула «Римское».

Задание на закрепление материала

Провести эксперименты со всеми вариантами, где возможно использование математических функций в Excel. Можно начать с простых, а потом усложнять запись со вставкой формулы в уже имеющейся.

Обработка данных,
хранимых в ячейках рабочих листов Excel,
осу­ществляется по формулам, определённым
пользователем. Для перехода в режим
создания формул необходимо активировать
ячейку, в которую будет записана формула,
и ввести знак «=».

В формулах при
вычислениях могут использоваться, как
различные операторы (см. табл. 1), так и
встроенные функции Excel
(см. ниже).

Таблица 1. Операторы
MS Excel

Арифметические операторы:	Операторы сравнения:	Операторы ссылок:
+ сложение	= равно	: двоеточие (оператор диапазона)
— вычитание	> больше
^ возведение в степень	< меньше	; точка с запятой (оператор объединения ссылок)
* умножение	>= больше или равно
/ деление	<= меньше или равно
% процент	<> не равно

При вычислении
математических выражений по формуле
Excel
руко­водствуются следующими
традиционными правилами, определяющими
приоритет выполнения операций:

• в первую очередь
вычисляются выражения внутри круглых
скобок;

• определяются
значения, возвращаемые встроенными
функциями;

• выполняются
операции возведения в степень (^), затем
умножения (*) и деления (/), а после —
сложения (+) и вычитания (-).

Необходимо отметить,
что операции с одинаковым приоритетом
вы­полняются слева направо.

В процессе выполнения
вычислительных операций возможны
ошибочные действия со стороны пользователя,
в результате которых в активной ячейке
появится запись с указанием причины
ошибки.

Математические функции ms Excel

В Excel
имеется целый ряд встроенных математических
функций, существенно облегчающих решение
задач. Синтаксис функций:

Имя Функции (Аргумент 1;…;Аргумент n).

Здесь в качестве
аргумента функции может использоваться
как непосредственное значение, так и
адрес ячейки или диапазона.

При использовании
в функции нескольких аргументов они
отделяются один от другого точкой с
запятой.

Например, формула

=ПРОИЗВЕД(А1;В2;С4)

означает, что
необходимо перемножить числа в ячейках
A1,
B2
и С4. Любой аргумент функции может быть
диапазоном, содержащим произвольное
число ячеек листа. Например, функция

=ПРОИЗВЕД(А1:А3;В2:В4)

имеет два аргумента,
но перемножает содержимое шести ячеек.

Аргументы не
обязательно должны образовывать
непрерывные диапазоны ячеек:

=ПРОИЗВЕД(А1:А3;В2;В4:В7).

Некоторые функции,
например ПИ(), не имеют аргументов.
Комбинацию функций можно использовать
для создания выражения, например

=CУMM(KOPEHЬ(16);COS(A1*ПИ())).

Перечень всех
встроенных математических функций с
их описанием можно посмотреть в Мастере
функций.
Некоторые из функций приведены в таблице.

Таблица 3. Встроенные
математические функции

№	Наименование	Обозначение	Примечание
2	Абсолютное значение	=ABS(x)	— число, ссылка на ячей­ку с числом или формула, возвращающая числовое значение
3	Сумма	=СУММ(х1;…;xn)	; игнорируются пустые ячейки, текстовые и логические значения
4	Произведение	=ПРОИЗВЕД(x1;…;хn)
5	Корень квадратный	=КОРЕНЬ(х)
1	Натуральный логарифм	=LN(х)	х>0, при возвраща­ется ошибочное значение #ЧИСЛО!
2	Десятичный ло­гарифм	=LOG10(x)	х>0, при х<0 возвраща­ется ошибочное значение #ЧИСЛО!
3	Логарифм по заданному ос­нованию	=LOG(х;основание)	х>0, при возвраща­ется ошибочное значение #ЧИСЛО! По умолчанию основание равно 10
4	Экспонента от х	=ЕХР(х)
1		=ПИ()	Возвращает значение  с 14 значащими разрядами после десятичной точки
Тригонометрические функции
4	sin x	=SIN(x)	х — угол в радианах
5	cos x	=COS(x)	х — угол в радианах
6	tg x	=TAN(x)	х — угол в радианах
7	arctg x	=ATAN(x)	Возвращаемое значение лежит на интервале между -/2 и /2 радиан
8	arcsin х	=ASIN(x)	Ограничения на аргумент: . Возвращае­мое значение лежит на ин­тервале между -/2 и /2 радиан
9	arccos x	=ACOS(x)	Ограничения на аргумент: . Возвращае­мое значение лежит на ин­тервале от 0 до  радиан
Логические функции
	И	=И(логическое значение1; логическое значение2;…)	Возвращает значение ИСТИНА, если все её аргументы принимают значение ИСТИНА. Если хотя бы один из её аргументов принимает значение ЛОЖЬ, функция И возвращает значение ЛОЖЬ.
	ИЛИ	=ИЛИ(логическое значение1; логическое значение2;…)	Возвращает значение ИСТИНА, если хотя бы один из её аргументов принимает значение ИСТИНА. Функция ИЛИ возвращает значение ЛОЖЬ только тогда, когда все её аргументы принимают значение ЛОЖЬ
	Отрицание	=НЕ(логическое значение)	Изменяет логическое значение своего аргумента на противоположное. Если аргумент этой функции принимает значение ЛОЖЬ, то функция НЕ возвращает значение ИСТИНА и наоборот.
	Условие	=ЕСЛИ(логическое выражение; действие1; действие2)	Если логическое выражение принимает значение ИСТИНА, то выполняется действие1, в противном случае выполняется действие2)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #