Содержание
- Применение математических функций
- СУММ
- СУММЕСЛИ
- ОКРУГЛ
- ПРОИЗВЕД
- ABS
- СТЕПЕНЬ
- КОРЕНЬ
- СЛУЧМЕЖДУ
- ЧАСТНОЕ
- РИМСКОЕ
- Вопросы и ответы
Чаще всего среди доступных групп функций пользователи Экселя обращаются к математическим. С помощью них можно производить различные арифметические и алгебраические действия. Их часто используют при планировании и научных вычислениях. Узнаем, что представляет собой данная группа операторов в целом, и более подробно остановимся на самых популярных из них.
Применение математических функций
С помощью математических функций можно проводить различные расчеты. Они будут полезны студентам и школьникам, инженерам, ученым, бухгалтерам, планировщикам. В эту группу входят около 80 операторов. Мы же подробно остановимся на десяти самых популярных из них.
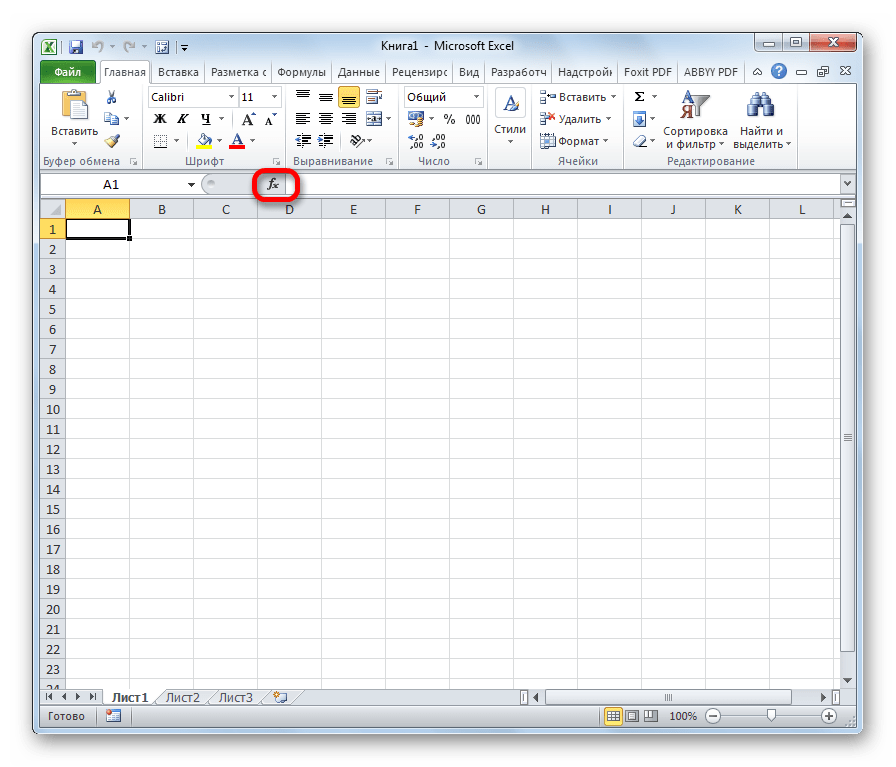
Открыть список математических формул можно несколькими путями. Проще всего запустить Мастер функций, нажав на кнопку «Вставить функцию», которая размещена слева от строки формул. При этом нужно предварительно выделить ячейку, куда будет выводиться результат обработки данных. Этот метод хорош тем, что его можно реализовать, находясь в любой вкладке.
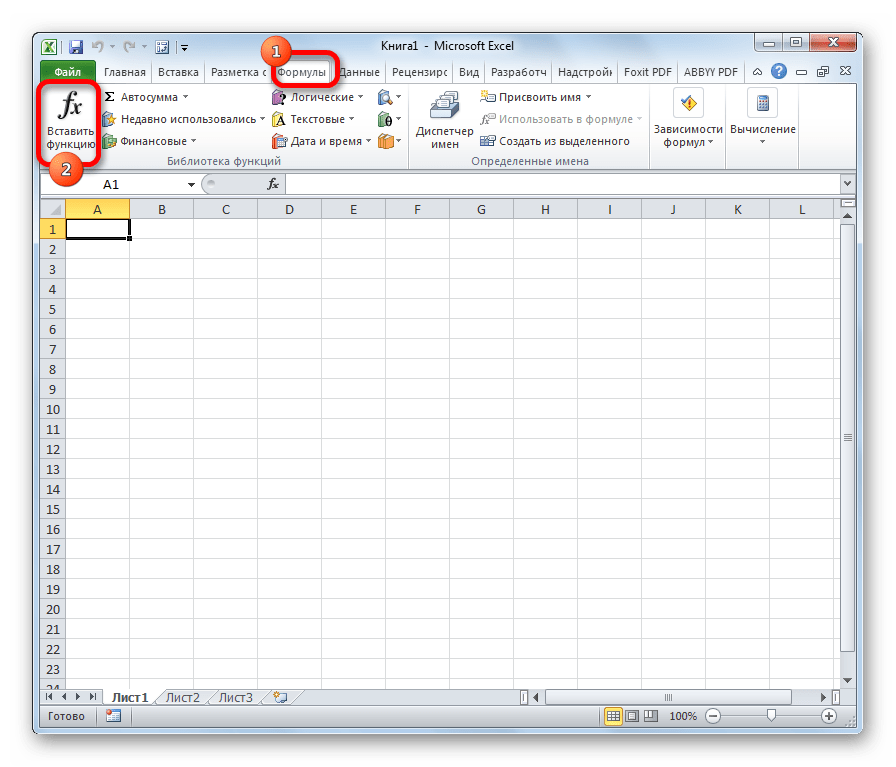
Также можно запустить Мастер функций, перейдя во вкладку «Формулы». Там нужно нажать на кнопку «Вставить функцию», расположенную на самом левом краю ленты в блоке инструментов «Библиотека функций».
Существует и третий способ активации Мастера функций. Он осуществляется с помощью нажатия комбинации клавиш на клавиатуре Shift+F3.
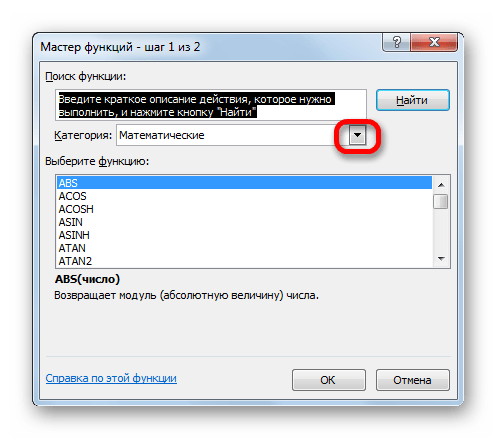
После того, как пользователь произвел любое из вышеуказанных действий, открывается Мастер функций. Кликаем по окну в поле «Категория».
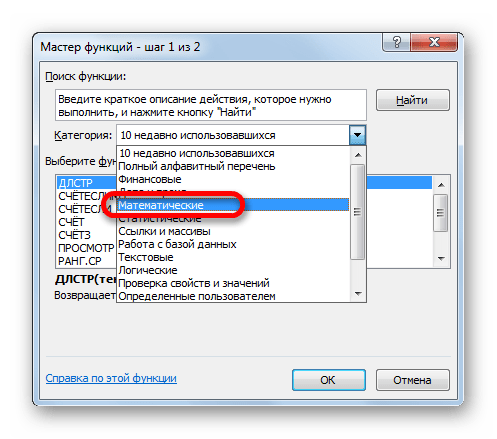
Открывается выпадающий список. Выбираем в нем позицию «Математические».
После этого в окне появляется список всех математических функций в Excel. Чтобы перейти к введению аргументов, выделяем конкретную из них и жмем на кнопку «OK».
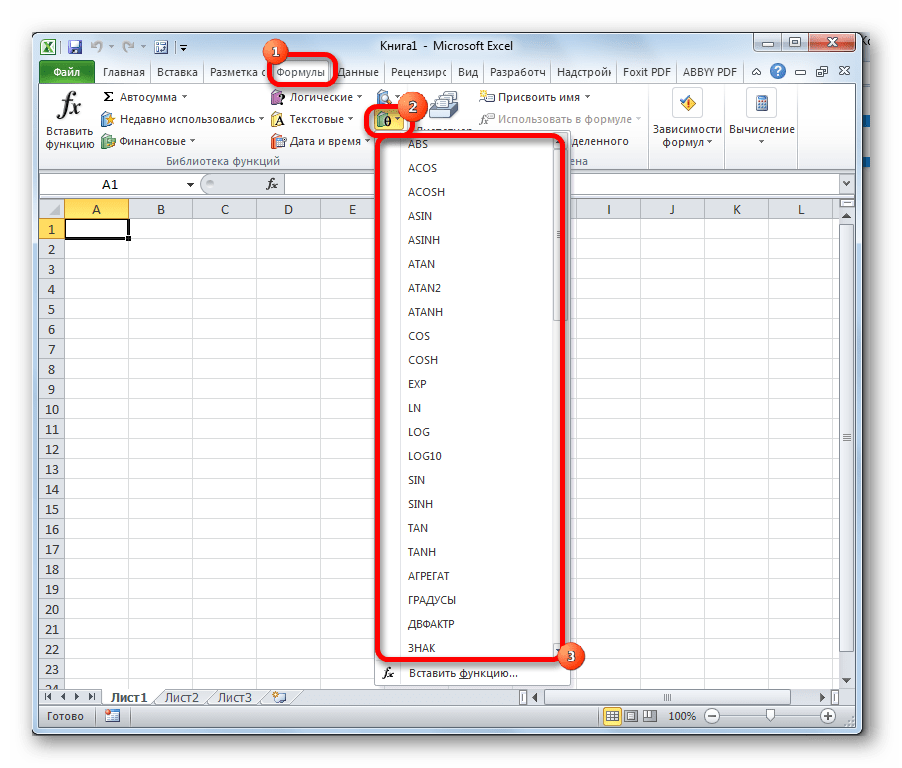
Существует также способ выбора конкретного математического оператора без открытия главного окна Мастера функций. Для этого переходим в уже знакомую для нас вкладку «Формулы» и жмем на кнопку «Математические», расположенную на ленте в группе инструментов «Библиотека функций». Открывается список, из которого нужно выбрать требуемую формулу для решения конкретной задачи, после чего откроется окно её аргументов.
Правда, нужно заметить, что в этом списке представлены не все формулы математической группы, хотя и большинство из них. Если вы не найдете нужного оператора, то следует кликнуть по пункту «Вставить функцию…» в самом низу списка, после чего откроется уже знакомый нам Мастер функций.
Урок: Мастер функций в Excel
СУММ
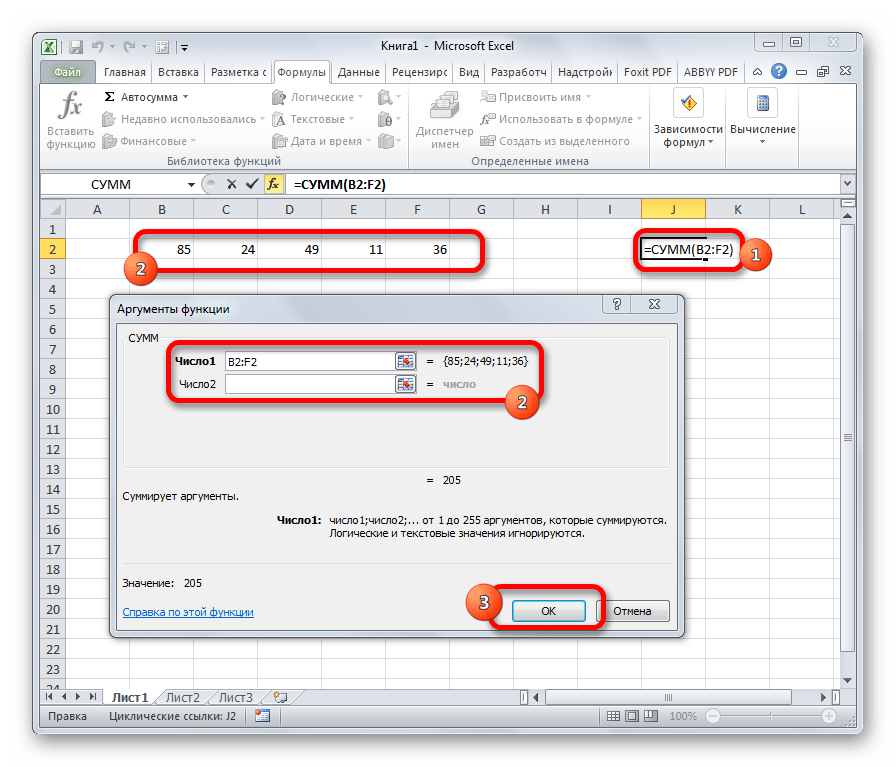
Наиболее часто используется функция СУММ. Этот оператор предназначен для сложения данных в нескольких ячейках. Хотя его можно использовать и для обычного суммирования чисел. Синтаксис, который можно применять при ручном вводе, выглядит следующим образом:
=СУММ(число1;число2;…)
В окне аргументов в поля следует вводить ссылки на ячейки с данными или на диапазоны. Оператор складывает содержимое и выводит общую сумму в отдельную ячейку.
Урок: Как посчитать сумму в Экселе
СУММЕСЛИ
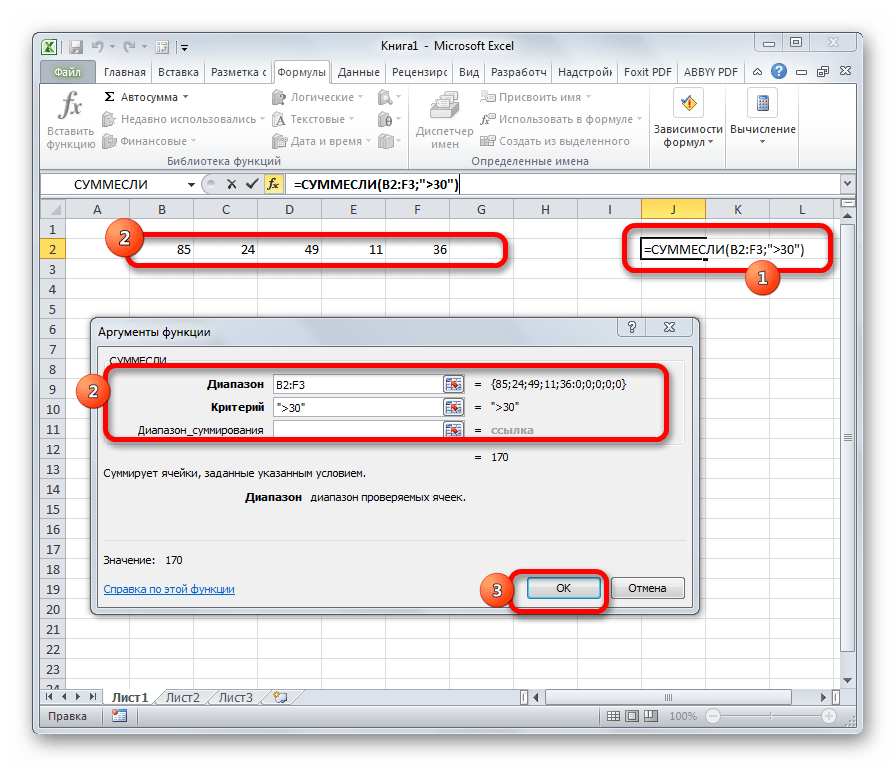
Оператор СУММЕСЛИ также подсчитывает общую сумму чисел в ячейках. Но, в отличие от предыдущей функции, в данном операторе можно задать условие, которое будет определять, какие именно значения участвуют в расчете, а какие нет. При указании условия можно использовать знаки «>» («больше»), «<» («меньше»), «< >» («не равно»). То есть, число, которое не соответствует заданному условию, во втором аргументе при подсчете суммы в расчет не берется. Кроме того, существует дополнительный аргумент «Диапазон суммирования», но он не является обязательным. Данная операция имеет следующий синтаксис:
=СУММЕСЛИ(Диапазон;Критерий;Диапазон_суммирования)
ОКРУГЛ
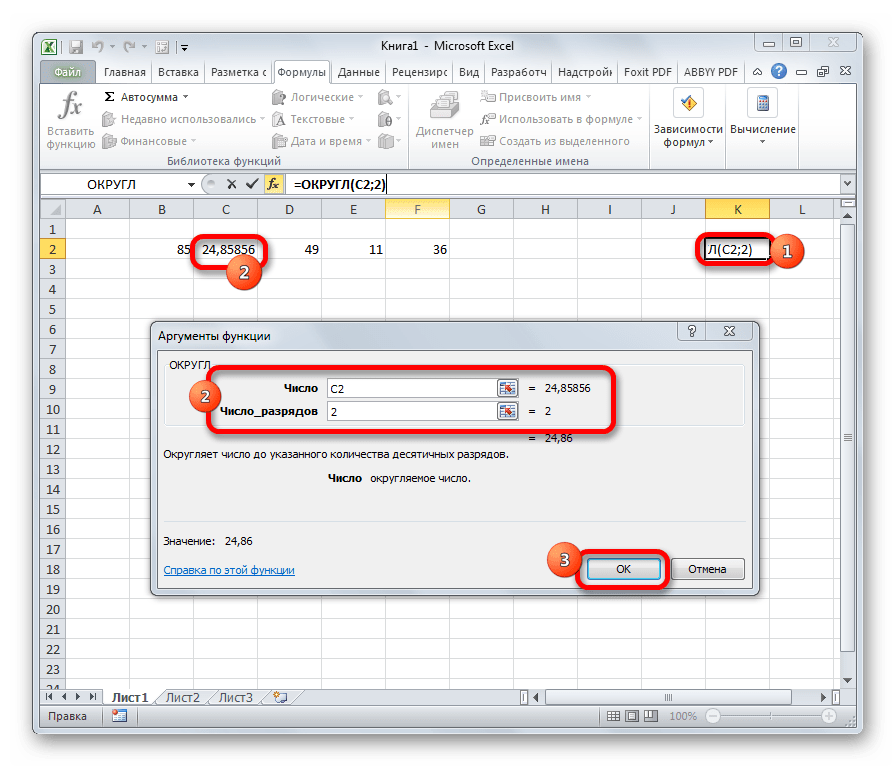
Как можно понять из названия функции ОКРУГЛ, служит она для округления чисел. Первым аргументом данного оператора является число или ссылка на ячейку, в которой содержится числовой элемент. В отличие от большинства других функций, у этой диапазон значением выступать не может. Вторым аргументом является количество десятичных знаков, до которых нужно произвести округление. Округления проводится по общематематическим правилам, то есть, к ближайшему по модулю числу. Синтаксис у этой формулы такой:
=ОКРУГЛ(число;число_разрядов)
Кроме того, в Экселе существуют такие функции, как ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, которые соответственно округляют числа до ближайшего большего и меньшего по модулю.
Урок: Округление чисел в Excel
ПРОИЗВЕД
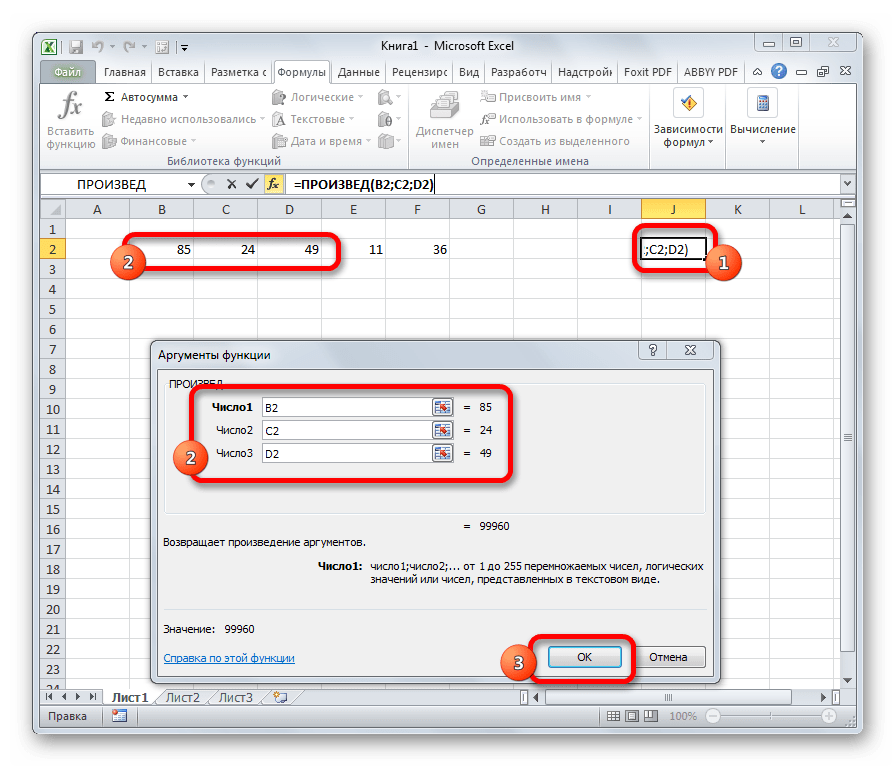
Задачей оператора ПРИЗВЕД является умножение отдельных чисел или тех, которые расположены в ячейках листа. Аргументами этой функции являются ссылки на ячейки, в которых содержатся данные для перемножения. Всего может быть использовано до 255 таких ссылок. Результат умножения выводится в отдельную ячейку. Синтаксис данного оператора выглядит так:
=ПРОИЗВЕД(число;число;…)
Урок: Как правильно умножать в Excel
ABS
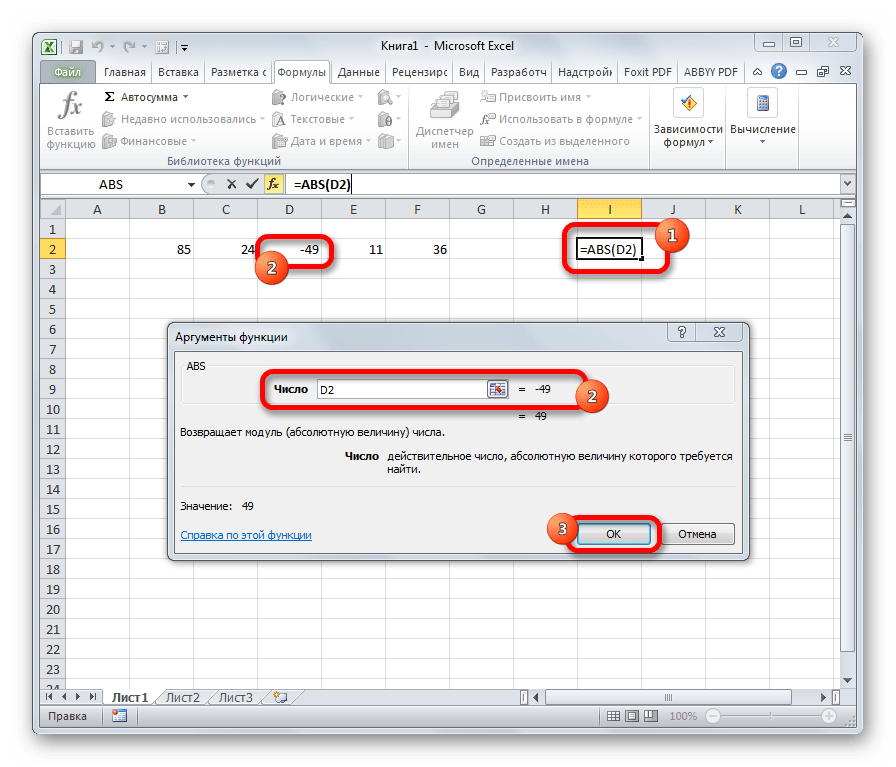
С помощью математической формулы ABS производится расчет числа по модулю. У этого оператора один аргумент – «Число», то есть, ссылка на ячейку, содержащую числовые данные. Диапазон в роли аргумента выступать не может. Синтаксис имеет следующий вид:
=ABS(число)
Урок: Функция модуля в Excel
СТЕПЕНЬ
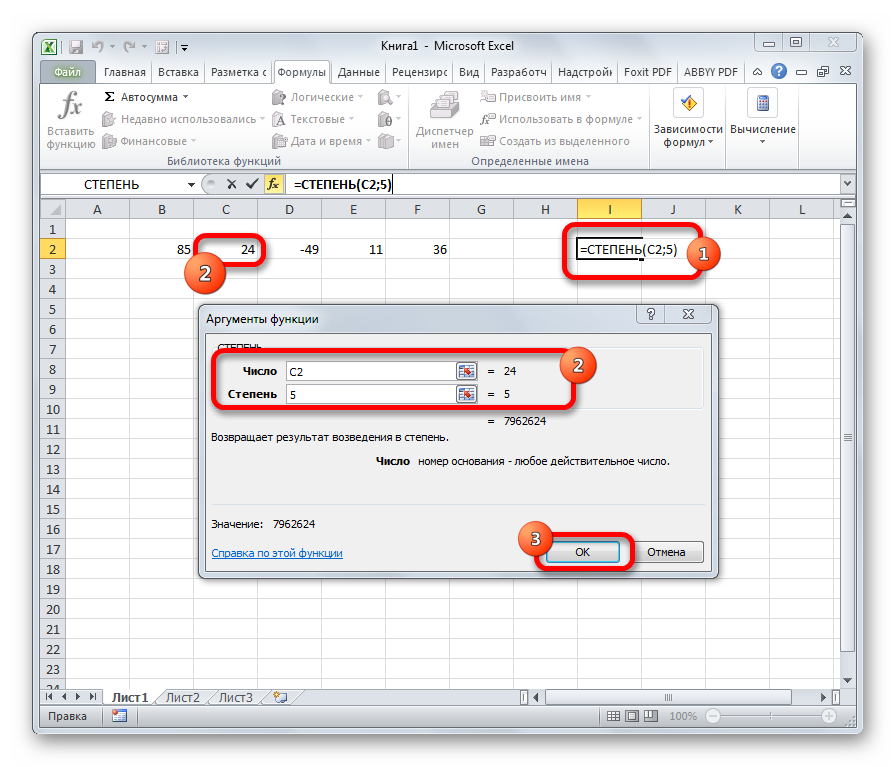
Из названия понятно, что задачей оператора СТЕПЕНЬ является возведение числа в заданную степень. У данной функции два аргумента: «Число» и «Степень». Первый из них может быть указан в виде ссылки на ячейку, содержащую числовую величину. Второй аргумент указывается степень возведения. Из всего вышесказанного следует, что синтаксис этого оператора имеет следующий вид:
=СТЕПЕНЬ(число;степень)
Урок: Как возводить в степень в Экселе
КОРЕНЬ
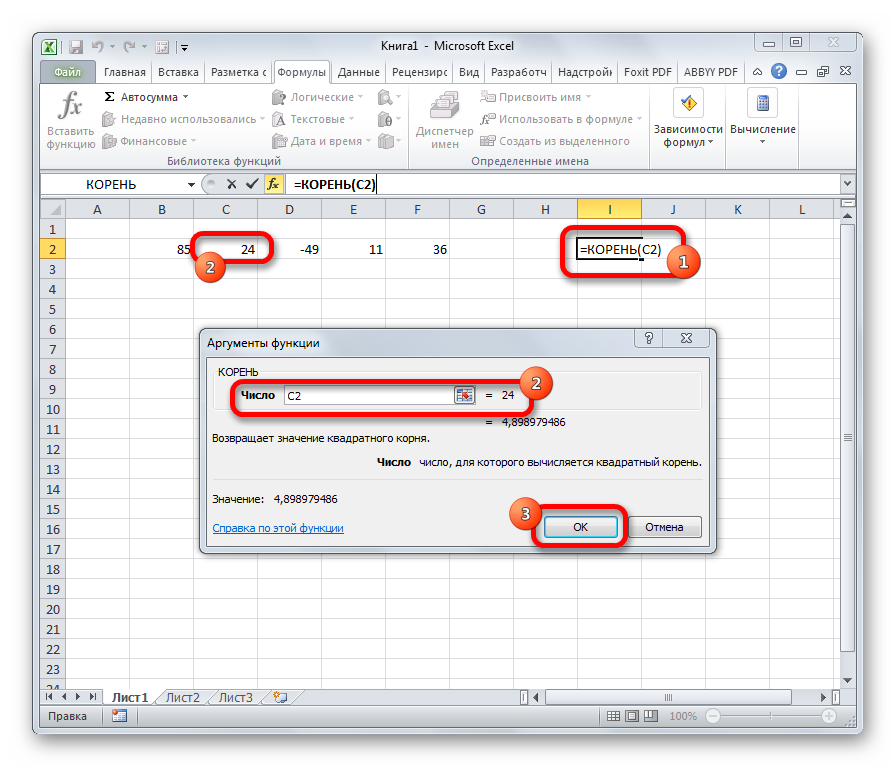
Задачей функции КОРЕНЬ является извлечение квадратного корня. Данный оператор имеет только один аргумент – «Число». В его роли может выступать ссылка на ячейку, содержащую данные. Синтаксис принимает такую форму:
=КОРЕНЬ(число)
Урок: Как посчитать корень в Экселе
СЛУЧМЕЖДУ
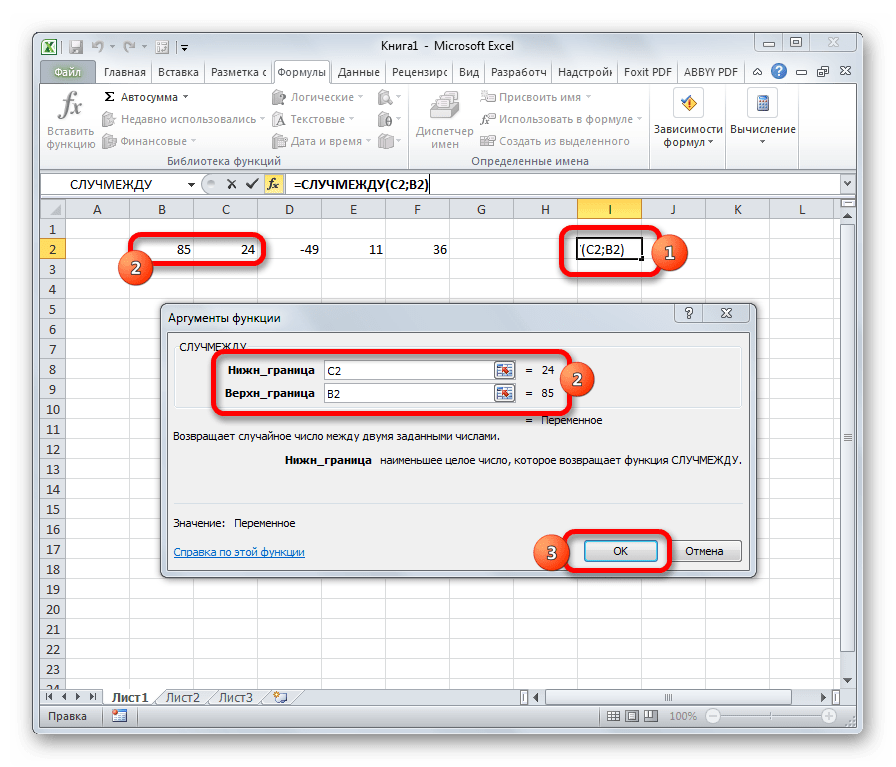
Довольно специфическая задача у формулы СЛУЧМЕЖДУ. Она состоит в том, чтобы выводить в указанную ячейку любое случайное число, находящееся между двумя заданными числами. Из описания функционала данного оператора понятно, что его аргументами является верхняя и нижняя границы интервала. Синтаксис у него такой:
=СЛУЧМЕЖДУ(Нижн_граница;Верхн_граница)
ЧАСТНОЕ
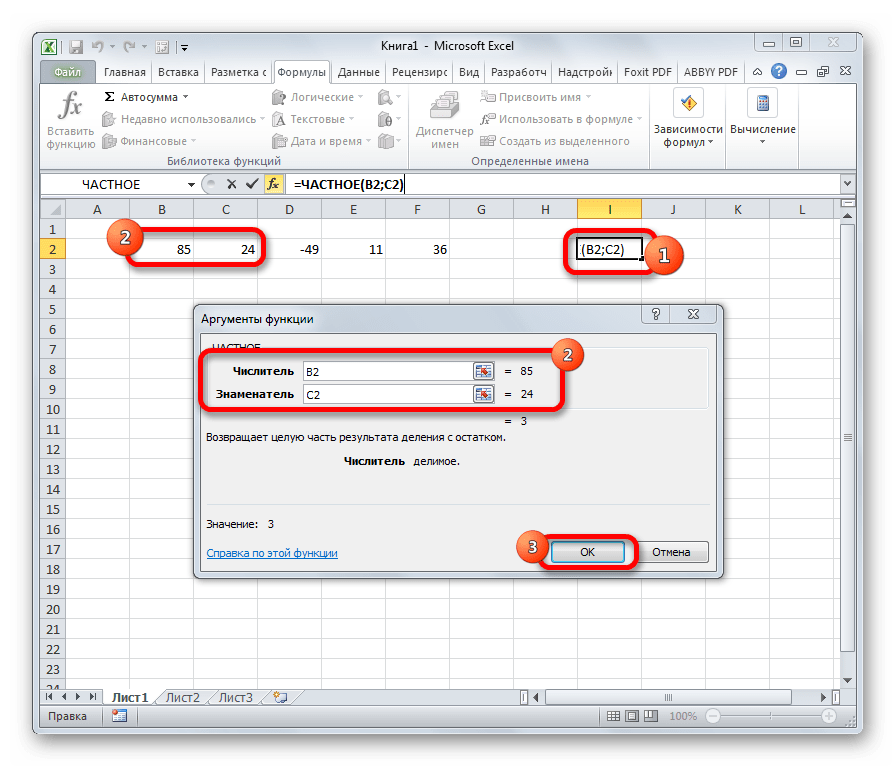
Оператор ЧАСТНОЕ применяется для деления чисел. Но в результатах деления он выводит только четное число, округленное к меньшему по модулю. Аргументами этой формулы являются ссылки на ячейки, содержащие делимое и делитель. Синтаксис следующий:
=ЧАСТНОЕ(Числитель;Знаменатель)
Урок: Формула деления в Экселе
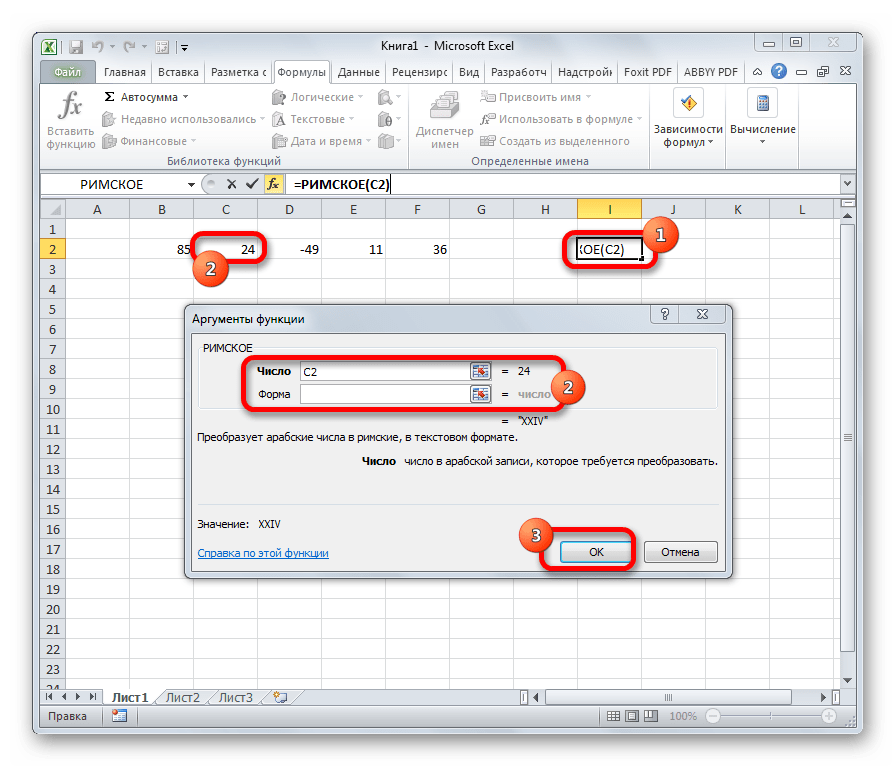
РИМСКОЕ
Данная функция позволяет преобразовать арабские числа, которыми по умолчанию оперирует Excel, в римские. У этого оператора два аргумента: ссылка на ячейку с преобразуемым числом и форма. Второй аргумент не является обязательным. Синтаксис имеет следующий вид:
=РИМСКОЕ(Число;Форма)
Выше были описаны только наиболее популярные математические функции Эксель. Они помогают в значительной мере упростить различные вычисления в данной программе. При помощи этих формул можно выполнять как простейшие арифметические действия, так и более сложные вычисления. Особенно они помогают в тех случаях, когда нужно производить массовые расчеты.
Чтобы просмотреть более подробные сведения о функции, щелкните ее название в первом столбце.
Примечание: Маркер версии обозначает версию Excel, в которой она впервые появилась. В более ранних версиях эта функция отсутствует. Например, маркер версии 2013 означает, что данная функция доступна в выпуске Excel 2013 и всех последующих версиях.
|
Функция |
Описание |
|
ABS |
Возвращает модуль (абсолютную величину) числа. |
|
ACOS |
Возвращает арккосинус числа. |
|
ACOSH |
Возвращает гиперболический арккосинус числа. |
|
ACOT |
Возвращает арккотангенс числа. |
|
ACOTH |
Возвращает гиперболический арккотангенс числа. |
|
АГРЕГАТ |
Возвращает агрегат для списка или базы данных. |
|
АРАБСКОЕ |
Преобразует римские числа в арабские в виде числа. |
|
ASIN |
Возвращает арксинус числа. |
|
ASINH |
Возвращает гиперболический арксинус числа. |
|
ATAN |
Возвращает арктангенс числа. |
|
ATAN2 |
Возвращает арктангенс для заданных координат x и y. |
|
ATANH |
Возвращает гиперболический арктангенс числа. |
|
ОСНОВАНИЕ |
Преобразует число в текстовое представление с данным основанием (базой). |
|
ОКРВВЕРХ |
Округляет число до ближайшего целого или кратного. |
|
ОКРВВЕРХ.МАТ |
Округляет число в большую сторону до ближайшего целого или кратного. |
|
ОКРВВЕРХ.ТОЧН |
Округляет число до ближайшего целого или кратного. Число округляется до большего значения вне зависимости от его знака. |
|
ЧИСЛКОМБ |
Возвращает количество комбинаций для заданного числа объектов. |
|
ЧИСЛКОМБА |
Возвращает количество комбинаций с повторами для заданного числа элементов. |
|
COS |
Возвращает косинус числа. |
|
COSH |
Возвращает гиперболический косинус числа. |
|
COT |
Возвращает котангенс угла. |
|
COTH |
Возвращает гиперболический котангенс числа. |
|
CSC |
Возвращает косеканс угла. |
|
CSCH |
Возвращает гиперболический косеканс угла. |
|
ДЕС |
Преобразует текстовое представление числа в заданном основании в десятичное число. |
|
ГРАДУСЫ |
Преобразует радианы в градусы. |
|
ЧЁТН |
Округляет число до ближайшего четного целого. |
|
EXP |
Возвращает число e, возведенное в указанную степень. |
|
ФАКТР |
Возвращает факториал числа. |
|
ДВФАКТР |
Возвращает двойной факториал числа. |
|
ОКРВНИЗ |
Округляет число до ближайшего меньшего по модулю значения. |
|
ОКРВНИЗ.МАТ |
Округляет число в меньшую сторону до ближайшего целого или кратного. |
|
ОКРВНИЗ.ТОЧН |
Округляет число в меньшую сторону до ближайшего целого или кратного. Число округляется в меньшую сторону независимо от знака. |
|
НОД |
Возвращает наибольший общий делитель. |
|
ЦЕЛОЕ |
Округляет число до ближайшего меньшего целого. |
|
ISO.ОКРВВЕРХ |
Округляет число в большую сторону до ближайшего целого или кратного. |
|
НОК |
Возвращает наименьшее общее кратное. |
|
LN |
Возвращает натуральный логарифм числа. |
|
LOG |
Возвращает логарифм числа по заданному основанию. |
|
LOG10 |
Возвращает десятичный логарифм числа. |
|
МОПРЕД |
Возвращает определитель матрицы массива. |
|
МОБР |
Возвращает обратную матрицу массива. |
|
МУМНОЖ |
Возвращает матричное произведение двух массивов. |
|
ОСТАТ |
Возвращает остаток от деления. |
|
ОКРУГЛТ |
Возвращает число, округленное с требуемой точностью. |
|
МУЛЬТИНОМ |
Возвращает мультиномиальный коэффициент множества чисел. |
|
МЕДИН |
Возвращает матрицу единицы или заданный размер. |
|
НЕЧЁТ |
Округляет число до ближайшего нечетного целого. |
|
ПИ |
Возвращает число пи. |
|
СТЕПЕНЬ |
Возвращает результат возведения числа в степень. |
|
ПРОИЗВЕД |
Возвращает произведение аргументов. |
|
ЧАСТНОЕ |
Возвращает целую часть частного при делении. |
|
РАДИАНЫ |
Преобразует градусы в радианы. |
|
СЛЧИС |
Возвращает случайное число в интервале от 0 до 1. |
|
Функция СЛУЧМАССИВ |
Возвращает массив случайных чисел в интервале от 0 до 1. Но вы можете указать количество заполняемых строк и столбцов, минимальное и максимальное значения, а также какие значения необходимо возвращать: целые или десятичные. |
|
Функция СЛУЧМЕЖДУ |
Возвращает случайное число в интервале между двумя заданными числами. |
|
РИМСКОЕ |
Преобразует арабские числа в римские в виде текста. |
|
ОКРУГЛ |
Округляет число до указанного количества десятичных разрядов. |
|
ОКРУГЛВНИЗ |
Округляет число до ближайшего меньшего по модулю значения. |
|
ОКРУГЛВВЕРХ |
Округляет число до ближайшего большего по модулю значения. |
|
SEC |
Возвращает секанс угла. |
|
SECH |
Возвращает гиперболический секанс угла. |
|
РЯД.СУММ |
Возвращает сумму степенного ряда, вычисленную по формуле. |
|
ЗНАК |
Возвращает знак числа. |
|
SIN |
Возвращает синус заданного угла. |
|
SINH |
Возвращает гиперболический синус числа. |
|
КОРЕНЬ |
Возвращает положительное значение квадратного корня. |
|
КОРЕНЬПИ |
Возвращает квадратный корень из значения выражения (число * пи). |
|
ПРОМЕЖУТОЧНЫЕ.ИТОГИ |
Возвращает промежуточный итог в списке или базе данных. |
|
СУММ |
Суммирует аргументы. |
|
СУММЕСЛИ |
Суммирует ячейки, удовлетворяющие заданному условию. |
|
СУММЕСЛИМН |
Суммирует ячейки в диапазоне, удовлетворяющие нескольким условиям. |
|
СУММПРОИЗВ |
Возвращает сумму произведений соответствующих элементов массивов. |
|
СУММКВ |
Возвращает сумму квадратов аргументов. |
|
СУММРАЗНКВ |
Возвращает сумму разностей квадратов соответствующих значений в двух массивах. |
|
СУММСУММКВ |
Возвращает сумму сумм квадратов соответствующих элементов двух массивов. |
|
СУММКВРАЗН |
Возвращает сумму квадратов разностей соответствующих значений в двух массивах. |
|
TAN |
Возвращает тангенс числа. |
|
TANH |
Возвращает гиперболический тангенс числа. |
|
ОТБР |
Отбрасывает дробную часть числа. |
Важно: Вычисляемые результаты формул и некоторые функции листа Excel могут несколько отличаться на компьютерах под управлением Windows с архитектурой x86 или x86-64 и компьютерах под управлением Windows RT с архитектурой ARM. Подробнее об этих различиях.
Перейти к содержимому
Статья посвящена тому, как добавлять математические формулы в документ «Эксель».
Иногда при оформлении таблиц в программе «Excel» приходится добавлять в ячейки математические формулы. Эти формулы не используются в расчетах, а несут функцию декоративных элементов таблицы. Можно конечно прописать формулы в строчку обычным шрифтом, но это будет не очень красиво.
Рассмотрим добавление формулы на лист «Excel» на примере формулы площади круга: Пи*D^2/4.
Как видите, выглядит она не очень презентабельно.
Попробуем отобразить ее в виде математической функции.
Шаг 1.
Устанавливаем курсор в нужную ячейку.
Шаг 2.
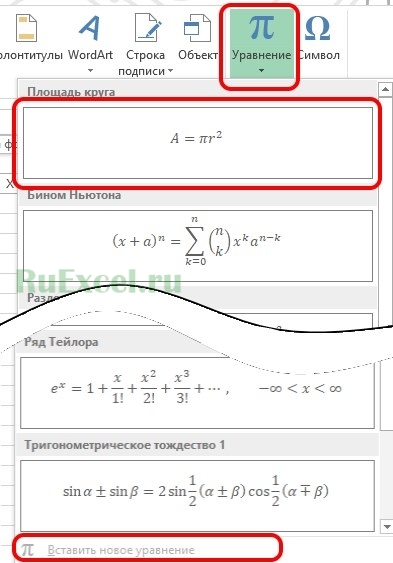
Во вкладке «Вставка» панели инструментов кликаем по значку «Уравнение».
Шаг 3.
При нажатии на значок «Уравнение» выпадает целый список готовых распространенных формул. Среди который есть и площадь круга, правда в ином формате.
Шаг 4.
Для того что бы записать формулу в том формате, который нам требуется, вставляем из списка уже готовое уравнение площади круга, а затем изменяем его при помощи пункта «Вставить новое уравнение»
Шаг 5.
После выбора пункта «Вставить новое уравнение» открывается конструктор с помощью которого можно изменить вид полученной формулы.
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Microsoft Excel – одна из самых популярных и легкодоступных программ для представителей разный специальностей. Сегодня мы рассмотрим, пожалуй, одну из самых используемых групп формул – математические формулы.
Начнем с того, как найти их среди прочего функционала. Есть несколько путей того, как открыть список математических формул.
Самый простой способ – нажать на кнопку «Формулы» на панели управления. Затем выбрать из перечня тип функций: «Математические».
Перед вами появится выпадающий длинный список всех существующих операторов:

Всего в Excel около 80 математических и тригонометрических функций. Мы рассмотрим не все, только самые распространенные из них, а также обратим внимание на некоторые нюансы, о которых вы, возможно, не знали. Если в статье вы не нашли нужную вам функцию, то скачивайте наш бесплатный гайд «Математические функции в Excel».
Для разминки вспомним самые простые формулы.
1. Формулы СУММ(), ПРОИЗВЕД()
Эти операции имеют схожую структуру и одинаковый тип аргументов, поэтому мы их объединили в один блок. СУММ() служит для сложения данных в нескольких ячейках, ПРОИЗВЕД() – очевидно, для нахождения произведения.
Аргументами этих функций могут быть числа, диапазоны, ссылки на ячейку, в которой содержится числовое значение. Количество элементов не может быть больше 30.
СУММ() и ПРОИЗВЕД() пропускают пустые ячейки, ячейки текстового формата и логические значения. Операторы вносят результат вычислений в отдельную, ранее выделенную курсором ячейку:

Аналогично для формулы ПРОИЗВЕД():

2. Формула ЧАСТНОЕ()
Тоже одна из простых операций в математике. В Excel выполняется тоже несложно: у функции ЧАСТНОЕ() есть два аргумента: делимое и делитель.
В выделенной ячейке выводится частное:

3. Формула СУММЕСЛИ()
Оператор СУММЕСЛИ() находит сумму чисел. Главное отличие этой функции от СУММ() в том, что здесь в качестве аргумента можно задавать условие (только одно), которое будет показывать, какие значения будут использованы в расчетах, а какие – нет.
В качестве условий могут выступать неравенства со знаками больше, меньше или не равно («>», «<», «< >»). Число, которое не соответствует введенному условию, не будет включен в суммирование.
На рисунке 5 изображено суммирование всех чисел, которые больше 0.
Оранжевым выделены те числа, которые будут включены в расчет функцией СУММЕСЛИ().
Остальные числа просто будут игнорироваться:

Кроме постоянных аргументов, существует еще и дополнительный – «Диапазон суммирования». Он добавляется тогда, когда необходимо просуммировать один диапазон, а условия выбирать по другому диапазону.
Например, нужно посчитать общую стоимость всех проданных фруктов.
Для этого воспользуемся следующей формулой:

То есть сначала пишем диапазон, по которому проверяем условие, затем само ограничение и в конце диапазон чисел, которые надо суммировать. В примере на рисунке 6 выше, соответственно, все строки из категории «Овощи» в расчет включены не будут.
4. Формулы ОКРУГЛ(), ОКРУГЛВВЕРХ(), ОКРУГЛВНИЗ()
Функция ОКРУГЛ() предназначена для округления значения до заданного количества знаков после запятой. В качестве первого аргумента выступают, как обычно, числа или диапазон ячеек, второго – разряд, до которого нужно округлить число.
Например, округление значения до второго знака после запятой:

Если в качестве второго аргумента выступает 0, то число будет округляться до ближайшего целого:

Второй аргумент может быть и отрицательным, тогда округление будет происходить до требуемого знака перед запятой:

Если необходимо округлить в сторону меньшего или большего по модулю числа используют функции ОКРУГЛВНИЗ(), ОКРУГЛВВЕРХ(), соответственно:


Замечание: многие могут решить, что функции округления бесполезны, так как можно просто убрать/добавить дополнительный знак после запятой с помощью кнопок увеличить/уменьшить разрядность.
На самом деле, это не так.
Дело в том, что увеличение или уменьшение разрядности влияет только на «внешний вид» ячейки, то есть на то, как мы число видим.
Само число, при этом, не меняется. Функции округления же полностью меняют вид числа, убирая лишние разряды.
5. Формулы ОТБР(), ЦЕЛОЕ()
Эти функции очень похожи на предыдущие, но работают немного по-другому.
ОТБР() убирает все цифры справа от запятой и у положительных, и у отрицательных чисел. На первом месте в скобках после оператора пишется значение, а на втором – разряд, после которого удалятся все знаки.
Если второй аргумент пропущен, то по умолчанию ставится 0:

ЦЕЛОЕ() – функция, которая выдает в качестве результата наименьшее целое число, стоящее перед аргументом:

На положительные числа операторы влияют почти одинаково, а вот на отрицательные – нет.
Функция ЦЕЛОЕ(-5,6) выдаст результат (-6), а ОТБР(-5,6;0) выдаст (-5), хотя в то же время для числа 5,3 результат обеих функций будет одинаковый – число (5).
6. Формула ABS()
Математическая формула ABS() позволяет получить число по модулю. Как обычно, аргументами оператора является число или ссылка на ячейку.

Эту функцию удобно использовать, например, когда необходимо найти количество дней между датами. Из школьной программы многие знают, что нужно из большего вычитать меньшее.
Но что делать если дана огромная таблица, где трудно определить, где какое значение? Здесь нам помогает оператор ABS(), который переводит отрицательное число в положительное.

7. Формула КОРЕНЬ()
КОРЕНЬ() – довольно легкая функция с одним аргументом (числом или ссылкой на ячейку), которая находит квадратный корень числа:

Замечание. Для извлечения корня другой степени (не квадратного) можно пользоваться функцией СТЕПЕНЬ().
8. Формула СТЕПЕНЬ()
Функция СТЕПЕНЬ() позволяет возвести число в любую степень, в том числе извлечь корень (то есть возвести число в дробную степень).
Например, чтобы извлечь кубический корень из числа 8, необходимо воспользоваться формулой, как на рисунке 17.1.


Помимо математической функции СТЕПЕНЬ(), можно пользоваться оператором “^”, но он выглядит менее опрятно в формулах.
Если вам интересно узнать больше о других математических функциях, напишите об этом ниже в комментариях. Записывайтесь на открытый онлайн-курс «Аналитика в Excel», если хотите научиться выполнять рутинную работу в программе быстрее.
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Блог SF Education
Investment Banking
5 примеров экономии времени в Excel
Содержание статьи Что для работодателя главное в сотруднике? Добросовестность, ответственность, профессионализм и, конечно же, умение пользоваться отведенным временем! Предлагаем познакомиться с очень нужными, на…
Как работает сотрудник одной из компаний «большой тройки»?
Ты работаешь в компании «большой тройки (имеются в виду три крупнейших консалтинговых компании: McKinsey, Boston Consulting Group и Bain & Company), в которых мечтают работать тысячи подписчиков наших каналов и читателей vc.ru. Что это значит для тебя?
Содержание
- Основные математические формулы в Excel (смотрите и учитесь)
- Основы Формул
- 1. Каждая формула в Excel начинается с “=”
- 2. Формулы показываются на панели формул Excel.
- 3. Как собрать формулу
- Базовая статистика
- Среднее
- Медиана
- Минимум
- Максимум
- Циклические вычисления
- Циклические вычисления и нахождение корней уравнения
- Функции ЧЁТН и НЕЧЁТ
- Функции ОКРВНИЗ, ОКРВВЕРХ
- Функции ЦЕЛОЕ и ОТБР
- Функция ПРОИЗВЕД
- Функция ОСТАТ
- Функция КОРЕНЬ
- Функция ЧИСЛОКОМБ
- Функция ЕЧИСЛО
- Формула ЧАСТНОЕ()
- Формула СУММЕСЛИ()
- Формулы ОКРУГЛ(), ОКРУГЛВВЕРХ(), ОКРУГЛВНИЗ()
- Использование ссылок
- ABS
- СТЕПЕНЬ
- СЛУЧМЕЖДУ
- РИМСКОЕ
- LOG
- Заключение
Если изучение по видеороликам, это ваш стиль, посмотрите видео ниже, чтобы пройти по этому уроку. В противном случае продолжайте читать подробное описание того, как работать с каждой математической формулой Excel.
Основы Формул
Прежде чем мы начнем, давайте рассмотрим, как использовать любую формулу в Microsoft Excel. Независимо от того, работаете ли вы с математическими формулами в этом учебнике или любыми другими, эти советы помогут вам овладеть Excel.
1. Каждая формула в Excel начинается с “=”
Чтобы ввести формулу, щелкните любую ячейку в Microsoft Excel и введите знак равенства на клавиатуре. Так начинается формула.
После знака равенства вы можете размещать в ячейке невероятно разнообразные вещи. Попробуйте ввести =4+4 в качестве вашей первой формулы и нажмите Enter, чтобы отобразить результат. Excel выведет 8, но формула останется за кулисами электронной таблицы.
2. Формулы показываются на панели формул Excel.
Когда вы вводите формулу в ячейку, вы можете увидеть результат в ячейке сразу после нажатия клавиши ввода. Но когда вы выбираете ячейку, вы можете увидеть формулу для этой ячейки на панели формул.
Чтобы использовать пример выше, ячейка отобразит «8», но когда мы нажмем на эту ячейку, панель формул покажет, что ячейка складывает 4 и 4.
3. Как собрать формулу
В приведенном выше примере мы набрали простую формулу для складывания двух чисел. Но вам не обязательно вводить числа, вы также можете ссылаться на другие ячейки.
Excel — это сетка ячеек, а столбцы идут слева направо, каждая назначена на букву, а строки пронумерованы. Каждая ячейка является пересечением строки и столбца. Например, ячейка, где пересекаются столбцы A и строка 3, называется A3.
Предположим, что у меня две ячейки с простыми числами, например 1 и 2, и они находятся в ячейках A2 и A3. Когда я набираю формулу, я могу начать формулу с «=», как всегда. Затем я могу ввести:
=A2+A3
…чтобы сложить эти два числа вместе. Очень распространено иметь лист со значениями и отдельный лист, где выполняются вычисления. Соблюдайте все эти советы при работе с этим руководством. Для каждой из формул вы можете ссылаться на ячейки или непосредственно вводить числовые значения в формулу.
Если вам нужно изменить формулу, которую вы уже набрали, дважды щелкните по ячейке. Вы сможете настроить значения в формуле.
Базовая статистика
Используйте вкладку “Basic Statistics” в книге для практики.
Теперь, когда вы знаете основные математические операторы, давайте перейдем к чему-то более продвинутому. Базовая статистика полезна для обзора набора данных и принятия обоснованных решений. Давайте рассмотрим несколько популярных простых статистических формул.
Среднее
Чтобы использовать формулу среднего в Excel, начните формулу с помощью =СРЗНАЧ(, а затем введите свои значения. Разделите каждое число запятой. Когда вы нажмёте клавишу ввода, Excel вычислит и выведет среднее значение.
=СРЗНАЧ(1;3;5;7;10)
Лучший способ рассчитать среднее это ввести ваши значения в отдельные ячейки в одном столбце.
=СРЗНАЧ(A2:A5)
Медиана
Медиана набора данных это значение, которое находится посередине. Если вы взяли числовые значения и выставили их в порядке от наименьшего к самому большому, медиана была бы ровно посередине этого списка.
=МЕДИАНА(1;3;5;7;10)
Я бы рекомендовал ввести ваши значения в список ячеек, а затем использовать формулу медианы над списком ячеек со значениями, введенными в них.
=МЕДИАНА(A2:A5)
Минимум
Если у вас есть набор данных и вы хотите держать на виду наименьшее значение, полезно использовать формулу МИН в Excel. Вы можете использовать формулу МИН со списком чисел, разделенных точкой с запятыми, чтобы найти самое маленькое значение в наборе. Это очень полезно при работе с большими наборами данных.
=МИН(1;3;5;7;9)
Возможно, вы захотите найти минимальное значение в списке данных, что вполне возможно с помощью такой формулы, как:
=МИН(A1:E1)
Максимум
Формула МАКС в Excel — полная противоположность МИН
=МАКС(1;3;5;7;9)
Или же, вы можете выбрать список значений в ячейках, и Excel вернет наибольшее из набора с этой формулой:
=МАКС(A1:E1)
Циклические вычисления
Если зависимые ячейки Excel образуют цикл, то говорят, что имеют место циклические ссылки (circular references). В обычном режиме Excel обнаруживает цикл и выдает сообщение о возникшей ситуации, требуя устранить циклические ссылки. Следуя обычной семантике, он не может провести вычисления, так как циклические ссылки порождают бесконечные вычисления. Есть два выхода из этой ситуации, – устранить циклические ссылки или изменить настройку в машине вычислений так, чтобы такие вычисления стали возможными. В последнем случае, естественно, требуется, чтобы число повторений цикла было конечным. Excel допускает переход к новой семантике, обеспечивающей проведение циклических вычислений. Вручную, для этого достаточно на вкладке Вычисления (меню Сервис, пункт Параметры) включить флажок Итерации и при необходимости изменить число повторений цикла в окошке “Максимум итераций”. Можно также задать точность вычислений в окошке “Максимальное изменение”, что также приводит к ограничению числа повторений цикла. По умолчанию максимальное число итераций и точность вычислений соответственно имеют значения 100 и 0,0001. Понятно, что включить циклические вычисления и задать значения параметров, определяющих окончание цикла, можно и программно.
Укажем, особенности семантики циклических вычислений:
- Формулы, связанные циклическими ссылками, вычисляются многократно.
- Запись формул на листе определяет порядок их вычисления. Формулы вычисляются сверху вниз, слева направо.
- Число повторений цикла определяется параметрами, заданными на вкладке Вычисления. Цикл заканчивается при достижении максимального числа итераций или, когда изменения значений во всех ячейках не превосходят заданной точности.
В каких же ситуациях требуется прибегать к циклическим вычислениям? Это, возможно, следует делать, когда речь идет о реализации итерационного процесса, вычислениях по рекуррентным соотношениям. У нас уже были примеры реализации итерационных процессов, например, вычисление суммы ряда, задающего экспоненту, в которых не применялись циклические ссылки. Платой за это было использование дополнительных ячеек таблицы Excel. Правда, появлялись и новые возможности, – возможность построить график, проанализировать процесс сходимости и т.д. Тем не менее, программисту, привыкшему к традиционным языкам, и привыкшему “с детства” экономить на переменных, может показаться странным предложенное решение задачи о нахождении корня уравнения, где на экран выводятся результаты всех приближений. В Excel экономия ячеек не главная задача. Тем не менее, при реализации итерационных процессов можно, конечно, и в Excel иметь одну единственную ячейку X, значение которой изменяется, начиная от начального приближения до искомого результата. Это в большей степени соответствует понятию переменной в языках программирования.
Циклические вычисления и нахождение корней уравнения
Покажем, как можно использовать циклические вычисления на примере задачи нахождения корня уравнения методом Ньютона. Для простоты я начну с квадратного уравнения, а позже рассмотрю и более “серьезные” уравнения. Итак, рассмотрим квадратное уравнение: X2 -5X+6 =0. Найти корень этого (и любого другого уравнения) можно, используя всего одну единственную ячейку Excel. Для этого достаточно включить режим циклических вычислений и ввести в произвольную ячейку с именем, скажем X, рекуррентную формулу, задающую вычисления по Ньютону:
где F и F1 задают соответственно выражения, вычисляющие функцию и производную. Для нашего квадратного уравнения после ввода формулы в ней появится значение 2, соответствующее одному из корней уравнения. А как получить второй корень? Обычно, это можно сделать путем изменения начального приближения. В нашем случае начальное приближение не задавалось, итерационный процесс вычислений начинался со значения, хранимого в ячейке X по умолчанию и равного нулю. Как же задать начальное приближение в циклических вычислениях? Возникшая проблема не связана с данной конкретной задачей. Она возникает всегда в циклических вычислениях, – до начала цикла надо задать начальные установки. В рекуррентных соотношениях всегда есть некоторый начальный отрезок. Решать задачу задания начальных установок в каждом случае можно по-разному. Я продемонстрирую один прием, основанный на использовании функции ЕСЛИ. Вот как выглядит “настоящее” решение этой задачи, использующее 4 ячейки, две из которых нужны по существу дела, а две используются для повышения наглядности процесса вычислений:
- В ячейку с именем Xinit я ввел начальное приближение.
- В ячейку Xcur, в которой и будет идти циклический счет, ввел формулу:
= ЕСЛИ(Xcur =0; Xinit; Xcur - (6- Xcur *(5- Xcur))/(2* Xcur -5))
- В две другие вспомогательные ячейки я поместил текст этой формулы и формулу, задающую вычисление функции в точке Xcur, позволяющую следить за качеством решения.
- Заметьте, что на первом шаге вычислений, функция IF (ЕСЛИ) поместит в ячейку Xcur начальное значение, а затем уже начнет счет по формуле на последующих шагах.
- Чтобы сменить начальное приближение, недостаточно изменить содержимое ячейки Xinit и запустить процесс вычислений. В этом случае вычисления будут продолжены, начиная с последнего вычисленного значения. Чтобы обнулить значение, хранящееся в ячейке Xcur, нужно заново записать туда формулу. Для этого достаточно выбрать ячейку и выделить текст формулы непосредственно в окне ее редактирования. Щелчок по Enter начнет вычисления с новым начальным приближением.
Функции ЧЁТН и НЕЧЁТ
Для выполнения операций округления можно использовать функции ЧЁТН (EVEN) и НЕЧЁТ (ODD). Функция ЧЁТН округляет число вверх до ближайшего четного целого числа. Функция НЕЧЁТ округляет число вверх до ближайшего нечетного целого числа. Отрицательные числа округляются не вверх, а вниз. Функции имеют следующий синтаксис:
=ЧЁТН(число)
=НЕЧЁТ(число)
Функции ОКРВНИЗ, ОКРВВЕРХ
Функции ОКРВНИЗ (FLOOR) и ОКРВВЕРХ (CEILING) тоже можно использовать для выполнения операций округления. Функция ОКРВНИЗ округляет число вниз до ближайшего кратного для заданного множителя, а функция ОКРВВЕРХ округляет число вверх до ближайшего кратного для заданного множителя. Эти функции имеют следующий синтаксис:
=ОКРВНИЗ(число;множитель)
=ОКРВВЕРХ(число;множитель)
Значения число и множитель должны быть числовыми и иметь один и тот же знак. Если они имеют различные знаки, то будет выдана ошибка.
Функции ЦЕЛОЕ и ОТБР
Функция ЦЕЛОЕ (INT) округляет число вниз до ближайшего целого и имеет следующий синтаксис:
=ЦЕЛОЕ(число)
Аргумент – число – это число, для которого надо найти следующее наименьшее целое число.
Рассмотрим формулу:
=ЦЕЛОЕ(10,0001)
Эта формула возвратит значение 10, как и следующая:
=ЦЕЛОЕ(10,999)
Функция ОТБР (TRUNC) отбрасывает все цифры справа от десятичной запятой независимо от знака числа. Необязательный аргумент количество_цифр задает позицию, после которой производится усечение. Функция имеет следующий синтаксис:
=ОТБР(число;количество_цифр)
Если второй аргумент опущен, он принимается равным нулю. Следующая формула возвращает значение 25:
=ОТБР(25,490)
Функции ОКРУГЛ, ЦЕЛОЕ и ОТБР удаляют ненужные десятичные знаки, но работают они различно. Функция ОКРУГЛ округляет вверх или вниз до заданного числа десятичных знаков. Функция ЦЕЛОЕ округляет вниз до ближайшего целого числа, а функция ОТБР отбрасывает десятичные разряды без округления. Основное различие между функциями ЦЕЛОЕ и ОТБР проявляется в обращении с отрицательными значениями. Если вы используете значение -10,900009 в функции ЦЕЛОЕ, результат оказывается равен -11, но при использовании этого же значения в функции ОТБР результат будет равен -10.
Функция ПРОИЗВЕД
Функция ПРОИЗВЕД (PRODUCT) перемножает все числа, задаваемые ее аргументами, и имеет следующий синтаксис:
=ПРОИЗВЕД(число1;число2…)
Эта функция может иметь до 30 аргументов. Excel игнорирует любые пустые ячейки, текстовые и логические значения.
Функция ОСТАТ
Функция ОСТАТ (MOD) возвращает остаток от деления и имеет следующий синтаксис:
=ОСТАТ(число;делитель)
Значение функции ОСТАТ – это остаток, получаемый при делении аргумента число на делитель. Например, следующая функция возвратит значение 1, то есть остаток, получаемый при делении 19 на 14:
=ОСТАТ(19;14)
Если число меньше чем делитель, то значение функции равно аргументу число. Например, следующая функция возвратит число 25:
=ОСТАТ(25;40)
Если число точно делится на делитель, функция возвращает 0. Если делитель равен 0, функция ОСТАТ возвращает ошибочное значение.
Функция КОРЕНЬ
Функция КОРЕНЬ (SQRT) возвращает положительный квадратный корень из числа и имеет следующий синтаксис:
=КОРЕНЬ(число)
Аргумент число должен быть положительным числом. Например, следующая функция возвращает значение 4:
КОРЕНЬ(16)
Если число отрицательное, КОРЕНЬ возвращает ошибочное значение.
Функция ЧИСЛОКОМБ
Функция ЧИСЛОКОМБ (COMBIN) определяет количество возможных комбинаций или групп для заданного числа элементов. Эта функция имеет следующий синтаксис:
=ЧИСЛОКОМБ(число;число_выбранных)
Аргумент число – это общее количество элементов, а число_выбранных – это количество элементов в каждой комбинации. Например, для определения количества команд с 5 игроками, которые могут быть образованы из 10 игроков, используется формула:
=ЧИСЛОКОМБ(10;5)
Результат будет равен 252. Т.е., может быть образовано 252 команды.
Функция ЕЧИСЛО
Функция ЕЧИСЛО (ISNUMBER) определяет, является ли значение числом, и имеет следующий синтаксис:
=ЕЧИСЛО(значение)
Пусть вы хотите узнать, является ли значение в ячейке А1 числом. Следующая формула возвращает значение ИСТИНА, если ячейка А1 содержит число или формулу, возвращающую число; в противном случае она возвращает ЛОЖЬ:
=ЕЧИСЛО(А1)
Формула ЧАСТНОЕ()
Тоже одна из простых операций в математике. В Экселе выполняется тоже несложно: у функции ЧАСТНОЕ() есть два аргумента: делимое и делитель.
В выделенной ячейке выводится частное:

Формула СУММЕСЛИ()
Оператор СУММЕСЛИ() находит сумму чисел. Главное отличие этой функции от СУММ() в том, что здесь в качестве аргумента можно задавать условие (только одно), которое будет показывать, какие значения будут использованы в расчетах, а какие — нет.
В качестве условий могут выступать неравенства со знаками больше, меньше или не равно («>», «<», «< >»). Число, которое не соответствует введенному условию, не будет включен в суммирование.
На рисунке изображено суммирование всех чисел, которые больше 0.
Оранжевым выделены те числа, которые будут включены в расчет функцией СУММЕСЛИ().
Остальные числа просто будут игнорироваться:

Например, нужно посчитать общую стоимость всех проданных фруктов.
Для этого воспользуемся следующей формулой:

Формулы ОКРУГЛ(), ОКРУГЛВВЕРХ(), ОКРУГЛВНИЗ()
Функция ОКРУГЛ() предназначена для округления значения до заданного количества знаков после запятой. В качестве первого аргумента выступают, как обычно, числа или диапазон ячеек, второго – разряд, до которого нужно округлить число.
Например, округление значения до второго знака после запятой:

Если в качестве второго аргумента выступает 0, то число будет округляться до ближайшего целого:

Второй аргумент может быть и отрицательным, тогда округление будет происходить до требуемого знака перед запятой:

Если необходимо округлить в сторону меньшего или большего по модулю числа используют функции ОКРУГЛВНИЗ(), ОКРУГЛВВЕРХ(), соответственно:


Замечание: многие могут решить, что функции округления бесполезны, так как можно просто убрать/добавить дополнительный знак после запятой с помощью кнопок увеличить/уменьшить разрядность.
На самом деле, это не так.
Дело в том, что увеличение или уменьшение разрядности влияет только на «внешний вид» ячейки, то есть на то, как мы число видим.
Само число, при этом, не меняется. Функции округления же полностью меняют вид числа, убирая лишние разряды.
Использование ссылок
При работе с Excel можно применять в работе различные виды ссылок. Начинающим пользователям доступны простейшие из них. Важно научиться использовать все форматы в своей работе.
Существуют:
- простые;
- ссылки на другой лист;
- абсолютные;
- относительные ссылки.
Простые адреса используются чаще всего. Простые ссылки могут быть выражены следующим образом:
- пересечение столбца и строки (А4);
- массив ячеек по столбцу А со строки 5 до 20 (А5:А20);
- диапазон клеток по строке 5 со столбца В до R (В5:R5);
- все ячейки строки (10:10);
- все клетки в диапазоне с 10 по 15 строку (10:15);
- по аналогии обозначаются и столбцы: В:В, В:К;
- все ячейки диапазона с А5 до С4 (А5:С4).
Следующий формат адресов: ссылки на другой лист. Оформляется это следующим образом: Лист2!А4:С6. Подобный адрес вставляется в любую функцию.
ABS
С помощью математической формулы ABS производится расчет числа по модулю. У этого оператора один аргумент – «Число», то есть, ссылка на ячейку, содержащую числовые данные. Диапазон в роли аргумента выступать не может. Синтаксис имеет следующий вид:
=ABS(число)
СТЕПЕНЬ
Из названия понятно, что задачей оператора СТЕПЕНЬ является возведение числа в заданную степень. У данной функции два аргумента: «Число» и «Степень». Первый из них может быть указан в виде ссылки на ячейку, содержащую числовую величину. Второй аргумент указывается степень возведения. Из всего вышесказанного следует, что синтаксис этого оператора имеет следующий вид:
=СТЕПЕНЬ(число;степень)
СЛУЧМЕЖДУ
Довольно специфическая задача у формулы СЛУЧМЕЖДУ. Она состоит в том, чтобы выводить в указанную ячейку любое случайное число, находящееся между двумя заданными числами. Из описания функционала данного оператора понятно, что его аргументами является верхняя и нижняя границы интервала. Синтаксис у него такой:
=СЛУЧМЕЖДУ(Нижн_граница;Верхн_граница)
РИМСКОЕ
Данная функция позволяет преобразовать арабские числа, которыми по умолчанию оперирует Excel, в римские. У этого оператора два аргумента: ссылка на ячейку с преобразуемым числом и форма. Второй аргумент не является обязательным. Синтаксис имеет следующий вид:
=РИМСКОЕ(Число;Форма)
LOG
С помощью этого оператора определяется логарифм числа по заданному основанию. Синтаксис функции представлен в виде:
=LOG(Число;Основание)
Необходимо заполнить два аргумента: Число и Основание логарифма (если его не указать, программа примет значение по умолчанию, равное 10).
Также для десятичного логарифма предусмотрена отдельная функция – LOG10.
Заключение
Таким образом, мы разобрали самые популярные математические функции, которые используются в Excel. Однако возможности программы гораздо шире, и в ее инструментарии можно найти функцию для успешного выполнения практически любой задачи.
Источники
- https://business.tutsplus.com/ru/tutorials/how-to-use-excel-math-formulas–cms-27554
- https://www.intuit.ru/studies/courses/114/114/lecture/3315
- http://on-line-teaching.com/excel/lsn021.html
- https://blog.sf.education/matematicheskie-funkczii-v-excel/
- https://FB.ru/article/445487/matematicheskie-funktsii-v-excel-osobennosti-i-primeryi
- https://lumpics.ru/mathematical-functions-in-excel/
- https://MicroExcel.ru/matematicheskie-funktsii/