Математическая обработка в таблице excel

Чаще всего среди доступных групп функций пользователи Экселя обращаются к математическим. С помощью них можно производить различные арифметические и алгебраические действия. Их часто используют при планировании и научных вычислениях. Узнаем, что представляет собой данная группа операторов в целом, и более подробно остановимся на самых популярных из них.

Применение математических функций

С помощью математических функций можно проводить различные расчеты. Они будут полезны студентам и школьникам, инженерам, ученым, бухгалтерам, планировщикам. В эту группу входят около 80 операторов. Мы же подробно остановимся на десяти самых популярных из них.

Открыть список математических формул можно несколькими путями. Проще всего запустить Мастер функций, нажав на кнопку «Вставить функцию», которая размещена слева от строки формул. При этом нужно предварительно выделить ячейку, куда будет выводиться результат обработки данных. Этот метод хорош тем, что его можно реализовать, находясь в любой вкладке.

Также можно запустить Мастер функций, перейдя во вкладку «Формулы». Там нужно нажать на кнопку «Вставить функцию», расположенную на самом левом краю ленты в блоке инструментов «Библиотека функций».

Существует и третий способ активации Мастера функций. Он осуществляется с помощью нажатия комбинации клавиш на клавиатуре Shift+F3.

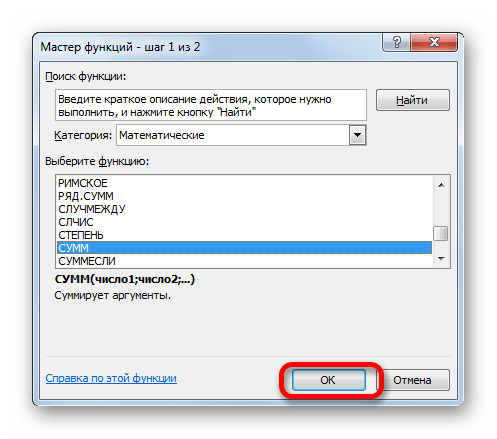
После того, как пользователь произвел любое из вышеуказанных действий, открывается Мастер функций. Кликаем по окну в поле «Категория».

Открывается выпадающий список. Выбираем в нем позицию «Математические».

После этого в окне появляется список всех математических функций в Excel. Чтобы перейти к введению аргументов, выделяем конкретную из них и жмем на кнопку «OK».

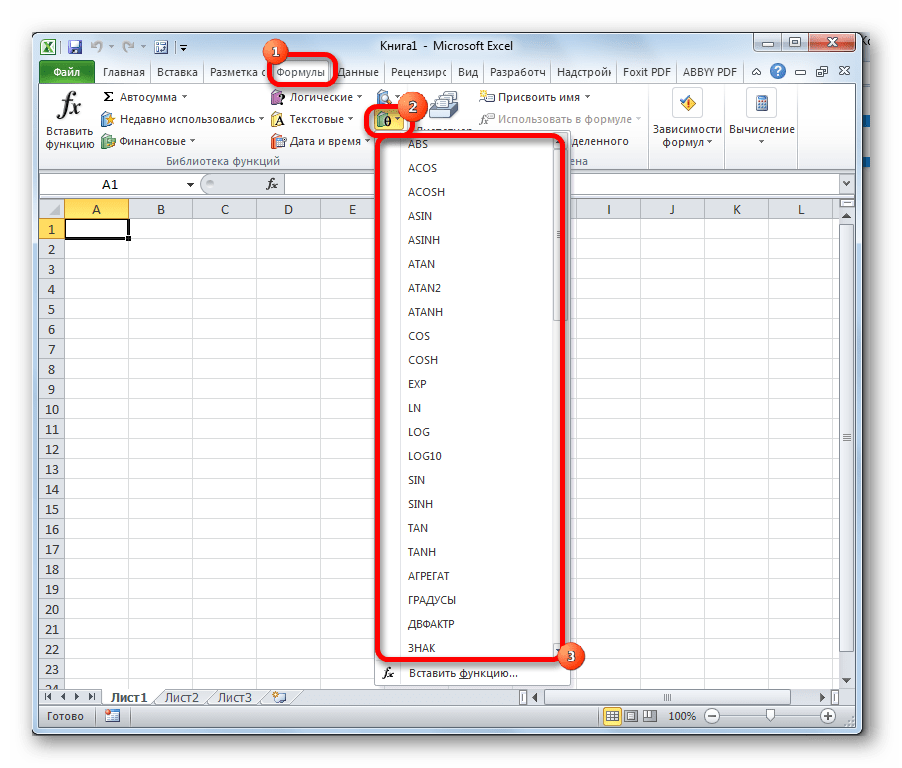
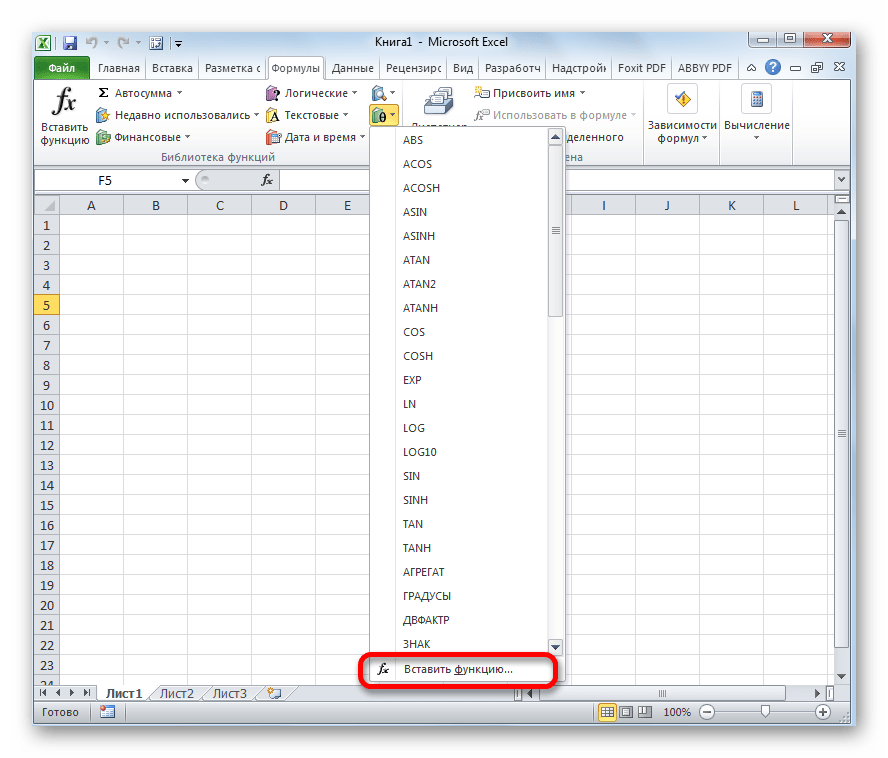
Существует также способ выбора конкретного математического оператора без открытия главного окна Мастера функций. Для этого переходим в уже знакомую для нас вкладку «Формулы» и жмем на кнопку «Математические», расположенную на ленте в группе инструментов «Библиотека функций». Открывается список, из которого нужно выбрать требуемую формулу для решения конкретной задачи, после чего откроется окно её аргументов.

Правда, нужно заметить, что в этом списке представлены не все формулы математической группы, хотя и большинство из них. Если вы не найдете нужного оператора, то следует кликнуть по пункту «Вставить функцию…» в самом низу списка, после чего откроется уже знакомый нам Мастер функций.

Урок: Мастер функций в Excel

СУММ

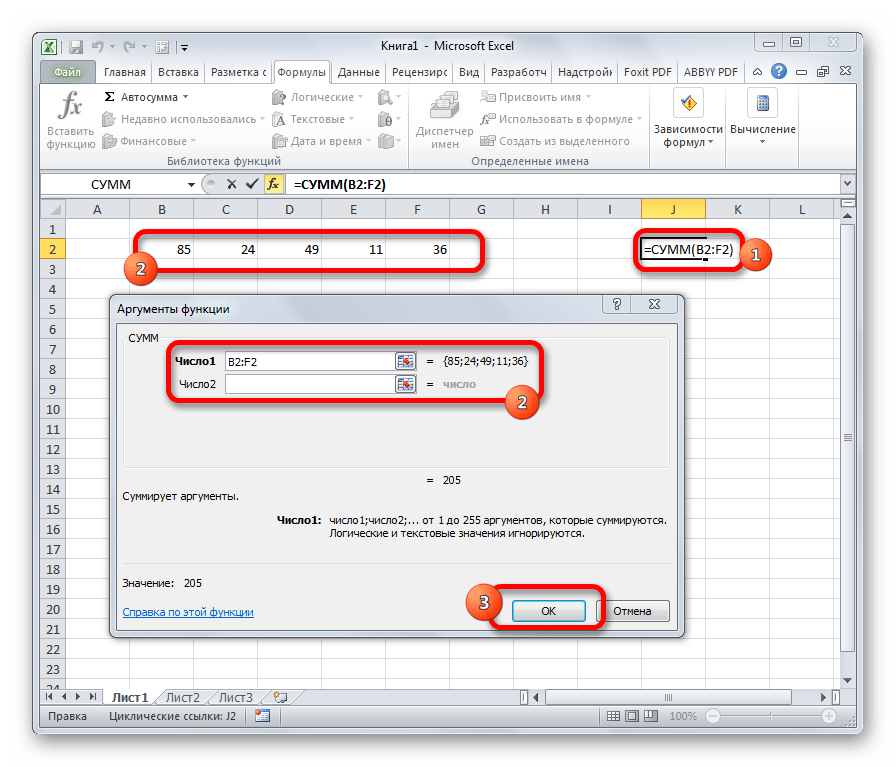
Наиболее часто используется функция СУММ. Этот оператор предназначен для сложения данных в нескольких ячейках. Хотя его можно использовать и для обычного суммирования чисел. Синтаксис, который можно применять при ручном вводе, выглядит следующим образом:

=СУММ(число1;число2;…)

В окне аргументов в поля следует вводить ссылки на ячейки с данными или на диапазоны. Оператор складывает содержимое и выводит общую сумму в отдельную ячейку.

Урок: Как посчитать сумму в Экселе

СУММЕСЛИ

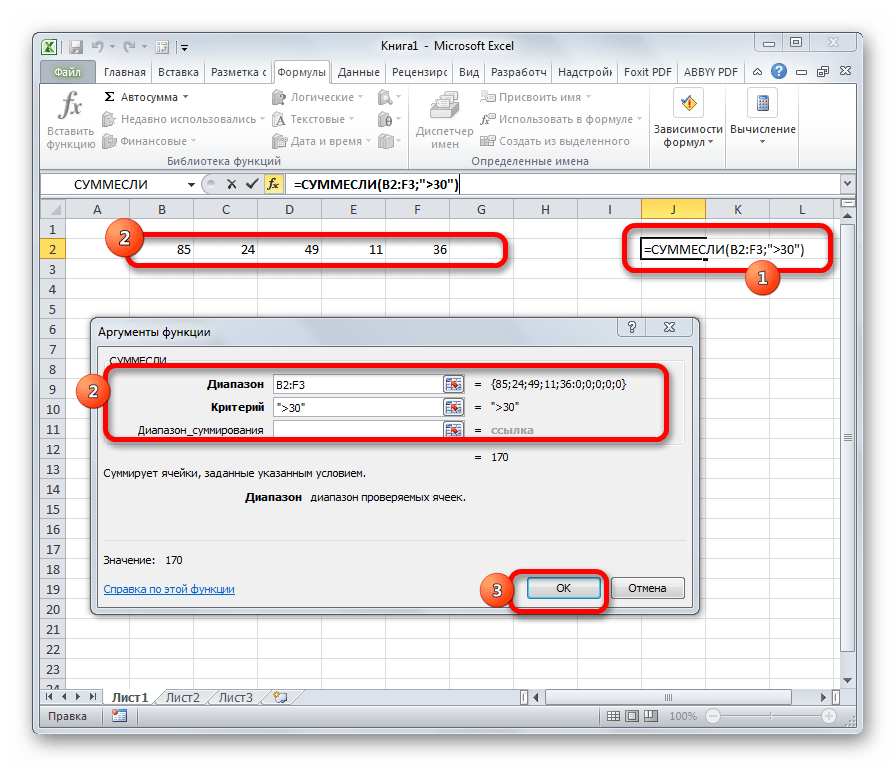
Оператор СУММЕСЛИ также подсчитывает общую сумму чисел в ячейках. Но, в отличие от предыдущей функции, в данном операторе можно задать условие, которое будет определять, какие именно значения участвуют в расчете, а какие нет. При указании условия можно использовать знаки «>» («больше»), «<» («меньше»), «< >» («не равно»). То есть, число, которое не соответствует заданному условию, во втором аргументе при подсчете суммы в расчет не берется. Кроме того, существует дополнительный аргумент «Диапазон суммирования», но он не является обязательным. Данная операция имеет следующий синтаксис:

=СУММЕСЛИ(Диапазон;Критерий;Диапазон_суммирования)

ОКРУГЛ

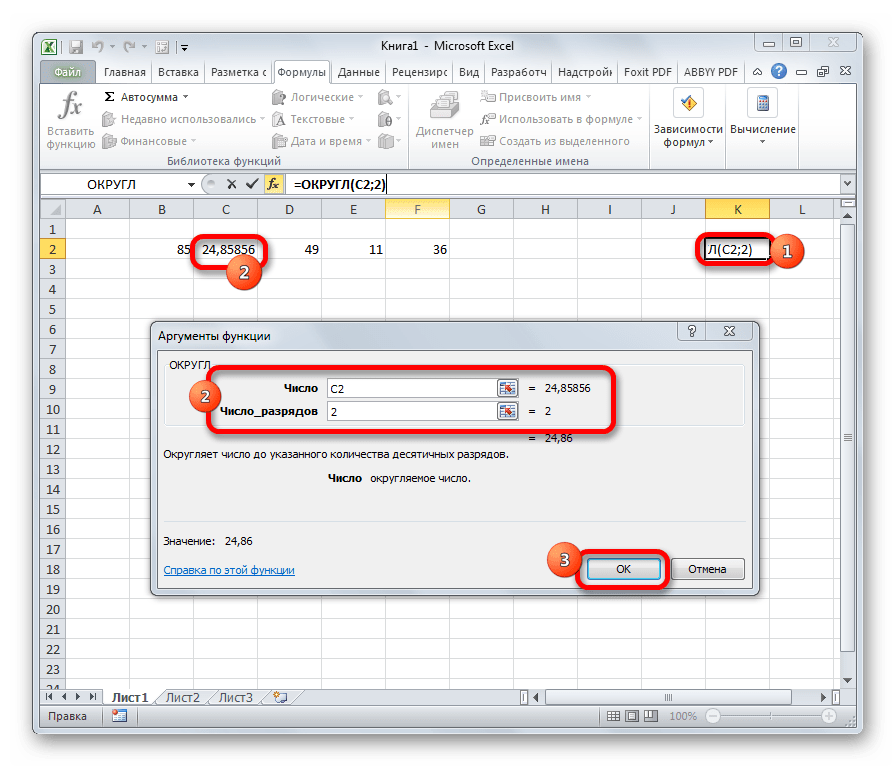
Как можно понять из названия функции ОКРУГЛ, служит она для округления чисел. Первым аргументом данного оператора является число или ссылка на ячейку, в которой содержится числовой элемент. В отличие от большинства других функций, у этой диапазон значением выступать не может. Вторым аргументом является количество десятичных знаков, до которых нужно произвести округление. Округления проводится по общематематическим правилам, то есть, к ближайшему по модулю числу. Синтаксис у этой формулы такой:

=ОКРУГЛ(число;число_разрядов)

Кроме того, в Экселе существуют такие функции, как ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, которые соответственно округляют числа до ближайшего большего и меньшего по модулю.

Урок: Округление чисел в Excel

ПРОИЗВЕД

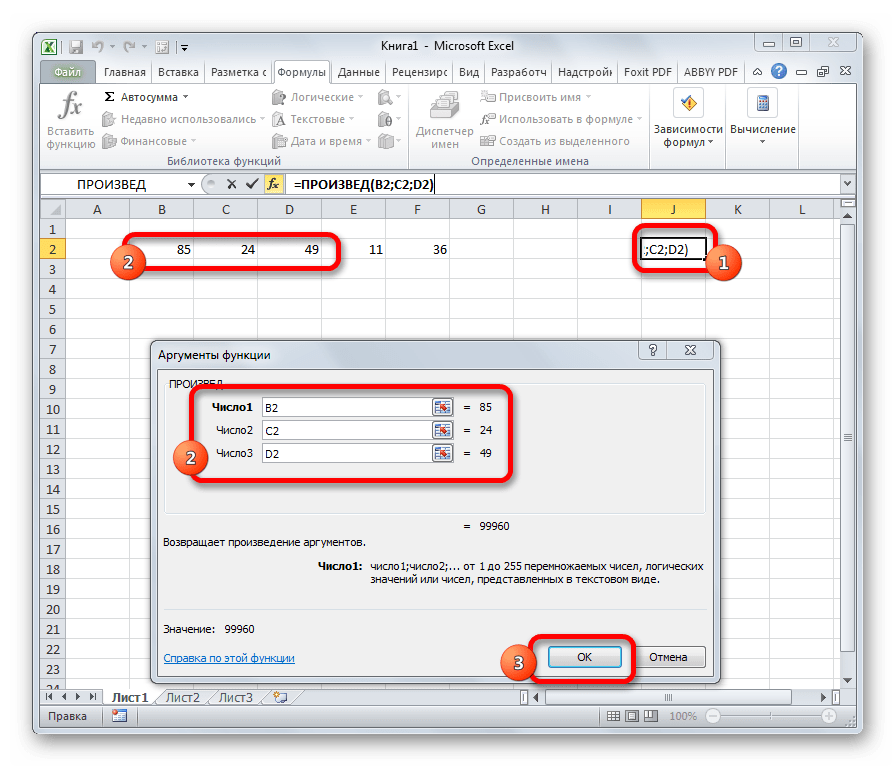
Задачей оператора ПРИЗВЕД является умножение отдельных чисел или тех, которые расположены в ячейках листа. Аргументами этой функции являются ссылки на ячейки, в которых содержатся данные для перемножения. Всего может быть использовано до 255 таких ссылок. Результат умножения выводится в отдельную ячейку. Синтаксис данного оператора выглядит так:

=ПРОИЗВЕД(число;число;…)

Урок: Как правильно умножать в Excel

ABS

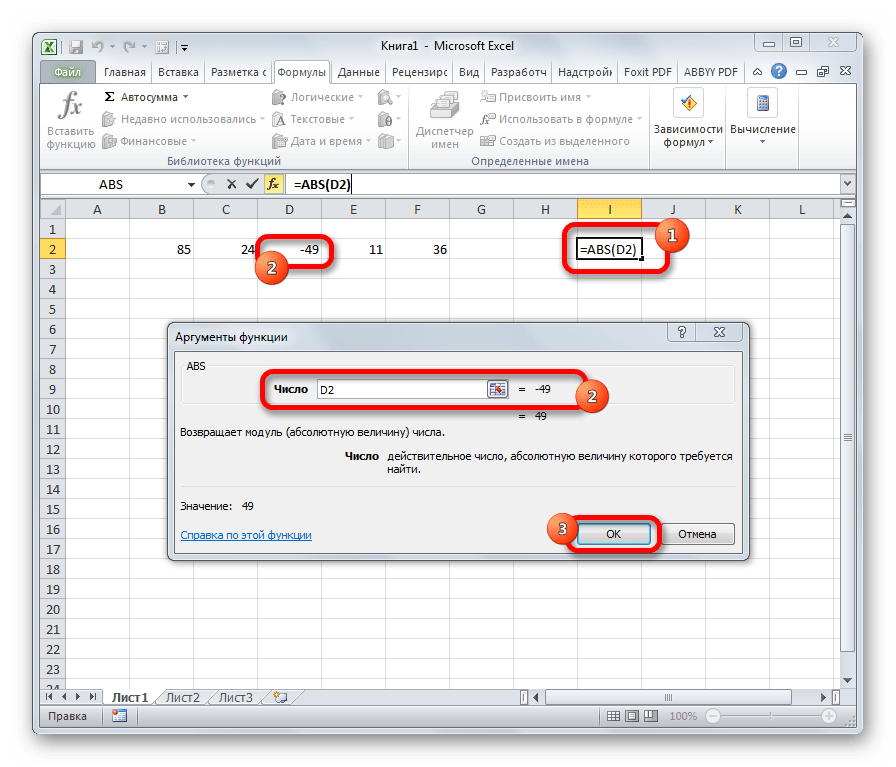
С помощью математической формулы ABS производится расчет числа по модулю. У этого оператора один аргумент – «Число», то есть, ссылка на ячейку, содержащую числовые данные. Диапазон в роли аргумента выступать не может. Синтаксис имеет следующий вид:

=ABS(число)

Урок: Функция модуля в Excel

СТЕПЕНЬ

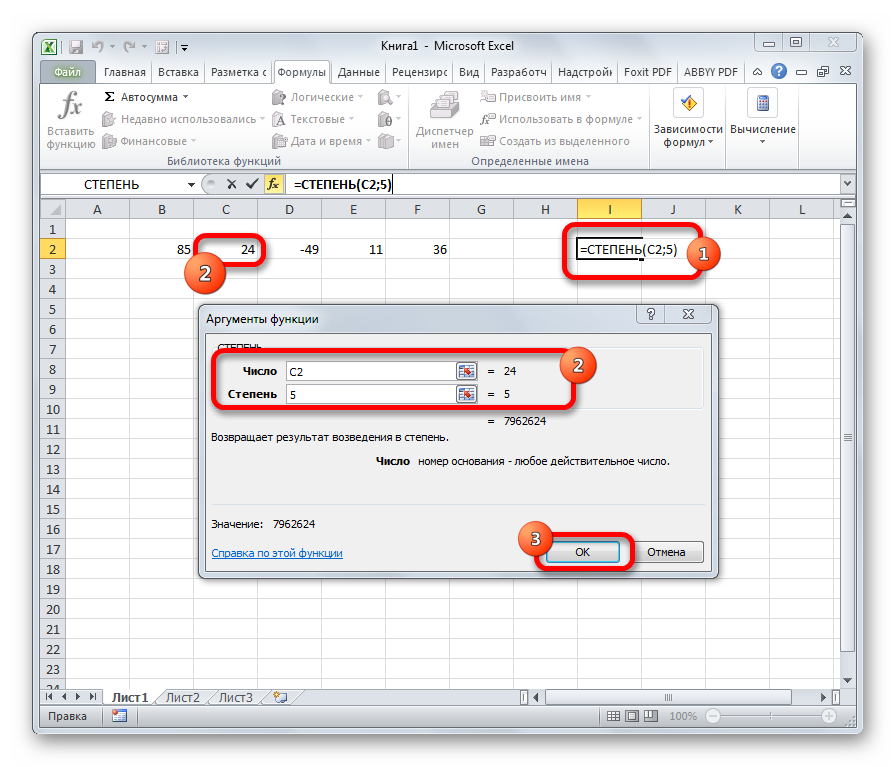
Из названия понятно, что задачей оператора СТЕПЕНЬ является возведение числа в заданную степень. У данной функции два аргумента: «Число» и «Степень». Первый из них может быть указан в виде ссылки на ячейку, содержащую числовую величину. Второй аргумент указывается степень возведения. Из всего вышесказанного следует, что синтаксис этого оператора имеет следующий вид:

=СТЕПЕНЬ(число;степень)

Урок: Как возводить в степень в Экселе

КОРЕНЬ

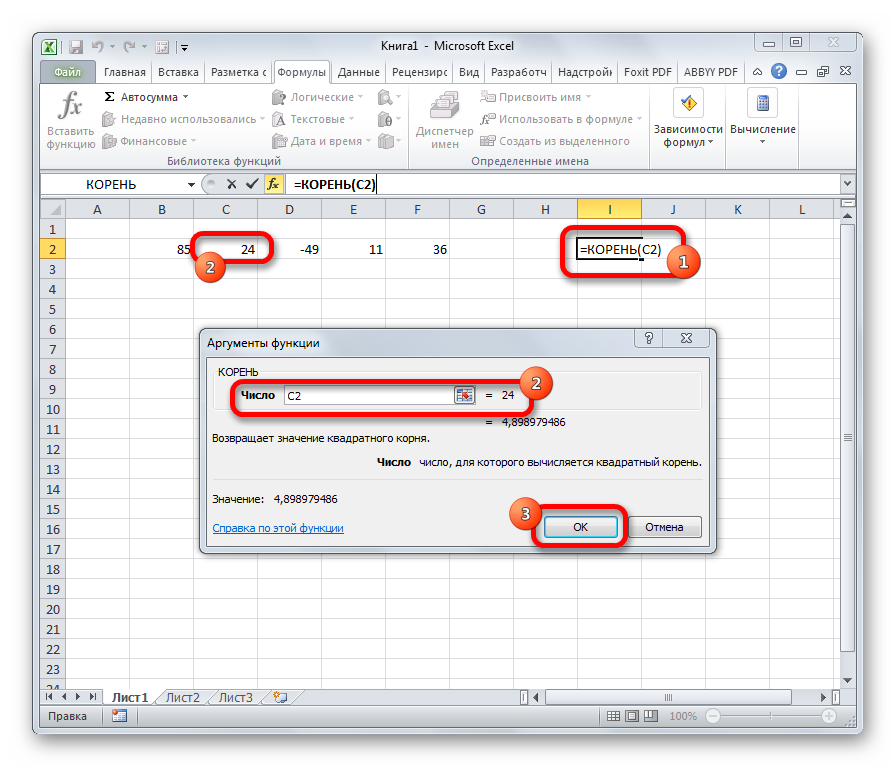
Задачей функции КОРЕНЬ является извлечение квадратного корня. Данный оператор имеет только один аргумент – «Число». В его роли может выступать ссылка на ячейку, содержащую данные. Синтаксис принимает такую форму:

=КОРЕНЬ(число)

Урок: Как посчитать корень в Экселе

СЛУЧМЕЖДУ

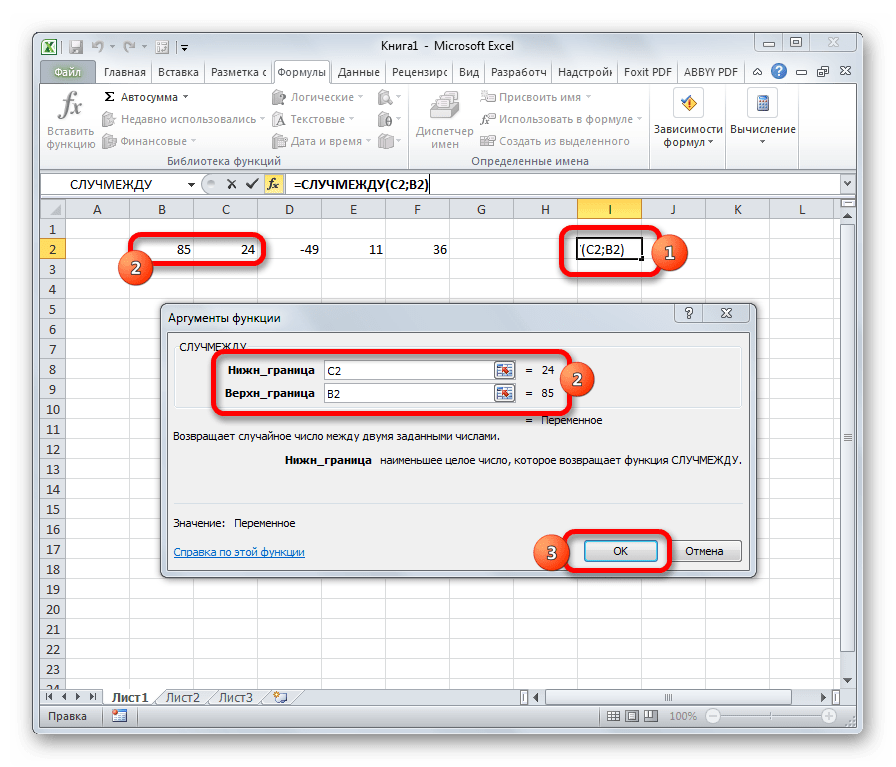
Довольно специфическая задача у формулы СЛУЧМЕЖДУ. Она состоит в том, чтобы выводить в указанную ячейку любое случайное число, находящееся между двумя заданными числами. Из описания функционала данного оператора понятно, что его аргументами является верхняя и нижняя границы интервала. Синтаксис у него такой:

=СЛУЧМЕЖДУ(Нижн_граница;Верхн_граница)

ЧАСТНОЕ

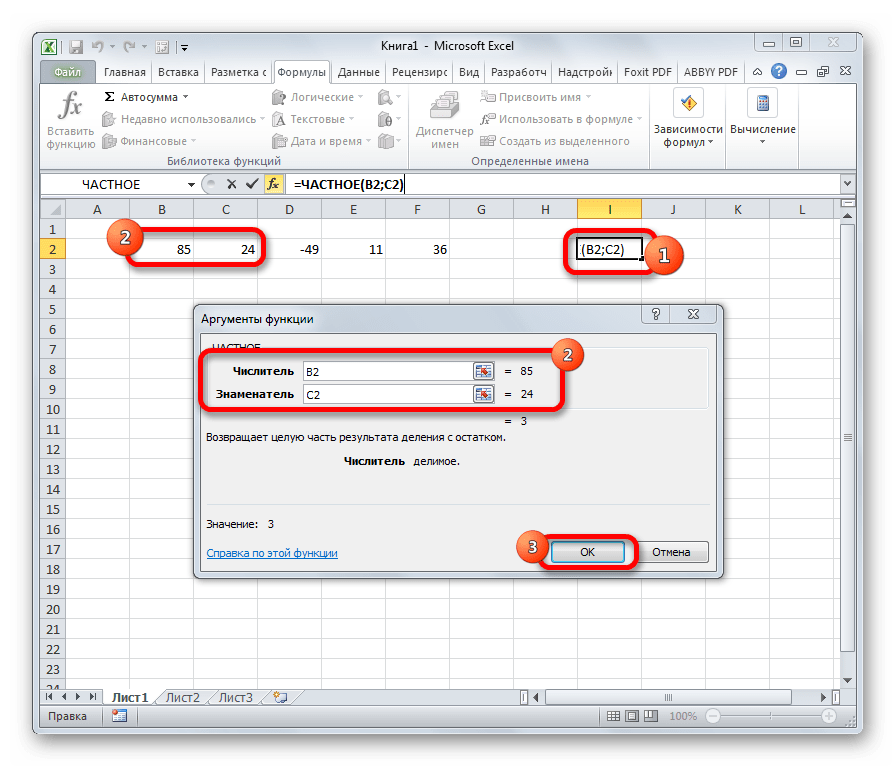
Оператор ЧАСТНОЕ применяется для деления чисел. Но в результатах деления он выводит только четное число, округленное к меньшему по модулю. Аргументами этой формулы являются ссылки на ячейки, содержащие делимое и делитель. Синтаксис следующий:

=ЧАСТНОЕ(Числитель;Знаменатель)

Урок: Формула деления в Экселе

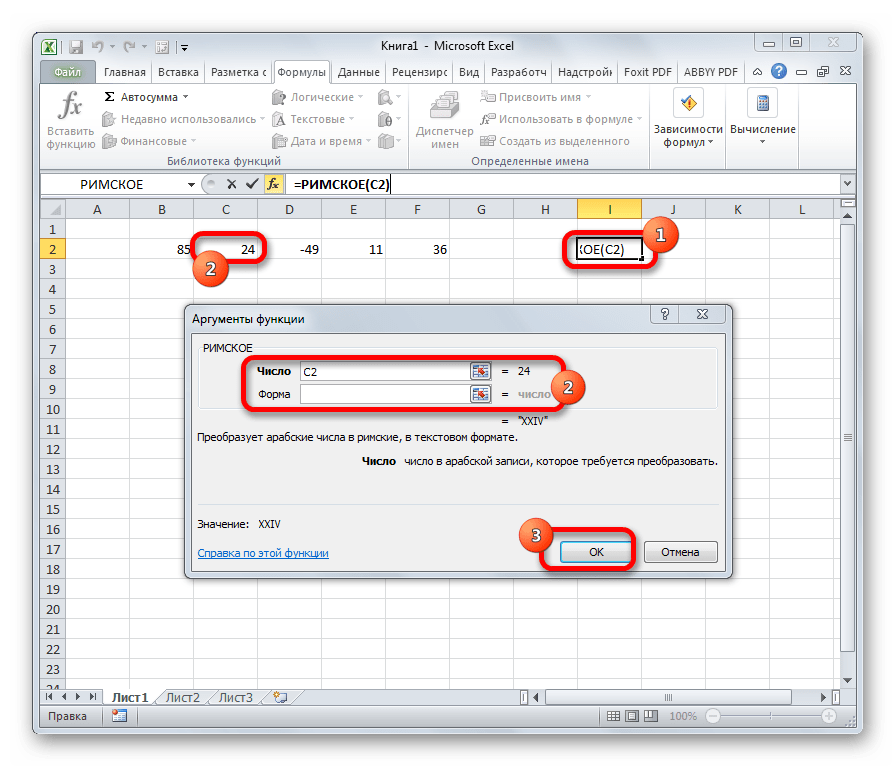
РИМСКОЕ

Данная функция позволяет преобразовать арабские числа, которыми по умолчанию оперирует Excel, в римские. У этого оператора два аргумента: ссылка на ячейку с преобразуемым числом и форма. Второй аргумент не является обязательным. Синтаксис имеет следующий вид:

=РИМСКОЕ(Число;Форма)

Выше были описаны только наиболее популярные математические функции Эксель. Они помогают в значительной мере упростить различные вычисления в данной программе. При помощи этих формул можно выполнять как простейшие арифметические действия, так и более сложные вычисления. Особенно они помогают в тех случаях, когда нужно производить массовые расчеты.

---

Статьи
Карта сайта
Главная страница

 

Ввод текста помогает оформлять заголовки таблиц, записывать
определенные пояснения. Допустим, нам надо рассчитать объем раствора по его
массе 10 г и плотности 1,25 г/мл, используя простейшую формулу V=m/d. Введем
в ячейки В5, С5, D5 заголовки столбцов будущей таблицы,
обозначения величин m, d и V, и приступим к вводу чисел. В
ячейку В6 введем численное значение массы 10. Заканчиваем ввод, нажимая Enter, и убеждаемся, что тест в ячейке, как правило, смещен к правой границе, а число к левой. Это удобно, так как позволяет замечать ошибки
ввода. В ячейку С6 введем дробное число 1,25. Здесь надо учесть, что в
зависимости от настройки конкретного компьютера для разделения целой и дробной
части числа может использоваться или запятая, или точка. При неправильном вводе
наши символы будут восприниматься как текст,  или даже как дата (янв.25).

Наконец, в ячейке D6 введем формулу, по
которой Excel будет проводить вычисления. Ввод формулы начинается со знака
равенства (=). Затем надо показать программе, где находится первое число в
нашей формуле, масса раствора, дать адрес этой ячейки  — В6. Конечно, можно
набрать этот адрес с клавиатуры, надо только учитывать, что В – это символ
английского алфавита. Поэтому, гораздо проще просто щелкнуть по нужной ячейке и
ее адрес будет введен автоматически (=В6). Далее надо ввести знак
арифметического действия. Эти знаки удобно вводить с правой части клавиатуры,
напоминающей клавиатуру калькулятора. Здесь есть клавиши со знаком сложения
(+), вычитания (-), умножения (*) и деления (/). И, наконец, надо показать
компьютеру, где находится делитель – щелкаем мышкой по ячейке С6 и получаем
окончательный вид формулы (=В6/С6). Нажимаем Enter, и,
если все было набрано правильно, получаем в ячейке D6 результат
(8). Таким образом, формулы возвращают в ячейку результат вычислений, число. Но
если щелкнуть по ячейке и посмотреть на строку формул, мы увидим, что на самом
деле находится в ней.

Иногда формула может возвращать и сообщение об ошибке. Щелкнем
по ячейке В6 и введем вместо числа 10 символы «10 г». В ячейке D6
тут же окажется сообщение #ЗНАЧ!, которое говорит о
неверном значении в одной из ячеек. Действительно, запись «10 г» воспринимается
уже как текст. Чтобы исправить ошибку надо снова вместо «10 г»  ввести число
10. (Для исправления неверных действий можно использовать и кнопку «Отменить»
на панели инструментов). Щелкнем теперь по ячейке С6 и нажмем клавишу “Del”. Этим мы удалим содержимое ячейки, и в соседней ячейке
тут же получим сообщение #ДЕЛ/0! (ошибка деления на 0). Действительно,
на ноль делить нельзя и ошибку надо исправить.

Итак, мы научились вводить числа и формулы, а значит и проводить
простейшие вычисления в Excel. Но как упростить эту процедуру, если таких
вычислений много? Здесь помогают приемы копирования, и автоматического
заполнения ячеек методом «протягивания». Пусть у нас 10 порций раствора массой 10 г, и в ячейки В6, В7 …, В16 надо ввести 10, 10, … и т.д. Щелкнем по ячейке В6, где число 10 уже
введено. В черной рамке выделенной ячейки, внизу справа, есть маленький черный
квадратик. При наведении на него указателя мышки, последний меняет форму. Если
в этот момент «взяться» (нажать левую кнопку мыши) и потянуть вниз, до ячейки
В16, то все десять ячеек окажутся автоматически заполнены нужным числом. Не
труднее заполнить и 100 ячеек!

А если массы растворов отличаются на некоторую постоянную
величину, например 10, 12,5, 15 г и т.д.? В этом случае достаточно ввести два
значения: число 10 в ячейку В6 и число 12,5 в ячейку В7. Теперь надо выделить
эти две ячейки. Для этого щелкаем по первой ячейке и, не отпуская кнопки, ведем
до второй. Теперь обе ячейки обведены жирной рамкой. Снова беремся за черный
квадратик и тянем вниз. Получаем ряд значений от 10 до 35.

Поскольку предполагается, что раствор у нас один и тот же,
оставим колонку С в покое и попробуем методом протягивания скопировать формулу,
которая у нас набрана в ячейке D6. Проделываем уже
описанную операцию: выделяем ячейку, беремся, протягиваем… и получаем во всех
ячейках, кроме первой, ошибку! Разберемся, почему это произошло, для чего
щелкнем по ячейке D7 и посмотрим на строку формул. В
ячейке D6 было написано «=В6/С6», а в ячейке D7 уже «=В7/С7»! То есть, при копировании формул Excel
автоматически меняет адреса ячеек, откуда он берет данные для расчетов. И это
совершенно правильно, когда речь идет о массе раствора. Но плотность раствора у
нас постоянная, как показать программе, что адрес этой ячейки менять не надо?

Для этого мы должны познакомиться с такими понятиями, как
относительный и абсолютный адрес. Те адреса, которые мы использовали,
называются относительными и меняются при копировании. Адрес в абсолютной форме
сопровождается знаками доллара и выглядит так: $C$6. Вот
эту поправку нам и надо внести в формулу в ячейке D6.

Исправлять записи в ячейках удобнее в строке формул. Щелкнем
сначала по ячейке D6, (формула появится в строке
формул), затем в нужном месте строки формул – там появится курсор. Конечно
знаки доллара можно ввести с клавиатуры, но проще, установив курсор на адресе
С6, нажать на клавиатуре клавишу F4. Понажимайте ее
несколько раз и посмотрите, как будет меняться адрес. Он может быть полностью
абсолютным, абсолютным по строчке, по колонке, и полностью относительным.
Добейтесь нужного вида и нажмите Enter. Формула
исправлена, теперь ее снова можно протянуть до ячейки D16.
Если все сделано правильно, вы получите ряд значений от 8 до 28 мл.

Итак, если Вы не только прочитали, но и проделали все, о чем шла
речь выше,  Вы научились многому. Вы умеете вводить текст, числа и формулы,
вносить исправления, устранять ошибки, копировать и заполнять ячейки рядами
данных. Не мешает сохранить результаты своей работы. Процедуры сохранения файла
и его открытия полностью совпадают с работой в Worde и не должны вызвать у Вас затруднений.

Формулы с
функциями.

Но в наших расчетах использовались только простейшие
арифметические действия. Для более сложных расчетов нужно научиться
использовать функции. Этим мы займемся на втором листе нашей книги.

Для перехода на нужный лист достаточно щелкнуть по его ярлычку.
Начнем работу с краткого повторения пройденного: дадим листу 2 имя «Ошибки», в
ячейку А3 введем текст «Данные эксперимента», в ячейки А5 и В5 — заголовки
новой таблицы «№» и «Х». Предполагается что мы проделали серию из 10 опытов,
измеряя некоторую величину Х (здесь не важно, что это, длина побега или объем
раствора). Номера опытов от 1 до 10 легко ввести протягиванием, а вот численные
значения Х надо последовательно ввести (табл.1).

Таблица 1. Примерный вид листа
«Ошибки»

Записи в колонках D и
Е – это подсказки, которые помогут разобраться с тем, какие характеристики мы
будем рассчитывать. Колонка F у
Вас должна быть пока пустой, в нее будем помещать наши формулы.

Обработку результатов начнем с расчета числа опытов n. Казалось бы это очевидное число, но в ходе работы, какой-то
результат мы можем отбросить, или провести еще пару опытов. Желательно, чтобы
нам не пришлось при этом переделывать все формулы. Для определения числа
значений используется специальная функция, которая называется СЧЕТ. Для ввода
формулы с функциями используется Мастер функций, который запускается командой
«Вставка функции» через меню «Вставка» – «Функция» или кнопкой на панели
инструментов с обозначением   f_x. Щелкнем мышкой по ячейке F6,
где должен находиться результат и запустим Мастер функций.

Первый шаг работы (рисунок 1) служит
для выбора нужной функции. Все функции разделены, в зависимости от своего
назначения на несколько категорий (математические, логические и др.). Для
обработки данных эксперимента используются в основном статистические функции.
Поэтому, прежде всего в списке категорий выбираем категорию «Статистические».
Во втором окне появляется список статистических функций. Если щелкнуть по любой
из них, внизу появляется краткое описание функции. Специальной ссылкой можно
вызвать систему помощи Excel, в которой данная функция будет разобрана
подробно, с примерами. Список функций упорядочен по алфавиту, что позволяет без
труда нужную нам функцию СЧЕТ («Подсчитывает количество чисел в списке
аргументов»). Выделив щелчком эту функцию, нажимаем кнопку Ok и переходим к шагу 2.

Второй шаг (рисунок 2) служит для задания аргументов функции. 
Функции СЧЕТ надо указать, какие числа ей надо пересчитывать, или в каких
ячейках находятся эти числа. Диапазон ячеек указывается адресами первой и
последней ячейки, записанными через двоеточие, в нашем случае данные находятся
в ячейках В6:В15. Как и в других случаях эти адреса лучше не вводить, а показать
мышкой. Для этого устанавливаем указатель мышки на первую ячейку, нажимаем
левую кнопку и ведем до последней. Обратите внимание, что окно аргументов можно
перемещать, если оно заслоняет нужную часть экрана. Кроме того, рядом с полем
для ввода есть маленькая кнопка с красной стрелочкой. При щелчке по ней окно
аргументов сворачивается до узкой полоски. Когда мы показываем в основном окне
диапазон ячеек, в окне аргументов появляется запись диапазона адресов, а рядом
с ним – значения чисел из первых ячеек. Предварительное значение функции тоже
показывается после ввода ее аргументов. Это помогает избегать ошибок. Помогает
работе с мастером функций и подсказка под полем для ввода аргументов, в которой
разъясняется их смысл и возможные значения. Заканчивается работа с мастером
функций нажатием кнопки “Ok” или клавиши “Enter”. Если все сделано правильно, в ячейке F6 появится нужное значение “10”.

Следующие два этапа обработки серии опытов проводятся
аналогично. В ячейке F7 c
помощью функции СРЗНАЧ рассчитывается
среднее значение выборки, в ячейке F8 – стандартное
отклонение выборки, с помощью функции СТАНДОТКЛОН.
. Будьте аккуратны при выборе функций
– среди них есть очень похожие по названию. Аргументами этих функций служит все
тот же диапазон ячеек.

Следующая формула сложная, частично она набирается как обычная
формула, начиная с символа ”=”. Указав, где находится делимое S и набрав знак операции (=F8/), вызываем
мастер функций. Функция КОРЕНЬ – математическая, поэтому на первом шаге
выбираем категорию математических функций. Аргументом этой функции служит число
опытов, которое мы рассчитали в ячейке F6. Окончательный
вид формулы “=F8/ КОРЕНЬ(F6)”.

Для расчета доверительного интервала необходимо определить
коэффициент Стьюдента. Он зависит от вероятности ошибки (при обычно задаваемой
надежности 95% вероятность ошибки составляет 5%), и от числа степеней свободы n-1). Для нахождения коэффициента Стьюдента используется
статистическая функция Excel СТЬЮДРАСПОБР (“Стьюдента распределение обратное“).
Особенностью этой функции является то, что первый аргумент, число 5% (или 0,05)
вводится в соответствующее окно с клавиатуры. Для второго указываем адрес
ячейки, где находится значение n,
затем дописываем в окне “-1”. Получаем запись “F6-1”.

Для нахождения
доверительного интервала используется обычная формула умножения. Конечно,
вместо букв там должны стоять адреса ячеек, где находятся коэффициент Стьюдента
и стандартное отклонение среднего. Как правило, значение доверительного
интервала округляется до одной значащей цифры, такой же порядок окружения
должен быть и у среднего. Поэтому окончательный результат можно записать так: с
95%-ной надежностью Х = 14,80±0,05. В заключение посчитаем относительную ошибку определения Х: d = ДИ / Х_ср (формула: “=F11/F7”).
Значение относительной ошибки обычно выражают в процентах, у нас 0,3%.

Если Вы впервые
работаете в Excel, описанная процедура обработки данных эксперимента может
показаться очень сложной.  Но на практике, вводить формулы, с помощью мастера
функций, ничуть не сложнее, чем обычные арифметические. К тому же, один раз
подготовив лист Excel для обработки данных, можно скопировать его, и ввести
результаты новой серии опытов в колонку В. Результаты будут тут же рассчитаны
автоматически.

Изучение
зависимостей.

Часто в исследованиях изучается зависимость некоторой величины
от другой. Характер этих зависимостей стремятся выразить математическими
формулами, коэффициенты которой могут иметь определенный физический смысл.
Наиболее употребительна и проста в обработке линейная зависимость, которую
можно выразить уравнением прямой у = kx + b. При этом коэффициент k показывает
степень влияния х на у, а b – некоторое
начальное значение у. Поскольку значения, полученные в ходе эксперимента,
всегда включают некоторую ошибку,  экспериментальные точки не лежат строго на
прямой. Как же провести по этим разбросанным точкам наилучшую линию. Для этого
используется статистический метод «наименьших квадратов» предлагающий
достаточно сложные функции для нахождения коэффициентов k и b, а также для оценки их
достоверности.

В Excel эта
задача решается при помощи статистических функций НАКЛОН (наклон прямой
относительно оси Х, коэффициент k) и ОТРЕЗОК  (отрезок
отсекаемый прямой на оси Y, коэффициент b). Кроме того, Excel позволяет
построить график зависимости, саму прямую, которая называется линией тренда, а
также вывести уравнение прямой на график.

Для знакомства с этим возможностями перейдем на Лист 3 нашей
книги, назовем его «Зависимость» и введем необходимые исходные данные (таблица
2).

Таблица 2. Примерный вид листа
«Зависимость»

В колонках В и С вводятся данные эксперимента по измерению
величин Х и У, записи в колонке Е играют роль подсказок, колонка F заполняется по мере обработки.
Начнем с ячейки F3.

Ввод формул проводится с помощью мастера функций так, как это
описывалось ранее. Маленькое отличие заключается в том, что у функций НАКЛОН и ОТРЕЗОК два
аргумента: диапазон ячеек со значениями Y и диапазон ячеек со значениями Х.
Щелкаем мышкой сначала по полю для ввода первого аргумента, показываем нужный
диапазон (С3:С13). Затем щелкаем по второму поля и повторяем ввод (В3:В13).
Также рассчитывается и значение функции ОТРЕЗОК в ячейке F4.

Для оценки достоверности можно использовать квадрат коэффициента
корреляции Пирсона (R²). Если он равен 1, то
имеет место полная корреляция с моделью, т.е. точки лежат строго на прямой. В
противоположном случае, если коэффициент  равен 0, то уравнение линейной
зависимости полностью неудачно. Для его нахождения используется статистическая
функция КВПИРСОН. Таким образом, данные
нашего эксперимента с достоверностью 0,98 описываются уравнением у = 1,42х+0,905.

Рассмотрим теперь второй метод обработки и представления
результатов эксперимента в виде графика. Для построения графиков и диаграмм в Excel’e используется
Мастер диаграмм, который можно запустить, используя меню Вставка – Диаграмма,
или кнопки на панели инструментов с условным изображением диаграммы.
Предварительно щелкнем мышкой по любой свободной ячейке нашего листа.

Рисунок 3. 

На первом шаге (рисунок 3) выбирается тип и вид диаграммы. Для
построения графика зависимости одной величины от другой используются точечные
диаграммы, причем лучше (из-за разброса точек) выбирать вид «Точки не
соединенные линиями». Заканчиваем выбор, щелкая по кнопке «Далее».

На втором шаге необходимо указать, где у нас находится
независимая величина Х и зависящая от нее Y (рисунок 4).
Для этого щелкаем по ярлычку вкладки «Ряд» и затем по кнопке «Добавить».

Рисунок 4.

Открываются поля для указания Х и Y. Ввод
значений адресов в эти поля не отличаются от работы с Мастером функций (только
при вводе Y предварительно
сотрите условное значение “={1}”. Если Вы правильно выполните эту часть работы,
на поле вверху уже появится примерный вид графика.

Следующие два шага имеют отношение к оформлению и размещению
графика. На первый раз можно, ничего не меняя, просто нажимать кнопки «Далее» и
«Готово». Полученный черновой вариант графика всегда можно редактировать,
изменять или удалять его отдельные элементы. Обычно для этого щелкают по
нужному элементу графика правой (!) кнопкой мышки. При этом открывается
контекстное меню, в котором выбирают подходящую команду.

Если правой кнопкой мышки щелкнуть по одной из точек графика, то
в контекстном меню можно увидеть команду «Добавить линию тренда». Это и есть
необходимая нам линия. Добавляется она тоже в два шага. На первом выбирается
тип (линейный), на втором – параметры. На вкладке Параметры нам важно поставить
галочки против слов: «показывать уравнение» и «поместить величину
достоверности». Если из теоретических предпосылок понятно, что прямая должна
проходить через начало координат (при нулевой концентрации скорость реакции,
очевидно, равна нулю) поставим галочку и в данном пункте. Примерный вид графика
после добавления линии тренда представлен на рисунке 5. Выведенное уравнение
прямой и величины достоверности совпадает с рассчитанными ранее.

Рисунок 5.

Итак, мы рассмотрели важнейшие приемы работы в Microsoft Excel, необходимые для качественной
обработки данных эксперимента. Разумеется эти приемы не исчерпывают всех
возможностей Excel, и могут развиваться в ходе работы.
Автор статьи с удовольствием ответит на все вопросы, связанные с работой в
данной программе. Желаю успеха!

Задать вопрос.

---

КУРС

EXCEL ACADEMY

Научитесь использовать все прикладные инструменты из функционала MS Excel.

Microsoft Excel – одна из самых популярных и легкодоступных программ для представителей разный специальностей. Сегодня мы рассмотрим, пожалуй, одну из самых используемых групп формул – математические формулы.

Начнем с того, как найти их среди прочего функционала. Есть несколько путей того, как открыть список математических формул.

Самый простой способ – нажать на кнопку «Формулы» на панели управления. Затем выбрать из перечня тип функций: «Математические».

Перед вами появится выпадающий длинный список всех существующих операторов:

Всего в Excel около 80 математических и тригонометрических функций. Мы рассмотрим не все, только самые распространенные из них, а также обратим внимание на некоторые нюансы, о которых вы, возможно, не знали. Если в статье вы не нашли нужную вам функцию, то скачивайте наш бесплатный гайд «Математические функции в Excel».

Для разминки вспомним самые простые формулы.

1. Формулы СУММ(), ПРОИЗВЕД()

Эти операции имеют схожую структуру и одинаковый тип аргументов, поэтому мы их объединили в один блок. СУММ() служит для сложения данных в нескольких ячейках, ПРОИЗВЕД() – очевидно, для нахождения произведения.

Аргументами этих функций могут быть числа, диапазоны, ссылки на ячейку, в которой содержится числовое значение. Количество элементов не может быть больше 30.

СУММ() и ПРОИЗВЕД() пропускают пустые ячейки, ячейки текстового формата и логические значения. Операторы вносят результат вычислений в отдельную, ранее выделенную курсором ячейку:

Аналогично для формулы ПРОИЗВЕД():

2. Формула ЧАСТНОЕ()

Тоже одна из простых операций в математике. В Excel выполняется тоже несложно: у функции ЧАСТНОЕ() есть два аргумента: делимое и делитель.

В выделенной ячейке выводится частное:

3. Формула СУММЕСЛИ()

Оператор СУММЕСЛИ() находит сумму чисел. Главное отличие этой функции от СУММ() в том, что здесь в качестве аргумента можно задавать условие (только одно), которое будет показывать, какие значения будут использованы в расчетах, а какие – нет.

В качестве условий могут выступать неравенства со знаками больше, меньше или не равно («>», «<», «< >»). Число, которое не соответствует введенному условию, не будет включен в суммирование.

На рисунке 5 изображено суммирование всех чисел, которые больше 0.

Оранжевым выделены те числа, которые будут включены в расчет функцией СУММЕСЛИ().

Остальные числа просто будут игнорироваться:

Кроме постоянных аргументов, существует еще и дополнительный – «Диапазон суммирования». Он добавляется тогда, когда необходимо просуммировать один диапазон, а условия выбирать по другому диапазону.

Например, нужно посчитать общую стоимость всех проданных фруктов.

Для этого воспользуемся следующей формулой:

То есть сначала пишем диапазон, по которому проверяем условие, затем само ограничение и в конце диапазон чисел, которые надо суммировать. В примере на рисунке 6 выше, соответственно, все строки из категории «Овощи» в расчет включены не будут.

4. Формулы ОКРУГЛ(), ОКРУГЛВВЕРХ(), ОКРУГЛВНИЗ()

Функция ОКРУГЛ() предназначена для округления значения до заданного количества знаков после запятой. В качестве первого аргумента выступают, как обычно, числа или диапазон ячеек, второго – разряд, до которого нужно округлить число.

Например, округление значения до второго знака после запятой:

Если в качестве второго аргумента выступает 0, то число будет округляться до ближайшего целого:

Второй аргумент может быть и отрицательным, тогда округление будет происходить до требуемого знака перед запятой:

Если необходимо округлить в сторону меньшего или большего по модулю числа используют функции ОКРУГЛВНИЗ(), ОКРУГЛВВЕРХ(), соответственно:

Замечание: многие могут решить, что функции округления бесполезны, так как можно просто убрать/добавить дополнительный знак после запятой с помощью кнопок увеличить/уменьшить разрядность.

На самом деле, это не так.

Дело в том, что увеличение или уменьшение разрядности влияет только на «внешний вид» ячейки, то есть на то, как мы число видим.

Само число, при этом, не меняется. Функции округления же полностью меняют вид числа, убирая лишние разряды.

5. Формулы ОТБР(), ЦЕЛОЕ()

Эти функции очень похожи на предыдущие, но работают немного по-другому.

ОТБР() убирает все цифры справа от запятой и у положительных, и у отрицательных чисел. На первом месте в скобках после оператора пишется значение, а на втором – разряд, после которого удалятся все знаки.

Если второй аргумент пропущен, то по умолчанию ставится 0:

ЦЕЛОЕ() – функция, которая выдает в качестве результата наименьшее целое число, стоящее перед аргументом:

На положительные числа операторы влияют почти одинаково, а вот на отрицательные – нет.

Функция ЦЕЛОЕ(-5,6) выдаст результат (-6), а ОТБР(-5,6;0) выдаст (-5), хотя в то же время для числа 5,3 результат обеих функций будет одинаковый – число (5).

6. Формула ABS()

Математическая формула ABS() позволяет получить число по модулю. Как обычно, аргументами оператора является число или ссылка на ячейку.

Эту функцию удобно использовать, например, когда необходимо найти количество дней между датами. Из школьной программы многие знают, что нужно из большего вычитать меньшее.

Но что делать если дана огромная таблица, где трудно определить, где какое значение? Здесь нам помогает оператор ABS(), который переводит отрицательное число в положительное.

7. Формула КОРЕНЬ()

КОРЕНЬ() – довольно легкая функция с одним аргументом (числом или ссылкой на ячейку), которая находит квадратный корень числа:

Замечание. Для извлечения корня другой степени (не квадратного) можно пользоваться функцией СТЕПЕНЬ().

8. Формула СТЕПЕНЬ()

Функция СТЕПЕНЬ() позволяет возвести число в любую степень, в том числе извлечь корень (то есть возвести число в дробную степень).

Например, чтобы извлечь кубический корень из числа 8, необходимо воспользоваться формулой, как на рисунке 17.1.

Помимо математической функции СТЕПЕНЬ(), можно пользоваться оператором “^”, но он выглядит менее опрятно в формулах.

Если вам интересно узнать больше о других математических функциях, напишите об этом ниже в комментариях. Записывайтесь на открытый онлайн-курс «Аналитика в Excel», если хотите научиться выполнять рутинную работу в программе быстрее.

КУРС

EXCEL ACADEMY

Научитесь использовать все прикладные инструменты из функционала MS Excel.

Блог SF Education

Investment Banking

5 примеров экономии времени в Excel

Содержание статьи Что для работодателя главное в сотруднике? Добросовестность, ответственность, профессионализм и, конечно же, умение пользоваться отведенным временем! Предлагаем познакомиться с очень нужными, на…

Как работает сотрудник одной из компаний «большой тройки»?

Ты работаешь в компании «большой тройки (имеются в виду три крупнейших консалтинговых компании: McKinsey, Boston Consulting Group и Bain & Company), в которых мечтают работать тысячи подписчиков наших каналов и читателей vc.ru. Что это значит для тебя?

Тема 4.2.  Математическая обработка числовых данных на примере MS Excel

3. Краткие теоретические сведения.

Представление данных в виде прямоугольных таблиц является удобным и привычным. В виде таблиц можно оформлять деловые документы: счета, накладные, ведомости и прочее. Для работы с табличными данными предназначены современные программы, называемые электронными таблицами. Примером электронных таблиц служат электронные таблицы MS Exсel.

Все данные таблицы размещаются в ячейках. Содержимым ячейки может быть текст, числовое значение или формула.

Вводить данные в электронные таблицы можно с помощью автозаполнения, а также используя другие приемы вставки строк и столбцов или приемы удаления строк, столбцов и ячеек. Текст и числа рассматриваются как константы. Изменить их можно только путем редактирования соответствующих ячеек. Формулы же автоматически пересчитывают свои значения, как только хотя бы один их операнд был изменен.

В Excel операции перемещения и копирования данных осуществляется с помощью Drag-and Drop („перетащить и бросить”) и буфера обмена. Для копирования в Excel используется маркер заполнения – рамка выделения в правом нижнем углу, имеющая утолщение, напоминающее прямоугольник. При помощи него можно скопировать содержимое в соседние ячейки.

Формула — это совокупность операндов, соединенных между собой знаками операций и круглых скобок. Операндом может быть число, текст, логичное значение, адрес ячейки (ссылка на ячейку), функция. В формулах различают арифметические операции и операции отношений.

Excel допускает арифметические операции «+» — сложение, «-» — вычитание, «*» — умножение,»/» — деление, «^» — возведение в степень; операции отношений: «>» — больше, «<» — меньше, «=» — равно, «<=» — меньше или равно, «>=» — больше или равно, «<>» — не равно.

Арифметические операции и операции отношений выполняются над числовыми операндами. Над текстовыми операндами выполняется единственная операция «&», которая к тексту первого операнда присоединяет текст второго операнда. Текстовые константы в формуле ограничиваются двойными кавычками. При вычислении формулы сначала выполняются операции в круглых скобках, потом арифметические операции, за ними операции отношений.

Адрес ячейки включает имя колонки и номер строки. Адреса ячеек (ссылки на ячейки) можно использовать в формулах. Возможны относительные, абсолютные и смешанные ссылки. Ссылка, которая включает имя колонки и номер строки, является относительной. При копировании формулы, а также редактировании листа такая ссылка будет модифицироваться. В абсолютных ссылках перед именем колонки и номером строки стоит символ $. Такие ссылки не модифицируются. В смешанных ссылках абсолютной является название колонки и относительной — номер строки, или наоборот (например, $А1, А$1). В них модифицируется только относительная часть ссылки.

В формуле может быть ссылка на диапазон ячеек. Диапазон может быть только прямоугольным. Указывая диапазон ячеек, задают адрес верхней левой ячейки и через двоеточие — адрес нижней правой ячейки. Если в формуле есть ссылки на ячейки, которые находятся на другом листе, то ссылка должна содержать имя листа, восклицательный знак и адрес ячейки: например, лист! А1.

Функции. Excel содержит более 400 встроенных функций. Функция имеет имя и список аргументов в круглых скобках. Аргументами могут быть числовые и текстовые константы, ячейки, диапазоны ячеек. Некоторые функции доступны только тогда, когда открыта соответствующая надстройка.

Ввести функции в формулу можно вручную или с использованием мастера функций. Для работы с мастером функций надо нажать кнопку Мастер функций панели инструментов Стандартная или выполнить команду Вставка — Функции. При этом открывается диалоговое окно Мастер функций шаг 1 из 2, в котором можно выбрать категорию функций. При выборе категории в поле Функция выводится список функций данной категории. В этом списке можно выбрать нужную функцию. В строке состояния выводится краткое описание функции.

После выбора функции надо нажать кнопку Далее, в результате чего откроется окно диалога Мастер функций шаг 2 из 2, в котором можно указать аргументы функции. В поле Значение выводится значение функции при указанных аргументах. После нажатия кнопки Готово формула вставляется в активную ячейку.

Для наглядного представления данных, входящих в электронные таблицы, служат диаграммы и графики. Они размещаются обычно на рабочем листе и позволяют проводить сравнение данных, находить закономерности. Excel предоставляет широкие возможности в построении различных видов диаграмм (линейчатых, круговых, кольцевых, лепестковых и т.д.).

Для построения диаграмм входят в меню Мастер диаграмм, где выбирается тип диаграммы, ее объемный вариант, диапазон данных и устанавливается название диаграммы и меняется цвет. При необходимости добавляется легенда – прямоугольник, в которой помещаются обозначения и названия рядов данных.

При построении графика функции следует выбрать тип диаграммы – точечный, со значениями, соединенными сглаживающими данными.

В программе Excel разработчиками заложено огромное количество различных функций, но, пользователи чаще всего пользуются математическими. Давайте рассмотрим их и подробнее остановимся на самых популярных.

Использование математических функций в программе

В категорию математических функций входит более 60 различных операторов, которые позволяют выполнять различные вычисления.

Вставить функцию в свободную ячейку таблицы можно по-разному:

1. Жмем кнопку “Вставить функцию” (fx) слева от строки формул. Выполнить данное действие можно, находясь в любой вкладке.
2. Переключаемся во вкладку “Формулы”. Здесь также представлена кнопка “Вставить функцию” – в левом углу ленты инструментов.
3. Нажимаем комбинацию клавиш Shift+F3, чтобы вызвать Мастер функций.

Результатом любого из вышеописанных способов будет открытие окна вставки функции. Здесь мы выбираем категорию “Математические”.

Теперь, когда категория выбрана, в поле ниже отмечаем требуемую функцию и щелкаем OK. 

После этого откроется окно с аргументами для заполнения.

Примечание: Если мы, находясь во вкладке “Формулы”, в группе инструментов “Библиотека функций” нажмем по значку математических функций, сразу откроется список операторов, которые мы можем выбрать, минуя окно вставки функции.

Стоит учитывать, что в предлагаемом перечне присутствуют не все операторы, но самые необходимые здесь все же есть, и в большинстве случаев их достаточно.

Теперь перейдем к детальному рассмотрению самых популярных функций.

СУММ

Пожалуй, это самая популярная функция, которая используется в Эксель. С помощью нее выполняется суммирование числовых данных. Формула функции:

=СУММ(число1;число2;...)

В аргументах можно указать как конкретные числа, так и ссылки на ячейки, содержащие числовые значения. Причем указать координаты можно вручную (с помощью клавиш клавиатуры) или методом клика/выделения непосредственно в самой таблице.

Для перехода к заполнению следующего аргумента достаточно кликнуть по полю напротив него или нажать клавишу Tab.

СУММЕСЛИ

Данная функция позволяет считать сумму чисел с заданным условиями, с помощью которых будет выполняться отбор значений, учитывающихся в суммировании. Формула выглядит следующим образом:

=СУММЕСЛИ(Диапазон;Критерий;Диапазон_суммирования)

В аргументах функции указывается диапазон ячеек (вручную или путем выделения в таблице), значения которых нужно просуммировать. В качестве критерия можно задать следующие условия (в кавычках):

• больше (“>”)
• меньше (“<“)
• не равно (“<>”)

Аргумент “Диапазон_сумирования” заполнять не обязательно.

ПРОИЗВЕД

С помощью данного оператора выполняется умножение чисел. Синтаксис выглядит следующим образом:

=ПРОИЗВЕД(число;число;…)

В аргументах функции, как и в СУММ, можно указывать как конкретные числа, так и адреса ячеек (диапазоны ячеек), которые содержат числовые значения.

ЧАСТНОЕ

Чаще всего для деления используется формула со знаком “/” между делимым и делителем: =Число1/Число2.

Однако в программе также есть отдельная функция для выполнения деления, синтаксис которой представлен ниже:

=ЧАСТНОЕ(Числитель;Знаменатель)

Заполнить нужно два аргумента: Числитель (Делимое) и Знаменатель (Делитель).

СТЕПЕНЬ

Оператор позволяет возвести число в указанную степень. Формула выглядит так:

=СТЕПЕНЬ(число;степень)

В аргументах функции указывается само число, а также, степень, в которую нужно его возвести.

КОРЕНЬ

С помощью данного оператора можно извлечь квадратный корень из числа. Синтаксис выглядит следующим образом:

=КОРЕНЬ(число)

Заполнить требуется только один аргумент – “Число”.

ОКРУГЛ

Функция применяется для выполнения еще одного распространенного математического действия – округления чисел (по общематематическим правилам, т.е., к ближайшему по модулю значению). Синтаксис функции представлен ниже:

=ОКРУГЛ(число;число_разрядов)

В аргументе “Число” указывается значение, которое требуется округлить. В числе разрядов, соответственно, пишем количество цифр, которые хотим оставить после запятой.

Также, в Excel доступны операторы ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, которые, как следует из их названий, используются для округления до ближайшего верхнего и нижнего числа, соответственно (по модулю).

ABS

Позволяет получить модуль числа. Формула функции представлена ниже:

=ABS(число)

Заполнить нужно всего один аргумент – “Число”, модуль которого требуется найти.

LOG

С помощью этого оператора определяется логарифм числа по заданному основанию. Синтаксис функции представлен в виде:

=LOG(Число;Основание)

Необходимо заполнить два аргумента: Число и Основание логарифма (если его не указать, программа примет значение по умолчанию, равное 10).

Также для десятичного логарифма предусмотрена отдельная функция – LOG10.

ОСТАТОК

Применяется для получения остатка от деления чисел. Формула оператора выглядит следующим образом:

=ОСТАТ(чило;делитель)

Для того, чтобы получить результат, требуется заполнить значения двух аргументов: Число и Делитель.

Заключение

Таким образом, мы разобрали самые популярные математические функции, которые используются в Excel. Однако возможности программы гораздо шире, и в ее инструментарии можно найти функцию для успешного выполнения практически любой задачи.