| title | description | author | manager | localization_priority | audience | ms.topic | ms.author | ms.reviewer | ms.custom | search.appverid | appliesto | ms.date | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Floating-point arithmetic may give inaccurate result in Excel |
Discusses that floating-point arithmetic may give inaccurate results in Excel. |
helenclu |
dcscontentpm |
Normal |
ITPro |
troubleshooting |
luche |
clayj |
CSSTroubleshoot |
MET150 |
|
3/31/2022 |
Floating-point arithmetic may give inaccurate results in Excel
Summary
This article discusses how Microsoft Excel stores and calculates floating-point numbers. This may affect the results of some numbers or formulas because of rounding or data truncation.
Overview
Microsoft Excel was designed around the IEEE 754 specification to determine how it stores and calculates floating-point numbers. IEEE is the Institute of Electrical and Electronics Engineers, an international body that, among other things, determines standards for computer software and hardware. The 754 specification is a very widely adopted specification that describes how floating-point numbers should be stored in a binary computer. It is popular because it allows floating-point numbers to be stored in a reasonable amount of space and calculations to occur relatively quickly. The 754 standard is used in the floating-point units and numeric data processors of nearly all of today’s PC-based microprocessors that implement floating-point math, including the Intel, Motorola, Sun, and MIPS processors.
When numbers are stored, a corresponding binary number can represent every number or fractional number. For example, the fraction 1/10 can be represented in a decimal number system as 0.1. However, the same number in binary format becomes the following repeating binary decimal:
0001100110011100110011 (and so on)
This can be infinitely repeated. This number cannot be represented in a finite (limited) amount of space. Therefore, this number is rounded down by approximately -2.8E-17 when it is stored.
However, there are some limitations of the IEEE 754 specification that fall into three general categories:
- Maximum/minimum limitations
- Precision
- Repeating binary numbers
More Information
Maximum/Minimum Limitations
All computers have a maximum and a minimum number that can be handled. Because the number of bits of memory in which the number is stored is finite, it follows that the maximum or minimum number that can be stored is also finite. For Excel, the maximum number that can be stored is 1.79769313486232E+308 and the minimum positive number that can be stored is 2.2250738585072E-308.
Cases in which we adhere to IEEE 754
- Underflow: Underflow occurs when a number is generated that is too small to be represented. In IEEE and Excel, the result is 0 (with the exception that IEEE has a concept of -0, and Excel does not).
- Overflow: Overflow occurs when a number is too large to be represented. Excel uses its own special representation for this case (#NUM!).
Cases in which we do not adhere to IEEE 754
-
Denormalized numbers: A denormalized number is indicated by an exponent of 0. In that case, the entire number is stored in the mantissa and the mantissa has no implicit leading 1. As a result, you lose precision, and the smaller the number, the more precision is lost. Numbers at the small end of this range have only one digit of precision.
Example: A normalized number has an implicit leading 1. For instance, if the mantissa represents 0011001, the normalized number becomes 10011001 because of the implied leading 1. A denormalized number does not have an implicit leading one, so in our example of 0011001, the denormalized number remains the same. In this case, the normalized number has eight significant digits (10011001) while the denormalized number has five significant digits (11001) with leading zeroes being insignificant.
Denormalized numbers are basically a workaround to allow numbers smaller than the normal lower limit to be stored. Microsoft does not implement this optional portion of the specification because denormalized numbers by their very nature have a variable number of significant digits. This can allow significant error to enter into calculations.
-
Positive/Negative Infinities: Infinities occur when you divide by 0. Excel does not support infinities, rather, it gives a #DIV/0! error in these cases.
-
Not-a-Number (NaN): NaN is used to represent invalid operations (such as infinity/infinity, infinity-infinity, or the square root of -1). NaNs allow a program to continue past an invalid operation. Excel instead immediately generates an error such as #NUM! or #DIV/0!.
Precision
A floating-point number is stored in binary in three parts within a 65-bit range: the sign, the exponent, and the mantissa.
| The sign | The exponent | The mantissa |
|---|---|---|
| 1 sign bit | 11 bits exponent | 1 implied bit + 52 bits fraction |
The sign stores the sign of the number (positive or negative), the exponent stores the power of 2 to which the number is raised or lowered (the maximum/minimum power of 2 is +1,023 and -1,022), and the mantissa stores the actual number. The finite storage area for the mantissa limits how close two adjacent floating point numbers can be (that is, the precision).
The mantissa and the exponent are both stored as separate components. As a result, the amount of precision possible may vary depending on the size of the number (the mantissa) being manipulated. In the case of Excel, although Excel can store numbers from 1.79769313486232E308 to 2.2250738585072E-308, it can only do so within 15 digits of precision. This limitation is a direct result of strictly following the IEEE 754 specification and is not a limitation of Excel. This level of precision is found in other spreadsheet programs as well.
Floating-point numbers are represented in the following form, where exponent is the binary exponent:
X = Fraction * 2^(exponent — bias)
Fraction is the normalized fractional part of the number, normalized because the exponent is adjusted so that the leading bit is always a 1. This way, it does not have to be stored, and you get one more bit of precision. This is why there is an implied bit. This is similar to scientific notation, where you manipulate the exponent to have one digit to the left of the decimal point; except in binary, you can always manipulate the exponent so that the first bit is a 1, because there are only 1s and 0s.
Bias is the bias value used to avoid having to store negative exponents. The bias for single-precision numbers is 127 and 1,023 (decimal) for double-precision numbers. Excel stores numbers using double-precision.
Example using very large numbers
Enter the following into a new workbook:
A1: 1.2E+200 B1: 1E+100 C1: =A1+B1
The resulting value in cell C1 would be 1.2E+200, the same value as cell A1. In fact if you compare cells A1 and C1 using the IF function, for example IF(A1=C1), the result will be TRUE. This is caused by the IEEE specification of storing only 15 significant digits of precision. To be able to store the calculation above, Excel would require at least 100 digits of precision.
Example using very small numbers
Enter the following into a new workbook:
A1: 0.000123456789012345 B1: 1 C1: =A1+B1
The resulting value in cell C1 would be 1.00012345678901 instead of 1.000123456789012345. This is caused by the IEEE specification of storing only 15 significant digits of precision. To be able to store the calculation above, Excel would require at least 19 digits of precision.
Correcting precision errors
Excel offers two basic methods to compensate for rounding errors: the ROUND function and the Precision as displayed or
Set precision as displayed workbook option.
Method 1: The ROUND function
Using the previous data, the following example uses the ROUND function to force a number to five digits. This lets you successfully compare the result to another value.
A1: 1.2E+200 B1: 1E+100 C1: =ROUND(A1+B1,5)
This results in 1.2E+200.
D1: =IF(C1=1.2E+200, TRUE, FALSE)
This results in the value TRUE.
Method 2: Precision as displayed
In some cases, you may be able to prevent rounding errors from affecting your work by using the Precision as displayed option. This option forces the value of each number in the worksheet to be the displayed value. To turn on this option, follow these steps.
- On the File menu, click Options, and then click the Advanced category.
- In the When calculating this workbook section, select the workbook that you want, and then select the Set precision as displayed check box.
For example, if you choose a number format that shows two decimal places, and then you turn on the Precision as displayed option, all accuracy beyond two decimal places is lost when you save your workbook. This option affects the active workbook including all worksheets. You cannot undo this option and recover the lost data. We recommend that you save your workbook before you enable this option.
Repeating binary numbers and calculations that have near-zero results
Another confusing problem that affects the storage of floating point numbers in binary format is that some numbers that are finite, non-repeating numbers in decimal base 10, are infinite, repeating numbers in binary. The most common example of this is the value 0.1 and its variations. Although these numbers can be represented perfectly in base 10, the same number in binary format becomes the following repeating binary number when it is stored in the mantissa:
000110011001100110011 (and so on)
The IEEE 754 specification makes no special allowance for any number. It stores what it can in the mantissa and truncates the rest. This results in an error of about -2.8E-17, or 0.000000000000000028 when it is stored.
Even common decimal fractions, such as decimal 0.0001, cannot be represented exactly in binary. (0.0001 is a repeating binary fraction that has a period of 104 bits). This is similar to why the fraction 1/3 cannot be exactly represented in decimal (a repeating 0.33333333333333333333).
For example, consider the following simple example in Microsoft Visual Basic for Applications:
Sub Main() MySum = 0 For I% = 1 To 10000 MySum = MySum + 0.0001 Next I% Debug.Print MySum End Sub
This will PRINT 0.999999999999996 as output. The small error in representing 0.0001 in binary propagates to the sum.
Example: Adding a negative number
-
Enter the following into a new workbook:
A1: =(43.1-43.2)+1
-
Right-click cell A1, and then click Format Cells. On the Number tab, click Scientific under Category. Set the Decimal places to 15.
Instead of displaying 0.9, Excel displays 0.899999999999999. Because (43.1-43.2) is calculated first, -0.1 is stored temporarily and the error from storing -0.1 is introduced into the calculation.
Example when a value reaches zero
-
In Excel 95 or earlier, enter the following into a new workbook:
A1: =1.333+1.225-1.333-1.225
-
Right-click cell A1, and then click Format Cells. On the Number tab, click Scientific under Category. Set the Decimal places to 15.
Instead of displaying 0, Excel 95 displays -2.22044604925031E-16.
Excel 97, however, introduced an optimization that attempts to correct for this problem. Should an addition or subtraction operation result in a value at or very close to zero, Excel 97 and later will compensate for any error introduced as a result of converting an operand to and from binary. The example above when performed in Excel 97 and later correctly displays 0 or 0.000000000000000E+00 in scientific notation.
For more information about floating-point numbers and the IEEE 754 specification, please see the following World Wide Web sites:
- https://www.ieee.org
- https://steve.hollasch.net/cgindex/coding/ieeefloat.html
This is a modification of Confounded’s excellent answer. I modified their function to be use the built-in function Hex rather than bit-wise operations to get the to the bit patterns, made it be able to handle both single and double precision flexibly, and return either the results in either hex (the default) or binary:
Type TDouble
Value As Double
End Type
Type TSingle
Value As Single
End Type
Type DArray
Value(1 To 8) As Byte
End Type
Type SArray
Value(1 To 4) As Byte
End Type
Function DoubleToArray(DPFloat As Double) As Variant
Dim A As TDouble
Dim B As DArray
A.Value = DPFloat
LSet B = A
DoubleToArray = B.Value
End Function
Function SingleToArray(SPFloat As Single) As Variant
Dim A As TSingle
Dim B As SArray
A.Value = SPFloat
LSet B = A
SingleToArray = B.Value
End Function
Function HexToBin(hDigit As String) As String
Select Case hDigit
Case "0": HexToBin = "0000"
Case "1": HexToBin = "0001"
Case "2": HexToBin = "0010"
Case "3": HexToBin = "0011"
Case "4": HexToBin = "0100"
Case "5": HexToBin = "0101"
Case "6": HexToBin = "0110"
Case "7": HexToBin = "0111"
Case "8": HexToBin = "1000"
Case "9": HexToBin = "1001"
Case "A": HexToBin = "1010"
Case "B": HexToBin = "1011"
Case "C": HexToBin = "1100"
Case "D": HexToBin = "1101"
Case "E": HexToBin = "1110"
Case "F": HexToBin = "1111"
End Select
End Function
Function ByteToString(B As Byte, Optional FullBinary As Boolean = False)
Dim BitString As String
BitString = Hex(B)
If Len(BitString) < 2 Then BitString = "0" & BitString
If FullBinary Then
BitString = HexToBin(Mid(BitString, 1, 1)) & HexToBin(Mid(BitString, 2, 1))
End If
ByteToString = BitString
End Function
Function FloatToBits(float As Variant, Optional FullBinary As Boolean = False) As String
Dim ByteArray() As Byte
Dim BitString As String
Dim i As Integer, n As Integer
Dim x As Double, y As Single
If TypeName(float) = "Double" Then
n = 8
x = float
ByteArray = DoubleToArray(x)
ElseIf TypeName(float) = "Single" Then
n = 4
y = float
ByteArray = SingleToArray(y)
Else
FloatToBits = "Error!"
Exit Function
End If
For i = n To 1 Step -1
BitString = BitString & ByteToString(ByteArray(i), FullBinary)
Next i
FloatToBits = BitString
End Function
Here is a test:
Sub test()
Dim x As Single, y As Double
x = Application.WorksheetFunction.Pi()
y = Application.WorksheetFunction.Pi()
Debug.Print FloatToBits(x)
Debug.Print FloatToBits(x, True)
Debug.Print FloatToBits(y)
Debug.Print FloatToBits(y, True)
End Sub
Output:
40490FDB
01000000010010010000111111011011
400921FB54442D18
0100000000001001001000011111101101010100010001000010110100011000
When I feed 400921FB54442D18 into this online tool I get back 3.141592653589793, which makes perfect sense.
Somewhat curiously, when I apply this to 10.4 I get
0100000000100100110011001100110011001100110011001100110011001101
which differs in the final place from the example in this excellent article on floats in Excel VBA. Both versions round to 10.4 (to many, many places). I don’t quite know what to make of the discrepancy.
Пользователи Excel часто озадачены очевидной неспособностью Excel выполнять простые математические операции. Это не ошибка программы: компьютеры по своей природе не обладают бесконечной точностью. Excel хранит числа в двоичном формате, используя 8 байт, которых хватает для обработки числа с 15 цифрами.
Некоторые числа не могут быть выражены именно с помощью 8 байт, поэтому хранятся в виде приближений. Чтобы продемонстрировать, как это ограничение может вызывать проблемы, введите следующую формулу в ячейку А1: =(5,1-5,2)+1.
Результат должен быть равен 0,9. Однако если вы отформатируете ячейку так, чтобы она отображала 15 знаков после запятой, то обнаружите, что программа вычисляет формулу с результатом 0,899999999999999 — значением, очень близким к 0,9, но никак не 0,9. Такой результат получается, поскольку операция в круглых скобках выполняется первой, и этот промежуточный результат сохраняется в двоичном формате с использованием приближения. Затем формула добавляет 1 к этому значению, а погрешность приближения распространяется на конечный результат.
Во многих случаях ошибки такого рода не представляют проблемы. Однако если вам необходимо проверить результат формулы с помощью логического оператора, это может стать головной болью. Например, следующая формула (которая предполагает, что предыдущая формула находится в ячейке А1) возвращает ЛОЖЬ: =A1-0,9.
Одно из решений этого типа ошибки заключается в использовании функции ОКРУГЛ. Следующая формула, например, возвращает ИСТИНА, поскольку сравнение выполняется с использованием значения в А1, округленного до одного знака после запятой: =ОКРУГЛ(А1;1)=0.9. Вот еще один пример проблемы точности. Попробуйте ввести следующую формулу: =(1,333-1,233)-(1,334-1,234). Эта формула должна возвращать 0, по вместо этого возвращает -2,22045Е-16 (число, очень близкое к нулю).
Если бы эта формула была в ячейке А1, то формула вернула бы Not Zero: =ЕСЛИ(А1=0;"Zero";"Not Zero"). Один способ справиться с такой ошибкой округления состоит в использовании формулы вроде этой: =ЕСЛИ(ABS(А1)<0.000001;"Zero";"Not Zero"). В данной формуле используется оператор «меньше чем» для сравнения абсолютного значения числа с очень малым числом. Эта формула будет возвращать Zero.
Другой вариант — указать Excel изменить значения листа в соответствии с их отображаемым форматом. Для этого откройте окно Параметры Excel (выберите Файл ► Параметры) и перейдите в раздел Дополнительно. Установите флажок Задать точность как на экране (который находится в области При пересчете этой книги).
Флажок Задать точность как на экране позволяет изменять числа в ваших листах так, что они постоянно будут соответствовать появлению на экране. Этот флажок применяется для всех листов активной книги. Такой вариант не всегда будет вам подходить. Убедитесь, что вы понимаете последствия установки флажка Задать точность как на экране.
As one of the most versatile calculators ever created, Excel is utilized to power innumerable business operations daily; however, can it ever fail to give you the correct results?
In the case of floating numbers, it can. The term floating point refers to the fact that there are no constant number of digits before or after the decimal point of a number. In other words, the decimal point itself can “float”.
Calculations may not show the correct results when dealing with high precision values. This is not a bug, but rather a design choice that affects every computing system to some degree.
Binary System
The main reason behind this behavior can be broken down to a fundamental design component of computer-based systems. Computer hardware and software communicate with one another using a binary system, consisting of values 1 and 0, as input and output data.
Therefore, the base-10 numerical system is also stored in binary format, which can cause issues with fractions. For example, the fraction of 2/10 is represented as 0.2 in the decimal number system, but identified by an infinitely repeating number 0.00110011001100110011 in the binary system. Data loss becomes inevitable when storing this number in a finite space. The data loss occurs after the 1E-15 point: more commonly known as the 15-digit limit in Excel.
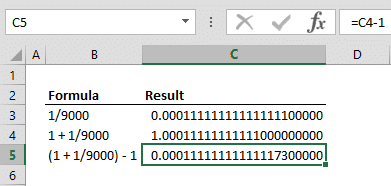
For instance, looking at the example below, you would agree that cells C3 and C5 are equal. However, adding a value of 1 to the value of C3 changes the precision level (i.e. there are eleven 1’s in cell C4, while there are fifteen in cell C3). Ultimately, we get a completely different result in C5, which supposedly contains the inverse function.
Standard
Excel uses a modified version of the IEEE 754-1985 standards. This is a technical standard for floating-point computation, established in 1985 by the Institute of Electrical and Electronics Engineers (IEEE). The 754 revision became very popular and is the most widely used format for floating-point computation by both software libraries and hardware components (i.e. CPUs). According to Microsoft, it is used in all of today’s PC-based microprocessors, including the Intel, Motorola, Sun, and MIPS processors.
Limitations
Maximum / Minimum
Excel only has a finite space to store data. This limitation affects the maximum and minimum numbers allowed by the software. Here are some examples[2]:
| Smallest allowed negative number | -2.2251E-308 |
| Smallest allowed positive number | 2.2251E-308 |
| Largest allowed positive number | 9.99999999999999E+307 |
| Largest allowed negative number | -9.99999999999999E+307 |
| Largest allowed positive number via formula | 1.7976931348623158e+308 |
| Largest allowed negative number via formula | -1.7976931348623158e+308 |
Source: https://support.office.com/en-us/article/excel-specifications-and-limits-1672b34d-7043-467e-8e27-269d656771c3
Excel returns the #NUM! error if a larger number is calculated. This behavior is called an overflow. Excel evaluates very small numbers as 0s, and this behavior is called as underflow. Both will result in data loss.
Excel does not support infinite numbers and provides a #DIV/0! error when a calculation results in an infinite number.
Precision
Although Excel can display more than 15 digits, displayed values are not the actual values that are used in calculations. The IEEE standard upholds storage to only 15 significant digits, which can cause inconsistent results when working with very large or very small numbers.
Very large numbers
In the example below, Excel finds the sum of B8 and B9 to be equal to the value of B8. The 15-digit limit causes Excel to evaluate the calculation with the 15 largest digits. This example would have required Excel to work with 100-digit precision to evaluate accurately.
Very small numbers
If we add the value 1 to 0.000123456789012345 (which has 18 significant digits but contains numeric values in its smallest 15 digits), the result should be 1.000123456789012345. However, Excel gives 1.00012345678901 because it ignores the digits following the 15th significant digit.
Repeating Binary Numbers
Storing repeating binary numbers as non-repeating decimal number can affect the final values in Excel. For example, the formula ‘=(73.1-73.2)+1’ evaluates to 0.899999999999991 when you format the decimal places to 15 digits.
Accuracy within VBA
Unlike Excel calculations, VBA can work with more than a single type of data. Excel uses 8-byte numbers, while VBA offers different data types that vary from 1 byte (Byte) to 16 bytes (Decimal), which can provide precision at the 28-digit level. You can choose a variable type based on your data storage, accuracy, and speed requirements.
Floating point calculations can be relatively challenging due to technical limitations. However, VBA and other mathematical methods offer workarounds to ensure that you don’t miss a decimal if you’re aware of the existing limitations.
|
Maxwell_R Пользователь Сообщений: 16 |
Приветствую! |
|
RAN Пользователь Сообщений: 7091 |
|
|
Maxwell_R Пользователь Сообщений: 16 |
Листы с этого файла у меня автоматически сохраняются в новую книгу. |
|
Казанский Пользователь Сообщений: 8839 |
#4 08.01.2018 21:52:34 Maxwell_R, без цикла по ячейкам
|
||
|
Maxwell_R Пользователь Сообщений: 16 |
Казанский, большое спасибо! Все работает! |
|
Казанский Пользователь Сообщений: 8839 |
#6 09.01.2018 00:44:13 Maxwell_R,
2) Если диапазон фиксирован, просто укажите его в 4 строке (можно с запасом)
иначе придумайте, как найти конец таблицы. |
||||
|
Maxwell_R Пользователь Сообщений: 16 |
#7 09.01.2018 00:59:48 Казанский, очень благодарен! Теперь идеально! |