Максимум прибыли в excel

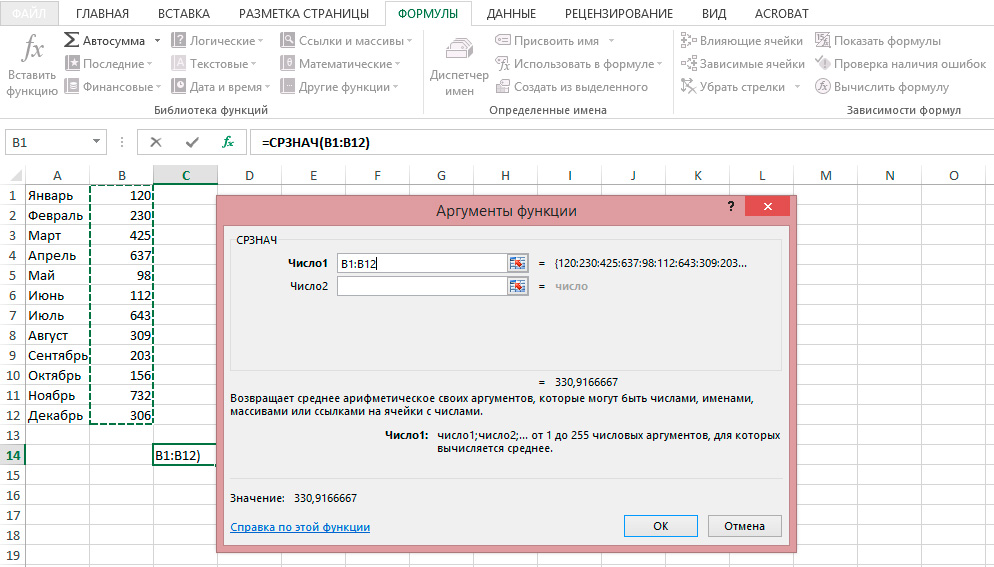
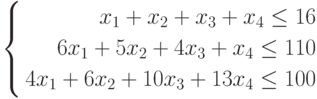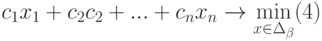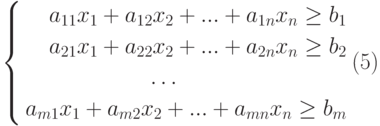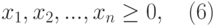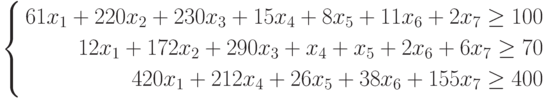Чтобы познакомиться с мощным инструментом Excel Поиск решения, рассмотрим и решим с вами задачу.

Необходимо найти оптимальные объемы выпуска трех видов продукции для получения максимальной прибыли от их продажи.

При решении данной задачи должны быть учтены следующие ограничения:

• общий объем производства – всего 300 изделий;
• должно быть произведено не менее 50 изделий А;
• должно быть произведено не менее 40 изделий В;
• должно быть произведено не более 40 изделий С.

Технология:

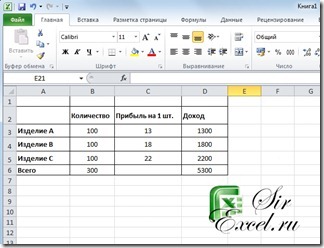
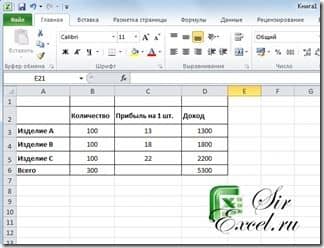
1. Внести в новый рабочий лист данные для вычисления прибыли от продажи трех видов продукции, причем в ячейки столбца D, и в ячейку B6 должны быть введены формулы.

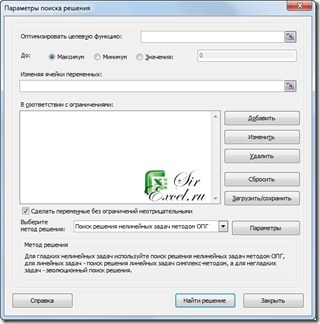
2. Запустить задачу поиска решений. Для этого: выполнить команду в Excel 2003 Сервис | Поиск решений … (В Excel 2007 и 2010 необходимо зайти в раздел Данные | Поиск решения)

и в окне “Поиск решений” ввести данные:

• в поле «Установить целевую ячейку» указать адрес D6;
• установить флажок «Равной максимальному значению»;
• в поле «Изменяя ячейки» определить изменяемые ячейки (B3:B5);
• в поле «Ограничения» по одному добавить каждое из следующих четырех ограничений задачи (B6=300; B3>=50; B4>=40; B5<=40). Для этого щелкнуть по кнопке «Добавить» и в появившемся окне «Добавление ограничения» ввести ссылку на ячейку (B6), оператор ограничения (=) и значение (300), для добавления следующего ограничения щелкнуть кнопку «Добавить» и повторить процедуру добавления ограничения; после ввода последнего ограничения щелкнуть кнопку «ОК».
• в диалоговом окне «Поиск решения» щелкнуть кнопку “Выполнить”;
• в диалоге “Результаты поиска решения” установить переключатель «Сохранить найденное решение», в окне «Тип отчета» выбрать «Результаты» и нажать кнопку “Ok”;

В результате с помощью средства Поиск решения будут найдены оптимальные объемы выпуска продукции для максимизации прибыли.

Скачать пример

Очень надеемся, что наша статья помогла Вам. Будем благодарны, если Вы нажмете +1 и/или Мне нравится внизу данной статьи или поделитесь с друзьями с помощью кнопок расположенных ниже.

Спасибо

Поиск решения в Excel – Получение максимальной прибыли

Чтобы познакомиться с мощным инструментом Excel Поиск решения, рассмотрим и решим с вами задачу.

Необходимо найти оптимальные объемы выпуска трех видов продукции для получения максимальной прибыли от их продажи.

При решении данной задачи должны быть учтены следующие ограничения:

• общий объем производства – всего 300 изделий;
• должно быть произведено не менее 50 изделий А;
• должно быть произведено не менее 40 изделий В;
• должно быть произведено не более 40 изделий С.

1. Внести в новый рабочий лист данные для вычисления прибыли от продажи трех видов продукции, причем в ячейки столбца D, и в ячейку B6 должны быть введены формулы.

2. Запустить задачу поиска решений. Для этого: выполнить команду в Excel 2003 Сервис | Поиск решений … (В Excel 2007 и 2010 необходимо зайти в раздел Данные | Поиск решения)

и в окне “Поиск решений” ввести данные:

• в поле «Установить целевую ячейку» указать адрес D6;
• установить флажок «Равной максимальному значению»;
• в поле «Изменяя ячейки» определить изменяемые ячейки (B3:B5);
• в поле «Ограничения» по одному добавить каждое из следующих четырех ограничений задачи (B6=300; B3>=50; B4>=40; B5 Поделиться:

Источник

Поиск решения в excel – получение максимальной прибыли

Видео: Поиск решения. Задача о выборе инвестиций

Чтобы познакомиться с мощным инструментом Excel Поиск решения, рассмотрим и решим с вами задачу.

Необходимо найти оптимальные объемы выпуска трех видов продукции для получения максимальной прибыли от их продажи.

При решении данной задачи должны быть учтены следующие ограничения:

• общий объем производства – всего 300 изделий;
• должно быть произведено не менее 50 изделий А;
• должно быть произведено не менее 40 изделий В;
• должно быть произведено не более 40 изделий С.

1. Внести в новый рабочий лист данные для вычисления прибыли от продажи трех видов продукции, причем в ячейки столбца D, и в ячейку B6 должны быть введены формулы.
2. Запустить задачу поиска решений. Для этого: выполнить команду в Excel 2003 Сервис | Поиск решений … (В Excel 2007 и 2010 необходимо зайти в раздел Данные | Поиск решения)

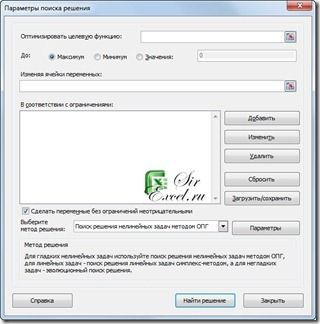
и в окне “Поиск решений” ввести данные:

Видео: Урок 1.Поиск решения, оптимизация, оптимальный план производства

• в поле «Установить целевую ячейку» указать адрес D6;
• установить флажок «Равной максимальному значению»;
• в поле «Изменяя ячейки» определить изменяемые ячейки (B3:B5);
• в поле «Ограничения» по одному добавить каждое из следующих четырех ограничений задачи (B6=300- B3>=50- B4>=40- B5 2018-09-15

Источник

Редактируйте фото онлайн бесплатно в редакторе фотографий

Теперь не нужно искать фотошоп, платить за услуги редактирования. В интернете это можно сделать самому и бесплатно. Онлайн фото-редактор поможет оригинально, качественно обработать необходимую фотографию.

Онлайн – редактор снимков, который объединил в себе наиболее востребованные и удобные функции редактирования.

Редактор не нужно загружать на компьютер или ноутбук. Пользователю достаточно посетить наш сайт и пользоваться программой в онлайн режиме.

Редактор на русском функционирует оперативно, позволяет оперативно редактировать габаритные снимки. Посетитель может выбрать любое фото с любых источников, в том числе из социальных сетей. После редактирования изображений их можно выставить обратно.

Редактор активно пользуются тысячи посетителей. Мы периодически совершенствуем функции редактора, делаем их эффективнее, увлекательнее, не сложнее в пользовании.

Редактор – многофункциональный редактор, где для обработки фотографий онлайн можно выбрать: разнообразные наклейки; текстуру; тексты; ретушь; оригинальные рамки; с эффектами; коллажи и др.

Редактирование фотографий абсолютно бесплатно, также можно бесплатно пользоваться этим фото в будущем.

Желаете без проблем и качественно отредактировать снимок прямо сейчас? онлайн редактор быстро исправит недостатки, и улучшит качество любого фото!

Человеку не подвластно время. Фотоснимок позволяет сохранить самые дорогие минуты нашей жизни в первозданном облике. Снимок улавливает и передает настроение, эмоции, все тонкие жизненные моменты. С iPhotor для рисования такие воспоминания станут более впечатлительными, яркими и незабываемыми!

Фотография – один из видов искусства. Сам процесс фотографирования простой, но он способен зафиксировать сложные моменты – красивое, хрупкое и быстротечное мгновенье. Это непросто передать с помощью обычных рисунков. Какого бы качества не были фото, редактор iPhotor преобразит даже самое обычные, снятые мобильным или простым фотоаппаратом.

Фотография лучше всего способна передать то, о чем вам хотелось рассказать людям. Фоторедактор iPhotor поможет поделиться с близкими впечатлениями, чувствами, отразит ваше вдохновение.

Возможности Редактора онлайн

Изменение размера, поворот, обрезка

Это самые востребованные операции в фото — редакторе, позволяющие вращать на 90 градусов снимок влево, вправо, по вертикали, горизонтали. Обработка делается оперативно и легко. Для обрезки выбираются границы обрезания фото.

Данное меню позволяет регулировать яркость, ретушь лица, коррекцию теней, светлых участков фото и т.п. Здесь также можно изменить оттенок, насыщенность, увеличить резкость картинок. Изменяя настройки каждого инструмента, можно наблюдать за изменениями в режиме онлайн.

Текст, стикеры, рамки

Графический редактор iPhotor позволяет создавать модные картинки, с прикольными стикерами, оригинальными фото рамками, текстовыми подписями.

Фото — эффекты, фото фильтры

С помощью редактора iPhotor можно бесплатно превратить цветное изображение в черно-белое, или наоборот, сделать виньетирование, наложение фото на фото, эффект пикселизации.

Воспользуйтесь уникальными возможностями фото — редактора онлайн прямо сейчас, сделайте вашу жизнь в реальности и на фото ярче!

Онлайн редактор приукрасит самые дорогие моменты вашей жизни!

Источник

Как рассчитать максимальную прибыль в excel

Поиск решения в Excel – Получение максимальной прибыли

Чтобы познакомиться с мощным инструментом Excel Поиск решения, рассмотрим и решим с вами задачу.

Необходимо найти оптимальные объемы выпуска трех видов продукции для получения максимальной прибыли от их продажи.

При решении данной задачи должны быть учтены следующие ограничения:

• общий объем производства – всего 300 изделий;
• должно быть произведено не менее 50 изделий А;
• должно быть произведено не менее 40 изделий В;
• должно быть произведено не более 40 изделий С.

1. Внести в новый рабочий лист данные для вычисления прибыли от продажи трех видов продукции, причем в ячейки столбца D, и в ячейку B6 должны быть введены формулы.

2. Запустить задачу поиска решений. Для этого: выполнить команду в Excel 2003 Сервис | Поиск решений … (В Excel 2007 и 2010 необходимо зайти в раздел Данные | Поиск решения)

и в окне “Поиск решений” ввести данные:

• в поле «Установить целевую ячейку» указать адрес D6;
• установить флажок «Равной максимальному значению»;
• в поле «Изменяя ячейки» определить изменяемые ячейки (B3:B5);
• в поле «Ограничения» по одному добавить каждое из следующих четырех ограничений задачи (B6=300; B3>=50; B4>=40; B5 Поделиться:

Пример функции ДОХОД для анализа доходности инвестиций в Excel

Финансовые показатели облигаций могут быстро рассчитываться в Excel. Для этого используется функция ДОХОД. С ее помощью вычисляется доходность ценных бумаг, по которым периодически выплачиваются проценты (дивиденды).

Как работает функция ДОХОД в Excel?

Облигации – это финансовый инструмент. Предприятие, выпустившее облигации, выступает в роли заемщика. Нуждаясь в привлечении средств, оно выпускает и выбрасывает на рынок такие ценные бумаги. Покупатель облигаций, фактически, является заимодавцем. Ставка купона – это процент, который получает покупатель облигации за то, что предоставил свои средства в пользование.

Как рассчитать доходность облигаций в Excel? Для решения данной задачи используется функция ДОХОД. Как и любая другая функция, ее синтаксис состоит из имени и аргументов. В строке формул сначала ставится знак равенства, после прописывается имя функции, а затем заполняем ее аргументы входящими значениями всех необходимых показателей.

Всего аргументов у сложной функции 7. Из них 6 обязательных для заполнения:

1. Дата_согл. Расчетный день, когда облигация продана. Дата, когда долговые обязательства переданы покупателю. Не стоит путать ее с датой выпуска облигации.
2. Дата_вступл_в_силу. День, когда заем возвращается покупателю. Это срок погашения облигации, когда истекает срок ее действия.
3. Ставка. Годовая ставка процентов по облигации. Процент, который получает покупатель ценных бумаг.
4. Цена. Показатель определяет цену облигации на 100 рублей номинала.
5. Погашение. Стоимость, по которой выкупаются ценные бумаги.
6. Частота. Число выплат по облигации в год. Может быть равна 1, 2 или 4.
7. Базис. Этот аргумент не является обязательным. Поэтому он заключается в квадратные скобки. Он определяет способ вычисления дней.

Существует 5 видов базиса:

• — 0 – Американский 30/360;
• — 1 – факт/факт;
• — 2 – факт/360;
• — 3 – факт/365;
• — 4 – Европейский 30/360.

Аргументы всегда берутся в круглые скобки. Все они перечисляются по порядку. Между ними ставится знак «;».

Синтаксис функции прописывается следующим образом:

=ДОХОД(дата_согл; дата_вступл_в_силу; ставка; цена; погашение; частота; [базис])

Обязательно учитывать то, что все даты в Excel записываются в виде последовательных чисел. Недопустимо использование текстового формата. За 1 принято 1 января 1900 года. Все последующие даты просто прибавляют число прошедших дней. Поэтому все значения рассчитываются с помощью функции «ДАТА».

Результатом применения функции является определение прибыльности облигаций. Программа может выдать не результат, а знак ошибки #ЧИСЛО! Это происходит в нескольких случаях:

• введены даты без использования функции «ДАТА»;
• значение ставки меньше нуля;
• указана цена меньше или равная нулю;
• погашение указано меньше или равно нулю;
• базис меньше нуля или больше четырех.

Примеры использования функции ДОХОД для анализа облигаций

Для вычисления доходности ценных бумаг нужно ввести в первый столбик таблицы все аргументы функции.

Пример 1. Необходимо вычислить доходность облигаций при следующих условиях:

1. Облигации были проданы 15 февраля 2008 года.
2. Срок погашения – 15 ноября 2016.
3. Ставка по купонам определена 5,75%.
4. Цена составляет 95.04 номиналов.
5. Выкупная стоимость — 100 номиналов.
6. Проценты выплачиваются раз в полгода.
7. Значение базиса – 0 (30/360).

Последовательно вводите все значения заполняя таблицу с данными:

В ячейку B9 вводите данные для аргументов функции ДОХОД. Формула будет выглядеть так:

Доходность облигаций составляет 4,26%.

Можно вводить формулу с клавиатуры или указывать соответствующие ячейки мышью. При этом прописать имя функции нужно вручную. Затем откройте скобку и последовательно через «пробел» укажите все ячейки, которые должны быть учтены.

Пример 2. Предприятие продало облигации 14 июля 2015. Установлен небольшой срок их погашения 14 июля 2017. Предлагается ставка 6%. Цена бумаг 97,4 номинальных значений. Стоимость для выкупа – 107 номиналов. Выплата процентов проводится 4 раза в год. Базис 2 – (48/360).

Для вычисления прибыльности облигации введите данные в таблицу по принципу, который стал понятен из примера 1:

В итоговой ячейке B9 приписываем функцию:

Это обозначает, что расчет доходности к погашению облигаций составляет (6,16% х 2года)=12,32%.

Пример 3. Ценные бумаги проданы 2 августа 2004. Погашение произошло 13 мая 2018. Купонная ставка по ним – 5,3%. Цена бумаг – 93 номинала. Стоимость для выкупа – 104 номинала. Проценты начисляются раз в год. Базис – 0 (30/360).

По аналогии составляем таблицу, используя функцию =ДОХОД():

Прибыльность акций оценена в 3,52%.

С помощью программы Excel удалось всего за несколько минут установить, что самыми прибыльными инвестициями являются облигации из второго примера.

Источник

Вычисление минимального, максимального и среднего значения в Microsoft Excel

В Microsoft Office Excel можно работать с цифрами и узнавать любое числовое значение. Этот табличный процессор справится практически со всеми расчётами. Он идеально подходит для бухгалтерского учёта. Для вычислений существуют специальные инструменты — формулы. Их можно применять к диапазону или к отдельным ячейкам. Чтобы узнать минимальную или максимальную цифру в группе клеток, необязательно искать их самостоятельно. Лучше воспользоваться предназначенными для этого опциями. Также полезно будет разобраться, как посчитать среднее значение в Excel.

Это особенно актуально в таблицах с большим объёмом данных. Если в столбце, например, указаны цены на продукцию торгового центра. И вам надо узнать, какой товар самый дешёвый. Если искать его «вручную», уйдёт очень много времени. Но в Экселе это можно сделать буквально за несколько кликов. Утилита также высчитывает среднее арифметическое. Ведь это две простые операции: сложение и деление.

В этой статье мы расскажем, как вычислить различные значения в Эксель

Максимальное и минимальное

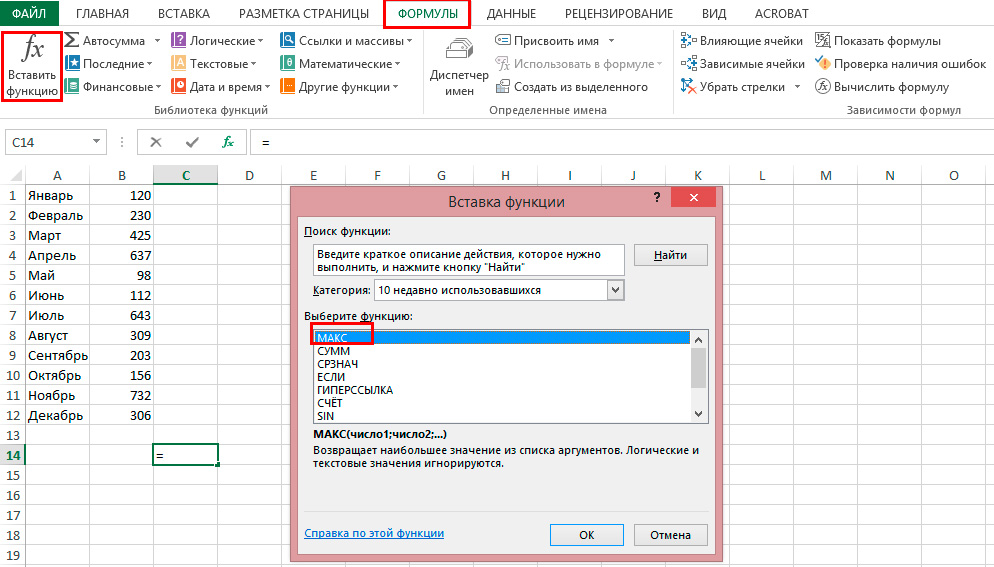
Вот как найти максимальное значение в Excel:

1. Поставьте курсор-ячейку в любое место.
2. Перейдите в меню «Формулы».
3. Нажмите «Вставить функцию».
4. В списке выберите «МАКС». Или напишите это слово в поле «Поиск» и нажмите «Найти».
5. В окне «Аргументы» введите адреса диапазона, максимальное значение которого вам нужно узнать. В Excel имена клеток состоят из буквы и цифры («B1», «F15», «W34»). А название диапазона — это первая и последняя ячейки, которые в него входят.
6. Вместо адреса можно написать несколько чисел. Тогда система покажет самое большее из них.
7. Нажмите «OK». В клетке, в которой стоял курсор, появится результат.

Следующий шаг — укажите диапазон значений

Теперь будет легче разобраться, как найти минимальное значение в Excel. Алгоритм действий полностью идентичен. Просто вместо «МАКС» выберите «МИН».

Среднее

Среднее арифметическое вычисляется так: сложить все цифры из множества и поделить на их количество. В Экселе можно посчитать суммы, узнать, сколько ячеек в строке и так далее. Но это слишком сложно и долго. Придётся использовать много разных функций. Держать в голове информацию. Или даже что-то записывать на листочек. Но можно упростить алгоритм.

Вот как найти среднее значение в Excel:

1. Поставьте ячейку курсор в любое свободное место таблицы.
2. Перейдите на вкладку «Формулы».
3. Нажмите на «Вставить функцию».
4. Выберите «СРЗНАЧ».
5. Если этого пункта нет в списке, откройте его с помощью опции «Найти».
6. В области «Число1» введите адрес диапазона. Или напишите несколько цифр в разных полях «Число2», «Число3».
7. Нажмите «OK». В ячейке появится нужное значение.

Нажмите ОК для подсчета

Так можно проводить расчёты не только с позициями в таблице, но и с произвольными множествами. Excel, по сути, играет роль продвинутого калькулятора.

Другие способы

Максимальное, минимальное и среднее можно узнать и другими способами.

1. Найдите панель функций с обозначением «Fx». Она над основной рабочей областью таблицы.
2. Поставьте курсор в любую ячейку.
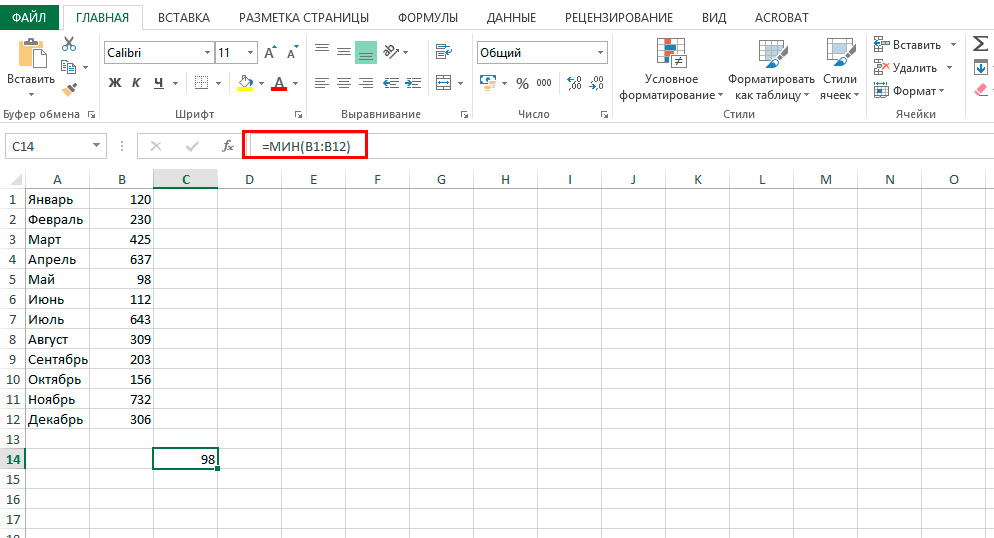
3. Введите в поле «Fx» аргумент. Он начинается со знака равенства. Потом идёт формула и адрес диапазона/клетки.
4. Должно получиться что-то вроде «=МАКС(B8:B11)» (максимальное), «=МИН(F7:V11)» (минимальное), «=СРЗНАЧ(D14:W15)» (среднее).
5. Кликните на «галочку» рядом с полем функций. Или просто нажмите Enter. В выделенной ячейке появится нужное значение.
6. Формулу можно скопировать непосредственно в саму клетку. Эффект будет тот же.

Впишите диапазон и нажмите Enter

Найти и вычислить поможет Excel-инструмент «Автофункции».

1. Поставьте курсор в ячейку.
2. Перейдите в раздел «Формулы».
3. Найдите кнопку, название которой начинается на «Авто». Это зависит от выбранной в Excel опции по умолчанию («Автосумма», «Авточисло», «Автосмещ», «Автоиндекс»).
4. Нажмите на чёрную стрелочку под ней.
5. Выберите «МИН» (минимальное значение), «МАКС» (максимальное) или «СРЗНАЧ» (среднее).
6. В отмеченной клетке появится формула. Кликните на любую другую ячейку — она будет добавлена в функцию. «Растяните» рамку вокруг неё, чтобы охватить диапазон. Или щёлкайте по сетке с зажатой клавишей Ctrl, чтобы выделять по одному элементу.
7. Когда закончите, нажмите Enter. Результат отобразится в клетке.

В Excel вычислить среднее значение достаточно легко. Не нужно складывать, а потом делить сумму. Для этого существует отдельная функция. Также можно найти минимум и максимум в множестве. Это намного легче, чем считать вручную или выискивать цифры в огромной таблице. Поэтому Эксель популярен во многих сферах деятельности, где требуется точность: бизнес, аудит, кадровое делопроизводство, финансы, торговля, математика, физика, астрономия, экономика, наука.

Источник

во втором поле выбрать оператор ограничения (>, Поиск решения).

Найденные решения (значения изменяемых ячеек) можно сохранить в качестве сценария. Для этого нужно:

1. В диалоговом окне Результаты поиска решения выбрать Сохранить сценарий.
2. В поле Название сценария ввести имя сценария. Просмотреть сценарии можно с помощью команды Данные > Работа с данными > Анализ что-если > Диспетчер сценариев > Сценарии.

С помощью программы Поиск решения можно создать три типа отчетов по результатам, полученным при успешном завершении процедуры решения.

Каждый отчет создается на отдельном листе текущей рабочей книги.

Для создания отчета надо в диалоговом окне Результаты поиска решения выбрать нужный тип отчета в поле Тип отчета. Можно выбрать сразу несколько типов (при выделении нескольких строк используется клавиша ).

• Результаты – отчет содержит целевую ячейку, список изменяемых ячеек, их исходные и конечные значения, ограничения и сведения о них.
• Устойчивость – отчет содержит сведения о степени зависимости модели от изменений величин, входящих в формулы, применяемые в задаче (формулы модели и формулы ограничений).
• Пределы – выводится целевая ячейка и ее значение, а также список изменяемых ячеек, их значений, нижних и верхних пределов и целевых результатов.

Рассмотрим применение процессора Excel для решения ЗЛП на примерах.

Задача 1. Планирование производства

Модель линейного программирования дает возможность определить наиболее выгодную производственную программу выпуска нескольких видов продукции при заданных ограничениях на ресурсы.

МП выпускает товары х₁,х₂,х₃,х₄, получая от реализации каждого прибыль в 60,70,120,130 руб. соответственно. Затраты на производство приведены в таблице.

Затраты	х1	х2	x3	х4	Всего
Трудовые	1	1	1	1	16
Сырьевые	6	5	4	1	110
Финансы	4	6	10	13	100

1. Максимум прибыли в зависимости от оптимального распределения затрат.
2. Минимум ресурсов, необходимых для получения максимальной прибыли.

Решение задачи средствами Excel состоит из 4 этапов:

1. Создание математической модели задачи ЛП.
2. Создание формы для ввода условий задачи, ввод в неё исходных данных и зависимостей из математической модели.
3. Ввод данных из формы в окно Excel Поиск решения из меню Данные.
4. Задание параметров поиска и решение задачи.

Создание математической модели задачи

Составим математическую модель процесса по описанию задачи:

— целевая функция прибыли.

— граничные условия модели, так как количество производимых товаров не может быть отрицательной величиной.

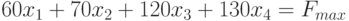
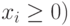
Для решения данной задачи c помощью программы MS Excel создадим новую книгу с именем Линейное программирование и изменим имя ее первого рабочего листа на Задача о производстве.

Создание формы

• Составление формы в виде:

A	B	C	D	E	F	G	H
1	Переменная	х7	х2	x3	х4	Формула	Знак	Св.член
2	Значение
3	Коэф. ЦФ	60	70	120	130	=СУММПРОИЗВ(В$2:Е$2;В3:Е3)	Max
4	Трудовые	1	1	1	1	=СУММПРОИЗВ(В$2:Е$2;В4:Е4)		16
5	Сырьевые	6	5	4	1	=СУММПРОИЗВ(В$2:Е$2;В5:Е5)		110
6	Финансы	4	6	10	13	=СУММПРОИЗВ(В$2:Е$2;В6:Е6)		100

• Запись в ячейки В3:Е3 коэффициентов целевой функции F (1), в В4:Е6 коэффициентов из системы ограничений (2) и в ячейки Н4:Н6 – свободных членов из системы (2).
• Ввод формул с помощью f_x – Мастера функций.

Для ввода формулы в целевую ячейку (целевой функции): щелкнуть левой клавишей мыши по ячейке F3 , затем по значку Мастера функций f_x на панели инструментов, в появившемся окне «Мастер функций, Шаг 1» выбрать категорию «Математические», далее выбрать функцию СУММПРОИЗВ, нажать клавишу ОК, в окне «Мастер функций Шаг 2» в поле Массив 1 ввести с клавиатуры В2:Е2 (ячейки, в которых будут варьироваться х₁..х₄), в поле Массив 2 ввести В3:Е3 (коэффициенты целевой функции ЦФ).

Примечание. Можно вводить В2:Е2 не с клавиатуры, а поставить курсор в окно Массив 1, а затем протащить курсор при нажатой левой клавише мыши по ячейкам В2:Е2, имена ячеек сами запишутся в окно. Аналогично поступить с полем Массив 2.

Нажать клавишу ОК, в ячейку F3 запишется формула 60х₁+70х₂+120х₃+ 130х₄ в виде СУММПРОИЗВ(В2:Е2;В3:Е3).

Чтобы не вводить формулы в другие ячейки, необходимо изменить тип адресации для ячеек В2:Е2 с относительной на абсолютную $B$2:$E$2 , установив курсор перед нужным адресом B2 и нажав функциональную клавишу F4 , затем повторить эти действия для адреса E2 . Формула примет следующий вид:

После внесенных изменений необходимо скопировать формулу в ячейки F4:F6 c помощью маркера заполнения. Для этого необходимо выделить ячейку F3 , содержащую нужную формулу, установить указатель мыши на черный квадратик в правом нижнем углу ячейки (он примет форму черного крестика) и протащить с помощью левой кнопки мыши на весь требуемый диапазон.

В результате копирования мы увидим следующие формулы:

• в ячейке F4 – СУММПРОИЗВ($В$2:$Е$2;В4:Е4),
• в ячейке F5 – СУММПРОИЗВ($В$2:$Е$2;В5:Е5),
• в ячейке F6 – СУММПРОИЗВ($В$2:$Е$2;В6:Е6).

Заполнение окна Поиск решения

Выбрать в пункте меню Данные команду Поиск решения, поставить курсор в поле целевой функции, выделить ячейку F3 в форме (или ввести F3 с клавиатуры), поставить переключатель в положение «Максимальному значению» (см. рис. 12.1 рис. 12.1). В поле «Изменяя ячейки» ввести $В$2:$Е$2(с клавиатуры или протащив мышью).

Нажать клавишу «Добавить», в окне «Добавление ограничения» в поле «Ссылка на ячейку» ввести F4 , выбрать через «стрелка вниз» знак ««, в поле справа ввести Н4 (рис. 12. рис. 12.2).

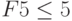
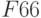
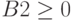
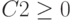
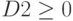
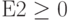
Аналогично через «Добавить» ввести , для системы ограничений (2), а также , , и .

Также необходимо добавить ограничения для получения целочисленных величин по количеству товаров: B2=цел, C2=цел, D2=цел и Е2=цел.

После ввода последнего граничного условия вместо «Добавить» нажать клавишу ОК, появится окно «Поиск решения».

Для изменения или удаления ограничений и граничных условий используются клавиши Изменить, Удалить.

Параметры поиска

В окне «Поиск решения» нажать клавишу «Параметры», выбрать по умолчанию Максимальное время – 100 с, число итераций – 100 (для большинства задач это количество просчётов подходит с большим запасом), установить флажок в строке «Линейная модель», нажать ОК, в появившемся окне Поиск Решения нажать Выполнить (рис. 12. рис. 12.3).

Результаты поиска решения с таблицей результатов:

A	B	C	D	E	F	G	H
1	Переменная	X1	X2	X3	X4	Формула	Знак	Св.член
2	Значение	10	0	6	0
3	Коэф. ЦФ	60	70	120	130	1320	Max
4	Трудовые	1	1	1	1	16		16
5	Сырьевые	6	5	4	1	84		110
6	Финансы	4	6	10	13	100		100

Таким образом оптимальный план Х(Х₁,Х₂,Х₃,Х₄)=(10,0,6,0) при минимальном использовании ресурсов

• Трудовые – 16 (У₁)
• Сырьевые – 84 (У₂)
• Финансы – 100 (У₃)

даёт максимум прибыли F в 1320 руб.

_Вывод: Максимальная прибыль F в 1320 руб. получается при выпуске только товаров Х₁ и Х₃ в количестве 10 и 6 штук соответственно, товары Х₃ и Х₄ выпускать не нужно (это приведёт к снижению прибыли). Трудовые (У₁) и финансовые (У₃) ресурсы используются полностью, по сырьевым ресурсам (У₂) есть запас в 110-84=26 ед.

Кроме того, это означает, что изменение трудовых ( y₁ ) и финансовых ( y₃ ) ресурсов приведёт к изменению прибыли F , а изменение сырьевых ресурсов ( y₂ ) – нет.

Разности между плановыми ресурсами и использованными являются двойственными переменными y₁, y₂ и y₃ сопряжённой задачи линейного программирования. В данном случае y₁=y₃=0 , а y₂=26 ед. Таким образом, ресурс y₂ можно уменьшить на 26 ед., тогда план по сырью тоже будет оптимальным.

Задача 2. Задача об оптимальной диете

Имеется n видов продуктов питания, в которых содержится m типов питательных веществ (белки, жиры, углеводы). В одной весовой единице продукта i-го типа содержится а_i единиц питательного вещества j-го вида . Известна минимальная суточная потребность b _j (j in <1,2. т>) человека в каждом из видов питательных веществ. Задана калорийность с_i одной весовой единицы i-го продукта ( i принадлежит <1, 2, . n>).

Требуется определить оптимальный состав рациона продуктов, такой, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.

Ведем в рассмотрение следующие переменные: х – весовое количество продукта питания i-го типа в суточном рационе.

Тогда в общем случае математическая постановка задачи об оптимальной диете может быть сформулирована следующим образом:

где множество допустимых альтернатив 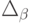формируется следующей системой ограничений типа неравенств:

Для решения задачи об оптимальной диете с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи.

Для определенности предположим, что в качестве исходных типов продуктов рассматриваются: хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3).

Калорийность одной весовой единицы каждого из продуктов следующая:с₁ = 2060,с₂= 2430,с₃= 3600,с₄= 890,с₅= 140,с₆= 230, с₇ = 650. Содержание питательных веществ в каждом из продуктов может быть задано в форме нижеприведенной таблицы.

Минимальная суточная потребность в питательных веществах следующая: в белках b ₁ = 100, в жирах b ₂= 70, в углеводах b3 = 400.

Для решения данной задачи c помощью программы MS Excel создадим новую книгу с именем Линейное программирование и изменим имя ее второго рабочего листа на Задача о диете.

Таблица 1. Содержание питательных веществ в продуктах питания

Продукты/питательные вещества	Хлеб ржаной	Мясо баранина	Сыр «Российский»	Банан	Огурцы	Помидоры	Виноград
Белки	61	220	230	15	8	11	6
Жиры	12	172	290	1	1	2	2
Углеводы	420	0	0	212	26	38	155

Создание математической модели задачи

Составим математическую модель процесса по описанию задачи:

– целевая функция (суммарная калорийность продуктов).

– граничные условия

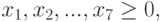
Создание формы

Для решения поставленной задачи выполним следующие подготовительные действия:

1. Внесем необходимые надписи в ячейки A1:I1, A2:A7, B4, I4, J4 .
2. В ячейки ВЗ:НЗ введем значения коэффициентов целевой функции: с₁ = 2060, с₂ = 2430, с₃ = 3600, с₄ = 890, с₅ = 140, с₆ = 230, с₇ = 650.
3. В ячейку I2 введем формулу: =СУММПРОИЗВ( b ₂:Н2;B3:H3), которая представляет целевую функцию (4).
4. В ячейки В5:Н7 введем значения коэффициентов ограничений, взятых из таблицы.

1. В ячейки J5 :J7 введем значения правых частей ограничений, соответствующих минимальной суточной потребности в питательных веществах: в белках b ₁=100 , жирах b ₂= 70 и углеводах b3 = 400.
2. В ячейку I5 введем формулу: =СУММПРОИЗВ($B$2:$H$2;В5:Н5), которая представляет левую часть первого ограничения (5).
3. Скопируем формулу, введенную в ячейку I5 , в ячейки I6 и I7 .
4. Внешний вид рабочего листа MS Office Excel с исходными данными для решения задачи об оптимальном рационе питания имеет следующий вид (pиc. 12.4).

Для отображения формул в ячейках рабочего листа необходимо выполнить команду меню: Формулы и на панели инструментов в группе Зависимости формул выбрать Показать формулы.

Заполнение окна Поиск решения

Для дальнейшего решения задачи следует вызвать мастер поиска решения, для чего необходимо выполнить операцию: Данные > Поиск решения.

После появления диалогового окна Поиск решения следует выполнить следующие действия:

1. В поле с именем Установить целевую ячейку: ввести абсолютный адрес ячейки $I$2 .
2. Для группы Равной: выбрать вариант поиска решения – минимальному значению.
3. В поле с именем Изменяя ячейки: ввести абсолютный адрес ячеек $B$2:$H$2 .
4. Добавить 3 ограничения, представляющие минимальные суточные потребности в питательных веществах. С этой целью выполнить следующие действия:
   • для задания первого ограничения в исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить (рис. 12.5 рис. 12.5, а);
   • в появившемся дополнительном окне выбрать ячейку $I$5 , которая должна отобразиться в поле с именем Ссылка на ячейку;
   • в качестве знака ограничения из выпадающего списка выбрать нестрогое неравенство » «;
   • в качестве значения правой части ограничения выбрать ячейку $J$5 ;
   • для добавления первого ограничения в дополнительном окне нажать кнопку с надписью Добавить;
   • аналогичным образом задать оставшиеся два ограничения (рис. 12.5 рис. 12.5, б).

Параметры

В окне «Поиск решения» нажать клавишу «Параметры», выбрать «Поиск решения Линейных задач симплекс-методом», нажать ОК, затем нажать Найти Решение (рис. 12.6 рис. 12.6, б).

После задания ограничений и целевой функции можно приступить к поиску численного решения, для чего следует нажать кнопку Выполнить. После выполнения расчетов программой MS Excel будет получено количественное решение, которое имеет вид, представленный на рис. 12. рис. 12.7.

Результатом решения задачи об оптимальной диете являются найденные оптимальные значения переменных: х₁ = 0, х₂ = 0,211, 3 = 0,109, х₄= 1,887, х₅ = 0, х₆ = 0, х₇ = 0, которым соответствует значение целевой функции: f_опт= 2587,140. При выполнении расчетов для ячеек В2:I2 был выбран числовой формат с 3 знаками после запятой.

Анализ найденного решения показывает, что для удовлетворения суточной потребности в питательных веществах (белки, жиры, углеводы) следует использовать 211 г мяса баранины, 109 г сыра и 1887 г бананов, совсем отказавшись от хлеба, огурцов, помидоров и винограда. При этом общая калорийность найденной оптимальной диеты будет приближенно равна 2590 ккал, что вполне соответствует малоактивному образу жизни без серьезных физических нагрузок. Напомним, что согласно медицинским данным, энергетические затраты работников интеллектуального труда (юристы, бухгалтера, врачи, педагоги) лежат в пределах 3000 ккал.

ЗАДАНИЕ

1. Составить математическую модель задачи линейного программирования.
2. Решить задачу линейного программирования в Excel с помощью Поиска решения.
3. Сохранить в виде модели установочные параметры.

Предприятие легкой промышленности выпускает две модели машин, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 80 изделий, второй линии – 85 изделий. На машину первой модели расходуются 12 однотипных элементов электронных схем, на машину второй модели – 6 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одной машины первой и второй моделей равна $30 и $40 соответственно. Определить оптимальный суточный объем производства первой и второй моделей.

Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех приборах. Время использования этих приборов для производства данных изделий ограничено 10 ч. в сутки. Найти оптимальный объем производства изделий каждого вида.

Фирма имеет возможность рекламировать свою продукции, используя местные радио- и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены $1000 в месяц. Каждая минута радиорекламы обходится в $5, а минута телерекламы – в $100. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.

Фирма производит два вида продукции – А и B . Объем сбыта продукции вида A составляет не менее 70% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 120 кг. Расход сырья на единицу продукции A составляет 3 кг, а на единицу продукции В – 5 кг. Цены продукции А и В равны $20 и $60 соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.

Фирма выпускает женские шляпы двух фасонов. Трудоемкость изготовления шляпы фасона 1 вдвое выше трудоемкости изготовления шляпы фасона 2. Если бы фирма выпускала только шляпы фасона 1, суточный объем производства мог бы составить 60 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 50 до 100 штук. Прибыль от продажи шляпы фасона 1 равна $6, а фасона 2 – $7. Определить какое количество шляп каждого фасона следует изготавливать, чтобы максимизировать прибыль.

Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков:

Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в машино-часах). Стоимость машино-часа составляет $10 и $15 для станка 1 и 2 соответственно. Допустимое время для использования станков для обработки изделий всех типов ограничено следующими значениями: 500 машино-часов – для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1,2,3 и 4 равны $65, $70, $55 и $45 соответственно. Составить план производства, максимизирующий чистую прибыль.

Завод выпускает изделия трех моделей ( I, II III ) Для их изготовления используется два вида ресурсов (А и В), запасы которых составляют – 5000 и 6000 единиц. Расходы ресурсов на одно изделие каждой модели:

Трудоемкость изготовления модели I вдвое больше, чем изделия модели II , и втрое больше, чем изделие модели III . Численность рабочих завода позволяет выпускать 1500 изделий I . Анализ условий сбыта показывает, что минимальный спрос на продукцию завода составляет 200, 200 и 150 изделий моделей I,II и III соответственно. Однако соотношение выпуска изделий моделей I,II и III должно быть равно 3:2:5. Удельная прибыль от реализации изделий моделей I,II и III составляет $30, $20 и $50 соответственно. Определить выпуск изделий, максимизирующий прибыль.

Требуется распределить имеющиеся денежные средства по четырем альтернативным вариантам. Игра имеет три исхода. Ниже приведены размеры выигрыша (или проигрыша) на каждый доллар, вложенный в соответствующий альтернативный вариант, для любого из трех исходов. У игрока имеется $500, причем, использовать в игре их можно только один раз. Точный исход игры заранее неизвестен, и, учитывая эту неопределенность, игрок решил распределить деньги так, чтобы максимизировать максимальную отдачу от этой суммы.

Бройлерное хозяйство птицеводческой фермы насчитывает 80000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Хотя недельный рацион цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 фунт.

Для того чтобы цыплята достигли к восьмой неделе необходимых весовых кондиций, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов или ингредиентов. Ограничим наше рассмотрение только тремя ингредиентами: известняком, зерном и соевыми бобами. Ниже приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента.

Смесь должна содержать:

• не менее 0.8%, но не более 1.2% кальция;
• не менее 22% белка;
• не более 5% клетчатки.

Необходимо определить количество каждого из трех ингредиентов, образующих смесь минимальной стоимости при соблюдении требований к общему расходу кормовой смеси и ее питательности.

Имеется n видов продуктов питания, в которых содержится m типов питательных веществ (белки, жиры, углеводы). В одной весовой единице продукта i-го типа содержится а_i единиц питательного вещества j-го вида . Известна минимальная суточная потребность b _j человека в каждом из видов питательных веществ. Задана калорийность сi одной весовой единицы i-го продукта ( i принадлежит <1, 2, . n >). Требуется определить оптимальный состав рациона продуктов, такой, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.

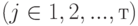
Для решения задачи об оптимальной диете с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи. Для определенности предположим, что в качестве исходных типов продуктов рассматриваются: хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3). Калорийность одной весовой единицы каждого из продуктов следующая:с₁ = 2060,с₂= 2430,с₃= 3600,с₄= 890,с₅= 140,с₆= 230, с₇ = 650. Содержание питательных веществ в каждом из продуктов может быть задано в форме следующей таблицы (см. табл.).

Таблица 1. Содержание питательных веществ в продуктах питания

Продукты/питательные вещества	Хлеб ржаной	Мясо баранина	Сыр «Российский»	Банан	Огурцы	Помидоры	Виноград
Белки	66	225	235	20	13	16	11
Жиры	17	177	295	1	1	7	7
Углеводы	425	0	0	217	31	43	200

Минимальная суточная потребность в питательных веществах следующая: в белках b ₁ = 105, в жирах b ₂ = 75, в углеводах b ₃ = 405.

Определить суточную потребности в питательных веществах (белки, жиры, углеводы) и общую калорийность оптимальной диеты.

Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 60 изделий, второй линии – 75 изделий. На радиоприемник первой модели расходуются 10 однотипных элементов электронных схем, на радиоприемник второй модели – 8 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одного радиоприемника первой и второй моделей равна $30 и $20 соответственно. Определить оптимальный суточный объем производства первой и второй моделей.

Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех станках. Время использования этих станков для производства данных изделий ограничено 10 ч. в сутки. Найти оптимальный объем производства изделий каждого вида.

Фирма имеет возможность рекламировать свою продукции, используя местные радио- и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены $1000 в месяц. Каждая минута радиорекламы обходится в $5, а минута телерекламы – в $100. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.

Фирма производит два вида продукции – A и B . Объем сбыта продукции вида A составляет не менее 60% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 100 кг. Расход сырья на единицу продукции A составляет 2 кг, а на единицу продукции В – 4 кг. Цены продукции А и В равны $20 и $40 соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.

Фирма выпускает ковбойские шляпы двух фасонов. Трудоемкость изготовления шляпы фасона 1 вдвое выше трудоемкости изготовления шляпы фасона 2. Если бы фирма выпускала только шляпы фасона 1, суточный объем производства мог бы составить 60 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 50 до 100 штук. Прибыль от продажи шляпы фасона 1 равна $8, а фасона 2 – $5. Определить какое количество шляп каждого фасона следует изготавливать, чтобы максимизировать прибыль.

Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков:

Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в машино-часах). Стоимость машино-часа составляет $10 и $15 для станка 1 и 2 соответственно. Допустимое время для использования станков для обработки изделий всех типов ограничено следующими значениями: 500 машино-часов – для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1,2,3 и 4 равны $65, $70, $55 и $45 соответственно. Составить план производства максимизирующий чистую прибыль.

Завод выпускает изделия трех моделей ( I, II III ). Для их изготовления используется два вида ресурсов (А и В), запасы которых составляют – 4000 и 6000 единиц. Расходы ресурсов на одно изделие каждой модели:

Трудоемкость изготовления модели I вдвое больше, чем изделия модели II , и втрое больше, чем изделие модели III . Численность рабочих завода позволяет выпускать 1500 изделий I . Анализ условий сбыта показывает, что минимальный спрос на продукцию завода составляет 200, 200 и 150 изделий моделей I,II и III соответственно. Однако соотношение выпуска изделий моделей I,II и III должно быть равно 3:2:5. Удельная прибыль от реализации изделий моделей I,II и III составляет $30, $20 и $50 соответственно. Определить выпуск изделий, максимизирующий прибыль.

Некоторое производственное предприятие выпускает три вида клея. Для производства клея используется 4 типа химических веществ: крахмал, желатин, квасцы и мел. Расход этих веществ в кг для получения 1 кг каждого вида клея и их запас на складе предприятия представлены в таблице.

Таблица 1. Расход химических веществ на изготовления клея, их запас на складе

Вид клея /Химические вещества	Клей № 1	Клей № 2	Клей № 3	Запас на складе
Крахмал	0,4	0,3	0,2	20
Желатин	0,2	0,3	0,4	35
Квасцы	0,05	0,07	0,1	7
Мел	0,01	0,05	0,15	10

Стоимость каждого вида клея для оптовых покупателей следующая:с₁ = 380 руб/кг,с₂ =430 руб/кг,с₃ = 460 руб/кг. Требуется определить оптимальный объем выпуска клея каждого вида, обеспечивающий максимум общей стоимости готовой продукции.

Бройлерное хозяйство птицеводческой фермы насчитывает 20000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Хотя недельный рацион цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 фунт.

Для того чтобы цыплята достигли к восьмой неделе необходимых весовых кондиций, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов или ингредиентов. Ограничим наше рассмотрение только тремя ингредиентами: известняком, зерном и соевыми бобами. Ниже приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента.

Смесь должна содержать:

• не менее 0.8%, но не более 1.2% кальция;
• не менее 22% белка;
• не более 5% клетчатки.

Необходимо определить количество каждого из трех ингредиентов, образующих смесь минимальной стоимости при соблюдении требований к общему расходу кормовой смеси и ее питательности.

Имеется конечное число видов продуктов питания: ананас, арбуз, грейпфрут, язык говяжий, сардельки говяжьи, хлеб «Бородинский», картофель ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3). Калорийность 1 кг каждого из продуктов следующая:с₁ = 470,с₂= 380,с₃ = 350,с₄ = 1460,с₅ = 2150,с₆ = 2070, с₇ = 800. Минимальная суточная потребность в питательных веществах следующая: в белках b ₁ = 100, в жирах b ₂ = 70, в углеводах b3 = 400. Содержание питательных веществ в каждом из продуктов может быть задано в форме нижеприведенной таблицы (табл.).

Требуется определить такой рацион питания, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.

Поиск решения задач в Excel с примерами

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.

Решение задач оптимизации в Excel

Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

1. Количество изделий нам пока неизвестно. Это переменные.
2. В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
3. Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
4. Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.

Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

1. Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
2. Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
3. Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
4. Тип – 0.
5. БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка) кпер . Подставим значения: ПС = 400 000 / (1 + 0,05) 16 = 183245.

Решение эконометрики в Excel

Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.

Дано 2 диапазона значений:

Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, =, Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

1. Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
2. Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
3. Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

1. Делаем таблицу со значениями матрицы А.
2. Выделяем на этом же листе область для обратной матрицы.
3. Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
4. В поле аргумента «Массив» вписываем диапазон матрицы А.
5. Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.

Чтобы познакомиться с мощным инструментом Excel Поиск решения, рассмотрим и решим с вами задачу.

Необходимо найти оптимальные объемы выпуска трех видов продукции для получения максимальной прибыли от их продажи.

При решении данной задачи должны быть учтены следующие ограничения:

• общий объем производства – всего 300 изделий;
• должно быть произведено не менее 50 изделий А;
• должно быть произведено не менее 40 изделий В;
• должно быть произведено не более 40 изделий С.

1. Внести в новый рабочий лист данные для вычисления прибыли от продажи трех видов продукции, причем в ячейки столбца D, и в ячейку B6 должны быть введены формулы.

2. Запустить задачу поиска решений. Для этого: выполнить команду в Excel 2003 Сервис | Поиск решений … (В Excel 2007 и 2010 необходимо зайти в раздел Данные | Поиск решения)

и в окне “Поиск решений” ввести данные:

• в поле «Установить целевую ячейку» указать адрес D6;
• установить флажок «Равной максимальному значению»;
• в поле «Изменяя ячейки» определить изменяемые ячейки (B3:B5);
• в поле «Ограничения» по одному добавить каждое из следующих четырех ограничений задачи (B6=300; B3>=50; B4>=40; B5 Поделиться:

Пример функции ДОХОД для анализа доходности инвестиций в Excel

Финансовые показатели облигаций могут быстро рассчитываться в Excel. Для этого используется функция ДОХОД. С ее помощью вычисляется доходность ценных бумаг, по которым периодически выплачиваются проценты (дивиденды).

Как работает функция ДОХОД в Excel?

Облигации – это финансовый инструмент. Предприятие, выпустившее облигации, выступает в роли заемщика. Нуждаясь в привлечении средств, оно выпускает и выбрасывает на рынок такие ценные бумаги. Покупатель облигаций, фактически, является заимодавцем. Ставка купона – это процент, который получает покупатель облигации за то, что предоставил свои средства в пользование.

Как рассчитать доходность облигаций в Excel? Для решения данной задачи используется функция ДОХОД. Как и любая другая функция, ее синтаксис состоит из имени и аргументов. В строке формул сначала ставится знак равенства, после прописывается имя функции, а затем заполняем ее аргументы входящими значениями всех необходимых показателей.

Всего аргументов у сложной функции 7. Из них 6 обязательных для заполнения:

1. Дата_согл. Расчетный день, когда облигация продана. Дата, когда долговые обязательства переданы покупателю. Не стоит путать ее с датой выпуска облигации.
2. Дата_вступл_в_силу. День, когда заем возвращается покупателю. Это срок погашения облигации, когда истекает срок ее действия.
3. Ставка. Годовая ставка процентов по облигации. Процент, который получает покупатель ценных бумаг.
4. Цена. Показатель определяет цену облигации на 100 рублей номинала.
5. Погашение. Стоимость, по которой выкупаются ценные бумаги.
6. Частота. Число выплат по облигации в год. Может быть равна 1, 2 или 4.
7. Базис. Этот аргумент не является обязательным. Поэтому он заключается в квадратные скобки. Он определяет способ вычисления дней.

Существует 5 видов базиса:

• — 0 – Американский 30/360;
• — 1 – факт/факт;
• — 2 – факт/360;
• — 3 – факт/365;
• — 4 – Европейский 30/360.

Аргументы всегда берутся в круглые скобки. Все они перечисляются по порядку. Между ними ставится знак «;».

Синтаксис функции прописывается следующим образом:

=ДОХОД(дата_согл; дата_вступл_в_силу; ставка; цена; погашение; частота; [базис])

Обязательно учитывать то, что все даты в Excel записываются в виде последовательных чисел. Недопустимо использование текстового формата. За 1 принято 1 января 1900 года. Все последующие даты просто прибавляют число прошедших дней. Поэтому все значения рассчитываются с помощью функции «ДАТА».

Результатом применения функции является определение прибыльности облигаций. Программа может выдать не результат, а знак ошибки #ЧИСЛО! Это происходит в нескольких случаях:

• введены даты без использования функции «ДАТА»;
• значение ставки меньше нуля;
• указана цена меньше или равная нулю;
• погашение указано меньше или равно нулю;
• базис меньше нуля или больше четырех.

Примеры использования функции ДОХОД для анализа облигаций

Для вычисления доходности ценных бумаг нужно ввести в первый столбик таблицы все аргументы функции.

Пример 1. Необходимо вычислить доходность облигаций при следующих условиях:

1. Облигации были проданы 15 февраля 2008 года.
2. Срок погашения – 15 ноября 2016.
3. Ставка по купонам определена 5,75%.
4. Цена составляет 95.04 номиналов.
5. Выкупная стоимость — 100 номиналов.
6. Проценты выплачиваются раз в полгода.
7. Значение базиса – 0 (30/360).

Последовательно вводите все значения заполняя таблицу с данными:

В ячейку B9 вводите данные для аргументов функции ДОХОД. Формула будет выглядеть так:

Доходность облигаций составляет 4,26%.

Можно вводить формулу с клавиатуры или указывать соответствующие ячейки мышью. При этом прописать имя функции нужно вручную. Затем откройте скобку и последовательно через «пробел» укажите все ячейки, которые должны быть учтены.

Пример 2. Предприятие продало облигации 14 июля 2015. Установлен небольшой срок их погашения 14 июля 2017. Предлагается ставка 6%. Цена бумаг 97,4 номинальных значений. Стоимость для выкупа – 107 номиналов. Выплата процентов проводится 4 раза в год. Базис 2 – (48/360).

Для вычисления прибыльности облигации введите данные в таблицу по принципу, который стал понятен из примера 1:

В итоговой ячейке B9 приписываем функцию:

Это обозначает, что расчет доходности к погашению облигаций составляет (6,16% х 2года)=12,32%.

Пример 3. Ценные бумаги проданы 2 августа 2004. Погашение произошло 13 мая 2018. Купонная ставка по ним – 5,3%. Цена бумаг – 93 номинала. Стоимость для выкупа – 104 номинала. Проценты начисляются раз в год. Базис – 0 (30/360).

По аналогии составляем таблицу, используя функцию =ДОХОД():

Прибыльность акций оценена в 3,52%.

С помощью программы Excel удалось всего за несколько минут установить, что самыми прибыльными инвестициями являются облигации из второго примера.

1. Решение задачи максимизации прибыли

Программа
Excel
имеет достаточный набор инструментальных
средств, для решения задач такого
класса. Рассмотрим задачу линейной
оптимизации на следующем примере.

Пример_1:
Предприятие
выпускает 4 вида продукции: П1, П2, П3, П4.
Для изготовления используется 3 вида
ресурсов: р1, р2, р3, объем которых ограничен.
Известны потребности в ресурсах для
каждого вида продукции, а также прибыль,
получаемая от ее реализации.

Требуется
определить оптимальное количество
выпуска каждого вида продукции, при
котором будет получена максимальная
прибыль для предприятия. Исходные данные
приведены в таблице 1.

Таблица
1

Исходные данные	Тип ограничения	Значение ограничения
Показатель	Вид продукции
П1	П2	П3	П4
Прибыль от ед. продукции	60	70	120	130
Ресурс р1	1	1	1	1	<=	16
Ресурс р2	4	6	10	13	<=	100
Ресурс р3	6	5	4	3	<=	110
Нижняя граница	1	2	2	1
Верхняя граница	4	—	—	1

Постановка
задачи.
Целью решения данной оптимизационной
задачи является нахождение максимальной
прибыли при оптимальном количестве
выпуска каждого вида продукции (n1,
n2, n3, n4) с учетом существующих ограничений.

Целевая
функция (прибыль):

60*n1+70*n2+120*n3+130*n4max.

1. Подготовка исходных данных

Создайте
на рабочем столе папку под своим именем
и скопируйте в нее файлы Максимизация
прибыли и Транспортная
задача с
жесткого диска, например с диска Е:
из папки
1550ПТ_1550_09.

1. Запустите
   программу Microsoft
   Excel.
   Откройте файл
   Максимизация прибыли.

2. В
   соответствии с данными таблицы 1,
   заполните ячейки таблицы:

• начальные
  значения объема производства изделий
  вида П1,
  П2,
  П3,
  П4,
  равные нулю, введите в
  C6:F6,

• значения
  единичной прибыли в ячейки C7:F7.

• нормы
  расходов ресурсов (р1 – р3) на каждый
  вид продукции в ячейки: C10:С12
  для П1, D10:D12
  для П2, E10:E12
  для П3, F10:F12
  для П4.

тип
ограничения в G10:G12,
значения ограничения на ресурсы – в
Н10:Н12.

• граничные
  условия в ячейки C14:F15.

1. В
   ячейку Н5
   введите целевую функцию:
   =C7*C6+D7*D6+E7*E6+F7*F6.

2. В
   ячейки I10:I12
   введите формулы
   для подсчета объема потребления каждого
   ресурса: р1 — C10*$C$6+D10*$D$6+E10*$E$6+F10*$F$6,

Р2
— C11*$C$6+D11*$D$6+E11*$E$6+F11*$F$6,

Р3
— C12*$C$6+D12*$D$6+E12*$E$6+F12*$F$6.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #