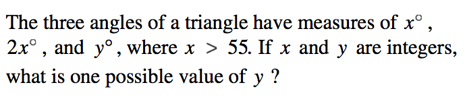Made up word problem - Word и Excel - помощь в работе с программами

Estimates of English’s total word count vary, but linguists agree the number ranks near the top of the world’s vocabularies. A May GrammarBook newsletter article cited English as having as many as 300,000 distinctly usable words.

With so many residents in a vernacular, impostors posing as real words are bound to slip in. They start as mistakes but last long enough to wiggle into pockets of speech. Before long, they spread out, gaining confidence and popularity until they set their sights on the real prize: placement in a dictionary.

While casual conversation provides the most refuge for these con artists, their common usage still often lets them cross into composition’s more-managed domain.

Here are but a few made-up words we and our readers have singled out as guilty from the line-up of suspects:

Imposter: administrate (v) Real Word: administer	Imposter: participator (n) Real Word: participant
Imposter: commentate (v) Real Word: comment	Imposter: preventative (adj) Real Word: preventive
Imposter: orientate (v) Real Word: orient	Imposter: supposably (adj, adv) Real Word: supposedly
Imposter: conversate (v) Real Word: converse	Imposter: undoubtably (adj, adv) Real Word: undoubtedly
Imposter: irregardless (adj, adv) Real Word: regardless	Imposter: vice-a-versa (adv) Real Word: vice versa
Imposter: exploitive (adj) Real Word: exploitative	Imposter: whole nother (adj) Real Words: another, whole other
Imposter: firstly (secondly, thirdly, etc.) (adv) Real Word: first (second, third, etc.)	Imposter: incentivize (v) Real Words: encourage, motivate, reward

A few of these invaders, such as irregardless and preventative, have already cleared the fence, crossed their covert tunnels, and arrived safely in dictionaries. That alone does not validate them, nor does it mean we should permit them into our writing.

You also probably noted several made-up words in the list include the suffix -ate. This is a common ploy some words will use to create more versions of themselves.

The suffix -ize operates much the same way. In addition to incentivize, keep an eye on words such as actualize, collectivize, intellectualize, and normalize. Some words, such as finalize, prioritize, memorize, and ostracize, need their three-letter caboose to deliver their meaning, but most -ize words are pitching tents where houses are built.

Made-up words present another call for us to lead the way in upholding concise, grammatical writing. By remaining vigilant, we can help halt the advance of the pretenders.

If the article or the existing discussions do not address a thought or question you have on the subject, please use the «Comment» box at the bottom of this page.

Источник

Math word problems can be a challenge for young learners. It’s particularly daunting for students who are struggling with reading comprehension or learning English as a second language. One way to level the playing field is to teach word problems visually. All of the common word problem types, such as part-part-whole, comparison, joining, separating, multiplication and division, can be expressed with simple but effective images that illustrate the numerical relationships within the word problems.

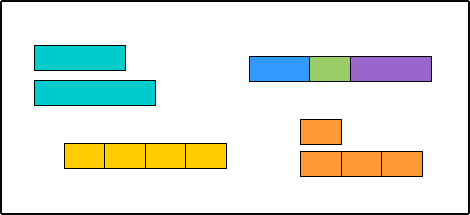
various Thinking Blocks models

Visuals, like the ones pictured above, are commonly known as bar models or tape diagrams. They’ve become quite popular in elementary classrooms in recent years. Bar models can be a very useful tool but only when clear representations are drawn.

For students in my 3rd grade math class, drawing advanced models proved to be difficult. They became frustrated with both the process and the errors that would inevitably arise. I wondered if conceptual understanding would increase if students could build bar models with blocks. What sort of the learning would take place once bar models became a more tactile experience? I used measuring blocks to help students physically model word problems. It was a good start but, like drawings, the unchanging nature of the blocks reduced their usefulness.

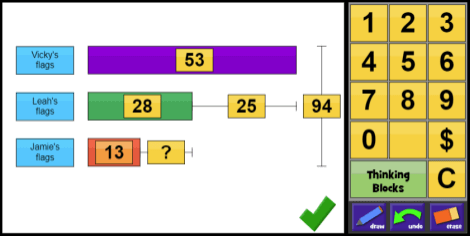
solving a multistep word problem

To overcome the limitations of the measuring blocks, I developed a system of virtual blocks that could be used to model almost any math word problem. These “thinking blocks” provided a powerful way to organize information and simplify problem solving. Thinking Blocks not only revealed what was to be solved, it illuminated the process as well. That was its superpower. Since then, Thinking Blocks has become a transformative math tool, teaching millions of students around the world how to model and solve word problems.

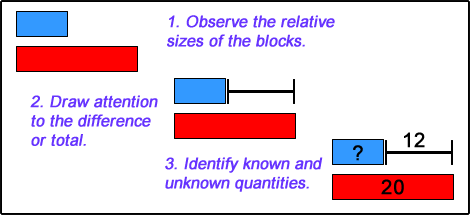
a three step approach

When introducing Thinking Blocks, I begin with a simple model and then, with help from my students, work backward to create a word problem. The model I use at first contains nothing more than blocks; it has no numbers, labels, or other visual information. I start by asking a series of guiding questions.

What do you notice about the blocks in the model?
The red block is longer the blue block.
The blue block is shorter than the red block.

I then add brackets to the model to draw attention to the difference.

What else could you ask about the blocks?
How much longer is the red block?
How much shorter is the blue block?

Now students are ready to identify known and unknown quantities. I vary the positions, asking my students each time what the question could be. Guiding students in this way provides the foundation they need to move toward higher level thinking.

From here, we look at more abstract problems. These are word problems in which the blocks represent other types of quantities such as the number of red and blue balloons, the weight of two different puppies, or the number of children who voted yes or no in a poll. Students make up word problems, personalize the stories, and change the known and unknown quantities. They are now well-prepared to complete the problems in Thinking Blocks.

4 Great Reasons to Use Thinking Blocks

Teach your students innovative and engaging problem-solving strategies.
Help your students solve multi-step word problems with mastery.
Accelerate your students’ math achievement.
Boost your students’ self-confidence.

Thinking Blocks and the Common Core

Represent and solve problems involving addition and subtraction.
Represent and solve problems involving multiplication and division.
Use the four operations with whole numbers to solve problems.
Build fractions from unit fractions.
Use equivalent fractions as a strategy to add and subtract fractions.
Understand ratio concepts and use ratio reasoning to solve problems.

How will you use Thinking Blocks in your classroom?

Источник

kansi

According to the publisher, “Lunario” “takes the name of a traditional farmer’s almanac to bring together several strands of work all relating to the moon.” The book is made up of photos Guidi created from 1968 to 1999. Throughout its pages, references to the moon manifest themselves in surprising ways — from the shape of a woman’s face to the glowing white orb of a young child’s ball and finally through a series of color photos Guidi took of a partial solar eclipse in August 1999.

Source: “This photographer spent decades..”, in The Washington Post

What’s the difference in meaning and nuance between that «made up of» and «composed of»?

They have exactly the same meaning, I guess.

<Source added, and bare link removed, by moderator (Florentia52)>

Last edited by a moderator: Jun 17, 2020

There is no difference. As we keep explaining to you, there are often multiple choices of words with the same or a very similar meaning in English, and each author chooses which one he wants to use in any context.

As usual, these two words have a slightly different ‘tone’. ‘composed of’ is slightly more elevated than ‘made up of’ because ‘composed’ has a Latin root and ‘made up of’ is good old basic Anglo-Saxon.

I’m sure this may be very different from how the Japanese language works, but to say the two phrases ‘mean the same’ is not satisfactory to us in English. The tone is very important and makes a big difference to which word you use in which context.

Yes, they mean basically the same.

is made of = consists of
is made up of = is composed of (heavily implies more than one constituent part)

e2efour

The verb you suggest (is composed) means the same as made up.

Strictly speaking, the book is also made up of text. So one should perhaps write The photos in the book are taken from those Guidi created …
Otherwise, the meaning might be that the book only consists of photos.

«Made up» is everyday words of Germanic origin; «compose» is a slightly more formal word of French or Latin origin. Apart from this stylistic difference, it would not make much difference which you used here.

kansi

As usual, these two words have a slightly different ‘tone’. ‘composed of’ is slightly more elevated than ‘made up of’ because ‘composed’ has a Latin root and ‘made up of’ is good old basic Anglo-Saxon.

I was just making sure that they mean same.

Thank you. That tone explanation is something I cannot know from a dictionavy.This article is
more like what some individual thinks about something.
So «compose of «which is more elevated toned isn’t necessary to be used, I guess?

isn’t necessary to be used

:confused: I suppose your writer did not feel the need to write in the most flowery language possible. Why would he/she?

kansi

«Made up» is everyday words of Germanic origin; «compose» is a slightly more formal word of French or Latin origin. Apart from this stylistic difference, it would not make much difference which you used here.

I see. There is a stylistic difference. Well if we use more Latin root words in a text, is it simple as that the text sounds fancier?

kansi

I see. it’s often so.
Thank you.

1.This big statue right there is actually composed of LEGO blocks.
2.This big statue right there is actually made up of LEGO blocks.

Both are idiomatic and if I want or need to make it sound more elevated toned because of the context then I would use 1,not 2.

What we have talked here is as sipmple as that?

Here we wouldn’t say ‘composed of’, or ‘made up of’, but simply ‘made of Lego’, or possibly ‘made out of Lego.’ (We call them ‘bricks, not blocks, but there’s no need to mention them at all)

In the case of #10, the difference is not merely stylistic.
A house is (literally) built or made of bricks. You would not normally use the word «compose» in such a literal, basic, concrete, physical context.

kansi

In the case of #10, the difference is not merely stylistic.
A house is (literally) built or made of bricks. You would not normally use the word «compose» in such a literal, basic, concrete, physical context.

I see..we won’t use it because we can acctually see what the LEGO statue in my example is made from?

For example,
This meal is (partly) made up of some vegetables I’ve grown in my yard.
This meal is (partly) composed of some vegetables I’ve grown in my yard.

Is the difference here merely stylistic and do I use the words correct?

Last edited: Jun 17, 2020

Both of those are unidiomatic. We wouldn’t talk about a meal in that way. This is the problem with constantly making up your own sentences and asking us to comment on them. They rarely prove the point you’re trying to make. You’ll learn more by finding actual examples of the usage you want to learn – such as the following, in all of which the verbs compose and make up are interchangeable:

A vegetable is composed of a root, stem, leaves, flowers, fruits, and seeds.
A human body is composed of organs, organs are composed of tissues, tissues are composed of cells, and so on.
Ancient Greeks thought matter was made up of four elements – earth, air, fire and water.
The third assumption is that future crews will be made up of people from different cultural backgrounds.

kansi

A vegetable is composed of a root, stem, leaves, flowers, fruits, and seeds.
A human body is composed of organs, organs are composed of tissues, tissues are composed of cells, and so on.
Ancient Greeks thought matter was made up of four elements – earth, air, fire and water.

I understand what sense these examples provide.

I found this example sentence and I couldn’t find this that different from that wrong example of mine..how are this and my example different?

●The force would be composed of troops from NATO countries.
(Collins dictionavy)

That, too, could be said using “would be made up of”.

kansi

That, too, could be said using “would be made up of”.

Yes I mean,
●The force would be composed of troops from NATO countries.
(Collins dictionavy)
●This meal is (partly) composed of some vegetables I’ve grown in my yard.(my wrong example)

I couldn’t see they are different.Where are they different?

I’ve already told you that we don’t talk about meals in that way! It would be idiomatic to describe a meal as consisting of (for example) soup, followed by a risotto and side salad, with ice cream for dessert.

kansi

a meal as consisting of (for example) soup, followed by a risotto and side salad, with ice cream for dessert.

Ah I see..a meal doesn’t consist of ingredients, but such as soup,salad or a main dish.

Источник

The English language is under serious threat from people who like to use made-up words that don’t really exist or who use words they don’t know the real meaning of.
The following seven words are completely made-up items of vocabulary that have crept into the English language and are misused on a very regular basis.

Irregardless.

You may think it means “regardless.” It is a non-standard word, and you should avoid using it.

Misunderestimate.

President Bush thinks it means to mistakenly underestimate something or someone: “They misunderestimated me.”

President Bush is wrong. It doesn’t mean a thing.

Refudiate.

Sarah Palin is a massive fan of this made-up word, and she has used it several times in interviews and tweets. Either she likes the word so much that she is trying to make it acceptable, or she doesn’t actually know that it isn’t a real word. We’re putting our money on the latter.

Supposably.

“Supposably” is a word that Americans often confuse with the word “supposedly.” “Supposably” can be used only when the meaning is “capable of being supposed,” and then only in the U.S.

“Author” is a noun that identifies the individual who wrote a document or book, it should not be used as a verb to describe the action of writing.

Alot.

“A lot” consists of two separate words. They should not be condensed down into one word in any circumstances.

Alright.

There’s no such word as “alright.” It should be two words: “all right.” As grammarian Bill Walsh puts it in his book Lapsing Into a Comma, “We word nerds have known since second grade that alright is not all right.”

What made-up words do you hear on a regular basis? Leave a comment and tell us all about them.

Need some help perfecting your written English? Check out our rewriting services.

In addition to made-up words being a major problem, there are also tons of people out there who use real words completely incorrectly. Are you one of them? Take a look at our guide to words you may think you know the meaning of, but probably don’t.

Источник

About 25% of your total SAT Math section will be word problems, meaning you will have to create your own visuals and equations to solve for your answers. Though the actual math topics can vary, SAT word problems share a few commonalities, and we’re here to walk you through how to best solve them.

This post will be your complete guide to SAT Math word problems. We’ll cover how to translate word problems into equations and diagrams, the different types of math word problems you’ll see on the test, and how to go about solving your word problems on test day.

Feature Image: Antonio Litterio/Wikimedia

What Are SAT Math Word Problems?

A word problem is any math problem based mostly or entirely on a written description. You will not be provided with an equation, diagram, or graph on a word problem and must instead use your reading skills to translate the words of the question into a workable math problem. Once you do this, you can then solve it.

You will be given word problems on the SAT Math section for a variety of reasons. For one, word problems test your reading comprehension and your ability to visualize information.

Secondly, these types of questions allow test makers to ask questions that’d be impossible to ask with just a diagram or an equation. For instance, if a math question asks you to fit as many small objects into a larger one as is possible, it’d be difficult to demonstrate and ask this with only a diagram.

Translating Math Word Problems Into Equations or Drawings

In order to translate your SAT word problems into actionable math equations you can solve, you’ll need to understand and know how to utilize some key math terms. Whenever you see these words, you can translate them into the proper mathematical action.

For instance, the word «sum» means the value when two or more items are added together. So if you need to find the sum of a and b, you’ll need to set up your equation like this: a+b.

Also, note that many mathematical actions have more than one term attached, which can be used interchangeably.

Here is a chart with all the key terms and symbols you should know for SAT Math word problems:

Key Terms	Mathematical Action
Sum, increased by, added to, more than, total of	+
Difference, decreased by, less than, subtracted from	−
Product, times, __ times as much, __ times as many (a number, e.g., “three times as many”)	* or x
Divided by, per, __ as many, __ as much (a fraction, e.g., “one-third as much”)	/ or ÷
Equals, is, are, equivalent	=
Is less than	<
Is greater than	>
Is less than or equal to	≤
Is greater than or equal to	≥

Now, let’s look at these math terms in action using a few official examples:

We can solve this problem by translating the information we’re given into algebra. We know the individual price of each salad and drink, and the total revenue made from selling 209 salads and drinks combined. So let’s write this out in algebraic form.

We’ll say that the number of salads sold = S, and the number of drinks sold = D. The problem tells us that 209 salads and drinks have been sold, which we can think of as this:

S + D = 209

Finally, we’ve been told that a certain number of S and D have been sold and have brought in a total revenue of 836 dollars and 50 cents. We don’t know the exact numbers of S and D, but we do know how much each unit costs. Therefore, we can write this equation:

6.50S + 2D = 836.5

We now have two equations with the same variables (S and D). Since we want to know how many salads were sold, we’ll need to solve for D so that we can use this information to solve for S. The first equation tells us what S and D equal when added together, but we can rearrange this to tell us what just D equals in terms of S:

S + D = 209

Now, just subtract S from both sides to get what D equals:

D = 209 − S

Finally, plug this expression in for D into our other equation, and then solve for S:

6.50S + 2(209 − S) = 836.5

6.50S + 418 − 2S = 836.5

6.50S − 2S = 418.5

4.5S = 418.5

S = 93

The correct answer choice is (B) 93.

This word problem asks us to solve for one possible solution (it asks for «a possible amount»), so we know right away that there will be multiple correct answers.

Wyatt can husk at least 12 dozen ears of corn and at most 18 dozen ears of corn per hour. If he husks 72 dozen at a rate of 12 dozen an hour, this is equal to 72 / 12 = 6 hours. You could therefore write 6 as your final answer.

If Wyatt husks 72 dozen at a rate of 18 dozen an hour (the highest rate possible he can do), this comes out to 72 / 18 = 4 hours. You could write 4 as your final answer.

Since the minimum time it takes Wyatt is 4 hours and the maximum time is 6 hours, any number from 4 to 6 would be correct.

Though the hardest SAT word problems might look like Latin to you right now, practice and study will soon have you translating them into workable questions.

Typical SAT Word Problems

Word problems on the SAT can be grouped into three major categories:

Word problems for which you must simply set up an equation
Word problems for which you must solve for a specific value
Word problems for which you must define the meaning of a value or variable

Below, we look at each world problem type and give you examples.

Word Problem Type 1: Setting Up an Equation

This is a fairly uncommon type of SAT word problem, but you’ll generally see it at least once on the Math section. You’ll also most likely see it first on the section.

For these problems, you must use the information you’re given and then set up the equation. No need to solve for the missing variable—this is as far as you need to go.

Almost always, you’ll see this type of question in the first four questions on the SAT Math section, meaning that the College Board consider these questions easy. This is due to the fact that you only have to provide the setup and not the execution.

To solve this problem, we’ll need to know both Armand’s and Tyrone’s situations, so let’s look at them separately:

Armand: Armand sent m text messages each hour for 5 hours, so we can write this as 5m—the number of texts he sent per hour multiplied by the total number of hours he texted.

Tyrone: Tyrone sent p text messages each hour for 4 hours, so we can write this as 4p—the number of texts he sent per hour multiplied by the total number of hours he texted.

We now know that Armand’s situation can be written algebraically as 5m, and Tyrone’s can be written as 4p. Since we’re being asked for the expression that represents the total number of texts sent by Armand and Tyrone, we must add together the two expressions:

5m + 4p

The correct answer is choice (C) 5m + 4p

Word Problem Type 2: Solving for a Missing Value

The vast majority of SAT Math word problem questions will fall into this category. For these questions, you must both set up your equation and solve for a specific piece of information.

Most (though not all) word problem questions of this type will be scenarios or stories covering all sorts of SAT Math topics, such as averages, single-variable equations, and ratios. You almost always must have a solid understanding of the math topic in question in order to solve the word problem on the topic.

Let’s try to think about this problem in terms of x. If Type A trees produced 20% more pears than Type B did, we can write this as an expression:

x + 0.2x = 1.2x = # of pears produced by Type A

In this equation, x is the number of pears produced by Type B trees. If we add 20% of x (0.2x) to x, we get the number of pears produced by Type A trees.

The problem tells us that Type A trees produced a total of 144 pears. Since we know that 1.2x is equal to the number of pears produced by Type A, we can write the following equation:

1.2x = 144

Now, all we have to do is divide both sides by 1.2 to find the number of pears produced by Type B trees:

x = 144 / 1.2

x = 120

The correct answer choice is (B) 120.

You might also get a geometry problem as a word problem, which might or might not be set up with a scenario, too. Geometry questions will be presented as word problems typically because the test makers felt the problem would be too easy to solve had you been given a diagram, or because the problem would be impossible to show with a diagram. (Note that geometry makes up a very small percentage of SAT Math.)

This is a case of a problem that is difficult to show visually, since x is not a set degree value but rather a value greater than 55; thus, it must be presented as a word problem.

Since we know that x must be an integer degree value greater than 55, let us assign it a value. In this case, let us call x 56°. (Why 56? There are other values x could be, but 56 is guaranteed to work since it’s the smallest integer larger than 55. Basically, it’s a safe bet!)

Now, because x = 56, the next angle in the triangle—2x—must measure the following:

56*2 = 112

Let’s make a rough (not to scale) sketch of what we know so far:

Now, we know that there are 180° in a triangle, so we can find the value of y by saying this:

y = 180 − 112 − 56

y = 12

One possible value for y is 12. (Other possible values are 3, 6, and 9.)

Word Problem Type 3: Explaining the Meaning of a Variable or Value

This type of problem will show up at least once. It asks you to define part of an equation provided by the word problem—generally the meaning of a specific variable or number.

This question might sound tricky at first, but it’s actually quite simple.

We know that P is the number of phones Kathy has left to fix, and d is the number of days she has worked in a week. If she’s worked 0 days (i.e., if we plug 0 into the equation), here’s what we get:

P = 108 − 23(0)

P = 108

This means that, without working any days of the week, Kathy has 108 phones to repair. The correct answer choice, therefore, is (B) Kathy starts each week with 108 phones to fix.

To help juggle all the various SAT word problems, let’s look at the math strategies and tips at our disposal.

Ready to go beyond just reading about the SAT? Then you’ll love the free five-day trial for our SAT Complete Prep program. Designed and written by PrepScholar SAT experts, our SAT program customizes to your skill level in over 40 subskills so that you can focus your studying on what will get you the biggest score gains.

Click on the button below to try it out!

SAT Math Strategies for Word Problems

Though you’ll see word problems on the SAT Math section on a variety of math topics, there are still a few techniques you can apply to solve word problems as a whole.

#1: Draw It Out

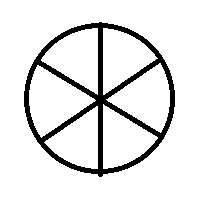
Whether your problem is a geometry problem or an algebra problem, sometimes making a quick sketch of the scene can help you understand what exactly you’re working with. For instance, let’s look at how a picture can help you solve a word problem about a circle (specifically, a pizza):

If you often have trouble visualizing problems such as these, draw it out. We know that we’re dealing with a circle since our focus is a pizza. We also know that the pizza weighs 3 pounds.

Because we’ll need to solve the weight of each slice in ounces, let’s first convert the total weight of our pizza from pounds into ounces. We’re given the conversion (1 pound = 16 ounces), so all we have to do is multiply our 3-pound pizza by 16 to get our answer:

3 * 16 = 48 ounces (for whole pizza)

Now, let’s draw a picture. First, the pizza is divided in half (not drawn to scale):

We now have two equal-sized pieces. Let’s continue drawing. The problem then says that we divide each half into three equal pieces (again, not drawn to scale):

This gives us a total of six equal-sized pieces. Since we know the total weight of the pizza is 48 ounces, all we have to do is divide by 6 (the number of pieces) to get the weight (in ounces) per piece of pizza:

48 / 6 = 8 ounces per piece

The correct answer choice is (C) 8.

As for geometry problems, remember that you might get a geometry word problem written as a word problem. In this case, make your own drawing of the scene. Even a rough sketch can help you visualize the math problem and keep all your information in order.

#2: Memorize Key Terms

If you’re not used to translating English words and descriptions into mathematical equations, then SAT word problems might be difficult to wrap your head around at first. Look at the chart we gave you above so you can learn how to translate keywords into their math equivalents. This way, you can understand exactly what a problem is asking you to find and how you’re supposed to find it.

There are free SAT Math questions available online, so memorize your terms and then practice on realistic SAT word problems to make sure you’ve got your definitions down and can apply them to the actual test.

#3: Underline and/or Write Out Important Information

The key to solving a word problem is to bring together all the key pieces of given information and put them in the right places. Make sure you write out all these givens on the diagram you’ve drawn (if the problem calls for a diagram) so that all your moving pieces are in order.

One of the best ways to keep all your pieces straight is to underline your key information in the problem, and then write them out yourself before you set up your equation. So take a moment to perform this step before you zero in on solving the question.

#4: Pay Close Attention to What’s Being Asked

It can be infuriating to find yourself solving for the wrong variable or writing in your given values in the wrong places. And yet this is entirely too easy to do when working with math word problems.

Make sure you pay strict attention to exactly what you’re meant to be solving for and exactly what pieces of information go where. Are you looking for the area or the perimeter? The value of x, 2x, or y?

It’s always better to double-check what you’re supposed to find before you start than to realize two minutes down the line that you have to begin solving the problem all over again.

#5: Brush Up on Any Specific Math Topic You Feel Weak In

You’re likely to see both a diagram/equation problem and a word problem for almost every SAT Math topic on the test. This is why there are so many different types of word problems and why you’ll need to know the ins and outs of every SAT Math topic in order to be able to solve a word problem about it.

For example, if you don’t know how to find an average given a set of numbers, you certainly won’t know how to solve a word problem that deals with averages!

Understand that solving an SAT Math word problem is a two-step process: it requires you to both understand how word problems work and to understand the math topic in question. If you have any areas of mathematical weakness, now’s a good time to brush up on them—or else SAT word problems might be trickier than you were expecting!

All set? Let’s go!

Test Your SAT Math Word Problem Knowledge

Finally, it’s time to test your word problem know-how against real SAT Math problems:

Word Problems

1. No Calculator

2. Calculator OK

3. Calculator OK

4. Calculator OK

Answers: C, B, A, 1160

Answer Explanations

1. For this problem, we have to use the information we’re given to set up an equation.

We know that Ken spent x dollars, and Paul spent 1 dollar more than Ken did. Therefore, we can write the following equation for Paul:

x + 1

Ken and Paul split the bill evenly. This means that we’ll have to solve for the total amount of both their sandwiches and then divide it by 2. Since Ken’s sandwich cost x dollars and Paul’s cost x + 1, here’s what our equation looks like when we combine the two expressions:

x + x + 1

2x + 1

Now, we can divide this expression by 2 to get the price each person paid:

(2x + 1) / 2

x + 0.5

But we’re not finished yet. We know that both Ken and Paul also paid a 20% tip on their bills. As a result, we have to multiply the total cost of one bill by 0.2, and then add this tip to the bill. Algebraically, this looks like this:

(x + 0.5) + 0.2(x + 0.5)

x + 0.5 + 0.2x + 0.1

1.2x + 0.6

The correct answer choice is (C) 1.2x + 0.6

2. You’ll have to be familiar with statistics in order to understand what this question is asking.

Since Nick surveyed a random sample of his freshman class, we can say that this sample will accurately reflect the opinion (and thus the same percentages) as the entire freshman class.

Of the 90 freshmen sampled, 25.6% said that they wanted the Fall Festival held in October. All we have to do now is find this percentage of the entire freshmen class (which consists of 225 students) to determine how many total freshmen would prefer an October festival:

225 * 0.256 = 57.6

Since the question is asking «about how many students»—and since we obviously can’t have a fraction of a person!—we’ll have to round this number to the nearest answer choice available, which is 60, or answer choice (B).

3. This is one of those problems that is asking you to define a value in the equation given. It might look confusing, but don’t be scared—it’s actually not as difficult as it appears!

First off, we know that t represents the number of seconds passed after an object is launched upward. But what if no time has passed yet? This would mean that t = 0. Here’s what happens to the equation when we plug in 0 for t:

h(0) = -16(0)2 + 110(0) + 72

h(0) = 0 + 0 + 72

h(0) = 72

As we can see, before the object is even launched, it has a height of 72 feet. This means that 72 must represent the initial height, in feet, of the object, or answer choice (A).

4. You might be tempted to draw a diagram for this problem since it’s talking about a pool (rectangle), but it’s actually quicker to just look at the numbers given and work from there.

We know that the pool currently holds 600 gallons of water and that water has been hosed into it at a rate of 8 gallons a minute for a total of 70 minutes.

To find the amount of water in the pool now, we’ll have to first solve for the amount of water added to the pool by hose. We know that 8 gallons were added each minute for 70 minutes, so all we have to do is multiply 8 by 70:

8 * 70 = 560 gallons

This tells us that 560 gallons of water were added to our already-filled, 600-gallon pool. To find the total amount of water, then, we simply add these two numbers together:

560 + 600 = 1160

The correct answer is 1160.

Aaaaaaaaaaand time for a nap.

Key Takeaways: Making Sense of SAT Math Word Problems

Word problems make up a significant portion of the SAT Math section, so it’s a good idea to understand how they work and how to translate the words on the page into a proper expression or equation. But this is still only half the battle.

Though you won’t know how to solve a word problem if you don’t know what a product is or how to draw a right triangle, you also won’t know how to solve a word problem about ratios if you don’t know how ratios work.

Therefore, be sure to learn not only how to approach math word problems as a whole, but also how to narrow your focus on any SAT Math topics you need help with. You can find links to all of our SAT Math topic guides here to help you in your studies.

What’s Next?

Want to brush up on SAT Math topics? Check out our individual math guides to get an overview of each and every topic on SAT Math. From polygons and slopes to probabilities and sequences, we’ve got you covered!

Running out of time on the SAT Math section? We have the know-how to help you beat the clock and maximize your score.

Been procrastinating on your SAT studying? Learn how you can overcome your desire to procrastinate and make a well-balanced prep plan.

Trying to get a perfect SAT score? Take a look at our guide to getting a perfect 800 on SAT Math, written by a perfect scorer.

Want to improve your SAT score by 160 points?

Check out our best-in-class online SAT prep program. We guarantee your money back if you don’t improve your SAT score by 160 points or more.

Our program is entirely online, and it customizes what you study to your strengths and weaknesses. If you liked this Math strategy guide, you’ll love our program. Along with more detailed lessons, you’ll get thousands of practice problems organized by individual skills so you learn most effectively. We’ll also give you a step-by-step program to follow so you’ll never be confused about what to study next.

Check out our 5-day free trial:

Have friends who also need help with test prep? Share this article!

About the Author

Courtney scored in the 99th percentile on the SAT in high school and went on to graduate from Stanford University with a degree in Cultural and Social Anthropology. She is passionate about bringing education and the tools to succeed to students from all backgrounds and walks of life, as she believes open education is one of the great societal equalizers. She has years of tutoring experience and writes creative works in her free time.

Источник

Most people have heard of word problems, but not as many have heard of the word problem. If you’re imagining that the word problem is some superlatively awful word problem, I can assure you it’s not. It’s both simpler and weirder than that.

The word problem is essentially about whether you can always apply algebraic rules in an automated way. The reason it is called the word problem is that you start by a description of your algebraic system in terms of symbols (“letters”) and concatenations of symbols (“words”) subject to certain rules, also called relations.

The word problem for groups

For example, you can describe a group by saying it contains a and b, and it satisfies the relations

a² = b²

and

a^-1ba = b^-1.

A couple things are implicit here. We’ve said this a group, and since every element in a group has an inverse, we’ve implied that a^-1 and b^-1 are in the group as well. Also from the definition of a group comes the assumption that multiplication is associative, that there’s an identity element, and that inverses work like they’re supposed to.

In the example above, you could derive everything about the group from the information given. In particular, someone could give you two words—strings made up of a, b, a^-1, and b^-1—and you could determine whether they are equal by applying the rules. But in general, this is not possible for groups.

Undecidable

The bad news is that in general this isn’t possible. In computer science terminology, the word problem is undecidable. There is no algorithm that can tell whether two words are equal given a list of relations, at least not in general. There are special cases where the word problem is solvable, but a general algorithm is not possible.

The word problem for semigroups

I presented the word problem above in the context of groups, but you could look at the word problem in more general contexts, such as semigroups. A semigroup is closed under some associative binary operation, and that’s it. There need not be any inverses or even an identity element.

Here’s a concrete example of a semigroup whose word problem has been proven to be undecidable. As before we have two symbols, a and b. And because we are in a semigroup, not a group, there are no inverses. Our semigroup consists of all finite sequences make out of a‘s and b‘s, subject to these five relations.

aba²b² = b²a²ba

a²bab²a = b²a³ba

aba³b² = ab²aba²

b³a²b²a²ba = b³a²b²a⁴

a⁴b²a²ba = b²a⁴

Source: Term Rewriting and All That

Experience

When I first saw groups presented this as symbols and relations, I got my hopes up that a large swath of group theory could be automated. A few minutes later my naive hopes were dashed. So in my mind I thought “Well, then this is hopeless.”

But that is not true. Sometimes the word problem is solvable. It’s like many other impossibility theorems. There’s no fifth degree analog of the quadratic equation in general, but there are fifth degree polynomials whose roots can be found in closed form. There’s no program that can tell whether any arbitrary program will halt, but that doesn’t mean you can’t tell whether some programs halt.

It didn’t occur to me at the time that it would be worthwhile to explore the boundaries, learning which word problems can or cannot be solved. It also didn’t occur to me that I would run into things like the word problem in practical applications, such as simplifying symbolic expressions and optimizing their evaluation. Undecidable problems lurk everywhere, but you can often step around them.

Источник

Скачать материал

Сейчас обучается 396 человек из 63 регионов

Описание презентации по отдельным слайдам:

1 слайд

GRAMMATICAL MEANING
OF THE WORD
2 слайд

1. The problem of word definition.
2. The notion of the word-form.
3. The notion of «grammatical meaning».
4. Types of grammatical meaning.
5. The notion of «grammatical category».
6. The notion of «opposition».

3
3 слайд

1.The Problem of Word Definition

The word is considered to be the central (though not the only) linguistic unit of language.
3
4 слайд

The Problem of Word Definition

In the written language words are clearly identified by spaces between them.

3
5 слайд

The Problem of Word Definition

In the spoken language the problem cannot be solved this way.
↓
If we listen to an unfamiliar language, we find it difficult to divide up the speech into single words.

3
6 слайд

The Problem of Word Definition

Approaches
to the problem of word definition:
the word is a semantic unit, a unit of meaning;
the word is a marked phonological unit;
the word is an indivisible unit.

3
7 слайд

The Problem of Word Definition

Semantic definition of the word:
“…a unit of a particular meaning with a particular complex of sounds capable of a particular grammatical employment».
↓
The word is a linguistic unit that has a single meaning.

3
8 слайд

The Problem of Word Definition

BUT:

heavy smoker ≠ heavy and
smoker
criminal lawyer;
the King of England’s hat.

3
9 слайд

The Problem of Word Definition

The problem:

the word is not always a single unit.

3
10 слайд

The Problem of Word Definition

A phonological criterion

that stuff that’s tough
a nice cakean ice cake
grey day Grade A
↓

3
11 слайд

The Problem of Word Definition

It is hard to distinguish the real meaning without a proper context.
3
12 слайд

The Problem of Word Definition

The word as an indivisible unit

“The word is a minimum free form“
(L. Bloomfield)
↓
The word is the smallest unit of speech that can occur in isolation.

3
13 слайд

The Problem of Word Definition

BUT:
a or the

3
14 слайд

The Problem of Word Definition

Thus,
the word is a linguistic unit larger than a morpheme but smaller than a phrase.

3
15 слайд

The Problem of Word Definition

In this case the word can be defined as:

• An orthographic word (something written with white spaces at both ends but no white space in the middle).

3
16 слайд

The Problem of Word Definition

• A phonological word (something pronounced as a single unit).

3
17 слайд

The Problem of Word Definition

• A lexical item, or lexeme, (a dictionary word).

3
18 слайд

The Problem of Word Definition

• A grammatical word-form (GWF) (or morphosyntactic word) (any one of the several forms which a lexical item may assume for grammatical purposes).

3
19 слайд

The Problem of Word Definition

The item ice cream is:
two orthographic words,
but
— a single phonological word (it is pronounced as a unit),
— a single lexical item (it has its own entry in a dictionary),
— a single GWF (indeed, it hardly has another form unless you think the plural ice cream is good English).

3
20 слайд

The Problem of Word Definition

The singular dog and the plural dogs:
— a single orthographic word,
— a single phonological word,
a single GWF,
but they both
— represent the same lexical item (only one entry in the dictionary).

3
21 слайд

The Problem of Word Definition

???
take, takes, took, taken, is taking:

3
22 слайд

The Problem of Word Definition

take, takes, took, taken and is taking:

— five orthographic words,
— five phonological words,
five GWFs (at least),
but only
— one lexical item.

3
23 слайд

The Problem of Word Definition

???
the contraction hasn’t

3
24 слайд

The Problem of Word Definition

The contraction hasn’t is:

— a single orthographic word,
a single phonological word,
— two lexical items (have and not),
— two GWFs (has and not).

3
25 слайд

The Problem of Word Definition

???
The phrasal verb make up (as in She made up her face)

3
26 слайд

The Problem of Word Definition

The phrasal verb make up (as in She made up her face):
— two orthographic words,
— two phonological words,
— one lexical item (because of its unpredictable meaning, it must be entered separately in the dictionary).
— has several GWFs (make up, makes up, made up, making up).

3
27 слайд

The Problem of Word Definition

???
make up
(She made up a story)

3
28 слайд

The Problem of Word Definition

make up (She made up a story):
— a different lexical item from the preceding one (a separate dictionary entry is required),
but
— this lexical item exhibits the same orthographic, phonological and grammatical forms as the first.

3
29 слайд

The Problem of Word Definition

So,
the word is not a clearly definable linguistic unit.

3
30 слайд

The Problem of Word Definition

For the sake of linguistic description, we will proceed from the following statements:
— the word is a meaningful unit differentiating word-groups at the upper level and integrating morphemes at the lower level;

3
31 слайд

The Problem of Word Definition

— the word is the main expressive unit of human language, which ensures the thought-forming function of language;

3
32 слайд

The Problem of Word Definition

the word It is also the basic nominative unit of language with the help of which the naming function of language is realized;

3
33 слайд

The Problem of Word Definition

in the structure of language the word belongs to the upper stage of the morphological level;

3
34 слайд

The Problem of Word Definition

the word is a unit of the sphere of «language» and it exists only through its speech actualization;

3
35 слайд

The Problem of Word Definition

one of the most characteristic features of the word is its indivisibility.

3
36 слайд

The Problem of Word Definition

the word is a bilateral entity

concept
WORD = ———————
sound image

3
37 слайд

2. The Notion of the Word -Form

The term «word-form“ shows that the word is a carrier of grammatical information.
E.g.: speaks — the present tense third
person singular
speak, spoke, is speaking
↓
Here the relational property of grammatical meaning is revealed.

3
38 слайд

The Notion of the Word -Form

Grammatical meanings of a word-form are very abstract and general.
They are peculiar of a whole class of words, unite it so that each word of the class expresses the corresponding grammatical meaning together with its individual, concrete semantics.

3
39 слайд

The Notion of the Word -Form

E.g.:
the meaning of the plural is rendered by the regular plural suffix –(e)s, phonemic interchange and a few lexeme-bound suffixes.

3
40 слайд

The Notion of the Word -Form

Due to the generalized character of the plural, we say that different groups of nouns «take» this form with strictly defined variations in the mode of expression.
The variations can be of more systemic (phonological conditioning) and less systemic (etymological conditioning) nature.

3
41 слайд

The Notion of the Word -Form

Cf.: faces, branches, matches, judges;
books, rockets, boats, chiefs, proofs;
dogs, beads, films, stones, hens;
lives, wives, thieves, leaves;
oxen, children, brethren;
swine, sheep, deer;
men, women, feet, teeth, geese, mice, lice;
formulae, antennae;
data, errata, strata, addenda, memoranda;
radii, genii, nuclei;
crises, bases, analyses, axes;
phenomena, criteria.

3
42 слайд

The Notion of the Word -Form

The lexical meaning of the word is irrelevant for the detection of the type of the word-form.

3
43 слайд

The Notion of the Word -Form

A word-form may be analytical by structure. In this case it is equivalent to one word as it expresses one unified content of a word, both from the point of view of grammatical and lexical meaning.
E.g.: has spoken

3
44 слайд

The Notion of the Word -Form

Words (as well as morphemes) are directly observable units by nature as they are characterized by a definite material structure of their own.

They can be registered and enumerated in any language.

3
45 слайд

The Notion of the Word -Form

The system of morphological units is a closed system. It means that all its items are on the surface and can be embraced in an inventory of forms.

3
46 слайд

The Notion of the Word -Form

Every word is a unit of grammar as a part of speech.

3
47 слайд

The Notion of the Word -Form

Parts of speech are usually considered a lexico-grammatical categories since:
they show lexical groupings of words;
these groupings present generalized classes, each with a unified, abstract meaning of its own.

3
48 слайд

3. The Notion of Grammatical Meaning

Notional words combine two meanings in their semantic structure:
lexical;
grammatical.

3
49 слайд

The Notion of Grammatical Meaning
Lexical meaning is the individual meaning of the word
E.g.: table — a definite piece of furniture with a flat top supported by one or more upright legs,
speak – to express thoughts aloud, using the voice.

3
50 слайд

The Notion of Grammatical Meaning
Grammatical (morphological) meaning is not individual.
↓
It is the meaning of the whole class or a subclass
E.g.: table (grammatical meaning of the class of nouns (thingness / substance) and the grammatical meaning of a subclass – countableness).

3
51 слайд

?

What are grammatical meanings of:
— verbs;
adjectives;
adverbs?

3
52 слайд

The Notion of Grammatical Meaning

There are some classes of words that are devoid of any lexical meaning and possess the grammatical meaning only.

3
54 слайд

The Notion of Grammatical Meaning

Function words

3
55 слайд

4.Types of Grammatical Meaning

The grammatical meaning may be:

explicit;
implicit.
3
56 слайд

Types of Grammatical Meaning
The implicit grammatical meaning is not expressed formally

E.g.: table (the meaning of inanimate object)

3
57 слайд

Types of Grammatical Meaning
The explicit grammatical meaning is always marked morphologically
E.g.: -s in cats (the grammatical meaning of plurality);
‘s in cat’s (the grammatical meaning of possessiveness);
is …ed in is asked (the grammatical meaning of passiveness)

3
58 слайд

Types of Grammatical Meaning
Types of the implicit grammatical meaning:
general
dependent

3
59 слайд

Types of Grammatical Meaning
general (the meaning of the whole word-class, of a part of speech)
E.g.: thingness of nouns

3
60 слайд

Types of Grammatical Meaning
dependent (the meaning of a subclass within the same part of speech)
E.g.: the verb (transitivity/ intransitivity,
terminativeness / non-terminativeness,
stativeness / non-stativeness);
the noun (countableness / uncountableness,
animateness / inanimateness)

3
61 слайд

Types of Grammatical Meaning
The dependent grammatical meaning influences the realization of grammatical categories restricting them to a subclass.
E.g.: the number category for the subclass of countable nouns;
the category of case for the subclass of animated nouns;
the category of voice for transitive verbs, etc.

3
62 слайд

Types of Grammatical Meaning

3
63 слайд

5. The Notion of Grammatical Category

A grammatical category is a linguistic category which has the effect of modifying the forms of some class of words in a language.

3
64 слайд

The Notion of Grammatical Category
Its structure displays two or more forms applied to a definite class of words and used in somewhat different grammatical circumstances.
↓↓

3
65 слайд

The Notion of Grammatical Category
Grammatical categories are made up by the unity of identical grammatical meanings that have the same form and meaning
E.g. singular : plural

3
66 слайд

The Notion of Grammatical Category
Due to dialectal unity of language and thought, grammatical categories correlate, on the one hand, with the conceptual categories and, on the other hand, with the objective reality:

3
67 слайд

The Notion of Grammatical Category
Thus,
grammatical categories are references of the corresponding objective categories.
E.g.: the objective category of time →
the grammatical category of tense,
the objective category of quantity → the grammatical category of number.

3
68 слайд

The Notion of Grammatical Category

Grammatical categories that have references in the objective reality are referential.
Objective correlate
↓
Lingual correlate

3
69 слайд

The Notion of Grammatical Category
Grammatical categories that do not correspond to anything in the objective reality and correlate only with conceptual matters are significational. They are few (e.g. the categories of mood and degree).
Conceptual correlate
↓
Lingual correlate

3
70 слайд

The Notion of Grammatical Category
Classifications of Gr. Categories

According to the referent relation:
immanent;
— reflective.
3
71 слайд

The Notion of Grammatical Category
Immanent gr. categories are:
1) innate for a given lexemic class, organically connected with its functional nature
E.g.: the number category of nouns,
the substantive-pronominal person
2) closed within a word-class
E.g.: the tense category of verbs,
the comparison of adjectives and adverbs

3
72 слайд

The Notion of Grammatical Category

Reflective gr. categories are of a secondary, derivative semantic value
E.g.: the number category of verbs,
the verbal person

3
73 слайд

The Notion of Grammatical Category
2. According to the changeability of the exposed feature
— unchangeable / derivational (constant feature categories)
E.g.: the gender category of nouns represented by the system of the 3rd person pronouns
— changeable / demutative (variable feature categories)
E.g.: the number category of nouns,
the degrees of comparison

3
74 слайд

The Notion of Grammatical Category

NB:
1. The notion of grammatical category applies to the plane of content of morphological paradigmatic units;

3
75 слайд

The Notion of Grammatical Category

2. It refers to grammatical meaning as a general notion;

3
76 слайд

The Notion of Grammatical Category

3. It does not nominate things but expresses relations, that is why it has to be studied in terms of oppositions;

3
77 слайд

The Notion of Grammatical Category

4. Grammatical categories of language represent a realization of universal categories produced by human thinking in a set of interrelated forms organized as oppositions;

3
78 слайд

The Notion of Grammatical Category

5. Grammatical categories are not uniform, they vary in accordance with the part of speech they belong to and the meaning they express;

3
79 слайд

The Notion of Grammatical Category

6. The expression of grammatical categories in language is based upon close interrelation between their forms and the meaning they convey.

3
80 слайд

6. The Notion of Opposition

The concept of opposition is that it distinguishes something.

↓
3
81 слайд

The Notion of Opposition
One thing can be distinguished from another only if it can be contrasted with something else or opposed to it.

3
82 слайд

The Notion of Opposition

Any grammatical category must be represented by at least two grammatical forms
E.g. the grammatical category of number: singular and plural forms.

3
83 слайд

The Notion of Opposition
Thus,
the relation between two grammatical forms that differ in meaning and external signs is called opposition.

3
84 слайд

The Notion of Opposition
The most widely known opposition is the binary «privative» opposition.

In it one member of the contrastive pair is characterized by the presence of a certain feature which the other member lacks

3
85 слайд

The Notion of Opposition
E.g. table::tables
↓ ↓
“unmarked” “marked”
(weak) member (strong) member
↓ ↓
non-plural plural
↓ ↓
more general and abstract more particular and
concrete
(used in a wider range of contexts)

3
86 слайд

The Notion of Opposition
FYI:
Some scholars, however, hold the opinion that oppositions can be
gradual (different degree of a feature)
E.g.: big — bigger — biggest
equipollent (different positive features)
E.g.: am — is — are.

3
87 слайд

The Notion of Opposition

NB:
A grammatical category is definable only on the basis of oppositions.

3
88 слайд

The Notion of Opposition

Means of realization of grammatical categories:
synthetic (near — nearer);
analytical (beautiful — more beautiful).

3

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 209 409 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

27.12.2020
4744
2

27.12.2020
4946
11

27.12.2020
5785
13

27.12.2020
5022
9

27.12.2020
4057
1

27.12.2020
3882
0

27.12.2020
3905
1

27.12.2020
3300
4

Вам будут интересны эти курсы:

Курс повышения квалификации «Основы местного самоуправления и муниципальной службы»
Курс профессиональной переподготовки «Организация и предоставление туристских услуг»
Курс профессиональной переподготовки «Клиническая психология: организация реабилитационной работы в социальной сфере»
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС педагогических направлений подготовки»
Курс повышения квалификации «Этика делового общения»
Курс повышения квалификации «Маркетинг в организации как средство привлечения новых клиентов»
Курс повышения квалификации «Правовое регулирование рекламной и PR-деятельности»
Курс повышения квалификации «Финансы предприятия: актуальные аспекты в оценке стоимости бизнеса»
Курс профессиональной переподготовки «Управление ресурсами информационных технологий»
Курс профессиональной переподготовки «Организация деятельности помощника-референта руководителя со знанием иностранных языков»
Курс профессиональной переподготовки «Организация деятельности секретаря руководителя со знанием английского языка»
Курс профессиональной переподготовки «Управление сервисами информационных технологий»
Курс профессиональной переподготовки «Эксплуатация и обслуживание общего имущества многоквартирного дома»
Курс профессиональной переподготовки «Техническая диагностика и контроль технического состояния автотранспортных средств»
Курс профессиональной переподготовки «Организация маркетинговой деятельности»

Источник

Word problems are a special kind of math challenge. Not only do they require computation skills, but they also test students’ reading comprehension and problem-solving abilities. This can be the perfect storm of frustration for many kids. But it doesn’t have to be so hard! Today, I’m sharing easy strategies for helping students master the word problem!

Start With Reading Comprehension

The first step in conquering word problems goes right back to good ol’ reading comprehension. Kids have a bad habit of reading word problems like they are just passing through words to get to the numbers. Blah, blah, blah. 127! Blah, blah, blah, 52! They search for numbers and then rush to DO something with those numbers.

If our students are going to find success with word problems, they need to use their good reading strategies! Teach your students to:

Reread: Slow down and reread as many times as needed

Visualize: Imagine what is taking place in the problem. What is the order of events?

Ask questions: What do I know? What do I need to find out?

Make predictions: What would be a reasonable result? Do I expect the answer to be more or less than the numbers I’m given?

Teach a Problem-Solving Routine

Help students form effective thinking habits by teaching and practicing a problem-solving process. I’m not talking about a rote set of steps like CUBES (Circle the numbers, Underline the question, Box key words, etc.). I’m talking about a THINKING routine that helps the child learn the critical thinking skills involved in solving real problems.

I’ve found a simple PLAN, SOLVE, CHECK format works best. With young children, the biggest issue I find is that they simply skip (or struggle with) one of these steps, which causes a breakdown in their ability to solve the problem. In fact, I form my guided math groups for word problems around those three categories (planning strategies, solving strategies, checking strategies.) **You can grab a FREE Word Problem Thinking Mat in the Preview File of my Tiered Word Problems Pack.

Compare Problem Structures

One of my favorite word problem teaching tools is something I call “Side-by-Sides.” This is simply where we solve two different problems and then compare the structure of the problem and the operation used.

When students model, solve, and discuss the different problem types, they grow a deeper understanding of how word problems work.

**You can grab FREE samples of side-by-side problems in the Preview File of my Side-by-Side Word Problems Pack or grab a FREE Side-by-Side Mat in the Preview File of my Tiered Word Problems Pack for 2nd Grade or 3rd Grade.

Example of Word Problem Comparison on Side-by-Side Mat (Click to view Side-by-Side Pack and grab your FREE mat in the Preview File.)

Start With the Easy Version

Differentiation isn’t just for reading! Many students get overwhelmed when they see large numbers in word problems, so why not meet them where they are? I use what I call “Tiered Word Problems” to help students understand word problem structures and grow confidence before tackling the on-level version.

In my Word Problem Solving Bundle, I provide all kinds of leveled word problems – Tiered Problem Pages, Task Cards, Exit Tickets, and more, that all increase in challenge from first through fifth grade. This allows me to scaffold instruction by student need, and throughout the school year.

**You can grab free goodies and sample pages from the Bundle in the Word Problem Solving Bundle Sampler Pack.

Example of Tiered Word Problems from my Addition and Subtraction Word Problem Pack (Click to learn more or download free samples pages.)

Use Problem-Solving Rounds

Problem-Solving Rounds changed math instruction in my classroom forever! This powerful routine encourages students to move through the problem-solving process I mentioned at the beginning of this post, to explain their thinking, and to reflect on other possible strategies and solutions.

Since using Problem-Solving Rounds, my students are more confident with word problems, have a deeper understanding of problem-types, and are better able to tackle new and challenging tasks.

The basic structure of the rounds follows the Problem-Solving Process I’ve shared. In Round 1, students read and discuss the problem with a focus on UNDERSTANDING. In Round 2, they turn to a partner and explain how they PLAN to solve the problem. They SOLVE the problem independently in Round 3, and in Round 4 they work with a partner and as a whole class to CHECK and reflect on their work. For a detailed guide to this process, check out my blog post all about Problem-Solving Rounds.

I’d love to hear from you! Comment below with your favorite word problem tips for teachers!

Источник