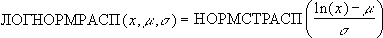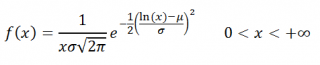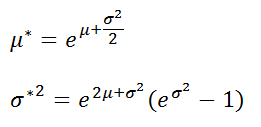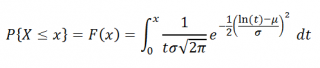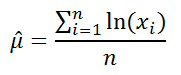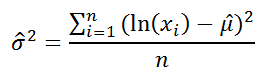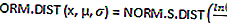Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ЛОГНОРМРАСП в Microsoft Excel.
Описание
Возвращает интегральное логнормальное распределение для x, где ln(x) является нормально распределенным с параметрами «среднее» и «стандартное_откл». Эта функция используется для анализа данных, которые были логарифмически преобразованы.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новом варианте этой функции см. в статье Функция ЛОГНОРМ.РАСП.
Синтаксис
ЛОГНОРМРАСП(x;среднее;стандартное_откл)
Аргументы функции ЛОГНОРМРАСП описаны ниже.
-
X — обязательный аргумент. Значение, для которого вычисляется функция.
-
Среднее Обязательный. Среднее ln(x).
-
Стандартное_отклонение Обязательный. Стандартное отклонение ln(x).
Замечания
-
Если какой-либо из аргументов не является числом, ЛОГНОРМДРАП возвращает #VALUE! значение ошибки.
-
Если x ≤ 0 или Standard_dev ≤ 0, то ЛОГНОРМIST возвращает #NUM! значение ошибки.
-
Уравнение для функции интегрального логарифмического нормального распределения имеет следующий вид:
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|
4 |
Значение, для которого рассчитывается функция (x) |
|
|
3,5 |
Среднее ln(x) |
|
|
1,2 |
Стандартное отклонение ln(x) |
|
|
Формула |
Описание |
Результат |
|
=ЛОГНОРМРАСП(A2;A3;A4) |
Интегральное логнормальное распределение при значении 4 в соответствии с приведенными выше условиями |
0,0390836 |
Нужна дополнительная помощь?
Рассмотрим Логнормальное распределение. С помощью функции MS EXCEL
ЛОГНОРМ
.РАСП()
построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел, распределенных по логнормальному закону, произведем оценку параметров распределения, среднего значения и стандартного отклонения.
Если случайная величина Х имеет
логнормальное распределение
(англ.
Lognormal
distribution
)
, то её логарифм Y=LN(X) имеет
нормальное распределение
. Справедливо и обратное утверждение: если случайная величина Y имеет
нормальное распределение
, то случайная величина X=EXP(Y) имеет
логнормальное распределение
. Из свойства логарифма следует, что X>0.
Сначала рассмотрим связь между
нормальным
и
логнормальным
распределениями.
Как известно,
нормальное распределение
чаще всего рассматривается как подходящая модель для описания такого процесса, когда действует большое число независимых случайных причин. Например, при производстве кускового мыла, вес каждого куска немного отличается от заданного в силу множества случайных причин, действующих на процесс: колебания температуры, состава исходного сырья, скачки напряжения на оборудовании и др. В этом случае плотность распределения случайной величины «вес мыла» имеет симметричную, колоколообразную форму.
Однако, в некоторых случаях наблюдения показывают, что случайная величина имеет заметно скошенное (несимметричное) распределение (см. раздел
Ассиметричность
в статье
Описательная статистика в MS EXCEL
), и, соответственно, не может быть описана
нормальным распределением
.
Скошенные распределения
имеют место когда, случайные величины не могут быть отрицательными или имеется другая естественная граница (не может быть меньше определенного значения).
Логнормальное распределение
является одним из примеров
скошенного распределения
.
В чем же состоит различие в процессах, приводящих к
нормальному
или
логнормальному
распределениям? Оба распределения имеют место, когда на описываемый объект воздействует множество случайных и независимых факторов. Если воздействия каждого из факторов складываются, т.е. имеется аддитивный характер их взаимодействия, то имеет место
нормальное распределение
(см. статью про
Центральную предельную теорему
).
Если воздействия каждого из факторов не складываются, а перемножаются, т.е. имеется мультипликативный характер взаимодействия, что часто соответствует
Логнормальному распределению.
Факторы также независимы как и в случае нормального распределения, но эффект от их воздействия накапливается в объекте в зависимости от предыдущего их количества.
Чтобы это пояснить, рассмотрим процесс износа подшипника. Понимание физического процесса позволит построить адекватную статистическую модель (распределение) и, в данном случае, оценить средний срок его работы до поломки.
Износ подшипника происходит из-за множества случайных независимых факторов: несовершенства формы шариков подшипника, внешних ударов, попадания грязи и пр. Пусть в определенный момент происходит случайное событие, например, удар, который приводит к микродефекту внешнего кольца удерживающего шарики, но поломка подшипника еще не происходит. Понятно, что с деформированным кольцом разрушение подшипника ускорится (например, за счет повышенного истирания). Теперь рассмотрим два вида взаимодействия воздействующих факторов: аддитивный и мультипликативный.
В первом случае, считается, что микродефекты просто складываются и поломка подшипника происходит при превышении некого порогового их воздействия (суммирование микродефектов). Т.е. в этой модели не учитывается, что каждый последующий микродефект воздействует уже не на новый подшипник, а на поврежденный.
Во втором случае (мультипликативное взаимодействие),
каждый последующий микродефект воздействует на подшипник пропорционально его текущему состоянию.
Т.е. одно и тоже воздействие будет приводить к разным последствиям (дефектам) в случае нового или уже поврежденного подшипника.
Как было сказано выше, модель аддитивного взаимодействия случайных факторов приводит к
нормальному распределению
(в данном случае она не применима для оценки срока работы подшипника). В нашем случае более адекватной моделью является модель мультипликативного взаимодействия, когда учитывается не только случайное воздействие фактора, но и состояние самой системы, на которую действует фактор. Мультипликативный эффект от всех случайных независимых воздействий на подшипник аккумулируется до тех пор пока не произойдет его разрушение.
Попытаемся вышесказанное изложить с помощью формул. По аналогии с
ЦПТ
и учитывая свойство логарифма
LN
(
x
1*
x
2*…*
xn
)=
LN
(
x
1)+
LN
(
x
2)+…
+LN(x
n
)
, можно предположить, что если x1, x2, x3, … xn – случайные независимые величины, и
y
=
x
1*
x
2*
x
3* … *
xn
, то случайная величина LN(y) будет распределена по
нормальному закону
. Если это условие выполняется, т.е.
LN
(
y
)
~
N
(μ;σ)
, то
y
имеет
логнормальное распределение
с параметрами μ и
σ
.
Примерами, когда имеет место
логнормальное распределение
могут служить следующие ситуации:
- сбой из-за химических реакций или деградации, таких как коррозия или диффузия, которые являются частой причиной отказа полупроводникового элемента;
- время до разрушения в металлах при условии роста усталостных трещин.
Ниже приведена функция плотности
логнормального распределения
:
СОВЕТ
: Подробнее о
Функции распределения
и
Плотности вероятности
см. статью
Функция распределения и плотность вероятности в MS EXCEL
.
Обратите внимание, что хотя μ и
σ
являются параметрами распределения, они НЕ являются
средним значением
(обозначим как μ*) и
стандартным отклонением
(
σ
*) этого распределения (как у
нормального распределения
).
Ниже приведены формулы для расчета
среднего
и
стандартного отклонения логнормального распределения
.
Примечание
: μ и
σ
являются параметрами
нормального распределения
LN(y) и, соответственно, его
средним
и
стандартным отклонением
.
Логнормальное распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для
Логнормального распределения
имеется функция
ЛОГНОРМ.РАСП()
, английское название — LOGNORM.DIST(), которая позволяет вычислить плотность вероятности (см. формулу выше) и
интегральную функцию распределения
(вероятность, что случайная величина X, распределенная по
логнормальному закону
, примет значение меньше или равное x). Вычисления в последнем случае производятся по следующей формуле:
Логнормальное распределение
имеет обозначение Ln
N
(μ;
σ
).
Примечание
: До MS EXCEL 2010 в EXCEL была функция
ЛОГНОРМРАСП()
, которая также позволяет вычислить
кумулятивную (интегральную) функцию распределения
, но не позволяет вычислить
плотность вероятности
.
ЛОГНОРМРАСП()
оставлена в MS EXCEL 2010 для совместимости. В
файле примера на листе Пример
приведены несколько альтернативных формул для вычисления
плотности вероятности
и
интегральной функции распределения
(использованы функции
НОРМ.СТ.РАСП()
и
НОРМ.РАСП()
.
Примечание
: Для удобства написания формул в
файле примера
созданы
Имена
для параметровраспределения: μ и
σ
.
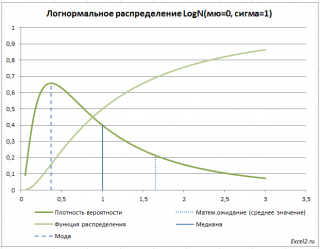
Графики функций
В
файле примера
приведены графики
плотности распределения вероятности
и
интегральной функции распределения
.
Примечание
: Для построения
функции распределения
и
плотности вероятности
можно использовать диаграмму типа
График
или
Точечная
(со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью
Основные типы диаграмм
.
Генерация случайных чисел
Для генерирования массива чисел, распределенных по
логнормальному закону
, можно использовать формулу
=ЛОГНОРМ.ОБР(СЛЧИС();μ;
σ
)
. Функция
СЛЧИС()
генерирует
непрерывное равномерное распределение
от 0 до 1, что как раз соответствует диапазону изменения вероятности (см.
файл примера лист Генерация
).
Оценку для μ (μ — параметр распределения, но не
среднее
) можно сделать с использованием формулы:
или с помощью формулы
=LN(СРГЕОМ(B16:B215))
, если значения массива размещены в диапазоне
B16:B215
.
Оценку для
σ
(
σ
— параметр распределения, но не
стандартное отклонение
) можно сделать с использованием формулы:
Задачи
Задача1.
Время жизни лазера имеет логнормальное распределение с μ=5 и
σ
=1 час. Какова вероятность того, что лазер проработает >400 часов?
Из определения
интегральной функции распределения
вычислим вероятность того, что лазер проработает меньше 400 часов. Это можно вычислить с помощью формулы (см.
файл примера лист Задачи
):
=ЛОГНОРМ.РАСП(400;5;1;ИСТИНА)=0,16
Тоже значение получим из формулы
=НОРМ.РАСП(LN(400);5;1;ИСТИНА)
Теперь найдем вероятность того, что лазер проработает больше 400 часов:
=1- ЛОГНОРМ.РАСП(400;5;1;ИСТИНА)
Задача2.
Учитывая условие Задачи1, вычислить какой срок жизни будет у 99% лазеров?
Если совокупность лазеров достаточно велика, то можно считать, что вопрос «
Какой срок жизни
x
будет у 99% лазеров?
» эквивалентен вопросу «
Какой срок жизни
x
будет у случайно взятого лазера с вероятностью 99%?
», т.е. вероятность, того что X>
x
равна 99%, где Х – случайная величина, соответствующая времени жизни лазера. Другими словами, после прошествия какого периода времени можно будет с уверенностью 99% сказать, что лазер еще работает. Здесь удобно перейти к дополнительному событию: вероятности того, что лазер сломается. Таким образом, в задаче нам необходимо вычислить значение
х
(время жизни), при котором 1% (1-99%) лазеров сломается, т.е. X<
x
.
Как и в предыдущей задаче, для формулировки условия задачи воспользуемся определением
интегральной функции распределения
: вероятность того, что лазер проработает меньше
x
часов равна 1%. Для вычисления
х
в MS EXCEL 2010 существует функция
ЛОГНОРМ.ОБР()
.
Формула
=ЛОГНОРМ.ОБР(1-99%;5;1)
вернет значение 14,49 часов, т.е. после 14,49 часов с начала работы 99% лазеров будут еще работать.
Примечание
: пользователям более ранних версий MS EXCEL можно посоветовать для расчетов воспользоваться формулами
=EXP(НОРМОБР(1-99%;5;1))
или
=ЛОГНОРМОБР(1-99%;5;1)
.
Задача3.
Учитывая условие Задачи1, вычислить среднее и стандартное отклонение времени жизни лазера.
Для заданных параметров
логнормального распределения
среднее
значение времени жизни лазера
=EXP(5+(1*1)/2)=244,69
часов, а
стандартное отклонение
=КОРЕНЬ((EXP(1*1)-1)*EXP(2*5+1*1))=320,75
часов.
Обратите внимание, что для
логнормального распределения
, как для типичного скошенного распределения,
стандартное отклонение
существенно больше
среднего
.
СОВЕТ
: О других распределениях MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
17 авг. 2022 г.
читать 2 мин
В этом пошаговом руководстве объясняется, как построить в Excel следующее логарифмически нормальное распределение:
Шаг 1: Определите значения X
Во-первых, давайте определим диапазон значений x для использования на нашем графике.
Шаг 2: Рассчитайте значения Y
Значения y на графике будут представлять значения PDF, связанные с логарифмически-нормальным распределением.
Мы можем ввести следующую формулу в ячейку B2 , чтобы вычислить значение PDF логарифмически нормального распределения, связанного со значением x, равным 0,01, средним значением, равным 1, и стандартным отклонением, равным 1:
=LOGNORM.DIST( A2 , $E$1 , $E$2 , FALSE)
Затем мы можем скопировать и вставить эту формулу в каждую оставшуюся ячейку в столбце B:
Шаг 3: Постройте логнормальное распределение
Затем выделите диапазон ячеек A2:B22 , затем щелкните вкладку « Вставка » на верхней ленте, затем щелкните параметр « Разброс » в группе « Диаграммы » и нажмите « Разброс с плавными линиями» :
Будет создана следующая диаграмма:
На оси X показаны значения случайной величины , которая соответствует логарифмически нормальному распределению со средним значением 1 и стандартным отклонением 1, а ось Y показывает соответствующие значения PDF логарифмически нормального распределения.
Обратите внимание, что если вы измените значения среднего или стандартного отклонения в ячейках E1 и E2 соответственно, график автоматически обновится.
Шаг 4: Измените внешний вид графика
Не стесняйтесь добавлять заголовок, метки осей и удалять линии сетки, чтобы сделать график более эстетичным:
Дополнительные ресурсы
В следующих руководствах объясняется, как построить другие распространенные распределения в Excel:
Как построить кривую нормального распределения в Excel
Как построить биномиальное распределение в Excel
Как построить распределение Пуассона в Excel
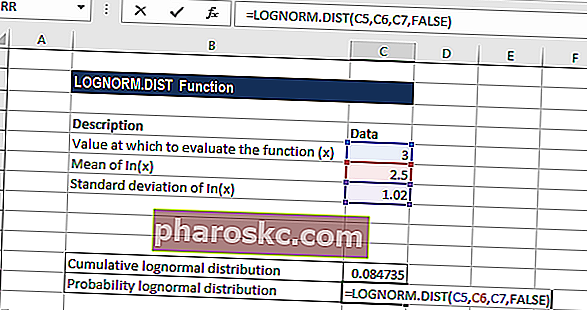
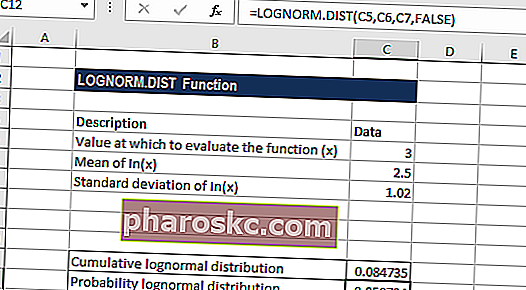
Calculates the cumulative log-normal distribution function at a given value of x
Lognormal Distribution Excel Function
The Lognormal Distribution Excel Function[1] is categorized under Excel Statistical functions. It will calculate the cumulative lognormal distribution function at a given value of x. We can use the function to analyze data that‘s been logarithmically transformed.
A variable x is log-normally distributed if its natural logarithm is normally distributed.
In terms of Excel functions:
Where μ is the mean of ln(x) and σ is the standard deviation of ln(x).
In financial analysis, the LOGNORM.DIST function is often used in analyzing stock prices, as normal distribution cannot be used to model stock prices. The normal distribution includes a negative side, but stock prices cannot fall below zero.
Also, the function is useful in pricing options. The Black-Scholes model uses the lognormal distribution as its basis to determine option prices.
Formula
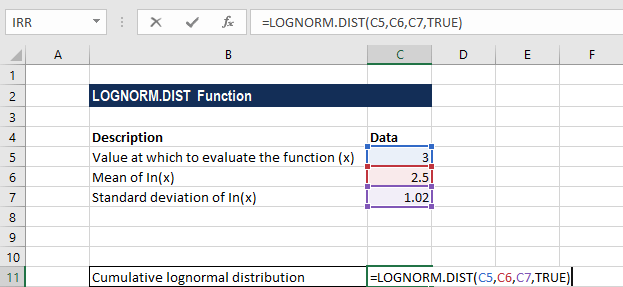
=LOGNORM.DIST(x,mean,standard_dev,cumulative)
The LOGNORM.DIST function uses the following arguments:
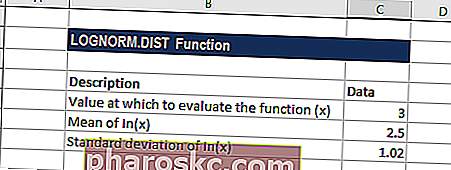
- X (required argument) – This is the value at which we wish to evaluate the function.
- Mean (required argument) – The mean of In(x).
- Standard_dev (required argument) – This is the standard deviation of In(x).
- Cumulative (optional argument) – This specifies the type of distribution to be used. It can be either TRUE (implies the cumulative distribution function) or FALSE (implies the normal probability density function).
To learn more, launch our free Excel crash course now!
How to use the Lognormal Distribution Excel Function
To understand the uses of the LOGNORM.DIST function, let’s consider an example:
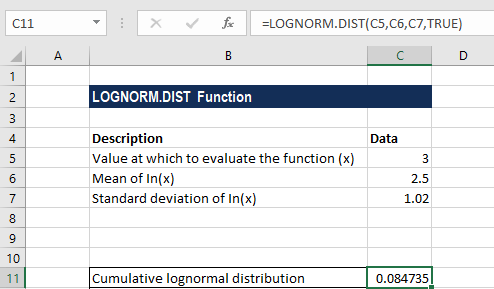
Lognormal Distribution Example
Suppose we are given the following data:
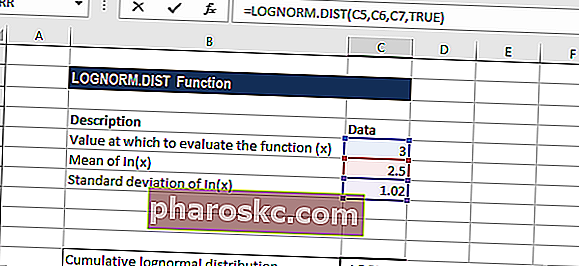
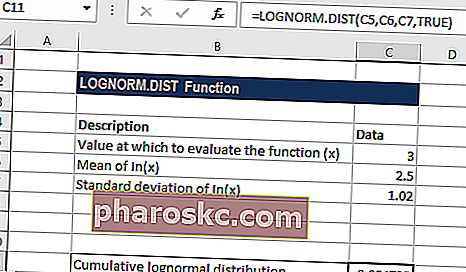
The formula for calculating cumulative lognormal distribution is shown below:
We get the result below:
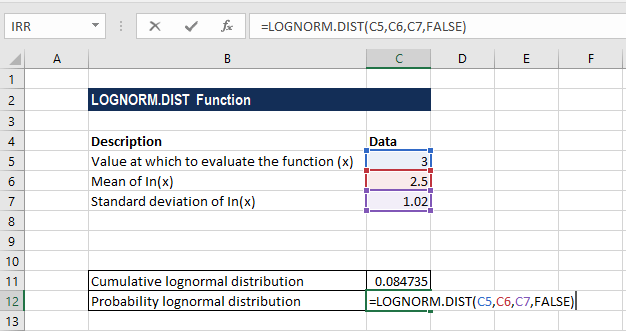
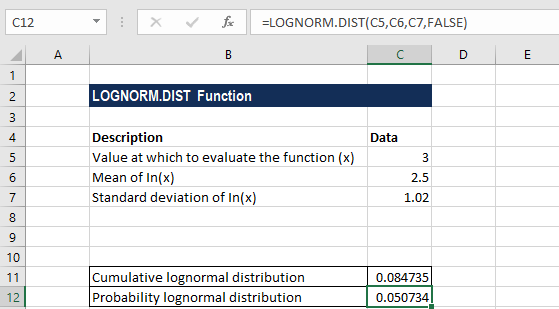
The formula for calculating probability lognormal distribution is shown below:
We get the result below:
Notes about the Excel Lognormal Distribution Function
- The LOGNORM.DIST function will truncate all numerical values to integers.
- #NUM! error – Occurs when:
- The argument x given is less than or equal to zero; or
- The argument standard_dev is less than or equal to zero.
- #VALUE! error – Occurs when any of given arguments is non-numeric.
- The LOGNORMAL.DIST function was introduced in Excel 2010 and hence is unavailable in earlier versions. For older versions, we can use the LOGNORMDIST function.
Free Excel Course
Check our Free Excel Crash Course to learn more about Excel functions using your own personal instructor. Master Excel functions to create more sophisticated financial analysis and modeling toward building a successful career as a financial analyst.
Additional Resources
Thanks for reading CFI’s guide to important Excel functions! By taking the time to learn and master these functions, you’ll significantly speed up your financial modeling. To learn more, check out these additional CFI resources:
- Excel Formulas for Finance
- Advanced Excel Class
- Advanced Excel Formulas List
- Excel Shortcuts List
- See all Excel resources
Функция Excel логнормального распределения относится к категории функций статистических функций Excel. Список наиболее важных функций Excel для финансовых аналитиков. Эта шпаргалка охватывает 100 функций, которые критически важно знать аналитику Excel. Он рассчитает кумулятивную функцию логнормального распределения при заданном значении x. Мы можем использовать эту функцию для анализа данных, которые были логарифмически преобразованы.
Переменная x имеет нормальное логарифмическое распределение, если ее натуральный логарифм имеет нормальное распределение.
Что касается функций Excel:
Где μ — среднее значение ln ( x ), а σ — стандартное отклонение ln ( x ).
В финансовом анализе Описание работы финансового аналитика В описании должности финансового аналитика ниже приводится типичный пример всех навыков, образования и опыта, необходимых для работы аналитиком в банке, учреждении или корпорации. Выполняйте финансовое прогнозирование, отчетность и отслеживание операционных показателей, анализируйте финансовые данные, создавайте финансовые модели, функция ЛОГНОР.РАСП часто используется при анализе цен на акции, поскольку нормальное распределение не может использоваться для моделирования цен на акции. Нормальное распределение включает отрицательную сторону, но цены на акции не могут опускаться ниже нуля.
Также функция полезна в вариантах ценообразования. Модель Блэка-Шоулза использует логнормальное распределение в качестве основы для определения цен опционов.
Формула
= ЛОГНОРМ.РАСП (x; среднее; стандартное_откл; совокупное)
Функция ЛОГНОРМ.РАСП использует следующие аргументы:
- X (обязательный аргумент) — это значение, при котором мы хотим оценить функцию.
- Среднее (обязательный аргумент) — среднее значение In (x).
- Standard_dev (обязательный аргумент) — это стандартное отклонение In (x).
- Накопительный (необязательный аргумент) — указывает тип используемого распределения. Это может быть ИСТИНА (подразумевает кумулятивную функцию распределения) или ЛОЖЬ (подразумевает нормальную функцию плотности вероятности).
Чтобы узнать больше, запустите наш бесплатный ускоренный курс по Excel прямо сейчас!
Как использовать функцию Excel логнормального распределения
Чтобы понять использование функции ЛОГНОРМ.РАСП, давайте рассмотрим пример:
Пример логнормального распределения
Допустим, нам даны следующие данные:
Формула для расчета кумулятивного логнормального распределения показана ниже:
Получаем результат ниже:
Формула для расчета логнормального распределения вероятностей показана ниже:
Получаем результат ниже:
Примечания о функции логнормального распределения Excel
- Функция ЛОГНОРМ.РАСП преобразует все числовые значения в целые.
- # ЧИСЛО! ошибка — возникает, когда:
- Заданный аргумент x меньше или равен нулю; или
- Аргумент standard_dev меньше или равен нулю.
- #ЦЕННОСТЬ! ошибка — возникает, когда любой из заданных аргументов не является числовым.
- Функция ЛОГНОР.РАСП была введена в Excel 2010 и поэтому недоступна в более ранних версиях. Для более старых версий мы можем использовать функцию ЛОГНОРМРАСП.
Бесплатный курс Excel
Посетите наш бесплатный ускоренный курс по Excel, чтобы узнать больше о функциях Excel с помощью личного инструктора. Освойте функции Excel для более сложного финансового анализа и моделирования для построения успешной карьеры финансового аналитика.
Дополнительные ресурсы
Спасибо за то, что прочитали руководство по важным функциям Excel! Потратив время на изучение и освоение этих функций, вы значительно ускорите свое финансовое моделирование. Чтобы узнать больше, ознакомьтесь с этими дополнительными финансовыми ресурсами:
- Формулы Excel для финансов Excel для финансов В этом руководстве по Excel для финансов представлены 10 основных формул и функций, которые вы должны знать, чтобы стать отличным финансовым аналитиком в Excel. В этом руководстве есть примеры, скриншоты и пошаговые инструкции. В конце скачайте бесплатный шаблон Excel, который включает в себя все финансовые функции, описанные в руководстве.
- Расширенный класс Excel
- Список расширенных формул Excel Расширенные формулы Excel, которые необходимо знать Эти расширенные формулы Excel очень важно знать и выведут ваши навыки финансового анализа на новый уровень. Вы должны знать дополнительные функции Excel. Изучите 10 лучших формул Excel, которые регулярно использует каждый финансовый аналитик мирового уровня. Эти навыки улучшат вашу работу с таблицами в любой карьере.
- Список ярлыков Excel Ярлыки Excel ПК Mac Ярлыки Excel — список наиболее важных и распространенных ярлыков MS Excel для пользователей ПК и Mac, специалистов в области финансов и бухгалтерского учета. Сочетания клавиш ускоряют ваши навыки моделирования и экономят время. Изучите редактирование, форматирование, навигацию, ленту, специальную вставку, манипулирование данными, редактирование формул и ячеек и другие краткие сведения.