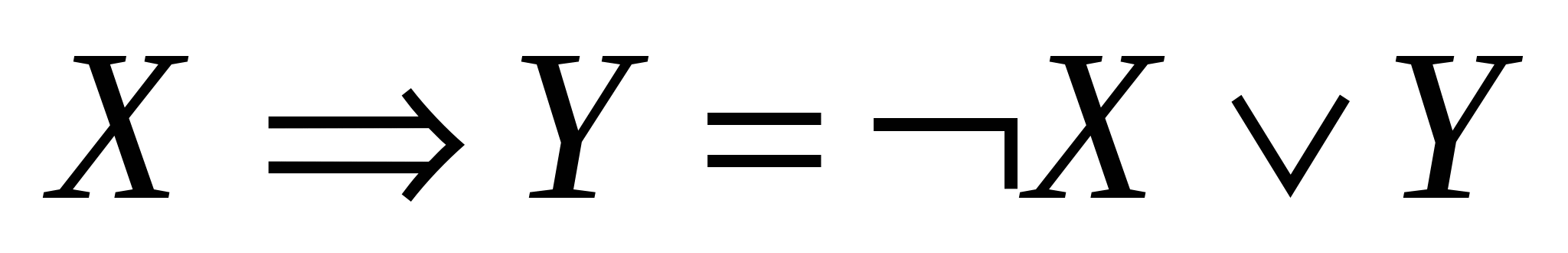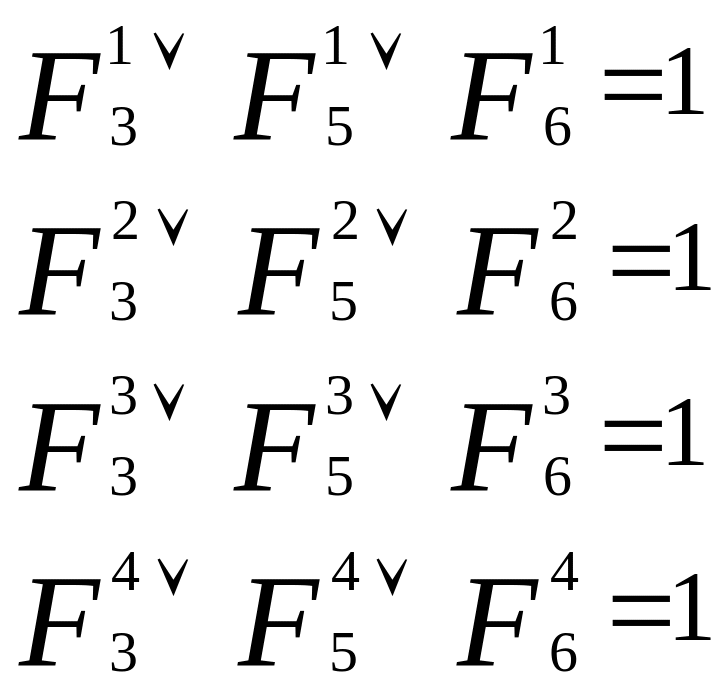Государственное бюджетное общеобразовательное учреждение Республики Крым «Керченская школа-интернат с усиленной физической подготовкой»
РАЗРАБОТКА УРОКА
«РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ С ПОМОЩЬЮ ЭЛЕКТРОННЫХ ТАБЛИЦ MS EXCEL»
РАЗДЕЛ «ЛОГИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ» ДЛЯ КУРСА ИНФОРМАТИКИ В СТАРШЕЙ ШКОЛЕ (10-11 КЛ.)
Учитель Романец К.С.
Керчь, 2016 год
-
обобщить и систематизировать знаний по темам «Таблицы истинности», «Преобразование логических выражений», «Решение логических задач»;
-
сформировать умения автоматизировать решение логических задач в электронных таблицах.
Задачи:
образовательные (по содержанию материала)
-
закрепить навыки применения программы MS Excel по форматированию ячеек, вставке логических функций (пользовательский и алгоритмический аспект),
-
повторить материал по использованию абсолютных и относительных ссылок в формулах, по копированию формул (пользовательский аспект),
-
ознакомить с методом защиты данных в ячейках от неквалифицированного ввода данных «fool proof» (пользовательский аспект),
-
закрепить навыки перевода выражений естественного языка на язык алгебры логики (теоретический аспект),
-
провести компьютерный эксперимент в электронных таблицах по решению задачи (мировоззренческий аспект).
развивающие (по деятельности учащихся)
-
формировать логическое мышление, внимание учащихся,
-
формировать информационную культуру,
-
формировать умение представить информацию в наглядной форме.
-
выработать умение создавать доступный и понятный по интерфейсу для других информационный продукт.
-
компьютеры, мультимедийный проектор, экран,
-
программное обеспечение WINDOWS XP, пакет MS OFFICE 2003,
-
презентация учителя для сопровождения урока по теме в POWER POINT, файл-тест, созданный учителем в EXCEL,
-
тексты заданий и тексты-памятки по технологии работы на уроке, распечатанные на принтере.
План урока
-
Сообщение темы и постановка целей урока (организация начала занятия). – 2 мин.
-
Актуализация знаний и умений учащихся к активной учебно-познавательной деятельности на основном этапе занятия.
-
Контроль и самопроверка знаний и способов действий в EXCEL (тест-разминка для каждого ученика). — мин.
-
Решение логической содержательной задачи в EXCEL. – 15 мин.
-
Физкульт-пауза. — 2 мин.
-
-
Практическая работа «Решение логических задач в EXCEL». – 10 мин.
-
Подведение итогов. 7 мин.
-
Домашнее задание. – 3 мин.
Ход урока
1.Сообщение темы и постановка целей и задач урока
Учитель сообщает тему урока обучающимся
2. Актуализация знаний и умений обучающихся
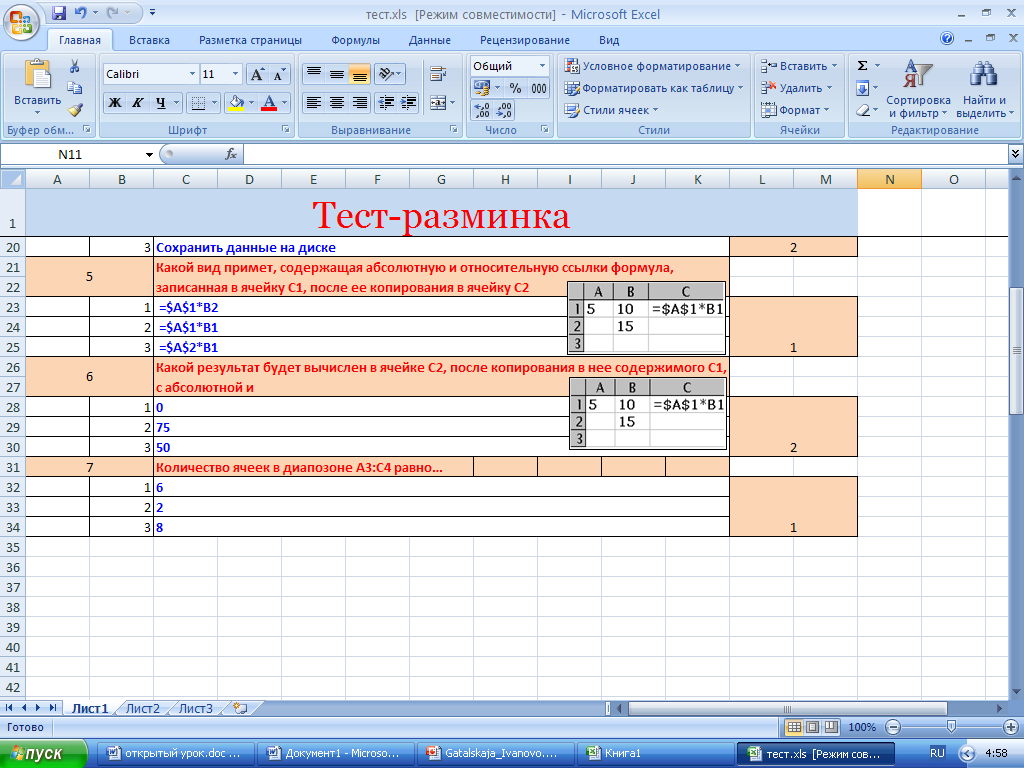
2.1. Тест-разминка на повторение материала.
Протестировать учащихся с помощью заранее созданного учителем мини-теста. Файл ученики берут на рабочем столе компьютера. Одновременно произвести тестирование на учительском компьютере кого-то из учеников с целью выявления после общей работы ошибок через подключенный проектор.
На примере теста
Вопрос учителя «Как организован тест? С помощью каких функций»
См. Приложение 1
Файл Excel (тест-разминка)
3. Мотивация
Мотивация: когда мы проходили тему «Построение таблиц истинности для сложных высказываний» мы видели, что чем больше логических переменных входит в состав сложного высказывания, тем с большим количеством строчек в таблице истинности мы работаем и тем самым увеличиваем время решения задачи и возникает вероятность того, что мы допустим ошибку в построении таблицы истинности.
Сегодня мы научимся автоматизировать процесс составления таблиц истинности средствами MS Excel и посмотрим преимущество автоматизированного решения в электронных таблицах
4. Ознакомление с новым материалом
Решение логической содержательной задачи.
Учитель использует презентацию для урока по теме. Так как обучающиеся уже достаточно хорошо знакомы с программой EXCEL (ориентируются в интерфейсе, умеют форматировать, вставлять функции, в том числе знакомы с логической функцией ЕСЛИ), то основной акцент – это логические функции ИСТИНА, ЛОЖЬ, И, ИЛИ, НЕ, соответствующие 0, 1, конъюнкции, дизъюнкции, инверсии в алгебре логики.
Задача
Четверо школьников, наблюдая за движущимся на большой высоте объектом, высказали свои предположения.
1-й сказал: «Высота объекта больше 10000 м или это перехватчик ПВО со скоростью выше скорости звука».
2-й предположил: «Если высота объекта больше 10 км, то это не перехватчик ПВО и скорость объекта ниже скорости звука».
3-й заявил: «Это НЛО или скорость объекта больше скорости звука».
4-й частично поддержал 3-его: «Если скорость объекта больше скорости звука, то это наверняка НЛО».
Если высказывания всех четырех истинны, то, что это был за объект, на какой высоте и с какой скоростью он летел?
Разбирается и решается коллективно средствами алгебры логики по технологическим картам (приложение )
Текст задачи обсуждается и записывается на языке алгебры логики для каждого высказывания на естественном языке.
В ходе выстраивания технологии решения задачи происходит:
повторение материала по формированию таблиц истинности (деятельность учеников – повторение материала),
обсуждение использования типового алгоритма вставки функций и использование его при вставке логических функций (коллективная деятельность).
5. Физкульт-пауза.
Ученики самостоятельно подходят и берут задачу и технологическую карту для практической работы, которые расположены на подоконнике. Условие: «Обязательно посмотреть в окно»
6. Практическая работа «Решение логических задач в EXCEL»
Решается следующая задача по аналогичной технологической карте, которая была обсуждена на уроке:
уровень воспроизводства — правильность, полнота, осознанность действий и использование новой технологии защиты данных;
Выбирается группа обучающихся (3 человека), которые решают задачу на бумаге, сами заполняют таблицу (приложение 4)
Один из знатоков алгебры логики, приглашая к себе в гости приятеля, решил проверить его способности в решении логических задач. Он охарактеризовал так принцип действия своего четырехкнопочного кодового замка: «Замок открывается, если выполняются следующие 4 условия:
1. Если не нажата кнопка 3, то нужно нажать кнопку 1 и не нажимать кнопку 4;
2.Если нажать кнопку 4, то нужно нажать кнопку 3 и не нажимать кнопку 2;
3.не верно, что нужно нажать кнопку2 или не нажимать кнопку 3, и все это притом, что не нажата кнопка 4;
4.Не нажимая кнопку 4, нажать кнопку 1 и кнопку 3».
Приятель знатока решил задачу.
Чему равно это решение?
К1=нажата кнопка 1, К2 = нажата кнопка 2 …
Дополнительная задача
Определить участника преступления, исходя из двух посылок:
1)Если Иванов не участвовал или Петров участвовал, то Сидоров участвовал
2)Если Иванов не участвовал, то Сидоров не участвовал
7. Подведение итогов.
Оценки учащимся выставляются следующим образом:
Ученикам, прошедшему тест-разминку за ПК, ученикам, активно работавшим на уроке, некоторым ученикам по практической работе (можно оценить всех по практической работе, при возможности сохранить в первоначальном виде их файлы и просмотреть впоследствии).
В ходе работы обнаруживается следующее: чем больше логических переменных, тем больше строк и столбцов таблицы надо заполнять вручную 0 и 1. Даже при наличии технологии защиты от неправильного ввода – это достаточно рутинная деятельность. Следовательно, у детей появится мотивация сделать впоследствии эту процедуру автоматической. Об этом непременно надо сообщить, на профильном уровне уместно заниматься VBA и научить работать с макросами в электронных таблицах.
Рефлексия. Заполнить анкеты Приложение 6
8. Домашнее задание
Запомнить технологию работы
Решить задачу на компьютере, расписав все этапы решения в тетради
Представим такую ситуацию: по телевизору синоптик объявляет прогноз погоды на завтра и утверждает следующее:
1)Если не будет ветра, то будет пасмурная погода без дождя.
2)Если будет дождь, то будет пасмурно и без ветра.
3)Если будет пасмурная погода, то будет дождь и не будет ветра.
Так какая же погода будет завтра?
Приложение 1
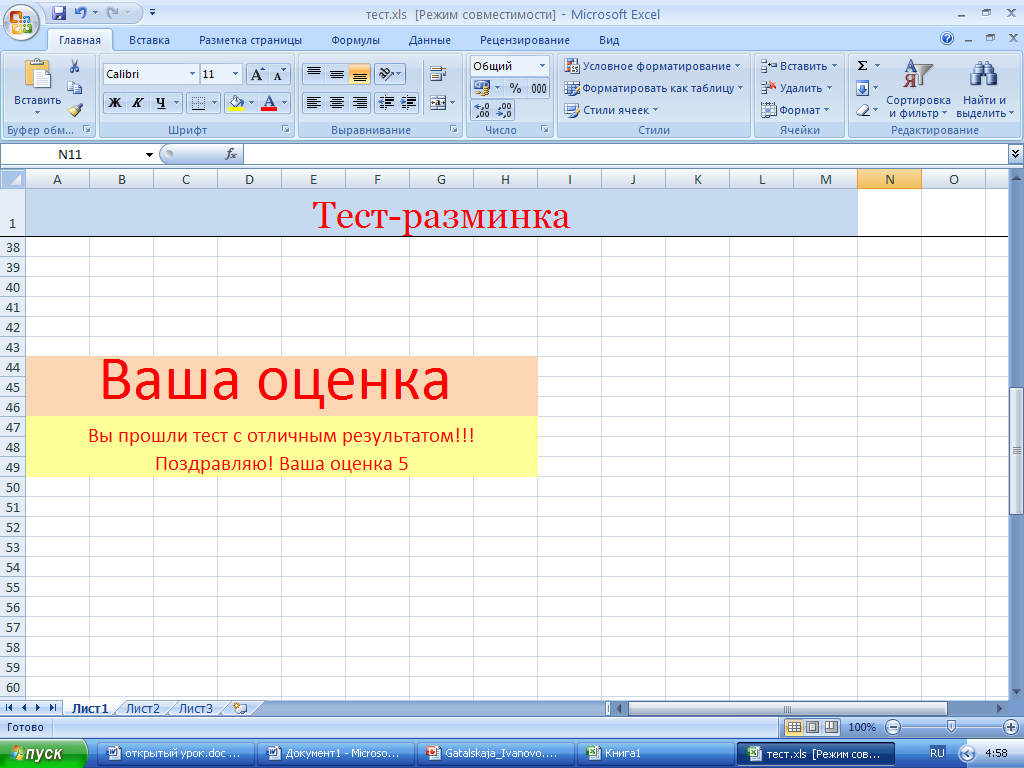
Тест –разминка
|
Вы прошли тест с отличным результатом!!! Поздравляю! |
|
|
Вам следует быть повнимательнее! Тест пройден с ошибками! |
|
|
Увы, тест не пройден. Прогресс обошел вас стороной, задумайтесь об этом! |
Приложение 2
Технологическая карта для задачи №1
Четверо школьников, наблюдая за движущимся на большой высоте объектом, высказали свои предположения.
1-й сказал: «Высота объекта больше 10000 м или это перехватчик ПВО со скоростью выше скорости звука».
2-й предположил: «Если высота объекта больше 10 км, то это не перехватчик ПВО и скорость объекта ниже скорости звука».
3-й заявил: «Это НЛО или скорость объекта больше скорости звука».
4-й частично поддержал 3-его: «Если скорость объекта больше скорости звука, то это наверняка НЛО».
Если высказывания всех четырех истинны, то, что это был за объект, на какой высоте и с какой скоростью он летел?
1. Выделим из условия задачи элементарные (простые) высказывания т обозначим их буквами
|
Имя логической переменной |
Значение |
|
H |
|
|
V |
|
|
P |
|
|
N |
-
Запишем логические формулы, соответствующие высказываниям школьников, и преобразуем их с учетом
|
Высказывание |
Логическая формула |
|
1 школьника (1) |
|
|
2 школьника (2) |
|
|
3 школьника (3) |
|
|
4 школьника (4) |
|
|
Объект не может быть одновременно НЛО и перехватчиком ПВО, тогда |
|
|
(5) |
|
|
Высказывания всех четырех школьников истинны (Ответ) |
-
Количество столбцов в Таблице истинности будет равно =_________________
(кол-во переменных + кол-во логических операций + ответ)
-
Количество строк равно____________________
-
Запустить MS EXCEL
-
На листе книги создать в первой строке таблицу со следующим заголовком:
-
Для 4-х логических переменных H,V,P,N ввести все возможные значения 1 (истина) и 0 (ложь) в диапазон ячеек A2:D17
-
Копируем все формулы строки 2 таким образом, чтобы заполнить весь диапазон E3:J17
-
Рассмотрим столбец «ответов» J. Указанные выражения принимают значение ИСТИНА только в одной строке. Она и есть искомое решение.
-
Ответ в задаче ______________________________________________________________________________________________________________________________________________________________
Приложение 3
Технологическая карта для задачи №2
Один из знатоков алгебры логики, приглашая к себе в гости приятеля, решил проверить его способности в решении логических задач. Он охарактеризовал так принцип действия своего четырехкнопочного кодового замка: «Замок открывается, если выполняются следующие 4 условия:
1. Если не нажата кнопка 3, то нужно нажать кнопку 1 и не нажимать кнопку 4;
2.Если нажать кнопку 4, то нужно нажать кнопку 3 и не нажимать кнопку 2;
3.не верно, что нужно нажать кнопку2 или не нажимать кнопку 3, и все это притом, что не нажата кнопка 4;
4.Не нажимая кнопку 4, нажать кнопку 1 и кнопку 3».
Приятель знатока решил задачу.
Чему равно это решение?
К1=нажата кнопка 1, К2 = нажата кнопка 2 …
-
Выделим из условия задачи элементарные (простые) высказывания т обозначим их буквами
|
Имя логической переменной |
Значение |
-
Запишем логические формулы, соответствующие высказываниям школьников, и преобразуем их с учетом
|
Высказывание |
Логическая формула |
-
Количество столбцов в Таблице истинности будет равно =_________________
(кол-во переменных + кол-во логических операций + ответ)
-
Количество строк равно____________________
-
Запустить MS EXCEL
-
На листе книги создать в первой строке таблицу со следующим заголовком, содержащим имена логических переменных, номера высказываний
-
Для 4-х логических переменных___________ ввести все возможные значения 1 (истина) и 0 (ложь) в диапазон ячеек ________
-
Копируем все формулы строки 2 таким образом, чтобы заполнить весь диапазон __________
-
Рассмотрим столбец «ответов»___. Указанные выражения принимают значение ИСТИНА только в одной строке. Она и есть искомое решение.
Ответ в задаче ______________________________________________________________________________________________________________________________________________________________
Приложение 4
|
К1 |
К2 |
К3 |
К4 |
(1) к3(к1к4) |
(2) к4(к3к2) |
(3) (к2к3)к4 |
(4) к4к1к3 |
(1)(2)(3)(4) |
|
1.На уроке я работал 7.Домашнее задание мне кажется |
активно / пассивно |
Приложение 5
Анкета для рефлексии
Приложение 6. Памятка.
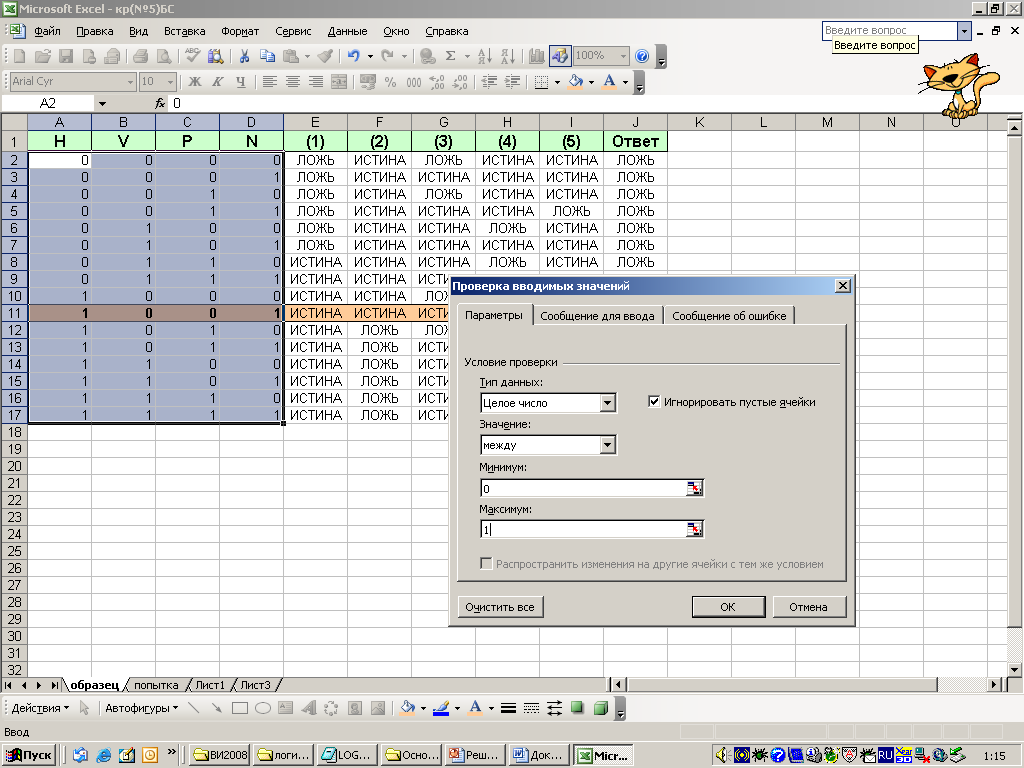
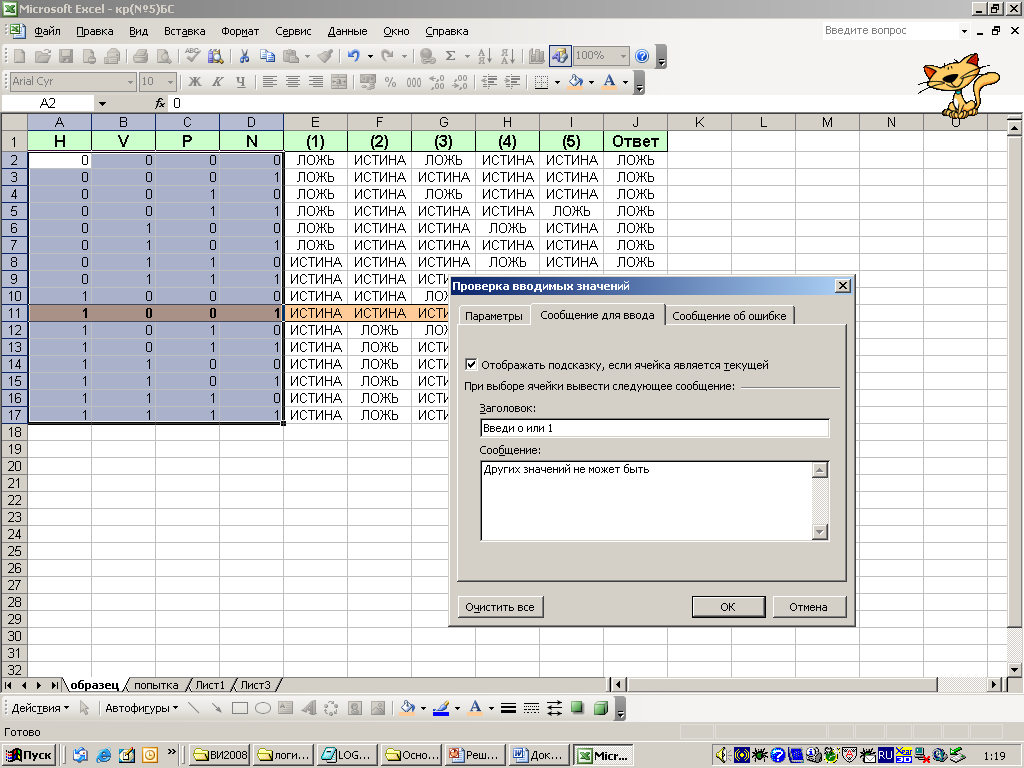
Как можно ввести в ячейки только 0 или 1, то есть выполнить защиту от «дурака»?
-
Воспользуемся строкой меню Данные→Проверка, выделив ячейки A2:D17
-
В окне диалога заполним Вкладку «Параметры»
-
Вкладку «Сообщение для ввода»
-
Вкладку «Сообщение об ошибке»
Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.
Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Решение финансовых задач в Excel
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
Заполнение аргументов:
- Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
- Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
- Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
- Тип – 0.
- БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)16 = 183245.
Решение эконометрики в Excel
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:
Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).
Решение логических задач в Excel
В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.
Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.
- Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
- Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
- Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».
Решение математических задач в Excel
Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).
Условие учебной задачи. Найти обратную матрицу В для матрицы А.
- Делаем таблицу со значениями матрицы А.
- Выделяем на этом же листе область для обратной матрицы.
- Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
- В поле аргумента «Массив» вписываем диапазон матрицы А.
- Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.
Скачать примеры
Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.
Антяскина Ольга
РЕШЕНИЕ ЗАДАЧ НА
НАХОЖДЕНИЕ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ В EXCEL
1.1 Логические выражения
в алгебре
Логическое выражение — это
символическая запись высказывания, состоящая из логических величин (констант
или переменных), объединенных логическими операциями (связками).
В математической логике не
рассматривается конкретное содержание высказывания, важно только, истинно оно
или ложно. Поэтому высказывание можно представить некоторой переменной
величиной, значением которой может быть только 0 или 1. Если высказывание
истинно, то его значение равно 1, если ложно — 0.
Связки «НЕ», «И»,
«ИЛИ» заменяются логическими операциями инверсия, конъюнкция,
дизъюнкция. Это основные логические операции, при помощи которых можно записать
любое логическое выражение.
Конъюнкция — логическое умножение
(соответствует союзу «И», в алгебре высказываний обозначается «&»). Конъюнкция
— это логическая операция, ставящая в соответствие каждым двум простым (или
исходным) высказываниям составное высказывание, являющееся истинным тогда и
только тогда, когда оба исходных высказывания истинны. Если хотя бы одно из
составляющих высказываний ложно, то и полученное из них с помощью союза «И»
сложное высказывание также считается ложным.
Дизъюнкция — логическое сложение (соответствует союзу «ИЛИ», в
алгебре высказываний обозначается «V»).Дизъюнкция — это
логическая операция, которая каждым двум простым (или исходным) высказываниям
ставит в соответствие составное высказывание, являющееся ложным тогда и только
тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из
двух образующих его высказываний истинно. Если два высказывания соединены
союзом «ИЛИ», то полученное сложное высказывание истинно, когда истинно,
хотя бы одно из составляющих высказываний.
Инверсия — отрицание (обозначается в
естественном языке словами «неверно, что…» и частице «не», в алгебре
высказываний обозначается «¬»)
Отрицание — логическая операция,
которая с помощью связки «не» каждому исходному высказыванию ставит в
соответствие составное высказывание, заключающееся в том, что исходное
высказывание отрицается.
Логическое следование (импликация): высказывание,
составленное из двух высказываний при помощи связки «если …, то …»,
называется логическим следованием, импликацией A => B.
Эквивалентность (логическое
тождество): высказывание, составленное из двух высказываний при помощи связки
«тогда и только тогда, когда», называется эквивалентностью A <=> B .
Новое высказывание, полученное с использованием эквивалентности, является
истинным тогда и только тогда, когда оба исходных высказывания одновременно
истинны или одновременно ложны.
В курсе математики решение задач,
связанных с логическими выражениями достаточно трудоемкая работа, однако она
значительно упрощается с использованием электронных таблиц, наибольшую
популярность среди которых приобрел MS Excel.
1.2 Использование логических функций в Microsoft Excel
2010
В Microsoft Excel 2010 имеется
возможность работы с различными типами функций, среди которых: математические,
логические, статистические, инженерные, аналитические, финансовые и т.д. С
учетом специфики нашего исследования более подробно остановимся на логических
функциях.
Для начала работы с ними необходимо:
1) использовать мастер «Вставить
функцию» (кнопка fx
слева от строки формул) Категория Логические.
2) другой способ – Вкладка Формулы
à Логические.
Категория Логические содержит семь
функций, в том числе функции ЕСЛИ и ЕСЛИОШИБКА. Использование логических
функций делает формулы более гибкими, а использование функции ЕСЛИ наделяет
формулу способностью «принимать решения». Благодаря этому функция ЕСЛИ стала
самой используемой логической функцией. Функция ЕСЛИОШИБКА имеется в библиотеке
встроенных функций только в Excel 2010 (2007).
Существуют особенности записи
логических операций в электронных таблицах: сначала записывается имя логической
операции (И, ИЛИ, НЕ), а затем в круглых скобках перечисляются логические
операнды.
Функция ЕСЛИ используется
при проверке условий для значений и формул. ЕСЛИ (лог_выражение,значение_если_истина,значение_если_ложь)
лог_выражение — любое значение или выражение, которое при вычислении
дает значение ИСТИНА или ЛОЖЬ;
значение_если_истина — значение,
которое возвращается, если аргумент лог_выражение — имеет значение ИСТИНА; если
аргумент лог_выражение имеет значение ИСТИНА и аргумент значение_если_истина
опущен, то возвращается значение ИСТИНА;
значение_если_ложь — значение,
которое возвращается, если аргумент лог_выражение имеет значение ЛОЖЬ. Если
аргумент лог_выражение имеет значение ЛОЖЬ и аргумент значение_если_ложь
опущен, то возвращается значение ЛОЖЬ.
Пример: 1)введем
в ячейку Е3 формулу = ЕСЛИ(Е1= 5; «Правильный ответ»; «Ошибка»).В строке лог_выражение
вводим Е1=5; значение_если_истина
вводим «Правильный ответ»; значение_если_ложь вводим «Ошибка».


Е3 появилась надпись «Правильный ответ». Такая конструкция позволяет
создавать достаточно сложные тестовые программы, например, такие, в которых
следует выбрать номер правильного варианта из многих.
3. Вводим в ячейку Е1 число ячейке
Е3 появилось слово «Ошибка».
Функция И
Возвращает значение ИСТИНА, если все
аргументы имеют значение ИСТИНА; возвращает значение ЛОЖЬ, если хотя бы один
аргумент имеет значение ЛОЖЬ.
Аргументы: логическое_значение1,
логическое_значение2,… — от 1 до 30 проверяемых условий, которые могут иметь
значение либо ИСТИНА, либо ЛОЖЬ. Аргументы должны быть логическими значениями,
массивами или ссылками, которые содержат логические значения. Если аргумент,
который является ссылкой или массивом, содержит тексты или пустые ячейки, то
такие значения игнорируются. Если указанный интервал не содержит логических
значений, то функция И возвращает значение ошибки #ЗНАЧ!
Функция ИЛИ
Возвращает значение ИСТИНА, если
хотя бы один из аргументов имеет значение ИСТИНА; возвращает значение ЛОЖЬ,
если все аргументы имеют значение ЛОЖЬ.
Аргументы: логическое_значение1,логическое_значение2,…
— от 1 до 30 проверяемых условий, которые могут иметь значение либо ИСТИНА,
либо ЛОЖЬ.
Функция НЕ
Заменяет
логическое значение аргумента на противоположное. Функция НЕ используется в тех
случаях, когда необходимо иметь уверенность в том, что значение не равно
некоторой конкретной величине.
Аргументы: логическое_значение — значение или выражение,
которое при вычислении дает значение ИСТИНА или ЛОЖЬ. Если аргумент
логическое_значение — имеет значение ЛОЖЬ, то функция НЕ возвращает значение
ИСТИНА; если аргумент логическое_значение имеет значение ИСТИНА, то функция НЕ
возвращает значение ЛОЖЬ.
Функции ИСТИНА и
ЛОЖЬ предоставляют альтернативный способ записи логических значений ИСТИНА и
ЛОЖЬ. Эти функции не имеют аргументов и выглядят следующим образом: =ИСТИНА(),
=ЛОЖЬ().
Функция
ЕСЛИОШИБКА
Данная функция
возвращает указанное значение, если вычисление по формуле вызывает ошибку; в
противном случае функция возвращает результат формулы. Функция ЕСЛИОШИБКА
позволяет перехватывать и обрабатывать ошибки в формулах.
Аргументы:Значение —
обязательный аргумент, проверяемый на возникновение ошибок. Значение_при_ошибке —
обязательный аргумент. Значение, возвращаемое при ошибке при вычислении по
формуле. Возможны следующие типы ошибок: #Н/Д, #ЗНАЧ!, #ССЫЛКА!, #ДЕЛ/0!,
#ЧИСЛО!, #ИМЯ? и #ПУСТО!
Как правильно
использовать логические формулы, а также решать конкретные задачи с их
использованием, покажем на следующих примерах.
1.3 Примеры задач,
связанные с нахождением решений логических выражений, средствами Excel
Отличительной особенностью задач,
связанных с нахождением логических выражений, является то, что ответом к ним
является не целочисленное значение, которое обычно мы привыкли указывать, а
установление истинности или ложности некоторой словесной формулировки,
отраженной в условии задачи. В этой связи, решая задачу средствами Excel, мы
можем ответить не только на этот вопрос, но и представить соответствующий
результат в виде графика, диаграммы и таблицы.
Рассмотрим некоторые примеры задач с
использованием логической операции ЕСЛИ.
Задача1.
Используя логическую функцию ЕСЛИ, определить кто из абитуриентов будет
зачислен, по результатам ЕГЭ, в университет. Абитуриент будет зачислен, если
сумма баллов за три экзамена составляет 270 и выше, и его балл по математике
должен быть не менее 80 баллов.
Решение: функция
ЕСЛИ выполняет проверку условия на истинность, и если оно верно — возвращает в
ячейку с формулой заданное нами значение для «ИСТИНА», иначе — другое
значение для «ЛОЖЬ».
Шаг 1. Используя логическую функцию ЕСЛИ,
выявим у кого из абитуриентов, сумма баллов превышает порог для
зачисления.
В столбце F будем вводить формулу о зачислении абитуриентов. В ячейку F3
введем формулу, для этого делаем её активной. Затем на ленте выбираем вкладку Формулы
à
Логические à Если. Заполняем поля аргументов,
следующим образом:
· Лог_выражение
— условие в форме логического выражения, которое в дальнейшем может принять два
варианта — Истина или Ложь. В этой строке мы зададим условие E3>=$B$1.
Ячейку B1 делаем абсолютной ссылкой — поскольку далее будем копировать
формулу.
· Значение_если_истина
— значение, которое выведет программа, если логическое выражение будет верно. В
этой строке мы пишем — «Да». Иначе говоря, если балл выше или равен
проходному, то в столбце «Зачисление» выведется слово Да.
· Значение_если_ложь
— значение, которое выведет программа, если логическое выражение будет НЕ
верно. В этой строке мы пишет — «Нет». Если балл будет ниже
проходного, то получим Нет.
После того как поля аргументов заполнены
, нажимаем ОК. В ячейки F3 получилось Да.
Для копирования формулы остальных ячеек, наведем указатель мыши на маркер,
который находится в нижнем правом углу рамки выделения. При этом он примет вид
черного плюсика. Щелкнем и, удерживая нажатием кнопку мыши, протянем рамку до
ячейки F8.
Получаем результаты:
Шаг
2. Выясним кто, из представленных условий задачи, будет студентом
университета.
Для
добавлений новых условий используем логическую функцию И, которая позволяет
добавлять новые условия истинности выражения и теперь выражение считается
истинным, только если оба условия выполняются.
Чтобы
вести второе условия, мы должны, щелкнуть ячейку F3,
затем в строке формул навести курсор на лог_выражение.
На
ленте выбрать вкладку Формулы àЛогические à
И.Заполним поля аргументов следующим образом:
В
строке лог_значение 1 вводим формулу: E3>=$B$1.
В
строке лог_значение 2 вводим формулу: В3>=80
После
того как поля аргументов заполнили наживаем ОК. В ячейки F3
получилось Да. Используем маркер автозаполнения для распространения формулы на
остальных абитуриентов. Получаем:
Ответ:
из условий задачи, зачисленными будут считаться абитуриенты Антонов, Синичкин,
Соколова.
Задача 2. Построить
график функции:
Решение: для
того чтобы построить данный график будем использовать функцию ЕСЛИ.

определений X∊[-2;2].Ячейку
А2 введем число -2, а в ячейку А3 -1,8. Далее выделяются эти две ячейки и
курсор мыши переводится в нижний правый угол выделенного диапазона до
появления черного крестика. Нажимается и, удерживая кнопку мыши, переводится
курсор на ячейку A22. Как видим, ячейки заполняются автоматически. Это одно из
преимуществ MS Excel.
В ячейках В2-В22 введем саму
фунцию зависищую от Х.В ячейку В2 введем формулу:
ЕСЛИ(A2<0;1+A2;ЕСЛИ(A2>=1;A2^2;EXP(A2)))
Заданная
функция зависит от переменной Х.Если Х принимает отрицательное значение то
график будет построен по уравнению 1+х, если x≥1
то x^2
в остальных случаях e^x.Получили
в ячейки В2 число -1. Для распространения формулы на остальные ячейки используем
маркер автозаполнения.
Теперь
строим график, для этого выделяются ячейки В2-В22. Выберем на ленте вкладку
Вставка àДиаграммы
àВставка
диаграммы àГрафикàОк.
Получим
график:
Ответ: с
помощью функции ЕСЛИ мы построили график функции.
Задача 3. Составить таблицу
истинности с помощью Excel.
Аня, Вика и Сергей решили пойти в
кино. Учитель, хорошо знавший
ребят, высказал предложения:
1. Аня пойдет в кино только тогда,
когда пойдут Вика и Сергей;
2. Аня и Сергей пойдут в кино вместе
или же оба останутся дома;
3. Чтобы Сергей пошел в кино,
необходимо, чтобы пошла Вика.
Когда ребята пошли в кино, оказалось,
что учитель немного ошибся: из трех его утверждений истинными оказались
только два. Кто из ребят пошел в кино?
Решение: обозначим
простые высказывания:
А — Аня пойдет в кино;
В — Вика пойдет в кино;
С — Сергей пойдет в кино.
Каждое составное
высказывание можно выразить в виде формулы — логического выражения:
1.Aó(B&C)
2. (A
& C)
A
& неC)
3. C óB

в Excel. Вводим функций в ячейках в виде ИСТИНА или ЛОЖЬ. Например для
заполнения ячейки А2 выберем на ленте вкладку Формулы Логические
Истина
Ок. Для
заполнения ячейки С2 выбираем на ленте вкладку Формулы → Логические →Ложь→Ок и
т.д.
Для нахождений логического выражения нам
потребуется вывести значения неА и неС. В ячейках D2-D8
найдем неА, а в ячейках Е2- Е8, неС. Чтобы получить неА в ячейке D2,
выбираем вкладку Формулы Логические
Не
А2
ОК. Получим
функцию Ложь. Для распространения формулы на остальные ячейки используем маркер
автозаполнения. Чтобы получить неС ячейке, Е2 выберем на ленте вкладку ФормулыЛогические
Не
С2
ОК. Получим функцию Истина.
Для распространения формулы на остальные ячейки используем маркер
автозаполнения. Получим:

Чтобы вывести формулу Aó(B&C)
:
1)
получим функцию в скобках. Для ячейки F2
выберем на ленте вкладку Формулы Логические
И
лог_значение1
выберем ячейку B2 лог_значение2
выберем ячейку С2 Ок. Получим Ложь. Автозаполнением
заполним остальные ячейки до ячейки F8.
2)
теперь получим фунцию всей формулы в ячейках G2-G8.
В ячейку G2 вводим =А2= F2.
Затем автозаполнением заполняем остальные ячейки. Получим:
Чтобы вывести формулу
(A
& C)
A
& неC)
нужно:
1)
получим функцию (A & C)в
ячейках Н2-Н8. Для ячейки H2
выберем на ленте вкладку Формулы Логические
И
лог_значение1 выберем
ячейку A2 лог_значение2 выберем
ячейку С2 Ок.
Получим Ложь. Автозаполнением заполним остальные ячейки.
2)
получим функцию (неA & неC)в
ячейках I2-I8.
Для ячейки I2 выберем на ленте
вкладку Формулы Логические
И
лог_значение1 выберем
ячейку D2 лог_значение2 выберем
ячейку E2 Ок. Получим Ложь. Автозаполнением
заполним остальные ячейки.
3) теперь получим
функцию всей формулы в ячейках J2-J8.
Для ячейки J2
выберем на ленте вкладку Формулы Логические
ИЛИ
лог_значение1 выберем
ячейку H2 лог_значение2 выберем
ячейку I2 Ок. Получим Ложь.
Автозаполнением заполним остальные ячейки.
Таблица примет вид:

Чтобы получить формулу C óB.
Вводим в ячейку К2 =С2= В2 и нажимаем ENTER.Затем
автозаполнением заполним остальные ячейки. Таблица примет вид:
Ответ:
т.к. два высказывания должны быть «истина», а одно «ложь», то правильный ответ
следующий: Аня и Сергей не пойдут в кино, а пойдет Вика.
СПИСОК ИСПОЛЬЗОВАННЫХ
ИСТОЧНИКОВ:
1.
Методическая разработка по курсу
«Информатика» для студентов всех форм обучения «Использование
табличного процессора Excel «. Составители: В.Ф. Билюба, В.Н. Ершов, С.Н.
Митяков, О.И. Митякова, С.П. Никитенкова, Н.Я. Николаев. 2010 год
2.
«Основные технологии работы с
табличным процессом Excel». Составители: Н.В. Зубов, И.В. Лапшин, С.Н.
Митяков, С.П. Никитенкова, А.Н. Демин.
3.
Электронный учебник, – «Электронные
таблицы Ехсеl» httр://www.lеssоns-tvа.infо/ дата обращения: 10.11.10
4.
«Microsoft Excel. Логические функции»-Астраханский
государственный университет, сост. Пономарева И.С 2010 г.
5.
Одинцова, Б.Е. Информатика в экономике :
Учеб. пособие / Под ред. проф. Б.Е. Одинцова, проф. А.Н. Романова – М. :
Вузовский учебник, 2010. – 476 с.
6.
Острейковский, В.А. Информатика : Учебник
для вузов.Высш. шк., 2000. – 511 с.
7.
Козырев, А.А. Информатика : Учебник для
вузов. – СПб. : Изд-во Михайлова В.А., 2008. – 511 с.
8.
Леонтьев, В.П. Новейшая энциклопедия
персонального компьютера 2003. – М. : ОЛМА-ПРЕСС, 2010. — 920 с.
9.
Информатика и информационные технологии.
Учебник / Н. Д. Угринович. – 3 изд. – М. : БИНОМ. 2010– 511 с.
10.
Маккормик, Д. Секреты работы в Windows,
Word, Excel. Полное руководство для начинающих. И. Тимонина. Харьков, 2010.– 240
с.
В настоящее время
методы математической логики внедряются
в гуманитарные знания как аппарат,
позволяющий быстро и эффективно
перерабатывать огромные объемы
информации. Эти методы, как правило, при
объяснении понятий и существующих между
ними отношений исключают ошибки,
проистекающие за счет неточного
толкования смысла понятий, благодаря
использованию логических операций.
Впервые с идеей
внедрения логики и математики в процесс
познания закономерностей между объектами
любой природы выступил немецкий философ
и математик Лейбниц (1646 – 1716). Он предвидел
возникновение новой области науки,
названной им философским исчислением.
Философское
исчисление, по идее Лейбница, должно
представлять такую логическую систему,
в которой все производные понятия
выражались бы символами, составленными
из известных простых символов, обозначающих
элементарные понятия на основании
строгих правил. Операции над символами
должны производиться по аналогии с
алгебраическими операциями так, чтобы
формальным путем можно было получать
все новые и новые понятия и умозаключения.
Грандиозный замысел
Лейбница долгое время оставался без
развития. Первый крупный шаг в осуществлении
идей Лейбница был сделан Джорджем Булем
(1815 – 1864). В период с 1847 по 1857 г. он
опубликовал три работы. Первые две
носили характер предварительных
исследований. В третьей работе (это
объемистая книга в 424 стр.) изложена, в
сущности, вся система Буля. Здесь он
демонстрирует, как при помощи символических
алгебраических методов можно строить
логические конструкции. Кроме того, он
показывает, как его система может быть
распространена на теорию вероятностей.
В этих работах
Буль преследует еще одну цель: найти
элементарные операции человеческого
мышления, выйдя за рамки дедуктивной и
индуктивной логики.
Выражаясь современным языком, его
исследования принадлежали к области
кибернетики.
Буль впервые
показал, что законы человеческого
мышления могут быть формализованы так,
что над понятиями могут производиться
те же операции, что и над целыми числами.
Но в отличие от арифметики, как он
показал, формальные операции над
понятиями подчиняются следующим двум
законам: два одних и тех же понятия
сложенные или перемноженные приводят
к тому же понятию (в современной Булевой
алгебре их называют – отсутствие
коэффициентов и степеней).
На формирование
Булевой алгебры как самостоятельной
научной дисциплины оказали влияние
исследования немецкого математика
Эрнста Шредера (1841–1902), который дал
математическую трактовку закона
исключенного третьего аристотелевской
логики.
Шредер допускал
наличие классов больше двух и для
оперирования с ними он сформулировал
следующее правило: если среди членов
некоторой суммы классов находится хотя
бы один, который оказывается отрицанием
другого, то вся сумма равна единице.
Легко показать, что с помощью этого
правила можно построить таблицу операции
отрицания Булевой алгебры.
Символическое
исчисление Буля Шредер называл логическим
исчислением и признавал только три
основных операции: сложение, умножение
и отрицание; вычитание он считал не
безусловно выполнимой операцией. Тем
самым Шредер поставил вопрос об
оптимальном количестве операций в
логике классов.
Однако гениальная
догадка Буля состояла в том, что только
на множестве числа М={0;1} символическое
исчисление не противоречит опыту
человеческого мышления. Вопрос же об
оптимальности количества операций и в
логике классов, и в исчислении Буля
решается неоднозначно.
Согласно современным
представлениям, алгеброй Буля
называют элементы множества М={0;1}
с заданными в нем операциями S={‘’,’’,’-‘}
дизъюнкции, конъюнкции и отрицания.
Обозначается алгебра Буля так:
=(М;S),
здесь М – множество, S – сигнатура
алгебры, т.е. набор операций. Переменные
будем называть булевыми переменными.
Эти переменные обозначают понятия или
высказывания как неделимые понятия,
если
,
то высказывание ложно, если же
,
высказывание истинно.
Рассмотрим следующие
логические задачи, которые решаются на
базе символического исчисления Буля.
Задача 1.
На уроке по гражданской обороне учитель
показывает макет гранаты. Необходимо
определить тип этой гранаты и радиус
разлета убойных осколков.
|
Характеристики осколочной гранаты |
|
|
Тип гранаты – Оборонительная Вес Вес разрывного Тип запала – УЗРГМ Время Радиус Радиус Средняя дальность броска |
|
|
Характеристики осколочной гранаты |
||
|
Тип гранаты: наступательная Вес Вес разрывного Тип запала УЗРГМ Время Радиус Радиус Средняя дальность броска |
|
|
|
Характеристики осколочной гранаты |
||
|
Тип гранаты – Оборонительная Вес Вес разрывного Тип запала – УДЗ Время Радиус Радиус Средняя дальность броска |
|
Были получены
следующие три ответа.
-
Это наступательная
граната с радиусом разлета 150 м. -
Это оборонительная
граната с радиусом разлета убойных
осколков 200м. -
Это не наступательная
граната с радиусом разлета осколков
25 м.:
Учитель сказал
ребятам, что каждый из них прав только
в одном из двух предложений. Какой же
тип и радиус разлета убойных осколков
представленной гранаты?
С помощью Булевой
переменной введем обозначения:
-
Это граната
наступательная –
; -
Радиус разлета
осколков равен 150 м.–
; -
Это граната
оборонительная –
; -
Радиус разлета
осколков равен 200 м. –
; -
Это граната не
наступательная –
; -
Радиус разлета
осколков равен 24 м. –
.
В этих обозначениях
ответы кодируются логическими функциями
следующим образом:
Ответ 1:
Ответ 2:
Ответ 3:
Кроме того, ясно,
что граната может быть только одного
типа и иметь определенный радиус разлета
убойных осколков. Эти условия позволяют
ввести дополнительные логические
функции:
,
Полученные таким
образом логические функции
представлены в совершенной дизъюнктивной
нормальной форме. Если придать всевозможные
значения наборам переменных, от которых
зависят указанные функции, то можно
получить таблицы для
.
Пусть все
,
тогда получим систему уравнений булевой
алгебры:
|
|
(1) |
Система (1)
представляет математическую модель
искомой задачи. Один из способов решения
(1) состоит в подборе тех единичных термов
логических функций
,
наборы переменных которых удовлетворяют
системе (1), а значения переменных
из этих наборов не противоречат друг
другу.
Для нахождения
всех единичных термов системы (1)
необходимо произвести вычисление таблиц
функций f1, f2, f3, f4, f5. Это можно сделать
с помощью программы Microsoft Excel. Для этого:
-
Включите компьютер;
-
После того, как
на экране монитора появится рабочий
стол операционной системы Windows,
откройте окно Microsoft Excel; -
Заполните ячейки
A1B4 таблицы,
перебрав все варианты значений логических
переменных х1 и х5; -
Постройте таблицу
истинности для функции f1,
воспользовавшись функциями НЕ, И,
ИЛИ, которые находятся в мастере
функций
в категории ЛОГИЧЕСКИЕ. Для этого:
-
активизируйте
ячейку С2; -
воспользуйтесь
функцией НЕ (см. рис. 1); -
автозаполнением
занесите полученные результаты в
ячейки С2С5 (рис.
2)
-
Аналогичным
способом достроим таблицу истинности
для функции f1, используя функции И,
ИЛИ. В результате получим значения для
х1 и х5, изображённые на рис. 3.

Рис. 3
Строя таблицы для
функций f2 – f5 и, проводя аналогичные
действия с переменными, получим следующие
таблицы (рис. 4):
Таблица 1. Таблица
2. Таблица 3.
-
x1
x5
f1
x2
x3
f2
x1
x4
f3
0
0
0
0
0
0
0
0
1
0
1
1
0
1
1
0
1
0
1
0
1
1
0
1
1
0
0
1
1
0
1
1
0
1
1
1
Таблица 4. Таблица 5.
-
x3
x4
x5
f4
x1
x2
f5
0
0
0
0
0
0
0
0
0
1
1
0
1
1
0
1
0
1
1
0
1
0
1
1
0
1
1
0
1
0
0
1
1
0
1
0
1
1
0
0
1
1
1
0
В таблицах
1 – 5 единичные наборы определяются теми
наборами переменных, при которых
логические функции имеют единичные
значения. Для решения поставленной
задачи
необходимо выбрать пять единичных
термов, значения переменных в которых
не противоречивы.
В
качестве таковых наборов переменных
возьмём следующие:

Из этих
наборов переменных следует, что решение
имеет вид:
(2)
Непротиворечивость
решения (2) надо понимать так: значение
х1=0
имеет место в наборах переменных для
функций f5,
f1,
f3
аналогично х5=1
имеет место для f1,
f4
и т.д.
Для проверки
решения (2) подставим его в систему (1) и
убедимся в том, что после этого уравнения
системы (1) превращаются в тождества.
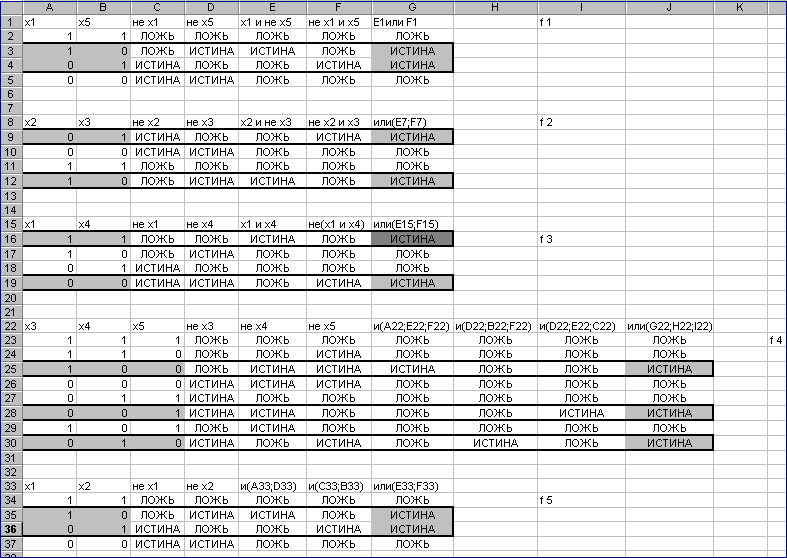
Рис.
4
Для воспроизведения
решения (2) в словесной форме необходимо
вспомнить высказывания, которые
кодировались символами хi. Из принятой
кодировки следует, что
означает, что граната – оборонительная,
а
– радиус разлета осколков равен 150 м.
Задача
2. В школе произошло чрезвычайное
происшествие: в классе кто-то из учеников
разбил окно. Учителем были опрошены
четыре ученика – Лёня, Дима, Толя и Миша.
Каждый из учеников сделал по три заявления
(см. таблицы 1–4). Учитель усомнился в
одном из трёх заявлений каждого из
опрошенных учеников. Последнее означает,
что у каждого одно из трёх заявлений
неверно. Из анализа всех заявлений
необходимо узнать – кто разбил
окно. Таблица 6.
|
№ |
Показания Лёни |
События |
Вероятности |
Переменные |
|
1 |
Я не виноват. |
|
|
|
|
2 |
Я не подходил к |
|
|
|
|
3 |
Миша знает, кто |
|
|
|
Таблица 7.
|
№ |
Показания Димы |
События |
Вероятности |
Переменные |
|
1 |
Стекло разбил не |
|
|
|
|
2 |
С Мишей я не был
поступления в |
|
|
|
|
3 |
Это сделал Толя. |
|
|
|
Таблица
8.
|
№ |
Показания Толи |
События |
Вероятности |
Переменные |
|
1 |
Я не виноват. |
|
|
|
|
2 |
Это сделал Миша. |
|
|
|
|
3 |
Дима говорит что я разбил окно. |
|
|
|
Таблица
9.
|
№ |
Показания Миши |
События |
Вероятности |
Переменные |
|
1 |
Я не виноват. |
|
|
|
|
2 |
Стекло разбил |
|
|
|
|
3 |
Дима может поручиться |
|
|
|
Для получения
вычислимого логического алгоритма
решения данной задачи необходимо
формализовать её условие, т.е. показаниям
всех учеников придать форму математических
соотношений, состоящих из символов,
обозначающих понятия, и знаков логических
операций, выполняемых над указанными
символами.
С
этой целью предположим, что каждое из
показаний Лёни есть события
,
,
,
которые могут произойти или не произойти.
Вероятности того, что каждое из названных
событий имело место, обозначим
соответственно
,
,
.
Вероятности же того, что события не
имели
место, обозначим через
,
,
.
При этом предполагается, что событие
противоположно событию
и т.д. применительно к оставшимся
событиям.
Событие
,
состоящее в том, что из трёх показаний
Лёни одно не верно, называется сложным
событием. Оно составляется как комбинация
простых событий следующим образом:
(3)
Здесь
операция суммы событий заменена операцией
дизъюнкции, а операция произведения –
конъюнкцией. Такие законы обоснованы
выше. Вероятность сложного события
обозначим через
.
В теории вероятностей значения вероятности
могут принимать весь спектр числовых
значений от нуля до единицы. Применительно
к данной задаче будем считать, что
вероятности
принимают только предельные значения:
нуль или единица. Это позволяет
отождествлять вероятность
с Булевой переменной
,
т.е. ввести обозначения:
,
,
,
,
В этом случае
означает истинность данного события,
а
–
ложность.
Аналогично
говорит об истинности
сложного события
,
а
— об его ложности.
Теперь,
согласно теоремам о вероятности суммы
и произведения нескольких событий,
вероятность
сложного события
определяется следующим образом:
(4)
Проводя
аналогичные рассуждения для показаний
остальных учеников, и используя
обозначения таблиц 2 – 4, заявления Димы,
Толи и Миши представим в форме следующих
математических соотношений:
(5)
(6)
(7)
Все
эти логические формулы однотипны и
представляют совершенную
дизъюнктивную нормальную форму
(СДНФ) одной и той же логической функции
.
(8)
Придавая
набору,
различные
комбинации из нулей и единиц, подставляя
их в (8) и производя вычисления с помощью
таблиц операций конъюнкции и дизъюнкции,
получаем таблицу 10 логической функции
.
Таблица
10.
|
|
|
|
|
0 1 2 3 |
0
0
0
0 |
0 0 0 1 |
|
4 5 6 7 |
1
1
1
1 |
0 1 1 0 |
В таблице 10 через
обозначен десятичный код набора
переменных, представляющего множество
трёхразрядных двоичных чисел.
Единичные значения
логической функции
называются единичными термами. Для них
введём новое обозначение
.
Единичные термы
можно вычислять с помощью операций
конъюнкции и отрицания по следующим
формулам:
(9)
Поскольку в формулах
(9) главной операцией считается операция
конъюнкции, то единичные термы называют
конъюнктивными термами. Если три
конъюнктивных терма объединить знаком
дизъюнкции, то согласно теории логических
функций, получим аналитическое
представление функции в форме СДНФ (8).
Для получения
явного вида конъюнктивных термов
логических функций
необходимо вычислить таблицы этих
функций с помощью программы Microsoft Excel.
Для этого:
6. В окне Microsoft Excel
заполните ячейки А12С49
таблицы, перебрав все варианты значений
логических переменных хj, уj, zj и sj;
Постройте таблицу
истинности для функций Fij,
воспользовавшись функциями НЕ, И, ИЛИ,
которые находятся в мастере функций ƒх
в категории ЛОГИЧЕСКИЕ. См. пп. 4 – 5.
В
конечном итоге получаем таблицу,
показанную на рис. 5.
Из
таблицы, изображённой на рис. 5, формируем
таблицу 11, состоящую из конъюнктивных
термов функций
и соответствующих им наборов переменных.
Таблица 11.
|
f1 |
f2 |
f3 |
f4 |
||||||||||||
|
x1 |
x2 |
x3 |
F1J |
y1 |
y2 |
y3 |
F2J |
z1 |
z2 |
z3 |
F3J |
s1 |
s2 |
s3 |
F4J |
|
0 |
1 |
1 |
F13 |
0 |
1 |
1 |
F23 |
0 |
1 |
1 |
F33 |
0 |
1 |
1 |
F43 |
|
1 |
0 |
1 |
F15 |
1 |
0 |
1 |
F25 |
1 |
0 |
1 |
F35 |
1 |
0 |
1 |
F45 |
|
1 |
1 |
0 |
F16 |
1 |
1 |
0 |
F26 |
1 |
1 |
0 |
F36 |
1 |
1 |
0 |
F46 |
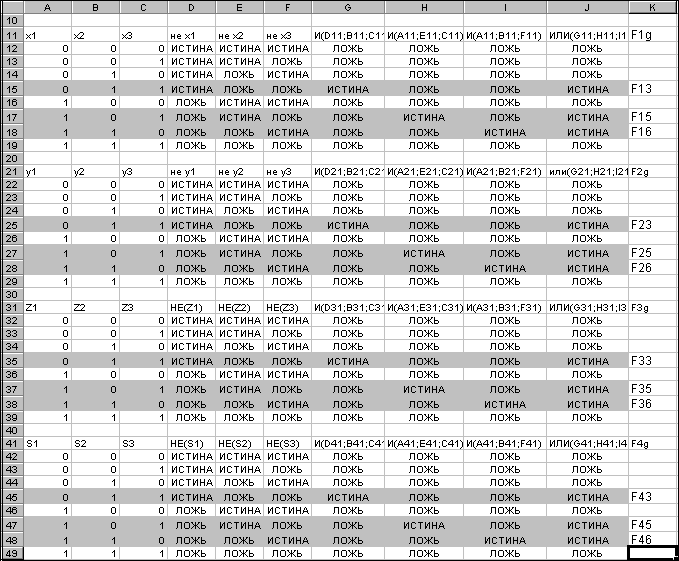
Рис.
5
Здесь применительно
к функции fi конъюнктивный терм
обозначен через Fij
так, что индекс i соответствует
номеру логической функции.
Если никто из
учеников не отказался от своих
высказываний, то значение всех логических
функций
надо положить равными единице, после
чего соотношения (4) – (7) примут вид
следующей системы алгебраических
уравнений для определения двенадцати
неизвестных, которые представляются
показаниями учеников в обозначениях
таблиц 6 – 9:
(10)
Здесь для обозначения
конъюнктивных термов, входящих в
использован символ
.
Соотношения (10) представляют математическую
модель показаний учеников и их следует
называть системой уравнений Булевой
алгебры, так как они определены на
множестве М={0;1} с использованием трёх
логических операций – дизъюнкции,
конъюнкции и отрицания. В этой системе
число неизвестных превышает число
уравнений. Однако, так как 10=1,
то решение системы (10) будет определяться
такими четырьмя термами: F1j, F2j, F3j, F4j
, (j=3, 5, 6), наборы переменных,
которых после
подстановки в (10) и проведения логических
вычислений превратят уравнение (10) в
тождества. При этом термы Fij
вычисляются по формуле (9) с учётом
обозначения переменных согласно таблице
11.
Среди комбинаций
из указанных четырёх термов могут
оказаться такие, значения наборов
переменных которых могут привести к
противоречивым показаниям учеников.
Например, рассмотрим термы F13, F23, F33, F43.
Наборы переменных,
соответствующие указанным термам,
определяются по таблице 11. В таблице 12
приведены значения переменных, найденные
из полученных наборов переменных, а
также показания учеников, соответствующие
данным значениям переменных.
Чтобы показать,
что значения переменных из таблицы 12
суть решение системы (10) необходимо для
этих значений вычислить по (9) строки и
подставить их в тождества.
Здесь же в таблице
12 даются высказывания мальчиков,
соответствующие рассмотренному решению.
Из них следует, что все ученики виноваты.
Последнее противоречит условию задачи.
Такое решение
задачи в дальнейшем будем называть
противоречивым
Таблица
12.
|
F13=1 |
Показания Лёни. |
|
x1=0 x2=1 x3=1 |
Я виноват.
Я не подходил к
Миша знает, кто |
|
F23=1 |
Показания Димы. |
|
y1=0 y2=1 y3=1 |
Стекло разбил я.
С Мишей я не был Это сделал Толя. |
|
F33=1 |
Показания Толи. |
|
z1=0 z2=1 z3=1 |
Я виноват. Это сделал Миша.
Дима говорит |
|
F43=1 |
Показания Миши. |
|
s1=0 s2=1 s3=1 |
Я виноват.
Стекло разбил
Дима может поручиться |
Рассмотрим другое
решение: F13=1, F26=1, F35=1, F46=1. Значения
переменных и показания учеников,
соответствующие этому решению, приведены
в таблице 13.
Таблица 13.
|
F13=1 |
Показания Лёни. |
|
x1=0 x2=1 x3=1 |
Я виноват.
Я не подходил к
Миша знает, кто |
|
F26=1 |
Показания Димы. |
|
y1=1 y2=1 y3=0 |
Стекло разбил я.
С Мишей я не был Это не сделал Толя. |
|
F35=1 |
Показания Толи. |
|
z1=1 z2=0 z3=1 |
Я не виноват. Это не сделал Миша.
Дима говорит |
|
F46=1 |
Показания Миши. |
|
s1=1 s2=1 s3=0 |
Я не виноват.
Стекло разбил
Дима не может |
Непротиворечивые
показания этой таблицы говорят о том,
что Лёня виноват и он разбил окно.
Решение, приводящее
к логически непротиворечивому результату,
назовём непротиворечивым.
Возникает вопрос:
Как из множества решений выбрать одно
– непротиворечивое?
Вернёмся к
первоначальным заявлениям учеников
(таблицы 6–9) и обратим внимание на то,
что из четырёх заявлений – x1, y1, z1, s1
одно не верно.
По
аналогии с рассуждениями, приводящими
к формулам (3) и (4), указанную особенность
четырёх заявлений можно выразить так:
(11)
Теперь значения
переменных из таблицы 13 подставим в
правую часть формулы (11) и произведём
вычисление f с помощью программы
Microsoft Excel. Для этого:
1. В ячейках А52–D52
запишите значения переменных x1, y1, z1
и s1 из таблицы 13.
2. Далее, с помощью
функций НЕ, И, ИЛИ найдём значение функции
f.
В
данном случае получим: f=fmax=1.
3. Аналогично
вычислим f по (11) с использованием
значений переменных из таблицы 12; тогда
будем иметь: f=fmin=0
(рис. 6).

Рис.
6
Таким
образом, непротиворечивое решение
приводит к максимальным значениям
логической функции (11). Последнее может
означать, что логическая функция (11)
представляется критерием отбора
непротиворечивого решения системы (10)
из множества решений. По аналогии с
экономическими задачами линейного и
нелинейного программирования, логическую
функцию (11) называют целевой
функцией.
Теперь
алгоритм решения данной задачи (10)–(11)
сводится к следующему: перебираем
всевозможные комбинации из четырёх
термов F1j,
F2j,
F3j,
F4j,
затем применительно к каждой выбранной
комбинации по таблице 11 определяем
значения переменных, по которым вычисляем
целевую функцию (11).
Тот
вариант из четырёх единичных термов,
который определит максимальное значение
целевой функции (11), следует признать в
качестве непротиворечивого решения.
Очевидно,
что такой алгоритм требует большого
объёма логических вычислений. Так,
например, в рассматриваемой задаче,
число комбинаций из четырех термов
будет определяться числом сочетаний
из двенадцати термов по четыре, т.е.
=495
Содержание
- Поиск решения задач в Excel с примерами
- Решение задач оптимизации в Excel
- Решение финансовых задач в Excel
- Решение эконометрики в Excel
- Решение логических задач в Excel
- Решение математических задач в Excel
- Проект «Решение задач при помощи электронных таблиц»
- Реализация межпредметных связей при обучении математике в системе основного и среднего общего образования
- Организация учебно-исследовательской деятельности учащихся как средство развития познавательной активности при обучении математике в условиях реализации ФГОС ООО и ФГОС СОО
- Ментальная арифметика: отрицательные числа, дроби, возведение в квадрат, извлечение квадратного корня
- Обучение школьников 5-9 классов решению текстовых задач по математике различными способами
- Описание презентации по отдельным слайдам:
- Опытные онлайн-репетиторы
- IV Международный практический «Инфофорум» для педагогов
- 2023 год педагога и наставника: вызовы и решения
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Онлайн-занятия с репетиторами
- Подарочные сертификаты
Поиск решения задач в Excel с примерами
Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.
Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Решение финансовых задач в Excel
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
- Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
- Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
- Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
- Тип – 0.
- БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка) кпер . Подставим значения: ПС = 400 000 / (1 + 0,05) 16 = 183245.
Решение эконометрики в Excel
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:
Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).
Решение логических задач в Excel
В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, =, Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.
- Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
- Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
- Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».
Решение математических задач в Excel
Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).
Условие учебной задачи. Найти обратную матрицу В для матрицы А.
- Делаем таблицу со значениями матрицы А.
- Выделяем на этом же листе область для обратной матрицы.
- Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
- В поле аргумента «Массив» вписываем диапазон матрицы А.
- Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.
Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.
Источник
Проект «Решение задач при помощи электронных таблиц»

Курс повышения квалификации
Реализация межпредметных связей при обучении математике в системе основного и среднего общего образования
- Сейчас обучается 21 человек из 13 регионов

Курс повышения квалификации
Организация учебно-исследовательской деятельности учащихся как средство развития познавательной активности при обучении математике в условиях реализации ФГОС ООО и ФГОС СОО
- Сейчас обучается 22 человека из 14 регионов

Курс повышения квалификации
Ментальная арифметика: отрицательные числа, дроби, возведение в квадрат, извлечение квадратного корня
- Сейчас обучается 92 человека из 37 регионов

Обучение школьников 5-9 классов решению текстовых задач по математике различными способами
Описание презентации по отдельным слайдам:
Решение задач при помощи электронных таблиц
Автор: Коротков Павел, 8 класс
Руководитель: Гончарук А.В.
МОУ Непецинская СОШ
Целью моей работы было рассмотреть задачи, решаемых при помощи электронных таблиц. Определить роль Excel в различных сферах деятельности, ведь знание Microsoft Excel стало обязательным требованием для офисных рабочих.
Для чего нужен EXCEL?
Во первых excel это самая популярная программа для быстрого и эффективного решения самых разных задач.
Программа способна создавать графики, решать самые различные рода задач: финансовые, экономические, математические, логические, оптимизационные и многие другие.
Например: если получать кредит на закупку товара в банке с более низкой процентной ставкой, а цену товара немного повысить – существенно ли возрастет прибыль при таких условиях?
РЕШЕНИЕ УРАВНЕНИЙ МЕТОДОМ ПОДБОРА ПАРАМЕТРОВ EXCEL
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
1. Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
2. Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
3. Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
4. После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
РЕШЕНИЕ ЗАДАЧ ОПТИМИЗАЦИИ В EXCEL
Подбор параметров («Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра») – находит значения, которые обеспечат нужный результат.
Поиск решения (надстройка Microsoft Excel; «Данные» — «Анализ») – рассчитывает оптимальную величину, учитывая переменные и ограничения. Диспетчер сценариев («Данные» — «Работа с данными» — «Анализ «что-если»» — «Диспетчер сценариев») – анализирует несколько вариантов исходных значений, создает и оценивает наборы сценариев.
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
Количество изделий нам пока неизвестно. Это переменные.
В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске
йогурта «3» и «1». Йогурт «2» производить не стоит.
РЕШЕНИЕ ФИНАНСОВЫХ ЗАДАЧ В EXCEL
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
Заполнение аргументов:
Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
Тип – 0.
БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
ПОСТРОЕНИЕ ГРАФИКОВ В EXCEL ПО ДАННЫМ ТАБЛИЦЫ
Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
ЗАКЛЮЧЕНИЕ
Excel – это самое полезное, универсальное и многофункциональное программное средство из пакета Office. Основное назначение Excel – хранение, анализ и визуализация данных, создание отчетов и проведение сложных расчетов.
СПАСИБО ЗА ВНИМАНИЕ!

Лучшее для учеников, педагогов и родителей
Опытные
онлайн-репетиторы
- По любым предметам 1-11 классов
- Подготовка к ЕГЭ и ОГЭ
Рабочие листы и материалы для учителей и воспитателей
Более 7 500 дидактических материалов для школьного и домашнего обучения
IV Международный практический «Инфофорум» для педагогов
2023 год педагога и наставника: вызовы и решения
Ценности гуманной педагогики
Открытая сессия для учителей и руководителей образовательных организаций
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 168 730 материалов в базе
Другие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 31.05.2018 3940
- PPTX 407.4 кбайт
- 65 скачиваний
- Рейтинг: 1 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Гончарук Анастасия Викторовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 4 месяца
- Подписчики: 0
- Всего просмотров: 9133
- Всего материалов: 7
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 490 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Онлайн-занятия с репетиторами
для весеннего интерьера
Как преуспеть в роли репетитора: запланируйте неудачу, чтобы проект получился удачным
Методическое сопровождение образовательного процесса
Оказание первой помощи при наружных кровотечениях и травмах
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Источник