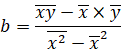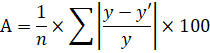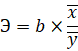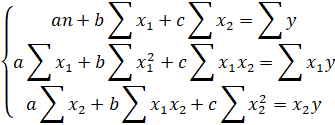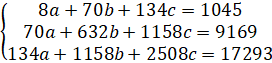17 авг. 2022 г.
читать 2 мин
Логарифмическая регрессия — это тип регрессии, используемый для моделирования ситуаций, когда рост или спад сначала быстро ускоряются, а затем со временем замедляются.
Например, следующий график демонстрирует пример логарифмического распада:
Для такого типа ситуации взаимосвязь между переменной-предиктором и переменной-откликом можно хорошо смоделировать с помощью логарифмической регрессии.
Уравнение модели логарифмической регрессии принимает следующий вид:
у = а + b*ln(x)
куда:
- y: переменная ответа
- x: предикторная переменная
- a, b: коэффициенты регрессии, описывающие взаимосвязь между x и y .
В следующем пошаговом примере показано, как выполнить логарифмическую регрессию в Excel.
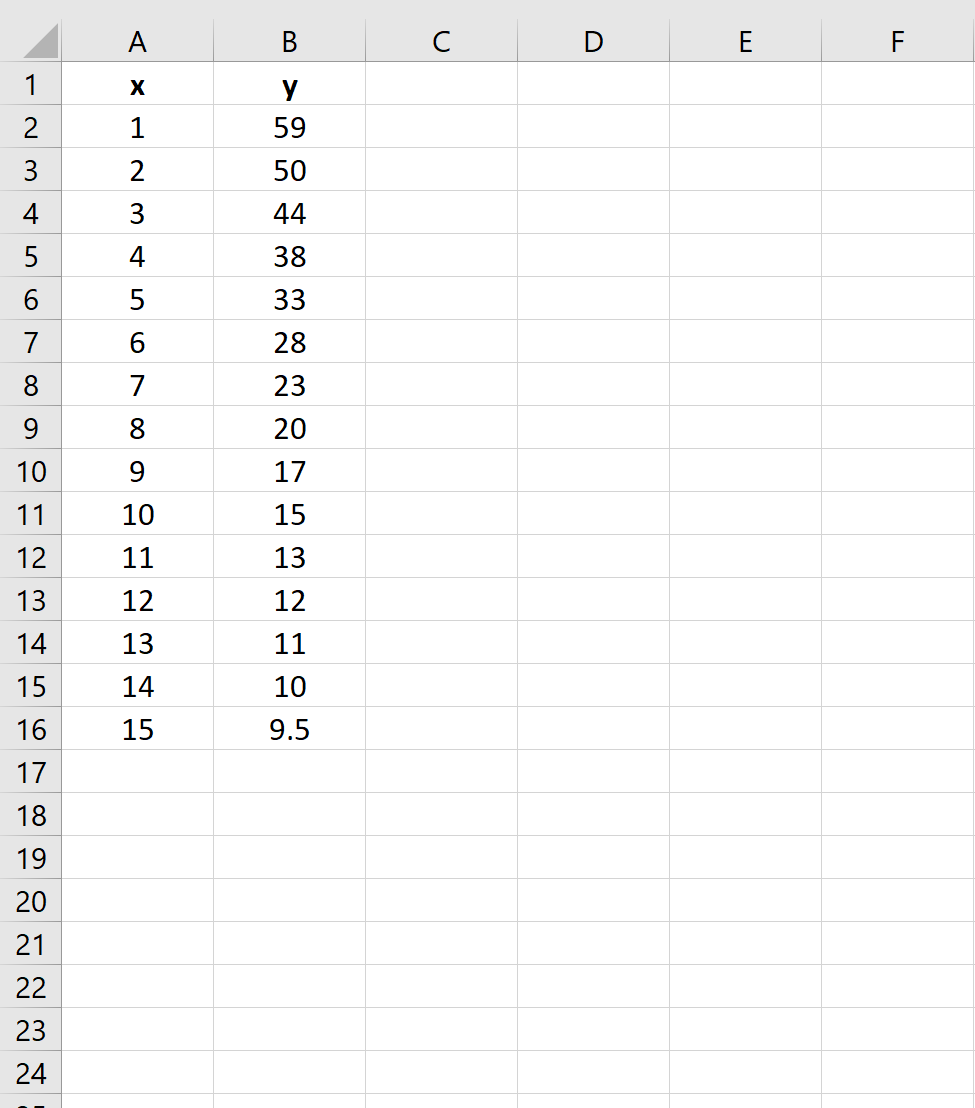
Шаг 1: Создайте данные
Во-первых, давайте создадим поддельные данные для двух переменных: x и y :
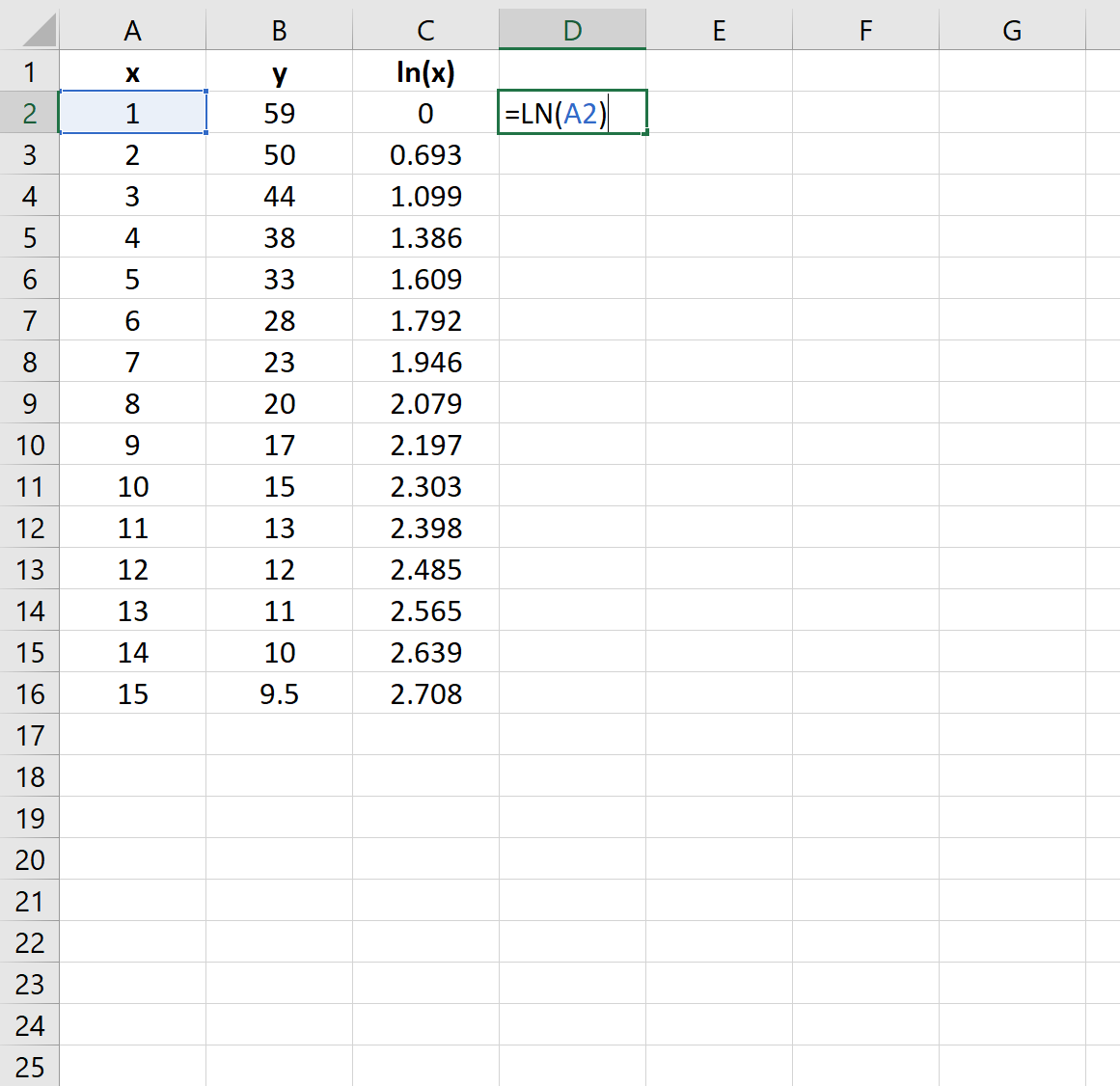
Шаг 2: возьмите натуральный логарифм переменной-предиктора
Далее нам нужно создать новый столбец, представляющий натуральный логарифм переменной-предиктора x :
Шаг 3: Подберите модель логарифмической регрессии
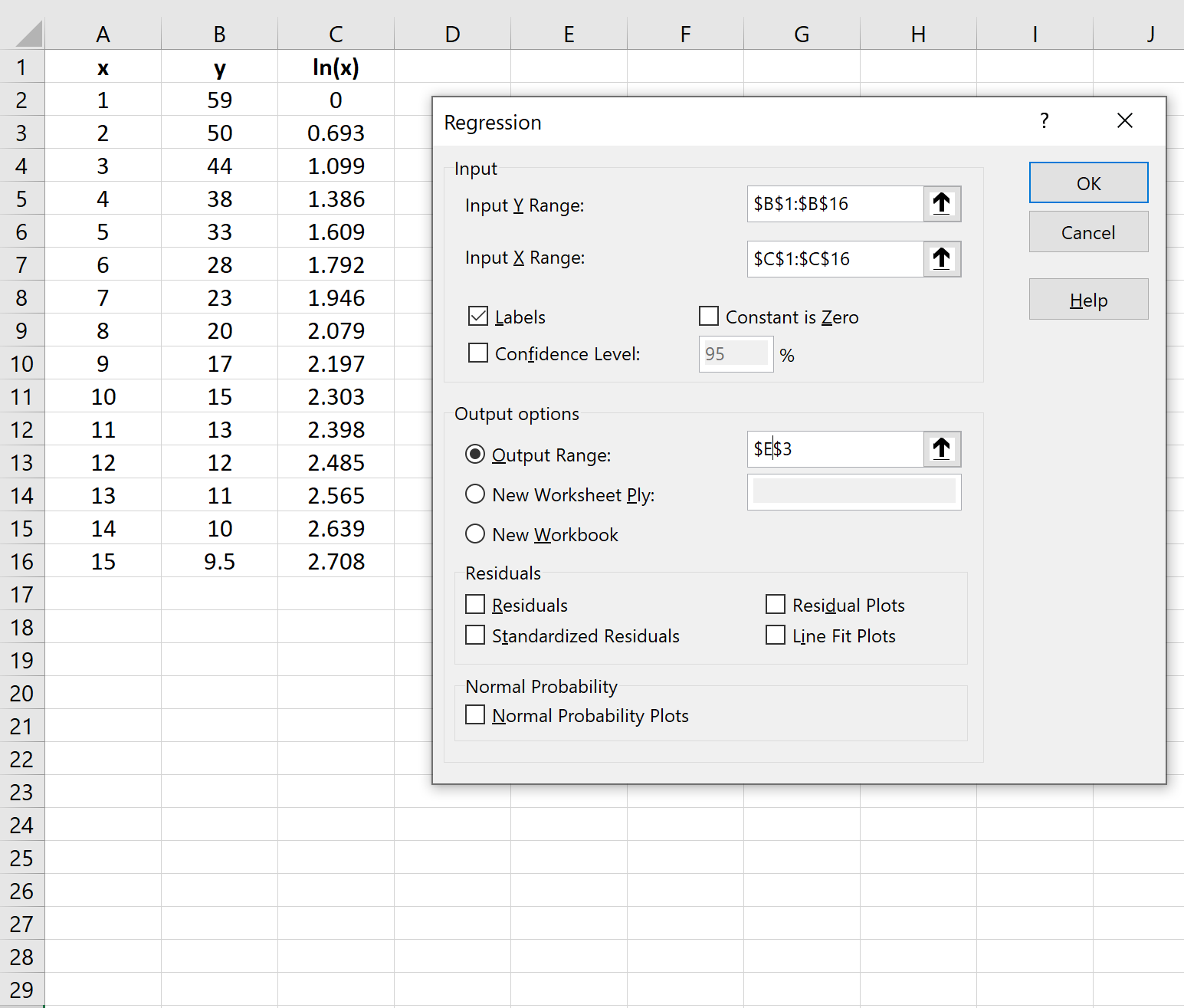
Далее мы подгоним модель логарифмической регрессии. Для этого щелкните вкладку « Данные » на верхней ленте, затем щелкните « Анализ данных» в группе « Анализ ».
Если вы не видите Data Analysis в качестве опции, вам нужно сначала загрузить Analysis ToolPak .
В появившемся окне нажмите Регрессия.В появившемся новом окне введите следующую информацию:
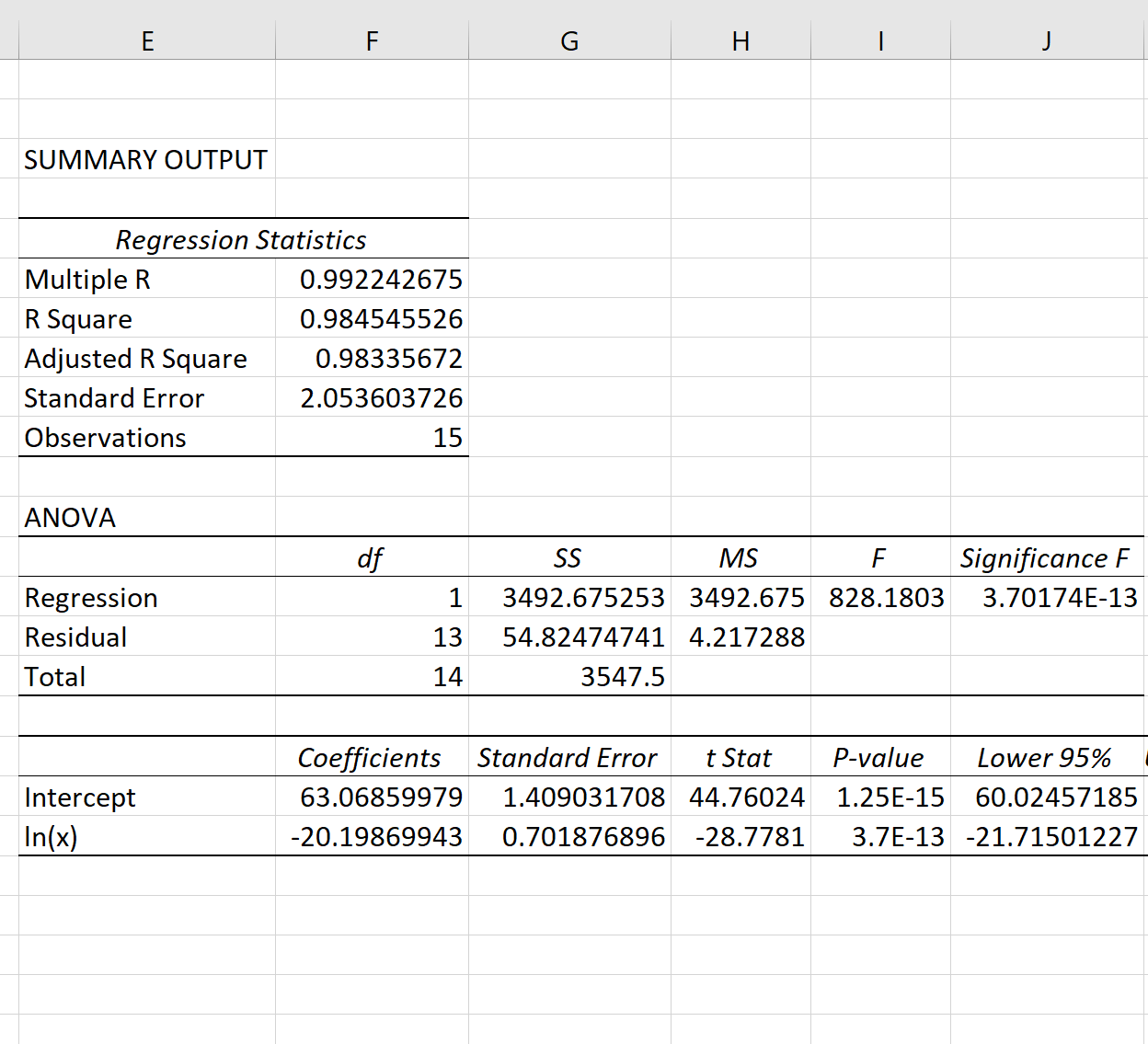
Как только вы нажмете OK , отобразятся выходные данные модели логарифмической регрессии:
Общее значение F модели составляет 828,18, а соответствующее значение p чрезвычайно мало (3,70174E-13), что указывает на то, что модель в целом полезна.
Используя коэффициенты из выходной таблицы, мы видим, что подобранное уравнение логарифмической регрессии:
у = 63,0686 – 20,1987 * ln(x)
Мы можем использовать это уравнение для прогнозирования переменной отклика y на основе значения переменной-предиктора x.Например, если x = 12, то мы предсказываем, что y будет 12,87 :
у = 63,0686 – 20,1987 * ln(12) = 12,87
Бонус: не стесняйтесь использовать этот онлайн- калькулятор логарифмической регрессии для автоматического вычисления уравнения логарифмической регрессии для заданного предиктора и переменной отклика.
Дополнительные ресурсы
Как выполнить простую линейную регрессию в Excel
Как выполнить множественную линейную регрессию в Excel
Как выполнить полиномиальную регрессию в Excel
Как выполнить экспоненциальную регрессию в Excel
Из данной статьи вы узнаете:
• Примеры применения логарифмического тренда в бизнесе;
• Логарифмический тренд y(x)=a*ln(x)+b разложим на запчасти;
• 5 способов расчета значений логарифмического тренда в Excel;
• Как можно скорректировать значения логарифмического тренда;
Логарифмический тренд применяется для прогнозирования временного ряда, данные которого вначале быстро растут или убывают, а затем постепенно стабилизируются.
Например, выводим новый товар на рынок, за счет роста клиентской базы продажи быстро растут, затем мы набираем постоянных клиентов, продажи стабилизируются, и новые клиенты уже не основной фактор роста, а основной фактор роста — это развитие продаж постоянным клиентам.
Или вводим продукцию в новую торговую точку, и по истечении определенного периода решаем увеличить количество фейсов на полке (т.е. увеличить размер полки для одного вида товара) (фейс — это единица продукции, которая стоит лицом к покупателю) или продублировать выкладку в другой части зала. Почему здесь лучше использовать логарифм? Потому что увеличение количества фейсингов на полке в 2 раза по одной группе товаров, к сожалению, не ведёт к увеличению продаж в 2 раза, причём с ростом количества фейсов темп прироста продаж уменьшаются для каждого последующего фейса. Именно поэтому для прогнозирования продаж для этой ситуации лучше всего использовать логарифмический тренд.
Логарифмический тренд – это функция y(x)=a*ln(x)+b, где
Значение x – это номера периода во временном ряду (например, номер месяца, квартала, дня; См. статью о временных рядах.)
y – это последовательность значений , которые мы анализируем и прогнозируем (например, объём продаж по месяцам.)
b – точка пересечения с осью y на графике;
a – это значение, на которое увеличивается следующее значение временного ряда;
Причем, если a>0, то динамика роста положительная,
Если а<0, то динамика тренда отрицательная.
При построении логарифмического тренда используют как положительные, так и отрицательные данные временных рядов.
Рассмотрим логарифмический тренд на примере построения прогноза продаж в Excel по месяцам.
Временной ряд — продажи по месяцам по новому товару
В этом временном раде у нас есть 2 переменных
1. Время — месяцы— x;
2. Объёмы продаж по месяцам — y;
Уравнение логарифмического тренда y(x)=a*ln(x)+b, где y — это объёмы продаж, x — месяцы.
5 способов расчета логарифмического тренда в Excel.
Как в Excel мы можем рассчитать коэффициенты логарифмического тренда?
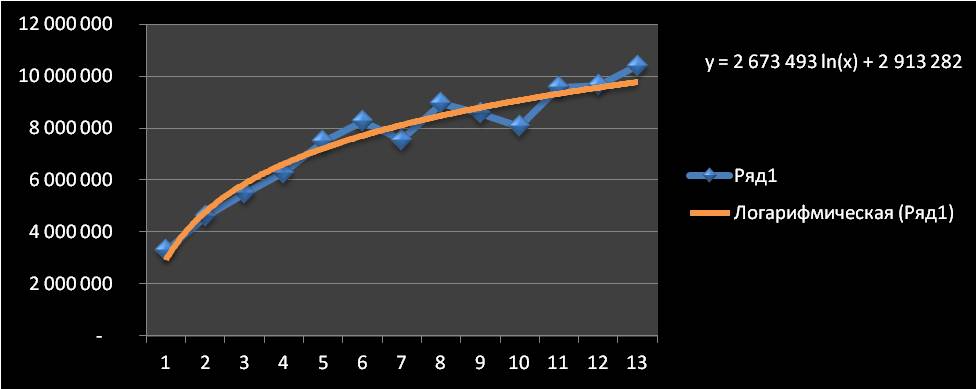
1-й способ — с помощью графика.
Строим график в Excel и видим по оси x — наш временной рад (1, 2, 3… — ноябрь, декабрь, январь …), по оси y объёмы продаж + добавляем на график линию тренда и уравнение тренда.
Получаем уравнение тренда y=2 673 493 ln(x) + 2 913 282
Для прогнозирования нам необходимо рассчитать значения тренда, как для анализируемых значений, так и для будущих периодов.
При расчете значений логарифмического тренда нам будут известны:
- Время — значение по оси Х;
- Значение «a» и «b» уравнения логарифмического тренда y(x)=a*ln(x)+b;
Рассчитываем значения тренда для каждого анализируемого периода времени от 1 до 13, а также для будущих периодов с 14 месяца до 20.
Например, для 14 месяца значение тренда рассчитывается по следующей схеме: в уравнение подставляем x=14 и получаем y=2 673 493 ln(14) + 2 913 282=9 968 782
20-го y=2 673 493 ln(20) + 2 913 282=10 922 350
И т.д.
Файл с примером вы можете скачать здесь.
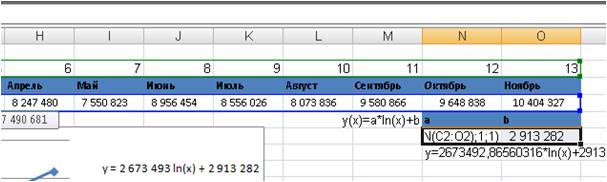
2-й способ — с помощью функции Excel =Линейн().
Для расчета коэффициентов логарифмического тренда воспользуемся функцией Excel =ЛИНЕЙН() .
Для этого в функцию =ЛИНЕЙН() введем:
1. известные значения y – объем продаж;
2. известные значения x – номера периодов, причём введенные, как LN(номера периодов);
3. константа – вводим 1 для расчёта коэффициента b уравнения y(x)=a*ln(x)+b;
4. Статистика — 1 или 0;
Формула будит выглядеть вот так =ЛИНЕЙН(C2:O2;LN(C1:O1);ИСТИНА;ИСТИНА)
Теперь формулу вводим как формулу массива, выделяем 2 ячейки (подробнее о формулах массива) и нажимаем F2, а затем одновременно — клавиши CTRL + SHIFT + ВВОД.
Коэффициенты «а» и «b» логарифмического тренда y(x)=a*ln(x)+b рассчитаны;
Получаем уравнение тренда y=2673492*ln(x)+2913281
Для прогнозирования нам необходимо продлить линию тренда и определить её значения. При её продлении нам будет известен только один параметр — это время, т.е. значения по оси X.
Рассчитываем значения тренда с 1-го месяца (ноябрь) до 20 (июнь)— y=2673492*ln(14)+2913281=9968782
17-го — y=2673492*ln(17)+2913281=10487857
И т.д.
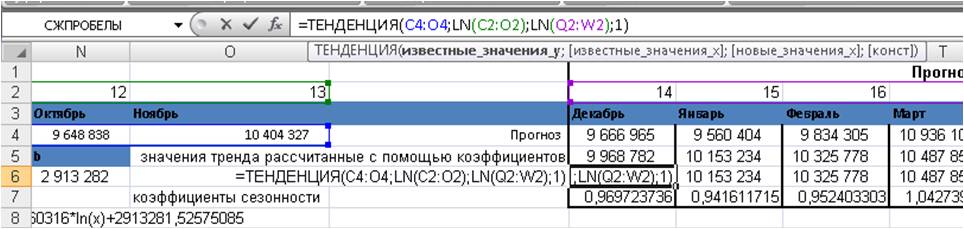
3-й способ — с помощью функции Excel =ТЕНДЕНЦИЯ().
Расчет значений логарифмического тренда с помощью функции Excel =ТЕНДЕНЦИЯ().
Для этого в функцию =ТЕНДЕНЦИЯ() вводим:
1. Известные значения y — объёмы продаж за анализируемый период;
2. Известные значений x — порядковые номера периодов (месяцев), причем введенные как LN(Известные значений x);
3. Новые значения x— порядковые номера периодов, для которых хотим рассчитать значения трендов, причем введенные как LN(Новые значения x);
4. Константа — ставим «1», если хотим рассчитать значения тренда y(x)=a*ln(x)+b с коэффициентом b.
Формула будет выглядеть вот так =ТЕНДЕНЦИЯ(C4:O4;LN(C2:O2);LN(Q2:W2);1)
Затем, вводим формулу =ТЕНДЕНЦИЯ(), как формулу массива. Для этого
1. Выделяем диапазон ячеек с 1-го по 20-й период, в первой ячейке введена формула =ТЕНДЕНЦИЯ();
2. Нажимаем F2, а затем одновременно — клавиши CTRL + SHIFT + ВВОД.
Значения логарифмического тренда с помощью формулы Excel =тенденция() рассчитаны.
Файл с примером вы можете скачать здесь.
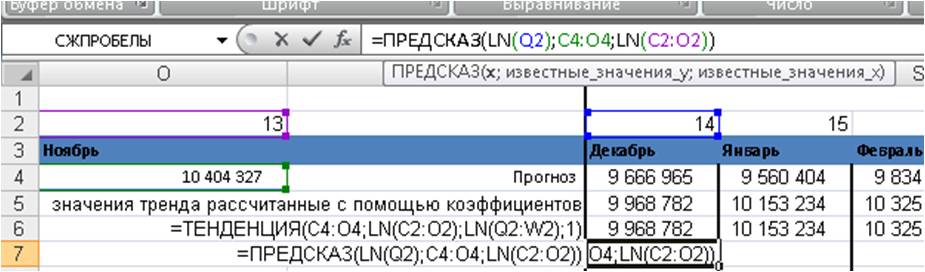
4-й способ — функция Excel =предсказ().
Расчёт значений логарифмического тренда — с помощью функции Excel =предсказ()
Для этого вводим в функцию =предсказ(
1. X — номер периода, для которого рассчитываем прогноз, причем вводим как LN(x);
2. Известные значения y — объёмы продаж по месяцам, фиксируем диапазон, выделяем его и нажимаем F4. Получаем ссылку, как на картинке:
3. Известные значения x — порядковые номера периодов, для которых хотим рассчитать значения логарифмического тренда, причем вводим как LN(Известные значения x) + фиксируем выделенный диапазон, выделяем его и нажимаем F4;
Получаем формулу =ПРЕДСКАЗ(LN(Q2);$C$4:$O$4;LN($C$2:$O$2))
Протягиваем формулу, значения логарифмического тренда рассчитаны.
5-й способ — Forecast4AC PRO
Расчет значений логарифмического тренда — с помощью программы Forecast4AC PRO.
1. Устанавливаем курсор в начало временного ряда, выбираем в настройках программы:
— Что рассчитываем — значения тренда;
— Тренд – Логарифмический тренд;
— Временной ряд — месячный;
и сохраняем;
2. Заходим в меню программы и нажимаем «Start_Forecast» — готово, значения логарифмического тренда рассчитаны!
Файл с примером вы можете скачать здесь.
Для того чтобы рассчитать прогноз с учетом роста и сезонности, мы умножаем рассчитанные значения тренда на коэффициенты сезонности.
Коэффициенты сезонности рассчитаем с помощью программы Forecast4AC PRO (лист » Лист2FYMLn «) или по аналоги, как описано в данной статье, только для рассчета коэффициентов сезонности вместо линейного тренда используем логарифмический.
Теперь значения тренда умножаем на коэффициенты сезонности и прогноз готов.
Отношение прогноза к предыдущему периоду получилось 116%, т.е. прогнозируется рост на 16%.
Как мы можем скорректировать прогнозные значения логарифмического тренда?
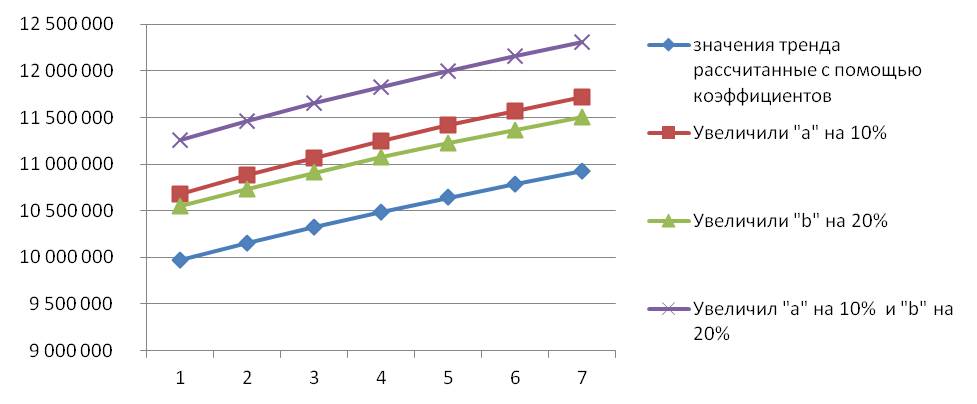
Если нас рост не устраивает, и мы планируем, что он будет больше, мы можем увеличить рост, скорректировав коэффициенты логарифмического тренда.
Скорректируем значение «a» и «b» рассчитанного нами выше тренда y=2673492*ln(x)+2913281
При изменении значений «a» и «b» логарифмического тренда y(x)=a*ln(x)+b, получаем увеличение значений тренда, причем увеличение коэффициента «а» на 10% даёт больший рост, чем увеличение коэффициента «b» на 20%.
Теперь рассчитаем коэффициенты сезонности для логарифмического тренда с помощью Forecast4AC PRO (лист » Лист2FYMLn «). Умножим скорректированные значения тренда на сезонность. Также при прогнозировании стоит учесть дополнительные факторы, которые значительно влияют на объём продаж. Прогноз продаж готов!
С помощью программы Forecast4AC PRO вы сможете в Excel одним нажатием клавиши рассчитать значения логарифмического тренда, коэффициенты сезонности и прогноз для более чем 5000 строк одновременно.
Точных вам прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel.
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Зарегистрируйтесь и скачайте решения
Статья полезная? Поделитесь с друзьями
Ниже приведены условия задач, и текстовый отчет о решении. Закачка полного решения(документы doc и xlsx в архиве zip) начнется автоматически через 10 секунд.
Задача 1. По данным приведенным в таблице 1 провести регрессионный анализ, используя следующие зависимости: линейную, квадратическую, гиперболическую, показательную, степенную, логарифмическую. Выбрать лучшую модель.
Таблица 1 – Исходные данные
|
№ п/п |
X |
Y |
|
1 |
1 |
12 |
|
2 |
2 |
18 |
|
3 |
3 |
15 |
|
4 |
4 |
25 |
|
5 |
5 |
26 |
|
6 |
6 |
34 |
|
7 |
7 |
37 |
|
8 |
8 |
47 |
Решение.
Для решения поставленной задачи и упрощения расчетов воспользуемся средствами табличного процессора MS Excel.
Первым этапом будет ввод исходных данных и построение линейной модели регрессии.
Рисунок 1 – Получение параметров линейной модели регрессии.
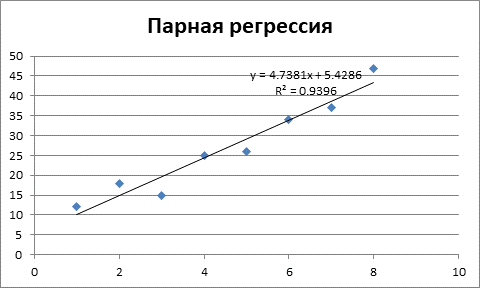
Таким образом, получили следующее линейное уравнение регрессии:
На рисунке 1 показано значение коэффициента детерминации R2 = 0,94. То есть 94% значений переменной Y объясняется значениями переменной X. Таким образом, можно говорить о высоком качестве уравнения регрессии.
Следующим этапом будет построение квадратического уравнения регрессии.
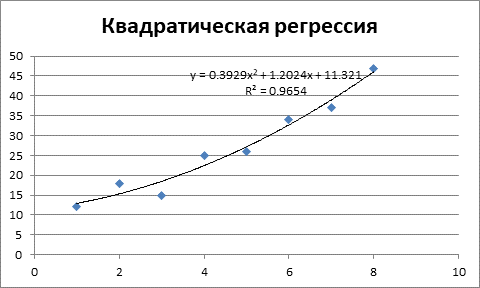
Рисунок 2 – Квадратическое уравнение регрессии и коэффициент детерминации.
Как видим из рисунка 2, коэффициент детерминации составляет R2 = 0,9654, то есть качество уравнения несколько выше линейного уравнения.
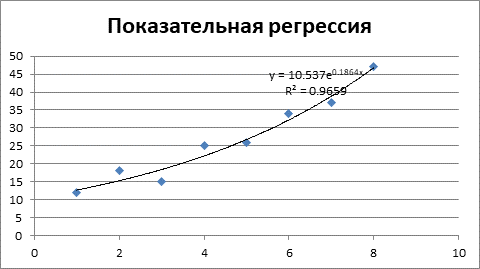
Следующим этапом будет получение показательного уравнения регрессии.
Рисунок 3 – Показательная регрессия и коэффициент детерминации.
Уравнение показательной регрессии объясняет 94,06% значений зависимой переменной Y от факторной переменной X.
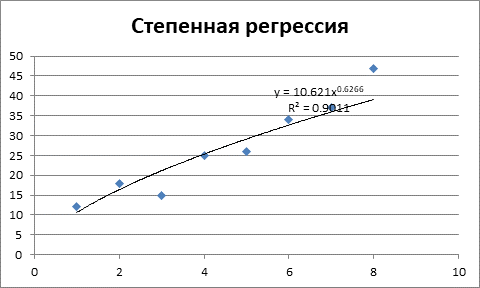
Рисунок 4 – Степенная регрессия и коэффициент детерминации.
Согласно рис. 4 полученное уравнение регрессии объясняет 87,7% значений зависимой переменной Y. Данное уравнение достаточно хуже по качеству, чем предыдущие.
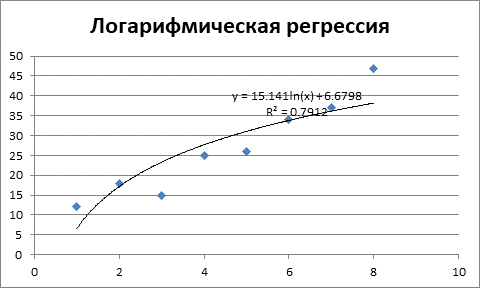
Рисунок 5 – Логарифмическая регрессия и коэффициент детерминации
Коэффициент детерминации логарифмического уравнения регрессии говорит о достаточно хорошем качестве уравнения регрессии, однако оно уступает по качеству предыдущим уравнениям.
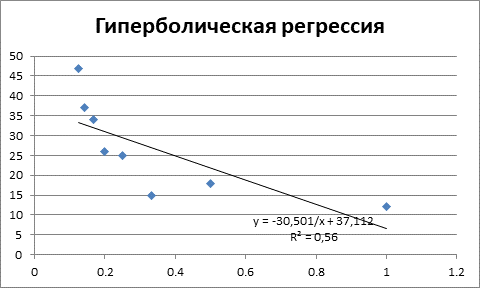
В заключении строим график гиперболической регрессии.
Рисунок 6 – Гиперболическая регрессия и коэффициент детерминации
Как видим данное уравнение регрессии является наихудшим по качеству, поскольку объясняет только 56% значений зависимой переменной Y.
Наилучшим по качеству уравнением регрессии в данной задаче является уравнение квадратической регрессии. Данное уравнение объясняет 96,54% значений зависимой переменной Y.
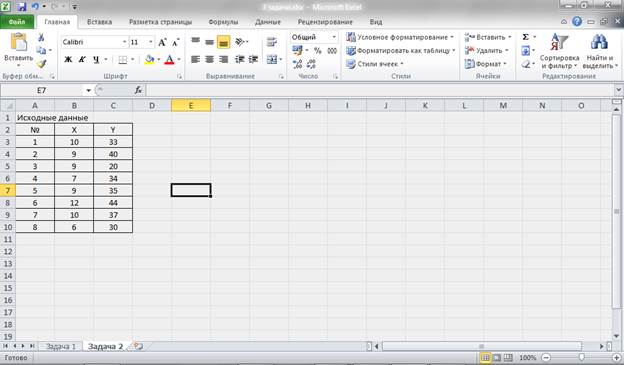
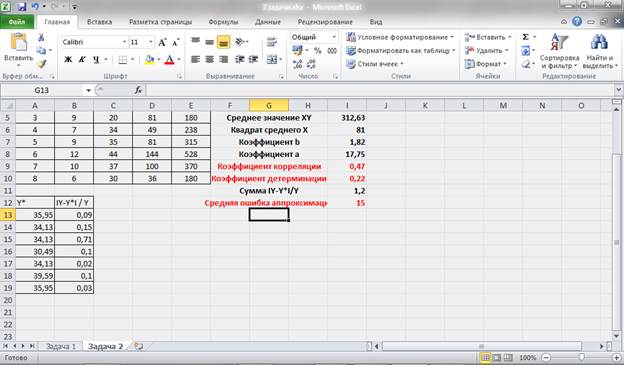
Задача 2. По данным приведенным в таблице 2 требуется:
1. Построить линейное уравнение регрессии Y по X.
2. Рассчитать линейный коэффициент корреляции, коэффициент детерминации и среднюю ошибку аппроксимации.
3. Рассчитать коэффициент эластичности.
Таблица 2 – Исходные данные
|
№ п / п |
X |
Y |
|
1 |
10 |
33 |
|
2 |
9 |
40 |
|
3 |
9 |
20 |
|
4 |
7 |
34 |
|
5 |
9 |
35 |
|
6 |
12 |
44 |
|
7 |
10 |
37 |
|
8 |
6 |
30 |
Решение.
Для решения поставленной задачи воспользуемся средствами табличного процессора MS Excel.
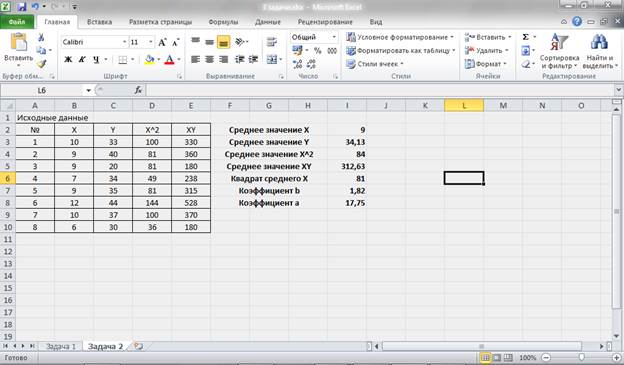
Для этого создаем новый лист и вводим исходные данные
Рисунок 7 – Исходные данные.
Уравнение парной регрессии имеет вид:
— x, y – факторная и зависимые переменные;
— a, b – коэффициенты уравнения.
Коэффициенты уравнения парной линейной регрессии будем искать с помощью метода наименьших квадратов и табличного процессора MS Excel. Согласно МНК коэффициенты уравнения находятся по следующим формулам:
Составим дополнительную таблицу и произведем промежуточные расчеты в табличном процессоре:
Рисунок 8 – Промежуточные расчеты и расчет коэффициентов уравнения.
В результате мы получили уравнение парной линейной регрессии:
Коэффициент корреляции, как правило используется для оценки направления и тесноты связи между зависимой и факторной переменными. Однако уже сейчас мы можем предположить направление связи между X и Y по знаку в уравнении регрессии.
Поскольку в уравнении стоит знак «+», то можно предположить наличие прямой связи между X и Y, т.е. значения Y напрямую зависят от значений X.
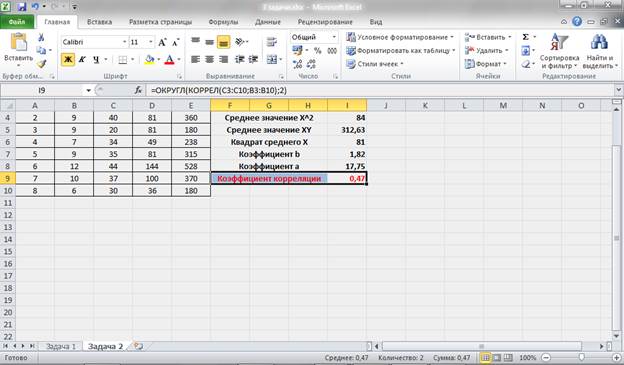
С помощью средств табличного процессора оценим тесноту этой связи:
Рисунок 9 – Оценка тесноты связи с помощью коэффициента корреляции.
Коэффициент корреляции ryx = 0,47. Отсюда можно сделать вывод, что между переменными X и Y существует умеренная связь. Положительное значение коэффициента корреляции подтверждает наше предположение о направлении связи – Y зависит от X.
Между коэффициентом корреляции и коэффициентом детерминации существует взаимосвязь:
Отсюда получаем значение коэффициента детерминации: R2 = 0,22. То есть уравнение регрессии объясняет 22% значений зависимой переменной. Можно говорить о невысоком качестве уравнения регрессии.
Для подтверждения наших выводов о качестве уравнения рассчитаем показатель средней ошибки аппроксимации:
Проведем дополнительные расчеты:
Рисунок 10 – Промежуточные расчеты и расчет средней ошибки аппроксимации.
Получаем, что средняя ошибка аппроксимации не попадает в предел до 5 – 8% (А = 15%), что подтверждает наш вывод о невысоком качестве уравнения регрессии.
Коэффициент эластичности определим по следующей формуле:
Рисунок 11 – Расчет коэффициента эластичности.
Таким образом, при изменении значения Х на 1% значение Y изменится на 0,48%.
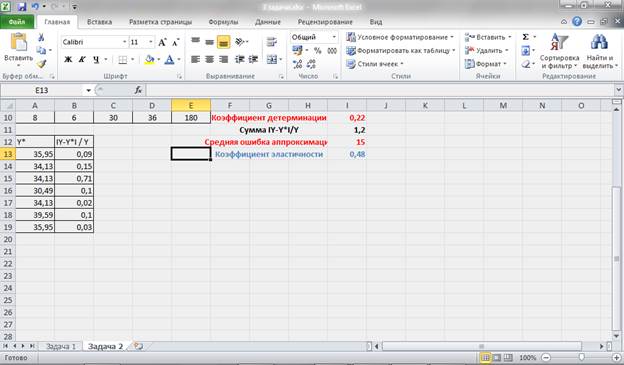
Задача 3. По данным приведенным в таблице 3 требуется:
1. Построить линейную модель множественной регрессии.
2. Записать стандартизированное уравнение множественной регрессии.
3. Рассчитать коэффициенты парной, частной и множественной корреляции. Проанализировать их.
Таблица 3 – Исходные данные
|
№ п / п |
Х1 |
X2 |
Y |
|
1 |
12 |
12 |
133 |
|
2 |
8 |
22 |
135 |
|
3 |
8 |
15 |
120 |
|
4 |
7 |
19 |
125 |
|
5 |
9 |
17 |
130 |
|
6 |
10 |
11 |
144 |
|
7 |
7 |
10 |
137 |
|
8 |
9 |
28 |
121 |
Решение.
Для решения поставленной задачи используем возможности и средства табличного процессора MS Excel. Вводим исходные данные.
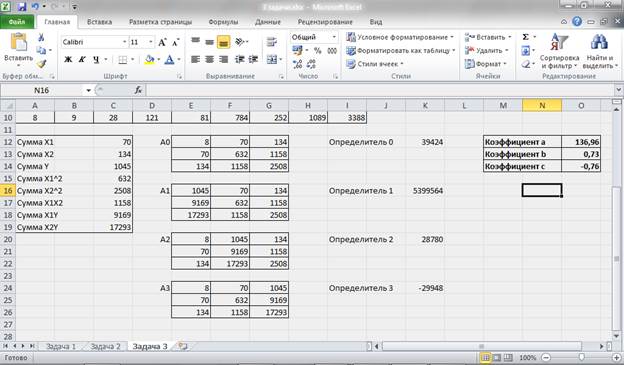
Для построения модели множественной регрессии проведем дополнительные расчеты:
Рисунок 12 – Промежуточные расчеты.
Параметры уравнения множественной регрессии для двухфакторной модели можно определить из системы уравнений:
Запишем действующую систему уравнений:
Данную систему можно решить методом Крамера при условии, что матрица, составленная из коэффициентов при неизвестных, не являтся вырожденной, т.е. Δ ≠ 0.
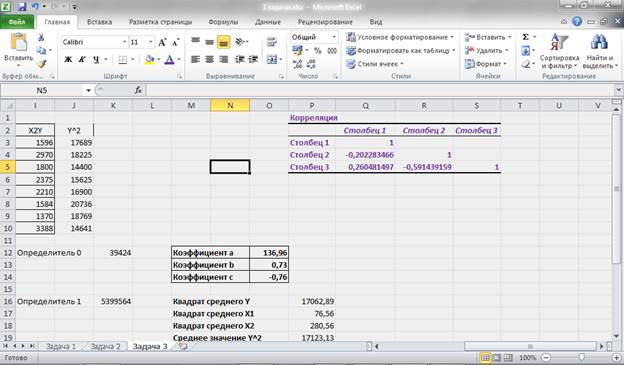
Для упрощения вычислений рассчитываем определитель матрицы, составленной из коэффициентов при неизвестных:
Δ = 39 424
Поскольку исходная матрица не является вырожденной система уравнений имеет решение.
Δ1 = 5 399 564
Δ2 = 28 780
Δ3 = -29 948
Отсюда находим коэффициенты при неизвестных в уравнении регрессии:
— a = 136,96
— b = 0,73
— c = -0,76.
Рисунок 13 – Расчет параметров уравнения множественной регрессии.
Таким образом, мы получаем следующее уравнение множественной регрессии:
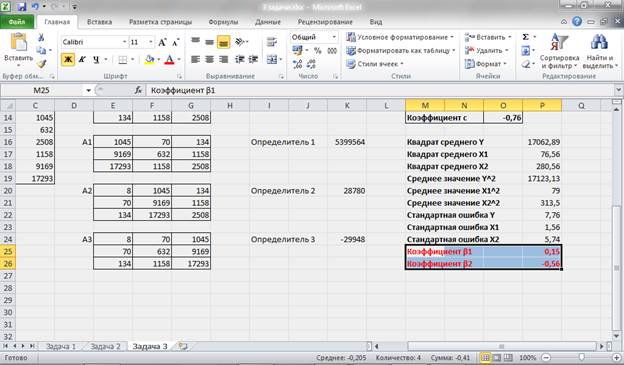
Для построения уравнения множественной регрессии в стандартизированной форме проведем расчет стандартных ошибок и коэффициентов стандартизированного уравнения:
Рисунок 14 – Расчет коэффициентов стандартизированного уравнения.
Таким образом, стандартизированное уравнение множественной регрессии примет вид: ty = 0,15tx1 – 0,56tx2
Для расчета парной, частной и множественной корреляции воспользуемся таким инструментом табличного процессора, как пакет анализа, для построения корреляционной матрицы:
Рисунок 15 – Расчет корреляционной матрицы.
Как видим из рис. 15. Наибольшая связь обратного направления присутствует между переменными Y и X2, т.е. по сути Х2 зависит от значений Y. Прямая же связь между Y и X1 хоть и присутствует, но она достаточно слабая.
Также присутствует слабая обратная связь между переменными X1 и X2.
Список литературы
Список литературы
1. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. Учебник для вузов. – М.ЮНИТИ, 1998. – с. 621 – 632; 751 – 766.
2. Бородич С.А. Эконометрика: Учебное пособие. – Мн.: Новое знание, 2001. – с. 98 – 115; 121 – 147; 200 – 222
3. Доугерти К. Введение в эконометрику: Пер. с англ. – М.: ИНФРА-М, 1999. – XIV, с. 53 – 111
4. Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов / Под ред. Проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2002. – с. 50 – 80
5. Кулинич Е.И. Эконометрия. – М.: Финансы и статистика, 2001. с. 43 – 83
6. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. Учебное пособие. 2-е изд. – М.: Дело, 1998. – с. 17 – 42
7. Практикум по эконометрике: Учебное пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2002. – с. 5 – 48
$begingroup$
Is it possible to perform logarithmic regression on multiple variables with Excel? If I just have a single independent variable than it’s very easy to do this using the best-fit line option (it lets me switch from linear to logarithmic). But this feature does not work for multiple variable regression and the regression feature under the Data Analysis plugin only seems to support linear multiple regression.
However, I have a table that has 3 columns containing 3 independent variables and 1 column with the corresponding dependent variable (outcome). I’m pretty sure there’s a logarithmic relationship, but I’m not sure how to use Excel to get the coefficients. Thanks!
asked Mar 24, 2011 at 5:30
$endgroup$
1
$begingroup$
If by logarithmic regression you mean the model log(y) = m1.x1 + m2.x2 + ... + b + (Error), you can use LOGEST and GROWTH with multiple independent variables. Note that if you want the estimated coefficients m1, m2, ..., b from LOGEST, you’ll have to enter the formula into multiple cells as an array. See Excel’s online help for the steps required.
Alternatively, you can log-transform your dependent variable and use LINEST/TREND which does the same thing under the hood.
ObWarning: Excel isn’t the best regression package in the world. See, for example, McCullough & Heiser (2008), On the accuracy of statistical procedures in Microsoft Excel 2007, Comp Stats & Data Analysis 52(10) pp.4570-4578.
answered Mar 24, 2011 at 6:26
Hong OoiHong Ooi
7,8593 gold badges30 silver badges53 bronze badges
$endgroup$
1
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
- линейной (у = а + bx);
- параболической (y = a + bx + cx2);
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а0 + а1х1 +…+акхк.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Пример:
- Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».
Теперь стали видны и данные регрессионного анализа.