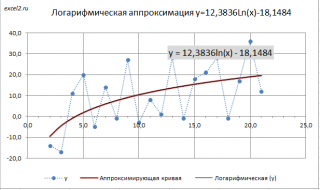
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью
логарифмической функции.
Метод наименьших квадратов
(англ.
Ordinary
Least
Squares
,
OLS
) является одним из базовых методов регрессионного анализа в части оценки неизвестных параметров
регрессионных моделей
по выборочным данным. Основная статья про МНК —
МНК: Метод Наименьших Квадратов в MS EXCEL
.
Иногда между переменными можно предположить логарифмическую зависимость y=a*Ln(x)+b для x>0. Логарифмическую зависимость можно свести к случаю
линейной зависимости
с помощью замены переменных u=Ln(x) (см.
файл примера
).
После замены переменной вычисления полностью аналогичны
линейному случаю
y=a*
u
+b
.
Примечание
: Построить
линию тренда
по методу наименьших квадратов можно и без замены переменной. Для этого нужно воспользоваться инструментом диаграммы
Линия тренда
(
Логарифмическая линия тренда
). Поставив в диалоговом окне галочку в поле «показывать уравнение на диаграмме» можно убедиться, что найденные выше параметры совпадают со значениями на диаграмме. Подробнее о диаграммах см. статью
Основы построения диаграмм в MS EXCEL
.
17 авг. 2022 г.
читать 2 мин
Логарифмическая регрессия — это тип регрессии, используемый для моделирования ситуаций, когда рост или спад сначала быстро ускоряются, а затем со временем замедляются.
Например, следующий график демонстрирует пример логарифмического распада:
Для такого типа ситуации взаимосвязь между переменной-предиктором и переменной-откликом можно хорошо смоделировать с помощью логарифмической регрессии.
Уравнение модели логарифмической регрессии принимает следующий вид:
у = а + b*ln(x)
куда:
- y: переменная ответа
- x: предикторная переменная
- a, b: коэффициенты регрессии, описывающие взаимосвязь между x и y .
В следующем пошаговом примере показано, как выполнить логарифмическую регрессию в Excel.
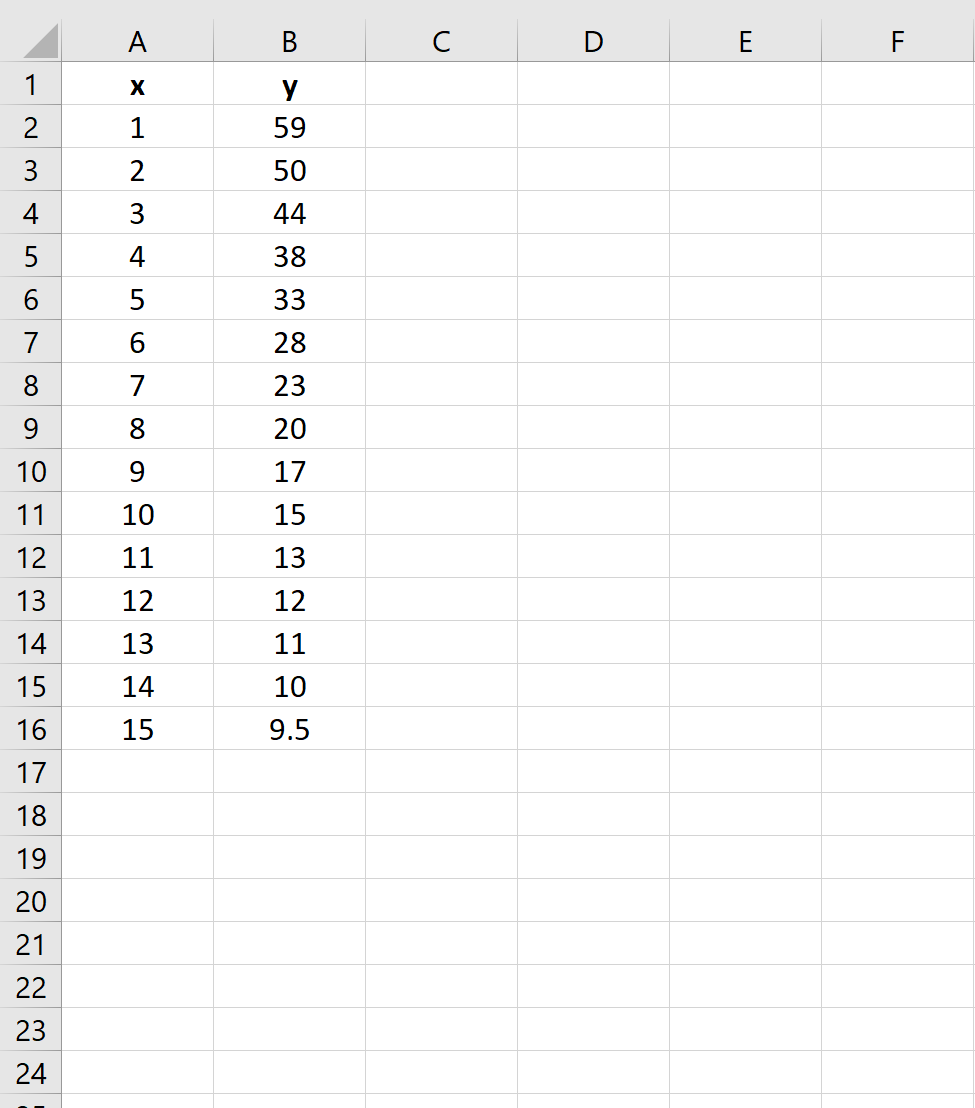
Шаг 1: Создайте данные
Во-первых, давайте создадим поддельные данные для двух переменных: x и y :
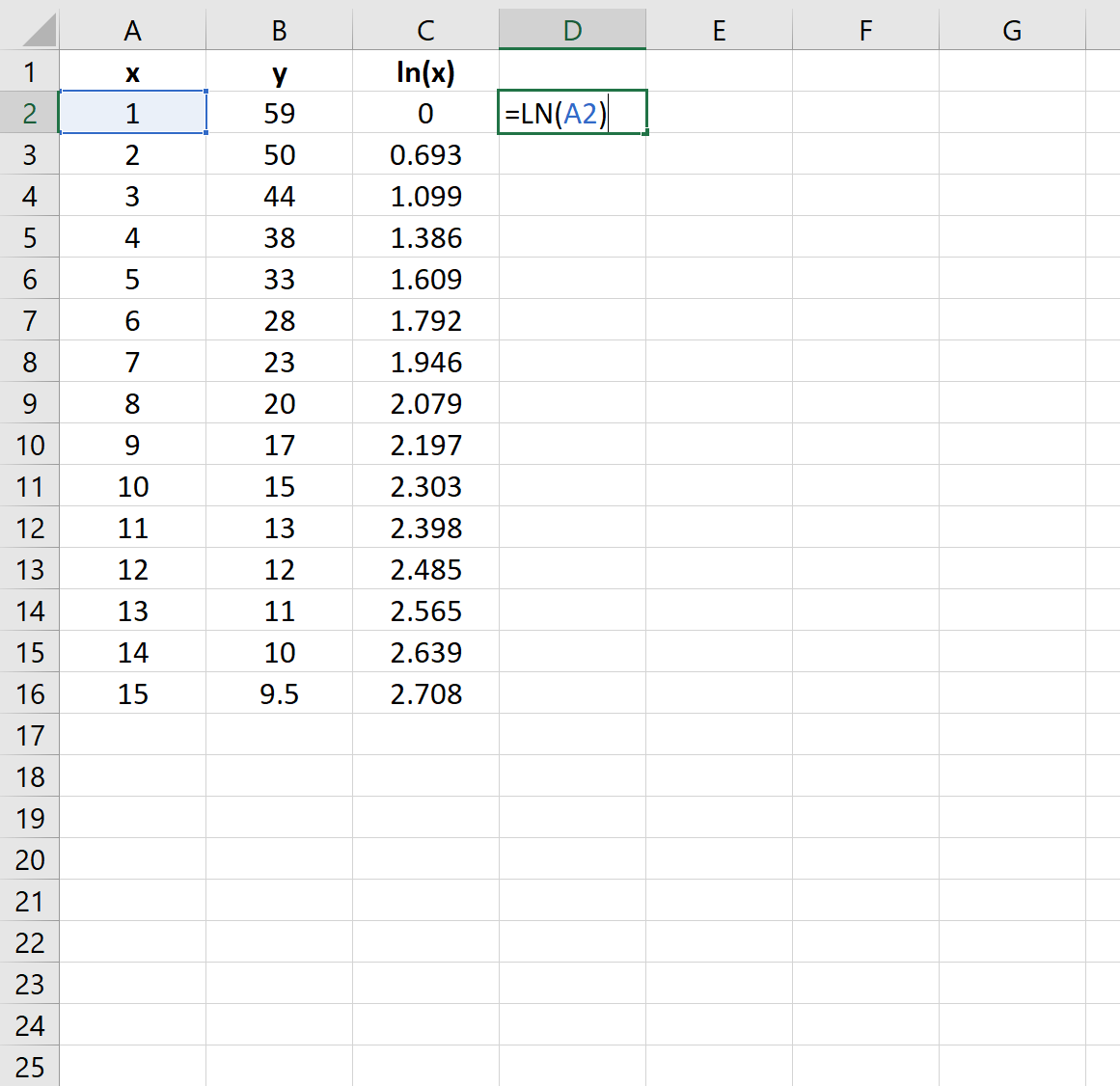
Шаг 2: возьмите натуральный логарифм переменной-предиктора
Далее нам нужно создать новый столбец, представляющий натуральный логарифм переменной-предиктора x :
Шаг 3: Подберите модель логарифмической регрессии
Далее мы подгоним модель логарифмической регрессии. Для этого щелкните вкладку « Данные » на верхней ленте, затем щелкните « Анализ данных» в группе « Анализ ».
Если вы не видите Data Analysis в качестве опции, вам нужно сначала загрузить Analysis ToolPak .
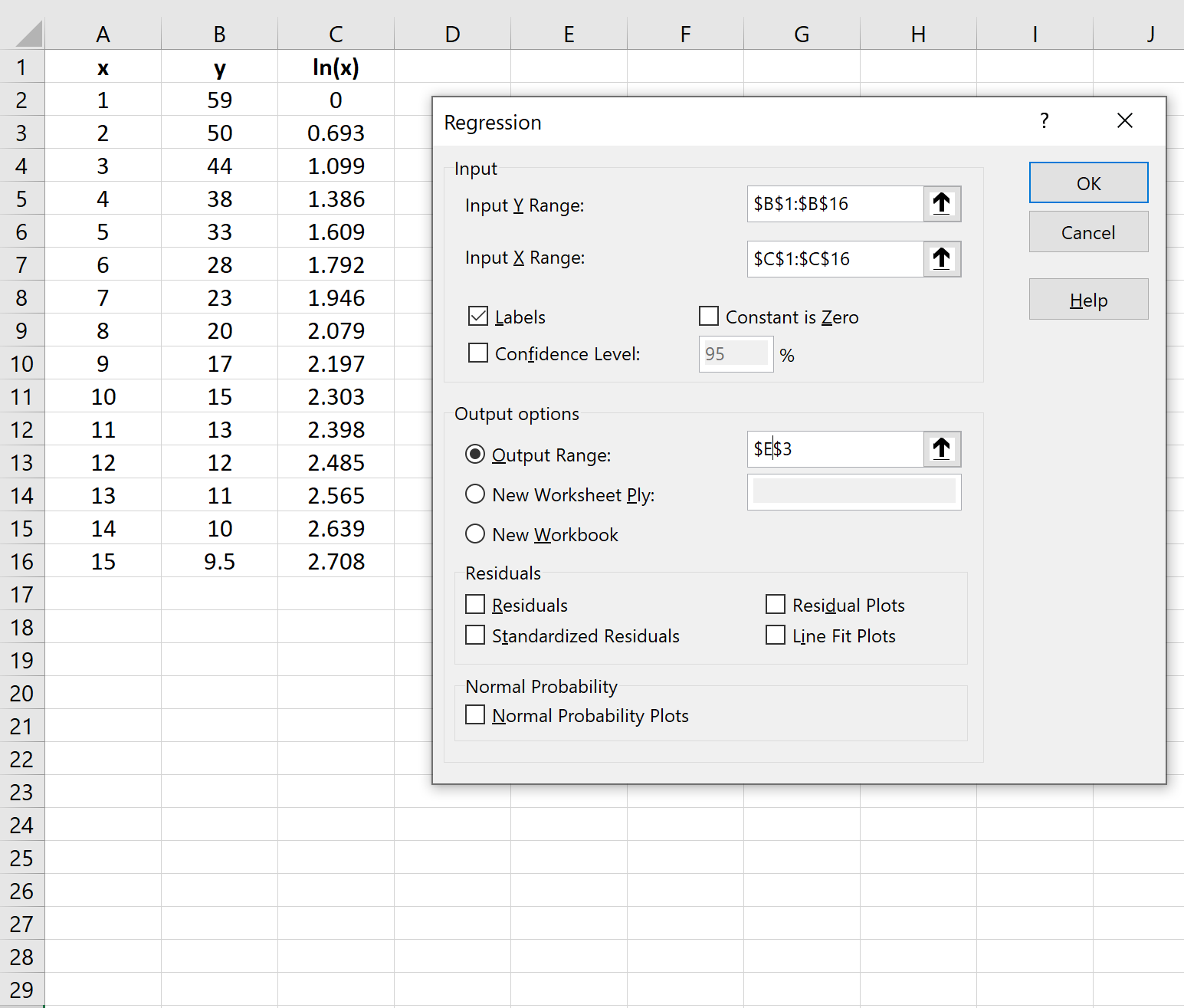
В появившемся окне нажмите Регрессия.В появившемся новом окне введите следующую информацию:
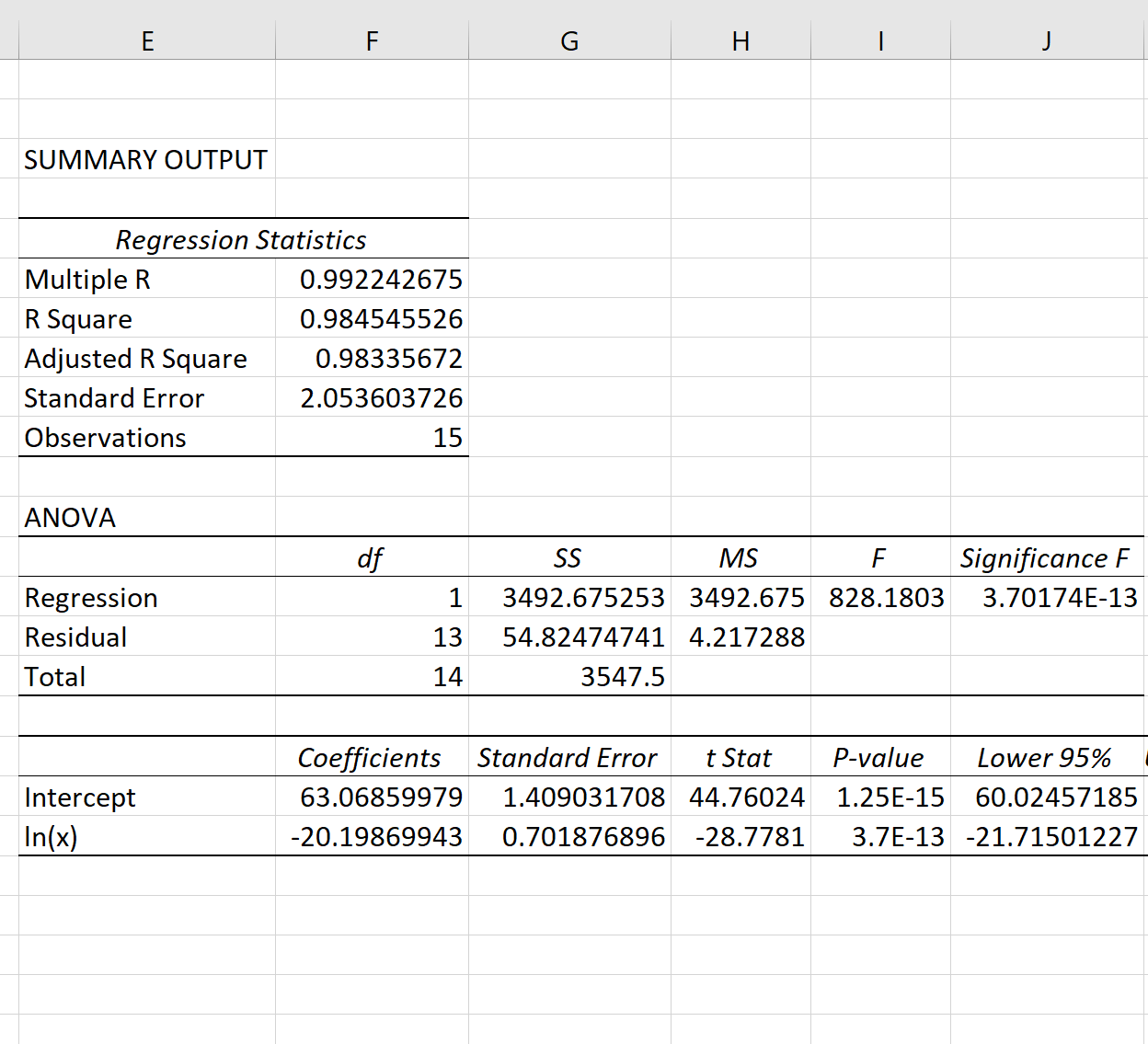
Как только вы нажмете OK , отобразятся выходные данные модели логарифмической регрессии:
Общее значение F модели составляет 828,18, а соответствующее значение p чрезвычайно мало (3,70174E-13), что указывает на то, что модель в целом полезна.
Используя коэффициенты из выходной таблицы, мы видим, что подобранное уравнение логарифмической регрессии:
у = 63,0686 – 20,1987 * ln(x)
Мы можем использовать это уравнение для прогнозирования переменной отклика y на основе значения переменной-предиктора x.Например, если x = 12, то мы предсказываем, что y будет 12,87 :
у = 63,0686 – 20,1987 * ln(12) = 12,87
Бонус: не стесняйтесь использовать этот онлайн- калькулятор логарифмической регрессии для автоматического вычисления уравнения логарифмической регрессии для заданного предиктора и переменной отклика.
Дополнительные ресурсы
Как выполнить простую линейную регрессию в Excel
Как выполнить множественную линейную регрессию в Excel
Как выполнить полиномиальную регрессию в Excel
Как выполнить экспоненциальную регрессию в Excel
Из данной статьи вы узнаете:
• Примеры применения логарифмического тренда в бизнесе;
• Логарифмический тренд y(x)=a*ln(x)+b разложим на запчасти;
• 5 способов расчета значений логарифмического тренда в Excel;
• Как можно скорректировать значения логарифмического тренда;
Логарифмический тренд применяется для прогнозирования временного ряда, данные которого вначале быстро растут или убывают, а затем постепенно стабилизируются.
Например, выводим новый товар на рынок, за счет роста клиентской базы продажи быстро растут, затем мы набираем постоянных клиентов, продажи стабилизируются, и новые клиенты уже не основной фактор роста, а основной фактор роста — это развитие продаж постоянным клиентам.
Или вводим продукцию в новую торговую точку, и по истечении определенного периода решаем увеличить количество фейсов на полке (т.е. увеличить размер полки для одного вида товара) (фейс — это единица продукции, которая стоит лицом к покупателю) или продублировать выкладку в другой части зала. Почему здесь лучше использовать логарифм? Потому что увеличение количества фейсингов на полке в 2 раза по одной группе товаров, к сожалению, не ведёт к увеличению продаж в 2 раза, причём с ростом количества фейсов темп прироста продаж уменьшаются для каждого последующего фейса. Именно поэтому для прогнозирования продаж для этой ситуации лучше всего использовать логарифмический тренд.
Логарифмический тренд – это функция y(x)=a*ln(x)+b, где
Значение x – это номера периода во временном ряду (например, номер месяца, квартала, дня; См. статью о временных рядах.)
y – это последовательность значений , которые мы анализируем и прогнозируем (например, объём продаж по месяцам.)
b – точка пересечения с осью y на графике;
a – это значение, на которое увеличивается следующее значение временного ряда;
Причем, если a>0, то динамика роста положительная,
Если а<0, то динамика тренда отрицательная.
При построении логарифмического тренда используют как положительные, так и отрицательные данные временных рядов.
Рассмотрим логарифмический тренд на примере построения прогноза продаж в Excel по месяцам.
Временной ряд — продажи по месяцам по новому товару
В этом временном раде у нас есть 2 переменных
1. Время — месяцы— x;
2. Объёмы продаж по месяцам — y;
Уравнение логарифмического тренда y(x)=a*ln(x)+b, где y — это объёмы продаж, x — месяцы.
5 способов расчета логарифмического тренда в Excel.
Как в Excel мы можем рассчитать коэффициенты логарифмического тренда?
1-й способ — с помощью графика.
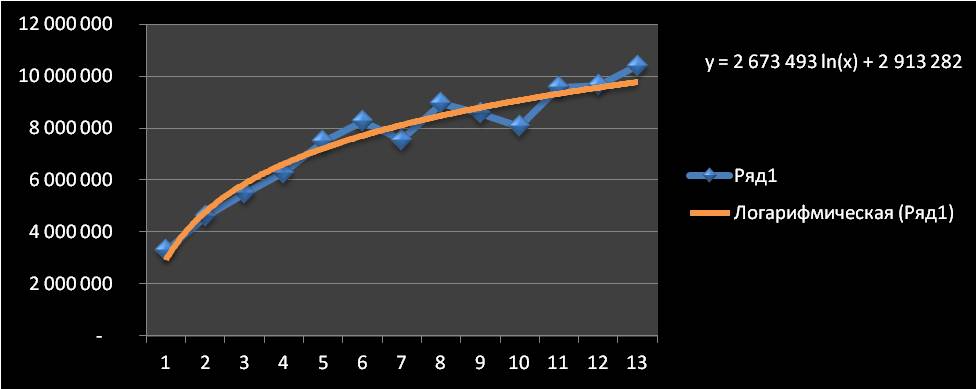
Строим график в Excel и видим по оси x — наш временной рад (1, 2, 3… — ноябрь, декабрь, январь …), по оси y объёмы продаж + добавляем на график линию тренда и уравнение тренда.
Получаем уравнение тренда y=2 673 493 ln(x) + 2 913 282
Для прогнозирования нам необходимо рассчитать значения тренда, как для анализируемых значений, так и для будущих периодов.
При расчете значений логарифмического тренда нам будут известны:
- Время — значение по оси Х;
- Значение «a» и «b» уравнения логарифмического тренда y(x)=a*ln(x)+b;
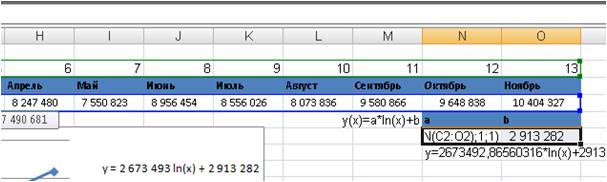
Рассчитываем значения тренда для каждого анализируемого периода времени от 1 до 13, а также для будущих периодов с 14 месяца до 20.
Например, для 14 месяца значение тренда рассчитывается по следующей схеме: в уравнение подставляем x=14 и получаем y=2 673 493 ln(14) + 2 913 282=9 968 782
20-го y=2 673 493 ln(20) + 2 913 282=10 922 350
И т.д.
Файл с примером вы можете скачать здесь.
2-й способ — с помощью функции Excel =Линейн().
Для расчета коэффициентов логарифмического тренда воспользуемся функцией Excel =ЛИНЕЙН() .
Для этого в функцию =ЛИНЕЙН() введем:
1. известные значения y – объем продаж;
2. известные значения x – номера периодов, причём введенные, как LN(номера периодов);
3. константа – вводим 1 для расчёта коэффициента b уравнения y(x)=a*ln(x)+b;
4. Статистика — 1 или 0;
Формула будит выглядеть вот так =ЛИНЕЙН(C2:O2;LN(C1:O1);ИСТИНА;ИСТИНА)
Теперь формулу вводим как формулу массива, выделяем 2 ячейки (подробнее о формулах массива) и нажимаем F2, а затем одновременно — клавиши CTRL + SHIFT + ВВОД.
Коэффициенты «а» и «b» логарифмического тренда y(x)=a*ln(x)+b рассчитаны;
Получаем уравнение тренда y=2673492*ln(x)+2913281
Для прогнозирования нам необходимо продлить линию тренда и определить её значения. При её продлении нам будет известен только один параметр — это время, т.е. значения по оси X.
Рассчитываем значения тренда с 1-го месяца (ноябрь) до 20 (июнь)— y=2673492*ln(14)+2913281=9968782
17-го — y=2673492*ln(17)+2913281=10487857
И т.д.
3-й способ — с помощью функции Excel =ТЕНДЕНЦИЯ().
Расчет значений логарифмического тренда с помощью функции Excel =ТЕНДЕНЦИЯ().
Для этого в функцию =ТЕНДЕНЦИЯ() вводим:
1. Известные значения y — объёмы продаж за анализируемый период;
2. Известные значений x — порядковые номера периодов (месяцев), причем введенные как LN(Известные значений x);
3. Новые значения x— порядковые номера периодов, для которых хотим рассчитать значения трендов, причем введенные как LN(Новые значения x);
4. Константа — ставим «1», если хотим рассчитать значения тренда y(x)=a*ln(x)+b с коэффициентом b.
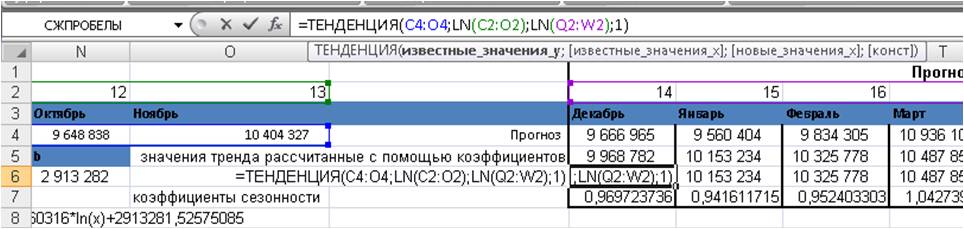
Формула будет выглядеть вот так =ТЕНДЕНЦИЯ(C4:O4;LN(C2:O2);LN(Q2:W2);1)
Затем, вводим формулу =ТЕНДЕНЦИЯ(), как формулу массива. Для этого
1. Выделяем диапазон ячеек с 1-го по 20-й период, в первой ячейке введена формула =ТЕНДЕНЦИЯ();
2. Нажимаем F2, а затем одновременно — клавиши CTRL + SHIFT + ВВОД.
Значения логарифмического тренда с помощью формулы Excel =тенденция() рассчитаны.
Файл с примером вы можете скачать здесь.
4-й способ — функция Excel =предсказ().
Расчёт значений логарифмического тренда — с помощью функции Excel =предсказ()
Для этого вводим в функцию =предсказ(
1. X — номер периода, для которого рассчитываем прогноз, причем вводим как LN(x);
2. Известные значения y — объёмы продаж по месяцам, фиксируем диапазон, выделяем его и нажимаем F4. Получаем ссылку, как на картинке:
3. Известные значения x — порядковые номера периодов, для которых хотим рассчитать значения логарифмического тренда, причем вводим как LN(Известные значения x) + фиксируем выделенный диапазон, выделяем его и нажимаем F4;
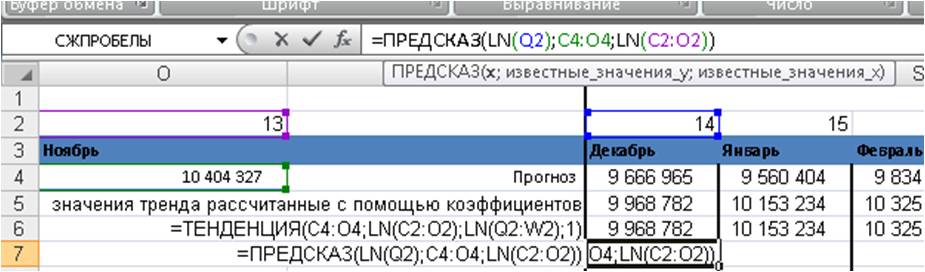
Получаем формулу =ПРЕДСКАЗ(LN(Q2);$C$4:$O$4;LN($C$2:$O$2))
Протягиваем формулу, значения логарифмического тренда рассчитаны.
5-й способ — Forecast4AC PRO
Расчет значений логарифмического тренда — с помощью программы Forecast4AC PRO.
1. Устанавливаем курсор в начало временного ряда, выбираем в настройках программы:
— Что рассчитываем — значения тренда;
— Тренд – Логарифмический тренд;
— Временной ряд — месячный;
и сохраняем;
2. Заходим в меню программы и нажимаем «Start_Forecast» — готово, значения логарифмического тренда рассчитаны!
Файл с примером вы можете скачать здесь.
Для того чтобы рассчитать прогноз с учетом роста и сезонности, мы умножаем рассчитанные значения тренда на коэффициенты сезонности.
Коэффициенты сезонности рассчитаем с помощью программы Forecast4AC PRO (лист » Лист2FYMLn «) или по аналоги, как описано в данной статье, только для рассчета коэффициентов сезонности вместо линейного тренда используем логарифмический.
Теперь значения тренда умножаем на коэффициенты сезонности и прогноз готов.
Отношение прогноза к предыдущему периоду получилось 116%, т.е. прогнозируется рост на 16%.
Как мы можем скорректировать прогнозные значения логарифмического тренда?
Если нас рост не устраивает, и мы планируем, что он будет больше, мы можем увеличить рост, скорректировав коэффициенты логарифмического тренда.
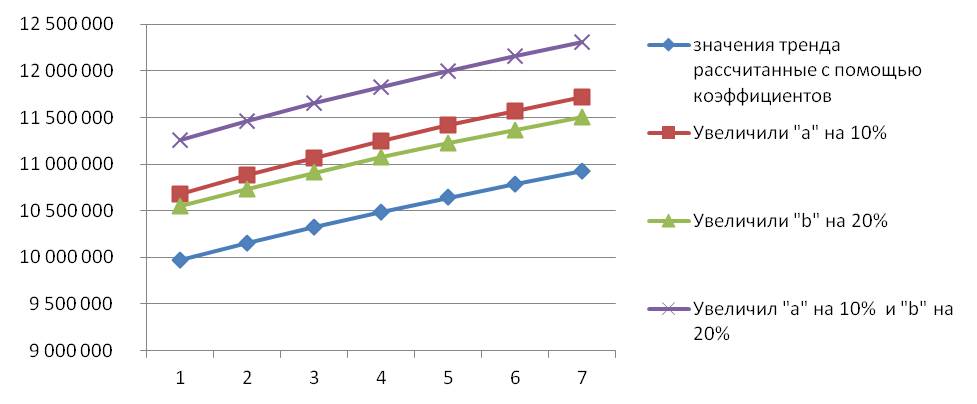
Скорректируем значение «a» и «b» рассчитанного нами выше тренда y=2673492*ln(x)+2913281
При изменении значений «a» и «b» логарифмического тренда y(x)=a*ln(x)+b, получаем увеличение значений тренда, причем увеличение коэффициента «а» на 10% даёт больший рост, чем увеличение коэффициента «b» на 20%.
Теперь рассчитаем коэффициенты сезонности для логарифмического тренда с помощью Forecast4AC PRO (лист » Лист2FYMLn «). Умножим скорректированные значения тренда на сезонность. Также при прогнозировании стоит учесть дополнительные факторы, которые значительно влияют на объём продаж. Прогноз продаж готов!
С помощью программы Forecast4AC PRO вы сможете в Excel одним нажатием клавиши рассчитать значения логарифмического тренда, коэффициенты сезонности и прогноз для более чем 5000 строк одновременно.
Точных вам прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel.
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Зарегистрируйтесь и скачайте решения
Статья полезная? Поделитесь с друзьями
Semi-log and log-log graphs can help you discover new relationships between your data. Here’s how to create them in Excel.
Semi-log and log-log graphs are useful tools for analyzing and finding exponential and power functions relations. Logarithmic graphs have the potential to give you a perspective of a relationship between your data that isn’t obvious on a plain graph.
While a semi-log graph is logarithmic on only one axis, a log-log graph is logarithmic on both axes. Each of these graphs has its own uses. With Excel, you can create semi-log and log-log charts and graphs with a few clicks to further analyze your data. Read on to find out how you can create such graphs in Excel.
How to Create a Semi-Log Graph in Excel
A semi-log graph is a graph that has one of the two axes on a logarithmic scale. Usually, the Y-axis is logarithmic. This means that the Y-axis grid lines will be exponential, while the X-axis gridlines stay even.
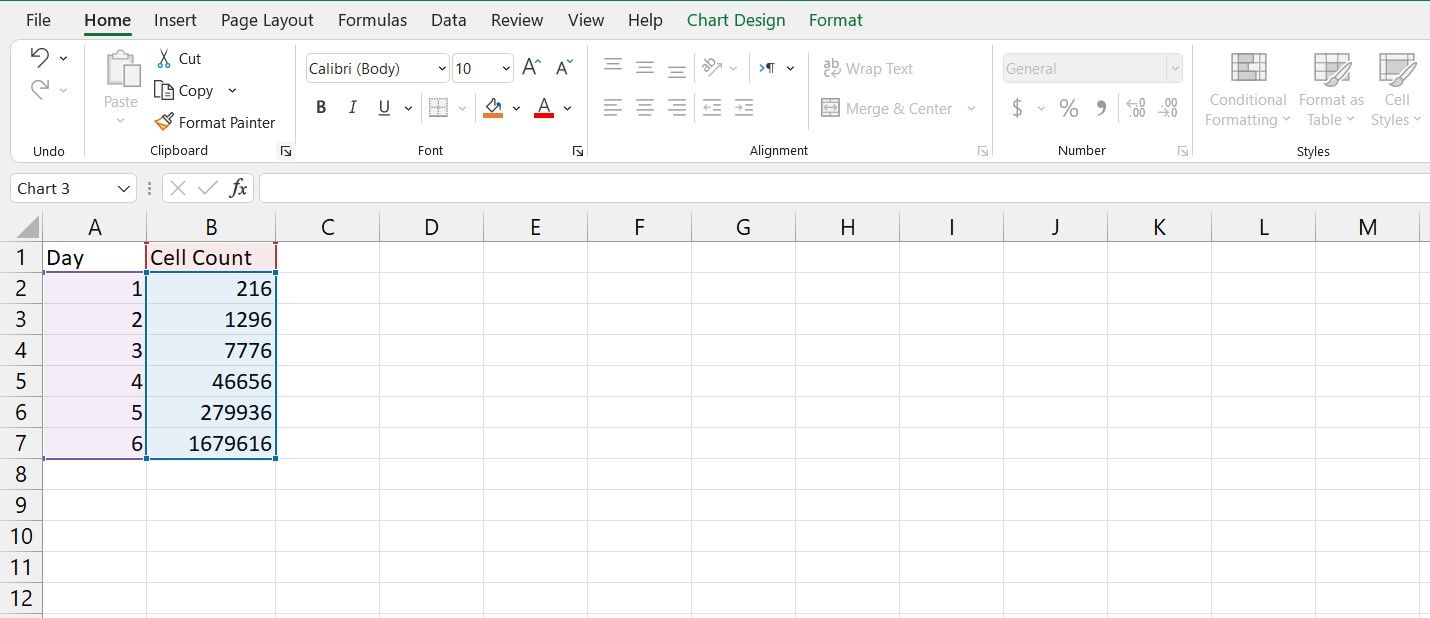
As an example, in this spreadsheet, we have the number of cells in a cell culture environment in an experiment on different days. The goal is to plot this data on a semi-log graph. If you’re not familiar with creating graphs in Excel, read our article on how to create graphs in Excel to get a good understanding of the process.
- Select the entire table. That will be cells A1 to B7 in this example.
- Go to the Insert menu.
- From the Charts section, click Insert Scatter (X, Y) or Bubble Chart.
- Select Scatter with Smooth Lines and Markers.
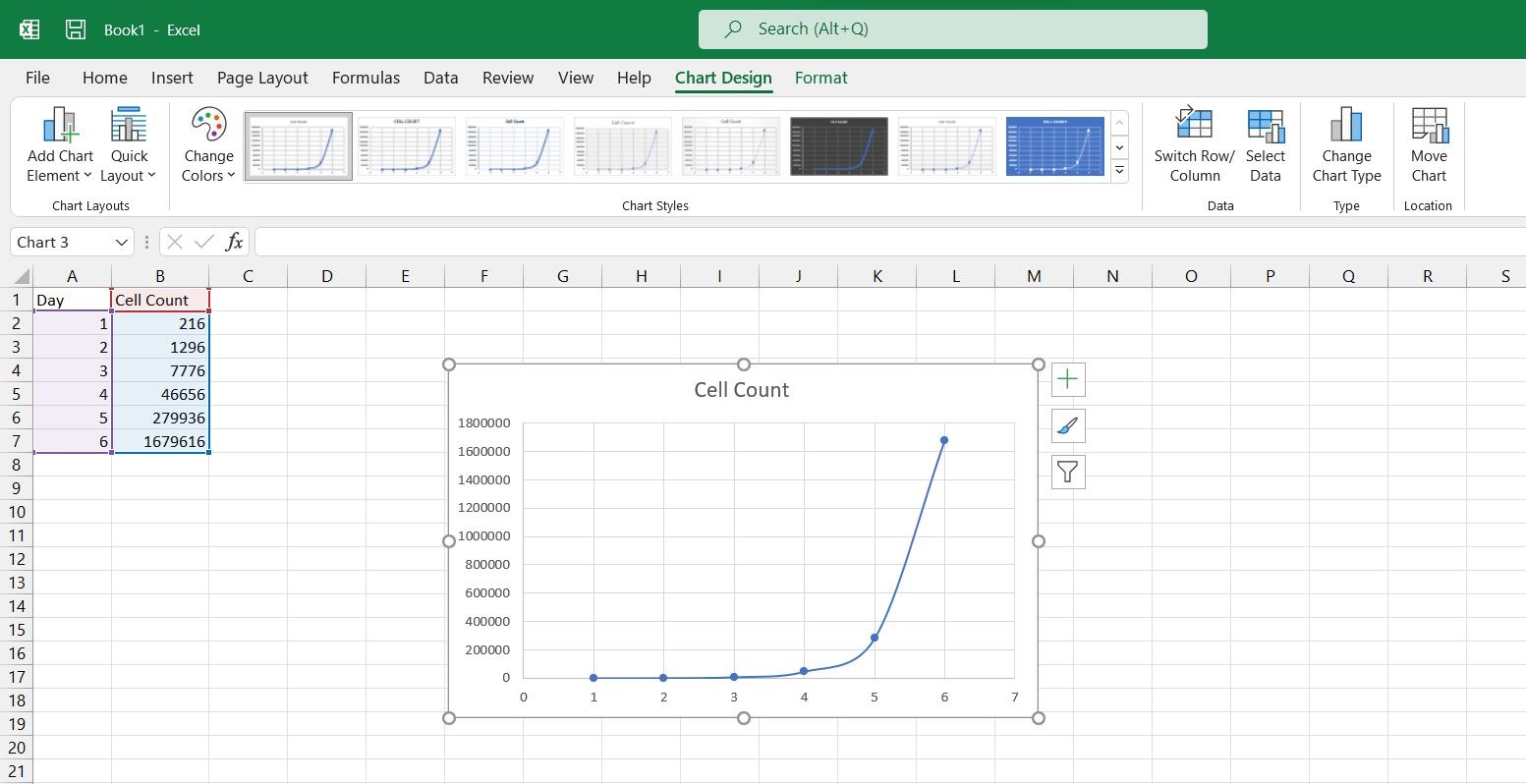
You now have a scatter chart of your data. Now it’s time to make it a semi-log one.
- Select the chart you just made.
- Double-click the Y-axis.
- In the Format Axis panel on the right, go to the Axis Options tab.
- In Axis Options, check Logarithmic Scale.
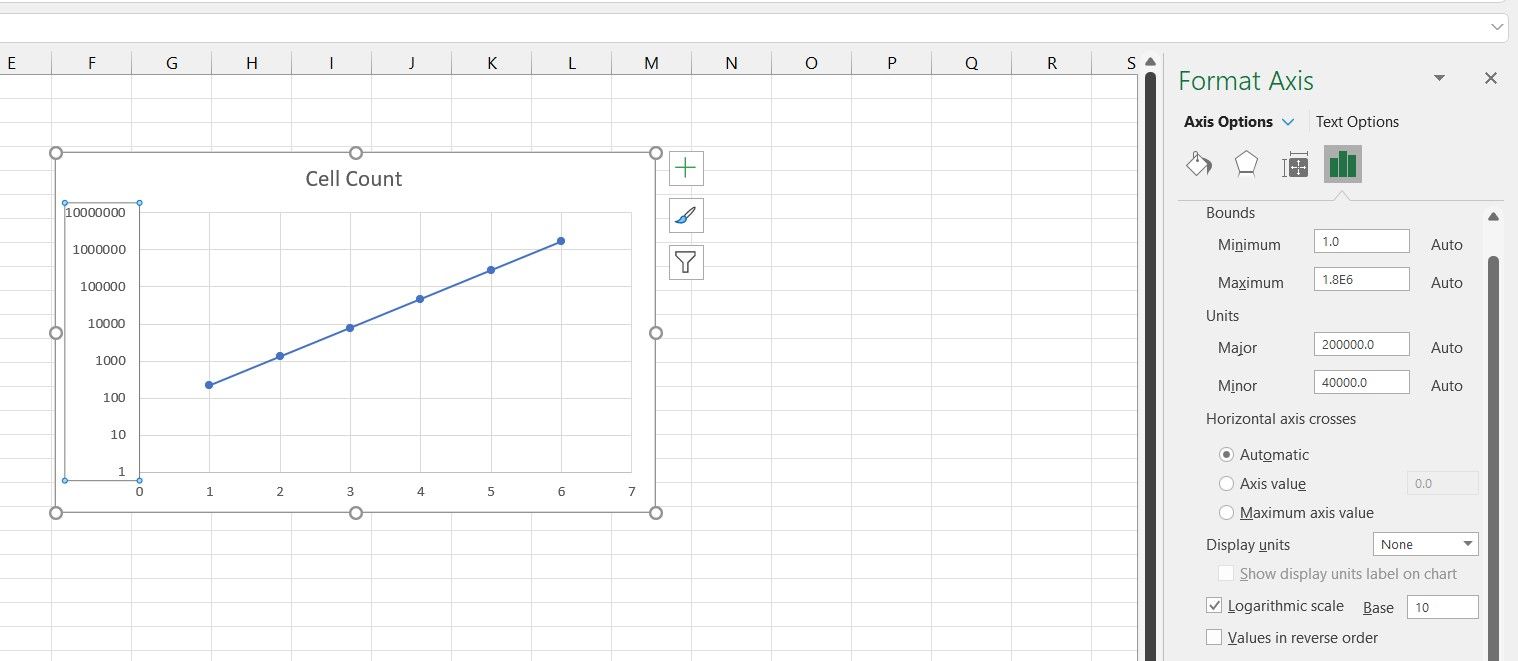
There’s your semi-log graph! Note that the graph is now a straight line now.
You can also alter the base from the default 10 to any other number that suits you better. That is because the cell count in the data table was exponential, as they are actually powers of six. You can further improve your graph’s readability by changing the logarithm base from 10 to 6.
How to Create a Log-Log Graph in Excel
A log-log graph is a graph that has both axes on a logarithmic scale. So then, the grid lines for both the X and Y axes are exponential and uneven in this graph. Let’s see the log-log graph in action with an example.
In a similar example, we have the cell counts on different days, but this time the days are exponential as well. A data table such as this practically begs for a log-log graph.
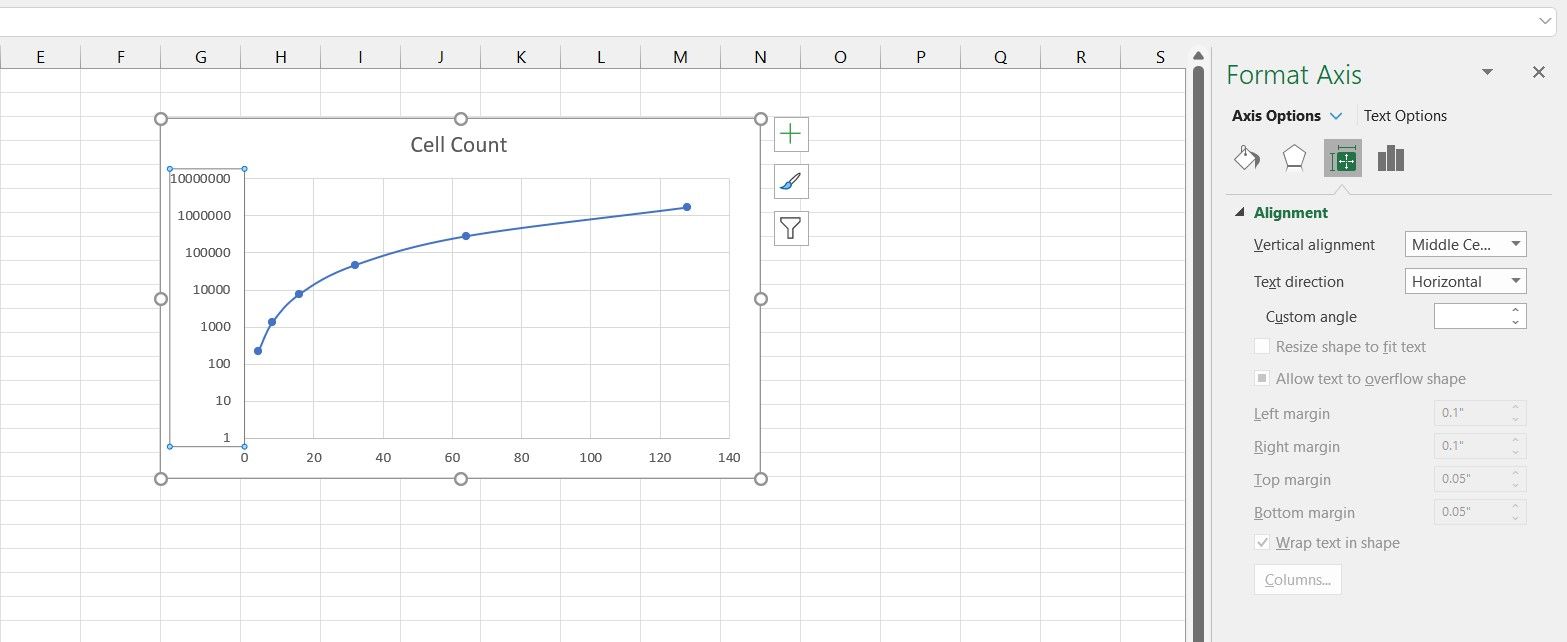
Just like the previous example, select the table and create a scatter chart for it. If you want to learn more about scatter charts, read our article on how to make a scatter plot in Excel to find out what exactly it is and when you should use it.
After you’ve created the scatter plot, change the Y-axis to log the way you learned in the previous section. You can see that the graph still isn’t a straight line. That’s because the X-axis (day number in this example) is exponential as well.
- Select the chart.
- Double-click the X-axis.
- From the Format Axis panel, click Axis Options.
- Under Axis Options, check Logarithmic Scale.
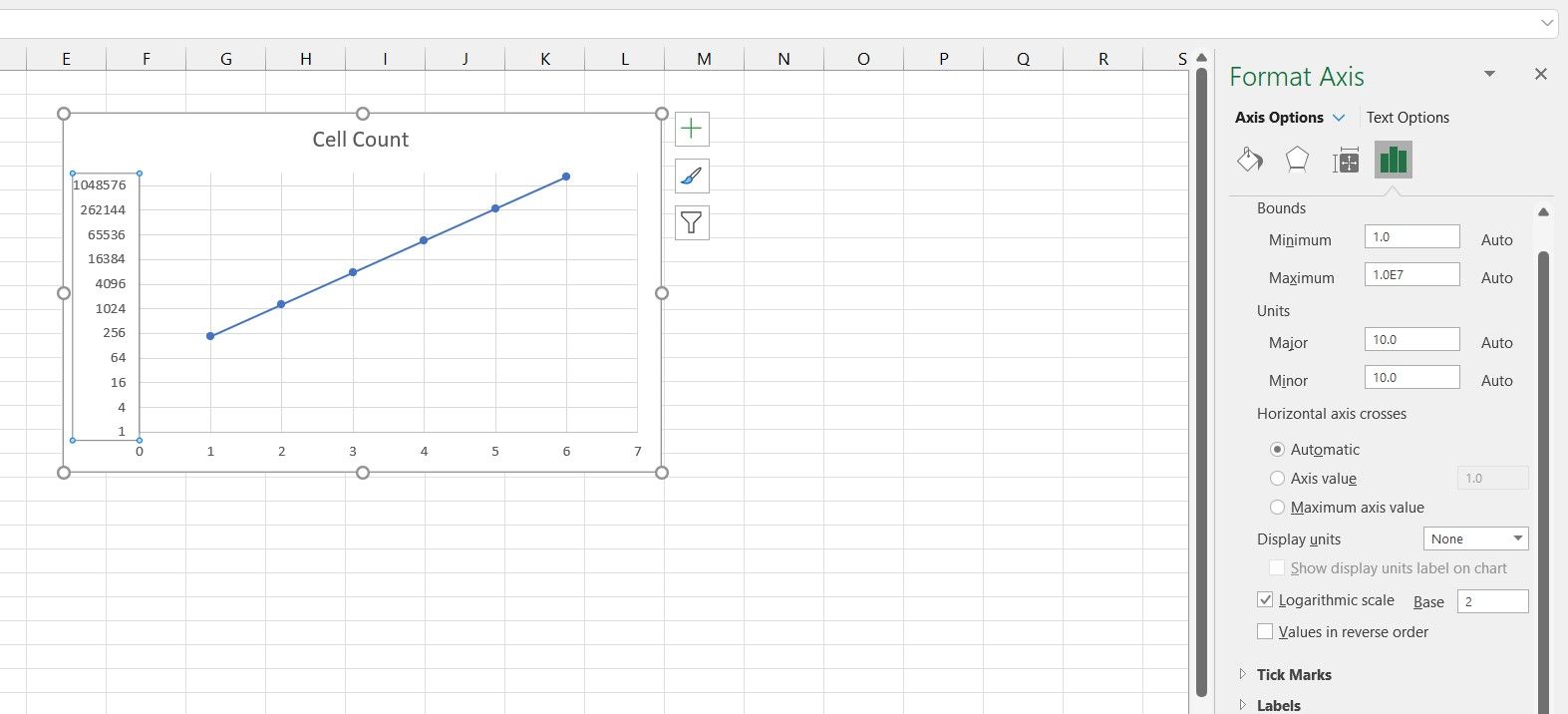
Now both your axes are on a logarithmic scale, and you can see that your graph has become a straight line as well. This is because the data on both axes are exponential.
Considering that the data on the X-axis are all powers of two, then changing the logarithm base to two will give you a better image of this graph.
Logarithmic Graphs in Excel
Semi-log and log-log graphs are useful assets that can help you discover new relations between your data. These tools are widely used in different areas, and though not immediately visible in the chart settings, Excel is also capable of creating semi-log and log-log graphs.
Now that you know how to create semi-log and log-log graphs in Excel, it’s time to use these graphs and see your data from a new perspective.
Содержание
- Выполнение аппроксимации
- Способ 1: линейное сглаживание
- Способ 2: экспоненциальная аппроксимация
- Способ 3: логарифмическое сглаживание
- Способ 4: полиномиальное сглаживание
- Способ 5: степенное сглаживание
- Вопросы и ответы
Среди различных методов прогнозирования нельзя не выделить аппроксимацию. С её помощью можно производить приблизительные подсчеты и вычислять планируемые показатели, путем замены исходных объектов на более простые. В Экселе тоже существует возможность использования данного метода для прогнозирования и анализа. Давайте рассмотрим, как этот метод можно применить в указанной программе встроенными инструментами.
Выполнение аппроксимации
Наименование данного метода происходит от латинского слова proxima – «ближайшая» Именно приближение путем упрощения и сглаживания известных показателей, выстраивание их в тенденцию и является его основой. Но данный метод можно использовать не только для прогнозирования, но и для исследования уже имеющихся результатов. Ведь аппроксимация является, по сути, упрощением исходных данных, а упрощенный вариант исследовать легче.
Главный инструмент, с помощью которого проводится сглаживания в Excel – это построение линии тренда. Суть состоит в том, что на основе уже имеющихся показателей достраивается график функции на будущие периоды. Основное предназначение линии тренда, как не трудно догадаться, это составление прогнозов или выявление общей тенденции.
Но она может быть построена с применением одного из пяти видов аппроксимации:
- Линейной;
- Экспоненциальной;
- Логарифмической;
- Полиномиальной;
- Степенной.
Рассмотрим каждый из вариантов более подробно в отдельности.
Урок: Как построить линию тренда в Excel
Способ 1: линейное сглаживание
Прежде всего, давайте рассмотрим самый простой вариант аппроксимации, а именно с помощью линейной функции. На нем мы остановимся подробнее всего, так как изложим общие моменты характерные и для других способов, а именно построение графика и некоторые другие нюансы, на которых при рассмотрении последующих вариантов уже останавливаться не будем.
Прежде всего, построим график, на основании которого будем проводить процедуру сглаживания. Для построения графика возьмем таблицу, в которой помесячно указана себестоимость единицы продукции, производимой предприятием, и соответствующая прибыль в данном периоде. Графическая функция, которую мы построим, будет отображать зависимость увеличения прибыли от уменьшения себестоимости продукции.
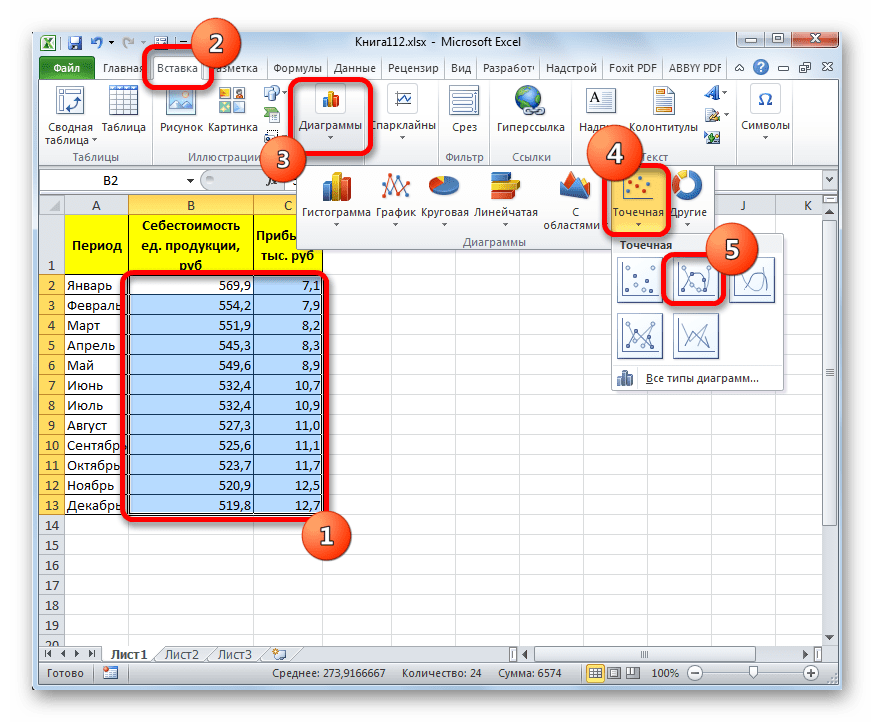
- Для построения графика, прежде всего, выделяем столбцы «Себестоимость единицы продукции» и «Прибыль». После этого перемещаемся во вкладку «Вставка». Далее на ленте в блоке инструментов «Диаграммы» щелкаем по кнопке «Точечная». В открывшемся списке выбираем наименование «Точечная с гладкими кривыми и маркерами». Именно данный вид диаграмм наиболее подходит для работы с линией тренда, а значит, и для применения метода аппроксимации в Excel.
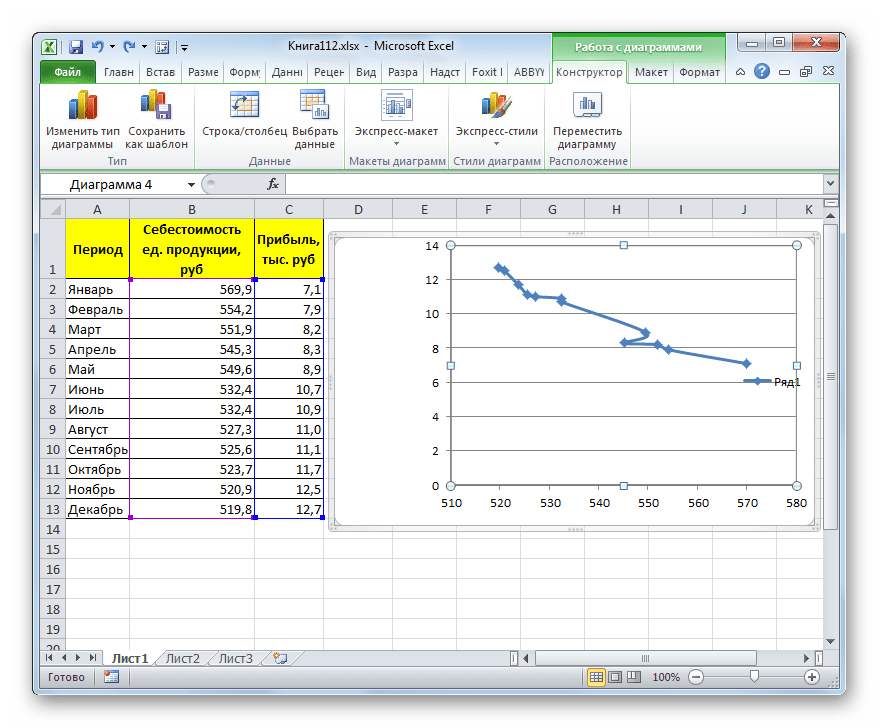
- График построен.
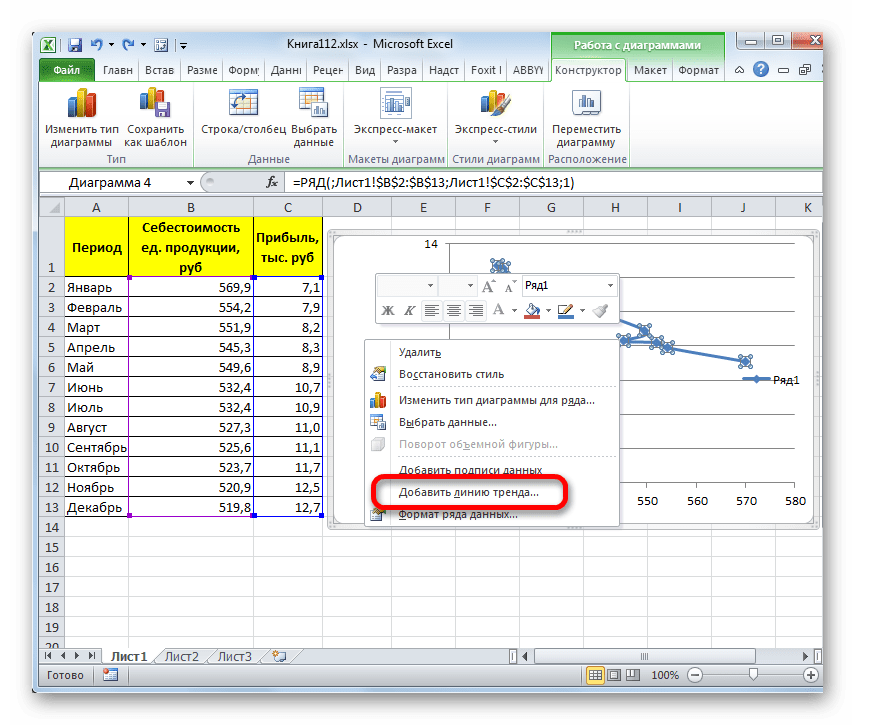
- Для добавления линии тренда выделяем его кликом правой кнопки мыши. Появляется контекстное меню. Выбираем в нем пункт «Добавить линию тренда…».
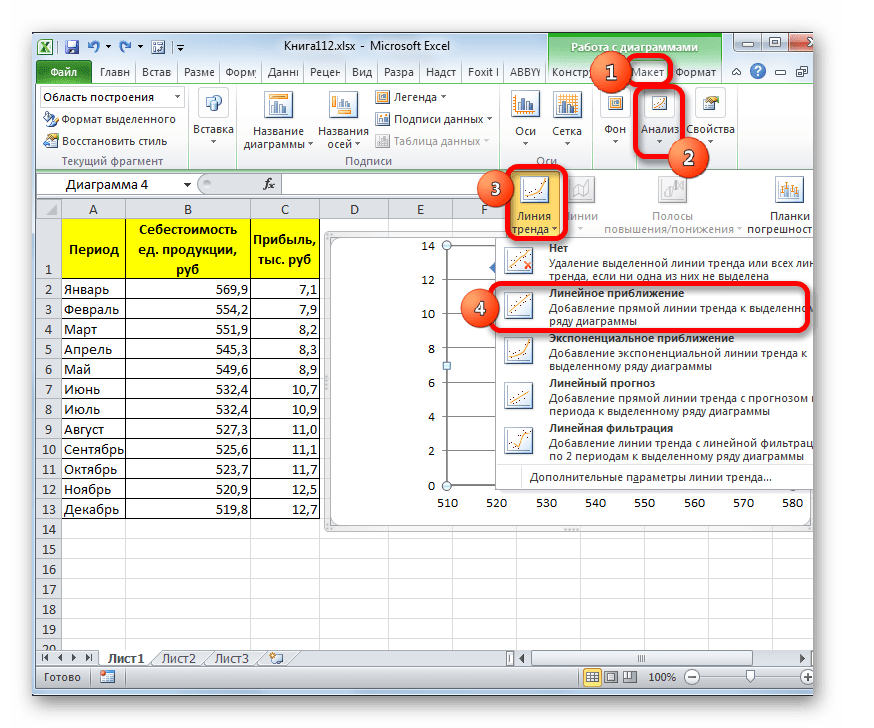
Существует ещё один вариант её добавления. В дополнительной группе вкладок на ленте «Работа с диаграммами» перемещаемся во вкладку «Макет». Далее в блоке инструментов «Анализ» щелкаем по кнопке «Линия тренда». Открывается список. Так как нам нужно применить линейную аппроксимацию, то из представленных позиций выбираем «Линейное приближение».
- Если же вы выбрали все-таки первый вариант действий с добавлением через контекстное меню, то откроется окно формата.
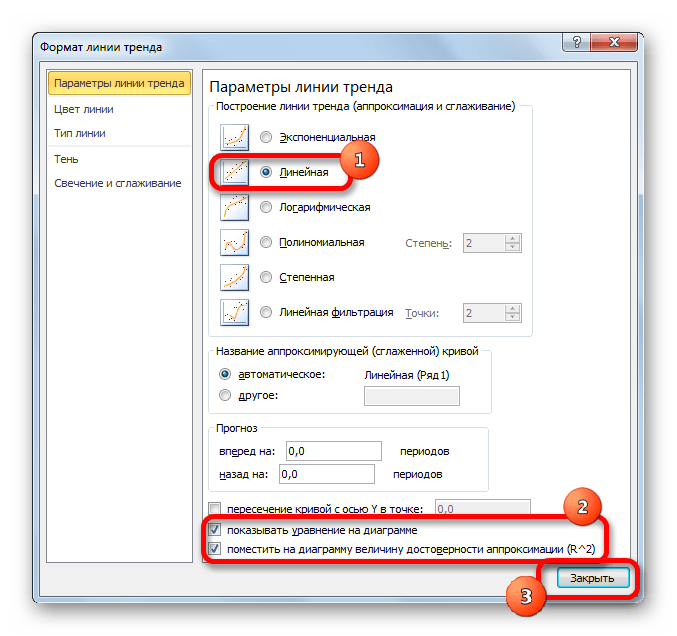
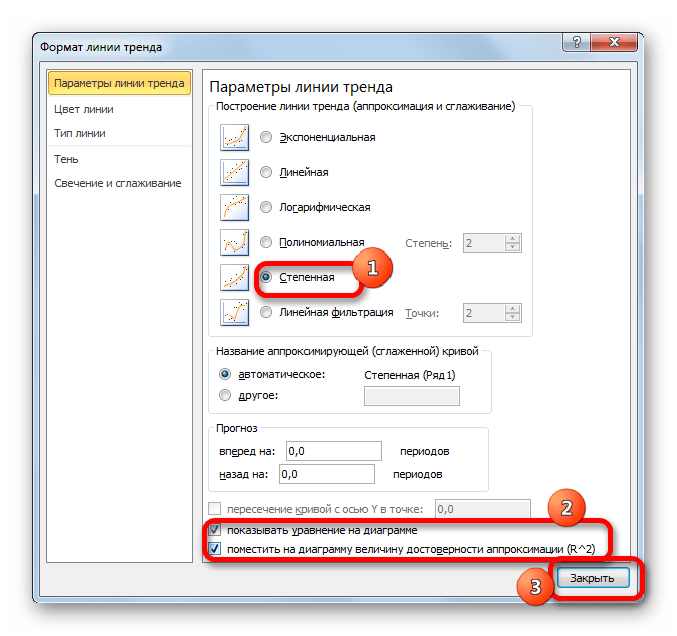
В блоке параметров «Построение линии тренда (аппроксимация и сглаживание)» устанавливаем переключатель в позицию «Линейная».
При желании можно установить галочку около позиции «Показывать уравнение на диаграмме». После этого на диаграмме будет отображаться уравнение сглаживающей функции.Также в нашем случае для сравнения различных вариантов аппроксимации важно установить галочку около пункта «Поместить на диаграмму величину достоверной аппроксимации (R^2)». Данный показатель может варьироваться от 0 до 1. Чем он выше, тем аппроксимация качественнее (достовернее). Считается, что при величине данного показателя 0,85 и выше сглаживание можно считать достоверным, а если показатель ниже, то – нет.
После того, как провели все вышеуказанные настройки. Жмем на кнопку «Закрыть», размещенную в нижней части окна.
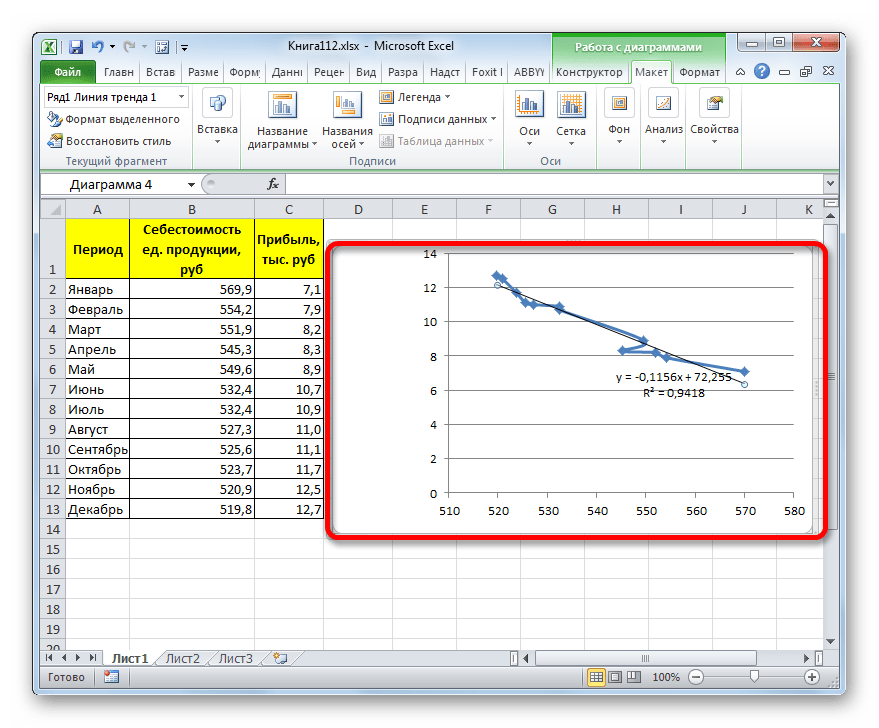
- Как видим, на графике линия тренда построена. При линейной аппроксимации она обозначается черной прямой полосой. Указанный вид сглаживания можно применять в наиболее простых случаях, когда данные изменяются довольно быстро и зависимость значения функции от аргумента очевидна.
Сглаживание, которое используется в данном случае, описывается следующей формулой:
y=ax+b
В конкретно нашем случае формула принимает такой вид:
y=-0,1156x+72,255
Величина достоверности аппроксимации у нас равна 0,9418, что является довольно приемлемым итогом, характеризующим сглаживание, как достоверное.
Способ 2: экспоненциальная аппроксимация
Теперь давайте рассмотрим экспоненциальный тип аппроксимации в Эксель.
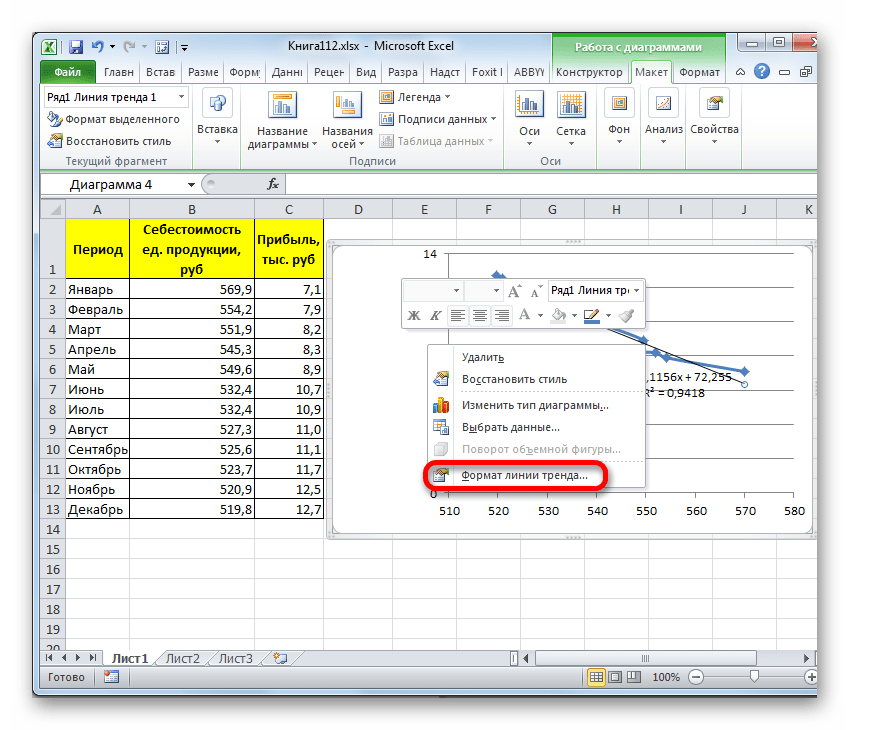
- Для того, чтобы изменить тип линии тренда, выделяем её кликом правой кнопки мыши и в раскрывшемся меню выбираем пункт «Формат линии тренда…».
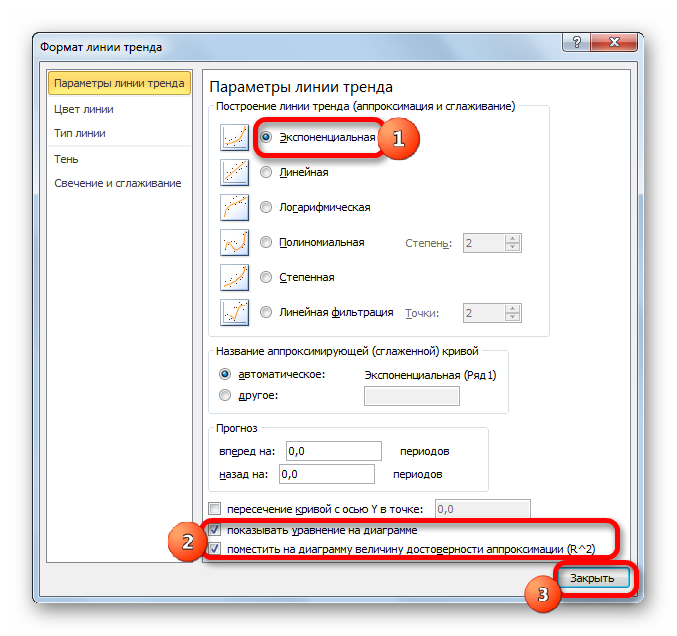
- После этого запускается уже знакомое нам окно формата. В блоке выбора типа аппроксимации устанавливаем переключатель в положение «Экспоненциальная». Остальные настройки оставим такими же, как и в первом случае. Щелкаем по кнопке «Закрыть».
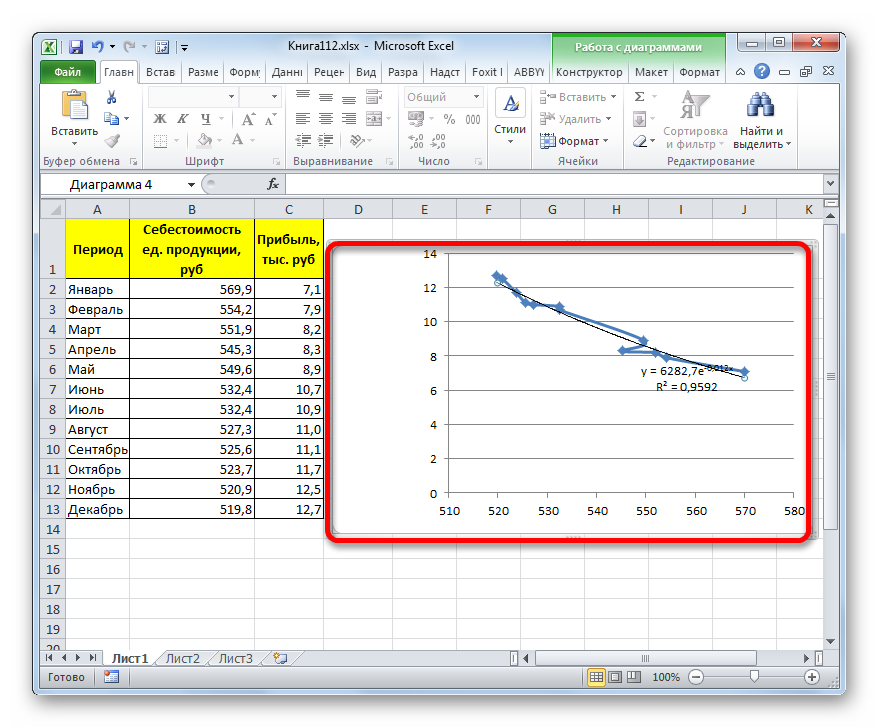
- После этого линия тренда будет построена на графике. Как видим, при использовании данного метода она имеет несколько изогнутую форму. При этом уровень достоверности равен 0,9592, что выше, чем при использовании линейной аппроксимации. Экспоненциальный метод лучше всего использовать в том случае, когда сначала значения быстро изменяются, а потом принимают сбалансированную форму.
Общий вид функции сглаживания при этом такой:
y=be^x
где e – это основание натурального логарифма.
В конкретно нашем случае формула приняла следующую форму:
y=6282,7*e^(-0,012*x)
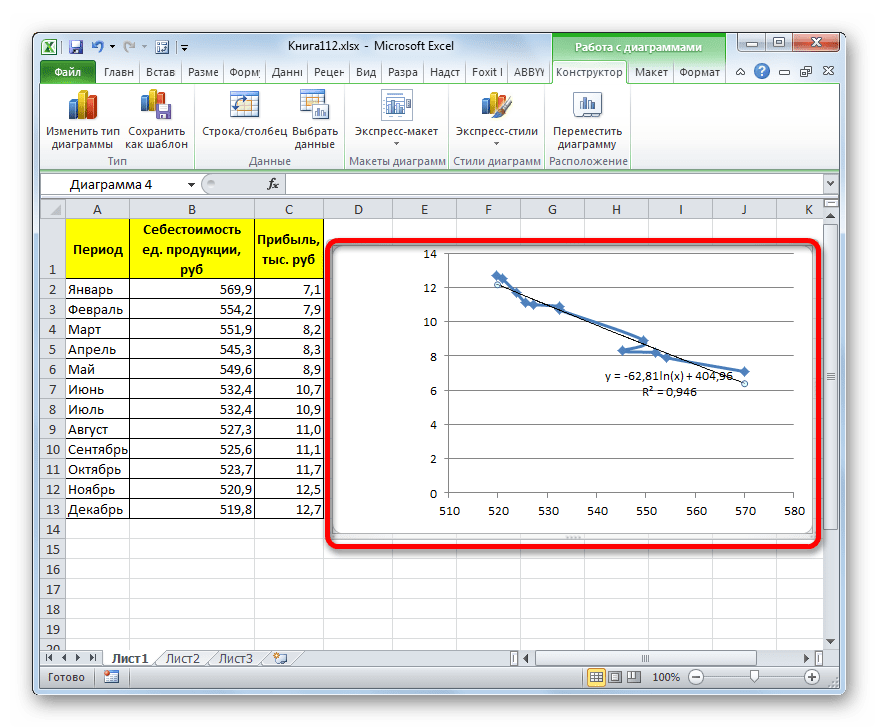
Способ 3: логарифмическое сглаживание
Теперь настала очередь рассмотреть метод логарифмической аппроксимации.
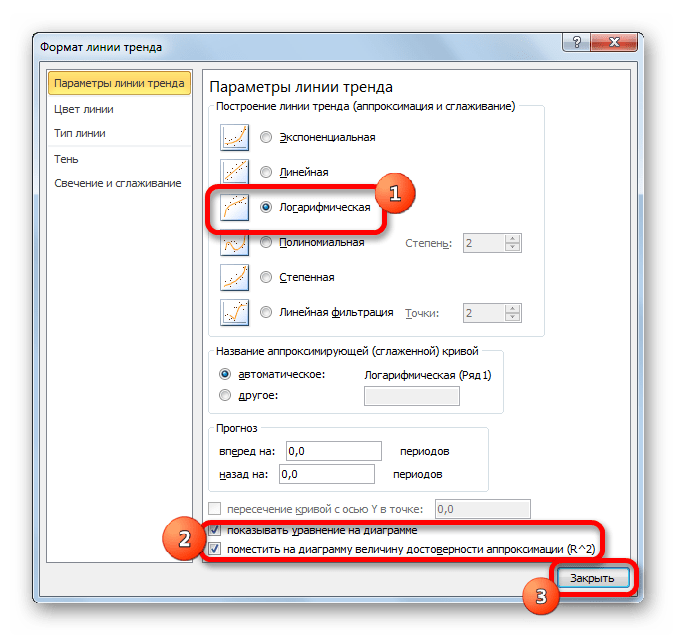
- Тем же способом, что и в предыдущий раз через контекстное меню запускаем окно формата линии тренда. Устанавливаем переключатель в позицию «Логарифмическая» и жмем на кнопку «Закрыть».
- Происходит процедура построения линии тренда с логарифмической аппроксимацией. Как и в предыдущем случае, такой вариант лучше использовать тогда, когда изначально данные быстро изменяются, а потом принимают сбалансированный вид. Как видим, уровень достоверности равен 0,946. Это выше, чем при использовании линейного метода, но ниже, чем качество линии тренда при экспоненциальном сглаживании.
В общем виде формула сглаживания выглядит так:
y=a*ln(x)+b
где ln – это величина натурального логарифма. Отсюда и наименование метода.
В нашем случае формула принимает следующий вид:
y=-62,81ln(x)+404,96
Способ 4: полиномиальное сглаживание
Настал черед рассмотреть метод полиномиального сглаживания.
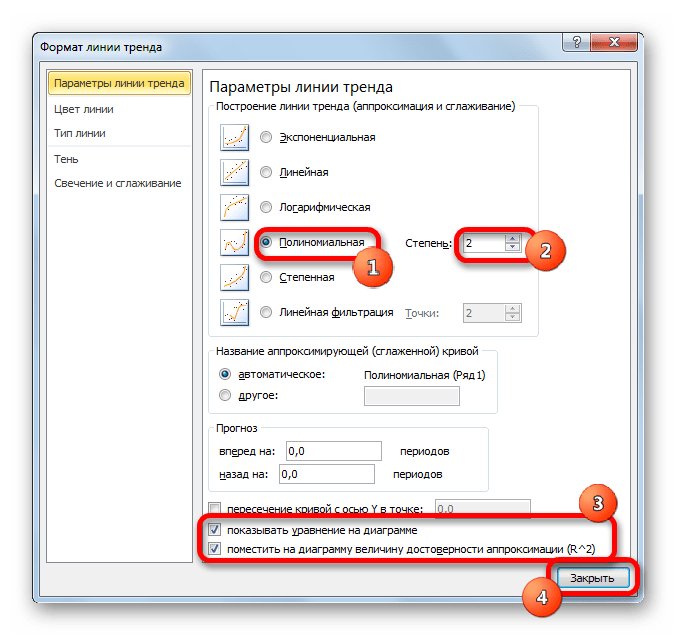
- Переходим в окно формата линии тренда, как уже делали не раз. В блоке «Построение линии тренда» устанавливаем переключатель в позицию «Полиномиальная». Справа от данного пункта расположено поле «Степень». При выборе значения «Полиномиальная» оно становится активным. Здесь можно указать любое степенное значение от 2 (установлено по умолчанию) до 6. Данный показатель определяет число максимумов и минимумов функции. При установке полинома второй степени описывается только один максимум, а при установке полинома шестой степени может быть описано до пяти максимумов. Для начала оставим настройки по умолчанию, то есть, укажем вторую степень. Остальные настройки оставляем такими же, какими мы выставляли их в предыдущих способах. Жмем на кнопку «Закрыть».
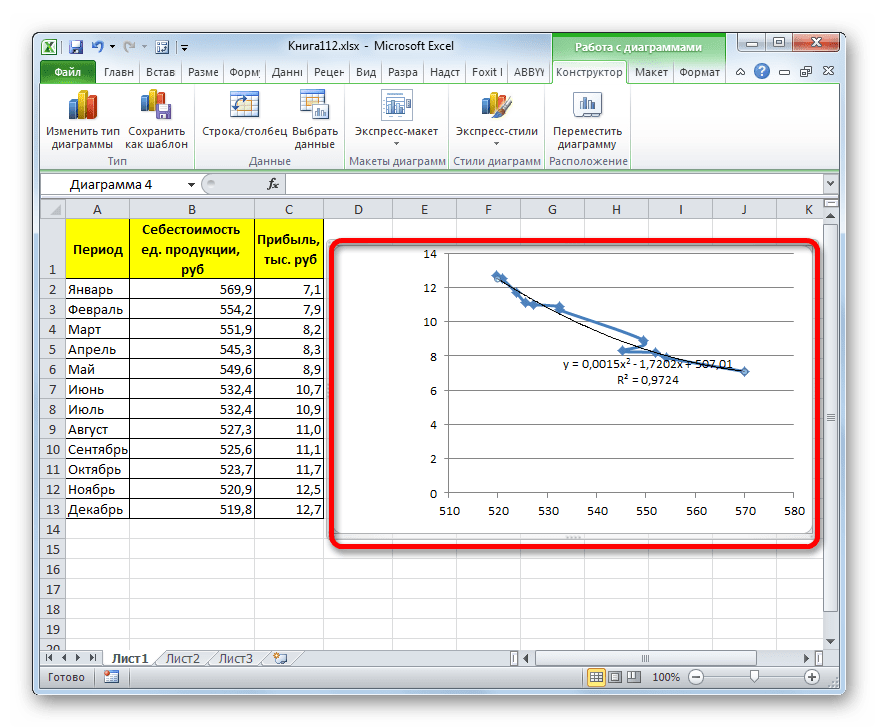
- Линия тренда с использованием данного метода построена. Как видим, она ещё более изогнута, чем при использовании экспоненциальной аппроксимации. Уровень достоверности выше, чем при любом из использованных ранее способов, и составляет 0,9724.
Данный метод наиболее успешно можно применять в том случае, если данные носят постоянно изменчивый характер. Функция, описывающая данный вид сглаживания, выглядит таким образом:
y=a1+a1*x+a2*x^2+…+an*x^nВ нашем случае формула приняла такой вид:
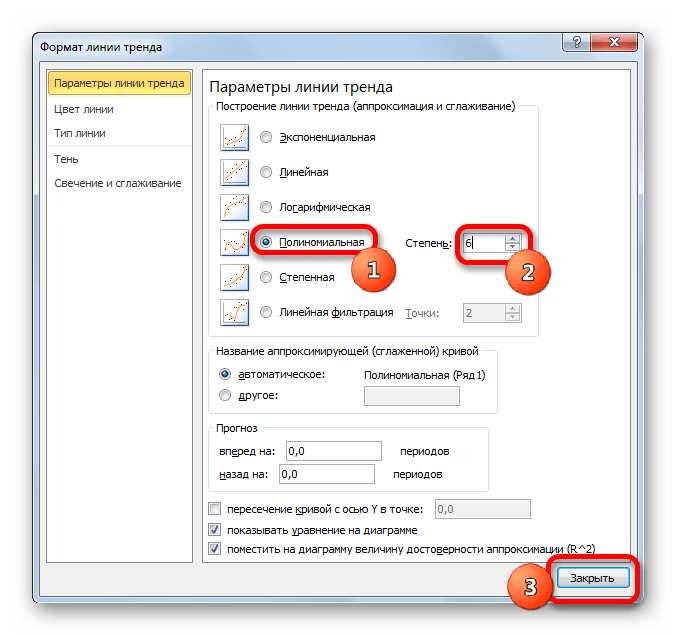
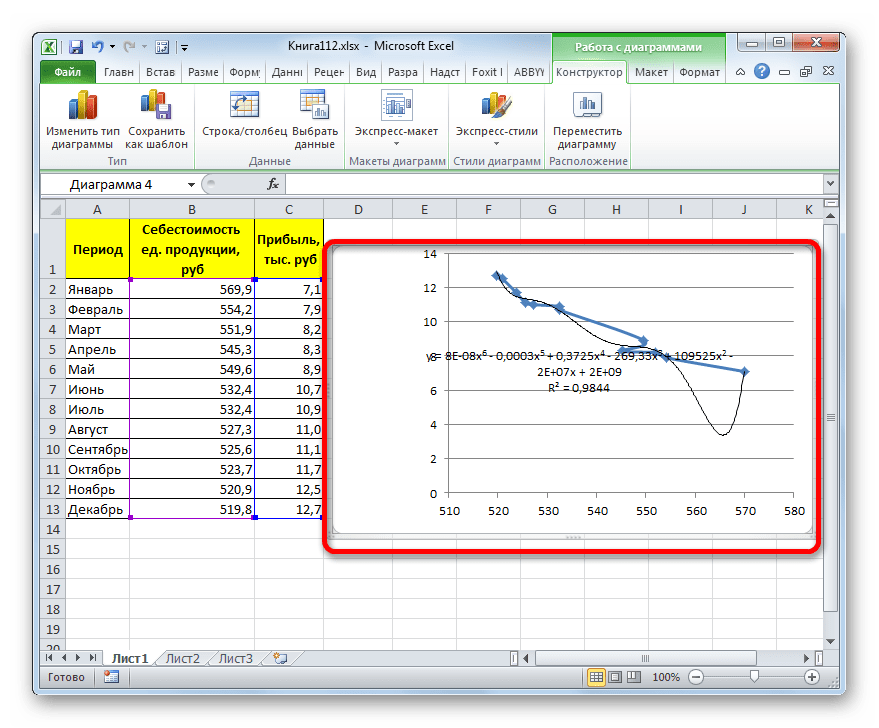
y=0,0015*x^2-1,7202*x+507,01 - Теперь давайте изменим степень полиномов, чтобы увидеть, будет ли отличаться результат. Возвращаемся в окно формата. Тип аппроксимации оставляем полиномиальным, но напротив него в окне степени устанавливаем максимально возможное значение – 6.
- Как видим, после этого наша линия тренда приняла форму ярко выраженной кривой, у которой число максимумов равно шести. Уровень достоверности повысился ещё больше, составив 0,9844.
Формула, которая описывает данный тип сглаживания, приняла следующий вид:
y=8E-08x^6-0,0003x^5+0,3725x^4-269,33x^3+109525x^2-2E+07x+2E+09
Способ 5: степенное сглаживание
В завершении рассмотрим метод степенной аппроксимации в Excel.
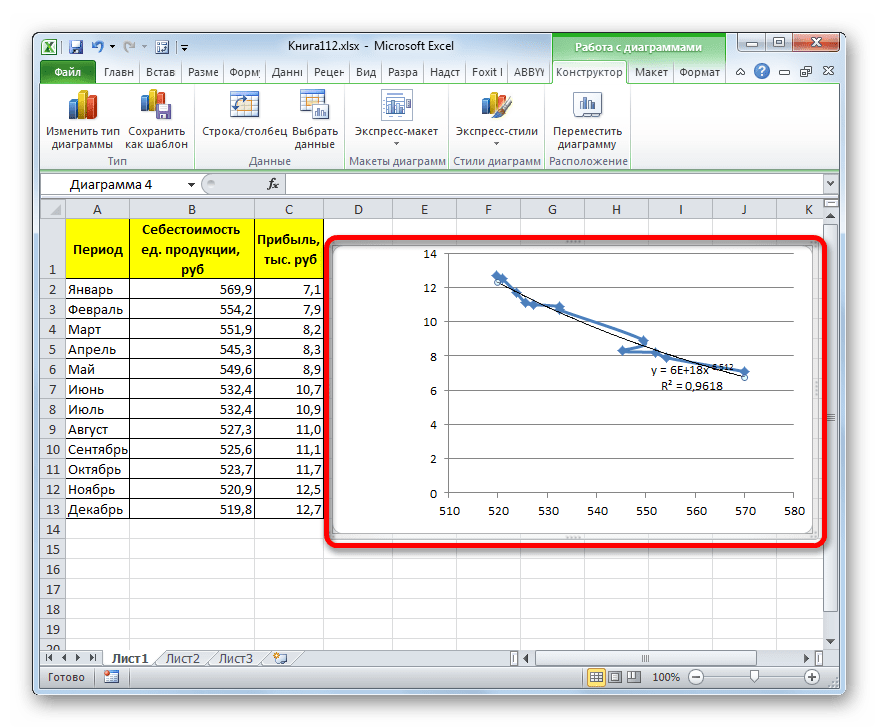
- Перемещаемся в окно «Формат линии тренда». Устанавливаем переключатель вида сглаживания в позицию «Степенная». Показ уравнения и уровня достоверности, как всегда, оставляем включенными. Жмем на кнопку «Закрыть».
- Программа формирует линию тренда. Как видим, в нашем случае она представляет собой линию с небольшим изгибом. Уровень достоверности равен 0,9618, что является довольно высоким показателем. Из всех вышеописанных способов уровень достоверности был выше только при использовании полиномиального метода.
Данный способ эффективно используется в случаях интенсивного изменения данных функции. Важно учесть, что этот вариант применим только при условии, что функция и аргумент не принимают отрицательных или нулевых значений.
Общая формула, описывающая данный метод имеет такой вид:
y=bx^n
В конкретно нашем случае она выглядит так:
y = 6E+18x^(-6,512)
Как видим, при использовании конкретных данных, которые мы применяли для примера, наибольший уровень достоверности показал метод полиномиальной аппроксимации с полиномом в шестой степени (0,9844), наименьший уровень достоверности у линейного метода (0,9418). Но это совсем не значит, что такая же тенденция будет при использовании других примеров. Нет, уровень эффективности у приведенных выше методов может значительно отличаться, в зависимости от конкретного вида функции, для которой будет строиться линия тренда. Поэтому, если для этой функции выбранный метод наиболее эффективен, то это совсем не означает, что он также будет оптимальным и в другой ситуации.
Если вы пока не можете сразу определить, основываясь на вышеприведенных рекомендациях, какой вид аппроксимации подойдет конкретно в вашем случае, то есть смысл попробовать все методы. После построения линии тренда и просмотра её уровня достоверности можно будет выбрать оптимальный вариант.