17 авг. 2022 г.
читать 2 мин
Логарифмическая регрессия — это тип регрессии, используемый для моделирования ситуаций, когда рост или спад сначала быстро ускоряются, а затем со временем замедляются.
Например, следующий график демонстрирует пример логарифмического распада:
Для такого типа ситуации взаимосвязь между переменной-предиктором и переменной-откликом можно хорошо смоделировать с помощью логарифмической регрессии.
Уравнение модели логарифмической регрессии принимает следующий вид:
у = а + b*ln(x)
куда:
- y: переменная ответа
- x: предикторная переменная
- a, b: коэффициенты регрессии, описывающие взаимосвязь между x и y .
В следующем пошаговом примере показано, как выполнить логарифмическую регрессию в Excel.
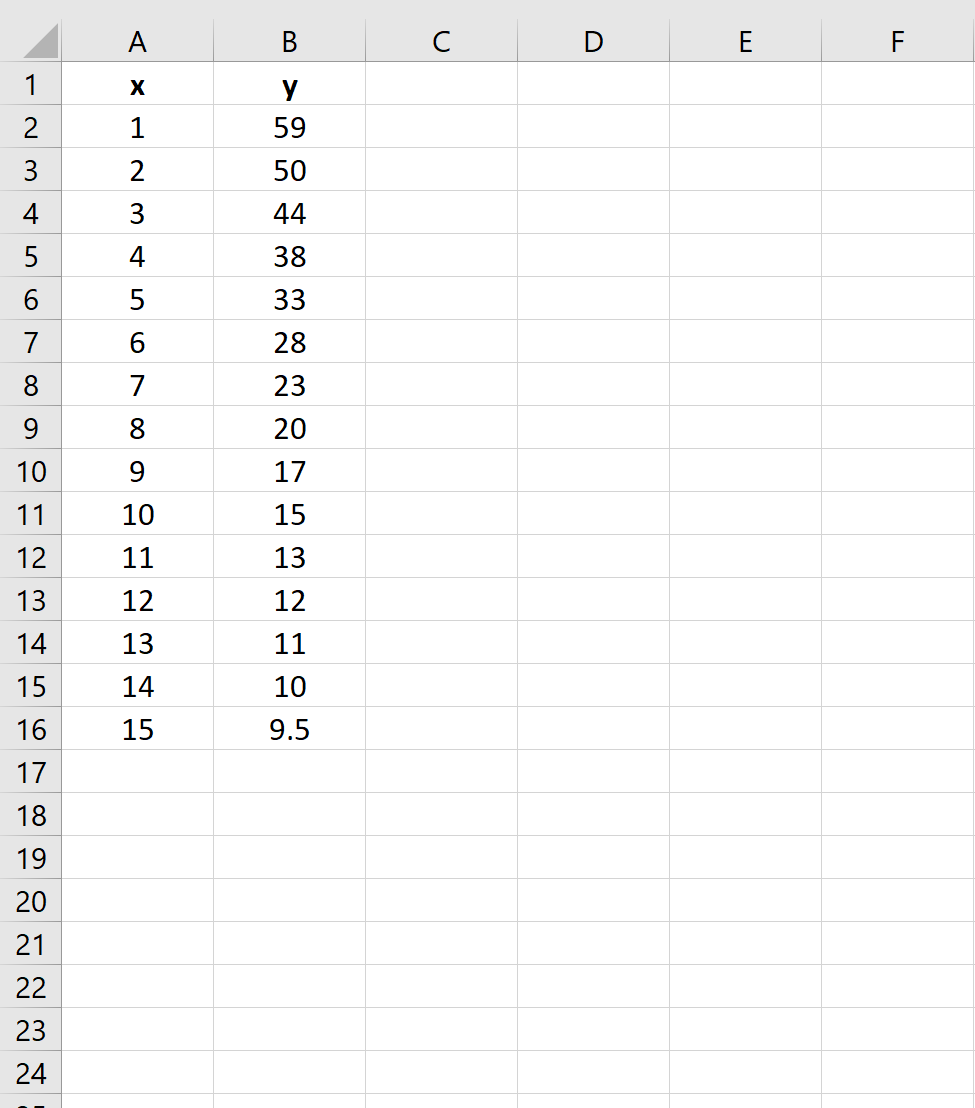
Шаг 1: Создайте данные
Во-первых, давайте создадим поддельные данные для двух переменных: x и y :
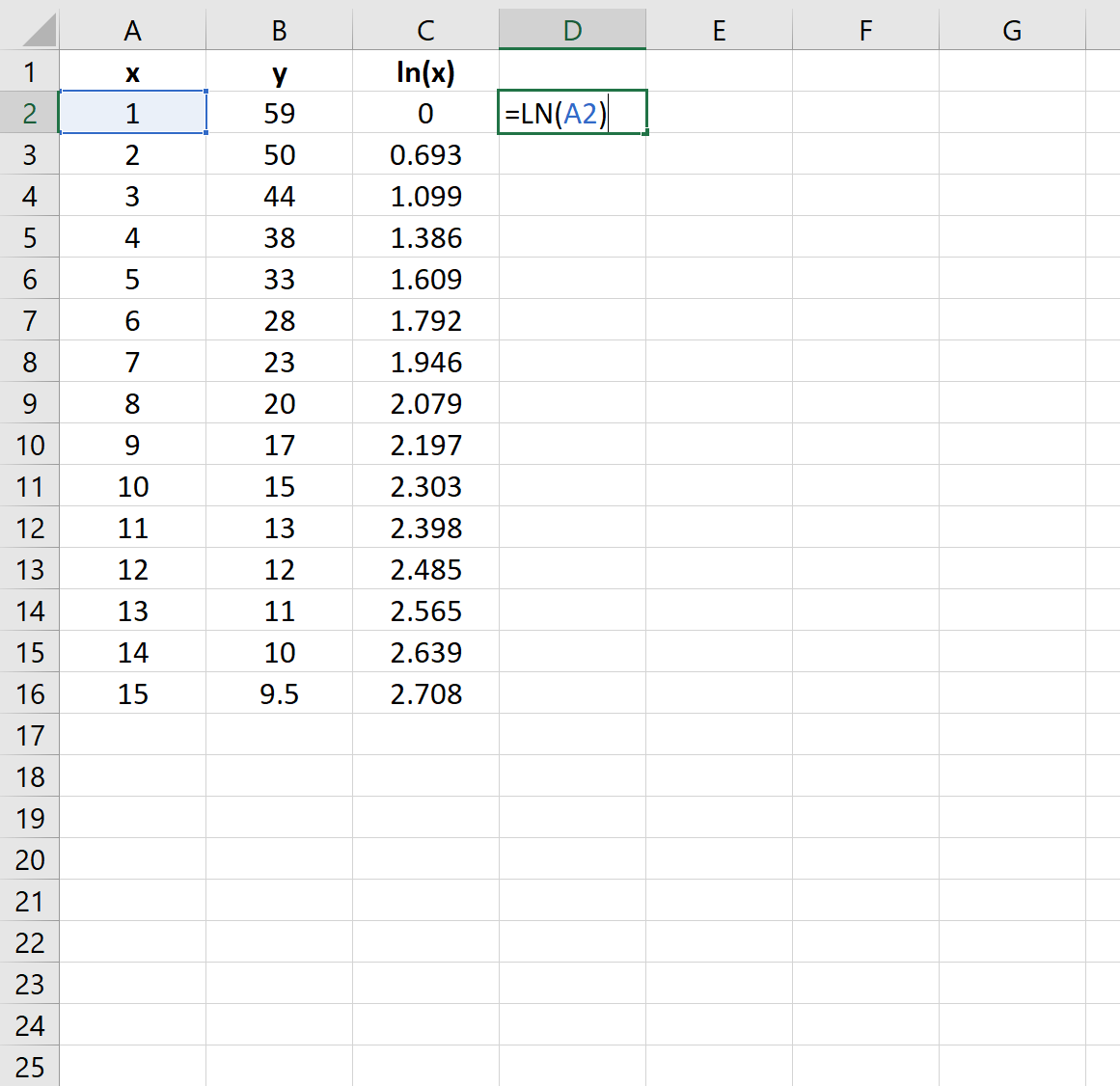
Шаг 2: возьмите натуральный логарифм переменной-предиктора
Далее нам нужно создать новый столбец, представляющий натуральный логарифм переменной-предиктора x :
Шаг 3: Подберите модель логарифмической регрессии
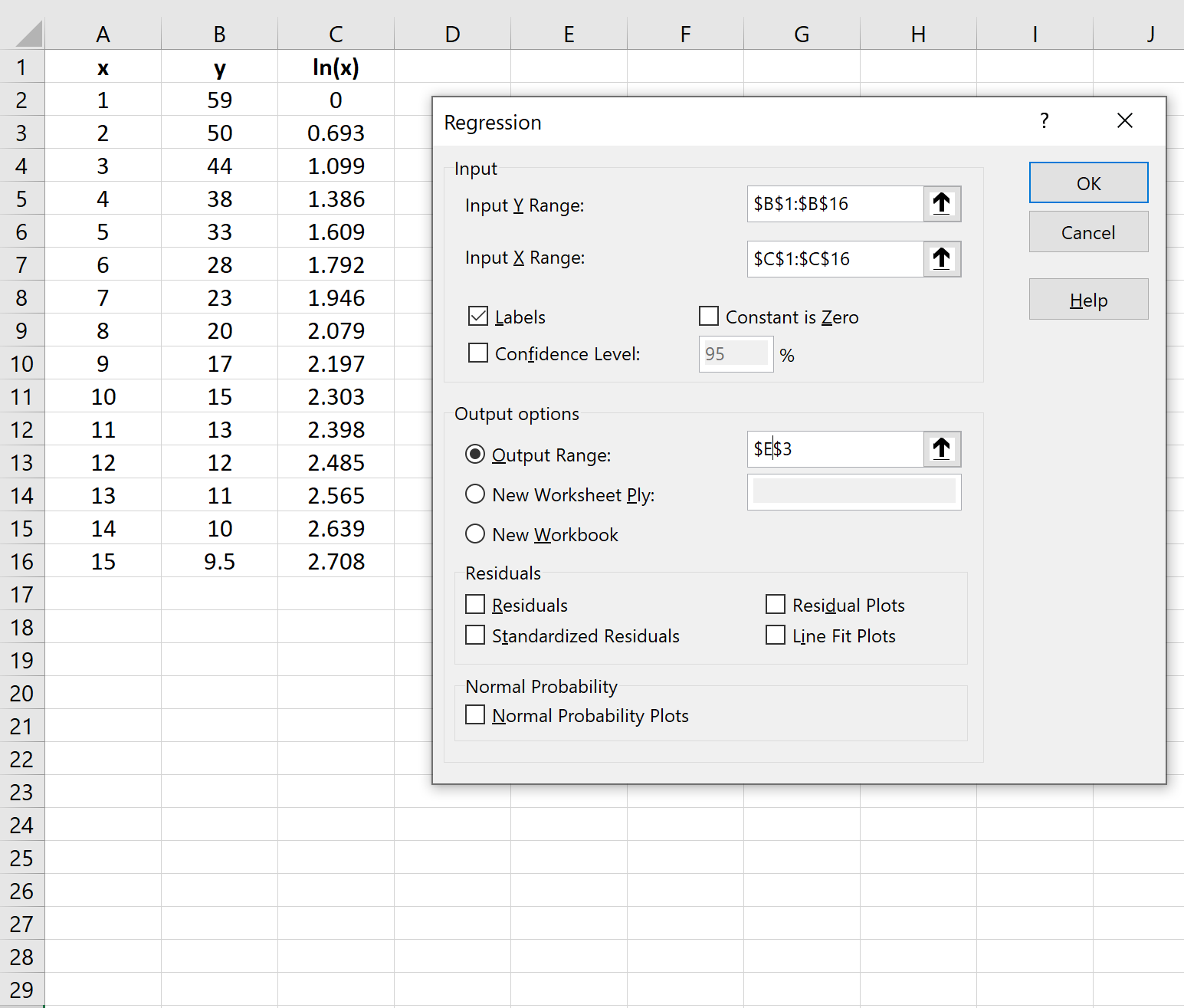
Далее мы подгоним модель логарифмической регрессии. Для этого щелкните вкладку « Данные » на верхней ленте, затем щелкните « Анализ данных» в группе « Анализ ».
Если вы не видите Data Analysis в качестве опции, вам нужно сначала загрузить Analysis ToolPak .
В появившемся окне нажмите Регрессия.В появившемся новом окне введите следующую информацию:
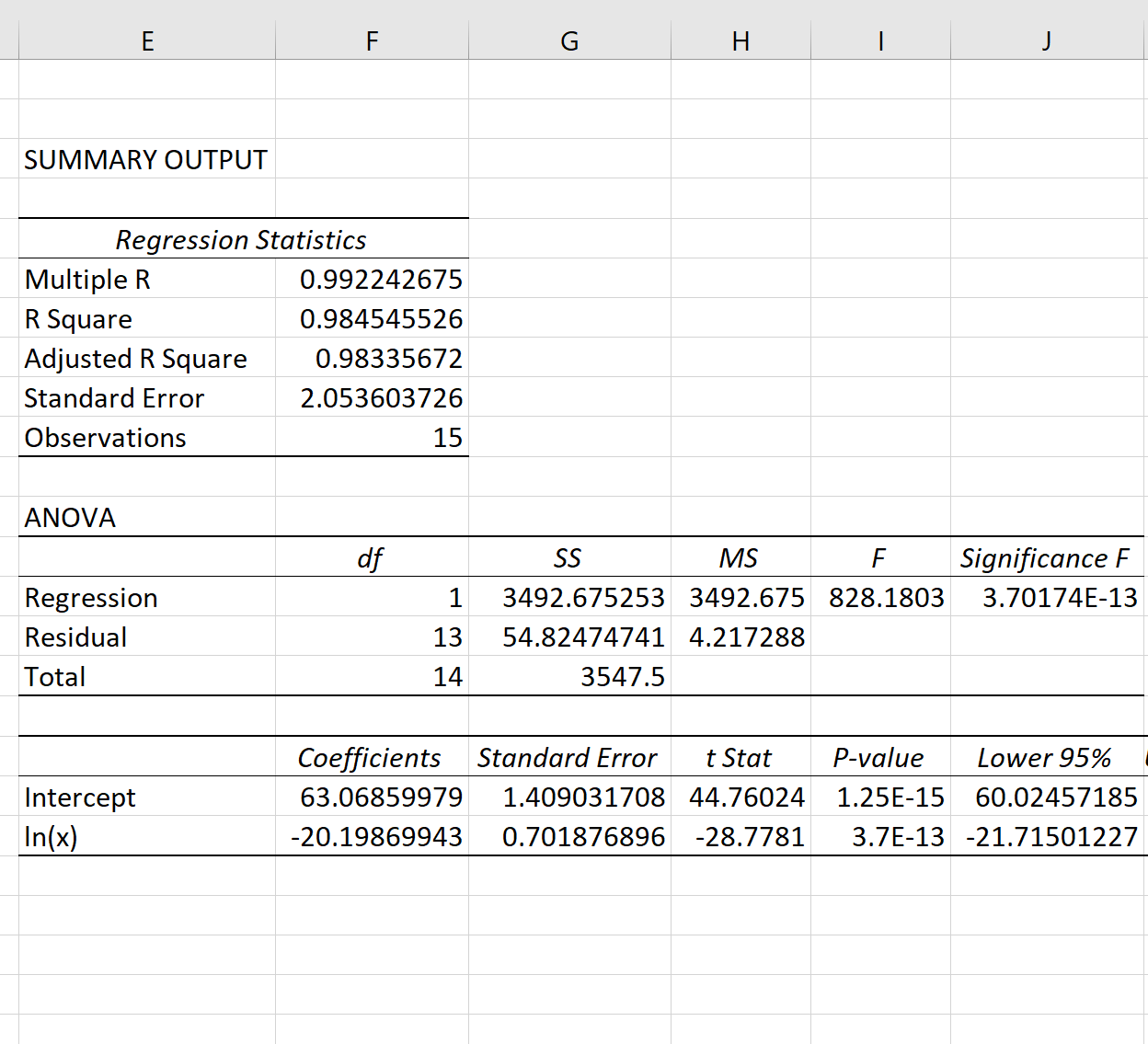
Как только вы нажмете OK , отобразятся выходные данные модели логарифмической регрессии:
Общее значение F модели составляет 828,18, а соответствующее значение p чрезвычайно мало (3,70174E-13), что указывает на то, что модель в целом полезна.
Используя коэффициенты из выходной таблицы, мы видим, что подобранное уравнение логарифмической регрессии:
у = 63,0686 – 20,1987 * ln(x)
Мы можем использовать это уравнение для прогнозирования переменной отклика y на основе значения переменной-предиктора x.Например, если x = 12, то мы предсказываем, что y будет 12,87 :
у = 63,0686 – 20,1987 * ln(12) = 12,87
Бонус: не стесняйтесь использовать этот онлайн- калькулятор логарифмической регрессии для автоматического вычисления уравнения логарифмической регрессии для заданного предиктора и переменной отклика.
Дополнительные ресурсы
Как выполнить простую линейную регрессию в Excel
Как выполнить множественную линейную регрессию в Excel
Как выполнить полиномиальную регрессию в Excel
Как выполнить экспоненциальную регрессию в Excel
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью
логарифмической функции.
Метод наименьших квадратов
(англ.
Ordinary
Least
Squares
,
OLS
) является одним из базовых методов регрессионного анализа в части оценки неизвестных параметров
регрессионных моделей
по выборочным данным. Основная статья про МНК —
МНК: Метод Наименьших Квадратов в MS EXCEL
.
Иногда между переменными можно предположить логарифмическую зависимость y=a*Ln(x)+b для x>0. Логарифмическую зависимость можно свести к случаю
линейной зависимости
с помощью замены переменных u=Ln(x) (см.
файл примера
).
После замены переменной вычисления полностью аналогичны
линейному случаю
y=a*
u
+b
.
Примечание
: Построить
линию тренда
по методу наименьших квадратов можно и без замены переменной. Для этого нужно воспользоваться инструментом диаграммы
Линия тренда
(
Логарифмическая линия тренда
). Поставив в диалоговом окне галочку в поле «показывать уравнение на диаграмме» можно убедиться, что найденные выше параметры совпадают со значениями на диаграмме. Подробнее о диаграммах см. статью
Основы построения диаграмм в MS EXCEL
.
Инфоурок
›
Другое
›Другие методич. материалы›Презентация по информатике на тему «Построение регрессионных моделей в Microsoft Excel»
Скачать материал

Скачать материал


- Сейчас обучается 264 человека из 64 регионов






Описание презентации по отдельным слайдам:
-
1 слайд
Презентация к уроку в 11 классе на тему
«Построение регрессионных моделей в Microsoft Excel»
Автор – Мирзоева Зитта МихайловнаМесто работы – ГБОУ ШКОЛА 1028
Должность – УЧИТЕЛЬ ИНФОРМАТИКИ
-
2 слайд
Тема урока
Построение регрессионных моделей в Microsoft Excel
Цель урока: освоение способов построения по экспериментальным данным регрессионной модели средствами ЭТ. -
3 слайд
Основные этапы компьютерного моделирования
1.Постановка задачи — описание объекта моделирования в общем виде, определение конечного результата моделирования и имеющихся условий.
2.Определение цели моделирования. От выбранной цели зависит, какие характеристики объекта моделирования считать существенными, какие методы лучше подходят для решения данной задачи.
3.Анализ объекта моделирования для выделения существенных свойств с точки зрения цели моделирования.
4.Формализация. Формами представления данных могут быть: словесное описание, чертеж, таблица, формула, схема, алгоритм, компьютерная программа.
Конечной целью этого этапа является создание информационной модели.
5.Разработка компьютерной модели для проведения эксперимента:
Разнообразное программное обеспечение позволяет преобразовать исходную информационную модель в компьютерную и провести компьютерный эксперимент.
6.Компьютерный эксперимент:
а) исследование модели;
б) анализ полученных результатов на соответствие цели моделирования;
в) уточнение модели.Конечная цель моделирования — принятие решения, которое должно быть выработано на основе всестороннего анализа результатов моделирования. Если результаты не соответствуют целям поставленной задачи, значит, на предыдущих этапах были допущены ошибки. Если такие ошибки выявлены, то требуется уточнение (корректировка) модели.
-
4 слайд
Контрольные вопросы по табличному редактору Excel
1.Назначение ЭТ.
для хранения и обработки числовых данных
для хранения таблиц
для обработки графической информации
для представления текстовой информации в табличном виде.
2. Укажите форматы следующих данных:
12345, Мир, 14 апреля 1998г., =А2+17.
3. Приведите примеры абсолютных и относительных ссылок.
4. В ячейку D13 ввели формулу =C12/$B$4. Данную формулу скопировали в ячейку F15. Какая формула содержится в F15.
5. Сколько ячеек содержит блок D5:I9.
6. Какие категории функций, используемых в ЭТ , вы знаете.
7. Какие статистические функции вы знаете. -
5 слайд
а)
б)
в)
г)
д)
е)
8. Назовите типы приведенных ниже диаграмм. -
6 слайд
Математическая обработка статистических данных, результатов эксперимента
Зависимости между параметрами некоторого объекта, процесса, явления могут быть выражены с помощью математических формул. Но в некоторых случаях коэффициенты в этих формулах могут быть получены в результате статистической обработки экспериментальных данных.
Статистика — это наука о сборе, измерении и анализе больших массивов данных. Статистические данные носят приближенный, усредненный характер, получаются путем многократных измерений. Статистические функции электронных таблиц позволяют обрабатывать статистические данные.
Статистический анализ данных широко используется:
в народном хозяйстве при: анализе результатов деятельности предприятий и организаций;
оценке состояния финансового, сырьевого и других рынков;
анализе прибыльности инвестиционной деятельности;
составлении краткосрочных планов и долгосрочных прогнозов;
• в научной деятельности для обработки результатов экспериментов, оценки их достоверности, проверки гипотез и пр.
Для обработки и представления результатов естественно-научного и математического эксперимента, экономических и экологических наблюдений, социальных опросов используются динамические (электронные) таблицы.
Для определения статистической зависимости необходимо выполнить два шага:
1.На основании физического смысла статистических данных выбрать вид функции таким образом, чтобы функция располагалась как можно ближе к экспериментальным данным.2.Выбрать метод вычисления параметров функции, определяющих конкретный вид принятой зависимости.
Полученная аналитическая зависимость называется регрессионной моделью.
-
7 слайд
Построение регрессионной модели.
Рассмотрим пример из медицинской статистики. Специалистами собраны сведения о средней концентрации угарного газа в атмосфере C и о заболеваемости астмой (число хронических больных на 1000 жителей) P. Полученные экспериментальные данные представим в табличной форме и в виде точечной диаграммы.
Как теперь построить математическую модель данного явления? Нужно получить формулу зависимости Р от С.
Основные требования к искомой функции:
— она должна быть достаточно простой для использования ее в дальнейших вычислениях;
график этой функции должен проходить вблизи экспериментальных точек так, чтобы отклонения этих точек о графика были минимальны и равномерны. -
8 слайд
Получение регрессионной модели происходит в два этапа:
— подбор вида функции;
вычисление параметров функции.Чаще всего выбор производится среди следующих функций:
-у=ах+b линейная функция;
— y=ax2+bx+c квадратичная функция;
— y=aln(x)+b логарифмическая функция;
y=aebx экспоненциальная функция;
— y=axb степенная функция.
Во всех этих формулах x – аргумент, y – значение функции, a, b, c – параметры функций.
При выборе одной из функций нужно подобрать параметры так, чтобы функция располагалась как можно ближе к экспериментальным точкам.Существует метод наименьших квадратов (МНК).
Суть – искомая функция должна быть построена так, чтобы сумма квадратов отклонений y-координат всех экспериментальных точек от y-координат графика функции была бы минимальна.
Графики регрессионной модели называются трендами. (Английское слово trend переводиться как общее направление или тенденция). -
9 слайд
Алгоритм получения с помощью MS Excel регрессионных моделей по МНК с построением тренда.
Ввести табличные данные.
Построить точечную диаграмму, где в качестве подписи к оси OX выбрать текст «Линейный тренд» (остальные надписи и легенду можно игнорировать).
Щелкнуть мышью по полю диаграммы; выполнить команду Диаграмма – Добавить линию тренда;
В открывшемся окне на закладке «Тип» выбрать «Линейный тренд»;
Перейти к закладке «Параметры» и установит галочки на флажках «показать уравнения на диаграмме» и «поместить на диаграмме величину достоверности ампроксикации R2» и щелкнуть OK.
Аналогично получаем и другие тренды.
Величина R2 определяет, насколько удачной является полученная регрессионная модель. Из трех построенных моделей самая неудачная – логарифмическая, наиболее удачная – степенная. -
10 слайд
Практическое задание для самостоятельного выполнения на получение регрессионных зависимостей.
В представленной таблице приводится прогноз средней дневной температуры на последнюю неделю мая в различных городах европейской части России. Города упорядочены по алфавиту. Указана также географическая широта этих городов.
Построить несколько вариантов регрессионных моделей (не менее трех), отражающих зависимость температуры от широты города. Выбрать наиболее подходящую регрессионную модель. -
11 слайд
Домашнее задание:
1. По данным из следующей таблицы постройте с помощью MS Excel линейную, квадратичную, экспоненциальную и логарифмическую регрессионные модели. Определите параметры, выберите модель.
2. Придумайте свои примеры практических задач, для которых имело бы смысл построение регрессионных моделей.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 211 186 материалов в базе
- Выберите категорию:
-
Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 30.12.2020
- 2600
- 2
- 13.12.2020
- 1900
- 0
- 07.12.2020
- 2008
- 0
- 04.12.2020
- 1993
- 0
- 22.11.2020
- 2028
- 2
- 16.10.2020
- 2055
- 12
- 16.10.2020
- 1631
- 1
- 06.08.2020
- 1111
- 0
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Подростковый возраст — важнейшая фаза становления личности»
-
Курс профессиональной переподготовки «Клиническая психология: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС педагогических направлений подготовки»
-
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС юридических направлений подготовки»
-
Курс профессиональной переподготовки «Логистика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Организация менеджмента в туризме»
-
Курс повышения квалификации «Финансы: управление структурой капитала»
-
Курс повышения квалификации «Источники финансов»
-
Курс профессиональной переподготовки «Управление информационной средой на основе инноваций»
-
Курс профессиональной переподготовки «Организация деятельности специалиста оценщика-эксперта по оценке имущества»
-
Курс профессиональной переподготовки «Политология: взаимодействие с органами государственной власти и управления, негосударственными и международными организациями»
-
Курс профессиональной переподготовки «Метрология, стандартизация и сертификация»
-
Курс профессиональной переподготовки «Организация деятельности по водоотведению и очистке сточных вод»
-
Курс профессиональной переподготовки «Организация и управление службой рекламы и PR»
-
Скачать материал
-
20.06.2020
650
-
PPTX
414.5 кбайт -
27
скачиваний -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Алексеев Алексей Викторович. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 2 года и 3 месяца
- Подписчики: 0
- Всего просмотров: 54746
-
Всего материалов:
235
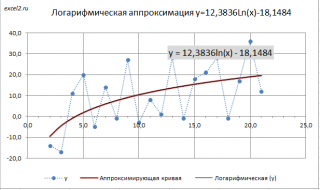
Фон: Многие предприятия не являются линейными ростом, и когда они растут в определенной степени, их скорость роста начнет замедляться.
1, подготовить данные
Данные подготовки в деле заключается в следующем
Excel2013 в качестве примера
Выберите данные «Вставить» график разброса, см. Следующее изображение
Увеличьте «линии тренда»
Выберите логарифмическую конфигурацию, выберите дисплей формул, вы можете увидеть формулу
Это также может быть предсказано вперед или более поздней версии, примеры прогнозируются с 5-фазы, и результаты показаны ниже.
$begingroup$
Is it possible to perform logarithmic regression on multiple variables with Excel? If I just have a single independent variable than it’s very easy to do this using the best-fit line option (it lets me switch from linear to logarithmic). But this feature does not work for multiple variable regression and the regression feature under the Data Analysis plugin only seems to support linear multiple regression.
However, I have a table that has 3 columns containing 3 independent variables and 1 column with the corresponding dependent variable (outcome). I’m pretty sure there’s a logarithmic relationship, but I’m not sure how to use Excel to get the coefficients. Thanks!
asked Mar 24, 2011 at 5:30
$endgroup$
1
$begingroup$
If by logarithmic regression you mean the model log(y) = m1.x1 + m2.x2 + ... + b + (Error), you can use LOGEST and GROWTH with multiple independent variables. Note that if you want the estimated coefficients m1, m2, ..., b from LOGEST, you’ll have to enter the formula into multiple cells as an array. See Excel’s online help for the steps required.
Alternatively, you can log-transform your dependent variable and use LINEST/TREND which does the same thing under the hood.
ObWarning: Excel isn’t the best regression package in the world. See, for example, McCullough & Heiser (2008), On the accuracy of statistical procedures in Microsoft Excel 2007, Comp Stats & Data Analysis 52(10) pp.4570-4578.
answered Mar 24, 2011 at 6:26
Hong OoiHong Ooi
7,8593 gold badges30 silver badges53 bronze badges
$endgroup$
1