17 авг. 2022 г.
читать 2 мин
Логарифмический график — это диаграмма рассеяния , в которой используются логарифмические шкалы как по оси X, так и по оси Y.
Этот тип графика полезен для визуализации двух переменных, когда истинная связь между ними подчиняется степенному закону. Это явление происходит во многих областях реальной жизни, включая астрономию, биологию, химию и физику.
В этом руководстве показано, как создать логарифмический график для двух переменных в Excel.
Пример: логарифмический график в Excel
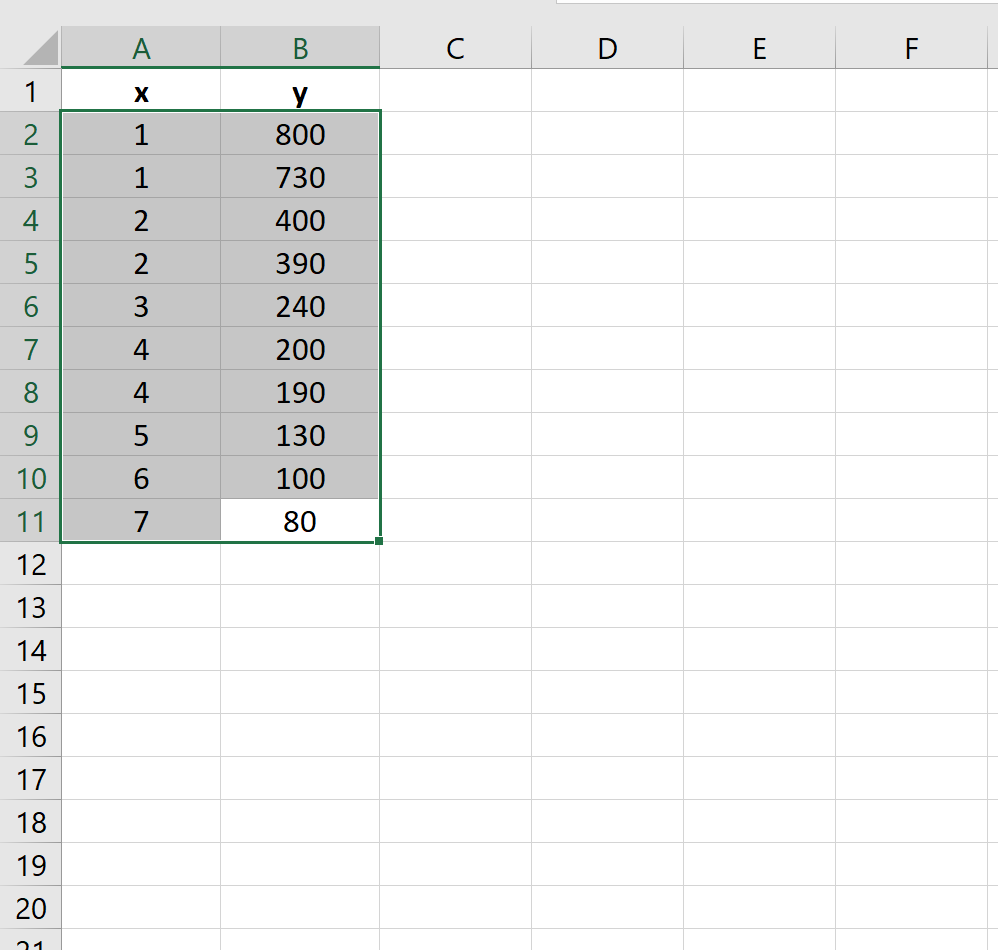
Предположим, у нас есть следующий набор данных в Excel, который показывает значения двух переменных, x и y:
Используйте следующие шаги, чтобы создать логарифмический график для этого набора данных:
Шаг 1: Создайте диаграмму рассеяния.
Выделите данные в диапазоне A2:B11 .
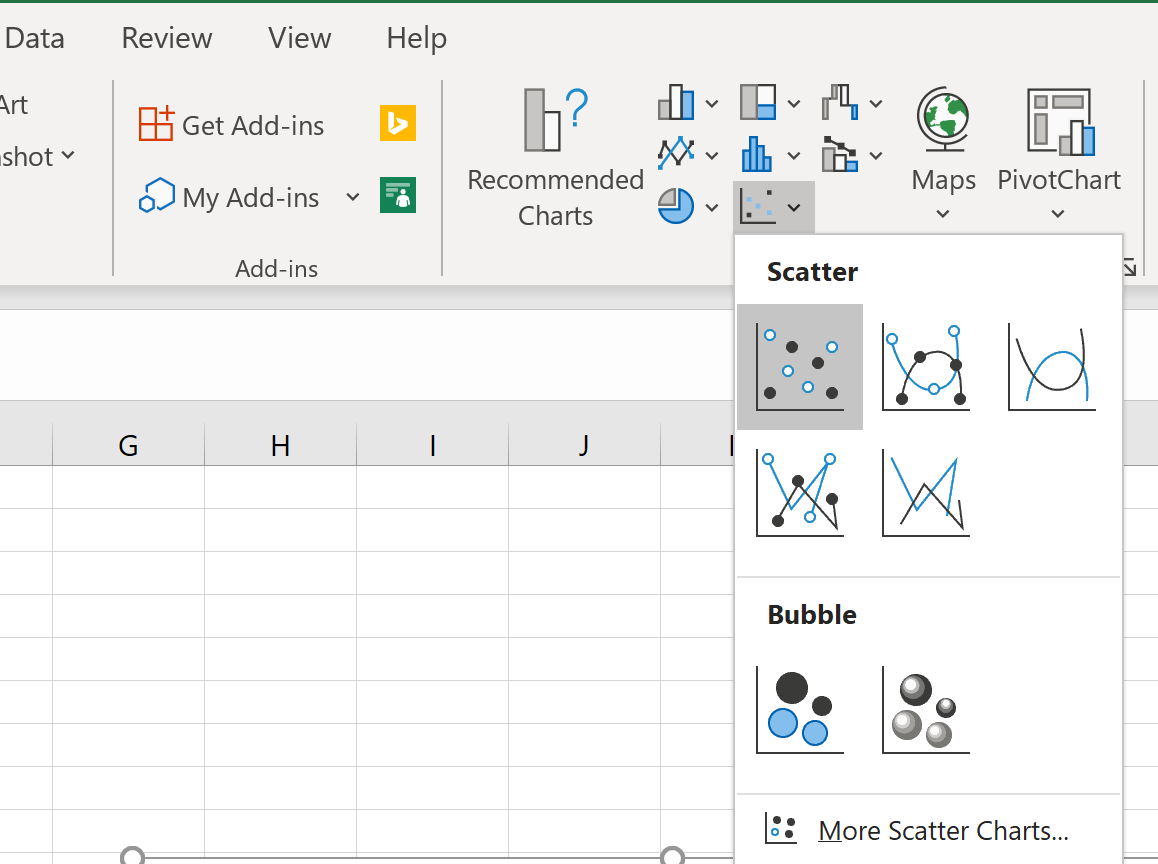
На верхней ленте щелкните вкладку « Вставка ». В группе « Графики » нажмите « Разброс ».
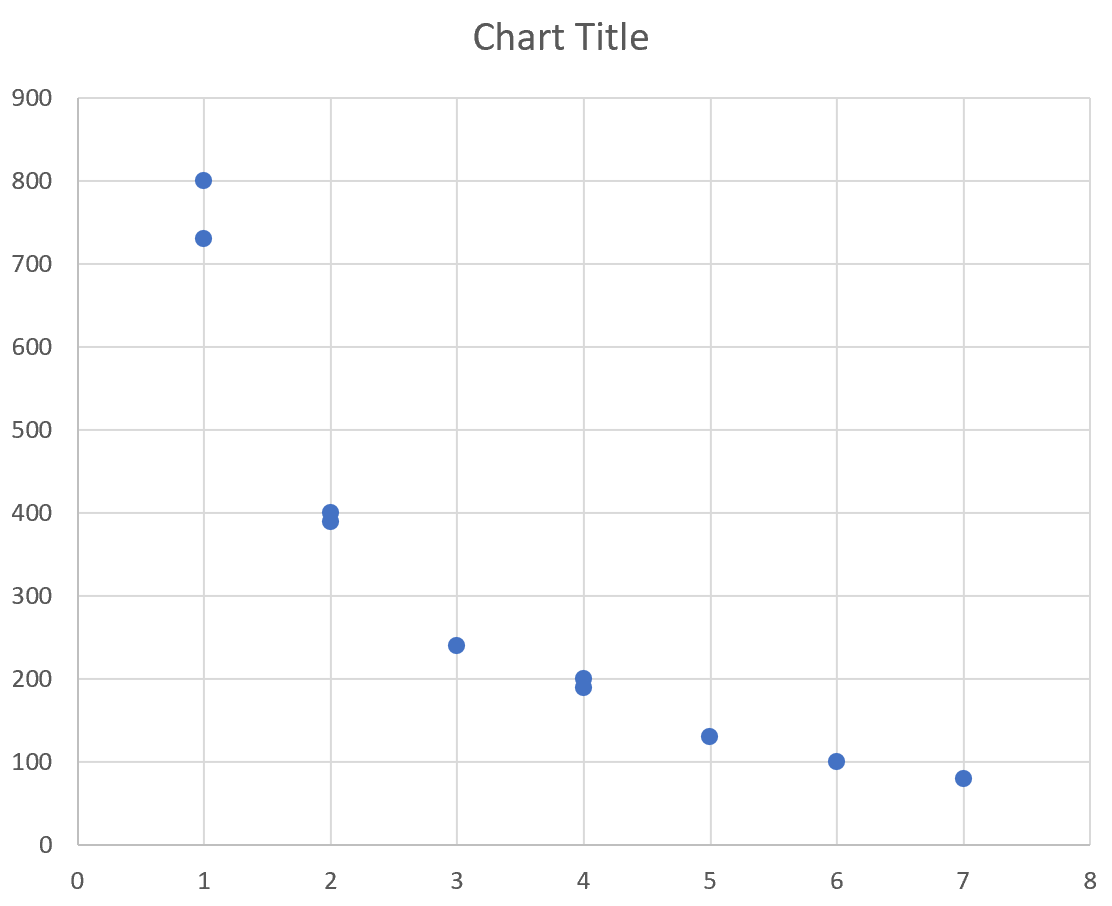
Автоматически появится следующая диаграмма рассеяния:
Шаг 2: Измените шкалу оси x на логарифмическую.
Щелкните правой кнопкой мыши значения вдоль оси x и выберите « Формат оси» .
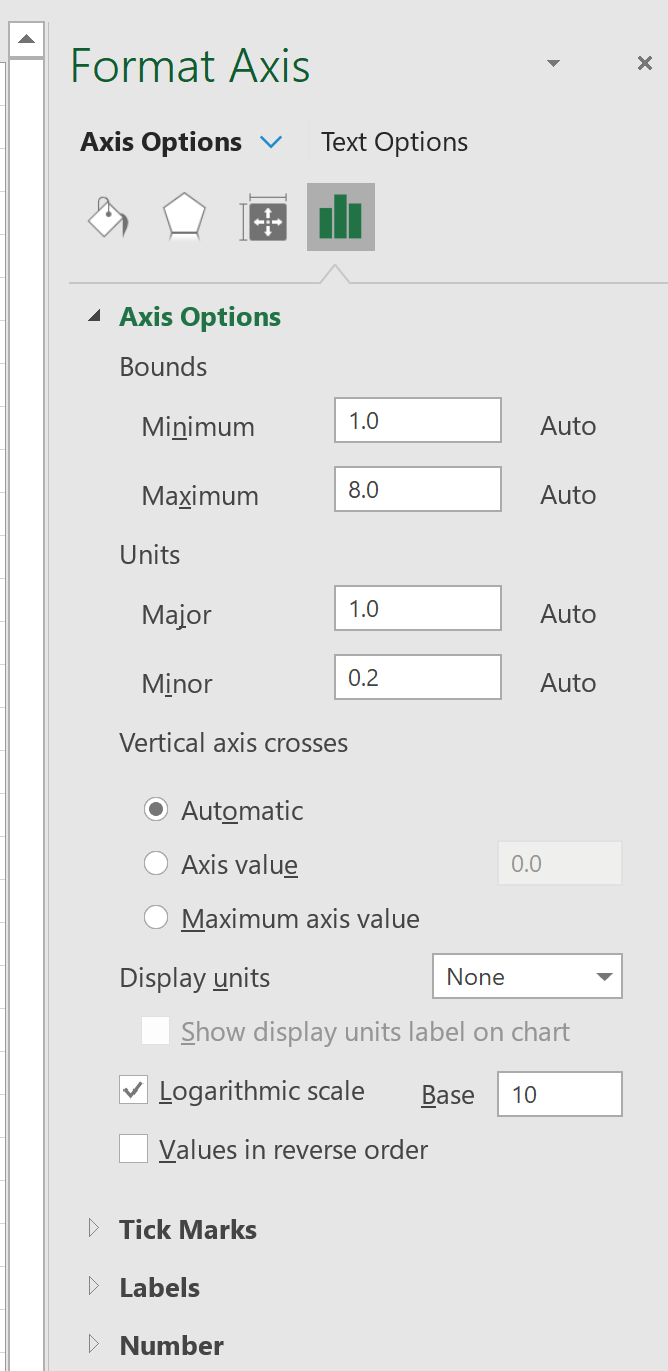
В новом всплывающем окне установите флажок рядом с Логарифмический масштаб , чтобы изменить масштаб по оси X.
Шаг 3: Измените шкалу оси Y на логарифмическую.
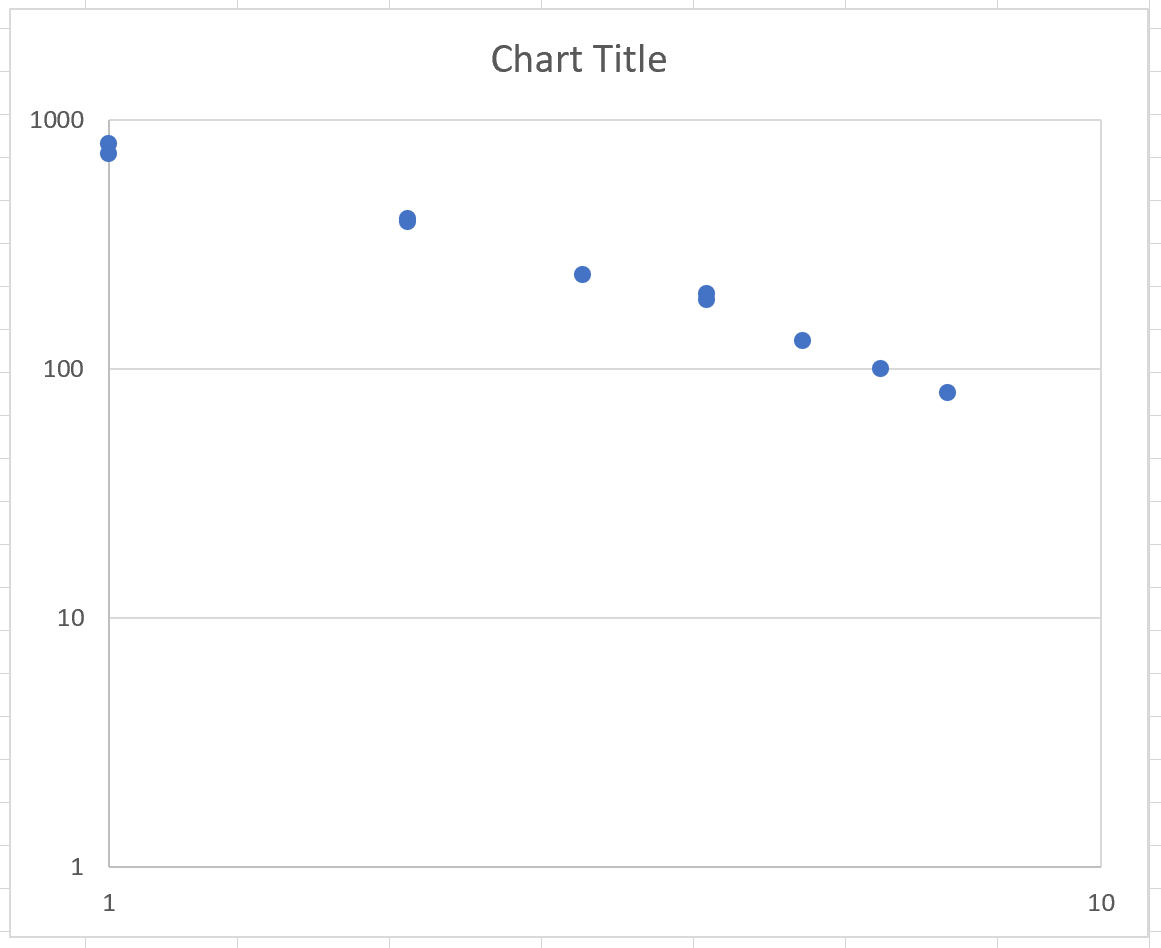
Затем щелкните по оси Y и повторите тот же шаг, чтобы изменить шкалу оси Y на логарифмическую. Результирующий график будет выглядеть так:
Обратите внимание, что ось x теперь охватывает от 1 до 10, а ось y — от 1 до 1000. Также обратите внимание, что связь между переменными x и y теперь выглядит более линейной. Это указывает на то, что две переменные действительно имеют степенную зависимость.
Вы можете найти больше учебников по Excel здесь .
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Semi-log and log-log graphs can help you discover new relationships between your data. Here’s how to create them in Excel.
Semi-log and log-log graphs are useful tools for analyzing and finding exponential and power functions relations. Logarithmic graphs have the potential to give you a perspective of a relationship between your data that isn’t obvious on a plain graph.
While a semi-log graph is logarithmic on only one axis, a log-log graph is logarithmic on both axes. Each of these graphs has its own uses. With Excel, you can create semi-log and log-log charts and graphs with a few clicks to further analyze your data. Read on to find out how you can create such graphs in Excel.
How to Create a Semi-Log Graph in Excel
A semi-log graph is a graph that has one of the two axes on a logarithmic scale. Usually, the Y-axis is logarithmic. This means that the Y-axis grid lines will be exponential, while the X-axis gridlines stay even.
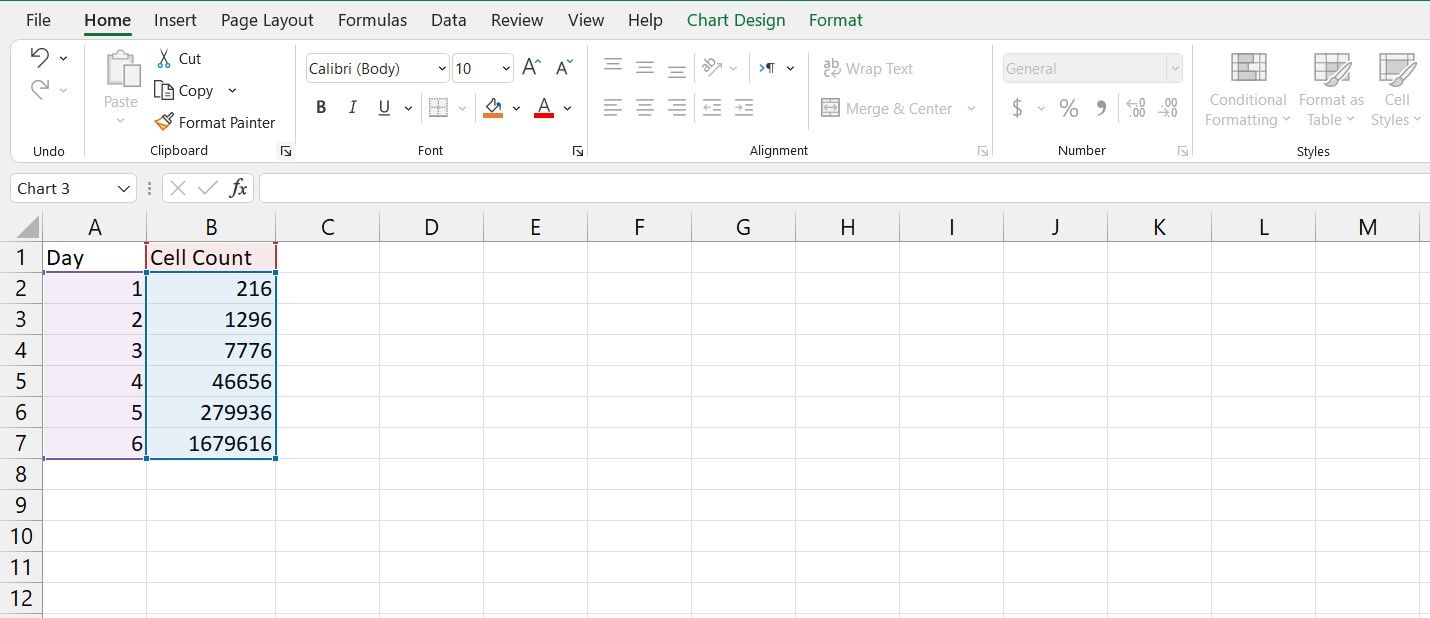
As an example, in this spreadsheet, we have the number of cells in a cell culture environment in an experiment on different days. The goal is to plot this data on a semi-log graph. If you’re not familiar with creating graphs in Excel, read our article on how to create graphs in Excel to get a good understanding of the process.
- Select the entire table. That will be cells A1 to B7 in this example.
- Go to the Insert menu.
- From the Charts section, click Insert Scatter (X, Y) or Bubble Chart.
- Select Scatter with Smooth Lines and Markers.
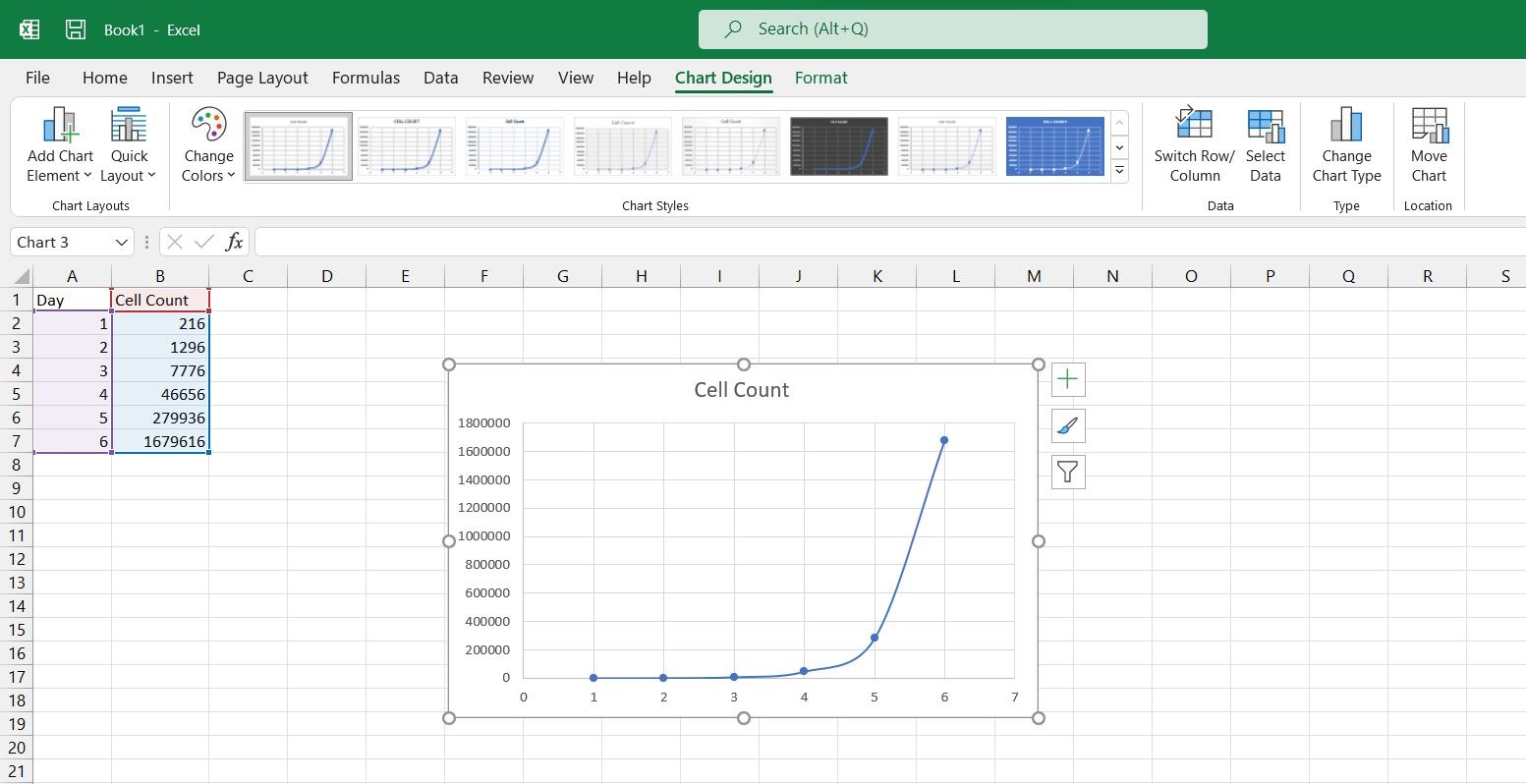
You now have a scatter chart of your data. Now it’s time to make it a semi-log one.
- Select the chart you just made.
- Double-click the Y-axis.
- In the Format Axis panel on the right, go to the Axis Options tab.
- In Axis Options, check Logarithmic Scale.
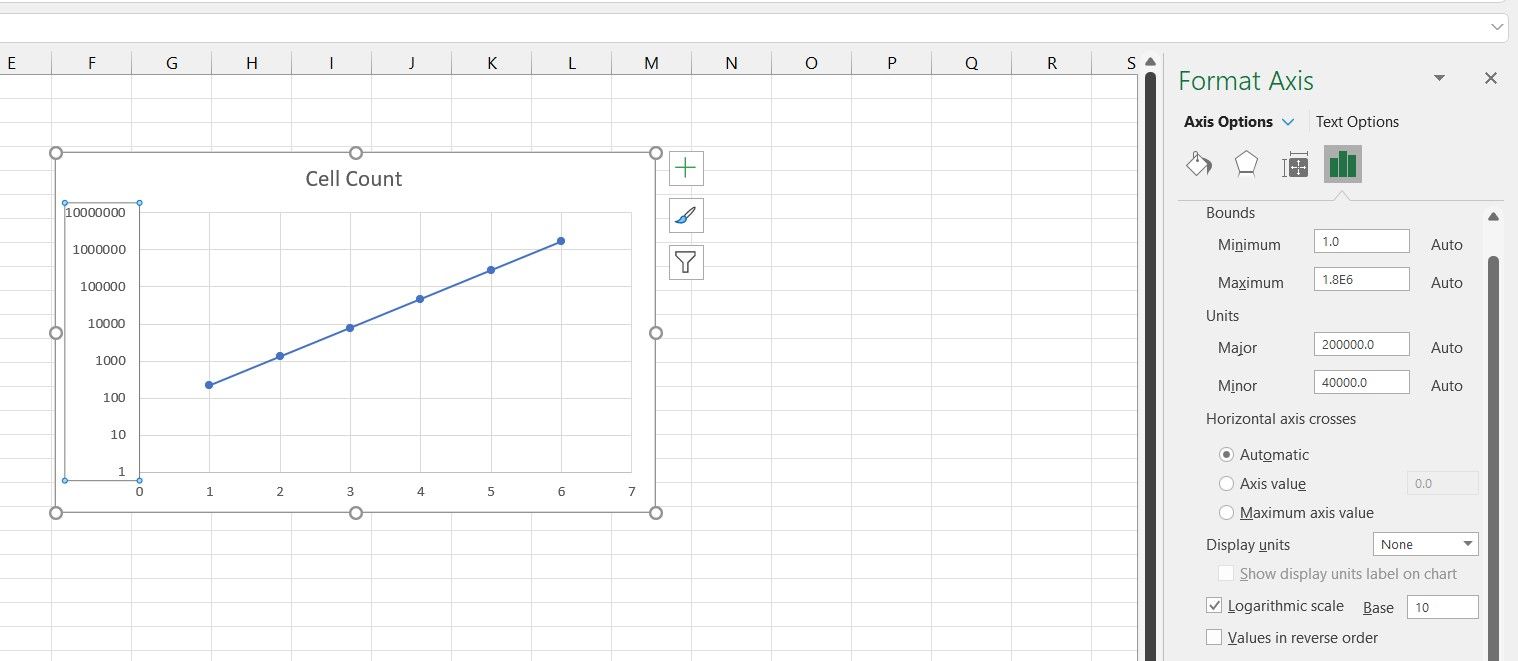
There’s your semi-log graph! Note that the graph is now a straight line now.
You can also alter the base from the default 10 to any other number that suits you better. That is because the cell count in the data table was exponential, as they are actually powers of six. You can further improve your graph’s readability by changing the logarithm base from 10 to 6.
How to Create a Log-Log Graph in Excel
A log-log graph is a graph that has both axes on a logarithmic scale. So then, the grid lines for both the X and Y axes are exponential and uneven in this graph. Let’s see the log-log graph in action with an example.
In a similar example, we have the cell counts on different days, but this time the days are exponential as well. A data table such as this practically begs for a log-log graph.
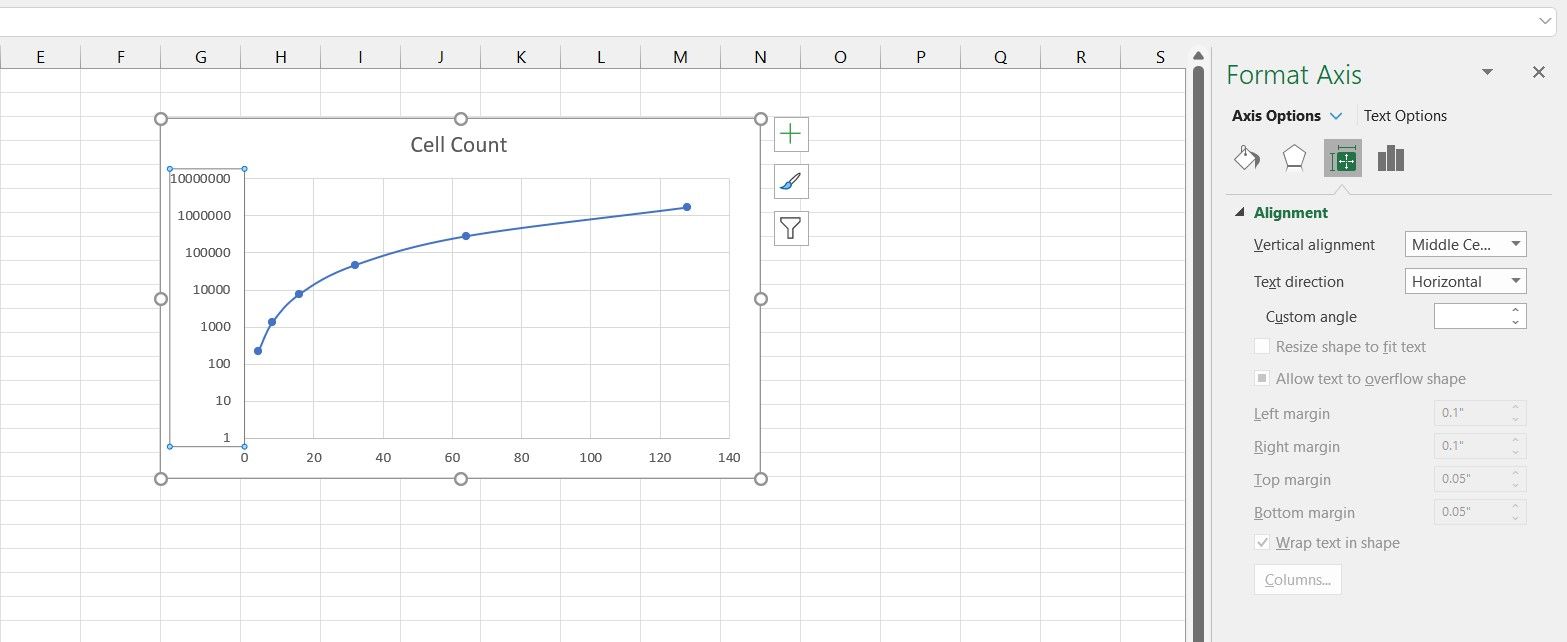
Just like the previous example, select the table and create a scatter chart for it. If you want to learn more about scatter charts, read our article on how to make a scatter plot in Excel to find out what exactly it is and when you should use it.
After you’ve created the scatter plot, change the Y-axis to log the way you learned in the previous section. You can see that the graph still isn’t a straight line. That’s because the X-axis (day number in this example) is exponential as well.
- Select the chart.
- Double-click the X-axis.
- From the Format Axis panel, click Axis Options.
- Under Axis Options, check Logarithmic Scale.
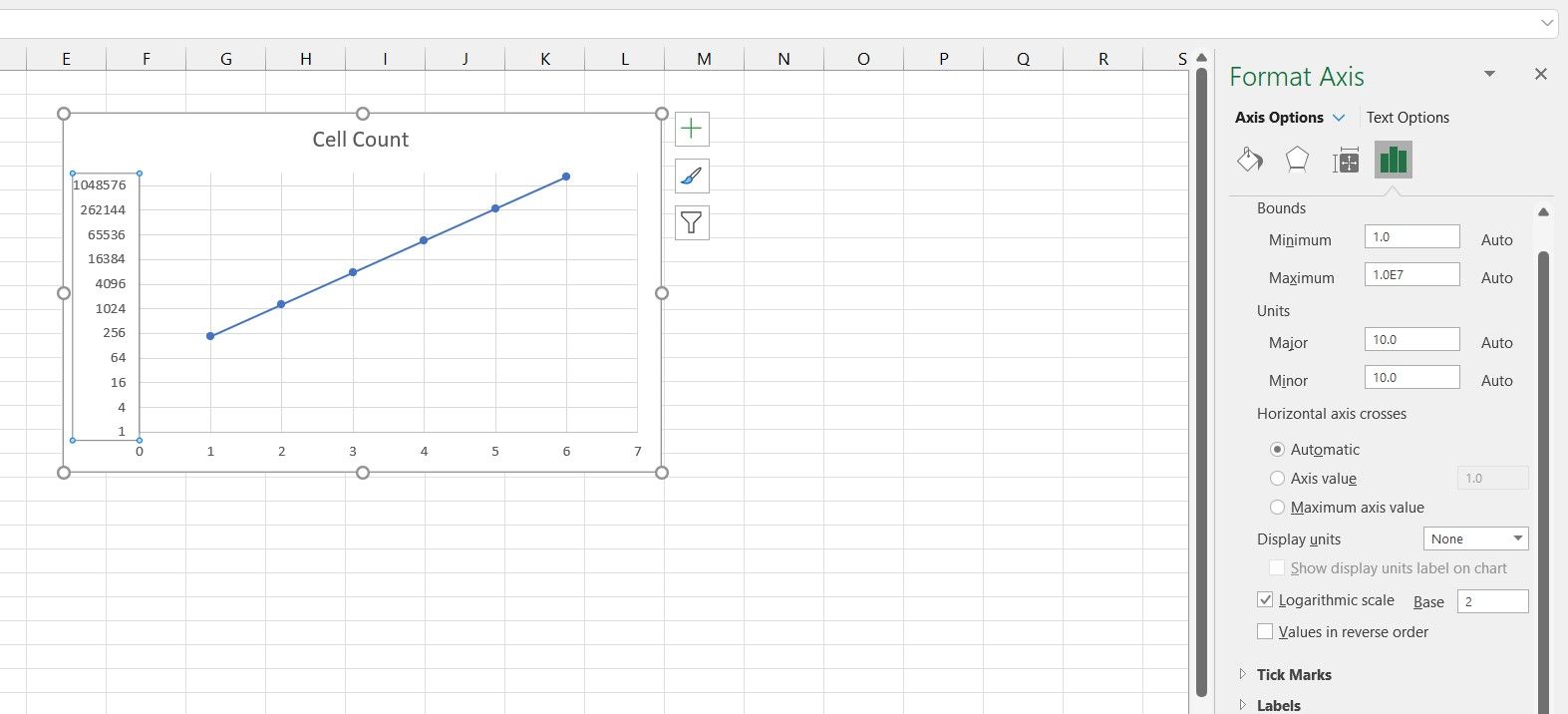
Now both your axes are on a logarithmic scale, and you can see that your graph has become a straight line as well. This is because the data on both axes are exponential.
Considering that the data on the X-axis are all powers of two, then changing the logarithm base to two will give you a better image of this graph.
Logarithmic Graphs in Excel
Semi-log and log-log graphs are useful assets that can help you discover new relations between your data. These tools are widely used in different areas, and though not immediately visible in the chart settings, Excel is also capable of creating semi-log and log-log graphs.
Now that you know how to create semi-log and log-log graphs in Excel, it’s time to use these graphs and see your data from a new perspective.
КАК ПОСТРОИТЬ ЛОГАРИФМИЧЕСКИЕ ФУНКЦИИ В EXCEL — ВОКРУГ-ДОМ — 2022
Видео: Excel 2010 Урок 20 Математические и Тригонометрические функции (Июнь 2022).
Microsoft Excel используется многими людьми для хранения информации и создания диаграмм, но его также можно использовать для построения графиков. Функции журнала не являются исключением. Используя комбинацию функции Excel (LOG ()) и инструмента регрессии, вы можете создать гладко выглядящий график журнала. С базовым пониманием Excel процесс занимает всего несколько минут.
кредит: gmast3r / iStock / Getty Images
Шаг 1
Введите в столбец «A» ряд значений, соответствующих маркерам оси X, которые вы хотите использовать. Например, если ваши данные находятся в диапазоне 0-100, вы можете ввести значения «x» 10, 20, 30 и т. Д. Просто убедитесь, что ваши значения «x» распределены и не сгруппированы близко друг к другу.
Шаг 2
Введите «= LOG (A1, base)» в ячейку B1, заменив base логарифмическим базовым числом, используемым вашей функцией. Большинство функций журнала используют базу 10. В качестве альтернативы, вы можете заменить «LOG» на «LN», если вы хотите использовать функцию натурального логарифма.
Шаг 3
Скопируйте эту формулу для всех оставшихся ячеек в столбце «B», для которых есть связанные значения «x» в столбце «A». Теперь у вас должна быть полная таблица значений. Эта таблица будет служить ориентиром для Excel для расчета гладкого графика.
Шаг 4
Нажмите на вкладку «Вставка» и из-под заголовка «Графики» выберите «Разброс только по маркерам».
Шаг 5
Нажмите на вкладку «Макет», нажмите «Линия тренда» и выберите «Дополнительные параметры линии тренда».
Шаг 6
Выберите «Логарифмический» и нажмите «Закрыть». Это создает гладкий график, который соответствует таблице данных, которую вы создали.
Шаг 7
(Необязательно) Щелкните правой кнопкой мыши одну из точек маркера и выберите «Форматировать ряд данных …».
Шаг 8
(Необязательно) Нажмите «Параметры маркера» и выберите «Нет». Это скрывает ориентиры, которые вы использовали для создания линии тренда.
Как построить кривую титрования в Excel
С точки зрения химии, кривая титрования отслеживает уровень pH раствора как вещества с известной концентрацией и объемом, добавляемым к нему. Этот тип кривой состоит из .
Как построить график анализа тренда в Microsoft Excel
Используйте инструмент линии тренда, чтобы отобразить тренд на данных в диаграмме Excel, проанализировать текущие данные и добавить прогноз на будущее.
Как построить стандартную кривую в Excel
Microsoft Excel предназначен не только для создания электронных таблиц — программное обеспечение более чем способно создать стандартный график кривой всего за несколько шагов. Чтобы сделать вашу стандартную кривую, вы .
КАК ИСПОЛЬЗОВАТЬ ЛОГАРИФМИЧЕСКОЕ МАСШТАБИРОВАНИЕ ДЛЯ АНАЛИЗА ДАННЫХ EXCEL — МАНЕКЕНЫ — СОЦИАЛЬНЫЕ МЕДИА — 2022
Видео: MATLAB 08 Расширенное построение графиков: особенности и приемы 2022.
Логарифмы и логарифмическое масштабирование — это инструменты, которые вы хотите использовать в своих диаграммах Excel, потому что они позволяют вам делать что-то очень мощное. При логарифмическом масштабировании вашей оси значений вы можете сравнить относительное изменение (а не абсолютное изменение) значений данных.
Например, скажите, что вы хотите сравнить продажи крупной компании, которая растет солидно, но медленно (10 процентов в год) при продажах небольшой фирмы, которая растет очень быстро (50 процентов в год). Поскольку типичная линейная диаграмма сравнивает значения абсолютных данных, если вы планируете продажи этих двух фирм в одной линейной диаграмме, вы полностью упускаете из виду тот факт, что одна фирма растет намного быстрее, чем другая фирма.
На этом рисунке показана традиционная простая линейная диаграмма. Эта линейная диаграмма не использует логарифмическое масштабирование оси значений.
Линейная диаграмма, которая отображает продажи двух конкурентов, но без логарифмического масштабирования.
Теперь взглянем на линейную диаграмму, показанную на следующем рисунке. Это та же информация в том же типе и подтипе диаграммы, но масштабирование оси значений изменяется для использования логарифмического масштабирования. При логарифмическом масштабировании показаны темпы роста, а не абсолютные значения. И когда вы определяете темпы роста, гораздо более быстрые темпы роста небольшой компании становятся ясными. Фактически, вы можете фактически экстраполировать темпы роста двух компаний и угадать, сколько времени потребуется маленькой компании, чтобы догнать крупную компанию. (Просто протяните линии.)
Простая линейная диаграмма, использующая логарифмическое масштабирование оси значений.
Чтобы сообщить Excel, что вы хотите использовать логарифмическое масштабирование доступа к значениям, выполните следующие действия:
Щелкните правой кнопкой мыши по оси значения (Y), а затем выберите команду Формат оси в появившемся контекстном меню.
Когда появится диалоговое окно «Формат оси», выберите пункт «Параметры оси» в списке.
Чтобы заставить Excel использовать логарифмическое масштабирование оси значения (Y), просто установите флажок «Логарифмическая шкала» и нажмите «ОК».
Excel снова масштабирует ось значений диаграммы для использования логарифмического масштабирования. Обратите внимание, что первоначально Excel использует логарифмическое масштабирование базы 10. Но вы можете изменить масштаб, введя другое значение в поле «Логарифмическая шкала».
Если вы строите графические данные с экспоненциальным ростом, такие как данные, описывающие рост бактериальной колонии, использование типичных декартовых осей может привести к тому, что вы не сможете легко увидеть тренды, такие как увеличения и уменьшения, на графике. В этих случаях полезно использовать графики с полулогарифмическими осями. После того, как вы использовали Excel для создания набора регулярных осей, преобразование осей в полулогарифмические оси в Excel становится совсем не сложным.
Введите имя вашей независимой переменной в начале столбца «А» в Excel. Например, если вы строите график зависимости времени от роста бактерий, введите «Время» в верхней части первого столбца.Аналогичным образом введите «Рост бактерий» в верхней части второго столбца (столбец «B»).
Используйте инструмент «Диаграмма», чтобы создать график, который отображает независимую переменную на оси X, а не на зависимую переменную на оси Y.
Решите, какую ось вы хотите сделать логарифмической: логарифмический граф делает обе оси логарифмическими, в то время как полулогарифмический граф делает только одну из осей логарифмической.
Дважды щелкните по этой оси. Нажмите на вкладку «Масштаб», затем установите флажок «Логарифмическая шкала». Ваш график теперь станет полулогарифмическим.
A semi-log graph is a type of graph that uses a logarithmic scale on the y-axis and a linear scale on the x-axis.
This type of graph is often used when the values for the y variable have much greater variability compared to the values for the x variable.
This occurs often in datasets in finance, economics, biology, and astronomy among other fields.
The following step-by-step example shows how to create a semi-log graph in Excel for a given dataset.
Step 1: Enter the Data
First, let’s enter the values for a fake dataset:
Step 2: Create a Scatterplot
Next, highlight the data values:
Along the top ribbon, click Insert. Then click the first option under the Scatter graph option:
The following scatterplot will automatically be displayed:
From the plot we can see that the values for the y variable have much higher variability than the values for the x variable.
This means it’s a good idea to convert the y-axis into a logarithmic scale to visualize the y-values more effectively.
Step 3: Modify the Y-Axis Scale
Next, right click the y-axis. In the dropdown menu that appears, click Format Axis:
In the window that appears on the right side of the screen, check the box next to Logarithmic scale:
The y-axis will automatically be converted to a logarithmic scale:
The x-axis remains on a linear scale, but the y-axis has been converted into a logarithmic scale.
Notice how much easier it is to interpret the y values in this graph compared to the previous graph.
Additional Resources
How to Create a Log-Log Plot in Excel
How to Transform Data in Excel (Log, Square Root, Cube Root)
How to Perform a Box-Cox Transformation in Excel
Логарифмическая функция
- Маеренкова Вера Васильевна, учитель математики
Разделы: Математика
Цели:
Оборудование: Компьютеры с выходом в сеть Интернет, интерактивная доска, мультимедийный проектор, документ-камера.
Тип урока: комбинированный (первичное ознакомление с материалом, образование понятий, установление связей и закономерностей, применение полученных знаний на практике).
План урока:
Ход урока
I. Организационный момент
Учитель приветствует учащихся, сообщает тему урока, ставит перед классом цель урока. (Приложение 1: слайды 1, 2, 3.)
II. Актуализация опорных знаний
Фронтальный опрос.
1) Дайте определение показательной функции 2) Изобразите график показательной функции:
а) при a > 1 (слайд 4) b) при 0 < a < 1 (слайд 6)
3) Перечислите свойства показательной функции:
a) при a > 1 (слайд 5) b) при 0 < a < 1 (слайд 7)
III. Объяснение нового материала
Вспомним теорему из курса алгебры:
Если функция y = f(x) определена и возрастает (или убывает) на промежутке Х и область ее определения является Y, то у нее существует обратная функция, причем обратная функция определена и возрастает (или убывает) на Y.
Вернемся к показательной функции и выясним, существует ли для нее обратная функция. Учащиеся должны обратить внимание, что показательная функция y = ax, где a >0, a 1 обладает всеми свойствами, которые гарантируют существование обратной функции.
Итак, мы выяснили, что у показательной функции существует обратная функция, давайте попробуем построить ее график.
Ранее было доказано, что графики данных функций являются симметричными относительно прямой y = x, поскольку состоят из точек, симметричных друг другу относительно указанной прямой. Например, если А(2,4) принадлежит графику y = ax при при х 0, то точка В(4,2) будет принадлежать графику обратной функции. (слайд 8)
Поскольку график показательной функции в зависимости от основания а имеет различный вид, то рассмотрим два случая: при a > 1; при 0 < a < 1.
Для этого разделим класс на две группы. Первая группа будет работать с графиками данных функций при a > 1, а вторая — при 0 < a < 1
Ребята рассаживаются за компьютеры и с помощью программы MS Excel строят сначала график показательной функции. У всех членов группы основания показательной функции различны.
Первая группа: y = ax, y = 3x, y = 6x…
Вторая группа: y = , y = , y = … (Приложение 2).
Далее, исходя из того что графики обратных функций симметричны относительно прямой y = x, построим график обратной функции. (слайд 9)
Для этого нам достаточно поменять местами координаты точек графика показательной функции. Если точка с координатами (x,y) принадлежала графику показательной функции, то точка с координатами (y,x) будет принадлежать обратной функции.
Итак, мы построили графики новой функции, которая называется логарифмической функцией и задается формулой y = logax.
Действительно, если точка с координатами (2,4) принадлежит графику функции y = 2x, то выполняется равенство 22 = 4, следовательно, точка с координатами (4,2) будет принадлежать графику обратной функции y = log2x, а значит, должно выполняться равенство log24 = 2. По определению логарифма имеем 22 = 4, 4=4. Равенство верно. Какими же свойствами обладает логарифмическая функция?
Используя построенные график, ребята перечисляют все свойства логарифмической функции.
Свойства логарифмической функции при a > 1 (слайд 10)
y > 0 при x (1; ) y < 0 при x (0;1)
- Функция экстремумов не имеет
- Функция возрастает при x (0;+ )
- Асимптота x = 0
Свойства логарифмической функции при 0 < a < 1 (слайд 12)
y > 0 при x (0;1) y < 0 при x (1; )
- Функция экстремумов не имеет
- Функция убывает при x (0;+ )
- Асимптота x = 0
IV. Закрепление изученного материала
1. Определите знак числа: (слайд 13)
a) ; b) ; c) log0,4 1,8; d) log0,1 0,3
2. Определите, какие из перечисленных ниже функций являются возрастающими, а какие убывающими? (слайд 14)
3. В одной координатной плоскости построить графики следующих функций:
1 группа (слайды 15, 16)
2 группа (слайды 17, 18)
Ребята делают вывод:
4. Опираясь на вывод, сделанный в задании 3, сравните: (слайд 19)
log3 5 и lg5 log3 0,5 и log50,5 log0,1 0,7 и log0,50,7 log0,36 и log0,56
V. Выполнение теста первичного закрепления материала
Условие теста выводится на интерактивную доску.
Проверка результатов теста осуществляется с помощью документ-камеры. Учащиеся самостоятельно оценивают выполненную работу, и результат сдают учителю.
VI. Работа в сети Интернет
На итерактивной доске записаны адреса сайтов, где учащиеся смогут найти тесты ЕГЭ:
http://www.ege-trener.ru/izbrannoe/ http://uztest.ru/simulator http://fipi.ru/view/sections/142/docs/
Ребята получают задание: Проанализировать задания тестов ЕГЭ: встречаются ли задания на применение свойств логарифмической функции, какие, сколько их может быть в одном тесте, в какой части теста, что нужно знать для их выполнения. В результате работы ребята должны сделать подборку заданий из тестов ЕГЭ для дальнейшего их решения. (слайды 20, 21)
VII. Решение заданий из тестов ЕГЭ
После того, как ребята сделают подборку заданий из тестов ЕГЭ, некоторые из них, если позволит время, можно решить на уроке.
За три минуты до звонка предложить учащимся разгадать кроссворд, где центральное слово по вертикали будет являться ключевым в теме урока.
По горизонтали: (слайды 22, 23, 24)
Ответы:
VII. Подведение итога урока
(слайд 25)