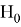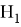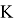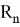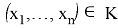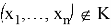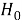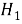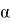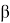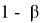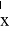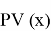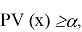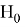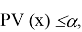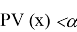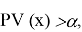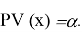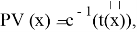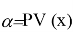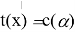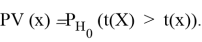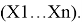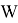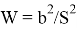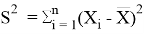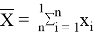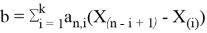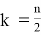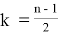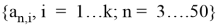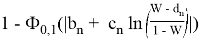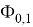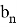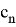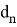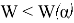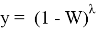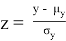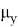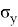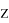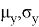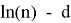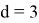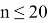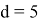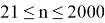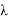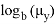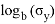Из данной статьи вы узнаете:
• Примеры применения логарифмического тренда в бизнесе;
• Логарифмический тренд y(x)=a*ln(x)+b разложим на запчасти;
• 5 способов расчета значений логарифмического тренда в Excel;
• Как можно скорректировать значения логарифмического тренда;
Логарифмический тренд применяется для прогнозирования временного ряда, данные которого вначале быстро растут или убывают, а затем постепенно стабилизируются.
Например, выводим новый товар на рынок, за счет роста клиентской базы продажи быстро растут, затем мы набираем постоянных клиентов, продажи стабилизируются, и новые клиенты уже не основной фактор роста, а основной фактор роста — это развитие продаж постоянным клиентам.
Или вводим продукцию в новую торговую точку, и по истечении определенного периода решаем увеличить количество фейсов на полке (т.е. увеличить размер полки для одного вида товара) (фейс — это единица продукции, которая стоит лицом к покупателю) или продублировать выкладку в другой части зала. Почему здесь лучше использовать логарифм? Потому что увеличение количества фейсингов на полке в 2 раза по одной группе товаров, к сожалению, не ведёт к увеличению продаж в 2 раза, причём с ростом количества фейсов темп прироста продаж уменьшаются для каждого последующего фейса. Именно поэтому для прогнозирования продаж для этой ситуации лучше всего использовать логарифмический тренд.
Логарифмический тренд – это функция y(x)=a*ln(x)+b, где
Значение x – это номера периода во временном ряду (например, номер месяца, квартала, дня; См. статью о временных рядах.)
y – это последовательность значений , которые мы анализируем и прогнозируем (например, объём продаж по месяцам.)
b – точка пересечения с осью y на графике;
a – это значение, на которое увеличивается следующее значение временного ряда;
Причем, если a>0, то динамика роста положительная,
Если а<0, то динамика тренда отрицательная.
При построении логарифмического тренда используют как положительные, так и отрицательные данные временных рядов.
Рассмотрим логарифмический тренд на примере построения прогноза продаж в Excel по месяцам.
Временной ряд — продажи по месяцам по новому товару
В этом временном раде у нас есть 2 переменных
1. Время — месяцы— x;
2. Объёмы продаж по месяцам — y;
Уравнение логарифмического тренда y(x)=a*ln(x)+b, где y — это объёмы продаж, x — месяцы.
5 способов расчета логарифмического тренда в Excel.
Как в Excel мы можем рассчитать коэффициенты логарифмического тренда?
1-й способ — с помощью графика.
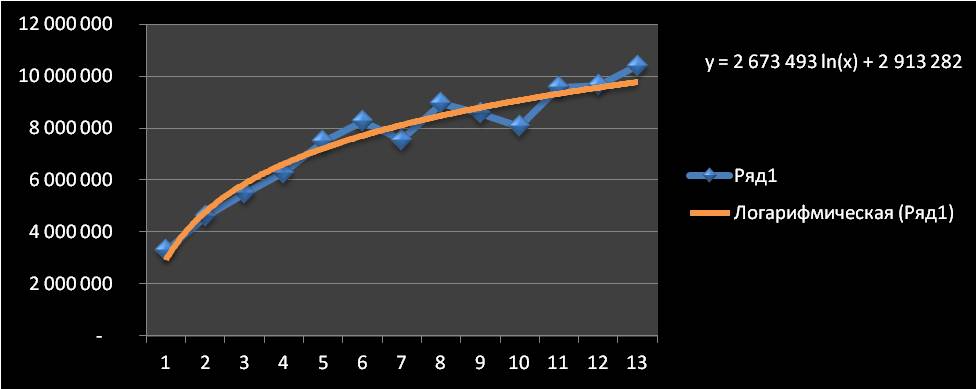
Строим график в Excel и видим по оси x — наш временной рад (1, 2, 3… — ноябрь, декабрь, январь …), по оси y объёмы продаж + добавляем на график линию тренда и уравнение тренда.
Получаем уравнение тренда y=2 673 493 ln(x) + 2 913 282
Для прогнозирования нам необходимо рассчитать значения тренда, как для анализируемых значений, так и для будущих периодов.
При расчете значений логарифмического тренда нам будут известны:
- Время — значение по оси Х;
- Значение «a» и «b» уравнения логарифмического тренда y(x)=a*ln(x)+b;
Рассчитываем значения тренда для каждого анализируемого периода времени от 1 до 13, а также для будущих периодов с 14 месяца до 20.
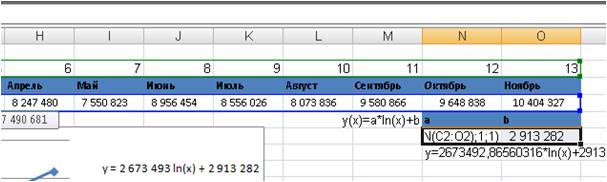
Например, для 14 месяца значение тренда рассчитывается по следующей схеме: в уравнение подставляем x=14 и получаем y=2 673 493 ln(14) + 2 913 282=9 968 782
20-го y=2 673 493 ln(20) + 2 913 282=10 922 350
И т.д.
Файл с примером вы можете скачать здесь.
2-й способ — с помощью функции Excel =Линейн().
Для расчета коэффициентов логарифмического тренда воспользуемся функцией Excel =ЛИНЕЙН() .
Для этого в функцию =ЛИНЕЙН() введем:
1. известные значения y – объем продаж;
2. известные значения x – номера периодов, причём введенные, как LN(номера периодов);
3. константа – вводим 1 для расчёта коэффициента b уравнения y(x)=a*ln(x)+b;
4. Статистика — 1 или 0;
Формула будит выглядеть вот так =ЛИНЕЙН(C2:O2;LN(C1:O1);ИСТИНА;ИСТИНА)
Теперь формулу вводим как формулу массива, выделяем 2 ячейки (подробнее о формулах массива) и нажимаем F2, а затем одновременно — клавиши CTRL + SHIFT + ВВОД.
Коэффициенты «а» и «b» логарифмического тренда y(x)=a*ln(x)+b рассчитаны;
Получаем уравнение тренда y=2673492*ln(x)+2913281
Для прогнозирования нам необходимо продлить линию тренда и определить её значения. При её продлении нам будет известен только один параметр — это время, т.е. значения по оси X.
Рассчитываем значения тренда с 1-го месяца (ноябрь) до 20 (июнь)— y=2673492*ln(14)+2913281=9968782
17-го — y=2673492*ln(17)+2913281=10487857
И т.д.
3-й способ — с помощью функции Excel =ТЕНДЕНЦИЯ().
Расчет значений логарифмического тренда с помощью функции Excel =ТЕНДЕНЦИЯ().
Для этого в функцию =ТЕНДЕНЦИЯ() вводим:
1. Известные значения y — объёмы продаж за анализируемый период;
2. Известные значений x — порядковые номера периодов (месяцев), причем введенные как LN(Известные значений x);
3. Новые значения x— порядковые номера периодов, для которых хотим рассчитать значения трендов, причем введенные как LN(Новые значения x);
4. Константа — ставим «1», если хотим рассчитать значения тренда y(x)=a*ln(x)+b с коэффициентом b.
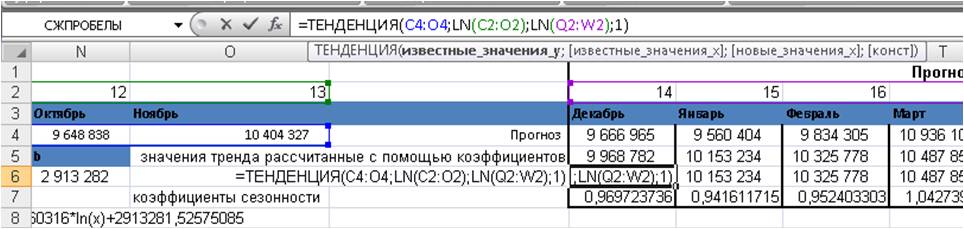
Формула будет выглядеть вот так =ТЕНДЕНЦИЯ(C4:O4;LN(C2:O2);LN(Q2:W2);1)
Затем, вводим формулу =ТЕНДЕНЦИЯ(), как формулу массива. Для этого
1. Выделяем диапазон ячеек с 1-го по 20-й период, в первой ячейке введена формула =ТЕНДЕНЦИЯ();
2. Нажимаем F2, а затем одновременно — клавиши CTRL + SHIFT + ВВОД.
Значения логарифмического тренда с помощью формулы Excel =тенденция() рассчитаны.
Файл с примером вы можете скачать здесь.
4-й способ — функция Excel =предсказ().
Расчёт значений логарифмического тренда — с помощью функции Excel =предсказ()
Для этого вводим в функцию =предсказ(
1. X — номер периода, для которого рассчитываем прогноз, причем вводим как LN(x);
2. Известные значения y — объёмы продаж по месяцам, фиксируем диапазон, выделяем его и нажимаем F4. Получаем ссылку, как на картинке:
3. Известные значения x — порядковые номера периодов, для которых хотим рассчитать значения логарифмического тренда, причем вводим как LN(Известные значения x) + фиксируем выделенный диапазон, выделяем его и нажимаем F4;
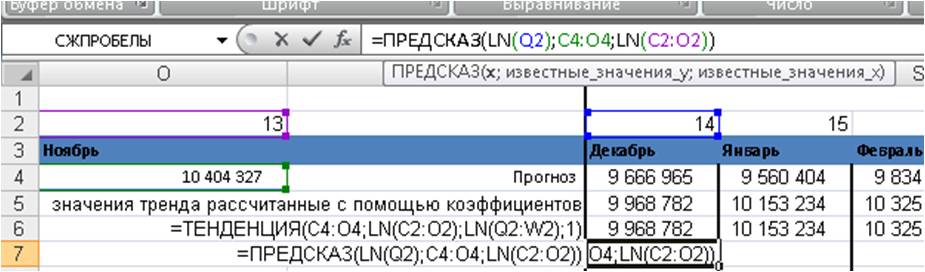
Получаем формулу =ПРЕДСКАЗ(LN(Q2);$C$4:$O$4;LN($C$2:$O$2))
Протягиваем формулу, значения логарифмического тренда рассчитаны.
5-й способ — Forecast4AC PRO
Расчет значений логарифмического тренда — с помощью программы Forecast4AC PRO.
1. Устанавливаем курсор в начало временного ряда, выбираем в настройках программы:
— Что рассчитываем — значения тренда;
— Тренд – Логарифмический тренд;
— Временной ряд — месячный;
и сохраняем;
2. Заходим в меню программы и нажимаем «Start_Forecast» — готово, значения логарифмического тренда рассчитаны!
Файл с примером вы можете скачать здесь.
Для того чтобы рассчитать прогноз с учетом роста и сезонности, мы умножаем рассчитанные значения тренда на коэффициенты сезонности.
Коэффициенты сезонности рассчитаем с помощью программы Forecast4AC PRO (лист » Лист2FYMLn «) или по аналоги, как описано в данной статье, только для рассчета коэффициентов сезонности вместо линейного тренда используем логарифмический.
Теперь значения тренда умножаем на коэффициенты сезонности и прогноз готов.
Отношение прогноза к предыдущему периоду получилось 116%, т.е. прогнозируется рост на 16%.
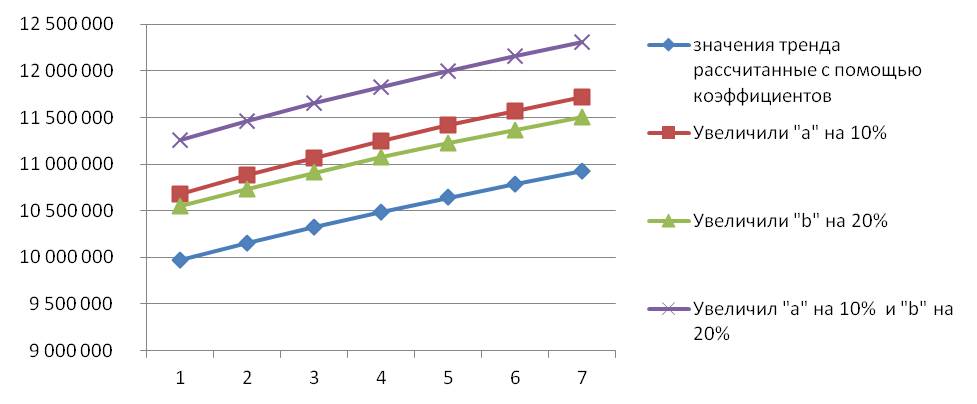
Как мы можем скорректировать прогнозные значения логарифмического тренда?
Если нас рост не устраивает, и мы планируем, что он будет больше, мы можем увеличить рост, скорректировав коэффициенты логарифмического тренда.
Скорректируем значение «a» и «b» рассчитанного нами выше тренда y=2673492*ln(x)+2913281
При изменении значений «a» и «b» логарифмического тренда y(x)=a*ln(x)+b, получаем увеличение значений тренда, причем увеличение коэффициента «а» на 10% даёт больший рост, чем увеличение коэффициента «b» на 20%.
Теперь рассчитаем коэффициенты сезонности для логарифмического тренда с помощью Forecast4AC PRO (лист » Лист2FYMLn «). Умножим скорректированные значения тренда на сезонность. Также при прогнозировании стоит учесть дополнительные факторы, которые значительно влияют на объём продаж. Прогноз продаж готов!
С помощью программы Forecast4AC PRO вы сможете в Excel одним нажатием клавиши рассчитать значения логарифмического тренда, коэффициенты сезонности и прогноз для более чем 5000 строк одновременно.
Точных вам прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel.
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Зарегистрируйтесь и скачайте решения
Статья полезная? Поделитесь с друзьями
I’m trying to compute the log returns of a stock using the formula:
X=log(pt)-log(pt-1)
The code I made, doesn’t work:
runtime error Q invalid procedure call or argument
Private Sub CommandButton1_Click()
Dim row As Integer
row = 9
Do While Cells(row, 2) <> ""
Cells(row, 4).Value = log(Cells(row + 1, 2).Value) - log(Cells(row, 2).Value)
row = row + 1
Loop
End Sub
asked Aug 4, 2016 at 16:15
2
You ran outside the bounds of your data. When Cells(row, 2) gets to the last row your data, you try to evaluate something equivalent to Log(Number) - Log(0) because Cells(row + 1, 2) is empty and defaults to 0. And of course, Log(0) is invalid and throws an error.
Fix this by adjusting your loop (start at second row and calculate with the cell above it).
Private Sub CommandButton1_Click()
Dim row As Integer
row = 10
Do While Cells(row, 2) <> ""
Cells(row - 1, 4).Value = Log(Cells(row, 2).Value) - Log(Cells(row - 1, 2).Value)
row = row + 1
Loop
End Sub
answered Aug 4, 2016 at 19:32
MikegrannMikegrann
1,0817 silver badges17 bronze badges
0
Термином «инвариант» в науке принято обозначать величину остающуюся неизменной при тех или иных преобразованиях объекта. К примеру, внешность человека может очень сильно меняться под воздействием возраста, грима или пластической хирургии, но его всегда можно опознать по ДНК. Код ДНК является инвариантом – неизменной характеристикой. Инварианты часто несут наиболее важную информацию о том или ином предмете или явлении.Какое отношение все это имеет к финансовым рынкам? Финансовые рынки хорошо известны своей необычайной подвижностью. Цены большинства инструментов меняются, чуть ли не ежесекундно. Естественным образом возникает вопрос: есть ли что-то неизменное в этом море хаоса и нестабильности?
Цена учла все… и заблудилась
Известный постулат технического анализа гласит: «Цена учитывает все». Многие трейдеры поэтому важнейшей характеристикой фининструмента считают его цену. Можно ли признать цену рыночным инвариантом? Не смотря на всю экономическую важность понятия «цена», ответ на этот вопрос отрицательный. Цена постоянно меняется, значит, по определению она не может быть инвариантом. А что же средняя цена? Скользящие средние – один из наиболее популярных методов анализа. Возможно, средняя цена демонстрирует качество неизменности и устойчивости? Оказывается, нет. В этом можно наглядно убедиться из следующей картинки.
Связано это с тем, что динамика цен многих инструментов неплохо описывается моделью так называемого «случайного блуждания со сносом». Возьмите тетрадку в клеточку. Киньте монетку. Если выпадет «орел», нарисуйте «свечку» вверх на две клеточки, если «решка» – на две клеточки вниз. Независимо от выпадения монеты всегда приплюсовывайте и к бычьей и к медвежьей свечке одну клеточку вверх – это и есть «снос» или, другими словами, тренд. Если не полениться и провести множество бросаний монеты, полученный график будет довольно похож на график цены какой-нибудь акции. При помощи компьютера можно добиться еще большего реализма, генерируя свечи вверх и вниз случайного размера. Гистограмма цены не содержит какого-либо выраженного паттерна по причине ее случайного блуждания. Нет никаких экономических механизмов, которые бы возвращали цену акции к ее среднему значению. По этой причине она блуждает сама по себе обычно с некоторым положительным трендом. Средняя цена, таким образом, не может быть инвариантом. Продолжим поиск…
Добавим смысла
Что если вместо самой цены рассматривать ее дневные приращения? Например, вместо самого значения индекса брать его дневные изменения в пунктах. Для акции это будет дневное изменение цены в рублях или долларах – логика при этом такая же.
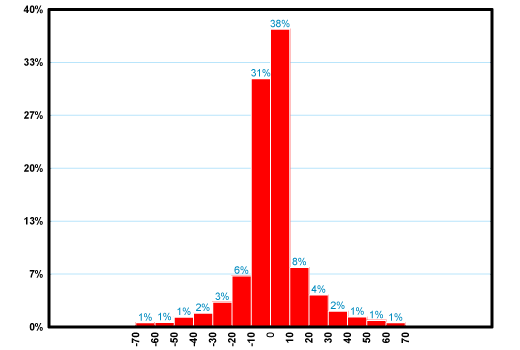
Гистограмма теперь имеет осмысленный вид. Среднее значение дневного приращения индекса – 0.43 пункта находится вблизи пика. В частности в интервал от -10 до +10 пунктов попадают 69% наблюдений. Таким образом, среднее приращение цены – это действительно наиболее ожидаемая величина (или очень близкая к ней).
Линейная доходность
Тем не менее, среднее изменение цены нельзя признать инвариантом. По мере роста цены акции или уровня индекса диапазон ее колебаний также будет расти. Допустим, некоторая акция торгуется сейчас в районе 10 рублей. Тогда увеличение ее цены на 1 рубль будет составлять 10%. Предположим, через несколько лет акция выросла до 100 рублей. Рост на 1 рубль для нее будет уже только 1%. Один рубль для 10-рублевой и 100-рублевой акции – совсем разные вещи, поэтому инвесторы ориентируются не на денежную, а на процентную доходность, т.е. не на абсолютные, а на относительные величины. Процентная доходность не зависит от текущего уровня цен. Она более устойчива и, следовательно, более достойна звания инварианта. Рассчитать процентную доходность очень просто. Для этого нужно знать лишь цену открытия (O) и цену закрытия (C):
(C/O — 1)*100%
Вообще говоря, доходность не является полностью статичной и меняется от года к году. В один год акция может давать 10%, в другой 15%, а в третий -20%. Однако в очень долгосрочной перспективе можно предположить, что средняя доходность фондовых рынков стабильна и не зависит от времени. Например, старейший фондовый индекс Доу Джонса за последние 80 лет в среднем показывал доходность около 4.5% годовых. Таким образом, в самом общем случае от американского фондового рынка можно ожидать такую цифру доходности.
Процентная доходность на первый взгляд кажется наиболее естественно характеристикой фининструмента. Она не зависит от уровня цены. Кроме того, на ней очень интуитивно отражается влияние кредитного плеча – она просто умножается на коэффициент рычага: 1% доходность при плече 1:2 превращается в 2% и т.п. По этой причине ее еще называют линейной доходностью, поскольку рычаг воздействует на нее линейным образом.
Однако линейная доходность имеет один недостаток. Цена не может быть отрицательным числом, а доходность не может быть меньше -1 (-100%). Это создает перекос в распределении линейной доходности. Он становится особенно заметен при больших цифрах. Напр., 100% росту соответствует 50% падение, а не 100% падение, как может ошибочно подумать новичок. Это легко проверить. 100-рублевая акция вырастает в 2 раза до 200 р.: 100*2 = 100*(1+1) = 200. Это рост на 100%. Чтобы вернуть ее обратно к 100 рублям, нужно 200 р. разделить на 2 или умножить на 0.5: 200/2 = 200*(1 — 0.5) = 100. Это 50% падение. Диапазон линейной доходности (от -1 до бесконечности) несимметричен относительно нуля, и эта асимметрия никак не связана с вероятностными свойствами цены, поэтому, по сути, она имеет искусственный характер. Как же ее устранить?
Логдоходность
Логарифмическая доходность (или просто логдоходность) лишена этого недостатка линейной доходности. Она рассчитывается по формуле:
ln(C/O) = ln(C) — ln(O)
и принимает значения от «минус» до «плюс бесконечности». Символ ln() обознает функцию натурального логарифма. Что это за функция? В математике кроме знаменитого числа π есть еще и число e. Оно приблизительно равно 2.7183. Натуральный логарифм – это степень, в которую нужно возвести число e, чтобы получить число под знаком логарифма. Например, если число e, 2.7183, возвести в квадрат (степень 2), получится: 2.718322 = 7.3891. Отсюда следует, что ln(7.3891) = 2. Собственно, чтобы пользоваться логарифмами, не обязательно знать все эти тонкости. Функция логарифма является стандартной, ее легко можно вычислить на компьютере, пользуясь калькулятором Windows или Excel и т.п.
Логдоходности удобны тем, что их можно складывать. Допустим, известны 5 дневных обычных доходностей за торговую неделю: 1%, -2%, 3%, -1%, 2%. Надо найти недельную доходность. Для этого нужно разделить доходности на 100%, прибавить к ним единицу и перемножить:
(1+1%/100%)*(1-2%/100%)*(1+3%/100%)*(1-1%/100%)*(1+2%/100%) =
(1+0.01)*(1-0.02)*(1+0.03)*(1-0.01)*(1+0.02) =
1.01*0.98*1.03*0.99*1.02 = 1.0295
За неделю цена выросла на 2.95%. Умножение, однако, не очень удобная и интуитивная операция. Если перейти к логдоходностям, можно заменить ее сложением:
0.0100 -0.0202 + 0.0296 -0.0101 + 0.0198 = 0.0291
Недельная логдоходность составляет 2.91%. Логдоходность всегда меньше обычной доходности. Величина этого различия становится заметной лишь при больших цифрах. К примеру, линейной доходности -50% соответствует логдоходность -69%, а -100% – «минус бесконечность».
Дорога домой
Итак, в поисках инвариантов мы проделали довольно долгий путь от цены, через ее приращения и линейные доходности к такой довольно абстрактной вещи как логдоходность. Гистограмма логдоходности как и гистограмма приращений имеет выраженный пик, поэтому средняя логдоходность является и наиболее ожидаемой, наиболее вероятной. Она, как и линейная доходность, не зависит от текущего уровня цен. И, наконец, она симметрична относительно нуля, поскольку может принимать любые отрицательные и положительные значения. Все это позволяют охарактеризовать ее как натуральный рыночный инвариант. Превратить же цены в логдоходности достаточно просто при помощи MATLAB, Excel или других табличных редакторов.
Сейчас существует большое количество программ для прогнозирования адресованных трейдерам, например, нейросетевых. Они просты в управлении и не требуют специальных знаний. Типичная ошибка новичка при использовании такого софта в том, что он пытается «предсказать» непосредственно будущую цену по прошлым ценам. Однако, как мы убедились, изучив гистограмму, прогнозирование самой цены «в лоб» лишено какого-либо вероятностного смысла. Лучше всего прогнозировать будущую логдоходность по прошлым логдоходностям того же самого инструмента или других инструментов, если предполагается межрыночное взаимодействие. Это максимально упростит работу программе, поскольку ей не надо будет тратить силы на поиск очевидных закономерностей: что приращения цены зависят от ее уровня, и что они скошены в положительную сторону.
Хорошо, допустим, все это сделано, и программа выдает прогноз: завтрашняя дневная логдоходность составит 0.03. Как это понимать и использовать на практике? Необходимо конвертировать прогноз логдоходности в прогноз цены при помощи обратного преобразования. Делается это очень просто. Предположим, что текущая цена акции 100 рублей. Тогда прогноз завтрашней цены можно получить по формуле:
100 р.*exp(0.03) = 100 р.*1.0305 = 103.05 р.
Функция exp() – это уже знакомое нам число e в степени икс. Это просто альтернативный вариант записи, часто используемый в компьютерных приложениях. Экспонента является обратной по отношению к логарифму функцией, поэтому, подставляя в нее логдоходность, сразу же получаем коэффициент роста, на него и надо умножить текущую цену, чтобы получить прогноз будущей.
Резюме
Таким образом, мы убедились, что логдоходности – очень удобный аналитический инструмент. Их можно складывать, они не зависят от уровня цен и симметричны относительно нуля. На практике, если нужно получить прогноз или исследовать какие-либо вероятности движения цен следует использовать именно логдоходности.
Логдоходности легко конвертируются из одного тайм-фрейма в другой. Например, если вы хотите перевести дневную логдоходность в годовую, нужно просто умножить ее на количество торговых дней (около 250). Если затем взять экспоненту от этого числа, будет получен годовой темп роста капитала для торговой стратегии. Его удобно сравнивать с текущими банковскими ставками, доходностью фондовых индексов и других эталонных инструментов.
————————————————————————
Источник:
http://q-trading.ru/index.php/articles/money-management/244-rynochnye-invarianty.html
17 авг. 2022 г.
читать 2 мин
Логарифмическая регрессия — это тип регрессии, используемый для моделирования ситуаций, когда рост или спад сначала быстро ускоряются, а затем со временем замедляются.
Например, следующий график демонстрирует пример логарифмического распада:
Для такого типа ситуации взаимосвязь между переменной-предиктором и переменной-откликом можно хорошо смоделировать с помощью логарифмической регрессии.
Уравнение модели логарифмической регрессии принимает следующий вид:
у = а + b*ln(x)
куда:
- y: переменная ответа
- x: предикторная переменная
- a, b: коэффициенты регрессии, описывающие взаимосвязь между x и y .
В следующем пошаговом примере показано, как выполнить логарифмическую регрессию в Excel.
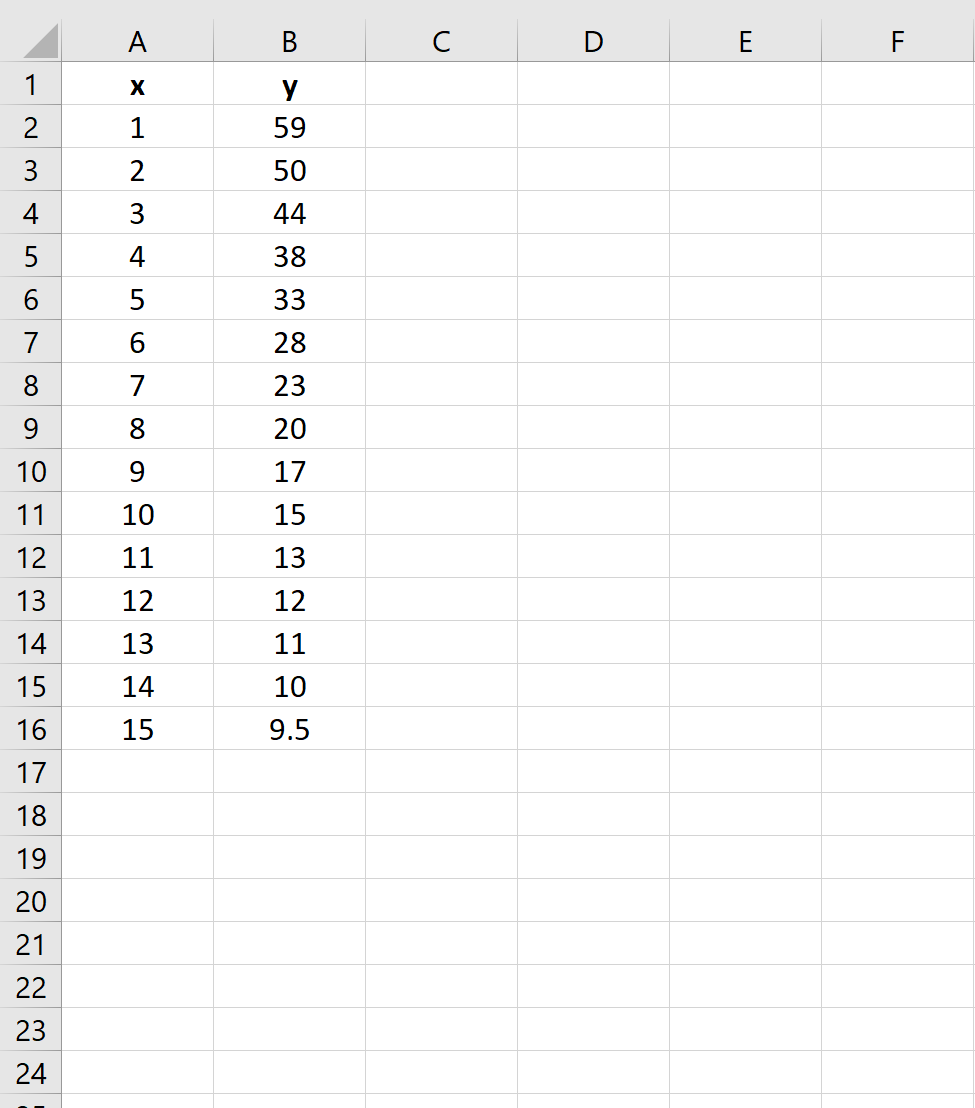
Шаг 1: Создайте данные
Во-первых, давайте создадим поддельные данные для двух переменных: x и y :
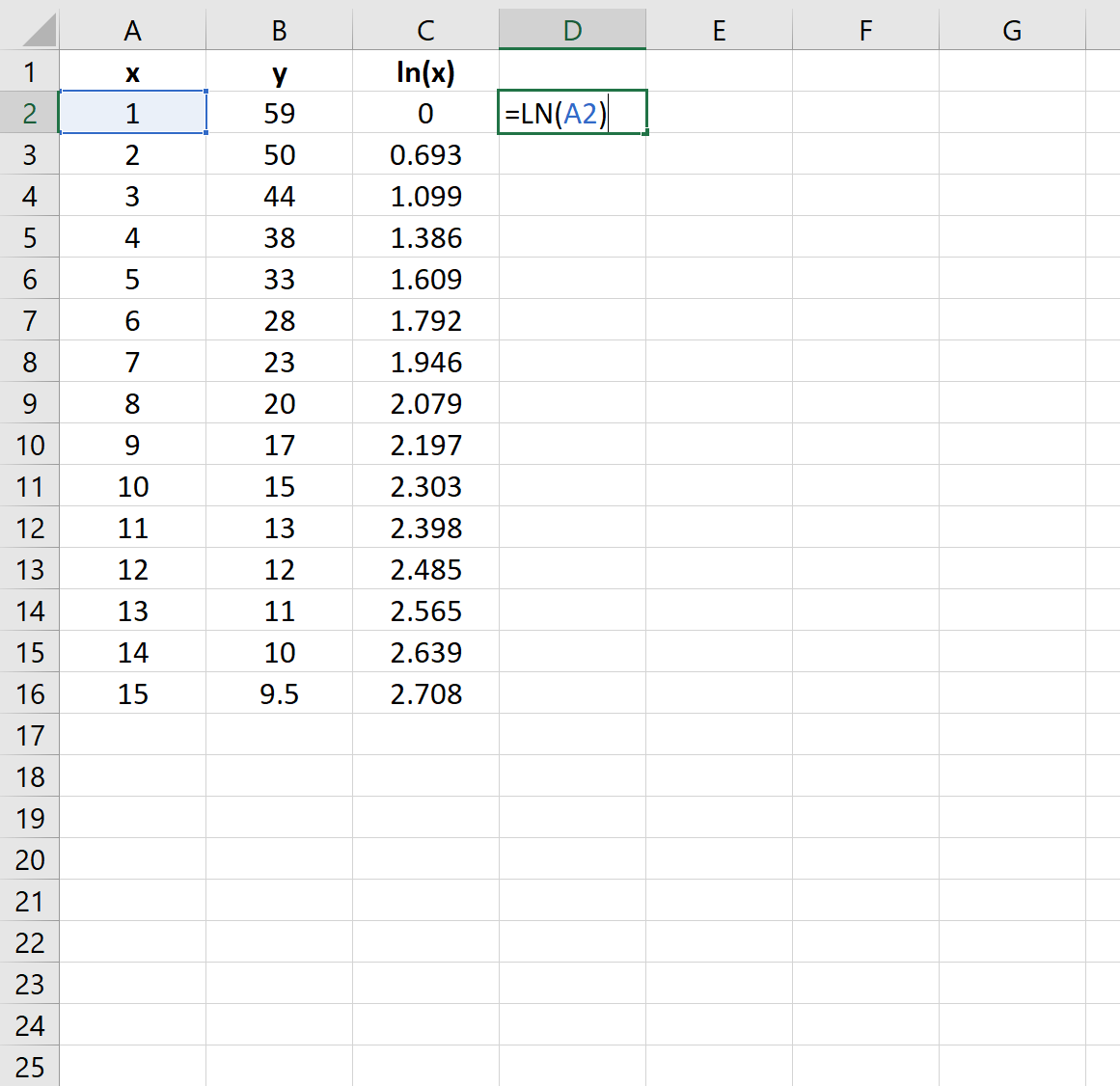
Шаг 2: возьмите натуральный логарифм переменной-предиктора
Далее нам нужно создать новый столбец, представляющий натуральный логарифм переменной-предиктора x :
Шаг 3: Подберите модель логарифмической регрессии
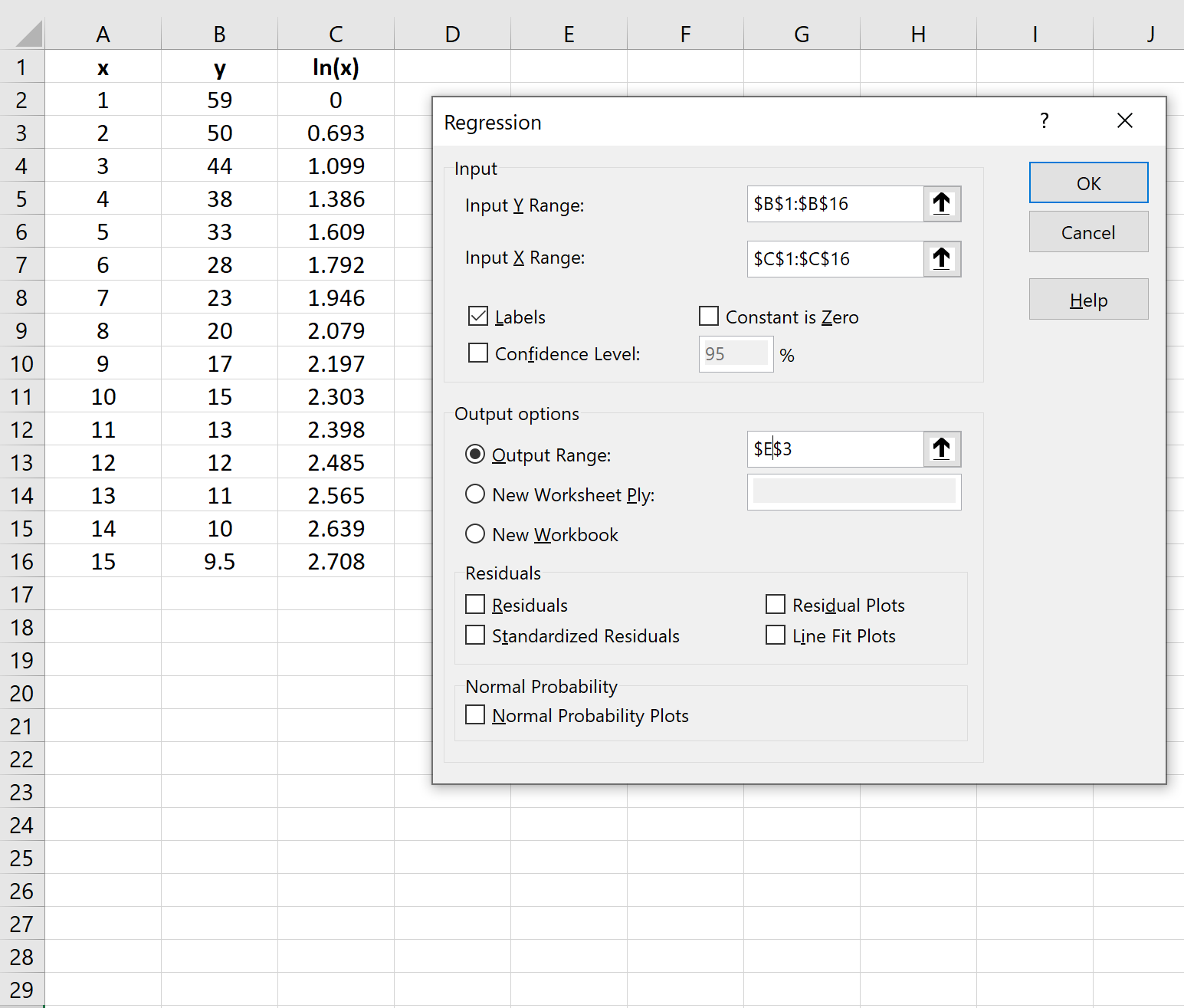
Далее мы подгоним модель логарифмической регрессии. Для этого щелкните вкладку « Данные » на верхней ленте, затем щелкните « Анализ данных» в группе « Анализ ».
Если вы не видите Data Analysis в качестве опции, вам нужно сначала загрузить Analysis ToolPak .
В появившемся окне нажмите Регрессия.В появившемся новом окне введите следующую информацию:
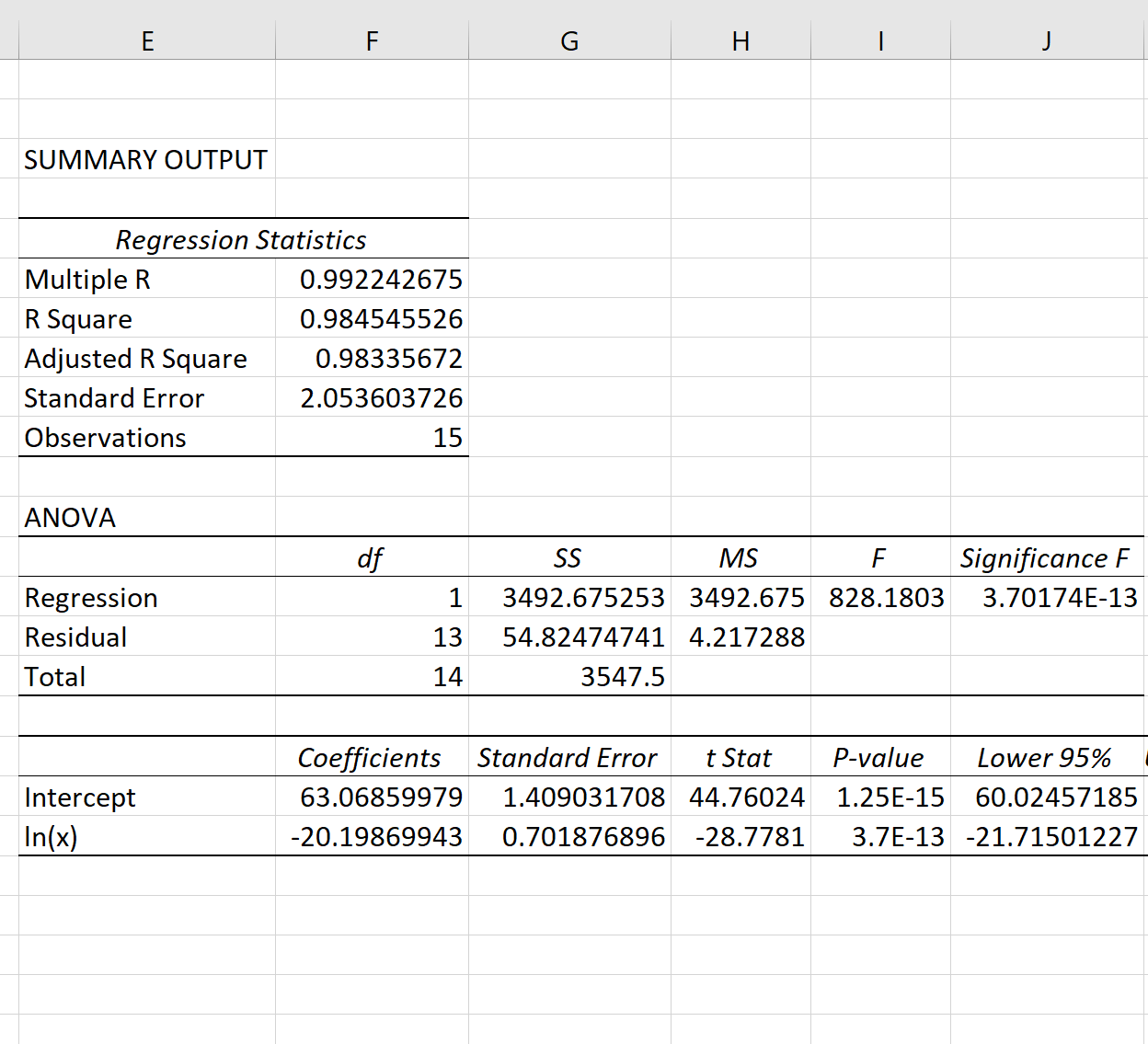
Как только вы нажмете OK , отобразятся выходные данные модели логарифмической регрессии:
Общее значение F модели составляет 828,18, а соответствующее значение p чрезвычайно мало (3,70174E-13), что указывает на то, что модель в целом полезна.
Используя коэффициенты из выходной таблицы, мы видим, что подобранное уравнение логарифмической регрессии:
у = 63,0686 – 20,1987 * ln(x)
Мы можем использовать это уравнение для прогнозирования переменной отклика y на основе значения переменной-предиктора x.Например, если x = 12, то мы предсказываем, что y будет 12,87 :
у = 63,0686 – 20,1987 * ln(12) = 12,87
Бонус: не стесняйтесь использовать этот онлайн- калькулятор логарифмической регрессии для автоматического вычисления уравнения логарифмической регрессии для заданного предиктора и переменной отклика.
Дополнительные ресурсы
Как выполнить простую линейную регрессию в Excel
Как выполнить множественную линейную регрессию в Excel
Как выполнить полиномиальную регрессию в Excel
Как выполнить экспоненциальную регрессию в Excel
Библиографическое описание:
Дручинин, Д. О. Проверка гипотезы о нормальном распределении логарифмической доходности по критерию Шапиро — Уилка / Д. О. Дручинин. — Текст : непосредственный // Молодой ученый. — 2023. — № 10 (457). — С. 6-9. — URL: https://moluch.ru/archive/457/100583/ (дата обращения: 16.04.2023).
Актуальность и цели. В данной работе производится анализ логарифмических доходностей акций, входящих в состав российского IT сектора. Предполагается, что дневная логарифмическая доходность распределена по нормальному закону. Цель работы — проверить гипотезу о нормальном распределении дневных логарифмических доходностей на реальных данных. С экономической точки зрения задача исследования — определить таймфреймы и промежутки времени, на которых логарифмические доходности будут иметь нормальное распределения, а также те, на которых условия не выполняются. Помимо этого, необходимо выяснить, как повлияло изменение цен акций в 2022 года на сектор информационных технологий. В дальнейшем эту информацию можно использовать для прогнозирования цен акций исследуемых компаний. Для проверки используется критерий Шапиро — Уилка, являющийся одним из наиболее эффективных критериев. После этого проверяется гипотеза на реальных данных и вычисляется процент проверок, в которых гипотеза будет приниматься при уровне значимости в 5 % и 1 %.
Временной отрезок для рассмотрения: 01.01.2022–31.12.2022
Ключевые слова
:
логарифмическая доходность, уровень значимости, нормальное распределение, проверка гипотезы
Введение
Информационный сектор играет важную роль в экономике России и является одной из самых быстро развивающихся отраслей. Он включает в себя производство и распространение информационных товаров и услуг, таких как программное обеспечение, интернет-сервисы, мультимедиа-контент и многое другое. Информационные технологии также широко применяются в других отраслях, таких как финансы, производство, здравоохранение, транспорт и телекоммуникации.
Вклад информационного сектора в экономику России растет из года в год. Согласно отчету Аналитического центра при Правительстве Российской Федерации, в 2020 году доля информационных технологий в ВВП России составила 4,5 %, а объем рынка информационных технологий оценивался в 3,4 трлн рублей.
Этот сектор является ключевым для развития экономики России, поскольку способствует созданию новых рабочих мест, привлечению инвестиций, улучшению качества жизни и повышению конкурентоспособности страны в мировом рынке. Более того, информационные технологии могут существенно повысить эффективность работы государственных органов и бизнеса, что в свою очередь ведет к увеличению производительности и экономического роста.
С экономической точки зрения, оценивается изменение цен акций в 2022 году в сектор информационных технологий. Определение на каких промежутках логарифмические доходности имели нормальное распределение позволит спрогнозировать дальнейшее изменение в данном секторе.
Основная часть
Для проверки критерия были взяты акции компаний, которые входят в сектор информационных технологий, а именно:
YNDX — Яндекс
HHRU — HeadHunter
VKCO — Вконтакте
OZON — Озон
MTSS — МТС
POSI — Positive Technologies
SFTL — Softline
Для того чтобы использовать эти данные для проверки нормальности по критерию Шапиро — Уилка, необходимо провести их предварительный анализ. В первую очередь, посчитаем логарифмические доходности акций.
1 Теоретическая справка по проверке гипотез
1.1 Статистическая проверка гипотез
Статистическая гипотеза — это любое утверждение о виде или параметрах генерального распределения. Гипотезу называют основной и обозначают
, если он утверждает, что отсутствуют различие между сравниваемыми характеристиками, а наблюдаемые отклонения объясняются лишь случайными колебаниями в выборках, которые используются для сравнения. Помимо основной гипотезы существует альтернативная ей гипотеза
. Стоит отметить, что
и
— являются взаимоисключающими статистическими гипотезами. Утверждение о справедливости одной из этих гипотез принимается в качестве предположения. Статистический критерий, который является случайной величиной с точным или приближенным известным распределением, используется для проверки гипотезы.
Пусть
— некоторое подмножество
. В этом случае правило, в соответствии с которым H
0
отвергается, если выборка
, и принимается, если
, называется статистическим критерием с критической областью К. Так как
и
являются гипотезами, которые исключают друг друга, принятие
ведет за собой отклонение
. Напротив, отклонение
приводит к принятию
из-за базисного предположения.
Использование статистического критерия может привести к ошибкам двух типов, которые приведены в таблице 1:
-
Ошибка первого рода заключается в том, что отвергается верная гипотеза
.
-
Ошибка второго рода заключается в том, что отвергается верная гипотеза
.
При этом, уровнем значимости критерия называется вероятность ошибки первого рода и обозначается
. Вероятность ошибки второго рода обозначается
, а величина
— это мощность критерия.
Таблица 1
Гипотезы
|
|
|
|
|
H |
Ошибка I рода |
+ |
|
H |
+ |
Ошибка II рода |
Для реализации
случайной выборки
, которая зафиксирована, P-значением критерия (P-value) называется такое число
, что
для любого уровня значимости α, при котором гипотеза
принимается и
для любого уровня значимости
, при котором
отвергается.
Предполагается, что Р-значение
уже каким-либо способом найдено. В этом случае решение о принятии или отклонении
для заданного
осуществляется на основе следующего простого правила: если
, гипотеза H
0
отвергается, а если
гипотеза
принимается.
Рассматривается отдельно случай
В этом случае
где c(- непрерывная убывающая функция, и для
имеет место равенство
, означающее, что
принимается. Отсюда уже легко получить широко применяемую формулу:
1.2 Критерий Шапиро — Уилка
В данной работе используется критерий Шапиро — Уилка. Он используется для проверки гипотезы H
0
: «случайная величина X распределена нормально».
Критерий Шапиро — Уилка основан на анализе линейной комбинации разностей порядковых статистик. Критерий применяется при объемах выборки от 3 ≤ n ≤ 50, так как табулированы константы, необходимые для вычисления статистики критерия и аппроксимации P-значения.
Пусть имеется выборка
Статистика
вычисляется по формулам:
, где
,
,
Значение k в последней формуле определяется следующим образом:
, если n — четное
, если n — нечетное
Нормальная аппроксимаций используется для вычисления реально достигнутого уровня значимости:
, где
— стандартное нормальное распределение, в котором
,
и
— константы, табличные значения которых известны, в зависимости от объема выборки. Значения приведены в таблице 2.
Если
, то нулевая гипотеза нормальности распределения отклоняется на уровне значимости .
Ж. П. Ройстон предложил другой способ вычисления P-значения для n вплоть до 2000:
и
, где z — стандартная нормальная случайная величина, а
и
ее матожидание и среднеквадратичное отклонение. Данная формула будет использована для нахождения уровня значимости и p — значений. Чтобы найти уровень значимости для конкретного
, необходимо посчитать вероятность того, что случайная величина
будет меньше
. Для проведения расчетов понадобятся следующие данные из таблицы. Значения
, аппроксимируются многочленами от
, где
, если
и
, если
.
Таблица 2
Коэффициенты
|
Параметр |
n |
|
||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
||
|
|
7–20 |
0,118898 |
0,133414 |
0,327907 |
||||
|
21–2000 |
0,480358 |
0,318828 |
0 |
-0,02417 |
0,008797 |
0,00299 |
||
|
|
7–20 |
-0,37542 |
0,492145 |
-1,12433 |
-0,19942 |
|||
|
21–2000 |
-1,91487 |
-1,37888 |
-0,04183 |
0,1066339 |
-0,03514 |
-0,01506 |
||
|
|
7–20 |
-3,15805 |
0,729399 |
3,01855 |
1,558776 |
|||
|
21–2000 |
-3,73538 |
-1,01581 |
-0,33189 |
0,1773538 |
-0,01639 |
-0,03215 |
0,003853 |
|
2 Проверка гипотезы на реальных данных
В данном разделе анализируются данные логарифмической доходности и применяется к ним критерий Шапиро — Уилка. Далее выбираются данные, в которых гипотеза принимается при 5 % и 1 % уровнях значимости. Строиться ряд гистограмм и делаются выводы.
Для удобства использования уровни значимости будут отмечаться следующим образом: 5 % —
0.12
, 1 % —
0.02
2.1 Гипотеза о нормальности распределения логарифмической доходности для периода в 6 месяцев
Далее анализируются данные на промежутке в 6 месяцев. Результаты приведены в таблице 3.
Таблица 3
Проверка критерия на промежутке в 6 месяцев
|
|
|
|
|
HHRU |
0.0 |
0.0 |
|
VKCO |
0.0 |
0.0 |
|
MTSS |
0.0 |
0.0 |
|
POSI |
0.0 |
0.000348 |
|
SFTL |
0.0 |
0.0 |
|
OZON |
0.0 |
0.0 |
|
YNDX |
0.0 |
0.000006 |
Из таблицы следует, что на временных промежутках в 6 месяцев p-значение выше 1 % не имела ни одна компания.
2.2 Гипотеза о нормальности распределения логарифмической доходности для периода в 3 месяца
Проверяются данные на промежутке в 3 месяца. Результаты приведены в таблице 4.
Таблица 4
Проверка критерия на промежутке в 3 месяца
|
|
|
|
|
|
|
HHRU |
0.000075 |
|
0.006304 |
0.000123 |
|
VKCO |
0.0 |
|
0.000557 |
|
|
MTSS |
0.0 |
0.0 |
0.0 |
|
|
POSI |
0.000001 |
0.000001 |
0.006477 |
|
|
SFTL |
0.0 |
0.001329 |
0.0 |
0.0 |
|
OZON |
0.006810 |
|
0.000477 |
0.0038 |
|
YNDX |
0.0 |
|
0.001316 |
|
Из таблиц видно, что с уменьшением исследуемого периода, возрастает количество логарифмических доходностей, которые имеют нормальное распределение.
Таблица 5
Итоговые результаты
|
|
|
|
|
5 % |
0 % |
25 % |
|
1 % |
0 % |
28,57 % |
Итоговые результаты показывают, что логарифмические доходности имели нормальное распределение лишь на промежутке в 3 месяца. Также следует отметить, что это было характерно только для 2 и 4 квартала.
Заключение
В данной работе проводился анализ логарифмических доходностей акций, входящих в состав сектора информационных технологий. В ходе работы были получены следующие результаты:
На промежутке в 1 год с таймфреймом 1 день не нашлось значений, которые имеют p-значение выше 5 %. На промежутке в 6 месяцев с таймфреймом 1 день количество значений, которые имеют нормальное распределение не увеличилось.
На промежутке в 3 месяца с таймфреймом 1 день, лишь 25 процентов акций имеют нормальное распределение. При этом, нормальное распределение акций встречалось только во втором и четвертом квартале.
Можно сделать вывод, что использование критерия Шапиро — Уилка для проверки нормальности распределения не позволяет выявить закономерности для предсказания будущих цен акций.
Литература:
1. Браилов А. В. Лекции по математической статистике. М.: Финакадемия, 2007
2. В. Е. Гмурман Теория вероятностей и математическая статистика, Юрайт, 2011
3. Фадеева Л. Н. Лебедев А. В. Теория вероятностей и математическая статистика, Эксмо, 2010
4. J. P. Royston, Extension of Shapiro and Wilk’s W Test for Normality to Large Samples, p. 118
5. Shapiro S. S., Wilk M. B. An analysis of variance test for normality (complete samples) Biometrika, 52 No. 3/4. (Dec., 1965), pp. 591–611
Основные термины (генерируются автоматически): нормальное распределение, уровень значимости, HHRU, MTSS, OZON, POSI, SFTL, VKCO, YNDX, Гипотеза.
логарифмическая доходность, уровень значимости, нормальное распределение, проверка гипотезы
Похожие статьи
Шаблон Excel для проверки законов распределения данных…
Критическое значение статистики U, которая имеет распределение с r степенями свободы
на рис. 4, задаваясь уровнем значимости (например, 0,05, что соответствует доверительной
7. Фаюстов А. А. Проверка гипотезы о нормальном распределении выборки по критерию
В силу аппроксимации значения индекса нормальным законом распределения, а также.
Метод оценки нормальности распределения результатов…
Критическое значение статистики U , которая имеет распределение χ 2 с f степенями
о нормальном распределении с помощью критерия Пирсона при уровне значимости 0,05.
Меняя закон распределения на этом листе можно проверить три гипотезы за несколько…
7. Фаюстов А. А. Проверка гипотезы о нормальном распределении выборки по критерию…
Отсеивание грубых погрешностей результатов измерений…
Задаются вероятностью Р или уровнем значимости α ( ) того, что результат наблюдения
Проверяемая гипотеза состоит в утверждении, что результат наблюдения x i не содержит
Квантили распределения статистики τ при уровнях значимости α = 0,10; 0,05; 0,025 и 0,01
о нормальном распределении с помощью критерия Пирсона при уровне значимости 0,05.
Обзор методик, используемых для оценки уровня…
В рамках данной статьи будут рассмотрены основные методики оценки уровня цифровой трансформации, применимые на практике деятельности коммерческих предприятий, на примере предприятий из банковской сферы.
Проверка нормальности распределения оценок параметров…
, где является стандартной нормально распределённой случайной величиной, параметр
При невысоком уровне шума можно рассчитывать на то, что в модели (3) остатки будут
Гипотеза отвергается, если статистика превышает квантиль распределения статистики заданного уровня значимости α.
Проверка статистических гипотез проводилась на уровне значимости .
Оценивание параметров генеральных совокупностей…
Однако, в отличие от теории нормального распределения, теория t —распределения для малых выборок не требует априорного знания или точных оценок математического ожидания и дисперсии генеральной совокупности.
Распределение Хотеллинга и его применение | Статья в сборнике…
Значение, соответствующее и выбранной степени свободы, представляет собой значение плотности распределения , правая часть которого имеет поверхность (рис. 6). Мы отвергнем нулевую гипотезу на уровне , если статистика больше критического значения в таблице
Использование языка R для эконометрического моделирования…
При данном уровне значимости P = 0.05 имеем нулевую гипотезу H0: r = 0 о равенстве нулю коэффициента корреляции и альтернативную гипотезу H1: r ≠ 0. Для проверки нулевой гипотезы используют величину (1), имеющую распределение Стьюдента с n-2 степенями…
Применение вектора Шепли и индекса Банзафа для определения…
…нормальным или патологическим состоянием и т. д. Разнообразие в профилях генной
полученные с помощью технологии микрочипов, с учетом уровня взаимодействия между
В [1] введен класс игр с микрочипами, позволяющий количественно оценить значимость каждого
Вывод. Результатом использования рассмотренного подхода является распределение вектора…