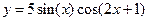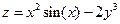Лист декарта в excel

Декартов лист – плоская кривая. Ее уравнение в декартовой прямоугольной системе координат имеет вид
х 3 + у 3 – 3аxу = 0. (*)

Таким образом, декартов лист – кривая третьего порядка. Она имеет асимптоту – прямую х + у + а = 0.

Положив у = хt (**), параметризуем кривую: из (*) и (**) получим параметрические уравнения декартова листа

В полярных координатах (ρ; φ) декартов лист имеет уравнение

Поскольку координаты х и у входят в уравнение декартова листа (*) симметрично, кривая расположена симметрично относительно прямой у = х – биссектрисы первого и третьего координатных углов. Начало координат – узловая точка декартова листа (называется также точкой самопересечения или кратной точкой).

Оси координат служат касательными к ветвям кривой в начале координат, поэтому кривая пересекает сама себя в начале координат под прямым углом.

Общий вид кривой см. на рис. Площадь S петли декартова листа равна 1,5а 2 .

Декартов лист впервые был упомянут в переписке Декарта с Ферма в 1638 г. Форма этой кривой была получена Робервалем, а окончательное исследование ее свойств было проведено в конце XVII в. Пойгенсом и И. Бернулли.

Лабораторная работа № 5

2015-05-10
5015

Построение различных типов диаграмм. Решение задач линейной оптимизации, применение сценариев.

Цель занятия: Закрепить умения по построению различных типов диаграмм, редактированию и изменению их типов. Решение задач линейной оптимизации, нахождению нескольких неизвестных параметров. Закрепить умения по составлению сценариев для осуществления прогноза.

Уокенбах, Джон. Microsoft Excel 2010. Библия пользователя.: Пер.с англ. – М.: ООО «И.Д.Вильямс», 2011.-312 с. : ил. – Парал.тит.англ.

Волков В.Б. Понятный самоучитель Excel 2010. – СПб.:Питер, 2010.-256с.:ил.

Кулешова О.В., Центр Компьютерного обучения «Специалист», Microsoft Excel 2010. Анализ и визуализация данных. Решения практических задач. Методическое пособие, 2012.

Задание 1. Построить график функции.

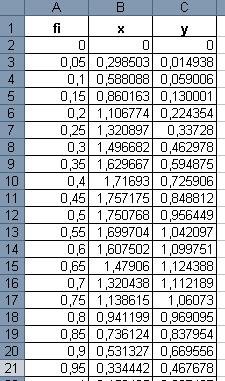
1.Построение трехлепестковой розы.

Построить функцию, заданную уравнением: , .

Для построения графика функции используется тип диаграммы Точечная. Выделяется только диапазон значений x и y.

Построим таблицу и произведем расчеты:

Для получения полной трехлепестковой розы значение fi должно быть от 0 до 3,2.

Формулы для вычисления:

Ячейка Формула
В2 =2*SIN(3*A2)*COS(A2)
С2 =2*SIN(3*A2)*SIN(A2)

2.Построить график функции:

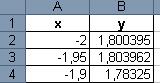
3.Построить график функции (Декартов лист): . Fi из диапазона -0,15 до 2 шагом 0,05.

4.Построить Верьсьеру: . Принять t от -5 до 5 шагом 0,3.

5.Построить Лемнискату Бернулли: . Fi возьмите из диапазона от -3 до 0 с шагом 0,1.

6.Построить Улитку Паскаля: . Fi от -2 до 4,3 с шагом 0,1.

7.Построить Астроиду: . Примите t от -3 до 3 с шагом 0,1.

8.Построить поверхность:

Задание 2. Фирма выпускает два типа строительных материалов: А и В. Продукция обоих видов поступает в продажу. Для производства материалов используются два исходных продукта I и II. Максимально возможные суточные запасы этих продуктов составляют 6 и 8 тонн соответственно. Расходы продуктов I и II на 1 тонну соответствующих материалов приведены в таблице

Изучение рынка сбыта показало, что суточный спрос на материал В никогда не превышает спроса на материал А более чем на 1 т. Кроме того, установлено, что спрос на материал А никогда не превышает 2 т в сутки. Оптовые цены одной тонны материалов равны: 3000 у.е. для В и 2000 у.е. для А. Какое количество материала каждого вида должна производить фабрика, чтобы доход от реализации был максимальным?

Источник

Построение
графиков 3-х видов в электронной таблице
Excel

1.
Построить несколько графиков параметрически
заданной функции при разных значениях
конcтант
а, b,
.
Оси графика – х и y,
которые зависят от аргумента t
или .

№

Название

кривой

Вид
графика

Параметри­ческие
уравнения

Диапазон

аргумента

Кол-во

граф.

Значения
констант

1

Циклоида

x = a(t — sin
t)

y = a(1 — cos
t)

t  0  6

шаг
0,5

5

a = 1;
1.25;
1.5; 1.75; 2

2

Циклоида

x = a(t — sin
t)

y = a(1 — cos
t)

t  0  6

шаг
0,5

6

a = 2

 = 0.4;
0.7; 1.0;
1.3; 1.6; 2.0

3

Трохоида

x = at — bsin
t

y = a — bcos
t

t  0  10

шаг
0,1

5

a = -1

b
= 0.1; 1; 2; 3; 4

4

Эпитрохоида

x = acos
(t)
— bcos
(t + t)

y = asin
(t)
— bsin
(t + t)

t  0  10

шаг
0,5

6

a = 0;
1; 2; 3; 10; 15

b = 2
 = 0.25

5

Гипотрохоида

x = acos
(t)
— bcos
(t — t)

y = asin
(t)
— bsin
(t — t)

t  0  10

шаг
0,5

6

a = 0;
1; 2; 3; 10; 15

b = 2
 = 0.25

6

Декартов

лист

x = at   / (1 + t3)

y = a
t2 / (1 + t3)

t  -6  6

шаг
0,3

6

a = 1;
2; 3; 4; 5; 6

7

Циссоида
Диоклеса

x = a
t2 / (1 + t2)

y = a
t3 / (1 + t2)

t  -6  6

шаг
0,2

6

a = 1;
2; 3; 4; 5; 6

8

Строфоида

x = a
 (t2 — 1) / (t2 + 1)

y = at(t2 — 1) / (t2 + 1)

t  -6  6

шаг
0,2

6

a = 1;
2; 3; 4; 5; 6

9

Конхоида

Никомеда

x = a + bcos
t

y = atg
t + bsin
t

t  0

10

шаг
0,2

5

a = 2

b
= 1; 10; 30; 50; 90

10

Улитка

Паскаля

x = acos2
t + bcos
t

y = a
cos
t sin
t + bsin
t

t  0  2

шаг
0,1

6

a = 1;
2; 3; 4; 5; 6

b
= 3

11

Эпици­клоида

x = (a + b)cos

— acos[(a + b)/a]

y = (a + b)
sin 
— a sin[(a + b)/a]

  0  2

Шаг
0,1

6

a
= 1

b = 1;
2; 3; 4; 5; 6

12

Эпици­клоида

x = (a + b)cos

— acos[(a + b)/a]

y = (a + b)
sin 
— a
sin[(a + b)/a]

  0  10

Шаг
0,2

6

a = 3;
b = 4

 = 0.5;
0.7; 1;
1.5; 2; 3

13

Эпици­клоида

x = (a + b)cos

— acos[(a + b)/a]

y = (a + b)
sin 
— a
sin[(a + b)/a]

  0  2

Шаг
0,1

6

a = 1;
b = 4

 = 0.5;
1; 1.5; 2; 4; 6

14

Эпици­клоида

x = (a + b)cos

— acos[(a + b)/a]

y = (a + b)
sin 
— a
sin[(a + b)/a]

  0  2

Шаг
0,1

6

a = 7;
b = 4

 = 0.5;
1; 2; 4; 6; 8

15

Гипоци­клоида

x = (b — a)cos

— acos[(b — a)/a]

y = (b — a)
sin 
— a sin[(b — a)/a]

  0  2

Шаг
0,1

6

a
= 1

b = 1.5;
2.5; 3;
3.5; 4; 5

16

Гипоци­клоида

x = (b — a)cos

— acos[(b — a)/a]

y = (b — a)
sin 
— a sin[(b — a)/a]

  0  6

Шаг
0,5

6

a
= 1.5; 2; 2.5;
3; 3,5; 4

b = 1

17

Гипоци­клоида

x = (b — a)cos

— acos[(b — a)/a]

y = (b — a)
sin 
— a
sin[(b — a)/a]

  0  2

Шаг
0,1

6

a = 1;
b = 4

 = 0.5;
1; 1.5; 2; 3; 4

18

Гипоци­клоида

x = (b — a)cos

— acos[(b — a)/a]

y = (b — a)
sin 
— a
sin[(b — a)/a]

  0  10

Шаг
0,2

6

a = 5;
b = 2

 = 0.2;
0.5; 0.7;
1; 1.5; 2

19

Спираль

x = atcos
t

y = btsin
t

t  0  10

Шаг
0,5

6

a
= 2

b = -2;
-1; 1; 2; 3; 4

20

Гиперболич.

спираль

x = (acos
t) / t

y = (b
sin
t) / t

t  -6  6

Шаг
0,3

5

a = 2

b = 1;
2; 3; 4; 5

21

Гиперболич.

спираль

x = (acos
t) / t

y = (b
sin
t) / t

t  0.5  20

Шаг
0,5

5

a = 3

b = 1;
2; 3; 4; 5

22

Астроида

x = acos3
(t / 4)

y = b
sin3
(t / 4)

t  0  8

Шаг
0,1

5

a
= 2

b = 1;
2;
3;
4;
5

23

Астроида

x = acos3
(t – b)

y = a
sin3
t

t  0  8

Шаг
0,2

5

a
= 2

b = 0;
1; 2; 3; 4

24

Астроида

x = acos3
(bt
)

y = a
sin3
t

t  0  8

Шаг
0,1

5

a
= 2

b = 0.5;
1; 1.5; 3; 3.5

25

Эволь­вента

x = acos
t + at
sin
t

y = a
sin
t + atcos
t

t  -10 10

Шаг
0,5

4

a
= -2;
-1; 1; 2

26

Эволь­вента

x = acos
t + at
sin
t

y = a
sin
t + atcos
t

t  0 20

Шаг
0,5

4

a
= -2;
-1; 1; 2

27

Эллипс

x = acos
t

y = b
sin
t

t  0  2

Шаг
0,5

5

a
= 7

b = 1;
4; 7; 10; 13

28

Эллипс

x = acos(c
+ t)

y = b
sin(c
— t)

t  0  2

Шаг
0,11

5

a
= 3 b = 2

b = 1;
2; 3; 4; 5

29

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Инфоурок

›

Информатика

›Другие методич. материалы›Лабораторная работа «MS Excel. Построение графиков и диаграмм»



Скачать материал



Скачать материал

  • Сейчас обучается 30 человек из 16 регионов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 211 186 материалов в базе

  • Выберите категорию:

  • Выберите учебник и тему

  • Выберите класс:

  • Тип материала:

    • Все материалы

    • Статьи

    • Научные работы

    • Видеоуроки

    • Презентации

    • Конспекты

    • Тесты

    • Рабочие программы

    • Другие методич. материалы

Найти материалы

Другие материалы

  • 10.12.2015
  • 2121
  • 6
  • 10.12.2015
  • 2020
  • 0
  • 10.12.2015
  • 543
  • 0
  • 10.12.2015
  • 1542
  • 1
  • 10.12.2015
  • 1061
  • 0
  • 10.12.2015
  • 743
  • 0
  • 10.12.2015
  • 626
  • 0

Вам будут интересны эти курсы:

  • Курс повышения квалификации «Информационные технологии в деятельности учителя физики»

  • Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»

  • Курс повышения квалификации «Организация работы по формированию медиаграмотности и повышению уровня информационных компетенций всех участников образовательного процесса»

  • Курс повышения квалификации «Облачные технологии в образовании»

  • Курс повышения квалификации «Сетевые и дистанционные (электронные) формы обучения в условиях реализации ФГОС по ТОП-50»

  • Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»

  • Курс повышения квалификации «Введение в программирование на языке С (СИ)»

  • Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»

  • Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

  • Курс повышения квалификации «Современные тенденции цифровизации образования»



  • Скачать материал


    • 10.12.2015


      8969
    • DOCX
      78.3 кбайт
    • 57
      скачиваний
    • Рейтинг:
      3 из 5
    • Оцените материал:





  • Настоящий материал опубликован пользователем Мельникова Анна Васильевна. Инфоурок является
    информационным посредником и предоставляет пользователям возможность размещать на сайте
    методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
    сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

    Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
    сайта, Вы можете оставить жалобу на материал.

    Удалить материал

  • Мельникова Анна Васильевна

    • На сайте: 7 лет и 4 месяца
    • Подписчики: 0
    • Всего просмотров: 46511
    • Всего материалов:

      14

  • Файлы

Файлы

Рабочий лист подходит для учеников 7 класса, работающих по учебнику «Информатика. ФГОС», автор Л….

Источник

Содержание

  1. Как построить декартовый лист в эксель
  2. Способ 1: Выбор таблицы для диаграммы
  3. Способ 2: Ручной ввод данных
  4. Лабораторная работа № 5
  5. Построение диаграмм в Excel

Как построить декартовый лист в эксель

Построение диаграммы в Microsoft Excel по таблице – основной вариант создания графиков и диаграмм другого типа, поскольку изначально у пользователя имеется диапазон данных, который и нужно заключить в такой тип визуального представления.

В Excel составить диаграмму по таблице можно двумя разными методами, о чем я и хочу рассказать в этой статье.

Способ 1: Выбор таблицы для диаграммы

Откройте необходимую таблицу и выделите ее, зажав левую кнопку мыши и проведя до завершения.

Вы должны увидеть, что все ячейки помечены серым цветом, значит, можно переходить на вкладку «Вставка».

Там нас интересует блок «Диаграммы», в котором можно выбрать одну из диаграмм или перейти в окно с рекомендуемыми.

Откройте вкладку «Все диаграммы» и отыщите среди типов ту, которая устраивает вас.

Справа отображаются виды выбранного типа графика, а при наведении курсора появляется увеличенный размер диаграммы. Дважды кликните по ней, чтобы добавить в таблицу.

Предыдущие действия позволили вставить диаграмму в Excel, после чего ее можно переместить по листку или изменить размер.

Дважды нажмите по названию графика, чтобы изменить его, поскольку установленное по умолчанию значение подходит далеко не всегда.

Не забывайте о том, что дополнительные опции отображаются после клика правой кнопкой мыши по графику. Так вы можете изменить шрифт, добавить данные или вырезать объект из листа.

Для определенных типов графиков доступно изменение стилей, что отобразится на вкладке «Конструктор» сразу после добавления объекта в таблицу.

Как видно, нет ничего сложного в том, чтобы сделать диаграмму по таблице, заранее выбрав ее на листе. В этом случае важно, чтобы все значения были указаны правильно и выбранный тип графика отображался корректно. В остальном же никаких трудностей при построении возникнуть не должно.

Способ 2: Ручной ввод данных

Преимущество этого типа построения диаграммы в Экселе заключается в том, что благодаря выполненным действиям вы поймете, как можно в любой момент расширить график или перенести в него совершенно другую таблицу. Суть метода заключается в том, что сначала составляется произвольная диаграмма, а после в нее вводятся необходимые значения. Пригодится такой подход тогда, когда уже сейчас нужно составить график на листе, а таблица со временем расширится или вовсе изменит свой формат.

На листе выберите любую свободную ячейку, перейдите на вкладку «Вставка» и откройте окно со всеми диаграммами.

В нем отыщите подходящую так, как это было продемонстрировано в предыдущем методе, после чего вставьте на лист и нажмите правой кнопкой мыши в любом месте текущего значения.

Из появившегося контекстного меню выберите пункт «Выбрать данные».

Задайте диапазон данных для диаграммы, указав необходимую таблицу. Вы можете вручную заполнить формулу с ячейками или кликнуть по значку со стрелкой, чтобы выбрать значения на листе.

В блоках «Элементы легенды (ряды)» и «Подписи горизонтальной оси (категории)» вы самостоятельно решаете, какие столбы с данными будут отображаться и как они подписаны. При помощи находящихся там кнопок можно изменять содержимое, добавляя или удаляя ряды и категории.

Обратите внимание на то, что пока активно окно «Выбор источника данных», захватываемые значения таблицы подсвечены на листе пунктиром, что позволит не потеряться.

По завершении редактирования вы увидите готовую диаграмму, которую можно изменить точно таким же образом, как это было сделано ранее.

Вам остается только понять, как сделать диаграмму в Excel по таблице проще или удобнее конкретно в вашем случае. Два представленных метода подойдут в совершенно разных ситуациях и в любом случае окажутся полезными, если вы часто взаимодействуете с графиками во время составления электронных таблиц. Следуйте приведенным инструкциям, и все обязательно получится!

Источник

Лабораторная работа № 5

Построение различных типов диаграмм. Решение задач линейной оптимизации, применение сценариев.

Цель занятия: Закрепить умения по построению различных типов диаграмм, редактированию и изменению их типов. Решение задач линейной оптимизации, нахождению нескольких неизвестных параметров. Закрепить умения по составлению сценариев для осуществления прогноза.

Уокенбах, Джон. Microsoft Excel 2010. Библия пользователя.: Пер.с англ. – М.: ООО «И.Д.Вильямс», 2011.-312 с.: ил. – Парал.тит.англ.

Волков В.Б. Понятный самоучитель Excel 2010. – СПб.:Питер, 2010.-256с.:ил.

Кулешова О.В., Центр Компьютерного обучения «Специалист», Microsoft Excel 2010. Анализ и визуализация данных. Решения практических задач. Методическое пособие, 2012.

Задание 1. Построить график функции.

1. Построение трехлепестковой розы.

Построить функцию, заданную уравнением: , .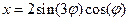

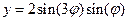
Для построения графика функции используется тип диаграммы Точечная. Выделяется только диапазон значений x и y.

Построим таблицу и произведем расчеты:

Для получения полной трехлепестковой розы значение fi должно быть от 0 до 3,2.

Формулы для вычисления:

Ячейка Формула
В2 =2*SIN(3*A2)*COS(A2)
С2 =2*SIN(3*A2)*SIN(A2)

2. Построить график функции:

3. Построить график функции (Декартов лист): 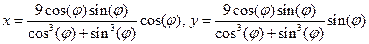. Fi из диапазона -0,15 до 2 шагом 0,05.

4. Построить Верьсьеру: 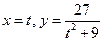. Принять t от -5 до 5 шагом 0,3.

5. Построить Лемнискату Бернулли: 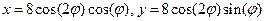. Fi возьмите из диапазона от -3 до 0 с шагом 0,1.

6. Построить Улитку Паскаля: 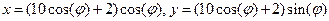. Fi от -2 до 4,3 с шагом 0,1.

7. Построить Астроиду: 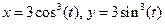. Примите t от -3 до 3 с шагом 0,1.

8. Построить поверхность:

Задание 2. Фирма выпускает два типа строительных материалов: А и В. Продукция обоих 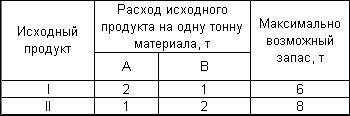видов поступает в продажу. Для производства материалов используются два исходных продукта I и II. Максимально возможные суточные запасы этих продуктов составляют 6 и 8 тонн соответственно. Расходы продуктов I и II на 1 тонну соответствующих материалов приведены в таблице

Изучение рынка сбыта показало, что суточный спрос на материал В никогда не превышает спроса на материал А более чем на 1 т. Кроме того, установлено, что спрос на материал А никогда не превышает 2 т в сутки. Оптовые цены одной тонны материалов равны: 3000 у.е. для В и 2000 у.е. для А. Какое количество материала каждого вида должна производить фабрика, чтобы доход от реализации был максимальным?

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник

Построение диаграмм в Excel

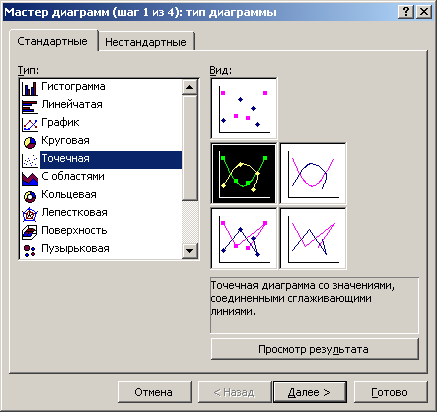
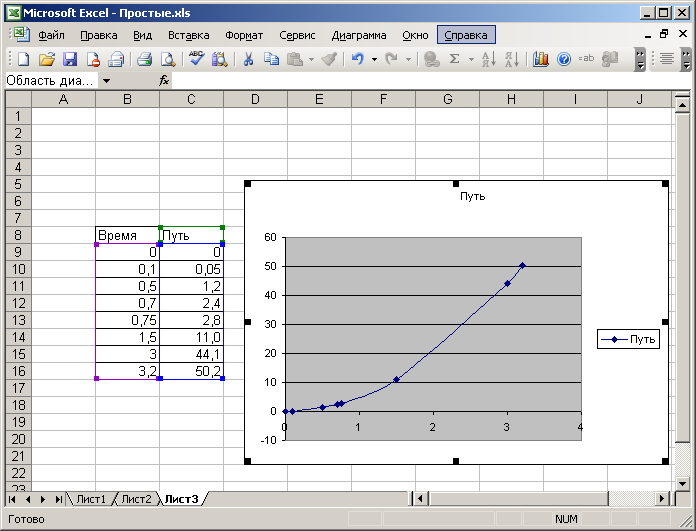
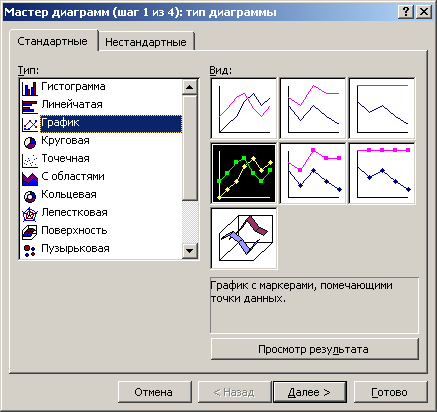
Для создания диаграммы в Excel необходима таблица значений. Рассмотрим построение декартовых графиков функциональной зависимости y=f(x). Пусть имеется экспериментальные данные измерения пройденного пути в зависимости от времени. Заполнив ими два соседних столбца (или строки) на рабочем листе Excel, выделим их вместе с названиями, вызовем «Мастер диаграмм» (пункт меню «Вставка» «Диаграмма»), и выберем тип диаграммы «Точечная».

Тип графика «Точечный»

Тип «Точечная» берёт значения из одного столбца (самого левого при таком способе построения) и откладывает их по оси «х», а соответствующие им из других столбцов по оси «y». Частой ошибкой бывает выбор для подобного типа диаграмм пункта «График». Посмотрим, что произойдёт при таком выборе.

Тип диаграммы «График»

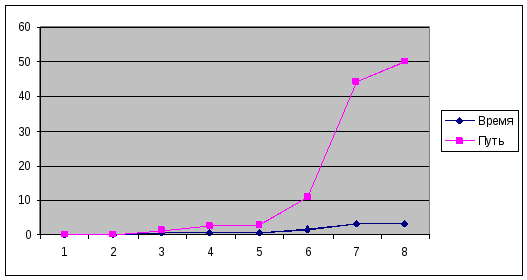
Полученный график не соответствует «Точечному» (и действительности). Значения расположены через равные промежутки, хотя в исходной таблице интервалы по оси «х» разные.

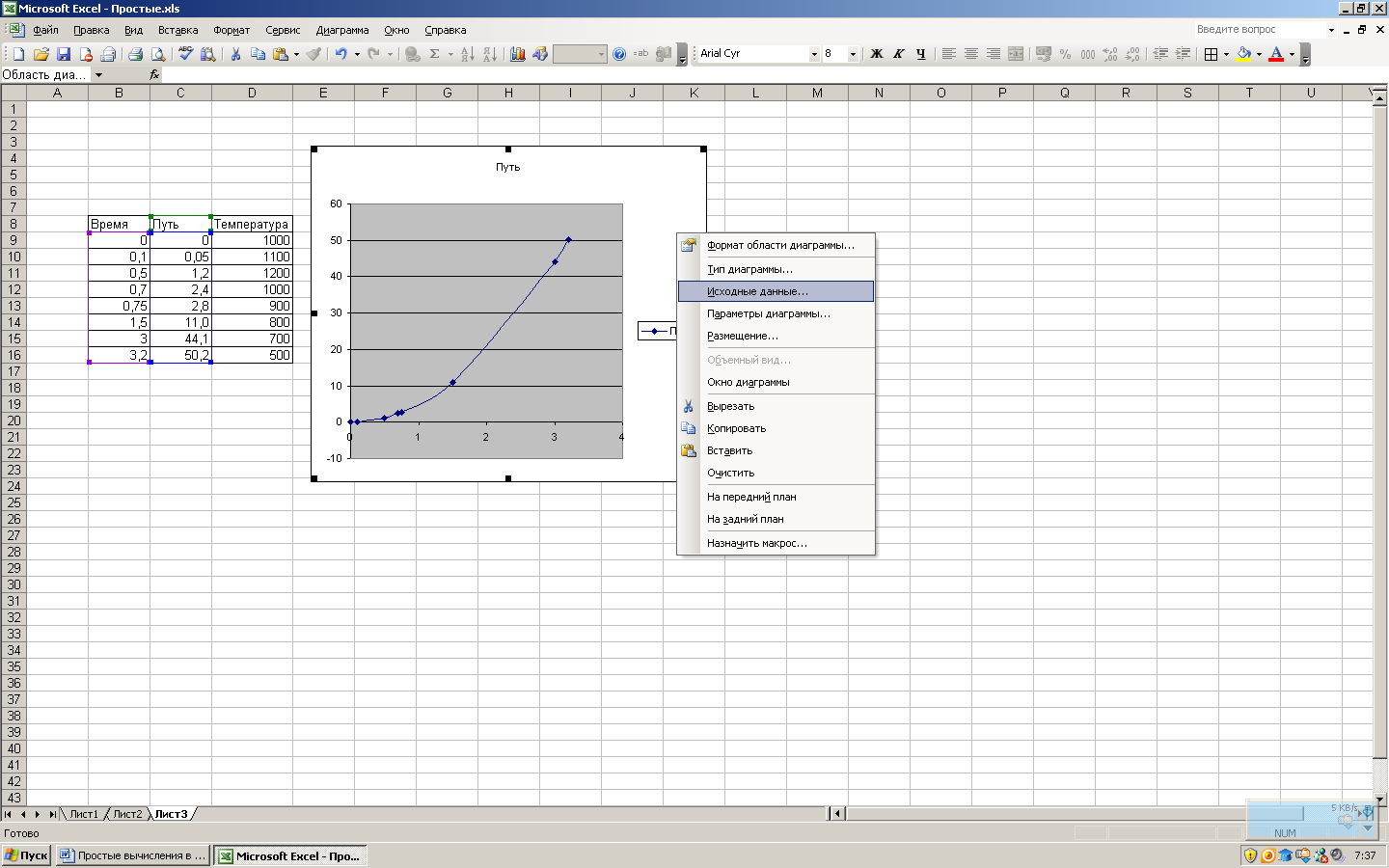
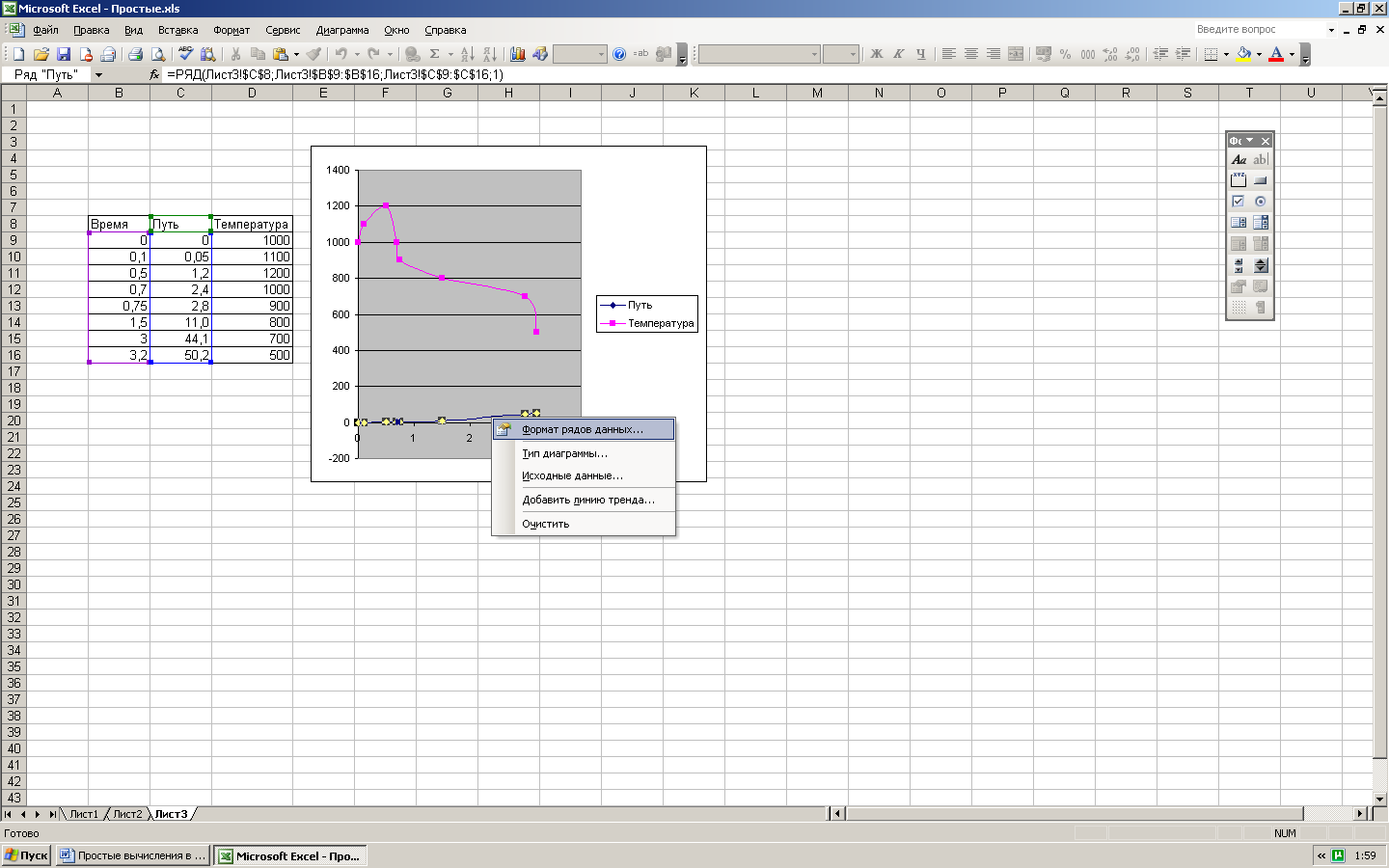
Возможно построение нескольких графиков в одном окне диаграммы. Пусть надо добавить новый ряд данных по температуре. Щелкнув правой кнопкой мыши в окне диаграммы, выбираем в контекстном меню пункт «Исходные данные»,

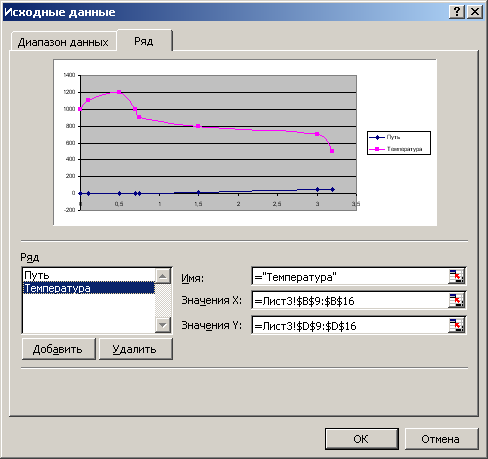
В диалоговом окне исходных данных на вкладке «Ряд», нажимаем кнопку «Добавить» и указываем в соответствующих полях диапазоны значений.

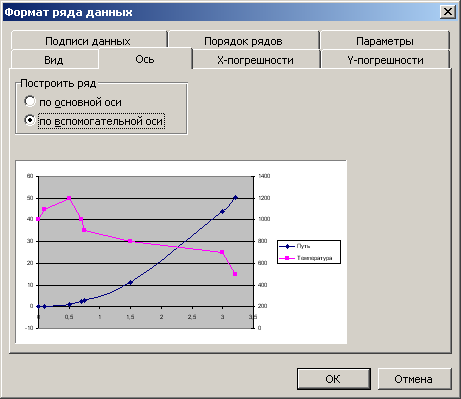
Так как данные в рядах «Путь» и «Температура» различаются на два порядка, вид графика для данных «Путь» мало показателен. В Excel существует возможность построить один из графиков во второй, вспомогательной оси. Для создания вспомогательной оси, надо щёлкнуть правой кнопкой по линии графика и, выделив её таким образом, в появившемся контекстном меню выбрать пункт «Формат рядов данных» и установить переключатель «по вспомогательной оси».

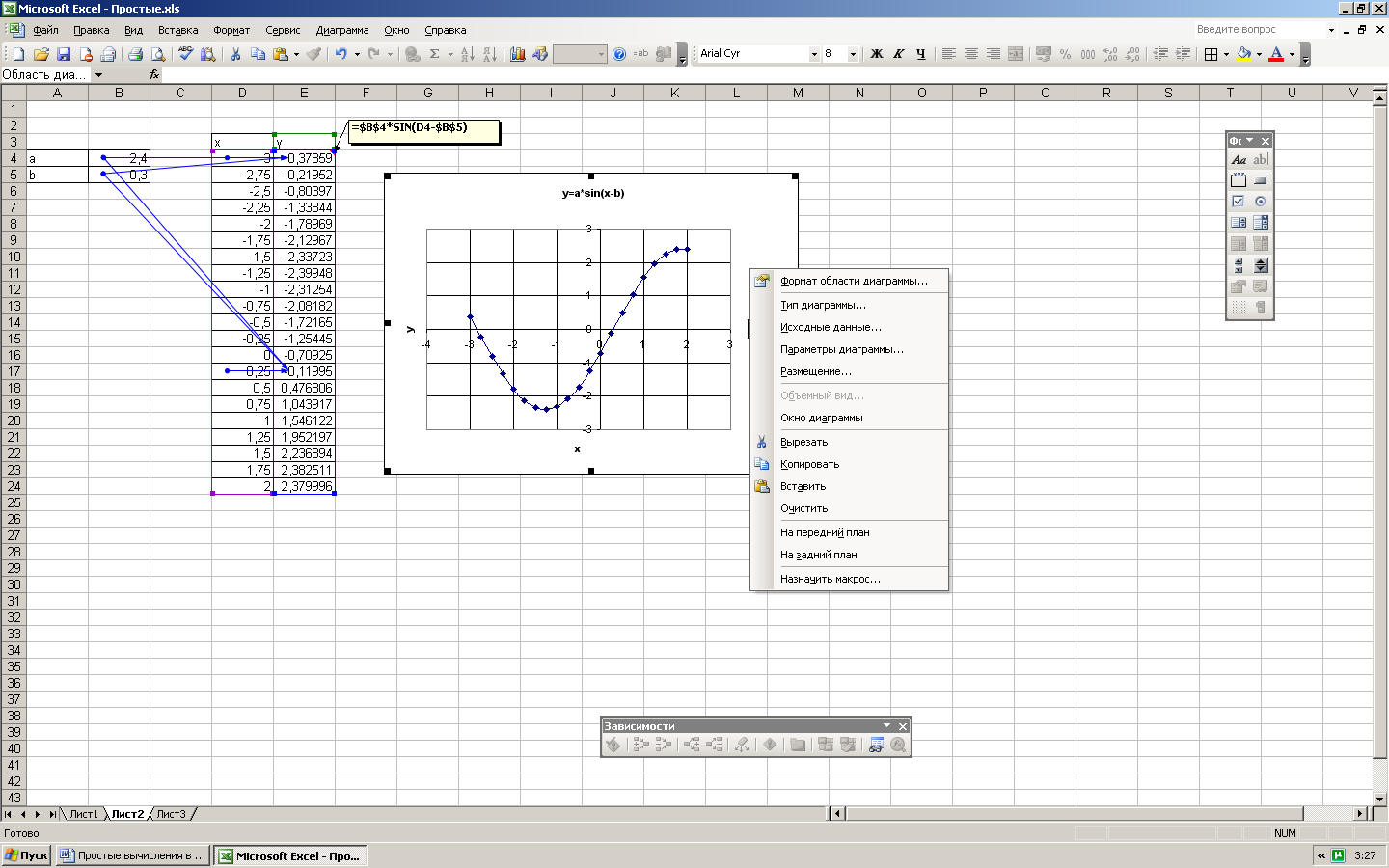
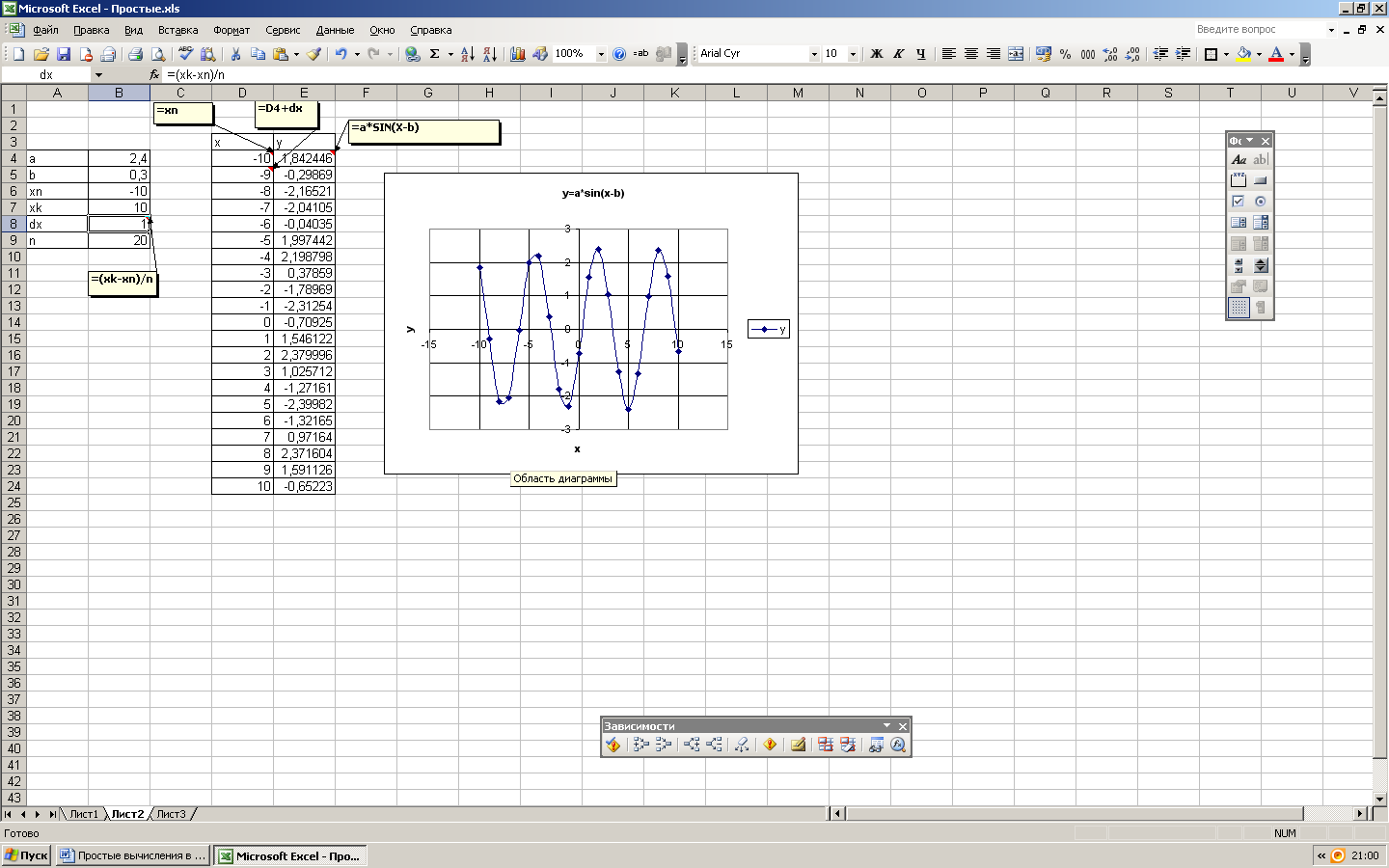
При построении графика функции заданной в аналитическом виде, например

таблицу значений можно построить следующим образом: в ячейку, например «D4», ввести начальное значение х то есть -3 , в ячейку «D5» ввести следующее значение ( для шага изменения по х равного 0,25 это будет -2,75 ), затем, выделив эти две ячейки, протянуть за правый нижний уголок , заполнив таким образом столбец значений по «x». Для значений «y» в ячейку «E4» вводим формулу «=$B$4*SIN(D4-$B$5)», где ««$B$4» и «$B$5» ссылки на ячейки со значениями «a» и «b» соответственно, эти адреса должны быть абсолютными, а «D4» — ссылка на ячейку со значениями «х», этот адрес должен быть относительным. Копируя методом протягивания ячейку «E4» вниз на нужное количество строк, получаем столбец значений «y». Затем строим график, выбирая тип «Точечный», и форматируем, задавая заголовки, линии сетки и т.п.

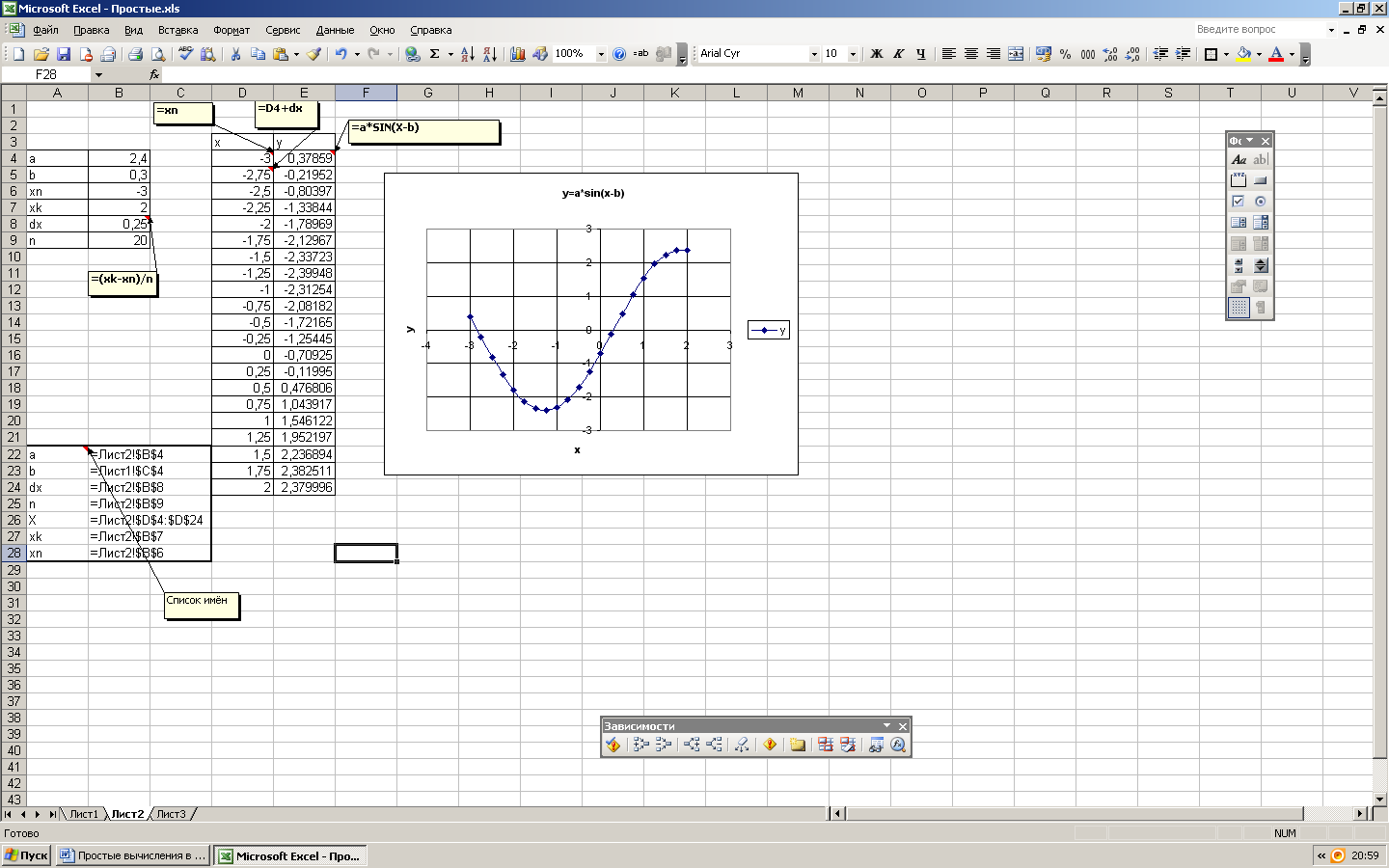
При построении и исследовании удобно применять имена диапазонов. Создадим таблицу входных значений для построения графика, где n – число точек. Выделив диапазон А4:В9 через пункты меню «Вставка» «Имя»  «Создать» дадим имена соответствующим ячейкам. В ячейку для dx введем формулу «=(xk-xn)/n». В ячейке D4 напишем «=xn» а в ячейку ниже (D5) – «=D4+dx» и скопируем ячейку D5 методом протаскивания до ячейки с адресом D24, заполнив, таким образом, 20 ячеек значениями x.

Выделив диапазон D4:D24, присвоим ему имя x. Теперь, при написании формул можно использовать не адреса ячеек, а имена. Это дает более наглядное написание формул.

Напишем в ячейке E4 формулу «=a*sin(x-b)» и, скопировав ее методом протаскивания до ячейки E24, заполним значениями функции.

При таком способе построения графиков, изменяя значения xn и xk можно исследовать любой нужный диапазон значений функций

Для построения графика функции, имеющего разный функциональный вид для разных значений аргумента (это задача «Развилка») используется логическая функция «=ЕСЛИ(условие; значение истинно; значение ложь)». Для графика функции заданной условием Y=a*sin(x) если x =-1 формула принимаем следующий вид

Источник

Источник

Понравилась статья? Поделить с друзьями:
  • Лист врачебных назначений скачать бланк word
  • Лист внутри листа excel
  • Лист в табличном процессоре excel это
  • Лист в книге excel как данные в ячейке
  • Лист в клеточку для word