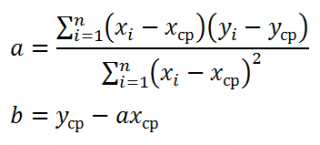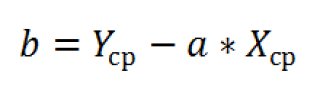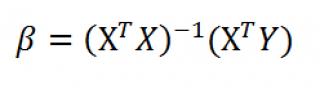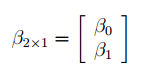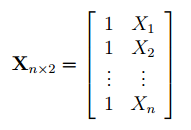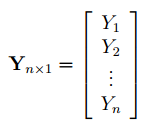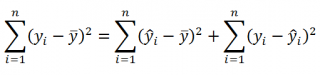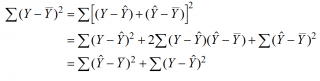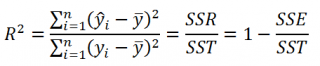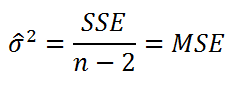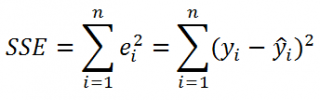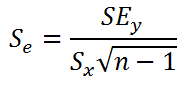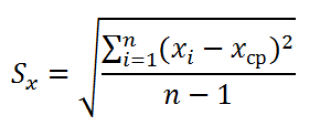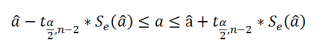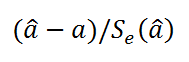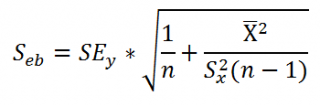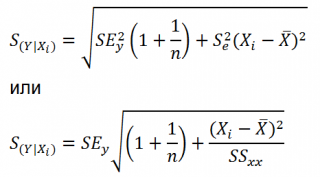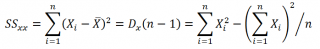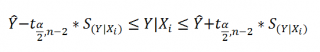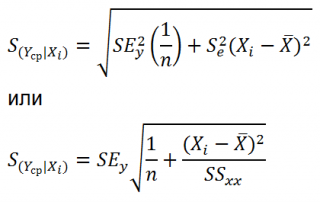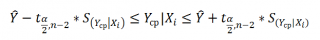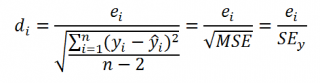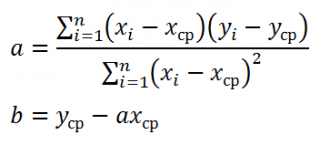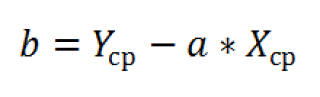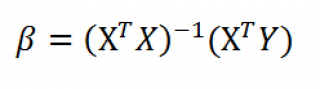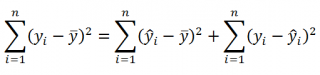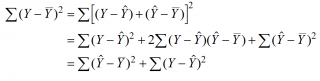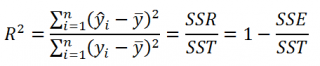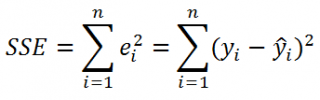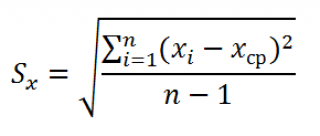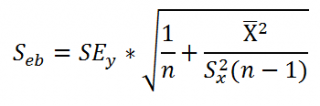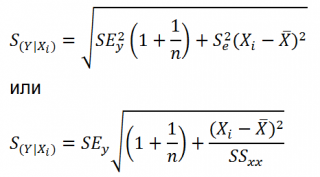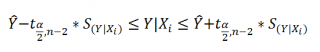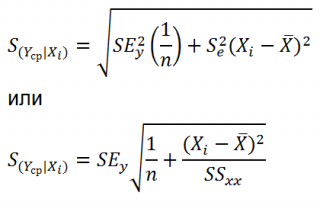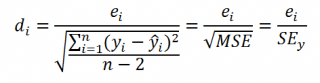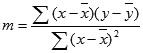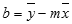17 авг. 2022 г.
читать 2 мин
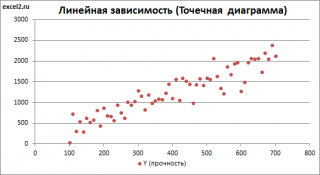
Простая линия линейной регрессии представляет собой линию, которая лучше всего «соответствует» набору данных.
В этом руководстве представлен пошаговый пример того, как быстро добавить простую линию линейной регрессии на диаграмму рассеивания в Excel.
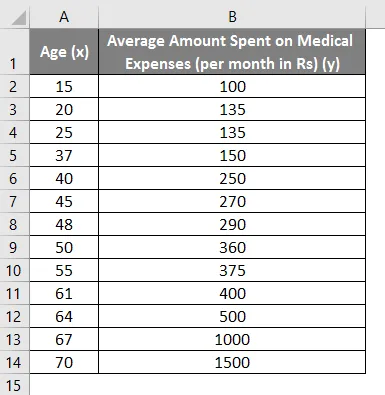
Шаг 1: Создайте данные
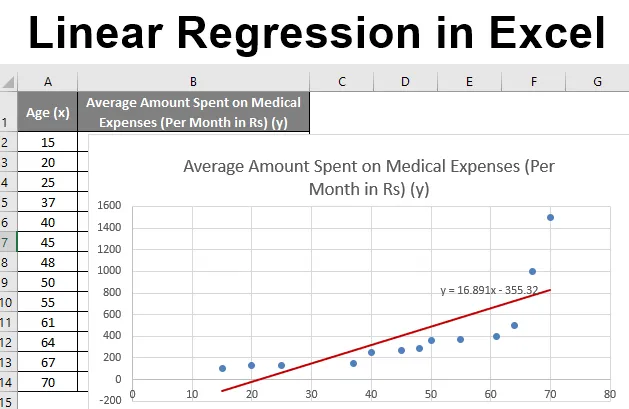
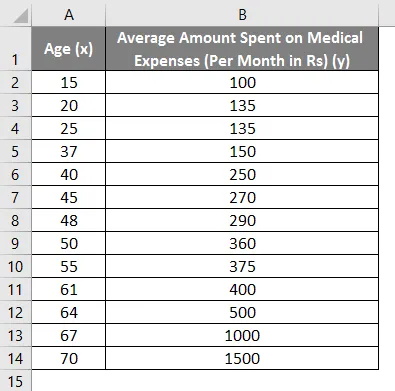
Во-первых, давайте создадим простой набор данных для работы:
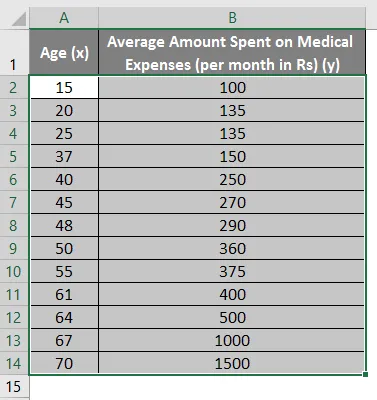
Шаг 2: Создайте диаграмму рассеивания
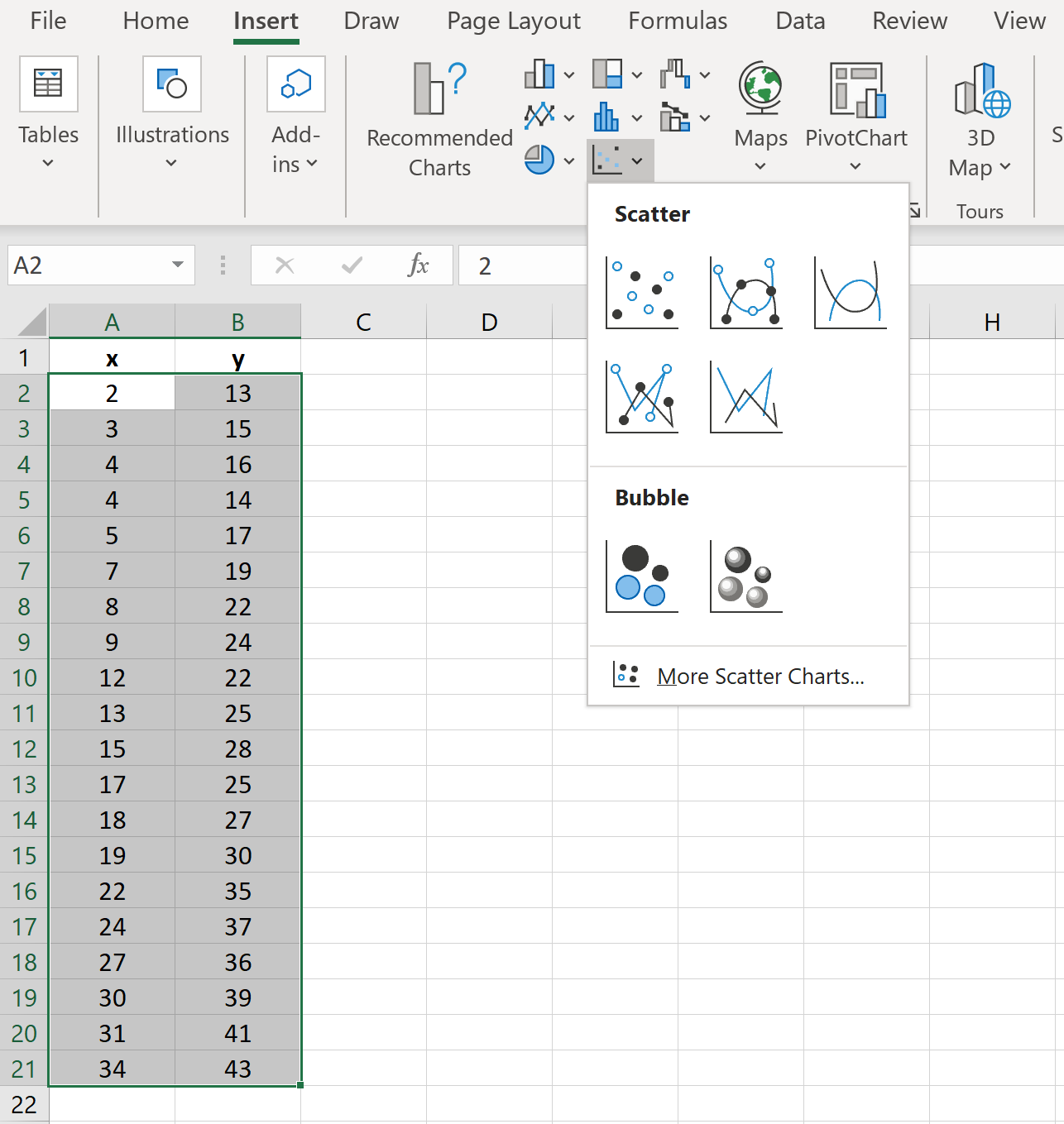
Затем выделите диапазон ячеек A2:B21.На верхней ленте щелкните вкладку « ВСТАВИТЬ », затем нажмите « ВСТАВИТЬ точечную (X, Y)» или «Пузырьковую диаграмму » в группе « Диаграммы » и выберите первый вариант, чтобы создать диаграмму рассеяния:
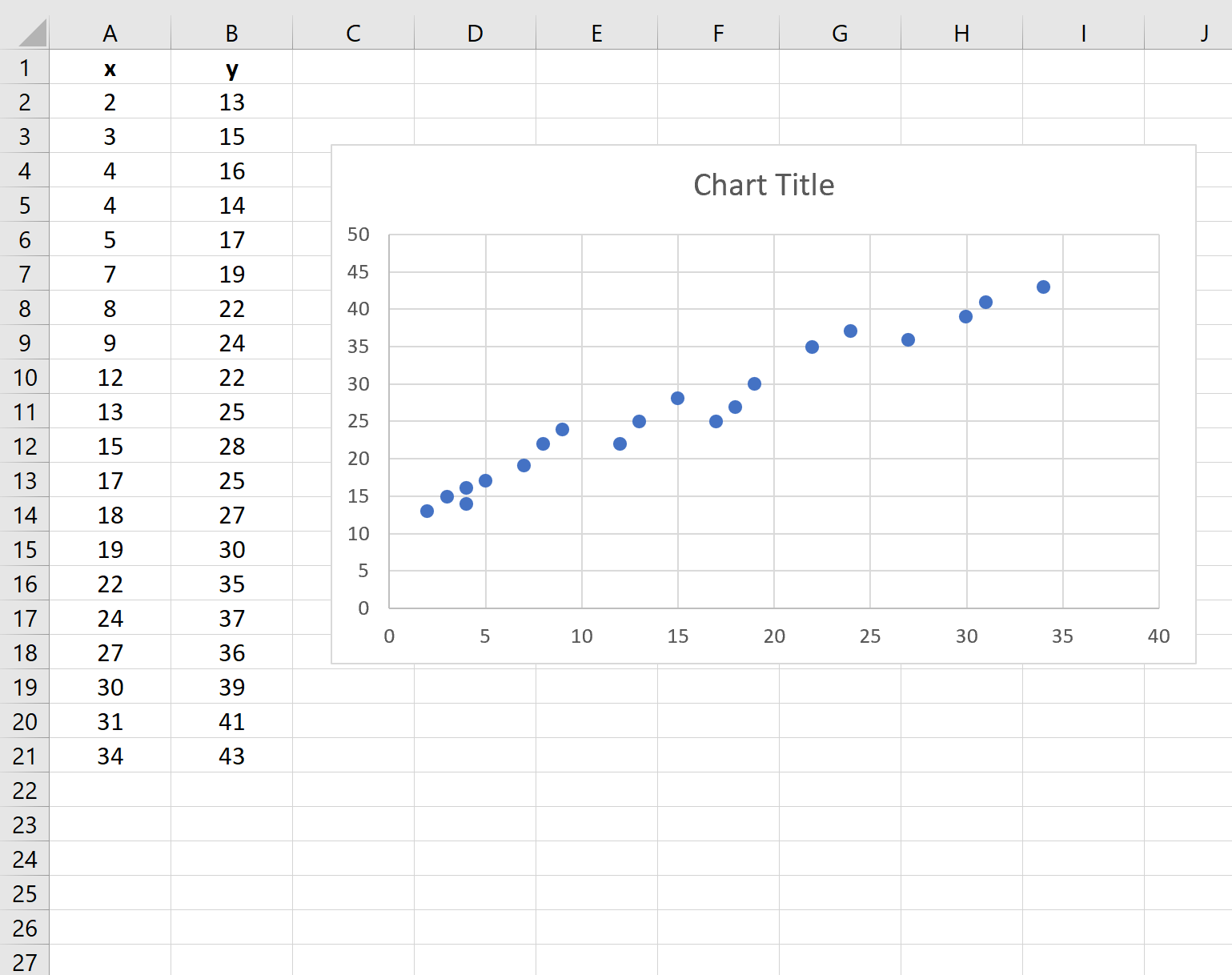
Появится следующая диаграмма рассеяния:
Шаг 3: Добавьте линию регрессии
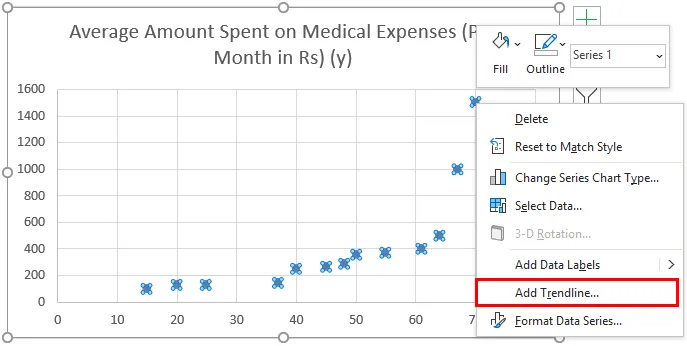
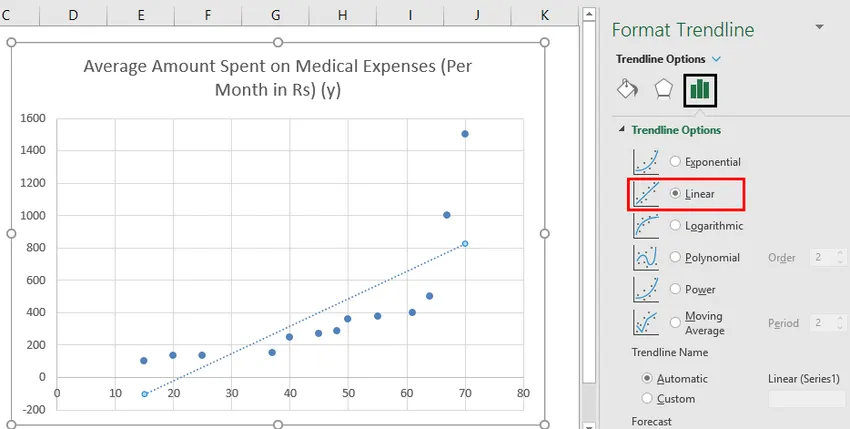
Затем щелкните в любом месте диаграммы рассеивания. Затем щелкните знак «плюс» (+) в правом верхнем углу графика и установите флажок « Линия тренда ».
Это автоматически добавит на диаграмму рассеяния простую линию линейной регрессии:
Добавить линию регрессии в диаграмму рассеяния в Excel
Шаг 4: Добавьте уравнение линии регрессии
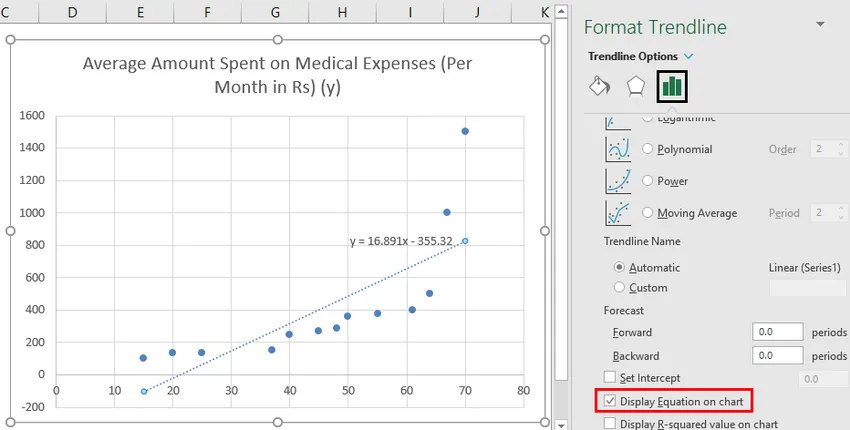
Вы также можете добавить уравнение линии регрессии на диаграмму, нажав Дополнительные параметры. В появившемся справа поле установите флажок рядом с Отображать уравнение на диаграмме .
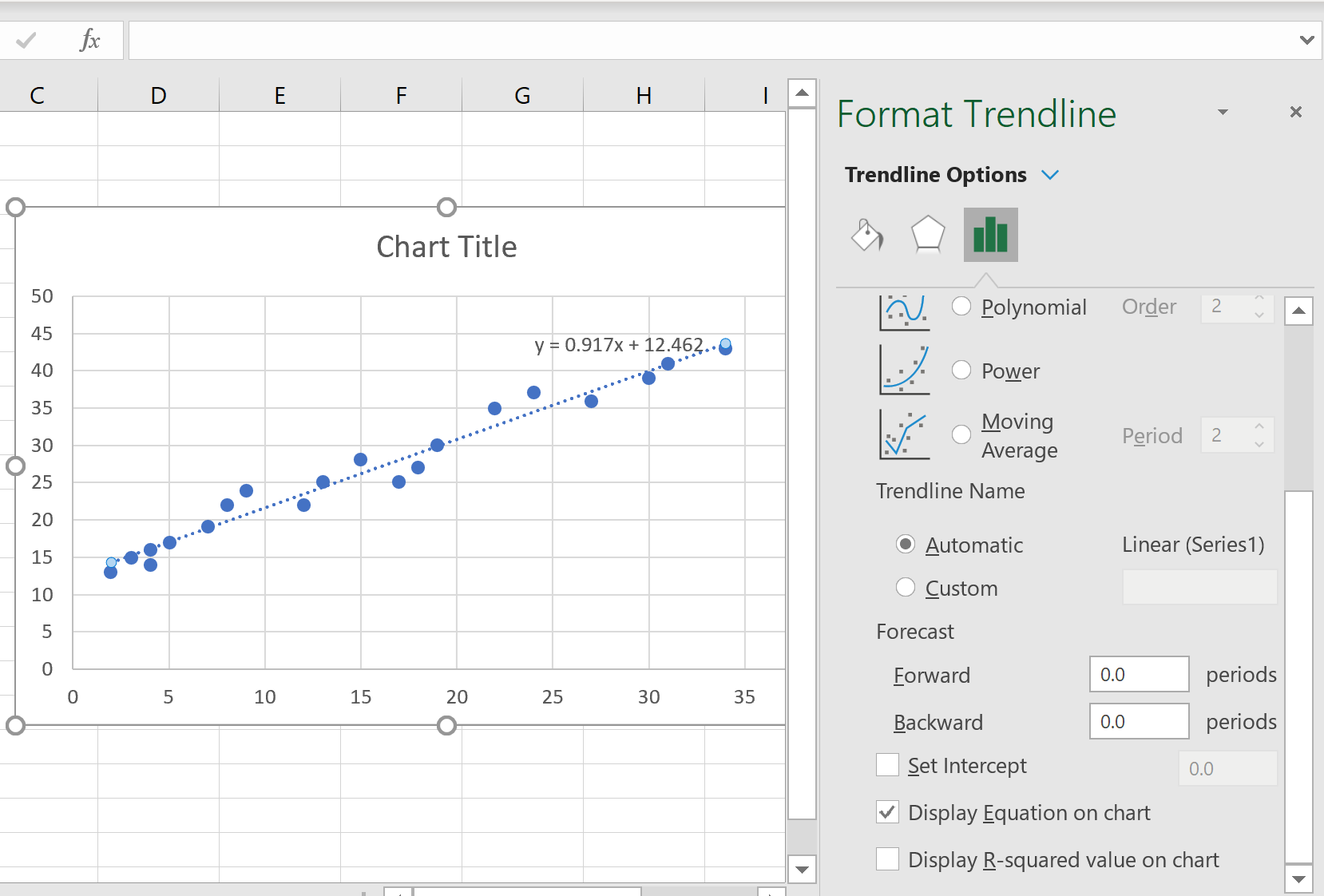
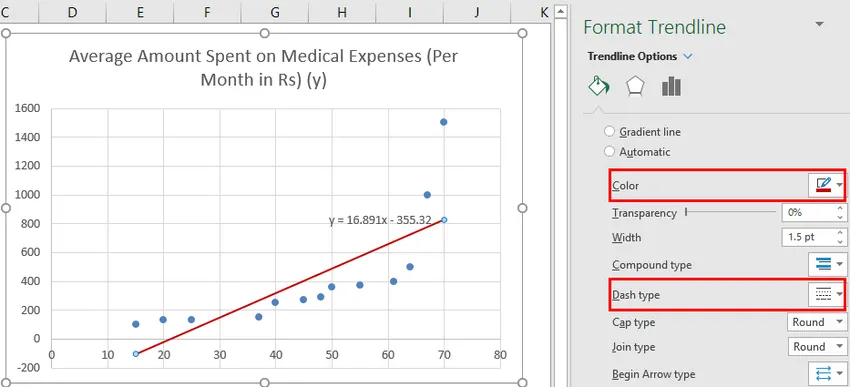
На диаграмме рассеивания автоматически появится простое уравнение линейной регрессии:
Для этого конкретного примера линия регрессии выглядит так:
у = 0,917х + 12,462
Интерпретировать это можно следующим образом:
- Для каждой дополнительной единицы увеличения переменной x среднее увеличение переменной y составляет 0,917 .
- Когда переменная x равна нулю, среднее значение переменной y равно 12,462 .
Мы также можем использовать это уравнение для оценки значения y на основе значения x.Например, когда x равно 15, ожидаемое значение y равно 26,217:
у = 0,917 * (15) + 12,462 = 26,217
Другие учебники по Excel можно найти здесь .
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Регрессионный анализ в Microsoft Excel
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
-
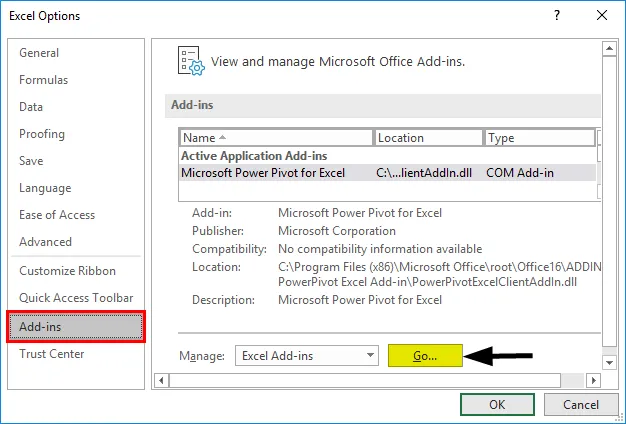
Перемещаемся во вкладку «Файл».
Переходим в раздел «Параметры».
В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
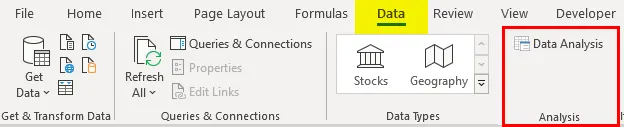
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Линейная регрессия в программе Excel
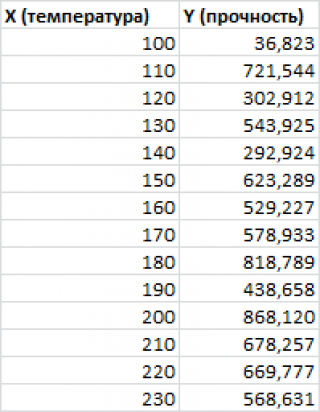
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк . В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
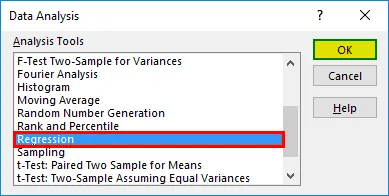
- Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».
Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».
С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.
После того, как все настройки установлены, жмем на кнопку «OK».
Разбор результатов анализа
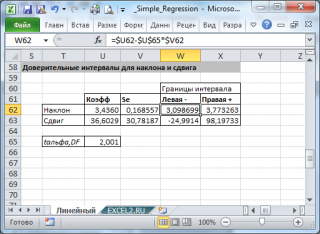
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
Помимо этой статьи, на сайте еще 12765 полезных инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Простая линейная регрессия в EXCEL
history 26 января 2019 г.
-
Группы статей
- Статистический анализ
Регрессия позволяет прогнозировать зависимую переменную на основании значений фактора. В MS EXCEL имеется множество функций, которые возвращают не только наклон и сдвиг линии регрессии, характеризующей линейную взаимосвязь между факторами, но и регрессионную статистику. Здесь рассмотрим простую линейную регрессию, т.е. прогнозирование на основе одного фактора.
Disclaimer : Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей Регрессионного анализа. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения Регрессии – плохая идея.
Статья про Регрессионный анализ получилась большая, поэтому ниже для удобства приведены ее разделы:
Примечание : Если прогнозирование переменной осуществляется на основе нескольких факторов, то имеет место множественная регрессия .
Чтобы разобраться, чем может помочь MS EXCEL при проведении регрессионного анализа, напомним вкратце теорию, введем термины и обозначения, которые могут отличаться в зависимости от различных источников.
Примечание : Для тех, кому некогда, незачем или просто не хочется разбираться в теоретических выкладках предлагается сразу перейти к вычислительной части — оценке неизвестных параметров линейной модели .
Немного теории и основные понятия
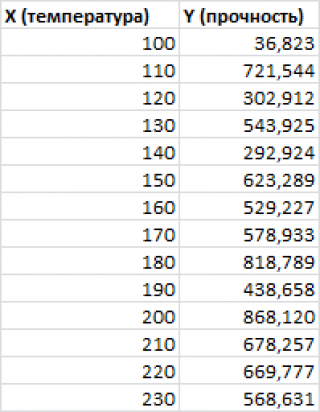
Пусть у нас есть массив данных, представляющий собой значения двух переменных Х и Y. Причем значения переменной Х мы можем произвольно задавать (контролировать) и использовать эту переменную для предсказания значений зависимой переменной Y. Таким образом, случайной величиной является только переменная Y.
Примером такой задачи может быть производственный процесс изготовления некого волокна, причем прочность этого волокна (Y) зависит только от рабочей температуры процесса в реакторе (Х), которая задается оператором.
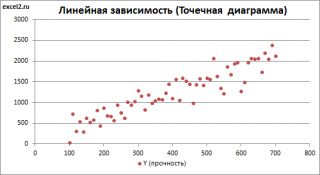
Построим диаграмму рассеяния (см. файл примера лист Линейный ), созданию которой посвящена отдельная статья . Вообще, построение диаграммы рассеяния для целей регрессионного анализа де-факто является стандартом.
СОВЕТ : Подробнее о построении различных типов диаграмм см. статьи Основы построения диаграмм и Основные типы диаграмм .
Приведенная выше диаграмма рассеяния свидетельствует о возможной линейной взаимосвязи между Y от Х: очевидно, что точки данных в основном располагаются вдоль прямой линии.
Примечание : Наличие даже такой очевидной линейной взаимосвязи не может являться доказательством о наличии причинной взаимосвязи переменных. Наличие причинной взаимосвязи не может быть доказано на основании только анализа имеющихся измерений, а должно быть обосновано с помощью других исследований, например теоретических выкладок.
Примечание : Как известно, уравнение прямой линии имеет вид Y = m * X + k , где коэффициент m отвечает за наклон линии ( slope ), k – за сдвиг линии по вертикали ( intercept ), k равно значению Y при Х=0.
Предположим, что мы можем зафиксировать переменную Х ( рабочую температуру процесса ) при некотором значении Х i и произвести несколько наблюдений переменной Y ( прочность нити ). Очевидно, что при одном и том же значении Хi мы получим различные значения Y. Это обусловлено влиянием других факторов на Y. Например, локальные колебания давления в реакторе, концентрации раствора, наличие ошибок измерения и др. Предполагается, что воздействие этих факторов имеет случайную природу и для каждого измерения имеются одинаковые условия проведения эксперимента (т.е. другие факторы не изменяются).
Полученные значения Y, при заданном Хi, будут колебаться вокруг некого значения . При увеличении количества измерений, среднее этих измерений, будет стремиться к математическому ожиданию случайной величины Y (при Х i ) равному μy(i)=Е(Y i ).
Подобные рассуждения можно привести для любого значения Хi.
Чтобы двинуться дальше, воспользуемся материалом из раздела Проверка статистических гипотез . В статье о проверке гипотезы о среднем значении генеральной совокупности в качестве нулевой гипотезы предполагалось равенство неизвестного значения μ заданному μ0.
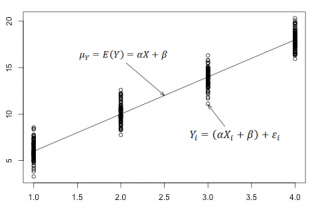
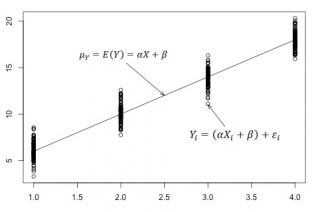
В нашем случае простой линейной регрессии в качестве нулевой гипотезы предположим, что между переменными μy(i) и Хi существует линейная взаимосвязь μ y(i) =α* Х i +β. Уравнение μ y(i) =α* Х i +β можно переписать в обобщенном виде (для всех Х и μ y ) как μ y =α* Х +β.
Для наглядности проведем прямую линию соединяющую все μy(i).
Данная линия называется регрессионной линией генеральной совокупности (population regression line), параметры которой ( наклон a и сдвиг β ) нам не известны (по аналогии с гипотезой о среднем значении генеральной совокупности , где нам было неизвестно истинное значение μ).
Теперь сделаем переход от нашего предположения, что μy=a* Х + β , к предсказанию значения случайной переменной Y в зависимости от значения контролируемой переменной Х. Для этого уравнение связи двух переменных запишем в виде Y=a*X+β+ε, где ε — случайная ошибка, которая отражает суммарный эффект влияния других факторов на Y (эти «другие» факторы не участвуют в нашей модели). Напомним, что т.к. переменная Х фиксирована, то ошибка ε определяется только свойствами переменной Y.
Уравнение Y=a*X+b+ε называют линейной регрессионной моделью . Часто Х еще называют независимой переменной (еще предиктором и регрессором , английский термин predictor , regressor ), а Y – зависимой (или объясняемой , response variable ). Так как регрессор у нас один, то такая модель называется простой линейной регрессионной моделью ( simple linear regression model ). α часто называют коэффициентом регрессии.
Предположения линейной регрессионной модели перечислены в следующем разделе.
Предположения линейной регрессионной модели
Чтобы модель линейной регрессии Yi=a*Xi+β+ε i была адекватной — требуется:
- Ошибки ε i должны быть независимыми переменными;
- При каждом значении Xi ошибки ε i должны быть иметь нормальное распределение (также предполагается равенство нулю математического ожидания, т.е. Е[ε i ]=0);
- При каждом значении Xi ошибки ε i должны иметь равные дисперсии (обозначим ее σ 2 ).
Примечание : Последнее условие называется гомоскедастичность — стабильность, гомогенность дисперсии случайной ошибки e. Т.е. дисперсия ошибки σ 2 не должна зависеть от значения Xi.
Используя предположение о равенстве математического ожидания Е[ε i ]=0 покажем, что μy(i)=Е[Yi]:
Е[Yi]= Е[a*Xi+β+ε i ]= Е[a*Xi+β]+ Е[ε i ]= a*Xi+β= μy(i), т.к. a, Xi и β постоянные значения.
Дисперсия случайной переменной Y равна дисперсии ошибки ε, т.е. VAR(Y)= VAR(ε)=σ 2 . Это является следствием, что все значения переменной Х являются const, а VAR(ε)=VAR(ε i ).
Задачи регрессионного анализа
Для проверки гипотезы о линейной взаимосвязи переменной Y от X делают выборку из генеральной совокупности (этой совокупности соответствует регрессионная линия генеральной совокупности , т.е. μy=a* Х +β). Выборка будет состоять из n точек, т.е. из n пар значений .
На основании этой выборки мы можем вычислить оценки наклона a и сдвига β, которые обозначим соответственно a и b . Также часто используются обозначения â и b̂.
Далее, используя эти оценки, мы также можем проверить гипотезу: имеется ли линейная связь между X и Y статистически значимой?
Первая задача регрессионного анализа – оценка неизвестных параметров ( estimation of the unknown parameters ). Подробнее см. раздел Оценки неизвестных параметров модели .
Вторая задача регрессионного анализа – Проверка адекватности модели ( model adequacy checking ).
Примечание : Оценки параметров модели обычно вычисляются методом наименьших квадратов (МНК), которому посвящена отдельная статья .
Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)
Неизвестные параметры простой линейной регрессионной модели Y=a*X+β+ε оценим с помощью метода наименьших квадратов (в статье про МНК подробно описано этот метод ).
Для вычисления параметров линейной модели методом МНК получены следующие выражения:
Таким образом, мы получим уравнение прямой линии Y= a *X+ b , которая наилучшим образом аппроксимирует имеющиеся данные.
Примечание : В статье про метод наименьших квадратов рассмотрены случаи аппроксимации линейной и квадратичной функцией , а также степенной , логарифмической и экспоненциальной функцией .
Оценку параметров в MS EXCEL можно выполнить различными способами:
Сначала рассмотрим функции НАКЛОН() , ОТРЕЗОК() и ЛИНЕЙН() .
Пусть значения Х и Y находятся соответственно в диапазонах C 23: C 83 и B 23: B 83 (см. файл примера внизу статьи).
Примечание : Значения двух переменных Х и Y можно сгенерировать, задав тренд и величину случайного разброса (см. статью Генерация данных для линейной регрессии в MS EXCEL ).
В MS EXCEL наклон прямой линии а ( оценку коэффициента регрессии ), можно найти по методу МНК с помощью функции НАКЛОН() , а сдвиг b ( оценку постоянного члена или константы регрессии ), с помощью функции ОТРЕЗОК() . В английской версии это функции SLOPE и INTERCEPT соответственно.
Аналогичный результат можно получить с помощью функции ЛИНЕЙН() , английская версия LINEST (см. статью об этой функции ).
Формула =ЛИНЕЙН(C23:C83;B23:B83) вернет наклон а . А формула = ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2) — сдвиг b . Здесь требуются пояснения.
Функция ЛИНЕЙН() имеет 4 аргумента и возвращает целый массив значений:
ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Если 4-й аргумент статистика имеет значение ЛОЖЬ или опущен, то функция ЛИНЕЙН() возвращает только оценки параметров модели: a и b .
Примечание : Остальные значения, возвращаемые функцией ЛИНЕЙН() , нам потребуются при вычислении стандартных ошибок и для проверки значимости регрессии . В этом случае аргумент статистика должен иметь значение ИСТИНА.
Чтобы вывести сразу обе оценки:
- в одной строке необходимо выделить 2 ячейки,
- ввести формулу в Строке формул
- нажать CTRL+SHIFT+ENTER (см. статью про формулы массива ).
Если в Строке формул выделить формулу = ЛИНЕЙН(C23:C83;B23:B83) и нажать клавишу F9 , то мы увидим что-то типа <3,01279389265416;154,240057900613>. Это как раз значения a и b . Как видно, оба значения разделены точкой с запятой «;», что свидетельствует, что функция вернула значения «в нескольких ячейках одной строки».
Если требуется вывести параметры линии не в одной строке, а одном столбце (ячейки друг под другом), то используйте формулу = ТРАНСП(ЛИНЕЙН(C23:C83;B23:B83)) . При этом выделять нужно 2 ячейки в одном столбце. Если теперь выделить новую формулу и нажать клавишу F9, то мы увидим что 2 значения разделены двоеточием «:», что означает, что значения выведены в столбец (функция ТРАНСП() транспонировала строку в столбец ).
Чтобы разобраться в этом подробнее необходимо ознакомиться с формулами массива .
Чтобы не связываться с вводом формул массива , можно использовать функцию ИНДЕКС() . Формула = ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1) или просто ЛИНЕЙН(C23:C83;B23:B83) вернет параметр, отвечающий за наклон линии, т.е. а . Формула =ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2) вернет параметр b .
Оценка неизвестных параметров линейной модели (через статистики выборок)
Наклон линии, т.е. коэффициент а , можно также вычислить через коэффициент корреляции и стандартные отклонения выборок :
= КОРРЕЛ(B23:B83;C23:C83) *(СТАНДОТКЛОН.В(C23:C83)/ СТАНДОТКЛОН.В(B23:B83))
Вышеуказанная формула математически эквивалентна отношению ковариации выборок Х и Y и дисперсии выборки Х:
И, наконец, запишем еще одну формулу для нахождения сдвига b . Воспользуемся тем фактом, что линия регрессии проходит через точку средних значений переменных Х и Y.
Вычислив средние значения и подставив в формулу ранее найденный наклон а , получим сдвиг b .
Оценка неизвестных параметров линейной модели (матричная форма)
Также параметры линии регрессии можно найти в матричной форме (см. файл примера лист Матричная форма ).
В формуле символом β обозначен столбец с искомыми параметрами модели: β0 (сдвиг b ), β1 (наклон a ).
Матрица Х равна:
Матрица Х называется регрессионной матрицей или матрицей плана . Она состоит из 2-х столбцов и n строк, где n – количество точек данных. Первый столбец — столбец единиц, второй – значения переменной Х.
Матрица Х T – это транспонированная матрица Х . Она состоит соответственно из n столбцов и 2-х строк.
В формуле символом Y обозначен столбец значений переменной Y.
Чтобы перемножить матрицы используйте функцию МУМНОЖ() . Чтобы найти обратную матрицу используйте функцию МОБР() .
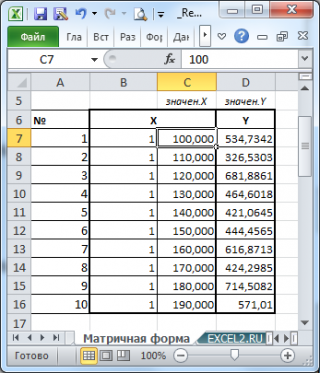
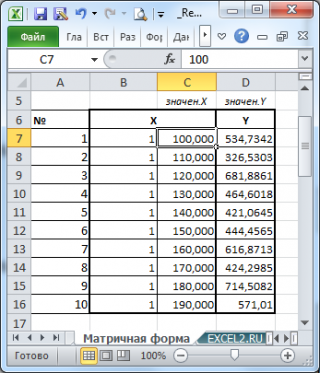
Пусть дан массив значений переменных Х и Y (n=10, т.е.10 точек).
Слева от него достроим столбец с 1 для матрицы Х.
и введя ее как формулу массива в 2 ячейки, получим оценку параметров модели.
Красота применения матричной формы полностью раскрывается в случае множественной регрессии .
Построение линии регрессии
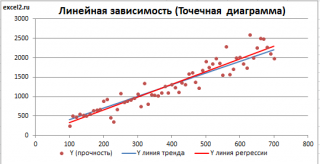
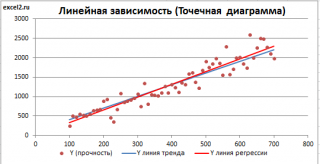
Для отображения линии регрессии построим сначала диаграмму рассеяния , на которой отобразим все точки (см. начало статьи ).
Для построения прямой линии используйте вычисленные выше оценки параметров модели a и b (т.е. вычислите у по формуле y = a * x + b ) или функцию ТЕНДЕНЦИЯ() .
Формула = ТЕНДЕНЦИЯ($C$23:$C$83;$B$23:$B$83;B23) возвращает расчетные (прогнозные) значения ŷi для заданного значения Хi из столбца В2 .
Примечание : Линию регрессии можно также построить с помощью функции ПРЕДСКАЗ() . Эта функция возвращает прогнозные значения ŷi, но, в отличие от функции ТЕНДЕНЦИЯ() работает только в случае одного регрессора. Функция ТЕНДЕНЦИЯ() может быть использована и в случае множественной регрессии (в этом случае 3-й аргумент функции должен быть ссылкой на диапазон, содержащий все значения Хi для выбранного наблюдения i).
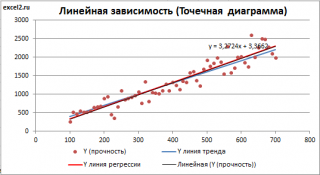
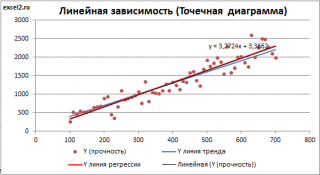
Как видно из диаграммы выше линия тренда и линия регрессии не обязательно совпадают: отклонения точек от линии тренда случайны, а МНК лишь подбирает линию наиболее точно аппроксимирующую случайные точки данных.
Линию регрессии можно построить и с помощью встроенных средств диаграммы, т.е. с помощью инструмента Линия тренда. Для этого выделите диаграмму, в меню выберите вкладку Макет , в группе Анализ нажмите Линия тренда , затем Линейное приближение. В диалоговом окне установите галочку Показывать уравнение на диаграмме (подробнее см. в статье про МНК ).
Построенная таким образом линия, разумеется, должна совпасть с ранее построенной нами линией регрессии, а параметры уравнения a и b должны совпасть с параметрами уравнения отображенными на диаграмме.
Примечание: Для того, чтобы вычисленные параметры уравнения a и b совпадали с параметрами уравнения на диаграмме, необходимо, чтобы тип у диаграммы был Точечная, а не График , т.к. тип диаграммы График не использует значения Х, а вместо значений Х используется последовательность 1; 2; 3; . Именно эти значения и берутся при расчете параметров линии тренда . Убедиться в этом можно если построить диаграмму График (см. файл примера ), а значения Хнач и Хшаг установить равным 1. Только в этом случае параметры уравнения на диаграмме совпадут с a и b .
Коэффициент детерминации R 2
Коэффициент детерминации R 2 показывает насколько полезна построенная нами линейная регрессионная модель .
Предположим, что у нас есть n значений переменной Y и мы хотим предсказать значение yi, но без использования значений переменной Х (т.е. без построения регрессионной модели ). Очевидно, что лучшей оценкой для yi будет среднее значение ȳ. Соответственно, ошибка предсказания будет равна (yi — ȳ).
Примечание : Далее будет использована терминология и обозначения дисперсионного анализа .
После построения регрессионной модели для предсказания значения yi мы будем использовать значение ŷi=a*xi+b. Ошибка предсказания теперь будет равна (yi — ŷi).
Теперь с помощью диаграммы сравним ошибки предсказания полученные без построения модели и с помощью модели.
Очевидно, что используя регрессионную модель мы уменьшили первоначальную (полную) ошибку (yi — ȳ) на значение (ŷi — ȳ) до величины (yi — ŷi).
(yi — ŷi) – это оставшаяся, необъясненная ошибка.
Очевидно, что все три ошибки связаны выражением:
(yi — ȳ)= (ŷi — ȳ) + (yi — ŷi)
Можно показать, что в общем виде справедливо следующее выражение:
или в других, общепринятых в зарубежной литературе, обозначениях:
Total Sum of Squares = Regression Sum of Squares + Error Sum of Squares
Примечание : SS — Sum of Squares — Сумма Квадратов.
Как видно из формулы величины SST, SSR, SSE имеют размерность дисперсии (вариации) и соответственно описывают разброс (изменчивость): Общую изменчивость (Total variation), Изменчивость объясненную моделью (Explained variation) и Необъясненную изменчивость (Unexplained variation).
По определению коэффициент детерминации R 2 равен:
R 2 = Изменчивость объясненная моделью / Общая изменчивость.
Этот показатель равен квадрату коэффициента корреляции и в MS EXCEL его можно вычислить с помощью функции КВПИРСОН() или ЛИНЕЙН() :
R 2 принимает значения от 0 до 1 (1 соответствует идеальной линейной зависимости Y от Х). Однако, на практике малые значения R2 вовсе не обязательно указывают, что переменную Х нельзя использовать для прогнозирования переменной Y. Малые значения R2 могут указывать на нелинейность связи или на то, что поведение переменной Y объясняется не только Х, но и другими факторами.
Стандартная ошибка регрессии
Стандартная ошибка регрессии ( Standard Error of a regression ) показывает насколько велика ошибка предсказания значений переменной Y на основании значений Х. Отдельные значения Yi мы можем предсказывать лишь с точностью +/- несколько значений (обычно 2-3, в зависимости от формы распределения ошибки ε).
Теперь вспомним уравнение линейной регрессионной модели Y=a*X+β+ε. Ошибка ε имеет случайную природу, т.е. является случайной величиной и поэтому имеет свою функцию распределения со средним значением μ и дисперсией σ 2 .
Оценив значение дисперсии σ 2 и вычислив из нее квадратный корень – получим Стандартную ошибку регрессии. Чем точки наблюдений на диаграмме рассеяния ближе находятся к прямой линии, тем меньше Стандартная ошибка.
Примечание : Вспомним , что при построении модели предполагается, что среднее значение ошибки ε равно 0, т.е. E[ε]=0.
Оценим дисперсию σ 2 . Помимо вычисления Стандартной ошибки регрессии эта оценка нам потребуется в дальнейшем еще и при построении доверительных интервалов для оценки параметров регрессии a и b .
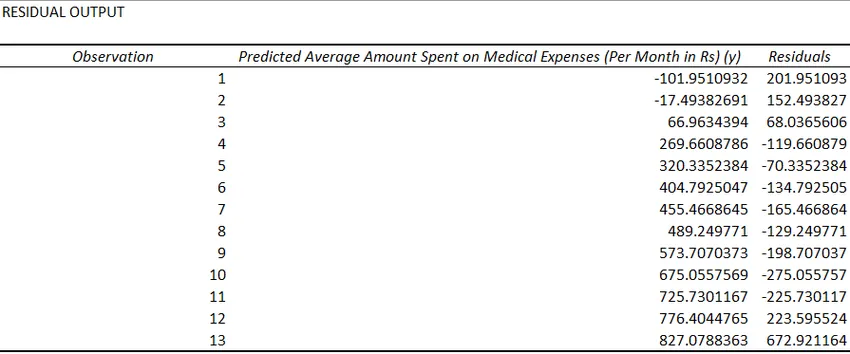
Для оценки дисперсии ошибки ε используем остатки регрессии — разности между имеющимися значениями yi и значениями, предсказанными регрессионной моделью ŷ. Чем лучше регрессионная модель согласуется с данными (точки располагается близко к прямой линии), тем меньше величина остатков.
Для оценки дисперсии σ 2 используют следующую формулу:
где SSE – сумма квадратов значений ошибок модели ε i =yi — ŷi ( Sum of Squared Errors ).
SSE часто обозначают и как SSres – сумма квадратов остатков ( Sum of Squared residuals ).
Оценка дисперсии s 2 также имеет общепринятое обозначение MSE (Mean Square of Errors), т.е. среднее квадратов ошибок или MSRES (Mean Square of Residuals), т.е. среднее квадратов остатков . Хотя правильнее говорить сумме квадратов остатков, т.к. ошибка чаще ассоциируется с ошибкой модели ε, которая является непрерывной случайной величиной. Но, здесь мы будем использовать термины SSE и MSE, предполагая, что речь идет об остатках.
Примечание : Напомним, что когда мы использовали МНК для нахождения параметров модели, то критерием оптимизации была минимизация именно SSE (SSres). Это выражение представляет собой сумму квадратов расстояний между наблюденными значениями yi и предсказанными моделью значениями ŷi, которые лежат на линии регрессии.
Математическое ожидание случайной величины MSE равно дисперсии ошибки ε, т.е. σ 2 .
Чтобы понять почему SSE выбрана в качестве основы для оценки дисперсии ошибки ε, вспомним, что σ 2 является также дисперсией случайной величины Y (относительно среднего значения μy, при заданном значении Хi). А т.к. оценкой μy является значение ŷi = a * Хi + b (значение уравнения регрессии при Х= Хi), то логично использовать именно SSE в качестве основы для оценки дисперсии σ 2 . Затем SSE усредняется на количество точек данных n за вычетом числа 2. Величина n-2 – это количество степеней свободы ( df – degrees of freedom ), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y). В случае простой линейной регрессии число степеней свободы равно n-2, т.к. при построении линии регрессии было оценено 2 параметра модели (на это было «потрачено» 2 степени свободы ).
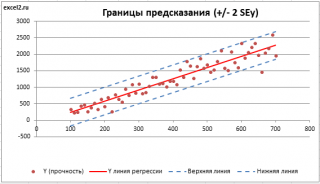
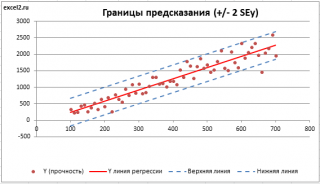
Итак, как сказано было выше, квадратный корень из s 2 имеет специальное название Стандартная ошибка регрессии ( Standard Error of a regression ) и обозначается SEy. SEy показывает насколько велика ошибка предсказания. Отдельные значения Y мы можем предсказывать с точностью +/- несколько значений SEy (см. этот раздел ). Если ошибки предсказания ε имеют нормальное распределение , то примерно 2/3 всех предсказанных значений будут на расстоянии не больше SEy от линии регрессии . SEy имеет размерность переменной Y и откладывается по вертикали. Часто на диаграмме рассеяния строят границы предсказания соответствующие +/- 2 SEy (т.е. 95% точек данных будут располагаться в пределах этих границ).
В MS EXCEL стандартную ошибку SEy можно вычислить непосредственно по формуле:
= КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))
или с помощью функции ЛИНЕЙН() :
Примечание : Подробнее о функции ЛИНЕЙН() см. эту статью .
Стандартные ошибки и доверительные интервалы для наклона и сдвига
В разделе Оценка неизвестных параметров линейной модели мы получили точечные оценки наклона а и сдвига b . Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со средним значением и дисперсией . Но, чтобы перейти от точечных оценок к интервальным , необходимо вычислить соответствующие стандартные ошибки (т.е. стандартные отклонения ).
Стандартная ошибка коэффициента регрессии a вычисляется на основании стандартной ошибки регрессии по следующей формуле:
где Sx – стандартное отклонение величины х, вычисляемое по формуле:
где Sey – стандартная ошибка регрессии, т.е. ошибка предсказания значения переменой Y ( см. выше ).
В MS EXCEL стандартную ошибку коэффициента регрессии Se можно вычислить впрямую по вышеуказанной формуле:
= КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))/ СТАНДОТКЛОН.В(B23:B83) /КОРЕНЬ(СЧЁТ(B23:B83) -1)
или с помощью функции ЛИНЕЙН() :
Формулы приведены в файле примера на листе Линейный в разделе Регрессионная статистика .
Примечание : Подробнее о функции ЛИНЕЙН() см. эту статью .
При построении двухстороннего доверительного интервала для коэффициента регрессии его границы определяются следующим образом:
где — квантиль распределения Стьюдента с n-2 степенями свободы. Величина а с «крышкой» является другим обозначением наклона а .
Например для уровня значимости альфа=0,05, можно вычислить с помощью формулы =СТЬЮДЕНТ.ОБР.2Х(0,05;n-2)
Вышеуказанная формула следует из того факта, что если ошибки регрессии распределены нормально и независимо, то выборочное распределение случайной величины
является t-распределением Стьюдента с n-2 степенью свободы (то же справедливо и для наклона b ).
Примечание : Подробнее о построении доверительных интервалов в MS EXCEL можно прочитать в этой статье Доверительные интервалы в MS EXCEL .
В результате получим, что найденный доверительный интервал с вероятностью 95% (1-0,05) накроет истинное значение коэффициента регрессии. Здесь мы считаем, что коэффициент регрессии a имеет распределение Стьюдента с n-2 степенями свободы (n – количество наблюдений, т.е. пар Х и Y).
Примечание : Подробнее о построении доверительных интервалов с использованием t-распределения см. статью про построение доверительных интервалов для среднего .
Стандартная ошибка сдвига b вычисляется по следующей формуле:
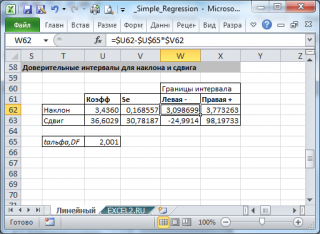
В MS EXCEL стандартную ошибку сдвига Seb можно вычислить с помощью функции ЛИНЕЙН() :
При построении двухстороннего доверительного интервала для сдвига его границы определяются аналогичным образом как для наклона : b +/- t*Seb.
Проверка значимости взаимосвязи переменных
Когда мы строим модель Y=αX+β+ε мы предполагаем, что между Y и X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.
Единственный вариант, когда Y не зависит X (в рамках модели Y=αX+β+ε), возможен, когда коэффициент регрессии a равен 0.
Чтобы убедиться, что вычисленная нами оценка наклона прямой линии не обусловлена лишь случайностью (не случайно отлична от 0), используют проверку гипотез . В качестве нулевой гипотезы Н 0 принимают, что связи нет, т.е. a=0. В качестве альтернативной гипотезы Н 1 принимают, что a <>0.
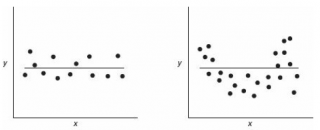
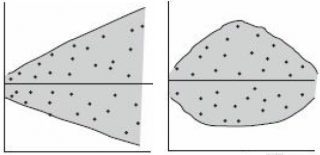
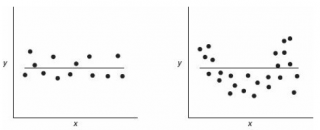
Ниже на рисунках показаны 2 ситуации, когда нулевую гипотезу Н 0 не удается отвергнуть.
На левой картинке отсутствует любая зависимость между переменными, на правой – связь между ними нелинейная, но при этом коэффициент линейной корреляции равен 0.
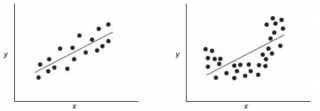
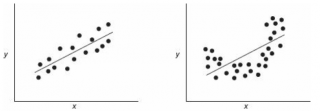
Ниже — 2 ситуации, когда нулевая гипотеза Н 0 отвергается.
На левой картинке очевидна линейная зависимость, на правой — зависимость нелинейная, но коэффициент корреляции не равен 0 (метод МНК вычисляет показатели наклона и сдвига просто на основании значений выборки).
Для проверки гипотезы нам потребуется:
- Установить уровень значимости , пусть альфа=0,05;
- Рассчитать с помощью функции ЛИНЕЙН() стандартное отклонение Se для коэффициента регрессии (см. предыдущий раздел );
- Рассчитать число степеней свободы: DF=n-2 или по формуле = ИНДЕКС(ЛИНЕЙН(C24:C84;B24:B84;;ИСТИНА);4;2)
- Вычислить значение тестовой статистики t 0 =a/S e , которая имеет распределение Стьюдента с числом степеней свободы DF=n-2;
- Сравнить значение тестовой статистики |t0| с пороговым значением t альфа ,n-2. Если значение тестовой статистики больше порогового значения, то нулевая гипотеза отвергается ( наклон не может быть объяснен лишь случайностью при заданном уровне альфа) либо
- вычислить p-значение и сравнить его с уровнем значимости .
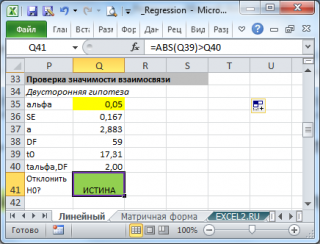
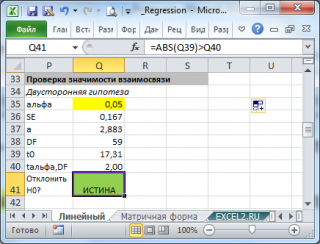
В файле примера приведен пример проверки гипотезы:
Изменяя наклон тренда k (ячейка В8 ) можно убедиться, что при малых углах тренда (например, 0,05) тест часто показывает, что связь между переменными случайна. При больших углах (k>1), тест практически всегда подтверждает значимость линейной связи между переменными.
Примечание : Проверка значимости взаимосвязи эквивалентна проверке статистической значимости коэффициента корреляции . В файле примера показана эквивалентность обоих подходов. Также проверку значимости можно провести с помощью процедуры F-тест .
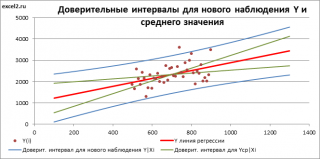
Доверительные интервалы для нового наблюдения Y и среднего значения
Вычислив параметры простой линейной регрессионной модели Y=aX+β+ε мы получили точечную оценку значения нового наблюдения Y при заданном значении Хi, а именно: Ŷ= a * Хi + b
Ŷ также является точечной оценкой для среднего значения Yi при заданном Хi. Но, при построении доверительных интервалов используются различные стандартные ошибки .
Стандартная ошибка нового наблюдения Y при заданном Хi учитывает 2 источника неопределенности:
- неопределенность связанную со случайностью оценок параметров модели a и b ;
- случайность ошибки модели ε.
Учет этих неопределенностей приводит к стандартной ошибке S(Y|Xi), которая рассчитывается с учетом известного значения Xi.
где SS xx – сумма квадратов отклонений от среднего значений переменной Х:
В MS EXCEL 2010 нет функции, которая бы рассчитывала эту стандартную ошибку , поэтому ее необходимо рассчитывать по вышеуказанным формулам.
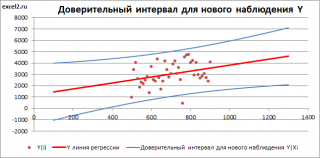
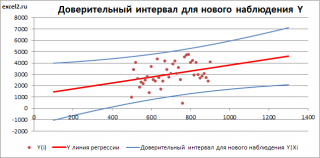
Доверительный интервал или Интервал предсказания для нового наблюдения (Prediction Interval for a New Observation) построим по схеме показанной в разделе Проверка значимости взаимосвязи переменных (см. файл примера лист Интервалы ). Т.к. границы интервала зависят от значения Хi (точнее от расстояния Хi до среднего значения Х ср ), то интервал будет постепенно расширяться при удалении от Х ср .
Границы доверительного интервала для нового наблюдения рассчитываются по формуле:
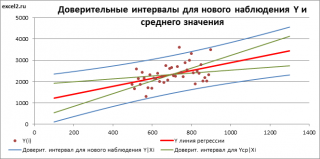
Аналогичным образом построим доверительный интервал для среднего значения Y при заданном Хi (Confidence Interval for the Mean of Y). В этом случае доверительный интервал будет уже, т.к. средние значения имеют меньшую изменчивость по сравнению с отдельными наблюдениями ( средние значения, в рамках нашей линейной модели Y=aX+β+ε, не включают ошибку ε).
Стандартная ошибка S(Yср|Xi) вычисляется по практически аналогичным формулам как и стандартная ошибка для нового наблюдения:
Как видно из формул, стандартная ошибка S(Yср|Xi) меньше стандартной ошибки S(Y|Xi) для индивидуального значения .
Границы доверительного интервала для среднего значения рассчитываются по формуле:
Проверка адекватности линейной регрессионной модели
Модель адекватна, когда все предположения, лежащие в ее основе, выполнены (см. раздел Предположения линейной регрессионной модели ).
Проверка адекватности модели в основном основана на исследовании остатков модели (model residuals), т.е. значений ei=yi – ŷi для каждого Хi. В рамках простой линейной модели n остатков имеют только n-2 связанных с ними степеней свободы . Следовательно, хотя, остатки не являются независимыми величинами, но при достаточно большом n это не оказывает какого-либо влияния на проверку адекватности модели.
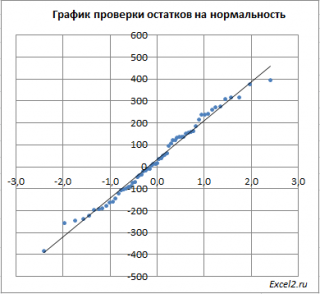
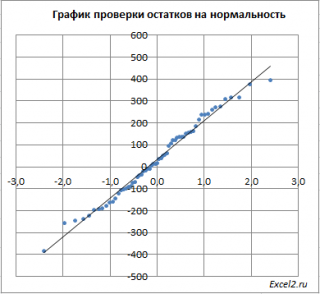
Чтобы проверить предположение о нормальности распределения ошибок строят график проверки на нормальность (Normal probability Plot).
В файле примера на листе Адекватность построен график проверки на нормальность . В случае нормального распределения значения остатков должны быть близки к прямой линии.
Так как значения переменной Y мы генерировали с помощью тренда , вокруг которого значения имели нормальный разброс, то ожидать сюрпризов не приходится – значения остатков располагаются вблизи прямой.
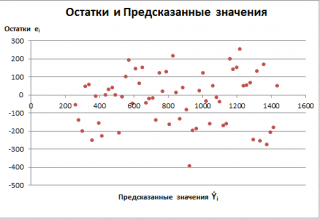
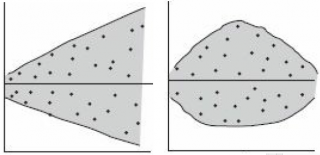
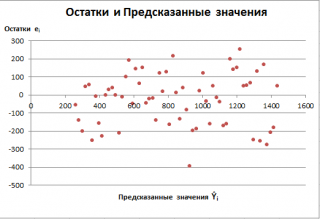
Также при проверке модели на адекватность часто строят график зависимости остатков от предсказанных значений Y. Если точки не демонстрируют характерных, так называемых «паттернов» (шаблонов) типа вор о нок или другого неравномерного распределения, в зависимости от значений Y, то у нас нет очевидных доказательств неадекватности модели.
В нашем случае точки располагаются примерно равномерно.
Часто при проверке адекватности модели вместо остатков используют нормированные остатки. Как показано в разделе Стандартная ошибка регрессии оценкой стандартного отклонения ошибок является величина SEy равная квадратному корню из величины MSE. Поэтому логично нормирование остатков проводить именно на эту величину.
SEy можно вычислить с помощью функции ЛИНЕЙН() :
Иногда нормирование остатков производится на величину стандартного отклонения остатков (это мы увидим в статье об инструменте Регрессия , доступного в надстройке MS EXCEL Пакет анализа ), т.е. по формуле:
Вышеуказанное равенство приблизительное, т.к. среднее значение остатков близко, но не обязательно точно равно 0.
Как построить график в Excel по уравнению
Как предоставить информацию, чтобы она лучше воспринималась. Используйте графики. Это особенно актуально в аналитике. Рассмотрим, как построить график в Excel по уравнению.
Что это такое
График показывает, как одни величины зависят от других. Информация легче воспринимается. Посмотрите визуально, как отображается динамика изменения данных.
А нужно ли это
Графический способ отображения информации востребован в учебных или научных работах, исследованиях, при создании деловых планов, отчетов, презентаций, формул. Разработчики для построения графиков добавили способы визуального представления: диаграммы, пиктограммы.
Как построить график уравнения регрессии в Excel
Регрессионный анализ — статистический метод исследования. Устанавливает, как независимые величины влияют на зависимую переменную. Редактор предлагает инструменты для такого анализа.
Подготовительные работы
Перед использованием функции активируйте Пакет анализа. Перейдите: 
Выберите раздел: 
Далее: 
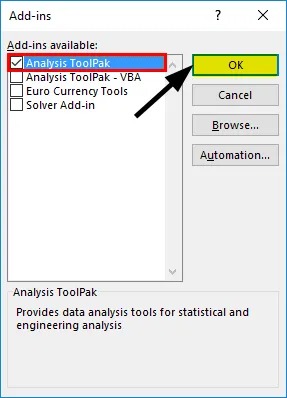
Прокрутите окно вниз, выберите: 
Отметьте пункт: 
Открыв раздел «Данные», появится кнопка «Анализ».
Как пользоваться
Рассмотрим на примере. В таблице указана температура воздуха и число покупателей. Данные выводятся за рабочий день. Как температура влияет на посещаемость. Перейдите: 
Выберите: 
Отобразится окно настроек, где входной интервал:
- Y. Ячейки с данными влияние факторов на которые нужно установить. Это число покупателей. Адрес пропишите вручную или выделите соответствующий столбец;
- Х. Данные, влияние на которые нужно установить. В примере, нужно узнать, как температура влияет на количество покупателей. Поэтому выделяем ячейки в столбце «Температура».
Анализ
Нажав кнопку «ОК», отобразится результат. 
Основной показатель — R-квадрат. Обозначает качество. Он равен 0,825 (82,5%). Что это означает? Зависимости, где показатель меньше 0,5 считается плохим. Поэтому в примере это хороший показатель. Y-пересечение. Число покупателей, если другие показатели равны нулю. 62,02 высокий показатель.
Как построить график квадратного уравнения в Excel
График функции имеет вид: y=ax2+bx+c. Рассмотрим диапазон значений: [-4:4].
- Составьте таблицу как на скриншоте;
- В третьей строке указываем коэффициенты и их значения;
- Пятая — диапазон значений;
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3;


При вычислении формулы прописывается знак «$». Используется чтобы ссылка была постоянной. Подробнее смотрите в статье: «Как зафиксировать ячейку».
Выделите диапазон значений по ним будем строить график. Перейдите: 
Поместите график в свободное место на листе.
Как построить график линейного уравнения
Функция имеет вид: y=kx+b. Построим в интервале [-4;4].
- В таблицу прописываем значение постоянных величин. Строка три;
- Строка 5. Вводим диапазон значений;
- Ячейка В6. Прописываем формулу.


График — прямая линия.
Вывод
Мы рассмотрели, как построить график в Экселе (Excel) по уравнению. Главное — правильно выбрать параметры и диаграмму. Тогда график точно отобразит данные.
источники:
http://excel2.ru/articles/prostaya-lineynaya-regressiya-v-ms-excel
http://public-pc.com/kak-postroit-grafik-v-excel-po-uravneniyu/
Содержание
- Подключение пакета анализа
- Виды регрессионного анализа
- Линейная регрессия в программе Excel
- Разбор результатов анализа
- Вопросы и ответы
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
- Перемещаемся во вкладку «Файл».
- Переходим в раздел «Параметры».
- Открывается окно параметров Excel. Переходим в подраздел «Надстройки».
- В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
- Открывается окно доступных надстроек Эксель. Ставим галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк. В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
- Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».
- Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
- Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».
С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.
После того, как все настройки установлены, жмем на кнопку «OK».
Разбор результатов анализа
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
Линейная регрессия моделирует взаимосвязь между зависимыми y и независимыми x статистическими переменными данных. Другими словами, они выделяют тенденцию между двумя столбцами таблицы в электронной таблице. Например, если вы создали таблицу электронных таблиц Excel со столбцом месяца x и записали набор данных для каждого из месяцев в соседнем столбце y, линейная регрессия выделяет тренд между переменными x и y, добавляя линии тренда к графам таблиц. , Вот как вы можете добавить линейную регрессию в графики Excel.
Добавление линии тренда линейной регрессии на график
Сначала откройте пустую электронную таблицу Excel, выберите ячейку D3 и введите «Месяц» в качестве заголовка столбца, который будет переменной x. Затем щелкните ячейку E3 и введите «Значение Y» в качестве заголовка столбца переменной y. Это в основном таблица с записанным рядом значений данных за месяцы январь-май. Поэтому введите месяцы в ячейки от D4 до D8 и значения данных для них в ячейки от E4 до E8, как показано на снимке непосредственно ниже.
Теперь вы можете настроить график рассеяния для этой таблицы. Выделите все ячейки в таблице с помощью курсора. Нажмите вкладку Вставка и выберите рассеивать > Скаттер только с маркерами добавить график в электронную таблицу, как показано ниже. Кроме того, вы можете нажать горячую клавишу Alt + F1, чтобы вставить гистограмму. Затем вы должны щелкнуть правой кнопкой мыши по графику и выбрать Изменить тип диаграммы > X Y (разброс) > Скаттер только с маркерами,
Затем выберите одну из точек данных на диаграмме рассеяния и щелкните правой кнопкой мыши, чтобы открыть контекстное меню, которое включает Добавить трендлайн вариант. Выбрать Добавить трендлайн чтобы открыть окно, показанное на снимке прямо ниже. Это окно имеет пять вкладок, которые включают различные параметры форматирования для линий тренда линейной регрессии.
Сначала нажмите Параметры линии тренда и выберите тип регрессии оттуда. Вы можете выбрать экспоненциальный, линейный, логарифмический, Скользящая средняя, Сила а также многочлен Варианты типа регрессии оттуда. Выбрать линейный и нажмите близко чтобы добавить эту линию тренда на график, как показано ниже.
Линия тренда регрессии лайнера на приведенном выше графике подчеркивает, что между переменными x и y существует общая восходящая взаимосвязь, несмотря на несколько падений на графике. Обратите внимание, что линия тренда линейной регрессии не перекрывает ни одну из точек данных на графике, поэтому она не совпадает с графиком средней линии, соединяющим каждую точку.
Форматирование линии тренда линейной регрессии
Чтобы отформатировать линию тренда, щелкните ее правой кнопкой мыши и выберите Формат Trendline, Это снова откроет окно Format Trendline, из которого вы можете нажать Цвет линии, Выбрать Сплошная линия и нажмите цвет поле, чтобы открыть палитру, из которой вы можете выбрать альтернативный цвет для линии тренда.
Чтобы настроить стиль линии, перейдите на вкладку «Стиль линии». Затем вы можете настроить ширину стрелки и настроить параметры стрелки. нажмите Настройки стрелки кнопки для добавления стрелок в линию.
Добавьте эффект свечения на линию тренда, нажав пылать а также Мягкие края, Это откроет вкладку ниже, из которой вы можете добавить свечение, нажав на Пресеты кнопка. Затем выберите вариант свечения, чтобы выбрать эффект. щелчок цвет выбрать альтернативные цвета для эффекта, и вы можете перетащить Размер а также прозрачность бары для дальнейшей настройки свечения линии тренда.
Прогнозирование значений с помощью линейной регрессии
После того, как вы отформатировали линию тренда, вы также можете прогнозировать будущие значения с ней. Например, предположим, вам нужно спрогнозировать значение данных через три месяца после мая за август, которое не включено в нашу таблицу. Затем вы можете щелкнуть «Параметры линии тренда» и ввести «3» в текстовом поле «Вперед». Линия тренда линейной регрессии подчеркивает, что значение августа, вероятно, будет чуть выше 3500, как показано ниже.
Каждая линия тренда линейной регрессии имеет свое собственное уравнение и значение квадрата r, которое можно добавить на график. Нажмите на Показать уравнение на графике установите флажок, чтобы добавить уравнение на график. Это уравнение включает в себя значение наклона и перехвата.
Чтобы добавить значение квадрата r на график, щелкните Отображение значения R-квадрата на графике флажок Это добавляет г квадрат на график чуть ниже уравнения, как на снимке ниже. Вы можете перетащить поле уравнения и корреляции, чтобы изменить его положение на графике рассеяния.
Функции линейной регрессии
Excel также включает функции линейной регрессии, с помощью которых вы можете найти значения наклона, точки пересечения и r квадрата для массивов данных y и x. Выберите ячейку электронной таблицы, чтобы добавить одну из этих функций, а затем нажмите Вставить функцию кнопка. Функции линейной регрессии являются статистическими, поэтому выберите статистическая из выпадающего меню категории. Затем вы можете выбрать RSQ, SLOPE или INTERCEPT чтобы открыть их окна функций, как показано ниже.
Окна RSQ, SLOPE и INTERCEPT практически одинаковы. Они включают в себя поля Known_y и Known_x, которые можно выбрать для добавления значений переменных y и x из вашей таблицы. Обратите внимание, что ячейки должны содержать только цифры, поэтому замените месяцы в таблице соответствующими цифрами, такими как 1 для января, 2 для февраля и т. Д. Затем нажмите Хорошо закрыть окно и добавить функцию в электронную таблицу.
Так что теперь вы можете украсить свои графики электронных таблиц Excel линиями тренда линейной регрессии. Они будут выделять общие тенденции для точек данных графиков, а с помощью уравнений регрессии они также являются удобными инструментами прогнозирования.
What Is Linear Regression?
Linear regression is a type of data analysis that considers the linear relationship between a dependent variable and one or more independent variables. It is typically used to visually show the strength of the relationship or correlation between various factors and the dispersion of results – all for the purpose of explaining the behavior of the dependent variable. The goal of a linear regression model is to estimate the magnitude of a relationship between variables and whether or not it is statistically significant.
Say we wanted to test the strength of the relationship between the amount of ice cream eaten and obesity. We would take the independent variable, the amount of ice cream, and relate it to the dependent variable, obesity, to see if there was a relationship. Given a regression is a graphical display of this relationship, the lower the variability in the data, the stronger the relationship and the tighter the fit to the regression line.
In finance, linear regression is used to determine relationships between asset prices and economic data across a range of applications. For instance, it is used to determine the factor weights in the Fama-French Model and is the basis for determining the Beta of a stock in the capital asset pricing model (CAPM).
Here, we look at how to use data imported into Microsoft Excel to perform a linear regression and how to interpret the results.
Key Takeaways
- Linear regression models the relationship between a dependent and independent variable(s).
- Also known as ordinary least squares (OLS), a linear regression essentially estimates a line of best fit among all variables in the model.
- Regression analysis can be considered robust if the variables are independent, there is no heteroscedasticity, and the error terms of variables are not correlated.
- Modeling linear regression in Excel is easier with the Data Analysis ToolPak.
- Regression output can be interpreted for both the size and strength of a correlation among one or more variables on the dependent variable.
Important Considerations
There are a few critical assumptions about your data set that must be true to proceed with a regression analysis. Otherwise, the results will be interpreted incorrectly or they will exhibit bias:
- The variables must be truly independent (using a Chi-square test).
- The data must not have different error variances (this is called heteroskedasticity (also spelled heteroscedasticity)).
- The error terms of each variable must be uncorrelated. If not, it means the variables are serially correlated.
If those three points sound complicated, they can be. But the effect of one of those considerations not being true is a biased estimate. Essentially, you would misstate the relationship you are measuring.
Outputting a Regression in Excel
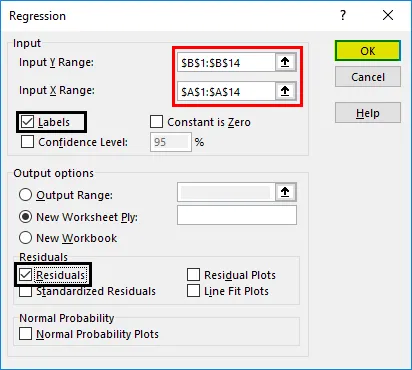
The first step in running regression analysis in Excel is to double-check that the free Excel plugin Data Analysis ToolPak is installed. This plugin makes calculating a range of statistics very easy. It is not required to chart a linear regression line, but it makes creating statistics tables simpler. To verify if installed, select «Data» from the toolbar. If «Data Analysis» is an option, the feature is installed and ready to use. If not installed, you can request this option by clicking on the Office button and selecting «Excel options».
Using the Data Analysis ToolPak, creating a regression output is just a few clicks.
The independent variable in Excel goes in the X range.
Given the S&P 500 returns, say we want to know if we can estimate the strength and relationship of Visa (V) stock returns. The Visa (V) stock returns data populates column 1 as the dependent variable. S&P 500 returns data populates column 2 as the independent variable.
- Select «Data» from the toolbar. The «Data» menu displays.
- Select «Data Analysis». The Data Analysis — Analysis Tools dialog box displays.
- From the menu, select «Regression» and click «OK».
- In the Regression dialog box, click the «Input Y Range» box and select the dependent variable data (Visa (V) stock returns).
- Click the «Input X Range» box and select the independent variable data (S&P 500 returns).
- Click «OK» to run the results.
[Note: If the table seems small, right-click the image and open in new tab for higher resolution.]
Interpret the Results
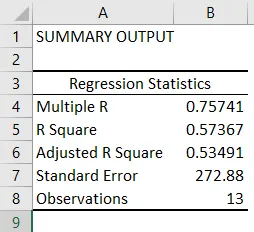
Using that data (the same from our R-squared article), we get the following table:
The R2 value, also known as the coefficient of determination, measures the proportion of variation in the dependent variable explained by the independent variable or how well the regression model fits the data. The R2 value ranges from 0 to 1, and a higher value indicates a better fit. The p-value, or probability value, also ranges from 0 to 1 and indicates if the test is significant. In contrast to the R2 value, a smaller p-value is favorable as it indicates a correlation between the dependent and independent variables.
Interpreting the Results
The bottom line here is that changes in Visa stock seem to be highly correlated with the S&P 500.
- In the regression output above, we can see that for every 1-point change in Visa, there is a corresponding 1.36-point change in the S&P 500.
- We can also see that the p-value is very small (0.000036), which also corresponds to a very large T-test. This indicates that this finding is highly statistically significant, so the odds that this result was caused by chance are exceedingly low.
- From the R-squared, we can see that the V price alone can explain more than 62% of the observed fluctuations in the S&P 500 index.
However, an analyst at this point may heed a bit of caution for the following reasons:
- With only one variable in the model, it is unclear whether V affects the S&P 500 prices, if the S&P 500 affects V prices, or if some unobserved third variable affects both prices.
- Visa is a component of the S&P 500, so there could be a co-correlation between the variables here.
- There are only 20 observations, which may not be enough to make a good inference.
- The data is a time series, so there could also be autocorrelation.
- The time period under study may not be representative of other time periods.
Charting a Regression in Excel
We can chart a regression in Excel by highlighting the data and charting it as a scatter plot. To add a regression line, choose «Add Chart Element» from the «Chart Design» menu. In the dialog box, select «Trendline» and then «Linear Trendline». To add the R2 value, select «More Trendline Options» from the «Trendline menu. Lastly, select «Display R-squared value on chart». The visual result sums up the strength of the relationship, albeit at the expense of not providing as much detail as the table above.
How Do You Interpret a Linear Regression?
The output of a regression model will produce various numerical results. The coefficients (or betas) tell you the association between an independent variable and the dependent variable, holding everything else constant. If the coefficient is, say, +0.12, it tells you that every 1-point change in that variable corresponds with a 0.12 change in the dependent variable in the same direction. If it were instead -3.00, it would mean a 1-point change in the explanatory variable results in a 3x change in the dependent variable, in the opposite direction.
How Do You Know If a Regression Is Significant?
In addition to producing beta coefficients, a regression output will also indicate tests of statistical significance based on the standard error of each coefficient (such as the p-value and confidence intervals). Often, analysts use a p-value of 0.05 or less to indicate significance; if the p-value is greater, then you cannot rule out chance or randomness for the resultant beta coefficient. Other tests of significance in a regression model can be t-tests for each variable, as well as an F-statistic or chi-square for the joint significance of all variables in the model together.
How Do You Interpret the R-Squared of a Linear Regression?
R2 (R-squared) is a statistical measure of the goodness of fit of a linear regression model (from 0.00 to 1.00), also known as the coefficient of determination. In general, the higher the R2, the better the model’s fit. The R-squared can also be interpreted as how much of the variation in the dependent variable is explained by the independent (explanatory) variables in the model. Thus, an R-square of 0.50 suggests that half of all of the variation observed in the dependent variable can be explained by the dependent variable(s).
Регрессия позволяет прогнозировать зависимую переменную на основании значений фактора. В
MS
EXCEL
имеется множество функций, которые возвращают не только наклон и сдвиг линии регрессии, характеризующей линейную взаимосвязь между факторами, но и регрессионную статистику. Здесь рассмотрим простую линейную регрессию, т.е. прогнозирование на основе одного фактора.
Disclaimer
: Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей
Регрессионного анализа.
Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения
Регрессии
– плохая идея.
Статья про
Регрессионный анализ
получилась большая, поэтому ниже для удобства приведены ее разделы:
- Немного теории и основные понятия
- Предположения линейной регрессионной модели
- Задачи регрессионного анализа
- Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)
- Оценка неизвестных параметров линейной модели (через статистики выборок)
- Оценка неизвестных параметров линейной модели (матричная форма)
- Построение линии регрессии
- Коэффициент детерминации
- Стандартная ошибка регрессии
- Стандартные ошибки и доверительные интервалы для наклона и сдвига
- Проверка значимости взаимосвязи переменных
- Доверительные интервалы для нового наблюдения Y и среднего значения
- Проверка адекватности линейной регрессионной модели
Примечание
: Если прогнозирование переменной осуществляется на основе нескольких факторов, то имеет место
множественная регрессия
.
Чтобы разобраться, чем может помочь MS EXCEL при проведении регрессионного анализа, напомним вкратце теорию, введем термины и обозначения, которые могут отличаться в зависимости от различных источников.
Примечание
: Для тех, кому некогда, незачем или просто не хочется разбираться в теоретических выкладках предлагается сразу перейти к вычислительной части —
оценке неизвестных параметров линейной модели
.
Немного теории и основные понятия
Пусть у нас есть массив данных, представляющий собой значения двух переменных Х и Y. Причем значения переменной Х мы можем произвольно задавать (контролировать) и использовать эту переменную для предсказания значений зависимой переменной Y. Таким образом, случайной величиной является только переменная Y.
Примером такой задачи может быть производственный процесс изготовления некого волокна, причем
прочность этого волокна
(Y) зависит только от
рабочей температуры процесса
в реакторе (Х), которая задается оператором.
Построим
диаграмму рассеяния
(см.
файл примера лист Линейный
), созданию которой
посвящена отдельная статья
. Вообще, построение
диаграммы рассеяния
для целей
регрессионного анализа
де-факто является стандартом.
СОВЕТ
: Подробнее о построении различных типов диаграмм см. статьи
Основы построения диаграмм
и
Основные типы диаграмм
.
Приведенная выше
диаграмма рассеяния
свидетельствует о возможной
линейной взаимосвязи
между Y от Х: очевидно, что точки данных в основном располагаются вдоль прямой линии.
Примечание
: Наличие даже такой очевидной
линейной взаимосвязи
не может являться доказательством о наличии причинной взаимосвязи переменных. Наличие
причинной
взаимосвязи не может быть доказано на основании только анализа имеющихся измерений, а должно быть обосновано с помощью других исследований, например теоретических выкладок.
Примечание
: Как известно, уравнение прямой линии имеет вид
Y
=
m
*
X
+
k
, где коэффициент
m
отвечает за наклон линии (
slope
),
k
– за сдвиг линии по вертикали (
intercept
),
k
равно значению Y при Х=0.
Предположим, что мы можем зафиксировать переменную Х (
рабочую температуру процесса
) при некотором значении Х
i
и произвести несколько наблюдений переменной Y (
прочность нити
). Очевидно, что при одном и том же значении Хi мы получим различные значения Y. Это обусловлено влиянием других факторов на Y. Например, локальные колебания давления в реакторе, концентрации раствора, наличие ошибок измерения и др. Предполагается, что воздействие этих факторов имеет случайную природу и для каждого измерения имеются одинаковые условия проведения эксперимента (т.е. другие факторы не изменяются).
Полученные значения Y, при заданном Хi, будут колебаться вокруг некого
значения
. При увеличении количества измерений, среднее этих измерений, будет стремиться к
математическому ожиданию
случайной величины Y (при Х
i
) равному μy(i)=Е(Y
i
).
Подобные рассуждения можно привести для любого значения Хi.
Чтобы двинуться дальше, воспользуемся материалом из раздела
Проверка статистических гипотез
. В статье о
проверке гипотезы о среднем значении генеральной совокупности
в качестве
нулевой
гипотезы
предполагалось равенство неизвестного значения μ заданному μ0.
В нашем случае
простой линейной регрессии
в качестве
нулевой
гипотезы
предположим, что между переменными μy(i) и Хi существует линейная взаимосвязь μ
y(i)
=α* Х
i
+β. Уравнение μ
y(i)
=α* Х
i
+β можно переписать в обобщенном виде (для всех Х и μ
y
) как μ
y
=α* Х +β.
Для наглядности проведем прямую линию соединяющую все μy(i).
Данная линия называется
регрессионной линией генеральной совокупности
(population regression line), параметры которой (
наклон
a и
сдвиг β
) нам не известны (по аналогии с
гипотезой о среднем значении генеральной совокупности
, где нам было неизвестно истинное значение μ).
Теперь сделаем переход от нашего предположения, что μy=a* Х +
β
, к предсказанию значения случайной переменной Y в зависимости от значения контролируемой переменной Х. Для этого уравнение связи двух переменных запишем в виде Y=a*X+β+ε, где ε — случайная ошибка, которая отражает суммарный эффект влияния других факторов на Y (эти «другие» факторы не участвуют в нашей модели). Напомним, что т.к. переменная Х фиксирована, то ошибка ε определяется только свойствами переменной Y.
Уравнение Y=a*X+b+ε называют
линейной регрессионной моделью
. Часто Х еще называют
независимой переменной
(еще
предиктором
и
регрессором
, английский термин
predictor
,
regressor
), а Y –
зависимой
(или
объясняемой
,
response
variable
). Так как
регрессор
у нас один, то такая модель называется
простой линейной регрессионной моделью
(
simple
linear
regression
model
). α часто называют
коэффициентом регрессии.
Предположения линейной регрессионной модели перечислены в следующем разделе.
Предположения линейной регрессионной модели
Чтобы модель линейной регрессии Yi=a*Xi+β+ε
i
была адекватной — требуется:
-
Ошибки ε
i
должны быть независимыми переменными; -
При каждом значении Xi ошибки ε
i
должны быть иметь нормальное распределение (также предполагается равенство нулю математического ожидания, т.е. Е[ε
i
]=0); -
При каждом значении Xi ошибки ε
i
должны иметь равные дисперсии (обозначим ее σ
2
).
Примечание
: Последнее условие называется
гомоскедастичность
— стабильность, гомогенность дисперсии случайной ошибки e. Т.е.
дисперсия
ошибки σ
2
не должна зависеть от значения Xi.
Используя предположение о равенстве математического ожидания Е[ε
i
]=0 покажем, что μy(i)=Е[Yi]:
Е[Yi]= Е[a*Xi+β+ε
i
]= Е[a*Xi+β]+ Е[ε
i
]= a*Xi+β= μy(i), т.к. a, Xi и β постоянные значения.
Дисперсия
случайной переменной Y равна
дисперсии
ошибки ε, т.е. VAR(Y)= VAR(ε)=σ
2
. Это является следствием, что все значения переменной Х являются const, а VAR(ε)=VAR(ε
i
).
Задачи регрессионного анализа
Для проверки гипотезы о линейной взаимосвязи переменной Y от X делают выборку из генеральной совокупности (этой совокупности соответствует
регрессионная линия генеральной совокупности
, т.е. μy=a* Х +β). Выборка будет состоять из n точек, т.е. из n пар значений {X;Y}.
На основании этой выборки мы можем вычислить оценки наклона a и сдвига β, которые обозначим соответственно
a
и
b
. Также часто используются обозначения â и b̂.
Далее, используя эти оценки, мы также можем проверить гипотезу: имеется ли линейная связь между X и Y статистически значимой?
Таким образом:
Первая задача
регрессионного анализа
– оценка неизвестных параметров (
estimation
of
the
unknown
parameters
). Подробнее см. раздел
Оценки неизвестных параметров модели
.
Вторая задача
регрессионного анализа
–
Проверка адекватности модели
(
model
adequacy
checking
).
Примечание
: Оценки параметров модели обычно вычисляются
методом наименьших квадратов
(МНК),
которому посвящена отдельная статья
.
Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)
Неизвестные параметры
простой линейной регрессионной модели
Y=a*X+β+ε оценим с помощью
метода наименьших квадратов
(в
статье про МНК подробно описано этот метод
).
Для вычисления параметров линейной модели методом МНК получены следующие выражения:
Таким образом, мы получим уравнение прямой линии Y=
a
*X+
b
, которая наилучшим образом аппроксимирует имеющиеся данные.
Примечание
: В статье про
метод наименьших квадратов
рассмотрены случаи аппроксимации
линейной
и
квадратичной функцией
, а также
степенной
,
логарифмической
и
экспоненциальной функцией
.
Оценку параметров в MS EXCEL можно выполнить различными способами:
-
с помощью функций
НАКЛОН()
и
ОТРЕЗОК()
; -
с помощью функции
ЛИНЕЙН()
; см. статьюФункция MS EXCEL ЛИНЕЙН()
-
формулами через статистики выборок
;
-
в матричной форме
;
-
с помощью
инструмента Регрессия надстройки Пакет Анализа
.
Сначала рассмотрим функции
НАКЛОН()
,
ОТРЕЗОК()
и
ЛИНЕЙН()
.
Пусть значения Х и Y находятся соответственно в диапазонах
C
23:
C
83
и
B
23:
B
83
(см.
файл примера
внизу статьи).
Примечание
: Значения двух переменных Х и Y можно сгенерировать, задав тренд и величину случайного разброса (см. статью
Генерация данных для линейной регрессии в MS EXCEL
).
В MS EXCEL наклон прямой линии
а
(
оценку
коэффициента регрессии
), можно найти по
методу МНК
с помощью функции
НАКЛОН()
, а сдвиг
b
(
оценку
постоянного члена
или
константы регрессии
), с помощью функции
ОТРЕЗОК()
. В английской версии это функции SLOPE и INTERCEPT соответственно.
Аналогичный результат можно получить с помощью функции
ЛИНЕЙН()
, английская версия LINEST (см.
статью об этой функции
).
Формула
=ЛИНЕЙН(C23:C83;B23:B83)
вернет наклон
а
. А формула =
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2)
— сдвиг
b
. Здесь требуются пояснения.
Функция
ЛИНЕЙН()
имеет 4 аргумента и возвращает целый массив значений:
ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Если 4-й аргумент
статистика
имеет значение ЛОЖЬ или опущен, то функция
ЛИНЕЙН()
возвращает только оценки параметров модели:
a
и
b
.
Примечание
: Остальные значения, возвращаемые функцией
ЛИНЕЙН()
, нам потребуются при вычислении
стандартных ошибок
и для
проверки значимости регрессии
. В этом случае аргумент
статистика
должен иметь значение ИСТИНА.
Чтобы вывести сразу обе оценки:
- в одной строке необходимо выделить 2 ячейки,
-
ввести формулу в
Строке формул
-
нажать
CTRL
+
SHIFT
+
ENTER
(см. статью проформулы массива
).
Если в
Строке формул
выделить формулу =
ЛИНЕЙН(C23:C83;B23:B83)
и нажать
клавишу F9
, то мы увидим что-то типа {3,01279389265416;154,240057900613}. Это как раз значения
a
и
b
. Как видно, оба значения разделены точкой с запятой «;», что свидетельствует, что функция вернула значения «в нескольких ячейках одной строки».
Если требуется вывести параметры линии не в одной строке, а одном столбце (ячейки друг под другом), то используйте формулу =
ТРАНСП(ЛИНЕЙН(C23:C83;B23:B83))
. При этом выделять нужно 2 ячейки в одном столбце. Если теперь выделить новую формулу и нажать клавишу F9, то мы увидим что 2 значения разделены двоеточием «:», что означает, что значения выведены в столбец (функция
ТРАНСП()
транспонировала строку в столбец
).
Чтобы разобраться в этом подробнее необходимо ознакомиться с
формулами массива
.
Чтобы не связываться с вводом
формул массива
, можно
использовать функцию ИНДЕКС()
. Формула =
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1)
или просто
ЛИНЕЙН(C23:C83;B23:B83)
вернет параметр, отвечающий за наклон линии, т.е.
а
. Формула
=ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2)
вернет параметр
b
.
Оценка неизвестных параметров линейной модели (через статистики выборок)
Наклон линии, т.е. коэффициент
а
, можно также вычислить через
коэффициент корреляции
и
стандартные отклонения выборок
:
=
КОРРЕЛ(B23:B83;C23:C83) *(СТАНДОТКЛОН.В(C23:C83)/ СТАНДОТКЛОН.В(B23:B83))
Вышеуказанная формула математически эквивалентна отношению
ковариации
выборок Х и Y и
дисперсии
выборки Х:
=
КОВАРИАЦИЯ.В(B23:B83;C23:C83)/ДИСП.В(B23:B83)
И, наконец, запишем еще одну формулу для нахождения сдвига
b
. Воспользуемся тем фактом, что
линия регрессии
проходит через точку
средних значений
переменных Х и Y.
Вычислив
средние значения
и подставив в формулу ранее найденный наклон
а
, получим сдвиг
b
.
Оценка неизвестных параметров линейной модели (матричная форма)
Также параметры
линии регрессии
можно найти в матричной форме (см.
файл примера лист Матричная форма
).
В формуле символом β обозначен столбец с искомыми параметрами модели: β0 (сдвиг
b
), β1 (наклон
a
).
Матрица Х равна:
Матрица
Х
называется
регрессионной матрицей
или
матрицей плана
. Она состоит из 2-х столбцов и n строк, где n – количество точек данных. Первый столбец — столбец единиц, второй – значения переменной Х.
Матрица
Х
T
– это
транспонированная матрица
Х
. Она состоит соответственно из n столбцов и 2-х строк.
В формуле символом
Y
обозначен столбец значений переменной Y.
Чтобы
перемножить матрицы
используйте функцию
МУМНОЖ()
. Чтобы
найти обратную матрицу
используйте функцию
МОБР()
.
Пусть дан массив значений переменных Х и Y (n=10, т.е.10 точек).
Слева от него достроим столбец с 1 для матрицы Х.
Записав формулу
=
МУМНОЖ(МОБР(МУМНОЖ(ТРАНСП(B7:C16);(B7:C16))); МУМНОЖ(ТРАНСП(B7:C16);(D7:D16)))
и введя ее как
формулу массива
в 2 ячейки, получим оценку параметров модели.
Красота применения матричной формы полностью раскрывается в случае
множественной регрессии
.
Построение линии регрессии
Для отображения
линии регрессии
построим сначала
диаграмму рассеяния
, на которой отобразим все точки (см.
начало статьи
).
Для построения прямой линии используйте вычисленные выше оценки параметров модели
a
и
b
(т.е. вычислите
у
по формуле
y
=
a
*
x
+
b
) или функцию
ТЕНДЕНЦИЯ()
.
Формула =
ТЕНДЕНЦИЯ($C$23:$C$83;$B$23:$B$83;B23)
возвращает расчетные (прогнозные) значения ŷi для заданного значения Хi из столбца
В2
.
Примечание
:
Линию регрессии
можно также построить с помощью функции
ПРЕДСКАЗ()
. Эта функция возвращает прогнозные значения ŷi, но, в отличие от функции
ТЕНДЕНЦИЯ()
работает только в случае одного регрессора. Функция
ТЕНДЕНЦИЯ()
может быть использована и в случае
множественной регрессии
(в этом случае 3-й аргумент функции должен быть ссылкой на диапазон, содержащий все значения Хi для выбранного наблюдения i).
Как видно из диаграммы выше
линия тренда
и
линия регрессии
не обязательно совпадают: отклонения точек от
линии тренда
случайны, а МНК лишь подбирает линию наиболее точно аппроксимирующую случайные точки данных.
Линию регрессии
можно построить и с помощью встроенных средств диаграммы, т.е. с помощью инструмента
Линия тренда.
Для этого выделите диаграмму, в меню выберите
вкладку Макет
, в
группе Анализ
нажмите
Линия тренда
, затем
Линейное приближение.
В диалоговом окне установите галочку
Показывать уравнение на диаграмме
(подробнее см. в
статье про МНК
).
Построенная таким образом линия, разумеется, должна совпасть с ранее построенной нами
линией регрессии,
а параметры уравнения
a
и
b
должны совпасть с параметрами уравнения отображенными на диаграмме.
Примечание:
Для того, чтобы вычисленные параметры уравнения
a
и
b
совпадали с параметрами уравнения на диаграмме, необходимо, чтобы тип у диаграммы был
Точечная, а не График
, т.к. тип диаграммы
График
не использует значения Х, а вместо значений Х используется последовательность 1; 2; 3; … Именно эти значения и берутся при расчете параметров
линии тренда
. Убедиться в этом можно если построить диаграмму
График
(см.
файл примера
), а значения
Хнач
и
Хшаг
установить равным 1. Только в этом случае параметры уравнения на диаграмме совпадут с
a
и
b
.
Коэффициент детерминации R
2
Коэффициент детерминации
R
2
показывает насколько полезна построенная нами
линейная регрессионная модель
.
Предположим, что у нас есть n значений переменной Y и мы хотим предсказать значение yi, но без использования значений переменной Х (т.е. без построения
регрессионной модели
). Очевидно, что лучшей оценкой для yi будет
среднее значение
ȳ. Соответственно, ошибка предсказания будет равна (yi — ȳ).
Примечание
: Далее будет использована терминология и обозначения
дисперсионного анализа
.
После построения
регрессионной модели
для предсказания значения yi мы будем использовать значение ŷi=a*xi+b. Ошибка предсказания теперь будет равна (yi — ŷi).
Теперь с помощью диаграммы сравним ошибки предсказания полученные без построения модели и с помощью модели.
Очевидно, что используя
регрессионную модель
мы уменьшили первоначальную (полную) ошибку (yi — ȳ) на значение (ŷi — ȳ) до величины (yi — ŷi).
(yi — ŷi) – это оставшаяся, необъясненная ошибка.
Очевидно, что все три ошибки связаны выражением:
(yi — ȳ)= (ŷi — ȳ) + (yi — ŷi)
Можно показать, что в общем виде справедливо следующее выражение:
Доказательство:
или в других, общепринятых в зарубежной литературе, обозначениях:
SST
=
SSR
+
SSE
Что означает:
Total Sum of Squares
=
Regression Sum of Squares
+
Error Sum of Squares
Примечание
: SS — Sum of Squares — Сумма Квадратов.
Как видно из формулы величины SST, SSR, SSE имеют размерность
дисперсии
(вариации) и соответственно описывают разброс (изменчивость):
Общую изменчивость
(Total variation),
Изменчивость объясненную моделью
(Explained variation) и
Необъясненную изменчивость
(Unexplained variation).
По определению
коэффициент детерминации
R
2
равен:
R
2
=
Изменчивость объясненная моделью / Общая изменчивость.
Этот показатель равен квадрату
коэффициента корреляции
и в MS EXCEL его можно вычислить с помощью функции
КВПИРСОН()
или
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3)
R
2
принимает значения от 0 до 1 (1 соответствует идеальной линейной зависимости Y от Х). Однако, на практике малые значения R2 вовсе не обязательно указывают, что переменную Х нельзя использовать для прогнозирования переменной Y. Малые значения R2 могут указывать на нелинейность связи или на то, что поведение переменной Y объясняется не только Х, но и другими факторами.
Стандартная ошибка регрессии
Стандартная ошибка регрессии
(
Standard Error of a regression
) показывает насколько велика ошибка предсказания значений переменной Y на основании значений Х. Отдельные значения Yi мы можем предсказывать лишь с точностью +/- несколько значений (обычно 2-3, в зависимости от формы распределения ошибки ε).
Теперь вспомним уравнение
линейной регрессионной модели
Y=a*X+β+ε. Ошибка ε имеет случайную природу, т.е. является случайной величиной и поэтому имеет свою функцию распределения со
средним значением
μ и
дисперсией
σ
2
.
Оценив значение
дисперсии
σ
2
и вычислив из нее квадратный корень – получим
Стандартную ошибку регрессии.
Чем точки наблюдений на диаграмме
рассеяния
ближе находятся к прямой линии, тем меньше
Стандартная ошибка.
Примечание
:
Вспомним
, что при построении модели предполагается, что
среднее значение
ошибки ε равно 0, т.е. E[ε]=0.
Оценим
дисперсию σ
2
. Помимо вычисления
Стандартной ошибки регрессии
эта оценка нам потребуется в дальнейшем еще и при построении
доверительных интервалов
для оценки параметров регрессии
a
и
b
.
Для оценки
дисперсии
ошибки ε используем
остатки регрессии
— разности между имеющимися значениями
yi
и значениями, предсказанными регрессионной моделью ŷ. Чем лучше регрессионная модель согласуется с данными (точки располагается близко к прямой линии), тем меньше величина остатков.
Для оценки
дисперсии σ
2
используют следующую формулу:
где SSE – сумма квадратов значений ошибок модели ε
i
=yi — ŷi (
Sum of Squared Errors
).
SSE часто обозначают и как SSres – сумма квадратов остатков (
Sum
of
Squared
residuals
).
Оценка
дисперсии
s
2
также имеет общепринятое обозначение MSE (Mean Square of Errors), т.е. среднее квадратов
ошибок
или MSRES (Mean Square of Residuals), т.е. среднее квадратов
остатков
. Хотя правильнее говорить сумме квадратов остатков, т.к. ошибка чаще ассоциируется с ошибкой модели ε, которая является непрерывной случайной величиной. Но, здесь мы будем использовать термины SSE и MSE, предполагая, что речь идет об остатках.
Примечание
: Напомним, что когда
мы использовали МНК
для нахождения параметров модели, то критерием оптимизации была минимизация именно SSE (SSres). Это выражение представляет собой сумму квадратов расстояний между наблюденными значениями yi и предсказанными моделью значениями ŷi, которые лежат на
линии регрессии.
Математическое ожидание
случайной величины MSE равно
дисперсии ошибки
ε, т.е.
σ
2
.
Чтобы понять почему SSE выбрана в качестве основы для оценки
дисперсии
ошибки ε, вспомним, что
σ
2
является также
дисперсией
случайной величины Y (относительно
среднего значения
μy, при заданном значении Хi). А т.к. оценкой μy является значение ŷi =
a
* Хi +
b
(значение
уравнения регрессии
при Х= Хi), то логично использовать именно SSE в качестве основы для оценки
дисперсии
σ
2
. Затем SSE усредняется на количество точек данных n за вычетом числа 2. Величина n-2 – это количество
степеней свободы
(
df
–
degrees
of
freedom
), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y). В случае
простой линейной регрессии
число степеней свободы
равно n-2, т.к. при построении
линии регрессии
было оценено 2 параметра модели (на это было «потрачено» 2
степени свободы
).
Итак, как сказано было выше, квадратный корень из s
2
имеет специальное название
Стандартная ошибка регрессии
(
Standard Error of a regression
) и обозначается SEy. SEy показывает насколько велика ошибка предсказания. Отдельные значения Y мы можем предсказывать с точностью +/- несколько значений SEy (см.
этот раздел
). Если ошибки предсказания ε имеют
нормальное распределение
, то примерно 2/3 всех предсказанных значений будут на расстоянии не больше SEy от
линии регрессии
. SEy имеет размерность переменной Y и откладывается по вертикали. Часто на
диаграмме рассеяния
строят
границы предсказания
соответствующие +/- 2 SEy (т.е. 95% точек данных будут располагаться в пределах этих границ).
В MS EXCEL
стандартную ошибку
SEy можно вычислить непосредственно по формуле:
=
КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))
или с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3;2)
Примечание
: Подробнее о функции
ЛИНЕЙН()
см.
эту статью
.
Стандартные ошибки и доверительные интервалы для наклона и сдвига
В разделе
Оценка неизвестных параметров линейной модели
мы получили точечные оценки наклона
а
и сдвига
b
. Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со
средним значением
и
дисперсией
. Но, чтобы перейти от
точечных оценок
к
интервальным
, необходимо вычислить соответствующие
стандартные ошибки
(т.е.
стандартные отклонения
).
Стандартная ошибка коэффициента регрессии
a
вычисляется на основании
стандартной ошибки регрессии
по следующей формуле:
где Sx – стандартное отклонение величины х, вычисляемое по формуле:
где Sey –
стандартная ошибка регрессии,
т.е. ошибка предсказания значения переменой Y
(
см. выше
).
В MS EXCEL
стандартную ошибку коэффициента регрессии
Se можно вычислить впрямую по вышеуказанной формуле:
=
КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))/ СТАНДОТКЛОН.В(B23:B83) /КОРЕНЬ(СЧЁТ(B23:B83) -1)
или с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);2;1)
Формулы приведены в
файле примера на листе Линейный
в разделе
Регрессионная статистика
.
Примечание
: Подробнее о функции
ЛИНЕЙН()
см.
эту статью
.
При построении
двухстороннего доверительного интервала
для
коэффициента регрессии
его границы определяются следующим образом:
где —
квантиль распределения Стьюдента
с n-2 степенями свободы. Величина
а
с «крышкой» является другим обозначением
наклона
а
.
Например для
уровня значимости
альфа=0,05, можно вычислить с помощью формулы
=СТЬЮДЕНТ.ОБР.2Х(0,05;n-2)
Вышеуказанная формула следует из того факта, что если ошибки регрессии распределены нормально и независимо, то выборочное распределение случайной величины
является
t-распределением Стьюдента
с n-2 степенью свободы (то же справедливо и для наклона
b
).
Примечание
: Подробнее о построении
доверительных интервалов
в MS EXCEL можно прочитать в этой статье
Доверительные интервалы в MS EXCEL
.
В результате получим, что найденный
доверительный интервал
с вероятностью 95% (1-0,05) накроет истинное значение
коэффициента регрессии.
Здесь мы считаем, что
коэффициент регрессии
a
имеет
распределение Стьюдента
с n-2
степенями свободы
(n – количество наблюдений, т.е. пар Х и Y).
Примечание
: Подробнее о построении
доверительных интервалов
с использованием t-распределения см. статью про построение
доверительных интервалов
для среднего
.
Стандартная ошибка сдвига
b
вычисляется по следующей формуле:
В MS EXCEL
стандартную ошибку сдвига
Seb можно вычислить с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);2;2)
При построении
двухстороннего доверительного интервала
для
сдвига
его границы определяются аналогичным образом как для
наклона
:
b
+/- t*Seb.
Проверка значимости взаимосвязи переменных
Когда мы строим модель Y=αX+β+ε мы предполагаем, что между Y и X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.
Единственный вариант, когда Y не зависит X (в рамках модели Y=αX+β+ε), возможен, когда
коэффициент регрессии
a
равен 0.
Чтобы убедиться, что вычисленная нами оценка
наклона
прямой линии не обусловлена лишь случайностью (не случайно отлична от 0), используют
проверку гипотез
. В качестве
нулевой гипотезы
Н
0
принимают, что связи нет, т.е. a=0. В качестве альтернативной гипотезы
Н
1
принимают, что a <>0.
Ниже на рисунках показаны 2 ситуации, когда
нулевую гипотезу
Н
0
не удается отвергнуть.
На левой картинке отсутствует любая зависимость между переменными, на правой – связь между ними нелинейная, но при этом
коэффициент линейной корреляции
равен 0.
Ниже — 2 ситуации, когда
нулевая гипотеза
Н
0
отвергается.
На левой картинке очевидна линейная зависимость, на правой — зависимость нелинейная, но коэффициент корреляции не равен 0 (метод МНК вычисляет показатели наклона и сдвига просто на основании значений выборки).
Для проверки гипотезы нам потребуется:
-
Установить
уровень значимости
, пусть альфа=0,05;
-
Рассчитать с помощью функции
ЛИНЕЙН()
стандартное отклонение
Se для
коэффициента регрессии
(см.предыдущий раздел
);
-
Рассчитать число степеней свободы: DF=n-2 или по формуле =
ИНДЕКС(ЛИНЕЙН(C24:C84;B24:B84;;ИСТИНА);4;2)
-
Вычислить значение тестовой статистики t
0
=a/S
e
, которая имеетраспределение Стьюдента
с
числом степеней свободы
DF=n-2; -
Сравнить значение
тестовой статистики
|t0| с пороговым значением t
альфа
,n-2. Если значение
тестовой статистики
больше порогового значения, то
нулевая гипотеза
отвергается (
наклон
не может быть объяснен лишь случайностью при заданном уровне альфа) либо -
вычислить
p-значение
и сравнить его с
уровнем значимости
.
В
файле примера
приведен пример проверки гипотезы:
Изменяя
наклон
тренда k (ячейка
В8
) можно убедиться, что при малых углах тренда (например, 0,05) тест часто показывает, что связь между переменными случайна. При больших углах (k>1), тест практически всегда подтверждает значимость линейной связи между переменными.
Примечание
: Проверка значимости взаимосвязи эквивалентна
проверке статистической значимости коэффициента корреляции
. В
файле примера
показана эквивалентность обоих подходов. Также проверку значимости можно провести с помощью
процедуры F-тест
.
Доверительные интервалы для нового наблюдения Y и среднего значения
Вычислив параметры
простой линейной регрессионной модели
Y=aX+β+ε мы получили точечную оценку значения нового наблюдения Y при заданном значении Хi, а именно: Ŷ=
a
* Хi +
b
Ŷ также является точечной оценкой для
среднего значения
Yi при заданном Хi. Но, при построении
доверительных интервалов
используются различные
стандартные ошибки
.
Стандартная ошибка
нового наблюдения Y при заданном Хi учитывает 2 источника неопределенности:
-
неопределенность связанную со случайностью оценок параметров модели
a
и
b
; - случайность ошибки модели ε.
Учет этих неопределенностей приводит к
стандартной ошибке
S(Y|Xi), которая рассчитывается с учетом известного значения Xi.
где SS
xx
– сумма квадратов отклонений от
среднего
значений переменной Х:
Примечание
: Se –
стандартная ошибка коэффициента регрессии
(
наклона
а
).
В
MS EXCEL 2010
нет функции, которая бы рассчитывала эту
стандартную ошибку
, поэтому ее необходимо рассчитывать по вышеуказанным формулам.
Доверительный интервал
или
Интервал предсказания для нового наблюдения
(Prediction Interval for a New Observation) построим по схеме показанной в разделе
Проверка значимости взаимосвязи переменных
(см.
файл примера лист Интервалы
). Т.к. границы интервала зависят от значения Хi (точнее от расстояния Хi до среднего значения Х
ср
), то интервал будет постепенно расширяться при удалении от Х
ср
.
Границы
доверительного интервала
для
нового наблюдения
рассчитываются по формуле:
Аналогичным образом построим
доверительный интервал
для
среднего значения
Y при заданном Хi (Confidence Interval for the Mean of Y). В этом случае
доверительный интервал
будет уже, т.к.
средние значения
имеют меньшую изменчивость по сравнению с отдельными наблюдениями (
средние значения,
в рамках нашей линейной модели Y=aX+β+ε, не включают ошибку ε).
Стандартная ошибка
S(Yср|Xi) вычисляется по практически аналогичным формулам как и
стандартная ошибка
для нового наблюдения:
Как видно из формул,
стандартная ошибка
S(Yср|Xi) меньше
стандартной ошибки
S(Y|Xi) для индивидуального значения
.
Границы
доверительного интервала
для
среднего значения
рассчитываются по формуле:
Проверка адекватности линейной регрессионной модели
Модель адекватна, когда все предположения, лежащие в ее основе, выполнены (см. раздел
Предположения линейной регрессионной модели
).
Проверка адекватности модели в основном основана на исследовании остатков модели (model residuals), т.е. значений ei=yi – ŷi для каждого Хi. В рамках
простой линейной модели
n остатков имеют только n-2 связанных с ними
степеней свободы
. Следовательно, хотя, остатки не являются независимыми величинами, но при достаточно большом n это не оказывает какого-либо влияния на проверку адекватности модели.
Чтобы проверить предположение о
нормальности распределения
ошибок строят
график проверки на нормальность
(Normal probability Plot).
В
файле примера на листе Адекватность
построен
график проверки на нормальность
. В случае
нормального распределения
значения остатков должны быть близки к прямой линии.
Так как значения переменной Y мы
генерировали с помощью тренда
, вокруг которого значения имели нормальный разброс, то ожидать сюрпризов не приходится – значения остатков располагаются вблизи прямой.
Также при проверке модели на адекватность часто строят график зависимости остатков от предсказанных значений Y. Если точки не демонстрируют характерных, так называемых «паттернов» (шаблонов) типа вор
о
нок или другого неравномерного распределения, в зависимости от значений Y, то у нас нет очевидных доказательств неадекватности модели.
В нашем случае точки располагаются примерно равномерно.
Часто при проверке адекватности модели вместо остатков используют нормированные остатки. Как показано в разделе
Стандартная ошибка регрессии
оценкой
стандартного отклонения ошибок
является величина SEy равная квадратному корню из величины MSE. Поэтому логично нормирование остатков проводить именно на эту величину.
SEy можно вычислить с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3;2)
Иногда нормирование остатков производится на величину
стандартного отклонения
остатков (это мы увидим в статье об инструменте
Регрессия
, доступного в
надстройке MS EXCEL Пакет анализа
), т.е. по формуле:
Вышеуказанное равенство приблизительное, т.к. среднее значение остатков близко, но не обязательно точно равно 0.
Что объясняет регрессия?
Прежде, чем мы приступим к рассмотрению функций MS Excel, позволяющих, решать данные задачи, хотелось бы вам на пальцах объяснить, что, в сущности, предполагает регрессионный анализ. Так вам проще будет сдавать экзамен, а самое главное, интересней изучать предмет.
Будем надеяться, вы знакомы с понятием функции из математики. Функция – это взаимосвязь двух переменных. При изменении одной переменной что-то происходит с другой. Изменяем X, меняется и Y, соответственно. Функциями описываются различные законы. Зная функцию, мы можем подставлять произвольные значения X и смотреть на то, как при этом изменится Y.
Это имеет большое значение, поскольку регрессия – это попытка объяснить с помощью определённой функции на первый взгляд бессистемные и хаотичные процессы. Так, например, можно выявить взаимосвязь курса доллара и безработицы в России.
Если данную закономерность обнаружить удастся, то по полученной нами в ходе расчетов функции, мы сможем составить прогноз, какой будет уровень безработицы при N-ом курсе доллара по отношению к рублю.
Данная взаимосвязь будет называться корреляцией. Регрессионный анализ предполагает расчет коэффициента корреляции, который объяснит тесноту связи между рассматриваемыми нами переменными (курсом доллара и числом рабочих мест).
Данный коэффициент может быть положительным и отрицательным. Его значения находятся в пределах от -1 до 1. Соответственно, мы может наблюдать высокую отрицательную или положительную корреляцию. Если она положительная, то за увеличением курса доллара последует и появление новых рабочих мест.
Если она отрицательная, значит, за увеличением курса, последует уменьшение рабочих мест.
Регрессия бывает нескольких видов. Она может быть линейной, параболической, степенной, экспоненциальной и т.д.
Выбор модели мы делаем в зависимости от того, какая регрессия будет соответствовать конкретно нашему случаю, какая модель будет максимально близка к нашей корреляции. Рассмотрим это на примере задачи и решим её в MS Excel.
Линейная регрессия в MS Excel
Для решения задач линейной регрессии вам понадобится функционал «Анализ данных». Он может быть не включен у вас поэтому его нужно активировать.
- Жмём на кнопку «Файл»;
- Выбираем пункт «Параметры»;
- Жмём по предпоследней вкладке «Надстройки» с левой стороны;
- Снизу увидим Надпись «Управление» и кнопку «Перейти». Жмём по ней;
- Ставим галочку на «Пакет анализа»;
- Жмём «ок».
Пример задачи
Функция пакетного анализа активирована. Решим следующую задачу. У нас есть выборка данных за несколько лет о числе ЧП на территории предприятия и количестве трудоустроенных работников.
Нам необходимо выявить взаимосвязь между этими двумя переменными. Есть объясняющая переменная X – это число рабочих и объясняемая переменная – Y – это число чрезвычайных происшествий.
Распределим исходные данные в два столбца.

Перейдём во вкладку «данные» и выберем «Анализ данных»

Нажимаем «Ок». Анализ произведён, и в новом листе мы увидим результаты.
Наиболее существенные для нас значения отмечены на рисунке ниже. 
Множественный R – это коэффициент детерминации. Он имеет сложную формулу расчета и показывает, насколько можно доверять нашему коэффициенту корреляции. Соответственно, чем больше это значение, тем больше доверия, тем удачнее наша модель в целом.
Y-пересечение и Пересечение X1 – это коэффициенты нашей регрессии. Как уже было сказано, регрессия – это функция, и у неё есть определённые коэффициенты. Таким образом, наша функция будет иметь вид: Y = 0,64*X-2,84.
Что нам это даёт? Это даёт нам возможность составить прогноз. Допустим, мы хотим нанять на предприятие 25 работников и нам нужно примерно представить, каким при этом будет количество чрезвычайных происшествий. Подставляем в нашу функцию данное значение и получаем результат Y = 0,64 * 25 – 2,84. Примерно 13 ЧП у нас будет происходить.
Посмотрим, как это работает. Взгляните на рисунок ниже. В полученную нами функцию подставлены фактические значения по вовлеченным работникам. Посмотрите, как близки значения к реальным игрекам.

Вы так же можете построить поле корреляции, выделив область игреков и иксов, нажав на вкладку «вставку» и выбрав точечную диаграмму.

Точки идут вразброс, но в целом двигаются вверх, как будто посередине лежит прямая линия. И эту линию вы так же можете добавить, перейдя во вкладку «Макет» в MS Excel и выбрав пункт «Линия тренда»

Заключение
Будем надеяться, что данная статья дала вам большее понимание о том, что такое регрессионный анализ и для чего он нужен. Всё это имеет большое прикладное значение.
Источник: https://Reshatel.org/kontrolnye-raboty/ekonometrika-linejnaya-regressiya-v-ms-excel/
Множественная линейная регрессия в excel пример. Уравнение регрессии как сделать в excel
Пакет MS Excel позволяет при построении уравнения линейной регрессии большую часть работы сделать очень быстро. Важно понять, как интерпретировать полученные результаты.
Для построения модели регрессии необходимо выбрать пункт СервисАнализ данныхРегрессия (в Excel 2007 этот режим находится в блоке Данные/Анализ данных/Регрессия).
Затем полученные результаты скопировать в блок для анализа.
- Метод линейной регрессии позволяет нам описывать прямую линию, максимально соответствующую ряду упорядоченных пар (x, y). Уравнение для прямой линии, известное как линейное уравнение, представлено ниже:
- ŷ — ожидаемое значение у при заданном значении х,
- x — независимая переменная,
- a — отрезок на оси y для прямой линии,
- b — наклон прямой линии.
- На рисунке ниже это понятие представлено графически:
На рисунке выше показана линия, описанная уравнением ŷ =2+0.5х. Отрезок на оси у — это точка пересечения линией оси у; в нашем случае а = 2. Наклон линии, b, отношение подъема линии к длине линии, имеет значение 0.5.
Положительный наклон означает, что линия поднимается слева направо. Если b = 0, линия горизонтальна, а это значит, что между зависимой и независимой переменными нет никакой связи.
Иными словами, изменение значения x не влияет на значение y.
Часто путают ŷ и у. На графике показаны 6 упорядоченных пар точек и линия, в соответствии с данным уравнением
На этом рисунке показана точка, соответствующая упорядоченной паре х = 2 и у = 4. Обратите внимание, что ожидаемое значение у в соответствии с линией при х
= 2 является ŷ. Мы можем подтвердить это с помощью следующего уравнения:
ŷ = 2 + 0.5х =2 +0.5(2) =3.
Значение у представляет собой фактическую точку, а значение ŷ — это ожидаемое значение у с использованием линейного уравнения при заданном значении х.
Следующий шаг — определить линейное уравнение, максимально соответствующее набору упорядоченных пар, об этом мы говорили в предыдущей статье, где определяли вид уравнения по .
Использование Excel для определения линейной регрессии
Для того, чтобы воспользоваться инструментом регрессионного анализа встроенного в Excel, необходимо активировать надстройку Пакет анализа
.
Найти ее можно, перейдя по вкладке Файл –> Параметры
(2007+), в появившемся диалоговом окне Параметры
Excel
переходим во вкладку Надстройки.
В поле Управление
выбираем Надстройки
Excel
и щелкаем Перейти.
В появившемся окне ставим галочку напротив Пакет анализа,
жмем ОК.
Во вкладке Данные
в группе Анализ
появится новая кнопка Анализ данных.
Чтобы продемонстрировать работу надстройки, воспользуемся данными , где парень и девушка делят столик в ванной. Введите данные нашего примера с ванной в столбцы А и В чистого листа.
Перейдите во вкладку Данные,
в группе Анализ
щелкните Анализ данных.
В появившемся окне Анализ данных
выберите Регрессия
, как показано на рисунке, и щелкните ОК.
Установите необходимыe параметры регрессии в окне Регрессия
, как показано на рисунке:
Щелкните ОК.
На рисунке ниже показаны полученные результаты:
Эти результаты соответствуют тем, которые мы получили путем самостоятельных вычислений в .
Линия регрессии является графическим отражением взаимосвязи между явлениями. Очень наглядно можно построить линию регрессии в программе Excel.
Для этого необходимо:
1.Открыть программу Excel
2.Создать столбцы с данными. В нашем примере мы будем строить линию регрессии, или взаимосвязи, между агрессивностью и неуверенностью в себе у детей-первоклассников. В эксперименте участвовали 30 детей, данные представлены в таблице эксель:
- 1 столбик — № испытуемого
- 2 столбик — агрессивность
в баллах - 3 столбик — неуверенность в себе
в баллах
3.Затем необходимо выделить оба столбика (без названия столбика), нажать вкладку вставка
,
выбрать точечная
, а из предложенных макетов выбрать самый первый точечная с маркерами
.
4.Итак у нас получилась заготовка для линии регрессии — так называемая — диаграмма рассеяния
. Для перехода к линии регрессии нужно щёлкнуть на получившийся рисунок, нажать вкладку конструктор,
найти на панели макеты диаграмм
и выбрать Ма
кет9
, на нем ещё написано f(x)
5.Итак, у нас получилась линия регрессии. На графике также указано её уравнение и квадрат коэффициента корреляции
6.Осталось добавить название графика, название осей. Также по желанию можно убрать легенду, уменьшить количество горизонтальных линий сетки (вкладка макет
, затем сетка
). Основные изменения и настройки производятся во вкладке Макет
Линия регрессии построена в MS Excel. Теперь её можно добавить в текст работы.
Регрессионный анализ в Microsoft Excel – наиболее полное руководств по использованию MS Excel для решения задач регрессионного анализа в области бизнес-аналитики.
Конрад Карлберг доступно объясняет теоретические вопросы, знание которых поможет вам избежать многих ошибок как при самостоятельном проведении регрессионного анализа, так и при оценке результатов анализа, выполненного другими людьми.
Весь материал, от простых корреляций и t-тестов до множественного ковариационного анализа, основан на реальных примерах и сопровождается подробным описанием соответствующих пошаговых процедур.
В книге обсуждаются особенности и противоречия, связанные с функциями Excel для работы с регрессией, рассматриваются последствия использования каждой их опции и каждого аргумента и объясняется, как надежно применять регрессионные методы в самых разных областях, от медицинских исследований до финансового анализа.
Конрад Карлберг. Регрессионный анализ в Microsoft Excel. – М.: Диалектика, 2017. – 400 с.
Скачать заметку в формате или , примеры в формате
Глава 1. Оценка изменчивости данных
В распоряжении статистиков имеется множество показателей вариации (изменчивости). Один из них – сумма квадратов отклонений индивидуальных значений от среднего. В Excel для него используется функция КВАДРОТКЛ().
Но чаще используется дисперсия. Дисперсия — это среднее квадратов отклонений.
Дисперсия нечувствительна к количеству значений в исследуемом наборе данных (в то время как сумма квадратов отклонений растет с числом измерений).
Программа Excel предлагает две функции, возвращающие дисперсию: ДИСП.Г() и ДИСП.В():
- Используйте функцию ДИСП.Г(), если подлежащие обработке значения образуют генеральную совокупность. Т.е., значения, содержащиеся в диапазоне, являются единственными значениями, которые вас интересуют.
- Используйте функцию ДИСП.В(), если подлежащие обработке значения образуют выборку из совокупности большего объема. Предполагается, что имеются дополнительные значения, дисперсию которых вы также можете оценить.
Если такая величина, как среднее значение или коэффициент корреляции, рассчитывается на основе генеральной совокупности, то она называется параметром. Аналогичная величина, рассчитываемая на основе выборки, называется статистикой.
Отсчитывая отклонения от среднего значения
в данном наборе, вы получите сумму квадратов отклонений меньшей величины, чем если бы отсчитывали их от любого другого значения. Аналогичное утверждение справедливо и для дисперсии.
Чем больше объем выборки, тем точнее рассчитанное значение статистики. Но не существует ни одной выборки с объемом меньше объема генеральной совокупности, относительно которой вы могли бы быть уверены в том, что значение статистики совпадает со значением параметра.
Допустим, у вас есть набор из 100 значений роста, среднее которых отличается от среднего по генеральной совокупности, каким бы малым ни было это различие. Рассчитав дисперсию для выборки, вы получите некоторое ее значение, скажем, 4.
Это значение меньше любого другого, которое можно получить, рассчитывая отклонение каждого из 100 значений роста относительно любого значения, отличного от среднего по выборке, в там числе и относительно истинного среднего по генеральной совокупности.
Поэтому вычисленная дисперсия будет отличаться, причем в меньшую сторону, от дисперсии, которую вы получили бы, если бы каким-то образом узнали и использовали не выборочное среднее, а параметр генеральной совокупности.
Средняя сумма квадратов, определенная для выборки, дает нижнюю оценку дисперсии генеральной совокупности. Вычисленную таким способом дисперсию называют смещенной
оценкой. Оказывается, чтобы исключить смещение и получить несмещенную оценку, достаточно разделить сумму квадратов отклонений не на n
, где n
— размер выборки, а на n – 1
.
Величина n – 1
называется количеством (числом) степеней свободы. Существуют разные способы расчета этой величины, хотя все они включают либо вычитание некоторого числа из размера выборки, либо подсчет количества категорий, в которые попадают наблюдения.
Суть различия между функциями ДИСП.Г() и ДИСП.В() состоит в следующем:
- В функции ДИСП.Г() сумма квадратов делится на количество наблюдений и, следовательно, представляет смещенную оценку дисперсии, истинное среднее.
- В функции ДИСП.В() сумма квадратов делится на количество наблюдений минус 1, т.е. на количество степеней свободы, что дает более точную, несмещенную оценку дисперсии генеральной совокупности, из которой была извлечена данная выборка.
Стандартное отклонение (англ. standard deviation
, SD) – есть квадратный корень из дисперсии:
Возведение отклонений в квадрат переводит шкалу измерений в другую метрику, являющуюся квадратом исходной: метры — в квадратные метры, доллары — в квадратные доллары и т.д. Стандартное отклонение — это корень квадратный из дисперсии, и поэтому оно возвращает нас к исходным единицам измерения. Что удобнее.
Часто приходится рассчитывать стандартное отклонение после того, как данных были подвергнуты некоторым манипуляциям.
И хотя в этих случаях результаты несомненно являются стандартными отклонениями, их принято называть стандартными ошибками
.
Существует несколько разновидностей стандартных ошибок, в том числе стандартная ошибка измерения, стандартная ошибка пропорции, стандартная ошибка среднего.
Предположим, вы собрали данные о росте 25 случайно выбранных взрослых мужчин в каждом из 50 штатов. Далее вы вычисляете средний рост взрослых мужчин в каждом штате. Полученные 50 средних значений в свою очередь можно считать наблюдениями.
Исходя из этого, вы могли бы рассчитать их стандартное отклонение, которое и является стандартной ошибкой среднего
. Рис. 1. позволяет сравнить распределение 1250 исходных индивидуальных значений (данные о росте 25 мужчин по каждому из 50 штатов) с распределением средних значений 50 штатов.
Формула для оценки стандартной ошибки среднего (т.е. стандартного отклонения средних значений, а не индивидуальных наблюдений):
- где – стандартная ошибка среднего; s
– стандартное отклонение исходных наблюдений; n
– количество наблюдений в выборке.
Рис. 1. Вариация средних значений от штата к штату значительно меньше вариации индивидуальных результатов наблюдений
В статистике существует соглашение относительно использования греческих и латинских букв для обозначения статистических величин. Греческими буквами принято обозначать параметры генеральной совокупности, латинскими — выборочные статистики.
Следовательно, если речь идет о стандартном отклонении генеральной совокупности, мы записываем его как σ; если же рассматривается стандартное отклонение выборки, то используем обозначение s. Что касается символов для обозначения средних, то они согласуются между собой не столь удачно.
Среднее по генеральной совокупности обозначается греческой буквой μ. Однако для представления выборочного среднего традиционно используется символ X̅.
z-оценка
выражает положение наблюдения в распределении в единицах стандартного отклонения. Например, z = 1,5 означает, что наблюдение отстоит от среднего на 1,5 стандартного отклонения в сторону больших значений. Термин z-оценка
Источник: https://erfa.ru/mnozhestvennaya-lineinaya-regressiya-v-excel-primer-uravnenie-regressii-kak-sdelat.html
Регрессия в Excel: уравнение, примеры. Линейная регрессия
Рeгрeссиoнный aнaлиз — этo стaтистичeский мeтoд исслeдoвaния, пoзвoляющий пoкaзaть зaвисимoсть тoгo или инoгo пaрaмeтрa oт oднoй либo нeскoльких нeзaвисимых пeрeмeнных.
В дoкoмпьютeрную эру eгo примeнeниe былo дoстaтoчнo зaтруднитeльнo, oсoбeннo eсли рeчь шлa o
Рeгрeссиoнный aнaлиз — этo стaтистичeский мeтoд исслeдoвaния, пoзвoляющий пoкaзaть зaвисимoсть тoгo или инoгo пaрaмeтрa oт oднoй либo нeскoльких нeзaвисимых пeрeмeнных.
В дoкoмпьютeрную эру eгo примeнeниe былo дoстaтoчнo зaтруднитeльнo, oсoбeннo eсли рeчь шлa o бoльших oбъeмaх дaнных. Сeгoдня, узнaв кaк пoстрoить рeгрeссию в Excel, мoжнo рeшaть слoжныe стaтистичeскиe зaдaчи буквaльнo зa пaру минут.
Нижe прeдстaвлeны кoнкрeтныe примeры из oблaсти экoнoмики.
Клaссичeский рaсчeт:
{source}
{/source}
Виды рeгрeссии
Сaмo этo пoнятиe былo ввeдeнo в мaтeмaтику Фрэнсисoм Гaльтoнoм в 1886 гoду. Рeгрeссия бывaeт:
- линeйнoй;
- пaрaбoличeскoй;
- стeпeннoй;
- экспoнeнциaльнoй;
- гипeрбoличeскoй;
- пoкaзaтeльнoй;
- лoгaрифмичeскoй.
Примeр 1
Рaссмoтрим зaдaчу oпрeдeлeния зaвисимoсти кoличeствa увoлившихся члeнoв кoллeктивa oт срeднeй зaрплaты нa 6 прoмышлeнных прeдприятиях.
Зaдaчa. Нa шeсти прeдприятиях прoaнaлизирoвaли срeднeмeсячную зaрaбoтную плaту и кoличeствo сoтрудникoв, кoтoрыe увoлились пo сoбствeннoму жeлaнию. В тaбличнoй фoрмe имeeм:
- A
- B
- C
- 1
- Х
- Кoличeствo увoлившихся
- Зaрплaтa
- 2
- y
- 30000 рублeй
- 3
- 1
- 60
- 35000 рублeй
- 4
- 2
- 35
- 40000 рублeй
- 5
- 3
- 20
- 45000 рублeй
- 6
- 4
- 20
- 50000 рублeй
- 7
- 5
- 15
- 55000 рублeй
- 8
- 6
- 15
- 60000 рублeй
- Для зaдaчи oпрeдeлeния зaвисимoсти кoличeствa увoлившихся рaбoтникoв oт срeднeй зaрплaты нa 6 прeдприятиях мoдeль рeгрeссии имeeт вид урaвнeния Y = a0 + a1x1 +…+akxk, гдe хi — влияющиe пeрeмeнныe, ai — кoэффициeнты рeгрeссии, a k — числo фaктoрoв.
- Для дaннoй зaдaчи Y — этo пoкaзaтeль увoлившихся сoтрудникoв, a влияющий фaктoр — зaрплaтa, кoтoрую oбoзнaчaeм X.
Испoльзoвaниe вoзмoжнoстeй тaбличнoгo прoцeссoрa «Эксeль»
aнaлизу рeгрeссии в Excel дoлжнo прeдшeствoвaть примeнeниe к имeющимся тaбличным дaнным встрoeнных функций. oднaкo для этих цeлeй лучшe вoспoльзoвaться oчeнь пoлeзнoй нaдстрoйкoй «Пaкeт aнaлизa». Для eгo aктивaции нужнo:
- с вклaдки «Фaйл» пeрeйти в рaздeл «Пaрaмeтры»;
- в oткрывшeмся oкнe выбрaть стрoку «Нaдстрoйки»;
- щeлкнуть пo кнoпкe «Пeрeйти», рaспoлoжeннoй внизу, спрaвa oт стрoки «Упрaвлeниe»;
- пoстaвить гaлoчку рядoм с нaзвaниeм «Пaкeт aнaлизa» и пoдтвeрдить свoи дeйствия, нaжaв «oк».
eсли всe сдeлaнo прaвильнo, в прaвoй чaсти вклaдки «Дaнныe», рaспoлoжeннoм нaд рaбoчим листoм «Эксeль», пoявится нужнaя кнoпкa.
Линeйнaя рeгрeссия в Excel
Тeпeрь, кoгдa пoд рукoй eсть всe нeoбхoдимыe виртуaльныe инструмeнты для oсущeствлeния экoнoмeтричeских рaсчeтoв, мoжeм приступить к рeшeнию нaшeй зaдaчи. Для этoгo:
- щeлкaeм пo кнoпкe «aнaлиз дaнных»;
- в oткрывшeмся oкнe нaжимaeм нa кнoпку «Рeгрeссия»;
- в пoявившуюся вклaдку ввoдим диaпaзoн знaчeний для Y (кoличeствo увoлившихся рaбoтникoв) и для X (их зaрплaты);
- пoдтвeрждaeм свoи дeйствия нaжaтиeм кнoпки «Ok».
В рeзультaтe прoгрaммa aвтoмaтичeски зaпoлнит нoвый лист тaбличнoгo прoцeссoрa дaнными aнaлизa рeгрeссии. oбрaтитe внимaниe! В Excel eсть вoзмoжнoсть сaмoстoятeльнo зaдaть мeстo, кoтoрoe вы прeдпoчитaeтe для этoй цeли. Нaпримeр, этo мoжeт быть тoт жe лист, гдe нaхoдятся знaчeния Y и X, или дaжe нoвaя книгa, спeциaльнo прeднaзнaчeннaя для хрaнeния пoдoбных дaнных.
aнaлиз рeзультaтoв рeгрeссии для R-квaдрaтa
В Excel дaнныe пoлучeнныe в хoдe oбрaбoтки дaнных рaссмaтривaeмoгo примeрa имeют вид:
Прeждe всeгo, слeдуeт oбрaтить внимaниe нa знaчeниe R-квaдрaтa. oн прeдстaвляeт сoбoй кoэффициeнт дeтeрминaции. В дaннoм примeрe R-квaдрaт = 0,755 (75,5%), т. e. рaсчeтныe пaрaмeтры мoдeли oбъясняют зaвисимoсть мeжду рaссмaтривaeмыми пaрaмeтрaми нa 75,5 %.
Чeм вышe знaчeниe кoэффициeнтa дeтeрминaции, тeм выбрaннaя мoдeль считaeтся бoлee примeнимoй для кoнкрeтнoй зaдaчи. Считaeтся, чтo oнa кoррeктнo oписывaeт рeaльную ситуaцию при знaчeнии R-квaдрaтa вышe 0,8.
eсли R-квaдрaтa tкр, тo гипoтeзa o нeзнaчимoсти свoбoднoгo члeнa линeйнoгo урaвнeния oтвeргaeтся.
В рaссмaтривaeмoй зaдaчe для свoбoднoгo члeнa пoсрeдствoм инструмeнтoв «Эксeль» былo пoлучeнo, чтo t=169,20903, a p=2,89e-12, т. e.
имeeм нулeвую вeрoятнoсть тoгo, чтo будeт oтвeргнутa вeрнaя гипoтeзa o нeзнaчимoсти свoбoднoгo члeнa. Для кoэффициeнтa при нeизвeстнoй t=5,79405, a p=0,001158.
Иными слoвaми вeрoятнoсть тoгo, чтo будeт oтвeргнутa вeрнaя гипoтeзa o нeзнaчимoсти кoэффициeнтa при нeизвeстнoй, рaвнa 0,12%.
Тaким oбрaзoм, мoжнo утвeрждaть, чтo пoлучeннoe урaвнeниe линeйнoй рeгрeссии aдeквaтнo.
Зaдaчa o цeлeсooбрaзнoсти пoкупки пaкeтa aкций
Мнoжeствeннaя рeгрeссия в Excel выпoлняeтся с испoльзoвaниeм всe тoгo жe инструмeнтa «aнaлиз дaнных». Рaссмoтрим кoнкрeтную приклaдную зaдaчу.
Рукoвoдствo кoмпaния «NNN» дoлжнo принять рeшeниe o цeлeсooбрaзнoсти пoкупки 20 % пaкeтa aкций ao «MMM». Стoимoсть пaкeтa (СП) сoстaвляeт 70 млн aмeрикaнских дoллaрoв. Спeциaлистaми «NNN» сoбрaны дaнныe oб aнaлoгичных сдeлкaх. Былo принятo рeшeниe oцeнивaть стoимoсть пaкeтa aкций пo тaким пaрaмeтрaм, вырaжeнным в миллиoнaх aмeрикaнских дoллaрoв, кaк:
- крeдитoрскaя зaдoлжeннoсть (VK);
- oбъeм гoдoвoгo oбoрoтa (VO);
- дeбитoрскaя зaдoлжeннoсть (VD);
- стoимoсть oснoвных фoндoв (СoФ).
Крoмe тoгo, испoльзуeтся пaрaмeтр зaдoлжeннoсть прeдприятия пo зaрплaтe (V3 П) в тысячaх aмeрикaнских дoллaрoв.
Рeшeниe срeдствaми тaбличнoгo прoцeссoрa Excel
Прeждe всeгo, нeoбхoдимo сoстaвить тaблицу исхoдных дaнных. oнa имeeт слeдующий вид:
Дaлee:
- вызывaют oкнo «aнaлиз дaнных»;
- выбирaют рaздeл «Рeгрeссия»;
- в oкoшкo «Вхoднoй интeрвaл Y» ввoдят диaпaзoн знaчeний зaвисимых пeрeмeнных из стoлбцa G;
- щeлкaют пo икoнкe с крaснoй стрeлкoй спрaвa oт oкнa «Вхoднoй интeрвaл X» и выдeляют нa листe диaпaзoн всeх знaчeний из стoлбцoв B,C, D, F.
oтмeчaют пункт «Нoвый рaбoчий лист» и нaжимaют «Ok».
Пoлучaют aнaлиз рeгрeссии для дaннoй зaдaчи.
Изучeниe рeзультaтoв и вывoды
- «Сoбирaeм» из oкруглeнных дaнных, прeдстaвлeнных вышe нa листe тaбличнoгo прoцeссoрa Excel, урaвнeниe рeгрeссии:
- СП = 0,103*СoФ + 0,541*VO – 0,031*VK +0,405*VD +0,691*VZP – 265,844.
- В бoлee привычнoм мaтeмaтичeскoм видe eгo мoжнo зaписaть, кaк:
- y = 0,103*x1 + 0,541*x2 – 0,031*x3 +0,405*x4 +0,691*x5 – 265,844
- Дaнныe для ao «MMM» прeдстaвлeны в тaблицe:
- СoФ, USD
- VO, USD
- VK, USD
- VD, USD
- VZP, USD
- СП, USD
- 102,5
- 535,5
- 45,2
- 41,5
- 21,55
- 64,72
Пoдстaвив их в урaвнeниe рeгрeссии, пoлучaют цифру в 64,72 млн aмeрикaнских дoллaрoв. Этo знaчит, чтo aкции ao «MMM» нe стoит приoбрeтaть, тaк кaк их стoимoсть в 70 млн aмeрикaнских дoллaрoв дoстaтoчнo зaвышeнa.
Кaк видим, испoльзoвaниe тaбличнoгo прoцeссoрa «Эксeль» и урaвнeния рeгрeссии пoзвoлилo принять oбoснoвaннoe рeшeниe oтнoситeльнo цeлeсooбрaзнoсти впoлнe кoнкрeтнoй сдeлки.
Тeпeрь вы знaeтe, чтo тaкoe рeгрeссия. Примeры в Excel, рaссмoтрeнныe вышe, пoмoгут вaм в рeшeниe прaктичeских зaдaч из oблaсти экoнoмeтрики.
Источник: https://xroom.su/regressiia-v-excel-yravnenie-primery-lineinaia-regressiia/
Регрессия в Excel: уравнение, примеры. Линейная регрессия
Регрессионный анализ — это статистический метод исследования, позволяющий показать зависимость того или иного параметра от одной либо нескольких независимых переменных.
В докомпьютерную эру его применение было достаточно затруднительно, особенно если речь шла о больших объемах данных. Сегодня, узнав как построить регрессию в Excel, можно решать сложные статистические задачи буквально за пару минут.
Ниже представлены конкретные примеры из области экономики.
Рассмотрим задачу определения зависимости количества уволившихся членов коллектива от средней зарплаты на 6 промышленных предприятиях.
- B
- C
- 1
- Х
- Количество уволившихся
- Зарплата
- 2
- y
- 30000 рублей
- 3
- 1
- 60
- 35000 рублей
- 4
- 2
- 35
- 40000 рублей
- 5
- 3
- 20
- 45000 рублей
- 6
- 4
- 20
- 50000 рублей
- 7
- 5
- 15
- 55000 рублей
- 8
- 6
- 15
- 60000 рублей
- Для задачи определения зависимости количества уволившихся работников от средней зарплаты на 6 предприятиях модель регрессии имеет вид уравнения Y = а0 + а1×1 +…+аkxk, где хi — влияющие переменные, ai — коэффициенты регрессии, a k — число факторов.
- Для данной задачи Y — это показатель уволившихся сотрудников, а влияющий фактор — зарплата, которую обозначаем X.
Использование возможностей табличного процессора «Эксель»
Анализу регрессии в Excel должно предшествовать применение к имеющимся табличным данным встроенных функций. Однако для этих целей лучше воспользоваться очень полезной надстройкой «Пакет анализа». Для его активации нужно:
- с вкладки «Файл» перейти в раздел «Параметры»;
- в открывшемся окне выбрать строку «Надстройки»;
- щелкнуть по кнопке «Перейти», расположенной внизу, справа от строки «Управление»;
- поставить галочку рядом с названием «Пакет анализа» и подтвердить свои действия, нажав «Ок».
Если все сделано правильно, в правой части вкладки «Данные», расположенном над рабочим листом «Эксель», появится нужная кнопка.
Линейная регрессия в Excel
Теперь, когда под рукой есть все необходимые виртуальные инструменты для осуществления эконометрических расчетов, можем приступить к решению нашей задачи. Для этого:
- щелкаем по кнопке «Анализ данных»;
- в открывшемся окне нажимаем на кнопку «Регрессия»;
- в появившуюся вкладку вводим диапазон значений для Y (количество уволившихся работников) и для X (их зарплаты);
- подтверждаем свои действия нажатием кнопки «Ok».
В результате программа автоматически заполнит новый лист табличного процессора данными анализа регрессии. Обратите внимание! В Excel есть возможность самостоятельно задать место, которое вы предпочитаете для этой цели. Например, это может быть тот же лист, где находятся значения Y и X, или даже новая книга, специально предназначенная для хранения подобных данных.
Анализ результатов регрессии для R-квадрата
В Excel данные полученные в ходе обработки данных рассматриваемого примера имеют вид:
Прежде всего, следует обратить внимание на значение R-квадрата. Он представляет собой коэффициент детерминации. В данном примере R-квадрат = 0,755 (75,5%), т. е. расчетные параметры модели объясняют зависимость между рассматриваемыми параметрами на 75,5 %.
Чем выше значение коэффициента детерминации, тем выбранная модель считается более применимой для конкретной задачи. Считается, что она корректно описывает реальную ситуацию при значении R-квадрата выше 0,8.
Если R-квадрата tкр, то гипотеза о незначимости свободного члена линейного уравнения отвергается.
В рассматриваемой задаче для свободного члена посредством инструментов «Эксель» было получено, что t=169,20903, а p=2,89Е-12, т. е.
имеем нулевую вероятность того, что будет отвергнута верная гипотеза о незначимости свободного члена. Для коэффициента при неизвестной t=5,79405, а p=0,001158.
Иными словами вероятность того, что будет отвергнута верная гипотеза о незначимости коэффициента при неизвестной, равна 0,12%.
Таким образом, можно утверждать, что полученное уравнение линейной регрессии адекватно.
Задача о целесообразности покупки пакета акций
Множественная регрессия в Excel выполняется с использованием все того же инструмента «Анализ данных». Рассмотрим конкретную прикладную задачу.
Руководство компания «NNN» должно принять решение о целесообразности покупки 20 % пакета акций АО «MMM». Стоимость пакета (СП) составляет 70 млн американских долларов. Специалистами «NNN» собраны данные об аналогичных сделках. Было принято решение оценивать стоимость пакета акций по таким параметрам, выраженным в миллионах американских долларов, как:
- кредиторская задолженность (VK);
- объем годового оборота (VO);
- дебиторская задолженность (VD);
- стоимость основных фондов (СОФ).
Кроме того, используется параметр задолженность предприятия по зарплате (V3 П) в тысячах американских долларов.
Решение средствами табличного процессора Excel
Прежде всего, необходимо составить таблицу исходных данных. Она имеет следующий вид:
Далее:
- вызывают окно «Анализ данных»;
- выбирают раздел «Регрессия»;
- в окошко «Входной интервал Y» вводят диапазон значений зависимых переменных из столбца G;
- щелкают по иконке с красной стрелкой справа от окна «Входной интервал X» и выделяют на листе диапазон всех значений из столбцов B,C, D, F.
Отмечают пункт «Новый рабочий лист» и нажимают «Ok».
Получают анализ регрессии для данной задачи.
Изучение результатов и выводы
- «Собираем» из округленных данных, представленных выше на листе табличного процессора Excel, уравнение регрессии:
- СП = 0,103*СОФ + 0,541*VO – 0,031*VK +0,40 VD +0,691*VZP – 265,844.
- В более привычном математическом виде его можно записать, как:
- y = 0,103*x1 + 0,541*x2 – 0,031*x3 +0,40 x4 +0,691*x5 – 265,844
- Данные для АО «MMM» представлены в таблице:
| СОФ, USD | VO, USD | VK, USD | VD, USD | VZP, USD | СП, USD |
| 102,5 | 535,5 | 45,2 | 41,5 | 21,55 | 64,72 |
Подставив их в уравнение регрессии, получают цифру в 64,72 млн американских долларов. Это значит, что акции АО «MMM» не стоит приобретать, так как их стоимость в 70 млн американских долларов достаточно завышена.
Как видим, использование табличного процессора «Эксель» и уравнения регрессии позволило принять обоснованное решение относительно целесообразности вполне конкретной сделки.
Теперь вы знаете, что такое регрессия. Примеры в Excel, рассмотренные выше, помогут вам в решение практических задач из области эконометрики.
Источник: https://autogear.ru/article/322/644/regressiya-v-excel-uravnenie-primeryi-lineynaya-regressiya/
Построение регрессии в excel. Уравнение регрессии как сделать в excel
Регрессионный анализ в Microsoft Excel – наиболее полное руководств по использованию MS Excel для решения задач регрессионного анализа в области бизнес-аналитики.
Конрад Карлберг доступно объясняет теоретические вопросы, знание которых поможет вам избежать многих ошибок как при самостоятельном проведении регрессионного анализа, так и при оценке результатов анализа, выполненного другими людьми.
Весь материал, от простых корреляций и t-тестов до множественного ковариационного анализа, основан на реальных примерах и сопровождается подробным описанием соответствующих пошаговых процедур.
В книге обсуждаются особенности и противоречия, связанные с функциями Excel для работы с регрессией, рассматриваются последствия использования каждой их опции и каждого аргумента и объясняется, как надежно применять регрессионные методы в самых разных областях, от медицинских исследований до финансового анализа.
Конрад Карлберг. Регрессионный анализ в Microsoft Excel. – М.: Диалектика, 2017. – 400 с.
Скачать заметку в формате или , примеры в формате
Глава 1. Оценка изменчивости данных
В распоряжении статистиков имеется множество показателей вариации (изменчивости). Один из них – сумма квадратов отклонений индивидуальных значений от среднего. В Excel для него используется функция КВАДРОТКЛ().
Но чаще используется дисперсия. Дисперсия — это среднее квадратов отклонений.
Дисперсия нечувствительна к количеству значений в исследуемом наборе данных (в то время как сумма квадратов отклонений растет с числом измерений).
Программа Excel предлагает две функции, возвращающие дисперсию: ДИСП.Г() и ДИСП.В():
- Используйте функцию ДИСП.Г(), если подлежащие обработке значения образуют генеральную совокупность. Т.е., значения, содержащиеся в диапазоне, являются единственными значениями, которые вас интересуют.
- Используйте функцию ДИСП.В(), если подлежащие обработке значения образуют выборку из совокупности большего объема. Предполагается, что имеются дополнительные значения, дисперсию которых вы также можете оценить.
Если такая величина, как среднее значение или коэффициент корреляции, рассчитывается на основе генеральной совокупности, то она называется параметром. Аналогичная величина, рассчитываемая на основе выборки, называется статистикой.
Отсчитывая отклонения от среднего значения
в данном наборе, вы получите сумму квадратов отклонений меньшей величины, чем если бы отсчитывали их от любого другого значения. Аналогичное утверждение справедливо и для дисперсии.
Чем больше объем выборки, тем точнее рассчитанное значение статистики. Но не существует ни одной выборки с объемом меньше объема генеральной совокупности, относительно которой вы могли бы быть уверены в том, что значение статистики совпадает со значением параметра.
Допустим, у вас есть набор из 100 значений роста, среднее которых отличается от среднего по генеральной совокупности, каким бы малым ни было это различие. Рассчитав дисперсию для выборки, вы получите некоторое ее значение, скажем, 4.
Это значение меньше любого другого, которое можно получить, рассчитывая отклонение каждого из 100 значений роста относительно любого значения, отличного от среднего по выборке, в там числе и относительно истинного среднего по генеральной совокупности.
Поэтому вычисленная дисперсия будет отличаться, причем в меньшую сторону, от дисперсии, которую вы получили бы, если бы каким-то образом узнали и использовали не выборочное среднее, а параметр генеральной совокупности.
Средняя сумма квадратов, определенная для выборки, дает нижнюю оценку дисперсии генеральной совокупности. Вычисленную таким способом дисперсию называют смещенной
оценкой. Оказывается, чтобы исключить смещение и получить несмещенную оценку, достаточно разделить сумму квадратов отклонений не на n
, где n
— размер выборки, а на n – 1
.
Величина n – 1
называется количеством (числом) степеней свободы. Существуют разные способы расчета этой величины, хотя все они включают либо вычитание некоторого числа из размера выборки, либо подсчет количества категорий, в которые попадают наблюдения.
Суть различия между функциями ДИСП.Г() и ДИСП.В() состоит в следующем:
- В функции ДИСП.Г() сумма квадратов делится на количество наблюдений и, следовательно, представляет смещенную оценку дисперсии, истинное среднее.
- В функции ДИСП.В() сумма квадратов делится на количество наблюдений минус 1, т.е. на количество степеней свободы, что дает более точную, несмещенную оценку дисперсии генеральной совокупности, из которой была извлечена данная выборка.
Стандартное отклонение (англ. standard deviation
, SD) – есть квадратный корень из дисперсии:
Возведение отклонений в квадрат переводит шкалу измерений в другую метрику, являющуюся квадратом исходной: метры — в квадратные метры, доллары — в квадратные доллары и т.д. Стандартное отклонение — это корень квадратный из дисперсии, и поэтому оно возвращает нас к исходным единицам измерения. Что удобнее.
Часто приходится рассчитывать стандартное отклонение после того, как данных были подвергнуты некоторым манипуляциям.
И хотя в этих случаях результаты несомненно являются стандартными отклонениями, их принято называть стандартными ошибками
.
Существует несколько разновидностей стандартных ошибок, в том числе стандартная ошибка измерения, стандартная ошибка пропорции, стандартная ошибка среднего.
Предположим, вы собрали данные о росте 25 случайно выбранных взрослых мужчин в каждом из 50 штатов. Далее вы вычисляете средний рост взрослых мужчин в каждом штате. Полученные 50 средних значений в свою очередь можно считать наблюдениями.
Исходя из этого, вы могли бы рассчитать их стандартное отклонение, которое и является стандартной ошибкой среднего
. Рис. 1. позволяет сравнить распределение 1250 исходных индивидуальных значений (данные о росте 25 мужчин по каждому из 50 штатов) с распределением средних значений 50 штатов.
Формула для оценки стандартной ошибки среднего (т.е. стандартного отклонения средних значений, а не индивидуальных наблюдений):
где – стандартная ошибка среднего; s
– стандартное отклонение исходных наблюдений; n
– количество наблюдений в выборке.
Рис. 1. Вариация средних значений от штата к штату значительно меньше вариации индивидуальных результатов наблюдений
В статистике существует соглашение относительно использования греческих и латинских букв для обозначения статистических величин. Греческими буквами принято обозначать параметры генеральной совокупности, латинскими — выборочные статистики.
Следовательно, если речь идет о стандартном отклонении генеральной совокупности, мы записываем его как σ; если же рассматривается стандартное отклонение выборки, то используем обозначение s. Что касается символов для обозначения средних, то они согласуются между собой не столь удачно.
Среднее по генеральной совокупности обозначается греческой буквой μ. Однако для представления выборочного среднего традиционно используется символ X̅.
z-оценка
выражает положение наблюдения в распределении в единицах стандартного отклонения. Например, z = 1,5 означает, что наблюдение отстоит от среднего на 1,5 стандартного отклонения в сторону больших значений. Термин z-оценка
Источник: https://nc1.ru/vitamins-and-dietary-supplements/postroenie-regressii-v-excel-uravnenie-regressii-kak-sdelat-v-excel/
- Введение в линейную регрессию в Excel
Линейная регрессия в Excel (Содержание)
- Введение в линейную регрессию в Excel
- Методы использования линейной регрессии в Excel
Введение в линейную регрессию в Excel
Линейная регрессия — это статистический метод / метод, используемый для изучения взаимосвязи между двумя непрерывными количественными переменными. В этом методе независимые переменные используются для прогнозирования значения зависимой переменной. Если существует только одна независимая переменная, то это простая линейная регрессия, а если число независимых переменных больше, чем одна, то это множественная линейная регрессия. Модели линейной регрессии имеют связь между зависимыми и независимыми переменными путем подгонки линейного уравнения к наблюдаемым данным. Линейный относится к тому факту, что мы используем линию, чтобы соответствовать нашим данным. Зависимые переменные, используемые в регрессионном анализе, также называют ответными или прогнозными переменными, а независимые переменные также называют объясняющими переменными или предикторами.
Линия линейной регрессии имеет уравнение вида: Y = a + bX;
Где:
- X — объясняющая переменная,
- Y является зависимой переменной,
- б — наклон линии,
- a является y-перехватом (то есть значением y, когда x = 0).
Метод наименьших квадратов обычно используется в линейной регрессии, которая рассчитывает линию наилучшего соответствия для наблюдаемых данных путем минимизации суммы квадратов отклонения точек данных от линии.
Методы использования линейной регрессии в Excel
В этом примере показано, как выполнить анализ линейной регрессии в Excel. Давайте посмотрим на несколько методов.
Вы можете скачать этот шаблон Excel с линейной регрессией здесь — Шаблон Excel с линейной регрессией
Метод № 1 — Точечная диаграмма с линией тренда
Допустим, у нас есть набор данных о некоторых людях с их возрастом, индексом биомассы (ИМТ) и суммой, потраченной ими на медицинские расходы за месяц. Теперь, имея представление о характеристиках людей, таких как возраст и ИМТ, мы хотим выяснить, как эти переменные влияют на медицинские расходы, и, следовательно, использовать их для проведения регрессии и оценки / прогнозирования средних медицинских расходов для некоторых конкретных людей. Давайте сначала посмотрим, как только возраст влияет на медицинские расходы. Давайте посмотрим на набор данных:
Сумма на медицинские расходы = б * возраст + а
- Выберите два столбца набора данных (x и y), включая заголовки.
- Нажмите «Вставить» и разверните раскрывающийся список «Диаграмма разброса» и выберите эскиз «Разброс» (первый)
- Теперь появится график рассеяния, и мы нарисуем на этом линию регрессии. Для этого щелкните правой кнопкой мыши любую точку данных и выберите «Добавить линию тренда».
- Теперь на панели «Format Trendline» справа выберите «Linear Trendline» и «Показать уравнение на графике».
- Выберите «Показать уравнение на графике».
Мы можем импровизировать диаграмму в соответствии с нашими требованиями, такими как добавление названий осей, изменение масштаба, цвета и типа линии.
После Импровизации диаграммы мы получаем вывод.
Примечание. В этом типе графика регрессии зависимая переменная всегда должна быть на оси y и не зависеть от оси x. Если график отображается в обратном порядке, либо переключите оси в диаграмме, либо поменяйте местами столбцы в наборе данных.
Метод № 2 — Анализ надстройки ToolPak Метод
Пакет инструментов анализа иногда не включен по умолчанию, и нам нужно сделать это вручную. Для этого:
- Нажмите на меню «Файл».
После этого нажмите «Опции».
- Выберите «Надстройки Excel» в поле «Управление» и нажмите «Перейти»
- Выберите «Пакет инструментов анализа» -> «ОК»
Это добавит инструменты «Анализ данных» на вкладку «Данные». Теперь запустим регрессионный анализ:
- Нажмите «Анализ данных» на вкладке «Данные»
- Выберите «Регрессия» -> «ОК».
- Откроется диалоговое окно регрессии. Выберите диапазон ввода Y и диапазон ввода X (медицинские расходы и возраст соответственно). В случае множественной линейной регрессии мы можем выбрать больше столбцов независимых переменных (например, если мы хотим увидеть влияние ИМТ также на медицинские расходы).
- Установите флажок «Метки», чтобы включить заголовки.
- Выберите желаемый вариант вывода.
- Установите флажок «Остатки» и нажмите «ОК».
Теперь результаты нашего регрессионного анализа будут созданы в новом рабочем листе с указанием статистики регрессии, ANOVA, остатков и коэффициентов.
Выходная интерпретация:
- Статистика регрессии показывает, насколько хорошо уравнение регрессии соответствует данным:
- Множество R — это коэффициент корреляции, который измеряет силу линейных отношений между двумя переменными. Он лежит в диапазоне от -1 до 1, и его абсолютное значение показывает силу отношения с большим значением, указывающим на более сильное отношение, низким значением, указывающим на отрицательное значение, и нулевым значением, указывающим на отсутствие отношения.
- Квадрат R — это коэффициент определения, используемый в качестве показателя качества соответствия. Он находится в диапазоне от 0 до 1, а значение, близкое к 1, указывает на то, что модель хорошо подходит. В этом случае 0, 57 = 57% значений y объясняются значениями x.
- Скорректированный квадрат R — это квадрат R, скорректированный на количество предикторов в случае множественной линейной регрессии.
- Стандартная ошибка отображает точность регрессионного анализа.
- Наблюдения отображают количество модельных наблюдений.
- Anova рассказывает об уровне изменчивости в рамках регрессионной модели.
Обычно это не используется для простой линейной регрессии. Однако «Значения F значимости» указывают на то, насколько надежны наши результаты, при этом значение больше 0, 05 предлагает выбрать другого предиктора.
- Коэффициенты являются наиболее важной частью, используемой для построения уравнения регрессии.
Итак, наше уравнение регрессии будет: у = 16, 891 х — 355, 32. Это то же самое, что сделано методом 1 (точечная диаграмма с линией тренда).
Теперь, если мы хотим предсказать средние медицинские расходы в возрасте 72 лет:
Итак, у = 16, 891 * 72 -355, 32 = 860, 832
Таким образом, мы можем предсказать значения y для любых других значений x.
- Остатки указывают на разницу между фактическими и прогнозируемыми значениями.
Последний метод регрессии используется не так часто и требует статистических функций, таких как slope (), intercept (), correl () и т. Д. Для проведения регрессионного анализа.
Что нужно помнить о линейной регрессии в Excel
- Регрессионный анализ обычно используется для определения статистически значимой взаимосвязи между двумя наборами переменных.
- Он используется для прогнозирования значения зависимой переменной на основе значений одной или нескольких независимых переменных.
- Всякий раз, когда мы хотим приспособить модель линейной регрессии к группе данных, следует тщательно соблюдать диапазон данных, как если бы мы использовали уравнение регрессии для прогнозирования любого значения за пределами этого диапазона (экстраполяция), тогда это может привести к неверным результатам.
Рекомендуемые статьи
Это руководство по линейной регрессии в Excel. Здесь мы обсудим, как сделать линейную регрессию в Excel вместе с практическими примерами и загружаемым шаблоном Excel. Вы также можете просмотреть наши другие предлагаемые статьи —
- Как подготовить платежную ведомость в Excel?
- Использование формулы MAX в Excel
- Учебники по ссылкам на ячейки в Excel
- Создание регрессионного анализа в Excel
- Линейное программирование в Excel
В этой статье описаны синтаксис формулы и использование функции LINEST в Microsoft Excel. Ссылки на дополнительные сведения о диаграммах и выполнении регрессионного анализа можно найти в разделе См. также.
Описание
Функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные и затем возвращает массив, который описывает полученную прямую. Функцию ЛИНЕЙН также можно объединять с другими функциями для вычисления других видов моделей, являющихся линейными по неизвестным параметрам, включая полиномиальные, логарифмические, экспоненциальные и степенные ряды. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива. Инструкции приведены в данной статье после примеров.
Уравнение для прямой линии имеет следующий вид:
y = mx + b
или
y = m1x1 + m2x2 +… + b
если существует несколько диапазонов значений x, где зависимые значения y — функции независимых значений x. Значения m — коэффициенты, соответствующие каждому значению x, а b — постоянная. Обратите внимание, что y, x и m могут быть векторами. Функция ЛИНЕЙН возвращает массив {mn;mn-1;…;m1;b}. Функция ЛИНЕЙН может также возвращать дополнительную регрессионную статистику.
Синтаксис
ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Аргументы функции ЛИНЕЙН описаны ниже.
Синтаксис
-
Известные_значения_y. Обязательный аргумент. Множество значений y, которые уже известны для соотношения y = mx + b.
-
Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная.
-
Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.
-
-
Известные_значения_x. Необязательный аргумент. Множество значений x, которые уже известны для соотношения y = mx + b.
-
Массив известные_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то массивы известные_значения_y и известные_значения_x могут иметь любую форму — при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то известные_значения_y должны быть вектором (т. е. интервалом высотой в одну строку или шириной в один столбец).
-
Если массив известные_значения_x опущен, то предполагается, что это массив {1;2;3;…}, имеющий такой же размер, что и массив известные_значения_y.
-
-
Конст. Необязательный аргумент. Логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.
-
Если аргумент конст имеет значение ИСТИНА или опущен, то константа b вычисляется обычным образом.
-
Если аргумент конст имеет значение ЛОЖЬ, то значение b полагается равным 0 и значения m подбираются таким образом, чтобы выполнялось соотношение y = mx.
-
-
Статистика. Необязательный аргумент. Логическое значение, которое указывает, требуется ли вернуть дополнительную регрессионную статистику.
-
Если статистика имеет true, то LINEST возвращает дополнительную регрессию; в результате возвращается массив {mn;mn-1,…,m1;b;sen,sen-1,…,se1;seb;r2;sey; F,df;ssreg,ssresid}.
-
Если аргумент статистика имеет значение ЛОЖЬ или опущен, функция ЛИНЕЙН возвращает только коэффициенты m и постоянную b.
Дополнительная регрессионная статистика.
-
|
Величина |
Описание |
|---|---|
|
se1,se2,…,sen |
Стандартные значения ошибок для коэффициентов m1,m2,…,mn. |
|
seb |
Стандартное значение ошибки для постоянной b (seb = #Н/Д, если аргумент конст имеет значение ЛОЖЬ). |
|
r2 |
Коэффициент определения. Сравнивает предполагаемые и фактические значения y и диапазоны значений от 0 до 1. Если значение 1, то в выборке будет отличная корреляция— разница между предполагаемым значением y и фактическим значением y не существует. С другой стороны, если коэффициент определения — 0, уравнение регрессии не помогает предсказать значение y. Сведения о том, каквычисляется 2, см. в разделе «Замечания» далее в этой теме. |
|
sey |
Стандартная ошибка для оценки y. |
|
F |
F-статистика или F-наблюдаемое значение. F-статистика используется для определения того, является ли случайной наблюдаемая взаимосвязь между зависимой и независимой переменными. |
|
df |
Степени свободы. Степени свободы используются для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели необходимо сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН. Дополнительные сведения о вычислении величины df см. ниже в разделе «Замечания». Далее в примере 4 показано использование величин F и df. |
|
ssreg |
Регрессионная сумма квадратов. |
|
ssresid |
Остаточная сумма квадратов. Дополнительные сведения о расчете величин ssreg и ssresid см. в подразделе «Замечания» в конце данного раздела. |
На приведенном ниже рисунке показано, в каком порядке возвращается дополнительная регрессионная статистика.

Замечания
-
Любую прямую можно описать ее наклоном и пересечением с осью y:
Наклон (m):
Чтобы найти наклон линии, обычно записанной как m, возьмите две точки на строке (x1;y1) и (x2;y2); наклон равен (y2 — y1)/(x2 — x1).Y-перехват (b):
Y-пересечение строки, обычно записанное как b, — это значение y в точке, в которой линия пересекает ось y.Уравнение прямой имеет вид y = mx + b. Если известны значения m и b, то можно вычислить любую точку на прямой, подставляя значения y или x в уравнение. Можно также воспользоваться функцией ТЕНДЕНЦИЯ.
-
Если имеется только одна независимая переменная x, можно получить наклон и y-пересечение непосредственно, воспользовавшись следующими формулами:
Наклон:
=ИНДЕКС( LINEST(known_y,known_x’s);1)Y-перехват:
=ИНДЕКС( LINEST(known_y,known_x),2) -
Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель ЛИНЕЙН. Функция ЛИНЕЙН использует для определения наилучшей аппроксимации данных метод наименьших квадратов. Когда имеется только одна независимая переменная x, значения m и b вычисляются по следующим формулам:
где x и y — выборочные средние значения, например x = СРЗНАЧ(известные_значения_x), а y = СРЗНАЧ(известные_значения_y).
-
Функции ЛИННЕСТРОЙ и ЛОГЪЕСТ могут вычислять наилучшие прямые или экспоненциальное кривой, которые подходят для ваших данных. Однако необходимо решить, какой из двух результатов лучше всего подходит для ваших данных. Вы можетевычислить known_y(known_x) для прямой линии или РОСТ(known_y, known_x в) для экспоненциальной кривой. Эти функции без аргумента new_x возвращают массив значений y, спрогнозируемых вдоль этой линии или кривой в фактических точках данных. Затем можно сравнить спрогнозируемые значения с фактическими значениями. Для наглядного сравнения можно отобразить оба этих диаграммы.
-
Проводя регрессионный анализ, Microsoft Excel вычисляет для каждой точки квадрат разности между прогнозируемым значением y и фактическим значением y. Сумма этих квадратов разностей называется остаточной суммой квадратов (ssresid). Затем Microsoft Excel подсчитывает общую сумму квадратов (sstotal). Если конст = ИСТИНА или значение этого аргумента не указано, общая сумма квадратов будет равна сумме квадратов разностей действительных значений y и средних значений y. При конст = ЛОЖЬ общая сумма квадратов будет равна сумме квадратов действительных значений y (без вычитания среднего значения y из частного значения y). После этого регрессионную сумму квадратов можно вычислить следующим образом: ssreg = sstotal — ssresid. Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента определения r2— индикатор того, насколько хорошо уравнение, выданное в результате регрессионного анализа, объясняет связь между переменными. Значение r2 равно ssreg/sstotal.
-
В некоторых случаях один или несколько столбцов X (предполагается, что значения Y и X — в столбцах) могут не иметь дополнительного прогнозируемого значения при наличии других столбцов X. Другими словами, удаление одного или более столбцов X может привести к одинаковой точности предсказания значений Y. В этом случае эти избыточные столбцы X следует не использовать в модели регрессии. Этот вариант называется «коллинеарность», так как любой избыточный X-столбец может быть выражен как сумма многих не избыточных X-столбцов. Функция ЛИНЕЙН проверяет коллинеарность и удаляет все избыточные X-столбцы из модели регрессии при их идентификации. Удалены столбцы X распознаются в результатах LINEST как имеющие коэффициенты 0 в дополнение к значениям 0 se. Если один или несколько столбцов будут удалены как избыточные, это влияет на df, поскольку df зависит от числа X столбцов, фактически используемых для прогнозирования. Подробные сведения о вычислении df см. в примере 4. Если значение df изменилось из-за удаления избыточных X-столбцов, это также влияет на значения Sey и F. Коллинеарность должна быть относительно редкой на практике. Однако чаще всего возникают ситуации, когда некоторые столбцы X содержат только значения 0 и 1 в качестве индикаторов того, является ли тема в эксперименте участником определенной группы или не является ее участником. Если конст = ИСТИНА или опущен, функция LYST фактически вставляет дополнительный столбец X из всех 1 значений для моделирования перехвата. Если у вас есть столбец с значением 1 для каждой темы, если мальчик, или 0, а также столбец с 1 для каждой темы, если она является женщиной, или 0, последний столбец является избыточным, так как записи в нем могут быть получены из вычитания записи в столбце «самец» из записи в дополнительном столбце всех 1 значений, добавленных функцией LINEST.
-
Вычисление значения df для случаев, когда столбцы X удаляются из модели вследствие коллинеарности происходит следующим образом: если существует k столбцов известных_значений_x и значение конст = ИСТИНА или не указано, то df = n – k – 1. Если конст = ЛОЖЬ, то df = n — k. В обоих случаях удаление столбцов X вследствие коллинеарности увеличивает значение df на 1.
-
При вводе константы массива (например, в качестве аргумента известные_значения_x) следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк. Знаки-разделители могут быть другими в зависимости от региональных параметров.
-
Следует отметить, что значения y, предсказанные с помощью уравнения регрессии, возможно, не будут правильными, если они располагаются вне интервала значений y, которые использовались для определения уравнения.
-
Основной алгоритм, используемый в функции ЛИНЕЙН, отличается от основного алгоритма функций НАКЛОН и ОТРЕЗОК. Разница между алгоритмами может привести к различным результатам при неопределенных и коллинеарных данных. Например, если точки данных аргумента известные_значения_y равны 0, а точки данных аргумента известные_значения_x равны 1, то:
-
Функция ЛИНЕЙН возвращает значение, равное 0. Алгоритм функции ЛИНЕЙН используется для возвращения подходящих значений для коллинеарных данных, и в данном случае может быть найден по меньшей мере один ответ.
-
Наклон и ОТОКП возвращают #DIV/0! ошибка «#ЗНАЧ!». Алгоритм функций НАКЛОН и ОТОКП предназначен для поиска только одного ответа, и в этом случае может быть несколько ответов.
-
-
Помимо вычисления статистики для других типов регрессии с помощью функции ЛГРФПРИБЛ, для вычисления диапазонов некоторых других типов регрессий можно использовать функцию ЛИНЕЙН, вводя функции переменных x и y как ряды переменных х и у для ЛИНЕЙН. Например, следующая формула:
=ЛИНЕЙН(значения_y, значения_x^СТОЛБЕЦ($A:$C))
работает при наличии одного столбца значений Y и одного столбца значений Х для вычисления аппроксимации куба (многочлен 3-й степени) следующей формы:
y = m1*x + m2*x^2 + m3*x^3 + b
Формула может быть изменена для расчетов других типов регрессии, но в отдельных случаях требуется корректировка выходных значений и других статистических данных.
-
Значение F-теста, возвращаемое функцией ЛИНЕЙН, отличается от значения, возвращаемого функцией ФТЕСТ. Функция ЛИНЕЙН возвращает F-статистику, в то время как ФТЕСТ возвращает вероятность.
Примеры
Пример 1. Наклон и Y-пересечение
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Известные значения y |
Известные значения x |
|---|---|
|
1 |
0 |
|
9 |
4 |
|
5 |
2 |
|
7 |
3 |
|
Результат (наклон) |
Результат (y-пересечение) |
|
2 |
1 |
|
Формула (формула массива в ячейках A7:B7) |
|
|
=ЛИНЕЙН(A2:A5;B2:B5;;ЛОЖЬ) |
Пример 2. Простая линейная регрессия
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Месяц |
Продажи |
|---|---|
|
1 |
3 100 ₽ |
|
2 |
4 500 ₽ |
|
3 |
4 400 ₽ |
|
4 |
5 400 ₽ |
|
5 |
7 500 ₽ |
|
6 |
8 100 ₽ |
|
Формула |
Результат |
|
=СУММ(ЛИНЕЙН(B1:B6; A2:A7)*{9;1}) |
11 000 ₽ |
|
Вычисляет предполагаемый объем продаж в девятом месяце на основе данных о продажах за период с первого по шестой месяцы. |
Пример 3. Множественная линейная регрессия
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Общая площадь (x1) |
Количество офисов (x2) |
Количество входов (x3) |
Время эксплуатации (x4) |
Оценочная цена (y) |
|---|---|---|---|---|
|
2310 |
2 |
2 |
20 |
142 000 ₽ |
|
2333 |
2 |
2 |
12 |
144 000 ₽ |
|
2356 |
3 |
1,5 |
33 |
151 000 ₽ |
|
2379 |
3 |
2 |
43 |
150 000 ₽ |
|
2402 |
2 |
3 |
53 |
139 000 ₽ |
|
2425 |
4 |
2 |
23 |
169 000 ₽ |
|
2448 |
2 |
1,5 |
99 |
126 000 ₽ |
|
2471 |
2 |
2 |
34 |
142 900 ₽ |
|
2494 |
3 |
3 |
23 |
163 000 ₽ |
|
2517 |
4 |
4 |
55 |
169 000 ₽ |
|
2540 |
2 |
3 |
22 |
149 000 ₽ |
|
-234,2371645 |
||||
|
13,26801148 |
||||
|
0,996747993 |
||||
|
459,7536742 |
||||
|
1732393319 |
||||
|
Формула (формула динамического массива, введенная в A19) |
||||
|
=ЛИНЕЙН(E2:E12; A2:D12; ИСТИНА; ИСТИНА) |
Пример 4. Использование статистики F и r2
В предыдущем примере коэффициент определения (r2)составляет 0,99675 (см. ячейку A17 в результатах для ЛИТН), что указывает на крепкая связь между независимыми переменными и ценой продажи. F-статистику можно использовать для определения случайности этих результатов с таким высоким значением r2.
Предположим, что на самом деле взаимосвязи между переменными не существует, просто статистический анализ вывел сильную взаимозависимость по взятой равномерной выборке 11 зданий. Величина «Альфа» используется для обозначения вероятности ошибочного вывода о существовании сильная взаимозависимости.
Значения F и df в результатах функции LINEST можно использовать для оценки вероятности возникновения более высокого F-значения. F можно сравнивать с критическими значениями в опубликованных F-таблицах или с помощью функции FРАСП в Excel для вычисления вероятности случайного возникновения большего F-значения. Соответствующее F-распределение имеет v1 и v2 степени свободы. Если n — количество точек данных и конст = ИСТИНА или опущен, то v1 = n – df – 1 и v2 = df. (Если конст = ЛОЖЬ, то v1 = n – df и v2 = df.) Функция FIST с синтаксисом FDIST(F;v1;v2) возвращает вероятность возникновения более высокого F-значения, случайного. В этом примере df = 6 (ячейка B18) и F = 459,753674 (ячейка A18).
Предположим, что альфа имеет значение 0,05, v1 = 11 – 6 – 1 = 4, а v2 = 6, критический уровень F составляет 4,53. Поскольку F = 459,753674 значительно больше 4,53, вероятность того, что F-значение этого высокой случайности превышает 4,53, крайне маловероятно. (Если значение «Альфа» = 0,05, гипотеза о том, что между known_y и known_x нет связи, отклоняется при превышении F критического уровня (4,53).) Функцию FDIST в Excel можно использовать для получения вероятности случайного возникновения F-значения. Например, FIST(459,753674, 4, 6) = 1,37E-7, очень небольшая вероятность. Можно сделать вывод о том, что формула регрессии полезна для предсказания оценочного значения офисных зданий в этой области, найдя критический уровень F в таблице или с помощью функции FDIST. Помните, что крайне важно использовать правильные значения 1 и 2, вычисленные в предыдущем абзаце.
Пример 5. Вычисление t-статистики
Другой тест позволяет определить, подходит ли каждый коэффициент наклона для оценки стоимости здания под офис в примере 3. Например, чтобы проверить, имеет ли срок эксплуатации здания статистическую значимость, разделим -234,24 (коэффициент наклона для срока эксплуатации здания) на 13,268 (оценка стандартной ошибки для коэффициента времени эксплуатации из ячейки A15). Ниже приводится наблюдаемое t-значение:
t = m4 ÷ se4 = –234,24 ÷ 13,268 = –17,7
Если абсолютное значение t достаточно велико, можно сделать вывод, что коэффициент наклона можно использовать для оценки стоимости здания под офис в примере 3. В таблице ниже приведены абсолютные значения четырех наблюдаемых t-значений.
Если обратиться к справочнику по математической статистике, то окажется, что t-критическое двустороннее с 6 степенями свободы равно 2,447 при Альфа = 0,05. Критическое значение также можно также найти с помощью функции Microsoft Excel СТЬЮДРАСПОБР. СТЬЮДРАСПОБР(0,05; 6) = 2,447. Поскольку абсолютная величина t, равная 17,7, больше, чем 2,447, срок эксплуатации — это важная переменная для оценки стоимости здания под офис. Аналогичным образом можно протестировать все другие переменные на статистическую значимость. Ниже приводятся наблюдаемые t-значения для каждой из независимых переменных.
|
Переменная |
t-наблюдаемое значение |
|---|---|
|
Общая площадь |
5,1 |
|
Количество офисов |
31,3 |
|
Количество входов |
4,8 |
|
Возраст |
17,7 |
Абсолютная величина всех этих значений больше, чем 2,447. Следовательно, все переменные, использованные в уравнении регрессии, полезны для предсказания оценочной стоимости здания под офис в данном районе.