В этой статье описаны синтаксис формулы и использование функции LINEST в Microsoft Excel. Ссылки на дополнительные сведения о диаграммах и выполнении регрессионного анализа можно найти в разделе См. также.
Описание
Функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные и затем возвращает массив, который описывает полученную прямую. Функцию ЛИНЕЙН также можно объединять с другими функциями для вычисления других видов моделей, являющихся линейными по неизвестным параметрам, включая полиномиальные, логарифмические, экспоненциальные и степенные ряды. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива. Инструкции приведены в данной статье после примеров.
Уравнение для прямой линии имеет следующий вид:
y = mx + b
или
y = m1x1 + m2x2 +… + b
если существует несколько диапазонов значений x, где зависимые значения y — функции независимых значений x. Значения m — коэффициенты, соответствующие каждому значению x, а b — постоянная. Обратите внимание, что y, x и m могут быть векторами. Функция ЛИНЕЙН возвращает массив {mn;mn-1;…;m1;b}. Функция ЛИНЕЙН может также возвращать дополнительную регрессионную статистику.
Синтаксис
ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Аргументы функции ЛИНЕЙН описаны ниже.
Синтаксис
-
Известные_значения_y. Обязательный аргумент. Множество значений y, которые уже известны для соотношения y = mx + b.
-
Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная.
-
Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.
-
-
Известные_значения_x. Необязательный аргумент. Множество значений x, которые уже известны для соотношения y = mx + b.
-
Массив известные_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то массивы известные_значения_y и известные_значения_x могут иметь любую форму — при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то известные_значения_y должны быть вектором (т. е. интервалом высотой в одну строку или шириной в один столбец).
-
Если массив известные_значения_x опущен, то предполагается, что это массив {1;2;3;…}, имеющий такой же размер, что и массив известные_значения_y.
-
-
Конст. Необязательный аргумент. Логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.
-
Если аргумент конст имеет значение ИСТИНА или опущен, то константа b вычисляется обычным образом.
-
Если аргумент конст имеет значение ЛОЖЬ, то значение b полагается равным 0 и значения m подбираются таким образом, чтобы выполнялось соотношение y = mx.
-
-
Статистика. Необязательный аргумент. Логическое значение, которое указывает, требуется ли вернуть дополнительную регрессионную статистику.
-
Если статистика имеет true, то LINEST возвращает дополнительную регрессию; в результате возвращается массив {mn;mn-1,…,m1;b;sen,sen-1,…,se1;seb;r2;sey; F,df;ssreg,ssresid}.
-
Если аргумент статистика имеет значение ЛОЖЬ или опущен, функция ЛИНЕЙН возвращает только коэффициенты m и постоянную b.
Дополнительная регрессионная статистика.
-
|
Величина |
Описание |
|---|---|
|
se1,se2,…,sen |
Стандартные значения ошибок для коэффициентов m1,m2,…,mn. |
|
seb |
Стандартное значение ошибки для постоянной b (seb = #Н/Д, если аргумент конст имеет значение ЛОЖЬ). |
|
r2 |
Коэффициент определения. Сравнивает предполагаемые и фактические значения y и диапазоны значений от 0 до 1. Если значение 1, то в выборке будет отличная корреляция— разница между предполагаемым значением y и фактическим значением y не существует. С другой стороны, если коэффициент определения — 0, уравнение регрессии не помогает предсказать значение y. Сведения о том, каквычисляется 2, см. в разделе «Замечания» далее в этой теме. |
|
sey |
Стандартная ошибка для оценки y. |
|
F |
F-статистика или F-наблюдаемое значение. F-статистика используется для определения того, является ли случайной наблюдаемая взаимосвязь между зависимой и независимой переменными. |
|
df |
Степени свободы. Степени свободы используются для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели необходимо сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН. Дополнительные сведения о вычислении величины df см. ниже в разделе «Замечания». Далее в примере 4 показано использование величин F и df. |
|
ssreg |
Регрессионная сумма квадратов. |
|
ssresid |
Остаточная сумма квадратов. Дополнительные сведения о расчете величин ssreg и ssresid см. в подразделе «Замечания» в конце данного раздела. |
На приведенном ниже рисунке показано, в каком порядке возвращается дополнительная регрессионная статистика.

Замечания
-
Любую прямую можно описать ее наклоном и пересечением с осью y:
Наклон (m):
Чтобы найти наклон линии, обычно записанной как m, возьмите две точки на строке (x1;y1) и (x2;y2); наклон равен (y2 — y1)/(x2 — x1).Y-перехват (b):
Y-пересечение строки, обычно записанное как b, — это значение y в точке, в которой линия пересекает ось y.Уравнение прямой имеет вид y = mx + b. Если известны значения m и b, то можно вычислить любую точку на прямой, подставляя значения y или x в уравнение. Можно также воспользоваться функцией ТЕНДЕНЦИЯ.
-
Если имеется только одна независимая переменная x, можно получить наклон и y-пересечение непосредственно, воспользовавшись следующими формулами:
Наклон:
=ИНДЕКС( LINEST(known_y,known_x’s);1)Y-перехват:
=ИНДЕКС( LINEST(known_y,known_x),2) -
Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель ЛИНЕЙН. Функция ЛИНЕЙН использует для определения наилучшей аппроксимации данных метод наименьших квадратов. Когда имеется только одна независимая переменная x, значения m и b вычисляются по следующим формулам:
где x и y — выборочные средние значения, например x = СРЗНАЧ(известные_значения_x), а y = СРЗНАЧ(известные_значения_y).
-
Функции ЛИННЕСТРОЙ и ЛОГЪЕСТ могут вычислять наилучшие прямые или экспоненциальное кривой, которые подходят для ваших данных. Однако необходимо решить, какой из двух результатов лучше всего подходит для ваших данных. Вы можетевычислить known_y(known_x) для прямой линии или РОСТ(known_y, known_x в) для экспоненциальной кривой. Эти функции без аргумента new_x возвращают массив значений y, спрогнозируемых вдоль этой линии или кривой в фактических точках данных. Затем можно сравнить спрогнозируемые значения с фактическими значениями. Для наглядного сравнения можно отобразить оба этих диаграммы.
-
Проводя регрессионный анализ, Microsoft Excel вычисляет для каждой точки квадрат разности между прогнозируемым значением y и фактическим значением y. Сумма этих квадратов разностей называется остаточной суммой квадратов (ssresid). Затем Microsoft Excel подсчитывает общую сумму квадратов (sstotal). Если конст = ИСТИНА или значение этого аргумента не указано, общая сумма квадратов будет равна сумме квадратов разностей действительных значений y и средних значений y. При конст = ЛОЖЬ общая сумма квадратов будет равна сумме квадратов действительных значений y (без вычитания среднего значения y из частного значения y). После этого регрессионную сумму квадратов можно вычислить следующим образом: ssreg = sstotal — ssresid. Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента определения r2— индикатор того, насколько хорошо уравнение, выданное в результате регрессионного анализа, объясняет связь между переменными. Значение r2 равно ssreg/sstotal.
-
В некоторых случаях один или несколько столбцов X (предполагается, что значения Y и X — в столбцах) могут не иметь дополнительного прогнозируемого значения при наличии других столбцов X. Другими словами, удаление одного или более столбцов X может привести к одинаковой точности предсказания значений Y. В этом случае эти избыточные столбцы X следует не использовать в модели регрессии. Этот вариант называется «коллинеарность», так как любой избыточный X-столбец может быть выражен как сумма многих не избыточных X-столбцов. Функция ЛИНЕЙН проверяет коллинеарность и удаляет все избыточные X-столбцы из модели регрессии при их идентификации. Удалены столбцы X распознаются в результатах LINEST как имеющие коэффициенты 0 в дополнение к значениям 0 se. Если один или несколько столбцов будут удалены как избыточные, это влияет на df, поскольку df зависит от числа X столбцов, фактически используемых для прогнозирования. Подробные сведения о вычислении df см. в примере 4. Если значение df изменилось из-за удаления избыточных X-столбцов, это также влияет на значения Sey и F. Коллинеарность должна быть относительно редкой на практике. Однако чаще всего возникают ситуации, когда некоторые столбцы X содержат только значения 0 и 1 в качестве индикаторов того, является ли тема в эксперименте участником определенной группы или не является ее участником. Если конст = ИСТИНА или опущен, функция LYST фактически вставляет дополнительный столбец X из всех 1 значений для моделирования перехвата. Если у вас есть столбец с значением 1 для каждой темы, если мальчик, или 0, а также столбец с 1 для каждой темы, если она является женщиной, или 0, последний столбец является избыточным, так как записи в нем могут быть получены из вычитания записи в столбце «самец» из записи в дополнительном столбце всех 1 значений, добавленных функцией LINEST.
-
Вычисление значения df для случаев, когда столбцы X удаляются из модели вследствие коллинеарности происходит следующим образом: если существует k столбцов известных_значений_x и значение конст = ИСТИНА или не указано, то df = n – k – 1. Если конст = ЛОЖЬ, то df = n — k. В обоих случаях удаление столбцов X вследствие коллинеарности увеличивает значение df на 1.
-
При вводе константы массива (например, в качестве аргумента известные_значения_x) следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк. Знаки-разделители могут быть другими в зависимости от региональных параметров.
-
Следует отметить, что значения y, предсказанные с помощью уравнения регрессии, возможно, не будут правильными, если они располагаются вне интервала значений y, которые использовались для определения уравнения.
-
Основной алгоритм, используемый в функции ЛИНЕЙН, отличается от основного алгоритма функций НАКЛОН и ОТРЕЗОК. Разница между алгоритмами может привести к различным результатам при неопределенных и коллинеарных данных. Например, если точки данных аргумента известные_значения_y равны 0, а точки данных аргумента известные_значения_x равны 1, то:
-
Функция ЛИНЕЙН возвращает значение, равное 0. Алгоритм функции ЛИНЕЙН используется для возвращения подходящих значений для коллинеарных данных, и в данном случае может быть найден по меньшей мере один ответ.
-
Наклон и ОТОКП возвращают #DIV/0! ошибка «#ЗНАЧ!». Алгоритм функций НАКЛОН и ОТОКП предназначен для поиска только одного ответа, и в этом случае может быть несколько ответов.
-
-
Помимо вычисления статистики для других типов регрессии с помощью функции ЛГРФПРИБЛ, для вычисления диапазонов некоторых других типов регрессий можно использовать функцию ЛИНЕЙН, вводя функции переменных x и y как ряды переменных х и у для ЛИНЕЙН. Например, следующая формула:
=ЛИНЕЙН(значения_y, значения_x^СТОЛБЕЦ($A:$C))
работает при наличии одного столбца значений Y и одного столбца значений Х для вычисления аппроксимации куба (многочлен 3-й степени) следующей формы:
y = m1*x + m2*x^2 + m3*x^3 + b
Формула может быть изменена для расчетов других типов регрессии, но в отдельных случаях требуется корректировка выходных значений и других статистических данных.
-
Значение F-теста, возвращаемое функцией ЛИНЕЙН, отличается от значения, возвращаемого функцией ФТЕСТ. Функция ЛИНЕЙН возвращает F-статистику, в то время как ФТЕСТ возвращает вероятность.
Примеры
Пример 1. Наклон и Y-пересечение
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Известные значения y |
Известные значения x |
|---|---|
|
1 |
0 |
|
9 |
4 |
|
5 |
2 |
|
7 |
3 |
|
Результат (наклон) |
Результат (y-пересечение) |
|
2 |
1 |
|
Формула (формула массива в ячейках A7:B7) |
|
|
=ЛИНЕЙН(A2:A5;B2:B5;;ЛОЖЬ) |
Пример 2. Простая линейная регрессия
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Месяц |
Продажи |
|---|---|
|
1 |
3 100 ₽ |
|
2 |
4 500 ₽ |
|
3 |
4 400 ₽ |
|
4 |
5 400 ₽ |
|
5 |
7 500 ₽ |
|
6 |
8 100 ₽ |
|
Формула |
Результат |
|
=СУММ(ЛИНЕЙН(B1:B6; A2:A7)*{9;1}) |
11 000 ₽ |
|
Вычисляет предполагаемый объем продаж в девятом месяце на основе данных о продажах за период с первого по шестой месяцы. |
Пример 3. Множественная линейная регрессия
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Общая площадь (x1) |
Количество офисов (x2) |
Количество входов (x3) |
Время эксплуатации (x4) |
Оценочная цена (y) |
|---|---|---|---|---|
|
2310 |
2 |
2 |
20 |
142 000 ₽ |
|
2333 |
2 |
2 |
12 |
144 000 ₽ |
|
2356 |
3 |
1,5 |
33 |
151 000 ₽ |
|
2379 |
3 |
2 |
43 |
150 000 ₽ |
|
2402 |
2 |
3 |
53 |
139 000 ₽ |
|
2425 |
4 |
2 |
23 |
169 000 ₽ |
|
2448 |
2 |
1,5 |
99 |
126 000 ₽ |
|
2471 |
2 |
2 |
34 |
142 900 ₽ |
|
2494 |
3 |
3 |
23 |
163 000 ₽ |
|
2517 |
4 |
4 |
55 |
169 000 ₽ |
|
2540 |
2 |
3 |
22 |
149 000 ₽ |
|
-234,2371645 |
||||
|
13,26801148 |
||||
|
0,996747993 |
||||
|
459,7536742 |
||||
|
1732393319 |
||||
|
Формула (формула динамического массива, введенная в A19) |
||||
|
=ЛИНЕЙН(E2:E12; A2:D12; ИСТИНА; ИСТИНА) |
Пример 4. Использование статистики F и r2
В предыдущем примере коэффициент определения (r2)составляет 0,99675 (см. ячейку A17 в результатах для ЛИТН), что указывает на крепкая связь между независимыми переменными и ценой продажи. F-статистику можно использовать для определения случайности этих результатов с таким высоким значением r2.
Предположим, что на самом деле взаимосвязи между переменными не существует, просто статистический анализ вывел сильную взаимозависимость по взятой равномерной выборке 11 зданий. Величина «Альфа» используется для обозначения вероятности ошибочного вывода о существовании сильная взаимозависимости.
Значения F и df в результатах функции LINEST можно использовать для оценки вероятности возникновения более высокого F-значения. F можно сравнивать с критическими значениями в опубликованных F-таблицах или с помощью функции FРАСП в Excel для вычисления вероятности случайного возникновения большего F-значения. Соответствующее F-распределение имеет v1 и v2 степени свободы. Если n — количество точек данных и конст = ИСТИНА или опущен, то v1 = n – df – 1 и v2 = df. (Если конст = ЛОЖЬ, то v1 = n – df и v2 = df.) Функция FIST с синтаксисом FDIST(F;v1;v2) возвращает вероятность возникновения более высокого F-значения, случайного. В этом примере df = 6 (ячейка B18) и F = 459,753674 (ячейка A18).
Предположим, что альфа имеет значение 0,05, v1 = 11 – 6 – 1 = 4, а v2 = 6, критический уровень F составляет 4,53. Поскольку F = 459,753674 значительно больше 4,53, вероятность того, что F-значение этого высокой случайности превышает 4,53, крайне маловероятно. (Если значение «Альфа» = 0,05, гипотеза о том, что между known_y и known_x нет связи, отклоняется при превышении F критического уровня (4,53).) Функцию FDIST в Excel можно использовать для получения вероятности случайного возникновения F-значения. Например, FIST(459,753674, 4, 6) = 1,37E-7, очень небольшая вероятность. Можно сделать вывод о том, что формула регрессии полезна для предсказания оценочного значения офисных зданий в этой области, найдя критический уровень F в таблице или с помощью функции FDIST. Помните, что крайне важно использовать правильные значения 1 и 2, вычисленные в предыдущем абзаце.
Пример 5. Вычисление t-статистики
Другой тест позволяет определить, подходит ли каждый коэффициент наклона для оценки стоимости здания под офис в примере 3. Например, чтобы проверить, имеет ли срок эксплуатации здания статистическую значимость, разделим -234,24 (коэффициент наклона для срока эксплуатации здания) на 13,268 (оценка стандартной ошибки для коэффициента времени эксплуатации из ячейки A15). Ниже приводится наблюдаемое t-значение:
t = m4 ÷ se4 = –234,24 ÷ 13,268 = –17,7
Если абсолютное значение t достаточно велико, можно сделать вывод, что коэффициент наклона можно использовать для оценки стоимости здания под офис в примере 3. В таблице ниже приведены абсолютные значения четырех наблюдаемых t-значений.
Если обратиться к справочнику по математической статистике, то окажется, что t-критическое двустороннее с 6 степенями свободы равно 2,447 при Альфа = 0,05. Критическое значение также можно также найти с помощью функции Microsoft Excel СТЬЮДРАСПОБР. СТЬЮДРАСПОБР(0,05; 6) = 2,447. Поскольку абсолютная величина t, равная 17,7, больше, чем 2,447, срок эксплуатации — это важная переменная для оценки стоимости здания под офис. Аналогичным образом можно протестировать все другие переменные на статистическую значимость. Ниже приводятся наблюдаемые t-значения для каждой из независимых переменных.
|
Переменная |
t-наблюдаемое значение |
|---|---|
|
Общая площадь |
5,1 |
|
Количество офисов |
31,3 |
|
Количество входов |
4,8 |
|
Возраст |
17,7 |
Абсолютная величина всех этих значений больше, чем 2,447. Следовательно, все переменные, использованные в уравнении регрессии, полезны для предсказания оценочной стоимости здания под офис в данном районе.
Возвращает обратное значение для F-распределения вероятности
Возвращает обратное значение для F-распределения вероятности
Возвращает F-распределение вероятности
Возвращает F-распределение вероятности
Возвращает результат F-теста
Возвращает обратное значение для F-распределения вероятности
Возвращает одностороннее значение вероятности z-теста
Возвращает обратную интегральную функцию указанного бета-распределения
Возвращает интегральную функцию бета-распределения
Возвращает наименьшее значение, для которого интегральное биномиальное распределение меньше заданного значения или равно ему
Возвращает отдельное значение вероятности биномиального распределения
Возвращает вероятность пробного результата с помощью биномиального распределения
Возвращает распределение Вейбулла
Возвращает вероятность того, что значение из диапазона находится внутри заданных пределов
Возвращает значение гамма-функции
Возвращает обратное значение интегрального гамма-распределения
Возвращает гамма-распределение
Возвращает натуральный логарифм гамма-функции, Г(x)
Возвращает натуральный логарифм гамма-функции, Г(x)
Возвращает значение на 0,5 меньше стандартного нормального распределения
Возвращает гипергеометрическое распределение
Оценивает дисперсию по выборке
Вычисляет дисперсию по генеральной совокупности
Оценивает дисперсию по выборке, включая числа, текст и логические значения
Вычисляет дисперсию для генеральной совокупности, включая числа, текст и логические значения
Возвращает доверительный интервал для среднего генеральной совокупности
Возвращает доверительный интервал для среднего генеральной совокупности, используя t-распределение Стьюдента
Возвращает сумму квадратов отклонений
Возвращает квартиль набора данных
Возвращает квартиль набора данных на основе значений процентили из диапазона от 0 до 1, исключая границы
Возвращает квадрат коэффициента корреляции Пирсона
Возвращает значение ковариации выборки, среднее попарных произведений отклонений для всех точек данных в двух наборах данных
Возвращает значение ковариации, среднее произведений парных отклонений
Возвращает коэффициент корреляции между двумя множествами данных
Возвращает параметры экспоненциального тренда
Возвращает обратное значение интегрального логарифмического нормального распределения
Возвращает интегральное логарифмическое нормальное распределение
Возвращает наибольшее значение в списке аргументов
Возвращает наибольшее значение в списке аргументов, включая числа, текст и логические значения
Возвращает максимальное значение из заданных определенными условиями или критериями ячеек
Возвращает медиану заданных чисел
Возвращает наименьшее значение в списке аргументов
Возвращает наименьшее значение в списке аргументов, включая числа, текст и логические значения
Возвращает минимальное значение из ячеек, заданных определенными условиями или критериями
Возвращает вертикальный массив наиболее часто встречающихся или повторяющихся значений в массиве или диапазоне данных
Возвращает значение моды набора данных
Возвращает k-ое наибольшее значение в множестве данных
Возвращает k-ое наименьшее значение в множестве данных
Возвращает наклон линии линейной регрессии
Возвращает нормальное интегральное распределение
Возвращает обратное значение стандартного нормального интегрального распределения
Возвращает стандартное нормальное интегральное распределение
Возвращает нормализованное значение
Возвращает обратное значение нормального интегрального распределения
Возвращает отрицательное биномиальное распределение
Возвращает отрезок, отсекаемый на оси линией линейной регрессии
Возвращает количество перестановок для заданного числа объектов
Возвращает количество перестановок для заданного числа объектов (с повторами), которые можно выбрать из общего числа объектов
Возвращает коэффициент корреляции Пирсона
Возвращает значение линейного тренда
Возвращает будущее значение на основе существующих (ретроспективных) данных с использованием версии AAA алгоритма экспоненциального сглаживания (ETS)
Возвращает длину повторяющегося фрагмента, обнаруженного программой Excel в заданном временном ряду
Возвращает статистическое значение, являющееся результатом прогнозирования временного ряда
Возвращает доверительный интервал для прогнозной величины на указанную дату
Возвращает будущее значение на основе существующих значений
Возвращает k-ю процентиль для значений диапазона
Возвращает k-ю процентиль значений в диапазоне, где k может принимать значения от 0 до 1, исключая границы
Возвращает процентную норму значения в наборе данных
Возвращает ранг значения в наборе данных как процентную долю набора (от 0 до 1, исключая границы)
Возвращает распределение Пуассона
Возвращает ранг числа в списке чисел
Возвращает ранг числа в списке чисел
Возвращает значения в соответствии с экспоненциальным трендом
Возвращает среднее значение (среднее арифметическое) всех ячеек, которые удовлетворяют нескольким условиям
Возвращает асимметрию распределения
Возвращает асимметрию распределения на основе заполнения: характеристика степени асимметрии распределения относительно его среднего
Возвращает среднее гармоническое
Возвращает среднее геометрическое
Возвращает среднее арифметическое аргументов
Возвращает среднее арифметическое аргументов, включая числа, текст и логические значения
Возвращает среднее значение (среднее арифметическое) всех ячеек в диапазоне, которые удовлетворяют заданному условию
Возвращает среднее арифметическое абсолютных значений отклонений точек данных от среднего
Оценивает стандартное отклонение по выборке
Вычисляет стандартное отклонение по генеральной совокупности
Оценивает стандартное отклонение по выборке, включая числа, текст и логические значения
Вычисляет стандартное отклонение по генеральной совокупности, включая числа, текст и логические значения
Возвращает стандартную ошибку предсказанных значений y для каждого значения x в регрессии
Возвращает значение t для t-распределения Стьюдента как функцию вероятности и степеней свободы
Возвращает обратное t-распределение Стьюдента
Возвращает процентные точки (вероятность) для t-распределения Стьюдента
Возвращает t-распределение Стьюдента
Возвращает вероятность, соответствующую проверке по критерию Стьюдента
Возвращает процентные точки (вероятность) для t-распределения Стьюдента
Подсчитывает количество чисел в списке аргументов
Подсчитывает количество ячеек в диапазоне, удовлетворяющих заданному условию
Подсчитывает количество ячеек внутри диапазона, удовлетворяющих нескольким условиям
Подсчитывает количество значений в списке аргументов
Подсчитывает количество пустых ячеек в диапазоне
Возвращает значения в соответствии с линейным трендом
Возвращает среднее внутренности множества данных
Возвращает значение функции плотности для стандартного нормального распределения
Возвращает преобразование Фишера
Возвращает обратное преобразование Фишера
Возвращает интегральную функцию плотности бета-вероятности
Возвращает обратное значение односторонней вероятности распределения хи-квадрат
Возвращает интегральную функцию плотности бета-вероятности
Возвращает одностороннюю вероятность распределения хи-квадрат
Возвращает тест на независимость
Возвращает распределение частот в виде вертикального массива
Возвращает экспоненциальное распределение
Возвращает эксцесс множества данных
| английском | русском |
|---|---|
| LINEST |
ЛИНЕЙН |
Описание
Функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные и затем возвращает массив, который описывает полученную прямую. Функцию ЛИНЕЙН также можно объединять с другими функциями для вычисления других видов моделей, являющихся линейными по неизвестным параметрам, включая полиномиальные, логарифмические, экспоненциальные и степенные ряды. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива. Инструкции приведены в данной статье после примеров.
Уравнение для прямой линии имеет следующий вид:
y = mx + b
или
y = m1x1 + m2x2 + ... + b
если существует несколько диапазонов значений x, где зависимые значения y — функции независимых значений x. Значения m — коэффициенты, соответствующие каждому значению x, а b — постоянная. Обратите внимание, что y, x и m могут быть векторами. Функция ЛИНЕЙН возвращает массив {mn;mn-1;…;m1;b}. Функция ЛИНЕЙН может также возвращать дополнительную регрессионную статистику.
Дополнительная информация (источник)
Содержание
- LINEST in excel (Формула, Примеры) — Как использовать функцию ЛИНЕЙН?
- ЛИНЕЙН в Excel
- ЛИНЕЙН Формула в Excel
- Шаги для использования функции ЛИНЕЙН в Excel:
- Как использовать функцию ЛИНЕЙН в Excel?
- Пример № 1 — один диапазон значений X
- Пример № 2
- Пример № 3 — ЛИНЕЙН-функционирование для нескольких значений X:
- Функция ЛИНЕЙН Используется в более ранней и последней версии.
- Что нужно помнить о функции ЛИНЕЙН в Excel
- Рекомендуемые статьи
- Метод WorksheetFunction.LinEst (Excel)
- Синтаксис
- Параметры
- Возвращаемое значение
- Примечания
- Поддержка и обратная связь
LINEST in excel (Формула, Примеры) — Как использовать функцию ЛИНЕЙН?
Функция ЛИНЕЙН в Excel (Содержание)
- ЛИНЕЙН в Excel
- ЛИНЕЙН Формула в Excel
- Как использовать функцию ЛИНЕЙН в Excel?
ЛИНЕЙН в Excel
Функция ЛИНЕЙН — это встроенная функция в Excel, которая относится к категории Статистической функции, которая использует метод «LEAST SQUARES», чтобы найти строку
действовать вписывается через набор значений массива, то есть значений x и y.
Эта функция LINEST является очень полезной функцией в Excel для подгонки линии (y = mx + b) к данным, чтобы идентифицировать связь между двумя значениями, то есть значениями x и y.
Функция LINEST использует следующее уравнение строки:
Y = mx + b (для одного диапазона значений x)
Y = m1x1 + m2x2 +…. + B (для нескольких значений x)
ЛИНЕЙН Формула в Excel
Ниже приведена формула ЛИНЕЙН в Excel:
Функция ЛИНЕЙН в Excel включает следующие параметры:
- known_y’s: известные y’s — это n диапазон или массив значений y из линейного уравнения.
- known_x’s: известные x — это диапазон или массив значений x из линейного уравнения. Если это значение x равно NULL, Excel примет эти значения x_values как 1, 2, 3 … с тем же количеством значений, что и значения y.
- const: const — это логическое значение, которое указывает «ИСТИНА» или «ЛОЖЬ».
- stats: stat — это логическое значение, которое указывает либо возвращать дополнительную статистику регрессии, т.е. «ИСТИНА» или «ЛОЖЬ», функция которой должна возвращать статистику по строке наилучшего соответствия.
Шаги для использования функции ЛИНЕЙН в Excel:
Нажмите вкладку формулы в меню. Выберите функцию вставки. Мы получим диалоговое окно, как показано ниже, и выберем статистическую опцию, под которой вы получите список функций, в которых мы можем найти ЛИНЕЙН.
В Excel 2010 и расширенной версии мы видим вкладку «Больше функций», где мы можем найти функцию ЛИНЕЙН под категорией «Статистические», и скриншот показан ниже.
Как использовать функцию ЛИНЕЙН в Excel?
Функция LINEST в Excel очень проста и удобна в использовании. Давайте рассмотрим работу функции LINEST в Excel на примере формулы LINEST.
Вы можете скачать этот ЛИНЕЙН — Шаблон функции Excel здесь — ЛИНЕЙН — Шаблон функции Excel
Пример № 1 — один диапазон значений X
Чтобы использовать ЛИНЕЙН в качестве формулы массива, вам необходимо выполнить следующие шаги:
- Выберите ячейку, в которой находится функция, и нажмите клавишу f2.
- Нажмите CTRL + SHIFT + ВВОД.
В этом примере функции LINEST в Excel мы увидим, как функция LINEST работает с данными. Введите данные в Excel с двумя заголовками данных, названными как X и Y.
Чтобы использовать функцию ЛИНЕЙН, чтобы найти точный результат, перейдите в Формулы и выберите функцию Больше. Выберите функцию ЛИНЕЙН под статистической категорией, как показано ниже.
Выберите функцию ЛИНЕЙН, и вы получите диалоговое окно, показанное ниже:
Как только появится диалоговое окно, выберите «Известные Y & Know X» и укажите логические значения «ИСТИНА» зависит от указанных данных. то есть выберите B2: B11 как Известные Y, A2: A11 как Известные X и укажите логическое условие как ИСТИНА, чтобы получить указанное значение. После того, как вы нажмете ОК.
Вы получите то же значение, которое является коэффициентом m в уравнении y = mx + b
Итак, результатом будет:
Как уже упоминалось выше, нам нужно нажать CTRL + SHIFT + ENTER, чтобы получить точные данные. Теперь мы можем видеть, что формула заключена в две круглые скобки, т. Е. () Где вычисляется функция LINEST.
Мы можем упомянуть прямую линию с уклоном и y-пересечением. Чтобы получить перехват и регрессию наклона, мы можем использовать функцию LINEST, которая позволяет увидеть пример с пошаговой процедурой.
Пример № 2
В этом примере мы увидим, как использовать функцию LINEST в Excel. Эта функция используется для расчета линии коэффициента.
Линия Уравнение: Y = mx + c
Используя функцию LINEST в Excel, мы рассчитаем:
- Линия градиента Best Fit
- Линия наилучшего соответствия перехвата
- Стандартная ошибка градиента
- Стандартная ошибка перехвата
- R2
- Регрессионная сумма квадратов
- Остаточная сумма квадратов.
Рассмотрим данные ниже, которые имеют значения X1 и Y1, показанные ниже:
Для расчета приведенного выше уравнения выберите ячейку и вставьте функцию ЛИНЕЙН, показанную ниже.
Используйте CTRL + SHIFT + ENTER, чтобы получить все значения, где мы видим, что формула содержит открывающую и закрывающую скобки.
Давайте посмотрим на те же данные, как мы можем вывести одно и то же уравнение на графике:
Выберите X1 и Y2 Data и Go, чтобы вставить опцию и выберите тип диаграммы, как показано ниже. И затем нажмите ОК.
Так что график точечной диаграммы будет отображаться с выбранными данными x и y.
Теперь мы собираемся добавить линию тренда, чтобы показать точно, выбрав разбросанный график, как показано ниже.
Щелкните правой кнопкой мыши на графике и выберите «Добавить TrendLine».
После того, как вы выбрали опцию «Добавить линию тренда», на график будет добавлена новая линия тренда, как показано ниже.
Снова щелкните правой кнопкой мыши и выберите « Форматировать линию тренда», и вы получите параметр «Линия тренда».
Где он показывает различные статистические параметры, такие как экспоненциальный, линейный, логарифмический и полиномиальный.
Здесь выберите полиномиальный вариант с порядком 2, как показано на скриншоте ниже.
Прокрутите вниз и установите флажок, чтобы отметить уравнение отображения на графике и отобразить значение R-квадрата на графике.
Таким образом, уравнение было отображено на графике, как показано ниже, с тем же уравнением линии.
Пример № 3 — ЛИНЕЙН-функционирование для нескольких значений X:
Рассмотрим приведенный ниже пример, который имеет те же данные X1 и Y и значения X2.
Следующая диаграмма была оценена с помощью рассеянного графика путем добавления функции линии тренда.
Предположим уравнение для Y = b + m1 * X1 + m2 * X2
Функция Lines: LINEST (Known_y’s, (Known_X’s), (const), (stats))
Рассмотрим приведенный ниже массив таблицы, который обозначает следующее:
- m1 — обозначает X
- m2- обозначает X 2
- Const- обозначает b
Функция ЛИНЕЙН Используется в более ранней и последней версии.
В более ранней версии функция LINEST использовалась как формула, которая неверна для определения общей суммы квадратов, если для третьего аргумента функции LINEST задано значение false, и это приводит к недопустимому значению для суммы квадратов регрессии, а также к неверным значениям. для другой выходной суммы квадратов и значения коллинеарности, вызванного раундом ошибки, стандартные ошибки коэффициента регрессии, которые не дают точных результатов, степени свободы, которые не подходят.
В Excel 2003 функция LINEST была улучшена и дала хороший результат, добавив функцию TREND, чтобы сделать ее подходящей.
Что нужно помнить о функции ЛИНЕЙН в Excel
- Функция ЛИНЕЙН в Excel должна использоваться с соответствующими значениями, если нет, мы не получим точный результат.
- Функция LINEST в Excel не будет работать, если массив Known_x не совпадает с массивом Known_y.
Рекомендуемые статьи
Это было руководство к ЛИНЕЙНУ в Excel. Здесь мы обсуждаем формулу LINEST в Excel и Как использовать функцию LINEST в Excel вместе с практическими примерами и загружаемым шаблоном Excel. Вы также можете просмотреть наши другие предлагаемые статьи —
- MS Excel: MATCH Excel Функция
- Использование функции PROPER в Excel
- Руководство по функции Excel COMBIN
- Функция NPV в Excel с примерами
Источник
Метод WorksheetFunction.LinEst (Excel)
Вычисляет статистику для линии с помощью метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом соответствует вашим данным, и возвращает массив, описывающий линию. Так как эта функция возвращает массив значений, его необходимо ввести в виде формулы массива.
Синтаксис
Выражение Переменная, представляющая объект WorksheetFunction .
Параметры
| Имя | Обязательный или необязательный | Тип данных | Описание |
|---|---|---|---|
| Arg1 | Обязательный | Variant | Known_y — набор значений y, которые вы уже знаете в связи y = mx + b. |
| Arg2 | Необязательный | Variant | Known_x — необязательный набор значений x, которые, возможно, уже известны в связи y = mx + b. |
| Arg3 | Необязательный | Variant | Const — логическое значение, указывающее, следует ли принудительно принудить константу b к 0. |
| Arg4 | Необязательный | Variant | Stats — логическое значение, указывающее, следует ли возвращать дополнительную статистику регрессии. |
Возвращаемое значение
Variant
Примечания
Уравнение для строки — y = mx + b или y = m1x1 + m2x2 + . + b (при наличии нескольких диапазонов значений x), где зависимое значение y является функцией независимых значений x. Значения m являются коэффициентами, соответствующими каждому значению x, а b — константным значением. Обратите внимание, что y, x и m могут быть векторами. Массив, возвращающий LinEst , имеет значение . LinEst также может возвращать дополнительную статистику регрессии.
Если массив known_y находится в одном столбце, каждый столбец known_x интерпретируется как отдельная переменная.
Если массив known_y находится в одной строке, каждая строка known_x интерпретируется как отдельная переменная.
Массив known_x может включать один или несколько наборов переменных. Если используется только одна переменная, known_y и known_x могут быть диапазонами любой формы, если они имеют равные размеры. Если используется несколько переменных, known_y должны быть вектором (то есть диапазоном высотой одной строки или шириной одного столбца).
Если known_x опущен, предполагается <1,2,3. >, что массив имеет тот же размер, что и known_y.
Если параметр const имеет значение True или опущен, b вычисляется обычно.
Если const имеет значение False, значение b равно 0, а значения m корректируются в соответствии с . y = mx
Если stats имеет значение True, LinEst возвращает дополнительную статистику регрессии, поэтому возвращаемый массив имеет значение .
Если значение stats равно False или опущено, LinEst возвращает только коэффициенты m и константа b.
Дополнительная статистика регрессии выглядит следующим образом.
| Статистика регрессии | Описание |
|---|---|
| se1,se2. sen | Стандартные значения ошибок для коэффициентов m1,m2. mn. |
| Seb | Стандартное значение ошибки для константы b (seb = #N/A, если const имеет значение False). |
| R2 | Коэффициент определения. Сравнивает оценочные и фактические значения y и диапазон в значении от 0 до 1. Если значение равно 1, в выборке имеется идеальная корреляция: между предполагаемым значением y и фактическим значением y нет никакой разницы. С другой стороны, если коэффициент определения равен 0, уравнение регрессии не полезен при прогнозировании значения Y. |
| Сей | Стандартная ошибка для оценки y. |
| F | Статистика F или наблюдаемое значение F. Используйте статистику F, чтобы определить, возникает ли наблюдаемая связь между зависимыми и независимыми переменными случайно. |
| Df | Степени свободы. Используйте степени свободы для поиска F-критических значений в статистической таблице. Сравните значения, которые вы найдете в таблице со статистикой F, возвращенной LinEst, чтобы определить уровень достоверности для модели. |
| ssreg | Сумма квадратов регрессии. |
| ssresid | Остаточная сумма квадратов. |
На следующем рисунке показан порядок возврата дополнительной статистики регрессии.
Можно описать любую прямую линию с наклоном и y-перехватом: Slope (m) . Чтобы найти наклон линии, часто написанной как m, возьмите две точки на линии( x1,y1) и (x2,y2); наклон равен (y2 – y1)/(x2 – x1). Y-intercept (b): y-intercept линии, часто записываемой как b, — это значение y в точке пересечения линии по оси Y. Уравнение прямой линии : y = mx + b. После того как вы узнаете значения m и b, вы можете вычислить любую точку в строке, включив значение y или x в это уравнение. Вы также можете использовать функцию TREND.
При наличии только одной независимой переменной x можно получить значения наклона и y-перехвата напрямую с помощью следующих формул:
- Уклона: =INDEX(LINEST(known_y’s,known_x’s),1)
- Y-intercept: =INDEX(LINEST(known_y’s,known_x’s),2)
Точность строки, вычисленной с помощью LinEst, зависит от степени точечной в данных. Чем линейнее данные, тем точнее модель LinEst . LinEst использует метод наименьших квадратов для определения оптимального соответствия данным. При наличии только одной независимой переменной x вычисления для m и b основаны на следующих формулах:
, что x = AVERAGE(известные x) и y = AVERAGE(known_y’s).
Функции подгонки линий и кривых LinEst и LogEst могут вычислить наилучшую прямую или экспоненциальную кривую, которая соответствует вашим данным. Однако вы должны решить, какой из двух результатов лучше всего подходит для ваших данных. Можно вычислить TREND(known_y’s,known_x’s) для прямой линии или GROWTH(known_y’s, known_x’s) для экспоненциальной кривой. Эти функции без аргумента new_x возвращают массив значений Y, прогнозируемых вдоль этой линии или кривой в фактических точках данных. Затем можно сравнить прогнозируемые значения с фактическими значениями. Вы можете создать диаграмму для визуального сравнения.
При анализе регрессии Microsoft Excel вычисляет для каждой точки квадратную разницу между предполагаемым значением Y для этой точки и его фактическим значением y. Сумма этих квадратных различий называется остаточной суммой квадратов, ssresid. Затем Excel вычисляет общую сумму квадратов( sstotal). Если const = TRUE или опущено, общая сумма квадратов — это сумма квадратных различий между фактическими значениями y и средним значением y-значений. Если const = FALSE, общая сумма квадратов — это сумма квадратов фактических значений y (без вычитания среднего значения y из каждого отдельного значения y). Затем регрессионные суммы квадратов , ssreg, можно найти в ssreg = sstotal — ssresid . Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента определения r2, что является показателем того, насколько хорошо уравнение, полученное в результате регрессии анализа, объясняет связь между переменными; r2 равно ssreg/sstotal.
В некоторых случаях один или несколько столбцов X (предполагается, что Y и X находятся в столбцах) могут не иметь дополнительного прогнозного значения в присутствии других столбцов X. Иными словами, исключение одного или нескольких X-столбцов может привести к прогнозируемым значениям Y с одинаковой точностью. В этом случае эти избыточные столбцы X следует исключить из модели регрессии. Это явление называется коллинарностью , так как любой избыточный столбец X может быть выражен в виде суммы кратных столбцов X. LinEst проверяет наличие коллинарности и удаляет все избыточные X-столбцы из модели регрессии при их идентификации. Удаленные столбцы X можно распознать в выходных данных LinEst как имеющие коэффициенты 0 и 0 se.
- Если один или несколько столбцов удаляются как избыточные, df затрагивается, так как df зависит от количества столбцов X, фактически используемых для прогнозирования. Если df изменяется из-за удаления избыточных столбцов X, также затрагиваются значения sey и F.
- Коллинеарность должна быть относительно редкой на практике. Однако один из случаев, когда это более вероятно, заключается в том, что некоторые столбцы X содержат только 0 и 1 в качестве индикаторов того, является ли субъект в эксперименте членом определенной группы. Если const = TRUE или опущен, LinEst фактически вставляет дополнительный столбец X всех 1 для моделирования перехвата. Если у вас есть столбец с 1 для каждого субъекта, если мужчина, или 0, если нет, и у вас также есть столбец с 1 для каждого субъекта, если женщина, или 0, если нет, этот столбец является избыточным, так как записи в нем можно получить, вычитая запись в мужском столбце индикатора из записи в дополнительном столбце всех 1, добавленных LinEst.
- df вычисляется следующим образом, если из модели не удаляются X-столбцы из-за коллинеарности: если есть k столбцов known_x и const = TRUE или опущен, df = n — k — 1 . Если const = FALSE, . df = n — k В обоих случаях каждый столбец X, удаленный из-за коллинеарности, увеличивает значение df на 1.
Формулы, возвращающие массивы, должны вводиться как формулы массива.
- При вводе константы массива, например known_x в качестве аргумента, используйте запятые для разделения значений в одной строке, а точки с запятой — для разделения строк. Символы разделителя могут отличаться в зависимости от параметра языкового стандарта в разделе Региональные и языковые параметрыв панель управления.
- Обратите внимание, что значения y, прогнозируемые уравнением регрессии, могут быть недопустимыми, если они находятся за пределами диапазона значений y, используемых для определения уравнения.
Базовый алгоритм, используемый в функции LinEst , отличается от базового алгоритма, используемого в функциях Наклон и Перехват . Разница между этими алгоритмами может привести к разным результатам, если данные не определены и коллинеарны. Например, если точки данных аргумента known_y имеют значение 0, а точки данных аргумента known_x — 1:
- LinEst возвращает значение 0. Алгоритм LinEst предназначен для возврата разумных результатов для коллинеарных данных, и в этом случае можно найти по крайней мере один ответ.
- Наклон и перехват возвращают #DIV/0! Ошибка. Алгоритм наклона и перехвата предназначен для поиска одного и только одного ответа, и в этом случае может быть несколько ответов.
Поддержка и обратная связь
Есть вопросы или отзывы, касающиеся Office VBA или этой статьи? Руководство по другим способам получения поддержки и отправки отзывов см. в статье Поддержка Office VBA и обратная связь.
Источник
Функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные и затем возвращает массив, который описывает полученную прямую.
Описание функции ЛИНЕЙН
Функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные и затем возвращает массив, который описывает полученную прямую.
Функцию ЛИНЕЙН также можно объединять с другими функциями для вычисления других видов моделей, являющихся линейными по неизвестным параметрам, включая полиномиальные, логарифмические, экспоненциальные и степенные ряды. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива.
Уравнение для прямой линии имеет следующий вид:
Синтаксис
=ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])Аргументы
известные_значения_yизвестные_значения_xконстстатистика
Обязательный аргумент. Множество значений y, которые уже известны для соотношения
y = mx + b- Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная.
- Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.
Необязательный аргумент. Множество значений x, которые уже известны для соотношения
y = mx + b- Массив известные_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то массивы известные_значения_y и известные_значения_x могут иметь любую форму — при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то известные_значения_y должны быть вектором (т. е. интервалом высотой в одну строку или шириной в один столбец).
- Если массив известные_значения_x опущен, то предполагается, что это массив {1;2;3;…}, имеющий такой же размер, что и массив известные_значения_y.
Необязательный аргумент. Логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.
- Если аргумент конст имеет значение ИСТИНА или опущен, то константа b вычисляется обычным образом.
- Если аргумент конст имеет значение ЛОЖЬ, то значение b полагается равным 0 и значения m подбираются таким образом, чтобы выполнялось соотношение y = mx.
Необязательный аргумент. Логическое значение, которое указывает, требуется ли возвратить дополнительную регрессионную статистику.
- Если аргумент статистика имеет значение ИСТИНА, функция ЛИНЕЙН возвращает дополнительную регрессионную статистику. Возвращаемый массив будет иметь следующий вид: {mn;mn-1;…;m1;b:sen;sen-1;…;se1;seb:r2;sey:F;df:ssreg;ssresid}.
- Если аргумент статистика имеет значение ЛОЖЬ или опущен, функция ЛИНЕЙН возвращает только коэффициенты m и постоянную b.
Дополнительная регрессионная статистика:
| Величина | Описание |
|---|---|
| se1,se2,…,sen | Стандартные значения ошибок для коэффициентов m1,m2,…,mn. |
| seb | Стандартное значение ошибки для постоянной b (seb = #Н/Д, если аргумент конст имеет значение ЛОЖЬ). |
| r2 | Коэффициент детерминированности. Сравниваются фактические значения y и значения, получаемые из уравнения прямой; по результатам сравнения вычисляется коэффициент детерминированности, нормированный от 0 до 1. Если он равен 1, то имеет место полная корреляция с моделью, т. е. различий между фактическим и оценочным значениями y нет. В противоположном случае, если коэффициент детерминированности равен 0, использовать уравнение регрессии для предсказания значений y не имеет смысла. |
| sey | Стандартная ошибка для оценки y. |
| F | F-статистика или F-наблюдаемое значение. F-статистика используется для определения того, является ли случайной наблюдаемая взаимосвязь между зависимой и независимой переменными. |
| df | Степени свободы. Степени свободы полезны для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели необходимо сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН. |
| ssreg | Регрессионная сумма квадратов. |
| ssresid | Остаточная сумма квадратов. Дополнительные сведения о расчете величин ssreg и ssresid см. в подразделе «Замечания» в конце данного раздела. |
На приведенном ниже рисунке показано, в каком порядке возвращается дополнительная регрессионная статистика:

Замечания
- Любую прямую можно описать ее наклоном и пересечением с осью y:
Наклон (m):
чтобы определить наклон прямой, обычно обозначаемый через m, нужно взять две точки прямой (x1,y1) и (x2,y2); наклон будет равен (y2 — y1)/(x2 — x1).Y-пересечение (b):
Y-пересечением прямой, обычно обозначаемым через b, является значение y для точки, в которой прямая пересекает ось y.Уравнение прямой имеет вид
y = mx + bЕсли известны значения m и b, то можно вычислить любую точку на прямой, подставляя значения y или x в уравнение. Можно также воспользоваться функцией ТЕНДЕНЦИЯ.
- Если имеется только одна независимая переменная x, можно получить наклон и y-пересечение непосредственно, воспользовавшись следующими формулами:
Наклон:
=ИНДЕКС(ЛИНЕЙН(известные_значения_y;известные_значения_x);1)Y-пересечение:
=ИНДЕКС(ЛИНЕЙН(известные_значения_y;известные_значения_x);2) - Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель, используемаяфункцией. Функция ЛИНЕЙН использует для определения наилучшей аппроксимации данных метод наименьших квадратов. Когда имеется только одна независимая переменная x, значения m и b вычисляются по следующим формулам:
где: $$overline{x}, overline{y}$$ — выборочные средние значения, например:x = СРЗНАЧ(известные_значения_x)а
y = СРЗНАЧ(известные_значения_y) - Функции аппроксимации ЛИНЕЙН и ЛГРФПРИБЛ позволяют вычислить прямую или экспоненциальную кривую, наилучшим образом описывающую данные. Однако они не дают ответа на вопрос, какой из двух результатов больше подходит для решения поставленной задачи. Можно также вычислить функцию
ТЕНДЕНЦИЯ(известные_значения_y; известные_значения_x)для прямой или функцию
РОСТ(известные_значения_y; известные_значения_x)для экспоненциальной кривой. Эти функции, если не задавать аргумент новые_значения_x, возвращают массив вычисленных значений y для фактических значений x в соответствии с прямой или кривой. После этого можно сравнить вычисленные значения с фактическими значениями. Можно также построить диаграммы для визуального сравнения.
- Проводя регрессионный анализ, Microsoft Excel вычисляет для каждой точки квадрат разности между прогнозируемым значением y и фактическим значением y. Сумма этих квадратов разностей называется остаточной суммой квадратов (ssresid).
Затем Microsoft Excel подсчитывает общую сумму квадратов (sstotal). Если конст = ИСТИНА или значение этого аргумента не указано, общая сумма квадратов будет равна сумме квадратов разностей действительных значений y и средних значений y. При конст = ЛОЖЬ общая сумма квадратов будет равна сумме квадратов действительных значений y (без вычитания среднего значения y из частного значения y). После этого регрессионную сумму квадратов можно вычислить следующим образом: ssreg = sstotal — ssresid. Чем меньше остаточная сумма квадратов, тем больше значение коэффициента детерминированности r2, который показывает, насколько хорошо уравнение, полученное с помощью регрессионного анализа, объясняет взаимосвязи между переменными. Коэффициент r2 равен отношению ssreg/sstotal. - В некоторых случаях один или более столбцов X (пусть значения Y и X находятся в столбцах) не оказывают влияния на результаты при наличии других столбцов X. Иными словами, удаление одного или более столбцов X может привести к вычислению значений Y с прежней точностью. В этом случае избыточные столбцы X будут исключены из модели регрессии. Это явление называется коллинеарностью, поскольку избыточные столбцы X могут быть представлены в виде суммы нескольких неизбыточных столбцов.
Функция ЛИНЕЙН проверяет на коллинеарность и удаляет из модели регрессии все избыточные столбцы X, если обнаруживает их. Удаленные столбцы X можно определить в выходных данных ЛИНЕЙН по коэффициенту, равному 0, и по значению se, равному 0. Удаление одного или более столбцов как избыточных изменяет величину df, поскольку она зависит от количества столбцов X, в действительности используемых для прогнозирования.
При изменении df вследствие удаления избыточных столбцов значения sey и F также изменяются. Часто использовать коллинеарность не рекомендуется. Однако ее следует применять, если некоторые столбцы X содержат 0 или 1 в качестве индикатора, указывающего, входит ли предмет эксперимента в отдельную группу. Если конст = ИСТИНА или значение этого аргумента не указано, функция ЛИНЕЙН вставляет дополнительный столбец X для моделирования точки пересечения.Если имеется столбец со значениями 1 для указания мужчин и 0 — для женщин, а также имеется столбец со значениями 1 для указания женщин и 0 — для мужчин, то последний столбец удаляется, поскольку его значения можно получить из столбца с «индикатором пола».
- Вычисление значения df для случаев, когда столбцы X удаляются из модели вследствие коллинеарности происходит следующим образом: если существует k столбцов известных_значений_x и значение конст = ИСТИНА или не указано, то df = n – k – 1. Если конст = ЛОЖЬ, то df = n — k. В обоих случаях удаление столбцов X вследствие коллинеарности увеличивает значение df на 1.
- Формулы, которые возвращают массивы, должны быть введены как формулы массива.
- При вводе константы массива (например, в качестве аргумента известные_значения_x) следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк. Знаки-разделители могут быть другими в зависимости от региональных параметров.
Следует отметить, что значения y, предсказанные с помощью уравнения регрессии, возможно, не будут правильными, если они располагаются вне интервала значений y, которые использовались для определения уравнения.
Основной алгоритм, используемый в функции ЛИНЕЙН, отличается от основного алгоритма функций НАКЛОН и ОТРЕЗОК. Разница между алгоритмами может привести к различным результатам при неопределенных и коллинеарных данных. Например, если точки данных аргумента известные_значения_y равны 0, а точки данных аргумента известные_значения_x равны 1, то:
- Функция ЛИНЕЙН возвращает значение, равное 0. Алгоритм функции ЛИНЕЙН используется для возвращения подходящих значений для коллинеарных данных, и в данном случае может быть найден по меньшей мере один ответ.
- Функции НАКЛОН и ОТРЕЗОК возвращают ошибку #ДЕЛ/0!. Алгоритм функций НАКЛОН и ОТРЕЗОК используется для поиска только одного ответа, а в данном случае их может быть несколько.
- Помимо вычисления статистики для других типов регрессии с помощью функции ЛГРФПРИБЛ, для вычисления диапазонов некоторых других типов регрессий можно использовать функцию ЛИНЕЙН, вводя функции переменных x и y как ряды переменных х и у для ЛИНЕЙН. Например, следующая формула:
=ЛИНЕЙН(значения_y, значения_x^СТОЛБЕЦ($A:$C))работает при наличии одного столбца значений Y и одного столбца значений Х для вычисления аппроксимации куба (многочлен 3-й степени) следующей формы:
y = m1*x + m2*x^2 + m3*x^3 + bФормула может быть изменена для расчетов других типов регрессии, но в отдельных случаях требуется корректировка выходных значений и других статистических данных.
- Значение F-теста, возвращаемое функцией ЛИНЕЙН, отличается от значения, которое возвращает функция ФТЕСТ. Функция ЛИНЕЙН возвращает F-статистику, тогда как ФТЕСТ возвращает вероятность.
Пример
Простая линейная регрессия
Функция ЛИНЕЙН
В этой статье описаны синтаксис формулы и использование функции LINEST в Microsoft Excel. Ссылки на дополнительные сведения о диаграммах и выполнении регрессионного анализа можно найти в разделе См. также.
Описание
Функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные и затем возвращает массив, который описывает полученную прямую. Функцию ЛИНЕЙН также можно объединять с другими функциями для вычисления других видов моделей, являющихся линейными по неизвестным параметрам, включая полиномиальные, логарифмические, экспоненциальные и степенные ряды. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива. Инструкции приведены в данной статье после примеров.
Уравнение для прямой линии имеет следующий вид:
y = m1x1 + m2x2 +. + b
если существует несколько диапазонов значений x, где зависимые значения y — функции независимых значений x. Значения m — коэффициенты, соответствующие каждому значению x, а b — постоянная. Обратите внимание, что y, x и m могут быть векторами. Функция ЛИНЕЙН возвращает массив . Функция ЛИНЕЙН может также возвращать дополнительную регрессионную статистику.
Синтаксис
ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Аргументы функции ЛИНЕЙН описаны ниже.
Синтаксис
Известные_значения_y. Обязательный аргумент. Множество значений y, которые уже известны для соотношения y = mx + b.
Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная.
Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.
Известные_значения_x. Необязательный аргумент. Множество значений x, которые уже известны для соотношения y = mx + b.
Массив известные_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то массивы известные_значения_y и известные_значения_x могут иметь любую форму — при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то известные_значения_y должны быть вектором (т. е. интервалом высотой в одну строку или шириной в один столбец).
Если массив известные_значения_x опущен, то предполагается, что это массив <1;2;3;. >, имеющий такой же размер, что и массив известные_значения_y.
Конст. Необязательный аргумент. Логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.
Если аргумент конст имеет значение ИСТИНА или опущен, то константа b вычисляется обычным образом.
Если аргумент конст имеет значение ЛОЖЬ, то значение b полагается равным 0 и значения m подбираются таким образом, чтобы выполнялось соотношение y = mx.
Статистика. Необязательный аргумент. Логическое значение, которое указывает, требуется ли вернуть дополнительную регрессионную статистику.
Если статистика имеет true, то LINEST возвращает дополнительную регрессию; в результате возвращается массив .
Если аргумент статистика имеет значение ЛОЖЬ или опущен, функция ЛИНЕЙН возвращает только коэффициенты m и постоянную b.
Дополнительная регрессионная статистика.
Стандартные значения ошибок для коэффициентов m1,m2. mn.
Стандартное значение ошибки для постоянной b (seb = #Н/Д, если аргумент конст имеет значение ЛОЖЬ).
Коэффициент определения. Сравнивает предполагаемые и фактические значения y и диапазоны значений от 0 до 1. Если значение 1, то в выборке будет отличная корреляция— разница между предполагаемым значением y и фактическим значением y не существует. С другой стороны, если коэффициент определения — 0, уравнение регрессии не помогает предсказать значение y. Сведения о том, как вычисляется 2, см. в разделе «Замечания» далее в этой теме.
Стандартная ошибка для оценки y.
F-статистика или F-наблюдаемое значение. F-статистика используется для определения того, является ли случайной наблюдаемая взаимосвязь между зависимой и независимой переменными.
Степени свободы. Степени свободы используются для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели необходимо сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН. Дополнительные сведения о вычислении величины df см. ниже в разделе «Замечания». Далее в примере 4 показано использование величин F и df.
Регрессионная сумма квадратов.
Остаточная сумма квадратов. Дополнительные сведения о расчете величин ssreg и ssresid см. в подразделе «Замечания» в конце данного раздела.
На приведенном ниже рисунке показано, в каком порядке возвращается дополнительная регрессионная статистика.
Замечания
Любую прямую можно описать ее наклоном и пересечением с осью y:
Наклон (m):
Чтобы найти наклон линии, обычно записанной как m, возьмите две точки на строке (x1;y1) и (x2;y2); наклон равен (y2 — y1)/(x2 — x1).
Y-перехват (b):
Y-пересечение строки, обычно записанное как b, — это значение y в точке, в которой линия пересекает ось y.
Уравнение прямой имеет вид y = mx + b. Если известны значения m и b, то можно вычислить любую точку на прямой, подставляя значения y или x в уравнение. Можно также воспользоваться функцией ТЕНДЕНЦИЯ.
Если имеется только одна независимая переменная x, можно получить наклон и y-пересечение непосредственно, воспользовавшись следующими формулами:
Наклон:
=ИНДЕКС( LINEST(known_y,known_x’s);1)
Y-перехват:
=ИНДЕКС( LINEST(known_y,known_x),2)
Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель ЛИНЕЙН. Функция ЛИНЕЙН использует для определения наилучшей аппроксимации данных метод наименьших квадратов. Когда имеется только одна независимая переменная x, значения m и b вычисляются по следующим формулам:
где x и y — выборочные средние значения, например x = СРЗНАЧ(известные_значения_x), а y = СРЗНАЧ( известные_значения_y ).
Функции ЛИННЕСТРОЙ и ЛОГЪЕСТ могут вычислять наилучшие прямые или экспоненциальное кривой, которые подходят для ваших данных. Однако необходимо решить, какой из двух результатов лучше всего подходит для ваших данных. Вы можетевычислить known_y( known_x) для прямой линии или РОСТ( known_y, known_x в ) для экспоненциальной кривой. Эти функции без аргумента new_x возвращают массив значений y, спрогнозируемых вдоль этой линии или кривой в фактических точках данных. Затем можно сравнить спрогнозируемые значения с фактическими значениями. Для наглядного сравнения можно отобразить оба этих диаграммы.
Проводя регрессионный анализ, Microsoft Excel вычисляет для каждой точки квадрат разности между прогнозируемым значением y и фактическим значением y. Сумма этих квадратов разностей называется остаточной суммой квадратов (ssresid). Затем Microsoft Excel подсчитывает общую сумму квадратов (sstotal). Если конст = ИСТИНА или значение этого аргумента не указано, общая сумма квадратов будет равна сумме квадратов разностей действительных значений y и средних значений y. При конст = ЛОЖЬ общая сумма квадратов будет равна сумме квадратов действительных значений y (без вычитания среднего значения y из частного значения y). После этого регрессионную сумму квадратов можно вычислить следующим образом: ssreg = sstotal — ssresid. Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента определения r 2 — индикатор того, насколько хорошо уравнение, выданное в результате регрессионного анализа, объясняет связь между переменными. Значение r 2 равно ssreg/sstotal.
В некоторых случаях один или несколько столбцов X (предполагается, что значения Y и X — в столбцах) могут не иметь дополнительного прогнозируемого значения при наличии других столбцов X. Другими словами, удаление одного или более столбцов X может привести к одинаковой точности предсказания значений Y. В этом случае эти избыточные столбцы X следует не использовать в модели регрессии. Этот вариант называется «коллинеарность», так как любой избыточный X-столбец может быть выражен как сумма многих не избыточных X-столбцов. Функция ЛИНЕЙН проверяет коллинеарность и удаляет все избыточные X-столбцы из модели регрессии при их идентификации. Удалены столбцы X распознаются в результатах LINEST как имеющие коэффициенты 0 в дополнение к значениям 0 se. Если один или несколько столбцов будут удалены как избыточные, это влияет на df, поскольку df зависит от числа X столбцов, фактически используемых для прогнозирования. Подробные сведения о вычислении df см. в примере 4. Если значение df изменилось из-за удаления избыточных X-столбцов, это также влияет на значения Sey и F. Коллинеарность должна быть относительно редкой на практике. Однако чаще всего возникают ситуации, когда некоторые столбцы X содержат только значения 0 и 1 в качестве индикаторов того, является ли тема в эксперименте участником определенной группы или не является ее участником. Если конст = ИСТИНА или опущен, функция LYST фактически вставляет дополнительный столбец X из всех 1 значений для моделирования перехвата. Если у вас есть столбец с значением 1 для каждой темы, если мальчик, или 0, а также столбец с 1 для каждой темы, если она является женщиной, или 0, последний столбец является избыточным, так как записи в нем могут быть получены из вычитания записи в столбце «самец» из записи в дополнительном столбце всех 1 значений, добавленных функцией LINEST.
Вычисление значения df для случаев, когда столбцы X удаляются из модели вследствие коллинеарности происходит следующим образом: если существует k столбцов известных_значений_x и значение конст = ИСТИНА или не указано, то df = n – k – 1. Если конст = ЛОЖЬ, то df = n — k. В обоих случаях удаление столбцов X вследствие коллинеарности увеличивает значение df на 1.
При вводе константы массива (например, в качестве аргумента известные_значения_x) следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк. Знаки-разделители могут быть другими в зависимости от региональных параметров.
Следует отметить, что значения y, предсказанные с помощью уравнения регрессии, возможно, не будут правильными, если они располагаются вне интервала значений y, которые использовались для определения уравнения.
Основной алгоритм, используемый в функции ЛИНЕЙН, отличается от основного алгоритма функций НАКЛОН и ОТРЕЗОК. Разница между алгоритмами может привести к различным результатам при неопределенных и коллинеарных данных. Например, если точки данных аргумента известные_значения_y равны 0, а точки данных аргумента известные_значения_x равны 1, то:
Функция ЛИНЕЙН возвращает значение, равное 0. Алгоритм функции ЛИНЕЙН используется для возвращения подходящих значений для коллинеарных данных, и в данном случае может быть найден по меньшей мере один ответ.
Наклон и ОТОКП возвращают #DIV/0! ошибка «#ЗНАЧ!». Алгоритм функций НАКЛОН и ОТОКП предназначен для поиска только одного ответа, и в этом случае может быть несколько ответов.
Помимо вычисления статистики для других типов регрессии с помощью функции ЛГРФПРИБЛ, для вычисления диапазонов некоторых других типов регрессий можно использовать функцию ЛИНЕЙН, вводя функции переменных x и y как ряды переменных х и у для ЛИНЕЙН. Например, следующая формула:
работает при наличии одного столбца значений Y и одного столбца значений Х для вычисления аппроксимации куба (многочлен 3-й степени) следующей формы:
y = m1*x + m2*x^2 + m3*x^3 + b
Формула может быть изменена для расчетов других типов регрессии, но в отдельных случаях требуется корректировка выходных значений и других статистических данных.
Значение F-теста, возвращаемое функцией ЛИНЕЙН, отличается от значения, возвращаемого функцией ФТЕСТ. Функция ЛИНЕЙН возвращает F-статистику, в то время как ФТЕСТ возвращает вероятность.
Примеры
Пример 1. Наклон и Y-пересечение
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Линия тренда в Excel на разных графиках
Для наглядной иллюстрации тенденций изменения цены применяется линия тренда. Элемент технического анализа представляет собой геометрическое изображение средних значений анализируемого показателя.
Рассмотрим, как добавить линию тренда на график в Excel.
Добавление линии тренда на график
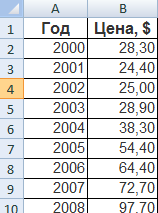
Для примера возьмем средние цены на нефть с 2000 года из открытых источников. Данные для анализа внесем в таблицу:
- Построим на основе таблицы график. Выделим диапазон – перейдем на вкладку «Вставка». Из предложенных типов диаграмм выберем простой график. По горизонтали – год, по вертикали – цена.
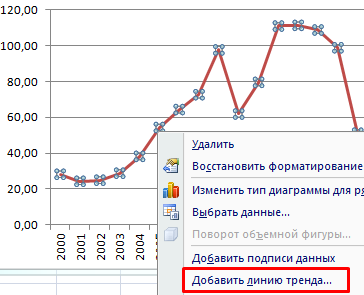
- Щелкаем правой кнопкой мыши по самому графику. Нажимаем «Добавить линию тренда».
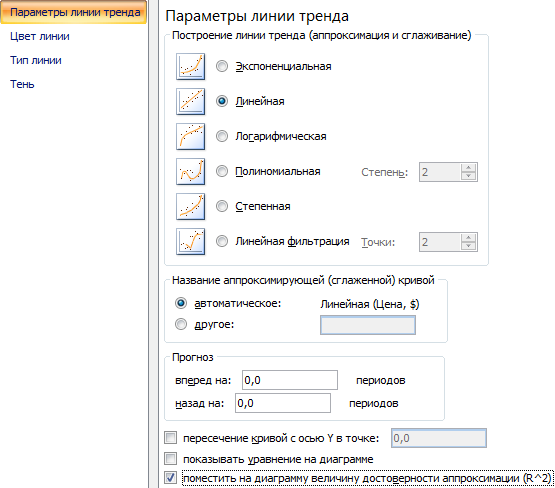
- Открывается окно для настройки параметров линии. Выберем линейный тип и поместим на график величину достоверности аппроксимации.
- На графике появляется косая линия.
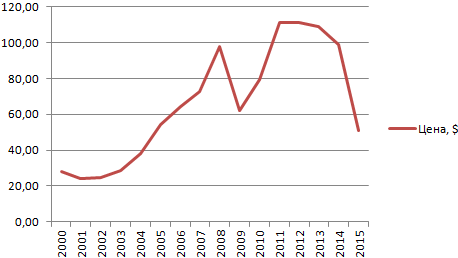
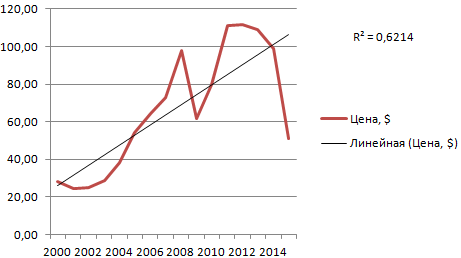
Линия тренда в Excel – это график аппроксимирующей функции. Для чего он нужен – для составления прогнозов на основе статистических данных. С этой целью необходимо продлить линию и определить ее значения.
Если R2 = 1, то ошибка аппроксимации равняется нулю. В нашем примере выбор линейной аппроксимации дал низкую достоверность и плохой результат. Прогноз будет неточным.
Внимание. Линию тренда нельзя добавить следующим типам графиков и диаграмм:
- лепестковый;
- круговой;
- поверхностный;
- кольцевой;
- объемный;
- с накоплением.
Уравнение линии тренда в Excel
В предложенном выше примере была выбрана линейная аппроксимация только для иллюстрации алгоритма. Как показала величина достоверности, выбор был не совсем удачным.
Следует выбирать тот тип отображения, который наиболее точно проиллюстрирует тенденцию изменений вводимых пользователем данных. Разберемся с вариантами.
Линейная аппроксимация
Ее геометрическое изображение – прямая. Следовательно, линейная аппроксимация применяется для иллюстрации показателя, который растет или уменьшается с постоянной скоростью.
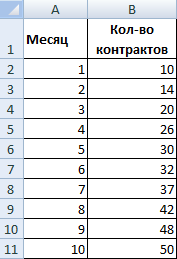
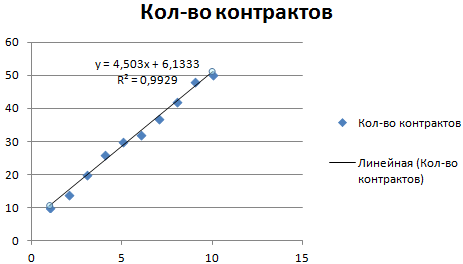
Рассмотрим условное количество заключенных менеджером контрактов на протяжении 10 месяцев:
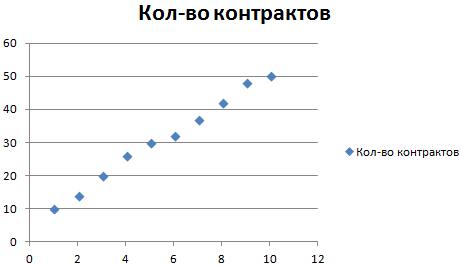
На основании данных в таблице Excel построим точечную диаграмму (она поможет проиллюстрировать линейный тип):
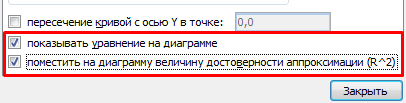
Выделяем диаграмму – «добавить линию тренда». В параметрах выбираем линейный тип. Добавляем величину достоверности аппроксимации и уравнение линии тренда в Excel (достаточно просто поставить галочки внизу окна «Параметры»).
Обратите внимание! При линейном типе аппроксимации точки данных расположены максимально близко к прямой. Данный вид использует следующее уравнение:
y = 4,503x + 6,1333
- где 4,503 – показатель наклона;
- 6,1333 – смещения;
- y – последовательность значений,
- х – номер периода.
Прямая линия на графике отображает стабильный рост качества работы менеджера. Величина достоверности аппроксимации равняется 0,9929, что указывает на хорошее совпадение расчетной прямой с исходными данными. Прогнозы должны получиться точными.
Чтобы спрогнозировать количество заключенных контрактов, например, в 11 периоде, нужно подставить в уравнение число 11 вместо х. В ходе расчетов узнаем, что в 11 периоде этот менеджер заключит 55-56 контрактов.
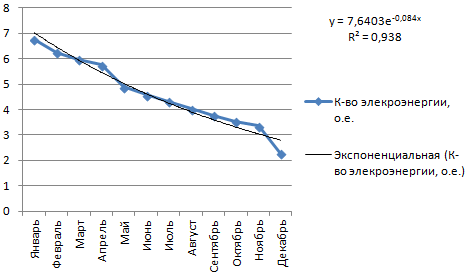
Экспоненциальная линия тренда
Данный тип будет полезен, если вводимые значения меняются с непрерывно возрастающей скоростью. Экспоненциальная аппроксимация не применяется при наличии нулевых или отрицательных характеристик.
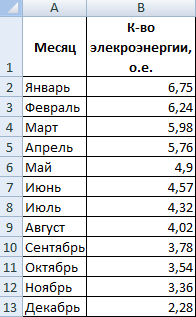
Построим экспоненциальную линию тренда в Excel. Возьмем для примера условные значения полезного отпуска электроэнергии в регионе Х:
Строим график. Добавляем экспоненциальную линию.
Уравнение имеет следующий вид:
- где 7,6403 и -0,084 – константы;
- е – основание натурального логарифма.
Показатель величины достоверности аппроксимации составил 0,938 – кривая соответствует данным, ошибка минимальна, прогнозы будут точными.
Логарифмическая линия тренда в Excel
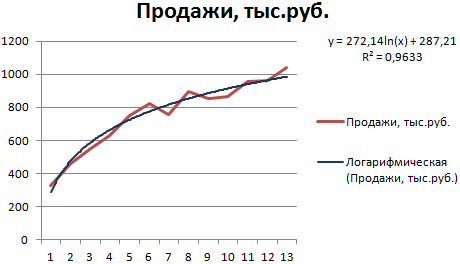
Используется при следующих изменениях показателя: сначала быстрый рост или убывание, потом – относительная стабильность. Оптимизированная кривая хорошо адаптируется к подобному «поведению» величины. Логарифмический тренд подходит для прогнозирования продаж нового товара, который только вводится на рынок.
На начальном этапе задача производителя – увеличение клиентской базы. Когда у товара будет свой покупатель, его нужно удержать, обслужить.
Построим график и добавим логарифмическую линию тренда для прогноза продаж условного продукта:
R2 близок по значению к 1 (0,9633), что указывает на минимальную ошибку аппроксимации. Спрогнозируем объемы продаж в последующие периоды. Для этого нужно в уравнение вместо х подставлять номер периода.
| Период | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Прогноз | 1005,4 | 1024,18 | 1041,74 | 1058,24 | 1073,8 | 1088,51 | 1102,47 |
Для расчета прогнозных цифр использовалась формула вида: =272,14*LN(B18)+287,21. Где В18 – номер периода.
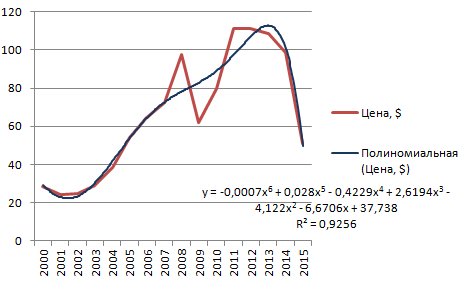
Полиномиальная линия тренда в Excel
Данной кривой свойственны переменные возрастание и убывание. Для полиномов (многочленов) определяется степень (по количеству максимальных и минимальных величин). К примеру, один экстремум (минимум и максимум) – это вторая степень, два экстремума – третья степень, три – четвертая.
Полиномиальный тренд в Excel применяется для анализа большого набора данных о нестабильной величине. Посмотрим на примере первого набора значений (цены на нефть).
Чтобы получить такую величину достоверности аппроксимации (0,9256), пришлось поставить 6 степень.
Зато такой тренд позволяет составлять более-менее точные прогнозы.
Как построить график в Excel по уравнению
Как предоставить информацию, чтобы она лучше воспринималась. Используйте графики. Это особенно актуально в аналитике. Рассмотрим, как построить график в Excel по уравнению.
Что это такое
График показывает, как одни величины зависят от других. Информация легче воспринимается. Посмотрите визуально, как отображается динамика изменения данных.
А нужно ли это
Графический способ отображения информации востребован в учебных или научных работах, исследованиях, при создании деловых планов, отчетов, презентаций, формул. Разработчики для построения графиков добавили способы визуального представления: диаграммы, пиктограммы.
Как построить график уравнения регрессии в Excel
Регрессионный анализ — статистический метод исследования. Устанавливает, как независимые величины влияют на зависимую переменную. Редактор предлагает инструменты для такого анализа.
Подготовительные работы
Перед использованием функции активируйте Пакет анализа. Перейдите: 
Выберите раздел: 
Далее: 
Прокрутите окно вниз, выберите: 
Отметьте пункт: 
Открыв раздел «Данные», появится кнопка «Анализ».
Как пользоваться
Рассмотрим на примере. В таблице указана температура воздуха и число покупателей. Данные выводятся за рабочий день. Как температура влияет на посещаемость. Перейдите: 
Выберите: 
Отобразится окно настроек, где входной интервал:
- Y. Ячейки с данными влияние факторов на которые нужно установить. Это число покупателей. Адрес пропишите вручную или выделите соответствующий столбец;
- Х. Данные, влияние на которые нужно установить. В примере, нужно узнать, как температура влияет на количество покупателей. Поэтому выделяем ячейки в столбце «Температура».
Анализ
Нажав кнопку «ОК», отобразится результат. 
Основной показатель — R-квадрат. Обозначает качество. Он равен 0,825 (82,5%). Что это означает? Зависимости, где показатель меньше 0,5 считается плохим. Поэтому в примере это хороший показатель. Y-пересечение. Число покупателей, если другие показатели равны нулю. 62,02 высокий показатель.
Как построить график квадратного уравнения в Excel
График функции имеет вид: y=ax2+bx+c. Рассмотрим диапазон значений: [-4:4].
- Составьте таблицу как на скриншоте;
- В третьей строке указываем коэффициенты и их значения;
- Пятая — диапазон значений;
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3;


При вычислении формулы прописывается знак «$». Используется чтобы ссылка была постоянной. Подробнее смотрите в статье: «Как зафиксировать ячейку».
Выделите диапазон значений по ним будем строить график. Перейдите: 
Поместите график в свободное место на листе.
Как построить график линейного уравнения
Функция имеет вид: y=kx+b. Построим в интервале [-4;4].
- В таблицу прописываем значение постоянных величин. Строка три;
- Строка 5. Вводим диапазон значений;
- Ячейка В6. Прописываем формулу.


График — прямая линия.
Вывод
Мы рассмотрели, как построить график в Экселе (Excel) по уравнению. Главное — правильно выбрать параметры и диаграмму. Тогда график точно отобразит данные.
источники:
http://exceltable.com/grafiki/liniya-trenda-v-excel
http://public-pc.com/kak-postroit-grafik-v-excel-po-uravneniyu/
В Excel реализовано большое количество функций, охватывающих математические вычисления, работу с текстом, статистику, аналитику, работу с базами данных, датой и временем, массивами и многим другим.
Для изучения функций в Excel пользователи часто обращаются к примерам и зачастую это примеры в Интернете на английском языке. Но при попытках использовать формулы (функции) из Интернета каждый раз возникают сообщения «В этой формуле обнаружена ошибка. Это не формула?».
Даже возникают вопросы, «почему в Excel отсутствует данная формула» и «как включить такую-то формулу в Excel»?
На самом деле ответ поразительный — формулы в Excel локализованы! Т.е. если у вас офисный пакет не на английском языке, то название функций переведено. Но всё ещё хуже — при этом оригинальные названия на английском не распознаются в Excel. То есть используя примеры в которых функции записаны английскими словами, нужно переводить их имена в русские эквиваленты.
Но и это ещё не всё! В английском написании формул Excel в качестве разделителя аргументов используется запятая, а в русском написании используется точка с запятой — вам нужно заменять и этот символ, чтобы функция Excel заработала.
Перевод функций (формул) Excel на русский
| A | Russian |
|---|---|
| ABS | ABS |
| ACCRINT | НАКОПДОХОД |
| ACCRINTM | НАКОПДОХОДПОГАШ |
| ACOS | ACOS |
| ACOSH | ACOSH |
| ACOT | ACOT |
| ACOTH | ACOTH |
| ADDRESS | АДРЕС |
| AGGREGATE | АГРЕГАТ |
| AMORDEGRC | АМОРУМ |
| AMORLINC | АМОРУВ |
| AND | И |
| ARABIC | АРАБСКОЕ |
| AREAS | ОБЛАСТИ |
| ASC | ASC |
| ASIN | ASIN |
| ASINH | ASINH |
| ATAN | ATAN |
| ATAN2 | ATAN2 |
| ATANH | ATANH |
| AVEDEV | СРОТКЛ |
| AVERAGE | СРЗНАЧ |
| AVERAGEA | СРЗНАЧА |
| AVERAGEIF | СРЗНАЧЕСЛИ |
| AVERAGEIFS | СРЗНАЧЕСЛИМН |
| B | Russian |
|---|---|
| BAHTTEXT | БАТТЕКСТ |
| BASE | ОСНОВАНИЕ |
| BESSELI | БЕССЕЛЬ.I |
| BESSELJ | БЕССЕЛЬ.J |
| BESSELK | БЕССЕЛЬ.K |
| BESSELY | БЕССЕЛЬ.Y |
| BETA.DIST | БЕТА.РАСП |
| BETA.INV | БЕТА.ОБР |
| BETADIST | БЕТАРАСП |
| BETAINV | БЕТАОБР |
| BIN2DEC | ДВ.В.ДЕС |
| BIN2HEX | ДВ.В.ШЕСТН |
| BIN2OCT | ДВ.В.ВОСЬМ |
| BINOM.DIST | БИНОМ.РАСП |
| BINOM.DIST.RANGE | БИНОМ.РАСП.ДИАП |
| BINOM.INV | БИНОМ.ОБР |
| BINOMDIST | БИНОМРАСП |
| BITAND | БИТ.И |
| BITLSHIFT | БИТ.СДВИГЛ |
| BITOR | БИТ.ИЛИ |
| BITRSHIFT | БИТ.СДВИГП |
| BITXOR | БИТ.ИСКЛИЛИ |
| C | Russian |
|---|---|
| CEILING | ОКРВВЕРХ |
| CEILING.MATH | ОКРВВЕРХ.МАТ |
| CEILING.PRECISE | ОКРВВЕРХ.ТОЧН |
| CELL | ЯЧЕЙКА |
| CHAR | СИМВОЛ |
| CHIDIST | ХИ2РАСП |
| CHIINV | ХИ2ОБР |
| CHISQ.DIST | ХИ2.РАСП |
| CHISQ.DIST.RT | ХИ2.РАСП.ПХ |
| CHISQ.INV | ХИ2.ОБР |
| CHISQ.INV.RT | ХИ2.ОБР.ПХ |
| CHISQ.TEST | ХИ2.ТЕСТ |
| CHITEST | ХИ2ТЕСТ |
| CHOOSE | ВЫБОР |
| CLEAN | ПЕЧСИМВ |
| CODE | КОДСИМВ |
| COLUMN | СТОЛБЕЦ |
| COLUMNS | ЧИСЛСТОЛБ |
| COMBIN | ЧИСЛКОМБ |
| COMBINA | ЧИСЛКОМБА |
| COMPLEX | КОМПЛЕКСН |
| CONCAT | СЦЕП |
| CONCATENATE | СЦЕПИТЬ |
| CONFIDENCE | ДОВЕРИТ |
| CONFIDENCE.NORM | ДОВЕРИТ.НОРМ |
| CONFIDENCE.T | ДОВЕРИТ.СТЬЮДЕНТ |
| CONVERT | ПРЕОБР |
| CORREL | КОРРЕЛ |
| COS | COS |
| COSH | COSH |
| COT | COT |
| COTH | COTH |
| COUNT | СЧЁТ |
| COUNTA | СЧЁТЗ |
| COUNTBLANK | СЧИТАТЬПУСТОТЫ |
| COUNTIF | СЧЁТЕСЛИ |
| COUNTIFS | СЧЁТЕСЛИМН |
| COUPDAYBS | ДНЕЙКУПОНДО |
| COUPDAYS | ДНЕЙКУПОН |
| COUPDAYSNC | ДНЕЙКУПОНПОСЛЕ |
| COUPNCD | ДАТАКУПОНПОСЛЕ |
| COUPNUM | ЧИСЛКУПОН |
| COUPPCD | ДАТАКУПОНДО |
| COVAR | КОВАР |
| COVARIANCE.P | КОВАРИАЦИЯ.Г |
| COVARIANCE.S | КОВАРИАЦИЯ.В |
| CRITBINOM | КРИТБИНОМ |
| CSC | CSC |
| CSCH | CSCH |
| CUBEKPIMEMBER | КУБЭЛЕМЕНТКИП |
| CUBEMEMBER | КУБЭЛЕМЕНТ |
| CUBEMEMBERPROPERTY | КУБСВОЙСТВОЭЛЕМЕНТА |
| CUBERANKEDMEMBER | КУБПОРЭЛЕМЕНТ |
| CUBESET | КУБМНОЖ |
| CUBESETCOUNT | КУБЧИСЛОЭЛМНОЖ |
| CUBEVALUE | КУБЗНАЧЕНИЕ |
| CUMIPMT | ОБЩПЛАТ |
| CUMPRINC | ОБЩДОХОД |
| D | Russian |
|---|---|
| DATE | ДАТА |
| DATEDIF | РАЗНДАТ |
| DATESTRING | СТРОКАДАННЫХ |
| DATEVALUE | ДАТАЗНАЧ |
| DAVERAGE | ДСРЗНАЧ |
| DAY | ДЕНЬ |
| DAYS | ДНИ |
| DAYS360 | ДНЕЙ360 |
| DB | ФУО |
| DBCS | БДЦС |
| DCOUNT | БСЧЁТ |
| DCOUNTA | БСЧЁТА |
| DDB | ДДОБ |
| DEC2BIN | ДЕС.В.ДВ |
| DEC2HEX | ДЕС.В.ШЕСТН |
| DEC2OCT | ДЕС.В.ВОСЬМ |
| DECIMAL | ДЕС |
| DEGREES | ГРАДУСЫ |
| DELTA | ДЕЛЬТА |
| DEVSQ | КВАДРОТКЛ |
| DGET | БИЗВЛЕЧЬ |
| DISC | СКИДКА |
| DMAX | ДМАКС |
| DMIN | ДМИН |
| DOLLAR | РУБЛЬ |
| DOLLARDE | РУБЛЬ.ДЕС |
| DOLLARFR | РУБЛЬ.ДРОБЬ |
| DPRODUCT | БДПРОИЗВЕД |
| DSTDEV | ДСТАНДОТКЛ |
| DSTDEVP | ДСТАНДОТКЛП |
| DSUM | БДСУММ |
| DURATION | ДЛИТ |
| DVAR | БДДИСП |
| DVARP | БДДИСПП |
| E | Russian |
|---|---|
| ECMA.CEILING | ECMA.ОКРВВЕРХ |
| EDATE | ДАТАМЕС |
| EFFECT | ЭФФЕКТ |
| ENCODEURL | КОДИР.URL |
| EOMONTH | КОНМЕСЯЦА |
| ERF | ФОШ |
| ERF.PRECISE | ФОШ.ТОЧН |
| ERFC | ДФОШ |
| ERFC.PRECISE | ДФОШ.ТОЧН |
| ERROR.TYPE | ТИП.ОШИБКИ |
| EVEN | ЧЁТН |
| EXACT | СОВПАД |
| EXP | EXP |
| EXPON.DIST | ЭКСП.РАСП |
| EXPONDIST | ЭКСПРАСП |
| F | Russian |
|---|---|
| F.DIST | F.РАСП |
| F.DIST.RT | F.РАСП.ПХ |
| F.INV | F.ОБР |
| F.INV.RT | F.ОБР.ПХ |
| F.TEST | F.ТЕСТ |
| FACT | ФАКТР |
| FACTDOUBLE | ДВФАКТР |
| FALSE | ЛОЖЬ |
| FDIST | FРАСП |
| FILTERXML | ФИЛЬТР.XML |
| FIND | НАЙТИ |
| FINDB | НАЙТИБ |
| FINV | FРАСПОБР |
| FISHER | ФИШЕР |
| FISHERINV | ФИШЕРОБР |
| FIXED | ФИКСИРОВАННЫЙ |
| FLOOR | ОКРВНИЗ |
| FLOOR.MATH | ОКРВНИЗ.МАТ |
| FLOOR.PRECISE | ОКРВНИЗ.ТОЧН |
| FORECAST | ПРЕДСКАЗ |
| FORECAST.ETS | ПРЕДСКАЗ.ETS |
| FORECAST.ETS.CONFINT | ПРЕДСКАЗ.ЕTS.ДОВИНТЕРВАЛ |
| FORECAST.ETS.SEASONALITY | ПРЕДСКАЗ.ETS.СЕЗОННОСТЬ |
| FORECAST.ETS.STAT | ПРЕДСКАЗ.ETS.СТАТ |
| FORECAST.LINEAR | ПРЕДСКАЗ.ЛИНЕЙН |
| FORMULATEXT | Ф.ТЕКСТ |
| FREQUENCY | ЧАСТОТА |
| FTEST | ФТЕСТ |
| FV | БС |
| FVSCHEDULE | БЗРАСПИС |
| G | Russian |
|---|---|
| GAMMA | ГАММА |
| GAMMA.DIST | ГАММА.РАСП |
| GAMMA.INV | ГАММА.ОБР |
| GAMMADIST | ГАММАРАСП |
| GAMMAINV | ГАММАОБР |
| GAMMALN | ГАММАНЛОГ |
| GAMMALN.PRECISE | ГАММАНЛОГ.ТОЧН |
| GAUSS | ГАУСС |
| GCD | НОД |
| GEOMEAN | СРГЕОМ |
| GESTEP | ПОРОГ |
| GETPIVOTDATA | ПОЛУЧИТЬ.ДАННЫЕ.СВОДНОЙ.ТАБЛИЦЫ |
| GROWTH | РОСТ |
| H | Russian |
|---|---|
| HARMEAN | СРГАРМ |
| HEX2BIN | ШЕСТН.В.ДВ |
| HEX2DEC | ШЕСТН.В.ДЕС |
| HEX2OCT | ШЕСТН.В.ВОСЬМ |
| HLOOKUP | ГПР |
| HOUR | ЧАС |
| HYPERLINK | ГИПЕРССЫЛКА |
| HYPGEOM.DIST | ГИПЕРГЕОМ.РАСП |
| HYPGEOMDIST | ГИПЕРГЕОМЕТ |
| I | Russian |
|---|---|
| IF | ЕСЛИ |
| IFERROR | ЕСЛИОШИБКА |
| IFNA | ЕСНД |
| IFS | УСЛОВИЯ |
| IMABS | МНИМ.ABS |
| IMAGINARY | МНИМ.ЧАСТЬ |
| IMARGUMENT | МНИМ.АРГУМЕНТ |
| IMCONJUGATE | МНИМ.СОПРЯЖ |
| IMCOS | МНИМ.COS |
| IMCOSH | МНИМ.COSH |
| IMCOT | МНИМ.COT |
| IMCSC | МНИМ.CSC |
| IMCSCH | МНИМ.CSCH |
| IMDIV | МНИМ.ДЕЛ |
| IMEXP | МНИМ.EXP |
| IMLN | МНИМ.LN |
| IMLOG10 | МНИМ.LOG10 |
| IMLOG2 | МНИМ.LOG2 |
| IMPOWER | МНИМ.СТЕПЕНЬ |
| IMPRODUCT | МНИМ.ПРОИЗВЕД |
| IMREAL | МНИМ.ВЕЩ |
| IMSEC | МНИМ.SEC |
| IMSECH | МНИМ.SECH |
| IMSIN | МНИМ.SIN |
| IMSINH | МНИМ.SINH |
| IMSQRT | МНИМ.КОРЕНЬ |
| IMSUB | МНИМ.РАЗН |
| IMSUM | МНИМ.СУММ |
| IMTAN | МНИМ.TAN |
| INDEX | ИНДЕКС |
| INDIRECT | ДВССЫЛ |
| INFO | ИНФОРМ |
| INT | ЦЕЛОЕ |
| INTERCEPT | ОТРЕЗОК |
| INTRATE | ИНОРМА |
| IPMT | ПРПЛТ |
| IRR | ВСД |
| ISBLANK | ЕПУСТО |
| ISERR | ЕОШ |
| ISERROR | ЕОШИБКА |
| ISEVEN | ЕЧЁТН |
| ISFORMULA | ЕФОРМУЛА |
| ISLOGICAL | ЕЛОГИЧ |
| ISNA | ЕНД |
| ISNONTEXT | ЕНЕТЕКСТ |
| ISNUMBER | ЕЧИСЛО |
| ISO.CEILING | ISO.ОКРВВЕРХ |
| ISODD | ЕНЕЧЁТ |
| ISOWEEKNUM | НОМНЕДЕЛИ.ISO |
| ISPMT | ПРОЦПЛАТ |
| ISREF | ЕССЫЛКА |
| ISTEXT | ЕТЕКСТ |
| ISTHAIDIGIT | ЕТАЙЦИФРЫ |
| K | Russian |
|---|---|
| KURT | ЭКСЦЕСС |
| L | Russian |
|---|---|
| LARGE | НАИБОЛЬШИЙ |
| LCM | НОК |
| LEFT | ЛЕВСИМВ |
| LEFTB | ЛЕВБ |
| LEN | ДЛСТР |
| LENB | ДЛИНБ |
| LINEST | ЛИНЕЙН |
| LN | LN |
| LOG | LOG |
| LOG10 | LOG10 |
| LOGEST | ЛГРФПРИБЛ |
| LOGINV | ЛОГНОРМОБР |
| LOGNORM.DIST | ЛОГНОРМ.РАСП |
| LOGNORM.INV | ЛОГНОРМ.ОБР |
| LOGNORMDIST | ЛОГНОРМРАСП |
| LOOKUP | ПРОСМОТР |
| LOWER | СТРОЧН |
| M | Russian |
|---|---|
| MATCH | ПОИСКПОЗ |
| MAX | МАКС |
| MAXA | МАКСА |
| MAXIFS | МАКСЕСЛИ |
| MDETERM | МОПРЕД |
| MDURATION | МДЛИТ |
| MEDIAN | МЕДИАНА |
| MID | ПСТР |
| MIDB | ПСТРБ |
| MIN | МИН |
| MINA | МИНА |
| MINIFS | МИНЕСЛИ |
| MINUTE | МИНУТЫ |
| MINVERSE | МОБР |
| MIRR | МВСД |
| MMULT | МУМНОЖ |
| MOD | ОСТАТ |
| MODE | МОДА |
| MODE.MULT | МОДА.НСК |
| MODE.SNGL | МОДА.ОДН |
| MONTH | МЕСЯЦ |
| MROUND | ОКРУГЛТ |
| MULTINOMIAL | МУЛЬТИНОМ |
| MUNIT | МЕДИН |
| N | Russian |
|---|---|
| N | Ч |
| NA | НД |
| NEGBINOM.DIST | ОТРБИНОМ.РАСП |
| NEGBINOMDIST | ОТРБИНОМРАСП |
| NETWORKDAYS | ЧИСТРАБДНИ |
| NETWORKDAYS.INTL | ЧИСТРАБДНИ.МЕЖД |
| NOMINAL | НОМИНАЛ |
| NORM.DIST | НОРМ.РАСП |
| NORM.INV | НОРМ.ОБР |
| NORM.S.DIST | НОРМ.СТ.РАСП |
| NORM.S.INV | НОРМ.СТ.ОБР |
| NORMDIST | НОРМРАСП |
| NORMINV | НОРМОБР |
| NORMSDIST | НОРМСТРАСП |
| NORMSINV | НОРМСТОБР |
| NOT | НЕ |
| NOW | ТДАТА |
| NPER | КПЕР |
| NPV | ЧПС |
| NUMBERSTRING | СТРОКАЧИСЕЛ |
| NUMBERVALUE | ЧЗНАЧ |
| O | Russian |
|---|---|
| OCT2BIN | ВОСЬМ.В.ДВ |
| OCT2DEC | ВОСЬМ.В.ДЕС |
| OCT2HEX | ВОСЬМ.В.ШЕСТН |
| ODD | НЕЧЁТ |
| ODDFPRICE | ЦЕНАПЕРВНЕРЕГ |
| ODDFYIELD | ДОХОДПЕРВНЕРЕГ |
| ODDLPRICE | ЦЕНАПОСЛНЕРЕГ |
| ODDLYIELD | ДОХОДПОСЛНЕРЕГ |
| OFFSET | СМЕЩ |
| OR | ИЛИ |
| P | Russian |
|---|---|
| PDURATION | ПДЛИТ |
| PEARSON | PEARSON |
| PERCENTILE | ПЕРСЕНТИЛЬ |
| PERCENTILE.EXC | ПРОЦЕНТИЛЬ.ИСКЛ |
| PERCENTILE.INC | ПРОЦЕНТИЛЬ.ВКЛ |
| PERCENTRANK | ПРОЦЕНТРАНГ |
| PERCENTRANK.EXC | ПРОЦЕНТРАНГ.ИСКЛ |
| PERCENTRANK.INC | ПРОЦЕНТРАНГ.ВКЛ |
| PERMUT | ПЕРЕСТ |
| PERMUTATIONA | ПЕРЕСТА |
| PHI | ФИ |
| PHONETIC | PHONETIC |
| PI | ПИ |
| PMT | ПЛТ |
| POISSON | ПУАССОН |
| POISSON.DIST | ПУАССОН.РАСП |
| POWER | СТЕПЕНЬ |
| PPMT | ОСПЛТ |
| PRICE | ЦЕНА |
| PRICEDISC | ЦЕНАСКИДКА |
| PRICEMAT | ЦЕНАПОГАШ |
| PROB | ВЕРОЯТНОСТЬ |
| PRODUCT | ПРОИЗВЕД |
| PROPER | ПРОПНАЧ |
| PV | ПС |
| Q | Russian |
|---|---|
| QUARTILE | КВАРТИЛЬ |
| QUARTILE.EXC | КВАРТИЛЬ.ИСКЛ |
| QUARTILE.INC | КВАРТИЛЬ.ВКЛ |
| QUOTIENT | ЧАСТНОЕ |
| R | Russian |
|---|---|
| RADIANS | РАДИАНЫ |
| RAND | СЛЧИС |
| RANDBETWEEN | СЛУЧМЕЖДУ |
| RANK | РАНГ |
| RANK.AVG | РАНГ.СР |
| RANK.EQ | РАНГ.РВ |
| RATE | СТАВКА |
| RECEIVED | ПОЛУЧЕНО |
| REPLACE | ЗАМЕНИТЬ |
| REPLACEB | ЗАМЕНИТЬБ |
| REPT | ПОВТОР |
| RIGHT | ПРАВСИМВ |
| RIGHTB | ПРАВБ |
| ROMAN | РИМСКОЕ |
| ROUND | ОКРУГЛ |
| ROUNDBAHTDOWN | ОКРУГЛБАТВНИЗ |
| ROUNDBAHTUP | ОКРУГЛБАТВВЕРХ |
| ROUNDDOWN | ОКРУГЛВНИЗ |
| ROUNDUP | ОКРУГЛВВЕРХ |
| ROW | СТРОКА |
| ROWS | ЧСТРОК |
| RRI | ЭКВ.СТАВКА |
| RSQ | КВПИРСОН |
| RTD | ДРВ |
| S | Russian |
|---|---|
| SEARCH | ПОИСК |
| SEARCHB | ПОИСКБ |
| SEC | SEC |
| SECH | SECH |
| SECOND | СЕКУНДЫ |
| SERIESSUM | РЯД.СУММ |
| SHEET | ЛИСТ |
| SHEETS | ЛИСТЫ |
| SIGN | ЗНАК |
| SIN | SIN |
| SINH | SINH |
| SKEW | СКОС |
| SKEW.P | СКОС.Г |
| SLN | АПЛ |
| SLOPE | НАКЛОН |
| SMALL | НАИМЕНЬШИЙ |
| SQRT | КОРЕНЬ |
| SQRTPI | КОРЕНЬПИ |
| STANDARDIZE | НОРМАЛИЗАЦИЯ |
| STDEV | СТАНДОТКЛОН |
| STDEV.P | СТАНДОТКЛОН.Г |
| STDEV.S | СТАНДОТКЛОН.В |
| STDEVA | СТАНДОТКЛОНА |
| STDEVP | СТАНДОТКЛОНП |
| STDEVPA | СТАНДОТКЛОНПА |
| STEYX | СТОШYX |
| SUBSTITUTE | ПОДСТАВИТЬ |
| SUBTOTAL | ПРОМЕЖУТОЧНЫЕ.ИТОГИ |
| SUM | СУММ |
| SUMIF | СУММЕСЛИ |
| SUMIFS | СУММЕСЛИМН |
| SUMPRODUCT | СУММПРОИЗВ |
| SUMSQ | СУММКВ |
| SUMX2MY2 | СУММРАЗНКВ |
| SUMX2PY2 | СУММСУММКВ |
| SUMXMY2 | СУММКВРАЗН |
| SWITCH | ПЕРЕКЛЮЧ |
| SYD | АСЧ |
| T | Russian |
|---|---|
| T | Т |
| T.DIST | СТЬЮДЕНТ.РАСП |
| T.DIST.2T | СТЬЮДЕНТ.РАСП.2Х |
| T.DIST.RT | СТЬЮДЕНТ.РАСП.ПХ |
| T.INV | СТЬЮДЕНТ.ОБР |
| T.INV.2T | СТЬЮДЕНТ.ОБР.2Х |
| T.TEST | СТЬЮДЕНТ.ТЕСТ |
| TAN | TAN |
| TANH | TANH |
| TBILLEQ | РАВНОКЧЕК |
| TBILLPRICE | ЦЕНАКЧЕК |
| TBILLYIELD | ДОХОДКЧЕК |
| TDIST | СТЬЮДРАСП |
| TEXT | ТЕКСТ |
| TEXTJOIN | ОБЪЕДИНИТЬ |
| THAIDAYOFWEEK | ТАЙДЕНЬНЕД |
| THAIDIGIT | ТАЙЦИФРА |
| THAIMONTHOFYEAR | ТАЙМЕСЯЦ |
| THAINUMSOUND | ТАЙЧИСЛОВЗВУК |
| THAINUMSTRING | ТАЙЧИСЛОВСТРОКУ |
| THAISTRINGLENGTH | ТАЙДЛИНАСТРОКИ |
| THAIYEAR | ТАЙГОД |
| TIME | ВРЕМЯ |
| TIMEVALUE | ВРЕМЗНАЧ |
| TINV | СТЬЮДРАСПОБР |
| TODAY | СЕГОДНЯ |
| TRANSPOSE | ТРАНСП |
| TREND | ТЕНДЕНЦИЯ |
| TRIM | СЖПРОБЕЛЫ |
| TRIMMEAN | УРЕЗСРЕДНЕЕ |
| TRUE | ИСТИНА |
| TRUNC | ОТБР |
| TTEST | ТТЕСТ |
| TYPE | ТИП |
| U | Russian |
|---|---|
| UNICHAR | ЮНИСИМВ |
| UNICODE | UNICODE |
| UPPER | ПРОПИСН |
| USDOLLAR | ДОЛЛСША |
| V | Russian |
|---|---|
| VALUE | ЗНАЧЕН |
| VAR | ДИСП |
| VAR.P | ДИСП.Г |
| VAR.S | ДИСП.В |
| VARA | ДИСПА |
| VARP | ДИСПР |
| VARPA | ДИСПРА |
| VDB | ПУО |
| VLOOKUP | ВПР |
| W | Russian |
|---|---|
| WEBSERVICE | ВЕБСЛУЖБА |
| WEEKDAY | ДЕНЬНЕД |
| WEEKNUM | НОМНЕДЕЛИ |
| WEIBULL | ВЕЙБУЛЛ |
| WEIBULL.DIST | ВЕЙБУЛЛ.РАСП |
| WORKDAY | РАБДЕНЬ |
| WORKDAY.INTL | РАБДЕНЬ.МЕЖД |
| X | Russian |
|---|---|
| XIRR | ЧИСТВНДОХ |
| XNPV | ЧИСТНЗ |
| XOR | ИСКЛИЛИ |
| Y | Russian |
|---|---|
| YEAR | ГОД |
| YEARFRAC | ДОЛЯГОДА |
| YIELD | ДОХОД |
| YIELDDISC | ДОХОДСКИДКА |
| YIELDMAT | ДОХОДПОГАШ |
| Z | Russian |
|---|---|
| Z.TEST | Z.ТЕСТ |
| ZTEST | ZТЕСТ |
Связанные статьи:
- Как в Excel заменить все точки в цифрах на запятые. Функция ПОДСТАВИТЬ (85%)
- Как конвертировать курсы валют в Microsoft Excel (85%)
- Расчёт процентов в Excel (65%)
- Как сделать палочковый график в Microsoft Excel (65%)
- Как создать интервальный график в Microsoft Excel (65%)
- Как сделать, чтобы офисные документы сохранялись по умолчанию на компьютер (RANDOM — 50%)
Updated: 05.05.2020 at 17:19
Английское название функции LINEST() было переведено на 19 языка/языков. Для всех остальных языков применяется английское название функции. Существуют различия в переводах в разных Excel версиях
Наличие
| Excel Версии | Наличие | Категория |
|---|---|---|
| Excel (Office 365) | Да | Статистические |
| Excel 2013 | Да | Статистические |
| Excel 2010 | Да | Статистические |
| Excel 2007 | Да | Статистические |
| Excel 2003 | Да | Статистические |
Ссылка язык
| язык | Обозначение |
|---|---|
| English | LINEST |
Переводы
| язык | Обозначение |
|---|---|
| Basque | ZENBATESPEN.LINEALA |
| Catalan | ESTIMACIO.LINEAL |
| Czech | LINREGRESE |
| Danish | LINREGR |
| Dutch | LIJNSCH |
| Finnish | LINREGR |
| French | DROITEREG |
| Galician | ESTLIN |
| German | RGP |
| Hungarian | LIN.ILL |
| Italian | REGR.LIN |
| Norwegian | RETTLINJE |
| Polish | REGLINP |
| Portuguese, Brazil | PROJ.LIN |
| Portuguese, Portugal | PROJ.LIN |
| Russian | ЛИНЕЙН |
| Spanish | ESTIMACION.LINEAL |
| Swedish | REGR |
| Turkish | DOT |
Ссылки на службу поддержки Microsoft для функции ЛИНЕЙН()
Примечание: Microsoft находится в процессе переработки ссылок и содержания службы поддержки . Поэтому в настоящее время не исключено, что некоторые из указанных ссылок не работают или ведут на ошибочную страницу. Ссылки будут актуализированы как только это будет возможно.
| язык | |||
|---|---|---|---|
| Arabic | Finnish | Kazakh | Russian |
| Basque | French | Konkani | Serbian |
| Bulgarian | Galician | Korean | Slovak |
| Catalan | German | Latvian | Slovenian |
| Chinese — Simplified | Greek | Lithuanian | Spanish |
| Chinese — Traditional | Gujarati | Malaysian | Swedish |
| Croatian | Hebrew | Marathi | Thai |
| Czech | Hindi | Norwegian | Turkish |
| Danish | Hungarian | Polish | Ukrainian |
| Dutch | Indonesian | Portuguese, Brazil | Vietnamese |
| English | Italian | Portuguese, Portugal | — |
| Estonian | Japanese | Romanian | — |

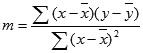
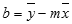


























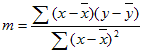
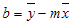 , что x = AVERAGE(известные x) и y = AVERAGE(known_y’s).
, что x = AVERAGE(известные x) и y = AVERAGE(known_y’s).