Линейный раскрой профиля в excel

Опубликовано 02 Дек 2015
Рубрика: Справочник Excel | 49 комментариев

Экономичный линейный раскрой материалов (раскрой погонажа) актуален для многих отраслей производства и в строительстве. Это — распил бревен и досок в деревообработке, резка прутков, арматурных стержней, уголков, швеллеров, труб, двутавров на заготовки…

…в производстве металлоконструкций и машиностроении, поперечный раскрой рулонов с бумагой и тканью в целлюлозной и легкой промышленности.

Не смотря на кажущуюся простоту, решение задач линейного раскроя является весьма не легким, но стоящим делом. Внедрение научного подхода к раскрою погонажных материалов позволяет снизить расходы на них иногда более чем на 10%! Дочитайте статью до конца и убедитесь в правоте этих слов.

Рассматриваемая тема относится к задачам линейного программирования. Для решения таких задач ученые в последние 70 лет придумали несколько различных методов.

Метод индексов Л.В. Канторовича и В.А. Залгаллера при определенном навыке позволяет «вручную» без использования вычислительной техники эффектно выполнять линейный раскрой. Любопытным читателям рекомендую с этим методом ознакомиться, прочитав книгу вышеназванных авторов «Рациональный раскрой промышленных материалов».

Симплекс-метод, основанный на идеях Л.В. Канторовича, был описан и детально разработан рядом ученых  из США в середине 20 века. Надстройка MS Excel «Поиск решения» (Solver) использует этот алгоритм. Именно с помощью этого метода и Excel мы будем в этой статье решать задачу линейного раскроя.

Позже появились и получили развитие генетический, жадный и муравьиный алгоритмы. Однако, ограничимся их перечислением и перейдем к делу, не забираясь в дебри теорий (хотя там, «в дебрях», очень интересно).

Включим Excel и на простом примере порезки металлических стержней на детали познакомимся с одним из способов решения практических задач линейного раскроя. Часто математики эту задачу называют «задачей о распиле».

Исходные данные для примера я не стал придумывать, а взял из статьи Покровского М.А. «Минимизация неизбежных потерь материалов в промышленном производстве при их раскрое на штучные заготовки» опубликованной в №5 (май 2015)  электронного научно-технического журнала «Инженерный вестник» издаваемого ФГБОУ ВПО «МГТУ им. Н.Э. Баумана» (ссылка: engbul.bmstu.ru/doc/775784.html).

Цель, которую я преследовал – сравнить полученные результаты решения задачи.

Пример решения задачи линейного раскроя в MS Excel.

Договоримся, что:

1. Заготовки – это исходный материал в виде прутков, полос, стержней и т.д. одинаковой длины.

2. Детали – это элементы, которые необходимо получить, разрезав исходные заготовки на части.

3. Ширина пила, реза, руба принята равной нулю.

Условие задачи:

Для комплектации одного из заказов заготовительный участок должен порубить на комбинированных ножницах из одинаковых прутков-заготовок длиной 1500 мм три типоразмера деталей:

151 штуку длиной 330 мм

206 штук длиной 270 мм

163 штуки длиной 190 мм

Требуется найти оптимальный план раскроя, использующий минимальное количество материала и дающий, соответственно, минимальное количество отходов.

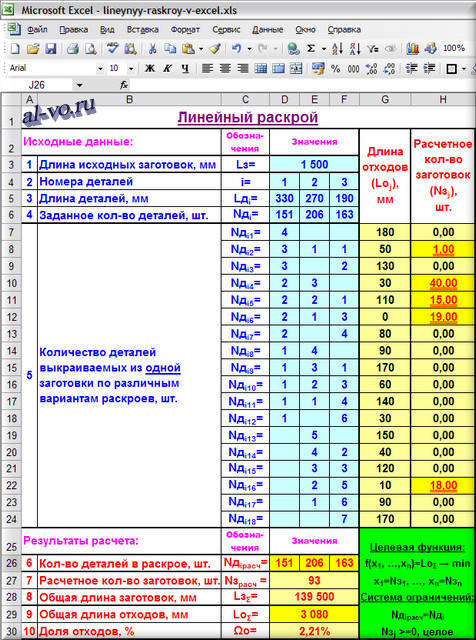
Исходные данные:

1. Длину исходных заготовок Lз в миллиметрах записываем в объединенную ячейку

D3E3F3: 1500

2. Присваиваем номера i всем типоразмерам деталей, начиная от самой длинной и заканчивая самой короткой в ячейках

D4; E4; F4: 1; 2; 3

3. Длины деталей Lд_i в миллиметрах пишем в

D5; E5; F5: 330; 270; 190

4. Количество деталей Nд_i в штуках заносим в

D6; E6; F6: 151; 206; 163

5.Приступаем к очень важному этапу – заполнению вариантов раскроев.

Необходимо запомнить и понять 2 принципа выполнения  этой работы.

1. Длины отходов должны быть меньше самой маленькой детали (0<Lo_j<Lд_min).

2. «Укладку» деталей в заготовку начинаем с самых больших деталей и с самого большого их количества, последовательно двигаясь в сторону уменьшения.

Если какого-нибудь типоразмера деталей в варианте раскроя нет, то ячейку оставляем пустой, ноль писать не будем для облегчения визуального восприятия таблицы.

Вариант раскроя №1:

Попытка выкроить из одной заготовки 5 деталей №1 невозможна, поэтому пишем в ячейку

D7: 4

Добавить в раскрой деталь №2 или деталь №3 также невозможно, поэтому оставляем пустыми ячейки

E7 и F7:

Вариант раскроя №2:

Уменьшаем на 1 от предыдущего варианта количество деталей №1 и записываем в

D8: 3

Пробуем добавить 2 детали №2 – не получается, поэтому дополняем в

E8: 1

Остается возможность дополнить раскрой деталью №3. Заносим в

F8: 1

Придерживаясь озвученных принципов, заполняем по аналогии все возможные в данном случае 18 вариантов раскроев.

Сделав пару-тройку таблиц вариантов раскроев самостоятельно, вы уясните логику действий и будете тратить считанные минуты на эту работу.

Если при раскрое не выполняется первый принцип, то ячейка с длиной отхода автоматически окрашивается в красный цвет. Условное форматирование, примененное к ячейкам G7…G24, наглядно поможет вам в этой работе.

В ячейках H7…H24 ничего не пишем! Они используются для вывода результата решения!

Ссылка на скачивание файла с примером: lineynyy-raskroy-v-excel (xls 38,5KB).

Подготовка к решению:

* В ячейках G7…G24 вычисляются длины отходов (обрезков), остающиеся в результате выполнения раскроев, по формуле

Lo_j=Lз— Σ(Lд_i*Nд_ij)

6. Количество деталей каждого типоразмера, изготовленных по всем примененным вариантам раскроя, будут подсчитываться в ячейках D26, E26 и F26 по формуле

Nд_iрасч=Σ(Nд_ij*Nз_j)

Количество деталей в найденном в конце решения плане раскроя должно полностью соответствовать заданному количеству деталей!

7. Необходимое число заготовок для выполнения оптимального плана раскроя будет определяться в объединенной ячейке D27E27F27 по формуле

Nз_расч=ΣNз_j

8. Общая длина всех заготовок, необходимых чтобы выполнить линейный раскрой всех деталей будет подсчитываться в объединенной ячейке D28E28F28 по формуле

Lз_Σ= Lз*Nз_расч

9. Общая длина всех отходов, получаемых при выполнении найденного плана раскроя, будет считаться в объединенной ячейке D29E29F29 по формуле

Lо_Σ= Σ(Lо_j*Nз_j)

10. Доля отходов, полученных при выполнении оптимального плана линейного раскроя от общего количества использованного материала, будет вычисляться в объединенной ячейке D30E30F30 по формуле

Ωo= Lо_Σ/Lз_Σ

Решение:

Подготовка завершена, определены 18 вариантов наиболее оптимальных раскроев одной заготовки на детали и вписаны все необходимые формулы. Теперь предстоит решить главную задачу: определить оптимальный план раскроя – сколько заготовок, и по каким вариантам раскроев резать, чтобы в итоге получить все необходимые детали в нужном количестве при минимуме отходов.

1. Выбираем в главном меню «Сервис» —  «Поиск решения…».

2. В появившемся одноименном окне  «Поиск решения» производим настройки.

2.1. Назначаем целевой функцией общую длину отходов Lо_Σ и вводим ссылку в окно целевой ячейки.

2.2. Устанавливаем переключатель «Равной:» в положение «минимальному значению».

2.3. Указываем ячейки с переменными Nз_j в окне «Изменяя ячейки».

2.4. Вводим ограничения в одноименное окно. В качестве условий указываем необходимость равенства заданного Nд_i и расчетного Nд_iрасч количества деталей, а так же на переменные Nз_j – расчетное количество заготовок по вариантам раскроев – накладываем ограничение: это должны быть целые числа.

3. Нажимаем кнопку «Параметры» и в выпавшем окне  «Параметры поиска решения» выполняем  настройки так, как показано на следующем скриншоте. Закрываем окно кнопкой «ОК».

4. В окне «Поиск решения» нажимаем кнопку «Выполнить» и ждем, пока Excel найдет решение. Это может длиться несколько минут.

5. После сохранения найденного решения кнопкой «ОК», результаты отобразятся в ячейках  H7…H24 на листе Excel.

На следующей картинке показан найденный оптимальный линейный раскройный план.

Что в итоге?

Линейный раскрой в Excel заготовок для задач подобных рассмотренной в этой статье выполняется описанным выше методом за 10-15 минут! «Вручную», не зная метод индексов Канторовича, за такое время решения не найдешь.

Запустив «Поиск решения» несколько раз при разных параметрах поиска, удалось найти 5 различных планов рубки заготовок. Все 5 планов требуют одинаковое число заготовок – 93 и дают отходов всего 2,21%!!! Эти планы почти на 6% лучше, чем план, рассчитанный Покровским и более чем на 10% экономичнее «Традиционного» плана (смотри ссылку на первоисточник в первой части статьи). Очень достойный результат достигнут быстро и без применения дорогостоящих программ.

Следует заметить, что надстройка Excel Solver («Поиск решения»), использующая симплекс-метод при решении задач линейного программирования, может работать не более чем с 200 переменными. В приложении к рассмотренной нами задаче линейного раскроя это означает, что количество раскроев не может превышать 200 вариантов. Для простых задач этого достаточно. Для более сложных задач следует попробовать применить «смесь» «жадного» алгоритма и симплексного метода Solver, отобрав из полного списка раскроев не более 200 самых экономичных. Далее запасаемся терпением и добиваемся результатов. Можно попытаться разбить сложную задачу на несколько простых, но «уровень оптимальности» найденного решения будет при этом, скорее всего, ниже.

Может быть, рассмотренный вариант решения вопросов линейного раскроя и не «высший пилотаж», но однозначно шаг вперед по сравнению с «традиционным» подходом на многих производствах.

Использование надстройки MS Excel «Поиск решения» (Solver) было на блоге уже однажды рассмотрено в статье «Бак для воды? «Поиск решения» в Excel!». Думаю, что этот замечательный инструмент достоин пристального внимания и еще не раз поможет изящно и быстро решить ряд новых нетривиальных задач.

P.S. Ссылки на лучшие из бесплатных программ линейного раскроя, найденных мной в Сети:

http://stroymaterial-buy.ru/raschet/70-raskroy-lineynih-izdeliy.html

http://forum-okna.ru/index.php?app=core&module=attach&section=attach &attach_id=7508

Программы по первым двум ссылкам решают рассмотренную задачу, используя 94 заготовки. Первая программа на  других тестах показала чуть лучшие результаты, чем вторая.

http://forum.dwg.ru/attachment.php?attachmentid=114501&d=13823277 74

http://www.planetcalc.ru/917/

Программы по последним двум ссылкам реализуют жадные эвристики и выполняют линейный раскрой в задаче из статьи, используя аж целых 103 заготовки. Применение жадных алгоритмов оправдано в случаях необходимости снижения общего времени операции резки при слишком большом количестве вариантов раскроев в более оптимальных планах.

Другие статьи автора блога

На главную

P. S. (11.06.2019)

В статье «Программа для раскроя в Excel и Calc» представлено решение автоматизации заполнения вариантов (схем) раскроев. Для поиска оптимального плана раскроя кроме надстройки Excel Solver использованы более мощные инструменты: NLPSolver и OpenSolver.

Статьи с близкой тематикой

Отзывы

Библиографическое описание:

Каюгина, С. М. Решение задач оптимального раскроя средствами MS Excel / С. М. Каюгина. — Текст : непосредственный // Молодой ученый. — 2016. — № 23 (127). — С. 54-57. — URL: https://moluch.ru/archive/127/35159/ (дата обращения: 16.04.2023).



В статье рассматривается методика решения задачи оптимального раскроя материалов на заготовки средствами MSExcel.

Ключевые слова: математическая модель, критерий оптимальности, рациональный способ раскроя

Большинство материалов, используемых в промышленности, поступает на производство в виде стандартных форм. Непосредственное использование таких материалов, как правило, невозможно. Предварительно их разделяют на заготовки необходимых размеров. Это можно сделать, используя различные способы раскроя материала.

Задача оптимального раскроя состоит в том, чтобы выбрать один или несколько способов раскроя материала и определить, какое количество материала следует раскраивать, применяя каждый из выбранных способов. В качестве критерия выбора оптимальных способов раскроя могут быть использованы минимум отходов, минимальный расход материалов, максимум комплектов, включающих заготовки различных видов.

Задачи такого типа возникают в строительстве, машиностроении, лесной, деревообрабатывающей и лёгкой промышленности. От успешности их решения зависят экономия материалов и снижение отходов.

Рассмотрим методику решения задачи раскроя листовых материалов средствами MSExcel.

Пример. На предприятии имеются древесностружечные плиты (ДСтП) нескольких форматов, приведенные в таблице 1. Спецификация заготовок приведена в таблице 2. Требуется составить оптимальный план раскроя плит ДСтП на заготовки по критерию минимума отходов, при условии выполнения заданной спецификации заготовок.

Таблица 1

Спецификация плит ДСтП

№п/п	Формат плиты, ммхмм	Количество плит, шт.
1	2440×1220	6000
2	1525×1525	8000

Таблица 2

Спецификация заготовок

№п/п	Формат плиты, ммхмм	Количество заготовок на годовую программу, шт.
1	1000×600	12000
2	800×600	12000
3	600×600	18000
4	300×450	12000
5	300×300	24000

На первом этапе решения задачи определяются рациональные способы раскроя материала. Разрабатываются карты раскроя, представляющие собой графическое расположение заготовок на стандартном формате раскраиваемого материала.

При разработке карт раскроя требуется соблюдать следующие условия:

− максимальный выход деталей;

− минимальное количество типоразмеров деталей при раскрое одного формата любого материала;

− минимальное повторение одних и тех же деталей в разных картах раскроя;

− обеспечение минимума отходов [2, c. 49].

В нашем примере использовано шесть карт раскроя, по три для каждого размера древесностружечных плит. В таблице 3 приведён выход заготовок и площадь отходов.

Таблица 3

Расчет количества заготовок

Размер заготовки	Количество заготовок, получаемых по карте раскроя, шт.
Плита 2440×1220	Плита 1525×1525
1	2	3	4	5	6
1000×600	4	—	—	—	2	—
800×600	—	4	—	—	—	2
600×600	—	—	8	—	—	2
300×450	—	5	—	6	5	—
300×300	—	—	—	15	—	—
Площадь отходов, м2	0,577	0,382	0,097	0,166	0,586	0,646

На втором этапе решается задача линейного программирования для определения интенсивности использования рациональных способов раскроя.

Составим математическую модель оптимизации.

В качестве неизвестных примем Х_{j —} количество плит раскраиваемых j-м способом.

Целевая функция (минимум отходов):

F=0,577Х₁+0,382Х₂+0,097Х₃+0,166Х₄+0,586Х₅+0,646Х₆min

Система ограничений:

1. по выпуску заготовок:

4Х₁+2Х₅=12000

4Х₂+2Х₆=12000

8Х₃+2Х₆=18000

5Х₂+6Х₄+5X₅=12000

15Х₄=24000

1. по запасам сырья:

Х₁+Х₂+Х₃<=6000

Х₄+Х₅+Х₆<=8000

1. по неотрицательности переменных:

Х₁,…, Х₆>=0

Симплекс-метод, основанный на идеях Л. В. Канторовича, был описан и детально разработан рядом ученых из США в середине 20 века. Надстройка MS Excel «Поиск решения» (Solver) использует этот алгоритм. Именно с помощью симплекс-метода и MS Excel мы будем решать задачу оптимального раскроя [3].

Оформим в MSExcel таблицу с исходными данными и введём формулы (рис.1):

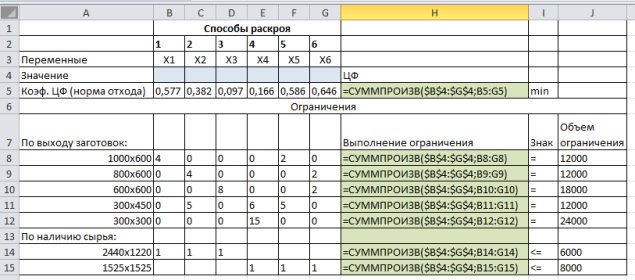
Рис. 1. Оформление таблицы с исходными данными в MSExcel

На вкладке «Данные» нажимаем кнопку «Поиск решения». Откроется диалоговое окно «Поиск решения», в котором указываем ячейку целевой функции, её направление, изменяемые ячейки и задаём ограничения задачи (рис. 2).

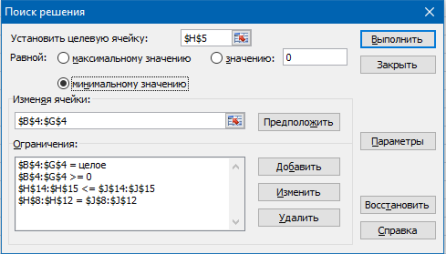
Рис. 2. Диалоговое окно «Поиск решения»

Щелчком по кнопке «Параметры» заходим в диалоговое окно «Параметры поиска решения» и устанавливаем флажок «Линейная модель». Нажимаем ОК. Выполняем поиск решения.

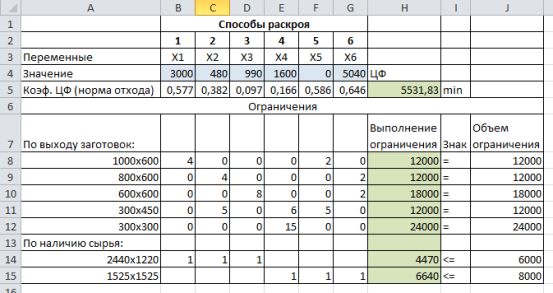
Рис. 3. Результат решения

На рисунке 3 показан оптимальный план раскроя. Следует раскроить древесностружечные плиты размера 2440х1220 первым способом 3000 шт., вторым способом 480 шт. и третьим способом 990 шт. Всего плит данного размера потребуется 4470 шт.

Древесностружечные плиты размера 1525х1525 следует раскроить четвертым способом 1600 шт. и шестым способом 5040 шт. Пятую карту раскроя использовать нерационально. Всего плит этого размера потребуется 6640 шт.

Полученный в оптимальном решении вариант использования карт раскроя плит обеспечит выполнение плана по выходу заготовок всех размеров. Отходы будут минимальными и составят 5531,83 м².

Литература:

1. Пижурин А. А. Основы моделирования и оптимизации процессов деревообработки / А. А. Пижурин. — М.: Лесная промышленность, 2004.
2. Яцун И. В., Чернышев О. Н. Моделирование и оптимизация процессов деревообработки. Часть 1. — Екатеринбург: Редакционно-издательский отдел УГЛТУ, 2011.
3. Линейный раскрой в Excel [Электронный ресурс] — Режим доступа: http://al-vo.ru/spravochnik-excel/linejnyj-raskroj-v-excel.html