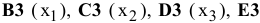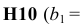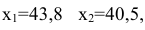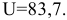- Download examples — 47.92 KB
Introduction
This article explains the use of Excel Solver for solving problems, specially the ones related to Linear Programming. If you do not know much about Linear programming it’s okay, this article will give you a little insight about that as well. However, the focus here is to make you aware of Excel Solver and let you know how to make use of it for solving interesting problems.
What is Solver and What Does It Do
In simple terms, Excel solver is an Add-in that solves problems for you. For a given problem, Excel solver can run various permutations and combinations and find out the best possible solution for you.
Enabling Solver in Excel
Go to options:
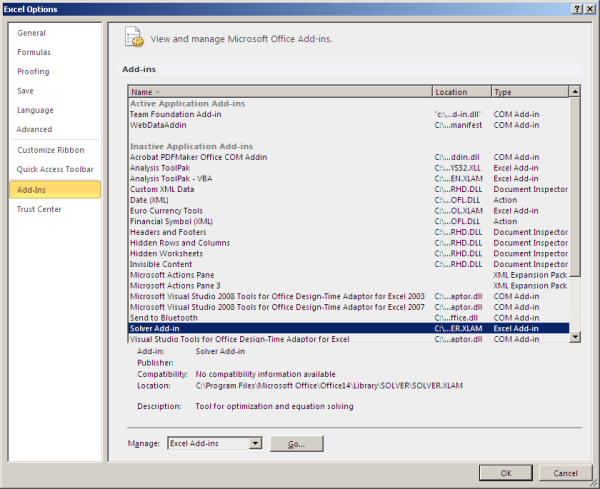
Select Add-In:
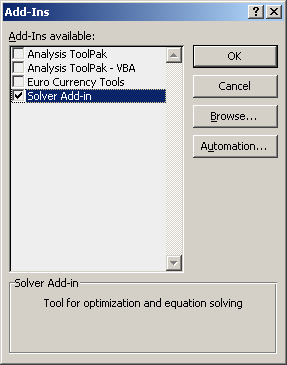
Click on ‘Go’ button, check Solver Add-in, click OK:
You should be able to see the Solver button in your Excel Data Ribbon:
What is Linear Programming
LP is a mathematical method for determining a way to achieve the best outcome (such as maximum profit or lowest cost) in a given mathematical model for some list of requirements represented as linear relationships.
Some Sample Problems that Solver can Solve
Problem 1
Let’s say we have a function e.g. f=x2-x+2 and we want to find out the minimum value of x where -1<= x <= 5.
Problem 2
A company manufactures desks and chairs. Each desk uses 4 units of wood, and each chair 3 units of wood. A desk contributes $40 to profit and a chair contributes $25. Marketing restrictions require that the number of chairs produced to be at least twice the number of desk produced. There are 20 units of wood available. What set of production will bring maximum profit.
Problem 3
Here is a more complex problem which is represented in terms of equations and solved through the matrix approach.
Maximize 50x1 + 30x2 + 25x3 + 30x4
Where
2x1 + 2.5x2 + 3x3 + 1.8x4 = 800
1.2x1 + 1x2 + 2x3 + 0.8x4 = 400
1.5x1 + 1.2x2 + 1.5x3 + 0.8x4 = 380
x2 = 50
x3 = 30
x1, x2, x3, x4 = 0
Solving the Problems using Excel Solver
Problem 1
The following image shows the solved example. Cell in green (C15) is the cell which gets the value through solver and is named as x.
Formula for cell C12 is x^2-x+2. By default, put 1 in cell C15 which is the initial value for variable x.
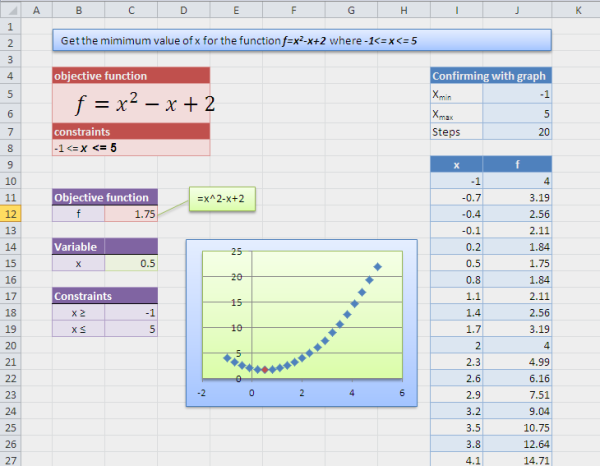
Objective field is f which is the name of cell C12 which we want to solve through solver. «By changing the variable cells» field has x which is cell C15, our variable. We have also set the constraints using add button x <= 5 and x>=-1. Just click the ‘solve’ button and it will give the value of x.
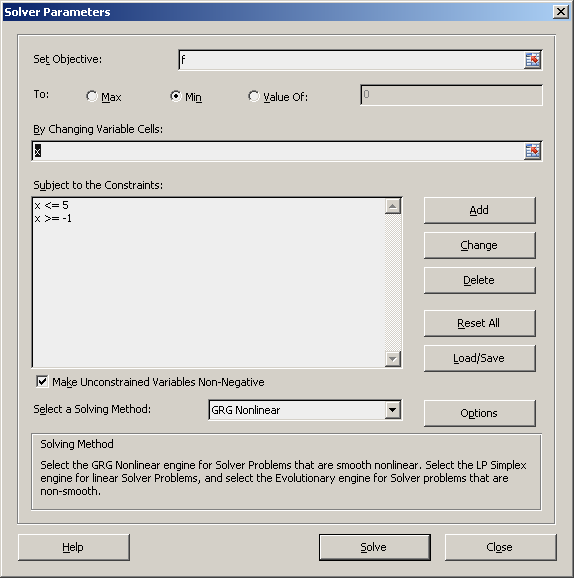
Problem 2
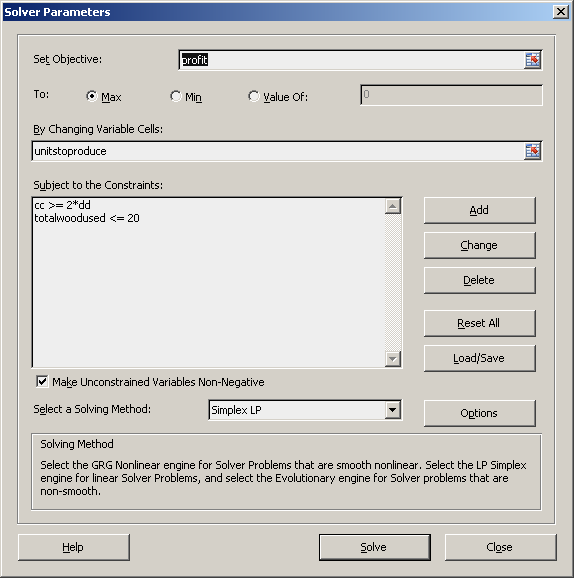
This problem is solved in a traditional way. Unitstoproduce is the range C18:C19. totoalwoodused is the name of cell F20.
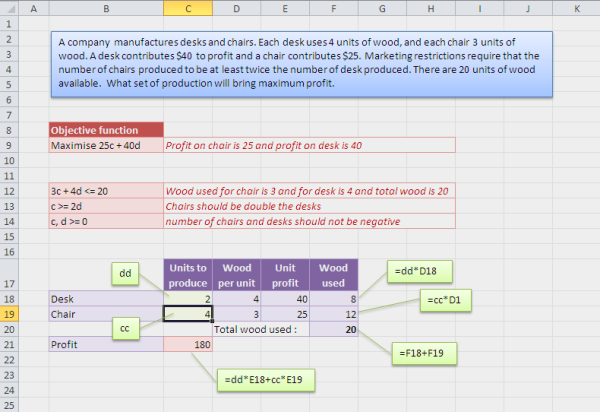
Here in the following figure, you can see the solver setting. Give 1 in green cells as initial values. Solver should be able to give you the correct values for them.
Problem 3
In real life, LP problems asre not as simple as in Problem 2. Therefore, we need to solve the problem using the matrix. In this problem, you can see many equations which you can relate to some equations in problem 2. To maximize the result of the equation, all we need to do is to Maximize (Transposed C) * x.
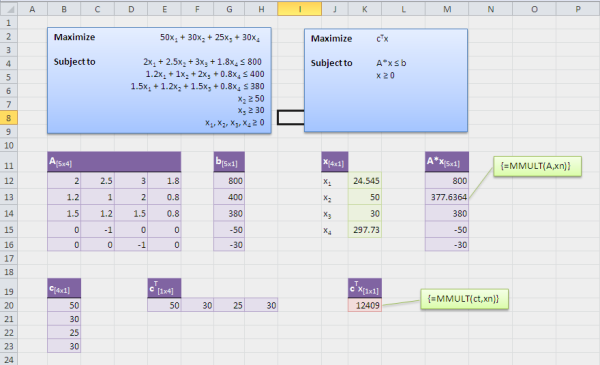
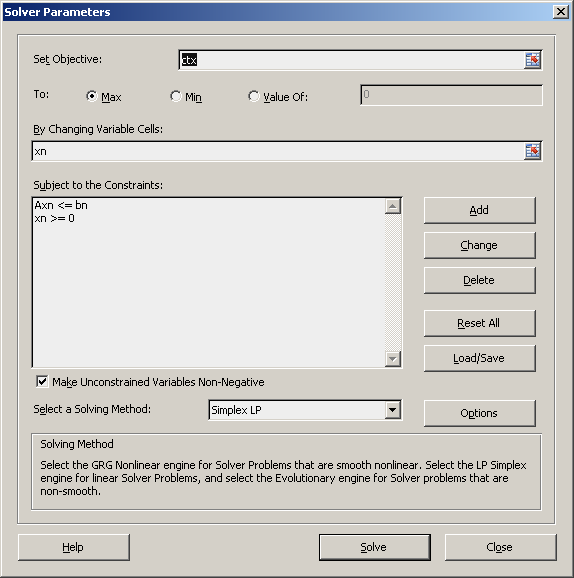
For the sake of uniqueness of the variable name, I named the matrix variable as xn, bn, etc. Values of x is what you want to get through solver. Give 1 as initial values for x1, x2, x3 and x4. When you run the solver, it will update those green cells with the solved values.
History
- 20th September, 2011: Initial post
Бизнес модели | 01.01.2022 |
Метки: Пошаговая инструкция | Матметоды в экономике | Эксель | Линейное программирование | Теория
Solver — важная надстройка в Excel, которая помогает решать экономические задачи продвинутого уровня (ранее такая функциональность была доступна только в специализированных компьютерных программах). Данный инструмент использует достижения такого раздела математики, как методы оптимизации (mathematical optimization), или по-другому, математическое программирование (Mathematical Programming, к обычному программированию компьютерных программ эта наука не имеет прямого отношения).
В экономике, как на уровне фирмы, так и на уровне государства, часто возникала проблема оптимального распределения ресурсов. Например, необходимо максимизировать прибыль, управляя ассортиментом выпускаемых изделий, при этом определенные ресурсы (количество имеющегося оборудования, сотрудников необходимой квалификации) зафиксированы. Или, к примеру, распределить доступный бюджет между различными видами рекламы, чтобы добиться максимального контакта с аудиторией. В математическую экономику такая задача вошла под названием задачи о размещении (распределении ресурсов) — также широко известно название Wyndor Glass Company problem.
Особенно ярко это проблема стояла перед социалистическими экономиками, где имелась возможность централизованно регулировать распределение ресурсов между отраслями. Поэтому неудивительно, что методы математического программирования были разработаны советским математиком Леонидом Канторовичем, который позднее получил за это Нобелевскую премию мира по экономике. И хотя в Советском Союзе они не помогли справиться с дефицитом и другими традиционными проблемами плановых экономик, на более низком уровне планирования разработанный математический аппарат оказался востребованным.
Основная задача математического программирования в общем виде
Основная задача математического программирования — максимизировать (или минимизировать) целевую функцию при условии выполнения определенных ограничений.
F(X1,X2,…,XN) -> max
при условии
f1(X1,X2,…,XN)1,
f1(X1,X2,…,XN)2,
…,
fM(X1,X2,…,XN)M
Иными словами, нам необходимо подобрать X1,X2,…,XN таким образом, чтобы целевая функция F достигла своего максимального значения при условии выполнения всех ограничений. Размерность задачи определяется количеством варьируемых переменных Х, а не количеством ограничений. В одномерном виде — это по существу широко известная из курса математического анализа задача максимизации (минимизации) функции на определенном интервале:
Математическое программирование в одномерном пространстве
В данном примере необходимо найти такое значение функции, при котором она принимает наименьшее значение. Переменная только одна — Х (по горизонтальной оси), а в роли ограничений выступают условия X>0 и X<8. Далее рассмотрим аналогичную двумерную задачу.
Математическое программирование в двумерном пространстве
На данном примере рассмотрена задача из области так называемого линейного программирования — важнейшего раздела математического программирования. Этот раздел работает с функциями, которые имеют линейный характер (такими, как Х2=kX1+b). Графически линейные функции описываются прямыми линиями (в двумерном пространстве), плоскостью (в трехмерном пространстве) и гиперплоскостью (в N-мерном пространстве). Линейными в этом случае должны быть как целевая функция, так и все функции ограничений.
На графике три ограничения (описаны сиреневыми линиями) совместно с требованиями на неотрицательность изменяемых переменных образуют многоугольник (светло-розового цвета) — область возможных решений (feasible solution). Целевая функция (желтого цвета) — описывается множеством линий (которые расположены параллельно по отношению к друг другу), чем выше и правее находится линия, тем большему значению целевой функции она соответствует. По существу, задача линейного программирования — найти наивысшее значение целевой функции, которое удовлетворяет множеству доступных решений. В данном примере максимум достигается в точке (5,5) и соответствует значению целевой функции, равному 15.
Данную двумерную задачу оптимизации графически можно описать и в трехмерном пространстве (тогда не придется двигать целевую функцию), это вопрос только удобства представления. Графически это будет выглядеть аналогично тому, как выше представлен одномерный случай (на графике отображена двумерная нелинейная целевая функция, линейная была бы в виде плоскости):
Математическое программирование в двумерном пространстве
То есть, вместо отрезка множество доступных множеств будет выглядеть как многогранник (на графике представлен вырожденный случай — квадрат), а целевая функция станет трехмерной (где по оси аппликат будет отложено целевое значение функции, а по осям абсцисс и ординат — возможные значения изменяемых (оптимизируемых) переменных.
Настройка Поиска решения в Excel
Обратим внимание, что по умолчанию Поиск решения (Solver) не входит в базовую версию Excel. Это надстройка, которую необходимо включить, после этого она появится в разделе Данные (Data). Solver также не стоит путать с функцией Goal seak. Solver позволяет найти максимальное или минимальное решение (оптимизация), в то время как Goal Seek помогает найти такую переменную, при которой функция принимает конкретное значение (не обязательно оптимальное решение). Goal Seek позволяет изменять только одну переменную, в то время как Solver позволяет изменять сразу несколько переменных. Упрощая, Goal Seak лучше использовать, когда Вам необходимо решить какое-то уравнение, в то время как Solver в основном заточен на решение оптимизационных задач (поиска максимума и минимума), хотя решить уравнение с его помощью также можно.
Отметим также, что Goal Seak в некоторых случаях также можно использовать для оптимизации. В этом случае нужно быть уверенным, что оптимальное значение находится именно в том месте, где целевую функцию пересекает ограничительное условие. Чаще всего это бывает в тех случаях, где есть уверенность в постоянном непрерывном возрастании (или убывании) целевой функции на всем множестве ее значений. Обычно это условие выполнено для линейных и некоторых других функций. В этом случае Goal Seak по существу ищет точку пересечения ограничения и целевой функции. Если функция имеет локальные максимумы и минимумы, то в этом нельзя быть уверенным. В любом случае, обычно проще всего все же использовать Solver.
При работе с Solver необходимо соблюдать определенные правила оформления. Как правила, целевые функция, изменяемые переменные и ограничения необходимо отобразить на одном листе Excel. Даже если сам расчет идет на другом листе, на том листе, где планируется запускать Solver, необходимо сослаться на этот расчет. Изменяемые переменные также располагают рядом, чтобы они представляли собой единый массив ячеек.
Выбор метода оптимизации в Excel
Самый важный момент при работе с Solver — выбор метода оптимизации. Если задача линейная, то рекомендуется выбрать вариант linear programming (Simplex LP). Для поиска оптимального решения в этом случае будет использован симплекс-метод — наиболее известный способ решения задач линейного программирования. Это наиболее быстрый метод, который обеспечивает максимально точное решение. Важно понимать, что линейными должны быть все изменяемые переменные (как внутри целевой функции, так и в каждом ограничении). Если хотя бы где-то изменяемая переменная возводится в квадрат, оказывается в знаменателе, участвует в условии вида IF, встречается внутри функции VLOOKUP, возводится в степень, от нее берется логарифм и пр., то линейное программирование использовать нельзя. Условие линейности также нарушается, если необходимо получить только целые значения изменяемых переменных.
В нелинейных случаях нужно выбирать из двух оставшихся вариантов. Если функция отвечает условию гладкости, то можно использовать вариант GRG Nonlinear (Generalized Reduced Gradient). Гладкость функции (smoothness) — более строгое условие, нежели непрерывность функции. Любая гладкая функция непрерывна, но не любая непрерывная функция гладкая. Например, функция константы непрерывная, но не гладкая. Гладкость бывает разного порядка — зависит от того, производную какого порядка можно от этой функции взять. Например, линейная функция — гладкая первого порядка, т.к. от нее можно взять только первую производную. Квадратичная функция — гладкая второго порядка, т.к. от нее можно взять первую и вторую производную.
На практике Вам необходимо в первую очередь понимать, является ли целевая функция непрерывной (то есть нет ли у нее разрывов или скачков значений в определенном месте). Если это полином (парабола и выше), степенная функция, логарифм, тригонометрическая функция и пр., то условие непрерывности выполнено. Непрерывность обычно нарушается, когда на разных интервалах значений изменяемой переменной функция описывается разной формулой (например, при Х<8 функция линейная, а при X>8 — квадратичная). Обычно в файлах Excel непрерывность нарушается при использовании конструкций вида IF и VLOOKUP (важно, чтобы аргументом этих расчетов была изменяемая переменная, во всех остальных случаях такие конструкции в файле не являются проблемой). В этом случае функция не будет непрерывной (и, как следствие, гладкой). А это значит, что GRG Nonlinear использовать нельзя.
GRG — достаточно быстрый метод. В его основе лежит расчет градиента — градиент функции в данной точке показывает направление ее наибольшего роста (снижения) в этой точке. Главная проблема этого метода — он останавливается в тот момент, когда находит локальный минимум функции. Например, возможна такая ситуация:
Ложный (локальный) минимум при поиске решения методом GRG Nonlinear
При поиске минимума данной функции метод может ложно остановиться в точке А (локальном минимуме функции), в то время как настоящий (глобальный) минимум функции находится в точке С. Таким образом, результат функции очень сильно зависит от начальных значений изменяемых переменных, и при разных начальных условиях Excel будет возвращать разный результат (не всегда правильный). При этом локальные минимумы и максимумы могут возникать у многих видов функций, например, у полиномов разной степени (Х3,X4,X5 и пр.). Чтобы использовать данный метод, нужно быть уверенным в непрерывно возрастающем или убывающем характере функции.
Если линейное программирование и градиентный метод не подходят, то можно использовать вариант Evolutionary. Этот метод реализует сложный итерационный вариант перебора возможных значений.
Отметим также, что существует компромиссный вариант между GRG и Evolutionary. Выбрав вариант GRG Nonlinear, можно зайти на вкладку Option и там указать опцию «Use multistart». В этом случае GRG стартует с нескольких начальных точек (система сама генерирует выборку распределенных случайным образом стартовых значений), далее выполняя свою стандартную процедуру поиска оптимального решения. В этом случае нахождение глобального максимума не гарантировано, но вероятность, что программа вернет именно его, существенно повышается.
Почему одни страны, города или компании добиваются экономического успеха, а другие — вынуждены влачить жалкое существование? Почему экономический рост такой слабый, а неравенство доходов все выше? Как новые технологии могут изменить глобальный экономический ландшафт? Присоединяйтесь к нашей группе ВКонтакте, чтобы получать больше информации о долгосрочных трендах в экономике и бизнесе.
Авторизация через:
Здесь пока нет комментариев. Чтобы их оставить, авторизуйтесь вверху страницы или с помощью аккаунта ВКонтакте либо зарегистрируйтесь .
1
- Введение в линейное программирование в Excel
Линейное программирование в Excel (Содержание)
- Введение в линейное программирование в Excel
- Методы решения линейного программирования с помощью Excel Solver
Введение в линейное программирование в Excel
Линейное программирование является наиболее важным, а также увлекательным аспектом прикладной математики, который помогает в оптимизации ресурсов (либо минимизации потерь, либо максимизации прибыли при данных ресурсах). Если у нас есть ограничения и целевая функция хорошо определены, мы можем использовать систему, чтобы предсказать оптимальное решение для данной проблемы. В Excel у нас есть Excel Solver, который помогает нам решать проблемы линейного программирования или LPP. В этой статье мы увидим, как использовать Excel Solver для оптимизации ресурсов, связанных с бизнес-задачами, с помощью линейного программирования.
Первое первым. Давайте посмотрим, как мы можем включить Excel Solver (ключевой компонент LPP в Excel).
Методы решения линейного программирования с помощью Excel Solver
Давайте разберемся, как использовать линейное программирование через Excel Solver с некоторыми методами.
Вы можете скачать этот шаблон Excel для линейного программирования здесь — Шаблон Excel для линейного программирования
Способ № 1 — Включение Солвера в Microsoft Excel
В Microsoft Excel мы можем найти Солвер на вкладке Данные, которую можно найти на ленте Excel, расположенной в самой верхней части, как показано ниже:
Если вы не можете увидеть этот инструмент утилиты там, вам нужно включить его через параметры Excel. Выполните следующие шаги, чтобы включить Solver в Excel.
Шаг 1: Перейдите к меню «Файл» и нажмите «Параметры», что является последним в этом списке.
Шаг 2: появится новое окно с именем Excel Options. Нажмите на Надстройки из списка опций, присутствующих в левой части окна.
Шаг 3: В разделе «Управление» в нижней части окна выберите «Надстройки Excel» из выпадающего списка и нажмите кнопку «Перейти…», расположенную рядом.
Шаг 4: Как только вы нажмете кнопку «Перейти…», вы сможете увидеть список всех надстроек, доступных в Excel, в новом окне. Установите флажок, чтобы выбрать надстройку Solver, чтобы использовать ее на вкладке «Данные» для решения уравнений. Нажмите кнопку ОК после того, как отметите выбор надстройки Solver.
Таким образом, вы можете включить Excel Solver в Microsoft Excel.
Метод № 2 — Решение проблемы линейного программирования с помощью Excel Solver
Теперь мы попытаемся решить задачу линейного программирования с помощью инструмента Excel Solver.
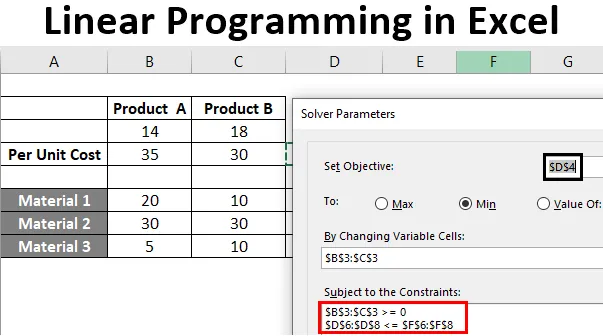
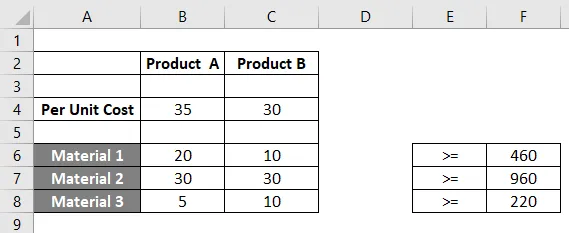
Пример: химический завод производит два продукта, а именно A и B. Этим двум продуктам требуется сырье, как показано ниже: продукту A требуется три вида сырья — материал_1 20 кг, материал_2 30 кг, материал_3 как 5 кг. Аналогичным образом, для продукта B требуется 10 кг материала_1, 30 кг материала_2 и 10 кг материала_3. Производитель требует минимум 460 кг или материала_1, 960 кг материала_2 и 220 кг материала_3. Если цена за единицу продукции для продукта A составляет 30 долларов США, а для продукта B — 35 долларов США, сколько продуктов производитель должен смешать, чтобы выполнить минимальные требования к материалам при минимально возможных затратах? Давайте использовать информацию, представленную в этом примере, для моделирования уравнений.
Шаг 1: Мы можем увидеть все ограничения уравнения, которые мы можем сформировать, используя информацию, представленную в примере выше.
Шаг 2: Используйте эти уравнения для добавления ограничений по ячейкам в Excel через A2: C8 данного листа. Смотрите на скриншот ниже:
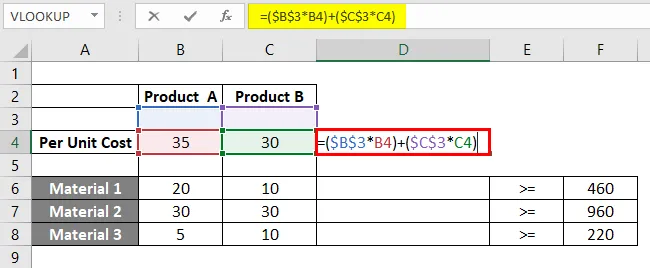
Шаг 3: Теперь нам нужно использовать формулу Количество * Стоимость единицы продукции и суммировать ее для обоих продуктов, чтобы получить фактические потребности в материалах. Вы можете увидеть это в столбце D для всех ячеек, содержащих ограничения B3, B4, C3). Пожалуйста, смотрите прикрепленный скриншот ниже:
Если вы внимательно посмотрите на эту формулу, мы использовали B3 и C3 в качестве фиксированных элементов для каждой формулы в разных ячейках столбца D. Это связано с тем, что B3 и C3 являются ячейками, обозначающими количества для Продукта A и Продукта B соответственно. Эти величины появятся, как только система уравнений будет решена с помощью Excel Solver.
Шаг 4: Нажмите на вкладку «Данные», а затем на Солвер, который присутствует в разделе «Анализ» на вкладке.
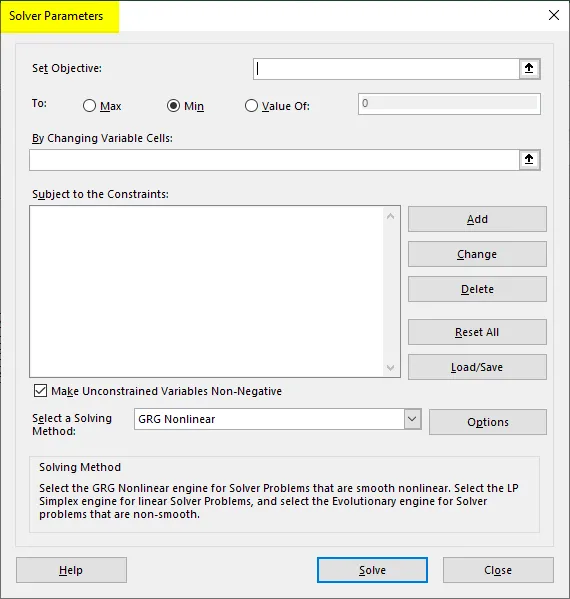
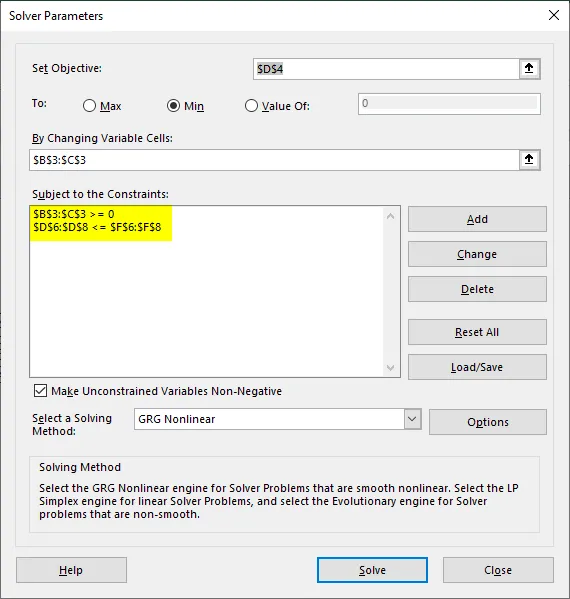
Шаг 5: После того, как вы нажмете на Solver, откроется новая вкладка с именем «Solver Parameter», в которой вам нужно установить параметры для этого набора уравнений, которые необходимо решить.
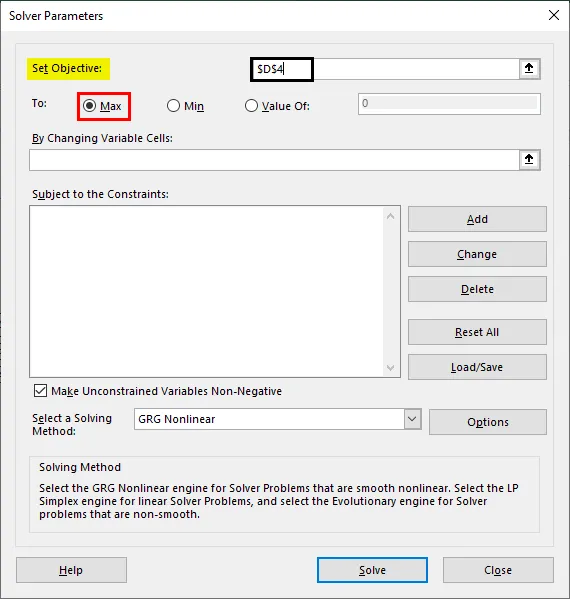
Шаг 6: Первое, что нам нужно определить, это установить цель: поскольку наша цель — определить общую стоимость, чтобы ее можно было минимизировать, установите для нее значение D4.
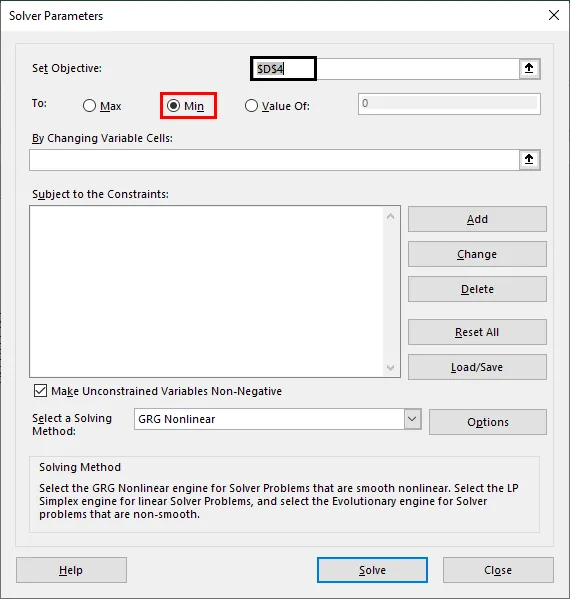
Шаг 7: Поскольку нам нужно минимизировать стоимость при максимально возможном производстве, установите следующий параметр как Мин. Вы можете сделать это, нажав кнопку Min.
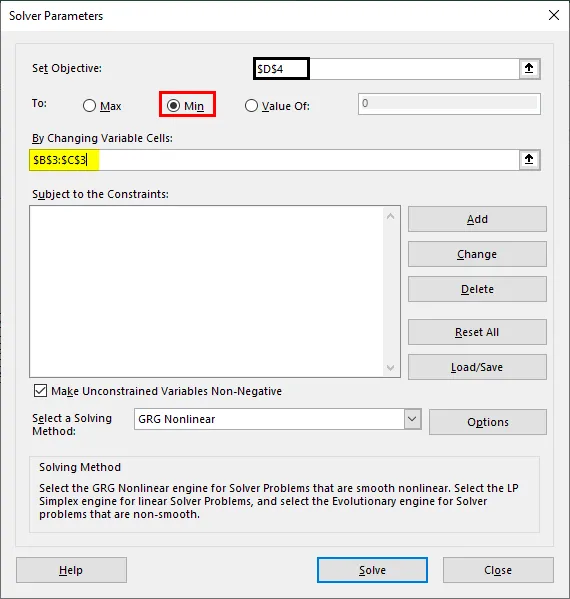
Шаг 8: в разделе «Изменение переменных ячеек» мы должны упомянуть B3 и C3, поскольку эти ячейки будут содержать количества для продукта A и продукта B соответственно после того, как проблема будет решена.
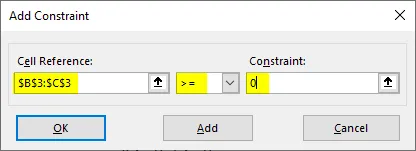
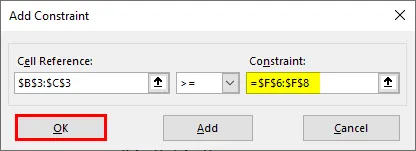
Шаг 9: Теперь добавьте ограничения. Нажмите кнопку «Добавить» в разделе «В зависимости от ограничений:», и откроется новое окно для добавления ограничений. Под этим окном — B3: C3 в качестве ссылки на ячейку, > = и 0 в качестве ограничений. Это мы и делаем, поскольку основное ограничение в любом LPP состоит в том, что X и Y должны быть больше нуля.
Шаг 10: Снова нажмите на кнопку «Добавить», и на этот раз используйте B3: C3 в качестве ссылки на ячейку и F6: F8 в качестве ограничения с неравенством как> =. Нажмите кнопку ОК, чтобы добавить это ограничение также под решатель.
Солвер теперь имеет все параметры, необходимые для решения этого набора линейных уравнений, и выглядит так:
Шаг 11: Теперь нажмите кнопку «Решить» в нижней части окна, чтобы решить это линейное уравнение и найти оптимальное решение.
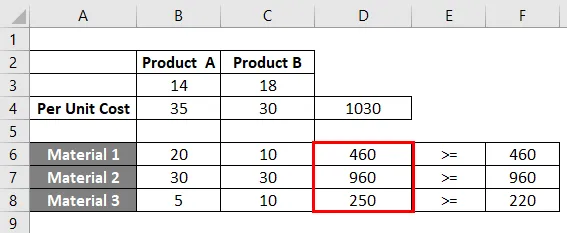
Как только мы нажимаем кнопку «решить», система начинает поиск оптимального решения для поставленной нами задачи, и мы получаем значения для B3, C3, используя которые мы также получаем значения в столбце F для F4, F6: F8. Каковы оптимальные затраты и материальные ценности, которые можно использовать для Продукта A и Продукта B.
Это решение информирует нас о том, что, если нам необходимо минимизировать стоимость производства для продукта A и продукта B при оптимальном использовании материалов_1, материалов_2 и материалов_3, мы должны произвести 14 количеств продукта A и 18 количеств продукта B.
Это из этой статьи. Давайте подведем итоги, чтобы запомнить некоторые моменты:
Что нужно помнить о линейном программировании в Excel
- Решение задач линейного программирования обязательно с помощью Excel Solver. Нет другого метода, который мы можем сделать, используя это.
- У нас всегда должны быть ограничения и переменная объекта, которая будет готова с нами.
- Если Солвер не включен, вы можете включить его в настройках надстройки Excel.
Рекомендуемые статьи
Это руководство по линейному программированию в Excel. Здесь мы обсуждаем, как использовать линейное программирование в Excel вместе с практическими примерами и загружаемым шаблоном Excel. Вы также можете просмотреть наши другие предлагаемые статьи —
- Интерполировать в Excel
- Программирование в Excel
- Перемещение столбцов в Excel
- Обратная матрица в Excel
Задачи линейного программирования относятся к широко распространённому классу задач, встречающихся в различных сферах деятельности: в бизнесе, на производстве, в быту. Как оптимально распорядиться бюджетом или за минимальное время добраться до нужного места в городе, как наилучшим образом спланировать деловые встречи, минимизировать риски капитальных вложений, определить оптимальные запасы сырья на складе – это те задачи, в которых нужно найти наилучшее из всех возможных решений.
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Линейное программирование
Линейное программирование – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Слово «программирование» заимствовано из зарубежной литературы, где оно используется в смысле «планирование».
Решение задач линейного программирования с использованием microsoft excel
Цель работы
Приобретение навыков решения задач линейного программирования (ЛП) в табличном редакторе Microsoft Excel.
Порядок выполнения работы
Для модели линейного программирования, соответствующей номеру Вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю.
Инструкция по использованию microsoft excel для решения задач линейного программирования
Для того чтобы решить задачу линейного программирования в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия.
Ввести условие задачи:
a) создать экранную форму для ввода условия задачи:
- переменных,
- целевой функции (ЦФ),
- ограничений,
- граничных условий;
b) ввести исходные данные в экранную форму:
- коэффициенты ЦФ,
- коэффициенты при переменных в ограничениях,
- правые части ограничений;
c) ввести зависимости из математической модели в экранную форму:
- формулу для расчета ЦФ,
- формулы для расчета значений левых частей ограничений;
d) задать ЦФ (в окне «Поиск решения»):
- целевую ячейку,
- направление оптимизации ЦФ;
e) ввести ограничения и граничные условия (в окне «Поиск решения»):
- ячейки со значениями переменных,
- граничные условия для допустимых значений переменных,
- соотношения между правыми и левыми частями ограничений.
Решить задачу:
a) установить параметры решения задачи (в окне «Поиск решения»);
b) запустить задачу на решение (в окне «Поиск решения»);
с) выбрать формат вывода решения (в окне «Результаты поиска решения»).
Возможно эта страница вам будет полезна:
Одноиндексные задачи линейного программирования
Рассмотрим пример нахождения решения для следующей одноиндексной задачи ЛП:
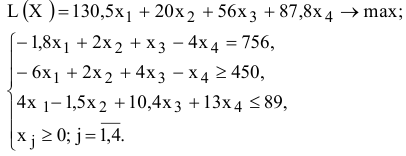
Ввод исходных данных
Создание экранной формы и ввод в нее условия задачи
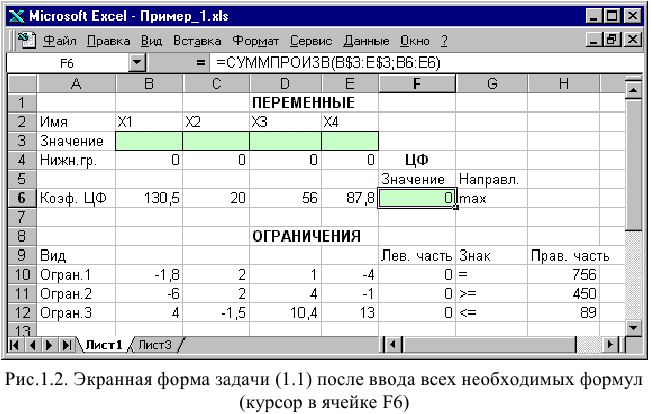
Экранная форма для ввода условий задачи (1.1) вместе с введенными в нее исходными данными представлена на рис. 1.1.
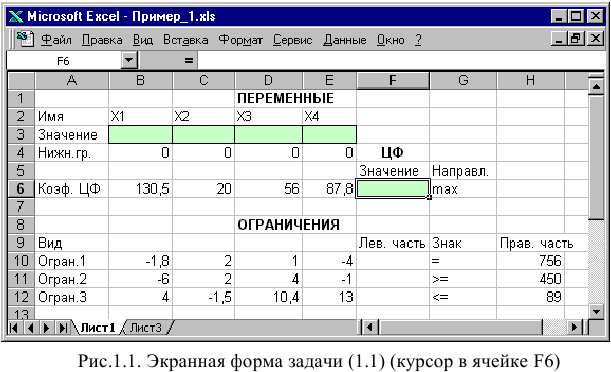
В экранной форме на рис. 1.1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Имя ячейки состоит из буквы, обозначающей столбец, и цифры, обозначающей строку, на пересечении которых находится объект задачи линейного программирования. Так, например, переменным задачи (1.1) соответствуют ячейки 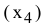
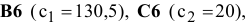
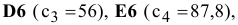
правым частям ограничений соответствуют ячейки
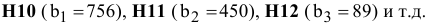
Ввод зависимостей из математической модели в экранную форму
Зависимость для ЦФ
В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1.1) значение ЦФ определяется выражением
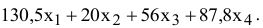
Используя обозначения соответствующих ячеек в Excel (см. рис. 1.1), формулу для расчета ЦФ (1.2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов ЦФ (В6, С6, D6, Е6), то есть
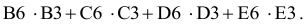
Чтобы задать формулу (1.3) необходимо в ячейку F6 ввести следующее выражение и нажать клавишу «Enter»
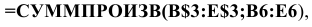
где символ $ перед номером строки 3 означает, что при копировании этой формулы в другие места листа Excel номер строки 3 не изменится;
символ : означает, что в формуле будут использованы все ячейки, расположенные между ячейками, указанными слева и справа от двоеточия (например, запись В6:Е6 указывает на ячейки В6, С6, D6 и Е6). После этого в целевой ячейке появится 0 (нулевое значение) (рис. 1.2).
Примечание 1.1. Существует другой способ задания функций в Excel с помощью режима «Вставка функций», который можно вызвать из меню «Вставка» или при нажатии кнопки «
• курсор в поле F6;
• нажав кнопку «
• выберите в окне «Категория» категорию «Математические»;
• в окне «Функция» выберите функцию СУММПРОИЗВ;
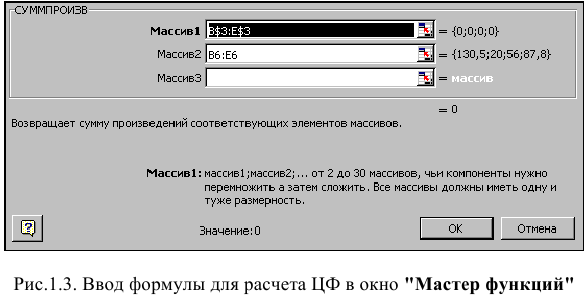
• в появившемся окне «СУММПРОИЗВ» в строку «Массив 1» введите выражение В$3:Е$3, а в строку «Массив 2» — выражение В6:Е6 (рис. 1.3);
• после ввода ячеек в строки «Массив 1» и «Массив 2» в окне «СУММПРОИЗВ» появятся числовые значения введенных массивов (см. рис. 1.3), а в экранной форме в ячейке F6 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).
Зависимости для левых частей ограничений
Левые части ограничений задачи (1.1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (В 10, СЮ, D10, ЕЮ — 1-е ограничение; В11, С11, D11, El 1 — 2-е ограничение и В12, С12, D12, Е12 — 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл. 1.1.

Как видно из табл. 1.1, формулы, задающие левые части ограничений задачи (1.1), отличаются друг от друга и от формулы (1.4) в целевой ячейке F6 только номером строки во втором массиве. Этот номер определяется той строкой, в которой ограничение записано в экранной форме. Поэтому для задания зависимостей для левых частей ограничений достаточно скопировать формулу из целевой ячейки в ячейки левых частей ограничений. Для этого необходимо:
• поместить курсор в поле целевой ячейки F6 и скопировать в буфер содержимое ячейки F6 (клавишами «Ctrl-Insert»);
• помещать курсор поочередно в поля левой части каждого из ограничений, то есть в F10, F11 и F12, и вставлять в эти поля содержимое буфера (клавишами «Shift-Insert») (при этом номер ячеек во втором массиве формулы будет меняться на номер той строки, в которую была произведена вставка из буфера);
• на экране в полях F10, F11 и F12 появится 0 (нулевое значение) (см. рис. 1.2).
Проверка правильности введения формул
Для проверки правильности введенных формул производите поочередно двойное нажатие левой клавиши мыши на ячейки с формулами. При этом на экране рамкой будут выделяться ячейки, используемые в формуле (рис. 1.4 и 1.5).

Задание ЦФ
Дальнейшие действия производятся в окне «Поиск решения», которое вызывается из меню «Сервис» (рис. 1.6):
• поставьте курсор в поле «Установить целевую ячейку»;
• введите адрес целевой ячейки $F$6 или сделайте одно нажатие левой клавиши мыши на целевую ячейку в экранной форме — это будет равносильно вводу адреса с клавиатуры;
• введите направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по селекторной кнопке «максимальному значению».
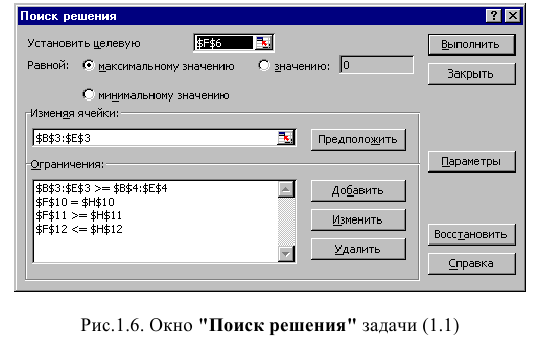
Ввод ограничений и граничных условий
Задание ячеек переменных
В окно «Поиск решения» в поле «Изменяя ячейки» впишите адреса $BS3:$E$3. Необходимые адреса можно вносить в поле «Изменяя ячейки» и автоматически путем выделения мышью соответствующих ячеек переменных непосредственно в экранной форме.
Задание граничных условий для допустимых значений переменных
В нашем случае на значения переменных накладывается только граничное условие неотрицательности, то есть их нижняя граница должна быть равна нулю (см. рис. 1.1).
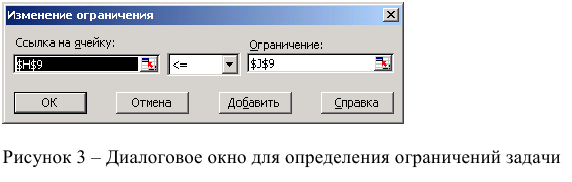
• Нажмите кнопку «Добавить», после чего появится окно «Добавление ограничения» (рис. 1.7).
• В поле «Ссылка на ячейку» введите адреса ячеек переменных $BS3:$E$3. Это можно сделать как с клавиатуры, так и путем выделения мышью всех ячеек переменных непосредственно в экранной форме.
• В поле знака откройте список предлагаемых знаков и выберите >.
• В поле «Ограничение» введите адреса ячеек нижней границы значений переменных, то есть $В$4:$Е$4. Их также можно ввести путем выделения мышью непосредственно в экранной форме.
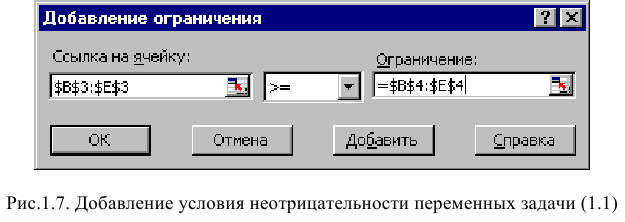
Задание знаков ограничений <. >, =
• Нажмите кнопку «Добавить» в окне «Добавление ограничения».
• В поле «Ссылка на ячейку» введите адрес ячейки левой части конкретного ограничения, например $F$10. Это можно сделать как с клавиатуры, так и путем выделения мышью нужной ячейки непосредственно в экранной форме.
• В соответствии с условием задачи (1.1) выбрать в поле знака необходимый знак, например =.
• В поле «Ограничение» введите адрес ячейки правой части рассматриваемого ограничения, например $Н$10.
• Аналогично введите ограничения: $F$11>=$Н$11, $F$12<=$H$12.
• Подтвердите ввод всех перечисленных выше условий нажатием кнопки ОК.
Окно «Поиск решения» после ввода всех необходимых данных задачи (1.1) представлено на рис. 1.6.
Если при вводе условия задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делают, нажав кнопки «Изменить» или «Удалить» (см. рис. 1.6).
Решение задачи
Установка параметров решения задачи
Задача запускается на решение в окне «Поиск решения». Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку «Параметры» и заполнить некоторые поля окна «Параметры поиска решения» (рис. 1.8).
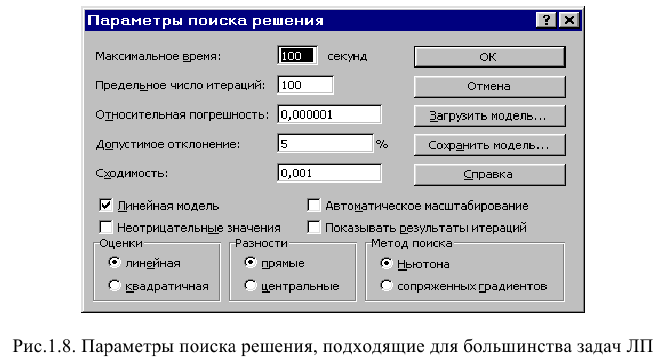
Параметр «Максимальное время» служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр «Предельное число итераций» служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32 767.
Параметр «Относительная погрешность» служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр «Допустимое отклонение» служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее.
Параметр «Сходимость» применяется только при решении нелинейных задач.
Установка флажка «Линейная модель» обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода.
Подтвердите установленные параметры нажатием кнопки «ОК».
Запуск задачи на решение
Запуск задачи на решение производится из окна «Поиск решения» путем нажатия кнопки «Выполнить».
После запуска на решение задачи линейного программирования на экране появляется окно «Результаты поиска решения» с одним из сообщений, представленных на рис. 1.9, 1.10 и 1.11.

Иногда сообщения, представленные на рис. 1.10 и 1.11, свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условий задачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует (см. ниже подразд.1.3.5).
Если при заполнении полей окна «Поиск решения» были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра «Относительная погрешность» не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.
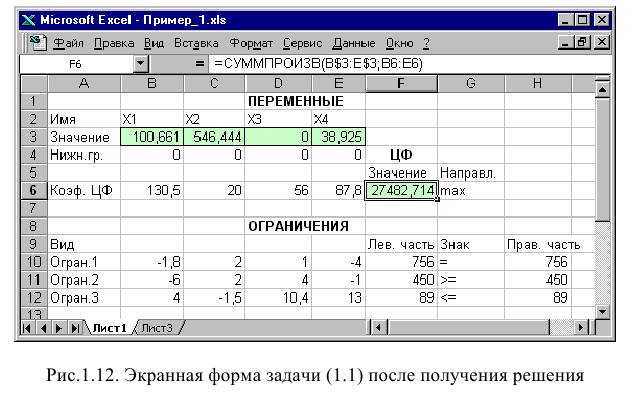
В окне «Результаты поиска решения» представлены названия трех типов отчетов: «Результаты», «Устойчивость», «Пределы». Они необходимы при анализе полученного решения на чувствительность (см. ниже подразд.3.3). Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку «ОК». После этого в экранной форме появляется оптимальное решение задачи (рис. 1.12).
Целочисленное программирование
Допустим, что к условию задачи (1.1) добавилось требование целочисленности значений всех переменных. В этом случае описанный выше процесс ввода условия задачи необходимо дополнить следующими шагами.
• В экранной форме укажите, на какие переменные накладывается требование целочисленности (этот шаг делается для наглядности восприятия условия задачи) (рис. 1.13).
• В окне «Поиск решения» (меню «Сервис»—>»Поиск решения»), нажмите кнопку «Добавить» и в появившемся окне «Добавление ограничений» введите ограничения следующим образом (рис.1.14):
- в поле «Ссылка на ячейку» введите адреса ячеек переменных задачи, то есть $В$3:$Е$3;
- в поле ввода знака ограничения установите «целое»;
- подтвердите ввод ограничения нажатием кнопки «ОК».
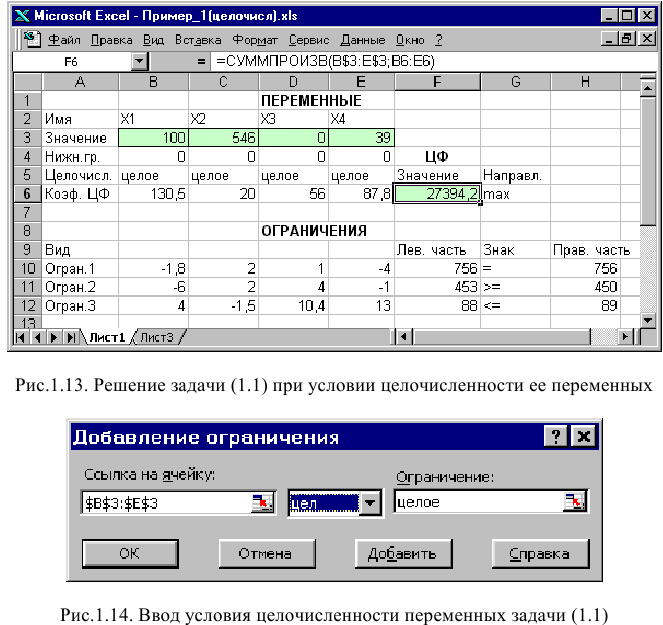
На рис. 1.13 представлено решение задачи (1.1), к ограничениям которой добавлено условие целочисленности значений ее переменных.
Двухиндексные задачи линейного программирования
Двухиндексные задачи линейного программирования вводятся и решаются в Excel аналогично одноиндексным задачам. Специфика ввода условия двухиндексной задачи ЛП состоит лишь в удобстве матричного задания переменных задачи и коэффициентов ЦФ.
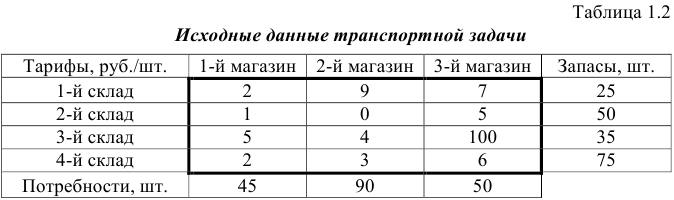
Рассмотрим решение двухиндексной задачи, суть которой заключается в оптимальной организации транспортных перевозок штучного товара со складов в магазины (табл. 1.2).
Целевая функция и ограничения данной задачи имеют вид
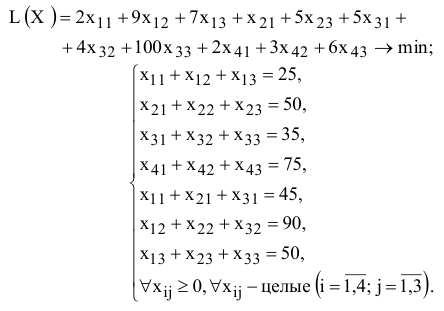
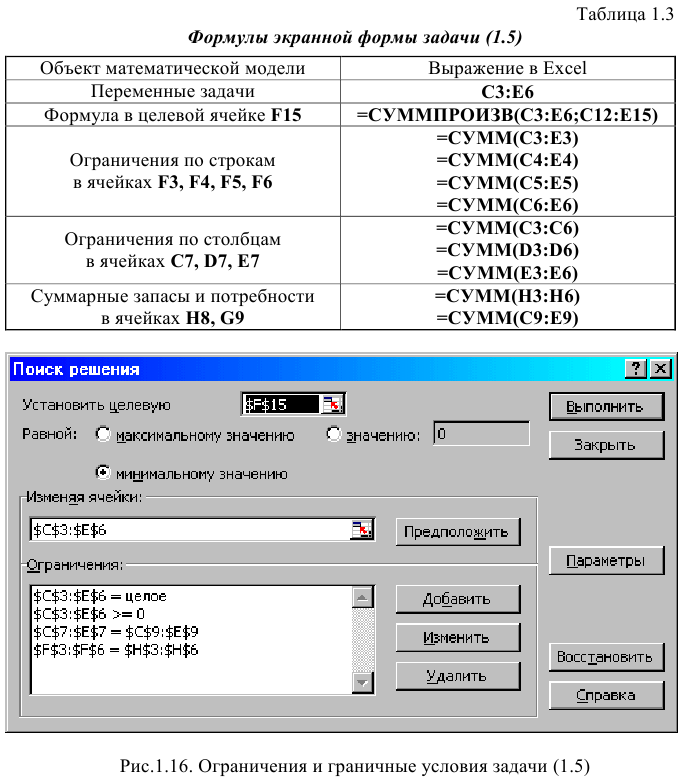
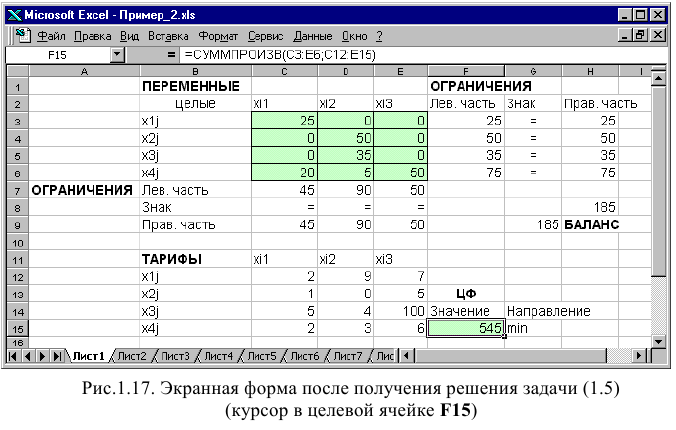
Экранные формы, задание переменных, целевой функции, ограничений и граничных условий двухиндексной задачи (1.5) и ее решение представлены на рис. 1.15, 1.16, 1.17 и в табл. 1.3.
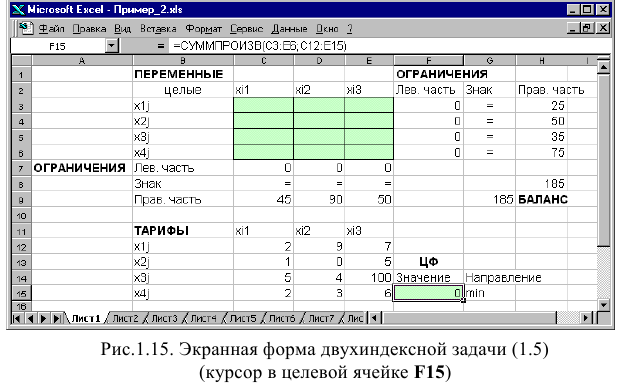
Задачи с булевыми переменными
Частным случаем задач с целочисленными переменными являются задачи, в результате решения которых искомые переменные 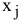
Рис. 1.18. Решение двухиндексной задачи с булевыми переменными
Помимо задания требования целочисленности (см. подразд.1.3.2) при вводе условия задач с булевыми переменными необходимо:
• для наглядности восприятия ввести в экранную форму слово «булевы» в качестве характеристики переменных (см. рис. 1.18);
• в окне «Поиск решения» добавить граничные условия, имеющие смысл ограничения значений переменных по их единичной верхней границе (рис. 1.19).
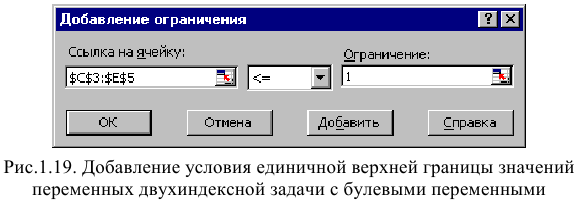
Вид окна «Поиск решения» для задачи с булевыми переменными, представленной на рис. 1.18, приведен на рис. 1.20.
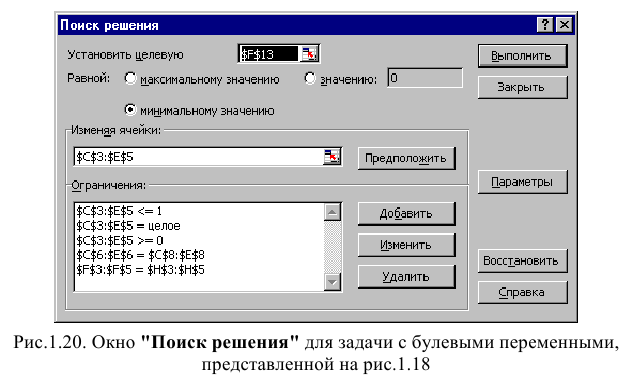
Возможные ошибки при вводе условий задач линейного программирования
Если при решении задачи линейного программирования выдается сообщение о невозможности нахождения решения, то возможно, что причина заключается в ошибках ввода условия задачи в Excel.
Как решить задачу линейного программирования в excel
Цель работы
Приобретение навыков решения задач линейного программирования (ЗЛП) в табличном редакторе Microsoft Excel. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Для модели линейного программирования, соответствующей номеру Вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю.
Инструкция по использованию microsoft excel для решения задач линейного программирования
Для того чтобы решить ЗЛП в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия. 1. Ввести условие задачи:
a) создать экранную форму для ввода условия задачи:
- • переменных,
- • целевой функции (ЦФ),
- • ограничений,
- • граничных условий;
b) ввести исходные данные в экранную форму:
- • коэффициенты ЦФ,
- • коэффициенты при переменных в ограничениях,
- • правые части ограничений;
c) ввести зависимости из математической модели в экранную форму:
- • формулу для расчета ЦФ,
- • формулы для расчета значений левых частей ограничений; с!) задать ЦФ (в окне «Поиск решения»):
- • целевую ячейку,
- • направление оптимизации ЦФ;
е) ввести ограничения и граничные условия (в окне «Поиск решения»):
- • ячейки со значениями переменных,
- • граничные условия для допустимых значений переменных,
- • соотношения между правыми и левыми частями ограничений. 2. Решить задачу:
a)установить параметры решения задачи (в окне «Поиск решения»,);
b) запустить задачу на решение (в окне «Поиск решения»,);
c) выбрать формат вывода решения (в окне «Результаты поиска решения»).
Одноиндексные ЗЛП
Рассмотрим пример нахождения решения для следующей одноиндексной ЗЛП:
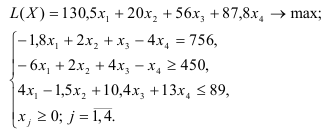
- Ввод исходных данных
Создание экранной формы и ввод в нее условия задачи
Экранная форма для ввода условий задачи (1) вместе с введенными в нее исходными данными представлена на рис.1.
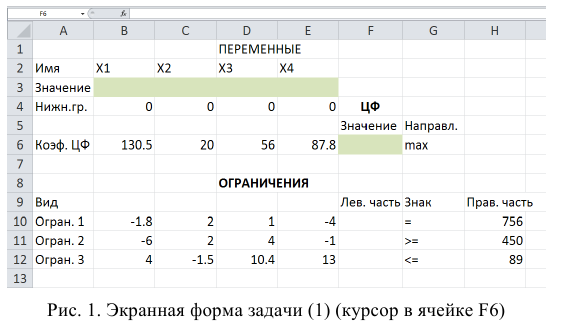
В экранной форме на рис. 1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Так, например, переменным задачи (1) соответствуют ячейки
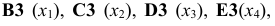
коэффициентам ЦФ соответствуют ячейки
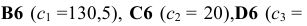
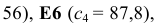
правым частям ограничений соответствуют ячейки
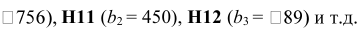
- Ввод зависимостей из математической модели в экранную форму
Зависимость для ЦФ.
В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1 (значение ЦФ определяется выражением
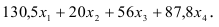
Используя обозначения соответствующих ячеек в Excel (см. рис. 1), формулу для расчета ЦФ (2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов ЦФ (В6, С6, D6,E6):
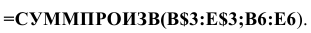
После этого в целевой ячейке появится 0 (нулевое значение) (рис. 2).
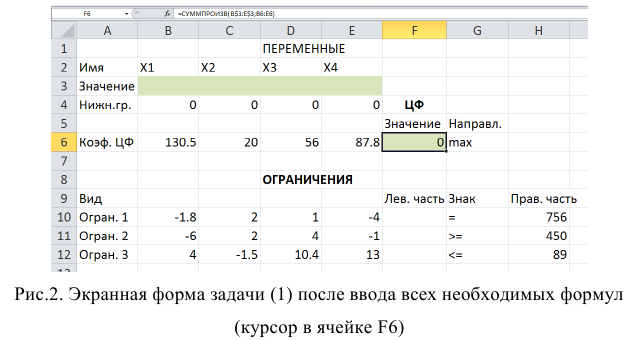
Зависимости для левых частей ограничений
Левые части ограничений задачи (1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи(ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B10, С10, D10, Е10 — 1-е ограничение; В11, C11,D11, Е11 — 2-е ограничение и В12, С12, D12, Е12 — 3-е ограничение). Формулы, соответствующие левым частям ограничений, записать самостоятельно. Проверка правильности введения формул
Для проверки правильности введенных формул производите поочередно двойное нажатие левой клавиши мыши на ячейки с формулами. При этом на экране рамкой будут выделяться ячейки, используемые в формуле. Дальнейшие действия производятся в окне «Поиск решения», которое вызывается из меню «Сервис». Решение задачи
Установка параметров решения задачи
Задача запускается на решение в окне «Поиск решения». Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку «Параметры»и заполнить некоторые поля окна «Параметры поиска решения».
Параметр «Максимальное время» служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр «Предельное число итераций» служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее32 767. Параметр «Относительная погрешность» служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр «Допустимое отклонение» служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее. Параметр «Сходимость» применяется только при решении нелинейных задач. Установка флажка «Линейная модель» обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода. Подтвердите установленные параметры нажатием кнопки «ОК». Запуск задачи на решение
Запуск задачи на решение производится из окна «Поиск решения» путем нажатия кнопки «Выполнить».
После запуска на решение задачи линейного программирования на экране появляется окно «Результаты поиска решения» с одним из сообщений:
• Сообщение об успешном решении задачи
• Сообщение при несовместной системе ограничений задачи
• Сообщение при неограниченности ЦФ в требуемом направлении Иногда второе и третье сообщения свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условийзадачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует.
Если при заполнении полей окна «Поиск решения» были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра»Относительная погрешность» не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.
В окне «Результаты поиска решения» представлены названия трех типов отчетов: «Результаты», «Устойчивость», «Пределы». Они необходимы при анализе полученного решения на чувствительность (будет рассмотрено позже). Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку «ОК». После этого в экранной форме появляется оптимальное решение задачи (рис.3).
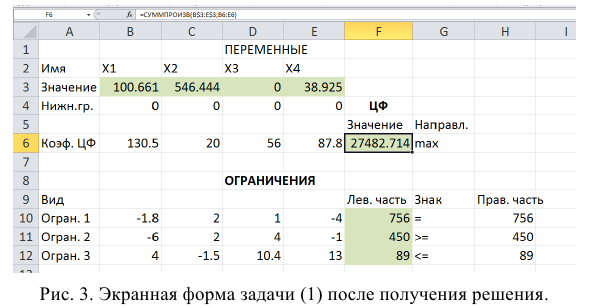
Целочисленное программирование
Допустим, что к условию задачи (1) добавилось требование целочисленности значений всех переменных. В этом случае описанный выше процесс ввода условия задачи необходимо дополнить следующими шагами.
• В экранной форме укажите, на какие переменные накладывается требование целочисленности (этот шаг делается для наглядности восприятия условия задачи) (рис. 4).
• В окне «Поиск решения» (меню «Сервис»—►»Поиск решения»), нажмите кнопку «Добавить» и в появившемся окне «Добавление ограничений» введите ограничения целочисленности. Сравните результаты.
Получите у преподавателя индивидуальные задания.
Примеры решения экономических задач Задача 1.
Средства очистки пола оценивают по следующим трем показателям:
- • очищающие свойства;
- • дезинфицирующие свойства;
- • раздражающее воздействие на кожу.
Каждый из этих показателей измеряется по линейной шкале от 0 до 100. Продукт на рынке должен иметь по крайней мере 60 ед. очищающих свойств и по крайней мере 60 ед. дезинфицирующих свойств по соответствующей шкале. При этом раздражающее воздействие на кожу должно быть минимальным. Конечный продукт должен быть смесью трех основных очистителей, характеристики которых приведены в таблице.
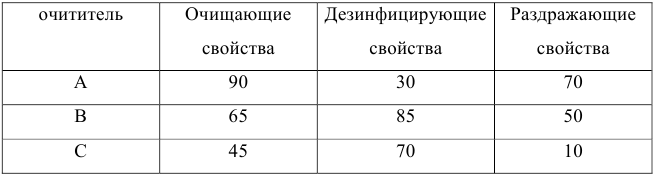
Составим математическую модель задачи. Пусть 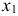
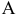
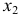
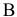
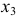
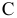
Целевая функция: 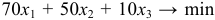
Ограничения:
Решение задачи с помощью MS Excel.
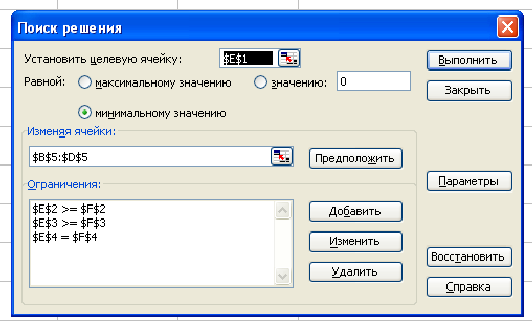
Заполним таблицу, содержащую исходные данные. Заполним диалоговое окно
«Поиск решения».
Щелкнув по кнопке ОК, мы получаем на месте исходной таблицы — таблицу с найденными оптимальными значениями. В результате в таблице получим значение целевой функции — 31,4 ед. раздражающего воздействия на кожу при
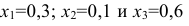
(т.е. очистители 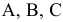
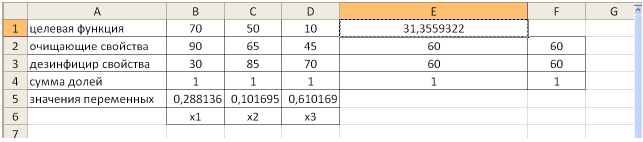
Задача 2.
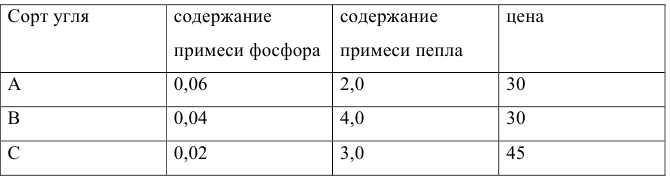
Фирме требуется уголь с содержанием фосфора не более 0,03% и с примесью пепла не более 3,25%. Доступны 3 сорта угля 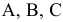
Как следует их смешать, чтобы удовлетворить ограничениям на примеси и минимизировать цену?
Решение задач математического программирования с помощью надстройки «Поиск решения» ЭТ Excel
Задачи линейного программирования, целочисленного программирования и ряд задач нелинейного программирования могут быть решены с помощью стандартного прикладного программного обеспечения. Например, в ЭТ MS Excel для этого имеется модуль «Поиск решения», вызываемый командой меню «Сервис/Поиск решения». Для активизации данного модуля необходимо выполнить команду «Сервис/Надстройки» и установить флажок напротив строки меню «Поиск решения».
Рассмотрим пример применения «Поиска решения» на основе решения задачи оптимизации портфеля ценных бумаг — одной из классических задач управления финансовыми средствами.
Постановка задачи. Перед инвестором стоит задача на основе информации, представленной в таблице 1, разместить имеющиеся средства так, чтобы получить максимальную прибыль за 1 период планирования (1 год), при этом должны быть выполнены следующие условия:
- Суммарный объем капитала составляет 100 000 $;
- доля средств, вложенная в один из объектов, не может превышать 25%;
- более 40% всех средств должны быть вложены в долгосрочные активы;
- доля высокорисковых активов не может превышать трети от суммарного объема.
Таблица 1 — Информация об объектах инвестирования
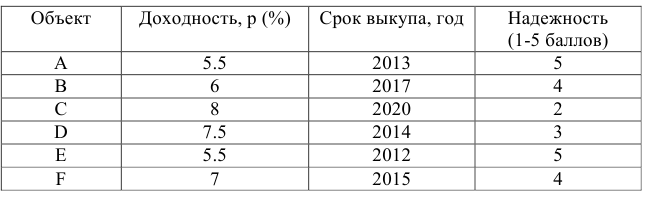
Построим экономико-математическую модель задачи.
Искомые переменные — объемы средств, вложенные в активы: 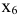
Прибыль, которую получит инвестор, задается целевой функцией:
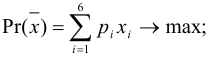
Сформируем ограничения:
Ограничения на суммарный объем активов —
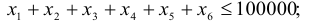
Ограничение на размер доли каждого актива
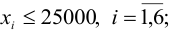
Необходимость долгосрочного инвестирования (например, более 3 лет)
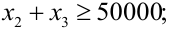
Учет необходимости снижения риска —
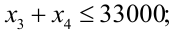
Естественное экономическое ограничение — неотрицательность искомых переменных —
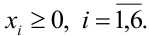
Для решения задачи выполним следующие шаги.
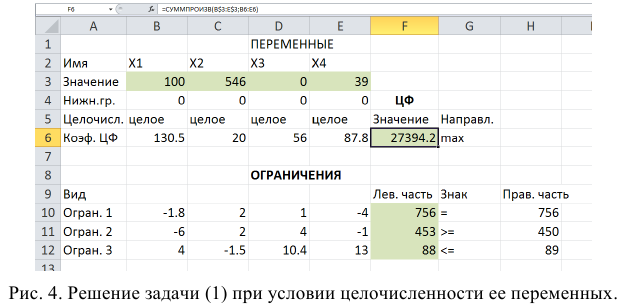
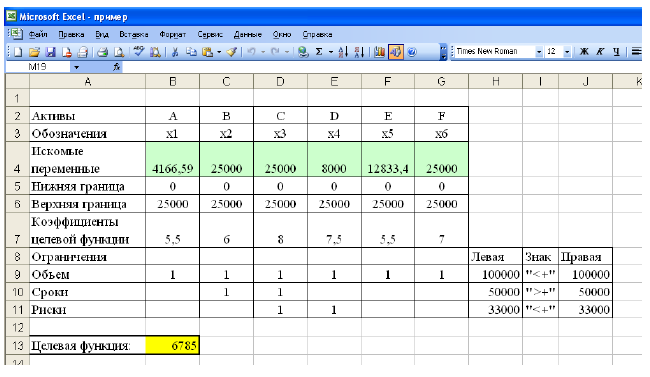
- На рабочем листе представим необходимую для решения информацию, согласно рисунку 1.
Ячейки В13, Н9-Н11 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае целесообразно использовать функцию Суммпроизв(…), аргументами которой являются диапазоны B4-G4 и диапазоны соответствующих параметров.
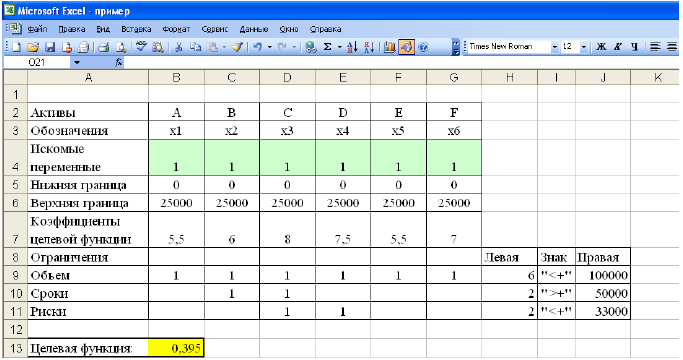
Рисунок 1 — Исходные данные для решения ЗЛП
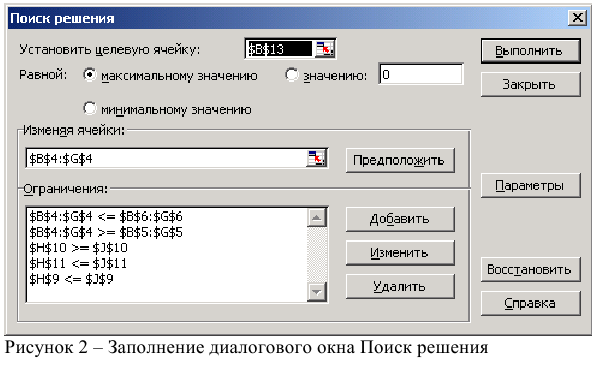
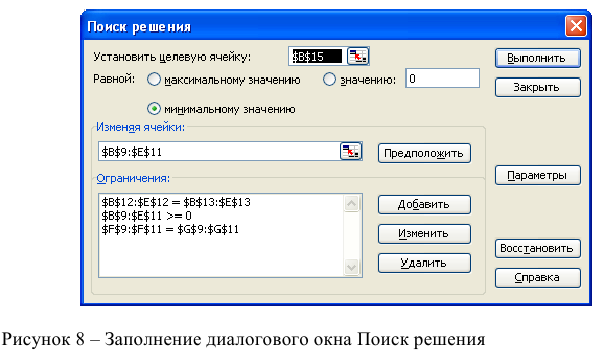
- Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:
Указать адрес ячейки (В 13), содержащей целевую функцию, указать тип целевой функции,
В поле «изменяя ячейки» указать адреса всех искомых переменных (от В4 до G4).
Затем последовательно заполнить все ограничения (Пример на рисунке 2.)
Если возникли ошибки ввода, то изменить или добавить ограничение можно с помощью командных кнопок «Добавить, изменить, удалить».
Далее, если это необходимо, устанавливаются особые значения параметров (кнопка «Параметры»).
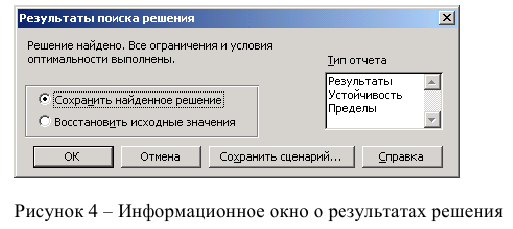
Результаты отражаются на рабочем листе. Результаты решения представлены на рисунке 5.
Рисунок 5 — Результаты решения задачи
На рисунке 6 представлена структура инвестиционного портфеля.
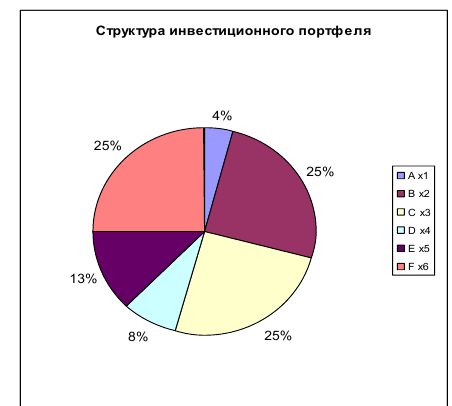
На основе решения проводится анализ, и принимаются соответствующие управленческие решения.
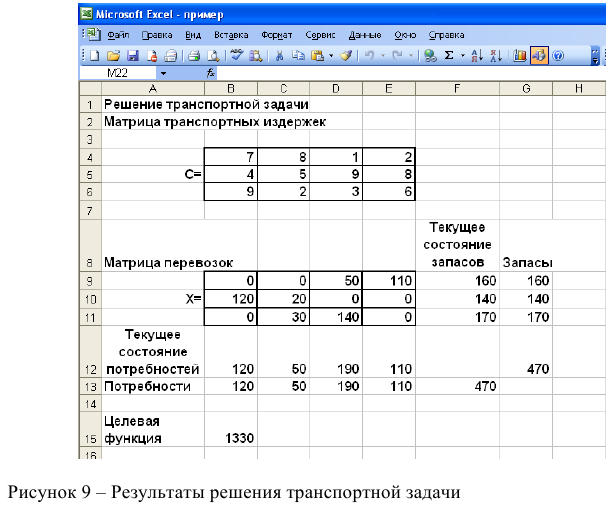
Технология решения транспортной задачи
1. На рабочем листе представим необходимую для решения информацию, согласно рисунку 7.
Ячейки В15 содержит формулу Суммпроизв(…), аргументами которой являются диапазоны В4-Е6 и В9-Е11. Ячейки F9-F11 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае целесообразно использовать функцию Сумм(…), аргументами которой являются диапазоны В9-Е9, В10-Е 10 и В11 -Е11. Аналогично определяются формулы в В12-Е 12.
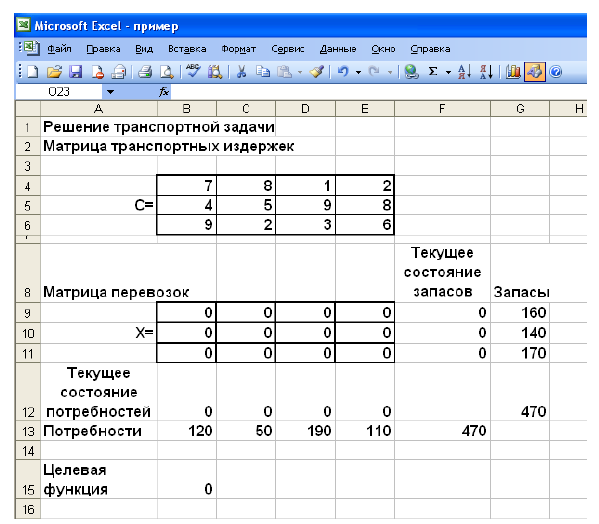
Рисунок 7 — Исходные данные для решения ЗЛП
- Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:
Указать адрес ячейки (В 15), содержащей целевую функцию, указать тип целевой функции (минимум),
В поле «изменяя ячейки» указать адреса всех искомых переменных (от В9 до Е11).
Затем последовательно заполнить все ограничения (Пример на рисунке 8.)
Если возникли ошибки ввода, то изменить или добавить ограничение можно с помощью командных кнопок «Добавить, изменить, удалить». Результаты отражаются на рабочем листе. Результаты решения представлены на рисунке 9.
Технология решения задачи нелинейного программирования
Построить математическую модель и решить задачу потребительского выбора для заданной функции полезности 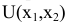
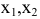
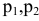
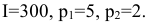
доходе I. Найти максимальное значение функции полезности.
Построим математическую модель задачи потребительского выбора:
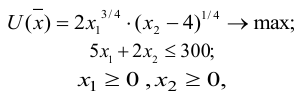
где 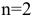
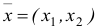
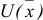
Набор, который является решением задачи потребительского выбора, называется оптимальным потребительским набором, или точкой локального рыночного равновесия потребителя. Поставленная задача — задача потребительского выбора — является задачей нелинейного программирования.
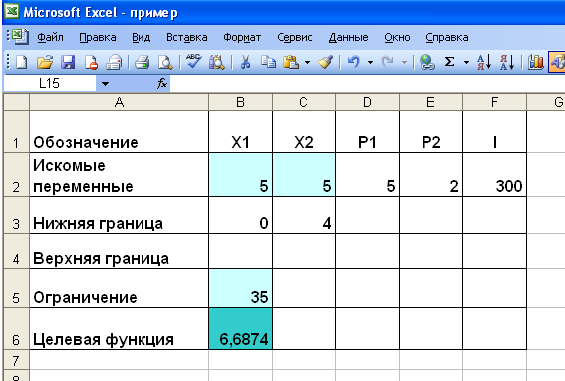
- На рабочем листе представим необходимую для решения информацию, согласно рисунку 10.
Ячейки В5, В6 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае ячейка В5 содержит формулу «=D2B2+E2C2», а ячейка В6 содержит формулу «=2В2Л(3/4)(С2-4)А(1/4)».
Рисунок 10 — Исходные данные для решения ЗНП
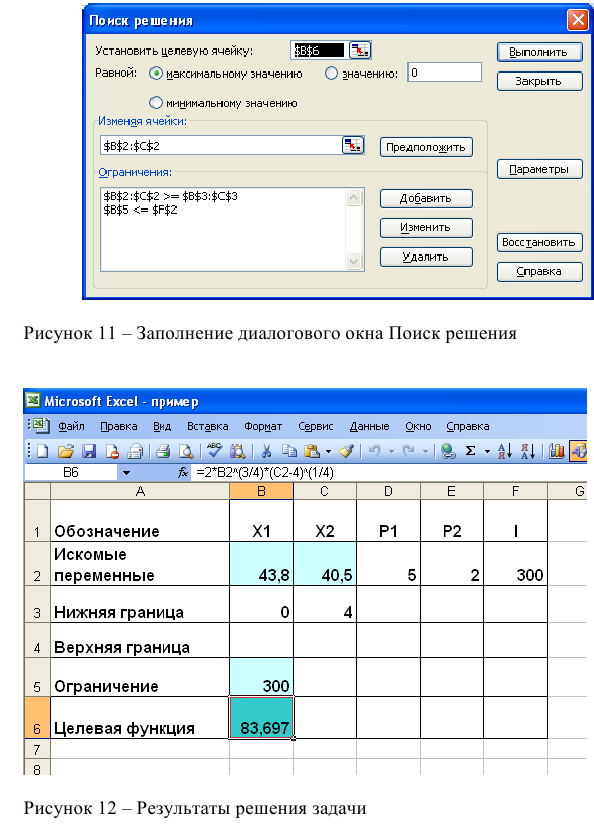
- Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:
Аналитическое решение задачи нелинейного программирования.
В рассматриваемом случае ограничение можно записать в виде строгого равенства, так как оптимальное решение достигается при полном использовании имеющихся средств.
Для решения классической задачи нелинейного программирования применим метод множителей Лагранжа, для этого составим функцию Лагранжа:
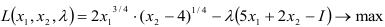
Найдем точки экстремума функции Лагранжа.
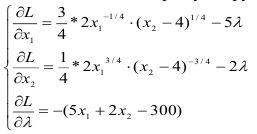
Приравняем каждое уравнение к 0:
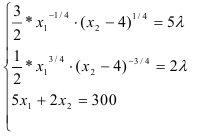
С помощью преобразований — разделим первое уравнение системы на второе, перейдем к системе:
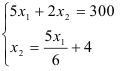
Подставим второе уравнение в первое и построим аналитические функции спроса:
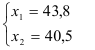
Максимальное значение функции полезности-
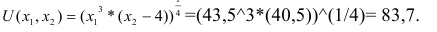
Решением задачи потребительского выбора будет набор
Возможно эти страницы вам будут полезны:
- Решение задач по математическому программированиюПримеры решения задач по математическому программированиюЗаказать работу по математическому программированиюПомощь по математическому программированиюЗадачи математического программированияЗадача линейного программированияРешение задач по линейному программированиюМетоды решения задач линейного программированияГрафическое решение задач линейного программированияГрафический метод решения задач линейного программированияЗаказать работу по линейному программированиюПомощь по линейному программированиюКонтрольная работа по линейному программированиюКурсовая работа по линейному программированию
Линейное программирование — это математический метод оптимизации результата в математической модели с использованием линейных уравнений в качестве ограничений. Для решения стандартной формы линейной программы используйте Microsoft Excel и надстройку Excel Solver. Excel Solver можно включить в Excel 2010, нажав кнопку «Файл» на панели инструментов, «Параметры» и «Надстройка». Установите флажок «Надстройка Солвера» и нажмите «ОК». Вы можете получить доступ к Solver на вкладке «Данные» на панели инструментов. Самая основная линейная программа для решения — стандартная форма.
-
Убедитесь, что все вычисления выполнены правильно, прежде чем запускать Солвер. Назовите все ячейки, которые будут использоваться в Солвере, такие как «target, x1, x2, A1x1 или b1».
Настройте линейную программу в виде:
Максимизировать c (транспонировать) x Подлежит: Ax ≤ b, x ≥ 0
где c, x, A и b — матрицы. Целевая функция также может быть минимизирована или равна некоторому числу z. Ограничения в линейной форме. X не должен иметь неотрицательное ограничение. Эти различия в линейной программе зависят от конкретной задачи. Однако обязательно, чтобы линейная программа была настроена правильно. Обязательно выполните все вычисления для матриц cTx, Ax и b в Excel, прежде чем решать линейную программу. Вы можете начать с установки всех значений x на 1 или оставив их неизвестными. Может быть полезно назвать ячейки, нажав «Вставить» на панели инструментов, «Имя» и «Определить». Имена ячеек могут быть введены непосредственно в Солвер.
Откройте Солвер и введите необходимые ячейки. Чтобы ввести ячейку, щелкните значок Excel справа от текстового поля, а затем щелкните нужную ячейку. «Задать целевую ячейку:» является целевой функцией. «Путем изменения ячеек:» — это переменные в вашей линейной программе, то есть матрица x. Нажмите «Добавить», чтобы добавить ограничение. Ссылка на ячейку — это матрица Ax. Выберите тип ограничения (больше или равно, меньше или равно или равно) в раскрывающемся меню. Ограничением является матрица b. Если x неотрицательный, добавьте это ограничение для каждого значения x.
Выберите правильную линейную модель в раскрывающемся меню «Выберите метод решения:». Линейные программы стандартной формы обычно используют метод решения LP Simplex. Если x имеет неотрицательное ограничение, установите флажок «Сделать неограниченные переменные неотрицательными».
Решите линейную программу, нажав «Решить». Позвольте Солверу задуматься на мгновение. Если Солвер находит решение, появится диалоговое окно с заголовком «Результаты Солвера». Вам предоставляется выбор оставить решающие решения или восстановить все ячейки до их первоначального значения.