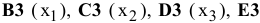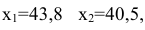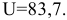Линейное программирование анализ что если в excel - Word и Excel

Линейное программирование
- Решение задач линейного программирования с использованием microsoft excel
  - Цель работы
  - Порядок выполнения работы
  - Инструкция по использованию microsoft excel для решения задач линейного программирования
- Одноиндексные задачи линейного программирования
  - Ввод исходных данных
- Решение задачи
- Целочисленное программирование
- Двухиндексные задачи линейного программирования
- Задачи с булевыми переменными
  - Возможные ошибки при вводе условий задач линейного программирования
- Как решить задачу линейного программирования в excel
  - Инструкция по использованию microsoft excel для решения задач линейного программирования
- Решение задач математического программирования с помощью надстройки «Поиск решения» ЭТ Excel
- Технология решения транспортной задачи

Задачи линейного программирования относятся к широко распространённому классу задач, встречающихся в различных сферах деятельности: в бизнесе, на производстве, в быту. Как оптимально распорядиться бюджетом или за минимальное время добраться до нужного места в городе, как наилучшим образом спланировать деловые встречи, минимизировать риски капитальных вложений, определить оптимальные запасы сырья на складе – это те задачи, в которых нужно найти наилучшее из всех возможных решений.

Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Линейное программирование

Линейное программирование – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Слово «программирование» заимствовано из зарубежной литературы, где оно используется в смысле «планирование».

Решение задач линейного программирования с использованием microsoft excel

Цель работы

Приобретение навыков решения задач линейного программирования (ЛП) в табличном редакторе Microsoft Excel.

Порядок выполнения работы

Для модели линейного программирования, соответствующей номеру Вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю.

Инструкция по использованию microsoft excel для решения задач линейного программирования

Для того чтобы решить задачу линейного программирования в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия.

Ввести условие задачи:

a) создать экранную форму для ввода условия задачи:

переменных,
целевой функции (ЦФ),
ограничений,
граничных условий;

b) ввести исходные данные в экранную форму:

коэффициенты ЦФ,
коэффициенты при переменных в ограничениях,
правые части ограничений;

c) ввести зависимости из математической модели в экранную форму:

формулу для расчета ЦФ,
формулы для расчета значений левых частей ограничений;

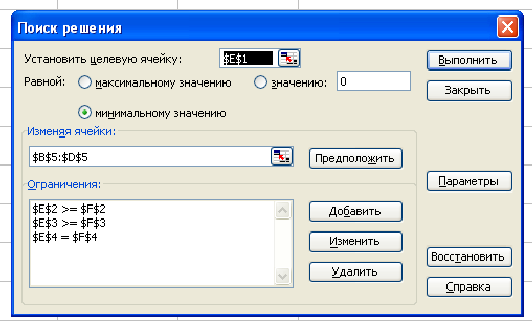
d) задать ЦФ (в окне «Поиск решения»):

целевую ячейку,
направление оптимизации ЦФ;

e) ввести ограничения и граничные условия (в окне «Поиск решения»):

ячейки со значениями переменных,
граничные условия для допустимых значений переменных,
соотношения между правыми и левыми частями ограничений.

Решить задачу:

a) установить параметры решения задачи (в окне «Поиск решения»);

b) запустить задачу на решение (в окне «Поиск решения»);

с) выбрать формат вывода решения (в окне «Результаты поиска решения»).

Возможно эта страница вам будет полезна:

Одноиндексные задачи линейного программирования

Рассмотрим пример нахождения решения для следующей одноиндексной задачи ЛП:

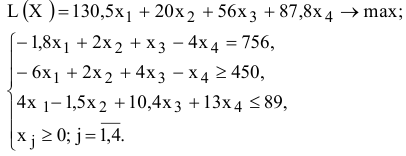
Линейное программирование в Excel задачи с решением

Ввод исходных данных

Создание экранной формы и ввод в нее условия задачи

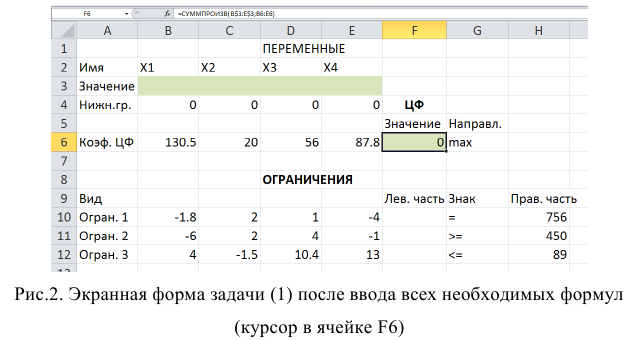
Экранная форма для ввода условий задачи (1.1) вместе с введенными в нее исходными данными представлена на рис. 1.1.

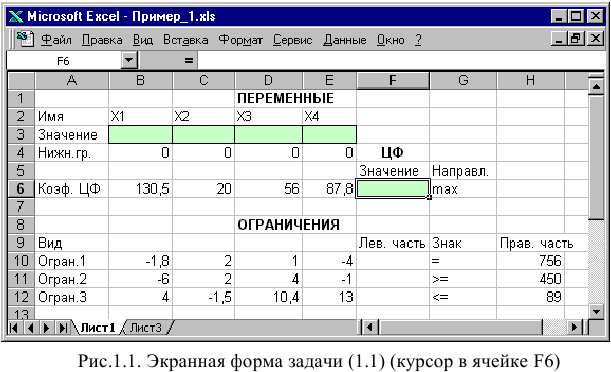
В экранной форме на рис. 1.1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Имя ячейки состоит из буквы, обозначающей столбец, и цифры, обозначающей строку, на пересечении которых находится объект задачи линейного программирования. Так, например, переменным задачи (1.1) соответствуют ячейки , коэффициентам ЦФ соответствуют ячейки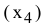

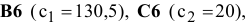
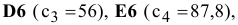
правым частям ограничений соответствуют ячейки

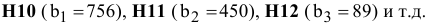
Ввод зависимостей из математической модели в экранную форму

Зависимость для ЦФ

В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1.1) значение ЦФ определяется выражением

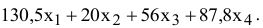
Используя обозначения соответствующих ячеек в Excel (см. рис. 1.1), формулу для расчета ЦФ (1.2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов ЦФ (В6, С6, D6, Е6), то есть

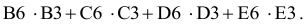
Чтобы задать формулу (1.3) необходимо в ячейку F6 ввести следующее выражение и нажать клавишу «Enter»

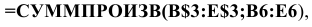
где символ $ перед номером строки 3 означает, что при копировании этой формулы в другие места листа Excel номер строки 3 не изменится;

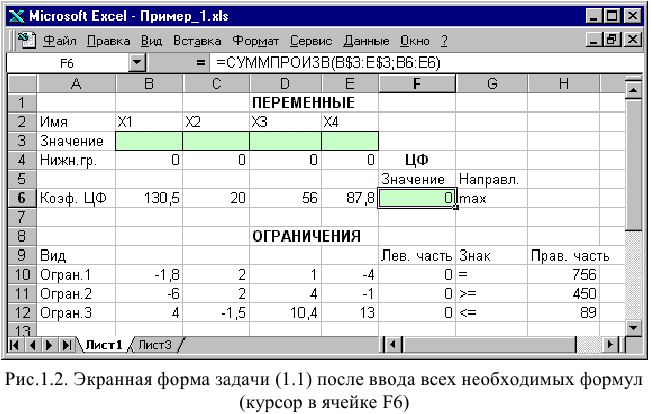
символ : означает, что в формуле будут использованы все ячейки, расположенные между ячейками, указанными слева и справа от двоеточия (например, запись В6:Е6 указывает на ячейки В6, С6, D6 и Е6). После этого в целевой ячейке появится 0 (нулевое значение) (рис. 1.2).

Примечание 1.1. Существует другой способ задания функций в Excel с помощью режима «Вставка функций», который можно вызвать из меню «Вставка» или при нажатии кнопки «» на стандартной панели инструментов. Так, например, формулу (1.4) можно задать следующим образом:

• курсор в поле F6;

• нажав кнопку «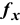«, вызовите окно «Мастер функций — шаг 1 из 2»;

• выберите в окне «Категория» категорию «Математические»;

• в окне «Функция» выберите функцию СУММПРОИЗВ;

• в появившемся окне «СУММПРОИЗВ» в строку «Массив 1» введите выражение В$3:Е$3, а в строку «Массив 2» — выражение В6:Е6 (рис. 1.3);

• после ввода ячеек в строки «Массив 1» и «Массив 2» в окне «СУММПРОИЗВ» появятся числовые значения введенных массивов (см. рис. 1.3), а в экранной форме в ячейке F6 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).

Зависимости для левых частей ограничений

Левые части ограничений задачи (1.1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (В 10, СЮ, D10, ЕЮ — 1-е ограничение; В11, С11, D11, El 1 — 2-е ограничение и В12, С12, D12, Е12 — 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл. 1.1.

Как видно из табл. 1.1, формулы, задающие левые части ограничений задачи (1.1), отличаются друг от друга и от формулы (1.4) в целевой ячейке F6 только номером строки во втором массиве. Этот номер определяется той строкой, в которой ограничение записано в экранной форме. Поэтому для задания зависимостей для левых частей ограничений достаточно скопировать формулу из целевой ячейки в ячейки левых частей ограничений. Для этого необходимо:

• поместить курсор в поле целевой ячейки F6 и скопировать в буфер содержимое ячейки F6 (клавишами «Ctrl-Insert»);

• помещать курсор поочередно в поля левой части каждого из ограничений, то есть в F10, F11 и F12, и вставлять в эти поля содержимое буфера (клавишами «Shift-Insert») (при этом номер ячеек во втором массиве формулы будет меняться на номер той строки, в которую была произведена вставка из буфера);

• на экране в полях F10, F11 и F12 появится 0 (нулевое значение) (см. рис. 1.2).

Проверка правильности введения формул

Задание ЦФ

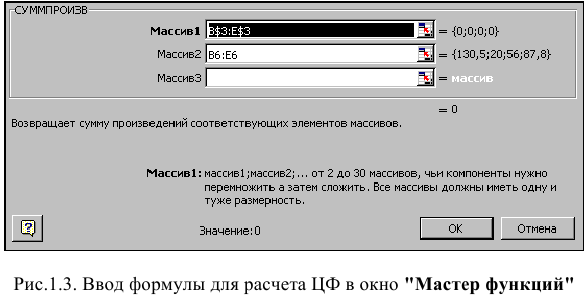
Дальнейшие действия производятся в окне «Поиск решения», которое вызывается из меню «Сервис» (рис. 1.6):

• поставьте курсор в поле «Установить целевую ячейку»;

• введите адрес целевой ячейки $F$6 или сделайте одно нажатие левой клавиши мыши на целевую ячейку в экранной форме — это будет равносильно вводу адреса с клавиатуры;

• введите направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по селекторной кнопке «максимальному значению».

Ввод ограничений и граничных условий

Задание ячеек переменных

В окно «Поиск решения» в поле «Изменяя ячейки» впишите адреса $BS3:$E$3. Необходимые адреса можно вносить в поле «Изменяя ячейки» и автоматически путем выделения мышью соответствующих ячеек переменных непосредственно в экранной форме.

Задание граничных условий для допустимых значений переменных

В нашем случае на значения переменных накладывается только граничное условие неотрицательности, то есть их нижняя граница должна быть равна нулю (см. рис. 1.1).

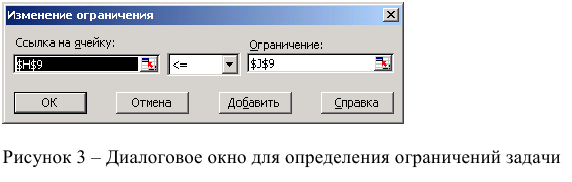
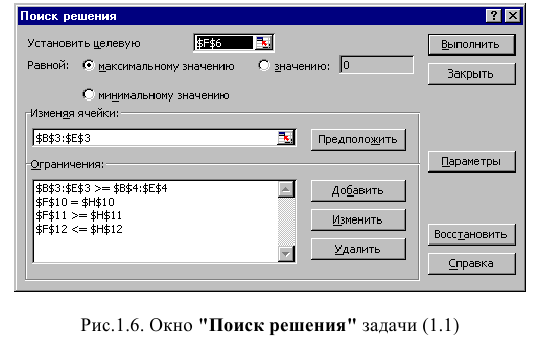
• Нажмите кнопку «Добавить», после чего появится окно «Добавление ограничения» (рис. 1.7).

• В поле «Ссылка на ячейку» введите адреса ячеек переменных $BS3:$E$3. Это можно сделать как с клавиатуры, так и путем выделения мышью всех ячеек переменных непосредственно в экранной форме.

• В поле знака откройте список предлагаемых знаков и выберите >.

• В поле «Ограничение» введите адреса ячеек нижней границы значений переменных, то есть $В$4:$Е$4. Их также можно ввести путем выделения мышью непосредственно в экранной форме.

Задание знаков ограничений <. >, =

• Нажмите кнопку «Добавить» в окне «Добавление ограничения».

• В поле «Ссылка на ячейку» введите адрес ячейки левой части конкретного ограничения, например $F$10. Это можно сделать как с клавиатуры, так и путем выделения мышью нужной ячейки непосредственно в экранной форме.

• В соответствии с условием задачи (1.1) выбрать в поле знака необходимый знак, например =.

• В поле «Ограничение» введите адрес ячейки правой части рассматриваемого ограничения, например $Н$10.

• Аналогично введите ограничения: $F$11>=$Н$11, $F$12<=$H$12.

• Подтвердите ввод всех перечисленных выше условий нажатием кнопки ОК.

Окно «Поиск решения» после ввода всех необходимых данных задачи (1.1) представлено на рис. 1.6.

Если при вводе условия задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делают, нажав кнопки «Изменить» или «Удалить» (см. рис. 1.6).

Решение задачи

Установка параметров решения задачи

Задача запускается на решение в окне «Поиск решения». Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку «Параметры» и заполнить некоторые поля окна «Параметры поиска решения» (рис. 1.8).

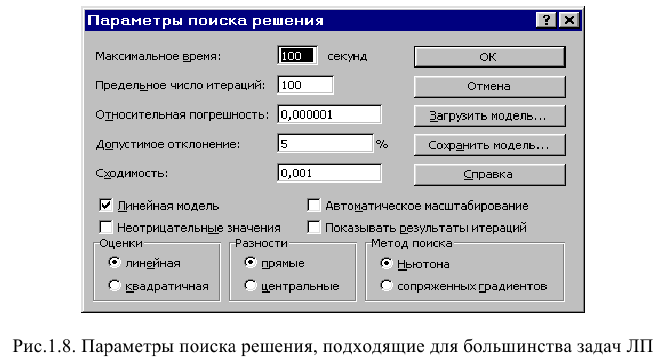
Параметр «Максимальное время» служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).

Параметр «Относительная погрешность» служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.

Параметр «Сходимость» применяется только при решении нелинейных задач.

Установка флажка «Линейная модель» обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода.

Подтвердите установленные параметры нажатием кнопки «ОК».

Запуск задачи на решение

Запуск задачи на решение производится из окна «Поиск решения» путем нажатия кнопки «Выполнить».

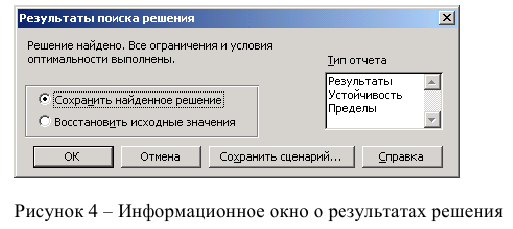
После запуска на решение задачи линейного программирования на экране появляется окно «Результаты поиска решения» с одним из сообщений, представленных на рис. 1.9, 1.10 и 1.11.

Иногда сообщения, представленные на рис. 1.10 и 1.11, свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условий задачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует (см. ниже подразд.1.3.5).

Если при заполнении полей окна «Поиск решения» были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра «Относительная погрешность» не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.

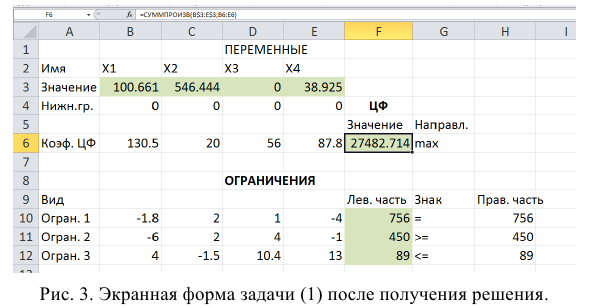
В окне «Результаты поиска решения» представлены названия трех типов отчетов: «Результаты», «Устойчивость», «Пределы». Они необходимы при анализе полученного решения на чувствительность (см. ниже подразд.3.3). Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку «ОК». После этого в экранной форме появляется оптимальное решение задачи (рис. 1.12).

Целочисленное программирование

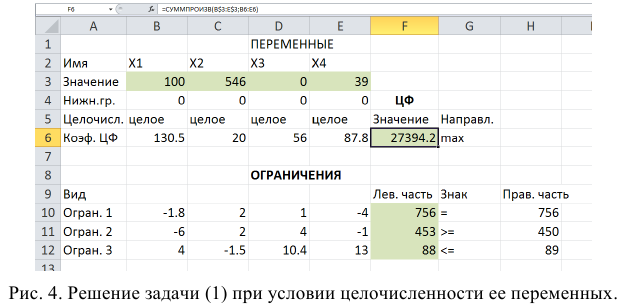
Допустим, что к условию задачи (1.1) добавилось требование целочисленности значений всех переменных. В этом случае описанный выше процесс ввода условия задачи необходимо дополнить следующими шагами.

• В экранной форме укажите, на какие переменные накладывается требование целочисленности (этот шаг делается для наглядности восприятия условия задачи) (рис. 1.13).

• В окне «Поиск решения» (меню «Сервис»—>»Поиск решения»), нажмите кнопку «Добавить» и в появившемся окне «Добавление ограничений» введите ограничения следующим образом (рис.1.14):

в поле «Ссылка на ячейку» введите адреса ячеек переменных задачи, то есть $В$3:$Е$3;
в поле ввода знака ограничения установите «целое»;
подтвердите ввод ограничения нажатием кнопки «ОК».

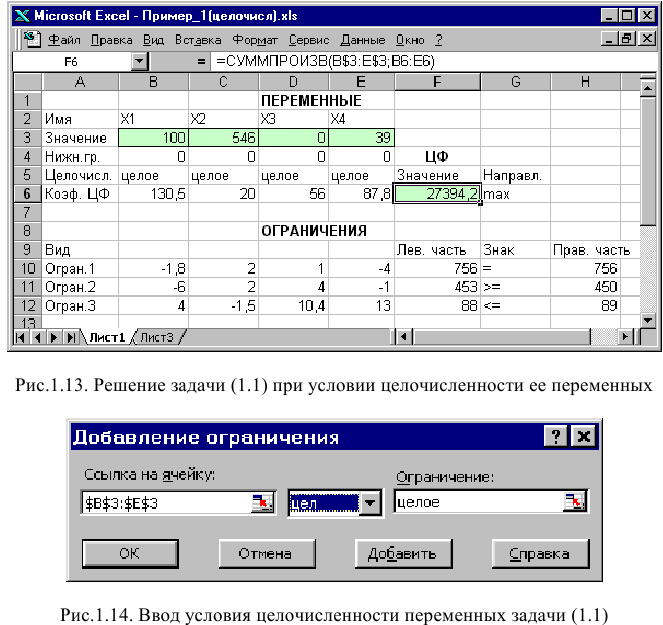
На рис. 1.13 представлено решение задачи (1.1), к ограничениям которой добавлено условие целочисленности значений ее переменных.

Двухиндексные задачи линейного программирования

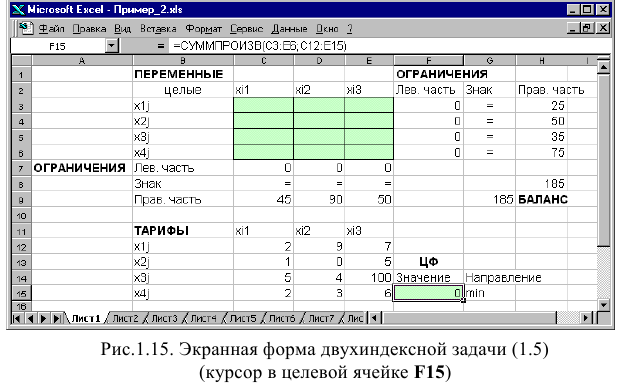
Двухиндексные задачи линейного программирования вводятся и решаются в Excel аналогично одноиндексным задачам. Специфика ввода условия двухиндексной задачи ЛП состоит лишь в удобстве матричного задания переменных задачи и коэффициентов ЦФ.

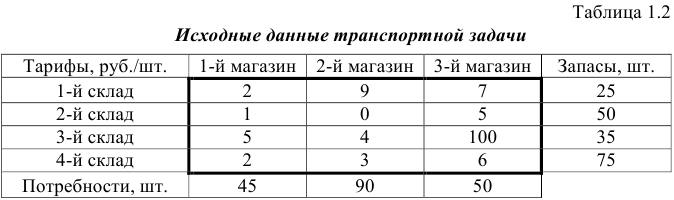
Рассмотрим решение двухиндексной задачи, суть которой заключается в оптимальной организации транспортных перевозок штучного товара со складов в магазины (табл. 1.2).

Целевая функция и ограничения данной задачи имеют вид

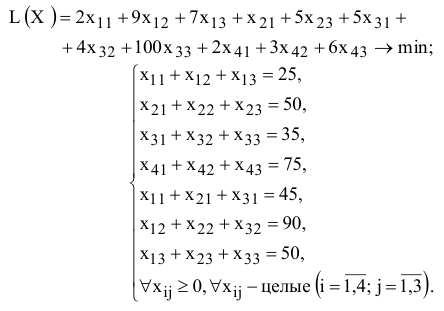
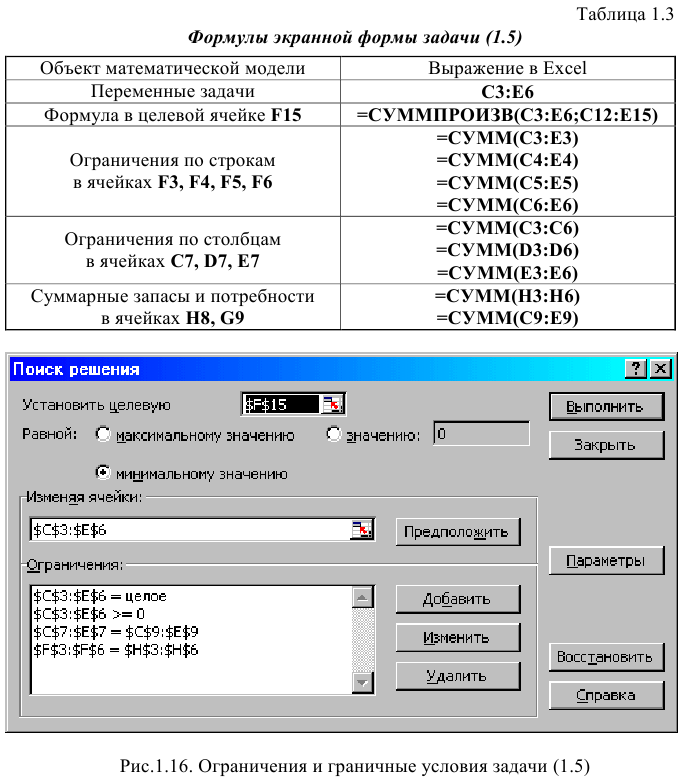
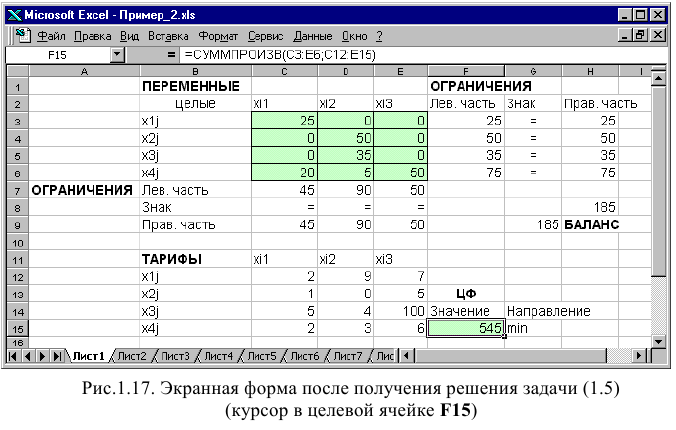
Экранные формы, задание переменных, целевой функции, ограничений и граничных условий двухиндексной задачи (1.5) и ее решение представлены на рис. 1.15, 1.16, 1.17 и в табл. 1.3.

Задачи с булевыми переменными

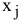
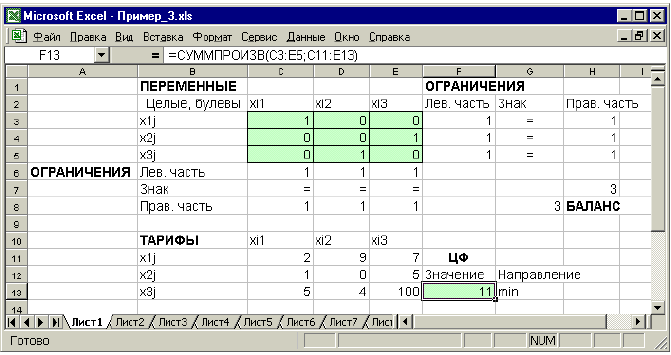
Частным случаем задач с целочисленными переменными являются задачи, в результате решения которых искомые переменные могут принимать только одно из двух значений: 0 или 1. Такие переменные в честь предложившего их английского математика Джорджа Буля называют булевыми. На рис. 1.18 представлена экранная форма с решением некоторой двухиндексной задачи с булевыми переменными.

Рис. 1.18. Решение двухиндексной задачи с булевыми переменными

Помимо задания требования целочисленности (см. подразд.1.3.2) при вводе условия задач с булевыми переменными необходимо:

• для наглядности восприятия ввести в экранную форму слово «булевы» в качестве характеристики переменных (см. рис. 1.18);

• в окне «Поиск решения» добавить граничные условия, имеющие смысл ограничения значений переменных по их единичной верхней границе (рис. 1.19).

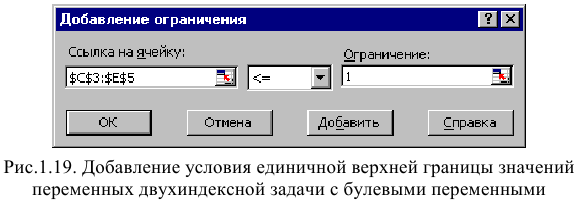
Вид окна «Поиск решения» для задачи с булевыми переменными, представленной на рис. 1.18, приведен на рис. 1.20.

Возможные ошибки при вводе условий задач линейного программирования

Если при решении задачи линейного программирования выдается сообщение о невозможности нахождения решения, то возможно, что причина заключается в ошибках ввода условия задачи в Excel.

Как решить задачу линейного программирования в excel

Цель работы

Приобретение навыков решения задач линейного программирования (ЗЛП) в табличном редакторе Microsoft Excel. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Инструкция по использованию microsoft excel для решения задач линейного программирования

Для того чтобы решить ЗЛП в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия. 1. Ввести условие задачи:

a) создать экранную форму для ввода условия задачи:

• переменных,
• целевой функции (ЦФ),
• ограничений,
• граничных условий;

b) ввести исходные данные в экранную форму:

• коэффициенты ЦФ,
• коэффициенты при переменных в ограничениях,
• правые части ограничений;

c) ввести зависимости из математической модели в экранную форму:

• формулу для расчета ЦФ,
• формулы для расчета значений левых частей ограничений; с!) задать ЦФ (в окне «Поиск решения»):
• целевую ячейку,
• направление оптимизации ЦФ;

е) ввести ограничения и граничные условия (в окне «Поиск решения»):

• ячейки со значениями переменных,
• граничные условия для допустимых значений переменных,
• соотношения между правыми и левыми частями ограничений. 2. Решить задачу:

a)установить параметры решения задачи (в окне «Поиск решения»,);

b) запустить задачу на решение (в окне «Поиск решения»,);

c) выбрать формат вывода решения (в окне «Результаты поиска решения»).

Одноиндексные ЗЛП

Рассмотрим пример нахождения решения для следующей одноиндексной ЗЛП:

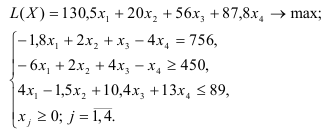
Ввод исходных данных

Создание экранной формы и ввод в нее условия задачи

Экранная форма для ввода условий задачи (1) вместе с введенными в нее исходными данными представлена на рис.1.

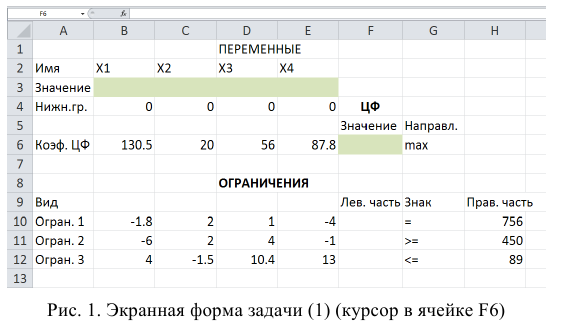
В экранной форме на рис. 1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Так, например, переменным задачи (1) соответствуют ячейки

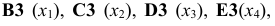
коэффициентам ЦФ соответствуют ячейки

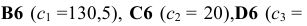
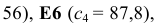
правым частям ограничений соответствуют ячейки

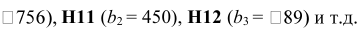
Ввод зависимостей из математической модели в экранную форму

Зависимость для ЦФ.

В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1 (значение ЦФ определяется выражением

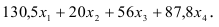
Используя обозначения соответствующих ячеек в Excel (см. рис. 1), формулу для расчета ЦФ (2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов ЦФ (В6, С6, D6,E6):

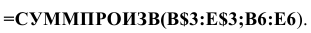
После этого в целевой ячейке появится 0 (нулевое значение) (рис. 2).

Зависимости для левых частей ограничений

Левые части ограничений задачи (1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи(ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B10, С10, D10, Е10 — 1-е ограничение; В11, C11,D11, Е11 — 2-е ограничение и В12, С12, D12, Е12 — 3-е ограничение). Формулы, соответствующие левым частям ограничений, записать самостоятельно. Проверка правильности введения формул

Для проверки правильности введенных формул производите поочередно двойное нажатие левой клавиши мыши на ячейки с формулами. При этом на экране рамкой будут выделяться ячейки, используемые в формуле. Дальнейшие действия производятся в окне «Поиск решения», которое вызывается из меню «Сервис». Решение задачи

Установка параметров решения задачи

Задача запускается на решение в окне «Поиск решения». Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку «Параметры»и заполнить некоторые поля окна «Параметры поиска решения».

Параметр «Предельное число итераций» служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее32 767. Параметр «Относительная погрешность» служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.

Параметр «Допустимое отклонение» служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее. Параметр «Сходимость» применяется только при решении нелинейных задач. Установка флажка «Линейная модель» обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода. Подтвердите установленные параметры нажатием кнопки «ОК». Запуск задачи на решение

Запуск задачи на решение производится из окна «Поиск решения» путем нажатия кнопки «Выполнить».

После запуска на решение задачи линейного программирования на экране появляется окно «Результаты поиска решения» с одним из сообщений:

• Сообщение об успешном решении задачи

• Сообщение при несовместной системе ограничений задачи

• Сообщение при неограниченности ЦФ в требуемом направлении Иногда второе и третье сообщения свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условийзадачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует.

Если при заполнении полей окна «Поиск решения» были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра»Относительная погрешность» не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.

В окне «Результаты поиска решения» представлены названия трех типов отчетов: «Результаты», «Устойчивость», «Пределы». Они необходимы при анализе полученного решения на чувствительность (будет рассмотрено позже). Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку «ОК». После этого в экранной форме появляется оптимальное решение задачи (рис.3).

Целочисленное программирование

Допустим, что к условию задачи (1) добавилось требование целочисленности значений всех переменных. В этом случае описанный выше процесс ввода условия задачи необходимо дополнить следующими шагами.

• В экранной форме укажите, на какие переменные накладывается требование целочисленности (этот шаг делается для наглядности восприятия условия задачи) (рис. 4).

• В окне «Поиск решения» (меню «Сервис»—►»Поиск решения»), нажмите кнопку «Добавить» и в появившемся окне «Добавление ограничений» введите ограничения целочисленности. Сравните результаты.

Получите у преподавателя индивидуальные задания.

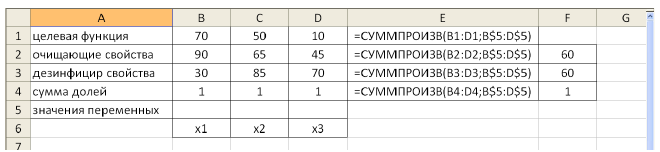
Примеры решения экономических задач Задача 1.

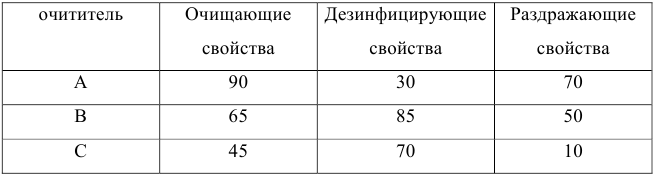
Средства очистки пола оценивают по следующим трем показателям:

• очищающие свойства;
• дезинфицирующие свойства;
• раздражающее воздействие на кожу.

Каждый из этих показателей измеряется по линейной шкале от 0 до 100. Продукт на рынке должен иметь по крайней мере 60 ед. очищающих свойств и по крайней мере 60 ед. дезинфицирующих свойств по соответствующей шкале. При этом раздражающее воздействие на кожу должно быть минимальным. Конечный продукт должен быть смесью трех основных очистителей, характеристики которых приведены в таблице.

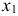
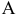
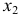
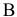
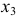
Составим математическую модель задачи. Пусть — доля очистителя в конечном продукте, — доля очистителя в конечном продукте, — доля очистителя в конечном продукте.

Целевая функция: 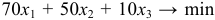(т.е. минимизируем раздражающее воздействие на кожу конечного продукта).

Ограничения:

Решение задачи с помощью MS Excel.

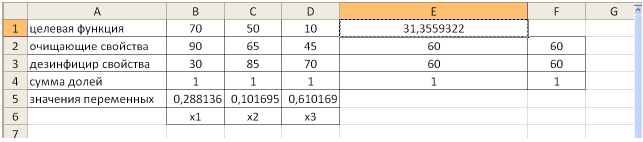
Заполним таблицу, содержащую исходные данные. Заполним диалоговое окно

«Поиск решения».

Щелкнув по кнопке ОК, мы получаем на месте исходной таблицы — таблицу с найденными оптимальными значениями. В результате в таблице получим значение целевой функции — 31,4 ед. раздражающего воздействия на кожу при

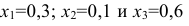
(т.е. очистители нужно брать в долях 30%, 10% и 60% соответственно).

Задача 2.

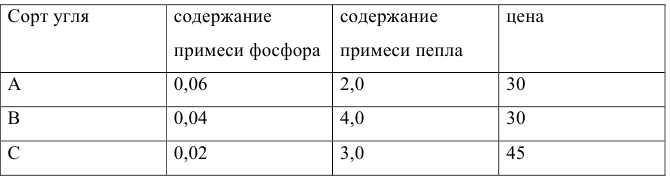
Фирме требуется уголь с содержанием фосфора не более 0,03% и с примесью пепла не более 3,25%. Доступны 3 сорта угля по следующим ценам (за тонну):

Как следует их смешать, чтобы удовлетворить ограничениям на примеси и минимизировать цену?

Решение задач математического программирования с помощью надстройки «Поиск решения» ЭТ Excel

Задачи линейного программирования, целочисленного программирования и ряд задач нелинейного программирования могут быть решены с помощью стандартного прикладного программного обеспечения. Например, в ЭТ MS Excel для этого имеется модуль «Поиск решения», вызываемый командой меню «Сервис/Поиск решения». Для активизации данного модуля необходимо выполнить команду «Сервис/Надстройки» и установить флажок напротив строки меню «Поиск решения».

Рассмотрим пример применения «Поиска решения» на основе решения задачи оптимизации портфеля ценных бумаг — одной из классических задач управления финансовыми средствами.

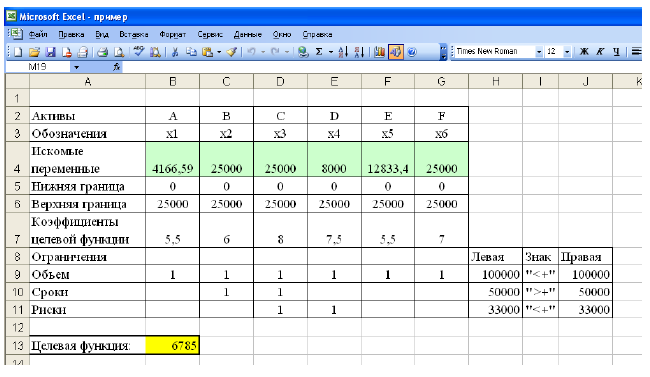
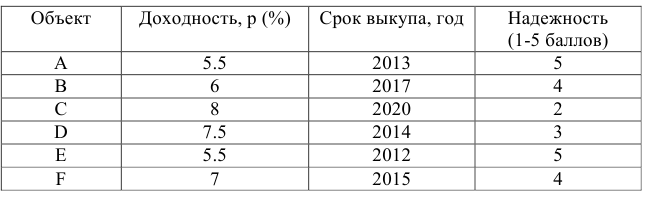
Постановка задачи. Перед инвестором стоит задача на основе информации, представленной в таблице 1, разместить имеющиеся средства так, чтобы получить максимальную прибыль за 1 период планирования (1 год), при этом должны быть выполнены следующие условия:

Суммарный объем капитала составляет 100 000 $;
доля средств, вложенная в один из объектов, не может превышать 25%;
более 40% всех средств должны быть вложены в долгосрочные активы;
доля высокорисковых активов не может превышать трети от суммарного объема.

Таблица 1 — Информация об объектах инвестирования

Построим экономико-математическую модель задачи.

Искомые переменные — объемы средств, вложенные в активы: .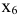

Прибыль, которую получит инвестор, задается целевой функцией:

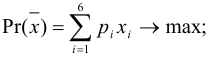
Сформируем ограничения:

Ограничения на суммарный объем активов —

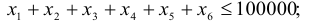
Ограничение на размер доли каждого актива

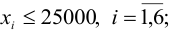
Необходимость долгосрочного инвестирования (например, более 3 лет)

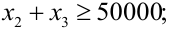
Учет необходимости снижения риска —

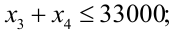
Естественное экономическое ограничение — неотрицательность искомых переменных —

Для решения задачи выполним следующие шаги.

На рабочем листе представим необходимую для решения информацию, согласно рисунку 1.

Ячейки В13, Н9-Н11 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае целесообразно использовать функцию Суммпроизв(…), аргументами которой являются диапазоны B4-G4 и диапазоны соответствующих параметров.

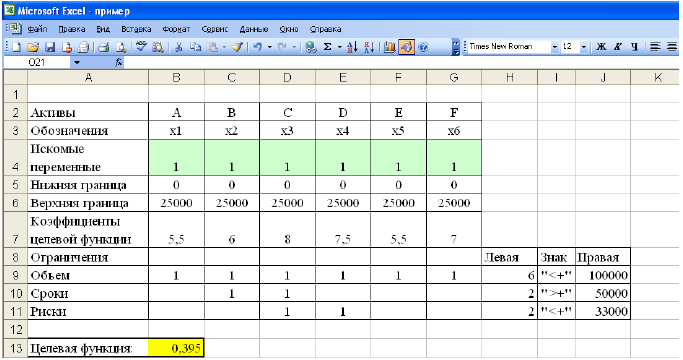
Рисунок 1 — Исходные данные для решения ЗЛП

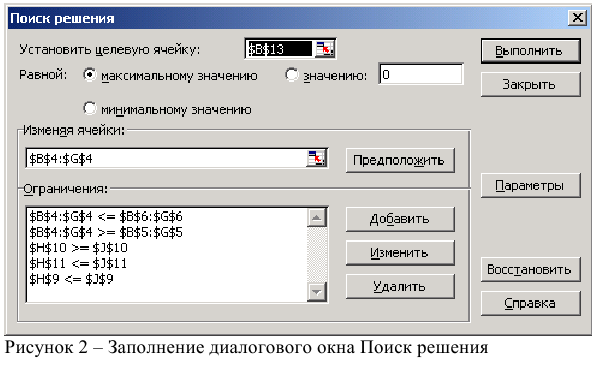
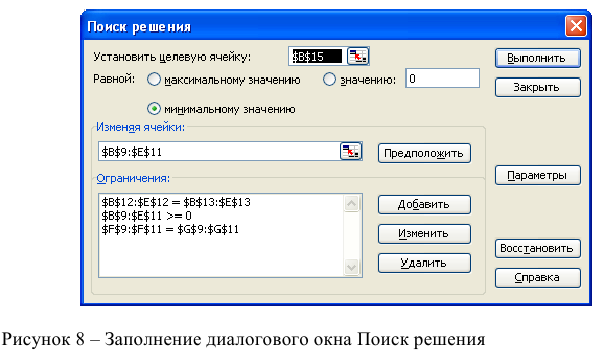
Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:

Указать адрес ячейки (В 13), содержащей целевую функцию, указать тип целевой функции,

В поле «изменяя ячейки» указать адреса всех искомых переменных (от В4 до G4).

Затем последовательно заполнить все ограничения (Пример на рисунке 2.)

Если возникли ошибки ввода, то изменить или добавить ограничение можно с помощью командных кнопок «Добавить, изменить, удалить».

Далее, если это необходимо, устанавливаются особые значения параметров (кнопка «Параметры»).

Результаты отражаются на рабочем листе. Результаты решения представлены на рисунке 5.

Рисунок 5 — Результаты решения задачи

На рисунке 6 представлена структура инвестиционного портфеля.

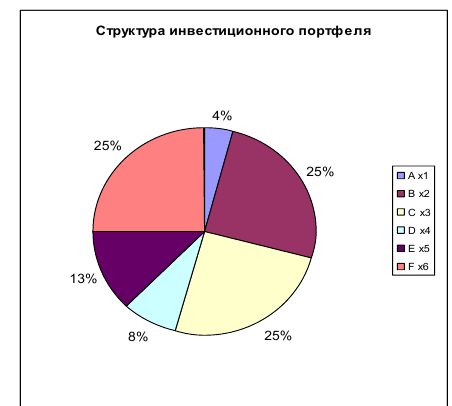
На основе решения проводится анализ, и принимаются соответствующие управленческие решения.

Технология решения транспортной задачи

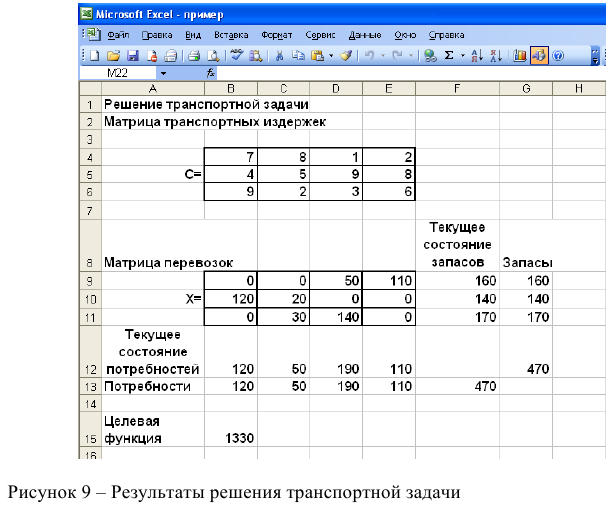
1. На рабочем листе представим необходимую для решения информацию, согласно рисунку 7.

Ячейки В15 содержит формулу Суммпроизв(…), аргументами которой являются диапазоны В4-Е6 и В9-Е11. Ячейки F9-F11 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае целесообразно использовать функцию Сумм(…), аргументами которой являются диапазоны В9-Е9, В10-Е 10 и В11 -Е11. Аналогично определяются формулы в В12-Е 12.

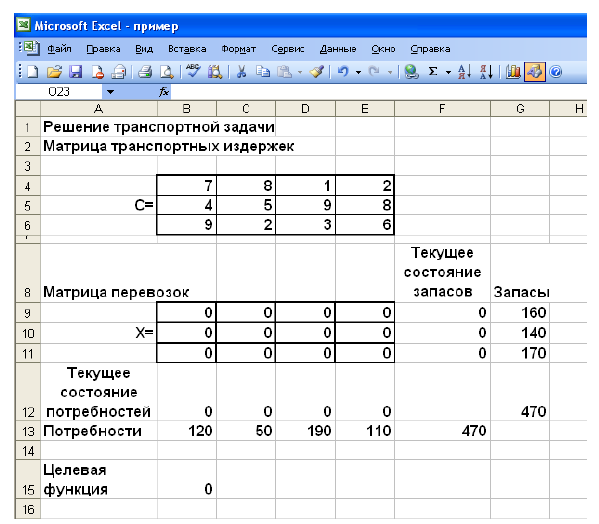
Рисунок 7 — Исходные данные для решения ЗЛП

Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:

Указать адрес ячейки (В 15), содержащей целевую функцию, указать тип целевой функции (минимум),

В поле «изменяя ячейки» указать адреса всех искомых переменных (от В9 до Е11).

Затем последовательно заполнить все ограничения (Пример на рисунке 8.)

Если возникли ошибки ввода, то изменить или добавить ограничение можно с помощью командных кнопок «Добавить, изменить, удалить». Результаты отражаются на рабочем листе. Результаты решения представлены на рисунке 9.

Технология решения задачи нелинейного программирования

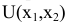
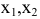
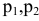
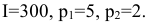
Построить математическую модель и решить задачу потребительского выбора для заданной функции полезности на товары , ценах и

доходе I. Найти максимальное значение функции полезности.

Построим математическую модель задачи потребительского выбора:

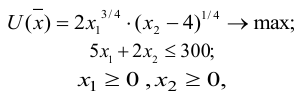
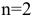
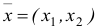
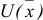
где — число потребляемых товаров или благ, — потребительский набор, — функция полезности потребителя.

Набор, который является решением задачи потребительского выбора, называется оптимальным потребительским набором, или точкой локального рыночного равновесия потребителя. Поставленная задача — задача потребительского выбора — является задачей нелинейного программирования.

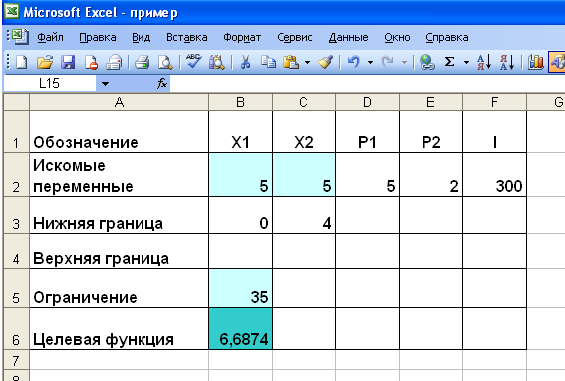
На рабочем листе представим необходимую для решения информацию, согласно рисунку 10.

Ячейки В5, В6 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае ячейка В5 содержит формулу «=D2B2+E2C2», а ячейка В6 содержит формулу «=2В2Л(3/4)(С2-4)А(1/4)».

Рисунок 10 — Исходные данные для решения ЗНП

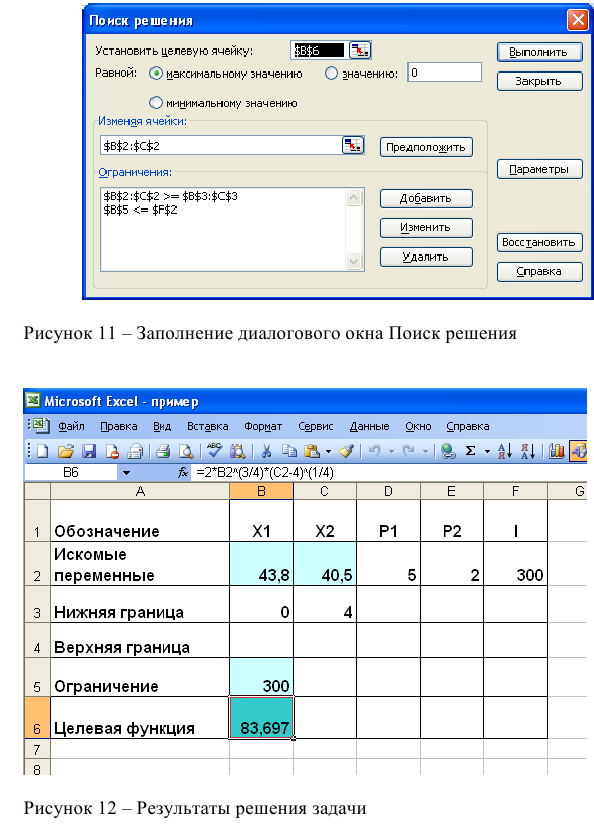
Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:

Аналитическое решение задачи нелинейного программирования.

В рассматриваемом случае ограничение можно записать в виде строгого равенства, так как оптимальное решение достигается при полном использовании имеющихся средств.

Для решения классической задачи нелинейного программирования применим метод множителей Лагранжа, для этого составим функцию Лагранжа:

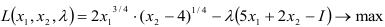
Найдем точки экстремума функции Лагранжа.

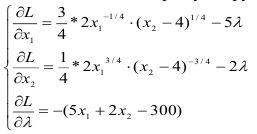
Приравняем каждое уравнение к 0:

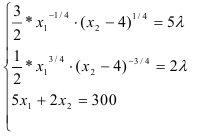
С помощью преобразований — разделим первое уравнение системы на второе, перейдем к системе:

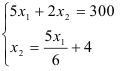
Подставим второе уравнение в первое и построим аналитические функции спроса:

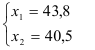
Максимальное значение функции полезности-

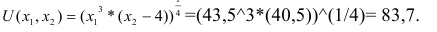
Решением задачи потребительского выбора будет набор

Возможно эти страницы вам будут полезны:

Решение задач по математическому программированиюПримеры решения задач по математическому программированиюЗаказать работу по математическому программированиюПомощь по математическому программированиюЗадачи математического программированияЗадача линейного программированияРешение задач по линейному программированиюМетоды решения задач линейного программированияГрафическое решение задач линейного программированияГрафический метод решения задач линейного программированияЗаказать работу по линейному программированиюПомощь по линейному программированиюКонтрольная работа по линейному программированиюКурсовая работа по линейному программированию

Источник

Ранее я писал, что для принятия решений с учетом ограничивающих факторов может использоваться линейное программирование. Напомню, что этот метод решает проблему распределения ограниченных ресурсов между конкурирующими видами деятельности с тем, чтобы максимизировать или минимизировать некоторые численные величины, такие как маржинальная прибыль или расходы.

При решении задач линейного программирования, во-первых, необходимо составить модель, то есть сформулировать условия на математическом языке. После этого решение может быть найдено графически (см., например, здесь), с использованием надстройки Excel «Поиск решения» (рассмотрено в настоящей заметке) или с помощью специализированных компьютерных программ (см., например, здесь).

Рассмотрим линейное программирование в Excel на примере задачи, ранее решенной графическим методом.

Задача. Николай Кузнецов управляет небольшим механическим заводом. В будущем месяце он планирует изготавливать два продукта (А и В), по которым удельная маржинальная прибыль оценивается в 2500 и 3500 руб., соответственно. Изготовление обоих продуктов требует затрат на машинную обработку, сырье и труд. На изготовление каждой единицы продукта А отводится 3 часа машинной обработки, 16 единиц сырья и 6 единиц труда. Соответствующие требования к единице продукта В составляют 10, 4 и 6. Николай прогнозирует, что в следующем месяце он может предоставить 330 часов машинной обработки, 400 единиц сырья и 240 единиц труда. Технология производственного процесса такова, что не менее 12 единиц продукта В необходимо изготавливать в каждый конкретный месяц. Необходимо определить количество единиц продуктов А и В, которые Николай доложен производить в следующем месяце для максимизации маржинальной прибыли.

Скачать заметку в формате Word, пример в формате Excel

1. Воспользуемся математической моделью построенной в упомянутой заметке. Вот эта модель:

Максимизировать: Z = 2500 * х₁+ 3500 *х₂

При условии, что: 3 * х₁ + 10 * х₂ ≤ 330

16 * х₁ + 4 * х₂ ≤ 400

6 * х₁ + 6 * х₂ ≤ 240

х₂ ≥ 12

х₁ ≥ 0

2. Создадим экранную форму и введем в нее исходные данные (рис. 1).

Рис. 1. Экранная форма для ввода данных задачи линейного программирования

Обратите внимание на формулу в ячейке С7. Это формула целевой функции. Аналогично, в ячейки С16:С18 введены формулы для расчета левой части ограничений.

3. Проверьте, если у вас установлена надстройка «Поиск решения» (рис. 2), пропустите этот пункт.

Рис. 2. Надстройка Поиск решения установлена; вкладка «Данные», группа «Анализ»

Если надстройки «Поиск решения» вы на ленте Excel не обнаружили, щелкните на кнопку Microsoft Office, а затем Параметры Excel (рис. 3).

Рис. 3. Параметры Excel

Выберите строку Надстройки, а затем в самом низу окна «Управление надстройками Microsoft Excel» выберите «Перейти» (рис. 4).

Рис. 4. Надстройки Excel

В окне «Надстройки» установите флажок «Поиск решения» и нажмите Ok (рис. 5). (Если «Поиск решения» отсутствует в списке поля «Надстройки», чтобы найти надстройку, нажмите кнопку Обзор. В случае появления сообщения о том, что надстройка для поиска решения не установлена на компьютере, нажмите кнопку Да, чтобы установить ее.)

Рис. 5. Активация надстройки «Поиск решения»

После загрузки надстройки для поиска решения в группе Анализ на вкладке Данные становится доступна команда Поиск решения (рис. 2).

4. Следующим этапом заполняем окно Excel «Поиск решения» (рис. 6)

Рис. 6. Заполнение окна «Поиск решения»

В поле «Установить целевую ячейку» выбираем ячейку со значением целевой функции – $C$7. Выбираем, максимизировать или минимизировать целевую функцию. В поле «Изменяя ячейки» выбираем ячейки со значениями искомых переменных $C$4:$D$4 (пока в них нули или пусто). В области «Ограничения» с помощью кнопки «Добавить» размещаем все ограничения нашей модели. Жмем «Выполнить». В появившемся окне «Результат поиска решения» выбираем все три типа отчета (рис. 7) и жмем Ok. Эти отчеты нужны для анализа полученного решения. Подробнее о данных, представленных в отчетах, можно почитать здесь.

Рис. 7. Выбор типов отчета

На основном листе появились значения максимизированной целевой функции – 130 000 руб. и изменяемых параметров х₁ = 10 и х₂ = 30. Таким образом, для максимизации маржинального дохода Николаю в следующем месяце следует произвести 10 единиц продукта А и 30 единиц продукта В.

Если вместо окна «Результат поиска решения» появилось что-то иное, Excel`ю найти решение не удалось. Проверьте правильность заполнения окна «Поиск решения». И еще одна маленькая хитрость. Попробуйте уменьшить точность поиска решения. Для этого в окне «Поиск решения» щелкните на Параметры (рис. 8.) и увеличьте погрешность вычисления, например, до 0,001. Иногда из-за высокой точности Excel не успевает за 100 итераций найти решение. Подробнее о параметрах поиска решения можно почитать здесь.

Рис. 8. Увеличение погрешности вычислений

Источник

При
рассмотрении симплексного метода было
показано, как решение задачи линейного
программирования выполнить с помощью
надстройки Excel
Поиск решения.

На
рис. 1.4 приведено найденное таким образом
решение задачи о выпуске продукции.

Кроме
этого решения, как было указано, Excel
позволяет представить результаты
поиска решений в форме отчета трех
типов:

Результаты.
В отчет включаются исходные и конечные
значения целевой и изменяемой ячеек,
дополнительные сведения об ограничениях.
Устойчивость.
Отчет, содержащий сведения о
чувствительности решения к малым
изменениям в изменяемых ячейках или в
формулах ограничений.
Пределы.
Помимо исходных и конечных значений
изменяемых и целевой ячеек, в отчет
включаются верхние и нижние границы
значений, которые могут принимать
влияющие ячейки при соблюдении
ограничений.

Содержание
указанных отчетов – в таблицах 1.1 –
1.3.

отчет
по результатам (табл.
1.1) состоит из трех таблиц:

таблица
1 приводит сведения о целевой функции.
В столбце Исходное
значение
приведены значения целевой функции до
начала вычислений;
таблица
2 приводит значения искомых переменных,
полученные в результате решения задачи;
таблица
3 показывает результаты оптимального
решения для ограничений и граничных
условий.

Таблица
1.1 – Содержание отчета по результатам.

Microsoft Excel 10.0 Отчет по результатам
Рабочий лист: [Книга1]Лист1
Отчет создан: 15.04.2006 1:22:43


Целевая ячейка (Максимум)
	Ячейка	Имя	Исходное значение	Результат
	$F$4	коэф.в ЦФ ЦФ	0	1320


Изменяемые ячейки
	Ячейка	Имя	Исходное значение	Результат
	$B$3	значение Х1	0	10
	$C$3	значение Х2	0	0
	$D$3	значение Х3	0	6
	$E$3	значение Х4	0	0


Ограничения
	Ячейка	Имя	Значение	Формула	Статус	Разница
	$F$7	труд левая часть	16	$F$7<=$H$7	связанное	0
	$F$8	оборудование левая часть	100	$F$8<=$H$8	связанное	0
	$F$9	полуфабрикаты левая часть	84	$F$9<=$H$9	не связан.	26

Для
ограничений
в графе формула
приведены зависимости, которые были
введены в диалоговой окно Поиск
решения;
в графе Значение
приведены величины использованного
ресурса; в графе Разница
показано количество неиспользованного
ресурса. Если ресурс используется
полностью, то в графе Состояние
указывается связанное;
при неполном
использовании ресурса в этой графе
указывается
не связан.

Для
граничных условий
приводятся величины с той лишь разницей,
что вместо величины неиспользованного
ресурса показана разность между значением
переменной в найденном оптимальном
решении и заданным для нее граничным
условием.

Итак,
в табл. 1.1 (в отчете по результатам)
содержатся оптимальные значения
переменных х₁,
х₂,
х₃,
х₄,
которые соответственно равны 10; 0; 6; 0;
значение целевой функции – 1320, а также
величина левых частей ограничений
соответственно полученному оптимальному
плану. Так, в рассматриваемой задаче
первое и второе ограничения выполнились
как равенства, а в третьем левая часть
(потребленное количество полуфабрикатов)
меньше правой части на 26 (столбец
Разница).

Решение
двойственной задачи можно найти, выбрав
команду Поиск
решений =>
Отчет
по устойчивости.
Этот отчет
для условий рассматриваемой задачи
приводится в табл.
1.2.

Отчет
по устойчивости состоит
из двух таблиц.

В
таблице 1 приводятся следующие значения
для переменных:

результат
решения задачи;
нормированная
стоимость, т.е. дополнительные двойственные
переменные, которые показывают, как
изменяется целевая функция при
принудительном включении единицы этой
продукции в оптимальное решение;
коэффициенты
целевой функции;
предельные
значения приращения коэффициентов c_j
целевой функции, при которых сохраняется
оптимальное решение.

В
таблице 2 приводятся аналогичные значения
для ограничений:

величина
использованных ресурсов;
теневая
цена, т.е. двойственные оценки y_i,
которые показывают, как изменится
целевая функция при изменении ресурсов
на единицу;
значение
приращения ресурсов b_i,
при которых сохраняется структура
базиса оптимального плана, а следовательно,
и величина оптимальных оценок.

Таблица
1.2 – Содержание отчета по устойчивости.

Microsoft Excel 10.0 Отчет по устойчивости
Рабочий лист: [Книга1]Лист1
Отчет создан: 15.04.2006 1:22:43


Изменяемые ячейки
			Результ.	Нормир.	Целевой	Допустимое	Допустимое
	Ячейка	Имя	значение	стоимость	Коэффициент	Увеличение	Уменьшение
	$B$3	значение Х1	10	0	60	40	12
	$C$3	значение Х2	0	-10	70	10	1E+30
	$D$3	значение Х3	6	0	120	30	13,33333333
	$E$3	значение Х4	0	-20	130	20	1E+30

Ограничения
			Результ.	Теневая	Ограничение	Допустимое	Допустимое
	Ячейка	Имя	значение	Цена	Правая часть	Увеличение	Уменьшение
	$F$7	труд левая часть	16	20	16	3,545454545	6
	$F$8	оборуд. левая часть	100	10	100	60	36
	$F$9	полуф. левая часть	84	0	110	1E+30	26

Так,
в первой таблице отчета
по устойчивости для рассматриваемой
задачи (табл.
1.2) нормированная стоимость для продукции
второго вида равна -10 ден.ед./шт. Это
означает, что если

мы, несмотря на
оптимальное решение (10; 0; 6; 0),
попробуем

включить
в план выпуска одно изделие второго
вида, то новый

план
выпуска принесет нам доход 1310 ден.ед.,
что на 10 ден.ед.

меньше,
чем прежнее оптимальное решение.

Предельные
значения приращения целевых коэффициентов
с_j,
при
которых сохраняется первоначальное
оптимальное решение,
показывают, что, например, допустимое
увеличение прибыльности продукции
первого вида равно
40 ден. ед./шт., а допустимое уменьшение
составляет 12 ден. ед. По изделию второго
вида допустимое
увеличение прибыльности составляет 10
ден. ед, а допустимое уменьшение —
практически не ограничено.
Это означает, что если прибыль на одно
изделие второго вида возрастет более
чем на 10 ден.ед./шт.,
то
оптимальное
решение изменится: станет целесообразным
выпускать
изделия второго вида.
А
если прибыльность второго изделия
будет снижаться вплоть до нуля, то
оптимальное
решение (10; 0; 6; 0) останется прежним.

вторая
часть табл. 1.2 содержит информацию,
относящуюся
к ограничениям. Так, в графе Допустимое
уменьшение
показано, на сколько можно уменьшить
(устранить
излишек) или увеличить (повысить
минимально необходимое
требование) ресурс, сохранив при этом
допустимое
решение и, что очень важно, оставив
неизменной величину оптимальной оценки
(«теневой цены»).

Рассмотрим
дефицитные
ресурсы.
Анализируя
отчет по результатам, мы установили,
что существуют причины
(ограничения), не позволяющие предприятию
выпускать больше
П₂,
чем в оптимальном решении, и получать
более высокий
доход. В рассматриваемой задаче такими
ограничениями
являются дефицитные ресурсы «труд» и
«оборудование».

Поскольку
знак ограничений этих запасов имеет
вид « 
», то

возникает
вопрос, на сколько максимально должен
возрасти

запас
этих ресурсов, чтобы обеспечить увеличение
выпуска продукции. Ответ на этот вопрос
показан в графе Допустимое
увеличение.
Ресурс «труд» имеет смысл увеличивать
не более, чем на 3,5 чел.-часа, а ресурс
«оборудование» – не более, чем на 60
станко-час.

Ценность
дополнительной единицы i-го
ресурса («теневая цена») рассчитывается
только для дефицитных ресурсов и
характеризует прирост результата в
расчете на одну дополнительную единицу
соответствующего ресурса.

Ценность
различных видов ресурсов нельзя
отождествлять с действительными ценами,
по которым осуществляется его закупка.
В данном случае речь идет о некоторой
мере, имеющей экономическую природу,
которая характеризует ценность ресурса
только относительно полученного
оптимального решения.

Таблица
1.3 – Содержание отчета по пределам

Microsoft Excel 10.0 Отчет по пределам
Рабочий лист: [Книга1]Отчет по пределам 1
Отчет создан: 15.04.2006 1:22:43


		Целевое
	Ячейка	Имя	Значение
	$F$4	коэф.в ЦФ	1320


		Изменяемое		Нижний	Целевой	Верхний	Целевой
	Ячейка	Имя	Значение	предел	результат	предел	результат
	$B$3	значение Х1	10	0	720	10	1320
	$C$3	значение Х2	0	0	1320	0	1320
	$D$3	значение Х3	6	0	600	6	1320
	$E$3	значение Х4	0	0	1320	0	1320

В
отчете по пределам
(табл. 1.3) показано, в каких пределах
может изменяться выпуск продукции,
вошедшей в оптимальный план, при
сохранении структуры оптимального
решения:

приводятся
значения x_j
в оптимальном решении;
приводятся
нижние пределы изменения значений x_j.

Кроме
этого, в отчете указаны значения целевой
функции при выпуске данного продукта
на нижнем пределе. Так, значение 720
соответствует следующей ситуации:

F
= c₁x₁+ c₃x₃
= 60 
0 + 120 
6 = 720.

Далее
приводятся верхние пределы изменения
x_j
и значения целевой функции при выпуске
продукции, вошедшей в оптимальный план
на верхнем пределе. Поэтому везде F
= 60 
10 + 120 
6 = 1320.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Изучив алгоритмы «ручного» решения задач линейного программирования, полезно познакомиться и со способом упростить этот процесс. Ясно, что чем сложнее задача, чем больше в ней переменных и условий, тем утомительнее и дольше ее решать. В таких случаях удобно использовать специальные математические пакеты, или доступную многим программу MS Excel (версии 2003, 2007, 2010, 2013 и др.).

Решить задачи линейного программирования в Excel достаточно просто:

составить математическую модель задачи,
внести исходные данные задачи и ограничения,
выделить место под ячейки решения и целевую функцию, ввести ее формулу,
запустить надстройку Поиск решения,
установить нужные параметры решения и запустить выполнение.

Программа подберёт оптимальное решение и покажет его в нужных ячейках, вычислит значение целевой функции. При необходимости можно построить отчеты для анализа решения задачи.

Подробнее все эти этапы с пояснениями и скриншотами разобраны ниже в примерах на разных задачах линейного программирования — изучайте, ищите похожие, решайте.

Помогаем студентам: Работы по линейному программированию на заказ

Понравилось? Добавьте в закладки

Линейное программирование: примеры в Excel

Задача 1. Построить математическую модель задачи и решить её средствами Excel. Записать сопряжённую задачу. Провести анализ и сделать выводы по полученным результатам.
Для производства столов и шкафов мебельная фабрика использует различные ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в таблице.
Определить, сколько столов и шкафов фабрике следует выпускать, чтобы прибыль от реализации была максимальной.

Задача 2. Цех производит 8 различных видов деталей для двигателей A, B, C1, C2, C3, D, E6, F имея в своем распоряжении перечисленный ниже парк из 7 видов универсальных станков: 2 шт. -ADF, 3 шт. -SHG, 3 шт. -BSD, 1 шт. -AVP, 1 шт. -BFG, 3 шт. -ABM, 2 шт. -RL.
Время, требуемое для обработки единицы каждого продукта на каждом станке, вклад в прибыль от производства единицы каждого продукта и рыночный спрос на каждый продукт за месяц даны в таблице.
Цех работает 12 часов в день. Каждый месяц содержит 26 рабочих дней. Для упрощения задачи считаем, что возможен произвольный порядок обработки деталей на различных станках.
Составьте оптимальный план производства.
Определите, производство каких продуктов лимитировано рынком, и каких – техническими возможностями цеха. Какие машинные ресурсы должны быть увеличены в первую очередь, чтобы добиться максимального увеличения прибыли (при заданных потребностях рынка)?
Есть ли продукт, который невыгодно производить? Почему? Что нужно изменить, чтобы все продукты стало выгодно производить?

Может пригодиться: транспортные задачи в Excel

Задача 3. Необходимо составить самый дешевый рацион питания цыплят, содержащий необходимое количество определенных питательных веществ тиамина Т и ниацина Н. Пищевая ценность рациона (в калориях) должна быть не менее заданной. Смесь для цыплят изготавливается из двух продуктов — К и С. Известно содержание тиамина и ниацина в этих продуктах, а также питательная ценность К и С (в калориях). Сколько К и С надо взять для одной порции куриного корма, чтобы цыплята получили необходимую им дозу веществ Н и Т и калорий (или больше), а стоимость порции была минимальна? Исходные данные для расчетов приведены в таблице.

Задача 4. Фирма «Компьютер-сервис» поставляет компьютеры под ключ четырех базовых комплектаций: «домашний», «игровой», «офисный» и «экстрим». Известны средние затраты времени на сборку, проверку и подключение компьютеров. Каждый компьютер приносит определенный уровень прибыли, но спрос ограничен. Кроме того, в плановом периоде ограничен ресурс человеко-часов, отведенных на выполнение каждой производственной операции. Определить, сколько компьютеров каждого типа необходимо произвести в плановом периоде, имея целью максимизировать прибыль.

Задача 5. На лесопилку поступают доски длиной 10 м. По контракту лесопилка должна поставить клиенту не менее 100 досок длиной 5 м, не менее 200 досок длиной 4 м и не менее 300 досок длиной 3 м. Как работникам лесопилки выполнить условия контракта, разрезав наименьшее количество досок?

Помогаем с контрольными по линейному программированию

Задача 6. Компания «Евростройтур» организует экскурсионные автобусные туры по странам Европы. Компания получила 4 новых автобуса и предполагает направить их на маршруты во Францию, Италию, Чехию и Испанию.
Каждый автобус обслуживают 2 водителя. Компанией приглашены 8 водителей, в различной степени знакомых с дорогами европейских стран (в % от экскурсионного маршрута).

Необходимо распределить водителей так, чтобы общий показатель освоения маршрутов был максимальным.

Задача 7. Решить задачу методом ветвей и границ, решая отдельные задачи линейного нецелочисленного программирования с помощью функции «Поиск решения» в Microsoft Excel (в случае, если первая же задача ЛП выдает целочисленное решение, не позволяя ветвить задачу, немного изменить начальные условия).

Состав еды рядовых регламентируется верховной ставкой главнокомандующего, которая устанавливает нижние нормы питания в сутки по основным компонентам: 1500 килокалорий, 100 г белков, 280 г углеводов, 90 г жиров, 1 кг воды. На складах есть 4 вида продуктов, которые выдают защитникам Родины сухим пайком: лимонад, тушенка в маленьких банках, унифицированные наборы горбушек и пирожки с ежевикой. Стоимость этих четырех продуктов соответственно 12 руб., 34 руб., 3 руб. и 20 руб. Какова минимальная сумма, которую должен затратить прапорщик на питание одного солдата?

Задача 8. Предприятие выпускает два вида продукции: Изделие 1 и Изделие 2. На изготовление единицы Изделия 1 требуется затратить a11 кг сырья первого типа, a21 кг сырья второго типа, a31 кг сырья третьего типа.
На изготовление единицы Изделия 2 требуется затратить a12 кг сырья первого типа, a22 кг сырья второго типа, a32 кг сырья третьего типа.
Производство обеспечено сырьем каждого типа в количестве b1 кг, b2 кг, b3 кг соответственно.
Рыночная цена единицы Изделия 1 составляет c1 тыс. руб., а единицы Изделия 2 — c2 тыс.руб.
Требуется:
1) построить экономико – математическую модель задачи;
2) составить план производства изделий, обеспечивающий максимальную выручку от их реализации при помощи графического метода решения задачи линейного программирования.
3) составить план производства изделий, обеспечивающий максимальную выручку от их реализации при помощи табличного симплекс – метода решения задачи линейного программирования.
4) составить план производства изделий, обеспечивающий максимальную выручку от их реализации, используя надстройку «Поиск решения» в среде MS EXCEL.

Полезные ссылки

Графическое решение ЗЛП
Симплекс-метод решения ЗЛП

Решенные контрольные по ЛП
Онлайн учебник по оптимальным решениям

Источник

Пример решения задачи линейного
программирования с помощью MS
Excel

Хозяйство специализируется в полеводстве на производстве
зерна, сахарной свеклы и подсолнечника. В с.-х. предприятии имеются 3200 га
пашни, трудовые ресурсы в объеме 7
000 чел.-дней и минеральные удобрения в
объеме 15000 ц.д.в. Требуется найти такое сочетание посевных площадей, которое
обеспечило бы получение максимума прибыли.

Следует также учесть, что

—
площадь посева технических культур (сахарной
свеклы и подсолнечника) не должна превышать 25% общей площади пашни;

—
хозяйством заключен договор на продажу зерна в объеме
65000 ц.

Для разработки экономико-математической модели
необходима подготовка входной информации (табл. 1).

Таблица 1

Показатели	Сельскохозяйственные культуры
зерновые	сахарная свекла	подсолнечник
Урожайность, ц/га
Цена реализации 1 ц продукции, руб./ц.
Стоимость товарной продукции с 1 га, тыс. руб.	5,59	20,62	6,73
Затраты на 1 га: МДС, тыс. руб.		12,7
труда, чел.-дней.
минеральных удобрений, ц.д.в.
Прибыль с 1 га, руб.	2,89	7,93	3,63

За неизвестные примем площади посева
сельскохозяйственных культур по видам:

X
1 —
зерновых культур

X
2 —
сахарной свеклы

X
3 —
подсолнечника

Для построения экономико-математической модели задачи
необходимо учесть все условия. В данном случае, по этим условиям можно составить
пять ограничений:

—
сумма площадей посева
сельскохозяйственных культур не должна превышать площади, имеющейся в хозяйстве
(3200 га). Коэффициентами при неизвестных в этом ограничении характеризуют
расход пашни на 1 га каждой сельскохозяйственной культуры. В данном случае
технико-экономические коэффициенты по неизвестным будут равняться единице. В
правой части записывается общая площадь пашни.

1) Х1+Х2+Х3<=3200

—
сумма площадей посева технических
культур не должна превышать площади, которая может быть отведена для этой цели
(3200*0,25=800 га). Коэффициентами при неизвестных в этом ограничении
характеризуют расход пашни, отведенной под посевы технических культур, на 1 га
каждой технической сельскохозяйственной культуры. В данном случае
технико-экономические коэффициенты по неизвестным Х2 и Х3 будут равняться
единице, а по нетехническим сельскохозяйственным культурам (Х3) — нулю. В правой
части записывается максимальная площадь пашни, которая может быть отведена под
посевы технических культур.

2) Х2+Х3<=800

—
третье и четвертое ограничения
гарантируют, что использование трудовых ресурсов и минеральных удобрений не
превысит их наличие в хозяйстве. Другими словами, сумма произведений норм затрат
ресурсов на 1 га на площади посева соответствующих сельскохозяйственных культур
не должна превышать объемов ресурсов, имеющихся в с.-х. предприятии.
Коэффициентами при неизвестных в этих ограничениях будут являться нормы расхода
ресурсов (в третьем ограничении – трудовых ресурсов, в четвертом – минеральных
удобрений) на 1 га площади посева сельскохозяйственных культур. В данном случае
технико-экономические коэффициенты взяты из таблицы 1. В правой части
записывается наличие этих ресурсов в хозяйстве.

3) 1,5Х1+4,5Х2+1,5Х3<=7000

4) 2Х1+15Х2+2,3Х3<=15000

—
пятое ограничение гарантирует
производство запланированного объема зерна. В качестве коэффициентов при
переменных выступает выход зерна с 1 га площади посева с.-х. культур. При
неизвестной Х1 это урожайность зерновых (таблица 1). При переменных Х2 и Х3 этот
коэффициент равен нулю. В правой части записывается план производства
зерна.

5) 26Х1>=65000

В результате получена система пяти линейных неравенств с
тремя неизвестными. Требуется найти такие неотрицательные значения этих
неизвестных Х1>=0; Х2>=0; Х3>=0, которые бы удовлетворяли данной
системе неравенств и обеспечивали получение максимума прибыли от отрасли
растениеводства в целом:

Z max =
2,89Х1+7,93Х2+3,53Х3

В качестве коэффициентов при неизвестных в целевой
функции выступает прибыль, получаемая с 1 га площади посева сельскохозяйственных
культур. Эти коэффициенты рассчитаны на основании данных таблицы 1.

Поскольку данная задача решается с помощью MS
Excel
, то и подготовку всей входной информации для построения
экономико-математической модели целесообразно осуществлять также с
использованием этого табличного процессора (рис 1). Это облегчает не только
расчеты технико-экономических коэффициентов и других данных, но и дает в
дальнейшем возможность автоматического обновления информации в
экономико-математической модели.

Рисунок 1

Вся разработанная информация сводится в развернутую
экономико-математическую модель и заносится в рабочий лист MS
Excel
.
(Рис. 2.)

Рисунок 2

Данные в модель рекомендуется заносить в виде ссылок на
ячейки с соответствующей информацией в расчетных рабочих листах или рабочих
листах с исходными сведениями. На рисунке 3 показано, как в ячейке F9
представлена информация по норме затрат удобрений на 1 га посева
подсолнечника.

Рисунок 3

В столбцы А
(«№»), В
(«Ограничения»),
С
(«Единицы измерения») и
H

(«Тип
ограничений») вводятся соответствующие данные непосредственно в модель (рис.1).
Они не используются в расчетах и служат для информативности и облегчения
понимания содержания модели. В столбец I
(«Объем ограничений») вводятся
ссылки на ячейки, содержащие соответствующую названию столбца информацию
(значения правых частей построенных ранее неравенств).

Для искомых величин переменных Х1
, Х2
,
Х3
нами были оставлены пустые ячейки — соответственно D5
,
E
5

,
F
5

. Изначально
пустые ячейки программа
MS
Excel
воспринимает как
ячейки, значение которых равно нулю. Столбец G
, названный нами «Сумма
произведений
», предназначен для определения суммы произведений значений
искомых неизвестных (ячейки D5
,
E
5

,
F
5

) и технико-экономических коэффициентов по
соответствующим ограничениям (строки 6-10) и целевой функции (строка 11). Таким
образом, в столбце G
определяется:

—
— количество используемых ресурсов (ячейка G6
–
общей площади пашни; G7
– пашни, которая может быть использована под
посевы технических культур; G8
– трудовых ресурсов; G9
–
минеральных удобрений);

—
— количество произведенного зерна (ячейка G10
);

—
— величина прибыли (ячейка G11
).

На рисунке 2 показано, как в ячейке G11
реализуется запись суммы произведений значений переменных (площадей посева
с.-х. культур — ячейки D5
,
E
5

,
F
5

) на соответствующие прибыли с 1 га их посева(ячейки D11
,
E
11

,
F
11

)с помощью функции MS
Excel

«СУММПРОИЗВ
». Так как при написании данной формулы использованы
абсолютные адресации на ячейки от D5
до
F
5

,эта формула может быть скопирована в другие
ячейки от
G
6

до
G10
.

Таким образом, построен опорный план (рис. 2) и получено
первое допустимое решение. Значения неизвестных Х1
, Х2
, Х3

равны нулю (ячейки D5
,
E
5

,
F
5 —

пустые ячейки), ячейки столбца G

«Сумма произведений» по всем ограничениям (строкам 6-10) и целевой строке
(строка 11) также имеют нулевые значения.

Экономическая интерпретация первого опорного плана
звучит следующим образом: в хозяйстве имеются ресурсы, рассчитаны все
технико-экономические коэффициенты, но процесс производства еще не начат;
ресурсы не использовались, и, соответственно, прибыли нет.

Для оптимизации имеющегося плана воспользуемся
инструментом Поиск решения,
который находится в меню Сервис
. Если
нет такой команды в меню Сервис,
необходимо в пункте Надстройка

поставить галочку напротив Поиск решения
. После этого данная процедура
станет доступной в меню Сервис
.

После выбора данной команды появится диалоговое окно
(рис. 4).

Рисунок 4

Поскольку в качестве критерия оптимизации нами выбрана
максимизация прибыли, в поле Установить целевую ячейку
введите ссылку на
ячейку, содержащую формулу расчета прибыли. В нашем случае это ячейка
$G$11
. Чтобы максимизировать значение конечной ячейки путем изменения
значений влияющих ячеек (влияющими, в данном случае это и изменяемые ячейки,
являются ячейки, которые предназначены для хранения значений искомых
неизвестных), переключатель установите в положение максимальному
значению
;

В поле Изменяя ячейки
введите ссылки на
изменяемые ячейки, разделяя их запятыми; либо, если ячейки находятся рядом,
указывая первую и последнюю ячейку, разделяя их двоеточием
($

D
$5:$
F
$5

В поле Ограничения
введите все ограничения,
накладываемые на поиск решения. Добавление ограничения рассмотрим на примере
добавления первого ограничения по общей площади пашни.

В разделе Ограничения
диалогового окна Поиск
решения
нажмите кнопку Добавить
. Появится следующее диалоговое окно
(рис. 5)

Рисунок 5

В поле Ссылка на ячейку
введите адрес ячейки, на
значение которой накладываются ограничения. В нашем случае, это ячейка
$

G
$6

, где
находится формула расчета используемой пашни в текущем плане.

Выберите из раскрывающегося списка условный оператор
<=
, который должен располагаться между ссылкой и ограничением.

В поле Ограничение
введите ссылку на ячейку, в
которой находится значение наличия площади пашни в хозяйстве, либо ссылка на это
значение. В нашем случае, это ячейка $

I
$6

В результате диалоговое окно примет следующий вид (рис.
6).

Рисунок 6

Чтобы принять ограничение и приступить к вводу нового,
нажмите кнопку Добавить
. Аналогично вводятся и другие ограничения. Чтобы
вернуться в диалоговое окно Поиск решения
, нажмите кнопку
OK
.

После выполнения вышеперечисленных инструкций диалоговое
окно
Поиск решения

будет иметь следующий вид (рис. 7).

Рисунок 7

Для изменения и удаления ограничений в списке
Ограничения
диалогового окна Поиск решения
укажите ограничение,
которое требуется изменить или удалить. Выберите команду Изменить
и
внесите изменения либо нажмите кнопку Удалить
.

Флажок Линейная модель
в диалоговом окне
Параметры
Поиска решения
(рис. позволяет задать любое
количество ограничений. Флажок Неотрицательные значения
позволит соблюсти
условие неотрицательности переменных (при решении нашей задачи – поставить
обязательно). Остальные параметры можно оставить без изменений, либо установить
нужные для вас параметры, при необходимости используя справку.

Рисунок 8

Для запуска задачи на решение нажмите кнопку
Выполнить
и выполните одно из следующих действий:

—
чтобы восстановить исходные данные, выберите вариант
Восстановить исходные значения
.

Рисунок 9

Для того чтобы прервать поиск решения, нажмите клавишу
ESC
.

Лист Microsoft Excel будет пересчитан с учетом найденных
значений влияющих ячеек. В результате решения и сохранения результатов поиска на
листе модель примет следующий вид (табл. 10).

Рисунок 10

В ячейках D5
—F5
получены значения искомых
неизвестных (площади посева равны: зерновых -2500 га, сахарной свеклы — 661 га,
подсолнечника – 39 га), в ячейках G6
—G9
определены объемы
используемых ресурсов (общей площади пашни – 3200 га; площади пашни, которая
может быть использована под посевы технических культур – 700 га; трудовых –
6781,9 чел.-дней; минеральных удобрений – 15000 ц.д.в.), в ячейке G10

установлено количество произведенного зерна (65000 ц.). При всех этих значениях
величина прибыли достигает 12603,5 тыс. руб. (ячейка G11
).

В случае если в результате поиска не было найдено
решение, удовлетворяющее заданным условиям, в диалоговом окне Результаты
поиска решения
появится соответствующее сообщение (рис. 11).

Рисунок 11

Одной из наиболее часто встречающихся причин
невозможности найти оптимальное решение является такая ситуация, когда в
результате решения задачи выясняется, что имеются ограничения, которые не
выполняются. Сохранив найденное решение на листе, требуется построчно сравнить
полученные значения столбцов «Сумма произведений» и «Объем ограничений» и
проверить, удовлетворяет ли отношение между ними ограничению, стоящему в столбце
«Тип ограничений». Найдя, таким образом, невыполняемые ограничения необходимо
найти и ликвидировать причины, обуславливающие невозможность соблюдения данного
конкретного условия (это может быть, например, слишком большие или, наоборот,
очень маленькие запланированные объемы ограничений и т.п.).

Если ограничений в модели очень много, то визуально
достаточно трудно сравнивать и проверять на верность каждую строку. Для
облегчения рекомендуется добавить в модель еще один столбец «Проверка», где с
помощью функций MS
Excel
«ЕСЛИ
» и «ОКРУГЛ
» можно
организовать автоматическую проверку (рис. 12).

Рисунок 12

Рассмотрим пример задачи линейного программирования.

Требуется определить, в каком количестве надо выпустить продукцию четырех типов Прод1, Прод2, Прод3, Прод4, для изготовления которой требуются ресурсы трех видов: трудовые, сырье и финансы. Количество ресурса каждого вида, необходимое для выпуска единицы продукции данного типа, называется нормой расхода. Нормы расхода, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены на рис. 1.

Ресурс	Прод1	Прод2	Прод3	Прод4	Знак	Наличие
Прибыль
Трудовые
Сырье
Финансы

Рисунок 1.

Математическая модель задачи имеет вид:

где x j – количество выпускаемой продукции j-го типа; F – функция цели; в левых частях выражений ограничений указаны величины потребного ресурса
, а правые части показывают количество имеющегося ресурса
.

Ввод условий задачи

Для решения задачи с помощью Excel следует создать форму для ввода исходных данных и ввести их. Форма ввода показана на рис. 2.

В ячейку F6 введено выражение целевой функции как суммы произведений значений прибыли от выпуска единицы продукции каждого типа на количество выпускаемой продукции соответствующего типа. Для наглядности на рис. 3 представлена форма ввода исходных данных в режиме вывода формул.

В ячейки F8:F10 введены левые части ограничений для ресурсов каждого вида.

Рисунок 2.

Рисунок 3.

Решение задачи линейного программирования

Для решения задач линейного программирования в Excel используется мощный инструмент, называемый Поиск решения

.
Обращение к Поиску решения осуществляется из меню Сервис

, на экран выводится диалоговое окно Поиска решения (рис. 4).

Рисунок 4.

Ввод условий задачи для поиска ее решения состоит из следующих шагов:

1 Назначить целевую функцию, для чего установить курсор в поле Установить целевую ячейку

окна Поиск решения и щелкнуть в ячейке F6 в форме ввода;

2 Включить переключатель значения целевой функции, т.е. указать ее Равной Максимальному значению

;

3 Ввести адреса изменяемых переменных (x j): для этого установить курсор в поле Изменяя ячейки

окна Поиск решения, а затем выделить диапазон ячеек B3:E3 в форме ввода;

4 Нажать кнопку Добавить

окна Поиск решения для ввода ограничений задачи линейного программирования; на экран выводится окно Добавление ограничения

(рис. 5)

:

Ввести граничные условия для переменных x j (x j ³0), для этого в поле Ссылка на ячейку

указать ячейку В3, соответствующую х 1 , выбрать из списка нужный знак (³), в поле Ограничение

указать ячейку формы ввода, в которой хранится соответствующее значение граничного условия, (ячейка В4), нажать кнопку Добавить

; повторить описанные действия для переменных х 2 , х 3 и х 4 ;

Ввести ограничения для каждого вида ресурса, для этого в поле Ссылка на ячейку

окна Добавление ограничения

указать ячейку F9 формы ввода, в которой содержится выражение левой части ограничения, наложенного на трудовые ресурсы, в полях Ограничение

указать знак £ и адрес Н9 правой части ограничения, нажать кнопку Добавить

; аналогично ввести ограничения на остальные виды ресурсов;

После ввода последнего ограничения вместо Добавить

нажать ОК

и возвратиться в окно Поиск решения.

Рисунок 5.

Решение задачи линейного программирования начинается с установки параметров поиска:

В окне Поиск решения

нажать кнопку Параметры

, на экран выводится окно Параметры поиска решения

(рис. 6);

Установить флажок Линейная модель,

что обеспечивает применение симплекс-метода;

Указать предельное число итераций (по умолчанию – 100, что подходит для решения большинства задач);

Установить флажок
, если необходимо просмотреть все этапы поиска оптимального решения;

Нажать ОК

, возврат в окно Поиск решения

.

Рисунок 6.

Для решения задачи нажать кнопку Выполнить

в окне Поиск решения

, на экране – окно Результаты поиска решения

(рис. 7), в котором содержится сообщение Решение найдено. Все ограничения и условия оптимальности выполнены.
Если условия задачи несовместны, то выводится сообщение Поиск не может найти подходящего решения
. Если целевая функция не ограничена, то появляется сообщение Значения целевой ячейки не сходятся
.

Рисунок 7.

Для рассматриваемого примера решение найдено и результат оптимального решения задачи выводится в форме ввода: значение целевой функции, соответствующее максимальной прибыли и равное 1320, указывается в ячейке F6 формы ввода,

оптимальный план выпуска продукции х 1 =10, х 2 =0, х 3 =6, х 4 =0 указывается в ячейках В3:С3 формы ввода (рис. 8).

Количество использованных для выпуска продукции ресурсов выводится в ячейки F9:F11: трудовых – 16, сырья – 84, финансов – 100.

Рисунок 8.

Если при установке параметров в окне Параметры поиска решения

(рис. 6) был установлен флажок Показывать результаты итераций

, то будут показаны последовательно все шаги поиска. На экран будет выводиться окно
(рис. 9). При этом текущие значения переменных и функции цели будут показаны в форме ввода. Так, результаты первой итерации поиска решения исходной задачи представлены в форме ввода на рисунке 10 .

Рисунок 9.

Рисунок 10.

Чтобы продолжить поиск решения, следует нажимать кнопку Продолжить

в окне Текущее состояние поиска решения

.

Анализ оптимального решения

Прежде чем, перейти к анализу результатов решения, представим исходную задачу в форме

введя дополнительные переменные у i , представляющие собой величины неиспользованных ресурсов.

Составим для исходной задачи двойственную задачу и введем дополнительные двойственные переменные v i .

Анализ результатов поиска решения позволит увязать их с переменными исходной и двойственной задач.

С помощью окна Результаты поиска решения

можно вызвать отчеты трех типов, позволяющие анализировать найденное оптимальное решение:

Результаты,

Устойчивость,

Пределы.

Для вызова отчета в поле Тип отчета

выделить название нужного типа и нажать ОК

.

1 Отчет по результатам
(рис. 11) состоит из трех таблиц:

Таблица 1 содержит сведения о целевой функции; в столбце Исходно
указывается значение целевой функции до начала вычислений;

Таблица 2 содержит значения искомых переменных x j , полученных в результате решения задачи (оптимальный план выпуска продукции);

Таблица 3 показывает результаты оптимального решения для ограничений и для граничных условий.

Для Ограничений
в графе Формула
приведены зависимости, которые были введены при задании ограничений в окне Поиск решения

; в графе Значение
указаны величины использованного ресурса; в графе Разница
показано количество неиспользованного ресурса. Если ресурс используется полностью, то в графе Состояние
выводится сообщение связанное

; при неполном использовании ресурса в этой графе указывается не связан.

Для Граничных условий
приводятся аналогичные величины с той лишь разницей, что вместо неиспользованного ресурса показана разность между значением переменной x j в найденном оптимальном решении и заданным для нее граничным условием (x j ³0).

Именно в графе Разница
можно увидеть значения дополнительных переменных y i исходной задачи в формулировке (2). Здесь у 1 =у 3 =0, т.е. величины неиспользованных трудовых и финансовых ресурсов равны нулю. Эти ресурсы используются полностью. Вместе с тем, величина неиспользованных ресурсов для сырья у 2 =26, значит, имеются излишки сырья.

Рисунок 11.

2 Отчет по устойчивости
(рис. 12)состоит из двух таблиц.

В таблице 1 приводятся следующие значения:

Результат решения задачи (оптимальный план выпуска);

— Нормир. стоимость
, т.е. величины, показывающие, насколько изменится целевая функция при принудительном включении единицы продукции соответствующего типа в оптимальный план;

Коэффициенты целевой функции;

Предельные значения приращения коэффициентов целевой функции, при которых сохраняется оптимальный план выпуска.

В таблице 2 содержатся аналогичные данные для ограничений:

Величины использованных ресурсов;

— Теневая цена
, показывающая, как изменится целевая функция при изменении величины соответствующего ресурса на единицу;

Допустимые значения приращений ресурсов, при которых сохраняется оптимальный план выпуска продукции.

Рисунок 12.

Отчет по устойчивости позволяет позволяет получить двойственные оценки.

Как известно, двойственные переменные z i показывают, как изменится целевая функция при изменении ресурса i-го типа на единицу. В отчете Excel двойственная оценка называется Теневой ценой
.

В нашем примере сырье не используется полностью и его ресурс у 2 =26. Очевидно, что увеличение количества сырья, например, до 111 не повлечет за собой увеличения целевой функции. Следовательно, для второго ограничения двойственная переменная z 2 =0. Таким образом, если по данному ресурсу есть резерв, то дополнительная переменная
будет больше нуля, а двойственная оценка
этого ограничения равна нулю.

В рассматриваемом примере трудовые ресурсы и финансы использовались полностью, поэтому их дополнительные переменные равны нулю (у 1 =у 3 =0). Если ресурс используется полностью, то его увеличение или уменьшение повлияет на объем выпускаемой продукции, и следовательно, на величину целевой функции. Двойственные оценки ограничений на трудовые и финансовые ресурсы отличны от нуля, т.е. z 1 =20, z 3 =10.

Значения двойственных оценок находим в Отчете по устойчивости
, в таблице 2, в графе Теневая цена
.

При увеличении (уменьшении) трудовых ресурсов на единицу целевая функция увеличится (уменьшится) на 20 единиц и будет равна

F=1320+20×1=1340 (при увеличении).

Аналогично, при увеличении объема финансов на единицу целевая функция будет

F=1320+10×1=1330.

Здесь же, в графах Допустимое увеличение
и Допустимое уменьшение
таблицы 2, показаны допустимые пределы изменения количества ресурсов j-го вида. Например, для при изменении приращения величины трудовых ресурсов в пределах от –6 до 3,55, как показано в таблице, структура оптимального решения сохраняется, т.е наибольшую прибыль обеспечивает выпуск Прод1 и Прод3, но в других количествах.

Дополнительные двойственные переменные также отражены в Отчете по устойчивости
в графе Нормир. стоимость
таблицы 1.

Если основные переменные не вошли в оптимальное решение, т.е. равны нулю (в примере х 2 =х 4 =0), то соответствующие им дополнительные переменные имеют положительные значения (v 2 =10, v 4 =20). Если же основные переменные вошли в оптимальное решение (х 1 =10, х 3 =6), то их дополнительные двойственные переменные равны нулю (v 1 =0, v 3 =0).

Эти величины показывают, насколько уменьшится (поэтому знак минус в значениях переменных v 2 и v 4) целевая функция при принудительном выпуске единицы данной продукции. Следовательно, если мы захотим принудительно выпустить единицу продукции вида Прод3, то целевая функция уменьшится на 10 единиц и будет равна 1320 -10×1 =1310.

Обозначим через Dс j изменение коэффициентов целевой функции в исходной модели (1). Эти коэффициенты определяют прибыль, получаемую при реализации единицы продукции j-го вида.

В графах Допустимое увеличение
и Допустимое Уменьшение
таблицы 1 Отчета по устойчивости
показаны пределы изменения Dс j , при которых сохраняется структура оптимального плана, т.е. будет выгодно по-прежнему выпускать продукцию вида Продj. Например, при изменении Dс 1 в пределах -12£ Dс 1 £ 40, как показано в отчете, по-прежнему будет выгодно выпускать продукцию вида Прод1. При этом значение целевой функции будет F=1320+x 1 ×Dс j =1320+10×Dс j .

3 Отчет по пределам
приведен на рис. 13. В нем показывается, в каких пределах могут изменяться значения x j , вошедшие в оптимальное решение, при сохранении структуры оптимального решения. Кроме этого, для каждого типа продукции приводятся значения целевой функции, получаемые при подстановке в оптимальное решение значения нижнего предела выпуска изделий соответствующего типа при неизменных значениях выпуска остальных типов. Например, если при оптимальном решении х 1 =10, х 2 =0, х 3 =6, х 4 =0 положить х 1 =0 (нижний предел) при неизменных х 2 , х 3 и х 4 , то значение целевой функции будет равно 60×0+70×0+120×6+130×0=720.

Размер: px

Начинать показ со страницы:

Транскрипт

1
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Тихоокеанский государственный университет» Решение задач линейного программирования в Microsoft Excel 00 Методические указания к выполнению лабораторных работ по информатике для обучающихся по всем программам бакалавриата и специалитета дневной формы обучения Хабаровск Издательство ТОГУ 05

2
УДК 68.58(076.5) Решение задач линейного программирования в Microsoft Excel 00: методические указания к выполнению лабораторных работ по информатике для обучающихся по всем программам бакалавриата и специалитета дневной формы обучения / сост. Н. Д. Берман, Н. И. Шадрина. Хабаровск: Изд-во Тихоокеан. гос. ун-та, с. Методические указания составлены на кафедре информатики. Включают общие сведения о задачах линейного программирования, задания для выполнения лабораторных работ с вариантами задач, рекомендательный библиографический список. Печатается в соответствии с решениями кафедры информатики и методического совета факультета компьютерных и фундаментальных наук. Тихоокеанский государственный университет, 05

3
. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ В MICROSOFT EXCEL 00. ОБЩИЕ СВЕДЕНИЯ Общая характеристика задач оптимизации Задачи линейной оптимизации относятся к широко распространённому классу задач, встречающихся в различных сферах деятельности: в бизнесе, на производстве, в быту. Как оптимально распорядиться бюджетом или за минимальное время добраться до нужного места в городе, как наилучшим образом спланировать деловые встречи, минимизировать риски капитальных вложений, определить оптимальные запасы сырья на складе это те задачи, в которых нужно найти наилучшее из всех возможных решений. Различают следующие типы линейных оптимизационных задач: задачи о перевозках, например, минимизация расходов по доставке товаров с нескольких фабрик в несколько магазинов с учетом спроса; задачи распределения рабочих мест, например, минимизация расходов на содержание штата с соблюдением требований, определенных законодательством; управление ассортиментом товаров: извлечение максимальной прибыли с помощью варьирования ассортиментным набором товаров (при соблюдении требований клиентов). Аналогичная задача возникает при продаже товаров с разной структурой затрат, рентабельностью и показателями спроса; замена или смешивание материалов, например, манипуляция материалами с целью снижения себестоимости, поддержания необходимого уровня качества и соблюдения требований потребителей; задача о диете. Из имеющихся в распоряжении продуктов требуется составить такую диету, которая, с одной стороны, удовлетворяла бы минимальным потребностям организма в питательных веществах (белки, жиры, углеводы, минеральные соли, витамины), с другой требовала бы наименьших затрат; задача распределения ресурсов, например, распределение ресурсов между работами таким образом, чтобы максимизировать прибыль, или минимизировать затраты, или определить такой состав работ, который можно выполнить, используя имеющиеся ресурсы, и при этом достичь максимума опре- 3

4
деленной меры эффективности, или рассчитать, какие ресурсы необходимы для того, чтобы выполнить заданные работы с наименьшими издержками. Математическая постановка задачи линейного программирования Рассмотрим наиболее распространенный класс оптимизационных задач задачи линейного программирования. К такому классу относятся задачи, описываемые линейными математическими моделями. Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции () при условиях: () () () (3) () (4) где заданные постоянные величины и Функция () называется целевой функцией задачи, а условия ()(4) ограничениями задачи. Совокупность чисел (), удовлетворяющих ограничениям задачи, называется допустимым решением. Решение, при котором целевая функция задачи принимает максимальное (минимальное) значение, называется оптимальным. Использование надстройки Excel для решения задач линейного программирования Поиск решения это надстройка EXCEL, которая позволяет решать оптимизационные задачи. Если команда Поиск решения или группа Анализ отсутствует, необходимо загрузить надстройку Поиск решения. 4

5
На вкладке Файл выберите команду Параметры, а затем категорию Надстройки (рис.). Рис. В поле Управление выберите значение Надстройки Excel и нажмите кнопку Перейти. В поле Доступные надстройки установите флажок рядом с пунктом Поиск решения (рис.) и нажмите кнопку ОК. Рис. Пример решения оптимизационных линейных задач в MS Excel 00 Схема решения задач линейного программирования в MS Excel 00 следующая: 5

6
. Составить математическую модель.. Ввести на рабочий лист Excel условия задачи: а) создать форму на рабочем листе для ввода условий задачи; б) ввести исходные данные, целевую функцию, ограничения и граничные условия. 3. Указать параметры в диалоговом окне Поиск решения. 4. Проанализировать полученные результаты. Рассмотрим решение задачи оптимизации на примере. Пример. Задача определения оптимального ассортимента продукции Предприятие изготавливает два вида продукции П и П, которая поступает в оптовую продажу. Для производства продукции используются два вида сырья А и В. Максимально возможные запасы сырья в сутки составляют 9 и 3 ед. соответственно. Расход сырья на единицу продукции вида П и П табл.. Таблица Сырье Расход сырья на ед. продукции П П Запас сырья, ед. А 3 9 В 3 3 Опыт работы показал, что суточный спрос на продукцию П никогда не превышает спроса на продукцию П более чем на ед. Кроме того, известно, что спрос на продукцию П никогда не превышает ед. в сутки. Оптовые цены единицы продукции равны: 3 д. е. для П и 4 д. е. для П. Какое количество продукции каждого вида должно производить предприятие, чтобы доход от реализации продукции был максимальным? Решение. Построим математическую модель для решения поставленной задачи. Предположим, что предприятие изготовит x единиц продукции П и x единиц продукции П. Поскольку производство продукции ограничено имеющимися в распоряжении предприятия сырьем каждого вида и спросом на данную продукцию, а также учитывая, что количество изготовляемых изделий не может быть отрицательным, должны выполняться следующие неравенства: 6

7
Доход от реализации x единиц продукции П и x единиц продукции П составит Cреди всех неотрицательных решений данной системы линейных неравенств требуется найти такое, при котором функция F принимает максимальное значения F max. Рассматриваемая задача относится к разряду типовых задач оптимизации производственной программы предприятия. В качестве критериев оптимальности в этих задачах могут быть также использованы: прибыль, себестоимость, номенклатура производимой продукции и затраты станочного времени. Создадим на рабочем листе форму для ввода исходных данных (рис. 3). Заливкой выделены ячейки для ввода функций. Рис. 3 В ячейку E5 введем формулу для целевой функции (рис. 4). Используя обозначения соответствующих ячеек в Excel, формулу для расчета целевой функции можно записать как сумму произведений каждой из ячеек, отведенной для значений переменных задачи (B3, C3), на соответствующие ячейки, отведенные для коэффициентов целевой функции (B5, C5). 7

8
Рис. 4 Аналогично в ячейки D0:D введены формулы для расчета левой части ограничений (рис. 5). Рис. 5 На вкладке Данные в группе Анализ выберем команду Поиск решения. В диалоговом окне Параметры поиска решения установим следующее (рис. 6): 8

9
в поле Оптимизировать целевую функцию выбираем ячейку со значением целевой функции Е5; выбираем, максимизировать или минимизировать целевую функцию; в поле Изменяя ячейки переменных выбираем ячейки со значениями искомых переменных B3:C3 (пока в них нули или пусто); в области В соответствии с ограничениями с помощью кнопки Добавить размещаем все ограничения нашей задачи (рис. 7); в поле Выберите метод решения указываем Поиск решения линейных задач симплекс-методом; нажимаем кнопку Найти решение. Рис. 6 9

10
Добавляем ограничения для нашей задачи. Для неравенств указываем в поле Ссылка на ячейки диапазон D0:D, выбираем в раскрывающемся списке знак неравенства, в поле Ограничение выделяем диапазон F0:F и нажимаем кнопку Добавить (рис. 7), чтобы принять ограничение и добавить следующее ограничение. Для принятия ограничения и возврата к диалоговому окну Поиск решения нажмите кнопку Ok. Рис. 7 Покажем окна для добавления ограничений: преобразуем в (рис. 8); Рис. 8 0

11
(рис. 9); Рис. 9, (рис. 0). Рис. 0 После выбора кнопки Найти решение появляется окно Результаты поиска решения (рис.). Рис.

12
Для сохранения полученного решения необходимо использовать переключатель Сохранить найденное решение в открывшемся окне диалога Результаты поиска решения. После чего рабочий лист примет вид, представленный на рис.. Рис. Сохранить модель поиска решения можно следующим образом:) при сохранении книги Excel после поиска решения все значения, введенные в окнах диалога Поиск решения, сохраняются вместе с данными рабочего листа. С каждым рабочим листом в рабочей книге можно сохранить один набор значений параметров Поиска решения;) если в пределах одного рабочего листа Excel необходимо рассмотреть несколько моделей оптимизации (например, найти максимум и минимум одной функции или максимальные значения нескольких функций), то удобнее сохранить эти модели, используя кнопку Загрузить/Сохранить окна Параметры поиска решения. Диапазон для сохраняемой модели содержит информацию о целевой ячейке, об изменяемых ячейках, о каждом из ограничений и все значения диалога Параметры. Выбор модели для решения конкретной оптимизационной задачи осуществляется с помощью кнопки Загрузить/сохранить диалогового окна Параметры поиска решения; 3) сохранить модель можно в виде именованных сценариев, для этого необходимо нажать на кнопку Сохранить сценарий диалогового окна Результаты поиска решений (см. рис.). Кроме вставки оптимальных значений в изменяемые ячейки, Поиск решения позволяет представлять результаты в виде трех отчетов (Результаты,

13
Устойчивость и Пределы). Для генерации одного или нескольких отчетов необходимо выделить их названия в окне диалога Результаты поиска решения (рис.). Рассмотрим более подробно каждый из них. Отчет по устойчивости (рис. 3) содержит информацию о том, насколько целевая ячейка чувствительна к изменениям ограничений и переменных. Этот отчет имеет два раздела: один для изменяемых ячеек, а второй для ограничений. Правый столбец в каждом разделе содержит информацию о чувствительности. Каждая изменяемая ячейка и ограничения приводятся в отдельной строке. При использовании целочисленных ограничений Excel выводит сообщение Отчеты об устойчивости и Пределы не применимы для задач с целочисленными ограничениями. Рис. 3 Отчет по результатам (рис. 4) содержит три таблицы: в первой приведены сведения о целевой функции до начала вычисления, во второй значения искомых переменных, полученные в результате решения задачи, в третьей результаты оптимального решения для ограничений. Этот отчет также содержит информацию о таких параметрах каждого ограничения, как статус и разница. Статус может принимать три состояния: связанное, несвязанное или невыполненное. Значение разницы это разность между значением, выводимым в ячейке ограничения при получении решения, и числом, заданным в правой части формулы ограничения. Связанное ограничение это ограничение, для которого значение разницы равно нулю. Несвязанное 3

14
ограничение это ограничение, которое было выполнено с ненулевым значением разницы. Рис. 4 Отчет по пределам (рис. 5) содержит информацию о том, в каких пределах значения изменяемых ячеек могут быть увеличены или уменьшены без нарушения ограничений задачи. Для каждой изменяемой ячейки этот отчет содержит оптимальное значение, а также наименьшие значения, которые ячейка может принимать без нарушения ограничений. Рис. 5 4

15
Полученное решение означает, что объем производства продукции вида П должен быть равен,4 ед., а продукции П,4 ед. продукции. Доход, получаемый в этом случае, составит,8 д. е. Допустим, что к условию задачи добавилось требование целочисленности значений всех переменных. В этом случае описанный выше процесс ввода условия задачи необходимо дополнить следующими шагами. В окне Поиск решения нажмите кнопку Добавить и в появившемся окне Добавление ограничений введите ограничения следующим образом (рис. 6): в поле Ссылка на ячейки введите адреса ячеек переменных задачи B3:C3; в поле ввода знака ограничения установите целое; подтвердите ввод ограничения нажатием кнопки OK. Рис. 6 Решение задачи при условии целочисленности ее переменных рис. 7. Рис. 7 5

16
. ЛАБОРАТОРНЫЕ РАБОТЫ Лабораторная работа Задание Найти максимум линейной функции при заданной системе ограничений. Вариант Целевая функция F Ограничения { { { { 3 { { 4 { { 5 { { 6 { { 7 { { 8 { { 9 { { 0 { { { { { { 3 { { 4 { { 5 { { 6

17
Лабораторная работа Задание. Построить математическую модель задачи.. Представить ее в табличной форме на листе Excel. 3. Найти решение задачи средствами надстройки Поиск решения. 4. Вывести отчеты по результатам и устойчивости. Вариант Для производства столов и шкафов мебельная фабрика использует необходимые ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида табл.. Таблица Ресурсы Древесина, м 3: -го вида -го вида Нормы затрат ресурсов на одно изделие Стол Шкаф 0, 0, 0, 0,3 Общее количество ресурсов Трудоемкость, чел.ч,5 37,4 Прибыль от реализации одного изделия, р. 6 8 Определить, сколько столов и шкафов следует изготавливать фабрике, чтобы прибыль от их реализации была максимальной. Ответ. Прибыль 940 р. при количестве столов и шкафов 0 и 66. Вариант Для производства двух видов изделий A и В используется токарное, фрезерное и шлифовальное оборудование. Нормы затрат времени для каждого из типов оборудования на одно изделие данного вида, общий фонд рабочего времени каждого из типов оборудования, а также прибыль от реализации одного изделия табл. 3. 7

18
Таблица 3 Затраты времени, стан.-ч, Тип оборудования на обработку одного изделия А В Фрезерное 0 8 Токарное 5 0 Шлифовальное 6 Прибыль от реализации одного изделия, р. 4 8 Общий фонд полезного рабочего времени оборудования, ч Найти план выпуска изделий А и В, обеспечивающий максимальную прибыль от их реализации. Ответ. Прибыль 76 р. при выпуске изделий и 6. Вариант 3 Для изготовления трех видов изделий А, В и С используется токарное, фрезерное, сварочное и шлифовальное оборудование. Затраты времени на обработку одного изделия для каждого из типов оборудования, общий фонд рабочего времени каждого из типов используемого оборудования, прибыль от реализации одного изделия данного вида табл. 4. Таблица 4 Тип оборудования Фрезерное Токарное Сварочное Шлифовальное Затраты времени, стан.-ч, на обработку одного изделия вида А В С Прибыль, р. 0 4 Общий фонд рабочего времени оборудования, ч Требуется определить, сколько изделий и какого вида следует изготовить предприятию, чтобы прибыль от их реализации была максимальной. Ответ. Прибыль 49 р. при выпуске изделий 4, 8, 0. 8

19
Вариант 4 Для поддержания нормальной жизнедеятельности человеку ежедневно необходимо потреблять не менее 8 г белков, 56 г жиров, 500 г углеводов, 8 г минеральных солей. Количество питательных веществ, содержащихся в кг каждого вида потребляемых продуктов, а также цена кг каждого из этих продуктов табл. 5 Таблица 5 Питательные вещества Содержание, г, питательных веществ в кг продуктов Мясо Рыба Молоко Масло Сыр Крупа Картофель Белки Жиры Углеводы Минеральные соли Цена кг продуктов, р.,8,0 0,8 3,4,9 0,5 0, Составить дневной рацион, содержащий не менее минимальной суточной нормы потребности человека в необходимых питательных веществах при минимальной общей стоимости потребляемых продуктов. Ответ. Минимальная общая стоимость 0, р. при количестве продуктов: мясо 0; рыба 0; молоко 0; масло 0,03335; сыр 0; крупа 0,9053; картофель 0. Вариант 5 Кондитерская фабрика для производства трех видов карамели А, В, и С использует три вида основного сырья: сахарный песок, патоку и фруктовое пюре. Нормы расхода сырья каждого вида на производство т карамели данного вида, общее количество сырья каждого вида, прибыль от реализации т карамели табл. 6. 9

20
Таблица 6 Вид сырья Сахарный песок Патока Фруктовое пюре Нормы расхода сырья, т, на т карамели А В С 0,8 0,4 0,5 0,4 0, 0,6 0,3 0, Прибыль от реализации т продукции, р Общее количество сырья, т Найти план производства карамели, обеспечивающий максимальную прибыль от ее реализации. Ответ. Максимальная прибыль р. при выпуске карамели 00, 0, 00 т. Вариант 6 На швейной фабрике для изготовления четырех видов изделий может быть использована ткань трех артикулов. Нормы расхода тканей всех артикулов на пошив одного изделия, имеющееся в распоряжении фабрики общее количество тканей каждого артикула и цена одного изделия данного вида табл. 7. Таблица 7 Артикул ткани I II III Норма расхода ткани, м, на одно изделие вида 3 4 Цена одного изделия, р Общее количество ткани, м Определить, сколько изделий каждого вида должна произвести фабрика, чтобы стоимость изготовленной продукции была максимальной. Ответ. Максимальная стоимость продукции 5 р. при выпуске изделий 95, 0, 0, 0. 0

21
Вариант 7 Предприятие выпускает четыре вида продукции и использует три типа основного оборудования: токарное, фрезерное и шлифовальное. Затраты времени на изготовление единицы продукции для каждого из типов оборудования, общий фонд рабочего времени каждого из типов оборудования и прибыль от реализации одного изделия данного вида табл. 8. Таблица 8 Затраты времени, стан.-ч, Тип оборудования на единицу продукции вида 3 4 Токарное Фрезерное Шлифовальное Прибыль от реализации 3 единицы продукции, р. 8 3 Общий фонд рабочего времени, стан.-ч Определить такой объем выпуска каждого из изделий, при котором общая прибыль от их реализации является максимальной. Ответ. Максимальная прибыль 965 р. при выпуске изделий 70, 35, 0, 0. Вариант 8 Торговое предприятие планирует организовать продажу четырех видов товара, используя при этом только два вида ресурсов: рабочее время продавцов в количестве 840 ч и площадь торгового зала 80 м. При этом известны плановые нормативы затрат этих ресурсов в расчете на единицу товаров и прибыль от их продажи табл. 9. Таблица 9 Показатели Расход рабочего времени на единицу товара, ч Использование площади торгового зала на единицу товара, м Товар А В С D 0,6 0,8 0,6 0,4 0, 0, 0,4 0, Прибыль от продажи единицы товара, р Общее количество ресурсов

22
Требуется определить оптимальную структуру товарооборота, обеспечивающую торговому предприятию максимальную прибыль. Ответ. Максимальная прибыль 6 00 р. при продаже товаров 0, 0, 0, 800. Вариант 9 Из трех видов сырья необходимо составить смесь, в состав которой должно входить не менее 6 ед. химического вещества А, 30 ед. вещества В и 4 ед. вещества С. Количество единиц химического вещества, содержащегося в кг сырья каждого вида, цена кг сырья каждого вида табл. 0 Таблица 0 Вещество А В С Цена кг сырья, р. Количество единиц вещества, содержащегося в кг сырья вида Составить смесь, содержащую не менее нужного количества веществ данного вида и имеющую минимальную стоимость. Ответ. Минимальная стоимость 6 р. при количестве 0; 0; 0; 6,5 кг. Вариант 0 Для производства трех видов продукции предприятие использует два типа технологического оборудования и два вида сырья. Нормы затрат сырья и времени на изготовление одного изделия каждого вида, общий фонд рабочего времени каждой из групп технологического оборудования, объемы имеющегося сырья каждого вида, цена одного изделия каждого вида, ограничения на возможный выпуск каждого из изделий табл..

23
Ресурсы Производительность оборудования в нормочасах: I типа II типа Сырье, кг: -го вида -го вида Цена одного изделия, р. Выпуск, шт.: минимальный максимальный Нормы затрат на одно изделие вида Таблица Общее количество ресурсов Составить план производства продукции, по которому будет изготовлено необходимое количество изделий каждого вида, при максимальной общей стоимости всей изготовляемой продукции. Ответ. Общая стоимость 495 р. при выпуске продукции 0, 33, 45. Вариант При производстве четырех видов кабеля выполняется пять групп технологических операций. Нормы затрат на км кабеля данного вида для каждой из групп операций, прибыль от реализации км каждого вида кабеля, а также общий фонд рабочего времени, в течение которого могут выполняться эти операции, табл. Таблица Технологическая операция Нормы затрат времени, ч, на обработку км кабеля вида 3 4 Волочение Наложение изоляций Скручивание элементов в кабель Освинцовывание Испытание и контроль,0 6,4 3,0,8 0,4 5,6,5,6 0,8 6,0,8 0,8,4 0,7 8,0,4 3,0 Прибыль от реализации км кабеля, р., 0,8,0,3 Общий фонд рабочего времени, ч

24
Определить план выпуска кабеля, при котором общая прибыль от реализации изготовляемой продукции является максимальной. Ответ. Общая прибыль от реализации 939,48 57 р. при выпуске 00; 64,8 57; 0; 0. Вариант Стальные прутья длиной 0 см необходимо разрезать на заготовки длиной 45, 35 и 50 см. Требуемое количество заготовок данного вида составляет соответственно 40, 30 и 0 шт. Возможные варианты разреза и величина отходов при каждом из них табл. 3. Таблица 3 Варианты разреза Длина заготовки, см Величина отходов, см Определить, сколько прутьев по каждому из возможных вариантов следует разрезать, чтобы получить не менее нужного количества заготовок каждого вида при минимальных отходах. Ответ. Минимальные отходы равны 550 см при количестве прутьев 0, 0, 0, 0, 0, 0 шт. Вариант 3 Для производства трех видов изделий А, В, С предприятие использует четыре вида сырья. Нормы затрат сырья каждого вида на производство единицы продукции данного вида, прибыль от реализации одного изделия каждого вида табл. 4. 4

25
Таблица 4 Нормы затрат сырья, кг, на единицу продукции Вид сырья А В С I II III IV Прибыль от реализации одного изделия Изделия А, В и С могут производиться в любых соотношениях (сбыт обеспечен), но для их производства предприятие может использовать сырье I вида не более 00 кг, II вида не более 0 кг, III вида не более 80 кг, IV вида не более 38 кг. Определить план производства продукции, при котором общая прибыль предприятия от реализации всей продукции была бы наибольшей. Ответ. План производства изделий 7, 5, 0 кг при общей прибыли 5 кг. Вариант 4 Туристическое агентство собирается заказать издательству выпуск художественных альбомов трех типов A, B, C. Их изготовление лимитируется затратами ресурсов трех видов, удельные расходы которых приведены в табл. 5. Вид ресурса Финансы, $ Бумага, л. Трудозатраты, чел. ч Таблица 5 Удельные затраты ресурсов на выпуск альбомов A B C 4 4 Издательство для выполнения заказа получило финансовые средства в объеме $ 3 600, имеет в наличии л. бумаги и может использовать трудовые ресурсы в объеме 00 чел. ч. Агентство платит за выпуск одного альбома типа А дол., за альбом В 8 дол., за альбом С 30 дол. 5

26
Сколько альбомов каждого типа должно выпустить издательство, чтобы получить наибольшую прибыль? Ответ. Максимальный суммарный доход дол., количество альбомов: 400; 800; 0 шт. Вариант 5 Предприятие оптовой торговли может реализовать T j, j, 4 группы товаров. Для этого используется несколько видов ресурсов. Исходные данные для построения математической модели табл. 6. Лимитирующие ресурсы и показатели Товарная группа T T T 3 T4 Объем ресурса Таблица 6 Складские площади, м Трудовые ресурсы, чел.ч Издержки обращения, ден. ед Товарные запасы, ден. ед План товарооборота, ден. ед Минимально допустимые значения товарооборота по j-й группе, ед. Прибыль в расчете на единицу товарооборота j-й группы, ден. ед. Вид огра ниче- ния Требуется рассчитать план хозяйственной деятельности торгового предприятия, обеспечивающий максимум прибыли при заданных ограничениях на складские площади, трудовые ресурсы, издержки обращения, товарные запасы, величину товарооборота, если торговая прибыль в расчете на единицу товарооборота j -й группы задана. Ответ. Максимальна прибыль ден. ед. Товарооборот по группам: Т 00 ед., Т 000 ед., Т ед., Т ед. 6

27
3. РЕКОМЕНДАТЕЛЬНЫЙ БИБЛИОГРАФИЧЕСКИЙ СПИСОК. Акулич, И. Л. Математическое программирование в примерах и задачах: учеб. пособие для студентов экон. спец. сузов / И. Л. Акулич. М. : Высш. шк., с.. Леоненков, А. В. Решение задач оптимизации в среде MS Excel / А. В. Леоненков. СПб. : БХВ-Петербург, с. 3. Васильев, А. Н. Финансовое моделирование и оптимизация средствами Excel007 / А. Н. Васильев. СПб. : Питер, с. 4. Уокенбах, Дж. Microsoft Excel 00. Библия пользователя: пер. с англ. / Дж. Уокенбах. М. : И. Д. Вильямс, 0. 9 с. 5. Уокенбах, Дж. Формулы в Microsoft Excel 00: пер. с англ. / Дж. Уокенбах. М. : И. Д. Вильямс, с. 6. Иванов, И. Microsoft Excel 00 для квалифицированного пользователя / И. Иванов. М. : Академия АЙТИ, с. 7. Справка и инструкции по Excel // Поддержка по Microsoft Office [Электронный ресурс]. Режим доступа: (дата обращения:). 8. Решение задач оптимизации управления с помощью MS Excel 00 // НОУ «ИНТУИТ» [Электронный ресурс]. Режим доступа: (дата обращения:). Оглавление. Задачи линейного программирования в Microsoft Excel 00. Общие сведения… 3 Общая характеристика задач оптимизации… 3 Математическая постановка задачи линейного программирования… 4 Использование надстройки Excel для решения задач линейного программирования… 4 Пример решения оптимизационных линейных задач в MS Excel Лабораторные работы… 6 Лабораторная работа… 6 Лабораторная работа Рекомендательный библиографический список

28
Решение задач линейного программирования в Microsoft Excel 00 Методические указания к выполнению лабораторных работ по информатике для обучающихся по всем программам бакалавриата и специалитета дневной формы обучения Нина Демидовна Берман Нина Ивановна Шадрина Главный редактор Л. А. Суевалова Редактор Е. Н. Ярулина Подписано в печать Формат 60 x 84 / 6. Бумага писчая. Гарнитура «Калибри». Печать цифровая. Усл. печ. л.,68. Тираж 60 экз. Заказ 70. Издательство Тихоокеанского государственного университета, Хабаровск, ул. Тихоокеанская, 36. Отдел оперативной полиграфии издательства Тихоокеанского государственного университета, Хабаровск, ул. Тихоокеанская, 36. 8

ОБЪЕМНОЕ ПЛАНИРОВАНИЕ РАБОТЫ ТЕХНОЛОГИЧЕСКИХ СТАНОЧНЫХ СИСТЕМ Х а б а р о в с к 2 0 0 9 Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования

Практическое занятие 3. 1. Для данных условий сформулируйте оптимизационную задачу, составьте математическую модель, найдите оптимальный план производства с помощью надстройки «Поиск решения» в EXCEL.

Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Тихоокеанский государственный университет» Н. И. Шадрина, Н.

Составление, решение и анализ задачи линейного программирования в Excel ЗАДАНИЕ. Построить математическую модель задачи и решить её средствами Excel. Записать сопряжённую задачу. Провести анализ и сделать

Задача распределения ресурсов предприятия Содержательная постановка задачи Фабрика выпускает сумки: женские, мужские, дорожные. Данные о материалах, используемых для производства сумок и месячный запас

Лабораторная работа 11 Решение задачи оптимального распределения ресурсов Задание Предприятие выпускает продукты нескольких видов. Для их изготовления используется сырье различного типа. Известны нормы

Лабораторная работа 3_9. Поиск и принятие решений в Excel. Что осваивается и изучается? Решение задачи определения оптимального плана и транспортной задачи при помощи надстройки «Поиск решения». Задание

Лабораторная работа 3. Поиск решения в Microsoft Excel Целью лабораторной работы является изучение возможностей средства Поиск решения MS Excel для решения оптимизационных задач. К защите лабораторной

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬ- НОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра «Технология

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «ТИХООКЕАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» Совместная работа

ЛАБОРАТОРНАЯ РАБОТА СРЕДСТВА ПОДДЕРЖКИ ПРИНЯТИЯ РЕШЕНИЙ КАК ФУНКЦИИ EXCEL Команда Подбор параметра Задание 1. Рассмотрим задачу, составленную на основании задачи по использованию функции ЧПС. Вас просят

ВАРИАНТ Для изготовления изделий двух видов имеется 00 кг металла. На одно изделие -го вида расходуется кг металла, а изделия -говида кг. Составить план производства, обеспечивающий получение наибольшей

Лабораторная работа 4 Тема работы: Решение задачи об оптимальном распределении ресурсов при выпуске продукции с использованием процедуры Поиск решения Microsoft Excel. Цель работы: Научиться использовать

Практическая работа 5.4. Решение задачи об оптимальном распределении ресурсов при выпуске продукции с использованием процедуры «Поиск решения» Microsoft Excel Цель работы. Выполнив эту работу, Вы научитесь:

Московская Государственная Академия Тонкой Химической Технологии имени М. В. Ломоносова Корнюшко В.Ф., Морозова О.А. Детерминированные модели экономических систем Методическое пособие по дисциплине Математические

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ КУРГАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА «ИНФОРМАТИКА» РЕАЛИЗАЦИЯ ОПТИМИЗАЦИОННЫХ МОДЕЛЕЙ В СРЕДЕ EXCEL Методические указания к проведению лабораторных

Оптимизация производственной программы Методические указания к лабораторной работе по экономике электротехнической промышленности Ульяновск 009 В 9 Васильев, В. Н. Оптимизация производственной программы

Экономико-математические методы и моделирование. Практическая работа 2. Симплексный метод решения задач линейного программирования. Решить задачу линейного программирования (ЛП) симплексным методом. Расчеты

РАБОТА 2 РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ Цель работы: ознакомление с методами решения задач линейного программирования в табличном процессоре Ecel. Решение экономических задач, как правило, связано

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования «Тихоокеанский государственный университет» Кафедра «Технология деревообработки» МОДЕЛИРОВАНИЕ

АНАЛИЗ ДАННЫХ В MS EXCEL Гедранович Валентина Васильевна 27 июня 2012 г. Аннотация Глава 11 из УМК: Гедранович, В.В. Основы компьютерных информационных технологий: учеб.-метод. комплекс / В.В. Гедранович,

Решение задачи линейного программирования графическим методом, симплекс-методом и через «Поиск решения» в Ecel ЗАДАНИЕ. Предприятие выпускает два вида продукции: Изделие и Изделие. На изготовление единицы

Лабораторная работа 3. Надстройка Поиск решения в Microsoft Excel. Диспетчер сценариев в Microsoft Excel. Целью данной лабораторной работы является изучение возможностей средства Поиск решения в Microsoft

Негосударственное образовательное частное учреждение высшего профессионального образования Уральский институт фондового рынка Кафедра Экономики предприятия ЭКОНОМИКА ФИРМЫ Сборник кейсов тема «Планирование

Практическое занятие 4. Для условий задачи cформулируйте двойственную задачу и найдите объективно обусловленные оценки. Проанализируйте использование ресурсов в оптимальном плане. Вариант 1. Для изготовления

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Курганский государственный университет» Кафедра

ЛАБОРАТОРНАЯ РАБОТА 6 Тема: Анализ данных в OpenOffice Calc 1. Основные понятия Процесс изменения значений ячеек и анализа влияния этих изменений на результат вычисления формул в OpenOffice.org Calc называется

Подбор параметра При обработке табличных данных часто возникает необходимость в прогнозировании результата на основе известных исходных данных или наоборот, в определении того, какими должны быть исходные

2 ПЛАН ЛЕКЦИИ: АНАЛИЗ ДАННЫХ В MS EXCEL Информатика 2 семестр Кондратенко Ольга Брониславовна [email protected] Инструмент анализа «что если» Инструмент анализа «что если» создание таблиц данных с одной

Практическая работа 13 Тема: ЗАДАЧИ ОПТИМИЗАЦИИ (ПОИСК РЕШЕНИЯ) В MICROSOFT EXCEL Цель занятия. Изучение технологии поиска решения для задач оптимизации (минимизации, максимизации). Задание 13.1. Минимизация

Приложение Содержимое кейса Задача 1 Одна вновь организованная коммерческая фирма решила выпускать два типа стульев х1 и х2. Для их производства необходимо два вида материалов: дерево и ткань. Фирма ежемесячно

ЛАБОРАТОРНАЯ РАБОТА 2 ИСПОЛЬЗОВАНИЕ MICROSOFT EXCEL 2007 ПРИ РЕШЕНИИ ПРАКТИЧЕСКИХ ЗАДАЧ (ДЛЯ СТУДЕНТОВ НАПРАВЛЕНИЯ 100800.62) 2.1 Решение задач оптимизации Задача. Завод производит электронные приборы

МОСКОВСКИЙ РАДИОТЕХНИЧЕСКИЙ КОЛЛЕДЖ им. А.А.Расплетина ЛАБОРАТОРНАЯ РАБОТА По предмету «Математические методы» «Двухиндексные задачи линейного программирования» Составил: Преподаватель МРТК им.а.а.расплетина

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ федеральное государственное автономное образовательное учреждение высшего образования «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» УТВЕРЖДАЮ

СОДЕРЖАНИЕ. ЗАДАНИЕ…. ЭТАПЫ РАБОТЫ….. Формирование математической модели задачи….. Решение прямой задачи симплекс-методом….. Построение двойственной задачи… 6.4. Решение прямой и двойственной

ЛАБОРАТОРНАЯ РАБОТА РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ИСПОЛЬЗОВАНИЕМ Microsoft Ecel ЦЕЛЬ РАБОТЫ Приобретение навыков решения задач линейного программирования (ЛП) в табличном редакторе Microsoft

МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра «Технология машиностроения»

Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Р.

Тверь Реферат Сервис Содержание Задача 1. Ассортимент продукции… 3 Условие задачи… 3 Математическая постановка задачи… 3 Табличная модель задачи… 5 Отчет о результатах решения задачи 1…. 6 Вывод…

ЗАДАНИЕ ПРАКТИЧЕСКОЙ РАБОТЫ 4 И ПРАКТИЧЕСКОЙ РАБОТЫ 5 Задачи линейной оптимизации Построение экономико-математических моделей (ЭММ). Решение задач линейной оптимизации с использованием информационных технологий.

ЛАБОРАТОРНЫЕ РАБОТЫ ПО MS EXCEL 2007 ЛАБОРАТОРНАЯ РАБОТА 1…. 1 ЛАБОРАТОРНАЯ РАБОТА 2… 3 ЛАБОРАТОРНАЯ РАБОТА 3… 4 ЛАБОРАТОРНАЯ РАБОТА 4… 7 ЛАБОРАТОРНАЯ РАБОТА 5… 8 ЛАБОРАТОРНАЯ РАБОТА 6… 10

Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Ульяновский государственный технический университет ИНФОРМАЦИОННЫЕ СИСТЕМЫ В ЭКОНОМИКЕ

1 Лабораторная работа 3 Решение задач. Подбор параметров, поиск решения 1. Реализация математической модели в Excel Математическая модель это описание состояния поведения некоторой реальной системы (объекта,

Gnumeric: электронная таблица для всех И.А.Хахаев, 2007-2010 7 Линейная оптимизация (поиск решения) 7.1 Оптимизация как задача линейного программирования Пусть имеется функция, называемая целевой, линейно

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА Государственное образовательное учреждение высшего профессионального образования «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ» Институт экономики

МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Самарский государственный технический университет» ИНЖЕНЕРНО-ЭКОНОМИЧЕСКИЙ ФАКУЛЬТЕТ КАФЕДРА ЭКОНОМИКИ

ЗАНЯТИЕ ПРИБЛИЖЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ Отделение корней Пусть дано уравнение f () 0, () где функция f () C[ a; Определение Число называется корнем уравнения () или нулем функции f (), если

Министерство образования и науки Российской Федерации Федеральное агентство по образованию Саратовский государственный технический университет РЕШЕНИЕ ЗАДАЧ ОПТИМИЗАЦИИ В СРЕДЕ MS EXCEL Методические указания

«Юго-Западный государственный университет» ЮЗГУ) Кафедра конструирования и технологии электронновычислительных средств МЕТОДЫ УСЛОВНОЙ ОПТИМИЗАЦИИ Методические указания по выполнению лабораторной работы

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Тихоокеанский государственный университет»

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ» (МИИТ)

МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Самарский государственный технический университет» (ФГБОУ ВПО «СамГТУ») Кафедра

Министерство образования и науки РФ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Уральский государственный лесотехнический университет Кафедра

Лабораторная работа 4 «Электронные таблицы Excel и автоматизация вычислений на ПК» РАЗДЕЛ 4. Решение систем уравнений и оптимизационных задач. Вычислительные возможности программы Excel достаточно широки,

Введение Линейное программирование раздел математики, в котором изучаются теория и численные методы решения задач нахождения экстремума (максимума или минимума) линейной функции многих переменных при наличии

ФЕДЕРАЛЬНОЕ АГЕНСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ

АНАЛИЗ УСТОЙЧИВОСТИ КОММЕРЧЕСКОЙ ДЕЯТЕЛЬНОСТИ ПРЕДПРИЯТИЯ Дегтярёва Нина Адамовна, к.э.н., доцент Коммерческая работа — это деятельность предприятия, направленная на решение особого комплекса задач. Изучение

ЛАБОРАТОРНАЯ РАБОТА 2 РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 1. Цели работы: построение математической модели задачи линейного программирования; решение задачи линейного программирования графическим

Изучив алгоритмы «ручного» решения задач линейного программирования, полезно познакомиться и со способом упростить этот процесс. Ясно, что чем сложнее задача, чем больше в ней переменных и условий, тем утомительнее и дольше ее решать. В таких случаях удобно использовать специальные математические пакеты, или доступную многим программу MS Excel.

Решить задачи линейного программирования в Excel
достаточно просто: 1) внести исходные данные задачи и ограничения, 2) запустить надстройку Поиск решения, 3) установить нужные параметры решения и запустить выполнение. Программа подберет оптимальное решение, выдаст отчеты для анализа решения задачи.

Подробнее все эти этапы с пояснениями и скриншотами разобраны ниже в примерах на разных задачах линейного программирования — изучайте, ищите похожие, решайте. Если вам нужна помощь в выполнении заданий, перейдите в раздел: Контрольные работы по линейному программированию .

Линейное программирование: примеры решений в Excel

Задача 1.
Построить математическую модель задачи и решить её средствами Excel. Записать сопряжённую задачу. Провести анализ и сделать выводы по полученным результатам.
Для производства столов и шкафов мебельная фабрика использует различные ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в таблице.
Определить, сколько столов и шкафов фабрике следует выпускать, чтобы прибыль от реализации была максимальной.

Задача 2.
Цех производит 8 различных видов деталей для двигателей A, B, C1, C2, C3, D, E6, F имея в своем распоряжении перечисленный ниже парк из 7 видов универсальных станков: 2 шт. -ADF, 3 шт. -SHG, 3 шт. -BSD, 1 шт. -AVP, 1 шт. -BFG, 3 шт. -ABM, 2 шт. -RL.
Время, требуемое для обработки единицы каждого продукта на каждом станке, вклад в прибыль от производства единицы каждого продукта и рыночный спрос на каждый продукт за месяц даны в таблице.
Цех работает 12 часов в день. Каждый месяц содержит 26 рабочих дней. Для упрощения задачи считаем, что возможен произвольный порядок обработки деталей на различных станках.
Составьте оптимальный план производства.
Определите, производство каких продуктов лимитировано рынком, и каких – техническими возможностями цеха. Какие машинные ресурсы должны быть увеличены в первую очередь, чтобы добиться максимального увеличения прибыли (при заданных потребностях рынка)?
Есть ли продукт, который невыгодно производить? Почему? Что нужно изменить, чтобы все продукты стало выгодно производить?

Задача 3.
Необходимо составить самый дешевый рацион питания цыплят, содержащий необходимое количество определенных питательных веществ тиамина Т и ниацина Н. Пищевая ценность рациона (в калориях) должна быть не менее заданной. Смесь для цыплят изготавливается из двух продуктов — К и С. Известно содержание тиамина и ниацина в этих продуктах, а также питательная ценность К и С (в калориях). Сколько К и С надо взять для одной порции куриного корма, чтобы цыплята получили необходимую им дозу веществ Н и Т и калорий (или больше), а стоимость порции была минимальна? Исходные данные для расчетов приведены в таблице.

Задача 4.
Фирма «Компьютер-сервис» поставляет компьютеры под ключ четырех базовых комплектаций: «домашний», «игровой», «офисный» и «экстрим». Известны средние затраты времени на сборку, проверку и подключение компьютеров. Каждый компьютер приносит определенный уровень прибыли, но спрос ограничен. Кроме того, в плановом периоде ограничен ресурс человеко-часов, отведенных на выполнение каждой производственной операции. Определить, сколько компьютеров каждого типа необходимо произвести в плановом периоде, имея целью максимизировать прибыль.

Задача 5.
На лесопилку поступают доски длиной 10 м. По контракту лесопилка должна поставить клиенту не менее 100 досок длиной 5 м, не менее 200 досок длиной 4 м и не менее 300 досок длиной 3 м. Как работникам лесопилки выполнить условия контракта, разрезав наименьшее количество досок?

Задача 6.
Компания «Евростройтур» организует экскурсионные автобусные туры по странам Европы. Компания получила 4 новых автобуса и предполагает направить их на маршруты во Францию, Италию, Чехию и Испанию.
Каждый автобус обслуживают 2 водителя. Компанией приглашены 8 водителей, в различной степени знакомых с дорогами европейских стран (в % от экскурсионного маршрута).
Необходимо распределить водителей так, чтобы общий показатель освоения маршрутов был максимальным.

Задача 7.
Решить задачу методом ветвей и границ, решая отдельные задачи линейного нецелочисленного программирования с помощью функции «Поиск решения» в Microsoft Excel (в случае, если первая же задача ЛП выдает целочисленное решение, не позволяя ветвить задачу, немного изменить начальные условия).
Состав еды рядовых регламентируется верховной ставкой главнокомандующего, которая устанавливает нижние нормы питания в сутки по основным компонентам: 1500 килокалорий, 100 г белков, 280 г углеводов, 90 г жиров, 1 кг воды. На складах есть 4 вида продуктов, которые выдают защитникам Родины сухим пайком: лимонад, тушенка в маленьких банках, унифицированные наборы горбушек и пирожки с ежевикой. Стоимость этих четырех продуктов соответственно 12 руб., 34 руб., 3 руб. и 20 руб. Какова минимальная сумма, которую должен затратить прапорщик на питание одного солдата?

Задача 8.
Предприятие выпускает два вида продукции: Изделие 1 и Изделие 2. На изготовление единицы Изделия 1 требуется затратить a11 кг сырья первого типа, a21 кг сырья второго типа, a31 кг сырья третьего типа.
На изготовление единицы Изделия 2 требуется затратить a12 кг сырья первого типа, a22 кг сырья второго типа, a32 кг сырья третьего типа.
Производство обеспечено сырьем каждого типа в количестве b1 кг, b2 кг, b3 кг соответственно.
Рыночная цена единицы Изделия 1 составляет c1 тыс. руб., а единицы Изделия 2 — c2 тыс.руб.
Требуется:
1) построить экономико – математическую модель задачи;
2) составить план производства изделий, обеспечивающий максимальную выручку от их реализации при помощи графического метода решения задачи линейного программирования.
3) составить план производства изделий, обеспечивающий максимальную выручку от их реализации при помощи табличного симплекс – метода решения задачи линейного программирования.
4) составить план производства изделий, обеспечивающий максимальную выручку от их реализации, используя надстройку «Поиск решения» в среде MS EXCEL.

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Размещено на http://www.allbest.ru/

Частное образовательное учреждение высшего образования «Санкт-Петербургский университет технологий управления и экономики»

Кафедра экономики и менеджмента

КОНТРОЛЬНАЯ РАБОТА

По дисциплине: МЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ

Выполнил:

Студент (ка) 3
курса, группа № 19731Д/3-2

Крюк Альбина Владимировна

Руководитель:

к.э.н., доцент Ж.М. Козлова.

Барнаул
2016

Введение
Заключение
ВВЕДЕНИЕ
Решение широкого круга задач электроэнергетики и других отраслей народного хозяйства основывается на оптимизации сложной совокупности зависимостей, описанных математически с помощью некоторой «целевой функции» (ЦФ). Подобные функции можно записать для определения затрат на топливо для электростанций, на потери электроэнергии при транспорте ее от электростанции к потребителям и многие другие проблемные задачи. В таких случаях требуется найти ЦФ при определенных ограничениях, накладываемых на ее переменные. Если ЦФ линейно зависит от входящих в ее состав переменных и все ограничения образуют линейную систему уравнений и неравенств, то такая частная форма оптимизационной задачи получила название «задачи линейного программирования».
Темы контрольной работы «Решение задач линейного программирования в MS Excel», получить практические навыки в использовании электронных таблиц Microsoft Excel и решения оптимизационных задач линейного программирования.

1. Типовые задачи оптимизации и их экономико-математические модели

Экономико-математическое моделирование представляет собой процесс выражения экономических явлений математическими моделями. Экономическая модель — это схематичное представление экономического явления или процесса с использованием научной абстракции, отражение их характерных черт. Математические модели — основное средство решения задач оптимизации любой деятельности. По своей сути эти модели — средство плановых расчетов. Ценность их для экономического анализа и оптимизации решений состоит в том, что они позволяют оценить напряженность плановых заданий, определить лимитирующую группу оборудования, видов ресурсов, получать оценки их дефицитности и т.п. Математическое моделирование экономических явлений и процессов дает возможность получить четкое представление об исследуемом объекте, охарактеризовать и количественно описать его внутреннюю структуру и внешние связи. Модель — условный образ объекта управления /1/.

Экономико-математическая модель должна быть адекватной действительности, отражать существенные стороны и связи изучаемого объекта. Отметим принципиальные черты, характерные для построения экономико-математической модели любого вида. Процесс моделирования можно условно подразделить на три этапа:

1) анализ теоретических закономерностей, свойственных изучаемому явлению или процессу и эмпирических данных о его структуре и особенностях; на основе такого анализа формируются модели;

2) определение методов, с помощью которых можно решить задачу;

3) анализ полученных результатов.

Важнейшим моментом первого этапа моделирования является четкая формулировка конечной цели построения модели, а также определение критерия, по которому будут сравниваться различные варианты решения. Такими критериями в системе менеджмента могут быть:

а) максимизация полезного эффекта товара при ограничении совокупности затрат;

б) максимизация прибыли фирмы при условии, что качество товара не снизится; в) снижение себестоимости товара при условии, что его качество не снизится, затраты у потребителя не увеличатся;

г) рост производительности труда, улучшение использования оборудования или материалов, повышение оборачиваемости оборотных средств при условии, что качество товара не снизится и другие критерии не ухудшатся.

Таким образом, в качестве критерия оптимизации может быть целое или любой компонент прибыли, эффективности товара, объема рынка при условии, что другие компоненты при этом не ухудшатся.

Например, уравнение целевой функции (L) и система ограничений по оптимизации прибыли фирмы (правда, у авторов нет ограничений по качеству товара) будет иметь следующий вид:

где хj — количество производимой продукции j-го вида в натуральных измерениях;

Пj — прибыль, получаемая от производства единицы продукции j-го вида;

аij — норма расхода i-го производственного ресурса на производство единицы j-го вида продукции;

щj — запасы i-го вида производственного ресурса на рассматриваемый период времени.

Не для всякой экономической задачи нужна собственная модель. Некоторые процессы с математической точки зрения однотипны и могут описываться одинаковыми моделями. Например, в линейном программировании, теории массового обслуживания и других существуют типовые модели, к которым приводится множество конкретных задач.

Вторым этапом моделирования экономических процессов является выбор наиболее рационального математического метода для решения задачи. Например, для решения задач линейного программирования известно много методов: симплексный, потенциалов и др. Лучшей моделью является не самая сложная и самая похожая на реальное явление, а та, которая позволяет получить самое рациональное решение и наиболее точные экономические оценки. Излишняя детализация затрудняет построение модели, а излишнее укрупнение модели приводит к потере существенной экономической информации, к неадекватному отражению реальности.

Третьим этапом моделирования является всесторонний анализ результата, полученного при изучении экономического явления. Окончательным критерием достоверности и качества модели являются практика, соответствие полученных результатов и выводов реальным условиям, экономическая содержательность полученных оценок. Если результаты не соответствуют реальным условиям, то необходим анализ причин несоответствия, в качестве которых могут быть недостоверность информации, несоответствие модели экономическим условиям и др. По результатам анализа причин несоответствия экономико-математическая модель корректируется и решение задачи повторяется.

Решим графическим методом типовую задачу оптимизации

Некоторая фирма выпускает два набора удобрений для газонов: обычный и улучшенный. В обычный набор входит 3 кг азотных, 4 кг фосфорных и 1 кг калийных удобрений, а в улучшенный — 2 кг азотных, 6 кг фосфорных и 3 кг калийных удобрений. Известно, что для некоторого газона требуется по меньшей мере 10 кг азотных, 20 кг фосфорных и 7 кг калийных удобрений. Обычный набор стоит 3 ден. Ед., а улучшенный — 4 ден. Ед. Какие и сколько наборов удобрений нужно купить, чтобы обеспечить эффективное питание почвы и минимизировать стоимость?

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на максимум, и почему?

Сформулируем прямую оптимизационную задачу.

Пусть х1 — количество обычных наборов удобрений;

х2 — количество улучшенных наборов удобрений.

А для некоторого газона требуется по крайней мере 10 кг азотных удобрений, следовательно:

3х1 + 2х2 ? 10

4х1 + 6х2 ? 20

Стоимость необходимых наборов удобрений составит:

Таким образом, получим следующую экономико-математическую модель задачи:

min (х) = 3х1 + 4х2

3х1 + 2х2 ? 10

4х1 + 6х2 ? 20

Построим область решений системы ограничений. Для этого рассмотрим равенства и построим их графики — прямые.

1) 3х1 + 2х2 ? 10

3х1 + 2х2 = 10

3) х1 + 3х2 ? 7

Неравенство не выполняется, значит, исходному неравенству соответствует полуплоскость, не содержащая точку О(0;0).

х1 = 0 — ось ОХ2.

х2 = 0 — ось ОХ1.

Следовательно, область решений системы ограничений находится только в первой четверти декартовой системы координат.

Рис.1. Графическое решение ЗЛП

Находим общую часть всех построенных полуплоскостей. Это выпуклая заштрихованная область.

Для нахождения оптимального решения задачи изобразим графически функцию цели:

(х) = d1x1 + d2x2

(х) = 3х1 + 4х2

Для этого строим вектор d, начало которого в точке (0;0), а конец в точке (d1;d2).

И строим одну из линий уровня функции цели (это линия, на которой функция цели принимает постоянное значение).

Для определения минимума данной функции, передвигаем линию уровня в направлении, противоположном вектору d, и видим, что она последний раз соприкасается с областью решений в точке В, где и будет достигнут min(х).

Определим координаты точки В:

3х1 + 2х2 = 10 *(-3)

4х1 + 6х2 = 20

9х1 — 6х2 = -30

4х1 + 6х2 = 20

Складываем почленно уравнения и получаем:

(х) = 3*2 + 4*2 = 14 (ден. ед.)

Таким образом, чтобы минимизировать стоимость удобрений, нужно купить 2 обычных набора удобрений и 2 улучшенных набора удобрений. При этом минимальные затраты на покупку удобрений составят 14 денежных единиц. microsoft excel программирование математический

Если решать данную задачу на максимум, то конечного оптимума не найдем, т.к. функция цели неограниченна, область решений системы ограничений бесконечна.

2. Задачи линейного программирования, решение средствами MS Excel

Линейное программирование является разделом, с которого начала развиваться дисциплина «математическое программирование». Термин «программирование» в названии дисциплины ничего общего с термином «программирование (т.е. составление программ) для ЭВМ» не имеет, так как дисциплина «линейное программирование» возникла еще до того времени, когда ЭВМ стали широко применяться при решении математических, инженерных, экономических и других задач. Термин «линейное программирование» возник в результате неточного перевода английского «linear programming». Одно из значений слова «programming» — составление планов, планирование. Следовательно, правильным переводом «linear programming» было бы не «линейное программирование», а «линейное планирование», что более точно отражает содержание дисциплины. Однако, термин линейное программирование, нелинейное программирование и т.д. в нашей литературе стали общепринятыми. Задачи линейного программирования является удобной математической моделью для большого числа экономических задач (планирование производства, расходование материалов, транспортные перевозки и т.д.). Использование метода линейного программирования представляет собой важность и ценность — оптимальный вариант выбирается из достаточно значительного количества альтернативных вариантов. Также все экономические задачи, решаемые с применением линейного программирования, отличаются альтернативностью решения и определенными ограничивающими условиями.
В электронных таблицах Excel с помощью функции поиска решения можно вести поиск значения в целевой ячейке, изменения значения переменных. При этом для каждой переменной можно задать ограничения, например верхнюю границу. Перед тем как запустить поиск решения, необходимо четко сформулировать в модели решаемую проблему, т.е. определить условия, выполняемые при оптимизации. Отправленной точкой при поиске оптимального решения является модель вычисления, созданная в рабочем листе. Программе поиска решения при этом необходимы следующие данные. 1. Целевая ячейка — это ячейка в модели вычисления, значения в которой должно быть максимизировано, минимизировано или же равняться определенному указанному значению. Она должна содержать формулу, которая прямо или косвенно ссылается на изменяемые ячейки, или же самой быть изменяемой. 2. Значения в изменяемых ячейках будут последовательно (методом итераций) изменяться до тех пор, пока не будет получено нужное значение в целевой ячейке. Эти ячейки, следовательно, прямо или косвенно должны влиять на значение целевой ячейки. 3. Вы можете задать как для целевой, так и для изменяемых ячеек, ограничения и граничные условия. Можно задать также ограничения для других ячеек. Прямо или косвенно присутствующих в модели. Программа предоставляет возможность задать специальные параметры, определяющие процесс поиска решения. После задания всех необходимых параметров можно запустить поиск решения. Функция поиска решения создаст по итогам своей работы три отчета, которые можно пометить в рабочую книгу.Ограничения — это условия, которые должны быть выполнены аппаратом поиска решения при оптимизации модели.

Изучение литературы показало, что:

1. Линейное программирование — это один из первых и наиболее подробно изученных разделов математического программирования. Именно линейное программирование явилось тем разделом, с которого начала развиваться сама дисциплина «математическое программирование».

Линейное программирование представляет собой наиболее часто используемый метод оптимизации. К числу задач линейного программирования можно отнести задачи:

· рационального использования сырья и материалов; задачи оптимизации раскроя;

· оптимизации производственной программы предприятий;

· оптимального размещения и концентрации производства;

· составления оптимального плана перевозок, работы транспорта;

· управления производственными запасами;

· и многие другие, принадлежащие сфере оптимального планирования.

2. Графический метод довольно прост и нагляден для решения задач линейного программирования с двумя переменными. Он основан на геометрическом представлении допустимых решений и ЦФ задачи.

Суть графического метода заключается в следующем. По направлению (против направления) вектора в ОДР производится поиск оптимальной точки. Оптимальной считается точка, через которую проходит линия уровня, соответствующая наибольшему (наименьшему) значению функции. Оптимальное решение всегда находится на границе ОДР, например, в последней вершине многоугольника ОДР, через которую пройдет целевая прямая, или на всей его стороне.

ЗАКЛЮЧЕНИЕ

С помощью правильной постановки задачи планирования производства и наличия основных производственных параметров, мы можем найти план выпуска продукции, при котором будет достигнута максимальная прибыль.

Благодаря программному продукту Excel, который входит в пакет MS Office, решение наших задач ускоряется в несколько десятков раз. А благодаря точным математическим расчетам данного ПО, мы можем без сомнения найти самые точные результаты исследований.

Размещено на Allbest.ru

…

Подобные документы

Краткие сведения об электронных таблицах MS Excel. Решение задачи линейного программирования. Решение с помощью средств Microsoft Excel экономической оптимизационной задачи, на примере «транспортной задачи». Особенности оформления документа MS Word.

курсовая работа , добавлен 27.08.2012

История развития и функции линейного программирования. Исследование условий типовых задач и возможностей табличного процессора. Решение задач о рационе питания, плане производства, раскрое материалов и рациональной перевозке груза в среде MS Excel.

курсовая работа , добавлен 28.04.2014

Принципы решения задач линейного программирования в среде электронных таблиц Excel, в среде пакета Mathcad. Порядок решения задачи о назначении в среде электронных таблиц Excel. Анализ экономических данных с помощью диаграмм Парето, оценка результатов.

лабораторная работа , добавлен 26.10.2013

Алгоритм решения задач линейного программирования симплекс-методом. Построение математической модели задачи линейного программирования. Решение задачи линейного программирования в Excel. Нахождение прибыли и оптимального плана выпуска продукции.

курсовая работа , добавлен 21.03.2012

Изучение и укрепление на практике всех моментов графического метода решения задач линейного программирования о производстве журналов «Автомеханик» и «Инструмент». Построение математической модели. Решение задачи с помощью электронной таблицы Excel.

курсовая работа , добавлен 10.06.2014

Общее понятие и характеристика задачи линейного программирования. Решение транспортной задачи с помощью программы MS Excel. Рекомендации по решению задач оптимизации с помощью надстройки «Поиск решения». Двойственная задача линейного программирования.

дипломная работа , добавлен 20.11.2010

Анализ метода линейного программирования для решения оптимизационных управленческих задач. Графический метод решения задачи линейного программирования. Проверка оптимального решения в среде MS Excel с использованием программной надстройки «Поиск решения».

курсовая работа , добавлен 29.05.2015

Разработка таблиц в Excel методами линейного программирования с целью оптимизации расходов ресурсов и запасов на изготовление продукции: определение переменных величин, структуры целевой функции, построение математической модели и блок-схем решения задач.

курсовая работа , добавлен 07.06.2010

Методы решения задач линейного программирования: планирования производства, составления рациона, задачи о раскрое материалов и транспортной. Разработка экономико-математической модели и решение задачи с использованием компьютерного моделирования.

курсовая работа , добавлен 13.03.2015

Графическое решение задач. Составление математической модели. Определение максимального значения целевой функции. Решение симплексным методом с искусственным базисом канонической задачи линейного программирования. Проверка оптимальности решения.

Источник