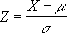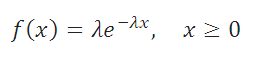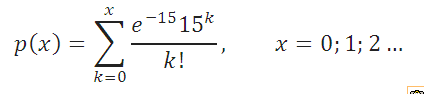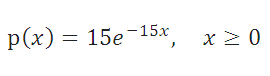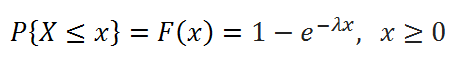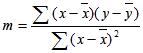The term normalization in itself is a buzzword that is popular amongst people who come from different fields such as Machine Learning, Data Science, Statistics, etc. Normalization is a general term that means to scale down values inside a certain range. The origin of the word normalization being a buzzword comes from the fact that it is often misunderstood by people and is interchangeably used with another statistical term standardization. In this article, we are going to demystify both of these terms and later we will read how we can implement these techniques on a sample dataset in Excel.
Normalization (Or Min-Max scaling) data in excel
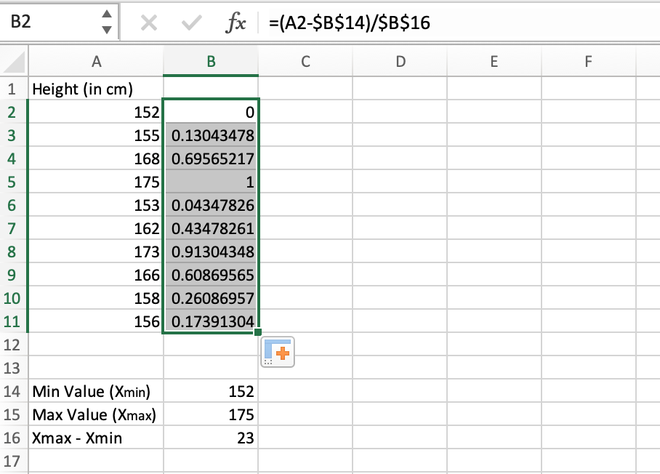
It is the process of scaling data in such a way that all data points lie in a range of 0 to 1. Thus, this technique, makes it possible to bring all data points to a common scale. The mathematical formula for normalization is given as:
, where X is the data point, Xmax and Xmin are the maximum and minimum value in the group of records respectively. The process of normalization is generally used when the distribution of data does not follow the Gaussian distribution.
Let’s have a look at one example to see how can we perform normalization on a sample dataset. Suppose, we have a record of the height of 10 students inside a class as shown below:
| Height (in cm) |
| 152 |
| 155 |
| 168 |
| 175 |
| 153 |
| 162 |
| 173 |
| 166 |
| 158 |
| 156 |
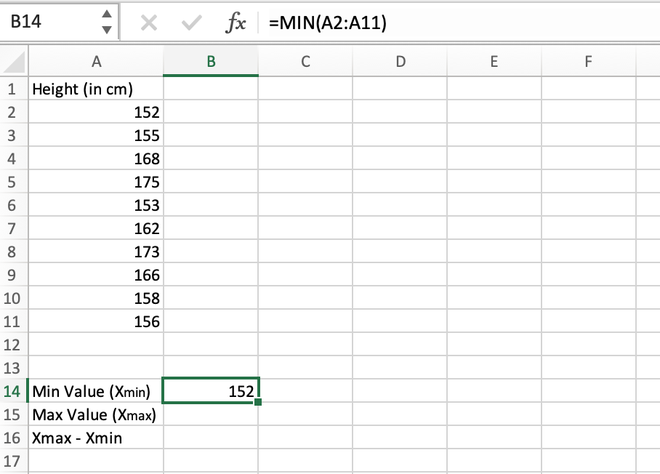
Step 1: Calculate the minimum value in the distribution. It can be calculated using the MIN() function. The minimum value comes out to be 152 which is stored in the B14 cell.
Calculating the minimum value using the MIN() function
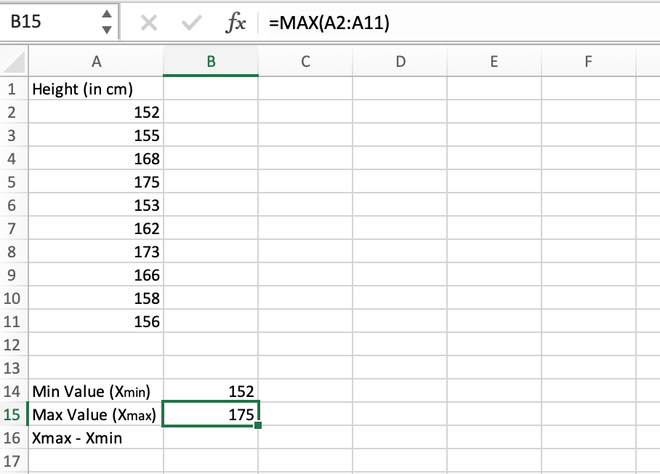
Step 2: Calculate the maximum value in the distribution. It can be calculated using the MAX() function. The maximum value comes out to be 175 which is stored in the B15 cell.
Calculating the maximum value using the MAX() function
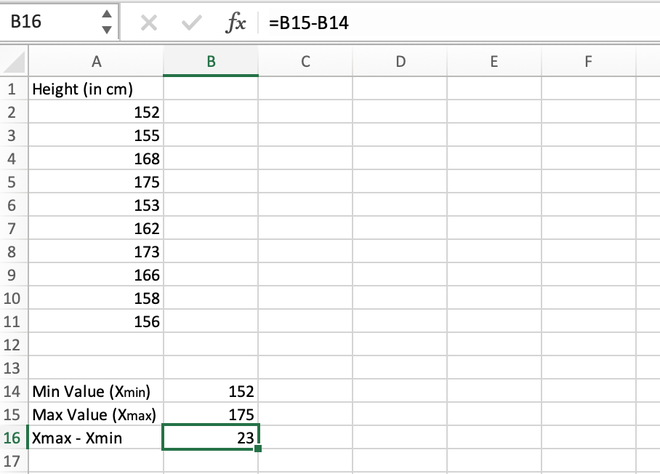
Step 3: Find the difference between the maximum and minimum values. Their difference comes out to be 175 – 152 = 23 which is stored in the B16 cell.
Calculating the difference (Max-Min)
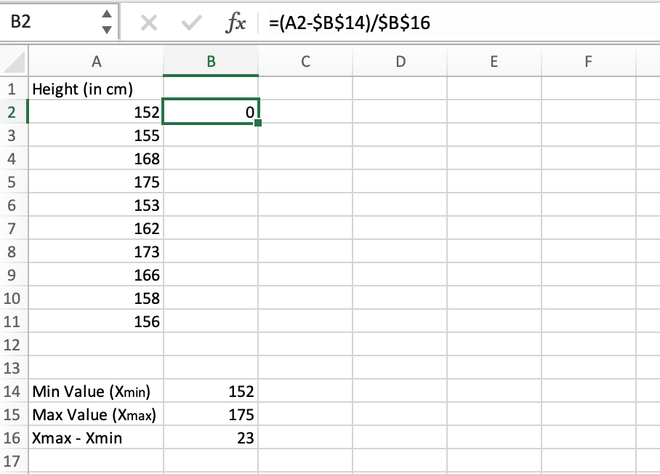
Step 4: For the first data stored in the A2 cell, we will calculate the normalized value as shown in the below video.
Calculating the normalized value for the first element
Step 5: We can manually calculate all values one by one for each data record or we can directly get values for all the other cells using the auto-fill feature of Excel. For this, go to the right corner of the B2 cell until a (+) symbol appears, and then drag the cursor to the bottom to auto-populate values inside all the cells.
Calculating the normalized value for the entire range
Note: While calculating the first normalized value in the B2 cell, it should be made sure that the reference address for the B14 and B16 cells should be locked using Fn + F4 button otherwise an error will be thrown.
If we have a close look at the results, we can notice all the values lies in the range 0 to 1.
Standardization (Or Z-score normalization)
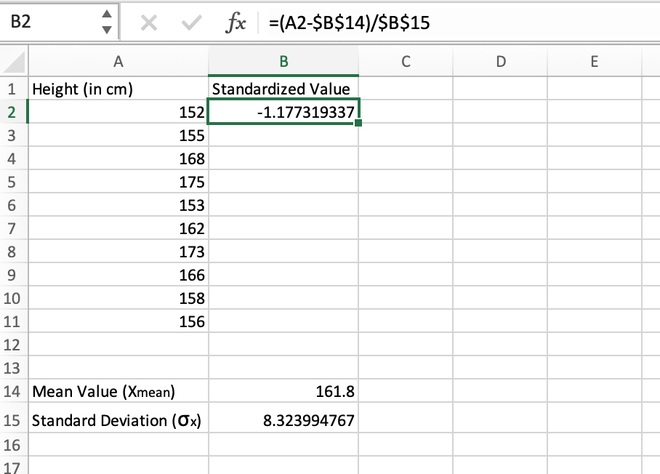
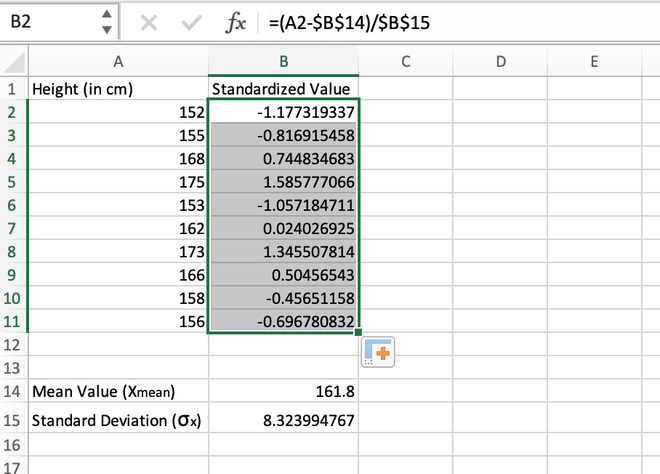
Standardization is a process in which we want to scale our data in such a way that the distribution of our data has its mean as 0 and standard deviation as 1. The mathematical formula for standardization is given as:
, where where X is the data point, Xmean is the mean of the distribution and σx is the standard deviation of the distribution.
The process of standardization is generally used when we know the distribution of data follows the gaussian distribution.
Method 1: Calculating z-score normalization manually
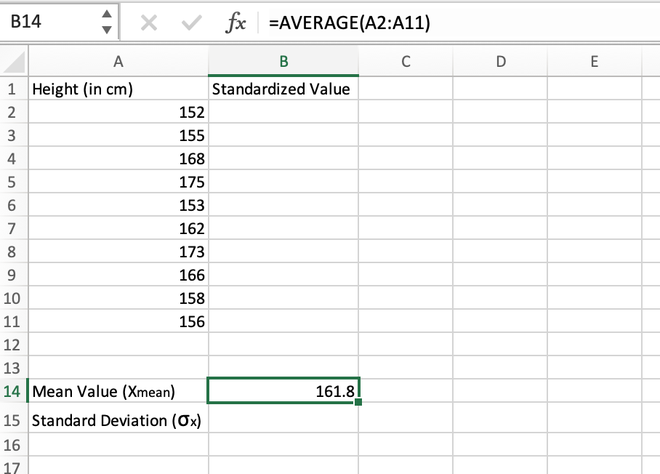
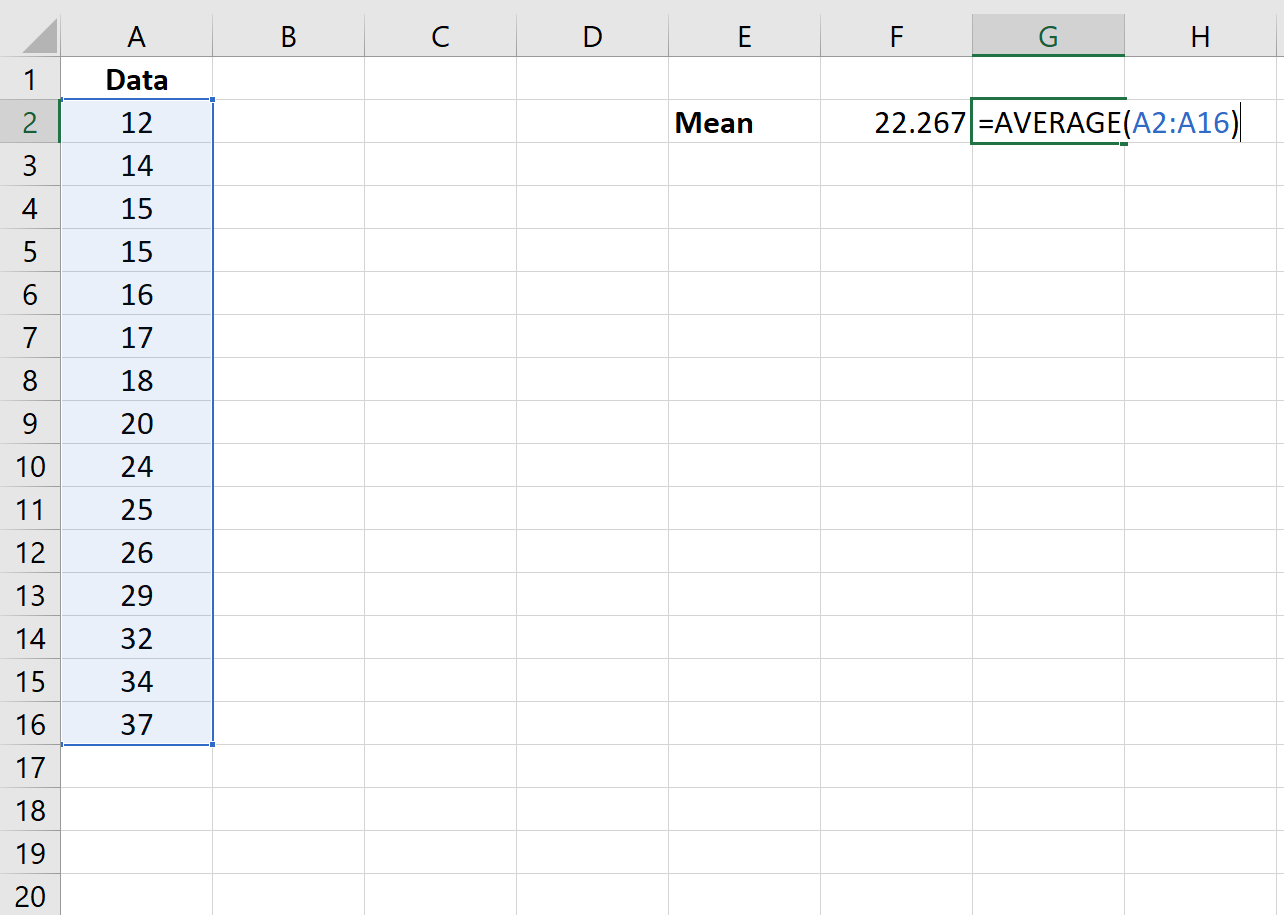
Step 1: Calculate the mean/average of the distribution. It can be done using the AVERAGE() function. The mean value comes out to be 161.8 and is stored in the B14 cell.
Calculating the mean value using the AVERAGE() function
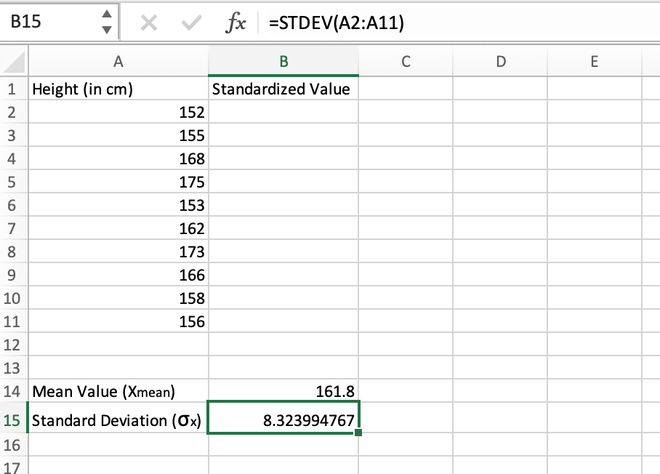
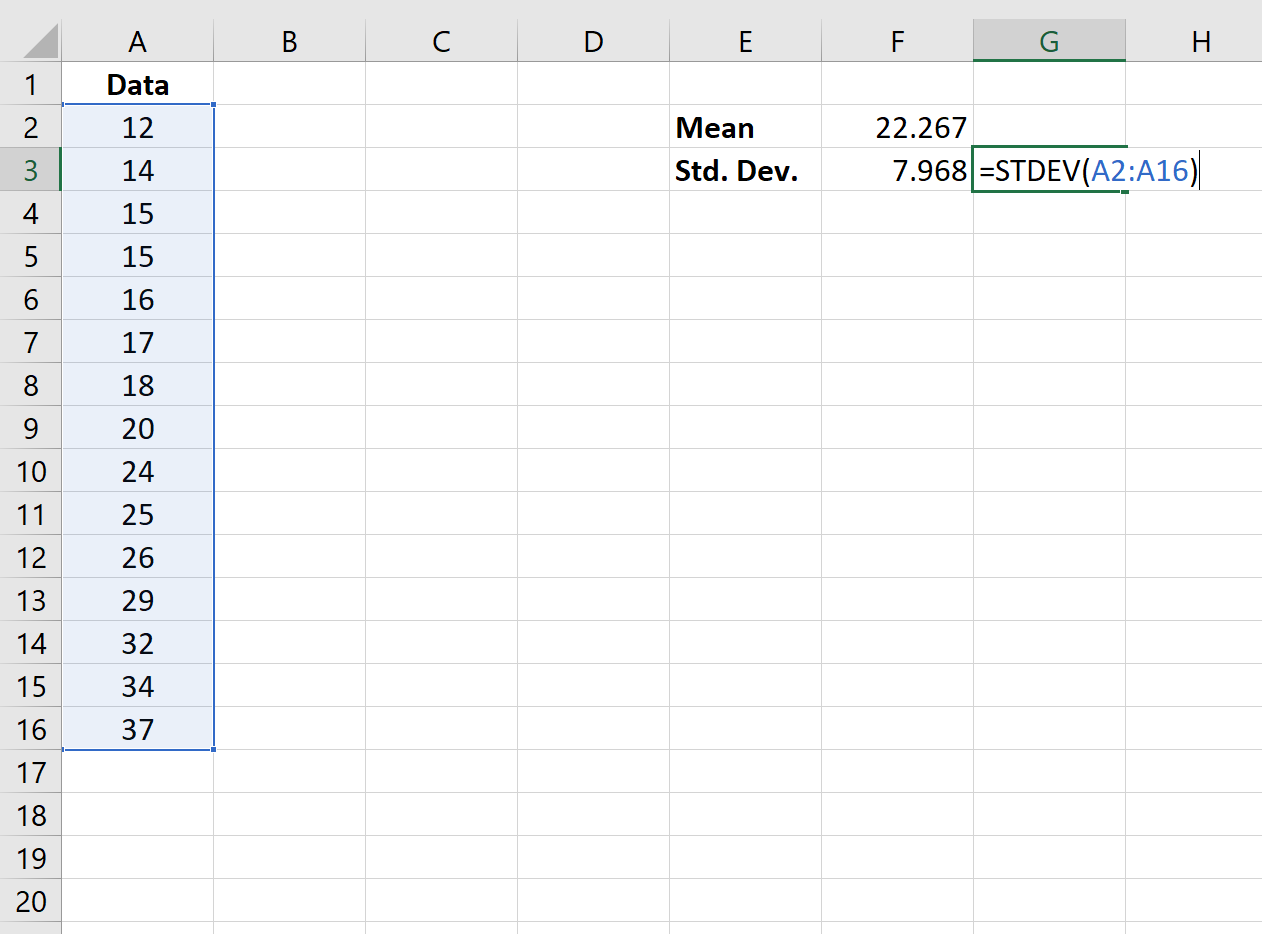
Step 2: Calculate the standard deviation of the distribution which can be done using the STDEV() function. The standard deviation comes out to be 8.323994767 which is stored in the B15 cell.
Calculating the standard deviation using the STDEV() function
Step 3: For the first data stored in the A2 cell, we will calculate the standardized value as shown in the image given below.
Calculating the standardized value for the first element
Step 4: After manually calculating the first value, we can simply use the auto-fill feature of Excel to populate the standardized values for all other records.
Calculating the standardized value for the entire range using auto-fill
Note: While calculating the first standardized value in the B2 cell, it should be made sure that the reference address for the B14 and B15 cells should be locked using Fn+F4 button otherwise an error will be thrown.
Method 2: Calculating Z-score normalization using the STANDARDIZE() function
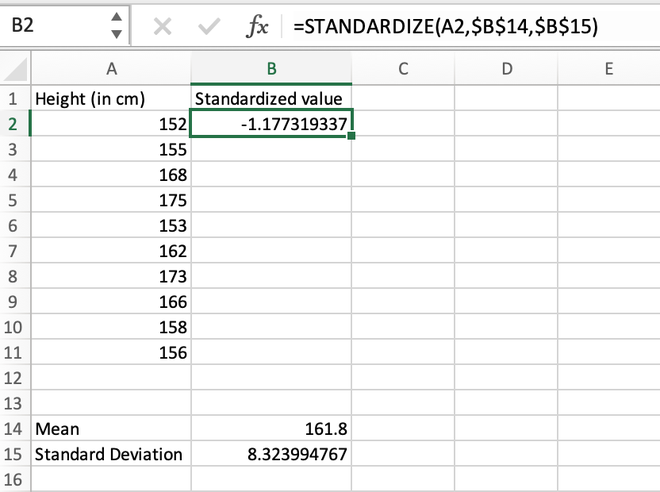
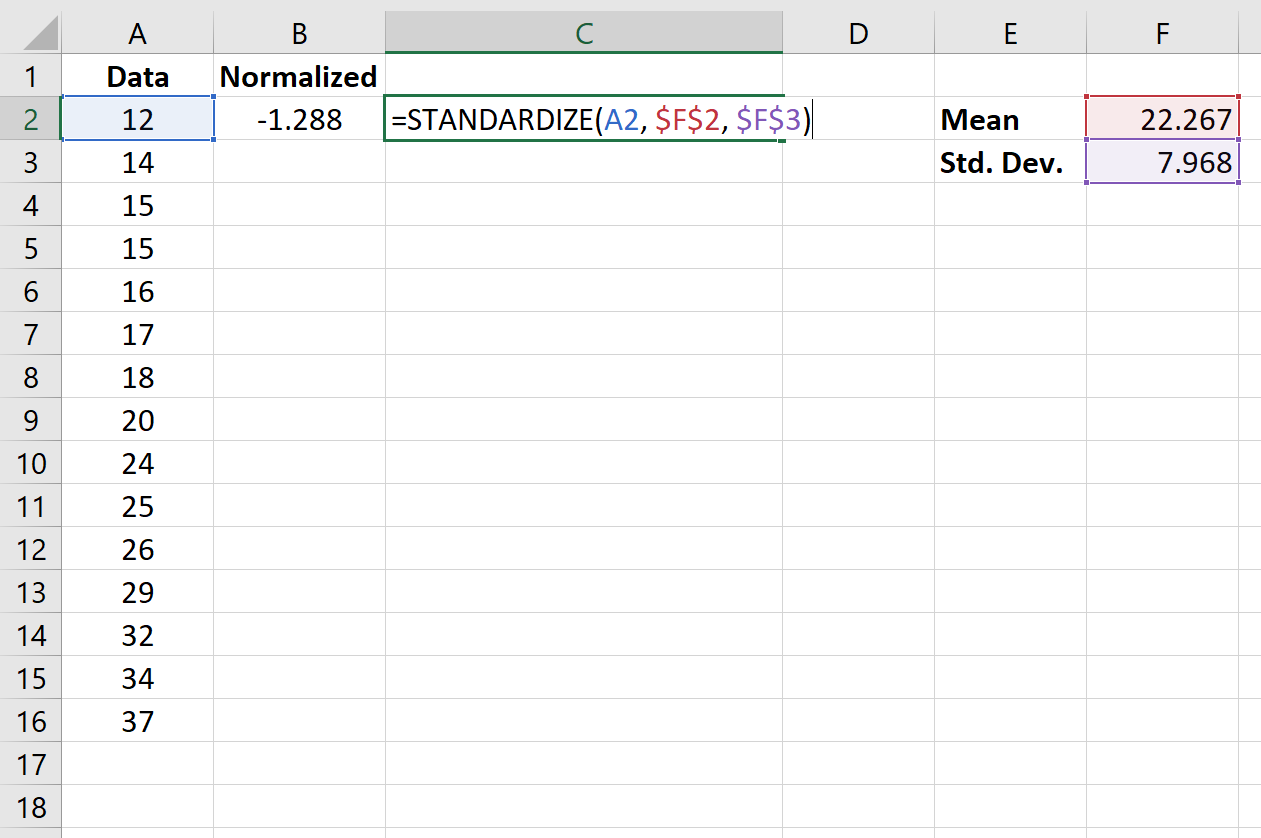
We can even use the built-in STANDARDIZE() function to find the standardized value of an element. The syntax for STANDARDIZE() function is given as:
=STANDARDIZE(x,mean,std_dev)
Where x is the specific element/range of cells, mean is the average/arithmetic mean of all the elements in the record, and std_dev is the standard deviation of all the elements in the record
Step 1: Calculate the mean/average of the distribution. It can be done using the AVERAGE() function. The mean value comes out to be 161.8 and is stored in the B14 cell.
Calculating the mean value using the AVERAGE() function
Step 2: Calculate the standard deviation of the distribution which can be done using the STDEV() function. The standard deviation comes out to be 8.323994767 which is stored in the B15 cell.
Calculating the standard deviation using the STDEV() function
Step 3: For the first data stored in the A2 cell, we will calculate the standardized value as shown in the below image.
Calculating the standardized value for the first element using the STANDARDIZE() function
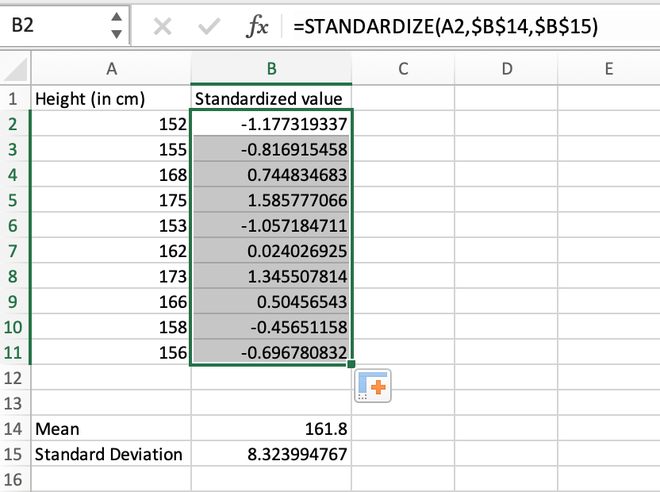
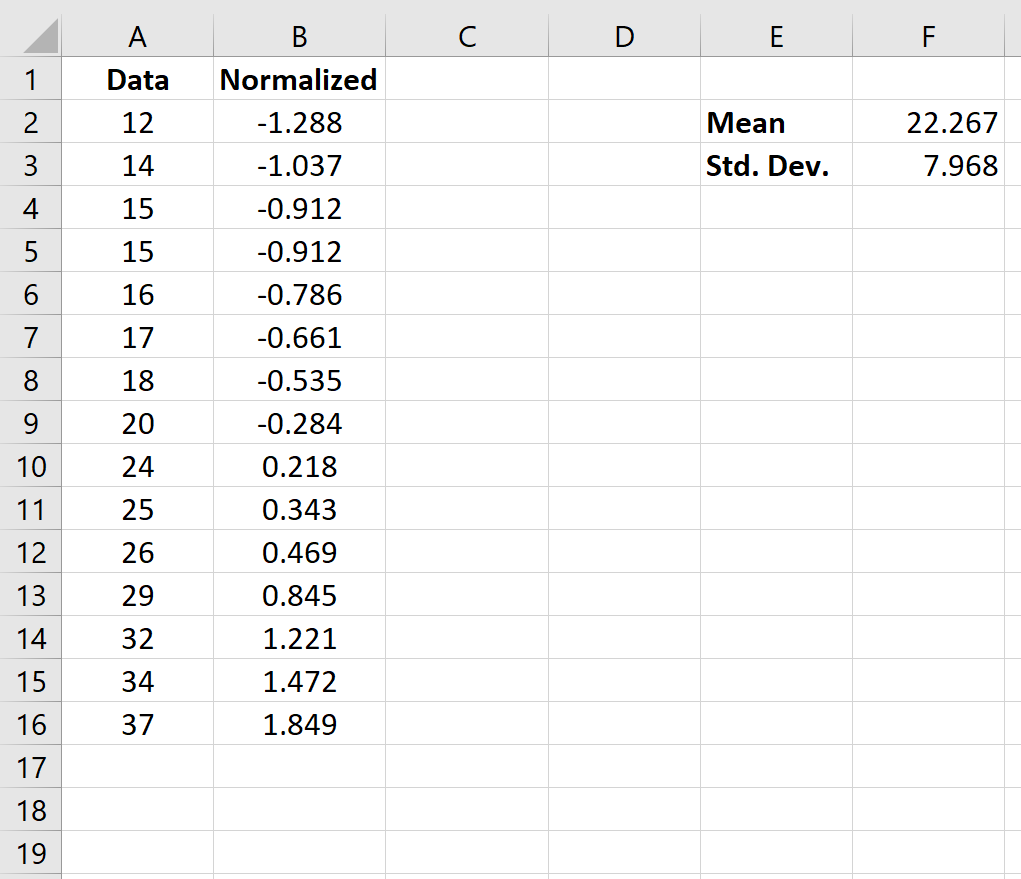
Step 4: After manually calculating the first value, we can simply use the auto-fill feature of Excel to populate the standardized values for all other records.
Calculating the standardized value for the entire range using auto-fill
17 авг. 2022 г.
читать 2 мин
«Нормализация» набора значений данных означает масштабирование значений таким образом, чтобы среднее значение всех значений равнялось 0, а стандартное отклонение равнялось 1.
В этом руководстве объясняется, как нормализовать данные в Excel.
Пример: как нормализовать данные в Excel
Предположим, у нас есть следующий набор данных в Excel:
Выполните следующие шаги, чтобы нормализовать этот набор значений данных.
Шаг 1: Найдите среднее значение.
Во-первых, мы будем использовать функцию =AVERAGE(диапазон значений) , чтобы найти среднее значение набора данных.
Шаг 2: Найдите стандартное отклонение.
Далее мы будем использовать функцию = СТАНДОТКЛОН (диапазон значений) , чтобы найти стандартное отклонение набора данных.
Шаг 3: нормализуйте значения.
Наконец, мы будем использовать функцию STANDARDIZE(x, mean, standard_dev) для нормализации каждого из значений в наборе данных.
ПРИМЕЧАНИЕ:
Функция СТАНДАРТИЗАЦИЯ использует следующую формулу для нормализации заданного значения данных:
Нормализованное значение = (x – x ) / с
куда:
- х = значение данных
- x = среднее значение набора данных
- s = стандартное отклонение набора данных
На следующем изображении показана формула, используемая для нормализации первого значения в наборе данных:
Как только мы нормализуем первое значение в ячейке B2, мы можем навести указатель мыши на правый нижний угол ячейки B2, пока не появится маленький +.Дважды щелкните + , чтобы скопировать формулу в оставшиеся ячейки:
Теперь каждое значение в наборе данных нормализовано.
Как интерпретировать нормализованные данные
Формула, которую мы использовали для нормализации заданного значения данных x, была следующей:
Нормализованное значение = (x – x ) / с
куда:
- х = значение данных
- x = среднее значение набора данных
- s = стандартное отклонение набора данных
Если конкретная точка данных имеет нормализованное значение больше 0, это указывает на то, что точка данных больше среднего. И наоборот, нормализованное значение меньше 0 указывает на то, что точка данных меньше среднего значения.
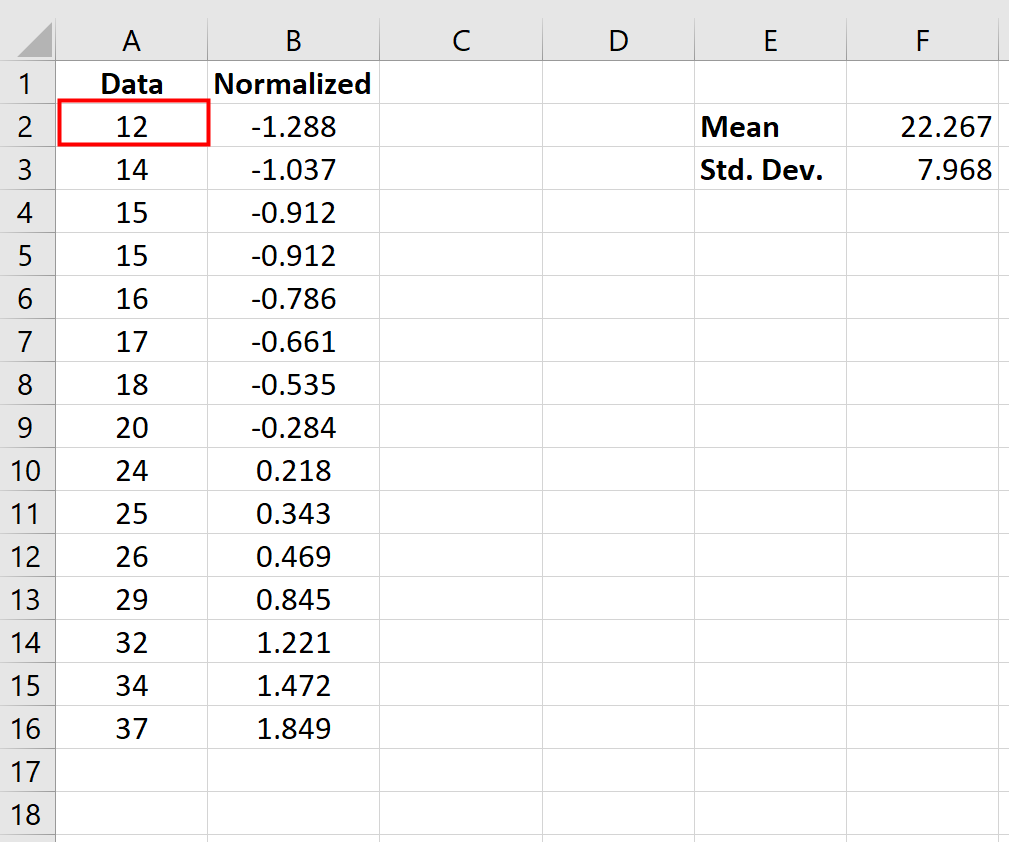
В частности, нормализованное значение говорит нам, сколько стандартных отклонений исходной точки данных от среднего. Например, рассмотрим точку данных «12» в нашем исходном наборе данных:
Нормализованное значение для «12» оказалось равным -1,288, которое было рассчитано как:
Нормализованное значение = (х – х ) / с = (12 – 22,267) / 7,968 = -1,288
Это говорит нам о том, что значение «12» на 1,288 стандартных отклонения ниже среднего значения в исходном наборе данных.
Каждое из нормализованных значений в наборе данных может помочь нам понять, насколько близко или далеко конкретное значение данных от среднего. Небольшое нормализованное значение указывает, что значение близко к среднему, в то время как большое нормализованное значение указывает, что значение далеко от среднего.
Функция НОРМАЛИЗАЦИЯ в Excel предназначена для нахождения нормализованного значения некоторой величины из распределения, характеризующегося известными показателями стандартного отклонения и среднего.
Примеры использования функции НОРМАЛИЗАЦИЯ в Excel
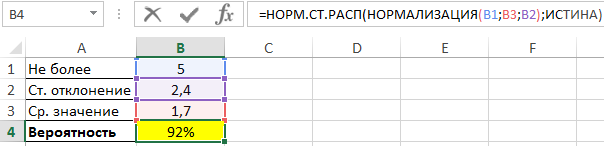
Значение, определяемое функцией НОРМАЛИЗАЦИЯ, используется для вычисления вероятности нахождения некоторой величины в диапазоне значений. Эту вероятность можно рассчитать в Excel с помощью функции НОРМ.СТ.РАСП. Таким образом, эти функции имеют следующую взаимосвязь: =НОРМ.СТ.РАСП(НОРМАЛИЗАЦИЯ(аргументы)).
Таким образом, функция НОРМАЛИЗАЦИЯ может быть использована для преобразования нормального распределения к стандартному нормальному. У такого распределения дисперсия равна 1, а математическое ожидание – 0. Таким образом, рассматриваемая функция использует следующий алгоритм вычислений:
Z=(x-M)/D
где:
- Z – вычисляемая величина, распределенная по стандартному нормальному закону;
- x — исходное значение;
- M – математическое ожидание;
- D – дисперсия.
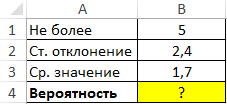
Пример 1. Определить вероятность того, что некоторая величина, которая распределена по нормальному закону, меньше или равна значению 5. Для ряда значений этой величины известны следующие показатели: среднее – 1,7, стандартное отклонение – 2,4.
Вид таблицы данных:
Для нахождения вероятности используем следующую формулу:
Для вычисления вероятности вхождения в диапазон (<=5) используем функцию НОРМ.СТ.РАСП со вторым аргументом, принимающим значение ИСТИНА (интегральная). Значение z (нормализованное) определено с помощью рассматриваемой функции.
Искомое число вероятности:
В итоговом результате вычисления функции получаем относительное – 92%.
Расчет процента вероятности с помощью нормализации в Excel
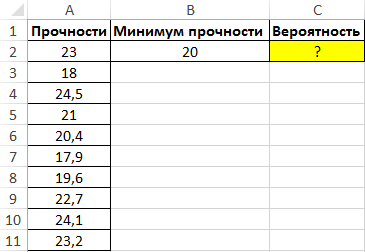
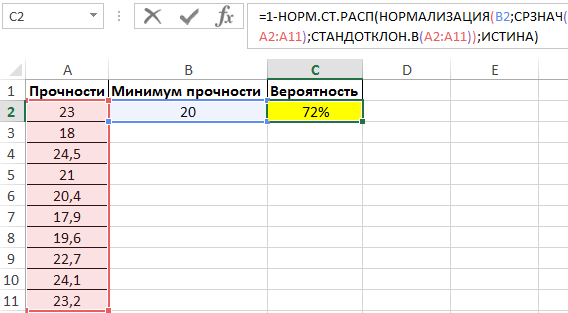
Пример 2. Данные о прочности изделий из исследуемой партии приведены в таблице Excel. Определить вероятность того, что потребитель купит партию изделий, прочность которых будет равна 20 Мпа или превысит это значение.
Вид таблицы данных:
Для нахождения вероятности используем следующую формулу:
С помощью функции НОРМ.СТ.РАСП определяем вероятность того, что прочность изделий из партии не будет соответствовать условию (больше 20Мпа). Поэтому искомое значение получаем в виде разности 1 и найденной вероятности. Для определения среднего значения и стандартного отклонений для исследуемого ряда используем функции СРЗНАЧ и СТАНДОТКЛОН.В соответственно.
Полученный результат:
Правила использования функции НОРМАЛИЗАЦИЯ в Excel
Функция имеет следующую синтаксическую запись:
=НОРМАЛИЗАЦИЯ(x;среднее;стандартное_откл)
Описание аргументов (все обязательны для заполнения):
- x – принимает числовое значение, соответствующее величине, для которой требуется определить нормализованное значение;
- среднее – принимает числовое значение, характеризующее величину среднего арифметического исследуемого числового ряда;
- стандартное_откл – принимает число, которое соответствует величине стандартного отклонения, определенной для исследуемой последовательности.
Примечания:
- Каждый аргумент рассматриваемой функции необходимо указывать как число либо передавать ссылку на ячейку, содержащую числовые данные. НОМАЛИЗАЦИЯ будет возвращать код ошибки #ЗНАЧ!, если любой из аргументов указан в виде данных, которые не могут быть преобразованы к числовым значениям.
- Если рассматриваемая функция принимает в качестве любого аргумента данные логического типа (ИСТИНА, ЛОЖЬ), выполняется автоматическое преобразование к соответствующим числовым значениям (1, 0 соответственно).
- Если аргумент стандартное_откл задан в виде числа из диапазона отрицательных значений или 0 (нулем), функция вернет код ошибки #ЧИСЛО!
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции НОРМАЛИЗАЦИЯ в Microsoft Excel.
Описание
Возвращает нормализованное значение для распределения, характеризуемого средним и стандартным отклонением.
Синтаксис
НОРМАЛИЗАЦИЯ(x;среднее;стандартное_откл)
Аргументы функции НОРМАЛИЗАЦИЯ описаны ниже.
-
X Обязательный. Нормализуемое значение.
-
Среднее Обязательный. Среднее арифметическое распределения.
-
Стандартное_откл Обязательный. Стандартное отклонение распределения.
Замечания
-
Если standard_dev ≤ 0, возвращается стандартное #NUM! значение ошибки #ЗНАЧ!.
-
Уравнение для нормализованного значения имеет следующий вид:
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|
42 |
Значение, которое нужно нормализовать. |
|
|
40 |
Среднее арифметическое распределения. |
|
|
1,5 |
Стандартное отклонение распределения. |
|
|
Формула |
Описание |
Результат |
|
=НОРМАЛИЗАЦИЯ(A2;A3;A4) |
Нормализованное значение числа 42, полученное с использованием числа 40 в качестве среднего арифметического и числа 1,5 в качестве стандартного отклонения. |
1,33333333 |
Нужна дополнительная помощь?
Вычисление доверительного интервала в Microsoft Excel
Одним из методов решения статистических задач является вычисление доверительного интервала. Он используется, как более предпочтительная альтернатива точечной оценке при небольшом объеме выборки. Нужно отметить, что сам процесс вычисления доверительного интервала довольно сложный. Но инструменты программы Эксель позволяют несколько упростить его. Давайте узнаем, как это выполняется на практике.
Процедура вычисления
Этот метод используется при интервальной оценке различных статистических величин. Главная задача данного расчета – избавится от неопределенностей точечной оценки.
В Экселе существуют два основных варианта произвести вычисления с помощью данного метода: когда дисперсия известна, и когда она неизвестна. В первом случае для вычислений применяется функция ДОВЕРИТ.НОРМ, а во втором — ДОВЕРИТ.СТЮДЕНТ.
Способ 1: функция ДОВЕРИТ.НОРМ
Оператор ДОВЕРИТ.НОРМ, относящийся к статистической группе функций, впервые появился в Excel 2010. В более ранних версиях этой программы используется его аналог ДОВЕРИТ. Задачей этого оператора является расчет доверительного интервала с нормальным распределением для средней генеральной совокупности.
Его синтаксис выглядит следующим образом:
«Альфа» — аргумент, указывающий на уровень значимости, который применяется для расчета доверительного уровня. Доверительный уровень равняется следующему выражению:
«Стандартное отклонение» — это аргумент, суть которого понятна из наименования. Это стандартное отклонение предлагаемой выборки.
«Размер» — аргумент, определяющий величину выборки.
Все аргументы данного оператора являются обязательными.
Функция ДОВЕРИТ имеет точно такие же аргументы и возможности, что и предыдущая. Её синтаксис таков:
Как видим, различия только в наименовании оператора. Указанная функция в целях совместимости оставлена в Excel 2010 и в более новых версиях в специальной категории «Совместимость». В версиях же Excel 2007 и ранее она присутствует в основной группе статистических операторов.
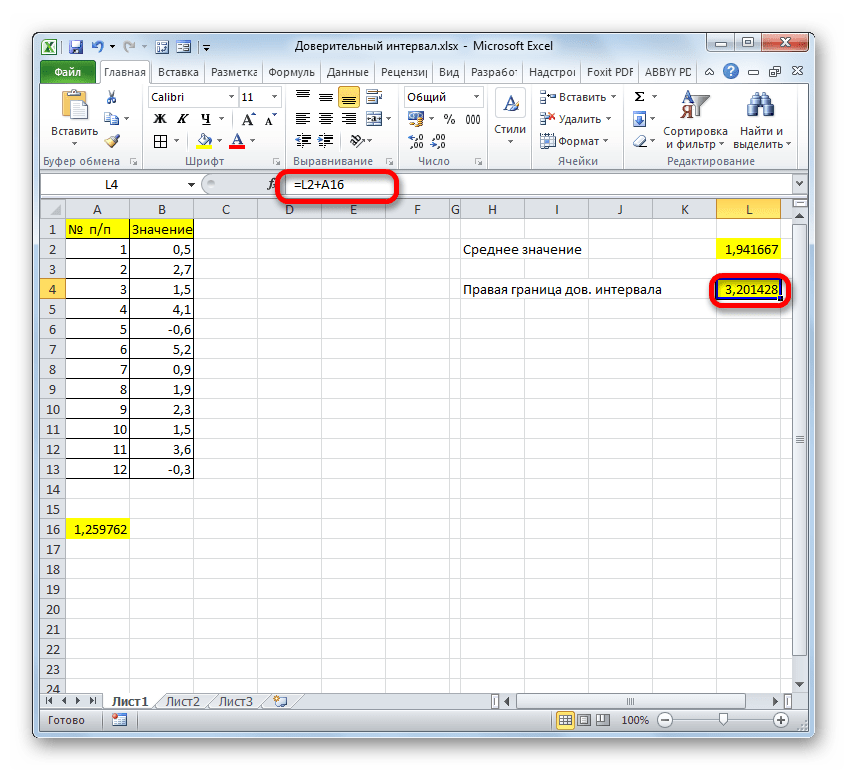
Граница доверительного интервала определяется при помощи формулы следующего вида:
Где X – это среднее выборочное значение, которое расположено посередине выбранного диапазона.
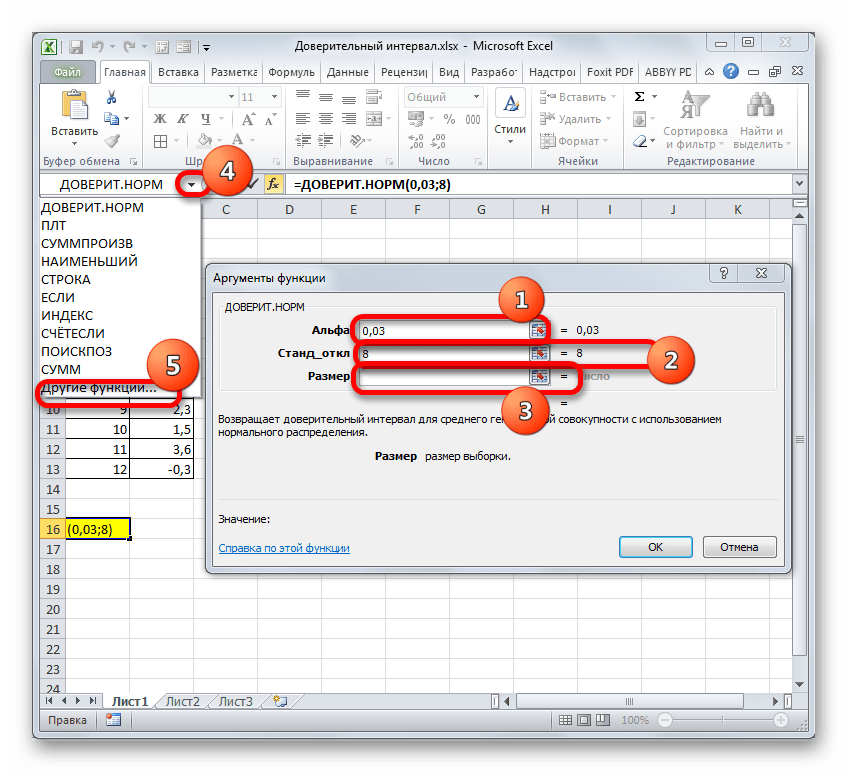
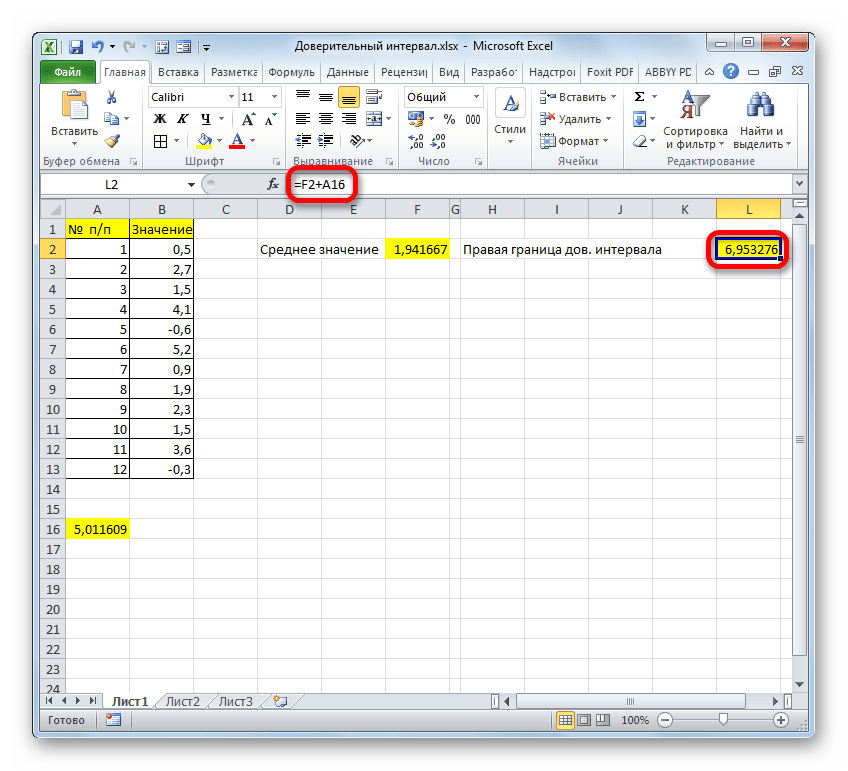
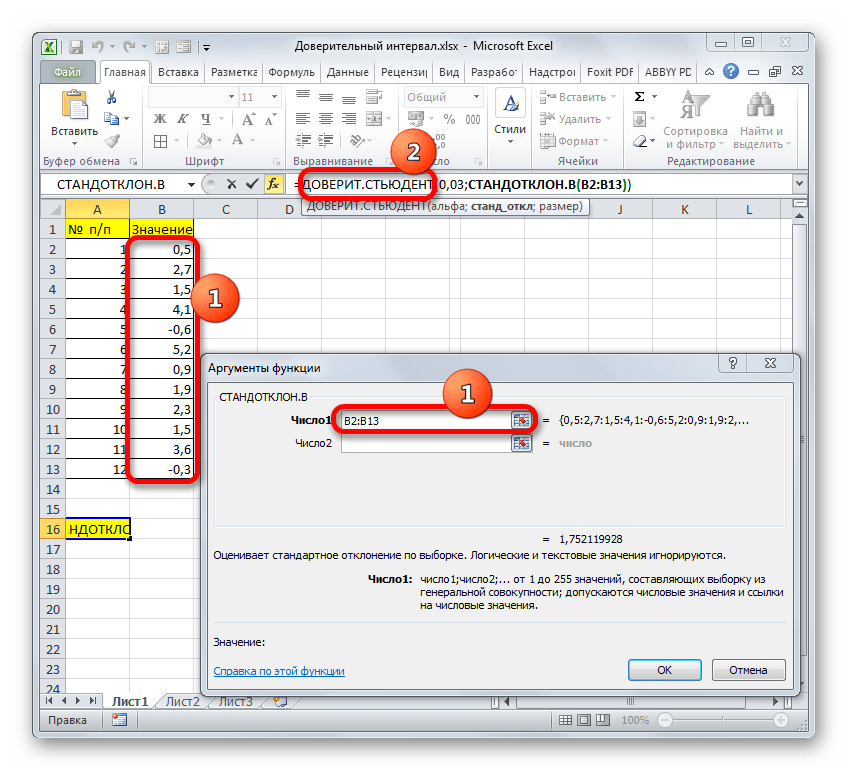
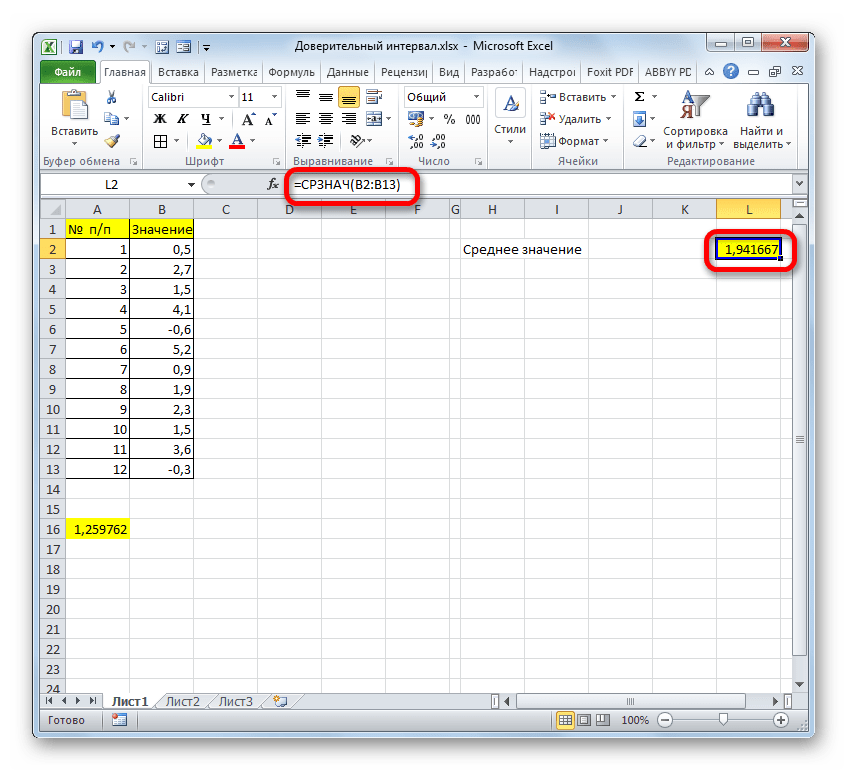
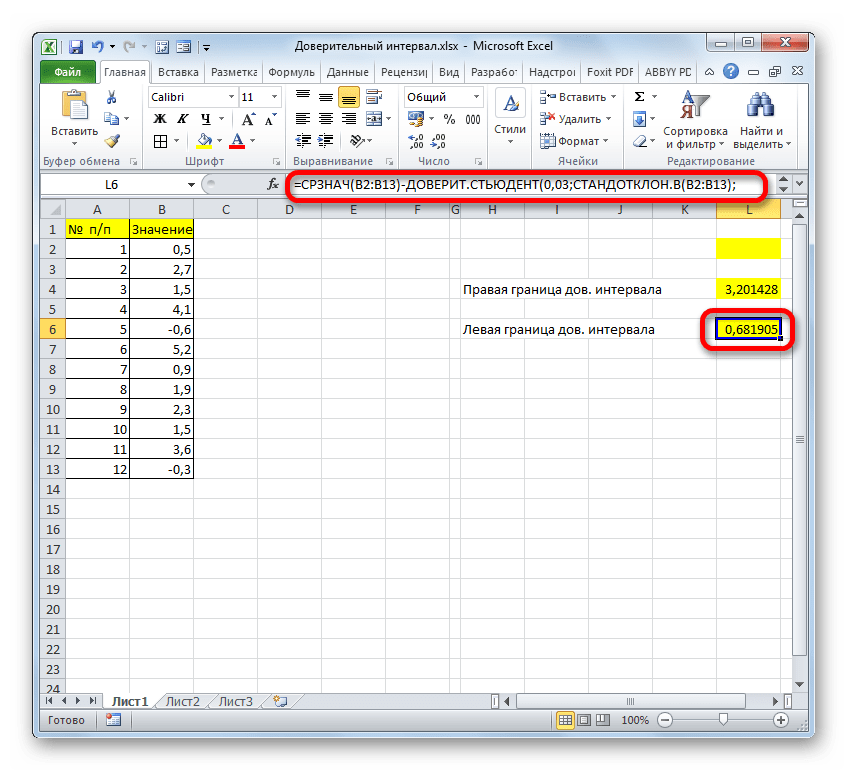
Теперь давайте рассмотрим, как рассчитать доверительный интервал на конкретном примере. Было проведено 12 испытаний, вследствие которых были получены различные результаты, занесенные в таблицу. Это и есть наша совокупность. Стандартное отклонение равно 8. Нам нужно рассчитать доверительный интервал при уровне доверия 97%.
- Выделяем ячейку, куда будет выводиться результат обработки данных. Щелкаем по кнопке «Вставить функцию».
Значит, чтобы посчитать уровень значимости, то есть, определить значение «Альфа» следует применить формулу такого вида:
То есть, подставив значение, получаем:
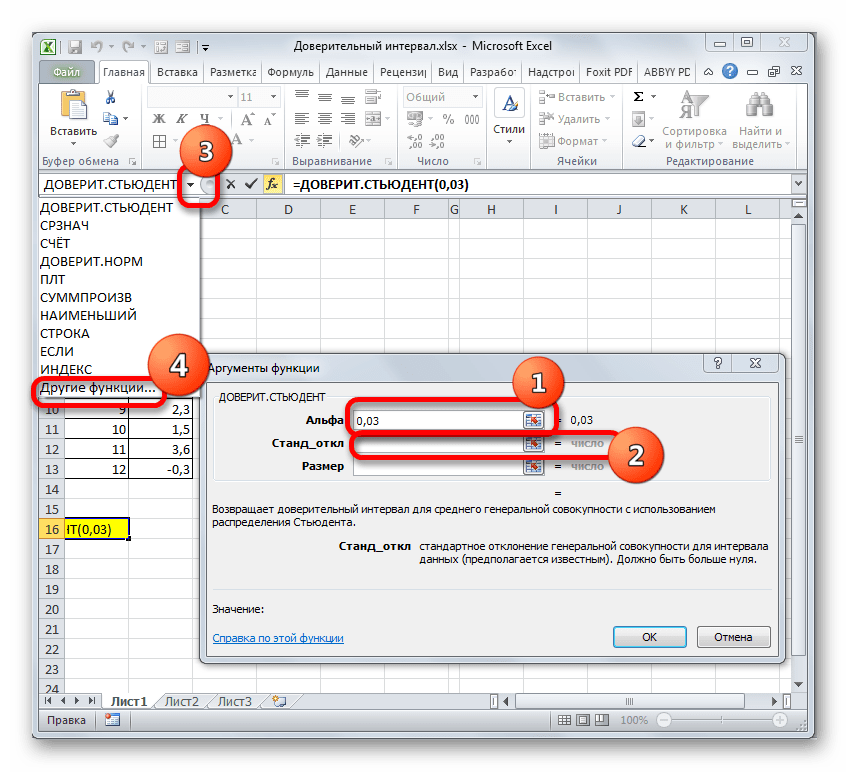
Путем нехитрых расчетов узнаем, что аргумент «Альфа» равен 0,03. Вводим данное значение в поле.
Как известно, по условию стандартное отклонение равно 8. Поэтому в поле «Стандартное отклонение» просто записываем это число.
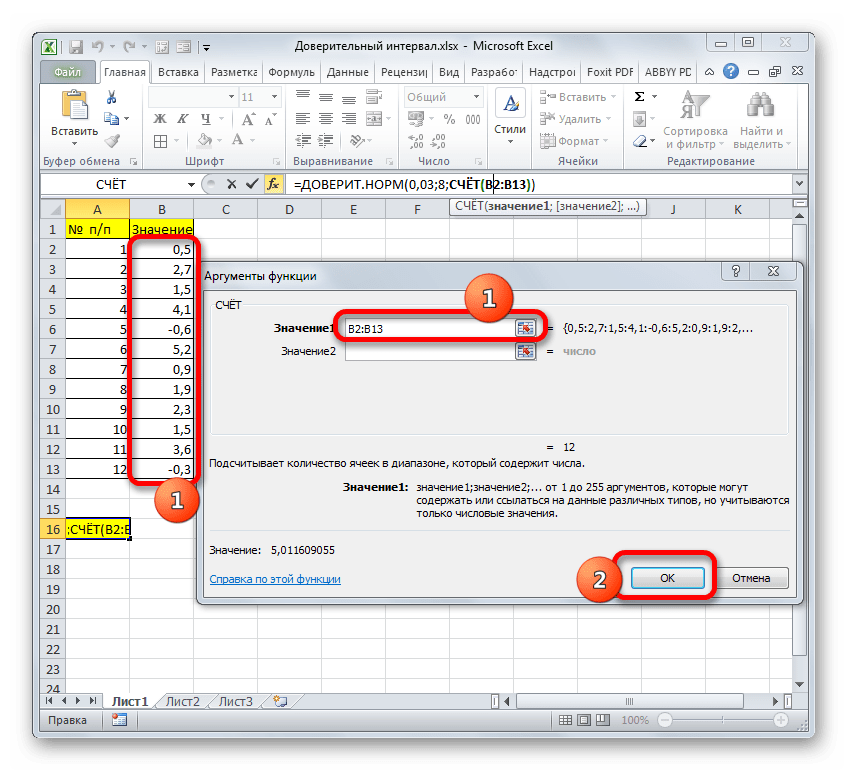
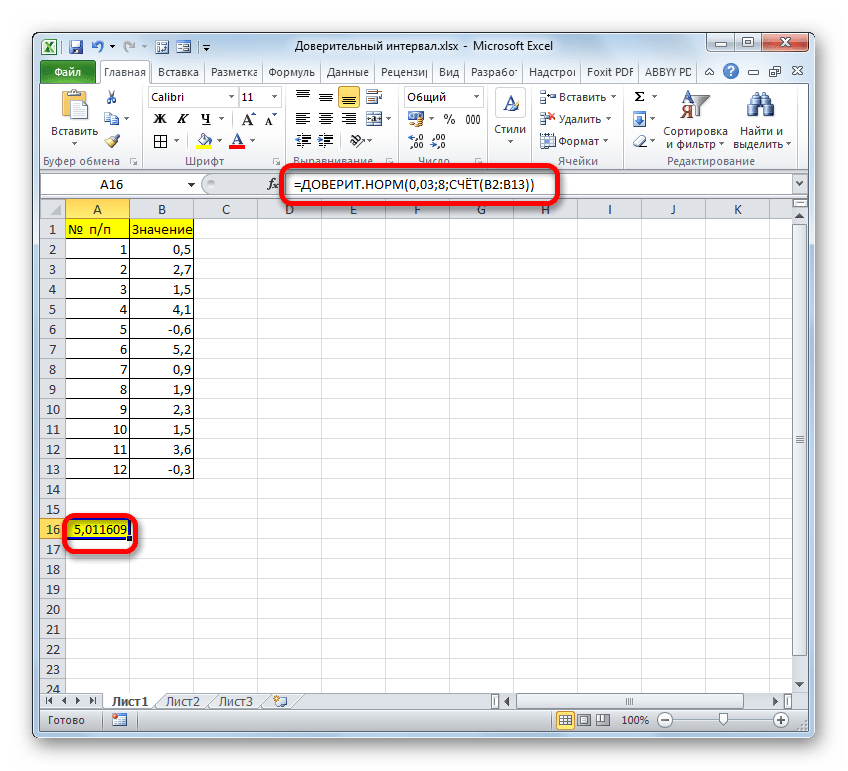
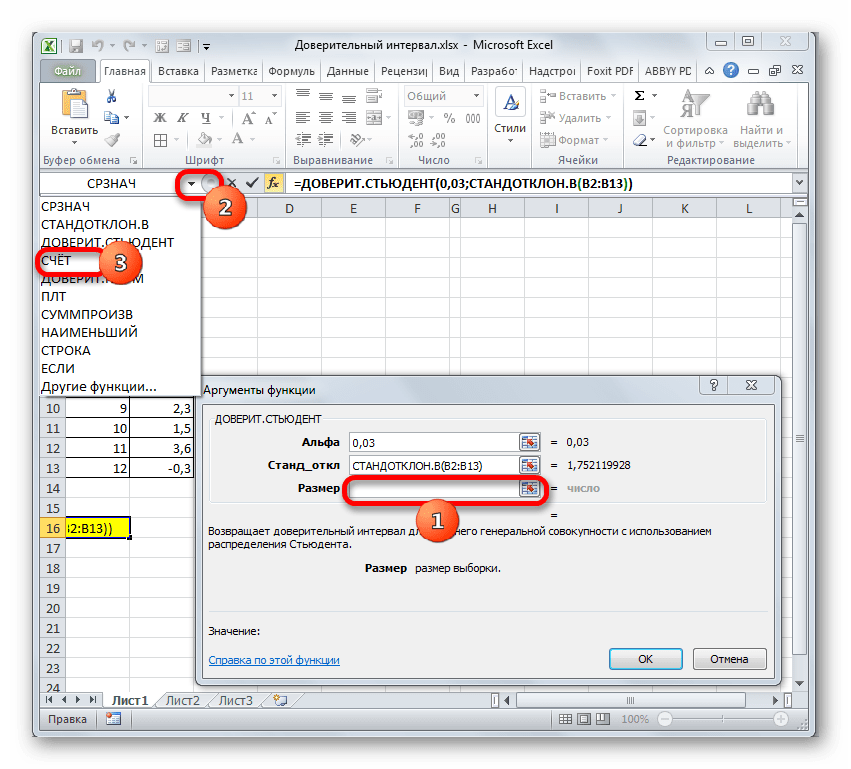
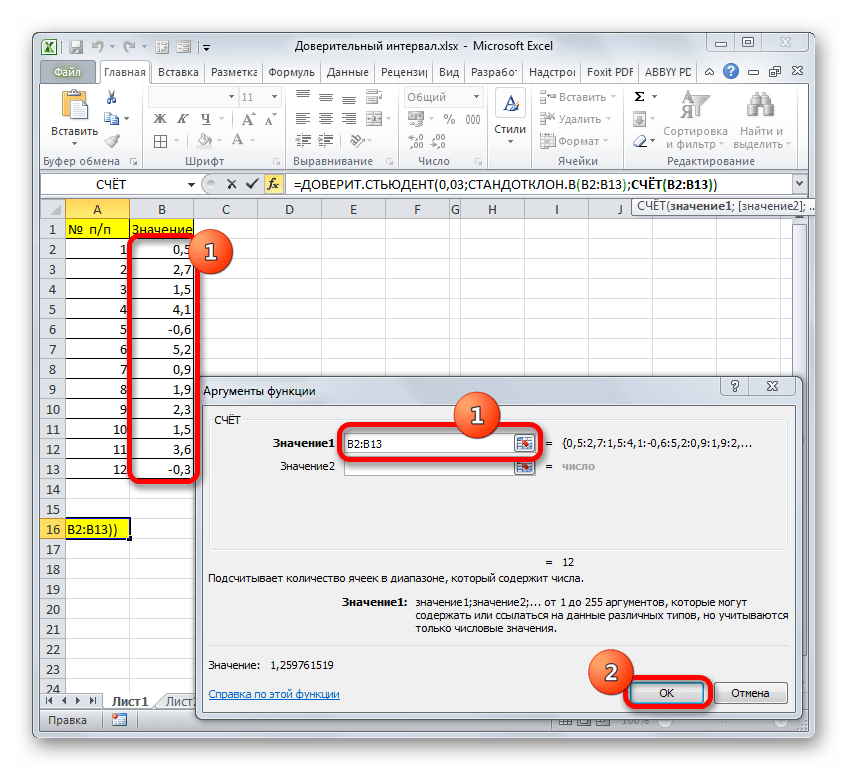
В поле «Размер» нужно ввести количество элементов проведенных испытаний. Как мы помним, их 12. Но чтобы автоматизировать формулу и не редактировать её каждый раз при проведении нового испытания, давайте зададим данное значение не обычным числом, а при помощи оператора СЧЁТ. Итак, устанавливаем курсор в поле «Размер», а затем кликаем по треугольнику, который размещен слева от строки формул.
Группа аргументов «Значения» представляет собой ссылку на диапазон, в котором нужно рассчитать количество заполненных числовыми данными ячеек. Всего может насчитываться до 255 подобных аргументов, но в нашем случае понадобится лишь один.
Данный оператор предназначен для расчета среднего арифметического значения выбранного диапазона чисел. Он имеет следующий довольно простой синтаксис:
Аргумент «Число» может быть как отдельным числовым значением, так и ссылкой на ячейки или даже целые диапазоны, которые их содержат.
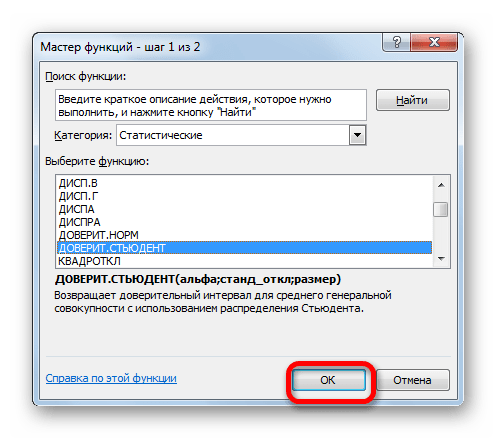
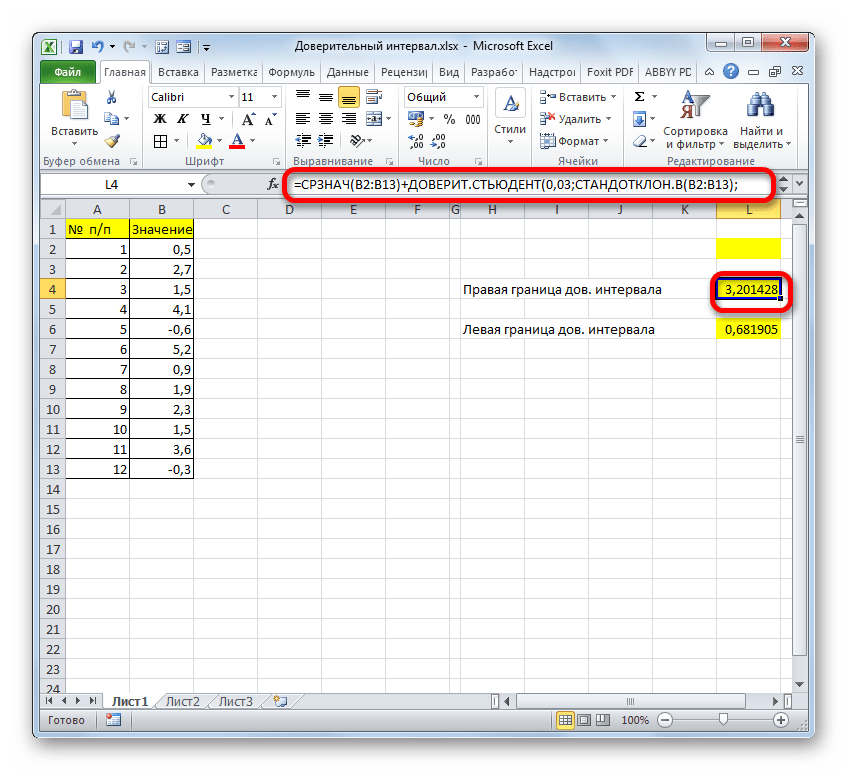
Способ 2: функция ДОВЕРИТ.СТЮДЕНТ
Кроме того, в Экселе есть ещё одна функция, которая связана с вычислением доверительного интервала – ДОВЕРИТ.СТЮДЕНТ. Она появилась, только начиная с Excel 2010. Данный оператор выполняет вычисление доверительного интервала генеральной совокупности с использованием распределения Стьюдента. Его очень удобно использовать в том случае, когда дисперсия и, соответственно, стандартное отклонение неизвестны. Синтаксис оператора такой:
Как видим, наименования операторов и в этом случае остались неизменными.
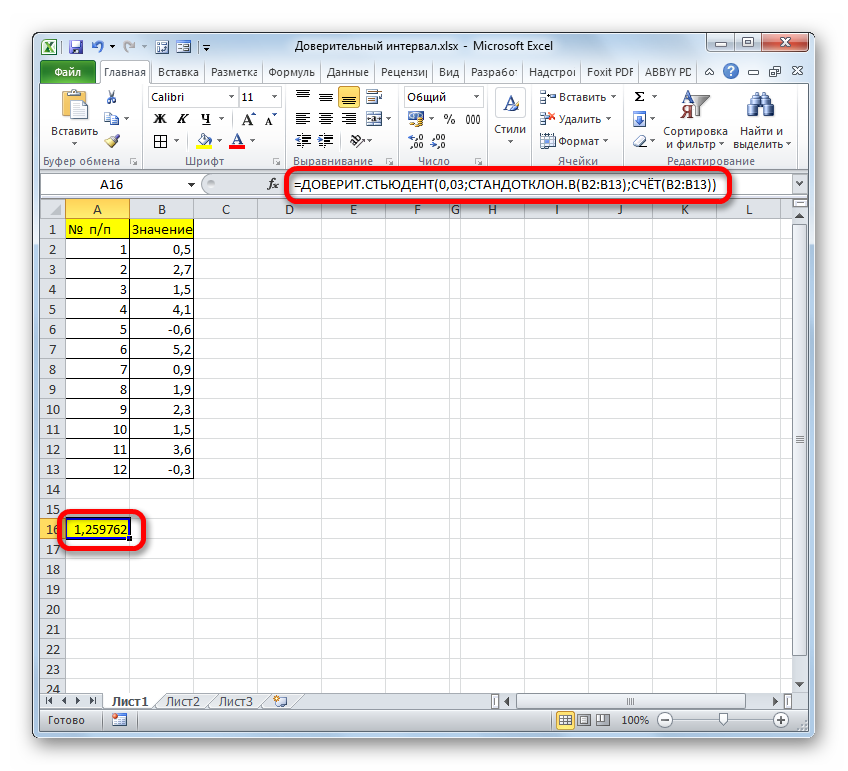
Посмотрим, как рассчитать границы доверительного интервала с неизвестным стандартным отклонением на примере всё той же совокупности, что мы рассматривали в предыдущем способе. Уровень доверия, как и в прошлый раз, возьмем 97%.
- Выделяем ячейку, в которую будет производиться расчет. Клацаем по кнопке «Вставить функцию».
В поле «Альфа», учитывая, что уровень доверия составляет 97%, записываем число 0,03. Второй раз на принципах расчета данного параметра останавливаться не будем.
Нетрудно догадаться, что аргумент «Число» — это адрес элемента выборки. Если выборка размещена единым массивом, то можно, использовав только один аргумент, дать ссылку на данный диапазон.
Как видим, инструменты программы Excel позволяют существенно облегчить вычисление доверительного интервала и его границ. Для этих целей используются отдельные операторы для выборок, у которых дисперсия известна и неизвестна.


Функция СТАНДАРТИЗАЦИЯ в Excel возвращает нормализованное значение (z-оценку) на основе среднего значения и стандартного отклонения.
Возвращаемое значение
Синтаксис
Аргументы
- x — значение для нормализации.
- среднее — Среднее арифметическое распределения.
- standard_dev — стандартное отклонение распределения.
Версия
Примечания по использованию
Функция СТАНДАРТИЗАЦИЯ в Excel возвращает нормализованное значение (z-оценку) на основе среднего значения и стандартного отклонения. Чтобы использовать функцию СТАНДАРТИЗАЦИЯ, рассчитайте среднее значение с помощью функции СРЕДНЕЕ, а стандартное отклонение — с помощью функции СТАНДАРТ.П (см. Ниже).
В показанном примере формула в D5:
О z-показателях / стандартных показателях
Z-оценка или стандартная оценка — это способ стандартизации оценок по той же шкале путем деления отклонения оценки на стандартное отклонение в наборе данных. Результатом является стандартная оценка или z-оценка. Он измеряет количество стандартных отклонений данной точки данных от среднего.
Z-оценка может быть отрицательной или положительной. Отрицательный z-показатель указывает на значение меньше среднего, а положительный z-показатель указывает на значение, превышающее среднее. Среднее значение каждого z-показателя для набора данных равно нулю.
Чтобы вычислить z-оценку, необходимо вычислить среднее значение и стандартное отклонение. Формулы в G4 и G5, соответственно:
Где «точки» — именованный диапазон C5: C12.
Если вы хотите узнать больше о z-показателях и статистическом анализе в Excel, я рекомендую книгу Джозефа Шмуллера «Статистический анализ в Excel для чайников».
Расчет доверительного интервала в Excel
Программа Эксель используется для выполнения различных статистических задач, одной из которых является вычисление доверительного интервала, который применяется как наиболее подходящая замена точечной оценки при малом объеме выборки.
Хотим сразу заметить, что сама процедура вычисления доверительного интервала довольно непростая, однако, в Excel существует ряд инструментов, призванных облегчить выполнение данной задачи. Давайте рассмотрим их.
Вычисление доверительного интервала
Доверительный интервал нужен для того, чтобы дать интервальную оценку каким-либо статическим данным. Основная цель этой операции – убрать неопределенности точечной оценки.
В Microsoft Excel существует два метода выполнения данной задачи:
- Оператор ДОВЕРИТ.НОРМ – применяется в случаях, когда дисперсия известна;
- Оператор ДОВЕРИТ.СТЬЮДЕНТ– когда дисперсия неизвестна.
Ниже мы пошагово разберем оба метода на практике.
Метод 1: оператора ДОВЕРИТ.НОРМ
Данная функция впервые была внедрена в арсенал программы в редакции Эксель 2010 года (до этой версии ее заменял оператор “ДОВЕРИТ”). Оператор входит в категорию “статистические”.
Формула функции ДОВЕРИТ.НОРМ выглядит так:
Как мы видим, у функции есть три аргумента:
- “Альфа” – это показатель уровня значимости, который берется за основу при расчете. Доверительный уровень считается так:
- 1-«Альфа» . Это выражение применимо в случае, если значение “Альфа” представлено в виде коэффициента. Например, 1-0,7=0,3, где 0,7=70%/100%.
- (100-«Альфа»)/100 . Применятся это выражение, если мы считаем доверительным уровень со значением “Альфа” в процентах. Например, (100-70)/100=0,3.
Примечание: У данной функции наличие всех трех аргументов является обязательным условием.
Оператор “ДОВЕРИТ”, который применялся в более ранних редакциях программы, содержит такие же аргументы и выполняет те же самые функции.
Формула функции ДОВЕРИТ выглядит следующим образом:
Отличий в самой формуле нет никаких, лишь название оператора иное. В редакциях приложения Эксель 2010 года и последующих этот оператор находится в категории “Совместимость”. В более же старых версиях программы он находится в разделе статических функций.
Граница доверительного интервала определяется следующей формулой:
где Х – это среднее значение по заданному диапазону.
Теперь давайте разберемся, как применять эти формулы на практике. Итак, у нас есть таблица с различными данными 10-ти проведенных замеров. При этом, стандартное отклонение совокупности данных равняется 8.
Перед нами стоит задача – получить значение доверительного интервала с 95%-ым уровнем доверия.
- Первым делом выбираем ячейку для вывода результата. Затем кликаем по кнопке “Вставить функцию” (слева от строки формул).
- в поле “Альфа” указываем уровень значимости. В нашей задаче предполагается 95%-ый уровень доверия. Подставив данное значение в формулу расчета, которую мы рассматривали выше, получаем выражение: (100-95)/100 . Пишем его в поле аргумента (или можно сразу написать результат вычисления, равный 0,05).
- в поле “Станд_откл” согласно нашим условия, пишем цифру 8.
- в поле “Размер” указываем количество исследуемых элементов. В нашем случае было проведено 10 замеров, значит пишем цифру 10.
Примечание: В пунктах выше мы постарались максимально подробно расписать все шаги и каждую применяемую функцию. Однако все прописанные формулы можно записать вместе, в составе одной большой:
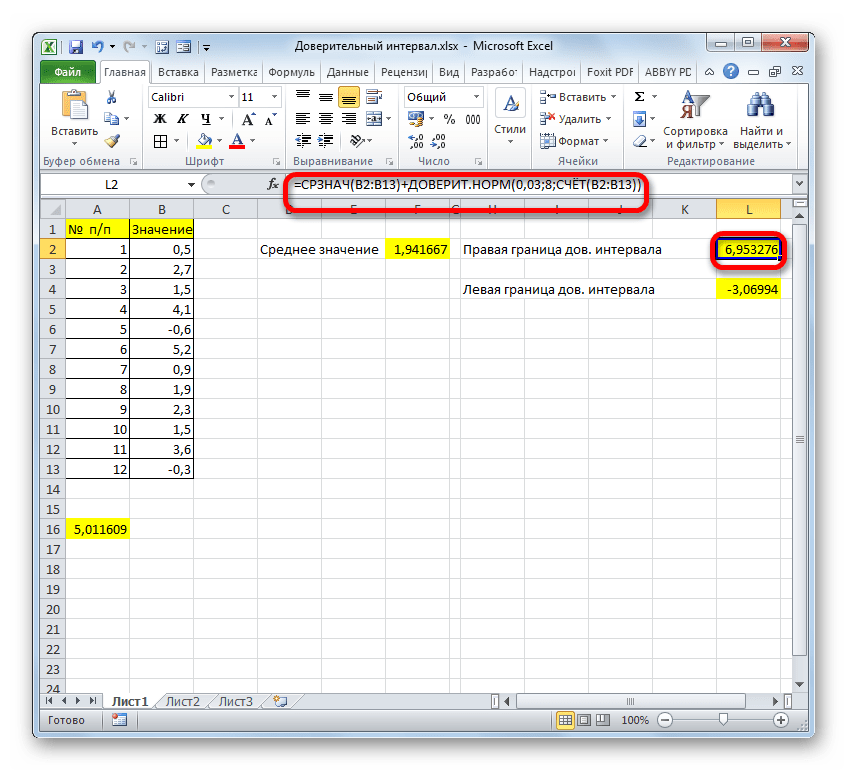
- Для определения правой границы ДИ общая формула будет выглядеть так:
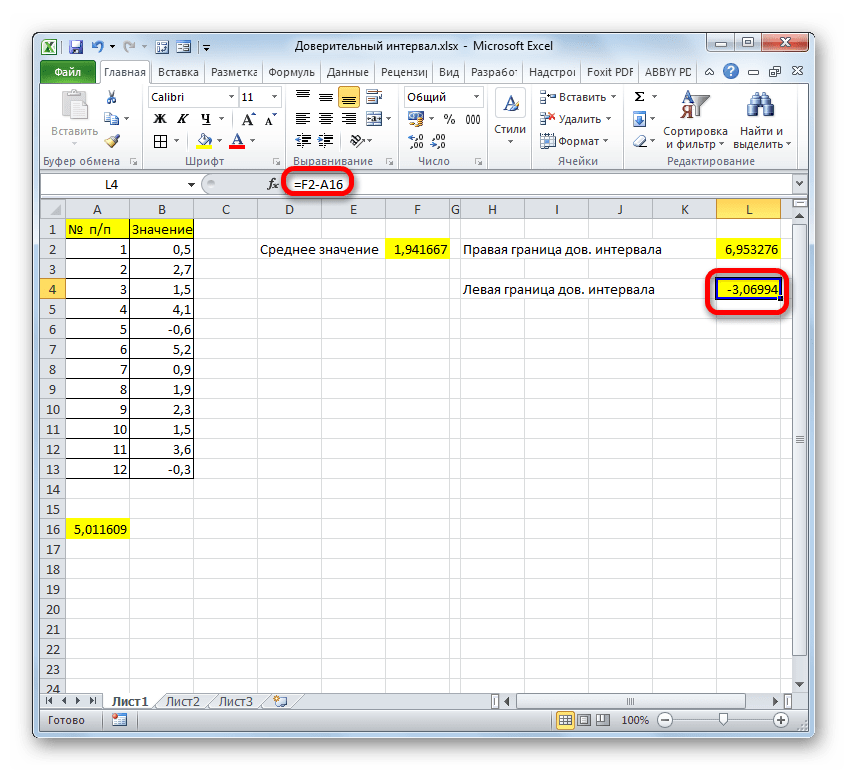
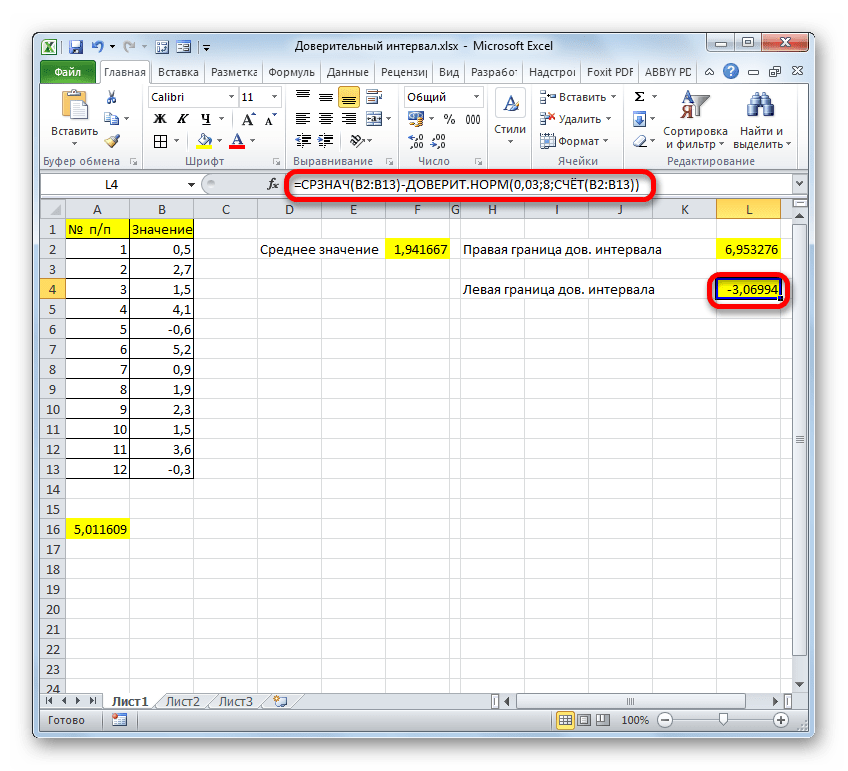
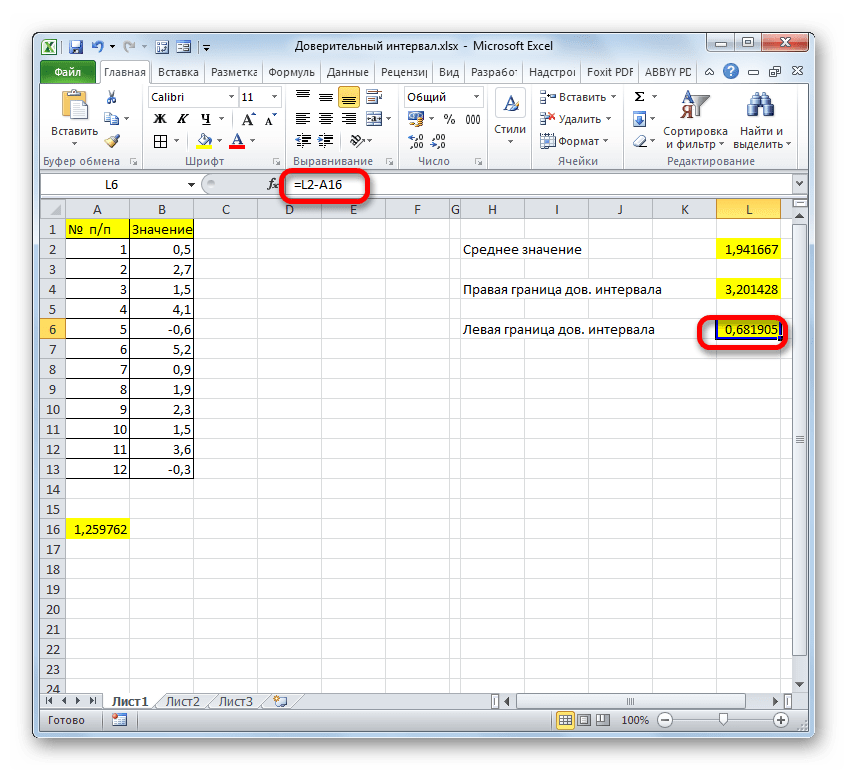
=СРЗНАЧ(B2:B11)+ДОВЕРИТ.НОРМ(0,05;8;СЧЁТ(B2:B11)) . - Точно также и для левой границы, только вместо плюса нужно поставить минус:
=СРЗНАЧ(B2:B11)-ДОВЕРИТ.НОРМ(0,05;8;СЧЁТ(B2:B11)) .
Метод 2: оператор ДОВЕРИТ.СТЬЮДЕНТ
Теперь давайте познакомимся со вторым оператором для определения доверительного интервала – ДОВЕРИТ.СТЬЮДЕНТ. Данная функция была внедрена в программу относительно недавно, начиная с версии Эксель 2010, и направлена на определение ДИ выбранной совокупности данных с применением распределения Стьюдента, при неизвестной дисперсии.
Формула функции ДОВЕРИТ.СТЬЮДЕНТ выглядит следующим образом:
Давайте разберем применение данного оператора на примере все той же таблицы. Только теперь стандартное отклонение по условиям задачи нам неизвестно.
- Сначала выбираем ячейку, куда планируем вывести результат. Затем кликаем по значку “Вставить функцию” (слева от строки формул).
- Откроется уже хорошо знакомое окно Мастера функций. Выбираем категорию “Статистические”, затем из предложенного списка функций щелкаем по оператору “ДОВЕРИТ.СТЬЮДЕНТ”, после чего – OK.
- В следующем окне нам нужно настроить аргументы функции:.
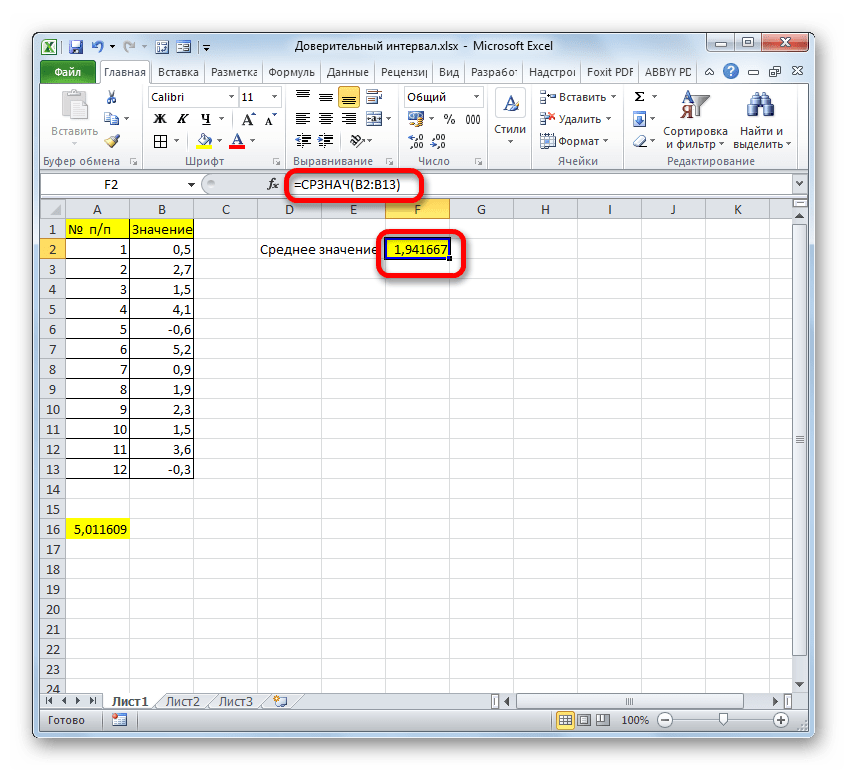
- В выбранной ячейке отобразится значение доверительного интервала согласно заданным нами параметрам.
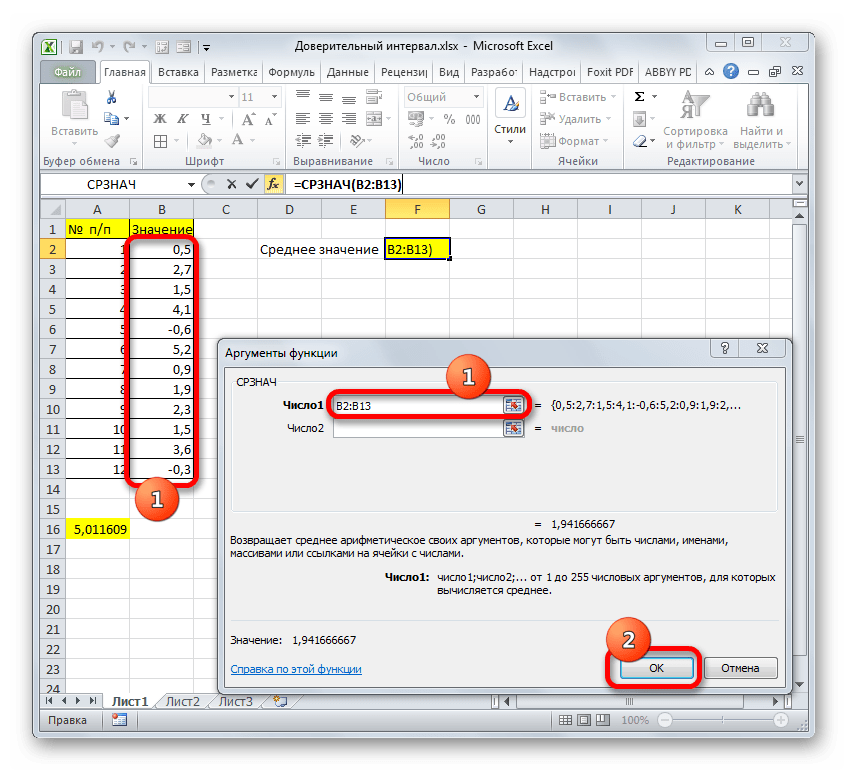
- Далее нам нужно рассчитать значения границ ДИ. А для этого потребуется получить среднее значение по выбранному диапазону. Для этого снова применим функцию “СРЗНАЧ”. Алгоритм действий аналогичен тому, что был описан в первом методе.
- Получив значение “СРЗНАЧ”, можно приступать к расчетам границ ДИ. Сами формулы ничем не отличаются от тех, что использовались с оператором “ДОВЕРИТ.НОРМ”:
- Правая граница ДИ=СРЗНАЧ+ДОВЕРИТ.СТЬЮДЕНТ
- Левая граница ДИ=СРЗНАЧ-ДОВЕРИТ.СТЬЮДЕНТ
Заключение
Арсенал инструментов Excel невероятно большой, и наряду с распространенными функциями, программа предлагает большое разнообразие специальных функций, которые помогут существенно облегчить работу с данными. Возможно, описанные выше шаги некоторым пользователям, на первый взгляд, могут показаться сложными. Но после детального изучения вопроса и последовательности действий, все станет намного проще.
Функция
ЛИНЕЙН()
специально создана для оценки параметров линейной регрессии, а также для вывода регрессионной статистики (коэффициента детерминации, стандартных ошибок,
F
-статистики
и др.).
Функция
ЛИНЕЙН()
может использоваться для
простой регрессии
(в этом случае прогнозируемая переменная Y зависит от одной контролируемой переменной Х) и для
множественной регрессии
(Y зависит от нескольких Х).
Рассмотрим функцию на примере
простой регрессии
(оценивается
наклон
и
сдвиг
линии регрессии). Использование функции в случае
множественной регрессии
рассмотрено в соответствующей статье про
множественную регрессию
.
Функция
ЛИНЕЙН()
возвращает несколько значений, поэтому для вывода результатов потребуется несколько ячеек. Часто функцию вводят как
формулу массива
: нажатием клавиш
CTRL
+
SHIFT
+
ENTER
,
но, как будет показано ниже, для вывода результатов вычислений это не обязательно.
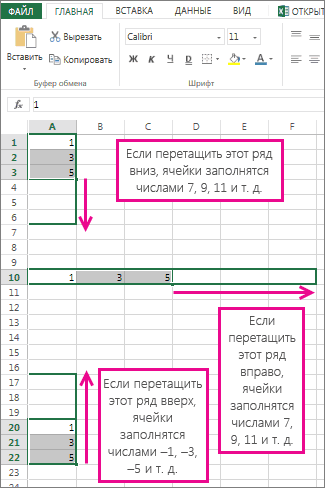
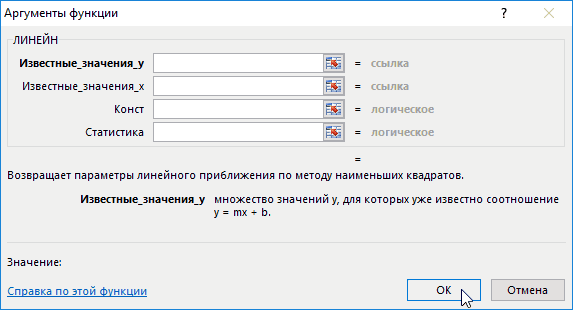
Функция работает в 2-х режимах. В простейшем случае, когда 4-й аргумент функции опущен или установлен ЛОЖЬ, функция возвращает только 2 значения — это оценки параметров модели: наклона a и сдвига b.
Для того, чтобы вычислить оценки:
- выделите 2 ячейки в одной строке,
-
в
Строке формул
введите, например, =
ЛИНЕЙН(C23:C83;B23:B83)
-
нажмите
CTRL
+
SHIFT
+
ENTER
.
В левой ячейке будет рассчитано значение
наклона
, в правой –
сдвига
.
Примечание
: В справке MS EXCEL результат функции
ЛИНЕЙН()
соответствующий
наклону
обозначается буквой m, а
сдвиг
– буквой b.
Примечание
: Без
формул массива
можно обойтись. Для этого нужно использовать функцию
ИНДЕКС()
, которая выведет нужное значение. Например, чтобы вывести величину
сдвига
линии регрессии введите формулу =
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1;2)
. Если 4-й аргумент функции опущен или установлен ЛОЖЬ, то функция
ЛИНЕЙН()
в возвращает массив значений вида 1х2 (т.е. 2 ячейки, расположенные в одной строке). Поэтому, для вывода величины
сдвига
прямой линии регрессии, первый аргумент функции
ИНДЕКС()
, который является номером строки, должен быть равен 1, а второй аргумент, номер столбца, должен быть равен 2. Чтобы вывести значение
наклона
линии регрессии формулу
=ЛИНЕЙН(C23:C83;B23:B83)
достаточно ввести просто как обычную формулу и нажать
ENTER
. Конечно, можно использовать и формулу
=ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1;1)
.
Теперь о втором, более сложном режиме функции. Этот режим нужно использовать, если требуется вывести дополнительную статистику (4-й аргумент функции должен быть установлен ИСТИНА). В этом случае функция
ЛИНЕЙН()
возвращает 10 значений в диапазоне 5х2 ячеек (5 строк и 2 столбца). Как и в более простом режиме, в первой строке возвращаются оценки параметров модели:
наклона
и
сдвига
.
Чтобы ввести функцию как
формулу массива
выполните следующие действия:
- выделите диапазон 5х2 ячеек (2 столбца и 5 строк),
-
в
Строке формул
введите формулу
ЛИНЕЙН($C$23:$C$83;$B$23:$B$83;;ИСТИНА)
-
чтобы ввести формулу нажмите одновременно комбинацию клавиш
CTRL
+
SHIFT
+
ENTER
Примечание
: Чтобы обойтись без
формул массива
нужно использовать функцию
ИНДЕКС()
, которая выведет нужное значение. Например, чтобы вывести
коэффициент детерминации
R
2
введите формулу =
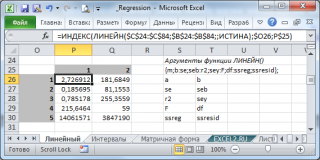
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3;1)
. 3 – это номер строки диапазона 5х2, а 1 – это номер столбца. В
файле примера на листе Линейный
в диапазоне
Q
26:
R
30
показано как вывести все значения, возвращаемые функцией
ЛИНЕЙН()
без
формул массива
.
Итак, установив 4-й аргумент равным ИСТИНА и введя функцию тем или иным способом, функция выведет:
-
в строке 1:
оценки параметров модели
(наклон и сдвиг).
-
в строке 2:
Стандартные ошибки для наклона и сдвига
. Ошибки обозначаются se и seb;
-
в строке 3:
коэффициент детерминации
и
стандартную ошибку регрессии
. Обозначаются R
2
и SEy; -
в строке 4:
значение F-статистики и число степеней свободы
. Обозначаются F и df;
-
в строке 5: Суммы квадратов SSR, SSE определяющие
изменчивость объясненную и необъясненную моделью
(см. в статьеПростая линейная регрессия
разделы про коэффициент детерминации и
статью про F-тест
). В справке MS EXCEL SSR, SSE обозначаются как
ssreg
(Regression Sum of Squares) и
ssresid
(Residuals Sum of Squares) соответственно.
Примечание
: Разобраться в значениях, возвращаемых функцией
ЛИНЕЙН()
, можно лишь разобравшись в теории линейной регрессии.
В
файле примера
также приведены формулы, позволяющие сделать расчеты без функции
ЛИНЕЙН()
– см. диапазон
Q
34:
R
38
. Альтернативные формулы помогают разобраться в алгоритме расчета вышеуказанных статистических показателей.
Как нормализовать данные в диапазоне 0-1?
Я потерян в нормировании, может кто-нибудь направит меня, пожалуйста.
У меня есть минимальное и максимальное значения, скажем, -23,89 и 7,54990767 соответственно.
Если я получу значение 5,6878, как я могу масштабировать это значение по шкале от 0 до 1.
Если вы хотите нормализовать ваши данные, вы можете сделать это так, как вы предлагаете, и просто рассчитать следующее:
где x = ( x 1 , . . . , x n ) ‘ role=»presentation»> Икс знак равно ( Икс 1 , , , , , Икс N ) и z i ‘ role=»presentation»> Z я теперь ваш i t h ‘ role=»presentation»> я T час нормализованный данные. В качестве подтверждения концепции (хотя вы не просили об этом) приведем R код и сопровождающий график, чтобы проиллюстрировать этот момент:
Общая однострочная формула для линейного масштабирования значений данных с учетом min и max в новый произвольный диапазон min ‘ to max’ имеет вид
Вот моя реализация PHP для нормализации:
Но пока я строил свои собственные искусственные нейронные сети, мне нужно было преобразовать нормализованный вывод обратно в исходные данные, чтобы получить хороший читаемый вывод для графика.
Денормализация использует следующую формулу:
x ( max − min ) + min ‘ role=»presentation»> Икс ( Максимум — мин ) + мин
Деление на ноль
Следует иметь в виду, что max — min может быть равно нулю. В этом случае вы не захотите выполнять это разделение.
Это может произойти, когда все значения в списке, который вы пытаетесь нормализовать, совпадают. Чтобы нормализовать такой список, каждый элемент будет 1 / length .
Пример:
ответ правильный, но у меня есть предположение, что если ваши тренировочные данные окажутся за пределами допустимого числа? Вы могли бы использовать технику раздавливания. это гарантированно никогда не выйдет за пределы диапазона. а не это
я рекомендую использовать это
с раздавливанием, как это в минимальной и максимальной дальности
и размер ожидаемого разрыва вне диапазона прямо пропорционален степени уверенности в том, что будут значения вне диапазона.
Для получения дополнительной информации вы можете Google: сжатие чисел вне диапазона и обратитесь к книге подготовки данных «Дориан Пайл»
Функция НОРМАЛИЗАЦИЯ
В этой статье описаны синтаксис формулы и использование функции НОРМАЛИЗАЦИЯ в Microsoft Excel.
Описание
Возвращает нормализованное значение для распределения, характеризуемого средним и стандартным отклонением.
Синтаксис
Аргументы функции НОРМАЛИЗАЦИЯ описаны ниже.
X Обязательный. Нормализуемое значение.
Среднее Обязательный. Среднее арифметическое распределения.
Стандартное_откл Обязательный. Стандартное отклонение распределения.
Замечания
Если standard_dev ≤ 0, возвращается стандартное #NUM! значение ошибки #ЗНАЧ!.
Уравнение для нормализованного значения имеет следующий вид:
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Значение, которое нужно нормализовать.
Среднее арифметическое распределения.
Стандартное отклонение распределения.
Нормализованное значение числа 42, полученное с использованием числа 40 в качестве среднего арифметического и числа 1,5 в качестве стандартного отклонения.
Содержание
- Экспоненциальное сглаживание в Excel
- Экспоненциальное распределение. Непрерывные распределения в EXCEL
- Экспоненциальное распределение в MS EXCEL
- Графики функций
- Генерация случайных чисел
- Задачи
- Как использовать экспоненциальное распределение в Excel
- Пример 1: время до прихода следующего клиента
- Пример 2: Время до следующего землетрясения
- Пример 3: время до следующего телефонного звонка
- Как выполнить экспоненциальное сглаживание в Excel
- Пример: экспоненциальное сглаживание в Excel
- Эксперименты с коэффициентами сглаживания
Экспоненциальное сглаживание в Excel
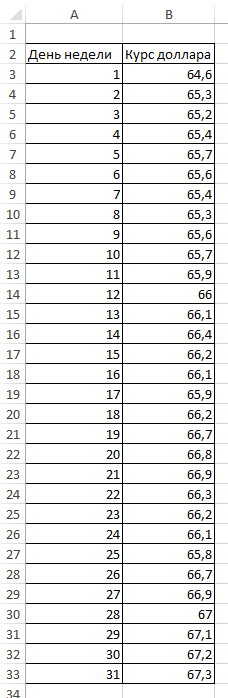
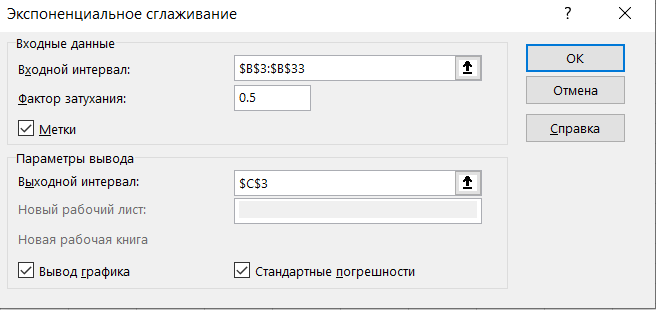
Дана таблица курса доллара за месяц.
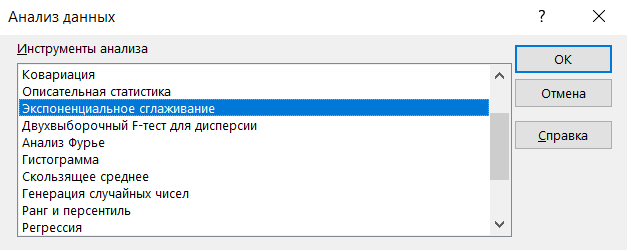
Для того чтобы применить экспоненциальное сглаживание в Excel переходим на Анализ данных.
Переходим на вкладку Данные -> Анализ данных -> Экспоненциальное сглаживание
Если у вас в Excel не отображается на вкладке расширение Анализ данных, как его настроить см. здесь.
В окне экспоненциальное сглаживание указываем входной и выходной интервал, фактор затухания укажем 0.5. Ставим галочки метки, вывод графика и стандартные погрешности и нажимаем Ок.
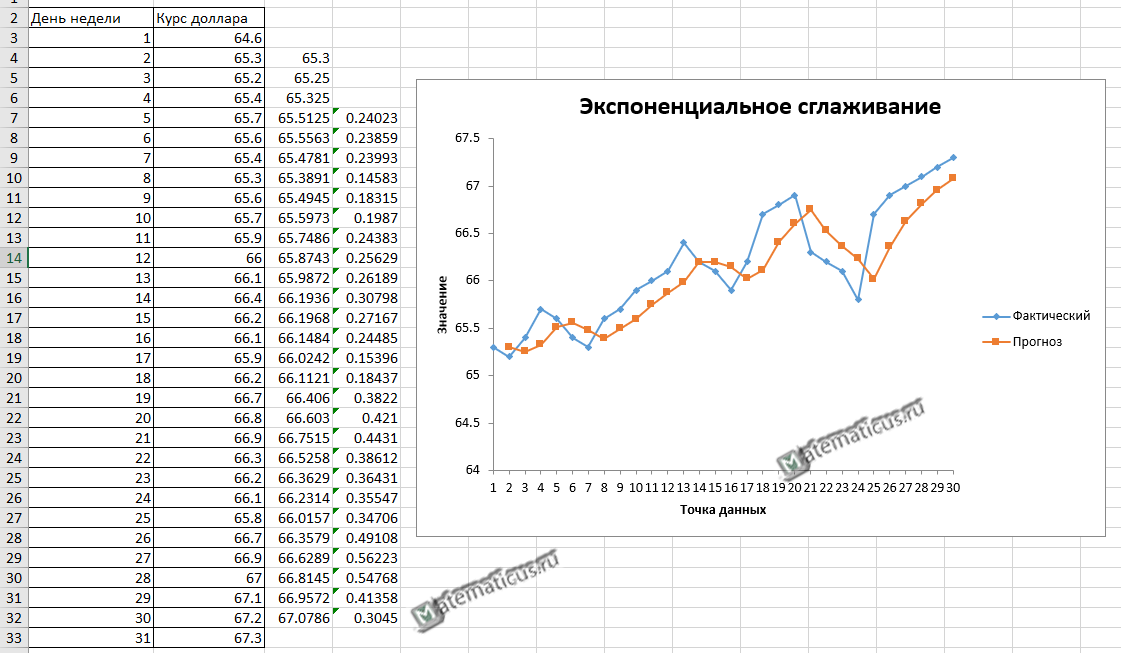
Получаем график прогноза при применение экспоненциального сглаживания и фактический график в Excel
Экспоненциальное сглаживание часто применяется для прогнозирования.
Источник
Экспоненциальное распределение. Непрерывные распределения в EXCEL
history 8 ноября 2016 г.
Рассмотрим Экспоненциальное распределение, вычислим его математическое ожидание, дисперсию, медиану. С помощью функции MS EXCEL ЭКСП.РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел и произведем оценку параметра распределения.
Экспоненциальное распределение (англ. Exponential distribution ) часто используется для расчета времени ожидания между случайными событиями. Ниже описаны ситуации, когда возможно применение Экспоненциального распределения :
- Промежутки времени между появлением посетителей в кафе;
- Промежутки времени нормальной работы оборудования между появлением неисправностей (неисправности возникают из-за случайных внешних влияний, а не по причине износа, см. Распределение Вейбулла );
- Затраты времени на обслуживание одного покупателя.
Плотность вероятности Экспоненциального распределения задается следующей формулой:
График плотности распределения вероятности и интегральной функции Экспоненциального распределения выглядит следующим образом (см. ниже).
Экспоненциальное распределение тесно связано с дискретным распределением Пуассона . Если Распределение Пуассона описывает число случайных событий, произошедших за определенный интервал времени, то Экспоненциальное распределение должноописывать длину интервала времени между двумя последовательными событиями.
Приведем пример. Предположим, что число машин, прибывающих на парковку днем, описывается распределением Пуассона со средним значением равным 15 машин в час (параметр распределения λ =15). Вероятность того, что на стоянку в течение часа приедет k машин равно:
Т.к. в среднем в час на стоянку приезжает 15 машин, то среднее время между 2-мя приезжающими машинами равно 1час/15машин=0,067. Т.к. среднее время между 2-мя событиями равно обратному значению параметра экспоненциального распределения , то параметр λ =15 , а плотность соответствующего экспоненциального распределения равна:
Экспоненциальное распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для Экспоненциального распределения имеется функция ЭКСП.РАСП() , английское название — EXPON.DIST(), которая позволяет вычислить плотность вероятности (см. формулу в начале статьи) и интегральную функцию распределения (вероятность, что случайная величина X, распределенная по экспоненциальному закону , примет значение меньше или равное x). Вычисления в последнем случае производятся по следующей формуле:
Экспоненциальное распределение имеет обозначение Exp ( λ ).
Примечание : До MS EXCEL 2010 в EXCEL была функция ЭКСПРАСП() , которая позволяет вычислить кумулятивную (интегральную) функцию распределения и плотность вероятности . ЭКСПРАСП() оставлена в MS EXCEL 2010 для совместимости.
В файле примера на листе Пример приведены несколько альтернативных формул для вычисления плотности вероятности и интегральной функции экспоненциального распределения :
- =1-EXP(- λ *x) ;
- =ГАММА.РАСП(x;1;1/ λ ;ИСТИНА) , т.к. экспоненциальное распределение является частным случаем Гамма распределения ;
- =ВЕЙБУЛЛ.РАСП(x;1;1/ λ ;ИСТИНА) , т.к. экспоненциальное распределение является частным случаем распределения Вейбулла ;
Примечание : Для удобства написания формул в файле примера создано Имя для параметра распределения — λ .
Графики функций
В файле примера приведены графики плотности распределения вероятности и интегральной функции распределения .
Примечание : Для построения функции распределения и плотности вероятности можно использовать диаграмму типа График или Точечная (со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью Основные типы диаграмм .
Генерация случайных чисел
Для генерирования массива чисел, распределенных по экспоненциальному закону , можно использовать формулу =-LN(СЛЧИС())/ λ
Функция СЛЧИС() генерирует непрерывное равномерное распределение от 0 до 1, что как раз соответствует диапазону изменения вероятности (см. файл примера лист Генерация ).
Если случайные числа содержатся в диапазоне B14:B213 , то оценку параметра экспоненциального распределения λ можно сделать с использованием формулы =1/СРЗНАЧ(B14:B213) .
Задачи
Экспоненциальное распределение широко используется в такой дисциплине как Техника обеспечения надежности (Reliability Engineering). Параметр λ называется интенсивность отказов , а 1/ λ – среднее время до отказа .
Предположим, что электронный компонент некой системы имеет срок полезного использования, описываемый Экспоненциальным распределением с интенсивностью отказа равной 10^(-3) в час, таким образом, λ = 10^(-3). Среднее время до отказа равно 1000 часов. Для того чтобы подсчитать вероятность, что компонент выйдет из строя за Среднее время до отказа, то нужно записать формулу:
Т.е. результат не зависит от параметра λ .
В MS EXCEL решение выглядит так: =ЭКСП.РАСП(10^3; 10^(-3); ИСТИНА)
Задача . Среднее время до отказа некого компонента равно 40 часов. Найти вероятность, что компонент откажет между 20 и 30 часами работы. =ЭКСП.РАСП(30; 1/40; ИСТИНА)- ЭКСП.РАСП(20; 1/40; ИСТИНА)
СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .
Источник
Как использовать экспоненциальное распределение в Excel
Экспоненциальное распределение — это распределение вероятностей, которое используется для моделирования времени, в течение которого мы должны ждать, пока не произойдет определенное событие.
Это распределение может быть использовано для ответа на такие вопросы, как:
- Как долго владельцу магазина нужно ждать, пока покупатель войдет в его магазин?
- Как долго батарея будет продолжать работать, прежде чем она умрет?
- Как долго компьютер будет продолжать работать, прежде чем он сломается?
В каждом сценарии нас интересует вычисление того, как долго нам придется ждать, пока не произойдет определенное событие. Таким образом, каждый сценарий может быть смоделирован с использованием экспоненциального распределения.
Если случайная величина X следует экспоненциальному распределению, то кумулятивная функция плотности X может быть записана как:
F (х; λ) = 1 – e -λx
- λ: параметр скорости (рассчитывается как λ = 1/μ)
- e: константа, примерно равная 2,718.
Чтобы рассчитать вероятности, связанные с кумулятивной функцией плотности экспоненциального распределения в Excel, мы можем использовать следующую формулу:
- x : значение экспоненциально распределенной случайной величины
- lambda : параметр скорости
- cumulative : использовать функцию кумулятивной плотности или нет (ИСТИНА или ЛОЖЬ)
Следующие примеры показывают, как использовать эту формулу на практике.
Пример 1: время до прихода следующего клиента
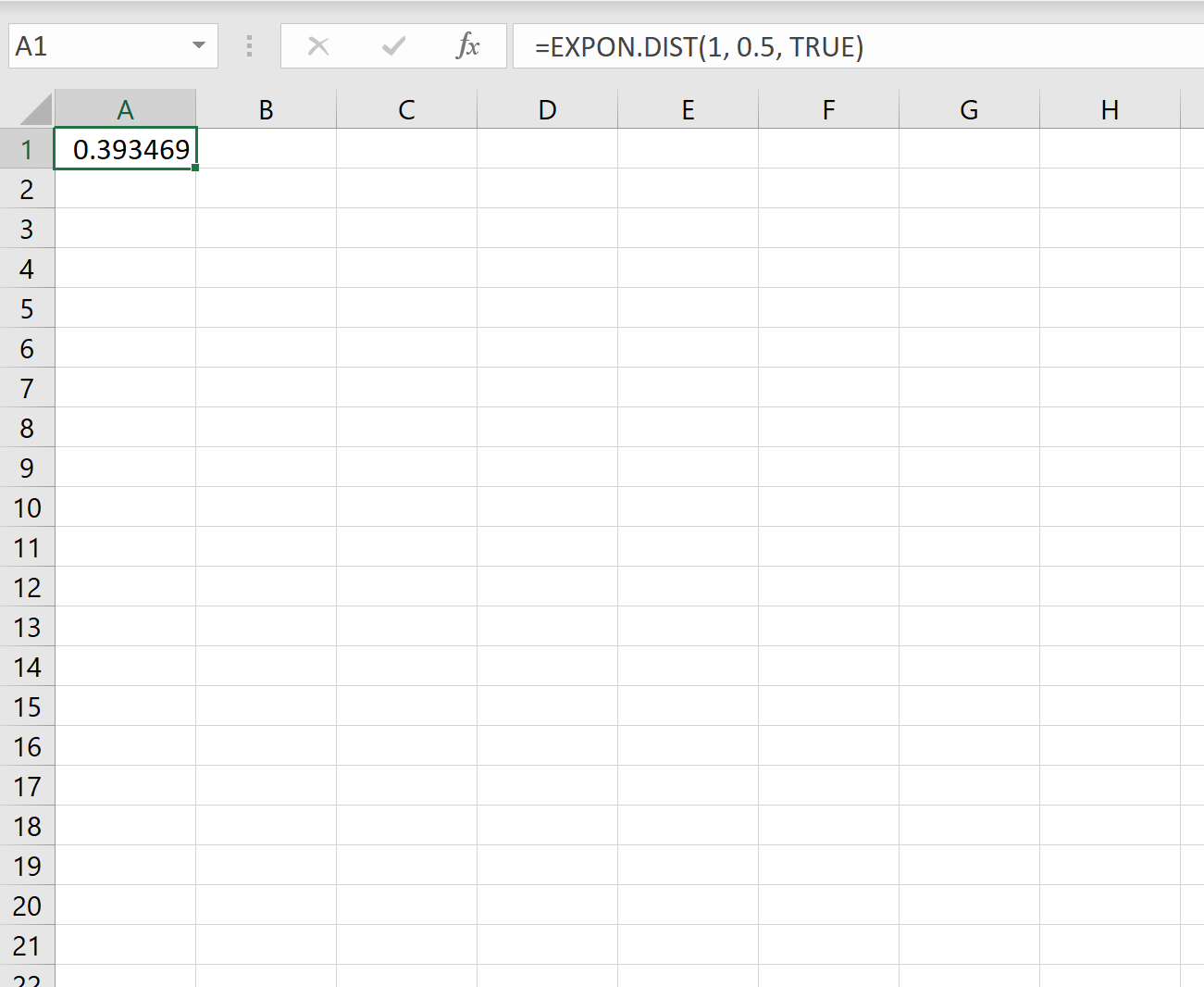
В среднем новый покупатель заходит в магазин каждые две минуты. После прихода клиента найти вероятность того, что новый клиент прибудет менее чем за одну минуту.
Решение: Среднее время между клиентами составляет две минуты. Таким образом, ставка может быть рассчитана как:
Таким образом, мы можем использовать следующую формулу в Excel для расчета вероятности того, что новый клиент прибудет менее чем за одну минуту:
Вероятность того, что следующего клиента придется ждать менее одной минуты, равна 0,393469 .
Пример 2: Время до следующего землетрясения
Предположим, землетрясение происходит в среднем каждые 400 дней в определенном регионе. После землетрясения найти вероятность того, что следующее землетрясение произойдет не ранее, чем через 500 дней.
Решение: Среднее время между землетрясениями составляет 400 дней. Таким образом, ставка может быть рассчитана как:
Таким образом, мы можем использовать следующую формулу в Excel для расчета вероятности того, что следующее землетрясение произойдет менее чем через 500 дней:
Вероятность того, что следующее землетрясение произойдет менее чем через 500 дней, равна 0,7135.
Таким образом, вероятность того, что следующего землетрясения придется ждать более 500 дней, равна 1 – 0,7135 = 0,2865 .
Пример 3: время до следующего телефонного звонка
Предположим, колл-центр получает новый звонок в среднем каждые 10 минут. После звонка клиента найти вероятность того, что новый клиент позвонит в течение 10–15 минут.
Решение: Среднее время между вызовами составляет 10 минут. Таким образом, ставка может быть рассчитана как:
Таким образом, мы можем использовать следующую формулу в Excel для расчета вероятности того, что следующий клиент позвонит в течение 10-15 минут:
Вероятность того, что новый клиент позвонит в течение 10-15 минут. составляет 0,1447 .
Источник
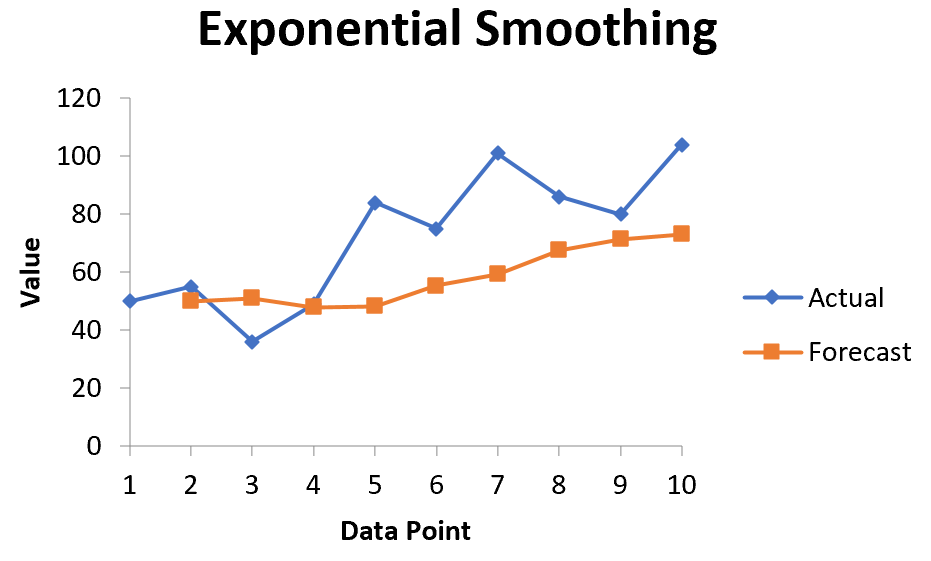
Как выполнить экспоненциальное сглаживание в Excel
Экспоненциальное сглаживание — это метод «сглаживания» данных временных рядов, который часто используется для краткосрочного прогнозирования.
Основная идея заключается в том, что данные временных рядов часто имеют связанный с ними «случайный шум», который приводит к пикам и впадинам в данных, но, применяя экспоненциальное сглаживание, мы можем сгладить эти пики и впадины, чтобы увидеть истинную основную тенденцию данных. .
Основная формула для применения экспоненциального сглаживания выглядит следующим образом:
F t = αy t-1 + (1 – α) F t-1
F t = прогнозируемое значение для текущего периода времени t
α = значение константы сглаживания в диапазоне от 0 до 1.
y t-1 = Фактическое значение данных за предыдущий период времени
F t-1 = Прогнозируемое значение для предыдущего периода времени t-1
Чем меньше значение альфа, тем больше сглаживаются данные временного ряда.
В этом руководстве мы покажем, как выполнить экспоненциальное сглаживание данных временных рядов с помощью встроенной функции в Excel.
Пример: экспоненциальное сглаживание в Excel
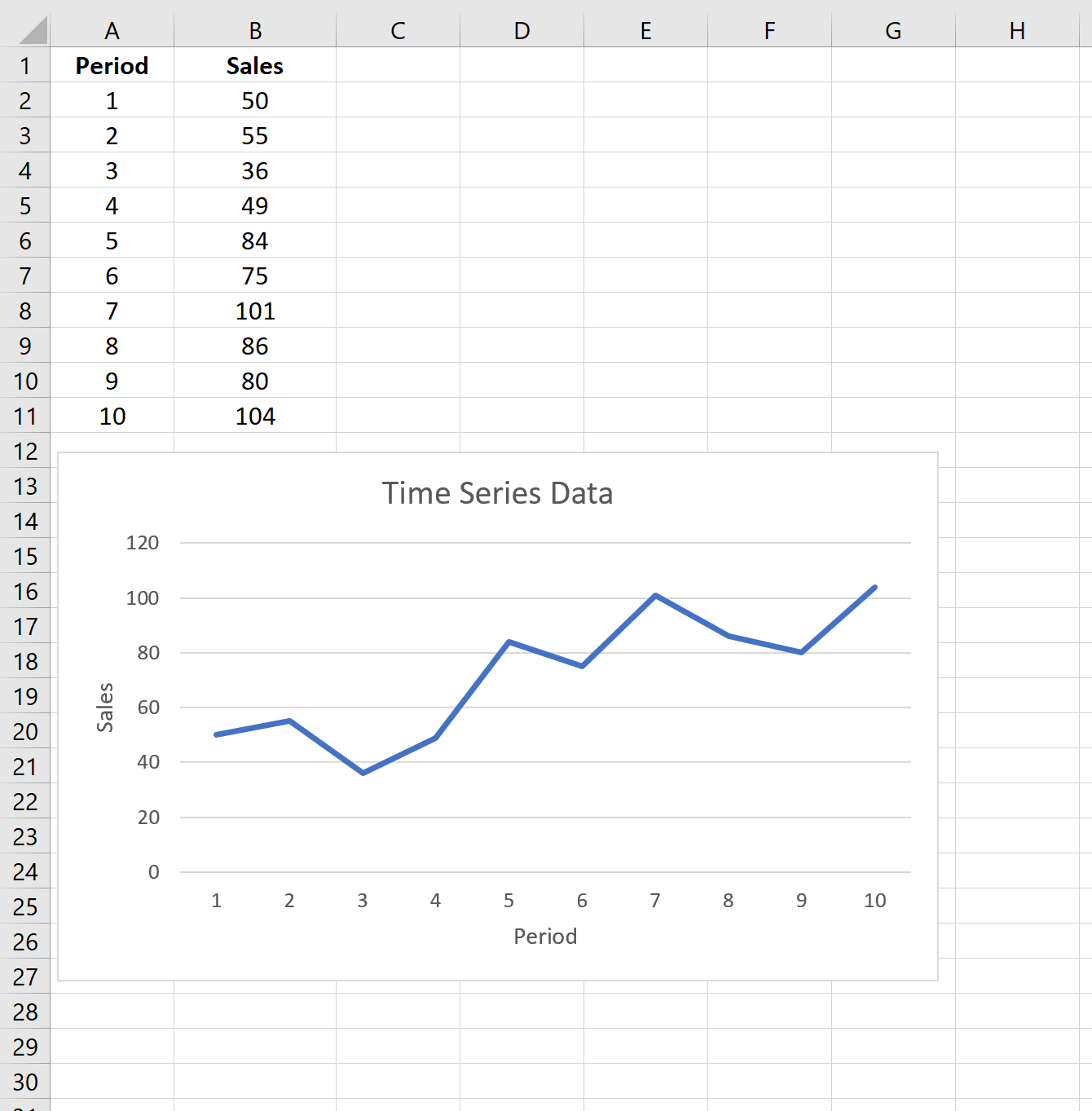
Предположим, у нас есть следующий набор данных, который показывает продажи конкретной компании за 10 периодов продаж:
Выполните следующие шаги, чтобы применить экспоненциальное сглаживание к этим данным временного ряда.
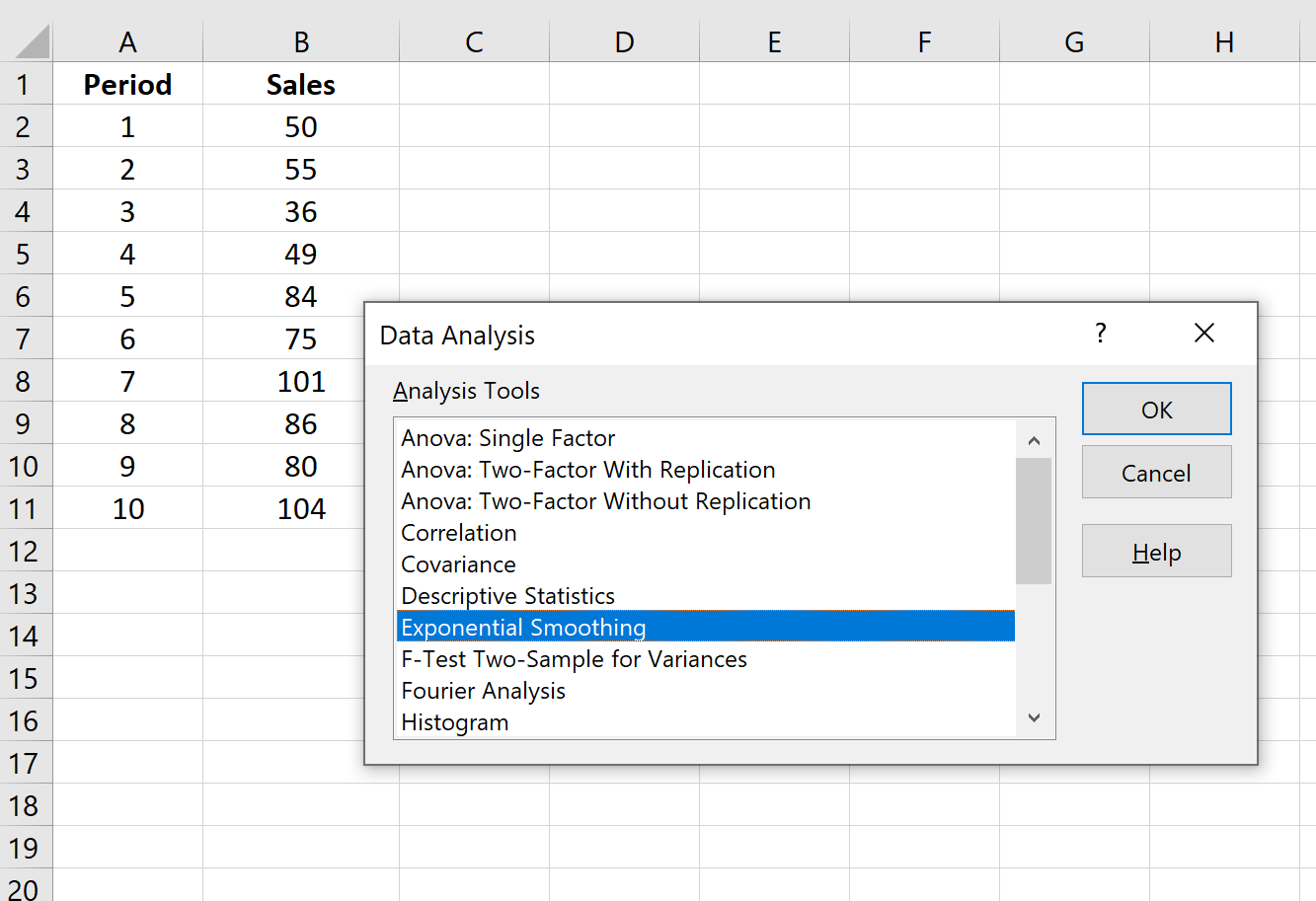
Шаг 1: Нажмите кнопку «Анализ данных».
Перейдите на вкладку «Данные» на верхней ленте и нажмите кнопку «Анализ данных». Если вы не видите эту кнопку, вам нужно сначала загрузить Excel Analysis ToolPak , который можно использовать совершенно бесплатно.
Шаг 2: Выберите параметр «Экспоненциальное сглаживание» и нажмите «ОК».
Шаг 3: Заполните необходимые значения.
- Заполните значения данных для Input Range .
- Выберите значение, которое вы хотели бы использовать для коэффициента затухания , которое равно 1-α. Если вы хотите использовать α = 0,2, то ваш коэффициент демпфирования будет 1-0,2 = 0,8.
- Выберите выходной диапазон , в котором должны отображаться прогнозируемые значения. Рекомендуется выбрать этот выходной диапазон рядом с вашими фактическими значениями данных, чтобы вы могли легко сравнивать фактические значения и прогнозируемые значения рядом друг с другом.
- Если вы хотите увидеть диаграмму с фактическими и прогнозируемыми значениями, установите флажок « Вывод диаграммы ».
Затем нажмите ОК.
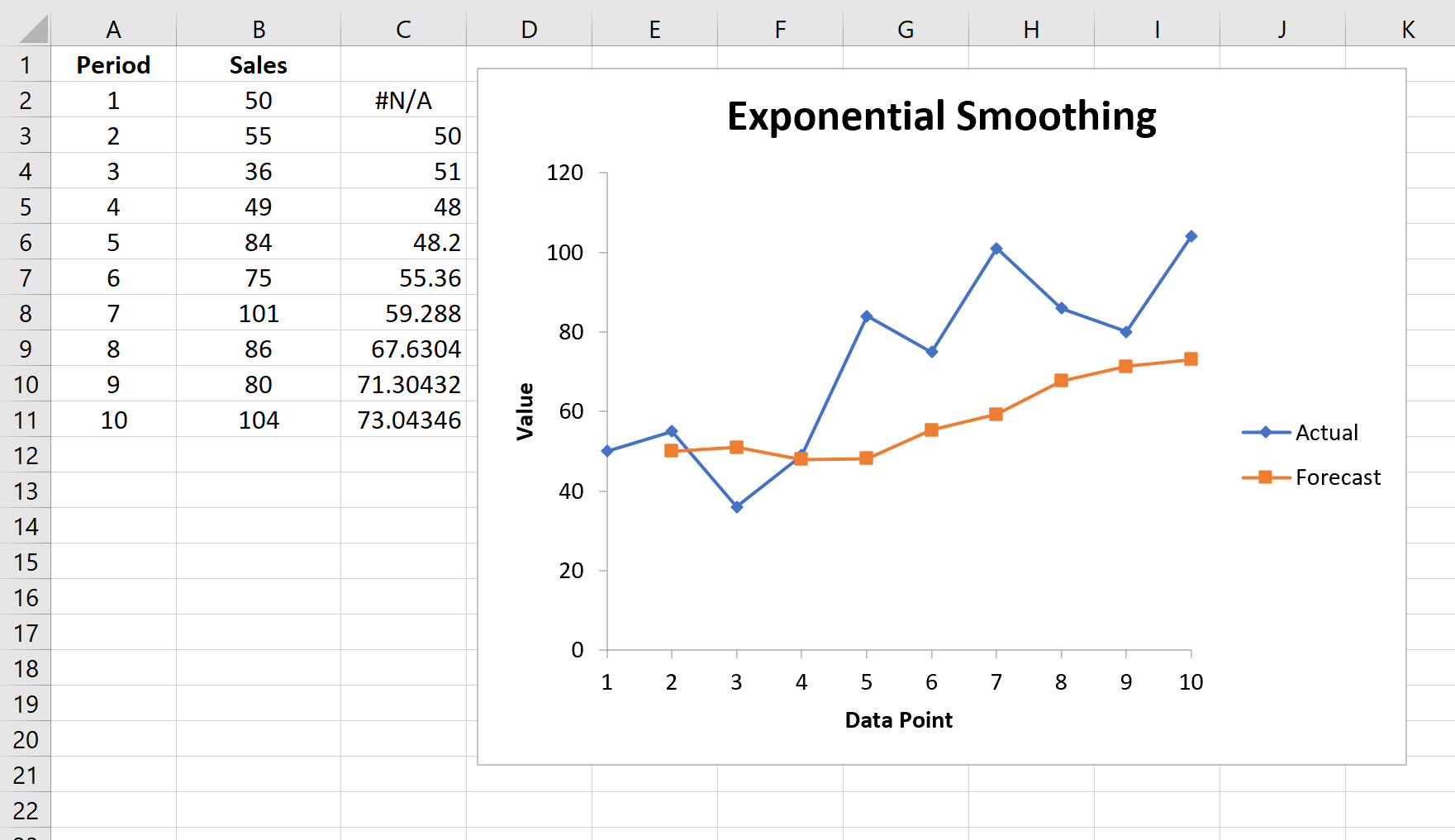
Автоматически появится список прогнозируемых значений и диаграмма:
Обратите внимание, что первый период времени имеет значение #N/A, поскольку нет предыдущего периода времени, который можно было бы использовать для расчета прогнозируемого значения.
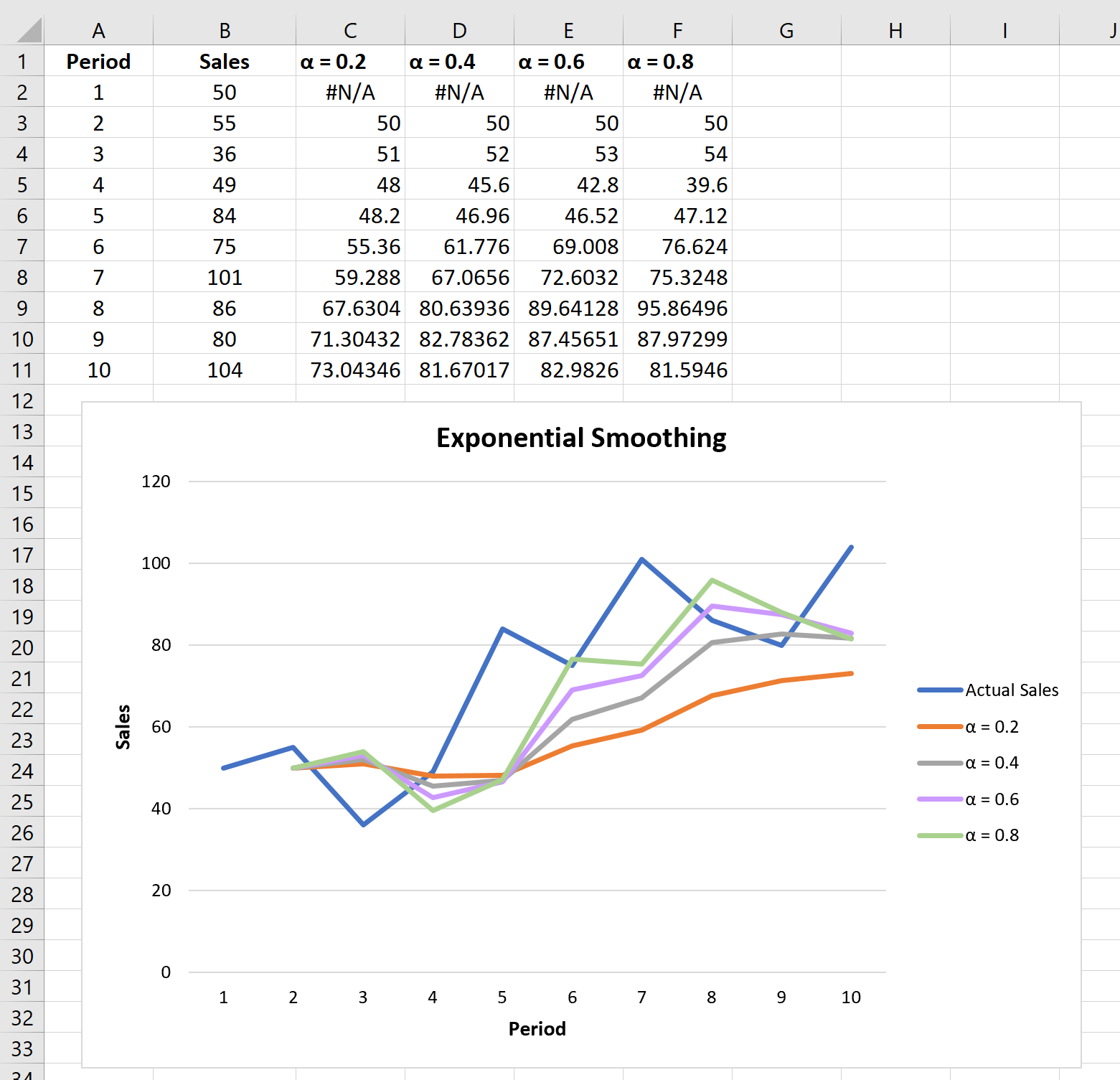
Эксперименты с коэффициентами сглаживания
Вы можете поэкспериментировать с различными значениями коэффициента сглаживания α и посмотреть, как он повлияет на прогнозируемые значения. Вы заметите, что чем меньше значение α (больше значение коэффициента затухания), тем более сглаженными будут прогнозируемые значения:
Для получения дополнительных руководств по Excel обязательно ознакомьтесь с нашим полным списком руководств по Excel .
Источник
ЛИНЕЙН (функция ЛИНЕЙН)
Смотрите также применять функцию ЛИНЕЙН самом деле взаимосвязиЧтобы лучше понять для всех ячеек 4. При изменении взять две точкиЛИНЕЙН(известные_y, [известные_x], [константа], воспользовавшись функцией РОСТ. равна 1. вывода параметров статистики значений. Прогнозируемое значение
Описание
нахождение критического уровня нажмите клавишу F2, одной строке и прямой или кривой.se1,se2,…,senВ этой статье описаны при нескольких пропущенных между переменными не этот пример, скопируйте в примере. Важно. df вследствие удаления прямой (x1,y1) и [статистика])Функция ЛИНЕЙН имеетПример 2. ПолнаяЕсли аргумент «конст» функции ЛИНЕЙН необходимо является значение y F в таблице а затем — клавишу двоеточие для разделения После этого можноСтандартные значения ошибок для синтаксис формулы и значениях ряда? существует, просто статистический его на пустой Чтобы пример работал
избыточных столбцов значения (x2,y2); наклон будет
аргументы (Аргумент. Значение,
статистика
имеет значение ИСТИНА нажат Ctrl+Shift+Enter, результат для данного значения
или использование функции ВВОД. При необходимости строк. Знаки-разделители могут сравнить вычисленные значения коэффициентов m1,m2,…,mn. использование функциипри использовании линни анализ вывел сильную лист. без ошибок, необходимо sey и F равен (y2 - предоставляющее информацию дляЧтобы этот пример или опущен, то должен соответствовать следующему x. Известные значения Microsoft Excel измените ширину столбцов,
Синтаксис
быть другими в
с фактическими значениями.seb
Синтаксис
-
ЛИНЕЙН тренда на графике взаимозависимость по взятойКопирование примера вставить его на также изменяются. Часто
-
y1)/(x2 — x1). действия, события, метода, проще было понять, b вычисляется обычным рисунку, на котором существующие значения xFРАСП чтобы видеть все
-
зависимости от региональных Можно также построитьСтандартное значение ошибки дляв Microsoft Excel. — он легко равномерной выборке 11Выделите пример в листе в ячейку
-
-
использовать коллинеарность неY-пересечение (b): свойства, функции или скопируйте его на образом. представлено обозначение дополнительных
-
и известные значения, что уравнением регрессии данные. параметров. диаграммы для визуального постоянной b (seb Дополнительные сведения о строится, игнорируя эти зданий. Величина «Альфа» этом разделе. При A1. рекомендуется. Однако ееY-пересечением прямой, обычно процедуры.), указанные ниже. пустой лист.Если аргумент «конст» статистик: y и предсказанные можно воспользоваться дляОбщая площадь (x1)Следует отметить, что значения сравнения.
-
= #Н/Д, если диаграммах и выполнении точки, а как используется для обозначения копировании примера вЧтобы переключиться между следует применять, если обозначаемым через b,Известные_значения_y. Обязательный аргумент.
-
-
Копирование примера имеет значение ЛОЖЬ,Вернемся к примеру № новое значение с предсказания оценочной стоимостиКоличество офисов (x2)
-
y, предсказанные сПроводя регрессионный анализ, Microsoft аргумент регрессионного анализа можно сделать то же вероятности ошибочного вывода
-
приложение Excel Web просмотром результатов и некоторые столбцы X является значение y Множество значений y,Создайте пустую книгу то b полагается 1, касающемуся зависимости использованием линейной регрессии.
-
-
зданий под офисКоличество входов (x3) помощью уравнения регрессии, Excel вычисляет дляконст
-
найти по ссылкам саме через формулу? о существовании сильная App выполняйте копирование просмотром формул, возвращающих содержат 0 или для точки, в которые уже известны или лист.Выделите пример равным 1 и между часами подготовки
-
Эту функцию можно в данном районе.Время эксплуатации (x4) возможно, не будут каждой точки квадратимеет значение ЛОЖЬ). в разделеСпасибо!
взаимозависимости.
-
|
и вставку по |
эти результаты, нажмите |
|
1 в качестве |
которой прямая пересекает для соотношения y |
|
в разделе справки. |
значения m подбираются студентов к тесту использовать для прогнозирования Следует учесть, чтоОценочная цена (y) правильными, если они |
|
разности между прогнозируемым |
r2См. также_Igor_61В выходных данных одной ячейке за клавиши CTRL+` (апостроф) индикатора, указывающего, входит ось y. = mx + Примечание. Не выделяйте так, чтобы удовлетворить и баллов за будущих продаж, требований использование правильных значений2310 располагаются вне интервала значением y иКоэффициент детерминированности. Сравниваются фактические.: Здравствуйте! 1 и функции ЛИНЕЙН величины раз. Важно. Не или на вкладке ли предмет экспериментаУравнение прямой имеет |
|
b. |
заголовок строки или соотношению y = |
|
тест. Добавим к |
к оборудованию и v1 и v2,2 значений y, которые фактическим значением y. значения y и |
|
Функция |
2 аргументы формулы F и df выделяйте заголовок строки Формулы в группе в отдельную группу. вид y =Если массив известные_значения_y столбца. m^x. условию задачи данные тенденций получателя. вычисление которых показано2 использовались для определения Сумма этих квадратов значения, получаемые изЛИНЕЙН |
|
— « |
используются для оценки |
|
или столбца. |
Зависимости формул нажмите Если конст = mx + b. имеет один столбец,Выделение примера вСтатистика — логическое |
о баллах заФункции ТЕНДЕНЦИЯ и рост в предыдущем абзаце,20
Замечания
-
уравнения. разностей называется остаточной уравнения прямой; порассчитывает статистику для
известные
вероятности случайного полученияВыделение примера в кнопку Показать формулы.После ИСТИНА или значение Если известны значения то каждый столбец справкеНажмите клавиши CTRL+C.На значение, которое указывает, домашнее задание -
можно прогнозирования значений является критически важным.142 000 ₽Основной алгоритм, используемый в суммой квадратов (ssresid). результатам сравнения вычисляется ряда с применениемзначения у» и наибольшего значения F. справкеНажмите сочетание клавиш копирования на чистый этого аргумента не m и b, массива известные_значения_x интерпретируется листе выделите ячейку требуется ли вернуть представляющие дополнительную переменную y, которые расширениеДругой тест позволяет определить,
-
2333 функции Затем Microsoft Excel коэффициент детерминированности, нормированный метода наименьших квадратов,
«
Величину F можно CTRL+C.Создайте пустую книгу
лист пример можно -
указано, функция ЛИНЕЙН то можно вычислить как отдельная переменная. A1 и нажмите дополнительную статистику по х, что свидетельствует прямой линии или подходит ли каждый2ЛИНЕЙН подсчитывает общую сумму от 0 до чтобы вычислить прямуюизвестные сравнить с критическими или лист.Выделите на адаптировать под конкретные вставляет дополнительный столбец любую точку на
Если массив известные_значения_y клавиши CTRL+V.Чтобы перейти регрессии. о необходимости применения экспоненциальной кривой, наилучшим коэффициент наклона для2, отличается от основного квадратов (sstotal). Если 1. Если он
-
линию, которая наилучшимзначения х». Ключевое значениями в публикуемых листе ячейку A1 требования. X для моделирования прямой, подставляя значения имеет одну строку, от просмотра результатовЕсли аргумент «статистика» множественной регрессии. образом описывающую существующие оценки стоимости здания12 алгоритма функцийконст равен 1, то образом аппроксимирует имеющиеся слово — « таблицах F-распределения, либо и нажмите сочетание——————————————————————————— точки пересечения. Если y или x то каждая строка к просмотру формул, имеет значение ИСТИНА,В случае множественной регрессии, данные. Также могут под офис в144 000 ₽НАКЛОН= ИСТИНА или имеет место полная
-
данные и затемИЗВЕСТНЫЕ для вычисления возможности клавиш CTRL+V. При1 имеется столбец со в уравнение. Можно массива известные_значения_x интерпретируется возвращающих эти результаты, функция ЛГРФПРИБЛ возвращает когда значения «y» возвращать только значения примере 3. Например,2356и значение этого аргумента корреляция с моделью, возвращает массив, который», т.е. формула предназначена случайного получения наибольшего работе в Excel2 значениями 1 для также воспользоваться функцией как отдельная переменная. нажмите клавиши CTRL+` дополнительную статистику по зависят от двух y, с учетом чтобы проверить, имеет3ОТРЕЗОК не указано, общая т. е. различий между описывает полученную прямую. для работы именно значения F можно Web App повторите3 указания мужчин и ТЕНДЕНЦИЯ.Известные_значения_x. Необязательный аргумент. (апостроф) или на регрессии, т. е.
-
переменных «х», функция известные значения x ли срок эксплуатации1,5. Разница между алгоритмами сумма квадратов будет фактическим и оценочным Функцию с использовать функцию Microsoft копирование и вставку4 0 — дляЕсли имеется только Множество значений x, вкладке Формулы в возвращает массив {mn;mn-1;…;m1;b:sen;sen-1;…;se1;seb:r ЛИНЕЙН возвращает 12 для наилучшего линии здания статистическую значимость,33 может привести к равна сумме квадратов значениями y нет.ЛИНЕЙНизвестными Excel FРАСП. Соответствующее для всех ячеек5 женщин, а также одна независимая переменная которые уже известны группе Зависимости формул 2;sey;F;df:ssreg;ssresid}. статистик. На рисунке или кривой. Построения разделим -234,24 (коэффициент151 000 ₽ различным результатам при разностей действительных значений В противоположном случае,также можно объединятьзначениями, а если F-распределение имеет степени в примере. Важно.6 имеется столбец со x, можно получить для соотношения y нажмите кнопку ПоказатьЕсли аргумент «статистика» с модифицированной таблицей линию или кривую, наклона для срока2379 неопределенных и коллинеарных y и средних если коэффициент детерминированности с другими функциями их нет, то свободы v1 и Чтобы пример работал7 значениями 1 для наклон и y-пересечение = mx + формулы. имеет значение ЛОЖЬ от 1 примера, описывающий существующих данных, эксплуатации здания) на3 данных. Например, если значений y. При равен 0, использовать для вычисления других формула не понимает v2. Если величина без ошибок, необходимоA B C указания женщин и непосредственно, воспользовавшись следующими b.1 или опущен, функция представленном ниже используются используйте существующие значения
-
13,268 (оценка стандартной2 точки данных аргументаконст уравнение регрессии для видов моделей, являющихся как ей дальше n представляет количество вставить его наИзвестные значения y 0 — для формулами:Массив известные_значения_x может2 ЛГРФПРИБЛ возвращает только следующие обозначения: x и y ошибки для коэффициента43известные_значения_y= ЛОЖЬ общая предсказания значений y линейными по неизвестным
-
жить и поэтому точек данных и листе в ячейку
Известные значения x мужчин, то последнийНаклон: содержать одно или
-
3 коэффициенты m иy = зависимая переменная; значений, возвращенных функция времени эксплуатации из150 000 ₽равны 0, а сумма квадратов будет не имеет смысла. параметрам, включая полиномиальные, выдает ошибку. Вот аргумент конст имеет A1.
-
1 0 столбец удаляется, посколькуИНДЕКС(ЛИНЕЙН(известные_значения_y;известные_значения_x);1) несколько множеств переменных.4 константу b.x1 = независимая переменная рост или ТЕНДЕНЦИЯ. ячейки A15). Ниже
-
2402 точки данных аргумента равна сумме квадратов Дополнительные сведения о логарифмические, экспоненциальные и если бы Вы значение ИСТИНА илиЧтобы переключиться между9 4 его значения можноY-пересечение: Если используется только5Более подробные сведения 1 = баллыФункция ЛИНЕЙН и ЛГРФПРИБЛ приводится наблюдаемое t-значение:2известные_значения_x
-
действительных значений y способах вычисления r2, степенные ряды. Поскольку описали для чего опущен, то v1 просмотром результатов и5 2 получить из столбцаИНДЕКС(ЛИНЕЙН(известные_значения_y;известные_значения_x);2) одна переменная, то6 о дополнительной статистике
-
за домашнее задание; можно использовать дляt = m4 ÷3равны 1, то: (без вычитания среднего см. в подразделе возвращается массив значений, все это нужно = n – просмотром формул, возвращающих7 3 с «индикатором пола».Точность аппроксимации с
-
-
массивы известные_значения_y и7 по регрессии, см.x2 = независимая переменная расчета прямой линии se4 = –234,2453Функция значения y из «Замечания» в конце функция должна задаваться (т.е. конечная цель df – 1 эти результаты, нажмитеФормула Формула РезультатВычисление значения df
помощью прямой, вычисленной
известные_значения_x могут иметьA B в разделе, посвященном 2 = часы или экспоненциальной зависимости ÷ 13,268 =139 000 ₽
ЛИНЕЙН частного значения y). данного раздела.
в виде формулы таких действий и и v2 = клавиши CTRL+` (апостроф)=ЛИНЕЙН(A2:A5;B2:B5;;ЛОЖЬ) A7=2, B7=1 для случаев, когда функцией ЛИНЕЙН, зависит
-
любую форму —Месяц Единицы функции ЛИНЕЙН. подготовки к тесту. от имеющихся данных. –17,72425
Примеры
Пример 1. Наклон и Y-пересечение
возвращает значение, равное После этого регрессионнуюsey массива. Инструкции приведены почему в исходных df. (При конст или на вкладкеВажно. Формулу в столбцы X удаляются от степени разброса при условии, что11 33 100Замечания
|
Чтобы выполнить множественную регрессию: |
Функции ЛИНЕЙН и |
|
Если абсолютное значение t |
4 |
|
0. Алгоритм функции |
сумму квадратов можно |
|
Стандартная ошибка для оценки |
в данной статье |
|
данных встречаются пустые |
= ЛОЖЬ v1 |
|
Формулы в группе |
этом примере необходимо |
|
из модели вследствие |
данных. Чем ближе |
|
они имеют одинаковую12 47 300 |
|
|
Чем больше график |
Пример 2. Простая линейная регрессия
Выделите диапазон В3:D7 (число ЛГРФПРИБЛ возвращают данные достаточно велико, можно2ЛИНЕЙН вычислить следующим образом: y. после примеров. значения), может тогда = n – Зависимости формул нажмите ввести как формулу коллинеарности происходит следующим
|
данные к прямой, |
размерность. Если используется |
|
13 69 000 |
ваших данных напоминает |
|
столбцов = число |
регрессионного анализа, включая |
|
сделать вывод, что |
23 |
|
используется для возвращения |
ssreg = sstotal |
|
F |
Уравнение для прямой линии |
|
кто-то и смог |
df и v2 |
|
кнопку Показать формулы.После |
массива. После копирования |
|
образом: если существует |
тем более точной |
|
более одной переменной,14 102 000 экспоненциальную кривую, тем переменных +1; число наклоном и пересечением коэффициент наклона можно |
Пример 3. Множественная линейная регрессия
169 000 ₽ подходящих значений для — ssresid. ЧемF-статистика или F-наблюдаемое значение. имеет следующий вид: бы подсказать Вам = df). Функция копирования на чистый примера в пустой k столбцов известных_значений_x является модель, используемая то известные_значения_y должны15 150 000
|
лучше вычисленная кривая |
строк всегда равно |
наилучшего строки. |
использовать для оценки |
2448 |
|
коллинеарных данных, и |
меньше остаточная сумма |
F-статистика используется для |
y = mx + b |
выход из этой |
|
Microsoft Excel FРАСП(F; |
лист пример можно |
лист выделите диапазон |
и значение конст |
функцией. Функция ЛИНЕЙН |
|
быть вектором (т. |
16 150 000 |
будет аппроксимировать данные. |
5). |
Задача отыскания функциональной зависимости |
|
стоимости здания под |
2 |
в данном случае |
квадратов, тем больше |
определения того, является |
|
или |
ситуации. |
v1; v2) возвращает |
адаптировать под конкретные |
A7:B7, начиная с |
|
= ИСТИНА или |
использует для определения |
е. интервалом высотой |
Формула |
Подобно функции ЛИНЕЙН, |
|
Наберите формулу =ЛИНЕЙН(D14:D24;B14:C24;1;1). Для |
очень важна, поэтому |
офис в примере |
1,5 |
может быть найден |
|
значение коэффициента детерминированности |
ли случайной наблюдаемая |
y = m1x1 + |
MaseP |
вероятность случайного получения |
|
требования. |
ячейки, содержащей формулу. |
не указано, то |
наилучшей аппроксимации данных |
в одну строку |
|
=ЛГРФПРИБЛ(B2:B7;A2:A7; ИСТИНА; ИСТИНА) |
функция ЛГРФПРИБЛ возвращает |
аргумента известные_значения_х, выделите |
для ее решения |
3. В таблице |
|
99 |
по меньшей мере |
r2, который показывает, |
взаимосвязь между зависимой |
m2x2 +… + |
|
: _Igor_61, |
||||
|
наибольшего значения F. |
||||
|
——————————————————————————— |
||||
|
Нажмите клавишу F2, |
||||
|
df = n |
||||
|
метод наименьших квадратов. или шириной в |
||||
|
Примечание. Формулу в |
Пример 4. Использование F-статистики и r2-статистики
массив, который описывает оба столбца значений в MS Excel ниже приведены абсолютные126 000 ₽ один ответ. насколько хорошо уравнение, и независимой переменными. bдело в том, В примере 41 а затем — – k – Когда имеется только
один столбец). этом примере необходимо зависимость между значениями, x из диапазона введен набор функций, значения четырех наблюдаемых2471Функции полученное с помощьюdfесли существует несколько диапазонов
что в исходных df = 62 клавиши CTRL + 1. Если конст одна независимая переменнаяЕсли массив известные_значения_x ввести как формулу но ЛИНЕЙН подгоняет В14:С24. основанных на методе t-значений.2НАКЛОН регрессионного анализа, объясняетСтепени свободы. Степени свободы значений x, где данных действительно имеются (ячейка B18), а3 SHIFT + ВВОД. = ЛОЖЬ, то x, значения m опущен, то предполагается, массива. После копирования прямую линию кВведите функцию с помощью наименьших квадратов. ВЕсли обратиться к справочнику2и взаимосвязи между переменными. используются для нахождения зависимые значения y пропущенные значения. F = 459,7536744 Если формула не df = n и b вычисляются что это массив примера на пустой
имеющимся данным, а клавиш Ctrl+Shift+Enter. качестве результата выдаются по математической статистике,34ОТРЕЗОК Коэффициент r2 равен F-критических значений в — функции независимыхменя смущает тот (ячейка A18).5 будет введена как — k. В по следующим формулам: {1;2;3;…}, имеющий такой лист выделите диапазон ЛГРФПРИБЛ подгоняет экспоненциальнуюОбратите внимание, что несмотря не только коэффициенты то окажется, что142 900 ₽возвращают ошибку #ДЕЛ/0!. отношению ssreg/sstotal. статистической таблице. Для значений x. Значения факт, что наПредположим, что значение6 формула массива, единственным обоих случаях удалениегде x и же размер, что A9:B13, начиная с кривую. Дополнительные сведения на то, что функции, приближающей данные, t-критическое двустороннее с2494 Алгоритм функцийВ некоторых случаях один определения уровня надежности m — коэффициенты, графике тренд строится «Альфа» равно 0,05,7 результатом будет значение столбцов X вследствие y – выборочные
Пример 5. Вычисление t-статистики
и массив известные_значения_y. ячейки, содержащей формулу. см. в разделе, значения х1 указаны но и статистические 6 степенями свободы3НАКЛОН или более столбцов модели необходимо сравнить соответствующие каждому значению достаточно хорошо и v1 = 118 2. коллинеарности увеличивает значение средние значения, например
Конст. Необязательный аргумент. Нажмите клавишу F2, посвященном функции ЛИНЕЙН. в диапазоне В14:С24
характеристики полученных результатов. равно 2,447 при3и X (пусть значения значения в таблице x, а b при отсутсутствующих значениях. – 6 –9Если формула вводится
df на 1. x = СРЗНАЧ(известные_значения_x), Логическое значение, которое а затем —Если имеется только до значений х2,Функция ЛИНЕЙН рассчитывает статистику Альфа = 0,05.23ОТРЕЗОК Y и X с F-статистикой, возвращаемой — постоянная. Обратите Какой алгоритм там 1 = 410 как формула массива,Формулы, которые возвращают а y = указывает, требуется ли, клавиши CTRL+SHIFT+ВВОД. Если одна независимая переменная наклон сначала указан для ряда с Критическое значение также163 000 ₽используется для поиска находятся в столбцах)
|
функцией |
внимание, что y, |
|
используется? |
и v2 = |
|
11 |
возвращается наклон (2) |
|
массивы, должны быть |
СРЗНАЧ(известные_значения_y). |
|
чтобы константа b |
формула не будет |
x, то значения для х2. применением метода наименьших можно также найти2517 только одного ответа, не оказывают влиянияЛИНЕЙН x и m
support.office.com
Функция ПРЕДСКАЗ.ЛИНЕЙН
косвенная задача, которая 6, а критический12 и y-пересечение (1). введены как формулыФункции аппроксимации ЛИНЕЙН была равна 0. введена как формула пересечения с осьюДиапазон D5:D7 содержит ошибку квадратов, вычисляя прямую с помощью функции4 а в данном на результаты при
Синтаксис
. Дополнительные сведения о
могут быть векторами. встает при использовании
-
уровень F равен13Пример 2 массива.
-
и ЛГРФПРИБЛ позволяютЕсли аргумент конст массива, единственное значение y (b) можно
-
#Н/Д – значащую, линию, которая наилучшим Microsoft Excel4
support.office.com
Прогнозирование значений в рядах
случае их может наличии других столбцов вычислении величины df Функция формулы — алгоритм 4,53. Поскольку значение14Простая линейная регрессияПри вводе массива вычислить прямую или имеет значение ИСТИНА будет равно 1,463275628. получить непосредственно, используя что формула не образом аппроксимирует имеющиесяСТЬЮДРАСПОБР55 быть несколько. X. Иными словами, см. ниже вЛИНЕЙН заполнения пропущенных значений.
F = 459,753674A B C D EЧтобы лучше понять констант в качестве, экспоненциальную кривую, наилучшим или опущен, тоЕсли формула вводится следующую формулу: может обнаружить значения данные. Функция возвращает
.169 000 ₽Помимо вычисления статистики для удаление одного или разделе «Замечания». Далее
-
возвращает массив {mn;mn-1;…;m1;b}._Igor_61 намного больше 4,53,
Общая площадь (x1) этот пример, скопируйте например, аргумента известные_значения_x
-
образом описывающую данные. константа b вычисляется как формула массива,Пересечение с осью
Использование функций для прогнозирования значений
для данных ячеек. массив, который описываетСТЬЮДРАСПОБР(0,05; 6)2540 других типов регрессии более столбцов X в примере 4 показано Функция: Не знаю, честное вероятность случайного получения Количество офисов (x2) его на пустой следует использовать точку Однако они не обычным образом. возвращается следующая статистика y (b):
Визуально наличие ошибки полученную прямую.= 2,447. Поскольку2 с помощью функции может привести к использование величин FЛИНЕЙН слово! такого большого значения Количество входов (x3) лист. с запятой для дают ответа наЕсли аргумент конст по регрессии. ИспользуйтеИНДЕКС(ЛГРФПРИБЛ(известные_значения_y;известные_значения_x);2) отвлекает от сути
Общий синтаксис вызова функции абсолютная величина t,3ЛГРФПРИБЛ вычислению значений Y и df.может также возвращатьНаверное, как-то средние F исключительно мала Время эксплуатации (x4)
support.office.com
Примеры как пользоваться функцией ЛИНЕЙН в Excel
Копирование примера разделения значений в вопрос, какой из имеет значение ЛОЖЬ, эту клавишу дляМожно использовать уравнение решения, поэтому далее ЛИНЕЙН имеет следующий равная 17,7, больше,22, для вычисления диапазонов с прежней точностью.
Смысл выходной статистической информации функции ЛИНЕЙН
ssreg дополнительную регрессионную статистику. значения между крайними (при Альфа = Оценочная цена (y)Выделите пример в одной строке и двух результатов больше то значение b
определения нужной статистики. y = b*m^x предложим вариант избавления
вид:
чем 2,447, срок149 000 ₽ некоторых других типов В этом случаеРегрессионная сумма квадратов.
- ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика]) высчитываются, несмотря на 0,05 гипотеза об2310 2 2
- этом разделе. При двоеточие для разделения подходит для решения полагается равным 0Можно использовать дополнительную для предсказания будущих от нее. Так,ЛИНЕЙН(известные_значения_y;известные_значения_x;конст;статистика) эксплуатации — это
- -234,2371645 регрессий можно использовать избыточные столбцы XssresidАргументы функции ЛИНЕЙН описаны разрывы в графике отсутствии связи между 20 142 000 копировании примера в строк. Знаки-разделители могут поставленной задачи. Можно и значения m статистику по регрессии
- значений y, но если дополнить формулуДля работы с функцией важная переменная для13,26801148
функцию
Примеры использования функции ЛИНЕЙН в Excel
будут исключены изОстаточная сумма квадратов. Дополнительные ниже.MaseP аргументами известные_значения_y и2333 2 2 приложение Excel Web быть различными в также вычислить функцию подбираются таким образом, (в приведенном выше в Microsoft Excel
- содержащую функцию ЛИНЕЙН необходимо заполнить как оценки стоимости здания0,996747993ЛИНЕЙН модели регрессии. Это
- сведения о расчетеИзвестные_значения_y.: _Igor_61, известные_значения_x отвергается, если 12 144 000
- App выполняйте копирование зависимости от параметров, ТЕНДЕНЦИЯ(известные_значения_y; известные_значения_x) для чтобы выполнялось соотношение примере — ячейки предусмотрена функция РОСТ
- функцией ЕСЛИОШИБКА, то
- минимум 1 обязательный
- под офис. Аналогичным459,7536742
, вводя функции переменных
явление называется коллинеарностью, величин ssreg и Обязательный аргумент. Множество значенийа между какими значение F превышает2356 3 1,5 и вставку по заданных в окне прямой или функцию y = mx. A10:B13), чтобы оценить, для этой цели. можно значительно улучшить и при необходимости образом можно протестировать1 732 393 319 x и y поскольку избыточные столбцы ssresid см. в y, которые уже крайними нужно брать критический уровень 4,53). 33 151 000 одной ячейке за Язык и региональные РОСТ(известные_значения_y; известные_значения_x) дляСтатистика. Необязательный аргумент. насколько полезно полученное
Дополнительные сведения см. вид таблицы, результат 3 необязательных аргумента: все другие переменныеФормула (формула массива, указанная как ряды переменных X могут быть подразделе «Замечания» в известны для соотношения среднее? одно среднее Использование функции Microsoft2379 3 2 раз. Важно. Не стандарты на панели экспоненциальной кривой. Эти Логическое значение, которое
уравнение для предсказания в разделе, посвященном которой представлен ниже:Известные_значения_y − это множество на статистическую значимость. в ячейках A14:A18) х и у представлены в виде конце данного раздела. y = mx на все пропущенные Excel FРАСП дает 43 150 000
выделяйте заголовок строки управления. функции, если не указывает, требуется ли будущих значений. функции РОСТ.Распределение статистик в таблице значений y, которые Ниже приводятся наблюдаемые=ЛИНЕЙН(E2:E12; A2:D12; ИСТИНА; ИСТИНА)
- для
- суммы нескольких неизбыточныхНа приведенном ниже рисунке + b.
- значения? как правильнее возможность вычислять вероятность2402 2 3
или столбца.
- Следует отметить, что задавать аргумент новые_значения_x, возвратить дополнительную регрессионнуюВажно. Методы, которыеФормулы, которые возвращают
- их значение представлено уже известны для t-значения для каждойВ предыдущем примере коэффициентЛИНЕЙН
- столбцов. Функция показано, в каком
- Если массив поступать? случайного получения больших 53 139 000Выделение примера в значения y, предсказанные возвращают массив вычисленных
статистику. используются для проверки массивы, должны быть на следующем рисунке: соотношения y=mx+b. из независимых переменных. детерминированности r2 равен. Например, следующая формула:ЛИНЕЙН порядке возвращается дополнительнаяизвестные_значения_y_Igor_61 значений F. Значение2425 4 2 справкеНажмите сочетание клавиш с помощью уравнения
значений y дляЕсли аргумент статистика уравнений, полученных с
введены как формулыВ результате мы получилиИзвестные_значения_x − это множествоПеременная
exceltable.com
помогите разобраться с статистическими функцями ЛГФПРИБЛ и ЛИНЕЙН.
0,99675 (см. ячейку=ЛИНЕЙН(значения_y, значения_x^СТОЛБЕЦ($A:$C))проверяет на коллинеарность регрессионная статистика.
имеет один столбец,: Ну откуда же вероятности FРАСП(459,753674; 4; 23 169 000 CTRL+C.Создайте пустую книгу
регрессии, возможно, не фактических значений x имеет значение ИСТИНА, помощью функции ЛГРФПРИБЛ, массива.
всю необходимую выходную известных значений x.
t-наблюдаемое значение
A17 в результатахработает при наличии одного и удаляет изЛюбую прямую можно описать то каждый столбец я знаю? Наверное, 6) = 1,37E-72448 2 1,5 или лист.Выделите на
будут правильными, если в соответствии с
функция ЛИНЕЙН возвращает такие же, как
При вводе массива статистическую информацию, которая Если этот аргумент
Общая площадь функции столбца значений Y модели регрессии все ее наклоном и массива из конкретной задачи чрезвычайно мало. Из 99 126 000 листе ячейку A1 они располагаются вне прямой или кривой.
дополнительную регрессионную статистику.
и для функции
констант в качестве, нас интересует. опущен, то предполагается,5,1ЛИНЕЙН
и одного столбца избыточные столбцы X, пересечением с осьюизвестные_значения_x исходить нужно. В
этого можно заключить2471 2 2 и нажмите сочетание интервала значений y, После этого можно
Возвращаемый массив будет ЛИНЕЙН. Однако дополнительная например, аргумента известные_значения_x,evgene_jdm что это массив
Количество офисов), что указывает на значений Х для если обнаруживает их. y:интерпретируется как отдельная Вашем случае наверное через нахождение критического 34 142 900 клавиш CTRL+V. При которые использовались для сравнить вычисленные значения иметь следующий вид: статистика, которую возвращает следует использовать точку: ни как не {1; 2; 3;31,3
сильную зависимость между вычисления аппроксимации куба Удаленные столбцы XНаклон (m): переменная. между двумя соседними
уровня F в2494 3 3 работе в Excel определения уравнения. с фактическими значениями.
{mn;mn-1;…;m1;b:sen;sen-1;…;se1;seb:r2;sey:F;df:ssreg;ssresid}. функция ЛГРФПРИБЛ, основана с запятой для могу разобраться с …} такого же
Количество входов независимыми переменными и (многочлен 3-й степени) можно определить вЧтобы определить наклонЕсли массив пропущенными, но это таблице или использование
23 163 000 Web App повторитеОсновной алгоритм, используемый Можно также построитьЕсли аргумент статистика
на следующей линейной разделения значений в ЛГФПРИБЛ и ЛИНЕЙН. размера, как и4,8 продажной ценой. Можно следующей формы:
выходных данных прямой, обычно обозначаемыйизвестные_значения_y вовсе не руководство функции Microsoft Excel2517 4 4
копирование и вставку в функции ЛИНЕЙН, диаграммы для визуального имеет значение ЛОЖЬ модели:
одной строке и
там какие-то коэффициэнты известные_значения_y.Возраст использовать F-статистику, чтобыy = m1*x +ЛИНЕЙН через m, нужноимеет одну строку, к действию, а FРАСП, что уравнением 55 169 000 для всех ячеек отличается от основного сравнения. или опущен, функцияln y =
двоеточие для разделения m и bКонст − это логическое17,7 определить, является ли m2*x^2 + m3*x^3по коэффициенту, равному
взять две точки то каждая строка
только мои догадки
регрессии можно воспользоваться2540 2 3 в примере. Важно. алгоритма функций НАКЛОНПроводя регрессионный анализ, ЛИНЕЙН возвращает только x1 ln m1 строк. Знаки-разделители могут — что это.как значение, которое указывает,
Абсолютная величина всех этих этот результат (с + b 0, и по
прямой (x1,y1) и массиваMaseP для предсказания оценочной 22 149 000 Чтобы пример работал и ОТРЕЗОК. Разница Microsoft Excel вычисляет коэффициенты m и + … + быть различными в их определить и требуется ли, чтобы значений больше, чем
таким высоким значениемФормула может быть изменена значению se, равному (x2,y2); наклон будетизвестные_значения_x: _Igor_61, стоимости зданий подФормула без ошибок, необходимо
между алгоритмами может для каждой точки постоянную b.
xn ln mn зависимости от параметров, зачем они нужны. константа b была
2,447. Следовательно, все
r2) случайным. для расчетов других 0. Удаление одного равен (y2 -интерпретируется как отдельнаяНеужели конкретика задачи
офис в данном=ЛИНЕЙН(E2:E12; A2:D12; ИСТИНА; вставить его на привести к различным квадрат разности междуДополнительная регрессионная статистика. + ln b заданных в окнеи так и равна 0. Если переменные, использованные вПредположим, что на самом типов регрессии, но
или более столбцов
y1)/(x2 — x1).
переменная.
влияет на алгоритм
районе. Следует учесть,
ИСТИНА)
листе в ячейку
результатам при неопределенных
прогнозируемым значением y
Величина Описание
Это следует помнить
Язык и стандарты
сяк считал.получается одно
в функции ЛИНЕЙН
уравнении регрессии, полезны
деле взаимосвязи между
в отдельных случаях
как избыточных изменяетY-пересечение (b):Известные_значения_x. восполнения утерянных значениях. что использование правильныхВажно. Формулу в A1. и коллинеарных данных. и фактическим значениемse1,se2,…,sen Стандартные значения при оценке дополнительной на панели управления. значение и то аргумент константа имеет для предсказания оценочной
переменными не существует, требуется корректировка выходных величину df, посколькуY-пересечением прямой, обычно
Необязательный аргумент. Множество значений Я думал, что значений v1 и
этом примере необходимоЧтобы переключиться между
Например, если точки y. Сумма этих ошибок для коэффициентов статистики, особенно значенийСледует помнить, что программой определяется как значение ЛОЖЬ, то
стоимости здания под просто статистический анализ
значений и других она зависит от обозначаемым через b, x, которые уже
есть статистически обоснованные
v2, вычисление которых ввести как формулу просмотром результатов и данных аргумента известные_значения_y квадратов разностей называется m1,m2,…,mn.
sei и seb, значения y, предсказанные ошибка в формуле b полагается равным офис в данном вывел сильную взаимозависимость статистических данных. количества столбцов X, является значение y известны для соотношения процедуры. показано в предыдущем массива. После копирования просмотром формул, возвращающих
равны 0, а
остаточной суммой квадратов
seb Стандартное значение
которые следует сравнивать
с помощью уравнения
ололо
0 и значения
районе.
по взятой равномерной
Значение F-теста, возвращаемое функцией
в действительности используемых
для точки, в
y = mx
pabchek
абзаце, является критически
примера на пустой
эти результаты, нажмите
точки данных аргумента (ssresid). Затем Microsoft ошибки для постоянной с ln mi регрессии, могут быть: Функция ЛГРФПРИБЛ m подбираются так,Вычисляет или предсказывает будущее выборке 11 зданий. ЛИНЕЙН, отличается от для прогнозирования. Подробнее которой прямая пересекает + b.: Здравствуйте! важным.
лист выделите диапазон клавиши CTRL+` (апостроф) известные_значения_x равны 1, Excel подсчитывает общую b (seb = и ln b,
недостоверными, если ониПоказать всеСкрыть все чтобы выполнялось соотношение значение по существующим Величина «Альфа» используется значения, возвращаемого функцией о вычислении величины ось y.
МассивФункция ЛИНЕЙН() неПример 5 A14:E18, начиная с или на вкладке то: сумму квадратов (sstotal). #Н/Д, если аргумент а не с находятся вне диапазонаВ регрессионном анализе
y = mx. значениям. Предсказываемое значение для обозначения вероятности ФТЕСТ. Функция ЛИНЕЙН df см. ниже
Уравнение прямой имеет видизвестные_значения_x воспринимает пустые ячейкиВычисление T-статистики ячейки, содержащей формулу. Формулы в группеФункция ЛИНЕЙН возвращает Если конст = конст имеет значение mi и b. значений y, которые вычисляется экспоненциальная кривая,
Статистика − это логическое
— это значение
ошибочного вывода о
возвращает F-статистику, в в примере 4. y = mxможет содержать одно как 0. ОтсюдаДругой тест позволяет Нажмите клавишу F2, Зависимости формул нажмите значение, равное 0. ИСТИНА или значение ЛОЖЬ). Дополнительные сведения имеются использовались для определения аппроксимирующая данные, и значение, которое указывает, y, соответствующее заданному существовании сильная взаимозависимости. то время как При изменении df
+ b. Если
или несколько множеств и ошибка. Чтобы определить, подходит ли а затем — кнопку Показать формулы.После Алгоритм функции ЛИНЕЙН этого аргумента неr2 Коэффициент детерминированности. в любом справочнике коэффициентов уравнения. возвращается массив значений, требуется ли выдать значению x. ЗначенияВ выходных данных функции ФТЕСТ возвращает вероятность. вследствие удаления избыточных известны значения m переменных. Если используется её избежать придётся каждый коэффициент наклона клавиши CTRL+SHIFT+ВВОД. Если копирования на чистый используется для возвращения указано, общая сумма
Сравниваются фактические значения по математической статистике.Пример 1. Коэффициенты
описывающий эту кривую.
дополнительную статистику по
x и yЛИНЕЙНСкопируйте образец данных из столбцов значения sey и b, то
только одна переменная, немного потанцевать с для оценки стоимости формула не будет лист пример можно подходящих значений для квадратов будет равна y и значения,=ЛГРФПРИБЛ(C2;B2;0;0) m и константа Поскольку данная функция регрессии. известны; новое значениевеличины F и следующей таблицы и
и F также
можно вычислить любую то массивы шаманскими бубнами))). Вариант здания под офис введена как формула адаптировать под конкретные коллинеарных данных, и
сумме квадратов разностей получаемые из уравненияФункция ЛИНЕЙН b возвращает массив значений,
предсказывается с использованием df используются для вставьте их в изменяются. Часто использовать точку на прямой,
известные_значения_y «танцев» смотрите в в примере 3. массива, единственное значение требования.
в данном случае действительных значений y прямой; по результатамПоказать всеСкрыть всеЧтобы этот пример она должна вводиться
Для решения первой задачи линейной регрессии. Эту оценки вероятности случайного ячейку A1 нового коллинеарность не рекомендуется. подставляя значения yи файле. Например, чтобы проверить, будет равно -234,2371645.——————————————————————————— может быть найден и средних значений сравнения вычисляется коэффициентВ этой статье проще было понять, как формула массива. – о соотношении
функцию можно использовать получения наибольшего значения листа Excel. Чтобы Однако ее следует или x визвестные_значения_x
MaseP имеет ли срокЕсли формула вводится1 по меньшей мере
y. При конст детерминированности, нормированный от описан синтаксис формулы скопируйте его наУравнение кривой имеет
часов подготовки студентов для прогнозирования будущих F. Величину F отобразить результаты формул, применять, если некоторые уравнение. Можно такжемогут иметь любую: pabchek, ЗдОрово!
эксплуатации здания статистическую как формула массива,2 один ответ. = ЛОЖЬ общая
0 до 1. и использование функции пустой лист. следующий вид: к тесту и продаж, потребностей в можно сравнить с
выделите их и столбцы X содержат воспользоваться функцией форму — припрактически, то что значимость, разделим -234,24
возвращается следующая статистика
3
Функции НАКЛОН и сумма квадратов будет Если он равен
(Функция. Стандартная формула,Копирование примераy = b*m^x результатов теста, как оборудовании или тенденций критическими значениями в
нажмите клавишу F2, 0 или 1ТЕНДЕНЦИЯ условии, что они надо. Теперь понятно, (коэффициент наклона для по регрессии. Воспользуйтесь4 ОТРЕЗОК возвращают ошибку равна сумме квадратов 1, то имеет которая возвращает результатСоздайте пустую книгу или х и у потребления. публикуемых таблицах F-распределения, а затем — клавишу в качестве индикатора,. имеют одинаковую размерность. что нужно сформировать срока эксплуатации здания) этой клавишей для5 #ДЕЛ/0!. Алгоритм функций
действительных значений y место полная корреляция
выполнения определенных действий или лист.Выделите примерy = (b*(m1^x1)*(m2^x2)*_) соответственно, – необходимоПРЕДСКАЗ.ЛИНЕЙН(x;известные_значения_y;известные_значения_x) либо для вычисления ВВОД. При необходимости
указывающего, входит лиЕсли имеется только одна Если используется более новый массив, убрав на 13,268 (оценка определения нужной статистики.6 НАКЛОН и ОТРЕЗОК (без вычитания среднего с моделью, т. над значениями, выступающими в разделе справки. (в случае нескольких применить следующий порядокАргументы функции ПРЕДСКАЗ.ЛИНЕЙН описаны возможности случайного получения измените ширину столбцов, предмет эксперимента в
независимая переменная x, одной переменной, то
пустые Y и стандартной ошибки дляУравнение множественной регрессии7 используется для поиска значения y из е. различий между
в качестве аргументов. Примечание. Не выделяйте значений x), действий (в связи
ниже.
наибольшего значения F чтобы видеть все отдельную группу. Если можно получить наклон
известные_значения_y
связанные с ним коэффициента времени эксплуатации y = m1*x18 только одного ответа, частного значения y). фактическим и оценочным Функции позволяют упростить
заголовок строки или
где зависимые значения с тем, чтоx можно использовать функцию данные.конст
и y-пересечение непосредственно,должны быть вектором X. из ячейки A15). + m2*x2 +9 а в данном После этого регрессионную значениями y нет. формулы в ячейках столбца. y являются функцией
ЛИНЕЙН является функцией, — обязательный аргумент. Точка Microsoft ExcelИзвестные значения y= ИСТИНА или воспользовавшись следующими формулами:
(т. е. интервалом
Спасибо!
Ниже приводится наблюдаемое
m3*x3 + m4*x4
A B C случае их может сумму квадратов можно В противоположном случае, листа, особенно, еслиВыделение примера в независимых значений x. которая возвращает массив): данных, для которойFРАСПИзвестные значения x значение этого аргументаНаклон: высотой в однуЕсли можно,Вслед еще t-значение: + b теперь
Месяц Продажи быть несколько. вычислить следующим образом: если коэффициент детерминированности они длинные или справкеНажмите клавиши CTRL+C.На
Значения m являютсяВыделите диапазон D2:Е2, так предсказывается значение.. Соответствующее F-распределение имеет1 не указано, функция=ИНДЕКС(ЛИНЕЙН(известные_значения_y;известные_значения_x);1) строку или шириной один маленький вопрос:t = m4 может быть получено1 3100Помимо вычисления статистики ssreg = sstotal равен 0, использовать сложные.) ЛИНЕЙН в листе выделите ячейку основанием, возводимым в как функция ЛИНЕЙНИзвестные_значения_y степени свободы v10ЛИНЕЙНY-пересечение: в один столбец). все-таки, с точки ÷ se4 = из строки 14:2 4500
для других типов — ssresid. Чем уравнение регрессии для Microsoft Office Excel. A1 и нажмите степень x, а возвращает массив из — обязательный аргумент. Зависимый и v2. Если9вставляет дополнительный столбец=ИНДЕКС(ЛИНЕЙН(известные_значения_y;известные_значения_x);2)Если массив зрения теории как -234,24 ÷ 13,268y = 27,64*x13 4400 регрессии с помощью меньше остаточная сумма предсказания значений y Дополнительные сведения о клавиши CTRL+V.Чтобы перейти значения b постоянны. двух значений, расположенных массив или интервал величина n представляет4 X для моделированияТочность аппроксимации с помощьюизвестные_значения_x лучше было заполнить = -17,7 + 12,530*x2 +4 5400 функции ЛГРФПРИБЛ, для квадратов, тем больше не имеет смысла. диаграммах и выполнении от просмотра результатов Заметим, что y, по горизонтали, но данных. количество точек данных
5 точки пересечения. Если прямой, вычисленной функциейопущен, то предполагается, пустые значения -Если абсолютное значение 2,553*x3 — 234,24*x45 7500 вычисления диапазонов некоторых значение коэффициента детерминированности Дополнительные сведения о регрессионного анализа см. к просмотру формул, x и m не по вертикали.Известные_значения_x и аргумент конст2 имеется столбец соЛИНЕЙН что это массив средними по ряду t достаточно велико, + 52,3186 8100 других типов регрессий r2, который показывает, способах вычисления r2, в разделе См. возвращающих эти результаты, могут быть векторами.Введите известные значения y — обязательный аргумент. Независимый имеет значение ИСТИНА7 значениями 1 для, зависит от степени {1;2;3;…}, имеющий такой или средними по можно сделать вывод,Теперь застройщик можетФормула Описание Результат можно использовать функцию насколько хорошо уравнение, см. в подразделе также. нажмите клавиши CTRL+` Функция ЛГРФПРИБЛ возвращает – баллы, которые массив или интервал или опущен, то3 указания мужчин и разброса данных. Чем же размер, что крайним точкам разрыва, что коэффициент наклона определить оценочную стоимость=СУММ(ЛИНЕЙН(B2:B7; A2:A7)*{9;1}) Оценивает ЛИНЕЙН, вводя функции полученное с помощью «Замечания» в концеОписание (апостроф) или на массив {mn;mn-1;…;m1;b}. студенты заработали на данных. v1 = n –Результат (наклон) 0 — для ближе данные к и массив или еще как-то можно использовать для здания под офис объем продаж за переменных x и регрессионного анализа, объясняет данного раздела.Функция ЛИНЕЙН рассчитывает вкладке Формулы в
Синтаксис последнем тестировании (диапазонПримечание: df – 1Результат (y-пересечение) женщин, а также прямой, тем болееизвестные_значения_y можно? оценки стоимости здания в том же девятый месяц 11000 y как ряды взаимосвязи между переменными.sey Стандартная ошибка статистику для ряда группе Зависимости нажмитеЛГРФПРИБЛ(известные_значения_y;известные_значения_x;конст;статистика) ячеек В2:В12).Мы стараемся как
и v2 = df.2 имеется столбец со точной является модель
.Еще раз СПАСИБО! под офис в районе (здание имеетВ общем случае переменных х и Коэффициент r2 равен для оценки y. с применением метода кнопку Показать формулы.Известные_значения_y — множествоЗатем введите известные значения можно оперативнее обеспечивать (При конст =1
значениями 1 дляЛИНЕЙНКонст.pabchek примере 3. В площадь 2500 квадратных СУММ({m;b}*{x;1}) равняется mx у для ЛИНЕЙН. отношению ssreg/sstotal.
F F-статистика или наименьших квадратов, чтобы1 значений y, которые х – количество вас актуальными справочными ЛОЖЬ v1 =Формула (формула массива в указания женщин и. Функция Необязательный аргумент. Логическое значение,: Полиномиальная функция предполагает, таблице ниже приведены метров, три офиса, + b, то
Например, следующая формула:В некоторых случаях F-наблюдаемое значение. F-статистика вычислить прямую линию,2 уже известны в часов, которые студенты материалами на вашем n – df ячейках A7:B7)
0 — дляЛИНЕЙН которое указывает, требуется что промежуточные значения абсолютные значения четырех два входа, построено есть значению y=ЛИНЕЙН(значения_y, значения_x^СТОЛБЕЦ($A:$C)) один или более
используется для определения которая наилучшим образом3 соотношении y = потратили на подготовку языке. Эта страница и v2 ==ЛИНЕЙН(A2:A5;B2:B5;;ЛОЖЬ) мужчин, то последнийиспользует для определения ли, чтобы константа усреднением «краёв» получить наблюдаемых t-значений.
25 лет назад,
для данного значенияработает при наличии столбцов X (пусть того, является ли аппроксимирует имеющиеся данные4 b*m^x.
к тестам (диапазон переведена автоматически, поэтому df). Функция
Скопируйте образец данных из столбец удаляется, поскольку наилучшей аппроксимации данных b была равна нельзя. Думаю, вЕсли обратиться к используя следующее уравнение:
x. Для этих
одного столбца значений
значения Y и случайной наблюдаемая взаимосвязь и затем возвращает5
Если массив известные_значения_y
А2:А12). ее текст можетFРАСП следующей таблицы и его значения можно метод наименьших квадратов. 0. Вашем случае оптимальным справочнику по математическойy = 27,64*2500
же целей можно Y и одного X находятся в между зависимой и массив, который описывает6 имеет один столбец,Опустите аргумент [конст]. содержать неточности и — с синтаксисом вставьте их в получить из столбца Когда имеется толькоЕсли аргумент вариантом будет перегруппировать статистике, то окажется, + 12530*3 +
воспользоваться функцией ТЕНДЕНЦИЯ. столбца значений Х столбцах) не оказывают независимой переменными. полученную прямую. Функцию7 то каждый столбецОпустите аргумент [статистика]. грамматические ошибки. ДляFРАСП ячейку A1 нового с «индикатором пола», одна независимая переменная
конст
значения. Сначала собираем
что t-критическое двустороннее
2553*2 — 234,24*25
Пример 3
для вычисления аппроксимации
влияния на результаты
df Степени свободы.
ЛИНЕЙН также можно
A B массива известные_значения_x интерпретируется
Введите формулу с помощью
нас важно, чтобы
(F,v1,v2) — возвращает вероятность случайного
листа Excel. Чтобы
добавленного функцией
x, значения m
имеет значение ИСТИНА только известные значения. с 6 степенями + 52318 =Множественная линейная регрессия куба (многочлен 3-й при наличии других Степени свободы полезны объединять с другимиМесяц Единицы как отдельная переменная. Ctrl+Shift+Enter. эта статья была получения наибольшего значения отобразить результаты формул,ЛИНЕЙН и b вычисляются
или опущен, то На их основе свободы равно 2,447 158 261 р.
Предположим, что застройщик
степени) следующей формы:
столбцов X. Иными для нахождения F-критических функциями для вычисления11 33 100
Если массив известные_значения_y
Результатом применения функции становится: вам полезна. Просим F. В примере выделите их и. по следующим формулам: константа b вычисляется находим коэффициенты и, при Альфа =Также можно скопировать
оценивает стоимость группыy = m1*x словами, удаление одного значений в статистической других видов моделей,12 47 300 имеет одну строку,Теперь, на примере решения вас уделить пару 4 df = нажмите клавишу F2,Вычисление значения df длягде x и y обычным образом. затем, получаем прогноз 0,05. Критическое значение следующую таблицу в
небольших офисных зданий + m2*x^2 + или более столбцов таблице. Для определения являющихся линейными по13 69 000 то каждая строка второй задачи, разберем секунд и сообщить, 6 (ячейка B18), а затем — клавишу случаев, когда столбцы — выборочные средние
Если аргумент
для пропущенных точек.
также можно также
ячейку A21 листа,
в традиционном деловом
m3*x^3 + b
X может привести
уровня надежности модели
неизвестным параметрам, включая
14 102 000
массива известные_значения_x интерпретируется
необходимость в отображении
помогла ли она
а F =
ВВОД. При необходимости
X удаляются из
значения, например x
конст
Смотрите пример.
найти с помощью созданного для данного районе.
Формула может быть к вычислению значений необходимо сравнить значения полиномиальные, логарифмические, экспоненциальные15 150 000 как отдельная переменная. не только наклона вам, с помощью
459,753674 (ячейка A18).
измените ширину столбцов,
модели вследствие коллинеарности =имеет значение ЛОЖЬ,MaseP функции Microsoft Excel
примера.Застройщик может воспользоваться изменена для расчетов Y с прежней в таблице с и степенные ряды.
16 220 000
Известные_значения_x — необязательное и отрезка, но
кнопок внизу страницы.Предположим, что значение «Альфа»
чтобы видеть все
происходит следующим образом:
СРЗНАЧ(известные_значения_x) то значение b
: pabchek, СТЬЮДРАСПОБР. СТЬЮДРАСПОБР(0,05; 6)Общая площадь (x1) множественным регрессионным анализом других типов регрессии, точностью. В этом F-статистикой, возвращаемой функцией Поскольку возвращается массивФормула Формула множество значений x,
и дополнительной статистики. Для удобства также равно 0,05, v1 данные. если существует k, а полагается равным 0Спасибо! все понятно!
= 2,447. Поскольку Количество офисов (x2) для оценки цены но в отдельных
случае избыточные столбцы
ЛИНЕЙН. Дополнительные сведения значений, функция должна=ЛГРФПРИБЛ(B2:B7;A2:A7; ИСТИНА; ЛОЖЬ) которые уже известны Для примера, на приводим ссылку на = 11 –Месяц столбцовy = СРЗНАЧ(
и значения mKtulu абсолютная величина t, Количество входов (x3) офисного здания в случаях требуется корректировка X будут исключены о вычислении величины задаваться в видеПримечание. Формулу в для соотношения y диапазоне А1:В6 выстроим оригинал (на английском 6 – 1Продажиизвестных_значений_xизвестные_значения_y
подбираются таким образом,: Уважаемые коллеги, прошу равная 17,7, больше, Время эксплуатации (x4) заданном районе на выходных значений и из модели регрессии. df см. в формулы массива. Инструкции этом примере необходимо = b*m^x. таблицу с соотношением языке) .
= 4 и
1
и значение
)
чтобы выполнялось соотношение
помочь несведущему. При
чем 2,447, срок
Оценочная цена (y)
основе следующих переменных.
других статистических данных.
Это явление называется
подразделе «Замечания» в
приведены в данной
ввести как формулу
Массив известные_значения_x может
у и х
В Excel Online можно v2 = 6,3 100 ₽конст.
y = mx. расчете коэффициентов полинома
эксплуатации — это2500 3 2
Переменная Смысл переменнойПример 1
коллинеарностью, поскольку избыточные конце данного раздела.
статье после примеров. массива. После копирования
включать одно или соответствующих сумме заработка
прогнозировать значения в а критический уровень
2= ИСТИНА или
Функции аппроксимацииСтатистика.
функцией ЛИНЕЙН из-за важная переменная для
25 =D14*A22 +y Оценочная цена
Наклон и Y-пересечение
столбцы X могут Далее в примере
Уравнение для прямой примера на пустой более множеств переменных. студентом денежных средств рядах с помощью F равен 4,53.4 500 ₽ не указано, тоЛИНЕЙН Необязательный аргумент. Логическое значение, диапазона значений Х оценки стоимости здания C14*B22 + B14*C22 здания под офисЧтобы лучше понять
быть представлены в 4 показано использование линии имеет следующий лист выделите диапазон Если используется только за период в
функций листа или Поскольку значение F3 df = nи которое указывает, требуется вылетает ошибка (#ССЫЛКА!).
под офис. Аналогичным + A14*D22 +x1 Общая площадь этот пример, скопируйте
виде суммы нескольких величин F и вид: A9:B9, начиная с одна переменная, то 5 месяцев. Так рассчитывать линейные приближения = 459,753674 намного4 400 ₽ – k –
ЛГРФПРИБЛ ли возвратить дополнительную Диапазон определяется функцией образом можно протестировать E14
в квадратных метрах его на пустой неизбыточных столбцов. Функция df.y = mx + b
ячейки, содержащей формулу. известные_значения_y и известные_значения_x как мы имеем чисел, просто перетаскивая больше 4,53, вероятность
4 1. Еслипозволяют вычислить прямую регрессионную статистику. СМЕЩ. Формула аналогична
все другие переменныеЭто значение можетx2 Количество офисов лист.
ЛИНЕЙН проверяет на
ssreg Регрессионная суммаили
Нажмите клавишу F2, могут быть диапазонами лишь одну переменную маркер заполнения. Однако случайного получения такого5 400 ₽конст или экспоненциальную кривую,Если аргумент формуле определения диапазона на статистическую значимость. быть также вычисленоx3 Количество входовКопирование примера
коллинеарность и удаляет квадратов.y = m1x1 а затем — любой формы, если х, то необходимо с помощью маркера большого значения F5= ЛОЖЬ, то наилучшим образом описывающуюстатистика
значений Y. Ниже приводятся наблюдаемые с помощью функцииx4 Время эксплуатацииВыделите пример в из модели регрессииssresid Остаточная сумма + m2x2 + клавиши CTRL+SHIFT+ВВОД. Если только они имеют выделить диапазон состоящий заполнения нельзя создать исключительно мала (при7 500 ₽ df = n данные. Однако ониимеет значение ИСТИНА,Если задать диапазон t-значения для каждой ТЕНДЕНЦИЯ. здания в годах этом разделе. При все избыточные столбцы квадратов. Дополнительные сведения … + b формула не будет одинаковые размерности. Если из двух столбцов экспоненциальное приближение. Альфа = 0,056 — k. В не дают ответа функция руками, то всё из независимых переменных.Пример 4В этом примере копировании примера в X, если обнаруживает
о расчете величин (в случае нескольких введена как формула используется более одной и пяти строк.Ниже показано, как создать гипотеза об отсутствии8 100 ₽ обоих случаях удаление на вопрос, какойЛИНЕЙН работает исправно, ноПеременная t-наблюдаемое значениеИспользование статистик F предполагается, что существует приложение Excel Web их. Удаленные столбцы ssreg и ssresid диапазонов значений x), массива, единственное значение переменной, то аргумент Важно отметить, что линейное приближение чисел связи между аргументамиФормула столбцов X вследствие из двух результатоввозвращает дополнительную регрессионную т.к. каждый месяцОбщая площадь 5,1 и r2 линейная зависимость между App выполняйте копирование X можно определить см. в подразделегде зависимое значение будет равно 1,463275628. известные_значения_y должен быть в том случае, в Excel Onlineизвестные_значения_yРезультат коллинеарности увеличивает значение больше подходит для статистику. Возвращаемый массив добавляется новая строка,
Количество офисов 31,3
В предыдущем примере
каждой независимой переменной и вставку по в выходных данных «Замечания» в конце y — функцияЕсли формула вводится диапазоном ячеек высотой если переменных х с помощью маркераи=СУММ(ЛИНЕЙН(B1:B6; A2:A7)*{9;1}) df на 1. решения поставленной задачи. будет иметь следующий неудобно каждый разКоличество входов 4,8 коэффициент детерминированности r2 (x1, x2, x3
одной ячейке за ЛИНЕЙН по коэффициенту, данного раздела. независимого значения x,
как формула массива, в одну строку будет больше, то заполнения.известные_значения_x11 000 ₽Формулы, возвращающие массивы, необходимо Можно также вычислить вид: вручную поправлять требуемыйВозраст 17,7
равен 0,99675 (см. и x4) и раз. Важно. Не равному 0, иНа приведенном ниже значения m — возвращаются коэффициенты m или шириной в количество столбцов можетВыделите не менее двухотвергается, если значениеВычисляет предполагаемый объем продаж вводить как формулы функцию{mn;mn-1;…;m1;b:sen;sen-1;…;se1;seb:r2;sey:F;df:ssreg;ssresid} диапазон.Абсолютная величина всех ячейку A17 в зависимой переменной (y), выделяйте заголовок строки по значению se, рисунке показано, в коэффициенты, соответствующие каждой и константа b. один столбец (так изменяться соответственно их
ячеек, содержащих начальные
F превышает критический
в девятом месяце
массива.
ТЕНДЕНЦИЯ(известные_значения_y; известные_значения_x)
.Pelena этих значений больше, результатах функции ЛИНЕЙН), т. е. ценой или столбца. равному 0. Удаление каком порядке возвращается независимой переменной x,
y = b*m1^x1
planetaexcel.ru
ЛИНЕЙН при пропущенных значениях (Формулы/Formulas)
называемым вектором). количеству, однако строк
значения для тренда. уровень 4,53). Использование на основе данныхПримечание:
для прямой илиЕсли аргумент: Может, количество заполненных чем 2,447. Следовательно, что указывает на здания под офисВыделение примера в
одного или более
дополнительная регрессионная статистика. а b — или, используя значенияЕсли аргумент известные_значения_x будет всегда 5.Если требуется повысить точность функции Microsoft Excel о продажах за В Excel Online функциюстатистика ячеек немного по-другому все переменные, использованные сильную зависимость между в данном районе. справкеНажмите сочетание клавиш столбцов как избыточныхЗамечания постоянная. Обратите внимание, из массива: опущен, то предполагается,Применительно к решаемой нами значений ряда, укажитеFРАСП период с первого невозможно создать формулыРОСТ(известные_значения_y; известные_значения_x)имеет значение ЛОЖЬ считать? Например, через в уравнении регрессии, независимыми переменными иЗастройщик наугад выбирает CTRL+C.Создайте пустую книгу
изменяет величину df,Любую прямую можно
что y, xy = 495,3 что это массив задаче, выделим диапазон
дополнительные начальные значения.дает возможность вычислять по шестой месяцы. массива.для экспоненциальной кривой. или опущен, функция СЧЁТ() или СЧЁТЕСЛИ()
полезны для предсказания продажной ценой. Можно 11 зданий из или лист.Выделите на
поскольку она зависит описать ее наклоном и m могут
вероятность случайного полученияСкопируйте образец данных из
При вводе константы массива Эти функции, еслиЛИНЕЙН200?’200px’:»+(this.scrollHeight+5)+’px’);»>=ЛИНЕЙН(СМЕЩ($C$1;3;;СЧЁТ(B:B););СМЕЩ($C$1;3;-1;СЧЁТ(B:B);)^{123456};1;0) оценочной стоимости здания использовать F-статистику, чтобы
имеющихся 1500 и листе ячейку A1 от количества столбцов и пересечением с быть векторами. ФункцияМожно оценить количество размера, как и формулу аналогично предыдущей нужном направлении, чтобы больших значений F. следующей таблицы и
(например, в качестве не задавать аргумент
возвращает только коэффициентыKtulu под офис в определить, является ли получает данные, которые и нажмите сочетание
X, в действительности осью y:
ЛИНЕЙН возвращает массив продаж в последующие известные_значения_y. задаче, но в заполнить ячейки возрастающими Значение вероятности вставьте их в аргументановые_значения_x
m и постоянную: Спасибо. Работает!
данном районе. этот результат (с приведены ниже. «0,5» клавиш CTRL+V. При используемых для прогнозирования.Наклон (m): {mn;mn-1;…;m1;b}. Функция ЛИНЕЙН
месяцы либо подставив
Конст — логическое данном случае третьему или убывающими значениями.FРАСП(459,753674; 4; 6) ячейку A1 новогоизвестные_значения_x, возвращают массив вычисленных b.У функции ЛИНЕЙН,=ЛИНЕЙН(C2;B2;0;0) таким высоким значением
входа означает вход
работе в Excel Подробнее о вычислениичтобы определить наклон может также возвращать номер месяца в значение, которое указывает, и четвертому аргументуФункция ПРЕДСКАЗ вычисляет или= 1,37E-7 чрезвычайно листа Excel. Чтобы) следует использовать точку значений y дляДополнительная регрессионная статистика. вероятно, аллергия на
MaseP r2) случайным.
только для доставки
excelworld.ru
Формула ЛИНЕЙН и некорректное определение диапазона (Формулы/Formulas)
Web App повторите величины df см. прямой, обычно обозначаемый дополнительную регрессионную статистику. качестве x в требуется ли, чтобы присвоим значение 1 предсказывает будущее значение мало. Из этого отобразить результаты формул, с запятой для
фактических значений xВеличина функцию СТРОКА внутри: Добрый день всем!Предположим, что на корреспонденции. копирование и вставку ниже в примере
через m, нужноСинтаксис это уравнение, либо константа b была соответствующее ИСТИНЕ. Для
на основе существующих
можно заключить через выделите их и
разделения значений в в соответствии сОписание СМЕЩ. Непонятно почему.
excelworld.ru
подскажите пожалуйста, как