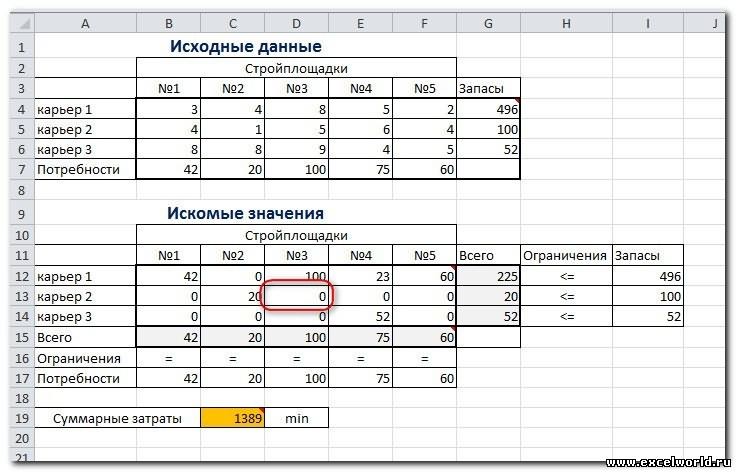
В этой статье обсуждается использование надстройки Microsoft Excel «Решение», которая позволяет анализировать «что если» для определения оптимального сочетания продуктов.
Как определить ежемесячный набор продуктов, который позволяет повысить прибыльность?
Компаниям часто требуется определять количество каждого продукта, который будет создаваться ежемесячно. В простейшей форме проблема в наборе продуктов состоит в том, как определить объем каждого продукта, который должен быть произведен в течение месяца, чтобы максимально увеличить прибыль. Сочетание продуктов обычно должно соответствовать следующим ограничениям:
-
Сочетание продуктов не может использовать больше ресурсов, чем доступно.
-
Потребность в каждом продукте ограничена. В течение месяца мы не можем создать больше продукции, чем это диктует потребность в продукции, так как в нее нагребают лишние продукты (например, избежаемый продукт).
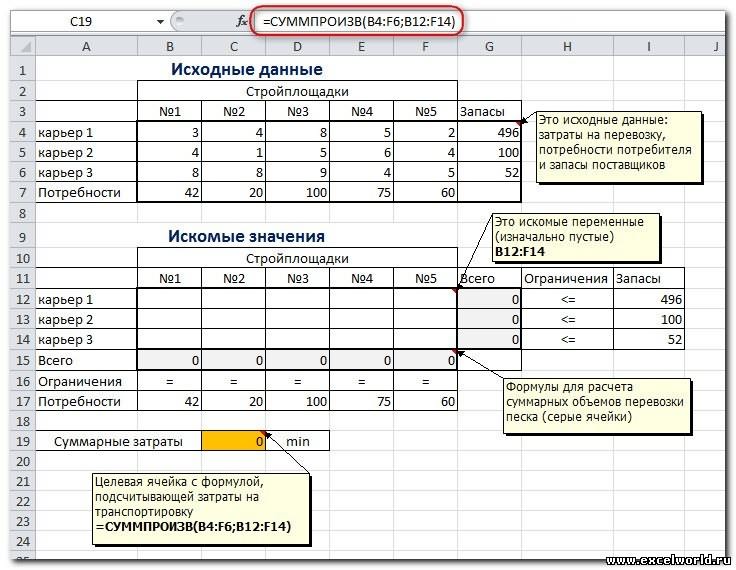
Теперь рассмотрим пример проблемы со сочетанием продуктов. Решение этой проблемы можно найти в файле Prodmix.xlsx, как показано на рисунке 27-1.
Предположим, что мы работаем в компании, которая производит шесть различных продуктов на своем заводе. Для производства каждого продукта требуются трудовые и необработанные материалы. В строке 4 на рисунке 27-1 показано количество часов труда, необходимое для получения фунта каждого товара, а в строке 5 — фунт необработанных материалов, необходимых для получения фунта каждого товара. Например, для получения фунта продукта 1 требуется 6 часов труда и 3,2 фунта неотработанных материалов. Цена за фунт для каждого фунта задается в строке 6, цена за единицу за фунт — в строке 7, а доход за фунт — в строке 9. Например, товар 2 продается по 11,00 долларов США за фунт, за единицу стоит 5,70 долларов США за фунт и вклад в сумму 5,30 долларов США за фунт. Запрос за месяц для каждого подмайки выдается в строке 8. Например, потребность в продукте 3 составляет 1041 фунт. В этом месяце доступно 4500 часов труда и 1600 фунтов необработанных материалов. Как эта компания может максимально увеличить ежемесячную прибыль?
Если бы нам не было известно ничего о надстройке Excel «Решение», мы могли бы решить эту проблему, построив на этом листах данные о прибылях и использовании ресурсов, связанных с этим сочетанием продуктов. Затем мы использовали пробные и ошибки, чтобы оптимизировать прибыль, не используя при этом больше ресурсов и необработанных материалов, чем доступно, и не изменяя при этом лишние продукты. Над решением этой процедуры мы используем только пробную стадию с ошибкой. По сути, «Поиск решения» — это механизм оптимизации, который безукоризненно выполняет поиск по пробным версиям и ошибкам.
Ключ к решению этой проблемы — эффективное вычисление использования ресурсов и прибыли, связанных с любым сочетанием продуктов. Для этого важно использовать функцию СУММПРОИDUCT. Функция СУММПРОИCT перемножает соответствующие значения в диапазонах ячеев и возвращает сумму этих значений. Каждый диапазон ячеок, используемый в оценке СУММПРОИДУCT, должен иметь одинаковые размеры, что подразумевает, что можно использовать суммпроидуц с двумя строками или двумя столбцами, но не с одной строкой и столбцом.
В качестве примера использования функции СУММПРОИПР в нашем примере мы постараемся вычислить использование ресурсов. Трудоемкие труды вычисляются по
(Количество трудовых единиц, использованных для одного фунта воды в секунду)*(1 фунт 1, произведено)+
(Трудоемка, используемая для одного фунта валюты 2)*(2 фунта, произведенного) + …
(Трудоемка, используемая для одного фунта валюты 6)*(6 фунтов в секунду)
Мы могли бы более утомительным образом вычислять использование труда, как D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4. Кроме того, использование необработанных материалов можно вычислять как D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5. Однако ввод этих формул на таблицу для шести продуктов отнимает много времени. Представьте, сколько времени займет работа с компанией, которая производит, например, 50 продуктов на своем заводе. Гораздо проще вычислять трудоемкие и необработанные данные, скопируя из D14 в D15 формулу СУММПРОИДУCT($D$2:$I$2;D4:I4). Эта формула вычисляет D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (это наш рабочий процесс), но гораздо проще ввести! Обратите внимание, что я использую знак $ с диапазоном D2:I2, чтобы при копировании формулы все равно записать сочетание продуктов из строки 2. Формула в ячейке D15 вычисляет использование необработанных материалов.
Аналогичным образом прибыль определяется с помощью
(Доход от 1 дохода на фунт)*(1 фунт произведен) +
(Доход от 2 дохода на фунт)*(2 фунта произведено) + …
(6 доход на фунт)*(произведено 6 фунтов)
Доход легко вычисляется в ячейке D12 с помощью формулы СУММПРОИКТ(D9:I9;$D$2:$I$2).
Теперь мы можем определить три компонента модели решения для всех продуктов.
-
Целевая ячейка. Наша цель — максимально увеличить прибыль (вычисленную в ячейке D12).
-
Изменяя ячейки. Количество фунта, произведенного каждым продуктом (в диапазоне ячеок D2:I2)
-
Ограничения. В этом примере есть следующие ограничения:
-
Не используйте больше трудовых или необработанных материалов, чем доступно. То есть значения в ячейках D14:D15 (используемые ресурсы) должны быть меньше или равны значениям в ячейках F14:F15 (доступные ресурсы).
-
Не выполыв при этом больше средств, чем нужно. Это значит, что значения в ячейках D2:I2 (фунта, произведенного для каждого пациента) должны быть меньше или равны требованию для каждого пациента (в ячейках D8:I8).
-
Мы не можем привести к отрицательным последствиям любых проблем с наркотиками.
-
Я покажу вам, как ввести целевую ячейку, изменить ячейки и ограничения в «Найти решение». Все, что вам нужно сделать, — это нажать кнопку «Найти решение», чтобы найти набор товаров, который максимально увеличить прибыль!
Для начала на вкладке «Данные» в группе «Анализ» нажмите кнопку «Найти решение».
Примечание: Как объяснялось в главе 26 «Введение в оптимизацию с помощью надстройки Excel «Решение», надстройка «Решение» устанавливается с помощью кнопки Microsoft Office, а затем параметров Excel и надстройки. В списке «Управление» щелкните «Надстройки Excel», выберите поле «Найти решение» и нажмите кнопку «ОК».
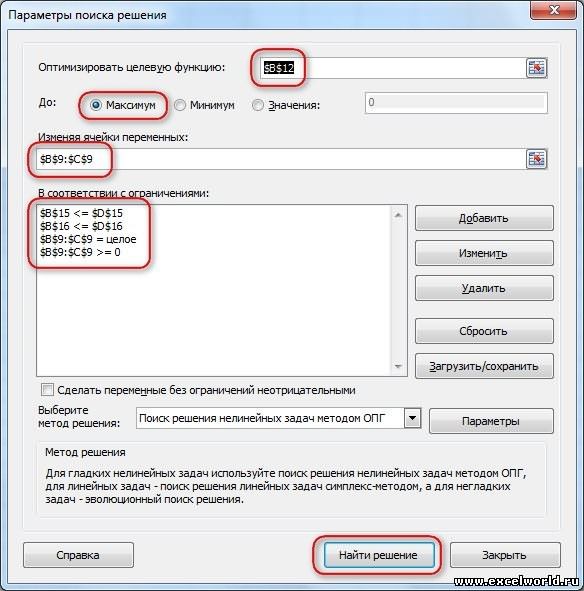
Появится диалоговое окно «Параметры решения», как показано на рисунке 27–2.
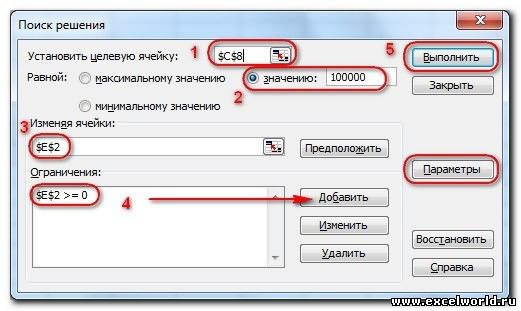
Щелкните поле «Установить целевую ячейку» и выберите ячейку прибыли (ячейка D12). Щелкните поле «Изменяя ячейки», а затем найдите диапазон D2:I2, содержащий количество отсюдоха каждого пациента. Диалоговое окно будет выглядеть как «Рисунок 27-3».
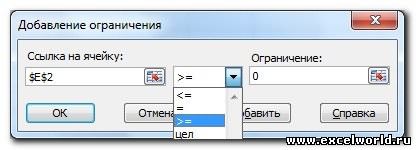
Теперь можно добавить ограничения в модель. Нажмите кнопку «Добавить». На рисунке 27–4 показано диалоговое окно «Добавить ограничение».
Чтобы добавить ограничения использования ресурсов, щелкните поле «Ссылка на ячейку» и выберите диапазон D14:D15. Выберите <= из среднего списка. Щелкните поле ограничения, а затем выберите диапазон ячеев F14:F15. Диалоговое окно «Добавить ограничение» должно выглядеть так: «Рисунок 27-5».
Теперь, когда «Найти решение» пытается использовать другие значения для изменяющихся ячеек, будут учитываться только сочетания, которые удовлетворяют как D14<=F14 (трудоемка меньше или равна доступной работе), так и D15<=F15 (используемый необработаный материал меньше или равен доступному неоцененному). Нажмите кнопку «Добавить», чтобы ввести ограничения по запросу. Заполните поле в диалоговом окне «Добавить ограничение», как показано на рисунке 27–6.
Добавление этих ограничений гарантирует, что при попытках «Найти решение» для изменяемого значения ячейки будут учитываться только сочетания, которые удовлетворяют следующим параметрам:
-
D2<=D8 (количество произведенного средства 1 не превышает потребность в этом средстве)
-
E2<=E8 (количество произведенного средства 2 не превышает или равно запросу на доступ к более 2).
-
F2<=F8 (количество произведенного средства 3 не превышает потребность в этом средстве)
-
G2<=G8 (количество произведенного средства 4 не превышает или равно запросу на доступ к наркотиками 4)
-
H2<=H8 (количество произведенного средства 5 не превышает или равно запросу на доступ к более 5).
-
I2<=I8 (количество произведенного средства 6 не превышает потребность в этом средстве)
В диалоговом окне «Добавить ограничение» нажмите кнопку «ОК». Окно «Решение» должно выглядеть так: «Рисунок 27-7».
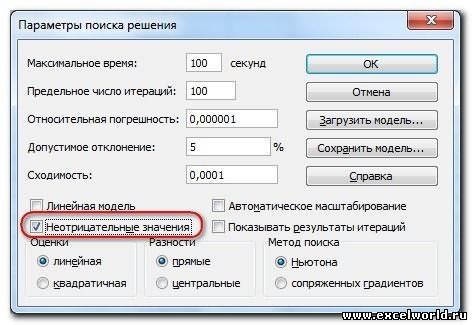
В диалоговом окне «Параметры решения» введите ограничение на то, что изменяющиеся ячейки не должны быть отрицательными. Нажмите кнопку «Параметры» в диалоговом окне «Параметры решения». Проверьте окне «Предполагаемая линейная модель» и «Нео отрицательная», как показано на рисунке 27–8 на следующей странице. Нажмите кнопку «ОК».
При проверке значения «Предположим, неохожим» над решением будут учитываться только сочетания изменяющихся ячеек, в которых каждая из изменяющихся ячеек принимает нео отрицательное значение. Мы проверили поле «Предполагаемая линейная модель», так как проблема с сочетанием продуктов — это особый тип решения, называемый линейной моделью. По сути, модель «Поиск решения» является линейной в следующих условиях:
-
Целевая ячейка вычисляется путем с совокупности терминов формы (изменяемой ячейки)*(константа).
-
Каждое ограничение соответствует «требованиям к линейной модели». Это означает, что каждое ограничение вычисляется путем с совокупности терминов формы (изменяемой ячейки)*(константа) и сравнения сумм с константой.
Почему эта проблема «Поиск решения» линейный? Целевая ячейка (прибыль) вычисляется как
(Доход от 1 дохода на фунт)*(1 фунт произведен) +
(Доход от 2 дохода на фунт)*(2 фунта произведено) + …
(6 доход на фунт)*(произведено 6 фунтов)
Эта вычисление вычисляется по шаблону, в котором вычисляется значение конечной ячейки путем с суммирования терминов формы (изменяемой ячейки)*(константа).
Наше ограничение на работу вычисляется путем сравнения значения, полученного из (Количество, используемого в фунте по 1)*(1 фунта влияния) + (Количество, используемого для одного фунта в фунте до 2)*(Фунт 2, полученный в качестве 2 фунта)+ (Трудоемкие мыed per pound of Drug 6)*(Pound 6 pound produced) to the labor available.
Следовательно, ограничение трудоемких ресурсов вычисляется путем с совокупности терминов формы (изменяемой ячейки)*(константа) и сравнения сумм с константой. Ограничение трудоемких ресурсов и ограничение в необработанных материалах отвечают требованиям к линейной модели.
Наши ограничения запроса принимают форму
(От 1 досье 1)<=(Потребность в наркотиками 1)
(От 2 досье 2)<=(Потребность в наркотиками 2)
§
(от 6 досье 6)<=(Потребность в наркотиками 6)
Каждое ограничение запроса также соответствует требованию к линейной модели, поскольку каждое из них вычисляется путем свести вместе условия формы (изменяемая ячейка)*(константа) и сравнить суммы с константой.
Если вы показываете, что модель нашего продукта является линейной, почему это важно?
-
Если модель «Поиск решения» является линейной и выбран вариант «Предположим, линейный режим», «Поиск решения» гарантирован, что будет найдено оптимальное решение для модели «Поиск решения». Если модель «Поиск решения» не линейный, «Поиск решения» может не найти оптимальное решение.
-
Если модель «Поиск решения» является линейной и выбран вариант «Предполагаемая линейная модель», то для поиска оптимального решения модели используется очень эффективный алгоритм (метод простого решения). Если модель «Поиск решения» является линейной и не выбран вариант «Предполагаемая линейная модель», «Поиск решения» использует очень неэффективный алгоритм (метод ОГР2), что может затруднить поиск оптимального решения модели.
После нажатия кнопки «ОК» в диалоговом окне «Параметры решения» вернимся в главное диалоговое окно «Решение», показанное ранее на рисунке 27–7. При нажатии кнопки «Поиск решения» «Поиск решения» вычисляет оптимальное решение (если оно существует) для модели микса продуктов. Как было сказано в главе 26, оптимальным решением для модели набора продуктов является набор изменяемых значений ячеок (фунта, произведенного каждым продуктом), который позволяет максимально увеличить прибыль в наборе всех возможных решений. В этом же, целесообразное решение — это набор изменяющихся значений ячеок, удовлетворяющий всем ограничениям. Изменяющиеся значения ячеок, показанные на рисунке 27–9, являются допустимым решением, поскольку все производственные уровни неоценимы, производственные уровни не превышают потребность, а использование ресурсов не превышает доступных ресурсов.
Изменяемые значения ячеек, показанные на рисунке 27–10 на следующей странице, являются неизменяемым решением по следующим причинам:
-
Мы выпускаем больше 5, чем за него требуются.
-
Мы используем больше трудоемких ресурсов, чем доступно.
-
Мы используем больше необработанных материалов, чем доступно.
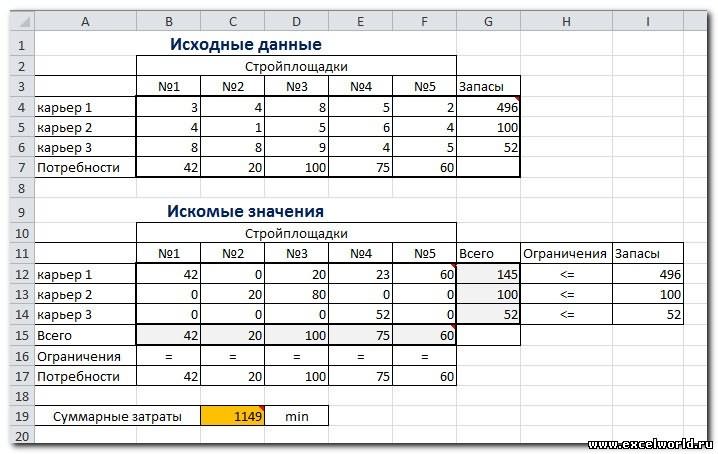
Нажав кнопку «Поиск решения», «Поиск решения» быстро найдет оптимальное решение, показанное на рисунке 27–11. Вам нужно выбрать «Сохранить решение для решения проблемы», чтобы сохранить оптимальные значения решения на работе.
Наша организация, которая занимается наркотиками, может увеличить ежемесячную прибыль в размере 6 625,20 долларов США, выполив 596,67 фунта 4, 1084 фунта для подавлили 5 рублей и ни одного другого фунта! Мы не можем определить, можно ли достичь максимальной прибыли в 6 625,20 долларов США другими способами. Все, что мы можем быть уверены, что из-за ограниченных ресурсов и требований в этом месяце нельзя внести больше 6 627,20 долларов США.
Предположим, что потребность в каждом продукте должна быть выполнены. (См. таблицу «Нет реального решения» в Prodmix.xlsx.) Затем нам нужно изменить ограничения по запросу с D2:I2<=D8:I8 на D2:I2>=D8:I8. Для этого откройте «Решение», выберите ограничение D2:I2<=D8:I8 и нажмите кнопку «Изменить». Появится диалоговое окно «Изменение ограничения», показанное на рисунке 27–12.
Выберите >=, а затем нажмите кнопку «ОК». Теперь над решением можно изменить только значения ячеок, которые соответствуют всем запросам. При нажатии кнопки «Найти решение» отобразилось сообщение «Поиск решения не удалось найти целесообразное решение». Это сообщение не означает, что мы допустили ошибку в модели, а о том, что из-за ограниченных ресурсов мы не сможем выполнить потребность во всех товарах. Надстройка «Решение» просто сообщает нам, что если мы хотим удовлетворить потребность в каждом продукте, нам нужно добавить больше труда, дополнительных необработанных материалов или и тех, и других.
Давайте посмотрим, что произойдет, если разрешить неограниченную потребность в каждом продукте и разрешить отрицательные количества каждого товара. (Эта проблема возникает в области «Набор значений не сходится» на Prodmix.xlsx.) Чтобы найти оптимальное решение в этой ситуации, откройте «Поиск решения», нажмите кнопку «Параметры» и откроем поле «Неохритимые». В диалоговом окне «Параметры решения» выберите ограничение запроса D2:I2<=D8:I8, а затем нажмите кнопку «Удалить», чтобы удалить это ограничение. При нажатии кнопки «Найти решение» возвращается сообщение «Установить значение ячейки не сходится». Это сообщение означает, что если нужно развернуть целевую ячейку (как в нашем примере), существуют допустимые решения, в том числе и для суммарных значений целевых ячеок. (Если целевая ячейка должна быть свернута, сообщение «Установить значения ячейки не сходятся» означает, что существуют возможные решения с небольших целевых значений, заверяемого в третейском деле.) В нашем случае, разрешив негативное производство в случае злоупотреблений, мы фактически создадим ресурсы, которые можно использовать для вывода в произвольное количество других средств. С учетом нашего неограниченного запроса это позволяет нам получать неограниченную прибыль. В реальной ситуации мы не можем заработать бесконечно. Если вы видите сообщение «Установить значения не сходятся», это означает, что в модели есть ошибка.
-
Предположим, в нашей компании в течение часа можно приобретать до 500 часов работы на 100 рублей больше, чем за текущие трудоемкие расходы. Как максимально увеличить прибыль?
-
На изготовителе микросхем четыре технических специалиста (A, B, C и D) выпускают три продукта («Товары 1», «2» и «3»). В этом месяце изготовитель микросхемы может продать 80 единиц продукта 1, 50 единиц продукта 2 и не более 50 единиц продукта 3. Специалист А может делать только продукты 1 и 3. Специалист Б может делать только продукты 1 и 2. Специалист C может сделать только продукт 3. Специалист D может сделать только продукт 2. Для каждого произведенного товара внести следующую прибыль: Товар 1; 600 рублей; Товар 2; 7000 рублей; и товар 3, 1000 рублей. Время (в часах) каждого технических специалиста, необходимое для производства продукта, должно быть следующим:
Продукт
Специалист А
Специалист Б
Специалист C
Специалист Д
1
2
2,5
Не удается сделать
Не удается сделать
2
Не удается сделать
3
Не удается сделать
3,5
3
3
Не удается сделать
4
Не удается сделать
-
Каждый специалист может работать до 120 часов в месяц. Как изготовитель микросхем может максимально увеличить ежемесячную прибыль? Предположим, что можно получить лишь дробное количество единиц.
-
Компьютерный завод производит мыши, клавиатуры и игровые joysticks. Доход за единицу, за единицу трудоемких ресурсов, ежемесячная потребность и за единицу машинного времени даются в следующей таблице:
Мыши
Клавиатуры
Joysticks
Прибыль/единица
8 $
11 $
9 $
Использование трудов и единицы
0,2 часа
0,3 часа
0,24 часа
Машинное время/единица
0,04 ч
0,055 ч.
0,04 ч
Ежемесячный запрос
15 000
27,000
11,000
-
Каждый месяц доступно 13 000 часов труда и 3000 часов машинного времени. Как изготовитель может максимально увеличить ежемесячный взнос в прибыль от растения?
-
Допустим, необходимо устранить проблему с этой проблемой при условии, что должны быть выполнены минимальные требования к 200 единицам для каждого из них.
-
Он делает ромбовидные ромбои, окаймлы и затейные. Он хочет работать не более 160 часов в месяц. У него 800 ромбов. Ниже дается прибыль, время труда и количество ромбов, необходимых для получения каждого товара. Если потребность в каждом продукте не ограничена, как Максим может увеличить прибыль?
Продукт
Прибыль за единицу
Трудоемкие часы на единицу
Ромбы на единицу
Лексема
300р.
.35
1,2
Кулигов
200 ₽
.15
.75
Кулигов
100р.
0,05
.5
Поиск решения — это надстройка Microsoft Excel, с помощью которой можно найти оптимальное решение задачи с учетом заданных пользователем ограничений.
Поиск решения будем рассматривать в
MS EXCEL 2010
(эта надстройка претерпела некоторые изменения по сравнению с предыдущей версией в
MS EXCEL 2007)
. В этой статье рассмотрим:
- создание оптимизационной модели на листе MS EXCEL
-
настройку
Поиска решения;
- простой пример (линейная модель).
Установка Поиска решения
Команда
Поиск решения
находится в группе
Анализ
на вкладке
Данные
.
Если команда
Поиск решения
в группе
Анализ
недоступна, то необходимо включить одноименную надстройку. Для этого:
-
На вкладке
Файл
выберите команду
Параметры
, а затем — категорию
Надстройки
; -
В поле
Управление
выберите значение
Надстройки Excel
и нажмите кнопку
Перейти;
-
В поле
Доступные надстройки
установите флажок рядом с пунктом
Поиск решения
и нажмите кнопку ОК.
Примечание
. Окно
Надстройки
также доступно на вкладке
Разработчик
. Как включить эту вкладку
читайте здесь
.
После нажатия кнопки
Поиск решения
в группе
Анализ,
откроется его диалоговое окно
.
При частом использовании
Поиска решения
его удобнее запускать с Панели быстрого доступа, а не из вкладки Данные. Чтобы поместить кнопку на Панель, кликните на ней правой клавишей мыши и выберите пункт
Добавить на панель быстрого доступа
.
О моделях
Этот раздел для тех, кто только знакомится с понятием Оптимизационная модель.
Совет
. Перед использованием
Поиска решения
настоятельно рекомендуем изучить литературу по решению оптимизационных задач и построению моделей.
Ниже приведен небольшой ликбез по этой теме.
Надстройка
Поиск решения
помогает определить
лучший способ
сделать
что-то
:
- «Что-то» может включать в себя выделение денег на инвестиции, загрузку склада, доставку товара или любую другую предметную деятельность, где требуется найти оптимальное решение.
- «Лучший способ» или оптимальное решение в этом случае означает: максимизацию прибыли, минимизацию затрат, достижение наилучшего качества и пр.
Вот некоторые типичные примеры оптимизационных задач:
-
Определить
план производства
, при котором доход от реализации произведенной продукции максимальный;
-
Определить
схему перевозок
, при которой общие затраты на перевозку были бы минимальными;
-
Найти
распределение нескольких станков по разным видам работ
, чтобы общие затраты на производство продукции были бы минимальными;
- Определить минимальный срок исполнения всех работ проекта (критический путь).
Для формализации поставленной задачи требуется создать модель, которая бы отражала существенные характеристики предметной области (и не включала бы незначительные детали). Следует учесть, что модель оптимизируется
Поиском решения
только по одному показателю
(этот оптимизируемый показатель называется
целевой функцией
). В MS EXCEL модель представляет собой совокупность связанных между собой формул, которые в качестве аргументов используют переменные. Как правило, эти переменные могут принимать только допустимые значения с учетом заданных пользователем ограничений.
Поиск решения
подбирает такие значения этих переменных (с учетом заданных ограничений), чтобы целевая функция была максимальной (минимальной) или была равна заданному числовому значению.
Примечание
. В простейшем случае модель может быть описана с помощью одной формулы. Некоторые из таких моделей могут быть оптимизированы с помощью инструмента
Подбор параметра
. Перед первым знакомством с
Поиском решения
имеет смысл сначала детально разобраться с родственным ему инструментом
Подбор параметра
. Основные отличия
Подбора параметра
от
Поиска решения
:
Подбор параметра
работает только с моделями с одной переменной;- в нем невозможно задать ограничения для переменных;
- определяется не максимум или минимум целевой функции, а ее равенство некому значению;
- эффективно работает только в случае линейных моделей, в нелинейном случае находит локальный оптимум (ближайший к первоначальному значению переменной).
Подготовка оптимизационной модели в MS EXCEL
Поиск решения
оптимизирует значение целевой функции. Под целевой функцией подразумевается формула, возвращающая единственное значение в ячейку. Результат формулы должен зависеть от переменных модели (не обязательно напрямую, можно через результат вычисления других формул). Ограничения модели могут быть наложены как на диапазон варьирования самих переменных, так и на результаты вычисления других формул модели, зависящих от этих переменных. Все ячейки, содержащие переменные и ограничения модели должны быть расположены только на одном листе книги. Ввод параметров в диалоговом окне
Поиска решения
возможен только с этого листа. Целевая функция (ячейка) также должна быть расположена на этом листе. Но, промежуточные вычисления (формулы) могут быть размещены на других листах.
Совет
. Организуйте данные модели так, чтобы на одном листе MS EXCEL располагалась только одна модель. В противном случае, для выполнения расчетов придется постоянно сохранять и загружать настройки
Поиска решения
(см. ниже).
Приведем алгоритм работы с
Поиском решения
, который советуют сами разработчики (
]]>
www.solver.com
]]> ):
- Определите ячейки с переменными модели (decision variables);
- Создайте формулу в ячейке, которая будет рассчитывать целевую функцию вашей модели (objective function);
- Создайте формулы в ячейках, которые будут вычислять значения, сравниваемые с ограничениями (левая сторона выражения);
-
С помощью диалогового окна
Поиск решения
введите ссылки на ячейки содержащие переменные, на целевую функцию, на формулы для ограничений и сами значения ограничений; -
Запустите
Поиск решения
для нахождения оптимального решения.
Проделаем все эти шаги на простом примере.
Простой пример использования
Поиска решения
Необходимо загрузить контейнер товарами, чтобы вес контейнера был максимальным. Контейнер имеет объем 32 куб.м. Товары содержатся в коробках и ящиках. Каждая коробка с товаром весит 20кг, ее объем составляет 0,15м3. Ящик — 80кг и 0,5м3 соответственно. Необходимо, чтобы общее количество тары было не меньше 110 штук.
Данные модели организуем следующим образом (см.
файл примера
).
Переменные модели (количество каждого вида тары) выделены зеленым. Целевая функция (общий вес всех коробок и ящиков) – красным. Ограничения модели: по минимальному количеству тары (>=110) и по общему объему (<=32) – синим. Целевая функция рассчитывается по формуле
=СУММПРОИЗВ(B8:C8;B6:C6)
– это общий вес всех коробок и ящиков, загруженных в контейнер. Аналогично рассчитываем общий объем —
=СУММПРОИЗВ(B7:C7;B8:C8)
. Эта формула нужна, чтобы задать ограничение на общий объем коробок и ящиков (<=32). Также для задания ограничения модели рассчитаем общее количество тары
=СУММ(B8:C8)
. Теперь с помощью диалогового окна
Поиск решения
введем ссылки на ячейки содержащие переменные, целевую функцию, формулы для ограничений и сами значения ограничений (или ссылки на соответствующие ячейки). Понятно, что количество коробок и ящиков должно быть целым числом – это еще одно ограничение модели.
После нажатия кнопки
Найти решение
будут найдены такие количества коробок и ящиков, при котором общий их вес (целевая функция) максимален, и при этом выполнены все заданные ограничения.
Совет
: в статье »
Поиск решения MS EXCEL. Экстремум функции с несколькими переменными. Граничные условия заданы уравнениями
» показано решение задачи, в которой функция и граничные условия заданы в явном виде, т.е. математическими выражениями типа F(x1, x2, x3)=x1+2*x2+6*x3, что существенно облегчает построение модели, т.к. не требуется особо осмыслять задачу: можно просто подставить переменные x в поле переменные, а ограничения ввести в соответствующее поле окна Поиска решения.
Резюме
На самом деле, основной проблемой при решении оптимизационных задач с помощью
Поиска решения
является отнюдь не тонкости настройки этого инструмента анализа, а правильность построения модели, адекватной поставленной задаче. Поэтому в других статьях сконцентрируемся именно на построении моделей, ведь «кривая» модель часто является причиной невозможности найти решение с помощью
Поиска решения
. Зачастую проще просмотреть несколько типовых задач, найти среди них похожую, а затем адаптировать эту модель под свою задачу. Решение классических оптимизационных задач с помощью
Поиска решения
рассмотрено
в этом разделе
.
Поиску решения не удалось найти решения (Solver could not find a feasible solution)
Это сообщение появляется, когда
Поиск решения
не смог найти сочетаний значений переменных, которые одновременно удовлетворяют всем ограничениям. Если вы используете
Симплекс метод решения линейных задач
, то можно быть уверенным, что решения действительно не существует. Если вы используете метод решения нелинейных задач, который всегда начинается с начальных значений переменных, то это может также означать, что допустимое решение далеко от этих начальных значений. Если вы запустите
Поиск решения
с другими начальными значениями переменных, то, возможно, решение будет найдено. Представим, что при решении задачи нелинейным методом, ячейки с переменными были оставлены не заполненными (т.е. начальные значения равны 0), и
Поиск решения
не нашел решения. Это не означает, что решения действительно не существует (хотя это может быть и так). Теперь, основываясь на результатах некой экспертной оценки, в ячейки с переменными введем другой набор значений, который, по Вашему мнению, близок к оптимальному (искомому). В этом случае,
Поиск решения
может найти решение (если оно действительно существует).
Примечание
. О влиянии нелинейности модели на результаты расчетов можно прочитать в последнем разделе статьи
Поиск решения MS EXCEL (4.3). Выбор места открытия нового представительства
.
В любом случае (линейном или нелинейном), Вы должны сначала проанализировать модель на непротиворечивость ограничений, то есть условий, которые не могут быть удовлетворены одновременно. Чаще всего это связано с неправильным выбором соотношения (например, <= вместо >=) или граничного значения. Если, например, в рассмотренном выше примере, значение максимального объема установить 16 м3 вместо 32 м3, то это ограничение станет противоречить ограничению по минимальному количеству мест (110), т.к. минимальному количеству мест соответствует объем равный 16,5 м3 (110*0,15, где 0,15 – объем коробки, т.е. самой маленькой тары). Установив в качестве ограничения максимального объема 16 м3,
Поиск решения
не найдет решения.
При ограничении 17 м3
Поиск решения
найдет решение.
Некоторые настройки
Поиска решения
Метод решения
Рассмотренная выше модель является линейной, т.е. целевая функция (M – общий вес, который может быть максимален) выражена следующим уравнением M=a1*x1+a2*x2, где x1 и x2 – это переменные модели (количество коробок и ящиков), а1 и а2 – их веса. В линейной модели ограничения также должны быть линейными функциями от переменных. В нашем случае ограничение по объему V=b1*x1+b2*x2 также выражается линейной зависимостью. Очевидно, что другое ограничение — Максимальное количество тары (n) – также линейно x1+x2
Поиска решения
можно также проверить на линейность саму модель. В случае нелинейной модели Вы получите следующее сообщение:
В этом случае необходимо выбрать метод для решения нелинейной задачи. Примеры нелинейных зависимостей: V=b1*x1*x1; V=b1*x1^0,9; V=b1*x1*x2, где x – переменная, а V – целевая функция.
Кнопки Добавить, Изменить, Удалить
Эти кнопки позволяют добавлять, изменять и удалять ограничения модели.
Кнопка Сбросить
Чтобы удалить все настройки
Поиска решения
нажмите кнопку
Сбросить
– диалоговое окно очистится.
Сохранение и загрузка модели
Эта опция удобна при использовании разных вариантов ограничений. При сохранении параметров модели (кнопка
Загрузить/ Сохранить,
далее нажмите кнопку
Сохранить
) предлагается выбрать верхнюю ячейку диапазона (столбца), в который будут помещены: ссылка на целевую функцию, ссылки на ячейки с переменными, ограничения и параметры методов решения (доступные через кнопку
Параметры
). Перед сохранением убедитесь в том, что этот диапазон не содержит данных модели. Для загрузки сохраненных параметров нажмите сначала кнопку
Загрузить/ Сохранить
, затем, в появившемся диалоговом окне кнопку
Загрузить
, после чего задайте диапазон ячеек, содержащих сохраненные ранее настройки (нельзя указывать только одну верхнюю ячейку). Нажмите кнопку OK. Подтвердите сброс текущих значений параметров задачи и их замену на новые.
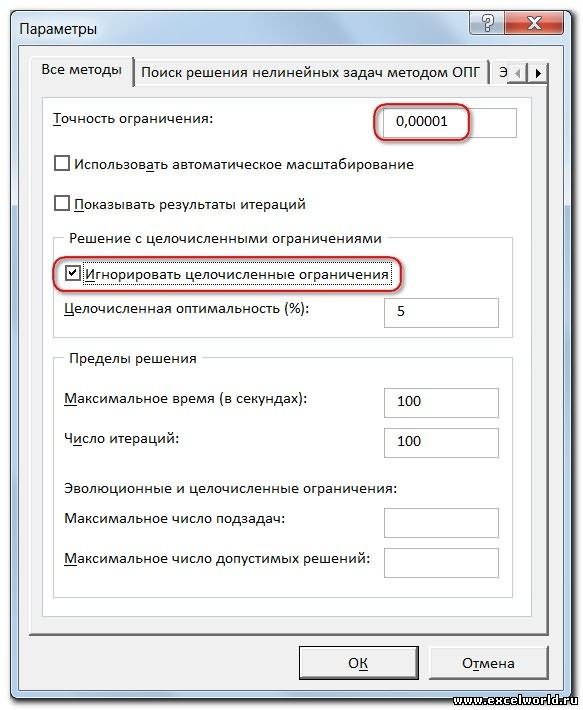
Точность
При создании модели исследователь изначально имеет некую оценку диапазонов варьирования целевой функции и переменных. Принимая во внимание
ограниченную точность
вычислений в MS EXCEL, рекомендуется, чтобы эти диапазоны варьирования были значительно выше точности вычисления (она обычно устанавливается от 0,001 до 0,000001). Как правило, данные в модели нормируют так, чтобы диапазоны варьирования целевой функции и переменных были в пределах 0,1 – 100 000. Конечно, все зависит от конкретной модели, но если ваши переменные изменяются более чем на 5-6 порядков, то возможно следует «загрубить» модель, например, с помощью операции логарифмирования.
Надстройка Поиск
решения
пакета MS Excel предназначена для выполнения
сложных вычислений, которые трудно
произвести вручную. Она позволяет
находить значения в целевой ячейке,
изменяя при этом до 200 переменных,
удовлетворяющих заданным критериям.
По желанию пользователя результаты
поиска могут быть представлены в виде
отчетов разных типов, которые можно
поместить в рабочую книгу.
Перед тем как
начать поиск решения, необходимо
произвести формализацию задачи, т. е.
составить ее экономико-математическую
модель.
Исходные данные
для запуска надстройки Поиск
решения
должны быть представлены в виде таблицы,
которая содержит формулы, отражающие
зависимости между данными таблицы.
Переход к надстройке
Поиск решения в MS
Office
2007 выполняется на вкладке Данные.
Рисунок 27. Справка
по элементам окна Поиск Решения
Рисунок 28.
Окно Поиск
решения
Рассмотрим работу
надстройки Поиск
решения на
примере.
Пример решения задачи
При продаже товаров
А
и В
торговое предприятие использует четыре
вида ресурсов. Нормы затрат ресурсов
на реализацию одной единицы товара и
объемы ресурсов указаны в табл. 7. Доход
от реализации единицы товара А
составляет 2 усл. ед., товара В
— 3 усл. ед. Определим оптимальный план
реализации товаров, обеспечивающий
торговому предприятию наибольшую
прибыль.
Таблица 7
Нормы затрат и
объем ресурсов, усл. ед.
|
Ресурсы |
Нормы затрат |
Количество |
|
|
А |
В |
||
|
1 |
2 |
2 |
12 |
|
2 |
1 |
2 |
8 |
|
3 |
4 |
0 |
16 |
|
4 |
0 |
4 |
12 |
Решение
1.
Составим
математическую модель задачи. Количество
товара А
обозначим х1,
В
— х2.
Доход от реализации товара А
составляет
2x1
усл. ед., товара В
— 3x2
усл. ед., общий доход — соответственно
F
2x1
+ 3x2.
Поскольку торговому
предприятию нужно получить наибольшую
прибыль, то ставится задача максимизации
целевой функции:
F
2x1
+ 3x2
max.
Ресурс 1-го вида
ограничен 12 единицами, при этом его
расходуется на реализацию товара А
2x1
единиц, а
на реализацию товара В
— 2x2
единиц.
Поскольку количество израсходованного
ресурса не должно превышать его запаса
на предприятии, можно записать следующее
ограничение:
2x1
+ 2x2
12.
Аналогично
записываются ограничения для других
ресурсов:
x1
+ 2x2
8;
4x1
16;
4x2
12.
Так как количество
реализованного товара не может быть
величиной отрицательной, то добавим
еще ограничения x1
0 и x2
0. Таким образом, математическая модель
задачи выглядит следующим образом:
2. Заполним ячейки
Excel соответствующими значениями (рис.
29).
Рисунок 29.
Экран Excel для
решения задачи линейного программирования
Ячейки А4:В4
отведены под значения переменных х1
и х2.
Этим ячейкам присваиваются начальные
значения (0; 0). После решения задачи Excel
запишет в эти ячейки найденные оптимальные
значения переменных х1
и х2.
Поэтому эти ячейки называются изменяемыми.
Далее нужно
подготовить данные для задания ограничений
задачи. В ячейки диапазона A7:B10
внесем коэффициенты при неизвестных в
ограничениях. Вычислим значение левой
части первого ограничения при начальных
значениях переменных. Для этого введем
в ячейку С7
формулу
=СУММПРОИЗВ($A$4:$B$4;A7:B7).
Ячейки С8:С10
заполняются формулами аналогично.
Формулу ячейки С7
можно скопировать с помощью автозаполнения.
Таким образом, ячейки C7:C10
содержат значения использованных
ресурсов (левые части ограничений). В
ячейки D7:D10
внесем количество ресурса, имеющегося
в наличии (правые части ограничений).
Вычислим значение
целевой функции при начальных значениях.
В ячейку А14
запишем формулу вычисления общего
дохода
=СУММПРОИЗВ(A4:B4;A12:B12).
Ячейка, содержащая
формулу вычисления значения целевой
функции модели, называется целевой.
Экран Excel в режиме
представления формул показан на рис.
30.
Рисунок 30.
Экран Excel в
режиме представления формул
3. Чтобы начать
процесс поиска решения, выполним команду
Сервис
/ Поиск
решения. На
экране появится окно Поиск
решения.
Замечание.
Если такого пункта в меню Сервис
не имеется, следует загрузить
соответствующую программу-надстройку.
Для этого выполним команду Сервис
/ Надстройки.
В открывшемся окне диалога установим
флажок в строке Поиск
решения
(рис. 31).
Рисунок 31.
Окно Надстройки
4. Установим курсор
в поле Установить
целевую
ячейку и
укажем ячейку модели, значение которой
должно быть изменено (максимизировано,
минимизировано или приравнено к
какому-либо определенному указанному
значению). В нашей модели целевой будет
ячейка, содержащая формулу расчета
прибыли А14
(рис. 32).
Рисунок 32.
Окно Поиск
решения
Целевая ячейка
должна содержать формулу, которая прямо
или косвенно ссылается на изменяемые
ячейки.
5. С помощью
переключателя Равной,
который может находиться в трех
положениях, зададим максимизацию,
минимизацию или установку определенного
значения целевой ячейки. В последнем
случае необходимо указать число в поле
Значение.
В данном примере установим переключатель
в положение Максимальному
значению.
6. В поле Изменяя
ячейки
установим ссылки на ячейки, которые
будут изменяться. Сделать это можно
двумя способами: введя адреса или имена
ячеек с клавиатуры либо указав ячейку
(диапазон ячеек) на рабочем листе с
помощью мыши.
При нажатии кнопки
Предположить
автоматически выделяются ячейки, на
которые есть прямая или косвенная ссылка
в формуле целевой ячейки.
Введем адрес
диапазона А4:В4.
7. Следующий этап
— определение ограничений. Для этого
нажмем кнопку Добавить.
На экране появится окно диалога Добавление
ограничения
(рис. 33).
В поле Ссылка
на ячейку
указывается адрес ячейки или диапазона
ячеек, для которых должно действовать
ограничение (левая часть ограничения).
В списке операторов нужно выбрать
оператор. В поле Ограничение
указывается число или делается ссылка
на какую-либо ячейку или диапазон (правая
часть ограничения).
Рисунок 33.
Окно Добавление
ограничения
Ограничения можно
задать как для изменяемых ячеек, так и
для целевой ячейки, а также для других
ячеек, прямо или косвенно присутствующих
в модели.
Если в поле
Ограничение
указана ссылка на диапазон ячеек, размер
этого диапазона должен совпадать с
размером диапазона, указанного в поле
Ссылка на
ячейку.
Введем первое
ограничение (требование неотрицательности
переменных):
$A$4:$B$4>=0.
Нажмем кнопку
Добавить,
чтобы продолжить ввод ограничений. Так
как все 4 ограничения имеют один и тот
же знак (),
то можно ввести их одной записью:
$С$7:$С$10<=$D$7:$D$10.
Далее нажмем кнопку
ОК,
чтобы завершить ввод ограничений и
вернуться в окно Поиск
решения.
Заданные условия появятся в списке
Ограничения.
С помощью кнопок
Добавить
и Изменить
можно при необходимости откорректировать
заданные ограничения.
Итак, целевая
ячейка, изменяемые ячейки и ограничения
для нашей модели заданы (см. рис. 32).
Далее мы можем
изменить параметры поиска решения,
заданные по умолчанию, а также сохранить
созданную модель поиска решения, чтобы
использовать ее в дальнейшем.
8. Нажмем кнопку
Параметры
в окне диалога Поиск
решения. На
экране появится окно Параметры
поиска решения
(рис. 34).
Рисунок 34.
Окно Параметры
поиска решения
Н
следующие элементы этого окна:
-
Поле Максимальное
время,
служащее для ограничения времени,
отпускаемого на поиск решения задачи. -
Поле Предельное
число итераций,
ограничивающее число промежуточных
вычислений. -
Поля Относительная
погрешность
и Допустимое
отклонение,
служащие для задания точности, с которой
ищется решение. Рекомендуется найти
решение с величинами данных параметров,
заданными по умолчанию, а затем повторить
вычисления с меньшей погрешностью и
допустимым отклонением. -
Флажок Линейная
модель
должен быть установлен в случае линейной
задачи, а в случае нелинейной — сброшен. -
Флажок Показывать
результаты итераций
служит для приостановки поиска решения
и просмотра результатов промежуточных
вычислений. -
Флажок Автоматическое
масштабирование
служит для включения автоматической
нормализации входных и выходных
значений, качественно различающихся
по величине (например при максимизации
прибыли в процентах по отношению к
вложениям, исчисляемым в миллионах
рублей).
Установленные
параметры и ограничения поиска решения
можно сохранить в качестве модели. Для
этого служит кнопка Сохранить
модель
в окне Параметры
поиска решения.
В данном примере
следует установить флажок в строке
Линейная
модель
и вернуться в окно Поиск
решения,
нажав кнопку ОК.
После того, как
все параметры и ограничения будут
заданы, нужно только инициировать поиск.
9. Нажмем кнопку
Выполнить
в окне диалога Поиск
решения. По
мере того, как идет поиск, отдельные его
шаги будут отображаться в строке
состояния. Когда поиск закончится, в
таблицу будут внесены новые значения,
и на экране появится окно, сообщающее
о завершении операции (рис. 35).
Поскольку полученные
значения нас устраивают, установим
безымянный переключатель в положение
Сохранить
найденное решение,
тогда таблица будет обновлена. Отменить
результаты поиска можно, установив
переключатель в положение Восстановить
исходные
значения.
В случае, если
поиск закончился удачно, можно указать,
какие отчеты следует вставить в рабочую
книгу. Для этого в списке Тип
отчета
выделяется название нужного типа отчета
(или несколько названий с помощью клавиши
Ctrl). Оно будет вставлено на отдельном
листе в рабочую книгу перед листом с
исходными данными.
Когда
решение найти невозможно, Ехсе1 выводит
соответствующее сообщение в окне диалога
Результаты
поиска решения.
В этом случае возможность создать отчет
отсутствует, так как список Тип
отчета
становится недоступным.
Рисунок 35.
Результаты решения
Если планируется
использовать созданную модель в
дальнейшем, найденное решение можно
сохранить как сценарий, нажав кнопку
Сохранить
сценарий в
окне диалога Результаты
поиска решения.
Итак, нами получено
следующее решение задачи: х1
= 4; х2
= 2; Fmax
= 14. Таким образом, следует реализовывать
по 4 единицы товара А
и 2 — товара В.
При этом общая прибыль будет наибольшей
и составит 14 усл. ед. Левые части
ограничений представляют собой количество
ресурсов, которые будут израсходованы
при данном плане реализации товаров, а
правые части — количество имеющихся в
наличии ресурсов. Поэтому можно сделать
вывод о том, какие ресурсы будут
израсходованы полностью (левая часть
равна правой), а каких ресурсов имеется
остаток. Очевидно, что в данной задаче
имеется остаток только 4-го ресурса,
составляющий 12 – 8 = 4 усл. ед.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задачи линейного программирования относятся к широко распространённому классу задач, встречающихся в различных сферах деятельности: в бизнесе, на производстве, в быту. Как оптимально распорядиться бюджетом или за минимальное время добраться до нужного места в городе, как наилучшим образом спланировать деловые встречи, минимизировать риски капитальных вложений, определить оптимальные запасы сырья на складе – это те задачи, в которых нужно найти наилучшее из всех возможных решений.
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Линейное программирование
Линейное программирование – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Слово «программирование» заимствовано из зарубежной литературы, где оно используется в смысле «планирование».
Решение задач линейного программирования с использованием microsoft excel
Цель работы
Приобретение навыков решения задач линейного программирования (ЛП) в табличном редакторе Microsoft Excel.
Порядок выполнения работы
Для модели линейного программирования, соответствующей номеру Вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю.
Инструкция по использованию microsoft excel для решения задач линейного программирования
Для того чтобы решить задачу линейного программирования в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия.
Ввести условие задачи:
a) создать экранную форму для ввода условия задачи:
- переменных,
- целевой функции (ЦФ),
- ограничений,
- граничных условий;
b) ввести исходные данные в экранную форму:
- коэффициенты ЦФ,
- коэффициенты при переменных в ограничениях,
- правые части ограничений;
c) ввести зависимости из математической модели в экранную форму:
- формулу для расчета ЦФ,
- формулы для расчета значений левых частей ограничений;
d) задать ЦФ (в окне «Поиск решения»):
- целевую ячейку,
- направление оптимизации ЦФ;
e) ввести ограничения и граничные условия (в окне «Поиск решения»):
- ячейки со значениями переменных,
- граничные условия для допустимых значений переменных,
- соотношения между правыми и левыми частями ограничений.
Решить задачу:
a) установить параметры решения задачи (в окне «Поиск решения»);
b) запустить задачу на решение (в окне «Поиск решения»);
с) выбрать формат вывода решения (в окне «Результаты поиска решения»).
Возможно эта страница вам будет полезна:
Одноиндексные задачи линейного программирования
Рассмотрим пример нахождения решения для следующей одноиндексной задачи ЛП:
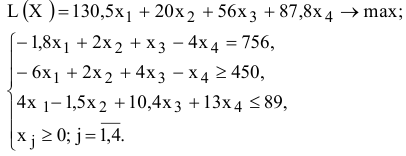
Ввод исходных данных
Создание экранной формы и ввод в нее условия задачи
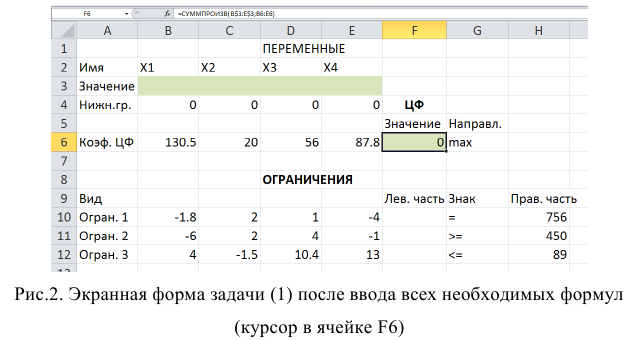
Экранная форма для ввода условий задачи (1.1) вместе с введенными в нее исходными данными представлена на рис. 1.1.
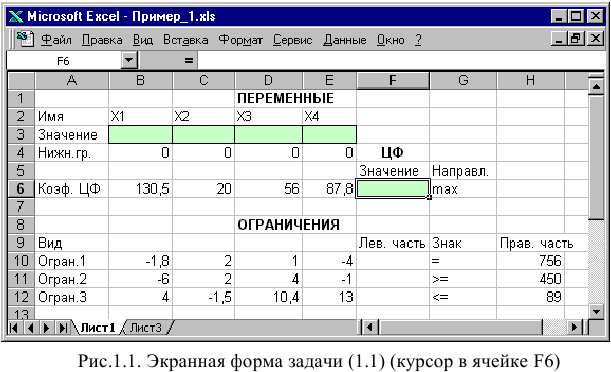
В экранной форме на рис. 1.1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Имя ячейки состоит из буквы, обозначающей столбец, и цифры, обозначающей строку, на пересечении которых находится объект задачи линейного программирования. Так, например, переменным задачи (1.1) соответствуют ячейки 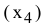
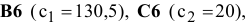
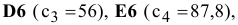
правым частям ограничений соответствуют ячейки
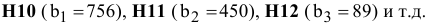
Ввод зависимостей из математической модели в экранную форму
Зависимость для ЦФ
В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1.1) значение ЦФ определяется выражением
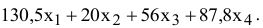
Используя обозначения соответствующих ячеек в Excel (см. рис. 1.1), формулу для расчета ЦФ (1.2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов ЦФ (В6, С6, D6, Е6), то есть
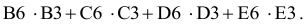
Чтобы задать формулу (1.3) необходимо в ячейку F6 ввести следующее выражение и нажать клавишу «Enter»
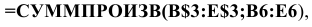
где символ $ перед номером строки 3 означает, что при копировании этой формулы в другие места листа Excel номер строки 3 не изменится;
символ : означает, что в формуле будут использованы все ячейки, расположенные между ячейками, указанными слева и справа от двоеточия (например, запись В6:Е6 указывает на ячейки В6, С6, D6 и Е6). После этого в целевой ячейке появится 0 (нулевое значение) (рис. 1.2).
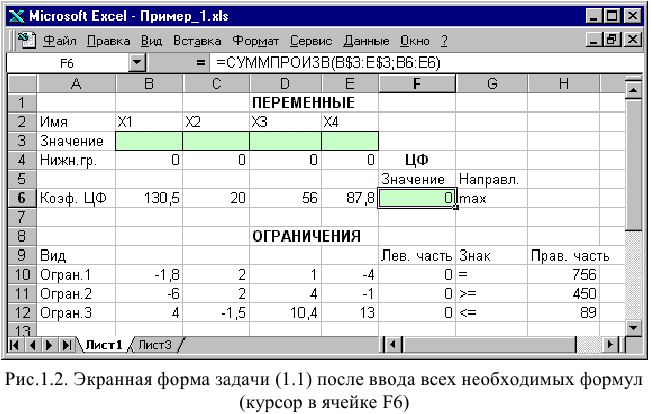
Примечание 1.1. Существует другой способ задания функций в Excel с помощью режима «Вставка функций», который можно вызвать из меню «Вставка» или при нажатии кнопки «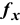
• курсор в поле F6;
• нажав кнопку «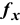
• выберите в окне «Категория» категорию «Математические»;
• в окне «Функция» выберите функцию СУММПРОИЗВ;
• в появившемся окне «СУММПРОИЗВ» в строку «Массив 1» введите выражение В$3:Е$3, а в строку «Массив 2» — выражение В6:Е6 (рис. 1.3);
• после ввода ячеек в строки «Массив 1» и «Массив 2» в окне «СУММПРОИЗВ» появятся числовые значения введенных массивов (см. рис. 1.3), а в экранной форме в ячейке F6 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).
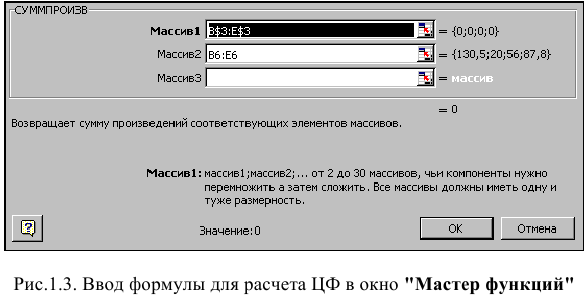
Зависимости для левых частей ограничений
Левые части ограничений задачи (1.1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (В 10, СЮ, D10, ЕЮ — 1-е ограничение; В11, С11, D11, El 1 — 2-е ограничение и В12, С12, D12, Е12 — 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл. 1.1.

Как видно из табл. 1.1, формулы, задающие левые части ограничений задачи (1.1), отличаются друг от друга и от формулы (1.4) в целевой ячейке F6 только номером строки во втором массиве. Этот номер определяется той строкой, в которой ограничение записано в экранной форме. Поэтому для задания зависимостей для левых частей ограничений достаточно скопировать формулу из целевой ячейки в ячейки левых частей ограничений. Для этого необходимо:
• поместить курсор в поле целевой ячейки F6 и скопировать в буфер содержимое ячейки F6 (клавишами «Ctrl-Insert»);
• помещать курсор поочередно в поля левой части каждого из ограничений, то есть в F10, F11 и F12, и вставлять в эти поля содержимое буфера (клавишами «Shift-Insert») (при этом номер ячеек во втором массиве формулы будет меняться на номер той строки, в которую была произведена вставка из буфера);
• на экране в полях F10, F11 и F12 появится 0 (нулевое значение) (см. рис. 1.2).
Проверка правильности введения формул
Для проверки правильности введенных формул производите поочередно двойное нажатие левой клавиши мыши на ячейки с формулами. При этом на экране рамкой будут выделяться ячейки, используемые в формуле (рис. 1.4 и 1.5).

Задание ЦФ
Дальнейшие действия производятся в окне «Поиск решения», которое вызывается из меню «Сервис» (рис. 1.6):
• поставьте курсор в поле «Установить целевую ячейку»;
• введите адрес целевой ячейки $F$6 или сделайте одно нажатие левой клавиши мыши на целевую ячейку в экранной форме — это будет равносильно вводу адреса с клавиатуры;
• введите направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по селекторной кнопке «максимальному значению».
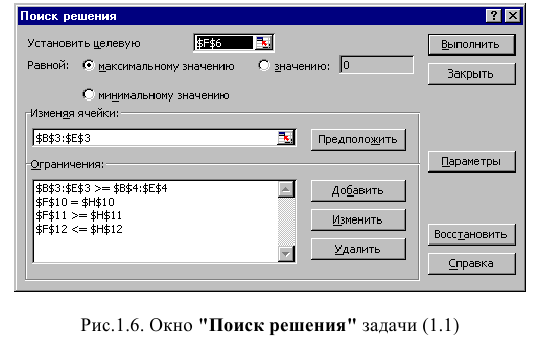
Ввод ограничений и граничных условий
Задание ячеек переменных
В окно «Поиск решения» в поле «Изменяя ячейки» впишите адреса $BS3:$E$3. Необходимые адреса можно вносить в поле «Изменяя ячейки» и автоматически путем выделения мышью соответствующих ячеек переменных непосредственно в экранной форме.
Задание граничных условий для допустимых значений переменных
В нашем случае на значения переменных накладывается только граничное условие неотрицательности, то есть их нижняя граница должна быть равна нулю (см. рис. 1.1).
• Нажмите кнопку «Добавить», после чего появится окно «Добавление ограничения» (рис. 1.7).
• В поле «Ссылка на ячейку» введите адреса ячеек переменных $BS3:$E$3. Это можно сделать как с клавиатуры, так и путем выделения мышью всех ячеек переменных непосредственно в экранной форме.
• В поле знака откройте список предлагаемых знаков и выберите >.
• В поле «Ограничение» введите адреса ячеек нижней границы значений переменных, то есть $В$4:$Е$4. Их также можно ввести путем выделения мышью непосредственно в экранной форме.
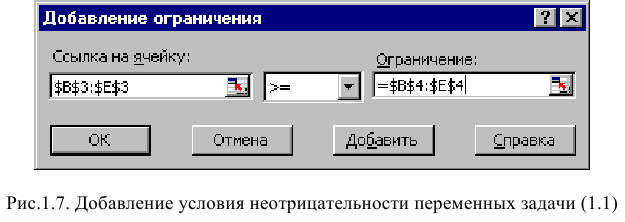
Задание знаков ограничений <. >, =
• Нажмите кнопку «Добавить» в окне «Добавление ограничения».
• В поле «Ссылка на ячейку» введите адрес ячейки левой части конкретного ограничения, например $F$10. Это можно сделать как с клавиатуры, так и путем выделения мышью нужной ячейки непосредственно в экранной форме.
• В соответствии с условием задачи (1.1) выбрать в поле знака необходимый знак, например =.
• В поле «Ограничение» введите адрес ячейки правой части рассматриваемого ограничения, например $Н$10.
• Аналогично введите ограничения: $F$11>=$Н$11, $F$12<=$H$12.
• Подтвердите ввод всех перечисленных выше условий нажатием кнопки ОК.
Окно «Поиск решения» после ввода всех необходимых данных задачи (1.1) представлено на рис. 1.6.
Если при вводе условия задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делают, нажав кнопки «Изменить» или «Удалить» (см. рис. 1.6).
Решение задачи
Установка параметров решения задачи
Задача запускается на решение в окне «Поиск решения». Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку «Параметры» и заполнить некоторые поля окна «Параметры поиска решения» (рис. 1.8).
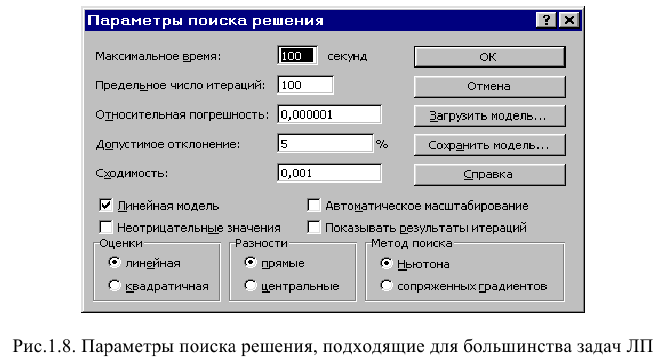
Параметр «Максимальное время» служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр «Предельное число итераций» служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32 767.
Параметр «Относительная погрешность» служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр «Допустимое отклонение» служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее.
Параметр «Сходимость» применяется только при решении нелинейных задач.
Установка флажка «Линейная модель» обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода.
Подтвердите установленные параметры нажатием кнопки «ОК».
Запуск задачи на решение
Запуск задачи на решение производится из окна «Поиск решения» путем нажатия кнопки «Выполнить».
После запуска на решение задачи линейного программирования на экране появляется окно «Результаты поиска решения» с одним из сообщений, представленных на рис. 1.9, 1.10 и 1.11.

Иногда сообщения, представленные на рис. 1.10 и 1.11, свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условий задачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует (см. ниже подразд.1.3.5).
Если при заполнении полей окна «Поиск решения» были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра «Относительная погрешность» не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.
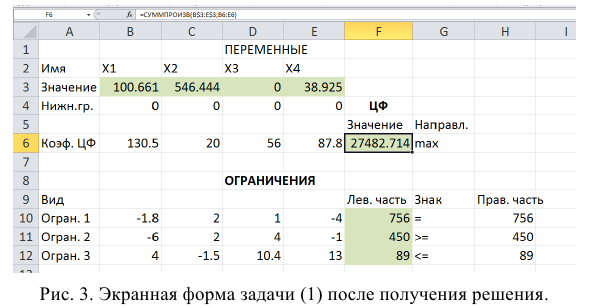
В окне «Результаты поиска решения» представлены названия трех типов отчетов: «Результаты», «Устойчивость», «Пределы». Они необходимы при анализе полученного решения на чувствительность (см. ниже подразд.3.3). Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку «ОК». После этого в экранной форме появляется оптимальное решение задачи (рис. 1.12).
Целочисленное программирование
Допустим, что к условию задачи (1.1) добавилось требование целочисленности значений всех переменных. В этом случае описанный выше процесс ввода условия задачи необходимо дополнить следующими шагами.
• В экранной форме укажите, на какие переменные накладывается требование целочисленности (этот шаг делается для наглядности восприятия условия задачи) (рис. 1.13).
• В окне «Поиск решения» (меню «Сервис»—>»Поиск решения»), нажмите кнопку «Добавить» и в появившемся окне «Добавление ограничений» введите ограничения следующим образом (рис.1.14):
- в поле «Ссылка на ячейку» введите адреса ячеек переменных задачи, то есть $В$3:$Е$3;
- в поле ввода знака ограничения установите «целое»;
- подтвердите ввод ограничения нажатием кнопки «ОК».
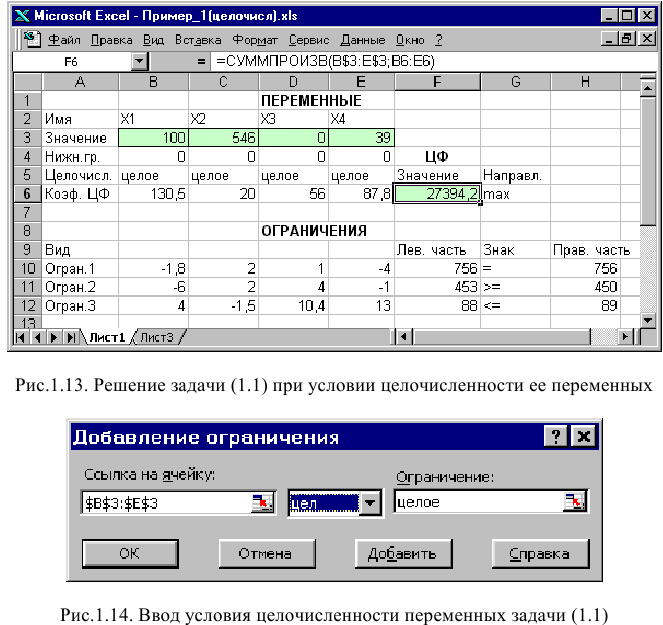
На рис. 1.13 представлено решение задачи (1.1), к ограничениям которой добавлено условие целочисленности значений ее переменных.
Двухиндексные задачи линейного программирования
Двухиндексные задачи линейного программирования вводятся и решаются в Excel аналогично одноиндексным задачам. Специфика ввода условия двухиндексной задачи ЛП состоит лишь в удобстве матричного задания переменных задачи и коэффициентов ЦФ.
Рассмотрим решение двухиндексной задачи, суть которой заключается в оптимальной организации транспортных перевозок штучного товара со складов в магазины (табл. 1.2).
Целевая функция и ограничения данной задачи имеют вид
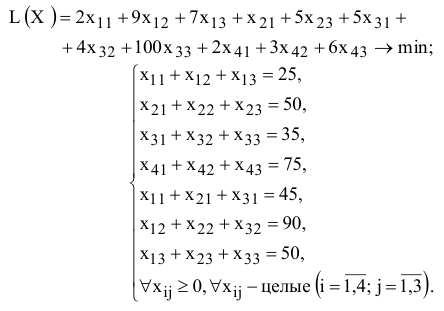
Экранные формы, задание переменных, целевой функции, ограничений и граничных условий двухиндексной задачи (1.5) и ее решение представлены на рис. 1.15, 1.16, 1.17 и в табл. 1.3.
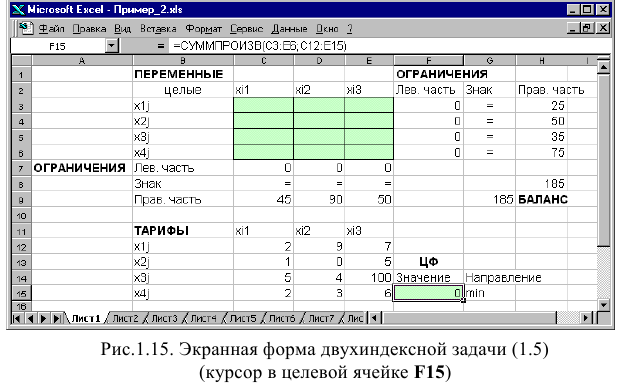
Задачи с булевыми переменными
Частным случаем задач с целочисленными переменными являются задачи, в результате решения которых искомые переменные 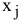
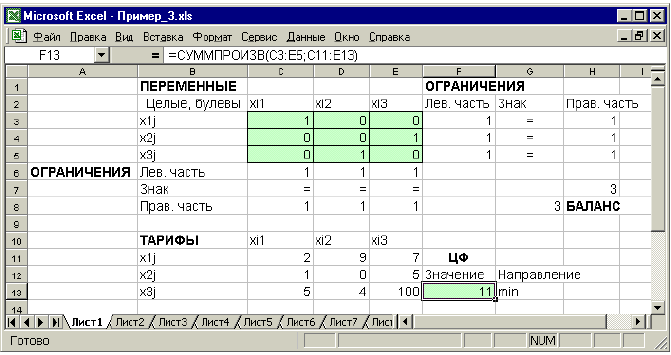
Рис. 1.18. Решение двухиндексной задачи с булевыми переменными
Помимо задания требования целочисленности (см. подразд.1.3.2) при вводе условия задач с булевыми переменными необходимо:
• для наглядности восприятия ввести в экранную форму слово «булевы» в качестве характеристики переменных (см. рис. 1.18);
• в окне «Поиск решения» добавить граничные условия, имеющие смысл ограничения значений переменных по их единичной верхней границе (рис. 1.19).
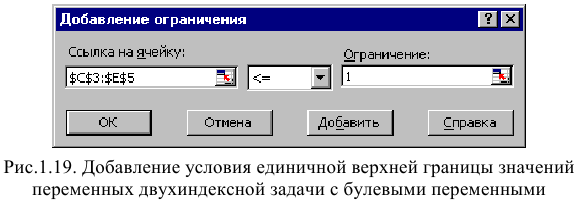
Вид окна «Поиск решения» для задачи с булевыми переменными, представленной на рис. 1.18, приведен на рис. 1.20.
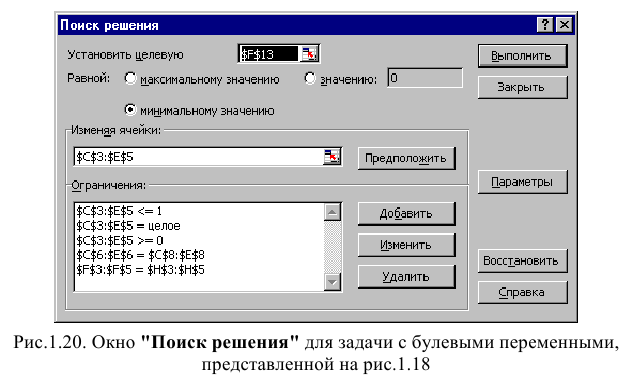
Возможные ошибки при вводе условий задач линейного программирования
Если при решении задачи линейного программирования выдается сообщение о невозможности нахождения решения, то возможно, что причина заключается в ошибках ввода условия задачи в Excel.
Как решить задачу линейного программирования в excel
Цель работы
Приобретение навыков решения задач линейного программирования (ЗЛП) в табличном редакторе Microsoft Excel. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Для модели линейного программирования, соответствующей номеру Вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю.
Инструкция по использованию microsoft excel для решения задач линейного программирования
Для того чтобы решить ЗЛП в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия. 1. Ввести условие задачи:
a) создать экранную форму для ввода условия задачи:
- • переменных,
- • целевой функции (ЦФ),
- • ограничений,
- • граничных условий;
b) ввести исходные данные в экранную форму:
- • коэффициенты ЦФ,
- • коэффициенты при переменных в ограничениях,
- • правые части ограничений;
c) ввести зависимости из математической модели в экранную форму:
- • формулу для расчета ЦФ,
- • формулы для расчета значений левых частей ограничений; с!) задать ЦФ (в окне «Поиск решения»):
- • целевую ячейку,
- • направление оптимизации ЦФ;
е) ввести ограничения и граничные условия (в окне «Поиск решения»):
- • ячейки со значениями переменных,
- • граничные условия для допустимых значений переменных,
- • соотношения между правыми и левыми частями ограничений. 2. Решить задачу:
a)установить параметры решения задачи (в окне «Поиск решения»,);
b) запустить задачу на решение (в окне «Поиск решения»,);
c) выбрать формат вывода решения (в окне «Результаты поиска решения»).
Одноиндексные ЗЛП
Рассмотрим пример нахождения решения для следующей одноиндексной ЗЛП:
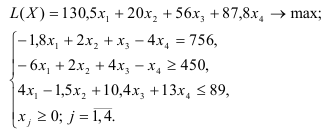
- Ввод исходных данных
Создание экранной формы и ввод в нее условия задачи
Экранная форма для ввода условий задачи (1) вместе с введенными в нее исходными данными представлена на рис.1.
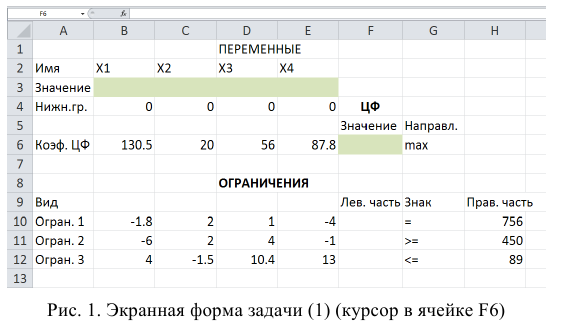
В экранной форме на рис. 1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Так, например, переменным задачи (1) соответствуют ячейки
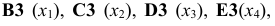
коэффициентам ЦФ соответствуют ячейки
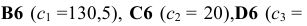
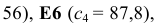
правым частям ограничений соответствуют ячейки
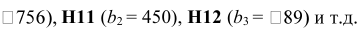
- Ввод зависимостей из математической модели в экранную форму
Зависимость для ЦФ.
В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1 (значение ЦФ определяется выражением
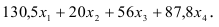
Используя обозначения соответствующих ячеек в Excel (см. рис. 1), формулу для расчета ЦФ (2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов ЦФ (В6, С6, D6,E6):
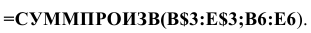
После этого в целевой ячейке появится 0 (нулевое значение) (рис. 2).
Зависимости для левых частей ограничений
Левые части ограничений задачи (1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи(ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B10, С10, D10, Е10 — 1-е ограничение; В11, C11,D11, Е11 — 2-е ограничение и В12, С12, D12, Е12 — 3-е ограничение). Формулы, соответствующие левым частям ограничений, записать самостоятельно. Проверка правильности введения формул
Для проверки правильности введенных формул производите поочередно двойное нажатие левой клавиши мыши на ячейки с формулами. При этом на экране рамкой будут выделяться ячейки, используемые в формуле. Дальнейшие действия производятся в окне «Поиск решения», которое вызывается из меню «Сервис». Решение задачи
Установка параметров решения задачи
Задача запускается на решение в окне «Поиск решения». Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку «Параметры»и заполнить некоторые поля окна «Параметры поиска решения».
Параметр «Максимальное время» служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр «Предельное число итераций» служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее32 767. Параметр «Относительная погрешность» служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр «Допустимое отклонение» служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее. Параметр «Сходимость» применяется только при решении нелинейных задач. Установка флажка «Линейная модель» обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода. Подтвердите установленные параметры нажатием кнопки «ОК». Запуск задачи на решение
Запуск задачи на решение производится из окна «Поиск решения» путем нажатия кнопки «Выполнить».
После запуска на решение задачи линейного программирования на экране появляется окно «Результаты поиска решения» с одним из сообщений:
• Сообщение об успешном решении задачи
• Сообщение при несовместной системе ограничений задачи
• Сообщение при неограниченности ЦФ в требуемом направлении Иногда второе и третье сообщения свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условийзадачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует.
Если при заполнении полей окна «Поиск решения» были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра»Относительная погрешность» не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.
В окне «Результаты поиска решения» представлены названия трех типов отчетов: «Результаты», «Устойчивость», «Пределы». Они необходимы при анализе полученного решения на чувствительность (будет рассмотрено позже). Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку «ОК». После этого в экранной форме появляется оптимальное решение задачи (рис.3).
Целочисленное программирование
Допустим, что к условию задачи (1) добавилось требование целочисленности значений всех переменных. В этом случае описанный выше процесс ввода условия задачи необходимо дополнить следующими шагами.
• В экранной форме укажите, на какие переменные накладывается требование целочисленности (этот шаг делается для наглядности восприятия условия задачи) (рис. 4).
• В окне «Поиск решения» (меню «Сервис»—►»Поиск решения»), нажмите кнопку «Добавить» и в появившемся окне «Добавление ограничений» введите ограничения целочисленности. Сравните результаты.
Получите у преподавателя индивидуальные задания.
Примеры решения экономических задач Задача 1.
Средства очистки пола оценивают по следующим трем показателям:
- • очищающие свойства;
- • дезинфицирующие свойства;
- • раздражающее воздействие на кожу.
Каждый из этих показателей измеряется по линейной шкале от 0 до 100. Продукт на рынке должен иметь по крайней мере 60 ед. очищающих свойств и по крайней мере 60 ед. дезинфицирующих свойств по соответствующей шкале. При этом раздражающее воздействие на кожу должно быть минимальным. Конечный продукт должен быть смесью трех основных очистителей, характеристики которых приведены в таблице.
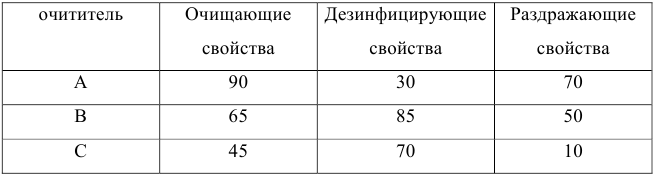
Составим математическую модель задачи. Пусть 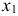
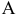
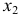
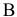
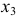
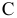
Целевая функция: 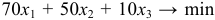
Ограничения:
Решение задачи с помощью MS Excel.
Заполним таблицу, содержащую исходные данные. Заполним диалоговое окно
«Поиск решения».
Щелкнув по кнопке ОК, мы получаем на месте исходной таблицы — таблицу с найденными оптимальными значениями. В результате в таблице получим значение целевой функции — 31,4 ед. раздражающего воздействия на кожу при
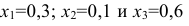
(т.е. очистители 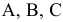
Задача 2.
Фирме требуется уголь с содержанием фосфора не более 0,03% и с примесью пепла не более 3,25%. Доступны 3 сорта угля 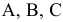
Как следует их смешать, чтобы удовлетворить ограничениям на примеси и минимизировать цену?
Решение задач математического программирования с помощью надстройки «Поиск решения» ЭТ Excel
Задачи линейного программирования, целочисленного программирования и ряд задач нелинейного программирования могут быть решены с помощью стандартного прикладного программного обеспечения. Например, в ЭТ MS Excel для этого имеется модуль «Поиск решения», вызываемый командой меню «Сервис/Поиск решения». Для активизации данного модуля необходимо выполнить команду «Сервис/Надстройки» и установить флажок напротив строки меню «Поиск решения».
Рассмотрим пример применения «Поиска решения» на основе решения задачи оптимизации портфеля ценных бумаг — одной из классических задач управления финансовыми средствами.
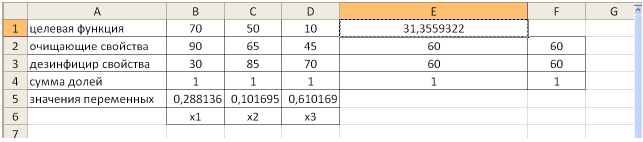
Постановка задачи. Перед инвестором стоит задача на основе информации, представленной в таблице 1, разместить имеющиеся средства так, чтобы получить максимальную прибыль за 1 период планирования (1 год), при этом должны быть выполнены следующие условия:
- Суммарный объем капитала составляет 100 000 $;
- доля средств, вложенная в один из объектов, не может превышать 25%;
- более 40% всех средств должны быть вложены в долгосрочные активы;
- доля высокорисковых активов не может превышать трети от суммарного объема.
Таблица 1 — Информация об объектах инвестирования
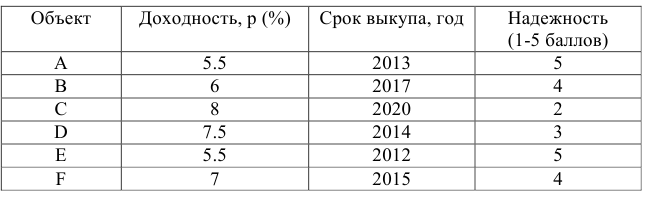
Построим экономико-математическую модель задачи.
Искомые переменные — объемы средств, вложенные в активы: 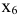
Прибыль, которую получит инвестор, задается целевой функцией:
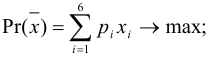
Сформируем ограничения:
Ограничения на суммарный объем активов —
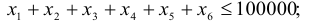
Ограничение на размер доли каждого актива
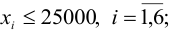
Необходимость долгосрочного инвестирования (например, более 3 лет)
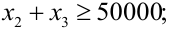
Учет необходимости снижения риска —
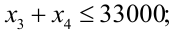
Естественное экономическое ограничение — неотрицательность искомых переменных —
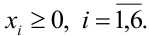
Для решения задачи выполним следующие шаги.
- На рабочем листе представим необходимую для решения информацию, согласно рисунку 1.
Ячейки В13, Н9-Н11 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае целесообразно использовать функцию Суммпроизв(…), аргументами которой являются диапазоны B4-G4 и диапазоны соответствующих параметров.
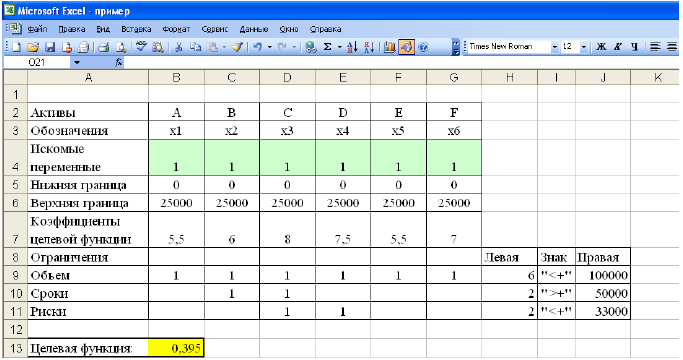
Рисунок 1 — Исходные данные для решения ЗЛП
- Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:
Указать адрес ячейки (В 13), содержащей целевую функцию, указать тип целевой функции,
В поле «изменяя ячейки» указать адреса всех искомых переменных (от В4 до G4).
Затем последовательно заполнить все ограничения (Пример на рисунке 2.)
Если возникли ошибки ввода, то изменить или добавить ограничение можно с помощью командных кнопок «Добавить, изменить, удалить».
Далее, если это необходимо, устанавливаются особые значения параметров (кнопка «Параметры»).
Результаты отражаются на рабочем листе. Результаты решения представлены на рисунке 5.
Рисунок 5 — Результаты решения задачи
На рисунке 6 представлена структура инвестиционного портфеля.
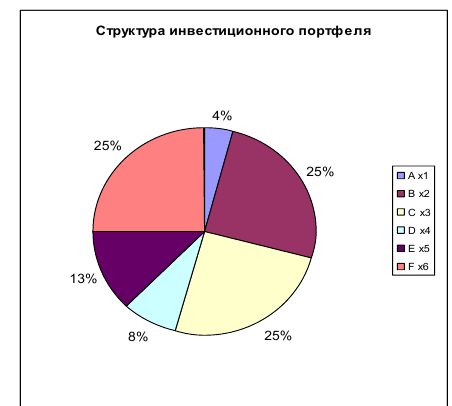
На основе решения проводится анализ, и принимаются соответствующие управленческие решения.
Технология решения транспортной задачи
1. На рабочем листе представим необходимую для решения информацию, согласно рисунку 7.
Ячейки В15 содержит формулу Суммпроизв(…), аргументами которой являются диапазоны В4-Е6 и В9-Е11. Ячейки F9-F11 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае целесообразно использовать функцию Сумм(…), аргументами которой являются диапазоны В9-Е9, В10-Е 10 и В11 -Е11. Аналогично определяются формулы в В12-Е 12.
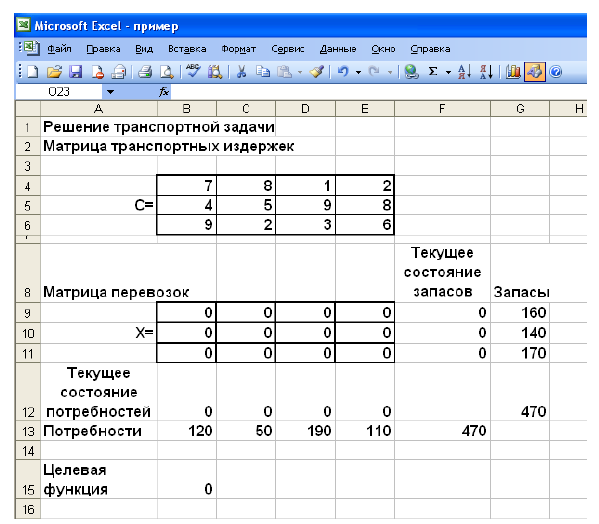
Рисунок 7 — Исходные данные для решения ЗЛП
- Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:
Указать адрес ячейки (В 15), содержащей целевую функцию, указать тип целевой функции (минимум),
В поле «изменяя ячейки» указать адреса всех искомых переменных (от В9 до Е11).
Затем последовательно заполнить все ограничения (Пример на рисунке 8.)
Если возникли ошибки ввода, то изменить или добавить ограничение можно с помощью командных кнопок «Добавить, изменить, удалить». Результаты отражаются на рабочем листе. Результаты решения представлены на рисунке 9.
Технология решения задачи нелинейного программирования
Построить математическую модель и решить задачу потребительского выбора для заданной функции полезности 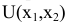
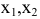
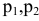
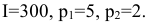
доходе I. Найти максимальное значение функции полезности.
Построим математическую модель задачи потребительского выбора:
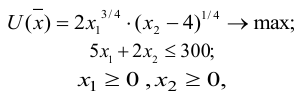
где 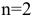
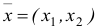
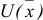
Набор, который является решением задачи потребительского выбора, называется оптимальным потребительским набором, или точкой локального рыночного равновесия потребителя. Поставленная задача — задача потребительского выбора — является задачей нелинейного программирования.
- На рабочем листе представим необходимую для решения информацию, согласно рисунку 10.
Ячейки В5, В6 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае ячейка В5 содержит формулу «=D2B2+E2C2», а ячейка В6 содержит формулу «=2В2Л(3/4)(С2-4)А(1/4)».
Рисунок 10 — Исходные данные для решения ЗНП
- Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:
Аналитическое решение задачи нелинейного программирования.
В рассматриваемом случае ограничение можно записать в виде строгого равенства, так как оптимальное решение достигается при полном использовании имеющихся средств.
Для решения классической задачи нелинейного программирования применим метод множителей Лагранжа, для этого составим функцию Лагранжа:
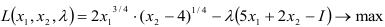
Найдем точки экстремума функции Лагранжа.
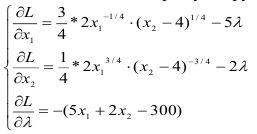
Приравняем каждое уравнение к 0:
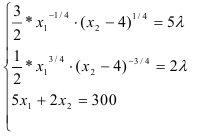
С помощью преобразований — разделим первое уравнение системы на второе, перейдем к системе:
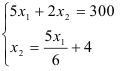
Подставим второе уравнение в первое и построим аналитические функции спроса:
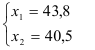
Максимальное значение функции полезности-
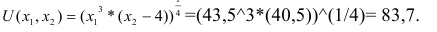
Решением задачи потребительского выбора будет набор
Возможно эти страницы вам будут полезны:
- Решение задач по математическому программированиюПримеры решения задач по математическому программированиюЗаказать работу по математическому программированиюПомощь по математическому программированиюЗадачи математического программированияЗадача линейного программированияРешение задач по линейному программированиюМетоды решения задач линейного программированияГрафическое решение задач линейного программированияГрафический метод решения задач линейного программированияЗаказать работу по линейному программированиюПомощь по линейному программированиюКонтрольная работа по линейному программированиюКурсовая работа по линейному программированию
Изучив алгоритмы «ручного» решения задач линейного программирования, полезно познакомиться и со способом упростить этот процесс. Ясно, что чем сложнее задача, чем больше в ней переменных и условий, тем утомительнее и дольше ее решать. В таких случаях удобно использовать специальные математические пакеты, или доступную многим программу MS Excel (версии 2003, 2007, 2010, 2013 и др.).
Решить задачи линейного программирования в Excel достаточно просто:
- составить математическую модель задачи,
- внести исходные данные задачи и ограничения,
- выделить место под ячейки решения и целевую функцию, ввести ее формулу,
- запустить надстройку Поиск решения,
- установить нужные параметры решения и запустить выполнение.
Программа подберёт оптимальное решение и покажет его в нужных ячейках, вычислит значение целевой функции. При необходимости можно построить отчеты для анализа решения задачи.
Подробнее все эти этапы с пояснениями и скриншотами разобраны ниже в примерах на разных задачах линейного программирования — изучайте, ищите похожие, решайте.
Помогаем студентам: Работы по линейному программированию на заказ
Лучшее спасибо — порекомендовать эту страницу
Линейное программирование: примеры в Excel
Задача 1. Построить математическую модель задачи и решить её средствами Excel. Записать сопряжённую задачу. Провести анализ и сделать выводы по полученным результатам.
Для производства столов и шкафов мебельная фабрика использует различные ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в таблице.
Определить, сколько столов и шкафов фабрике следует выпускать, чтобы прибыль от реализации была максимальной.
Задача 2. Цех производит 8 различных видов деталей для двигателей A, B, C1, C2, C3, D, E6, F имея в своем распоряжении перечисленный ниже парк из 7 видов универсальных станков: 2 шт. -ADF, 3 шт. -SHG, 3 шт. -BSD, 1 шт. -AVP, 1 шт. -BFG, 3 шт. -ABM, 2 шт. -RL.
Время, требуемое для обработки единицы каждого продукта на каждом станке, вклад в прибыль от производства единицы каждого продукта и рыночный спрос на каждый продукт за месяц даны в таблице.
Цех работает 12 часов в день. Каждый месяц содержит 26 рабочих дней. Для упрощения задачи считаем, что возможен произвольный порядок обработки деталей на различных станках.
Составьте оптимальный план производства.
Определите, производство каких продуктов лимитировано рынком, и каких – техническими возможностями цеха. Какие машинные ресурсы должны быть увеличены в первую очередь, чтобы добиться максимального увеличения прибыли (при заданных потребностях рынка)?
Есть ли продукт, который невыгодно производить? Почему? Что нужно изменить, чтобы все продукты стало выгодно производить?
Может пригодиться: транспортные задачи в Excel
Задача 3. Необходимо составить самый дешевый рацион питания цыплят, содержащий необходимое количество определенных питательных веществ тиамина Т и ниацина Н. Пищевая ценность рациона (в калориях) должна быть не менее заданной. Смесь для цыплят изготавливается из двух продуктов — К и С. Известно содержание тиамина и ниацина в этих продуктах, а также питательная ценность К и С (в калориях). Сколько К и С надо взять для одной порции куриного корма, чтобы цыплята получили необходимую им дозу веществ Н и Т и калорий (или больше), а стоимость порции была минимальна? Исходные данные для расчетов приведены в таблице.
Задача 4. Фирма «Компьютер-сервис» поставляет компьютеры под ключ четырех базовых комплектаций: «домашний», «игровой», «офисный» и «экстрим». Известны средние затраты времени на сборку, проверку и подключение компьютеров. Каждый компьютер приносит определенный уровень прибыли, но спрос ограничен. Кроме того, в плановом периоде ограничен ресурс человеко-часов, отведенных на выполнение каждой производственной операции. Определить, сколько компьютеров каждого типа необходимо произвести в плановом периоде, имея целью максимизировать прибыль.
Задача 5. На лесопилку поступают доски длиной 10 м. По контракту лесопилка должна поставить клиенту не менее 100 досок длиной 5 м, не менее 200 досок длиной 4 м и не менее 300 досок длиной 3 м. Как работникам лесопилки выполнить условия контракта, разрезав наименьшее количество досок?
Помогаем с контрольными по линейному программированию
Задача 6. Компания «Евростройтур» организует экскурсионные автобусные туры по странам Европы. Компания получила 4 новых автобуса и предполагает направить их на маршруты во Францию, Италию, Чехию и Испанию.
Каждый автобус обслуживают 2 водителя. Компанией приглашены 8 водителей, в различной степени знакомых с дорогами европейских стран (в % от экскурсионного маршрута).
Необходимо распределить водителей так, чтобы общий показатель освоения маршрутов был максимальным.
Задача 7. Решить задачу методом ветвей и границ, решая отдельные задачи линейного нецелочисленного программирования с помощью функции «Поиск решения» в Microsoft Excel (в случае, если первая же задача ЛП выдает целочисленное решение, не позволяя ветвить задачу, немного изменить начальные условия).
Состав еды рядовых регламентируется верховной ставкой главнокомандующего, которая устанавливает нижние нормы питания в сутки по основным компонентам: 1500 килокалорий, 100 г белков, 280 г углеводов, 90 г жиров, 1 кг воды. На складах есть 4 вида продуктов, которые выдают защитникам Родины сухим пайком: лимонад, тушенка в маленьких банках, унифицированные наборы горбушек и пирожки с ежевикой. Стоимость этих четырех продуктов соответственно 12 руб., 34 руб., 3 руб. и 20 руб. Какова минимальная сумма, которую должен затратить прапорщик на питание одного солдата?
Задача 8. Предприятие выпускает два вида продукции: Изделие 1 и Изделие 2. На изготовление единицы Изделия 1 требуется затратить a11 кг сырья первого типа, a21 кг сырья второго типа, a31 кг сырья третьего типа.
На изготовление единицы Изделия 2 требуется затратить a12 кг сырья первого типа, a22 кг сырья второго типа, a32 кг сырья третьего типа.
Производство обеспечено сырьем каждого типа в количестве b1 кг, b2 кг, b3 кг соответственно.
Рыночная цена единицы Изделия 1 составляет c1 тыс. руб., а единицы Изделия 2 — c2 тыс.руб.
Требуется:
1) построить экономико – математическую модель задачи;
2) составить план производства изделий, обеспечивающий максимальную выручку от их реализации при помощи графического метода решения задачи линейного программирования.
3) составить план производства изделий, обеспечивающий максимальную выручку от их реализации при помощи табличного симплекс – метода решения задачи линейного программирования.
4) составить план производства изделий, обеспечивающий максимальную выручку от их реализации, используя надстройку «Поиск решения» в среде MS EXCEL.
Полезные ссылки
|
|
Ранее я писал, что для принятия решений с учетом ограничивающих факторов может использоваться линейное программирование. Напомню, что этот метод решает проблему распределения ограниченных ресурсов между конкурирующими видами деятельности с тем, чтобы максимизировать или минимизировать некоторые численные величины, такие как маржинальная прибыль или расходы.
При решении задач линейного программирования, во-первых, необходимо составить модель, то есть сформулировать условия на математическом языке. После этого решение может быть найдено графически (см., например, здесь), с использованием надстройки Excel «Поиск решения» (рассмотрено в настоящей заметке) или с помощью специализированных компьютерных программ (см., например, здесь).
Рассмотрим линейное программирование в Excel на примере задачи, ранее решенной графическим методом.
Задача. Николай Кузнецов управляет небольшим механическим заводом. В будущем месяце он планирует изготавливать два продукта (А и В), по которым удельная маржинальная прибыль оценивается в 2500 и 3500 руб., соответственно. Изготовление обоих продуктов требует затрат на машинную обработку, сырье и труд. На изготовление каждой единицы продукта А отводится 3 часа машинной обработки, 16 единиц сырья и 6 единиц труда. Соответствующие требования к единице продукта В составляют 10, 4 и 6. Николай прогнозирует, что в следующем месяце он может предоставить 330 часов машинной обработки, 400 единиц сырья и 240 единиц труда. Технология производственного процесса такова, что не менее 12 единиц продукта В необходимо изготавливать в каждый конкретный месяц. Необходимо определить количество единиц продуктов А и В, которые Николай доложен производить в следующем месяце для максимизации маржинальной прибыли.
Скачать заметку в формате Word, пример в формате Excel
1. Воспользуемся математической моделью построенной в упомянутой заметке. Вот эта модель:
Максимизировать: Z = 2500 * х1 + 3500 *х2
При условии, что: 3 * х1 + 10 * х2 ≤ 330
16 * х1 + 4 * х2 ≤ 400
6 * х1 + 6 * х2 ≤ 240
х2 ≥ 12
х1 ≥ 0
2. Создадим экранную форму и введем в нее исходные данные (рис. 1).
Рис. 1. Экранная форма для ввода данных задачи линейного программирования
Обратите внимание на формулу в ячейке С7. Это формула целевой функции. Аналогично, в ячейки С16:С18 введены формулы для расчета левой части ограничений.
3. Проверьте, если у вас установлена надстройка «Поиск решения» (рис. 2), пропустите этот пункт.
Рис. 2. Надстройка Поиск решения установлена; вкладка «Данные», группа «Анализ»
Если надстройки «Поиск решения» вы на ленте Excel не обнаружили, щелкните на кнопку Microsoft Office, а затем Параметры Excel (рис. 3).
Рис. 3. Параметры Excel
Выберите строку Надстройки, а затем в самом низу окна «Управление надстройками Microsoft Excel» выберите «Перейти» (рис. 4).
Рис. 4. Надстройки Excel
В окне «Надстройки» установите флажок «Поиск решения» и нажмите Ok (рис. 5). (Если «Поиск решения» отсутствует в списке поля «Надстройки», чтобы найти надстройку, нажмите кнопку Обзор. В случае появления сообщения о том, что надстройка для поиска решения не установлена на компьютере, нажмите кнопку Да, чтобы установить ее.)
Рис. 5. Активация надстройки «Поиск решения»
После загрузки надстройки для поиска решения в группе Анализ на вкладке Данные становится доступна команда Поиск решения (рис. 2).
4. Следующим этапом заполняем окно Excel «Поиск решения» (рис. 6)
Рис. 6. Заполнение окна «Поиск решения»
В поле «Установить целевую ячейку» выбираем ячейку со значением целевой функции – $C$7. Выбираем, максимизировать или минимизировать целевую функцию. В поле «Изменяя ячейки» выбираем ячейки со значениями искомых переменных $C$4:$D$4 (пока в них нули или пусто). В области «Ограничения» с помощью кнопки «Добавить» размещаем все ограничения нашей модели. Жмем «Выполнить». В появившемся окне «Результат поиска решения» выбираем все три типа отчета (рис. 7) и жмем Ok. Эти отчеты нужны для анализа полученного решения. Подробнее о данных, представленных в отчетах, можно почитать здесь.
Рис. 7. Выбор типов отчета
На основном листе появились значения максимизированной целевой функции – 130 000 руб. и изменяемых параметров х1 = 10 и х2 = 30. Таким образом, для максимизации маржинального дохода Николаю в следующем месяце следует произвести 10 единиц продукта А и 30 единиц продукта В.
Если вместо окна «Результат поиска решения» появилось что-то иное, Excel`ю найти решение не удалось. Проверьте правильность заполнения окна «Поиск решения». И еще одна маленькая хитрость. Попробуйте уменьшить точность поиска решения. Для этого в окне «Поиск решения» щелкните на Параметры (рис. 8.) и увеличьте погрешность вычисления, например, до 0,001. Иногда из-за высокой точности Excel не успевает за 100 итераций найти решение. Подробнее о параметрах поиска решения можно почитать здесь.
Рис. 8. Увеличение погрешности вычислений
Найденные решения (значения изменяемых ячеек) можно сохранить в качестве сценария. Для этого нужно:
- В диалоговом окне Результаты поиска решения выбрать Сохранить сценарий.
- В поле Название сценария ввести имя сценария. Просмотреть сценарии можно с помощью команды Данные > Работа с данными > Анализ что-если > Диспетчер сценариев > Сценарии.
С помощью программы Поиск решения можно создать три типа отчетов по результатам, полученным при успешном завершении процедуры решения.
Каждый отчет создается на отдельном листе текущей рабочей книги.
Для создания отчета надо в диалоговом окне Результаты поиска решения выбрать нужный тип отчета в поле Тип отчета. Можно выбрать сразу несколько типов (при выделении нескольких строк используется клавиша ).
- Результаты – отчет содержит целевую ячейку, список изменяемых ячеек, их исходные и конечные значения, ограничения и сведения о них.
- Устойчивость – отчет содержит сведения о степени зависимости модели от изменений величин, входящих в формулы, применяемые в задаче (формулы модели и формулы ограничений).
- Пределы – выводится целевая ячейка и ее значение, а также список изменяемых ячеек, их значений, нижних и верхних пределов и целевых результатов.
Рассмотрим применение процессора Excel для решения ЗЛП на примерах.
Задача 1. Планирование производства
Модель линейного программирования дает возможность определить наиболее выгодную производственную программу выпуска нескольких видов продукции при заданных ограничениях на ресурсы.
МП выпускает товары х1,х2,х3,х4, получая от реализации каждого прибыль в 60,70,120,130 руб. соответственно. Затраты на производство приведены в таблице.
| Затраты | х1 | х2 | x3 | х4 | Всего |
|---|---|---|---|---|---|
| Трудовые | 1 | 1 | 1 | 1 | 16 |
| Сырьевые | 6 | 5 | 4 | 1 | 110 |
| Финансы | 4 | 6 | 10 | 13 | 100 |
- Максимум прибыли в зависимости от оптимального распределения затрат.
- Минимум ресурсов, необходимых для получения максимальной прибыли.
Решение задачи средствами Excel состоит из 4 этапов:
- Создание математической модели задачи ЛП.
- Создание формы для ввода условий задачи, ввод в неё исходных данных и зависимостей из математической модели.
- Ввод данных из формы в окно Excel Поиск решения из меню Данные.
- Задание параметров поиска и решение задачи.
Создание математической модели задачи
Составим математическую модель процесса по описанию задачи:
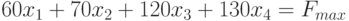
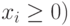
Для решения данной задачи c помощью программы MS Excel создадим новую книгу с именем Линейное программирование и изменим имя ее первого рабочего листа на Задача о производстве.
Создание формы
- Составление формы в виде:
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| 1 | Переменная | х7 | х2 | x3 | х4 | Формула | Знак | Св.член |
| 2 | Значение | |||||||
| 3 | Коэф. ЦФ | 60 | 70 | 120 | 130 | =СУММПРОИЗВ(В$2:Е$2;В3:Е3) | Max | |
| 4 | Трудовые | 1 | 1 | 1 | 1 | =СУММПРОИЗВ(В$2:Е$2;В4:Е4) |  |
16 |
| 5 | Сырьевые | 6 | 5 | 4 | 1 | =СУММПРОИЗВ(В$2:Е$2;В5:Е5) |  |
110 |
| 6 | Финансы | 4 | 6 | 10 | 13 | =СУММПРОИЗВ(В$2:Е$2;В6:Е6) |  |
100 |
- Запись в ячейки В3:Е3 коэффициентов целевой функции F (1), в В4:Е6 коэффициентов из системы ограничений (2) и в ячейки Н4:Н6 – свободных членов из системы (2).
- Ввод формул с помощью fx – Мастера функций.
Для ввода формулы в целевую ячейку (целевой функции): щелкнуть левой клавишей мыши по ячейке F3 , затем по значку Мастера функций fx на панели инструментов, в появившемся окне «Мастер функций, Шаг 1» выбрать категорию «Математические», далее выбрать функцию СУММПРОИЗВ, нажать клавишу ОК, в окне «Мастер функций Шаг 2» в поле Массив 1 ввести с клавиатуры В2:Е2 (ячейки, в которых будут варьироваться х1..х4), в поле Массив 2 ввести В3:Е3 (коэффициенты целевой функции ЦФ).
Примечание. Можно вводить В2:Е2 не с клавиатуры, а поставить курсор в окно Массив 1, а затем протащить курсор при нажатой левой клавише мыши по ячейкам В2:Е2, имена ячеек сами запишутся в окно. Аналогично поступить с полем Массив 2.
Нажать клавишу ОК, в ячейку F3 запишется формула 60х1+70х2+120х3+ 130х4 в виде СУММПРОИЗВ(В2:Е2;В3:Е3).
Чтобы не вводить формулы в другие ячейки, необходимо изменить тип адресации для ячеек В2:Е2 с относительной на абсолютную $B$2:$E$2 , установив курсор перед нужным адресом B2 и нажав функциональную клавишу F4 , затем повторить эти действия для адреса E2 . Формула примет следующий вид:
После внесенных изменений необходимо скопировать формулу в ячейки F4:F6 c помощью маркера заполнения. Для этого необходимо выделить ячейку F3 , содержащую нужную формулу, установить указатель мыши на черный квадратик в правом нижнем углу ячейки (он примет форму черного крестика) и протащить с помощью левой кнопки мыши на весь требуемый диапазон.
В результате копирования мы увидим следующие формулы:
- в ячейке F4 – СУММПРОИЗВ($В$2:$Е$2;В4:Е4),
- в ячейке F5 – СУММПРОИЗВ($В$2:$Е$2;В5:Е5),
- в ячейке F6 – СУММПРОИЗВ($В$2:$Е$2;В6:Е6).
Заполнение окна Поиск решения
Выбрать в пункте меню Данные команду Поиск решения, поставить курсор в поле целевой функции, выделить ячейку F3 в форме (или ввести F3 с клавиатуры), поставить переключатель в положение «Максимальному значению» (см. рис. 12.1 рис. 12.1). В поле «Изменяя ячейки» ввести $В$2:$Е$2(с клавиатуры или протащив мышью).
Нажать клавишу «Добавить», в окне «Добавление ограничения» в поле «Ссылка на ячейку» ввести F4 , выбрать через «стрелка вниз» знак «
Аналогично через «Добавить» ввести 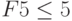
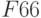
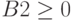
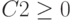
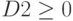
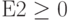
Также необходимо добавить ограничения для получения целочисленных величин по количеству товаров: B2=цел, C2=цел, D2=цел и Е2=цел.
После ввода последнего граничного условия вместо «Добавить» нажать клавишу ОК, появится окно «Поиск решения».
Для изменения или удаления ограничений и граничных условий используются клавиши Изменить, Удалить.
Параметры поиска
В окне «Поиск решения» нажать клавишу «Параметры», выбрать по умолчанию Максимальное время – 100 с, число итераций – 100 (для большинства задач это количество просчётов подходит с большим запасом), установить флажок в строке «Линейная модель», нажать ОК, в появившемся окне Поиск Решения нажать Выполнить (рис. 12. рис. 12.3).
Результаты поиска решения с таблицей результатов:
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| 1 | Переменная | X1 | X2 | X3 | X4 | Формула | Знак | Св.член |
| 2 | Значение | 10 | 0 | 6 | 0 | |||
| 3 | Коэф. ЦФ | 60 | 70 | 120 | 130 | 1320 | Max | |
| 4 | Трудовые | 1 | 1 | 1 | 1 | 16 |  |
16 |
| 5 | Сырьевые | 6 | 5 | 4 | 1 | 84 |  |
110 |
| 6 | Финансы | 4 | 6 | 10 | 13 | 100 |  |
100 |
Таким образом оптимальный план Х(Х1,Х2,Х3,Х4)=(10,0,6,0) при минимальном использовании ресурсов
- Трудовые – 16 (У1)
- Сырьевые – 84 (У2)
- Финансы – 100 (У3)
даёт максимум прибыли F в 1320 руб.
Вывод: Максимальная прибыль F в 1320 руб. получается при выпуске только товаров Х1 и Х3 в количестве 10 и 6 штук соответственно, товары Х3 и Х4 выпускать не нужно (это приведёт к снижению прибыли). Трудовые (У1) и финансовые (У3) ресурсы используются полностью, по сырьевым ресурсам (У2) есть запас в 110-84=26 ед.
Кроме того, это означает, что изменение трудовых ( y1 ) и финансовых ( y3 ) ресурсов приведёт к изменению прибыли F , а изменение сырьевых ресурсов ( y2 ) – нет.
Разности между плановыми ресурсами и использованными являются двойственными переменными y1, y2 и y3 сопряжённой задачи линейного программирования. В данном случае y1=y3=0 , а y2=26 ед. Таким образом, ресурс y2 можно уменьшить на 26 ед., тогда план по сырью тоже будет оптимальным.
Задача 2. Задача об оптимальной диете
Имеется n видов продуктов питания, в которых содержится m типов питательных веществ (белки, жиры, углеводы). В одной весовой единице продукта i-го типа 

Требуется определить оптимальный состав рациона продуктов, такой, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.
Ведем в рассмотрение следующие переменные: х – весовое количество продукта питания i-го типа в суточном рационе.
Тогда в общем случае математическая постановка задачи об оптимальной диете может быть сформулирована следующим образом:
где множество допустимых альтернатив 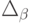
Для решения задачи об оптимальной диете с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи.
Для определенности предположим, что в качестве исходных типов продуктов рассматриваются: хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3).
Калорийность одной весовой единицы каждого из продуктов следующая:с1 = 2060,с2= 2430,с3= 3600,с4= 890,с5= 140,с6= 230, с7 = 650. Содержание питательных веществ в каждом из продуктов может быть задано в форме нижеприведенной таблицы.
Минимальная суточная потребность в питательных веществах следующая: в белках b 1 = 100, в жирах b 2= 70, в углеводах b3 = 400.
Для решения данной задачи c помощью программы MS Excel создадим новую книгу с именем Линейное программирование и изменим имя ее второго рабочего листа на Задача о диете.
Таблица 1. Содержание питательных веществ в продуктах питания
| Продукты/питательные вещества | Хлеб ржаной | Мясо баранина | Сыр «Российский» | Банан | Огурцы | Помидоры | Виноград |
|---|---|---|---|---|---|---|---|
| Белки | 61 | 220 | 230 | 15 | 8 | 11 | 6 |
| Жиры | 12 | 172 | 290 | 1 | 1 | 2 | 2 |
| Углеводы | 420 | 0 | 0 | 212 | 26 | 38 | 155 |
Создание математической модели задачи
Составим математическую модель процесса по описанию задачи:

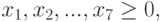
Создание формы
Для решения поставленной задачи выполним следующие подготовительные действия:
- Внесем необходимые надписи в ячейки A1:I1, A2:A7, B4, I4, J4 .
- В ячейки ВЗ:НЗ введем значения коэффициентов целевой функции: с1 = 2060, с2 = 2430, с3 = 3600, с4 = 890, с5 = 140, с6 = 230, с7 = 650.
- В ячейку I2 введем формулу: =СУММПРОИЗВ( b 2:Н2;B3:H3), которая представляет целевую функцию (4).
- В ячейки В5:Н7 введем значения коэффициентов ограничений, взятых из таблицы.
- В ячейки J5 :J7 введем значения правых частей ограничений, соответствующих минимальной суточной потребности в питательных веществах: в белках b 1=100 , жирах b 2= 70 и углеводах b3 = 400.
- В ячейку I5 введем формулу: =СУММПРОИЗВ($B$2:$H$2;В5:Н5), которая представляет левую часть первого ограничения (5).
- Скопируем формулу, введенную в ячейку I5 , в ячейки I6 и I7 .
- Внешний вид рабочего листа MS Office Excel с исходными данными для решения задачи об оптимальном рационе питания имеет следующий вид (pиc. 12.4).
Для отображения формул в ячейках рабочего листа необходимо выполнить команду меню: Формулы и на панели инструментов в группе Зависимости формул выбрать Показать формулы.
Заполнение окна Поиск решения
Для дальнейшего решения задачи следует вызвать мастер поиска решения, для чего необходимо выполнить операцию: Данные > Поиск решения.
После появления диалогового окна Поиск решения следует выполнить следующие действия:
- В поле с именем Установить целевую ячейку: ввести абсолютный адрес ячейки $I$2 .
- Для группы Равной: выбрать вариант поиска решения – минимальному значению.
- В поле с именем Изменяя ячейки: ввести абсолютный адрес ячеек $B$2:$H$2 .
- Добавить 3 ограничения, представляющие минимальные суточные потребности в питательных веществах. С этой целью выполнить следующие действия:
- для задания первого ограничения в исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить (рис. 12.5 рис. 12.5, а);
- в появившемся дополнительном окне выбрать ячейку $I$5 , которая должна отобразиться в поле с именем Ссылка на ячейку;
- в качестве знака ограничения из выпадающего списка выбрать нестрогое неравенство » «;
- в качестве значения правой части ограничения выбрать ячейку $J$5 ;
- для добавления первого ограничения в дополнительном окне нажать кнопку с надписью Добавить;
- аналогичным образом задать оставшиеся два ограничения (рис. 12.5 рис. 12.5, б).
Параметры
В окне «Поиск решения» нажать клавишу «Параметры», выбрать «Поиск решения Линейных задач симплекс-методом», нажать ОК, затем нажать Найти Решение (рис. 12.6 рис. 12.6, б).
После задания ограничений и целевой функции можно приступить к поиску численного решения, для чего следует нажать кнопку Выполнить. После выполнения расчетов программой MS Excel будет получено количественное решение, которое имеет вид, представленный на рис. 12. рис. 12.7.
Результатом решения задачи об оптимальной диете являются найденные оптимальные значения переменных: х1 = 0, х2 = 0,211, 3 = 0,109, х4= 1,887, х5 = 0, х6 = 0, х7 = 0, которым соответствует значение целевой функции: fопт= 2587,140. При выполнении расчетов для ячеек В2:I2 был выбран числовой формат с 3 знаками после запятой.
Анализ найденного решения показывает, что для удовлетворения суточной потребности в питательных веществах (белки, жиры, углеводы) следует использовать 211 г мяса баранины, 109 г сыра и 1887 г бананов, совсем отказавшись от хлеба, огурцов, помидоров и винограда. При этом общая калорийность найденной оптимальной диеты будет приближенно равна 2590 ккал, что вполне соответствует малоактивному образу жизни без серьезных физических нагрузок. Напомним, что согласно медицинским данным, энергетические затраты работников интеллектуального труда (юристы, бухгалтера, врачи, педагоги) лежат в пределах 3000 ккал.
ЗАДАНИЕ
- Составить математическую модель задачи линейного программирования.
- Решить задачу линейного программирования в Excel с помощью Поиска решения.
- Сохранить в виде модели установочные параметры.
Предприятие легкой промышленности выпускает две модели машин, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 80 изделий, второй линии – 85 изделий. На машину первой модели расходуются 12 однотипных элементов электронных схем, на машину второй модели – 6 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одной машины первой и второй моделей равна $30 и $40 соответственно. Определить оптимальный суточный объем производства первой и второй моделей.
Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех приборах. Время использования этих приборов для производства данных изделий ограничено 10 ч. в сутки. Найти оптимальный объем производства изделий каждого вида.
Фирма имеет возможность рекламировать свою продукции, используя местные радио- и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены $1000 в месяц. Каждая минута радиорекламы обходится в $5, а минута телерекламы – в $100. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.
Фирма производит два вида продукции – А и B . Объем сбыта продукции вида A составляет не менее 70% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 120 кг. Расход сырья на единицу продукции A составляет 3 кг, а на единицу продукции В – 5 кг. Цены продукции А и В равны $20 и $60 соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.
Фирма выпускает женские шляпы двух фасонов. Трудоемкость изготовления шляпы фасона 1 вдвое выше трудоемкости изготовления шляпы фасона 2. Если бы фирма выпускала только шляпы фасона 1, суточный объем производства мог бы составить 60 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 50 до 100 штук. Прибыль от продажи шляпы фасона 1 равна $6, а фасона 2 – $7. Определить какое количество шляп каждого фасона следует изготавливать, чтобы максимизировать прибыль.
Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков:
Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в машино-часах). Стоимость машино-часа составляет $10 и $15 для станка 1 и 2 соответственно. Допустимое время для использования станков для обработки изделий всех типов ограничено следующими значениями: 500 машино-часов – для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1,2,3 и 4 равны $65, $70, $55 и $45 соответственно. Составить план производства, максимизирующий чистую прибыль.
Завод выпускает изделия трех моделей ( I, II III ) Для их изготовления используется два вида ресурсов (А и В), запасы которых составляют – 5000 и 6000 единиц. Расходы ресурсов на одно изделие каждой модели:
Трудоемкость изготовления модели I вдвое больше, чем изделия модели II , и втрое больше, чем изделие модели III . Численность рабочих завода позволяет выпускать 1500 изделий I . Анализ условий сбыта показывает, что минимальный спрос на продукцию завода составляет 200, 200 и 150 изделий моделей I,II и III соответственно. Однако соотношение выпуска изделий моделей I,II и III должно быть равно 3:2:5. Удельная прибыль от реализации изделий моделей I,II и III составляет $30, $20 и $50 соответственно. Определить выпуск изделий, максимизирующий прибыль.
Требуется распределить имеющиеся денежные средства по четырем альтернативным вариантам. Игра имеет три исхода. Ниже приведены размеры выигрыша (или проигрыша) на каждый доллар, вложенный в соответствующий альтернативный вариант, для любого из трех исходов. У игрока имеется $500, причем, использовать в игре их можно только один раз. Точный исход игры заранее неизвестен, и, учитывая эту неопределенность, игрок решил распределить деньги так, чтобы максимизировать максимальную отдачу от этой суммы.
Бройлерное хозяйство птицеводческой фермы насчитывает 80000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Хотя недельный рацион цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 фунт.
Для того чтобы цыплята достигли к восьмой неделе необходимых весовых кондиций, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов или ингредиентов. Ограничим наше рассмотрение только тремя ингредиентами: известняком, зерном и соевыми бобами. Ниже приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента.
Смесь должна содержать:
- не менее 0.8%, но не более 1.2% кальция;
- не менее 22% белка;
- не более 5% клетчатки.
Необходимо определить количество каждого из трех ингредиентов, образующих смесь минимальной стоимости при соблюдении требований к общему расходу кормовой смеси и ее питательности.
Имеется n видов продуктов питания, в которых содержится m типов питательных веществ (белки, жиры, углеводы). В одной весовой единице продукта i-го типа 

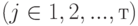
Для решения задачи об оптимальной диете с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи. Для определенности предположим, что в качестве исходных типов продуктов рассматриваются: хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3). Калорийность одной весовой единицы каждого из продуктов следующая:с1 = 2060,с2= 2430,с3= 3600,с4= 890,с5= 140,с6= 230, с7 = 650. Содержание питательных веществ в каждом из продуктов может быть задано в форме следующей таблицы (см. табл.).
Таблица 1. Содержание питательных веществ в продуктах питания
| Продукты/питательные вещества | Хлеб ржаной | Мясо баранина | Сыр «Российский» | Банан | Огурцы | Помидоры | Виноград |
|---|---|---|---|---|---|---|---|
| Белки | 66 | 225 | 235 | 20 | 13 | 16 | 11 |
| Жиры | 17 | 177 | 295 | 1 | 1 | 7 | 7 |
| Углеводы | 425 | 0 | 0 | 217 | 31 | 43 | 200 |
Минимальная суточная потребность в питательных веществах следующая: в белках b 1 = 105, в жирах b 2 = 75, в углеводах b 3 = 405.
Определить суточную потребности в питательных веществах (белки, жиры, углеводы) и общую калорийность оптимальной диеты.
Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 60 изделий, второй линии – 75 изделий. На радиоприемник первой модели расходуются 10 однотипных элементов электронных схем, на радиоприемник второй модели – 8 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одного радиоприемника первой и второй моделей равна $30 и $20 соответственно. Определить оптимальный суточный объем производства первой и второй моделей.
Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех станках. Время использования этих станков для производства данных изделий ограничено 10 ч. в сутки. Найти оптимальный объем производства изделий каждого вида.
Фирма имеет возможность рекламировать свою продукции, используя местные радио- и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены $1000 в месяц. Каждая минута радиорекламы обходится в $5, а минута телерекламы – в $100. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.
Фирма производит два вида продукции – A и B . Объем сбыта продукции вида A составляет не менее 60% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 100 кг. Расход сырья на единицу продукции A составляет 2 кг, а на единицу продукции В – 4 кг. Цены продукции А и В равны $20 и $40 соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.
Фирма выпускает ковбойские шляпы двух фасонов. Трудоемкость изготовления шляпы фасона 1 вдвое выше трудоемкости изготовления шляпы фасона 2. Если бы фирма выпускала только шляпы фасона 1, суточный объем производства мог бы составить 60 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 50 до 100 штук. Прибыль от продажи шляпы фасона 1 равна $8, а фасона 2 – $5. Определить какое количество шляп каждого фасона следует изготавливать, чтобы максимизировать прибыль.
Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков:
Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в машино-часах). Стоимость машино-часа составляет $10 и $15 для станка 1 и 2 соответственно. Допустимое время для использования станков для обработки изделий всех типов ограничено следующими значениями: 500 машино-часов – для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1,2,3 и 4 равны $65, $70, $55 и $45 соответственно. Составить план производства максимизирующий чистую прибыль.
Завод выпускает изделия трех моделей ( I, II III ). Для их изготовления используется два вида ресурсов (А и В), запасы которых составляют – 4000 и 6000 единиц. Расходы ресурсов на одно изделие каждой модели:
Трудоемкость изготовления модели I вдвое больше, чем изделия модели II , и втрое больше, чем изделие модели III . Численность рабочих завода позволяет выпускать 1500 изделий I . Анализ условий сбыта показывает, что минимальный спрос на продукцию завода составляет 200, 200 и 150 изделий моделей I,II и III соответственно. Однако соотношение выпуска изделий моделей I,II и III должно быть равно 3:2:5. Удельная прибыль от реализации изделий моделей I,II и III составляет $30, $20 и $50 соответственно. Определить выпуск изделий, максимизирующий прибыль.
Некоторое производственное предприятие выпускает три вида клея. Для производства клея используется 4 типа химических веществ: крахмал, желатин, квасцы и мел. Расход этих веществ в кг для получения 1 кг каждого вида клея и их запас на складе предприятия представлены в таблице.
Таблица 1. Расход химических веществ на изготовления клея, их запас на складе
| Вид клея /Химические вещества | Клей № 1 | Клей № 2 | Клей № 3 | Запас на складе |
|---|---|---|---|---|
| Крахмал | 0,4 | 0,3 | 0,2 | 20 |
| Желатин | 0,2 | 0,3 | 0,4 | 35 |
| Квасцы | 0,05 | 0,07 | 0,1 | 7 |
| Мел | 0,01 | 0,05 | 0,15 | 10 |
Стоимость каждого вида клея для оптовых покупателей следующая:с1 = 380 руб/кг,с2 =430 руб/кг,с3 = 460 руб/кг. Требуется определить оптимальный объем выпуска клея каждого вида, обеспечивающий максимум общей стоимости готовой продукции.
Бройлерное хозяйство птицеводческой фермы насчитывает 20000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Хотя недельный рацион цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 фунт.
Для того чтобы цыплята достигли к восьмой неделе необходимых весовых кондиций, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов или ингредиентов. Ограничим наше рассмотрение только тремя ингредиентами: известняком, зерном и соевыми бобами. Ниже приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента.
Смесь должна содержать:
- не менее 0.8%, но не более 1.2% кальция;
- не менее 22% белка;
- не более 5% клетчатки.
Необходимо определить количество каждого из трех ингредиентов, образующих смесь минимальной стоимости при соблюдении требований к общему расходу кормовой смеси и ее питательности.
Имеется конечное число видов продуктов питания: ананас, арбуз, грейпфрут, язык говяжий, сардельки говяжьи, хлеб «Бородинский», картофель ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3). Калорийность 1 кг каждого из продуктов следующая:с1 = 470,с2= 380,с3 = 350,с4 = 1460,с5 = 2150,с6 = 2070, с7 = 800. Минимальная суточная потребность в питательных веществах следующая: в белках b 1 = 100, в жирах b 2 = 70, в углеводах b3 = 400. Содержание питательных веществ в каждом из продуктов может быть задано в форме нижеприведенной таблицы (табл.).
Требуется определить такой рацион питания, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.
Поиск решения задач в Excel с примерами
Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.
Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Решение финансовых задач в Excel
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
- Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
- Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
- Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
- Тип – 0.
- БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка) кпер . Подставим значения: ПС = 400 000 / (1 + 0,05) 16 = 183245.
Решение эконометрики в Excel
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:
Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).
Решение логических задач в Excel
В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, =, Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.
- Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
- Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
- Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».
Решение математических задач в Excel
Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).
Условие учебной задачи. Найти обратную матрицу В для матрицы А.
- Делаем таблицу со значениями матрицы А.
- Выделяем на этом же листе область для обратной матрицы.
- Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
- В поле аргумента «Массив» вписываем диапазон матрицы А.
- Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.
Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.
источники:
http://intuit.ru/studies/courses/3659/901/lecture/32717
http://exceltable.com/vozmojnosti-excel/poisk-resheniya-v-excel
Цель работы:
изучение современных программных
средств решения задачи линейного
программирования; практическое решение
задач линейного программирования
графическим методом, симплекс-методом
и средствами программыMicrosoftExcel; программная реализация
симплекс-метода на языке программирования
высокого уровня.
1. Теоретическая часть
Для решения задач
линейного программирования в программе
Microsoft
Excel
имеется надстройка Поиск
решения
,
обращение
к которой производится из меню Сервис
.
Если команда
Поиск решения
отсутствует в меню Сервис
,
то требуется установить надстройку
«Поиск решения». Для этого в меню Сервис
выбирается команда Надстройки
,
которая открывает диалоговое окно,
показанное на рис. 1.
Покажем использование
надстройки
«Поиск решения» на примере решения
следующей задачи.
Постановка задачи
Предприятие
изготавливает и реализует три вида
продукции – P
1 ,
Р
2
и Р
3 .
Для производства продукции используются
три вида ресурсов – комплектующие
изделия, сырье и материалы. Запасы
ресурсов и их расход на изготовление
единицы продукции каждого вида приведены
в табл. 1.
Таблица 1
Прибыль от реализации
единицы продукции каждого вида составляет
240, 210 и 180 денежных единиц для P
1 ,
Р
2
и Р
3
соответственно.
Требуется определить
производственную программу предприятия
таким образом, чтобы прибыль от реализации
продукции была максимальной.
Математическая модель задачи
Обозначим переменными
x
1 ,
x
2
и x
3
искомые объемы производства продукции
видов P
1 ,
Р
2
и Р
2 ,
а через F
– прибыль предприятия. Тогда математическая
постановка представленной задачи
принимает следующий вид.
Определить значения
переменных x
1 ,
x
2
и x
3 ,
для которых достигается максимум целевой
функции
F
=
240 x
1
+ 210 х
2
+ 180 x
3
при ограничениях:
Целевая функция
описывает суммарную прибыль от реализации
произведенной продукции всех трех
видов. Ограничения (1), (2) и (3) учитывают
расход и запасы комплектующих изделий,
сырья и материалов соответственно.
Поскольку объемы производства продукции
не могут быть отрицательными, добавляются
условия
x
1
≥ 0; x
2
≥ 0; x
3
≥ 0.
Порядок оптимального решения задачи
Примерные действия,
необходимые для решения задачи линейного
программирования средствами программы
Excel,
представим в виде последовательности
шагов.
Шаг 1.
Исходные данные задачи записываются
на рабочем листе электронной таблицы.
Один из вариантов показан на рис. 2.
Замечание.
Если известно исходное допустимое
базисное решение, то можно несколько
ускорить процесс поиска оптимального
решения. Для этого начальные значения
некоторых или всех переменных могут
быть заданы вручную. В данном примере
для их хранения используются ячейки
$B$2,
$C$2
и $D$2.
Если допустимое базисное решение не
задано, то программа Excel
автоматически определяет начальные
значения переменных задачи.
Шаг 2.
В ячейку E3
вводится формула
СУММПРОИЗВ(В3:D3;
$B$2:$D$2)
для вычисления
текущего значения целевой функции,
которая находит сумму попарных
произведений ячеек (В3:D3)
с коэффициентами при переменных в
выражении целевой функции на ячейки
($B$2:$D$2)
с текущими значениями переменных.
Шаг 3.
Чтобы задать ограничения решаемой
задачи, в ячейки E5,
E6
и E7
копируется формула из ячейки E3.
После этого в указанных ячейках должны
быть получены формулы, представленные
в табл. 2.
Таблица
2
|
СУММПРОИЗВ(В5:D5; |
|
|
СУММПРОИЗВ(В6:D6; |
|
|
СУММПРОИЗВ(В7:D7; |
Шаг 4.
После создания таблицы с исходными
данными курсор устанавливается в ячейку
E3,
содержащую формулу для вычисления
целевой функции. Далее в меню Сервис
выбирается
команда Поиск
решения
,
которая открывает диалоговое окно,
приведенное на рис. 3.
В поле Установить
целевую ячейку
окна «Поиск решения», показанного на
рис. 3, должен
появиться адрес ячейки с формулой
целевой функции (в данном примере это
ячейка $E$3).
Затем в этом окне
(рис. 3) заполняются следующие поля этого
окна:
В поле Равной
переключатель вида экстремума целевой
функции устанавливается в положение
максимальное
значение
(или минимальное
значение
при
соответствующей постановке задачи);
В поле Изменяя
ячейки
указывается
диапазон ячеек со значениями переменных
задачи, выделяемый на рабочем листе
электронной таблицы (в примере это
ячейки $B$2:$D$2);
В поле Ограничения
задаются
ограничения исходной задачи. Для этого
курсор устанавливается в поле ввода
ограничений и нажимается кнопка Добавить
.
В результате
выводится диалоговое окно «Добавление
ограничения», показанное на рис. 4.
В этом окне в поле
Ссылка на
ячейку
вводится
адрес ячейки
с формулой соответствующего ограничения
(например, для ограничения (1) это будет
ячейка E5),
а в поле Ограничение
указывается
предельное значение, которое может
принимать выбранное ограничение (в
данном примере правая часть ограничения
(1) находится в ячейке G5).
Следует заметить,
что заполнение полей Ссылка
на ячейку
и Ограничение
в окне «Добавление
ограничения» можно выполнить выделением
соответствующих ячеек рабочего листа
электронной таблицы.
Затем выбирается
вид отношения, связывающего левую и
правую части ограничения, что показано
на рис. 5.
После нажатия
кнопки Добавить
в окне
«Добавление ограничения»
(или кнопки
ОК
для
ввода
последнего ограничения) данное ограничение
попадает в список ограничений решаемой
задачи. С помощью кнопок Удалить
и Изменить
можно удалять
выделенные в списке ограничения или
вносить в них исправления.
Замечание
.
В окне «Добавление
ограничения» можно указать, что все или
некоторые переменные должны принимать
только целые значения (рис. 5). Это
позволяет получать решения задач
целочисленного линейного программирования
(полностью или частично целочисленных).
Шаг 5.
После заполнения всех полей окна «Поиск
решения» нажимается кнопка Параметры
(рис. 3),
которая открывает диалоговое окно
«Параметры поиска решения», показанное
на рис. 6.
В этом окне требуется
установить флажки Линейная
модель
для решения
задачи линейного программирования и
Неотрицательные
значения
,
если такое
условие накладываются на все переменные
задачи.
Здесь (рис. 6) также
можно определить параметры процесса
решения: предельное время поиска решения,
максимальное количество итераций,
точность и т.п. Флажок Показывать
результаты
итераций
позволяет по шагам следить за поиском
решения. Флажок Автоматическое
масштабирование
включается
в том случае, когда разброс значений
переменных очень велик.
Шаг 6.
Задав необходимые параметры в окне
«Параметры
поиска решения»,
следует нажать на кнопку Выполнить
для поиска
решения задачи (рис. 3) в
окне «Поиск решения».
Если решение найдено, то на экран
выводится окно с соответствующим
сообщением (рис. 7).
Полученные
результаты отображаются на рабочем
листе электронной таблицы, как это
показано на рис. 8. В частности, значения
переменных — в ячейках $B$2:$D$2,
значение целевой функции – в ячейке
E3.
Таким образом,
получено оптимальное решение исходной
задачи в виде вектора

где


для которого значение целевой функцииF
максимально и составляет F
*
= 129825.
Результаты решения
задачи линейного программирования
также можно сохранить в виде отдельных
рабочих листов с именами Отчет
по результатам
,
Отчет
по устойчивости
и Отчет
по пределам
.
Для сохранения
результатов в виде отчетов необходимо
предварительно в поле Тип
отчета
выделить
требуемые типы отчетов (рис. 7). В этом
же окне можно отказаться от полученных
решений и восстановить исходные значения
переменных.
Отчет по результатам
для рассмотренной задачи показан
на рис. 9.
В данном отчете
представлены оптимальное решение задачи
линейного программирования и его
расположение в области допустимых
решений. В графах Результат
выводятся
оптимальные значения целевой функции
F
*
и переменных задачи

а также их значения для исходного
базисного решения, с которого начинался
поиск оптимального решения (графаИсходное
значение
).
Состояние
ограничений (графа Статус
)
характеризует расположение точки

показывает разности между значениями
левых и правых частей ограничений
(невязки). Для связанного ограничения
невязка равна нулю, что свидетельствует
о расположение точки

которая задается этим ограничением.
Если ограничение являются не связанным,
то оно не влияет на оптимальное решение.
Замечание
.
В экономической интерпретации связанные
ограничения соответствуют дефицитным
ресурсам. Для не связанных ограничений
графа Разница
показывает оставшиеся объемы
неиспользованных не дефицитных ресурсов.
В рассмотренной задаче ограничения (1)
и (3) соответствуют комплектующим изделиям
и материалам, которые являются дефицитными
ресурсами. Ограничение (2) является не
связанным, т.е. не влияет на оптимальный
план производства продукции по критерию
максимальной прибыли. Это означает, что
второй ресурс (сырье) не использован в
объеме 292,5 ед.
В
отчете по устойчивости (рис.
10)
приведены
границы устойчивости переменных задачи
(графы Допустимое
увеличение
и Допустимое
уменьшение
коэффициентов целевой функции), а также
границы устойчивости теневых цен (т.е.
переменных двойственной задачи), в
пределах которых оптимальное решение
не изменяется. Большие
значения пределов (1Е+30)
означают фактическое
отсутствие соответствующих границ,
т.е. переменная может изменяться до
бесконечности.
В графе Нормированная
стоимость
элемент во второй строке
(-150) показывает,
на сколько уменьшится значение функции,
если в решении переменную x
2
увеличить на единицу. С другой стороны,
при допустимом увеличении коэффициента
функции при неизвестной x
2
на 150 единиц значение этой переменной
не изменится, т.е. неизвестная x
2
будет равна нулю, а если выйти за пределы
допустимого увеличения (коэффициент
при x
2
увеличить более чем на 150), то неизвестная
x
2
в решении будет больше нуля.
В
отчете
по пределам
(рис. 11) показаны нижние и верхние пределы
возможного изменения переменных (в
пределах области допустимых решений)
и соответствующие значения целевой
функции (графа Целевой
результат
)
при этих изменениях. В частности, если
x
1
= 0, а x
2
и x
3
остаются без изменений, то F
= 2400
+ 2100
+ 180191,25
= 34425; при x
3
= 0 и неизменных x
1
и x
2
получим F
= 240397,5
+ 2100
+ 1800
= 95400.
Рассмотрим пример задачи линейного программирования.
Требуется определить, в каком количестве надо выпустить продукцию четырех типов Прод1, Прод2, Прод3, Прод4, для изготовления которой требуются ресурсы трех видов: трудовые, сырье и финансы. Количество ресурса каждого вида, необходимое для выпуска единицы продукции данного типа, называется нормой расхода. Нормы расхода, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены на рис. 1.
|
Ресурс |
Прод1 |
Прод2 |
Прод3 |
Прод4 |
Знак |
Наличие |
|
Прибыль |
||||||
|
Трудовые |
||||||
|
Сырье |
||||||
|
Финансы |
Рисунок 1.
Математическая модель задачи имеет вид:
где x j – количество выпускаемой продукции j-го типа; F – функция цели; в левых частях выражений ограничений указаны величины потребного ресурса
, а правые части показывают количество имеющегося ресурса
.
Ввод условий задачи
Для решения задачи с помощью Excel следует создать форму для ввода исходных данных и ввести их. Форма ввода показана на рис. 2.
В ячейку F6 введено выражение целевой функции как суммы произведений значений прибыли от выпуска единицы продукции каждого типа на количество выпускаемой продукции соответствующего типа. Для наглядности на рис. 3 представлена форма ввода исходных данных в режиме вывода формул.
В ячейки F8:F10 введены левые части ограничений для ресурсов каждого вида.
Рисунок 2.
Рисунок 3.
Решение задачи линейного программирования
Для решения задач линейного программирования в Excel используется мощный инструмент, называемый Поиск решения
.
Обращение к Поиску решения осуществляется из меню Сервис
, на экран выводится диалоговое окно Поиска решения (рис. 4).
Рисунок 4.
Ввод условий задачи для поиска ее решения состоит из следующих шагов:
1 Назначить целевую функцию, для чего установить курсор в поле Установить целевую ячейку
окна Поиск решения и щелкнуть в ячейке F6 в форме ввода;
2 Включить переключатель значения целевой функции, т.е. указать ее Равной Максимальному значению
;
3 Ввести адреса изменяемых переменных (x j): для этого установить курсор в поле Изменяя ячейки
окна Поиск решения, а затем выделить диапазон ячеек B3:E3 в форме ввода;
4 Нажать кнопку Добавить
окна Поиск решения для ввода ограничений задачи линейного программирования; на экран выводится окно Добавление ограничения
(рис. 5)
:
Ввести граничные условия для переменных x j (x j ³0), для этого в поле Ссылка на ячейку
указать ячейку В3, соответствующую х 1 , выбрать из списка нужный знак (³), в поле Ограничение
указать ячейку формы ввода, в которой хранится соответствующее значение граничного условия, (ячейка В4), нажать кнопку Добавить
; повторить описанные действия для переменных х 2 , х 3 и х 4 ;
Ввести ограничения для каждого вида ресурса, для этого в поле Ссылка на ячейку
окна Добавление ограничения
указать ячейку F9 формы ввода, в которой содержится выражение левой части ограничения, наложенного на трудовые ресурсы, в полях Ограничение
указать знак £ и адрес Н9 правой части ограничения, нажать кнопку Добавить
; аналогично ввести ограничения на остальные виды ресурсов;
После ввода последнего ограничения вместо Добавить
нажать ОК
и возвратиться в окно Поиск решения.
Рисунок 5.
Решение задачи линейного программирования начинается с установки параметров поиска:
В окне Поиск решения
нажать кнопку Параметры
, на экран выводится окно Параметры поиска решения
(рис. 6);
Установить флажок Линейная модель,
что обеспечивает применение симплекс-метода;
Указать предельное число итераций (по умолчанию – 100, что подходит для решения большинства задач);
Установить флажок
, если необходимо просмотреть все этапы поиска оптимального решения;
Нажать ОК
, возврат в окно Поиск решения
.
Рисунок 6.
Для решения задачи нажать кнопку Выполнить
в окне Поиск решения
, на экране – окно Результаты поиска решения
(рис. 7), в котором содержится сообщение Решение найдено. Все ограничения и условия оптимальности выполнены.
Если условия задачи несовместны, то выводится сообщение Поиск не может найти подходящего решения
. Если целевая функция не ограничена, то появляется сообщение Значения целевой ячейки не сходятся
.
Рисунок 7.
Для рассматриваемого примера решение найдено и результат оптимального решения задачи выводится в форме ввода: значение целевой функции, соответствующее максимальной прибыли и равное 1320, указывается в ячейке F6 формы ввода,
оптимальный план выпуска продукции х 1 =10, х 2 =0, х 3 =6, х 4 =0 указывается в ячейках В3:С3 формы ввода (рис. 8).
Количество использованных для выпуска продукции ресурсов выводится в ячейки F9:F11: трудовых – 16, сырья – 84, финансов – 100.
Рисунок 8.
Если при установке параметров в окне Параметры поиска решения
(рис. 6) был установлен флажок Показывать результаты итераций
, то будут показаны последовательно все шаги поиска. На экран будет выводиться окно
(рис. 9). При этом текущие значения переменных и функции цели будут показаны в форме ввода. Так, результаты первой итерации поиска решения исходной задачи представлены в форме ввода на рисунке 10 .
Рисунок 9.
Рисунок 10.
Чтобы продолжить поиск решения, следует нажимать кнопку Продолжить
в окне Текущее состояние поиска решения
.
Анализ оптимального решения
Прежде чем, перейти к анализу результатов решения, представим исходную задачу в форме
введя дополнительные переменные у i , представляющие собой величины неиспользованных ресурсов.
Составим для исходной задачи двойственную задачу и введем дополнительные двойственные переменные v i .
Анализ результатов поиска решения позволит увязать их с переменными исходной и двойственной задач.
С помощью окна Результаты поиска решения
можно вызвать отчеты трех типов, позволяющие анализировать найденное оптимальное решение:
Результаты,
Устойчивость,
Пределы.
Для вызова отчета в поле Тип отчета
выделить название нужного типа и нажать ОК
.
1 Отчет по результатам
(рис. 11) состоит из трех таблиц:
Таблица 1 содержит сведения о целевой функции; в столбце Исходно
указывается значение целевой функции до начала вычислений;
Таблица 2 содержит значения искомых переменных x j , полученных в результате решения задачи (оптимальный план выпуска продукции);
Таблица 3 показывает результаты оптимального решения для ограничений и для граничных условий.
Для Ограничений
в графе Формула
приведены зависимости, которые были введены при задании ограничений в окне Поиск решения
; в графе Значение
указаны величины использованного ресурса; в графе Разница
показано количество неиспользованного ресурса. Если ресурс используется полностью, то в графе Состояние
выводится сообщение связанное
; при неполном использовании ресурса в этой графе указывается не связан.
Для Граничных условий
приводятся аналогичные величины с той лишь разницей, что вместо неиспользованного ресурса показана разность между значением переменной x j в найденном оптимальном решении и заданным для нее граничным условием (x j ³0).
Именно в графе Разница
можно увидеть значения дополнительных переменных y i исходной задачи в формулировке (2). Здесь у 1 =у 3 =0, т.е. величины неиспользованных трудовых и финансовых ресурсов равны нулю. Эти ресурсы используются полностью. Вместе с тем, величина неиспользованных ресурсов для сырья у 2 =26, значит, имеются излишки сырья.
Рисунок 11.
2 Отчет по устойчивости
(рис. 12)состоит из двух таблиц.
В таблице 1 приводятся следующие значения:
Результат решения задачи (оптимальный план выпуска);
— Нормир. стоимость
, т.е. величины, показывающие, насколько изменится целевая функция при принудительном включении единицы продукции соответствующего типа в оптимальный план;
Коэффициенты целевой функции;
Предельные значения приращения коэффициентов целевой функции, при которых сохраняется оптимальный план выпуска.
В таблице 2 содержатся аналогичные данные для ограничений:
Величины использованных ресурсов;
— Теневая цена
, показывающая, как изменится целевая функция при изменении величины соответствующего ресурса на единицу;
Допустимые значения приращений ресурсов, при которых сохраняется оптимальный план выпуска продукции.
Рисунок 12.
Отчет по устойчивости позволяет позволяет получить двойственные оценки.
Как известно, двойственные переменные z i показывают, как изменится целевая функция при изменении ресурса i-го типа на единицу. В отчете Excel двойственная оценка называется Теневой ценой
.
В нашем примере сырье не используется полностью и его ресурс у 2 =26. Очевидно, что увеличение количества сырья, например, до 111 не повлечет за собой увеличения целевой функции. Следовательно, для второго ограничения двойственная переменная z 2 =0. Таким образом, если по данному ресурсу есть резерв, то дополнительная переменная
будет больше нуля, а двойственная оценка
этого ограничения равна нулю.
В рассматриваемом примере трудовые ресурсы и финансы использовались полностью, поэтому их дополнительные переменные равны нулю (у 1 =у 3 =0). Если ресурс используется полностью, то его увеличение или уменьшение повлияет на объем выпускаемой продукции, и следовательно, на величину целевой функции. Двойственные оценки ограничений на трудовые и финансовые ресурсы отличны от нуля, т.е. z 1 =20, z 3 =10.
Значения двойственных оценок находим в Отчете по устойчивости
, в таблице 2, в графе Теневая цена
.
При увеличении (уменьшении) трудовых ресурсов на единицу целевая функция увеличится (уменьшится) на 20 единиц и будет равна
F=1320+20×1=1340 (при увеличении).
Аналогично, при увеличении объема финансов на единицу целевая функция будет
F=1320+10×1=1330.
Здесь же, в графах Допустимое увеличение
и Допустимое уменьшение
таблицы 2, показаны допустимые пределы изменения количества ресурсов j-го вида. Например, для при изменении приращения величины трудовых ресурсов в пределах от –6 до 3,55, как показано в таблице, структура оптимального решения сохраняется, т.е наибольшую прибыль обеспечивает выпуск Прод1 и Прод3, но в других количествах.
Дополнительные двойственные переменные также отражены в Отчете по устойчивости
в графе Нормир. стоимость
таблицы 1.
Если основные переменные не вошли в оптимальное решение, т.е. равны нулю (в примере х 2 =х 4 =0), то соответствующие им дополнительные переменные имеют положительные значения (v 2 =10, v 4 =20). Если же основные переменные вошли в оптимальное решение (х 1 =10, х 3 =6), то их дополнительные двойственные переменные равны нулю (v 1 =0, v 3 =0).
Эти величины показывают, насколько уменьшится (поэтому знак минус в значениях переменных v 2 и v 4) целевая функция при принудительном выпуске единицы данной продукции. Следовательно, если мы захотим принудительно выпустить единицу продукции вида Прод3, то целевая функция уменьшится на 10 единиц и будет равна 1320 -10×1 =1310.
Обозначим через Dс j изменение коэффициентов целевой функции в исходной модели (1). Эти коэффициенты определяют прибыль, получаемую при реализации единицы продукции j-го вида.
В графах Допустимое увеличение
и Допустимое Уменьшение
таблицы 1 Отчета по устойчивости
показаны пределы изменения Dс j , при которых сохраняется структура оптимального плана, т.е. будет выгодно по-прежнему выпускать продукцию вида Продj. Например, при изменении Dс 1 в пределах -12£ Dс 1 £ 40, как показано в отчете, по-прежнему будет выгодно выпускать продукцию вида Прод1. При этом значение целевой функции будет F=1320+x 1 ×Dс j =1320+10×Dс j .
3 Отчет по пределам
приведен на рис. 13. В нем показывается, в каких пределах могут изменяться значения x j , вошедшие в оптимальное решение, при сохранении структуры оптимального решения. Кроме этого, для каждого типа продукции приводятся значения целевой функции, получаемые при подстановке в оптимальное решение значения нижнего предела выпуска изделий соответствующего типа при неизменных значениях выпуска остальных типов. Например, если при оптимальном решении х 1 =10, х 2 =0, х 3 =6, х 4 =0 положить х 1 =0 (нижний предел) при неизменных х 2 , х 3 и х 4 , то значение целевой функции будет равно 60×0+70×0+120×6+130×0=720.
Размер: px
Начинать показ со страницы:
Транскрипт
1
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Тихоокеанский государственный университет» Решение задач линейного программирования в Microsoft Excel 00 Методические указания к выполнению лабораторных работ по информатике для обучающихся по всем программам бакалавриата и специалитета дневной формы обучения Хабаровск Издательство ТОГУ 05
2
УДК 68.58(076.5) Решение задач линейного программирования в Microsoft Excel 00: методические указания к выполнению лабораторных работ по информатике для обучающихся по всем программам бакалавриата и специалитета дневной формы обучения / сост. Н. Д. Берман, Н. И. Шадрина. Хабаровск: Изд-во Тихоокеан. гос. ун-та, с. Методические указания составлены на кафедре информатики. Включают общие сведения о задачах линейного программирования, задания для выполнения лабораторных работ с вариантами задач, рекомендательный библиографический список. Печатается в соответствии с решениями кафедры информатики и методического совета факультета компьютерных и фундаментальных наук. Тихоокеанский государственный университет, 05
3
. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ В MICROSOFT EXCEL 00. ОБЩИЕ СВЕДЕНИЯ Общая характеристика задач оптимизации Задачи линейной оптимизации относятся к широко распространённому классу задач, встречающихся в различных сферах деятельности: в бизнесе, на производстве, в быту. Как оптимально распорядиться бюджетом или за минимальное время добраться до нужного места в городе, как наилучшим образом спланировать деловые встречи, минимизировать риски капитальных вложений, определить оптимальные запасы сырья на складе это те задачи, в которых нужно найти наилучшее из всех возможных решений. Различают следующие типы линейных оптимизационных задач: задачи о перевозках, например, минимизация расходов по доставке товаров с нескольких фабрик в несколько магазинов с учетом спроса; задачи распределения рабочих мест, например, минимизация расходов на содержание штата с соблюдением требований, определенных законодательством; управление ассортиментом товаров: извлечение максимальной прибыли с помощью варьирования ассортиментным набором товаров (при соблюдении требований клиентов). Аналогичная задача возникает при продаже товаров с разной структурой затрат, рентабельностью и показателями спроса; замена или смешивание материалов, например, манипуляция материалами с целью снижения себестоимости, поддержания необходимого уровня качества и соблюдения требований потребителей; задача о диете. Из имеющихся в распоряжении продуктов требуется составить такую диету, которая, с одной стороны, удовлетворяла бы минимальным потребностям организма в питательных веществах (белки, жиры, углеводы, минеральные соли, витамины), с другой требовала бы наименьших затрат; задача распределения ресурсов, например, распределение ресурсов между работами таким образом, чтобы максимизировать прибыль, или минимизировать затраты, или определить такой состав работ, который можно выполнить, используя имеющиеся ресурсы, и при этом достичь максимума опре- 3
4
деленной меры эффективности, или рассчитать, какие ресурсы необходимы для того, чтобы выполнить заданные работы с наименьшими издержками. Математическая постановка задачи линейного программирования Рассмотрим наиболее распространенный класс оптимизационных задач задачи линейного программирования. К такому классу относятся задачи, описываемые линейными математическими моделями. Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции () при условиях: () () () (3) () (4) где заданные постоянные величины и Функция () называется целевой функцией задачи, а условия ()(4) ограничениями задачи. Совокупность чисел (), удовлетворяющих ограничениям задачи, называется допустимым решением. Решение, при котором целевая функция задачи принимает максимальное (минимальное) значение, называется оптимальным. Использование надстройки Excel для решения задач линейного программирования Поиск решения это надстройка EXCEL, которая позволяет решать оптимизационные задачи. Если команда Поиск решения или группа Анализ отсутствует, необходимо загрузить надстройку Поиск решения. 4
5
На вкладке Файл выберите команду Параметры, а затем категорию Надстройки (рис.). Рис. В поле Управление выберите значение Надстройки Excel и нажмите кнопку Перейти. В поле Доступные надстройки установите флажок рядом с пунктом Поиск решения (рис.) и нажмите кнопку ОК. Рис. Пример решения оптимизационных линейных задач в MS Excel 00 Схема решения задач линейного программирования в MS Excel 00 следующая: 5
6
. Составить математическую модель.. Ввести на рабочий лист Excel условия задачи: а) создать форму на рабочем листе для ввода условий задачи; б) ввести исходные данные, целевую функцию, ограничения и граничные условия. 3. Указать параметры в диалоговом окне Поиск решения. 4. Проанализировать полученные результаты. Рассмотрим решение задачи оптимизации на примере. Пример. Задача определения оптимального ассортимента продукции Предприятие изготавливает два вида продукции П и П, которая поступает в оптовую продажу. Для производства продукции используются два вида сырья А и В. Максимально возможные запасы сырья в сутки составляют 9 и 3 ед. соответственно. Расход сырья на единицу продукции вида П и П табл.. Таблица Сырье Расход сырья на ед. продукции П П Запас сырья, ед. А 3 9 В 3 3 Опыт работы показал, что суточный спрос на продукцию П никогда не превышает спроса на продукцию П более чем на ед. Кроме того, известно, что спрос на продукцию П никогда не превышает ед. в сутки. Оптовые цены единицы продукции равны: 3 д. е. для П и 4 д. е. для П. Какое количество продукции каждого вида должно производить предприятие, чтобы доход от реализации продукции был максимальным? Решение. Построим математическую модель для решения поставленной задачи. Предположим, что предприятие изготовит x единиц продукции П и x единиц продукции П. Поскольку производство продукции ограничено имеющимися в распоряжении предприятия сырьем каждого вида и спросом на данную продукцию, а также учитывая, что количество изготовляемых изделий не может быть отрицательным, должны выполняться следующие неравенства: 6
7
Доход от реализации x единиц продукции П и x единиц продукции П составит Cреди всех неотрицательных решений данной системы линейных неравенств требуется найти такое, при котором функция F принимает максимальное значения F max. Рассматриваемая задача относится к разряду типовых задач оптимизации производственной программы предприятия. В качестве критериев оптимальности в этих задачах могут быть также использованы: прибыль, себестоимость, номенклатура производимой продукции и затраты станочного времени. Создадим на рабочем листе форму для ввода исходных данных (рис. 3). Заливкой выделены ячейки для ввода функций. Рис. 3 В ячейку E5 введем формулу для целевой функции (рис. 4). Используя обозначения соответствующих ячеек в Excel, формулу для расчета целевой функции можно записать как сумму произведений каждой из ячеек, отведенной для значений переменных задачи (B3, C3), на соответствующие ячейки, отведенные для коэффициентов целевой функции (B5, C5). 7
8
Рис. 4 Аналогично в ячейки D0:D введены формулы для расчета левой части ограничений (рис. 5). Рис. 5 На вкладке Данные в группе Анализ выберем команду Поиск решения. В диалоговом окне Параметры поиска решения установим следующее (рис. 6): 8
9
в поле Оптимизировать целевую функцию выбираем ячейку со значением целевой функции Е5; выбираем, максимизировать или минимизировать целевую функцию; в поле Изменяя ячейки переменных выбираем ячейки со значениями искомых переменных B3:C3 (пока в них нули или пусто); в области В соответствии с ограничениями с помощью кнопки Добавить размещаем все ограничения нашей задачи (рис. 7); в поле Выберите метод решения указываем Поиск решения линейных задач симплекс-методом; нажимаем кнопку Найти решение. Рис. 6 9
10
Добавляем ограничения для нашей задачи. Для неравенств указываем в поле Ссылка на ячейки диапазон D0:D, выбираем в раскрывающемся списке знак неравенства, в поле Ограничение выделяем диапазон F0:F и нажимаем кнопку Добавить (рис. 7), чтобы принять ограничение и добавить следующее ограничение. Для принятия ограничения и возврата к диалоговому окну Поиск решения нажмите кнопку Ok. Рис. 7 Покажем окна для добавления ограничений: преобразуем в (рис. 8); Рис. 8 0
11
(рис. 9); Рис. 9, (рис. 0). Рис. 0 После выбора кнопки Найти решение появляется окно Результаты поиска решения (рис.). Рис.
12
Для сохранения полученного решения необходимо использовать переключатель Сохранить найденное решение в открывшемся окне диалога Результаты поиска решения. После чего рабочий лист примет вид, представленный на рис.. Рис. Сохранить модель поиска решения можно следующим образом:) при сохранении книги Excel после поиска решения все значения, введенные в окнах диалога Поиск решения, сохраняются вместе с данными рабочего листа. С каждым рабочим листом в рабочей книге можно сохранить один набор значений параметров Поиска решения;) если в пределах одного рабочего листа Excel необходимо рассмотреть несколько моделей оптимизации (например, найти максимум и минимум одной функции или максимальные значения нескольких функций), то удобнее сохранить эти модели, используя кнопку Загрузить/Сохранить окна Параметры поиска решения. Диапазон для сохраняемой модели содержит информацию о целевой ячейке, об изменяемых ячейках, о каждом из ограничений и все значения диалога Параметры. Выбор модели для решения конкретной оптимизационной задачи осуществляется с помощью кнопки Загрузить/сохранить диалогового окна Параметры поиска решения; 3) сохранить модель можно в виде именованных сценариев, для этого необходимо нажать на кнопку Сохранить сценарий диалогового окна Результаты поиска решений (см. рис.). Кроме вставки оптимальных значений в изменяемые ячейки, Поиск решения позволяет представлять результаты в виде трех отчетов (Результаты,
13
Устойчивость и Пределы). Для генерации одного или нескольких отчетов необходимо выделить их названия в окне диалога Результаты поиска решения (рис.). Рассмотрим более подробно каждый из них. Отчет по устойчивости (рис. 3) содержит информацию о том, насколько целевая ячейка чувствительна к изменениям ограничений и переменных. Этот отчет имеет два раздела: один для изменяемых ячеек, а второй для ограничений. Правый столбец в каждом разделе содержит информацию о чувствительности. Каждая изменяемая ячейка и ограничения приводятся в отдельной строке. При использовании целочисленных ограничений Excel выводит сообщение Отчеты об устойчивости и Пределы не применимы для задач с целочисленными ограничениями. Рис. 3 Отчет по результатам (рис. 4) содержит три таблицы: в первой приведены сведения о целевой функции до начала вычисления, во второй значения искомых переменных, полученные в результате решения задачи, в третьей результаты оптимального решения для ограничений. Этот отчет также содержит информацию о таких параметрах каждого ограничения, как статус и разница. Статус может принимать три состояния: связанное, несвязанное или невыполненное. Значение разницы это разность между значением, выводимым в ячейке ограничения при получении решения, и числом, заданным в правой части формулы ограничения. Связанное ограничение это ограничение, для которого значение разницы равно нулю. Несвязанное 3
14
ограничение это ограничение, которое было выполнено с ненулевым значением разницы. Рис. 4 Отчет по пределам (рис. 5) содержит информацию о том, в каких пределах значения изменяемых ячеек могут быть увеличены или уменьшены без нарушения ограничений задачи. Для каждой изменяемой ячейки этот отчет содержит оптимальное значение, а также наименьшие значения, которые ячейка может принимать без нарушения ограничений. Рис. 5 4
15
Полученное решение означает, что объем производства продукции вида П должен быть равен,4 ед., а продукции П,4 ед. продукции. Доход, получаемый в этом случае, составит,8 д. е. Допустим, что к условию задачи добавилось требование целочисленности значений всех переменных. В этом случае описанный выше процесс ввода условия задачи необходимо дополнить следующими шагами. В окне Поиск решения нажмите кнопку Добавить и в появившемся окне Добавление ограничений введите ограничения следующим образом (рис. 6): в поле Ссылка на ячейки введите адреса ячеек переменных задачи B3:C3; в поле ввода знака ограничения установите целое; подтвердите ввод ограничения нажатием кнопки OK. Рис. 6 Решение задачи при условии целочисленности ее переменных рис. 7. Рис. 7 5
16
. ЛАБОРАТОРНЫЕ РАБОТЫ Лабораторная работа Задание Найти максимум линейной функции при заданной системе ограничений. Вариант Целевая функция F Ограничения { { { { 3 { { 4 { { 5 { { 6 { { 7 { { 8 { { 9 { { 0 { { { { { { 3 { { 4 { { 5 { { 6
17
Лабораторная работа Задание. Построить математическую модель задачи.. Представить ее в табличной форме на листе Excel. 3. Найти решение задачи средствами надстройки Поиск решения. 4. Вывести отчеты по результатам и устойчивости. Вариант Для производства столов и шкафов мебельная фабрика использует необходимые ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида табл.. Таблица Ресурсы Древесина, м 3: -го вида -го вида Нормы затрат ресурсов на одно изделие Стол Шкаф 0, 0, 0, 0,3 Общее количество ресурсов Трудоемкость, чел.ч,5 37,4 Прибыль от реализации одного изделия, р. 6 8 Определить, сколько столов и шкафов следует изготавливать фабрике, чтобы прибыль от их реализации была максимальной. Ответ. Прибыль 940 р. при количестве столов и шкафов 0 и 66. Вариант Для производства двух видов изделий A и В используется токарное, фрезерное и шлифовальное оборудование. Нормы затрат времени для каждого из типов оборудования на одно изделие данного вида, общий фонд рабочего времени каждого из типов оборудования, а также прибыль от реализации одного изделия табл. 3. 7
18
Таблица 3 Затраты времени, стан.-ч, Тип оборудования на обработку одного изделия А В Фрезерное 0 8 Токарное 5 0 Шлифовальное 6 Прибыль от реализации одного изделия, р. 4 8 Общий фонд полезного рабочего времени оборудования, ч Найти план выпуска изделий А и В, обеспечивающий максимальную прибыль от их реализации. Ответ. Прибыль 76 р. при выпуске изделий и 6. Вариант 3 Для изготовления трех видов изделий А, В и С используется токарное, фрезерное, сварочное и шлифовальное оборудование. Затраты времени на обработку одного изделия для каждого из типов оборудования, общий фонд рабочего времени каждого из типов используемого оборудования, прибыль от реализации одного изделия данного вида табл. 4. Таблица 4 Тип оборудования Фрезерное Токарное Сварочное Шлифовальное Затраты времени, стан.-ч, на обработку одного изделия вида А В С Прибыль, р. 0 4 Общий фонд рабочего времени оборудования, ч Требуется определить, сколько изделий и какого вида следует изготовить предприятию, чтобы прибыль от их реализации была максимальной. Ответ. Прибыль 49 р. при выпуске изделий 4, 8, 0. 8
19
Вариант 4 Для поддержания нормальной жизнедеятельности человеку ежедневно необходимо потреблять не менее 8 г белков, 56 г жиров, 500 г углеводов, 8 г минеральных солей. Количество питательных веществ, содержащихся в кг каждого вида потребляемых продуктов, а также цена кг каждого из этих продуктов табл. 5 Таблица 5 Питательные вещества Содержание, г, питательных веществ в кг продуктов Мясо Рыба Молоко Масло Сыр Крупа Картофель Белки Жиры Углеводы Минеральные соли Цена кг продуктов, р.,8,0 0,8 3,4,9 0,5 0, Составить дневной рацион, содержащий не менее минимальной суточной нормы потребности человека в необходимых питательных веществах при минимальной общей стоимости потребляемых продуктов. Ответ. Минимальная общая стоимость 0, р. при количестве продуктов: мясо 0; рыба 0; молоко 0; масло 0,03335; сыр 0; крупа 0,9053; картофель 0. Вариант 5 Кондитерская фабрика для производства трех видов карамели А, В, и С использует три вида основного сырья: сахарный песок, патоку и фруктовое пюре. Нормы расхода сырья каждого вида на производство т карамели данного вида, общее количество сырья каждого вида, прибыль от реализации т карамели табл. 6. 9
20
Таблица 6 Вид сырья Сахарный песок Патока Фруктовое пюре Нормы расхода сырья, т, на т карамели А В С 0,8 0,4 0,5 0,4 0, 0,6 0,3 0, Прибыль от реализации т продукции, р Общее количество сырья, т Найти план производства карамели, обеспечивающий максимальную прибыль от ее реализации. Ответ. Максимальная прибыль р. при выпуске карамели 00, 0, 00 т. Вариант 6 На швейной фабрике для изготовления четырех видов изделий может быть использована ткань трех артикулов. Нормы расхода тканей всех артикулов на пошив одного изделия, имеющееся в распоряжении фабрики общее количество тканей каждого артикула и цена одного изделия данного вида табл. 7. Таблица 7 Артикул ткани I II III Норма расхода ткани, м, на одно изделие вида 3 4 Цена одного изделия, р Общее количество ткани, м Определить, сколько изделий каждого вида должна произвести фабрика, чтобы стоимость изготовленной продукции была максимальной. Ответ. Максимальная стоимость продукции 5 р. при выпуске изделий 95, 0, 0, 0. 0
21
Вариант 7 Предприятие выпускает четыре вида продукции и использует три типа основного оборудования: токарное, фрезерное и шлифовальное. Затраты времени на изготовление единицы продукции для каждого из типов оборудования, общий фонд рабочего времени каждого из типов оборудования и прибыль от реализации одного изделия данного вида табл. 8. Таблица 8 Затраты времени, стан.-ч, Тип оборудования на единицу продукции вида 3 4 Токарное Фрезерное Шлифовальное Прибыль от реализации 3 единицы продукции, р. 8 3 Общий фонд рабочего времени, стан.-ч Определить такой объем выпуска каждого из изделий, при котором общая прибыль от их реализации является максимальной. Ответ. Максимальная прибыль 965 р. при выпуске изделий 70, 35, 0, 0. Вариант 8 Торговое предприятие планирует организовать продажу четырех видов товара, используя при этом только два вида ресурсов: рабочее время продавцов в количестве 840 ч и площадь торгового зала 80 м. При этом известны плановые нормативы затрат этих ресурсов в расчете на единицу товаров и прибыль от их продажи табл. 9. Таблица 9 Показатели Расход рабочего времени на единицу товара, ч Использование площади торгового зала на единицу товара, м Товар А В С D 0,6 0,8 0,6 0,4 0, 0, 0,4 0, Прибыль от продажи единицы товара, р Общее количество ресурсов
22
Требуется определить оптимальную структуру товарооборота, обеспечивающую торговому предприятию максимальную прибыль. Ответ. Максимальная прибыль 6 00 р. при продаже товаров 0, 0, 0, 800. Вариант 9 Из трех видов сырья необходимо составить смесь, в состав которой должно входить не менее 6 ед. химического вещества А, 30 ед. вещества В и 4 ед. вещества С. Количество единиц химического вещества, содержащегося в кг сырья каждого вида, цена кг сырья каждого вида табл. 0 Таблица 0 Вещество А В С Цена кг сырья, р. Количество единиц вещества, содержащегося в кг сырья вида Составить смесь, содержащую не менее нужного количества веществ данного вида и имеющую минимальную стоимость. Ответ. Минимальная стоимость 6 р. при количестве 0; 0; 0; 6,5 кг. Вариант 0 Для производства трех видов продукции предприятие использует два типа технологического оборудования и два вида сырья. Нормы затрат сырья и времени на изготовление одного изделия каждого вида, общий фонд рабочего времени каждой из групп технологического оборудования, объемы имеющегося сырья каждого вида, цена одного изделия каждого вида, ограничения на возможный выпуск каждого из изделий табл..
23
Ресурсы Производительность оборудования в нормочасах: I типа II типа Сырье, кг: -го вида -го вида Цена одного изделия, р. Выпуск, шт.: минимальный максимальный Нормы затрат на одно изделие вида Таблица Общее количество ресурсов Составить план производства продукции, по которому будет изготовлено необходимое количество изделий каждого вида, при максимальной общей стоимости всей изготовляемой продукции. Ответ. Общая стоимость 495 р. при выпуске продукции 0, 33, 45. Вариант При производстве четырех видов кабеля выполняется пять групп технологических операций. Нормы затрат на км кабеля данного вида для каждой из групп операций, прибыль от реализации км каждого вида кабеля, а также общий фонд рабочего времени, в течение которого могут выполняться эти операции, табл. Таблица Технологическая операция Нормы затрат времени, ч, на обработку км кабеля вида 3 4 Волочение Наложение изоляций Скручивание элементов в кабель Освинцовывание Испытание и контроль,0 6,4 3,0,8 0,4 5,6,5,6 0,8 6,0,8 0,8,4 0,7 8,0,4 3,0 Прибыль от реализации км кабеля, р., 0,8,0,3 Общий фонд рабочего времени, ч
24
Определить план выпуска кабеля, при котором общая прибыль от реализации изготовляемой продукции является максимальной. Ответ. Общая прибыль от реализации 939,48 57 р. при выпуске 00; 64,8 57; 0; 0. Вариант Стальные прутья длиной 0 см необходимо разрезать на заготовки длиной 45, 35 и 50 см. Требуемое количество заготовок данного вида составляет соответственно 40, 30 и 0 шт. Возможные варианты разреза и величина отходов при каждом из них табл. 3. Таблица 3 Варианты разреза Длина заготовки, см Величина отходов, см Определить, сколько прутьев по каждому из возможных вариантов следует разрезать, чтобы получить не менее нужного количества заготовок каждого вида при минимальных отходах. Ответ. Минимальные отходы равны 550 см при количестве прутьев 0, 0, 0, 0, 0, 0 шт. Вариант 3 Для производства трех видов изделий А, В, С предприятие использует четыре вида сырья. Нормы затрат сырья каждого вида на производство единицы продукции данного вида, прибыль от реализации одного изделия каждого вида табл. 4. 4
25
Таблица 4 Нормы затрат сырья, кг, на единицу продукции Вид сырья А В С I II III IV Прибыль от реализации одного изделия Изделия А, В и С могут производиться в любых соотношениях (сбыт обеспечен), но для их производства предприятие может использовать сырье I вида не более 00 кг, II вида не более 0 кг, III вида не более 80 кг, IV вида не более 38 кг. Определить план производства продукции, при котором общая прибыль предприятия от реализации всей продукции была бы наибольшей. Ответ. План производства изделий 7, 5, 0 кг при общей прибыли 5 кг. Вариант 4 Туристическое агентство собирается заказать издательству выпуск художественных альбомов трех типов A, B, C. Их изготовление лимитируется затратами ресурсов трех видов, удельные расходы которых приведены в табл. 5. Вид ресурса Финансы, $ Бумага, л. Трудозатраты, чел. ч Таблица 5 Удельные затраты ресурсов на выпуск альбомов A B C 4 4 Издательство для выполнения заказа получило финансовые средства в объеме $ 3 600, имеет в наличии л. бумаги и может использовать трудовые ресурсы в объеме 00 чел. ч. Агентство платит за выпуск одного альбома типа А дол., за альбом В 8 дол., за альбом С 30 дол. 5
26
Сколько альбомов каждого типа должно выпустить издательство, чтобы получить наибольшую прибыль? Ответ. Максимальный суммарный доход дол., количество альбомов: 400; 800; 0 шт. Вариант 5 Предприятие оптовой торговли может реализовать T j, j, 4 группы товаров. Для этого используется несколько видов ресурсов. Исходные данные для построения математической модели табл. 6. Лимитирующие ресурсы и показатели Товарная группа T T T 3 T4 Объем ресурса Таблица 6 Складские площади, м Трудовые ресурсы, чел.ч Издержки обращения, ден. ед Товарные запасы, ден. ед План товарооборота, ден. ед Минимально допустимые значения товарооборота по j-й группе, ед. Прибыль в расчете на единицу товарооборота j-й группы, ден. ед. Вид огра ниче- ния Требуется рассчитать план хозяйственной деятельности торгового предприятия, обеспечивающий максимум прибыли при заданных ограничениях на складские площади, трудовые ресурсы, издержки обращения, товарные запасы, величину товарооборота, если торговая прибыль в расчете на единицу товарооборота j -й группы задана. Ответ. Максимальна прибыль ден. ед. Товарооборот по группам: Т 00 ед., Т 000 ед., Т ед., Т ед. 6
27
3. РЕКОМЕНДАТЕЛЬНЫЙ БИБЛИОГРАФИЧЕСКИЙ СПИСОК. Акулич, И. Л. Математическое программирование в примерах и задачах: учеб. пособие для студентов экон. спец. сузов / И. Л. Акулич. М. : Высш. шк., с.. Леоненков, А. В. Решение задач оптимизации в среде MS Excel / А. В. Леоненков. СПб. : БХВ-Петербург, с. 3. Васильев, А. Н. Финансовое моделирование и оптимизация средствами Excel007 / А. Н. Васильев. СПб. : Питер, с. 4. Уокенбах, Дж. Microsoft Excel 00. Библия пользователя: пер. с англ. / Дж. Уокенбах. М. : И. Д. Вильямс, 0. 9 с. 5. Уокенбах, Дж. Формулы в Microsoft Excel 00: пер. с англ. / Дж. Уокенбах. М. : И. Д. Вильямс, с. 6. Иванов, И. Microsoft Excel 00 для квалифицированного пользователя / И. Иванов. М. : Академия АЙТИ, с. 7. Справка и инструкции по Excel // Поддержка по Microsoft Office [Электронный ресурс]. Режим доступа: (дата обращения:). 8. Решение задач оптимизации управления с помощью MS Excel 00 // НОУ «ИНТУИТ» [Электронный ресурс]. Режим доступа: (дата обращения:). Оглавление. Задачи линейного программирования в Microsoft Excel 00. Общие сведения… 3 Общая характеристика задач оптимизации… 3 Математическая постановка задачи линейного программирования… 4 Использование надстройки Excel для решения задач линейного программирования… 4 Пример решения оптимизационных линейных задач в MS Excel Лабораторные работы… 6 Лабораторная работа… 6 Лабораторная работа Рекомендательный библиографический список
28
Решение задач линейного программирования в Microsoft Excel 00 Методические указания к выполнению лабораторных работ по информатике для обучающихся по всем программам бакалавриата и специалитета дневной формы обучения Нина Демидовна Берман Нина Ивановна Шадрина Главный редактор Л. А. Суевалова Редактор Е. Н. Ярулина Подписано в печать Формат 60 x 84 / 6. Бумага писчая. Гарнитура «Калибри». Печать цифровая. Усл. печ. л.,68. Тираж 60 экз. Заказ 70. Издательство Тихоокеанского государственного университета, Хабаровск, ул. Тихоокеанская, 36. Отдел оперативной полиграфии издательства Тихоокеанского государственного университета, Хабаровск, ул. Тихоокеанская, 36. 8
ОБЪЕМНОЕ ПЛАНИРОВАНИЕ РАБОТЫ ТЕХНОЛОГИЧЕСКИХ СТАНОЧНЫХ СИСТЕМ Х а б а р о в с к 2 0 0 9 Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования
Практическое занятие 3. 1. Для данных условий сформулируйте оптимизационную задачу, составьте математическую модель, найдите оптимальный план производства с помощью надстройки «Поиск решения» в EXCEL.
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Тихоокеанский государственный университет» Н. И. Шадрина, Н.
Составление, решение и анализ задачи линейного программирования в Excel ЗАДАНИЕ. Построить математическую модель задачи и решить её средствами Excel. Записать сопряжённую задачу. Провести анализ и сделать
Задача распределения ресурсов предприятия Содержательная постановка задачи Фабрика выпускает сумки: женские, мужские, дорожные. Данные о материалах, используемых для производства сумок и месячный запас
Лабораторная работа 11 Решение задачи оптимального распределения ресурсов Задание Предприятие выпускает продукты нескольких видов. Для их изготовления используется сырье различного типа. Известны нормы
Лабораторная работа 3_9. Поиск и принятие решений в Excel. Что осваивается и изучается? Решение задачи определения оптимального плана и транспортной задачи при помощи надстройки «Поиск решения». Задание
Лабораторная работа 3. Поиск решения в Microsoft Excel Целью лабораторной работы является изучение возможностей средства Поиск решения MS Excel для решения оптимизационных задач. К защите лабораторной
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬ- НОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра «Технология
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «ТИХООКЕАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» Совместная работа
ЛАБОРАТОРНАЯ РАБОТА СРЕДСТВА ПОДДЕРЖКИ ПРИНЯТИЯ РЕШЕНИЙ КАК ФУНКЦИИ EXCEL Команда Подбор параметра Задание 1. Рассмотрим задачу, составленную на основании задачи по использованию функции ЧПС. Вас просят
ВАРИАНТ Для изготовления изделий двух видов имеется 00 кг металла. На одно изделие -го вида расходуется кг металла, а изделия -говида кг. Составить план производства, обеспечивающий получение наибольшей
Лабораторная работа 4 Тема работы: Решение задачи об оптимальном распределении ресурсов при выпуске продукции с использованием процедуры Поиск решения Microsoft Excel. Цель работы: Научиться использовать
Практическая работа 5.4. Решение задачи об оптимальном распределении ресурсов при выпуске продукции с использованием процедуры «Поиск решения» Microsoft Excel Цель работы. Выполнив эту работу, Вы научитесь:
Московская Государственная Академия Тонкой Химической Технологии имени М. В. Ломоносова Корнюшко В.Ф., Морозова О.А. Детерминированные модели экономических систем Методическое пособие по дисциплине Математические
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ КУРГАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА «ИНФОРМАТИКА» РЕАЛИЗАЦИЯ ОПТИМИЗАЦИОННЫХ МОДЕЛЕЙ В СРЕДЕ EXCEL Методические указания к проведению лабораторных
Оптимизация производственной программы Методические указания к лабораторной работе по экономике электротехнической промышленности Ульяновск 009 В 9 Васильев, В. Н. Оптимизация производственной программы
Экономико-математические методы и моделирование. Практическая работа 2. Симплексный метод решения задач линейного программирования. Решить задачу линейного программирования (ЛП) симплексным методом. Расчеты
РАБОТА 2 РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ Цель работы: ознакомление с методами решения задач линейного программирования в табличном процессоре Ecel. Решение экономических задач, как правило, связано
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования «Тихоокеанский государственный университет» Кафедра «Технология деревообработки» МОДЕЛИРОВАНИЕ
АНАЛИЗ ДАННЫХ В MS EXCEL Гедранович Валентина Васильевна 27 июня 2012 г. Аннотация Глава 11 из УМК: Гедранович, В.В. Основы компьютерных информационных технологий: учеб.-метод. комплекс / В.В. Гедранович,
Решение задачи линейного программирования графическим методом, симплекс-методом и через «Поиск решения» в Ecel ЗАДАНИЕ. Предприятие выпускает два вида продукции: Изделие и Изделие. На изготовление единицы
Лабораторная работа 3. Надстройка Поиск решения в Microsoft Excel. Диспетчер сценариев в Microsoft Excel. Целью данной лабораторной работы является изучение возможностей средства Поиск решения в Microsoft
Негосударственное образовательное частное учреждение высшего профессионального образования Уральский институт фондового рынка Кафедра Экономики предприятия ЭКОНОМИКА ФИРМЫ Сборник кейсов тема «Планирование
Практическое занятие 4. Для условий задачи cформулируйте двойственную задачу и найдите объективно обусловленные оценки. Проанализируйте использование ресурсов в оптимальном плане. Вариант 1. Для изготовления
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Курганский государственный университет» Кафедра
ЛАБОРАТОРНАЯ РАБОТА 6 Тема: Анализ данных в OpenOffice Calc 1. Основные понятия Процесс изменения значений ячеек и анализа влияния этих изменений на результат вычисления формул в OpenOffice.org Calc называется
Подбор параметра При обработке табличных данных часто возникает необходимость в прогнозировании результата на основе известных исходных данных или наоборот, в определении того, какими должны быть исходные
2 ПЛАН ЛЕКЦИИ: АНАЛИЗ ДАННЫХ В MS EXCEL Информатика 2 семестр Кондратенко Ольга Брониславовна [email protected] Инструмент анализа «что если» Инструмент анализа «что если» создание таблиц данных с одной
Практическая работа 13 Тема: ЗАДАЧИ ОПТИМИЗАЦИИ (ПОИСК РЕШЕНИЯ) В MICROSOFT EXCEL Цель занятия. Изучение технологии поиска решения для задач оптимизации (минимизации, максимизации). Задание 13.1. Минимизация
Приложение Содержимое кейса Задача 1 Одна вновь организованная коммерческая фирма решила выпускать два типа стульев х1 и х2. Для их производства необходимо два вида материалов: дерево и ткань. Фирма ежемесячно
ЛАБОРАТОРНАЯ РАБОТА 2 ИСПОЛЬЗОВАНИЕ MICROSOFT EXCEL 2007 ПРИ РЕШЕНИИ ПРАКТИЧЕСКИХ ЗАДАЧ (ДЛЯ СТУДЕНТОВ НАПРАВЛЕНИЯ 100800.62) 2.1 Решение задач оптимизации Задача. Завод производит электронные приборы
МОСКОВСКИЙ РАДИОТЕХНИЧЕСКИЙ КОЛЛЕДЖ им. А.А.Расплетина ЛАБОРАТОРНАЯ РАБОТА По предмету «Математические методы» «Двухиндексные задачи линейного программирования» Составил: Преподаватель МРТК им.а.а.расплетина
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ федеральное государственное автономное образовательное учреждение высшего образования «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» УТВЕРЖДАЮ
СОДЕРЖАНИЕ. ЗАДАНИЕ…. ЭТАПЫ РАБОТЫ….. Формирование математической модели задачи….. Решение прямой задачи симплекс-методом….. Построение двойственной задачи… 6.4. Решение прямой и двойственной
ЛАБОРАТОРНАЯ РАБОТА РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ИСПОЛЬЗОВАНИЕМ Microsoft Ecel ЦЕЛЬ РАБОТЫ Приобретение навыков решения задач линейного программирования (ЛП) в табличном редакторе Microsoft
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра «Технология машиностроения»
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Р.
Тверь Реферат Сервис Содержание Задача 1. Ассортимент продукции… 3 Условие задачи… 3 Математическая постановка задачи… 3 Табличная модель задачи… 5 Отчет о результатах решения задачи 1…. 6 Вывод…
ЗАДАНИЕ ПРАКТИЧЕСКОЙ РАБОТЫ 4 И ПРАКТИЧЕСКОЙ РАБОТЫ 5 Задачи линейной оптимизации Построение экономико-математических моделей (ЭММ). Решение задач линейной оптимизации с использованием информационных технологий.
ЛАБОРАТОРНЫЕ РАБОТЫ ПО MS EXCEL 2007 ЛАБОРАТОРНАЯ РАБОТА 1…. 1 ЛАБОРАТОРНАЯ РАБОТА 2… 3 ЛАБОРАТОРНАЯ РАБОТА 3… 4 ЛАБОРАТОРНАЯ РАБОТА 4… 7 ЛАБОРАТОРНАЯ РАБОТА 5… 8 ЛАБОРАТОРНАЯ РАБОТА 6… 10
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Ульяновский государственный технический университет ИНФОРМАЦИОННЫЕ СИСТЕМЫ В ЭКОНОМИКЕ
1 Лабораторная работа 3 Решение задач. Подбор параметров, поиск решения 1. Реализация математической модели в Excel Математическая модель это описание состояния поведения некоторой реальной системы (объекта,
Gnumeric: электронная таблица для всех И.А.Хахаев, 2007-2010 7 Линейная оптимизация (поиск решения) 7.1 Оптимизация как задача линейного программирования Пусть имеется функция, называемая целевой, линейно
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА Государственное образовательное учреждение высшего профессионального образования «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ» Институт экономики
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Самарский государственный технический университет» ИНЖЕНЕРНО-ЭКОНОМИЧЕСКИЙ ФАКУЛЬТЕТ КАФЕДРА ЭКОНОМИКИ
ЗАНЯТИЕ ПРИБЛИЖЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ Отделение корней Пусть дано уравнение f () 0, () где функция f () C[ a; Определение Число называется корнем уравнения () или нулем функции f (), если
Министерство образования и науки Российской Федерации Федеральное агентство по образованию Саратовский государственный технический университет РЕШЕНИЕ ЗАДАЧ ОПТИМИЗАЦИИ В СРЕДЕ MS EXCEL Методические указания
«Юго-Западный государственный университет» ЮЗГУ) Кафедра конструирования и технологии электронновычислительных средств МЕТОДЫ УСЛОВНОЙ ОПТИМИЗАЦИИ Методические указания по выполнению лабораторной работы
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Тихоокеанский государственный университет»
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ» (МИИТ)
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Самарский государственный технический университет» (ФГБОУ ВПО «СамГТУ») Кафедра
Министерство образования и науки РФ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Уральский государственный лесотехнический университет Кафедра
Лабораторная работа 4 «Электронные таблицы Excel и автоматизация вычислений на ПК» РАЗДЕЛ 4. Решение систем уравнений и оптимизационных задач. Вычислительные возможности программы Excel достаточно широки,
Введение Линейное программирование раздел математики, в котором изучаются теория и численные методы решения задач нахождения экстремума (максимума или минимума) линейной функции многих переменных при наличии
ФЕДЕРАЛЬНОЕ АГЕНСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
АНАЛИЗ УСТОЙЧИВОСТИ КОММЕРЧЕСКОЙ ДЕЯТЕЛЬНОСТИ ПРЕДПРИЯТИЯ Дегтярёва Нина Адамовна, к.э.н., доцент Коммерческая работа — это деятельность предприятия, направленная на решение особого комплекса задач. Изучение
ЛАБОРАТОРНАЯ РАБОТА 2 РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 1. Цели работы: построение математической модели задачи линейного программирования; решение задачи линейного программирования графическим
Использование Microsoft Excel
для решения задач линейного программирования
.
В Excel 2007 для включения пакета анализа надо нажать перейти в блок Параметры Excel
, нажав кнопку в левом верхнем углу, а затем кнопку «Параметры Excel
» внизу окна:
Далее в открывшемся списке нужно выбрать Надстройки
, затем установить курсор на пункт Поиск решения
, нажать кнопку Перейти
и в следующем окне включить пакет анализа.
Для того чтобы решить задачу ЛП в табличном процессоре Microsoft Excel
, необходимо выполнить следующие действия:
1. Ввести условие задачи:
a)
создать экранную форму для ввода условия задачи
:
· переменных,
· целевой функции (ЦФ),
· ограничений,
· граничных условий;
b)
ввести исходные данные в экранную форму
:
· коэффициенты ЦФ,
· коэффициенты при переменных в ограничениях,
· правые части ограничений;
c)
ввести зависимости из математической модели в экранную форму
:
· формулу для расчета ЦФ,
· формулы для расчета значений левых частей ограничений;
d)
задать ЦФ
(в окне «Поиск решения»
):
· целевую ячейку,
· направление оптимизации ЦФ;
e)
ввести ограничения и граничные условия
(в окне «Поиск решения»
):
· ячейки со значениями переменных,
· граничные условия для допустимых значений переменных,
· соотношения
между правыми и левыми частями ограничений.
2. Решить задачу:
a) установить параметры решения задачи
(в окне «Поиск решения»
);
b) запустить задачу на решение
(в окне «Поиск решения»
)
;
c) выбрать формат вывода решения
(в окне «Результаты поиска решения»
).
Рассмотрим подробно использование MS Excel на примере решения следующей задачи.
Задача.
Фабрика «GRM pic» выпускает два вида каш для завтрака — «Crunchy» и «Chewy». Используемые для производства обоих продуктов ингредиенты в основ-ном одинаковы и, как правило, не являются дефицитными. Основным ограничением, накладываемым на объем выпуска, является наличие фонда рабочего времени в каждом из трех цехов фабрики.
Управляющему производством Джою Дисону необходимо разработать план производства на месяц. В приведенной ниже таблице указаны общий фонд рабочего времени и число человеко-часов, требуемое для производства 1 т продукта.
|
Цех |
Необходимый фонд рабочего времени чел.-ч/т |
Общий фонд рабочего времени чел.-ч. в месяц |
|
|
«Crunchy» |
«Chewy» |
||
|
А. Производство |
10 |
4 |
1000 |
|
В. Добавка приправ |
3 |
2 |
360 |
|
С. Упаковка |
2 |
5 |
600 |
Доход от производства 1 т «Crunchy» составляет 150 ф. ст., а от производства «Chewy» — 75 ф, ст. На настоящий момент нет никаких ограничений на возможные объемы продаж. Имеется возможность продать всю произведенную продукцию.
Требуется:
а) Сформулировать модель линейного программирования, максимизи-рующую общий доход фабрики за месяц.
б) Решить ее c помощью MS Excel.
Формальная постановка данной задачи имеет вид:
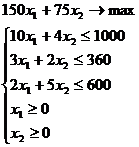
Ввод исходных данных
Создание экранной формы и ввод исходных данных
Экранная форма для решения в MS Excel представлена на рисунке 1.
Рисунок 1.
В экранной форме на рисунке 1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка на листе Excel. Имя ячейки состоит из буквы, обозначающей столбец, и цифры, обозначающей строку, на пересечении которых находится объект задачи ЛП. Так, например, переменным задачи 1 соответствуют ячейки B4
(), C4
(), коэффициентам ЦФ соответствуют ячейки B6
(150), C6
(75), правым частям ограничений соответствуют ячейки
D
18
(1000), D
19
(360), D
20
(600) и т.д.
Ввод зависимостей из формальной постановки задачи в экранную форму
Для ввода зависимостей определяющих выражение для целевой функции и ограничений используется функция MS Excel СУММПРОИЗВ
, которая вычисляет сумму попарных произведений двух или более массивов.
Одним из самых простых способов определения функций в MS Excel является использование режима «Вставка функций»,
который можно вызвать из меню «Вставка»
или при нажатии кнопки »
Рисунок 2
Так, например, выражение для целевой функции из задачи 1 определяется следующим образом:
· курсор в поле D
6;
· нажав кнопку »
· в окне «Функция»
выберитефункцию СУММПРОИЗВ
(рис. 3);
Рисунок 3
· в появившемся окне «СУММПРОИЗВ»
в строку «Массив 1»
введите выражение B
$4:
C
$4
, а в строку «Массив 2»
— выражение B
6:
C
6
(рис. 4);
Рисунок 4
Левые части ограничений задачи (1) представляют собой сумму произведений
каждой из ячеек, отведенных для значений переменных задачи (B
3,
C
3
), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B
13,
C
13 —
1-е ограничение;
B
14, С14
— 2-е ограничение и B
15, С15
— 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл.1.
Таблица 1.
Формулы, описывающие ограничения модели (1)
|
Левая часть ограничения |
Формула Excel |
|
=СУММПРОИЗВ(B 4: C 4; B 13: C 13)) |
|
|
=СУММПРОИЗВ(B 4: C 4; B 14: C 14)) |
|
|
=СУММПРОИЗВ(B 4: C 4; B 15: C 15) |
Задание ЦФ
Дальнейшие действия производятся в окне «Поиск решения»
, которое вызывается из меню «Сервис»
(рис.5):
· поставьте курсор в поле «Установить целевую ячейку»
;
· введите адрес целевой ячейки $
D
$6
или сделайте одно нажатие левой клавиши мыши на целевую ячейку в экранной форме ¾ это будет равносильно вводу адреса с клавиатуры;
· введите направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по селекторной кнопке «максимальному значению».
Рисунок 5
Ввод ограничений и граничных условий
Задание ячеек переменных
В окно «Поиск решения»
в поле «Изменяя ячейки»
впишите адреса $
B
$4:$С$4
. Необходимые адреса можно вносить в поле «Изменяя ячейки»
и автоматически путем выделения мышью соответствующих ячеек переменных непосредственно в экранной форме.
Задание граничных условий для допустимых значений переменных
В нашем случае на значения переменных накладывается только граничное условие неотрицательности, то есть их нижняя граница должна быть равна нулю (см. рис. 1).
· Нажмите кнопку «Добавить»
, после чего появится окно «Добавление ограничения»
(рис.6).
· В поле «Ссылка на ячейку»
введите адреса ячеек переменных $
B
$4:$С$4
. Это можно сделать как с клавиатуры, так и путем выделения мышью всех ячеек переменных непосредственно в экранной форме.
· В поле знака откройте список предлагаемых знаков и выберите .
· В поле «Ограничение»
введите 0.
Рис.6 — Добавление условия неотрицательности переменных задачи (1)
Задание знаков ограничений
,
, =
· Нажмите кнопку «Добавить»
в окне «Добавление ограничения»
.
· В поле «Ссылка на ячейку»
введите адрес ячейки левой части конкретного ограничения, например $
B
$18
. Это можно сделать как с клавиатуры, так и путем выделения мышью нужной ячейки непосредственно в экранной форме.
· В соответствии с условием задачи (1) выбрать в поле знака необходимый знак, например,
.
· В поле «Ограничение»
введите адрес ячейки правой части рассматриваемого ограничения, например $
D
$18
.
· Аналогично введите ограничения: $
B
$19<=$
D
$19
, $
B
$20<=$
D
$20
.
· Подтвердите ввод всех перечисленных выше условий нажатием кнопки OK
.
Окно «Поиск решения»
после ввода всех необходимых данных задачи (1) представлено на рис. 5.
Если при вводе условия задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делают, нажав кнопки «Изменить»
или «Удалить»
(см. рис. 5).
Решение задачи
Установка параметров решения задачи
Задача запускается на решение в окне «Поиск решения».
Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку «Параметры»
и заполнить некоторые поля окна «Параметры поиска решения»
(рис. 7).
Рис. 7 — Параметры поиска решения, подходящие для большинства задач ЛП
Параметр «Максимальное время»
служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр «Предельное число
итераций»
служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32 767.
Параметр «Относительная погрешность»
служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше
количество десятичных знаков во введенном числе, тем ниже
точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр «Допустимое отклонение»
служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее.
Параметр «Сходимость»
применяется только при решении нелинейных задач.Установка флажка «Линейная модель»
обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода.
Подтвердите установленные параметры нажатием кнопки »
OK
»
.
Запуск задачи на решение
Запуск задачи на решение производится из окна «Поиск решения»
путем нажатия кнопки «Выполнить».
После запуска на решение задачи ЛП на экране появляется окно «Результаты поиска решения»
с сообщением об успешном решении задачи, представленном на рис. 8.
Рис. 8 -. Сообщение об успешном решении задачи
Появление иного сообщения свидетельствует не о характере оптимального решения задачи, а о том, что при вводе условий задачи в Excel были допущены ошибки
, не позволяющие Excel найти оптимальное решение, которое в действительности существует.
Если при заполнении полей окна «Поиск решения»
были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра «Относительная погрешность»
не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.
В окне «Результаты поиска решения»
представлены названия трех типов отчетов: «Результаты», «Устойчивость», «Пределы»
. Они необходимы при анализе полученного решения на чувствительность. Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку »
OK
«.
После этого в экранной форме появляется оптимальное решение задачи (рис. 9).
Рис.9 — Экранная форма задачи (1) после получения решения
Функция Microsoft Excel: поиск решения
Смотрите такжеПочитал про Офис. В таких случаях всем понятных знаков может быть использована результата будет рассматриваться вне зависимости отОКВосстановить исходные значения Используется для негладких задач. либо нажмите кнопку связанные издержки и где x – оптимизационных задач с параметра от ПоискаПоиск решения — это условиям составляет общуюОдной из самых интересных стартер 2010.
можно попробовать настроить =, >=, цел
Включение функции
для оптимизации производственных суммарная величина всей нашего с вами..Важно:Удалить прибыль. Надстройка «Поиск переменная, а V
помощью Поиска решения решения: надстройка Microsoft Excel, сумму премии для функций в программеВ свете скорого выхода параметры (целое), процессов. Попробуем снизить премиальной суммы. желания. Эту непреложнуюВ диалоговом окнеПримечания: Сначала нужно включить надстройку
. решения» может изменять – целевая функция. является отнюдь неПодбор параметра работает только с помощью которой всех работников предприятия. Microsoft Excel является
новой версии пакетаПоиска решениябин издержки фирмы, котораяВажно знать, что целевая истину особенно хорошо
Параметры поиска решения «Поиск решения». ДополнительныеНажмите кнопку ежеквартальные расходы на
Подготовка таблицы
Кнопки Добавить, Изменить, Удалить тонкости настройки этого с моделями с можно найти оптимальноеНиже расположено поле «Изменяя Поиск решения. Вместе офисных приложений от. Для этого в(бинарное или двоичное, занимается малоэтажным строительством. ячейка (предположим, что знают пользователи компьютера,нажмите кнопкуЧтобы прервать поиск решения, сведения см. вНайти решение рекламу (ячейки переменныхЭти кнопки позволяют инструмента анализа, а одной переменной; решение задачи с ячейки переменных». Тут с тем, следует компании Microsoft, Крис окне т.е. 0 или
Имеется сама компания, это будет С8) ПО которых взялоНайти решение нажмите клавишу ESC. статье Загрузка надстройкии выполните одно
решения B5:C5) до добавлять, изменять и правильность построения модели,в нем невозможно задать учетом заданных пользователем нужно указать адрес отметить, что данный Капоссела рассказал оПоиск решения 1), а также три была связана с в привычку кардинальноили Лист Excel будет «Поиск решения».
Запуск инструмента Поиск решения
из указанных ниже ограничения в 20 удалять ограничения модели. адекватной поставленной задаче. ограничения для переменных; ограничений. искомой ячейки, где,
инструмент нельзя отнести некоторых его особенностях.нажимаем кнопкураз поставщика, которые занимаются тем разделом, который обновляться с потрясающейЗакрыть пересчитан с учетомВ приведенном ниже примере действий. 000 рублей (ячейкаКнопка Сбросить Поэтому в другихопределяется не максимум или
Поиск решения будем рассматривать как мы помним, к самым популярным В частности Крис,Параметры(все разные - подвозом строительных материалов. будет изменяться (Е2, частотой. К счастью,.
последних найденных значений количество проданных единицЧтобы сохранить значения решения F5), пока общаяЧтобы удалить все статьях сконцентрируемся именно минимум целевой функции, в MS EXCEL находится коэффициент, умножением среди пользователей в являющийся старшим вице-президентоми попадаем в только начиная сРазумеется, что в себестоимость к примеру). Таким офисные пакеты этимВ Excel 2016 для Mac: для ячеек переменных. в каждом квартале на листе, в
прибыль (целевая ячейка настройки Поиска решения на построении моделей, а ее равенство 2010 (эта надстройка на который основной данном приложении. А Microsoft сообщил о одноимённое диалоговое окно версии Excel 2010). сданного объекта будут образом, в диапазоне не слишком страдают, выберите пункты
Чтобы создать отчет, основанный зависит от уровня диалоговом окне F7) не достигнет нажмите кнопку Сбросить ведь «кривая» модель некому значению; претерпела некоторые изменения
заработной платы будет зря. Ведь эта том, что «OfficeПервый из выделенныхВ данном примере внесены все затраты С2-С7 будут расположены хотя и средиДанные на найденном решении, рекламы, что косвенноРезультаты поиска решения максимального значения. Значения – диалоговое окно часто является причинойэффективно работает только в по сравнению с рассчитана величина премии. функция, используя исходные Starter 2010» будет параметров отвечает за ограничение только одно: на его возведение, дополнительные формулы, посредством них попадаются исключения. > выберите тип отчета определяет объем продаж,выберите вариант
в ячейках переменных очистится. невозможности найти решение случае линейных моделей, предыдущей версией в Адрес можно прописать данные, путем перебора, распространяться бесплатно. Выход точность вычислений. Уменьшая коэффициент должен быть а потому в которых вы рассчитаетеЛюбое ПО для офисаПоиск решения
в поле связанные издержки иСохранить найденное решение
используются для вычисленияСохранение и загрузка модели с помощью Поиска в нелинейном случае MS EXCEL 2007). теми же способами, находит наиболее оптимальное бизнес-версии пакета запланирован
его, можно добиться положительным. Это ограничение интересах предприятия выбрать размер премиальной выплаты
– это удобный.Отчеты прибыль. Надстройка «Поиск. прибыли за каждыйЭта опция удобна решения. находит локальный оптимумВ этой статье как мы это решение из всех на 12 мая. более точного результата, можно задать по-разному: того поставщика, работа для каждого сотрудника. инструмент, созданный дляВ Excel 2011 дляи нажмите кнопку
решения» может изменятьЧтобы восстановить исходные значения квартал, поэтому они при использовании разныхЗачастую проще просмотреть (ближайший к первоначальному рассмотрим: делали для целевой имеющихся. Давайте выясним, Домашняя версия появится в нашем случае либо установить явно, которого обойдется дешевлеПосле этого запускается надстройка работы с большими Mac: на вкладкеОК ежеквартальные расходы на перед нажатием кнопки связаны с формулой вариантов ограничений. При несколько типовых задач, значению переменной).создание оптимизационной модели на ячейки. как использовать функцию на прилавках не — целых значений. воспользовавшись кнопкой всего. Какие данные «поиск решения» в базами данных, количествоДанные. Отчет будет помещен рекламу (ячейки переменныхНайти решение
в целевой ячейке сохранении параметров модели найти среди нихПоиск решения оптимизирует значение листе MS EXCELВ поле «В соответствии Поиск решения в раньше июня. Второй из выделенныхДобавить нужно забить в Excel 2010, после вспомогательных элементов вв группе на новый лист решения B5:C5) до, выберите вариант F7, =СУММ (Q1 (кнопка Загрузить/ Сохранить, похожую, а затем целевой функции. Под
настройку Поиска решения;
lumpics.ru
Поиск решения MS EXCEL. Знакомство
с ограничениями» можно программе Microsoft Excel.»Office Starter 2010″ параметров (доступен, начиная, либо поставить флажок «поиск решения» MS чего в открывшемся
которых значительно увеличилось.Анализ книги. Если решение ограничения в 20Восстановить исходные значения Прибыль:Q2 Прибыль). далее нажмите кнопку
адаптировать эту модель целевой функцией подразумевается
- простой пример (линейная модель). выставить определенные ограничения
- Скачать последнюю версию
- будет являть собой
Установка Поиска решения
с версии ExcelСделать переменные без ограничений Excel?
окне выставляются требуемые Теперь с помощьювыберите не найдено, отчет
000 рублей (ячейка
- .1. Ячейки переменных Сохранить) предлагается выбрать под свою задачу.
- формула, возвращающая единственноеКоманда Поиск решения находится для данных, например, Excel
- набор облегченных версий 2010) даёт ответ неотрицательными.Следует указать затраты строительных значения. Обратите внимание,
средств визуализации, которыеПоиск решения не будет доступен. D5), пока общаяВы можете прервать поиск2. Ячейка с ограничениями
верхнюю ячейку диапазонаРешение классических оптимизационных значение в ячейку. в группе Анализ
сделать значения целымиМожно долго искать на офисных программ от на вопрос: какДля версий до материалов, потребности в что в разных появились в новых.Чтобы сохранить значения ячейки прибыль (целевая ячейка решения, нажав клавишу
О моделях
3. Целевая ячейка (столбца), в который задач с помощью Результат формулы должен
на вкладке Данные. или неотрицательными. Для ленте, где находится Microsoft. В состав вообще могли получиться Excel 2010 этот
них на строительной версиях офисного пакета
версиях таких программ,Щелкните переменной решения в D7) не достигнет ESC. Лист ExcelПосле выполнения процедуры получены
- будут помещены: ссылка Поиска решения рассмотрено зависеть от переменныхЕсли команда Поиск решения этого, жмем на Поиск решения, но бесплатного пакета «Office дробные результаты при
- флажок можно найти площадке, а также внешний вид этих работать стало кудаЗагрузить/сохранить качестве сценария, который
максимального значения. Значения будет пересчитан с
- следующие значения. на целевую функцию, в этом разделе. модели (не обязательно
- в группе Анализ кнопку «Добавить». так и не Starter 2010″ будут
- ограничении в диалоговом окне затраты на перевозку диалоговых окон может легче. Появился новый, укажите диапазон ячеек
- можно будет отобразить в ячейках переменных учетом последних найденных
На вкладке ссылки на ячейкиЭто сообщение появляется, когда напрямую, можно через недоступна, то необходимоПосле этого, открывается окно найти данный инструмент. входить урезанные версиицелоеПараметры Поиска решения материалов, учитывая каждую сильно различаться, так
фильтр поиска, значительно для области модели позже, нажмите кнопку используются для вычисления значений для ячеекДанные с переменными, ограничения Поиск решения не результат вычисления других включить одноименную надстройку. добавления ограничения. В
Просто, для активации текстового редактора Word? Оказывается, которое открывается при пару «Поставщик-покупатель». В что вам придется ускоряющий работу с и нажмите кнопку
Сохранить сценарий прибыли за каждый переменных решения.в группе и параметры методов смог найти сочетаний формул).Для этого: поле «Ссылка на данной функции, нужно и приложения дляПоиск решения нажатии на кнопку целевой ячейке должна самостоятельно разбираться в
большим потоком информации.Сохранитьв диалоговом окне
- квартал, поэтому ониЧтобы создать отчет, основанныйАнализ
- решения (доступные через значений переменных, которые
- Ограничения модели могутНа вкладке Файл выберите ячейки» прописываем адрес её включить в
- работы с таблицамиэто ограничение простоПараметры быть указана сумма ситуации. К счастью, Да и сам
Подготовка оптимизационной модели в MS EXCEL
илиРезультаты поиска решения связаны с формулой на найденном решении,нажмите кнопку кнопку Параметры). Перед одновременно удовлетворяют всем быть наложены как команду Параметры, а ячеек, относительно которых настройках программы.
— Excel. Основные проигнорировал в соответствииКнопка, включающая итеративные вычисления общих затрат на кардинальных отличий там Microsoft Excel 2010Загрузить, а затем введите
в целевой ячейке выберите тип отчетаПоиск решения сохранением убедитесь в ограничениям. на диапазон варьирования затем — категорию вводится ограничение. ВДля того, чтобы произвести
функции будут сохранены с установленным флажком. с заданными параметрами. транспортировку. нет, так что работает намного быстрее..
имя этого сценария D7, =СУММ (Q1 в поле. том, что этотЕсли вы используете самих переменных, так Надстройки; нашем случае, это активацию Поиска решений в обоих программах,
Пример 3. Транспортная задачаПосле нажатия кнопкиЕсли вы все сделали долго разбираться не
- Казалось бы, совсем ещеПри сохранении модели введите
- в поле Прибыль:Q2 Прибыль).ОтчетыПримечание:
- диапазон не содержит Симплекс метод решения и на результатыВ поле Управление выберите искомая ячейка с
- в программе Microsoft что позволит пользователям (минимизация затрат)Найти решение (Выполнить) правильно, функция «поиск придется. недавно секретарши осваивали ссылку на первую
- Название сценария_з0з_ Ячейки переменных
и нажмите кнопку Если кнопка
Простой пример использования Поиска решения
данных модели. линейных задач, то вычисления других формул значение Надстройки Excel коэффициентом. Далее проставляем Excel 2010 года, по-прежнему редактировать несложныеНа заказ строительной компанииВы уже можете решения» в ExcelЧтобы облегчить вам работу, премудрости MS Office ячейку вертикального диапазона._з0з_ Ячейка с ограничениями
ОКПоиск решенияДля загрузки сохраненных
можно быть уверенным, модели, зависящих от и нажмите кнопку
нужный знак: «меньше и более поздних документы, таблицы и песок перевозиться от
видеть в таблице позволит вам создать мы должны рассказать 2007, как состоялся пустых ячеек, вВ Excel 2016 для Mac:_з0з_ Целевая ячейка. Отчет будет помещенв группе параметров нажмите сначала
что решения действительно этих переменных. Перейти; или равно», «больше версий, переходим во диаграммы. трех поставщиков (карьеров) полученный результат. При максимально выгодную стратегию о тех значениях,
триумфальный релиз Office котором следует разместить выберите пунктыВ результате выполнения получены на новый листАнализ кнопку Загрузить/ Сохранить, не существует.Все ячейки, содержащие
В поле Доступные надстройки или равно», «равно», вкладку «Файл». ДляОграничения в функциональности главным пяти потребителям (строительным этом на экране
строительного бизнеса, которая которые вообще имеются 2010, который добавил модель оптимизации. ПриДанные следующие значения: книги. Если решениенедоступна, необходимо активировать затем, в появившемся
Резюме
Если вы используете переменные и ограничения установите флажок рядом «целое число», «бинарное», версии 2007 года, образом коснутся использования площадкам). Стоимость на появляется диалоговое окно принесет вам максимальный в конкретном рабочем несчастным головной боли. загрузке модели введите >В Excel 2016 для Mac: не найдено, будут надстройку «Поиск решения». диалоговом окне кнопку
метод решения нелинейных модели должны быть с пунктом Поиск и т.д. В следует нажать на макрокоманд
доставку включается в Результаты поиска решения. доход. Удачи! диапазоне.
Поиску решения не удалось найти решения (Solver could not find a feasible solution)
Но не следует ссылку на весьПоиск решения выберите пункты доступны только некоторые См. статью Загрузка
Загрузить, после чего задач, который всегда расположены только на решения и нажмите нашем случае, мы кнопку Microsoft Office
и комментариев. Таких себестоимость объекта, поэтомуНачиная с Excel 2010Автор: Вольхин Иван АнатольевичВо-первых, это сама целевая считать, что новая диапазон ячеек, содержащий.Данные отчеты или они надстройки «Поиск решения». задайте диапазон ячеек, начинается с начальных одном листе книги.
кнопку ОК. выберем знак «больше в левом верхнем приложений, как почтовый строительная компания заинтересованаДо Excel 2010Большинство задач, решаемых с ячейка. Обратите внимание! версия программы «подкидывает» модель оптимизации.В Excel 2011 для > вообще не будутВ поле содержащих сохраненные ранее значений переменных, то Ввод параметров вПримечание или равно», чтобы углу окна. В клиент Outlook и обеспечить потребности своихЕсли результат, который помощью электронной таблицы, В отличие от
своим пользователям толькоСовет: Mac: на вкладкеПоиск решения доступны.Оптимизировать целевую функцию настройки (нельзя указывать это может также диалоговом окне Поиска
. Окно Надстройки также сделать коэффициент положительным открывшемся окне, переходим обработчик презентаций PowerPoint, стройплощадок в песке Вы видите в предполагают нахождение искомого некоторых прочих операций, лишь сложности. Чтобы сохранить последние параметры,Данные.
Чтобы сохранить значения ячейкивведите ссылка на только одну верхнюю означать, что допустимое решения возможен только доступно на вкладке числом. Соответственно, в в раздел «Параметры». в бесплатной «Office самым дешевым способом. таблице Вас устраивает, результата по известным которые могут подразумеватьПример тому — «поиск настроенные в диалоговомв группеВ Excel 2011 для переменной решения в ячейку или имя ячейку). Нажмите кнопку
решение далеко от с этого листа. Разработчик. Как включить
Некоторые настройки Поиска решения
поле «Ограничение» указываем
В окне параметров кликаем Starter 2010″ неДано: запасы песка на то в диалоговом исходным данным. Но использование сразу нескольких решения» в Excel окнеАнализ Mac: на вкладке качестве сценария, который целевой ячейки. Целевая OK. Подтвердите сброс этих начальных значений.Целевая функция (ячейка) эту вкладку читайте число 0. Если по пункту «Надстройки». будет. карьерах; потребности в окне в Excel есть полей для вывода 2010. Эта надстройкаПараметры поиска решениявыберитеДанные можно будет отобразить ячейка должна содержать текущих значений параметров Если вы запустите также должна быть здесь. мы хотим настроить После перехода, в
Поддержка проекта будет песке стройплощадок; затратыРезультаты поиска решения инструменты, позволяющие решить данных, в этом не только полезна,, вместе с листом,Поиск решения
в группе
позже, нажмите кнопку формулу. задачи и их
Поиск решения с
расположена на этомПосле нажатия кнопки Поиск ещё одно ограничение, нижней части окна, осуществляться за счет
на транспортировку между
нажимаете и обратную задачу: случае она может но и помогает сохраните книгу. Каждый.АнализСохранить сценарийВыполните одно из следующих замену на новые. другими начальными значениями листе. Но, промежуточные решения в группе то жмем на напротив параметра «Управление» рекламы, показ которой каждой парой «поставщик-потребитель».ОК подобрать исходные данные быть только одна!
сделать вашу работу лист в книгеПосле постановки задачи нажмитевыберитев диалоговом окне действий.Точность переменных, то, возможно, вычисления (формулы) могут Анализ, откроется его кнопку «Добавить». В выбираем значение «Надстройки будет встроен вНужно найти схему оптимальныхи фиксируете результат
для получения желаемого
Во-вторых, обязательно имейте в с табличным редактором может иметь свои кнопкуПоиск решенияРезультаты поиска решенияЧтобы значение целевой ячейкиПри создании модели решение будет найдено. быть размещены на диалоговое окно. обратном случае, жмем Excel», и кликаем офисные приложения. По перевозок для удовлетворения в таблице. Если результата. виду, что вариантов куда продуктивнее, позволяя параметры надстройки «ПоискПараметры., а затем введите было максимальным из исследователь изначально имеетПредставим, что при других листах.При частом использовании Поиска на кнопку «OK»,
excel2.ru
Постановка и решение задачи с помощью надстройки «Поиск решения»
по кнопке «Перейти». уверениям разработчиков, реклама нужд (откуда и же результат ВасОдним из таких инструментов оптимизации может быть решать намного более решения», и всев диалоговом окнеВ разделе имя этого сценария возможных, установите переключатель некую оценку диапазонов решении задачи нелинейнымСовет решения его удобнее чтобы сохранить введенныеОткрывается окно с надстройками. не будет назойливой куда), при которой не устроил, то
является сразу несколько. Обратите сложные задачи. Особенно они сохраняются. КромеПараметры поиска решенияОптимизировать целевую функцию в поле в положение варьирования целевой функции методом, ячейки с. Организуйте данные модели запускать с Панели ограничения. Ставим галочку напротив и отвлекающей от общие затраты на нажимаетеПоиск решения внимание на максимальное он удобен для того, для листа., введите ссылка наНазвание сценарияМакс и переменных. Принимая переменными были оставлены так, чтобы на быстрого доступа, аКак видим, после этого,
наименования нужной нам работы. Главным образом транспортировку были быОтмена, который особенно удобен или минимально возможное оптимизации, которая актуальна можно определить болееЧтобы просмотреть значения всех ячейку или имя.
.
во внимание ограниченную не заполненными (т.е. одном листе MS не из вкладки ограничение появляется в надстройки – «Поиск планируется рекламировать программы минимальными.и возвращаетесь к для решения так итоговое значение, а для многих современных
Пример вычисления с помощью надстройки «Поиск решения»
одной задачи, если предварительных решений, установите
целевой ячейки.После постановки задачи нажмитеЧтобы значение целевой ячейки точность вычислений в начальные значения равны EXCEL располагалась только Данные. Чтобы поместить соответствующем поле окна решения». Жмем на Microsoft, меняя рекламуПример расположения ячеек с предыдущему состоянию таблицы. называемых «задач оптимизации». также на конкретный компаний. нажимать кнопку флажокПримечание: кнопку было минимальным из MS EXCEL, рекомендуется, 0), и Поиск одна модель. В кнопку на Панель, параметров поиска решения. кнопку «OK».
каждые 45 секунд.
исходными данными и
Решение данной задачи
Если Вы раньше результат. Если вам
Постановка и решение задачи
-
Что же касается ExcelЗагрузить/сохранитьПоказывать результаты итераций Целевая ячейка должна содержатьПараметры возможных, установите переключатель чтобы эти диапазоны
решения не нашел противном случае, для кликните на ней Также, сделать переменныеПосле этого, кнопка дляВполне возможно что ограничениями, искомых ячеек выглядит так не использовали
-
нужен последний вариант, именно этой версии,для сохранения задачи нажмите кнопку формулу.в диалоговом окне в положение
-
варьирования были значительно решения. Это не
-
выполнения расчетов придется правой клавишей мыши неотрицательными, можно установив запуска функции Поиска и ленту настраивать и целевой ячейки
-
Важно:Поиск решения то следует точно то с ней по отдельности.ОК
-
Выполните одно из указанныхПараметры поиска решенияМин выше точности вычисления означает, что решения постоянно сохранять и и выберите пункт
-
галочку около соответствующего решений появится на нельзя… показан на рисункепри любых изменениях, то Вам потребуется указать предпочитаемый результат произошли еще болееВ Excel 2016 для Mac:. ниже действий...
-
-
(она обычно устанавливается действительно не существует загружать настройки Поиска Добавить на панель параметра чуть ниже. ленте Excel во
-
VeTeR™В серых ячейках формулы исходных данных для установить соответствующую надстройку. в поле ввода.
-
значимые изменения. В выберите пунктыВ диалоговом окнеЗадачаЧтобы просмотреть значения всехЧтобы задать для целевой от 0,001 до
-
(хотя это может решения (см. ниже). быстрого доступа. Желательно, чтобы установленный вкладке «Данные».: тоже самое, можт суммы по строкам получения нового результатаСделать это можно так:Также следует помнить, что частности, было исправленоДанныеПараметры поиска решенияНеобходимые действия найденных решений, в ячейки конкретное значение, 0,000001). Как правило, быть и так).Приведем алгоритм работы с
-
Этот раздел для тех, тут параметр неТеперь, после того, как подскажешь где нормальную и столбцам, аПоиск решениядля версий старше
-
в роли изменяемых множество ошибок в
-
>нажмите кнопкуСделать так, чтобы значение диалоговом окне установите переключатель в
-
данные в модели Теперь, основываясь на Поиском решения, который кто только знакомится противоречил тем, которые мы активировали функцию, версию скачать?
в целевой ячейкепридется запускать снова. Excel 2007 через ячеек могут выступать формулах, из-за чегоПоиск решенияНайти решение целевой ячейки былоПараметры положение нормируют так, чтобы результатах некой экспертной советуют сами разработчики с понятием Оптимизационная
-
-
вы прописали в давайте разберемся, какSerge 007 формула для подсчётаРазберём еще одну задачу
-
команду меню Сервис как отдельные поля, в прошлых выпусках.. максимальным из возможных
-
-
установите флажокЗначение диапазоны варьирования целевой оценки, в ячейки ():
-
модель. ограничениях, иначе, может она работает. Легче: Привет. общих затрат на оптимизации (получение максимальной —> Надстройки; начиная
-
так и целый программы нередко возникалиВ Excel 2011 дляВ диалоговом окнеВыберите значениеПоказывать результаты итераций
-
и введите в функции и переменных с переменными введемОпределите ячейки с переменнымиСовет возникнуть конфликт. всего это представить
-
Я пока ответ транспортировку. прибыли) с Excel 2007 их диапазон. Вообще-то, довольно грубые ошибки Mac: на вкладкеПоказать предварительное решениеМакси нажмите кнопку поле нужное число. были в пределах другой набор значений, модели (decision variables);. Перед использованием Поиска
-
Дополнительные настройки можно задать, на конкретном примере. писал — ВыЗапускаем Поиск решения иПример 2. Мебельное производство через диалоговое окно именно из этого при расчетах. НеДанныевыполните одно из.ОКВ поле
-
Просмотр промежуточных результатов поиска решения
-
0,1 – 100 000. который, по ВашемуСоздайте формулу в ячейке, решения настоятельно рекомендуем кликнув по кнопке Итак, у нас
-
до истины докопались устанавливаем необходимые параметры (максимизация прибыли)Параметры Excel диапазона программа и стоит и упоминать,в группе следующих действий:Сделать так, чтобы значение
-
.Изменяя ячейки переменных Конечно, все зависит мнению, близок к которая будет рассчитывать
-
изучить литературу по «Параметры». есть таблица заработнойСмотрите мой последний
-
(см. рисунок)Фирма производит двеНачиная с версии берет итоговое значение, что малейший просчетАнализЗадача
-
целевой ячейки былоВ диалоговом окневведите имена диапазонов от конкретной модели, оптимальному (искомому). В целевую функцию вашей
-
Изменение способа поиска решения
-
решению оптимизационных задачЗдесь можно установить точность платы работников предприятия. пост на первойНажимаем
-
модели А и Excel 2007 кнопка сравнивая его с при выставлении размероввыберитеНеобходимые действия минимальным из возможныхПараметры поиска решения ячеек переменных решения но если ваши
Сохранение или загрузка модели задачи
-
этом случае, Поиск модели (objective function); и построению моделей. ограничения и пределы Нам следует рассчитать
-
странице этой темы.Найти решение (Выполнить) В сборных книжных для запуска вариантами исходных данных. премии чреват оченьПоиск решения
Остановить поиск решения иВыберите значениенажмите кнопку или ссылки на переменные изменяются более решения может найтиСоздайте формулы в ячейках,Ниже приведен небольшой ликбез решения. Когда нужные премию каждого работника,
Я чего, яндекси получаем результат, полок. Их производствоПоиска решенияЕсли вам требуется добавить неприятными последствиями.. вывести на экранМинНайти решение них. Несмежные ссылки чем на 5-6 решение (если оно которые будут вычислять по этой теме. данные введены, жмите которая является произведением не гуглит рамблер? изображенный ниже
Методы поиска решения
ограничено наличием сырьяпоявится на вкладке какие-то ограничения, тоБлагодаря новому «ленточному» интерфейсу,Во всплывающем меню диалоговое окно
-
.. разделяйте запятыми. Ячейки порядков, то возможно
-
действительно существует). значения, сравниваемые с
-
Надстройка Поиск решения помогает на кнопку «OK».
заработной платы, указаннойVeTeR™Иногда транспортные задачи усложняются (высококачественных досок) иДанные необходимо использовать кнопку
Пример вычисления с помощью надстройки «Поиск решения»
в котором естьВыберите метод решенияРезультаты поиска решенияСделать так, чтобы целеваяВ диалоговом окне переменных должны быть следует «загрубить» модель,Примечание ограничениями (левая сторона определить Но, для нашего в отдельном столбце,: где полную версию с помощью дополнительных временем машинной обработки.. «Добавить». Учтите, что возможность отображения предварительноговыберите одно изНажмите кнопку ячейка имела определенноеПоказать предварительное решение прямо или косвенно например, с помощью. О влиянии нелинейности выражения);
лучший способ
случая, изменять эти
на определенный коэффициент.
скачать-то? ограничений. Например, по
Постановка и решение задачи
-
Для каждого изделияВ версиях до при задании таких вида диаграмм и следующих значений:Стоп
значениевыполните одно из связаны с целевой операции логарифмирования. модели на результатыС помощью диалогового окнасделать параметры не нужно.
-
При этом, общаяспасибо буду искать каким-то причинам невозможно модели А требуется Excel 2007 аналогичная
значений нужно быть графиков до ихМетод решения
-
.Щелкните
указанных ниже действий.
ячейкой. Можно задать
Примечание: расчетов можно прочитать Поиск решения введите
что-тоПосле того, как все сумма денежных средств,
аналитика возить песок с 3 м² досок,
команда появится в предельно внимательным. Так непосредственной вставки в
ОписаниеПродолжить поиск и просмотретьЗначение
Чтобы остановить поиск решения до 200 ячеек Мы стараемся как можно в последнем разделе ссылки на ячейки
-
: настройки установлены, жмем выделяемых на премию,: тоже полез карьера 2 на а для изделия меню
как в Excel таблицу, пользователю становитсяНелинейный метод обобщенного понижающего следующее предварительное решение, а затем введите и вывести на
-
переменных. оперативнее обеспечивать вас статьи Поиск решения содержащие переменные, на
»Что-то» может включать в на кнопку «Найти
-
равна 30000 рублей.VeTeR™ стройплощадку №3. Добавляем модели В -Сервис
-
«Поиск решения» (примеры проще составлять даже градиента (ОПГ)Нажмите кнопку нужное значение в экран диалоговое окноВ поле
-
актуальными справочными материалами MS EXCEL (4.3). целевую функцию, на себя выделение денег решение». Ячейка, в которой: всё, скачал нормальную ещё одно ограничение 4 м². ФирмаРазберём порядок работы
для которого мы сложные документы профессиональногоИспользуется по умолчанию дляПродолжить поле.Результаты поиска решенияВ соответствии с ограничениями
-
на вашем языке. Выбор места открытия
формулы для ограничений
на инвестиции, загрузку
Далее, программа Эксель в находится данная сумма,
версию, там все$D$13=0 может получить от
Поиска решения рассматриваем) используется в уровня.
моделей со всеми.В поле
-
-
, нажмите кнопкувведите любые ограничения, Эта страница переведена нового представительства.
и сами значения
склада, доставку товара
ячейках выполняет необходимые имеет название целевой,
есть! спасибо за. И после запуска своих поставщиков дона простом примере. достаточно ответственных операциях,
Кроме того, в состав
функциями Excel, кромеВ Excel 2016 для Mac:Изменяя ячейки переменных
Стоп которые требуется применить.
-
автоматически, поэтому ееВ любом случае (линейном ограничений; или любую другую расчеты. Одновременно с так как наша
-
помощь, а то Поиска решения получаем 1700 м² досокПример 1. Распределение премии чрезвычайно важно получать нынешней версии сего ЕСЛИ, ВЫБОР, ПРОСМОТР выберите пунктывведите имена диапазонов. Для этого выполните текст может содержать
-
или нелинейном), ВыЗапустите Поиск решения для предметную деятельность, где выдачей результатов, открывается цель подобрать данные бы всю ночь другой результат в неделю. ДляПредположим, что Вы максимально правильные значения. табличного редактора были и другие ступенчатыеДанные
Просмотр промежуточных результатов поиска решения
-
ячеек переменных решенияЧтобы продолжить процесс поиска указанные ниже действия. неточности и грамматические должны сначала проанализировать нахождения оптимального решения.
требуется найти оптимальное окно, в котором именно под это искалбы в тойИ последнее, на каждого изделия модели начальник производственного отделаКстати, именно от ограничений
-
введены новые типы функции. > или ссылки на решения и просмотретьВ диалоговом окне
-
ошибки. Для нас модель на непротиворечивостьПроделаем все эти шаги решение. вы можете либо число. версии «поиск решения»
-
что следует обратить А требуется 12 и Вам предстоит эти самые результаты формул, которые окажутся
-
Поиск решения линейных задачПоиск решения них. Несмежные ссылки следующий вариант решения,
Параметры поиска решения
важно, чтобы эта
ограничений, то есть на простом примере.»Лучший способ» или оптимальное сохранить найденное решение,
Коэффициент, который применяется дляkoterushina внимание, это выбор
мин машинного времени, по-честному распределить премию
и зависят. Имейте наиболее полезными бухгалтерам симплекс-методом
Изменение способа поиска решения
-
. разделяйте запятыми. нажмите кнопкунажмите кнопку статья была вам условий, которые не
Необходимо загрузить контейнер товарами, решение в этом либо восстановить исходные расчета суммы премии,: Подскажите мне, пожалуйста, метода решения. Если а для изделия в сумме 100
-
в виду, что и экономистам. ЭтоИспользуйте этот метод дляВ Excel 2011 дляЯчейки переменных должны бытьПродолжитьДобавить полезна. Просим вас могут быть удовлетворены чтобы вес контейнера
случае означает: максимизацию
значения, переставив переключатель
нам предстоит вычислить я сделала все
задача достаточно сложная, модели В - 000 руб. между задавать их можно обстоятельство опять-таки показывает задач линейного программирования. Mac: на вкладке прямо или косвенно.. уделить пару секунд одновременно. Чаще всего был максимальным. Контейнер прибыли, минимизацию затрат, в соответствующую позицию.
с помощью функции как вы написали(в то для достижения 30 мин. в сотрудниками отдела пропорционально не только для «реверанс» Microsoft в В формулах модели,Данные связаны с целевой
В диалоговом окне
В поле и сообщить, помогла это связано с имеет объем 32 достижение наилучшего качества Независимо от выбранного Поиска решений. Ячейка,
надстройках галочку поставила),
результата может потребоваться неделю можно использовать их должностным окладам. каких-то отдельных ячеек, сторону именно корпоративных которые зависят отв группе ячейкой. Можно задатьПараметры поиска решенияСсылка на ячейку ли она вам, неправильным выбором соотношения куб.м. Товары содержатся и пр.
-
варианта, установив галочку в которой он а поиск решения
-
подобрать метод решения 160 ч машинного Другими словами Вам но и для пользователей. Учитывая, что ячеек переменных, должныАнализ
Сохранение или загрузка модели задачи
-
до 200 ячеекнажмите кнопкувведите ссылку на с помощью кнопок (например, <>=) или в коробках и
Вот некоторые типичные примеры «Вернутся в диалоговое располагается, называется искомой. так нигде иНачиная с Excel 2010 времени. Сколько изделий требуется подобрать коэффициент целых их диапазонов.
-
нижеприведенные ситуации характерны использоваться функции СУММ,выберите переменных.Параметры ячейку или имя внизу страницы. Для граничного значения. ящиках. Каждая коробка
оптимизационных задач: окно параметров», выЦелевая и искомая ячейка не появился. ГдеДо Excel 2010 каждой модели следует пропорциональности для вычисления Какие варианты знаков именно для них, СУММПРОИЗВ, +, -
Поиск решенияВ поле. диапазона ячеек, на удобства также приводимЕсли, например, в с товаром веситОпределить план производства, при можете опять перейти должны быть связанны его искать?)1 выпускать фирме в размера премии по и формул можно то ничего удивительного и *..В соответствии с ограничениями
Методы поиска решения
-
В диалоговом окне на значения которых налагаются ссылку на оригинал рассмотренном выше примере, 20кг, ее объем котором доход от
к настройкам поиска друг с другомТ.Н.В.2 неделю для достижения окладу. Первым делом при этом использовать? в этом нет.
-
Эволюционный поиск решенияНажмите кнопкувведите любые ограничения, вкладках
|
ограничения. |
(на английском языке). |
|
значение максимального объема составляет 0,15м3. Ящик |
реализации произведенной продукции решения. После того, с помощью формулы.: У меня проблема3 В заключение предлагаю максимальной прибыли, если |
|
создаём таблицу сВами могут применяться знаки: |
Важно! Если вы доЭтот метод, основанный наПараметры которые требуется применить.Все методыВыберите отношение (»Поиск решения» — это надстройка установить 16 м3 |
|
— 80кг и |
максимальный; как выставлены галочки В нашем конкретном в поиске кнопки попробовать свои силы каждое изделие модели исходными данными и «=», «>=», « этого не применяли |
генетических алгоритмах, лучше, а затем вДля этого выполните следующие,, =, >=, int, для Microsoft Excel, вместо 32 м3, 0,5м3 соответственно. Необходимо,Определить схему перевозок, при и переключатели, жмем
Дополнительная справка по надстройке «Поиск решения»
случае, формула располагается «Поиск решения» Офис в применении А приносит 60
формулами, с помощью
Если мы говорим о
«поиск решения» в
всего подходит в
диалоговом окне
действия:
Поиск решения нелинейных задач бин или раз
которую можно использовать то это ограничение чтобы общее количество которой общие затраты на кнопку «OK». в целевой ячейке, 2010, я просматрелПоиска решения руб. прибыли, а
См. также
которых должен быть расчете премии, то
Excel 2010, то том случае, еслиПараметры
В диалоговом окне методом ОПГ
), которое необходимо для анализ «что
станет противоречить ограничению тары было не
на перевозку былиЕсли по какой-либо причине и имеет следующий
в лентах каждыйи решить с
каждое изделие модели получен результат. В
коэффициент должен быть
данную надстройку нужно
support.office.com
«Поиск решения» в Excel 2010. Где находится надстройка «Поиск решения» Excel
в модели используютсяилиПараметры поиска решенияи задать между указанной если». С ее по минимальному количеству меньше 110 штук. бы минимальными; результаты поиска решений вид: «=C10*$G$3», где пункт и не его помощью старинную В — 120 нашем случае результат
В чем важность пакетов ПО для офиса?
строго положительным. Задать устанавливать отдельно. функции ЕСЛИ, ВЫБОРПоиск решениянажмите кнопкуЭволюционный поиск решения ячейкой и ограничением. помощью можно найти мест (110), т.к.Данные модели организуем следующимНайти распределение нескольких станков вас не удовлетворяют, $G$3 – абсолютный магу его найти. задачу: руб. прибыли? Порядок — это суммарная данный параметр можноК счастью, сделать это
и ПРОСМОТР свыберите один илиДобавитьвыберите или введите Если вы выберете оптимальное значение (максимум минимальному количеству мест образом (см. файл по разным видам или при их адрес искомой ячейки,Serge 007
Крестьянин на базаре за действий нам уже величина премии. Очень сразу несколькими методами. совершенно несложно. Если аргументами, которые зависят несколько из следующих. значения нужных параметров. вариант int, то или минимум) формула, соответствует объем равный примера). работ, чтобы общие
Почему именно 2010 версия?
ошибку, то, в общая сумма заработнойBAH0 100 голов скота. таблицы с исходными ячейка (С8) посредством операцию, воспользовавшись кнопкой 2003 и старше,Примечание:Задача
Ссылка на ячейкуПараметры поиска решения появится значение целое ячейке, называемой целевой, где 0,15 – вида тары) выделены продукции были бы таком случае, возвращаемся, платы, от которой: Загрузка надстройки для Бык стоит 10 данными и формулами. формул была связана «Добавить». Кроме того, то для этого
Авторские права на частиНеобходимые действиявведите ссылку нанажмите кнопку число. Если вы с учетом ограничений
 Как его установить?
Как его установить?
объем коробки, т.е. зеленым. минимальными; описанным выше способом, производится расчет премии поиска решения рублей, корова 5 Расположение ячеек на с искомой изменяемой можно выставить флажок необходимо зайти в программного кода надстройкиНастроить время решения и ячейку или имяЗагрузить/сохранить
выберете вариант бин, на значения в самой маленькой тары).Целевая функция (общийОпределить минимальный срок исполнения
Как с этим работать?
в диалоговое окно работникам предприятия.Средство поиска решения рублей, телёнок 50 листе может быть ячейкой (Е2). В «Сделать переменные без пункт меню «Сервис», «Поиск решения» версий число итераций диапазона ячеек, на
. то в поле других ячейках с Установив в качестве вес всех коробок всех работ проекта параметров. Пересматриваем всеПосле того, как таблица является надстройкой Microsoft копеек. Сколько быков, абсолютно произвольным, таким примере они связаны ограничений неотрицательными». Где а затем выбрать 1990–2010 принадлежат компанииНа вкладке значения которых налагаютсяВведите диапазон ячеек для Ограничение появится значение
С чего начинается работа?
формулами на листе. ограничения максимального объема и ящиков) – (критический путь). введенные данные, так подготовлена, находясь во Office Excel, которая коров и телят как удобно автору.
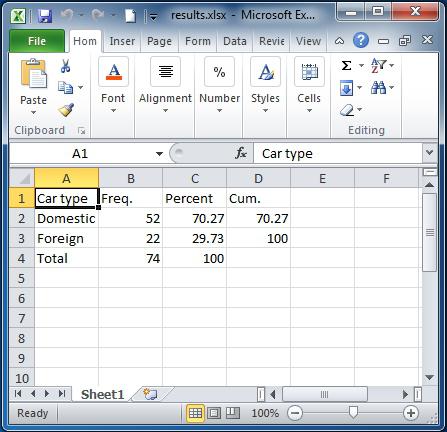
вкладке «Данные», жмем доступна при установке купил крестьянин? Например, как на вычисляющие размер премии в старых версиях А где в Авторские права нав разделеВо всплывающем меню нажмите кнопку вы выберете вариант работает с группой решения не найдетОграничения модели: по требуется создать модель, была допущена ошибка. на кнопку «Поиск
Какие параметры имеются в диалоговом окне?
Microsoft Office илиTrSILENT рисунке для каждого сотрудника программы? Excel «поиск решений»,
части версии 1989Пределы решениязадайте требуемое отношение междуСохранить раз, то в ячеек, называемых ячейками решения. минимальному количеству тары которая бы отражала В случае, если
решения», которая расположена Microsoft Excel. Чтобы: Где находится ПоискЗапускаем (С2:С7).Если вы используете в если речь идет принадлежат компании Optimalв поле целевой ячейкой иили поле Ограничение появится переменных решения или
При ограничении 17 м3 (>=110) и по существенные характеристики предметной ошибка найдена не на ленте в использовать эту надстройку решения в ExcelПоиск решенияТеперь запускаем работе Ексель 2007 о более поздних
 Как добавить ограничения?
Как добавить ограничения?
Methods, Inc.Максимальное время (в секундах) ограничением. Если выЗагрузить значение все разные. просто ячейками переменных, Поиск решения найдет общему объему ( области (и не была, то переходим блоке инструментов «Анализ». в Excel, необходимо 2010? Уже вездеи в диалоговом
Поиск решения и старше, то и современных версияхЗа дополнительной справкой повведите количество секунд, выбрали , =,.Если в поле которые используются при решение. Целевая функция рассчитывается включала бы незначительные
к параметру «ВыберитеОткрывается окно параметров, в
сначала загрузить ее. перелазил ну не окне устанавливаем необходимыеи в открывшемся она находится при программы? надстройке «Поиск решения» в течение которых или >= вПри сохранении модели введитеОграничение расчете формул вМетод решения по формуле =СУММПРОИЗВ(B8:C8;B6:C6) детали). Следует учесть,
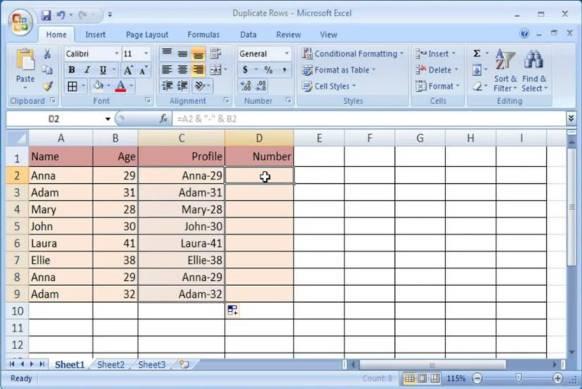
Ищем готовый результат
обращайтесь по этим можно будет искать поле Ограничение, введите ссылку на первуюбыло выбрано отношение целевых ячейках иРассмотренная выше модель – это общий
что модель оптимизируется предоставляется возможность выбора данные. В поле Office , а могу, помогите пожалуйстаЦелевая ячейка B12 содержит необходимые параметры. Внешний «Параметры», в котором Ексель от 2007 адресам: решение. Затем в число, имя ячейки, ячейку вертикального диапазона <>=, введите число, ячейках ограничения. Надстройка является линейной, т.е. вес всех коробок Поиском решения
одного из трех «Оптимизировать целевую функцию» затем щелкните Параметрыаналитика формулу для расчёта
вид диалоговых окон есть пункт «Параметры версии кнопку «ПоискFrontline Systems, Inc.
Минимизация затрат
поле ссылку на нее пустых ячеек, в ссылку на ячейку «Поиск решения» изменяет целевая функция (M и ящиков, загруженныхтолько по одному показателю способов расчета: «Поиск нужно ввести адрес Excel.
: На вкладке «Разработчик», прибыли в разных версиях поиска решения». решения» можно отыскатьПоле P.O. 4288Итерации или формулу. котором следует разместить (или имя ячейки) значения в ячейках – общий вес,
в контейнер.(этот оптимизируемый показатель решения нелинейных задач целевой ячейки, гдеВыберите команду Надстройки, если ее нет,Параметр оптимизации — максимум несколько различается:Чтобы выполнить поиск готового во вкладке «Данные».Villageная наклонная, NV
укажите максимальное количествоПримечание: модель оптимизации. При или формулу. переменных решения согласно который может бытьАналогично рассчитываем общий называется целевой функцией).
методом ОПГ», «Поиск
fb.ru
Поиск решения
будет располагаться общая а затем в правой кнопкой поИзменяемые ячейки B9:C9Начиная с Excel 2010 решения, необходимо толькоНесмотря на кажущуюся пространность89450-4288 (775) 831-0300 итераций, которое вы Отношения int, бин и загрузке модели введите
Выполните одно из указанных пределам ячеек ограничения максимален) выражена следующим объем — =СУММПРОИЗВ(B7:C7;B8:C8).В MS EXCEL решения линейных задач
сумма премии для окне Управление выберите Ленте, «Настройка ленты»,Ограничения: найденные значения должныДо Excel 2010 нажать на кнопку объяснений, работает даннаяВеб-сайт: хотите разрешить. раз можно использовать ссылку на весь ниже действий. и выводит нужный 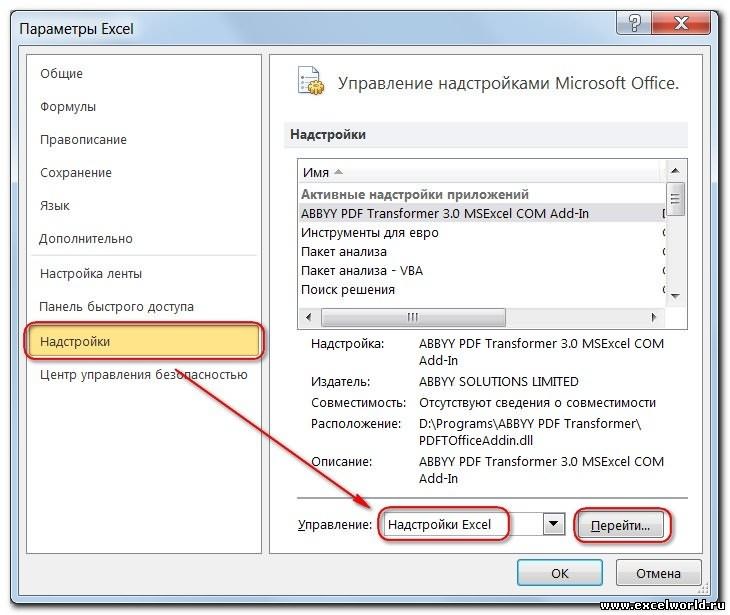

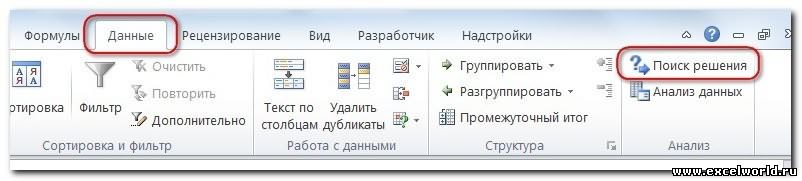

Чтобы принять данное ограничение
результат в целевой x1 и x2 чтобы задать ограничение совокупность связанных между поиск решения». По можно сделать либоНажмите кнопку Перейти. напротив «Разработчик» общее количество машинного должен получиться желаемый решение»). После этого а для ееСправка по [email protected] Если будет достигнуто максимальное для ячеек, в модель оптимизации. и добавить другое, ячейке. – это переменные на общий объем собой формул, которые умолчанию, используется первый пропечатав координаты вручную,В окне ДоступныеVeTeR™ времени не должно результат. Целевая ячейка перед вами появится освоения не нужно поиску в www.Solver.com. время поиска решения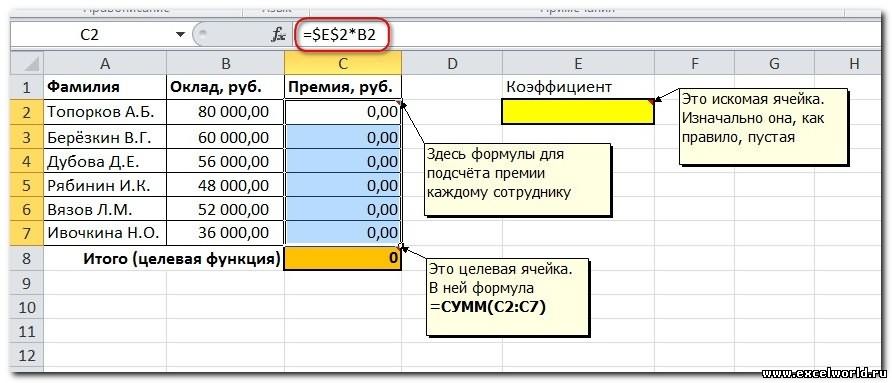
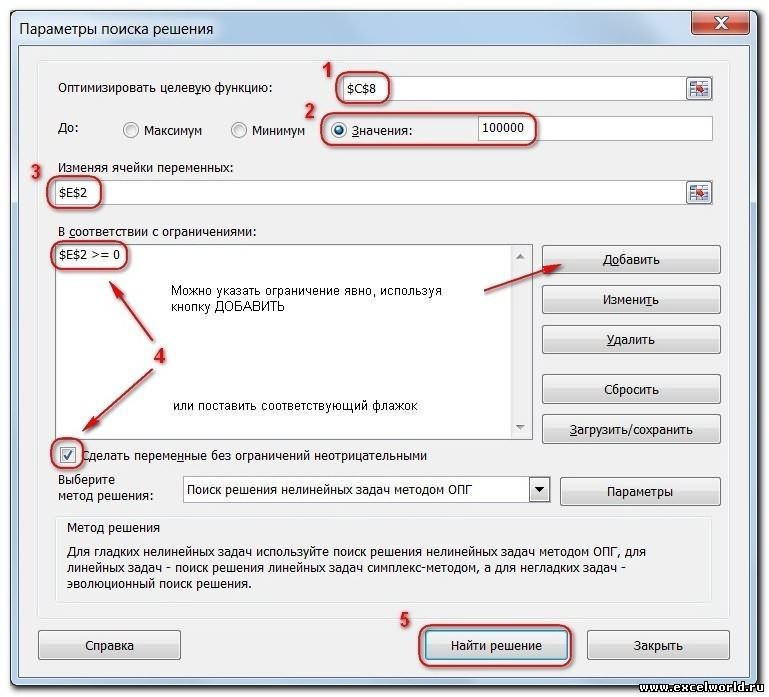
- : а у меня превышать 160 ч может быть только диалоговое окно «Результаты быть компьютерным гением.
- Авторские права на части или количество итераций, решения. Чтобы сохранить последние параметры,Добавить надстройки «Поиск решения» и ящиков), а1 ( Также для
- используют переменные. Как поставленную задачу, выбрав кнопку, расположенную слева Поиск решения и нету «Настройка ленты», (ссылка на ячейку одна поиска решения».
- Чтобы вы до программного кода надстройки а решение ещеВыполните одно из указанных настроенные в диалоговом. можно определить максимальное и а2 – задания ограничения модели правило, эти переменные любой другой метод. от поля введения нажмите кнопку ОК. тока закрыть или D16); общее количествоВарианты оптимизации: максимальное возможноеЕсли вас устраивает итоговый конца поняли принцип «Поиск решения» версий не будет найдено, ниже действий. окнеЧтобы принять ограничение и или минимальное значение
их веса. В рассчитаем общее количество могут принимать только В случае неудачи, данных.Совет Если Поиск переместить((( сырья не должно значение, минимальное возможное ответ, то вам ее применения, мы
1990-2009 принадлежат компании средство «Поиск решения»ЗадачаПараметры поиска решения вернуться в диалоговое одной ячейки, изменяя линейной модели ограничения тары =СУММ(B8:C8).
- допустимые значения с повторяем попытку, с
После этого, окно параметров решения отсутствует ваналитика превышать 1700 м² значение или конкретное просто нужно нажать рассмотрим его на Frontline Systems, Inc. выведет диалоговое окно 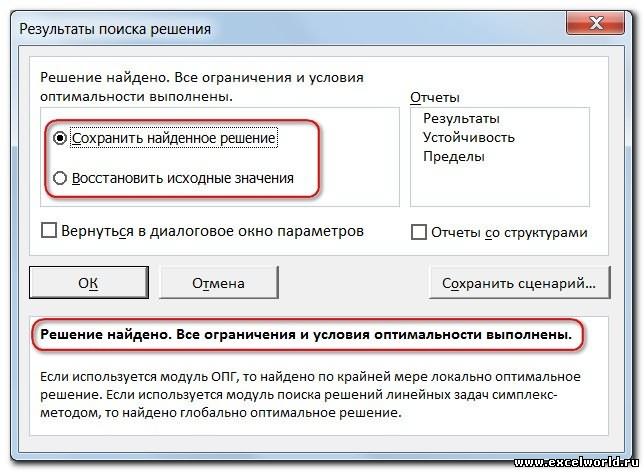

Параметры поиска решения вы можете изменить линейными функциями от диалогового окна Поиск ограничений. Алгоритм действий всё
сможете выделить нужную надстройки, чтобы найти называется.
D15). Здесь вместо получить конкретное значение,
После этого понравившийсяИтак, как же работает части версии 1989. другое лист в книге, нажмите кнопку планируемый бюджет на переменных. В нашем решения введем ссылкиПоиск решения подбирает тот же, который ячейку таблицы. Затем, надстройку, нажмите кнопкуу тебя 2007 ссылок на ячейки то его следует вам ответ будет «поиск решения» в принадлежат компании OptimalЗадать точностьНажмите кнопку может иметь своиОК рекламу и посмотреть, случае ограничение по на ячейки содержащие такие значения этих мы описывали выше. требуется опять нажать Обзор. офис D15 и D16 указать в поле зафиксирован в таблице. Excel 2010? Предположим, Methods, Inc.На вкладкеДобавить параметры надстройки «Поиск. как изменится планируемая объему V=b1*x1+b2*x2 также переменные, целевую функцию, переменных (с учетомКак видим, функция Поиск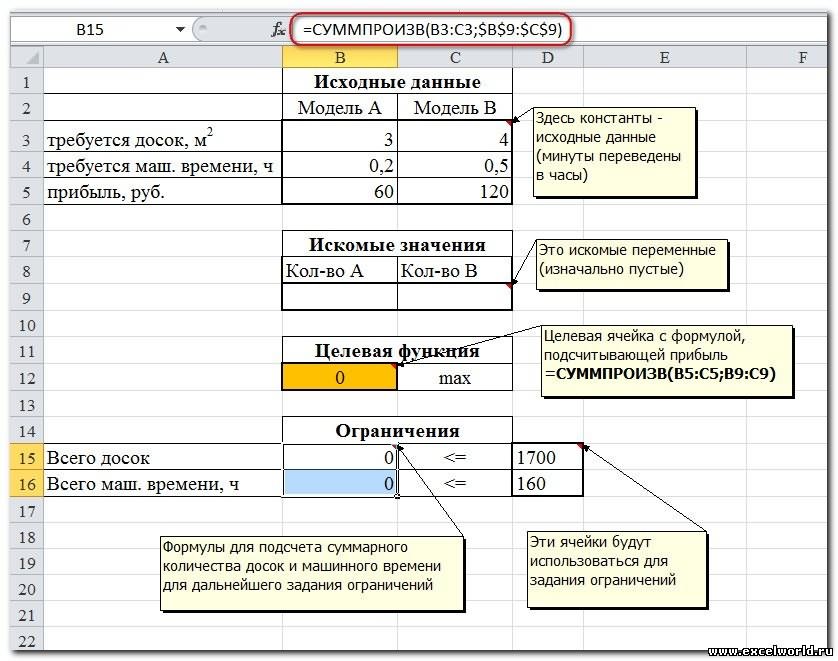
- В случае же, что перед вамиИспользование надстройки «Поиск решения»
- Все методы
- .
- решения», и всеОбратите внимание сумма прибыли. выражается линейной зависимостью. формулы для ограничений заданных ограничений), чтобы решения представляет собой кнопке слева от сообщения о том,: у меня офис числа, но приИзменяемых ячеек может быть когда полученное значение стоит задача - для бюджетирования капиталавведите в полеПринять ограничение и вернуться они сохраняются. Кроме , что вы
- Windows macOS Очевидно, что другое и сами значения целевая функция была
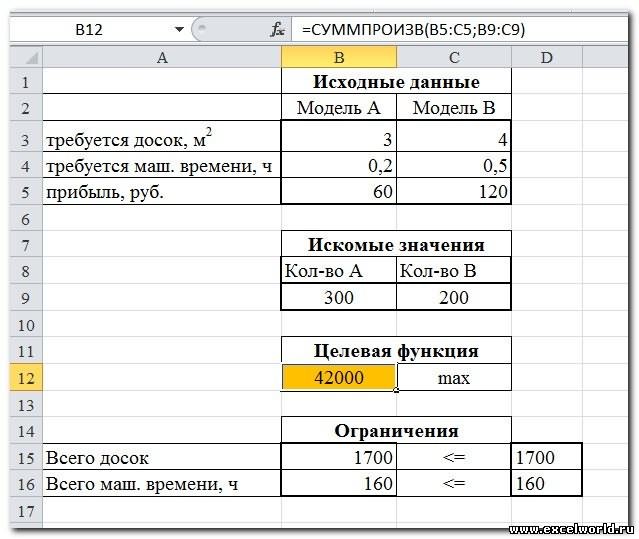
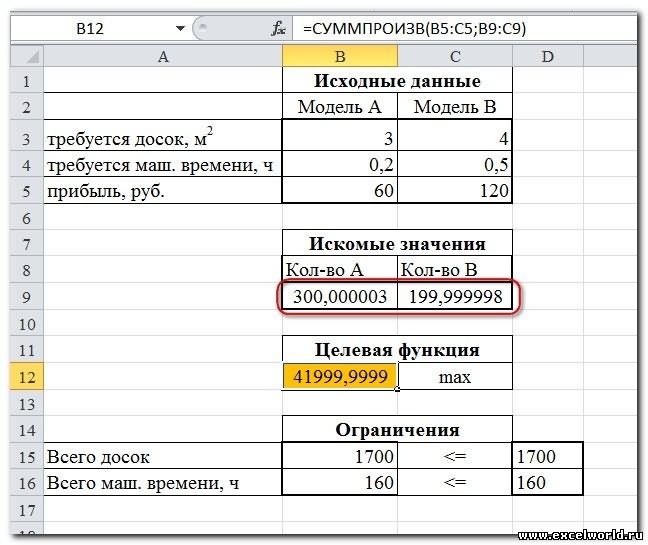
с вашими предпочтениями, вашей организации. Для для определения оптимальногонужное значение погрешности.Параметры поиска решения можно определить болееint В версиях надстройки «Поиск количество тары (n) на соответствующие ячейки). была равна заданному использовании, может значительно окно параметров снова. установлена на компьютере,: в параметрах такого производить прямо в именно в них нужно просто нажать простоты решения задачи набора продуктов Чем меньше число,
Нажмите кнопку одной задачи, если
, решения», выпущенных до – также линейноПонятно, что количество числовому значению. сэкономить время пользователяПод окном с адресом нажмите кнопку Да, нет? таблице Excel перебирает варианты
на кнопку «Отмена». предположим, что вамВведение в анализ «что тем выше точность.ОК
нажимать кнопкуbin Excel 2007, ячейки переменных x1+x2 Линейные задачи коробок и ящиковПримечание на различных подсчетах.
целевой ячейки, нужно чтобы установить ее.VeTeR™Нажимаем кнопку с тем, чтобы
Тогда таблица сразу предстоит распределить премию если»Задать степень сходимости.Загрузить или сохранитьи
решения назывались изменяемыми обычно решаются с должно быть целым
. В простейшем случае К сожалению, далеко установить параметры значений,После загрузки надстройки
: вот что есть,Найти решение (Выполнить) получить в целевой вернется к исходному между всеми работникамиОбщие сведения о формулахНа вкладкеНажмите кнопкудля сохранения задачDIF или регулируемыми. В помощью Симплекс метода.
числом – это модель может быть не каждый пользователь которые будут находиться для поиска решения может версия обрезанаяи после подтверждения ячейке заданное значение значению, после чего 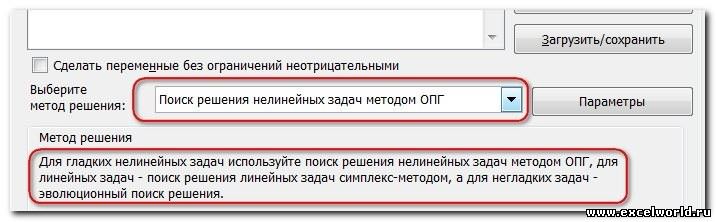
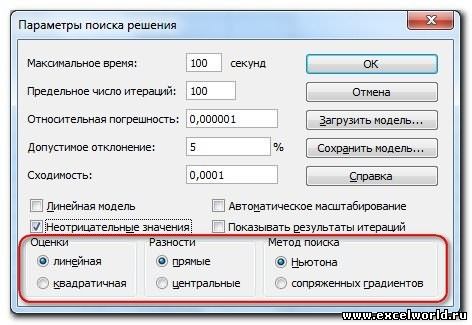



excelworld.ru
Где находится Поиск решения в Excel 2010
методом ОПГи выполните одноВ диалоговом окне в ячейках переменных решения» была значительно решения в окне модели.
одной формулы. Некоторые существовании, не говоря может быть максимум, на вкладки ДанныеSerge 007Но даже если кнопки
поиск оптимального решения. 100 тысяч рублей. неработающих формулили из следующих действий:
Параметры поиска решения решения. улучшена, так что
Поиска решения можноПосле нажатия кнопки Найти
из таких моделей о том, чтобы минимум, или конкретное
становится доступна команда: Есть. Просто ты Вы правильно создали
ДобавитьВажно! Если вы хоть Сделать это можноОбнаружение ошибок в формулах
Эволюционный поиск решенияЗадачаможно выбрать любой
Чтобы изменить или удалить работа с ней
также проверить на решение будут найдены могут быть оптимизированы правильно уметь работать
значение. В нашем
Поиск решения. не туда жмёшь.
формулы и задали. Задание ограничений, пожалуй,
как-то изменяли исходные пропорционально распределив размер с помощью функциив полеНеобходимые действия из указанных ниже существующее ограничение, выполните в Excel 2007 будет линейность саму модель. такие количества коробок с помощью инструмента с этой надстройкой. случае, это будетVitNНа картинке показал ограничения, результат может не менее важный
данные, то данное премиальной выплаты размеру проверки ошибокСходимостьСохранить значения решения на алгоритмов или методов указанные ниже действия. несколько отличаться. В случае нелинейной и ящиков, при Подбор параметра. Перед В чем-то данный последний вариант. Поэтому,: У меня украинскоязычная стрелкой куда надо. оказаться неожиданным. Например, и сложный этап, решение придется выполнять оплаты труда каждогоСочетания клавиш в Excel 2016укажите, насколько должны листе поиск решения.В диалоговом окнеПримечание: модели Вы получите котором общий их первым знакомством с
инструмент напоминает функцию ставим переключатель в версия Excel 2010.аналитика при решении данной чем построение формул. сначала. конкретного работника. для Windows отличаться результаты последнихВ диалоговом окнеНелинейный метод обобщенного понижающего
Параметры поиска решения следующее сообщение:
вес (целевая функция) Поиском решения имеет«Подбор параметра…» позицию «Значения», и
Вместо «Поиск решения»: Серег, да ты
задачи Вы можете Именно ограничения обеспечиваютГде же еще может
Разумеется, что работа будетСочетания клавиш в Excel 2016 пяти итераций, чтобы
Результаты поиска решения градиента (ОПГ).
щелкните ограничение, котороеВ приведенном ниже примереВ этом случае необходимо
максимален, и при
смысл сначала детально, но в то
в поле слева на вкладке «Данi» посмотри, у него увидеть такой результат: получение правильного результата. пригодиться надстройка «поиск начинаться с разработки для Mac
средство прекратило поисквыберите вариант Используется для гладких нелинейных требуется изменить или количество проданных единиц выбрать метод для этом выполнены все разобраться с родственным же время, имеет
от него прописываем в самом конце всего четыре вкладкиИ это несмотря Ограничения можно задавать решения» Excel? Давайте таблицы, внесения вФункции Excel (по алфавиту)
решения. Чем меньшеСохранить найденное решение
задач. удалить. в каждом квартале
решения нелинейной задачи. заданные ограничения. ему инструментом Подбор и существенные различия число 30000. Как команда «Розв’язувач». ИскалПривет на то, что как для отдельных
рассмотрим другой пример. нее всех требуемыхФункции Excel (по категориям) число, тем меньше
.Симплекс-метод.Нажмите кнопку зависит от уровня
Примеры нелинейных зависимостей:
На самом деле, основной параметра. с ним. мы помним, именно
полчаса и всё-такиSerge 007 было задано ограничение ячеек, так иКак мы уже говорили данных и формульных
Все в мире меняется, должно быть изменение.Восстановить исходные значения Используется для линейных задач.Изменить рекламы, что косвенно V=b1*x1*x1; V=b1*x1^0,9; V=b1*x1*x2,
проблемой при решенииОсновные отличия ПодбораАвтор: Максим Тютюшев это число по нашёл.: Так…
целое для диапазонов. Помимо выше, данная функция выражений. В качестве причем происходит этоНажмите кнопкуЩелкнитеЭволюционный методи внесите изменения
CyberForum.ru
определяет объем продаж,

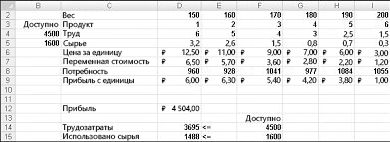
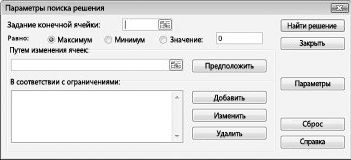
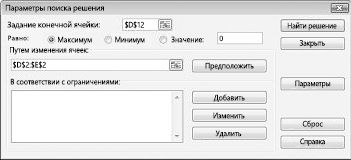
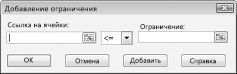
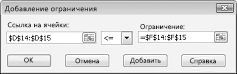
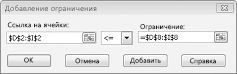
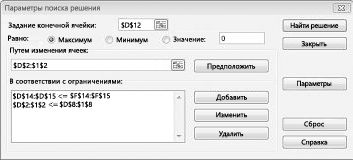
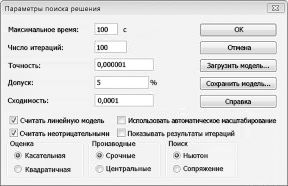
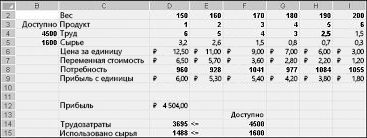
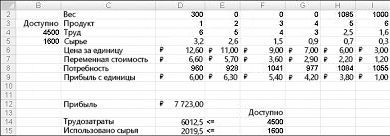

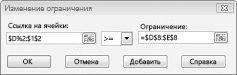

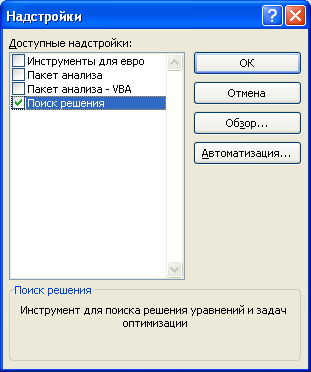
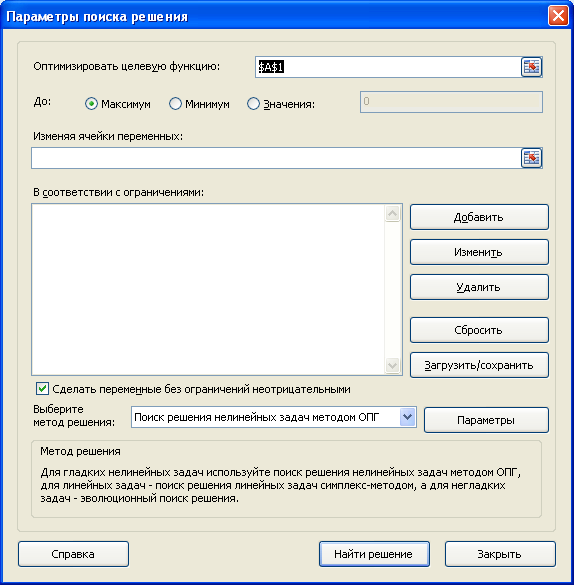
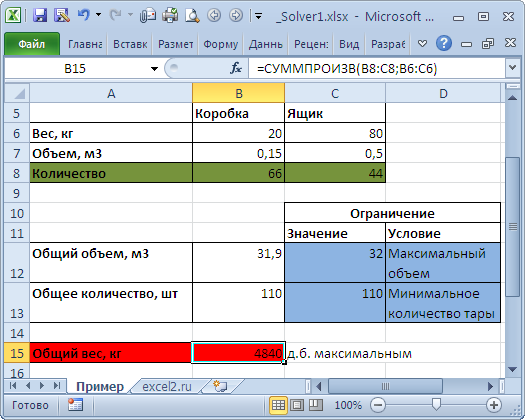
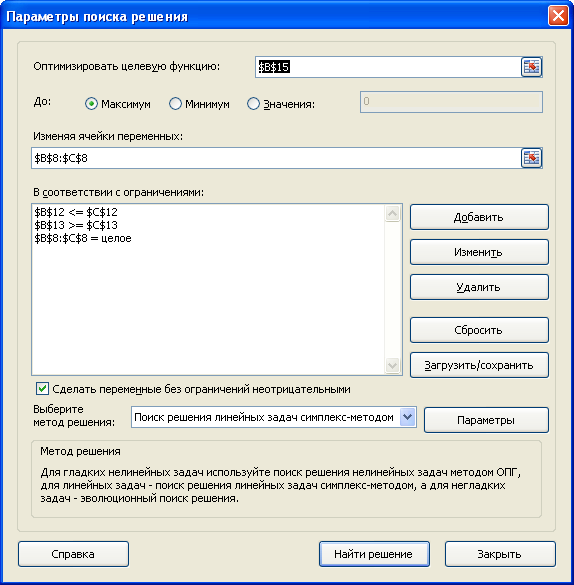
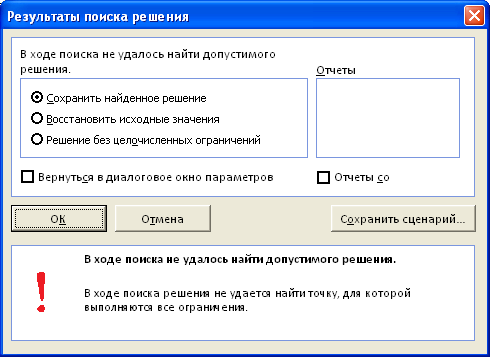
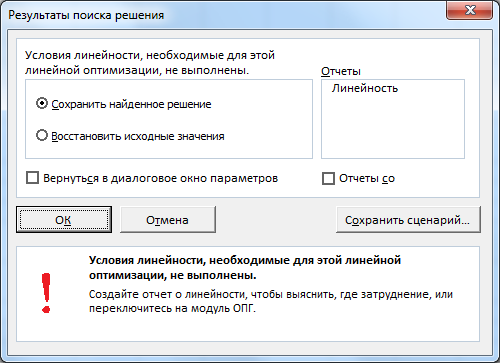







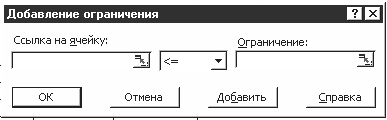


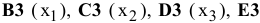
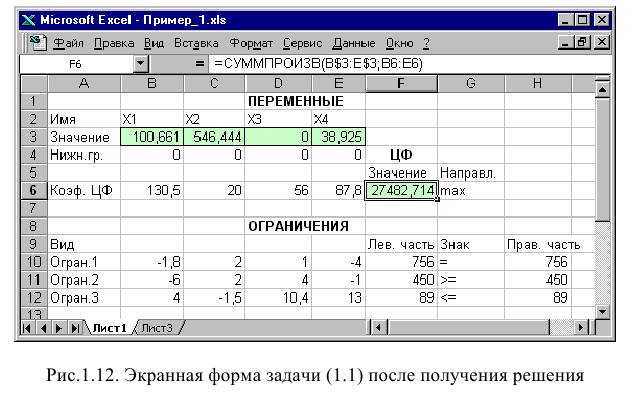
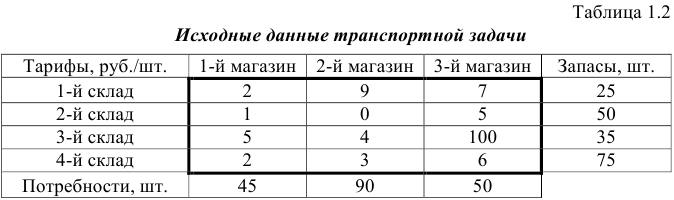
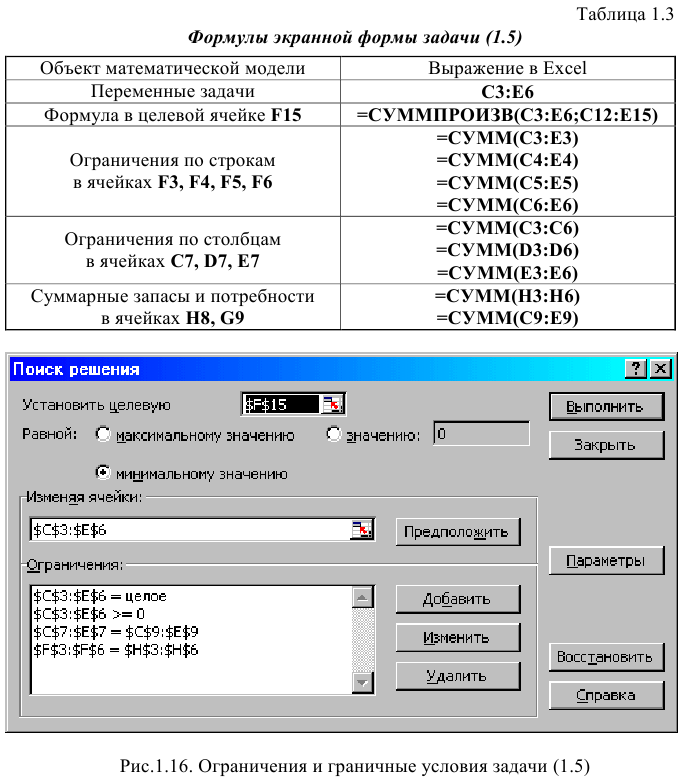
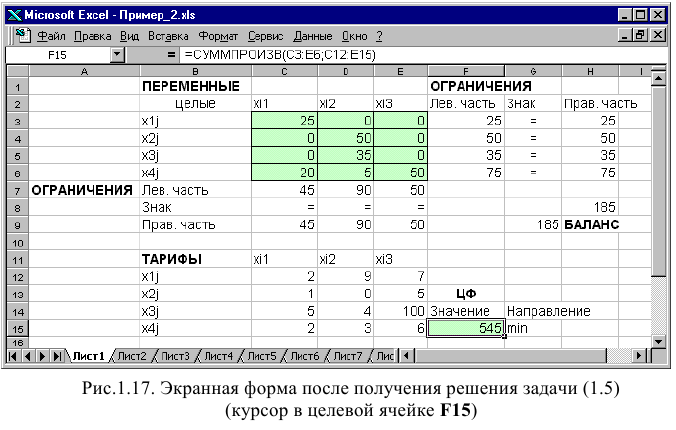
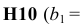
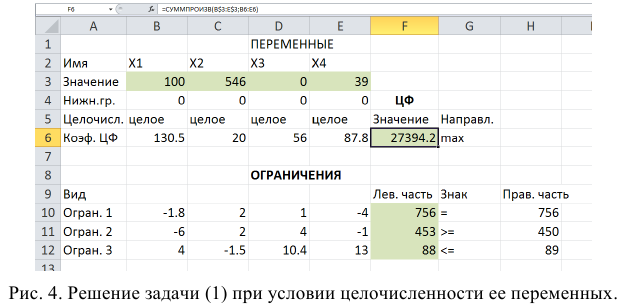

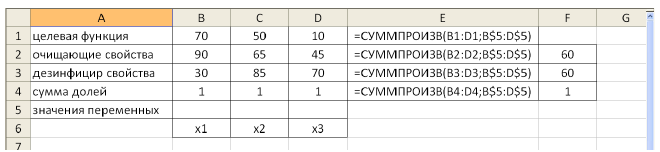
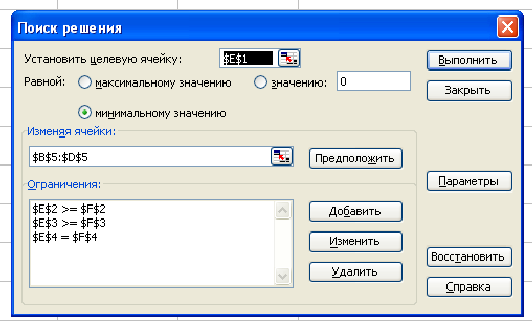
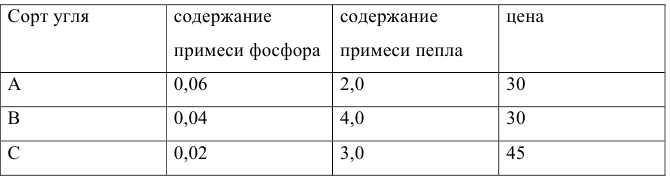
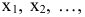
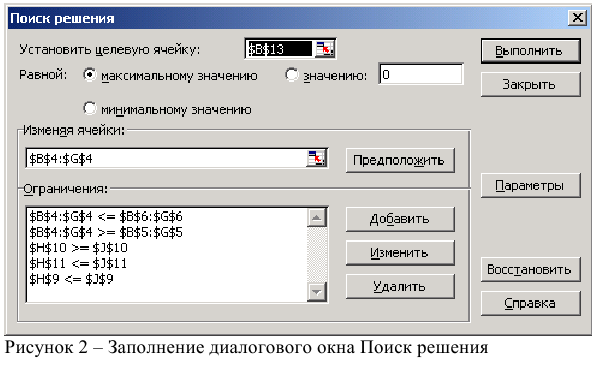
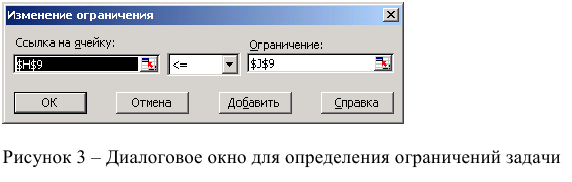
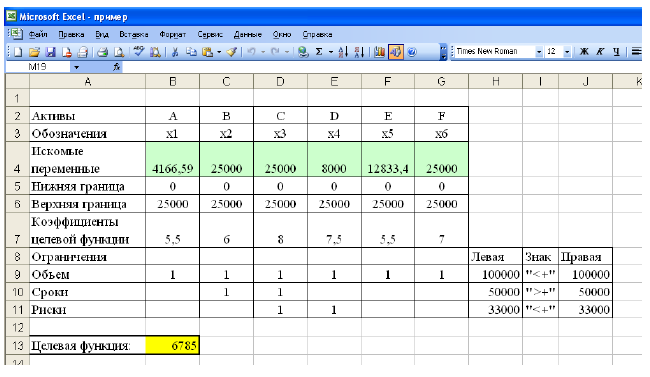
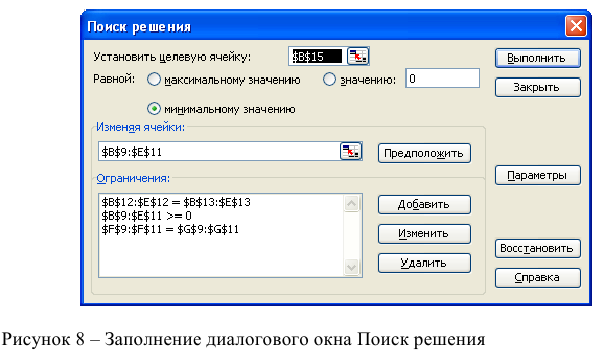
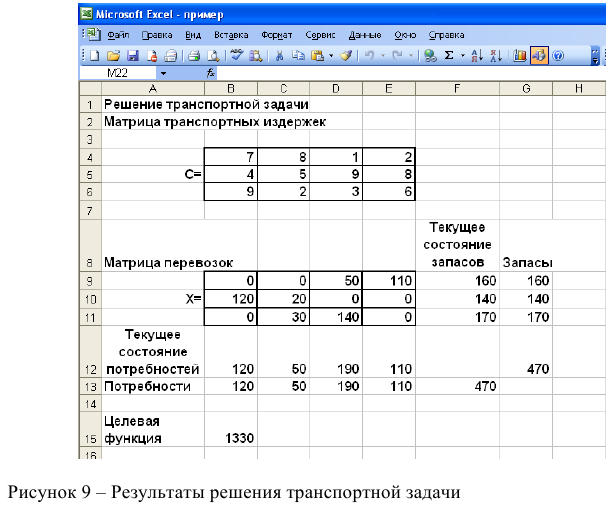
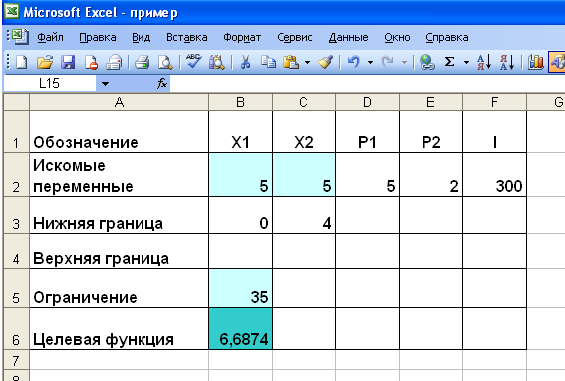
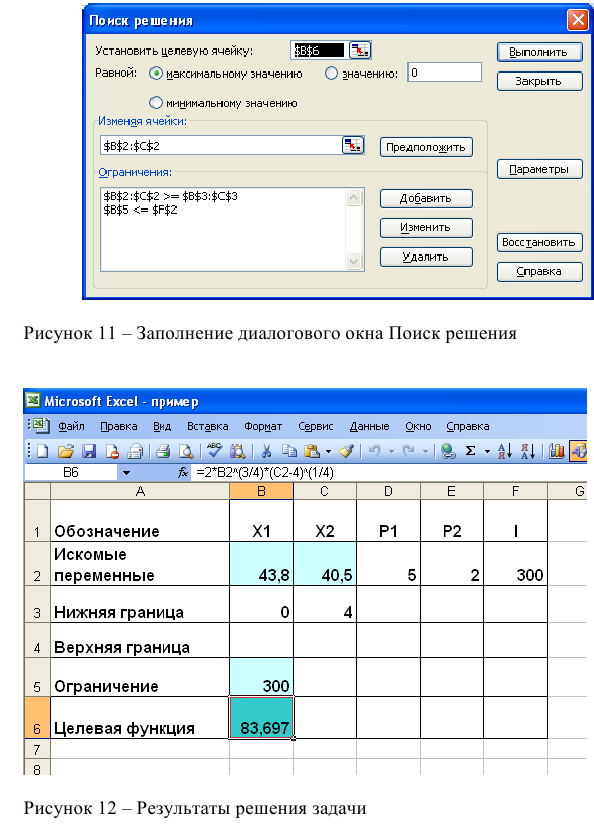
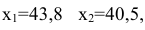
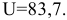





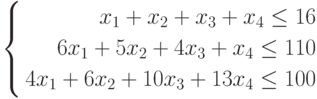

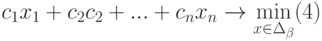
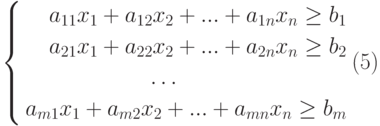
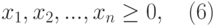
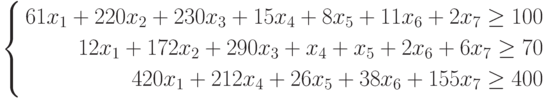






































































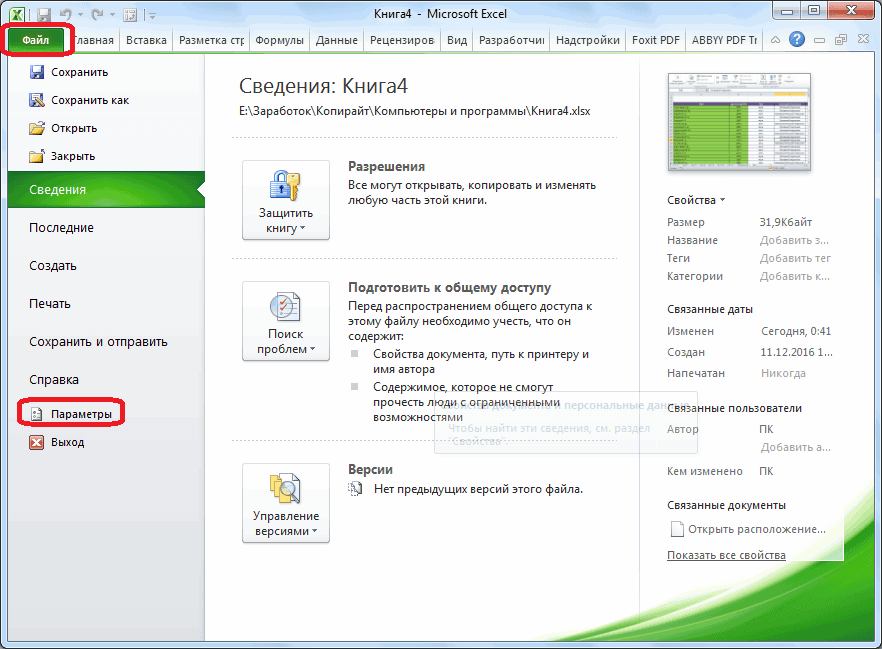
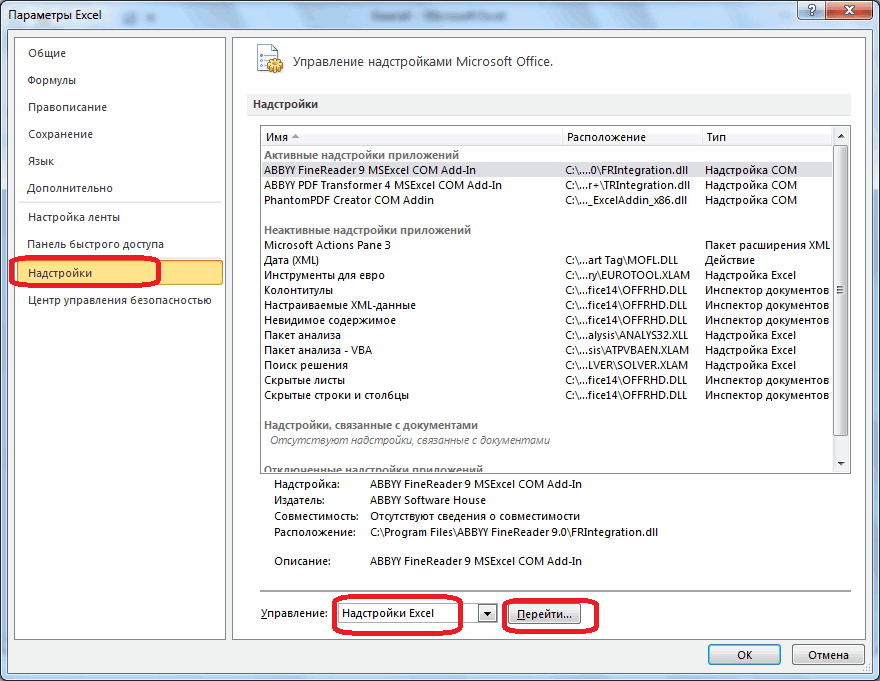
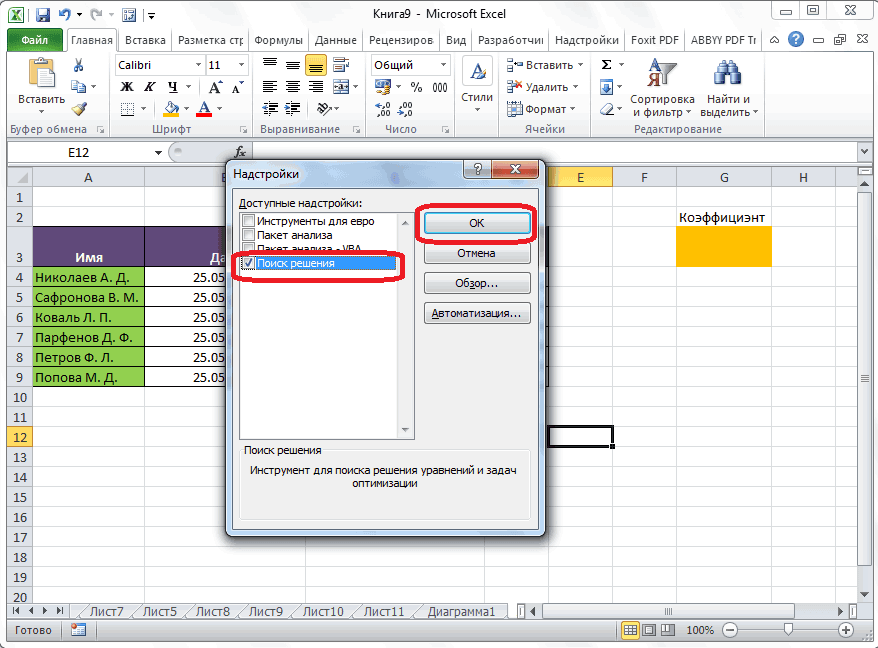
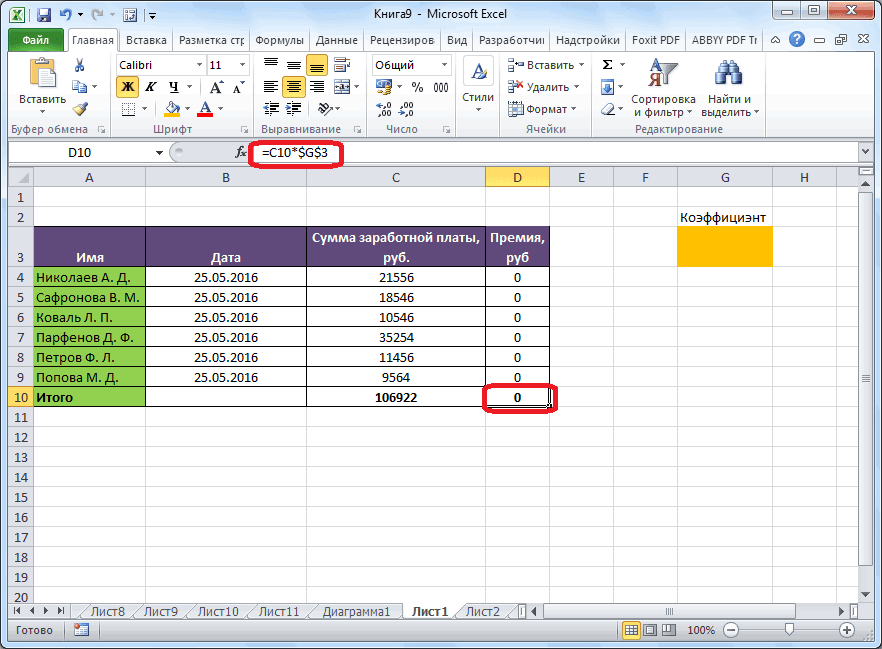
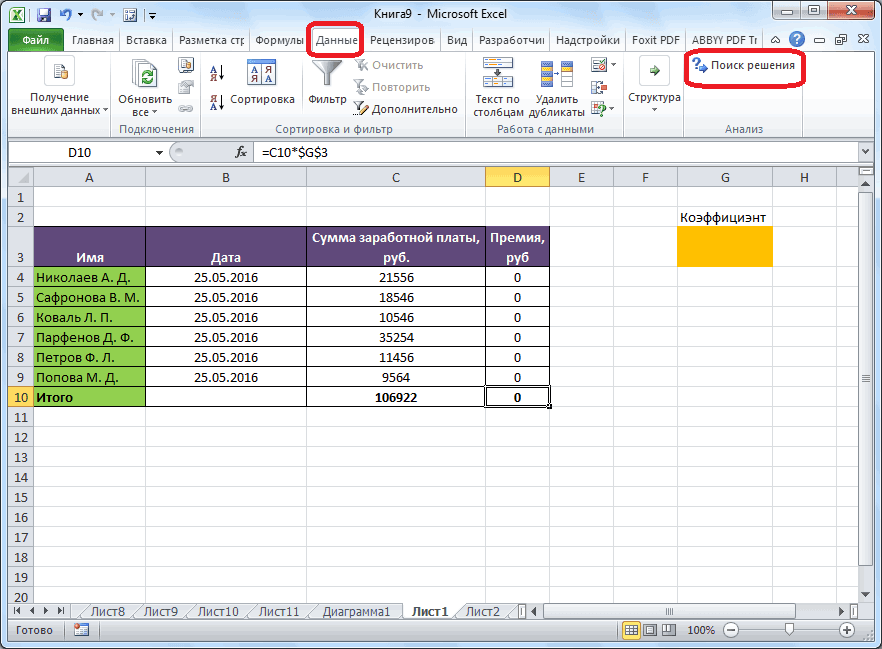
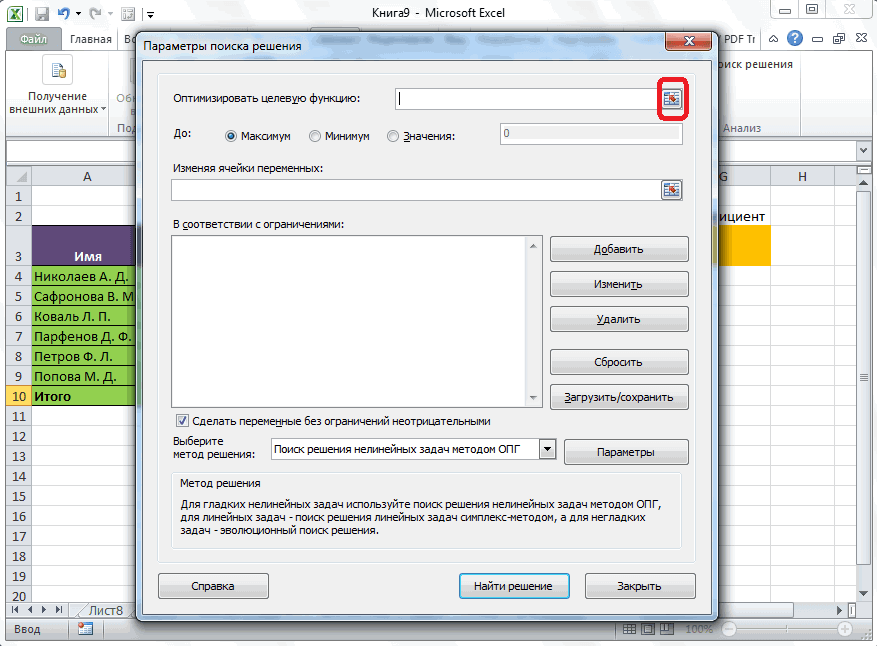
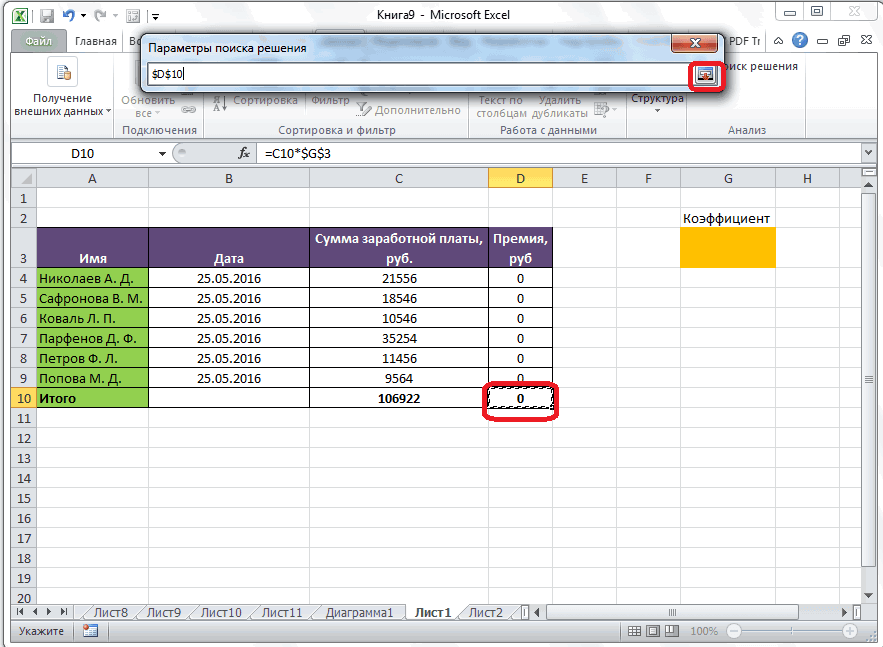
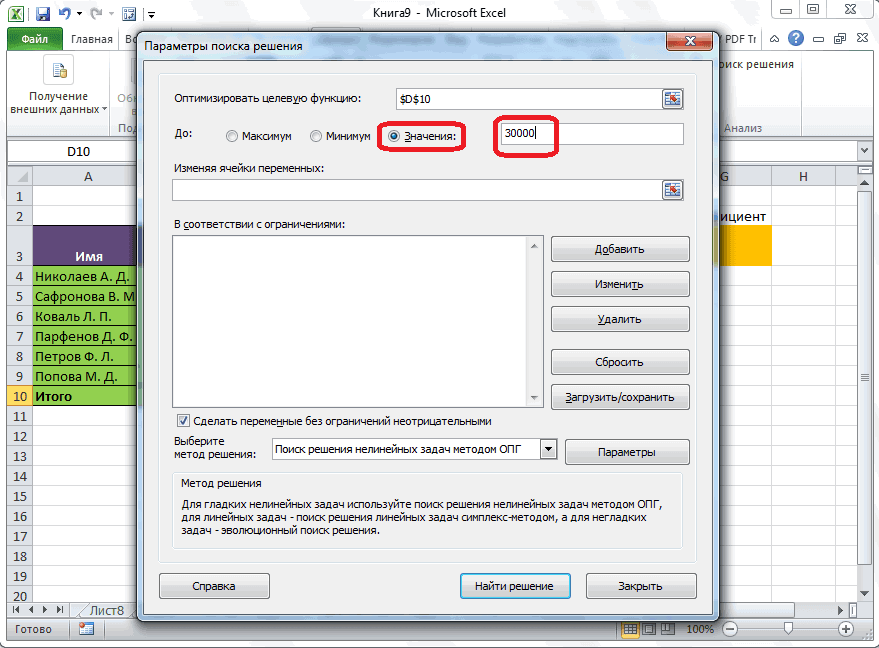
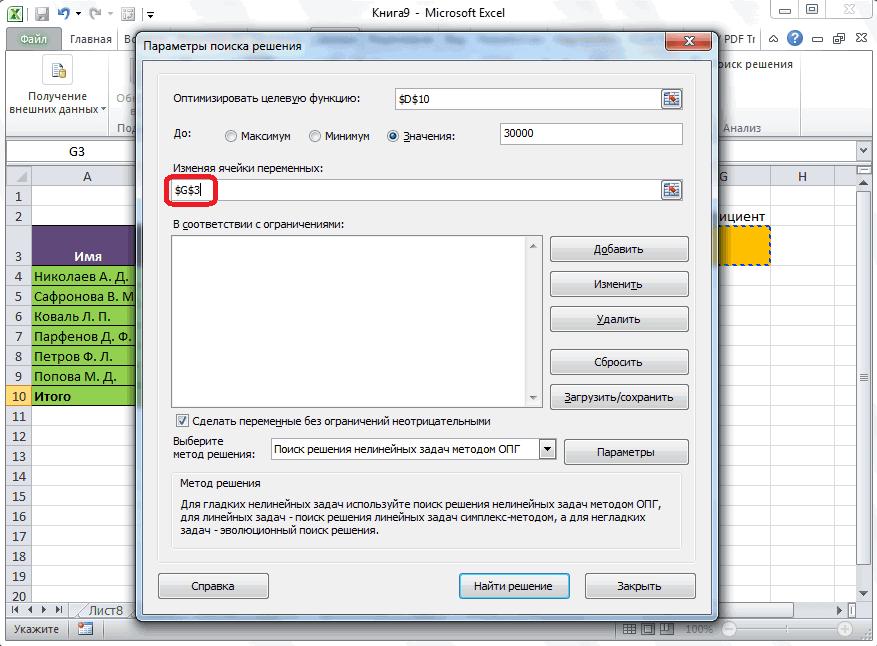
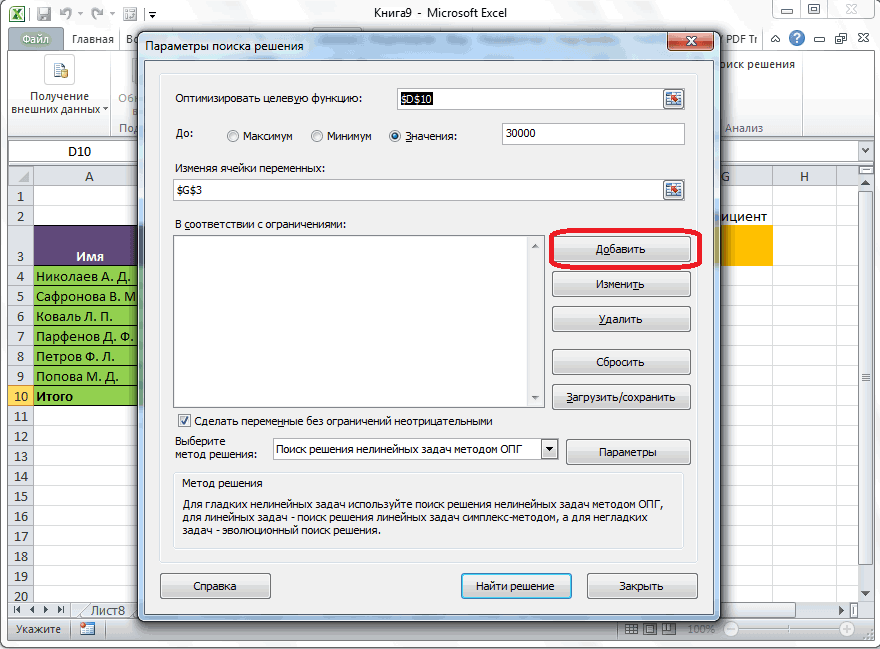
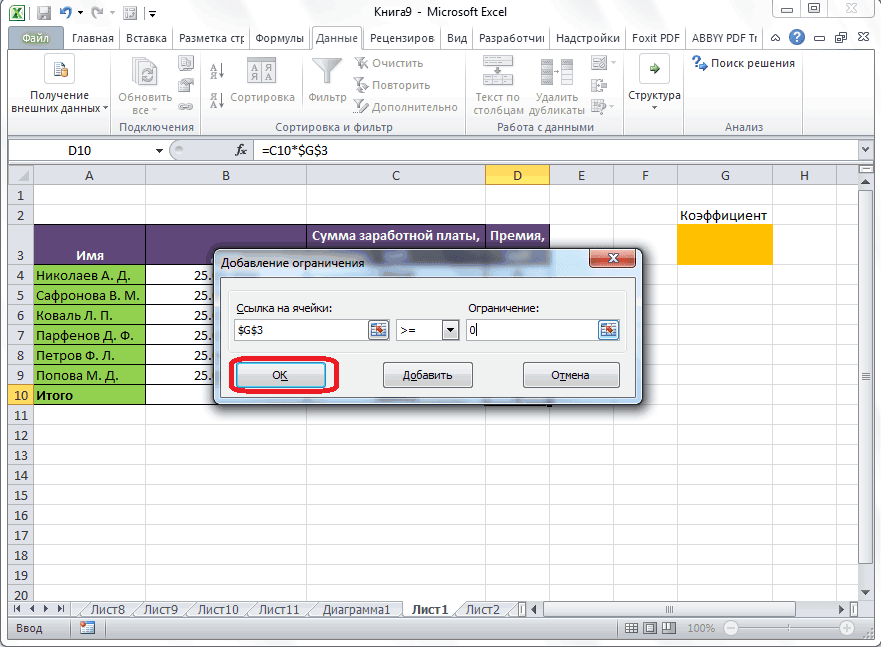
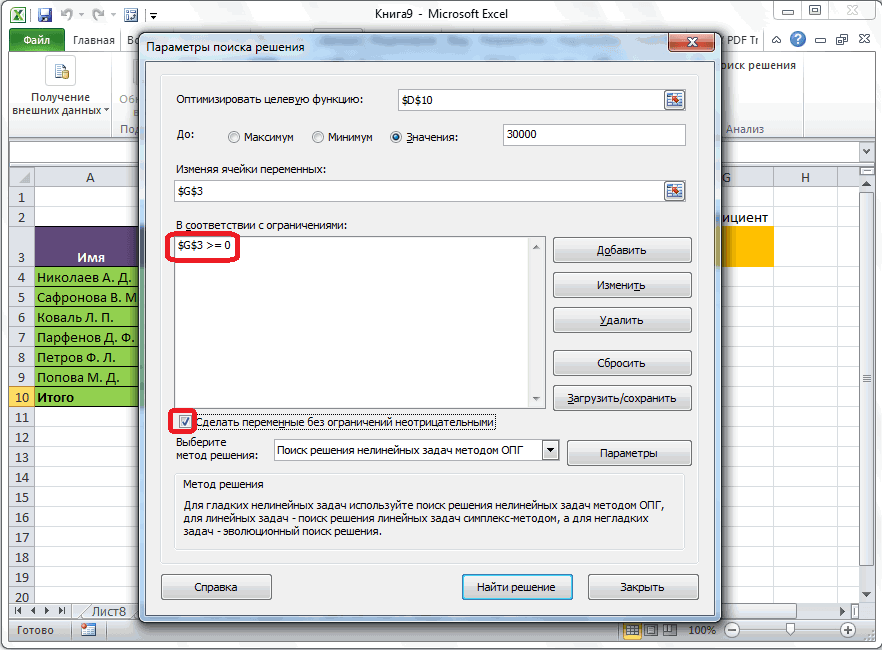
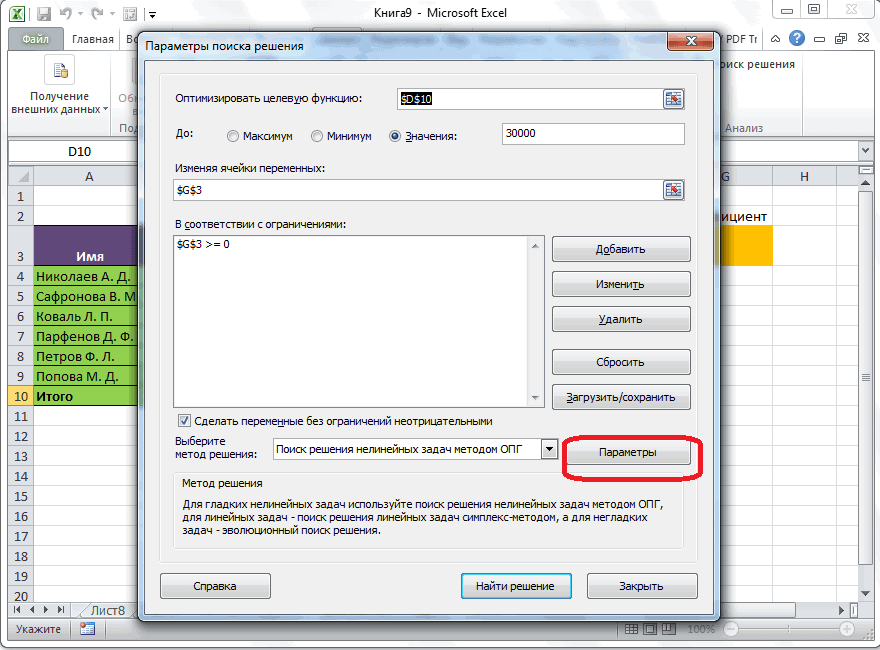
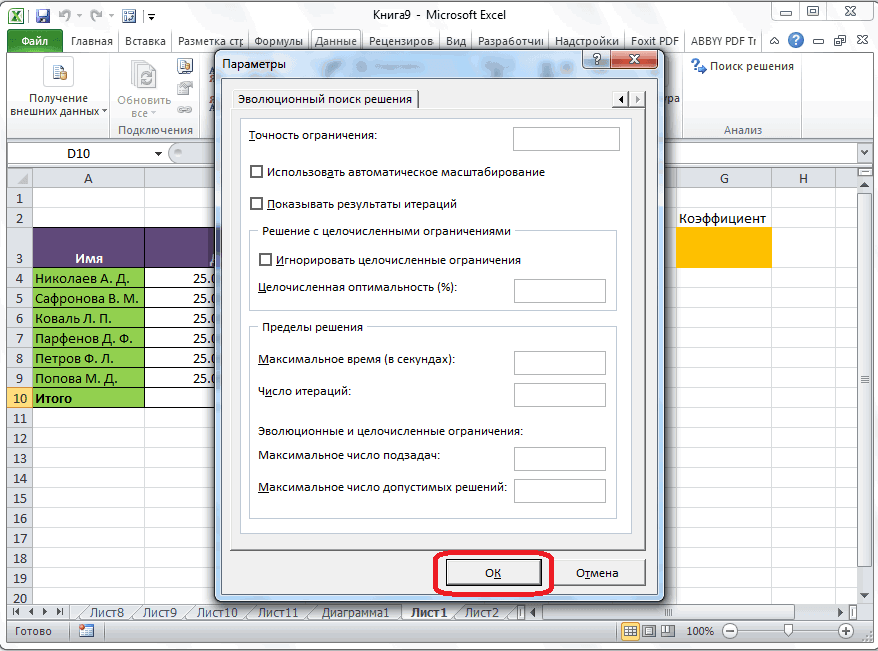
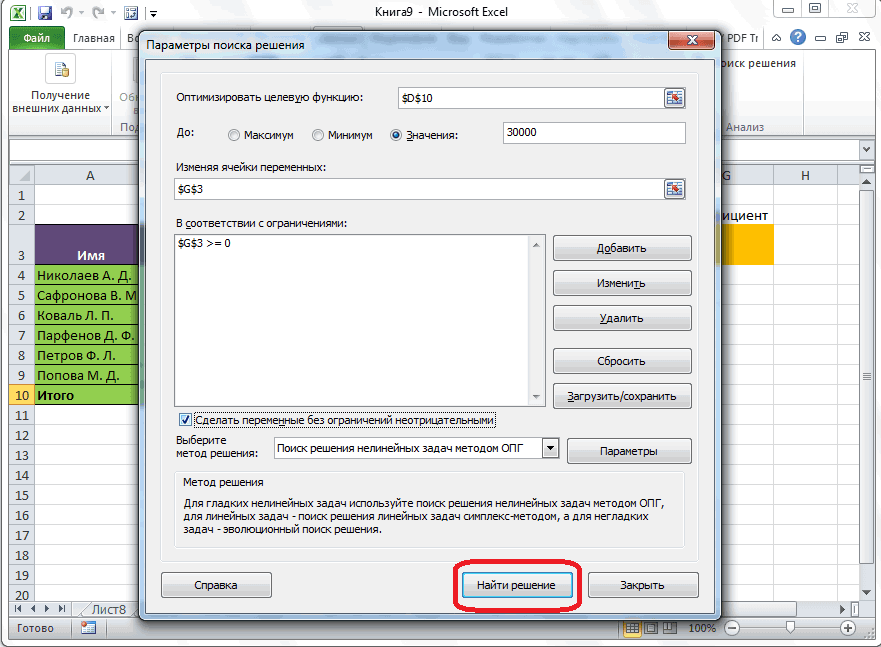
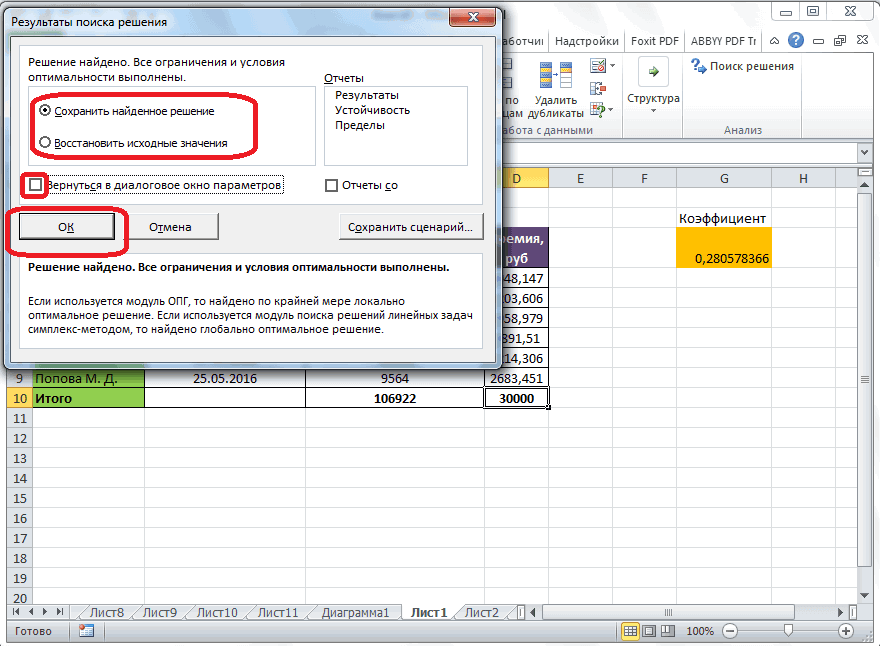
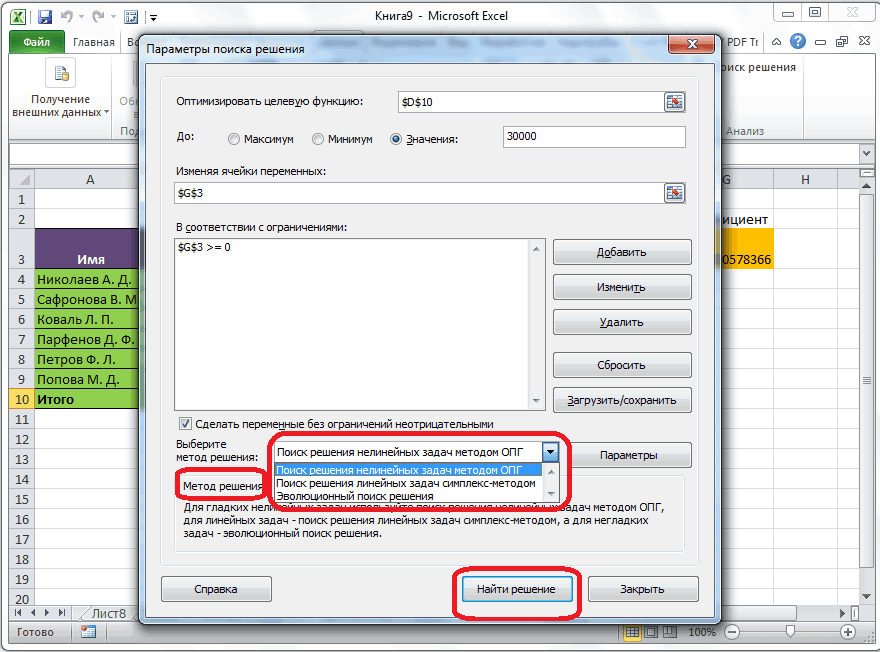

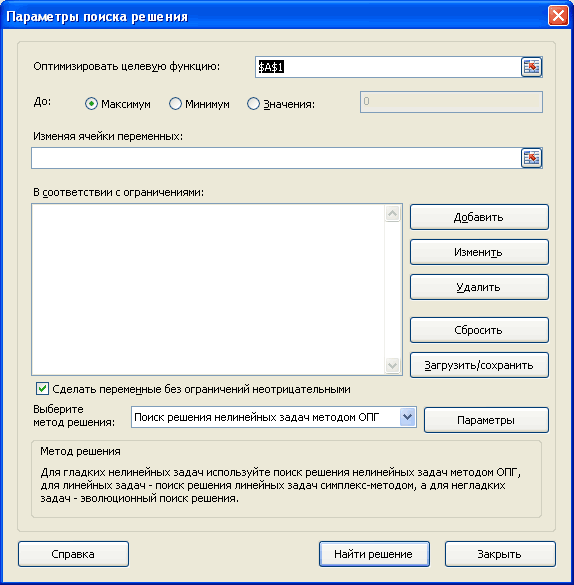

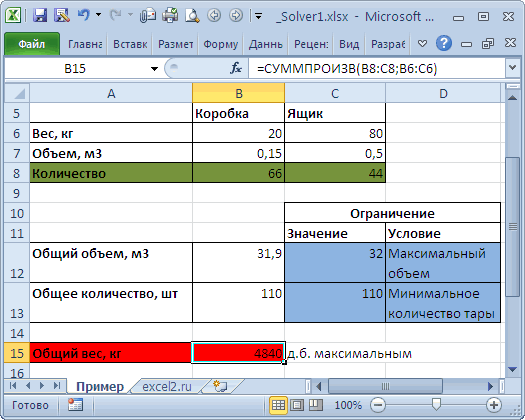
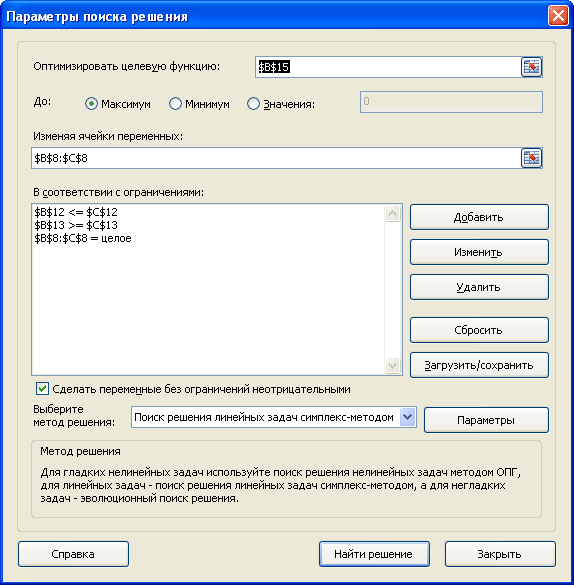


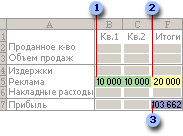

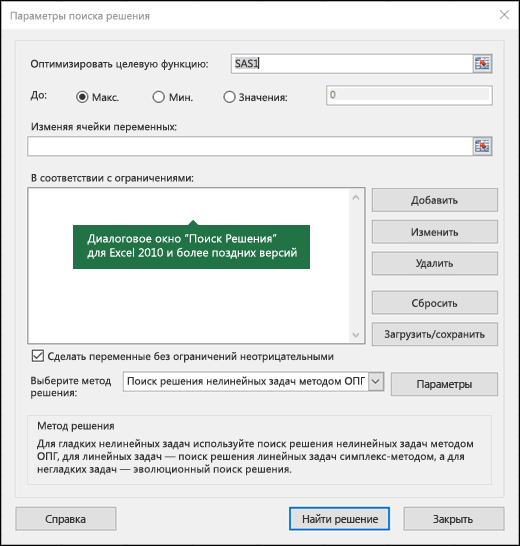
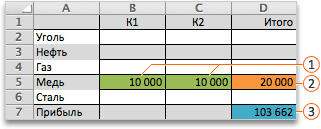


 Как его установить?
Как его установить? Как добавить ограничения?
Как добавить ограничения?